| Скачать .docx | Скачать .pdf |
Курсовая работа: Проверка истинности моделей множественной регрессии
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. И.И. ПОЛЗУНОВА
ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ РЕГИОНАЛЬНЫМ РАЗВИТИЕМ
Расчётное задание
по дисциплине: Эконометрика
Проверка истинности моделей множественной регрессии
Выполнил:
Филатов М.И.
2010
Исходные данные
| Численность студентов (на 1000 человек населения) | Динамика Валового Внутреннего Продукта (в постоянных ценах) | Динамика валового накопления основного капитала (в постоянных ценах) | |
| x1 | y | x2 | |
| Россия | 64 | 131,2 | 103 |
| Австралия | 50 | 123 | 169 |
| Австрия | 29 | 117 | 115 |
| Азербайджан | 22 | 177,3 | 103,4 |
| Армения | 34 | 184,1 | 263,5 |
| Беларусь | 195 | 164,9 | 162,2 |
| Бельгия | 39 | 115 | 120 |
| Венгрия | 42 | 139 | 178 |
| Германия | 28 | 110 | 102 |
| Грузия | 42 | 169,3 | 112,4 |
| Дания | 40 | 114 | 134 |
| Италия | 34 | 111 | 125 |
| Казахстан | 61 | 163,4 | 126,7 |
| Канада | 42 | 121 | 156 |
| Киргизия | 46 | 134,7 | 83,3 |
| Китай | 15 | 184 | 420 |
| Мексика | 22 | 122 | 175 |
| Нидерланды | 33 | 119 | 129 |
| Норвегия | 47 | 120 | 130 |
| Польша | 54 | 140 | 154 |
| Республика Молдова | 34 | 129,1 | 134,1 |
| Румыния | 32 | 115 | 132 |
| Соединенное Королевство Великобритания | 38 | 122 | 146 |
| США | 58 | 117 | 143 |
| Таджикистан | 21 | 116,4 | 143,5 |
| Украина | 51 | 122,7 | 122,6 |
| Финляндия | 58 | 130 | 154 |
| Франция | 36 | 115 | 129 |
| Швеция | 48 | 121 | 129 |
| Япония | 32 | 105 | 91¹ |
Все данные взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели.
2003. Федеральная служба государственной статистики Построение модели множественной регрессии
Расчет параметров
Рассчитаем необходимые параметры:
| Признак | Ср. знач. | СКО | Характеристики тесноты связи | βi | bi | Коэф-ты частной корр. | F-критерий фактический | Табличный F-критерий | |
| y | 131,77 | 22,74 | Ryx1x2 =0,5963 | ||||||
| x1 | 44,9 | 30,41 | ryx1 =0,2152 | 0,2639 | 0,1973 | 0,0672 | ryx1 х2 =0,3112 | Fx1 факт =2,8954 | 4,21 |
| x2 | 146,19 | 60,57 | ryx2 =0,5353 | 0,5583 | 0,2097 | 0,2326 | ryx 2х1 =0,5695 | Fx 2факт =12,95 | 4,21 |
| rx1x2 =-0,0872 | a=92,26 | rx1 х2у =-0,2453 | Fфакт =7,45 | 3,35 |
Уравнение регрессии в стандартизованном масштабе:
ty =2639tx 1 +0,5583tx 2
Уравнение множественной регрессии в естественной форме:
yтеор =92,26+0,1973x1 +0,2097x2
Рассчитаем по этой формуле теоретические значения динамики ВВП и определим среднюю ошибку аппроксимации. Она равна 9,5254.
Выбор фактора, оказывающего большее влияние
1. Динамика валового накопления основного капитала оказывает большее влияние на динамику ВВП, чем численность студентов, так как
|β2 |=0,5583 > |β1 |=0,2639.
2. С помощью средних коэффициентов эластичности можно оценить относительную силу влияния динамики валового накопления основного капитала (х2 ) и числа студентов (х1) на динамику ВВП (у):
![]() =0,0672,
=0,0672, ![]() =0,2326,
=0,2326,
следовательно, с увеличением валового накопления основного капитала на 1% от их среднего значения, динамика ВВП возрастает на 0,23% от своего среднего значения. А при увеличении числа студентов на 1% от своего среднего значения, динамика ВВП увеличится на 0,067% от своего среднего значения. Очевидно, что сила влияния второго фактора (динамики валового накопления основного капитала) на результативный признак (динамику ВВП) значительно больше, чем сила влияния первого фактора (числа студентов).
3.Сравнивая коэффициенты парной и частной корреляции
| ryx1 | 0,2152 | ryx2 | 0,5353 |
| ryx1x2 | 0,3112 | ryx2x1 | 0,5695 |
Коэффициенты парной и частной корреляции отличаются незначительно что говорит о слабой межфакторной связи. Связь между динамикой валового накопления основного капитала и динамикой валового внутреннего продукта (связь прямая и средне тесная) выше, чем связь между числом студентов и динамикой ВВП (связь прямая слабая).
4. По коэффициенту множественной корреляции: Rуx1x2 =0,5963 можно сделать вывод, что зависимость динамики ВВП от динамики валового накопления основного капитала и числа студентов характеризуется как средне тесная, в которой 59,63% вариации результативного признака определяется вариацией учтённых в модели факторов. Прочие факторы, не включённые в модель, составляют соответственно 35,56% от общей вариации.
4. Так как F – критерий Фишера превышает табличное значение:
Fфакт =7,45>Fтабл =3,35
то можно говорить о статистической значимости и надёжности уравнения регрессии.
5. Сравнивая частные F – критерии фактические с пороговой константой Fтабл =4,21, делаем вывод: Fх2факт =12,95 > Fтабл , следовательно статистически подтверждена целесообразность включения в модель динамики валового накопления основного капитала, после числа студентов, т.к. этот фактор оказывает большее влияние.
Построение парных моделей регрессии
Представим данные полученные при построении парных моделей в таблице:
| Модель | Aср. | r (ρ) | Уравнение | Fфакт |
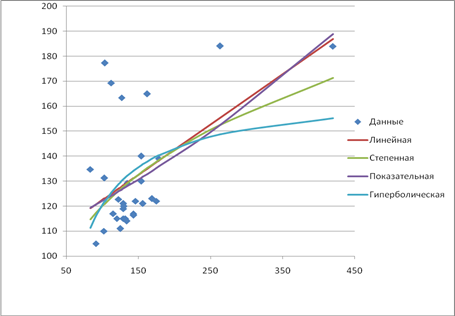
| Линейная | 10,89 | 0,5353 | у=102,38+0,201х1 | 11,24 |
| Степенная | 11,008 | 0,4934 | у=38,26×х1 0,2481 | 9,01 |
| Показательная | 10,47 | 0,5350 | у=106,53×1,001х1 | 11,23 |
| Гиперболическая | 12,59 | 0,3786 | у=165,92-4546,04/х1 | 4,68 |
Определение лучшей модели
1. Недопустимую ошибку аппроксимации имеют все 4 модели, однако у показательной модели она наименьшая, это говорит о том что линейная модель лучше аппроксимирует исходные данные чем остальные модели.
2. У линейной модели теснота связи самая сильная по сравнению с другими моделями. Это говорит о том, что показательная модель лучше подходит к нашим данным.
3. Проверив гипотезу о стат. значимости и надежности, получив значения Fфакт больше табличного во всех случаях, получаем, что все 4 уравнения являются стат. значимыми и надежными. Хотя линейная модель имеет наибольшее Fфакт по сравнению с другими моделями, это говорит о большей точности линейной модели.
По двум показателям линейная модель лучше остальных, это говорит о том, что линейная модель лучше аппроксимирует исходные данные. Однако множественная модель, на мой взгляд, лучше аппроксимирует данные, чем линейная, потому что множественная модель имеет допустимую ошибку аппроксимации и большую тесноту связи.
Проверка предпосылок МНК
1.Первую предпосылку проверим путём вычисления суммы значений остатков:
| x1 | x2 | y | x1x2 | yx1 | yx2 | y^x | y-y^x |
| 64 | 103 | 131,2 | 6592 | 8396,8 | 13513,6 | 126,48 | 4,72 |
| 50 | 169 | 123 | 8450 | 6150 | 20787 | 137,56 | -14,56 |
| 29 | 115 | 117 | 3335 | 3393 | 13455 | 122,09 | -5,09 |
| 22 | 103,4 | 177,3 | 2274,8 | 3900,6 | 18332,82 | 118,28 | 59,02 |
| 34 | 263,5 | 184,1 | 8959 | 6259,4 | 48510,35 | 154,21 | 29,89 |
| 195 | 162,2 | 164,9 | 31629 | 32155,5 | 26746,78 | 164,75 | 0,15 |
| 39 | 120 | 115 | 4680 | 4485 | 13800 | 125,11 | -10,11 |
| 42 | 178 | 139 | 7476 | 5838 | 24742 | 137,87 | 1,13 |
| 28 | 102 | 110 | 2856 | 3080 | 11220 | 119,17 | -9,17 |
| 42 | 112,4 | 169,3 | 4720,8 | 7110,6 | 19029,32 | 124,11 | 45,19 |
| 40 | 134 | 114 | 5360 | 4560 | 15276 | 128,25 | -14,25 |
| 34 | 125 | 111 | 4250 | 3774 | 13875 | 125,18 | -14,18 |
| 61 | 126,7 | 163,4 | 7728,7 | 9967,4 | 20702,78 | 130,86 | 32,54 |
| 42 | 156 | 121 | 6552 | 5082 | 18876 | 133,25 | -12,25 |
| 46 | 83,3 | 134,7 | 3831,8 | 6196,2 | 11220,51 | 118,80 | 15,90 |
| 15 | 420 | 184 | 6300 | 2760 | 77280 | 183,27 | 0,73 |
| 22 | 175 | 122 | 3850 | 2684 | 21350 | 133,29 | -11,29 |
| 33 | 129 | 119 | 4257 | 3927 | 15351 | 125,82 | -6,82 |
| 47 | 130 | 120 | 6110 | 5640 | 15600 | 128,79 | -8,79 |
| 54 | 154 | 140 | 8316 | 7560 | 21560 | 135,20 | 4,80 |
| 34 | 134,1 | 129,1 | 4559,4 | 4389,4 | 17312,31 | 127,08 | 2,02 |
| 32 | 132 | 115 | 4224 | 3680 | 15180 | 126,25 | -11,25 |
| 38 | 146 | 122 | 5548 | 4636 | 17812 | 130,37 | -8,37 |
| 58 | 143 | 117 | 8294 | 6786 | 16731 | 133,69 | -16,69 |
| 21 | 143,5 | 116,4 | 3013,5 | 2444,4 | 16703,4 | 126,49 | -10,09 |
| 51 | 122,6 | 122,7 | 6252,6 | 6257,7 | 15043,02 | 128,03 | -5,33 |
| 58 | 154 | 130 | 8932 | 7540 | 20020 | 135,99 | -5,99 |
| 36 | 129 | 115 | 4644 | 4140 | 14835 | 126,41 | -11,41 |
| 48 | 129 | 121 | 6192 | 5808 | 15609 | 128,78 | -7,78 |
| 32 | 91 | 105 | 2912 | 3360 | 9555 | 117,65 | -12,65 |
| сумма | 0,0000 |
2.Случайный характер остатков. Проверим графически:
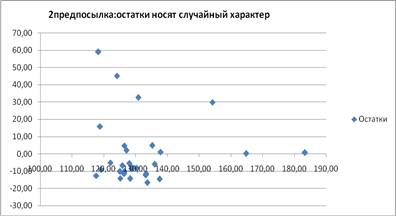
Из графика зависимости остатков εi от теоретических значений результативного признака видно, что точки распределены случайно, следовательно, εi представляют собой случайные величины и МНК оправдан.
3. Наличие гомоскедастичности. Воспользуемся методом Гольдфельда – Квандта. Число исключаемых центральных наблюдений примем равным 8. Тогда в каждой группе будет по 11 наблюдений. Результаты расчетов представим в таблице:
| x1 | x2 | y | x1x2 | yx1 | yx2 | y^x | y-y^x | Ai | (y-y^x)^2 |
| 46 | 83,3 | 134,7 | 3831,8 | 6196,2 | 11220,51 | 132,15 | 2,55 | 1,8961 | 6,52 |
| 32 | 91 | 105 | 2912 | 3360 | 9555 | 128,41 | -23,41 | 22,2973 | 548,13 |
| 28 | 102 | 110 | 2856 | 3080 | 11220 | 127,98 | -17,98 | 16,3451 | 323,27 |
| 64 | 103 | 131,2 | 6592 | 8396,8 | 13513,6 | 139,08 | -7,88 | 6,0058 | 62,09 |
| 22 | 103,4 | 177,3 | 2274,8 | 3900,6 | 18332,82 | 126,24 | 51,06 | 28,7972 | 2606,87 |
| 42 | 112,4 | 169,3 | 4720,8 | 7110,6 | 19029,32 | 133,02 | 36,28 | 21,4308 | 1316,41 |
| 29 | 115 | 117 | 3335 | 3393 | 13455 | 129,22 | -12,22 | 10,4468 | 149,40 |
| 39 | 120 | 115 | 4680 | 4485 | 13800 | 132,65 | -17,65 | 15,3447 | 311,40 |
| 51 | 122,6 | 122,7 | 6252,6 | 6257,7 | 15043,02 | 136,51 | -13,81 | 11,2549 | 190,71 |
| 34 | 125 | 111 | 4250 | 3774 | 13875 | 131,48 | -20,48 | 18,4460 | 419,23 |
| 61 | 126,7 | 163,4 | 7728,7 | 9967,4 | 20702,78 | 139,87 | 23,53 | 14,4012 | 553,73 |
| 0,0000 | 15,1514 | 6487,74 |
| x1 | x2 | y | x1x2 | yx1 | yx2 | y^x | y-y^x | Ai | (y-y^x)^2 |
| 21 | 143,5 | 116,4 | 3013,5 | 2444,4 | 16703,4 | 119,32 | -2,92 | 2,5060 | 8,51 |
| 38 | 146 | 122 | 5548 | 4636 | 17812 | 124,14 | -2,14 | 1,7530 | 4,57 |
| 58 | 154 | 130 | 8932 | 7540 | 20020 | 131,22 | -1,22 | 0,9407 | 1,50 |
| 54 | 154 | 140 | 8316 | 7560 | 21560 | 130,25 | 9,75 | 6,9625 | 95,01 |
| 42 | 156 | 121 | 6552 | 5082 | 18876 | 127,90 | -6,90 | 5,7020 | 47,60 |
| 195 | 162,2 | 164,9 | 31629 | 32155,5 | 26746,78 | 166,75 | -1,85 | 1,1203 | 3,41 |
| 50 | 169 | 123 | 8450 | 6150 | 20787 | 133,47 | -10,47 | 8,5103 | 109,57 |
| 22 | 175 | 122 | 3850 | 2684 | 21350 | 128,35 | -6,35 | 5,2041 | 40,31 |
| 42 | 178 | 139 | 7476 | 5838 | 24742 | 134,04 | 4,96 | 3,5697 | 24,62 |
| 34 | 263,5 | 184,1 | 8959 | 6259,4 | 48510,35 | 155,95 | 28,15 | 15,2883 | 792,18 |
| 15 | 420 | 184 | 6300 | 2760 | 77280 | 195,01 | -11,01 | 5,9854 | 121,29 |
| 0,0000 | 5,2311 | 1248,57 |
Величина R=0,1924 (1248,57/6487,74), меньше табличного значения F-критерия, следовательно, наличие гомоскедастичности и отсутствие гетероскедастичности.
4.Отсутствие автокорреляции. Тест Дарбина–Уотсона:
| x1 | x2 | y | y^ | lу-у^l | (lу-у^l/у)*100 | у-у^ | ei-ei-1 | (ei-ei-1)^2 | (у-у^)^2 |
| 64 | 103 | 131 | 126,48 | 4,715497 | 3,594 | -4,715 | -4,7155 | 22,2 | 22,24 |
| 50 | 169 | 123 | 137,56 | 14,55865 | 11,836 | 14,559 | 19,27414 | 371,5 | 211,95 |
| 29 | 115 | 117 | 122,09 | 5,093094 | 4,353 | 5,093 | -9,46555 | 89,6 | 25,94 |
| 22 | 103 | 177 | 118,28 | 59,02032 | 33,288 | -59,020 | -64,1134 | 4110,5 | 3483,40 |
| 34 | 264 | 184 | 154,21 | 29,88682 | 16,234 | -29,887 | 29,13349 | 848,8 | 893,22 |
| 195 | 162 | 165 | 164,75 | 0,151302 | 0,092 | -0,151 | 29,73552 | 884,2 | 0,02 |
| 39 | 120 | 115 | 125,11 | 10,11485 | 8,796 | 10,115 | 10,26615 | 105,4 | 102,31 |
| 42 | 178 | 139 | 137,87 | 1,133281 | 0,815 | -1,133 | -11,2481 | 126,5 | 1,28 |
| 28 | 102 | 110 | 119,17 | 9,170267 | 8,337 | 9,170 | 10,30355 | 106,2 | 84,09 |
| 42 | 112 | 169 | 124,11 | 45,18646 | 26,690 | -45,186 | -54,3567 | 2954,7 | 2041,82 |
| 40 | 134 | 114 | 128,25 | 14,24733 | 12,498 | 14,247 | 59,43379 | 3532,4 | 202,99 |
| 34 | 125 | 111 | 125,18 | 14,17636 | 12,771 | 14,176 | -0,07097 | 0,0 | 200,97 |
| 61 | 127 | 163 | 130,86 | 32,53879 | 19,914 | -32,539 | -46,7152 | 2182,3 | 1058,77 |
| 42 | 156 | 121 | 133,25 | 12,25437 | 10,128 | 12,254 | 44,79316 | 2006,4 | 150,17 |
| 46 | 83,3 | 135 | 118,80 | 15,89794 | 11,802 | -15,898 | -28,1523 | 792,6 | 252,74 |
| 15 | 420 | 184 | 183,27 | 0,725914 | 0,395 | -0,726 | 15,17202 | 230,2 | 0,53 |
| 22 | 175 | 122 | 133,29 | 11,29077 | 9,255 | 11,291 | 12,01669 | 144,4 | 127,48 |
| 33 | 129 | 119 | 125,82 | 6,817621 | 5,729 | 6,818 | -4,47315 | 20,0 | 46,48 |
| 47 | 130 | 120 | 128,79 | 8,790167 | 7,325 | 8,790 | 1,972546 | 3,9 | 77,27 |
| 54 | 154 | 140 | 135,20 | 4,796736 | 3,426 | -4,797 | -13,5869 | 184,6 | 23,01 |
| 34 | 134 | 129 | 127,08 | 2,015804 | 1,561 | -2,016 | 2,780932 | 7,7 | 4,06 |
| 32 | 132 | 115 | 126,25 | 11,24923 | 9,782 | 11,249 | 13,26503 | 176,0 | 126,55 |
| 38 | 146 | 122 | 130,37 | 8,368454 | 6,859 | 8,368 | -2,88077 | 8,3 | 70,03 |
| 58 | 143 | 117 | 133,69 | 16,68649 | 14,262 | 16,686 | 8,318035 | 69,2 | 278,44 |
| 21 | 144 | 116 | 126,49 | 10,08938 | 8,668 | 10,089 | -6,59711 | 43,5 | 101,80 |
| 51 | 123 | 123 | 128,03 | 5,32814 | 4,342 | 5,328 | -4,76124 | 22,7 | 28,39 |
| 58 | 154 | 130 | 135,99 | 5,992662 | 4,610 | 5,993 | 0,664522 | 0,4 | 35,91 |
| 36 | 129 | 115 | 126,41 | 11,40967 | 9,921 | 11,410 | 5,417008 | 29,3 | 130,18 |
| 48 | 129 | 121 | 128,78 | 7,777864 | 6,428 | 7,778 | -3,63181 | 13,2 | 60,50 |
| 32 | 91 | 105 | 117,65 | 12,65349 | 12,051 | 12,653 | 4,875628 | 23,8 | 160,11 |
| 19110,43 | 10002,65 |
Исходя из статистики Дарбина-Уотсона, можно сделать вывод, что автокорреляция отсутствует, так как 1,91 находится в промежутке (1,339;2,661) (d2 ; 4-d2 ). Следовательно, значения остатков распределены независимо друг от друга. Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
Таким образом, не все предпосылки выполнились, это говорит о недостаточной надежности уравнения множественной регрессии. Возможно, можно было бы и получить надежную модель, если исключить из данных страны значение динамики ВВП, которых сильно отличается от других.