| Скачать .docx | Скачать .pdf |
Реферат: Линейная парная регрессия
1. Линейная парная регрессия
1.1. Основные понятия и определения
Корреляционная зависимость может быть представлена в виде
Mx (Y ) = j(x ) (1)
или My (X ) = y(у ), где j(x ) ¹const, y(у ) ¹const.
В регрессионном анализе рассматривается односторонняя зависимость случайной переменной Y от одной (или нескольких) неслучайной независимой переменной Х . Такая зависимость Y от X (иногда ее называют регрессионной ) может быть также представлена в виде модельного уравнения регрессии Y от X (1). При этом зависимую переменную Y называют также функцией отклика (объясняемой, выходной, результирующей, эндогенной переменной, результативным признаком), а независимую переменную Х – объясняющей (входной, предсказывающей, предикторной, экзогенной переменной, фактором, регрессором, факторным признаком).
Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная Х примет значение х , т.е. Х = х . В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (xi , yi ) ограниченного объема n . В этом случае речь может идти об оценке (приближенном выражении, аппроксимации) по выборке функции регрессии. Такой оценкой является выборочная линия (кривая) регрессии :
![]() =
= ![]() ( x
, b
0
, b
1
, …, bp
) (2)
( x
, b
0
, b
1
, …, bp
) (2)
где ![]() - условная (групповая) средняя переменной Y
при фиксированном значении переменной X
= x
;
b
0
, b
1
, …, bp
– параметры кривой.
- условная (групповая) средняя переменной Y
при фиксированном значении переменной X
= x
;
b
0
, b
1
, …, bp
– параметры кривой.
Уравнение (2) называется выборочным уравнением регрессии .
В дальнейшем рассмотрим линейную модель и представим ее в виде
![]() = b
0
+ b
1
x
. (3)
= b
0
+ b
1
x
. (3)
Для решения поставленной задачи определим формулы расчета неизвестных параметров уравнения линейной регрессии (b 0 , b 1 ).
Согласно методу наименьших квадратов (МНК)
неизвестные параметры b
0
и b
1
выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значенийyi
от значений ![]() , найденных по уравнению регрессии (3), была минимальной:
, найденных по уравнению регрессии (3), была минимальной:
![]() . (4)
. (4)
На основании необходимого условия экстремума функции двух переменных S = S (b 0 , b 1 ) (4) приравняем к нулю ее частные производные, т.е.
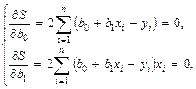
откуда после преобразований получим систему нормальных уравнений для определения параметров линейной регрессии:
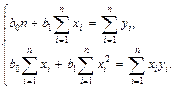 (5)
(5)
Теперь, разделив обе части уравнений (5) на n , получим систему нормальных уравнений в следующем виде:
![]() (6)
(6)
где соответствующие средние определяются по формулам:
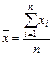 ; (7)
; (7) 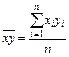 ; (9)
; (9)
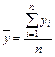 ; (8)
; (8) 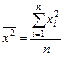 . (10)
. (10)
Решая систему (6), найдем
![]() , (11)
, (11)
где ![]() - выборочная дисперсия переменной Х
:
- выборочная дисперсия переменной Х
:
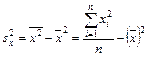 , (12)
, (12)
![]() - выборочный корреляционный момент или выборочная ковариация:
- выборочный корреляционный момент или выборочная ковариация:
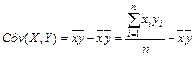 . (13)
. (13)
Коэффициент b 1 называется выборочным коэффициентом регрессии Y по X .
Коэффициент регрессии Y по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.
Отметим, что из уравнения регрессии ![]() следует, что линия регрессии проходит через точку
следует, что линия регрессии проходит через точку ![]() , т.е.
, т.е. ![]() = b
0
+ b
1
= b
0
+ b
1
![]() .
.
На первый взгляд, подходящим измерителем тесноты связи Y
от Х
является коэффициент регрессии b
1
. Однако b
1
зависит от единиц измерения переменных. Очевидно, что для "исправления" b
1
как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Если представить уравнение ![]() в эквивалентном виде:
в эквивалентном виде:
![]() . (14)
. (14)
В этой системе величина ![]() называется выборочный коэффициент корреляции
и является показателем тесноты связи.
называется выборочный коэффициент корреляции
и является показателем тесноты связи.
Если r > 0 (b 1 > 0), то корреляционная связь между переменными называется прямой, если r < 0 (b 1 < 0), - обратной.
Учитывая (7)–(13) получим следующие формулы для расчета коэффициента корреляции:
![]() ; (15)
; (15)
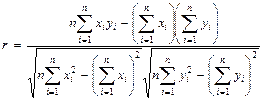 . (16)
. (16)
Выборочный коэффициент корреляции обладает следующими свойствами:
1.Коэффициент корреляции принимает значения на отрезке [-1: 1], т.е. -1 ≤ r ≥ 1.
2.Приr =±1 корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдения располагаются на прямой линии.
3. При r = 0 линейная корреляционная связь отсутствует. При этом линия регрессии параллельна оси ОХ .
В силу воздействия неучтенных факторов и причин отдельные наблюдения переменной Y будут в большей или меньшей мере отклоняться от функции регрессии j(Х ). В этом случае уравнение взаимосвязи двух переменных (парная регрессионная модель) может быть представлена в виде:
Y = j(X ) + e,
где e-случайная переменная (случайный член), характеризующая отклонение от функции регрессии.
Рассмотрим линейный регрессионный анализ, для которого унция j(Х ) линейна относительно оцениваемых параметров:
Mx (Y ) = b0 + b1 x .(17)
Предположим, что для оценки параметров линейной функции регрессии (17) взята выборка, содержащая п пар значений переменных (xi , yi ), где i = 1, 2, …, п . В этом случае линейная парная регрессионная модель имеет вид:
yi = b0 + b1 xi + ei . (18)
Отметим основные предпосылки регрессионного анализа (условия Гаусса-Маркова) .
1. В моделиyi = b0 + b1 xi + ei возмущение ei есть величина случайная, а объясняющая переменная xi – величина неслучайная.
2. Математическое ожидание возмущения ei равно нулю:
M (ei ) = 0. (19)
3. Дисперсия возмущения ei постоянна для любого i :
D (ei ) = s2 . (20)
4. Возмущения ei и ej не коррелированны:
M (ei ej ) = 0 (i ¹j ). (21)
5. Возмущения ei есть нормально распределенная случайная величина.
Оценкой модели (18) по выборке является уравнение регрессии ![]() = b
0
+ b
1
x
. Параметры этого уравнения b
0
и b
1
определяются на основе МНК. Воздействие неучтенных случайных факторов и ошибок наблюдений в модели (18) определяется с помощью дисперсии возмущений (ошибок)
или остаточной дисперсии
(см. табл. 1).
= b
0
+ b
1
x
. Параметры этого уравнения b
0
и b
1
определяются на основе МНК. Воздействие неучтенных случайных факторов и ошибок наблюдений в модели (18) определяется с помощью дисперсии возмущений (ошибок)
или остаточной дисперсии
(см. табл. 1).
Теорема Гаусса
-
Маркова
. Если регрессионная модель
yi
= b0
+ b1
xi
+ ei
удовлетворяет предпосылкам 1-5, то оценкиb
0
, b
1
имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.
Таким образом, оценки b 0 и b 1 в определенном смысле являются наиболее эффективными линейными оценками параметров b0 и b1 .
Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Для проверки значимости выдвигают нулевую гипотезу о надежности параметров. Вспомним основные понятия и определения необходимые для анализа значимости параметров регрессии.
Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным.
Нулевая гипотеза Н 0 – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияние фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п.
Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой.
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость проверить ее. Так как проверку производят статистическими методами, то данная проверка называется статистической.
При проверке статистических гипотез возможны ошибки (ошибочные суждения) двух видов:
- можно отвергнуть нулевую гипотезу, когда она на самом деле верна (так называемая ошибка первого рода );
- можно принять нулевую гипотезу, когда она на самом деле не верна (так называемая ошибка второго рода ).
Допустимая вероятность ошибки первого рода может быть равна 5% или 1% (0,05 или 0,01).
Уровень значимости – это вероятность ошибки первого рода при принятии решения (вероятность ошибочного отклонения нулевой гипотезы).
Альтернативные гипотезы принимаются тогда и только тогда, когда опровергается нулевая гипотеза. Это бывает в случаях, когда различия в средних арифметических экспериментальной и контрольной групп настолько значимы (статистически достоверны), что риск ошибки отвергнуть нулевую гипотезу и принять альтернативную не превышает одного из трех принятых уровней значимости статистического вывода:
1-йуровень - 5% (a = 0,05), где допускается риск ошибки в выводе в пяти случаях из ста теоретически возможных таких же экспериментов при строго случайном отборе для каждого эксперимента;
2-й уровень - 1% (a = 0,01), т. е. соответственно допускается риск ошибиться только в одном случае из ста;
3-й уровень - 0,1% (a = 0,01), т. е. допускается риск ошибиться только в одном случае из тысячи.
Последний уровень значимости предъявляет очень высокие требования к обоснованию достоверности результатов эксперимента и потому редко используется. В эконометрических исследованиях, не нуждающихся в очень высоком уровне достоверности, представляется разумным принять 5%-й уровень значимости.
Статистика критерия - некоторая функция от исходных данных, по значению которой проверяется нулевая гипотеза. Чаще всего статистика критерия является числовой функцией.
Всякое правило, на основе которого отклоняется или принимается нулевая гипотеза, называется критерием проверки данной гипотезы. Статистический критерий – это случайная величина, которая служит для проверки статистических гипотез.
Критическая область – совокупность значений критерия, при котором нулевую гипотезу отвергают. Область принятия нулевой гипотезы (область допустимых значений) – совокупность значений критерия, при котором нулевую гипотезу принимают. При справедливости нулевой гипотезы вероятность того, что статистика критерия попадает в область принятия нулевой гипотезы должна быть равна 1.
Процедура проверки нулевой гипотезы в общем случае включает следующие этапы:
- задается допустимая вероятность ошибки первого рода (a = 0,05);
- выбирается статистика критерия;
- ищется область допустимых значений;
- по исходным данным вычисляется значение статистики;
- если статистика критерияпринадлежит области принятия нулевой гипотезы, то нулевая гипотеза принимается (корректнее говоря, делается заключение, что исходные данные не противоречат нулевой гипотезе), а в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза. Это основной принцип проверки всех статистических гипотез.
В современных эконометрических программах (например, EViews) используются не стандартные уровни значимости, а уровни, подсчитываемые непосредственно в процессе работы с соответствующим статистическим методом. Эти уровни, обозначенные обычно Prob , могут иметь различное числовое выражение в интервале от 0 до 1, например, 0,7, 0,23 или 0,012. Понятно, что в первых двух случаях, полученные уровни значимости слишком велики и говорить о том, что результат значим нельзя. В последнем случае результаты значимы на уровне двенадцати тысячных.
Если вычисленное значение Р rob превосходит выбранный уровень Р rob кр , то принимается нулевая гипотеза, а в противном случае - альтернативная гипотеза. Чем меньше вычисленное значение Р rob , тем более исходные данные противоречат нулевой гипотезе.
Число степеней свободы у какого-либо параметра определяют как размер выборки, по которой рассчитан данный параметр, минус количество выбранных переменных.
Величина W называется мощностью критерия и представляет собой вероятность отклонения неверной нулевой гипотезы, т.е. вероятность правильного решения. Мощность критерия – вероятность попадания критерия в критическую область при условии, что справедлива альтернативная гипотеза. Чем больше W , тем вероятность ошибки второго рода меньше.
Коэффициент регрессии (b 1 ) является случайной величиной. Отсюда после вычисления возникает необходимость проверки гипотезы о значимости полученного значения. Выдвигаем нулевую гипотеза (Н 0 ) о равенстве нулю коэффициента регрессии (Н 0 :b 1 = 0) против альтернативной гипотезы (Н 1 ) о неравенстве нулю коэффициента регрессии (Н 1 :b 1 ¹ 0). Для проверки гипотезы Н 0 против альтернативы используется t -статистика, которая имеет распределение Стьюдента с (n - 2) степенями свободы (парная линейная регрессия).
Коэффициент регрессии надежно отличается от нуля (отвергается нулевая гипотеза Н0 ), если t набл > t a ; n -2 . В этом случае вероятность нулевой гипотезы (Prob . ) будет меньше выбранного уровня значимости. t a ; n -2 - критическая точка, определяемая по математико-статистическим таблицам.
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
Согласно основной идее дисперсионного анализа
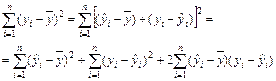 (22)
(22)
или
Q = QR + Qe , (23)
где Q – общая сумма квадратов отклонений зависимой переменной от средней, а QR и Qe – соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов.
Схема дисперсионного анализа имеет вид, представленный в табл. 1.
Средние квадраты ![]() и s
2
(табл. 1) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной Х
и воздействием неучтенных случайных факторов и ошибок; m
– число оцениваемых параметров уравнения регрессии; п
– число наблюдений.
и s
2
(табл. 1) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной Х
и воздействием неучтенных случайных факторов и ошибок; m
– число оцениваемых параметров уравнения регрессии; п
– число наблюдений.
При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины ![]() и
и ![]() имеют c2
-распределение соответственно с т
– 1 и п
– т
степенями свободы.
имеют c2
-распределение соответственно с т
– 1 и п
– т
степенями свободы.
Таблица 1
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы |
Средние квадраты |
| Регрессия | m – 1 | ||
| Остаточная | n – m | ||
| Общая | n – 1 |
Поэтому уравнение регрессии значимо на уровне a, если фактически наблюдаемое значение статистики
![]() , (24)
, (24)
где ![]() - табличное значение F
-критерия Фишера-Снедекора, определяемое на уровне значимости a при k
1
= m
– 1 и k
2
= n
– m
степенях свободы.
- табличное значение F
-критерия Фишера-Снедекора, определяемое на уровне значимости a при k
1
= m
– 1 и k
2
= n
– m
степенях свободы.
Учитывая смысл величин ![]() и s
2
, можно сказать, что значение F
показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
и s
2
, можно сказать, что значение F
показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.
Для парной линейно регрессии т = 2, и уравнение регрессии значимо на уровне a (отвергается нулевая гипотеза), если
![]() . (25)
. (25)
Следует отметить, что значимость уравнения парной линейной регрессии может быть проведена и другим способом, если оценить значимость коэффициента регрессии
b
1
, который имеет
t
-распределение Стьюдента с k
= n
– 2 степенями свободы.
Уравнение парной регрессии или коэффициент регрессии b
1
значимы на уровне a (иначе – гипотеза Н
0
о равенстве параметра b
1
нулю, т.е.
Н
0
:b
1
= 0, отвергается), если фактически наблюдаемое значение статистики
![]() (26)
(26)
больше критического (по абсолютной величине), т.е. |t | > t 1 - a ; n - 2 .
Коэффициент корреляции r значим на уровне a (Н 0 : r = 0), если
![]() . (27)
. (27)
Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации , определяемый по формуле:
![]() . (28)
. (28)
Величина R 2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату корреляции, т.е. R 2 = r 2 .
Доверительный интервал для индивидуальных значений зависимой переменной
![]() .
.
![]() -t
1 –
a
;
n
-
2
×
-t
1 –
a
;
n
-
2
×![]() £
£![]() £
£![]() + t
1
-
a
;
n
-
2
×
+ t
1
-
a
;
n
-
2
×![]() , (29)
, (29)
где 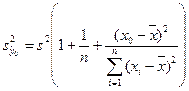 - оценка дисперсии индивидуальных значений у
0
при х
= х
0
.
- оценка дисперсии индивидуальных значений у
0
при х
= х
0
.
Доверительный интервал для параметров регрессионной модели .
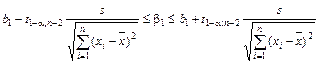 (30)
(30)
1.4. Типичный пример анализа экономических процессов
с использованием пространственных данных
По 28 предприятиям концерна изучается зависимость дневной выработки (ед.) у от уровня механизации труда (%) х по следующим данным (табл. 2).
Таблица 2
| Номер пред-приятия | Уровень механизации, %, х | Дневная выработка, ед., у | Номер пред-приятия | Уровень механизации, %, х | Дневная выработка, ед., у |
| 1 | 15 | 5 | 15 | 63 | 24 |
| 2 | 24 | 6 | 16 | 64 | 25 |
| 3 | 42 | 6 | 17 | 66 | 25 |
| 4 | 46 | 9 | 18 | 70 | 27 |
| 5 | 48 | 15 | 19 | 72 | 31 |
| 6 | 48 | 14 | 20 | 75 | 33 |
| 7 | 50 | 17 | 21 | 76 | 33 |
| 8 | 52 | 17 | 22 | 80 | 42 |
| 9 | 53 | 22 | 23 | 82 | 41 |
| 10 | 54 | 21 | 24 | 87 | 44 |
| 11 | 55 | 22 | 25 | 90 | 53 |
| 12 | 60 | 23 | 26 | 93 | 55 |
| 13 | 61 | 23 | 27 | 95 | 57 |
| 14 | 62 | 24 | 28 | 99 | 62 |
При анализе статистических зависимостей широко используются графические методы, которые задают направление его дальнейшего анализа. В Excel для этого можно использовать средство Мастер диаграмм . Для создания диаграммы необходимо выделить данные, запустить мастер диаграмм, выбрать тип и вид диаграммы (для нашего примера тип диаграммы – Точечная), выбрать и уточнить ориентацию диапазона данных и ряда, настроить параметры диаграммы.
Для описания закономерностей в исследуемой выборке наблюдений строится линия тренда .
Для добавления линии тренда в диаграмму необходимо выполнить следующие действия:
1) щелкнуть правой кнопкой мыши по ряду данных;
2) в динамическом меню выбрать команду Добавить линию тренда. На экране появится окно Линия тренда (рис. 2);
3) выбрать вид зависимости регрессии. Для нашего примера тип тренда определим, как Линейный;
4) перейти на вкладку Параметры. В поле Показать уравнение на диаграмме установить подтверждение;
5) в случае необходимости можно задать остальные параметры.
Рис. 2. Диалоговое окно для выбора типа тренда
Изобразим полученную зависимость графически точками координатной плоскости (рис. 3). Такое изображение статистической зависимости называется полем корреляции .
По расположению эмпирических точек можно предполагать наличие линейной корреляционной (регрессионной) зависимости между переменными х и у .
По данным табл. 2 найдем уравнение регрессии у по х . Расчеты произведем в Excel по формулам (7)–(13), промежуточные вычисления представим в табл. 3.
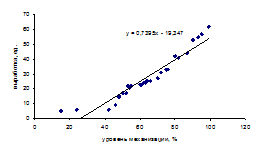
Рис. 3. Поле корреляции
Таблица 3
| N | X | Y | X*Y | X*X | Y*Y |
| 1 | 15 | 5 | 75 | 225 | 25 |
| 2 | 24 | 6 | 144 | 576 | 36 |
| 3 | 42 | 6 | 252 | 1764 | 36 |
| 4 | 46 | 9 | 414 | 2116 | 81 |
| 5 | 48 | 15 | 720 | 2304 | 225 |
| 6 | 48 | 14 | 672 | 2304 | 196 |
| 7 | 50 | 17 | 850 | 2500 | 289 |
| 8 | 52 | 17 | 884 | 2704 | 289 |
| 9 | 53 | 22 | 1166 | 2809 | 484 |
| 10 | 54 | 21 | 1134 | 2916 | 441 |
| 11 | 55 | 22 | 1210 | 3025 | 484 |
| 12 | 60 | 23 | 1380 | 3600 | 529 |
| 13 | 61 | 23 | 1403 | 3721 | 529 |
| 14 | 62 | 24 | 1488 | 3844 | 576 |
| 15 | 63 | 24 | 1512 | 3969 | 576 |
| 16 | 64 | 25 | 1600 | 4096 | 625 |
| 17 | 66 | 25 | 1650 | 4356 | 625 |
| 18 | 70 | 27 | 1890 | 4900 | 729 |
| 19 | 72 | 31 | 2232 | 5184 | 961 |
| 20 | 75 | 33 | 2475 | 5625 | 1089 |
| 21 | 76 | 33 | 2508 | 5776 | 1089 |
| 22 | 80 | 42 | 3360 | 6400 | 1764 |
| 23 | 82 | 41 | 3362 | 6724 | 1681 |
| 24 | 87 | 44 | 3828 | 7569 | 1936 |
| 25 | 90 | 53 | 4770 | 8100 | 2809 |
| 26 | 93 | 55 | 5115 | 8649 | 3025 |
| 27 | 95 | 57 | 5415 | 9025 | 3249 |
| 28 | 99 | 62 | 6138 | 9801 | 3844 |
| Сумма | 1782 | 776 | 57647 | 124582 | 28222 |
| Среднее | 63,64286 | 27,71429 | 2058,821 | 4449,357 | |
| Дисперсия | 398,9439 | 239,8469 | b1 | 0,739465 | |
| Cov(x,y) | 295,0051 | b0 | -19,3474 |
Итак, уравнение регрессии у по х :
![]() = -19,37 + 0,74x
.
= -19,37 + 0,74x
.
Из полученного уравнения регрессии следует, что при увеличении уровня механизации х на 1% выработка у увеличивается в среднем на 0,74 ед.
По исходным данным вычислим коэффициент корреляции.
Расчеты произведем в Excel, промежуточные вычисления см. табл. 3 и формулы (15), (16).
![]() = 0,954,
= 0,954,
т.е. связь между переменными тесная.
Оценим на уровне значимости a = 0,05 значимость уравнения регрессии у по х .
1-й способ . Используя данные табл. 4 вычислим необходимые суммы по формулам табл. 1:
![]() = 6715,71 (см. столбец 6);
= 6715,71 (см. столбец 6);
QR
= ![]() = 6108,09 (см. столбец 7);
= 6108,09 (см. столбец 7);
Qe = Q -QR = 6715,71 – 6108,09 = 607,63
Таблица 4
| N | X | Y | Yрег | Yi-Yрег | (Yi-Yср)^2 | (Yрег-Yср)^2 | (Xi-Xcp)^2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 15 | 5 | -8,25541 | 13,2554 | 515,9388 | 1293,8192 | 2366,12755 |
| 2 | 24 | 6 | -1,60023 | 7,6002 | 471,5102 | 859,3406 | 1571,55612 |
| 3 | 42 | 6 | 11,71015 | -5,7101 | 471,5102 | 256,1325 | 468,413265 |
| 4 | 46 | 9 | 14,66801 | -5,6680 | 350,2245 | 170,2054 | 311,270408 |
| 5 | 48 | 15 | 16,14694 | -1,1469 | 161,6531 | 133,8035 | 244,69898 |
| 6 | 48 | 14 | 16,14694 | -2,1469 | 188,0816 | 133,8035 | 244,69898 |
| 7 | 50 | 17 | 17,62587 | -0,6259 | 114,7959 | 101,7762 | 186,127551 |
| 8 | 52 | 17 | 19,1048 | -2,1048 | 114,7959 | 74,1233 | 135,556122 |
| 9 | 53 | 22 | 19,84426 | 2,1557 | 32,6531 | 61,9372 | 113,270408 |
| 10 | 54 | 21 | 20,58373 | 0,4163 | 45,0816 | 50,8448 | 92,9846939 |
| 11 | 55 | 22 | 21,32319 | 0,6768 | 32,6531 | 40,8461 | 74,6989796 |
| 12 | 60 | 23 | 25,02052 | -2,0205 | 22,2245 | 7,2564 | 13,2704082 |
| 13 | 61 | 23 | 25,75998 | -2,7600 | 22,2245 | 3,8193 | 6,98469388 |
| 14 | 62 | 24 | 26,49945 | -2,4995 | 13,7959 | 1,4758 | 2,69897959 |
| 15 | 63 | 24 | 27,23892 | -3,2389 | 13,7959 | 0,2260 | 0,41326531 |
| 16 | 64 | 25 | 27,97838 | -2,9784 | 7,3673 | 0,0697 | 0,12755102 |
| 17 | 66 | 25 | 29,45731 | -4,4573 | 7,3673 | 3,0381 | 5,55612245 |
| 18 | 70 | 27 | 32,41517 | -5,4152 | 0,5102 | 22,0983 | 40,4132653 |
| 19 | 72 | 31 | 33,8941 | -2,8941 | 10,7959 | 38,1901 | 69,8418367 |
| 20 | 75 | 33 | 36,1125 | -3,1125 | 27,9388 | 70,5300 | 128,984694 |
| 21 | 76 | 33 | 36,85196 | -3,8520 | 27,9388 | 83,4971 | 152,69898 |
| 22 | 80 | 42 | 39,80982 | 2,1902 | 204,0816 | 146,3020 | 267,556122 |
| 23 | 82 | 41 | 41,28875 | -0,2888 | 176,5102 | 184,2662 | 336,984694 |
| 24 | 87 | 44 | 44,98608 | -0,9861 | 265,2245 | 298,3149 | 545,556122 |
| 25 | 90 | 53 | 47,20447 | 5,7955 | 639,3673 | 379,8675 | 694,69898 |
| 26 | 93 | 55 | 49,42287 | 5,5771 | 744,5102 | 471,2626 | 861,841837 |
| 27 | 95 | 57 | 50,9018 | 6,0982 | 857,6531 | 537,6608 | 983,270408 |
| 28 | 99 | 62 | 53,85966 | 8,1403 | 1175,5102 | 683,5807 | 1250,12755 |
| Сумма | 1782 | 776 | 0,00 | 6715,7143 | 6108,0879 | 11170,4286 | |
| Среднее | 63,64286 | 27,71429 | |||||
| b1 | 0,739465 | ||||||
| b0 | -19,3474 |
F
= ![]() = 261,36.
= 261,36.
По статистическим таблицам F
-распределения F0,05;1;26
= 4,22. Так как
F
> F
0,05;1;26
, то уравнение регрессии значимо.
2-й способ
. Учитывая, что b
1
= 0,739, ![]() = 11170,43
= 11170,43
(табл. 4), ![]() =
= ![]() =23,37 (табл. 4), по формуле (26)
=23,37 (табл. 4), по формуле (26)
t
= ![]() = 16,17.
= 16,17.
По таблице t -распределения t 0,95;26 = 2,06. Так как t > t 0,95;26 , то коэффициент регрессии b 1 , а значит, и уравнение парной линейной регрессии значимо.
Найдем коэффициент детерминации и поясним его смысл. Ранее было получено QR
= 6108,09, Q
= 6715,71. По формуле (28) ![]() = 0,9095 (или R
2
= r
2
= 0,9542
= 0,9095). Это означает, что изменения зависимой переменной у
– дневная выработка – на 90% объясняется вариацией объясняющей переменной х
– уровнем механизации.
= 0,9095 (или R
2
= r
2
= 0,9542
= 0,9095). Это означает, что изменения зависимой переменной у
– дневная выработка – на 90% объясняется вариацией объясняющей переменной х
– уровнем механизации.
Найдем 95%-ные доверительные интервалы для индивидуального значения прибыли при уровне механизации равной 65%.
Ранее было получено уравнение регрессии
![]() = -19,37 + 0,74x
.
= -19,37 + 0,74x
.
Чтобы построить доверительный интервал для индивидуального значения ![]() , найдем точечное значение признака
, найдем точечное значение признака ![]() = -19,37 + 0,74∙65 = 28,718.
= -19,37 + 0,74∙65 = 28,718.
Затем найдем дисперсию оценки:
![]() =23,370
=23,370![]() = 0,839
= 0,839
и ![]() = 0,916.
= 0,916.
Далее искомый доверительный интервал получим по (29):
28,718 – 2,06∙0,916 £![]() £ 28,718 + 2,06∙0,916
£ 28,718 + 2,06∙0,916
26,832 £![]() £ 30,604
£ 30,604
Таким образом, дневная выработка при уровне механизации равной 65% с надежностью 0,95 находится в пределах от 26,832 ед. до
30,604 ед.
Найдем 95%-ный доверительный интервал для параметра b1 .
По формуле (30)
0,74 – 2,06![]() £b1
£ 0,74 + 2,06
£b1
£ 0,74 + 2,06![]() ,
,
0,645 £b1 £ 0,834,
т.е. с надежностью 0,95 при изменении уровня механизации x на 1% дневная выработка y будет изменяться на величину, заключенную в интервале от 0,645 до 0,834 (ед.).
Исследуем полученную модель на наличие гетероскедастичности.
Тест Голфреда - Квандта .
Упорядочим п
наблюдений по мере возрастания переменной х
. Исключим из рассмотрения С
= 6 центральных наблюдений (условие
(п
-С
)/2 = (28 – 6)/2 = 11 > р
= 1 выполняется). Разделим совокупность из (п
-С
) = (28 – 6) = 22 наблюдений на две группы (соответственно с малыми и большими значениями фактора х
по 11 наблюдений) и определим по каждой из групп уравнения регрессии. Для первой группы оно составит ![]() = -3,70 + 0,39x
. Для второй группы:
= -3,70 + 0,39x
. Для второй группы: ![]() = 1,16 + 53,11x
. Определим остаточные суммы квадратов для первой (S
1
) и второй (S
2
) групп. Промежуточные расчеты занесем в табл. 5.
= 1,16 + 53,11x
. Определим остаточные суммы квадратов для первой (S
1
) и второй (S
2
) групп. Промежуточные расчеты занесем в табл. 5.
| N | X | Y | Yрег = -3,70 + 0,39Х | e=Y-Yрег | e^2 |
| 1 | 15 | 5 | 2,15 | 2,85 | 8,1225 |
| 2 | 24 | 6 | 5,66 | 0,34 | 0,1156 |
| 3 | 42 | 6 | 12,68 | -6,68 | 44,6224 |
| 4 | 46 | 9 | 14,24 | -5,24 | 27,4576 |
| 5 | 48 | 15 | 15,02 | -0,02 | 0,0004 |
| 6 | 48 | 14 | 15,02 | -1,02 | 1,0404 |
| 7 | 50 | 17 | 15,8 | 1,2 | 1,44 |
| 8 | 52 | 17 | 16,58 | 0,42 | 0,1764 |
| 9 | 53 | 22 | 16,97 | 5,03 | 25,3009 |
| 10 | 54 | 21 | 17,36 | 3,64 | 13,2496 |
| S1 | 121,5258 | ||||
| N | X | Y | Yрег = -53,11 + 1,16Х | e=Y-Yрег | e^2 |
| 17 | 66 | 25 | 23,45 | 1,55 | 2,4025 |
| 18 | 70 | 27 | 28,09 | -1,09 | 1,1881 |
| 19 | 72 | 31 | 30,41 | 0,59 | 0,3481 |
| 20 | 75 | 33 | 33,89 | -0,89 | 0,7921 |
| 21 | 76 | 33 | 35,05 | -2,05 | 4,2025 |
| 22 | 80 | 42 | 39,69 | 2,31 | 5,3361 |
| 23 | 82 | 41 | 42,01 | -1,01 | 1,0201 |
| 24 | 87 | 44 | 47,81 | -3,81 | 14,5161 |
| 25 | 90 | 53 | 51,29 | 1,71 | 2,9241 |
| 26 | 93 | 55 | 54,77 | 0,23 | 0,0529 |
| 27 | 95 | 57 | 57,09 | -0,09 | 0,0081 |
| 28 | 99 | 62 | 61,73 | 0,27 | 0,0729 |
| S 2 | 32,8636 |
Тест ранговой корреляции Спирмэна
Проранжируем значения х i и абсолютные величины остатков в порядке возрастания, расчеты занесем в табл. 6.
Найдем коэффициент ранговой корреляции Спирмэна:
![]() = 0,108.
= 0,108.
Таблица 6
| N | X | Ei | Расчет ранговой корреляции | |||
| Ранг Х | Ранг |Ei| | d | d^2 | |||
| 1 | 15 | 13,27 | 1 | 28 | -27 | 729 |
| 2 | 24 | 7,61 | 2 | 26 | -24 | 576 |
| 3 | 42 | -5,71 | 3 | 23 | -20 | 400 |
| 4 | 46 | -5,67 | 4 | 22 | -18 | 324 |
| 5 | 48 | -1,15 | 5 | 6 | -1 | 1 |
| 6 | 48 | -2,15 | 6 | 9 | -3 | 9 |
| 7 | 50 | -0,63 | 7 | 3 | 4 | 16 |
| 8 | 52 | -2,11 | 8 | 8 | 0 | 0 |
| 9 | 53 | 2,15 | 9 | 10 | -1 | 1 |
| 10 | 54 | 0,41 | 10 | 2 | 8 | 64 |
| 11 | 55 | 0,67 | 11 | 4 | 7 | 49 |
| 12 | 60 | -2,03 | 12 | 7 | 5 | 25 |
| 13 | 61 | -2,77 | 13 | 13 | 0 | 0 |
| 14 | 62 | -2,51 | 14 | 12 | 2 | 4 |
| 15 | 63 | -3,25 | 15 | 17 | -2 | 4 |
| 16 | 64 | -2,99 | 16 | 15 | 1 | 1 |
| 17 | 66 | -4,47 | 17 | 19 | -2 | 4 |
| 18 | 70 | -5,43 | 18 | 20 | -2 | 4 |
| 19 | 72 | -2,91 | 19 | 14 | 5 | 25 |
| 20 | 75 | -3,13 | 20 | 16 | 4 | 16 |
| 21 | 76 | -3,87 | 21 | 18 | 3 | 9 |
| 22 | 80 | 2,17 | 22 | 11 | 11 | 121 |
| 23 | 82 | -0,31 | 23 | 1 | 22 | 484 |
| 24 | 87 | -1,01 | 24 | 5 | 19 | 361 |
| 25 | 90 | 5,77 | 25 | 24 | 1 | 1 |
| 26 | 93 | 5,55 | 26 | 21 | 5 | 25 |
| 27 | 95 | 6,07 | 27 | 25 | 2 | 4 |
| 28 | 99 | 8,11 | 28 | 27 | 1 | 1 |
| Сумма | 0, 00 | 3258 | ||||
Найдем t -критерий для ранговой корреляции:
![]() = 0,556.
= 0,556.
Сравним полученное значение t
r
с табличным значением
t
0,95; 26
= 2,06. Так как t
r
< t
0,95; 26
, то на уровне значимости 5% принимается гипотеза об отсутствии гетероскедастичности.
Использование теста Уайта рассмотрим во второй части методических указаний.
Тест Парка Тест предполагает, что дисперсия остатков связана со значениями факторов функций ln e2 = а + b lnх + и . Проверяется значимость коэффициента регрессии b по t -критерию Стьюдента. Если коэффициент регрессии для уравнения lne2 окажется статистически значимым, то, следовательно, существует зависимость lne2 от lnх , т.е. имеет место гетероскедастичность остатков.
Чтобы построить зависимость ln e2
= а
+ b
lnх
введем замены:
ln e2
= у
, lnх
= z
. Построим линейную регрессию у
= а
+ bz
. Для этого воспользуемся пакетом анализа MicrosoftExcel (Сервис + Анализ данных + + Регрессия). В результате получим следующую модель:
ln e2 = 5,635 - 0,901 lnх .
Проверка уравнения на значимость показывает: R 2 = 0,039; F = 1,056; ta = 1,565 и tb = 1,028. По тесту Парка зависимость дисперсии остатков от х проявляется ненадежно: все параметры статистически нее значимы, R 2 очень низкий, t -критерий и F -статистика меньше табличных значений (t 0,95;26 = 2,06; F 0,05;1;26 = 4,23). Тест Парка показал отсутствие гетероскедастичности.
Тест Гейзера
Тест оценивает зависимость абсолютных значений остатков от значений фактора х в виде функции: |e| = a + b ∙ xc , где с задается определенным числом степени. Для нашего примера используем значения с равные -2;-1; -0,5; 0,5; 1;2.
Для построения моделей регрессий воспользуемся пакетом анализа Microsoft Excel. Получили следующие результаты:
при с = -2 |e| = 2,62 + 2327,52x -2 R 2 = 0,460; F = 22,14
(5,61) (4,71)
при с = -1 |e| = 0,87 + 153,09x -1 R 2 = 0,360; F = 14,61
(1,01) (3,82)
при с = -0,5 |e| = -2,40 + 46,10x -0,5 R 2 = 0,271; F = 9,65
(1,19) (3,11)
при с = 0,5 |e| = 8,58 - 0,62x 0,5 R 2 = 0,090; F = 2,56
(2,76) (1,60)
при с = 1 |e| = 5,39 - 0,03x R 2 = 0,035; F = 0,945
(2,97) (0,97)
Из теста Гейзера следует, что абсолютная величина остатков достаточно сильно зависит от х -2 .