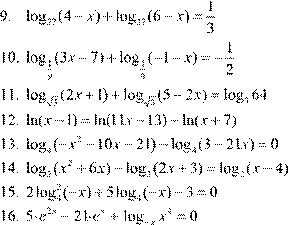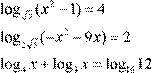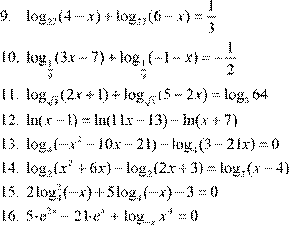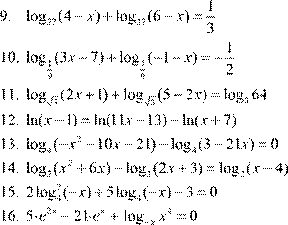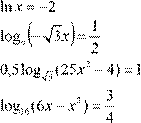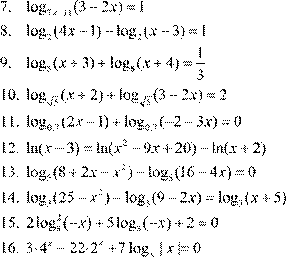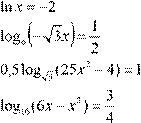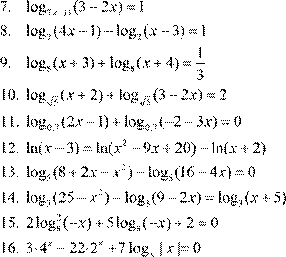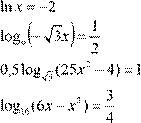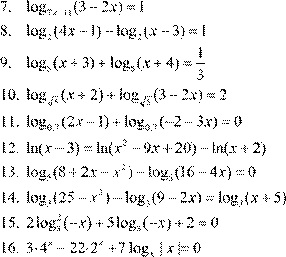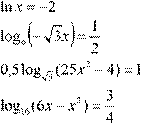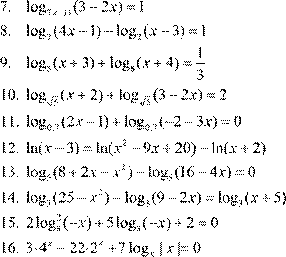| Скачать .docx | Скачать .pdf |
Реферат: Логарифмические уравнения
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
Данная система упражнений может быть использована в качестве дополнения при изучении темы «Логарифмические
уравнения» к любому учебнику по алгебре для 10-го класса.
Система состоит из 5 таблиц, содержащих 64 упражнения в каждой, для устной работы и 16 равноценных вариантов, имеющих по 16 упражнений не выше среднего уровня сложности, для письменной работы.
Для того, чтобы работать по таблице, необходимо сделать ее копию на каждую парту (или один большой плакат для всего класса). Таблица позволяет учителю организовать отработку навыков решения простейших заданий, предполагающих применение какого-либо одного правила (свойства) или 2-3 простейших правил одновременно. Каждая таблица имеет вид шахматной доски, на каждом поле которой записано одно задание. Давая задание, необходимо указать (как в шахматах) поле, на котором оно находится, например: а5, а8, b4, b1, сЗ, f7 и т. д. Имея подобные таблицы, учитель может организовать фронтальную групповую, индивидуальную работы с учениками, а также при необходимости проводить письменные мини-диктанты по 8 вариантам: столбцы таблицы от а до h. Можно также организовать работу сразу по нескольким таблицам.
Варианты для письменной работы содержат основные типы логарифмических уравнений с применением всех свойств логарифмов. При решении уравнения одного варианта учащиеся сталкиваются со всеми возможными случаями при выборе правильного ответа:
1) все найденные корни входят в ОДЗ;
2) часть корней входит в ОДЗ, а часть - нет (посторонние корни);
3) все найденные корни не входят в ОДЗ; 4) ОДЗ пуста.
В случаях 3 и 4 об уравнении делается вывод: нет решения.
Для удобства при проверке имеется таблица ответов.
Приведем пример решения одного из вариантов для письменной работы.


 |
 |


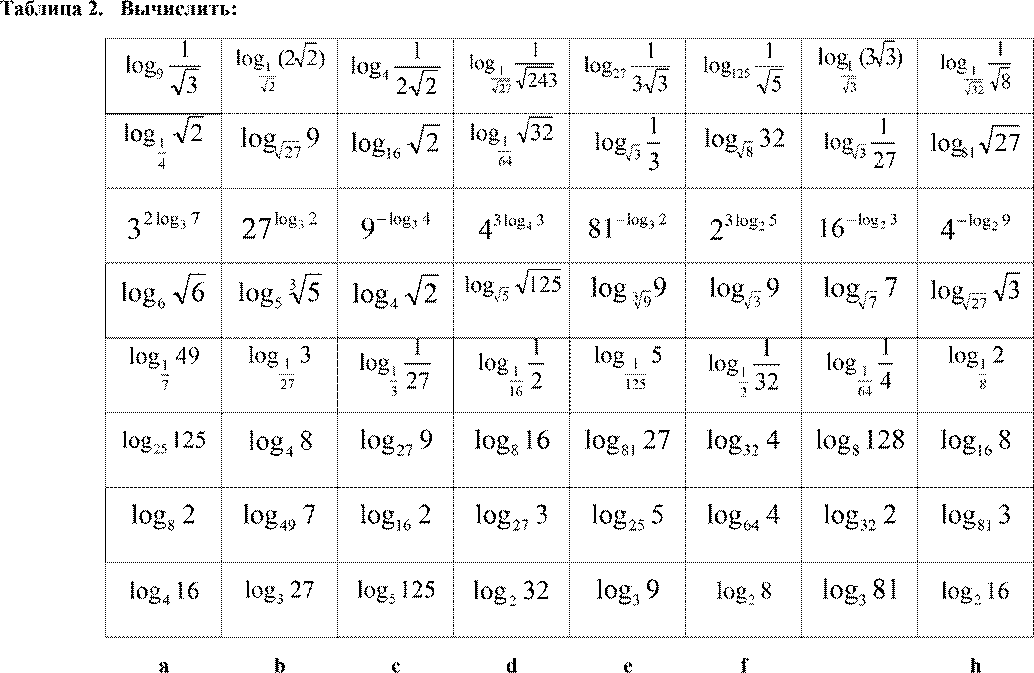
Таблица 1. Вычислить:
|
⎜⎟ ⎝ ⎠ |
4 −3 2 |
64 |
3 32 −5 |
⎜ ⎝ ⎠ |
32 |
⎜ ⎝ ⎠ |
3 16 −4 |
| 1 4 −2 |
1 ⎛1⎞− 2 ⎜ ⎝9⎠ |
1 125 −3 |
1 ⎛1 ⎞⎟−3 ⎜ ⎝8⎠ |
1 16 −4 |
1 ⎛ 1 ⎞⎟−2 ⎜ ⎝16⎠ |
1 81 −4 |
1 ⎛ 1 ⎞⎟−3 ⎜ ⎝ 27⎠ |
| 16 |
64 |
8 |
32 |
1 27 3 |
81 |
64 |
25 |
|
|
|
|
|
|
|
|
|
| ⎛ 3⎞−3 ⎜ ⎝ 2⎠ |
⎛ 2 ⎞⎟−2 ⎜ ⎝ 5⎠ |
⎛ 3⎞−3 ⎜ ⎝ 4⎠ |
⎛ 1 ⎞⎟−5 ⎜ ⎝ 2⎠ |
⎛1 ⎞⎟−1 ⎜ ⎝3⎠ |
⎛ 2 ⎞⎟−4 ⎜ ⎝ 3⎠ |
⎛ 3⎞−1 ⎜ ⎝ 4⎠ |
⎛ 1 ⎞⎟−4 ⎜ ⎝ 2⎠ |
| 6–2 |
2–4 |
3–3 |
5–1 |
3–4 |
2–3 |
7–2 |
4–1 |
| ⎛ 1⎞ 5 ⎜ ⎝ 2⎠ |
⎛ 2 ⎞⎟3 ⎜ ⎝ 3⎠ |
⎛3 ⎞⎟2 ⎜ ⎝5⎠ |
⎛ 3 ⎞⎟1 ⎜ ⎝ 2⎠ |
⎛ 4⎞3 ⎜ ⎝ 3⎠ |
⎛1⎞4 ⎜ ⎝3⎠ |
⎛ 2⎞3 ⎜ ⎟ ⎝ 5⎠ |
⎛ 3⎞2 ⎜ ⎝ 4⎠ |
| 34 |
43 |
24 |
53 |
25 |
33 |
50 |
23 |
8
7
6
5
4
3
2
1
a b c d e f g h
![]() 1
1
| 2 |
|
32 |
|
3 |
16 |
2 |
|
|
|
3 |
|
2 |
|
4 |
|
3 |
| 2 |
8 |
2 |
2 |
3 |
3 |
4 |
5 |
| 7 |
16 |
25 |
32 |
36 |
8 |
9 |
1 |
|
|
|
|
32 |
3 |
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 81 |
64 |
16 |
125 |
32 |
27 |
1 |
8 |
8
7
6
5
4
3
2
1
 8
8
7
6
5
4
3
2
1
![]() 2
2
| − |
–3 |
− |
|
− |
− |
–3 |
|
| − |
|
|
− |
–2 |
|
–6 |
|
| 49 |
8 |
|
27 |
|
125 |
|
|
|
|
|
|
3 |
3 |
4 |
2 |
|
| –2 |
− |
3 |
|
− |
5 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
3 |
3 |
5 |
2 |
3 |
4 |
4 |
7
6
5
4
3
2
1
3. Упростить:
|
|
|
|
|
|
|
|
|
|
|
log 92
log 5 log 32 ⋅ 5 |
|
|
|
|
|
|
|
+ log 43 |
lg9 log 274
− lg4 |
lg54 ln6
lg5 ln5 |
1 log 52
+ lg2 |
log 3 log 22 ⋅ 3 |
ln30 lg2
ln3 lg3 |
1
log4 e |
log 5 log 39 ⋅ 5 |
|
|
|
|
|
|
|
|
|
|
|
1 lg2 + 2 |
1 2 |
|
1 2 |
1 ln 3 + 2 |
|
|
| 2log 2 log3 + 3 5 |
log 3 2log 95 − 5 |
2log 4 log3 − 3 8 |
log 4 3log 29 + 9 |
log 2 3log 37 + 7 |
2log 6 log3 − 3 4 |
log 4 2log 57 + 7 |
log 123 −2log3 2 |
| log 24 log 45 − 5 |
log 40 log 83 − 3 |
log 45 log 97 − 7 |
log 30 log 53 − 3 |
log 35 log 72 − 2 |
log 63 log 78 − 8 |
log 32 log 43 − 3 |
log 36 log 97 − 7 |
| log 76 + log 86 |
log 32 +log 92 |
log 65 +log 75 |
log 8 log 97 + 7 |
log 73 + log 43 |
log 95 + log 65 |
log 69 +log 89 |
log 35 + log 85 |
7
6
5
4
3
2
![]() 3
3
| log 43 |
log 4002 |
log 167 |
lg16 |
log 69 |
3 |
lg9 |
lg3 |
| 1 |
2 |
log 92 |
|
1 |
log 25 |
3 |
1 |
| log 354 |
log 34 |
log 95 |
log 502 |
1 |
log 153 |
ln32 |
|
| log 35 |
log 43 |
log 98 |
lg2 |
log 125 |
ln 45 |
log 26 |
log 67 |
| lg3 |
lg12 |
ln6 |
ln2 |
lg2 |
ln21 |
ln2 |
lg15 |
| log 203 |
1 log5 27 |
log 23 |
log 329 |
log 547 |
2 |
log 1007 |
1 |
| log 65 |
log 53 |
log 57 |
log 63 |
log 52 |
log 98 |
log 83 |
log 47 |
| log 566 |
log 272 |
log 425 |
log 727 |
log 283 |
log 545 |
log 489 |
log 245 |
7
6
5
4
3
2
1
4. Решить уравнения:
| log4 x = log 58 |
−log5 x = log25 9 |
2log3 x = log 169 |
−log4 x = log 316 |
|
3log2 x =log 274 |
|
log27 x = log 49 |
| log3 x = log 29 |
log25 x = log 95 |
log4 x = log 72 |
log3 x = log27 2 |
log2 x = log 38 |
log27 x = log 23 |
log9 x = log 83 |
log16 x = log 32 |
| log3 x = log 23 |
log5 x 2 = log 45 |
log (4 x −1)=log 34 |
log (2 x +2)=log 52 |
|
1 log7
|
x log3
|
log (3 )4 x =log 54 |
| x log3
5 |
log (54 − =x ) 1 |
log (7 )2 x =1 |
log (5 x − 2) =1 |
log (2 x +2) =1 |
log5⎛⎜− ⎝ 8⎠ |
log (3 − − =x 1) 1 |
log ( 4 )2 − =x 1 |
| log (62 −x ) = 0 |
log (5 )4 x = 0 |
log (3 x −3) = 0 |
x log2
3 |
log ( 3 )4 − x = 0 |
log (46 +x ) = 0 |
log2⎛⎜− ⎝ 2⎠ |
log (5 − − =x 2) 0 |
| log 4x = 2 |
log− x 9 = 2 |
log 27x = 3 |
log 25 2− x = |
log 36x =−2 |
log 49− x =−2 |
log 16x =−2 |
log 64− x =−3 |
| log2 x = 5 |
log (3 − =x ) 2 |
log4 x = 3 |
log (2 −x )=−4 |
log8 x =−2 |
log (5 −x )=3 |
log3 x =−3 |
log (2 − =−x ) 1 |
| 3x = 5 |
6x = 4 |
7x = 8 |
2x = 9 |
8x = 3 |
4x = 7 |
9x = 5 |
5x = 2 |
7
6
5
4
3
2
![]() 4
4
|
|
|
2 |
|
|
|
|
8 |
|
|
81 |
49 |
|
|
8 |
64 |
81 |
| 2 |
± 2 |
4 |
3 |
16 |
|
35 |
|
| 15 |
1 |
|
7 |
0 |
–40 |
–4 |
− |
| 5 |
|
4 |
3 |
− |
–3 |
–2 |
–3 |
| 2 |
–3 |
3 |
–5 |
− |
− |
||
| 32 |
–9 |
64 |
− |
|
–125 |
|
− |
| log 53 |
log 46 |
log 87 |
log 92 |
log 38 |
log 74 |
log 59 |
log 25 |
7
6
5
4
3
2
1
a b c d e f g h
5. Решить уравнения:
|
= 1−x |
(x 2 −4)log2 x =0 |
x 2 −x
log2 x |
(5x x − 2 )log5 x 2 =0 |
x 2 −9
1−log3 x |
log3 x 2 0 =
|
x 2 + 4x
log (2 x +5) |
1− | x |
|
|
|
|
log 58 x =x 2 |
log 32
x
=− |
|
1 x
⎝3⎠ x |
log 43
|
log 4 |
| log 8| |x = 3 |
log 91 =−2
| |x |
log 81x 2 =−2 |
log 1 12 = 2 − x |
log 3| |x =−2 |
log3x 2 18= 2 |
log 1 25= 4
|
log 49x
2 = |
| log 2x x 2−3 = 0 |
1
log 25 x = 0 |
|
log 5x x 2 − +4 3x = 0 |
log 4x 1−x 2 = 0 |
log 5x | | 2x + = 0 |
logx 2+13x x 3− = 0 |
log|x +1| 2x 2+2x = 0 |
| 4x
2 = |
1 10−| |x
=
9 |
3−2x =4 |
1
7| |x =3 |
2
6 x = 2 |
1 5−x
2 =
3 |
8−| |x =5 |
2 − 3 x =10 |
| log2−x x = 0 |
log1 − x (x − =2) 0 |
log (x x −1) = 0 |
log (2− x −x ) = 0 |
log1 2− x (2 )x = 0 |
x log3−x
2 |
log2 + x (−x ) = 0 |
log (2−x x + =2) 0 |
| 1 log3
x |
log (4 x 2 + =2) 0 |
log9 x 2 =1 |
2 log4
x |
log 53 x = 0 |
log (5 x 2 + =1) 1 |
log 62 x =1 |
log2 x 2 = 0 |
| log (3 x +1) = 2 |
log (14 − =x ) 2 |
log (3 x −1) =−2 |
log (2 −x −1) =−3 |
log (22 −x ) = 2 |
log (3 −x −2) =3 |
log (3 x +2) =−3 |
log (4 x − =−2) 2 |
7
6
5
4
3
2
![]() 5
5
| –1 |
1; 2 |
нет решения |
± 1; 5 |
нет решения |
1 |
0 |
нет решения |
|
|
0; log 43 |
0; log 58 |
нет решения |
|
log 23 |
нет решения |
0; log 45 |
| ± 2 |
± 3 |
± |
1
2 3 |
1 ± |
|
|
± 49 |
|
|
нет решения |
2 |
3 |
нет решения |
нет решения |
± 1 |
нет решения |
| нет решения |
±lg9 |
−log 23 |
±log 73 |
log 362 |
|
нет решения |
−lg9 |
| нет решения |
нет решения |
2 |
нет решения |
нет решения |
нет решения |
нет решения |
− |
|
|
нет решения |
± 3 |
2 |
0 |
± 2 |
log 26 |
± 1 |
| 8 |
–15 |
1 |
−1 |
–2 |
–29 |
−1 |
2 |
7
6
5
4
3
2
1
a b c d e f g h
| Вариант 1. |
Вариант 1. |
| 6.
7. log 2x + 9 (x +5)=1 3x −2 8.
lg 3 4− x
|
6.
7. log 2 x + 9 (x +5)=1 3x −2 8.
lg 3 4− x
|
| Вариант 1. |
Вариант 1. |
| 6.
7. log 2 x + 9 (x +5)=1 3x −2 8.
lg 3 4− x
|
6.
7. log 2 x + 9 (x +5)=1 3x −2 8.
lg 3 4− x
|
| Вариант 2. |
Вариант 2. |
| 12. lg(− x −4)= lg( 5 )− x − lg 9( − x ) 2 13. log 5 (x + 5x −6)− log 5 (− 20−4x )= 0 2 14. log 4 (x +8)− log 4 (x −2)= log 4 (2x +1)
16. 2 0,16⋅ x − 7 0⋅ ,4x +logx x 3 = 0 |
12. lg(− x −4)= lg( 5 )− x − lg 9( − x ) 2 13. log 5 (x + 5x −6)− log 5 (− 20−4x )= 0 2 14. log 4 (x +8)− log 4 (x −2)= log 4 (2x +1)
16. 2 0,16⋅ x − 7 0⋅ ,4x +logx x 3 = 0 |
| Вариант 2. |
Вариант 2. |
| 12. lg(− x −4)= lg( 5 )− x − lg 9( − x ) 2 13. log 5 (x + 5x −6)− log 5 (− 20−4x )= 0 2 14. log 4 (x +8)− log 4 (x −2)= log 4 (2x +1)
16. 2 0,16⋅ x − 7 0⋅ ,4x +logx x 3 = 0 |
12. lg(− x −4)= lg( 5 )− x − lg 9( − x ) 2 13. log 5 (x + 5x −6)− log 5 (− 20−4x )= 0 2 14. log 4 (x +8)− log 4 (x −2)= log 4 (2x +1)
16. 2 0,16⋅ x − 7 0⋅ ,4x +logx x 3 = 0 |
|
|
|
|
|
|
| Вариант 4. |
Вариант 4. |
| 11. lg 1( + 6x ) + lg(− −x 1) = 0 13.
14. log 2 (12 − 2x 2 )− log 2 (2 − x ) = log 2 (x + 6)
16. 6⋅⎜ ⎟ − ⎝9⎠ ⎝3⎠ |
11. lg 1( + 6x ) + lg(−x −1) = 0 13.
14. log 2 (12 − 2x 2 )− log 2 (2 − x ) = log 2 (x + 6)
16. 6⋅⎜ ⎟ − ⎝9⎠ ⎝3⎠ |
| Вариант 4. |
Вариант 4. |
| 12. lg 5( x − 49) − lg(x −8) = lg(x + 3) 13. log 5 (x 2 − 8x +12)− log 5 (x + 4) = 0 14. log 2 (12 − 2x 2 )− log 2 (2 − x ) = log 2 (x + 6)
16. 6⋅ − ⎝9⎠ ⎝3⎠ |
12. lg 5( x − 49) − lg(x −8) = lg(x + 3) 13. log 5 (x 2 − 8x +12)− log 5 (x + 4) = 0 14. log 2 (12 − 2x 2 )− log 2 (2 − x ) = log 2 (x + 6)
16. 6⋅ − ⎝9⎠ ⎝3⎠ |
|
|
|
|
|
|
|
|
|
| Вариант 6. 1. 2.
4. 5. 6. 7. 8. lg( 4− x −1) − lg(8x + 3) = 0
12. lg(x − =3) lg(6 − −x ) lg(x − 2) 13. log (6 x 2 −9x +18) − log ( 186 − x + 4) = 0 14. log (32 x x − 2 ) − log (22 x −3) = log (2 − −x 1) 15. 2log2 − x 4 + 3log− x 4 − 2 = 0 16. 3⋅⎛⎜ ⎝36⎠ ⎝ 6⎠ |
Вариант 6.
2. 3. 4. 5. 6. 7. 8. lg( 4− x −1) − lg(8x + 3) = 0
12. lg(x −3) = lg(6 −x ) − lg(x − 2) 13. log (6 x 2 −9x +18) − log ( 186 − x + 4) = 0 14. log (32 x x − 2 ) − log (22 x −3) = log (2 − −x 1) 15. 2log2 − x 4 + 3log− x 4 − 2 = 0 x x 16. 3⋅⎛⎜ ⎝36⎠ ⎝ 6⎠ |
| Вариант 6.
2. 3. 4. 5. 6. 7. 8. lg( 4− x −1) − lg(8x + 3) = 0
12. lg(x − =3) lg(6 − −x ) lg(x − 2) 13. log (6 x 2 −9x +18) − log ( 186 − x + 4) = 0 14. log (32 x x − 2 ) − log (22 x −3) = log (2 − −x 1) 15. 2log2 − x 4 + 3log− x 4 − 2 = 0 16. 3⋅⎛⎜ ⎝36⎠ ⎝ 6⎠ |
Вариант 6.
2. 3. 4. 5. 6. 7. 8. lg( 4− x −1) − lg(8x + 3) = 0
12. lg(x −3) = lg(6 −x ) − lg(x − 2) 13. log (6 x 2 −9x +18) − log ( 186 − x + 4) = 0 14. log (32 x x − 2 ) − log (22 x −3) = log (2 − −x 1) 15. 2log2 − x 4 + 3log− x 4 − 2 = 0 x x 16. 3⋅⎛⎜ ⎝36⎠ ⎝ 6⎠ |
| 1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 7.
lg(3x
− 6)⋅lg(2x
−3) = 0 log− −
7 2x
(4x
+17) =1 lg
|
1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 7.
lg(3x
− 6)⋅lg(2x
−3) = 0 log− −
7 2x
(4x
+17) =1 lg
|
| 1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 7.
lg(3x
− 6)⋅lg(2x
−3) = 0 log− −
7 2x
(4x
+17) =1 lg
|
1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 7.
lg(3x
− 6)⋅lg(2x
−3) = 0 log− −7 2
x
(4x
+17) =1 lg
|
| Вариант 8.
12. lg(3− x ) = lg20 − lg(− 5) 13. log (6 x 2 + 7x +12) − log (46 x +10) = 0 14. log (22 + x x − 2 ) − log (2 x −1) = log (2 x +1) 15. log 252 x − 4 = 0 x x 16. 6⋅⎛⎜ ⎝ 4⎠ ⎝ 2⎠ |
Вариант 8.
3. 4. 5. 6. 7. 8. 9. lg(3− x ) = lg20 − lg(− −x 5) 13. log (6 x 2 + 7x +12) − log (46 x +10) = 0 14. log (22 + x x − 2 ) − log (2 x −1) = log (2 x +1) 15. log 252 x − 4 = 0 x x 16. 6⋅⎛⎜ ⎝ 4⎠ ⎝ 2⎠ |
||
| Вариант 8.
5. 8. lg(3− x ) = lg20 − lg(−x −5) 13. log (6 x 2 + 7x +12) − log (46 x +10) = 0 14. log (22 + x x − 2 ) − log (2 x −1) = log (2 x +1) 15. log 252 x − 4 = 0 x x 16. 6⋅⎛⎜ ⎝ 4⎠ ⎝ 2⎠ |
3. 6. 9.
12. lg(3 13. log (6 x 14. log (22 15. log 252 x 16. 6⋅⎛⎜ ⎝ 4⎠ |
2 7 + + − 4 x − 19 |
Вариант 8.
lg20 − lg(− −x 5) x +12) − log (46 x +10) = 0 x x − 2 ) − log (2 x −1) = log (2 x +1) = 0 x ⎛ 1 ⎞ ⋅⎜ |
| 1. 2. 3. 4. 5. 6. |
Вариант 9.
lg(3x + 2)⋅lg( 1− −3 )x = 0
|
Вариант 9.
2.
5. 6. lg(3x + 2)⋅lg( 1− −3 )x = 0
|
| 1. 2. 3. 4. 5. 6. |
Вариант 9.
lg(3x + 2)⋅lg( 1− −3 )x = 0
|
Вариант 9.
2.
5. 6. lg(3x + 2)⋅lg( 1− −3 )x = 0
|
| Вариант 10.
7. 8. 9.
12. lg(x +1) = lg(3− x ) − lg(x + 3) 13. log (5 x 2 − x − 20) − log (45 x + 4) = 0 14. log (263 − 2x 2 ) − log ( 23 − − x ) = log (3 x +1) 15. log 162 x + 2logx 16 −8 = 0 16. 7 0⋅ ,04x − 23 0,2⋅ x + 6logx x = 0 |
Вариант 10.
12. lg(x +1) = lg(3− x ) − lg(x + 3) 13. log (5 x 2 − x − 20) − log (45 x + 4) = 0 14. log (263 − 2x 2 ) − log ( 23 − − x ) = log (3 x +1) 15. log 162 x + 2logx 16 −8 = 0 16. 7 0⋅ ,04x − 23 0,2⋅ x + 6logx x = 0 |
| Вариант 10.
12. lg(x +1) = lg(3− x ) − lg(x + 3) 13. log (5 x 2 − x − 20) − log (45 x + 4) = 0 14. log (263 − 2x 2 ) − log ( 23 − − x ) = log (3 x +1) 15. log 162 x + 2logx 16 −8 = 0 16. 7 0⋅ ,04x − 23 0,2⋅ x + 6logx x = 0 |
Вариант 10.
12. lg(x +1) = lg(3− x ) − lg(x + 3) 13. log (5 x 2 − x − 20) − log (45 x + 4) = 0 14. log (263 − 2x 2 ) − log ( 23 − − x ) = log (3 x +1) 15. log 162 x + 2logx 16 −8 = 0 16. 7 0⋅ ,04x − 23 0,2⋅ x + 6logx x = 0 |
| 1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 11.
lg( 4− x − 7)⋅lg(2x + 4) = 0 log5x − 19 (3x − =11) 1 lg(12x + 7) − lg(3x + 2) = 0
|
1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 11.
lg( 4− x − 7)⋅lg(2x + 4) = 0 log5x − 19 (3x −11) =1 lg(12x + 7) − lg(3x + 2) = 0
|
| 1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 11.
lg( 4− x − 7)⋅lg(2x + 4) = 0 log5x − 19 (3x −11) =1 lg(12x + 7) − lg(3x + 2) = 0
|
1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 11.
lg( 4− x − 7)⋅lg(2x + 4) = 0 log5x − 19 (3x −11) =1 lg(12x + 7) − lg(3x + 2) = 0
|
| Вариант 12.
2. 3. 4. 5. 6. 8. 9. 11. lg(x
12. lg(3− x ) = lg(5− x 2 ) − lg(x +1) 13. log (103 x − 21− x 2 ) − log (193 x −1) = 0 14. log (2 x 2 − 4 )x − log (22 x + 7) = log (2 x + 2) 15. log2 − x 27 − 7log− x 27 + 6 = 0 16. ⎝16⎠ ⎝ 4⎠ |
Вариант 12.
2. 11. lg(x
12. lg(3− x ) = lg(5− x 2 ) − lg(x +1) 13. log (103 x − 21− x 2 ) − log (193 x −1) = 0 14. log (2 x 2 − 4 )x − log (22 x + 7) = log (2 x + 2) 15. log2 − x 27 − 7log− x 27 + 6 = 0 x x 16. ⎝16⎠ ⎝ 4⎠ |
||
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 11. lg(x 4) 12. lg(3− x ) = 13. log (103 x − 14. log (2 x 2 − 15. log2 − x 27 −
16. 3⋅⎛⎜ ⎞⎟ ⎝16⎠ |
Вариант 12.
lg(5− x 2 ) − lg(x +1) 21− x 2 ) − log (193 x −1) = 0 4 )x − log (22 x + 7) = log (2 x + 2) 7log− x 27 + 6 = 0 x
|
1. 3. 4. 5. 6. 8. 9. 11. lg(x 4) 12. lg(3− x ) = 13. log (103 x 14. log (2 x 2 − 15. log− 2 x 27 −
16. 3⋅⎛⎜ ⎞⎟ ⎝16⎠ |
Вариант 12.
lg(5− x 2 ) − lg(x +1) − 21− x 2 ) − log (193 x −1) = 0 4 )x − log (22 x + 7) = log (2 x + 2) 7log− x 27 + 6 = 0
− ⎝ 4⎠ |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. |
Вариант 13. 6log64 (− =x ) 5
3 ⎝ 6 ⎠
lg( 2− x −1)⋅lg(2x + 3) = 0 log8x + 9 (4x − =1) 1 5 lg 1+ 2x
|
1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 13. 6log64 (−x ) = 5 log1 ⎛⎜
lg( 2− x
−1)⋅lg(2x
+ 3) = 0 log8x
+
9
(4x
−1) =1 lg 5 1+ 2x
|
| 1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 13. 6log64 (−x ) = 5
3 ⎝ 6 ⎠
lg( 2− x
−1)⋅lg(2x
+ 3) = 0 log8x
+
9
(4x
−1) =1 lg 5 1+ 2x
|
1. 2. 3. 4. 5. 6. 7. 8. |
Вариант 13. 6log64 (−x ) = 5 log1 ⎛⎜
lg( 2− x −1)⋅lg(2x + 3) = 0 log8 x +9 (4x −1) =1 5 lg 1+ 2x
|
| Вариант 14.
2. 3. 4. 5. 8. 5 11. lg(2 −3 )x + lg(2x + =1) 0 12. lg(x − =6) lg(x 2 − − −5x 14) lg(x − 2) 13. log (116 x x − 2 −18) − log (86 x −36) = 0 14. log (163 − x 2 ) − log (3 x − 4) = log ( 23 − x −1) 15. log 492 x − 6logx 49 +8 = 0 16. 4 0⋅ ,36x −15 0,6⋅ x + 9 = log− x 1 |
Вариант 14.
3. 4. 5. 6. 7. 5 11. lg(2 −3 )x + lg(2x +1) = 0 12. lg(x − 6) = lg(x 2 −5x −14) − lg(x − 2) 13. log (116 x x − 2 −18) − log (86 x −36) = 0 14. log (163 − x 2 ) − log (3 x − 4) = log ( 23 − x −1) 15. log 492 x − 6logx 49 +8 = 0 16. 4 0⋅ ,36x −15 0,6⋅ x + 9 = log− x 1 |
| Вариант 14.
4. 5. 7. 5 11. lg(2 −3 )x + lg(2x +1) = 0 12. lg(x − 6) = lg(x 2 −5x −14) − lg(x − 2) 13. log (116 x x − 2 −18) − log (86 x −36) = 0 14. log (163 − x 2 ) − log (3 x − 4) = log ( 23 − x −1) 15. log 492 x − 6logx 49 +8 = 0 16. 4 0⋅ ,36x −15 0,6⋅ x + 9 = log− x 1 |
Вариант 14.
3. 4. 5. 6. 7. 5 11. lg(2 −3 )x + lg(2x +1) = 0 12. lg(x − 6) = lg(x 2 −5x −14) − lg(x − 2) 13. log (116 x x − 2 −18) − log (86 x −36) = 0 14. log (163 − x 2 ) − log (3 x − 4) = log ( 23 − x −1) 15. log 492 x − 6logx 49 +8 = 0 16. 4 0⋅ ,36x −15 0,6⋅ x + 9 = log− x 1 |
| 1. 2. 3. 4. 5. 6. |
Вариант 15.
lgx + log5 x = log100 50 lg( 2− x −5)⋅lg( 7− − 2 )x = 0
|
1. 2. 3. 4. 5. 6. |
Вариант 15.
lgx + log5 x = log100 50 lg( 2− x −5)⋅lg( 7− − 2 )x = 0
|
| 1. 2. 3. 4. 5. 6. |
Вариант 15.
lgx + log5 x = log100 50 lg( 2− x −5)⋅lg( 7− − 2 )x = 0
|
1. 2. 3. 4. 5. 6. |
Вариант 15.
lgx + log5 x = log100 50 lg( 2− x −5)⋅lg( 7− − 2 )x = 0
|
| Вариант 16.
2. 3. 4. 5. 6. 7. 8. 9. ln3 11. log (12
+ x
) + log ( 92
− − 2 )x
= 12. lg(8− x ) = lg(32 − 4 )x − lg(x + 4) 13. log (66 x −8− x 2 ) − log (46 x − 23) = 0 14. log (323 − 2x 2 ) − log (63 − x ) = log (3 x + 5) 15. log 362 x + 2logx 36 = 0 x x 16. 5⋅⎛⎜ ⎝ 25⎠ ⎝ 5⎠ |
Вариант 16.
4. 6. 8. ln3 11. log (12
+ x
) + log ( 92
− − 2 )x
= 12. lg(8− x ) = lg(32 − 4 )x − lg(x + 4) 13. log (66 x −8− x 2 ) − log (46 x − 23) = 0 14. log (323 − 2x 2 ) − log (63 − x ) = log (3 x + 5) 15. log 362 x + 2logx 36 = 0
16. 5⋅⎜ ⎟ − ⎝ 25⎠ ⎝ 5⎠ |
| Вариант 16.
4. 6. 7. 8. 9. ln3 11. log (12
+ x
) + log ( 92
− − 2 )x
= 12. lg(8− x ) = lg(32 − 4 )x − lg(x + 4) 13. log (66 x −8− x 2 ) − log (46 x − 23) = 0 14. log (323 − 2x 2 ) − log (63 − x ) = log (3 x + 5) 15. log 362 x + 2logx 36 = 0 x x 16. 5⋅⎛⎜ ⎝ 25⎠ ⎝ 5⎠ |
Вариант 16.
4. 5. 7. ln3 11. log (12
+ x
) + log ( 92
− − 2 )x
= 12. lg(8− x ) = lg(32 − 4 )x − lg(x + 4) 13. log (66 x −8− x 2 ) − log (46 x − 23) = 0 14. log (323 − 2x 2 ) − log (63 − x ) = log (3 x + 5) 15. log 362 x + 2logx 36 = 0
16. 5⋅⎜ ⎟ − ⎝ 25⎠ ⎝ 5⎠ |
![]()
 lg 3( x
−1)⋅lg(6x
−3)= 0
lg 3( x
−1)⋅lg(6x
−3)= 0
 lg 3( x
−1)⋅lg(6x
−3)= 0
lg 3( x
−1)⋅lg(6x
−3)= 0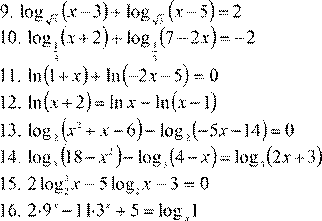
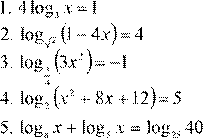 lg 3( x
−1)⋅lg(6x
−3)= 0
lg 3( x
−1)⋅lg(6x
−3)= 0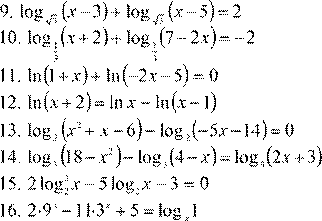
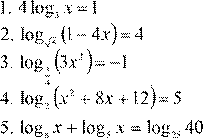 lg 3( x
−1)⋅lg(6x
−3)= 0
lg 3( x
−1)⋅lg(6x
−3)= 0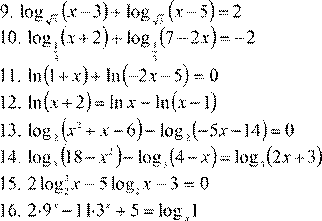
 5
5
 5
5
 5
5
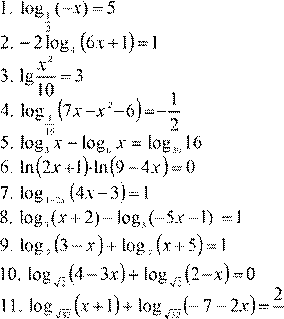 5
5
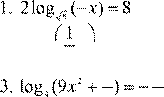
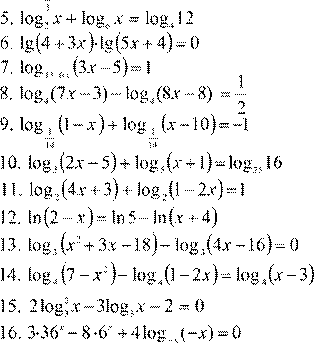
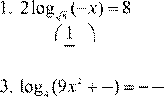
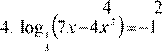
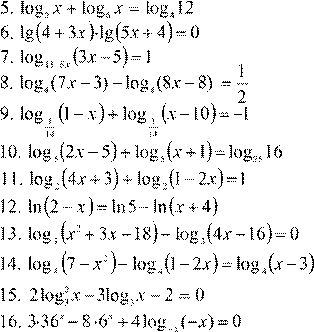
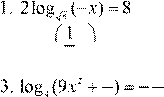
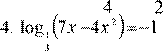
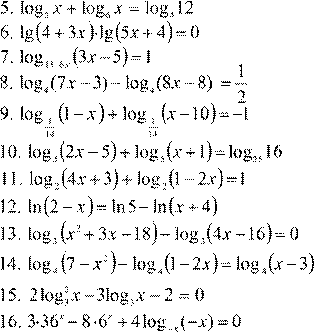
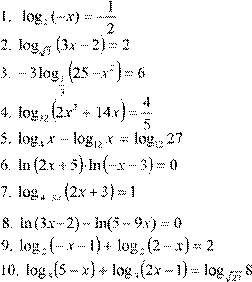
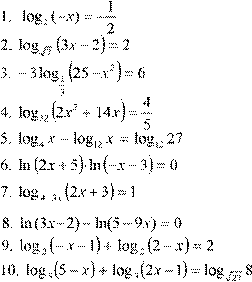
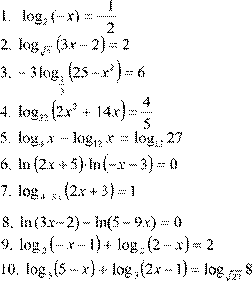
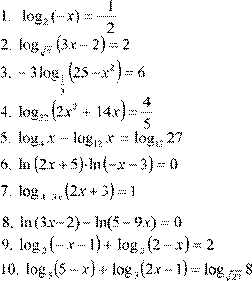
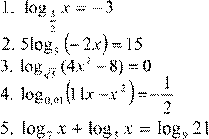 Вариант 5.
Вариант 5.
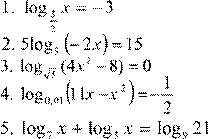 Вариант 5.
Вариант 5.
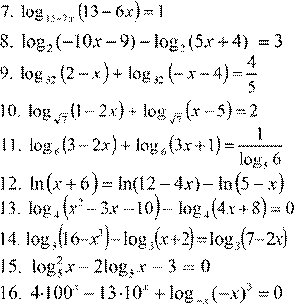 6. lg 2( x
−1)⋅lg(1− x
) = 0
6. lg 2( x
−1)⋅lg(1− x
) = 0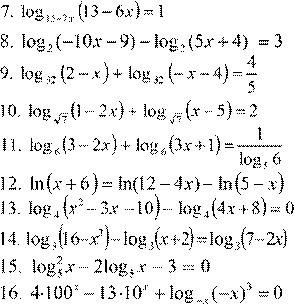 6. lg 2( x
−1)⋅lg(1− x
) = 0
6. lg 2( x
−1)⋅lg(1− x
) = 0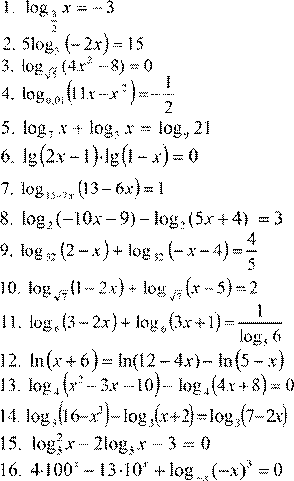 Вариант 5.
Вариант 5.
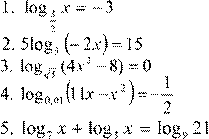 Вариант 5.
Вариант 5.
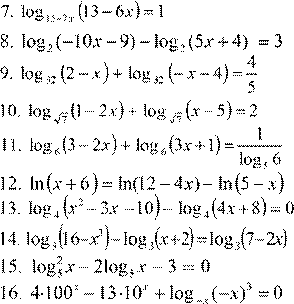 6. lg 2( x
−1)⋅lg(1− x
) = 0
6. lg 2( x
−1)⋅lg(1− x
) = 0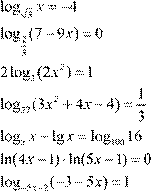 3.
3.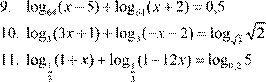
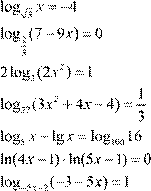 1.
1.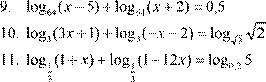
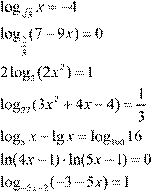 1.
1.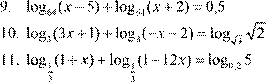
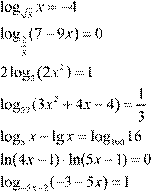 1.
1.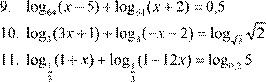
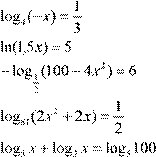
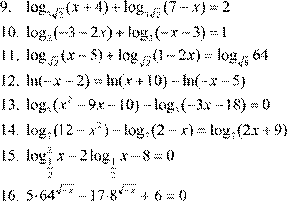
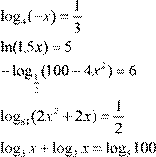

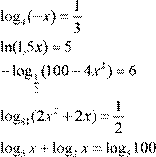
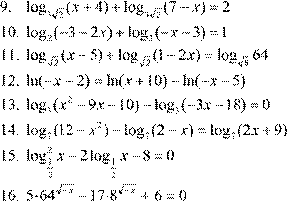
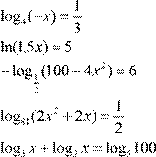
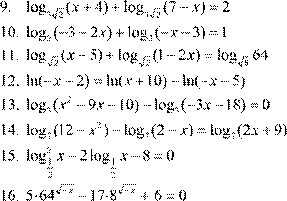
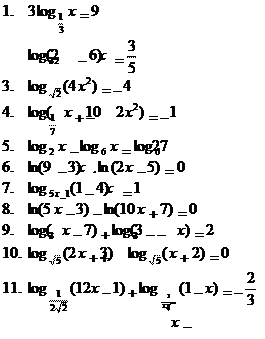 2.
2.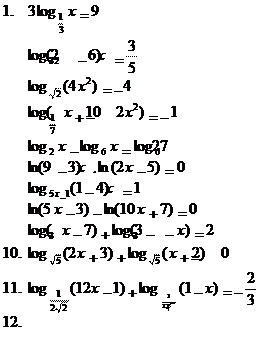 2.
2.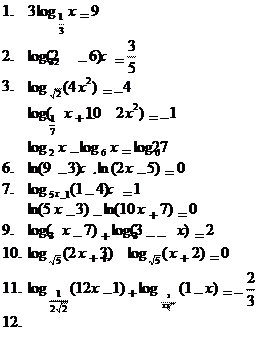 4.
4.
 log 2
⎜ x
⎟ = −3
log 2
⎜ x
⎟ = −3 
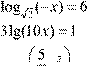 1.
1. 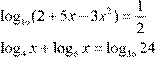 4.
4.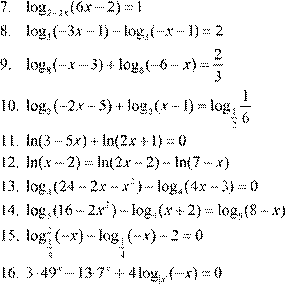
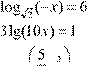 log 2
⎜ x
⎟ = −3
log 2
⎜ x
⎟ = −3 
 1.
1.  4.
4.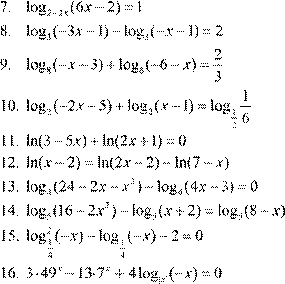
 5.
5.
 3.
3.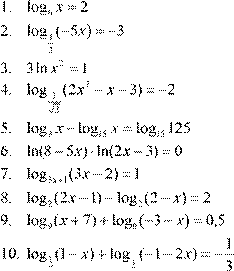
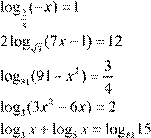
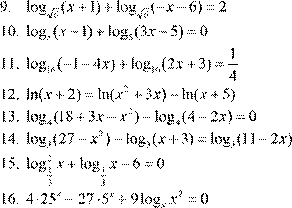
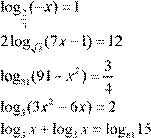
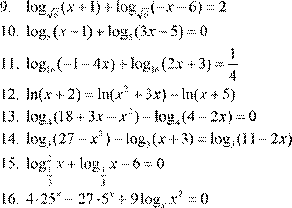
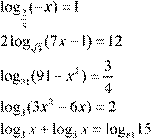
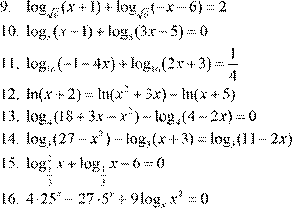
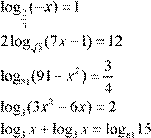
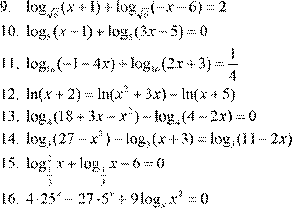
 1.
1. 1.
1.
 ⎝ 6 ⎠
⎝ 6 ⎠