| Скачать .pdf |
Книга: Оптимальное управление линейными динамическими объектами
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОУВПО «Пермский государственный университет»
С.В. Лутманов
ЛИНЕЙНЫЕ ЗАДАЧИ
ОПТИМИЗАЦИИ
Часть 2
Оптимальное управление линейными динамическими объектами
Учебное пособие
Рекомендовано УМС по математике и механике УМО по классическому университетскому образованию РФ в качестве учебного пособия для студентов высших учебных заведений, обучающихся по группе направлений и специальностей «Механика»
Пермь 2005
БК 22. 161.8
Л 86
УДК 519.9
Лутманов, С.В.
Л 86 Линейные задачи оптимизации: учеб. пособие [Электронный ресурс] /Перм. ун.-т. – Пермь, 2005.- Ч.2. Оптимальное управление линейными динамическими объектами. – 195 с.
ISBN 5-7944-0565-1
В учебном пособии рассматриваются задачи теории оптимального управления линейными динамическими объектами. В частности, подробно исследован случай управления с терминальным критерием качества и случай управления по критерию предельного быстродействия. Изучается возможность сведения задачи теории оптимального управления к функциональной проблеме моментов. Вывод необходимых условий оптимальности управляющих воздействий опирается на математический аппарат выпуклого анализа. Указываются эффективные достаточные условия оптимальности программных управлений. Само построение оптимальных управлений осуществляется либо аналитическим путем, либо с применением систем аналитических вычислений, реализуемых в интерактивном режиме на ЭВМ. Весь излагаемый материал поясняется на примерах, большинство из которых решено с применением пакета MATHEMATICA 4.2 Пособие предназначено для студентов, магистрантов и аспирантов математических специальностей, изучающих курсы, связанные с вопросами оптимизации.
Ил. 34. Библиогр. 32 назв.
Печатается в соответствии с решением редакционно-издательского совета Пермского государственного университета
Рецензенты: кафедра дифференциальных уравнений Удмуртского государственного университета; профессор кафедры «Математическое моделирование систем и процессов» Пермского государственного технического университета, д.т.н. В.Ю. Столбов
ISBN 5-7944-0565-1 © Лутманов С.В., 2005
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ…………………………………………………………………. 5 1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ ДИНАМИЧЕСКИЕ ОБЪЕКТЫ……….8
1.1. Примеры линейных управляемых динамических объектов …………………8
1.2. Системы однородных линейных дифференциальных уравнений …………16
1.3. Фундаментальная матрица Коши ……………................................................20
1.4. Допустимые реализации вектора управляющих параметров ………………26
1.5. Формула Коши …………………………...........................................................31
1.6. Критерии качества управления динамическими объектами………………..33
1.7. Программные стратегии ……………………………………………………...36
1.8. Постановка и существование решения задачи теории оптимального управ-
ления ……………………………………………………………………………….39
1.9. Область достижимости линейного управляемого динамического объекта 45
2. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЛИНЕЙНЫМИ ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ С ФИКСИРОВАННЫМ ВРЕМЕНЕМ И ТЕРМИНАЛЬНЫМ КРИТЕРИЕМ КАЧЕСТВА……………………………………..49
2.1. Случай закрепленного левого конца и свободного правого конца траекто-
рии ………………………………………………………………………………….49
2.2. Поведение функции Л.С. Понтрягина вдоль оптимальной пары…………..53
2.3. Частные случаи геометрических ограничений на вектор управляющих па-
раметров……………………………………………………………………………56
2.4. Минимизация расстояния до целевого множества…………………………67
2.5. Случай подвижного левого и свободного правого конца траектории……85
2.6. Минимизация расстояния до целевого множества в случае подвижного ле-
вого конца траектории…………………………………………………………….96
3. ЗАДАЧА ЛИНЕЙНОГО ПРЕДЕЛЬНОГО БЫСТРОДЕЙСТВИЯ…….107
3.1. Постановка задачи линейного предельного быстродействия и существова-
ние ее решения.……………………………………………………………………107
3.2. Необходимые условия оптимальности программной стратегии ………….108
4. ЛИНЕЙНАЯ ЗАДАЧА ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ КАК ФУНКЦИОНАЛЬНАЯ ПРОБЛЕМА МОМЕНТОВ………………….117
4.1. Сведение задачи теории оптимального управления к функциональной про-
блеме моментов…………………………………………………………………..117
4.2. Управляемость линейной динамической системы…………………………125
4.3. Управление по критерию «минимум энергии»…………………………….128
4.4. Управление по критерию «минимум силы»……………………………….134
ПРИЛОЖЕНИЕ…………………………………………………………………142 БИБЛИОГРАФИЧЕСКИЙ СПИСОК …………………………………...192
ПРЕДИСЛОВИЕ
Предлагаемое учебное пособие написано на основе спецкурса «Линейные задачи оптимизации», который автор читает для студентов и магистрантов (специальность «Механика») механико-математического факультета Пермского государственного университета. Оно представляет собой конспект лекций той части курса, которая посвящена задачам оптимального управления линейными динамическими системами. Линейные динамические системы с выпуклыми геометрическими ограничениями на управляющие параметры являются удобными объектами исследования в теории оптимального управления. Вывод необходимых условий оптимальности управляющих воздействий для таких систем опирается на математический аппарат выпуклого анализа и требует существенно меньших усилий, чем для нелинейных систем. В ряде случаев удается сформулировать эффективные достаточные условия оптимальности. Само построение оптимальных управлений осуществляется либо аналитическим путем, либо с применением систем аналитических вычислений, реализуемых в интерактивном режиме на ЭВМ.
Пособие состоит из четырех разделов и приложения. В первом разделе изучаются основные свойства систем линейных дифференциальных уравнений, вводится понятие фундаментальной матрицы Коши системы однородных линейных дифференциальных уравнений и доказывается формула Коши. Здесь же приводится постановка задачи теории оптимального управления в классе программных стратегий, оговаривается класс допустимых стратегий и доказывается теорема существования решения задачи теории оптимального управления.
Во втором разделе для задач управления с терминальным критерием качества и фиксированным временем выводятся необходимые условия оптимальности программного управления в форме принципа максимума Л.С. Понтрягина. В частности, когда минимизируемый функционал имеет смысл расстояния от целевого множества до фазового вектора объекта в финальный момент времени, эти условия записываются в форме прицеливания на опорный вектор к области достижимости динамического объекта. Для этого случая формулируются и доказываются эффективные достаточные условия оптимальности. Рассмотрены ситуации, когда левый конец траектории закреплен и когда он является подвижным. В последнем случае принимается, что множество начальных положений объекта описывается системой дифференцируемых неравенств.
Третий раздел посвящен задачам линейного быстродействия. Оптимальное время перехода определяется здесь как разность между первым моментом времени, для которого пересечение области достижимости управляемого объекта и целевого множества не является пустым, и начальным моментом времени. Оптимальная программная стратегия строится из условия прицеливания на соответствующий опорный вектор к области достижимости объекта.
В четвертом разделе изучается возможность сведения задачи теории оптимального управления к функциональной проблеме моментов. Приводятся необходимые и достаточные условия разрешимости проблемы моментов. На их основе доказывается критерий полной управляемости динамическим объектом и реализуется конструктивный алгоритм решения задачи теории оптимального управления по критерию «минимум энергии» и «минимум силы».
В каждом разделе пособия дается подробный алгоритм решения соответствующего класса задач теории оптимального управления. Реализация алгоритма поясняется на конкретных примерах. Большинство из них решается с применением пакета MATHEMATICA 4.2. Заголовки примеров, решение которых требует обращения к компьютеру, помечены звездочкой. Для них в приложении приводятся тексты программ, обеспечивающие решение этих примеров.
По тематике книги существует обширная библиография. Приведенный в конце книги библиографический список содержит лишь те источники, которые непосредственно использовались при написании данного учебного пособия. Пособие разбито на разделы, внутри которых принята самостоятельная нумерация задач, лемм, рисунков, примеров и теорем. В свою очередь, раздел разбит на пункты, в которых ведется независимая нумерация формул. Ссылки на материалы (за исключением формул), расположенные в пределах данного раздела, нумеруются одним числом, вне данного раздела – двумя числами. Ссылки на формулы нумеруются одним числом только в пределах данного пункта. Вне данного пункта, но в пределах данного раздела, они нумеруются двумя числами, вне данного раздела – тремя числами.
1. ЛИНЕЙНЫЕ УПРАВЛЯЕМЫЕ ДИНАМИЧЕСКИЕ ОБЪЕКТЫ
1.1. Примеры линейных управляемых динамических объектов. Рас-
смотрим управляемые объекты, состояние которых в каждый момент времени t ∈ R 1 характеризуется набором величин x 1 ,",x n . Эти величины называются фазовыми координатами объекта. Управление объектом осуществляется посредством воздействий u 1 ,",u r , которые будем называть управляющими параметрами объекта. Принимаем, что изменение фазовых координат во времени описывается системой обыкновенных линейных дифференциальных уравнений вида
x 1 = a 11 (t x ) 1 + +" a 1n (t x ) n +b 11 (t u ) 1 + +" b 1r (t u ) r +c t 1 ( ),
.......................................................................................... (1)
x n = a n 1 (t x ) 1 + +" a nn (t x ) n +b n 1 (t u ) 1 + +" b nr (t u ) r +c n (t ),
где a ij = a ij (t ), b ik = b ik ( )t , c i = c t i ( ), t ∈ R i j 1 , , =1,", ,n k =1,",r - известные непрерывные функции времени.
Система дифференциальных уравнений (1) допускает векторноматричную запись
x = A t x ( ) +B t u ( ) +C t ( ). (2)
Здесь обозначено
⎛⎜ x ⎞
x = ⎜⎜⎜⎜⎜⎜"x 1n ⎠⎟⎟⎟⎟⎟⎟⎟⎟, u =⎛⎝⎜⎜⎜⎜⎜⎜⎜"uu 1r ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, A t ( )= ⎜⎛⎝⎜⎜⎜⎜⎜⎜⎜aa 11n "1( )( )tt """ aa 1nn "n ( )( )tt ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, B t ( )=⎜⎛⎝⎜⎜⎜⎜⎜⎜⎜bb 11n "1( )( )tt """ bb 1nr "r ( )( )tt ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, C t ( )=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜cc t 1n "( )( )t ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟.
⎝
Векторы x ∈ R n и u ∈ R r называются фазовым вектором и вектором управляющих параметров объекта, соответственно.
Система дифференциальных уравнений (1), или ее векторно-матричная форма (2), является математической моделью (с той или иной степенью точности) реального управляемого физического объекта. В дальнейшем эту математическую модель будем называть линейным управляемым динамическим объектом. Следуя [17], приведем примеры линейных управляемых динамических объектов.
Пример 1. Рассмотрим материальную точку массы m , движущуюся в вертикальной плоскости ξ η , в однородном поле тяжести (см. рис. 1 ). Управ-
ляющее воздействие на точку M осуществляет-

![]() ся посредством реактивной силы
f
, возникающей в результате отделения от точки частиц с элементарной массой
dm
. Тогда масса точки
M
является величиной переменной, а движение точки описывается векторным дифференциальным
ся посредством реактивной силы
f
, возникающей в результате отделения от точки частиц с элементарной массой
dm
. Тогда масса точки
M
является величиной переменной, а движение точки описывается векторным дифференциальным
ξ уравнением Мещерского
Рис. 1
![]()
![]() m dv
= +mg
dm
a
r
,
(3) dt dt
m dv
= +mg
dm
a
r
,
(3) dt dt
![]() где
a
r
- вектор относительной скорости отде-
где
a
r
- вектор относительной скорости отде-
ляющихся частиц. Проектируя уравнение (3) на оси выбранной системы координат, получим
mξ = ma cosα ξ , (4) mη = ma cosα η −mg .
Здесь α α ξ , η - углы, которые составляет вектор относительной скорости отделяющихся частиц с соответствующими координатными осями. Запишем систему (4) в нормальной форме
x 1 = x 3 ,
x 2 = x 4 , (5) x 3 = u 1 , x 4 = u 2 − g ,
где
![]()
![]() x
1
= = = = =ξ
, x
2
η
, x
3
ξ
, x
4
η
, u
1
a m
cosα
ξ
, u
2
= a
m
m
cosα
η
. m
x
1
= = = = =ξ
, x
2
η
, x
3
ξ
, x
4
η
, u
1
a m
cosα
ξ
, u
2
= a
m
m
cosα
η
. m
Векторно-матричная форма системы дифференциальных уравнений (5) имеет вид
⎛⎜⎜x ⎞⎟
⎜⎜⎜x
⎜⎝⎜⎜⎜⎜⎜⎜xx 12 43⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛000 0 000 0 1000 1000 ⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜x x x x 12 43⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟+⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜1 00 0 1 000 ⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎜⎝⎜⎜⎛u u 1 2 ⎠⎞⎟⎟⎟⎟+⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜−000g ⎟⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎠⎟.
 Обычно физический объект можно моделировать линейными дифференциальными уравнениями лишь в дополнительных предположениях об области изменения его фазовых координат.
Обычно физический объект можно моделировать линейными дифференциальными уравнениями лишь в дополнительных предположениях об области изменения его фазовых координат.
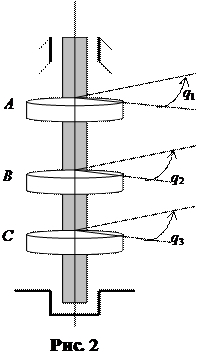
Пример 2. Рассмотрим упругий вал, несущий жестко насаженные маховики A B , и C (см. рис. 2 ). Система вращается вокруг оси вала с постоянной угловой скоростью ω , однако вследствие возмущений возникают крутильные колебания, которые необходимо успокоить управ-
ляющими моментами u u 1 , 2 , приложенными к ма-
ховикам A и C соответственно. Система имеет три степени свободы. В качестве обобщенных координат выбираются следующие величины: q 2 - угол отклонения маховика B от заданного движения системы ψ (t )=ωt t , ≥t 0 ; q q 1 , 3 - суть углы закручивания маховиков A и C соответственно относительно маховика B .
Пусть I A ,I B ,I C - моменты инерции маховиков. Вычислим кинетическую энергию всей системы. Имеем
T = 1 2 I A (ω + + +q 1 q 2 )2 1 2 I B (ω + +q 2 )2 1 2 I C (ω + +q 3 q 2 )2 .
Обозначим через c c 1 , 2 крутильные жесткости соответствующих участков вала. Принимаем, что система работает в пределах деформаций, подчиняющихся закону Гука. Тогда потенциальная энергия системы определяется равенством
Π = 1 2 c q 1 12 + 1 2 c q 2 32 .
Из выражения для элементарной работы
δA =Q q 1 δ 1 +Q q 2 δ 2 +Q q 3 δ 3 = + +u q 1 δ 1 (u 1 u 2 )δq 2 +u q 2 δ 3
следует, что обобщенные силы Q i i , =1,2,3 выражаются равенствами
Q 1 = u Q 1 , 2 = +u 1 u 2 ,Q 3 = u 3 .
Составим уравнения Лагранжа
![]() d
⎛⎜⎜∂
T
⎞⎟
d
⎛⎜⎜∂
T
⎞⎟
dt ⎜⎜⎝∂q i ⎠⎟⎟⎟−∂∂ q T i =Q i −∂Π ∂q i , i =1,2,3.
Получаем следующие три дифференциальных уравнения второго порядка:
I q A 1 + =I q A 2 −c q 1 1 +u 1 ,
I A q 1 + + +(I A I B I C )q 2 + = +I q C 3 u 1 u 2 , (6)
I q C 2 + =I q C 3 −c q 2 3 +u 2 .
Разрешим систему дифференциальных уравнений (6) относительно старших производных
![]() q
1 = − c
1(I
A
+ I
B
)q
1 − c
2
q
3 +
q
1 = − c
1(I
A
+ I
B
)q
1 − c
2
q
3 + ![]() 1 u
1,
1 u
1,
I I A B I B I A
q 2 = +c 1 q 1 c 2 q 3 , (7)
![]() I
B
I
B
q
3 = − c
1
q
1 − c
2 (I
B
+ I
C
)q
3 + 1 u
2.
I
B
I
B
q
3 = − c
1
q
1 − c
2 (I
B
+ I
C
)q
3 + 1 u
2.
I B I B + I C I C
Проведя замену переменных
x 1 = q 1 , x 2 = q 2 , x 3 = q 3 , x 4 = q 1, x 5 = q 2, x 6 = q 3 ,
запишем систему (7) в нормальной форме
x 1 = x 4 , x 2 = x 5 , x 3 = x 6 ,
![]() x
4 = − c
1 (I
A
+ I
B
) x
1 − c
2
x
3 +
x
4 = − c
1 (I
A
+ I
B
) x
1 − c
2
x
3 + ![]() 1 u
1,
1 u
1,
I I A B I B I A
x 5 = +c 1 x 1 c 2 x 3,
I B I B
![]() x
6 = − c
1
x
1 − c
2 (I
B
+ I
C
) x
3 + 1 u
2. (8)
x
6 = − c
1
x
1 − c
2 (I
B
+ I
C
) x
3 + 1 u
2. (8)
I B I B +I C I C
Векторно-матричная форма системы дифференциальных уравнений (8) имеет вид
⎜⎜⎜⎜⎛ 00 00 00 10 10 00⎞⎟⎟⎟⎟⎟ ⎜⎛ 0 0 ⎞
⎜
![]() ⎟⎟ ⎜⎜⎜⎜⎜⎜⎜ 0 0 0 0 0 1⎟⎟⎟⎟⎜⎛ x
⎞
⎟⎟ ⎜⎜⎜⎜⎜⎜⎜ 0 0 0 0 0 1⎟⎟⎟⎟⎜⎛ x
⎞
⎜⎜⎜xx ⎟⎟⎟⎟⎟⎟ = ⎜⎜⎜⎜⎜− c ( II I + I ) 0 − Ic 0 0 0⎟⎟⎟⎟⎟⎟⎟⎟⎜⎜⎜⎜⎜⎜⎜xx ⎟⎟⎟ ⎜⎜⎜ ⎟
⎟ ![]()
![]() ⎜⎜⎜⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜x
xx
x
12
4653
⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜ 1
−Ic
A
I
A B
B
1
c
B
1
B
00
− c
2 I
(B
IIc
B
+B
2
B
2
+I
C
I
C
) 00 00 00
⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜xxx
1
652
43
⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟+⎜⎜⎜⎜⎜⎜⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜ I
10
000
A
I
1
0000
C
⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎛⎜⎜⎜⎝u
u
1
2⎞⎠⎟⎟⎟⎟.
⎜⎜⎜⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜x
xx
x
12
4653
⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜ 1
−Ic
A
I
A B
B
1
c
B
1
B
00
− c
2 I
(B
IIc
B
+B
2
B
2
+I
C
I
C
) 00 00 00
⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜xxx
1
652
43
⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟+⎜⎜⎜⎜⎜⎜⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜ I
10
000
A
I
1
0000
C
⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎛⎜⎜⎜⎝u
u
1
2⎞⎠⎟⎟⎟⎟.
⎜⎜
![]()
⎜⎝⎜⎜ ⎟
Заметим, что в разобранном примере математическая модель, представленная системой дифференциальных уравнений (8), адекватна физическому объекту только в пределах деформаций, удовлетворяющих закону Гука, т.е. ес-
ли фазовые координаты x 1 ,x 2 ,x 3 достаточно малы по абсолютной величине.
К дифференциальным уравнениям вида (2) можно прийти и в результате линеаризации исходных нелинейных дифференциальных уравнений движения объекта. Опишем процедуру линеаризации.
Пусть математической моделью управляемого динамического объекта служит система нелинейных дифференциальных уравнений
y =Y t y v ( , , ) , t ∈[t T 0 , ], y ∈ R n , v ∈ R r . (9) Относительно функции Y :[t 0 ,T ]× R n + r → R n предполагается существование непрерывных частных производных не ниже второго порядка включительно по каждому из аргументов.
Допустим, что некоторой функции v ∗ :[t T 0 , ]→ R r отвечает решение y ∗ ()⋅ = y ∗ (⋅,t 0 , y 0 ,v ∗ ()⋅ ) дифференциального уравнения (9), удовлетворяющее начальному условию y t ( 0)= y 0 . Предположим, что именно эта функция y ∗ (⋅) является требуемым законом движения для управляемого объекта. Однако при физической реализации указанного управления v ∗ (⋅) закон движения y ()⋅ реального динамического объекта вследствие ряда факторов (неадекватность математической модели, наличие неконтролируемых возмущений, невозможность в точности удовлетворить начальным условиям и др.) будет отличаться от идеального движения y ∗ ()⋅ . Для реализаций управляющих воздействий и отвечающих им движений примем следующее представление:
![]() y
(⋅)= y
∗
(⋅)+ x
(⋅), v
(⋅)= v
∗
(⋅)+ u
(⋅). (10) Здесь величины x
()⋅ , u
()⋅ полагаются малыми. Подставим выражения (10) в уравнения (9). В результате получим
y
(⋅)= y
∗
(⋅)+ x
(⋅), v
(⋅)= v
∗
(⋅)+ u
(⋅). (10) Здесь величины x
()⋅ , u
()⋅ полагаются малыми. Подставим выражения (10) в уравнения (9). В результате получим
![]() y
∗
( )t
+ x
( )t
= Y
(t
, y
∗
(t
)+ x
(t
),v
∗
(t
)+ u
(t
)), t
∈[t
0
,T
]. (11) С точностью до величин второго порядка малости по отношению к x
(⋅) , u
(⋅) из (11) выводим
y
∗
( )t
+ x
( )t
= Y
(t
, y
∗
(t
)+ x
(t
),v
∗
(t
)+ u
(t
)), t
∈[t
0
,T
]. (11) С точностью до величин второго порядка малости по отношению к x
(⋅) , u
(⋅) из (11) выводим
![]() y
∗
( )t
+ x
( )t
=Y
( ) ( )
y
∗
( )t
+ x
( )t
=Y
( ) ( ) ![]()
![]() [ ,T
]. y v
[ ,T
]. y v
Обозначая
A
( )t
= ![]() ∂
Y
(t
, y
∗
( )t
,v
∗
( )t
), B
( )t
=
∂
Y
(t
, y
∗
( )t
,v
∗
( )t
), B
( )t
= ![]() ∂
Y
(t
, y
∗
( )t
,v
∗
( )t
), t
∈[t
0
,T
] (12)
∂
Y
(t
, y
∗
( )t
,v
∗
( )t
), t
∈[t
0
,T
] (12)
∂y ∂v
и учитывая, что
y ∗ ( )t = Y (t , y ∗ (t ), v ∗ (t )), t ∈ [t 0 ,T ],
приходим к уравнениям (2), в которых C t ( )= 0, t ∈[t T 0 , ].
Пример 3*. На горизонтальный плоскости находится двухзвенный механический манипулятор, каждое звено которого представляет собой абсолют-
 но жесткий стержень длиной
но жесткий стержень длиной
l i ,i =1,2. Первое звено соединено с неподвижным основанием манипулятора вращательной парой O 1 , а со вторым звеном – враща-
Рис. 3 тельной парой O 2 . Масса схвата
манипулятора – m , центр масс i -го звена находится в середине стержня – точке C i , его масса – m i , момент инерции i -го звена относительно своего центра масс – I i ,i =1,2. В соединительных парах могут развиваться управляющие вращательные моменты, соответственно, v 1 и v 2 ,
На горизонтальной плоскости, в которой расположен манипулятор, введем прямолинейную ось O 1 x . Обозначим через ϕi угол, образованный i -м звеном манипулятора, i =1,2, с осью O 1 x . Запишем дифференциальные уравнения движения манипулятора в форме уравнений Лагранжа второго рода, в которых в качестве обобщенных координат берутся углы ϕi ,i =1,2 . Кинетическая энергия манипулятора определяется по формуле
T = T 1 + T 2 + T c , (13)
где T i – кинетическая энергия i -го, i =1,2, звена, а T c – кинетическая энергия схвата манипулятора. Последовательно вычисляем
![]()
![]()
![]() 1 ( 2 21
)( 2 2 2 ) 4I
1 + m
1l
12
2
1 ( 2 21
)( 2 2 2 ) 4I
1 + m
1l
12
2
T 1 = I 1 ϕ1 + m 1 v C = 4I 1 ϕ1 + m 1 l 1 ϕ1 = ϕ1 ,
28
T
2 = ![]() (I
2ϕ22 + m
2 v
C
22 )=
(I
2ϕ22 + m
2 v
C
22 )= ![]() [4I
2ϕ22 + 4m
2 l
12ϕ12 + m
2 l
22ϕ22 + 4m
2 l
1l
2ϕ1ϕ2 cos(ϕ1 −ϕ2 )],
[4I
2ϕ22 + 4m
2 l
12ϕ12 + m
2 l
22ϕ22 + 4m
2 l
1l
2ϕ1ϕ2 cos(ϕ1 −ϕ2 )],
T
c
= ![]() mv
c
2 =
mv
c
2 = ![]() m
[l
12ϕ12 + l
22ϕ22 + 2l
1l
2ϕ1ϕ2 cos(ϕ1 −ϕ2 )].
m
[l
12ϕ12 + l
22ϕ22 + 2l
1l
2ϕ1ϕ2 cos(ϕ1 −ϕ2 )].
Подставляя найденные величины энергий составных частей манипулятора в (13), находим
![]() T
=
T
= ![]() 1ϕ1
2
[l
1
2
(m
1
+ 4m
2
+ 4m
)+ 4I
1
]+
1ϕ1
2
[l
1
2
(m
1
+ 4m
2
+ 4m
)+ 4I
1
]+
![]() 1
ϕ2
2
[l
2
2
(m
2
+ 4m
)+ 4I
2
]+ (2m
+ m
2
)l
1
l
2
ϕ1
ϕ2
cos(ϕ1
−ϕ2
).
1
ϕ2
2
[l
2
2
(m
2
+ 4m
)+ 4I
2
]+ (2m
+ m
2
)l
1
l
2
ϕ1
ϕ2
cos(ϕ1
−ϕ2
).
8 8
Введем обозначения
![]() a
=
a
= ![]() 1 [l
1
2
(m
1
+ 4m
2
+ 4m
)+ 4I
1
], b
=
1 [l
1
2
(m
1
+ 4m
2
+ 4m
)+ 4I
1
], b
= ![]() 1
[l
2
2
(m
2
+ 4m
)+ 4I
2
], c
= (2m
+ m
2
)l
1
l
2
.
1
[l
2
2
(m
2
+ 4m
)+ 4I
2
], c
= (2m
+ m
2
)l
1
l
2
.
4 4
Тогда выражение для кинетической энергии манипулятора принимает вид
T
=
![]() [a
ϕ1
2
+ 2c
ϕ1
ϕ2
cos(ϕ1
−ϕ2
)+ b
ϕ2
2
].
[a
ϕ1
2
+ 2c
ϕ1
ϕ2
cos(ϕ1
−ϕ2
)+ b
ϕ2
2
].
Справедливы равенства
∂T d ∂T
![]() = a
ϕ1
+ c
ϕ2
cos(ϕ1
−ϕ2
),
= a
ϕ1
+ c
ϕ2
cos(ϕ1
−ϕ2
), ![]() = a
ϕ1
+ c
ϕ2
cos(ϕ1
−ϕ2
)− c
ϕ2
(ϕ1
−ϕ2
)sin(ϕ1
−ϕ2
),
= a
ϕ1
+ c
ϕ2
cos(ϕ1
−ϕ2
)− c
ϕ2
(ϕ1
−ϕ2
)sin(ϕ1
−ϕ2
),
∂ϕ1 dt ∂ϕ1
∂T d ∂T
![]() = b
ϕ2
+ c
ϕ1
cos(ϕ1
−ϕ2
),
= b
ϕ2
+ c
ϕ1
cos(ϕ1
−ϕ2
), ![]() = b
ϕ2
+ c
ϕ1
cos(ϕ1
−ϕ2
)− c
ϕ1
(ϕ1
−ϕ2
)sin(ϕ1
−ϕ2
),
= b
ϕ2
+ c
ϕ1
cos(ϕ1
−ϕ2
)− c
ϕ1
(ϕ1
−ϕ2
)sin(ϕ1
−ϕ2
),
∂ϕ2 dt ∂ϕ2
![]() ∂T
= −c
ϕ1
ϕ2
sin(ϕ1
−ϕ2
),
∂T
= −c
ϕ1
ϕ2
sin(ϕ1
−ϕ2
), ![]() ∂T
= c
ϕ1
ϕ2
sin(ϕ1
−ϕ2
).
(14)
∂T
= c
ϕ1
ϕ2
sin(ϕ1
−ϕ2
).
(14)
∂ϕ1 ∂ϕ2
Обобщенной силой Q i , отвечающей обобщенной координате ϕi , является управляющий вращательный момент v i , i =1,2.
Используя формулы (14), выпишем уравнения Лагранжа
d ∂T ∂T
![]() − = Q
i
, i
=1,2.
− = Q
i
, i
=1,2.
dt ∂ϕi ∂ϕi
В результате получим
a ϕ 1 +c ϕ 2 cos (ϕ ϕ 1 − 2)+c ϕ 2[1] sin (ϕ ϕ 1 − 2)= v 1 , c ϕ 1 cos (ϕ ϕ 1 − 2)+b ϕ 2 −c ϕ 12 sin (ϕ ϕ 1 − 2)= v 2 . (15)
Разрешим дифференциальные уравнения (15) относительно старших производных
![]()
![]() 2 2 ⎡
⎣ ⎤
⎦ ,
2 2 ⎡
⎣ ⎤
⎦ ,
1
![]() 2 ab
−c
cos (ϕ ϕ
1 − 2 )
2 ab
−c
cos (ϕ ϕ
1 − 2 )
![]()
![]() 2 2 ⎡
⎣ ⎤
⎦ .
2 2 ⎡
⎣ ⎤
⎦ .
2
![]() 2 ab
−c
cos (ϕ ϕ
1 − 2 )
2 ab
−c
cos (ϕ ϕ
1 − 2 )
Полученную систему двух дифференциальных уравнений второго порядка от-
носительно переменных ϕ1 ,ϕ2 заменой переменных
y 1 =ϕ 1, y 2 =ϕ 2, y 3 =ϕ 1, y 4 =ϕ 2
сведем к системе четырех дифференциальных уравнений первого порядка
y 1 = y 3 , y 2 = y 4 ,
1 2bv −2bcy sin y − y −2cv cos y − y −c y sin 2
![]() y
3 = ⋅ 1 4
2
( 1 2
) 2 2 2 ( 1 2
) 2
3
2
⎡
⎣
(y
1
− y
2
)⎤
⎦ ,
y
3 = ⋅ 1 4
2
( 1 2
) 2 2 2 ( 1 2
) 2
3
2
⎡
⎣
(y
1
− y
2
)⎤
⎦ ,
2 ab −c cos (y 1 − y 2 )
y 4 = 1 ⋅ 2av 2 +2acy 32 sin(y 1 − y 2 )−2cv 2 1 cos2 (y 1 − y 2 )+c y 2 42 sin 2⎡⎣ (y 1 − y 2 )⎤⎦ (16)
⎛ ⎞⎜⎜⎜0 ⎟⎟
⎜
v ∗( )t ≡ ⎛ ⎞⎜⎝ ⎠⎜ ⎜0 0 ⎟⎟⎟⎟, y ∗( )t = ⎜⎜⎜⎜⎜⎝ ⎠⎜0 00 ⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟.
⎜
По формулам (10) находим
⎛⎜⎜ ⎜⎜ 0 0 1 0⎞⎟
![]() A
= ⎜⎜
⎜⎜⎜⎜00
0
0
00 0
00
1
00
⎠⎟⎟⎟⎟
⎟⎟⎟⎟
⎟⎟⎟ , B
= ⎜⎜
⎜
⎜⎛⎜⎜⎜
⎜⎜⎜⎝⎜⎜⎜ab cab c
−
00
−−
b
c
22 ab cab c
−
00
−−
a
c
22 ⎞⎠⎟⎟⎟
⎟⎟⎟⎟
⎟⎟⎟
⎟⎟
⎟⎟.
A
= ⎜⎜
⎜⎜⎜⎜00
0
0
00 0
00
1
00
⎠⎟⎟⎟⎟
⎟⎟⎟⎟
⎟⎟⎟ , B
= ⎜⎜
⎜
⎜⎛⎜⎜⎜
⎜⎜⎜⎝⎜⎜⎜ab cab c
−
00
−−
b
c
22 ab cab c
−
00
−−
a
c
22 ⎞⎠⎟⎟⎟
⎟⎟⎟⎟
⎟⎟⎟
⎟⎟
⎟⎟.
⎜⎝⎜
Таким образом, линеаризованные уравнения здесь имеют вид
⎜⎜⎛ x ⎞
⎜⎜⎜⎜⎜xx ⎟⎟⎟⎟
![]() ⎜⎜⎜⎜⎜⎝x
1423⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟ = ⎜⎜⎜⎜⎝⎜⎜⎜⎜⎜⎜⎜⎛0000 0000 1000 1000⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜xxxx
1423⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟+⎜⎜⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛ab cab c
−
00−−bc
22 ab cab c
−
00−−ac
22 ⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎝⎜⎜⎛⎜uu
12 ⎞⎟⎟⎟⎟⎠.
⎜⎜⎜⎜⎜⎝x
1423⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟ = ⎜⎜⎜⎜⎝⎜⎜⎜⎜⎜⎜⎜⎛0000 0000 1000 1000⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜xxxx
1423⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟+⎜⎜⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛ab cab c
−
00−−bc
22 ab cab c
−
00−−ac
22 ⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎝⎜⎜⎛⎜uu
12 ⎞⎟⎟⎟⎟⎠.
1.2. Системы однородных линейных дифференциальных уравнений
Системе дифференциальных уравнений (1.1) поставим в соответствие однородную систему уравнений
x 1 = a 11 (t x ) 1 + +" a 1n (t x ) n ,
.............................................. x n = a n 1 (t x ) 1 + +" a nn (t x ) n .
или ее векторно-матричный аналог
x = A t x ( ) . (1)
Установим некоторые простейшие свойства дифференциального уравнения (1).
Свойство 1. Пусть x (⋅) - решение дифференциального уравнения (1) и x t ( 0)= 0 для некоторого значения t 0 ∈ R 1 . Тогда x ( )t ≡ 0, t ∈ R 1 .
Доказательство. Справедливость свойства следует непосредственно из теоремы существования и единственности решения дифференциальных уравнений.
Свойство 2. Пусть x ( 1 ) (⋅),",x ( s ) (⋅) - система решений уравнения (1). Тогда для всех α 1,",α s ∈ R 1 выражение
x ˆ()⋅ =∑s α i x ( )i ()⋅
i =1
будет также решением дифференциального уравнения (1).
Доказательство. Действительно,
![]()
![]() dx t
ˆ( ) ⎛ ⎞ ⎛ ⎞
dx t
ˆ( ) ⎛ ⎞ ⎛ ⎞
.
dt dt ⎝ i = 1 ⎠ i = 1 i = 1 ⎝ i = 1 ⎠
Определение 1. Система решений x ( 1 ) (⋅),",x ( s ) (⋅) уравнения (1) называется линейно зависимой, если существуют такие константы α 1,",α s ∈ R 1 , не обращающиеся одновременно в нуль, что
∑s α i x ( ) i ( )t ≡ 0, t ∈ R 1 .
i =1
В противном случае система решений x ( 1 ) (⋅),",x ( s ) (⋅) называется линейно независимой.
Заметим, что для зависимой системы решений x ( 1 ) (⋅),",x ( s ) (⋅) набор векторов x ( 1 ) (t ),",x ( s ) (t ) является линейно зависимым при всех t ∈ R 1 . Это утверждение может быть обращено следующим образом.
Лемма 1. Пусть для некоторого значения t 0 ∈ R 1 набор векторов
x ( 1 ) (t 0 ),",x ( s ) (t 0 ) линейно зависим. Тогда система решений x ( 1 ) (⋅),",x ( s ) (⋅) уравнения (1) является линейно зависимой.
Доказательство. Из линейной зависимости векторов x ( 1 ) (t 0 ),",x ( s ) (t 0 ) следует существование ненулевого набора констант α 1,",α s ∈ R 1 , для которого
∑s α i x ( ) i ( )t 0 = 0 . (2)
i =1
Полагаем
x ˆ()⋅ =∑s α i x ( )i ()⋅ .
i =1
По свойству 2 функция x ˆ()⋅ является решением уравнения (1), при этом в силу
(2) справедливо равенство x t ˆ( 0)= 0. Тогда по свойству 1 должно выполняться
s
x ˆ( )t =∑α i x ( ) i ( )t ≡ 0, t ∈ R 1 ,
i =1
что и означает искомую линейную зависимость системы решений
x ( 1 ) (⋅),",x ( s ) (⋅). Лемма доказана.
Следствие. Пусть система решений x ( 1 ) (⋅),",x ( s ) (⋅) линейно независима.
Тогда набор векторов x ( 1 ) ( )t ,",x ( s ) ( )t является линейно независимым при всех t ∈ R 1 .
Доказательство.
От противного приходим к существованию некоторого значения
t
![]() R
, для которого набор векторов
x
(
1
)
( )t
,",x
(
s
)
( )t
является линейно зависимым. Тогда по
лемме 1
система решений
x
(
1
)
(⋅),",x
(
s
)
(⋅) должна быть зависимой, что противоречит исходным предположениям.
R
, для которого набор векторов
x
(
1
)
( )t
,",x
(
s
)
( )t
является линейно зависимым. Тогда по
лемме 1
система решений
x
(
1
)
(⋅),",x
(
s
)
(⋅) должна быть зависимой, что противоречит исходным предположениям.
Установим критерий линейной зависимости и независимости системы
решений x ( 1 ) (⋅),",x ( s ) (⋅) уравнения (1).
Теорема 1. Система решений x ( 1 ) (⋅),",x ( s ) (⋅) уравнения (1) является линейно зависимой или линейно независимой, тогда и только тогда когда соответственно линейно зависим или линейно независим набор векторов x ( 1 ) (t 0 ),",x ( s ) (t 0 ) хотя бы при одном значении t 0 ∈ R 1 .
Доказательство.
Необходимость теоремы вытекает непосредственно из
определения 1
и
следствия
из
леммы 1
. Достаточность в части линейной зависимости системы решений
x
(
1
)
(⋅),",x
(
s
)
(⋅) доказана в
лемме 1
. Наконец, если набор векторов
x
(
1
)
(t
0
),",x
(
s
)
(t
0
) является линейно независимым при некотором значении
t
![]() R
, то для системы решений
x
(
1
)
(⋅),",x
(
s
)
(⋅)равенство
R
, то для системы решений
x
(
1
)
(⋅),",x
(
s
)
(⋅)равенство
∑s α i x ( )i ( )t 0 = 0
i =1
невозможно ни при каких ненулевых наборах констант α 1,",α s ∈ R 1 . Это означает, что система решений x ( 1 ) (⋅),",x ( s ) (⋅) не является линейно зависимой, и поэтому она линейно независима. Теорема доказана.
Определение 2. Линейно независимая система решений
x ( 1 ) (⋅),",x ( n ) (⋅) (3)
дифференциального уравнения (1), где n - размерность вектора x , называется фундаментальной системой решений дифференциального уравнения (1). Теорема 2. Для уравнения (1) существует фундаментальная система решений, и любое решение этого уравнения может быть представлено как линейная комбинация решений, составляющих фундаментальную систему. Доказательство. Пусть набор векторов
e 1,",e n ∈ R n
образует базис в R n . Определим систему решений (3) условиями
x ( i ) (t 0 )= =e i i , 1,",n .
По теореме 1 из линейной независимости векторов x ( 1 ) (t 0 ),",x ( n ) (t 0 ) вытекает линейная независимость системы решений (3). Таким образом, существование фундаментальной системы решений для уравнения (1) установлено.
Покажем, что каждое решение x ()⋅ уравнения (1) можно представить в виде
x ( )t =∑n α i x ( ) i ( )t , t ∈ R 1 .
i =1
Набор векторов x ( 1 ) (t 0 ),",x ( n ) (t 0 ) является базисом в R n . Тогда для любого решения x (⋅) уравнения (1) найдется набор констант α 1,",α n ∈ R 1 такой, что
n x ( )t 0 =∑α i x ( )i ( )t 0 .
i =1
Решения x ()⋅ и ∑n α i x ( ) i ()⋅ имеют общее начальное условие и потому совпадают.
i =1
Теорема доказана.
Пример 4*. Рассмотрим однородную линейную систему дифференциальных уравнений третьего порядка
x 1 = + +x 1 4x 2 x 3 ,
x 2 = + +x 1 x 2 x 3 , (4) x 3 = 2x 1 −4x 2 + x 3 .
Приведем векторно-матричную форму записи этой системы
⎜⎝⎛⎜⎜⎜xx 123⎞⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜112 −144 111⎠⎝⎞⎛⎟⎟⎟⎟⎟⎟⎟⎟⎜⎜⎜⎜⎜⎜⎜⎜xxx 123⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟.
⎜⎜x ⎠
⎜⎜
Покажем, что следующая система решений этого уравнения
⎜⎛2e ⎞
x ( )1 ( )t =⎜⎜⎜⎜⎜⎜⎝ e 033tt ⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟, x ( )2 ( )t =⎜⎜⎜⎛⎜⎜⎜⎜⎜⎝7coscos−10t −t +cos2sinsint tt ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, x ( )3 ( )t =⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜−43coscos−t sint −+sint 2sint t ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, t ∈ R 1
⎜
образует фундаментальную систему решений.
Сначала непосредственно проверяем, что каждый член системы
| 2e 3t D t ( )= e 3t 0 |
7cost +sint cost −2sint −10cost |
3cost −sint −sint . −4cost +2sint |
![]()
![]() x
(
1
)
(⋅),x
(
2
)
(⋅),x
(
3
)
(⋅) является решением уравнений (2). Далее составим определитель
x
(
1
)
(⋅),x
(
2
)
(⋅),x
(
3
)
(⋅) является решением уравнений (2). Далее составим определитель
Вычислим его значение при t = 0. Имеем
![]()
![]() 2 7 3
2 7 3
D ( )0 =1 1 0= −10 ≠ 0.
0 −10 −4
Таким образом, D ( )0 ≠ 0 и набор векторов x ( 1 ) (0), x ( 2 ) (0), x ( 3 ) (0) является линейно независимым. Тогда по теореме 1 система решений x ( 1 ) (⋅),x ( 2 ) (⋅),x ( 3 ) (⋅) уравнений
(2) является фундаментальной системой решений.
1.3. Фундаментальная матрица Коши. Пусть
x ( )1 ()⋅ =⎜⎜⎜⎜⎜⎜⎛x 1n ( )( )"11 ((⋅⋅))⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟,",x ( )n ()⋅ =⎝⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜xx 1n ( )( )"nn ((⋅⋅))⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟ ⎝⎜⎜⎜x
фундаментальная система решений однородного дифференциального уравнения (2.1). Для всех t ∈ R 1 построим квадратную матрицу Z (t ) следующего вида
| Z t ( )=⎛⎜⎜⎜⎜⎜x 1( )"1 (t ) |
" " |
x 1( )n (t )⎞⎟⎟⎟⎟⎟⎟⎟. " |
⎜
⎝⎜⎜⎜x n ( )1 (t ) " x n ( )n (t )⎠⎟⎟⎟
Из теоремы 1 следует, что матрица Z (t ) является невырожденной при всех t ∈ R 1 и, следовательно, для всех t ∈ R 1 существует обратная матрица
| ⎛ ζ1( )1 ( )t ⎜ Z − 1 ( )t = ⎜ ⎜⎜ζn ( )1 ( )t ⎝ Полагаем |
ζ1( )n ( )t ⎞ ⎟ ⎟. ζn ( )n ( )t ⎟⎟⎠ |
| X [t ,τ ]= Z t Z ( ) ( )τ = −1 ⎛⎜⎜⎜⎜⎜⎜⎜⎜⎜⎝xx 1n ( )( )11"[[tt ,,ττ ]] |
" x 1n ( )( )nn [[tt ,,ττ ]]⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟, t ,τ ∈ R 1 . " " " x |
Определение 3 . Матрица X [t ,τ ] , t ,τ ∈ R 1 называется фундаментальной матрицей Коши для однородного дифференциального уравнения (2.1).
Установим ряд свойств фундаментальной матрицы Коши.
Теорема 3. Для всех t , ,τ s ∈ R 1 имеют место равенства
⎛⎜ ⎜⎜" " "1 " 0 ⎞⎟
X s s [ , ]= =E ⎜⎝⎜⎜⎜ ⎜ 0 " 1 ⎠⎟⎟⎟⎟⎟⎟⎟ , . (1)
(X [t ,τ ])−1 = X [τ , ,t ] (2)
d
![]() X
[t
,
τ
]= A t X t
( )
[ ,
τ
], (3)
X
[t
,
τ
]= A t X t
( )
[ ,
τ
], (3)
dt
d
![]() dτ X t
[ ,τ
]=−X t
[ ,τ
] ( )A τ
. (
4)
dτ X t
[ ,τ
]=−X t
[ ,τ
] ( )A τ
. (
4)
Доказательство. Равенство (1) является простым следствием определения 3 . Докажем равенство (2). Имеем
(X [t ,τ ])−1 =(Z t ( ) Z −1 ( )τ )−1 =(Z −1 ( )τ )−1 Z −1 ( )τ = Z ( )τ Z −1 ( )t = X [τ ,t ] .
Для вывода равенства (3) замечаем, что
n
x
i
( )
j
[t
,τ
]=![]() x
i
( )
s
( )t ζ
s
( )
j
( )τ
, ,i j
=1,",n
.
x
i
( )
s
( )t ζ
s
( )
j
( )τ
, ,i j
=1,",n
.
s =1
Тогда
⎜⎜⎛x
( )[t
,τ
]⎞ ![]()
x
( )j
[t
,τ
]=⎜⎜⎜⎜ 1n
( )jj
"[t
,τ
]⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=![]() s
=n
1 ζ
j
τ
⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜xx
i
( )"ss
( )tt
⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟.
s
=n
1 ζ
j
τ
⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜xx
i
( )"ss
( )tt
⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟.
⎜⎜⎜x
⎝
Таким образом, столбцы матрицы X [t ,τ], t ,τ∈[t 0 ,T ] являются линейными комбинациями столбцов матрицы Z (t ) и поэтому представляют собой решения уравнения (2.1). Последнее означает, что
![]() d
x
( )
i
[t
,τ
]= A t x
( ) ( )
i
[t
,τ
] , i
=1,",n
⇒
d
x
( )
i
[t
,τ
]= A t x
( ) ( )
i
[t
,τ
] , i
=1,",n
⇒ ![]() d
X t
[ ,τ
]= A t X t
( ) [ ,τ
].
(5) dt dt
d
X t
[ ,τ
]= A t X t
( ) [ ,τ
].
(5) dt dt
Для вывода равенства (4) продифференцируем по переменной τ очевидное тождество X [t ,τ] [X τ,t ]= E . Имеем
⎛
⎜ ![]() d
X
[t
,τ]⎞
⎟
X
[τ,t
]+ X
[t
,τ]
d
X
[t
,τ]⎞
⎟
X
[τ,t
]+ X
[t
,τ] ![]() d
X
[τ,t
]= 0 .
d
X
[τ,t
]= 0 .
⎝d τ ⎠ d τ
Перепишем последнее равенство с учетом (5):
⎛
⎜ ![]() d
X
[t
,τ]
⎞
⎟ X
[τ,t
]= −X
[t
,τ]A
( )τ X
[τ,t
].
(6)
d
X
[t
,τ]
⎞
⎟ X
[τ,t
]= −X
[t
,τ]A
( )τ X
[τ,t
].
(6)
⎝ d τ ⎠
Умножим равенство (6) на матрицу X − 1 [τ,t ] справа. В результате получим искомое равенство (4) Теорема доказана.
![]()
![]() Равенству (4) в доказанной теореме можно дать следующую трактовку: d X t
[ ,τ
]=−X t
[ ,τ
] ( ) d
−1[τ
,t
]=−X
−1[τ
,t A
] ( )τ
⇒
Равенству (4) в доказанной теореме можно дать следующую трактовку: d X t
[ ,τ
]=−X t
[ ,τ
] ( ) d
−1[τ
,t
]=−X
−1[τ
,t A
] ( )τ
⇒
A τ ⇒ X dτ dτ
![]() d
{ −1[τ
,t
]}Tр
=−A
Tр
( )τ
{X
−1[τ
,t
]}Tр
.
d
{ −1[τ
,t
]}Tр
=−A
Tр
( )τ
{X
−1[τ
,t
]}Tр
.
X
dτ
Таким образом, матрица {X −1 [t ,τ ]}T является фундаментальной матрицей Коши для линейной однородной системы дифференциальных уравнений
d ψ Tр
![]() = −A
( )t
ψ. (7)
= −A
( )t
ψ. (7)
dt
В дальнейшем систему (7) будем называть сопряженной системой дифференциальных уравнений по отношению к системе (2.1).
Укажем один способ построения фундаментальной матрицы Коши для случая, когда известна фундаментальная система решений x ( 1 ) ( )⋅ , ,x ( n ) (⋅) дифференциального уравнения (2.1), не связанный с вычислением обратной матрицы для матрицы
Z ( )⋅ = (x ( ) 1 ( )⋅ , ,x ( ) n ( )⋅ ).
Для каждого номера i ∈{1, ,n } составим систему линейных алгебраических уравнений
c x 1 1(1) (τ)+ +c x n 1(n ) (τ) = 0,
…………………………..
c x 1 i (1) (τ)+ +c x n i (n ) (τ) =1,
………………………….
c x 1 n (1) (τ)+ +c x n n (n ) (τ) = 0,
τ∈[t 0 ,T ] (8)
относительно переменных c 1 , ,c n . Эта система имеет решение при всех τ∈[t 0 ,T ], т. к. ее определитель отличен от нуля при всех τ∈[t 0 ,T ]. Пусть c k ( i ) ( )τ , k i , =1, , ,n τ∈[t 0 ,T ] – решение системы (8). Положим
⎛c 1( )i ( )τ x 1( )1 ( )t + +c n ( )i ( )τ x 1( )n ( )t ⎞
( )i ⎜ ⎟ x [t ,τ] = ⎜ ................................ ⎟ , t ,τ∈[t T 0 , ] , i =1, ,n .
⎜⎜⎝c
![]() x t c x t
⎟⎟⎠
x t c x t
⎟⎟⎠
Вектор x ( ) i [t ,τ] представляет собой i -й, i =1, ,n , столбец фундаментальной матрицы Коши.
В случае, когда матрица A постоянна в алгоритме построения фундаментальной матрицы Коши система алгебраических уравнений (8) заменяется на следующую систему:
c x 1 1(1) (0)+ +c x n 1(n ) (0) = 0,
…………………………..
c x 1 i (1) (0)+ +c x n i (n ) (0) =1,
………………………….
c x 1 n (1) (0)+ +c x n n (n ) (0) = 0.
Пусть c k ( i ) , ,i k =1, ,n – ее решение. Столбцы фундаментальной матрицы Коши строятся по формуле
⎛c x
1( )i
1![]() ( ) t c x
i
1n
t
⎞
( ) t c x
i
1n
t
⎞
⎜⎟
( )i
x
[t
,τ] = ⎜ ................................ ⎟ , t
,τ∈[t T
0
, ] , i
=1, ,n
. (9) ⎜⎜⎝c x
1( )i
1![]() ( ) t c x
i
1n
t
⎟⎟⎠
( ) t c x
i
1n
t
⎟⎟⎠
Пример 5*. Требуется построить фундаментальную матрицу Коши для однородного дифференциального уравнения из примера 4 и проверить для нее выполнение равенств (1)-(4).
Выше было показано, что система решений
⎜⎛2e ⎞
x ( )1 ( )t =⎜⎜⎜⎜ e 33tt ⎟⎟⎟⎟⎟⎟⎟⎟, x ( )2 ( )t =⎜⎜⎜⎛⎜⎜⎜⎜⎜⎝7coscos−10t −t +cos2sinsint tt ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, x ( )3 ( )t =⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜−43coscos−t sint −+sint 2sint t ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, t ∈ R 1
⎜⎜⎜⎝ 0 ⎠⎟⎟
этого уравнения является фундаментальной. Построим фундаментальную матрицу Коши непосредственно следуя ее определению. Имеем
X t [ ,τ ]=⎛⎜⎜2e 33tt 7cost +sint 3cost −sint ⎞ ⎛⎟⎟⎟⎟⎟⎟⋅⎜⎜⎜⎜⎜⎜⎜⎜⎜2ee 033ττ 7coscos−τ 10τ −cos+2sinsinτ ττ −34coscos−ττ sin−+τ sin2sinττ ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟−1 = ⎜⎜⎜⎜⎜⎝⎜⎜ e 0 cos−10t −cos2sint t −4cos−sint +t 2sint ⎠ ⎝⎟⎟⎟⎟
⎛⎜⎜⎜ 54 e 3(t −τ ) + 1 5 cos(t −τ )− 52 e 3(t −τ ) − 52 cos(t −τ )+ 53 e 3(t −τ ) − 53 cos(t −τ )− ⎟⎟⎟⎟⎞⎟
⎜⎜⎜![]()
![]()
![]()
⎜⎜⎜⎜⎟⎟⎟⎟
| ⎜⎜⎜⎜ ⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎝⎜⎜ 2sin (t −τ ) ⎜ |
−4sin(t −τ ) |
⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎠⎟⎟⎟ cos(t −τ )+sin(t −τ ) |
![]() ⎜⎜⎜⎜⎜⎜⎜⎜−52
e
1
53(sint
−τ
)(−t
−52
τ
cos) (t
−τ
)− +1
5 e
52
3 sint
−τ
(+t
−54
cosτ
) (t
−τ
)+ 103
e
10
1
3sin
t
−τ
(−t
103 τ
cos)
(t
−τ
)+⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
⎟. (10)
⎜⎜⎜⎜⎜⎜⎜⎜−52
e
1
53(sint
−τ
)(−t
−52
τ
cos) (t
−τ
)− +1
5 e
52
3 sint
−τ
(+t
−54
cosτ
) (t
−τ
)+ 103
e
10
1
3sin
t
−τ
(−t
103 τ
cos)
(t
−τ
)+⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟
⎟. (10)
=
Осуществим построение фундаментальной матрицы Коши, не прибегая к обращению матрицы Z ( )⋅ . Для этого последовательно решаем три системы линейных алгебраических уравнений
2c 11−+ + =+107c c 222 −34c c 33==10., ⎜⎝⎜⎛⎜⎜⎜cc 132( )(111)⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎜⎜⎛⎜⎝⎜⎜⎜⎜−152 52 ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟, 2cc 11−+ + =+107ccc 222 −34cc 33 ==010,, ⇒ ⎜⎜⎛⎜⎜⎜⎝⎜⎜⎜⎜ccc 132( )(( )222)⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎜⎛⎜⎝⎜⎜⎜⎜⎜−1 554 2⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟. c c 0, ⇒ ⎜⎜
⎜⎜c ( )⎠⎟⎟
2c 11−+ + =107cc 222 34cc 33 01, ⎜⎛⎜⎜c 132( )(333)⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎜⎜⎜⎜⎜⎜⎝⎜−101 23 103 ⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟. c + c = 0, ⇒ ⎜⎜⎜⎜c
− = ⎜⎝⎜c ( )⎠
По формуле (9) определяем столбцы фундаментальной матрицы Коши
( )1 ⎛ ⎜2e 33 t ( −t τ− τ) ⎞ ⎟ 2 ⎛⎜7cos(t −τ)+sin(t −τ)⎞⎟ ⎜⎛ 3cos(t −τ)−sin(t −τ) ⎟⎞
2 ( )
x
[t
,τ] = ![]() ⋅⎜ e
⎟−
⋅⎜ e
⎟− ![]() (t
−τ)⋅⎜cos(t
−τ)− 2sin(t
−τ)⎟+⎜ −sin(t
−τ) ⎟ =
(t
−τ)⋅⎜cos(t
−τ)− 2sin(t
−τ)⎟+⎜ −sin(t
−τ) ⎟ =
5 ⎜⎜ 0 ⎟⎟ 5 ⎜⎝ −10cos ⎟⎠ ⎜⎝−4cos(t −τ)+ 2sin(t −τ)⎟⎠
⎝ ⎠
⎛ 54 e 3(t −τ) + 1 5 cos(t −τ)− 7 5 sin(t −τ)⎞
⎜ ⎟
= ⎜ 5 2 e 3 ( t − τ) − 5 2 cos(t −τ)− 1 5 sin(t −τ)⎟,
⎜ ⎟ ⎜ 2sin(t −τ) ⎟
⎝ ⎠
( )2 ⎜⎛ 2e 33 t ( −t τ− τ) ⎟⎞ 4 ⎜⎛7cos(t −τ)+sin(t −τ)⎟⎞ ⎛⎜ 3cos(t −τ)−sin(t −τ) ⎟⎞
1 ( )
x
[t
,τ] = ![]() ⋅⎜ e
⎟+
⋅⎜ e
⎟+ ![]() ⋅⎜cos(t
−τ)−2sin(t
−τ)⎟− 2⋅⎜ −sin(t
−τ) ⎟ =
⋅⎜cos(t
−τ)−2sin(t
−τ)⎟− 2⋅⎜ −sin(t
−τ) ⎟ =
5 ⎜⎜ 0 ⎟ ⎟ 5 ⎜⎝ −10cos(t −τ) ⎠⎟ ⎜⎝−4cos(t −τ)+ 2sin(t −τ)⎟⎠
⎝ ⎠
⎛ 52 e 3(t −τ) − 52 cos(t −τ)+ 14 5 sin(t −τ)⎞
⎜ ⎟
= ⎜ 1 5 e 3 ( t − τ) + 5 4 cos(t −τ)+ 5 2 sin(t −τ) ⎟,
⎜ ⎟ ⎜ −4sin(t −τ) ⎟
⎝ ⎠
( )3 ⎛ ⎜2e 33 t ( −t τ− τ) ⎞ ⎟ 3 ⎛⎜7cos(t −τ)+sin(t −τ)⎟⎞ 1 ⎛⎜ 3cos(t −τ)−sin(t −τ) ⎞⎟
3 ( )
![]()
![]()
![]() x
[t
,τ] = ⋅⎜ e
⎟−⎟ ⋅⎜⎝cos(t
−τ)−2sin(t
−τ)⎟+ 2 ⋅⎜⎜−4cos(−t
−sinτ)(+t
−2τsin) (t
−τ)⎟⎠⎟ =
x
[t
,τ] = ⋅⎜ e
⎟−⎟ ⋅⎜⎝cos(t
−τ)−2sin(t
−τ)⎟+ 2 ⋅⎜⎜−4cos(−t
−sinτ)(+t
−2τsin) (t
−τ)⎟⎠⎟ =
10 ⎜ ⎟ 10 ⎜ −10cos(t −τ) ⎠⎟ ⎝
⎜ 0
⎝ ⎠
⎛ 53 e 3(t −τ) − 53 cos(t −τ)− 54 sin(t −τ) ⎞
⎜ ⎟
= ⎜ 103 e 3(t −τ) − 103 cos(t −τ)+ 101 sin(t −τ)⎟ . ⎜ ⎟ ⎜ cos(t −τ)+sin(t −τ) ⎟
⎝ ⎠
Получили совпадение с формулой (10). Непосредственно убеждаемся, что равенства (1)-(4) выполняются (см. приложение).
В случае A = const дадим другую интерпретацию для фундаментальной матрицы Коши.
Определение 4. Квадратная матрица e tA , определенная степенным рядом
e tA = + + + + + +E 1!A t A 2!2 t 2 A 3!3 t 3 " A k k ! t k " , (11)
где E - единичная матрица размера n ×n , называется экспоненциалом матрицы A .
Покажем, что ряд (11) сходится абсолютно для любого фиксированного t ∈ R 1 . Действительно, с одной стороны,
![]() A
k
k
! t
k
≤ Ak
!k
t
k
, k
= 0,1,2,",
A
k
k
! t
k
≤ Ak
!k
t
k
, k
= 0,1,2,",
а с другой стороны, степенной ряд
![]()
![]() 1+ + + + + +1!A
t
A
2!2 t
2 A
3!3 t
3 " Ak
!k
t
k
"
1+ + + + + +1!A
t
A
2!2 t
2 A
3!3 t
3 " Ak
!k
t
k
"
сходится абсолютно при всех t ∈ R 1 .
Из абсолютной сходимости ряда (11) следует, что его можно почленно дифференцировать. Вычисляем
d
![]() tA
d
A A
2 2 A
3 3 A
k
k A
2 A
3 2 A
k
k
tA
d
A A
2 2 A
3 3 A
k
k A
2 A
3 2 A
k
k
e = (E + + + + + + = + + + + + =1! t 2! t 3! t " k ! t ") A 1! t 2! t " k ! t "
dt dt
![]() = + + + + +A
(E
1!A
t
A
2!2 t
2 A
3!3 t
3 " (kA
−k
−1 !1) t
k
−1 + =") Ae
At
. (12)
= + + + + +A
(E
1!A
t
A
2!2 t
2 A
3!3 t
3 " (kA
−k
−1 !1) t
k
−1 + =") Ae
At
. (12)
Из (12) вытекает справедливость матричного равенства
d tA At
![]() e
= Ae
, dt
e
= Ae
, dt
которое означает, что столбцы экспоненциала матрицы A являются решениями однородного дифференциального уравнения
x = Ax . (13)
![]() В силу очевидного равенства e
At
t
0 = E
эти столбцы образуют фундаменталь-
В силу очевидного равенства e
At
t
0 = E
эти столбцы образуют фундаменталь-
=
ную систему решений дифференциального уравнения (13). Таким образом,
X [t ,τ ]= e (t −τ )A , t ,τ ∈ R 1 .
1.4. Допустимые реализации вектора управляющих параметров.
Пусть управление динамическим объектом осуществляется на промежутке времени [t T 0 , ]. Начальную точку траектории x 0 называют левым концом траектории, а конечную x T – правым концом траектории. Начальный t 0 и конечный
T
моменты времени в общем случае не являются фиксированными. Предполагается, что t
0
∈θ
0 ⊂ R
1
, T
![]() R t t
. На левый и правый концы траектории обычно накладываются ограничение в форме включений
R t t
. На левый и правый концы траектории обычно накладываются ограничение в форме включений
x 0 ∈S 0 ( )t 0 ⊂ R n , t 0 ∈θ0 , x T ∈S T 1 ( ) ⊂ R n , T ∈θ1 .
В задачах теории оптимального управления принята следующая терминология: если множество S 0 (множество S 1 ) состоит из одной точки и не зависит от t 0 ∈θ0 (T ∈θ1 ), то говорят, что левый (правый) конец траектории закреплен; если S 0 (t 0 ) = R n , t 0 ∈θ0 , (S 1 (T ) = R n ,T ∈θ1 ), то левый (правый) конец траектории называют свободным.
Реализация вектора управляющих параметров не является произвольной функцией времени. Эта функция должна быть достаточно «гладкой» и в любой момент времени удовлетворять геометрическим ограничениям
u t ( )∈ P ⊂ R r , t ∈[t T 0 , ].
Оба приведенных требования обусловливаются техническими возможностями механизмов, осуществляющих управляющие воздействия на объект.
С другой стороны, слишком «бедное» множество возможных реализаций вектора управляющих воздействий может не обеспечить достижение поставленной цели управления. В частности, таковым является класс непрерывных на отрезке времени [t T 0 , ] функций. Покажем это на примере.
Пример 6. Рассмотрим поезд, движущийся от станции A к станции B в соответствии с уравнениями
x 1 = x 2 , x 2 =u ,
![]() где
x
1
- расстояние от станции
A
до поезда;
u
- тяга поезда, которой можно управлять. На величину тяги наложено ограничение
u
≤1. Требуется так выбрать управление, чтобы поезд преодолел путь между станциями за наименьшее время. При этом скорость в начальный и конечный моменты времени должна быть нулевой.
где
x
1
- расстояние от станции
A
до поезда;
u
- тяга поезда, которой можно управлять. На величину тяги наложено ограничение
u
≤1. Требуется так выбрать управление, чтобы поезд преодолел путь между станциями за наименьшее время. При этом скорость в начальный и конечный моменты времени должна быть нулевой.
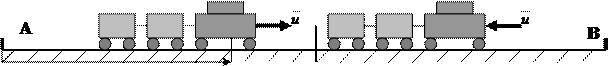 x
1
x
1
Рис. 4
Нетрудно сообразить, что время перехода будет минимальным, когда поезд до половины пути разгоняется с максимальным ускорением u t ( )=+1, а вторую половину максимально затормаживается, т.е. u t ( )=−1. Таким образом, реализация оптимального управления в данном случае имеет вид
![]()
![]() 0
1, , , u t
0
1, , , u t
1, , ,
Функция
u
0
(t
), t
∈[t T
0
, ] терпит разрыв в точке
![]() T
.
T
.
Из опыта решения прикладных задач следует, что реализации вектора управляющих воздействий принадлежат классу C 0 [t T 0 , ] – кусочно-непрерывных функций, то есть таких функций u :[t 0 ,T ]→ R r , которые непрерывны в каждой точке t ∈[t 0 ,T ], за исключением, быть может, конечного числа точек τ1 , ,τm ∈[t 0 ,T ], в которых функция u ()⋅ терпит разрывы первого рода. В этих точках существуют конечные пределы
t →limτi −0 u (t ) = u (τi − 0), t →limτi +0 u (t ) = u (τi + 0),
но u (τi − 0)≠ u (τi + 0),i =1, ,m . В теории оптимального управления принимается, что в точках разрыва реализации вектора управляющих воздействий непрерывны справа. Таким образом,
t →limτi +0 u (t ) = u (τi ),i =1, ,m .
Определение 5. Реализация u ()⋅ вектора управляющих воздействий называется допустимой, если u ()⋅ ∈C t T 0 [ 0, ], функция u ()⋅ непрерывна справа в точках разрыва и выполнено условие u t ( )∈ P ⊂ R r , t ∈[t T 0 , ].
Определение 6. Движением линейного динамического объекта, отвечающим допустимой реализации вектора управляющих воздействий u ()⋅ и выходящим из начального положения x 0 ∈ S 0 (t 0 ), называется решение следующей задачи Коши для векторного дифференциального уравнения
x = A t x ( ) +B t u t ( ) ( )+C t ( ), x t ( 0)= x 0 . (1)
Это движение будем обозначать символом x (⋅, ,t 0 x u 0 , ()⋅ ).
Кусочно-непрерывная реализация вектора управляющих воздействий не гарантирует непрерывность по переменной t правой части дифференциального уравнения (1), поэтому условия классической теоремы существования и единственности решения задачи Коши для дифференциального уравнения здесь не выполняются. В связи с этим предлагается следующая процедура построения движения динамического объекта, отвечающего реализации вектора управляющих воздействий u ( )⋅ ∈C 0 [t T 0 , ] и выходящего из начального положения x 0 ∈ S 0 ( )t 0 . Пусть τ1 , ,τm ∈[t 0 ,T ] - точки разрыва функции u (⋅). Движение объекта на полуинтервале [t 0 ,τ1 ) отождествим с решением задачи Коши
x = A t x ( ) +B t u t ( ) ( )+C t ( ), x t ( )0 = x 0 , t ∈[t 0 ,τ 1).
В силу непрерывности управления u (⋅) на полуинтервале [t 0 ,τ1 ) сформулированная задача Коши имеет решение и притом единственное. Доопределим фазовый вектор в момент времени τ1 по непрерывности, положив
x 1 = x (τ1 )= lim x (t ) .
t →τ 1 −0
Движение объекта на полуинтервале [τ1 ,τ2 ) отождествим с решением задачи Коши x = =x A t x ( ) +B t u t ( ) ( )+C t ( ) , x (τ 1) = x 1 , t ∈[τ τ 1, 2 ),
которое также существует и единственно. Фазовый вектор в момент времени τ2 снова доопределим по непрерывности
x 2 = x ( )τ2 = lim x (t ).
t →τ2 −0
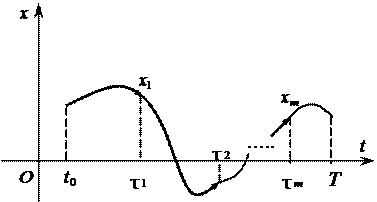 Аналогичные построения производятся на каждом полуинтервале времени
Аналогичные построения производятся на каждом полуинтервале времени
[τi − 1 ,τi ),i =1, ,m .
В результате получим искомое движение динамиче-
x 2 ского объекта (см. рис 5 ). В Рис. 5 книге [7] приводится теорема существования и единственности такого движения. Заметим, что для любого момента времени t ∈[t 0 ,T ] имеет место равенство
τ τ τ x ( )t = +x 0 ∫ A ( ) ( )τ x τ τd +∫ B ( ) ( )τ u τ τd +∫ C ( )τ τd . (2)
t 0 t 0 t 0
Равенство (2) может служить и непосредственным определением движения x (⋅, ,t 0 x u 0 , ()⋅ ). Таким образом, движение объекта принадлежит классу D t T 0 [ 0, ]- классу кусочно-дифференцируемых на промежутке [t T 0 , ] функций и удовлетворяет дифференциальному уравнению (1) во всех точках промежутка [t T 0 , ] за исключением тех, где реализация вектора управляющих воздействий терпит разрыв. Пример 7*. Рассмотрим линейный управляемый динамический объект
x =u x , ∈ R 1 , u ∈ R 1 , [t T 0 , ]=[0,4 ,] x 0 = 0.
Пусть реализация управляющего воздействия имеет вид
⎧ 1, t ∈[0,1),
⎪ ⎪ t , t ∈[1,2),
u (t ) = ⎨
⎪ − t , t ∈[2,3), ⎪⎩ −1, t ∈[3,4].
Построим движение, отвечающее данной реализации управляющего воздействия и выходящее из начального положения x 0 = 0. Полагаем
τ0 = 0,τ1 =1,τ2 = 2,τ3 = 3 и проводим необходимые построения на каждом полуинтервале [τi ,τi + 1 ),i = 0,1,2,3. Последовательно определяем
i = 0, x 0 = 0, x (t ) = t , t ∈[0,1),
i
![]() ,
,
i
= 2, x
2
= ![]() , x
, x
![]() ,
,
i = 3, x 3 = 0, x (t ) = 3−t , t ∈[3,4].
![]()
Рис 6.
Итоговая конструкция изображена на рис. 6 .
1.5. Формула Коши. Рассмотрим линейный управляемый динамический объект, динамика которого описывается дифференциальным уравнением (1.2).
Пусть t s , ∈ R 1 ,x ∗ ∈ R n , u (⋅ ∈) C 0 ⎡ ⎢⎣R 1 ⎥⎦⎤ . Для движения x ( )⋅ = x (⋅, ,s x u ∗ , (⋅)) этого объекта справедливо следующее утверждение.
Теорема 4 (Формула Коши). Для всех t ∈R 1 , в которых реализация вектора управляющих воздействий u ( )⋅ непрерывна, имеет место равенство
t t
x ( )t = X t s x [ , ] ∗ +∫ X t [ ,τ ] ( ) ( )B τ u τ τd +∫ X t [ ,τ ] ( )C τ τd , t ∈ R 1 . (1)
s s
Доказательство. Требуется доказать следующие два равенства:
x (s ) = x ∗ ,
d
1
![]() dt x
( )t
= A t x t
( ) ( )+B t u t
( ) ( )+C t
( ), t
∈ R
.
dt x
( )t
= A t x t
( ) ( )+B t u t
( ) ( )+C t
( ), t
∈ R
.
Первое из них следует непосредственно из теоремы 3 (равенство (3.1)), а второе доказывается путем дифференцирования по аргументу t правой части равенства (1). Действительно,
d d d t d t
![]() dt x t
( )=
dt x t
( )=
![]() dt
X t s x
[ , ] ∗ +
dt
X t s x
[ , ] ∗ +
![]() dt
∫s
X t
[ ,τ
] ( ) ( )B τ u τ τd
+
dt
∫s
X t
[ ,τ
] ( ) ( )B τ u τ τd
+
![]() dt
∫s
X t
[ ,τ
] C
( )τ τd
=
dt
∫s
X t
[ ,τ
] C
( )τ τd
=
t
= A ( )t X t s x [ , ] ∗ + X t t B t u t [ , ] ( ) ( )+∫ A t X t ( ) [ ,τ ] ( ) ( )B τ u τ τd + X t t [ , ] C t ( )+
s
t
+∫ A t X t ( ) [ ,τ ] C ( )τ τd =
s
⎡
= A ( )t ⎢⎢⎢⎣X t s x [ , ] ∗ +∫st X t [ ,τ τ ] ( ) ( )B u τ τd +∫st X t [ ,τ ] C ( )τ τd ⎤⎥⎥⎦⎥ +B t u t ( ) ( )+ =W t ( )
= A t x t ( ) ( )+B t u t ( ) ( )+C t ( ), t ∈ R 1 .
Теорема доказана.
Для однородной системы дифференциальных уравнений (т.е., если B t ( ) ≡ 0, C t ( ) ≡ 0) формула Коши принимает вид
x ( )t = X t s x [ , ] ∗, t ∈ R 1 .
Тогда решение ψ(⋅) сопряженной системы дифференциальных уравнений (3.7), удовлетворяющее условию ψ(s ) =ψ∗ , можно записать в виде
ψ( )t ={X − 1 [t s , ]}T ψ∗ , t ∈R 1 . (2)
Пример 8*. Рассмотрим линейную управляемую систему
x 1 = x 2 +u 1 , x 2 = u 2 , t ∈R 1 (3)
с начальными условиями
x 1 (0)=1, x 2 (0)=1. (4)
В качестве реализации вектора управляющих воздействий выберем вектор-
функцию u R : 1 → R 2 , определенную формулой
⎛u t 1 ( )⎞ ⎛ ⎞t 1 u t ( )=⎜ ⎟=⎜ ⎟ , t ∈R .
⎝u 2 ( )t ⎠ ⎝ ⎠2t
Нетрудно видеть, что после подстановки этой функции в (1) и интегрирования полученной системы дифференциальных уравнений с начальными условиями (4) получим
x
![]() .
(5)
.
(5)
Покажем, что движение x (⋅), определенное формулой Коши (1), совпадает с выражением (5). Действительно, для данного примера имеем
C t ( ) = 0, B t ( ) = ⎛⎜⎜⎝⎜10 10⎞⎠⎟⎟⎟⎟ , X t [ ,τ ]=⎛⎝⎜⎜⎜10 t −1τ ⎞⎠⎟⎟⎟⎟ , t ,τ ∈ R 1 .
Подставляя последние выражения в формулу (1), получим
⎛ x 1 ( )t ⎞ ⎛1 t ⎞⎛1⎞ t ⎛1 t −τ⎞⎛1 0⎞⎛ τ ⎞
⎜⎜x 2 ( )t ⎟⎟⎠ = ⎜⎜⎝0 1⎟⎠⎟⎜⎝⎜1⎟⎠⎟ + ∫0 ⎝⎜⎜0 1 ⎟⎠⎟⎜⎜⎝0 1⎟⎠⎟⎜⎜⎝2τ⎟⎟⎠d τ= ⎝
⎛1+ t ⎞ t ⎛1 t −τ⎞ ⎛ τ ⎞ ⎛1+ t ⎞ t ⎛τ+ 2t τ− 2τ2 ⎞
=⎜⎜⎝ 1 ⎟⎠⎟ + ∫ 0 ⎝⎜⎜0 1 ⎟⎟⎠ ⎜⎝⎜2τ ⎟⎠⎟d τ= ⎜⎝⎜ 1 ⎠⎟⎟ + ∫ 0 ⎜⎜⎝ 2τ ⎟⎠⎟ d τ=
⎛ 1 2 3 2 3 ⎞ ⎛1 3 1 2 ⎞
![]()
![]()
![]() = ⎜
⎛1+t
⎟
⎞+
⎜⎜⎜⎝ 2t
+t
t
2 − 3t
⎟⎟⎟⎠ = ⎜⎜⎜⎝ 3t
+t
22 +t
1+ +t
1⎟⎟⎟⎠, t
∈R
1 .
= ⎜
⎛1+t
⎟
⎞+
⎜⎜⎜⎝ 2t
+t
t
2 − 3t
⎟⎟⎟⎠ = ⎜⎜⎜⎝ 3t
+t
22 +t
1+ +t
1⎟⎟⎟⎠, t
∈R
1 .
⎝ 1 ⎠
Искомое совпадение установлено.
1.6. Критерии качества управления динамическими объектами. Цель управления динамическим объектом состоит в оптимизации некоторого критерия качества, который формализуется в виде функционала, определенного на множестве реализаций вектора управляющих параметров и отвечающих им движений объекта. Обычно функционал представляет собой следующее выражение:
T
∫ f 0 (τ,x ( ) ( )τ ,u τ )d τ+ Φ(t 0 ,x 0 ,T ,x ( ))T , (1)
t 0
где f 0 : R n + r + 1 → R 1 , Φ : R 2 ( n + 1 ) → R 1 - заданные функции, непрерывные по совокупности своих аргументов. Первое слагаемое в (1) называется интегральным, а второе – терминальным.
Определение 7. Функционал (1) называется функционалом Больца. В частности, если f 0 ≡ 0, то функционал (1) называют функционалом Майера, а если Φ≡ 0 , то - функционалом Лагранжа.
Задача управления, в которой критерий качества имеет вид функционала Лагранжа с подынтегральной функцией f 0 ≡1, называется задачей на предельное быстродействие.
Пусть задан критерий (1). Уточним схему, в соответствии с которой, можно оценить качество управления динамическим объектом в случае, когда известно дифференциальное уравнение движения объекта (1.2), промежуток времени процесса управления [t T 0 , ], начальное положение объекта x 0 ∈ S 0 ( )t 0 и реализация вектора управляющих параметров
u (⋅ ∈) D t T 0 [ 0, ], u t ( )∈ P ⊂ R r , t ∈[t T 0 , ].
Сначала определяется движение x (⋅)= x (⋅, ,t 0 x u 0 , (⋅)) динамического объекта, отвечающее реализации вектора управляющих воздействий u (⋅ ∈) D t T 0 [ 0, ], u t ( )∈ P , t ∈[t T 0 , ] и выходящее из начального положения x 0 ∈ S 0 ( )t 0 . Оно находится в результате решения задачи Коши (4.1), например, с помощью формулы Коши (5.1). В конечный момент времени T это движение должно удовлетворять граничному условию x (T )∈ S T 1 ( ). В противном случае оценивать качество управления динамическим объектом не имеет смысла. Далее для пары (u () ()⋅ ,x ⋅ ) вычисляется значение функционала (1). Полученное число и является количественной оценкой качества управления динамическим объектом.
Пример 9*. Рассмотрим линейный управляемый динамический объект
| ⎛⎜⎜⎜⎜⎜⎜⎜⎜xxx 123⎟⎟⎟⎟⎟⎟⎟⎟⎠⎞=⎜⎜⎜⎜⎜⎜⎜⎜⎛⎝112 ⎝ для которого |
4 1 −4 |
1 11 ⎞⎛⎠⎝⎟⎟⎟⎟⎟⎟⎟⎟⎜⎜⎜⎜⎜⎜⎜⎜x x x 123⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟+⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜1 0 0 |
0 1 0 |
100⎞⎛⎟⎟⎟⎟⎟⎟⎟⎟⎜⎜⎜⎜⎜⎜⎜⎜uuu 123⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟, ⎠⎝ |
| ⎛1 4 1⎞ |
⎛1 0 0⎞ |
⎛ ⎞0 |
![]() ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
.
⎜⎜⎜⎝2 −4 1⎠⎟ ⎟ ⎝⎜⎜⎜0 0 1⎠⎟⎟ ⎝ ⎠⎜⎜⎜0⎟⎟
Полагаем
⎧⎪
θ
0 = ={t
0
} {0
},
θ
1 = ={T
} {1
},
,S
0 = ={x
0} ⎪⎩⎪⎪⎨⎪⎪⎪⎪⎝ ⎠⎜⎜⎜⎜⎜⎜⎛ ⎞⎜111⎟⎟⎟⎟⎟⎟⎟⎟⎪⎭⎪⎬⎪⎪⎪⎪⎪⎫⎪∈ R
3, S
1 ={x
T
∈ R
n
![]() ≤ 50},
≤ 50},
![]() T
I
⎡⎣
u
()⋅ ,x
()⋅ ⎤⎦
=∫
t
u t
( ),x t
( ) dt
+ x t
( )0 2
+ x T
( ) 2
,
T
I
⎡⎣
u
()⋅ ,x
()⋅ ⎤⎦
=∫
t
u t
( ),x t
( ) dt
+ x t
( )0 2
+ x T
( ) 2
,
0
⎛
![]() P
={u
∈ R
3 u
≤ 2}, u t
ˆ( )=⎜⎜⎜⎜⎜⎜cossint tt
⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟, t
∈[0,1].
P
={u
∈ R
3 u
≤ 2}, u t
ˆ( )=⎜⎜⎜⎜⎜⎜cossint tt
⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟, t
∈[0,1].
⎜⎝
Реализуем описанную выше схему оценки качества управления динамическим объектом для рассматриваемого случая. В примере 5 для однородной системы дифференциальных уравнений
⎛⎜⎜⎜⎜⎜xx 123⎞⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜112 −144 111⎞⎛⎠⎝⎟⎟⎟⎟⎟⎟⎟⎟⎜⎜⎜⎜⎜⎜⎜⎜xxx 123⎠⎞⎟⎟⎟⎟⎟⎟⎟⎟
⎜⎜⎝⎜x ⎠
была построена фундаментальная матрица Коши
| X t [ ,τ ]= ⎛⎜⎜ ⎜⎜⎜ ⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜ ⎜⎜⎜⎜ ⎜⎜⎜⎜⎜⎜⎝−−54 5 2 e e 7 1 55 33 (( sin sint t −− τ τ )) ((2 −+t t sin −−5 21 5 ττ cos cos()t )−((t tτ −−) τ τ ) )− − ⎜ |
52 e 3(t −τ ) − 52 cos(t −τ )+ + 14 5 sin(t −τ ) 1 5 e 3(t −τ ) + 54 cos(t −τ )+ + 52 sin(t −τ ) −4sin(t −τ ) |
− sin(t −τ ) e ( −τ ) − cos(t −τ )+ + sin(t −τ ) cos(t −τ )+sin(t −τ ) 103 53 e 101 54 33(tt −τ ) − 10533 cos(t −τ )− ⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎠⎟⎟⎟⎟⎟. ⎟ |
| Для управления u ˆ(⋅) по формуле (5.1) находим x t ˆ( ) = x t t x u ( , 0 , 0 , ˆ(⋅)) = |
||
![]() ⎛⎞
⎛⎞
⎜⎟ ⎛ ⎞1
| ⎜ ⎜ ⎝ |
2sint |
−4sint |
⎟ ⎜ ⎟1 cost +sint ⎟⎝ ⎠ ⎠ |
=![]() ⎜ 2 −2cos −sin 2 + 4cos + 2sin 3 −3cos +sin ⎟⎜ ⎟
⎜ ⎟1 +
⎜ 2 −2cos −sin 2 + 4cos + 2sin 3 −3cos +sin ⎟⎜ ⎟
⎜ ⎟1 +
⎛ 54 e 3(t −τ) + 1 5 cos(t −τ)− ⎜
⎜− 7 5 sin(t −τ)
⎜
⎜
⎜ 2 e 3(t −τ) − 2 cos(t −τ)− t ⎜ 5 5
+∫⎜− 1 5 sin(t −τ)
0 ⎜
⎜
⎜ ⎜ 2sin(t −τ)
⎜
⎜
⎜
⎝
52 e 3(t −τ) − 52 cos(t −τ)+ + 14 5 sin(t −τ)
1 5 e 3(t −τ) + 54 cos(t −τ)+
+ 5 2 sin(t −τ)
−4sin(t −τ)
3 e 3(t −τ) − 3 cos(t −τ)− ⎞
5 5
⎟
− 5 4 sin(t −τ) ⎟
⎟
⎟
103 e 3(t −τ) − 103 cos(t −τ)+⎟⎟ ⎛ sinτ⎞
+ 101 sin(t −τ) ⎟ ⎜⎜cosτ⎟⎟ d τ= .
⎟⎟ ⎜⎝ τ ⎟⎠ cos(t −τ)+sin(t −τ) ⎟ ⎟
⎟
⎟ ⎟ ⎠
⎛ 301 ⎡⎣−20+62e 3t +3(− +4 5t )cost +9 1( +5t )sint ⎦⎤⎞⎟ ⎜
![]() = ⎜ ⎡⎣−10+31e
+3 3+5t
cost
+12sint
⎦⎤ ⎟⎟, t
∈[0,1]
= ⎜ ⎡⎣−10+31e
+3 3+5t
cost
+12sint
⎦⎤ ⎟⎟, t
∈[0,1]
⎜
⎜ 1+ −t t cost −(1+ 2t )sint ⎟
⎝ ⎠
Далее полагаем
![]() ⎛ 41.4121 ⎞ x
ˆ
( )1 = ⎜
⎜
21.1906 ⎟
⎟
,
x
ˆ(1) = 46.531...< 50.
⎛ 41.4121 ⎞ x
ˆ
( )1 = ⎜
⎜
21.1906 ⎟
⎟
,
x
ˆ(1) = 46.531...< 50.
⎜ ⎝−1.06472⎟ ⎠
Последнее неравенство означает, что для движения x ˆ(⋅) выполнены граничные условия на правом конце. Величина критерия качества процесса вычисляется по формуле
1
![]() I u
⎣⎡ ˆ()⋅ , x
ˆ()⋅ ⎦⎤ =∫0 u t
ˆ( ), x t dt
ˆ( ) + x
ˆ( )0 2
+ x
ˆ( )1 2
= 49.7931.
I u
⎣⎡ ˆ()⋅ , x
ˆ()⋅ ⎦⎤ =∫0 u t
ˆ( ), x t dt
ˆ( ) + x
ˆ( )0 2
+ x
ˆ( )1 2
= 49.7931.
1.7. Программные стратегии. Различают два типа стратегий управления динамическим объектом: позиционный и программный. Первый из них предполагает, что при назначении вектора управляющих параметров используется информация о текущем времени и о значении фазового вектора объекта; второй - только информация о текущем времени. В математическом плане программные стратегии можно отождествить с функциями одного переменного (текущего времени), а позиционные стратегии с функциями n +1 переменного, где n - размерность фазового вектора. Таким образом, множество программных стратегий формально включено в множество позиционных стратегий. Вместе с тем задача программного управления представляет и самостоятельный интерес. Это объясняется тем, что в ряде случаев результат управления, достигаемый в классе позиционных стратегий, может быть получен и в классе программных стратегий. В то же время техническая реализация программного управления значительно проще позиционного. Кроме того, решение задачи программного управления может быть использовано как вспомогательное средство решения задачи позиционного управления. Сами позиционные стратегии обычно применяются в тех случаях, когда дифференциальные уравнения движения объекта с недостаточной степенью точности описывают динамику управляемого процесса.
Другой сферой применения позиционных стратегий являются конфликтноуправляемые динамические объекты, математическими моделями которых служат дифференциальные игры. Позиционные стратегии управления не являются предметом изучения данного пособия.
Пусть P ⊂ R r - область изменения вектора управляющих параметров.
Определение 8. Программной стратегией управления динамическим объектом на промежутке времени [t T 0 , ]⊂ R 1 называется функция вида
U :[t T 0 , ]→ P ⊂ R r .
Обычно оговаривается класс допустимых программных стратегий. В частности, если им является класс кусочно-непрерывных (в точках разрыва непрерывных справа) функций, то допустимые программные управления можно отождествить с допустимыми реализациями вектора управляющих параметров. В этом случае программные стратегии будем также называть программными управлениями и обозначать строчными буквами.
![]() В теоретических исследованиях программные стратегии обычно принадлежат более широким, классам функций, таким, как например, пространство L t T
r
p
[ 0, ], p
∈[1,∞]. Здесь символом L
r
p
[t T
0
, ], p
∈[1,∞) обозначено пространство измеримых вектор функций u t T
:[ 0, ]→ P
⊂ R
r
, для которых функция u
()⋅ p
суммируема на промежутке [t T
0
, ] в смысле Лебега, с нормой
В теоретических исследованиях программные стратегии обычно принадлежат более широким, классам функций, таким, как например, пространство L t T
r
p
[ 0, ], p
∈[1,∞]. Здесь символом L
r
p
[t T
0
, ], p
∈[1,∞) обозначено пространство измеримых вектор функций u t T
:[ 0, ]→ P
⊂ R
r
, для которых функция u
()⋅ p
суммируема на промежутке [t T
0
, ] в смысле Лебега, с нормой
1
⎛
![]()
![]() u
L
p
= ⎜⎜⎜⎜⎜⎝∫tT
0 u t
( ) p
dt
⎞⎠⎟⎟⎟⎟⎟⎟p
.
u
L
p
= ⎜⎜⎜⎜⎜⎝∫tT
0 u t
( ) p
dt
⎞⎠⎟⎟⎟⎟⎟⎟p
.
При p = ∞ под символом L r ∞ [t T 0 , ] понимается пространство ограниченных измеримых функций, u :[t T 0 , ]→ P ⊂ R r с нормой
![]()
![]()
![]() u
L
∞ = ess
t
∈sup[t T
0, ] U t
( ) = inf supv
()
⋅
t
∈
[
t T
0, ]
v t
( ) ,
u
L
∞ = ess
t
∈sup[t T
0, ] U t
( ) = inf supv
()
⋅
t
∈
[
t T
0, ]
v t
( ) ,
где v (⋅) пробегает множество всех измеримых функций, совпадающих с функцией u ()⋅ почти всюду на отрезке [t T 0 , ].
Класс допустимых программных стратегий должен удовлетворять следующему свойству: любую допустимую программную стратегию U ()⋅ можно сколь угодно точно приблизить (в смысле сходимости в среднем
![]() T
∫
T
∫![]() u
s
( )t
−U t dt
( ) → 0, s
→ ∞ ) реализацией вектора управляющих параметров
u
s
( )t
−U t dt
( ) → 0, s
→ ∞ ) реализацией вектора управляющих параметров
t 0
u s (t ), s =1,2, , t ∈[t T 0 , ].
В частности, пусть класс допустимых программных стратегий принадлежит пространству L t T r p [ 0, ], p ∈[1,∞]. Тогда указанное свойство следует из того, что множество непрерывных функций всюду плотно в L t T 1 r [ 0, ] [16 ].
В дальнейшем, если не оговорено противное, множество допустимых программных стратегий будем считать принадлежащим пространству суммируемых по Лебегу функций.
Определение 9. Движением динамического объекта на интервале времени [t T 0 , ], выходящим из начального положения {t x 0 , 0 }и порожденным допустимой программной стратегией U (⋅), называется функция x :[t T 0 , ]→ R n , определенная равенством
t t
x ( )t = X t t x [ , 0 ] 0 +∫ X t [ ,τ ] ( )B τ U ( )τ τd +∫ X t [ ,τ ] ( )C τ τd , t ∈[t T 0 , ]. (1)
t 0 t 0
В общем случае интегралы в формуле (1) следует понимать в смысле Лебега. Движение объекта, определенное формулой (1), обозначим символом
x (⋅) = x (⋅,t x U 0 , 0 , (⋅)).
Пусть {u s ( )⋅ } - последовательность реализаций вектора управляющих воздействий, аппроксимирующая программное управление U ( )⋅ , и x s ( )⋅ движение объекта, отвечающее реализации u s (⋅), s =1,2, . Тогда справедлива оценка
![]()
![]() tT
tT
![]()
![]() x
( )t
− x
s
( )t
∫ X t
[ ,τ]B
( )τ τ⎣
⎡U
( )−u
s
( )τ τ⎤⎦
d
≤ M
∫
x
( )t
− x
s
( )t
∫ X t
[ ,τ]B
( )τ τ⎣
⎡U
( )−u
s
( )τ τ⎤⎦
d
≤ M
∫ ![]() U
( )τ −u
s
( )τ τd
,
U
( )τ −u
s
( )τ τd
,
t 0t 0
t ∈[t T 0 , ], M = const .
Из нее следует, что последовательность функций ϕs (⋅), определенных формулой
ϕs
( )t
=![]() x t
( )− x
s
(t
)
x t
( )− x
s
(t
) ![]() , t
∈[t T
0
, ], s
=1,2,
, t
∈[t T
0
, ], s
=1,2,
равномерно сходится к нулю на отрезке времени [t T 0 , ].
Таким образом, любое движение динамического объекта можно рассматривать как равномерный предел движений объекта, порожденных соответствующими допустимыми реализациями вектора управляющих воздействий. При этом оно принадлежит классу абсолютно непрерывных на промежутке [t T 0 , ] функций и удовлетворяет на нем дифференциальному уравнению x = A t x ( ) +B t U t ( ) ( )+C t ( )
почти всюду.
1.8. Постановка и существование решения задачи теории оптимального управления. Пусть заданы дифференциальные уравнения (1.2) движения динамического объекта, критерий качества (6.1), множество начальных и конечных моментов времени θ0 ⊂ R 1 , θ1 ⊂ R 1 , infθ0 ≤ sup, θ1 , область изменения вектора управляющих параметров P ⊂ R r , ограничения на левый конец S 0 ( )t 0 ⊂ R n , t 0 ∈θ0 и правый конец S T 1 ( ), T ∈θ1 фазовой траектории динамического объекта, и допустимая программная стратегия U (⋅).
Определение 10. Набор (t T x U 0 , , 0 , ( )⋅ ,x ( )⋅ ) назовем допустимым, если t 0 ∈θ0 , T ∈θ1 , t 0 <T , x ( )⋅ = x (⋅,t x U 0 , 0 , ( )⋅ ), x 0 ∈S 0 (t 0 ), x (T )∈S 1 (T ) .
На множестве допустимых наборов посредством формулы (6.1) определим функционал I :(t T x U 0 , , 0 , ( )⋅ , x ( )⋅ ) → I t T x U [ 0 , , 0 , ( )⋅ , x ( )⋅ ] и поставим следующую задачу.
Задача 1.
Определить допустимый набор
![]() такой, что для
такой, что для
любого другого допустимого набора (t T x U 0 , , 0 , ( )⋅ ,x ( )⋅ ) выполнялось бы неравенство
I
⎡⎣
t
![]() T x U x
⎤⎦
I t T x U x
.
T x U x
⎤⎦
I t T x U x
.
Допустимый набор ![]() назовем решением задачи оптимального
назовем решением задачи оптимального
управления, U 0 ( )⋅ – оптимальной программной стратегией, x 0 ()⋅ – оптимальной траекторией. В задаче 1 требуется минимизировать функционал I . Случай максимизации функционала сводится к эквивалентной задаче минимизации функ-
ционала − I .
Сформулированная задача 1 оптимального управления динамическим объектом не всегда имеет решение. Покажем это на примере.
Пример 10. Рассмотрим управляемый динамический объект
![]() 1
⎧⎫
1
⎧⎫
x = u , x ∈R , u ∈ −[ 1,1 ,] θ0 ={ }0 , θ1 = (0,+∞) , S 0 ={ }0 , S 1 ( )T = ⎨x = 0, T ∈θ1 ⎬,
| I [T ,u (⋅)]= x (T ). 1 Очевидно, что I T U ⎡⎣ , ( )⋅ ⎤⎦ = T > 0. Для каждого T ˆ > 0 положим |
|
| ⎧0, ⎪ u ˆ ( )t = ⎨ T ⎪⎩1 |
t ∈⎡t T 0 , ˆ ⎤ , ⎣ ⎦ t >T ˆ . |
![]() ⎩⎭
⎩⎭
![]() Траектория движения, отвечающая программному управле-
Траектория движения, отвечающая программному управле-
нию u T ˆ (⋅), изображена на рис. 7 .
Момент времени T окончания процесса в данном случае удов-
летворяет неравенству T >T ˆ , и
![]() Рис. 7
1 1 поэтому
< . Выбирая вели-
Рис. 7
1 1 поэтому
< . Выбирая вели-
T T ˆ
чину
T
ˆ
достаточно большой, значение функционала
I T u
⎡⎣
ˆ
, T
ˆ ( )⋅ ⎦
⎤ = ![]() T
1
ˆ
можно сделать сколь угодно малым. Однако программной стратегии
U
( )⋅ , для которой
I T U
⎡⎣
, ( )⋅ ⎤⎦
= 0, не существует в классе
L t T
r
p
[ 0, ], p
∈[1,∞]. Отсюда заключаем, что рассматриваемая задача оптимального управления решения не имеет.
Для задачи теории оптимального управления
T
1
ˆ
можно сделать сколь угодно малым. Однако программной стратегии
U
( )⋅ , для которой
I T U
⎡⎣
, ( )⋅ ⎤⎦
= 0, не существует в классе
L t T
r
p
[ 0, ], p
∈[1,∞]. Отсюда заключаем, что рассматриваемая задача оптимального управления решения не имеет.
Для задачи теории оптимального управления
x = A t x ( ) + B t u ( ) +C t ( ),
t
![]() t T t t t T T T t T
,
t T t t t T T T t T
,
x ∈R n , u ∈P ⊂ R r , x 0 ∈S 0 (t 0 ) , t 0 ∈θ0 , x T ( )∈S T 1 ( ) , T ∈θ1 ,
I [t 0 ,T , x 0 ,u (⋅), x (⋅)]= Φ(t 0 ,T , x 0 , x (T ))
выведем достаточные условия существования ее решения в классе интегрируемых по Лебегу программных стратегий.
Теорема 5 (существование решения задачи теории оптимального управления).
Пусть выполнены следующие предположения:
1) множество P ⊂ R r компактно и выпукло;
2)
множество
Ξ = {e
= (t
0
,T
, x
0
,x
T
)![]() x
0
∈ S
0
(t
0
), x
T
∈ S
1
(T
), t
0
∈θ0
, T
∈θ1
}⊂ R
2
(
n
+
1
)
компактно;
x
0
∈ S
0
(t
0
), x
T
∈ S
1
(T
), t
0
∈θ0
, T
∈θ1
}⊂ R
2
(
n
+
1
)
компактно;
3) множество допустимых наборов G ={(t T x U 0 , , 0 , ( )⋅ , x ( )⋅ )} содержит хотя бы один элемент;
4) множество допустимых программных стратегий принадлежит пространству функций, интегрируемых по Лебегу на интервале управления.
Тогда существует
допустимый набор
![]() t T x U x G
, на котором
t T x U x G
, на котором
функционал I достигает минимума.
Доказательству теоремы предпошлем лемму.
Лемма 2. Пусть R :[t 0 ,t ]→ K ⊂ R n – интегрируемая по Лебегу функция и множество K - выпуклый компакт. Тогда
1 t
![]() ∫
R
( )τ d
τ∈K
.
(1)
∫
R
( )τ d
τ∈K
.
(1)
t − t 0 t 0
Доказательство. Известно [16], что для всякой интегрируемой по Лебегу функции R , определенной на интервале [t 0 ,t ], найдется последовательность ступенчатых функций { }R s , определенных и равномерно сходящихся на этом интервале к функции R , причем справедливо равенство
t t
![]() ( ) R
( )τ d
τ.
(2)
( ) R
( )τ d
τ.
(2)
t 0 t 0
Покажем, что включение (1) справедливо для всякой ступенчатой функции
R :[t 0 ,T ]→ K . Напомним, что функция называется ступенчатой, если она принимает конечное число значений R ( 1 ) , ,R ( k ) ∈K . Обозначим
T
j
= {τ∈[t
0
,t
]![]() R
(τ) = R
(
j
)
}, j
=1, ,k
.
R
(τ) = R
(
j
)
}, j
=1, ,k
.
Тогда
![]() 1 t
1 t
![]() ∫
R
( )τ d
τ= .
(3)
∫
R
( )τ d
τ= .
(3)
t − t 0 t 0 t − t 0 j =1
Здесь µ (T j ) – мера множества T j , j =1, ,k . Заметим, что
![]()
![]() .
t
.
t
Выражение (3) представляет собой выпуклую комбинацию векторов R ( j ) ∈K , j =1, ,k . Отсюда следует справедливость включения (1) для случая, когда функция R ступенчатая. Доказательство общего случая использует предельный переход в (2) и условие компактности множества K .
Доказательство теоремы. B силу компактности множества Ξ функционал I ограничен на множестве допустимых наборов G . Из условия G ≠∅ следует существование для функционала I минимизирующей последовательности {(t 0 s ,T s ,x U 0 s , s ( )⋅ ,x s ( )⋅ )}, (t 0 s ,T s ,x U 0 s , s ( )⋅ ,x s (⋅))∈G , s =1,2, , т.е. такой последовательности, что
![]() lims
→∞ I t T
⎡
⎣ 0s
, s
,x U
0
s
, s
( )⋅ ,x
s
( )⋅ ⎦
⎤
=
(
t T x U
0, , 0inf
, ( )⋅ ,x
( )
⋅ ∈)
G
I t T x U
⎣
⎡ 0
, , 0
, ( )⋅ ,x
(⋅)
⎦
⎤ = I
∗
, I
∗
< ∞ .
lims
→∞ I t T
⎡
⎣ 0s
, s
,x U
0
s
, s
( )⋅ ,x
s
( )⋅ ⎦
⎤
=
(
t T x U
0, , 0inf
, ( )⋅ ,x
( )
⋅ ∈)
G
I t T x U
⎣
⎡ 0
, , 0
, ( )⋅ ,x
(⋅)
⎦
⎤ = I
∗
, I
∗
< ∞ .
В силу 2) из последовательности {(t T 0 s , s , x x 0 s , s (T s ))}, s =1,2, можно извлечь сходящуюся. Не теряя общности, считаем, что
{(t T 0 s , s , x x 0 s , s (T s ))} → (t T 0 0 , 0 , x 0 0 ,x T 0 )∈Ξ .
Рассмотрим последовательность движений
{x ( ) s ( )⋅ }, x ( ) s ( )⋅ = x (⋅,t 0 s , x U 0 s , s ( )⋅ ), s =1,2,
Для всех номеров s =1,2, справедливо равенство
t t
x ( ) s ( )t = X t t ⎡ ⎢⎣ , 0 s ⎦⎤ ⎥ x 0 s +∫t X t [ ,τ ] ( )B τ U s ( )τ τd +∫t X t [ ,τ ] ( )C τ τd , t ∈⎡ ⎣ t 0 s ,T s ⎦ ⎤ . (4)
0 0
Полагаем
⎧⎪ x 0s , t ∈⎡⎣t 0∗,t 0s ) , x ( ) s ∗ ( )t = ⎨ ⎪ x ( ) s ( )t , t ∈⎡⎣ t 0 s ,T s ⎤⎦ , (5)
⎪ ( )s s s ∗
⎪⎩ x (T ), t ∈(T ,T ⎤⎦ .
Из компактности множеств Ξ, P и формул (4) (5) следует, что функции, образующие последовательность {x ( ) s ∗ ( )⋅ }, равномерно ограничены и равностепенно непрерывны на отрезке ⎡⎣ t 0 ∗ ,T ∗ ⎤⎦ . По теореме Арцела (при необходимости следует перейти к подпоследовательности) эта последовательность равномерно сходится на отрезке ⎡⎣ t 0 ∗ ,T ∗ ⎤⎦ к некоторой абсолютно непрерывной функции x 0 ∗ ( )⋅ . Очевидно, что
x
![]() .
.
Обозначим через x 0 ( )⋅ сужение функции x 0 ∗ (⋅) на отрезке ⎣ ⎡t 0 0 ,T 0 ⎦ ⎤ и докажем существование допустимой программной стратегии U 0 ( )⋅ , для которой почти всюду на отрезке ⎡⎣ t 0 0 ,T 0 ⎤⎦ выполняется равенство
x 0 ( )t = A t x ( ) 0 (t )+ B t U ( ) 0 (t )+C t ( ). (6)
Пусть t ∈(t T 0 , 0 ) – точка, где функция x 0 (⋅) имеет производную. Для достаточно больших номеров s =1,2, и малых положительных чисел h будет
выполнено вложение [t t , + h ]⊂ ⎡⎣ t 0 s ,T s ⎤⎦ . Из равенства
t t t
x
( )![]()
t 0∗ t 0∗ t 0∗
следует
![]() x
(s
) (t
+ hh
)− x
(s
) (t
) = 1h
t h
+t
⎡A
( )τ x
( )s
( )τ + B
( )τ U
s
( )τ +C
( )τ ⎤⎦d
τ. (7) ∫ ⎣
x
(s
) (t
+ hh
)− x
(s
) (t
) = 1h
t h
+t
⎡A
( )τ x
( )s
( )τ + B
( )τ U
s
( )τ +C
( )τ ⎤⎦d
τ. (7) ∫ ⎣
В силу равномерной сходимости последовательности функций {x ( ) s ( )⋅ } к функции x 0 ( )⋅ , для любого ε> 0 и достаточно малого h > 0 , начиная с некоторого номера s , будет выполняться включение
A ( )τ x ( s ) ( )τ + B ( )τ U s (τ)+C (τ)∈K x ( 0 (t ),ε),τ∈[t t , + h ],
где
![]()
K x ( 0 ( )t ,ε) = A t x ( ) 0 (t )+ B t P ( ) +C t ( )+O (0,ε).
Множество K x ( 0 (t ),ε) является выпуклым компактом. Тогда по лемме 2 следует, что
1 t h + s s 0
![]() h
t
⎣
A
( )τ x
( )τ τ τ τ τ+ B
( )U
( )+C
( )⎤⎦
d
∈K x
( ( )t
,ε). ∫
⎡
h
t
⎣
A
( )τ x
( )τ τ τ τ τ+ B
( )U
( )+C
( )⎤⎦
d
∈K x
( ( )t
,ε). ∫
⎡
Отсюда и из равенства (7) выводим
x
(s
) (t
+ h
)− x
(s
) (t
) 0 ![]()
![]() ∈ A t x
( ) ( )t
+ B t P
( ) +C t
( )+O
(0,ε). h
∈ A t x
( ) ( )t
+ B t P
( ) +C t
( )+O
(0,ε). h
Переходя в нем к пределу при s → ∞, получим
x
0
(t
+ h
)− x
0
(t
) 0
![]()
![]() ∈ A t x
( ) ( )t
+ B t P
( ) +C t
( )+O
(0,ε). (8)
∈ A t x
( ) ( )t
+ B t P
( ) +C t
( )+O
(0,ε). (8)
h
Из существования производной функции x 0 (⋅) в точке t вытекает возможность предельного перехода в левой части равенства (8) при h → 0. В результате такого перехода получим
![]()
x 0 ( )t ∈ A t x ( ) 0 (t )+ B t P ( ) +C t ( )+O (0,ε).
Отсюда в силу произвольности ε> 0 выводим
x 0 ( )t ∈ A t x ( ) 0 (t )+ B t P ( ) +C t ( ).
Итак, установлено, что для каждого момента времени t ∈⎡⎣ t 0 0 ,T 0 ⎤⎦ , в который существует производная функции x 0 (⋅), найдется вектор u 0 ( )t ∈P , удовлетворяющий равенству (6). По лемме об измеримом выборе [31] функция u 0 (⋅) может быть выбрана интегрируемой по Лебегу. Допустимую программную стратегию U 0 ( )⋅ отождествим с функцией u 0 (⋅).
Очевидно, что набор
![]() является допустимым, и при этом
является допустимым, и при этом
I ∗ = lims →∞ I t T ⎡⎣ 0s , s , x U 0 s , s ( )⋅ , x s ( )⋅ ⎦ ⎤ = lims →∞ Φ( t T 0 s , s ,x x 0 s , s (T s ))) = Φ( t T 0 0 , 0 ,x 0 0 , x 0 (T 0 )) =
![]() .
.
Теорема доказана.
1.9. Область достижимости линейного управляемого динамического объекта. Важной характеристикой управляемого объекта является его область достижимости. Пусть t 0 ∈θ0 , x 0 ∈S 0 (t 0 ),T ∈θ1 . Символом Π[t T 0 , ] обозначим множество всех допустимых программных стратегий вида U :[t T 0 , ]→ P .
Определение 11. Множество
G t
( 0
,x T
0
, ) ={q
= x T t
( , 0
,x U
0
, ( )⋅)![]() U
( )⋅ ∈Π[t T
0
, ]} ⊂ R
n
U
( )⋅ ∈Π[t T
0
, ]} ⊂ R
n
называется областью достижимости управляемого динамического объекта в момент времени T для начального положения {t 0 , x 0 }.
Теорема 6. Пусть множество P ⊂ R r выпукло и компактно. Тогда область достижимости является выпуклым компактным множеством в пространст-
ве R n .
Доказательство. Из определения области достижимости для всякого q ∈G t x T ( 0 , 0 , ) следует существование программной стратегии U ( )⋅ ∈Π[t T 0 , ] такой, что
T T
q = X T t [ , 0 ]x 0 + ∫ X T [ ,τ]B ( )τ τ τU ( )d + ∫ X T [ ,τ τ τ]C ( )d , (1)
t 0 t 0
где X [s ,t ], s ,t ∈[t 0 ,T ]– фундаментальная матрица Коши, отвечающая однородному дифференциальному уравнению x = A (t )x , t ∈[t 0 ,T ]. Оценим по норме вектор q . Имеем
T T
![]()
![]()
![]()
![]() q
≤ X T t
[ , 0
] x
0
+ ∫ X T
[ ,τ] B
( )τ τ τU
( ) d
+ ∫
q
≤ X T t
[ , 0
] x
0
+ ∫ X T
[ ,τ] B
( )τ τ τU
( ) d
+ ∫![]() X T
[ ,τ τ τ] C
( ) d
.
X T
[ ,τ τ τ] C
( ) d
.
t 0 t 0
В силу ограниченности множества P ⊂ R n из последнего неравенства вытекает ограниченность области достижимости. Пусть q ~ – предельная точка области достижимости и {q ( ) s } → q q , ( ) s ∈G t ( 0 ,x T 0 , ). Из равенства (1) следует, что для всех s =1,2, будет справедливо
T T
q ( ) s = X T t [ , 0 ]x 0 + ∫ X T [ ,τ]B ( )τ U ( ) s ( )τ τd + ∫ X T [ ,τ τ τ]C ( )d , (2)
t 0 t 0
где U ( s ) ( )⋅ ∈Π[t T 0 , ]. В силу слабой компактности множества Π[t T 0 , ] [16 ] из последовательности функций {U ( ) s ( )⋅ } можно извлечь подпоследовательность, слабо сходящуюся к функции U (⋅ ∈Π) [t T 0 , ]. Переходя к пределу по подходящей подпоследовательности индексов в (2), получаем равенство
T T
q ∗ = X T t [ , 0 ]x 0 + ∫ X T [ ,τ]B ( )τ τ τU ( )d + ∫ X [T ,τ]C ( )τ τd . (3)
t 0 t 0
Равенство (3) означает, что q ∗ ∈G t x T ( 0 , 0 , ). Отсюда следует замкнутость области достижимости. Докажем ее выпуклость. Пусть q ( ) 1 ,q ( ) 2 ∈ ∈G t x T ( 0 , 0 , ). Это означает, что существуют функции U ( 1 ) (⋅),U ( 2 ) (⋅ ∈Π) [t T 0 , ], для которых справедливы равенства
T T
q ( ) i = X T t [ , 0 ]x 0 + ∫ X T [ ,τ]B ( )τ τ τU ( ) i ( )d +∫ X T [ ,τ τ τ]C ( )d , i =1,2. (4)
t 0 t 0
Для любого α∈[0,1] положим q α =αq ( 1 ) + (1−α)q ( 2 ) . В силу (1) имеем
T T
α 0 0 ∫ X [T ,τ] B ( )τ α τ⎣ ⎡ U ( ) 1 ( ) (+ 1−α)U ( ) 2 ( )τ τ⎤⎦ d + ∫ X T [ ,τ τ τ]C ( )d . (5)
q = X T t [ , ]x +
t 0 t 0
Из выпуклости множества P следует, что α τU ( 1 ) ( )+(1−α)U ( 2 ) ( )τ ∈P для всех
τ∈[t T 0 , ] . Это означает справедливость включения
αU ( 1 ) ( ) (⋅ + 1−α)U ( 2 ) (⋅ ∈Π) [t T 0 , ]. Тогда в силу (5) заключаем, что q α ∈G t x T ( 0 , 0 , ). Таким образом, область достижимости выпукла. Теорема доказана.
Упражнения для самостоятельной работы
Даны дифференциальные уравнения движения управляемых линейных динамических объектов
x 1 = −3x 1 + 4x 2 − 6x 3 + u 1 , x 1 = −2x 1 − 4x 2 − 60x 3 + u 1 ,
а) x 2 = x 1 − 2x 2 + 2x 3 + u 2 , б) x 2 = −4x 1 − x 2 −51x 3 + u 2 , x 3 = 2x 1 − x 2 + 3x 3 + u 3 , x 3 = 2x 1 − 2x 2 + x 3 + u 3 ,
x 1 = 2x 1 + 4x 2 −16x 3 + u 1 , x 1 = −3x 1 − x 2 −5x 3 +u 1 ,
в) x 2 = 2x 1 − x 2 + 21x 3 + u 2 , г) x 2 = x 1 − x 2 +u 2 , x 3 = −2x 1 − 2x 2 + x 3 + u 3 , x 3 = x 1 + x 2 + 2x 3 +u 3 .
1. Записать дифференциальные уравнения движения в матричной форме.
2. Для однородных систем линейных дифференциальных уравнений, соответствующих заданным неоднородным системам, построить фундаментальную матрицу Коши двумя способами: с использованием операции обращения матрицы и без использования. Убедиться в том, что оба метода строят одну и ту же матрицу. Проверить выполнение свойств (3.1)-(3.4) фундаментальной матрицы Коши.
3. Проверить справедливость формулы Коши (5.1) при следующих дополнительных данных:
⎛ ⎞1 ⎛−1⎞
⎜ ⎟ ⎜ ⎟
x =
а) 0 ⎜ ⎟⎜ ⎟⎝ ⎠11 , t 0 = 0,T =1, б) x 0 = ⎜⎝⎜−11⎟⎠⎟, t 0 = 0,T =1,
u 1 ( )t = sin ,t u 2 ( )t = cos ,t u 3 ( )t = e t , u 1 ( )t = t u , 2 ( )t = e − t , u 3 ( )t = cos ,t
⎛ 1 ⎞ ⎛−1⎞
⎜ ⎟ ⎜ ⎟
в) x 0 = −⎜⎜⎝ 11⎟⎠, t 0 = 0,T =1, г) x 0 = −⎜⎜⎝ 11⎠⎟⎟, t 0 = 0,T =1,
⎟
u 1 ( )t = sin ,t u 2 ( )t = t 2 , u 3 ( )t = e t , u 1 ( )t = e u t , 2 ( )t = sin ,t u 3 ( )t = −cos .t
4. Вычислить критерии оптимальности для движений, отвечающих указанным в пункте 3 задания управлениям и выходящих из приведенных там же начальных положений
I u ⎡⎣ ( )⋅ ⎤⎦ = I u ⎡⎣ (⋅)⎤⎦ =
а) ![]() б)
б) ![]()
I u ⎡⎣ ( )⋅ ⎤⎦ = I u ⎡⎣ (⋅)⎤⎦ =
в) ![]() г)
г) ![]()
2. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ ЛИНЕЙНЫМИ
ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ С ФИКСИРОВАННЫМ
ВРЕМЕНЕМ И ТЕРМИНАЛЬНЫМ КРИТЕРИЕМ КАЧЕСТВА
2.1. Случай закрепленного левого конца и свободного правого конца траектории. Рассматривается следующая задача теории оптимального управления.
Задача 1. Найти допустимую программную стратегию U 0 ( )⋅ ∈Π[t T 0 , ], доставляющую минимум функционалу
I ⎡⎣ U (⋅)⎤⎦ = Φ(x T ( )), Φ∈C 1 (R 1 )
при ограничениях
x = A t x ( ) + B t u ( ) +C t ( ), x ∈R n , u ∈P ⊂ R r , θ0 ={t 0 },θ1 ={T }, S 0 ={x 0 }, S 1 = R n ,
где множество P ⊂ R n является выпуклым компактом.
По теореме 1.6 область достижимости G t ( 0 ,x T 0 , ) является компактом в пространстве R n . Тогда в силу непрерывности функции Φ решение задачи 1 существует.
Пусть U 0 ( )⋅ - оптимальная программная стратегия. Обозначим через x 0 ( )⋅ = x (⋅,t 0 ,x U 0 , 0 ( )⋅ ) оптимальное движение объекта, а через ψ0 ( )⋅ - решение сопряженной системы дифференциальных уравнений (1.3.7), удовлетворяющее условию
![]() .
.
Теорема 1 ( принцип максимума Л.С. Понтрягина). Оптимальная программная стратегия U 0 ( )⋅ удовлетворяет следующему условию максимума:
![]() B
( )t U
0
(t
),ψ0
(t
)
B
( )t U
0
(t
),ψ0
(t
) ![]() = max
= max ![]() B t u
( ) ,ψ0
(t
)
B t u
( ) ,ψ0
(t
)![]() (1)
(1)
u P ∈
для почти всех t ∈[t T 0 , ].
Доказательство. Из выпуклости области достижимости G t ( 0 ,x T 0 , ) в силу [7 ] следует, что для всех q ∈G t ( 0 ,x T 0 , ) имеет место неравенство
![]() ∂Φ 0 00 00 00
∂Φ 0 00 00 00
![]()
![]()
![]()
![]() 0 ≤(x
( )T
),q
− x
( )T
= − ψ ( )T
,q
− x
( )T
= ψ ( )T
,x
( )T
− ψ ( )T
,q
. (2)
0 ≤(x
( )T
),q
− x
( )T
= − ψ ( )T
,q
− x
( )T
= ψ ( )T
,x
( )T
− ψ ( )T
,q
. (2)
∂x
Тогда для всех u ( )⋅ ∈Π[t T 0 , ] должно выполняться
![]()
![]() T T
T T
ψ0 ( )T , X T t [ , 0 ]x 0 + ∫ X T [ ,τ τ τ τ]B ( )U 0 ( )d + ∫ X T [ ,τ τ τ]C ( )d −
t 0 t 0
T T
− ψ0 ( )T , X T t [ , 0 ]x 0 + ∫ X T [ ,τ τ τ τ]B ( ) ( )u d + ∫ X T [ ,τ τ τ]C ( )d =
t 0 t 0
TT
![]() = ψ ( )T
,∫ X T
[ ,τ τ τ τ ψ]B
( )U
0
( )d
− 0
( )T
,∫ X T
[ ,τ τ τ τ]B
( ) ( )u d
≥ 0.
= ψ ( )T
,∫ X T
[ ,τ τ τ τ ψ]B
( )U
0
( )d
− 0
( )T
,∫ X T
[ ,τ τ τ τ]B
( ) ( )u d
≥ 0.
t 0t 0
Последнее возможно, только если
![]()
![]()
![]()
![]() TT
TT
ψ0 ( )T ,∫ X T [ ,τ τ τ τ]B ( )U 0 ( )d = u ( ) ⋅ ∈Πmax[ t T 0, ] ψ0 ( )T ,∫ X T [ ,τ τ τ τ]B ( ) ( )u d . (3)
t 0t 0
Последовательно преобразуем левую и правую части равенства (3). Имеем
T
![]()
![]() ψ0
( )T
, X T
[ ,τ τ τ τ]B
( )U
0
( ) d
= u
⋅ ∈Πmaxt T
0, ∫ ψ0
( )T
, X T
[ ,τ τ τ τ]B
( ) ( )u d
⇒
ψ0
( )T
, X T
[ ,τ τ τ τ]B
( )U
0
( ) d
= u
⋅ ∈Πmaxt T
0, ∫ ψ0
( )T
, X T
[ ,τ τ τ τ]B
( ) ( )u d
⇒
( ) [ ]
t 0
T
ψ0 ( )T , X − 1 [τ,T B ] ( )τ τ τU 0 ( ) d = u ⋅ ∈Πmaxt T 0, ∫ ψ0 ( )T , X − 1 [τ,T B ] ( ) ( )τ τ τud ⇒
( ) [ ]
t 0
T
![]()
![]()
![]() ∫ X
[τ,T
]}Tр
ψ0
( )T
, B
( )τ τ τU
0
( ) d
= u
( )
⋅ ∈Πmax[
t T
0, ]
{X
−
1
[τ ψ,T
]}Tр
0
( )T
, B
( ) ( )τ τ τud
.
∫ X
[τ,T
]}Tр
ψ0
( )T
, B
( )τ τ τU
0
( ) d
= u
( )
⋅ ∈Πmax[
t T
0, ]
{X
−
1
[τ ψ,T
]}Tр
0
( )T
, B
( ) ( )τ τ τud
.
t 0 0
Отсюда в силу (1.5.2) выводим
T T
![]()
![]()
![]()
![]() ∫ψ0
( )τ τ τ τ, B
( )U
0
( )d
= u
( )
⋅ ∈Πmax[
t T
0, ]
∫ψ τ τ τ τ0
( ), B
( ) ( )ud
∫ψ0
( )τ τ τ τ, B
( )U
0
( )d
= u
( )
⋅ ∈Πmax[
t T
0, ]
∫ψ τ τ τ τ0
( ), B
( ) ( )ud
t 0 t 0
В книге [18 ] показано, что
![]()
![]()
![]()
![]() T T
max ∫ψ0
( )τ τ τ τ,B
( ) ( )ud
= ∫maxψ τ τ τ0
( ), B
( )u d
.
T T
max ∫ψ0
( )τ τ τ τ,B
( ) ( )ud
= ∫maxψ τ τ τ0
( ), B
( )u d
.
u ( ) ⋅ ∈Π[ t T 0, ] u P ∈ t 0 t 0
Тогда
T
![]()
![]()
![]() ∫
⎡⎣
ψ τ τ τ0
( ), B
( )U
0
( )
∫
⎡⎣
ψ τ τ τ0
( ), B
( )U
0
( )![]() −maxu P
∈ ψ τ τ τ0
( ), B
( )u
⎤⎦
d
= 0,
−maxu P
∈ ψ τ τ τ0
( ), B
( )u
⎤⎦
d
= 0,
t 0
![]()
![]() что и означает выполнение условия (1). Теорема доказана.
что и означает выполнение условия (1). Теорема доказана.
Функция
H t x u ( , , ,ψ) =A t x ( ) + B t u ( ) +C t ( ),ψ
представляет собой функцию Л.С. Понтрягина [25] для рассматриваемого управляемого динамического объекта. Таким образом, доказанная теорема утверждает, что на оптимальном управлении функция Л.С. Понтрягина достигает максимального значения.
Заметим, что для выпуклых функций Φ неравенство (2) является доста-
точным условием минимума функции Φ на множестве G t ( 0 ,x T 0 , ). Тогда усло-
![]() вие (1) будет не только необходимым, но и достаточным для оптимальности программной стратегии
вие (1) будет не только необходимым, но и достаточным для оптимальности программной стратегии
U 0 (⋅).
![]() Пример 1.
Рассмотрим линейный управляемый динамический объект
Пример 1.
Рассмотрим линейный управляемый динамический объект
x 1 ⎛u 1 ⎞ ⎧⎪⎛u 1 ⎞ x 1 = u 1 , x 2 = u 2 , u = ⎜ ⎟∈P = ⎨⎜ ⎟
⎝u 2 ⎠ ⎩⎪⎝u 2 ⎠
⎛ x 10 ⎞ ⎛ ⎞0
⎜ ⎟ = ⎜ ⎟, t 0 = 0,T =1, Φ( )x =
⎝ x 20 ⎠ ⎝ ⎠0
Рис. 1
Оптимальное управление объектом, как вид-
но из рис. 1 , здесь состоит в том, чтобы перевести управляемую точку из на-
⎛ x 10 (1)⎞ ⎛ ⎞1
![]() чала координат в положение
M
∗
÷⎜⎜
⎝ x
20 ( )1
⎠
⎟⎟
= ⎜ ⎟⎝ ⎠
0
. Это можно осуществить только программной стратегией вида
чала координат в положение
M
∗
÷⎜⎜
⎝ x
20 ( )1
⎠
⎟⎟
= ⎜ ⎟⎝ ⎠
0
. Это можно осуществить только программной стратегией вида
U t u d t . (4)
⎝ 1 ⎠ 0
Проверим выполнение условий теоремы 1 для таких стратегий. Сопряженная система дифференциальных уравнений и граничные условия для нее здесь имеют вид
ψ1 = 0,ψ2 = 0,
x 10 (1)
ψ1 ( )1 = −= 0,
(x 1 0 ( )1 )2 +(x 2 0 ( )1 −2)2
![]() x
2
0
( )1 −2 ψ2
( )1 = −=1.
x
2
0
( )1 −2 ψ2
( )1 = −=1.
(x 1 0 ( )1 )2 +(x 2 0 ( )1 −2)2
Интегрируя, находим, что
![]() .
.
Выпишем функцию Л.С. Понтрягина, вычисленную вдоль оптимальной пары
(x 0 ( )⋅ ,ψ0 ( )⋅ ). Имеем
H t x
![]() t u t t u t u u t
.
t u t t u t u u t
.
Отсюда следует, что
![]()
![]() maxu P
∈ H t x
( , 0
( )t
, ,u
ψ0
(t
)) = u
1max≤1,u
2 ≤1(ψ1
0
(t u
) 1
+ψ1
0
(t u
) 2
) = maxu
2 ≤1 u
2
=1, t
∈[0,1]. (5)
maxu P
∈ H t x
( , 0
( )t
, ,u
ψ0
(t
)) = u
1max≤1,u
2 ≤1(ψ1
0
(t u
) 1
+ψ1
0
(t u
) 2
) = maxu
2 ≤1 u
2
=1, t
∈[0,1]. (5)
Очевидно, что программное управление (4) доставляет максимум в (5) и, следовательно, удовлетворяет условию (1).
Практическое применение теоремы 1 для поиска решения задачи управления осуществляется следующим образом.
Для каждого фиксированной пары (t ,ψ)∈[t T 0 , ]×R n решается задача математического программирования
![]() B
Tр
(t
)ψ, u
B
Tр
(t
)ψ, u
![]() → max, u
∈P
. (6)
→ max, u
∈P
. (6)
Распишем подробнее левую часть условия (6). Имеем
| ⎛b 11 ( )t B Tр ( )t ψ= ⎜⎜ ⎜b 1r ( )t ⎝ |
⎛ n ⎞ b t ψ b n 1 ( )t ⎞⎛⎜ ψ1 ⎞⎟ ⎜⎜ ∑ k =1 k 1 ( ) k ⎟⎟ ⎟ ⎟⎜ ⎟ = ⎜ ⎟ . b nr ( )t ⎟⎠⎜⎝ψn ⎟⎠ ⎜⎜∑n b kr ( )t ψk ⎟⎟⎟ ⎜ ⎝ k =1 ⎠ |
Тогда задача математического программирования принимает вид
n n ⎛u 1 ⎞ ⎛ ⎞ ⎛ ⎞ ⎜ ⎟
u 1 ⎜∑b k 1 ( )t ψk ⎟ + +u r ⎜∑b kr ( )t ψk ⎟ → max, ⎜ ⎟ ∈P . (7)
⎝ k =1 ⎠ ⎝ k =1 ⎠ ⎜ ⎝u r ⎟ ⎠
По теореме Вейерштрасса максимум в условии (7) существует для любой пары (t ,ψ)∈[t T 0 , ]×R n . Следовательно, можно определить вектор-функцию
U ˆ :[t T 0 , ]×R n → P , (8)
которая каждой паре (t ,ψ)∈[t T 0 , ]×R n ставит в соответствие вектор U t ˆ ( ,ψ)∈P , доставляющий максимум в условии (7).
Пусть функция U ˆ уже построена. Рассмотрим систему из 2n обыкновенных дифференциальных уравнений
⎧⎪⎨x = A t x ( ) + B t U t ( ) ˆTр ( ,ψ)+C t ( ), (10)
⎪⎩ ψ= −A ψ.
относительно 2n неизвестных x ,ψ с 2n граничными условиями
![]() x
( ) ( )
x
( ) ( ) ![]() . (11) x
. (11) x
Заметим, что в общем случае эта система нелинейная. Более того, функция U ˆ может оказаться разрывной по переменной ψ, и тогда для системы дифференциальных уравнений (10) не будут выполняться условия существования решения. В случае, когда все же для задачи (10), (11) получено решение x 0 (⋅),ψ0 (⋅), программная стратегия U 0 ( )⋅ =U ˆ (⋅,ψ0 (⋅)) будет удовлетворять условиям теоремы 1 , т.е. являться стратегией подозрительной на оптимальную стратегию.
2.2. Поведение функции Л.С. Понтрягина вдоль оптимальной пары
В предыдущем пункте (теорема 1 ) было доказано, что функция Понтрягина на оптимальном управлении принимает максимальное значение. Установим ниже некоторые общие свойства функции максимума (минимума).
Пусть F : X ×Y → R 1 , X ⊂ R n ,Y ⊂ R m – некоторая функция, непрерывная по совокупности своих переменных в каждой точке области определения. При этом множество Y компактное, а множество X – открытое. Положим
F 0 (x )= max F (x , y ), x ∈ X , (1)
y ∈Y
![]() Y
0
( )x
=
{y
0
(x
)F
(x
, y
0
(x
))= F
0
(x
)
}, x
∈ X
.
Y
0
( )x
=
{y
0
(x
)F
(x
, y
0
(x
))= F
0
(x
)
}, x
∈ X
.
Лемма 1. Функция F 0 : X → R 1 , определенная равенством (1), является непрерывной в каждой точке x ∈X .
Доказательство. Пусть x ∈ X . Для всякого ∆x ∈R n , x + ∆x ∈ X положим
∆F 0 (x ) = F 0 (x + ∆x )− F 0 (x )= F (x + ∆x , y 0 (x + ∆x ))− F (x , y 0 ( )x ).
Справедливо двойное неравенство
F (x + ∆x , y 0 (x ))− F (x , y 0 ( )x )≤ ∆F 0 (x ) ≤ F (x + ∆x , y 0 (x + ∆x ))− F (x , y 0 (x + ∆x )), (2) из которого следует, что ∆F 0 (x ) → 0 при ∆x → 0. Лемма доказана.
Определение 1. Будем говорить, что многозначное отображение χ: X → 2Y , где через 2Y обозначено множество всех подмножеств множества Y , называется полунепрерывным сверху по включению в точке x ∗ ∈ X , если для всякой последовательности {x ( ) s } → x ∗ и {y ( ) s } → y ∗ , y ( ) s ∈χ(x ( ) s ), s =1,2, имеет место включение y ∗ ∈χ(x ∗ ).
Заметим, что если отображение χ однозначно, т.е. множество χ(x ) состоит ровно из одного элемента при всех x ∈ X , то из полунепрерывности сверху по включению этого отображения следует его непрерывность в обычном смысле.
Лемма 2. Многозначное отображение Y 0 : X → 2Y полунепрерывно сверху по включению в каждой точке x ∈X .
Доказательство. От противного приходим к существованию точки x ∗ ∈ X и таких последовательностей
{ }x
s
→ x
∗
, x
s
![]() Y
, y
s
0
∈Y
0
(x
s
), s
=1,2 ,
Y
, y
s
0
∈Y
0
(x
s
), s
=1,2 ,
что y ∗ ∉Y 0 ( )x ∗ . Тогда найдется число ε> 0, для которого
F 0 (x ∗ )− F (x ∗ , y ∗ )=ε. (3)
Из непрерывности функций F ,F 0 и сходимости последовательностей {x s },{y s } к точкам x ∗ , y ∗ , соответственно, для достаточно больших номеров s будут справедливы неравенства
![]()
![]()
![]() F
0
( )x
∗
− F
0
( )x
s
F
(x
∗
, y
∗
)− F
(x
s
, y
s
0
) <
ε
.
(4)
F
0
( )x
∗
− F
0
( )x
s
F
(x
∗
, y
∗
)− F
(x
s
, y
s
0
) <
ε
.
(4)
3
Учитывая, что
F
![]() , , из соотношений (3),(4) выводим
, , из соотношений (3),(4) выводим
ε= F
0
( )x
∗
− F
(x
∗
, y
∗
)=![]() F
0
(x
∗
)− F
(x
∗
, y
∗
) ≤
F
0
(x
∗
)− F
(x
∗
, y
∗
) ≤
![]()
![]() ≤
≤![]() F
0 ( )x
∗ − F
0 (x
s
) + F
(x
s
, y
s
0 )− F
(x
∗, y
∗) < ε + ε = 2ε<ε.
F
0 ( )x
∗ − F
0 (x
s
) + F
(x
s
, y
s
0 )− F
(x
∗, y
∗) < ε + ε = 2ε<ε.
3 3 3
Получили противоречие, которое и доказывает лемму.
Дополнительно предположим, что функция F непрерывно дифференцируема по переменной x в области X , а множество Y 0 (x ) состоит ровно из одного элемента y 0 (x ) при всех x ∈ X . Тогда, как отмечалось выше, функция y 0 : X → R m будет непрерывной в каждой точке x ∈ X .
Теорема 2. В принятых предположениях функция F 0 : X → R 1 непрерывно дифференцируема в каждой точке области определения и при этом имеет место равенство
∂ 0 ∂∗ 0
![]() F
( )x
=
F
( )x
= ![]() ∗
F
(x
, y
( )x
), x
∈ X
,
(5) ∂x
∂ x
∗
F
(x
, y
( )x
), x
∈ X
,
(5) ∂x
∂ x
где индекс « ∗» в обозначении производной по векторному аргументу x в правой части (5) означает, что эта производная вычисляется без учета зависимости y 0 от x ∈ X .
Доказательство. По формуле конечных приращений [7] из двойного неравенства (2) находим
![]()
![]()
![]() F
(x
, y
0
(x
+ ∆x
)), ∆x
+ o
∆x
≤ ∆F
0
( )x
≤
F
(x
, y
0
(x
+ ∆x
)), ∆x
+ o
∆x
≤ ∆F
0
( )x
≤ ![]() F
(x
, y
0
( )x
), ∆x
+ o
∆x
.
(6)
F
(x
, y
0
( )x
), ∆x
+ o
∆x
.
(6)
Из соотношений (6) с учетом непрерывности функции y 0 следует, что
![]() ∆F
0
( )x
=
∆F
0
( )x
= ![]() F
(x
, y
0
( )x
), ∆x
+ o
∆x
.
F
(x
, y
0
( )x
), ∆x
+ o
∆x
.
Последнее условие означает дифференцируемость функции F 0 в точке x ∈X и справедливость равенства (5). Из непрерывности правой части равенства (5) следует непрерывность и его левой части. Теорема доказана.
Докажем одно важное свойство функции Л.С. Понтрягина.
Теорема 3. Пусть A = const B , = const C , = const и тройка U 0 ( )⋅ ,x 0 (⋅),ψ0 (⋅) удовлетворяет условиям теоремы 1 . Тогда функция Л.С. Понтрягина
![]() H t x
( , 0
( )t
,U
0
( )t
,ψ0
( )t
) = ψ0
( )t
, Ax
0
( )t
+ BU t
ˆ ( ,ψ0
( )t
)+C
H t x
( , 0
( )t
,U
0
( )t
,ψ0
( )t
) = ψ0
( )t
, Ax
0
( )t
+ BU t
ˆ ( ,ψ0
( )t
)+C
![]() ,
,
вычисленная вдоль оптимальной пары (x 0 (⋅),ψ0 (⋅)), остается постоянной на всем промежутке времени [t T 0 , ].
Доказательство . Вычисляем
![]()
![]() d
0 0 0 d
0 0 d
0 0
d
0 0 0 d
0 0 d
0 0
![]() ψ ( )t
, Ax
( )t
+ BU
( )t
+C
= ψ ( )t
, Ax
( )t
+ ψ ( )t
, BU
( )t
+C
=
ψ ( )t
, Ax
( )t
+ BU
( )t
+C
= ψ ( )t
, Ax
( )t
+ ψ ( )t
, BU
( )t
+C
=
dt dt dt
![]() 0 00 0
d
0
ˆ (ψ0
( )t
)+C
=
0 00 0
d
0
ˆ (ψ0
( )t
)+C
=
![]()
![]()
![]() = ψ ( )t
, Ax
( )t
+ ψ ( )t
, Ax
( )t
+ ψ ( )t
, BU dt
Тр
0 0Тр
0 0
d
0
ˆ (ψ0
( )t
)
= ψ ( )t
, Ax
( )t
+ ψ ( )t
, Ax
( )t
+ ψ ( )t
, BU dt
Тр
0 0Тр
0 0
d
0
ˆ (ψ0
( )t
)
= −A ψ ( )t , Ax ( )t + A ψ ( )t , x ( )t + ψ ( )t , BU
dt
![]()
![]() = −A
Тр
ψ0
( )t
, Ax
0
( )t
+ A
Тр
ψ0
( )t
, Ax
0
( )t
+ BU
ˆ (ψ0
( )t
)+C
+
d
ψ0
( )t
, BU
ˆ (ψ0
( )t
)+C
= −A
Тр
ψ0
( )t
, Ax
0
( )t
+ A
Тр
ψ0
( )t
, Ax
0
( )t
+ BU
ˆ (ψ0
( )t
)+C
+
d
ψ0
( )t
, BU
ˆ (ψ0
( )t
)+C
![]() =
=
dt
![]() = − ψ ( )t
, BU
ˆ (ψ0
( )t
)+C
+
d
ψ0
( )t
, BU
ˆ (ψ0
( )t
)+C
=
= − ψ ( )t
, BU
ˆ (ψ0
( )t
)+C
+
d
ψ0
( )t
, BU
ˆ (ψ0
( )t
)+C
=
dt
![]()
![]() 0
ˆ
(ψ0
( )t
) + d
ψ0
( )t
, BU
ˆ
(ψ0
( )t
). (12) = −ψ ( )t
, BU
0
ˆ
(ψ0
( )t
) + d
ψ0
( )t
, BU
ˆ
(ψ0
( )t
). (12) = −ψ ( )t
, BU
dt
В силу теоремы 2 справедливо равенство
![]()
![]()
![]() d
ψ0
( )t
, BU
ˆ (ψ0
( )t
) =
∂
∗
∗
ψ0
( )t
, BU
ˆ (ψ0
( )t
) = ψ0
( )t
, BU
ˆ (ψ0
( )t
)
d
ψ0
( )t
, BU
ˆ (ψ0
( )t
) =
∂
∗
∗
ψ0
( )t
, BU
ˆ (ψ0
( )t
) = ψ0
( )t
, BU
ˆ (ψ0
( )t
)![]() . dt
∂ t
. dt
∂ t
Тогда из (12) следует, что
![]()
![]()
![]()
![]() d
0 0 00 0 0 ψ ( )t
, Ax
( )t
+ BU
( )t
+C
= 0 ⇒ψ ( )t
, Ax
( )t
+ BU
( )t
+C
= const
.t
∈[t T
0
, ].
d
0 0 00 0 0 ψ ( )t
, Ax
( )t
+ BU
( )t
+C
= 0 ⇒ψ ( )t
, Ax
( )t
+ BU
( )t
+C
= const
.t
∈[t T
0
, ].
dt
Теорема доказана.
2.3 Частные случаи геометрических ограничений на вектор управляющих параметров. Иногда функция (1.8) может быть выписана в явном виде. Рассмотрим два таких частных случая.
Случай 1. Пусть
⎧ r r ( )u i 2 ⎫⎪
⎪
![]() P
= ⎨u
∈R
∑ 2 ≤1⎬, a
i
> 0, i
=1, ,r
.
⎪⎩ i
=1 ( )a
i
⎪⎭
P
= ⎨u
∈R
∑ 2 ≤1⎬, a
i
> 0, i
=1, ,r
.
⎪⎩ i
=1 ( )a
i
⎪⎭
Задача математического программирования по определению функции U ˆ состоит в максимизации линейной формы (1,7) при квадратичных ограничениях
2 ![]()
![]() 1.
1.
i =1 ( )a i 2
Решение этой задачи приводится в примере 1.4.3 книги [22]. Ее решением при ус-
⎛U ˆ 1 (t ,ψ)⎞
⎜ ⎟
ловии, что ψ≠ 0, служит вектор U t ˆ ( ,ψ) = ⎜ ⎟∈P , для которого
⎜⎜⎝U ˆ r (t ,ψ)⎟⎟⎠
2 ⎛ n ⎞ a i ⎜∑b ki ( )t ψk ⎟
U ˆ i (t ,ψ) = ⎝ k = 1 ⎠ , i =1, ,r . (1)
2
n ⎛ n ⎞ 2
![]() ∑ ∑⎜ b
ks
( )t
ψk
⎟ a
s
∑ ∑⎜ b
ks
( )t
ψk
⎟ a
s
s =1 ⎝ k =1 ⎠
В частности, если a 1 = = a r = a , то формула (1) принимает вид
⎛ n ⎞
⎜∑b ki ( )t ψk ⎟
U ˆ i (t ,ψ) = a ⎝ k = 1 ⎠ , i =1, ,r .
2 n ⎛ n ⎞
![]() ∑∑⎜
b
ks
( )t
ψk
⎟
∑∑⎜
b
ks
( )t
ψk
⎟
s =1 ⎝ k =1 ⎠
Пример 2*. Рассмотрим линейный управляемый динамический объект
x 1 = x 2 +u x 1 , 2 = −x 1 +u 2 , t ∈[0,π];
⎛u 1 ⎞ ⎧ ⎛u 1 ⎞ 22 2 ⎫
u
= ⎜ ⎟, u
∈P
= ⎨u
= ⎜ ⎟∈R
![]() u
1
+u
2
≤1⎬, x
1
( )0 = −3, x
2
( )0 = 2;
u
1
+u
2
≤1⎬, x
1
( )0 = −3, x
2
( )0 = 2;
⎝u 2 ⎠ ⎩ ⎝u 2 ⎠ ⎭
I U
⎡⎣
![]() ⎤⎦
x x
.
⎤⎦
x x
.
Здесь
| ⎛ 0 A = ⎜ ⎝−1 |
1⎞ ⎟, 0⎠ |
⎛1 B = ⎜ ⎝0 |
0⎞ ⎟, 1⎠ |
Φ( )x = 3x 1 2 + 2x 2 2 |
Сформулируем задачу математического программирования (1.7)
![]()
Функция (1.8) здесь имеет вид
⎛ ψ1 ⎞
![]() ⎜⎟
⎜⎟
U t ˆ ( ,ψ) = ⎜ ⎜ ⎟ ⎟ ,ψ≠ 0, (2)
⎜⎟
⎜⎟
⎝⎠
система дифференциальных уравнений (1.10) и граничные условия (1.11) записываются так:
ψ1
x 1 = x 2 +,
![]() ψ ψ12 + 22 ψ2
ψ ψ12 + 22 ψ2
x 2 = −x 1 +, (3)
ψ12 +ψ22
ψ1 = −ψ2 , ψ2 =ψ1 ,
x 1 ( )0 = −3, x 2 ( )0 = 2,ψ1 (π) = −6x 1 (π ψ π), 2 ( ) = −4x 2 ( )π . (4)
Общее решение сопряженной системы находится независимо от остальных уравнений системы
ψ1 (t c c , 1 , 2 ) = c 1 cost +c 2 sin ,t ψ2 (t c c , 1 , 2 ) = c 2 cost −c 1 sint . (5)
Преобразуем первые два уравнения в (3) с учетом (5)
![]() (c
cost
+c
sint
)
(c
cost
+c
sint
)
и проинтегрируем полученную систему
tc 1 cost tc 2 sint
![]()
![]() x
1
(t c c c c
, 1
, 2
, 3
, 4
) = +c
3
cost
+ + c
4
sint
,
c
+c c
+c
x
1
(t c c c c
, 1
, 2
, 3
, 4
) = +c
3
cost
+ + c
4
sint
,
c
+c c
+c
x 2 (t c c c c , 1 , 2 , 3 , 4 +c 4 cost − −c 3 sint . (6)
Граничные условия (4) принимают вид
⎛ π c 1 ⎞ ⎛ π c 2 ⎞
c 3 = −3, c 4 = 2, −c 1 = 6⎜+ c 3 ⎟, −c 2 = 4 ⎜+ c 4 ⎟ . (7)
![]()
![]() ⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
Решением нелинейной системы уравнений (7) будут числа
c 1 ∗ = 2.0562, c 2 ∗ = −1.2967, c 3 ∗ = −3, c 4 ∗ = 2. . (8)
Подставляя найденные константы в (5) определяем вектр-функцию ψ0 (⋅), а из
(2) - оптимальное программное управление
⎛ ![]() ⎞ ⎛ c
1
∗
cost
+c
2
∗
sint
⎞
⎞ ⎛ c
1
∗
cost
+c
2
∗
sint
⎞
![]() ⎜ 02 02 ⎟ ⎜ ∗2 ∗2 ⎟ 0 0
⎜ ψ1
( )t
+ψ2
( )t
⎟ ⎜
c
1
+c
2
⎟
⎜ 02 02 ⎟ ⎜ ∗2 ∗2 ⎟ 0 0
⎜ ψ1
( )t
+ψ2
( )t
⎟ ⎜
c
1
+c
2
⎟
u ( )t =U t ˆ ( ,ψ ( )t ) = ⎜ 0 ⎟ = ⎜ ∗ ∗ ⎟ , t ∈[0,π]. (9)
⎜ ψ2 ⎟ ⎜ c 2 cost −c 1 sint ⎟
⎜⎜ ψ102 ( )t +ψ202 ( )t ⎟⎟⎠ ⎜⎝ c 1∗2 +c 2∗2 ⎟⎠
⎝
Аналогично из (8) находим оптимальную траекторию
![]() 2
⎜ +c
4
∗
cost
− −c
3
∗
sint
⎟
2
⎜ +c
4
∗
cost
− −c
3
∗
sint
⎟
Ниже на рис. 2 приводятся графики изменения каждой из компонент вектора ψ0 ( )t от времени
![]()
Рис. 2
Из графиков видно, что вектор ψ0 (t ) не является нулевым вектором на всем промежутке времени [t T 0 , ], и программное управление, удовлетворяющее условиям принципа максимума, единственное. В силу выпуклости функции Φ программное управление u 0 ( )⋅ и движение объекта x 0 (⋅), определенные равенствами (9) и (10) соответственно, являются оптимальными. Вычислим значение функционала на оптимальном управлении
I u
⎡⎣ ![]() ⎤⎦ x x
.
⎤⎦ x x
.
Для сравнения вычислим значение функционала на допустимом программном управлении
![]()
 ⎜ ⎟
⎜ ⎟
Имеем
I u ⎡⎣ (⋅)⎤⎦ = 0.598124 .
Итак,
I u ⎡⎣ ( )⋅ ⎤⎦ = 0.598124 > 0.56252 = I u ⎡⎣ 0 (⋅)⎤⎦.
Оптимальная траектория объекта показана на рис. 3
![]()
Рис. 3
Заметим, что в соответствии с теоремой 3 функция Понтрягина
H t x ( , 0 ( )t ,u 0 ( )t ,ψ0 ( )t ) =ψ1 0 (t )(x 2 0 (t )+u 1 0 (t ))+ψ2 0 (t )(−x 1 0 ( )t +u 2 0 ( )t ),
должна оставаться постоянной на всем промежутке времени [0,π]. Действительно, ниже на рис. 4 приводится график функции
H t x ( , 0 (t ),u 0 (t ),ψ0 (t )) =
⎡ 0 ⎤ ⎡ 0 ⎤ 0 ⎢ 0 ψ1 ( )t ⎥ 0 ⎢ 0 ψ2 ( )t ⎥
=ψ1 ( )t ⎢x 2 ( )t + 2 2 ⎥ +ψ2 ( )t ⎢−x 1 ( )t + 2 2 ⎥
![]()
![]() ⎢⎣
(ψ1
0
( )t
) +(ψ2
0
( )t
) ⎥⎦
⎢⎣
(ψ1
0
( )t
) +(ψ2
0
( )t
) ⎥⎦
⎢⎣
(ψ1
0
( )t
) +(ψ2
0
( )t
) ⎥⎦
⎢⎣
(ψ1
0
( )t
) +(ψ2
0
( )t
) ⎥⎦
3
2.5 2
1.5 1
0.5
0.2 0.4 0.6 0.8 1
Рис. 4
который подтверждает факт постоянства функции Л.С. Понтрягина.
Случай 2. Геометрические ограничения на вектор управляющих параметров имеют вид
![]() ⎧ ⎛u
1
⎞⎫
⎧ ⎛u
1
⎞⎫
⎪ ⎜ ⎟r ⎪
P = ⎨u = ⎜ ⎟∈R αi ≤ u i ≤ βi ,i =1, ,r ⎬ .
⎪⎩ ⎜⎝u r ⎟⎠⎪⎭
⎛U ˆ 1 (t ,ψ)⎞
⎜ ⎟
Решением задачи (1.7) будет служить вектор U t ˆ ( ,ψ) = ⎜ ⎟∈P , для которого
⎜⎜⎝U ˆ r (t ,ψ)⎟⎟⎠
⎧
⎪ βi ,
⎪
U ˆ i (t ,ψ) = ⎪ ⎨∀u i ∈[αβi , i ],
⎪
⎪
⎪ αi , ⎩
n
∑b ki ( )t ψk > 0,
k =1
n
∑b ki ( )t ψk = 0, i =1, ,r ,
k =1 n
∑b ki ( )t ψk < 0.
k =1
Отсюда следует, что оптимальное управление u 0 (t ) =U t ˆ ( ,ψ0 ( )t ), t ∈[t T 0 , ] имеет кусочно-постоянные компоненты. При дополнительных предположениях относительно матриц A и B можно дать оценку сверху для числа переключений каждой из компонент оптимального управления.
Теорема 4 (А. А. Фельдбаума). Пусть в задаче линейного быстродействия
A = const B , = const , множество P имеет вид (1), все собственные значения матрицы A - действительные числа и вектор-функция ψ0 (⋅) не является тривиальным решением сопряженной системы дифференциальных уравнений (1.3.7). Тогда каждая компонента оптимального управления u 0 (t ) =U t ˆ ( ,ψ0 ( )t ), t ∈[t T 0 , ] имеет не более n −1 переключений, где n -размерность фазового вектора.
Доказательству теоремы предпошлем лемму.
Лемма 3. Пусть λ1 , ,λm – действительные попарно различные числа, а f 1 , , f m – многочлены с действительными коэффициентами, имеющие степень k 1 , ,k m , соответственно. Тогда функция F : R 1 → R 1 , определенная форму-
лой
F (t ) = f 1 (t )e λ 1 t + + f m (t )e λ m t , t ∈R 1 , (11)
имеет не более чем k 1 + + k m + m −1 корней.
Доказательство. Проведем индукцию по числу m . При m =1 лемма очевидно справедлива, ибо функция F тогда имеет вид F (t ) = f 1 (t )e λ 1 t , t ∈ R 1 , ее действительные корни совпадают с действительными корнями полинома f 1 и их число не более чем k 1 . Предположим, что лемма уже доказана для случая, когда в формуле (11) содержится меньше чем m слагаемых.
От противного будем считать, что функция F имеет, по крайней мере, k 1 + + k m + m действительных корней. Построим функцию F 1 : R 1 → R 1 по фор-
муле
F 1(t ) = F (t )e −λm t = f 1(t )e (λ1−λm )t + + f m −1(t )e (λm −1−λm )t + f m (t ), t ∈R 1.
Функции F и F 1 имеют одни и те же действительные корни. Так как между каждыми двумя действительными корнями функции лежит, по крайней мере, один корень ее производной, то производная (k m +1)-го порядка функции F 1 имеет по крайней мере
(k 1 + + k m + m )−(k m +1) = k 1 + + k m − 1 + m −1
действительных корней. С другой стороны, эта производная имеет вид
F 1(k m +1)( )t = g 1(t )e (λ1−λm )t + + g m −1(t )e (λm −1−λm )t , t ∈R 1 ,
где числа λ1 −λm , ,λm − 1 −λm попарно различны, а степень многочлена g i равна k i ,i =1, ,m −1. Согласно предположению индукции функция F 1 ( k m + 1 ) имеет не более
k 1 + + k m +(m −1)− =1 k 1 + + k m + m − 2
действительных корней, вопреки тому, что было установлено выше. Полученное противоречие завершает индукцию. Лемма доказана.
Доказательство теоремы 4. Достаточно установить, что для всех
n
i =1, ,r функция V i ( )⋅ = ∑b ki ψk 0 ( )⋅ имеет не более чем n −1 действительных
k =1
корней. Напомним, что вектор-функция ψ0 (⋅) является решением линейного дифференциального уравнения
ψ= −A T ψ.
Каждое собственное число матрицы −A T представляет собой собственное число матрицы A , взятое с противоположным знаком, и поэтому является действительным числом. Тогда
ψk 0 ( )t = g 1k ( )t e λ 1 t + + g mk ( )t e λ k t , t ∈R 1 , k =1, ,n ,
где λ1 , ,λm – все попарно различные собственные значения матрицы −A T , а g jk ( )⋅ – многочлен степени r j −1, где r j – кратность корня λj , j =1, ,m , k =1, ,n . Таким образом,
V t
![]() ( ) = f
( )t e
λ
t
+ + f
( )t e
λ
m
t
, t
∈R
1
, i
=1, ,r
.
( ) = f
( )t e
λ
t
+ + f
( )t e
λ
m
t
, t
∈R
1
, i
=1, ,r
.
Здесь f ji – многочлен степени r j −1, j =1, ,m . По лемме 3 функция V s (⋅) имеет не более чем
(r 1 −1)+ + (r m −1)+ m −1= r 1 + + r m −1= n −1
действительных корней. Теорема доказана.
Пример 3* . Рассмотрим линейный управляемый динамический объект
x 1 = 2x 1 + 2x 2 −30x 3 +u 1 , x 2 =10x 1 − x 2 −35x 3 +u 2 , x 3 = 2x 1 − x 2 + x 3 +u 3 ,
⎛u 1 ⎞ ⎧ ⎛u 1 ⎞ ⎫
⎜ ⎟ ⎪ ⎜ ⎟ 3 ⎪
![]() u
= ⎜u
2 ⎟, u
∈P
= ⎨u
= ⎜
u
2
⎟
∈R u
i
≤1, i
=1,2,3 ,⎬ x
1
( )0 = −3, x
2
( )0 = 2, x
3
( )0 =1;
u
= ⎜u
2 ⎟, u
∈P
= ⎨u
= ⎜
u
2
⎟
∈R u
i
≤1, i
=1,2,3 ,⎬ x
1
( )0 = −3, x
2
( )0 = 2, x
3
( )0 =1;
| ⎜u 3 ⎟⎠ ⎝ Здесь |
⎪ ⎩ |
⎜u 3 ⎟⎠ ⎪⎭ ⎝ I U ⎡⎣ ( )⋅ ⎤⎦ = x 1 (1)+ 2x 2 (1)− x 3 (1) → min . |
| ⎛ 2 ⎜ A = ⎜ 10 ⎜ 2 ⎝ |
2 −1 −1 |
−30⎞ ⎛1 0 0⎞ ⎟ ⎜ ⎟ −35⎟ , B = ⎜ 0 1 0⎟ , Φ( )x = x 1 ( )1 + 2x 2 ( )1 − x 3 ( )1 . 1 ⎟⎠ ⎜⎝0 0 1⎟⎠ |
Сформулируем задачу математического программирования (1.7)
![]() ψ1 1
u
+ψ ψ2
u
2
+ 3
u
3
→ min, u
i
≤1, i
=1,2,3
ψ1 1
u
+ψ ψ2
u
2
+ 3
u
3
→ min, u
i
≤1, i
=1,2,3
и решим ее. Функция (1.8) здесь имеет вид
ˆ ( ,ψ) = ⎜⎛⎜U U ˆˆ12 ((t t , ,ψ ψ))⎟⎞ ⎟,U ˆi (t ,ψ) = ⎪ ⎪⎨⎧любоечислоsign [ψi ], ψψii =<00,
U t
⎜U
⎜⎝ ˆ3 (t ,ψ)⎟⎟⎠ ⎩⎪⎪из −[0sign ,1],[ψ ψi ], i > 0.
Система дифференциальных уравнений (1.10) и граничные условия (1.11) записываются так:
x 1 = 2x 1 + 2x 2 −30x 3 +U ˆ 1 (t ,ψ), x 2 =10x 1 − x 2 −35x 3 +U ˆ 2 (t ,ψ), x 3 = 2x 1 − x 2 + x 3 +U ˆ 3 (t ,ψ),
ψ1 = −2ψ ψ ψ1 −10 2 −2 3 , ψ2 = −2ψ ψ ψ1 + 2 + 3 , ψ3 = 30ψ ψ ψ1 +35 2 − 3 ,
x 1 ( )0 = −3, x 2 ( )0 = 2, x 3 (0) =1, ψ1 (1) = −1,ψ2 (1) = −2,ψ3 ( )1 =1.
В данном примере сопряженная система дифференциальных уравнений интегрируется независимо от основной системы. В результате с учетом граничных условий получим вектор-функцию ψ0 (t ), t ∈[0,1]
Ниже на рис. 5 приводятся графики зависимости компонент этой вектор-функции от времени
ψ1 ψ2

Рис. 5
Из приведенных графиков видно, что вектор ψ0 (t ), t ∈[0,1] не является тождественным нулем. Тогда функция (8) определяется однозначно и представляет собой оптимальное программное управление. Компоненты
![]() вектора
ψ0
(t
) знакопостоянны, поэтому для построения
вектора
ψ0
(t
) знакопостоянны, поэтому для построения
оптимальной программной стратегии достаточно определить момент времени t ˆ∈[0,1], в который происходит переключение первой компоненты вектора ψ0 ( )t . В результате решения уравнения ψ1 0 (t ) = 0 приходим к равенству
t ˆ = 0.741061.
Таким образом, оптимальное программное управление имеет вид
⎧ 1, t ∈⎡⎣0, t ˆ),
⎪
⎪произвольноечисло
u
![]() t
= ⎨ t
= t
ˆ, , u
t
= ⎨ t
= t
ˆ, , u
![]() t u t
t u t
⎪ из [−1,1 ,]
⎪ ⎩ −1, t ∈(t ˆ,1 .⎤⎦
Подставим оптимальное управление в основную систему дифференциальных уравнений и проинтегрируем ее с соответствующими начальными условиями. В результате получим оптимальное движение x 0 ( )t , t ∈[0,1].
Вычислим значение функционала на оптимальном программном управле-
нии
I u ⎡⎣ 0 ( )⋅ ⎤⎦ = x 1 0 (1)+ 2x 2 0 (1)− x 3 0 (1) = −366.188
Для сравнения вычислим значение функционала на допустимом про-
⎛ 1 ⎞
граммном управлении u t ( ) = −⎜ ⎜ 1⎟ ⎟ , t ∈[0,1]. Пусть x (⋅) = x (⋅,t x u 0 , 0 , ( )⋅ ). Тогда ⎜⎝ 1 ⎟⎠
I u ⎡⎣ ( )⋅ ⎤⎦ = x 1 (1)+ 2x 2 (1)− x 3 (1) = −365.348.
Таким образом,
I u ⎡⎣ ( )⋅ ⎤⎦ = −365.348 > −366.188 = I u ⎡⎣ 0 (⋅)⎤⎦ .
Наконец, в соответствии с теоремой 3 проверим постоянство функции Понтрягина, вычисленной вдоль оптимальной пары (x 0 (t ),ψ0 ( )t ) на промежутке времени [0,1]. Действительно, ниже на рис. 6 приводится график функции
H t x ( , 0 ( )t ,u 0 ( )t ,ψ0 (t )) =ψ1 0 (t )(2x 1 0 (t )+ 2x 2 0 (t )−30x 3 0 ( )t +u 1 0 ( )t )+
+ψ2 0 ( )t (10x 1 0 (t )− x 2 0 ( )t −35x 3 0 (t )+u 2 0 (t ))+ψ3 0 (t )(2x 1 0 (t )− x 2 0 (t )+ x 3 0 ( )t +u 1 0 ( )t ),

Рис. 6
который подтверждает факт постоянства функции Л.С. Понтрягина.
2.4. Минимизация расстояния до целевого множества. Рассмотрим частный случай задачи 1, исследованной в предыдущем пункте. Именно, будем предполагать, что функция Φ , определяющая критерий качества, имеет смысл евклидового расстояния от проекции фазового вектора на часть своих (k первых, k ≤ n ) координат до некоторого выпуклого компактного множества M ⊂ R k .
Таким образом,
![]() Φ( )x
= ρ
({ }x
k
,M
) = minm M
∈ ρ
({ }x
k
,m
) = minm M
∈ m
−{ }x
k
,m
−{ }x
k
, k
≤ n M
, ⊂ R
k
. Здесь символ {⋅}k
означает проекцию вектора из пространства R
n
на свои первые k
≤ n
координат.
Φ( )x
= ρ
({ }x
k
,M
) = minm M
∈ ρ
({ }x
k
,m
) = minm M
∈ m
−{ }x
k
,m
−{ }x
k
, k
≤ n M
, ⊂ R
k
. Здесь символ {⋅}k
означает проекцию вектора из пространства R
n
на свои первые k
≤ n
координат.
В дальнейшем множество M ⊂ R k будем называть целевым.
Проекцию области достижимости G t x T ( 0 , 0 , ) ⊂ R n на подпространство R k обозначим символом {G t ( 0 ,x T 0 , )}k . Предположим, что выполняется условие
{G t ( 0 ,x T 0 , )}k ∩ M = ∅. Полагаем
ε0
= min{ε> 0![]() {G t
( 0
,x
0
)}k
∩ M
ε
≠ ∅},
{G t
( 0
,x
0
)}k
∩ M
ε
≠ ∅},
где символом M ε обозначена замкнутая ε−окрестность целевого множества. Из компактности множества {G t ( 0 ,x T 0 , )}k следует существование минимума в правой части последнего равенства и справедливость соотношения
ε0 = I U ⎣ ⎡ 0 (⋅) ⎦ ⎤ > 0.
Вычислим величину ε0 . По теореме 1.30 [22] условие {G t ( 0 ,x T 0 , )}k ∩ M ε ≠ ∅ будет иметь место тогда и только тогда, когда
![]()
![]() G t
min0 0,x T
, l q
, ≤χ
(M
ε
, ),l
∀ l
∈ S
(0, 1)=
{s
∈ R
k
s
=1}.
G t
min0 0,x T
, l q
, ≤χ
(M
ε
, ),l
∀ l
∈ S
(0, 1)=
{s
∈ R
k
s
=1}.
q ∈ { ( )}k
![]() Здесь χ(M
ε
,⋅) - опорная функция множества M
ε
. Тогда
Здесь χ(M
ε
,⋅) - опорная функция множества M
ε
. Тогда
![]() ε0
= min⎨⎧ε> 0min l q
, ≤ χ(M
ε
, )l
∀ ∈l S
(0, 1) ⎫
⎬
. (1)
ε0
= min⎨⎧ε> 0min l q
, ≤ χ(M
ε
, )l
∀ ∈l S
(0, 1) ⎫
⎬
. (1)
⎩q ∈ {G t ( 0 0 ,x T , )} k ⎭
В силу равенства
![]()
![]() χ
(M
ε
, )l
= max m l
, = +ε
maxm M
m l
, m M
∈ α
∈
χ
(M
ε
, )l
= max m l
, = +ε
maxm M
m l
, m M
∈ α
∈
из (1) выводим, что
![]()
![]() 0 ⎡⎤
0 ⎡⎤
![]()
![]() ε = l S
max∈ (0,1) ⎢⎣−maxm M
∈m l
,+ q
∈{G t
min( 0 0,x T
, )}k
q l
, ⎦⎥ . (2) Пусть максимум в (2) достигается на векторе l
0
∈S
(0,1). Покажем, что вектор l
0
∈S
(0,1) определяется однозначно. Действительно, от противного приходим к существованию векторов l
(
1
)
,l
(
2
)
∈S
(0,1 ,) l
(
1
)
≠ l
(
2
)
, для которых
ε = l S
max∈ (0,1) ⎢⎣−maxm M
∈m l
,+ q
∈{G t
min( 0 0,x T
, )}k
q l
, ⎦⎥ . (2) Пусть максимум в (2) достигается на векторе l
0
∈S
(0,1). Покажем, что вектор l
0
∈S
(0,1) определяется однозначно. Действительно, от противного приходим к существованию векторов l
(
1
)
,l
(
2
)
∈S
(0,1 ,) l
(
1
)
≠ l
(
2
)
, для которых
![]()
![]()
![]() = −max m l
, ( )
1
+ min q l
, ( )
1
,
= −max m l
, ( )
1
+ min q l
, ( )
1
,
q ∈ {G t ( 0 0 ,x T , )}
k
= −max m l , ( ) 2 + min q l , ( ) 2 .
q ∈ {G t ( 0 0 ,x T , )}
k
Сложим эти равенства почленно
![]()
![]()
![]()
![]() 2ε0
= −max m l
, ( )
1
+ min q l
, ( )
1
− max m l
, + min q l
, ( )
2
2ε0
= −max m l
, ( )
1
+ min q l
, ( )
1
− max m l
, + min q l
, ( )
2
![]() ≤ m M
∈q
∈
{G t
( 0 0
,x T
, )}
k
m M
∈q
∈
{G t
( 0 0
,x T
, )}
≤ m M
∈q
∈
{G t
( 0 0
,x T
, )}
k
m M
∈q
∈
{G t
( 0 0
,x T
, )}
≤ −max m l , ( )1 +l ( )2 + min q l , ( ) 1 +l ( ) 2 (3)
m M ∈q ∈{G t ( 0 0 k
Из неравенства (3) следует, что l
(
1
)
≠ −l
(
2
)
, а из условия l
(
1
)
≠ l
(
2
)
следует, что ![]() l
( )
1
+l
( )
2
l
( )
1
+l
( )
2
![]() < 2. Полагаем
< 2. Полагаем
(1) (2)
∗ l +l
![]() l
= ( )1 ( )2 ∈S
(0,1). l
+l
l
= ( )1 ( )2 ∈S
(0,1). l
+l
Тогда из (3) выводим
2ε0 0
![]()
![]() ε <≤ −max m
, l
( )1 +l
( )2 m M
∈
ε <≤ −max m
, l
( )1 +l
( )2 m M
∈
![]() + min=
+ min=
q ∈{G t ( 0 0 ,x T , )} k
![]()
![]()
![]()
![]() −maxm M
∈ m l
, ∗ + q
∈{G t
min( 0 0,x T
, )}k
q l
, ∗ ≤ l S
max∈ (0,1) ⎡⎢⎣−maxm M
∈ m l
, + q
∈{G t
min( 0 0,x T
, )}k
q l
, ⎤⎦⎥ =ε0 .
−maxm M
∈ m l
, ∗ + q
∈{G t
min( 0 0,x T
, )}k
q l
, ∗ ≤ l S
max∈ (0,1) ⎡⎢⎣−maxm M
∈ m l
, + q
∈{G t
min( 0 0,x T
, )}k
q l
, ⎤⎦⎥ =ε0 .
Получили противоречие, которое и доказывает единственность максими-
зирующего вектора l 0 ∈S (0,1).
Геометрическая интерпретация полученного результата (см. рис. 7 ) состоит в том, что вектор l 0 является опорным к множеству M , а вектор −l 0 -
опорным к множеству {G t ( 0 ,x 0 )}k .
Используя формулу Коши, придадим равенству (2) другую форму
ε0 =
![]()
![]()
![]()
![]() ⎡T T
⎫
⎪⎤⎥ =
⎡T T
⎫
⎪⎤⎥ =
![]()
![]() = max ⎢−max m l
, +X T t
[ , 0
]x
0
+ ∫ X T
[ ,τ τ τ τ]B
( ) ( )u d
+ ∫ X t
[ ,τ τ τ]C
( )d
⎬⎥
= max ⎢−max m l
, +X T t
[ , 0
]x
0
+ ∫ X T
[ ,τ τ τ τ]B
( ) ( )u d
+ ∫ X t
[ ,τ τ τ]C
( )d
⎬⎥
l =1 ⎢ m M ∈t 0 t 0 ⎪⎭k ⎦
⎣
⎡T T
![]()
![]() = max ⎢−max m l
, +X T t
[ , 0
]x
0
+ ∫ X T
[ ,τ τ τ τ]B
( ) ( )u d
+ ∫ X t
[ ,τ τ τ]C
( )d
, l
∗
⎥ =
= max ⎢−max m l
, +X T t
[ , 0
]x
0
+ ∫ X T
[ ,τ τ τ τ]B
( ) ( )u d
+ ∫ X t
[ ,τ τ τ]C
( )d
, l
∗
⎥ =
l =1 m M ∈
⎢⎣t 0 t 0
⎡T
![]() = max1 ⎢−max m l
, + X T t
[ , 0
]x l
0
, ∗
= max1 ⎢−max m l
, + X T t
[ , 0
]x l
0
, ∗
![]() + ∫ X T
[ ,τ]B
( ) ( )τ τu
, l
∗
d
τ+ l
= m M
∈
+ ∫ X T
[ ,τ]B
( ) ( )τ τu
, l
∗
d
τ+ l
= m M
∈
⎢⎣ t 0
⎡
= max ⎢−max m l ,
![]() l
=1 m M
∈ u P
∈
l
=1 m M
∈ u P
∈
⎢⎣
![]() T
T
![]() +∫C
( )τ , X
Тр
[T
,τ τ]l
∗
d
. (4)
+∫C
( )τ , X
Тр
[T
,τ τ]l
∗
d
. (4)
t 0
⎛ l ⎞
⎜ ⎟
Здесь обозначено l ∗ = ⎜ 0 ⎟ ∈R n .
⎜ ⎟
⎜⎜⎝ 0 ⎟⎟⎠
Теорема 5. Пусть ε0 > 0 и U 0 (⋅ ∈Π) [t T 0 , ] - оптимальная программная стратегия. Тогда
![]() B
( )t U
0
( )t
, X
Тр
[T t l
, ] 0
∗
B
( )t U
0
( )t
, X
Тр
[T t l
, ] 0
∗
![]() = min
= min ![]() B t u
( ) , X
Тр
[T t l
, ] 0
∗
B t u
( ) , X
Тр
[T t l
, ] 0
∗
![]() (5)
(5)
u P ∈
⎛l 0 ⎞
⎜ ⎟
при почти всех t ∈[t T 0 , ], где l 0 ∗ = ⎜ 0 ⎟ ∈R n .
⎜ ⎟
⎜⎜⎝ 0 ⎟⎟⎠
![]()
![]()
![]()
![]() Доказательство.
Допустим, что условие (5) нарушается. Тогда существует множество
T
∈[t T
0
, ] ненулевой меры, на котором выполняется неравенство
Доказательство.
Допустим, что условие (5) нарушается. Тогда существует множество
T
∈[t T
0
, ] ненулевой меры, на котором выполняется неравенство
B (t U ) 0 ( )t , X Тр [T t l , ] 0 ∗ > minB t u ( ) , X Тр [T t l , ] 0 ∗ , t ∈T .
u P ∈
![]() Из последнего соотношения вытекает, что
Из последнего соотношения вытекает, что
![]() T T
T T
![]()
![]() ∫B
( )τ U
0
( )τ , X
Тр
[T
,τ τ]l
0
∗
d
> ∫minu P
∈B
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0
∗
d
. (6)
∫B
( )τ U
0
( )τ , X
Тр
[T
,τ τ]l
0
∗
d
> ∫minu P
∈B
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0
∗
d
. (6)
t 0 t 0
![]() Подставим вектор
l
0
∈S
(0,1) в правую часть равенства (4). Имеем
Подставим вектор
l
0
∈S
(0,1) в правую часть равенства (4). Имеем
![]() T
T
![]()
![]()
![]()
![]() 0
= −max m l
, 0
+ x
0
, X
Тр
[T t l
, 0
] 0
∗
+ ∫minB
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0
∗
d
+
0
= −max m l
, 0
+ x
0
, X
Тр
[T t l
, 0
] 0
∗
+ ∫minB
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0
∗
d
+
t 0 u P ∈
![]() T
T
+∫C ( )τ , X Тр [t ,τ τ]l 0 ∗ d .
t 0
С учетом неравенства (6) выводим
![]()
![]()
![]()
![]()
![]() ε0
= I U
⎡⎣
0
( )⋅ ⎤⎦
= ρ
({x
0
( )T
}k
,M
) = maxl
=1 ⎣⎢
⎡
−maxm M
∈ m l
, + {x
0
( )T
}k
,l
⎦⎥
⎤
= l
1 ⎡⎢−max m l
, X T t
[ , 0
]x
0
+ tT
∫
0 X T
[ ,τ τ τ τ]B
( )U
0
( )d
+ tT
∫
0 X t
[ ,τ τ τ]C
( )d
⎪
⎬⎫k
⎥⎤⎥ ≥
ε0
= I U
⎡⎣
0
( )⋅ ⎤⎦
= ρ
({x
0
( )T
}k
,M
) = maxl
=1 ⎣⎢
⎡
−maxm M
∈ m l
, + {x
0
( )T
}k
,l
⎦⎥
⎤
= l
1 ⎡⎢−max m l
, X T t
[ , 0
]x
0
+ tT
∫
0 X T
[ ,τ τ τ τ]B
( )U
0
( )d
+ tT
∫
0 X t
[ ,τ τ τ]C
( )d
⎪
⎬⎫k
⎥⎤⎥ ≥
= max
= ⎢ ⎣⎪⎭ ⎦
T 0 T ⎫ ⎪
≥ −max m l , X T t [ , 0 ]x 0 + ∫ X T [ ,τ τ τ τ]B ( )U ( )d + ∫ X t [ ,τ τ τ]C ( )d ⎬ , l =
t 0 t 0 ⎪⎭k
T T
= −max m l , X T t [ , 0 ]x 0 + ∫ X T [ ,τ τ τ τ]B ( )U 0 ( )d + ∫ X t [ ,τ τ τ]C ( )d , l 0 ∗
t 0 t 0
T
![]()
![]() + x
0
, X
Тр
[T t l
, 0
] 0
∗
+ ∫ B
( )τ U
0
( )τ , X
Тр
[T
,τ τ]ld
+
+ x
0
, X
Тр
[T t l
, 0
] 0
∗
+ ∫ B
( )τ U
0
( )τ , X
Тр
[T
,τ τ]ld
+
t 0
![]() C
( )τ , X
Тр
[t
,τ τ]l
0
∗
d
> −max m l
, 0
+ x
0
, X
Тр
[T t l
, 0
] 0
∗
+
C
( )τ , X
Тр
[t
,τ τ]l
0
∗
d
> −max m l
, 0
+ x
0
, X
Тр
[T t l
, 0
] 0
∗
+
m M ∈
0
T T
![]()
![]() +∫minu P
∈
+∫minu P
∈![]() B
( )τ u X
, Тр
[T
,τ τ]l
0
∗
d
+ ∫
B
( )τ u X
, Тр
[T
,τ τ]l
0
∗
d
+ ∫ ![]() C
( )τ , X
Тр
[t
,τ τ ε]l
0
∗
d
= 0
.
C
( )τ , X
Тр
[t
,τ τ ε]l
0
∗
d
= 0
.
t 0 t 0
Получили противоречие. Теорема доказана.
![]() Очевидно (см. рис. 7
), что
Очевидно (см. рис. 7
), что
0 {x 0 ( )T }k −m 0 l =.
![]() {x
0
( )T
}k
−m
0
{x
0
( )T
}k
−m
0
Представим функцию Φ в виде
![]() Φ( )x
= minm M
∈ { }x
k
−m
,{ }x
k
−m
=
Φ( )x
= minm M
∈ { }x
k
−m
,{ }x
k
−m
=
= { }x k −m 0 ( ) { }x , x k −m 0 ( )x ,
Рис. 7 x ∈R n .
Из теоремы 3 следует, что
⎧∂Φ(x )⎫
![]() ⎨ ⎬ =
⎨ ⎬ =
⎩ ∂x ⎭k
⎧ ∂ ⎫ {x } −m 0 (x ) {x } −m 0 ( )x
![]() = ⎨ { }x
k
−m
,{ }x
k
−m
m m
= 0 x
⎬ = 0 k
0 = k
0 = l
0
.
= ⎨ { }x
k
−m
,{ }x
k
−m
m m
= 0 x
⎬ = 0 k
0 = k
0 = l
0
.
![]() ⎩∂x
( ) ⎭k
{ }x
k
−m
( ) { }x
, x
k
−m
( )x
{ }x
k
−m
( )x
⎩∂x
( ) ⎭k
{ }x
k
−m
( ) { }x
, x
k
−m
( )x
{ }x
k
−m
( )x
При x = x 0 ( )T отсюда выводим
⎧⎪ ∂Φ(x 0 ( )T )⎫⎪ {x 0 (T )}k −m 0 (x 0 (T )) 0 ∂Φ(x 0 ( )T ) 0∗
![]() ⎨ ⎬ = 0 0 0 = l
⇒ = l
.
⎨ ⎬ = 0 0 0 = l
⇒ = l
.
![]() ⎪⎩ ∂x
⎪⎭k
{x
( )T
}k
−m
(x
( )T
) ∂x
⎪⎩ ∂x
⎪⎭k
{x
( )T
}k
−m
(x
( )T
) ∂x
![]()
![]()
![]() Тогда условие (5) эквивалентно следующему:
Тогда условие (5) эквивалентно следующему:
0 ТрТр ∂Φ(x 0 ( )T )
![]() B
( )t U
( )t
, −X
[T t
, ]= maxB t u
( ) , −X
[T t
, ], t
∈[t T
0
, ].
B
( )t U
( )t
, −X
[T t
, ]= maxB t u
( ) , −X
[T t
, ], t
∈[t T
0
, ].
u P ∈∂x
В силу равенства
0 Тр ∂Φ(x 0 (T ))
![]() ψ ( )t
= −X
[T t
, ] , t
∈[t T
0
, ]
ψ ( )t
= −X
[T t
, ] , t
∈[t T
0
, ]
∂x
необходимые условия оптимальности программного управления, доказанные в теореме 6, совпадают с аналогичными условиями принципа максимума Л.С. Понтрягина (теорема 1 ). Из теоремы 5 также следует, что если величина Φ(x 0 ( )T ), вычисленная в результате интегрирования исходной системы дифференциальных уравнений после подстановки в нее программного управления, определенного из условия (4), совпадает с величиной ε0 , вычисленной по формуле (5), то это программное управление является оптимальным.
![]() Пример 4.
Рассмотрим линейный управляемый динамический объект из
примера 1
. Терминальный критерий качества
Φ( )x
= x
1
2
+(x
2
−2)2
можно трактовать как расстояние в конечный момент времени от фазового вектора
Пример 4.
Рассмотрим линейный управляемый динамический объект из
примера 1
. Терминальный критерий качества
Φ( )x
= x
1
2
+(x
2
−2)2
можно трактовать как расстояние в конечный момент времени от фазового вектора
⎛ ⎞0 до точки m = ⎜ ⎟. Для данного примера выполнены равенства
⎝ ⎠2
| ⎛1 k = 2, X t [ ,τ] = ⎜ ⎝0 Последовательно вычисляем |
0⎞ ⎟, 1⎠ |
⎛1 B t ( ) = ⎜ ⎝0 T |
0⎞ 0∗ 0 ⎟ , l = l . 1⎠ |
![]()
![]() ∫minu P
∈
∫minu P
∈ ![]() X T
[ ,τ τ]B
( )u l d
, 0
τ=
X T
[ ,τ τ]B
( )u l d
, 0
τ=
t 0
⎤ ⎡ 1 ⎤
![]()
![]() d
τ⎥ = max
l
=1 ⎢−2l
2
− ∫( l
1
+ l
2
)d
τ
⎥ =
d
τ⎥ = max
l
=1 ⎢−2l
2
− ∫( l
1
+ l
2
)d
τ
⎥ =
⎦⎥⎣ 0 ⎦
⎛l 1 0 ⎞ ⎛ 0 ⎞
![]()
![]() =1 ⎤ =1, ⎜ 0
⎟ = ⎜ ⎟ . l
⎝l
2
⎠ ⎝−1⎠
=1 ⎤ =1, ⎜ 0
⎟ = ⎜ ⎟ . l
⎝l
2
⎠ ⎝−1⎠
Необходимые условия оптимальности программного управления здесь принимают вид
u
![]() t sign l u t sign l t
. (7)
t sign l u t sign l t
. (7)
В силу l 1 0 = 0 условия(7) определяют программную стратегию неоднозначно. В частности, им удовлетворяет стратегия
U
![]() t u d t
.
t u d t
.
⎝ 1 ⎠ 0
При этом
I U ⎣ ⎡ 0 (⋅) ⎦ ⎤ =1=ε0 .
Следовательно, стратегия U 0 (⋅) является оптимальной.
Приведем последовательность действий по решению задачи управления динамической системой на основе теоремы 5.
В начале строится фундаментальная матрица Коши для однородной системы дифференциальных уравнений и вычисляется опорная функция χ (M , )⋅ целевого множества M по формуле
![]() χ
(M l
, ) = maxm M
∈
m l
, , l
∈ S
(0,1).
χ
(M l
, ) = maxm M
∈
m l
, , l
∈ S
(0,1).
Далее для произвольного l ∈S (0,1) решается задача математического программирования
![]()
![]() ⎛ l
⎞
⎛ l
⎞
⎜ ⎟
Tр Тр 0
B ( )t X [T t , ]⎜ ⎟ , u → min, u ∈P . (8)
⎜ ⎟
⎜⎜⎝ 0 ⎟⎟⎠
По теореме Вейерштрасса минимум в левой части равенства (8) существует для любой пары (t l , )∈[t T 0 , ]×S (0,1). Таким образом, определена векторфункция
U ˆ :[t T 0 , ]×S (0,1) → P , (9)
которая каждой паре (t l , )∈[t T 0 , ]×S (0,1) ставит в соответствие вектор U t l ˆ ( , )∈P , доставляющий минимум в условии (8). Явная запись этой функции возможна для частных случаев управляемой системы, рассмотренных в предыдущем пункте. Пусть функция U ˆ уже построена. Тогда приходим к следующей задаче математического программирования:
![]()
![]()
![]() ⎛ l
⎞⎛ l
⎞
⎛ l
⎞⎛ l
⎞
⎜ ⎟⎜ ⎟
Тр 0Tр Тр 0 ε( )l = −χ(M l , )+[T t , 0 ]⎜ ⎟ U (τ,l ), B ( )t X [T ,τ]⎜ ⎟ d τ+
⎜ ⎟⎜ ⎟
⎜⎜⎝ 0 ⎟⎟⎠⎜⎜⎝ 0 ⎟⎟⎠
![]() C
( )τ , X
Тр
[d
τ→ max , l
=1. (10)
C
( )τ , X
Тр
[d
τ→ max , l
=1. (10)
Эта задача всегда имеет решение, а в случае когда ε ε0 = ( )l 0 > 0 , ее решение единственное. Заметим, что приведенная задача математического программирования осложнена наличием определенных интегралов в выражении для целевой функции. Эти интегралы обычно не берутся
аналитически даже, если функция U ˆ определена явно.
Пусть ε0 > 0 и l 0 ∈S (0,1) - максимизирующий вектор. Тогда программное управление, удовлетворяющее необходимому условию оптимальности, определяется по формуле
U 0 (⋅) =U ˆ (⋅,l 0 ). (11)
После подстановки этого управления в исходные дифференциальные уравнения движения объекта, последние могут быть проинтегрированы с заданными начальными условиями. Далее проверяется справедливость равенства
ε0 = I U ⎡⎣ 0 (⋅)⎤⎦ .
В случае его выполнения программная стратегия, определенная равенством (11), является оптимальной.
Пример 5*. Рассматривается следующая управляемая динамическая система
![]() x
1 = 2x
1 +9x
2 +u
1, ⎧⎪⎛u
1 ⎞22 2 ⎫⎪
x
1 = 2x
1 +9x
2 +u
1, ⎧⎪⎛u
1 ⎞22 2 ⎫⎪
, u ∈P = ⎨⎜ ⎟ ∈R u 1 +u 2 ≤1⎬, t ∈[0,1],
x 2 = x 1 + 2x 2 +u 2 ⎪⎩⎝u 2 ⎠⎪⎭
![]() ⎧⎪⎛ m
1 ⎞⎫⎪
⎧⎪⎛ m
1 ⎞⎫⎪
M = ⎨⎜ ⎟ ≤1⎬ , k = n = 2, x 1 (0) = x 2 ( )0 = 0.
⎪⎩⎝m 2 ⎠⎪⎭
Фундаментальная матрица Коши для однородной системы дифференциальных уравнений здесь имеет вид
⎛ 1 2 e −(t −τ) (1+e 6(t −τ) ) 3 2 e −(t −τ) (− +1 e 6(t −τ) )⎞
X t [ ,τ] = ⎜⎜⎜ ⎟⎟⎟ .
⎝![]() ⎠
⎠
Вычислим опорную функцию χ(M ,⋅)терминального множества M . Име-
ем
ml
1 1
+ m l
2 2
→ ![]() .
.
Обозначим n 1 = m 1 −50, n 2 = m 2 −12. Тогда
n 2 n 2
(n
1
+50)l
1
+(n
2
+12)l
2
= nl
1 1
+ n l
2 2
+50l
1
+30l
2
→ max,![]() .
.
Отсюда выводим
2 2 ⎛l ⎞ 2
![]() χ(M
,l
) = 4l
+9l
+50l
+30l l
, = ∈R
.
χ(M
,l
) = 4l
+9l
+50l
+30l l
, = ∈R
.
Выражение ε( )l здесь принимает вид
![]() T
T
![]() ε( )l
= −max m l
, 0
+ X T t
[ , 0
]x
∗
, l
0
+ ∫minu P
∈
ε( )l
= −max m l
, 0
+ X T t
[ , 0
]x
∗
, l
0
+ ∫minu P
∈
t 0
+ ⎜
![]() ⎝
⎝
![]()
⎝l 2 ⎠
X T
[ ,τ τ τ]B
( ) ( )u
, l
0
![]() =
=
![]() 3
e
−(1(−1τ−τ) )(− +1 e
6 1( −τ) )⎟⎞⎛ ⎞⎜ ⎟0 , ⎛⎜l
1 ⎞⎟+
3
e
−(1(−1τ−τ) )(− +1 e
6 1( −τ) )⎟⎞⎛ ⎞⎜ ⎟0 , ⎛⎜l
1 ⎞⎟+
2
1 2 e − (1+e 6 1( −τ) ) ⎟⎠⎟⎝ ⎠0 ⎝l 2 ⎠
⎛u 1 ⎞ ⎜
![]() ⎝u
⎠ )
⎝u
⎠ )
⎝
1
![]() ) ∫ ⎡⎡ 1
e
−(1−τ) (1+ e
6 1( −τ) )l
1 + 1
6 e
−(1−τ) (− +1 e
6 1( −τ) )l
2 ⎤⎦2 +
) ∫ ⎡⎡ 1
e
−(1−τ) (1+ e
6 1( −τ) )l
1 + 1
6 e
−(1−τ) (− +1 e
6 1( −τ) )l
2 ⎤⎦2 +
= −4l +9l +50l 1 +30l 2 − ⎢⎣ 2
0 ⎣
2
![]() +⎡
⎣ 23
e
−(1−τ)
(− +1 e
6 1( −τ)
)l
1 + 1
2 e
−(1−τ)
(1+e
6 1( −τ)
)l
2 ⎤
⎦
⎤
⎥⎦
d
τ=
+⎡
⎣ 23
e
−(1−τ)
(− +1 e
6 1( −τ)
)l
1 + 1
2 e
−(1−τ)
(1+e
6 1( −τ)
)l
2 ⎤
⎦
⎤
⎥⎦
d
τ=
,
где обозначено
2
![]() Ε(τ, ,l l
1 2 ) = ⎢⎣⎡⎣⎡ 1
2 e
−(1−τ) (1+e
6 1( −τ) )l
1 + 1
6 e
−(1−τ) (− +1 e
6 1( −τ) )l
2 ⎦⎤ +
Ε(τ, ,l l
1 2 ) = ⎢⎣⎡⎣⎡ 1
2 e
−(1−τ) (1+e
6 1( −τ) )l
1 + 1
6 e
−(1−τ) (− +1 e
6 1( −τ) )l
2 ⎦⎤ +
2
+⎡ 23 e −(1−τ) (− +1 e 6 1( −τ) )l 1 + 1 2 e −(1−τ) (1+e 6 1( −τ) )l 2 ⎤ ⎦ ⎤ ⎥⎦ . ⎣
Функция U ˆ , доставляющая минимум в выражении (8), определяется формулой
⎛ 1 e −(1−τ) (1+e 6 1( −τ) )l 1 + 1 6 e −(1−τ) (− +1 e 6 1( −τ) )l 2 ⎞
2
⎜− ![]() ⎟
⎟
ˆ ( , ) = ⎜⎜ Ε(τ, ,l l 1 2 ) ⎟⎟. (12)
U t l
⎜ 23 e −(1−τ) (− +1 e 6 1( −τ) )l 1 + 1 2 e −(1−τ) (1+ e 6 1( −τ) )l 2 ⎟
⎜− ![]() ⎟
⎟
⎜⎝ Ε(τ, ,l l 1 2 ) ⎟⎠
Задача математического программирования (10) формулируется следующим образом:
![]() .
.
![]() Ее решение в силу равенства
l
2
= ± 1−l
1
2
сводится к проблеме максимизации функции одного переменного
l
1
∈ −[ 1,1]. Максимум целевой функции и вектор, на котором этот максимум достигается, соответственно имеют вид
Ее решение в силу равенства
l
2
= ± 1−l
1
2
сводится к проблеме максимизации функции одного переменного
l
1
∈ −[ 1,1]. Максимум целевой функции и вектор, на котором этот максимум достигается, соответственно имеют вид
0
0 0 0 ⎛l 1 ⎞ ⎛−0.316⎞
ε ε= ( )l =11.874 > 0, l = ⎜ 0 ⎟ = ⎜ ⎟ .
⎝l 2 ⎠ ⎝−0.949⎠
Подставляя l 0 в (12,) находим управление
⎛ 1 e −(1−τ) (1+e 6 1( −τ) )l 1 0 + 1 6 e −(1−τ) (− +1 e 6 1( −τl ) )l 2 0 ⎞
2
⎜− ![]() ⎟
⎟
⎜ Ε(τ,l l 1 0 , 2 0 ) ⎟
U 0 ( )t = ⎜ ⎟,
⎜ 3 e −(1−τ) (− +1 e 6 1( −τ) )l 1 0 + 1 2 e −(1−τ) (1+e 6 1( −τ) )l 2 0 ⎟
2
⎜ − ![]() ⎟
⎟
⎜⎝ Ε(τ,l l 10, 20 ) ⎟⎠
удовлетворяющее необходимым условиям оптимальности.
Подставим это управление в исходное дифференциальное уравнение и проинтегрируем полученное уравнение с заданными начальными условиями.
Ниже на рис. 8 приводятся графики изменения фазовых координат по времени для найденного закона движения объекта
![]()
Рис. 8
Вычислим координаты фазового вектора в конечный момент времени и финальное расстояние от него до целевого множества
0 ⎛ x 1 0 ( )1 ⎞ ⎛45.817⎞ 0 0
x ( )1 = ⎜⎜ x 20 ( )1 ⎠ ⎟⎟ = ⎜⎝ 15.805 ⎟⎠ , I U ⎡⎣ ( )⋅ ⎤⎦ = ρ (x ( )1 ,M ) =11.874. ⎝
Непосредственно убеждаемся в справедливости равенства
ε ε0 = (l 0 ) = I U ⎡⎣ 0 (⋅)⎤⎦ .
Таким образом, стратегия U 0 является оптимальной стратегией, а отвечающая ей траектория движения объекта – оптимальной траекторией. Для сравнения вычислим финальное расстояние от фазового вектора до терминального множества в случае, когда в качестве допустимого программного управления взята вектор- функция
⎛ 1
2 e
−(1−τ) (1+e
6 1( −τ) )l
10 + 1
6 e
−(1−τ) (− +1 e
6 1( −τl
) )l
20 −0.5⎞ ⎜− ![]() ⎟
⎟
⎜ Ε1 (τ,l 1 0 ,l 2 0 ) ⎟ u t ( ) = ⎜ ⎟,
⎜ 23
e
−(1−τ) (− +1 e
6 1( −τ) )l
10 + 1
2 e
−(1−τ) (1+e
6 1( −τ) )l
20 + 0.5 ⎟ ⎜ − ![]() ⎟
⎟
⎜⎝ Ε1 (τ,l 1 0 ,l 2 0 ) ⎟⎠
где
Ε1 (τ, ,l l 1 2 ) = ⎡⎡ 1 2 e −(1−τ) (1+e 6 1( −τ) )l 1 + 1 6 e −(1−τ) (− +1 e 6 1( −τ) )l 2 −0.5⎤2 +
⎢⎣⎣ ⎦
2![]()
+⎡⎣ 23 e −(1−τ) (− +1 e 6 1( −τ) )l 1 + 1 2 e −(1−τ) (1+ e 6 1( −τ) )l 2 + 0.5⎤⎦ ⎤⎦⎥ .
Пусть x ( )⋅ = x (⋅,t 0 ,x V 0 . ( )⋅ ). Тогда
⎛ x 1 ( )1 ⎞ ⎛45.878⎞
⎜ x 2 ( )1 ⎟⎠ = ⎜⎝ ⎟, I u ⎡⎣ ( )⋅ ⎤ =⎦ 11.923.
⎝ 15.733⎠
Таким образом,
I u ⎡⎣ ( )⋅ ⎤⎦ =11.923 >11.8735 = I U ⎡⎣ 0 (⋅)⎤⎦ .
Пример 6*. В условиях предыдущего примера принимается, что
![]() ⎧⎪⎛u
1
⎞ 2
⎫⎪ P
= ⎨⎜ ⎟∈R
≤1⎬.
⎧⎪⎛u
1
⎞ 2
⎫⎪ P
= ⎨⎜ ⎟∈R
≤1⎬.
⎪⎩⎝u 2 ⎠⎭⎪
Тогда
1
![]()
![]() ε( )l
== −
ε( )l
== − ![]() 4l
+9l
+50l
1 +30l
2
4l
+9l
+50l
1 +30l
2 ![]() − ∫
− ∫![]() 1
2 e
−(1−τ) (1+ e
6 1( −τ) )l
1 + 1
6 e
−(1−τ) (− +1 e
6 1( −τ) )l d
2 τ−
1
2 e
−(1−τ) (1+ e
6 1( −τ) )l
1 + 1
6 e
−(1−τ) (− +1 e
6 1( −τ) )l d
2 τ−
0
![]() 3
e
−(1−τ)
(− +1 e
6 1( −τ)
)l
1
+ 1
2
e
−(1−τ)
(1+ e
6 1( −τ)
)l d
2
τ.
3
e
−(1−τ)
(− +1 e
6 1( −τ)
)l
1
+ 1
2
e
−(1−τ)
(1+ e
6 1( −τ)
)l d
2
τ.
0
Функция U ˆ , доставляющая минимум в выражении (8), определяется формулой
ˆ ( , ) = ⎛⎜ ⎝⎜⎜ −−signsign ⎡⎣⎡⎣ 1 2 3 2 ee −−((11−−ττ)) ((1− ++1e 6 1e ( 6 1−(τ−)τ))l 1)l +1 +1 6 e 1 2 −e (1−−(τ1)−τ()− +(11 + e e 6 16 1(( −−ττ)) ))l l 22 ⎤⎦⎦⎤ ⎟⎞⎠⎟ ⎟ , (13)
U t l
а задача математического программирования (10) формулируется следующим образом:
ε(l ) → max, l 1 2 +l 2 2 =1.
Ниже приводится ее численное решение
⎛l 0 ⎞ ⎛ 0.304 ⎞ l = ⎜ 0 ⎟ = ⎜ ⎟ , ε ε= ( )l = 9.036 > 0.
0 1 0 0
⎝l 2 ⎠ ⎝−0.953⎠
Подставляя l 0 в (13), находим программное управление
U 0 ( )t = ⎜⎛ −sign z ⎣⎡ 1 ( )t ⎦⎤ ⎟⎞, (14)
⎜⎝−sign z ⎡⎣ 2 ( )t ⎤⎦⎟⎠
где
z
![]() t e e l e e l
, z
t e e l e e l
, z
![]() t e e l e e l t
.
t e e l e e l t
.
Моменты переключений управления (14) определим из анализа графиков
функций z 1 ( )t ,z 2 ( )t , t ∈[0,1], представленных на рис. 9.

Рис. 9
Из условия z 1 ( )t = 0 находим момент времени t ≈ 0.36245, в который происходит переключение первой компоненты вектора оптимального управления. Очевидно, что вторая компонента этого вектора все время остается постоянной.
Приведем (см. рис. 10 ) графики зависимостей компонент вектора управления (14) от времени
U1 U2

Рис. 10
Финальное расстояние от фазового вектора до терминального множества при управлении (12) равно I U ⎡⎣ 0 ⎤⎦ = ρ(x 0 (1),M ) = 9.036. Соотношение
I ⎡⎣ U 0 ⎤⎦ =ε ε0 = (l 0 )
здесь снова выполняется и, следовательно, управление (12) является оптимальным. Финальное расстояние до терминального множества оказалось меньше того, что было получено в примере 5 . Этот результат ожидаемый, так как область изменения вектора управляющих параметров в рассматриваемом случае шире, чем в примере 5.
Для сравнения вычислим финальное расстояние от фазового вектора до терминального множества, когда в качестве допустимого программного управления взята вектор- функция
.
![]() ⎝ ⎠
⎝ ⎠
Пусть x ( )⋅ = x (⋅,t 0 ,x u 0 , ( )⋅ ). Тогда
⎛ x 1 ( )1 ⎞ ⎛58.334⎞
⎜ x 2 ( )1 ⎟⎠ = ⎜⎝19.866⎟ ⎠, I u ⎡⎣ ( )⋅ ⎤⎦ =10.513. ⎝
Таким образом,
I u ⎡⎣ ( )⋅ ⎤⎦ =10.513 > 9.036 = I U ⎡⎣ 0 (⋅)⎦⎤ .
Рассмотрим управляемый объект, динамика которого описывается линейными дифференциальными уравнениями с переменными коэффициентами.
Пример 7*.
x 1 = x 3 ,
x 2 = x 4 ,
x 3 = (cost x ) 3 +tx 4 +u 1 ,
1
x
2
= ![]() x
3
+(sint x
) 4
+u
2
, t
+1
x
3
+(sint x
) 4
+u
2
, t
+1
⎧⎪⎛u 1 ⎞22 2 ⎫⎪
![]() u
∈P
= ⎨⎜ ⎟∈R u
1
+u
2
≤1⎬, t
∈[0,1],
u
∈P
= ⎨⎜ ⎟∈R u
1
+u
2
≤1⎬, t
∈[0,1],
⎪⎩⎝u 2 ⎠⎪⎭
⎧⎪⎛ m 1 ⎞ 22 2 ⎫ ⎪
k = 2, M = ⎨⎜ ⎟ ∈R (m 1 −5) +(m 2 − 4) ≤1⎬ ,
⎩⎪⎝m 2 ⎠⎭⎪
x 1 ( )0 = x 2 (0) = x 3 (0) = x 4 (0) = 0.
Построим фундаментальную матрицу Коши для однородной системы дифференциальных уравнений и запишем выражение (4) для данного случая
![]()
![]()
![]() ε0
= max ⎡
⎢−max m l
, + min q l
, ⎤
⎥ = max ⎡
⎢−max(l n
1 1
+l n
2 2
+5l
1
+ 4l
2
)+
ε0
= max ⎡
⎢−max m l
, + min q l
, ⎤
⎥ = max ⎡
⎢−max(l n
1 1
+l n
2 2
+5l
1
+ 4l
2
)+
l
![]()
![]() S
∈ (0,1)
⎣ m M
∈q
∈
{G t
( 0 0
,x T
, )}
2
⎦ l S
∈ (0,1)
⎣n
=1
S
∈ (0,1)
⎣ m M
∈q
∈
{G t
( 0 0
,x T
, )}
2
⎦ l S
∈ (0,1)
⎣n
=1
⎛0 0⎞ ⎛ x 11 (1,τ) x 12 (1,τ) x 13 (1,τ) x 14 (1,τ)⎞Tр ⎤
![]() ⎜ ⎟ ⎜ ⎟⎥
⎜ ⎟ ⎜ ⎟⎥
+ min⎜⎜10 00⎟⎟⎜⎛⎝uu 12 ⎟⎞⎠, ⎜⎜ xx 3121 ((11,,ττ)) xx 32 22 ((11,,ττ)) xx 33 23 ((11,,ττ)) xx 34 24 ((11,,ττ))⎟⎟d τ⎥⎥⎥ =
![]() ⎜⎜0 1⎟⎟⎠ ⎜⎜⎝ x
41 (1,τ) x
42
(1,τ) x
43
(1,τ) x
44
(1,τ)⎟
⎠
⎟⎦⎥
⎜⎜0 1⎟⎟⎠ ⎜⎜⎝ x
41 (1,τ) x
42
(1,τ) x
43
(1,τ) x
44
(1,τ)⎟
⎠
⎟⎦⎥
⎝
⎛ 0 ⎞ ⎛l x 1 11 (τ)+l x 2 21 (τ)⎞
⎜ ⎟ ⎜ ⎟
1 2 1⎜ 0 ⎟,⎜l x 1 12 ( )τ +l x 2 22 ( )τ ⎟
= max0,1 ⎡− −⎣ 1 (5l + 4l )+ ∫0 minu P ∈⎜u 1 ⎟ ⎜l x 1 13 ( )τ +l x 2 23 ( )τ ⎟ l S ∈ ( )
⎜⎜⎝u 2 ⎟⎟⎠ ⎜⎜⎝l x 1 14 ( )τ +l x 2 24 ( )τ ⎟⎟⎠
⎡⎤
![]() = − +1 l S
max∈ (0,1) ⎢ −(5l
1
+ 4l
2
)+ ⎡⎣
x
13
(1, )l
1
+ x
23
(1,τ)l
2
⎤ + ⎡⎦
2
⎣
x
14
(1,τ)l
1
+ x
24
(1,τ)l
2
⎦
⎤2
d
τ
⎥.
= − +1 l S
max∈ (0,1) ⎢ −(5l
1
+ 4l
2
)+ ⎡⎣
x
13
(1, )l
1
+ x
23
(1,τ)l
2
⎤ + ⎡⎦
2
⎣
x
14
(1,τ)l
1
+ x
24
(1,τ)l
2
⎦
⎤2
d
τ
⎥.
⎣ 0 ⎦
Задача математического программирования (10) здесь принимает вид
![]() ε(l
) = − −1 (5l
1
+ 4l
2
)−
ε(l
) = − −1 (5l
1
+ 4l
2
)−
![]() − d
→ max, l
=1.
− d
→ max, l
=1.
Приведем ее решение
0 ⎛−0.779⎞ 0
l = ⎜ ⎟ , ε( )l = 4.596.
⎝−0.627⎠
Заметим, что построить фундаментальную матрицу Коши в аналитическом виде в данном примере не удается. Это обстоятельство в некоторой степени осложняет численное решение задачи математического программирования. Программная стратегия, удовлетворяющая необходимым условиям оптимальности, определяется по формуле
⎛ x 13 (1,t l ) 1 0 + x 23 (1,t l ) 2 0 ⎞
![]() ⎜−⎟
⎜−⎟
0 ⎜⎟
U ( )t = ⎜ 0 0 ⎟ , (15)
![]() ⎜
−
x
14
(1,t l
) 1
+ x
24
(1,t l
) 2
⎟
⎜
−
x
14
(1,t l
) 1
+ x
24
(1,t l
) 2
⎟
⎜⎟
⎝⎠
где
![]() Ε(t l
, 1
0
,l
2
0
) = (x
13
(1,t l
) 1
0
+ x
23
(1,t l
) 2
0
)2
+(x
14
(1,t l
) 1
0
+ x
24
(1,t l
) 2
0
)2
.
Ε(t l
, 1
0
,l
2
0
) = (x
13
(1,t l
) 1
0
+ x
23
(1,t l
) 2
0
)2
+(x
14
(1,t l
) 1
0
+ x
24
(1,t l
) 2
0
)2
.
Закон движения объекта определяется путем интегрирования основной системы дифференциальных уравнений с заданными начальными условиями, в которую подставлено программное управление (15). Ниже на рис. 11 приводятся графики изменения первых двух координат фазового вектора от времени
![]()
Рис. 11
Финальное значение проекции фазового вектора на первые две координаты и расстояние от нее до терминального множества задается равенствами
{x 0 ( )1 }2 = ⎜⎜⎛ xx 1200 ( )( )11 ⎟⎟⎠⎞ = ⎜⎝⎛0.4910.641⎠⎟⎞, I U ⎣⎡ 0 ( )⋅ ⎤⎦ = ρ({x 0 ( )1 }2 ,M ) = 4.596 . ⎝
Непосредственно проверяется, что
ε ε0 = (l 0 ) = I U ⎡⎣ 0 (⋅)⎤⎦
и устанавливается, что программное управление U 0 (⋅) является оптимальным.
Для сравнения вычислим финальное расстояние от проекции фазового вектора на первые две координаты до терминального множества для случая, когда в качестве допустимого программного управления взята вектор функция
⎛ x
![]() t l x t l
⎞
t l x t l
⎞
⎜− ![]() 0 0 ⎟
0 0 ⎟
⎜ Ε1 (t l , 1 ,l 2 ) ⎟ u t ( ) = ⎜⎟ , t ∈[0,1].
⎜ x
![]() t l x t l
⎟
t l x t l
⎟
![]() ⎜⎟
⎜⎟
⎝⎠
Здесь
![]() .
.
Пусть x ( )⋅ = x (⋅,t 0 ,x u 0 , ( )⋅ ). Тогда
⎛ x 1 ( )1 ⎞ ⎛0.703⎞
⎝ x 2 ( )1 ⎟⎠ = ⎜⎝0.193⎟⎠, I u ⎡⎣ ( )⋅ ⎤⎦ = 4.74077 ⎜
Таким образом,
I u ⎡⎣ ( )⋅ ⎤⎦ = 4.74077 > 4.596 = I U ⎡⎣ 0 (⋅)⎤⎦ .
Пример 8*. В условиях предыдущего примера принимается, что
![]() ⎧⎪⎛u
1
⎞ 2
⎫⎪ P
= ⎨⎜ ⎟∈R
≤1⎬.
⎧⎪⎛u
1
⎞ 2
⎫⎪ P
= ⎨⎜ ⎟∈R
≤1⎬.
⎪⎩⎝u 2 ⎠⎭⎪
Тогда
0 ![]() ⎡ 1 ⎤
⎡ 1 ⎤
![]() ε = − +1 l S
max∈ 0,1 ⎢ −(5l
1
+ 4l
2
)− ∫
ε = − +1 l S
max∈ 0,1 ⎢ −(5l
1
+ 4l
2
)− ∫![]() x
13
(1,τ)l
1
+ x
23
(1,τ)l
2
+ x
14
(1,τ)l
1
+ x
24
(1,τ τ)l d
2
⎥.
x
13
(1,τ)l
1
+ x
23
(1,τ)l
2
+ x
14
(1,τ)l
1
+ x
24
(1,τ τ)l d
2
⎥.
( )
⎣ 0 ⎦
Вектор- функция U ˆ определяется формулой
U t l l ˆ ( , ,1 2 ) = ⎛⎜−sign x ⎣⎡ 13 (1,τ)l 1 + x 23 (1,τ)l 2 ⎤⎦⎞⎟, (14)
⎜⎝−sign x ⎡⎣ 14 (1,τ)l 1 + x 24 (1,τ)l 2 ⎤⎦ ⎟⎠
а задача математического программирования (8) здесь принимает вид
1
![]()
![]()
![]() ε( )l
= − −1 (5l
1
+ 4l
2
)− ∫ ⎡⎣
ε( )l
= − −1 (5l
1
+ 4l
2
)− ∫ ⎡⎣
![]() x
13
(1,τ)l
1
+ x
23
(1,τ)l
2
+ x
14
(1,τ)l
1
+ x
24
(1,τ τ)l
2
⎤⎦
d
→ max, l
=1.
x
13
(1,τ)l
1
+ x
23
(1,τ)l
2
+ x
14
(1,τ)l
1
+ x
24
(1,τ τ)l
2
⎤⎦
d
→ max, l
=1.
0
Приведем ее решение
0 ⎛ −0.791⎞ 0
l = ⎜ ⎟ , ε( )l = 4.282.
⎝−0.612⎠
Подставляя l 0 в (12), находим управление
![]() ⎛−sign x
⎡ 13
(1,τ)l
1
0
+ x
23
(1,τ)l
2
0
⎤⎞
⎛−sign x
⎡ 13
(1,τ)l
1
0
+ x
23
(1,τ)l
2
0
⎤⎞
U 0 ( )t t . (15)
⎜⎝−sign x ⎡⎣ 14 (1,τ)l 1 0 + x 24 (1,τ)l 2 0 ⎤⎦ ⎟⎠ ⎝ ⎠1
Из графиков компонент вектора управления (15), представленных на
рис. 12
U1 U2
0.2 0.4 0.6 0.8 1 0.2 0.4 0.6 0.8 1
Рис. 12.
видно, что оптимальное управление постоянно на всем промежутке времени [0,1]. Оптимальный закон движения объекта определяется путем интегрирования основной системы дифференциальных уравнений с заданными начальными условиями, в которую подставлено оптимальное программное управление (15). Ниже на рис 13 приводятся графики изменения первых двух координат фазового вектора от времени
![]()
Рис. 13
Финальное значение проекции фазового вектора на первые две координаты и расстояние от нее до терминального множества задается равенствами
0 ⎛ x 1 0 ( )1 ⎞ ⎛0.821⎞ 0 0
{x ( )1 }2 = ⎜⎜ x 20 ( )1 ⎟⎟⎠ = ⎝ ⎜0.771 ⎠ ⎟, I U ⎣ ⎡ ( )⋅ ⎤⎦ = ρ ({x ( )1 }2 ,M ) = 4.282 . ⎝
Вновь подтверждается выполнение равенства
I ⎡⎣ U 0 (⋅)⎤⎦ =ε ε0 = (l 0 ).
Найденное расстояние меньше того, что было получено в примере 7 . Этот результат ожидаемый, так как область изменения вектора управляющих параметров в рассматриваемом примере шире, чем в примере 7.
Для сравнения вычислим финальное расстояние от проекции фазового вектора на первые две координаты до терминального множества для случая, когда в качестве допустимого программного управления взята вектор- функция
![]() 1, 0, 0.1 1, [0, 0.9)
1, 0, 0.1 1, [0, 0.9)
u t = ⎜ ⎟ u 1 ( )t = u 2 t = .
⎝u 2 ( )t ⎠ ⎪⎩ 1 t ∈[0.1,1] ⎪⎩−1 t ∈[0.9,1]
Пусть x ( )⋅ = x (⋅,t 0 ,x U 0 , ( )⋅ ). Тогда
⎛ x 1 ( )1 ⎞ ⎛0.499⎞
⎜ x 2 ( )1 ⎟⎠ = ⎜⎝0.652⎟ ⎠, I U ⎡⎣ ( )⋅ ⎤⎦ = 4.60949 . ⎝
Таким образом, I u ⎡⎣ ( )⋅ ⎤⎦ = 4.60949 > 4.282 = I U ⎡⎣ 0 (⋅)⎤⎦ .
2.5. Случай подвижного левого и свободного правого конца траектории. Будем предполагать, что в постановке задачи 1 множество S 0 ⊂ R n содержит более одной точки и является компактным множеством в R n . Сформулируем получившуюся задачу.
Задача 2. Найти допустимую программную стратегию U 0 ( )⋅ ∈Π[t T 0 , ], доставляющую минимум функционалу
I ⎡⎣ U (⋅)⎤⎦ = Φ(x T ( )), Φ∈C 1 (R 1 )
при ограничениях
x = A t x ( ) + B t u ( ) +C t ( ), x ∈R n , u ∈P ⊂ R r , θ0 ={t 0 },θ1 ={T }, x 0 ∈S 0 ⊂ R n , S 1 = R n .
Обозначим
Γ(t S T 0 , 0 , ) = ∪ G t x T ( 0 , 0 , ).
x 0∈S 0
Из непрерывной зависимости области достижимости от начального положения x 0 ∈S 0 (см. формулу Коши) и компактности множества S 0 следует, что множество Γ(t S T 0 , 0 , ) ⊂ R n также является компактным, поэтому решение задачи
2 существует.
Пусть пара ![]() доставляет решение задачи 2.
доставляет решение задачи 2.
Очевидно, что программная стратегия U 0 (⋅ ∈Π) [t T 0 , ] будет оптимальной для задачи 1, если принять S 0 ={x 0 0 }, а остальные условия задачи 1 считать совпадающими с соответствующими условиями задачи 2. Тогда по теореме 4 должно выполняться
![]() B
( )t U
0
(t
),ψ0
(t
)
B
( )t U
0
(t
),ψ0
(t
) ![]() = max
= max ![]() B t u
( ) ,ψ0
(t
)
B t u
( ) ,ψ0
(t
)![]() (1)
(1)
u P ∈
для почти всех t ∈[t T 0 , ], где
![]() . (2)
. (2)
Условия (1) и (2) не позволяют однозначно определить программную стратегию управления, претендующую на решение задачи 2, поскольку они содержат n неизвестных параметров, образующих вектор начальных условий
x
![]() . Для их определения выведем так называемые условия трансверсальности на левом конце траектории.
. Для их определения выведем так называемые условия трансверсальности на левом конце траектории.
Пусть
S
0
={x
∈R
n
![]() ϕi
( )x
≤ 0, i
=1, ,m
},
ϕi
( )x
≤ 0, i
=1, ,m
},
где ϕi : R n → R 1 , i =1, ,m -заданные непрерывно дифференцируемые по совокупности аргументов функции. Дополнительно предположим, что для множества
S 0 выполнено следующее условие регулярности: для всех x ∈S 0 набор векторов
∂ϕi ( )x 0
![]() , i
∈I
( )x
={i
∈{1, ,m
}
, i
∈I
( )x
={i
∈{1, ,m
}![]() ϕi
( )x
= 0}
ϕi
( )x
= 0}
∂x
является линейно независимым.
Оптимальное начальное положение фазового вектора x 0 0 удовлетворяет равенству
⎛ T T ⎞
Φ ![]() x T
= Φ⎜⎜ X T t
, x
+ X T
,τ τ τ τB U d
+ X T
[ ,τ τ τ]C
( )d
⎟⎟ =
x T
= Φ⎜⎜ X T t
, x
+ X T
,τ τ τ τB U d
+ X T
[ ,τ τ τ]C
( )d
⎟⎟ =
⎝ t 0 t 0 ⎠
⎛ T T ⎞
= minx 0∈S 0 Φ⎜⎜ X [T t , 0 ]x 0 + ∫ X T [ ,τ]B ( )τ τ τU 0 ( )d + ∫ X T [ ,τ τ τ]C ( )d ⎟ ⎟.
⎝ t 0 t 0 ⎠
⎧µ0 ⎫
⎪ ⎪
⎪µ1 ⎪
По теореме Кароша – Джона [22] существует вектор ⎨ ⎬ ≠ 0, для которого
⎪ ⎪
⎪⎩µm ⎪⎭
справедливы соотношения
⎛ T T ⎞
∂Φ⎜⎜ X T t [ , 0 ]x 0 0 + ∫ X T [ ,τ τ τ τ]B ( )U 0 ( )d + ∫ X T [ ,τ τ τ]C ( )d ⎟⎟
![]() µ0 ⎝ t
0 t
0 ⎠ +
µ0 ⎝ t
0 t
0 ⎠ +
∂x 0
![]() m
∂ϕi
m
∂ϕi
+
∑
i
=1 µi
![]() ∂
x
0 ; (3)
∂
x
0 ; (3)
µϕi i
![]() 0, µi
0, i
1, ,m
; (4)
0, µi
0, i
1, ,m
; (4)
µ0 ∈{0,1}. (5)
Заметим, что в силу регулярности множества S 0 , в условии (5) можно сразу записать µ0 =1. Действительно, пусть µ0 = 0 . Тогда из условий (3) и (4) следует, что
![]() µ
µ ![]() = 0 ⇒ µ = 0 , (6)
= 0 ⇒ µ = 0 , (6)
i
=1 ![]() x
0 x
0
x
0 x
0
причем среди чисел µi , i ∈I 0 ( )x есть числа, отличные от нуля. Равенство (6) про-
тиворечит линейной независимости набора векторов ![]() . Остается
. Остается
признать, что µ0 =1.
Вычисляем
![]() ∂Φ ⎛ T
0
T
⎞
∂Φ ⎛ T
0
T
⎞
![]() ⎜ X T t
[ , ]x
+ ∫
X T
[ ,τ τ τ τ]B
( )U
( )d
+ ∫
X T
[ ,τ τ τ]C
( )d
⎟ =
⎜ X T t
[ , ]x
+ ∫
X T
[ ,τ τ τ τ]B
( )U
( )d
+ ∫
X T
[ ,τ τ τ]C
( )d
⎟ =
∂ x 0 ⎝ ⎜ 0 0 t 0 t 0 ⎟⎠ x 0=x 00
![]() = X
Tp
= X
Tp
![]() = − .
= − .
x
Теперь условие (3) можно переписать в виде
0 m
∂ϕi
![]()
ψ ( )t
0
= ∑
i
=1 µi
![]() ∂
x
.
∂
x
.
Таким образом, доказана следующая теорема.
Теорема 6.
Пусть пара
![]() доставляет ре-
доставляет ре-
шение задачи 2. Тогда необходимо
![]() B
( )t U
0
(t
),ψ0
(t
)
B
( )t U
0
(t
),ψ0
(t
) ![]() = max
= max ![]() B t u
( ) ,ψ0
(t
)
B t u
( ) ,ψ0
(t
)![]()
u P ∈
при почти всех t ∈[t T 0 , ]. В случае, когда для множества S 0 выполнены условия регулярности, существует набор чисел µ1 ≥ 0, ,µm ≥ 0 таких, что
0 m
∂ϕi
![]() 0
0
ψ ( )t
0
= ∑
i
=1 µi
![]() ∂
x
, µϕi i
(x
0
) = 0, i
=1, ,m
.
∂
x
, µϕi i
(x
0
) = 0, i
=1, ,m
.
Пример 9*. Рассмотрим линейный управляемый динамический объект
x 1 = x 2 +u x 1 , 2 = −x 1 +u 2 , t ∈[0,π];
⎛u 1 ⎞ ⎧ ⎛u 1 ⎞ 22 2 ⎫
u
= ⎜ ⎟, u
∈P
= ⎨u
= ⎜ ⎟∈R
![]() u
1
+u
2
≤1⎬,
u
1
+u
2
≤1⎬,
⎝u 2 ⎠ ⎩ ⎝u 2 ⎠ ⎭
⎧⎪⎛ x 1 ⎞ 2 ⎫⎪
![]() S
0
= ⎨⎜ ⎟∈R
− 25− x
+ x
2
≤ 0, x
1
− x
2
+5 ≤ 0⎬
S
0
= ⎨⎜ ⎟∈R
− 25− x
+ x
2
≤ 0, x
1
− x
2
+5 ≤ 0⎬
⎪⎩⎝ x 2 ⎠⎪⎭
I U
⎡⎣ ![]() ⎤⎦ x x
.
⎤⎦ x x
.
Условия рассматриваемого примера совпадают с условиями примера 2 за исключением граничных условий на левом конце траектории. В данном примере множество S 0 содержит более одной точки. Множество S 0 показано на
рис. 14 .
x2
![]()
Рис. 14
Повторяя выкладки из примера 2, приходим к тому, что
⎛ ψ1 ⎞
![]() ⎜⎟
⎜⎟
U t ˆ ( ,ψ) = ⎜ ⎜ ⎟ ⎟ ,ψ≠ 0,
⎜⎟
⎜⎟
⎝⎠
а объединенная система дифференциальных уравнений имеет вид
ψ1
x 1 = x 2 +,
![]() ψ ψ12 + 22 ψ2
ψ ψ12 + 22 ψ2
x 2 = −x 1 +, (7)
ψ12 +ψ22
ψ1 = −ψ2 , ψ2 =ψ1 .
Выпишем граничные условия. На правом конце траектории они тождественны условиям, полученным в примере 2
ψ1 ( )π = −6x 1 (π),ψ2 (π) = −4x 2 (π). (8)
В соответствии с теоремой 6 выпишем граничные условия на левом конце траектории
![]() ψ0 ( )0 =µ1 ∂ ⎛⎜− 4⋅ 25− x
12 + x
2 ⎟⎞+µ2
ψ0 ( )0 =µ1 ∂ ⎛⎜− 4⋅ 25− x
12 + x
2 ⎟⎞+µ2 ![]() ∂ (x
1 − x
2 +5) =
∂ (x
1 − x
2 +5) =
∂x ⎝ 5 ⎠ ∂x
⎛ 4x 1 ⎞ ⎛ 4x 1 ⎞
⎜ 2 ⎟ ⎛ 1 ⎞ ⎜µ1 2 +µ2 ⎟
![]()
![]() = µ1 ⎜ 5 25− x
1 ⎟+µ2 ⎝⎜−1⎟⎠ = ⎜⎜ 5 25µ µ1 −− x
12 ⎟⎟⎠ ,
= µ1 ⎜ 5 25− x
1 ⎟+µ2 ⎝⎜−1⎟⎠ = ⎜⎜ 5 25µ µ1 −− x
12 ⎟⎟⎠ ,
⎜ 1 ⎟⎠ ⎝
⎝
⎛ 4 2 ⎞
![]() µ1
⎜
− ⋅ 25− x
1
+ x
2
⎟
= 0, µ2
(x
1
− x
2
+5) = 0, µ µ1
≥ 0, 2
≥ 0 .
µ1
⎜
− ⋅ 25− x
1
+ x
2
⎟
= 0, µ2
(x
1
− x
2
+5) = 0, µ µ1
≥ 0, 2
≥ 0 .
⎝ 5 ⎠
Общее решение системы дифференциальных уравнений (7) имеет вид
ψ1 (t c c , 1 , 2 ) = c 1 cost +c 2 sint , ψ2 (t c c , 1 , 2 ) = c 2 cost −c 1 sint ,
tc 1 cost tc 2 sint ,
![]()
![]() x
1
(t c c c c
, 1
, 2
, 3
, 4
) = +c
3
cost
+ + c
4
sint c
+c c
+c
x
1
(t c c c c
, 1
, 2
, 3
, 4
) = +c
3
cost
+ + c
4
sint c
+c c
+c
x 2 (t c c c c , 1 , 2 , 3 , 4 +c 4 cost − −c 3 sint . (9)
Выпишем граничные условия с учетом равенств (9).
На левом конце
4x
![]() 10
,
c
2
= µ µ1
− 2
,
+µ2
10
,
c
2
= µ µ1
− 2
,
+µ2
| c 3 = x 10, На правом конце |
c 4 = x 20 , µ1 ≥ 0, |
µ2 ≥ 0. |
(10) |
⎛⎜ πc 1 + c 3 ⎞⎟, −c 2 = 4⎛⎜ πc 2 +c 4 ⎞⎟. (11)
−c 1 = 6
![]()
![]() ⎜ c
12 +c
22 ⎟
⎠
⎜
⎝
c
12 +c
22 ⎟
⎠
⎜ c
12 +c
22 ⎟
⎠
⎜
⎝
c
12 +c
22 ⎟
⎠
⎝
В результате получилась система из восьми уравнений относительно восьми c c c c 1 , 2 , 3 , 4 ,µ1 ,µ2 , x 10 ,x 20 неизвестных. Последовательно рассмотрим четыре случая: 1) µ µ1 = 0, 2 = 0, : 2) µ µ1 > 0, 2 = 0, : 1) µ µ1 = 0, 2 > 0, : 1) µ µ1 > 0, 2 > 0.
Случай 1. Из первых двух равенств в (10) вытекает, что
c 1 = c 2 = 0 ⇒ ψ0 (t ) ≡ 0, t ∈[0,π].
Из граничных условий (8) следуют равенства x 1 (π) = x 2 (π) = 0. Покажем, что
⎛ ⎞0
⎜ ⎟ ∉Γ(0,S 0 ,π). Для этого достаточно установить справедливость неравенст-
⎝ ⎠0 ва
![]()
![]() l S
max
∈ (0,1) ⎣⎢⎡
q G t
∈ min
( 0 0,x T
, ) q l
,
⎤ =
l S
max
∈ (0,1 ⎢⎡min
x
0∈S
0
l S
max
∈ (0,1) ⎣⎢⎡
q G t
∈ min
( 0 0,x T
, ) q l
,
⎤ =
l S
max
∈ (0,1 ⎢⎡min
x
0∈S
0 ![]() X
[π,0]x l
0
,
X
[π,0]x l
0
, ![]() +π
∫
0 min
u P
∈
+π
∫
0 min
u P
∈ ![]() X
[πτ, ]u l d
, τ
⎥⎤ > 0. (12)
X
[πτ, ]u l d
, τ
⎥⎤ > 0. (12)
⎥⎦ ) ⎣⎦
Последовательно вычисляем
⎛ cos(t −τ) sin(t −τ)⎞
X
[t
,τ] = ⎜ ⎟,![]() X
[π,0]x
0
, l
X
[π,0]x
0
, l
![]() = −l x
1 10
−l x
2 20
,
= −l x
1 10
−l x
2 20
,
⎝ −sin(t −τ) cos(t −τ) ⎠
![]() min
min ![]() X
[πτ,
X
[πτ, ![]() ]u l
, 1.
]u l
, 1.
u P ∈
В результате неравенство (12) принимает вид
![]() l
max minl
⎢⎣⎡ x
∈S
(−l x
1 10 −l x
2 20 )⎥⎦⎤ >π. (13)
l
max minl
⎢⎣⎡ x
∈S
(−l x
1 10 −l x
2 20 )⎥⎦⎤ >π. (13)
Минимум линейной формы, стоящей в левой части неравенства (13), может достигаться лишь в тех начальных позициях, которые лежат на дуге эллипса.
Тогда левая часть неравенства (13) вычисляется по формуле
![]()
= 3.527 >π,
и неравенство (13) имеет место. Таким образом, случай 1 не дает решения задачи оптимального управления.
Случай 2). Граничные условия принимают вид
![]() 4x
10
4
4x
10
4
c 1 =µ1 , c 2 =µ1 , , x 10 − x 20 +5 ≤ 0, (14)
![]() 5 25− x
102
5 25− x
102
⎛ πc 1 ⎞ ⎛ πc 2 ⎞
![]()
![]() c
3
= x
10
, c
4
= x
20
,
µ1
> 0 ,
−c
1
= 6⎜+ c
3
⎟, −c
2
= 4⎜+c
4
⎟.
(15) ⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
c
3
= x
10
, c
4
= x
20
,
µ1
> 0 ,
−c
1
= 6⎜+ c
3
⎟, −c
2
= 4⎜+c
4
⎟.
(15) ⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
Эти условия противоречивы, так как в силу второго равенства в (14) выполняется c 2 > 0. Тогда из второго и четвертого равенств в (15) следует, что x 20 < 0 и x 0 ∉S 0 .
Случай 3). Граничные условия принимают вид
c
1
=µ2
,
c
2
= −µ2
,
![]() ,
x
10
− x
20
+5 = 0 ,
(16)
,
x
10
− x
20
+5 = 0 ,
(16)
⎛ πc 1 ⎞ ⎛ πc 2 ⎞
c 3 = x 10 , c 4 = x 20 , µ2 > 0 , −c 1 = 6⎜+ c 3 ⎟, −c 2 = 4⎜+c 4 ⎟. (17)
![]()
![]() ⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
Решением системы (16), (17) будут числа c 1 =1.337, c 2 = −1.337, c 3 = −2.444, c 4 = 2.556,µ2 =1.337 > 0, x 10 = −2.444, x 20 = 2.556.
Подставляя их в (7), определяем оптимальную программную стратегию и оптимальную траекторию объекта. Ниже на рис. 15 приводится вид этой траектории. x2
![]()
Рис. 15
Оптимальное значение функционала равно
I U
⎡⎣
![]() ⎤⎦
x x
.
⎤⎦
x x
.
В примере 4 значение функционала на оптимальном управлении было
«хуже» и равнялось величине 0.562 . Такой результат является ожидаемым,
⎛−3⎞ так как начальная точка x 0 = ⎜ ⎟ из примера 4 принадлежит множеству S 0 ⎝ 2 ⎠
данного примера.
Случай 4). Граничные условия принимают вид
![]() 4x
10
4
4x
10
4
c 1 =µ1 +µ2 , c , x 10 − x 20 +5 = 0 ,
![]() 5 25− x
102
5 25− x
102
⎛ πc 1 ⎞ ⎛ πc 2 ⎞
c 3 = x 10 , c 4 = x 20 , µ1 > 0, µ2 > 0 , −c 1 = 6⎜+ c 3 ⎟, −c 2 = 4⎜+c 4 ⎟.
![]()
![]() ⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
⎜⎝ c
12 +c
22 ⎟⎠ ⎜⎝ c
12 +c
22 ⎟⎠
Эта система имеет два решения.
Первое решение
c 1 =11.150, c 2 = 0, c 3 = −5, c 4 = 0, µ1 = −8.79 10⋅ − 7 , µ2 = −8.79 10⋅ − 7 ,
x 10 = −5, x 20 = 0 .
Второе решение
c 1 =1.093, c 2 = −3.589, c 3 = −1.098, c 4 = 3.902,µ1 = −3.043< 0,µ2 = 0.545,
x 10 = −1.098, x 20 = 3.902 .
Оба решения не удовлетворяют предположениям четвертого случая.
Таким образом, задача оптимального управления имеет единственное решение, которое было получено в третьем случае.
Пример 10* . Рассмотрим линейный управляемый динамический объект
x 1 = 2x 1 + 2x 2 −30x 3 +u 1 , x 2 =10x 1 − x 2 −35x 3 +u 2 , x 3 = 2x 1 − x 2 + x 3 +u 3 ,
⎧ ⎛u 1 ⎞ ⎫
⎪ ⎜ ⎟ 3 ⎪
![]() u
∈P
= ⎨u
= ⎜
u
2
⎟
∈R u
i
≤1, i
=1,2,3⎬
, t
∈[0,1]
u
∈P
= ⎨u
= ⎜
u
2
⎟
∈R u
i
≤1, i
=1,2,3⎬
, t
∈[0,1]
⎪ ⎜⎝u 3 ⎟⎠ ⎪⎭
⎩
![]() ⎧⎛ x
1
⎞⎫
⎧⎛ x
1
⎞⎫
⎪⎜ ⎟ 3x 2 x 3 ⎪
x 0 ∈S 0 = ⎨⎪⎜⎜ x 2 ⎟∈R + 6 + 3 ≤1, x 1 ≤ 0, − x 2 ≤ 0, − x 3 ≤ 0⎪⎬;
⎩⎝ x 3 ⎟⎠⎭
I U ⎡⎣ ( )⋅ ⎤⎦ = x 1 (1)+ 2x 2 (1)− x 3 (1) → min .
Условия рассматриваемого примера совпадают с условиями примера 3 за исключением граничных условий на левом конце траектории. В данном примере множество S 0 содержит более одной точки. Множество S 0 показано на
рис. 16 .

Рис. 16
Повторяя выкладки из примера 3, приходим к тому, что
⎛U ˆ1 (t ,ψ)⎞ ⎧⎪ sign [ψi ], ψi < 0
ˆ ( ,ψ) = ⎜⎜U ˆ2 (t ,ψ)⎟⎟,U ˆi (t ,ψ) = ⎪⎨любоечисло ψi = 0,
U t
⎜⎜⎝U ˆ3 (t ,ψ)⎟⎟⎠ ⎩⎪⎪из −[0sign ,1],[ψ ψi ], i > 0.
Объединенная система дифференциальных уравнений принимает вид
x 1 = 2x 1 + 2x 2 −30x 3 +U ˆ 1 (t ,ψ), x 2 =10x 1 − x 2 −35x 3 +U ˆ 2 (t ,ψ), x 3 = 2x 1 − x 2 + x 3 +U ˆ 3 (t ,ψ),
ψ1 = −2ψ ψ ψ1 −10 2 −2 3 , ψ2 = −2ψ ψ ψ1 + 2 + 3 , ψ3 = 30ψ ψ ψ1 +35 2 − 3 .
В данном примере сопряженная система дифференциальных уравнений интегрируется независимо от основной системы. В результате с учетом граничных условий
ψ1 (1) = −1,ψ2 (1) = −2,ψ3 (1) =1
получим вектор-функцию ψ0 (t ), t ∈[0,1]. Эта функция тождественна той, что была построена в примере 3.
Тогда оптимальная программная стратегия имеет вид
⎧ 1, t ∈⎡⎣ 0, t ˆ),
⎪
⎪произвольноечисло
U
![]() t
= ⎨ t
= t
ˆ, , U
t
= ⎨ t
= t
ˆ, , U
![]() t U t t
,
t U t t
,
⎪ из [−1,1 ,]
⎪ ⎩ −1, t ∈(t ˆ,1 .⎤⎦
где t ˆ = 0.741061.
Подставим ее в исходную систему дифференциальных уравнений
x 1 = 2x 1 + 2x 2 −30x 3 +U 1 0 (t ),
x 2 =10x 1 − x 2 −35x 3 +U 2 0 ( )t , (18)
x 3 = 2x 1 − x 2 + x 3 +U 3 0 ( )t ,
В соответствии с теоремой 6 выпишем граничные условия на левом конце траектории. С учетом равенств
x
1
x
3
x
2
ϕ1
(x x x
1
, 2
, 3
) = ![]() + + −1,, (−9) 6 3
+ + −1,, (−9) 6 3
ϕ2 (x 1 ,x x 2 , 3 ) = x 1 , ϕ3 (x x x 1 , 2 , 3 ) = −x 2 , ϕ4 (x x x 1 , 2 , 3 ) = −x 3 ,
имеем
− 1 9 µ µ ψ1 + 2 = 1 ( )0 , 1 6 µ µ ψ1 − 3 = 2 (0), 1 3 µ µ ψ1 − 4 = 3 ( )0 ,
⎡ x 1 x 3 x 2 ⎤
µ1
⎢ ![]() + + −1⎥ = 0, µ2
x
1
= 0, µ3
x
2
= 0, µ4
x
3
= 0,
+ + −1⎥ = 0, µ2
x
1
= 0, µ3
x
2
= 0, µ4
x
3
= 0,
⎣ (−9) 6 3 ⎦
µ1 ≥ 0, µ2 ≥ 0, µ3 ≥ 0, µ4 ≥ 0 . (19)
Условия (19) однозначно определяют следующий набор параметров:
µ1 = 2050.13,µ2 = 346.69,µ3 = 468.885,µ4 = 0, x 10 0 = 0, x 20 0 = 0, x 30 0 = 3.0 .
Проинтегрируем систему(18) с полученными начальными условиями
⎛ x 10 0 ⎞ ⎛ ⎞0
⎜ 0 ⎟ ⎜ ⎟
x ( )0 = ⎜ x 20 ⎟ = ⎜ ⎟0
⎜⎝ x 300 ⎟⎠ ⎜ ⎟⎝ ⎠ 3
и вычислим значение функционала на оптимальном управлении. Имеем
I U ⎡⎣ 0 (⋅)⎤⎦ = −2344.02.
В примере 3 значение функционала на оптимальном управлении было «хуже» и равнялось величине −366.188. Такой результат является ожидаемым, так как
⎛−3⎞
начальная точка x 0 = ⎜ ⎜ 2 ⎟ ⎟ из примера 3 принадлежит множеству S 0 данного
⎜⎝ 1 ⎟⎠
примера.
2.6. Минимизация расстояния до целевого множества в случае подвижного левого конца траектории. Рассмотрим частный случай задачи 2, исследованной в пункте 2.5. Именно, будем предполагать, что функция Φ , определяющая критерий качества, имеет смысл евклидового расстояния от проекции фазового вектора на часть своих (k первых (k ≤ n )) координат до некоторого выпуклого компактного множества M ⊂ R k . Относительно множества S 0 ∈R n дополнительно предположим, что оно выпукло.
Пусть
Γ(t S T 0 , 0 , ) = ∪ G t x T ( 0 , 0 , ).
x 0∈S 0
Из непрерывной зависимости области достижимости от начального положения x 0 ∈S 0 (см. формулу Коши) компактности и выпуклости множества S 0 следует, что множество Γ(t S T 0 , 0 , ) ⊂ R n также является компактным и выпуклым. Предположим, что выполняется {Γ(t 0 ,S T 0 , )}k ∩ M = ∅. Полагаем
ε0
= min{ε> 0![]() {Γ(t
0
,S T
0
, )}k
∩ M
ε
≠ ∅}.
{Γ(t
0
,S T
0
, )}k
∩ M
ε
≠ ∅}.
Из компактности множества Γ(t S T 0 , 0 , ) следует существование минимума в правой части последнего равенства и справедливость соотношения
ε0 = I U ⎡⎣ 0 (⋅)⎤⎦ > 0.
Вычислим величину ε0 . По теореме 1.30 [22] условие
{Γ(t 0 ,S T 0 , )}k ∩ M ε ≠ ∅ будет иметь место тогда и только тогда, когда
![]()
![]() q
∈ Γ{ min(t S T
0 0, , )}k
l q
, ≤χ
(M
ε
, ),l
∀ l
∈ S
(0, 1)=
{s
∈ R
k
s
=1}.
q
∈ Γ{ min(t S T
0 0, , )}k
l q
, ≤χ
(M
ε
, ),l
∀ l
∈ S
(0, 1)=
{s
∈ R
k
s
=1}.
Отсюда следует, что
![]() ε0
= min⎨⎧ε> 0
ε0
= min⎨⎧ε> 0![]() min l q
, ≤ χ(M
ε
, )l
∀ ∈l S
(0, 1) ⎬
⎫
=
min l q
, ≤ χ(M
ε
, )l
∀ ∈l S
(0, 1) ⎬
⎫
=
⎩q ∈ Γ{ (t 0 0 ,S T , )} k ⎭
⎡⎤
![]()
![]() = max ⎢−maxm M
∈ m l
, + q
∈ Γ{ min(t S T
0 0, , )}k
q l
, ⎥⎦ . (1) l S
∈ (0,1) ⎣
= max ⎢−maxm M
∈ m l
, + q
∈ Γ{ min(t S T
0 0, , )}k
q l
, ⎥⎦ . (1) l S
∈ (0,1) ⎣
По аналогии с пунктом 2.4. можно показать, что максимум в (1) достигается на единственном векторе l 0 ∈S (0,1) и получить другую форму записи равенства (1)
![]()
![]()
![]() ⎡Тр
∗T Тр
∗
⎡Тр
∗T Тр
∗
0
![]()
![]()
![]() ε = maxl
=1 ⎢−maxm M
∈ m l
, + minx
0∈S
0x
0
, X T t
[ , 0
] l
+
∫minu P
∈B
( )τ u X
, [T
,τ τ]ld
+
ε = maxl
=1 ⎢−maxm M
∈ m l
, + minx
0∈S
0x
0
, X T t
[ , 0
] l
+
∫minu P
∈B
( )τ u X
, [T
,τ τ]ld
+
⎢⎣ t 0
T ⎤
![]() +∫
+∫![]() C
( )τ , X
Тр
[T
,τ τ]l
∗
d
⎥ . (2) t
0 ⎥⎦
C
( )τ , X
Тр
[T
,τ τ]l
∗
d
⎥ . (2) t
0 ⎥⎦
⎛ l ⎞
⎜ ⎟
∗ ⎜ 0 ⎟ ∈R n .
Здесь обозначено l =
⎜ ⎟
⎜⎜⎝ 0 ⎟⎟⎠
Теорема 7.
Пусть
ε0
> 0 и пара
![]() ,
U
0
( )⋅ ∈Π[t T
0
, ] является
,
U
0
( )⋅ ∈Π[t T
0
, ] является
решением задачи оптимального управления. Тогда
![]()
![]()
![]()
![]() x
0
0
, X
Тр
[T t
, 0
]l
0
∗
= min x
0
, X
Тр
[T t
, 0
]l
0
∗
(3)
x
0
0
, X
Тр
[T t
, 0
]l
0
∗
= min x
0
, X
Тр
[T t
, 0
]l
0
∗
(3)
x 0∈S 0
![]() B
( )t U
0
( )t
, X
Тр
[T t l
, ] 0
∗
= min B t u
( ) , X
Тр
[ (4)
B
( )t U
0
( )t
, X
Тр
[T t l
, ] 0
∗
= min B t u
( ) , X
Тр
[ (4)
u P ∈
⎛l 0 ⎞
⎜ ⎟
при почти всех t ∈[t T 0 , ], где l 0 ∗ = ⎜ ⎜ 0 ⎟ ⎟ ∈R n .
⎜⎜⎝ 0 ⎟⎟⎠
Доказательство. Из равенства (2) при l ∗ = l 0 ∗ выводим
T
![]()
![]()
![]()
![]() 0 = −max m l
, 0 + minx
0∈S
0
0 = −max m l
, 0 + minx
0∈S
0 ![]() x
0
, X
Тр
[T t l
, 0
] 0∗
x
0
, X
Тр
[T t l
, 0
] 0∗ ![]() + ∫minu P
∈ B
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0∗ d
+
+ ∫minu P
∈ B
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0∗ d
+
t 0
T
+∫![]() C
( )τ , X
Тр
[t
,τ τ]l
0
∗
d
.
C
( )τ , X
Тр
[t
,τ τ]l
0
∗
d
.
t 0
Пусть нарушается какое-либо из условий (3) - (4). Тогда одно из неравенств (или оба сразу)
![]() x
00, X
Тр
[T t l
, 0 ] 0∗ ≥ min x X
0, Тр
[T t l
, 0 ] 0∗
x
00, X
Тр
[T t l
, 0 ] 0∗ ≥ min x X
0, Тр
[T t l
, 0 ] 0∗ ![]() ,
,
x 0∈S 0
TT
![]()
![]()
![]() ∫
∫![]() B
( )τ U
0
( )τ , X
Тр
[T
,τ τ]l
0
∗
d
≥ ∫minu P
∈ B
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0
∗
d
.
(5)
B
( )τ U
0
( )τ , X
Тр
[T
,τ τ]l
0
∗
d
≥ ∫minu P
∈ B
( ) ( )τ τu
, X
Тр
[T
,τ τ]l
0
∗
d
.
(5)
t 0 t 0
![]() будет строгим. По аналогии с
пунктом 2.4
с учетом условия (5) вычисляем
будет строгим. По аналогии с
пунктом 2.4
с учетом условия (5) вычисляем
0 0 0 0 ⎡0⎤
ε = I x U ⎡⎣ 0 ,
m M ∈
T
![]()
![]()
![]()
![]() ( )⋅ ⎤⎦
= ρ
({x
( )T
}k
,M
) = maxl
=1 ⎣⎢
−maxm M
∈ m l
, + {x
( )T
}k
,l
⎥
⎦ =
( )⋅ ⎤⎦
= ρ
({x
( )T
}k
,M
) = maxl
=1 ⎣⎢
−maxm M
∈ m l
, + {x
( )T
}k
,l
⎥
⎦ =
t 0
+ x 0 0 , X Тр [T t l , 0 ] 0 ∗ B ( )τ U 0 ( )τ ,
![]() X
Тр
[t
,τ τ]l
0
∗
d
> −max m l
, + min x
0
,
X
Тр
[t
,τ τ]l
0
∗
d
> −max m l
, + min x
0
,
m M ∈ x 0 ∈S 0
T T
![]()
![]() +∫minu P
∈
+∫minu P
∈![]() B
( )τ u X
, Тр
[T
,τ τ]l
0
∗
d
+ ∫
B
( )τ u X
, Тр
[T
,τ τ]l
0
∗
d
+ ∫ ![]() C
( )τ , X
Тр
[t
,τ τ ε]l
0
∗
d
= 0
.
C
( )τ , X
Тр
[t
,τ τ ε]l
0
∗
d
= 0
.
t 0 t 0
Получили противоречие. Теорема доказана.
Последовательность действий по решению задачи управления динамической системой на основе теоремы 7 в целом аналогична той, что была описана в пункте 2.4. Отличие состоит лишь в том, что задача математического программирования (4.7) здесь принимает вид
![]()
![]()
![]() ⎛ l
⎞⎛ l
⎞
⎛ l
⎞⎛ l
⎞
⎜ ⎟⎜ ⎟
ε( )l = −χ(M l , )+ min X T t [ , 0 ]x 0 ,⎜ 0 ⎟ X T [ ,τ τ τ]B ( )U ˆ ( ,l ), ⎜ 0 ⎟ d τ+
x 0 ∈S 0 ⎜ ⎟⎜ ⎟
⎜⎜⎝ 0 ⎟⎟⎠⎜⎜⎝ 0 ⎟⎟⎠
![]() +X t
[ ,τ τ]C
( ), d
τ→ max , l
=1. (6)
+X t
[ ,τ τ]C
( ), d
τ→ max , l
=1. (6)
Эта задача всегда имеет решение, а в случае когда ε ε0 = ( )l 0 > 0 , это решение единственное. Другое отличие касается начальных условий для фазового вектора: их следует выбирать из соотношения (3). Также как и в пункте 2.4, достаточным условием оптимальности найденного управления будет являться совпадения величины ε0 и значения функционала на этом управлении.
Пример 11*. Рассматривается следующая управляемая система:
x 1 = x 3 ,
x 2 = x 4 ,
x 3 = (cost x ) 3 +tx 4 +u 1 ,
1
x
2
= ![]() x
3
+(sint x
) 4
+u
2
, t
+1
x
3
+(sint x
) 4
+u
2
, t
+1
![]() ⎪⎧⎛u
1 ⎞ 2 2 2 ⎪⎫
⎪⎧⎛u
1 ⎞ 2 2 2 ⎪⎫
u ∈P = ⎨⎜ ⎟∈R u 1 +u 2 ≤1⎬, t ∈[0,1],
⎪⎩⎝u 2 ⎠ ⎪⎭
⎧⎪⎛ m 1 ⎞ 2 2 2 ⎫ ⎪
k = 2, M = ⎨⎜ ⎟ ∈R (m 1 −5) +(m 2 − 4) ≤1⎬ ,
Фундаментальная матрица Коши для однородной системы дифференциальных уравнений, опорная функция множества M и функция U ˆ здесь совпадают с теми, что были построены в примере 7. Вычисляем
![]()
![]() ⎛ x
10
⎞ ⎛l
1
⎞
⎛ x
10
⎞ ⎛l
1
⎞
⎜ ⎟ ⎜ ⎟
min![]() x
0
, ψ0
∗
( )T
x
0
, ψ0
∗
( )T
![]() = min X
[1,0]⎜
x
20
⎟
,⎜
l
2
⎟
=
= min X
[1,0]⎜
x
20
⎟
,⎜
l
2
⎟
=
x 0∈S 0x 0∈S 0⎜ x 30 ⎟ ⎜ 0 ⎟
⎜⎜ x 40 ⎟⎟⎠ ⎜⎜⎝ 0 ⎟⎟⎠
⎝ = min0 0 ⎡⎣ l 1 (x 11 [1,0]x 10 + x 12 [1,0]x 20 + x 13 [1,0]x 30 + x 14 [1,0]x 40 )+ x ∈S
+l 2 (x 21 [1,0]x 10 + x 22 [1,0]x 20 + x 23 [1,0]x 30 + x 24 [1,0]x 40 )⎤⎦ =
= min0 0 ⎡⎣ x 10 (l x 1 11 [1,0]+l x 2 21 [1,0])+ x 20 (l x 1 12 [1,0]+l x 2 22 [1,0])+ x ∈S
+x
![]() + + + = =
+ + + = =
0∈ 0
i =1
![]() = − (0.2)2
β1
2
(l l
1
, 2
) (+ 0.1)2
β2
2
(l l
1
, 2
) (+ 0.1)2
β3
2
(l l
1
, 2
) (+ 0.2)2
β4
2
(l l
1
, 2
) = −Ξ(l l
1
, 2
), где обозначено
= − (0.2)2
β1
2
(l l
1
, 2
) (+ 0.1)2
β2
2
(l l
1
, 2
) (+ 0.1)2
β3
2
(l l
1
, 2
) (+ 0.2)2
β4
2
(l l
1
, 2
) = −Ξ(l l
1
, 2
), где обозначено
βi (l l 1 , 2 ) = l x 1 1i [1,0]+l x 2 2i [1,0 ,] i =1,2,3,4 .
При этом
β1 (l l 1, 2 ) (⋅ 0.2)2 β2 (l l 1, 2 ) (⋅ 0.1)2
x
10 (l l
1, 2 ) = − ![]() , x
20 (l l
1, 2 ) = −
, x
20 (l l
1, 2 ) = − ![]() , Ξ(l l
1
, 2
) Ξ(l l
1
, 2
)
, Ξ(l l
1
, 2
) Ξ(l l
1
, 2
)
β3 (l l 1 , 2 ) (⋅ 0.2)2 β4 (l l 1 , 2 ) (⋅ 0.1)2
x
30
(l l
1
, 2
) = − ![]() , x
40
(l l
1
, 2
) = −
, x
40
(l l
1
, 2
) = − ![]() . (7) Ξ(l l
1
, 2
) Ξ(l l
1
, 2
)
. (7) Ξ(l l
1
, 2
) Ξ(l l
1
, 2
)
Выпишем задачу математического программирования (6)
T
![]() ε( )l
= − −1 (5l
1
+ 4l
2
)−Ξ(l l
1
, 2
)− Ε∫
(τ,l l
1
0
, 2
0
)d
τ→ max, l
=1,
ε( )l
= − −1 (5l
1
+ 4l
2
)−Ξ(l l
1
, 2
)− Ε∫
(τ,l l
1
0
, 2
0
)d
τ→ max, l
=1,
t 0
где
![]() Ε(t l
, 1
0
,l
2
0
) = (x
13
(1,t l
) 1
0
+ x
23
(1,t l
) 2
0
)2
+(x
14
(1,t l
) 1
0
+ x
24
(1,t l
) 2
0
)2
.
Ε(t l
, 1
0
,l
2
0
) = (x
13
(1,t l
) 1
0
+ x
23
(1,t l
) 2
0
)2
+(x
14
(1,t l
) 1
0
+ x
24
(1,t l
) 2
0
)2
.
Решением этой задачи будет
l 1 0 = −0.781, l 2 0 = −0.625,ε(l 0 ) = 4.287.
Подставляя вектор l 0 в (7), находим оптимальное начальное положение фазового вектора
x 1 0 = 0.101, x 2 0 = 0.202, x 3 0 = 0.057, x 4 0 = 0.123. (8)
Оптимальная программная стратегия задается формулой
⎛ x 13 (1,t l ) 1 0 + x 23 (1,t l ) 2 0 ⎞
![]() ⎜−⎟
⎜−⎟
0 ⎜⎟
U ( )t = ⎜ 0 0 ⎟ . (9)
⎜ − x 14 (1,t l ) 1 + x 24 (1,t l ) 2 ⎟
![]() ⎜⎟
⎜⎟
⎝⎠
Оптимальный закон движения объекта определяется путем интегрирования основной системы дифференциальных уравнений с начальными условиями (8), в которую подставлено оптимальное программное управление (9). Ниже на рис. 16 приводятся графики изменения первых двух координат фазового вектора от времени
![]()
Рис. 16
Финальное значение проекции фазового вектора на первые две координаты и расстояние от нее до целевого множества задаются равенствами
0 ⎛ x 1 0 ( )1 ⎞ ⎛0.872⎞ 0 0 0
{x ( )1 }2 = ⎜⎜ x 20 ( )1 ⎟⎟⎠ = ⎜⎝ 0.697 ⎠ ⎟, ρ (x (1),M ) = 4.287 =ε ( )l =ε .
⎝
Последнее равенство означает оптимальность найденного программного управления.
В примере 7 значение функционала на оптимальном управлении было
«хуже» и равнялось величине 4.596 . Этот результат объясняется тем, что
⎛ ⎞0
⎜ ⎟
0 начальная точка x 0 = ⎜ ⎟ из примера 7 принадлежит множеству S 0 данного
⎜ ⎟0
⎜ ⎟⎜ ⎟⎝ ⎠0
примера.
Пример 12*. В условиях предыдущего примера принимается, что
![]() ⎧⎪⎛u
1
⎞ 2
⎫⎪ P
= ⎨⎜ ⎟∈R
≤1⎬.
⎧⎪⎛u
1
⎞ 2
⎫⎪ P
= ⎨⎜ ⎟∈R
≤1⎬.
⎩⎪⎝u 2 ⎠⎭⎪
Тогда вектор функция U ˆ определяется формулой
U t l l ˆ ( , ,1 2 ) = ⎛⎜−sign x ⎣⎡ 13 (1,τ)l 1 + x 23 (1,τ)l 2 ⎦⎤⎞⎟, (10)
⎜⎝−sign x ⎡⎣ 14 (1,τ)l 1 + x 24 (1,τ)l 2 ⎤⎦ ⎟⎠
а задача математического программирования (6) здесь принимает вид
ε( )l = − −1 (5l 1 + 4l 2 )−Ξ(l l 1 , 2 )−
1
![]()
![]()
![]() −∫⎡⎣
−∫⎡⎣
![]() x
13
(1,τ)l
1
+ x
23
(1,τ)l
2
+ x
14
(1,τ)l
1
+ x
24
(1,τ τ)l
2
⎤⎦
d
→ max, l
=1.
x
13
(1,τ)l
1
+ x
23
(1,τ)l
2
+ x
14
(1,τ)l
1
+ x
24
(1,τ τ)l
2
⎤⎦
d
→ max, l
=1.
0
Решением этой задачи будут числа
l 1 0 = −0.794, l 2 0 = −0.608,ε(l 0 ) = 3.973.
Подставляя вектор l 0 в (7), находим оптимальное начальное положение фазового вектора
x 1 0 = 0.103, x 2 0 = 0.197, x 3 0 = 0.057, x 4 0 = 0.121. (11)
Оптимальная программная стратегия задается формулой
U 0 ( )t = ⎛⎜−sign x ⎡⎣ 13 (1,τ)l 10 + x 23 (1,τ)l 20 ⎤⎦⎟⎞, t ∈[0,1]. (12)
⎜⎝−sign x ⎡⎣ 14 (1,τ)l 1 0 + x 24 (1,τ)l 2 0 ⎤⎦ ⎟⎠
Из графиков компонент вектора оптимального управления, представленных на
рис. 17,
U1 U2

0.2 0.4 0.6 0.8 1 0.2 0.4 0.6 0.8 1
Рис. 17.
видно, что оптимальное управление постоянно на всем промежутке времени [0,1]. Оптимальный закон движения объекта определяется путем интегрирования основной системы дифференциальных уравнений с начальными условиями (11), в которую подставлено оптимальное программное управление (12). Ниже приводятся графики изменения первых двух координат фазового вектора от времени.
![]()
Рис. 18
Финальное значение проекции фазового вектора на первые две координаты и расстояние от нее до терминального множества задаются равенствами
0 ⎛ x 1 0 ( )1 ⎞ ⎛1.053⎞ 0 0 0
{x ( )1 }2 = ⎜⎜ x 20 ( )1 ⎠ ⎟⎟ = ⎜⎝ 0.975 ⎟⎠ , ρ (x (1),M ) = 3.973 =ε ( )l =ε .
⎝
Последнее равенство означает оптимальность найденного программного управления.
Полученный результат лучше, чем в примере 8 ( 4.282 ) и лучше, чем в примере 11 ( 4.287 ). Это объясняется тем, что в первом случае точка x 0 из примера 8 принадлежит множеству S 0 данного примера, а во втором случае тем, что множество P из примера 11 вложено в множество P данного примера.
Упражнения для самостоятельной работы
1. Найти ошибку в рассуждениях.
Рассмотрим управляемый динамический объект
![]() ⎛u
1
⎞ ⎧⎪⎛u
⎛u
1
⎞ ⎧⎪⎛u
x 1 = u 1 , x 2 = u 2 , u = ⎜ ⎟∈P = ⎨⎜
⎝u 2 ⎠ ⎪⎩⎝
⎛ x 10 ⎞ ⎛ ⎞0
⎜ ⎟ = ⎜ ⎟ , t 0 = 0,T =1, Φ( )x = (x −0.25) +(x − 2) .
⎝ x 20 ⎠ ⎝ ⎠0
Критерий качества Φ здесь имеет смысл расстояния от финального положения фазового вектора до точки M , положение которой задается вектором
⎛0.25⎞
![]() r
M
= ⎜ ⎟. Тогда оптимальное управление (одно из возможных) имеет вид
r
M
= ⎜ ⎟. Тогда оптимальное управление (одно из возможных) имеет вид
⎝ 2 ⎠
0 ⎛0.25⎞
u ( )t = ⎜ ⎟ , t ∈[0,1].
⎝ 1 ⎠
![]()
Покажем, что управление u 0 (⋅) не удовлетворяет условиям принципа максимума Л.С. Понтрягина. Действительно, выпишем функцию Л.С. Понтрягина
H t x u ( , , ,ψ ψ ψ) = 1 1 u + 2 u 2 .
Максимум этой функции достигается, когда
u ˆ1 = sign (ψ1 ), u ˆ2 = sign (ψ2 ).
Сопряженная система здесь записывается так:
ψ1 = 0,ψ2 = 0 ⇒ψ1 0 (t ) = c 1 ,ψ2 0 (t ) = c 2 .
Управления, подозрительные на оптимальность, удовлетворяют условию
u ˆ1 = sign c ( 1 ) = const u , ˆ2 = sign c ( 2 ) = const .
После подстановки управлений u u ˆ1 , ˆ2 в основную систему дифференциальных уравнений получим
x 1 = sign c ( 1 ), x 2 = sign c ( 2 ).
Интегрируя основную систему, с учетом начальных условий находим
x 1 0 ( )t = sign c t ( )1 , x 2 0 ( )t = sign c ( 2 )t ⇒ x 1 0 (1) = sign c ( 1 ), x 2 0 ( )1 = sign c ( )2 .
Выпишем условия трансверсальности в конечный момент времени
![]() − ⇒
− ⇒
⎛
⎜
⎝⎛⎜⎜ψψ1200 ( )( )11 ⎠⎞ ⎜⎜
⎟⎟ = −⎜
⎜
⎜⎜
⎝
x 1 0 (1)−0.25 ⎞
⎟
(x 1 0 ( )1 −0.1)2 +(x 2 0 ( )1 −2)2 ⎟
⎟ ⇒ x 2 0 ( )1 −2 ⎟
![]() ⎟ (x
1
0
( )1 −0.1)2
+(x
2
0
( )1 −2)2
⎟⎟⎠
⎟ (x
1
0
( )1 −0.1)2
+(x
2
0
( )1 −2)2
⎟⎟⎠
⎧ sign c ( 1 )−0.25
⎪c 1 = − 2 2 ,
⎪⎪ (sign c ( )1 −0.1 ) +(sign c ( )2 −2 )
⎨
![]() ⎪c
2 = −
sign c
( )2
−2 .
⎪c
2 = −
sign c
( )2
−2 .
⎪ 2 2
![]() ⎪⎩
(sign c
( )1
−0.1) +(sign c
( )2
−2)
⎪⎩
(sign c
( )1
−0.1) +(sign c
( )2
−2)
Пусть c 1 0 ,c 2 0 - решение этой системы. Очевидно, что c c . Тогда оптимальное управление должно привести управляемую точку в вершины квадрата. Управление u 0 (⋅) этому условию не удовлетворяет.
2. Для линейных управляемых динамических систем, описанных в упражнениях раздела 1 (дифференциальные уравнения движения, начальные условия, отрезок времени управления), решить задачу оптимального управления со следующими функционалами:
Рассмотреть два случая геометрических ограничений на вектор управляющих параметров
![]() ⎧⎛u
1
⎞
⎧⎛u
1
⎞
⎪⎜ ⎟
1) P = ⎨⎜u 2 ⎟
⎪⎩⎜⎝u 3 ⎟⎠
⎫ ⎧⎛u 1 ⎞ 2 2 2 ⎪ ⎪⎜ ⎟ u 1 +u 2 +u 3 ≤1⎬, 2) P = ⎨⎜ u 2 ⎟
⎪⎭ ⎪⎩⎜⎝u 3 ⎟⎠
⎫
⎪
![]() u
≤1, i
=1,2,3⎬.
u
≤1, i
=1,2,3⎬.
⎪ ⎭
Убедиться, что результат управления во втором случае будет «лучше», чем в первом случае. Задачу оптимального управления следует решить двумя способами. Первый способ состоит в использовании необходимых условий оптимальности в форме принципа максимума Л.С. Понтрягина, второй способ – в форме прицеливания на опорный вектор к множеству области достижимости.
Проверить выполнение достаточных условий оптимальности.
3. Решить приведенные выше задачи оптимального управления в предположении, что начальное положение фазового вектора не фиксировано. Считать, что

3. ЗАДАЧА ЛИНЕЙНОГО ПРЕДЕЛЬНОГО БЫСТРОДЕЙСТВИЯ
3.1. Постановка задачи линейного предельного быстродействия и существование ее решения. Линейную задачу теории оптимального управления назовем задачей линейного быстродействия, если:
1) минимизируемый функционал имеет форму Лагранжа с подынтеграль-
ной функцией f 0 ≡1;
2) начальный момент времени фиксирован θ0 ={t 0 };
3) конечный момент времени не фиксирован θ1
∈{T
![]() T
> t
0
};
T
> t
0
};
4) левый и правый конец траектории закреплены S 0 ={x 0 }, S 1 ={0}, x 0 ≠ 0 ,
5) область изменения управляющих параметров P ⊂ R r выпукла.
Теорема 1 (Существование решения задачи линейного быстродействия.) Пусть для некоторого момента времени T ∗ > t 0 выполнено включение
0∈G t ( 0,x T 0 , ∗ ),
где G t x T ( 0 , 0 , ),T > t 0 - область достижимости управляемого объекта. Тогда задача линейного быстродействия имеет решение .
Доказательство. По предположению теоремы
Τ ={T
> t
0
![]() 0∈G t
( 0
,x T
0
, )} ≠ ∅ .
0∈G t
( 0
,x T
0
, )} ≠ ∅ .
Обозначим T 0 = inf T . Достаточно показать, что
T ∈Τ
0∈G t ( 0,x T 0 , 0 ). (1)
Рассмотрим последовательность
{T k } →T 0 , T k ∈Τ, k =1,2,
Включение (1) следует из замкнутости области достижимости, непрерывной зависимости ее от T и включений
0∈G t x T ( 0 , 0 , k ), k =1,2,
Теорема доказана.
Момент времени T 0 будем называть оптимальным временем перехода.
3.2. Необходимые условия оптимальности программной стратегии.
Пусть выполнены условия теоремы 1. Полагаем
![]()
![]() ε[ ]T
= maxl
=1 ⎡
⎢
⎣q G t
∈ min(
0 0,x T
, )
q l
, ⎥⎦
⎤
= maxl
=1 F l T
( , ), T
≥ t
0
, (1)
ε[ ]T
= maxl
=1 ⎡
⎢
⎣q G t
∈ min(
0 0,x T
, )
q l
, ⎥⎦
⎤
= maxl
=1 F l T
( , ), T
≥ t
0
, (1)
L T 0 ( ) ={l 0 ( )T ∈S (0,1) F l ( 0 ( )T ,T )= l S max∈ ( 0,1) F l T ( , ) }, T ≥ t 0 ,
где
T T
![]()
![]() F l T
( , ) =
F l T
( , ) =![]() X T t
[ , 0
]x
0
, l
X T t
[ , 0
]x
0
, l
![]() + ∫minu P
∈
+ ∫minu P
∈ ![]() X T
[ ,τ]B
( )τ u l d
, τ+ ∫
X T
[ ,τ]B
( )τ u l d
, τ+ ∫ ![]() X t
[ ,τ τ τ]C
( ), l d
.
X t
[ ,τ τ τ]C
( ), l d
.
t 0 t 0
По лемме 2.1 функция ε является непрерывной. Условие ε[T ] > 0 будет необходимым и достаточным для того, чтобы 0∉G t x T ( 0 , 0 , ). Отсюда следует, что оптимальное время перехода T 0 совпадает с наименьшим из корней уравнения ε[T ] = 0 , лежащим правее начального момента времени t 0 .
Теорема 2 ( необходимые условия оптимальности). Пусть T 0 - оптимальное время перехода и U 0 ( )⋅ - программное управление, решающее задачу линейного быстродействия. Тогда
![]() B
( )t U
0
( )t
, X
Тр
⎡⎣
T
0
,t l
⎤⎦
0
B
( )t U
0
( )t
, X
Тр
⎡⎣
T
0
,t l
⎤⎦
0
![]() = minu P
∈
= minu P
∈ ![]() B t u X
( ) , Тр
⎡⎣
T
0
,t l
⎦
⎤ 0
B t u X
( ) , Тр
⎡⎣
T
0
,t l
⎦
⎤ 0
![]() , (2)
, (2)
для всех l 0 ∈L 0 (T 0 ) и при почти всех t ∈⎣ ⎡t T 0 , 0 ⎤⎦ .
Доказательство. Допустим, что условие (2) нарушается. Тогда существует вектор l 0 ∈L T 0 ( ) и множество T ∈⎡⎣ t T 0 , 0 ⎦ ⎤ ненулевой меры, на котором выполняется неравенство
![]() B
(t U
) 0
( )t
, X
Тр
[T t l
, ] 0
B
(t U
) 0
( )t
, X
Тр
[T t l
, ] 0
![]() > min
> min ![]() B t u
( ) , X
Тр
[T t l
, ] 0
B t u
( ) , X
Тр
[T t l
, ] 0
![]() , t
∈T
.
, t
∈T
.
u P ∈
Следовательно,
T 0 T 0
![]()
![]() ∫
∫![]() B
( )τ U
0
( )τ , X
Тр
⎡⎣
T
0
,τ τ⎤⎦
l
0
d
> ∫ minu P
∈
B
( )τ U
0
( )τ , X
Тр
⎡⎣
T
0
,τ τ⎤⎦
l
0
d
> ∫ minu P
∈ ![]() B
( )τ u
, X
Тр
⎡⎣
T
0
,τ τ⎤⎦
l
0
d
. (3)
B
( )τ u
, X
Тр
⎡⎣
T
0
,τ τ⎤⎦
l
0
d
. (3)
t 0 t 0
Из равенства x 0 (T 0 ) = 0 и условия (3) выводим
![]() 0 =
0 =![]() x
0
(T
0
),l
0
x
0
(T
0
),l
0
T 0T 0
![]() X T
⎡⎣
0
,t
0
⎤⎦
x
0
, l
0
X T
⎡⎣
0
,t
0
⎤⎦
x
0
, l
0
![]() X T
⎡⎣
0
,τ⎦
⎤ B
( )τ τU
0
( ), l d
τ+ ∫
X T
⎡⎣
0
,τ⎦
⎤ B
( )τ τU
0
( ), l d
τ+ ∫ ![]() X T
⎣
⎡ 0
,τ τ⎤⎦
C
( ), l
0
X T
⎣
⎡ 0
,τ τ⎤⎦
C
( ), l
0
![]() d
τ=
d
τ=
0 t 0
T 0 T 0
![]()
![]()
![]()
![]()
![]() =X T
⎡⎣
0
,t
0
⎤⎦
x
0
, l
0
B
( )τ U
0
( )τ , X
Тр
⎡⎣
T
0
,τ τ⎤⎦
l
0
d
+ ∫X T
⎡⎣
0
,τ τ⎦
⎤C
( ), ld
τ>
=X T
⎡⎣
0
,t
0
⎤⎦
x
0
, l
0
B
( )τ U
0
( )τ , X
Тр
⎡⎣
T
0
,τ τ⎤⎦
l
0
d
+ ∫X T
⎡⎣
0
,τ τ⎦
⎤C
( ), ld
τ>
t
T 0
> X T
⎡⎣
0
,t
0
⎤⎦
x
0
, l
0
minu P
∈![]() B
( )τ u
, X
Тр
⎣
⎡T
0
,τ τ⎤⎦
l
0
d
+ ∫ X T
⎡⎣
0
,τ τ⎤⎦
C
( ), l
0
d
τ>=
B
( )τ u
, X
Тр
⎣
⎡T
0
,τ τ⎤⎦
l
0
d
+ ∫ X T
⎡⎣
0
,τ τ⎤⎦
C
( ), l
0
d
τ>=
0 t 0
=ε(T 0 ) = 0.
Получили противоречие, которое и доказывает справедливость теоремы.
Заметим, что условие (2) доказанной теоремы должно выполняться обязательно для всех векторов l 0 ∈L 0 (T 0 ). Покажем это на примере.
Пример 1. Рассмотрим следующую задачу линейного быстродействия:
![]() ⎛u
1
⎞ ⎧⎪⎛u
1
⎞ 2
⎫⎪
⎛u
1
⎞ ⎧⎪⎛u
1
⎞ 2
⎫⎪
x 1 = u 1 , x 2 = u 2 , u = ⎜ ⎟∈P = ⎨⎜ ⎟∈R ≤1⎬,
⎝u 2 ⎠ ⎪⎩⎝u 2 ⎠⎭⎪
⎛ x 10 ⎞ ⎛ ⎞1
⎜ ⎟ = ⎜ ⎟, t 0 = 0, .
⎝ x 20 ⎠ ⎝ ⎠1
![]() Очевидно, что здесь оптимальное время перехода
T
0
=1, а оптимальное программное управление (см.
рис. 1)
имеет вид
Очевидно, что здесь оптимальное время перехода
T
0
=1, а оптимальное программное управление (см.
рис. 1)
имеет вид
0 ⎛−1⎞
U ( )t = ⎜ ⎟ , t ∈[0,1].
⎝−1⎠
Проверим выполнение условий теоремы 2. Имеем
⎡ T ⎤
![]() ε[ ]T
= maxl
=1 ⎢l
1
+l
2
+ ∫ u
1min≤1,u
2 ≤1(u l
1 1
+u l d
2 2
) τ
⎥ =
ε[ ]T
= maxl
=1 ⎢l
1
+l
2
+ ∫ u
1min≤1,u
2 ≤1(u l
1 1
+u l d
2 2
) τ
⎥ =
⎣ 0⎦
![]()
![]() = maxl
=1 ⎡⎣
l
1
+l
2
−( l
+ l T
⎤⎦
.
= maxl
=1 ⎡⎣
l
1
+l
2
−( l
+ l T
⎤⎦
.
Наименьшим корнем уравнения ε[T ] = 0 является момент времени T 0 =1. При этом
![]() L
0 (T
0 ) = ⎪⎨⎧l
= ⎛⎜l
1 ⎞⎟ l
=1, l
1 ≥ 0,l
2 ≥ 0 ⎫⎪⎬.
L
0 (T
0 ) = ⎪⎨⎧l
= ⎛⎜l
1 ⎞⎟ l
=1, l
1 ≥ 0,l
2 ≥ 0 ⎫⎪⎬.
⎩⎪ ⎝l 2 ⎠⎭⎪
Условие (2) здесь принимает вид
![]() l U
1
0
1
0
( )t
+l U
2
0
2
0
(t
) = u
1min≤1,u
2 ≤1(l u
1
0
1
+l u
2
0
2
), t
∈[0,1 ,] . (4)
l U
1
0
1
0
( )t
+l U
2
0
2
0
(t
) = u
1min≤1,u
2 ≤1(l u
1
0
1
+l u
2
0
2
), t
∈[0,1 ,] . (4)
Очевидно, что оптимальное управление U 0 удовлетворяет соотношению (4),
![]() ⎛l
0
⎞ 0
⎛ ⎞1 0 0
при всех векторах
⎜ ⎟ . Однако, для одного вектора
l
= ⎜ ⎟
∈L
(T
)
⎛l
0
⎞ 0
⎛ ⎞1 0 0
при всех векторах
⎜ ⎟ . Однако, для одного вектора
l
= ⎜ ⎟
∈L
(T
)
⎝l 2 ⎠ ⎝ ⎠0
∗ ⎛−1⎞ этому условию удовлетворяет, например, управление U ( )t = ⎜ ⎟ , t ∈[0,1], кото ⎝+1⎠
рое заведомо не является оптимальным.
Приведем последовательность действий по решению задачи управления динамической системой на основе теоремы 2. По формуле (1) находим выражение для функции ε. Решаем уравнение ε[T ] = 0 . Наименьший корень T 0 > t 0 , если таковой найдется, будет оптимальным временем перехода. Далее определяется множество L 0 (T 0 ), которое является не пустым в силу непрерывности функции F и компактности множества S (0,1). Для каждого вектора l 0 ∈L 0 (T 0 ) по формуле (2) строится программное управление. По теореме 2 среди построенных управлений обязательно содержится управление U 0 ( )⋅ , для которого выполняется равенство x t ( 0,x U 0 , 0 (⋅),T 0 ) = 0. Управление U 0 (⋅) и будет оптимальным. Приведенный алгоритм будет эффективным, если множество L 0 (T 0 ) содержит ровно один элемент l 0 , а условие (2) определяет управление U 0 однозначно по существу.
Пример 2*. Рассмотрим следующую задачу линейного быстродействия
x 1 = x 2 +u 1 ,
x 2 = −x 1 +u 2 ,
![]() ⎧⎪⎛u
1 ⎞22 2 ⎫⎪
⎧⎪⎛u
1 ⎞22 2 ⎫⎪
u ∈P = ⎨⎜ ⎟∈R u 1 +u 2 ≤1⎬,
⎩⎪⎝u 2 ⎠⎭⎪
t 0 = 0, x 10 =1, x 20 =1.
Фундаментальная матрица Коши здесь имеет вид
⎛ cos(t − s ) sin(t − s )⎞
X t s [ , ] = ⎜ ⎟.
⎝ −sin(t − s ) cos(t − s ) ⎠
Вычисляем
⎡ ⎛ cosT
![]() = maxl
=1 ⎢⎣⎢ ⎝⎜−sinT
= maxl
=1 ⎢⎣⎢ ⎝⎜−sinT
![]()
![]()
![]() ε[T
] =
ε[T
] =
sinT ⎞⎛ ⎞1 ⎛l 1 ⎞T ⎛u 1 ⎞ ⎛cos(T −τ) −sin(T −τ)⎞ ⎛l 1 ⎞⎤
![]() cosT
⎠⎝ ⎠⎟⎜ ⎟1 , ⎝⎜l
2 ⎠⎟+ ∫min⎝⎜u
2 ⎠⎟, ⎝⎜ sin(T
−τ) cos(T
−τ) ⎟⎠ ⎝⎜l
2 ⎟⎠d
τ⎥⎦⎥ =
cosT
⎠⎝ ⎠⎟⎜ ⎟1 , ⎝⎜l
2 ⎠⎟+ ∫min⎝⎜u
2 ⎠⎟, ⎝⎜ sin(T
−τ) cos(T
−τ) ⎟⎠ ⎝⎜l
2 ⎟⎠d
τ⎥⎦⎥ =
![]() = max ⎡l
(cosT
+sinT
)+l
(−sinT
+ cosT
)−
= max ⎡l
(cosT
+sinT
)+l
(−sinT
+ cosT
)−
⎣
T ⎤
−∫ d ⎥ .
0 ⎦
Минимум подынтегрального выражения достигается на векторе
ˆ (τ, ,l T ) = −⎛⎜l 1 cos(T −τ)−l 2 sin(T −τ)⎞⎟∈P ,τ∈[0,T ].
U
⎝ l 1 sin(T −τ)+l 2 cos(T −τ) ⎠
Выражение для функции ε здесь принимает вид
![]() ε[T
] = max ⎡⎣l
(cosT
+sinT
)+l
(−sinT
+cosT
)−T
⎦⎤ =
ε[T
] = max ⎡⎣l
(cosT
+sinT
)+l
(−sinT
+cosT
)−T
⎦⎤ =
![]() 2 −T
,
2 −T
,
где
![]() L
0
( )T
={l
0
( )T
}, l
0
( )T
= 1 ⎛⎜
cosT
+sinT
⎞⎟
.
L
0
( )T
={l
0
( )T
}, l
0
( )T
= 1 ⎛⎜
cosT
+sinT
⎞⎟
.
⎝−sinT +cosT ⎠
Таким образом,
![]() ε0
[T
] = 0 ⇒T
0
= 2 .
ε0
[T
] = 0 ⇒T
0
= 2 .
Вычисляем оптимальное управление
1 ⎛−(cos 2 +sin 2)cos( 2 −t )+ −( sin 2 + cos 2)sin( 2 −t )⎞
![]()
![]()
![]() U
0 ( )t
=⎜⎜ ( ) ( ) ( ) ( ) ⎟⎟⎟.
U
0 ( )t
=⎜⎜ ( ) ( ) ( ) ( ) ⎟⎟⎟.
⎜ − cos 2 +sin 2 sin 2 −t − −sin 2 +cosT cos 2 −t
⎝⎠
Подставляя его в дифференциальные уравнения движения и интегрируя последние с заданными начальными условиями, находим
![]()
![]() x
1
0
( )t
= − 1
2
(− +2 2t
)(cost
+sint
), x
2
0
( )t
= − 1
2
(− +2 2t
)(cost
−sint
).
x
1
0
( )t
= − 1
2
(− +2 2t
)(cost
+sint
), x
2
0
( )t
= − 1
2
(− +2 2t
)(cost
−sint
).
Очевидно, что
![]()
![]() x
1
0
( 2) = x
2
0
( 2) = 0.
x
1
0
( 2) = x
2
0
( 2) = 0.
Таким образом, построенное управление U 0 (t ) является оптимальным.
Ниже на рис. 2 приводится оптимальная траектория движения
![]()
Рис. 2
Рассмотрим задачу линейного быстродействия для управляемого объекта, динамика которого описывается линейными дифференциальными уравнениями с переменными коэффициентами. Пример 3*
x 1 = (cost x ) 1 +tx 2 +u 1 ,
1 (5)
x
2
= ![]() x
1
+(sint x
) 2
+u
2
, t
+1
x
1
+(sint x
) 2
+u
2
, t
+1
![]() ⎧⎪⎛u
1 ⎞22 2 ⎫⎪
⎧⎪⎛u
1 ⎞22 2 ⎫⎪
u ∈P = ⎨⎜ ⎟∈R u 1 +u 2 ≤ 3⎬,
⎩⎪⎝u 2 ⎠⎭⎪
t 0 = 0, x 10 =1, x 20 =1.
Построим фундаментальную матрицу Коши для однородной системы дифференциальных уравнений и запишем выражение для функции ε. Имеем
![]()
![]()
![]() ⎡
⎛ x
11
[T
,0] x
12
[T
,0]⎞⎛ x
10
⎞ ⎛l
⎞ ⎛u
1
⎞ ⎛ x
11
[T
,τ] x
12
[T
,τ]⎞Тр
⎛l
1
⎞⎤
⎡
⎛ x
11
[T
,0] x
12
[T
,0]⎞⎛ x
10
⎞ ⎛l
⎞ ⎛u
1
⎞ ⎛ x
11
[T
,τ] x
12
[T
,τ]⎞Тр
⎛l
1
⎞⎤
![]() ε[ ]T
= maxl
=
1
⎢
⎜ ⎟⎜ ⎟, ⎜⎜ ⎟ ⎜, ⎟ ⎜ ⎟d
τ⎥
=
ε[ ]T
= maxl
=
1
⎢
⎜ ⎟⎜ ⎟, ⎜⎜ ⎟ ⎜, ⎟ ⎜ ⎟d
τ⎥
=
⎢⎣ ⎝ x 21 [T ,0] x 22 [T ,0]⎠⎝ x 20 ⎠ ⎝ 2 ⎠ ⎝u 2 ⎠ ⎝ x 21 [T ,τ] x 22 [T ,τ]⎠ ⎝l 2 ⎠⎥⎦
⎡ ⎛ x 11 [T ,0]+ x 12 [T ,0]⎞ ⎛l 1 ⎞⎞ ⎛l x 1 11 [T ,τ]+l x 2 21 [T ,τ]⎞⎤
= maxl =1 ⎢ ⎜ ⎟ ⎜, ⎟⎟ ⎜, ⎟d τ⎥ =
⎢⎣ ⎝ x 21 [T ,0]+ x 22 [T ,0]⎠ ⎝l 2 ⎠2 ⎠ ⎝l x 1 12 [T ,τ]+l x 2 21 [T ,τ]⎠⎥⎦
![]() = max ⎡⎣(x
[T
,0]+ x
[T
,0])l
+(x
[T
,0]+ x
[T
,0])l
−
= max ⎡⎣(x
[T
,0]+ x
[T
,0])l
+(x
[T
,0]+ x
[T
,0])l
−
T ⎤
−3⋅∫⎥ .
0 ⎦
Программная стратегия, удовлетворяющая необходимым условиям оптимальности, определяется по формуле
⎛ x
![]() ⎞ ⎜−
⎞ ⎜−![]() ⎟
⎟
⎜ ![]() ⎟
⎟
U 0 ( )t = 3⋅⎜ 0 0 0 0 ⎟, t ∈⎡⎣ t T 0 , 0 ⎤⎦ , l 0 ∈L 0 (T 0 ), (6)
⎜ x 14 (T ,t l ) 1 + x 24 (T ,t l ) 2 ⎟
⎜−![]() ⎟
⎟
![]() ⎜⎟
⎜⎟
⎝⎠
где
![]() Ε(t l
, 1
0
,l
2
0
,T
0
) = (x
13
(T
0
,t l
) 10
+ x
23
(T
0
,t l
) 20
)2
+(x
14
(T
0
,t l
) 10
+ x
24
(T
0
,t l
) 20
)2
.
Ε(t l
, 1
0
,l
2
0
,T
0
) = (x
13
(T
0
,t l
) 10
+ x
23
(T
0
,t l
) 20
)2
+(x
14
(T
0
,t l
) 10
+ x
24
(T
0
,t l
) 20
)2
.
В данном случае
0 0 0 0 0 ⎛ 0.617752⎞
T = 0.662, L (T ) { }= l , l = ⎜ ⎟ .
⎝0.786372⎠
Подставим управление (6) в дифференциальные уравнения (5) и проинтегрируем их с заданными начальными условиями. Непосредственно проверяется, что для полученного закона движения x 0 (t ), t ∈⎣ ⎡0,T 0 ⎤⎦ выполняется
0 ⎛−0.0000134271⎞ ⎛ ⎞0
x (0.662) = ⎜ ⎟ ≈ ⎜ ⎟.
⎝−0.0000148833⎠ ⎝ ⎠0
Таким образом, построенное управление U 0 (t ) является оптимальным. Ниже на рис. 3 приводится оптимальная траектория движения
![]()
Рис. 3
Пример 4*.
x 1 = −x 1 + 2x 2 −2x 3 +u 2 +u 3 , x 2 = x 1 −3x 2 − x 3 +u 1 +u 3 , x 3 = −x 1 + 4x 2 −2x 3 +u 1 +u 2 , t 0 = 0, x 10 =1, x 20 =1, x 30 =1.
В данном примере матрицы A и B имеют вид
| ⎛−1 ⎜ A = ⎜ 1 ⎜−1 ⎝ |
2 −3 4 |
−2⎞ ⎟ −1⎟, −2⎟⎠ |
⎛0 ⎜ B = ⎜1 ⎜1 ⎝ |
1 0 1 |
1⎞ ⎟ 1⎟ . 0⎟⎠ |
Заметим, что собственными числами матрицы A являются действительные числа -1, -2, -3.
Построим фундаментальную матрицу Коши для однородной системы дифференциальных уравнений и запишем выражение для функции ε. Имеем
⎛e −3(T −τ) (2−4e T −τ +3e 2(T −τ) ) −e −3(T −τ) (5−8e T −τ +3e 2(T −τ) ) −e −3(T −τ) (1− 4e T −τ +3e 2(T −τ) )⎞
⎜ ⎟
X t [ ,τ] = ⎜⎜ e −2(T −τ) (− +1 e T −τ) −e −2(T −τ) (− +2 e T −τ) −e −2(T −τ) (− +1 e T −τ) ⎟⎟
⎜ −3(T −τ) T −τ 2(T −τ) −3(T −τ) T −τ 2(T −τ) −3(T −τ) T −τ 2(T −τ) ⎟
⎜ e (2−3e +e ) −e (5−6e + e ) −e (1−3e + e ) ⎟
⎝ ⎠
⎡ 3 T ⎤
![]() ε[ ]T
= max ⎢m l l l T
( 1
, 2
, ,3
)+ ∑∫mini
k l l l T
i
( 1
, 2
, , ,3
τ τ)u d
i
⎥ =
ε[ ]T
= max ⎢m l l l T
( 1
, 2
, ,3
)+ ∑∫mini
k l l l T
i
( 1
, 2
, , ,3
τ τ)u d
i
⎥ =
l =1 u ≤1
⎣ i =1 0 ⎦
⎡ 3 T ⎤
![]()
![]() = max ⎢m l l l T
( 1
, 2
, ,3
)+ ∑∫ k l l l T
i
( 1
, 2
, , ,3
τ)
= max ⎢m l l l T
( 1
, 2
, ,3
)+ ∑∫ k l l l T
i
( 1
, 2
, , ,3
τ)![]() d
τ
⎥ ,
d
τ
⎥ ,
l =1 ⎣ i =1 0 ⎦
где
m l l l T ( 1, 2, ,3 ) = −( 4e −3T +8e −2T −3e −T )l 1 +(2e −2T −e −T )l 2 + −( 4e −3T + 6e −2T −e −T )l 3 , k 1 (l l l T 1, 2, , ,3 τ) = −6e −3(T −τ) (l 1 +l 3 )−2e −(T −τ) (3l 1 +l 2 +l 3 )+3e −2(T −τ) (4l 1 +l 2 +3l 3 ),
k 2 (l l l T 1, 2, , ,3 τ) = e −3(T −τ) (l 1 +l 3 ),
k 3 (l l l T 1, 2, , ,3 τ) = −3e −3(T −τ) (l 1 +l 3 )+e −2(T −τ) (4l 1 +l 2 +3l 3 ) .
Программная стратегия, удовлетворяющая необходимым условиям оптимальности, определяется по формуле
U
i
![]() t sign k
i
l l l T t t T i
.
t sign k
i
l l l T t t T i
.
В данном случае
⎛ 0.332184 ⎞
T 0 = 0.44738, L T 0 ( 0 ) { }= l 0 , l 0 = −⎜ ⎜ 0.705538⎟ ⎟ .
⎜ ⎝ 0.625998 ⎟ ⎠
По теореме 2.4 каждая из компонент оптимального программного управления должна иметь не более трех переключений. Убедимся в этом, приведя графики их изменения на промежутке времени ⎡⎣ 0,T 0 ⎤⎦ .
u1 u1
1.5 1.5
| 1 0.5 |
||
| 0.1 0.2 0.3 0.4 |
t -0.5 -1 |
0.1 0.2 0.3 0.4 |
1 0.5
t -0.5
-1
-1.5 -1.5
![]()
Рис. 4
На рис. 4 видно, что первая компонента оптимального программного управления переключается в момент времени t ∗ = 0.426649, третья компонента – в момент времени t ∗∗ = 308253, а вторая компонента остается все время постоянной.
Непосредственно проверяется, что для полученного закона движения x 0 ( )t , t ∈⎡⎣ 0,T 0 ⎤⎦ выполняется
⎛−0.000568689⎞ ⎛ ⎞0
x 0 (0.44738) = −⎜ ⎜ 0.000411838⎟ ⎟ ≈ ⎜ ⎟ ⎜ ⎟ 0 .
⎜⎝−0.000184312⎟⎠ ⎜ ⎟⎝ ⎠0
Таким образом, построенное управление U 0 (t ) является оптимальным.
Ниже на рис. 5 приводится оптимальная траектория движения
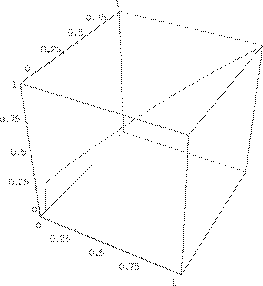
Рис. 5.
Упражнения для самостоятельной работы
Для линейных управляемых динамических систем
x 1 = −3x 1 + 4x 2 −6x 3 +u 1 , x 1 = −2x 1 −4x 2 −60x 3 +u 1 , x 2 = x 1 −2x 2 + 2x 3 +u 2 , x 2 = −4x 1 − x 2 −51x 3 +u 2 ,
а) x 3 = 2x 1 − x 2 +3x 3 +u 3 , б) x 3 = 2x 1 −2x 2 + x 3 +u 3 , t 0 = 0, x 10 = −1.43859, t 0 = 0, x 10 = 3.84645,
x 20 = 0.580455, x 30 =1.35472, x 20 = 4.12477, x 30 = −0.591971,
x 1 = 2x 1 + 4x 2 −16x 3 +u 1 , x 1 = −3x 1 − x 2 −5x 3 +u 1 , x 2 = 2x 1 − x 2 + 21x 3 +u 2 , x 2 = x 1 − x 2 +u 2 ,
в) x 3 = −2x 1 −2x 2 + x 3 +u 3 , г) x 3 = x 1 + x 2 + 2x 3 +u 3 , t 0 = 0, x 10 =15.3151, t 0 = 0, x 10 = −1.56927,
x 20 = −11.9799, x 30 = 3.9094 x 20 = −0.473713, x 30 =1.2287
решить задачу быстродействия. Рассмотреть два случая:
![]()
![]() ⎧⎛u
1
⎞⎫ ⎧⎛u
1
⎞ ⎫
⎧⎛u
1
⎞⎫ ⎧⎛u
1
⎞ ⎫
1) P = ⎨⎪⎜⎜u 2 ⎟⎟∈R u 312 +u 22 +u 32 =1⎪⎬, 2) P = ⎪⎨⎜⎜u 2 ⎟⎟∈R 3 ⎪⎬
⎪⎜⎝u 3 ⎟⎠⎪⎭ ⎩⎪⎜⎝u 3 ⎟⎠ ⎭⎪
⎩
Показать, что оптимальное время перехода в первом случае больше, чем во втором. Обосновать этот результат.
4. ЛИНЕЙНАЯ ЗАДАЧА ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕ-
НИЯ КАК ФУНКЦИОНАЛЬНАЯ ПРОБЛЕМА МОМЕНТОВ
4.1. Сведение задачи теории оптимального управления к функциональной проблеме моментов. Рассмотрим задачу теории оптимального управления, в которой θ0 ={ }t 0 ,θ1 ={T }, S 0 ={x 0 }, S 1 ={x T }, P = R r , а минимизируемый функционал имеет вид
T
I [u ()⋅ ]= ∫ f 0 (u ( )τ )d τ. (1)
t 0
Класс программных стратегий отождествим с множеством L r p [t 0 ,T ] измеримых по Лебегу r -мерных вектор-функций U :[t T 0 , ]→ R r , для которых функция
![]() U
( )⋅
p
, p
∈[1,∞) суммируема на [t
0
,T
] в смысле Лебега.
U
( )⋅
p
, p
∈[1,∞) суммируема на [t
0
,T
] в смысле Лебега.
Относительно минимизируемого функционала I дополнительно предположим:
1) для всех U
( )![]() L t T
справедливо неравенство I U
⎡⎣ ( )⋅ ⎤⎦
≥ 0, причем
L t T
справедливо неравенство I U
⎡⎣ ( )⋅ ⎤⎦
≥ 0, причем
I U ⎡⎣ ( )⋅ ⎤⎦ = 0 тогда и только тогда, когда U t ( ) = 0 почти всюду на [t 0 ,T ];
2) для всех U
1
( )![]() U
2
( ) L t T
0
справедливо неравенство
U
2
( ) L t T
0
справедливо неравенство
I U ⎡⎣ 1 (⋅)+U 2 (⋅)⎤⎦ ≤ I U ⎡⎣ 1 (⋅)⎦ ⎤ + I U ⎡⎣ 2 (⋅)⎤⎦ ;
3) для всех U ( )⋅ ∈L t T r p [ 0 , ] , λ∈R 1 имеет место равенство
![]() I
⎡⎣
λU
(⋅)⎤⎦
= λI U
⎡⎣
(⋅)⎤⎦
.
I
⎡⎣
λU
(⋅)⎤⎦
= λI U
⎡⎣
(⋅)⎤⎦
.
Условия 1)-3) позволяют истолковать функционал I как некоторую норму
на функциональном пространстве L r p [t 0 ,T ].
Следуя [17], осуществим сведение задачи теории оптимального управления к функциональной проблеме моментов. Пусть U
![]() L t T
– некоторое программное управление, переводящее фазовый вектор из положения x
0
в момент времени t
0
в положение x
T
в момент времени T
, и x
( )⋅ = x
(⋅,t x U
0
, 0
, (⋅)). Тогда с учетом x
( )T
= x
T
по формуле Коши получим
L t T
– некоторое программное управление, переводящее фазовый вектор из положения x
0
в момент времени t
0
в положение x
T
в момент времени T
, и x
( )⋅ = x
(⋅,t x U
0
, 0
, (⋅)). Тогда с учетом x
( )T
= x
T
по формуле Коши получим
T T
x T = X T t [ , 0 ]x 0 + ∫ X t [ ,τ]B ( ) ( )τ τ τu d + ∫ X t [ ,τ τ τ] W ( )d . (2)
t 0 t 0
Введем обозначения
H T [ ,τ] = X T [ ,τ τ τ]B ( ), ,t ∈[t T 0 , ],
T
c = x T − X [T ,t 0 ]x 0 − ∫ X [t ,τ]W ( )τ d τ.
t 0
Определение 1. Матрицу H [T ,τ], t ,τ∈[t 0 ,T ] будем называть переходной матрицей объекта.
Условие (2) перепишем с учетом введенных обозначений
T с = ∫ H [t ,τ]u ( )τ d τ.
t 0
Пусть h ( i ) [t ,τ τ] , ,t ∈[t T 0 , ] , i =1, ,n – строки переходной матрицы. Тогда последнее равенство в координатной форме имеет вид
T
![]() с
i
= ∫
с
i
= ∫
![]() (h
( )
i
[t
,τ]
)T
, U
( )τ τd
, i
=1, ,n
. (3)
(h
( )
i
[t
,τ]
)T
, U
( )τ τd
, i
=1, ,n
. (3)
t 0
Вектор-функции h [ ] i ( )⋅ = (h ( ) i [T ,⋅])T , i =1, ,n отождествим с элементами линейно-
![]() го функционального пространства L
q
r
[t
0
,T
], где 1
+ 1
= 1. Такое предположение
го функционального пространства L
q
r
[t
0
,T
], где 1
+ 1
= 1. Такое предположение
p q
правомерно, так как функции h [ i ] (⋅), i =1, ,n непрерывны на [t 0 ,T ]. В дальнейшем это пространство функций будем называть основным для рассматриваемой задачи оптимального управления. Обозначим его символом Ω[t 0 ,T ].
На основании теоремы о представлении линейных функционалов на пространстве функций [16] можно установить взаимно однозначное соответствие между линейными функционалами ϕ, определенными на пространстве Ω[t 0 ,T ] и программными управлениями u (⋅) формулой
T
ϕu
[h
()⋅ ]= ∫![]() h
( )τ , u
( )τ
h
( )τ , u
( )τ ![]() d
τ, h
()⋅ ∈Ω[t
0
,T
]. (4)
d
τ, h
()⋅ ∈Ω[t
0
,T
]. (4)
t 0
Формула (4) позволяет отождествить совокупность программных управлений с пространством Ω∗ [t 0 ,T ], сопряженным к основному пространству, т.е. с пространством линейных функционалов, определенных на Ω[t 0 ,T ]. Превратим линейное пространство Ω[t 0 ,T ] в нормированное, определив для каждого его элемента h ()⋅ ∈Ω[t 0 ,T ] норму
![]() T
h
()⋅ = sup ∫
T
h
()⋅ = sup ∫
![]() h
( )τ , u
( )τ
h
( )τ , u
( )τ ![]() d
τ, I
[u
()⋅ ]≤1. (5)
d
τ, I
[u
()⋅ ]≤1. (5)
u
( )
![]() t
0
t
0
![]() В силу предположений 1)-3) формула (5) действительно определяет некоторую норму ⋅ на основном пространстве Ω[t
0
,T
] [16], при этом естественная норма
В силу предположений 1)-3) формула (5) действительно определяет некоторую норму ⋅ на основном пространстве Ω[t
0
,T
] [16], при этом естественная норма
![]() ∗
в сопряженном пространстве Ω∗
[t
0
,T
] совпадает с функционалом I
[u
(⋅)]. Таким образом, задача об оптимальном управлении свелась к следующей функциональной проблеме моментов.
∗
в сопряженном пространстве Ω∗
[t
0
,T
] совпадает с функционалом I
[u
(⋅)]. Таким образом, задача об оптимальном управлении свелась к следующей функциональной проблеме моментов.
Задача 1. Пусть h [ ] 1 , ,h [ n ] ∈H , где H – линейное нормированное простран-
ство и c 1 , ,c n ∈R 1 . Требуется найти линейный функционал ϕ0 ∈H ∗ , для которого
ϕ0 [h [ i ] ]= c i ,i =1, ,n , (6)
![]() и такой, что среди всех других функционалов
ϕ∈H
∗
, удовлетворяющих условию (6), он имел бы наименьшую норму
⋅
∗
.
и такой, что среди всех других функционалов
ϕ∈H
∗
, удовлетворяющих условию (6), он имел бы наименьшую норму
⋅
∗
.
Выведем необходимые и достаточные условия разрешимости задачи 1. Прежде всего, заметим, что если c 1 = = c n = 0 , то решением проблемы моментов будет тривиальный функционал. Поэтому в дальнейшем этот случай рассматривать не будем. Полагаем
![]() ⎧ n
[ ]
i
1 n
⎫
⎧ n
[ ]
i
1 n
⎫
Q = ⎨h = ∑l i hl i ∈R ,i =1, ,n , ∑l i c i =1⎬.
⎩ i =1 i =1 ⎭
Справедливы следующие утверждения.
Лемма 1. Пусть ϕ∈H ∗ линейный функционал, удовлетворяющий условию
(6). Тогда
ϕ[h ]=1, ∀h ∈Q .
Доказательство. Для всех h ∈Q имеем
n n n
![]() .
.
⎣ i =1 ⎦ i =1 i =1
Лемма доказана.
Лемма 2. Существует элемент h 0 ∈Q , удовлетворяющий условию
![]()
![]() = min h
.
(7)
= min h
.
(7)
h ∈Q
Доказательство. Сначала предположим, что элементы h [ ] i , i =1, ,n ли-
n нейного пространства H независимы, т. е., что для них равенство ∑αi h [ ] i = 0
i =1
возможно лишь при нулевом наборе констант αi ∈ R 1 , i =1, ,n .
В линейном пространстве H рассмотрим последовательность элементов
n n
{ }h s , h s = ∑l is h [ ] i ∈ H , ∑c i l is =1, s =1,2, , (8)
i =1 i =1
![]() для которой
lim h
s
= inf h
. Заметим, что справедливо неравенство
для которой
lim h
s
= inf h
. Заметим, что справедливо неравенство
s →∞ h ∈Q
![]() 0 ≤ inf h
< +∞. (9)
0 ≤ inf h
< +∞. (9)
h ∈Q
Для каждого номера s =1,2, обозначим
![]()
![]() l
s
max = max l
is
.
l
s
max = max l
is
.
i ∈{1, ,n }
![]() Достаточно показать, что последовательность
{l
s
max
} ограничена. Допустим противное. Полагаем
Достаточно показать, что последовательность
{l
s
max
} ограничена. Допустим противное. Полагаем
∗ l is
l
is
= ![]() max , i
=1, ,n
, s
=1,2,
max , i
=1, ,n
, s
=1,2,
l s
![]() Очевидно, что
l
is
∗
≤1, i
=1, ,n
, и для всех номеров
s
=1,2, среди чисел
l
1
∗
s
, ,l
ns
∗
Очевидно, что
l
is
∗
≤1, i
=1, ,n
, и для всех номеров
s
=1,2, среди чисел
l
1
∗
s
, ,l
ns
∗
⎛l 1∗s ⎞
⎜ ⎟
хотя бы одно является единицей. Тогда последовательность векторов l s ∗ = ⎜ ⎟
⎜ ∗ ⎟
⎝l ns ⎠
⎛l 10∗ ⎞
⎜ ⎟
имеет предельную точку
l
![]() ⎜ ⎟ ≠ 0. В силу линейной независимости элемен-
⎜ ⎟ ≠ 0. В силу линейной независимости элемен-
⎜ ∗ ⎟
⎝l n 0 ⎠
n
тов
h
[ ]
i
∈ H
, i
=1, ,n
, будет выполнено
![]() . Каждый член последователь-
. Каждый член последователь-
i =1
ности (8) можно представить в виде
![]() h
s
= l
s
max ⎛⎜∑n
l
is
∗ h
[ ]i
⎞
⎟, s
=1,2, .
h
s
= l
s
max ⎛⎜∑n
l
is
∗ h
[ ]i
⎞
⎟, s
=1,2, .
⎝ i =1 ⎠
Переходя к пределу в равенстве
![]()
![]() n
n
∑l is ∗ h [ ]i , s =1,2,
i =1
по подходящей подпоследовательности, получим противоречие с условием (9). Случай, когда набор элементов h [ i ] ∈ H , i =1, ,n не является независимым, сводится к предыдущему случаю путем замены в (8) зависимых элементов линейными комбинациями независимых элементов. Лемма доказана. Определение 2. Элемент
n
h 0 = ∑l i 0h [ ]i ,
i =1
удовлетворяющий условию (7), назовем «минимальным», а его норму обозначим
символом ρ0 .
Теорема 1 (необходимые условия разрешимости проблемы моментов). Пусть функционал ϕ0 ∈H ∗ решает функциональную проблему моментов ( задачу
1 ). Тогда
0 0 1
![]() ρ > 0 и
ϕ ≥ 0
.
ρ > 0 и
ϕ ≥ 0
.
ρ
Доказательство. Предположим, что ρ0 = 0 . Тогда h 0 = 0. Последнее невозможно. Действительно, с одной стороны, из линейности функционала ϕ0 вытекает, что ϕ0 [h 0 ]= 0 , а, с другой стороны, в силу h 0 ∈Q и леммы 1 должно быть ϕ0 [h 0 ]=1. Таким образом, ρ0 > 0 .
∗
С учетом вложения Q ⊂ H дадим оценку для величины ϕ0 . Имеем:
0 ∗ ϕ(h ) ϕ(h ) 1 1 1
![]()
![]()
![]()
![]() ϕ = sup≥ sup= sup = = 0
.
h
∈H
h
h
∈Q
h
h
∈Q
h
inf h
ρ
ϕ = sup≥ sup= sup = = 0
.
h
∈H
h
h
∈Q
h
h
∈Q
h
inf h
ρ
h ∈Q
Теорема доказана.
Обозначим через
![]() ~ ⎧ n
[ ]
i
1
⎫
~ ⎧ n
[ ]
i
1
⎫
H = ⎨h = ∑l i hl i ∈R ,i =1, ,n , ⎬
⎩ i =1 ⎭
~ подпространство пространства H . Заметим, что для произвольного h ∈H разложение
n
h = ∑l i h [ ] i (10)
i =1
не всегда однозначно. Тем не менее, справедливо следующее утверждение.
0 ~ n
Лемма 3. Пусть ρ > 0 . Тогда для любого h ∈H величина ∑l i c i , где l 1 , ,l n
i =1
– коэффициенты разложения (10), полностью определяется элементом h ∈ H ∗ и не зависит от конкретного вида разложения (10).
~
Доказательство. Допустим противное. Тогда найдется h ∈H , для кото-
рого
n n n n
h = ∑l i 'h [ ] i = ∑l i ''h [ ] i , ∑l i 'c i ≠ ∑l i ''c i . (11)
i =1 i =1 i =1 i =1
Из условий (11) выводим, что
| ∑(l i '−l i '')h [ ] i = 0, ∑(l i '−l i '')c i ≠ 0 . (12) i =1 i =1 n Первое равенство в (12) разделим на величину ∑(l i '−l i '')c i ≠ 0. Имеем |
|||
| i =1 |
|||
| n (l i '−l i '') [ ]i ∑ h = 0. n i =1 ( ) ∑ l j '−l j '' c j j =1 Обозначим (l '−l '') l i = n i i , i = 1, ,n . ∑(l j '−l j '')c j j =1 n Тогда ∑l i c i =1 и равенство (13) запишется в виде i =1 n n ∑l i h [ ] i = 0, ∑l i c i =1. i =1 i =1 |
(13) |
||
![]()
![]() n n
n n
Последнее означает, что 0∈Q , а это противоречит условию ρ0 > 0 . Лемма доказана.
Теорема 2 (достаточные условия разрешимости проблемы моментов). Пусть ρ0 > 0 . Тогда проблема моментов имеет решение – функционал ϕ0 . При этом
0 ∗ 1
![]() ϕ = 0
.
ϕ = 0
.
ρ
Доказательство. Определим функционал ϕ ~ : H ~ → R 1 , положив
ϕ ~ [ ]h = ∑n l i c i , h ∈H ~ . (14)
i =1
Здесь l i ,i =1, ,n – коэффициенты разложения (10). В силу леммы 3 функционал (14) определен однозначно. Кроме того, он линеен. Действительно, для всех
~
α,β∈R
1
, h
,g
∈H
имеет место равенство
ϕ
~[αh
+ βg
]=ϕ
~⎡⎢
α∑n
l
i
[ ]h
h
[ ]i
+ β∑n
l
i
[ ]g
h
[ ]i
⎤⎥
=ϕ
~⎡⎢
∑n
![]() [ ] [ ]
c
i
=
[ ] [ ]
c
i
=
⎣ i =1 i =1 ⎦ ⎣ i =1 ⎦ i =1
n n
=α∑l i [ ]h с i + β∑l i [ ]g c i =αϕ~[ ]h + βϕ~[ ]g .
i =1 i =1
Выполнение равенств
ϕ~[h [i ]]=ϕ~[0⋅h [ ]1 + +1⋅h [i ] + + 0⋅h [n ]]= c i , i =1, ,n .
для функционала ϕ ~ очевидно.
Обозначим
⎛ l 1 ⎞n
![]() ⎜ ⎟ ⎧⎫
⎜ ⎟ ⎧⎫
l = ⎜ ⎟, L = ⎨l ∑l i c i =1⎬
⎜⎝l n ⎟⎠ ⎩i =1 ⎭
и вычислим норму функционала ϕ ~ как линейного функционала, определенного
~ на линейном нормированном пространстве H . Имеем:
![]()
![]() =
=
По следствию из теоремы Хана-Банаха [16 ] линейный функционал ϕ ~
~ может быть продолжен с подпространства H на все пространство H без увеличения его нормы. Обозначим это продолжение через ϕ0 . Легко видеть, что для функционала ϕ0 выполнены условия (6), а величина его нормы совпадает с нижней оценкой из теоремы 1 для нормы функционала, решающего задачу 1. Следовательно, функционал ϕ0 является искомым. Теорема доказана. Теорема 3 (принцип максимина). Пусть ϕ0 ∈H ∗ – решение задачи 1 , h 0 ∈Q
⎧ ∗ ⎫
![]() – «минимальный» элемент и
G
= ⎨ϕ∈H
ϕ ⎬. Тогда
– «минимальный» элемент и
G
= ⎨ϕ∈H
ϕ ⎬. Тогда
⎩⎭
ϕ0 (h 0 )= maxϕ [h 0 ].
ϕ∈G
Доказательство. Для всякого функционала ϕ∈G справедливо
![]() ϕ(h
0 ) ≤ ϕ ∗ h
0 = 10 ⋅ρ0 =1.
ρ
ϕ(h
0 ) ≤ ϕ ∗ h
0 = 10 ⋅ρ0 =1.
ρ
С другой стороны, в силу леммы 1 имеет место равенство ϕ (h 0 )=1. Теорема доказана.
Применим теоремы 1-3 к рассматриваемой линейной задаче теории оптимального управления. В результате получим следующее утверждение.
![]() Теорема 4.
Задача оптимального управления имеет решение тогда и только тогда, когда для
r
-мерной вектор-функции
h
0
(⋅), найденной из условия (7), где
⋅ определяется формулой (5), а
Теорема 4.
Задача оптимального управления имеет решение тогда и только тогда, когда для
r
-мерной вектор-функции
h
0
(⋅), найденной из условия (7), где
⋅ определяется формулой (5), а
⎧ n [ ]i ⎫
Q
= ⎨h
( )⋅ =
∑l h
i
( )⋅![]() l
∈L
⎬,
l
∈L
⎬,
⎩ i =1 ⎭
![]() справедливо неравенство
h
= ρ0
> 0. При этом
I
справедливо неравенство
h
= ρ0
> 0. При этом
I
![]() , и оптимальное
, и оптимальное
управление на минимальном элементе h 0 обладает свойством максимума
T T
∫![]() h
0
( )τ , u
0
( )τ
h
0
( )τ , u
0
( )τ ![]() d
τ= max ∫
d
τ= max ∫ ![]() h
0
( ) ( )τ , u
τ
h
0
( ) ( )τ , u
τ ![]() d
τ.
(15)
d
τ.
(15)
I
![]()
t 0 ρ t 0
Опираясь на утверждение теоремы 4 , сформулируем правило решения задачи об оптимальном управлении.
На первом этапе следует посредством формулы (5) ввести норму на линейном пространстве r -мерных функций Ω[t 0 ,T ]. На втором – строится «минимальный» элемент h 0 ()⋅ из условия (7), и на третьем – из условия (15) определяется оптимальное управление u 0 (⋅).
4.2. Управляемость линейной динамической системы. Важной характеристикой динамической системы является ее управляемость. Определение 3. Линейная динамическая система
x = A t x ( ) + B t u ( ) (1)
называется вполне управляемой на промежутке времени [t T 0 , ], если для любых векторов x 0 ,x T ∈R n существует такое программное управление u ( )⋅ , что для него выполняется равенство
x (⋅,t x u 0 , 0 , (⋅)) = x T .
Относительно системы (1) дополнительно предположим, что элементы матриц A t ( ) и B ( )t непрерывно дифференцируемы не менее чем n −1 раз по переменной t на промежутке времени [t T 0 , ]. Полагаем
d d
L t
1
( ) = B t
( ), L
2
( )t
= A t L t
( ) 1
( )− ![]() L t
1
( ), ,L
n
( )t
= A t L
( ) n
−
1
( )t
−
L t
1
( ), ,L
n
( )t
= A t L
( ) n
−
1
( )t
− ![]() L
n
−
1
( )t
. dt dt
L
n
−
1
( )t
. dt dt
Сконструируем матрицу
K t ( ) = (L t 1 ( ), ,L n (t ))
размера n ×(r n ⋅ ).
Теорема 5. Пусть существует момент времени t ∗ ∈[t T 0 , ] такой, что rang K t ⎡⎣ ( )∗ ⎤⎦ = n . Тогда система (1) вполне управляема на промежутке времени
[t T 0 , ].
Доказательство. Достаточно установить, что для всех c ∈R n , c ≠ 0 спра-
ведливо неравенство
![]()
![]() n
n
ρ0
( )c
=![]() h
0
(c
,⋅)
h
0
(c
,⋅) ![]() = minn
∑l h
i
[ ]
i
( )⋅
= minn
∑l h
i
[ ]
i
( )⋅
∑l ci i =1i =1
i =1
= minn
![]() (X T
[ ,⋅]B
( )⋅ )T
l
(X T
[ ,⋅]B
( )⋅ )T
l
![]() =
=
∑l ci i =1
i =1
=![]() (X T
[ ,⋅]B
( )⋅ )T
l
0
( )c
(X T
[ ,⋅]B
( )⋅ )T
l
0
( )c
![]() > 0.
> 0.
Допустим противное. Тогда существует вектор c ∗ ∈R n такой, что ρ0 (c ∗ ) = 0. Это возможно, если по переменной t на промежутке [t T 0 , ] выполняется тождество
(X T t B t [ , ] ( ))T l 0 ( )c ∗ = (X T t L t [ , ] 1 ( ))T l 0 (c ∗ ) = (L t 1 ( ))T (X T t [ , ])T l 0 ( )c ∗ = 0 . (2)
Продифференцируем (2) по переменной t . Имеем
![]() d
⎡(L t
( ))T
(X T t
[ , ])T
l
0
( )c
∗
⎤ =
d
⎡(L t
( ))T
(X T t
[ , ])T
l
0
( )c
∗
⎤ = ![]() d
⎡(X T t B t
[ , ] ( ))T
l
0
( )c
∗
⎤ = dt
⎣
1
⎦
dt
⎣ ⎦
d
⎡(X T t B t
[ , ] ( ))T
l
0
( )c
∗
⎤ = dt
⎣
1
⎦
dt
⎣ ⎦
⎛ d ⎞T 0 ∗ ⎛ d ⎞T T 0 ∗
= −⎜
X T t A t B t
[ , ] ( ) ( )+ X T t
[ , ] ![]() B t
( )⎟
l
( )c
= −⎜
A t B t
( ) ( )+
B t
( )⎟
l
( )c
= −⎜
A t B t
( ) ( )+ ![]() B t
( )⎟
(X T t
[ , ]) l
( )c
=
B t
( )⎟
(X T t
[ , ]) l
( )c
=
⎝ dt ⎠ ⎝ dt ⎠
⎛ d ⎞T T 0 ∗ T T 0 ∗
= −⎜
A t L t
( ) 1
( )+ ![]() L t
1
( )⎟
(X T t
[ , ]) l
( )c
= (L
2
( )t
) (X T t
[ , ]) l
( )c
= 0 . (3)
L t
1
( )⎟
(X T t
[ , ]) l
( )c
= (L
2
( )t
) (X T t
[ , ]) l
( )c
= 0 . (3)
⎝ dt ⎠
Дифференцируя (3) по переменной t еще n −2 раза включительно по аналогии получим
![]() dt
d
⎣⎡(L
2
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
⎦
⎤ = (L
3
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
= 0,
dt
d
⎣⎡(L
2
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
⎦
⎤ = (L
3
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
= 0,
………………………………………………………
![]() d
⎡(L
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
⎤ = (L
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
= 0 .
d
⎡(L
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
⎤ = (L
( )t
)T
(X T t
[ , ])T
l
0
( )c
∗
= 0 .
dt ⎣ n − 1 ⎦ n
t ∈[t T 0 , ]. (4)
Обозначим
g c t ( ∗ , ) = (X T t [ , ])T l 0 (c ∗ )∈R n , t ∈[t T 0 , ].
Заметим, что g c t ( ∗ , ) ≠ 0 для всех t ∈[t T 0 , ]. Перепишем тождества (2)-(4) в виде
(L t 1 ( ))T g c t ( ∗ , ) = 0, (L 2 ( )t )T g c t ( ∗ , ) = 0, ,(L n ( )t )T g c t ( ∗ , ) = 0, t ∈[t T 0 , ]. (5) Из равенств (5) следует, что в любой момент времени t ∈[t T 0 , ] ненулевой n −мерный вектор g c t ( ∗ , ) ортогонален каждому из столбцов матрицы K t ( ). В том числе и в момент времени t ∗ ∈[t T 0 , ] он ортогонален каждому из n линейно независимых столбцов матрицы K t ( ∗ ). Последнее невозможно. Следовательно, ρ0 ( )c ∗ ≠ 0. Теорема доказана.
Пример 1. Покажем, что динамическая система из примера 2.7.
x 1 = x 3 ,
x 2 = x 4 ,
x 3 = (cost x ) 3 +tx 4 +u 1 ,
1
x
2
= ![]() x
3
+(sint x
) 4
+u
2
t
+1
x
3
+(sint x
) 4
+u
2
t
+1
| но находим |
|||||
| ⎛0 ⎜ ⎜0 A t ( ) = ⎜0 ⎜ ⎜0 ⎜ ⎝ |
0 0 0 0 |
1 0 cost 1 1+t |
0 ⎞ ⎟ ⎛0 1 ⎜ ⎟ 0 t ⎟, L t 1 ( ) = B = ⎜ ⎟ ⎜1 sint ⎟⎟ ⎜⎜⎝0 ⎠ |
⎛ 1 0⎞ ⎜ ⎟ 0 d ⎜ 0 ⎟, L 2 ( )t = A t L t ( ) 1 ( )− L t 1 ( ) = ⎜cost 0⎟ dt ⎜ ⎟ 1⎟⎠ ⎜⎜ 1 ⎝1+t |
0 ⎞ ⎟ 1 ⎟ t ⎟, ⎟ sint ⎟ ⎟ ⎠ |
| ⎛0 ⎜ ⎜0 K t ( ) = ⎜1 ⎜ ⎜0 ⎜ ⎝ |
0 1 0 ⎞ ⎟ 0 0 1 ⎟ 0 cost t ⎟ . ⎟ 1 ⎟ 1 sint ⎟ 1+t ⎠ |
||||
| Вычислим определитель матрицы K t ( ). Имеем |
|||||
![]()
![]()
![]()
![]() является вполне управляемой. Действительно, достаточно установить линейную независимость первых четырех столбцов матрицы
K t
( ). Последователь-
является вполне управляемой. Действительно, достаточно установить линейную независимость первых четырех столбцов матрицы
K t
( ). Последователь-
0 ![]()
![]()
![]()
![]() 0 1 0
0 1 0
0 0 0 1 0 0 1
1 0
1 0 cost t 0 t =1≠ 0 .
0 1
1 0 1 sint
0 1 ![]() sint
sint
1+t
Таким образом, ранг матрицы K t ( ) равен четырем при всех t ∈[0,1] и рассматриваемая динамическая система является вполне управляемой.
В частности, пусть A = const , B = const . Тогда K = (B AB , , , A n − 1 B ) и проверка полной управляемости системы (1) сводится к доказательству равенства rang K [ ] = n .
Пример 2. Покажем, что динамическая система из примера 2.3.
x 1 = 2x 1 + 2x 2 −30x 3 +u 1 , x 2 =10x 1 − x 2 −35x 3 +u 2 , x 3 = 2x 1 − x 2 + x 3 +u 3 ,
является вполне управляемой. Действительно, достаточно установить линейную независимость первых трех столбцов матрицы K . В силу
| ⎛1 ⎜ B = ⎜0 ⎜0 ⎝ этот факт очевиден. |
0 1 0 |
0⎞ ⎟ 0⎟ 1⎟⎠ |
4.3. Управление по критерию «минимум энергии». Конкретизируем процедуру построения оптимального управления, описанную выше, для случая, когда минимизируемый функционал имеет вид
⎡T
⎤![]()
I
[u
()⋅ ]= ⎢∫![]() u
( ) ( )τ , u
τ
u
( ) ( )τ , u
τ ![]() d
τ⎥ . (1)
d
τ⎥ . (1)
⎢⎣t 0 ⎥ ⎦
Эта величина играет роль оценки количества энергии, затрачиваемой в процессе управления динамическим объектом. Нетрудно видеть, что функционал (1) удовлетворяет условиям 1)-3) предыдущего пункта.
Для реализации первого этапа процедуры построения оптимального управления необходимо решить следующую задачу:
T T
∫![]() u
( )τ , h
( )τ
u
( )τ , h
( )τ ![]() d
τ→ max, ∫
d
τ→ max, ∫ ![]() u
( )τ , u
( )τ
u
( )τ , u
( )τ ![]() d
τ=1.
d
τ=1.
t 0 t 0
Эта задача является изопериметрической задачей вариационного исчисления. Ее решение записывается в виде
u
h
()![]() ,
,
где постоянная λ∈R 1 вычисляется путем подстановки управления u h (⋅) в уравнение связи. В результате вычислений получим
1 ⎡T
⎤![]() ⎡T
⎤
⎡T
⎤![]()
![]() λ= − 2 ⎢⎢⎣t
∫0 h
( ) ( )τ, h
τ
λ= − 2 ⎢⎢⎣t
∫0 h
( ) ( )τ, h
τ![]() d
τ⎥⎥⎦ , u
h
()⋅ = h
()⋅ ⎣⎢⎢t
∫0
d
τ⎥⎥⎦ , u
h
()⋅ = h
()⋅ ⎣⎢⎢t
∫0 ![]() h
( ) ( )τ , h
τ
h
( ) ( )τ , h
τ ![]() d
τ⎦⎥⎥ .
d
τ⎦⎥⎥ .
Тогда норма на пространстве Ω[t 0 ,T ] определяется формулой
![]() ⎡T
⎤
⎡T
⎤ ![]() ⎡T
⎤
⎡T
⎤ ![]() h
()⋅ = ⎢∫ u
h
( )τ, u
h
( )τ
h
()⋅ = ⎢∫ u
h
( )τ, u
h
( )τ![]() d
τ⎥ = ⎢∫
d
τ⎥ = ⎢∫ ![]() h
( ) ( )τ, h
τ
h
( ) ( )τ, h
τ ![]() d
τ⎥ .
d
τ⎥ .
⎢⎣t 0 ⎥⎦ ⎢⎣t 0 ⎥⎦
Второй этап процедуры, состоящий в построении «минимального» элемента h 0 ()⋅ , сводится к задаче математического программирования следующего ви-
да:
![]() Tn nn
⎡T
⎤
Tn nn
⎡T
⎤
![]()
![]() ∫ ∑l h
i
[ ]
i
( )τ ,∑l h
i
[ ]
i
( )τ τd
= ∑ ⎢∫
∫ ∑l h
i
[ ]
i
( )τ ,∑l h
i
[ ]
i
( )τ τd
= ∑ ⎢∫![]() h
[ ]
i
( )τ , h
[ ]
j
( )τ τd
⎥ l l
i j
→ min, l
∈L
.
h
[ ]
i
( )τ , h
[ ]
j
( )τ τd
⎥ l l
i j
→ min, l
∈L
.
t 0i =1 i =1i j , =1 ⎢ ⎣t 0 ⎥ ⎦
Или по-другому:
n n
i ∑, j =1αij l i l j → min, ∑i =1 c i l i =1,
где
T
![]() αij
= ∫
αij
= ∫![]() h
[ ]
i
( )τ , h
[ ]
j
( )τ τd
, ,i j
=1, ,n
. (2)
h
[ ]
i
( )τ , h
[ ]
j
( )τ τd
, ,i j
=1, ,n
. (2)
t 0
⎛l 10 ⎞
⎜ ⎟
Пусть вектор l 0 = ⎜ ⎟ – решение этой задачи. Тогда «минимальный» элемент
⎜⎝l n 0 ⎟⎠
вычисляется по формуле
n
h
![]() l h
.
l h
.
i =1
Заключительный третий этап построения оптимального управления снова сводится к решению изопериметрической задачи вариационного исчисления
![]() t
T
∫
t
T
∫![]() u
( )τ , h
0
( )τ
u
( )τ , h
0
( )τ ![]() d
τ→ max, t
T
∫0
d
τ→ max, t
T
∫0
![]() u
( )τ , u
( )τ d
τ= ( 1
0 )2 .
u
( )τ , u
( )τ d
τ= ( 1
0 )2 .
0 ρ
Ее решением является вектор-функция
0 1 0 1
U
( )⋅ = − ![]() h
( )⋅ , µ∈R
, 2µ
h
( )⋅ , µ∈R
, 2µ
где
![]()
![]() ⎡T
⎤
⎡T
⎤![]()
µ ⎢∫![]() h
0
( )τ , h
0
( )τ
h
0
( )τ , h
0
( )τ ![]() d
τ⎥ ρ0
= − .
d
τ⎥ ρ0
= − .
⎢⎣t 0 ⎥ ⎦
Таким образом, оптимальное управление, решающее задачу теории оптимального управления, имеет вид
U
![]() h l h h
, (3)
h l h h
, (3)
(ρ0 ) (ρ0 ) i =1 i =1
0 l i 0
где νi
= ![]() 2
,i
=1, ,n
. Очевидно, что
2
,i
=1, ,n
. Очевидно, что
(ρ0 )
![]()
0 ⎡T 0 0 ⎤1
![]() I U
⎡⎣
( )⋅ ⎤⎦
= ⎢⎢⎣t
∫
0
I U
⎡⎣
( )⋅ ⎤⎦
= ⎢⎢⎣t
∫
0 ![]() U
( )τ , u
( )τ τd
⎥⎦⎥ =
U
( )τ , u
( )τ τd
⎥⎦⎥ = ![]() ρ
0 .
ρ
0 .
Воспользовавшись соотношениями (3), укажем другой способ формирования оптимального управления, который быстрее и проще приводит к цели. Подставив выражение (3) в равенство (1.3), получим
![]() Tnn Tn
Tnn Tn
![]()
![]() c
i
= ∫ h
[ ]
i
( )τ ν τ τ ν, ∑ 0
j
h
[ ]
j
( ) d
= ∑ 0
j
∫
c
i
= ∫ h
[ ]
i
( )τ ν τ τ ν, ∑ 0
j
h
[ ]
j
( ) d
= ∑ 0
j
∫![]() h
[ ]
i
( )τ , h
[ ]
j
( )τ τ ναd
= ∑ 0
j ij
, i
=1, ,n
. (4)
h
[ ]
i
( )τ , h
[ ]
j
( )τ τ ναd
= ∑ 0
j ij
, i
=1, ,n
. (4)
t 0 =1j =1 t 0 j =1 j
Таким образом, решение задачи об оптимальном управлении можно начинать непосредственно с решения системы линейных алгебраических уравнений
(4), а оптимальное программное управление вычислять по формуле (3).
Итак, оптимальное управление для случая минимизации «энергии» единственно, непрерывно в каждой точке интервала [t 0 ,T ], пропорционально «минимальному» элементу h 0 ()⋅ и зависит линейно от краевых условий. Пример 3* . Рассмотрим линейный управляемый динамический объект
x 1 = 2x 1 + 2x 2 −30x 3 +u 1 , x 2 =10x 1 − x 2 −35x 3 +u 2 , x 3 = 2x 1 − x 2 + x 3 +u 3 , t 0 = 0,T =1;
x 10 = −3, x 20 = 2, x 30 =1; x T 1 = −80.7746, x T 2 = −147,179, x T 3 = −8.94415;
![]() ⎡ 1
⎤
⎡ 1
⎤![]()
I U ⎣ ⎡ ( )⎦ ⎤ u ( ) u ( ) u ( ) . (5)
⎣ 0 ⎦
В рассматриваемом примере дифференциальные уравнения движения динамического объекта и начальное положение фазового вектора взяты из примера 2.3. Конечное положение фазового вектора совпадает с той точкой фазового пространства, в которую переводит в конечный момент времени фазовый вектор оптимальное управление из примера 2.3.
Последовательно вычисляем
⎛ x 11 [t ,τ] x 12 [t ,τ] x 13 [t ,τ]⎞
X t [ ,τ] = ⎜ ⎜ x 21 [t ,τ] x 22 [t ,τ] x 23 [t ,τ] ⎟ ⎟ , H t [ ,τ] = X t [ ,τ]B = X t [ ,τ],
⎜ ⎝ x 31 [t ,τ] x 32 [t ,τ] x 33 [t ,τ]⎟ ⎠
⎛ x 11 [1,τ]⎞ ⎛ x 21 [1,τ]⎞ ⎛ x 31 [1,τ]⎞
h [ ]1 ( )τ = ⎜⎜ x 12 [1,τ]⎟⎟ , h [ ]2 ( )τ = ⎜⎜ x 22 [1,τ]⎟⎟ , h [ ]3 ( )τ = ⎜⎜ x 32 [1,τ τ]⎟⎟, ∈[0,1],
⎜⎝ x 13 [1,τ]⎠⎟ ⎝⎜ x 23 [1,τ]⎟⎠ ⎝⎜ x 33 [1,τ]⎠⎟
1 ⎛α α α11 12 13 ⎞ ⎛4770.34 8405.45 469.812⎞
![]()
![]() ⎜ ⎟ ⎜ ⎟ αij
= ∫h
[ ]
1
( )τ , h
[ ]
i
( )τ τd
, ,i j
=1,2,3 ⇒ ⎜
α α α21 22 23
⎟
= ⎜
8405.45 14824.4 832.786⎟
.
⎜ ⎟ ⎜ ⎟ αij
= ∫h
[ ]
1
( )τ , h
[ ]
i
( )τ τd
, ,i j
=1,2,3 ⇒ ⎜
α α α21 22 23
⎟
= ⎜
8405.45 14824.4 832.786⎟
.
0 ⎜⎝α α α31 32 33 ⎟⎠ ⎜⎝469.812 832.786 48.3062⎟⎠
⎛c 1 ⎞ ⎛ x T 1 ⎞ ⎛ x 10 ⎞ ⎛−67.4743⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜c 2 ⎟ = ⎜ x T 2 ⎟− X [1,0]⎜ x 20 ⎟ = −⎜ 115.885⎟.
⎝⎜c 3 ⎠⎟ ⎝⎜ x T 3 ⎟⎠ ⎜⎝ x 30 ⎟⎠ ⎜⎝−5.34546⎠⎟
Запишем систему линейных алгебраических уравнений (4)
α11 1ν αν αν+ 12 2 + 13 3 = c 1, αν αν αν21 1 + 22 2 + 23 3 = c 2, . αν αν αν31 1 + 32 2 + 33 3 = c 3
Ее решением будут числа
ν1 0 = 0.0682083, ν2 0 = −0.0954224, ν3 0 = 0.871024 .
Тогда оптимальное управление определяется по следующей формуле:
U
![]() t h h h t
.
t h h h t
.
Вычислим функционал (5) на оптимальном управлении
![]()
0 ⎡ 1 0 0 ⎤
![]() I U
⎣
⎡ ( )⋅
⎦
⎤ = ⎢
∫
I U
⎣
⎡ ( )⋅
⎦
⎤ = ⎢
∫![]() U
( )τ ,U
( )τ τd
⎥ =1.34153.
U
( )τ ,U
( )τ τd
⎥ =1.34153.
⎣ 0 ⎦
![]() Заметим, что для оптимального управления из
примера 2.3
функционал (5) принимает значение
3 =1.73205 >1.34153. Такой результат является естественным, поскольку оптимальное управление в
примере 2.3
определялось из условия минимума другого критерия, а не функционала (5).
Заметим, что для оптимального управления из
примера 2.3
функционал (5) принимает значение
3 =1.73205 >1.34153. Такой результат является естественным, поскольку оптимальное управление в
примере 2.3
определялось из условия минимума другого критерия, а не функционала (5).
Проверим проведенные вычисления. Покажем, что полученное управление переводит фазовый вектор из положения x 0 в положение x T за время [0,1]. Действительно проинтегрируем систему дифференциальных уравнений
x 1 = 2x 1 + 2x 2 −30x 3 +U 1 0 (t ), x 2 =10x 1 − x 2 −35x 3 +U 2 0 ( )t , x 3 = 2x 1 − x 2 + x 3 +U 3 0 ( )t
с начальными условиями x 10 = −3, x 20 = 2, x 30 =1. В результате получим
⎛0.000303⎞
x 0 ( )1 − x T = ⎜ ⎜0.000484⎟ ⎟ ≈ 0 .
⎜ ⎝0.000011⎟ ⎠
Пример 4* . Дифференциальные уравнения движения динамического объекта имеют вид
x 1 = x 3 ,
x 2 = x 4 ,
x 3 = (cost x ) 3 +tx 4 +u 1 ,
1
x
2
= ![]() x
3
+(sint x
) 4
+u
2
, t
+1 t
0
= 0,T
=1,
x
3
+(sint x
) 4
+u
2
, t
+1 t
0
= 0,T
=1,
x 10 = x 20 = x 30 = x 40 = 0, x T 1 = 0.640532, x T 2 = 0.491302, x T 3 =1.61672, x T 4 =1.31002,
![]() ⎡ 1
⎤
⎡ 1
⎤![]()
I U ⎣ ⎡ ( )⎤⎦ u ( ) u ( ) . (6)
⎣ 0 ⎦
В рассматриваемом примере дифференциальные уравнения движения динамического объекта и начальное положение фазового вектора взяты из примера 2.7. Конечное же положение фазового вектора совпадает с той точкой фазового пространства, в которую переводит в конечный момент времени фазовый вектор оптимальное управление из примера 2.
Последовательно вычисляем
⎛ x 11 [t ,τ] x 12 [t ,τ] x 13 [t ,τ] x 14 [t ,τ]⎞ ⎛0 0⎞ ⎛ x 13 [t ,τ] x 14 [t ,τ]⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
X t [ ,τ] = ⎜⎜ xx 3121 [[tt ,,ττ]] xx 3222 [[tt ,,ττ]] xx 3323 [[tt ,,ττ]] xx 34 24 [[tt ,,ττ]]⎟⎟, H t [ ,τ] = X t [ ,τ] ⎜⎜10 00⎟⎟ = ⎜⎜ x x 3323 [[t t , ,τ τ]] xx 34 24 [[tt ,,ττ]]⎟⎟
⎜⎜⎝ x 41 [t ,τ] x 42 [t ,τ] x 43 [t ,τ] x 44 [t ,τ]⎟⎠⎟ ⎜⎜⎝0 1⎟⎟⎠ ⎝⎜⎜ x 43 [t ,τ] x 44 [t ,τ]⎟⎟⎠
![]() ⎛ x
[1,τ]⎞ ⎛ x
[1,τ]⎞
⎛ x
[1,τ]⎞ ⎛ x
[1,τ]⎞
h [ ]1 ( )τ = ⎛ x 13 [1,τ]⎞ , h [ ]2 τ
14 1,τ
αij
⎛ x 23 [1,τ]⎞ [ ] 3 33 [ ] 4 43
= , h τ = , h τ = , τ∈[0,1],
24 [1,τ] 34 [1,τ] 44 [1,τ]
![]() 1
1
![]() = ∫h
[ ]
1
( )τ , h
[ ]
i
( )τ τd
, i j
, =1,2,3,4 ⇒
= ∫h
[ ]
1
( )τ , h
[ ]
i
( )τ τd
, i j
, =1,2,3,4 ⇒
0
| ⎛α α α α11 12 13 14 ⎞ ⎛0.766436 ⎜ ⎟ ⎜ ⎜α α α α21 22 23 24 ⎟ = ⎜0.303602 ⎜α α α α31 32 33 34 ⎟ ⎜ 1.51071 ⎜⎜α α α α41 42 43 44 ⎟⎟⎠ ⎜⎜⎝0.779061 ⎝ |
0.303602 0.557218 0.764328 1.12012 |
1.51071 0.764328 3.3364 1.89574 |
0.779061⎞ ⎟ 1.12012 ⎟ , 1.89574 ⎟ ⎟ 2.6037 ⎟ ⎠ |
⎛c 1 ⎞ ⎛ x T 1 ⎞ ⎛ x 10 ⎞ ⎛0.640532⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ 2 ⎟ = ⎜ T 2 ⎟− X [1,0]⎜ x 20 ⎟ = ⎜0.491302⎟. c x
⎜c 3 ⎟ ⎜ x T 3 ⎟ ⎜ x 30 ⎟ ⎜ 1.61672 ⎟
⎜⎜⎝c 4 ⎟⎟⎠ ⎜⎜⎝ x T 4 ⎟⎟⎠ ⎝⎜⎜ x 40 ⎟⎠⎟ ⎜⎜⎝ 1.31002 ⎟⎟⎠
Запишем систему линейных алгебраических уравнений (4)
α11 1ν αν αν αν+ 12 2 + 13 3 + 14 4 = c 1, αν αν αν αν21 1 + 22 2 + 23 3 + 24 4 = c 2,
αν αν αν αν31 1 + 32 2 + 33 3 + 34 4 = c 3, αν αν αν αν41 1 + 42 2 + 43 3 + 44 4 = c 4.
Ее решением будут числа
ν1 0 = −0.982227, ν2 0 = −0.833006, ν3 0 = 0.790821, ν4 0 = 0.579604 .
Тогда оптимальное управление определяется по следующей формуле:
U
![]() t h h h h t
.
t h h h h t
.
Вычислим функционал (5) на оптимальном управлении
⎡ 1 ⎤![]()
![]() 00 0
00 0
![]() I U
⎡⎣
( )⋅ ⎤⎦
= ⎢
∫U
( )τ ,U
( )τ τd
⎥ = 0.999712.
I U
⎡⎣
( )⋅ ⎤⎦
= ⎢
∫U
( )τ ,U
( )τ τd
⎥ = 0.999712.
⎣ 0 ⎦
Заметим, что для оптимального управления из примера 2.7 функционал
(6) принимает значение 1.0 > 0.999712. Такой результат является естественным, поскольку оптимальное управление в примере 2.7 определялось из условия минимума другого критерия, а не функционала (6).
Проверим проведенные вычисления. Покажем, что полученное управление
U 0 ( )⋅ переводит фазовый вектор из положения x 0 в положение x T за время [0,1]. Действительно проинтегрируем систему дифференциальных уравнений
x 1 = x 3 ,
x 2 = x 4 ,
x 3 = (cost x ) 3 +tx 4 +U 1 0 (t ),
1 0
x
2
= ![]() x
3
+(sint x
) 4
+U
2
( )t
, t
+1
x
3
+(sint x
) 4
+U
2
( )t
, t
+1
с начальными условиями x 10 = x 20 = x 30 = x 40 = 0. В результате получим
⎛ −1.68561⎞
⎜ ⎟ x
![]() x
.
x
.
⎜ −1.6007 ⎟
⎜⎜⎝−2.40392⎟⎟⎠
4.4. Управление по критерию «минимум силы». Конкретизируем процедуру построения оптимального управления, описанную выше, для случая, когда минимизируемый функционал имеет вид
![]()
![]() I u
⎡⎣
( )⋅ ⎤⎦
= vrai
max u
( )τ = vrai
max u
( )τ τ, u
( ) . (1)
I u
⎡⎣
( )⋅ ⎤⎦
= vrai
max u
( )τ = vrai
max u
( )τ τ, u
( ) . (1)
τ∈[t T 0, ]τ∈[t T 0, ]
В случае, когда вектор управляющих параметров представляет собой силу (обобщенную силу), функционал (1) оценивает наибольшее значение по модулю этой силы. Отсюда следует вынесенное в заголовок параграфа название рассматриваемого функционала. Нетрудно видеть, что функционал (1) удовлетворяет условиям 1)-3) пункта 4.2.
Для реализации первого этапа процедуры построения оптимального управления необходимо решить следующую задачу:
T
![]()
![]() t
∫
0
t
∫
0 ![]() u
( )τ , h
( )τ τd
→ max, vray
τ∈[
t T
0max, ]
u
( )τ τ, u
( ) =1. (2)
u
( )τ , h
( )τ τd
→ max, vray
τ∈[
t T
0max, ]
u
( )τ τ, u
( ) =1. (2)
Максимум интеграла в (2) достигается, когда подынтегральная функция принимает максимальное значение почти всюду на промежутке [t T 0 , ]. Максимальное значение этой функции можно получить, решив следующую задачу математического программирования:
![]()
![]() u h
, → max, u u
, =1, u h
, ∈R
s
. (3)
u h
, → max, u u
, =1, u h
, ∈R
s
. (3)
![]() Максимальным значением целевой функции в (3) служит величина h h
, . Тогда норма на пространстве Ω[t
0
,T
] определяется формулой
Максимальным значением целевой функции в (3) служит величина h h
, . Тогда норма на пространстве Ω[t
0
,T
] определяется формулой
![]() T
h
( )⋅ = ∫ h
( )τ , h
( )τ τd
.
T
h
( )⋅ = ∫ h
( )τ , h
( )τ τd
.
t 0
Второй этап процедуры – построение «минимального» элемента h 0 (⋅) – сводится к задаче математического программирования следующего вида:
T n n T n
![]()
![]() ∫ ∑l h
i
[ ]
i
( )τ , ∑l h
i
[ ]
i
( )τ τd
= ∫∑ h
[ ]
i
( )τ , h
[ ]
j
( )τ ll d
i j
τ→ min, l
∈L
,
∫ ∑l h
i
[ ]
i
( )τ , ∑l h
i
[ ]
i
( )τ τd
= ∫∑ h
[ ]
i
( )τ , h
[ ]
j
( )τ ll d
i j
τ→ min, l
∈L
,
t 0 =1 i =1 t 0 i j , =1 i
⎛l 10 ⎞
⎜ ⎟
Пусть вектор l 0 = ⎜ ⎟ – решение этой задачи. Тогда «минимальный» элемент и
⎜⎝l n 0 ⎟⎠
его норма вычисляются по формулам
n T
![]() h
h
![]() l h
0
h
0
( )τ , h
0
( )τ τd
l h
0
h
0
( )τ , h
0
( )τ τd
i =1 t 0
соответственно.
Заключительный третий этап построения оптимального управления сводится к следующей задаче на максимум:
T 0 1
![]()
![]() t
∫
0
t
∫
0 ![]() u
( )τ , h
( )τ τd
→ max, vrai
τ∈[
t T
0max, ]
u
( )τ τ, u
( ) = ρ
0 .
u
( )τ , h
( )τ τd
→ max, vrai
τ∈[
t T
0max, ]
u
( )τ τ, u
( ) = ρ
0 .
Ее решением является вектор-функция
0 1 h 0 (τ) 0
u ( )τ = 0 ⋅ , h (τ τ) ≠ 0, ∈[t T 0 , ], (4)
![]() ρ
h
0
( )τ , h
0
( )τ
ρ
h
0
( )τ , h
0
( )τ
которая и будет оптимальным в смысле функционала (1) управлением. Очевидно, что
![]()
![]() I u
⎡⎣
0
( )⋅ ⎤⎦
= vrai
max u
0
( )τ τ, u
0
( ) =.
I u
⎡⎣
0
( )⋅ ⎤⎦
= vrai
max u
0
( )τ τ, u
0
( ) =.
τ∈[t T 0, ]
Для сравнения заметим, что критерий качества (3.1) («минимум энергии»), вычисленный на программном управлении (4) принимает значение:
T 1 h 0 ( )τ 1 h 0 ( )τ 1 T h 0 ( )τ τ, h 0 ( ) T −t 0
![]() t
∫0 ρ0 ⋅ h
0 ( )τ τ, h
0 ( ) , ρ0 ⋅ h
0 ( )τ τ, h
0 ( ) d
τ= ρ0 t
∫0 h
0 ( )τ τ, h
0 ( ) d
τ= ρ0 . (5)
t
∫0 ρ0 ⋅ h
0 ( )τ τ, h
0 ( ) , ρ0 ⋅ h
0 ( )τ τ, h
0 ( ) d
τ= ρ0 t
∫0 h
0 ( )τ τ, h
0 ( ) d
τ= ρ0 . (5)
Пример 5* . Рассмотрим линейный управляемый динамический объект из
примера 4
x 1 = 2x 1 + 2x 2 −30x 3 +u 1 , x 2 =10x 1 − x 2 −35x 3 +u 2 , x 3 = 2x 1 − x 2 + x 3 +u 3 , t 0 = 0,T =1;
x 10 = −3, x 20 = 2, x 30 =1; x T 1 = −80.7746, x T 2 = −147,179, x T 3 = −8.94415. Поставим задачу управления этим объектом по критерию качества «минимум силы»
I U
⎡⎣ ( )![]() ⎤⎦
. (6)
⎤⎦
. (6)
Для решения задачи управления последовательно вычисляем
⎛ x 11 [t ,τ]
X t [ ,τ] = ⎜ ⎜ x 21 [t ,τ]
⎜ ⎝ x 31 [t ,τ]
⎛ x 11 [1,τ]⎞ h [ ]1 ( )τ = ⎜⎜ x 12 [1,τ]⎟⎟ ,
⎜⎝ x 13 [1,τ]⎟⎠
⎛c 1 ⎞
⎜ ⎟
x 12 [t ,τ] x 13 [t ,τ]⎞
x 22 [t ,τ] x 23 [t ,τ] ⎟ ⎟ , H t [ ,τ] = X t [ ,τ]B = X t [ ,τ], x 32 [t ,τ] x 33 [t ,τ]⎟ ⎠
⎛ x 21 [1,τ]⎞ ⎛ x 31 [1,τ]⎞
h [ ]2 ( )τ = ⎜⎜ x 22 [1,τ]⎟⎟ , h [ ] 3 ( )τ = ⎜ ⎜ x 32 [1,τ τ] ⎟ ⎟ , ∈[0,1],
⎜⎝ x 23 [1,τ]⎟⎠ ⎜⎝ x 33 [1,τ]⎟⎠
⎛ x T 1 ⎞ ⎛ x 10 ⎞ ⎛−67.4743⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
⎜c 2 ⎟ = ⎜ x T 2 ⎟− X [1,0]⎜ x 20 ⎟ = −⎜ 115.885⎟.
⎝⎜c 3 ⎠⎟ ⎜⎝ x T 3 ⎠⎟ ⎝⎜ x 30 ⎟⎠ ⎜⎝−5.34546⎠⎟
Запишем задачу математического программирования по определению
минимального элемента h 0 ( )⋅ ∈Ω[0,1]. Имеем
1
![]() ∫ l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ , l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ τd
→ min,
∫ l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ , l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ τd
→ min,
0
l c 2 2 +l c 3 3 . (7)
l c 1 1 +l c 2 2 +l c 3 3 =1⇔ l 1 =
c 1
Эта задача эквивалентна следующей задаче на безусловный минимум
![]() ∫10 l c
2 2
c
+1 l c
3 3
h
[ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ , l c
2 2
c
+1 l c
3 3
h
[ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ τd
→ min по переменным
l
2
и
l
3
. Ее решением будут числа
∫10 l c
2 2
c
+1 l c
3 3
h
[ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ , l c
2 2
c
+1 l c
3 3
h
[ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ τd
→ min по переменным
l
2
и
l
3
. Ее решением будут числа
l 2 0 = −0.038468, l 3 0 = 0.28735.
Из равенства (6) находим
l 1 0 = −0.103653.
Тогда
h
![]() t l h l h l h t
,
t l h l h l h t
,
1
![]() ρ0
= ∫ h
0
( )τ τ τ, h
0
( ) d
= 0.731198.
ρ0
= ∫ h
0
( )τ τ τ, h
0
( ) d
= 0.731198.
0
Оптимальное управление определяется по формуле (4). При этом
0 1
I U
⎡⎣
( )⋅ ⎤⎦
= ![]() ρ
0 =1.36762.
ρ
0 =1.36762.

Рис. 1
Из него видно, что функционал (6) для этого управления принимает значение
1.53213 >1.36762 = I U ⎡⎣ 0 ( )⋅ ⎤⎦ . Такой результат является естественным, поскольку оптимальное управление в примере 3 определялось для критерия «минимум энергии», а не «минимум силы». Обратно, из формулы (5) следует, что критерий «минимум энергии» на управлении U 0 (⋅) принимает значение 1.36762. Этот результат «хуже», чем величина 1.34153, которая была получена на оптимальном в смысле критерия «минимум энергии» управлении в примере 3 .
Для проверки проведенных вычислений, покажем, что полученное управление U 0 ( )⋅ переводит фазовый вектор из положения x 0 в положение x T за время [0,1]. Действительно, проинтегрируем систему дифференциальных уравнений
x 1 = 2x 1 + 2x 2 −30x 3 +U 1 0 (t ), x 2 =10x 1 − x 2 −35x 3 +U 2 0 ( )t , x 3 = 2x 1 − x 2 + x 3 +U 3 0 ( )t
с начальными условиями x 10 = −3, x 20 = 2, x 30 =1. В результате получим
⎛0.0000773993⎞
x 0 ( )1 − x T = ⎜ ⎜ 0.000215504 ⎟ ⎟ ≈ 0 .
⎜ ⎝0.0000639765⎟ ⎠
Пример 6* . Дифференциальные уравнения движения динамического объекта имеют вид
x 1 = x 3 ,
x 2 = x 4 ,
x 3 = (cost x ) 3 +tx 4 +u 1 ,
1
x
2
= ![]() x
3
+(sint x
) 4
+u
2
, t
+1 t
0
= 0,T
=1,
x
3
+(sint x
) 4
+u
2
, t
+1 t
0
= 0,T
=1,
x 10 = x 20 = x 30 = x 40 = 0, x T 1 = 0.640532, x T 2 = 0.491302, x T 3 =1.61672, x T 4 =1.31002. Поставим задачу управления этим объектом по критерию качества «минимум силы»
I U
⎡
⎣ ( )![]() ⎤
⎦
. (8)
⎤
⎦
. (8)
Для решения задачи управления последовательно вычисляем
⎛ x 11 [t ,τ] x 12 [t ,τ] x 13 [t ,τ] x 14 [t ,τ]⎞ ⎛0 0⎞ ⎛ x 13 [t ,τ] x 14 [t ,τ]⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟
X t [ ,τ] = ⎜⎜ xx 3121 [[tt ,,ττ]] xx 3222 [[tt ,,ττ]] xx 3323 [[tt ,,ττ]] xx 3424 [[tt ,,ττ]]⎟⎟, H t [ ,τ] = X t [ ,τ]⎜⎜10 00⎟⎟ = ⎜⎜ xx 3323 [[tt ,,ττ]] xx 34 24 [[tt ,,ττ]]⎟⎟
⎜⎜⎝ x 41 [t ,τ] x 42 [t ,τ] x 43 [t ,τ] x 44 [t ,τ]⎟⎠⎟ ⎜⎜⎝0 1⎠⎟⎟ ⎝⎜⎜ x 43 [t ,τ] x 44 [t ,τ]⎟⎟⎠
[ ] 1 ⎛ x 13 [1,τ]⎞ [ ] 2 ⎛ x 23 [1,τ]⎞ [ ] 3 ⎛ x 33 [1,τ]⎞ [ ] 4 ⎛ x 43 [1,τ]⎞
![]() h
( ) = h
( ) = h
( ) = h
( ) = ∈[ ],
h
( ) = h
( ) = h
( ) = h
( ) = ∈[ ],
1,τ [1,τ] [1,τ] [1,τ]
14 24 34 44
⎛c 1 ⎞ ⎛ x T 1 ⎞ ⎛ x 10 ⎞ ⎛0.640532⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎜ 2 ⎟ = ⎜ T 2 ⎟− X [1,0]⎜ x 20 ⎟ = ⎜0.491302⎟. c x
⎜c 3 ⎟ ⎜ x T 3 ⎟ ⎜ x 30 ⎟ ⎜ 1.61672 ⎟
⎜⎜c 4 ⎟⎟⎠ ⎜⎜⎝ x T 4 ⎟⎟⎠ ⎝⎜⎜ x 40 ⎟⎠⎟ ⎜⎜⎝ 1.31002 ⎟⎟⎠ ⎝
Запишем задачу математического программирования по определению мини-
мального элемента h 0 ( )⋅ ∈Ω[0,1]. Имеем
1
![]() ∫ l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ , l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ +l h
4 [ ]4 ( )τ τd
→ min ,
∫ l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ , l h
1 [ ]1 ( )τ +l h
2 [ ]2 ( )τ +l h
3 [ ]3 ( )τ +l h
4 [ ]4 ( )τ τd
→ min ,
0
l c 2 2 +l c 3 3 +l c 4 4 . (9)
l c 1 1 +l c 2 2 +l c 3 3 +l c 4 4 =1⇔ l 1 =
c 1
Эта задача эквивалентна следующей задаче на безусловный минимум:
1 4 4
![]() ∫
l c
2 2
+l c
3
c
13
+l c
4 4
h
[ ]1
( )τ + ∑
i
=2 l h
i
[ ]i
( )τ ,
l c
2 2
+l c
3 3
c
1 +l c
4 4
h
[ ]1
( )τ + ∑
i
=2 l h
i
[ ]i
( )τ τd
→ min
∫
l c
2 2
+l c
3
c
13
+l c
4 4
h
[ ]1
( )τ + ∑
i
=2 l h
i
[ ]i
( )τ ,
l c
2 2
+l c
3 3
c
1 +l c
4 4
h
[ ]1
( )τ + ∑
i
=2 l h
i
[ ]i
( )τ τd
→ min
0
по переменным l l 2 , 3 и l 4 . Ее решением будут числа
l 2 0 = 0.76217, l 3 0 = 0.00721295, l 4 0 = 0.947403.
Из равенства (9) находим
l 1 0 = 0.947403.
Тогда
h
![]() t l h l h l h l h t
,
t l h l h l h l h t
,
1
![]() ρ0
= ∫ h
0
( )τ τ τ, h
0
( ) d
= 0.999996
ρ0
= ∫ h
0
( )τ τ τ, h
0
( ) d
= 0.999996
0
Оптимальное управление определяется по формуле (4). При этом
0 1
I U
⎡⎣
( )⋅ ⎤⎦
= ![]() ρ
0 =1.00000
ρ
0 =1.00000
На
рис. 2
приведен график изменения величины
![]() для
для
оптимального управления из примера 4
![]()
Рис. 2
Из него видно, что функционал (8) для этого управления принимает значение 1.01073 >1.00000 . Такой результат является естественным, поскольку оптимальное управление в примере 4 определялось для критерия «минимум энергии», а не «минимум силы». Обратно, из формулы (5) следует, что критерий «минимум энергии» на управлении U 0 (⋅) принимает значение 1.00000. Этот результат «хуже», чем величина 0.999712 , которая была получена на оптимальном в смысле критерия «минимум энергии» управлении в примере 4 .
Для проверки проведенных вычислений, покажем, что полученное управление U 0 ( )⋅ переводит фазовый вектор из положения x 0 в положение x T за время [0,1]. Действительно, проинтегрируем систему дифференциальных уравнений
x 1 = x 3 ,
x 2 = x 4 ,
x 3 = (cost x ) 3 +tx 4 +U 1 0 ,
1 0
x
2
= ![]() x
3
+(sint x
) 4
+U
2
t
+1
x
3
+(sint x
) 4
+U
2
t
+1
с начальными условиями x 10 = x 20 = x 30 = x 40 = 0. В результате получим
⎛ 0.0000221525 ⎞
⎜ ⎟
x 0 ( )1 − x T = ⎜−0.0000337122⎟ ≈ 0.
⎜ −0.000318149 ⎟
⎜⎜ ⎝ 0.000376441 ⎟⎟ ⎠
Упражнения для самостоятельной работы
Для линейных управляемых динамических систем
x 1 = −3x 1 + 4x 2 −6x 3 +u 1 , x 1 = −2x 1 −4x 2 −60x 3 +u 1 , x 2 = x 1 −2x 2 + 2x 3 +u 2 , x 2 = −4x 1 − x 2 −51x 3 +u 2 ,
а) x 3 = 2x 1 − x 2 +3x 3 +u 3 , б) x 3 = 2x 1 −2x 2 + x 3 +u 3 , t 0 = 0,T =1, t 0 = 0,T =1,
x 10 = 0, x 20 = 0, x 30 = 0, x 10 = 0, x 20 = 0, x 30 = 0,
x 1 = 2x 1 + 4x 2 −16x 3 +u 1 , x 1 = −3x 1 − x 2 −5x 3 +u 1 , x 2 = 2x 1 − x 2 + 21x 3 +u 2 , x 2 = x 1 − x 2 +u 2 ,
в) x 3 = −2x 1 −2x 2 + x 3 +u 3 , г) x 3 = x 1 + x 2 + 2x 3 +u 3 , t 0 = 0,T =1, t 0 = 0,T =1, x 10 = 0, x 20 = 0, x 30 = 0, x 10 = 0, x 20 = 0, x 30 = 0.
решить задачу оптимального управления по критерию «минимум энергии»
⎡ 1 3 ⎤![]()
I u ⎡⎣ ( )⋅ ⎤⎦ = ⎢∫∑u i ( )τ d τ ⎥
⎣ 0 i =1 ⎦
и по критерию «минимум силы»
![]() I
⎡⎣u
( )⋅ ⎤⎦ = vrai d
.
I
⎡⎣u
( )⋅ ⎤⎦ = vrai d
.
τ∈[t T 0 , ] 0
В каждом случае сравнить оптимальную величину функционала с его значением на управлении, найденном из условия оптимальности другого критерия.
ПРИЛОЖЕНИЕ
Пример 1.3.
Ввод правых частей дифференциальных уравнений
![]()
![]()
![]()
![]()
![]()
![]() =
=
| H |
![]() 2 b v1 2
∗
b
∗
c
∗
y4^2
∗
Sin
@
y1
−
y2
D −
2 b v1 2
∗
b
∗
c
∗
y4^2
∗
Sin
@
y1
−
y2
D −
∗
![]() ∗ −
y2
∗ −
y2
![]() H
y2
D
^2
LDLê
,
H H @ @@ HD D @LDLêLLLL< D
H
y2
D
^2
LDLê
,
H H @ @@ HD D @LDLêLLLL< D
H@ Sin y1 − y2 −
− y2 +
∗ − y2
2 a ∗ b − c^2 ∗ Cos y1 − y2 ^2 ;
Вычисление матрицы А
A = Transpose ∂ y1 Y1,Y2,Y3,Y4 ,
![]() ∂
y2
@8 8 <
∂
y2
@8 8 <
∂ y3
∂ y4 88 <<<D ;
MatrixForm
8
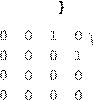 v2
→
0
@ Dê
y1
→
0,y4
→
0,v1
→
0,
v2
→
0
@ Dê
y1
→
0,y4
→
0,v1
→
0,
![]()
![]()
![]()
![]() i
i![]()
Вычисление{ матрицы В
B = Transpose ∂ v1 ,
∂ v2 8 Y1,Y2,Y3,Y4 @8Dê
MatrixForm.
| 8 |
y1 → 0,y2 0,y3 → 0, v2 → 0
![]() 0− 0<
− y
0− 0<
− y
00
![]() abbc2 −
abcc2 k{
abbc2 −
abcc2 k{
−
Пример 1.4.
Построение матрицы X ( )t = (x ( ) 1 ( )t ,x ( ) 2 ( )t ,x ( ) 3 ( )t ) и ввод матрицы A
X
![]()
![]() t t
t t
![]()
![]() @
;
@
;
0 @ DD −@ 10 D@∗ Cos D @ t D@@ DD − 4 ∗ Cos @@ t DD+@ 2 D∗ Sin @ @D t Dy{
1 4 1
![]()
![]() A
=
1 1 1;
A
=
1 1 1;
i 2 − 4 1 {y
k Проверка того факта, что каждый столбец матрицы X является решением
дифференциального уравнения
![]()
![]() X' t
−
A.X t
X' t
−
A.X t
0,0, D 0 @ DD
матрицы X (0)
Det X 0 −10@ @ DD
Пример 1.5.
Построение Фундаментальной матрицы Коши
2 ∗ Exp 3 ∗ t 7 ∗ Cos t + Sin t 3 ∗ Cos t − Sin t
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Z
@
Z
@
![]() t
t
 D
=
τk
Exp
@
3
@∗
t
DD
Cos
@
t
D@
−
D
2
∗
Sin
@
D
@
@@
DLt
@
DD
DDê
−
@@
Sin
LDD
D
@
t
D
@
@
D
D
y
{
;
D
=
τk
Exp
@
3
@∗
t
DD
Cos
@
t
D@
−
D
2
∗
Sin
@
D
@
@@
DLt
@
DD
DDê
−
@@
Sin
LDD
D
@
t
D
@
@
D
D
y
{
;
0 − 10 ∗ Cos t − 4 ∗ Cos t + 2 ∗ Sin t
X_ = Z t . Inverse Z t .t → τ
7Sin t − τ ,
− − τ + @− τ , ![]() H @ D ,
H @ D ,
1 H2 3t−3τ − 2Cos@t − τD − @− τ DL=,
2Sin@t − τDL,
![]() 101H 3 3t−3τ − 3Cos@ t − τD + Sin@ t − τDL ,
101H 3 3t−3τ − 3Cos@ t − τD + Sin@ t − τDL ,
82SinH @t − τ D, −4Sin@ @t − τ D D,Cos@@t − τ DDL=+ Sin@t − τ D<=.
Проверка равенства (1)
Simplify MatrixForm X s,s
![]()
![]()
![]() 1 0 0
@@ @ DDD
k0 0 1y{
1 0 0
@@ @ DDD
k0 0 1y{
0 1 0
Проверка равенства (2)
![]()
![]() Simplify MatrixForm Inverse X t,
τ −
X
τ
,t
Simplify MatrixForm Inverse X t,
τ −
X
τ
,t
![]() 0 0 0@ @ @ @ DD @ DDD
0 0 0@ @ @ @ DD @ DDD
0 0 0
| k |
![]() 0 0 0y{
0 0 0y{
Проверка равенства (3)
1 4 1
![]() A
=
1 1 1;Simplify MatrixForm
∂
t
X t,
τ −
A.X t,
τ
A
=
1 1 1;Simplify MatrixForm
∂
t
X t,
τ −
A.X t,
τ
2 − 4 1
| i |
![]()
![]() 0 0 0k
y{ {
y
@ @ @ D @ DDD
0 0 0k
y{ {
y
@ @ @ D @ DDD
0 0 0
0 0 0
![]() k Проверка равенства (4)
k Проверка равенства (4)
![]()
![]() Simplify MatrixForm
∂τ
X t,
τ +
X t,
τ
.A
k
Simplify MatrixForm
∂τ
X t,
τ +
X t,
τ
.A
k![]() 0 0 0y
{@
@ @ D @ D DD
0 0 0y
{@
@ @ D @ D DD
0 0 0
0 0 0
Пример 1.7. Определение движения на промежутке [0,1)
u0 t_ = 1;Dv0 = DSolve x' t u0 t ,x 0 0 ,x t ,t ;
t @@ DD @ Dê @ @8 @ DD @ D @ D < @ D D x0 t_ = x t .Part Dv0,1,1
Определение движения на промежутке [1,[2] )
u1 t_ = t;Dv1 = DSolve x' t u1 t ,x 1 == x0 1 ,x t ,t ;
x1 @@ Ht_ 1+DD t= x L@ t Dê .Part @ Dv1,1,1 @8 @ DD @ D @ D @ D< @ D D
1 2
u2 t_ = − t;Dv2 = DSolve x' t u2 t ,x 2 == x1 2 ,x t ,t ;
x2 1@@ Ht_ 9 −DD = x L@ t Dê .Part @ Dv2,1,1 @8 @DD @ D @ D @ D< @ D D
![]() 2 t2
2 t2
Определение движения на промежутке [3,4]
u3 t_ = − 1;Dv3 = DSolve x' t u3 t ,x 3 == x2 3 ,x t ,t ; x3 @@ t_ DD = x @ t Dê .Part @ Dv3,1,1 @8 @DD @ D @ D @ D< @ D D
3 − t
![]() Построение движения в целом на промежутке [0,4] x t_ :
=
x0 t ;t
≥
0 t
<
1 x
@
t_
DDDD@
:
@=
x1
D @@@@8
t
DêDêDêDê
;t
≥<D
1
flflfl
t
<
2
Построение движения в целом на промежутке [0,4] x t_ :
=
x0 t ;t
≥
0 t
<
1 x
@
t_
DDDD@
:
@=
x1
D @@@@8
t
DêDêDêDê
;t
≥<D
1
flflfl
t
<
2
x @@@ t_ : = x2 t ;t ≥ 2 t < 3 x t_ : = x3 t ;t ≥ 3
Plot x t , t,0,4
Пример 1.8.
Ввод программного управления
![]()
![]() ,u2
@
t_
D<
=
8
t,2
∗
t
<
,u2
@
t_
D<
=
8
t,2
∗
t
<
Решение задачи Коши
x1' t
![]() 998
x2'
@
t@8
t
D
→ 1@
H@D<
2
==D D @ D
1,x
L2
@ D <
, x1 t
@
,x2 t
998
x2'
@
t@8
t
D
→ 1@
H@D<
2
==D D @ D
1,x
L2
@ D <
, x1 t
@
,x2 t
x1 D DD 6 6 + 6t + 3t2 + 2t3 , x2@@t → 1 + t
Ввод фундаментальной матрицы Коши и начального положения фазового вектора
![]()
![]()
![]()
![]()
![]()
![]() B;X t,
τ
_
=
1 t
− τ
; uu1
N@@ττDD@N
;
D J
0 1
N
B;X t,
τ
_
=
1 t
− τ
; uu1
N@@ττDD@N
;
D J
0 1
N
u2
=
Формула Коши
t
X τ .B.u @τD τ 1 + t
99
Пример 1.9.
Ввод программного управления Sin
![]()
![]() D i
t
u t_
=
Cos
D i
t
u t_
=
Cos
![]()
Sin t , Cos t , t
![]() 88 Ввод@ D<k
фундаментальной8@ D
@{
D< 8 << матрицы Коши и начального положения фазового
88 Ввод@ D<k
фундаментальной8@ D
@{
D< 8 << матрицы Коши и начального положения фазового
вектора Z
![]()
![]()
![]()
![]()
![]() X
k
X
k
![]() t_,
i τ
_
@D = yD @@
Z
D@
t
D
.
H@
Inverse
D@ D @
Z
@
t
DDê@
.t
D → τ@ DLD
;
@ D{y i
;
t_,
i τ
_
@D = yD @@
Z
D@
t
D
.
H@
Inverse
D@ D @
Z
@
t
DDê@
.t
D → τ@ DLD
;
@ D{y i
;
1 0 0
B = 0 1 0;
0 0 1
| k |
![]() i
1
{
i
1
{
![]() 1
y
x0
=
1 ;
1
y
x0
=
1 ;
Формула{ Коши
t
X1 @ t_ D = X @ t,0 D .x0 + ‡ 0 X @ t, τ D .B.u @ τ D τ ;
Проверка граничных условий на правом конце траектории
1
N
AH
Part
@
Transpose
@
X1
@
1
DD
.X1
@
1
D
,1,1
DL
^
![]() 2
E
2
E
46.531
Вычисление функционала
49.7931
Пример 2.2.
Решение сопряженной системы дифференциальных уравнений
![]()
![]()
![]() Sopr
=
DSolve
ψ
1' t
ψ
2 t ,
ψ
2' t
−ψ
1 t ,
ψ
1
ψ
2
@
;
D @ D @ D @ D<
Sopr
=
DSolve
ψ
1' t
ψ
2 t ,
ψ
2' t
−ψ
1 t ,
ψ
1
ψ
2
@
;
D @ D @ D @ D<
1t .Sopr, ψ 2 t .Sopr Cos@ @ tD Dê − C@ 1D Sin@ tD<< @ Dê <
системы дифференциальных уравнений с оптималь-
ными управлениями
![]()
![]()
![]()
![]() Osn
=
DSolvet t
ψ
^21
@
+ ψ
t
D
2
@
t
D
^2
, x2'
@ D @ D è @ D @ D
@
@
t
D
D
^2
=
,
Osn
=
DSolvet t
ψ
^21
@
+ ψ
t
D
2
@
t
D
^2
, x2'
@ D @ D è @ D @ D
@
@
t
D
D
^2
=
,
t t ,t
x1 = t .Osn
tDê D>, <
![]()
![]() ::è@
::è@
:è @@DD + @@DD @ D @ D è @@DD2 + @@DD2 − C@3DSin@tD>>
Решение нелинейной системы уравнений Относительно неизвестных
C C 1 , 2
![]()
![]()
![]()
![]() =
.
=
.
Fin 3,Ax20
 ∗
Ax1
π
,
88
∗
Ax1
π
,
88
![]() ψ<
2
π8 −<
4
@8∗8
Ax2
<π 8
,
<< ê<D <
ψ<
2
π8 −<
4
@8∗8
Ax2
<π 8
,
<< ê<D <
C1 , C2 , C3 , C4 =
.Fin,C4 .Fin 88 < 8 <, 8 <, 8 <<
147
Подстановка найденных констант в общее решение объединенной системы дифференциальных уравнений
| 8 |
x10 t_ ,x20 t_ , ψ 10 t_ , ψ 20 t_ =
C 1 → C1,C 2 → C2,C 3 → C3,C 4 → C4
![]()
![]() 3x1
.Cos@@@
@t
@tDDD
D,x2
D
@ D @
t
D@
,
@ ψDD
1
@@
@@Dt
DD
D,
@ψ
2
@@
@D
@t
DDD<ê
D @.
@
D D<@ D
@@DD@ <
D<
3x1
.Cos@@@
@t
@tDDD
D,x2
D
@ D @
t
D@
,
@ ψDD
1
@@
@@Dt
DD
D,
@ψ
2
@@
@D
@t
DDD<ê
D @.
@
D D<@ D
@@DD@ <
D<
−8 +0.845845tCos t +2.Sin t −0.533429tSin t ,
2.Cos t −0.533429tCos t +3.Sin t −0.845845tSin t ,
2.0562Cos t −1.29673Sin t ,−1.29673Cos t −2.0562Sin t
ParametricPlot x10 t ,x20 t , t,0, π ,
![]() AxesLabel
→
8
"x
@8
1
","x
@
2
D
"
<D @ D< 8 <
AxesLabel
→
8
"x
@8
1
","x
@
2
D
"
<D @ D< 8 <
Graphics
Исследование поведения решения сопряженной системы
Plot ψ 10 t , ψ 20 t , t,0, π ,
AxesLabel @8 @ →D8 "t"," @ D<ψ 1, ψ 2 8 " <D <
![]()
Graphics
Вычисление оптимального значения функционала
3 ∗ x10 π ^2 + 2 ∗ x20 π ^2
0.56252@ D @ D
Проверка постоянства функции Понтрягина
![]()
![]()
![]()
![]() Q
@
t_20
D
= ψ
10
@
t
D
∗
ik
@
x20
D @
t
èD
+
è
@
ψ
D @ D
+ ψ
@ D y{
^2
y
{ +
Q
@
t_20
D
= ψ
10
@
t
D
∗
ik
@
x20
D @
t
èD
+
è
@
ψ
D @ D
+ ψ
@ D y{
^2
y
{ +
ψ t ∗ik−8 x10 t + ψ 20 ;
t
Graphics
Вычисление значения функционала на произвольном управлении
Srav =
NDSolve
![]()
![]()
![]() @
y1
D<
D
t
A
t
DD
D
+8
y2
è
@@
t
H
DD<<@+
@
Dè
D
8=@8
L
Dê@
@
D
D
ψ
H
10
@
t
@
@
D
+
D<+
D
@
0.1
ψ
20
Dê
8
@
t
L
D −
0.1
<<EL
^2 ,
@
y1
D<
D
t
A
t
DD
D
+8
y2
è
@@
t
H
DD<<@+
@
Dè
D
8=@8
L
Dê@
@
D
D
ψ
H
10
@
t
@
@
D
+
D<+
D
@
0.1
ψ
20
Dê
8
@
t
L
D −
0.1
<<EL
^2 ,
![]() t
t
− @ @ ψ 10 t 0.1 ^2 ,
y1 0 == − 3,y2 0 2 , y1 t ,y2 t , t,0, π ;
y1 t_ , = y1 t .Srav,y2 t .Srav ;
3 88∗ y1 @@πD ^2 + 2 y2 @ D ^2
0.598124
Пример 2.3.
Интегрирование сопряженной системы с граничными условиями
![]()
![]()
![]()
![]() Sopr
=
DSolve
@
Sopr
=
DSolve
@
| @ |
, t D ,
,
t D ψ 1 t_ , t_ , ψ 3 @ D<<@ D<=
Re.Sopr , Re @ Dê D
@ @ Dê D< решения сопряженной системы
![]()
![]() Plot
ψ
1 t , t,0,1 , AxesLabel
@ D →88
"t","
ψ<
1
"
<D
Plot
ψ
1 t , t,0,1 , AxesLabel
@ D →88
"t","
ψ<
1
"
<D
ψ1
Graphics
![]()
![]() Plot
ψ
2 t , t,0,1 , AxesLabel
@ D →88
"t","
ψ<
2
"
<D
Plot
ψ
2 t , t,0,1 , AxesLabel
@ D →88
"t","
ψ<
2
"
<D
ψ2
Graphics
![]()
![]() Plot
ψ
3 t , t,0,1 , AxesLabel
@ D →88
"t","
ψ<
3
"
<D
Plot
ψ
3 t , t,0,1 , AxesLabel
@ D →88
"t","
ψ<
3
"
<D
700ψ3
Graphics
Определение момента переключения управления
![]() FindRoot
ψ
1 t 0, t,0.6,0.8
t → 0.741061@ @
<D
8 <D
FindRoot
ψ
1 t 0, t,0.6,0.8
t → 0.741061@ @
<D
8 <D
Интегрирование основной системой с полностью определенными оптимальными управлениями и с начальными условиями
Osn =
![]()
![]()
![]() NDSolve
@
NDSolve
@
x2' t 10 x1 t x2 t 35 ∗ x3 t D −
1,
8 x1t_ D − , 3.,x2 @ @ 0 DD 2 @ ,x D 3 @ 0 D@ == < DD 1. < ,
88
x1
@
DD
D<@@ DêDê
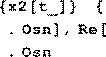 @ D D<
,
@@ DêD<< = D
x1
@
,x2 t ,x3 t ;
@ D D<
,
@@ DêD<< = D
x1
@
,x2 t ,x3 t ;
Re @@ x1 t,
8 Re @ x3 t
Вычислениеоптимального значения функционала
x1 1 + 2 ∗ x2 1 − x3 1
−366.188 @ D @ D @ D
Сравнение с неоптимальным управлением
Srav =
![]()
![]()
![]()
![]() DSolve
@
DSolve
@
t D −
1, y10 @ DD− 3.,y2 @ @ 0 D @ D D< 2 @ @ ,y @DD 3 D<<Dê@ 0 D@ == D 1. D< ,
t t ,t ; D , y3 t_ =
Re y1 @ y2 t .Srav ,
y1
−365.348 @ D @ D @ D
Проверка постоянства функции Понтрягина
![]()
![]() Plot
Q
H
PlotRange
HH
2t_210
∗
D∗
x1
∗=
x1
@
@
x1
Q
@
t
@
D
@
tt
Plot
Q
H
PlotRange
HH
2t_210
∗
D∗
x1
∗=
x1
@
@
x1
Q
@
t
@
D
@
tt
![]() +
D
+
D
![]() D
x2
→8
@ D
8
862,864
∗
x3
<
@
1
,
D∗ψ
<
3
D
@L
t
D
2
@
t
D
@
t
+DDL∗ψ
1
@
t
D+
D
x2
→8
@ D
8
862,864
∗
x3
<
@
1
,
D∗ψ
<
3
D
@L
t
D
2
@
t
D
@
t
+DDL∗ψ
1
@
t
D+
Graphics
Пример 2.5.
Построение фундаментальной матрицы Коши
Resh1 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() DSolve x11' t 2
∗
x11 t
+
9
∗
x21'
@8@
D
t
D
x11
@
@
D@
D<
t
D
+
D
2
∗
x21
@
@D
t, t ,x21 t ,t ; x12't 2
∗
x12 t
+
9
∗
x22 t ,
DSolve x11' t 2
∗
x11 t
+
9
∗
x21'
@8@
D
t
D
x11
@
@
D@
D<
t
D
+
D
2
∗
x21
@
@D
t, t ,x21 t ,t ; x12't 2
∗
x12 t
+
9
∗
x22 t ,
@ D t;
x22' @8 t x12 D@ D< t D + 2 ∗ Dê x22 @ @@ D D< t D 8 @ @D D<<@ D Dê < ,
tx21 t ,
t .Resh2,x21 t .Resh1,
X = .t → 1 − τ
::  подынтегральногоD
−1+τNê
H−1+ 6H1−τLL>,: и61 внеинтегрального−1+τH−1+ 6H1−τLL, 12 −1выражений+τH1+ 6H1−τLL>> функции
подынтегральногоD
−1+τNê
H−1+ 6H1−τLL>,: и61 внеинтегрального−1+τH−1+ 6H1−τLL, 12 −1выражений+τH1+ 6H1−τLL>> функции
ипсилон
XT = Transpose X ;L = l1 ;
![]()
![]()
![]()
![]()
![]() = −
4
∗ @ D+
9
∗
l2^2
J
l2
N+
50
∗
l1
+
30
∗
l2
= −
4
∗ @ D+
9
∗
l2^2
J
l2
N+
50
∗
l1
+
30
∗
l2
;
τ
=
Построениедвух ветвей функции ипсилон
Eps1 l1_; Eps2 @ @ l1_ D D = Dob2 − NIntegrate @ @ D 8 < < D D ;
Решение задачи математического
u = − 1;If Eps1 − 1 < Eps2 − 1 ,S = Eps2 − 1 = u;
![]()
l20 = − u^2 ;
![]()
![]() Do
A
u
= è
1
−
1000.u^2
è
A
@ @
D
u
D
;
DE
Do
A
u
= è
1
−
1000.u^2
è
A
@ @
D
u
D
;
DE
m10 = u;m20 = − 1 − u^2,P
m20 E ;If P > S,S @ D m20 ,
",l10," ","l20 = ",l20,
l10 D
Построение оптимального управления
![]()
![]()
![]() f2^2, ;
f2^2, ;
x1 @ t @DD< ,x2 @D D8 @@ D<<D< 88
@8
Координаты фазового вектора в конечный момент времени
| 8 |
x1 1 ,x2 1
| 8 |
45.817,15.8054@ D @ <D<
Вычисление финального расстояния
F ϕ _ =
![]()
![]()
![]() @HH
x1
D
@
1
DL
^2
L
^
@HH
x1
D
@
1
DL
^2
L
^
![]() 2
1;
2
1;
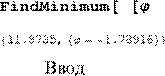
![]()
![]()
![]()
![]()
![]() NDSolve y1' t,
NDSolve y1' t,
y2' t
@8
D
y1
@
@@
@D<
t
DD
D<<+
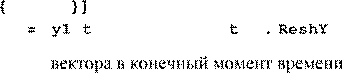 2
∗
8
@
@
D
Dê @ D
@
@
D
Dê
0,y2
@
0
D
<
0
<
,
2
∗
8
@
@
D
Dê @ D
@
@
D
Dê
0,y2
@
0
D
<
0
<
,
t ,
y2 t_ .ReshY,y2
Координаты фазового y1 1 ,y2 1 @ D @ D<
финального расстояния
FY ϕ _ =
@
y1
D
@
1
D −
y2
@
1
D −
30
−
3
∗
Sin
@
ϕ
DL
^2
L
^
![]() 1
2
;
1
2
;
![]() FindMinimum
HH
FindMinimum
HH
811.923, 8ϕ → −1.78491 @ @ << D 8 Пример < D 2.6.
Построение фундаментальной матрицы Коши
Resh1 =
![]()
![]()
![]()
![]() DSolve x11' t 2
∗
x11 t
+
9
∗
x21'
@8@
D
t
D
x11
@
@
D@
D<
t
D
+
D
2
∗
x21
@
@D
t, t ,x21 t ,t ; x12' t 2
∗
x12 t
+
9
∗
x22 t ,
DSolve x11' t 2
∗
x11 t
+
9
∗
x21'
@8@
D
t
D
x11
@
@
D@
D<
t
D
+
D
2
∗
x21
@
@D
t, t ,x21 t ,t ; x12' t 2
∗
x12 t
+
9
∗
x22 t ,
88
![]() =
J
x22'x11t
@8@D
tt,
D8
x12x12
@@@D@D<
tt
D<D + D8
2
@∗Dê
x22
@@@DD<
t
D 8 @@DD<<@DDê <
,
@ Dê <
x12 t ,x22 t ,t ;
=
J
x22'x11t
@8@D
tt,
D8
x12x12
@@@D@D<
tt
D<D + D8
2
@∗Dê
x22
@@@DD<
t
D 8 @@DD<<@DDê <
,
@ Dê <
x12 t ,x22 t ,t ;
x11 8 @@ x12 t , x21 t , X x21 @ D<Dê@@ t DD x22 @@ t DDNê .t → 1 − τ x11 t .Resh1,x12 t .Resh2,x21 t .Resh1,x22 t .Resh2 ;
Построение подынтегрального и внеинтегрального выражений функции
ипсилон
![]()
 двух ветвей
двух ветвей
l10 0.304 l 0.952672 Eps0 9.03586
Анализ оптимального управления
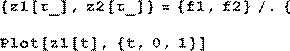 τ →
t,l1
→
l10,l2
→
l20
<
τ →
t,l1
→
l10,l2
→
l20
<
![]()
Graphics
![]()
![]()
![]() Plotz2t , t,0,1 ,PlotRange
→ −
4,0
Plotz2t , t,0,1 ,PlotRange
→ −
4,0
D 8 < -0.5 0.2 0.4 8 0.6 0.8 <D
-1
-1.5
-2 -2.5
Graphics
Определение момента переключения
FindRoot z1 t 0, t, 0,1
![]() Построение@ @
< D
оптимального8 8
управления<<D
Построение@ @
< D
оптимального8 8
управления<<D
t → 0.36245
![]()
![]() U10 t_ ,U20 t_
= −
Sign z1 t ,
−
Sign z2 t
Plot
@
U10
D
@
t
D
,
@
8
t,0,1
D<
8
<
,AxesLabel
@ @ DD
→
8
"t","U
@
1
"
@
<DDD<
U10 t_ ,U20 t_
= −
Sign z1 t ,
−
Sign z2 t
Plot
@
U10
D
@
t
D
,
@
8
t,0,1
D<
8
<
,AxesLabel
@ @ DD
→
8
"t","U
@
1
"
@
<DDD<
@ U1
Graphics
Plot @ U20 @ t D , 8 t,0,1 < ,AxesLabel → 8 "t","U 2 " < ,PlotRange → 8− 1,1 <D
![]()
Graphics
Интегрирование уравнений движения для оптимального управления

Graphics
Координаты фазового вектора в конечный момент времени
x1 1 ,x2 1
![]()
![]()
![]()
![]() 53.2155,18.4742@ D= @ D< −
< − ∗ ϕ + − − ∗ ϕ
53.2155,18.4742@ D= @ D< −
< − ∗ ϕ + − − ∗ ϕ
Вычисление финального расстояния
1
ϕ
_ x1 1 50 2 Cos ^2 x2 1 30 3 Sin ^2 ^
![]() ; FindMinimum
HH @@
F
D@ϕD
,
; FindMinimum
HH @@
F
D@ϕD
,
 ,0,2
@ DL<D H @ D @ DL L
,0,2
@ DL<D H @ D @ DL L
2
ϕ → −1.35749 произвольного
![]()
системы уравнений с введенным управлением
![]() NDSolve y1' t 2
∗ +
V1,
888
NDSolve y1' t 2
∗ +
V1,
888
![]() y2'
@@DD<
t
@8D 8
y1
@@@@D<
t
DDD<<+8 ∗ 8 <@DDDê D
0
@
,y
Dê
2
@
0
D
0
<<
,
y2'
@@DD<
t
@8D 8
y1
@@@@D<
t
DDD<<+8 ∗ 8 <@DDDê D
0
@
,y
Dê
2
@
0
D
0
<<
,
.ReshY,y2 t .ReshY
@ Координаты фазового вектора в конечный момент времени
y1 1 ,y2 1
![]()
![]() 8
58.3336,19.866@ D @ D<
8
58.3336,19.866@ D @ D<
финального расстояния
FY 50
−
2
∗
Cos
ϕ
^2
+
y2 1
−
30
−
3
∗
Sin
ϕ
^2 ^
![]() 1
;
1
;
![]() FindMinimum
@ D HH @
FY
@ @D
<< @ DL<D H @ D @ DL L
2
FindMinimum
@ D HH @
FY
@ @D
<< @ DL<D H @ D @ DL L
2
10.5125, ϕ→−1.00394
![]() 8
8
Пример 2.7.
Построение фундаментальной матрицы Коши
Resh1 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() NDSolve x11'
==
x41 t , x31'
A9
,
@ D
NDSolve x11'
==
x41 t , x31'
A9
,
@ D
x41'x41 t ,x11 0 1,
0,x31 0 == 0,x41 @ D @ D
;
Resh2 <E
, t D
![]() ,x12 0 0,
,x12 0 0,
1,x32
![]() 0
==@
0
D
,x42
@ D @ D
0
==@
0
D
,x42
@ D @ D
;
Resh3 <E
,
D ,x13 0 0,
![]() D
1
@
,x43
@ D @ D @ D D @ D
D
1
@
,x43
@ D @ D @ D D @ D
;
![]() Resh4
<E
Resh4
<E
,
![]() +
t
∗
x44
t
D
+
t
∗
x44
t
D
![]()
![]() ,x14 0 0,
,x14 0 0,
![]()
![]()
![]() 0,x44
@ D
0,x44
@ D
![]() @D<Dê
D
D
,x24, t;
@
tt
@D<Dê
D
D
,x24, t;
@
tt
![]() 8 @ Dê
.Resh2t;,
@ Dê
8 @ Dê
.Resh2t;,
@ Dê
![]() 8
8
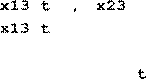 @@ DêDê
.Resh4,x24
< @ Dê
@@ DêDê
.Resh4,x24
< @ Dê
@ Dê <
![]() t;
D<<@ Dê
.Resh1,
<E
t;
D<<@ Dê
.Resh1,
<E
t = D<< @ t Dê .Resh2,
x43 t = D<< @ t Dê .Resh3,
t =
D<< @ t Dê .Resh4,
x11 t x12 t x13 t x14 t
![]()
![]() X t_
=
x21x31
@
@@@
tt
D
DDD
@
x22x32
D @
@
@
@
tt
D
D
D
D
x33x23
@
@@@
tt
D
D
D
D
x34
x24
@
@@@
t
t
DDD
D
y
{
;Y
@
s
D =
Inverse
@
X
@
s
DD
;
X t_
=
x21x31
@
@@@
tt
D
DDD
@
x22x32
D @
@
@
@
tt
D
D
D
D
x33x23
@
@@@
tt
D
D
D
D
x34
x24
@
@@@
t
t
DDD
D
y
{
;Y
@
s
D =
Inverse
@
X
@
s
DD
;
@ D x41 t x42 t x43 t x44 t
![]() MK s_
=k
X
@
1
D
.Y s ;
MK s_
=k
X
@
1
D
.Y s ;
@ ПостроениеD подынтегрального и внеинтегрального выражений функции ипсилон
![]() l1 0 0
l1 0 0
![]()
![]()
![]()
![]() −
l1^2 ;
−
l1^2 ;
двух ветвей функции ипсилон @
Print "l10 = ",l10," ","l20 = ",l20," ","Eps0 = ",
S l10 D =−0.779 l20 =−0.627024 Eps0=4.59607
Построение оптимального управления
![]() −
f1
−
f2
;
−
f1
−
f2
;
| 8 |
![]() U10
U10
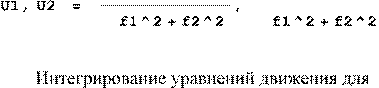 t_
<
D
,U20
9
è
@
t_
D<
=
8
U1,U2
<
è
ê
.
8τ →
t,l1
→
=
l10,l2
→
l20
<
;
t_
<
D
,U20
9
è
@
t_
D<
=
8
U1,U2
<
è
ê
.
8τ →
t,l1
→
=
l10,l2
→
l20
<
;
@ оптимального управления
Resh =
![]()
![]()
![]()
![]()
![]()
![]() NDSolve x1'x4 t , x3'
A9+
U10
@ D
@
t
D
,
@ D @ D
NDSolve x1'x4 t , x3'
A9+
U10
@ D
@
t
D
,
@ D @ D
x4't + U20 t ,x1 0 0,
t,0,1 ;
![]() 88
x2
@@@DDD< 8@ D@@D<D@@Dê8D8 @@D<D<< ==88@
0
@Dê
,
@D<<D<E 8 @ Dê <D<
88
x2
@@@DDD< 8@ D@@D<D@@Dê8D8 @@D<D<< ==88@
0
@Dê
,
@D<<D<E 8 @ Dê <D<
, x2 t_ ,t_ =
@ Dê@ .Resh,x2 D @ D< t .Resh,x3 t .Resh,x4 t .Resh
Plot 8 @8 x1 t ,x2 t , t,0,1 ,AxesLabel → "t","x1 ,x2 "
x1,x2
Graphics
Координаты фазового вектора в конечный момент времени x1 1 ,x2 1
| 8 |
![]() 0.640532,0.491302@ D @ D<
< 1
0.640532,0.491302@ D @ D<
< 1
Вычисление финального расстояния
x1 1
−
5 ^2
+
x2 1
−
4 ^2 ^
![]() 2
−
1
2
−
1
4.59606HH @ D L H @ D L L
Ввод произвольного управления
V1,V2 = − f1 + 0.5 ,
![]()
![]()
![]()
![]() è
@H <D 9è@−HL
f2
−
f1
D<−+
0.5
H
0.5
L
^2
+ HL−
f2
−=
;0.5
L
^2
<
è
@H <D 9è@−HL
f2
−
f1
D<−+
0.5
H
0.5
L
^2
+ HL−
f2
−=
;0.5
L
^2
<
− f1 + 0.5 ^2 + − f2 − 0.5 ^2
V10 t_ ,V20 t_ τ → t,l1 → l10,l2 → l20 ;
![]() Интегрирование уравнений с введенным управлением
Интегрирование уравнений с введенным управлением
ReshY =
NDSolve y1' t y3 t ,y2' t
![]() ,
,
![]()
![]()
![]() 888
888
![]() y3'
@
@@Dê
@
DD<A9D 8@
D
@
y3'
@
@@Dê
@
DD<A9D 8@
D
@
 D<∗
y3
@
D<∗
y3
@
 DêD<<<@
E
t
D
,
@ D @@DêD <
y4'
DêD<<<@
E
t
D
,
@ D @@DêD <
y4'
![]() +
1 t
+
Sin t
∗
V20 t ,y1 0 0,
+
1 t
+
Sin t
∗
V20 t ,y1 0 0,
y2 0,y3 0 == 0,y4 0 == 0
,y2 t;
, y2t_ =
y1 t .ReshY,y2t .ReshY,y4 t .ReshY
Координаты фазового конечный момент времени y1 1 ,y2 1
![]()
![]() 8
0.70276,0.193406@ D @ D<
< 1
8
0.70276,0.193406@ D @ D<
< 1
Вычисление финального расстояния
HH
y1
@ L
^2
L
^
![]() 2
−
1
2
−
1
4.74077
Пример 2.8.
Построение фундаментальной матрицы Коши
Resh1 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() NDSolve x11' t x31 t ,x21' t
==
x41 t , x31'
A9 +
1 t
D
,
@ D
NDSolve x11' t x31 t ,x21' t
==
x41 t , x31'
A9 +
1 t
D
,
@ D
x41' ∗ x31 t + Sin t ∗
| 8 |
x110,x31 0 == 0,x41 0 == 0 , x11 @@ D @<E ; =
Resh2 =
![]() NDSolve x12' t, x32'
A9
@ D @ D @ D
,
@ D
NDSolve x12' t, x32'
A9
@ D @ D @ D
,
@ D
x42'
| 8 |
x12
![]() 1,x32 0
==
0,x42 0
==
0 , x12
@@ D @<E
;
=
1,x32 0
==
0,x42 0
==
0 , x12
@@ D @<E
;
=
Resh3 =
NDSolve x13' t == , x33' A9 t Cos t @ D
x43'
![]() ,
,
x13
![]() ,
,
Resh4 =@ DD @ D@ D @ D @@DD< 8 @ D<E = x13 @ t
NDSolve x14' t x34 t ,x24' t == x44 t , x34' A9@ D
x44' ,
![]()
![]()
![]()
![]()
![]()
![]() x14
x14
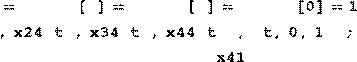 0,x34 ,
888
x41
@@
0,x34 ,
888
x41
@@
![]() t
@Dê
D<
DêDD
t
@Dê
D<
DêDD
 @
D
;
@
@DêD @
D< @
@
8D<<
D<<
@
@
Dê
Dê
<E =
@
D
;
@
@DêD @
D< @
@
8D<<
D<<
@
@
Dê
Dê
<E =
x11 8 t @ , t t = x14 t
x11 t .Resh1,x31 t .Resh1,
t x42 t =
.Resh2,x32 t .Resh2, .Resh2 ; @
t , x43 t =
@@ DêDê < @ Dê .Resh3,x33 @@ D<<D<<@@ t DêDê .Resh3,
x44 t =
.Resh4,x24 .Resh4,x34 t .Resh4,
@ Dê <
x11 t x12 t x13 t x14 t
X
![]()
![]() t_
=
x21x31
@@@
@
ttt
@DD
DD
@@
x22x32x42
DDD@
@
@
@
t
tt
D
D
D
D
x23x33
@@
@
@
tt
D
D
D
D
x24x34
@@
@
@
t
t
D
DD
Dy
{
;
t_
=
x21x31
@@@
@
ttt
@DD
DD
@@
x22x32x42
DDD@
@
@
@
t
tt
D
D
D
D
x23x33
@@
@
@
tt
D
D
D
D
x24x34
@@
@
@
t
t
D
DD
Dy
{
;
@ D x41 x43 t x44 t
Y
![]() s
=
Inverse
k
X s ;
s
=
Inverse
k
X s ;
MK @@D s_ D = X @ 1 D .Y s ;
Построение подынтегрального и внеинтегрального выражений функции ипсилон
l1 0 0
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() L
=
l20
y
;B
=i
0 01 0
y
;
L
=
l20
y
;B
=i
0 01 0
y
;
00 1
f2 Transpose B .
τ
.L ;
 @DD
f2
DLL
;
@DD
f2
DLL
;
=
двух ветвей функции ипсилон
Eps1 l1_ = Dob1 − ; Eps2 < < D D ;
u = − u;
![]()
![]()
![]()
![]()
![]()
![]()
![]() l20
AA
= −
èèA
1 u^2,S
@ D
Eps1
@@
1
DD
;l10
@ D D
u;l20
8@ D
=
èè
1
− <
u^2
E EE
;
l20
AA
= −
èèA
1 u^2,S
@ D
Eps1
@@
1
DD
;l10
@ D D
u;l20
8@ D
=
èè
1
− <
u^2
E EE
;
Do u 1000.
If = ;m10 = u;
m20Eps1 u ;m10 = u;m20 = 1 − u^2 ;
If P > m10;l20 = m20 , i,200,220 ;
Print @ @ "l10 = ",l10," ","l D 20 = ",l20," ",
"Eps0 = ",S
l10 =−0.791 l20 =−0.611816 Eps0=4.28152
Построение оптимального управления f1 , − Sign f2 ;
| 8 |
![]() U10 t_
@ =D @ D<
U10 t_
@ =D @ D<
8 @ D<ê
.
8@ D<
t,l1
→
l10,l2
→
![]() ;
;
Анализ оптимального управления
![]()
![]() PlotU10 t , t,0,1 ,AxesLabel
→
"t","U1
"
PlotU10 t , t,0,1 ,AxesLabel
→
"t","U1
"
Graphics
![]()
![]() PlotU20 t , t,0,1 ,AxesLabel
→
"t","U2
"
PlotU20 t , t,0,1 ,AxesLabel
→
"t","U2
"
Graphics
Интегрирование уравнений движения для оптимального управления
Resh =
![]()
![]()
![]()
![]() NDSolve t x3 t ,x2' t x4 t ,
NDSolve t x3 t ,x2' t x4 t ,
x3' t
![]() U10
D@
t
D
,
D
U10
D@
t
D
,
D
x4' t
![]() t , x1
t , x1
![]() 0,x3 ,
0,x3 ,
88
x1
@@
t
DD
,x2
 8@
t
D@ D<@DêD8 @@D<D< 88@@DêD<<<E
x1
8
t_
@ D<=
8@
t
D@ D<@DêD8 @@D<D< 88@@DêD<<<E
x1
8
t_
@ D<=
x1 tt .Resh,x3 t .Resh, 8 x4 @@ t DêDê@ D 8 @ D< 8 <D <
Plot x1t,0,1 ,
AxesLabel @8 1 ,x2 "
x1,x2
![]()
Graphics
Координаты фазового вектора в конечный момент времени x1 1 ,x2 1
| 8 |
![]() 0.820538,0.770994@ D @ D<
<
0.820538,0.770994@ D @ D<
<
Вычисление финального расстояния
x1 1
−
5 ^2
+
x2 1
−
4 ^2 ^
![]() 1
2
−
1
1
2
−
1
4.28151HH @ D L H @ D L L
Ввод произвольного управления
![]() V10 t_ ,V20 t_
=
V10 t_ ,V20 t_
=
1, D< 1 D ,If @ t > 0.9, − 1,1 D<
Интегрирование системы уравнений с введенным управлением
=
![]()
![]()
![]()
![]()
![]() NDSolve t y3 t ,y2' t y4 t ,
NDSolve t y3 t ,y2' t y4 t ,
y3' t + t ,
y4' t
![]() ∗ @ D
t
D
,
∗ @ D
t
D
,
y1,
@ t D ,y2 t =
88 @ @ t_ @DêDD< , 8 y2 @ D@<D<@8Dê@ D< 8 @@ DêD<< =
t .ReshY,y2 t .ReshY,
8 y4t Dê .ReshY
Координаты фазового вектора в конечный момент времени y1 1 ,y2 1
| 8 |
![]() 0.499235,0.651947@ D @
D<
< 1
0.499235,0.651947@ D @
D<
< 1
Вычисление финального расстояния HH
y1
@
1
D −
5
L
^2
+
H
y2
@
1
D −
4
L
^2
L
^
![]() 2
−
1
2
−
1
4.60949
Пример 2.9
Область начальных положений фазового вектора
a = 5;b = 4;k = 1;
![]()
![]() Plot
∗
a^2
−
x^2,2
+
k
∗
x
+
3 , x,
−
a,a ,
Plot
∗
a^2
−
x^2,2
+
k
∗
x
+
3 , x,
−
a,a ,
a
AxesLabel → "x ","x "
![]() Уравнения, описывающие границы области начальных положений фазового вектора 4
è
Уравнения, описывающие границы области начальных положений фазового вектора 4
è
![]()
![]() ϕ
1x1,x2
=
x2
− ∗
25
−
x1^2;
ϕ
1x1,x2
=
x2
− ∗
25
−
x1^2;
5
ϕ 2x1,x2 = x1 − x2 + 5;
@ ОпределениеD точек пересечения прямой и эллипса
Gran = NSolve ϕ 1 x1,x2 0, ϕ 2 x1,x2 0 , x1,x2
88x1 → −5.,x2@8 → 0.@ <, 8x1D → −1.09756,x2@ → D 3.90244< 8 << <D
Решение совместной системы дифференциальных уравнений для оптимальных управлений
![]()
![]() Sopr
=
DSolve
ψ
1' t
ψ
2 t ,
ψ
2' t
−ψ
1 t ,
8
ψ
=
1
@
DSolve
@
t
t
,
ψ
−
2
@8
t
x1x1'
D<@
t
,t
@@
t
+
D
DD<<D
;
x2
@
8
@
t
D
D
@
+
ψ
Dê
2
è
C
@
t
@D@D@D
ψ
D
1C
@
@
t
@=DDêD<@
D
<
Sopr
=
DSolve
ψ
1' t
ψ
2 t ,
ψ
2' t
−ψ
1 t ,
8
ψ
=
1
@
DSolve
@
t
t
,
ψ
−
2
@8
t
x1x1'
D<@
t
,t
@@
t
+
D
DD<<D
;
x2
@
8
@
t
D
D
@
+
ψ
Dê
2
è
C
@
t
@D@D@D
ψ
D
1C
@
@
t
@=DDêD<@
D
<
ψ 1C t_ , ψ 2C t_ = ψ 1 t .Sopr, ψ 2 t .Sopr ;
88 Osn D D< A9 @ 8 ψ 1 C t ^2 + ψ 2C t ^2 ,
x2' @ D @ D ψ 1C t ^2 + ψ 2C t ^2 ,
![]()
![]() 88
x1
@
t_
@
1
@
@
DD
DD<
D
,x2
→
C1,C
@8
t_
@@DD<@
,
@D
2
DψD<<
1
→E@
C2,Ct_
è8
,
ψ@
32
@@Dê
t_
D@D<D<ê= @ D @ Dê< <
x1 t ,x2 t ,t ;
88
x1
@
t_
@
1
@
@
DD
DD<
D
,x2
→
C1,C
@8
t_
@@DD<@
,
@D
2
DψD<<
1
→E@
C2,Ct_
è8
,
ψ@
32
@@Dê
t_
D@D<D<ê= @ D @ Dê< <
x1 t ,x2 t ,t ;
x1C 8 t , x2C t = x1 t .Osn,x2 t .Osn ;
8 x1C t ,x2C t , ψ 1C t , ψ 2C t .
8 C @DD@ D → C3,C 4 → C4
Случай 1
Построение фундаментальной матрицы Коши
Resh1 =
DSolve x11' t x21 t ,x21' t − x11 t ,
x11 @ 00 @8 D 10,x,x @ 2122 D @ 00 D @ 01 <D ,, 8 x11 @@ t DD ,x21 @ t D<@ ,t D D ;
Resh2 =
DSolve x12' t x22 t ,x22' t − x12 t ,
x12 @ @@8 @ D D8@@Dê<D@8D< x12 @8@ t DD ,x22 @ D<<@@Dê t D<@ ,t D D ; 88 88X 8@ t_, @ @τ t_ Dê Dê D< − τDD = DJ8 ,Sinx21x11 @ @@ @< tt tD< @ DD − τx12x22 D<,@@ tt 8DD −SinNê .t @t − τ→ t D− τ @ D<< x11 t , x12 t , x21 t , x22 t =
x11 t .Resh1,x12 t .Resh2,x21 t .Resh1, x22 t .Resh2 ;
Cos ,Cos t − τ
Вычисление@ внеинтегрального слагаемого
X0 = x10 ;L = l1 ;U = u1 ; 88Transpose l1x10J x20 N@ X @π ,0 JD <<l2 .X0 N D .L J u2 N
− − l2x20
Вычисление подынтегрального слагаемого
Collect Part Transpose X π , τ .U .L,1,1 , u1,u2
![]() u2 −l2Cos@=
@H
τD−
D@
l2Cos
+ l1Sin@τ@D
@τEDL<@
DL@
+ u1H@D
−DL
l1CosD
@τD −D
l2Sin8
@τDL<D
a1,a2
H < è@8 +
l1Sin
τ
,
u2 −l2Cos@=
@H
τD−
D@
l2Cos
+ l1Sin@τ@D
@τEDL<@
DL@
+ u1H@D
−DL
l1CosD
@τD −D
l2Sin8
@τDL<D
a1,a2
H < è@8 +
l1Sin
τ
,
− l1Cos τ − l2Sin τ ;
![]() Simplify
H A
a1^2
+
a2^2
Simplify
H A
a1^2
+
a2^2
![]()
| " |
l12+l22
Вычисление максимина
Aw = Array aw,200 ;Bw Array ;
![]()
![]() F x_,l1_
@= −
l1
∗
x
D+
è
è
1
∗
4
∗ è
25
D −
x^2;
F x_,l1_
@= −
l1
∗
x
D+
è
è
1
∗
4
∗ è
25
D −
x^2;
@ D = − l1 ∗ x − 1 − l1^2 ∗ 5 ∗ 25 − x^2;
= −
1
+
![]() = −
5;S
=
F x,l1
= −
5;S
=
F x,l1
![]()
![]() Do
A @@
If
@@
F
@
x,l1
@ DD>
F
@
x
@+ δ ∗
i,l1
@@
D
,S
D <<
D
EE@ @
i,l1
DD
,
DD
Do
A @@
If
@@
F
@
x,l1
@ DD>
F
@
x
@+ δ ∗
i,l1
@@
D
,S
D <<
D
EE@ @
i,l1
DD
,
DD
= j,0,200
Do F1 x,l1 ;
Do i,l1 ,S = F1 x + δ ∗ i,l1 ,
j,0,200 ;
Max
3.52737
Случай 3
Prim =
NSolve C1 µ 2,C2 == −µ 2,x10 − x20 + 5 0,C3 == x10,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() C4
==
A9
x20,
iè−
C1
π ∗
6
∗
i
kè
C1^2
π ∗
C1
y{=
y
{
,
C4
==
A9
x20,
iè−
C1
π ∗
6
∗
i
kè
C1^2
π ∗
C1
y{=
y
{
,
− C2 4 ∗ C1^2 + C2C2^2 + C4,
µ 2,x10,x20 ;
C1 , C2 ,C3 , C4 , µ 2 , x10 , x20 = .Prim,C4 ê <<8ê .Prim, <<
.Prim ê значения функционала
3 ∗ x1 π ^2 + 2 ∗ x2 π ^2
0.372455@ D @ D
Оптимальная траектория
ParametricPlot @8 x1 @ t D ,x2 @ t D< , 8 t,0,1 <D
![]()
Graphics
Случай 4
Clear C1,C2,C3,C4, µ 2,x10,x20
Первое@ решение D
Gran,1,2
− µ 2, D<
![]()
![]() C3 x1,C4 x2, C1 6C3,
C3 x1,C4 x2, C1 6C3,
C1^2 C2^2
![]()
![]()
![]()
![]()
![]() 88 ==A9 ∗ == π ∗ è− +∗ iky{è= 8π ∗+
C1
+y{ µ µ <E
88 ==A9 ∗ == π ∗ è− +∗ iky{è= 8π ∗+
C1
+y{ µ µ <E
C2
− C2 4C4, C1,C2,C3,C4, 1, 2
| è |
C1^2 + C2^2
→ k → →− →
→−× −7 µ →− ×
![]()
![]() C3 x1,C4 x2, C1 6C3,
C3 x1,C4 x2, C1 6C3,
C1^2 C2^2
![]()
![]()
![]() 88 →→==A9 ∗ k
88 →→==A9 ∗ k
![]() ==
µπ ∗
→−→−è− +∗ ik{y
µè=
→−→8π ∗+
C1
+ {y µ µ <E
==
µπ ∗
→−→−è− +∗ ik{y
µè=
→−→8π ∗+
C1
+ {y µ µ <E
C2
− C2 4C4, C1,C2,C3,C4, 1, 2
C1^2 + C2^2
C1 1.09307,C2 3.58865,C3 1.09756,
C4 3.90244, 1 3.04339, 2 0.545264 <<
Пример 2.10
Множество S 0
Plot3D 3
∗
1
+
![]() 1
∗
x1
−
1
∗
x1
−
![]() 1
x2 , x1,
−
9,0 ,
1
x2 , x1,
−
9,0 ,
![]() 8
x2,0,6
A <J
,AxesLabel9
→
6
8
"x
N
1
","x
8
2
","x
3
<
"
<E
8
x2,0,6
A <J
,AxesLabel9
→
6
8
"x
N
1
","x
8
2
","x
3
<
"
<E
SurfaceGraphics
Интегрирование сопряженной системы
Sopr =
![]()
![]()
![]()
![]()
![]()
![]()
![]() NDSolve
NDSolve
![]() @
D @ D @ D @
t
D
,
@
D @ D @ D @
t
D
,
∗ ψ ∗ ψ ,
1. D ,
;
888![]() @
D< 8 @
ψ
2
D<
@
t
Dê
8
@88@88@
0D<<
.,ψ
1.@
<<<<<<Dê
.Sopr
D@D@D@ D<D<<D<<
@
D< 8 @
ψ
2
D<
@
t
Dê
8
@88@88@
0D<<
.,ψ
1.@
<<<<<<Dê
.Sopr
D@D@D@ D<D<<D<<
InterpolatingFunction@ Dê , <> t ,
InterpolatingFunction 0.,1. , <> t ,
InterpolatingFunction@88 , <> t
Определение начальных
Nach =
NSolve
−
![]() 1
∗ µ
1
+ µ
2
ψ
1 0 ,
1
∗ µ
1
+ µ
2
ψ
1 0 ,
![]() 1
∗ µ
1
− µ
3
ψ
2 0 ,
1
∗ µ
1
− µ
3
ψ
2 0 ,
![]()
![]() A9− µ
94
ψ
3 0 ,
@ D
6
@ D
A9− µ
94
ψ
3 0 ,
@ D
6
@ D
µ ∗ −
![]()
![]()
![]() 1
0,
1
0,
µ 2 ∗ 0, µ 3 ∗ x20 0, µ 4 ∗ x30 0 ,
8µ 1, 2, µ 3, µ 4,x10,x20,x30
µ1 → −1070.08, µ2 → 0., µ3 → −51.1497,
![]() 88µ4 → −1040.07,x10 → −9.,x20 → 0.,x30 → 0. ,
88µ4 → −1040.07,x10 → −9.,x20 → 0.,x30 → 0. ,
µ1 → 2050.13, µ2 → 346.69, µ3 → 468.885, <
,
| 8 |
µ4 → −937.77,x10 → 0.,x20 → 6.,x30 → 0. ,
µ1 → 0., µ2 → 118.898, µ3 → 127.197, < 8µ4 → −683.376,x10 → 0.,x20 → 0.,x30 → 0.<< ![]() x10,x20,x30
=
x10,x20,x30 .Part Nach,2
x10,x20,x30
=
x10,x20,x30 .Part Nach,2
Интегрирование основной системы дифференциальных уравнений с оптимальными
80.,0.,3. <управлениями < 8 и оптимальными<ê начальными@ D условиями
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Osn
=
NDSolve
@
Osn
=
NDSolve
@
+
x3'
@ D ∗ @ D− @ D @ D ψ
3 t ,
x1
@@ D @@DD< @8
 D<< <D @ DD
D<< <D @ DD
t
, @ D , x3 t_ 888 @ DêD< .Osn,x2 @ t Dê .Osn,x3 @88 t
InterpolatingFunctiont , 88InterpolatingFunction@88@880.,1.<<<< <>D@D@D@tD<D<<D<
InterpolatingFunction 0.,1.t ,
8 Вычисление оптимального значенияфункционала x1 1 + 2 ∗ x2 1 − x3 1 −2344.02 @ D @ D @ D
Пример 2.11
Построение столбцов матрицы Коши
Resh1 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() NDSolve x11'
==
x41 t , x31'
A9
,
@ D
NDSolve x11'
==
x41 t , x31'
A9
,
@ D
x41'x41 t ,x11 0 1,
0,x31 0 == 0,x41 @ D @ D
;
Resh2 <E
, t D
![]() ,x12 0 0,
,x12 0 0,
1,x32
![]() 0
==@
0,x
D
42
@ D @ D
0
==@
0,x
D
42
@ D @ D
;
Resh3 <E
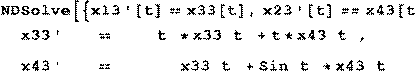 ,
,
![]() @ D @@DD @DD @ @D D @=D @ D
,x13
<DE @
0
D
0,
@ D @@DD @DD @ @D D @=D @ D
,x13
<DE @
0
D
0,
x231,x43 ,
;
Resh4 , t D
,x14 0 0,
,x24 t t ;
@DêD<
D
D
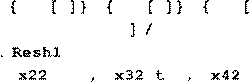 @
0,x44
D<<
@ Dê <E @ D
@
0,x44
D<<
@ Dê <E @ D
,
t .Resh1,
; t t =
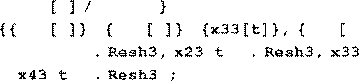 @ Dê @
t
Dê
D<<
@
t
Dê
.Resh2,
@ Dê @
t
Dê
D<<
@
t
Dê
.Resh2,
.Resh2 ;
t , x43 t =
8 @ D<< @ t Dê .Resh3,
888 @@ DêDêDê < @ x34 Dê@ t D< , 8 x44 @ t D<<@ Dê=
.Resh4,x24 t .Resh4,x34 t .Resh4,
x44 t .Resh4 ; @ Dê
фундаментальной матрицы Коши X[1,s]
x11 t x12 t x13 t x14 t
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() X t_s_
D
=
=
x21x31
@D
@
@
@
tt
D
D
D
D
@
x22x32
D @@
@@
tt
D
DD
D
x33x23
@@@@
tt
DD
D
D
x24x34
@@@
@
t
t
DDD
D
y
{
;Y
@
s
D =
Inverse
@
X
@
s
DD
;
X t_s_
D
=
=
x21x31
@D
@
@
@
tt
D
D
D
D
@
x22x32
D @@
@@
tt
D
DD
D
x33x23
@@@@
tt
DD
D
D
x24x34
@@@
@
t
t
DDD
D
y
{
;Y
@
s
D =
Inverse
@
X
@
s
DD
;
@D x41 @ t x42 t x43 t x44 t
![]() MK
k
X 1 .Y s ;
MK
k
X 1 .Y s ;
Построение слагаемого для начальных условий
x10 l1
![]() x0
=
x20x30
y
;l
=
i
l20
y
;
x0
=
x20x30
y
;l
=
i
l20
y
;
x400
Z = H Part H @ MK { @ 0 D .x0 D .l,1,1 D L L
l1 1.x10 @ 1.7491x30 + 0.243323x40 + l2 0.x10
x0 Array α ,4 ;Array β ,4 ;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
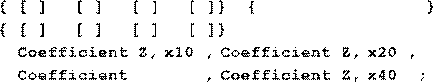
![]() @ D @ D
;
8
K
8
=
ki‚α@
i
D
^2
@@∗ β@
i
D<−β
^2
D
D@
@ D @ D
;
8
K
8
=
ki‚α@
i
D
^2
@@∗ β@
i
D<−β
^2
D
D@
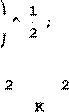 D∗ α@ D
^2
,
@
@
−β@
3
D∗ αD<
D
@ D
D∗ α@ D
^2
,
@
@
−β@
3
D∗ αD<
D
@ D
Z,x30
4
i = 1
x10,x20,x30,x40 =
1 ^23 ^2
, K ,
4 D ^2
Построениеподыинтегрального выражения и оптимальной стратегии
, f3 t_ , f4 t_ = Transpose MK t .l;
![]()
![]() s ^2;U1
@
D<
s_,l1_,l2_
= −
f3ss ;
s ^2;U1
@
D<
s_,l1_,l2_
= −
f3ss ;
![]() U2
@ D
f
@
s
s
DDD
;
@8 @
D<<
D
f
@@D
@
D @ DD
U2
@ D
f
@
s
s
DDD
;
@8 @
D<<
D
f
@@D
@
D @ DD
Решение задачиматематического программирования
l1 = − 1;l2 = 0;
S = − 1 − 5 ∗ l1 + 4 ∗ 1 − l1^2 − K − NIntegrate f s , s,0,1 ;
![]()
![]()
![]() j
=
0;l10
=
l1;l20
è=
l2;
@ @ D 8 <D
j
=
0;l10
=
l1;l20
è=
l2;
@ @ D 8 <D
Do l1 = − 1 + i ;l2 = − 1 − l1^2;
W A = − W1 >− S,S5 ∗ l1 = 1000. W;l10 − 4 ∗ l2 =− l1;l20K − è NIntegrate = l2;j @= fi @ D s D , 88 s,0,1 D <D ; <E
If , i,215,220 ;
Print @ @ j," ",l10," ",l20," ","S = ",S
219 −0.781 −0.624531 S=4.28676
Построение оптимальной траектории и оптимального начального положения
l1,l2 = l10,l20 ; x10,x20,x30,x40
![]()
![]()
![]()
![]() < 8 < 8 <
< 8 < 8 <
![]() t ,
8 @
@
@@
t ,
8 @
@
@@
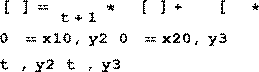 DD
t
8
Cos
@ D
t
DD
t
8
Cos
@ D
t
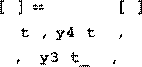 ∗@
y3
D
t
+@
t
D<∗
y4 t
+
U1 t,l10,l20
@@DDê D
,
<D
∗@
y3
D
t
+@
t
D<∗
y4 t
+
U1 t,l10,l20
@@DDê D
,
<D
+ t,l10,l20 ,
![]()
![]() 8
8
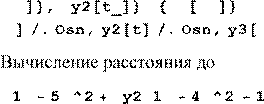 D
0
8 @@D<<D<E @
0
D
x40
=
,
D
0
8 @@D<<D<E @
0
D
x40
=
,
y1; @
y1 t_ =
88 y1 t 8 t Dê .Osn,y4 t .Osn ;
терминального множества
| H |
y1
4.28675@ D L H @ D L
![]() Оптимальный закон движения Plot
@8
y1
@
t
D
,y2
@
t
D<
,
8
t,0,1
<D
Оптимальный закон движения Plot
@8
y1
@
t
D
,y2
@
t
D<
,
8
t,0,1
<D
0.8
0.6
0.4
0.2 0.4 0.6 0.8 1
Graphics
Пример 2.12
Построение столбцов матрицы Коши
Resh1 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() NDSolve x11'
==
x41 t , x31'
A9
,
@ D
NDSolve x11'
==
x41 t , x31'
A9
,
@ D
x41'x41 t ,x11 0 1,
0,x31 0 == 0,x41 @ D @ D
;
Resh2 <E
, t D
![]() ,x12 0 0,
,x12 0 0,
1,x32
![]() 0
==@
0
D
,x42
@ D @ D
0
==@
0
D
,x42
@ D @ D
;
Resh3 <E
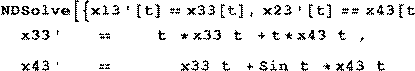 ,
,
![]() @ D @@DD @DD @ @D D @=D @ D
,x13
<DE @
0
D
0,
@ D @@DD @DD @ @D D @=D @ D
,x13
<DE @
0
D
0,
x231,x43 ,
;
Resh4 , t D
,x14 0 0,
0,x 44 @ D
@DêD<DD
,x24
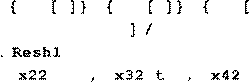 @
t t
D<<@ Dê <E
;
@
t t
D<<@ Dê <E
;
,
t .Resh1,
; t t =
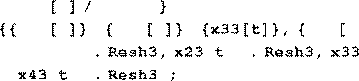 @ Dê @
t
Dê
D<<
@
t
Dê
.Resh2,
@ Dê @
t
Dê
D<<
@
t
Dê
.Resh2,
.Resh2 ;
t , x43 t =
8 @ D<< @ t Dê .Resh3,
88 @ DêDê < @ x34 Dê@ t D< , 8 x44 @ t D<<@ Dê=
.Resh4,x24 t .Resh4,x34 t .Resh4,
8 x44 @ t Dê .Resh4 @ Dê
фундаментальной матрицы Коши X[1,s]
x11 t x12 t x13 t x14 t
![]()
![]()
![]()
![]()
![]()
![]()
![]() X
@@
t_
D D
=
i
x21x31
@ @
@@
@
tt
@
D
D
D
D
X
@@
x22x32
DDD@@
@@
tt
D
DD
D
x33
x23
@
@@
@
t
t
D
DD
D
x34x24
@@
@@
tt
D
DD
D
y
{
;
X
@@
t_
D D
=
i
x21x31
@ @
@@
@
tt
@
D
D
D
D
X
@@
x22x32
DDD@@
@@
tt
D
DD
D
x33
x23
@
@@
@
t
t
D
DD
D
x34x24
@@
@@
tt
D
DD
D
y
{
;
D x41 t x42 t x43 t x44 t
Y s = Inverse k s ;
MKs_ = X 1 .Y s ;
ПостроениеD слагаемого для начальных условий
x10 l1
![]() x0
=
x20
y
;l
=
i
l20
y
;
x0
=
x20
y
;l
=
i
l20
y
;
x30
x400
Z = Part Transpose { k @ MK { @ 0 D .x0 D .l,1,1 D ;
![]() Решение@
задачи минимизации Z по переменным x0 Array
α
,4 ;Array
β
,4 ;
Решение@
задачи минимизации Z по переменным x0 Array
α
,4 ;Array
β
,4 ;
![]() @ D @ D
;
@ D @ D
;
@ D @ D< и оптимальное начальное
положение (в зависимости от l)
4
![]()
![]()
![]()
![]() K
=
i
α
@
i
D
^2
∗ β
@
i
D
^2
y
^
K
=
i
α
@
i
D
^2
∗ β
@
i
D
^2
y
^
![]() ;
;
i = 1
=
![]()
![]() 8∗ α@
2
D
^2,
−β@
3
D∗ α@
3
D
^2,
8∗ α@
2
D
^2,
−β@
3
D∗ α@
3
D
^2,
@ D @ DD = ; @ D K K
Построение подынтегрального выражения и оптимальной стратегии f1 t_ ,
![]() f4 t_
=
f4 t_
=
![]()
![]() Transpose
Transpose
![]() @
D< @
DD @@ @@ DDDD @
f3
@
@
s
DD<<+
f4
@
s
DD
;
@
D< @
DD @@ @@ DDDD @
f3
@
@
s
DD<<+
f4
@
s
DD
;
s_,l1_,l2_
s_,l1_,l2_
![]() Решение задачи математического программирования
Решение задачи математического программирования
l1 = − 1;l2 = 0;
S = − 1 − 5 ∗ l1 + 4 ∗ 1 − l1^2 − K −
![]()
![]()
![]()
![]()
![]() NIntegrate s
è
, s,0,1 ;j
=
0;l10
= =
l2;
NIntegrate s
è
, s,0,1 ;j
=
0;l10
= =
l2;
Do
 W
A<D
;
<E
W
A<D
;
<E
If > ; Print @ @ D
206 −0.794 −0.607918 S=3.97259
Анализ оптимального управления
![]() Plot
@8
U1
@
t,l10,l20
D
,U2
@
t,l10,l20
D<
,
8
t,0,1
<D
Plot
@8
U1
@
t,l10,l20
D
,U2
@
t,l10,l20
D<
,
8
t,0,1
<D
2
1.5
0.5
Graphics
Построение оптимального начального положения
![]() 8 закона <
8 закона <
Osny4 t ,
t,l10,l20 ,
![]()
![]()
![]() y4'
@
t
DD A9
1
@ D∗@
y3
D@
t
@DD+
Sin
@ D@
t
D@∗
y4
D@@D
t
D@+
U2
@@@
t,l10,l20
DD D= D
,
y4'
@
t
DD A9
1
@ D∗@
y3
D@
t
@DD+
Sin
@ D@
t
D@∗
y4
D@@D
t
D@+
U2
@@@
t,l10,l20
DD D= D
,
y1 x10,y2 0 x20,y3 0 x30,y4 0 x40 ,
88
Plot
8 @@@8@@Dê
y1
DD<@
t
D8
,y2
@ D@@
t
D<
![]() @ 8D @@D<D<<D@
88Dê@ D<<<E @ Dê <
y1t ; y1
8
t_ ,
=
@ 8D @@D<D<<D@
88Dê@ D<<<E @ Dê <
y1t ; y1
8
t_ ,
=
y1 t .Osn,y2t .Osn,y4 t .Osn ;
![]()
Graphics
Вычисление оптимального расстояния до терминального множества
y1 1 − 5 ^2 + y2 1 − 4 ^2 − 1
![]() 3.97259
3.97259![]() @ D
L H @ D L
@ D
L H @ D L
Пример 3.1.
Построение фундаментальной матрицы Коши
Resh1 =
![]() DSolve t x21 t ,x21' t
−
x11 t ,x11 0
==
1, x21
D < 8 @ D
,x21
D @
t
D<@
,t
DD
;
@ D @ D
DSolve t x21 t ,x21' t
−
x11 t ,x11 0
==
1, x21
D < 8 @ D
,x21
D @
t
D<@
,t
DD
;
@ D @ D
Resh2 =@
![]()
![]()
![]()
![]()
![]() DSolve x12' t x22 t ,x22' t
−
x12 t ,x12 0 0, x22
@
0
@8D<D @ D @
,x22
D @
t
D<@
,t
DD
;
@ D @ D
DSolve x12' t x22 t ,x22' t
−
x12 t ,x12 0 0, x22
@
0
@8D<D @ D @
,x22
D @
t
D<@
,t
DD
;
@ D @ D
x11 t .Resh1,x21 t .Resh1 ;
888 @ D<< 8 x12 @@ t DêDê .Resh2,x22 @@ t DêDê .Resh2 << ;
.t → t − s;
J X @@ DD @@ DDNê
J@ CosSin@@ssВвод−−D ttDD − CosSinоптимального@ −−tD N DD управления
![]()
![]()
![]() Интегрирование уравнений движения для оптимального управления
Интегрирование уравнений движения для оптимального управления
Fin = DSolve x1' t x2 t + u10 t ,x2' t − x1 t + u20 t , 8 x1 @ @ @ 0 D< D< D == 1 @8 ,x @ @ Dê Dê 2 @@ 0 DD 1 < , @ 8 x1 D @ t D ,x2 @ D @ t D< ,t @ DD ; @ D @ D
x1 t_ = x1 t .Fin;
x2 t_ = x2 t .Fin;
![]() Оптимальная траектория
Оптимальная траектория
![]() ParametricPlot
A8
x1
@
t
D
,x2
@
t
D<
,
9
t,0,
è
2
=E
ParametricPlot
A8
x1
@
t
D
,x2
@
t
D<
,
9
t,0,
è
2
=E
Graphics
Пример 3.2. Ввод начальных условий
![]() x0
1 J
, 1N
x0
1 J
, 1N
88 < 8 Построение<< фундаментальной матрицы Коши
Resh1 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() NDSolve x11' t Cos t
∗
x11 t
+
t
∗
x21 t , x21'
@
A9
t
D
=
NDSolve x11' t Cos t
∗
x11 t
+
t
∗
x21 t , x21'
@
A9
t
D
=
![]() t
8 ∗
x21
@
t
D
<E
,x11
@
D
@
0
D
1,
t
8 ∗
x21
@
t
D
<E
,x11
@
D
@
0
D
1,
x21 0 @D 0 ,;
Resh2 =
NDSolve x12' + ∗ t ,
![]() x22'
@@A9
D
t
D
x22'
@@A9
D
t
D
![]() t
@+
1
D ∗
x12
@
t
D+
Sin
@
t
D∗
x22
@
t
<@E
,x12
@
@@
DD
DDêDê
@
0
D
0,
<<
t
@+
1
D ∗
x12
@
t
D+
Sin
@
t
D∗
x22
@
t
<@E
,x12
@
@@
DD
DDêDê
@
0
D
0,
<<
x22 0 1 ,;
x11x11 t t .Resh1 ; t .Resh2 ;
Inverse X s ;
![]()
![]() JD
@
@@
D
DD @@@DDDN @ D
JD
@
@@
D
DD @@@DDDN @ D
@ Построение функции ипсилон
l = l l2 1 ;Vne = PartTranspose MKT,0.x0 .l,1,1;Vsp = Transpose MKT,s .l;
Pod
J
T_,s_,l1_,l2_
N @ =
Part Vsp,1,1
@H @ D
^2
+LD
Part Vsp,2,1
D
^2 ^
![]() 12;
@ @ DD
Eps
@
@
T_,l1_,l2_
D=
Vne
D
H
−
3
∗
NIntegrate
@ D
@
Pod
@
T,s,l1,l2
@
D
,
8D
s,0,T
L
<D
12;
@ @ DD
Eps
@
@
T_,l1_,l2_
D=
Vne
D
H
−
3
∗
NIntegrate
@ D
@
Pod
@
T,s,l1,l2
@
D
,
8D
s,0,T
L
<D
2.27631l1+ 2.08901l2− 3NIntegrate Pod T,s,l1,l2 , s,0,T Ввод оптимального времени@ @ переходаD 8 <D
T = 0.662;
Определение опорного вектора
A = FindMinimum − EpsT,l1,l2 + 100 ∗ l1^2 + l2^2 − 1 ^2, l1,0.1,0.2, l2,0.1,0.2 ; l10,l20 8 <= 8 l1 < @ ê .Part @ @ A,2,1 D D ,l2 ê .Part H @ A,2,2 D< ; L 8 < 8 <D
![]() l0
=
l10,l20
l0
=
l10,l20
0.617752,0.786373
8EpsT,l10,l20 <
−0.0000122584@ D
Построение оптимального управления
![]()
![]()
![]() Upr
=
t_Transpose3
∗
@
PartMK
@@
T,tUpr,1
DD
.l0;u10Part^2
+
@
Upr,2Part
@
t_
@D
Upr,2
D
=−
3
∗
D
Part
L
Upr,1
Par
^2
t
+@
Part
Upr,
@
1
Upr,2
D
D
^2
L
^
2
1
; u20
@
D
=−
H D H
^2 ^
;
D
Upr
=
t_Transpose3
∗
@
PartMK
@@
T,tUpr,1
DD
.l0;u10Part^2
+
@
Upr,2Part
@
t_
@D
Upr,2
D
=−
3
∗
D
Part
L
Upr,1
Par
^2
t
+@
Part
Upr,
@
1
Upr,2
D
D
^2
L
^
2
1
; u20
@
D
=−
H D H
^2 ^
;
D
Интегрирование уравнений движения для оптимального управления
Fin = NDSolve x1' t Cos t ∗ x1 t + t ∗ x2 t + u10 t ,
![]()
![]() 8
8
![]() x2'
@
@
@
D<D< A9@@
1
DêDê @ D @
D
@
D
<E+
u20
@
@
t
D
D
,x1
@@
0
DD
1,
x2'
@
@
@
D<D< A9@@
1
DêDê @ D @
D
@
D
<E+
u20
@
@
t
D
D
,x1
@@
0
DD
1,
x2 0 t,0,T ;
x1 t_ 8
x2 t_ = t
Оптимальная траектория
![]() ParametricPlot
@8
x1
@
t
D
,x2
@
t
D<
,
8
t,0,T
<D
ParametricPlot
@8
x1
@
t
D
,x2
@
t
D<
,
8
t,0,T
<D
Graphics
Проверка попадания в начало координат
8 x1 −0.0000134271@ T D ,x2 @ T D< , −0.0000148833
8 <
Пример 4.3
Ввод начального и конечного положений фазового вектора
X0
![]()
![]() XT 80.7746,
−
147.179,
−
8.94415
XT 80.7746,
−
147.179,
−
8.94415
80.7746,
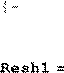 < матрицы Коши
< матрицы Коши
![]()
![]()
![]()
![]() DSolve x11'
DSolve x11'
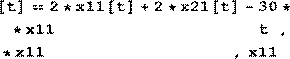 x31 t , x21'
D @@8@@D
tx12'
DD
t
@ D < 8 @ D @ DD@
x32
D @@ D<D
x31' t 20 1,
x31 t , x21'
D @@8@@D
tx12'
DD
t
@ D < 8 @ D @ DD@
x32
D @@ D<D
x31' t 20 1,
x21 0 0,x31 0 t ,x31 t ,
t ; Resh2 =
DSolvet , x22' @8D @ D < 8 @ D @ DD@ D @@ D<D
x32' + t 0,
x22 1,x32 t ,x32 t ,
t ; @
Resh3 D =
![]()
![]()
![]()
![]()
![]()
![]()
![]() DSolve t x33 t , x23'
@8
DSolve t x33 t , x23'
@8


 @ D 8888888
x33'
D@@@@@
@ D 8888888
x33'
D@@@@@
 @@@@@@DDD<DDêDDêDDê8 @@@DD<
@@@@@@DDD<DDêDDêDDê8 @@@DD<
 D<ê<@@888@@@D +@DDêDDê<@D<<D<<@ @ DD<<
0
@
0
D<
, x23 0t ,x23t , t ; x21 t,
D<ê<@@888@@@D +@DDêDDê<@D<<D<<@ @ DD<<
0
@
0
D<
, x23 0t ,x23t , t ; x21 t,
Re x11 x21 .Resh1,
Re x31 .
x12 t, τ , x22 t, τ , x32 t, = Re x12 t .Resh2,Re .Resh2,
Re @ x32 t .Resh2 . − τ ; x13 t, τ x23 t, τ , x33 t, τ =
Re .Resh3,
Re. X t,
τ =
![]()
![]() ;
;
@ D k @@ DD @@ D @ {
Построение матрицы перехода
![]() MK
τ = τ
.t
→
1;
MK
τ = τ
.t
→
1;
| 8 |
h1 @ @ D @ _ Dê D ,h3 @τ _ D< = MK @ τ D ;
коэффициентов в системе линейных алгебраических уравнений ,
![]()
![]()
![]()
![]()
![]() h1
<D@τD
.h3
@τD
,
8τ
,0,1
<D<
h1
<D@τD
.h3
@τD
,
8τ
,0,1
<D<
= NIntegrateh2 τ .h1 τ , τ ,0,1 ,
h2 <D@τD .h3 @τD , 8τ ,0,1 <D<
8a31,a32,a33 = <
| 8 |
NIntegrate h3 < @τDD < .h1 @ D , 8 ,0,1 <<<DDD< , NIntegrate @ h3 @@ ,
NIntegrate @@ h3 τ
469.812,832.786,48.3062
![]() Решение системы алгебраических уравнений
Решение системы алгебраических уравнений
![]()
![]()
![]()
![]()
![]()
![]() c1,c2,c3.X0;
c1,c2,c3.X0;
V = Solvea13 ∗ v3, c2 a21 @8
c3 a31, v1,v2,v3 ;
88.V < <D ê
оптимального ![]()
h3 t ;
@ D значения@ D функционала
![]() NIntegrate u10 t ,u20 t ,u30 t .
H 8
u10
@
t
D
,u20
@8
@@
t
DD
,u30
@@
t
D<D
,
8
t,0,1
@
D<
<DL
^
NIntegrate u10 t ,u20 t ,u30 t .
H 8
u10
@
t
D
,u20
@8
@@
t
DD
,u30
@@
t
D<D
,
8
t,0,1
@
D<
<DL
^
![]() 2
1
2
1
1.34153
Вычисление критерия "минимум силы" на построенном управлении для примера 2
Plot
AH
u10
@
t
D
^2
+
u20
@
t
D
^2
+
u30
@
t
D
^2
L
^
 <E
<E
![]()
![]()
![]() Graphics FindMinimum
−
u10t ^2
+
u20t ^2
+
u30t ^2 ^
1
2, t,0,1
A H @ D
@ D @ D L 8 <E
Graphics FindMinimum
−
u10t ^2
+
u20t ^2
+
u30t ^2 ^
1
2, t,0,1
A H @ D
@ D @ D L 8 <E
оптимального закона движения
Resh0 =
![]()
![]()
![]()
![]()
![]()
![]() NDSolve
@ +
u10
@D
t
D
,
NDSolve
@ +
u10
@D
t
D
,
u20 t ,
D @ D @ D @< @ t D , @
t,0,1 t_ =
88 D<< Dê .Resh0 D ,
вычислений XT − x10 1 ,x20 1 ,x30 1 8 @ D @ D @ D<
Пример 4.4
Ввод матрицы В и конечного положения фазового вектора
0 0
![]()
![]() B
=
0 0
1 0
y{
;XT
=
8
0.640532,0.491302,1.61672,1.31002
<
;
B
=
0 0
1 0
y{
;XT
=
8
0.640532,0.491302,1.61672,1.31002
<
;
| k |
![]() 0 1
0 1
Построение матрицы Коши и матрицы перехода
Resh1 =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() NDSolve x11'
==
x41 t , x31'
A9
,
@ D
NDSolve x11'
==
x41 t , x31'
A9
,
@ D
x41'x41 t ,x11 0 1,
0,x31 0 == 0,x41 @ D @ D
;
Resh2 <E
, t D
![]() ,x12 0 0,
,x12 0 0,
1,x32
![]() 0
==@
0
D
,x42
@ D @ D
0
==@
0
D
,x42
@ D @ D
;
Resh3 <E
,
D ,x13 0 0,
![]() D
1
@
,x43
@ D @ D @ D D @ D
D
1
@
,x43
@ D @ D @ D D @ D
;
Resh4 <E
,
![]()
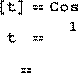
![]()
![]() @ D
+
Sin t
∗
@
,x14
D
0 0,
@
D @ D
0,x44 1
@ D <E @ D
t , t,0,1 ;
@ D
+
Sin t
∗
@
,x14
D
0 0,
@
D @ D
0,x44 1
@ D <E @ D
t , t,0,1 ;
D<Dê @ t D .Resh1,x31 @ D< 8D<<@ t Dê .Resh1,
Dê
t
D<<
![]() Dê=
Dê=
t .Resh2,
![]() , x43 t
=
, x43 t
=
D<<@ t Dê .Resh3,
8 @ DêDê t < @ Dê t D<<@ Dê=
.Resh4,x24 t .Resh4,
x44 @@ t DêDê .Resh4 < ; @ Dê
x11 t x12 t x13 t x14 t
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() @ D
@ D
![]() x41x31 t x42 t t
x41x31 t x42 t t
X
@
ts
D
@ ==
Inverse
D
x21
@@@@@
tt
DDDD@HD
x22x32
@ @@Dê@DD
 @@@DDD< @@DD{D
;
@@@DDD< @@DD{D
;
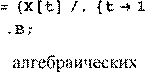 <L @ D
<L @ D
Y k X t ..Y s ; h1 s_ ,h2 s_ ,h3 s_ s_ = MK s
Построение и решение линейных уравнений a11,a12,a13,a14 =
| 8 |
![]() NIntegrate h1
τ τ τ
,0,1 NIntegrate
@@@@
h1
@@ DD @@ DD 88 <<<DDD<
NIntegrate h1
τ τ τ
,0,1 NIntegrate
@@@@
h1
@@ DD @@ DD 88 <<<DDD<
NIntegrate h1, NIntegrate h1 τ .h4 τ , τ ,0,1
=
,
| 8 |
NIntegrate @@@ @@ DD @ D 8 <D
NIntegrate
τ .h4 τ , τ ,0,1
=
,
![]()
![]()
![]()
![]() @@@τDDDD
.h3
@@@@τDDDD
,
8888τ
,0,1
<<<<
<DDDD<
,
@@@τDDDD
.h3
@@@@τDDDD
,
8888τ
,0,1
<<<<
<DDDD<
,
1.51071,0.764328,3.3364,1.89574@ τ τ τ
| 8 |
a41,a42,a43,a44 =
NIntegrate h4 τ < .h1 @@τDD , 88τ ,0,1 <<DD ,
8 NIntegrate @@@ h4 @@@@τDD .h2 τ , τ ,0,1
NIntegrate h4,
0.779061,1.12012,1.89574,2.6037
V = @8 < ∗ v1 + a12 ∗ v2 + a13 ∗ v3 + a14 ∗ v4, c2 a21 ∗ v1 + a22 ∗ v2 + a23 ∗ v3 + a24 ∗ v4, c3 a31 ∗ v1 + a32 ∗ v2 + a33 ∗ v3 + a34 ∗ v4,
![]() ∗
; v1 , v2
<D
∗
; v1 , v2
<D
Построение оптимального управления
u10 t_ ,u20 t_ = v1 ∗ h1 t + v2 ∗ h2 t + v3 ∗ h3 t + v4 ∗ h4 t ;
![]() @
ВычислениеD @
оптимальногоD< @
значенияD
функционала@ D
@ D @ D H
NIntegrate
@8
u10
@
t
D
,u20
@
t
D<
.
8
u10
@
t
D
,u20
@
t
D<
,
8
t,0,1
<DL
^
@
ВычислениеD @
оптимальногоD< @
значенияD
функционала@ D
@ D @ D H
NIntegrate
@8
u10
@
t
D
,u20
@
t
D<
.
8
u10
@
t
D
,u20
@
t
D<
,
8
t,0,1
<DL
^
![]()
0.999712
Построение оптимального закона движения
Resh0 =
![]() NDSolve t x30 t ,x20' t x40 t ,
NDSolve t x30 t ,x20' t x40 t ,
![]()
![]()
![]()
![]()
![]() x30'
x30'
![]() @@DDDD @@DD @@DD @
@@DDDD @@DD @@DD @
 D @ D @
t
DD
D @ D @
t
DD
![]() ,
@
D
,
@
D
x40' + 1 ∗ + ∗ + u20 t , x100,x30 @ D D== 0 ,
x10t ,x20 t ,x40 @ t ,
8 @ @ x30 D t_ @ D< , 8 @@DêD<< <E Dê .Resh0,x30 @ D< t .Resh0,
правильности вычислений
−1.68561 1.60071 × 10− 6 , −2.40392 × 10− 6
![]() <
<
Пример 4.5
Ввод начального и конечного положений фазового вектора
![]()
![]() X0;
X0;
XT 80.7746,
8−80.7746, 147.179, < матрицы Коши
Resh1 =
![]()
![]() DSolve x11'x31 t , x21'
@8@
t
@ D
DSolve x11'x31 t , x21'
@8@
t
@ D
x31' D t DD @@DD < @8D @ D@ D @ DD@ 0 D @ 1, D<
x21 0 @D 0,x31 0 t ,x31 t ,
t ; @
Resh2 =
![]()
![]()
![]() DSolve x12' tx32 t , x22'
@8@ D
x32'
+
t 0,
DSolve x12' tx32 t , x22'
@8@ D
x32'
+
t 0,
x22 1,x32 0 @ DD== 0 < , @ 8 x12 D @ t D ,x22 @ D @ D ,x32 @ D @ t D< , t D ; @ D @
Resh3 =
![]()
![]()
![]()
![]() DSolve t x33 t , x23'
DSolve t x33 t , x23'
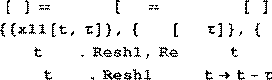 @8@@ DDDDê @D@DD <@ 8@@@DDDDê@@ @ D @@D<D
@8@@ DDDDê @D@DD <@ 8@@@DDDDê@@ @ D @@D<D
![]()
![]()
![]()
![]()
![]()
![]()
![]() x33'
+
0 0, x23 0t ,x23t , t ; x21 t, x31
888888
Re
D@@
x11
@
@
x12x32
@@
t
@D<DDê
t
DDê8 @@ <<D<D<êê@
x21
x33'
+
0 0, x23 0t ,x23t , t ; x21 t, x31
888888
Re
D@@
x11
@
@
x12x32
@@
t
@D<DDê
t
DDê8 @@ <<D<D<êê@
x21
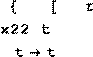 888 @ @DDê<<
.Resh1,
D<<D<< D<<
888 @ @DDê<<
.Resh1,
D<<D<< D<<
Re x31 . ;
x12 t, τ , x22 t, τ , x32 t, = Re .Resh2,Re .Resh2, Re.Resh2 . − τ ;
x13 t, τ x23 t, τ , x33 t, τ = Re .Resh3,Re.Resh3, 8 Re @@ @DDê .
X t,
τ =
![]()
![]() ;
@ D@ @ {
;
@ D@ @ {
Построение
MK τ = τ 1;
![]() J
J
Ro @ l2_,l3_ D= NIntegrate @ Pod @τ ,l2,l3 D , 8τ ,0,1 <D
![]() NIntegrateMinel
=
FindMinimum
@Pod@τ,l2,l3D,
NIntegrateMinel
=
FindMinimum
@Pod@τ,l2,l3D,![]() <D
<D
0.731198, l2→
0.038468,l3 <D
 Minel,1
D
Minel,1
D
![]() l20,l30
=
Minel,2,1,l3 .Part Minel,2,2 ;
l20,l30
=
Minel,2,1,l3 .Part Minel,2,2 ;
![]() @
c3
L D ê @ D< H
@
c3
L D ê @ D< H
−0.103653 l10,l20,l30 <
| 8 |
−0.103653,0.038468,0.28735
![]() ;
;
![]()
![]() Построение@ D
оптимального@ D @
управленияD
Построение@ D
оптимального@ D @
управленияD
![]() u0
τ =
1
∗
h0
τ
;
u0
τ =
1
∗
h0
τ
;
![]()
![]() @ D
Ronol
è @ D D
@ D
Ronol
è @ D D
τ _ ,u20 τ ,u30 τ _ = u0 τ ;
ВычислениеD @ оптимальногоD @ D< значения@ D функционала
Part @ Minel,1 D
0.731198
Построение оптимального закона движения
Resh0 =
NDSolve
![]()
![]()
![]()
![]() @ +
u10
@
t
D
,
@ +
u10
@
t
D
,
u20 t ,
8 @ @ < @ t D , @ D
@ D @ D@ t 8 t,0,1 @ D <D
t_ =
88 D<<Dê .Resh0 D ,
вычислений
XT − x10 1 ,x20 1 ,x30 1
80.0000773993,0.000215504,0.00006397658 @ D @ D @ D< <
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Алексеев В. М., Тихомиров В. М., Фомин С.В. Оптимальное управление. М.: Наука, 1979. 432 с.
2. Афонасьев А.П., Дикуссар В.В., Милютин А.А., Чуканов С.В. Необходимые условия в оптимальном управлении. М.: Наука. 1990. 318 с.
3. Беллман Р. Процессы регулирования с адаптацией. М.: Наука, 1964. – 360 с.
4. Благодатских В.И. Введение в оптимальное управление. М.: Высшая школа, 2001, 239 с.
5. Болтянский В. Г. Математические методы оптимального управления. – М.:
Наука, 1969. 408 с.
6. Варга Дж. Оптимальное управление дифференциальными и функциональными уравнениями. М.: Наука, 1977. 624 с.
7. Васильев Ф. П. Численные методы решения экстремальных задач. М.: Наука, 1988. 549 с.
8. Габасов Р. Ф., Кириллова Ф. М. Оптимизация линейных систем. Минск: Изд.во БГУ, 1973. 246 с.
9. Габасов Р. Ф., Кириллова Ф. М. Принцип максимума в теории оптимального управления. Минск: Наука и техника, 1974. 272 с.
10. Гамкрелидзе Р.В. Основы оптимального управления. Тбилиси: Изд-во ТГУ, 1977. 254 с.
11. Дикуссар В.В. Милютин А.А. Качественные и численные методы в принципе максимума М.: Наука, 1989. 144 с.
12. Дьяконов В.П. Математика 4.: Учебный курс. СПб.; М., Харьков, Минск, 2001. 654 с.
13. Зеликин М.И. Оптимальное управление и вариационное исчисление. М.:
Изд.-во МГУ, 1985
14. Канторович Л. В., Акилов Г. П. Функциональный анализ. М.: Наука, 1977. 741 с
15. Карманов В. Г. Математическое программирование. М.: Наука, 1986. 288 с.
16. Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. – М.: Наука, 1976. – 544 с.
17. Красовский Н. Н. Теория управления движением. М.: Наука, 1968. 476 с.
18. Красовский Н. Н. Игровые задачи о встрече движений М.: Наука, 1970. 420 с.
19. Красовский Н. Н., Субботин А. И., Позиционные дифференциальные игры
М.: Наука, 1974. 456 с.
20. Кротов В. Ф. Основы теории оптимального управления. М.: Высшая школа, 1990. 429 с.
21. Лутманов С. В. Программное оптимальное управление динамическими объектами. Пермь: Изд.-во ПГУ, 1994. 120 с.
22. Лутманов С.В. Курс лекций по методам оптимизации. Ижевск: РХД 2001.
363 с.
23. Матвеев А.С., Якубович В.А. Оптимальные системы управления: обыкновенные дифференциальные уравнения. Специальные задачи.- СПб.: Изд.-во СПбГУ, 2003. 537 с.
24. Милютин А.А., Илютович А.Е., Осмоловский Н.П., Чуканов С.В. Оптимальное управление в линейных системах. М.: Наука, 1974. 268 с.
25. Понтрягин Л. С., Болтянский В.Г., Гамкрелидзе Р. В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука. 1993. 392 с.
26. Понтрягин Л. С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1983. – 332 с.
27. Поляк Б. Т. Введение в оптимизацию. М.: Наука, 1983. 384 с.
28. Пшеничный Б.Н. Выпуклый анализ и экстремальные задачи. М.: Наука,
1980. 320 с.
29. Рокафеллер Р. Выпуклый анализ. М.: Мир. 1973. 470 с.
30. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. М.: Наука, 1986. 328 с.
31. Флеминг У., Ришел Р. Оптимальное управление детерминированными и стохастическими системами. М.: Мир, 1978. 318 с.
32. Янг Л. Лекции по вариационному исчислению и оптимальному управлению. М.: Мир, 1974. 448 с.
Учебное издание
Сергей Викторович Лутманов
ЛИНЕЙНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ
ЧАСТЬ 2
Оптимальное управление линейными динамическими объектами
Редактор Л.Л. Савенкова
Корректор А.Ю. Морскова
Компьютерная верстка С.В. Лутманов
Подписано в печать 14.09. 2005. Усл. печ. л. 11.39. Уч.-изд. л. 10.5 Размер 1 МБ
Редакционно-издательский отдел Пермского государственного университета 614990 Пермь, ул. Букирева, 15
Электронный адрес в Интернете: info @ psu. ru
[1] ab−c cos (y1 − y2 )
относительно переменных y1 , y2 , y3 , y4 .
Проведем линеаризацию дифференциальных уравнений (16) в окрестности пары
[2] Определение движения на промежутке [2,3)