| Скачать .docx | Скачать .pdf |
Доклад: Элементы специальной теории относительности
В своей работе «К электродинамике движущихся тел», опубликованной в 1905г., Эйнштейн сформулировал более точную теорию механики быстродвижущихся тел - специальную теорию относительности.(1)
Специальная теория относительности (СТО) применима для тел, движущихся со скоростью, близкой к скорости света в вакууме (v~с). Основные следствия этой теории следующие.
Масса частицы зависит от скорости ее движения:
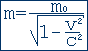
m0- масса покоя частицы.
Продольная длина тел сокращается, согласно формуле:
![]()
l0- cобственная длина тела при V=0.
Движущиеся часы идут медленнее:
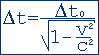
?t0- собственное время, измеренное по неподвижным относительно наблюдателя часам.
Кинетическая энергия релятивистской частицы:
![]()
где ![]() - полная энергия частицы,
- полная энергия частицы,
![]() - энергия покоя.
- энергия покоя.
Закон взаимосвязи массы частицы с ее полной энергией записывается как
![]() (2)
(2)
Исходными для построения теории относительности являются два закона природы, получившие подтверждение в самых различных явлениях движения. Эти законы были сформулированы Эйнштейном в следующем виде:
1. «Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, находящихся относительно друг друга в равномерном поступательном движении, эти изменения состояния относятся».
2. «Каждый луч света движется в «покоящейся» системе координат с определенной скоростью, независимо от того, испускается этот луч света покоящимся или движущимся телом».
Первый закон распространяет закон эквивалентности инерциальных систем(закон относительности классической механики Галилея - Ньютон) на широкий класс физических явлений. Второй закон устанавливает постоянство скорости света независимо от скорости движения источника света.(1)
Второй закон кажется наиболее парадоксальным. В самом деле, при изучении движения тел со скоростями, малыми по сравнению со скоростью света, мы убеждаемся и теоретически, и экспериментально, что скорость тела относительно неподвижной системы координат зависит от движения «платформы», с которой бросание тела производится. Так мяч, брошенный в направлении движения поезда, будет иметь по отношению к Земле большую скорость, нежели мяч, брошенный с неподвижного поезда. Для случая прямолинейного движения результирующая скорость будет равна алгебраической сумме слагаемых скоростей. При движении платформы и тела в одну сторону результирующая скорость будет равна арифметической сумме скоростей и будет подсчитываться по формуле:
![]() рез.=
рез.=![]() ,
,
где vрез. Есть результирующая скорость тела по отношению к Земле, ![]() - скорость платформы,
- скорость платформы, ![]() - скорость тела по отношению к платформе.
- скорость тела по отношению к платформе.
Из этого уравнения следует, что результирующая скорость всегда меньше скорости света. Даже в предельном случае, когда ![]() =с,
=с, ![]() =с,
=с,
Существенные изменения претерпевают и другие понятия механики. Масса тела в задачах специальной теории относительности зависит от скорости движения тела:

В этой формуле ![]() - масса тела при v=0 (масса «покоя»), m- масса тела, движущегося со скоростью v, и масса тела неограниченно возрастает, если его скорость приближается к скорости света.
- масса тела при v=0 (масса «покоя»), m- масса тела, движущегося со скоростью v, и масса тела неограниченно возрастает, если его скорость приближается к скорости света.
Время в теории относительности не является универсальным; для движущегося наблюдателя время течет медленнее, чем для неподвижного. Связь времен, показываемых покоящимися и движущимися часами, определяется формулой, где ![]() - время, отсчитываемое неподвижными часами, а t- время, показываемое часами, движущимися со скоростью v относительно неподвижной системы. Для обычных задач механики величина очень мала по сравнению с единицей, и механика Ньютона дает весьма точные результаты.
- время, отсчитываемое неподвижными часами, а t- время, показываемое часами, движущимися со скоростью v относительно неподвижной системы. Для обычных задач механики величина очень мала по сравнению с единицей, и механика Ньютона дает весьма точные результаты.
При скоростях, близких к скорости света, уточнения, даваемые теорией относительности, приобретают принципиальный характер и в настоящее время, например, конструирование ускорителей, определение времени жизни элементарных частиц и экспериментальное определение массы быстродвижущихся тел не могут быть произведены без учета результатов, вытекающих из специальной теории относительности.(3)
Список литературы
1.<Детская энциклопедия> том 3
2 А.И.Маркушевич, А.М.Кузнецова, И.В.Петрянов<Вещество и энергия>.
3. Сополов Е.Ф. <КСЕ>.