| Скачать .docx | Скачать .pdf |
Реферат: Шпаргалка по Математике 3
дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле: ![]()
В свою очередь ускорение a является производной по времени t от скорости V , которая также является производной по времени t от перемещения S . Т.е.
![]()
Тогда получаем: ![]() - уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
- уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение . Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
![]() - обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается
- обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается ![]() .
.
![]() - обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается
- обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается ![]()
![]()
- дифференциальное уравнение в частных производных первого порядка.
Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0 , у(х0 ) = у0 существует такое значение С = С0 , при котором решением дифференциального уравнения является функция у = j(х, С0 ).
Определение. Решение вида у = j(х, С0 ) называется частным решением дифференциального уравнения.
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С0 ), удовлетворяющего начальным условиям у(х0 ) = у0 .
Теорема Коши . (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если функция
f
(
x
,
y
) непрерывна в некоторой области
D
в плоскости
XOY
и имеет в этой области непрерывную частную производную ![]() , то какова бы не была точка (х0
, у0
) в области
D
, существует единственное решение
, то какова бы не была точка (х0
, у0
) в области
D
, существует единственное решение ![]() уравнения
уравнения ![]() , определенное в некотором интервале, содержащем точку х0
, принимающее при х = х0
значение
j
(х0
) = у0
, т.е. существует единственное решение дифференциального уравнения.
, определенное в некотором интервале, содержащем точку х0
, принимающее при х = х0
значение
j
(х0
) = у0
, т.е. существует единственное решение дифференциального уравнения.
Определение. Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.
Пример. Найти общее решение дифференциального уравнения ![]() .
.
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
![]()
![]()
![]()
Теперь интегрируем: ![]()
![]()
![]()
![]()
![]()
![]() - это общее решение исходного дифференциального уравнения.
- это общее решение исходного дифференциального уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
![]()
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
![]()
Определение. Интегральной кривой называется график y = j(x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального уравнения: ![]() Найти особое решение, если оно существует.
Найти особое решение, если оно существует.
![]()
![]()
![]()
![]()
![]()
![]()
Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C 1 = eC ¹ 0.
Диф. Уранения первого порядка
Дифференциальным уравнением первого порядка
называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:![]()
Решение:
![]() ;
; ![]()
Функцию f(x,y) представим в виде: ![]() тогда при подстановке в полученное выше уравнение имеем:
тогда при подстановке в полученное выше уравнение имеем: ![]()
Уравнения с разделяющимися переменными
Дифференциальное уравнение ![]() называется уравнением с разделяющимися переменными
, если его можно записать в виде
называется уравнением с разделяющимися переменными
, если его можно записать в виде![]() .
.
Такое уравнение можно представить также в виде:
![]()
Перейдем к новым обозначениям ![]()
Получаем: ![]()
![]()
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
![]()
![]()
![]()
Однородные уравнения.
Функция f(x, y) называется однородной
относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество: ![]()
Является ли однородной функция ![]()
![]() функция f(x, y) является однородной 3- го порядка.
функция f(x, y) является однородной 3- го порядка.
Любое уравнение вида ![]() является однородным, если функции P
(
x
,
y
)
и Q
(
x
,
y
)
– однородные функции одинакового измерения.
является однородным, если функции P
(
x
,
y
)
и Q
(
x
,
y
)
– однородные функции одинакового измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Рассмотрим однородное уравнение ![]()
Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать: ![]()
Т.к. параметр t вообще говоря произвольный, предположим, что ![]() . Получаем:
. Получаем: ![]()
Правая часть полученного равенства зависит фактически только от одного аргумента ![]() , т.е.
, т.е. ![]()
Исходное дифференциальное уравнение таким образом можно записать в виде: ![]()
Далее заменяем y
=
ux
, ![]() .
.![]()
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u. ![]()
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
Решить уравнение ![]() .
.
Введем вспомогательную функцию u .
![]() .
.
Отметим, что введенная нами функция u
всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее ![]() .
.
Подставляем в исходное уравнение:
![]()
Разделяем переменные: ![]()
Интегрируя, получаем: ![]()
Переходя от вспомогательной функции обратно к функции у, получаем общее решение:
![]()
Уравнения в полных дифференциалах.
Дифференциальное уравнение первого порядка вида: ![]()
называется уравнением в полных дифференциалах
, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции ![]()
Интегрирование такого уравнения сводится к нахождению функции u
, после чего решение находится в виде: ![]()
Если дифференциальная форма ![]() является полным дифференциалом некоторой функции u
, то можно записать:
является полным дифференциалом некоторой функции u
, то можно записать: ![]() Т.е
Т.е
Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у
, а второе – по х
: 
Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется условием тотальности.
![]()
Теперь рассмотрим вопрос о нахождении собственно функции u .
Проинтегрируем равенство ![]() :
:![]()
Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т.к. при интегрировании переменная у полагается постоянным параметром.
Определим функцию С(у).
Продифференцируем полученное равенство по у .
![]()
Откуда получаем: ![]()
Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х . Это условие будет выполнено, если производная этой функции по х равна нулю.

Теперь определяем функцию С(у):
![]()
Подставляя этот результат в выражение для функции u , получаем:
![]()
Тогда общий интеграл исходного дифференциального уравнения будет иметь вид:
![]()
Следует отметить, что при решении уравнений в полных дифференциалах не обязательно использовать полученную формулу. Решение может получиться более компактным, если просто следовать методу, которым формула была получена.
Линейные уравнения.
Дифференциальное уравнение называется линейным
относительно неизвестной функции и ее производной, если оно может быть записано в виде: ![]()
при этом, если правая часть Q ( x ) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q ( x ) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.
P ( x ) и Q ( x )- функции непрерывные на некотором промежутке a < x < b.
Линейные однородные дифференциальные уравнения.
общее решение линейного однородного дифференциального уравнения первого порядка вида![]()
Рзделение переменных
![]()
![]()
![]()
Общее решение: ![]()
Линейные неоднородные дифференциальные уравнения.
Для интегрирования линейных неоднородных уравнений (Q ( x ) ¹ 0) применяются в основном два метода: метод Бернулли и метод Лагранжа.
Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций ![]() .
.
![]() - дифференцирование по частям.
- дифференцирование по частям.
Подставляя в исходное уравнение, получаем:
![]()
![]()
т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.
Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение ![]() .
.
можно получить функцию u , проинтегрировав, полученное соотношение как однородное дифференциальное уравнение
![]()
![]()
Для нахождения второй неизвестной функции v
подставим поученное выражение для функции u
в исходное уравнение ![]() с учетом того, что выражение, стоящее в скобках, равно нулю.
с учетом того, что выражение, стоящее в скобках, равно нулю.
![]()
Интегрируя, можем найти функцию v
: ![]()
![]()
Подставляя полученные значения, получаем:
![]()
Окончательно получаем формулу:
![]() , С2
- произвольный коэффициент.
, С2
- произвольный коэффициент.
Пример.
Решить уравнение ![]()
Разделим уравнение на xy
2
: ![]()
Полагаем ![]()
![]() .
.
Полагаем ![]()
![]()
![]()
![]()
Произведя обратную подстановку, получаем:
![]()
Метод Лагранжа решения неоднородных линейных дифференциальных уравнений
![]()
Правея часть =0 ![]()
![]() .
.
Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С1 некоторой функцией от х.
Тогда по правилам дифференцирования произведения функций получаем:
![]()
Подставляем полученное соотношение в исходное уравнение
![]()
![]()
Из этого уравнения определим переменную функцию С1
(х): ![]()
Интегрируя, получаем: ![]()
Подставляя это значение в исходное уравнение, получаем:
![]() .
.
Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.
При выборе метода решения линейных дифференциальных уравнений следует руководствоваться простотой интегрирования функций, входящих в исходный интеграл.
Решить уравнение ![]()
Сначала приведем данное уравнение к стандартному виду: ![]()
Применим полученную выше формулу: ![]()


![]()
Уравнения, допускающие понижение порядка.
Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.
Уравнения вида y ( n ) = f ( x ).
Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.
![]()
![]()
…………………………………………………………….
![]()
Уравнения, допускающие понижение порядка
одним из методов интегрирования ДУ высших порядков является ме-тод понижения порядка. Суть метода состоит в том, что с помощью заме-ны переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.
Рассмотрим три типа уравнений, допускающих понижение порядка.
I. Пусть дано уравнение
![]()
Порядок можно понизить, введя новую функцию р(х), положив у'=р(х). Тогда у''=p'(x) и получаем ДУ первого порядка: p'=ƒ(х). Решив его, т. е. найдя функцию р=р(х), решим уравнение y'=р(х). Получим общее решение заданного уравнения (3.6).
На практике поступают иначе: порядок понижается непосредственно путем последовательного интегрирования уравнения.
Так как уравнение ![]() можно записать в виде dy'=ƒ(х) dx. Тогда, интегрируя уравнение y''=ƒ(х), получаем: y'=
можно записать в виде dy'=ƒ(х) dx. Тогда, интегрируя уравнение y''=ƒ(х), получаем: y'= ![]() или y'=j1 (x)+с1. Далее, интегрируя полученное уравнение по х, находим:
или y'=j1 (x)+с1. Далее, интегрируя полученное уравнение по х, находим: ![]() - общее решение данного уравнения. Если дано уравнение
- общее решение данного уравнения. Если дано уравнение ![]() то, проинтегрировав его последовательно n раз, найдем общее решение уравнения:
то, проинтегрировав его последовательно n раз, найдем общее решение уравнения: ![]()
Линейным однородным дифференциальным уравнением второго порядка называется уравнение вида![]()
коэффициенты которого![]() и
и ![]() – непрерывные функции.
– непрерывные функции.
Пусть![]() и
и ![]() – частные решения уравнения, т.е. не содержат произвольных констант.
– частные решения уравнения, т.е. не содержат произвольных констант.
Два решения ![]() и
и ![]() называются линейно независимыми, если можно подобрать постоянные числа
называются линейно независимыми, если можно подобрать постоянные числа ![]() и
и ![]() , не равные одновременно нулю, такие, что линейная комбинация этих функций тождественно равна нулю, т.е.
, не равные одновременно нулю, такие, что линейная комбинация этих функций тождественно равна нулю, т.е. ![]()
В противном случае, если таких чисел подобрать нельзя, решения ![]() и
и ![]() называются линейно независимыми, т.е. если функции и линейно независимые и имеет место тождество
называются линейно независимыми, т.е. если функции и линейно независимые и имеет место тождество![]() , то
, то![]()
Постоянные коэфициенты
Если y1 и y2 – линейно независимые частные решения линейного однородного уравнения второго порядка ![]() , то общее решение данного уравнения есть линейная комбинация этих частных решений, т.е. общее решение уравнение имеет вид
, то общее решение данного уравнения есть линейная комбинация этих частных решений, т.е. общее решение уравнение имеет вид
![]()
Где C1 и C2 – произвольные постоянные.
Пусть линейное однородное дифференциальное уравнение ![]()
имеет постоянные коэффициенты p и q .
Будем искать частное решение данного уравнения в виде ![]()
Где k – постоянное число, которое нужно найти. Дифференцируя получаем ![]()
и![]() .
.
Подставляя и в уравнение, получим ![]()
или, сокращая на множитель ![]() , который не равен нулю, находим
, который не равен нулю, находим ![]()
которого определяется число k , называется характеристическим уравнением данного линейного уравнения второго порядка с постоянными коэффициентами
Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида ![]()
где p и q – данные постоянные числа и ![]() (правая часть уравнения) – известная функция от x .
(правая часть уравнения) – известная функция от x .
Общее решение линейного неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения ![]()
и частного решения данного неоднородного уравнения.
Интегрирование
4.1. Интегрирование ЛОДУ второго порядка с постоянными коэффициентами
Частным случаем рассмотренных выше линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами.
Пусть дано ЛОДУ второго порядка ![]()
где р и q постоянны.
Для нахождения общего решения уравнения (4.1) достаточно найти два его частных решения.
Будем искать частные решения уравнения (4.1) в виде ![]()
Дифференцируя эту функцию два раза и подставляя выражения для у, у' и у" в уравнение (4.1),получим: ![]()
![]()
Уравнение (4.2) называется характеристическим уравнением ДУ (для его составления достаточно в уравнении (4.1) заменить у", у' и у соответственно на k2, k1).
При решении характеристического уравнения (4.2) возможны следующие три случая.
Случай 1. Корни k1 и k2 уравнения (4.2) действительные и различные:
![]()
общее решение уравнения (4.1), имеет вид ![]()
Случай 2. Корни k1 и k2 характеристического уравнения (4.2) действительные и равные:
![]()
В этом случае имеем лишь одно частное решение y1=ek1x. Покажем, что наряду с у1 решением уравнения (4.1) будет и у2=хеk1x. Действительно, подставим функцию у2 в уравнение (4.1). Имеем:
![]()
Но k12+pk1+q=0, т. к. k1 есть корень уравнения (4.2); р+2k1=0, т. к. по условию![]()
Поэтому y''2+Py'2+qy2=0, т. е. функция у2=хеk1x является решением уравнения (4.1).
Частные решения ![]() образуют фундаментальную систему решений: W(x)=e2k1x≠0. Следовательно, в этом случае общее решение ЛОДУ (4.1) имеет вид
образуют фундаментальную систему решений: W(x)=e2k1x≠0. Следовательно, в этом случае общее решение ЛОДУ (4.1) имеет вид![]()
Случай3. Корни k1 и k2 уравнения (4.2) комплексные![]()
В этом случае частными решениями уравнения (4.1) являются функции![]()
имеем
![]()
Найдем два действительных частных решения уравнения (4.1). Для этого составим две линейные комбинации решений y1 и у2:
![]()
Функции ![]() являются решениями уравнения (4.1).Поэтому общее решение уравнения (4.1) запишется в виде
являются решениями уравнения (4.1).Поэтому общее решение уравнения (4.1) запишется в виде ![]() или
или
![]()
Интегрирование ЛНДУ второго порядка с постоянными коэффициентами и правой частью специального вида
Рассмотрим ЛНДУ второго порядка с постоянными коэффициентами,
![]()
где р и q - некоторые числа.
Для уравнений с постоянными коэффициентами существует способ нахождения у*, если правая часть ƒ(х) уравнения имеет так называемый «специальный вид»:
I.![]() или
или
II.![]()
Случай 1.
Правая часть (5.10) имеет вид![]() где а є R, Рn
(х) - многочлен степени n. Уравнение (5.10) запишется в виде
где а є R, Рn
(х) - многочлен степени n. Уравнение (5.10) запишется в виде
![]()
В этом случае частное решение у* ищем в виде:
![]()
где r - число, равное кратности а как корня характеристического уравнения ![]() (т.е. r - число, показывающее, сколько раз а является корнем уравнения
(т.е. r - число, показывающее, сколько раз а является корнем уравнения ![]()
- многочлен степени n, записанный с неопределенными коэффициентами Аi (i=l,2,...,n).
а) Пусть а не является корнем характеристического уравнения ![]() т. е.
т. е.![]() Следовательно,
Следовательно,
![]()
После подстановки функции у* и ее производных в уравнение (5.11), сокращения на![]() , получим:
, получим:
![]()
Слева - многочлен степени n с неопределенными коэффициентами, справа - многочлен степени n, но с известными
коэффициентами. Приравнивая коэффициенты при одинаковых степенях х, получим систему (n+1) алгебраических уравнений для определения коэффициентов Ао , А1 ,..., Аn .
б) Пусть а является однократным (простым) корнем характеристического уравнения ![]()
В этом случае искать решение в форме![]() нельзя, т. к.
нельзя, т. к. ![]() и уравнение (5.13) принимает вид
и уравнение (5.13) принимает вид
![]() В левой части - многочлен степени (n-1), в правой части - многочлен степени n. Чтобы получить тождество многочленов в решении у*, нужно иметь многочлен степени (n+1). Поэтому частное решение у* следует искать в виде
В левой части - многочлен степени (n-1), в правой части - многочлен степени n. Чтобы получить тождество многочленов в решении у*, нужно иметь многочлен степени (n+1). Поэтому частное решение у* следует искать в виде ![]() (в равенстве (5.12) положить r=1).
(в равенстве (5.12) положить r=1).
в) Пусть а является двукратным корнем характеристического уравнения k2
+рк+q=0, т. е. а=k1
=k2
. В этом случае а2
+ра+q=0 и 2а+р=0, а поэтомy уравнение (5.13) принимает вид![]()
Слева стоит многочлен степени n-2. Понятно, чтобы иметь слева многочлен степени n, частное решение у* следует искать в виде
![]()
(в равенстве (5.12) положить r=2).
Случай 2. Правая часть (5.10) имеет вид
![]()
где Рn (х) и Qm (x) - многочлены степени n и m соответственно, а и β - действительные числа. Уравнение (5.10) запишется в виде
![]()
Можно показать, что в этом случае частное решение у* уравнения (5.14) следует искать в виде
![]()
где r - число, равное кратности а+βi как корня характеристического уравнения ![]() - многочлены степени l с неопределенными коэффициентами, l - наивысшая степень многочленов Рn
(х) и
- многочлены степени l с неопределенными коэффициентами, l - наивысшая степень многочленов Рn
(х) и ![]()
Замечания.
1. После подстановки функции (5.15) в (5.14) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения.
2. Форма (5.15) сохраняется и в случаях, когда![]()
3. Если правая часть уравнения (5.10) есть сумма функций вида I или II, то для нахождения у* следует использовать теорему 5.2 о наложении решений.
Пример 5.2. Найти общее решение уравнения![]()
Решение: Найдем общее решение![]() ЛОДУ
ЛОДУ![]() Характеристическое уравнение k2
-2k+1=0 имеет корень k1
=1 кратнoсти 2. Значит,
Характеристическое уравнение k2
-2k+1=0 имеет корень k1
=1 кратнoсти 2. Значит,![]() Находим частное решение исходного уравнения. В нем правая часть
Находим частное решение исходного уравнения. В нем правая часть![]() есть формула вида
есть формула вида ![]() причем а=0, не является корнем характеристического уравнения:
причем а=0, не является корнем характеристического уравнения: ![]() . Поэтому, согласно формуле (5.12), частное решение у* ищем в виде
. Поэтому, согласно формуле (5.12), частное решение у* ищем в виде ![]() - неопределенные коэффициенты. Тогда
- неопределенные коэффициенты. Тогда ![]() Подставив
Подставив ![]() в исходноеуравнение, получим
в исходноеуравнение, получим![]() Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:![]()
Отсюда А=1, В=-2. Поэтому частное решение данного уравнения имеет вид у* =х-2. Следовательно,![]() искомое общее решение уравнения.
искомое общее решение уравнения.
Элементы теории вероятности
Случайные события и их классификация.
Если некоторый производится опыт, исход которогго предсказать заранее нельзя, то такие эксперементы называются случайными. При этом рассматриваются только те эксперементы, которые можно повторять многократно при одних и тех же условиях.
Случайным событием называется любой исход опыта, который может произойти или не произойти.
События как правило обозначаются заглавными буквами А, В, С..
Пример, бросоние игральной кости:
А – выпадение 5 очков
В - выпадение четного числа очков
С – 7 очков
D– выпадение целого числа очков
Е – неменее 3х очков
Непосредственные исходы опыта называются элементарными событиями и обозначаются W.
Все возможные исходы называются пространством элементарных событий. И обозначаются Λ.
· Сбытие называется достоверным, если оно обязательно наступит в результате опыта. (D)
· Событие называется невозможным, если он зав6едомо не произойдет в результате проведения опыта. (С)
· 2 события называются несовместными, если появление одного из них исключает появлене другого события в одном и том же опыте. (А и В)
· В противном случае, если событие дополняет появление другого, то они будут совместными. (В и Е); (D и Е); (А и Е).
· Полную группу случайных событий образуют все возможные, попарно-несовместные события для данного опыта. События А1, А2…, Ан, называются попарно-несовместимыми если любые дщва из них несовместимы.
Действия над событиями.
Завтра будет дождливое (В) утро (А).
1. Суммой событий А и В называется событие С, С = А+В, состоящее в наступлении хотя бы одного из них ( или А, или В, или А и В вместе). Дождя нет
2. Произведением событий А и В называется событие С, С = А*В, состоящее в совместном наступлении этих событий ( и А и В одновременно). Дождь есть
3. Разностью событий А и В называется событие С, С= А –В, происходящее тогда и только тогда, когда происходит событие А , но не происходит событие В. Нет дождя
4. Противоположным событию А называется событие не наступление события Ā. А →Ā
Операции над событиями обладают следующими свойствами:
· А+В=В+А; А*В=В*А (переместительное)
· (А+В)*С=А*С+В*С; А*В+С=(А+С)*(В+С) (распеределительное)
· (А+В) +С = А+ (В +С); (А*В)*С =А*(В*С) (сочетательное)
· А+А=А; А*А=А
· А-В=А*Ḃ
· Ā +Ḃ =Ā *Ḃ и Ā *Ḃ = Ā +Ḃ
Алгебра событий.
Множество Ω = { w } всех вохможных взаимоисключающих исходов данного опыта называется пространством элементарных событий, а сами исходы w – элементарными событиями.
Случайным событием А называется любое подмножество множества Ω, если Ω конечно или счетно: А принадлежит Ω. Элементарные события, входящие в подмножество А пространства Ω, называются благоприятствующими событию А. Множество Ω называется достоверным событием. Ему благоприятствует любое элементарное событие, в результате опыта оно обязательно произойдет. Пустое множество ø называется невозможным событием, в результате опыта оно произойти не может.
Над событиями можно производить все операции, выполняемые для множеств.
Сумма (или объединение) двух событий А+В - это множество, которое содержит элементы, принадлежащие хотя бы одному из событий А и В.
Произведение двух событий А*В - это множество, которое содержит элементы, принадлежащие хотя бы одному из событий А и В.
Разность событий А – В - это множество, которое содержит элементы события А, не принадлежащие событию В.
Противоположное событию А принадлежит Ω событие Ā = Ω\А.
Событие А влечет событие В, если каждый элемент события А содержится в В.
Статистическое определение вероятности.
Статистической вероятностью события А называется число, около которого колеблется относительная частота события А при достаточно ьольшом числе испытаний (опытов).
Вероятность события А обозначается символом Р(А). Согласно данному определению Р(А)≈ Р*(А) = nA /n, где nA – число наступления событий в данном испытании, n– общее кол-во испытаний.
Свойства:
1.Вероятность любого события заключена между 0 и 1, т.е. 0 ≤ Р(А) ≤ 1
2.Вероятность невозможного события равна 0, т.е. Р(ᴓ) = 0
3.Вероятность достоверного события равна единице, т.е. Р(Ω) = 1.
4.Вероятность суммы несовместных событий равна сумме вероятностейэтих событий, т.е. если А*В =ᴓ, то Р (А + В) = Р (А) + Р(В)
Классическое определение вероятности.
Пусть проводится опыт с nисходами, которые можно представить в видепоолной группы несовместных равновозможных событий. Такие исходы называются случаями, шансами, элементарными событиями, опыт – классическим. Случай w, который приводит к наступлению события А, называется благоприятным (или – благоприятствующим) ему, т.е. случай w влечет за собой событие А.
Вероятностью события А называется отношение числа mслучаев, благоприятсвующих этому событию, к общему числу n случаев, т.е. Р(А) = m/n, где m–кол-во случаев благоприятствующих этому событию, n –кол-во всех событий.
Свойства:
1. Вероятность любого события заключена между 0 и 1, т.е. 0 ≤ Р(А) ≤ 1
2. Вероятность невозможного события равна 0, т.е. Р(ᴓ) = 0
3. Вероятность достоверного события равна единице, т.е. Р(Ω) = 1.
4. Вероятность суммы несовместных событий равна сумме вероятностейэтих событий, т.е. если А*В =ᴓ, то Р (А + В) = Р (А) + Р(В)
Пример: В урне 12 белых и 8 черных шаров. Какова вероятность того, что на удачу вынутый шар будет белым?
Пусть А – событие, состоящее в том, что вынут белый шар. Ясно что n = 12+8=20 – число всех возможных случаев. Число благоприят –х событию А, равно12. След-но по формуле Р(А) = 12/20 = 0,6.
Геометрическое определение вероятности.
Геометрической вероятностью события А называется отношение площади области Dк площади области Ω, т.е. Р(А) = SD /SΩ .
Геометрическое определение вероятности события применимо и в случае, когда области ΩиD обе линейные и объемные. В первом случае Р(А) = lD /lΩ . Во втором Р(А) = VD /VΩ , где l– длина, V – объем соответствующей области.
Все три формулы можно записать в виде Р(А) = mesD/mesΩ, где mes – мера (S,l,V) области.
Свойства:
1.Вероятность любого события заключена между 0 и 1, т.е. 0 ≤ Р(А) ≤ 1
2.Вероятность невозможного события равна 0, т.е. Р(ᴓ) = 0
3.Вероятность достоверного события равна единице, т.е. Р(Ω) = 1.
4.Вероятность суммы несовместных событий равна сумме вероятностейэтих событий, т.е. если А*В =ᴓ, то Р (А + В) = Р (А) + Р(В)
Свойства вероятностей
1. Вероятность невозможного события равна нулю, т.е. Р(ᴓ) = 0
2. Сумма вероятностей противотоложных событий равна единице, т.е. Р(А) +Р(Ā) = 1
3. Вероятность любого события не превосходит единицы, т.е. Р(А) ≤1
4. Если событие А влечет за собой событие В, то Р(А)≤Р(В)
5. Если события А1, А2, ..Ан образуют полную группу несовместных событий , ![]()
![]()
Условные вероятности
Пусть А и В – два события, рассматриваемые в данном опыте. Наступление одного события (А), может влиять на возможность наступления другого (В). Для зхарактеристи зависимости одних событий от других вводится понятие условной вероятности.
Условной вероятностью события В при условии, что произошлособытие А, называется отношение вероятности произведения этих событий к вероятности события А, причем Р(А) ≠0, обозначается символом Р(В/А).
Таким образом по определению Р(В/А)= Р(А*В)÷Р(А), Р(А) ≠0.
Вероятность Р(В), в отличие от условной, называется безусловной вероятностью.
Аналогично определяется вероятность события А, при условии В, т.е.Р(А/В)
Р(А/В)=Р(А*В)÷Р(В), Р(В) ≠0.
Пример : в урне 2 белых и 7 черных шаров. Из нее последовательно вынимают 2 шара. Какова вероятность того, что 2 шар окажется белым при условии, что 1 был черным. Решение: Пусть А – 1 шар черный, В – 2 белый. Т к событие А произошло, в урне осталось 8 шаров, из которых 2 белых. Поэтому (В/А) = 2/8=1/4.
Вероятность произведения событий
Вероятность произведения 2х событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое произошло. Р(А*В) = Р(А) * Р(В/А) = Р(В) * Р(А/В) – правило или теорема умножения вероятностей.
Правило умножения вероятностей имеет простой вид если события, образующие произведение, независимы. Событие А называется независимым от события В, если его условная вероятность равна безусловной, т.е. если выполняется равенство Р(А/В) = Р(А).
Лемма: Если событие А не зависит от события В, то и событие В не зависит от события А.
Два события называются независимыми, если появления одного из них не меняет вероятность появления другого. Для независимых событий правило вероятности имеет вид: Р(А*В) = Р(А) * Р(В), т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
События А1 , А2 ,….Аn называются независимыми, если каждое из них не зависит от произведения любого числа остальных событий и от каждого в отдельности. В противном случае события А1 , А2 ,….Аn , называются зависимыми. Для независимых событий их условные вероятности равны безусловным, а формула упрощается
Р(А1 *А2 ….Аn )=Р(А1 )*Р(А2 )*……*Р(Аn )
Пример: в коробке 4 белых,3 синих, 2 черных шара. Наудачу послед-но вынимают 3 шара. Какова вероят-ть что 1й шар будет белым, 2й –синим, 3й- черным. Решение: событие А1 – 1м вытащили белый шар, А2 – 2м вытащили синий шар, 3м вытащили черный шар. Тогда А=А1*А2*А3. По правилу умнож-я вер-й :Р(А) =Р(А1)*Р(А2/А1)*Р(А3/А2*А1) . То Р(А1) = 4/9, Р(А2/А1)=3/8, Р(А3/А2*А1)=2/7. Р(А)= 1/21=0,05.
Вероятность суммы событий.
Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения, Р(А+В) = Р(А) + Р(В) – Р(А*В).
Можно получить формулу вероятности суммы трех и большего числа совместных событий; для 3х событий она имеет вид: Р(А+В+С) = Р(А) +Р(В)+Р(С) – Р(А*В) –Р(А*С) –Р(В*С) +Р(А*В*С).
Основные формулы комбинаторики.
При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. Определим основные такие комбинации.
Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок
Рп = п ! (1.3)
Пример. Сколько различных списков (отличающихся порядком фамилий) можно составить из 7 различных фамилий?
Решение. Р 7 = 7! = 2·3·4·5·6·7 = 5040.
Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений
![]() (1.4)
(1.4)
Пример. Сколько возможно различных вариантов пьедестала почета (первое, второе, третье места), если в соревнованиях принимают участие 10 человек?
Решение. ![]()
Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний
![]() (1.5)
(1.5)
Пример. В отборочных соревнованиях принимают участие 10 человек, из которых в финал выходят трое. Сколько может быть различных троек финалистов?
Решение. В отличие от предыдущего примера, здесь не важен порядок финалистов, следовательно, ищем число сочетаний из 10 по 3:
![]()
Формула полной вероятности
Пусть события Н1, Н2,….Нn образуют полную группу. Тогда для любого события А имеет место формула полной вероятности или средней вероятности.
![]()
Пример. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбран-ной урны наудачу вынут шар. Найти вероятность того, что он белый.
Решение. Будем считать гипотезами Н
1
, Н
2
и Н
3
выбор урны с соответствующим номером. Так как по условию задачи все гипотезы равновозможны, то![]() Найдем условную вероятность А
при реализации каждой гипотезы:
Найдем условную вероятность А
при реализации каждой гипотезы: ![]()
![]() Тогда
Тогда ![]()
Формула Байеса
Она позволяет переоценить вероятность гипотез Нi , принятых до опыта и называемых априорными, по результатам уже проведенного опыта, т.е. найти условные вероятности Р(Нi /А), которые называются апостериорными.
Теорема: Пусть события Н1, Н2,…Нn образуют полную группу событий. Тогда условная вероятность события Нk (k=l,n- по модулю) при условии, что событие А произошло, задается формулой
![]()
Где ![]() - формула полной вероятности.
- формула полной вероятности.
Пример. После двух выстрелов двух стрелков, вероятности попаданий которых равны 0,6 и 0,7, в мишени оказалась одна пробоина. Найти вероятность того, что попал первый стрелок.
Решение. Пусть событиеА – одно попадание при двух выстрелах, а гипотезы: Н 1 – первый попал, а второй промахнулся, Н 2 – первый промахнулся, а второй попал, Н 3 – оба попали, Н 4 – оба промахнулись. Вероятности гипотез: р(Н 1 ) = 0,6·0,3 = 0,18, р (Н 2 ) = 0,4·0,7 = 0,28, р (Н 3 ) = 0,6·0,7 = 0,42, р (Н 4 ) = 0,4·0,3 = 0,12.Тогда р (А/Н 1 ) = р (А/Н 2 ) = 1, р (А/Н 3 ) = р (А/Н 4 ) = 0. Следовательно, полная вероятность р (А ) = 0,18·1 + 0,28·1 + 0,42·0 + 0,12·0 = 0,46. Применяя формулу Байеса, получим:
![]()
Формула Бернулли
Теорема: Если производится n независимых испытаний, в каждом из которых вероятность появления события А равна р, а вероятность его непоявления равна q = 1 –p, то вероятность того, что событие А произойдет mраз определяется формулой.Pn (m) = Cm n * pm * qn - m , m = 0, 1,2….n.
Пример: Производится 3 независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны р = 0,9. Какова вероятность: а) промаха, б) одного попадания, в) 2х попаданий, г) трех попаданий? Если вероятности попадания при разных случаях различны: р1 = 0,7, р2 = 0,8, р3 = 0,9
В данном случае n = 3, p = 0.9, q = 0.1
А) Р(0) = С0 3 × 0,90 × 0,13 = 0,001 – вероятность 3х промахов
Б) Р (1) = С1 3 × 0,91 × 0,12 = 0,027 - вероятность одного попадания
В) Р (2) = С2 3 × 0,92 × 0,11 = 0,243 - вероятность 2х попаданий
Г) Р (3) = С3 3 × 0,93 × 0,10 = 0,729 – вероятность 3х попаданий
Предельные теоремы в схеме Бернулли
Использование формулы Бернулли при больших значениях nи mвызывает большие трудности, так как оно связано с громоздкими вычислениями. Вычисление Рn (m) вызывает затруднения также при малых значениях р (q).
Теоремма Пуассона .
Если число испытыний неограничено увеличиваетя (n – 0) и вероятность р наступления события А в каждом испытании неограниченно уменьшается ( р – 0), но так, что их произведение np является постоянной величиной (np = a = const), то вероятность Рn (m) удовлетворяет предельному равенству limPn (m) = am e- a /m! (n→∞).
Пример : Завод отправил 1500 бутылок. Вероятность того что бутылка в пути может разбиться равна 0,002. Найти вероятность того, что в пути будет разбито не более 4х бутылок - Р(А).
Искомая вероятность равна Р1500 (0)+Р1500 (1) + Р1500 (2)+ Р1500 (3)+Р1500 (4)
Так как n = 1500, p = 0,002, то а = (np) = 3
Р(А) = 30 * е-3 /0! +31 * е-3 /1! +32 * е-3 /2!+ 33 * е-3 /3! +34 * е-3 /4! = 0,815.
Формулу пуассона можно считать математической моделью простейшего потока событий.
Потоком событий называют последовательность событий, наступающих в случайные моменты времени (поток посетителей в парикхмахерской, поток вызовов, поток отказов элементов).
Можно доказать что вероятность появления m событий простейшего потока за время продолжительностью tопределяется формулой Пуассона
Рt (m) = p (m) = (λt)m *e- λt /m!
Локальная и интегральная теоремы Муавра-Лапласа.
Локальная теорема: Если вероятность р наступления события А в каждом испытании постояннаи отлична от 0 и 1, а число независимых испытаний достаточно велико, то вероятность Рn (m) может быть вычислена по приближенной формуле
Pn (m) = 1/ √npq * 1/ √2П * е-х2/2 , где х=m-np/ √npq
Выражение 1/ √2П * е-х2/2 = ɸ(x) называется функцией Гаусса, а ее график кривой вероятностей.
Равенство можно расписать в виде Pn (m) = 1/ √npq *ɸ(x), где х=m-np/ √npq
Интегральная теорема : Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Рn (k1 ≤m≤ k2 ) может быть найдена по приближенной формуле
Рn (k1 ≤m≤ k2 ) = 1/ √2П∫х2 х1 е-х2/2 dx, где х1 =k1 -np/ √npq, х2 =k2 -np/ √npq
Равенство принимает вид Рn (k1 ≤ m ≤ k2 ) = Ф0 (х2 ) – Ф0 (х1 ), гдех1 =k1 -np/ √npq, х2 =k2 -np/ √npq
Наряду с номированной функцией Лапласа используют функцию , ɸ(x) =1/ √2П ∫х -∞ е- t 2/2 dt, Ф (х) =0,5 +Ф0 (х)
Понятие случайной величины.
Одним из важнейших понятий теории вероятностей (наряду со случайным событием и вероятностью) является понятие случайной величины.
Под случайной величиной понимают величину, которая в результате опыта принимает то или иное значение, причем неизвестно заранее, какое именно.
Случайные величины (сокращенно: св.) обозначаются прописными латинскими буквами X, У, Z , ... а принимаемые ими значения
Х1,Х2,Х3…..У1,У2,У3….
Примерами с. в. могут служить: 1) X — число очков, появляющихся при бросании игральной кости; 2) Y — число выстрелов до первого попадания в цель; 3) Z — время безотказной работы прибора и т.п. (рост человека, курс доллара, количество бракованных деталей в партии, температура воздуха, выигрыш игрока, координата точки при случайном выборе ее на [0; 1], прибыль фирмы, ...).
То есть д. с. в. принимает отдельные изолированные друг от друга значения, а н. с. в. может принимать любые значения из некоторого промежутка (например, значения на отрезке, на всей числовой прямой и т.д.). Случайные величины X и Y (примеры 1) и 2)) являются дискретными. С. в. Z (пример 3)) является непрерывной: ее возможные значения принадлежат промежутку То есть д. с. в. принимает отдельные изолированные друг от друга значения, а н. с. в. может принимать любые значения из некоторого промежутка (например, значения на отрезке, на всей числовой прямой и т.д.). Случайные величины X и Y (примеры 1) и 2)) являются дискретными. С. в. Z (пример 3)) является непрерывной: ее возможные значения принадлежат промежутку [0, t), где t >= 0, правая граница не определена (теоретически t = +оо). Отметим, что рассматриваются также с. в. смешанного типа.
Дадим теперь строгое определение св., исходя из теоретике-множественной трактовки основных понятий теории вероятностей.
Случайной величиной X называется числовая функция, определенная на пространстве элементарных событий J2, которая каждому элементарному событию w ставит в соответствие число X ( w ), т.е. X = X ( w ), теП (или X = f ( w )).
Пример. Опыт состоит в бросании монеты 2 раза. На ПЭС fi — = {wi,w2,W3,W4}, гд -е W 1 = ГГ, W 2 = ГР, Wз = РГ, W4 = РР, можно рассмотреть с.в. X — число появлений герба. Св. X является функцией от элементарного события wt : X ( w \) = 2, X ( w 2 ) — 1, X ( w 3) ~ 1, X ( w 4 ) = 0; X — д.с. в. со значениями х-\ = 0, х2 = 1, хз = 2.
Закон распределения случайной величины
Пусть X — д. с. в., которая принимает значения х1 , х2 , х3 ,..., хп ,... (множество этих значений конечно или счетно) с некоторой вероятностью р i , где i = 1,2,3,...,n,— Закон распределения д. с. в. удобно задавать с помощью формулы р i = Р{Х = xit }, i = 1,2,3,..., n,..., определяющей вероятность того, что в результате опыта с. в. X примет значение хг . Для д. с. в. X закон распределения может быть задан в виде таблицы распределения:
| X |
Xi |
х2 |
… |
Хп |
… |
| р |
Р\ |
Р2 |
… |
Рп |
… |
где первая строка содержит все возможные значения (обычно в порядке возрастания) с. в., а вторая — их вероятности. Такую таблицу называют рядом распределения.
Так как события {X = х1}, {X — х2 } ... несовместны и образуют полную группу, то сумма их вероятностей равна единице т.е. сумма Pi = 1
Закон распределения д. с. в. можно задать графически, если на оси абсцисс отложить возможные значения с. в., а на оси ординат — вероятности этих значений. Ломаную, соединяющую последовательно точки ( xi , p 1) y (х2 ,р2 ), называют многоугольником (или полигоном) распределения
Характеристики дискретной случайной величины
Числовые характеристики ДСВХ.
Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относятся математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическое ожидание .
Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон распределения, но для решения подобных задач ее бывает достаточно.
Математическое ожидание ДСВХ равно сумме произведений всех ее возможных значений на их вероятности, т
.е. ![]()
Если ДСВХ принимает счетное множество значений, то ![]()
Свойства математического ожидания
1. М(С) =С, где С=const;
2. М(СХ)= СМ(Х);
3. М(XY) =M(X)M(Y), где Х и У- независимые случайные величины;
4. М(Х+У) = М(Х) +М(У), где Х и У- независимые случайные величины.
Заметим, что математическое ожидание для данной ДСВХ есть величина постоянная.
Дисперсия.
Для полного представления о ДСВХ недостаточно знать только математическое ожидание. Иногда математические ожидания случайных величин равны , а их возможные значения резко отличаются дру от друга. Приведем пример. Даны ряды распределения двух случайных величин Х и У:
Х -0,01 0,01
р 0,5 0,5
У -100 100
р 0,5 0,5
Здесь математические ожидания случайных величин равны: М(Х) = М(У) = 0, но возможные значения ДСВХ близки к М(Х), а возможные значения ДСВУ далеки от М(У). По М(У) нельзя судить о значениях ДСВУ.
По этой причине вводят числовую характеристику, которая называется дисперсией. Эта характеристика оценивает рассеяние случайной величины вокруг своего математического ожидания.
Дисперсией ДСВХ (D(X)) называют математическое ожидание квадрата отклонения СВ от ее математического ожидания, т.е.
![]()
Для вычисления D(X) удобнее пользоваться следующей формулой, которая выводится на основании свойств математического ожидания:
![]()
Свойства дисперсии
1. D(C) =0 , где С = const;
2. D(CX) = C2D(X);
Среднеквадратическое откланение
Дисперсия величины имеет размерность, что в сравнительных целях неудобно,поэтому вводят Ср.от.
СКО позволяет сравнивать отклонения различные по размерным величинам
![]()
Пример:
х -1 0 1 2
р 0,2 0,1 0,3 0,4
Мх= (-1*0,2)+0,1*0+0,3+2*0,4=0,9
Dx= (-1-9)^2*0,2+0,9^2*0,1+(1-0,9)^2*0,3+(2*0,9)^2*0,4=1,29
σх= √1,29~1,14
Свойства характеристик случайной величины.
Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:
М ( Х ) = х1 · р1 + х2 · р2 + х3 · р3 + ... + хn· рn .
Свойства математического ожидания:
1) М ( с · Х ) = с · М ( Х ) , c![]() R ,
R ,
2) М ( Х + Y ) = М ( Х ) + М ( Y ) , Х , Y ![]() Е ,
Е ,
3) М ( Х · Y ) = М ( Х ) · М ( Y ) для независимых случайных величин Х и Y .
Дисперсией случайной величины Х называется число:
D ( Х ) = М{ [ Х – М ( Х )] 2 }= М ( Х 2 ) – [М ( Х )] 2 .
Свойства дисперсии:
1) D ( с · Х ) = с 2 · D ( Х ) , c ![]() R ,
R ,
2) D ( Х + Y ) = D ( Х ) + D ( Y ) для независимых случайных величин Х и Y .
Среднее квадратичное отклонение: ![]()
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!ИЛИ ЭТО!!!!!!!!!!!!!!!!!!!!!!!!!!!
Числовыми характеристиками случайных величин являются математическое ожидание и дисперсия, а так же и моменты случайных величин
Математическое ожиданием М(Х) называется средняя величина возможных значений случайных величин, взвешенных по их вероятности. Выражается формулой: ![]()
Свойство 1. Мат. ожидание постоянной равно этой постоянной.
Свойство 2. Мат. ожидание суммы случайных величин равно сумме их мат. ожиданий: ![]()
Из этого свойства следует следствие:
Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий: ![]()
Свойство 3. Математическое ожидание произведения независимых случайных величин Х и Y равно произведению математических ожиданий этих вел. M(XY)=M(X)·(M)Y.
Следствие. Постоянный множитель можно вынести за знак математических ожидания: М(сХ) = сМ(Х)
Дисперсией называется математическое ожидание квадрата отклонения случайных величин от математического ожидания:
D[Х]=M[X-M(X)]2
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. постоянную величину можно вынести за знак дисперсии, предварительно возведя ее в квадрат:
D(cX) = c2D(X)
Свойство 3. Дисперсия суммы независимых случайных величин Х и Y равна сумме их дисперсий:
D(X+Y) = D(X) + D(Y), от сюда следствие:
если х1, х2, ..., хn - случайные величины, каждая из которых независима от суммы остальных, то
D(X1+X2+...+Xn) = D(X1) + D(X2)+...+D(Xn).
Моментом k-порядка называется математическое ожидание k-й степени отклонения случайной величины Х от некоторой постоянной с.
Если в качестве с берется нуль, моменты называются начальными
νk = М(Х)k
Если с = М(Х), то моменты называются центральными
μ = M[X – M(X)]k
Непрерывные случайные величины
Непрерывной случайной величиной (НСВ) называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Множество возможных значений непрерывной случайной величины бесконечно и несчетно.
F(х)
f(x)=F’(x)
Случайная величина называется непрерывной, если для нее существует неотрицательная кусочно-непрерывная функция* ![]() , удовлетворяющая для любых значений x равенству
, удовлетворяющая для любых значений x равенству
![]()
Функция ![]() называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x1<x2,
называется плотностью распределения вероятностей, или кратко, плотностью распределения. Если x1<x2,
f(x)>=0
![]()
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств ![]()
равна площади криволинейной трапеции с основанием [x1,x2], ограниченной сверху кривой ![]()
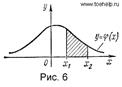
![]()
![]()
Функция распределения непрерывной случайной величины
Универсальной формой задания распределения двумерной случайной величины является функция распределения (или «интегральная функция»), пригодная как для дискретной, так и для непрерывной случайной величины, обозначаемая Fx , y { x , y ) или просто F ( x , y ).
Функцией распределения двумерной случайной величины (X, У) называется функция F ( x , у), которая для любых действительных чисел х и у равна вероятности совместного выполнения двух событий {X < х) и {У < у].
Таким образом, по определению
F ( x , y ) = P { X < x , Y <у}
(событие {X < x , Y < у] означает произведение событий {X < х} и { Y < y })
Функция распределения двумерной случайной величины (x,y) находится суммированием всех вероятностей
Плотность вероятности непрерывной случайной величины
Двумерная случайная величина называется непрерывной, если ее
функция распределения F ( x , y ) есть непрерывная функция, дифференцируемая по каждому из аргументов, у которой существует вторая смешанная производная F " y ( x , y ).
Плотностью распределения вероятностей (или совместной плот-
ностью) непрерывной двумерной случайной величины (X, У) называется вторая смешанная производная ее функции распределения.
Обозначается совместная плотность системы двух непрерывных случайных величин (X, У) через f ( x , y ) (или р(х,у)). Таким образом, по определению
![]()
Плотность распределения вероятностей непрерывной двумерной случайной величины (X, Y ) есть предел отношения вероятности попадания случайной точки (X, Y ) в элементарный прямоугольник со сторонами дельтаХ и дельтаУ примыкающий к точке (х,у), к площади этого прямоугольника, когда его размеры дельтах и дельта у стремятся к нулю

Свойства плотности вероятностей
Плотность распределения f (х, у) обладает следующими свойствами:
1. Плотность распределения двумерной случайной величины неотрицательна, т. е. ![]()
2. Вероятность попадания случайной точки (X, Y ) в область D равна двойному интегралу от плотности по области D , т.е.
![]()
3. Функция распределения двумерной случайной величины может быть выражена через ее плотность распределения по формуле:
![]()
4. Условие нормировки: двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной с. в. равен единице, т. е.
![]()
5. Плотности распределения одномерных составляющих X и У могут быть найдены по формулам:
-
![]()
Математическое ожидание и дисперсия
На практике чаще всего используются моменты I и II порядков: математическое ожидание (м. о.), дисперсия и корреляционный момент. Математическое ожидание и дисперсия двумерной случайной величины служат соответственно средним значением и мерой рассеяния. Корреляционный момент выражает меру взаимного влияния случайных величин, входящих в систему (X, У).
Математическим ожиданием двумерной св. ( X , Y ) называется совокупность двух м.о. MX и MY , определяемых равенствами:
![]()
если (Х,У) — дискретная система с. в. (здесь р ij — Р{Х = Xi , Y = yj }); и
![]()
если (X, Y ) — непрерывная система св. (здесь j ( x , y ) — плотность распределения системы).
Дисперсией системы со. (Х.У) называется совокупность двух дисперсий DX н DY , определяемых равенствами:
![]()
если ( X , Y )- дискретная случайная величина
![]()
если ( X , Y ) — непрерывная система с. в.
Дисперсии DX и DY характеризуют рассеяние (разброс) случайной точки {X, У) и в направлении осей Ох и Оу вокруг точки (тх ,ту ) на плоскости Оху — центра рассеяния.
Математические ожидания mx, и mу являются частными случаями начального момента a порядка k + в системы (X. У), определяемого равенством
Aks, = M [ Xk Ys );
![]()
Дисперсии DX
и DY
являются частными случаями начального
.момента Aks порядка к +
s системы {X,
У), определяемого равенство![]()
Математическое ожидание св. u
{
X
,
Y
),
являющейся функцией компонент X и У двумерной с. в. (X, У) находится, аналогично, по формулам ![]()
для непрерывного случая и ![]()
для дискретного случая.
Начальный момент II порядка a1,1 = MXY часто встречается в приложениях. Вычисляется по формуле
![]()
для дискретных с.в
![]()
для непрерывных с. в.