| Скачать .docx | Скачать .pdf |
Реферат: Приближенное вычисление интеграла
Содержание
Введение 2
1. Различные методы вычисления определенных интегралов 3
1.1. Метод Симпсона для интегрирования функций F (x ) по
заданному промежутку и его реализация на языке Pascal 4
1.2. Метод Симпсона для интегрирования функции от двух
переменных F (x ,y ) по прямоугольной двумерной области и его
реализация на языке Pascal 5
1.3. Метод Ромберга и его реализация на языке Pascal 7
1.4. Метод Гаусса и его реализация на языке Pascal 10
Заключение 16
Литература 17
Введение
Система программирования Турбо Паскаль представляет собой единство двух в известной степени самостоятельных начал: компилятора с языка программирования Паскаль (язык назван в честь выдающегося французского математика и философа Блеза Паскаля (1623-1662)) и некоторой инструментальной программной оболочки, способствующей повышению эффективности создания программ.
Паскаль – гибкий и развитый в отношении типов данных язык. Привлекательны его рекурсивные возможности, а также поддержка технологии объектно-ориентированного программирования.
Изучение программирования на языке Паскаль может дать хороший старт в огромный и увлекательный мир программирования. Обучение языку программирования проходит намного более эффективно с изучением примеров.
В данной работе рассмотрен пример использования языка программирования высокого уровня Pascal для вычисления определенных интегралов.
1. Различные методы вычисления определенных интегралов.
Приближенное вычисление интеграла,
I
= 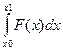 ,
,
Основано на его замене конечной суммой:
I
n
= ![]() k
F
(xk
),
k
F
(xk
),
где wk – числовые коэффициенты, а xk – точки отрезка [x 0 ,x 1 ]. Приближенное равенство
I ≈ I n называется квадратурной формулой , точки xk – узлами квадратурной формулы, а числа wk – коэффициентами квадратурной формулы. Разные методы приближенного интегрирования отличаются выбором узлов коэффициентов. От этого выбора зависит погрешность квадратурной формулы.
R
n
= ![]() .
.
В модуле integral реализовано несколько методов численного интегрирования как для простых (одномерных), так и для кратных (многомерных) интегралов.
В функции simpson реализован стандартный метод Симпсона для интегрирования функции F (x ) по заданному промежутку, когда число разбиений интервала выбирается заранее. Функция double_simpson является прямым обобщением метода Симпсона на случай интегрирования функции от двух переменных F (x ,y ) по прямоугольной двумерной области.
Функция adaptive_simpson служит для вычисления простых интегралов, она корректирует число и размер разбиений интервала, чтобы ошибка вычисления интеграла попала в заранее заданный интервал. Этот метод называется адаптивным интегрированием . Все современные программы интегрирования так или иначе адаптивны.
В функции romberg запрограммирован еще один метод адаптивного интегрирования – метод Ромберга, в настоящее время, вероятно, один из наиболее популярных. Имеются также функция gauss – одномерная версия метода интегрирования Гаусса. Интерфейсная секция модуля integral приведена в листинге 1.1.
Листинг 1 .1 . Интерфейсная секция модуля integral.
Unit integral;
Interface
Const
Max_dim =10;
Max_deg=96;
Type
Real_fun=function(x:real):real;
Real_fun2=function(x,y:real):real;
Real_vec=array[1..max_dim+1] of real;
Index=array[1..max_dim+1] of word;
Vec_fun=function(j:word; x:real_vec):real;
Var
no_evaluations, highest_level:word;
function simpson(F:real_fun; x0,x1:real; div_no:word):real;
function double_simpson(F:real_fun2; x0,x1,y0,y1:real; x_div,y_div:word):real;
function adaptive_simpson(F:real_fun;x0,x1,eps,eta:real):real;
function romberg(f:real_fun; x0,x1,eps,eta:real; min,max:word):real;
function gauss3(F:real_fun;x0,x1:real; n:word):real;
procedure compute_gauss_coeffs(deg:word);
function gauss(Freal_fun:x0,x1:real; deg:word):real;
1.1. Метод Симпсона для интегрирования функций F ( x ) по заданному промежутку и его реализация на языке Pascal.
Перейдем к секции реализации. Она начинается описанием функции simpson. Стоит сказать несколько слов о выборе узлов и коэффициентов квадратурной формулы Симпсона. Идея трехточечного метода Симпсона заключается в следующем.
Пусть x m – это средняя точка интервала [x 0 , x 1 ] и пусть Q (x ) – единственный полином второй степени, который интерполирует (приближает) подынтегральную функцию F (x ) по точкам x 0 , x m и x 1 . Искомый интеграл аппроксимируется интегралом от функции Q (x ):
I≈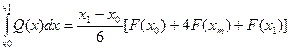 .
.
Это оценка точна, если F (x ) является полиномом степени 3.
В функции simpson интервал интегрирования делится на div_no равных частей, а трехточечная формула Симпсона применяется к каждому такому интервалу. Параметрами функции simpson (листинг1.2) являются, по порядку, подынтегральная функция, нижняя и верхняя границы интервала интегрирования и количество подынтервалов.
Листинг 1.2. Функция simpson модуля integral
Implementation
Uses crt;
Var
zero, weight:array [1..max_deg] of real;
Function simpson(F:real_fun; x0,x1:real; div_no:word):real;
Var
x, dx, sum:real;
j:word;
begin
dx:=(x1-x0)/(2.0*div_no);
sum:=F(x0)+F(x1);
x:=x0;
for j:=1 to 2*div_no-1 do
begin
x:=x+dx;
if Odd (j) then
sum:=sum+4.0*F(x)
else
sum:=sum+2.0*F(x);
end;
simpson:=dx*sum/3.0;
end;
1.2. Метод Симпсона для интегрирования функции от двух переменных F ( x , y ) по прямоугольной двумерной области и его реализация на языке Pascal.
Функция double_simpson (листинг 1.3.) является, по существу, прямым обобщением одномерного метода Симпсона на случай вычисления двойного интеграла по прямоугольной области.
Листинг 1.3. Функции double_simpson и simple_simpson модуля integral
Function double_simpson(F:real_fun2; x0,x1,y0,y1:real; x_div,y_div:word):real;
var
dx,dy,x,sum:real;
i:word;
function simple_simpson(x:real):real;
var
y,sum:real;
j,v:word;
begin
sum:=F(x,y0)+F(x,y1);
y:=y0;
for j:=1 to 2*y_div-1 do
begin
y:=y+dy;
if Odd(j) then
sum:=sum+4.0*F(x,y)
else
sum:=sum+2.0*F(x,y);
end;
simple_simpson:=sum;
end;{simple_simpson}
begin{doudle_simpson}
dx:=(x1-x0)/(2.0*x_div);
dy:=(y1-y0)/(2.0*y_div);
x:=x0;
sum:=simple_simpson(x0)+simple_simpon(x1);
for i:=1 to 2*x_div-1 do
begin
x:=x+dx;
if Odd(i) then
sum:=sum+4.0*simple_simpson(x)
else
sum:=sum+2.0*simple_simpson(x);
end;
double_simpson:=dx+dy*sum/9.0;
end;{double_simpson}
Недостатком рассмотренных функций интегрирования является то, что они не дают возможности явно задать точность вычисления интеграла. Точность связана с количеством точек разбиения, но ее значение в этих функциях не определяется с адаптивным выбором шага разбиения. Такой функцией является adaptive_simpson. Параметры eps и eta задают соответственно абсолютную и относительную погрешности. Их роль поясняется следующим неравенством:
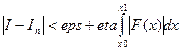 .
.
Функция adaptive_simpson (листинг1.4) использует рекурсивную процедуру simpson3point, которая вычисляет значение интеграла по интервалу [x 0 , x 0 +δ x ], где x0 – не обязательно исходная левая граничная точка.
Если трехточечный метод Симпсона не дает достаточную точность на данном интервале, этот интервал делится на три равные части, и метод вновь применяется к каждой из полученных частей. В результате получим 7 точек разбиения, но вычислять функцию F (x ) придется только в четырех из них, поскольку значения в других трех точках уже известны.
При адаптивном разбиении имеется одна тонкость. При переходе к подынтервалам, составляющим одну треть от исходного, чтобы получить новые абсолютную и относительную погрешности, надо поделить eps и eta на ![]() .
.
Листинг 1.4. Функция adaptive_simpson модуля integral
Function adaptive_simpson(F:real_fun:x0,x1,eps,eta:real):real;
const
max_level=35;
var
k,nest_level:word;
integral_abs:real;
function simpson3poin(x0,delta_x, estimate, integral_abs,
eps,eta,left,middle,right:real):real;
var
dx3,sum,eps3,eta3,factor,left_integ,
middle_integ, right_integ,F1,F2,F4,F5:real;
begin
Inc(nest_level);
dx3:=delta_x/3.0;
F1:=F(x0+0.5*dx3);
F2:=F(x0+dx3);
F:=F(x0+2.0*dx3);
F5:=F(x0+2.5*dx3);
Inc(no_evaluations,4);
factor:=dx3/6.0;
left_integ:=factor*(left+4.0*F1+F2);
middle_integ:=factor*(F2+4.0*middle+F4);
right_integ:=factor*(F4+4.0*F5+right);
sum:=left_integ+middle_integ+right_integ;
integral_abs:=integral_abs- Abs(eastimate)+Abs(left_integ)+Abs(middle_integ)+Abs(right_integ);
if (nest_level>1) and ((nest_level=max_level) or
(Abs(sum- estimate)<=eps+eta*integral_abs)) then simpson3point:=sum
else
Begin
If nest_level>highest_level then
Inc(highest_level);
Eps3:=0.577*eps;
Eta3:=0.577*eta;
Left_integ:=simpson3point(x0,dx3,left_integ,integral_abs,eps3,eta3, left,F1,F2);
middle_integ:=simpson3point(x0+dx3,dx3,middle_integ, integral_abs,eps3,eta3,F2,middle,F4);
right_integ:=simpson3point(x0+2.0*dx3,dx3,right_integ,integral_abs,eps3,eta3,F4,F5,right);
simpson3poin:=left_integ+middle_integ+right_integ;
end;
Dec(nest_level);
End; {simpson3point}
Begin {adaptive_simpson}
nest_level:=1;
highest_level:=1;
no_evaluations:=3;
adaptive_simpson:=simpson3point(x0,x1-x0,0.0,0.0,eps,eta,F(x0),F(x0+0.5*(x1-x0)),F(x1));
end;{adaptive_simpson}
1.3. Метод Ромберга и его реализация на языке Pascal.
Интегрирование следующим методом – методом Ромберга – основано на правиле трапеций, использующем кусочно-линейное приближение для интегрируемой функции. Основной факт относительно погрешности в методе трапеций следующий.
Теорема
. Пусть F
(x
) – гладкая функция на интервале [a
,b
], и этот интервал делится на т равных частей, каждая длиной h
=![]() . Пусть I
(h
) обозначает соответствующее приближение метода трапеций:
. Пусть I
(h
) обозначает соответствующее приближение метода трапеций:
I
(h
) = ![]() ,
,
где f i =F (a +jh ) – значение интегрируемой функции в точке a +jh .
Тогда
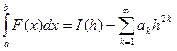 ,
,
Где ak – некоторая константа.
Основное здесь то, что погрешность в методе трапеций может быть выражена рядом по четным степеням шага интегрирования h . Построим таблицу значений T ik :
![]()

![]()
В нулевой строке T 0 k = I ((b – a )/2k ), так что T 00 ,T 01 ,… являются последовательными приближениями метода трапеций для интеграла, каждое с удвоенным по сравнению с предыдущим числом интервалов. Согласно приведенной выше теореме,
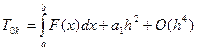 ,
,
где h = ((b – a )/2k.
Отсюда следует, что
 ,
,
Поэтому положим
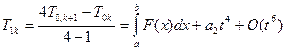 .
.
В общем случае строим j-ю строку таблицы Ромберга по формуле
![]() ,
,
а оценка погрешности имеет вид
 ,
,
где h = (b – a )/2k .
Для работы понадобится не целая таблица, а только последняя вычисленная строка. Число точек выборки на каждом шаге удваивается. Обратите внимание на то, что функцию следует вычислять только в новых точках, которые являются средними точками предыдущих подынтервалов:
F 0 + 2F 1 + 2F 2 + …+ 2F 2n-1 + F 2n =
= (F 0 + 2F 2 + 2F 4 + …+ 2F 2 n-2 + F 2 n ) + 2(F 1 + F 3 +…+F 2 n-1 ).
Таким образом, чтобы модифицировать предыдущее приближение, необходимо вычислить сумму значений функции в новых средних точках. Это делается в цикле со счетчиком k. Метод Ромберга реализован в функции romberg (листинг1.5).
Листинг 1.5. Функция romberg модуля integral
Function romberg (F:real_fun;x0,x1,eps,eta:real; min,max:word):real;
const
abs_max=30;
var
p,dx,error,F_of_x0, F_of_x1, F_of_xk,
roundoff_error,integral_abs,tolerance,
previous_estimate,current_estimate,
mid_sum, temp_sum, mid_sum_abs:real;
table:array[0..abs_max] of real;
j,n:word;
k,r:longint;
done:Boolean;
denom:array[1..abs_max] of real;
begin
p:=1.0;
for k:=1 to abs_max do
begin
p:=4.0*p;
denom[k]:=1.0/(p-1.0);
end;
dx:=x1-x0;
F_of_x0:=F(x0);
F_of_x1:=F(x1);
current_estimate:=0.0;
previos_estimate:=0.0;
done:=False;
table[0]:=0.5*dx*(F_of_x0+F_of_x1);
integral_abs:=0.5*Abs(dx)*(Abs(F_of_x0)+Abs(F_of_x1));
n:=1;
r:=1;
repeat
dx:=0.5*dx;
mid_sum:=0.0;
mid_sum_abs:=0.0;
roundoff_error:=0.0;
for k:=1 to r do
begin
F_of_xk:=F(x0+(2*k-1)*dx);
mid_sum_abs:=mid_sum_abs+Abs(F_of_xk);
F_of_xk:=F_of_xk+roundof_eroor;
temp_sum:=mid_sum+F_of_xk;
roundof_error:=(mid_sum-temp_sum)+F_of_xk;
mid_sum:=temp_sum;
if KeyPressed then
Halt;
end;
table[n]:=0.5*table[n-1]+dx*mid_sum;
integral_abs:=0.5*integral_abs+Abs(dx)*mid_sum_abs;
for j:=n-1 downto 0 do
table[j]:=table[j+1]+denom[n-j]*(table[j+1]-table[j]);
if n>=min then
begin
tolerance:=eta*integral_abs+eps;
error:=Abs(table[0]-current_estimate)+Abs(current_estimate-previos_estimate);
done:=(error<tolerance);
end;
Inc(n);
done:=done or(n>max);
previous_estimate:=current_estimate;
current_estimate:=table[0];
r:=r+r;
until done;
romberg:=current_estimate;
end;
1.4. Метод Гаусса и его реализация на языке Pascal.
Теперь перейдем к гауссовским квадратурам – семейству правил интегрирования, основанных на неравномерном разбиении основного интервала интегрирования. Вообще, метод гаусса с n точками точен для полиномов степени 2n – 1. В функции gauss3 (листинг1.6.) основной трехточечный алгоритм Гаусса применяется к каждой из n равных частей интервала. Для интервала [-1,1] узлами квадратурной формулы являются нули полинома Лежандра третьей степени P 3 = (5x 3 – 3x )/2, а коэффициенты выбираются специальным образом.
Листинг 1.6. Функция gauss3 модуля integral
Function gaus3(F:real_fun; x0,x1:real; n:word):real;
var
t,sum,x,z,dx:real;
i,k:word;
gzero,gweight:array[1..3] of real;
procedure initialize_constants;
var
s,t:real;
j:word;
begin
gzero[1]:=-sqrt(0.6);
gzero[2]:=0.0;
gzero[3]:=sqrt(0.6);
gweight[1]:=5.0/9.0;
gweight[2]:=8.0/9.0
gweight[3]:=5.0/9.0;
for j:=1 to 3 do
begin
gzero[j]:=0.5*(1.0+gzero[j]);
gweight[j]:=0.5*gweight[j]);
end;
end; {initialize_constants}
begin {gauss3}
initialize_constants;
dx:=(x1-x0)/n;
x:=x0;
sum:=0.0;
for i:=0 to n-1 do
begin
t:=0.0;
for k:=1 to 3 do
begin
z:=x+dx*gzero[k];
t:=t+gweight[k]*F(z);
end;
sum:=sum+dx*t;
x:=x+dx;
end;
gauss3:=sum;
end;{gauss3}
Дадим некоторый обзор некоторых свойств полиномов Лежандра. Рекурсивное определение полиномов Лежандра приводилось ранее в этой работе. Они образуют ортогональное (но не ортонормированное)семейство на промежутке [-1,1], то есть
![]() , m
≠n
,
, m
≠n
,
![]() .
.
Величина второго интеграла определяет нормировку для этих полиномов. Имеет место также следующее представление полиномов Лежандра:
![]() .
.
Другая явная формула:
![]() .
.
Приведем несколько первых полиномов Лежандра:
P 0 (x ) = 1,
P 1 (x ) = x ,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Очевидно, что в общем случае полиномы Лежандра нечетной степени являются нечетными функциями, а четной степени – четными функциями.
Нам требуется найти нули полинома Pn (x ). Важно здесь то, что эти нули являются простыми и принадлежат открытому интервалу (-1,1). Таким образом,
-1<x 1 <x 2 <…<xn <1, Pn (xj ) = 0.
Соответствующая формула гаусовского интегрировании (с остатком) имеет следующий вид:
![]() .
.
В этой формуле
![]() ,
,
Где -1 <![]() <1.
<1.
Веса задаются несколькими эквивалентными формулами
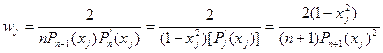 .
.
Процедура compute_gauss_coeffs (листинг1.7). предназначена для вычисления нулей и весов квадратурной формулы Гаусса. Подпрограмма legendre_poly вычисляет значения Pn (x ), Pn -1 (x ) и Pn ’(x ). Последнее получается дифференцированием основной рекуррентной формулы для Pn (x ):
![]() .
.
Нули находятся предварительным делением интервала и применением метода секущих, после чего следует ньютоновские итерации, в которых используются значения производных. Затем применяется первая формула для весов, в которой вновь используются значения производных. Здесь zero – массив нулей полинома Лежандра n -й степени, а weight – массив соответствующих весов.
Метод вычислений нулей полинома заключается в том, чтобы поделить интервал [0,1] на маленькие подынтервалы и проверить каждый из них на изменение знака полинома. Если изменение знака имеет место, то однократное применение метода секущих позволяет достаточно хорошо определить положение нуля. Для уточнения этого значения применяется метод Ньютона. Для обработки интервала [-1,0] учитывается симметрия.
Листинг 1.7. Процедура compute_gauss_coeffs модуля integral
procedure compute_gauss_coeffs(deg:word);
const
eps=6.0e-20;
var
i,index:word;
P0k, P0k_1,D0k, P1k,P1k_1, D1k,
x0,x1,y,z,dx,x,u:real;
procedure legendre_poly(n:word; x:real; var Pk,Pk_1,Dk:real);
var
Pk_2,Dk_1,Dk_2:real;
i,j,k:word;
begin
If n=0 then
Begin
Pk:=1.0;
Dk:=0.0;
end
else
begin
Pk_1:=1.0;
Pk:=x;
Dk_1:=0.0;
Dk:=1.0;
i:==3;
j:=1;
for k:=2 to n do
begin
Pk_2:=Pk_1;
Pk_1:=Pk;
Dk_2:=Dk_1;
Dk_1:=Dk;
Pk:=(i*x*Pk_1-j*Pk_2)/k;
Dk:=(i*(Pk_1+x*Dk_1)-j*Dk_2)/k;
Inc(I,2);
Inc(j);
end;
end
end;{legendre_poly}
begin{computr_gauss_coeffs}
index:=(deg+1) div 2;
dx:=1.0/(10.0*deg);
x0:=0.0;
x1:=x0+dx;
if Odd(deg) then
begin
zero[index]:=0.0;
legendre_poly(deg,x0,P0k, P0k_1,D0k);
weight[index]:=2.0/(P0k_1*D0k*deg);
end;
for i:=0 to 10*deg-1 do
begin
x0:=x1;
x1:=x1+dx;
legendre_poly(deg,x0,P0k_1,D0k);
legendre_poly(deg,x1,P1k,P1k_1,D1k);
if P0k*P1k<=0.0 then
begin
x:=x0-P0k*dx/(P1k-P0k);
legendre_poly(deg,x,P0k,P0k_1,D0k);
u:=P0k/D0k;
y:=x-u;
while Abs(x-y)>=eps do
begin
if keyPressed then begin
writeln(‘>=eps loop:’,x:10:10,’ ‘, y:10:10,’ ‘,Abs(x-y):10);
readln;
end;
x:=y;
legendre_poly(deg,x,P0k,P0k_1,D0k);
u:=P0k/D0k;
y:=x-u;
end;
inc(index);
legendre_poly(deg,y,P0k,P0k_1,D0k);
zero[index]:=y;
weight[index]:=2.0/(P0k_1*D0k*deg);
if index=deg then
Break;
end;
end;
For i:=1 to deg div 2 do
begin
Zero[i]:=zero[deg-i+1];
Weight[i]:=weight[deg-i+1];
end;
end;{compute_gauss_coeffs}
В функции gauss (листинг 1.8.) запрограммирован один гауссовский шаг на заданном интервале. Конечно, серьезная прикладная программа будет делить интервал на меньшие подынтервалы, применять эту процедуру к каждому из них адаптивным способом.
Листинг 1.8. Функция gauss модуля integral
Function gauss(F:real_fun;x0,x1:real;deg:word):real;
var
Index:word;
a,b,sum:real;
begin
a:=0.5*(x1-x0);
b:=0.5*(x1+x0);
sum:=0.0;
for index:=1 to deg do begin
sum:=sum+F(a*zero[index]+b)*weight[index];
if KeyPressed then
Halt;
end;
gauss:=a*sum;
end;
end.
Заключение
В данной работе были рассмотрены различные методы интегрирования определенных интегралов и их реализация на языке программирования высокого уровня Pascal. Таким образом было показано, что данный язык программирования возможно использовать для решения различных задач из области высшей математики и численных методов. В данной работе затронута лишь одна проблема – проблема вычисления интегралов, но Pascal позволяет решать и такие проблемы как: решение дифференциальных уравнений, вычисление с полиномами, решение нелинейных уравнений, вычисления связанные с линейной алгеброй.
Литература
1. Немнюгин С.А. Turbo Pascal, 2 - издание – С-П.: Питер, 2003-544 с.
2. Большой энциклопедический словарь: под редакцией Ю.В. Прохорова – М.: Большая Российская энциклопедия, 2000. – 845 с.