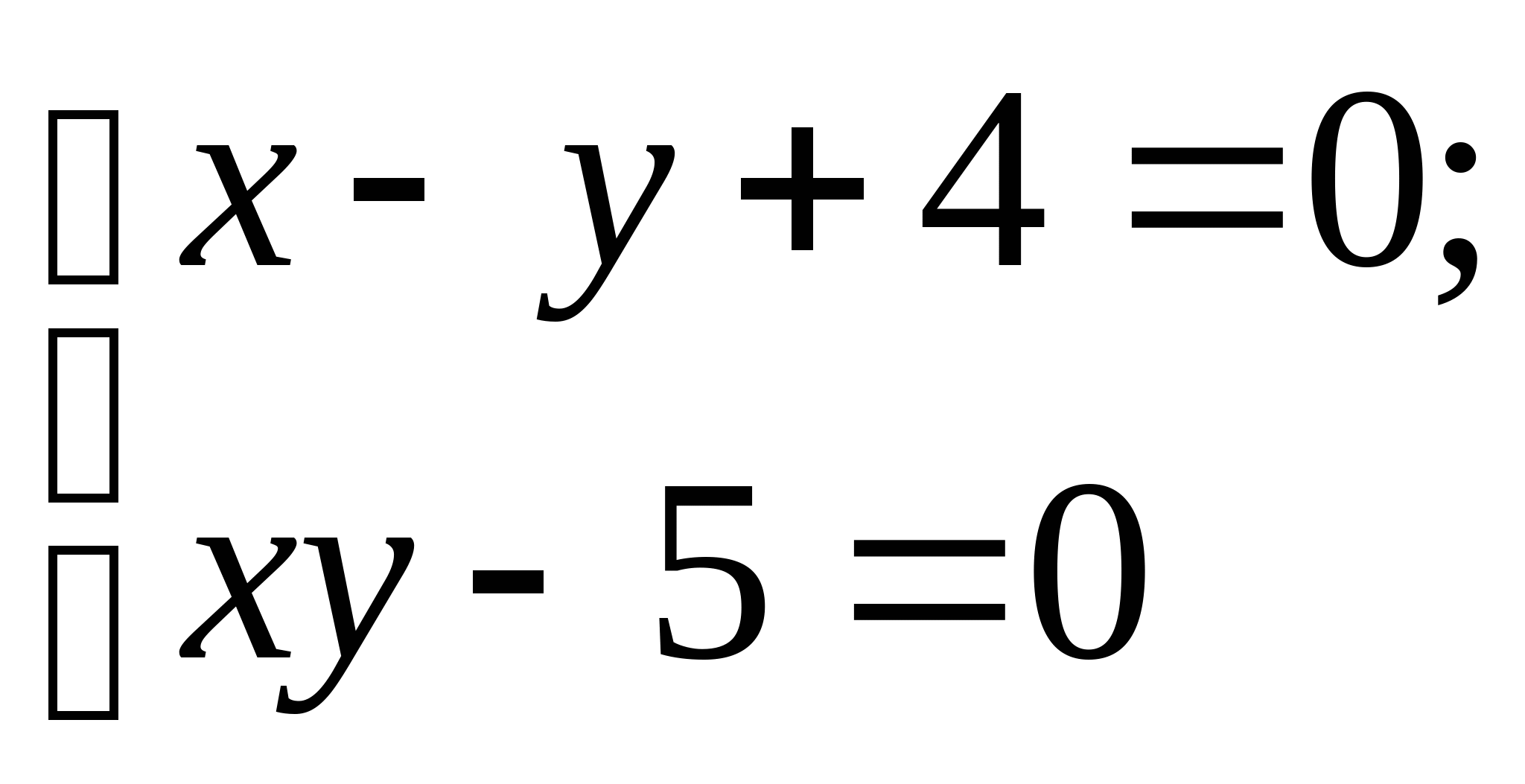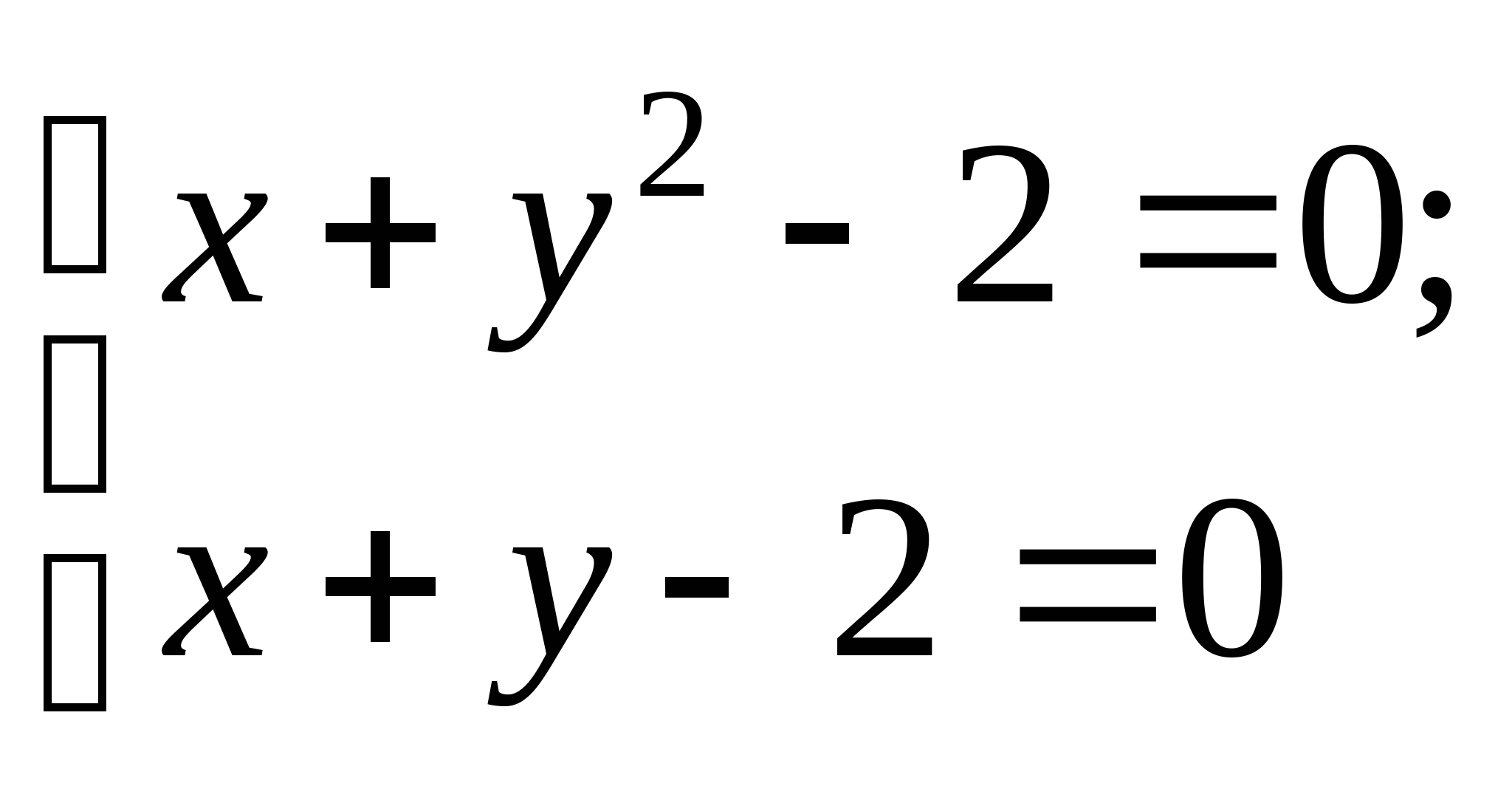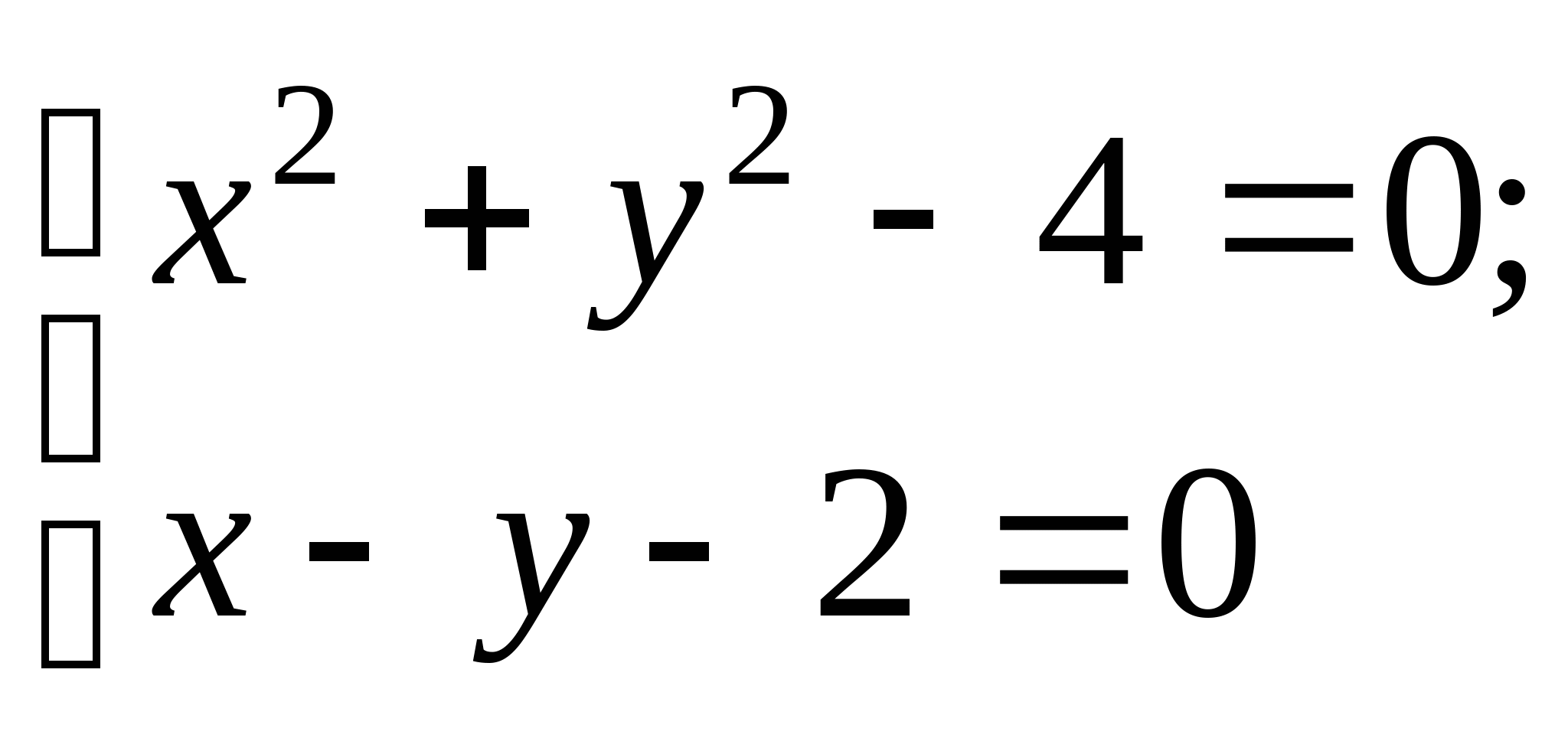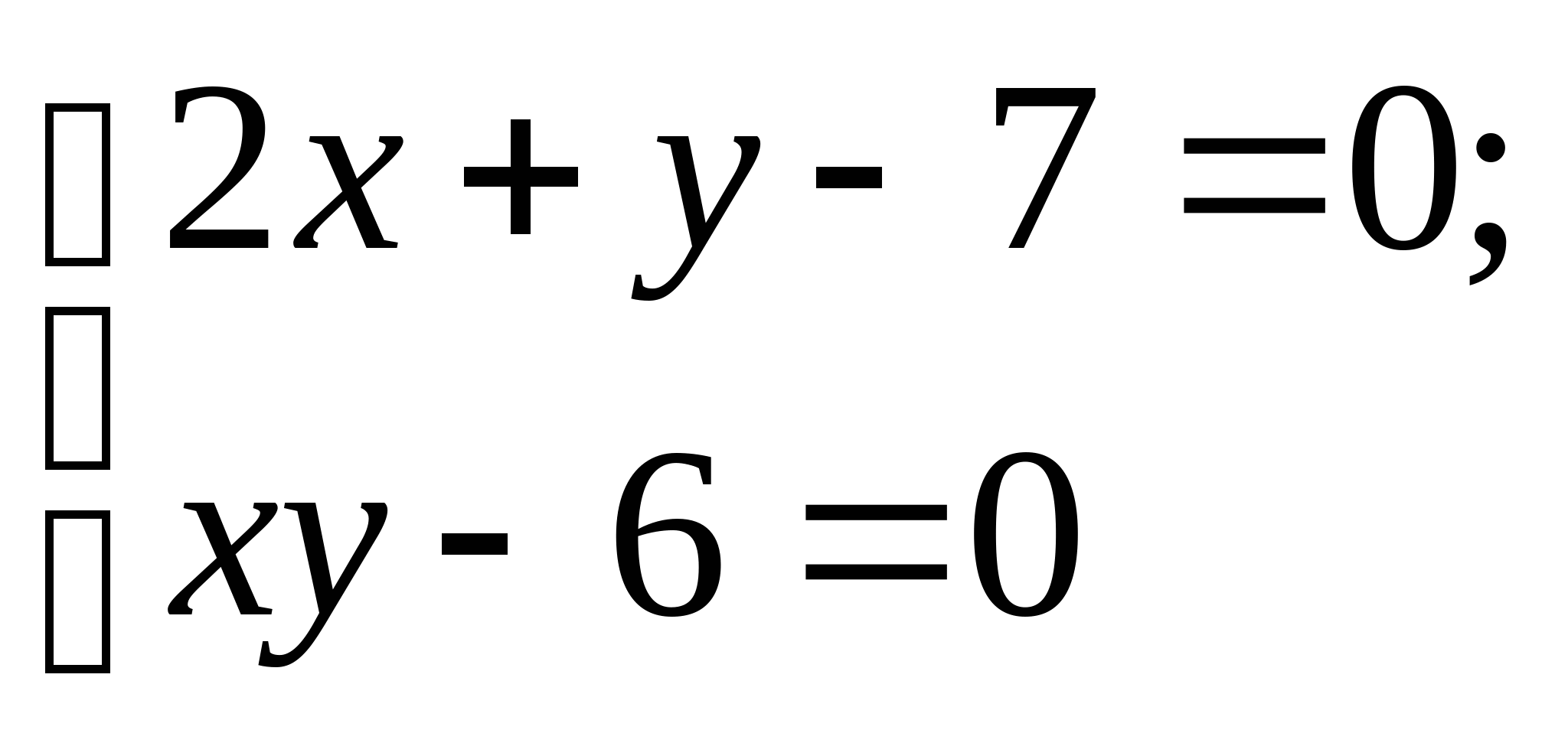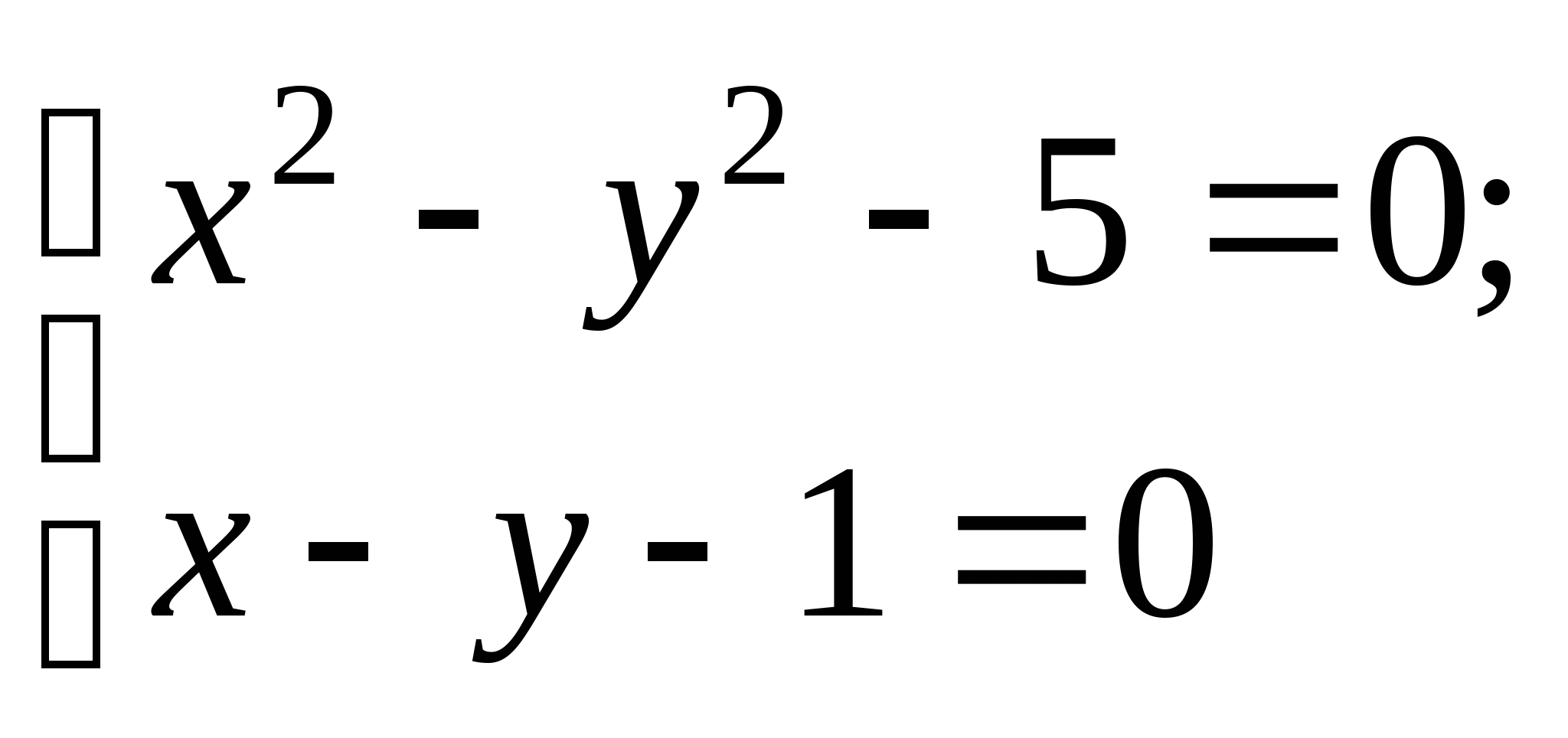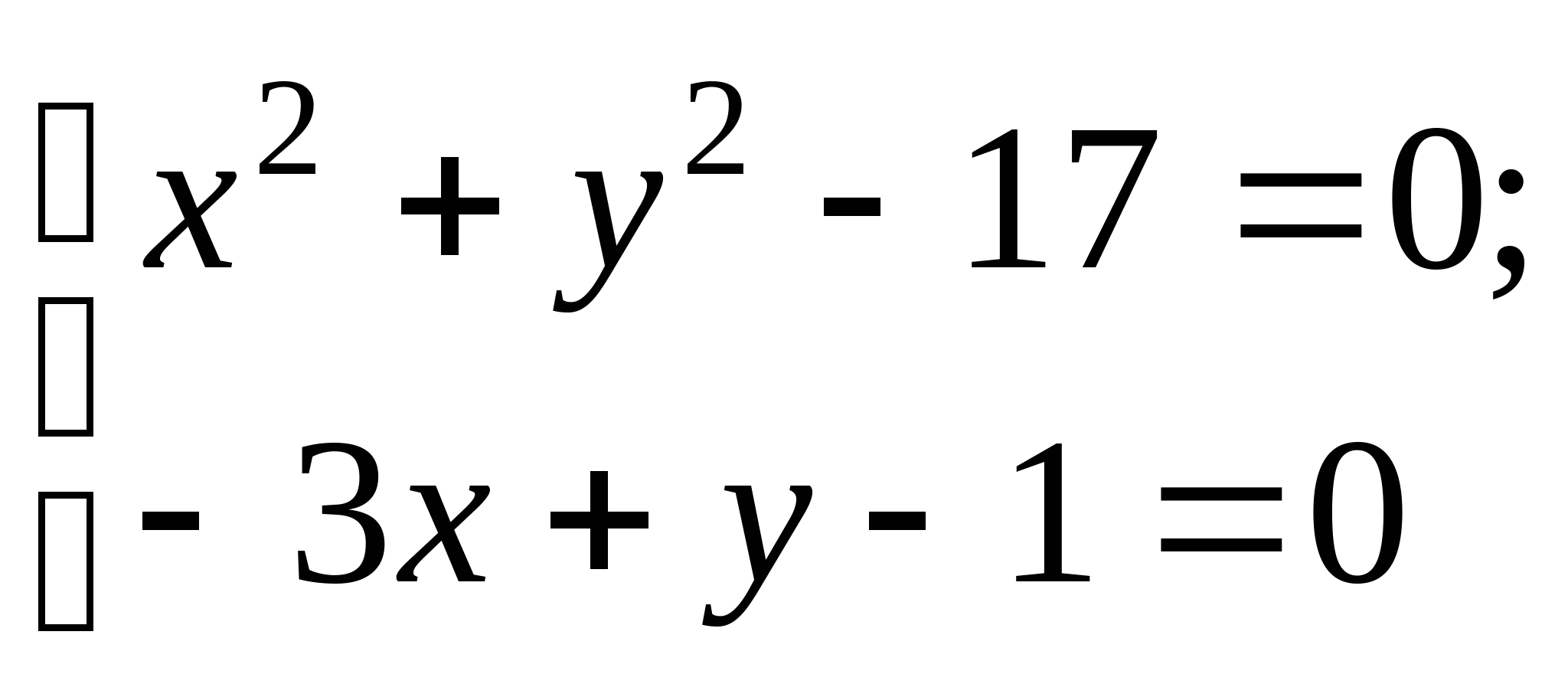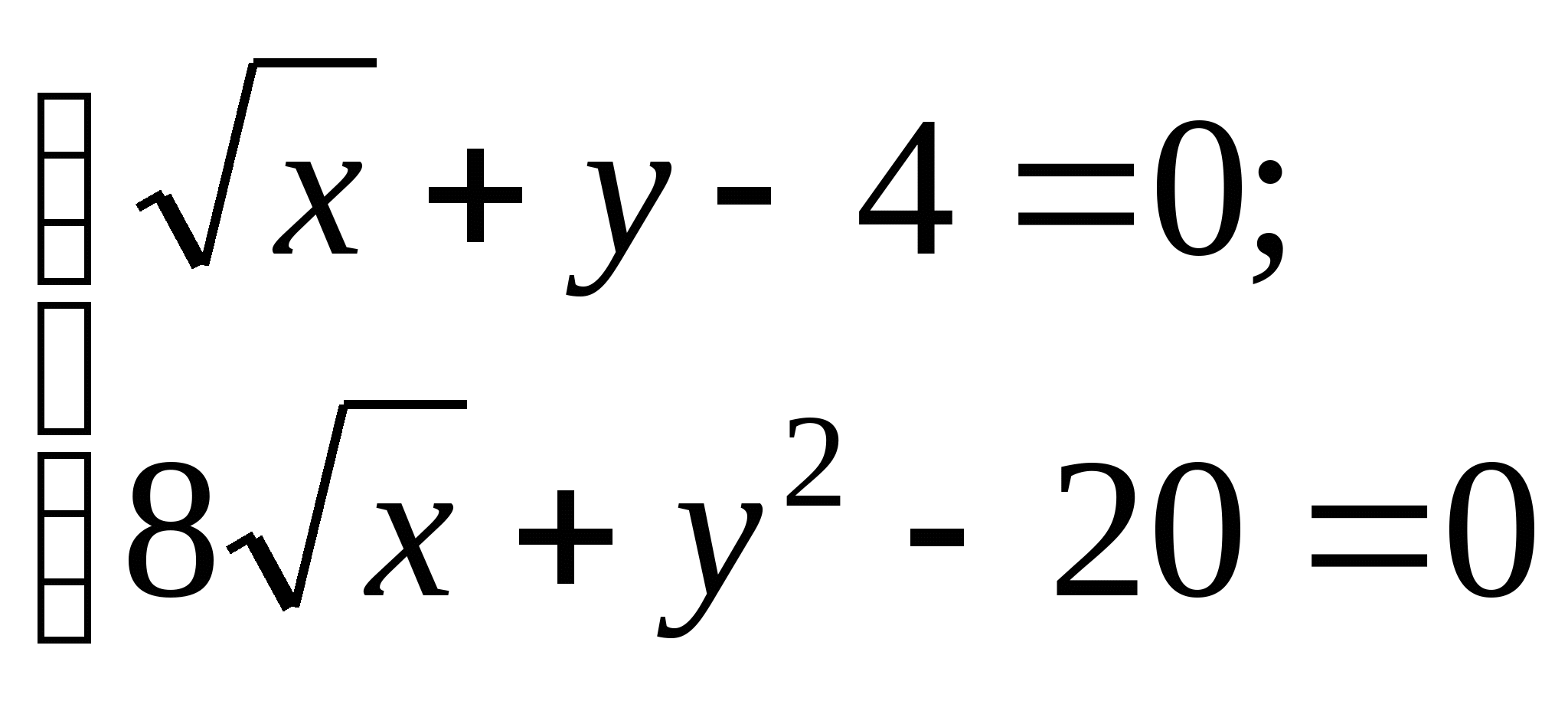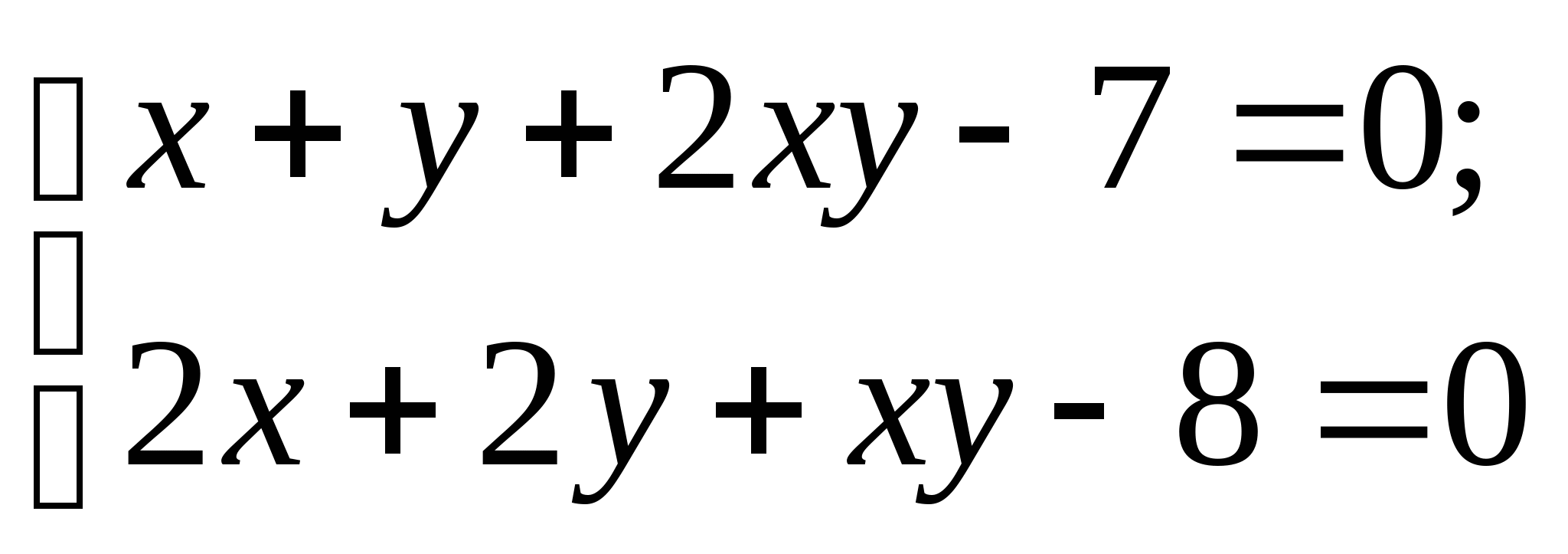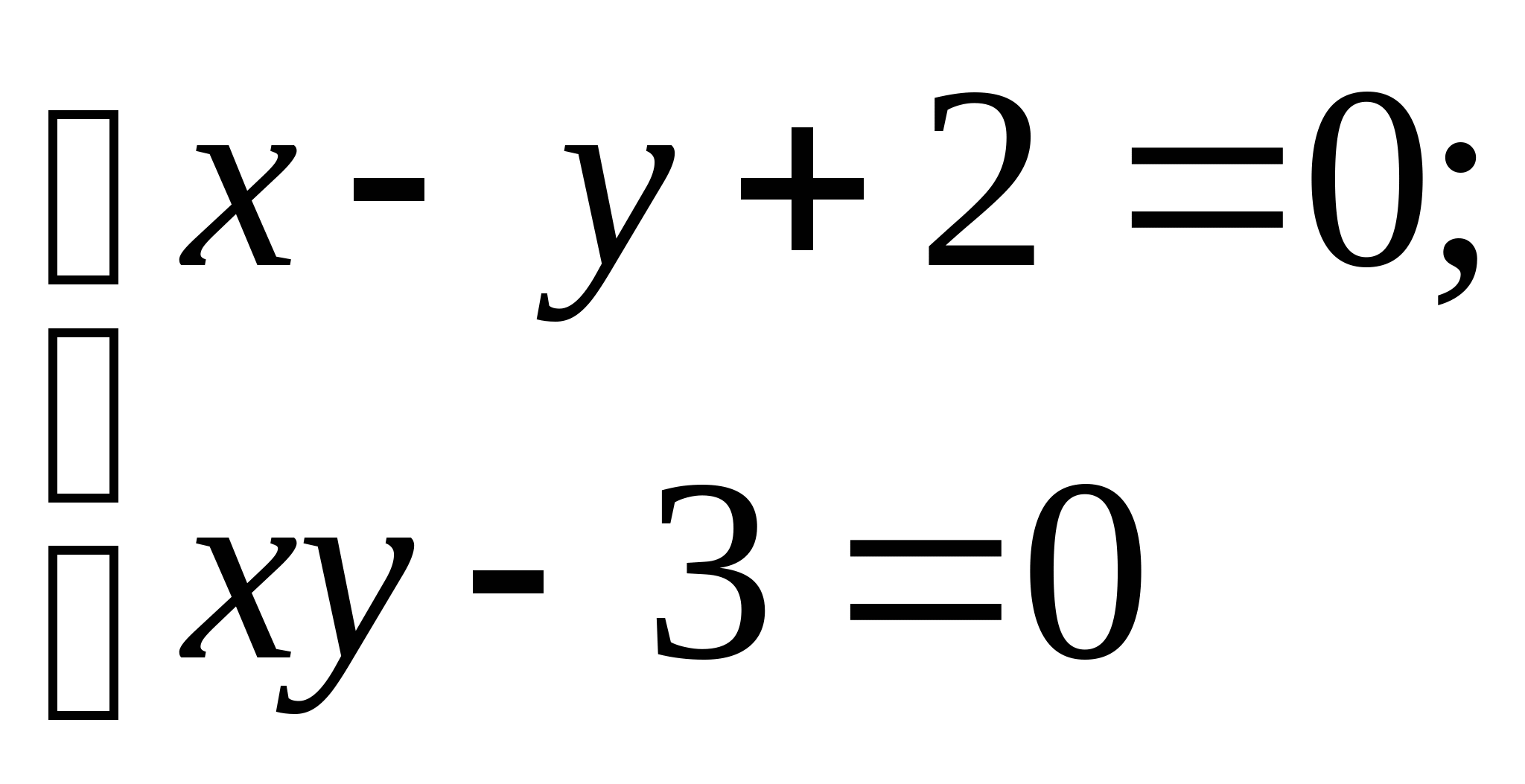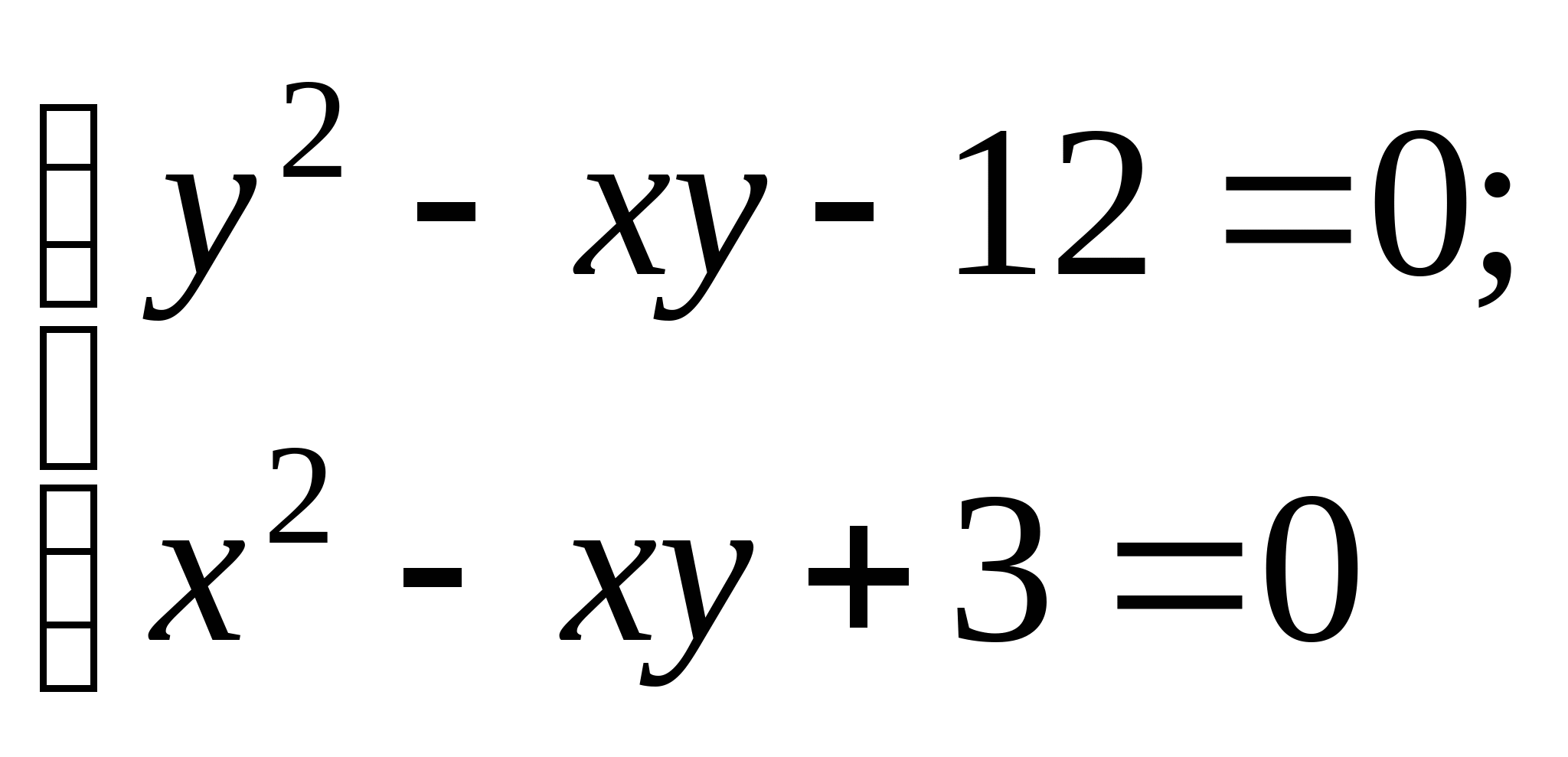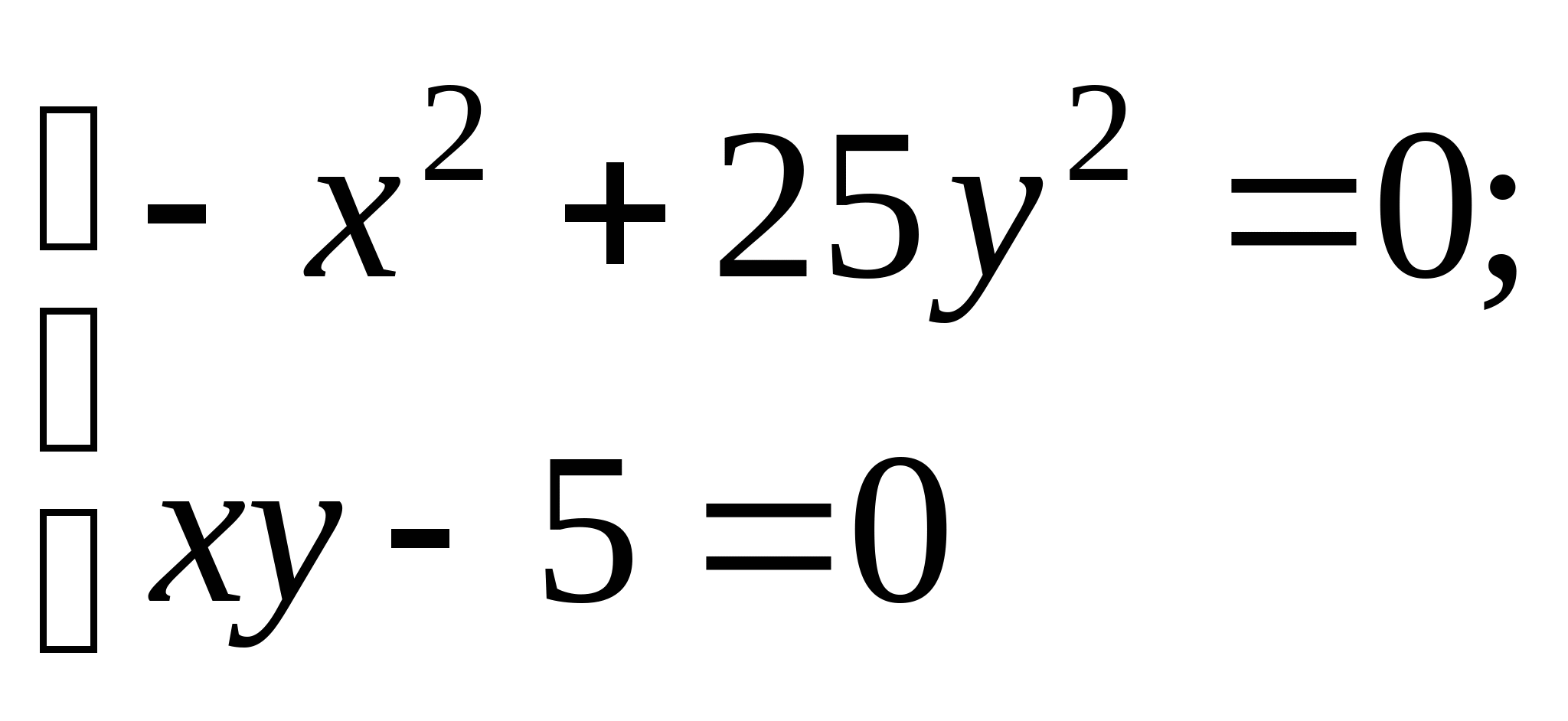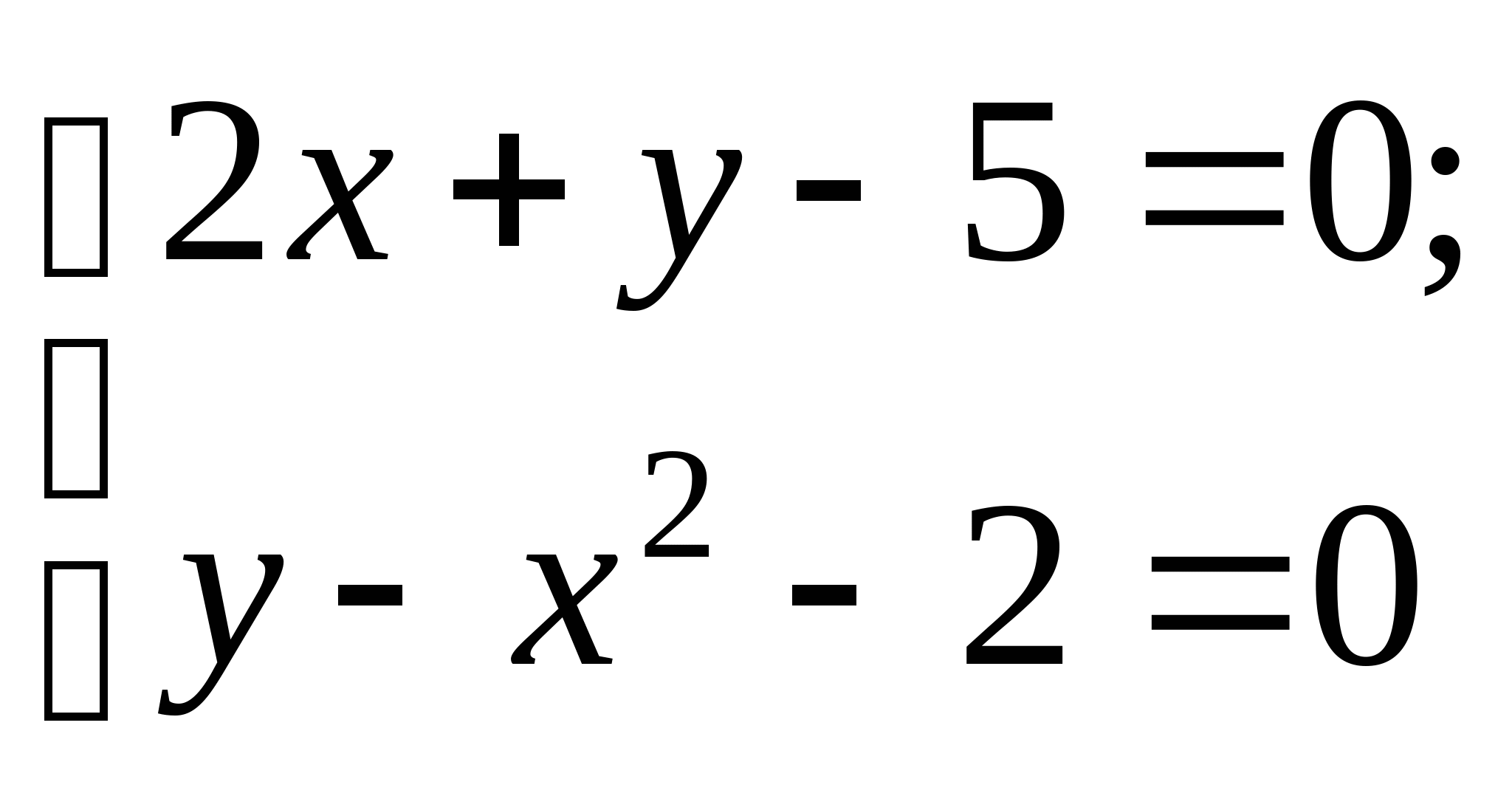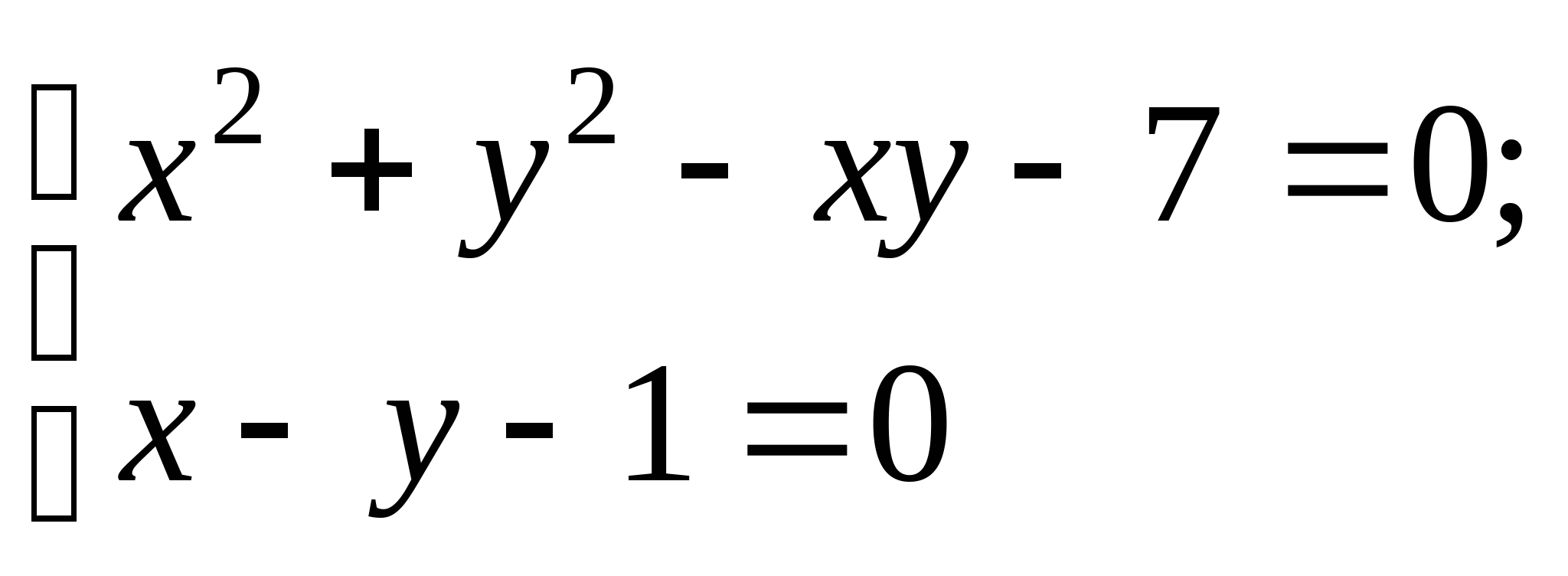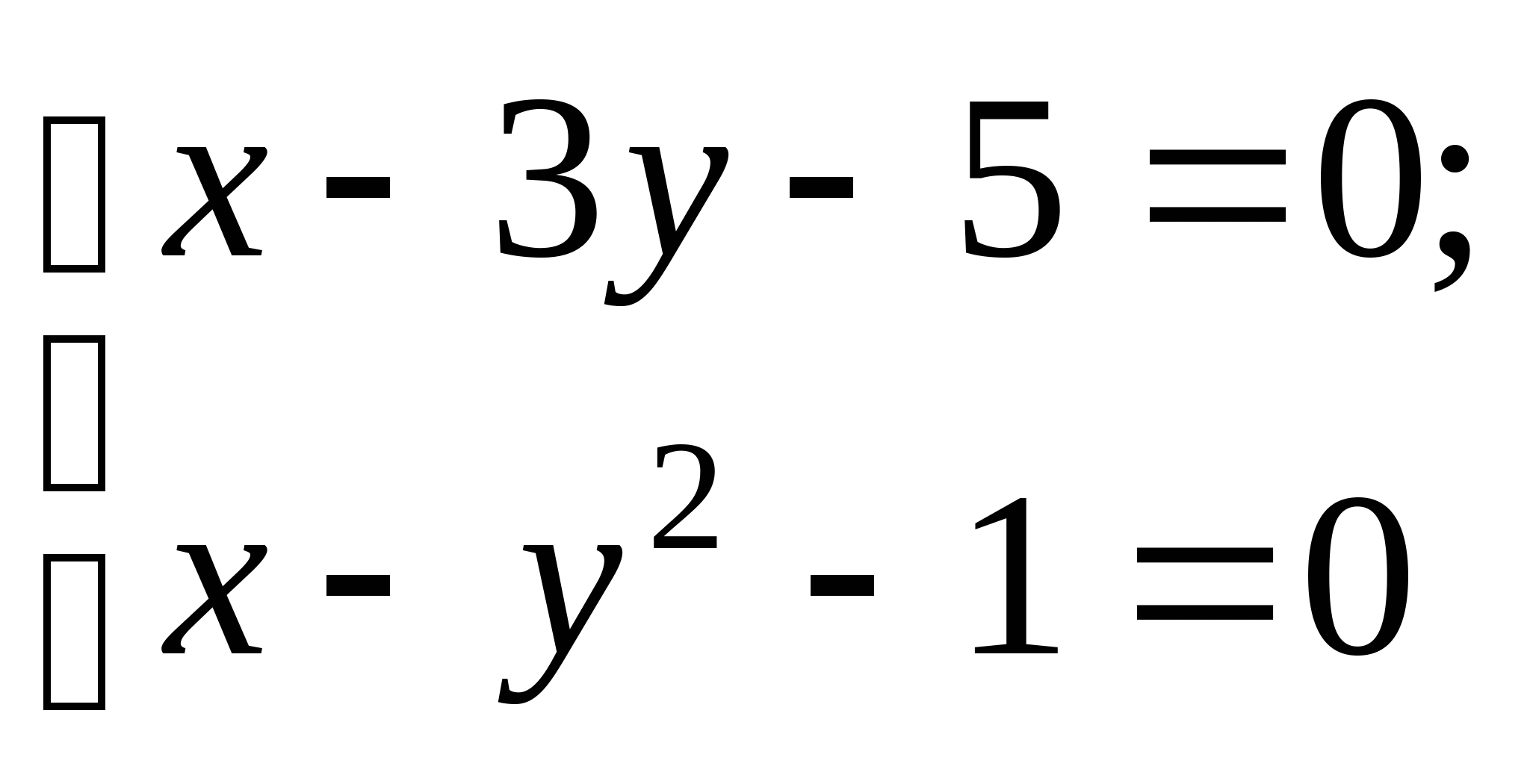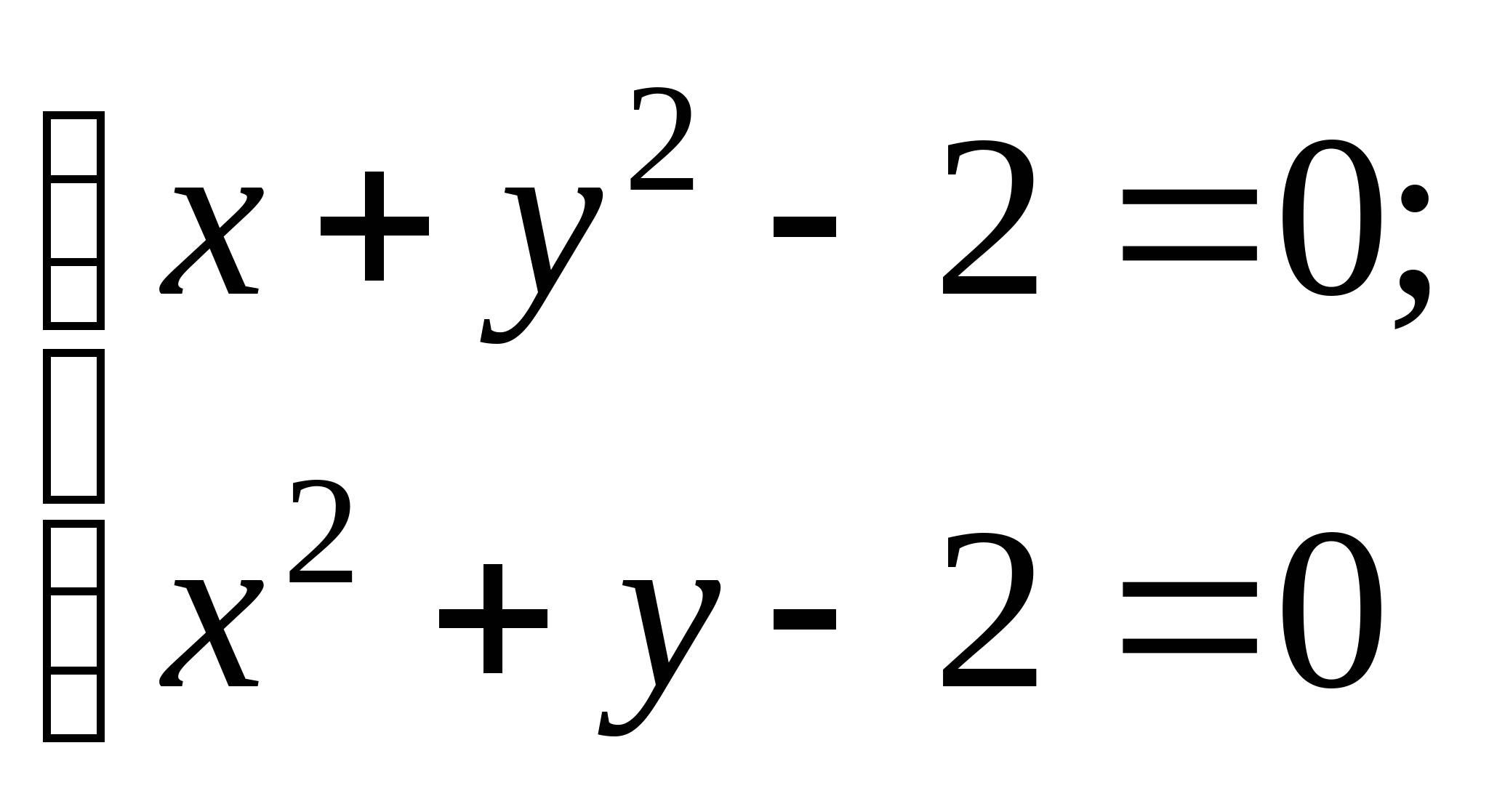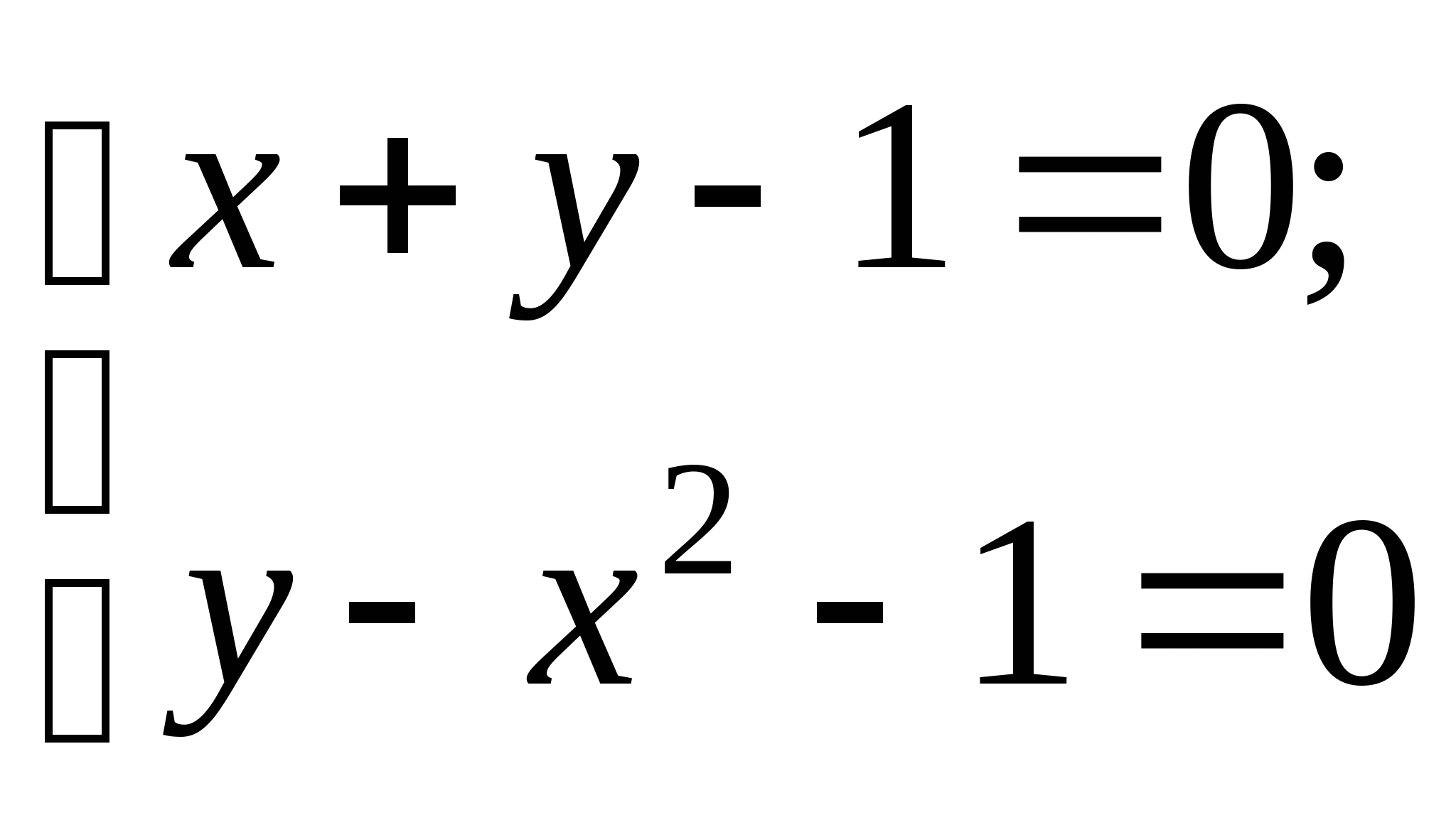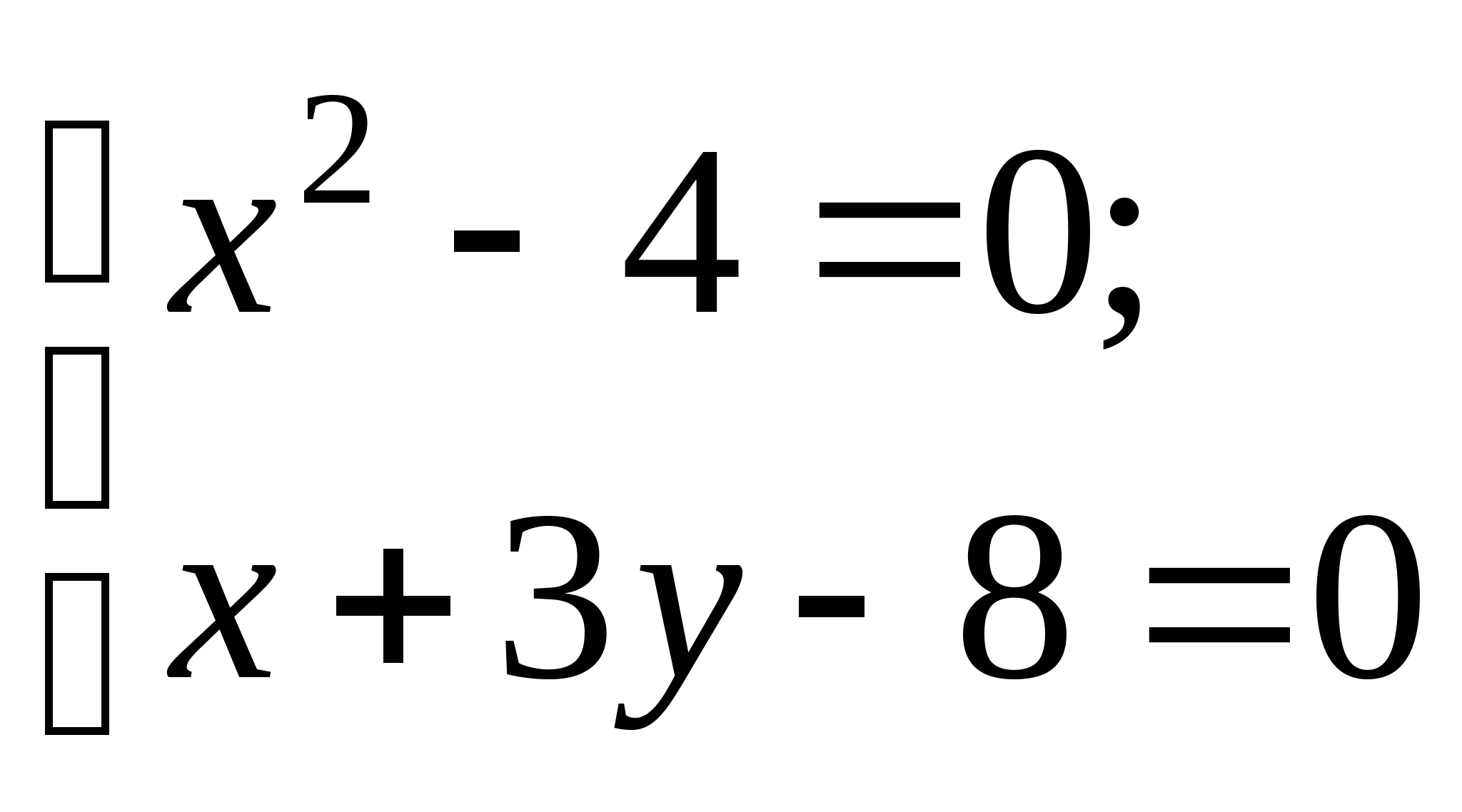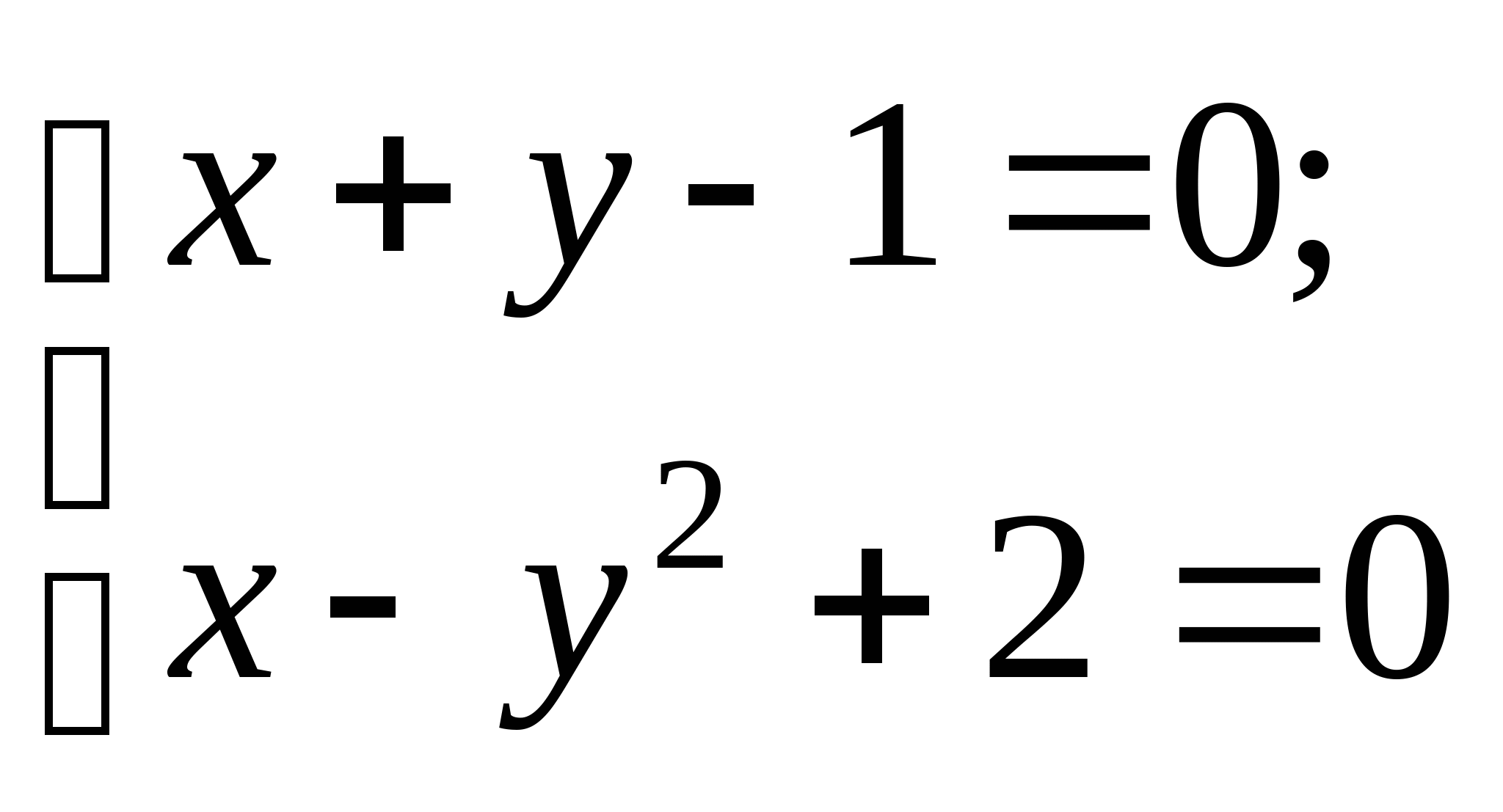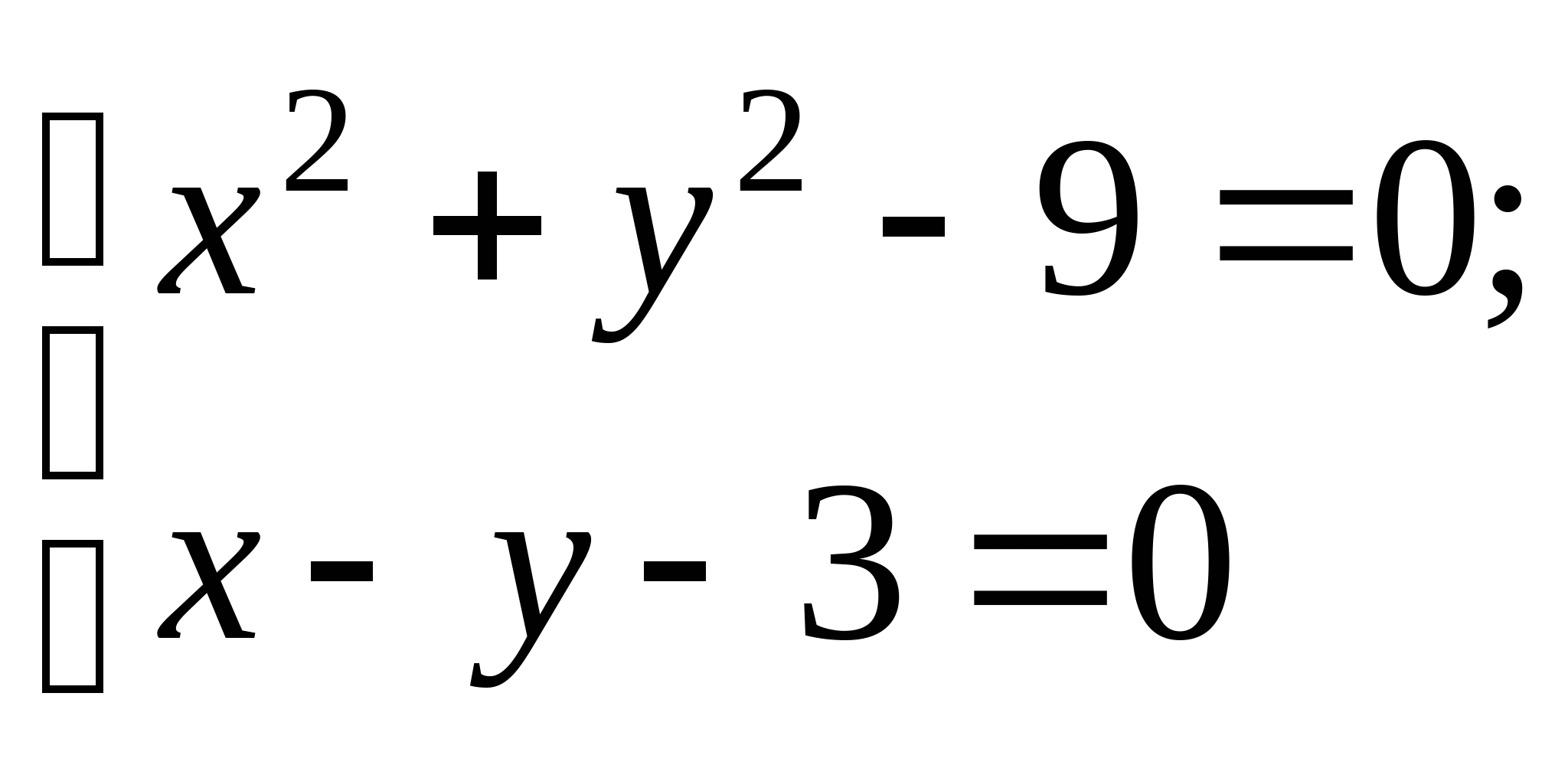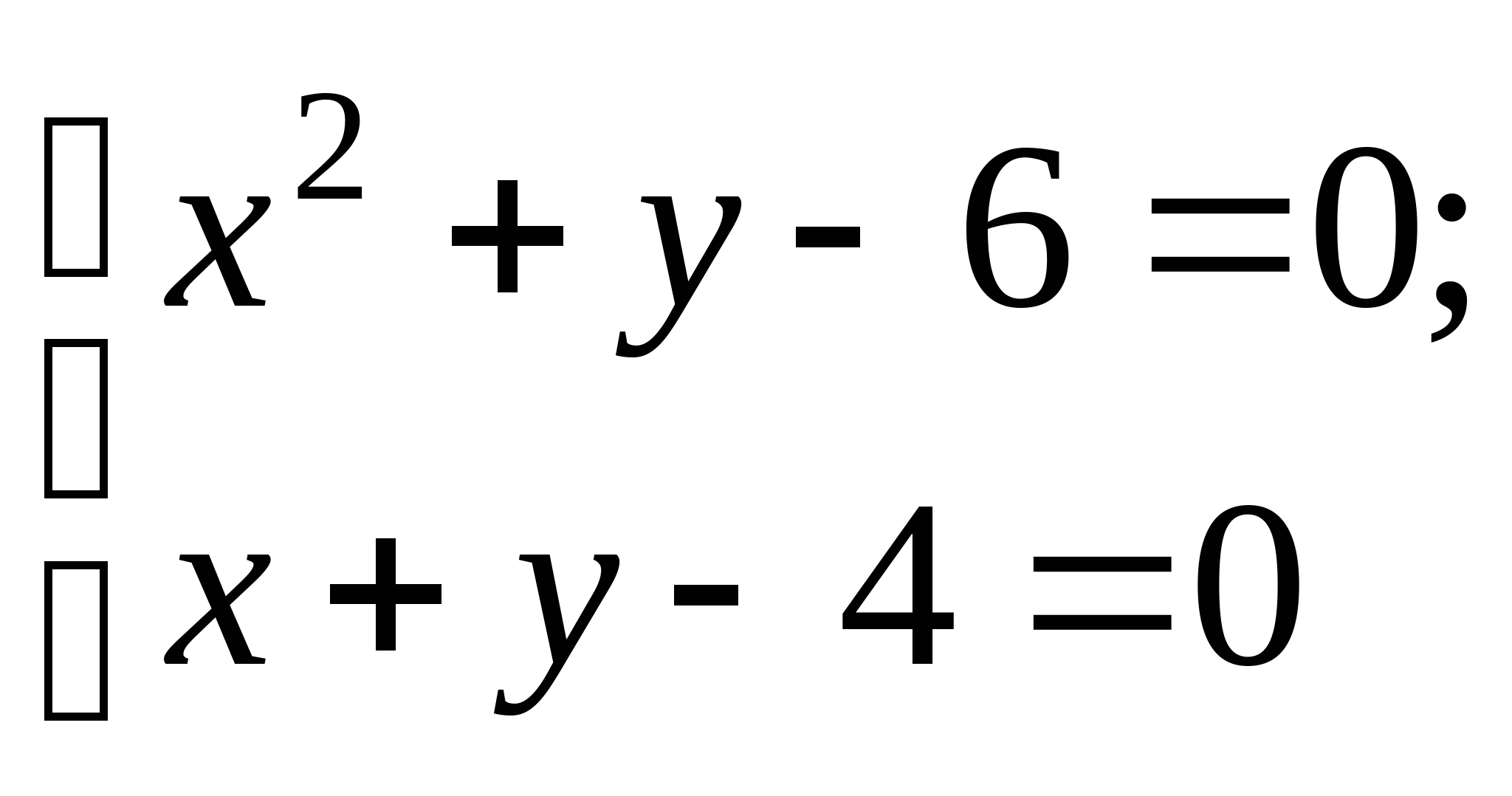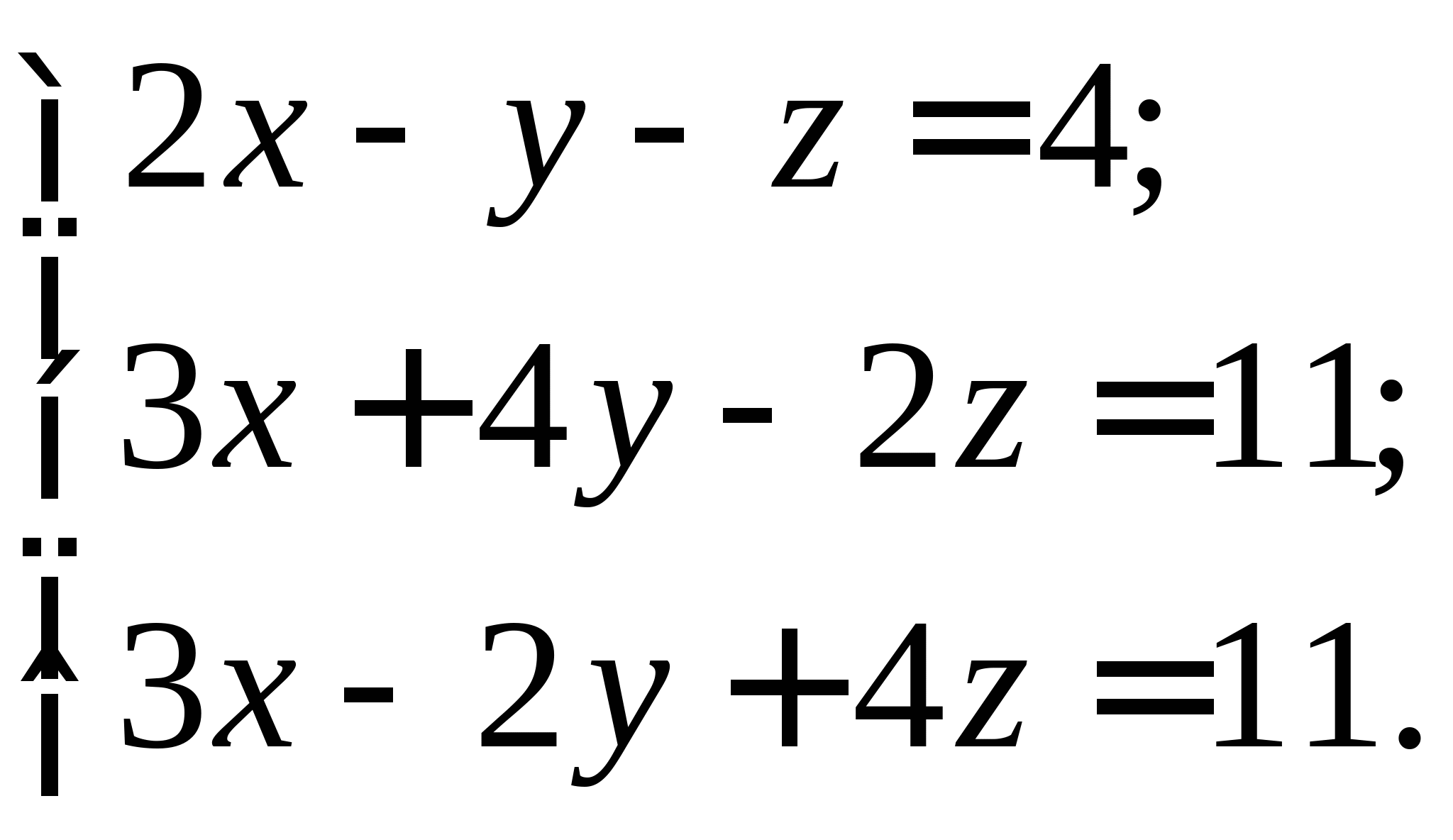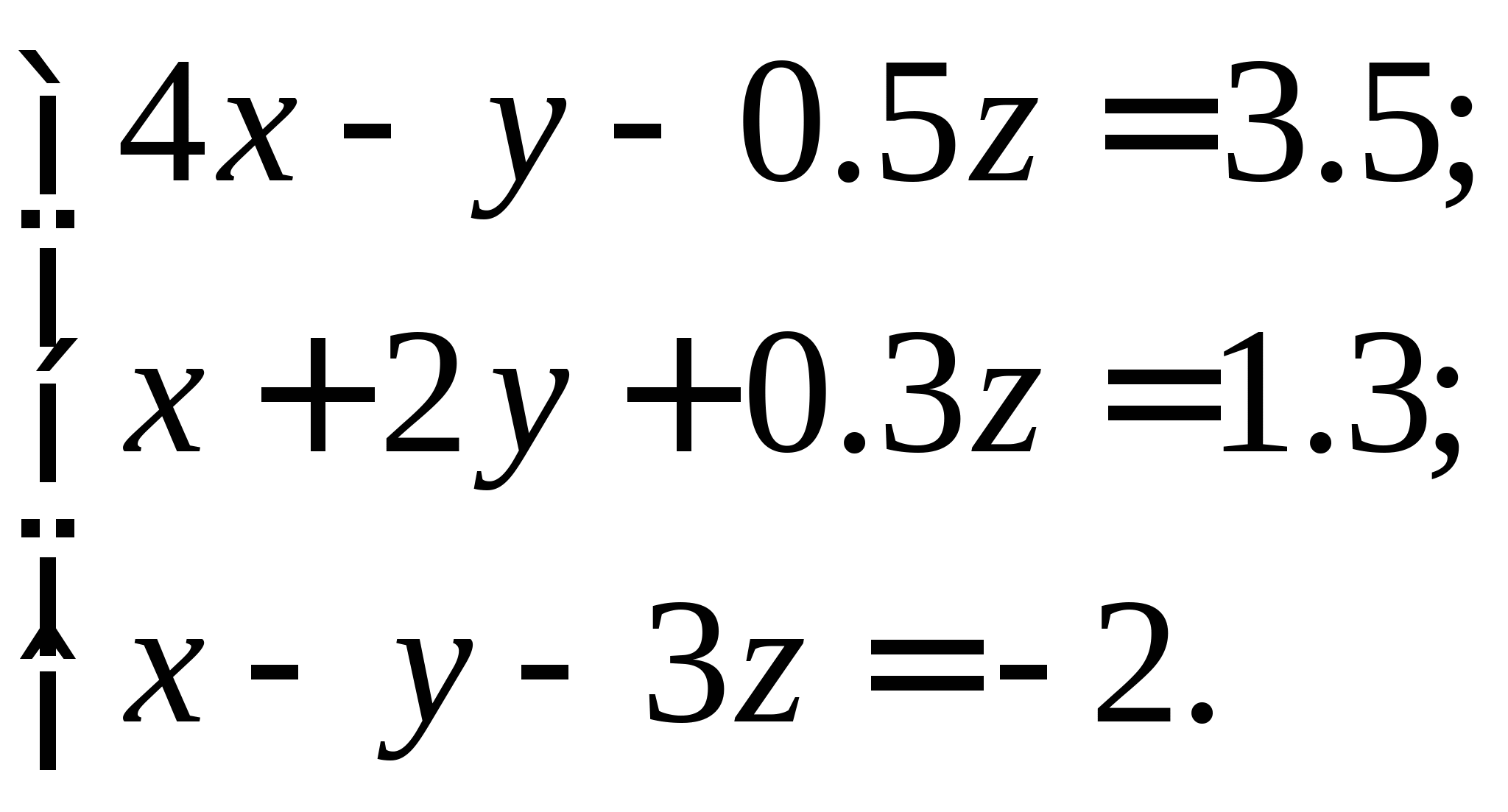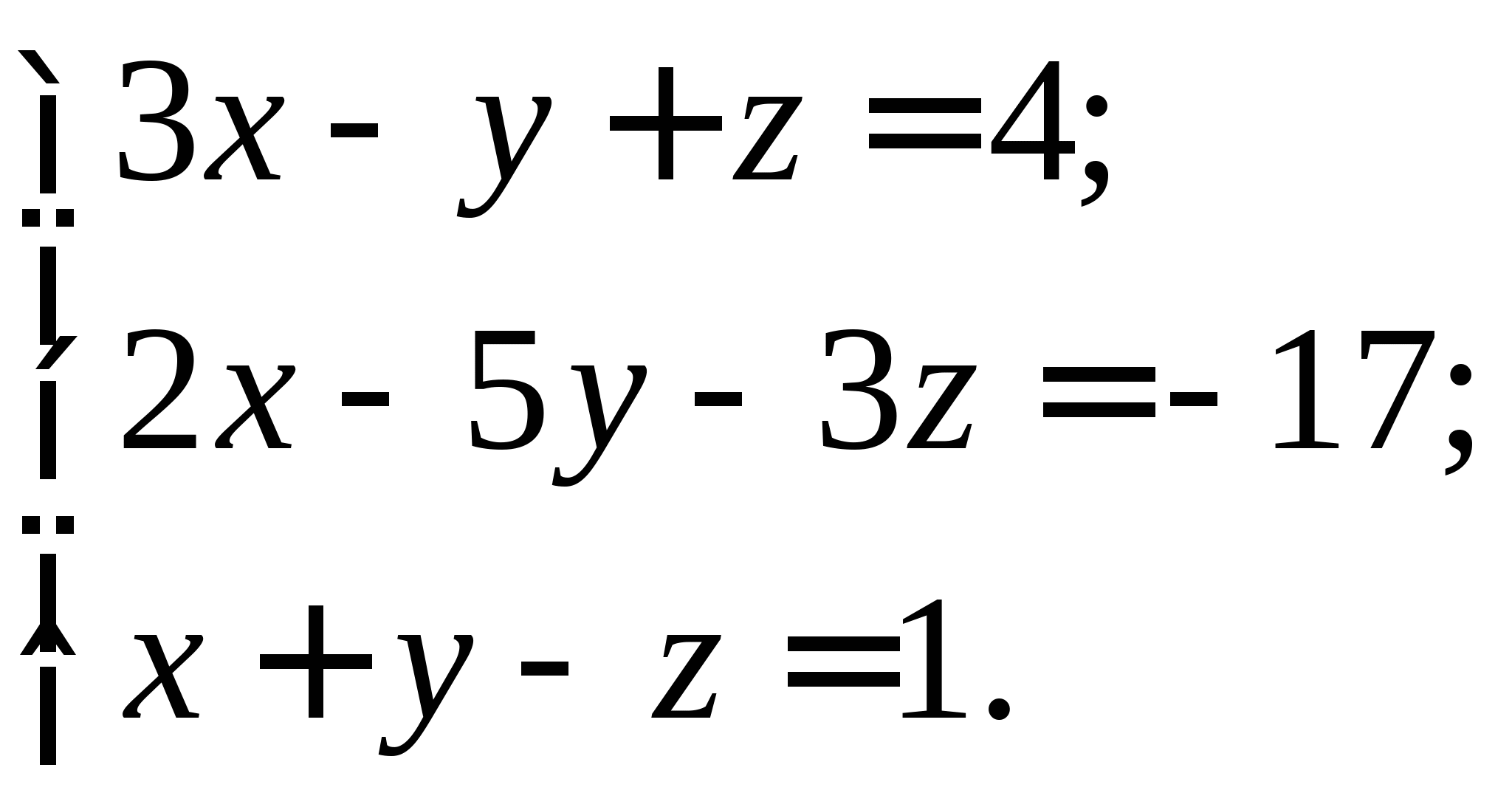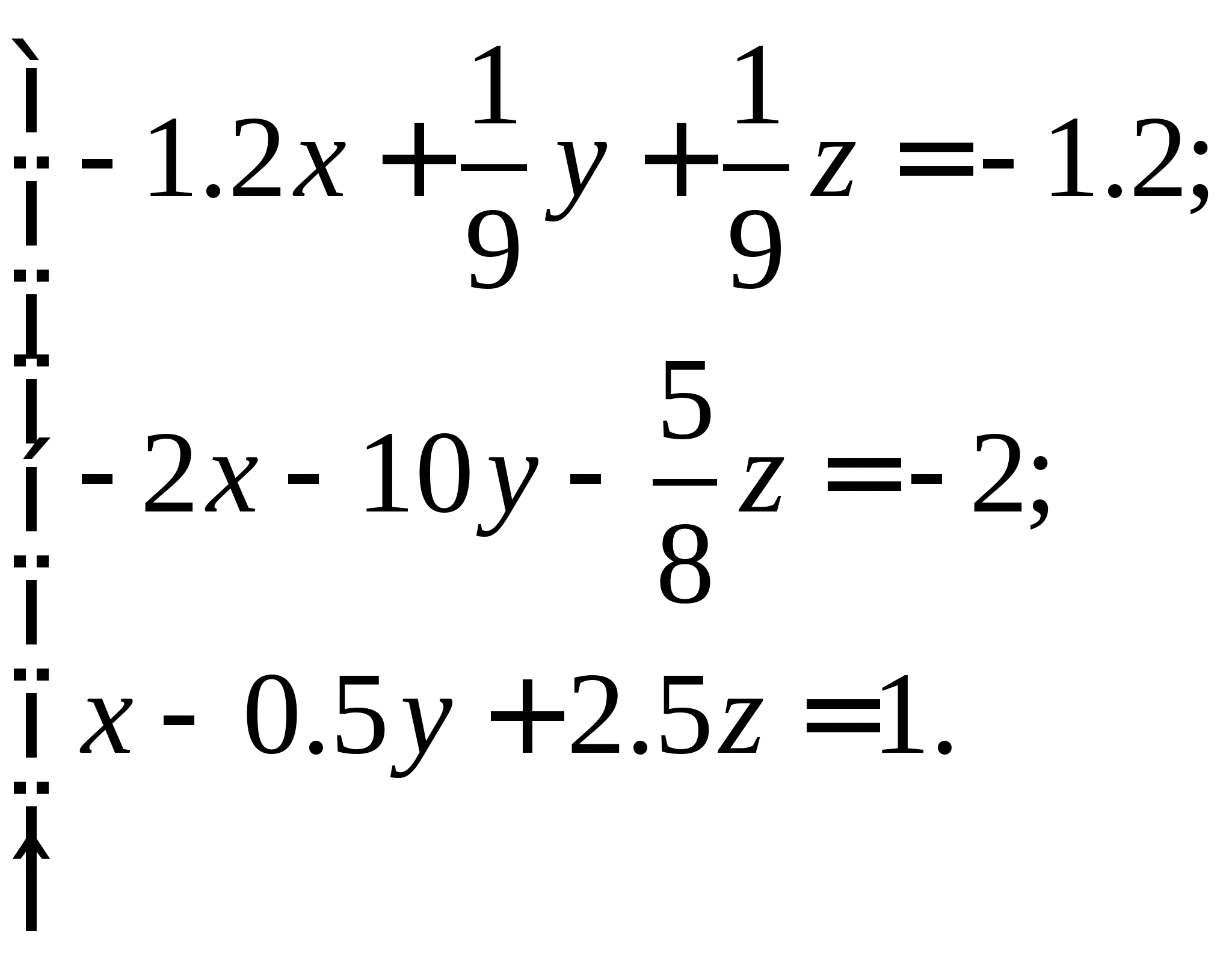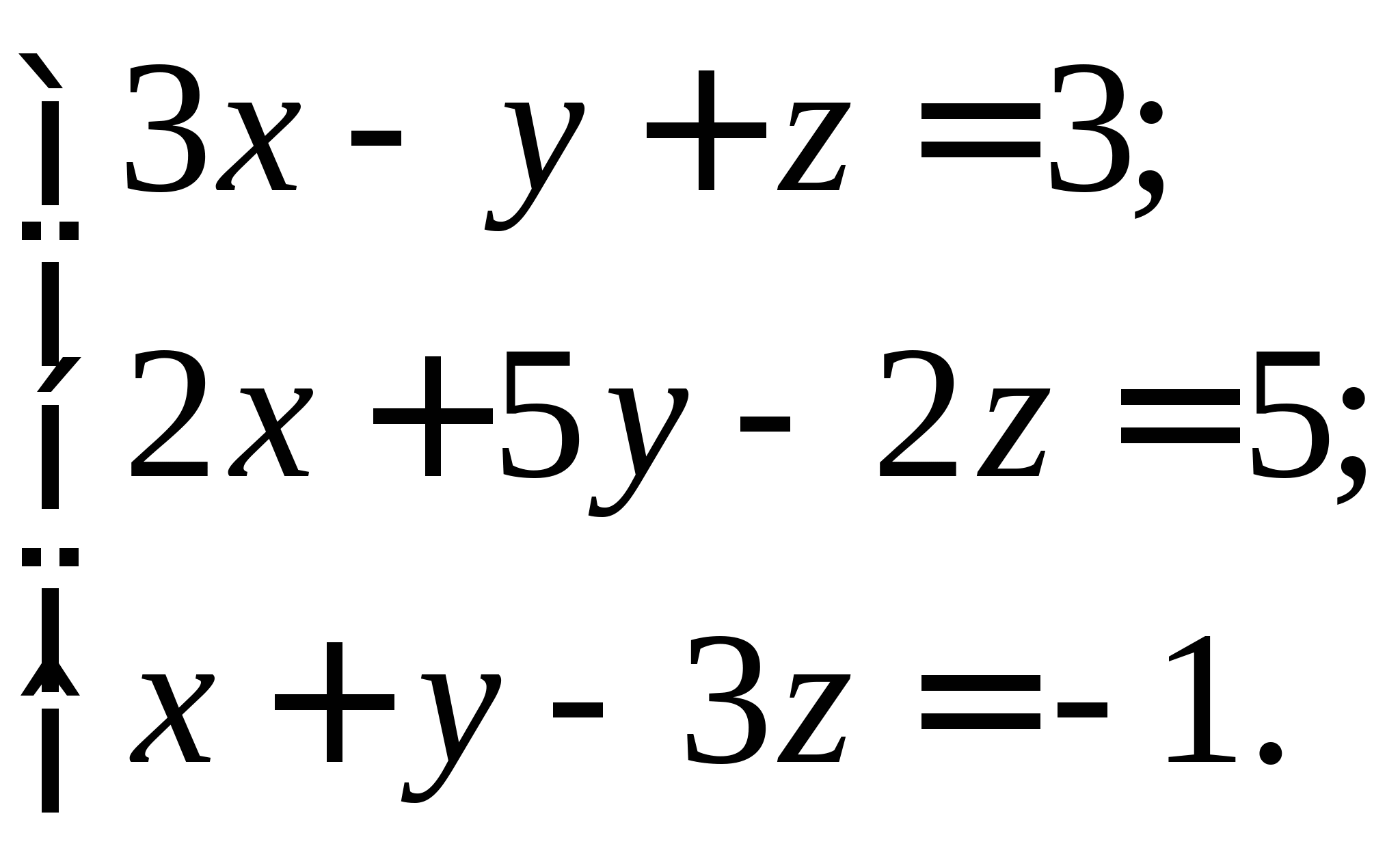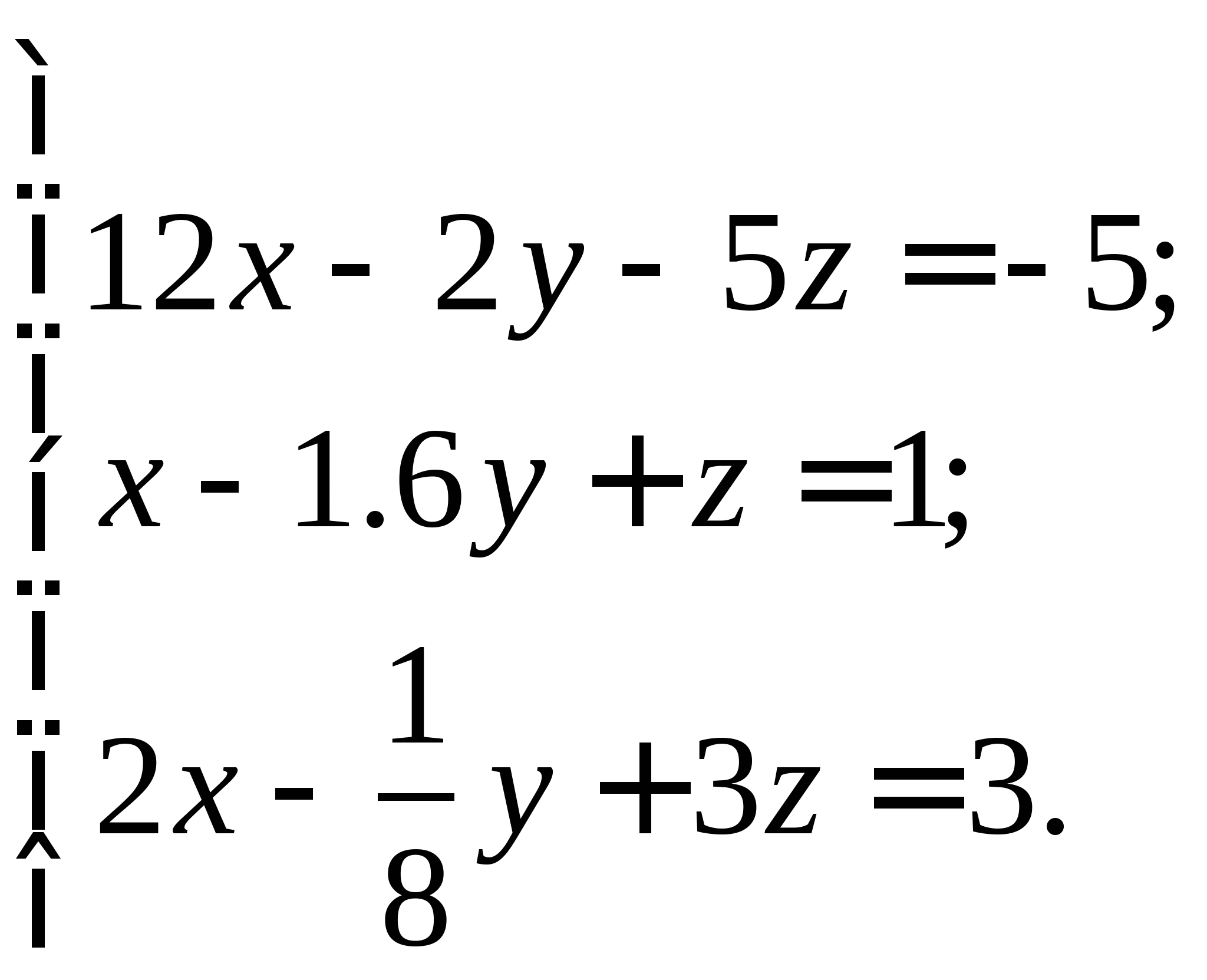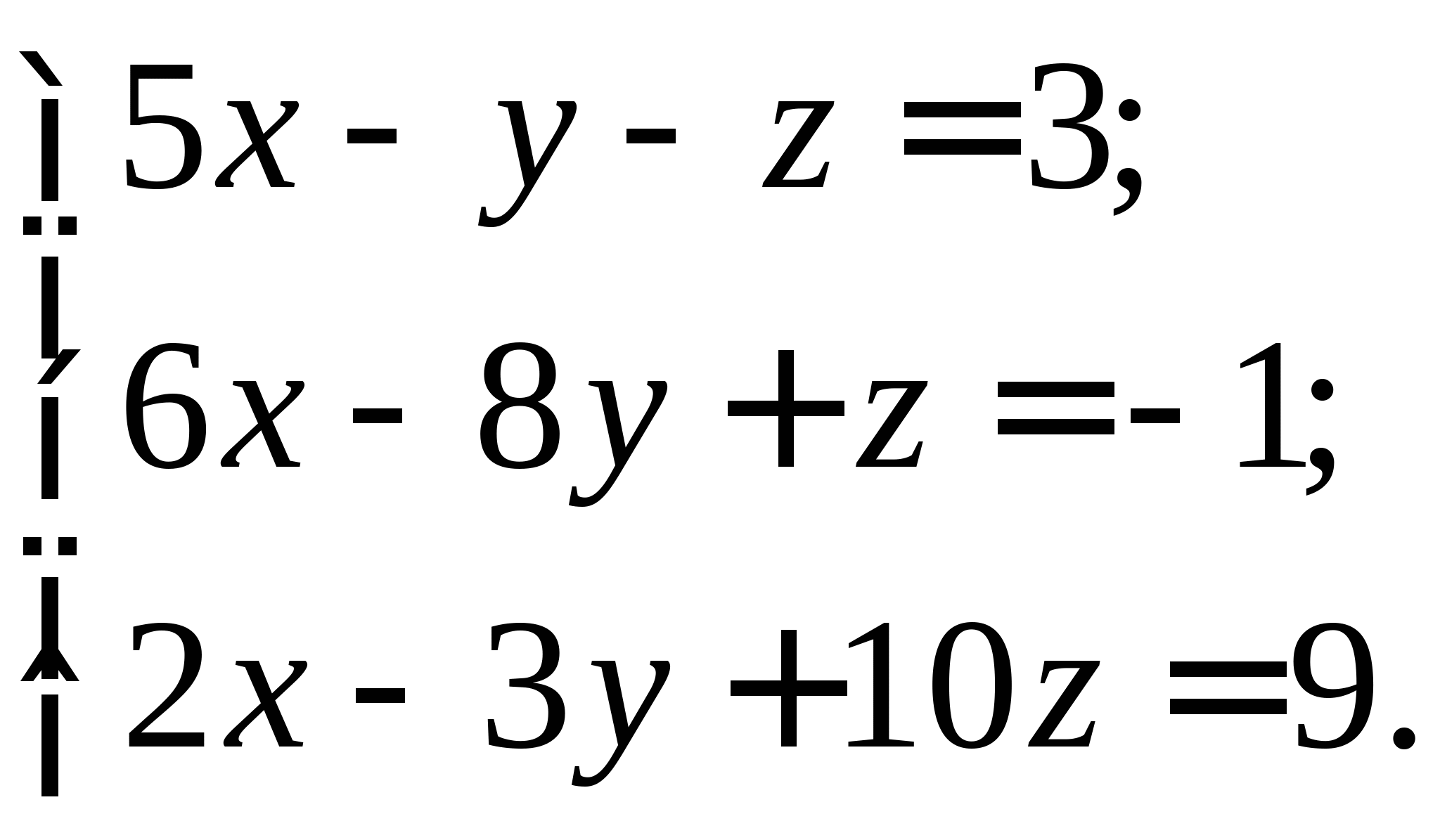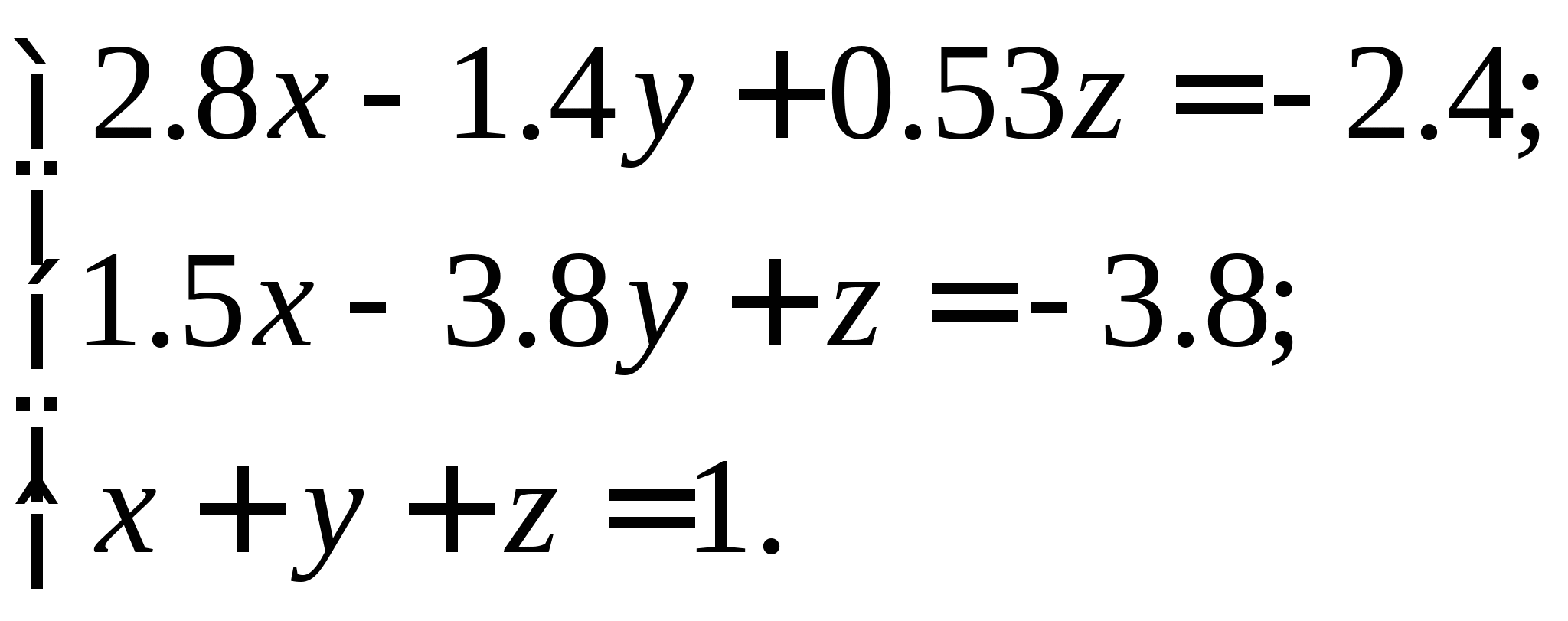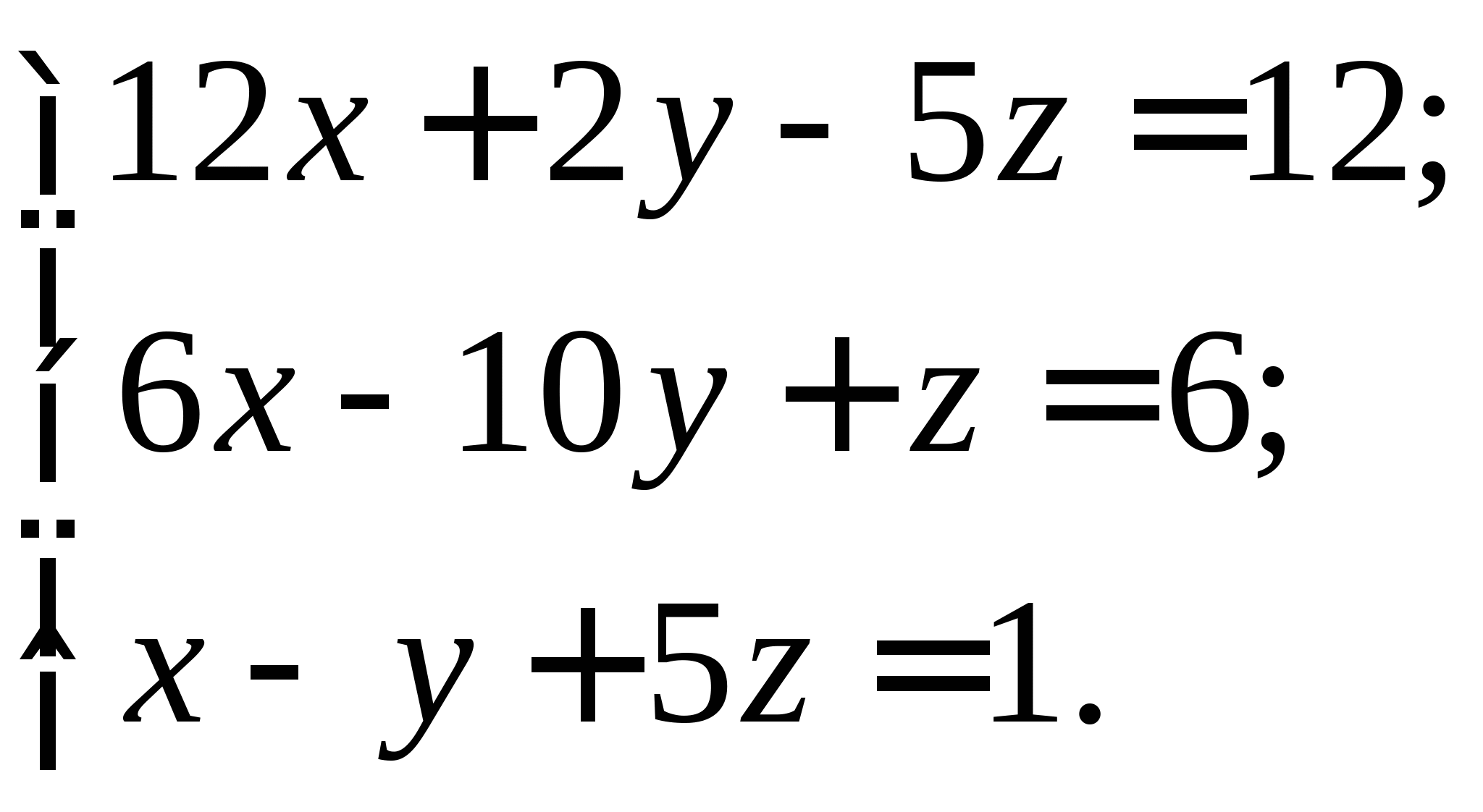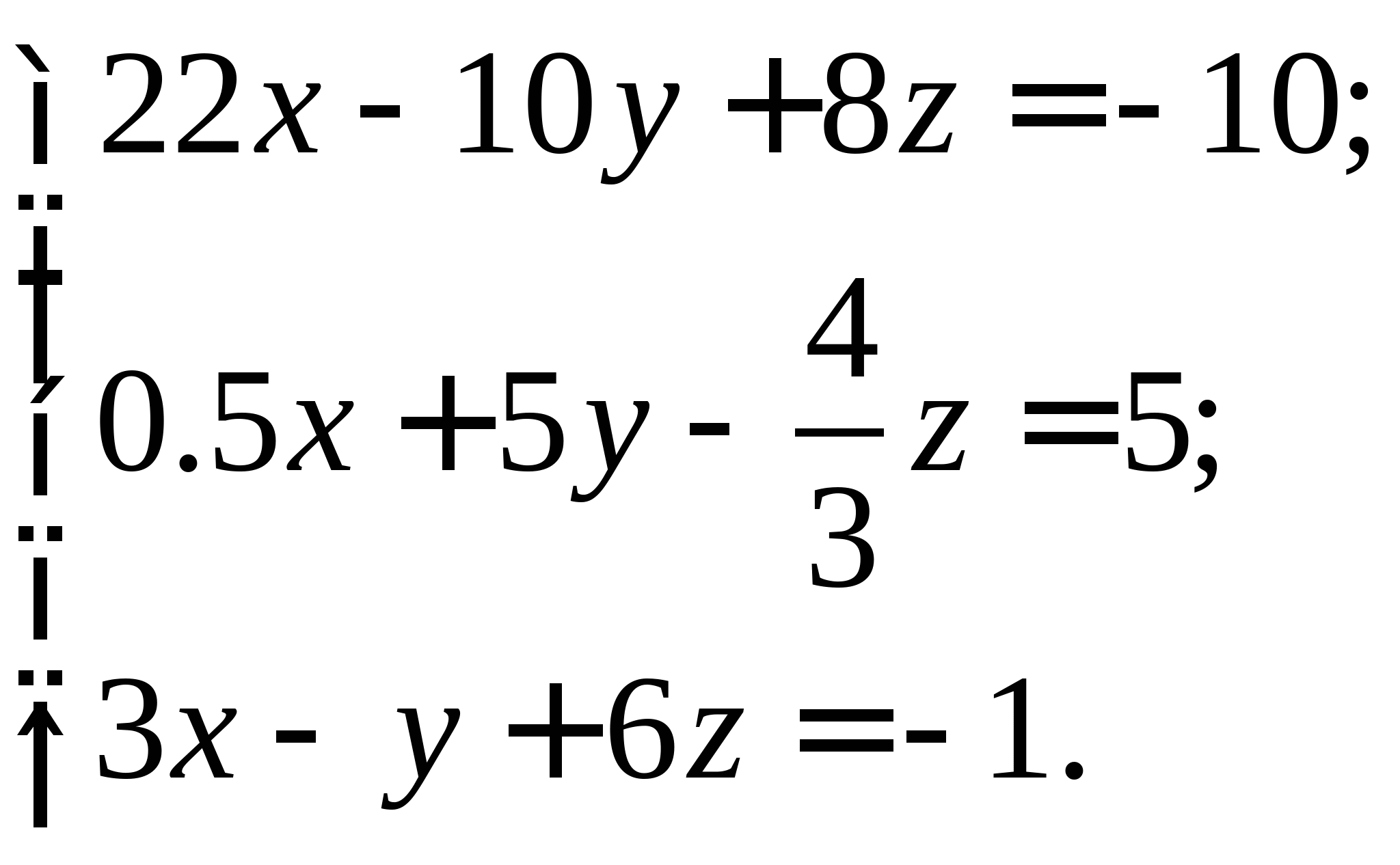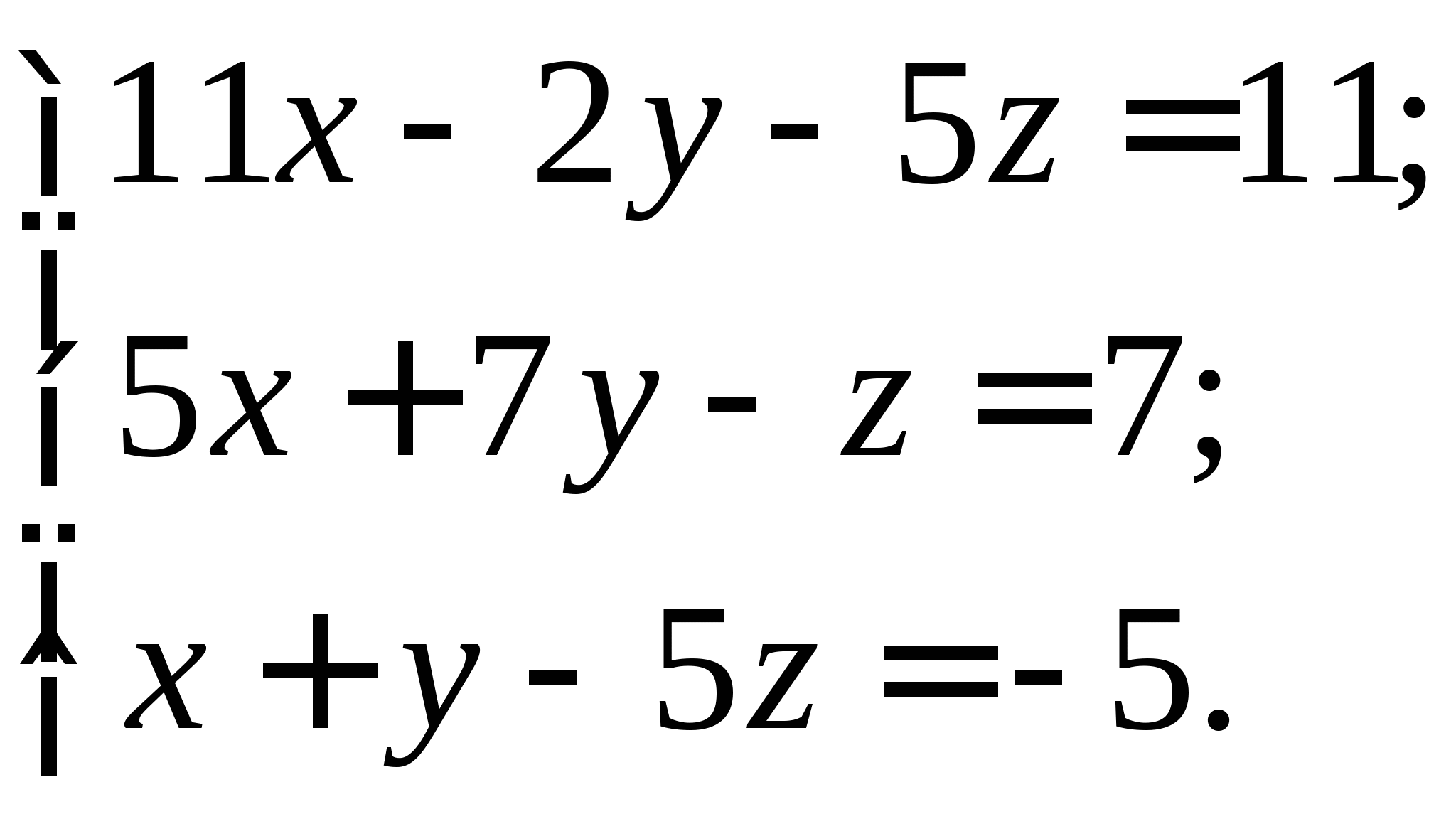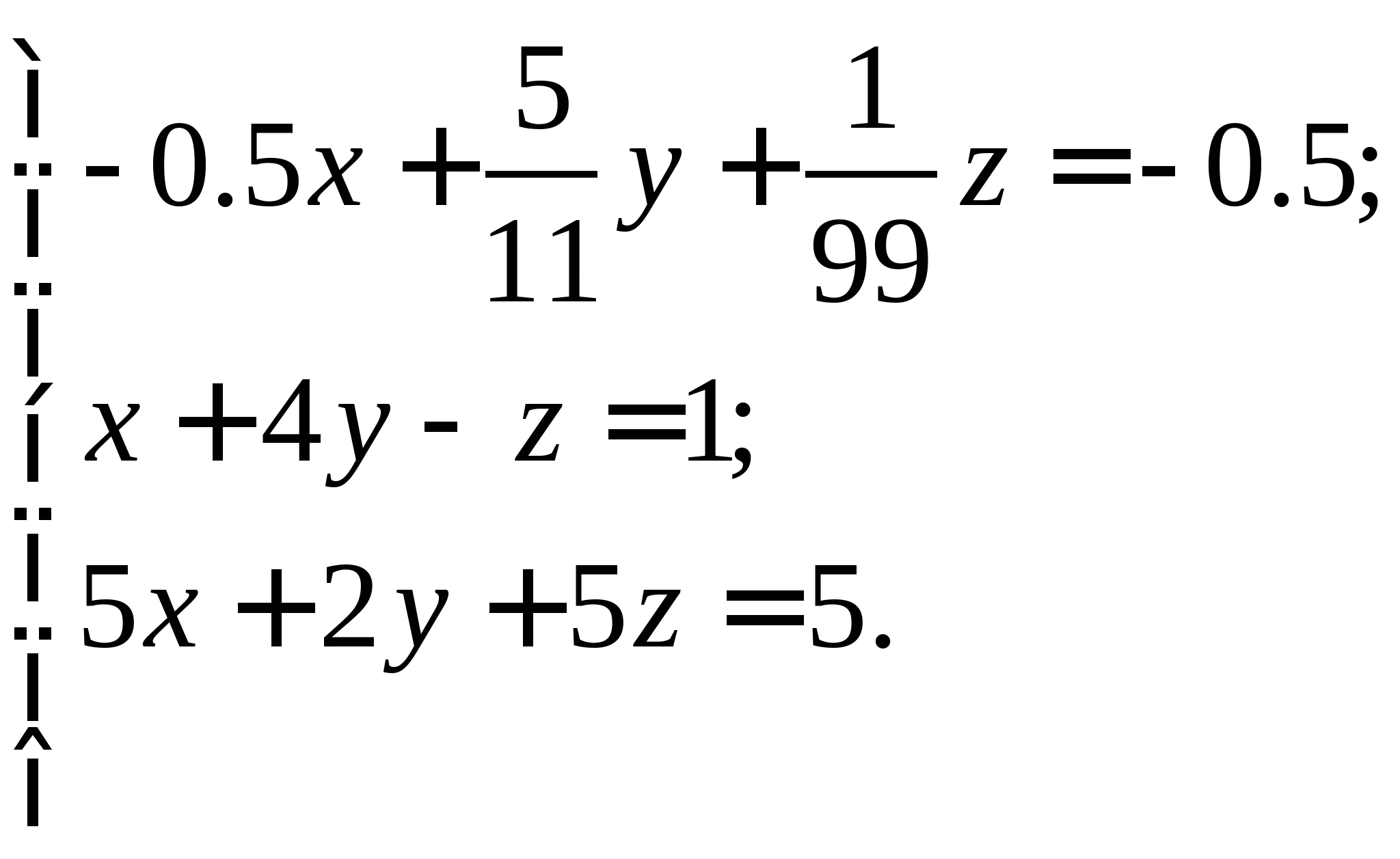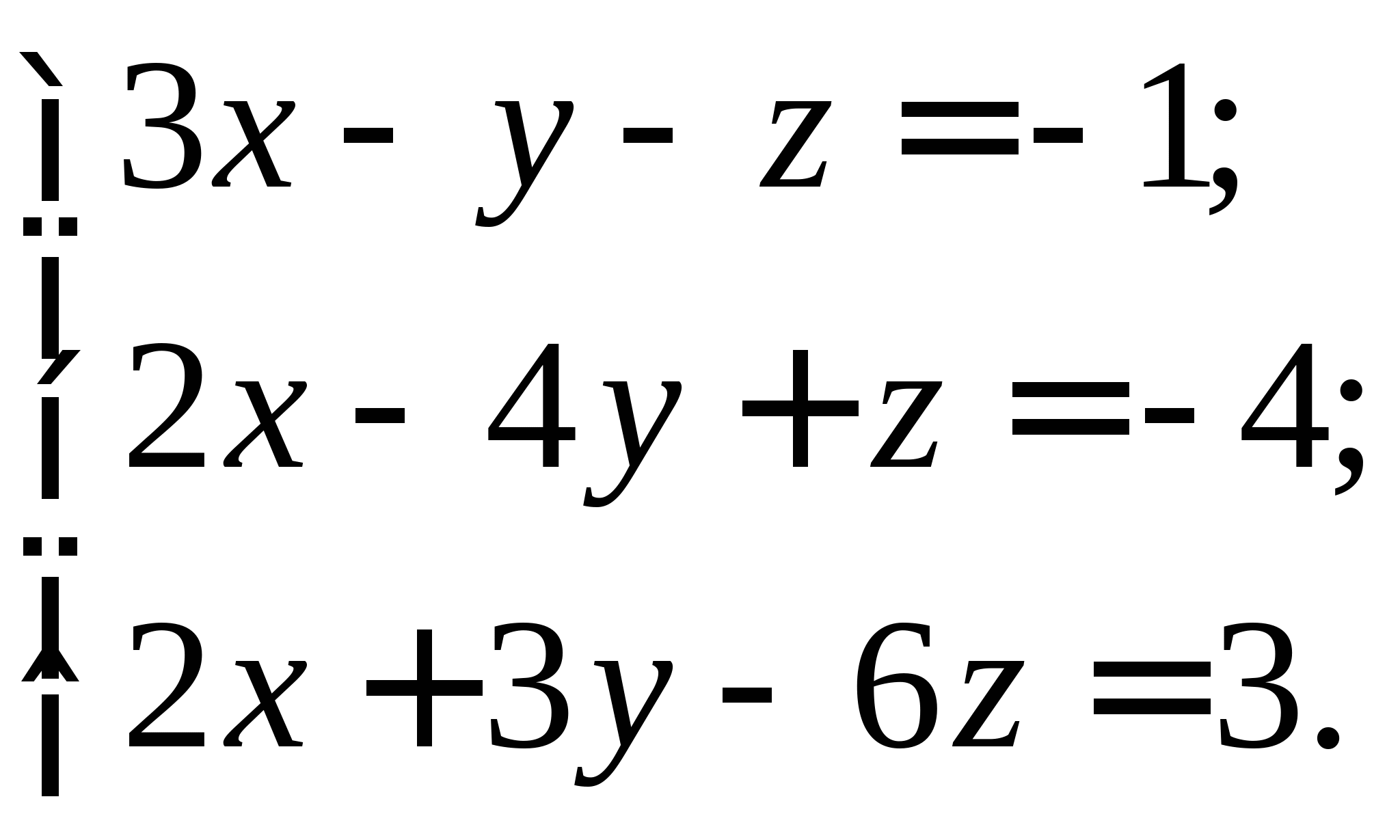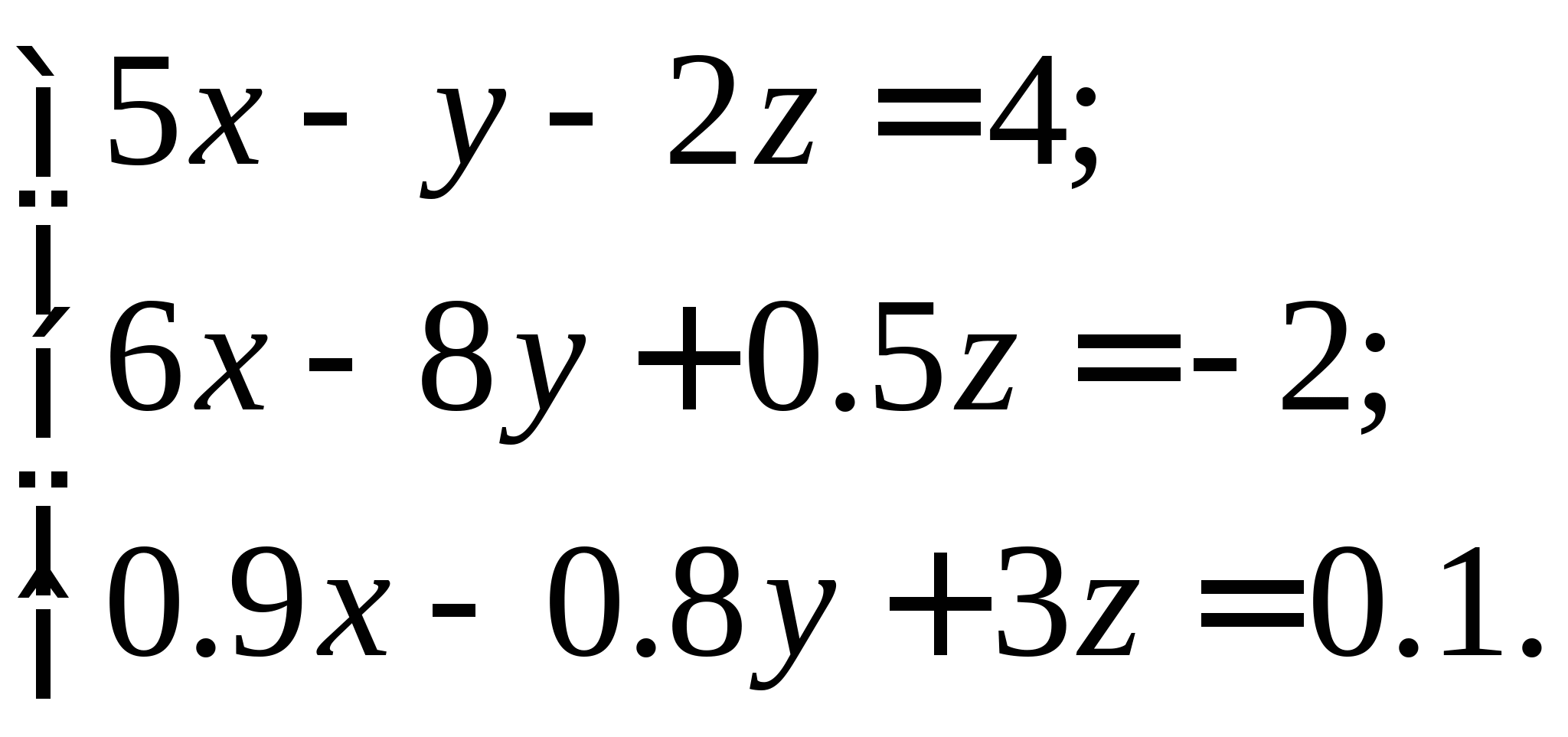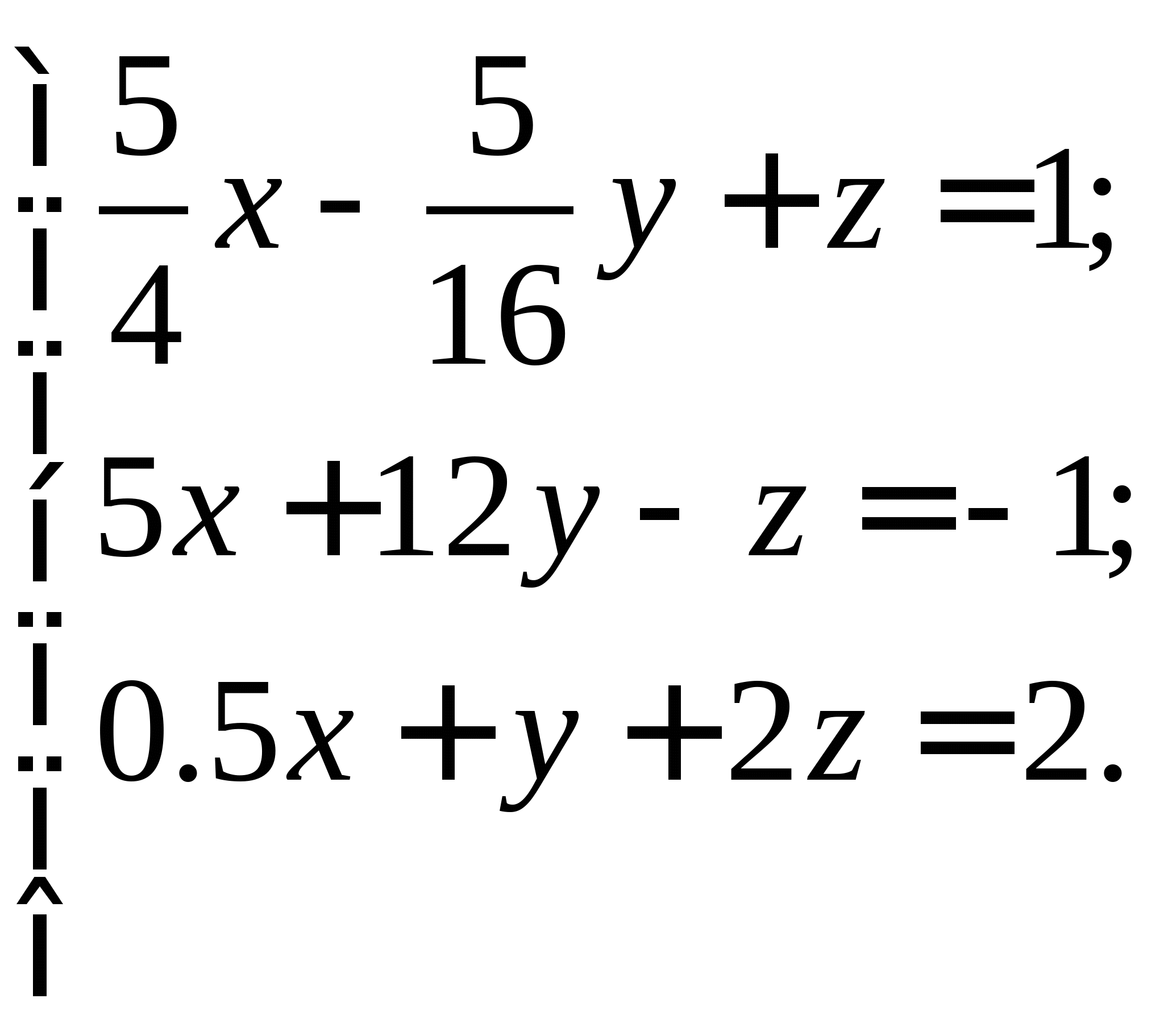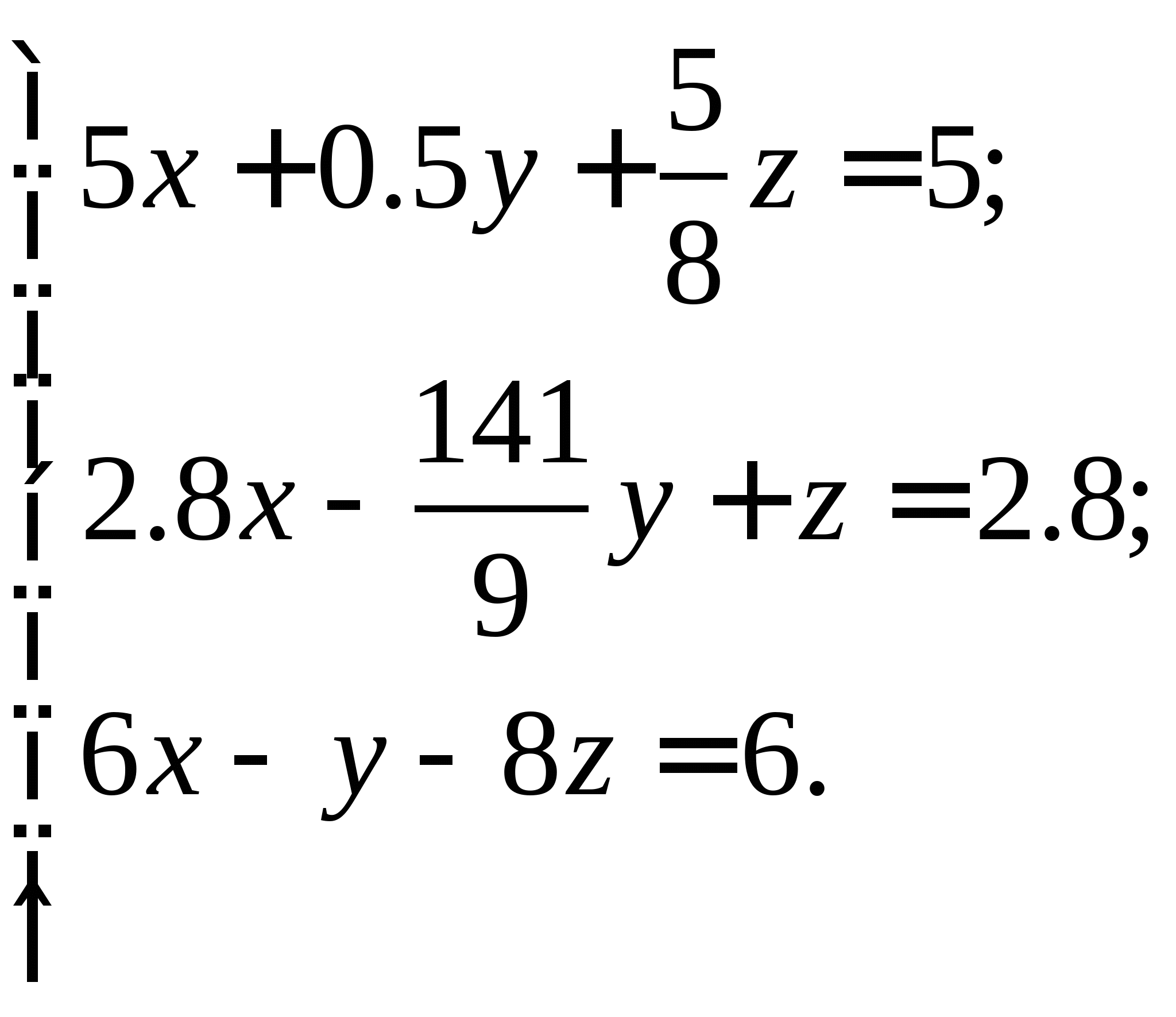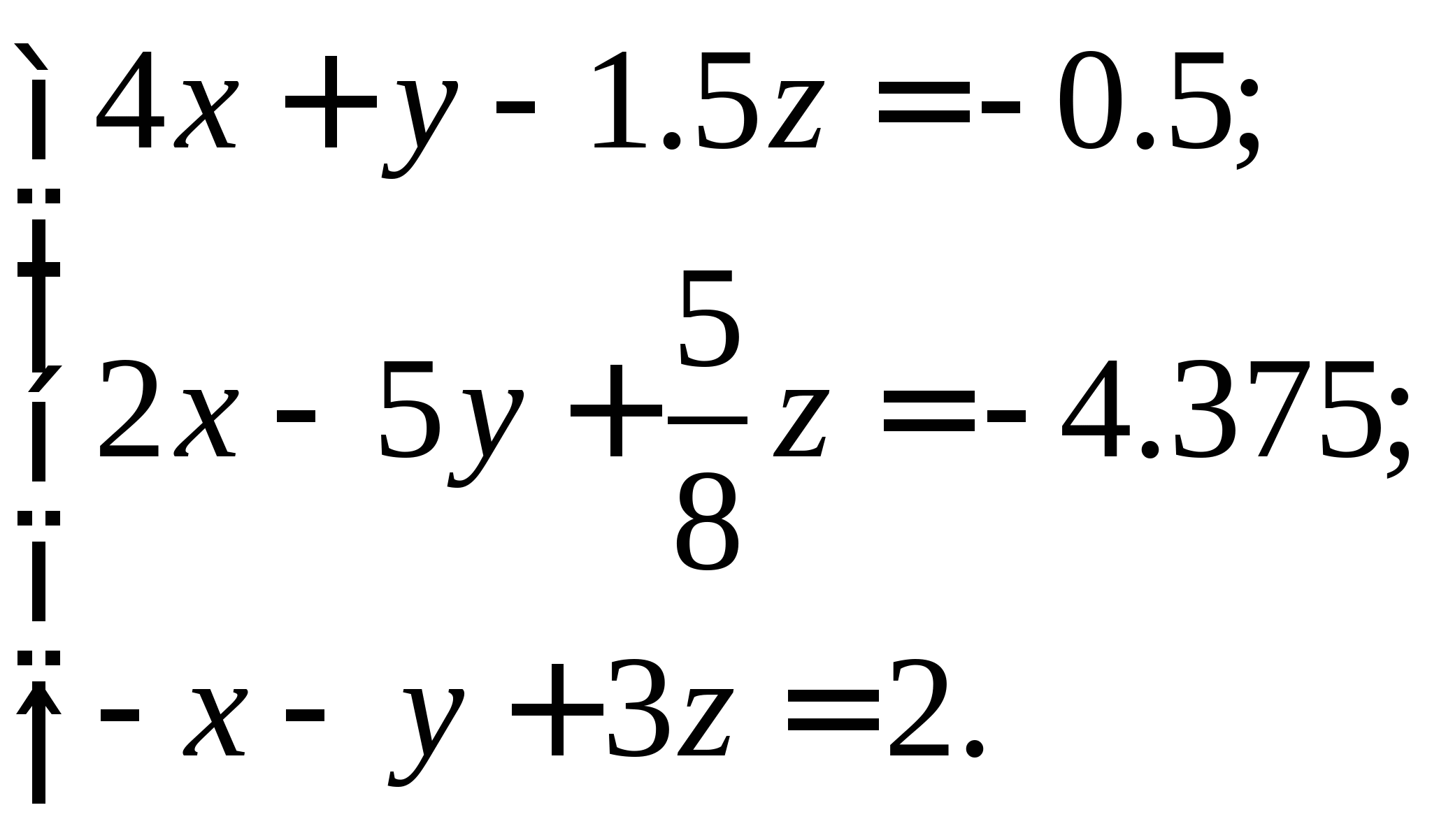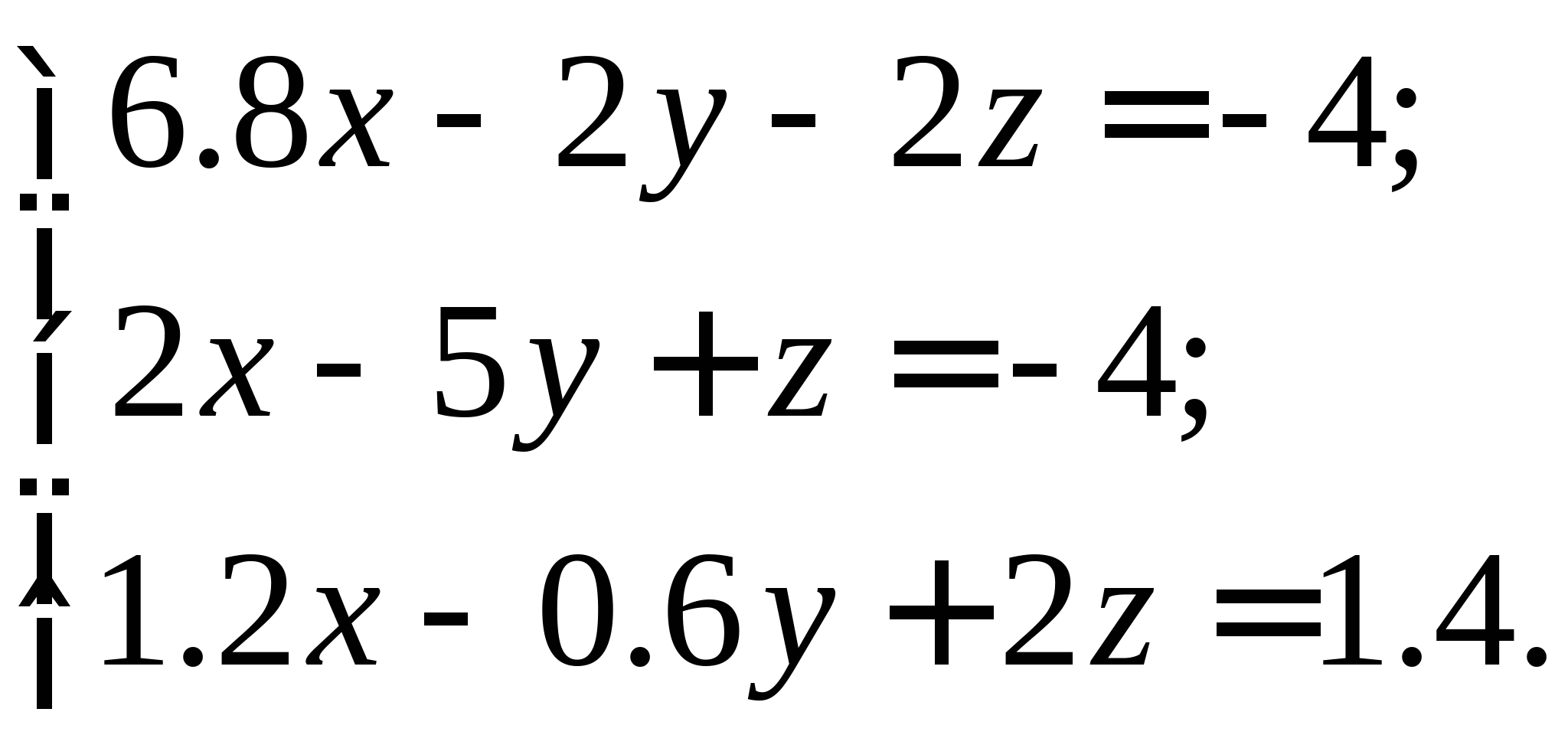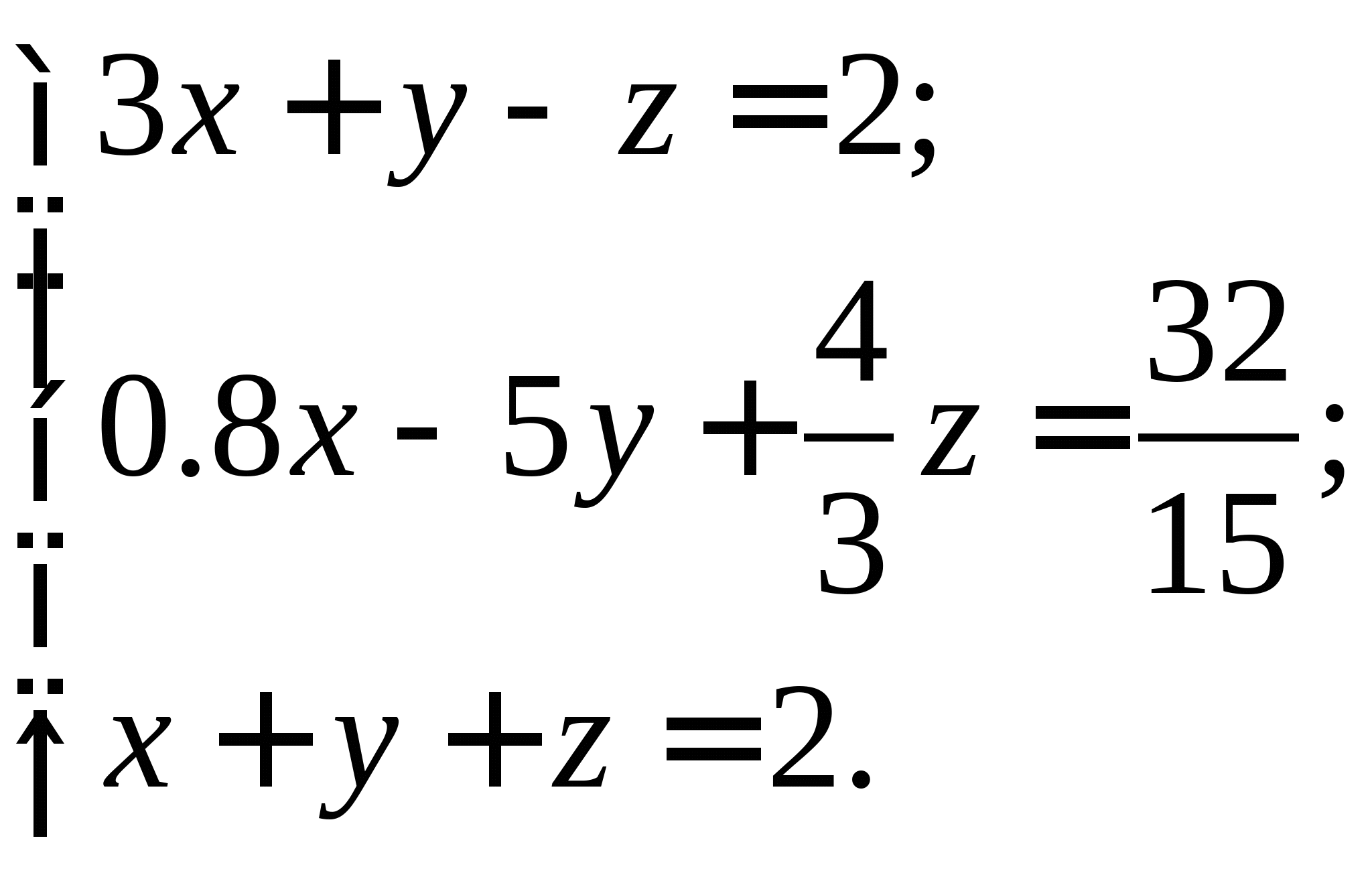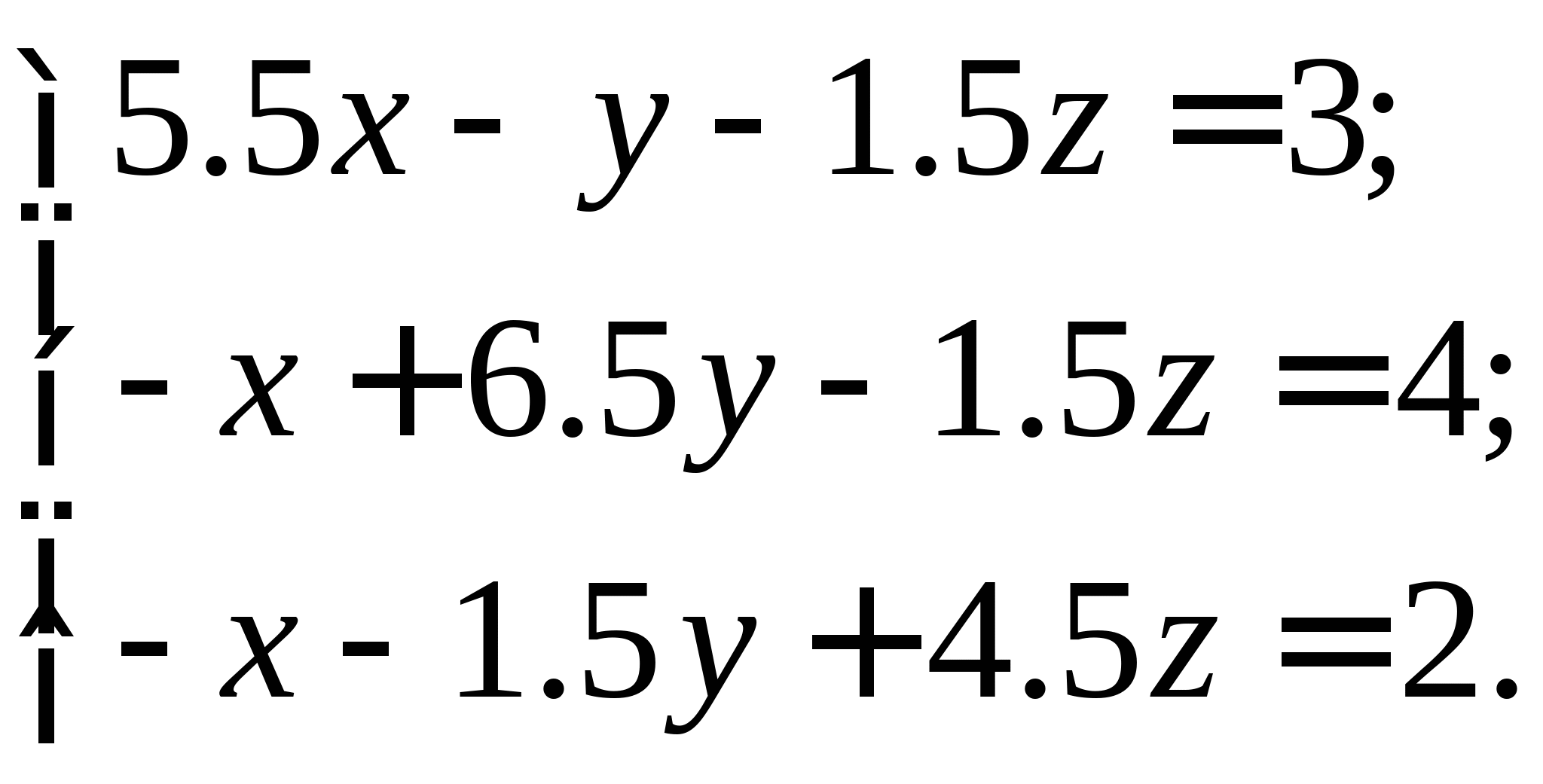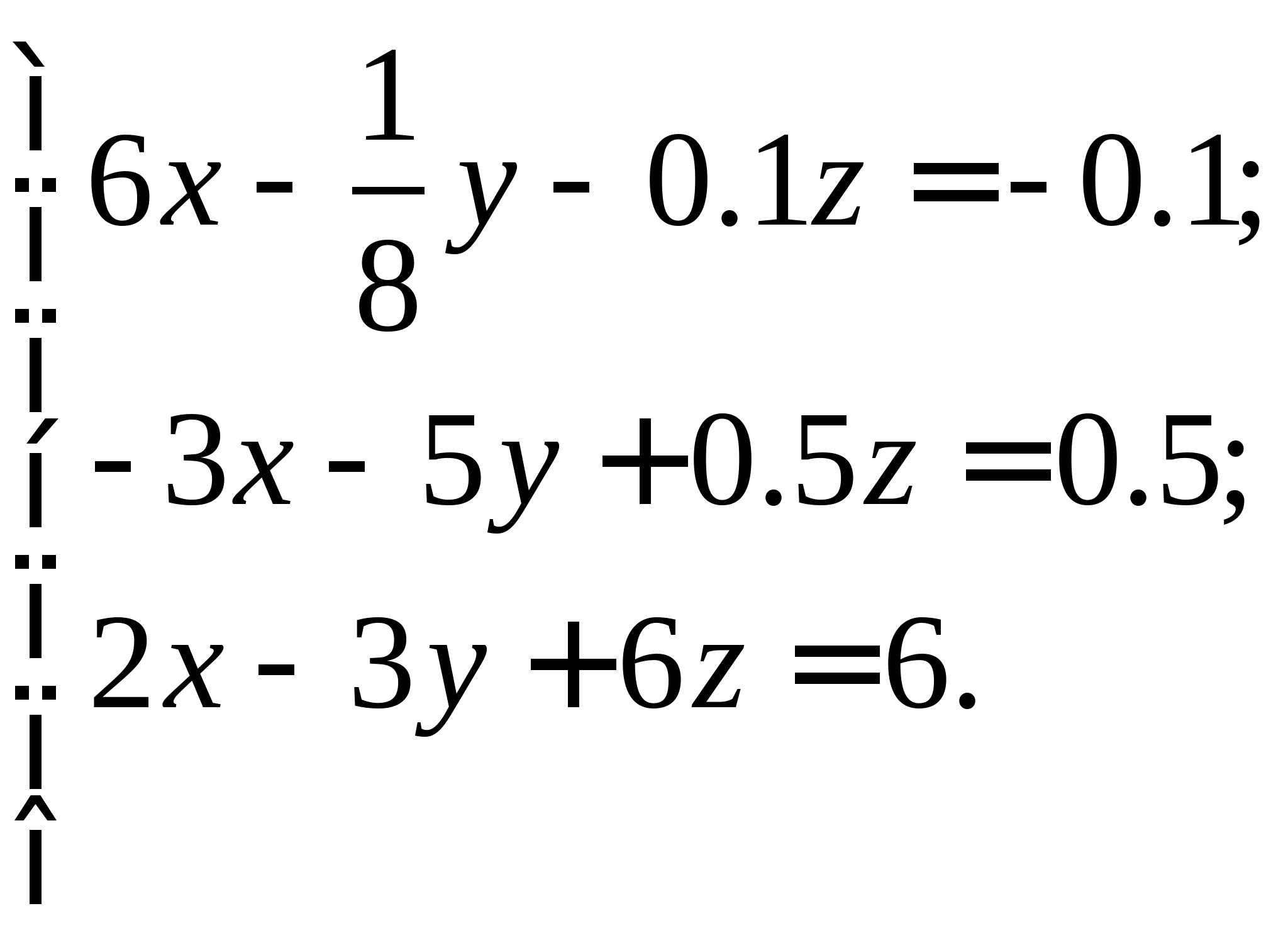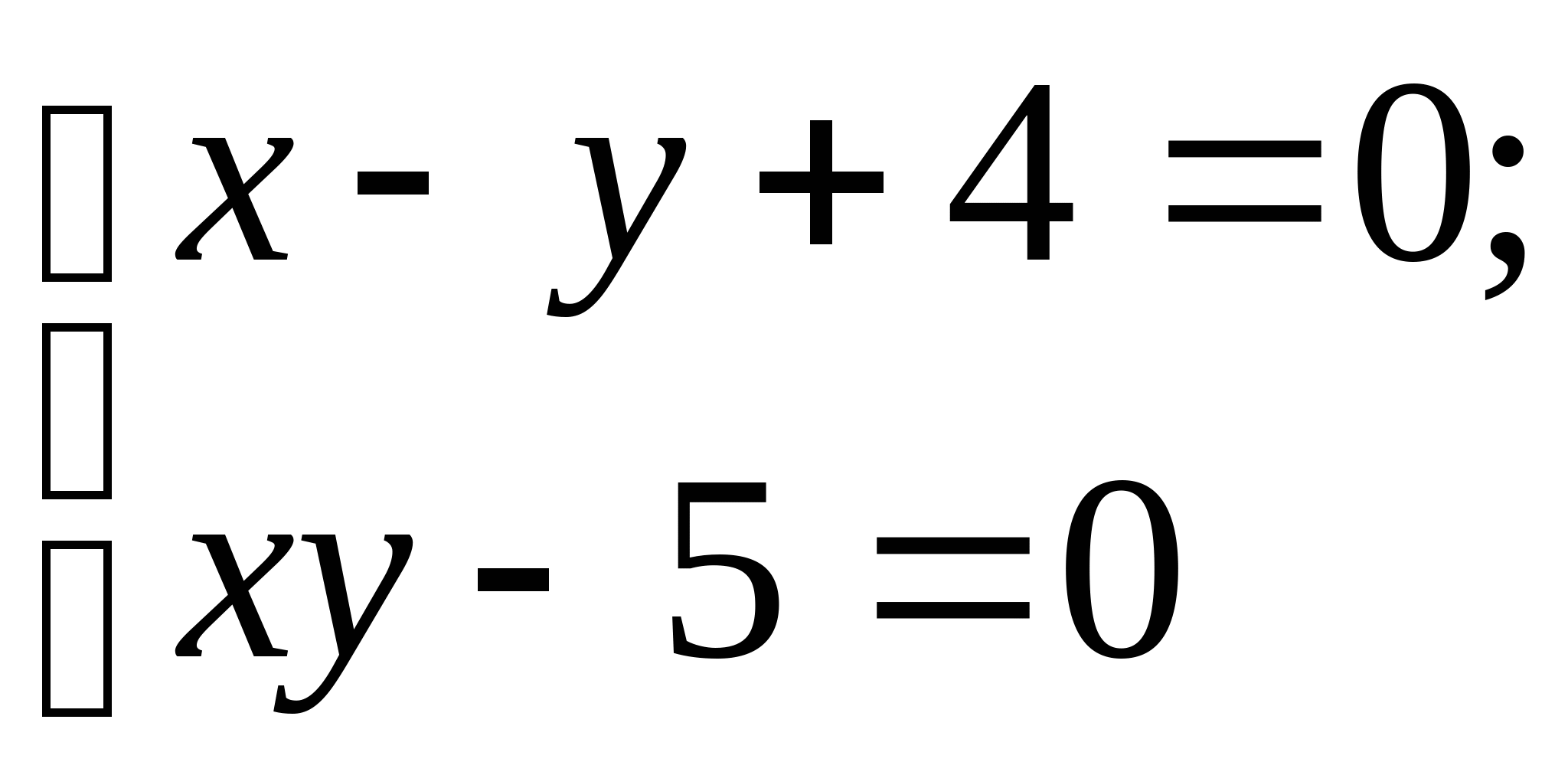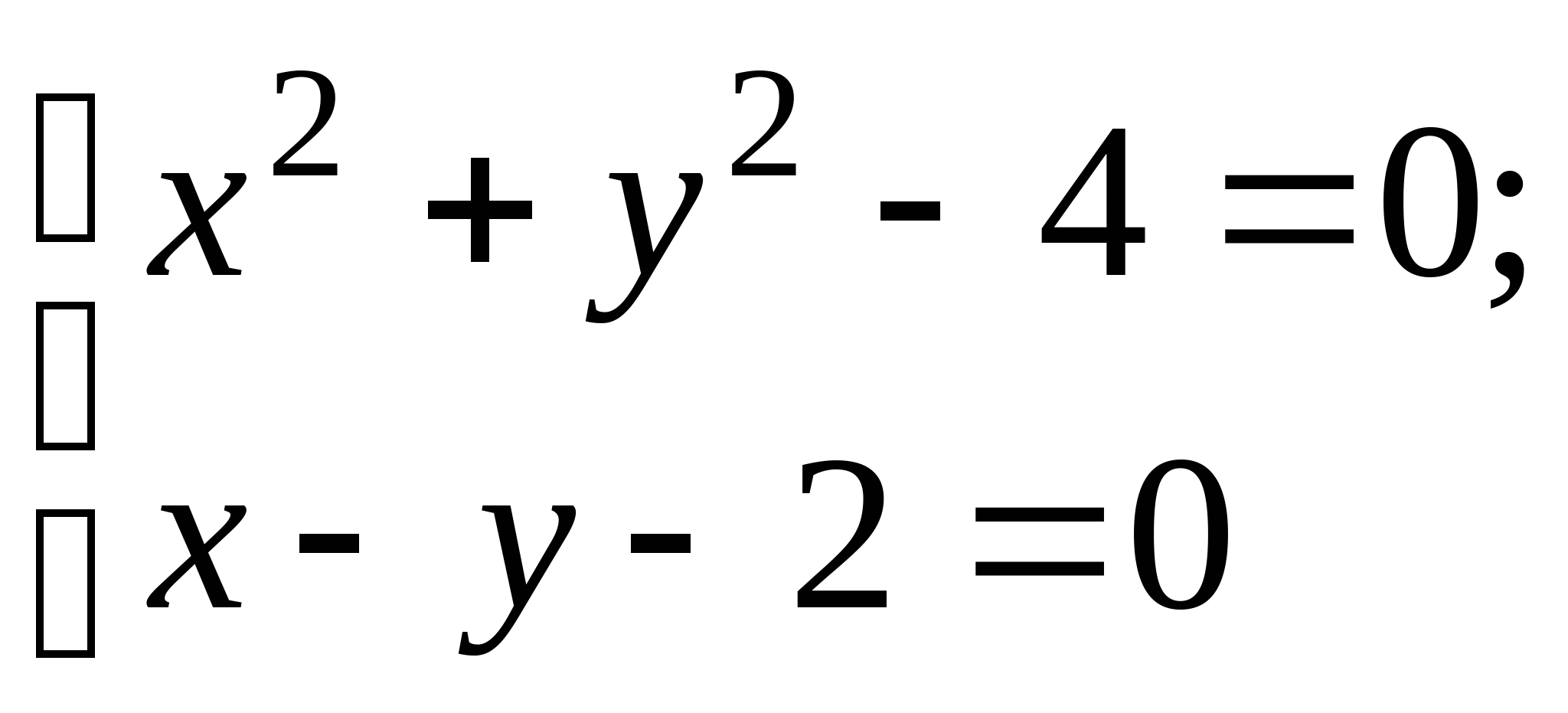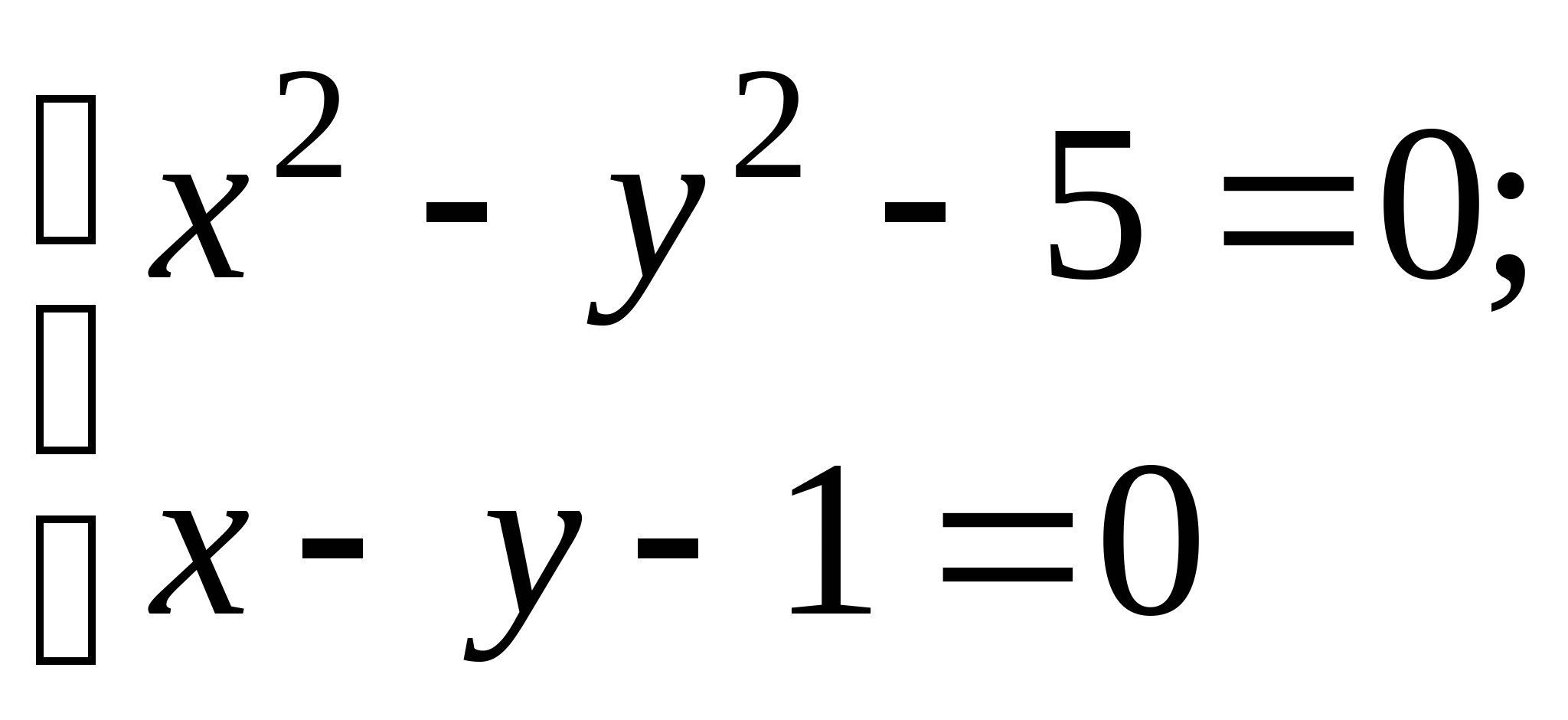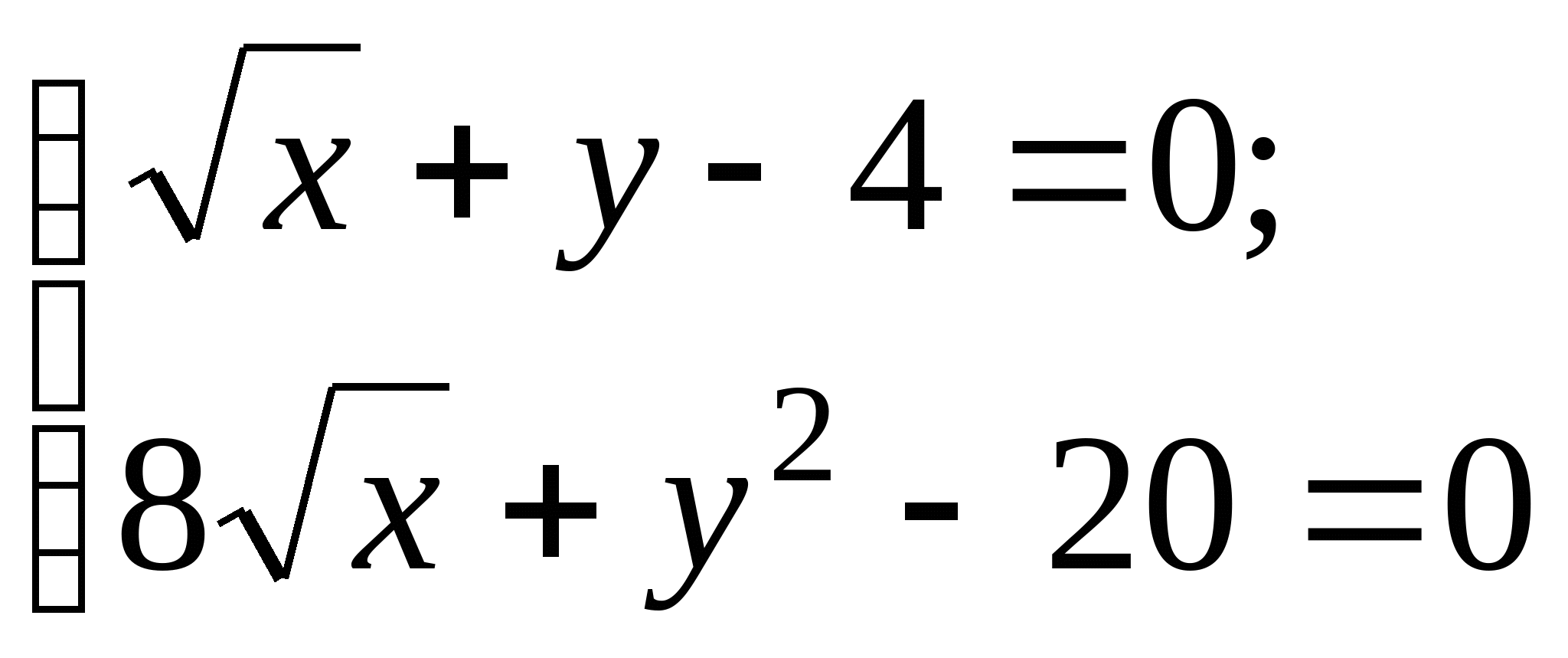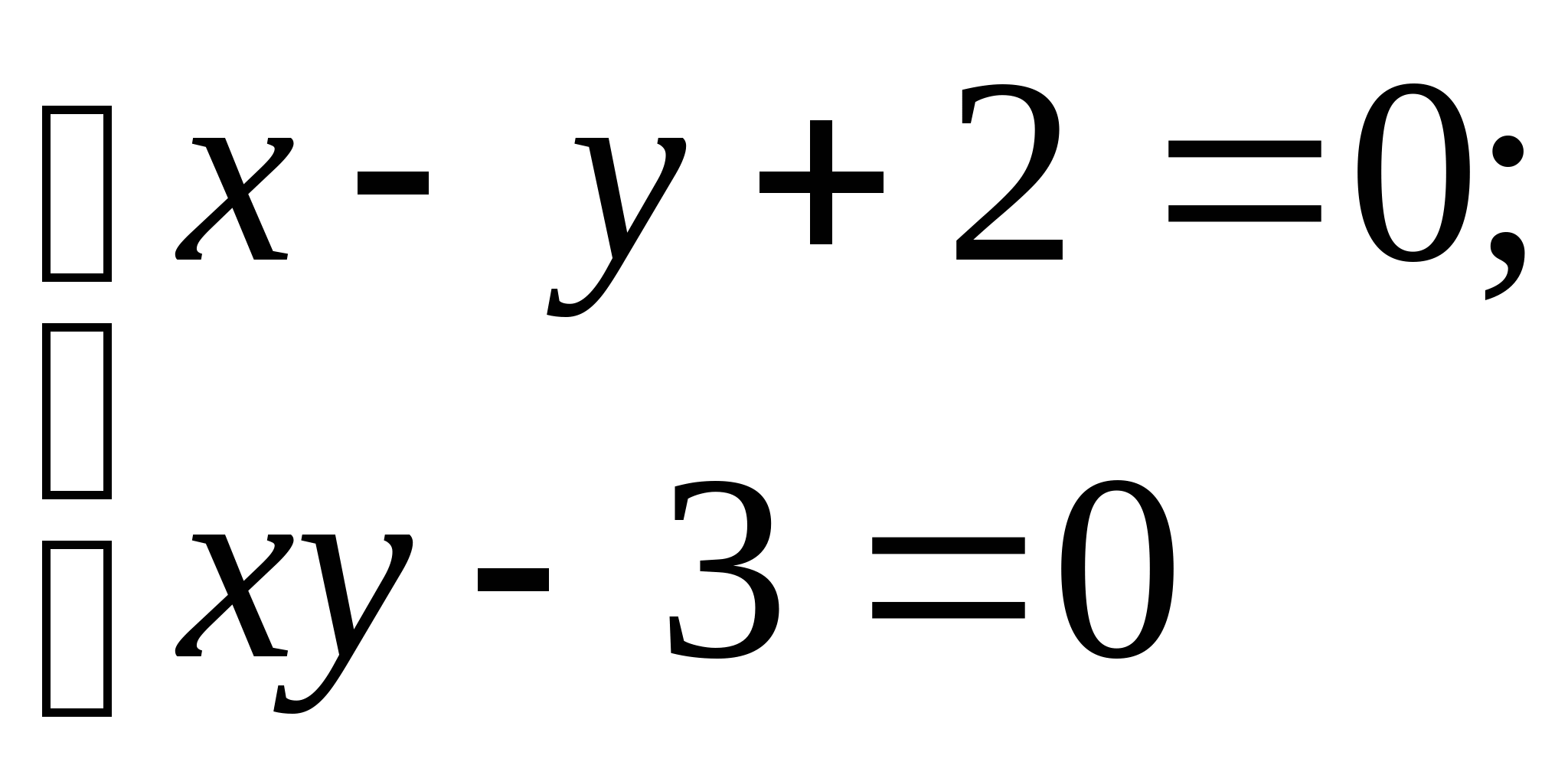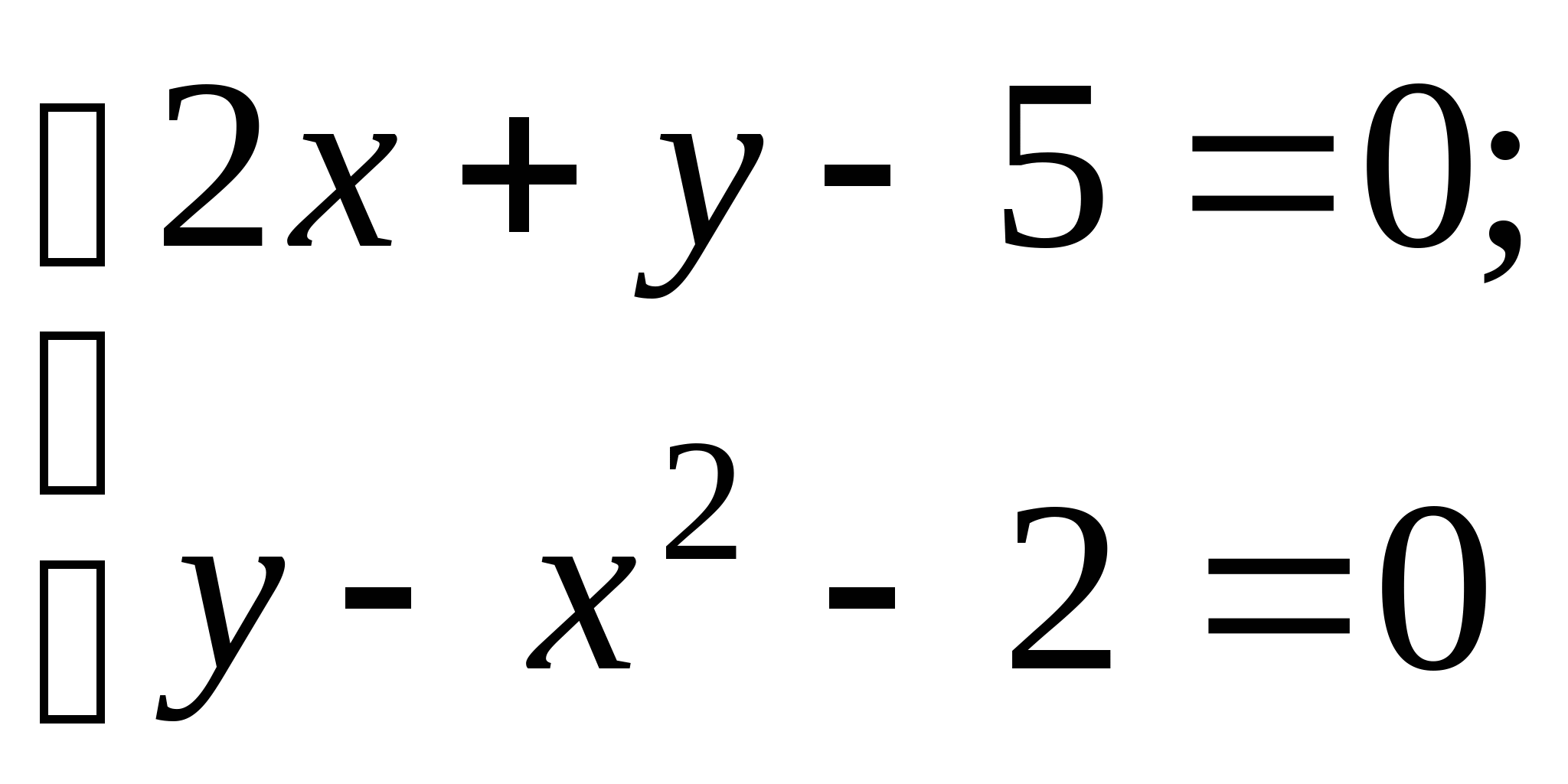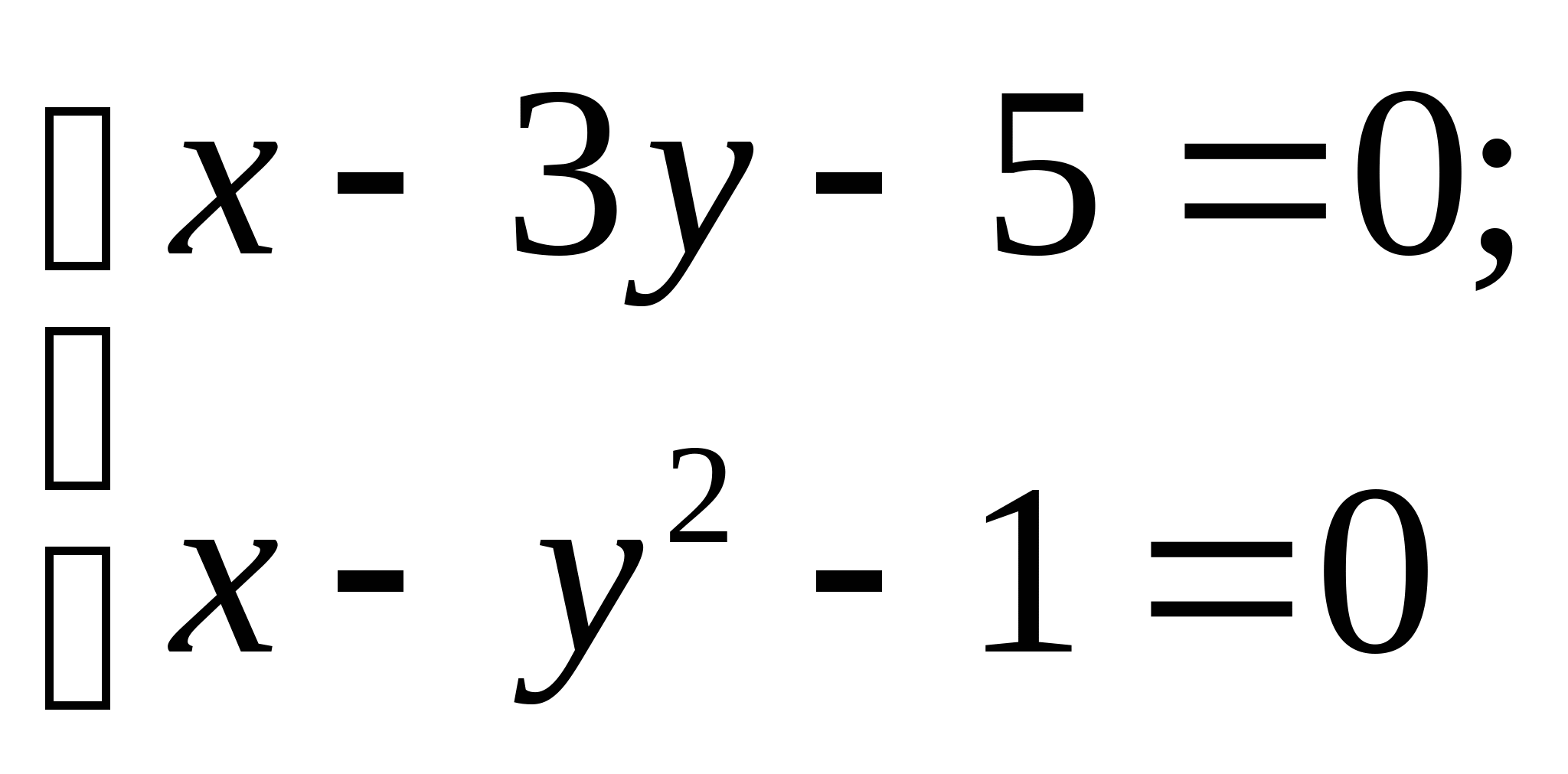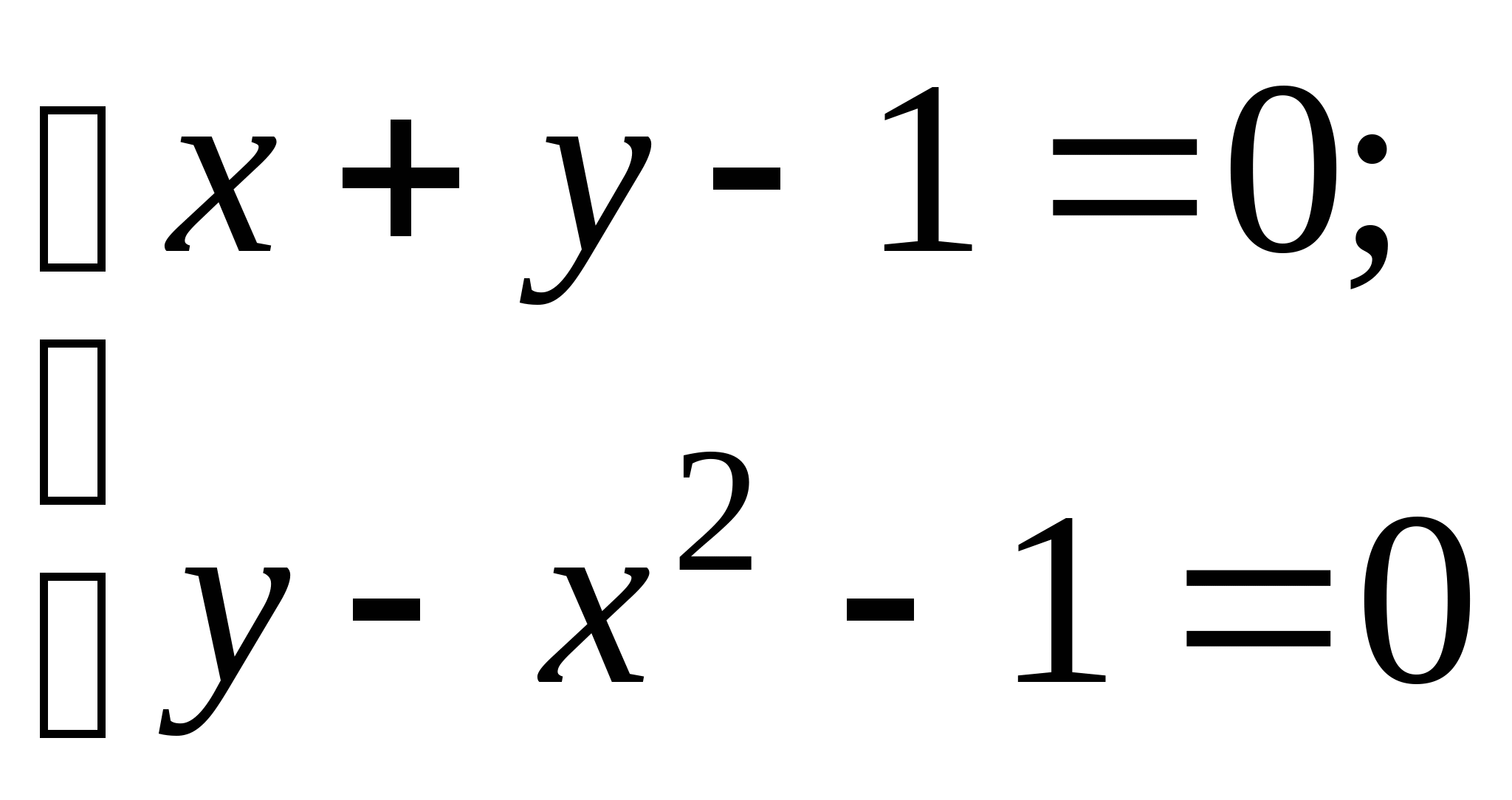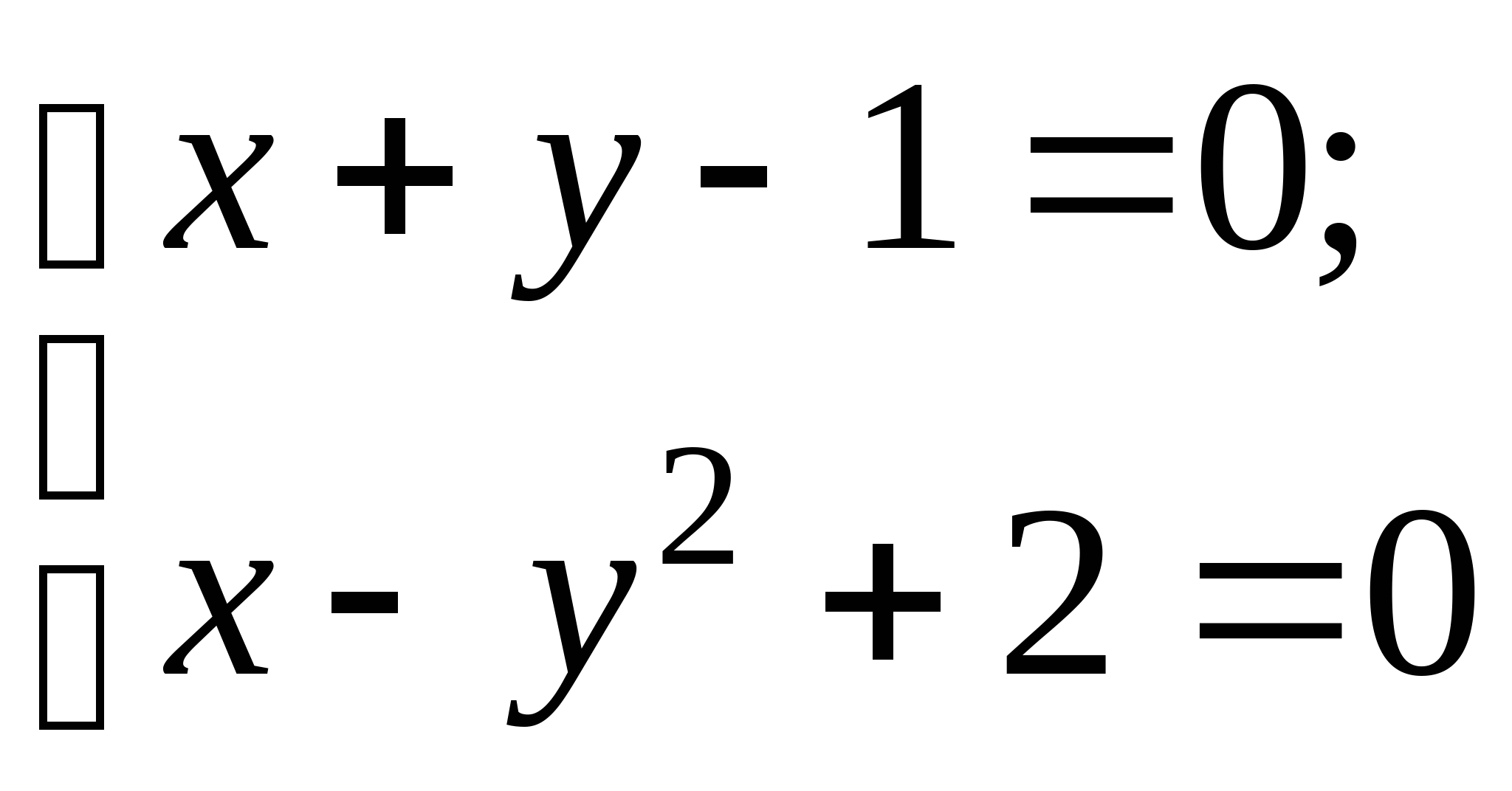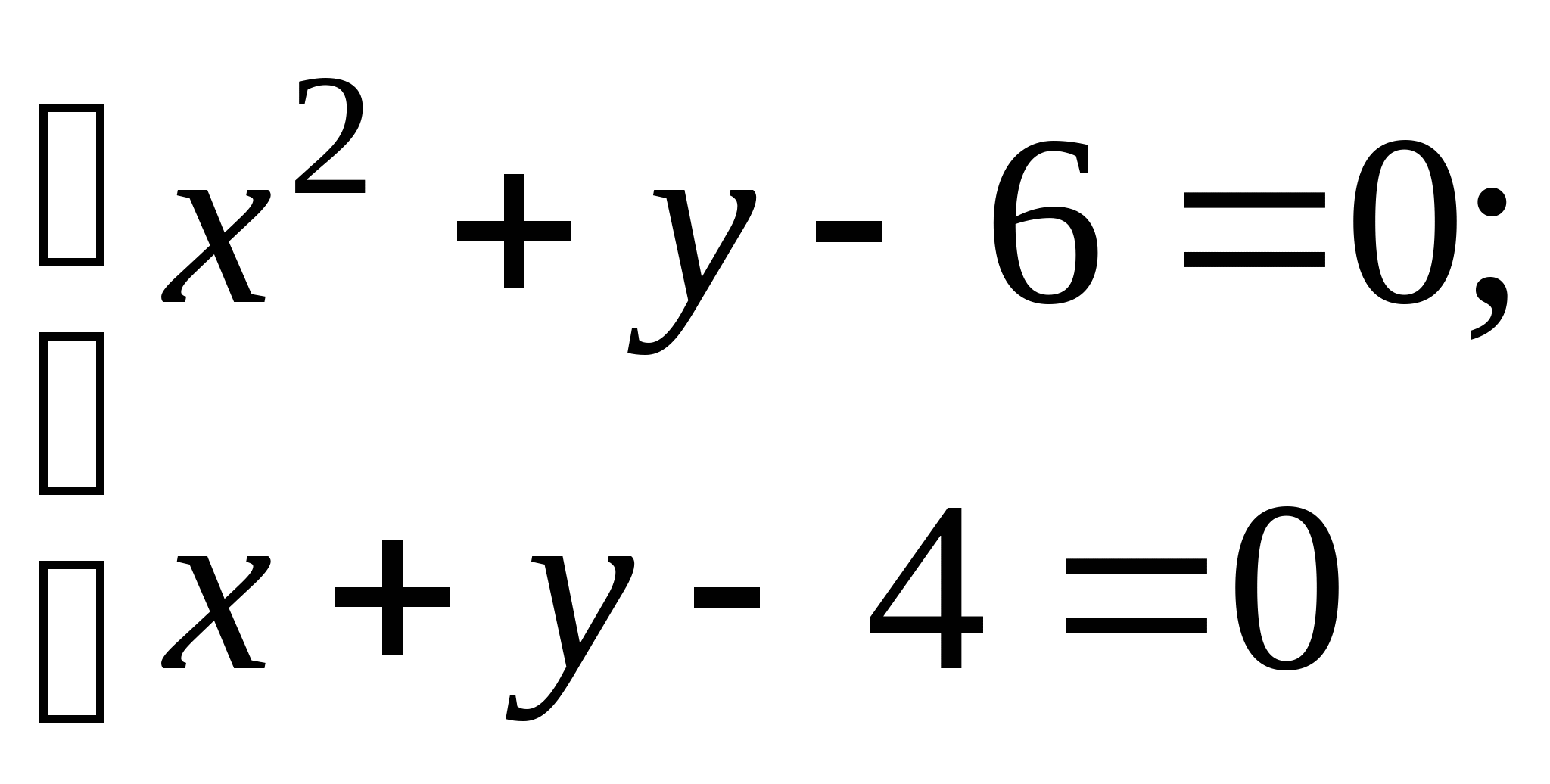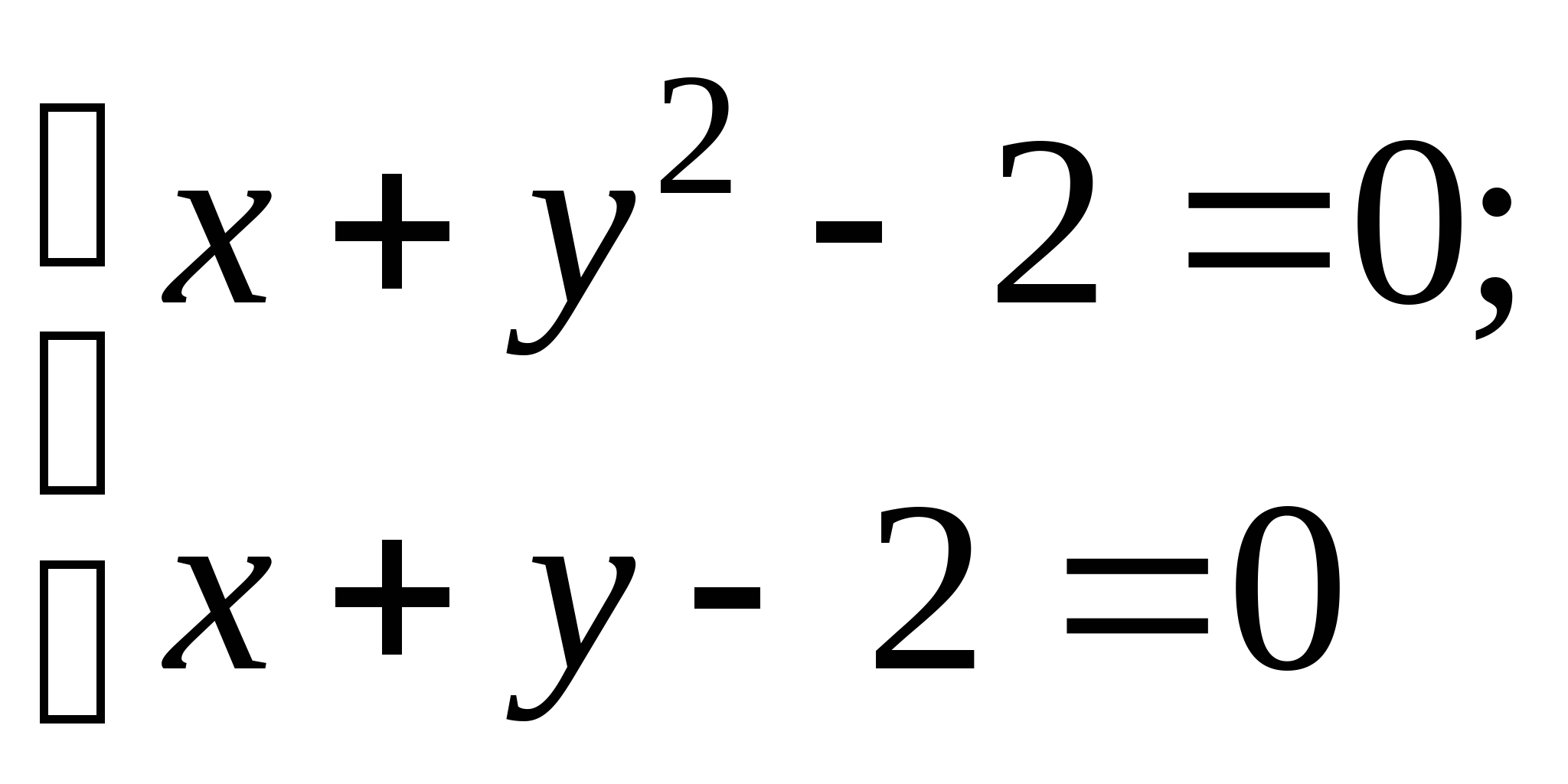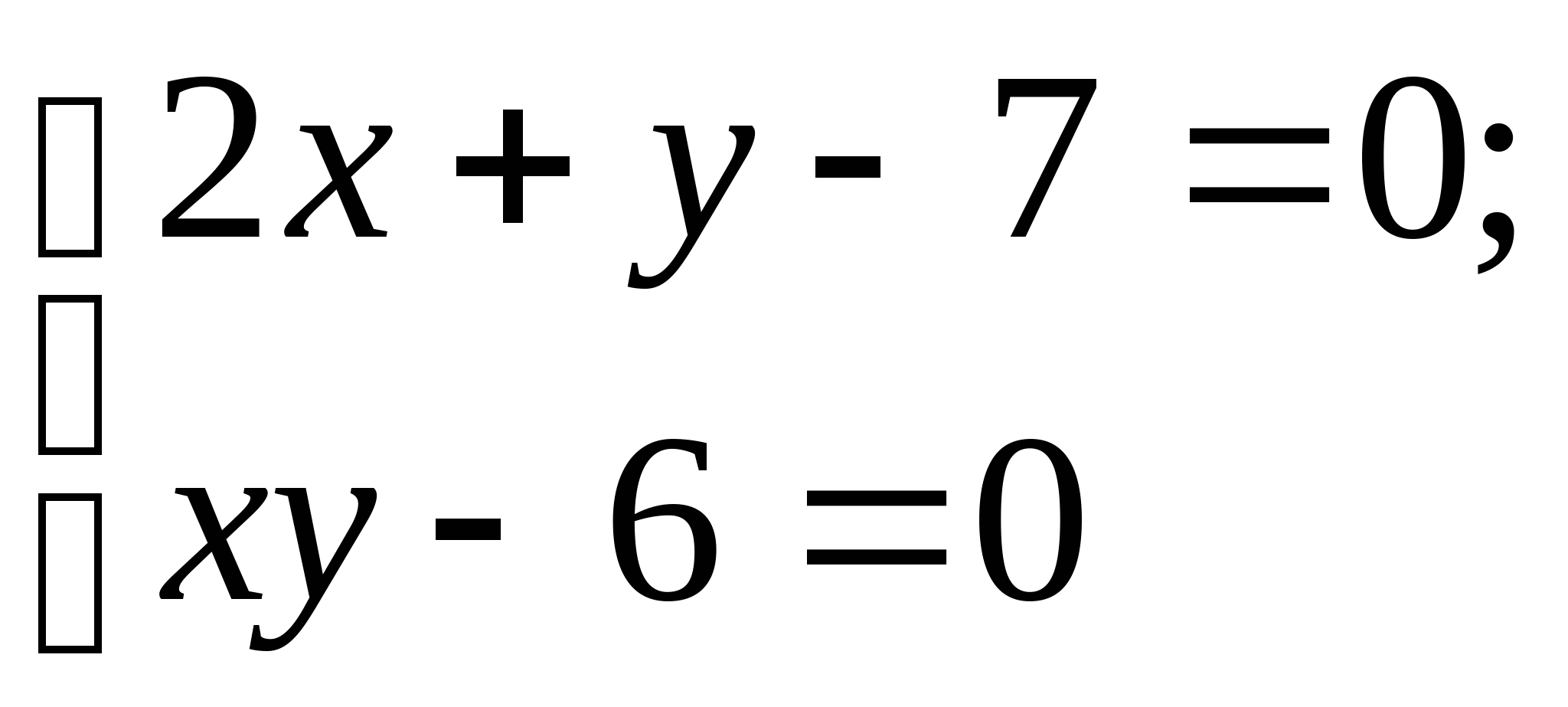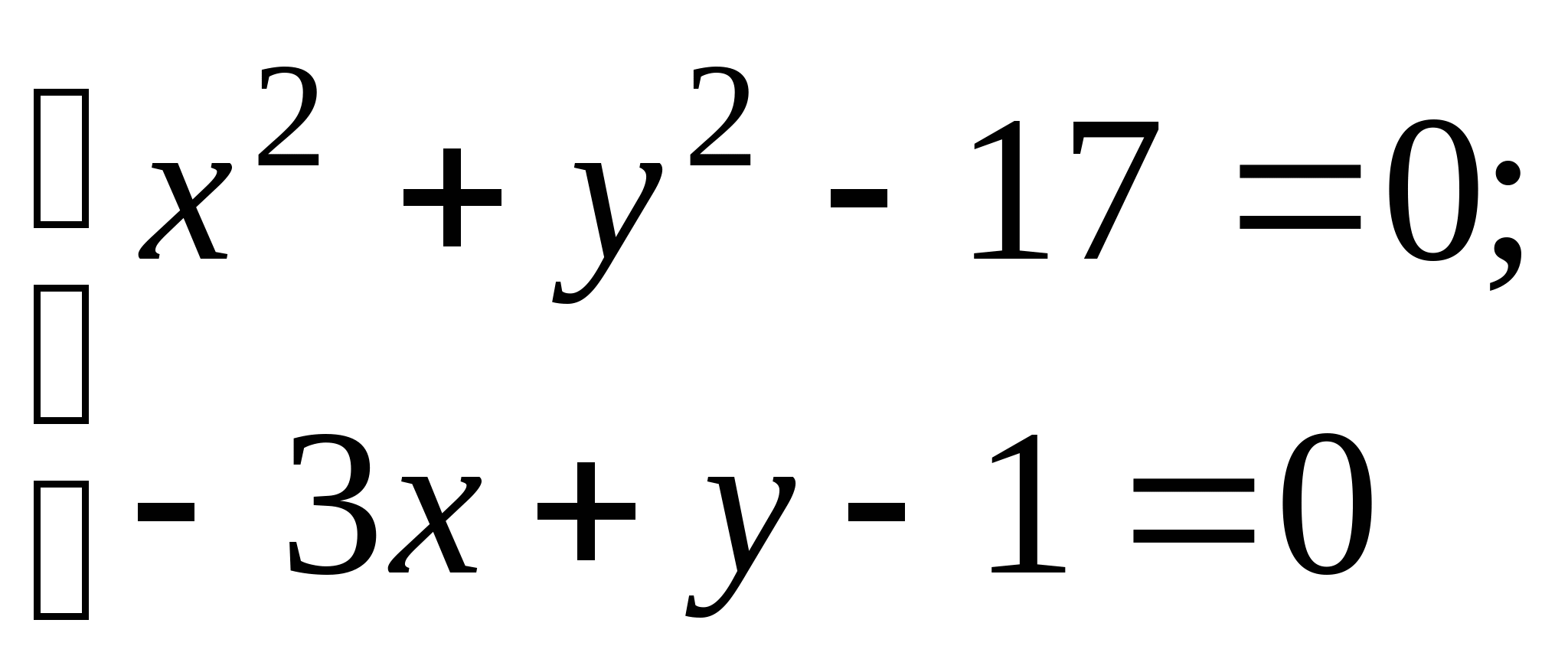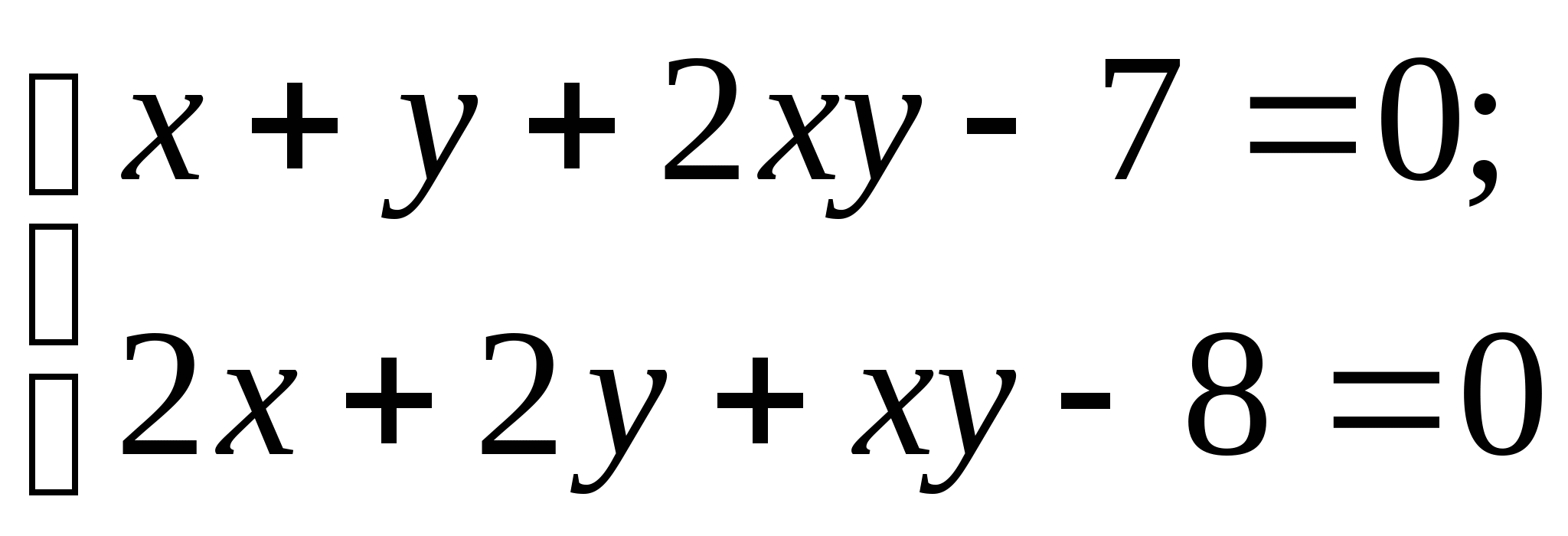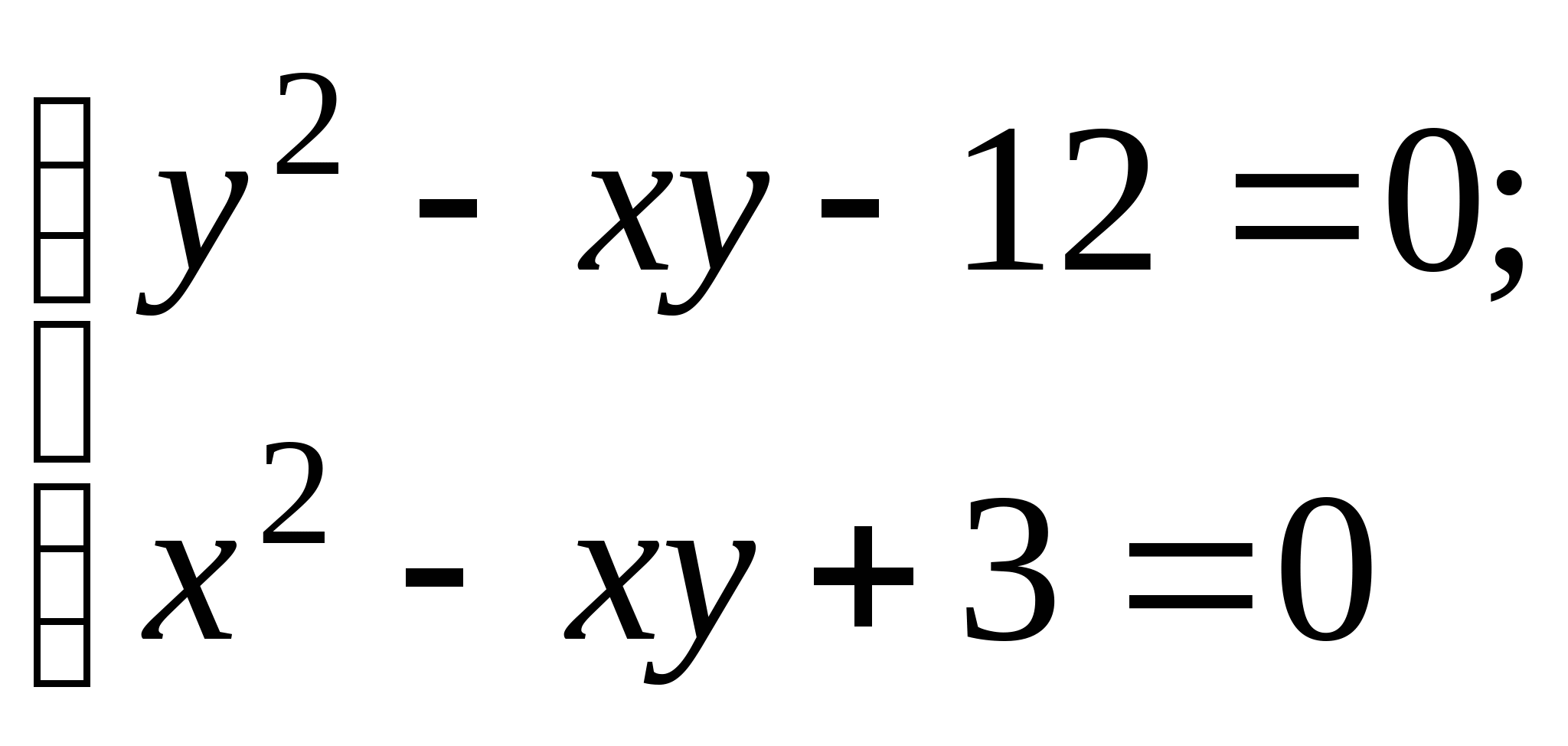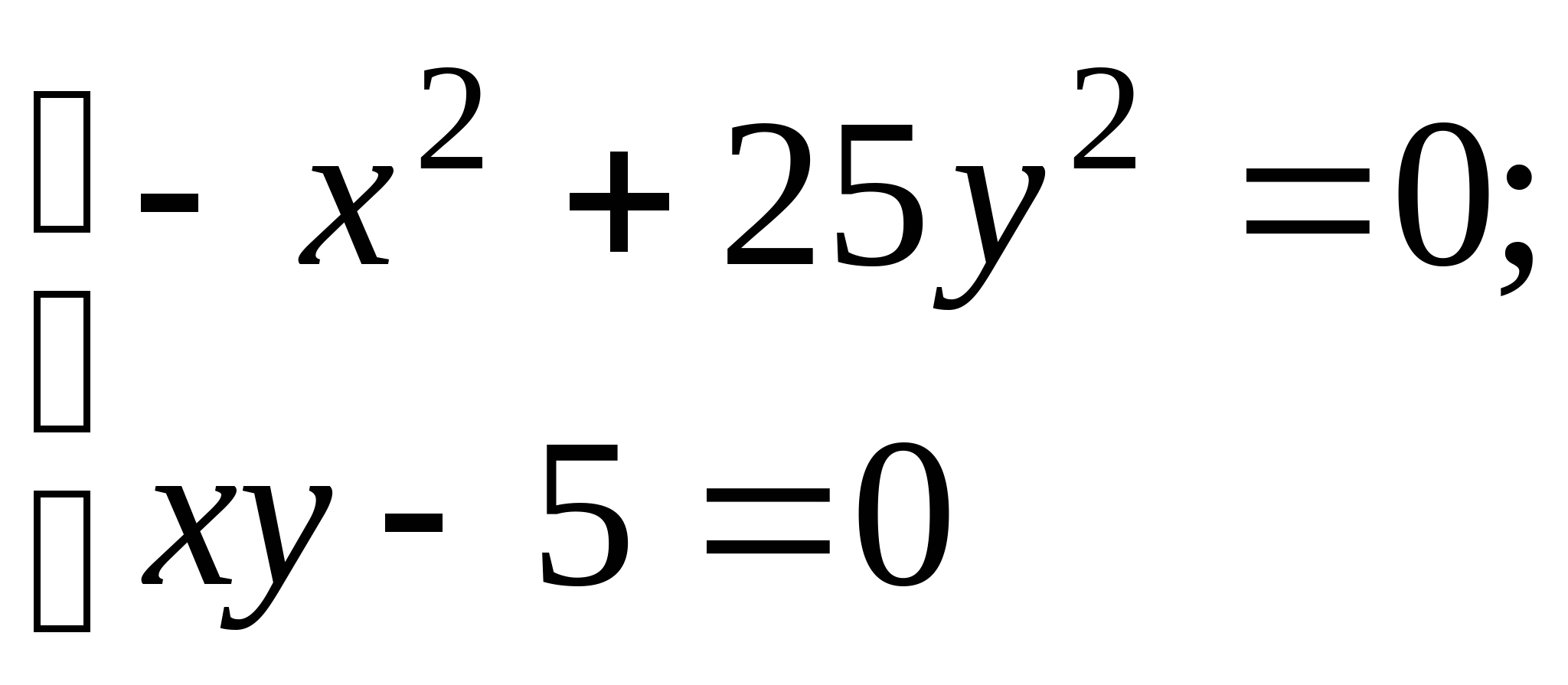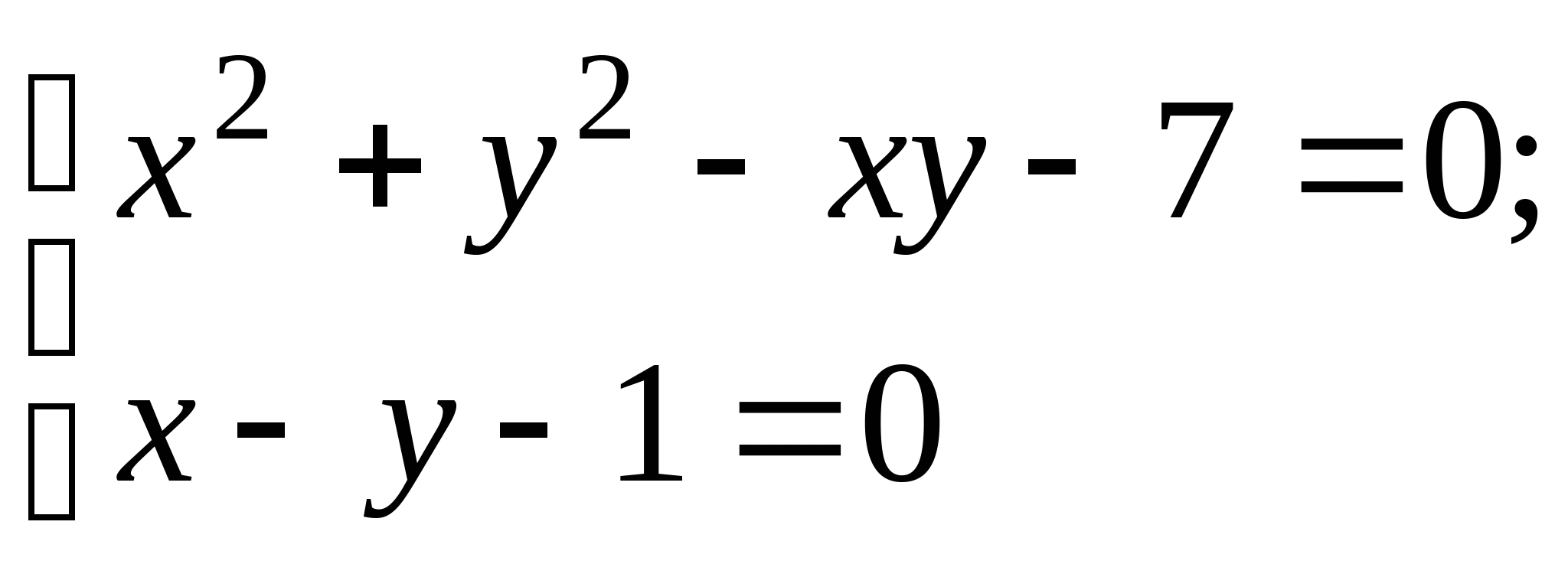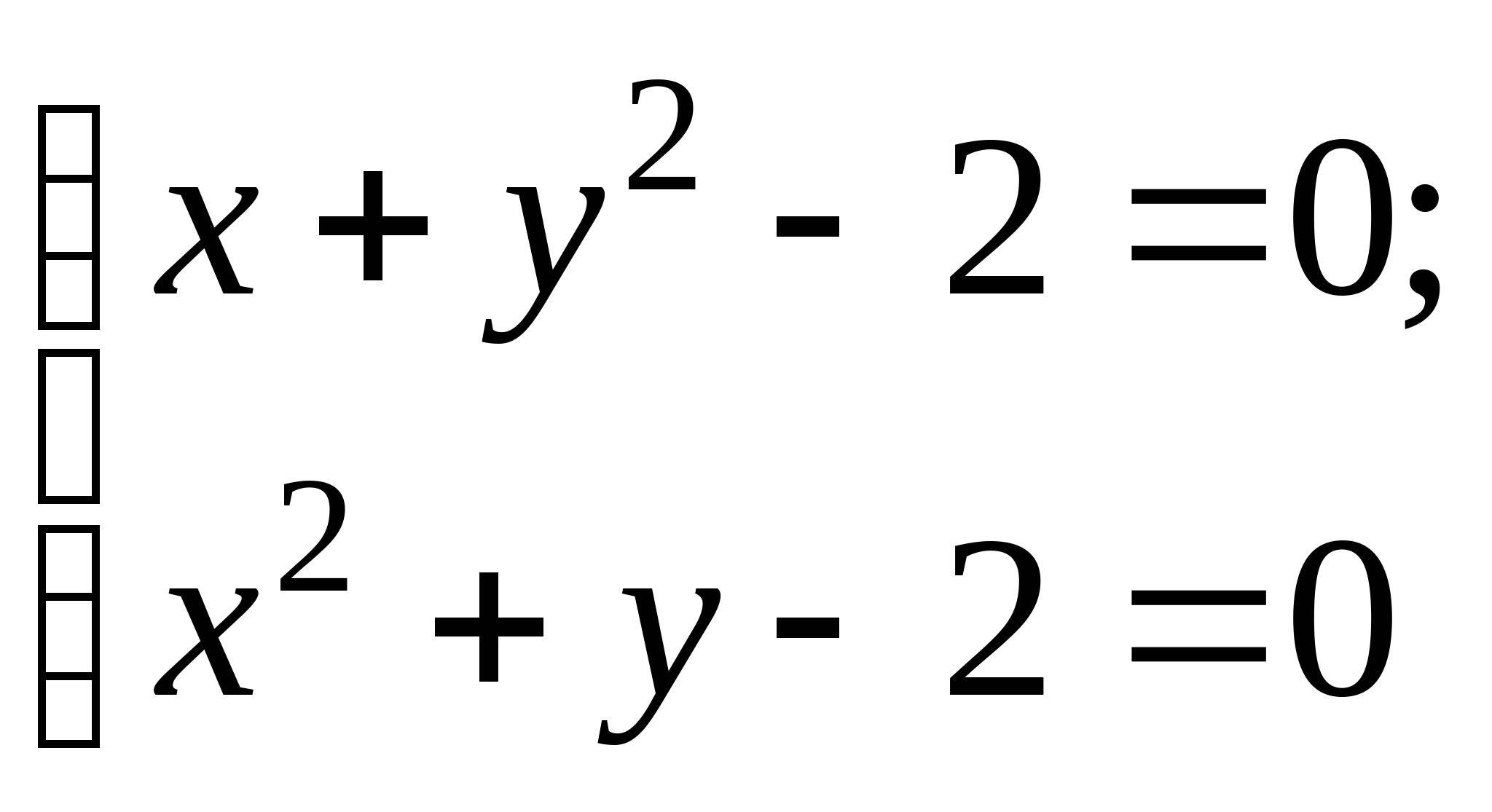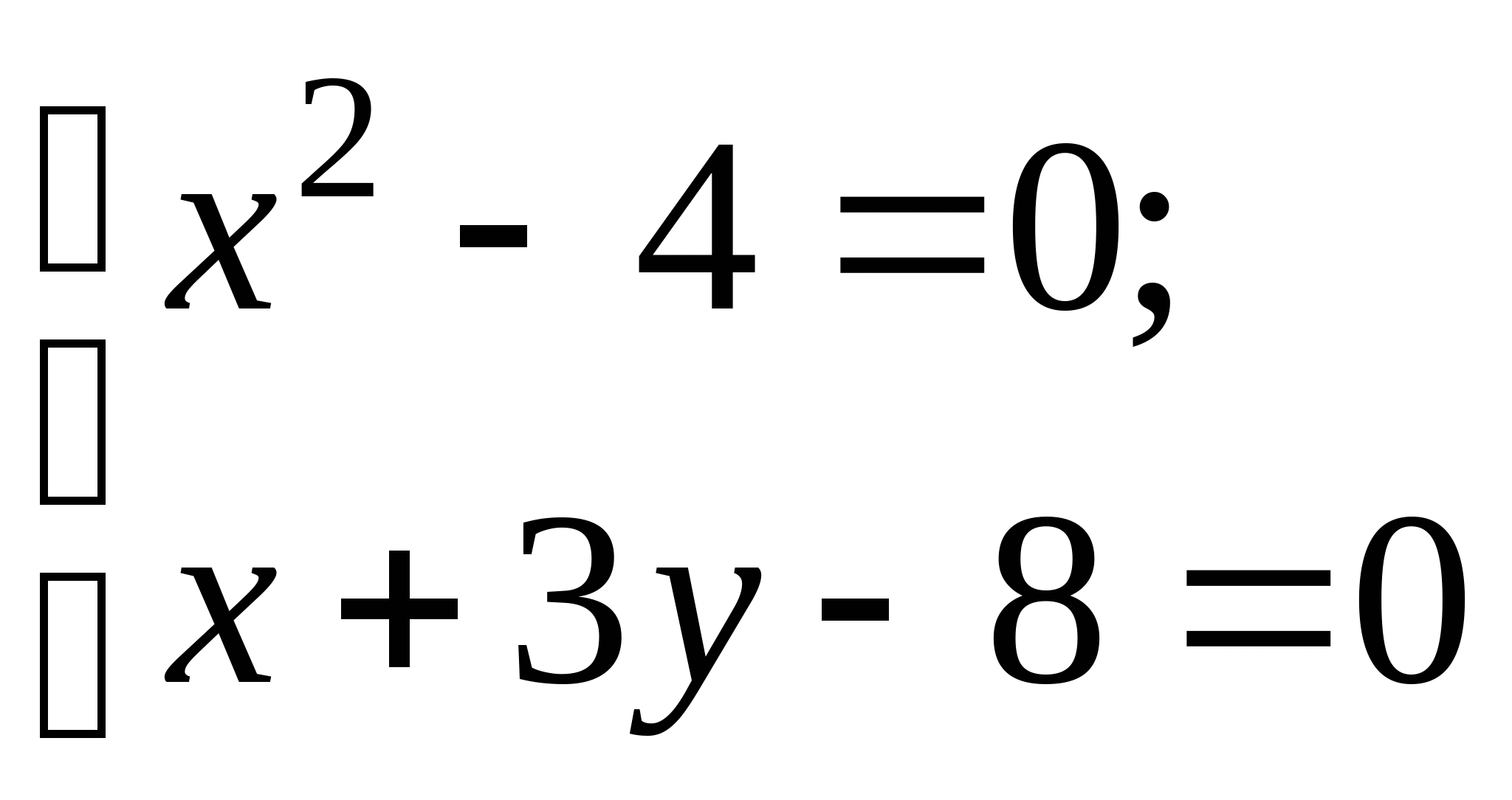| Скачать .zip |
Реферат: Итерациональные методы решения нелинейных уравнений
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. А.Н. ТУПОЛЕВА
УТВЕРЖДАЮ:
Проректор по учебной и методической
работе
_________________ И.К. Насыров
«_____» _______________ 2007 г.
ПРОГРАММА ДИСЦИПЛИНЫ
ЕН.Ф.01.05 "ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА"
Рекомендуется УМЦ КГТУ им. А.Н. Туполева для направлений
(специальностей)
направления: 654600 (230100 )* “Информатика и вычислительная техника”
654700 (230200)* «Информационные системы»
специальности:220200 (230102)* «Автоматизированные системы обработки
информации и управления»
071900 (230201)* «Информационные системы и технологии»
специализации: «Автоматизированные системы в административно-
организационном управлении»
«Информационные системы и технологии
в компьютерных сетях»
формы обучения: очная, очно – заочная и заочная
*) коды направлений и специальностей указаны по Общероссийскому классификатору специальностей по образованию (ОК 009-2003)
Цели и задачи дисциплиныЦелью и задачами дисциплины является изучение основных положений вычислительной математики, знакомство с приближенными методами решения реальных инженерных задач на ЭВМ, современными методами решения задач, связанных с дифференциальными уравнениями, в объеме, достаточном для квалифицированного решения основных профессиональных задач будущими инженерами.
Материал курса основан на знаниях, навыках и умениях полученных при обучении в среднем образовательном учреждении, а также получаемых студентами при изучении дисциплин: «Алгебра и геометрия», «Математический анализ», «Дифференциальные уравнения», «Программирование на языках высокого уровня», «Информатика».
Студенты должны быть знакомы с основными алгебраическими структурами («Алгебра и геометрия»); с понятиями функции и ее непрерывности, с понятиями множества, отношения («Математический анализ»); с понятиями обыкновенных и систем обыкновенных дифференциальных уравнений, аналитическими методами их решения («Дифференциальные уравнения»); способами записи алгоритма, стандартными типами данных («Программирование на языках высокого уровня»); с основными приемами работы в операционных системах MS DOS и Windows, а также с основными офисными системами MS Word и MS Excel («Информатика»).
Студенты должны иметь практические навыки решения линейных алгебраических и нелинейных уравнений и систем («Алгебра и геометрия»), решения обыкновенных и систем обыкновенных дифференциальных уравнений («Дифференциальные уравнения»), уметь строить схемы алгоритмов и программ («Программирование на языках высокого уровня»).
Знания, умения и навыки, полученные в процессе изучения данного курса, могут быть использованы студентами для изучения дисциплин «Технологии программирования», «Операционные системы», «Базы данных», «Управление данными», «Информационные технологии», «Сетевые технологии», «Теория принятия решений», а также при прохождении вычислительной практики студентами второго курса очной формы обучения.
Требования к уровню освоения содержания дисциплины
В результате изучения дисциплины студенты должны:
знать:основные численные методы решения нелинейных уравнений, систем нелинейных и линейных алгебраических уравнений;
методы интерполирования, аппроксимирования и экстраполирования функций;
методы численного решения задачи Коши для обыкновенных дифференциальных уравнений;
условий сходимости методов, областей применения численных методов, условий окончания итерационных процессов по каждому методу.
уметь:выводить итерационные формулы для решения конкретной задачи выбранным методом;
составлять и отлаживать программу для конкретного метода;
объяснять полученные результаты.
иметь опыт выбора метода численного решения конкретной задачи. иметь представление:о вычислительной математике как науке о численных (приближенных) методах решения математических и реальных инженерных задач;
о методах и алгоритмах численного решения задач, сходимости методов, погрешностях вычислений, теоретическом обосновании ряда методов, достоинствах и недостатках методов;
о состоянии и тенденциях развития вычислительной математики.
Объем дисциплины и виды учебной работы
| Виды учебной работы | Очное | Очно-заочное | Заочное | |
| Всего | Семестры | Семестры | Семестры | |
| 3 | 3 | 3 | ||
| Общая трудоемкость дисциплины | 140 | 140 | 140 | 140 |
| Аудиторные занятия (всего) | 68 | 68 | 51 | 18 |
| Лекции | 34 | 34 | 34 | 12 |
| Практические занятия (ПЗ) | 0 | 0 | 0 | 0 |
| Семинары (С) | 0 | 0 | 0 | 0 |
| Лабораторные работы (ЛР) | 34 | 34 | 17 | 6 |
| Другие виды аудиторных занятий | 0 | 0 | 0 | 0 |
| Самостоятельная работа (всего) | 72 | 72 | 89 | 122 |
| Курсовой проект (работа) | 0 | 0 | 0 | 0 |
| Расчетно-графические работы | 0 | 0 | 0 | 0 |
| Реферат | 0 | 0 | 0 | 0 |
| Другие виды самостоятельной работы | 72 | 72 | 89 | 92 |
| Вид итогового контроля | Экзамен | Экзамен | Экзамен | |
Содержание дисциплины
Тематический план *):
| № пп | Наименование тем | Очное | Очно-заочное | Заочное | |||
| ЛК | ЛБ | ЛК | ЛБ | ЛК | ЛБ | ||
| 1 | Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. | 4 | 4 | 4 | - | 1 | - |
| 2 | Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений. | 14 | 16 | 14 | 8 | 3 | 3 |
| 3 | Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. | 10 | 10 | 10 | 5 | 2 | 2 |
| 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. | 6 | 4 | 6 | 4 | 2 | 1 |
| Всего | 34 | 34 | 34 | 17 | 12 | 6 | |
*) Используемые сокращения: ЛК –лекции, ЛБ – лабораторные работы, ПЗ – практические занятия.
Содержание тем
1. Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. (очное: 4/8ч.; очно-заочное: 4/11ч.; заочное:2/15ч.).
1.1. Основные понятия дисциплины (очное: 1/2ч.; очно-заочное: 1/1ч.; заочное: 1/1ч.).
Понятие приближенных (численных) методов решения математических задач. Место численных методов в математическом анализе. Понятие вычислительной математики, предмет изучения вычислительной математики. Понятия итерационных методов и погрешностей вычислений, вычислительной схемы. Проблема «устойчивости вычислительных методов» и сложности алгоритма.
1.2. Учет погрешностей при вычислениях (очное: 2/4ч.; очно-заочное: 2/6ч.; заочное: 1/8ч.).
Источники и классификация погрешностей. Основные понятия и определения теории погрешностей. Округление чисел. Погрешности алгебраической суммы, произведения, частного, степени, корня, функции. Правило сложения приближенных чисел. Обратная задача теории погрешностей.
1.3. Вычислительные программные системы (очное: 1/2ч.; очно-заочное: 1/4ч.; заочное: 0/6ч.).Основы работы с MS Excel, MathCad, MathLab с точки зрения решения задач вычислительной математики.
2. Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений (очное: 14/30ч.; очно-заочное: 14/36ч.; заочное: 4/50ч.). 2.1. Приближенные методы решения нелинейных уравнений (очное: 8/10ч.; очно-заочное: 8/12ч.; заочное: 2/15ч.). Понятия отделения и уточнения корней нелинейных уравнений на отрезке. Графический и аналитический методы отделения корней. Геометрическая интерпретация графического и аналитического методов. Методы уточнения корней: метод дихотомии, метод простых итераций, метод Ньютона (касательных), модифицированный метод Ньютона.
Метод простых итераций: понятия начального приближения и итерационного процесса; достаточное условие сходимости итерационного процесса; критерии останова итерационного процесса. Геометрическая интерпретация метода простых итераций. Приведение нелинейного уравнения к виду, допускающего сходящиеся итерации. Достоинства и недостатки метода простых итераций.
Метод Ньютона, его геометрическая интерпретация, рабочая формула, выбор начального приближения. Достаточное условие сходимости. Критерий останова итерационного процесса. Достоинства и недостатки метода Ньютона. Модифицированный метод Ньютона, его геометрическая интерпретация и рабочая формула.
2.2. Приближенные методы решения систем нелинейных уравнений (очное: 3/8ч.; очно-заочное: 2/12ч.; заочное: 2/15ч.).Понятие системы нелинейных уравнений (СНУ). Проблема отделения корней СНУ. Приближенные методы решения СНУ. Метод простых итераций, понятия начального приближения, итерационного процесса. Достаточные условия сходимости итерационного процесса. Критерий останова итерационного процесса. Приведение исходной системы к системе, допускающей сходящиеся итерации на примере системы второго порядка. Достоинства и недостатки метода простых итераций для решения СНУ.
Метод Ньютона для решения СНУ, его рабочая формула и критерий останова итерационного процесса. Достаточное условие сходимости. Достоинства и недостатки метода Ньютона. Рабочая формула модифицированного метода Ньютона.
2.3. Приближенные методы решения систем линейных алгебраических уравнений (очное: 3/10ч.; очно-заочное: 3/12ч.; заочное: 0/20ч.).Методы решения систем линейных алгебраических уравнений. Метод простых итераций, его рабочие формулы и критерий останова; выбор начального приближения; достаточные условия и необходимые и достаточные условия сходимости итерационного процесса; приведение исходной системы к системе, допускающей сходящиеся итерации; достоинства и недостатки метода простых итераций.
Рабочие формулы методы Зейделя, критерий останова, необходимые и достаточные условия сходимости метода. Достоинства и недостатки метода.
Метод релаксации. Приведение исходной системы к виду, пригодному для релаксации. Понятие невязки. Рабочие формулы метода. Критерии останова процесса.3. Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. (очное: 10/20ч.; очно-заочное: 10/26ч.; заочное: 4/35ч.). 3.1. Построение интерполяционных формул Лагранжа, первой и второй формул Ньютона (очное: 3/7ч.; очно-заочное: 3/9ч.; заочное: 3/10ч.).
Постановка задачи интерполирования функций по заданной системе точек, понятие равноотстоящих и неравноотстоящих узловых точек. Принципы построения интерполяционной формулы Лагранжа, первой и второй интерполяционной формулы Ньютона, их форма записи и погрешности вычислений по ним. Формулы линейной и квадратичной интерполяции. Понятие табличных разностей различных порядков.
3.2. Основные приложения теории интерполяции (очное: 4/6ч.; очно-заочное: 4/8ч.; заочное: 0/15ч.).Понятие численного дифференцирования. Основные принципы решения задачи численного дифференцирования на примере использования таблицы узловых точек и интерполяционных полиномов. Погрешность построенных формул.
Понятие численного интегрирования, квадратурных формул. Построение квадратурной формулы Ньютона-Котеса с использованием интерполяционных формул, коэффициенты Котеса. Частные случаи формулы Ньютона-Котеса (формула трапеций и формула Симпсона) и их геометрическая интерпретация. Погрешность построенных формул. Понятие несобственных интегралов. Приближенное вычисление несобственных интегралов. Случаи бесконечного отрезка интегрирования с непрерывной подынтегральной функцией и разрывной на конечном отрезке интегрирования подынтегральной функцией, их геометрическая интерпретация.
Приближенное вычисление двойных интегралов: понятие кубатурных формул; вывод кубатурной и обобщенной кубатурной формул типа Симпсона для различных видов областей интегрирования. 3.3. Метод наименьших квадратов для обработки результатов экспериментов (очное: 3/7ч.; очно-заочное: 3/9ч.; заочное: 1/10ч.).Задача аппроксимирования функций по заданной системе точек. Общая идея метода наименьших квадратов. Понятие отклонения искомой функции от экспериментальной в узловых точках. Алгоритм метода наименьших квадратов и его теоретическое обоснование.
Аппроксимация с помощью экспоненциальных функций.
4. Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. (очное: 6/14ч.; очно-заочное: 6/16ч.; заочное: 2/22ч.). 4.1. Приближенное решение обыкновенных дифференциальных уравнений и систем (очное: 3/5ч.; очно-заочное: 3/4ч.; заочное: 1/6ч.).
Классификация методов решения и численных методов интегрирования дифференциальных уравнений. Понятия задачи Коши и шага интегрирования. Метод последовательных приближений (метод Пиккара). Метод Эйлера: общая идея метода, его графическая интерпретация и рабочая формула. Достоинства и недостатки метода. Рабочие формулы метода Эйлера для решения системы второго порядка дифференциальных уравнений.
Метод Рунге-Кутта. Общая идея методов Рунге-Кутта второго и четвертого порядков, их рабочие формулы. Достоинства и недостатки методов. Решение задачи Коши для системы второго порядка методом Рунге-Кутта четвертого порядка.
Метод Адамса. Достоинства и недостатки метода Адамса. Экстраполяционная и интерполяционная формулы Адамса для решения дифференциальных уравнений.
Непрерывные схемы решения нелинейных уравнений, условие их применения. Дифференциальное уравнение в отклонениях, его решение. Достоинства и недостатки непрерывных схем. Дифференциальное уравнение с малым параметром, его решение. Достоинства и недостатки методов решения нелинейных уравнений с использованием дифференциальных уравнений с малым параметром.
4.2. Приближенное решение краевых задач для дифференциальных уравнений второго порядка (очное: 1/4ч.; очно-заочное: 1/6ч.; заочное: 1/8ч.).
Метод конечных разностей. Понятие краевой задачи для дифференциального уравнения второго порядка и ее геометрическая интерпретация при различных краевых условиях. Понятие двухточечной краевой задачи для линейного дифференциального уравнения второго порядка и ее форма записи. Метод конечных разностей для решения двухточечной краевой задачи для линейного дифференциального уравнения второго порядка.
Метод прогонки. Конечно-разностная и каноническая формы записи двухточечной краевой задачи для линейного дифференциального уравнения второго порядка. Алгоритм метода прогонки прямым и обратным ходом вычислений.
4.3. Приближенное решение краевых задач для дифференциальных уравнений в частных производных первого порядка (очное: 2/5ч.; очно-заочное: 2/6ч.; заочное: 1/8ч.).
Методы моделирования и Монте-Карло для решения задачи Дирихле. Понятие дифференциального уравнения в частных производных первого порядка эллиптического типа. Понятие краевых задач для уравнений эллиптического типа. Понятие задачи Дирихле. Решение задачи Дирихле методом моделирования и Монте-Карло.
Метод сеток и метод прогонки для решения уравнений параболического типа. Понятие дифференциального уравнения в частных производных первого порядка параболического типа. Метод сеток и метод прогонки для решения уравнений параболического типа.
Метод сеток для решения уравнений гиперболического типа. Понятие дифференциального уравнения в частных производных первого порядка гиперболического типа. Метод сеток для решения уравнений гиперболического типа.
Лабораторный практикум
| №п/п | Номер темы дисцип-лины | Объем в часах | Наименование лабораторных работ | ||
| Очное | Очно-заочное | Заочное | |||
| 1. | 3 | 4 | - | Основы работы с MS Excel, MathCad, MathLab | |
| 2. | 1 | 6 | 4 | Итерационные методы решения нелинейных уравнений | |
| 2 | 2 | 6 | 2 | Итерационные методы решения систем нелинейных уравнений | |
| 2. | 3 | 4 | 2 | Итерационные методы решения систем линейных алгебраических уравнений | |
| 3 | 1, 3 | 8 | 5 | Решение задач интерполирования и аппроксимации функций | |
| 3 | 2 | 2 | - | Численное интегрирование | |
| 4 | 1 | 4 | 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем | |
Курсовой проект (работа) и его содержание
Курсовой проект и курсовая работа не предусмотрены.
Контрольная работа.
Контрольная работа предусмотрена для заочной формы обучения. На выполнение контрольной работы отводится 30 часов самостоятельной работы студентов. Задания контрольной работы включает решение задач по темам 2 и 3 (см. приложение 6 и 7).
Подготовка реферата.Реферат не предусмотрен.
5. Учебно-методическое обеспечение дисциплины
5.1 Рекомендуемая литература
а) основная литература:
| | Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Учебно-методическое пособие, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 48с. |
| | Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. |
| | Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматгиз, 1966. |
| | Калиткин Н.Н. Численные методы. М.: Наука, 1978. |
| | Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Наука, 1967. |
б) дополнительная литература:
1. Иванов В.С., Ляшев А.С. Лабораторный практикум по дисциплине «Вычислительная техника в инженерных и экономических расчетах». Казань, КАИ, 1984.
2. Вахонина Г.С. Методическое руководство к выполнению лабораторных работ по дисциплине “Методы вычислений”. – Казань: КАИ, 1982.
3. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Лабораторный практикум, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 44с.
4. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Методические указания для студентов заочной формы обучения, Казань, Изд-во Казан. гос. техн. ун-та, 2001, 40с.
5. «Журнал вычислительной математики».
6. «Математическое моделирование».
7. «Программирование».
8. «Математика. Реферативный журнал».
9. http://meth.ras.ru («Журналы Отделения Математики РАН»).
10. http://www.exponenta.ru («Образовательный математический сайт»).
5.2 Средства обеспечения освоения дисциплины
Программное обеспечение для выполнения лабораторных работ и самостоятельной работы студентов:
Windows 98 или более поздних версий.
Автоматизированная вычислительная система «MathCad».
Автоматизированная вычислительная система «MathLab».
MS Excel 97 или более поздних версий.
MS Word 97 или более поздних версий.
Системы программирования Turbo C V6.0 или 7.0, Borland C++ V6.0 или 7.0.
Системы программирования Turbo Pascal V6.0 или 7.0, Borland Pascal V6.0 или 7.0.
6. Материально-техническое обеспечение дисциплины
Для проведения лабораторных работ и организации самостоятельной работы студентов необходимо иметь учебный класс оснащенный ПЭВМ со стандартной комплектацией.
7. Методические рекомендации по организации изучения дисциплины
7.1. Организация изучения дисциплины при очной форме обучения
Обучение проводится в течение одного семестра. Темы 1-4 и все указанные лабораторные работы рассматриваются в семестре № 3.
При проведении лабораторных работ используются программные комплексы, поддерживающие языки программирования Pascal и C, как в учебных лабораториях кафедры, оснащенных компьютерами, так и в ВЦ.
При изучении дисциплины используется балльно - рейтинговая система оценки знаний. Контрольные тестирования организуются на 6, 12 и 17 неделях каждого семестра. Каждое тестирование включает задания, предусматривающие ответы на теоретические и практические вопросы (см. приложение № 5).
7.2. Организация изучения дисциплины при заочной форме обучения
Изучение дисциплины проводится в течение осеннего семестра и охватывает следующие формы обучения и виды занятий:
Установочные лекции (4 часа) охватывают темы № 2,3 (сентябрь);
Выполнение контрольной работы по темам №2-4. Задания контрольных работ приведены в приложении № 6. Требования к оформлению контрольных работ приведены в приложении № 7 (октябрь - декабрь);
Самостоятельное изучение теоретического материала по теме №1 и некоторых параграфов по темам №2-4 и подготовка к теоретическому экзамену. Список вопросов теоретического курса приведен в приложении № 8.
Консультации с преподавателем в университете в последнюю субботу каждого месяца и ежедневные консультации с использованием электронной почты (октябрь - декабрь);
Тестирование с целью определения усвоения тем № 2 и № 3. Список тестов приведен в приложении № 4 (январь);
Лекции (8 часов) по темам № 1-4 (январь);
Выполнение лабораторных работ (январь);
Повторение теоретического материала и подготовка к итоговому экзамену (январь).
Итоговый экзамен (январь).
Программу составили:
Горбунов Д.А., к.т.н., доцент каф. ПМИ КГТУ им. А.Н. Туполева
_____________________
Программа обсуждена и одобрена на заседании кафедры ПМИ
«____» ______________2007г., протокол № __.
Зав. кафедрой ПМИ Н.Е. Роднищев
д.т.н., профессор
Председатель Учебно-методической В.А. Суздальцев
комиссии факультета, доцент
Декан факультета Л.Ю.Емалетдинова
д.т.н., профессор
Согласовано: Л.М.Шарнин
зав.кафедрой АСОиУ
д.т.н., профессор
ПРИЛОЖЕНИЕ 5
ТЕСТЫ ПО ДИСЦИПЛИНЕ «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
Вопрос 1. Сделайте вывод о сходимости итерационного процесса ![]() , построенного для решения нелинейного уравнения
, построенного для решения нелинейного уравнения ![]() методом простых итераций на отрезке
методом простых итераций на отрезке ![]() .
.
сходится для любой точки из отрезка;
сходится только из определенной точки отрезка;
сходится только для одной из граничных точек отрезка;
расходится на всем отрезке;
расходится на всей числовой оси.
Вопрос 2. Чему равно значение ![]() , вычисленное по итерационной формуле
, вычисленное по итерационной формуле ![]() при
при ![]() ?
?
0.5;
0.875;
0.4;
0.8;
0.9.
Вопрос 3. Если итерационный процесс, построенный по методу простых итераций для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() сходится, то в качестве начальной точки может быть выбрана:
сходится, то в качестве начальной точки может быть выбрана:
одна из граничных точек отрезка;
обе граничные точки отрезка;
середина отрезка;
любая точка отрезка;
все ответы правильные.
Вопрос 4. По какой из итерационных формул осуществляется решение нелинейных уравнений вида ![]() методом Ньютона?
методом Ньютона?
1. ![]() ;
;
2. ![]() ;
;
3. 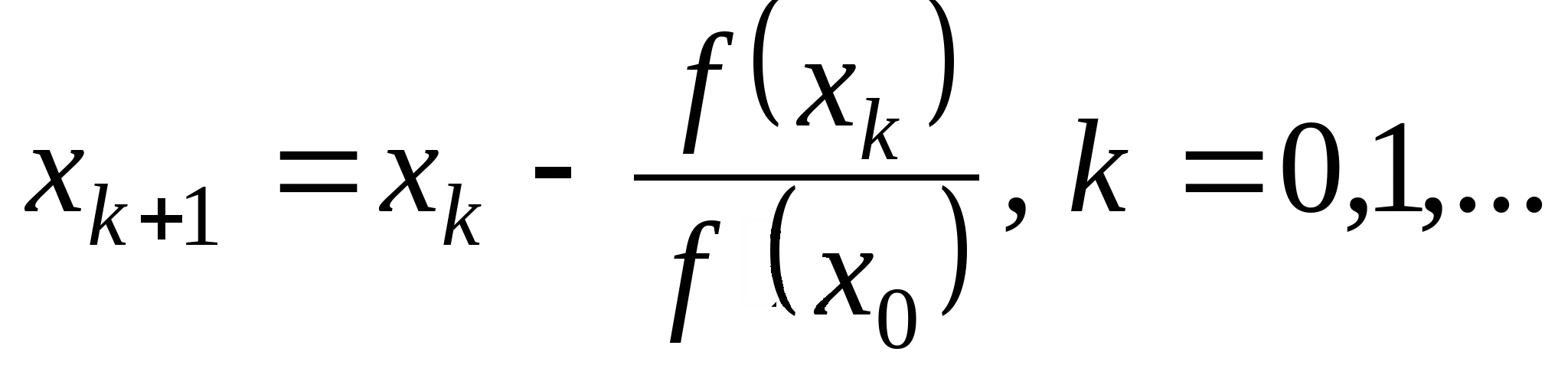 ;
;
4. 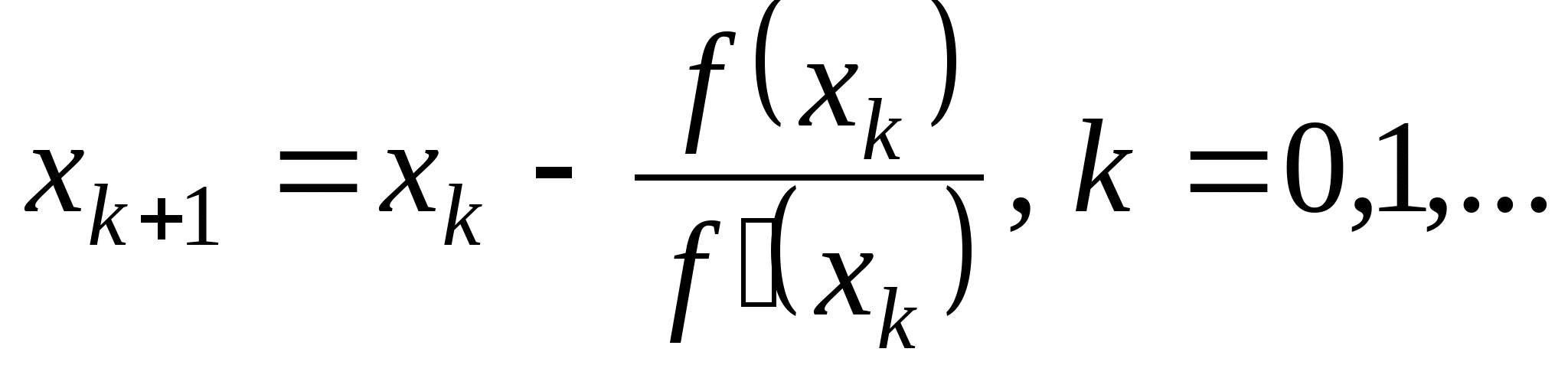 ;
;
5. 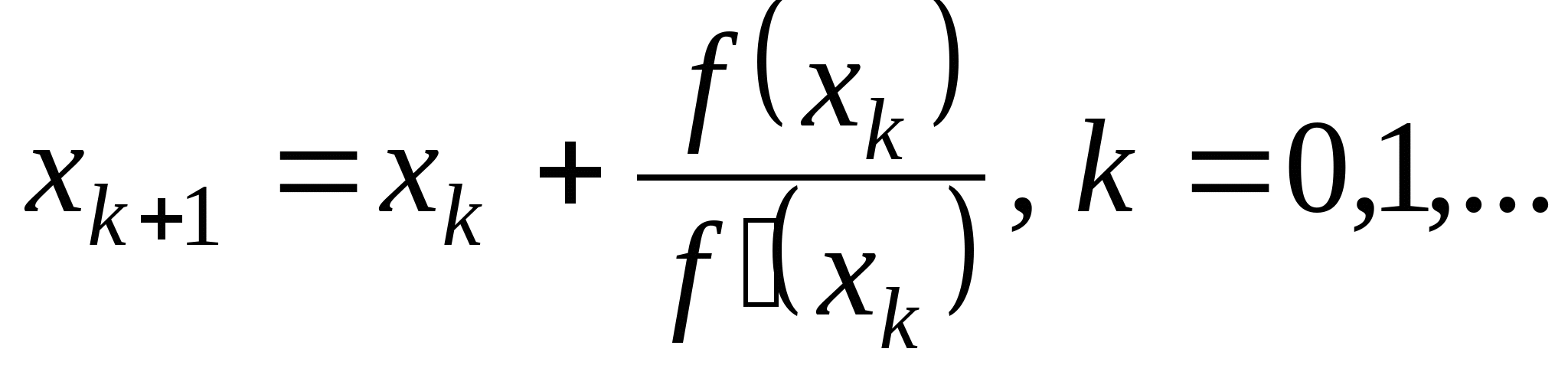 .
.
Вопрос 5. Сформулируйте теорему о существовании хотя бы одного корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() где
где ![]() - произвольная нелинейная функция.
- произвольная нелинейная функция.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на отрезке содержится хотя бы один корень.
, то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка не меняет знак (
и на концах отрезка не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка меняет знак (
и на концах отрезка меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() не меняет знак (
не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() меняет знак (
меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Вопрос 6. Какое условие является достаточным для сходимости итерационного процесса ![]() решения нелинейного уравнения
решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 7. При нахождении корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом Ньютона в качестве начального приближения нужно выбрать
методом Ньютона в качестве начального приближения нужно выбрать ![]() равное:
равное:
0.5;
2;
1;
любой из концов отрезка;
любое значение из отрезка.
Вопрос 8.К какому виду, допускающему сходящиеся итерации, нужно привести систему нелинейных уравнений второго порядка 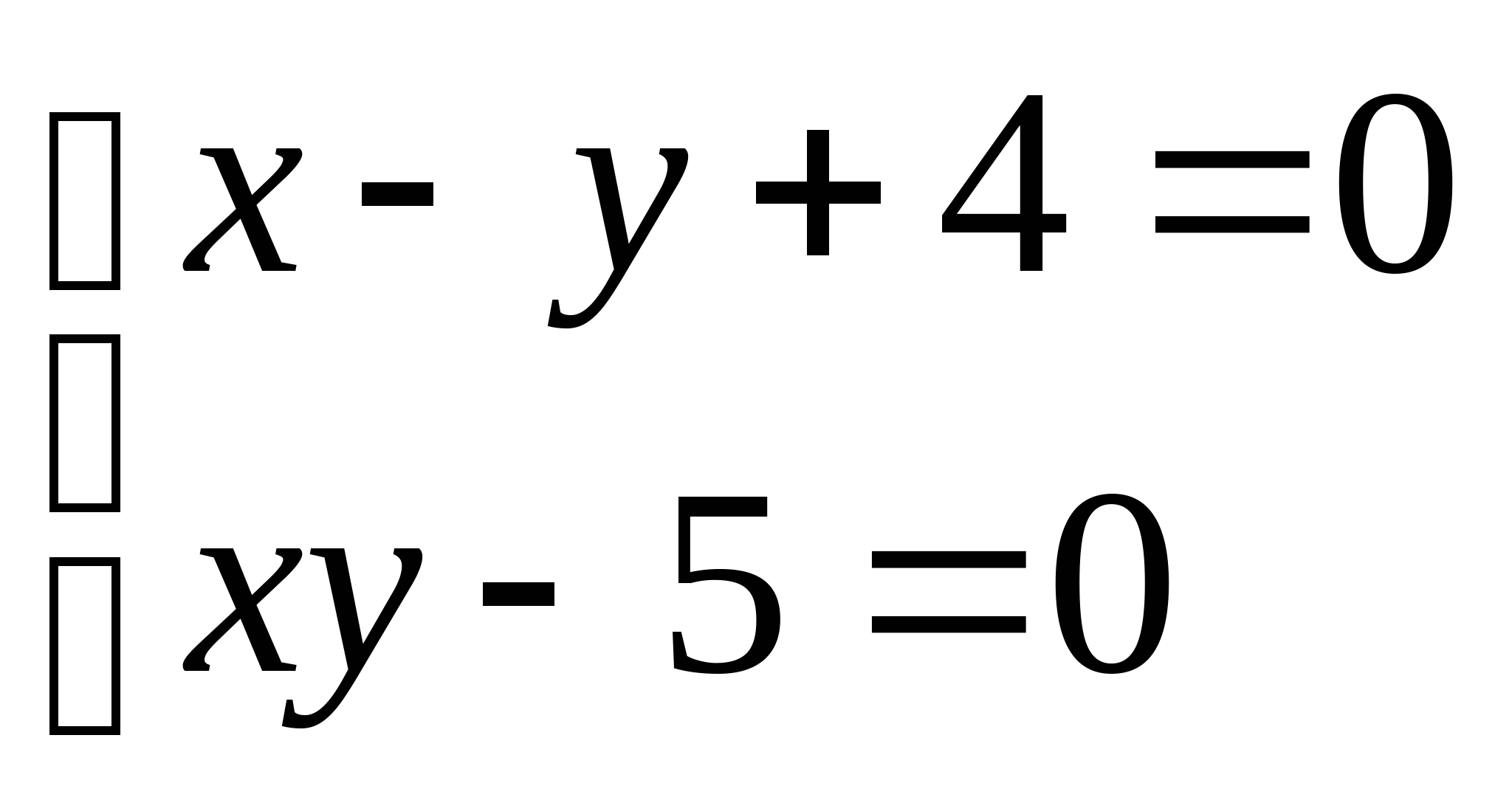 ?
?
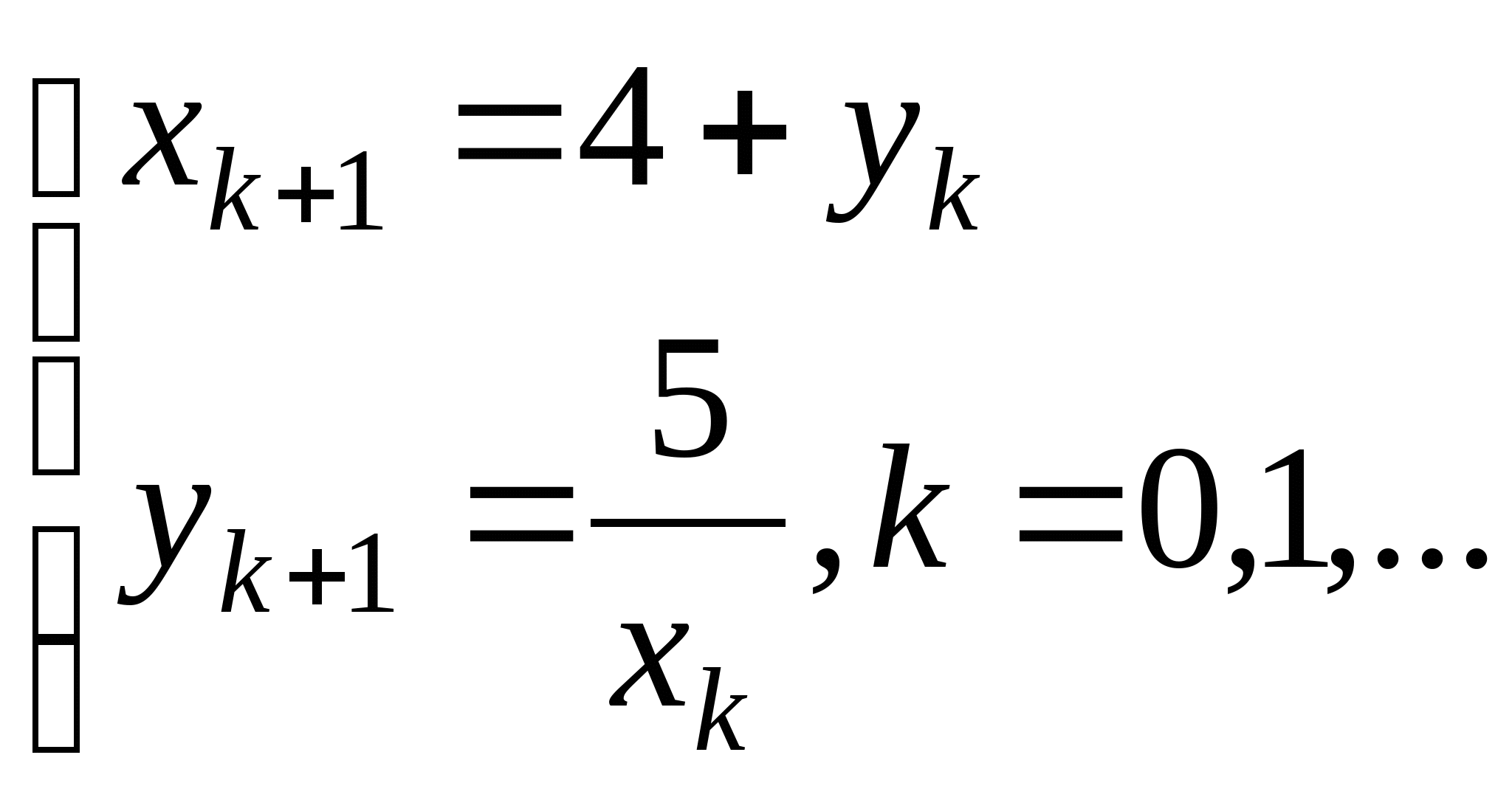 ;
;
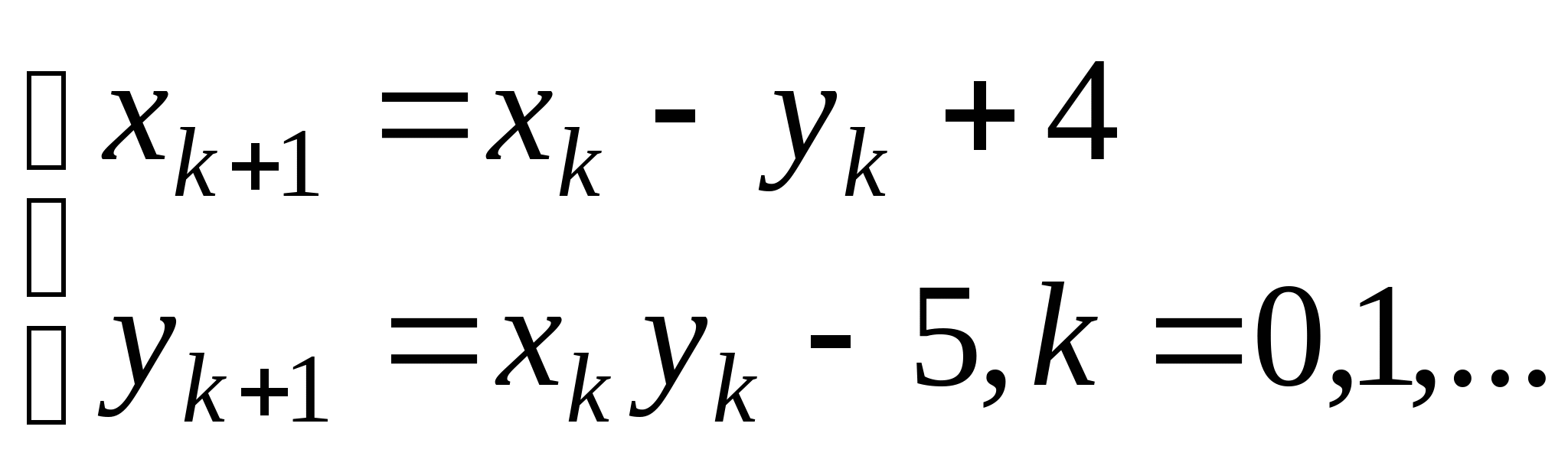 ;
;
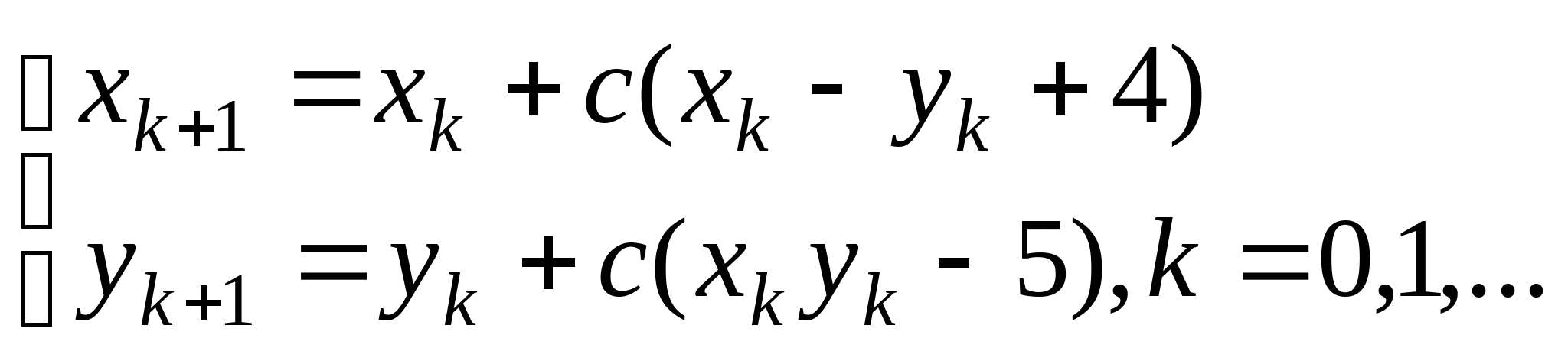 , где константа
, где константа ![]() выбирается из достаточных условий сходимости итерационного процесса;
выбирается из достаточных условий сходимости итерационного процесса;
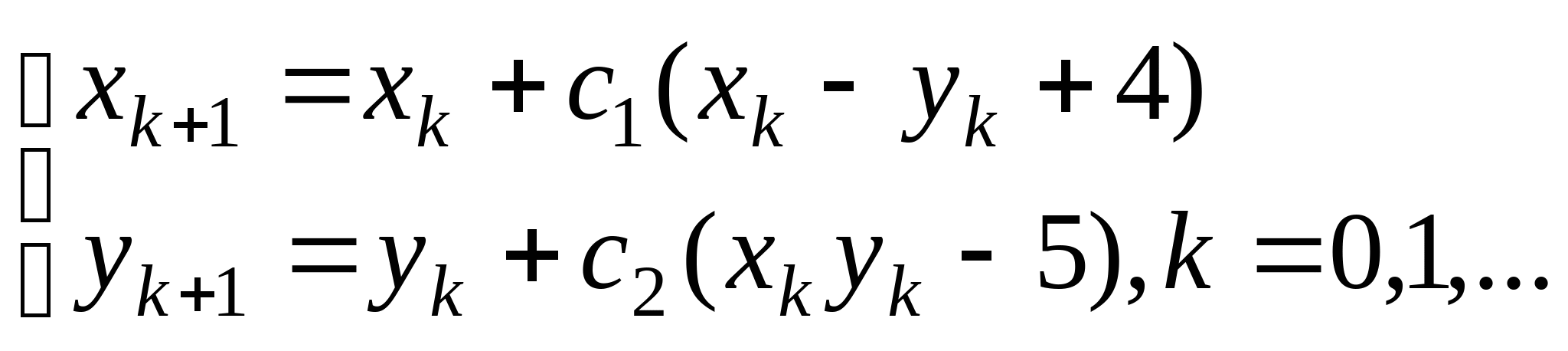 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса;
выбираются из достаточных условий сходимости итерационного процесса;
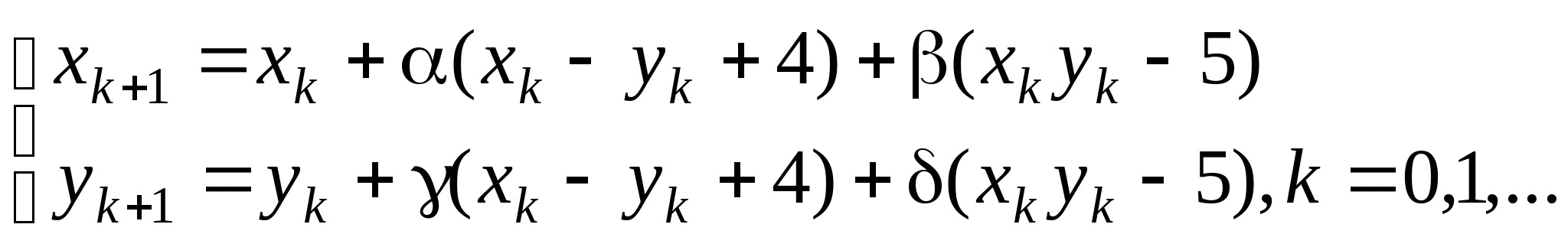 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса.
выбираются из достаточных условий сходимости итерационного процесса.
Вопрос 9. При решении какого класса задач достаточные условия сходимости итерационного процесса имеют вид: ![]() или
или ![]() ?
?
решение нелинейных уравнений;
решение систем нелинейных уравнений;
решение систем линейных алгебраических уравнений;
решение линейных уравнений;
все ответы правильные.
Вопрос 10. При численном решении СЛАУ ![]() ее необходимо привести к виду, допускающему сходящиеся итерации
ее необходимо привести к виду, допускающему сходящиеся итерации ![]() . Чему равно значение коэффициента
. Чему равно значение коэффициента ![]() для СЛАУ вида
для СЛАУ вида 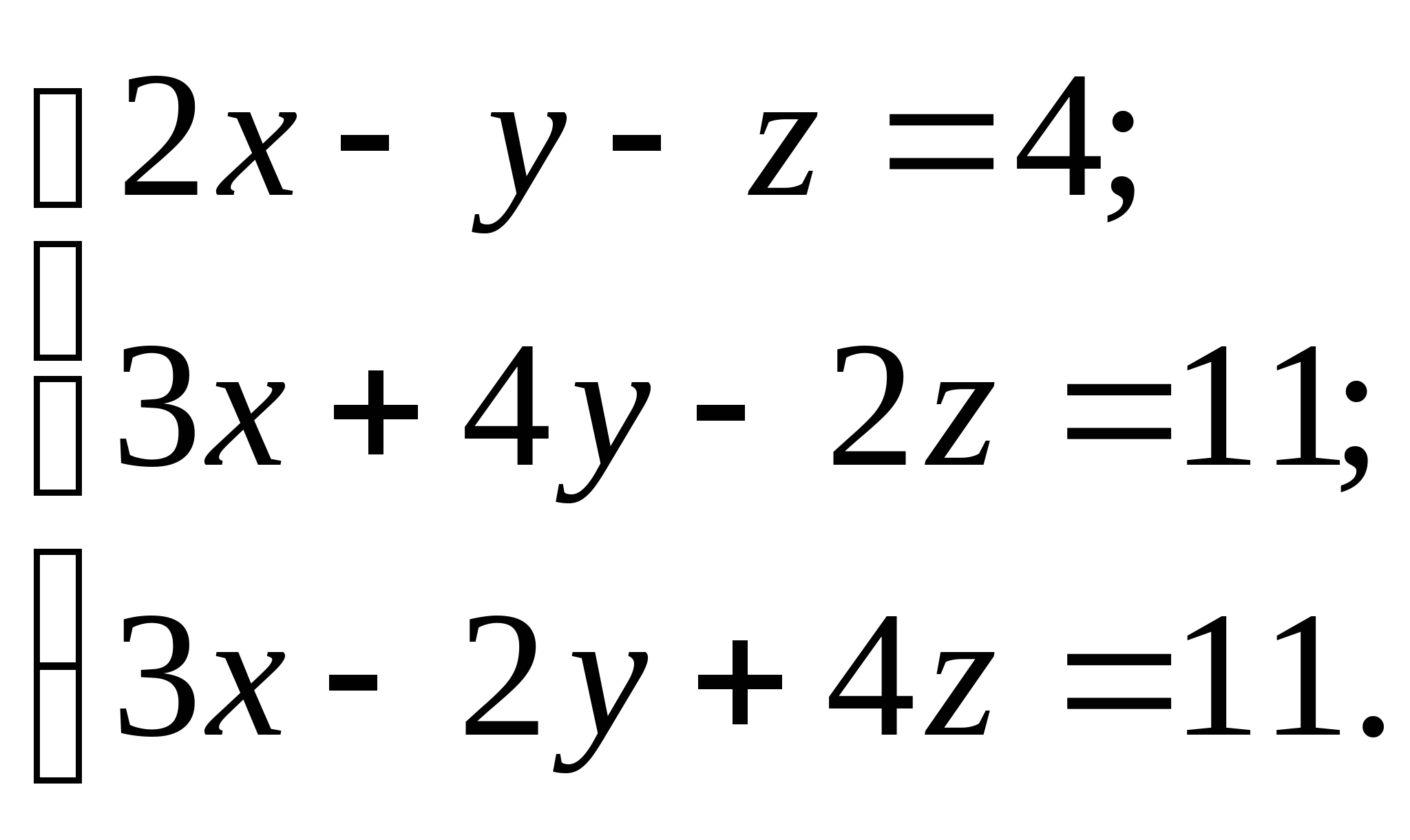 ?
?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
1.
Вопрос 11. Чему равно следующее приближение ![]() , вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида
, вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида 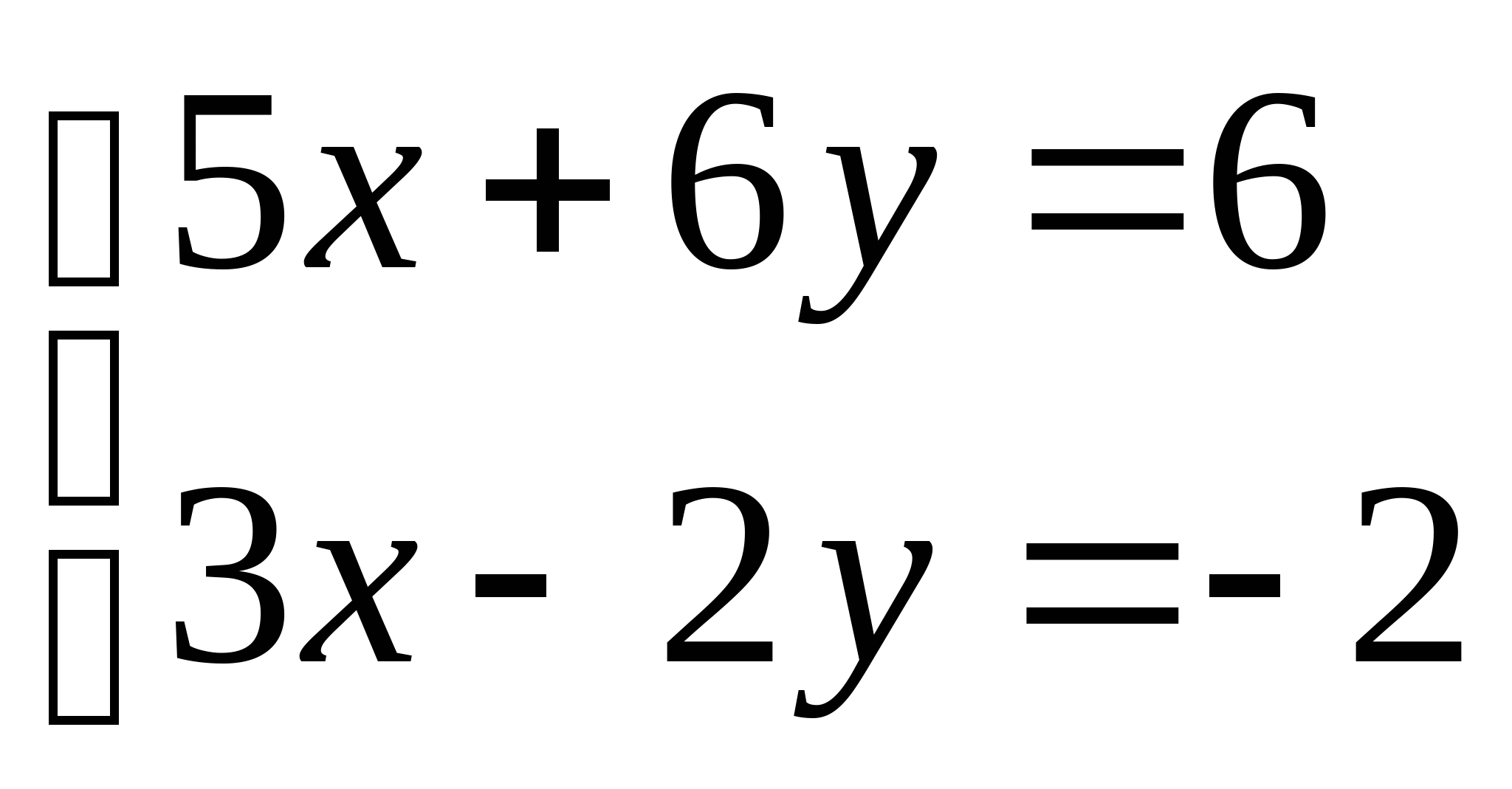 при
при ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 12. Задача интерполяции функций возникает в тех случаях, когда:
необходимо знать значения функции для промежуточных значений аргументов между узловыми точками;
необходимо знать значения функции для точек, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблично;
необходимо представить в более простом виде сложную аналитически заданную функцию;
все ответы правильные.
Вопрос 13. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1 | 0 | 1 |
можно построить интерполяционный полином Лагранжа второго порядка вида:
![]() . Чему будет равен коэффициент
. Чему будет равен коэффициент ![]() ?
?
0;
0.5;
1;
0.4;
0.35.
Вопрос 14. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1.5 | 0.9 | 0.4 |
найти табличную разность второго порядка ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 15. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() :
: ![]() .
.
Строится и решается СЛАУ относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
Вопрос 16. Как называется следующая квадратурная формула: 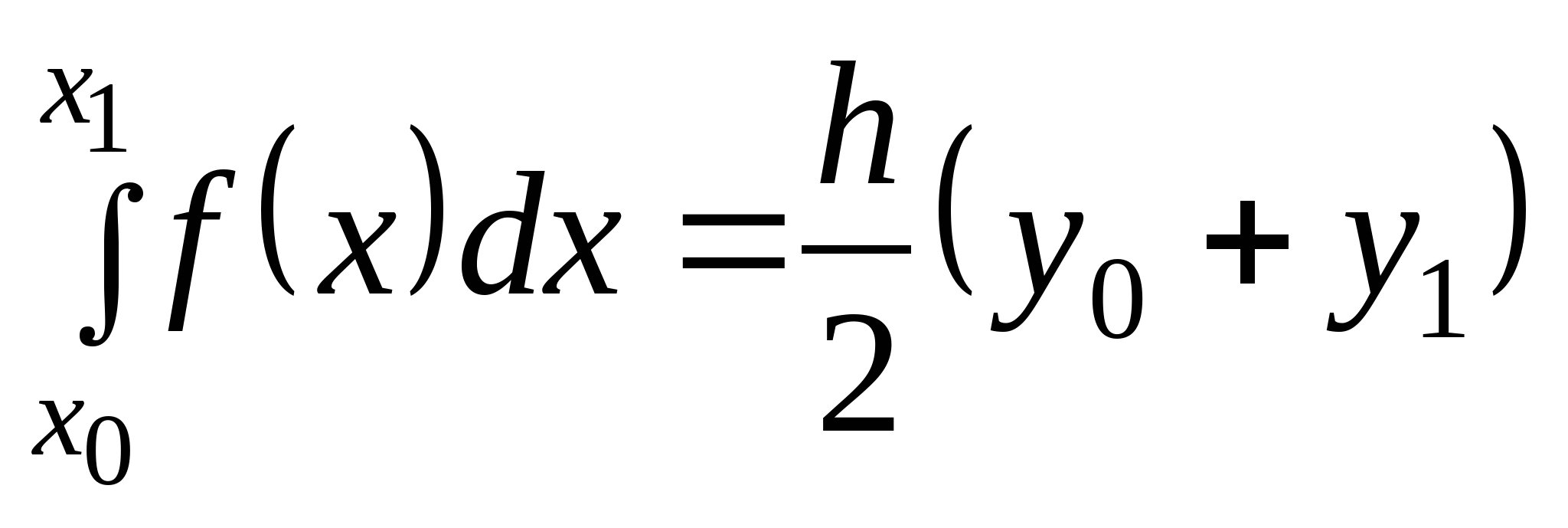 ?
?
формула Ньютона-Котеса;
формула трапеций;
формула Симпсона;
формула Ньютона;
формула Котеса.
Вопрос 17. Как называется следующая интерполяционная формула, построенная для неравноотстоящих узлов:
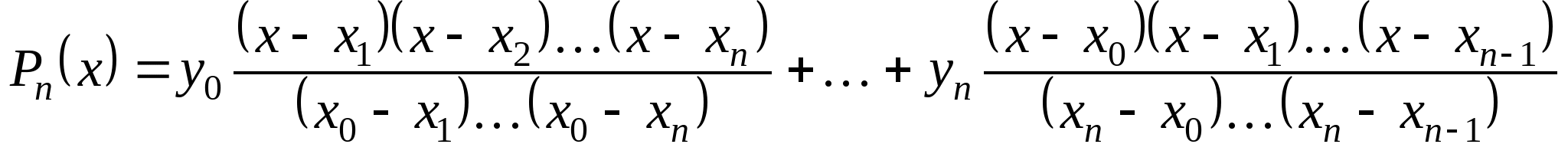 ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула квадратичной интерполяции;
формула линейной интерполяции.
ПРИЛОЖЕНИЕ 6
ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ.
Задание № 1. Доказать графическим и аналитическим методами существование единственного корня нелинейного уравнения на отрезке; построить итерационные формулы по методу простых итераций, методу Ньютона и модифицированному методу Ньютона для поиска корня на отрезке; составить программу на любом языке программирования, реализующую построенные итерационные процессы (см. Таблицу 1).
Таблица 1
| № варианта | Нелинейное уравнение | Отрезок | № варианта | Нелинейное уравнение | Отрезок |
| |
|
| 12 |
|
|
| |
|
| 13 |
|
|
| |
|
| 14 |
|
|
| |
|
| 15 |
|
|
| |
|
| 16 |
|
|
| |
|
| 17 |
|
|
| |
|
| 18 |
|
|
| |
|
| 19 |
|
|
| |
|
| 20 |
|
|
| |
|
| 21 |
|
|
| |
|
|
Задание № 2. Построить итерационные формулы по методу простых итераций и методу Ньютона для приближенного решения системы нелинейных уравнений второго порядка с указанного начального приближения; составить программу на любом языке программирования, реализующую построенные итерационные процессы (см. Таблицу 2).
Таблица 2
| № варианта | Система нелинейных уравнений | Начальное приближение | № варианта | Система нелинейных уравнений | Начальное приближение |
| |
|
| 12 |
|
|
| |
|
| 13 |
|
|
| |
|
| 14 |
|
|
| |
|
| 15 |
|
|
| |
|
| 16 |
|
|
| |
|
| 17 |
|
|
| |
|
| 18 |
|
|
| |
|
| 19 |
|
|
| |
|
| 20 |
|
|
| |
|
| 21 |
|
|
| |
|
|
Задание № 3. Вычислить таблицу значений экспериментальной функции для равноотстоящей системы из трех узловых точек на отрезке из области допустимых значений функции; по сформированной системе точек построить интерполяционную формулу Лагранжа, первую и вторую интерполяционные формулы Ньютона, аппроксимационный полином второго порядка; составить программу на любом языке программирования, реализующую процесс построения указанных полиномов для заданной системы точек (см. Таблицу 3).
Таблица 3
| № варианта |
| № варианта |
|
| |
| 12 |
|
| |
| 13 |
|
| |
| 14 |
|
| |
| 15 |
|
| |
| 16 |
|
| |
| 17 |
|
| |
| 18 |
|
| |
| 19 |
|
| |
| 20 |
|
| |
| 21 |
|
| |
|
ПРИЛОЖЕНИЕ 7
Требования к оформлению контрольной работы.
Задания выполняются в тонкой тетради в клетку (18-24 листа). Поля обязательны. Тетрадь должна быть подписана ( указать: КГТУ им. А.Н. Туполева, кафедра ПМиИ, дисциплина: "Вычислительная математика", номер группы, фамилия, имя, отчество; учебный год, город проживания студента, адрес электронной почты).
Оформление выполнения каждого задания необходимо начинать с номера и текста задания.
Помарки и зачеркивания не допускаются. Писать необходимо с интервалом через строку. При записи числа каждую цифру числа писать в одной клетке.
Необходимо использовать пасту или чернила черного, синего или фиолетового цвета.
Графические работы (схемы, таблицы) выполнять только карандашом, использовать линейку.
Текст, поясняющий выполнение заданий, должен быть связанным, логически последовательным. Сокращения слов не допускаются. Особое внимание уделить пунктуации.
Все вычисления должны сопровождаться связующим текстом с указанием объекта, вычислений и исходных данных. Например: «Докажем аналитическим методом единственность корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() ».
».
Контрольная работа пересылается в КГТУ им. А.Н. Туполева, кафедра ПМиИ , или по электронной почте (admdo@mail.ru) для проверки.
ПРИЛОЖЕНИЕ 8.
СПИСОК ВОПРОСОВ ДЛЯ ПОВТОРЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Источники и классификация погрешностей.
2. Основные понятия и определения теории погрешностей.
3. Значащая и верная цифра приближенной величины. Округление чисел.
4. Погрешность алгебраической суммы.
5. Погрешность произведения и частного.
6. Погрешность степени и корня.
7. Погрешность функции.
8. Обратная задача теории погрешностей.
9. Основные этапы решения нелинейных уравнений.
10. Метод половинного деления.
11. Метод простых итераций для решения нелинейных уравнений.
12. Метод Ньютона (метод касательных) для решения нелинейных уравнений.
13. Модифицированный метод Ньютона для решения нелинейных уравнений.
14. Метод простых итераций для решения систем нелинейных уравнений.
15. Метод Ньютона для решения систем нелинейных уравнений.
16. Модифицированный метод Ньютона для решения систем нелинейных уравнений.
17. Метод простых итераций для решения систем линейных алгебраических уравнений.
18. Метод Зейделя.
19. Метод релаксации.
20. Интерполяционная формула Лагранжа.
21. Первая интерполяционная формула Ньютона.
22. Вторая интерполяционная формула Ньютона.
23. Численное дифференцирование.
24. Квадратурная формула Ньютона-Котеса.
25. Формула трапеций.
26. Квадратурная формула Симпсона.
27. Приближенное вычисление несобственных интегралов.
28. Метод наименьших квадратов.
29. Метод Эйлера.
30. Метод Рунге-Кутта.
31. Метод Адамса.
СПИСОК ЛИТЕРАТУРЫ.
1. Вержбицкий В.М. Численные методы (линейная алгебра и нелинейные уравнения). –М.: Высшая школа, 2000, 370с.
2. Вержбицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения). –М.:ОНИКС 212 век, 2005, 400с.
3. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Казань, Изд-во Казан. гос. техн. ун-та, 2001, 40с.
4. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Учебное пособие. Казань: Изд-во Казан. гос. техн. ун-та, 2002, 48с.
5. Горбунов Д.А., Вахонина Г.С. Численные методы. Лабораторный практикум. Казань: Изд-во Казан. гос. техн. ун-та, 2002, 44с.
6. Демидович Б.П., Марон И.А. Основы вычислительной математики. -М.: Наука, 1970, 664с..
7. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. -М.: Наука, 1967, 368с.
8. Канторович Л.В. О методе Ньютона. Труды Матем. ин-та им. Стеклова, т.XXVIII, 1949, с.104-144.
9. Лапчик М.П., Рагулина М.И., Хеннер Е.К. Численные методы. –М.: Academia, 2004, 384с.
10. Самарский А.А., Гулин А.В. Численные методы. –М.: Наука, 1989, 432с.
11. Моисеев В.С., Нестерова Л.Е., Горбунов Д.А. Основные численные методы интегрирования обыкновенных дифференциальных уравнений. Учебно-методическое пособие по выполнению курсовой работы по дисциплине “Дифференциальные уравнения”. Казань: Изд-во Казан. гос. техн. ун-та, 1999, 25с.
147
Содержание. Об истории возникновения предмета «Вычислительная математика». 5 Глава 1. Учет погрешностей при вычислениях. §1.1. Источники и классификация погрешностей. 7 §1.2. Основные понятия и определения теории погрешностей. 8 §1.3. Значащая и верная цифра приближенной величины. Округление
чисел. 9 §1.4. Погрешность алгебраической суммы. 11 §1.5. Погрешность произведения и частного. 13 §1.6. Погрешность степени и корня. 15 §1.7. Погрешность функции. 16 §1.8. Обратная задача теории погрешностей. 17 Глава 2. Итерационные методы решения нелинейных уравнений. §2.1. Основные этапы решения нелинейных уравнений. 19 §2.2. Метод половинного деления. 21 §2.3. Метод простых итераций. 22 §2.4. Метод Ньютона (метод касательных). 28 §2.5. Модифицированный метод Ньютона. 32 §2.6. Непрерывные схемы решения нелинейных уравнений. 33 Глава 3. Итерационные методы решения систем нелинейных
уравнений. §3.1. Метод простых итераций для решения систем нелинейных
уравнений. 36 §3.2. Метод Ньютона для решения систем нелинейных уравнений. 40 Глава 4. Итерационные методы решения систем линейных
алгебраических уравнений. §4.1. Метод простых итераций для решения систем линейных
алгебраических уравнений. 44 §4.2. Метод Зейделя. 47 §4.3. Метод релаксации. 49 Глава 5. Методы приближения функций. §5.1. Постановка задачи аппроксимации и интерполяции функций. 53 §5.2. Конечные разности. Обобщенная степень. 55 §5.3. Первая интерполяционная формула Ньютона. 57 §5.4. Вторая интерполяционная формула Ньютона. 59 §5.5. Интерполяционная формула Лагранжа. 61 §5.6. Метод наименьших квадратов для обработки результатов
экспериментов. 65 §5.7.Обработка экспериментальных данных некоторыми другими
функциями. 67 Глава 6. Численное дифференцирование. §6.1. Постановка вопроса. 70 §6.2. Формулы приближенного дифференцирования, основанные на
первой интерполяционной формуле Ньютона. 70 §6.3. Формулы численного дифференцирования для равноотстоящих
точек, основанные на интерполяционной формуле Лагранжа. 72 Глава 7. Приближенное интегрирование функций. §7.1. Квадратурная формула Ньютона-Котеса. 74 §7.2. Частные случаи квадратурной формулы Ньютона-Котеса. 76 §7.3. Квадратурная формула Гаусса. 79 §7.4. Приближенное вычисление несобственных интегралов. 82 §7.5. Кубатурные формулы типа Симпсона. 84 Глава 8. Приближенное решение обыкновенных дифференциальных
уравнений и систем. §8.1. Метод Эйлера. 88 §8.2. Метод Рунге-Кутта. 91 §8.3. Метод Адамса. 93 Глава 9. Краевые задачи для дифференциальных уравнений второго
порядка. 95 §9.1. Решение краевой задачи для обыкновенного дифференциального
уравнения второго порядка методом конечных разностей. 96 §9.2. Метод прогонки. 98 Глава 10.Численные методы решения краевых задач для дифференци-
альных уравнений с частными производными. §10.1. Классификация дифференциальных уравнений с частными
производными. 101 §10.2. Уравнение Лапласа в конечных разностях. 103 §10.3. Решение задачи Дирихле методом сеток. 105 §10.4. Метод сеток для уравнения параболического типа. 108 §10.5. Метод сеток для уравнений гиперболического типа. 113 Лабораторная работа № 1-2.
Итерационные методы решения нелинейных уравнений. 115 Лабораторная работа № 3-4.
Итерационные методы решения систем нелинейных уравнений. 121 Лабораторная работа № 5.
Итерационные методы решения систем линейных алгебраи-
ческих уравнений. 128 Лабораторная работа № 6-7.
Интерполяция и аппроксимация функций. 133 Лабораторная работа № 8.
Приближенное решение обыкновенных дифференциальных
уравнений. 138 Приложение 1. 143 Приложение 2. 146 Список литературы 147
4
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. А.Н. ТУПОЛЕВА
УТВЕРЖДАЮ:
Проректор по учебной и методической
работе
_________________ И.К. Насыров
«_____» _______________ 2007 г.
ПРОГРАММА ДИСЦИПЛИНЫ
ЕН.Ф.01.05 "ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА"
Рекомендуется УМЦ КГТУ им. А.Н. Туполева для направлений
(специальностей)
направления: 552800 (230000 )* “Информатика и вычислительная техника”
специальности: 220100 (230101)* «Вычислительные машины, комплексы,
системы и сети»
формы обучения: очная, очно – заочная
*) коды направлений и специальностей указаны по Общероссийскому классификатору специальностей по образованию (ОК 009-2003)
Цели и задачи дисциплины
Целью и задачами дисциплины является изучение основных положений вычислительной математики, знакомство с приближенными методами решения реальных инженерных задач на ЭВМ, современными методами решения задач, связанных с дифференциальными уравнениями, в объеме, достаточном для квалифицированного решения основных профессиональных задач будущими инженерами.
Материал курса основан на знаниях, навыках и умениях полученных при обучении в среднем образовательном учреждении, а также получаемых студентами при изучении дисциплин: «Алгебра и геометрия», «Математический анализ», «Дифференциальные уравнения», «Программирование на языках высокого уровня», «Информатика».
Студенты должны быть знакомы с основными алгебраическими структурами («Алгебра и геометрия»); с понятиями функции и ее непрерывности, с понятиями множества, отношения («Математический анализ»); с понятиями обыкновенных и систем обыкновенных дифференциальных уравнений, аналитическими методами их решения («Дифференциальные уравнения»); способами записи алгоритма, стандартными типами данных («Программирование на языках высокого уровня»); с основными приемами работы в операционных системах MS DOS и Windows, а также с основными офисными системами MS Word и MS Excel («Информатика»).
Студенты должны иметь практические навыки решения линейных алгебраических и нелинейных уравнений и систем («Алгебра и геометрия»), решения обыкновенных и систем обыкновенных дифференциальных уравнений («Дифференциальные уравнения»), уметь строить схемы алгоритмов и программ («Программирование на языках высокого уровня»).
Знания, умения и навыки, полученные в процессе изучения данного курса, могут быть использованы студентами для изучения дисциплин «Технологии программирования», «Операционные системы», «Базы данных», «Управление данными», «Информационные технологии», «Сетевые технологии», «Теория принятия решений», а также при прохождении вычислительной практики студентами второго курса очной формы обучения.
Требования к уровню освоения содержания дисциплины
В результате изучения дисциплины студенты должны:
знать:основные численные методы решения нелинейных уравнений, систем нелинейных и линейных алгебраических уравнений;
методы интерполирования, аппроксимирования и экстраполирования функций;
методы численного решения задачи Коши для обыкновенных дифференциальных уравнений;
условий сходимости методов, областей применения численных методов, условий окончания итерационных процессов по каждому методу.
уметь:выводить итерационные формулы для решения конкретной задачи выбранным методом;
составлять и отлаживать программу для конкретного метода;
объяснять полученные результаты.
иметь опыт выбора метода численного решения конкретной задачи. иметь представление:о вычислительной математике как науке о численных (приближенных) методах решения математических и реальных инженерных задач;
о методах и алгоритмах численного решения задач, сходимости методов, погрешностях вычислений, теоретическом обосновании ряда методов, достоинствах и недостатках методов;
о состоянии и тенденциях развития вычислительной математики.
Объем дисциплины и виды учебной работы
| Виды учебной работы | Очное | Очно-заочное | |
| Всего | Семестры | Семестры | |
| 3 | 3 | ||
| Общая трудоемкость дисциплины | 140 | 140 | 140 |
| Аудиторные занятия (всего) | 68 | 68 | 51 |
| Лекции | 34 | 34 | 34 |
| Практические занятия (ПЗ) | 0 | 0 | 0 |
| Семинары (С) | 0 | 0 | 0 |
| Лабораторные работы (ЛР) | 34 | 34 | 17 |
| Другие виды аудиторных занятий | 0 | 0 | 0 |
| Самостоятельная работа (всего) | 72 | 72 | 89 |
| Курсовой проект (работа) | 0 | 0 | 0 |
| Расчетно-графические работы | 0 | 0 | 0 |
| Реферат | 0 | 0 | 0 |
| Другие виды самостоятельной работы | 72 | 72 | 89 |
| Вид итогового контроля | Экзамен | Экзамен | |
Содержание дисциплины
Тематический план *):
| № пп | Наименование тем | Очное | Очно-заочное | ||
| ЛК | ЛБ | ЛК | ЛБ | ||
| 1 | Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. | 4 | 4 | 4 | - |
| 2 | Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений. | 14 | 16 | 14 | 8 |
| 3 | Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. | 10 | 10 | 10 | 5 |
| 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. | 6 | 4 | 6 | 4 |
| Всего | 34 | 34 | 34 | 17 | |
*) Используемые сокращения: ЛК –лекции, ЛБ – лабораторные работы, ПЗ – практические занятия.
Содержание тем
1. Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. (очное: 4/8ч.; очно-заочное: 4/11ч.).
1.1. Основные понятия дисциплины (очное: 1/2ч.; очно-заочное: 1/1ч.).
Понятие приближенных (численных) методов решения математических задач. Место численных методов в математическом анализе. Понятие вычислительной математики, предмет изучения вычислительной математики. Понятия итерационных методов и погрешностей вычислений, вычислительной схемы. Проблема «устойчивости вычислительных методов» и сложности алгоритма.
1.2. Учет погрешностей при вычислениях (очное: 2/4ч.; очно-заочное: 2/6ч.).
Источники и классификация погрешностей. Основные понятия и определения теории погрешностей. Округление чисел. Погрешности алгебраической суммы, произведения, частного, степени, корня, функции. Правило сложения приближенных чисел. Обратная задача теории погрешностей.
1.3. Вычислительные программные системы (очное: 1/2ч.; очно-заочное: 1/4ч.).Основы работы с MS Excel, MathCad, MathLab с точки зрения решения задач вычислительной математики.
2. Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений (очное: 14/30ч.; очно-заочное: 14/36ч.). 2.1. Приближенные методы решения нелинейных уравнений (очное: 8/10ч.; очно-заочное: 8/12ч.). Понятия отделения и уточнения корней нелинейных уравнений на отрезке. Графический и аналитический методы отделения корней. Геометрическая интерпретация графического и аналитического методов. Методы уточнения корней: метод дихотомии, метод простых итераций, метод Ньютона (касательных), модифицированный метод Ньютона.
Метод простых итераций: понятия начального приближения и итерационного процесса; достаточное условие сходимости итерационного процесса; критерии останова итерационного процесса. Геометрическая интерпретация метода простых итераций. Приведение нелинейного уравнения к виду, допускающего сходящиеся итерации. Достоинства и недостатки метода простых итераций.
Метод Ньютона, его геометрическая интерпретация, рабочая формула, выбор начального приближения. Достаточное условие сходимости. Критерий останова итерационного процесса. Достоинства и недостатки метода Ньютона. Модифицированный метод Ньютона, его геометрическая интерпретация и рабочая формула.
2.2. Приближенные методы решения систем нелинейных уравнений (очное: 3/8ч.; очно-заочное: 2/12ч.).Понятие системы нелинейных уравнений (СНУ). Проблема отделения корней СНУ. Приближенные методы решения СНУ. Метод простых итераций, понятия начального приближения, итерационного процесса. Достаточные условия сходимости итерационного процесса. Критерий останова итерационного процесса. Приведение исходной системы к системе, допускающей сходящиеся итерации на примере системы второго порядка. Достоинства и недостатки метода простых итераций для решения СНУ.
Метод Ньютона для решения СНУ, его рабочая формула и критерий останова итерационного процесса. Достаточное условие сходимости. Достоинства и недостатки метода Ньютона. Рабочая формула модифицированного метода Ньютона.
2.3. Приближенные методы решения систем линейных алгебраических уравнений (очное: 3/10ч.; очно-заочное: 3/12ч.).Методы решения систем линейных алгебраических уравнений. Метод простых итераций, его рабочие формулы и критерий останова; выбор начального приближения; достаточные условия и необходимые и достаточные условия сходимости итерационного процесса; приведение исходной системы к системе, допускающей сходящиеся итерации; достоинства и недостатки метода простых итераций.
Рабочие формулы методы Зейделя, критерий останова, необходимые и достаточные условия сходимости метода. Достоинства и недостатки метода.
Метод релаксации. Приведение исходной системы к виду, пригодному для релаксации. Понятие невязки. Рабочие формулы метода. Критерии останова процесса.3. Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. (очное: 10/20ч.; очно-заочное: 10/26ч.). 3.1. Построение интерполяционных формул Лагранжа, первой и второй формул Ньютона (очное: 3/7ч.; очно-заочное: 3/9ч.).
Постановка задачи интерполирования функций по заданной системе точек, понятие равноотстоящих и неравноотстоящих узловых точек. Принципы построения интерполяционной формулы Лагранжа, первой и второй интерполяционной формулы Ньютона, их форма записи и погрешности вычислений по ним. Формулы линейной и квадратичной интерполяции. Понятие табличных разностей различных порядков.
3.2. Основные приложения теории интерполяции (очное: 4/6ч.; очно-заочное: 4/8ч.).Понятие численного дифференцирования. Основные принципы решения задачи численного дифференцирования на примере использования таблицы узловых точек и интерполяционных полиномов. Погрешность построенных формул.
Понятие численного интегрирования, квадратурных формул. Построение квадратурной формулы Ньютона-Котеса с использованием интерполяционных формул, коэффициенты Котеса. Частные случаи формулы Ньютона-Котеса (формула трапеций и формула Симпсона) и их геометрическая интерпретация. Погрешность построенных формул. Понятие несобственных интегралов. Приближенное вычисление несобственных интегралов. Случаи бесконечного отрезка интегрирования с непрерывной подынтегральной функцией и разрывной на конечном отрезке интегрирования подынтегральной функцией, их геометрическая интерпретация.
Приближенное вычисление двойных интегралов: понятие кубатурных формул; вывод кубатурной и обобщенной кубатурной формул типа Симпсона для различных видов областей интегрирования. 3.3. Метод наименьших квадратов для обработки результатов экспериментов (очное: 3/7ч.; очно-заочное: 3/9ч.).Задача аппроксимирования функций по заданной системе точек. Общая идея метода наименьших квадратов. Понятие отклонения искомой функции от экспериментальной в узловых точках. Алгоритм метода наименьших квадратов и его теоретическое обоснование.
Аппроксимация с помощью экспоненциальных функций.
4. Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. (очное: 6/14ч.; очно-заочное: 6/16ч.). 4.1. Приближенное решение обыкновенных дифференциальных уравнений и систем (очное: 3/5ч.; очно-заочное: 3/4ч).
Классификация методов решения и численных методов интегрирования дифференциальных уравнений. Понятия задачи Коши и шага интегрирования. Метод последовательных приближений (метод Пиккара). Метод Эйлера: общая идея метода, его графическая интерпретация и рабочая формула. Достоинства и недостатки метода. Рабочие формулы метода Эйлера для решения системы второго порядка дифференциальных уравнений.
Метод Рунге-Кутта. Общая идея методов Рунге-Кутта второго и четвертого порядков, их рабочие формулы. Достоинства и недостатки методов. Решение задачи Коши для системы второго порядка методом Рунге-Кутта четвертого порядка.
Метод Адамса. Достоинства и недостатки метода Адамса. Экстраполяционная и интерполяционная формулы Адамса для решения дифференциальных уравнений.
Непрерывные схемы решения нелинейных уравнений, условие их применения. Дифференциальное уравнение в отклонениях, его решение. Достоинства и недостатки непрерывных схем. Дифференциальное уравнение с малым параметром, его решение. Достоинства и недостатки методов решения нелинейных уравнений с использованием дифференциальных уравнений с малым параметром.
4.2. Приближенное решение краевых задач для дифференциальных уравнений второго порядка (очное: 1/4ч.; очно-заочное: 1/6ч.).
Метод конечных разностей. Понятие краевой задачи для дифференциального уравнения второго порядка и ее геометрическая интерпретация при различных краевых условиях. Понятие двухточечной краевой задачи для линейного дифференциального уравнения второго порядка и ее форма записи. Метод конечных разностей для решения двухточечной краевой задачи для линейного дифференциального уравнения второго порядка.
Метод прогонки. Конечно-разностная и каноническая формы записи двухточечной краевой задачи для линейного дифференциального уравнения второго порядка. Алгоритм метода прогонки прямым и обратным ходом вычислений.
4.3. Приближенное решение краевых задач для дифференциальных уравнений в частных производных первого порядка (очное: 2/5ч.; очно-заочное: 2/6ч.).
Методы моделирования и Монте-Карло для решения задачи Дирихле. Понятие дифференциального уравнения в частных производных первого порядка эллиптического типа. Понятие краевых задач для уравнений эллиптического типа. Понятие задачи Дирихле. Решение задачи Дирихле методом моделирования и Монте-Карло.
Метод сеток и метод прогонки для решения уравнений параболического типа. Понятие дифференциального уравнения в частных производных первого порядка параболического типа. Метод сеток и метод прогонки для решения уравнений параболического типа.
Метод сеток для решения уравнений гиперболического типа. Понятие дифференциального уравнения в частных производных первого порядка гиперболического типа. Метод сеток для решения уравнений гиперболического типа.
Лабораторный практикум
| №п/п | Номер темы дисцип-лины | Объем в часах | Наименование лабораторных работ | ||
| Очное | Очно-заочное | Заочное | |||
| 1. | 3 | 4 | - | Основы работы с MS Excel, MathCad, MathLab | |
| 2. | 1 | 6 | 4 | Итерационные методы решения нелинейных уравнений | |
| 2 | 2 | 6 | 2 | Итерационные методы решения систем нелинейных уравнений | |
| 2. | 3 | 4 | 2 | Итерационные методы решения систем линейных алгебраических уравнений | |
| 3 | 1, 3 | 8 | 5 | Решение задач интерполирования и аппроксимации функций | |
| 3 | 2 | 2 | - | Численное интегрирование | |
| 4 | 1 | 4 | 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем | |
Курсовой проект (работа) и его содержание
Курсовой проект и курсовая работа не предусмотрены.
Контрольная работа.
Контрольная работа не предусмотрена.
Подготовка реферата.Реферат не предусмотрен.
5. Учебно-методическое обеспечение дисциплины
5.1 Рекомендуемая литература
а) основная литература:
| | Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Учебно-методическое пособие, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 48с. |
| | Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. |
| | Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматгиз, 1966. |
| | Калиткин Н.Н. Численные методы. М.: Наука, 1978. |
| | Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Наука, 1967. |
б) дополнительная литература:
1. Иванов В.С., Ляшев А.С. Лабораторный практикум по дисциплине «Вычислительная техника в инженерных и экономических расчетах». Казань, КАИ, 1984.
2. Вахонина Г.С. Методическое руководство к выполнению лабораторных работ по дисциплине “Методы вычислений”. – Казань: КАИ, 1982.
3. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Лабораторный практикум, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 44с.
4. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Методические указания для студентов заочной формы обучения, Казань, Изд-во Казан. гос. техн. ун-та, 2001, 40с.
5. «Журнал вычислительной математики».
6. «Математическое моделирование».
7. «Программирование».
8. «Математика. Реферативный журнал».
9. http://meth.ras.ru («Журналы Отделения Математики РАН»).
10. http://www.exponenta.ru («Образовательный математический сайт»).
5.2 Средства обеспечения освоения дисциплины
Программное обеспечение для выполнения лабораторных работ и самостоятельной работы студентов:
Windows 98 или более поздних версий.
Автоматизированная вычислительная система «MathCad».
Автоматизированная вычислительная система «MathLab».
MS Excel 97 или более поздних версий.
MS Word 97 или более поздних версий.
Системы программирования Turbo C V6.0 или 7.0, Borland C++ V6.0 или 7.0.
Системы программирования Turbo Pascal V6.0 или 7.0, Borland Pascal V6.0 или 7.0.
6. Материально-техническое обеспечение дисциплины
Для проведения лабораторных работ и организации самостоятельной работы студентов необходимо иметь учебный класс оснащенный ПЭВМ со стандартной комплектацией.
7. Методические рекомендации по организации изучения дисциплины
7.1. Организация изучения дисциплины при очной форме обучения
Обучение проводится в течение одного семестра. Темы 1-4 и все указанные лабораторные работы рассматриваются в семестре № 3.
При проведении лабораторных работ используются программные комплексы, поддерживающие языки программирования Pascal и C, как в учебных лабораториях кафедры, оснащенных компьютерами, так и в ВЦ.
При изучении дисциплины используется балльно - рейтинговая система оценки знаний. Контрольные тестирования организуются на 6, 12 и 17 неделях каждого семестра. Каждое тестирование включает задания, предусматривающие ответы на теоретические и практические вопросы (см. приложение № 5).
Программу составили:
Горбунов Д.А., к.т.н., доцент каф. ПМИ КГТУ им. А.Н. Туполева
_____________________
Программа обсуждена и одобрена на заседании кафедры ПМИ
«____» ______________2007г., протокол № __.
Зав. кафедрой ПМИ Н.Е. Роднищев
д.т.н., профессор
Председатель Учебно-методической В.А. Суздальцев
комиссии факультета, доцент
Декан факультета Л.Ю.Емалетдинова
д.т.н., профессор
Согласовано: В.А.Песошин
зав.кафедрой КС
д.т.н., профессор
ПРИЛОЖЕНИЕ 5
ТЕСТЫ ПО ДИСЦИПЛИНЕ «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
Вопрос 1. Сделайте вывод о сходимости итерационного процесса ![]() , построенного для решения нелинейного уравнения
, построенного для решения нелинейного уравнения ![]() методом простых итераций на отрезке
методом простых итераций на отрезке ![]() .
.
сходится для любой точки из отрезка;
сходится только из определенной точки отрезка;
сходится только для одной из граничных точек отрезка;
расходится на всем отрезке;
расходится на всей числовой оси.
Вопрос 2. Чему равно значение ![]() , вычисленное по итерационной формуле
, вычисленное по итерационной формуле ![]() при
при ![]() ?
?
0.5;
0.875;
0.4;
0.8;
0.9.
Вопрос 3. Если итерационный процесс, построенный по методу простых итераций для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() сходится, то в качестве начальной точки может быть выбрана:
сходится, то в качестве начальной точки может быть выбрана:
одна из граничных точек отрезка;
обе граничные точки отрезка;
середина отрезка;
любая точка отрезка;
все ответы правильные.
Вопрос 4. По какой из итерационных формул осуществляется решение нелинейных уравнений вида ![]() методом Ньютона?
методом Ньютона?
1. ![]() ;
;
2. ![]() ;
;
3. 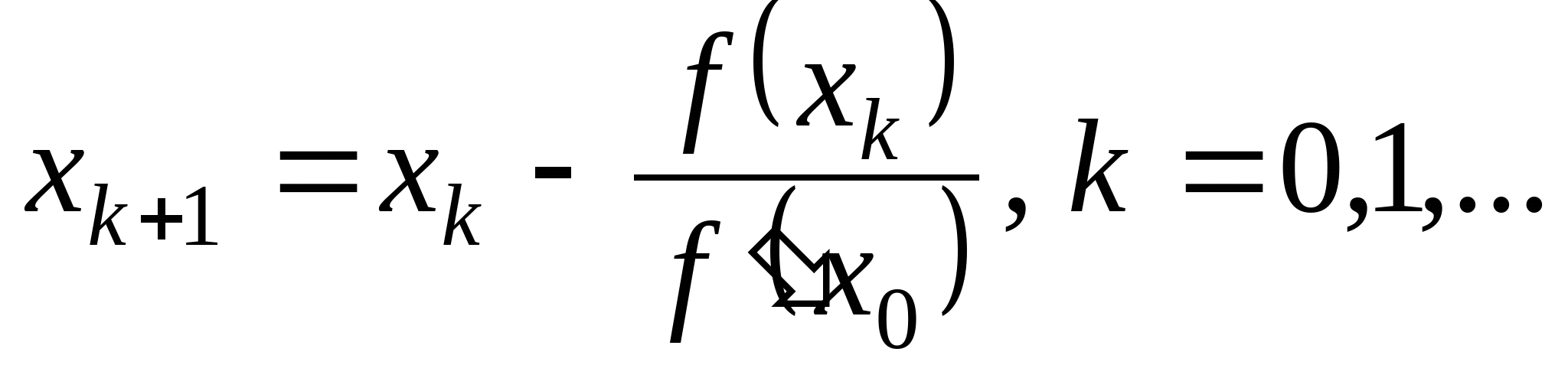 ;
;
4. 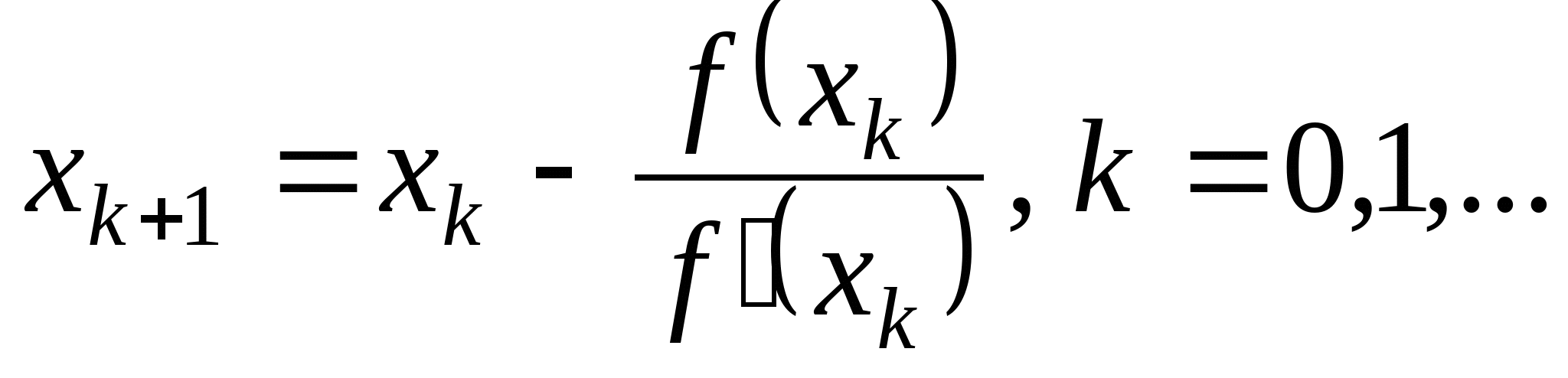 ;
;
5. 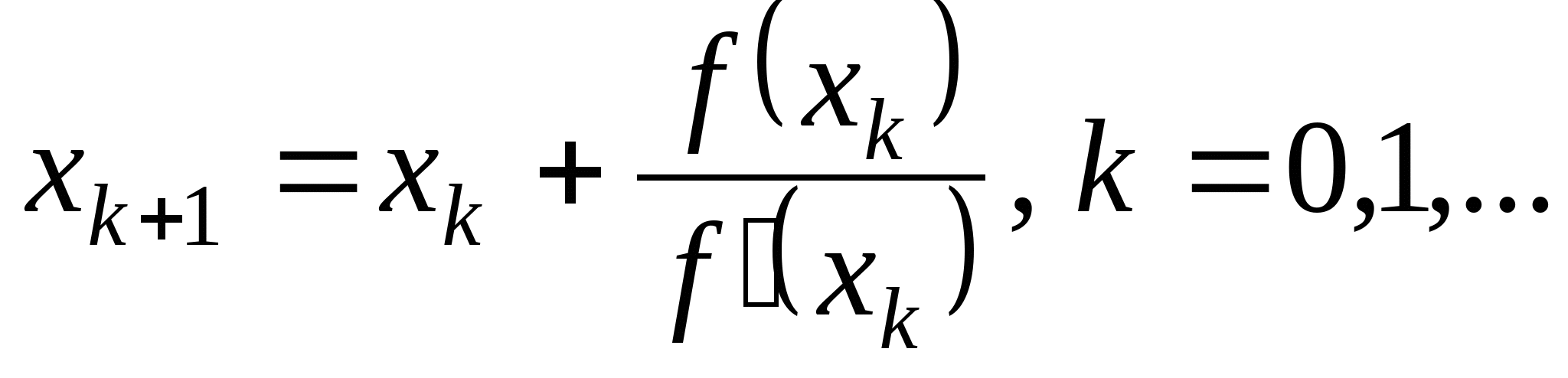 .
.
Вопрос 5. Сформулируйте теорему о существовании хотя бы одного корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() где
где ![]() - произвольная нелинейная функция.
- произвольная нелинейная функция.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на отрезке содержится хотя бы один корень.
, то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка не меняет знак (
и на концах отрезка не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка меняет знак (
и на концах отрезка меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() не меняет знак (
не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() меняет знак (
меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Вопрос 6. Какое условие является достаточным для сходимости итерационного процесса ![]() решения нелинейного уравнения
решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 7. При нахождении корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом Ньютона в качестве начального приближения нужно выбрать
методом Ньютона в качестве начального приближения нужно выбрать ![]() равное:
равное:
0.5;
2;
1;
любой из концов отрезка;
любое значение из отрезка.
Вопрос 8.К какому виду, допускающему сходящиеся итерации, нужно привести систему нелинейных уравнений второго порядка 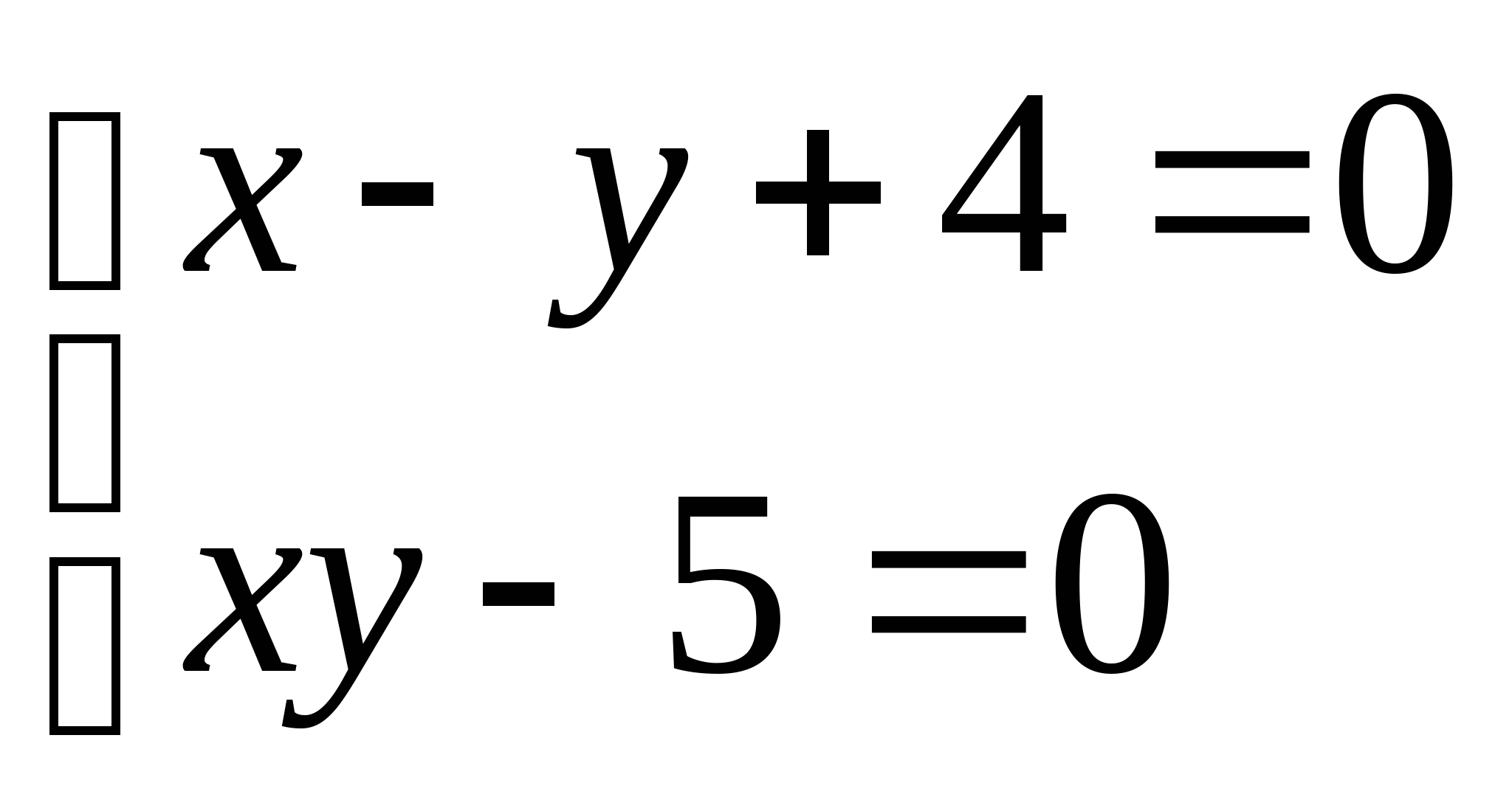 ?
?
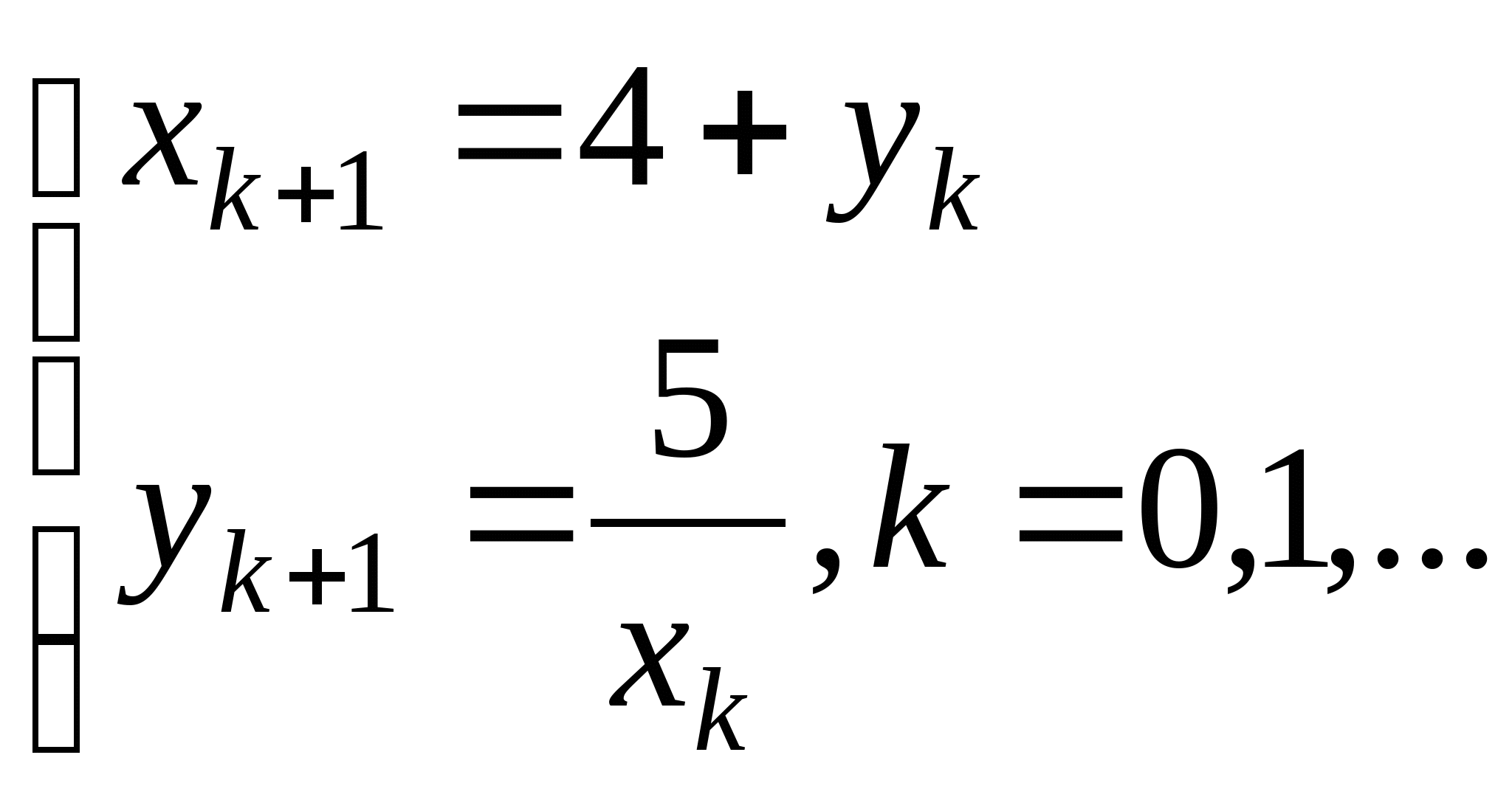 ;
;
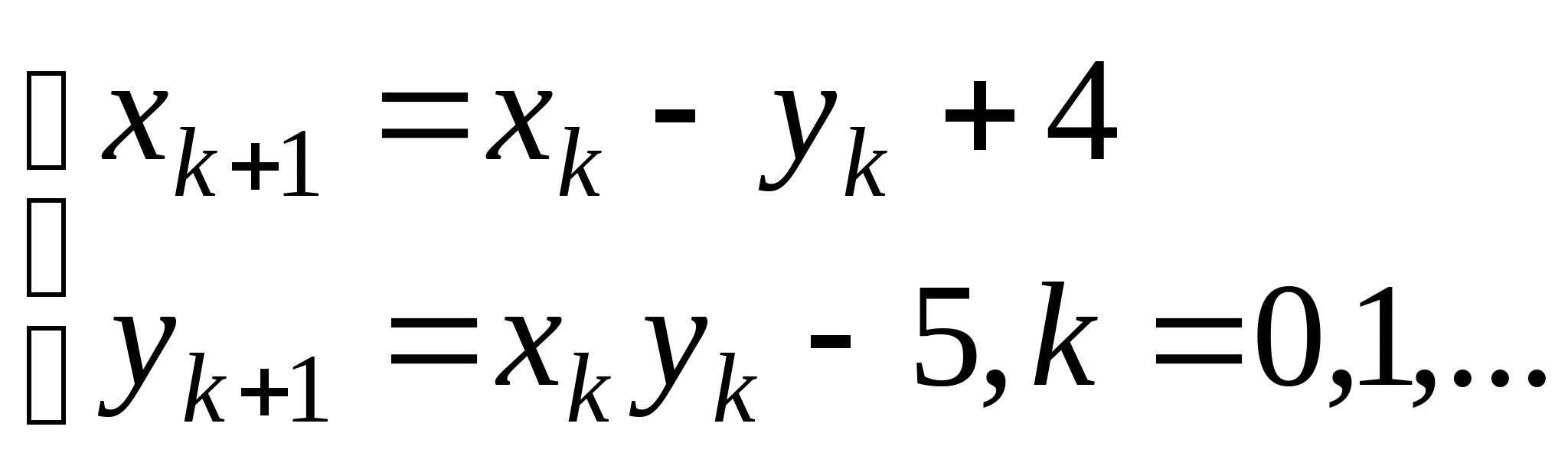 ;
;
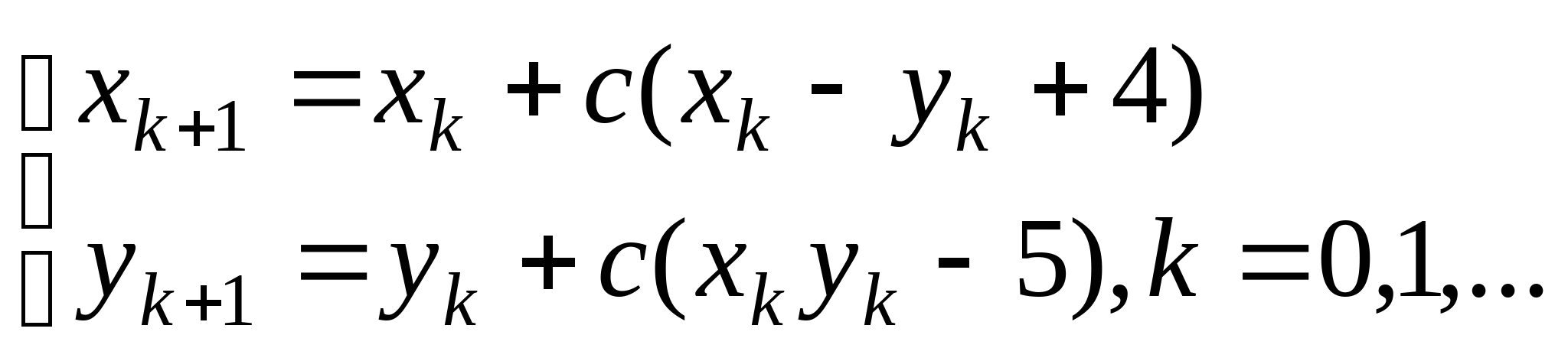 , где константа
, где константа ![]() выбирается из достаточных условий сходимости итерационного процесса;
выбирается из достаточных условий сходимости итерационного процесса;
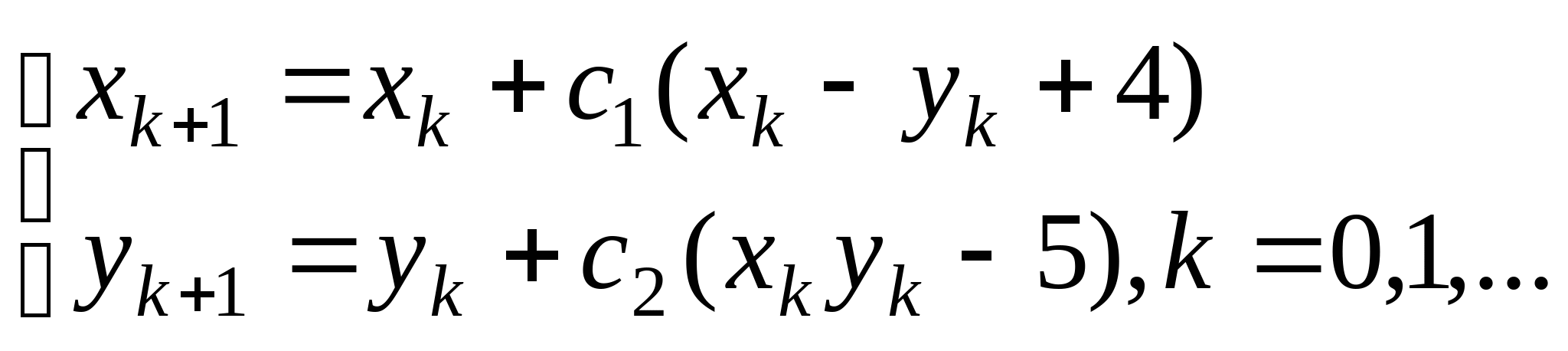 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса;
выбираются из достаточных условий сходимости итерационного процесса;
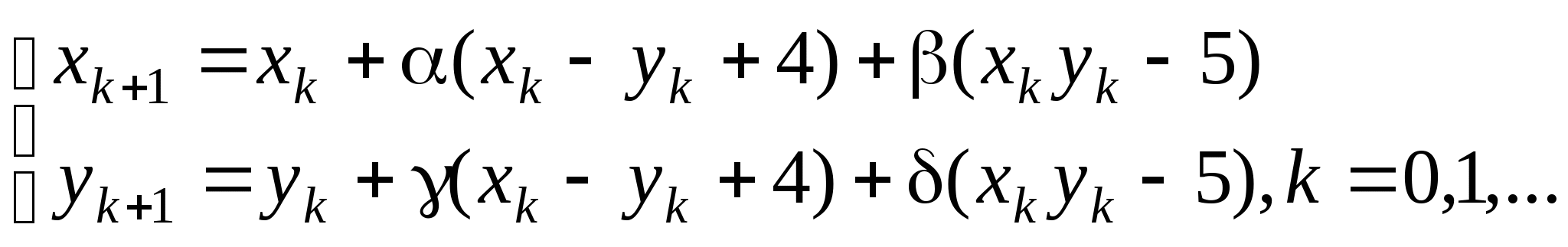 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса.
выбираются из достаточных условий сходимости итерационного процесса.
Вопрос 9. При решении какого класса задач достаточные условия сходимости итерационного процесса имеют вид: ![]() или
или ![]() ?
?
решение нелинейных уравнений;
решение систем нелинейных уравнений;
решение систем линейных алгебраических уравнений;
решение линейных уравнений;
все ответы правильные.
Вопрос 10. При численном решении СЛАУ ![]() ее необходимо привести к виду, допускающему сходящиеся итерации
ее необходимо привести к виду, допускающему сходящиеся итерации ![]() . Чему равно значение коэффициента
. Чему равно значение коэффициента ![]() для СЛАУ вида
для СЛАУ вида 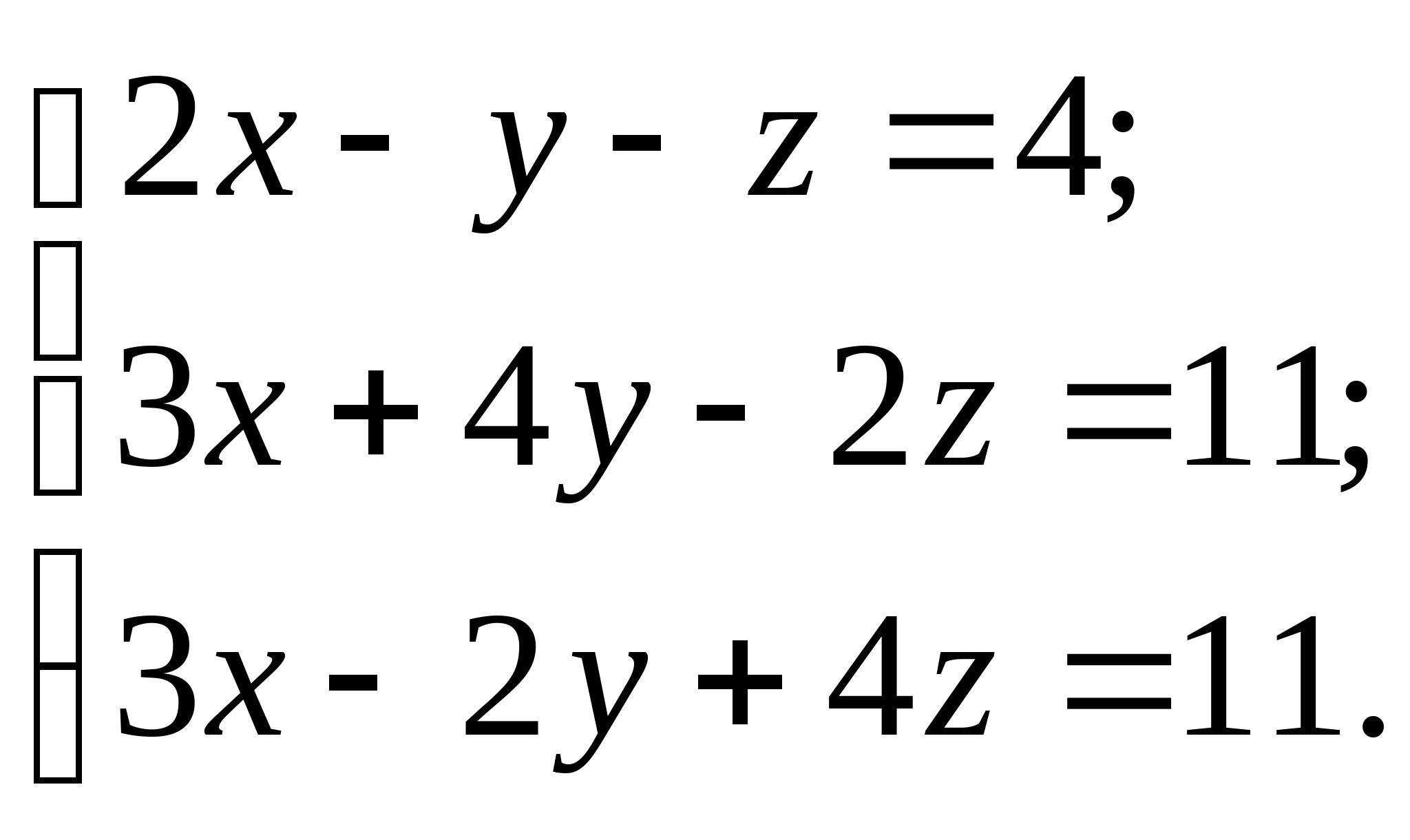 ?
?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
1.
Вопрос 11. Чему равно следующее приближение ![]() , вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида
, вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида 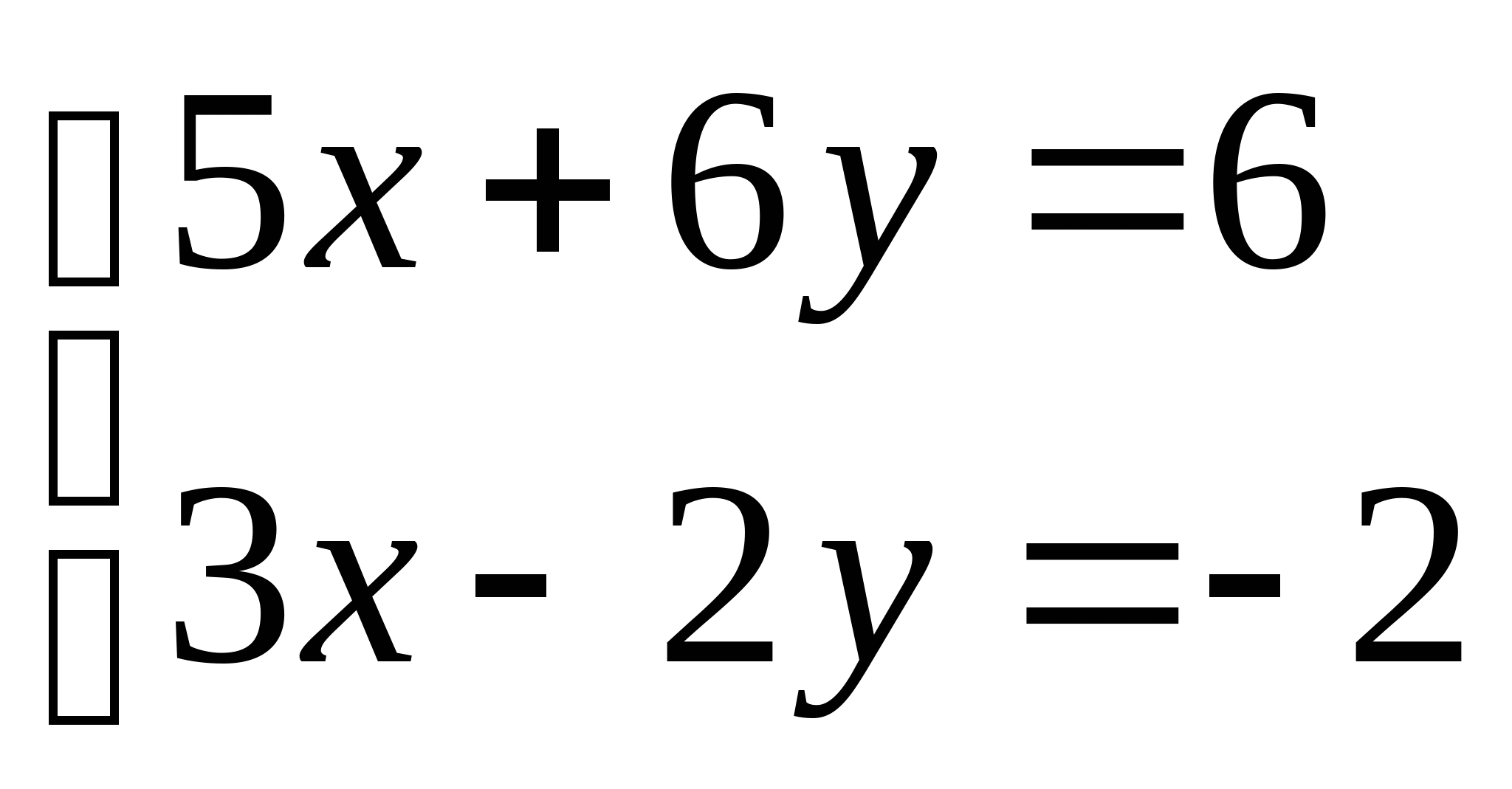 при
при ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 12. Задача интерполяции функций возникает в тех случаях, когда:
необходимо знать значения функции для промежуточных значений аргументов между узловыми точками;
необходимо знать значения функции для точек, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблично;
необходимо представить в более простом виде сложную аналитически заданную функцию;
все ответы правильные.
Вопрос 13. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1 | 0 | 1 |
можно построить интерполяционный полином Лагранжа второго порядка вида:
![]() . Чему будет равен коэффициент
. Чему будет равен коэффициент ![]() ?
?
0;
0.5;
1;
0.4;
0.35.
Вопрос 14. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1.5 | 0.9 | 0.4 |
найти табличную разность второго порядка ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 15. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() :
: ![]() .
.
Строится и решается СЛАУ относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
Вопрос 16. Как называется следующая квадратурная формула: 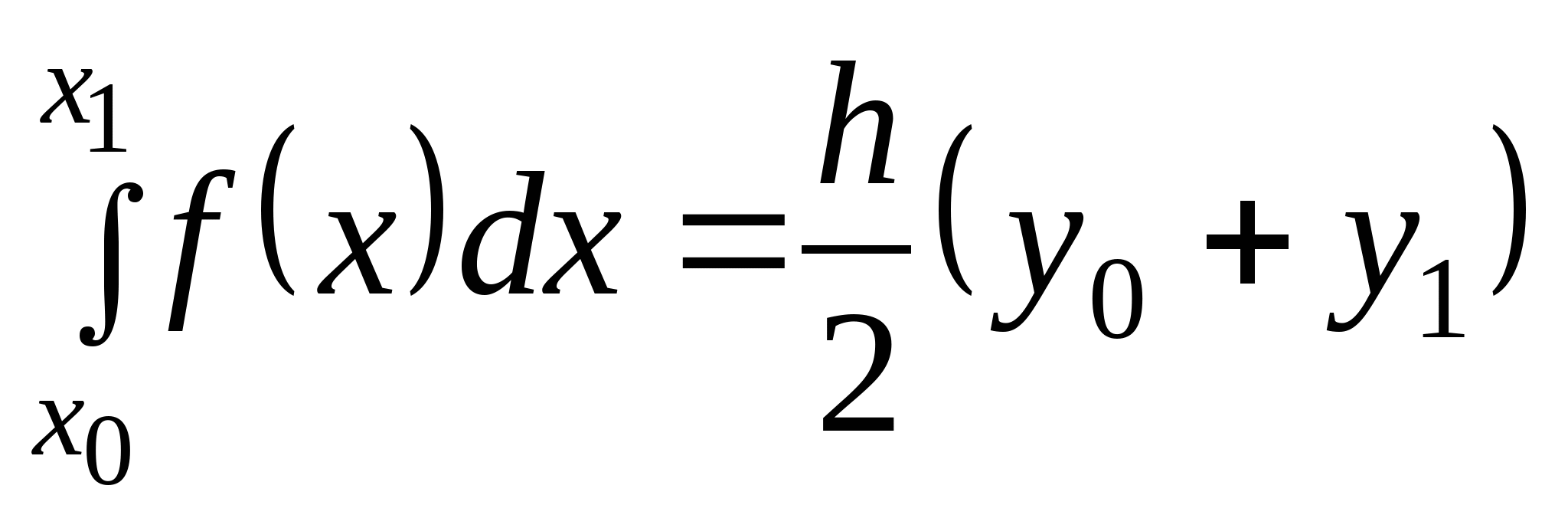 ?
?
формула Ньютона-Котеса;
формула трапеций;
формула Симпсона;
формула Ньютона;
формула Котеса.
Вопрос 17. Как называется следующая интерполяционная формула, построенная для неравноотстоящих узлов:
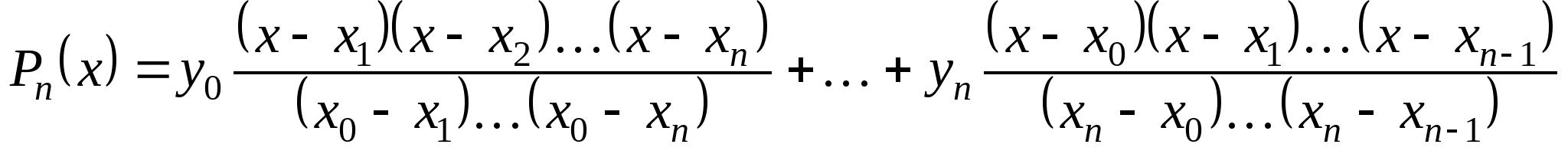 ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула квадратичной интерполяции;
формула линейной интерполяции.
ПРИЛОЖЕНИЕ 8.
СПИСОК ВОПРОСОВ ДЛЯ ПОВТОРЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Источники и классификация погрешностей.
2. Основные понятия и определения теории погрешностей.
3. Значащая и верная цифра приближенной величины. Округление чисел.
4. Погрешность алгебраической суммы.
5. Погрешность произведения и частного.
6. Погрешность степени и корня.
7. Погрешность функции.
8. Обратная задача теории погрешностей.
9. Основные этапы решения нелинейных уравнений.
10. Метод половинного деления.
11. Метод простых итераций для решения нелинейных уравнений.
12. Метод Ньютона (метод касательных) для решения нелинейных уравнений.
13. Модифицированный метод Ньютона для решения нелинейных уравнений.
14. Метод простых итераций для решения систем нелинейных уравнений.
15. Метод Ньютона для решения систем нелинейных уравнений.
16. Модифицированный метод Ньютона для решения систем нелинейных уравнений.
17. Метод простых итераций для решения систем линейных алгебраических уравнений.
18. Метод Зейделя.
19. Метод релаксации.
20. Интерполяционная формула Лагранжа.
21. Первая интерполяционная формула Ньютона.
22. Вторая интерполяционная формула Ньютона.
23. Численное дифференцирование.
24. Квадратурная формула Ньютона-Котеса.
25. Формула трапеций.
26. Квадратурная формула Симпсона.
27. Приближенное вычисление несобственных интегралов.
28. Метод наименьших квадратов.
29. Метод Эйлера.
30. Метод Рунге-Кутта.
31. Метод Адамса.
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. А.Н. ТУПОЛЕВА
УТВЕРЖДАЮ:
Проректор по учебной и методической
работе
_________________ И.К. Насыров
«_____» _______________ 2007 г.
ПРОГРАММА ДИСЦИПЛИНЫ
ЕН.Р.01 "ЧИСЛЕННЫЕ МЕТОДЫ"
Рекомендуется УМЦ КГТУ им. А.Н. Туполева для направлений
(специальностей)
направления: 090100 * “Информационная безопасность”
специальности: 075400 (090104)* «Комплексная защита объектов
информатизации»
формы обучения: очная
*) коды направлений и специальностей указаны по Общероссийскому классификатору специальностей по образованию (ОК 009-2003)
Цели и задачи дисциплины
Целью и задачами дисциплины является изучение основных положений вычислительной математики, знакомство с приближенными методами решения реальных инженерных задач на ЭВМ, современными методами решения задач, связанных с дифференциальными уравнениями, в объеме, достаточном для квалифицированного решения основных профессиональных задач будущими инженерами.
Материал курса основан на знаниях, навыках и умениях полученных при обучении в среднем образовательном учреждении, а также получаемых студентами при изучении дисциплин: «Алгебра и геометрия», «Математический анализ», «Дифференциальные уравнения», «Программирование на языках высокого уровня», «Информатика».
Студенты должны быть знакомы с основными алгебраическими структурами («Алгебра и геометрия»); с понятиями функции и ее непрерывности, с понятиями множества, отношения («Математический анализ»); с понятиями обыкновенных и систем обыкновенных дифференциальных уравнений, аналитическими методами их решения («Дифференциальные уравнения»); способами записи алгоритма, стандартными типами данных («Программирование на языках высокого уровня»); с основными приемами работы в операционных системах MS DOS и Windows, а также с основными офисными системами MS Word и MS Excel («Информатика»).
Студенты должны иметь практические навыки решения линейных алгебраических и нелинейных уравнений и систем («Алгебра и геометрия»), решения обыкновенных и систем обыкновенных дифференциальных уравнений («Дифференциальные уравнения»), уметь строить схемы алгоритмов и программ («Программирование на языках высокого уровня»).
Знания, умения и навыки, полученные в процессе изучения данного курса, могут быть использованы студентами для изучения дисциплин «Технологии программирования», «Операционные системы», «Базы данных», «Управление данными», «Информационные технологии», «Сетевые технологии», «Теория принятия решений», а также при прохождении вычислительной практики студентами второго курса очной формы обучения.
Требования к уровню освоения содержания дисциплины
В результате изучения дисциплины студенты должны:
знать:основные численные методы решения нелинейных уравнений, систем нелинейных и линейных алгебраических уравнений;
методы интерполирования, аппроксимирования и экстраполирования функций;
методы численного решения задачи Коши для обыкновенных дифференциальных уравнений;
условий сходимости методов, областей применения численных методов, условий окончания итерационных процессов по каждому методу.
уметь:выводить итерационные формулы для решения конкретной задачи выбранным методом;
составлять и отлаживать программу для конкретного метода;
объяснять полученные результаты.
иметь опыт выбора метода численного решения конкретной задачи. иметь представление:о вычислительной математике как науке о численных (приближенных) методах решения математических и реальных инженерных задач;
о методах и алгоритмах численного решения задач, сходимости методов, погрешностях вычислений, теоретическом обосновании ряда методов, достоинствах и недостатках методов;
о состоянии и тенденциях развития вычислительной математики.
Объем дисциплины и виды учебной работы
| Виды учебной работы | Очное | |
| Всего | Семестры | |
| 3 | ||
| Общая трудоемкость дисциплины | 130 | 130 |
| Аудиторные занятия (всего) | 68 | 68 |
| Лекции | 34 | 34 |
| Практические занятия (ПЗ) | 0 | 0 |
| Семинары (С) | 0 | 0 |
| Лабораторные работы (ЛР) | 34 | 34 |
| Другие виды аудиторных занятий | 0 | 0 |
| Самостоятельная работа (всего) | 62 | 62 |
| Курсовой проект (работа) | 0 | 0 |
| Расчетно-графические работы | 0 | 0 |
| Реферат | 0 | 0 |
| Другие виды самостоятельной работы | 62 | 62 |
| Вид итогового контроля | Экзамен | |
Содержание дисциплины
Тематический план *):
| № пп | Наименование тем | Очное | |
| ЛК | ЛБ | ||
| 1 | Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. | 4 | 4 |
| 2 | Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений. | 14 | 16 |
| 3 | Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. | 10 | 10 |
| 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных второго порядка. | 6 | 4 |
| Всего | 34 | 34 | |
*) Используемые сокращения: ЛК –лекции, ЛБ – лабораторные работы, ПЗ – практические занятия.
Содержание тем
1. Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. (4/4ч.).
1.1. Основные понятия дисциплины (1/1ч.).
Понятие приближенных (численных) методов решения математических задач. Место численных методов в математическом анализе. Понятие вычислительной математики, предмет изучения вычислительной математики. Понятия итерационных методов и погрешностей вычислений, вычислительной схемы. Проблема «устойчивости вычислительных методов» и сложности алгоритма.
1.2. Учет погрешностей при вычислениях (2/2ч.).
Источники и классификация погрешностей. Основные понятия и определения теории погрешностей. Округление чисел. Погрешности алгебраической суммы, произведения, частного, степени, корня, функции. Правило сложения приближенных чисел. Обратная задача теории погрешностей.
1.3. Вычислительные программные системы (1/1ч.).Основы работы с MS Excel, MathCad, MathLab с точки зрения решения задач вычислительной математики.
2. Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений (14/30ч.). 2.1. Приближенные методы решения нелинейных уравнений (8/10ч.). Понятия отделения и уточнения корней нелинейных уравнений на отрезке. Графический и аналитический методы отделения корней. Геометрическая интерпретация графического и аналитического методов. Методы уточнения корней: метод дихотомии, метод простых итераций, метод Ньютона (касательных), модифицированный метод Ньютона.
Метод простых итераций: понятия начального приближения и итерационного процесса; достаточное условие сходимости итерационного процесса; критерии останова итерационного процесса. Геометрическая интерпретация метода простых итераций. Приведение нелинейного уравнения к виду, допускающего сходящиеся итерации. Достоинства и недостатки метода простых итераций.
Метод Ньютона, его геометрическая интерпретация, рабочая формула, выбор начального приближения. Достаточное условие сходимости. Критерий останова итерационного процесса. Достоинства и недостатки метода Ньютона. Модифицированный метод Ньютона, его геометрическая интерпретация и рабочая формула.
2.2. Приближенные методы решения систем нелинейных уравнений (3/10ч.).Понятие системы нелинейных уравнений (СНУ). Проблема отделения корней СНУ. Приближенные методы решения СНУ. Метод простых итераций, понятия начального приближения, итерационного процесса. Достаточные условия сходимости итерационного процесса. Критерий останова итерационного процесса. Приведение исходной системы к системе, допускающей сходящиеся итерации на примере системы второго порядка. Достоинства и недостатки метода простых итераций для решения СНУ.
Метод Ньютона для решения СНУ, его рабочая формула и критерий останова итерационного процесса. Достаточное условие сходимости. Достоинства и недостатки метода Ньютона. Рабочая формула модифицированного метода Ньютона.
2.3. Приближенные методы решения систем линейных алгебраических уравнений (3/10ч.).Методы решения систем линейных алгебраических уравнений. Метод простых итераций, его рабочие формулы и критерий останова; выбор начального приближения; достаточные условия и необходимые и достаточные условия сходимости итерационного процесса; приведение исходной системы к системе, допускающей сходящиеся итерации; достоинства и недостатки метода простых итераций.
Рабочие формулы методы Зейделя, критерий останова, необходимые и достаточные условия сходимости метода. Достоинства и недостатки метода.
Метод релаксации. Приведение исходной системы к виду, пригодному для релаксации. Понятие невязки. Рабочие формулы метода. Критерии останова процесса.3. Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. (10/18ч.). 3.1. Построение интерполяционных формул Лагранжа, первой и второй формул Ньютона (3/7ч.).
Постановка задачи интерполирования функций по заданной системе точек, понятие равноотстоящих и неравноотстоящих узловых точек. Принципы построения интерполяционной формулы Лагранжа, первой и второй интерполяционной формулы Ньютона, их форма записи и погрешности вычислений по ним. Формулы линейной и квадратичной интерполяции. Понятие табличных разностей различных порядков.
3.2. Основные приложения теории интерполяции (4/6ч.).Понятие численного дифференцирования. Основные принципы решения задачи численного дифференцирования на примере использования таблицы узловых точек и интерполяционных полиномов. Погрешность построенных формул.
Понятие численного интегрирования, квадратурных формул. Построение квадратурной формулы Ньютона-Котеса с использованием интерполяционных формул, коэффициенты Котеса. Частные случаи формулы Ньютона-Котеса (формула трапеций и формула Симпсона) и их геометрическая интерпретация. Погрешность построенных формул. Понятие несобственных интегралов. Приближенное вычисление несобственных интегралов. Случаи бесконечного отрезка интегрирования с непрерывной подынтегральной функцией и разрывной на конечном отрезке интегрирования подынтегральной функцией, их геометрическая интерпретация.
Приближенное вычисление двойных интегралов: понятие кубатурных формул; вывод кубатурной и обобщенной кубатурной формул типа Симпсона для различных видов областей интегрирования. 3.3. Метод наименьших квадратов для обработки результатов экспериментов (3/5ч.).Задача аппроксимирования функций по заданной системе точек. Общая идея метода наименьших квадратов. Понятие отклонения искомой функции от экспериментальной в узловых точках. Алгоритм метода наименьших квадратов и его теоретическое обоснование.
Аппроксимация с помощью экспоненциальных функций.
4. Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. (6/10ч.). 4.1. Приближенное решение обыкновенных дифференциальных уравнений и систем (3/5ч.).
Классификация методов решения и численных методов интегрирования дифференциальных уравнений. Понятия задачи Коши и шага интегрирования. Метод последовательных приближений (метод Пиккара). Метод Эйлера: общая идея метода, его графическая интерпретация и рабочая формула. Достоинства и недостатки метода. Рабочие формулы метода Эйлера для решения системы второго порядка дифференциальных уравнений.
Метод Рунге-Кутта. Общая идея методов Рунге-Кутта второго и четвертого порядков, их рабочие формулы. Достоинства и недостатки методов. Решение задачи Коши для системы второго порядка методом Рунге-Кутта четвертого порядка.
Метод Адамса. Достоинства и недостатки метода Адамса. Экстраполяционная и интерполяционная формулы Адамса для решения дифференциальных уравнений.
Непрерывные схемы решения нелинейных уравнений, условие их применения. Дифференциальное уравнение в отклонениях, его решение. Достоинства и недостатки непрерывных схем. Дифференциальное уравнение с малым параметром, его решение. Достоинства и недостатки методов решения нелинейных уравнений с использованием дифференциальных уравнений с малым параметром.
4.2. Приближенное решение краевых задач для дифференциальных уравнений второго порядка (1/2ч.).
Метод конечных разностей. Понятие краевой задачи для дифференциального уравнения второго порядка и ее геометрическая интерпретация при различных краевых условиях. Понятие двухточечной краевой задачи для линейного дифференциального уравнения второго порядка и ее форма записи. Метод конечных разностей для решения двухточечной краевой задачи для линейного дифференциального уравнения второго порядка.
Метод прогонки. Конечно-разностная и каноническая формы записи двухточечной краевой задачи для линейного дифференциального уравнения второго порядка. Алгоритм метода прогонки прямым и обратным ходом вычислений.
4.3. Приближенное решение краевых задач для дифференциальных уравнений в частных производных второго порядка (2/3ч.).
Понятие дифференциального уравнения в частных производных второго порядка эллиптического типа. Понятие краевых задач для уравнений эллиптического типа. Задача Дирихле. Решение задачи Дирихле методом сеток.
Понятие дифференциального уравнения в частных производных второго порядка параболического типа. Метод сеток для решения уравнений параболического типа.
Понятие дифференциального уравнения в частных производных второго порядка гиперболического типа. Метод сеток для решения уравнений гиперболического типа.
Лабораторный практикум
| №п/п | Номер темы дисцип-лины | Объем в часах | Наименование лабораторных работ | ||
| Очное | Очно-заочное | Заочное | |||
| 1. | 3 | 4 | Основы работы с MS Excel, MathCad, MathLab | ||
| 2. | 1 | 6 | Итерационные методы решения нелинейных уравнений | ||
| 2 | 2 | 6 | Итерационные методы решения систем нелинейных уравнений | ||
| 2. | 3 | 4 | Итерационные методы решения систем линейных алгебраических уравнений | ||
| 3 | 1, 3 | 8 | Решение задач интерполирования и аппроксимации функций | ||
| 3 | 2 | 2 | Численное интегрирование | ||
| 4 | 1 | 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем | ||
Курсовой проект (работа) и его содержание
Курсовой проект и курсовая работа не предусмотрены.
Контрольная работа.
Контрольная работа не предусмотрена.
Подготовка реферата.Реферат не предусмотрен.
5. Учебно-методическое обеспечение дисциплины
5.1 Рекомендуемая литература
а) основная литература:
| | Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Учебно-методическое пособие, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 48с. |
| | Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. |
| | Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматгиз, 1966. |
| | Калиткин Н.Н. Численные методы. М.: Наука, 1978. |
| | Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Наука, 1967. |
б) дополнительная литература:
1. Иванов В.С., Ляшев А.С. Лабораторный практикум по дисциплине «Вычислительная техника в инженерных и экономических расчетах». Казань, КАИ, 1984.
2. Вахонина Г.С. Методическое руководство к выполнению лабораторных работ по дисциплине “Методы вычислений”. – Казань: КАИ, 1982.
3. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Лабораторный практикум, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 44с.
4. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Методические указания для студентов заочной формы обучения, Казань, Изд-во Казан. гос. техн. ун-та, 2001, 40с.
5. «Журнал вычислительной математики».
6. «Математическое моделирование».
7. «Программирование».
8. «Математика. Реферативный журнал».
9. http://meth.ras.ru («Журналы Отделения Математики РАН»).
10. http://www.exponenta.ru («Образовательный математический сайт»).
5.2 Средства обеспечения освоения дисциплины
Программное обеспечение для выполнения лабораторных работ и самостоятельной работы студентов:
Windows 98 или более поздних версий.
Автоматизированная вычислительная система «MathCad».
Автоматизированная вычислительная система «MathLab».
MS Excel 97 или более поздних версий.
MS Word 97 или более поздних версий.
Системы программирования Turbo C V6.0 или 7.0, Borland C++ V6.0 или 7.0.
Системы программирования Turbo Pascal V6.0 или 7.0, Borland Pascal V6.0 или 7.0.
6. Материально-техническое обеспечение дисциплины
Для проведения лабораторных работ и организации самостоятельной работы студентов необходимо иметь учебный класс оснащенный ПЭВМ со стандартной комплектацией.
7. Методические рекомендации по организации изучения дисциплины
7.1. Организация изучения дисциплины при очной форме обучения
Обучение проводится в течение одного семестра. Темы 1-4 и все указанные лабораторные работы рассматриваются в семестре № 3.
При проведении лабораторных работ используются программные комплексы, поддерживающие языки программирования Pascal и C, как в учебных лабораториях кафедры, оснащенных компьютерами, так и в ВЦ.
При изучении дисциплины используется балльно - рейтинговая система оценки знаний. Контрольные тестирования организуются на 6, 12 и 17 неделях каждого семестра. Каждое тестирование включает задания, предусматривающие ответы на теоретические и практические вопросы (см. приложение № 5).
Программу составили:
Горбунов Д.А., к.т.н., доцент каф. ПМИ КГТУ им. А.Н. Туполева
_____________________
Программа обсуждена и одобрена на заседании кафедры ПМИ
«____» ______________2007г., протокол № __.
Зав. кафедрой ПМИ Н.Е. Роднищев
д.т.н., профессор
Председатель Учебно-методической В.А. Суздальцев
комиссии факультета, доцент
Декан факультета Л.Ю.Емалетдинова
д.т.н., профессор
Согласовано: В.И.Глова
зав.кафедрой СИБ
д.т.н., профессор
ПРИЛОЖЕНИЕ 5
ТЕСТЫ ПО ДИСЦИПЛИНЕ «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
Вопрос 1. Сделайте вывод о сходимости итерационного процесса ![]() , построенного для решения нелинейного уравнения
, построенного для решения нелинейного уравнения ![]() методом простых итераций на отрезке
методом простых итераций на отрезке ![]() .
.
сходится для любой точки из отрезка;
сходится только из определенной точки отрезка;
сходится только для одной из граничных точек отрезка;
расходится на всем отрезке;
расходится на всей числовой оси.
Вопрос 2. Чему равно значение ![]() , вычисленное по итерационной формуле
, вычисленное по итерационной формуле ![]() при
при ![]() ?
?
0.5;
0.875;
0.4;
0.8;
0.9.
Вопрос 3. Если итерационный процесс, построенный по методу простых итераций для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() сходится, то в качестве начальной точки может быть выбрана:
сходится, то в качестве начальной точки может быть выбрана:
одна из граничных точек отрезка;
обе граничные точки отрезка;
середина отрезка;
любая точка отрезка;
все ответы правильные.
Вопрос 4. По какой из итерационных формул осуществляется решение нелинейных уравнений вида ![]() методом Ньютона?
методом Ньютона?
1. ![]() ;
;
2. ![]() ;
;
3. 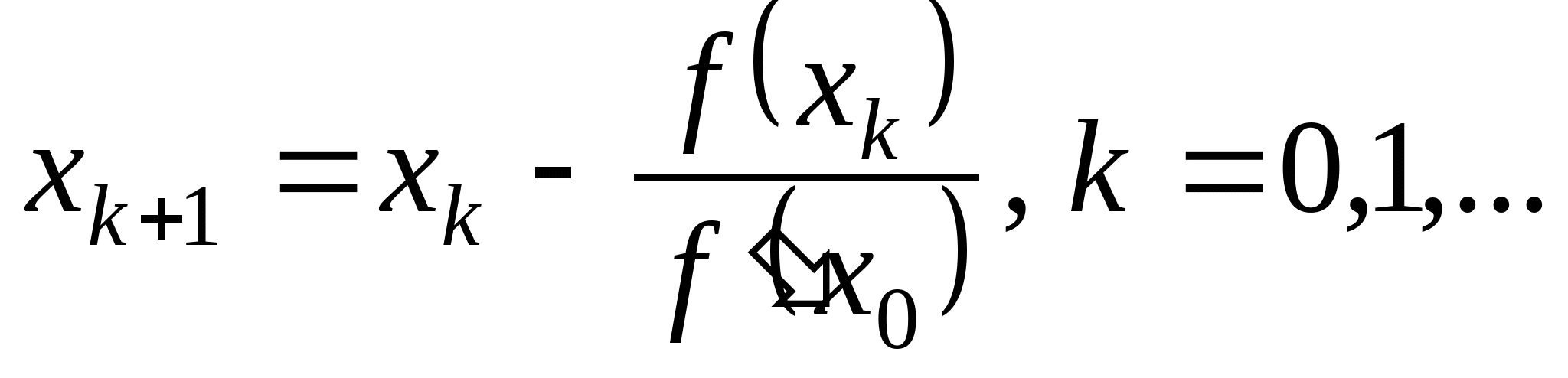 ;
;
4. 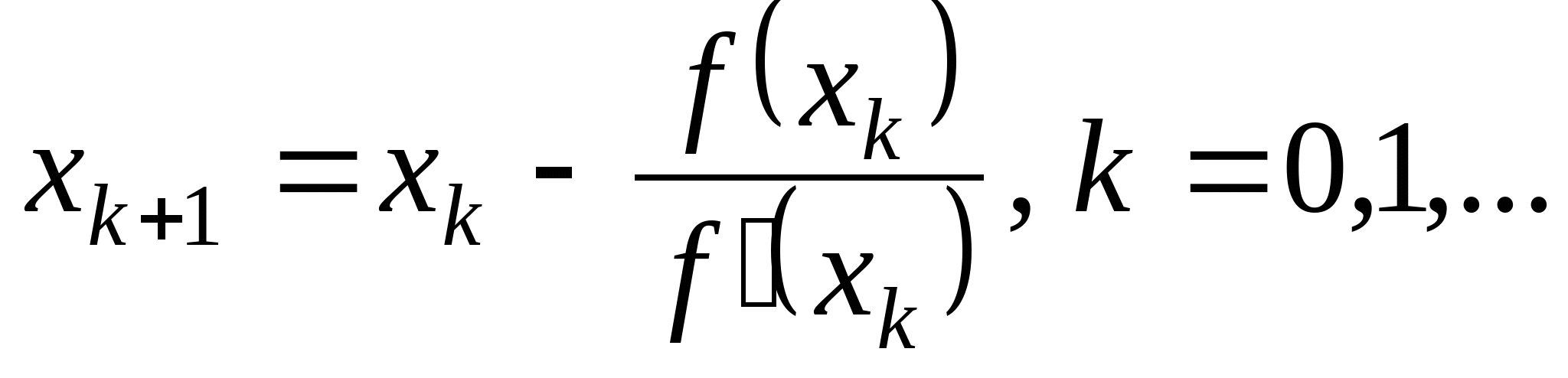 ;
;
5. 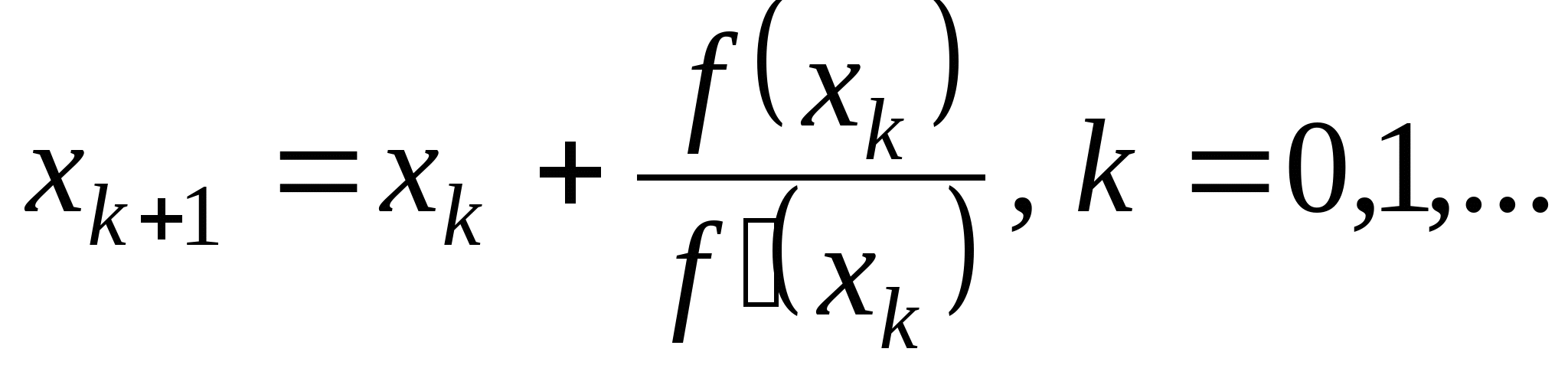 .
.
Вопрос 5. Сформулируйте теорему о существовании хотя бы одного корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() где
где ![]() - произвольная нелинейная функция.
- произвольная нелинейная функция.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на отрезке содержится хотя бы один корень.
, то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка не меняет знак (
и на концах отрезка не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка меняет знак (
и на концах отрезка меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() не меняет знак (
не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() меняет знак (
меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Вопрос 6. Какое условие является достаточным для сходимости итерационного процесса ![]() решения нелинейного уравнения
решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 7. При нахождении корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом Ньютона в качестве начального приближения нужно выбрать
методом Ньютона в качестве начального приближения нужно выбрать ![]() равное:
равное:
0.5;
2;
1;
любой из концов отрезка;
любое значение из отрезка.
Вопрос 8.К какому виду, допускающему сходящиеся итерации, нужно привести систему нелинейных уравнений второго порядка 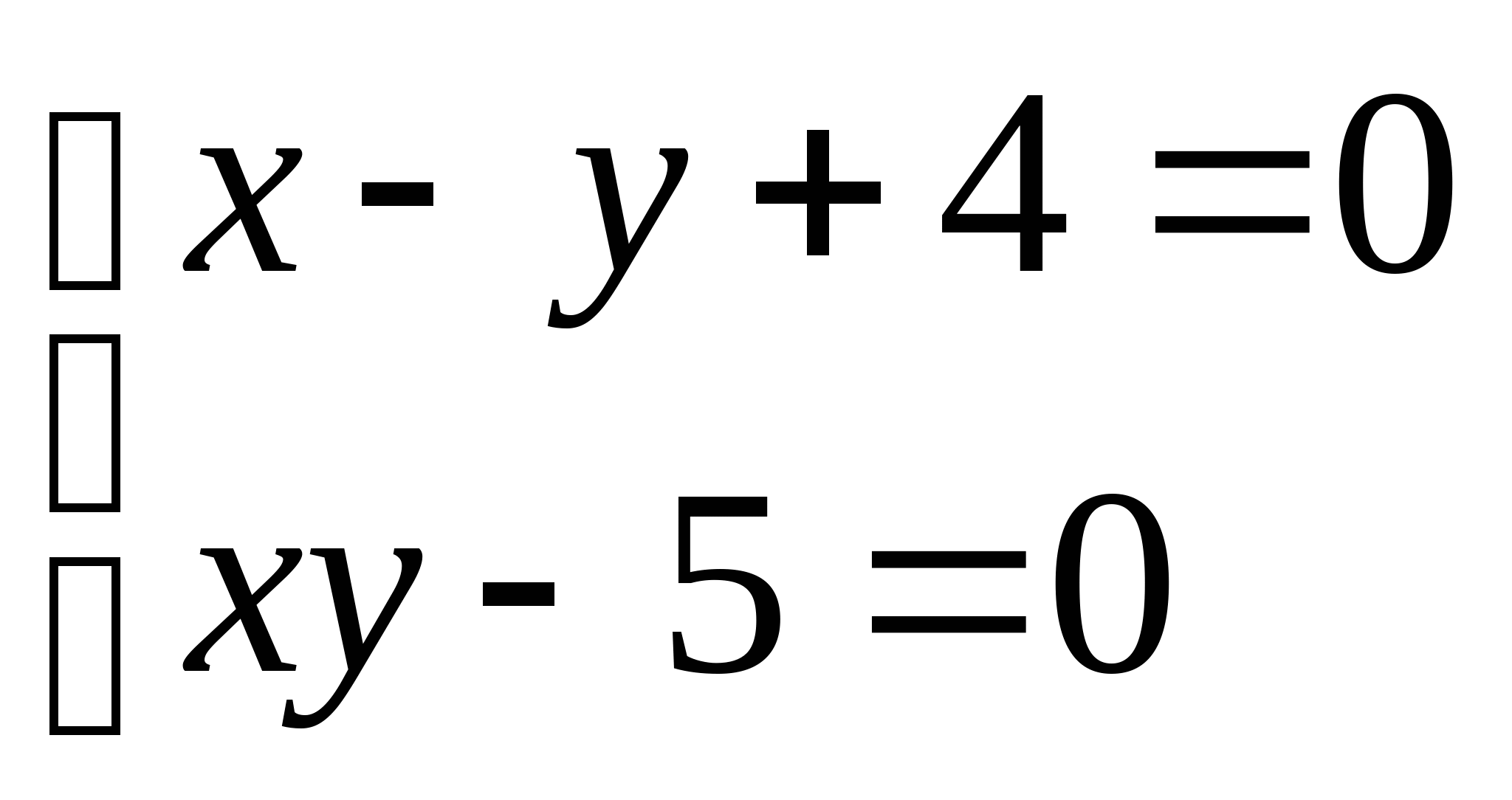 ?
?
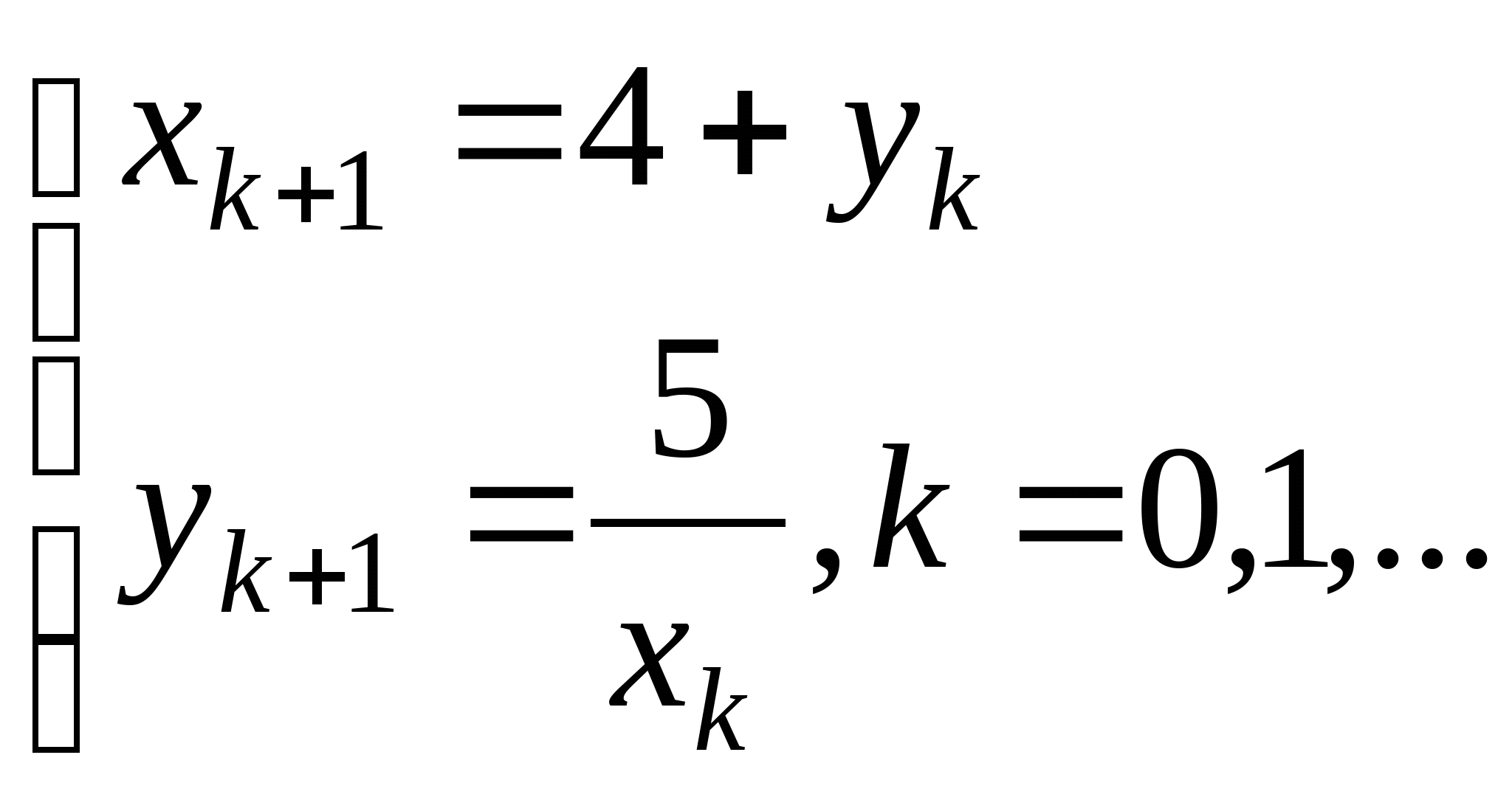 ;
;
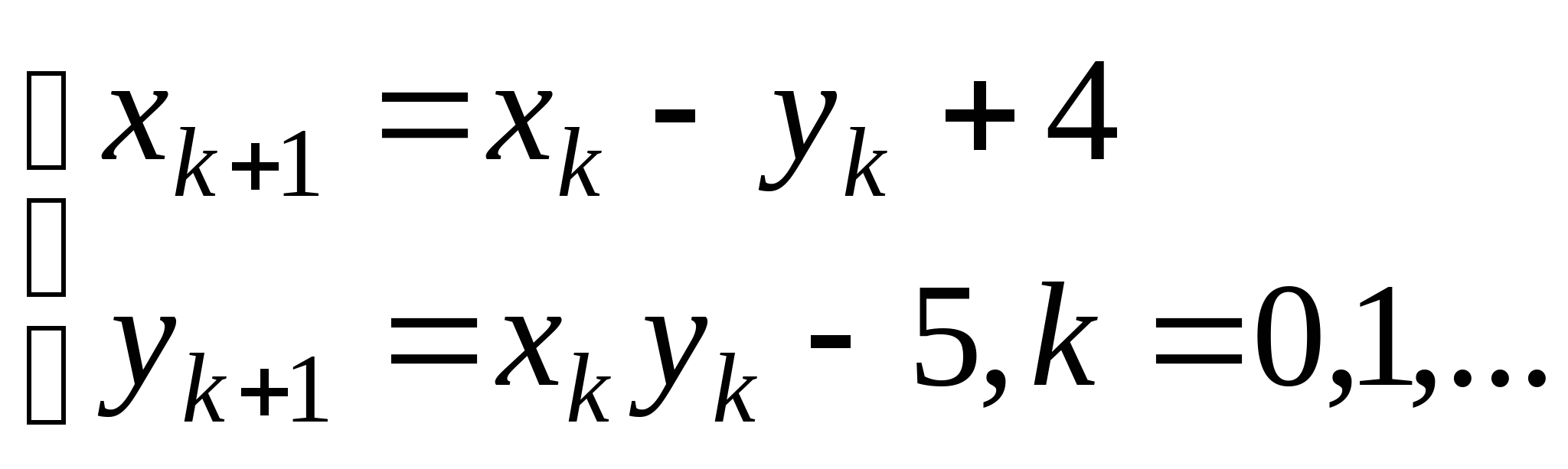 ;
;
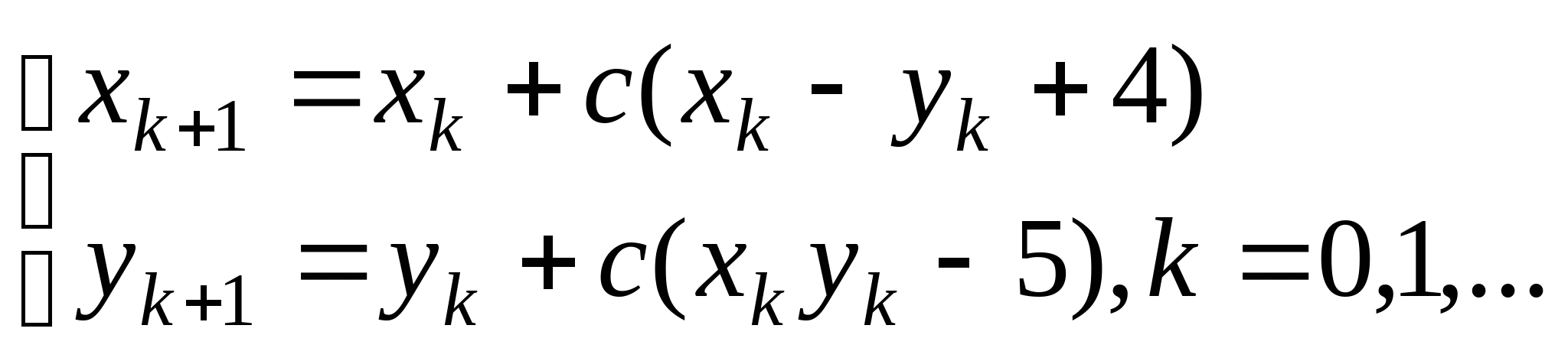 , где константа
, где константа ![]() выбирается из достаточных условий сходимости итерационного процесса;
выбирается из достаточных условий сходимости итерационного процесса;
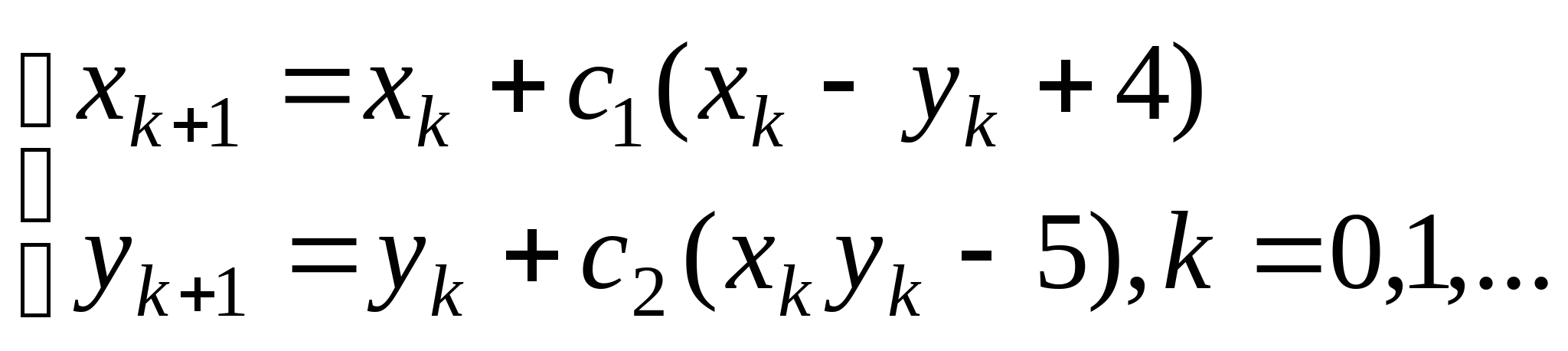 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса;
выбираются из достаточных условий сходимости итерационного процесса;
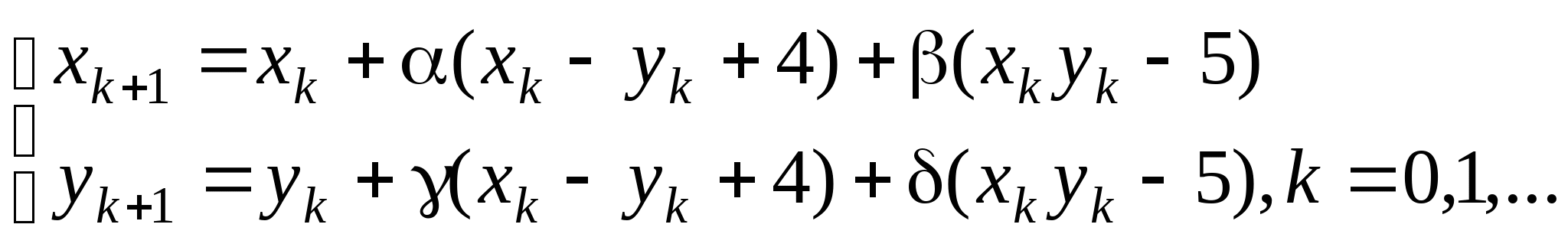 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса.
выбираются из достаточных условий сходимости итерационного процесса.
Вопрос 9. При решении какого класса задач достаточные условия сходимости итерационного процесса имеют вид: ![]() или
или ![]() ?
?
решение нелинейных уравнений;
решение систем нелинейных уравнений;
решение систем линейных алгебраических уравнений;
решение линейных уравнений;
все ответы правильные.
Вопрос 10. При численном решении СЛАУ ![]() ее необходимо привести к виду, допускающему сходящиеся итерации
ее необходимо привести к виду, допускающему сходящиеся итерации ![]() . Чему равно значение коэффициента
. Чему равно значение коэффициента ![]() для СЛАУ вида
для СЛАУ вида 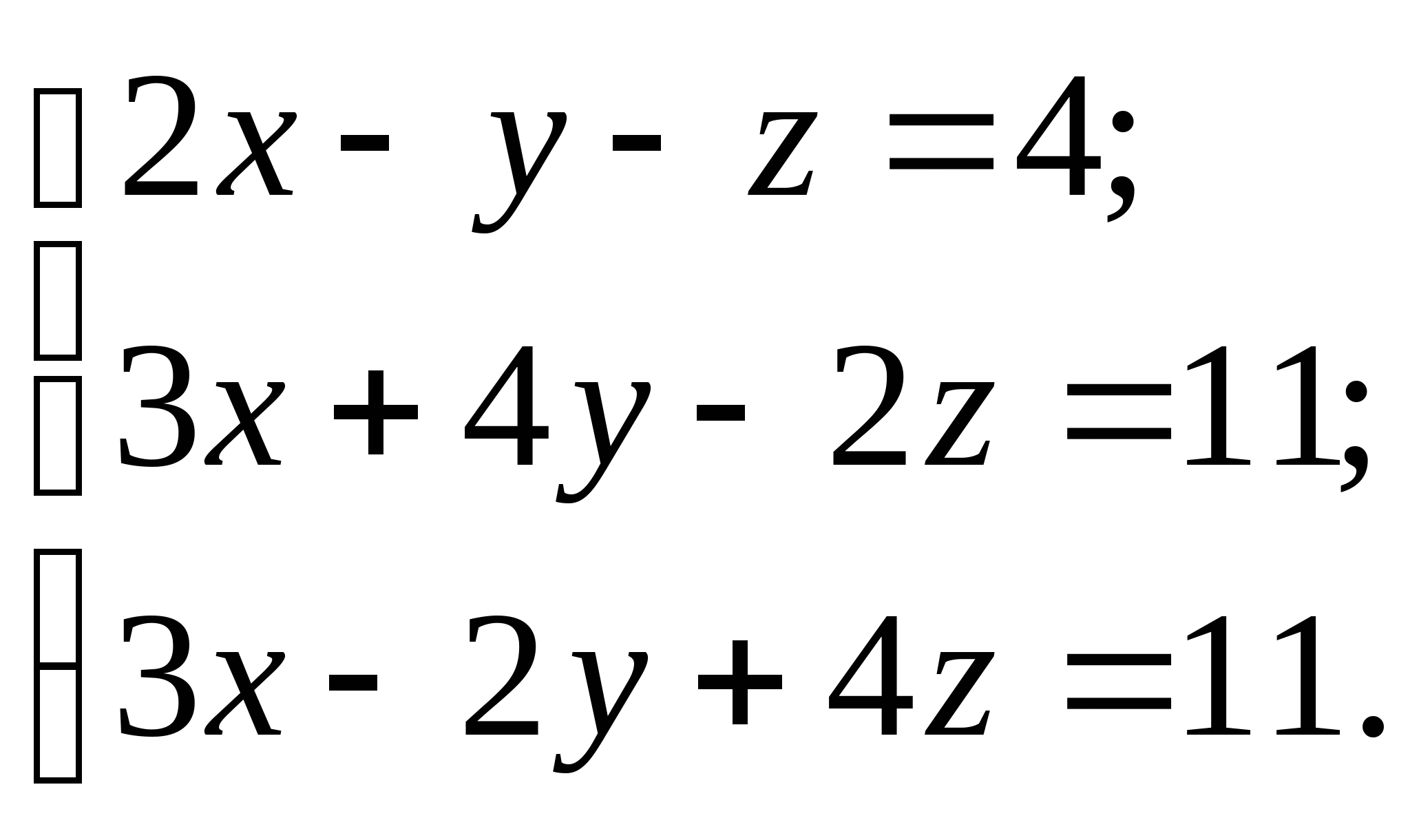 ?
?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
1.
Вопрос 11. Чему равно следующее приближение ![]() , вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида
, вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида 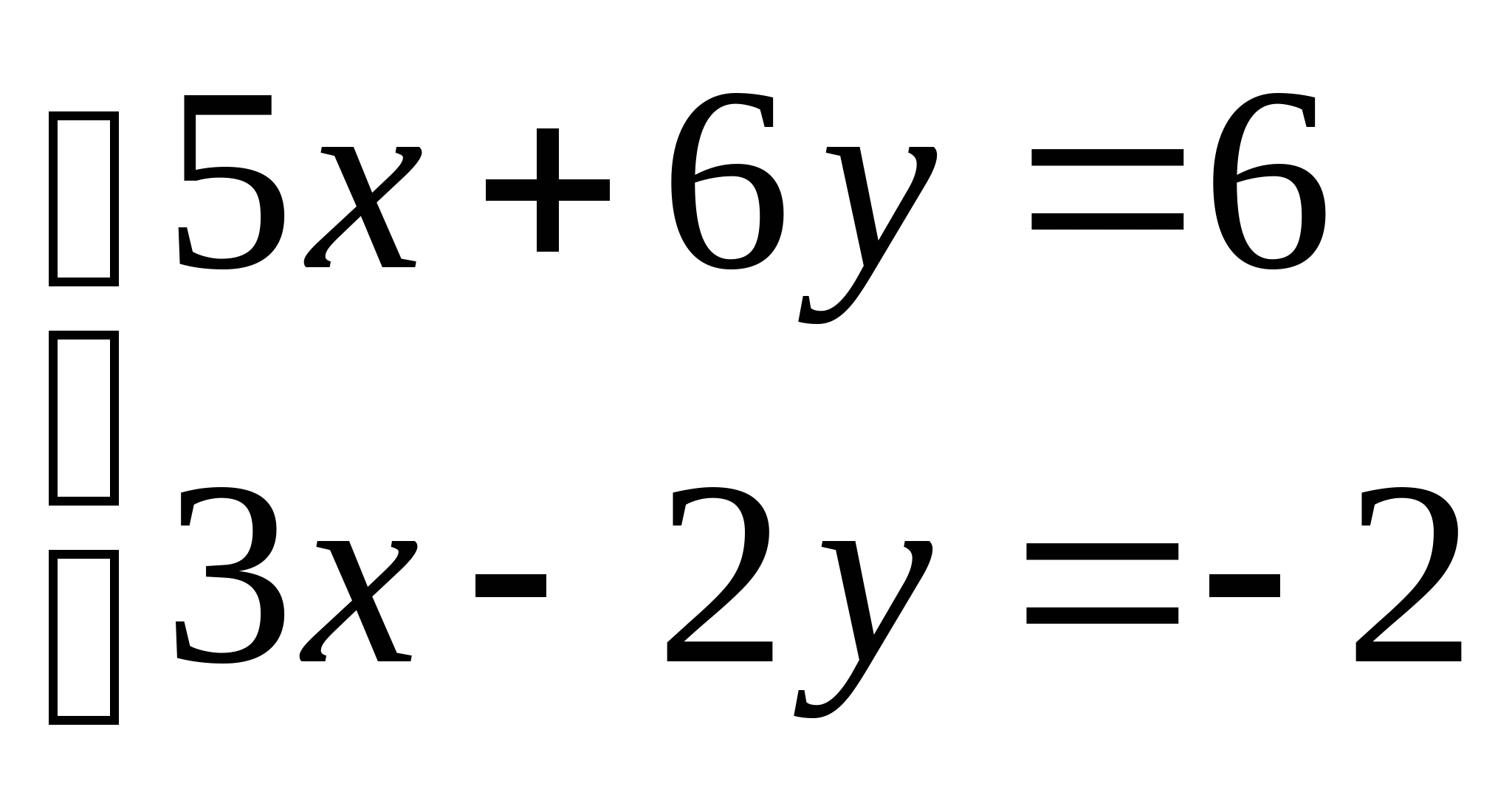 при
при ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 12. Задача интерполяции функций возникает в тех случаях, когда:
необходимо знать значения функции для промежуточных значений аргументов между узловыми точками;
необходимо знать значения функции для точек, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблично;
необходимо представить в более простом виде сложную аналитически заданную функцию;
все ответы правильные.
Вопрос 13. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1 | 0 | 1 |
можно построить интерполяционный полином Лагранжа второго порядка вида:
![]() . Чему будет равен коэффициент
. Чему будет равен коэффициент ![]() ?
?
0;
0.5;
1;
0.4;
0.35.
Вопрос 14. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1.5 | 0.9 | 0.4 |
найти табличную разность второго порядка ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 15. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() :
: ![]() .
.
Строится и решается СЛАУ относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
Вопрос 16. Как называется следующая квадратурная формула: 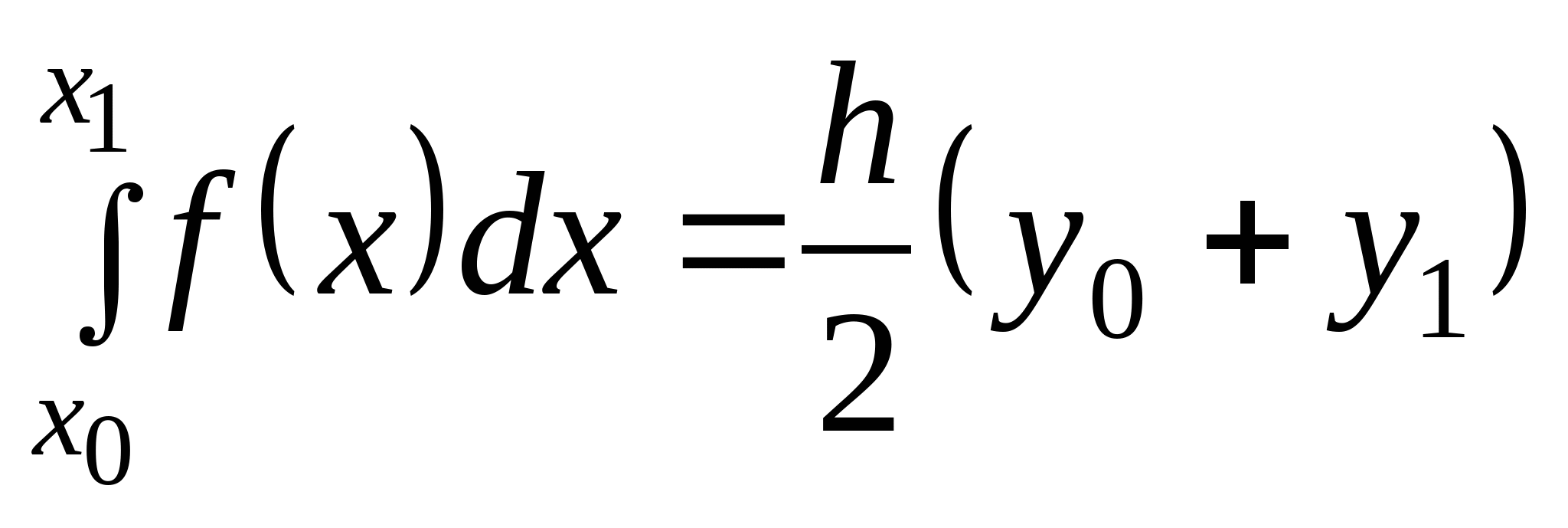 ?
?
формула Ньютона-Котеса;
формула трапеций;
формула Симпсона;
формула Ньютона;
формула Котеса.
Вопрос 17. Как называется следующая интерполяционная формула, построенная для неравноотстоящих узлов:
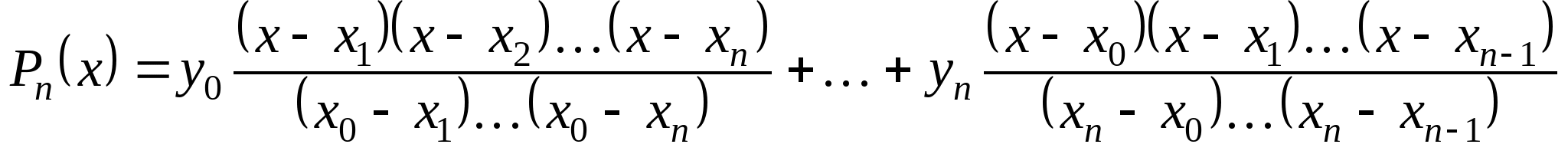 ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула квадратичной интерполяции;
формула линейной интерполяции.
ПРИЛОЖЕНИЕ 8.
СПИСОК ВОПРОСОВ ДЛЯ ПОВТОРЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Источники и классификация погрешностей.
2. Основные понятия и определения теории погрешностей.
3. Значащая и верная цифра приближенной величины. Округление чисел.
4. Погрешность алгебраической суммы.
5. Погрешность произведения и частного.
6. Погрешность степени и корня.
7. Погрешность функции.
8. Обратная задача теории погрешностей.
9. Основные этапы решения нелинейных уравнений.
10. Метод половинного деления.
11. Метод простых итераций для решения нелинейных уравнений.
12. Метод Ньютона (метод касательных) для решения нелинейных уравнений.
13. Модифицированный метод Ньютона для решения нелинейных уравнений.
14. Метод простых итераций для решения систем нелинейных уравнений.
15. Метод Ньютона для решения систем нелинейных уравнений.
16. Модифицированный метод Ньютона для решения систем нелинейных уравнений.
17. Метод простых итераций для решения систем линейных алгебраических уравнений.
18. Метод Зейделя.
19. Метод релаксации.
20. Интерполяционная формула Лагранжа.
21. Первая интерполяционная формула Ньютона.
22. Вторая интерполяционная формула Ньютона.
23. Численное дифференцирование.
24. Квадратурная формула Ньютона-Котеса.
25. Формула трапеций.
26. Квадратурная формула Симпсона.
27. Приближенное вычисление несобственных интегралов.
28. Метод наименьших квадратов.
29. Метод Эйлера.
30. Метод Рунге-Кутта.
31. Метод Адамса.
32. Метод конечных разностей.
33. Метод прогонки.
34. Решение задачи Дирихле методом сеток.
35. Метод сеток для дифференциального уравнения параболического типа.
36. Метод сеток для дифференциального уравнения гиперболического типа.
1. Задача интерполяции функций возникает в тех случаях, когда:
необходимо знать значения функции для промежуточных значений аргументов между узловыми точками;
необходимо знать значения функции для точек, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблично;
необходимо представить в более простом виде сложную аналитически заданную функцию;
все ответы правильные.
2. Какой из подходов используется для уплотнения таблицы узловых точек?
1. построение интерполяционной формулы Лагранжа;
2. построение первой интерполяционной формулы Ньютона;
3. построение второй интерполяционной формулы Ньютона;
4. построение аппроксимационного полинома;
5. все ответы правильные.
3. В задаче интерполяция функций для произвольно заданных узлов используется:
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
интерполяционная формула Лагранжа;
формула линейной интерполяции;
формула квадратичной интерполяции.
4. Какой из подходов применяется при вычислении значений таблично заданной функции в точках, расположенных ближе к началу таблицы?
построение интерполяционной формулы Лагранжа;
построение первой интерполяционной формулы Ньютона;
построение второй интерполяционной формулы Ньютона;
построение аппроксимационного полинома;
все ответы правильные.
5. Какой из подходов применяется при вычислении значений таблично заданной функции в точках, расположенных ближе к концу таблицы, и для продолжения таблицы?
построение интерполяционной формулы Лагранжа;
построение первой интерполяционной формулы Ньютона;
построение второй интерполяционной формулы Ньютона;
построение аппроксимационного полинома;
все ответы правильные.
6. Как называется интерполяционная формула, построенная для равноотстоящих узлов: ![]() ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула линейной интерполяции;
формула квадратичной интерполяции.
7. Как называется интерполяционная формула, построенная для равноотстоящих узлов: ![]() ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула квадратичной интерполяции;
формула линейной интерполяции.
8. Как называется интерполяционная формула, построенная для неравноотстоящих узлов: 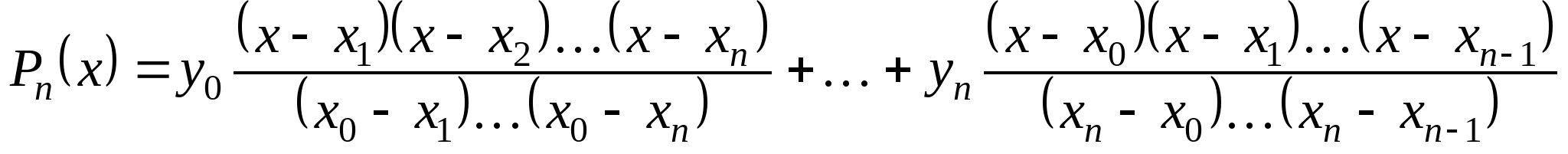 ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула квадратичной интерполяции;
формула линейной интерполяции.
9. Какая из формул называется интерполяционной формулой Лагранжа?
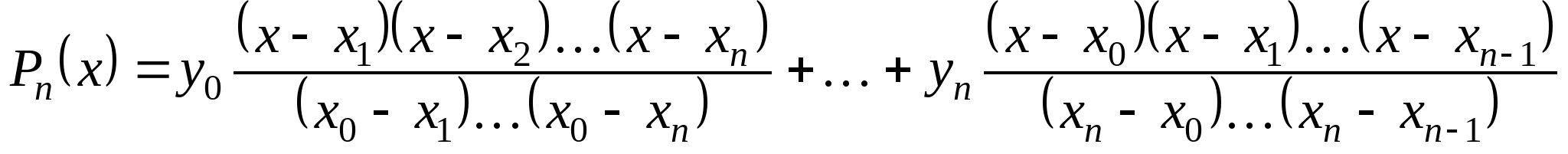 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
10. Какая из формул называется первой интерполяционной формулой Ньютона?
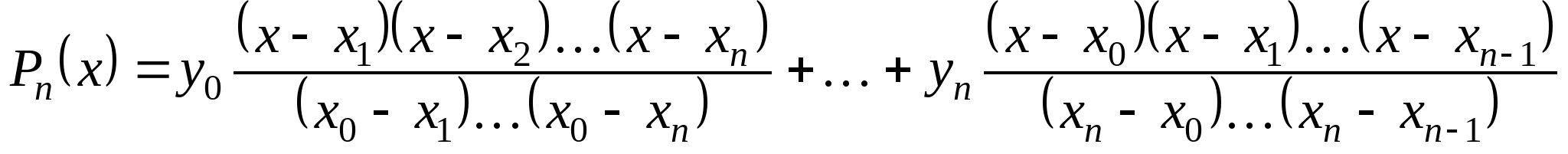 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
11. Какая из формул называется второй интерполяционной формулой Ньютона?
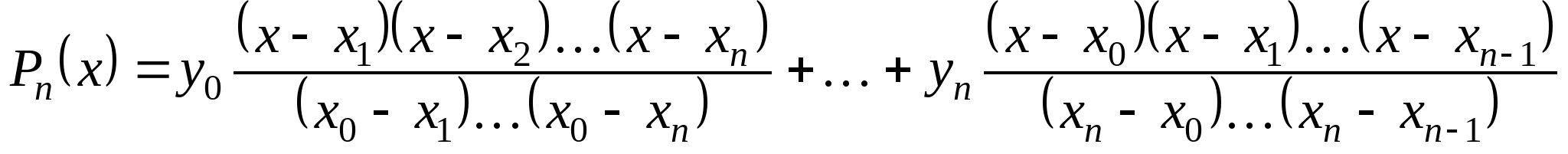 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
12. Какая из формул называется формулой линейной интерполяции?
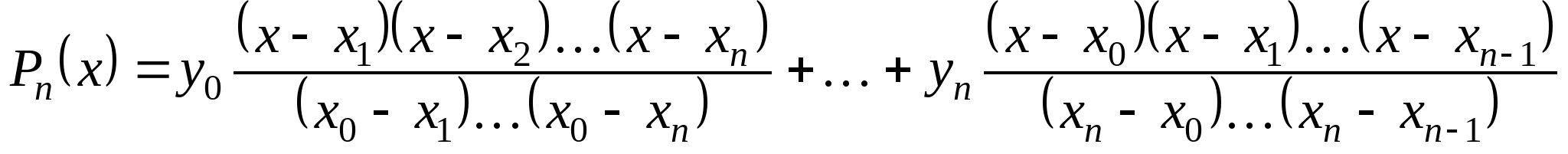 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
13. Какая из формул называется формулой квадратичной интерполяции?
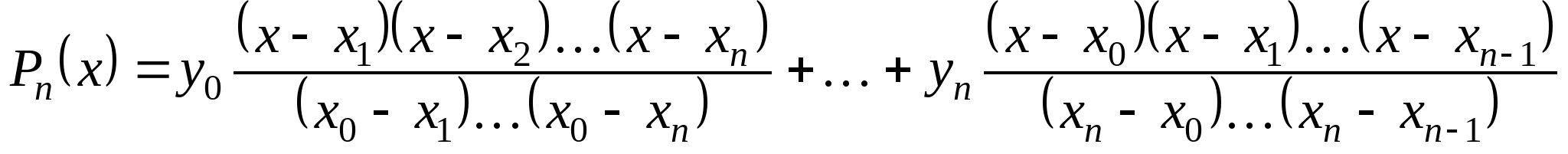 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
14. Как называется интерполяционная формула ![]() , построенная для равноотстоящих узлов:
, построенная для равноотстоящих узлов:
1. интерполяционная формула Лагранжа;
2. первая интерполяционная формула Ньютона;
3. вторая интерполяционная формула Ньютона;
4. формула квадратичной интерполяции;
5. формула линейной интерполяции.
15. Как называется интерполяционная формула ![]() , построенная для равноотстоящих узлов:
, построенная для равноотстоящих узлов:
1. интерполяционная формула Лагранжа;
2. первая интерполяционная формула Ньютона;
3. вторая интерполяционная формула Ньютона;
4. формула квадратичной интерполяции;
5. формула линейной интерполяции.
16. По таблице из трех узловых точек
|
| 0.1 | 0.2 | 0.3 |
|
| 0.1 | 0.2 | 0.3 |
можно построить интерполяционный полином Лагранжа второго порядка. Чему будут равны коэффициенты ![]() ?
?
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
17. По таблице из трех равноотстоящих узловых точек
|
| 0.1 | 0.2 | 0.3 |
|
| 0.1 | 0.2 | 0.3 |
найти табличные разности первого и второго порядка.
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]() .
.
18. Какое из приведенных ниже понятий не используется в теории численного интегрирования?
квадратурные и кубатурные формулы;
квадратурная формула Ньютона-Котеса;
коэффициенты Котеса;
достаточные условия сходимости;
формула Симпсона.
19. Как называется частный случай квадратурной формулы Ньютона-Котеса при ![]() ?
?
формула Ньютона;
формула Котеса;
формула трапеций;
формула Симпсона;
формула Эйлера.
20. Как называется частный случай квадратурной формулы Ньютона-Котеса при ![]() ?
?
формула Ньютона;
формула Котеса;
формула трапеций;
формула Симпсона;
формула Эйлера.
21. Как называется следующая квадратурная формула: 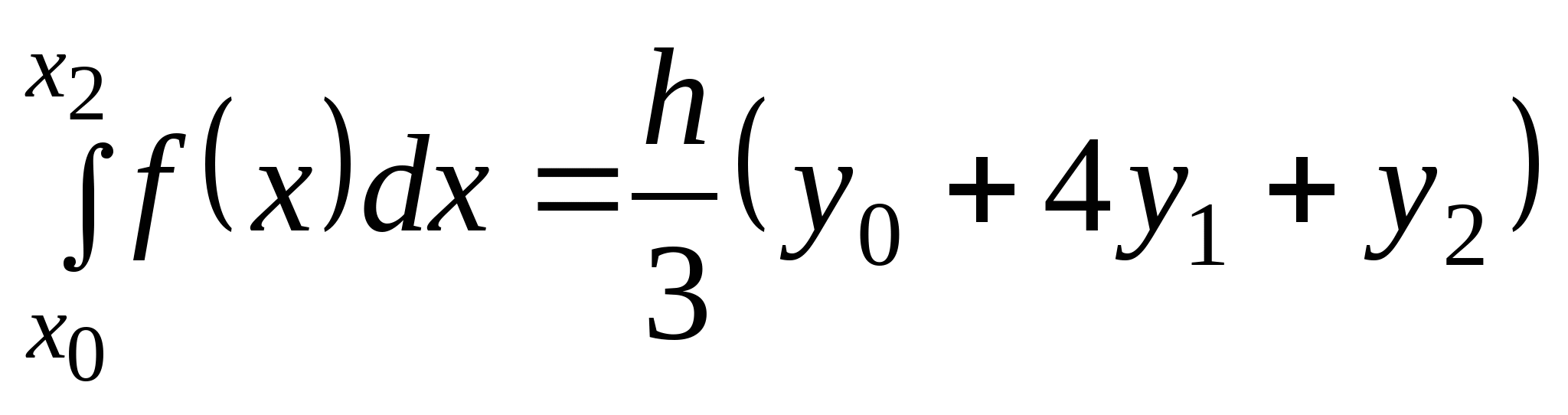 ?
?
формула Ньютона-Котеса;
формула трапеций;
формула Симпсона;
формула Ньютона;
формула Котеса.
22. Как называются коэффициенты вида: ![]() ,
, ![]() , используемые в теории численного интегрирования?
, используемые в теории численного интегрирования?
коэффициенты Лагранжа;
коэффициенты Ньютона;
коэффициенты Ньютона-Котеса;
коэффициенты Котеса;
коэффициенты Симпсона.
23. Как называется следующая квадратурная формула: ![]() ?
?
формула Котеса;
формула Ньютона-Котеса;
формула Симпсона;
формула трапеций;
формула Ньютона.
24. Как называются величины ![]() , используемые в теории интерполирования функций?
, используемые в теории интерполирования функций?
табличные разности первого порядка;
табличные разности второго порядка;
табличные разности различных порядков;
равноотстоящие узловые точки;
неравноотстоящие узловые точки.
25. Как называется величина ![]() , используемая в теории интерполирования функций?
, используемая в теории интерполирования функций?
табличные разности первого порядка;
табличные разности второго порядка;
табличные разности различных порядков;
равноотстоящие узловые точки;
неравноотстоящие узловые точки.
26. Как называется величина ![]() , используемая в теории интерполирования функций?
, используемая в теории интерполирования функций?
табличные разности первого порядка;
табличные разности второго порядка;
табличные разности различных порядков;
равноотстоящие узловые точки;
неравноотстоящие узловые точки.
27. Какие понятия используются в задаче аппроксимации?
отклонение построенной функции от экспериментальной;
узловые точки;
полином ![]() -й степени;
-й степени;
коэффициенты полинома;
все ответы правильные.
28. Какие понятия используются в теории численного интегрирования?
однократные и двукратные интегралы;
квадратурные и кубатурные формулы;
квадратурные формулы Ньютона-Котеса, трапеций, Симпсона;
обобщенная кубатурная формула Симпсона;
все ответы правильные.
29. Как называется следующая квадратурная формула: 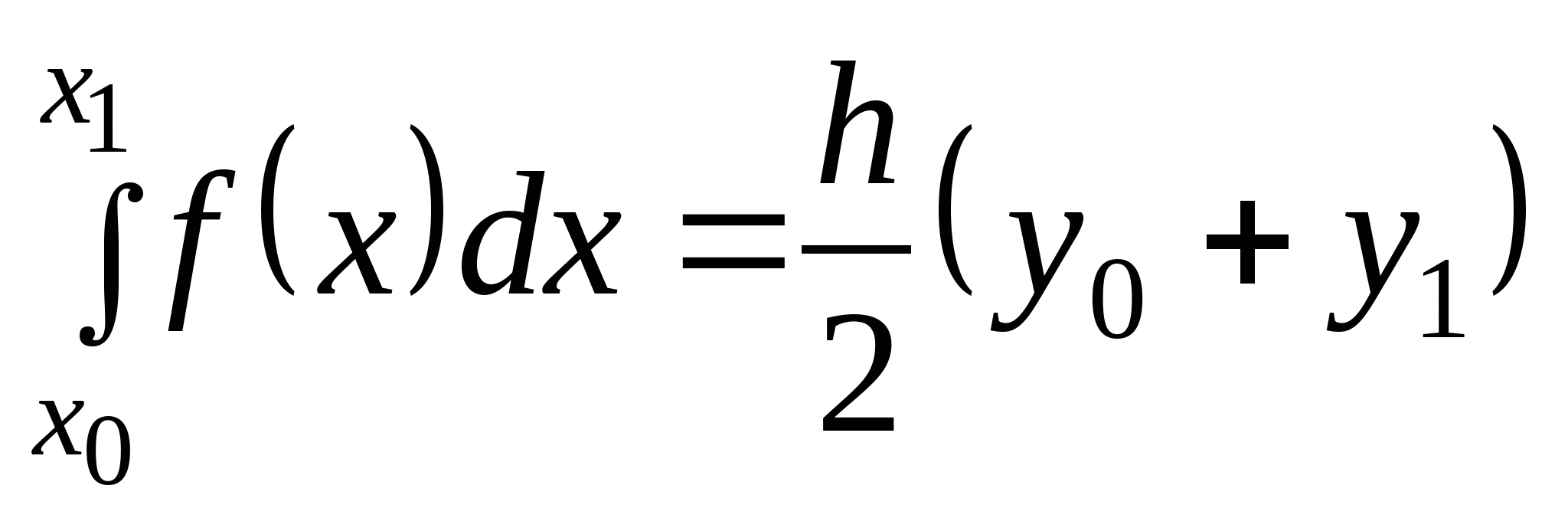 ?
?
формула Ньютона;
формула Котеса;
формула Симпсона;
формула Лагранжа;
формула трапеций.
30. В чем состоит основная идея метода наименьших квадратов?
по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция проходила через узловые точки;
по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция не проходила через узловые точки;
по заданной таблице значений построить приближенно функцию таким образом, чтобы построенная функция могла как проходить через узловые точки, так и не проходить через них;
по данным эксперимента построить приближенно функцию таким образом, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальна;
по данным эксперимента построить приближенно функцию таким образом, чтобы сумма отклонений построенной функции от экспериментальной в узловых точках была минимальна.
31. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() .
.
Строится и решается СЛАУ относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
32. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() .
.
Строится и решается СЛАУ относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
33. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() .
.
Строится и решается система нелинейных уравнений относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
34. Когда возникает задача численного дифференцирования?
необходимо знать значения производных в узловых точках для функций, заданных таблицей, или для функций, имеющих сложный аналитический вид;
необходимо знать значения функции между узловыми точками;
необходимо знать значения функции в точках, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблично;
необходимо представить в более простом виде сложную аналитически заданную функцию.
35. Продолжите определение собственного интеграла: «Интеграл вида ![]() называется собственным, если:
называется собственным, если:
промежуток интегрирования ![]() конечен и подынтегральная функция
конечен и подынтегральная функция ![]() разрывна на
разрывна на ![]() »;
»;
промежуток интегрирования ![]() бесконечен и подынтегральная функция
бесконечен и подынтегральная функция ![]() разрывна на
разрывна на ![]() »;
»;
промежуток интегрирования ![]() конечен и подынтегральная функция
конечен и подынтегральная функция ![]() непрерывна на
непрерывна на ![]() »;
»;
промежуток интегрирования ![]() бесконечен и подынтегральная функция
бесконечен и подынтегральная функция ![]() непрерывна на
непрерывна на ![]() »;
»;
промежуток интегрирования ![]() бесконечен или подынтегральная функция
бесконечен или подынтегральная функция ![]() разрывна на
разрывна на ![]() ».
».
36. Продолжите определение несобственного интеграла: «Интеграл вида ![]() называется несобственным, если:
называется несобственным, если:
промежуток интегрирования ![]() бесконечен или подынтегральная функция
бесконечен или подынтегральная функция ![]() разрывна на
разрывна на ![]() »;
»;
промежуток интегрирования ![]() бесконечен и (или) подынтегральная функция
бесконечен и (или) подынтегральная функция ![]() разрывна на
разрывна на ![]() »;
»;
промежуток интегрирования ![]() бесконечен и подынтегральная функция
бесконечен и подынтегральная функция ![]() разрывна на
разрывна на ![]() »;
»;
промежуток интегрирования ![]() конечен и подынтегральная функция
конечен и подынтегральная функция ![]() непрерывна на
непрерывна на ![]() »;
»;
промежуток интегрирования ![]() бесконечен или подынтегральная функция
бесконечен или подынтегральная функция ![]() непрерывна на
непрерывна на ![]() ».
».
37. В чем состоит принципиальное отличие теорий интерполяции и аппроксимации функций?
в задаче интерполяции искомый полином проходит через узловые точки; в задаче аппроксимации – не проходит через них;
в задаче интерполяции искомый полином проходит через узловые точки; в задаче аппроксимации – проходит на расстоянии, минимально удаленном от узловых точек;
в задаче интерполяции искомый полином не проходит через узловые точки; в задаче аппроксимации – проходит;
в задаче интерполяции искомый полином не проходит через узловые точки; в задаче аппроксимации – проходит на расстоянии, минимально удаленном от узловых точек;
принципиальных отличий нет.
38. Когда возникает задача численного интегрирования?
необходимо знать значения функции между узловыми точками;
необходимо знать значения функции для точек, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблицей;
необходимо представить в более простом виде сложную аналитически заданную функцию;
необходимо вычислить определенный интеграл от функций, заданных таблицей, или от функций, имеющих сложный аналитический вид.
39. По таблице узловых точек
|
| 0.1 | 0.11 | 0.14 |
|
| 0.1 | 0.3 | 0.9 |
|
|
|
|
|
| 0.35 | 0.042 | 1.3 | 0.169 |
1. ![]() .
.
2. ![]() .
.
3. ![]() .
.
4. ![]() .
.
5. ![]() .
.
40. По таблице узловых точек
|
| 0.1 | 0.11 | 0.14 |
|
| 0.1 | 0.3 | 0.9 |
|
|
|
|
|
|
|
|
| 0.35 | 0.042 | 0.1 | 0.04 | 1.3 | 0.169 | 0.022 |
1. 0.05;
2. -0.004;
3. 0.002;
4. 1.0;
5. 0.1.
1. Сделайте вывод о сходимости итерационного процесса ![]() , построенного для решения нелинейного уравнения
, построенного для решения нелинейного уравнения ![]() методом простых итераций на отрезке
методом простых итераций на отрезке ![]() .
.
сходится для любой точки из отрезка;
сходится только из определенной точки отрезка;
сходится только для одной из граничных точек отрезка;
расходится на всем отрезке;
расходится на всей числовой оси.
2. Чему равно значение ![]() , вычисленное по итерационной формуле
, вычисленное по итерационной формуле ![]() при
при ![]() ?
?
0.5;
0.875;
0.4;
0.8;
0.9.
3. Чему равно значение ![]() , вычисленное по итерационной формуле метода Ньютона для решения нелинейного уравнения
, вычисленное по итерационной формуле метода Ньютона для решения нелинейного уравнения ![]() при
при ![]() ?
?
0.636;
0.543;
1.8;
1.85;
1.9.
4. При нахождении корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом Ньютона в качестве начального приближения нужно выбрать
методом Ньютона в качестве начального приближения нужно выбрать ![]() равное:
равное:
0.5;
2;
1;
любой из концов отрезка;
любое значение из отрезка.
5. Для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом простых итераций в качестве начальной точки
методом простых итераций в качестве начальной точки ![]() можно выбрать:
можно выбрать:
любую точку из отрезка;
только одну из граничных точек, в которых выполняется достаточное условие сходимости ![]() ;
;
любую точку из отрезка, кроме граничных точек;
любую точку отрезка, если выполняется достаточное условие сходимости ![]() ;
;
любую точку вне отрезка.
6. Какой из приведенных ниже итерационных методов обладает квадратичной скоростью сходимости?
метод простых итераций;
метод Ньютона;
модифицированных метод Ньютона;
метод дихотомии;
метод Зейделя.
7. Итерационный процесс для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом простых итераций называется расходящимся, если:
методом простых итераций называется расходящимся, если:
процесс расходится хотя бы для одной начальной точки из отрезка.
процесс расходится для любой начальной точки из отрезка.
процесс расходится для любой начальной точки вне отрезка.
процесс расходится для любой начальной точки из отрезка, а вне его - сходится.
процесс сходится для любой начальной точки из отрезка, а вне его - расходится.
8. Какой из приведенных ниже итерационных методов является универсальным, самоисправляющимся и простым для реализации на ЭВМ?
метод простых итераций;
метод Ньютона;
модифицированных метод Ньютона;
метод дихотомии;
метод Зейделя.
9. Итерационный процесс для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом простых итераций называется сходящимся, если:
методом простых итераций называется сходящимся, если:
процесс сходится для любой начальной точки из отрезка.
процесс сходится для конкретной начальной точки из отрезка.
процесс сходится для одной из граничных точек отрезка, выбираемой в качестве начальной.
процесс сходится для любой начальной точки вне отрезка.
процесс сходится для обеих граничных точек отрезка, выбираемых в качестве начальных.
10. В каком из приведенных ниже итерационных методов для вычисления ![]() -го приближения каждой
-го приближения каждой ![]() -й компоненты вектора решения используются предыдущие компоненты от первой до
-й компоненты вектора решения используются предыдущие компоненты от первой до ![]() -й также
-й также ![]() -го приближения, а для остальных компонент от
-го приближения, а для остальных компонент от ![]() -й до
-й до ![]() -й используется
-й используется ![]() -е приближение?
-е приближение?
метод простых итераций;
метод Ньютона;
модифицированный метод Ньютона;
метод Зейделя;
метод дихотомии.
11. Если итерационный процесс, построенный по методу простых итераций для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() сходится, то в качестве начальной точки может быть выбрана:
сходится, то в качестве начальной точки может быть выбрана:
одна из граничных точек отрезка;
обе граничные точки отрезка;
середина отрезка;
любая точка отрезка;
все ответы правильные.
12. Для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом Ньютона в качестве начальной точки может быть выбрана:
методом Ньютона в качестве начальной точки может быть выбрана:
любая точка из отрезка;
любая из граничных точек отрезка;
одна из граничных точек отрезка;
середина отрезка;
одна из граничных точек отрезка, удовлетворяющая условиям ![]() ,
, ![]() .
.
13. По какой из итерационных формул осуществляется решение нелинейных уравнений вида ![]() методом Ньютона?
методом Ньютона?
1. ![]() ;
;
2. ![]() ;
;
3. 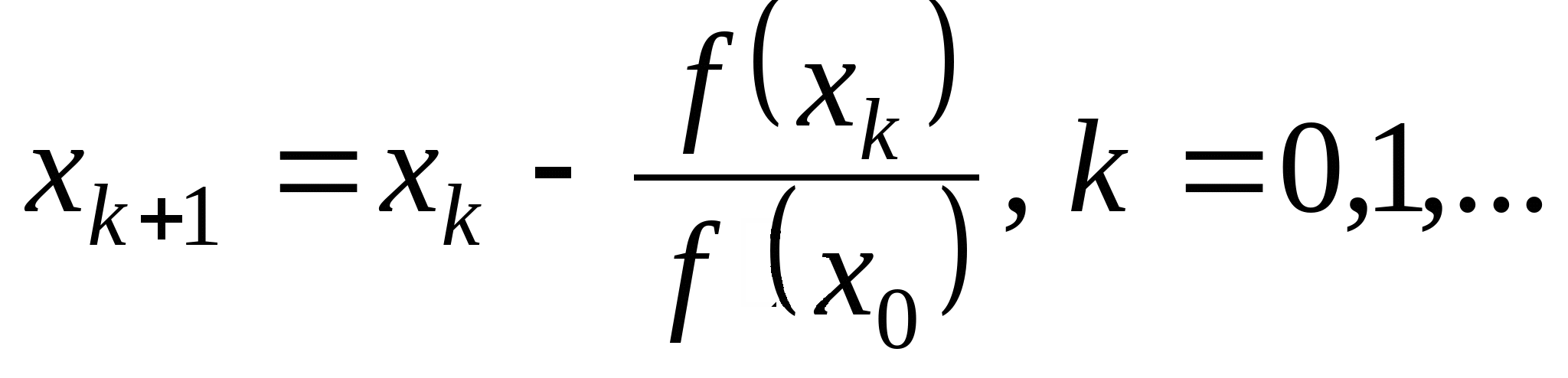 ;
;
4. 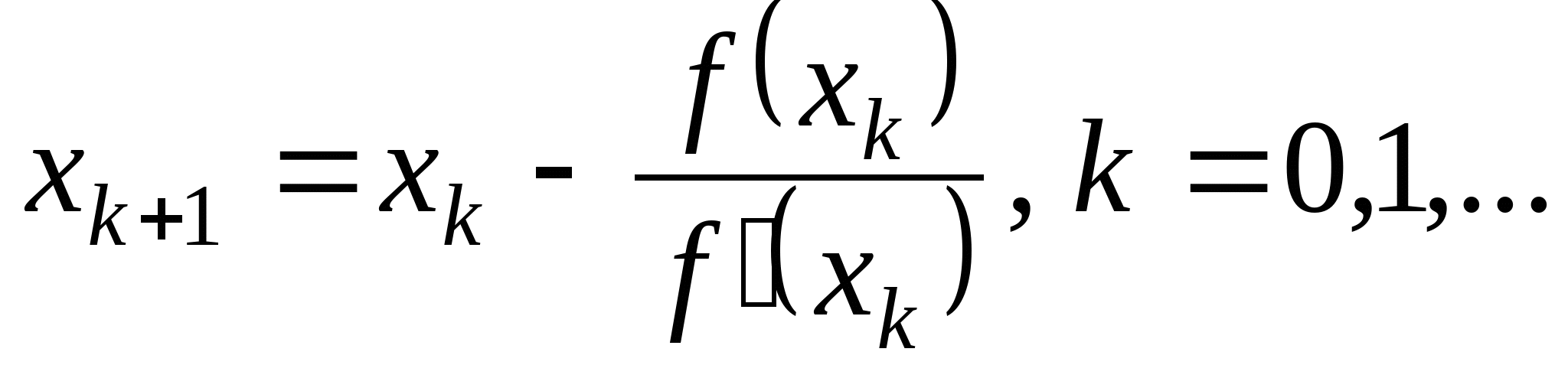 ;
;
5. 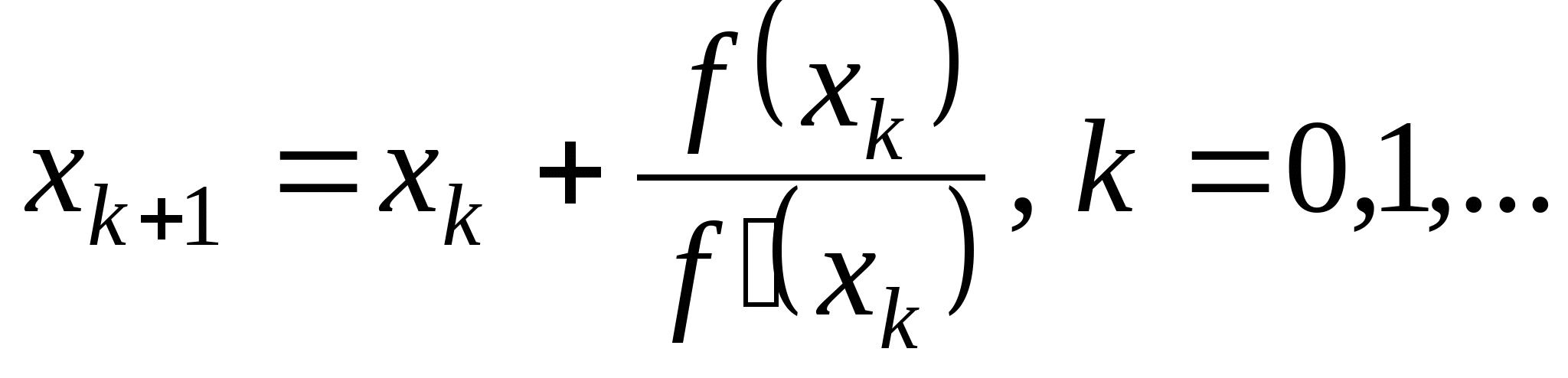 .
.
14. Какое число неизвестных постоянных необходимо определить для построения сходящегося итерационного процесса при решении системы нелинейных уравнений третьего порядка методом простых итераций?
1;
2;
4;
9;
16.
15. Что не характерно для графического метода отделения корней нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
представление функции ![]() в виде двух более простых функций
в виде двух более простых функций ![]() и
и ![]() ;
;
построение графиков функций ![]() и
и ![]() ;
;
построение графика функции ![]() и определение точек пересечения графика с осью абсцисс;
и определение точек пересечения графика с осью абсцисс;
определение точек пересечения графиков функций ![]() и
и ![]() ;
;
определение интервалов, в которых находится единственный корень.
16. Для чего предназначен этап отделения корней нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
для доказательства единственности корня на отрезке;
для доказательства существования корней на отрезке;
для доказательства отсутствия корней на отрезке;
для определения количества корней уравнения на отрезке ![]() и разбиения отрезка таким образом, чтобы каждый интервал содержал единственный корень;
и разбиения отрезка таким образом, чтобы каждый интервал содержал единственный корень;
для непосредственного определения значения корня на отрезке ![]() .
.
17. Итерационной формулой решения нелинейных уравнений вида ![]() является формула вида:
является формула вида:
![]() , где
, где ![]() ;
;
![]() где
где ![]() ;
;
![]() ;
;
![]() ;
;
все ответы правильные.
18. В чем состоит принципиальное отличие метода Ньютона от метода простых итераций для решения нелинейных уравнений и систем нелинейных уравнений?
другая итерационная формула;
требование к существованию производных (частных производных) от функций в левых частях уравнений (систем уравнений) на всей области;
более быстрая скорость сходимости, близкая к квадратичной;
трудность в выборе начальных условий;
все ответы правильные.
19. Какое условие является достаточным для сходимости итерационного процесса ![]() решения нелинейного уравнения
решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
20. Приведите условие окончания итерационного процесса по методу простых итераций для решения нелинейного уравнения ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
одновременное выполнение условий ![]() и
и ![]() ;
;
![]() .
.
21. Решение нелинейного уравнения ![]() начинается с:
начинается с:
определения знака производной ![]() на отрезке
на отрезке ![]() ;
;
записи итерационной формулы ![]() и проверки условия сходимости итерационного процесса на отрезке
и проверки условия сходимости итерационного процесса на отрезке ![]() ;
;
записи итерационной формулы ![]() , где значение постоянной
, где значение постоянной ![]() определяется из условий сходимости итерационного процесса;
определяется из условий сходимости итерационного процесса;
отделения корней исходного нелинейного уравнения;
определение начальных условий для начала итерационного процесса.
22. По какой из итерационных формул осуществляется решение нелинейного уравнения вида ![]() модифицированным методом Ньютона?
модифицированным методом Ньютона?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
23. При решении какого класса задач достаточные условия сходимости итерационного процесса имеют вид: ![]() или
или ![]() ?
?
1. решение нелинейных уравнений;
2. решение систем нелинейных уравнений;
3. решение систем линейных алгебраических уравнений;
4. решение линейных уравнений;
5. все ответы правильные.
24. К какому виду, допускающему сходящиеся итерации, необходимо привести СЛАУ ![]() для решения ее методом простых итераций?
для решения ее методом простых итераций?
![]() , где матрица
, где матрица ![]() определяется из достаточных условий сходимости;
определяется из достаточных условий сходимости;
![]() , где матрица
, где матрица ![]() определяется из достаточных условий сходимости;
определяется из достаточных условий сходимости;
![]() ,
, ![]() ;
;
![]() ;
;
все ответы правильные.
25. Решение системы нелинейных уравнений ![]() методом простых итераций в заданной области осуществляется по итерационным формулам вида:
методом простых итераций в заданной области осуществляется по итерационным формулам вида:
![]() , где функции
, где функции ![]() удовлетворяют достаточным условиям сходимости;
удовлетворяют достаточным условиям сходимости;
![]() , где функции
, где функции ![]() удовлетворяют достаточным условиям сходимости;
удовлетворяют достаточным условиям сходимости;
![]() , где функции
, где функции ![]() удовлетворяют достаточным условиям сходимости;
удовлетворяют достаточным условиям сходимости;
![]() , где функции
, где функции ![]() удовлетворяют достаточным условиям сходимости;
удовлетворяют достаточным условиям сходимости;
![]() , где функции
, где функции ![]() удовлетворяют достаточным условиям сходимости.
удовлетворяют достаточным условиям сходимости.
26. Продолжите формулировку теоремы, применяемой для отделения корней нелинейного уравнения ![]() на отрезке
на отрезке ![]() : «Если функция
: «Если функция ![]() является многочленом
является многочленом ![]() -й степени и на концах отрезка
-й степени и на концах отрезка ![]() меняет знак (
меняет знак (![]() ), то:
), то:
на отрезке содержится единственный корень».
на отрезке содержится хотя бы один корень».
на отрезке корней нет».
на отрезке содержится четное число корней».
на отрезке содержится нечетное число корней».
27. Продолжите формулировку теоремы, применяемой для отделения корней нелинейного уравнения ![]() на отрезке
на отрезке ![]() : «Если функция
: «Если функция ![]() является многочленом
является многочленом ![]() -й степени и на концах отрезка
-й степени и на концах отрезка ![]() не меняет знак (
не меняет знак (![]() ), то:
), то:
на отрезке либо не имеется корней, либо имеется четное число корней».
на отрезке либо имеется единственный корень, либо имеется нечетное число корней».
на отрезке корней нет».
на отрезке содержится хотя бы один корень».
на отрезке содержится единственный корень».
28. Сформулируйте теорему о существовании хотя бы одного корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() где
где ![]() - произвольная нелинейная функция.
- произвольная нелинейная функция.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на отрезке содержится хотя бы один корень.
, то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка не меняет знак (
и на концах отрезка не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка меняет знак (
и на концах отрезка меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() не меняет знак (
не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() меняет знак (
меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
29. Сформулируйте теорему о существовании единственного корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() где
где ![]() - произвольная нелинейная функция.
- произвольная нелинейная функция.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , на концах отрезка меняет знак (
, на концах отрезка меняет знак (![]() ), то на отрезке содержится единственный корень.
), то на отрезке содержится единственный корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и производная
и производная ![]() на отрезке знак сохраняет, то на отрезке содержится единственный корень.
на отрезке знак сохраняет, то на отрезке содержится единственный корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() меняет знак (
меняет знак (![]() ) и производная
) и производная ![]() на отрезке знак сохраняет, то на отрезке содержится единственный корень.
на отрезке знак сохраняет, то на отрезке содержится единственный корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка не меняет знак (
и на концах отрезка не меняет знак (![]() ), то на отрезке содержится единственный корень.
), то на отрезке содержится единственный корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , на концах отрезка меняет знак (
, на концах отрезка меняет знак (![]() ) и производная
) и производная ![]() на отрезке знак сохраняет, то на отрезке содержится единственный корень.
на отрезке знак сохраняет, то на отрезке содержится единственный корень.
30. При решении какого класса задач достаточные условия сходимости итерационного процесса имеют вид: ![]() или
или ![]() ?
?
решение нелинейных уравнений;
решение систем нелинейных уравнений;
решение систем линейных алгебраических уравнений;
задача интерполяции функций;
задача численного интегрирования.
31. Продолжите формулировку теоремы, применяемой для отделения корней нелинейного уравнения ![]() на отрезке
на отрезке ![]() в случае произвольной нелинейной функции
в случае произвольной нелинейной функции ![]() : «Если функция
: «Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , на концах отрезка меняет знак (
, на концах отрезка меняет знак (![]() ) и производная
) и производная ![]() на отрезке знак сохраняет, то:
на отрезке знак сохраняет, то:
на отрезке содержится единственный корень».
на отрезке содержится хотя бы один корень».
на отрезке корней нет».
на отрезке содержится четное число корней».
на отрезке содержится нечетное число корней».
32. Продолжите формулировку теоремы, применяемой для отделения корней нелинейного уравнения ![]() на отрезке
на отрезке ![]() в случае произвольной нелинейной функции
в случае произвольной нелинейной функции ![]() : «Если функция
: «Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка меняет знак (
и на концах отрезка меняет знак (![]() ), то:
), то:
на отрезке содержится единственный корень».
на отрезке содержится хотя бы один корень».
на отрезке корней нет».
на отрезке содержится четное число корней».
на отрезке содержится нечетное число корней».
33. К какому виду, допускающему сходящиеся итерации, нужно привести систему нелинейных уравнений второго порядка?
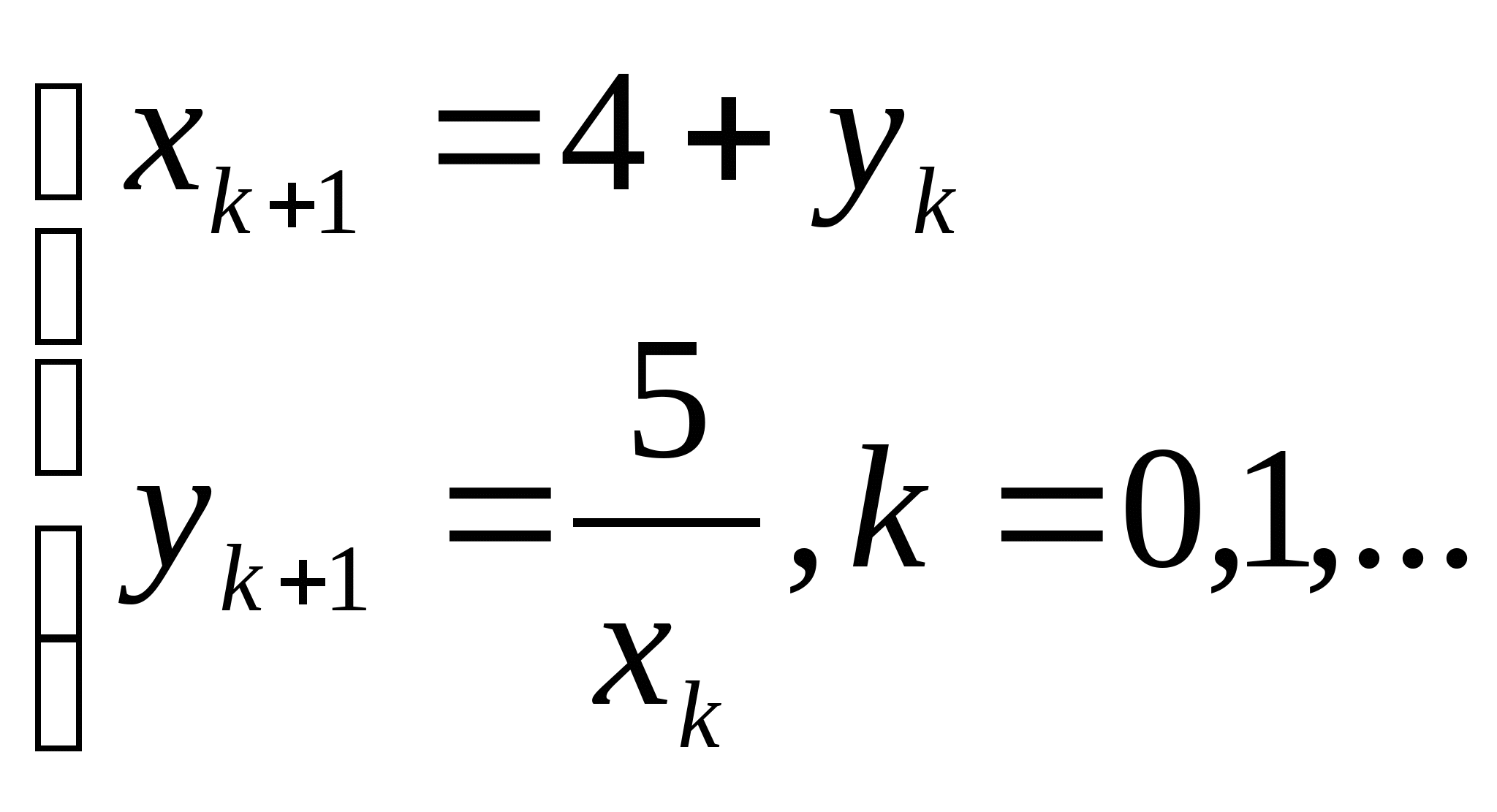 ;
;
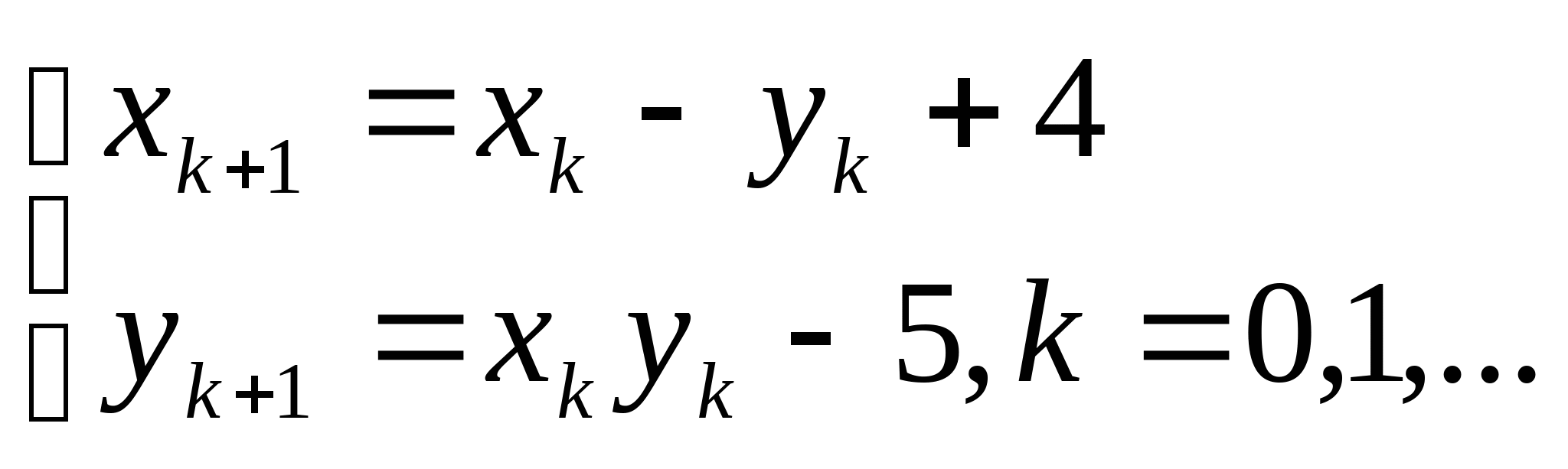 ;
;
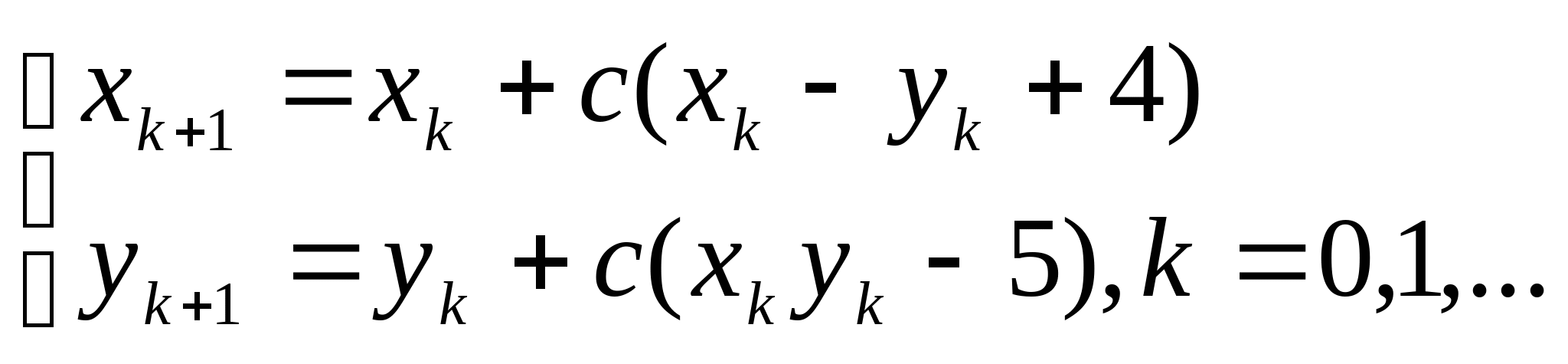 , где константа
, где константа ![]() выбирается из достаточных условий сходимости итерационного процесса;
выбирается из достаточных условий сходимости итерационного процесса;
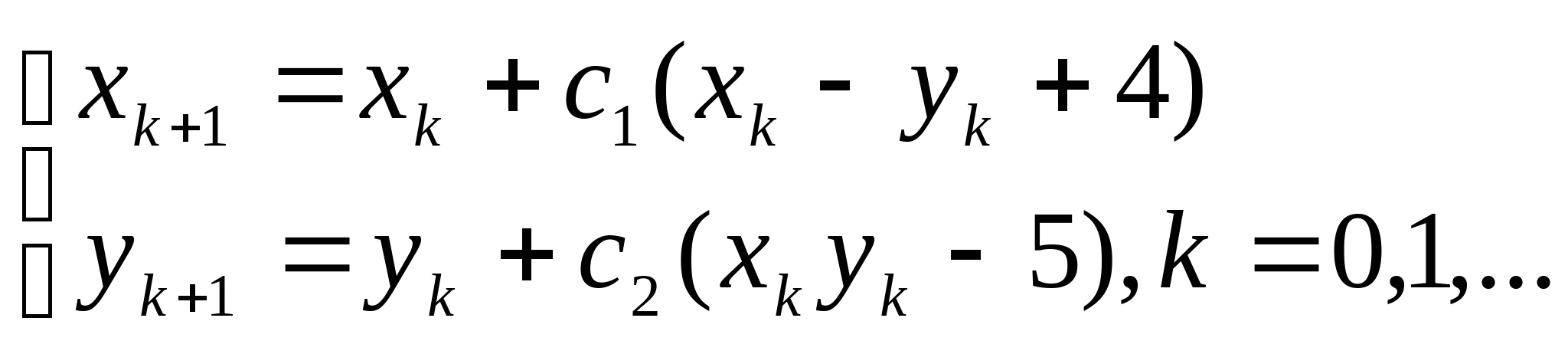 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса;
выбираются из достаточных условий сходимости итерационного процесса;
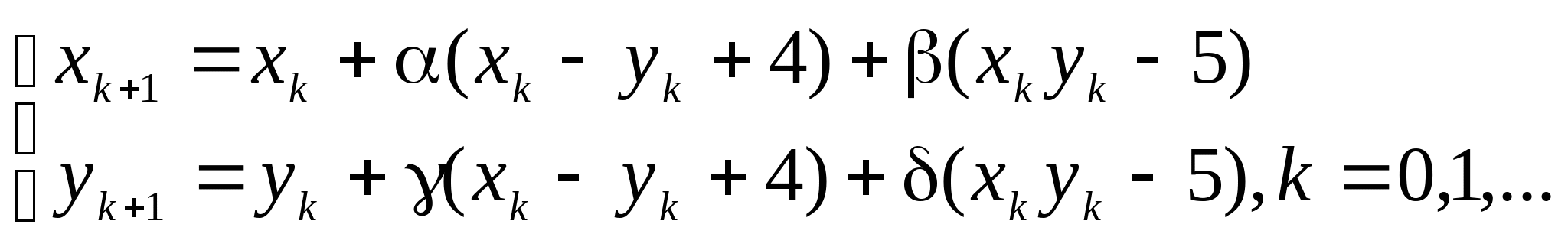 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса.
выбираются из достаточных условий сходимости итерационного процесса.
34. Чему равно следующее приближение ![]() , вычисленное по итерационной формуле
, вычисленное по итерационной формуле 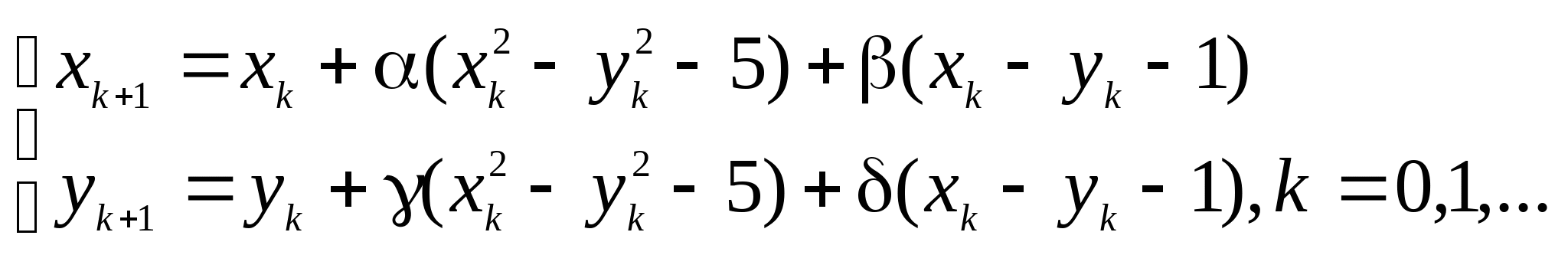 при
при ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
35. Чему равно следующее приближение ![]() , вычисленное по итерационной формуле метода Зейделя для решения СЛАУ вида
, вычисленное по итерационной формуле метода Зейделя для решения СЛАУ вида 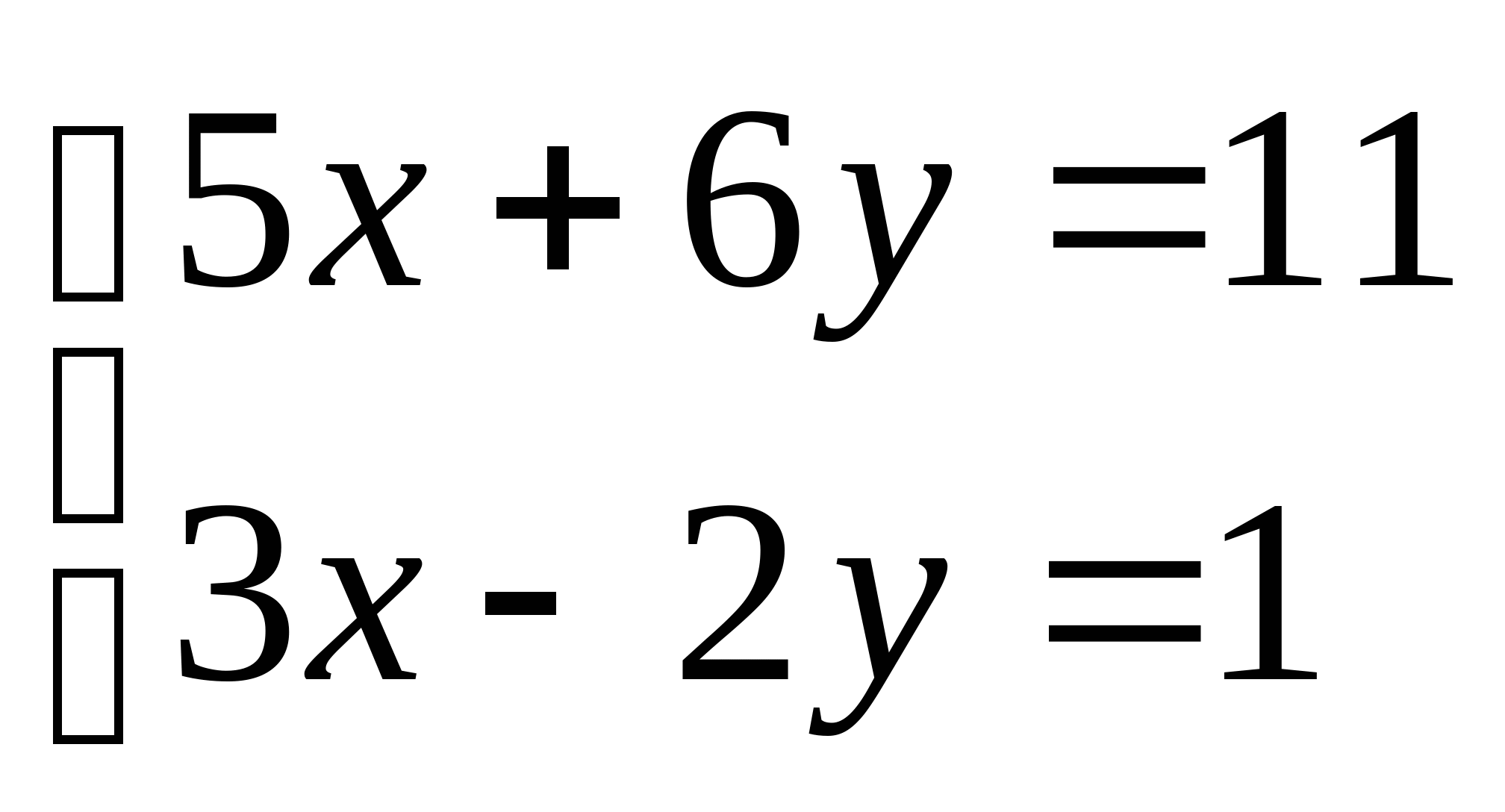 при
при ![]() ?
?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() .
.
36. При численном решении СЛАУ ![]() ее необходимо привести к виду, допускающему сходящиеся итерации
ее необходимо привести к виду, допускающему сходящиеся итерации ![]() . Чему равно значение коэффициента
. Чему равно значение коэффициента ![]() для СЛАУ вида
для СЛАУ вида 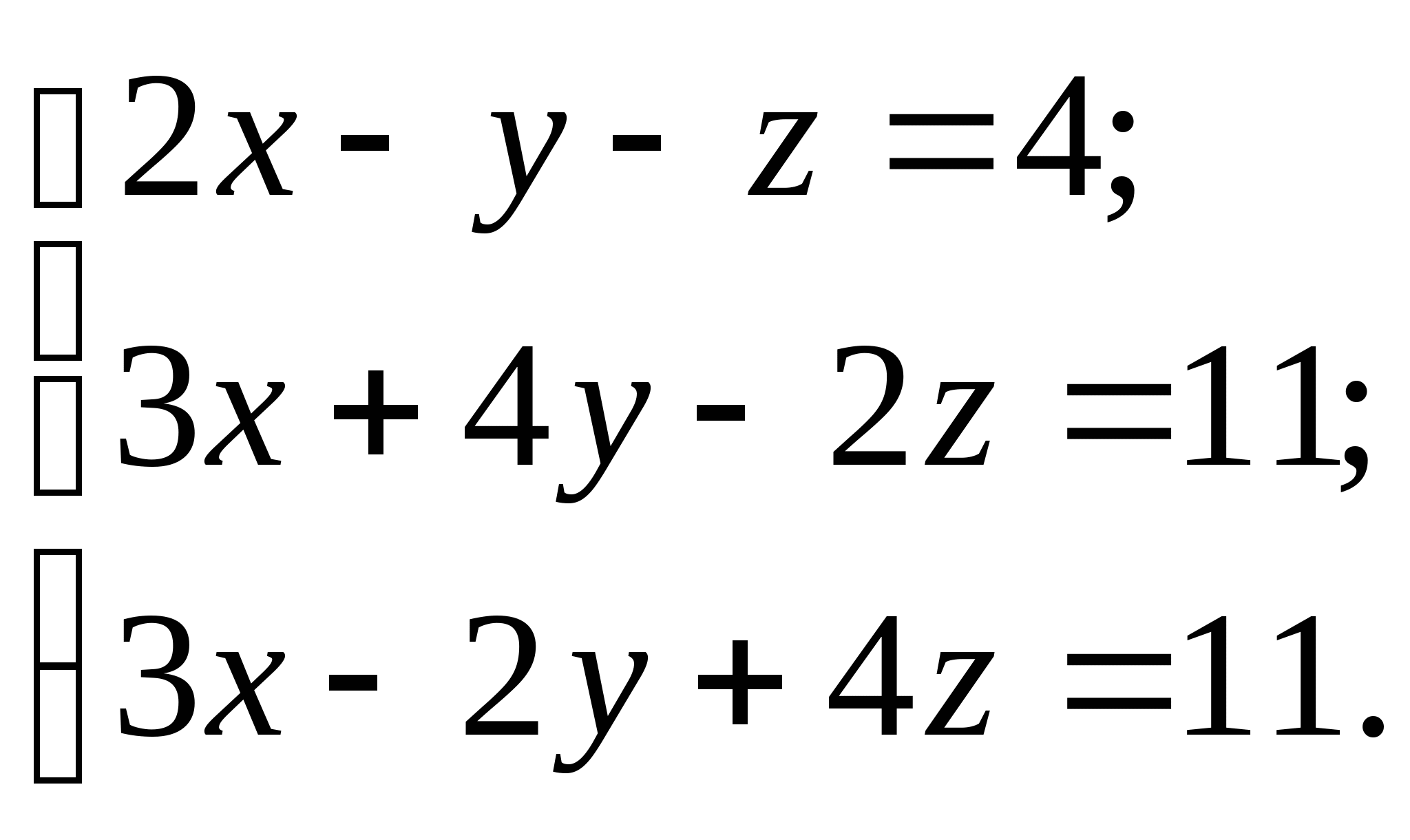 ?
?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. 1.
37. Для приближенного решения нелинейных уравнений применяется:
1. метод деления отрезка пополам;
2. метод простых итераций;
3. метод Ньютона;
4. модифицированный метод Ньютона;
5. все ответы правильные.
38. Какой метод приближенного решения нелинейных уравнений ![]() на отрезке
на отрезке ![]() приведен на рисунке:
приведен на рисунке:
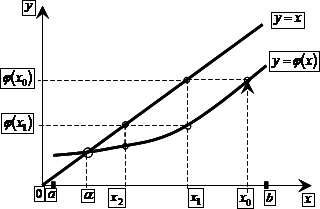
1. метод простых итераций (сходимость типа «лестница»);
2. метод простых итераций (сходимость типа «спираль»);
3. метод простых итераций (расходящийся процесс);
4. метод Ньютона;
5. модифицированный метод Ньютона.
39. Какой метод приближенного решения нелинейных уравнений ![]() на отрезке
на отрезке ![]() приведен на рисунке:
приведен на рисунке:
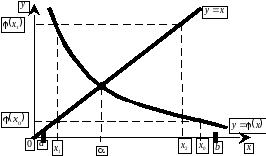
1. метод простых итераций (сходимость типа «лестница»);
2. метод простых итераций (сходимость типа «спираль»);
3. метод простых итераций (расходящийся процесс);
4. метод Ньютона;
5. модифицированный метод Ньютона.
40. Какой метод приближенного решения нелинейных уравнений ![]() на отрезке
на отрезке ![]() приведен на рисунке:
приведен на рисунке:
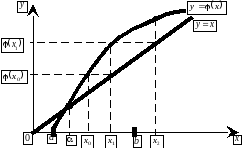
1. метод простых итераций (сходимость типа «лестница»);
2. метод простых итераций (сходимость типа «спираль»);
3. метод простых итераций (расходящийся процесс);
4. метод Ньютона;
5. модифицированный метод Ньютона.
41. Какой метод приближенного решения нелинейных уравнений ![]() на отрезке
на отрезке ![]() приведен на рисунке:
приведен на рисунке:
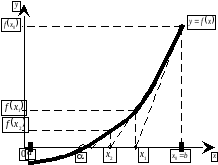
1. метод простых итераций (сходимость типа «лестница»);
2. метод простых итераций (сходимость типа «спираль»);
3. метод простых итераций (расходящийся процесс);
4. метод Ньютона;
5. модифицированный метод Ньютона.
42. Какой метод приближенного решения нелинейных уравнений ![]() на отрезке
на отрезке ![]() приведен на рисунке:
приведен на рисунке:
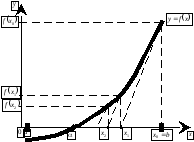
1. метод простых итераций (сходимость типа «лестница»);
2. метод простых итераций (сходимость типа «спираль»);
3. метод простых итераций (расходящийся процесс);
4. метод Ньютона;
5. модифицированный метод Ньютона.
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. А.Н. ТУПОЛЕВА
УТВЕРЖДАЮ:
Проректор по учебной и методической
работе
_________________ И.К. Насыров
«_____» _______________ 2007 г.
ПРОГРАММА ДИСЦИПЛИНЫ
ЕН.Ф.04 "ЧИСЛЕННЫЕ МЕТОДЫ И МАТЕМАТИЧЕСКОЕ
МОДЕЛИРОВАНИЕ"
Рекомендуется УМЦ КГТУ им. А.Н. Туполева для направлений
(специальностей)
специальности: 010400 (010701)* «Физика»
формы обучения: очная
*) коды направлений и специальностей указаны по Общероссийскому классификатору специальностей по образованию (ОК 009-2003)
Цели и задачи дисциплиныЦелью и задачами дисциплины является изучение основных положений вычислительной математики, знакомство с приближенными методами решения реальных инженерных задач на ЭВМ, современными методами решения задач, связанных с дифференциальными уравнениями, в объеме, достаточном для квалифицированного решения основных профессиональных задач будущими инженерами.
Материал курса основан на знаниях, навыках и умениях полученных при обучении в среднем образовательном учреждении, а также получаемых студентами при изучении дисциплин: «Алгебра и геометрия», «Математический анализ», «Дифференциальные уравнения», «Программирование на языках высокого уровня», «Информатика».
Студенты должны быть знакомы с основными алгебраическими структурами («Алгебра и геометрия»); с понятиями функции и ее непрерывности, с понятиями множества, отношения («Математический анализ»); с понятиями обыкновенных и систем обыкновенных дифференциальных уравнений, аналитическими методами их решения («Дифференциальные уравнения»); способами записи алгоритма, стандартными типами данных («Программирование на языках высокого уровня»); с основными приемами работы в операционных системах MS DOS и Windows, а также с основными офисными системами MS Word и MS Excel («Информатика»).
Студенты должны иметь практические навыки решения линейных алгебраических и нелинейных уравнений и систем («Алгебра и геометрия»), решения обыкновенных и систем обыкновенных дифференциальных уравнений («Дифференциальные уравнения»), уметь строить схемы алгоритмов и программ («Программирование на языках высокого уровня»).
Знания, умения и навыки, полученные в процессе изучения данного курса, могут быть использованы студентами для изучения дисциплин «Технологии программирования», «Операционные системы», «Базы данных», «Управление данными», «Информационные технологии», «Сетевые технологии», «Теория принятия решений», а также при прохождении вычислительной практики студентами второго курса очной формы обучения.
Требования к уровню освоения содержания дисциплины
В результате изучения дисциплины студенты должны:
знать:основные численные методы решения нелинейных уравнений, систем нелинейных и линейных алгебраических уравнений;
методы интерполирования, аппроксимирования и экстраполирования функций;
методы численного решения задачи Коши для обыкновенных дифференциальных уравнений;
условий сходимости методов, областей применения численных методов, условий окончания итерационных процессов по каждому методу.
уметь:выводить итерационные формулы для решения конкретной задачи выбранным методом;
составлять и отлаживать программу для конкретного метода;
объяснять полученные результаты.
иметь опыт выбора метода численного решения конкретной задачи. иметь представление:о вычислительной математике как науке о численных (приближенных) методах решения математических и реальных инженерных задач;
о методах и алгоритмах численного решения задач, сходимости методов, погрешностях вычислений, теоретическом обосновании ряда методов, достоинствах и недостатках методов;
о состоянии и тенденциях развития вычислительной математики.
Объем дисциплины и виды учебной работы
| Виды учебной работы | Очное | |
| Всего | Семестры | |
| 3 | ||
| Общая трудоемкость дисциплины | 65 | 65 |
| Аудиторные занятия (всего) | 51 | 51 |
| Лекции | 34 | 34 |
| Практические занятия (ПЗ) | 0 | 0 |
| Семинары (С) | 0 | 0 |
| Лабораторные работы (ЛР) | 17 | 17 |
| Другие виды аудиторных занятий | 0 | 0 |
| Самостоятельная работа (всего) | 14 | 14 |
| Курсовой проект (работа) | 0 | 0 |
| Расчетно-графические работы | 0 | 0 |
| Реферат | 0 | 0 |
| Другие виды самостоятельной работы | 0 | 0 |
| Вид итогового контроля | Зачет | |
Содержание дисциплины
Тематический план *):
| № пп | Наименование тем | Очное | |
| ЛК | ЛБ | ||
| 1 | Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. | 4 | 0 |
| 2 | Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений. | 14 | 7 |
| 3 | Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. | 10 | 6 |
| 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. | 6 | 4 |
| Всего | 34 | 17 | |
*) Используемые сокращения: ЛК –лекции, ЛБ – лабораторные работы.
Содержание тем
1. Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. (4/1ч.).
1.1. Основные понятия дисциплины (1/0ч.).
Понятие приближенных (численных) методов решения математических задач. Место численных методов в математическом анализе. Понятие вычислительной математики, предмет изучения вычислительной математики. Понятия итерационных методов и погрешностей вычислений, вычислительной схемы. Проблема «устойчивости вычислительных методов» и сложности алгоритма.
1.2. Учет погрешностей при вычислениях (2/1ч.).
Источники и классификация погрешностей. Основные понятия и определения теории погрешностей. Округление чисел. Погрешности алгебраической суммы, произведения, частного, степени, корня, функции. Правило сложения приближенных чисел. Обратная задача теории погрешностей.
1.3. Вычислительные программные системы (1/0ч.).Основы работы с MS Excel, MathCad, MathLab с точки зрения решения задач вычислительной математики.
2. Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений (14/7ч.). 2.1. Приближенные методы решения нелинейных уравнений (8/4ч.). Понятия отделения и уточнения корней нелинейных уравнений на отрезке. Графический и аналитический методы отделения корней. Геометрическая интерпретация графического и аналитического методов. Методы уточнения корней: метод дихотомии, метод простых итераций, метод Ньютона (касательных), модифицированный метод Ньютона.
Метод простых итераций: понятия начального приближения и итерационного процесса; достаточное условие сходимости итерационного процесса; критерии останова итерационного процесса. Геометрическая интерпретация метода простых итераций. Приведение нелинейного уравнения к виду, допускающего сходящиеся итерации. Достоинства и недостатки метода простых итераций.
Метод Ньютона, его геометрическая интерпретация, рабочая формула, выбор начального приближения. Достаточное условие сходимости. Критерий останова итерационного процесса. Достоинства и недостатки метода Ньютона. Модифицированный метод Ньютона, его геометрическая интерпретация и рабочая формула.
2.2. Приближенные методы решения систем нелинейных уравнений (3/2ч.).Понятие системы нелинейных уравнений (СНУ). Проблема отделения корней СНУ. Приближенные методы решения СНУ. Метод простых итераций, понятия начального приближения, итерационного процесса. Достаточные условия сходимости итерационного процесса. Критерий останова итерационного процесса. Приведение исходной системы к системе, допускающей сходящиеся итерации на примере системы второго порядка. Достоинства и недостатки метода простых итераций для решения СНУ.
Метод Ньютона для решения СНУ, его рабочая формула и критерий останова итерационного процесса. Достаточное условие сходимости. Достоинства и недостатки метода Ньютона. Рабочая формула модифицированного метода Ньютона.
2.3. Приближенные методы решения систем линейных алгебраических уравнений (3/1ч).Методы решения систем линейных алгебраических уравнений. Метод простых итераций, его рабочие формулы и критерий останова; выбор начального приближения; достаточные условия и необходимые и достаточные условия сходимости итерационного процесса; приведение исходной системы к системе, допускающей сходящиеся итерации; достоинства и недостатки метода простых итераций.
Рабочие формулы методы Зейделя, критерий останова, необходимые и достаточные условия сходимости метода. Достоинства и недостатки метода.
Метод релаксации. Приведение исходной системы к виду, пригодному для релаксации. Понятие невязки. Рабочие формулы метода. Критерии останова процесса.3. Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. (10/3ч.). 3.1. Построение интерполяционных формул Лагранжа, первой и второй формул Ньютона (3/1ч.).
Постановка задачи интерполирования функций по заданной системе точек, понятие равноотстоящих и неравноотстоящих узловых точек. Принципы построения интерполяционной формулы Лагранжа, первой и второй интерполяционной формулы Ньютона, их форма записи и погрешности вычислений по ним. Формулы линейной и квадратичной интерполяции. Понятие табличных разностей различных порядков.
3.2. Основные приложения теории интерполяции (4/1ч.).Понятие численного дифференцирования. Основные принципы решения задачи численного дифференцирования на примере использования таблицы узловых точек и интерполяционных полиномов. Погрешность построенных формул.
Понятие численного интегрирования, квадратурных формул. Построение квадратурной формулы Ньютона-Котеса с использованием интерполяционных формул, коэффициенты Котеса. Частные случаи формулы Ньютона-Котеса (формула трапеций и формула Симпсона) и их геометрическая интерпретация. Погрешность построенных формул. Понятие несобственных интегралов. Приближенное вычисление несобственных интегралов. Случаи бесконечного отрезка интегрирования с непрерывной подынтегральной функцией и разрывной на конечном отрезке интегрирования подынтегральной функцией, их геометрическая интерпретация.
Приближенное вычисление двойных интегралов: понятие кубатурных формул; вывод кубатурной и обобщенной кубатурной формул типа Симпсона для различных видов областей интегрирования. 3.3. Метод наименьших квадратов для обработки результатов экспериментов (3/1ч.).Задача аппроксимирования функций по заданной системе точек. Общая идея метода наименьших квадратов. Понятие отклонения искомой функции от экспериментальной в узловых точках. Алгоритм метода наименьших квадратов и его теоретическое обоснование.
Аппроксимация с помощью экспоненциальных функций.
4. Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. (6/3ч.). 4.1. Приближенное решение обыкновенных дифференциальных уравнений и систем (3/0ч.).
Классификация методов решения и численных методов интегрирования дифференциальных уравнений. Понятия задачи Коши и шага интегрирования. Метод последовательных приближений (метод Пиккара). Метод Эйлера: общая идея метода, его графическая интерпретация и рабочая формула. Достоинства и недостатки метода. Рабочие формулы метода Эйлера для решения системы второго порядка дифференциальных уравнений.
Метод Рунге-Кутта. Общая идея методов Рунге-Кутта второго и четвертого порядков, их рабочие формулы. Достоинства и недостатки методов. Решение задачи Коши для системы второго порядка методом Рунге-Кутта четвертого порядка.
Метод Адамса. Достоинства и недостатки метода Адамса. Экстраполяционная и интерполяционная формулы Адамса для решения дифференциальных уравнений.
Непрерывные схемы решения нелинейных уравнений, условие их применения. Дифференциальное уравнение в отклонениях, его решение. Достоинства и недостатки непрерывных схем. Дифференциальное уравнение с малым параметром, его решение. Достоинства и недостатки методов решения нелинейных уравнений с использованием дифференциальных уравнений с малым параметром.
4.2. Приближенное решение краевых задач для дифференциальных уравнений второго порядка (1/1ч.).
Метод конечных разностей. Понятие краевой задачи для дифференциального уравнения второго порядка и ее геометрическая интерпретация при различных краевых условиях. Понятие двухточечной краевой задачи для линейного дифференциального уравнения второго порядка и ее форма записи. Метод конечных разностей для решения двухточечной краевой задачи для линейного дифференциального уравнения второго порядка.
Метод прогонки. Конечно-разностная и каноническая формы записи двухточечной краевой задачи для линейного дифференциального уравнения второго порядка. Алгоритм метода прогонки прямым и обратным ходом вычислений.
4.3. Приближенное решение краевых задач для дифференциальных уравнений в частных производных первого порядка (2/2ч.).
Методы моделирования и Монте-Карло для решения задачи Дирихле. Понятие дифференциального уравнения в частных производных первого порядка эллиптического типа. Понятие краевых задач для уравнений эллиптического типа. Понятие задачи Дирихле. Решение задачи Дирихле методом моделирования и Монте-Карло.
Метод сеток и метод прогонки для решения уравнений параболического типа. Понятие дифференциального уравнения в частных производных первого порядка параболического типа. Метод сеток и метод прогонки для решения уравнений параболического типа.
Метод сеток для решения уравнений гиперболического типа. Понятие дифференциального уравнения в частных производных первого порядка гиперболического типа. Метод сеток для решения уравнений гиперболического типа.
Лабораторный практикум
| №п/п | Номер темы дисциплины | Объем в часах | Наименование лабораторных работ |
| Очное | |||
| 2. | 1 | 3 | Итерационные методы решения нелинейных уравнений |
| 2 | 2 | 2 | Итерационные методы решения систем нелинейных уравнений |
| 2. | 3 | 1 | Итерационные методы решения систем линейных алгебраических уравнений |
| 3 | 1, 3 | 6 | Решение задач интерполирования и аппроксимации функций |
| 4 | 1 | 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем |
Курсовой проект (работа) и его содержание
Курсовой проект и курсовая работа не предусмотрены.
Контрольная работа.
Контрольная работа не предусмотрена.
Подготовка реферата.Реферат не предусмотрен.
5. Учебно-методическое обеспечение дисциплины
5.1 Рекомендуемая литература
а) основная литература:
| | Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Учебно-методическое пособие, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 48с. |
| | Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. |
| | Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматгиз, 1966. |
| | Калиткин Н.Н. Численные методы. М.: Наука, 1978. |
| | Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Наука, 1967. |
б) дополнительная литература:
1. Иванов В.С., Ляшев А.С. Лабораторный практикум по дисциплине «Вычислительная техника в инженерных и экономических расчетах». Казань, КАИ, 1984.
2. Вахонина Г.С. Методическое руководство к выполнению лабораторных работ по дисциплине “Методы вычислений”. – Казань: КАИ, 1982.
3. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Лабораторный практикум, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 44с.
4. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Методические указания для студентов заочной формы обучения, Казань, Изд-во Казан. гос. техн. ун-та, 2001, 40с.
5. «Журнал вычислительной математики».
6. «Математическое моделирование».
7. «Программирование».
8. «Математика. Реферативный журнал».
9. http://meth.ras.ru («Журналы Отделения Математики РАН»).
10. http://www.exponenta.ru («Образовательный математический сайт»).
5.2 Средства обеспечения освоения дисциплины
Программное обеспечение для выполнения лабораторных работ и самостоятельной работы студентов:
Windows 98 или более поздних версий.
Автоматизированная вычислительная система «MathCad».
Автоматизированная вычислительная система «MathLab».
MS Excel 97 или более поздних версий.
MS Word 97 или более поздних версий.
Системы программирования Turbo C V6.0 или 7.0, Borland C++ V6.0 или 7.0.
Системы программирования Turbo Pascal V6.0 или 7.0, Borland Pascal V6.0 или 7.0.
6. Материально-техническое обеспечение дисциплины
Для проведения лабораторных работ и организации самостоятельной работы студентов необходимо иметь учебный класс оснащенный ПЭВМ со стандартной комплектацией.
7. Методические рекомендации по организации изучения дисциплины
7.1. Организация изучения дисциплины при очной форме обучения
Обучение проводится в течение одного семестра. Темы 1-4 и все указанные лабораторные работы рассматриваются в семестре № 3.
При проведении лабораторных работ используются программные комплексы, поддерживающие языки программирования Pascal и C, как в учебных лабораториях кафедры, оснащенных компьютерами, так и в ВЦ.
При изучении дисциплины используется балльно - рейтинговая система оценки знаний. Контрольные тестирования организуются на 6, 12 и 17 неделях каждого семестра. Каждое тестирование включает задания, предусматривающие ответы на теоретические и практические вопросы (см. приложение № 5).
Программу составили:
Горбунов Д.А., к.т.н., доцент каф. ПМИ КГТУ им. А.Н. Туполева
_____________________
Программа обсуждена и одобрена на заседании кафедры ПМИ
«____» ______________2007г., протокол № __.
Зав. Кафедрой ПМИ Н.Е. Роднищев
д.т.н., профессор
Председатель Учебно-методической
комиссии факультета
Декан факультета
ПРИЛОЖЕНИЕ 5
ТЕСТЫ ПО ДИСЦИПЛИНЕ «ЧИСЛЕННЫЕ МЕТОДЫ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ»
Вопрос 1. Сделайте вывод о сходимости итерационного процесса ![]() , построенного для решения нелинейного уравнения
, построенного для решения нелинейного уравнения ![]() методом простых итераций на отрезке
методом простых итераций на отрезке ![]() .
.
сходится для любой точки из отрезка;
сходится только из определенной точки отрезка;
сходится только для одной из граничных точек отрезка;
расходится на всем отрезке;
расходится на всей числовой оси.
Вопрос 2. Чему равно значение ![]() , вычисленное по итерационной формуле
, вычисленное по итерационной формуле ![]() при
при ![]() ?
?
0.5;
0.875;
0.4;
0.8;
0.9.
Вопрос 3. Если итерационный процесс, построенный по методу простых итераций для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() сходится, то в качестве начальной точки может быть выбрана:
сходится, то в качестве начальной точки может быть выбрана:
одна из граничных точек отрезка;
обе граничные точки отрезка;
середина отрезка;
любая точка отрезка;
все ответы правильные.
Вопрос 4. По какой из итерационных формул осуществляется решение нелинейных уравнений вида ![]() методом Ньютона?
методом Ньютона?
1. ![]() ;
;
2. ![]() ;
;
3. 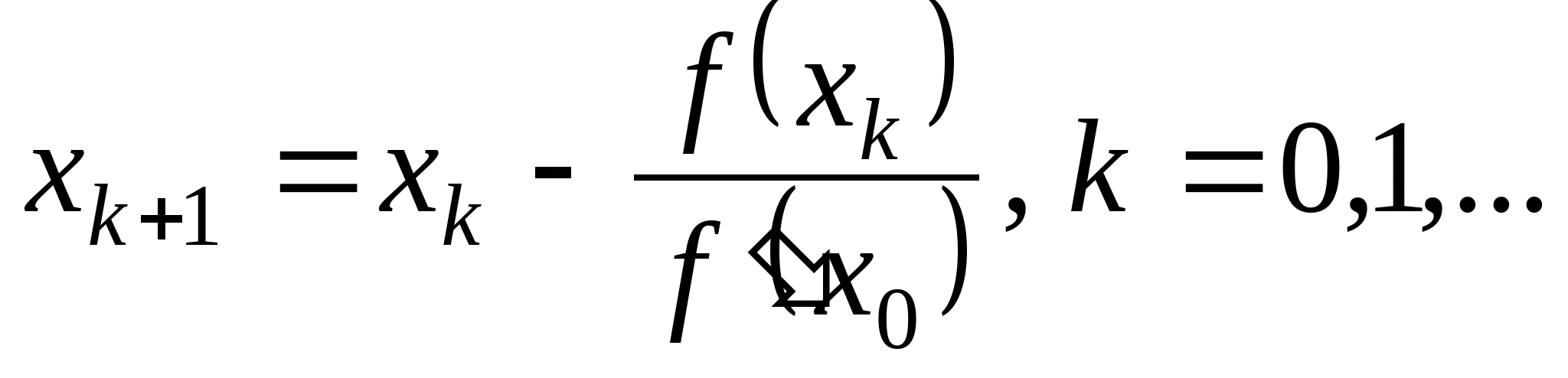 ;
;
4. 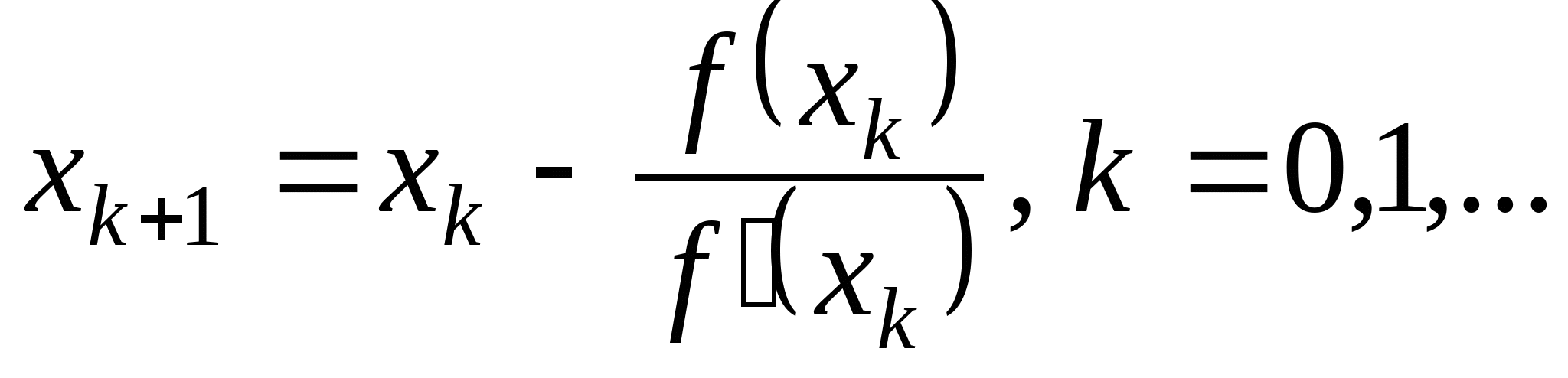 ;
;
5. 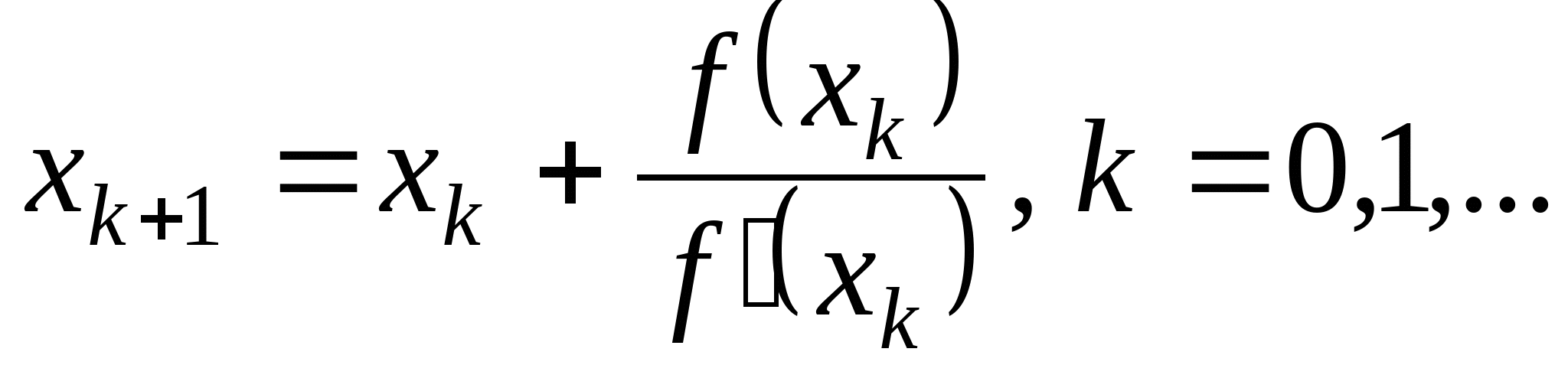 .
.
Вопрос 5. Сформулируйте теорему о существовании хотя бы одного корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() где
где ![]() - произвольная нелинейная функция.
- произвольная нелинейная функция.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на отрезке содержится хотя бы один корень.
, то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка не меняет знак (
и на концах отрезка не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка меняет знак (
и на концах отрезка меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() не меняет знак (
не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() меняет знак (
меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Вопрос 6. Какое условие является достаточным для сходимости итерационного процесса ![]() решения нелинейного уравнения
решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 7. При нахождении корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом Ньютона в качестве начального приближения нужно выбрать
методом Ньютона в качестве начального приближения нужно выбрать ![]() равное:
равное:
0.5;
2;
1;
любой из концов отрезка;
любое значение из отрезка.
Вопрос 8.К какому виду, допускающему сходящиеся итерации, нужно привести систему нелинейных уравнений второго порядка 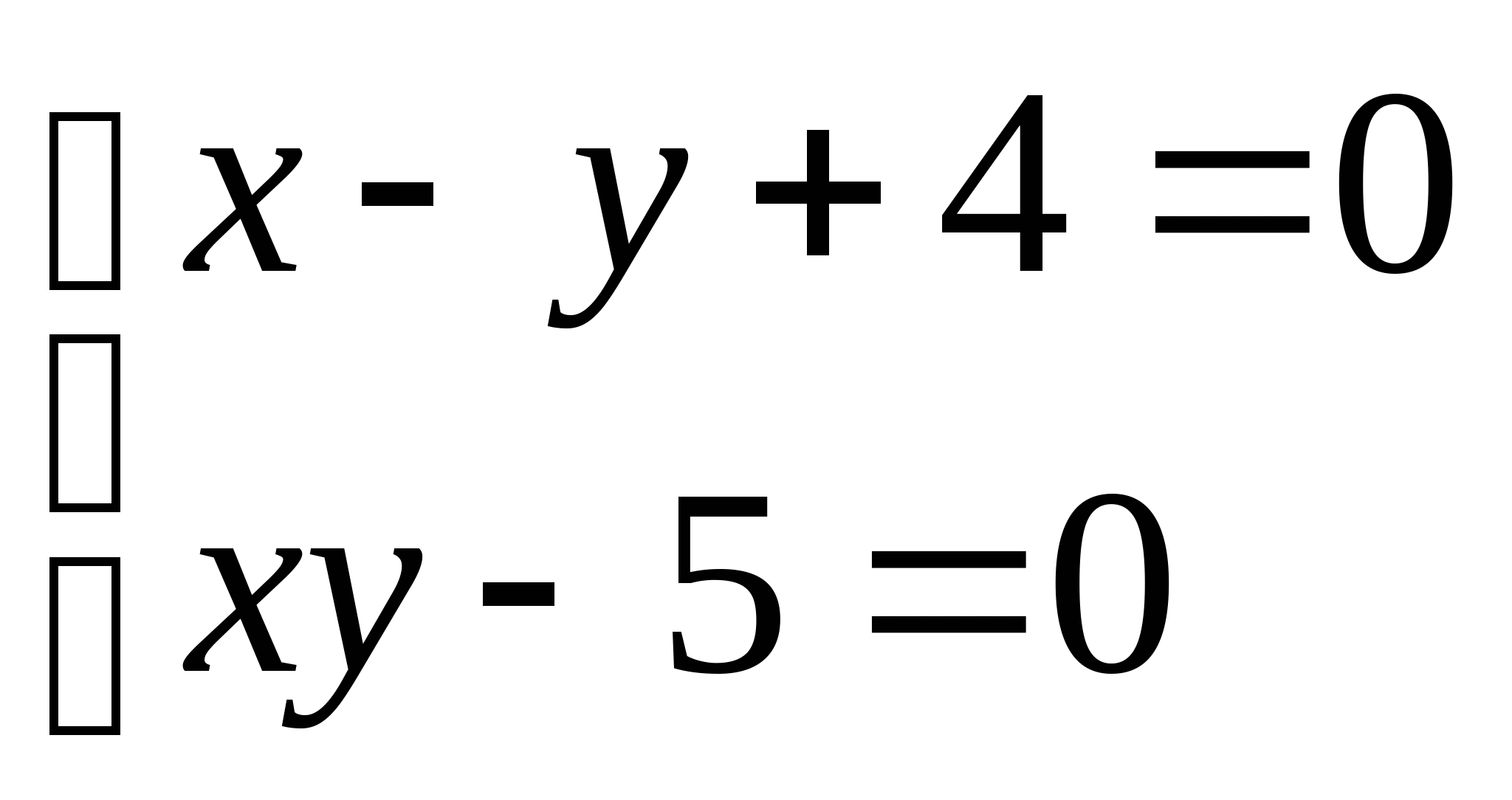 ?
?
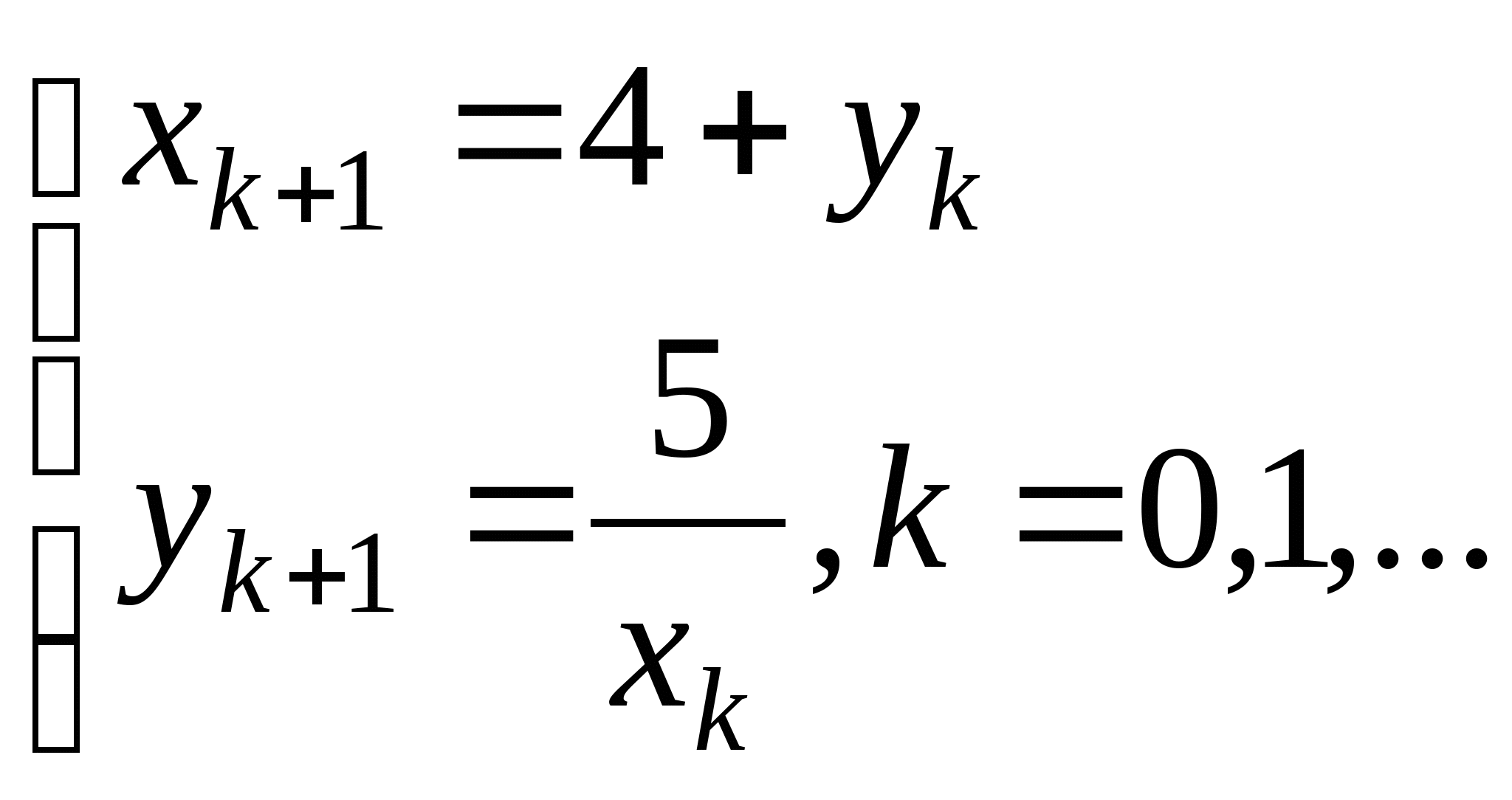 ;
;
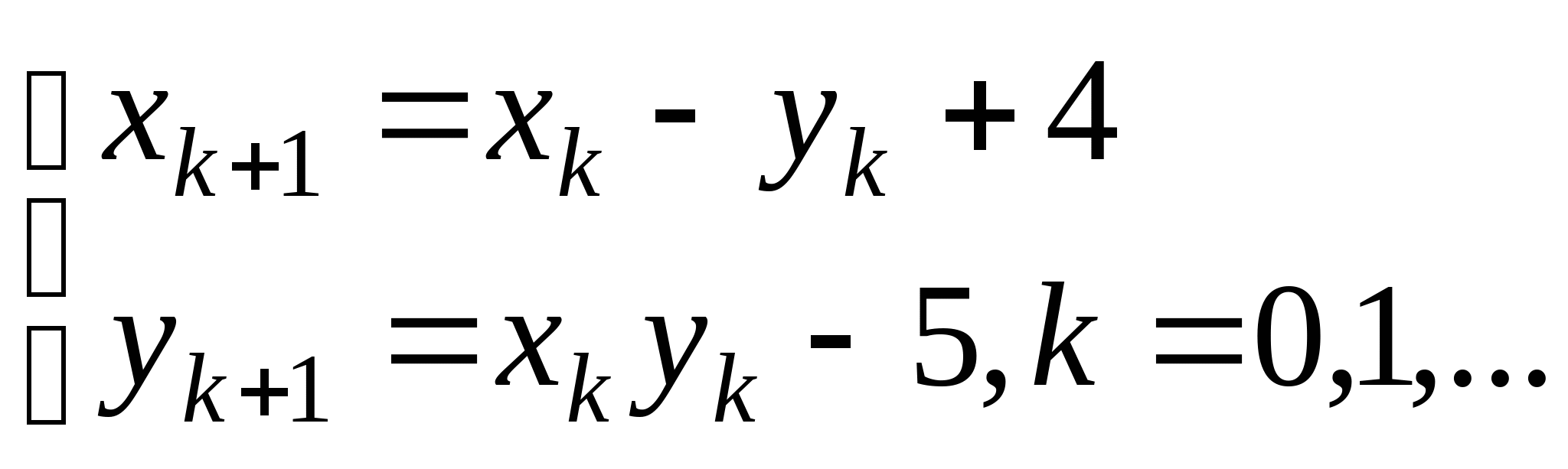 ;
;
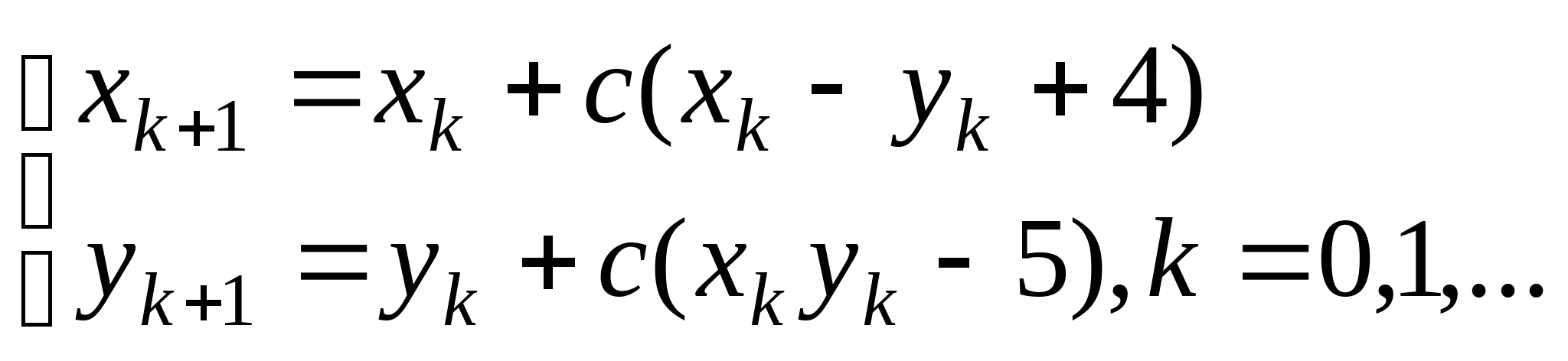 , где константа
, где константа ![]() выбирается из достаточных условий сходимости итерационного процесса;
выбирается из достаточных условий сходимости итерационного процесса;
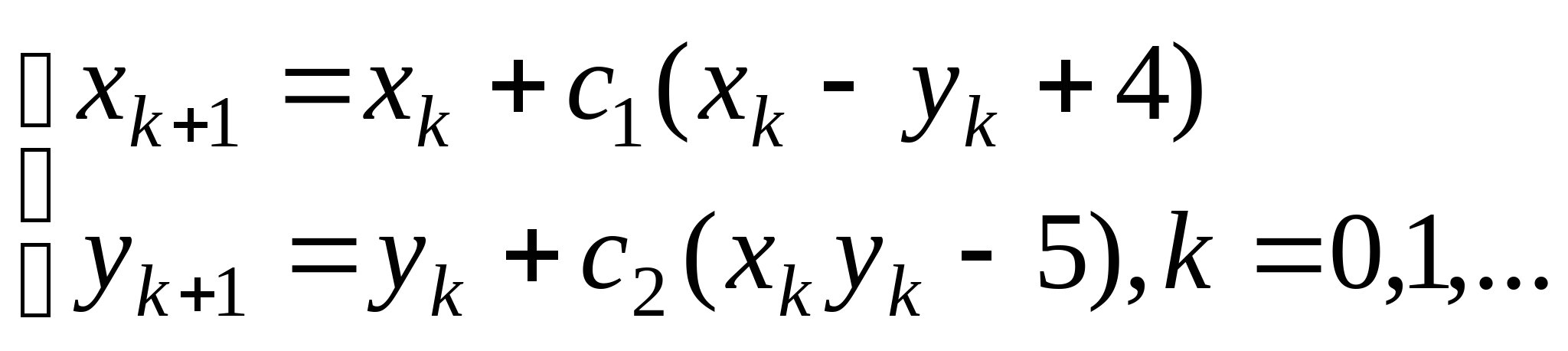 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса;
выбираются из достаточных условий сходимости итерационного процесса;
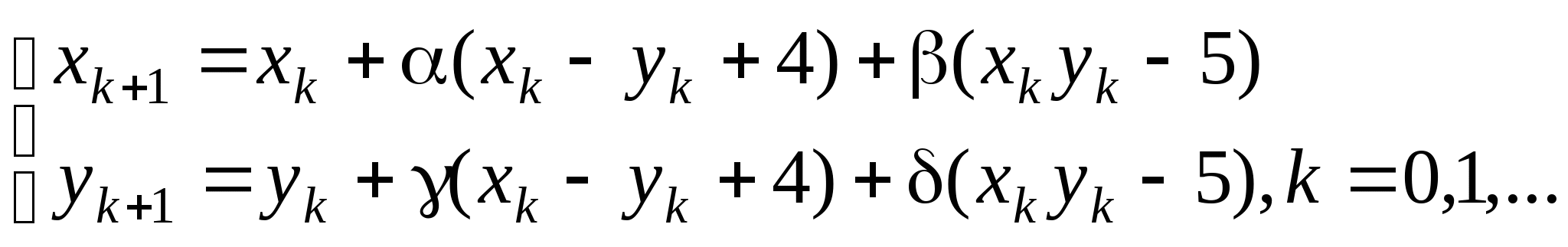 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса.
выбираются из достаточных условий сходимости итерационного процесса.
Вопрос 9. При решении какого класса задач достаточные условия сходимости итерационного процесса имеют вид: ![]() или
или ![]() ?
?
решение нелинейных уравнений;
решение систем нелинейных уравнений;
решение систем линейных алгебраических уравнений;
решение линейных уравнений;
все ответы правильные.
Вопрос 10. При численном решении СЛАУ ![]() ее необходимо привести к виду, допускающему сходящиеся итерации
ее необходимо привести к виду, допускающему сходящиеся итерации ![]() . Чему равно значение коэффициента
. Чему равно значение коэффициента ![]() для СЛАУ вида
для СЛАУ вида 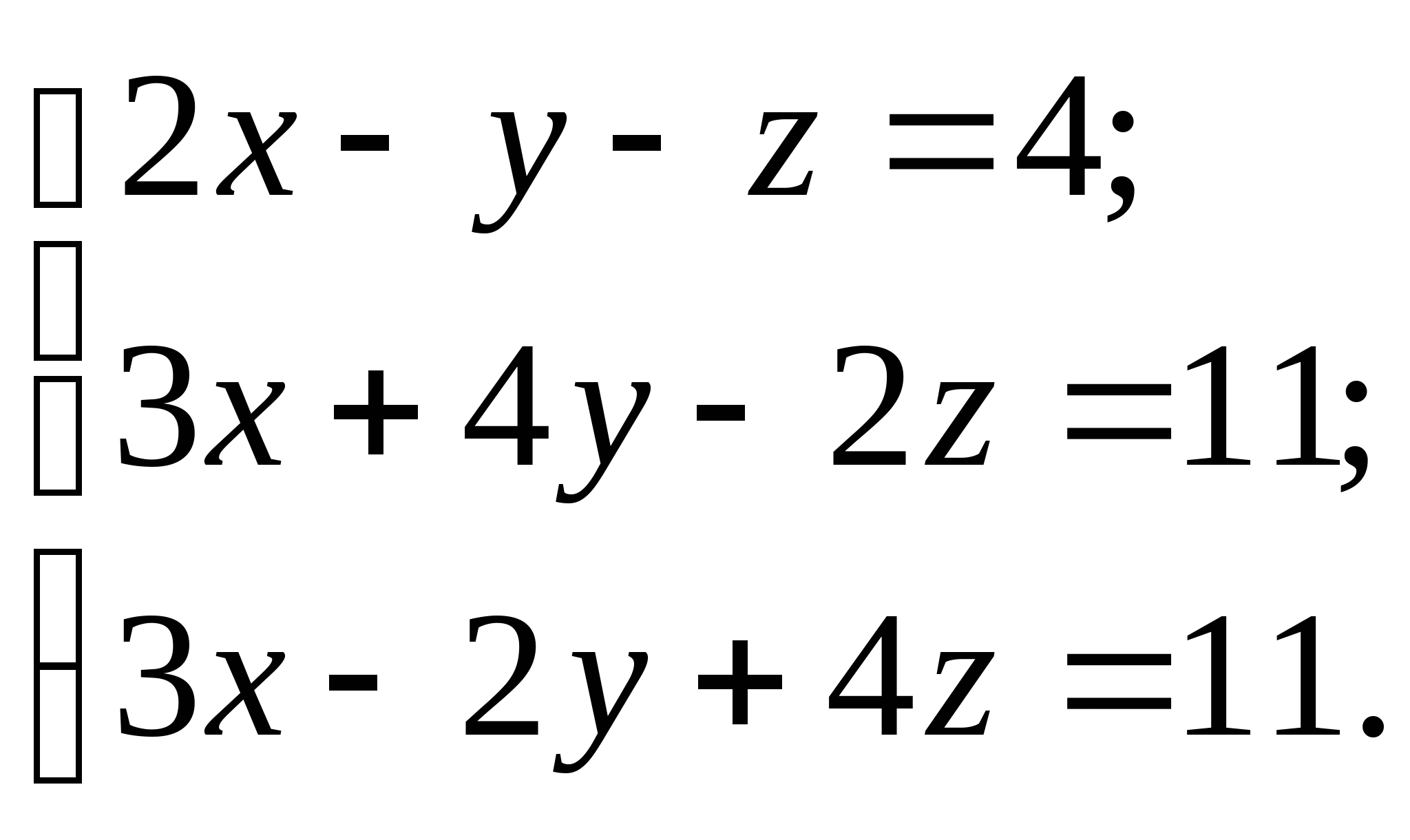 ?
?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
1.
Вопрос 11. Чему равно следующее приближение ![]() , вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида
, вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида 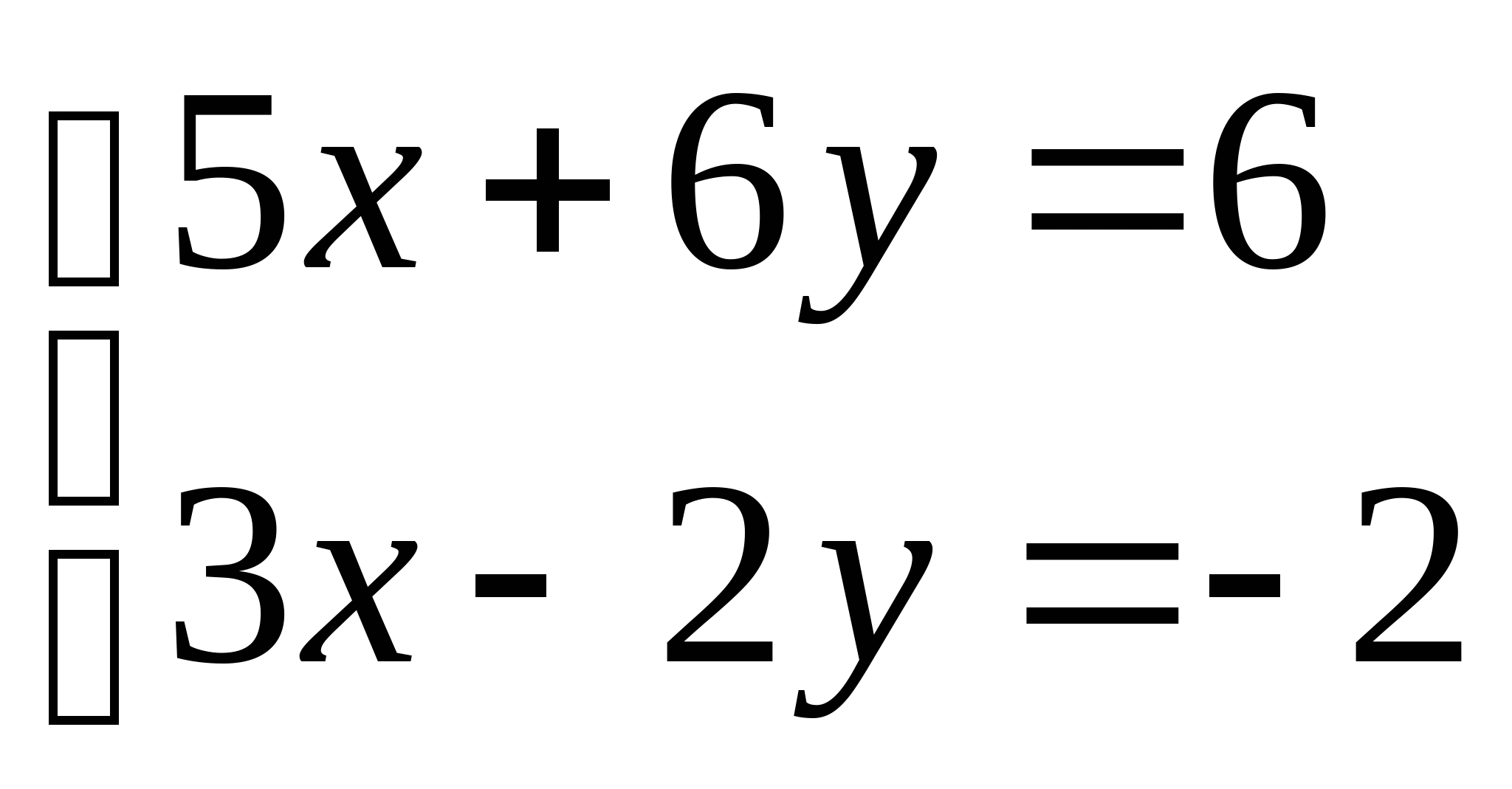 при
при ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 12. Задача интерполяции функций возникает в тех случаях, когда:
необходимо знать значения функции для промежуточных значений аргументов между узловыми точками;
необходимо знать значения функции для точек, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблично;
необходимо представить в более простом виде сложную аналитически заданную функцию;
все ответы правильные.
Вопрос 13. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1 | 0 | 1 |
можно построить интерполяционный полином Лагранжа второго порядка вида:
![]() . Чему будет равен коэффициент
. Чему будет равен коэффициент ![]() ?
?
0;
0.5;
1;
0.4;
0.35.
Вопрос 14. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1.5 | 0.9 | 0.4 |
найти табличную разность второго порядка ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 15. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() :
: ![]() .
.
Строится и решается СЛАУ относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
Вопрос 16. Как называется следующая квадратурная формула: 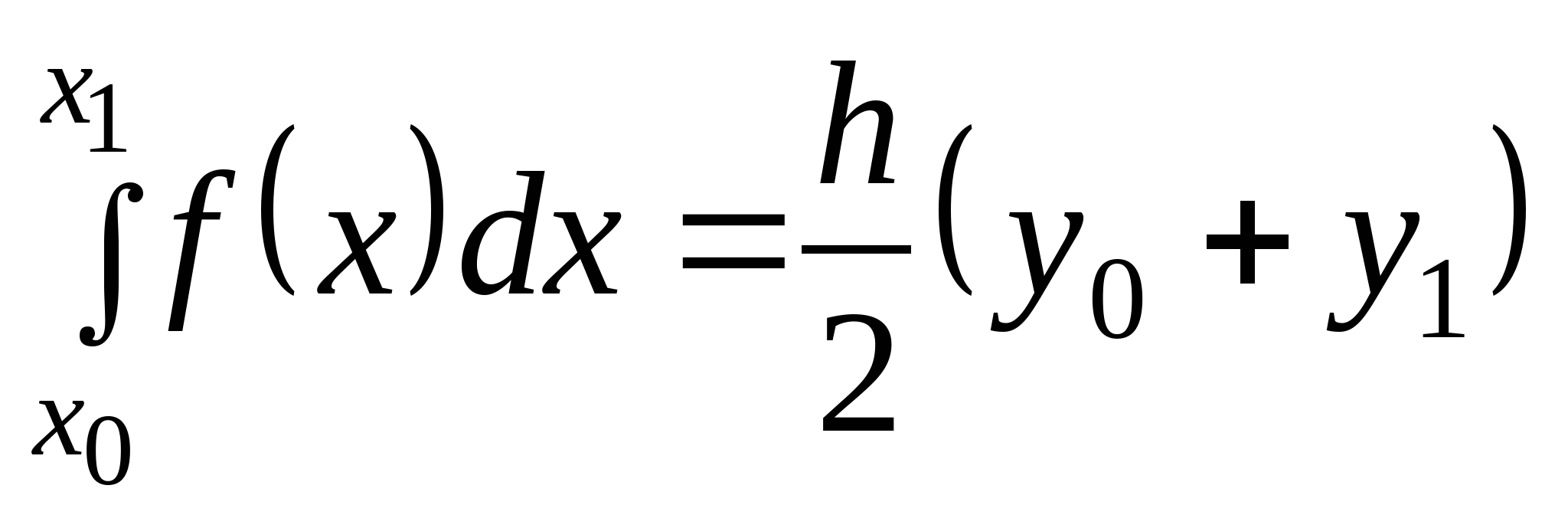 ?
?
формула Ньютона-Котеса;
формула трапеций;
формула Симпсона;
формула Ньютона;
формула Котеса.
Вопрос 17. Как называется следующая интерполяционная формула, построенная для неравноотстоящих узлов:
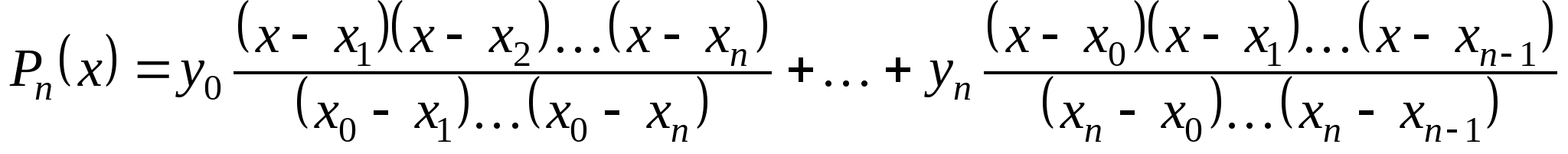 ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула квадратичной интерполяции;
формула линейной интерполяции.
ПРИЛОЖЕНИЕ 8.
СПИСОК ВОПРОСОВ ДЛЯ ПОВТОРЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Источники и классификация погрешностей.
2. Основные понятия и определения теории погрешностей.
3. Значащая и верная цифра приближенной величины. Округление чисел.
4. Погрешность алгебраической суммы.
5. Погрешность произведения и частного.
6. Погрешность степени и корня.
7. Погрешность функции.
8. Обратная задача теории погрешностей.
9. Основные этапы решения нелинейных уравнений.
10. Метод половинного деления.
11. Метод простых итераций для решения нелинейных уравнений.
12. Метод Ньютона (метод касательных) для решения нелинейных уравнений.
13. Модифицированный метод Ньютона для решения нелинейных уравнений.
14. Метод простых итераций для решения систем нелинейных уравнений.
15. Метод Ньютона для решения систем нелинейных уравнений.
16. Модифицированный метод Ньютона для решения систем нелинейных уравнений.
17. Метод простых итераций для решения систем линейных алгебраических уравнений.
18. Метод Зейделя.
19. Метод релаксации.
20. Интерполяционная формула Лагранжа.
21. Первая интерполяционная формула Ньютона.
22. Вторая интерполяционная формула Ньютона.
23. Численное дифференцирование.
24. Квадратурная формула Ньютона-Котеса.
25. Формула трапеций.
26. Квадратурная формула Симпсона.
27. Приближенное вычисление несобственных интегралов.
28. Метод наименьших квадратов.
29. Метод Эйлера.
30. Метод Рунге-Кутта.
31. Метод Адамса.
КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. А.Н. ТУПОЛЕВА
УТВЕРЖДАЮ:
Проректор по учебной и методической
работе
_________________ И.К. Насыров
«_____» _______________ 2007 г.
ПРОГРАММА ДИСЦИПЛИНЫ
ЕН.Ф.06 "ЧИСЛЕННЫЕ МЕТОДЫ"
Рекомендуется УМЦ КГТУ им. А.Н. Туполева для направлений
(специальностей)
направления: 090100 * “Информационная безопасность”
специальности: 075600 (090106)* «Информационная безопасность
телекоммуникационных систем»
формы обучения: очная
*) коды направлений и специальностей указаны по Общероссийскому классификатору специальностей по образованию (ОК 009-2003)
Цели и задачи дисциплины
Целью и задачами дисциплины является изучение основных положений вычислительной математики, знакомство с приближенными методами решения реальных инженерных задач на ЭВМ, современными методами решения задач, связанных с дифференциальными уравнениями, в объеме, достаточном для квалифицированного решения основных профессиональных задач будущими инженерами.
Материал курса основан на знаниях, навыках и умениях полученных при обучении в среднем образовательном учреждении, а также получаемых студентами при изучении дисциплин: «Алгебра и геометрия», «Математический анализ», «Дифференциальные уравнения», «Программирование на языках высокого уровня», «Информатика».
Студенты должны быть знакомы с основными алгебраическими структурами («Алгебра и геометрия»); с понятиями функции и ее непрерывности, с понятиями множества, отношения («Математический анализ»); с понятиями обыкновенных и систем обыкновенных дифференциальных уравнений, аналитическими методами их решения («Дифференциальные уравнения»); способами записи алгоритма, стандартными типами данных («Программирование на языках высокого уровня»); с основными приемами работы в операционных системах MS DOS и Windows, а также с основными офисными системами MS Word и MS Excel («Информатика»).
Студенты должны иметь практические навыки решения линейных алгебраических и нелинейных уравнений и систем («Алгебра и геометрия»), решения обыкновенных и систем обыкновенных дифференциальных уравнений («Дифференциальные уравнения»), уметь строить схемы алгоритмов и программ («Программирование на языках высокого уровня»).
Знания, умения и навыки, полученные в процессе изучения данного курса, могут быть использованы студентами для изучения дисциплин «Технологии программирования», «Операционные системы», «Базы данных», «Управление данными», «Информационные технологии», «Сетевые технологии», «Теория принятия решений», а также при прохождении вычислительной практики студентами второго курса очной формы обучения.
Требования к уровню освоения содержания дисциплины
В результате изучения дисциплины студенты должны:
знать:основные численные методы решения нелинейных уравнений, систем нелинейных и линейных алгебраических уравнений;
методы интерполирования, аппроксимирования и экстраполирования функций;
методы численного решения задачи Коши для обыкновенных дифференциальных уравнений;
условий сходимости методов, областей применения численных методов, условий окончания итерационных процессов по каждому методу.
уметь:выводить итерационные формулы для решения конкретной задачи выбранным методом;
составлять и отлаживать программу для конкретного метода;
объяснять полученные результаты.
иметь опыт выбора метода численного решения конкретной задачи. иметь представление:о вычислительной математике как науке о численных (приближенных) методах решения математических и реальных инженерных задач;
о методах и алгоритмах численного решения задач, сходимости методов, погрешностях вычислений, теоретическом обосновании ряда методов, достоинствах и недостатках методов;
о состоянии и тенденциях развития вычислительной математики.
Объем дисциплины и виды учебной работы
| Виды учебной работы | Очное | |
| Всего | Семестры | |
| 3 | ||
| Общая трудоемкость дисциплины | 120 | 120 |
| Аудиторные занятия (всего) | 68 | 68 |
| Лекции | 34 | 34 |
| Практические занятия (ПЗ) | 0 | 0 |
| Семинары (С) | 0 | 0 |
| Лабораторные работы (ЛР) | 34 | 34 |
| Другие виды аудиторных занятий | 0 | 0 |
| Самостоятельная работа (всего) | 52 | 52 |
| Курсовой проект (работа) | 0 | 0 |
| Расчетно-графические работы | 0 | 0 |
| Реферат | 0 | 0 |
| Другие виды самостоятельной работы | 52 | 52 |
| Вид итогового контроля | Экзамен | |
Содержание дисциплины
Тематический план *):
| № пп | Наименование тем | Очное | |
| ЛК | ЛБ | ||
| 1 | Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. | 4 | 4 |
| 2 | Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений. | 14 | 16 |
| 3 | Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. | 10 | 10 |
| 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. | 6 | 4 |
| Всего | 34 | 34 | |
*) Используемые сокращения: ЛК –лекции, ЛБ – лабораторные работы, ПЗ – практические занятия.
Содержание тем
1. Введение, понятие приближенных (численных) методов решения инженерных задач на ЭВМ. Учет погрешностей при вычислениях. Вычислительные программные системы. (4/8ч.).
1.1. Основные понятия дисциплины (1/2ч.).
Понятие приближенных (численных) методов решения математических задач. Место численных методов в математическом анализе. Понятие вычислительной математики, предмет изучения вычислительной математики. Понятия итерационных методов и погрешностей вычислений, вычислительной схемы. Проблема «устойчивости вычислительных методов» и сложности алгоритма.
1.2. Учет погрешностей при вычислениях (2/4ч.).
Источники и классификация погрешностей. Основные понятия и определения теории погрешностей. Округление чисел. Погрешности алгебраической суммы, произведения, частного, степени, корня, функции. Правило сложения приближенных чисел. Обратная задача теории погрешностей.
1.3. Вычислительные программные системы (1/2ч.).Основы работы с MS Excel, MathCad, MathLab с точки зрения решения задач вычислительной математики.
2. Приближенные методы решения нелинейных уравнений, систем нелинейных уравнений и систем линейных алгебраических уравнений (14/23ч.). 2.1. Приближенные методы решения нелинейных уравнений (8/8ч.). Понятия отделения и уточнения корней нелинейных уравнений на отрезке. Графический и аналитический методы отделения корней. Геометрическая интерпретация графического и аналитического методов. Методы уточнения корней: метод дихотомии, метод простых итераций, метод Ньютона (касательных), модифицированный метод Ньютона.
Метод простых итераций: понятия начального приближения и итерационного процесса; достаточное условие сходимости итерационного процесса; критерии останова итерационного процесса. Геометрическая интерпретация метода простых итераций. Приведение нелинейного уравнения к виду, допускающего сходящиеся итерации. Достоинства и недостатки метода простых итераций.
Метод Ньютона, его геометрическая интерпретация, рабочая формула, выбор начального приближения. Достаточное условие сходимости. Критерий останова итерационного процесса. Достоинства и недостатки метода Ньютона. Модифицированный метод Ньютона, его геометрическая интерпретация и рабочая формула.
2.2. Приближенные методы решения систем нелинейных уравнений (3/7ч.).Понятие системы нелинейных уравнений (СНУ). Проблема отделения корней СНУ. Приближенные методы решения СНУ. Метод простых итераций, понятия начального приближения, итерационного процесса. Достаточные условия сходимости итерационного процесса. Критерий останова итерационного процесса. Приведение исходной системы к системе, допускающей сходящиеся итерации на примере системы второго порядка. Достоинства и недостатки метода простых итераций для решения СНУ.
Метод Ньютона для решения СНУ, его рабочая формула и критерий останова итерационного процесса. Достаточное условие сходимости. Достоинства и недостатки метода Ньютона. Рабочая формула модифицированного метода Ньютона.
2.3. Приближенные методы решения систем линейных алгебраических уравнений (3/8ч.).Методы решения систем линейных алгебраических уравнений. Метод простых итераций, его рабочие формулы и критерий останова; выбор начального приближения; достаточные условия и необходимые и достаточные условия сходимости итерационного процесса; приведение исходной системы к системе, допускающей сходящиеся итерации; достоинства и недостатки метода простых итераций.
Рабочие формулы методы Зейделя, критерий останова, необходимые и достаточные условия сходимости метода. Достоинства и недостатки метода.
Метод релаксации. Приведение исходной системы к виду, пригодному для релаксации. Понятие невязки. Рабочие формулы метода. Критерии останова процесса.3. Задачи интерполяции, экстраполяции и аппроксимации функций. Основные приложения теории интерполяции. (10/15ч.). 3.1. Построение интерполяционных формул Лагранжа, первой и второй формул Ньютона (3/6ч.).
Постановка задачи интерполирования функций по заданной системе точек, понятие равноотстоящих и неравноотстоящих узловых точек. Принципы построения интерполяционной формулы Лагранжа, первой и второй интерполяционной формулы Ньютона, их форма записи и погрешности вычислений по ним. Формулы линейной и квадратичной интерполяции. Понятие табличных разностей различных порядков.
3.2. Основные приложения теории интерполяции (4/5ч.).Понятие численного дифференцирования. Основные принципы решения задачи численного дифференцирования на примере использования таблицы узловых точек и интерполяционных полиномов. Погрешность построенных формул.
Понятие численного интегрирования, квадратурных формул. Построение квадратурной формулы Ньютона-Котеса с использованием интерполяционных формул, коэффициенты Котеса. Частные случаи формулы Ньютона-Котеса (формула трапеций и формула Симпсона) и их геометрическая интерпретация. Погрешность построенных формул. Понятие несобственных интегралов. Приближенное вычисление несобственных интегралов. Случаи бесконечного отрезка интегрирования с непрерывной подынтегральной функцией и разрывной на конечном отрезке интегрирования подынтегральной функцией, их геометрическая интерпретация.
Приближенное вычисление двойных интегралов: понятие кубатурных формул; вывод кубатурной и обобщенной кубатурной формул типа Симпсона для различных видов областей интегрирования. 3.3. Метод наименьших квадратов для обработки результатов экспериментов (3/4ч.).Задача аппроксимирования функций по заданной системе точек. Общая идея метода наименьших квадратов. Понятие отклонения искомой функции от экспериментальной в узловых точках. Алгоритм метода наименьших квадратов и его теоретическое обоснование.
Аппроксимация с помощью экспоненциальных функций.
4. Приближенное решение обыкновенных дифференциальных уравнений и систем, краевых задач для решения дифференциальных уравнений второго порядка и дифференциальных уравнений в частных производных первого порядка. (6/6ч.). 4.1. Приближенное решение обыкновенных дифференциальных уравнений и систем (3/3ч.).
Классификация методов решения и численных методов интегрирования дифференциальных уравнений. Понятия задачи Коши и шага интегрирования. Метод последовательных приближений (метод Пиккара). Метод Эйлера: общая идея метода, его графическая интерпретация и рабочая формула. Достоинства и недостатки метода. Рабочие формулы метода Эйлера для решения системы второго порядка дифференциальных уравнений.
Метод Рунге-Кутта. Общая идея методов Рунге-Кутта второго и четвертого порядков, их рабочие формулы. Достоинства и недостатки методов. Решение задачи Коши для системы второго порядка методом Рунге-Кутта четвертого порядка.
Метод Адамса. Достоинства и недостатки метода Адамса. Экстраполяционная и интерполяционная формулы Адамса для решения дифференциальных уравнений.
Непрерывные схемы решения нелинейных уравнений, условие их применения. Дифференциальное уравнение в отклонениях, его решение. Достоинства и недостатки непрерывных схем. Дифференциальное уравнение с малым параметром, его решение. Достоинства и недостатки методов решения нелинейных уравнений с использованием дифференциальных уравнений с малым параметром.
4.2. Приближенное решение краевых задач для дифференциальных уравнений второго порядка (1/2ч.).
Метод конечных разностей. Понятие краевой задачи для дифференциального уравнения второго порядка и ее геометрическая интерпретация при различных краевых условиях. Понятие двухточечной краевой задачи для линейного дифференциального уравнения второго порядка и ее форма записи. Метод конечных разностей для решения двухточечной краевой задачи для линейного дифференциального уравнения второго порядка.
Метод прогонки. Конечно-разностная и каноническая формы записи двухточечной краевой задачи для линейного дифференциального уравнения второго порядка. Алгоритм метода прогонки прямым и обратным ходом вычислений.
4.3. Приближенное решение краевых задач для дифференциальных уравнений в частных производных первого порядка (2/1ч.).
Методы моделирования и Монте-Карло для решения задачи Дирихле. Понятие дифференциального уравнения в частных производных первого порядка эллиптического типа. Понятие краевых задач для уравнений эллиптического типа. Понятие задачи Дирихле. Решение задачи Дирихле методом моделирования и Монте-Карло.
Метод сеток и метод прогонки для решения уравнений параболического типа. Понятие дифференциального уравнения в частных производных первого порядка параболического типа. Метод сеток и метод прогонки для решения уравнений параболического типа.
Метод сеток для решения уравнений гиперболического типа. Понятие дифференциального уравнения в частных производных первого порядка гиперболического типа. Метод сеток для решения уравнений гиперболического типа.
Лабораторный практикум
| №п/п | Номер темы дисцип-лины | Объем в часах | Наименование лабораторных работ | ||
| Очное | Очно-заочное | Заочное | |||
| 1. | 3 | 4 | Основы работы с MS Excel, MathCad, MathLab | ||
| 2. | 1 | 6 | Итерационные методы решения нелинейных уравнений | ||
| 2 | 2 | 6 | Итерационные методы решения систем нелинейных уравнений | ||
| 2. | 3 | 4 | Итерационные методы решения систем линейных алгебраических уравнений | ||
| 3 | 1, 3 | 8 | Решение задач интерполирования и аппроксимации функций | ||
| 3 | 2 | 2 | Численное интегрирование | ||
| 4 | 1 | 4 | Приближенное решение обыкновенных дифференциальных уравнений и систем | ||
Курсовой проект (работа) и его содержание
Курсовой проект и курсовая работа не предусмотрены.
Контрольная работа.
Контрольная работа не предусмотрена.
Подготовка реферата.Реферат не предусмотрен.
5. Учебно-методическое обеспечение дисциплины
5.1 Рекомендуемая литература
а) основная литература:
| | Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Учебно-методическое пособие, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 48с. |
| | Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. |
| | Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматгиз, 1966. |
| | Калиткин Н.Н. Численные методы. М.: Наука, 1978. |
| | Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Наука, 1967. |
б) дополнительная литература:
1. Иванов В.С., Ляшев А.С. Лабораторный практикум по дисциплине «Вычислительная техника в инженерных и экономических расчетах». Казань, КАИ, 1984.
2. Вахонина Г.С. Методическое руководство к выполнению лабораторных работ по дисциплине “Методы вычислений”. – Казань: КАИ, 1982.
3. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Лабораторный практикум, Казань, Изд-во Казан. гос. техн. ун-та, 2002, 44с.
4. Горбунов Д.А., Вахонина Г.С. Применение численных методов для решения инженерных задач на ЭВМ. Методические указания для студентов заочной формы обучения, Казань, Изд-во Казан. гос. техн. ун-та, 2001, 40с.
5. «Журнал вычислительной математики».
6. «Математическое моделирование».
7. «Программирование».
8. «Математика. Реферативный журнал».
9. http://meth.ras.ru («Журналы Отделения Математики РАН»).
10. http://www.exponenta.ru («Образовательный математический сайт»).
5.2 Средства обеспечения освоения дисциплины
Программное обеспечение для выполнения лабораторных работ и самостоятельной работы студентов:
Windows 98 или более поздних версий.
Автоматизированная вычислительная система «MathCad».
Автоматизированная вычислительная система «MathLab».
MS Excel 97 или более поздних версий.
MS Word 97 или более поздних версий.
Системы программирования Turbo C V6.0 или 7.0, Borland C++ V6.0 или 7.0.
Системы программирования Turbo Pascal V6.0 или 7.0, Borland Pascal V6.0 или 7.0.
6. Материально-техническое обеспечение дисциплины
Для проведения лабораторных работ и организации самостоятельной работы студентов необходимо иметь учебный класс оснащенный ПЭВМ со стандартной комплектацией.
7. Методические рекомендации по организации изучения дисциплины
7.1. Организация изучения дисциплины при очной форме обучения
Обучение проводится в течение одного семестра. Темы 1-4 и все указанные лабораторные работы рассматриваются в семестре № 3.
При проведении лабораторных работ используются программные комплексы, поддерживающие языки программирования Pascal и C, как в учебных лабораториях кафедры, оснащенных компьютерами, так и в ВЦ.
При изучении дисциплины используется балльно - рейтинговая система оценки знаний. Контрольные тестирования организуются на 6, 12 и 17 неделях каждого семестра. Каждое тестирование включает задания, предусматривающие ответы на теоретические и практические вопросы (см. приложение № 5).
Программу составили:
Горбунов Д.А., к.т.н., доцент каф. ПМИ КГТУ им. А.Н. Туполева
_____________________
Программа обсуждена и одобрена на заседании кафедры ПМИ
«____» ______________2007г., протокол № __.
Зав. кафедрой ПМИ Н.Е. Роднищев
д.т.н., профессор
Председатель Учебно-методической В.А. Суздальцев
комиссии факультета, доцент
Декан факультета Л.Ю.Емалетдинова
д.т.н., профессор
Согласовано: В.И.Глова
зав.кафедрой СИБ
д.т.н., профессор
ПРИЛОЖЕНИЕ 5
ТЕСТЫ ПО ДИСЦИПЛИНЕ «ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА»
Вопрос 1. Сделайте вывод о сходимости итерационного процесса ![]() , построенного для решения нелинейного уравнения
, построенного для решения нелинейного уравнения ![]() методом простых итераций на отрезке
методом простых итераций на отрезке ![]() .
.
сходится для любой точки из отрезка;
сходится только из определенной точки отрезка;
сходится только для одной из граничных точек отрезка;
расходится на всем отрезке;
расходится на всей числовой оси.
Вопрос 2. Чему равно значение ![]() , вычисленное по итерационной формуле
, вычисленное по итерационной формуле ![]() при
при ![]() ?
?
0.5;
0.875;
0.4;
0.8;
0.9.
Вопрос 3. Если итерационный процесс, построенный по методу простых итераций для решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() сходится, то в качестве начальной точки может быть выбрана:
сходится, то в качестве начальной точки может быть выбрана:
одна из граничных точек отрезка;
обе граничные точки отрезка;
середина отрезка;
любая точка отрезка;
все ответы правильные.
Вопрос 4. По какой из итерационных формул осуществляется решение нелинейных уравнений вида ![]() методом Ньютона?
методом Ньютона?
1. ![]() ;
;
2. ![]() ;
;
3. 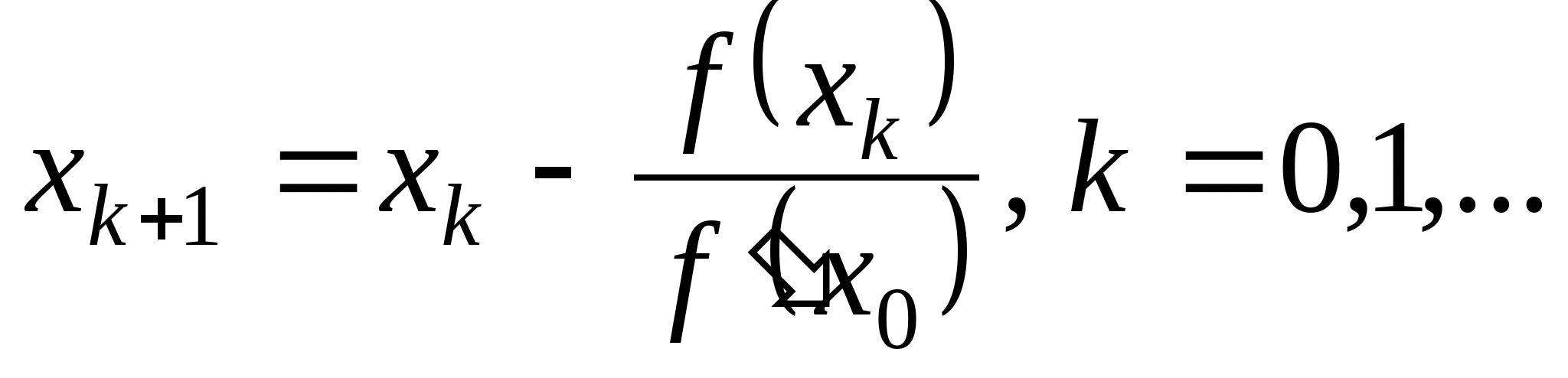 ;
;
4. 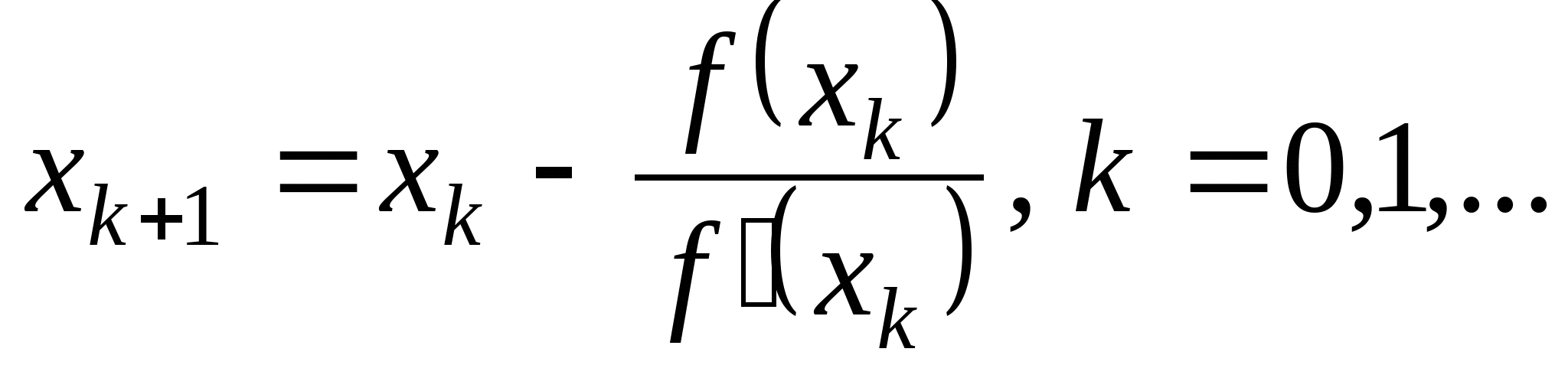 ;
;
5. 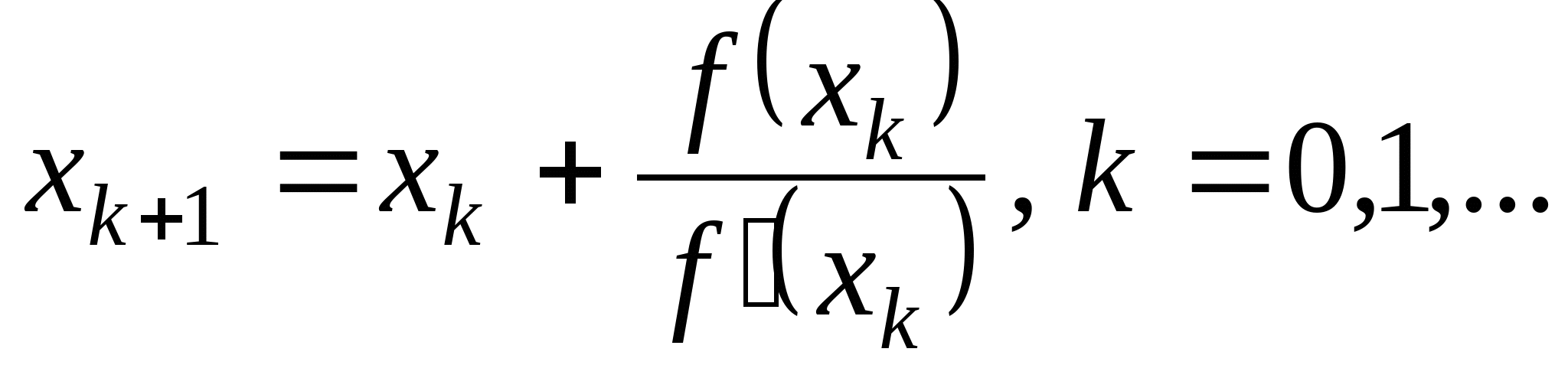 .
.
Вопрос 5. Сформулируйте теорему о существовании хотя бы одного корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() где
где ![]() - произвольная нелинейная функция.
- произвольная нелинейная функция.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , то на отрезке содержится хотя бы один корень.
, то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка не меняет знак (
и на концах отрезка не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка меняет знак (
и на концах отрезка меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() не меняет знак (
не меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Если функция ![]() на концах отрезка
на концах отрезка ![]() меняет знак (
меняет знак (![]() ), то на отрезке содержится хотя бы один корень.
), то на отрезке содержится хотя бы один корень.
Вопрос 6. Какое условие является достаточным для сходимости итерационного процесса ![]() решения нелинейного уравнения
решения нелинейного уравнения ![]() на отрезке
на отрезке ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 7. При нахождении корня нелинейного уравнения ![]() на отрезке
на отрезке ![]() методом Ньютона в качестве начального приближения нужно выбрать
методом Ньютона в качестве начального приближения нужно выбрать ![]() равное:
равное:
0.5;
2;
1;
любой из концов отрезка;
любое значение из отрезка.
Вопрос 8.К какому виду, допускающему сходящиеся итерации, нужно привести систему нелинейных уравнений второго порядка 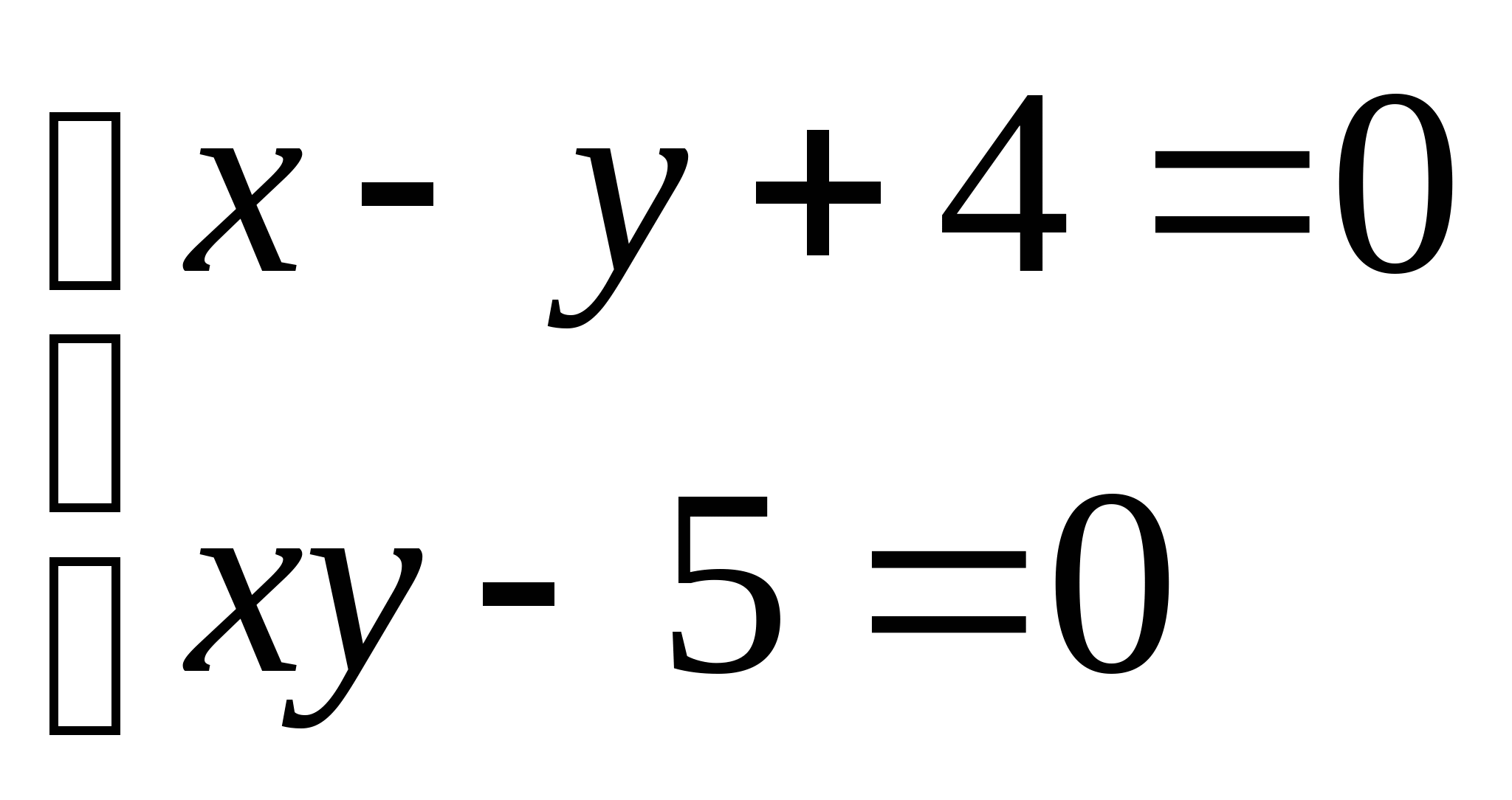 ?
?
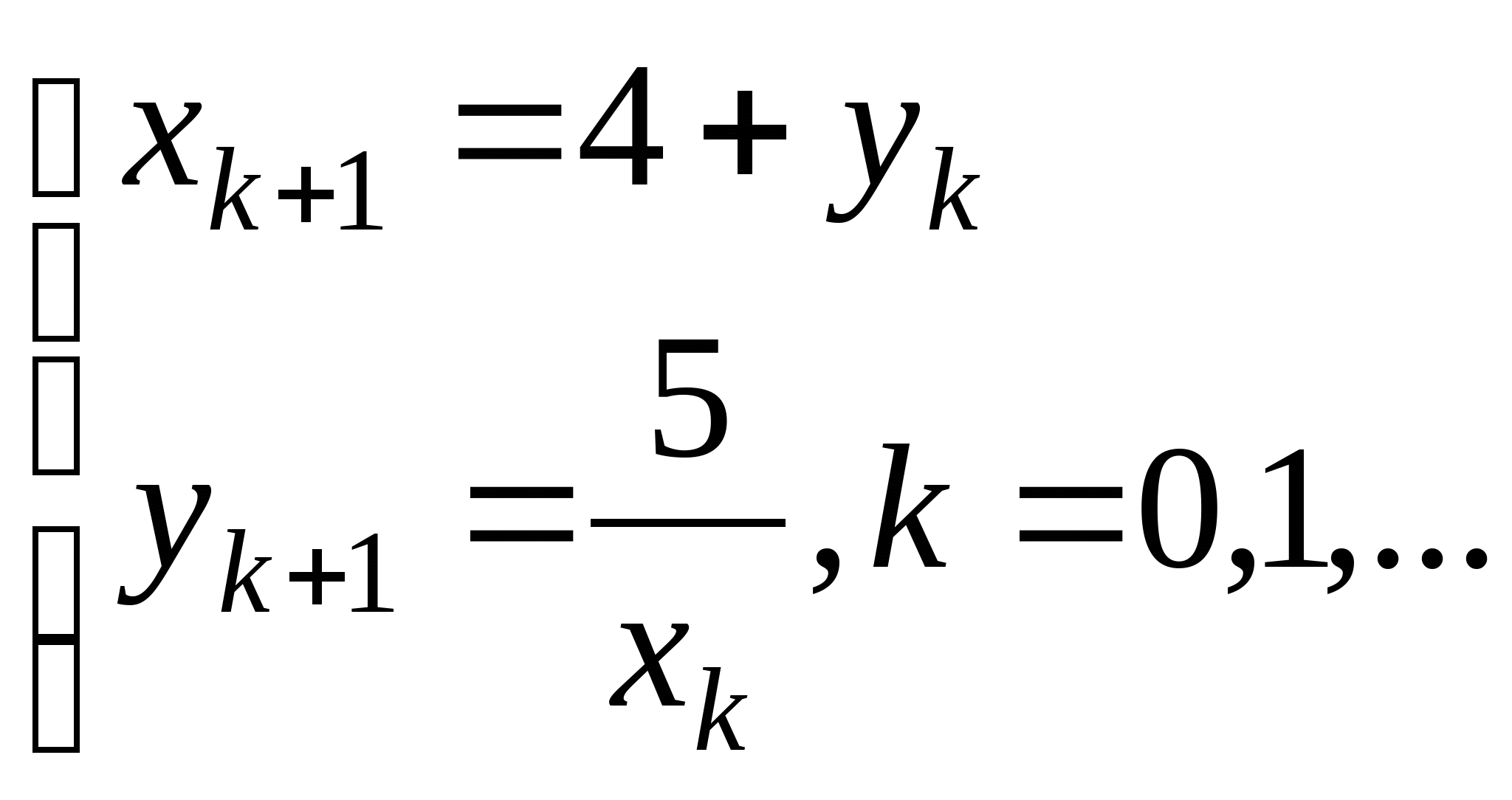 ;
;
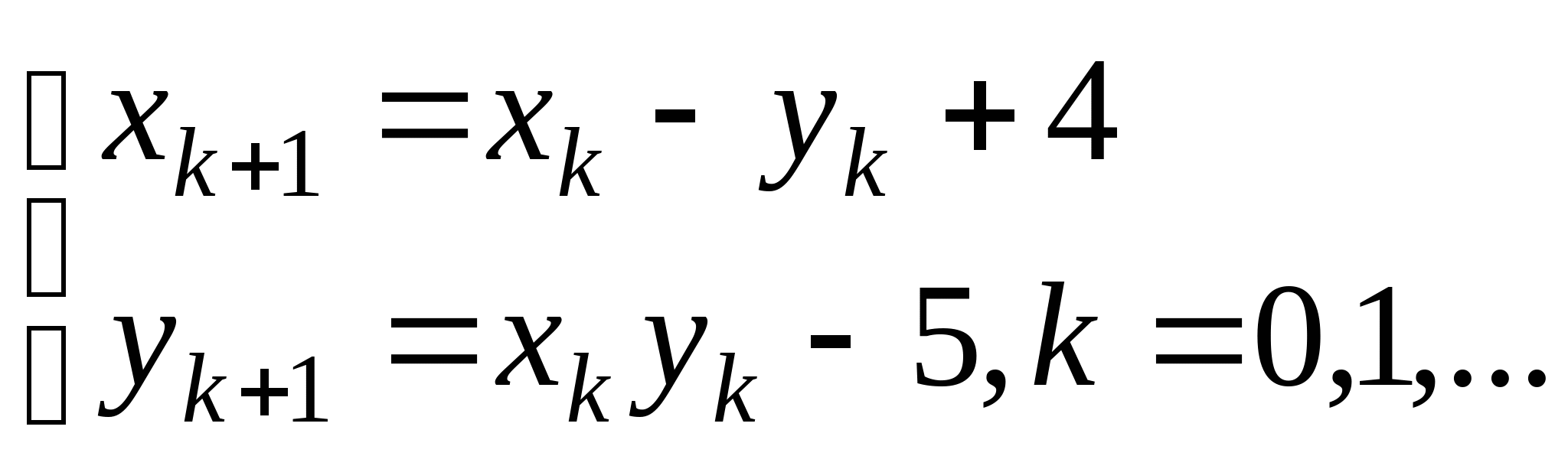 ;
;
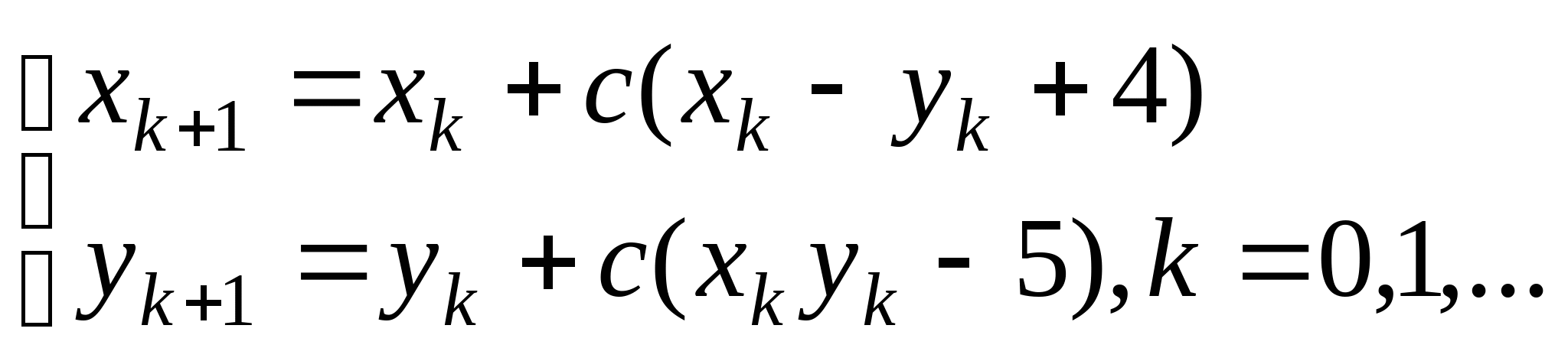 , где константа
, где константа ![]() выбирается из достаточных условий сходимости итерационного процесса;
выбирается из достаточных условий сходимости итерационного процесса;
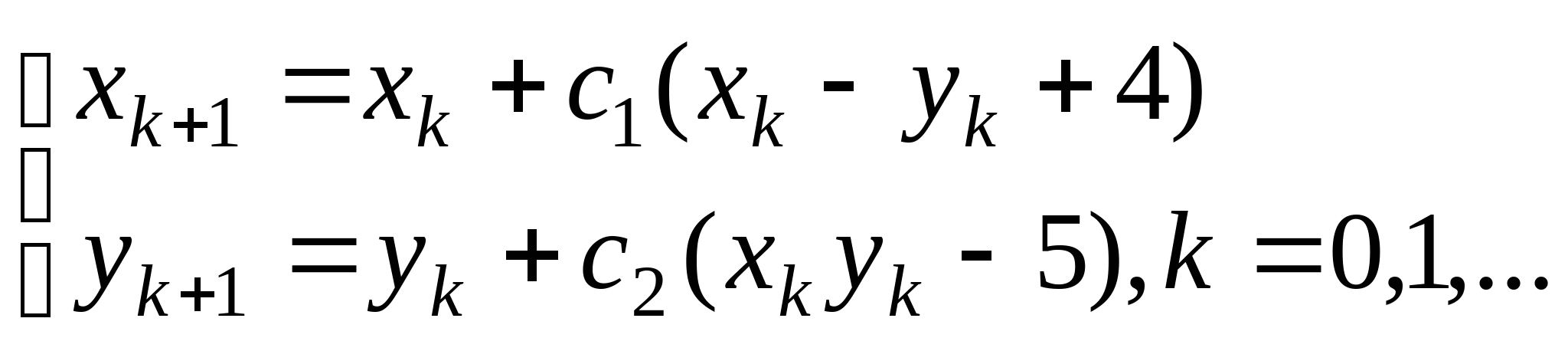 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса;
выбираются из достаточных условий сходимости итерационного процесса;
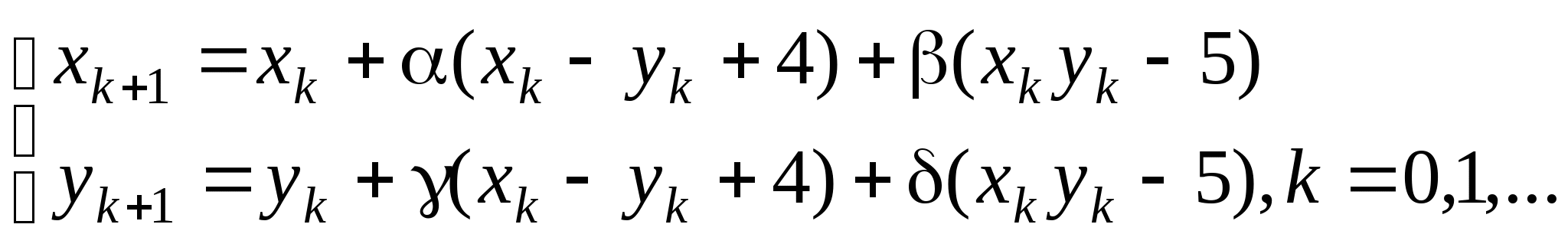 , где константы
, где константы ![]() выбираются из достаточных условий сходимости итерационного процесса.
выбираются из достаточных условий сходимости итерационного процесса.
Вопрос 9. При решении какого класса задач достаточные условия сходимости итерационного процесса имеют вид: ![]() или
или ![]() ?
?
решение нелинейных уравнений;
решение систем нелинейных уравнений;
решение систем линейных алгебраических уравнений;
решение линейных уравнений;
все ответы правильные.
Вопрос 10. При численном решении СЛАУ ![]() ее необходимо привести к виду, допускающему сходящиеся итерации
ее необходимо привести к виду, допускающему сходящиеся итерации ![]() . Чему равно значение коэффициента
. Чему равно значение коэффициента ![]() для СЛАУ вида
для СЛАУ вида 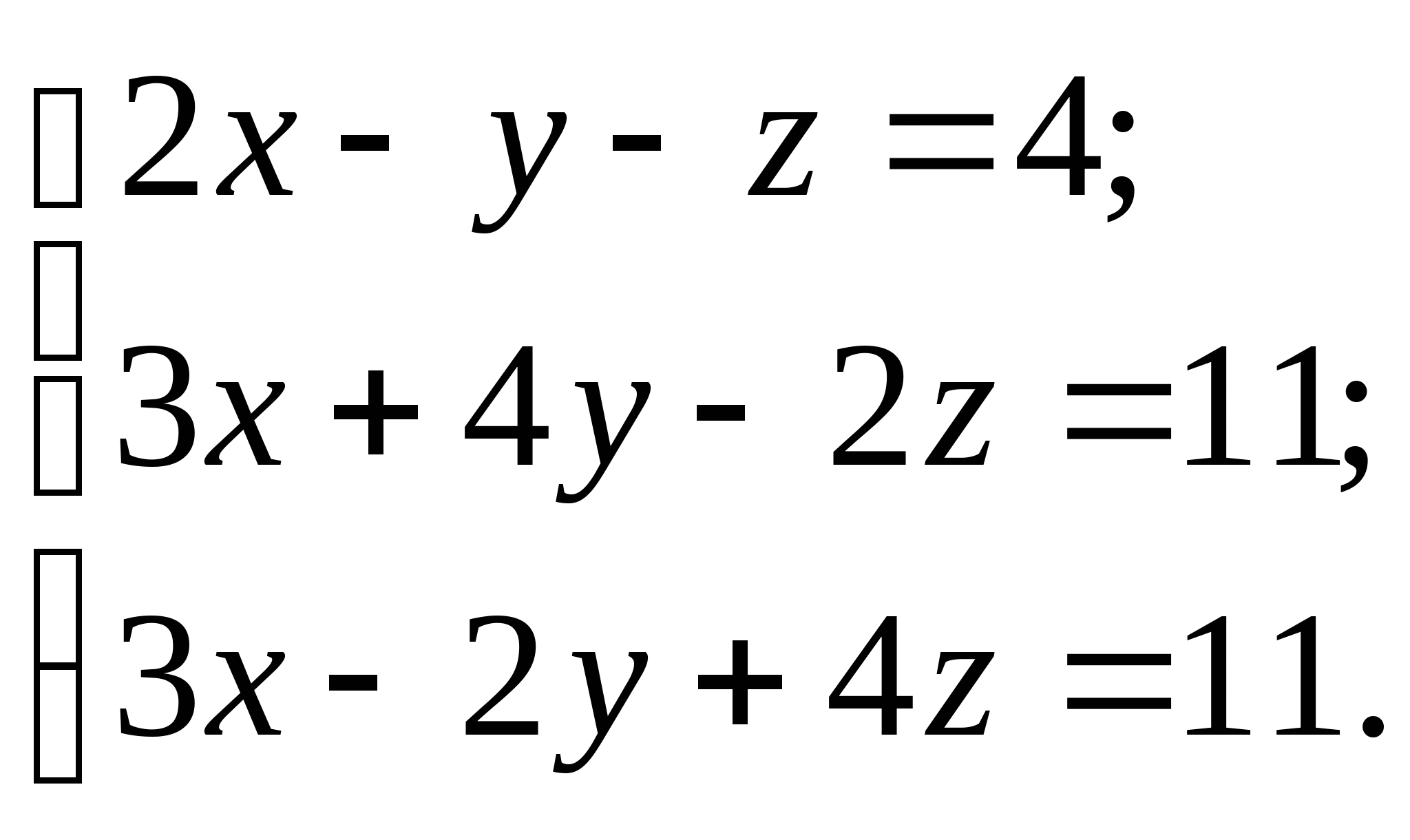 ?
?
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
1.
Вопрос 11. Чему равно следующее приближение ![]() , вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида
, вычисленное по итерационной формуле метода простых итераций для решения СЛАУ вида 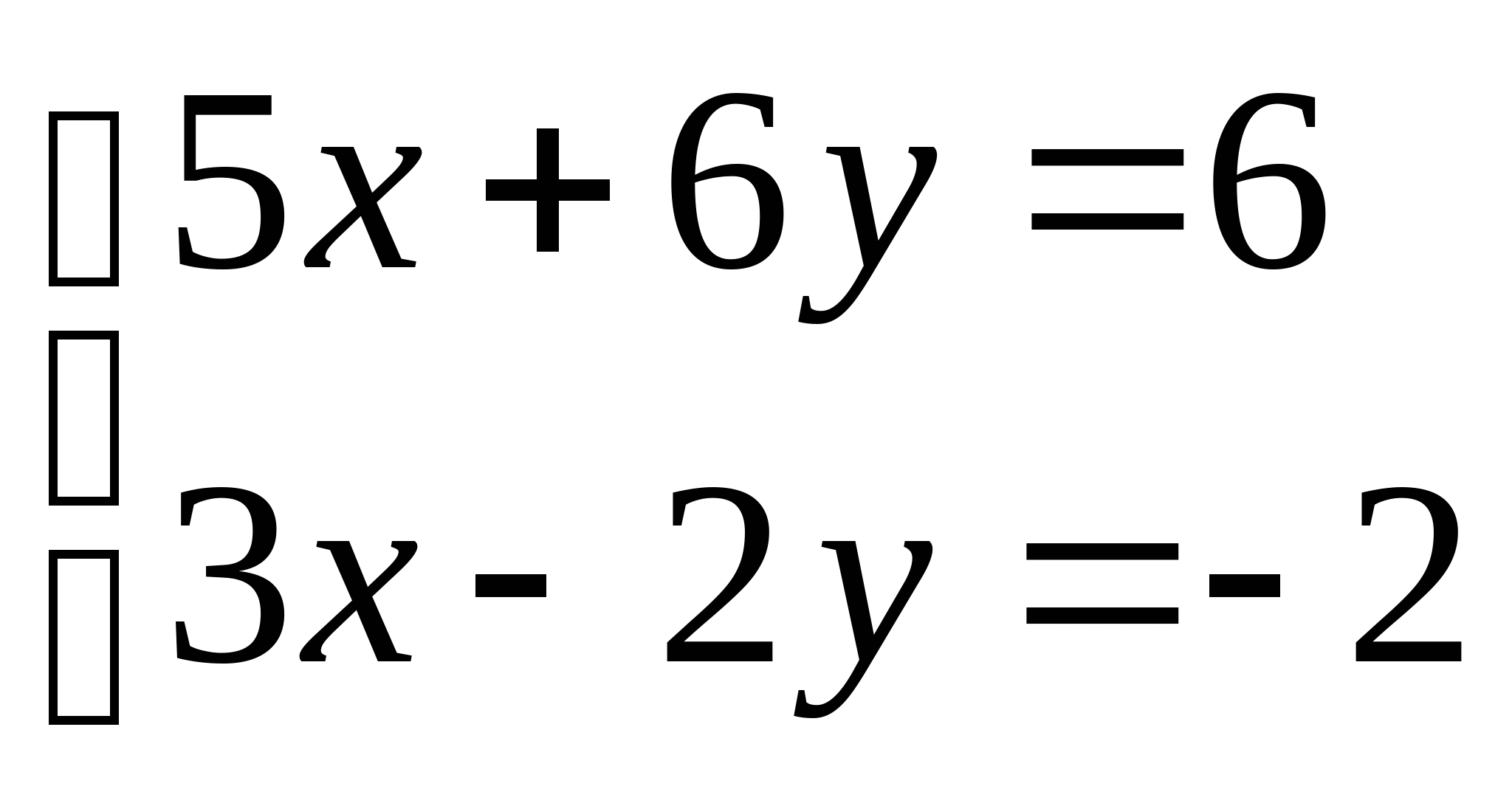 при
при ![]() ?
?
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 12. Задача интерполяции функций возникает в тех случаях, когда:
необходимо знать значения функции для промежуточных значений аргументов между узловыми точками;
необходимо знать значения функции для точек, расположенных в начале или в конце таблицы;
необходимо представить в аналитическом виде функцию, заданную таблично;
необходимо представить в более простом виде сложную аналитически заданную функцию;
все ответы правильные.
Вопрос 13. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1 | 0 | 1 |
можно построить интерполяционный полином Лагранжа второго порядка вида:
![]() . Чему будет равен коэффициент
. Чему будет равен коэффициент ![]() ?
?
0;
0.5;
1;
0.4;
0.35.
Вопрос 14. По таблице из трех узловых точек
|
| -1 | 0 | 1 |
|
| 1.5 | 0.9 | 0.4 |
найти табличную разность второго порядка ![]() .
.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вопрос 15. В каком пункте алгоритма метода наименьших квадратов допущена ошибка?
Задается таблица чисел ![]() .
.
Вводится функция ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Находятся необходимые условия экстремума функции ![]() :
: ![]() .
.
Строится и решается СЛАУ относительно неизвестных коэффициентов ![]() ;
;
Записывается искомый многочлен в виде
![]() .
.
Вопрос 16. Как называется следующая квадратурная формула: 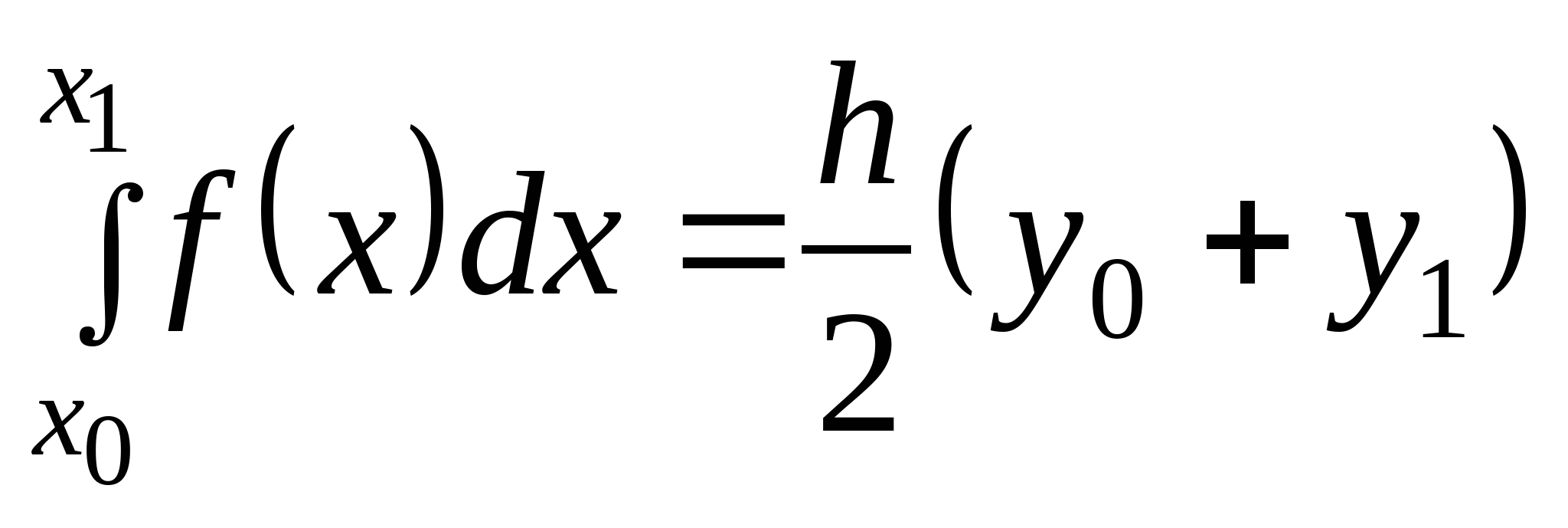 ?
?
формула Ньютона-Котеса;
формула трапеций;
формула Симпсона;
формула Ньютона;
формула Котеса.
Вопрос 17. Как называется следующая интерполяционная формула, построенная для неравноотстоящих узлов:
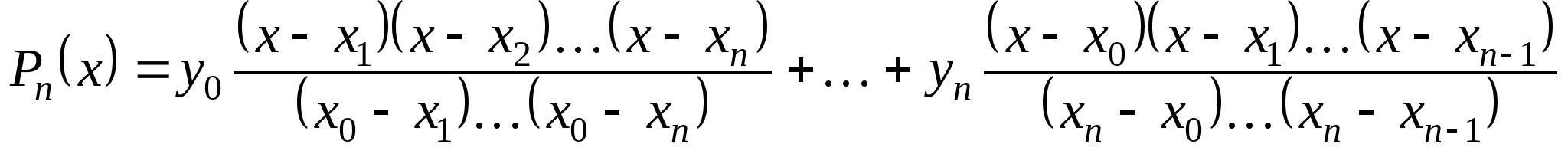 ?
?
интерполяционная формула Лагранжа;
первая интерполяционная формула Ньютона;
вторая интерполяционная формула Ньютона;
формула квадратичной интерполяции;
формула линейной интерполяции.
ПРИЛОЖЕНИЕ 8.
СПИСОК ВОПРОСОВ ДЛЯ ПОВТОРЕНИЯ УЧЕБНОГО МАТЕРИАЛА
1. Источники и классификация погрешностей.
2. Основные понятия и определения теории погрешностей.
3. Значащая и верная цифра приближенной величины. Округление чисел.
4. Погрешность алгебраической суммы.
5. Погрешность произведения и частного.
6. Погрешность степени и корня.
7. Погрешность функции.
8. Обратная задача теории погрешностей.
9. Основные этапы решения нелинейных уравнений.
10. Метод половинного деления.
11. Метод простых итераций для решения нелинейных уравнений.
12. Метод Ньютона (метод касательных) для решения нелинейных уравнений.
13. Модифицированный метод Ньютона для решения нелинейных уравнений.
14. Метод простых итераций для решения систем нелинейных уравнений.
15. Метод Ньютона для решения систем нелинейных уравнений.
16. Модифицированный метод Ньютона для решения систем нелинейных уравнений.
17. Метод простых итераций для решения систем линейных алгебраических уравнений.
18. Метод Зейделя.
19. Метод релаксации.
20. Интерполяционная формула Лагранжа.
21. Первая интерполяционная формула Ньютона.
22. Вторая интерполяционная формула Ньютона.
23. Численное дифференцирование.
24. Квадратурная формула Ньютона-Котеса.
25. Формула трапеций.
26. Квадратурная формула Симпсона.
27. Приближенное вычисление несобственных интегралов.
28. Метод наименьших квадратов.
29. Метод Эйлера.
30. Метод Рунге-Кутта.
31. Метод Адамса.
ГЛАВА 8. ПРИБЛИЖЕННОЕ Решение ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И СИСТЕМ.
Дифференциальные уравнения являются основным математическим инструментом моделирования и анализа разнообразных явлений и процессов в науке и технике.
Методы их решения подразделяются на два класса:
аналитические методы, в которых решение получается в виде аналитических функций;
численные (приближенные) методы, где искомые интегральные кривые получают в виде таблиц их числовых значений.
Применение аналитических методов позволяет исследовать полученные решения методами математического анализа и сделать соответствующие выводы о свойствах моделируемого явления или процесса. К сожалению, с помощью таких методов можно решать достаточно ограниченный круг реальных задач. Численные методы позволяют получить с определенной точностью приближенное решение практически любой задачи.
Решить дифференциальное уравнение
![]() (8.1)
(8.1)
численным методом означает, что для заданной последовательности аргументов ![]() и числа
и числа ![]() , не определяя аналитического вида функции
, не определяя аналитического вида функции ![]() , найти значения
, найти значения ![]() , удовлетворяющие условиям:
, удовлетворяющие условиям:
![]() .
.
Рассмотрим три наиболее распространенных при решении практических задач численных метода интегрирования: метод Эйлера, метод Рунге-Кутта и метод Адамса.
§8.1. Метод Эйлера.
Этот метод обладает малой точностью и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других численных методов.
Пусть дано дифференциальное уравнение с начальным условием (задача Коши)
![]() ,
, ![]() (8.2)
(8.2)
и выполняются условия существования и единственности решения.
Теорема Пиккара (теорема о существовании и единственности решения задачи Коши).
Если в уравнении (8.1) функция ![]() непрерывна в прямоугольнике
непрерывна в прямоугольнике ![]() и удовлетворяет в
и удовлетворяет в ![]() условию Липшица
условию Липшица
![]() ,
,
где ![]() - константа Липшица, то существует единственное решение
- константа Липшица, то существует единственное решение ![]() ,
, ![]() , уравнения (8.1), удовлетворяющее условию
, уравнения (8.1), удовлетворяющее условию ![]() , где
, где 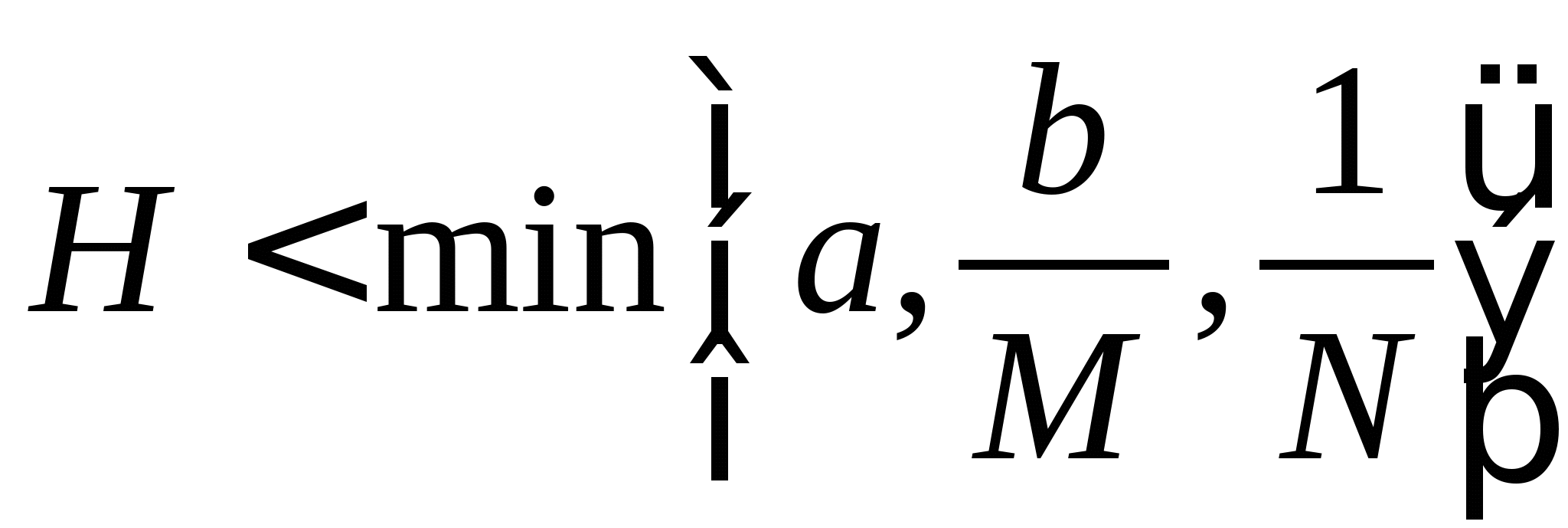 ,
, ![]() в
в ![]() .
.
Требуется найти решение ![]() задачи Коши (8.2).
задачи Коши (8.2).
Выбрав шаг ![]() - достаточно малый, равный
- достаточно малый, равный ![]() , строим систему равноотстоящих точек
, строим систему равноотстоящих точек ![]() .
.
И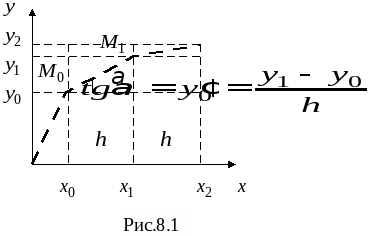
скомую интегральную кривую ![]() , проходящую через точку
, проходящую через точку ![]() , приближенно заменим ломаной Эйлера с вершинами
, приближенно заменим ломаной Эйлера с вершинами ![]() (Рис.8.1).
(Рис.8.1).
Звено ломаной ![]() , заключенное между
, заключенное между ![]() и
и ![]() , наклонено к оси
, наклонено к оси ![]() под углом
под углом ![]() . Тангенс этого угла вычисляется по формуле:
. Тангенс этого угла вычисляется по формуле:
![]() .
.
Сделав преобразование, получим формулу Эйлера:
![]() . (8.3)
. (8.3)
Вычисление значений ![]() осуществляется с использованием формулы (8.3) следующим образом. По заданным начальным условиям
осуществляется с использованием формулы (8.3) следующим образом. По заданным начальным условиям ![]() и
и ![]() полагая
полагая ![]() в выражении (8.3) вычисляется значение
в выражении (8.3) вычисляется значение
![]() . (8.4)
. (8.4)
Далее определяя значение аргумента ![]() по формуле
по формуле ![]() , используя найденное значение
, используя найденное значение ![]() и полагая в формуле (8.3)
и полагая в формуле (8.3) ![]() вычисляем следующее приближенное значение интегральной кривой
вычисляем следующее приближенное значение интегральной кривой ![]() :
:
![]() . (8.5)
. (8.5)
Поступая аналогичным образом при ![]() определяем все остальные значения
определяем все остальные значения ![]() , в том числе последнее значение
, в том числе последнее значение ![]() , которое соответствует значению аргумента
, которое соответствует значению аргумента ![]() .
.
Таким образом, соединяя на координатной плоскости точки ![]() отрезками прямых, получаем ломаную линию с вершинами в точках
отрезками прямых, получаем ломаную линию с вершинами в точках ![]() .
.
Запишем разложение ![]() в ряд Тейлора:
в ряд Тейлора:
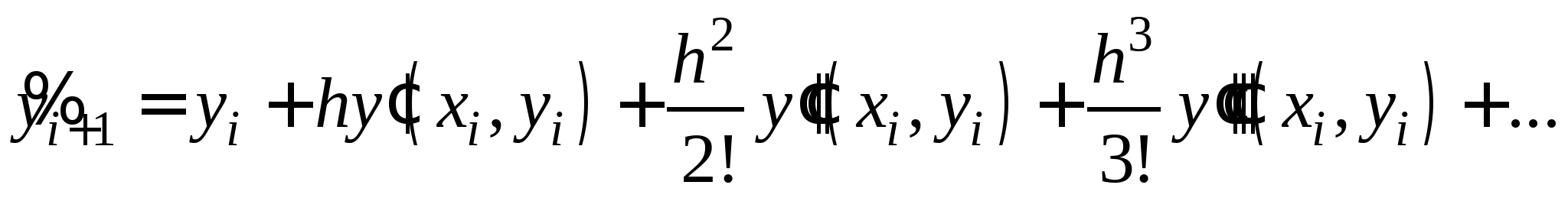 (8.6)
(8.6)
Учитывая формулы (8.3) и (8.6), получим
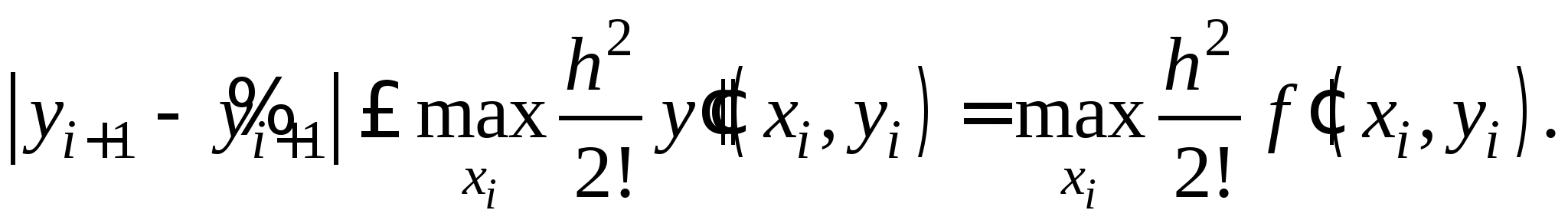 (8.7)
(8.7)
Соотношение (8.7) может быть использовано для выбора шага ![]() . Как правило, шаг
. Как правило, шаг ![]() выбирают таким образом, чтобы
выбирают таким образом, чтобы ![]() , где
, где ![]() - заданная точность.
- заданная точность.
Метод Эйлера может быть применен к решению систем дифференциальных уравнений.
Пусть задана система двух дифференциальных уравнений первого порядка
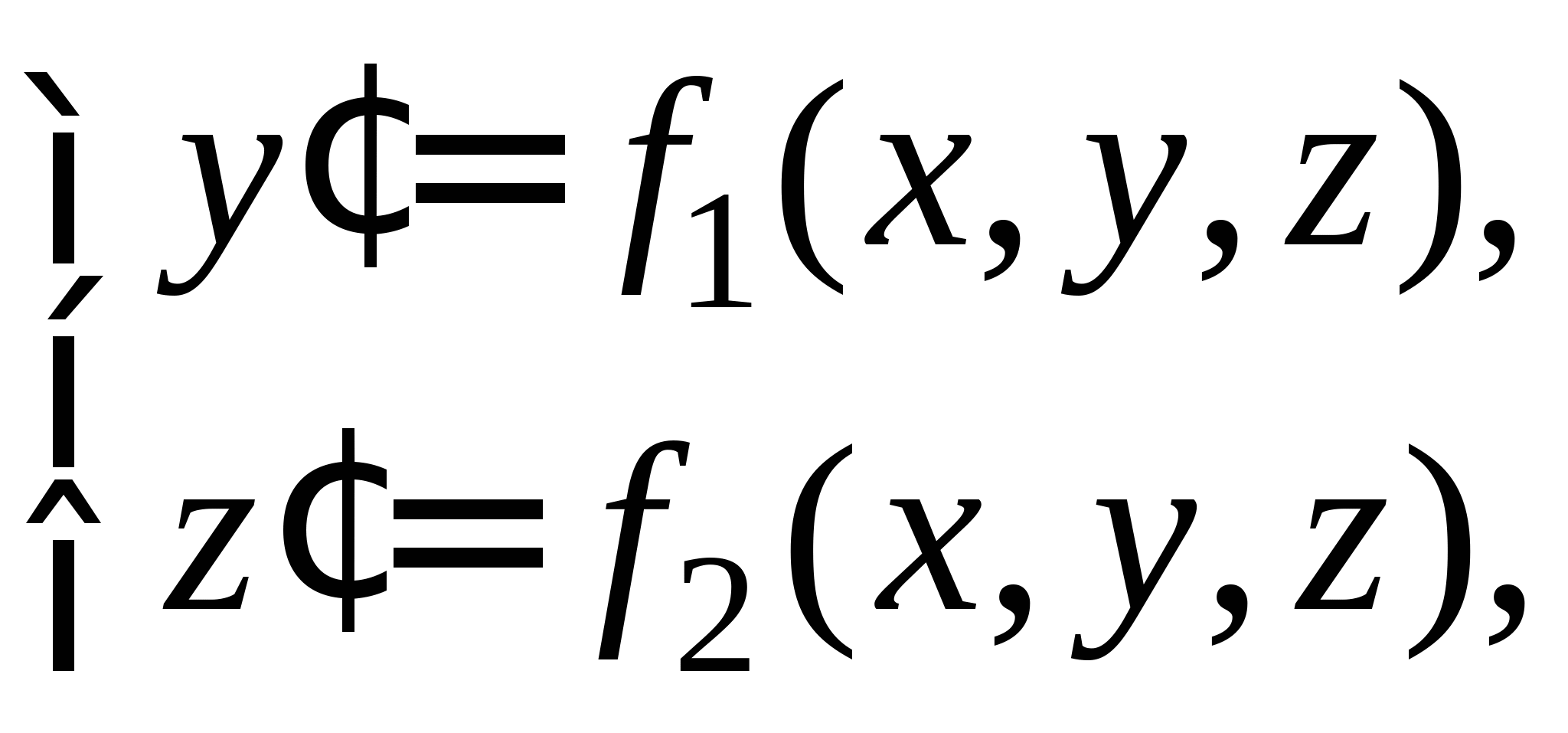 (8.8)
(8.8)
с начальными условиями
![]() .
.
Необходимо найти решение этой задачи Коши. Проводя аналогичные рассуждения, получаем расчетные формулы вида:
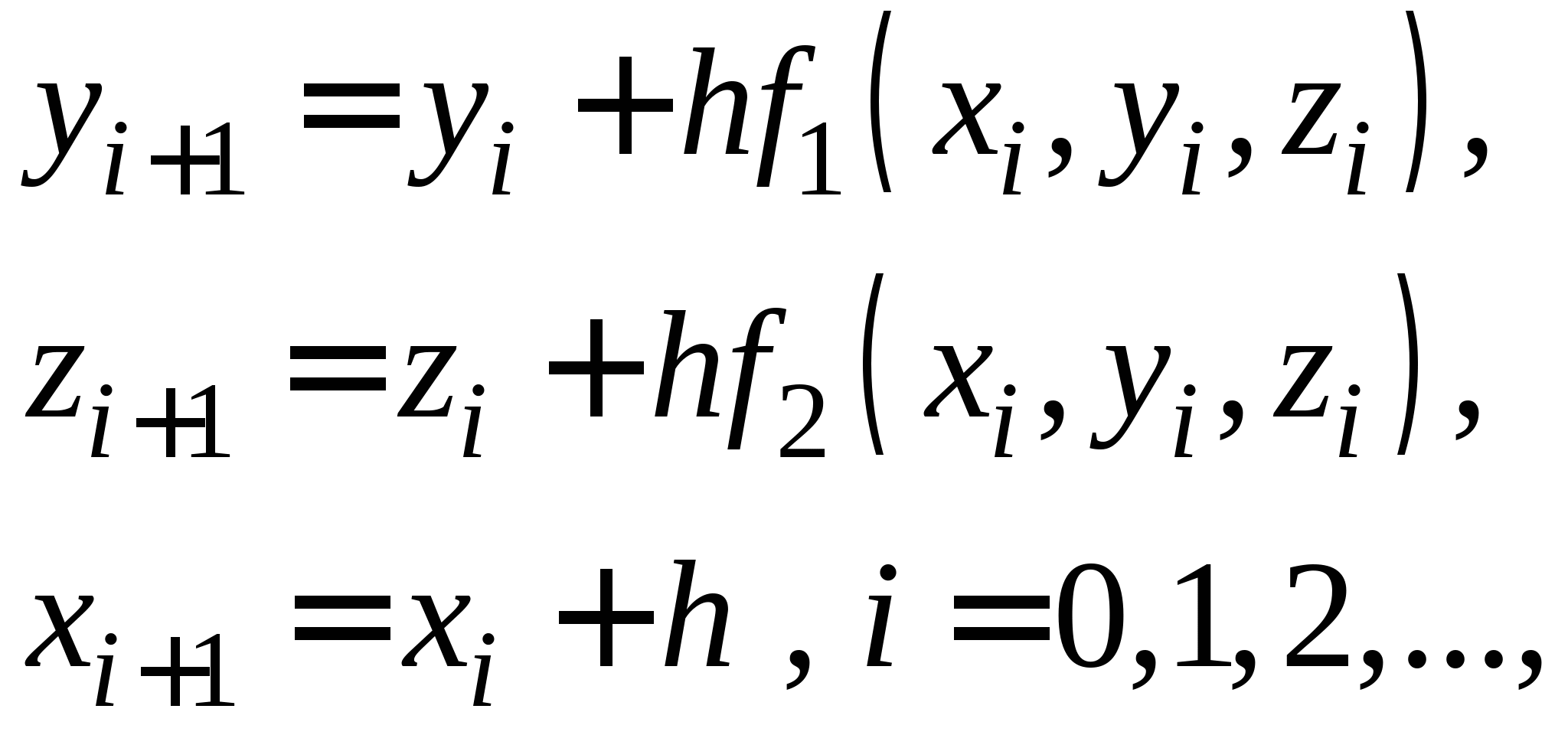 (8.9)
(8.9)
где ![]() шаг интегрирования.
шаг интегрирования.
В результате применения расчетной схемы (8.9) получается приближенное представление интегральных кривых ![]() и
и ![]() в форме двух ломаных Эйлера, построенных по полученным точкам
в форме двух ломаных Эйлера, построенных по полученным точкам ![]() .
.
Достоинством метода Эйлера является его простота и высокая скорость поиска решения. Недостатками метода Эйлера являются малая точность и систематическое накопление ошибок, так как при вычислении значений на каждом последующем шаге исходные данные не являются точными и содержат погрешности, зависящие от неточности предшествующих вычислений.
§8.2. Метод Рунге-Кутта.
Данный метод является одним из наиболее распространенных численных методов интегрирования обыкновенных дифференциальных уравнений. По сравнению с описанным выше методом Эйлера метод Рунге-Кутта имеет более высокую точность, но невысокую скорость поиска решения, так как метод относится к классу многошаговых методов.
Пусть дано дифференциальное уравнение первого порядка
![]() , (8.10)
, (8.10)
с начальным условием
![]() . (8.11)
. (8.11)
Выберем шаг ![]() и для краткости введем обозначения
и для краткости введем обозначения ![]() ,
, ![]() , где
, где ![]() .
.
Рассмотрим числа:
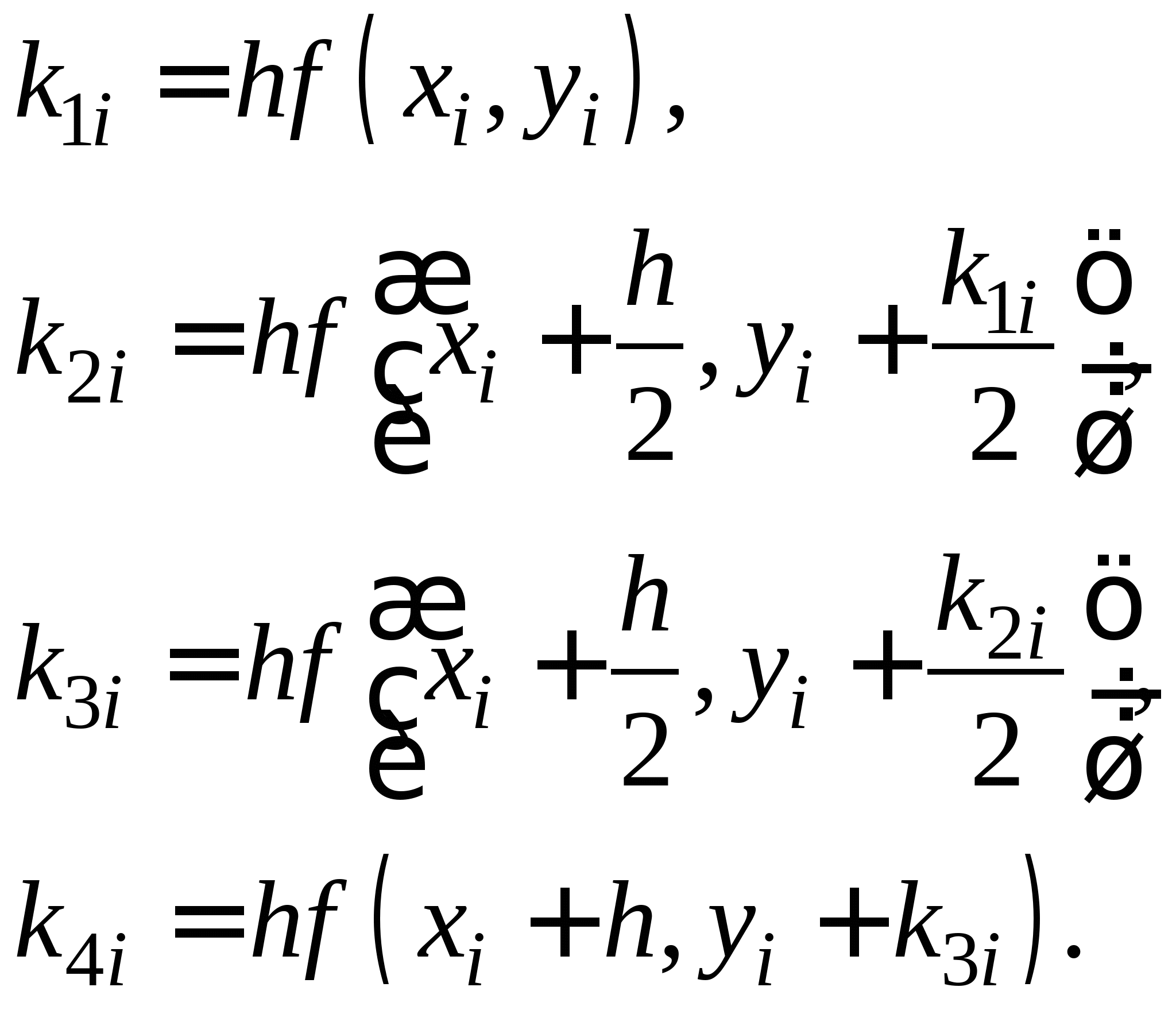 (8.12)
(8.12)
По методу Рунге-Кутта последовательные значения ![]() искомой функции
искомой функции ![]() определяются по формуле:
определяются по формуле:
![]() . (8.13)
. (8.13)
Погрешность метода Рунге-Кутта, заданного формулой (8.13), на каждом шаге есть величина порядка ![]() (в предположении, что
(в предположении, что ![]() ).
).
Формулу (8.13) еще называют формулой Рунге-Кутта четвертого порядка точности.
Помимо формулы (8.13) существуют еще другие формулы типа Рунге-Кутта с иными порядками точности. В частности формула ![]() формула Рунге-Кутта второго порядка точности. Эта формула на каждом шаге дает погрешность порядка
формула Рунге-Кутта второго порядка точности. Эта формула на каждом шаге дает погрешность порядка ![]() .
.
Для определения правильности выбора шага ![]() на практике обычно на каждом этапе из двух шагов применяют двойной пересчет. Исходя из текущего верного значения
на практике обычно на каждом этапе из двух шагов применяют двойной пересчет. Исходя из текущего верного значения ![]() , вычисляют
, вычисляют ![]() двумя способами: вначале с шагом
двумя способами: вначале с шагом ![]() , а затем с шагом
, а затем с шагом ![]() . Если расхождение полученных результатов не превышает допустимой погрешности, то шаг
. Если расхождение полученных результатов не превышает допустимой погрешности, то шаг ![]() для данного этапа выбран правильно и полученное с его помощью значение можно принять за
для данного этапа выбран правильно и полученное с его помощью значение можно принять за ![]() . В противном случае шаг уменьшается в два раза. Эту вычислительную схему легко запрограммировать на ЭВМ.
. В противном случае шаг уменьшается в два раза. Эту вычислительную схему легко запрограммировать на ЭВМ.
Метод Рунге-Кутта может быть использован и при решении систем дифференциальных уравнений. Рассмотрим задачу Коши для системы двух дифференциальных уравнений:
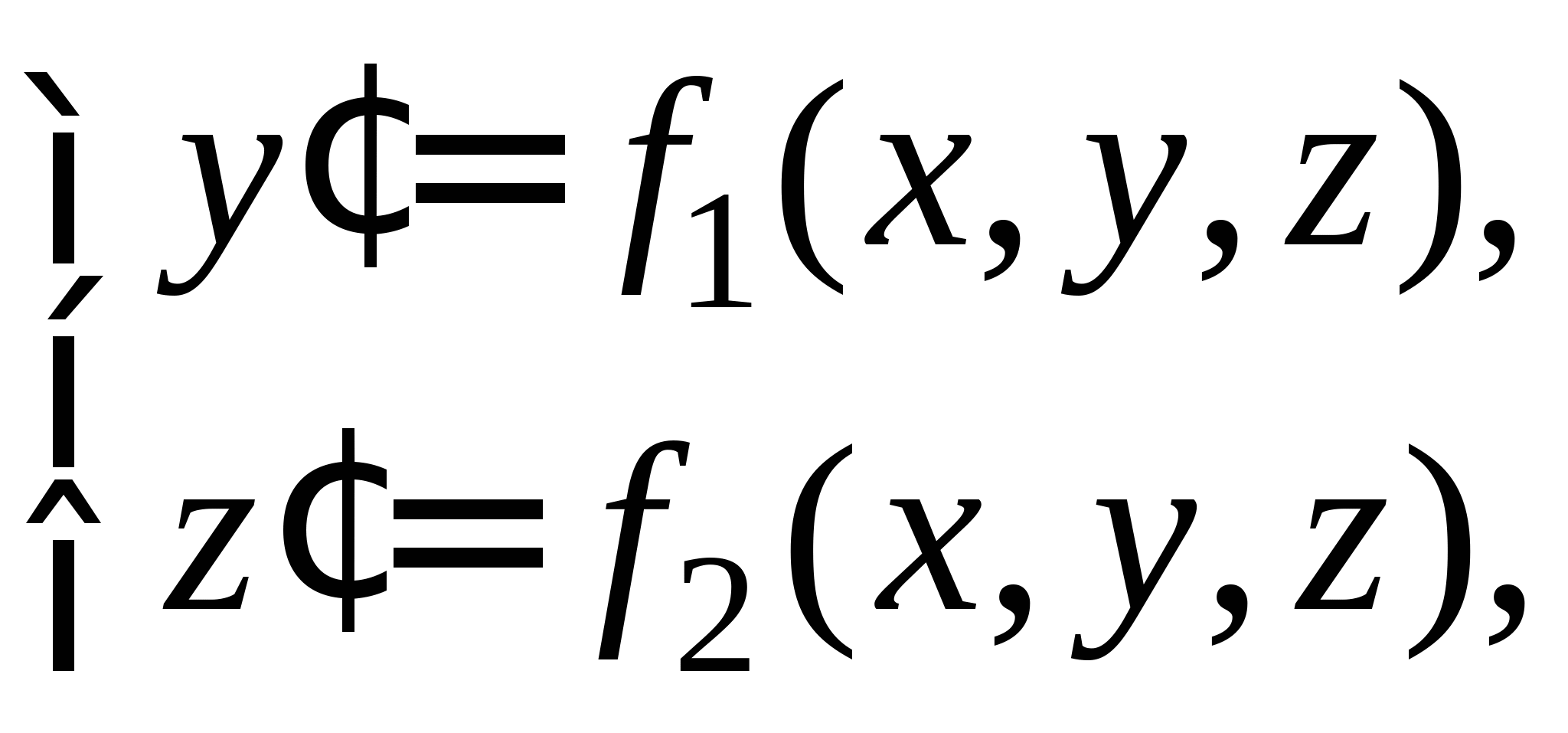
с начальными условиями
![]() .
.
Формулы метода Рунге-Кутта для данной системы примут вид:
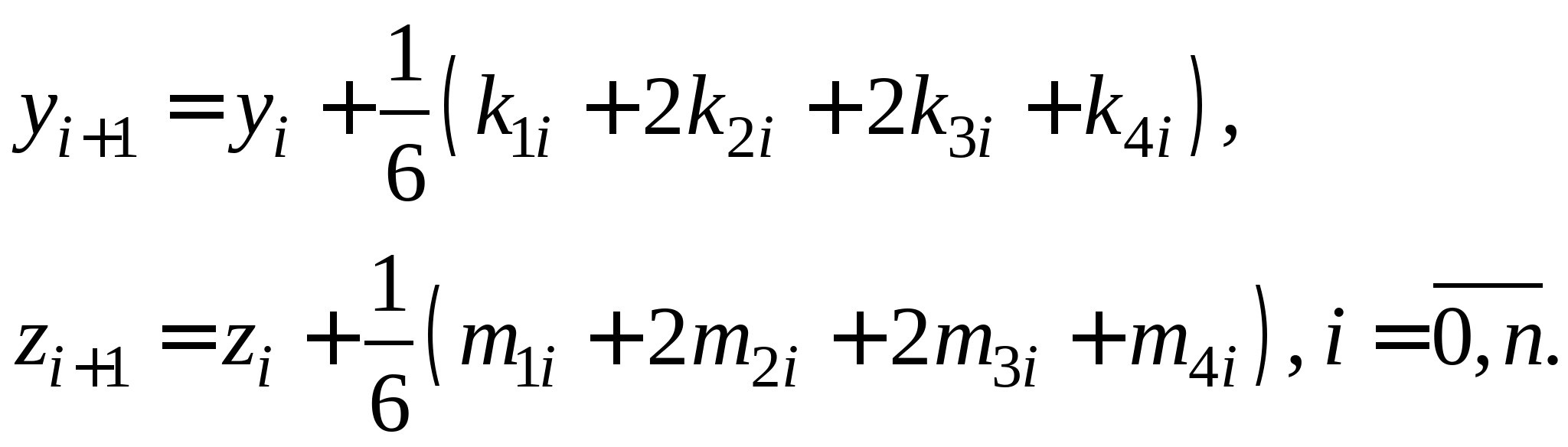
где
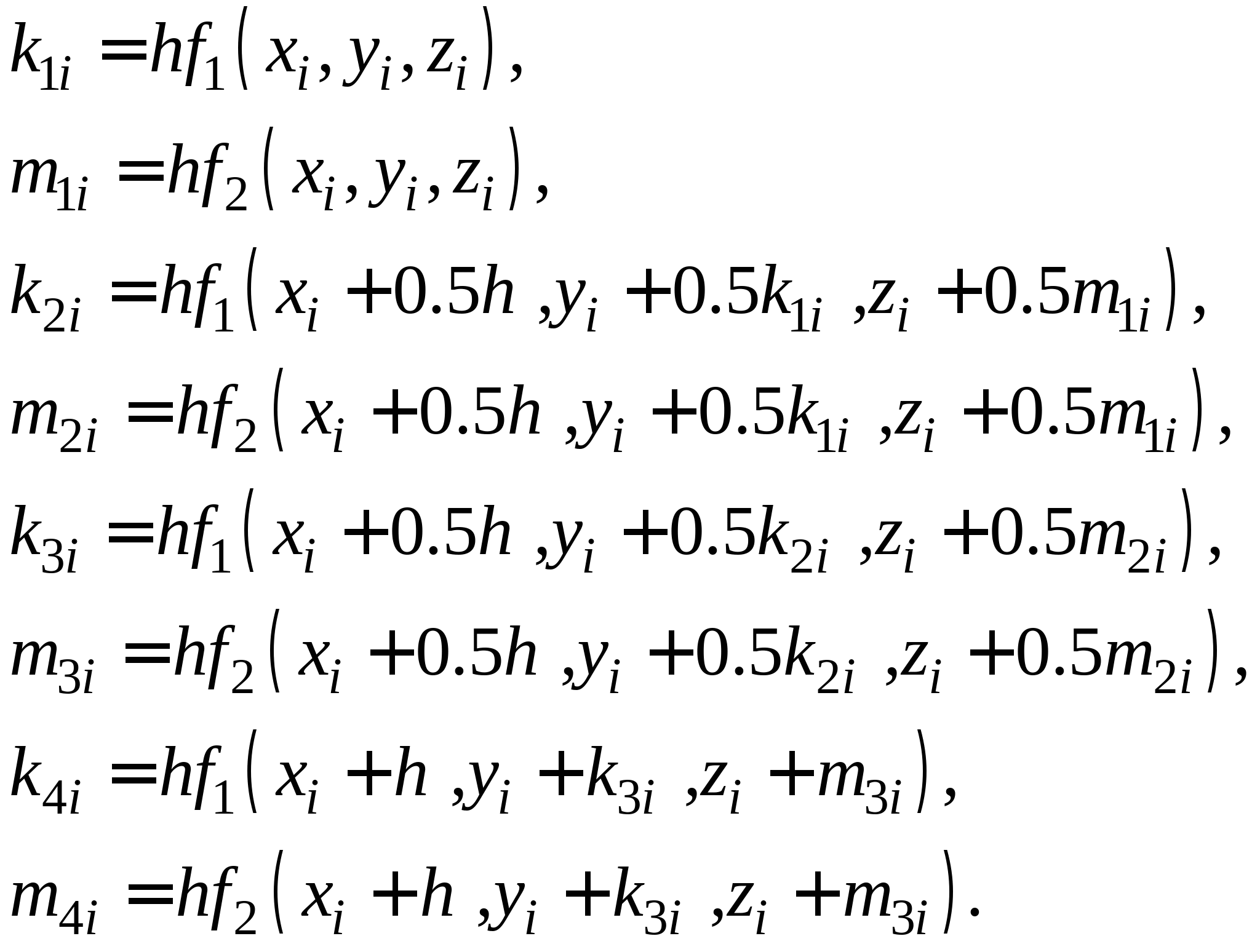
Метод Рунге-Кутта обладает значительной точностью и, несмотря на свою трудоемкость, широко используется при численном решении дифференциальных уравнений и систем. Важным преимуществом этого метода является возможность применения переменного шага, что позволяет учитывать локальные особенности искомой функции.
§8.3. Метод Адамса.
Этот метод численного интегрирования разработан Адамсом в 1855 году по просьбе известного английского артиллериста Башфорта, который занимался баллистикой. В последствии этот метод был забыт и вновь открыт в начале XX века норвежским математиком Штермером. Популяризация метода Адамса и дальнейшее его усовершенствование связано с именем А.Н. Крылова.
Пусть дано дифференциальное уравнение первого порядка
![]() , (8.14)
, (8.14)
с начальным условием
![]() . (8.15)
. (8.15)
Пусть ![]() система равноотстоящих значений с шагом
система равноотстоящих значений с шагом ![]() и
и ![]() . Очевидно, что
. Очевидно, что
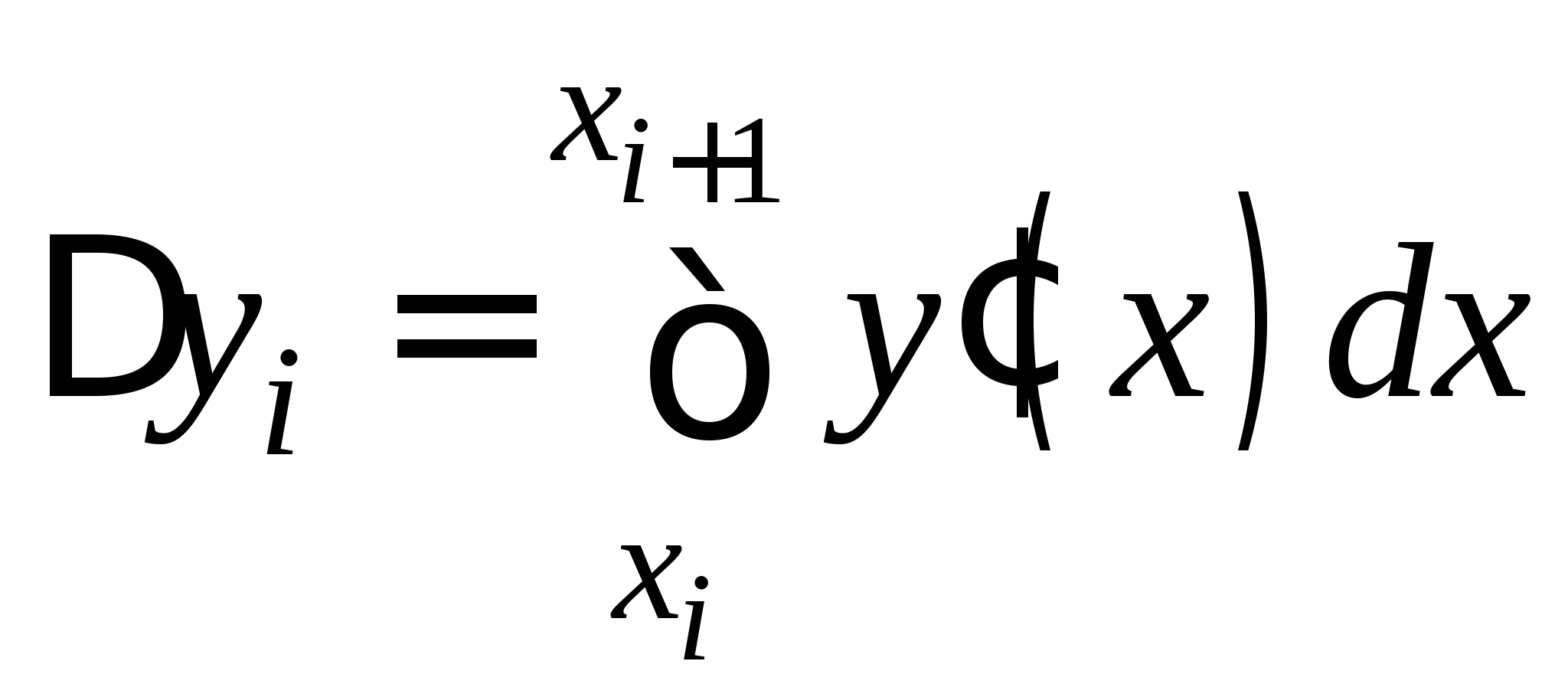 . (8.16)
. (8.16)
Запишем вторую интерполяционную формулу Ньютона с точностью до разностей четвертого порядка:
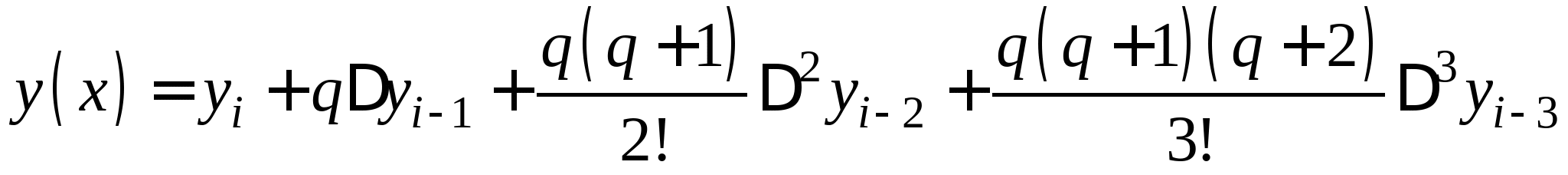 , (8.17)
, (8.17)
где ![]() .
.
В формуле (8.17) функцию ![]() заменим на производную
заменим на производную ![]() , получим:
, получим:
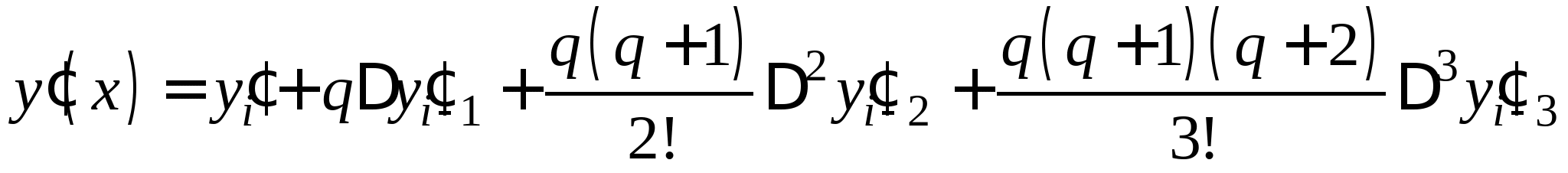 . (8.18)
. (8.18)
Так как ![]() , то подставив (8.18) в (8.16), получим:
, то подставив (8.18) в (8.16), получим:
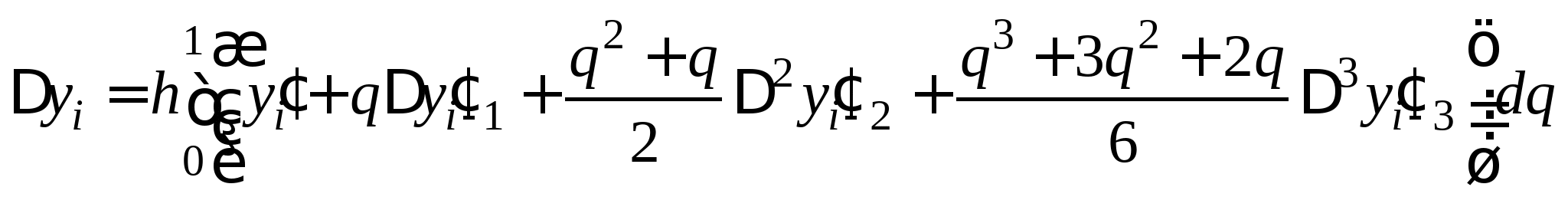 .
.
После преобразований будем иметь:
![]() . (8.19)
. (8.19)
Формула (8.19) называется экстраполяционной формулой Адамса.
Для начала итерационного процесса нужно знать начальные значения ![]() , так называемый начальный отрезок, который определяют, исходя из начального условия (8.15), каким-либо численным методом (например, методом Рунге-Кутта). Зная значения
, так называемый начальный отрезок, который определяют, исходя из начального условия (8.15), каким-либо численным методом (например, методом Рунге-Кутта). Зная значения ![]() из (8.14) находят
из (8.14) находят ![]() и составляют таблицу разностей:
и составляют таблицу разностей:
![]() . (8.20)
. (8.20)
Дальнейшие значения ![]() искомого решения можно шаг за шагом вычислять по формуле Адамса (8.19), пополняя по мере необходимости таблицу разностей (8.20).
искомого решения можно шаг за шагом вычислять по формуле Адамса (8.19), пополняя по мере необходимости таблицу разностей (8.20).
Для работы на ЭВМ формулу Адамса применяют в раскрытом виде. Так как
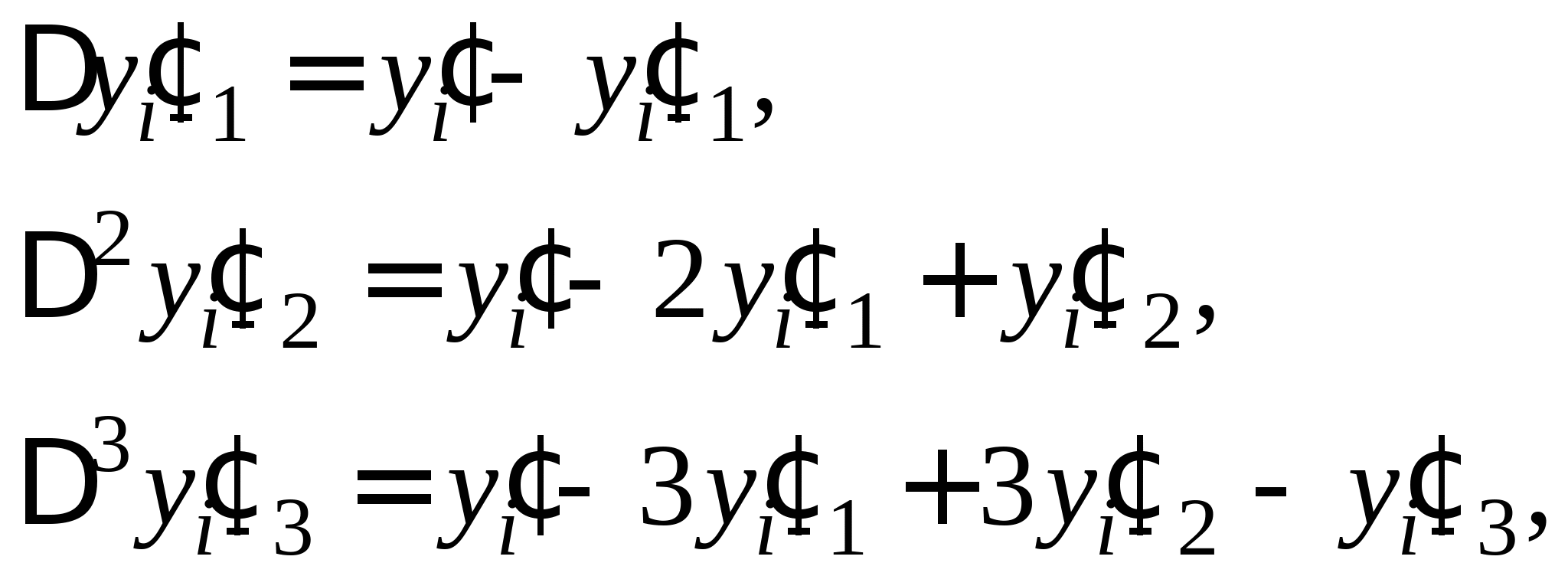
то после приведения подобных членов имеем:
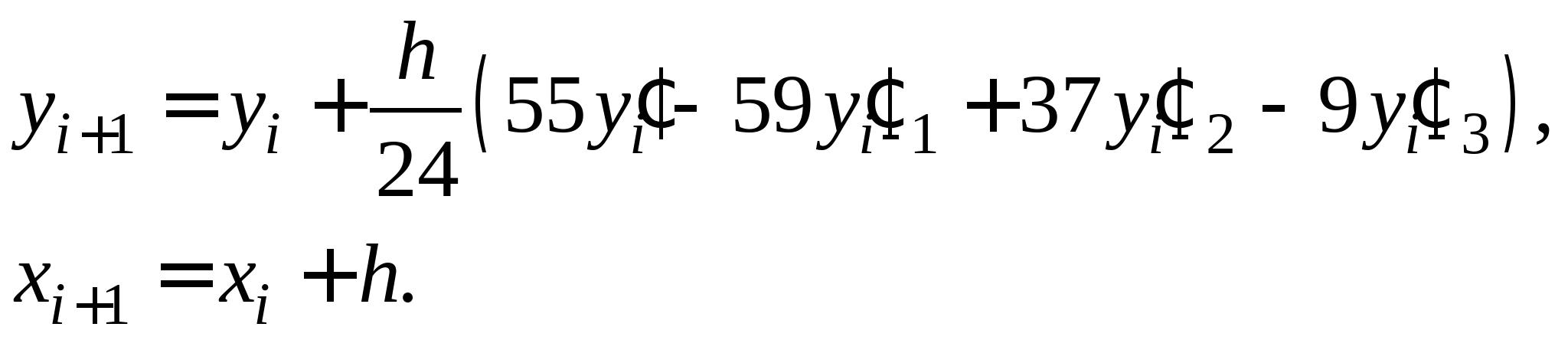 (8.21)
(8.21)
На практике шаг ![]() выбирают так, чтобы можно было пренебречь величиной
выбирают так, чтобы можно было пренебречь величиной
![]() .
.
Метод Адамса легко распространяется на системы дифференциальных уравнений. Погрешность метода Адамса имеет тот же порядок, что и метод Рунге-Кутта.
94
ГЛАВА 6. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ.
§6.1. Постановка вопроса.
При решении практических задач часто требуется найти производные указанных порядков от функции ![]() , заданной таблично, или в силу сложности аналитического выражения функции
, заданной таблично, или в силу сложности аналитического выражения функции ![]() непосредственное ее дифференцирование затруднено. В этих случаях прибегают к приближенному дифференцированию.
непосредственное ее дифференцирование затруднено. В этих случаях прибегают к приближенному дифференцированию.
Для этого на отрезке ![]() функцию
функцию ![]() заменяют интерполирующей функцией
заменяют интерполирующей функцией ![]() (чаще всего интерполирующим полиномом
(чаще всего интерполирующим полиномом ![]() ), затем полагают
), затем полагают ![]() при
при ![]() . Аналогично поступают при нахождении производных высших порядков от функции
. Аналогично поступают при нахождении производных высших порядков от функции ![]() .
.
Если для интерполирующей функции известна погрешность
![]() ,
,
то погрешность производной
![]() ,
,
т.е. погрешность производной интерполирующей функции равна производной от погрешности этой функции. То же справедливо для производных высших порядков.
Приближенное дифференцирование является менее точной операцией, чем интерполирование. Близость друг к другу ординат двух кривых ![]() и
и ![]() на отрезке
на отрезке ![]() еще не гарантирует близости на этом отрезке их производных
еще не гарантирует близости на этом отрезке их производных ![]() и
и ![]() , то есть малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.
, то есть малого расхождения угловых коэффициентов касательных к рассматриваемым кривым при одинаковых значениях аргумента.
§6.2. Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона.
Пусть на отрезке ![]() заданы равноотстоящие точки
заданы равноотстоящие точки ![]() :
: ![]() ,
, ![]() , и известны значения функции в этих точках
, и известны значения функции в этих точках ![]() . Требуется найти производные
. Требуется найти производные ![]() на отрезке
на отрезке ![]() (заранее известно, что эти производные существуют).
(заранее известно, что эти производные существуют).
Заменим функцию ![]() интерполяционным полиномом Ньютона, построенным для узлов
интерполяционным полиномом Ньютона, построенным для узлов ![]() , воспользовавшись первой интерполяционной формулой Ньютона:
, воспользовавшись первой интерполяционной формулой Ньютона:
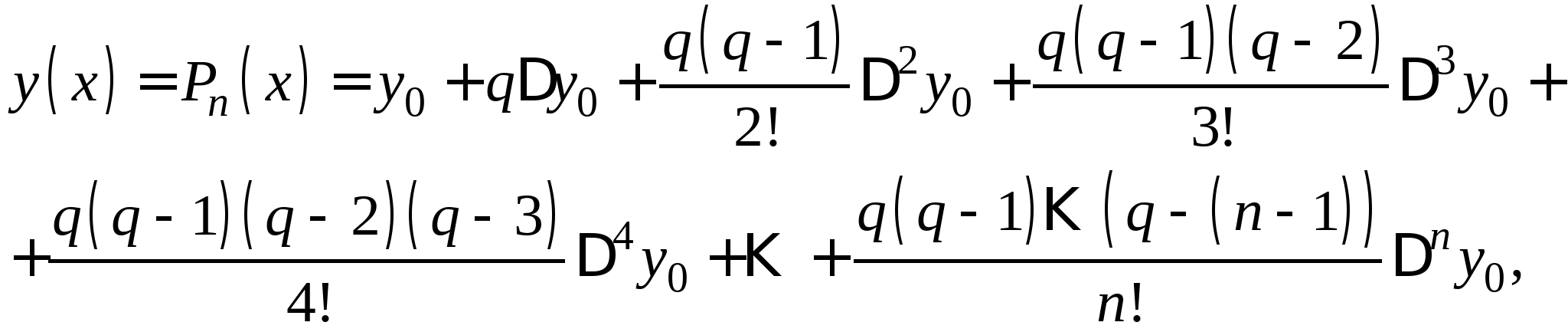 (6.1)
(6.1)
где ![]() .
.
Произведя перемножение биномов и приведя подобные, получим:
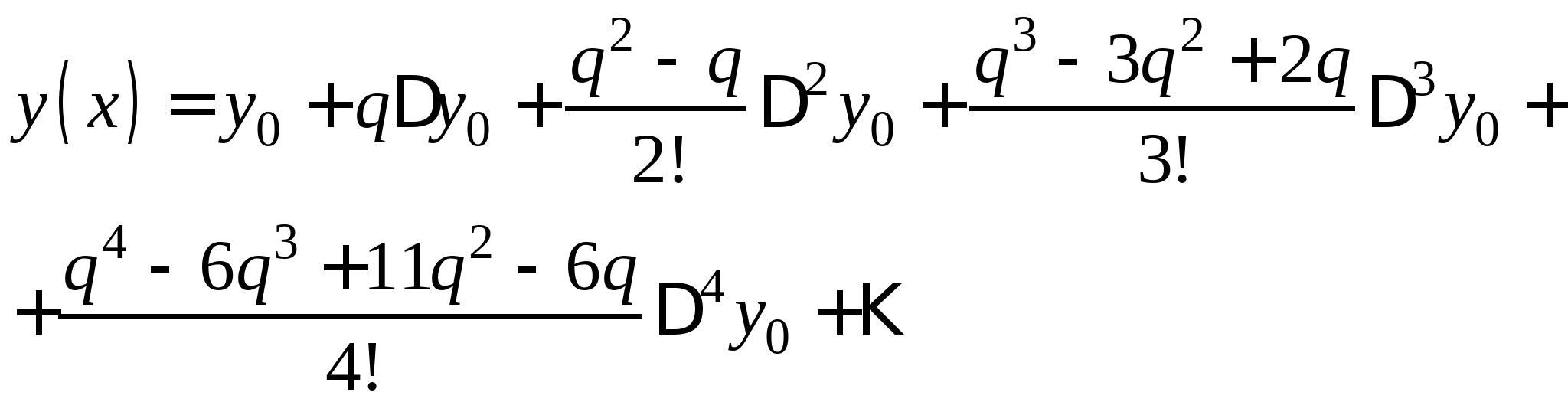 (6.2)
(6.2)
Так как
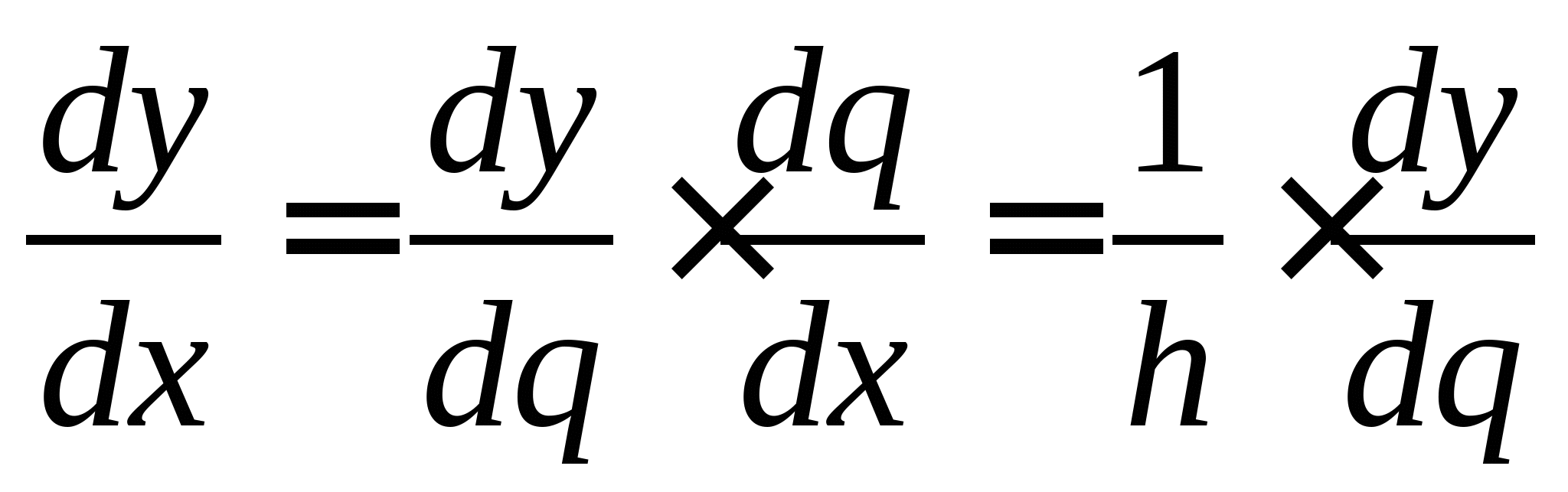 ,
,
то
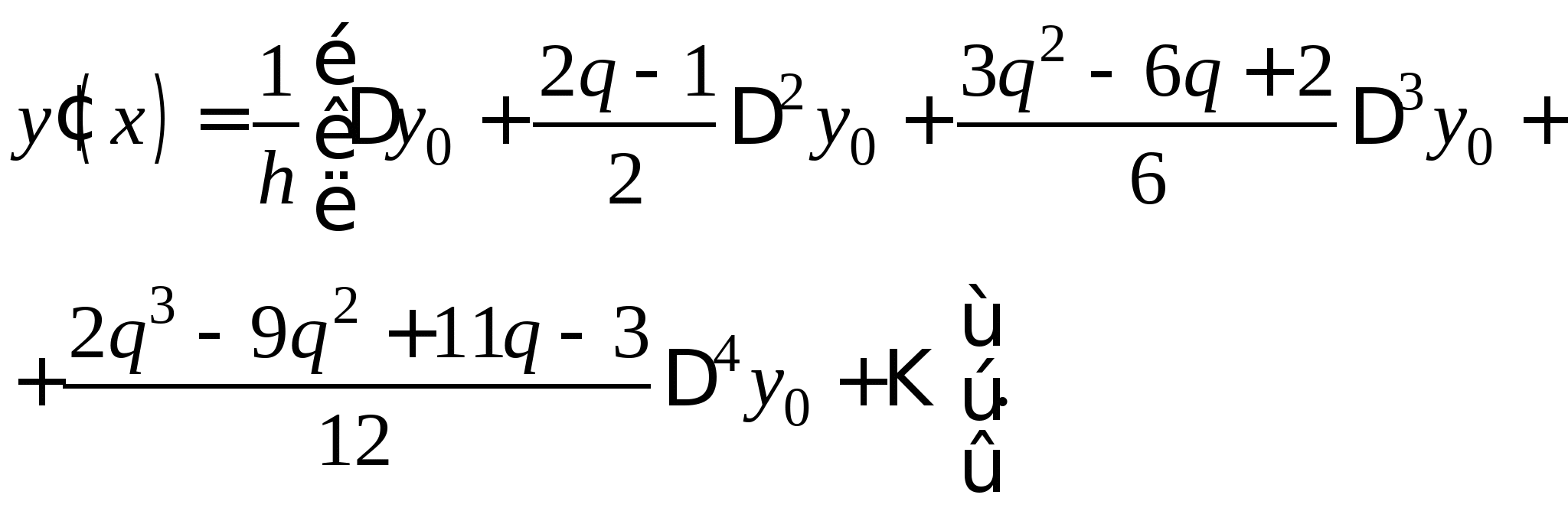 (6.3)
(6.3)
Аналогично, так как
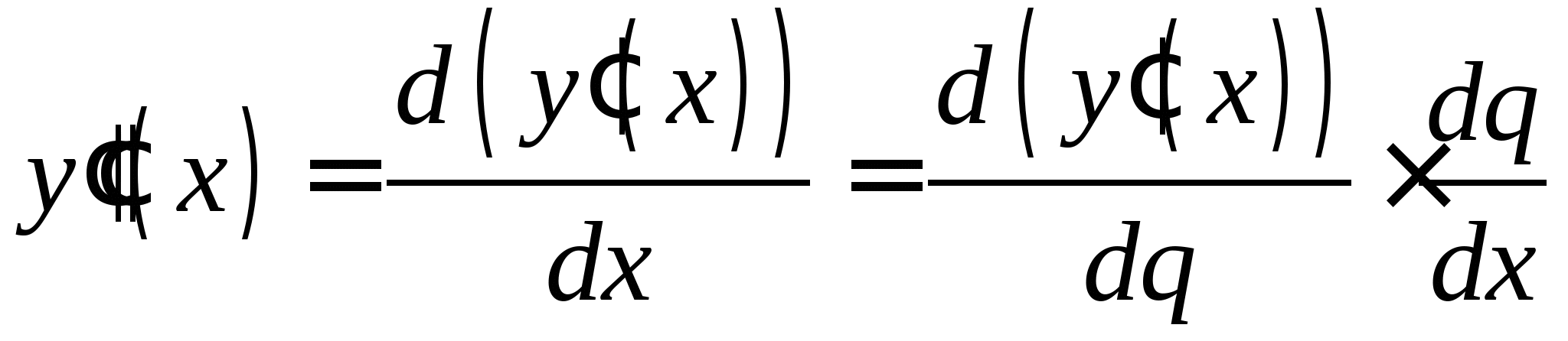 ,
,
то
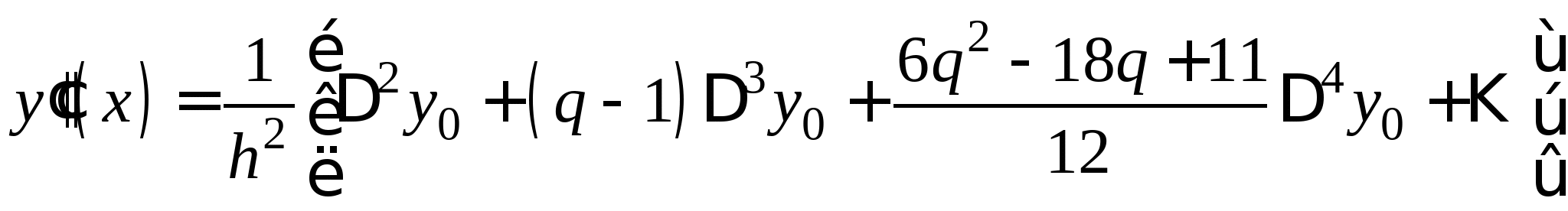 . (6.4)
. (6.4)
Таким способом можно вычислить производную любого порядка.
При нахождении производных ![]() в фиксированной точке
в фиксированной точке ![]() в качестве
в качестве ![]() следует брать ближайшее к
следует брать ближайшее к ![]() табличное значение аргумента.
табличное значение аргумента.
Формулы (6.3) и (6.4) упрощаются, если нужно подсчитать производные в узлах интерполяции. Полагая ![]() ,
, ![]() , получаем:
, получаем:
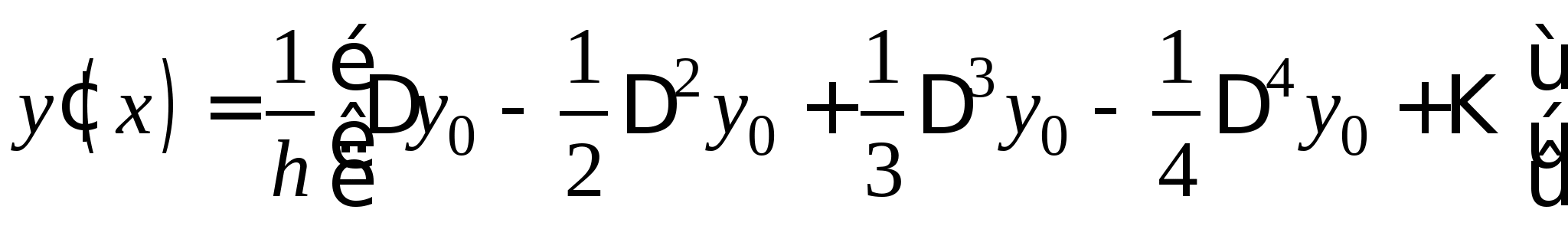 , (6.5)
, (6.5)
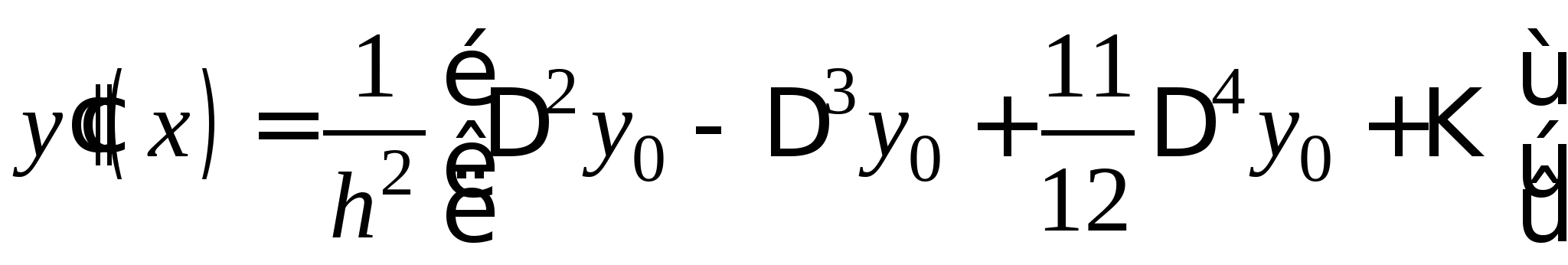 . (6.6)
. (6.6)
Пусть ![]() - интерполяционный полином Ньютона, содержащий конечные разности
- интерполяционный полином Ньютона, содержащий конечные разности ![]() и
и ![]() , тогда
, тогда ![]() . Но
. Но 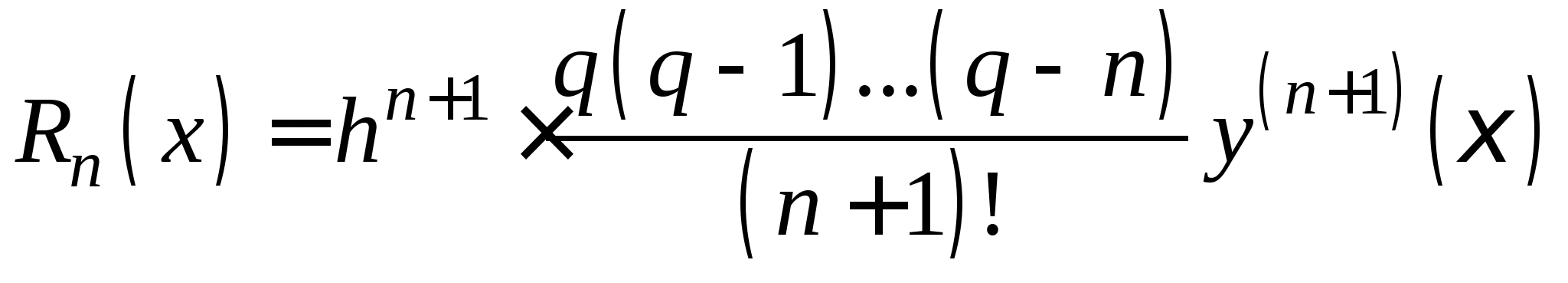 .
.
Тогда, если ![]() , то
, то
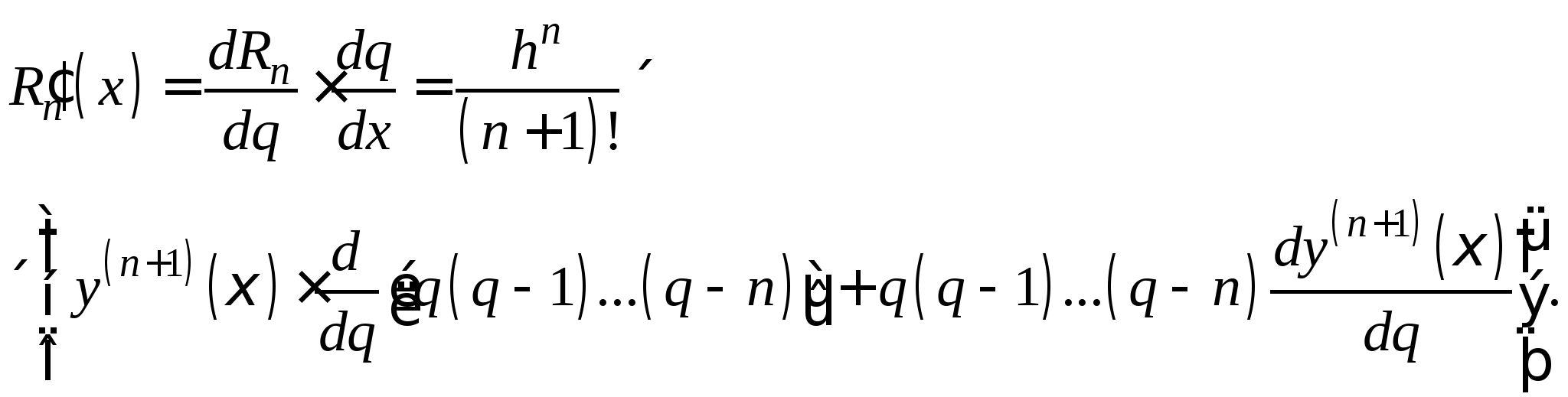 (6.7)
(6.7)
Полагая 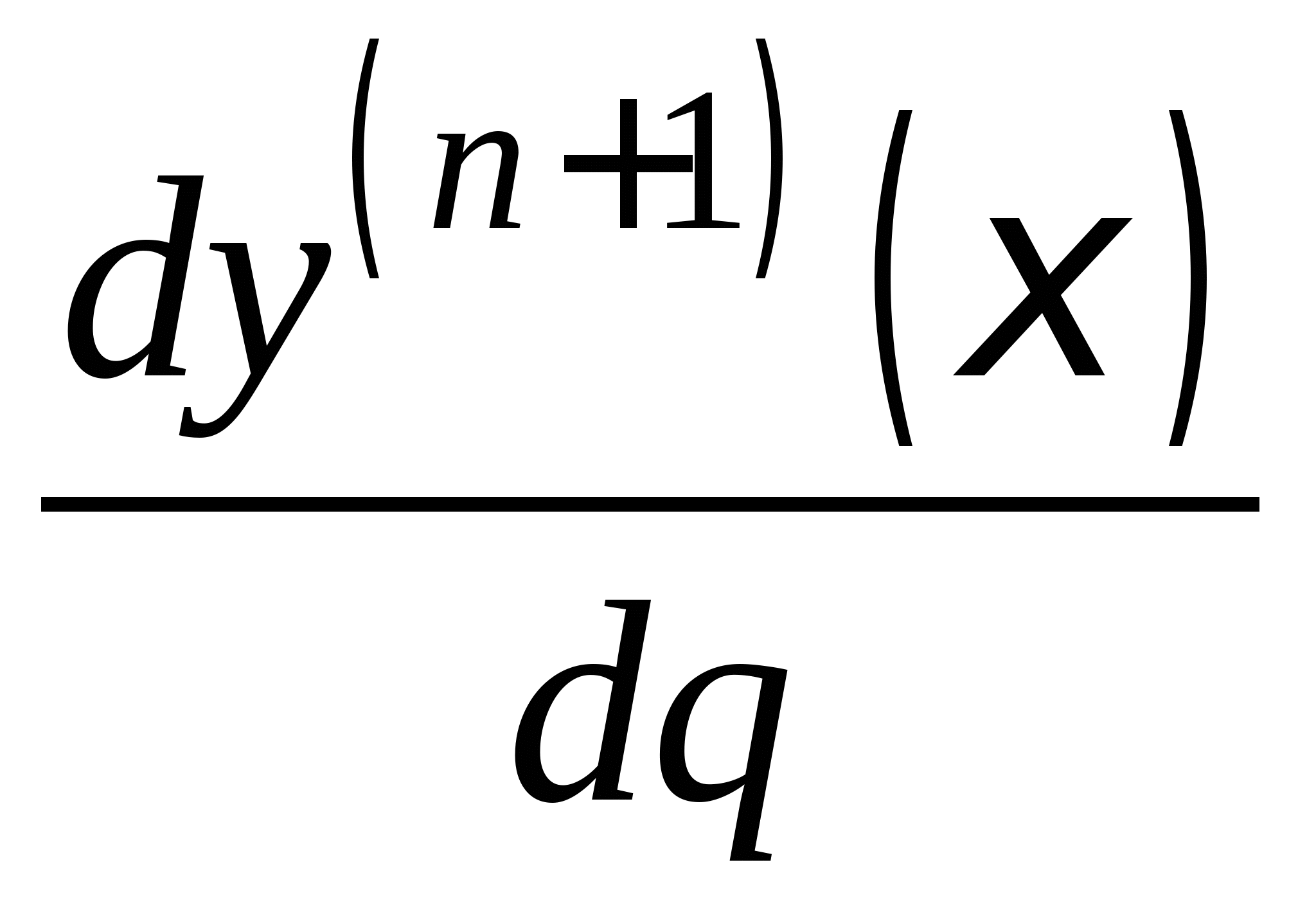 - ограниченной и учитывая, что
- ограниченной и учитывая, что
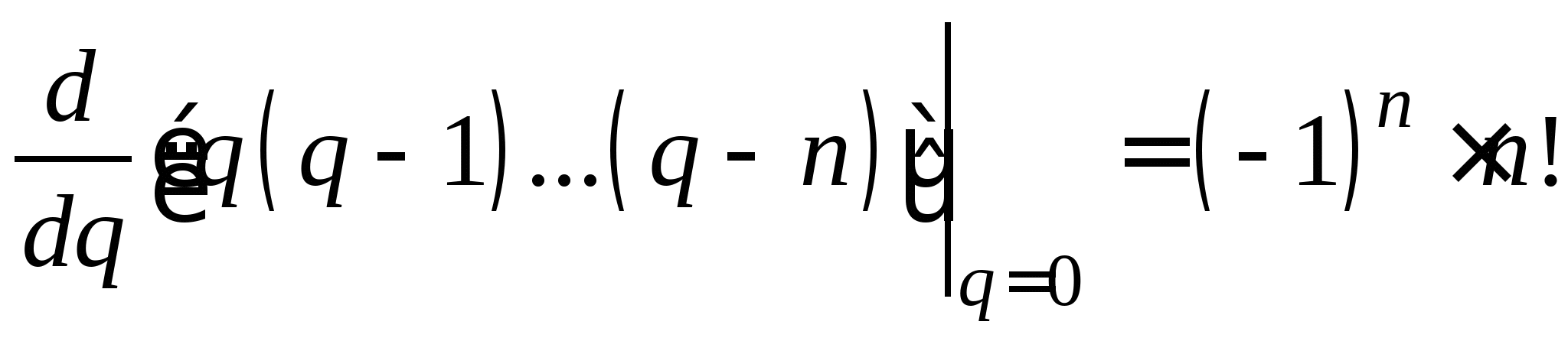 ,
,
получаем при ![]() ,
, ![]() :
:
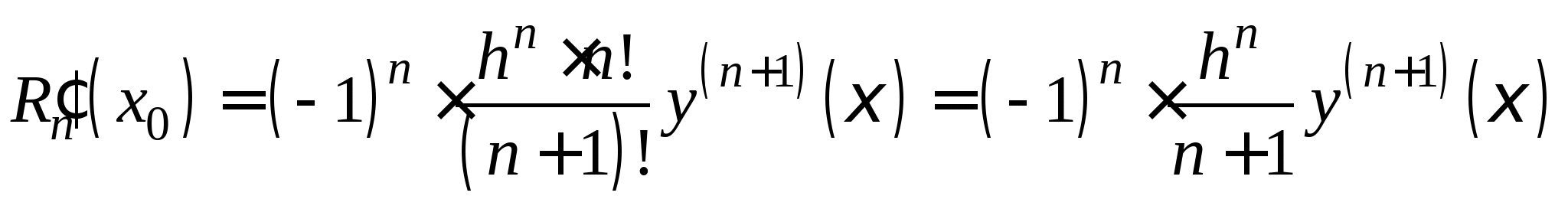 . (6.8)
. (6.8)
Так как ![]() сложно определить, то при малом шаге
сложно определить, то при малом шаге ![]() принято считать
принято считать 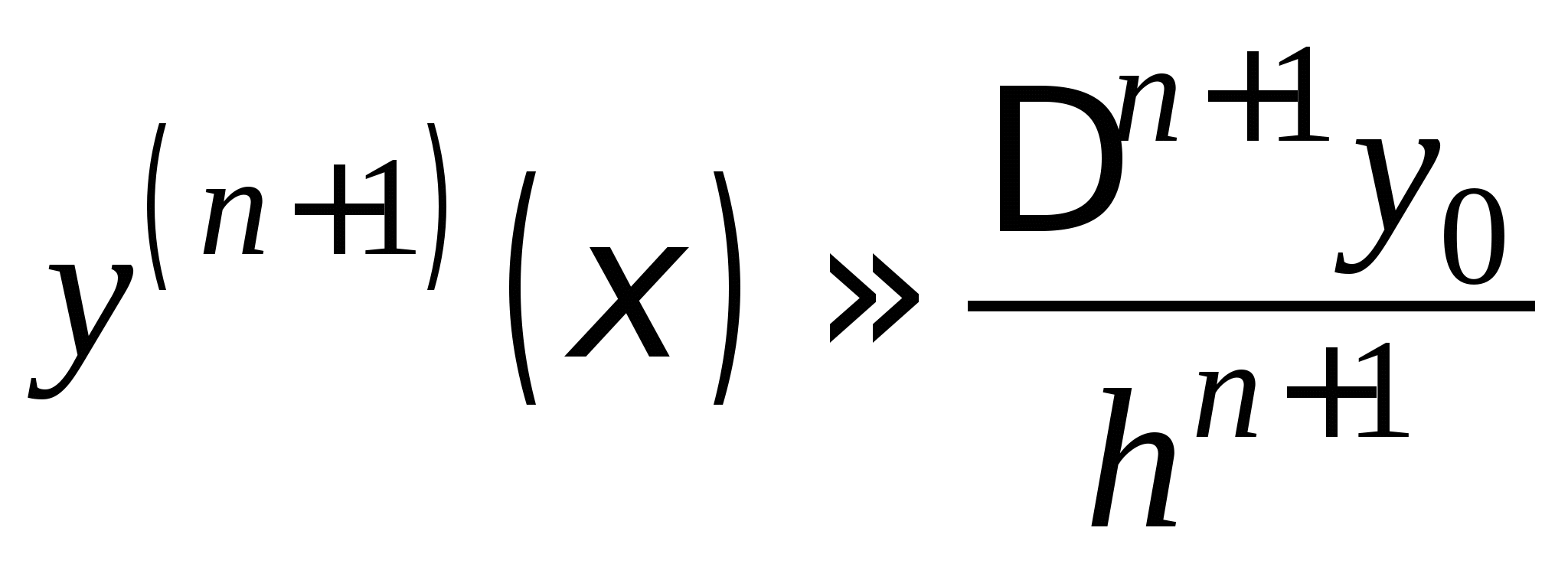 . Тогда (6.8) примет вид:
. Тогда (6.8) примет вид:
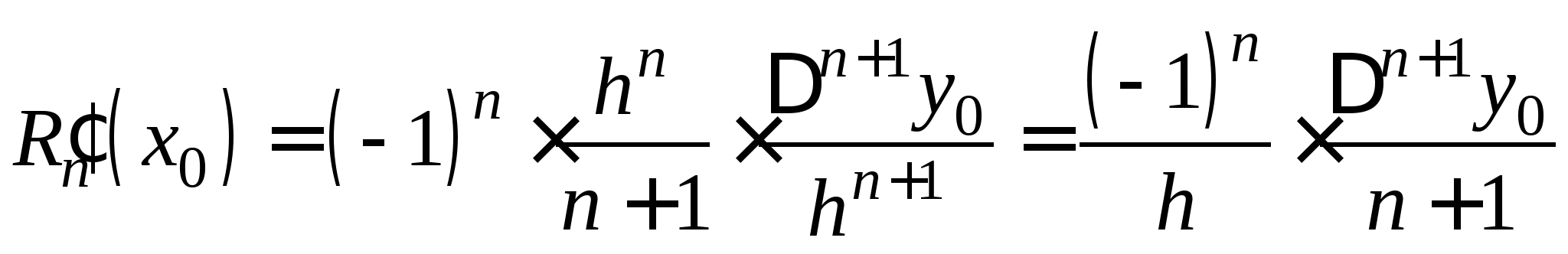 . (6.9)
. (6.9)
Аналогично находится ![]() и так далее.
и так далее.
Формулы приближенного дифференцирования аналогичным образом можно получить, используя вторую интерполяционную формулу Ньютона.
§6.3. Формулы численного дифференцирования для равноотстоящих точек, основанные на интерполяционной формуле Лагранжа.
Пусть даны равноотстоящие точки ![]() , такие, что
, такие, что ![]() , и известны значения функции в этих точках
, и известны значения функции в этих точках ![]() . Для данной системы узлов
. Для данной системы узлов ![]() построим интерполяционный полином Лагранжа:
построим интерполяционный полином Лагранжа:
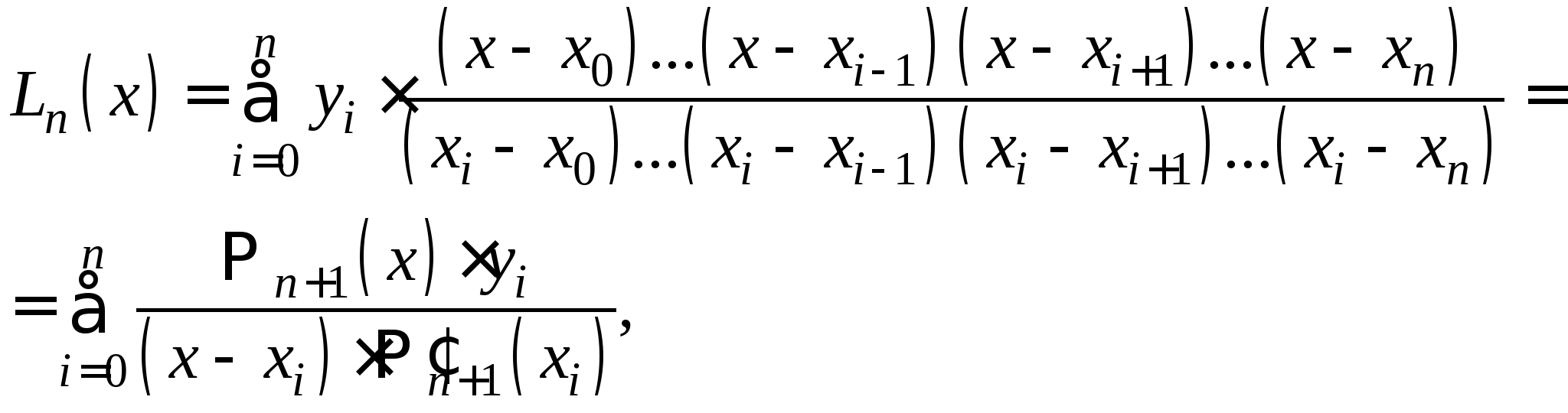 (6.10)
(6.10)
где ![]() .
.
Для ![]() справедливо соотношение
справедливо соотношение
![]() .
.
Введем новую переменную ![]() , тогда
, тогда
![]() , (6.11)
, (6.11)
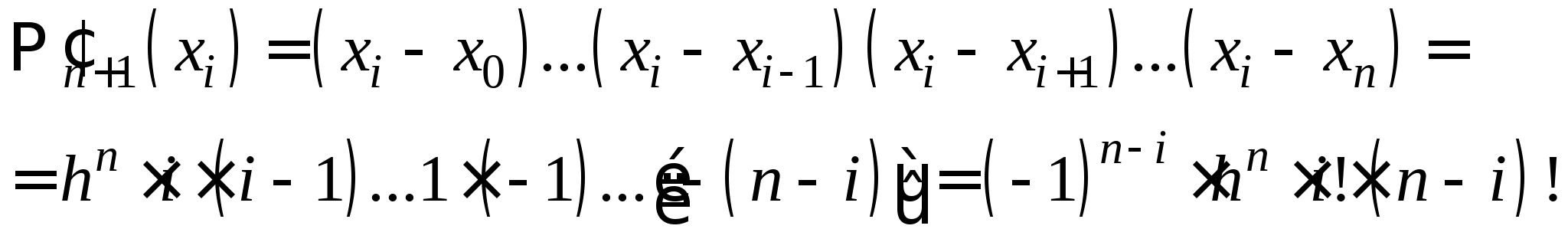 (6.12)
(6.12)
Подставив (6.11), (6.12) в (6.10), получим:
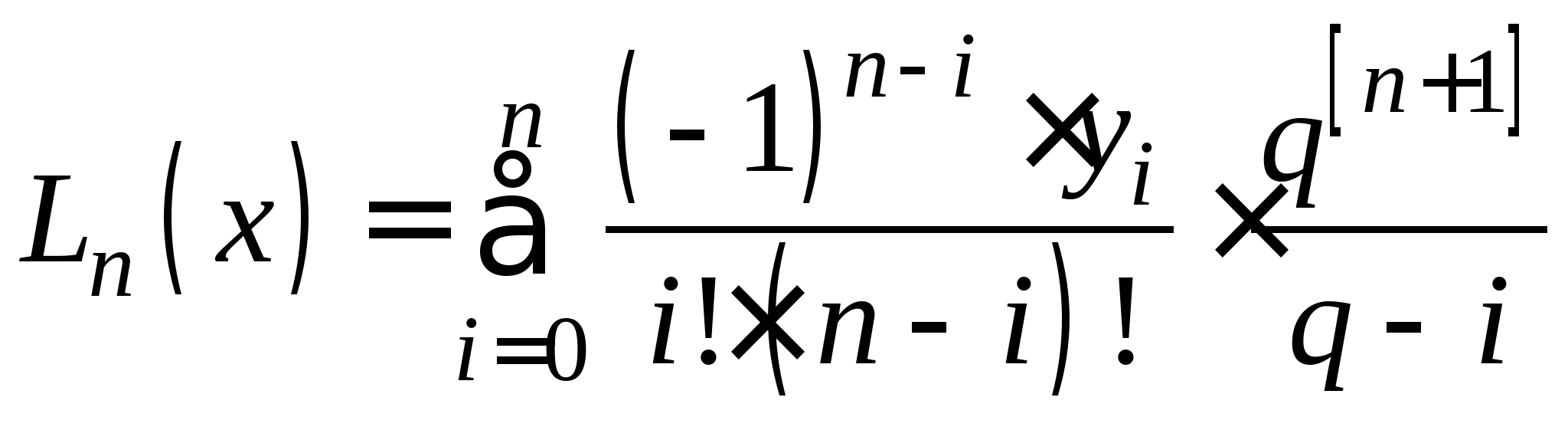 . (6.13)
. (6.13)
Заменив функцию ![]() интерполяционным полиномом Лагранжа
интерполяционным полиномом Лагранжа ![]() и учитывая, что
и учитывая, что 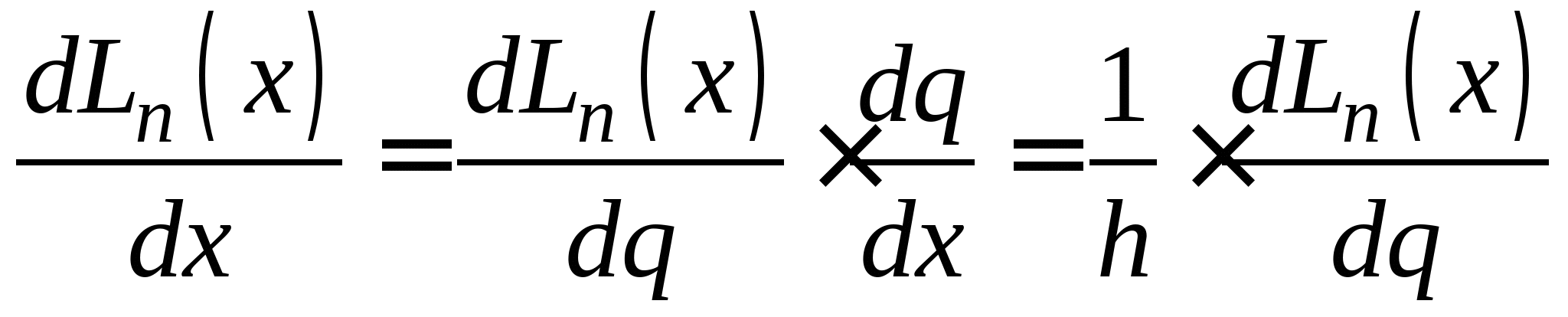 , из соотношения (6.13) получим:
, из соотношения (6.13) получим:
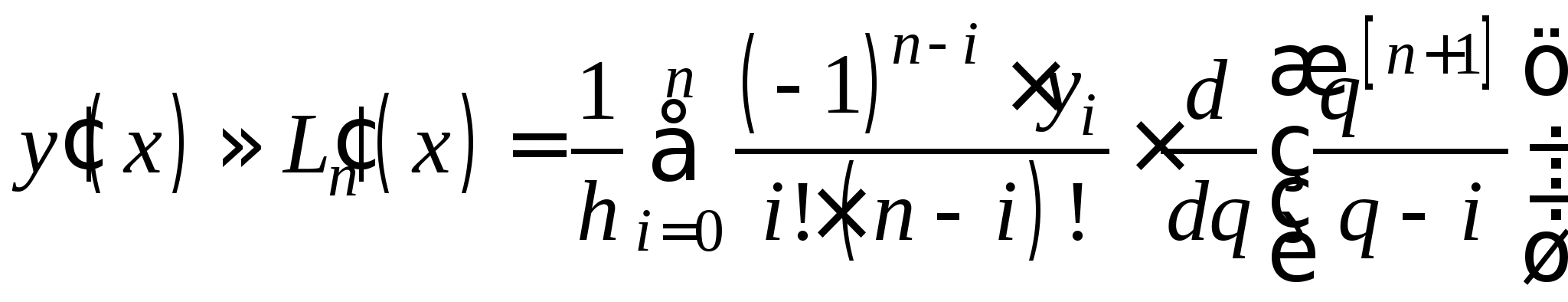 . (6.14)
. (6.14)
Аналогично можно найти ![]() и так далее.
и так далее.
Для оценки погрешности ![]() воспользуемся формулой погрешности интерполяционной формулы Лагранжа:
воспользуемся формулой погрешности интерполяционной формулы Лагранжа:
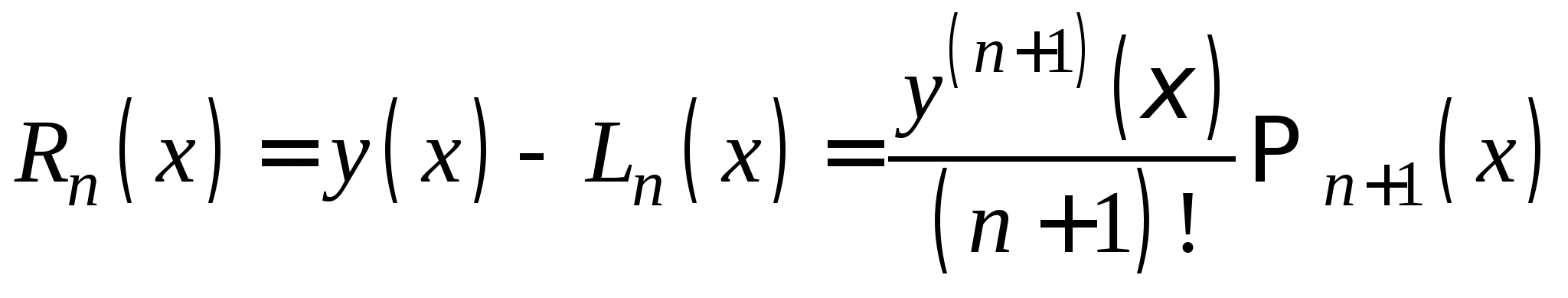 ,
,
где ![]() - промежуточное значение между
- промежуточное значение между ![]() и узлами интерполяции
и узлами интерполяции ![]() .
.
Предположим, что ![]() , тогда
, тогда
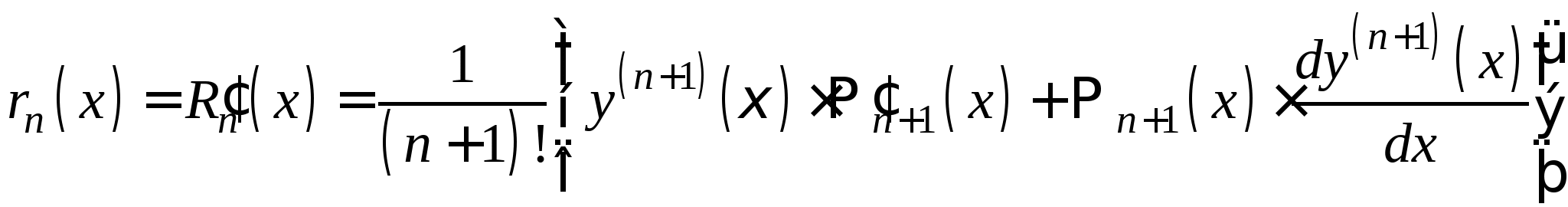 . (6.15)
. (6.15)
Учитывая соотношение (6.12) и предполагая 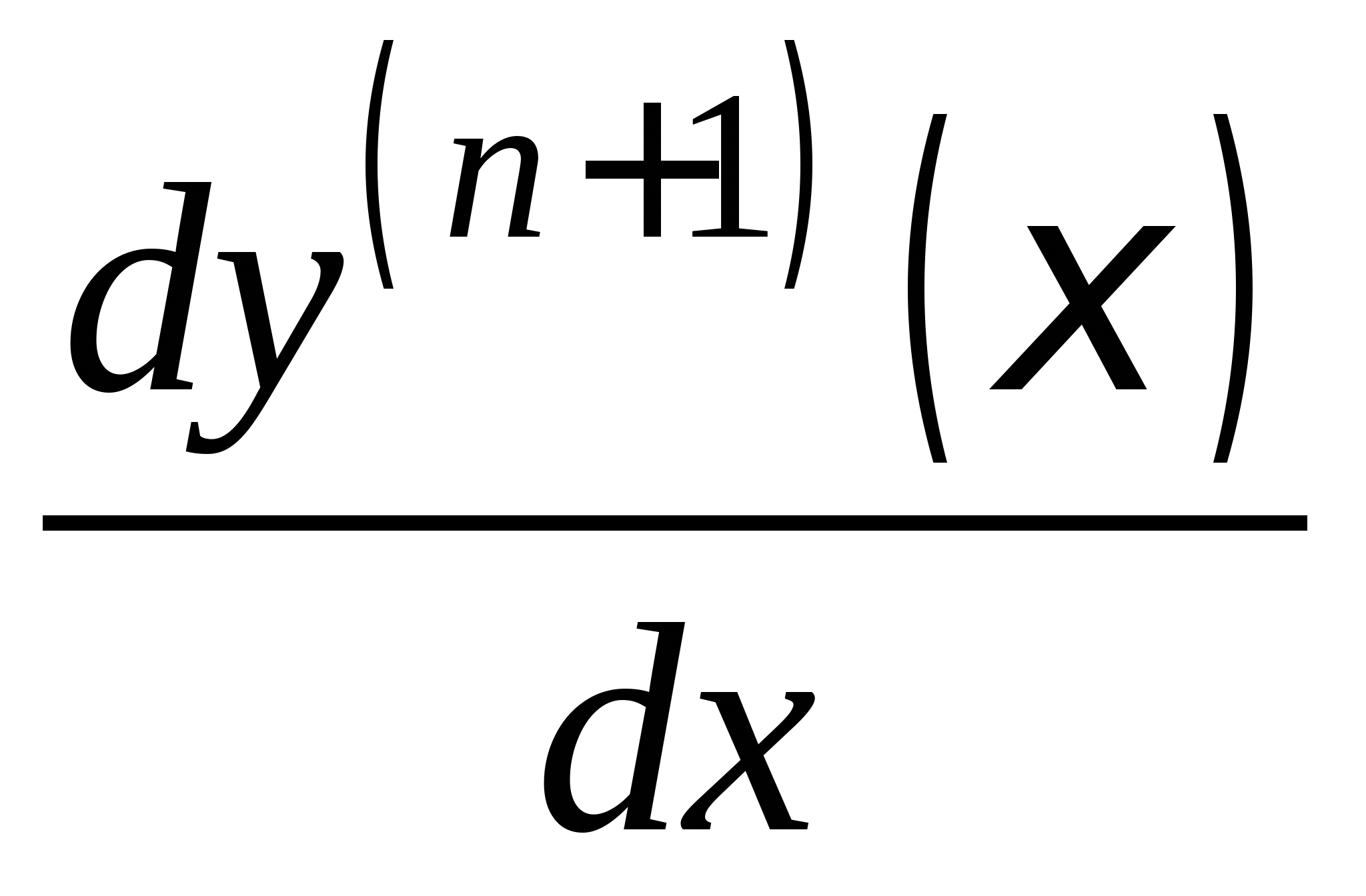 - ограниченной, из соотношения (6.15) получим оценку погрешности в узлах интерполяции:
- ограниченной, из соотношения (6.15) получим оценку погрешности в узлах интерполяции:
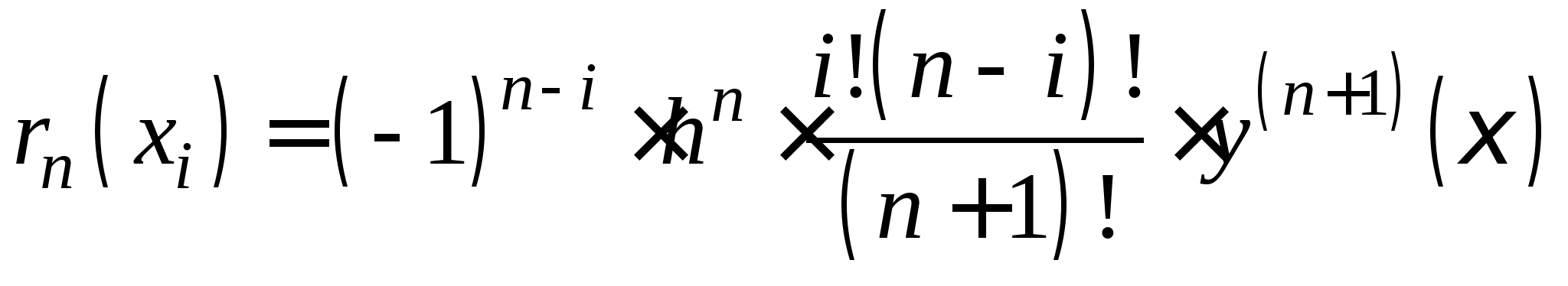 . (6.16)
. (6.16)
ГЛАВА 7. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ.
§7.1. Квадратурная формула Ньютона-Котеса.
Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и известна ее первообразная
и известна ее первообразная ![]() , то определенный интеграл от этой функции в пределах от
, то определенный интеграл от этой функции в пределах от ![]() до
до ![]() может быть вычислен по формуле Ньютона-Лейбница:
может быть вычислен по формуле Ньютона-Лейбница:
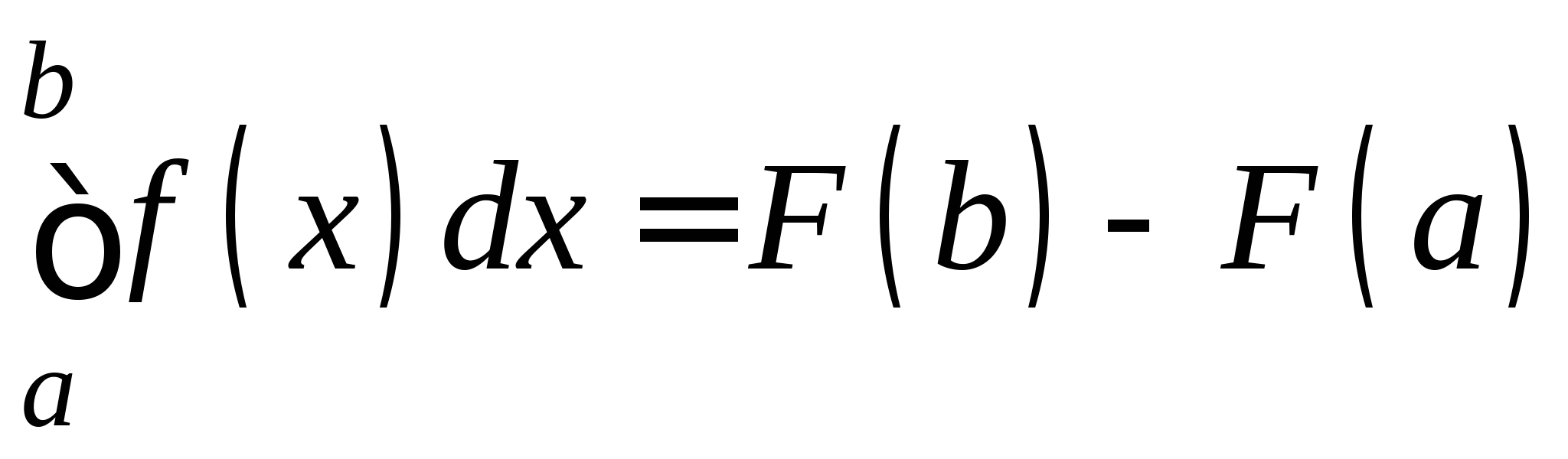 (7.1)
(7.1)
Однако во многих случаях первообразная ![]() не может быть найдена с помощью элементарных средств или является слишком сложной; вследствие этого вычисление определенного интеграла по формуле (7.1) может быть затруднено или быть практически невыполнимым. Кроме того, на практике подынтегральная функция
не может быть найдена с помощью элементарных средств или является слишком сложной; вследствие этого вычисление определенного интеграла по формуле (7.1) может быть затруднено или быть практически невыполнимым. Кроме того, на практике подынтегральная функция ![]() часто задается таблично и тогда само понятие первообразной теряет смысл. Поэтому, важное значение приобретают численные методы вычисления определенных интегралов, использующие ряд значений подынтегральной функции в точках
часто задается таблично и тогда само понятие первообразной теряет смысл. Поэтому, важное значение приобретают численные методы вычисления определенных интегралов, использующие ряд значений подынтегральной функции в точках ![]() , где
, где ![]() .
.
Определение 7.1.
Численное вычисление однократного интеграла называется механической квадратурой, двойного интеграла механической кубатурой. Соответствующие формулы называются квадратурными и кубатурными формулами.
Рассмотрим один из способов вычисления определенных интегралов.
Если воспользоваться, например, интерполяционным полиномом Лагранжа, то, заменяя функцию ![]() полиномом
полиномом ![]() , получим равенство
, получим равенство
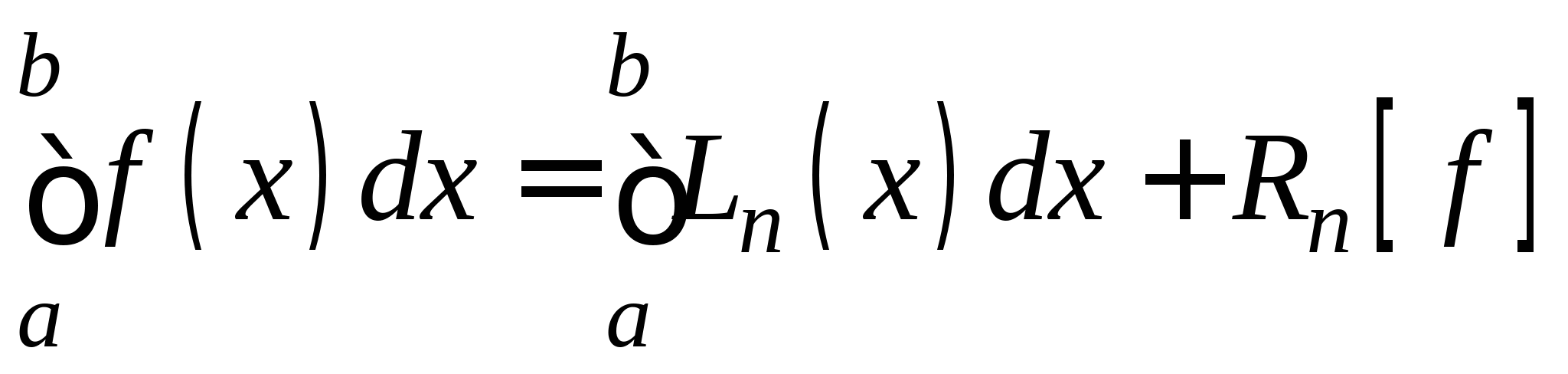 (7.2)
(7.2)
где ![]() - ошибка этой интерполяционной формулы.
- ошибка этой интерполяционной формулы.
Требуется вычислить интеграл ![]() , где
, где ![]() . Выбрав шаг
. Выбрав шаг ![]() , разобьем отрезок
, разобьем отрезок ![]() на
на ![]() равных частей с помощью равноотстоящих точек
равных частей с помощью равноотстоящих точек ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Заменим подынтегральную функцию
. Заменим подынтегральную функцию ![]() интерполяционным полиномом Лагранжа
интерполяционным полиномом Лагранжа ![]() и получим приближенную квадратурную формулу
и получим приближенную квадратурную формулу
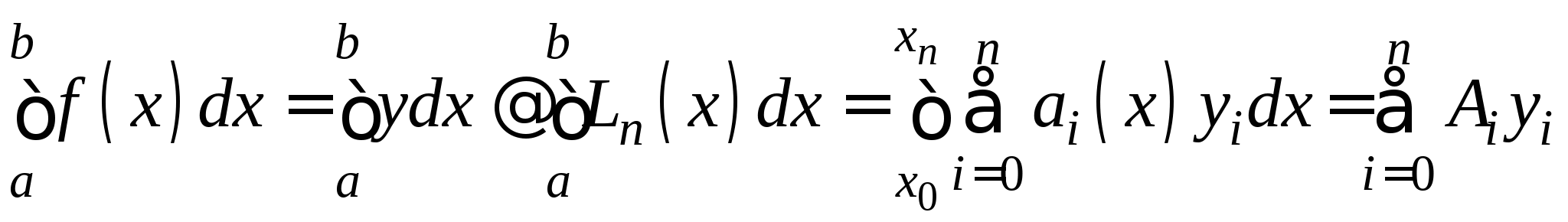 , (7.3)
, (7.3)
где ![]() - некоторые постоянные коэффициенты.
- некоторые постоянные коэффициенты.
Выведем явные выражения для коэффициентов ![]() формулы (7.3). Многочлен Лагранжа
формулы (7.3). Многочлен Лагранжа ![]() имеет коэффициенты
имеет коэффициенты
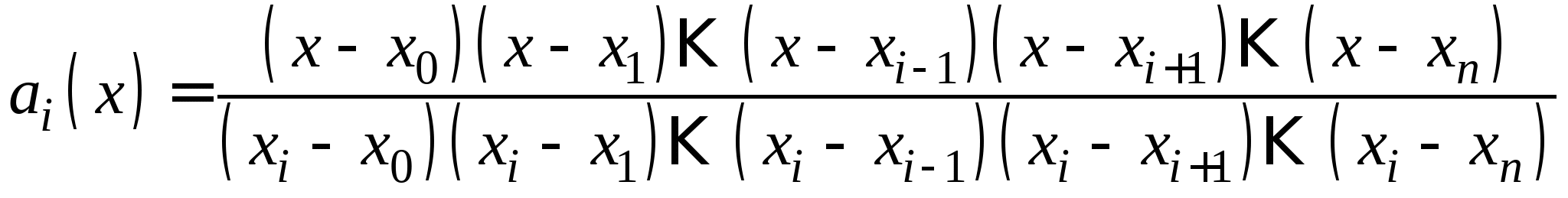 .
.
Введем обозначения ![]() и
и ![]() . Тогда многочлен Лагранжа запишется в виде:
. Тогда многочлен Лагранжа запишется в виде:
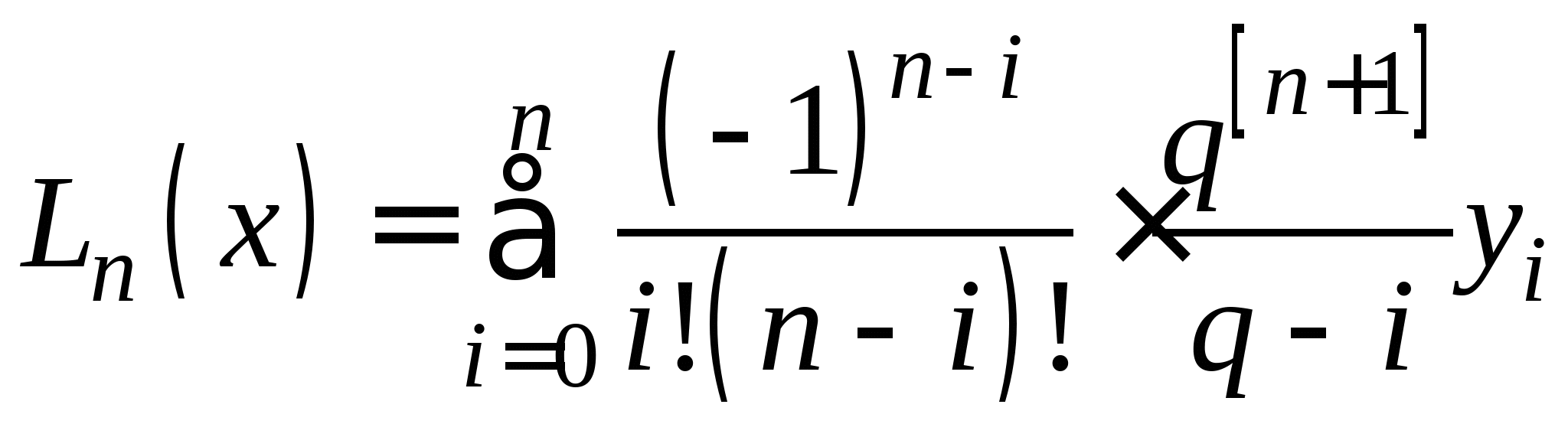 . (7.4)
. (7.4)
Заменяя в (7.3) функцию ![]() полиномом
полиномом ![]() по формуле (7.4), получим:
по формуле (7.4), получим:
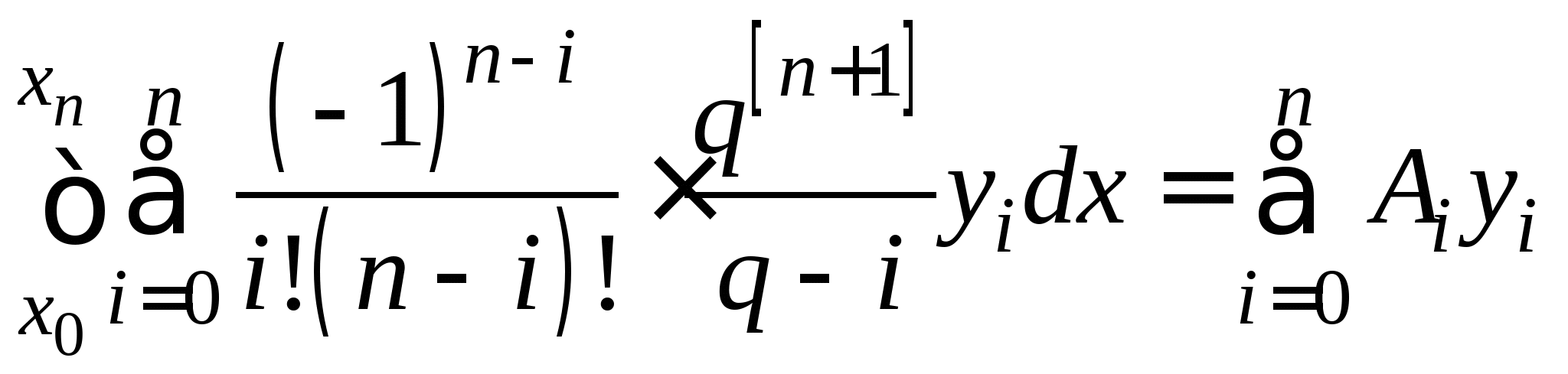 ,
,
где 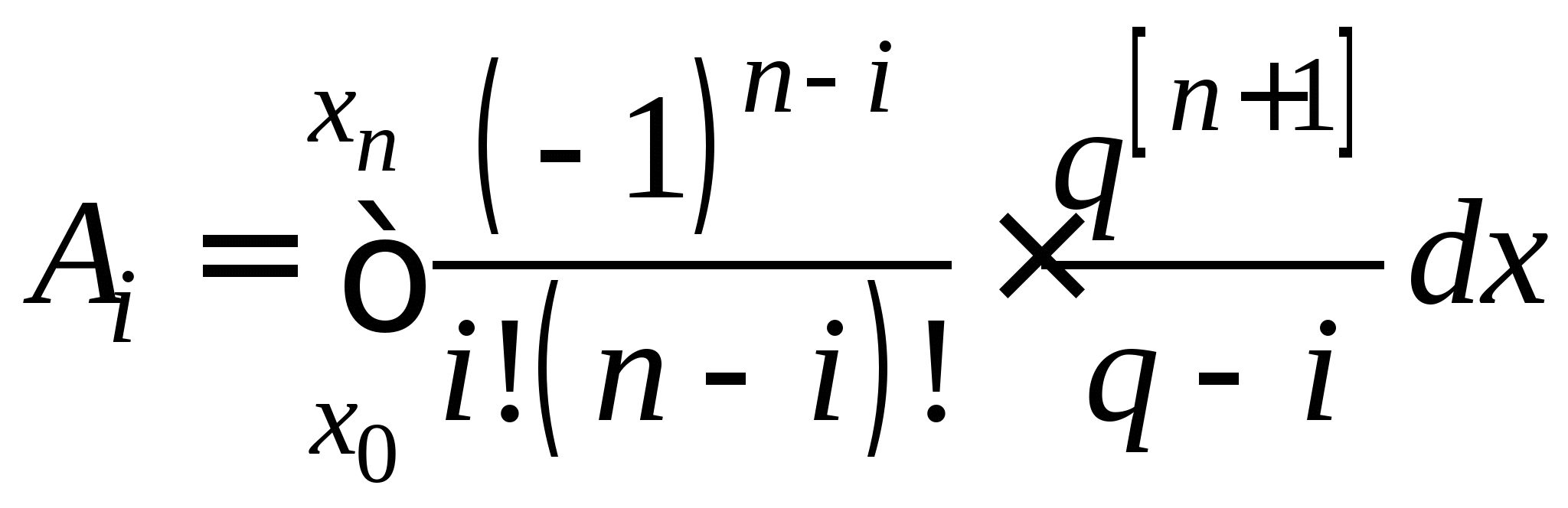 .
.
Так как ![]() и
и ![]() , то сделав замену переменных в определенном интеграле, будем иметь:
, то сделав замену переменных в определенном интеграле, будем иметь:
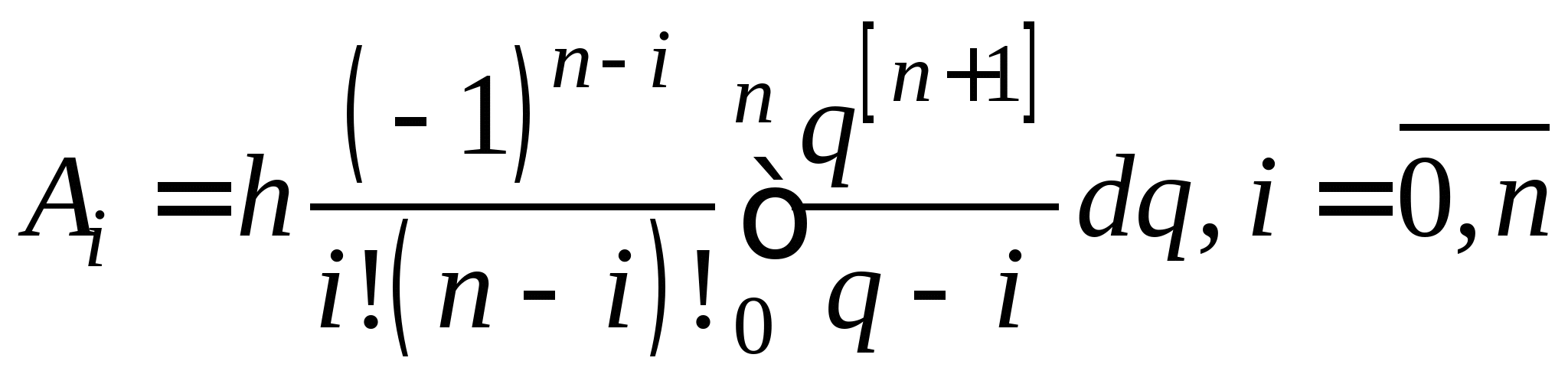 .
.
Так как ![]() , где коэффициенты
, где коэффициенты
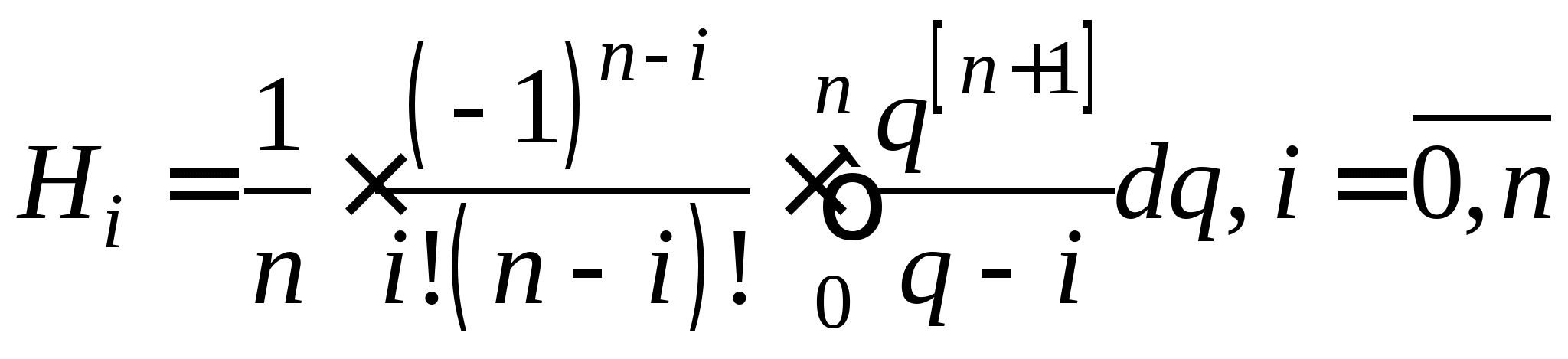 (7.5)
(7.5)
называются коэффициентами Котеса, то можно записать следующую квадратурную формулу:
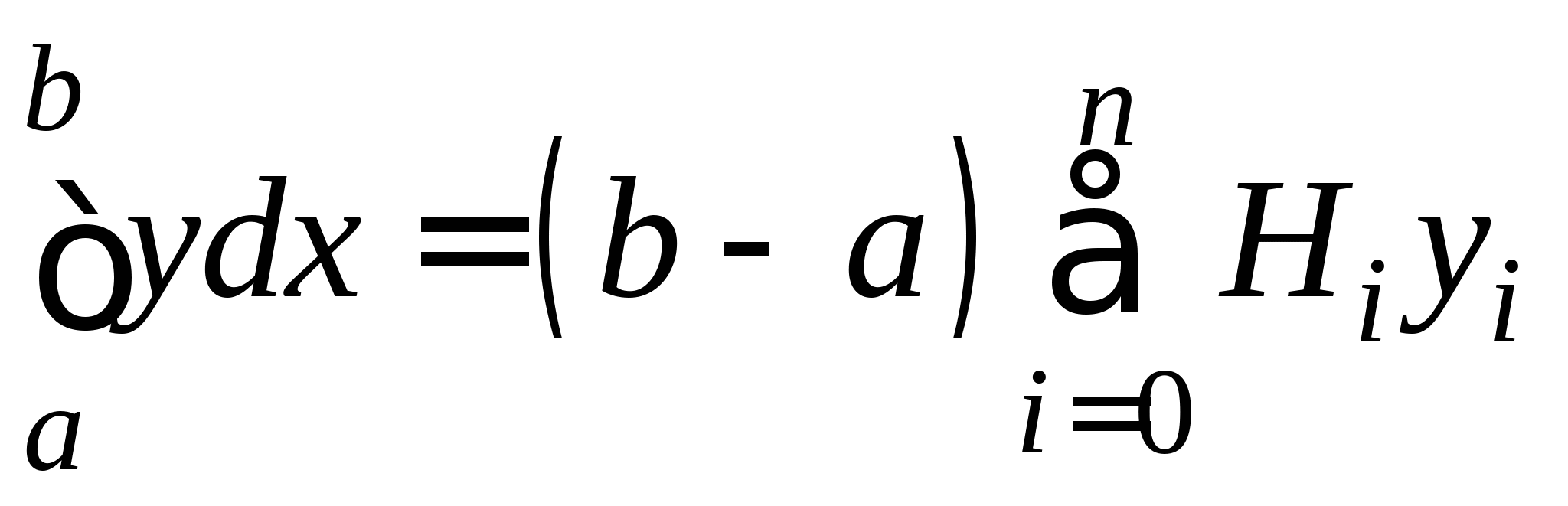 . (7.6)
. (7.6)
Формула (7.6) называется квадратурной формулой Ньютона-Котеса.
Нетрудно проверить, что для коэффициентов Котеса справедливы соотношения:
1) ![]() ;
;
2) ![]() .
.
§7.2. Частные случаи квадратурной формулы Ньютона-Котеса.
7.2.1. Формула трапеций.
а) Пусть отрезок ![]() достаточно мал. Положим
достаточно мал. Положим ![]() . Тогда по формуле (7.5) при
. Тогда по формуле (7.5) при ![]() вычислим:
вычислим:
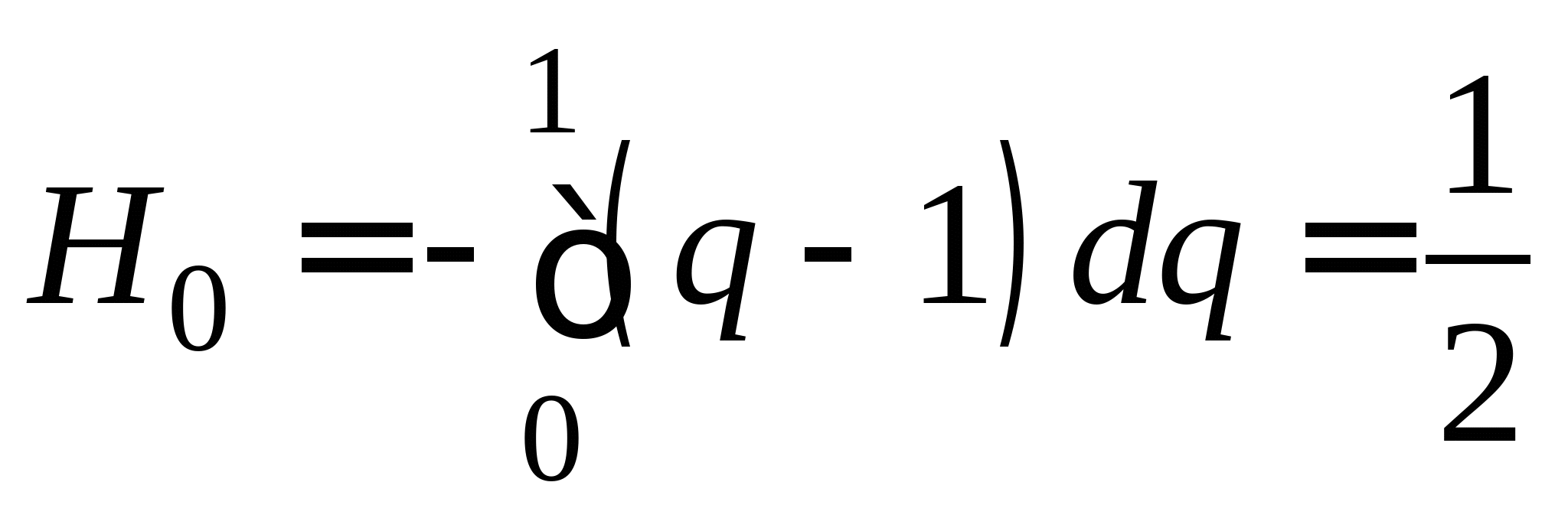 ,
,
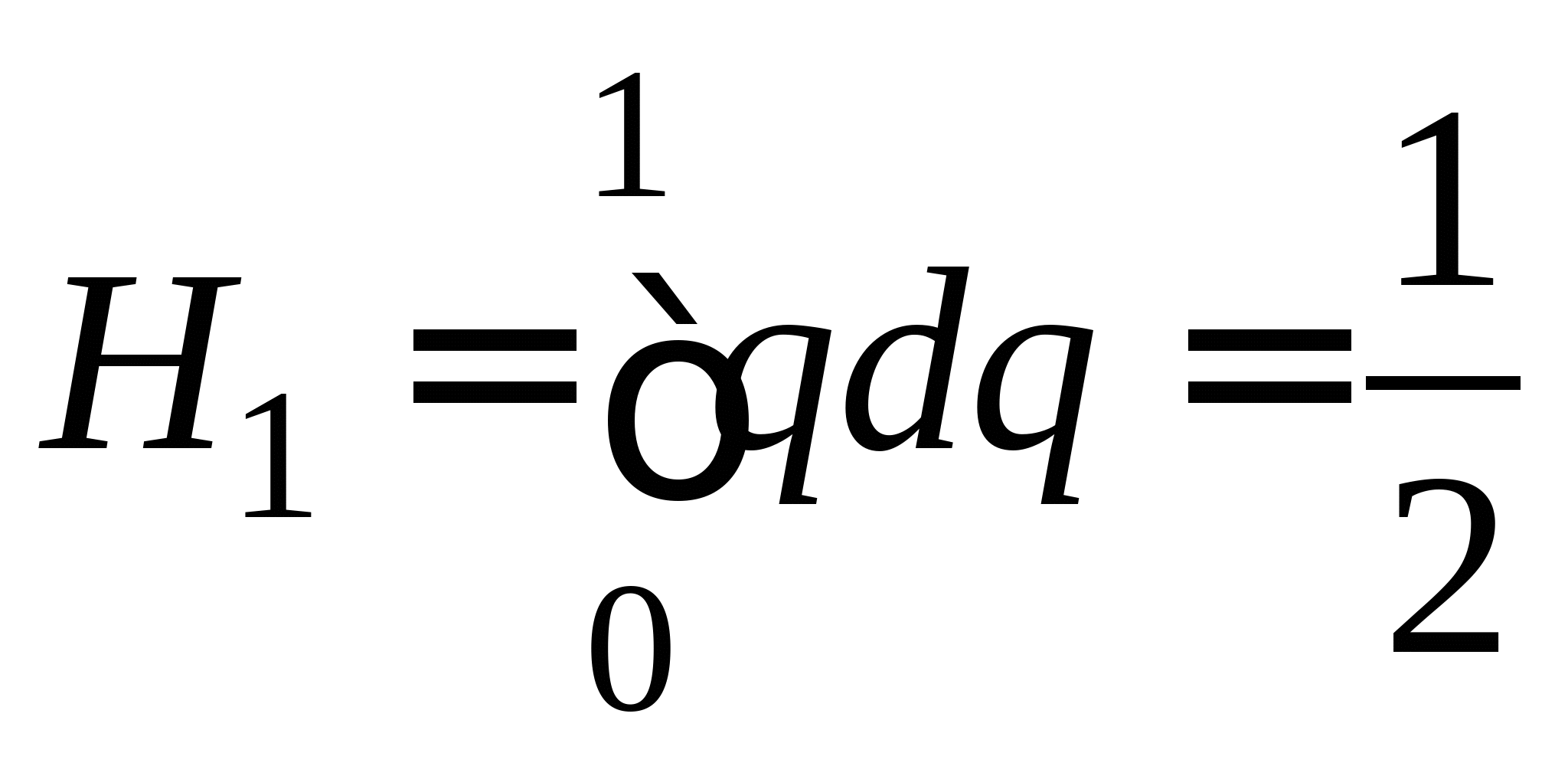 ,
,
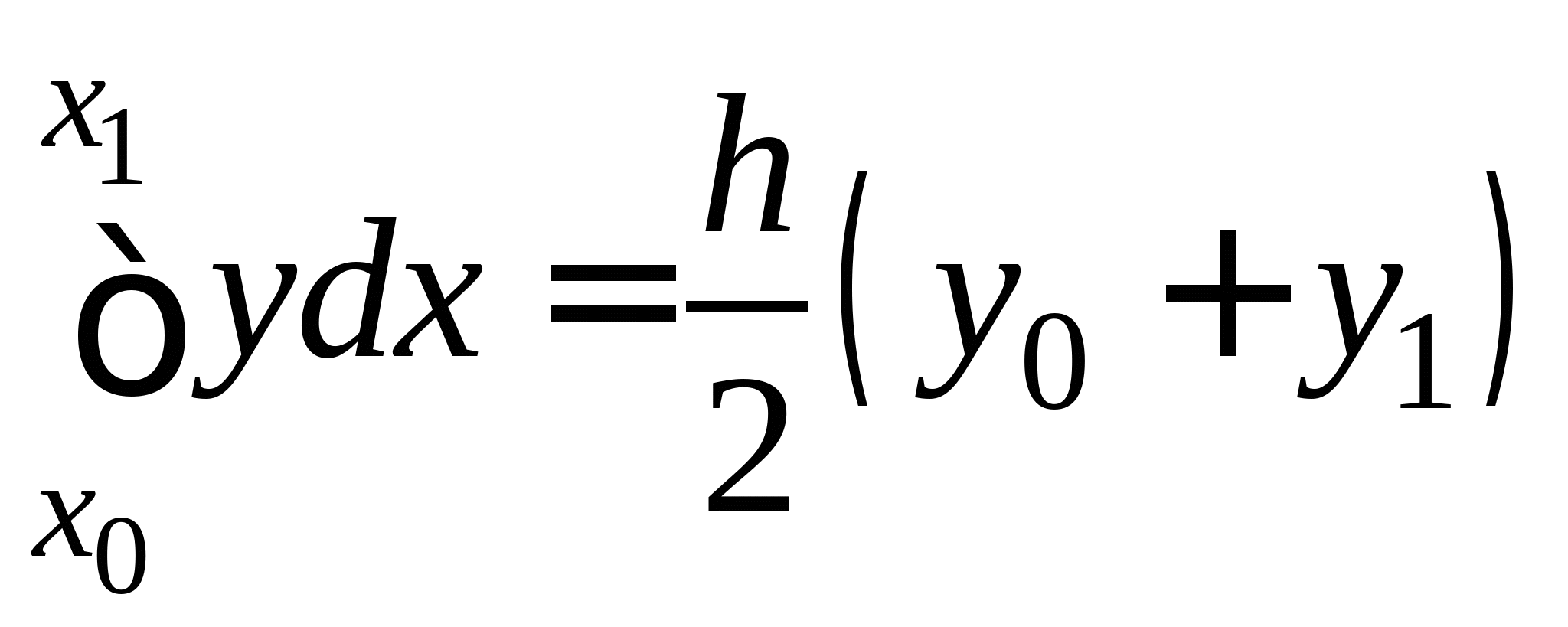 . (7.7)
. (7.7)
П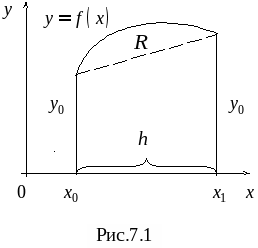
олученная формула (7.7) называется формулой трапеций для приближенного вычисления определенного интеграла (Рис.7.1).
Погрешность квадратурной формулы (7.7) равна:
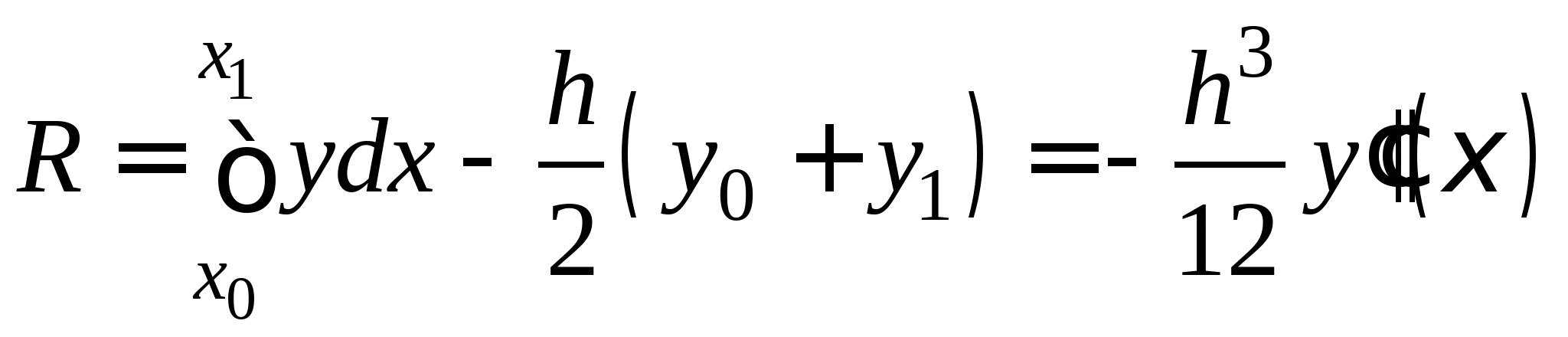 , где
, где ![]() . (7.8)
. (7.8)
Если ![]() , то формула (7.7) дает значение интеграла с избытком, если
, то формула (7.7) дает значение интеграла с избытком, если ![]() то с недостатком.
то с недостатком.
б) Рассмотрим общий случай, когда отрезок ![]() произвольной длины.
произвольной длины.
Разделим отрезок ![]() на
на ![]() равных частей
равных частей ![]() ,
, ![]() , …,
, …, ![]() и к каждому из них применим формулу трапеций:
и к каждому из них применим формулу трапеций:
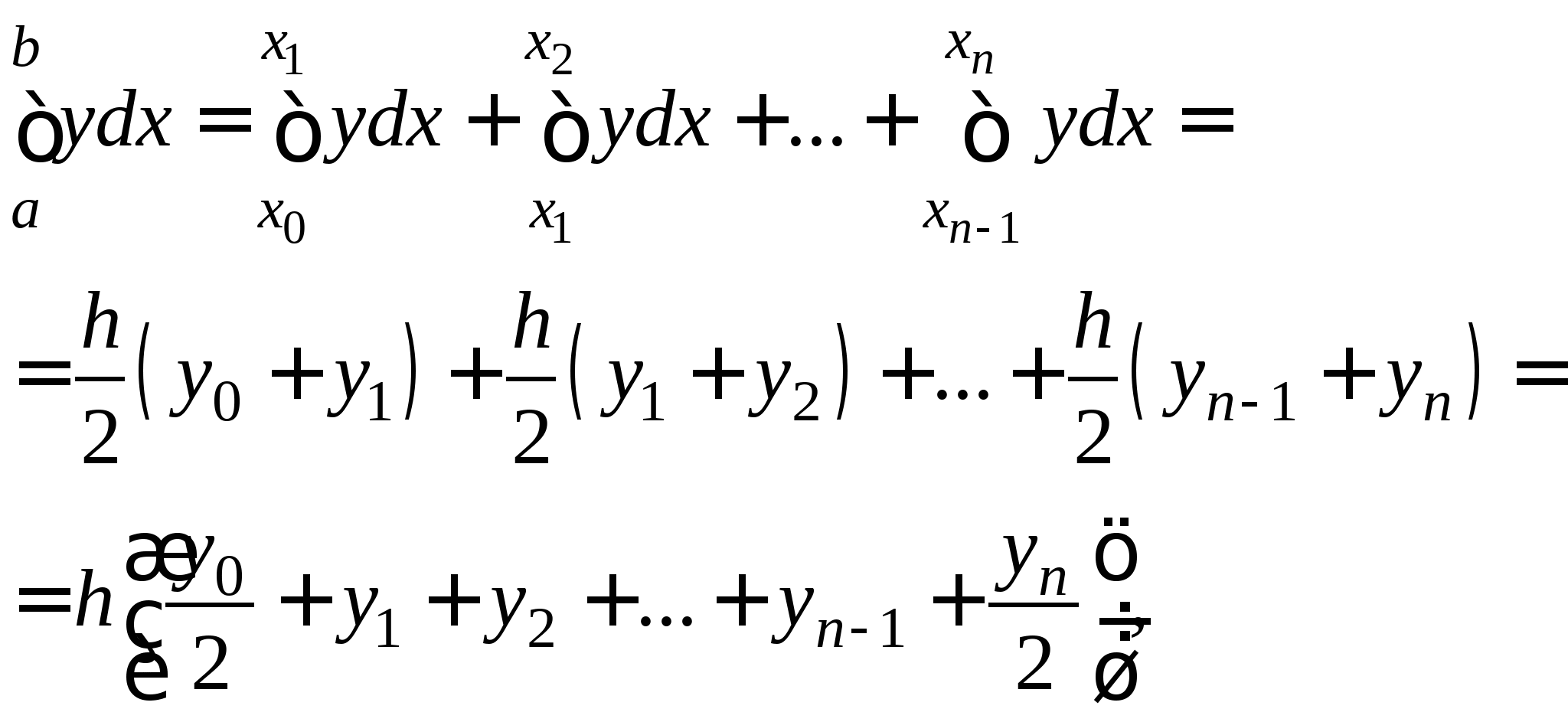 (7.9)
(7.9)
где ![]() .
.
Формула (7.9) называется общей формулой трапеций. Для нее справедлива оценка погрешности:
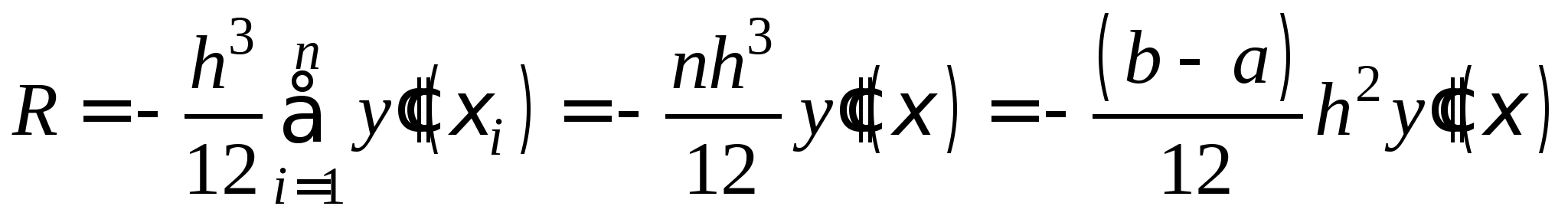 , (7.10)
, (7.10)
где ![]() ,
, ![]() ,
, ![]() .
.
7.2.2. Квадратурная формула Симпсона.
а) По формуле (7.5) при ![]() вычислим коэффициенты Котеса:
вычислим коэффициенты Котеса:
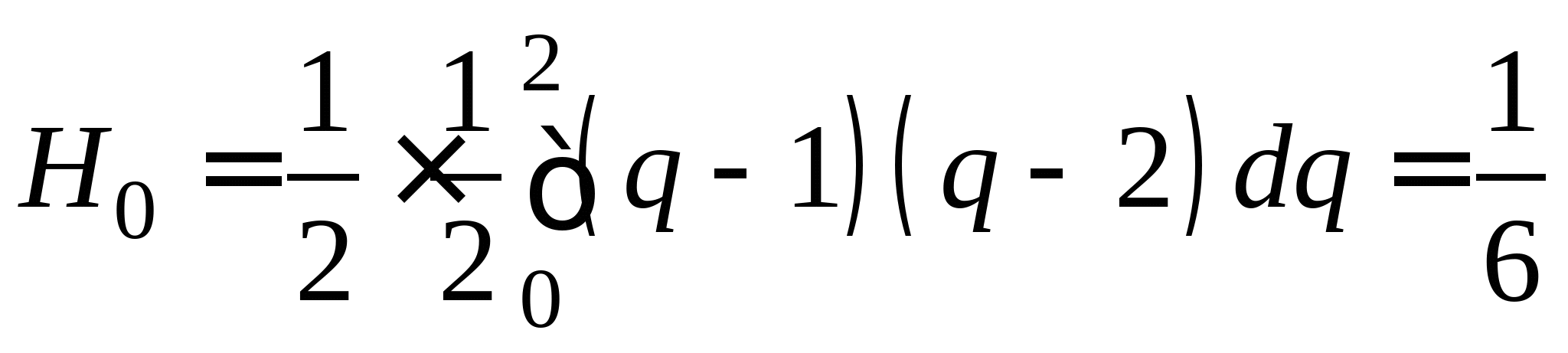 ,
,
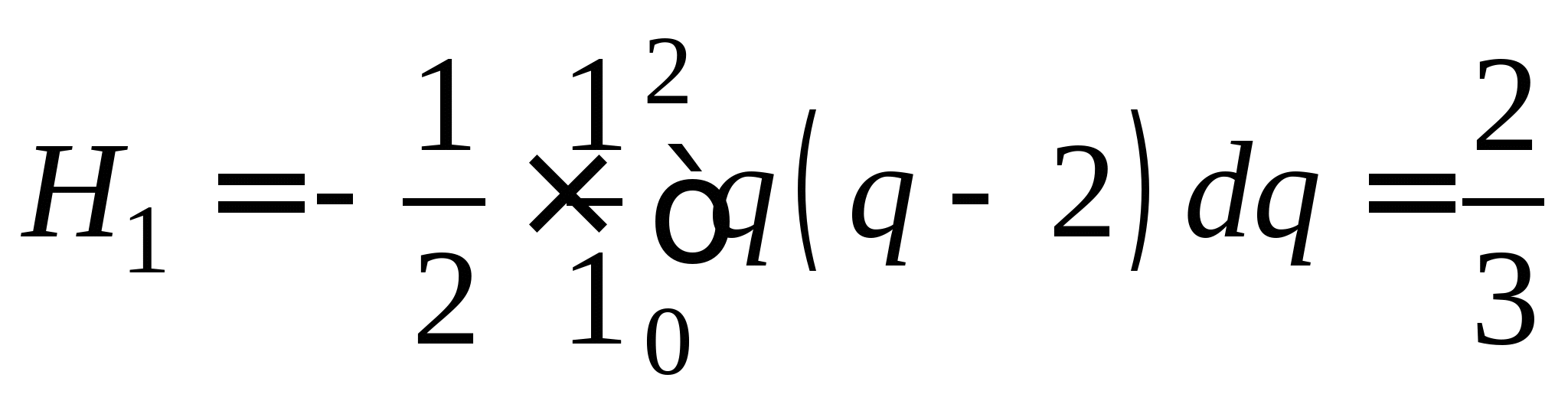 ,
,
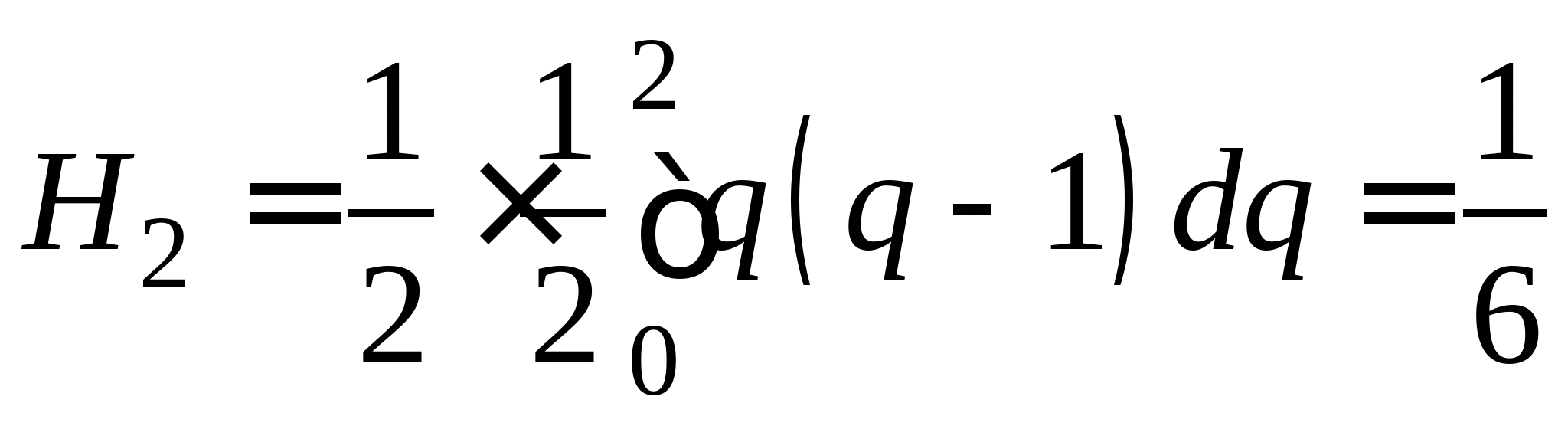 .
.
Так как ![]() , то квадратурная формула для вычисления интеграла примет вид
, то квадратурная формула для вычисления интеграла примет вид
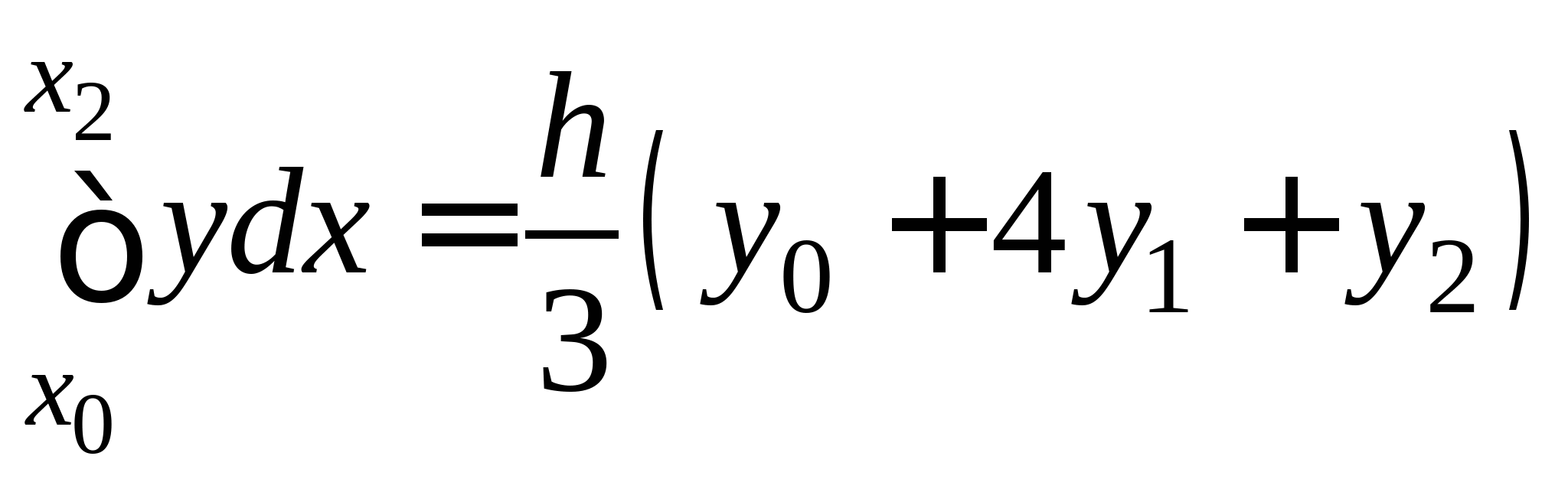 . (7.11)
. (7.11)
Ф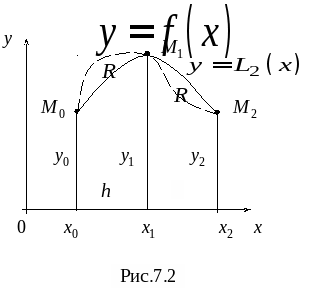
ормула (7.11) называется квадратурной формулой Симпсона. Геометрическая интерпретация формулы состоит в том, что происходит замена данной кривой ![]() параболой
параболой ![]() , проходящей через три точки
, проходящей через три точки ![]() (Рис.7.2).
(Рис.7.2).
Погрешность квадратурной формулы Симпсона равна:
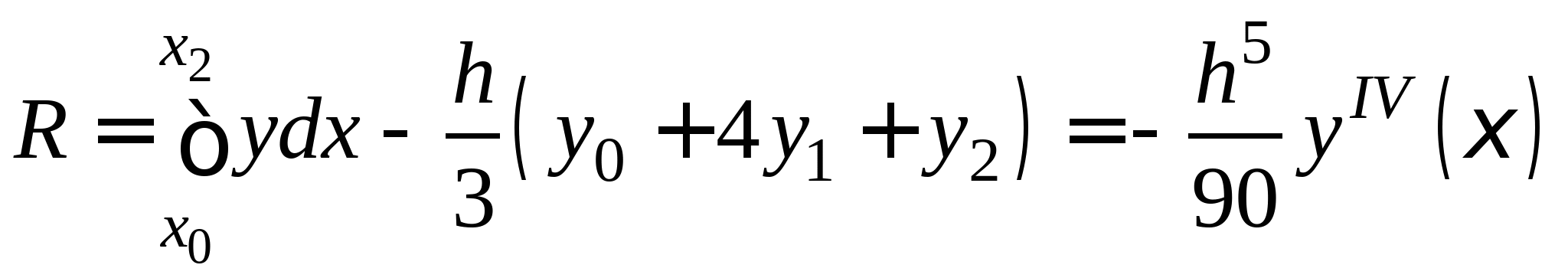 , где
, где ![]() . (7.12)
. (7.12)
Квадратурная формула Симпсона является точной для полиномов второй и третьей степени.
б) Общая формула Симпсона.
Пусть ![]() четное число, и
четное число, и ![]() значения функции
значения функции ![]() для равноотстоящих точек
для равноотстоящих точек ![]() с шагом
с шагом ![]() ,
, ![]() .
.
Применяя квадратурную формулу Симпсона (7.11) к каждому сдвоенному промежутку ![]() ,
, ![]() , …
, … ![]() длины
длины ![]() , будем иметь:
, будем иметь:
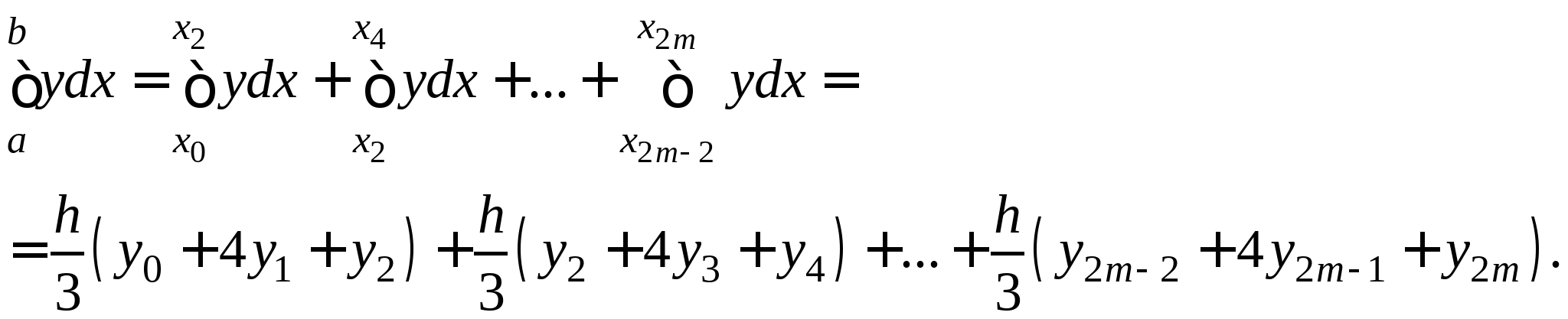
Отсюда получим общую квадратурную формулу Симпсона:
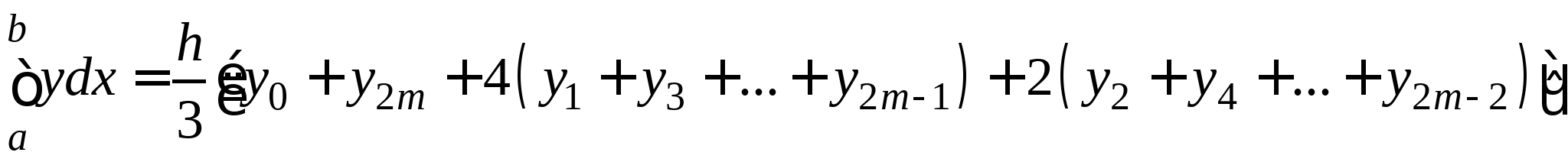 . (7.13)
. (7.13)
Остаточный член формулы (7.13) равен:
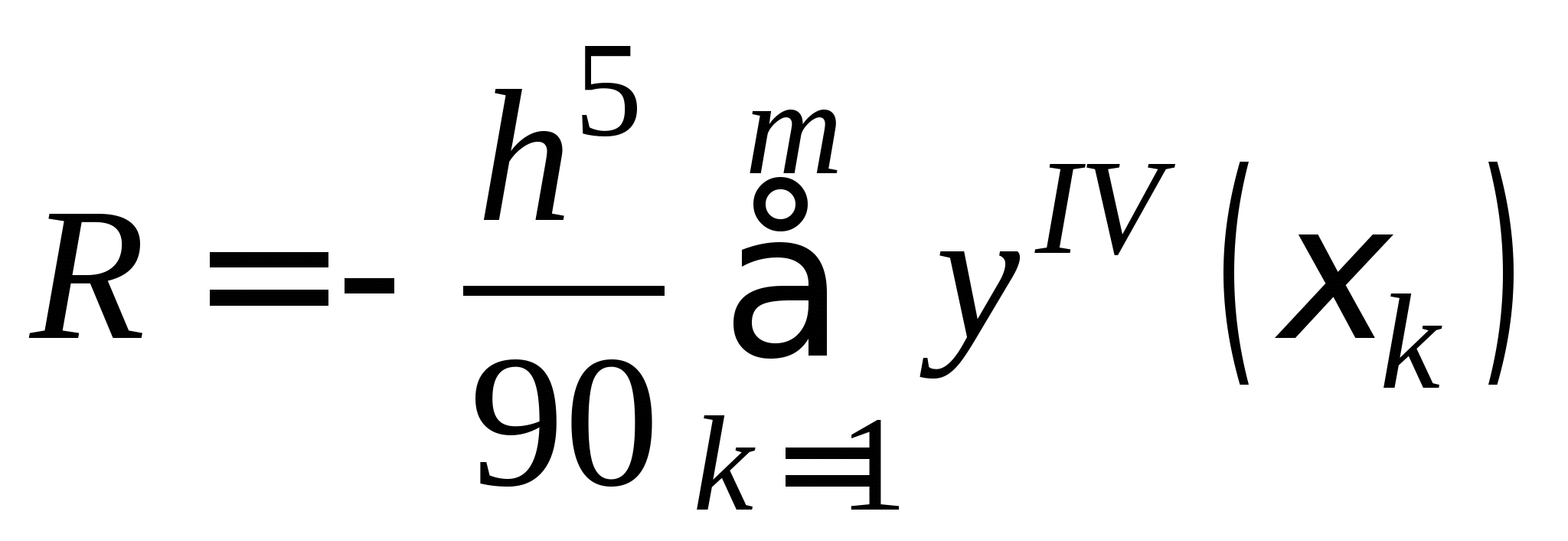 .
.
В силу непрерывности ![]() на отрезке
на отрезке ![]() найдется точка
найдется точка ![]() такая, что
такая, что
![]() .
.
Поэтому будем иметь:
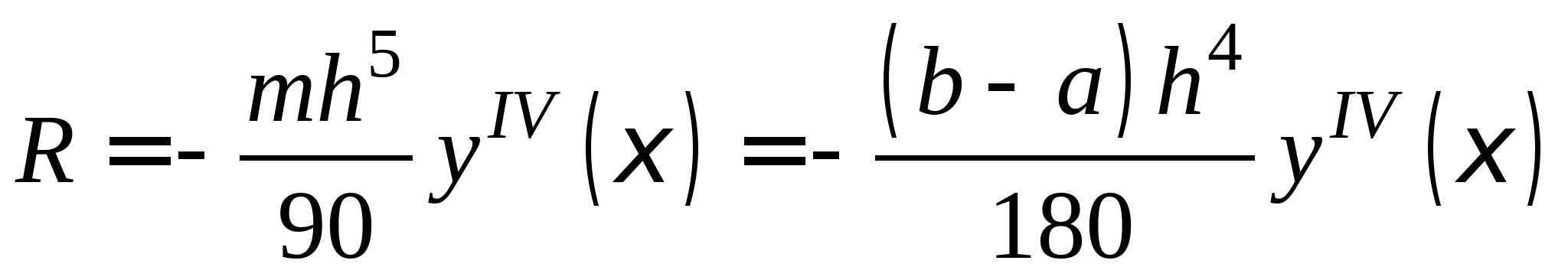 , (7.14)
, (7.14)
где ![]() .
.
§7.3. Квадратурная формула Гаусса.
Для вывода квадратурной формулы Гаусса потребуются некоторые сведения о полиномах Лежандра.
Определение 7.2.
Полиномы вида
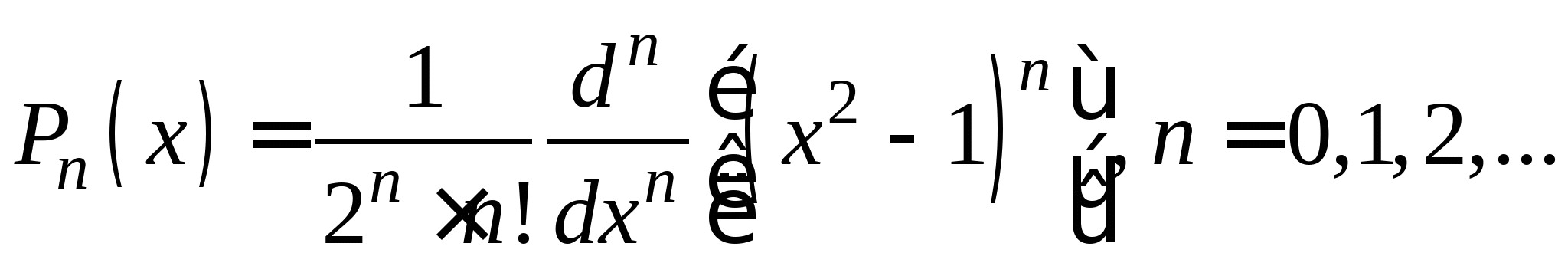
называются полиномами Лежандра.
Полиномы Лежандра обладают следующими свойствами:
1) ![]() ;
;
2) 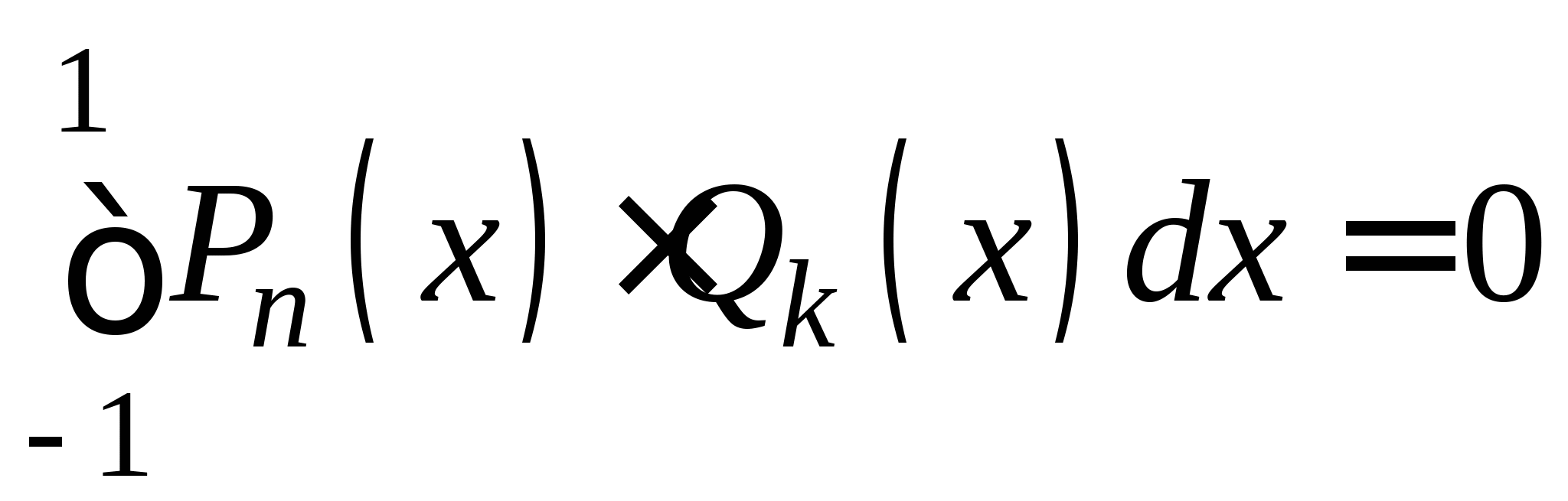 , где
, где ![]() любой полином степени
любой полином степени ![]() , меньшей
, меньшей ![]() ;
;
3) полином Лежандра ![]() имеет
имеет ![]() различных и действительных корней, которые расположены на интервале
различных и действительных корней, которые расположены на интервале ![]() .
.
Свойство 2 называется свойством ортогональности полиномов Лежандра.
Перейдем к выводу квадратурной формулы Гаусса.
Рассмотрим сначала функцию ![]() , заданную на отрезке
, заданную на отрезке ![]() .
.
Поставим задачу: как нужно подобрать точки ![]() и коэффициенты
и коэффициенты ![]() , чтобы квадратурная формула
, чтобы квадратурная формула
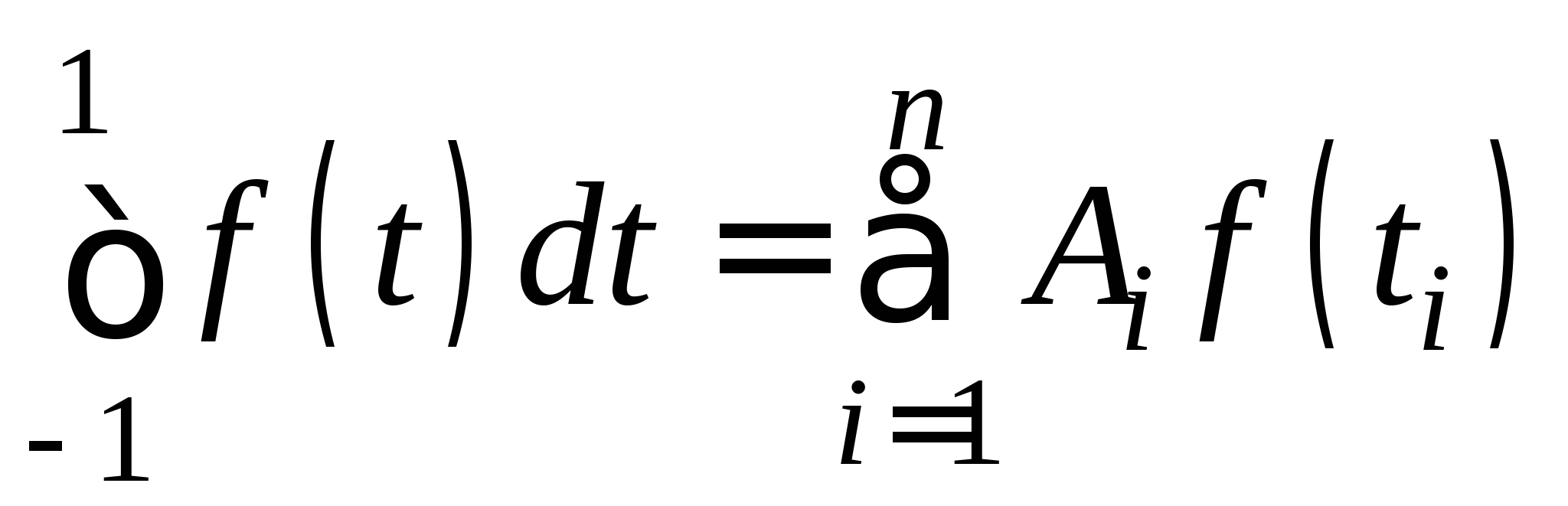 (7.15)
(7.15)
была точной для всех полиномов ![]() наивысшей возможной степени
наивысшей возможной степени ![]() .
.
Так как в распоряжении имеется ![]() постоянных
постоянных ![]() и
и ![]() , а полином степени
, а полином степени ![]() определяется
определяется ![]() коэффициентами, то эта наивысшая степень в общем случае равна
коэффициентами, то эта наивысшая степень в общем случае равна ![]() .
.
Для обеспечения равенства (7.15) необходимо и достаточно, чтобы оно было верным при ![]() .
.
Действительно, полагая
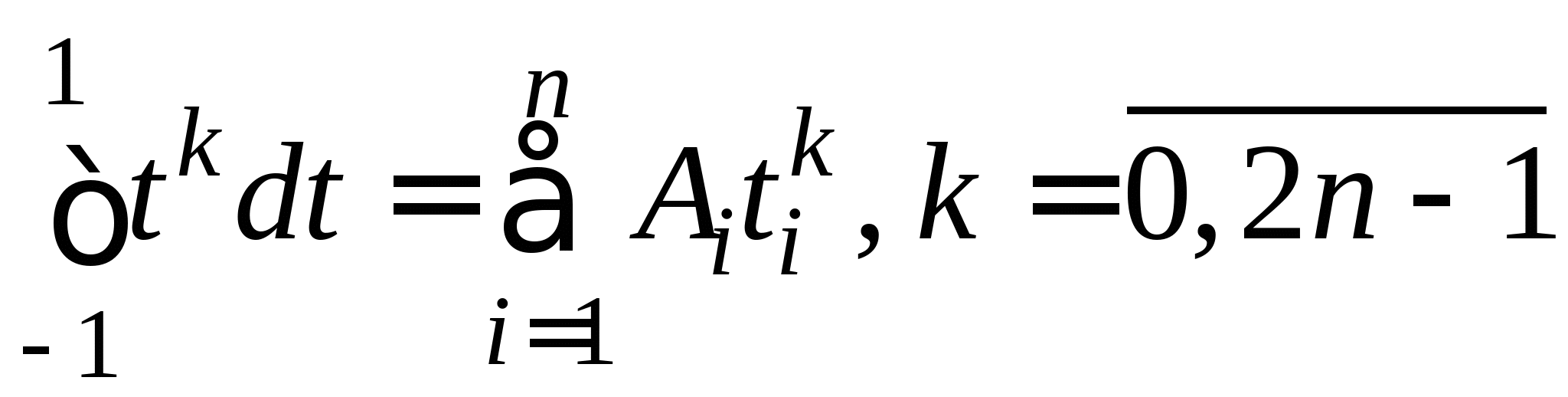 (7.16)
(7.16)
и
![]() ,
,
будем иметь:
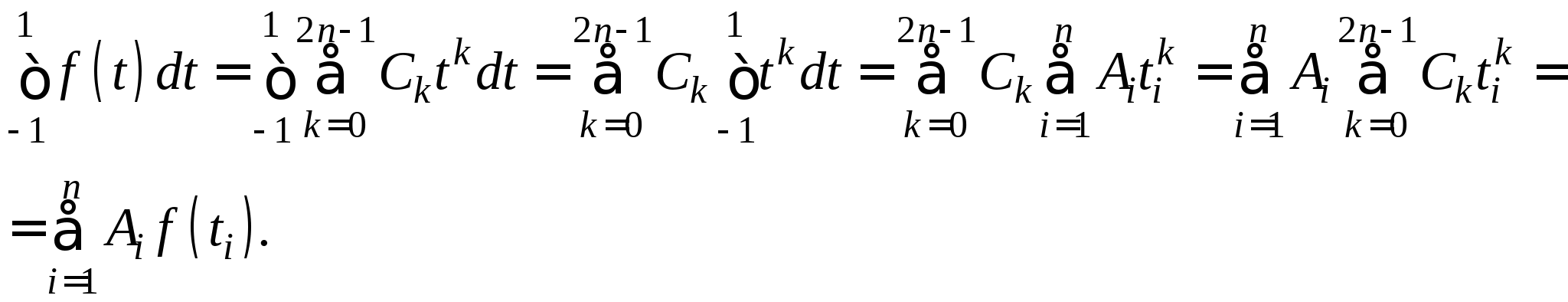 .
.
Таким образом, учитывая соотношения:
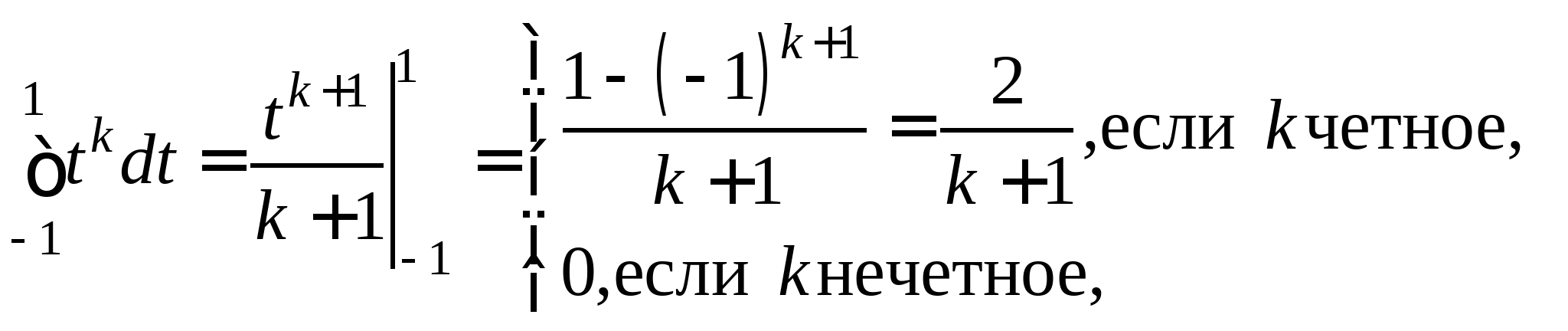
заключаем, что для решения поставленной задачи достаточно определить ![]() и
и ![]() из системы
из системы ![]() уравнений
уравнений
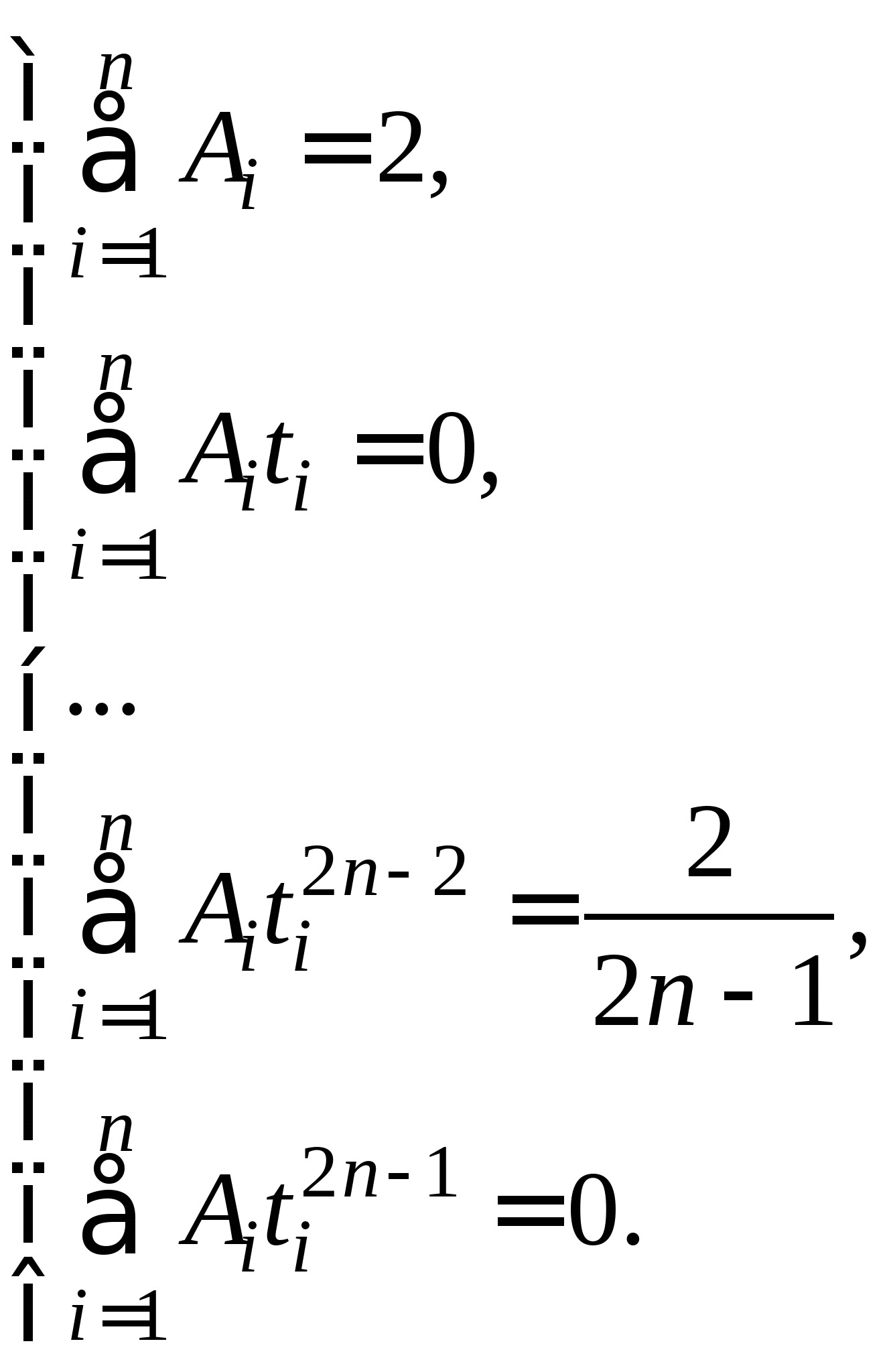 (7.17)
(7.17)
Система (7.17) – нелинейная система, состоящая из ![]() уравнений с
уравнений с ![]() неизвестными
неизвестными ![]() и
и ![]() . Решение ее обычным путем представляет большие математические трудности. Поэтому применяют искусственный прием.
. Решение ее обычным путем представляет большие математические трудности. Поэтому применяют искусственный прием.
Рассмотрим полиномы
![]() ,
,
где ![]() - полином Лежандра.
- полином Лежандра.
Так как степени этих полиномов не превышают ![]() , то на основании системы (7.17) для них должна быть справедлива формула (7.15):
, то на основании системы (7.17) для них должна быть справедлива формула (7.15):
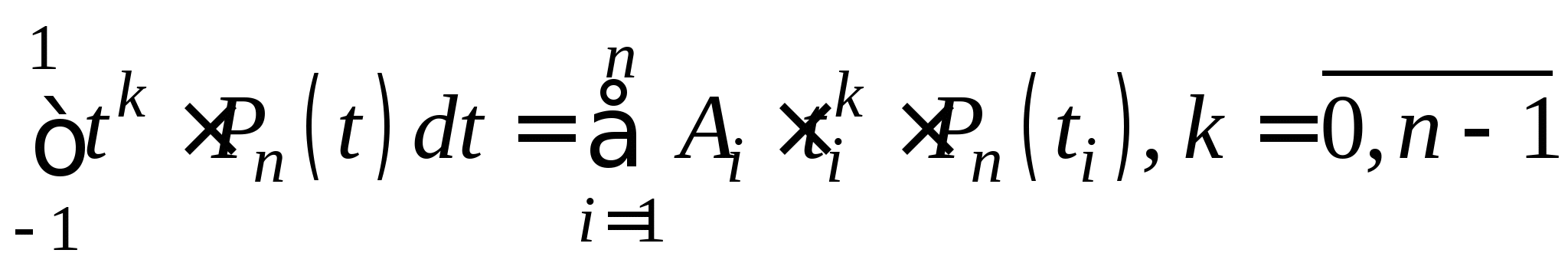 . (7.18)
. (7.18)
С другой стороны, в силу свойства ортогональности полиномов Лежандра выполнены равенства:
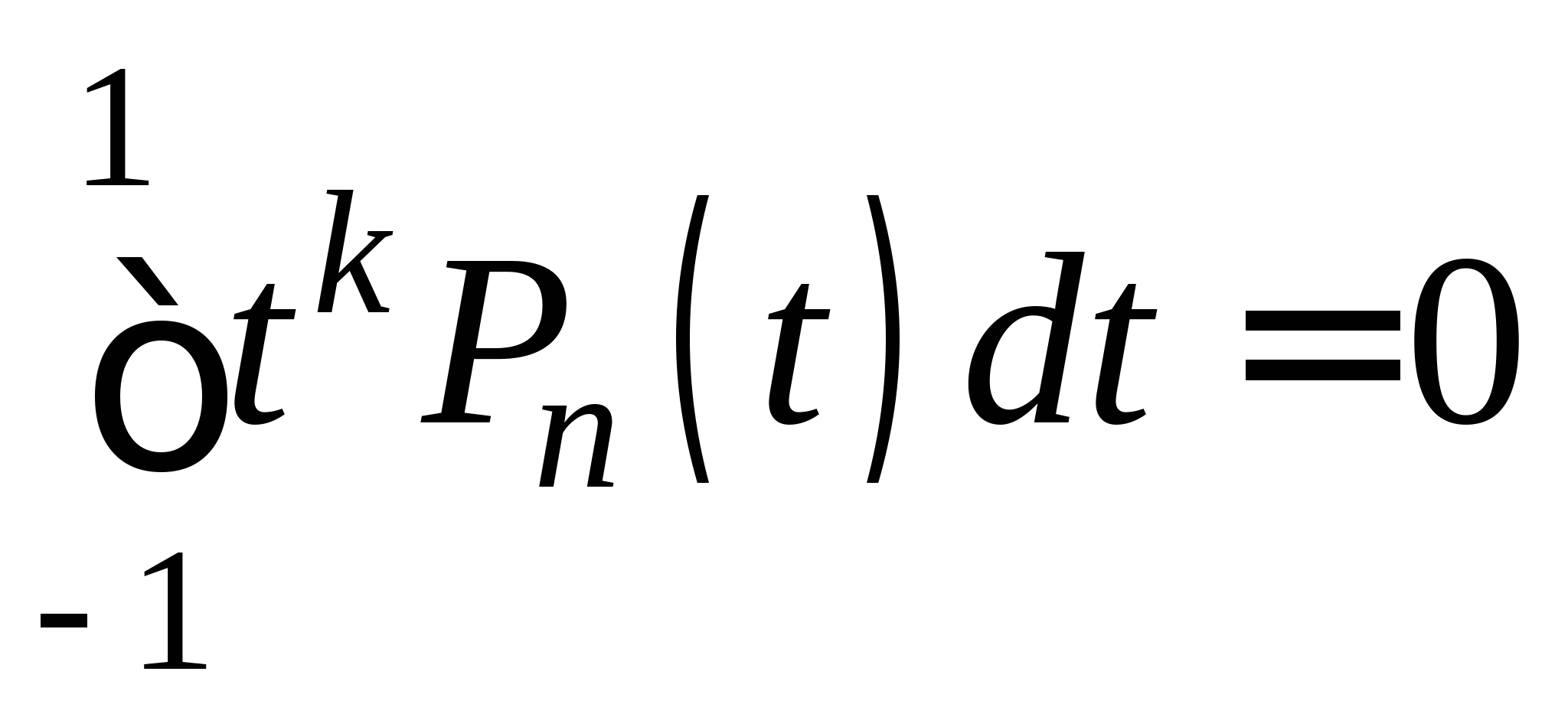 , при
, при ![]() ,
,
поэтому в силу (7.18)
![]() (7.19)
(7.19)
Если положить ![]() , то соотношения (7.19) будут выполняться при любых значениях
, то соотношения (7.19) будут выполняться при любых значениях ![]() .
.
Таким образом, для достижения наивысшей точности квадратурной формулы (7.15) в качестве точек ![]() достаточно взять нули соответствующего полинома Лежандра. В силу свойства 3 эти нули действительны, различны и расположены на интервале
достаточно взять нули соответствующего полинома Лежандра. В силу свойства 3 эти нули действительны, различны и расположены на интервале ![]() . Подставив найденные значения
. Подставив найденные значения ![]() в систему (7.17), которая при этом становится линейной, из первых
в систему (7.17), которая при этом становится линейной, из первых ![]() уравнений можно найти коэффициенты
уравнений можно найти коэффициенты ![]() .
.
Определитель этой подсистемы является определителем Вандермонда
![]() ,
,
и, следовательно, коэффициенты ![]() определяются однозначно.
определяются однозначно.
Формула (7.15), где ![]() - нули полинома Лежандра
- нули полинома Лежандра ![]() и
и ![]() определяются из системы (7.17), называется квадратурной формулой Гаусса.
определяются из системы (7.17), называется квадратурной формулой Гаусса.
Неудобство применения квадратурной формулы Гаусса состоит в том, что абсциссы точек ![]() и коэффициенты
и коэффициенты ![]() - вообще говоря, иррациональные числа. Этот недостаток отчасти искупается ее высокой точностью при сравнительно малом числе ординат.
- вообще говоря, иррациональные числа. Этот недостаток отчасти искупается ее высокой точностью при сравнительно малом числе ординат.
Для вычисления общего интеграла 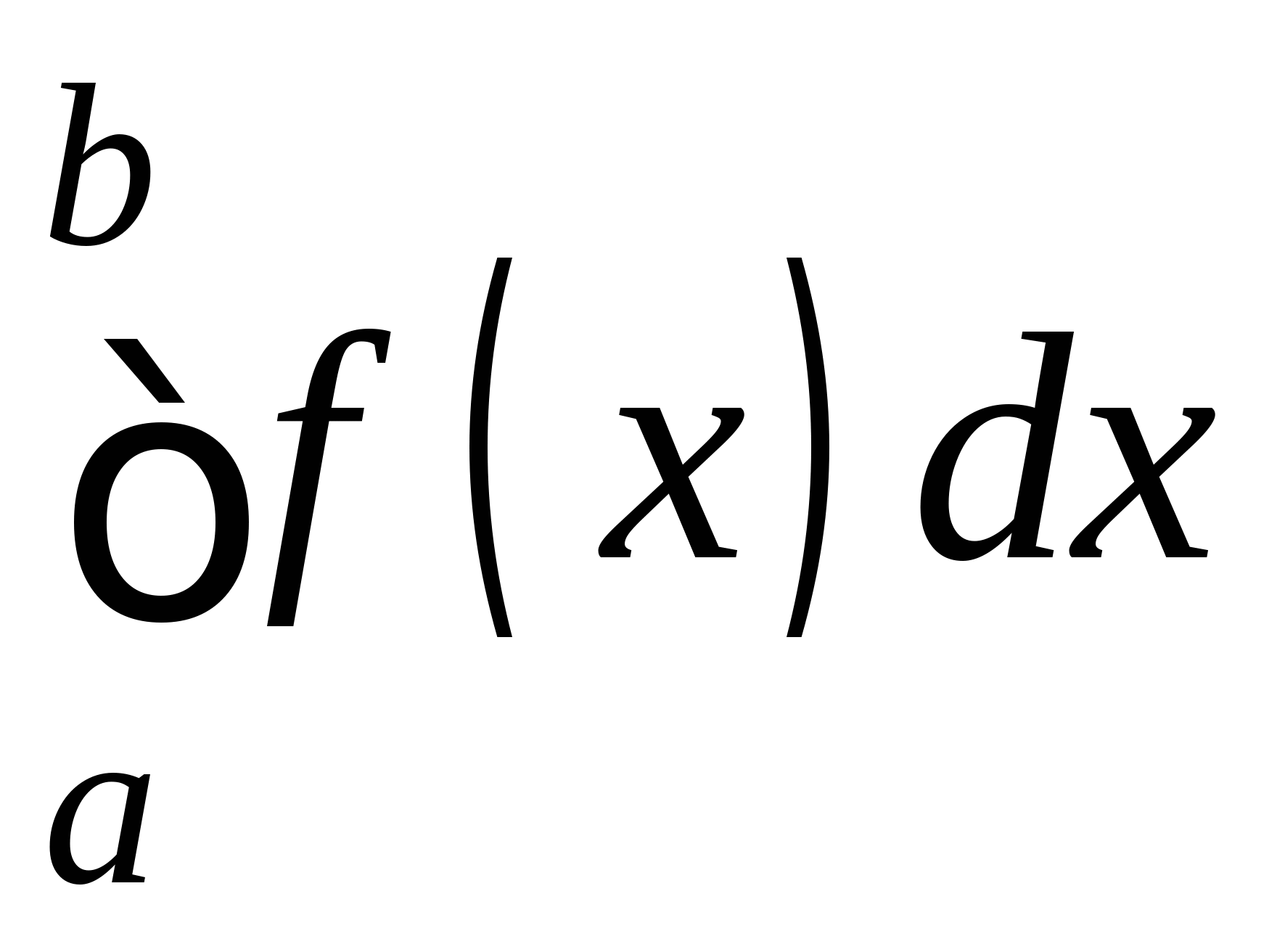 по квадратурной формуле Гаусса делают замену
по квадратурной формуле Гаусса делают замену
![]() .
.
Тогда
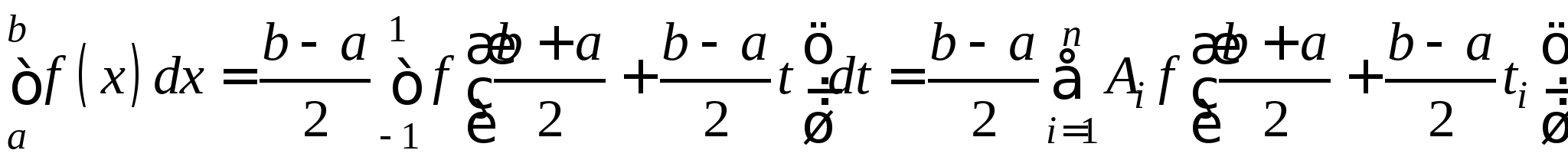 , (7.20)
, (7.20)
где ![]() - нули полинома Лежандра,
- нули полинома Лежандра, ![]() .
.
Соотношение (7.20) – квадратурная формула Гаусса для вычисления произвольного интеграла.
Остаточный член квадратурной формулы Гаусса (7.20) с ![]() узлами выражается следующим образом:
узлами выражается следующим образом:
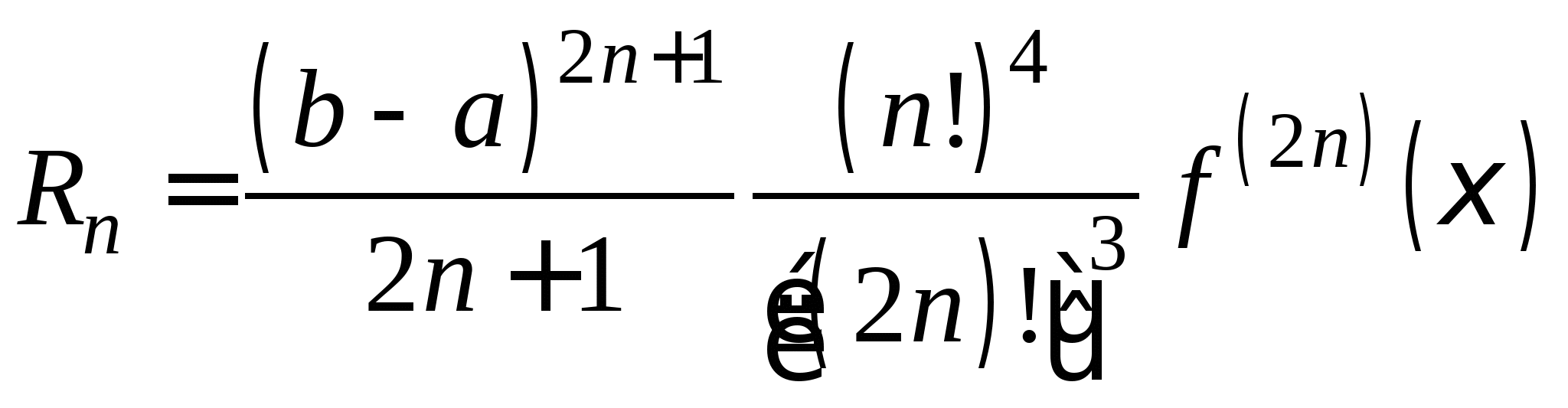 . (7.21)
. (7.21)
§7.4. Приближенное вычисление несобственных интегралов.
Определение 7.3. Интеграл
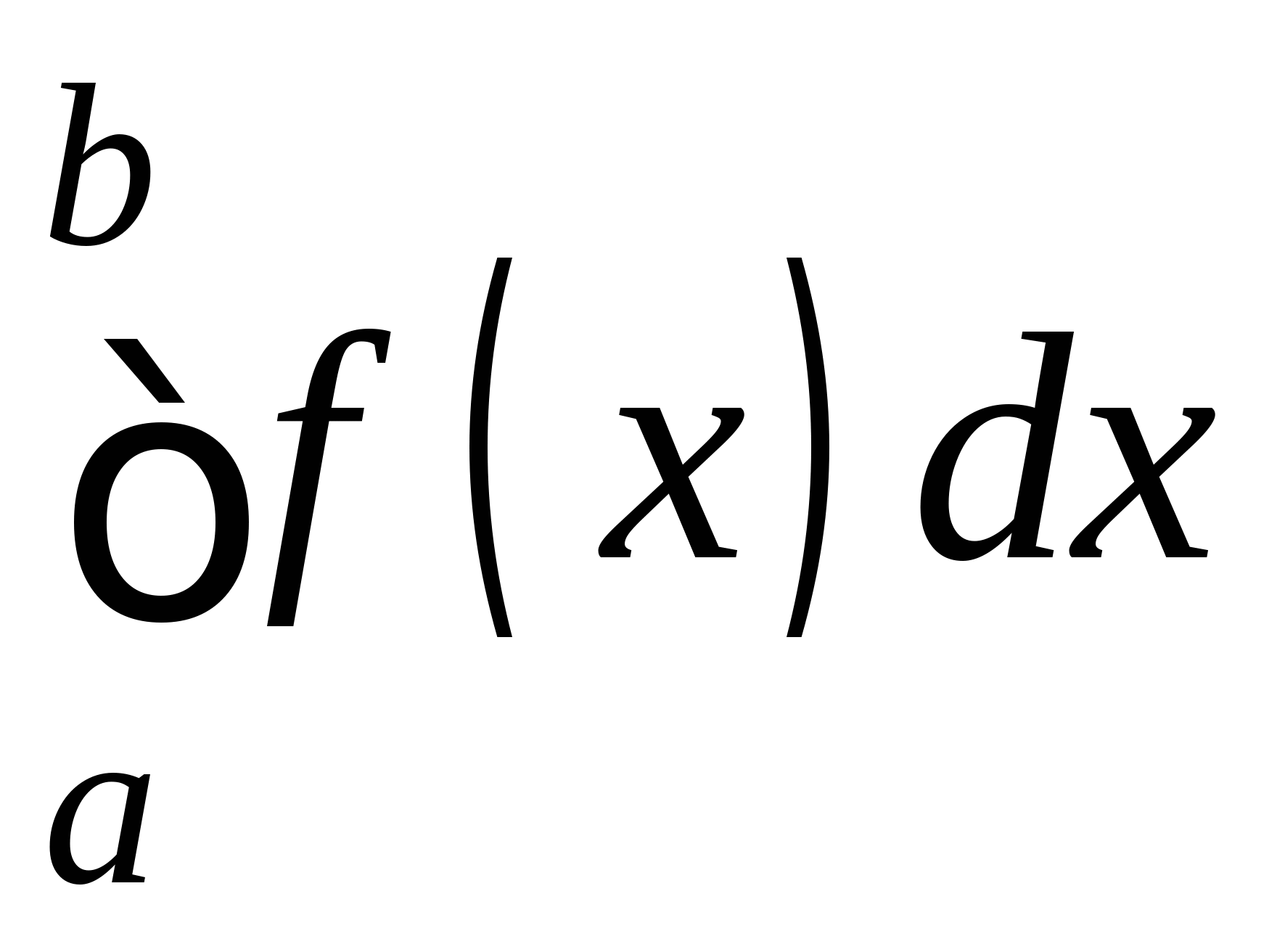 (7.22)
(7.22) называется собственным, если
промежуток интегрирования ![]() конечен;
конечен;
подынтегральная функция ![]() непрерывна на
непрерывна на ![]() .
.
В противном случае, интеграл (7.22) называется несобственным.
а). Рассмотрим приближенное вычисление несобственного интеграла
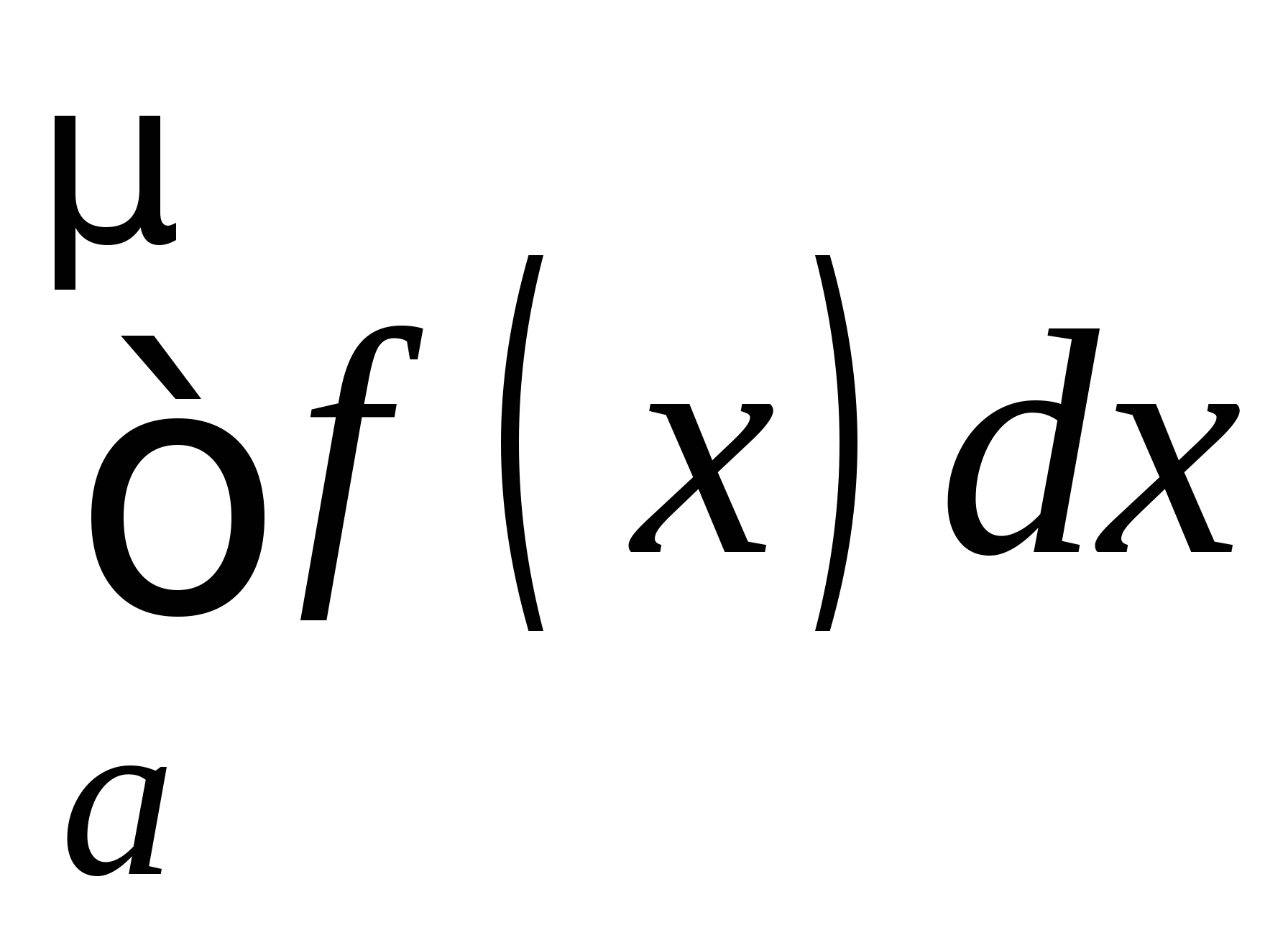 (7.23)
(7.23) с бесконечным промежутком интегрирования, где функция ![]() непрерывна при
непрерывна при ![]() .
.
Определение 7.4.
И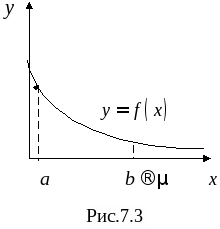
нтеграл (7.23) называется сходящимся (Рис.7.3), если существует конечный предел
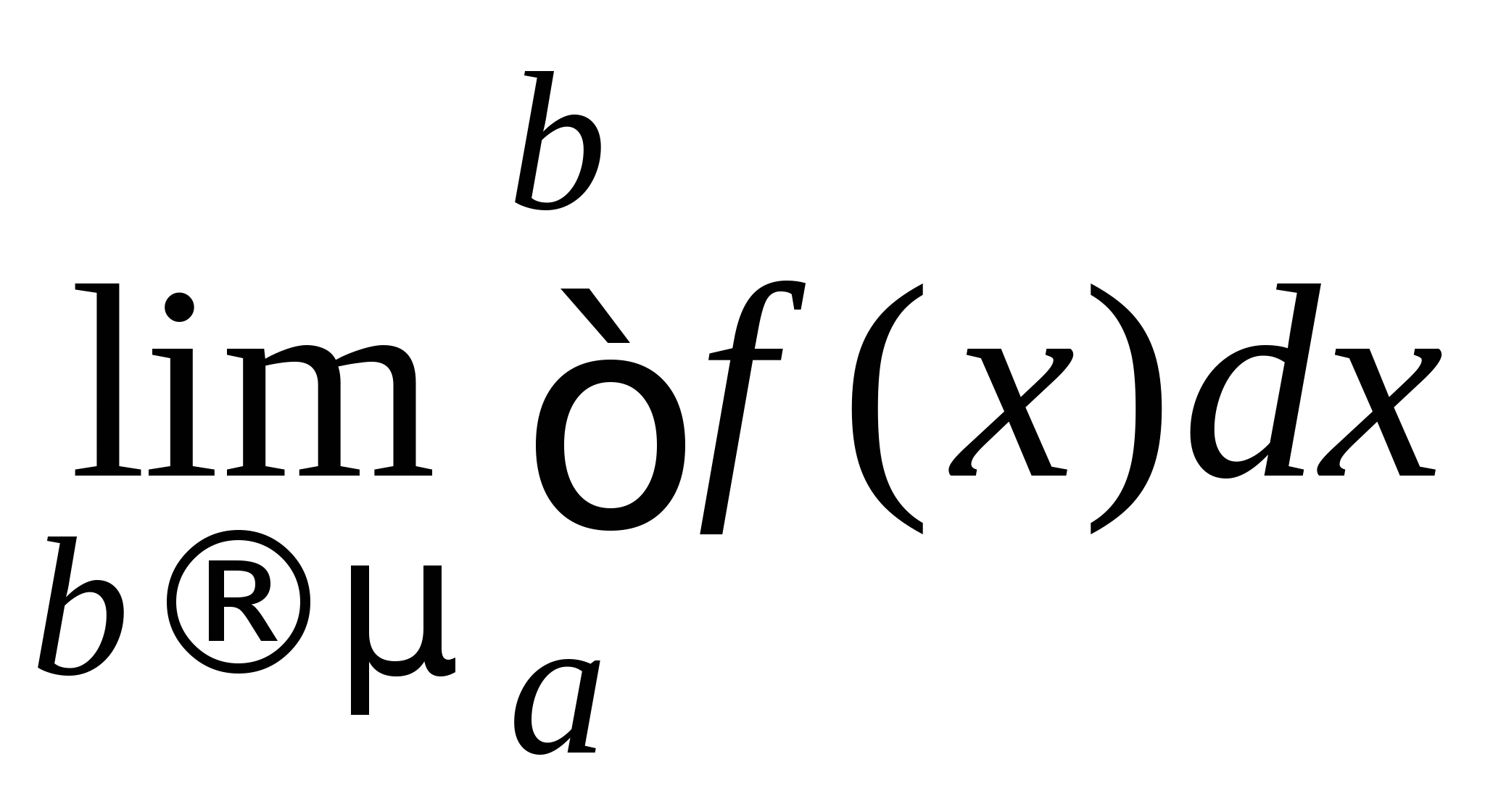 (7.24)
(7.24) и по определению полагают
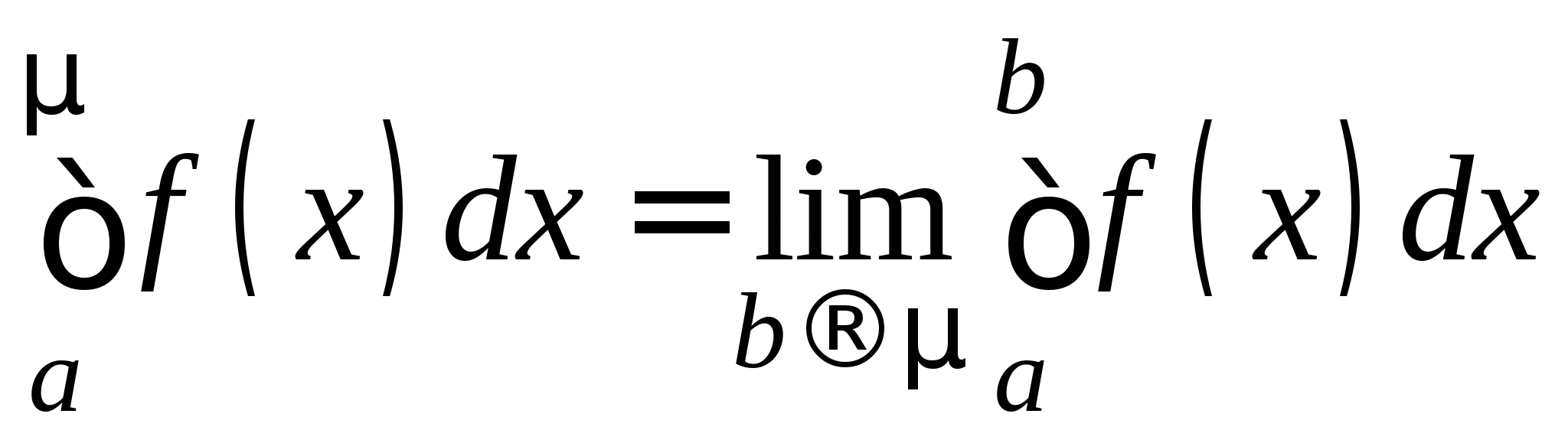 (7.25)
(7.25) Если предел (7.24) не существует, то интеграл (7.23) называется расходящимся. Поэтому, прежде чем приступить к вычислению несобственного интеграла, нужно предварительно убедиться, что этот интеграл сходится.
Чтобы вычислить сходящийся несобственный интеграл (7.23) с заданной точностью ![]() , представим его в виде
, представим его в виде
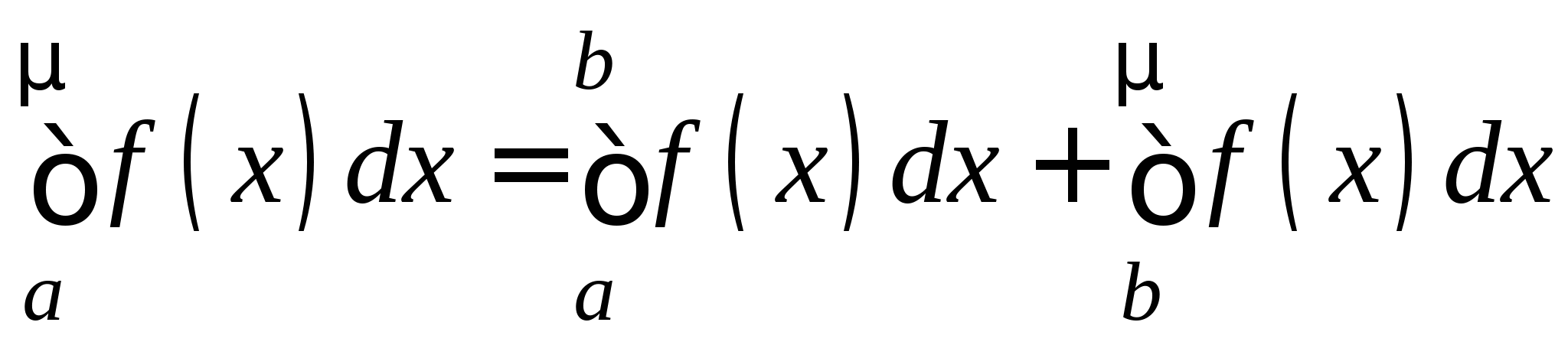 (7.26)
(7.26) В силу сходимости интеграла число ![]() можно выбрать столь большим, чтобы имело место неравенство
можно выбрать столь большим, чтобы имело место неравенство
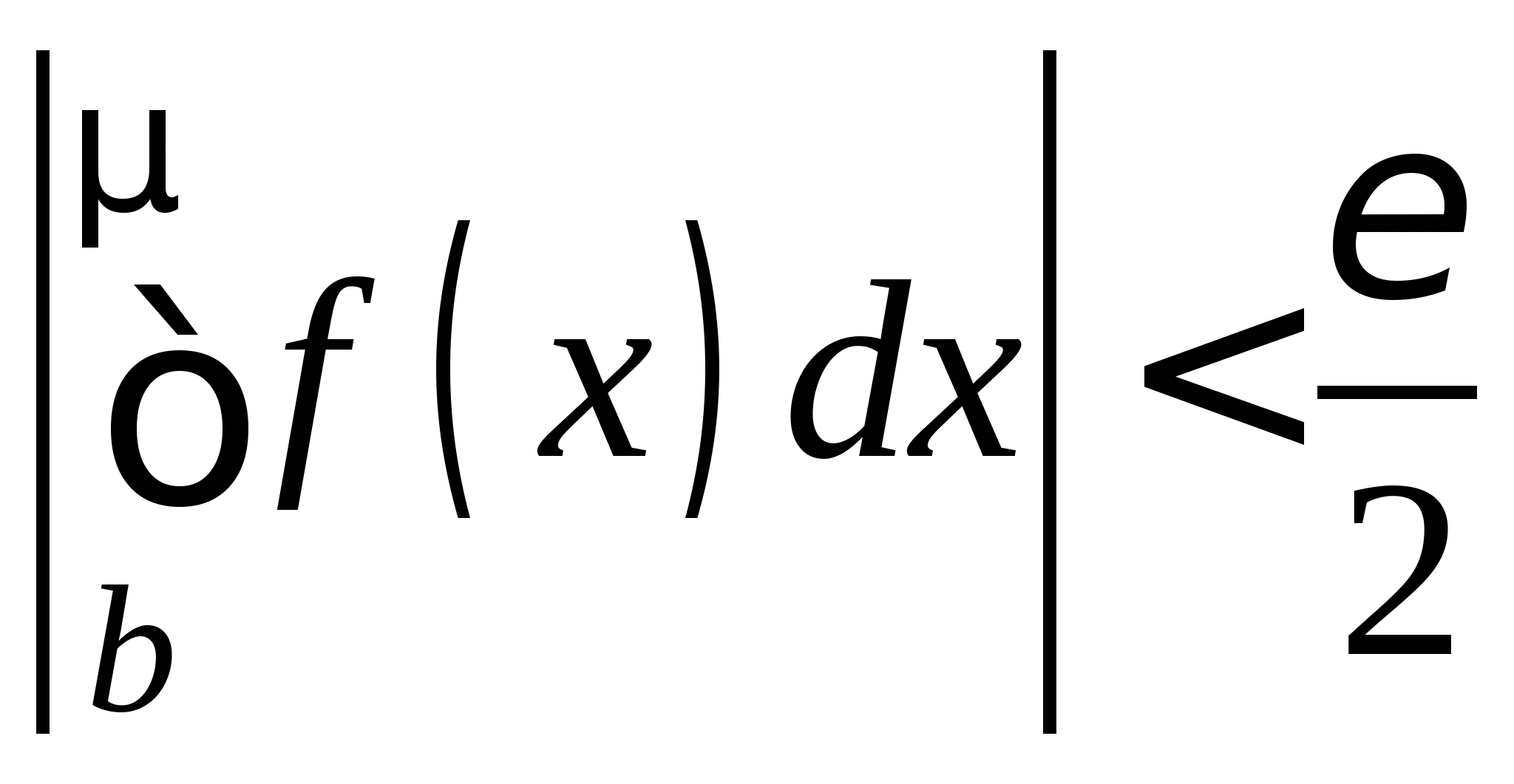 (7.27)
(7.27)
Собственный интеграл 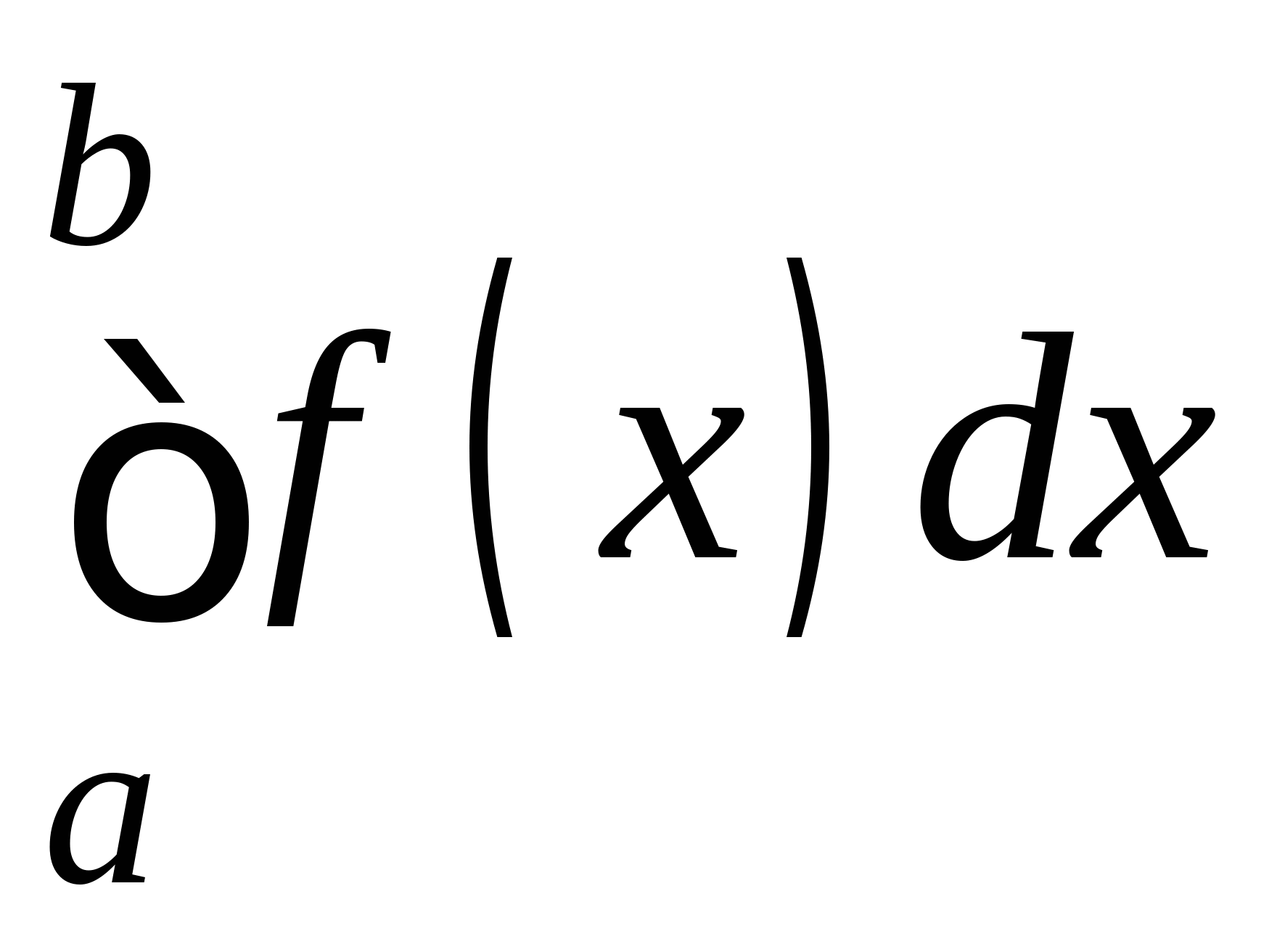 можно вычислить по одной из квадратурных формул. Пусть
можно вычислить по одной из квадратурных формул. Пусть ![]() - приближенное значение этого интеграла с точностью до
- приближенное значение этого интеграла с точностью до ![]() , т.е.
, т.е.
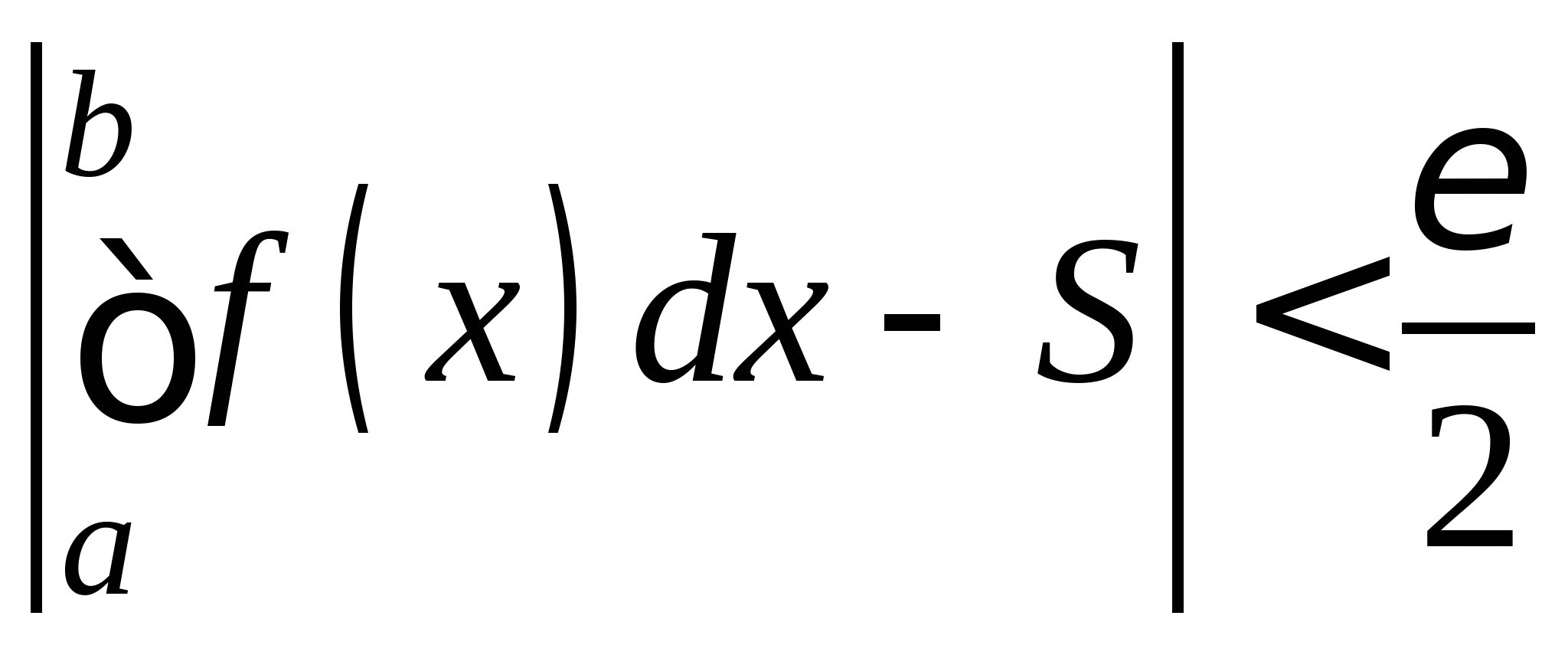 . (7.28)
. (7.28)
Из формул (7.26)-(7.28) имеем
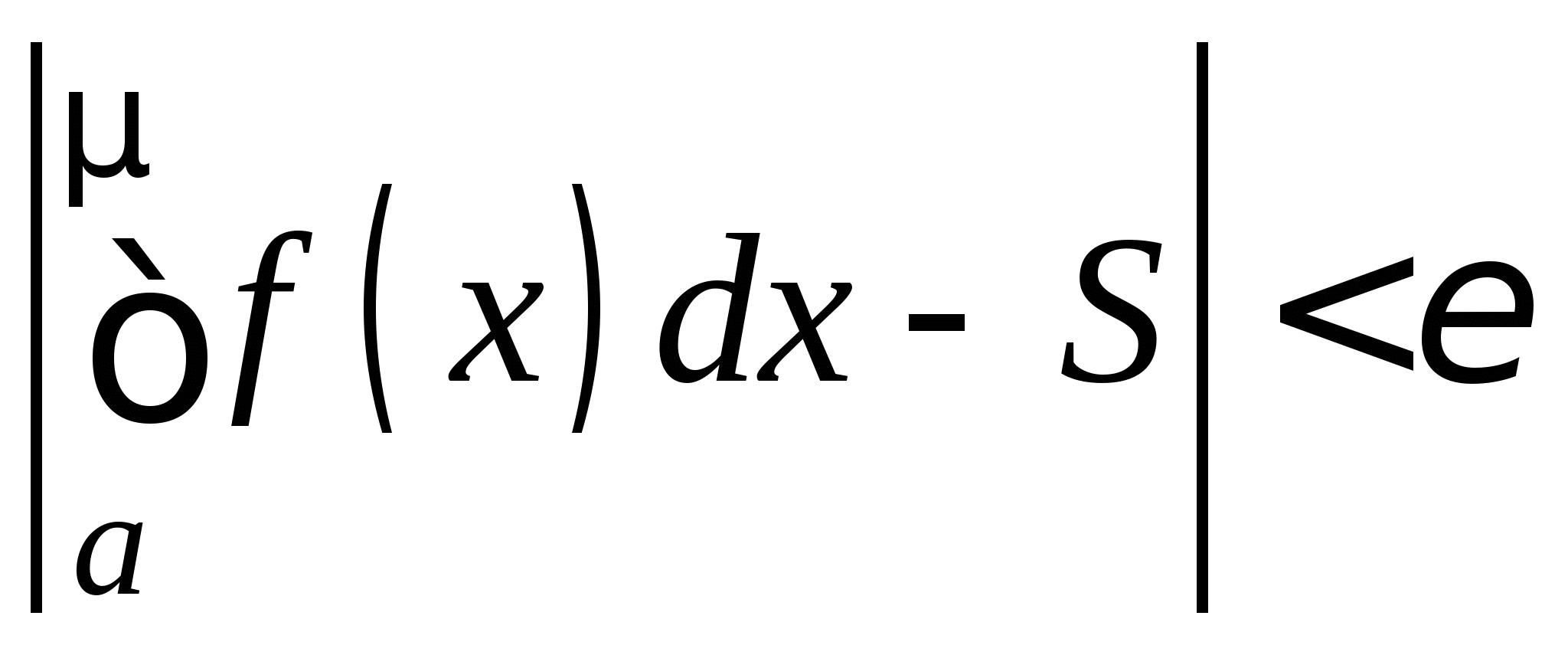 ,
,
т.е. поставленная задача решена.
б). Допустим теперь, что отрезок ![]() конечен, а функция
конечен, а функция ![]() имеет конечное число точек разрыва на
имеет конечное число точек разрыва на ![]() . Эти точки назовем «особыми» и обозначим
. Эти точки назовем «особыми» и обозначим ![]() . Такими особыми точками могут быть или один из концов отрезка, или оба конца отрезка, либо одна или несколько точек внутри отрезка.
. Такими особыми точками могут быть или один из концов отрезка, или оба конца отрезка, либо одна или несколько точек внутри отрезка.
Так как промежуток интегрирования можно разбить на частичные промежутки с единственной точкой разрыва подынтегральной функции, то достаточно разобрать лишь случай, когда на ![]() имеется единственная точка разрыва
имеется единственная точка разрыва ![]() функции
функции ![]() , причем второго рода.
, причем второго рода.
Если ![]() есть внутренняя точка отрезка
есть внутренняя точка отрезка ![]() , то по определению полагают:
, то по определению полагают:
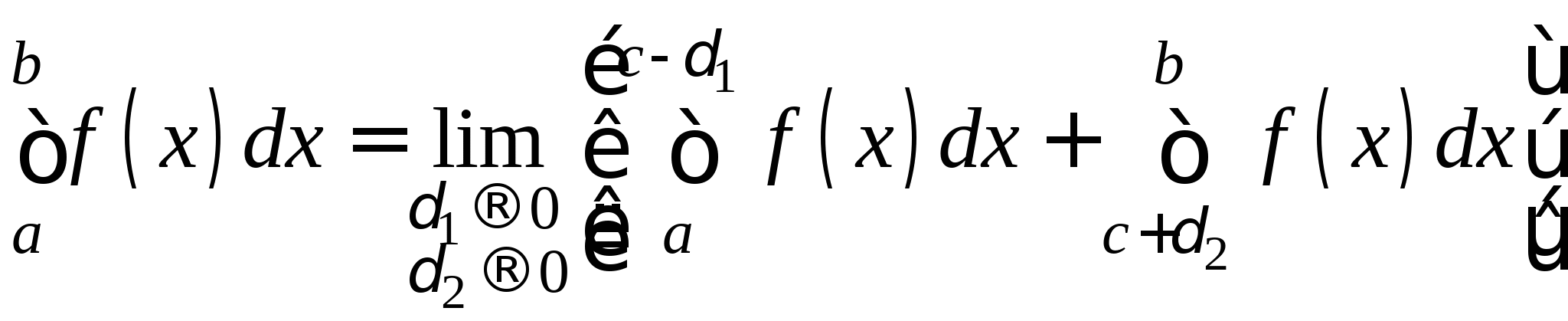 , (7.29)
, (7.29)
и в случае существования этого предела интеграл называют сходящимся, в противном случае – расходящимся.
Аналогично определяется сходимость несобственного интеграла, если точка разрыва ![]() подынтегральной функции
подынтегральной функции ![]() совпадает с одним из концов промежутка интегрирования
совпадает с одним из концов промежутка интегрирования ![]() .
.
Для приближенного вычисления с заданной точностью ![]() сходящегося несобственного интеграла (7.29), где точка разрыва
сходящегося несобственного интеграла (7.29), где точка разрыва ![]() , выбирают положительные числа
, выбирают положительные числа ![]() и
и ![]() столь малыми, чтобы имело место неравенство:
столь малыми, чтобы имело место неравенство:
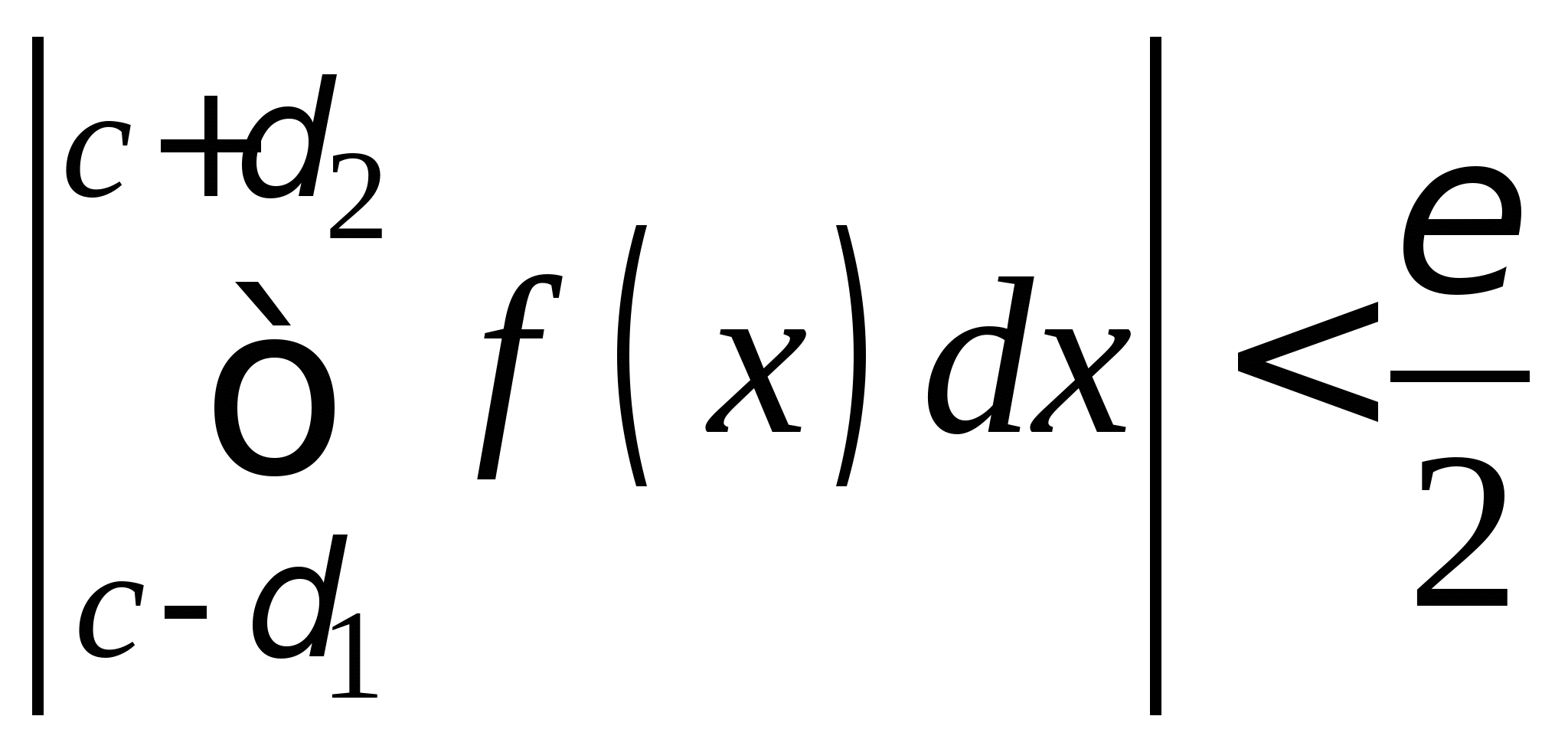 .
.
Затем по известным квадратурным формулам вычисляют определенные интегралы 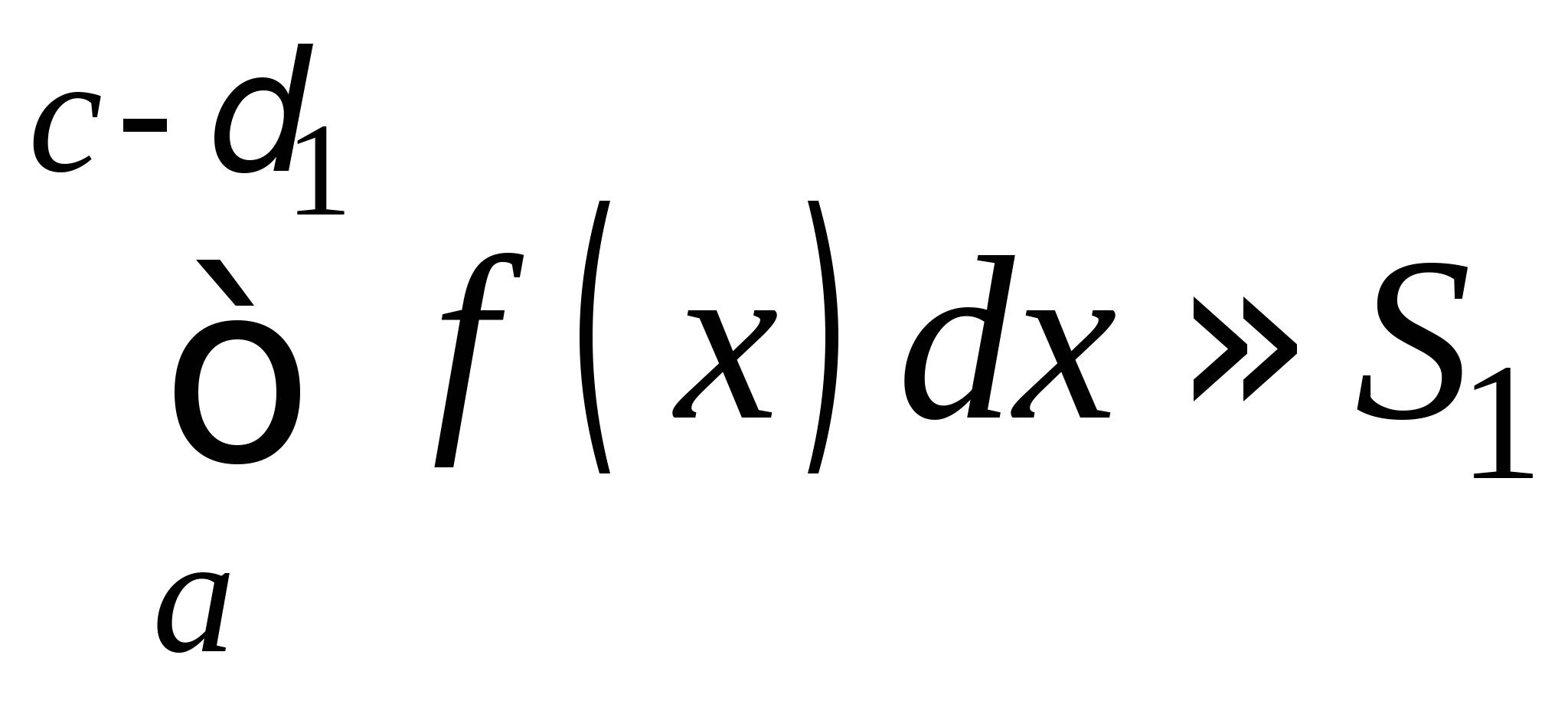 ,
, 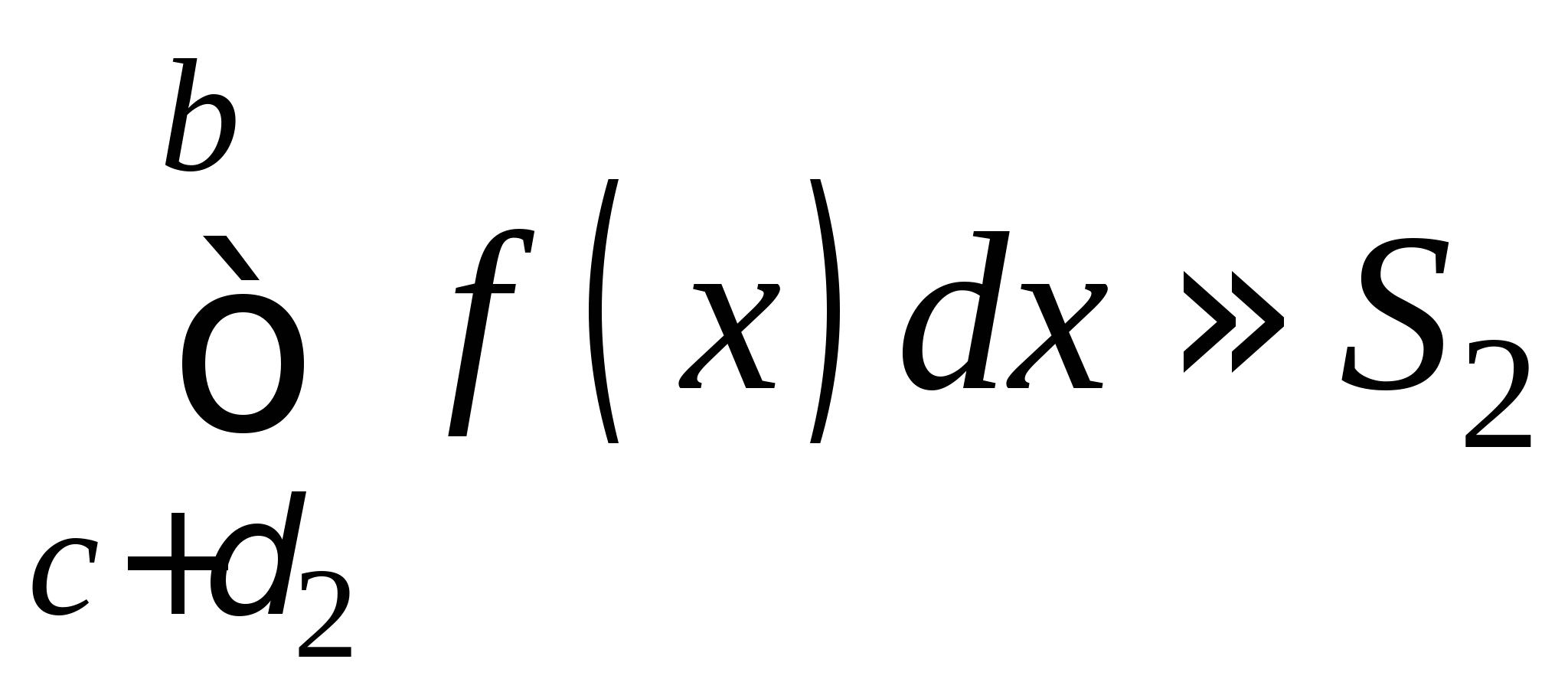 с точностью
с точностью ![]() . Тогда
. Тогда 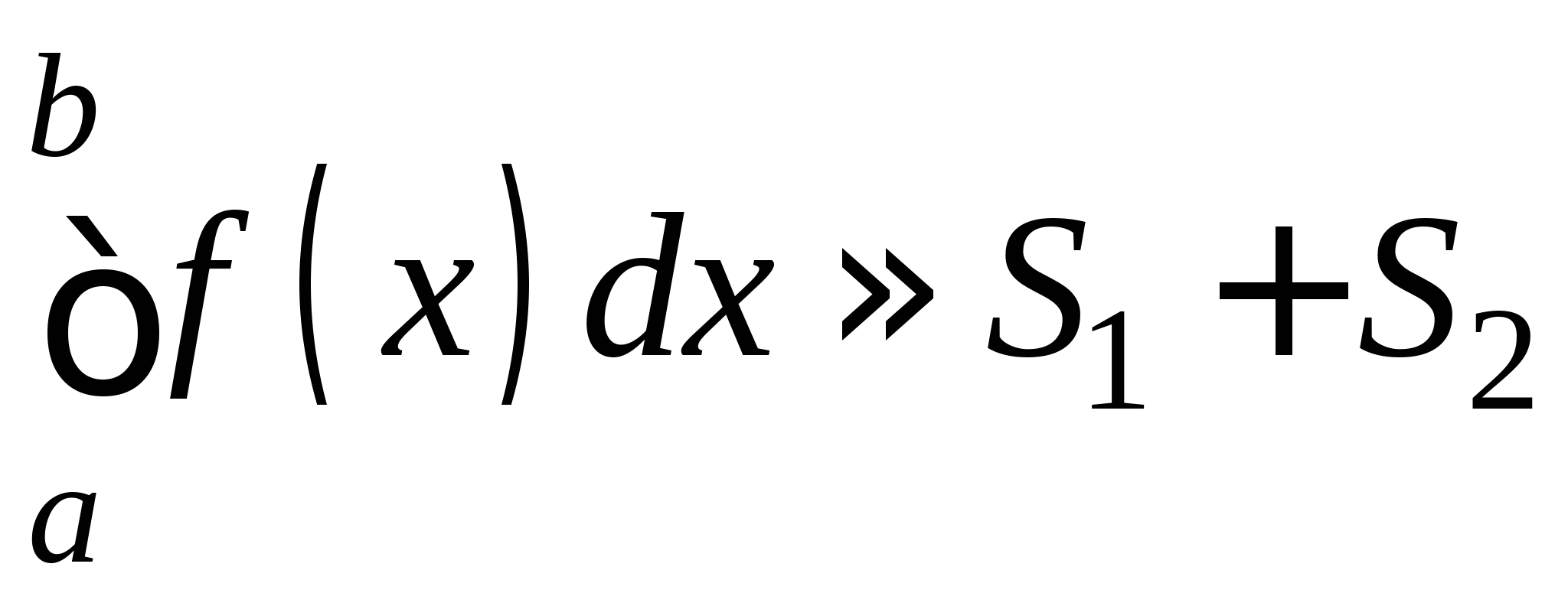 с точностью
с точностью ![]() , т.е.
, т.е.
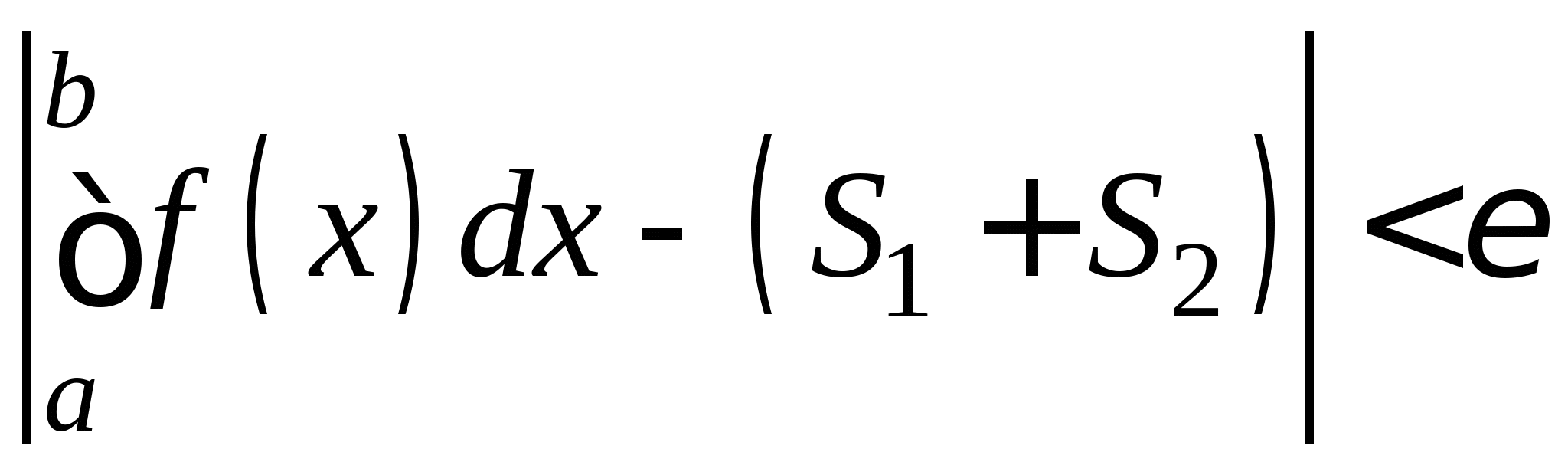 .
.
Если точка разрыва ![]() подынтегральной функции
подынтегральной функции ![]() является концевой для промежутка интегрирования
является концевой для промежутка интегрирования ![]() , то методика вычисления очевидным образом видоизменяется.
, то методика вычисления очевидным образом видоизменяется.
§7.5. Кубатурные формулы типа Симпсона.
Рассмотрим один из методов приближенного вычисления двойного интеграла.
Так как двойной интеграл вычисляется через повторный, то при приближенном вычислении двойного интеграла используется квадратурная формула Симпсона.
1) Вычислим ![]() , где область
, где область ![]() – это прямоугольник вида:
– это прямоугольник вида:
![]() .
.
Каждый отрезок ![]() ,
, ![]() разобьем пополам точками
разобьем пополам точками
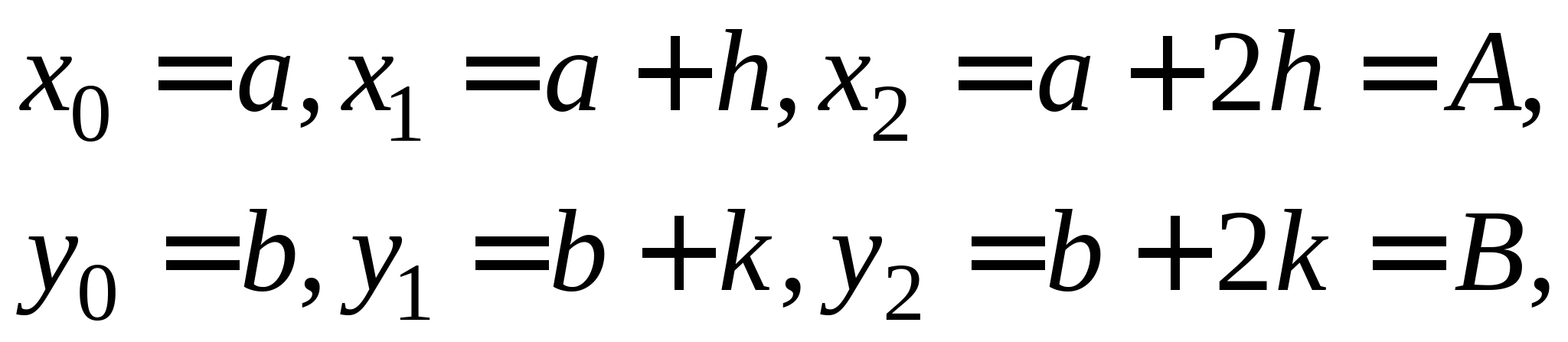
г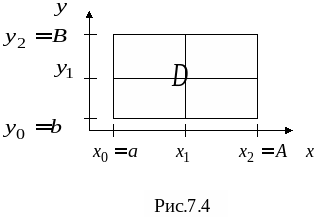
де ![]() ,
, ![]() .
.
Получим девять точек с координатами ![]() (Рис.7.4).
(Рис.7.4).
Расписав двойной интеграл через повторный и применив два раза квадратурную формулу Симпсона, получим:
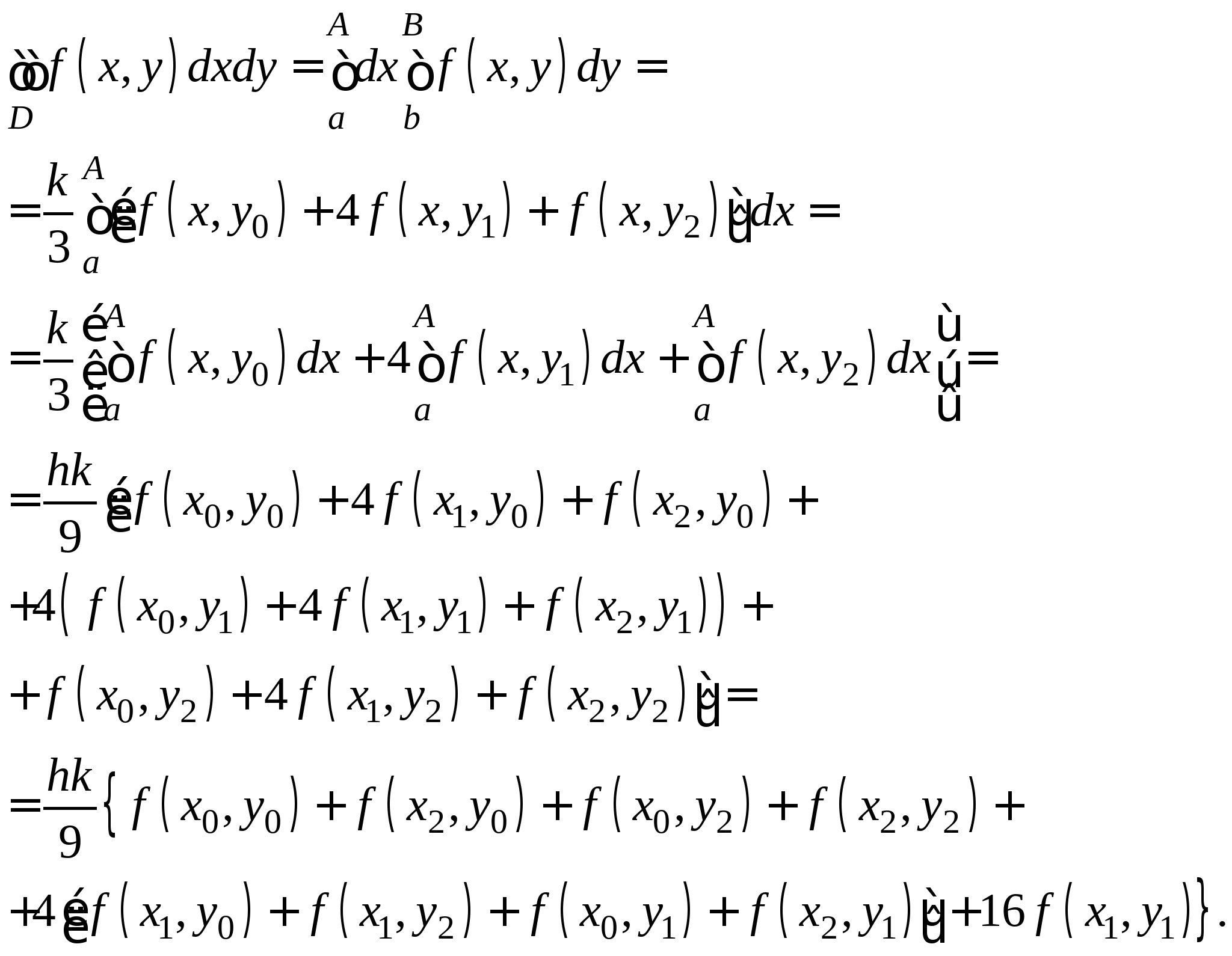 (7.30)
(7.30)
Формула (7.30) называется кубатурной формулой Симпсона.
2) Пусть теперь область ![]() представляет собой прямоугольник, стороны которого достаточно велики. Тогда отрезок
представляет собой прямоугольник, стороны которого достаточно велики. Тогда отрезок ![]() разобьем на
разобьем на ![]() равных частей, отрезок
равных частей, отрезок ![]() – на
– на ![]() равных частей. Выбирая шаги
равных частей. Выбирая шаги ![]()
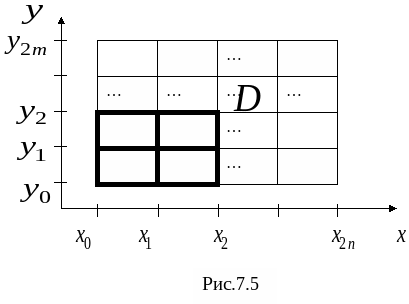
и ![]() , делим прямоугольник на четное число прямоугольников (Рис.7.5).
, делим прямоугольник на четное число прямоугольников (Рис.7.5).
Введем обозначения ![]() ,
, ![]() ,
, ![]() . Применяя кубатурную формулу Симпсона (7.30) к каждым четырем соседним прямоугольникам, получим:
. Применяя кубатурную формулу Симпсона (7.30) к каждым четырем соседним прямоугольникам, получим:
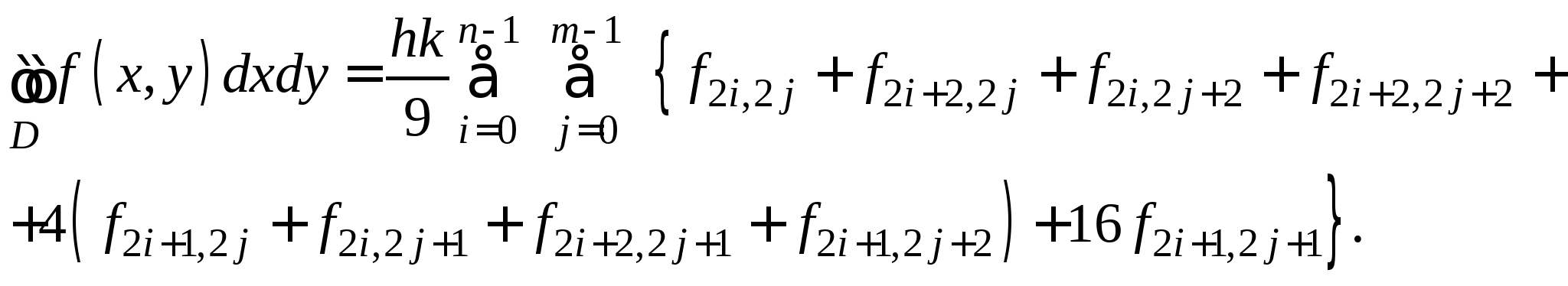
Приведя подобные, получим:
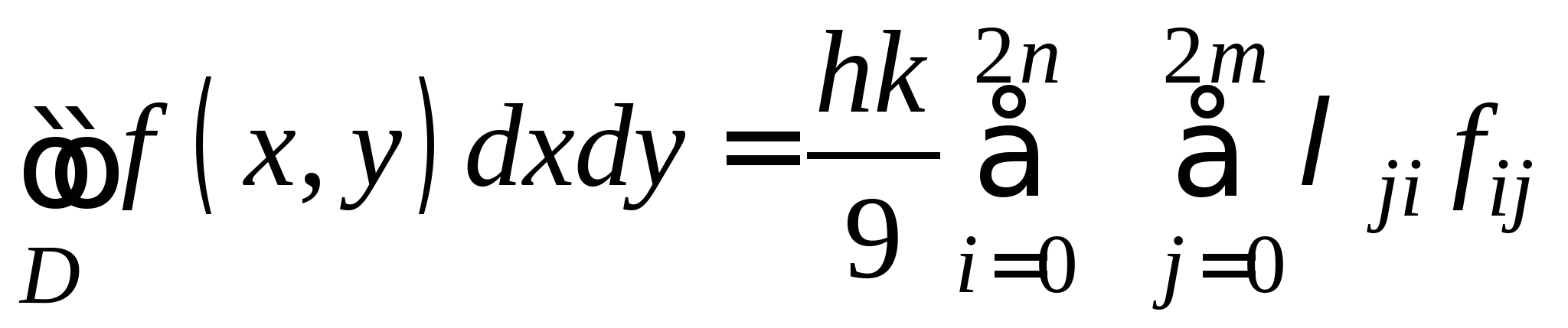 , (7.31)
, (7.31)
где коэффициенты ![]() являются соответствующими элементами матрицы
являются соответствующими элементами матрицы
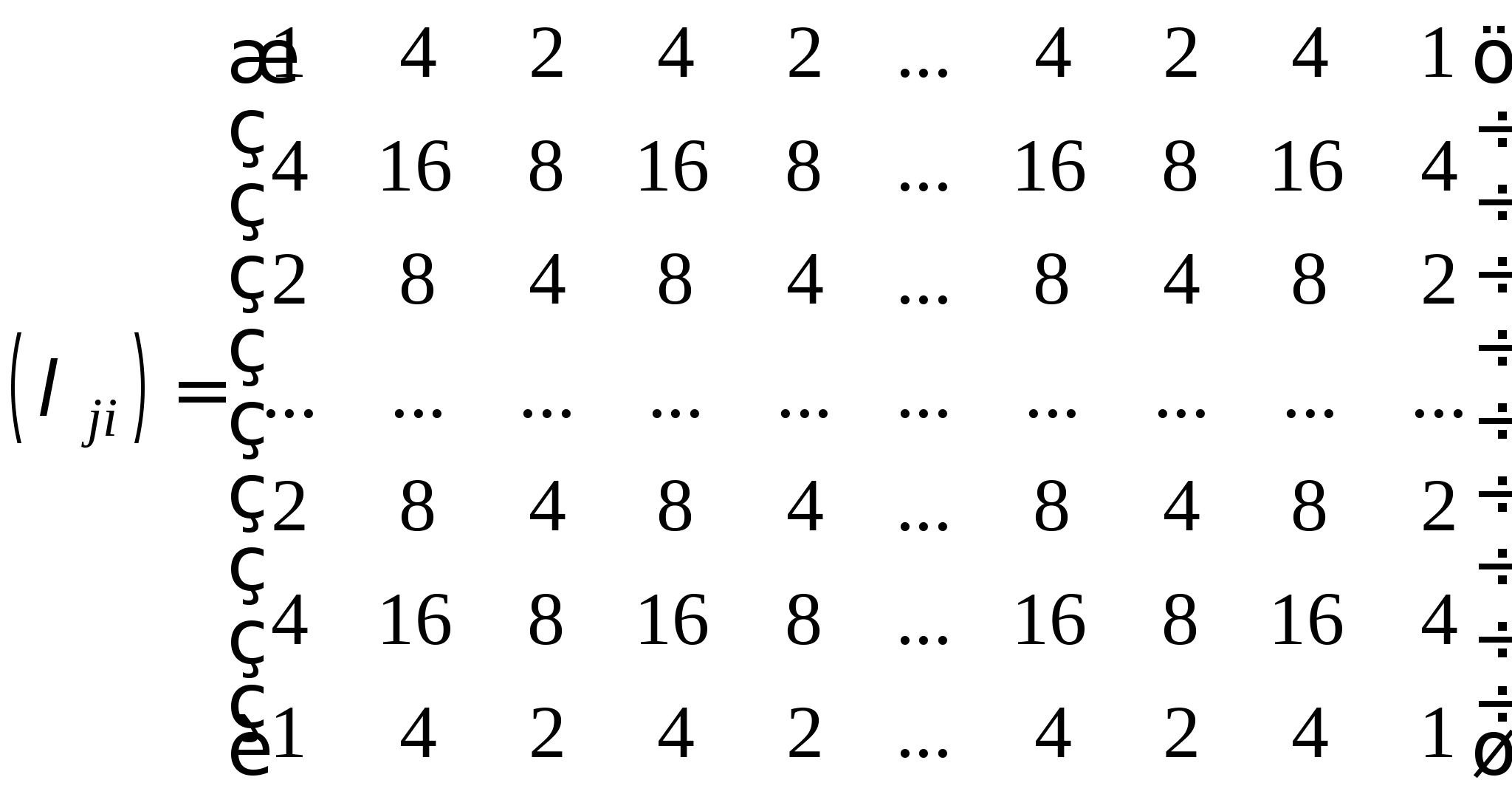 .
.
3) Если область ![]() – произвольная криволинейная область, то строится прямоугольник
– произвольная криволинейная область, то строится прямоугольник ![]() , содержащий область
, содержащий область ![]() , причем стороны прямоугольника
, причем стороны прямоугольника ![]() параллельны осям координат (Рис.7.6).
параллельны осям координат (Рис.7.6).
Р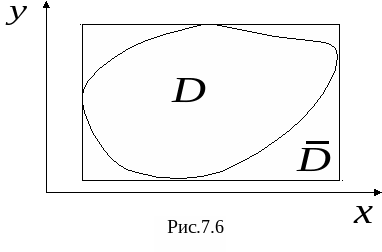
ассматривается вспомогательная функция
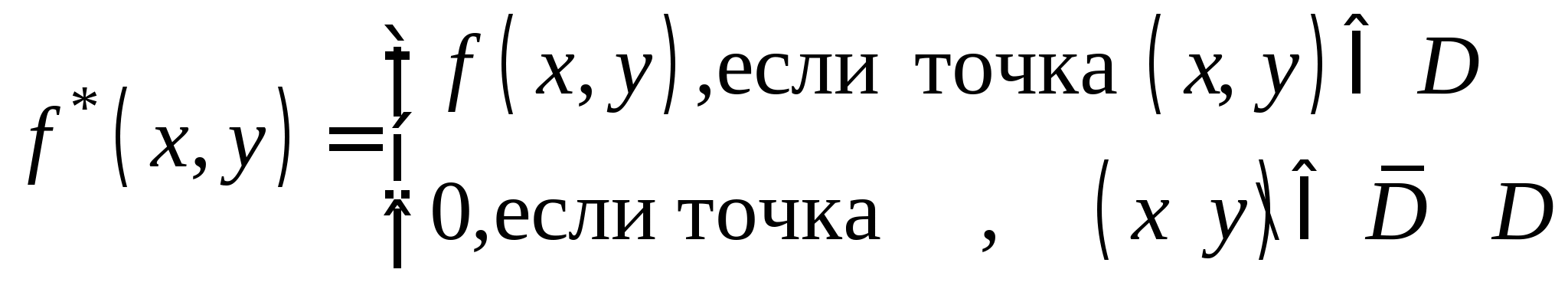 .
.
Тогда ![]() и, применяя к последнему интегралу общую кубатурную формулу Симпсона (7.31), получим приближенное значение двойного интеграла по произвольной области
и, применяя к последнему интегралу общую кубатурную формулу Симпсона (7.31), получим приближенное значение двойного интеграла по произвольной области ![]() .
.
87
ЛАБОРАТОРНАЯ РАБОТА №8. Приближенное решение обыкновенных дифференциальных уравнений.
Цель работы: научиться решать обыкновенные дифференциальные уравнения (ОДУ) методами Эйлера и Рунге-Кутта с помощью ЭВМ.
Содержание работы:
1. Изучить методы Эйлера и Рунге-Кутта для приближенного решения ОДУ.
2. На конкретном примере усвоить порядок решения ОДУ указанными методами с помощью ЭВМ.
3. Составить программу на любом языке программирования, реализующую процесс приближенного решения ОДУ указанными методами.
4. Сделать вывод о точности используемых методов.
5. Составить отчет о проделанной работе.
ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Задание.
1. Аналитически решить задачу Коши вида:
![]() (1)
(1)
![]() (2)
(2)
2. Записать рабочие формулы метода Эйлера и метода Рунге-Кутта 4 порядка точности для численного решения системы (1) при начальном условии (2) на отрезке
![]() . (3)
. (3)
3. Составить программу на любом языке программирования, реализующую построенные процессы.
Решение.
1. ОДУ (1) является дифференциальным уравнением с разделяющимися переменными. Его аналитическим решением являются интегральные кривые вида ![]() , где постоянная
, где постоянная ![]() определяется из начального условия (2) и равна
определяется из начального условия (2) и равна ![]() . Таким образом, решением задачи Коши (1)-(2) является интегральная кривая
. Таким образом, решением задачи Коши (1)-(2) является интегральная кривая ![]() .
.
2. Для построения рабочих формул методов Эйлера и Рунге-Кутта 4 порядка точности разделим отрезок (3) на ![]() равных частей и сформируем систему равноотстоящих точек
равных частей и сформируем систему равноотстоящих точек ![]() ,
, ![]() , где
, где ![]() ,
, ![]() , шаг интегрирования
, шаг интегрирования ![]() .
.
Рабочая формула метода Эйлера в общем случае имеет вид:
![]() .
.
Для поставленной задачи данная формула запишется так:
![]() (4)
(4)
Для вычислений по методу Рунге-Кутта 4 порядка необходимо предварительно вычислить 4 коэффициента:
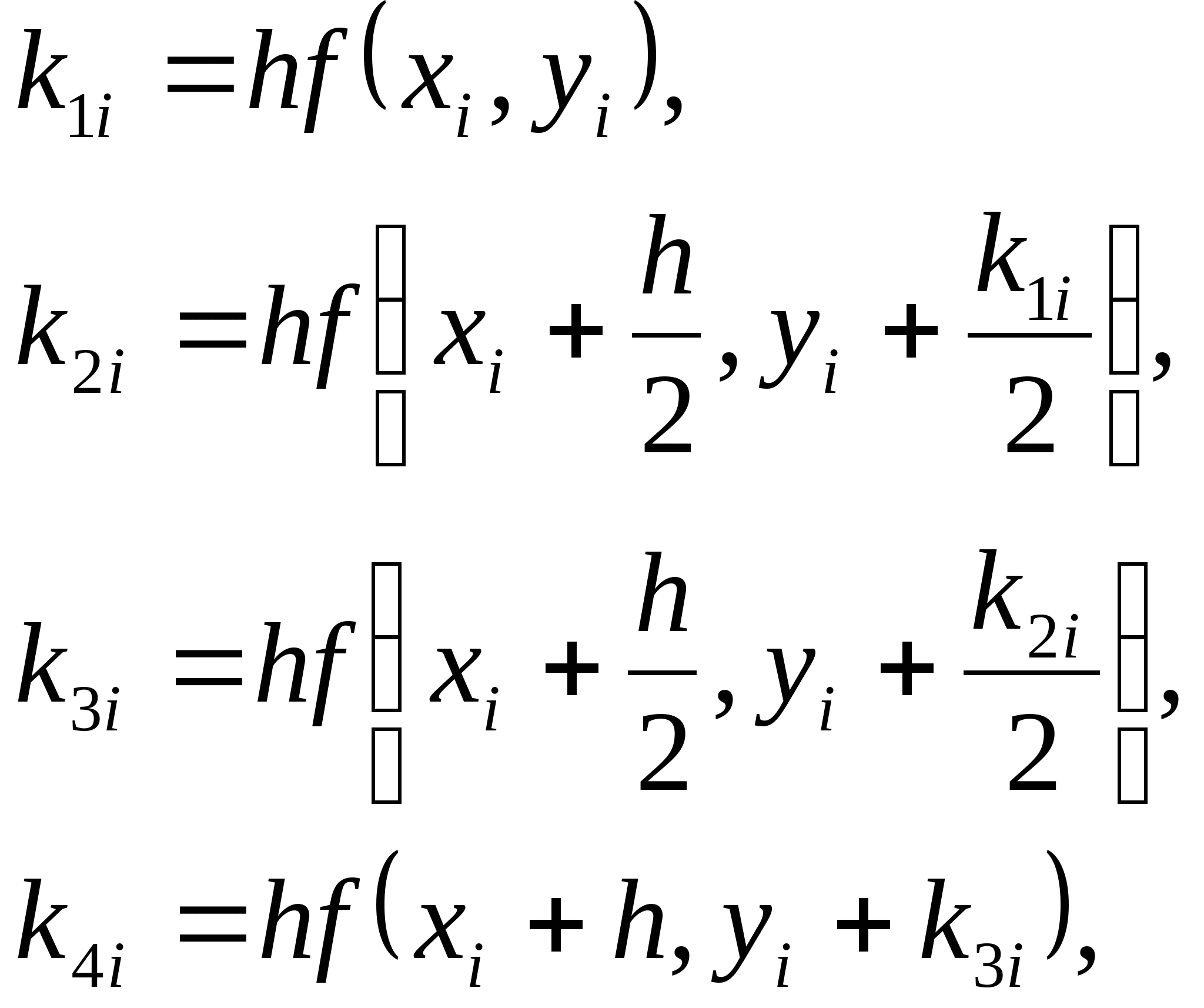
а рабочая формула имеет вид:
![]() . (5)
. (5)
Для рассматриваемого примера коэффициенты запишутся так:
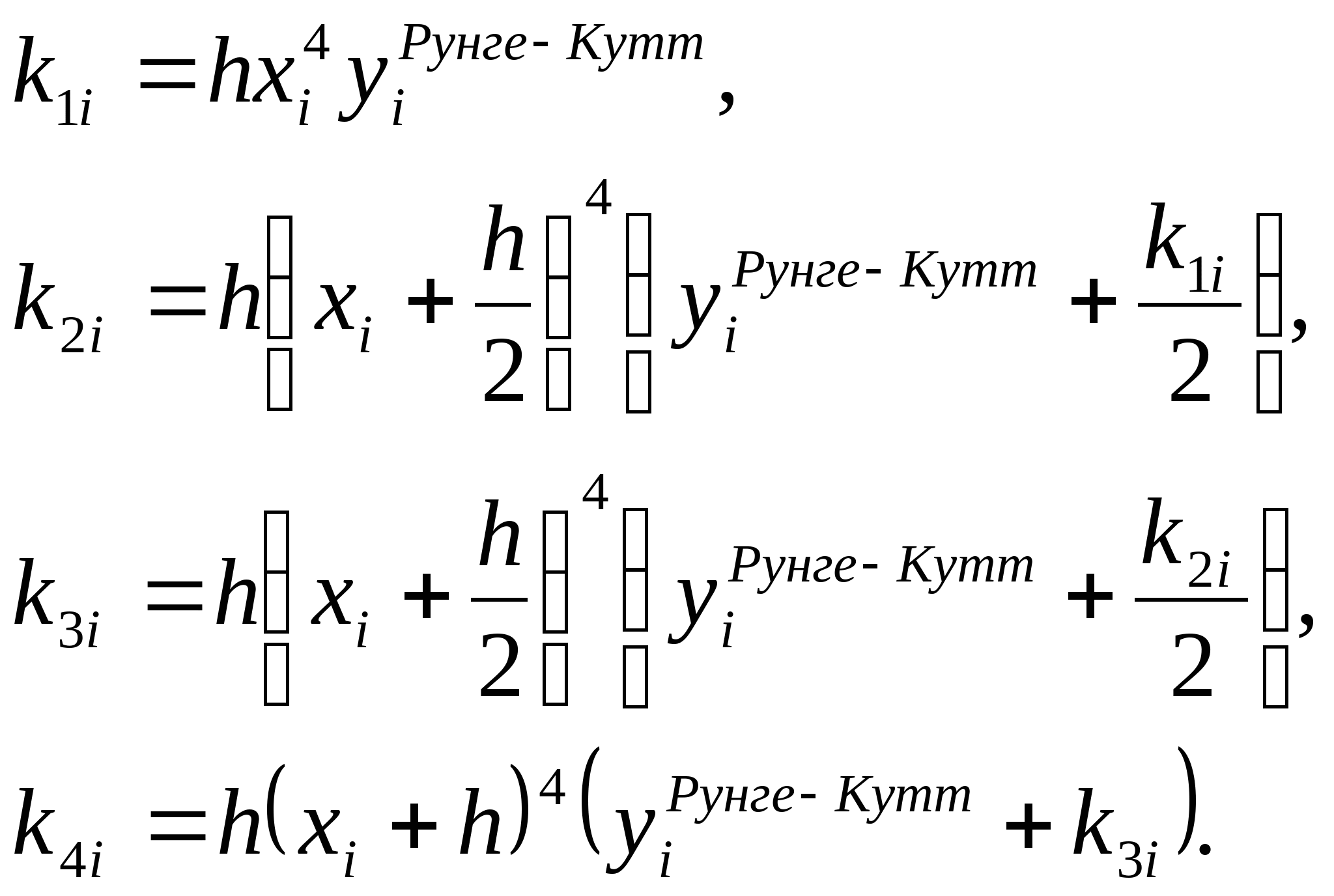 . (6)
. (6)
Итерационные процессы, заданные формулами (4), (5) и (6), можно начать, задав начальное условие (2). Процессы заканчиваются при достижении конца отрезка (3). В этом случае построенные интегральные кривые ![]() являются приближенными решениями задачи Коши (1)-(2) на отрезке (3) рассматриваемыми методами.
являются приближенными решениями задачи Коши (1)-(2) на отрезке (3) рассматриваемыми методами.
3. Блок-схема построения приближенного решения задачи Коши методами Эйлера и Рунге-Кутта приведена на рисунке 1.
Решение: результаты решения сформулированной задачи в виде графиков приведены на рисунке 2.
4. Содержание отчета.
Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод итерационных формул); листинг программы; таблицу результатов; графики, выводы о проделанной работе.
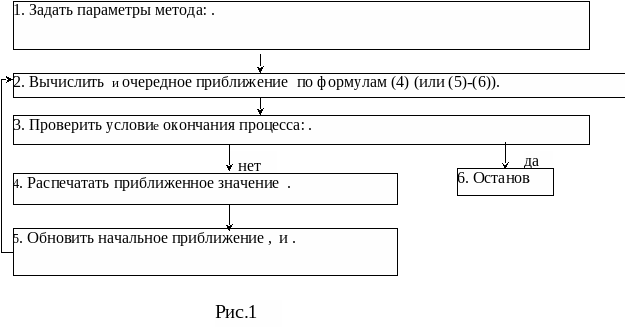
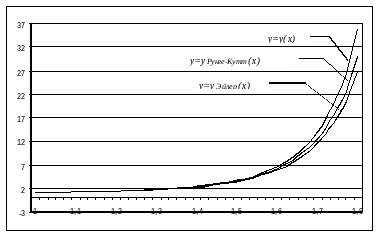
Рис.2
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Аналитически решить задачу Коши (1)-(2).
2. Записать рабочие формулы методов Эйлера и Рунге-Кутта 4 порядка для приближенного решения сформулированной задачи на отрезке (3).
3. Используя блок-схему (Рис.1), составить программу на любом языке программирования, реализующую метод Эйлера и метод Рунге-Кутта для задачи Коши. Печать результатов должна осуществляться на каждом шаге итераций в виде следующей таблицы:
|
|
|
|
|
|
|
|
4. Провести вычисления при ![]() .
.
5. Построить графики точного решения и двух приближенных (методы Эйлера и Рунге-Кутта).
6. Составить отчет о проделанной работе.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
| № варианта | Задача Коши | Отрезок |
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
142
ЛАБОРАТОРНАЯ РАБОТА №6-7. ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ ФУНКЦИЙ.
Цель работы: научиться строить интерполяционные и аппроксимационные многочлены по заданной системе точек с помощью ЭВМ.
Содержание работы:
1. Изучить принципы построения интерполяционной формулы Лагранжа, I и II интерполяционных формул Ньютона и аппроксимационного полинома.
2. На конкретном примере усвоить порядок построения указанных полиномов с помощью ЭВМ.
3. Составить программу на любом языке программирования, реализующую процесс построения указанных полиномов второго порядка для системы из трех равноотстоящих узловых точек.
4. Сделать вывод о точности построения полиномов.
5. Составить отчет о проделанной работе.
ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Задание.
1. Составить таблицу значений экспериментальной функции ![]() с точностью
с точностью ![]() для равноотстоящей системы из трех узловых точек
для равноотстоящей системы из трех узловых точек ![]() ,
, ![]() на отрезке
на отрезке ![]() из области допустимых значений функции, где
из области допустимых значений функции, где ![]() .
.
2. По сформированной системе точек построить интерполяционную формулу Лагранжа, I и II интерполяционные формулы Ньютона и аппроксимационный полином второго порядка.
3. Составить программу на любом языке программирования, реализующую процесс построения указанных полиномов для заданной системы точек.
Решение.
1. Таблица значений функции ![]() с точностью
с точностью ![]() для равноотстоящей системы из трех узловых точек
для равноотстоящей системы из трех узловых точек ![]() ,
, ![]() на отрезке
на отрезке ![]() , где
, где ![]() , имеет вид:
, имеет вид:
|
| 0.524 | 1.047 | 1.571 |
| | 0.500 | 0.866 | 1.000 |
2. Интерполяционный полином Лагранжа.
Замечание. Так как данный полином строится для произвольной системы узловых точек, то запишем этот полином для равноотстоящих узловых точек:
![]() ,
,
где коэффициенты ![]() вычисляются так:
вычисляются так:
![]() ;
;
![]() ;
;
![]() .
.
Тогда искомый многочлен Лагранжа второго порядка будет иметь вид:
![]() ,
,
где ![]() .
.
I интерполяционная формула Ньютона второго порядка по заданной системе точек строится в виде:
![]() .
.
Здесь величины ![]() ,
, ![]() называются табличными разностями первого и второго порядков соответственно,
называются табличными разностями первого и второго порядков соответственно, ![]() .
.
II интерполяционная формула Ньютона второго порядка по заданной системе точек строится в виде:
![]() .
.
Здесь величины ![]() и
и ![]() вводятся аналогично случаю, рассмотренному выше,
вводятся аналогично случаю, рассмотренному выше, ![]() .
.
При построении аппроксимационного многочлена методом наименьших квадратов необходимо, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальна. Будем строить функцию в виде многочлена второго порядка
![]() .
.
Согласно алгоритму метода наименьших квадратов, для построения многочлена второй степени необходимо вычислить следующие суммы:
![]()
![]() ,
,
и решить систему линейных алгебраических уравнений 3-го порядка вида
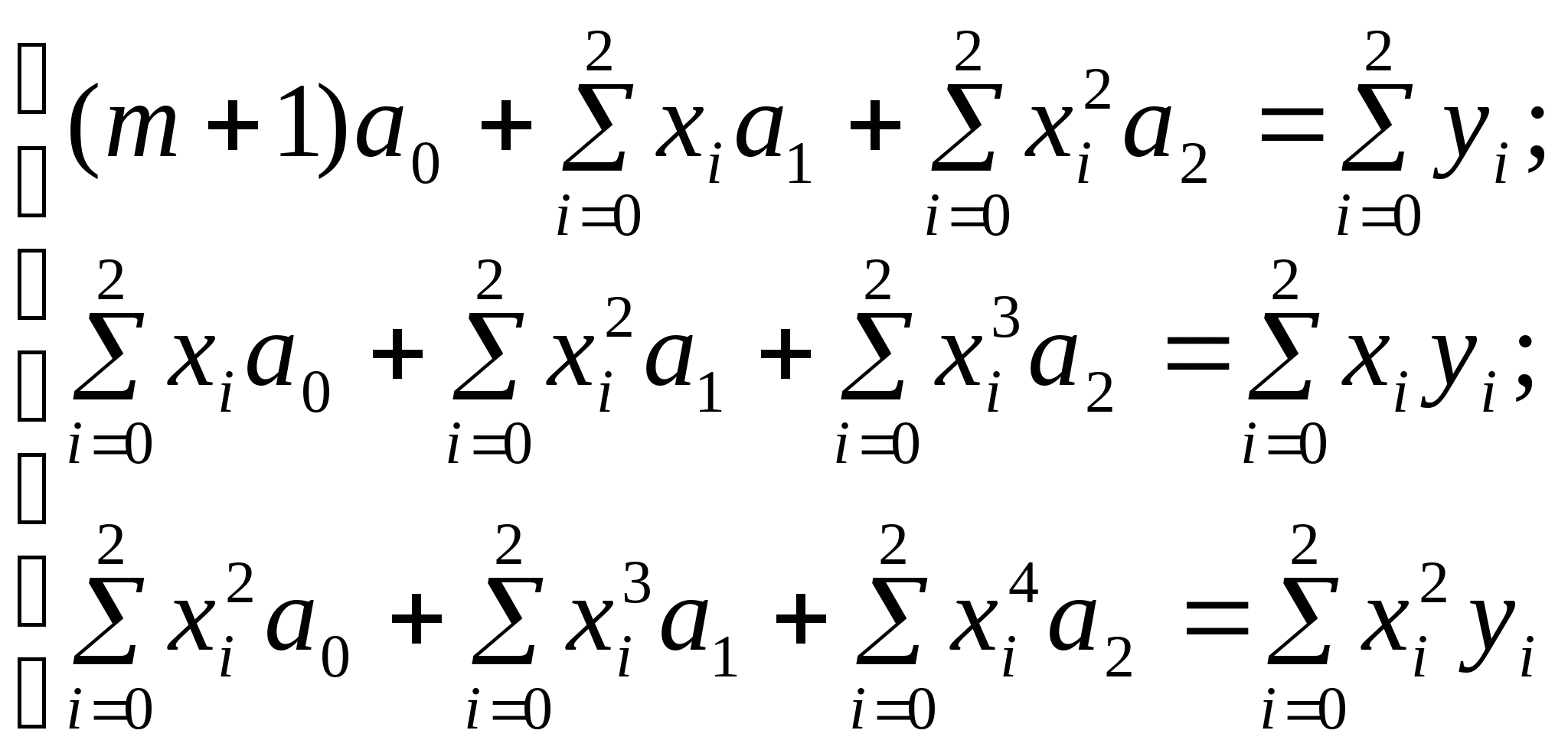 (1)
(1)
относительно неизвестных коэффициентов ![]() . В данном случае система (1) будет выглядеть так
. В данном случае система (1) будет выглядеть так
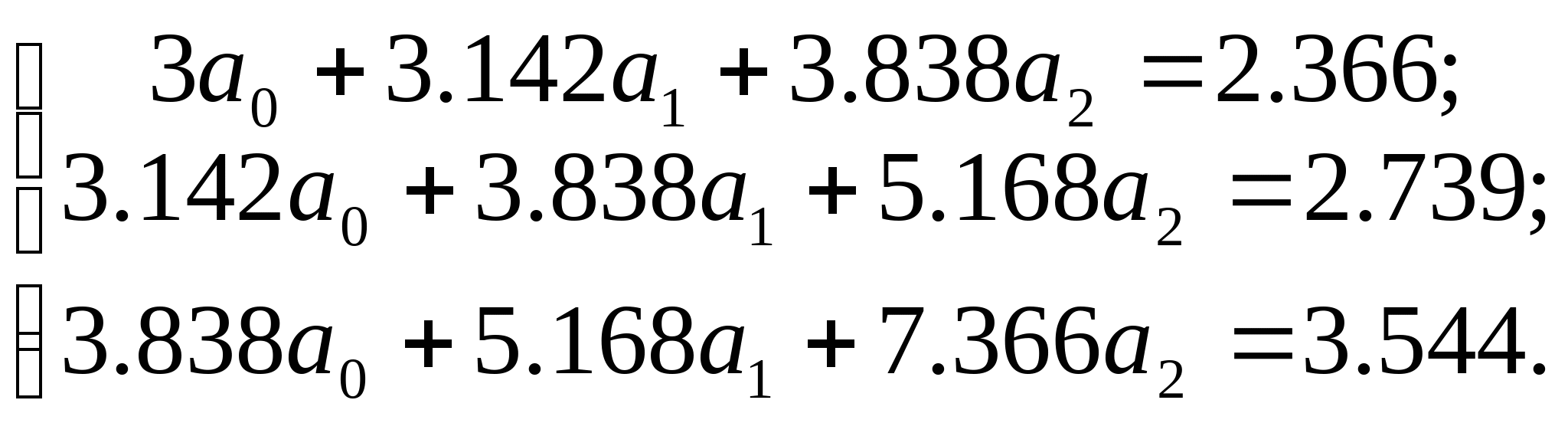 (2)
(2)
Для ее решения можно воспользоваться любым известным методом, например, методом Крамера. Для этого необходимо вычислить четыре определителя системы (2) вида:
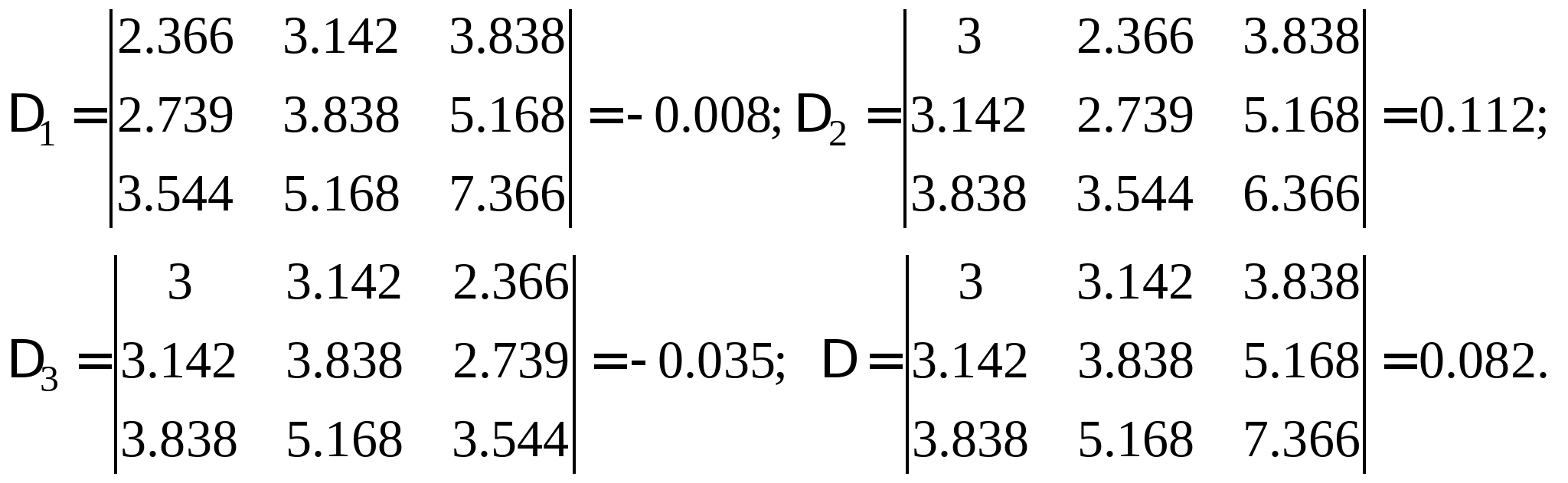
Значения искомых коэффициентов вычисляются по формулам:
![]() .
.
Искомый многочлен второго порядка будет иметь вид:
![]() .
.
Для проверки правильности построения полиномов необходимо провести программно процесс табулирования четырех построенных полиномов и экспериментальной функции при ![]() с одинаковым шагом табулирования.
с одинаковым шагом табулирования.
Графики этих функций представлены на рисунке 1. Из графика видно, что искомые полиномы на отрезке практически совпадают с экспериментальной функцией и проходят через узловые точки.
З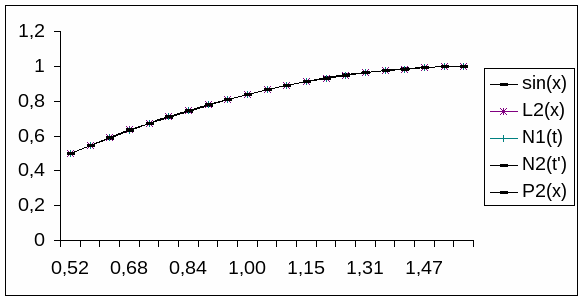
амечание. Аппроксимационный полином в общем случае не проходит через узловые точки и для системы из трех узловых точек может давать погрешность, превышающую погрешность построения остальных полиномов.
Рис.1.
3. Содержание отчета.
Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод интерполяционных и аппроксимационного полиномов); графики; листинг программы; таблицу результатов; выводы о проделанной работе.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Составить программу на любом языке программирования, реализующую процесс построения указанных полиномов:
1.1. Сформировать таблицу значений экспериментальной функции ![]() с точностью
с точностью ![]() для равноотстоящей системы из трех узловых точек
для равноотстоящей системы из трех узловых точек ![]() ,
, ![]() на отрезке
на отрезке ![]() из области допустимых значений функции, где
из области допустимых значений функции, где ![]() .
.
1.2. Вычислить значения коэффициентов интерполяционной формулы Лагранжа ![]() и записать непосредственно полином.
и записать непосредственно полином.
1.3. Вычислить значения табличных разностей первого и второго порядков, необходимых для построения I и II интерполяционных формул Ньютона и записать непосредственно полиномы.
1.4. Для построения аппроксимационного полинома второго порядка вычислить необходимые суммы, сформировать СЛАУ 3-го порядка, решить ее любым известным методом и записать непосредственно полином.
1.5. Осуществить процесс табулирования четырех построенных полиномов и экспериментальной функции при ![]() с одинаковым шагом табулирования. Печать результатов табулирования должна осуществляться на каждом шаге в виде следующей таблицы:
с одинаковым шагом табулирования. Печать результатов табулирования должна осуществляться на каждом шаге в виде следующей таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
2. Провести вычислительные эксперименты.
3. Построить графики всех приведенных в таблице функций.
4. Составить отчет о проделанной работе.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
| № варианта |
| № варианта |
|
| 1 |
| 12 |
|
| 2 |
| 13 |
|
| 3 |
| 14 |
|
| 4 |
| 15 |
|
| 5 |
| 16 |
|
| 6 |
| 17 |
|
| 7 |
| 18 |
|
| 8 |
| 19 |
|
| 9 |
| 20 |
|
| 10 |
| 21 |
|
| 11 |
|
137
ЛАБОРАТОРНАЯ РАБОТА №5. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Цель работы: научиться решать системы линейных алгебраических уравнений (СЛАУ) методом простых итераций (МПИ) и методом Зейделя с помощью ЭВМ.
Содержание работы:
1. Изучить метод простых итераций и метод Зейделя для решения СЛАУ.
2. На конкретном примере усвоить порядок решения СЛАУ с помощью ЭВМ указанными методами.
3. Составить программу и с ее помощью решить СЛАУ с точностью ![]() . Сравнить скорости сходимости метода простых итераций и метода Зейделя.
. Сравнить скорости сходимости метода простых итераций и метода Зейделя.
4. Изменить ![]() и снова решить задачу. Сделать вывод о влиянии точности на количество итераций.
и снова решить задачу. Сделать вывод о влиянии точности на количество итераций.
5. Решить СЛАУ с точностью ё и ![]() , выбрав другие начальные приближения для неизвестных системы. Сделать вывод о том, как выбор начального приближения влияет на скорость сходимости рассматриваемых методов.
, выбрав другие начальные приближения для неизвестных системы. Сделать вывод о том, как выбор начального приближения влияет на скорость сходимости рассматриваемых методов.
6. Составить отчет о работе.
ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Задание.
1. Аналитически решить СЛАУ вида:
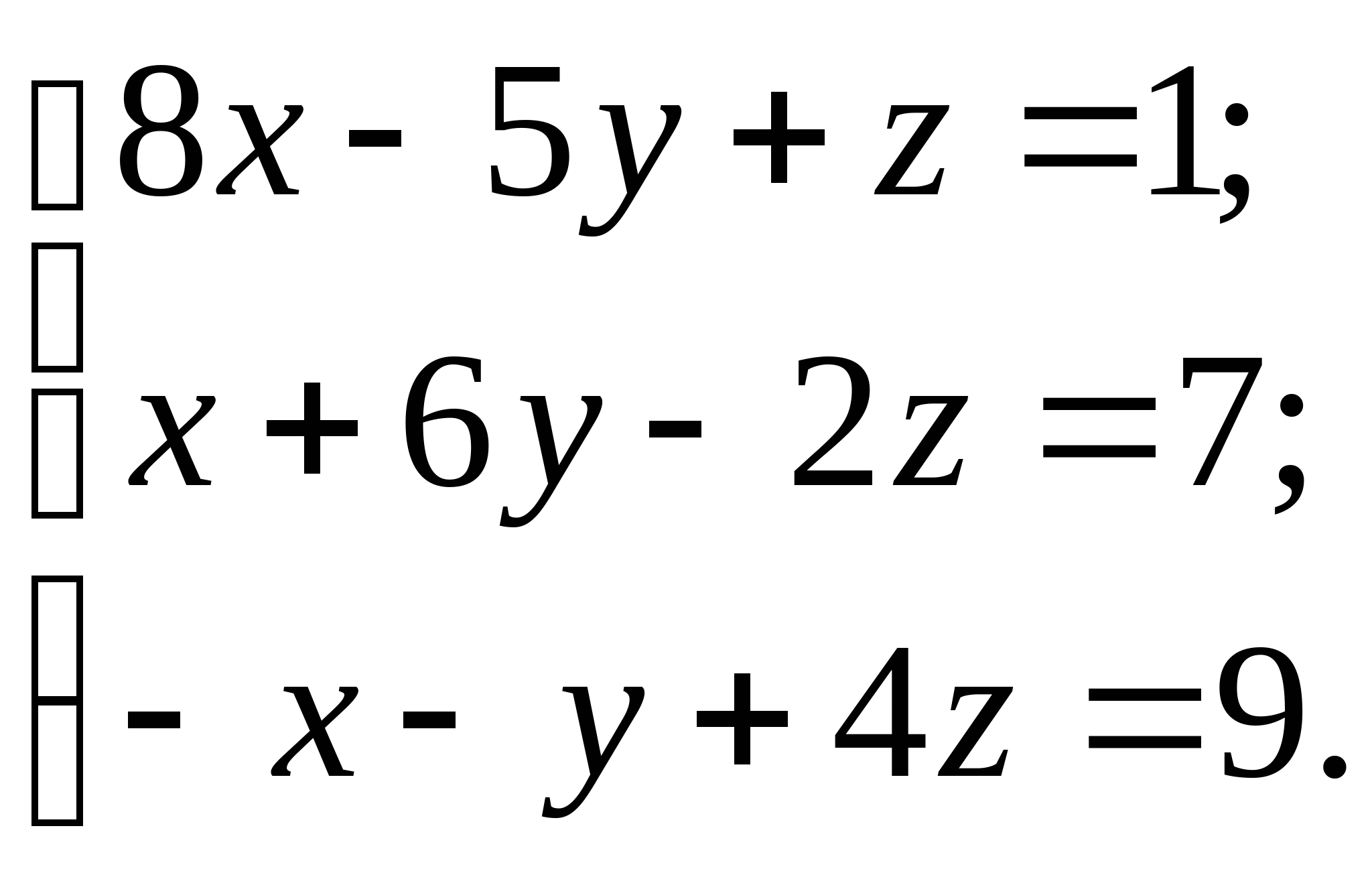 (1)
(1)
2. Построить рабочие формулы МПИ и метода Зейделя для численного решения системы (1).
3. Составить программу(ы) на любом языке программирования, реализующую(ие) построенные итерационные процессы.
Решение.
1. Аналитическим решением системы являются значения: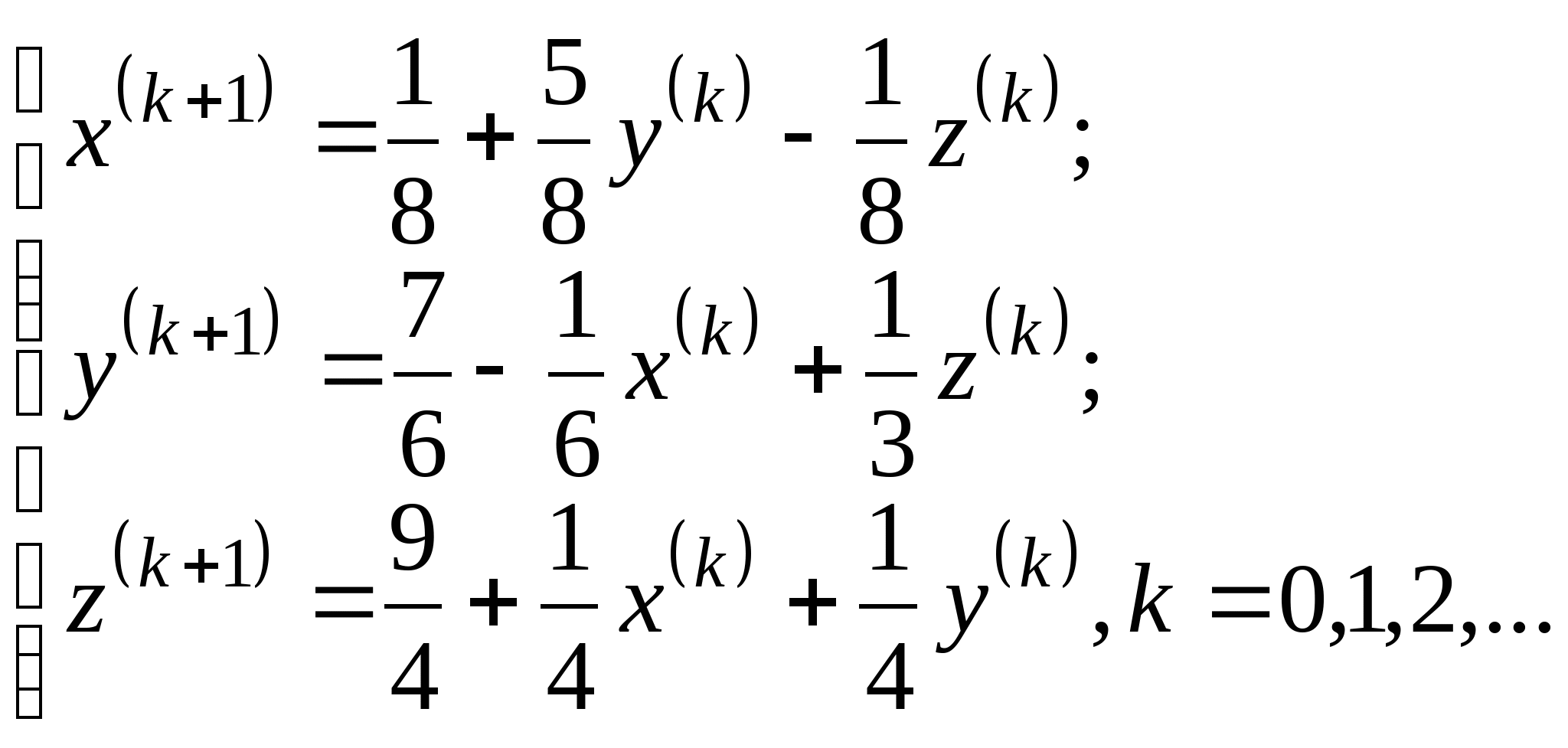 (2)
(2)
Начальное приближение обычно выбирают равным столбцу свободных членов преобразованной системы ![]() . Процесс (2) заканчивается при одновременном выполнении трех условий:
. Процесс (2) заканчивается при одновременном выполнении трех условий:
![]() ,
, ![]() ,
, ![]() .
.
В этом случае значения ![]() являются приближенными значениями решения СЛАУ (1).
являются приближенными значениями решения СЛАУ (1).
Метод Зейделя. Более быструю скорость сходимости имеет метод Зейделя, в котором найденное ![]() -е приближение сразу же используется для получения
-е приближение сразу же используется для получения ![]() -го приближения последующих координат (Рис.1).
-го приближения последующих координат (Рис.1).
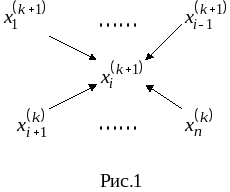
Рабочие формулы метода Зейделя запишутся так:
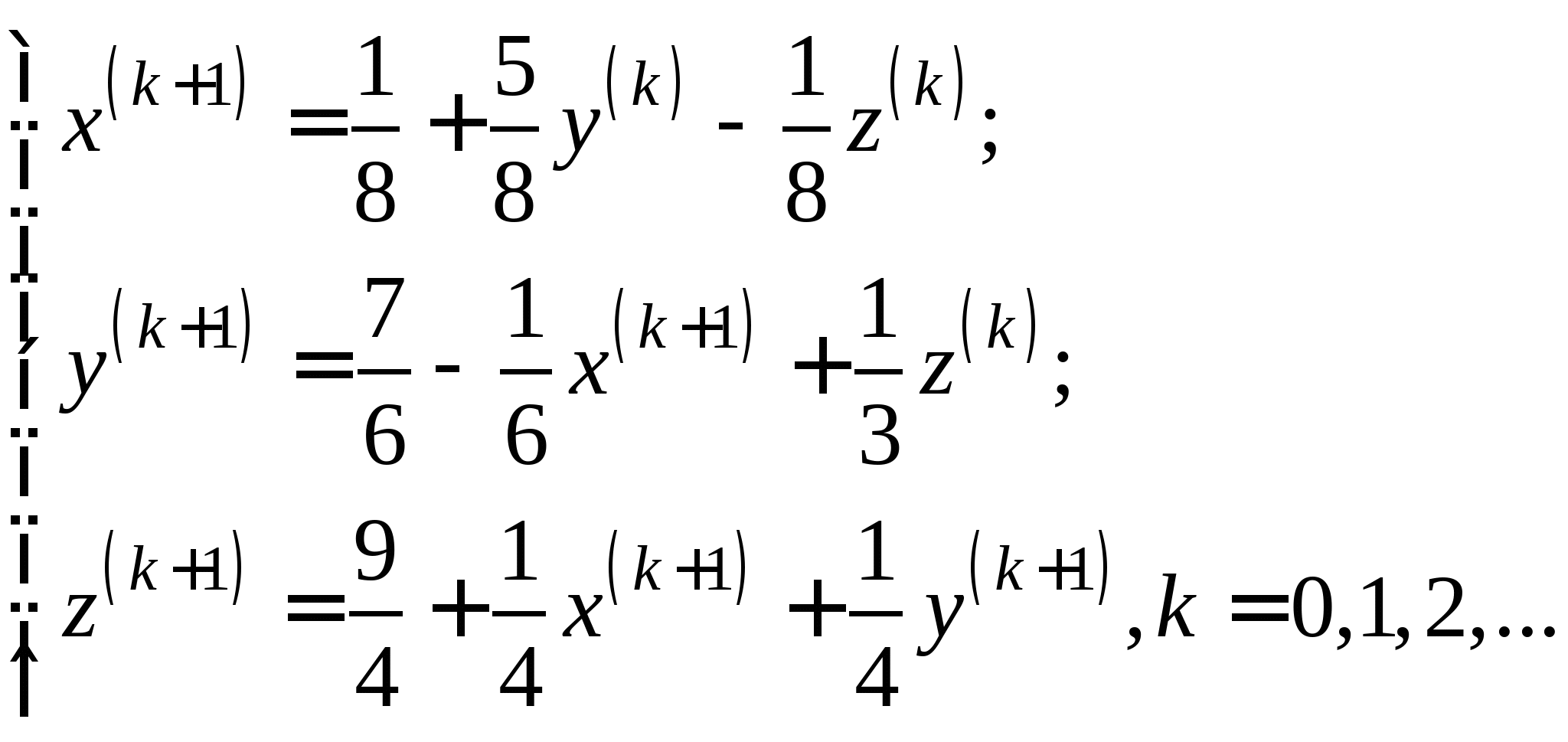 (3)
(3)
Условия выхода итерационного процесса (3) и выбор начального приближения аналогичны МПИ.
3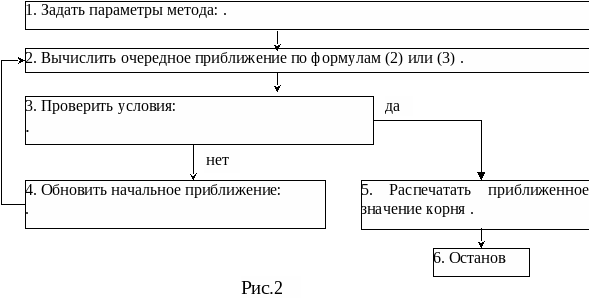
. Блок-схема метода простых итераций и метода Зейделя приведена на рисунке 2.
Решение: в результате решения СЛАУ (1) методом простых итераций с точностью ![]() получено решение
получено решение ![]() , методом Зейделя с той же точностью
, методом Зейделя с той же точностью ![]() .
.
4. Содержание отчета.
Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод итерационных формул); листинг(и) программ(ы); таблицы результатов (в случае, если число итераций в таблице достаточно большое, в отчет занести две первых и две последних итерации); выводы о проделанной работе.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Определить аналитическое решение исходной СЛАУ.
2. Если исходная СЛАУ не является системой с преобладающими диагональными коэффициентами, то путем элементарных преобразований привести ее к этому виду.
3. Построить итерационные формулы, реализующие процесс поиска решения СЛАУ методом простых итераций и методом Зейделя.
4. Составить программу(ы) на любом языке программирования, реализующую(ие) построенные итерационные процессы, используя приведенный на рисунке 2 алгоритм методов. Печать результатов должна осуществляться на каждом шаге итераций в виде следующей таблицы:
|
|
|
|
|
|
|
|
|
|
|
5. Провести вычислительные эксперименты.
6. Составить отчет о проделанной работе.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
| № варианта | Система линейных алгебраических уравнений | № варианта | Система линейных алгебраических уравнений |
| 1 |
| 12 |
|
| 2 |
| 13 |
|
| 3 |
| 14 |
|
| 4 |
| 15 |
|
| 5 |
| 16 |
|
| 6 |
| 17 |
|
| 7 |
| 18 |
|
| 8 |
| 19 |
|
| 9 |
| 20 |
|
| 10 |
| 21 |
|
| 11 |
|
132
ЛАБОРАТОРНАЯ РАБОТА №3-4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Цель работы: научиться решать системы нелинейных уравнений (СНУ) методом простых итераций (МПИ) и методом Ньютона с помощью ЭВМ.
Содержание работы:
1. Изучить МПИ и метод Ньютона для решения систем нелинейных уравнений.
2. На конкретном примере усвоить порядок решения систем нелинейных уравнений МПИ и методом Ньютона с помощью ЭВМ.
3. Составить программу и с ее помощью решить систему уравнений с точностью ![]() .
.
4. Изменить ![]() и снова решить задачу. Сделать вывод о влиянии точности на количество итераций.
и снова решить задачу. Сделать вывод о влиянии точности на количество итераций.
5. Составить отчет о проделанной работе.
ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Задание.
1. Аналитически решить СНУ вида:
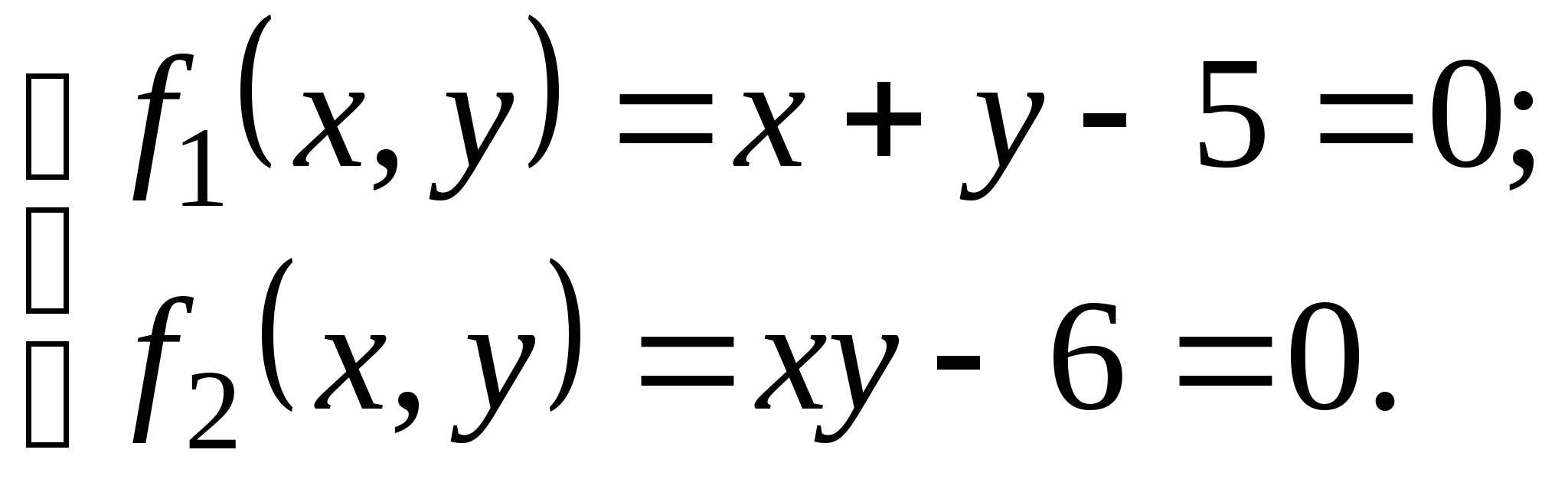 (1)
(1)
2. Построить рабочие формулы МПИ и метода Ньютона для численного решения системы (1) при начальном приближении
![]() . (2)
. (2)
3. Составить программу на любом языке программирования, реализующую построенный итерационный процесс.
Решение.
1. Аналитическим решением СНУ (1) являются точки ![]() и
и ![]() .
.
2. Для построения рабочих формул МПИ для численного решения системы (1) необходимо вначале привести ее к виду:
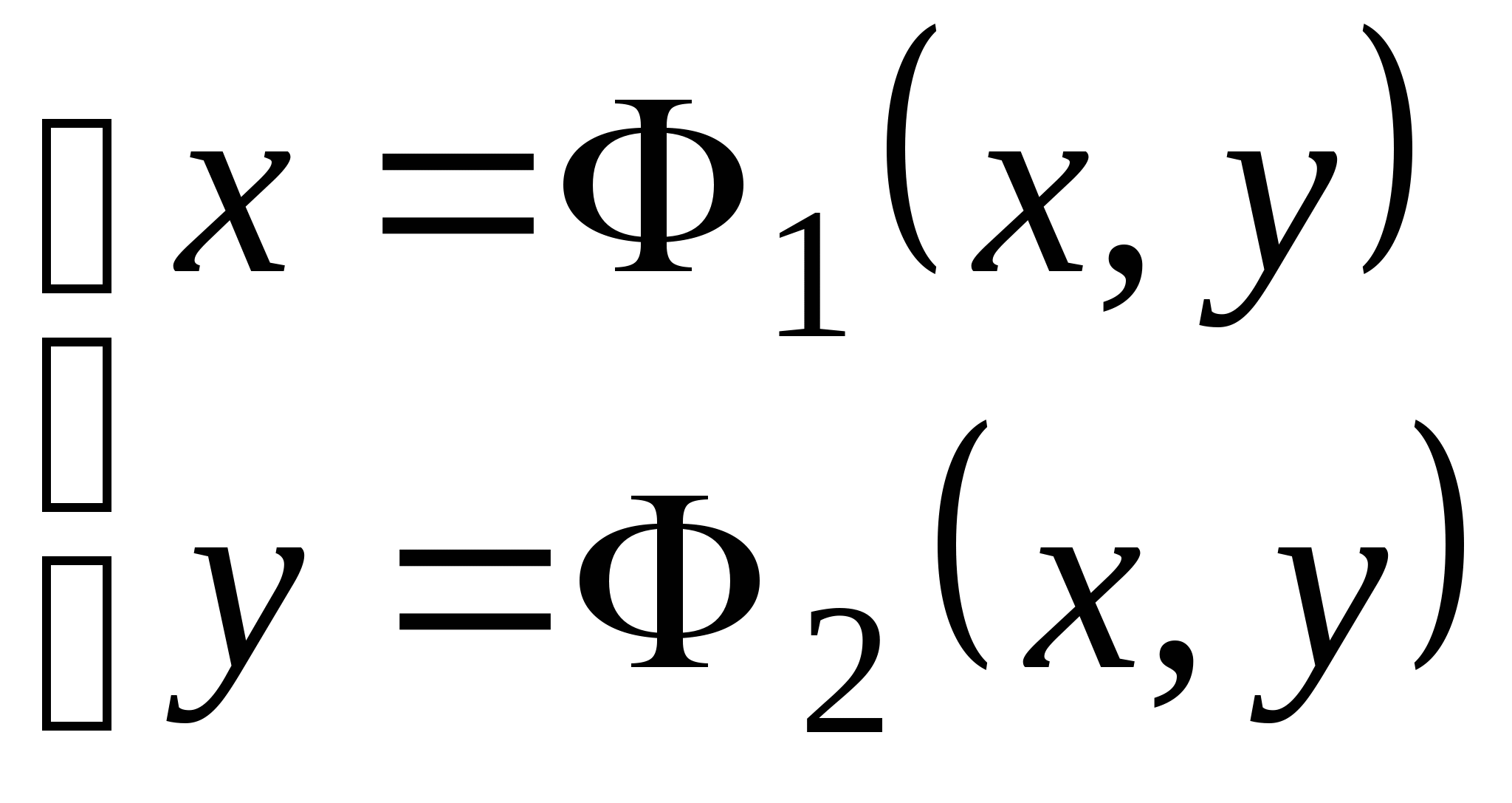 (3)
(3)
Для этого умножим первое уравнение системы (1) на неизвестную постоянную ![]() , второе - на
, второе - на ![]() , затем сложим их и добавим в обе части уравнения
, затем сложим их и добавим в обе части уравнения ![]() . Получим первое уравнение преобразуемой системы
. Получим первое уравнение преобразуемой системы
![]() (4)
(4)
где ![]() . Далее, умножим первое уравнение системы (1) на неизвестную постоянную
. Далее, умножим первое уравнение системы (1) на неизвестную постоянную ![]() , второе - на
, второе - на ![]() , затем сложим их и добавим в обе части уравнения
, затем сложим их и добавим в обе части уравнения ![]() . Тогда второе уравнение преобразуемой системы будет иметь вид:
. Тогда второе уравнение преобразуемой системы будет иметь вид:
![]() (5)
(5)
где ![]() .
.
Неизвестные постоянные ![]() определим из достаточных условий сходимости итерационного процесса:
определим из достаточных условий сходимости итерационного процесса:
![]() и
и ![]() .
.
Запишем эти условия более подробно:
![]()
![]()
Полагая равными нулю выражения под знаком модуля, получим систему линейных алгебраических уравнений (СЛАУ) 4 порядка с 4 неизвестными ![]() :
:
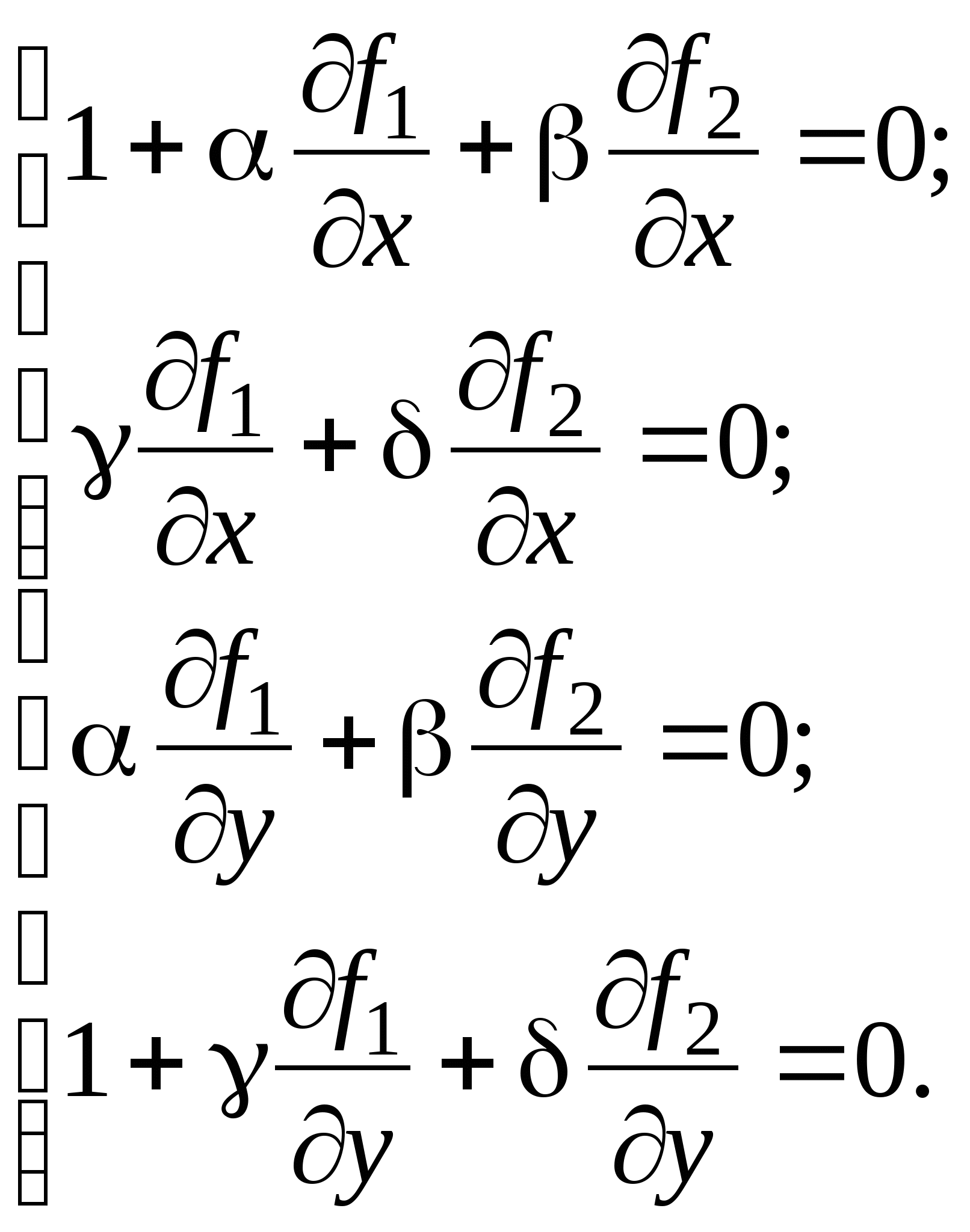 (6)
(6)
Для решения системы (6) необходимо вычислить частные производные ![]() :
:
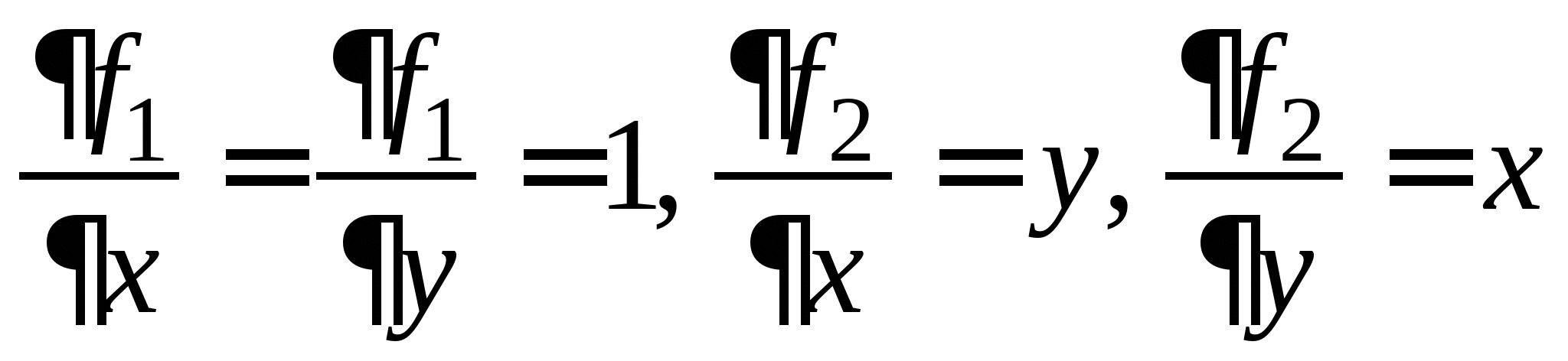 .
.
Тогда СЛАУ (6) запишется так:
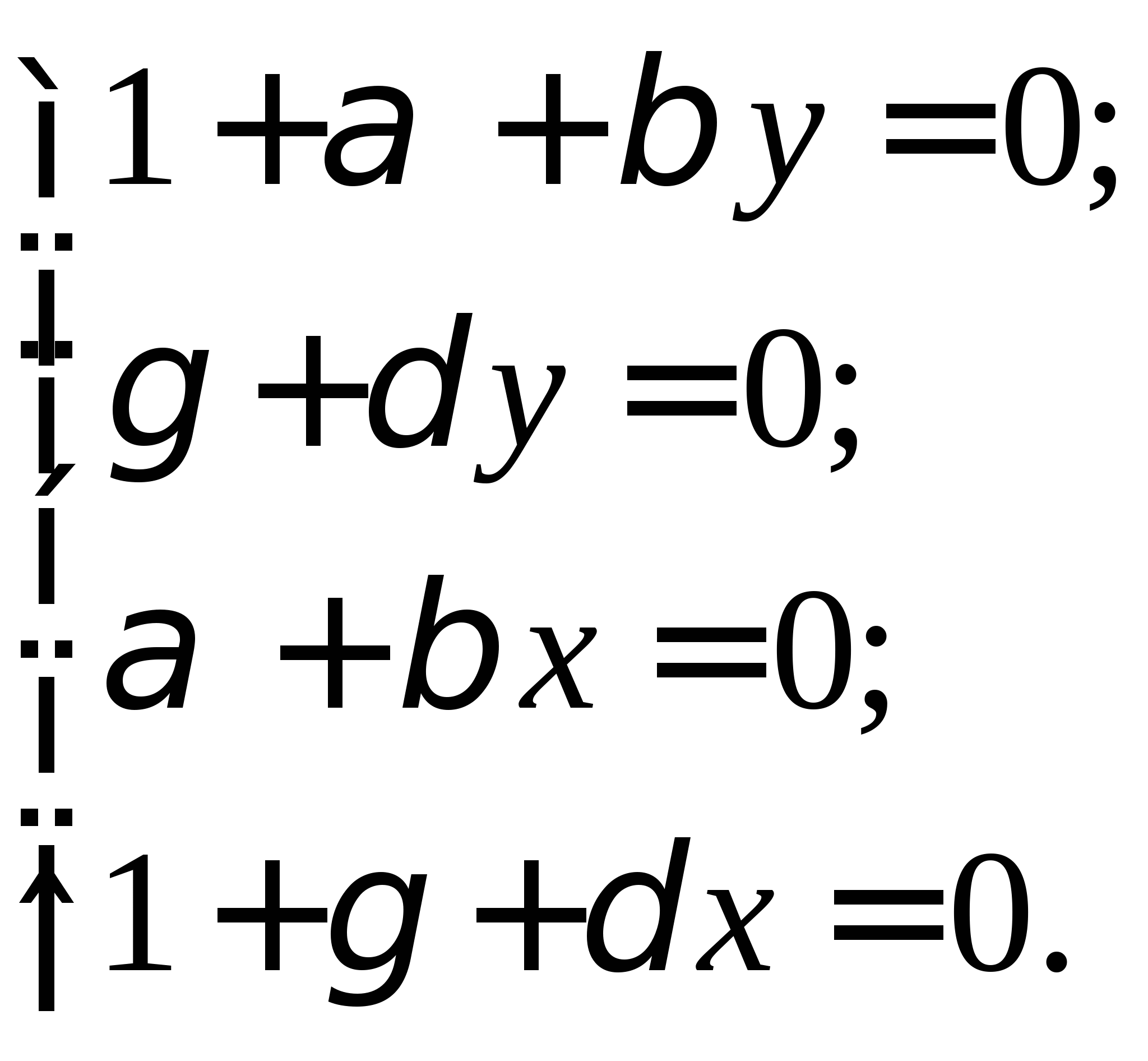
Решением этой системы являются следующие значения: 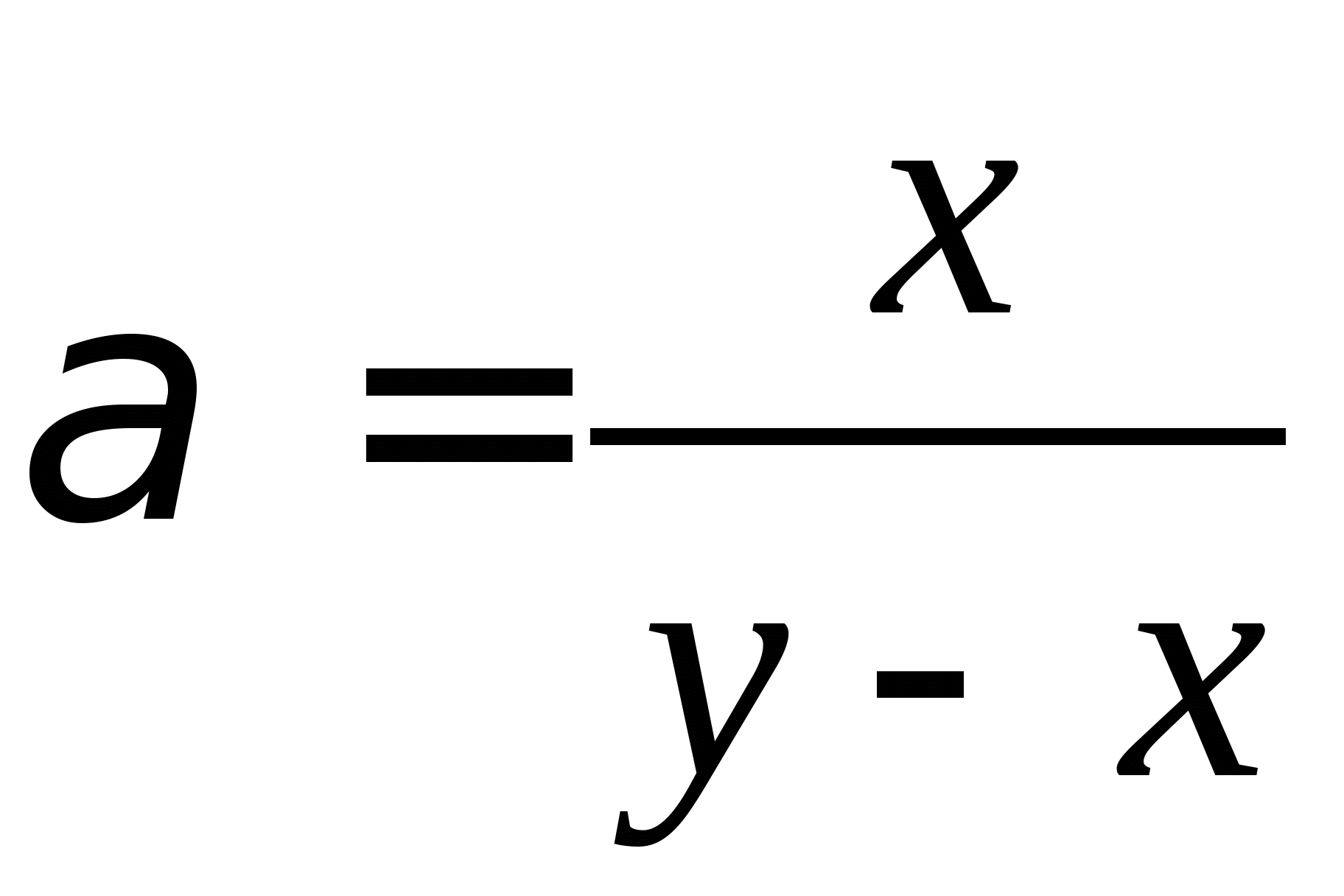 ,
, 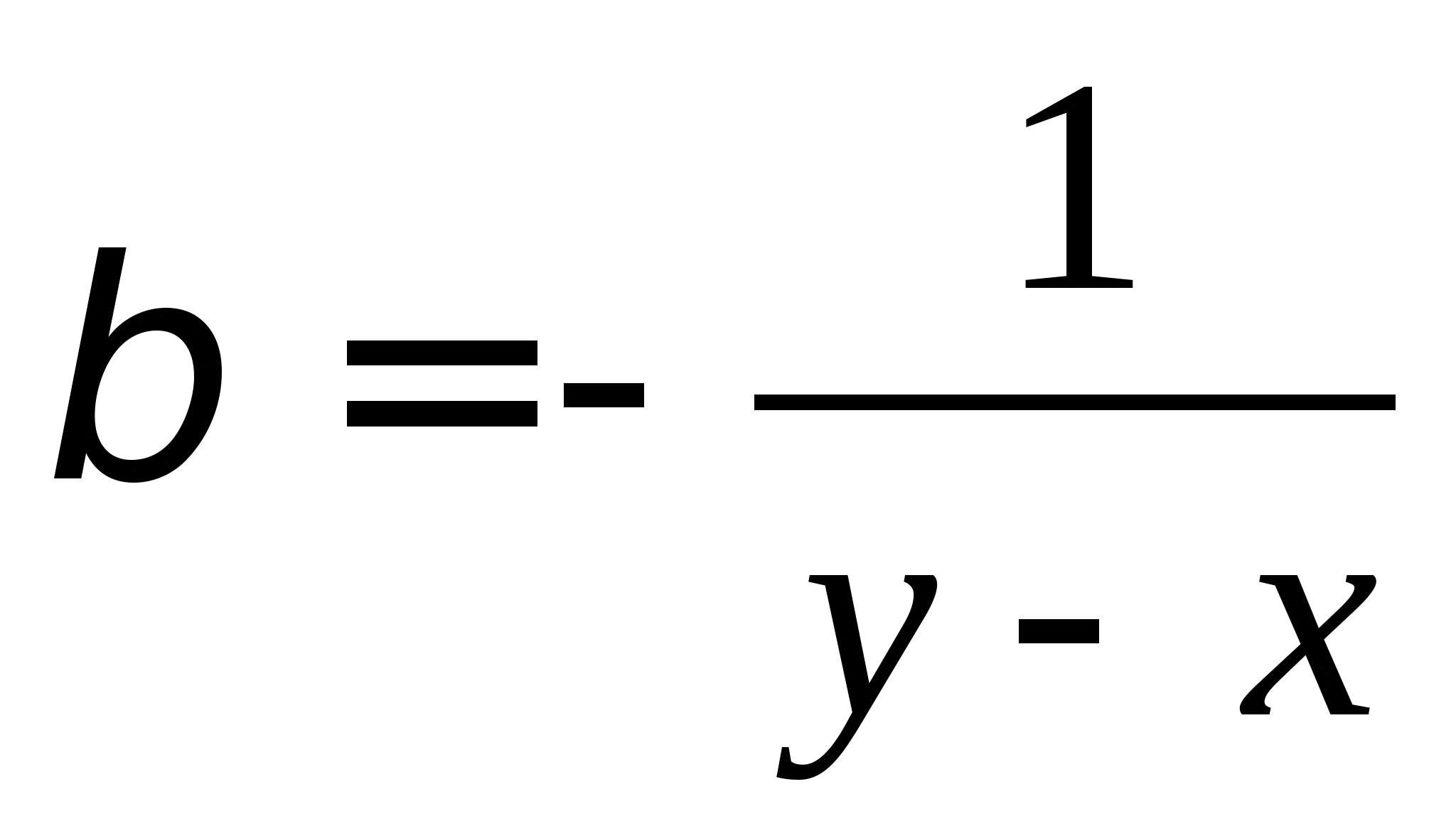 ,
, 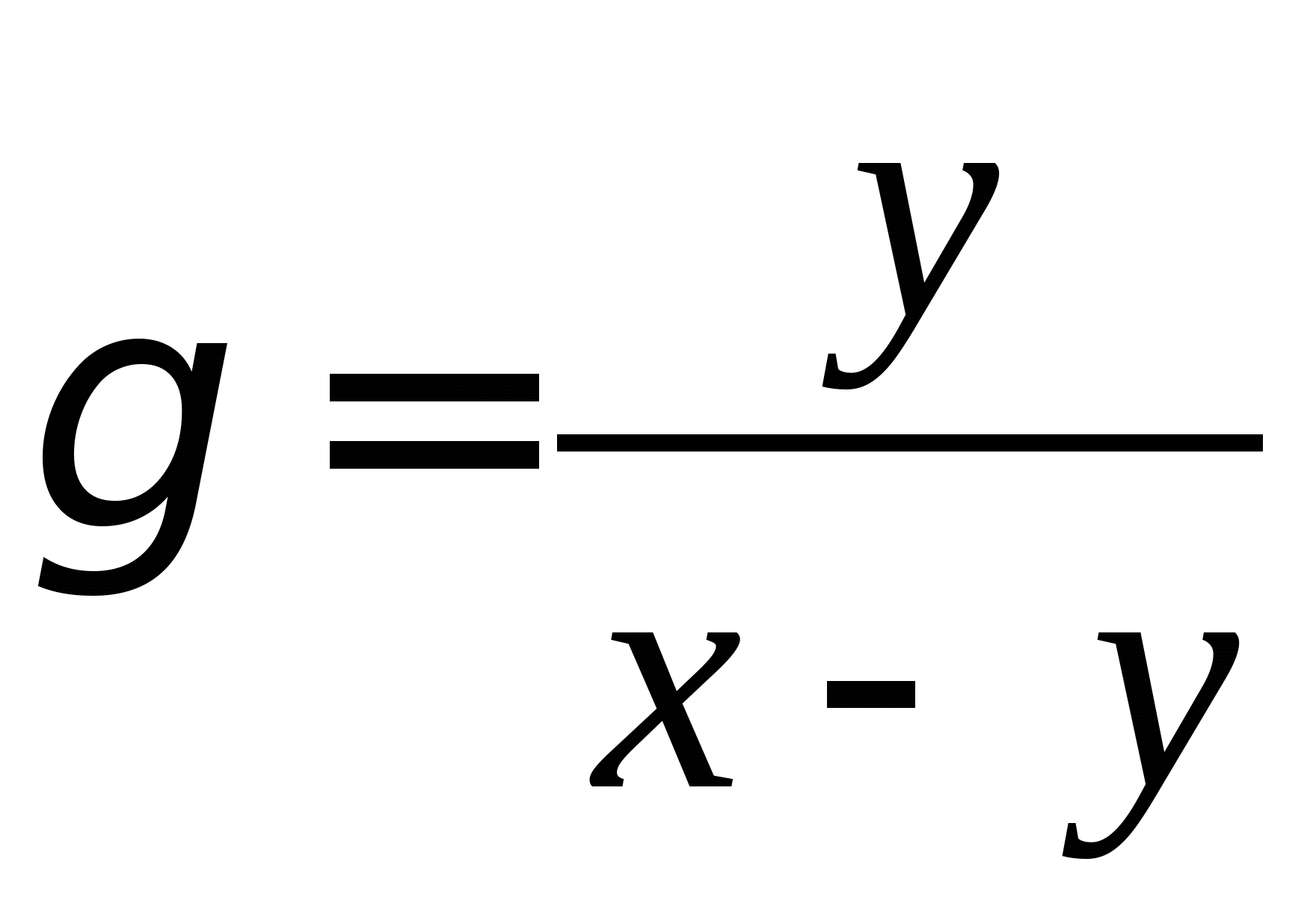 ,
, 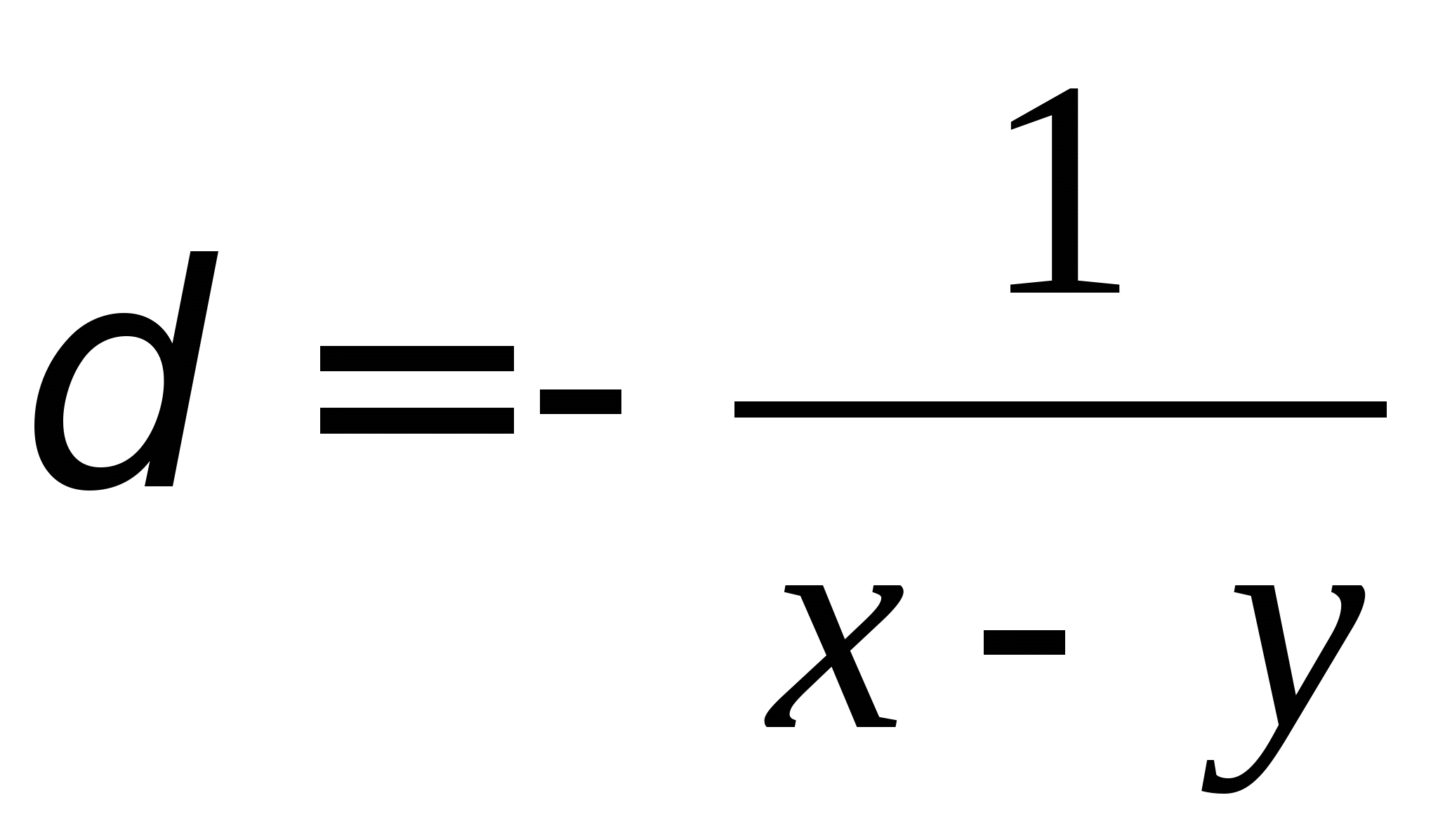 . Тогда рабочие формулы (4), (5) для решения СНУ (1) примут вид:
. Тогда рабочие формулы (4), (5) для решения СНУ (1) примут вид:
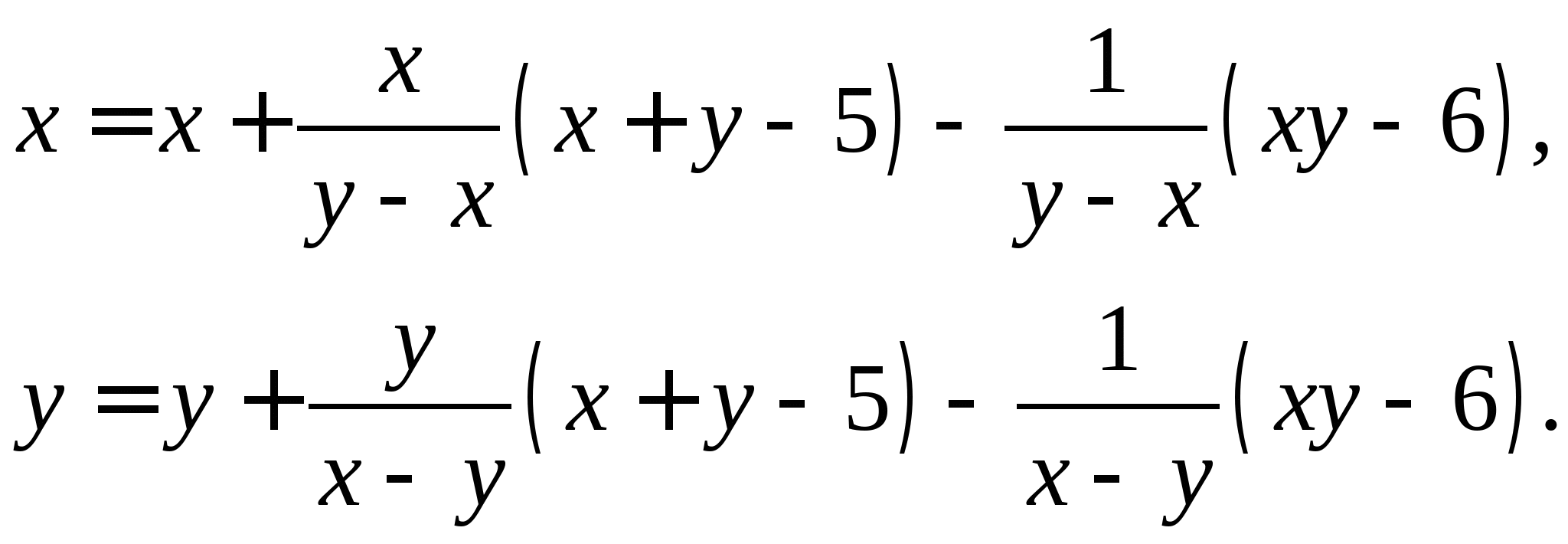
Для реализации на ЭВМ рабочие формулы можно переписать так:
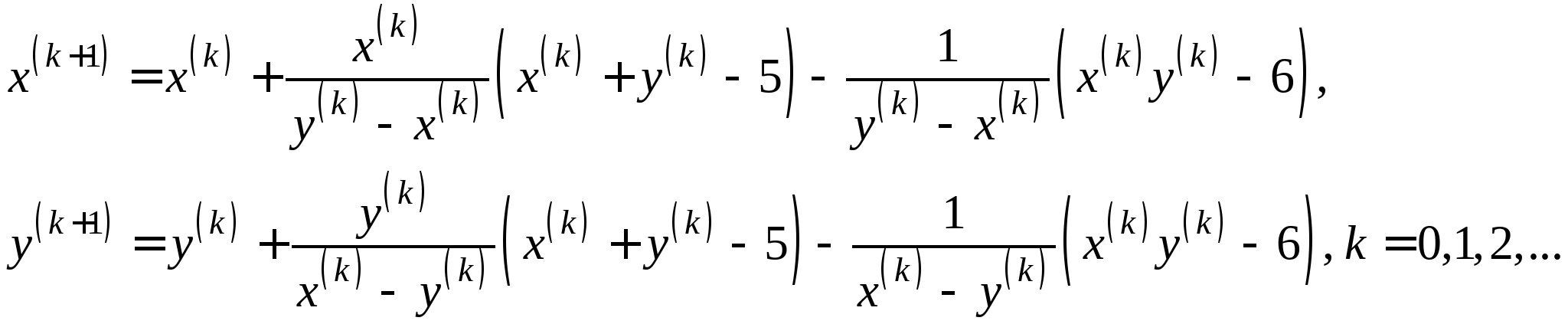
После несложных преобразований данные формулы примут вид:
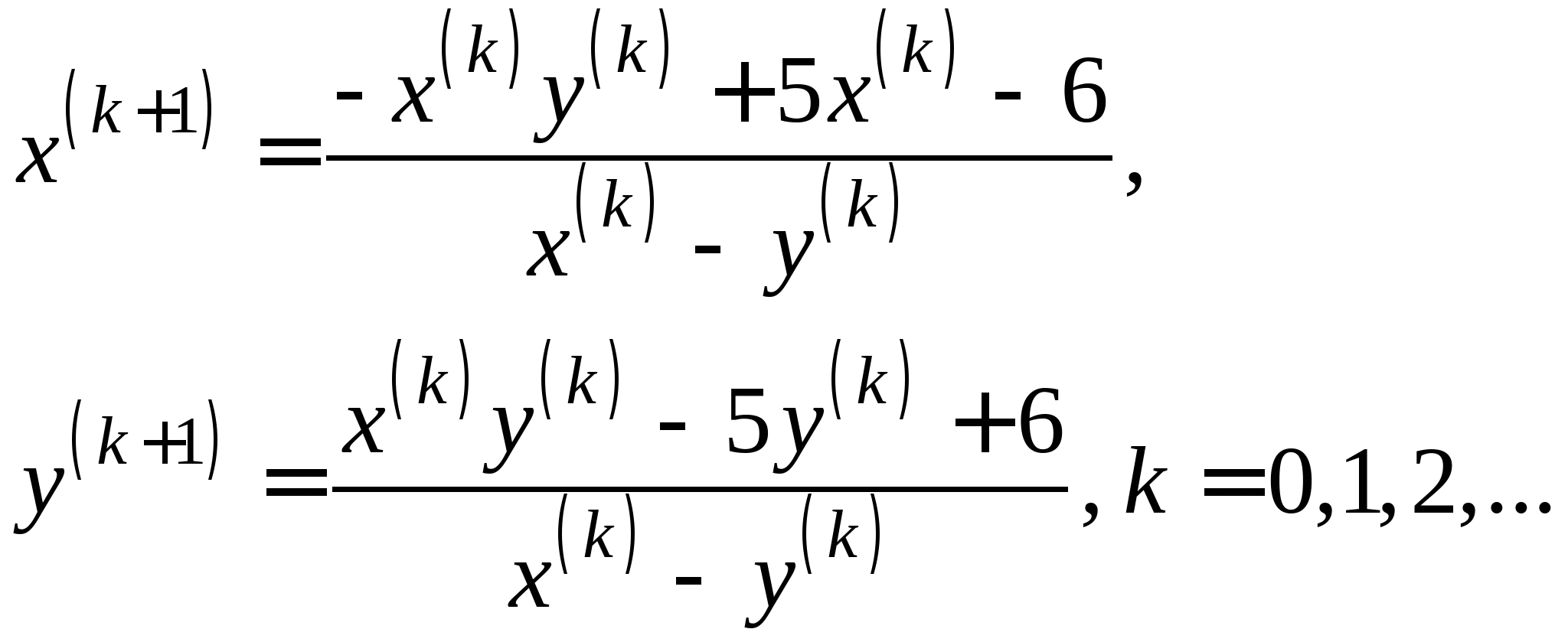
Заметим, что если частные производные ![]() мало изменяются в окрестности начального приближения (2), то:
мало изменяются в окрестности начального приближения (2), то:
![]() .
.
Тогда СЛАУ (6) запишется так:
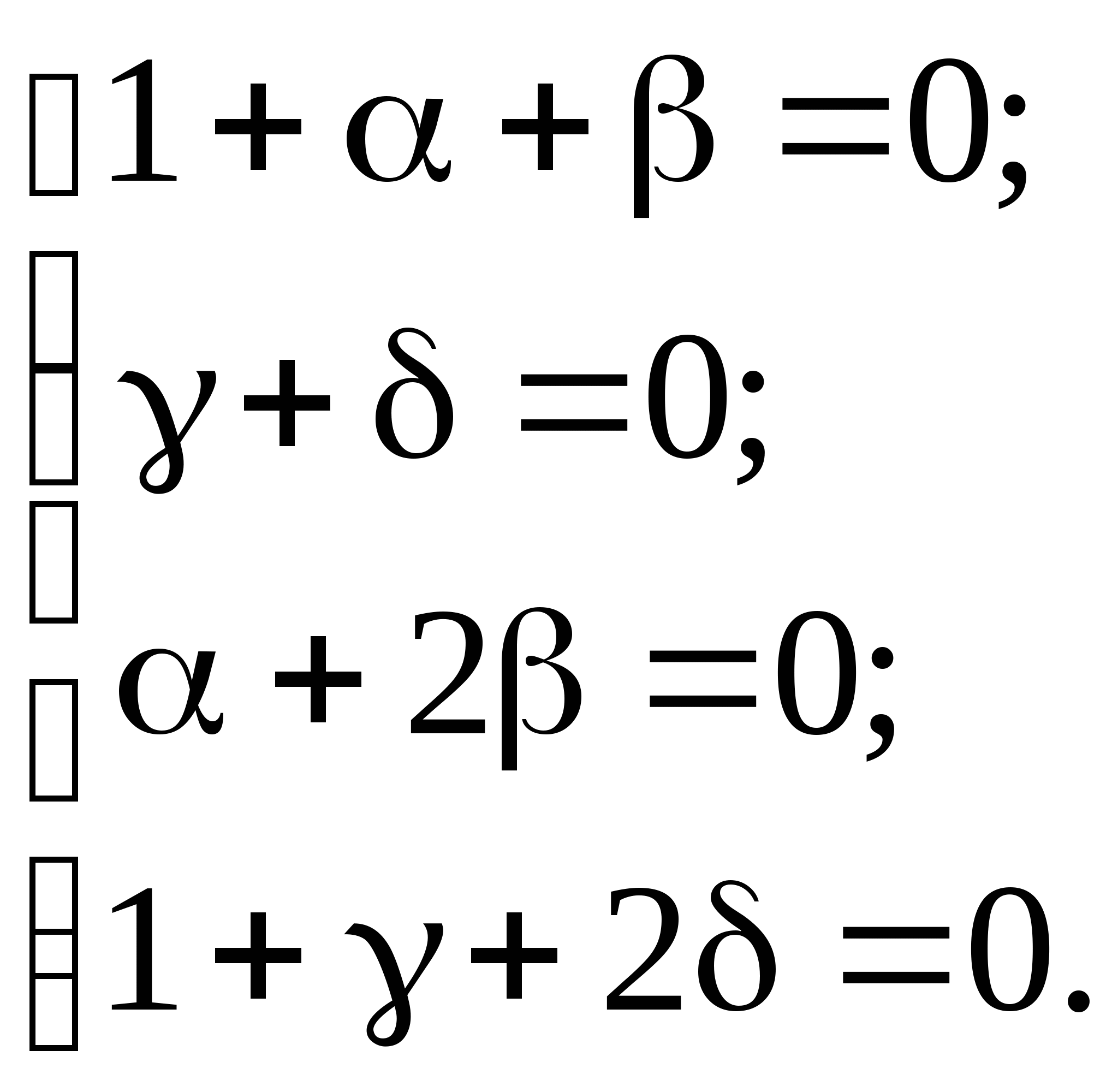
Решением этой системы являются точки ![]() ,
, ![]() ,
, ![]() . Тогда рабочие формулы (4), (5) МПИ для решения СНУ (1) примут вид:
. Тогда рабочие формулы (4), (5) МПИ для решения СНУ (1) примут вид:
![]()
Для реализации на ЭВМ рабочие формулы можно переписать так:
![]() (7)
(7)
Итерационный процесс (7) можно начать, задав начальное приближение (2). Процесс (7) заканчивается при одновременном выполнении двух условий: ![]() и
и ![]() . В этом случае значения
. В этом случае значения ![]() и
и ![]() являются приближенным значением одного из решений СНУ (1).
являются приближенным значением одного из решений СНУ (1).
3. Для построения рабочих формул метода Ньютона в виде
![]() (8)
(8)
где 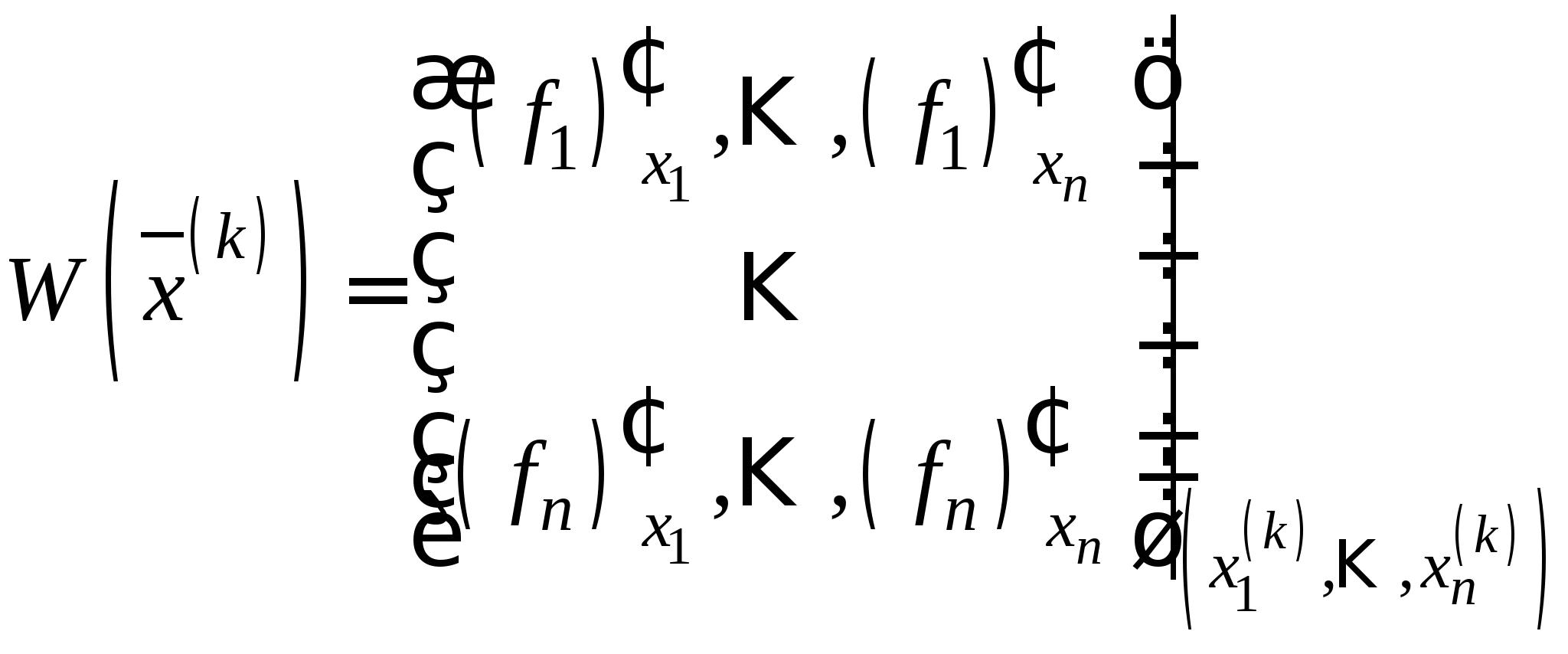 ,
,
необходимо:
1. Найти матрицу частных производных 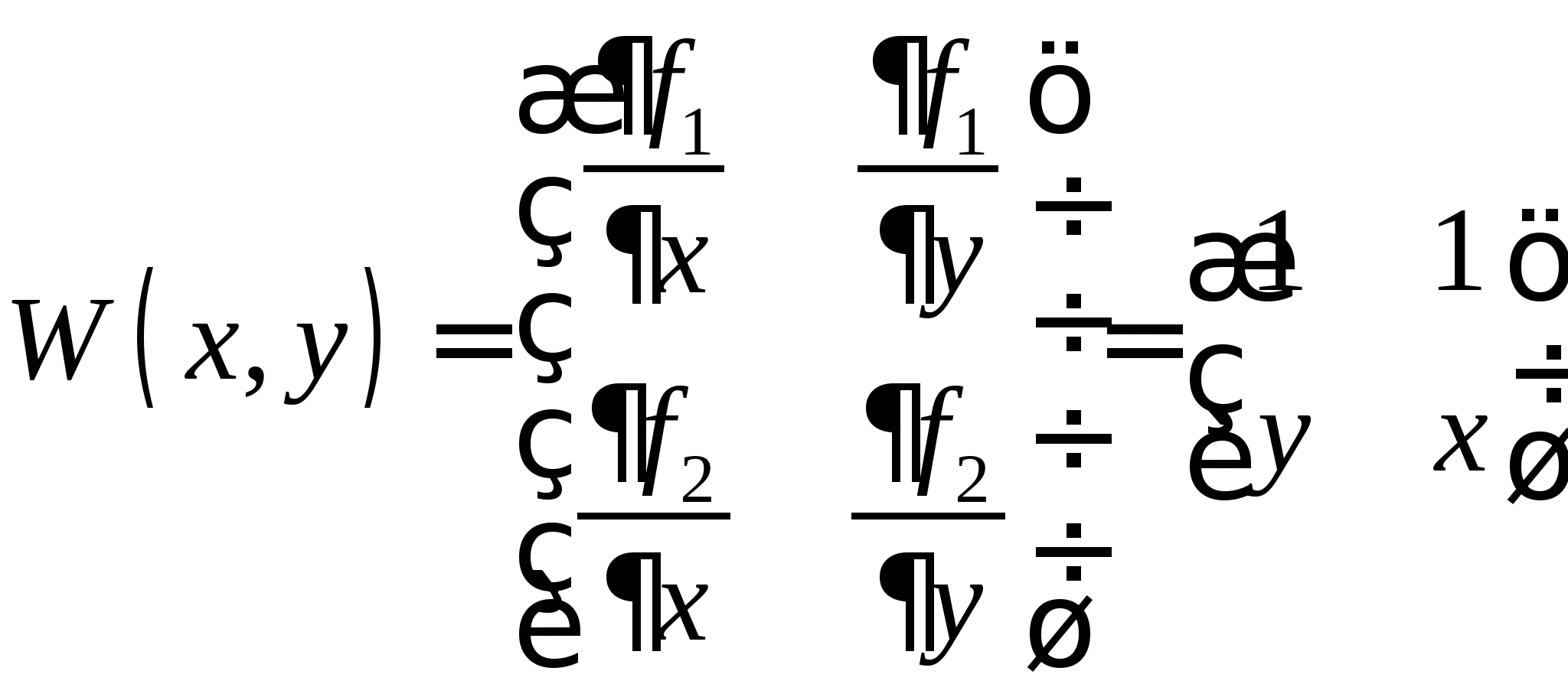 .
.
2. Найти определитель этой матрицы:
![]() .
.
3. Определить обратную матрицу:
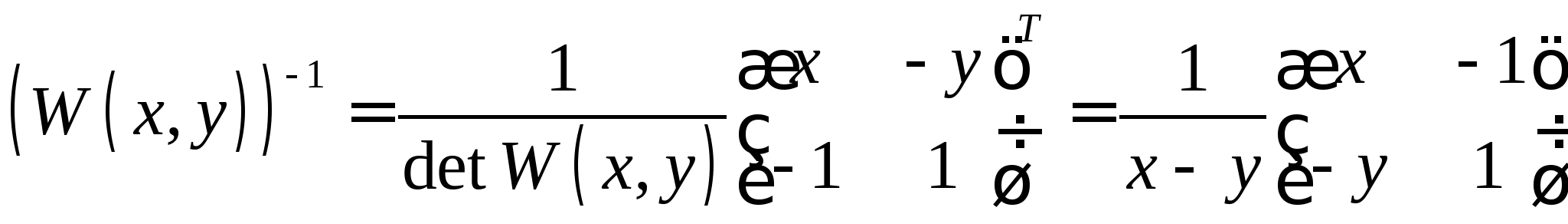 .
.
Проведя несложные преобразования получим рабочую формулу метода Ньютона (8) в виде:
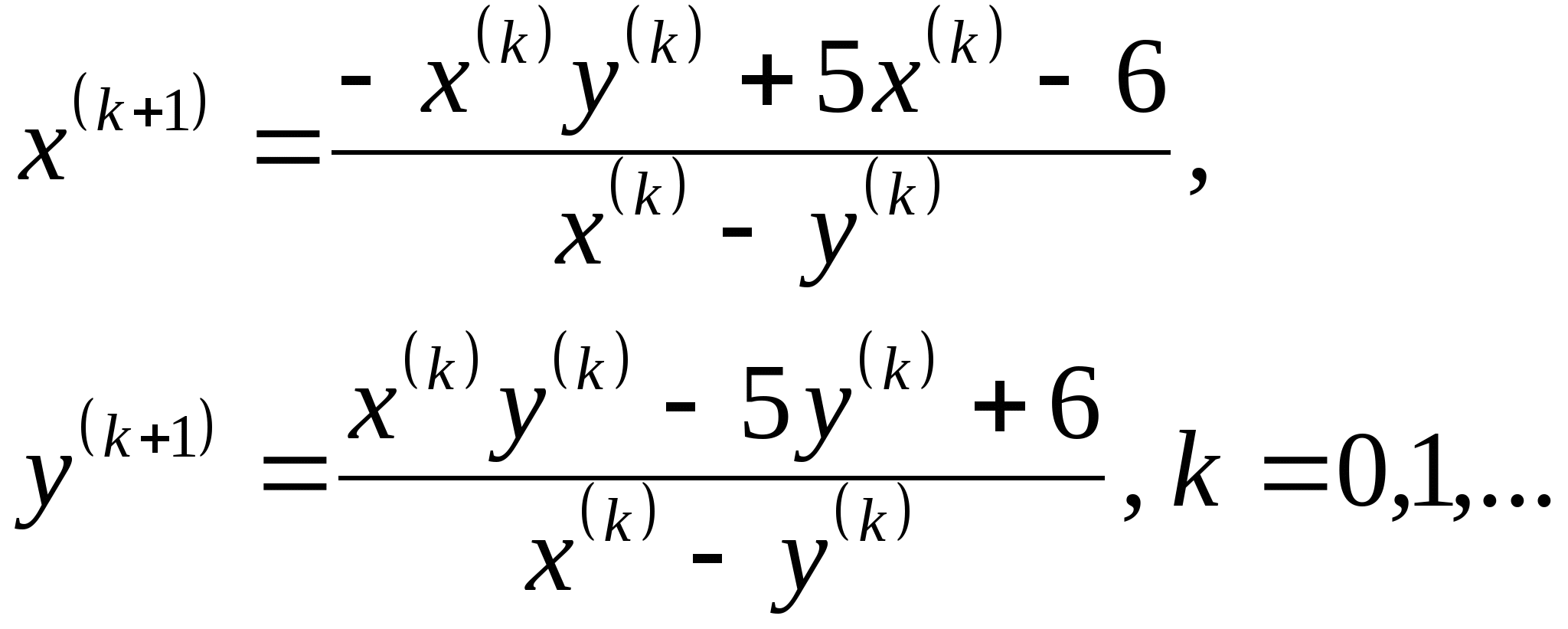
3. Блок-схема МПИ и метода Ньютона для решения СНУ приведена на рисунке 1.
Решение: в результате решения СНУ (1) при начальном приближении (2) методом простых итераций с точностью ![]() получено решение
получено решение ![]() , а методом Ньютона
, а методом Ньютона ![]() .
.
4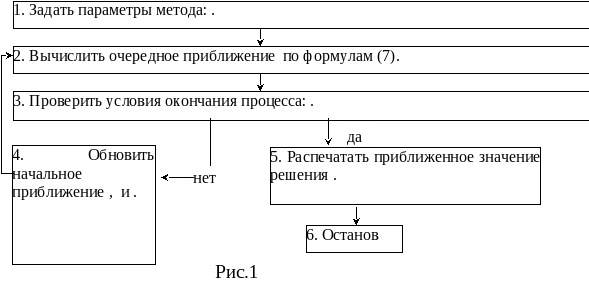
. Содержание отчета.
Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод итерационных формул); листинг программы; таблицу результатов; выводы о проделанной работе.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Определить аналитическое(ие) решение(я) исходной системы нелинейных уравнений.
2. Построить итерационные формулы, реализующие процесс поиска одного из решений системы нелинейных уравнений методом простых итераций и методом Ньютона.
3. Составить программу на любом языке программирования, реализующую построенные итерационные процессы, используя алгоритм методов, приведенный на рисунке 1. Печать результатов должна осуществляться на каждом шаге итераций в виде следующей таблицы:
|
|
|
|
|
|
|
|
4. Провести вычислительные эксперименты.
5. Составить отчет о проделанной работе.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
| № варианта | Система нелинейных уравнений | Начальное приближение |
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
127
Введение
Развитие новой вычислительной техники привело к тому, что инженерная практика наших дней все чаще и чаще встречается с математическими задачами, точное решение которых получить весьма сложно или невозможно. В этих случаях обычно прибегают к тем или иным приближенным вычислениям. Вот почему приближенные и численные методы математического анализа получили за последние годы широкое развитие и приобрели исключительно важное значение.
ЭВМ способна выполнять очень большое, но конечное число операций. По этой причине точные предельные процессы решения задач, связанные с бесконечным числом операций, при работе на ЭВМ должны быть заменены приближенными алгоритмами, содержащими лишь конечное число действий. Кроме того, ЭВМ обладает конечной памятью и может оперировать с числами только конечной длины, поэтому промежуточные результаты округляются, из-за этого даже точный метод с конечным числом действий становится приближенным.
Высокая производительность ЭВМ существенным образом изменила подход к оценке того или иного вычислительного метода. Новые вычислительные средства вызвали переоценку известных методов решения задач с точки зрения целесообразности их реализации на ЭВМ и стимулировали создание более эффективных. Наиболее ценными становятся методы, которые являются наиболее универсальными и допускают простую реализацию на ЭВМ. Поэтому в последнее время большое распространение получили итерационные, разностные, вариационные, вероятностные и тому подобные методы решения задач, допускающие достаточно простую реализацию на ЭВМ и применимые к широкому кругу инженерных задач.
При приближенном решении задач необходима оценка погрешности полученного результата. Приспособление какого-либо метода для работы на ЭВМ, когда используются вычисления с большим числом шагов, выдвинуло специфическую проблему устойчивости вычислительной схемы. Неизбежные погрешности округления могут быстро накапливаться, делая вычислительную схему неустойчивой и непригодной для практики. Допустимо использовать для решения задач только устойчивые вычислительные схемы, когда погрешности округлений взаимно компенсируются и вызываемая ими ошибка результата остается малой для всего процесса вычислений.
Предметом изучения вычислительной математики являются численные методы решения задач математического анализа: изучение алгоритма метода, условий сходимости итерационных методов и границ применимости методов, исследования оценок погрешностей методов и вычислений. Главным разделом вычислительной математики является реализация численных методов на ЭВМ, т.е. составление программы для требуемого алгоритма и решения конкретной задачи с помощью составленной программы. Поэтому можно сказать: вычислительная математика это ЭВМ плюс численные методы.
Любая прикладная задача формируется, исходя из определенного физического смысла некоторого процесса (распределение тепла в стержне, описание траектории движения объектов). Прикладная математическая задача может быть сформулирована, например, из описания некоторой экономической модели (задача распределения ресурсов, задача планирования производства, транспортная задача перевозки грузов, оптимальных в заданном смысле). Следовательно, для постановки любой прикладной задачи нужна математическая модель, поэтому можно выделить следующие этапы решения задач на ЭВМ:
1) описание математической модели задачи на основе физической или экономической модели;
2) изучение методов решения поставленной математической модели задачи и создание новых методов;
3) выбор метода решения задачи исходя из заданной точности решения и особенностей задачи;
4) составление блок-схемы программы для решения задачи на ЭВМ;
5) отладка программы и оценка полученных результатов. Подстановка решения в уравнение (например, при решении нелинейных уравнений и систем, при решении систем линейных алгебраических уравнений). Решение одной и той же задачи разными методами и решение задачи различными пользователями. Проверка соответствия решения математической и физической модели задачи. В случае несоответствия решений происходит возврат на более ранние этапы решения задачи;
6) решение задачи на ЭВМ, построение графиков, получение оценки погрешностей и обоснование результатов.
6
Глава 1. Учет ПОГРЕШНОСТЕй при ВЫЧИСЛЕНИях
§1.1. Источники и классификация погрешностей
При всевозможных расчетах, в том числе и на ЭВМ, всегда получается некоторое приближенное значение истинной величины. Отличие приближенного значения от истинного характеризует ошибку вычислений (погрешность). Ошибки появляются:
1) из-за неточностей в исходных данных. Данная погрешность является неустранимой, возникает при округлении (![]() при расчетах, а в реальности
при расчетах, а в реальности ![]() .) или при использовании экспериментальных данных;
.) или при использовании экспериментальных данных;
2) из-за использования итерационных методов для получения результата, где теоретически можно получить точное решение, совершая бесконечное число шагов вычислений. Так как число шагов ограничено искусственно, то в вычисления вносится погрешность;
3) из-за погрешностей самих методов.
Существует следующая классификация погрешностей.
1. Погрешности задачи – погрешности, возникающие при постановке математической задачи. Математические модели задачи редко точно отображают реальные явления. При изучении тех или иных явлений природы принимают некоторые условия, которые упрощают задачу, но влекут появление погрешностей.
2. Погрешность метода – это погрешность, возникающая при замене точной задачи на близкую по результатам приближенную задачу.
3. Остаточная погрешность – погрешность, связанная с наличием бесконечных процессов в математическом анализе.
4. Начальная погрешность – это погрешность, связанная с наличием в формулах числовых параметров, значения которых могут быть определены лишь приближенно.
5. Погрешность округления – это погрешность, связанная с системой счисления. Например, ![]() .
.
6. Погрешность действий – это погрешность, связанная с действиями над приближенными числами.
При решении конкретной задачи те или иные погрешности иногда отсутствуют или влияние их ничтожно мало. Для полного анализа погрешностей следует учитывать все их виды.
В предлагаемом курсе будут рассматриваться погрешности действий и погрешности методов.
§1.2. Основные понятия и определения теории погрешностей
Обозначим через ![]() - точные числа, через
- точные числа, через ![]() - приближенные значения.
- приближенные значения.
Определение 1.1. Приближенным числом ![]() называется число, незначительно отличающееся от точного числа
называется число, незначительно отличающееся от точного числа ![]() и заменяющее его в вычислениях.
и заменяющее его в вычислениях.
Если ![]() , то
, то ![]() называется приближенным числом с избытком.
называется приближенным числом с избытком.
Если ![]() , то
, то ![]() - приближенное число с недостатком.
- приближенное число с недостатком.
Определение 1.2. Погрешностью (ошибкой) ![]() приближенного числа
приближенного числа ![]() называется разность между соответствующим точным числом
называется разность между соответствующим точным числом ![]() и данным приближенным, т.е.
и данным приближенным, т.е. ![]() .
.
Чтобы получить точное число ![]() , нужно к приближенному числу
, нужно к приближенному числу ![]() прибавить его ошибку
прибавить его ошибку ![]() , т.е.
, т.е. ![]() .
.
Точное число ![]() можно рассматривать как приближенное число с погрешностью, равной нулю.
можно рассматривать как приближенное число с погрешностью, равной нулю.
Если ![]() , то
, то ![]() .
.
Если ![]() , то
, то ![]() .
.
Во многих случаях знак ошибки неизвестен, поэтому целесообразно пользоваться абсолютной погрешностью приближенного числа ![]() .
.
Определение 1.3. Абсолютной погрешностью приближенного числа ![]() называется абсолютная величина разности между
называется абсолютная величина разности между ![]() и
и ![]() , т.е.
, т.е. ![]() .
.
Абсолютная погрешность недостаточна для характеристики точности измерения или вычисления.
Определение 1.4. Относительной погрешностью приближенного числа ![]() называется отношение абсолютной погрешности этого числа к модулю соответствующего точного числа
называется отношение абсолютной погрешности этого числа к модулю соответствующего точного числа ![]() (
(![]() ):
):
![]() .
.
Следовательно, ![]() .
.
Как правило, число ![]() не известно, следовательно, нельзя определить и абсолютную погрешность
не известно, следовательно, нельзя определить и абсолютную погрешность ![]() . Поэтому вместо неизвестной абсолютной погрешности
. Поэтому вместо неизвестной абсолютной погрешности ![]() используют ее оценку сверху, так называемую предельную абсолютную погрешность.
используют ее оценку сверху, так называемую предельную абсолютную погрешность.
Определение 1.5. Предельной абсолютной погрешностью ![]() называется всякое число, которое не меньше абсолютной погрешности этого числа, т.е. удовлетворяющее неравенству:
называется всякое число, которое не меньше абсолютной погрешности этого числа, т.е. удовлетворяющее неравенству: ![]() .
.
Определение 1.6. Предельной относительной погрешностью ![]() приближенного числа
приближенного числа ![]() называется всякое число, которое не меньше относительной погрешности этого числа
называется всякое число, которое не меньше относительной погрешности этого числа ![]() , т.е.
, т.е. ![]() , следовательно,
, следовательно, ![]() .
.
За предельную абсолютную погрешность числа ![]() можно принять:
можно принять:
![]() .
.
§1.3. Значащая и верная цифра приближенной величины. Округление чисел
Определение 1.7. Значащей цифрой приближенного числа называется всякая цифра в его десятичном изображении, отличная от нуля, и нуль, если он находится между значащими цифрами или является представителем сохраненного десятичного разряда. Все остальные нули не являются значащими цифрами.
Определение 1.8 (первое определение верной цифры). Верной цифрой приближенной величины называется такая цифра, если абсолютная погрешность не превосходит единицы разряда этой цифры. Например, ![]() ,
, ![]() ,
, ![]() верные цифры.
верные цифры.
Приближенные числа принято записывать так, чтобы они содержали только верные цифры. В технических таблицах допускается одна сомнительная цифра. Во всех математических таблицах содержатся только верные цифры, соответствующие второму более строгому определению верной цифры.
Определение 1.9 (второе определение верной цифры). Если абсолютная погрешность приближенного числа ![]() не превышает половины единицы разряда, выражаемого
не превышает половины единицы разряда, выражаемого ![]() -й значащей цифрой (считая слева направо), то говорят, что
-й значащей цифрой (считая слева направо), то говорят, что ![]() первых значащих цифр приближенного числа
первых значащих цифр приближенного числа ![]() являются верными.
являются верными.
Любое положительное число может быть представлено в виде
![]() .
.
Если ![]() , то
, то ![]() являются верными.
являются верными.
Пример 1.1. Например, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() верные цифры.
верные цифры.
Пример 1.2. ![]() ,
, ![]() .
.
По первому определению: ![]() верные цифры.
верные цифры.
По второму определению: ![]() верные цифры.
верные цифры.
Пример 1.3. ![]() ,
, ![]() .
.
![]() , тогда
, тогда ![]() имеет 4 значащих цифры, но только 3 из них – верные.
имеет 4 значащих цифры, но только 3 из них – верные.
Округление чисел
Чтобы округлить приближенное число ![]() до
до ![]() значащих цифр, отбрасывают все цифры, стоящие справа от
значащих цифр, отбрасывают все цифры, стоящие справа от ![]() -й значащей цифры, или, если нужно для сохранения разрядов, заменяют их нулями. При этом, если первая из отброшенных цифр:
-й значащей цифры, или, если нужно для сохранения разрядов, заменяют их нулями. При этом, если первая из отброшенных цифр:
1) меньше 5, то оставшиеся десятичные знаки сохраняются без изменения;
2) больше 5, то к последней оставшейся цифре прибавляется единица;
3) равна 5 и среди остальных отброшенных есть неравные нулю, то последняя оставшаяся цифра увеличивается на единицу;
4) равна 5 и все остальные отброшенные цифры равны нулю, то последняя оставшаяся цифра остается неизменной, если она четная, и увеличивается на единицу, если она нечетная (правило четной цифры).
Пример 1.4. Округлить до ![]() значащих цифр число:
значащих цифр число:
а) = 3.14159266535;
![]() ;
;
![]() ;
;
![]() ;
;
б) ![]() ;
;
![]() ;
;
с) ![]() ;
;
![]() .
.
Теорема 1.1 (устанавливает связь относительной погрешности приближенного числа с количеством верных знаков этого числа).
Если положительное приближенное число ![]() имеет
имеет ![]() верных десятичных знаков (в смысле определения 1.9), то относительная погрешность
верных десятичных знаков (в смысле определения 1.9), то относительная погрешность ![]() этого числа не превосходит одной десятой в степени
этого числа не превосходит одной десятой в степени ![]() , деленной на первую значащую цифру числа
, деленной на первую значащую цифру числа ![]() , т.е.
, т.е. ![]() , где
, где ![]() – первая значащая цифра числа
– первая значащая цифра числа ![]() .
.
Доказательство.
Пусть ![]() является приближенным числом точного числа
является приближенным числом точного числа ![]() . Для определенности будем считать
. Для определенности будем считать ![]() . Любое положительное число может быть представлено в виде:
. Любое положительное число может быть представлено в виде:
![]() .
.
Так как ![]() имеет
имеет ![]() верных знаков, то по определению
верных знаков, то по определению ![]() или
или ![]() . Следовательно,
. Следовательно, ![]() . Так как
. Так как ![]() , то
, то
![]() .
.
Правая часть достигает наименьшего значения при ![]() . Следовательно,
. Следовательно, ![]() . Так как
. Так как ![]() , то в силу последнего соотношения
, то в силу последнего соотношения ![]() . Тогда для относительной погрешности справедливо соотношение:
. Тогда для относительной погрешности справедливо соотношение:
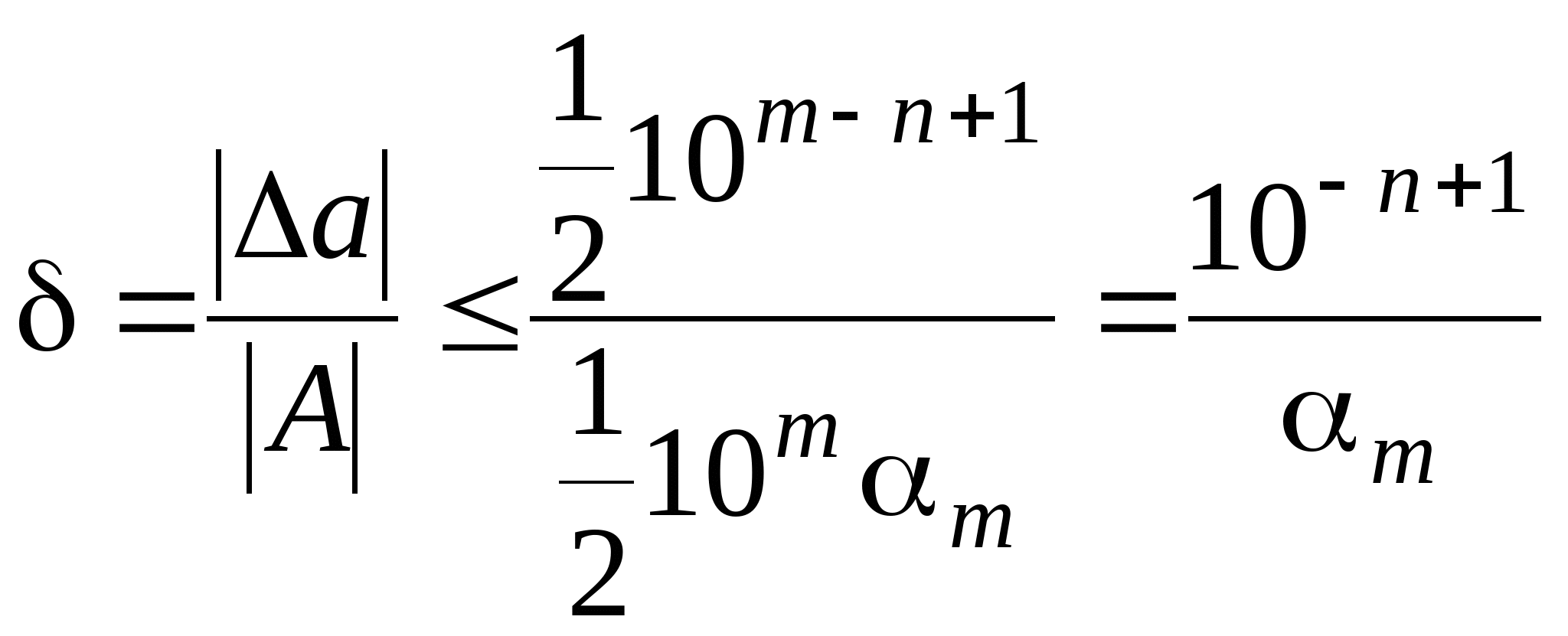 ,
,
т.е. ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Следствие. За предельную относительную погрешность числа ![]() можно принять:
можно принять:
![]() ,
,
где ![]() первая значащая цифра числа
первая значащая цифра числа ![]() .
.
§1.4. Погрешность алгебраической суммы
Теорема 1.2. Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел.
Доказательство.
Пусть ![]() приближенные числа. Рассмотрим их алгебраическую сумму
приближенные числа. Рассмотрим их алгебраическую сумму
![]() .
.
Очевидно, что
![]()
Следовательно
![]() .
.
Следствие. За предельную абсолютную погрешность алгебраической суммы можно принять сумму предельных абсолютных погрешностей слагаемых:
![]() .
.
Правило сложения приближенных чисел
Чтобы сложить числа различной абсолютной точности, следует:
выделить числа, десятичная запись которых обрывается раньше других, и оставить их без изменения;
остальные числа округлить по образцу выделенных, сохраняя один или два запасных десятичных знака;
произвести сложение чисел, учитывая все сохраненные знаки;
полученный результат округлить на один знак.
Пример 1.5.
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
Числа наименьшей точности: ![]() ,
, ![]() , их абсолютная погрешность может достигать 0.1. Округлим остальные числа до 0.01, получим:
, их абсолютная погрешность может достигать 0.1. Округлим остальные числа до 0.01, получим:
![]() (по правилу четной цифры).
(по правилу четной цифры).
Подсчитаем погрешность:
1) сумма предельных погрешностей исходных данных:
![]()
3) ![]() погрешность округления:
погрешность округления:
=1+2+30.222+0.009+0.050=0.2810.3.
Поэтому в качестве абсолютной погрешности следует взять значение ![]() . Тогда искомая сумма
. Тогда искомая сумма
![]() .
.
Доказательство.
Пусть ![]() приближенные числа,
приближенные числа, ![]() соответствующие точные числа, где
соответствующие точные числа, где ![]() .
.
Рассмотрим сумму приближенных ![]() и точных чисел
и точных чисел ![]() . Тогда
. Тогда
![]() .
.
Так как ![]() , то
, то ![]() .
.
![]() .
.
Пусть ![]() , тогда
, тогда
![]() ,
,
т.е. ![]() , что и требовалось доказать.
, что и требовалось доказать.
§1.5. Погрешность произведения и частного
Теорема 1.4. Относительная погрешность произведения нескольких приближенных чисел, отличных от нуля, не превышает суммы относительных погрешностей этих чисел.
Доказательство:
Пусть ![]() – приближенные числа, причем
– приближенные числа, причем ![]() .
.
Рассмотрим произведение ![]() , тогда
, тогда
![]() .
.
Так как ![]() , то
, то
![]() ;
;
![]() .
.
Так как ![]() и
и ![]() малы по сравнению с
малы по сравнению с ![]() , то приближенно можно положить, что
, то приближенно можно положить, что ![]() и
и ![]() .
.
Тогда ![]() , что и требовалось доказать.
, что и требовалось доказать.
Замечание. Соотношение ![]() остается верным, если сомножители
остается верным, если сомножители ![]() имеют различные знаки.
имеют различные знаки.
![]() .
.
Следствие 2. При умножении приближенного числа ![]() на точный множитель
на точный множитель ![]() предельная относительная погрешность не изменяется, а предельная абсолютная погрешность увеличивается в модуль
предельная относительная погрешность не изменяется, а предельная абсолютная погрешность увеличивается в модуль ![]() раз.
раз.
Пусть ![]() . Тогда
. Тогда
![]() ,
, ![]() .
.
Погрешность частного
Теорема 1.5. Относительная погрешность частного не превышает суммы относительных погрешностей делимого и делителя, т.е. ![]() .
.
Доказательство.
Пусть ![]() , где
, где ![]() – приближенные числа, тогда
– приближенные числа, тогда ![]() ,
, ![]() . Отсюда
. Отсюда ![]() .
.
Следовательно, ![]() , где
, где ![]() - относительные погрешности
- относительные погрешности ![]() соответственно.
соответственно.
Следствие. Если ![]() , то предельная относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя
, то предельная относительная погрешность частного равна сумме предельных относительных погрешностей делимого и делителя ![]() .
.
§1.6. Погрешность степени и корня
Погрешность степени
Теорема 1.6. Предельная относительная погрешность ![]() -й степени числа
-й степени числа ![]() в
в ![]() раз больше предельной относительной погрешности самого этого числа.
раз больше предельной относительной погрешности самого этого числа.
Доказательство.
Пусть ![]() , где
, где ![]() – натуральное число. Тогда
– натуральное число. Тогда ![]() ,
, ![]() . Следовательно,
. Следовательно, ![]() , т.е. относительная погрешность
, т.е. относительная погрешность ![]() -й степени числа в
-й степени числа в ![]() раз больше относительной погрешности самого числа. Тогда, в силу определения предельной относительной погрешности, получаем:
раз больше относительной погрешности самого числа. Тогда, в силу определения предельной относительной погрешности, получаем:
![]() .
.
Погрешность корня
Теорема 1.7. Предельная относительная погрешность корня ![]() -й степени числа
-й степени числа ![]() в
в ![]() раз меньше предельной относительной погрешности самого числа
раз меньше предельной относительной погрешности самого числа ![]() .
.
Доказательство.
Пусть ![]() , где
, где ![]() – натуральное число. Тогда
– натуральное число. Тогда ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() , т.е. относительная погрешность корня
, т.е. относительная погрешность корня ![]() -й степени числа
-й степени числа ![]() в
в ![]() раз меньше относительной погрешности самого числа
раз меньше относительной погрешности самого числа ![]() . Тогда, в силу определения предельной относительной погрешности, получим
. Тогда, в силу определения предельной относительной погрешности, получим
![]() .
.
§1.7. Погрешность функции
Рассмотрим частный случай функции одной переменной. Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и имеет на
и имеет на ![]() непрерывную первую производную. Выберем две точки на
непрерывную первую производную. Выберем две точки на ![]() :
: ![]() ,
, ![]() и вычислим разность
и вычислим разность ![]() , где
, где ![]() ,
, ![]() . Следовательно,
. Следовательно,
![]()
Таким образом, абсолютная погрешность функции пропорциональна абсолютной погрешности аргумента с коэффициентом пропорциональности ![]() .
.
Пример 1.6. Пусть задана функция ![]() и известна
и известна ![]() . Тогда абсолютная погрешность
. Тогда абсолютная погрешность ![]() .
.
Пусть требуется определить относительную погрешность ![]() функции
функции ![]() . По определению
. По определению ![]() . Так как
. Так как ![]() , то
, то ![]() и
и ![]() . Таким образом, относительная погрешность функции пропорциональна абсолютной погрешности аргумента с коэффициентом пропорциональности
. Таким образом, относительная погрешность функции пропорциональна абсолютной погрешности аргумента с коэффициентом пропорциональности ![]() .
.
Обобщим сделанные выкладки на случай функции многих переменных.
Пусть ![]() дифференцируемая функция,
дифференцируемая функция, ![]() абсолютная погрешность аргумента
абсолютная погрешность аргумента ![]() , тогда
, тогда
![]() .
.
Если ![]() достаточно малы, то их произведениями, квадратами, кубами и т.д. можно пренебречь. Тогда
достаточно малы, то их произведениями, квадратами, кубами и т.д. можно пренебречь. Тогда
![]() .
.
Следовательно,
![]() . (1.1)
. (1.1)
Тогда
![]() ,
,
где ![]() предельные абсолютные погрешности. Обе части (1.1) поделим на
предельные абсолютные погрешности. Обе части (1.1) поделим на ![]() , получим
, получим
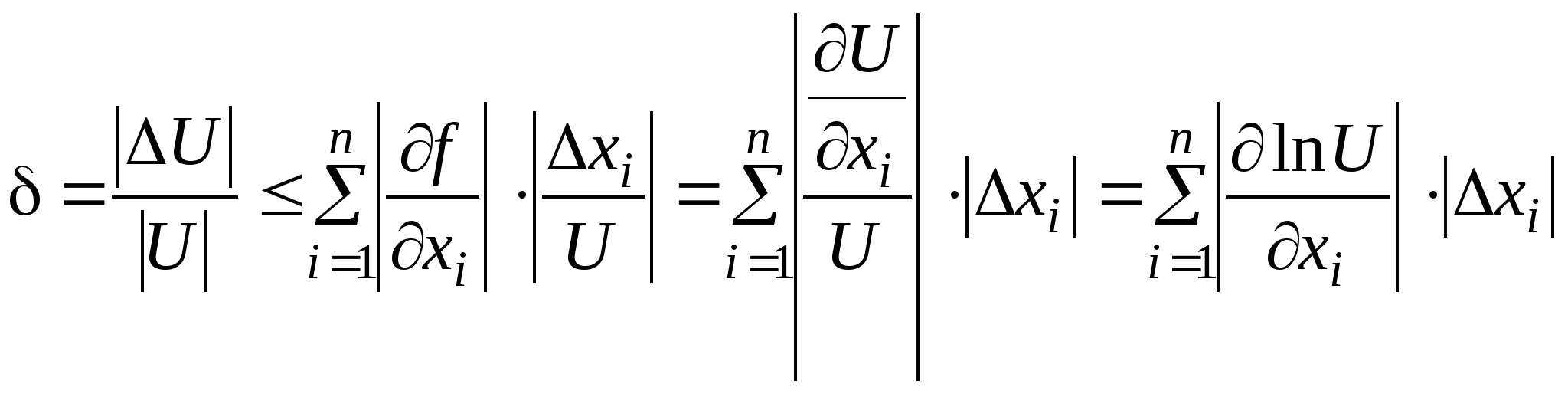 ,
,
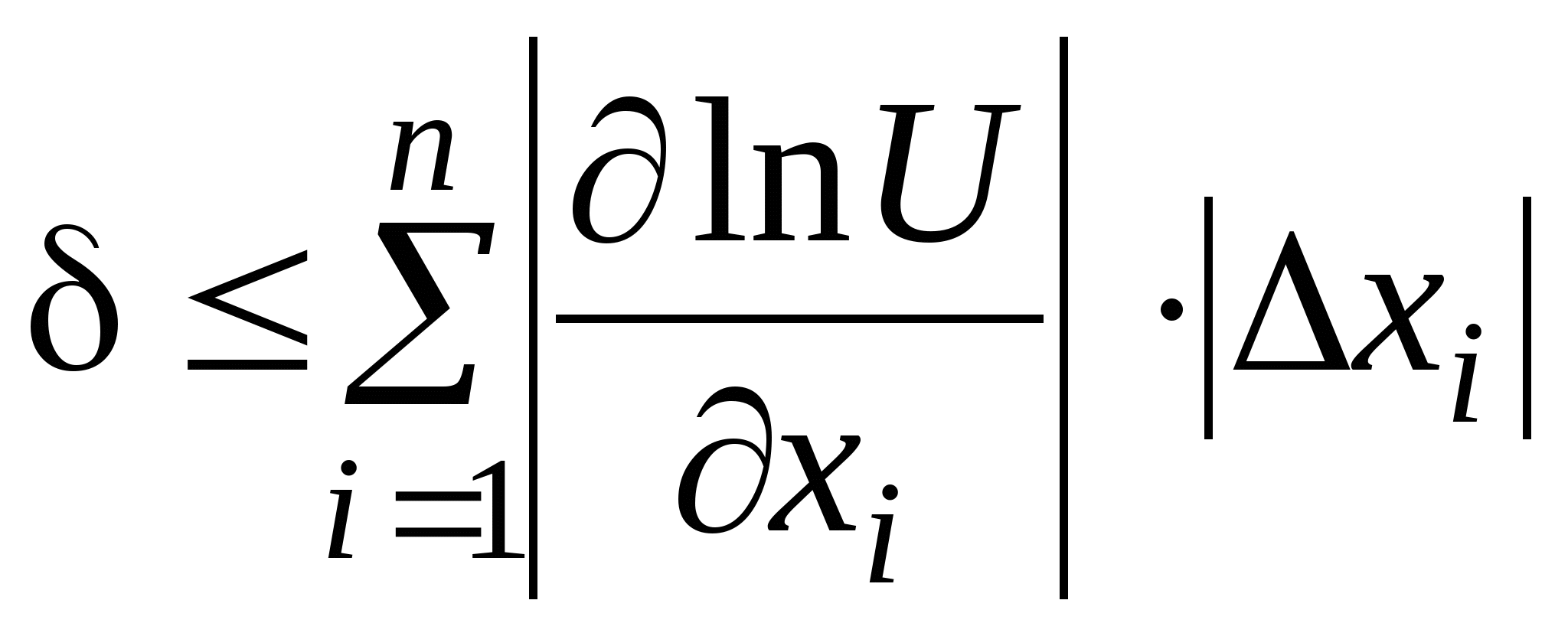 .
.
Окончательно получим
![]() .
.
§1.8. Обратная задача теории погрешностей
Встречаются задачи, когда нужно определить абсолютные погрешности аргумента функции, чтобы абсолютная погрешность самой функции ![]() не превышала заданной величины. При решении этих задач пользуются принципом равных влияний.
не превышала заданной величины. При решении этих задач пользуются принципом равных влияний.
Предполагается, что частные дифференциалы ![]() одинаково влияют на образование предельной абсолютной погрешности
одинаково влияют на образование предельной абсолютной погрешности ![]() .
.
Так как ![]() , то
, то
![]()
и тогда
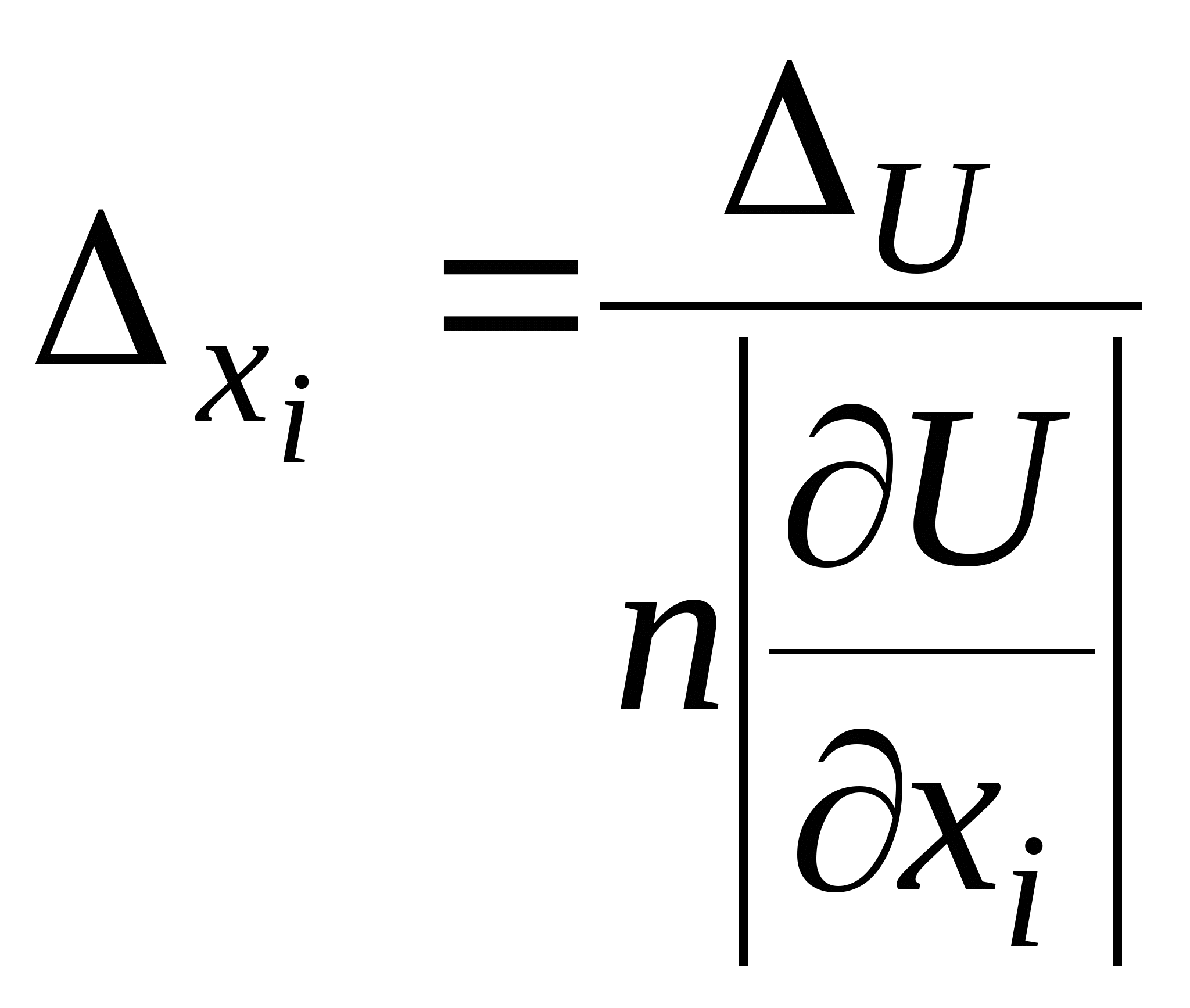 .
.
Замечание 1. Если требуется получить результат с ![]() верными знаками, то исходные данные при вычислениях должны содержать
верными знаками, то исходные данные при вычислениях должны содержать ![]() или
или ![]() знака. Зная теорию погрешностей, можно решить две задачи:
знака. Зная теорию погрешностей, можно решить две задачи:
1) с какой точностью должны быть заданы исходные данные, чтобы получить заданную точность результатов вычислений;
2) с какой точностью получен результат вычислений, если известны погрешности исходных данных.
Замечание 2. Если в исходных данных есть ошибка, то в результате вычислений она распространится на все действия и накопится в результате погрешностей округлений и вычислений и в силу ограниченности разрядной сетки ЭВМ.
| | | | |
| | | | |
| | |||
| | | ||
| | |||
| | | | |
| | | | |
| | | |
Из таблицы видно, что особенно эта ошибка распространяется, если используются конечные разности.
ГЛАВА 5. Методы приближения ФУНКЦИЙ.
§5.1. Постановка задачи аппроксимации и интерполяции функций.
В вычислительной математике нередки случаи, когда одну функцию приходится заменять другой, более простой и удобной для дальнейшей работы. Такую задачу называют аппроксимацией функции.
Поводом для аппроксимации функции может послужить, в частности, табличный способ ее задания. Предположим, что в результате некоторого эксперимента для конечного набора значений ![]() величины
величины ![]() из отрезка
из отрезка ![]()
![]()
получен набор значений ![]() величины
величины ![]() . Если допустить, что между
. Если допустить, что между ![]() и
и ![]() существует функциональная зависимость
существует функциональная зависимость ![]() , можно поставить вопрос о поиске аналитического представления функции
, можно поставить вопрос о поиске аналитического представления функции ![]() .
.
Повод для аппроксимации может возникнуть даже тогда, когда аналитическое выражение некоторой функции ![]() имеется, однако оно оказывается мало пригодным для решения поставленной задачи, потому что операция, которую требуется осуществить над этой функцией, трудновыполнима или невыполнима совсем. Например, вычисление значения трансцендентной функции «вручную». Действительно, чтобы вычислить
имеется, однако оно оказывается мало пригодным для решения поставленной задачи, потому что операция, которую требуется осуществить над этой функцией, трудновыполнима или невыполнима совсем. Например, вычисление значения трансцендентной функции «вручную». Действительно, чтобы вычислить ![]() , проще всего воспользоваться степенным разложением функции, т.е. заменить трансцендентную функцию степенным рядом. При этом получается приближенное значение функции.
, проще всего воспользоваться степенным разложением функции, т.е. заменить трансцендентную функцию степенным рядом. При этом получается приближенное значение функции.
Другая ситуация, когда может потребоваться аппроксимация аналитически заданной функции – дифференцирование функции, вычисление определенных и неопределенных интегралов. Если аналитическое выражение функции достаточно сложное, то поставленная задача трудно выполнима, а иногда и невыполнима с помощью элементарных приемов. Например, интеграл 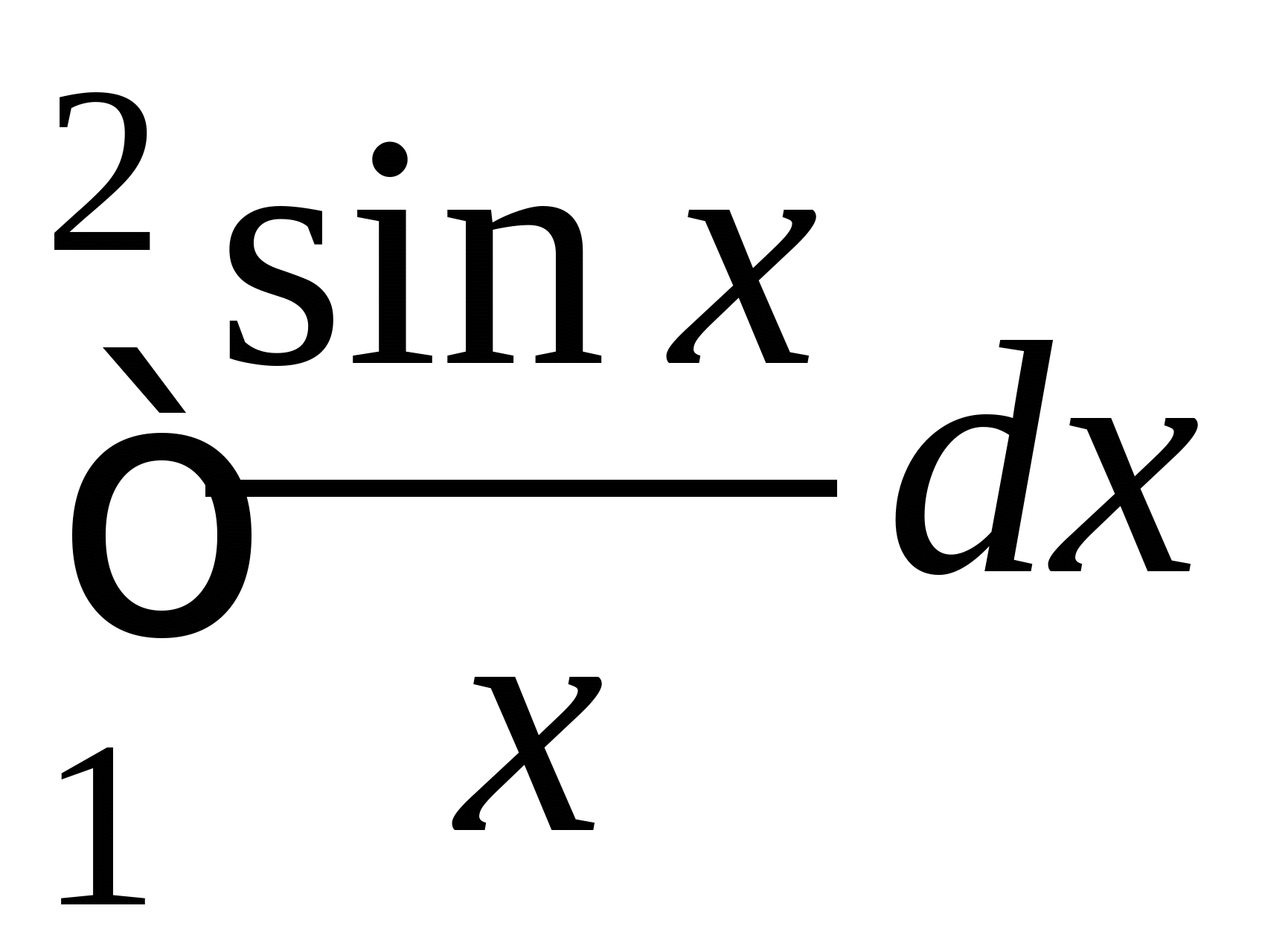 существует, но по формуле Ньютона-Лейбница практически вычислен быть не может, т.к. первообразная
существует, но по формуле Ньютона-Лейбница практически вычислен быть не может, т.к. первообразная ![]() не выражается в элементарных функциях. Аппроксимация подынтегральной функции – один из возможных приемов.
не выражается в элементарных функциях. Аппроксимация подынтегральной функции – один из возможных приемов.
Классический подход к численному решению подобных задач заключается в том, чтобы, опираясь на информацию о функции ![]() , по некоторому алгоритму подобрать аппроксимирующую функцию
, по некоторому алгоритму подобрать аппроксимирующую функцию ![]() , в определенном смысле «близкую» к
, в определенном смысле «близкую» к ![]() .
.
Для оценки «близости» функций выбирают тот или иной критерий согласия. Эти критерии основаны на использовании той или иной метрики, т.е. способа введения расстояния между функциями, принадлежащими тому или иному классу: ![]() . Например, для функций, ограниченных на отрезке
. Например, для функций, ограниченных на отрезке ![]() , расстояние может быть введено следующим образом:
, расстояние может быть введено следующим образом: ![]() ; для функций, непрерывных на отрезке
; для функций, непрерывных на отрезке ![]() , по формуле
, по формуле 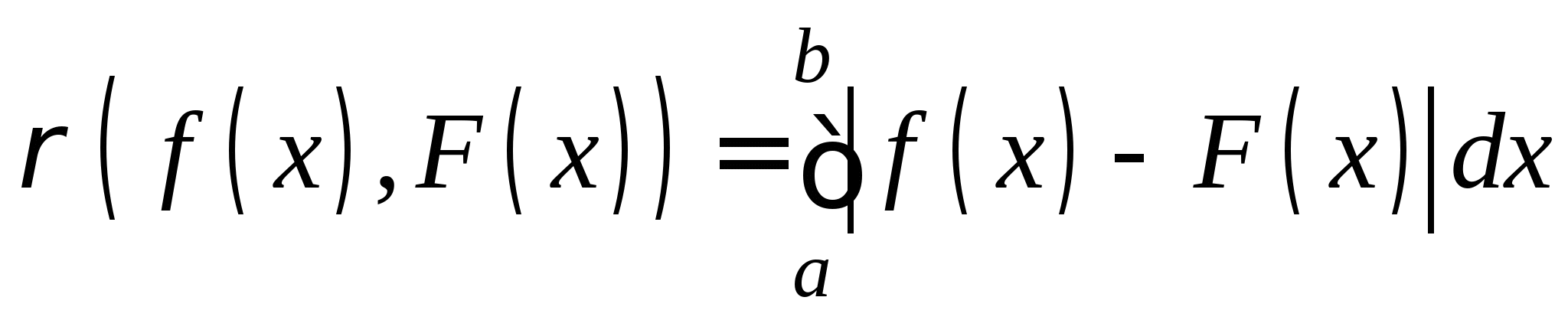 .
.
Часто процедура аппроксимации связана с другим критерием согласия:
![]() .
.
Применяемый на его основе способ аппроксимации получил название метода наименьших квадратов.
Для функций, заданных таблично, достаточно распространенным критерием согласия является критерий Чебышева, который определяет расстояние ![]() между аппроксимируемой и аппроксимирующей функциями как максимум величины отклонения между этими функциями в узлах сетки:
между аппроксимируемой и аппроксимирующей функциями как максимум величины отклонения между этими функциями в узлах сетки:
![]() .
.
Если ![]() , т.е.
, т.е. ![]() , то соответствующий способ аппроксимации называют интерполяцией, а процедуру вычисления значений
, то соответствующий способ аппроксимации называют интерполяцией, а процедуру вычисления значений ![]() с помощью
с помощью ![]() в точках, не являющихся узлами сетки, интерполированием.
в точках, не являющихся узлами сетки, интерполированием.
Задача интерполирования состоит в следующем.
На отрезке ![]() заданы
заданы ![]() точки
точки ![]() , которые называются узлами интерполяции, и значения некоторой функции
, которые называются узлами интерполяции, и значения некоторой функции ![]() в этих точках:
в этих точках:
![]() . (5.1)
. (5.1)
Необходимо построить функцию ![]() - интерполирующую функцию, принадлежащую некоторому классу и принимающую в узлах интерполяции заданные значения (5.1), т.е.
- интерполирующую функцию, принадлежащую некоторому классу и принимающую в узлах интерполяции заданные значения (5.1), т.е.
![]() . (5.2)
. (5.2)
Геометрически это означает, что нужно найти кривую ![]() определенного типа, проходящую через заданные точки
определенного типа, проходящую через заданные точки ![]() .
.
В такой общей постановке задача может иметь бесконечное множество решений или совсем их не иметь.
Сформулированная задача становится однозначной, если вместо произвольной функции ![]() искать полином
искать полином ![]() степени не выше
степени не выше ![]() , удовлетворяющий условиям (5.2), т.е.
, удовлетворяющий условиям (5.2), т.е.
![]() .
.
Полученную интерполяционную функцию ![]() используют для приближенного вычисления значений данной функции
используют для приближенного вычисления значений данной функции ![]() в точках, отличных от узлов интерполяции. Такая операция называется интерполированием функции.
в точках, отличных от узлов интерполяции. Такая операция называется интерполированием функции.
Различают интерполирование в узком смысле, т.е. когда ![]() , и экстраполирование, т.е. когда
, и экстраполирование, т.е. когда ![]() . В дальнейшем, под термином интерполирование будет пониматься как первая, так и вторая операции.
. В дальнейшем, под термином интерполирование будет пониматься как первая, так и вторая операции.
§5.2. Конечные разности. Обобщенная степень.
Пусть задана функция ![]() . Обозначим через
. Обозначим через ![]() фиксированную величину приращения аргумента (шаг). Тогда выражение
фиксированную величину приращения аргумента (шаг). Тогда выражение
![]() (5.3)
(5.3)
называется первой конечной разностью функции ![]() . Аналогично определяются конечные разности высших порядков
. Аналогично определяются конечные разности высших порядков ![]()
Например:
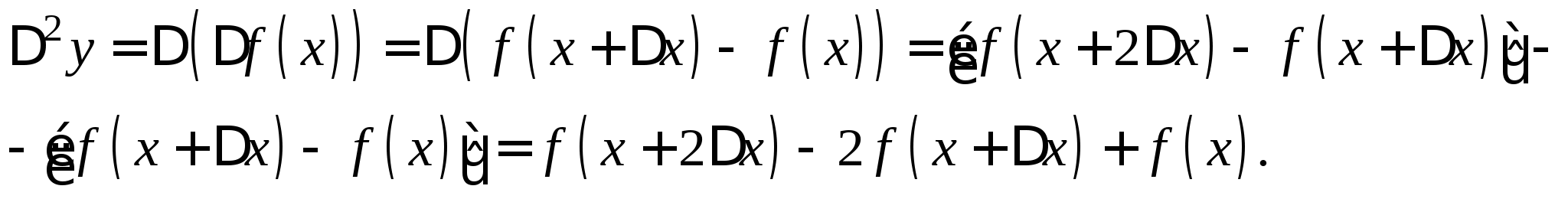 (5.4)
(5.4)
Символ ![]() (дельта) можно рассматривать как оператор, ставящий в соответствие функции
(дельта) можно рассматривать как оператор, ставящий в соответствие функции ![]() функцию
функцию ![]() .
.
Легко проверить основные свойства оператора ![]() :
:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() , где
, где ![]() (целые неотрицательные числа), причем
(целые неотрицательные числа), причем ![]() .
.
Из формулы (5.3) имеем:
![]() .
.
Отсюда, рассматривая ![]() как символический множитель, получим:
как символический множитель, получим:
![]() . (5.5)
. (5.5)
Из формулы (5.4):
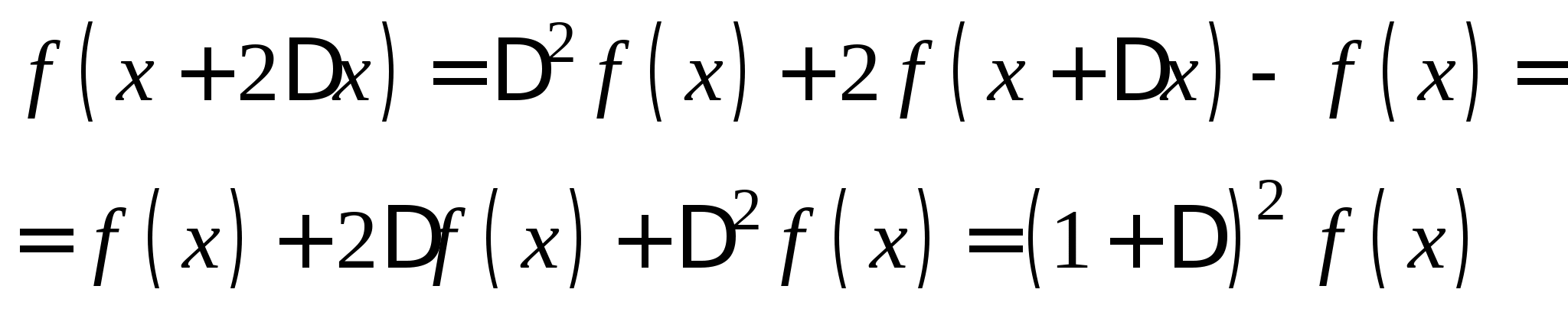 ; (5.6)
; (5.6)
и т.д. Окончательно получим:
![]() . (5.7)
. (5.7)
В дальнейшем нам понадобится понятие обобщенной степени.
Определение.
Обобщенной ![]() -степенью числа
-степенью числа ![]() называется произведение
называется произведение ![]() сомножителей, первый из которых равен
сомножителей, первый из которых равен ![]() , а каждый следующий на
, а каждый следующий на ![]() меньше предыдущего:
меньше предыдущего:
![]() , (5.8)
, (5.8)
где ![]() .
.
Полагают, что ![]() . При
. При ![]() обобщенная степень совпадает с обычной:
обобщенная степень совпадает с обычной: ![]() .
.
Вычислим конечные разности для обобщенной степени, полагая ![]() . Для первой конечной разности имеем:
. Для первой конечной разности имеем:
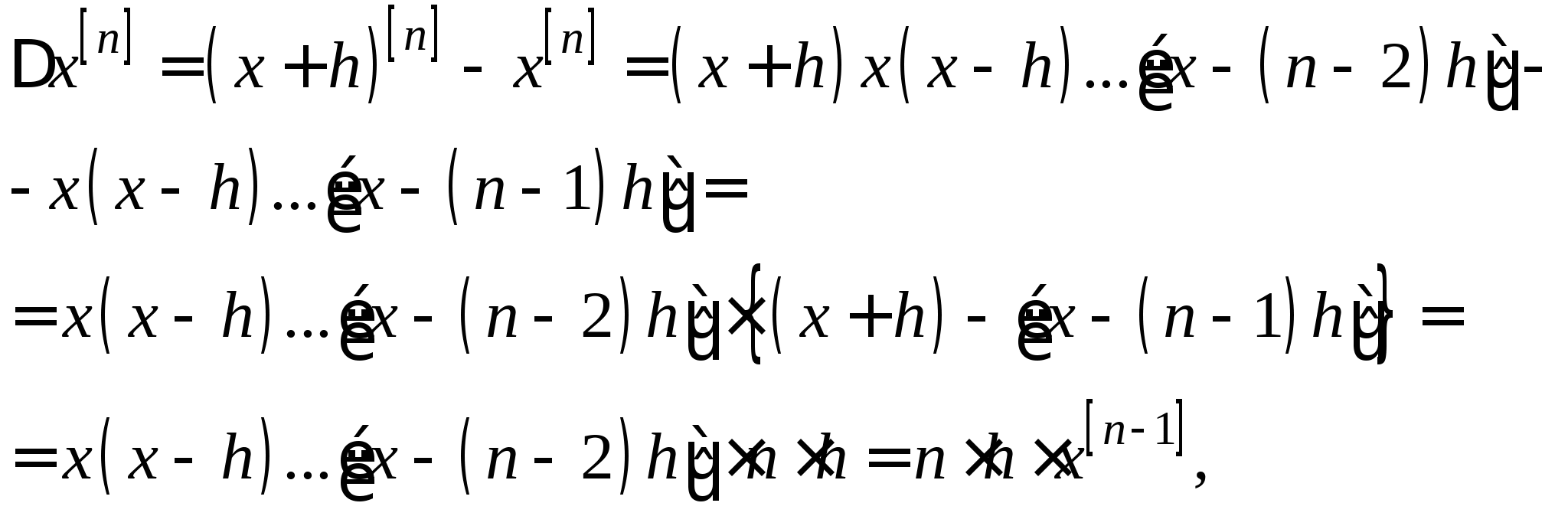
то есть
![]() . (5.9)
. (5.9)
Для второй конечной разности:
![]() ,
,
то есть
![]() . (5.10)
. (5.10)
Аналогично,
![]() ,
,
и так далее.
Окончательно будем иметь:
![]() , (5.11)
, (5.11)
![]() , если
, если ![]() . (5.12)
. (5.12)
§5.3. Первая интерполяционная формула Ньютона.
Пусть для функции ![]() заданы значения
заданы значения ![]() для равноотстоящих значений независимой переменной
для равноотстоящих значений независимой переменной ![]() , где
, где ![]() - шаг интерполяции. Требуется подобрать полином
- шаг интерполяции. Требуется подобрать полином ![]() степени не выше
степени не выше ![]() , принимающий в точках
, принимающий в точках ![]() значения
значения
![]() . (5.13)
. (5.13)
Условия (5.13) эквивалентны тому, что
![]() . (5.14)
. (5.14)
Будем искать полином в виде
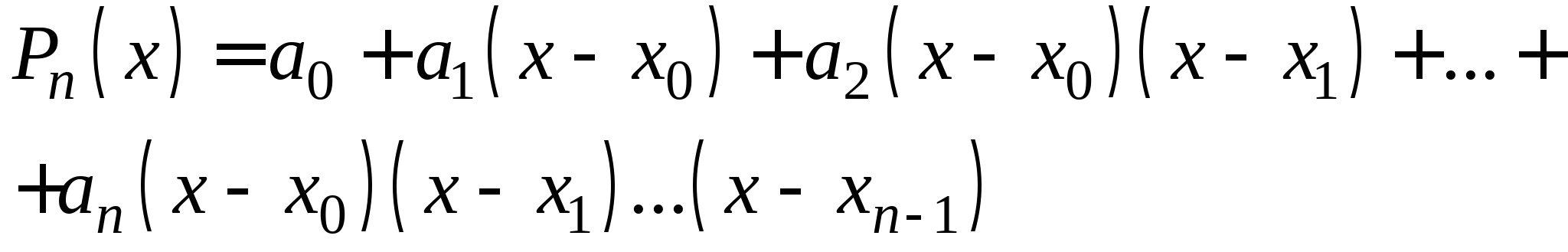 . (5.15)
. (5.15)
Используя понятие обобщенной степени, запишем выражение (5.15) в виде:
![]() . (5.16)
. (5.16)
Чтобы полином был определен, нужно найти коэффициенты ![]() . Полагая
. Полагая ![]() в выражении (5.16), получим
в выражении (5.16), получим
![]() . (5.17)
. (5.17)
Чтобы найти коэффициент ![]() , составим первую конечную разность:
, составим первую конечную разность:
![]() .
.
Полагая ![]() , получим:
, получим:
![]() ,
,
откуда
![]() . (5.18)
. (5.18)
Для определения коэффициента ![]() составим вторую конечную разность:
составим вторую конечную разность:
![]() .
.
Положив ![]() , получим:
, получим:
![]() ,
,
откуда
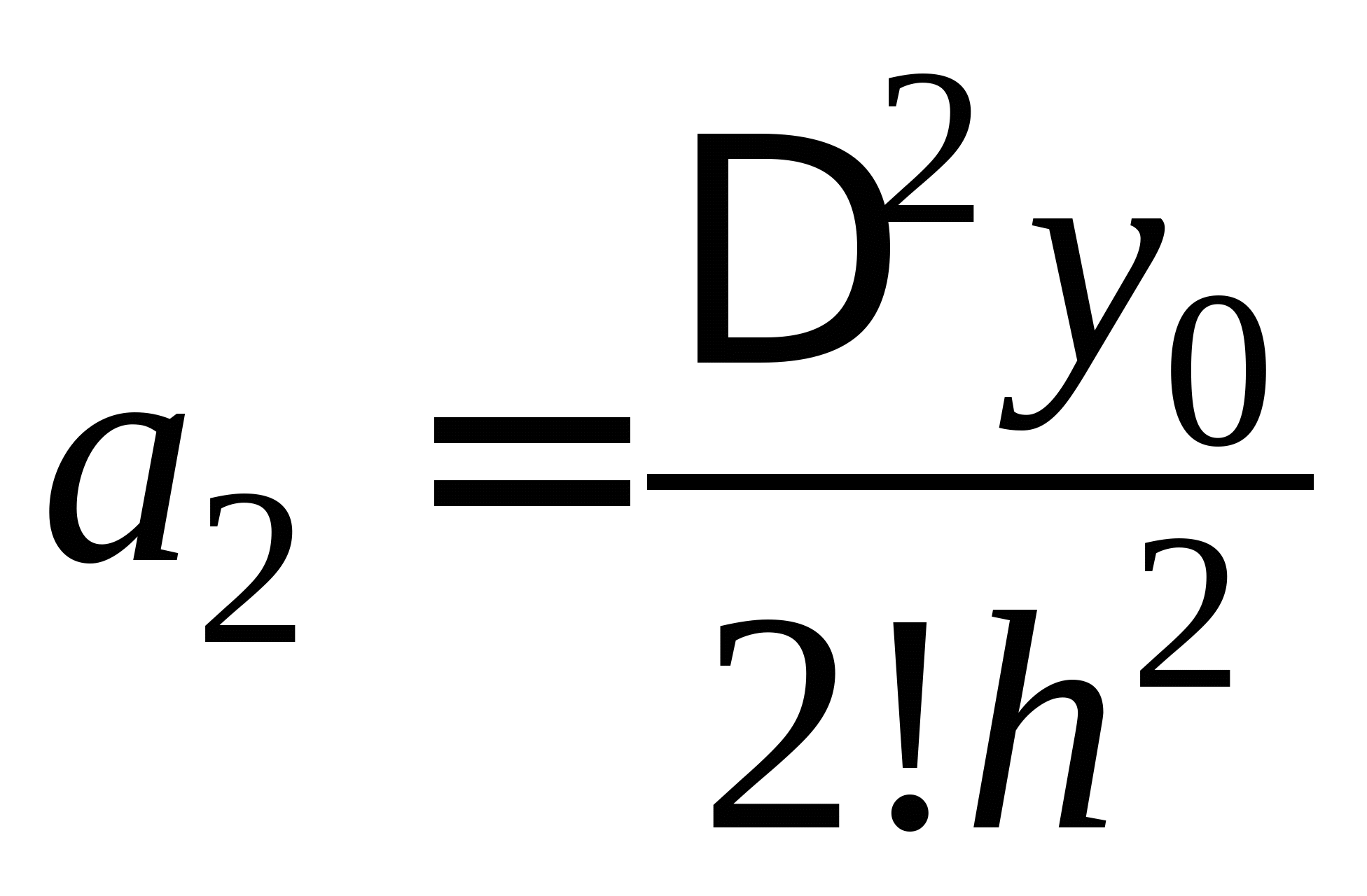 . (5.19)
. (5.19)
Продолжая процесс, получим:
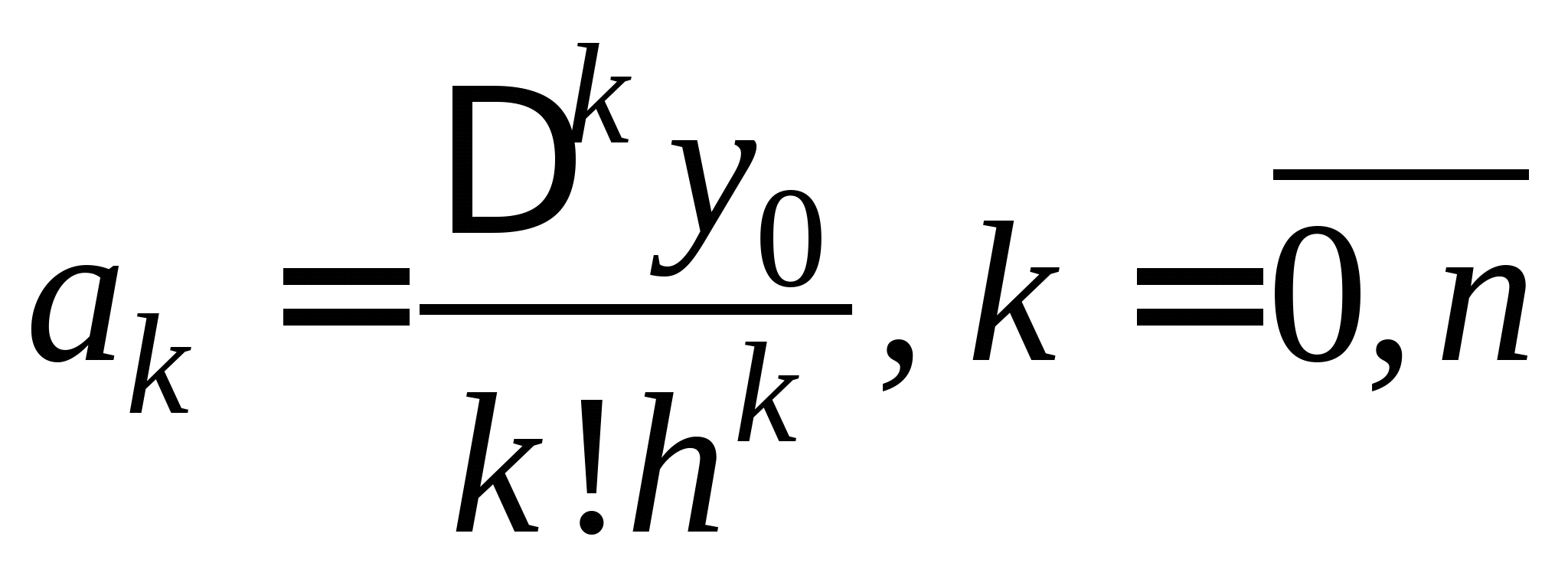 , (5.20)
, (5.20)
причем ![]() .
.
Подставляя найденные значения коэффициентов ![]() в выражение (5.16), получим интерполяционный полином Ньютона:
в выражение (5.16), получим интерполяционный полином Ньютона:
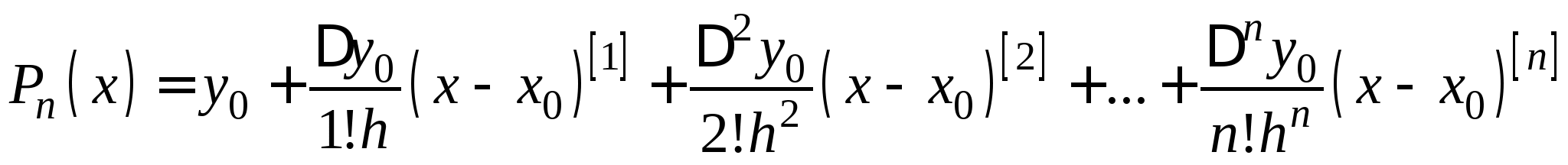 . (5.21)
. (5.21)
Этот полином полностью удовлетворяет требованиям поставленной задачи. Действительно, степень полинома ![]() не выше
не выше ![]() ;
; ![]() ;
;
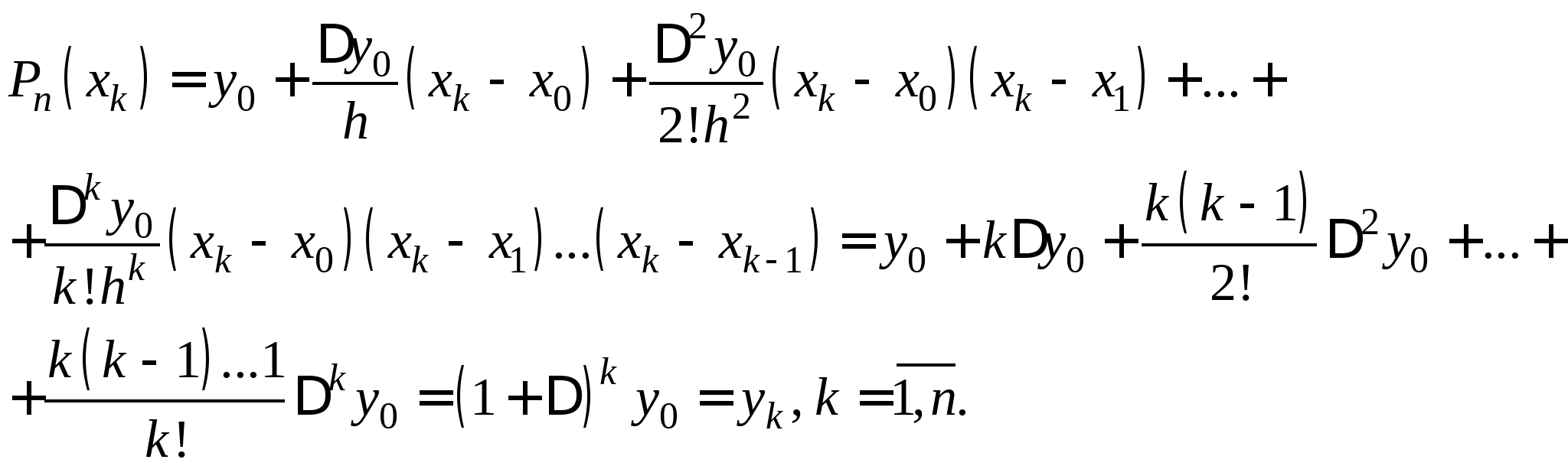
Для практического использования первую интерполяционную формулу Ньютона записывают в несколько преобразованном виде. Для этого введем новую переменную
![]() . (5.22)
. (5.22)
Тогда
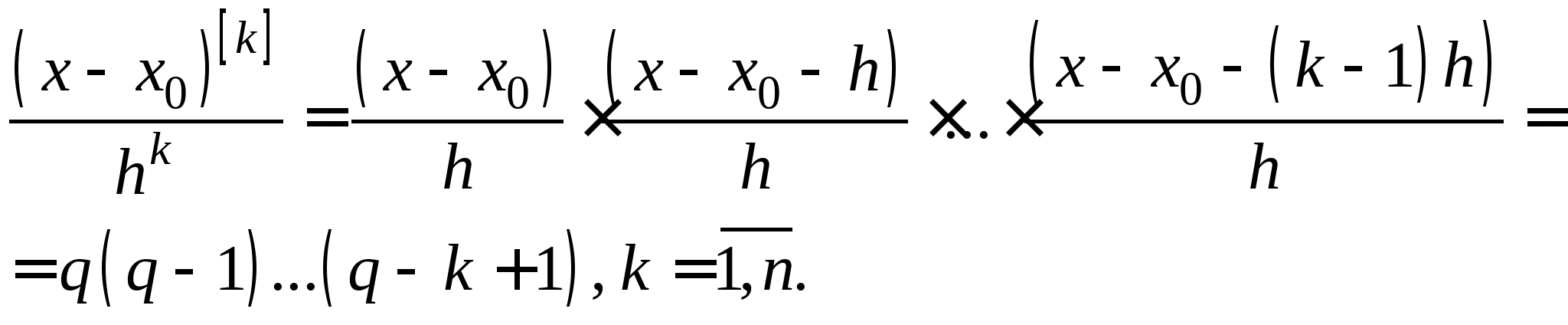 (5.23)
(5.23)
Подставляя (5.23) в (5.21), получим окончательный вид первой интерполяционной формулы Ньютона:
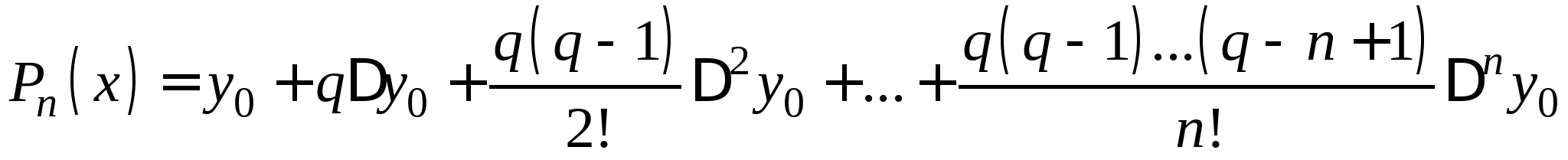 . (5.24)
. (5.24)
Если в формуле (5.24) положить ![]() , то получим формулу линейного интерполирования:
, то получим формулу линейного интерполирования:
![]() . (5.25)
. (5.25)
При ![]() получим формулу параболического или квадратичного интерполирования:
получим формулу параболического или квадратичного интерполирования:
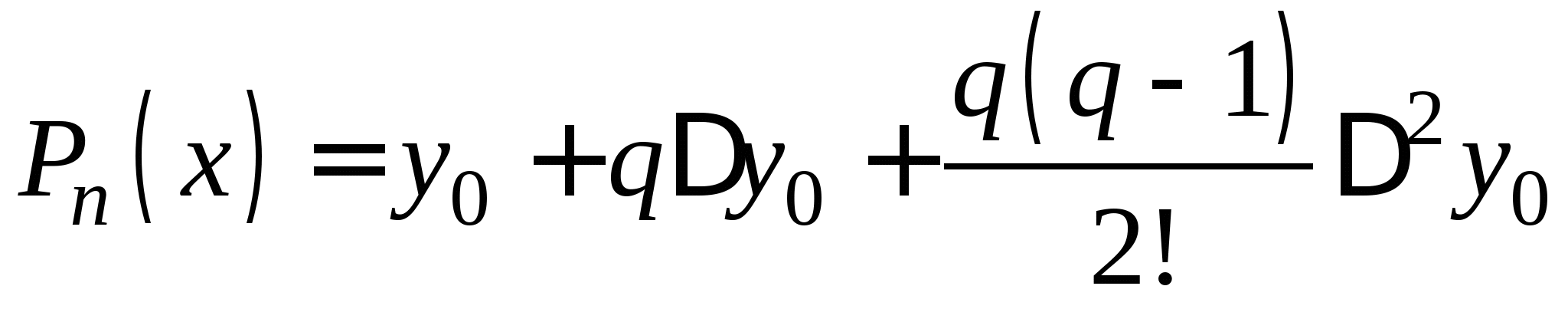 . (5.26)
. (5.26)
Первую интерполяционную формулу Ньютона используют для интерполирования функции в окрестности начальной точки ![]() , где
, где ![]() мало по абсолютной величине и представляет собой число шагов, необходимых для достижения точки
мало по абсолютной величине и представляет собой число шагов, необходимых для достижения точки ![]() , исходя из точки
, исходя из точки ![]() .
.
Остаточный член первой интерполяционной формулы Ньютона:
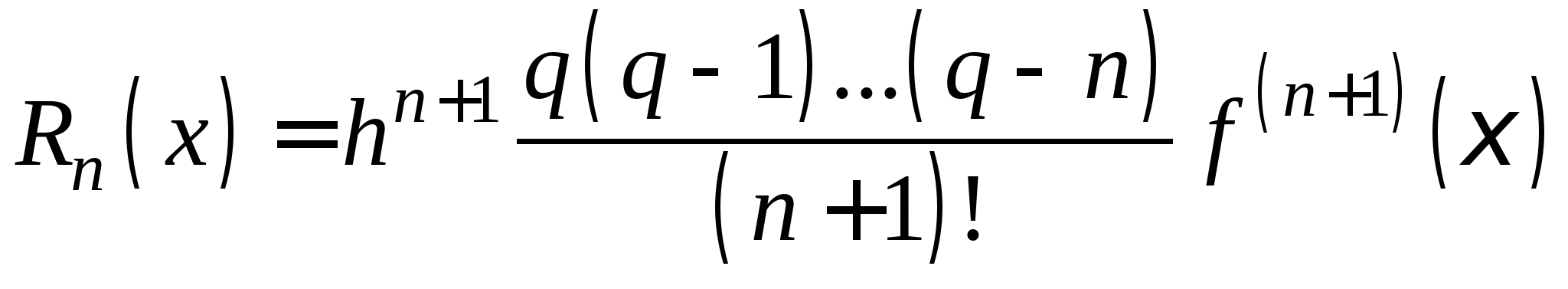 , (5.27)
, (5.27)
где ![]() - некоторое промежуточное значение между узлами интерполирования
- некоторое промежуточное значение между узлами интерполирования ![]() и рассматриваемой точкой
и рассматриваемой точкой ![]() .
.
Учитывая, что 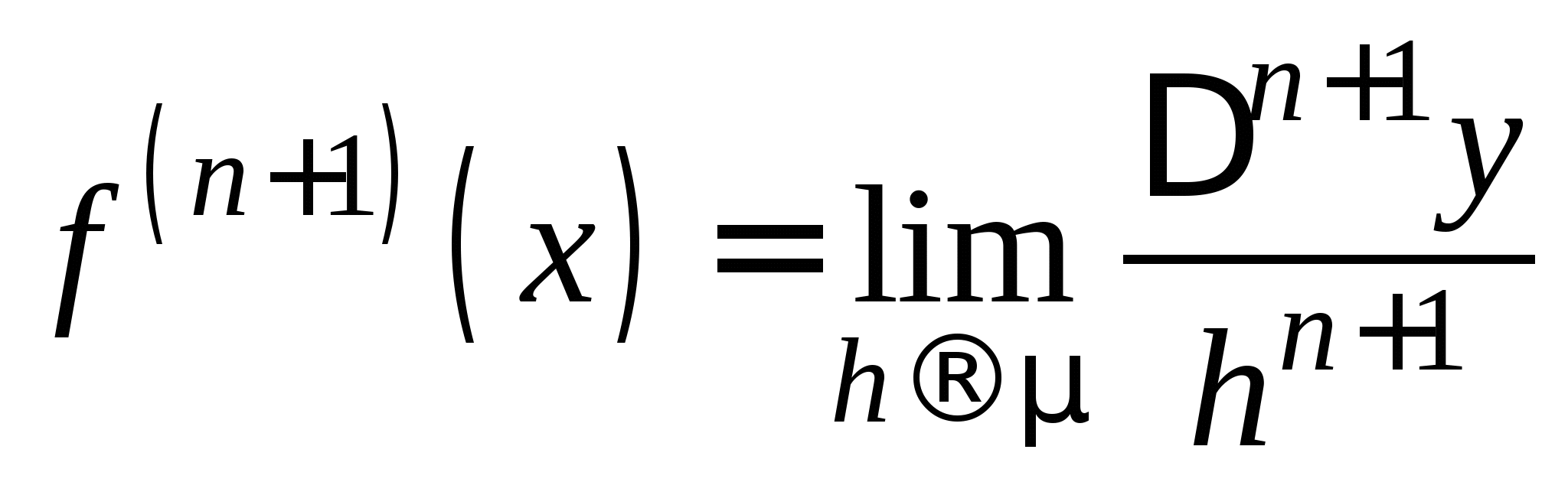 , приближенно можно положить:
, приближенно можно положить:
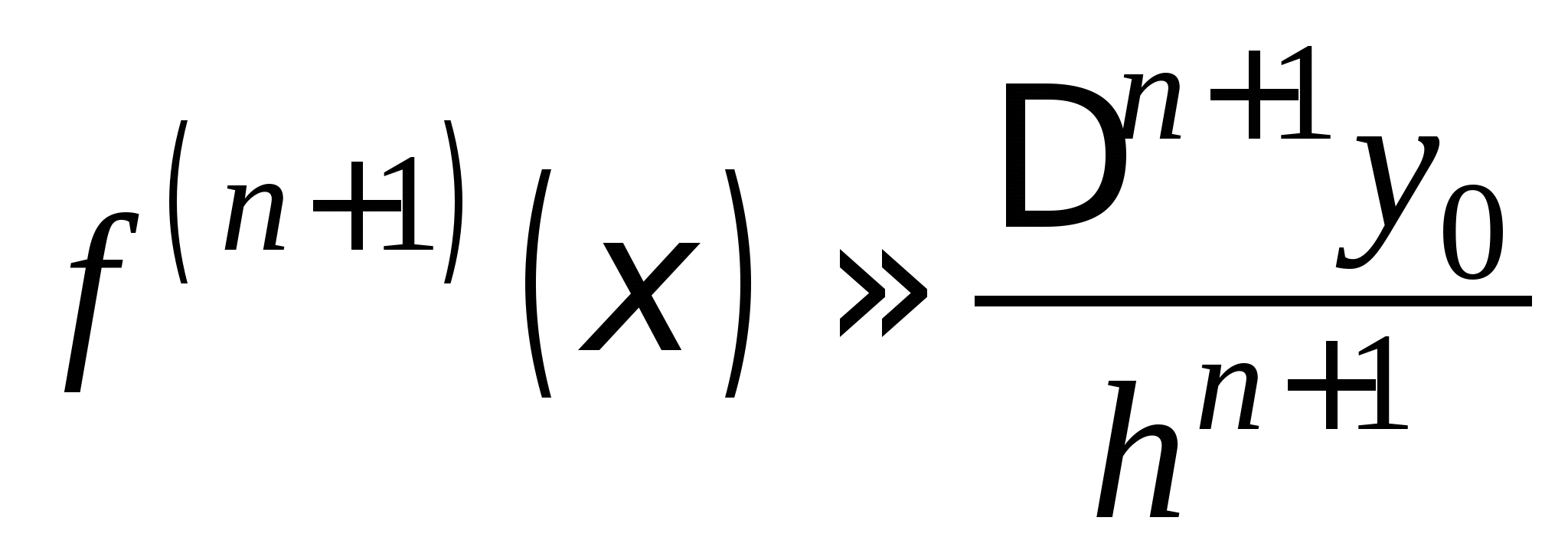 .
.
В этом случае соотношение (5.27) примет вид:
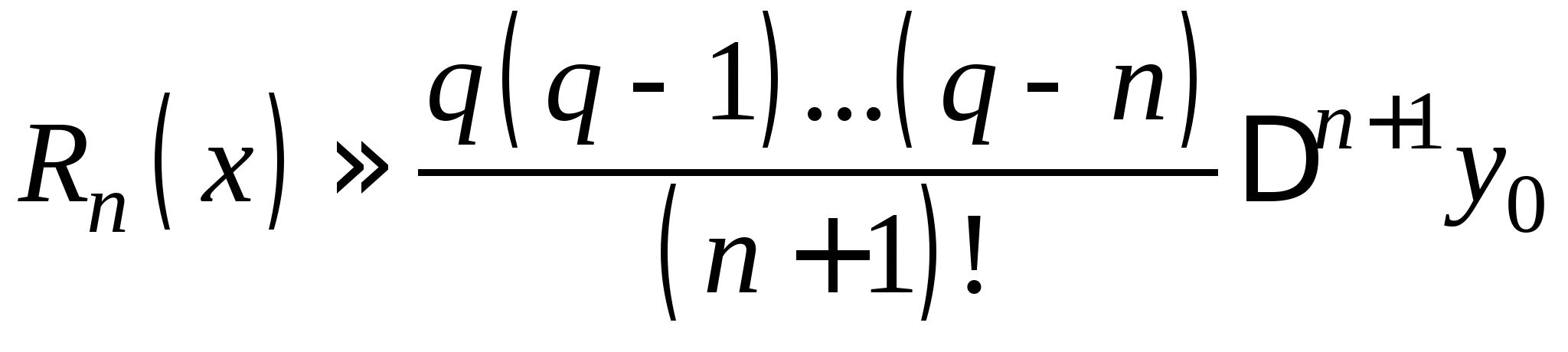 . (5.28)
. (5.28)
§5.4. Вторая интерполяционная формула Ньютона.
Вторая интерполяционная формула Ньютона применяется для интерполирования в окрестности конечного значения ![]() .
.
Пусть для функции ![]() заданы значения
заданы значения ![]() для равноотстоящих значений независимой переменной
для равноотстоящих значений независимой переменной ![]() . Построим полином следующего вида:
. Построим полином следующего вида:
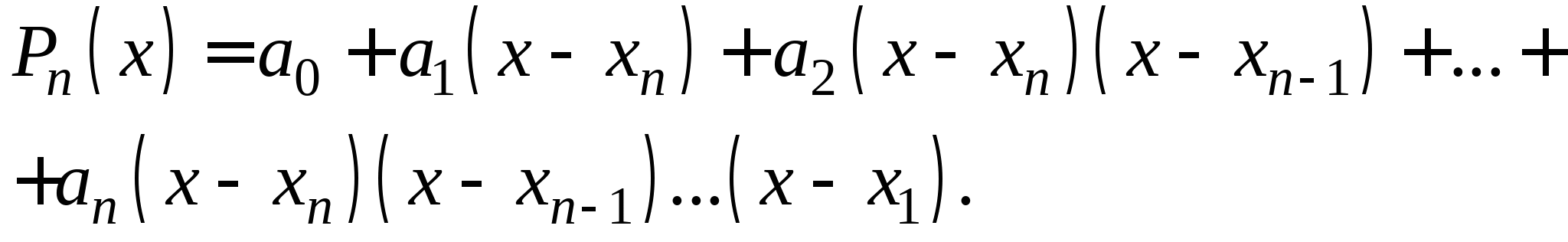 (5.29)
(5.29)
Используя обобщенную степень, получим:
![]() . (5.30)
. (5.30)
Найдем коэффициенты ![]() из условий
из условий ![]() . Эти условия равносильны
. Эти условия равносильны
![]() . (5.31)
. (5.31)
Полагая ![]() в выражении (5.30), получим
в выражении (5.30), получим
![]() . (5.32)
. (5.32)
Чтобы найти коэффициент ![]() , составим первую конечную разность:
, составим первую конечную разность:
![]() .
.
Полагая ![]() , получим:
, получим:
![]() .
.
Отсюда
![]() . (5.33)
. (5.33)
Из второй конечной разности
![]()
при ![]() находим:
находим:
![]() .
.
Следовательно,
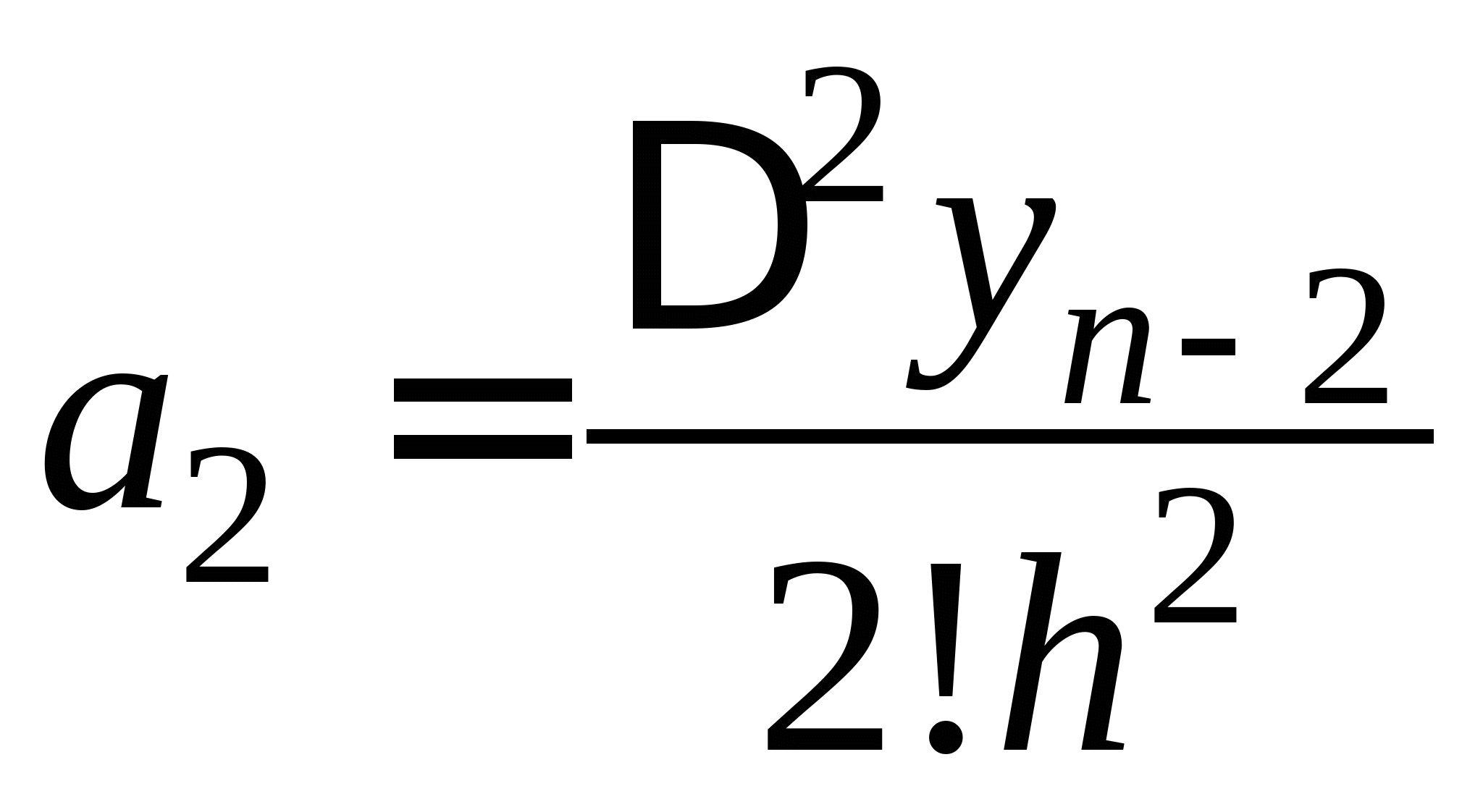 . (5.34)
. (5.34)
Продолжая дальнейшее вычисление конечных разностей, получим:
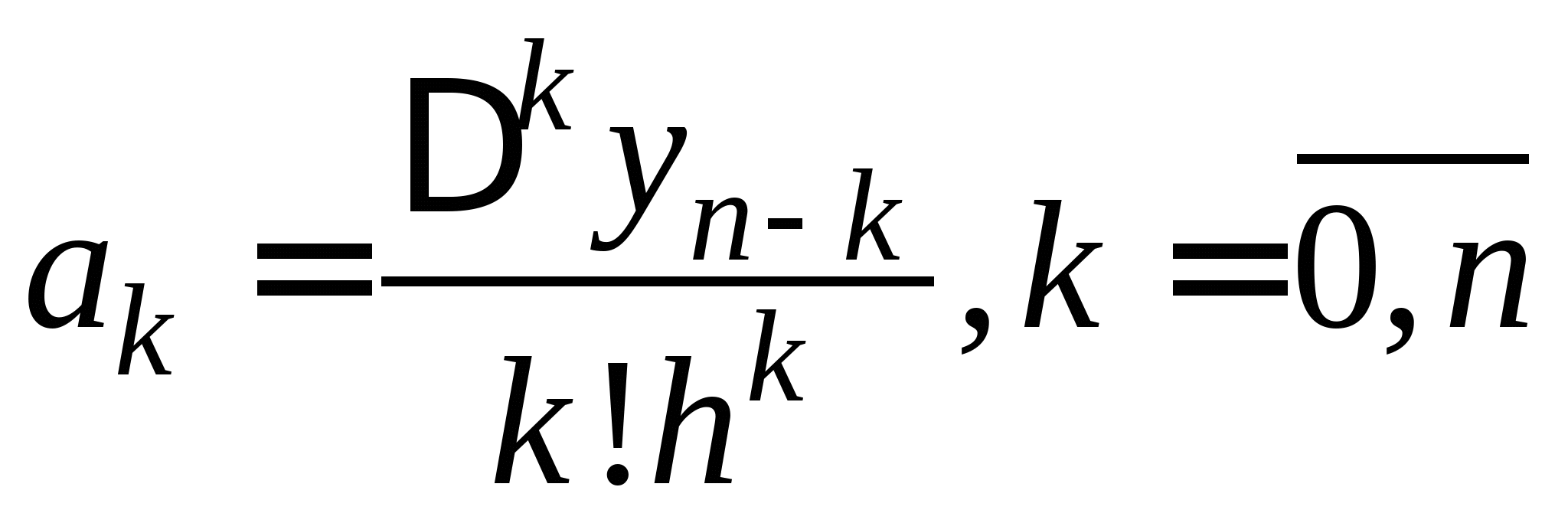 . (5.35)
. (5.35)
Подставляя найденные значения коэффициентов ![]() в выражение (5.29), получим вторую интерполяционную формулу Ньютона:
в выражение (5.29), получим вторую интерполяционную формулу Ньютона:
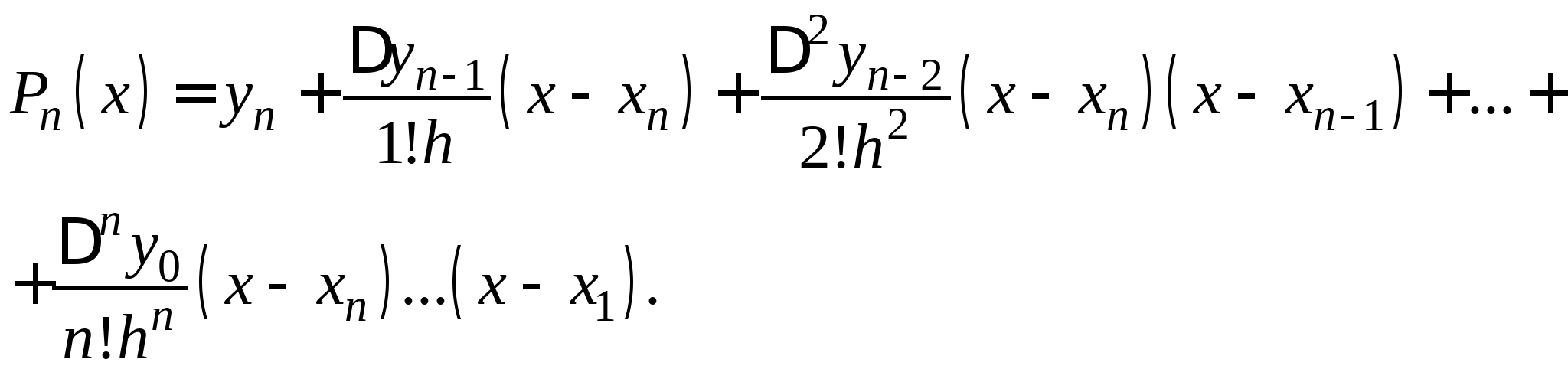 (5.36)
(5.36)
Введем новую переменную
![]() , (5.37)
, (5.37)
тогда
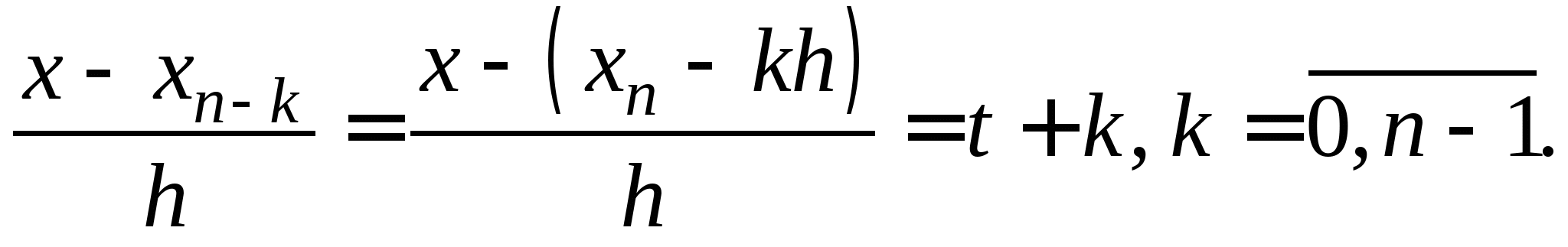 (5.38)
(5.38)
С учетом (5.38) вторая интерполяционная формула Ньютона примет вид:
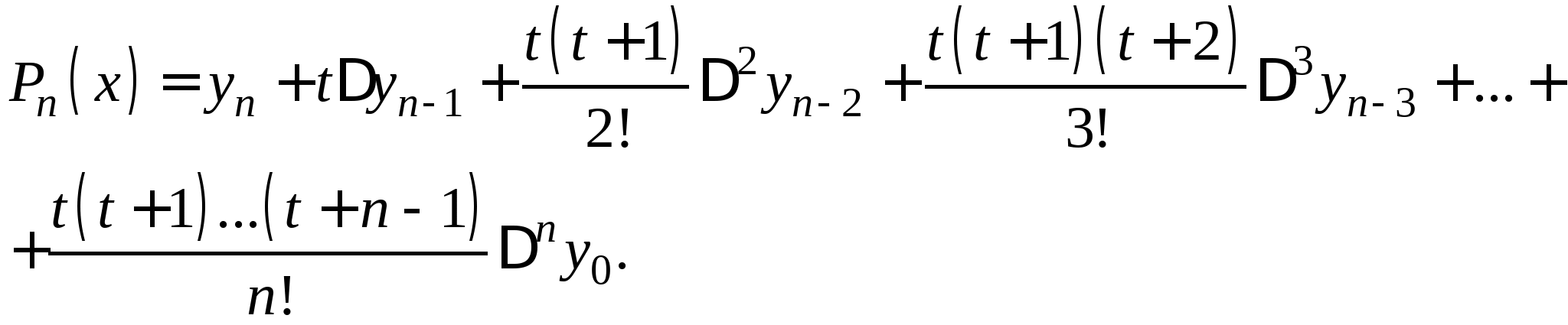 . (5.39)
. (5.39)
Остаточный член второй интерполяционной формулы Ньютона:
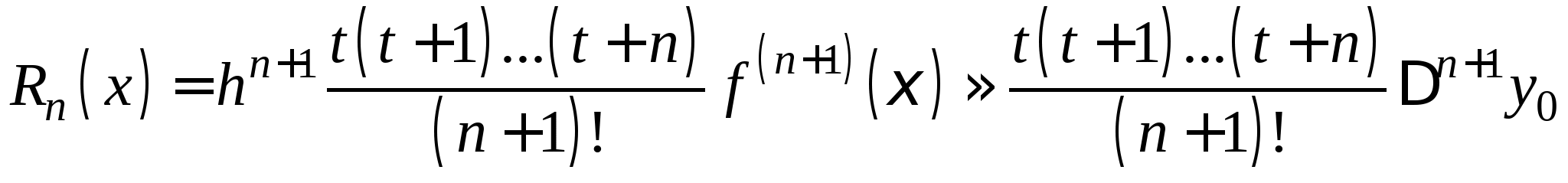 , (5.40)
, (5.40)
где ![]() - промежуточное значение между узлами интерполирования
- промежуточное значение между узлами интерполирования ![]() и точкой
и точкой ![]() .
.
§5.5. Интерполяционная формула Лагранжа.
Пусть на отрезке ![]() задана произвольная система точек
задана произвольная система точек ![]() , в которых известны значения функции
, в которых известны значения функции ![]() . То есть, задана следующая таблица
. То есть, задана следующая таблица
Таблица 5.1.
|
|
|
| … |
|
|
|
|
| … |
|
Установим зависимость ![]() одного ряда чисел от другого и построим новую функцию, которая с определенной степенью точности будет приближена к заданной.
одного ряда чисел от другого и построим новую функцию, которая с определенной степенью точности будет приближена к заданной.
Построим многочлен ![]() таким образом, чтобы его значения совпали со значениями функции, заданными в таблице, для тех же аргументов, то есть
таким образом, чтобы его значения совпали со значениями функции, заданными в таблице, для тех же аргументов, то есть
![]() . (5.41)
. (5.41)
Лагранж предложил строить многочлен ![]() -й степени в виде:
-й степени в виде:
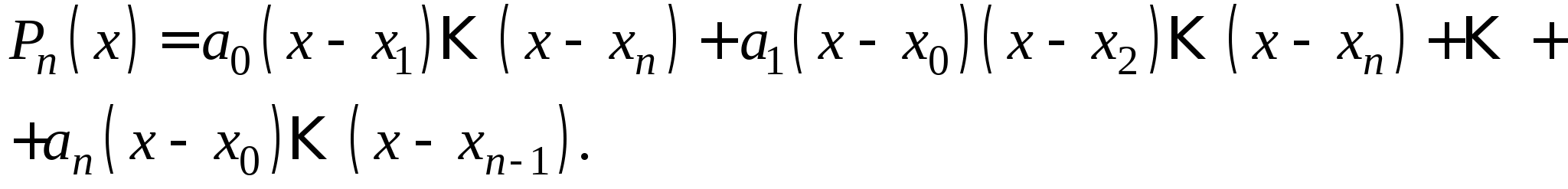 (5.42)
(5.42)
Здесь в каждом слагаемом отсутствует скобка ![]() , которой соответствует коэффициент
, которой соответствует коэффициент ![]() .
.
Найдем неизвестные коэффициенты ![]() , называемые коэффициентами Лагранжа, используя условие (5.41).
, называемые коэффициентами Лагранжа, используя условие (5.41).
При ![]() :
: ![]() .
.
![]() .
.
Следовательно, коэффициент ![]() вычисляется по следующей формуле:
вычисляется по следующей формуле:
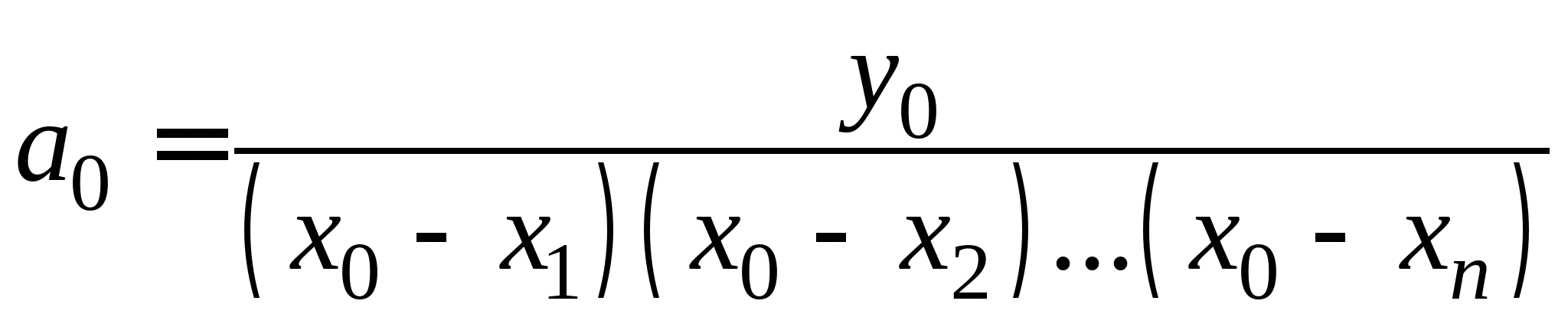 .
.
При ![]() :
: ![]() .
.
![]() .
.
Следовательно, коэффициент ![]() вычисляется по следующей формуле:
вычисляется по следующей формуле:
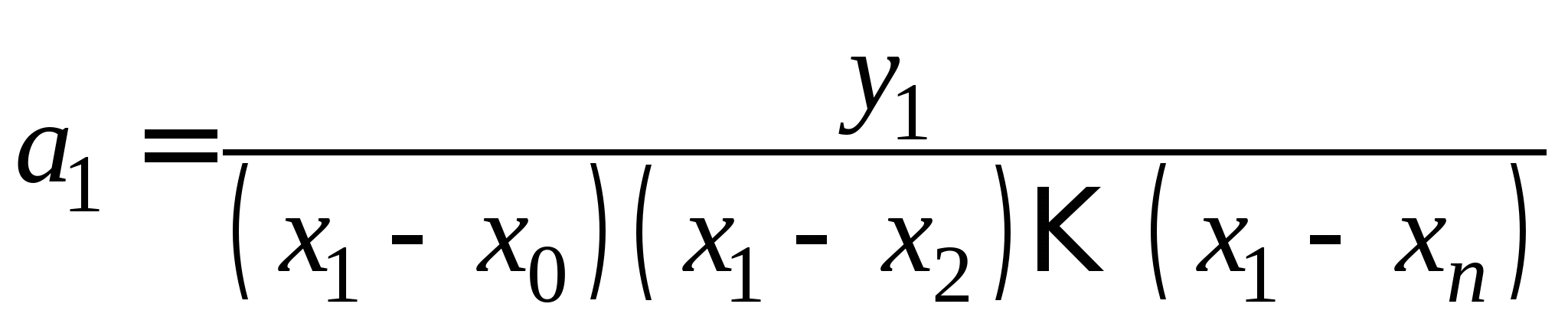 .
.
Таким образом, коэффициенты ![]() вычисляются по формулам:
вычисляются по формулам:
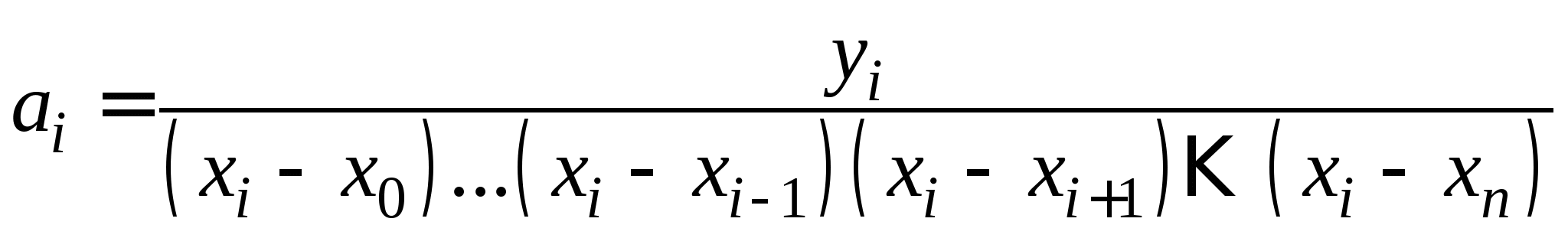 .
.
С учетом найденных коэффициентов интерполяционный полином Лагранжа запишется в виде
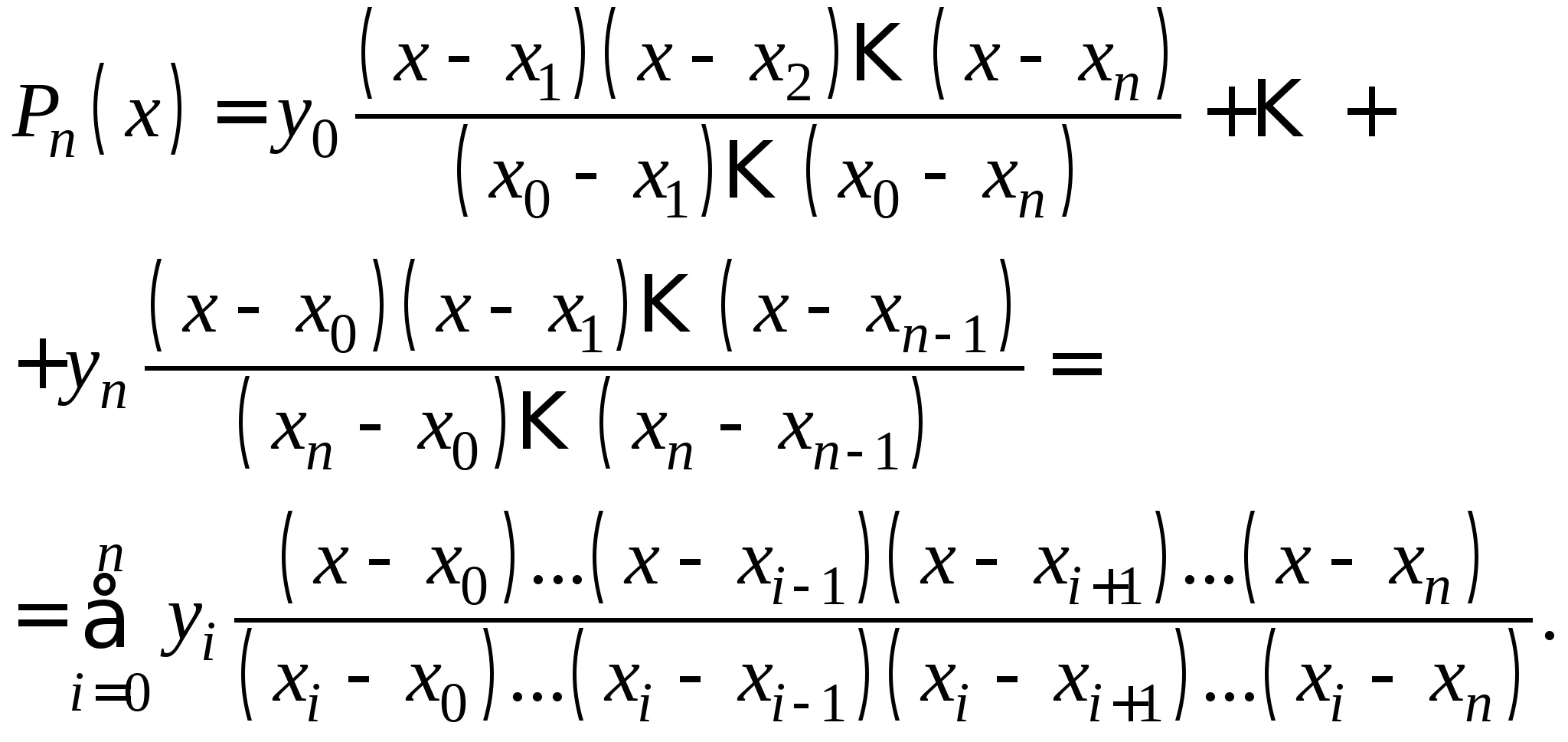 . (5.43)
. (5.43)
Для интерполяционной формулы Лагранжа справедлива оценка погрешности:
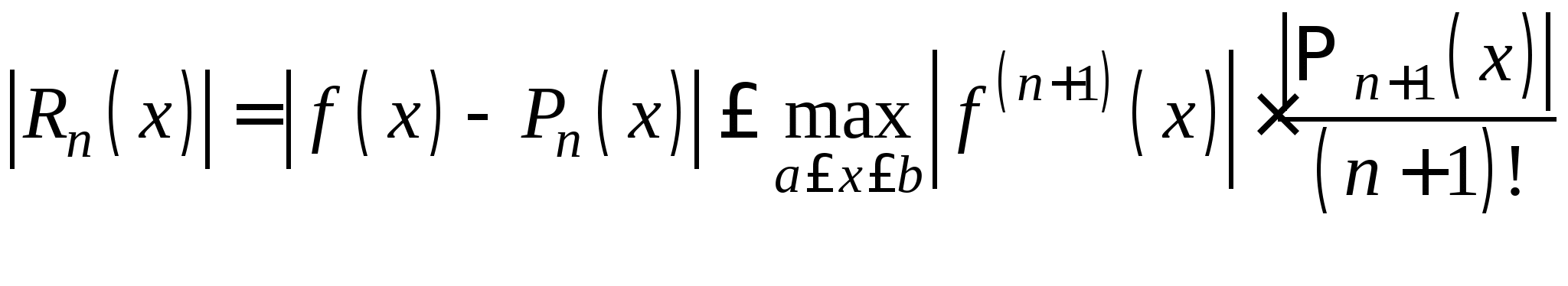 , (5.44)
, (5.44)
где ![]() .
.
Пример 5.1. По заданной системе точек
Таблица 5.2.
|
|
|
|
|
|
|
|
|
|
построить интерполяционный многочлен Лагранжа второго порядка вида:
![]() .
.
Коэффициенты этого многочлена будут вычислены по следующим формулам:
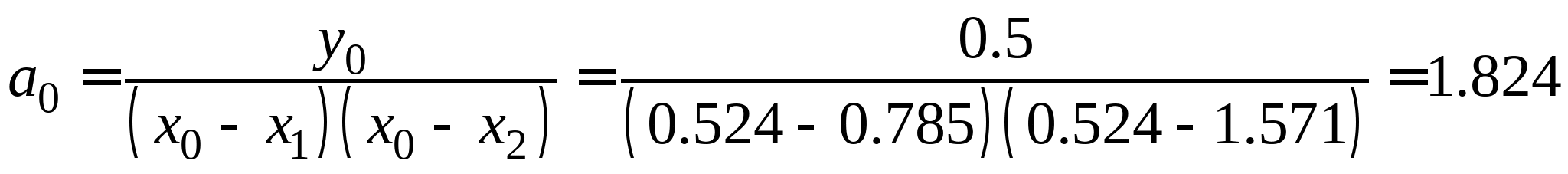 ,
,
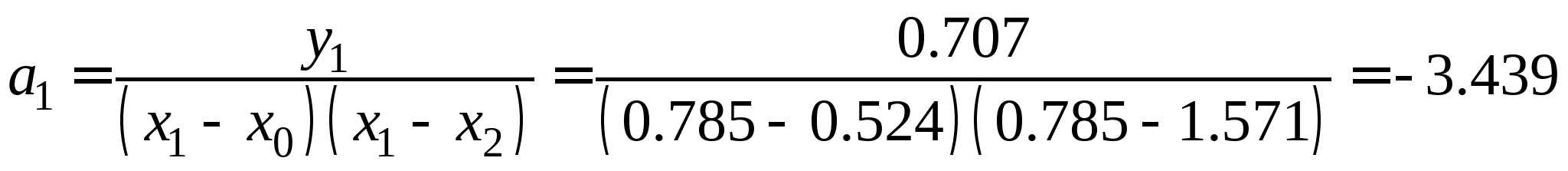 ,
,
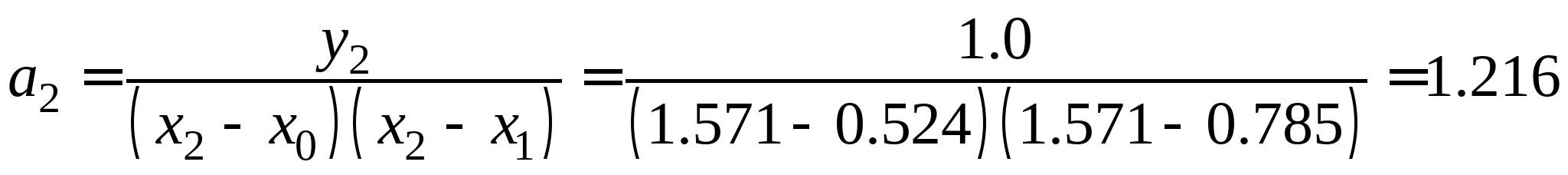 .
.
Тогда многочлен Лагранжа второго порядка будет иметь вид:
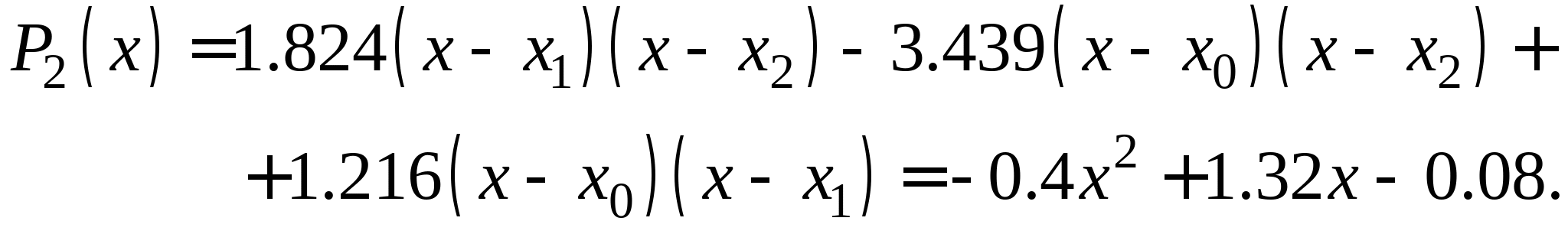
Учитывая, что таблица приведена для функции ![]() , вычисленной в узловых точках
, вычисленной в узловых точках ![]() , сравним погрешность вычислений данной функции и построенного многочлена в контрольной точке
, сравним погрешность вычислений данной функции и построенного многочлена в контрольной точке ![]() :
:
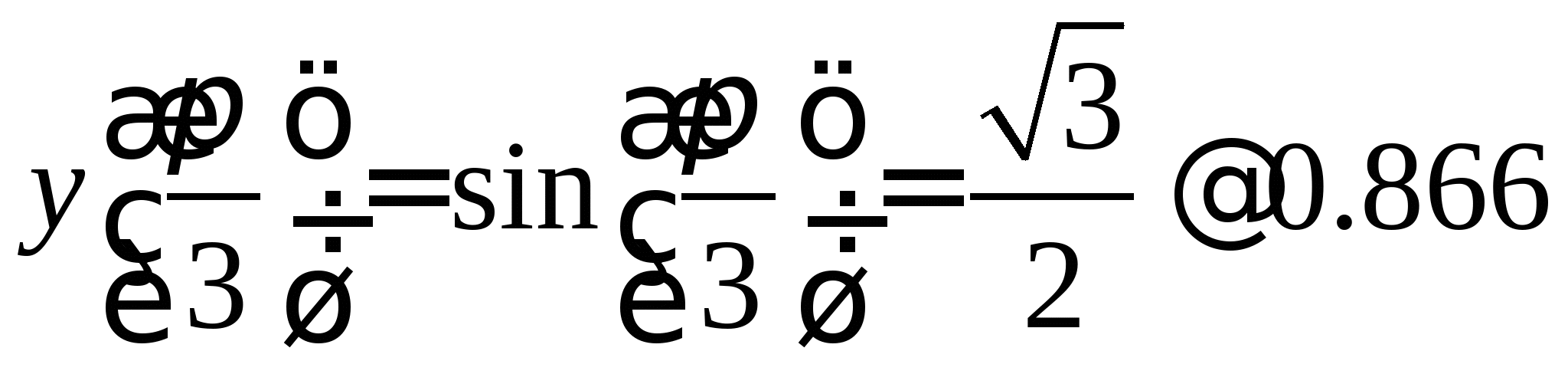 и
и 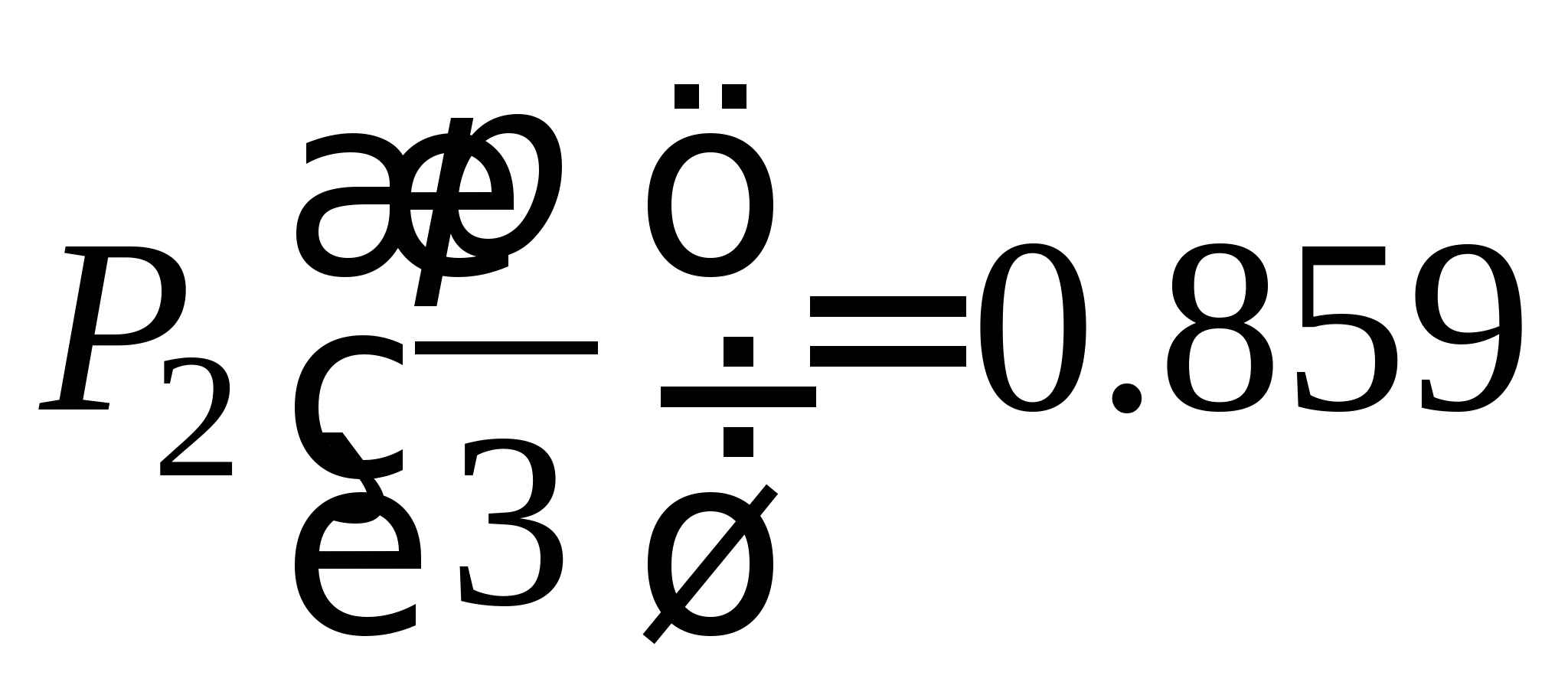 .
.
Погрешность вычислений равна
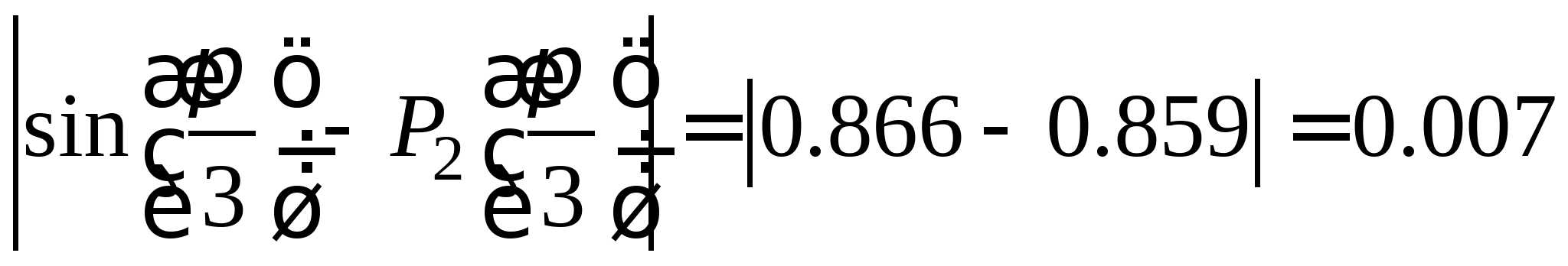 .
.
Н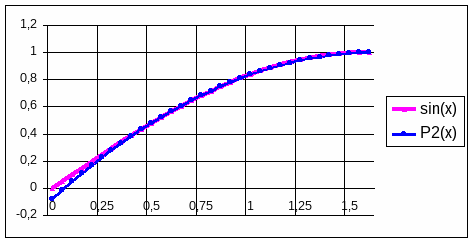
иже приведены графики функции ![]() и построенного полинома Лагранжа на заданном интервале. Из рисунка 5.1 видно, что многочлен второго порядка обеспечивает достаточно высокую точность построения синусоиды на заданном отрезке
и построенного полинома Лагранжа на заданном интервале. Из рисунка 5.1 видно, что многочлен второго порядка обеспечивает достаточно высокую точность построения синусоиды на заданном отрезке 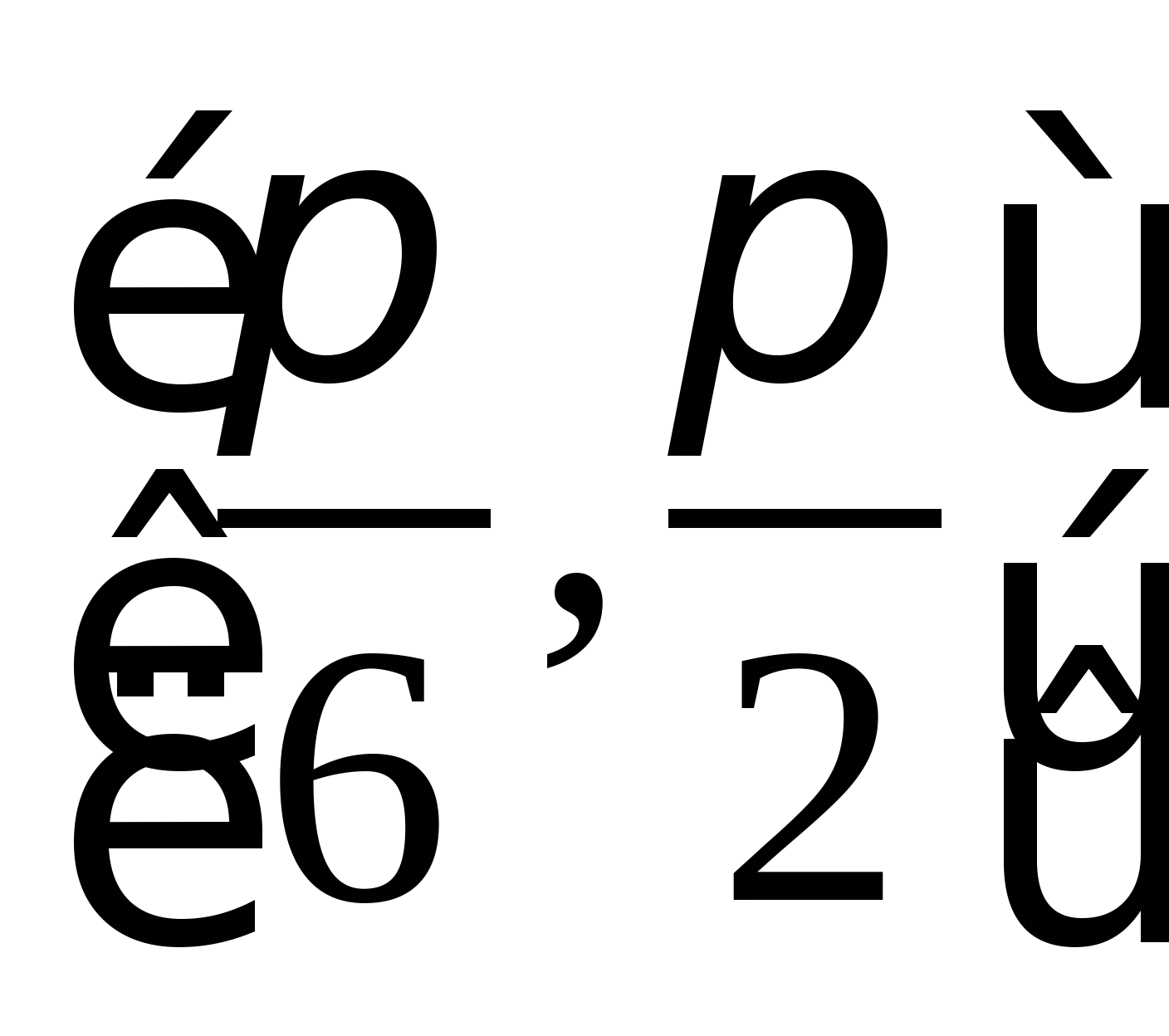 .
.
Рис.5.1.
Если таблица 5.1, для которой построена формула Лагранжа, задана для равноотстоящих узлов ![]() , то формула Лагранжа упрощается. Обозначим через
, то формула Лагранжа упрощается. Обозначим через ![]() . Тогда
. Тогда
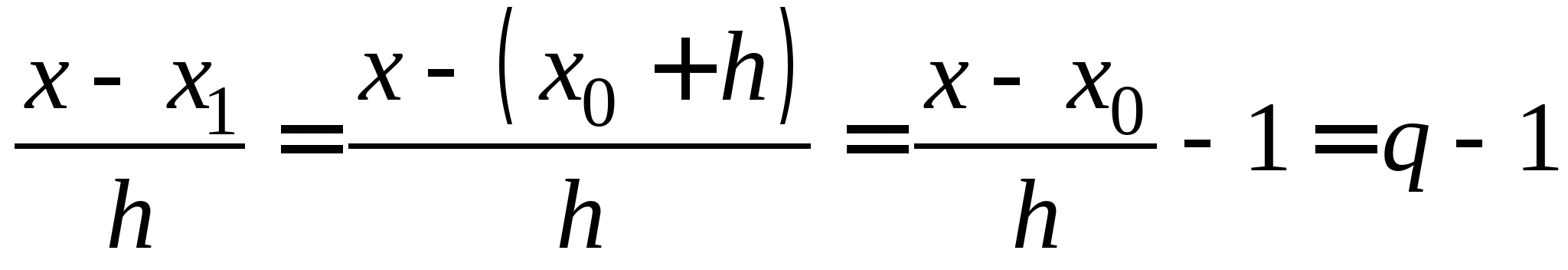 ,
,
![]() ,…,
,…,
![]() .
.
С учетом введенных обозначений формула Лагранжа запишется так:
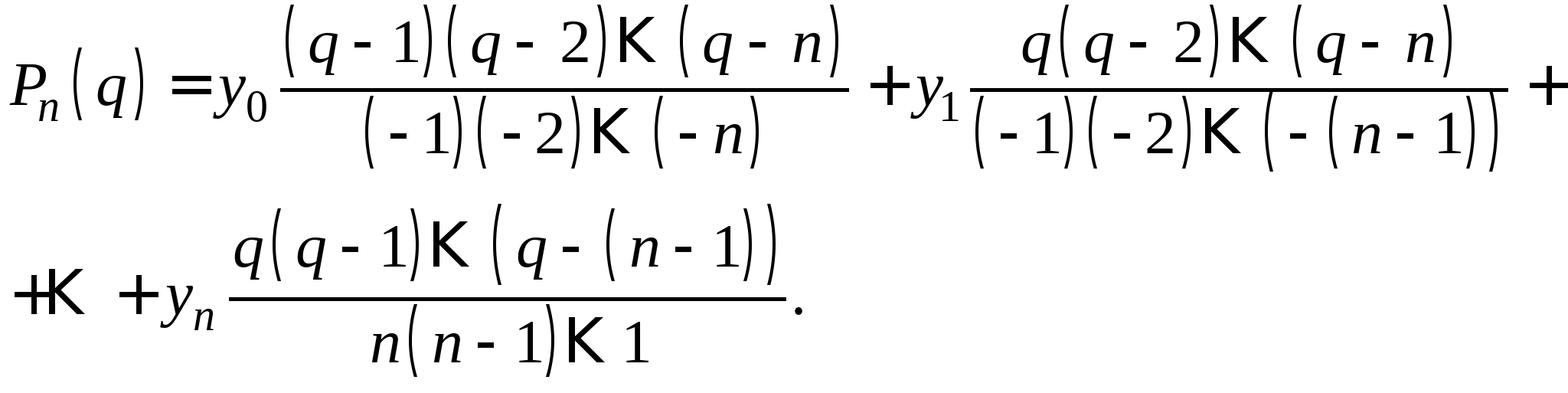
Запишем формулу Лагранжа в случае, если ![]() :
:
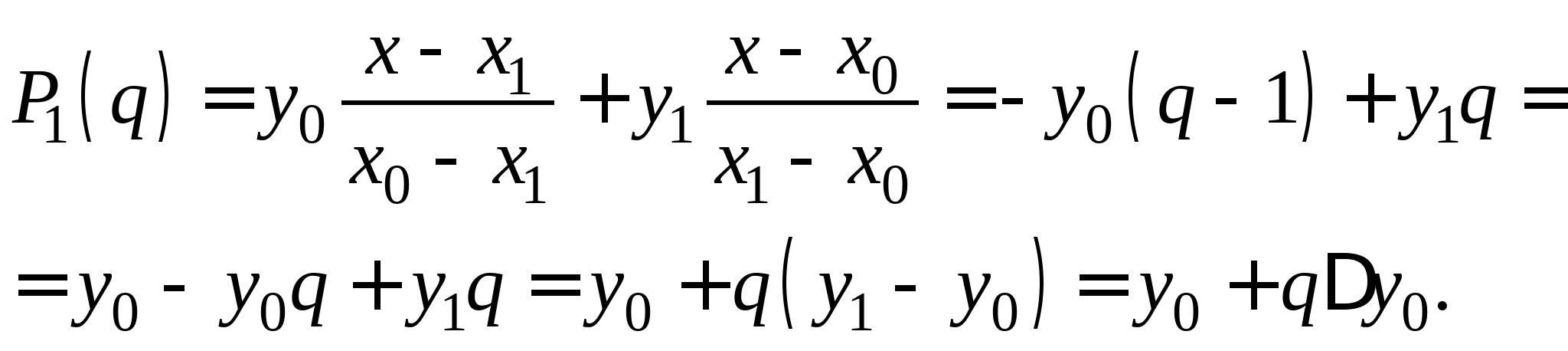
Получили формулу линейной интерполяции (5.25):
![]() .
.
Здесь ![]() - табличные разности первого порядка.
- табличные разности первого порядка.
При ![]() получаем формулу квадратичной интерполяции (5.26):
получаем формулу квадратичной интерполяции (5.26):
![]() .
.
Здесь ![]() - табличные разности второго порядка, и так далее. Продолжая этот процесс, окончательно получим:
- табличные разности второго порядка, и так далее. Продолжая этот процесс, окончательно получим:
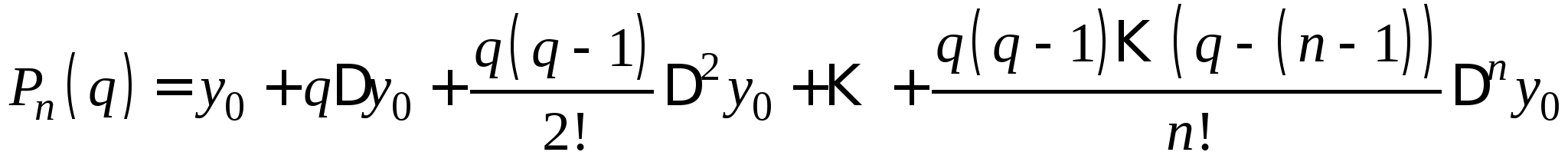 .
.
Эта формула называется первой интерполяционной формулой Ньютона (сравните с формулой (5.24)). Для нее справедлива оценка остаточного члена (5.27) и (5.28).
Если обозначить через ![]() , то с учетом введенного обозначения, получим:
, то с учетом введенного обозначения, получим:
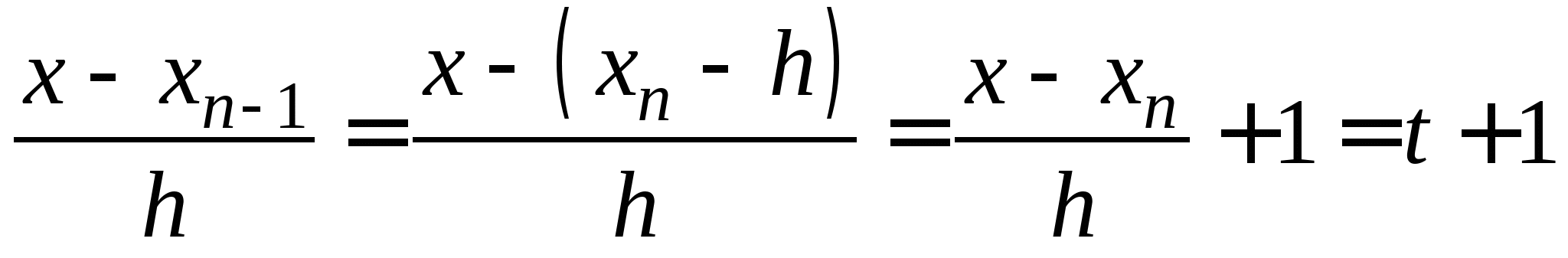 , …,
, …,
![]() .
.
Тогда формула (5.43) примет вид:
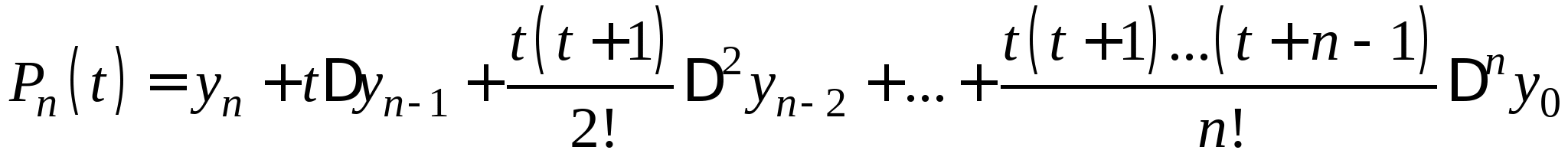 .
.
Эта формула называется второй интерполяционной формулой Ньютона (сравните с формулой (5.39)). Для нее справедлива оценка остаточного члена (5.40).
§5.6. Метод наименьших квадратов для обработки результатов экспериментов.
Данный метод относится к классу аппроксимационных методов. Идея метода состоит в том, чтобы по данным эксперимента построить приближенно функцию, отображающую зависимость ее от ![]() , в виде многочлена с тем расчетом, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальна. Будем строить функцию в виде многочлена
, в виде многочлена с тем расчетом, чтобы сумма квадратов отклонений построенной функции от экспериментальной в узловых точках была минимальна. Будем строить функцию в виде многочлена
![]() .
.
Используем для построения результаты эксперимента:
Таблица 5.3
|
|
|
| … |
|
|
|
|
| … |
|
Построить многочлен, значит, определить его коэффициенты ![]() . Для этого введем функцию
. Для этого введем функцию ![]() и потребуем, чтобы
и потребуем, чтобы ![]() , где
, где ![]() - отклонение функции от экспериментальной в узлах
- отклонение функции от экспериментальной в узлах ![]() .
.
Используя вид ![]() , получим:
, получим:
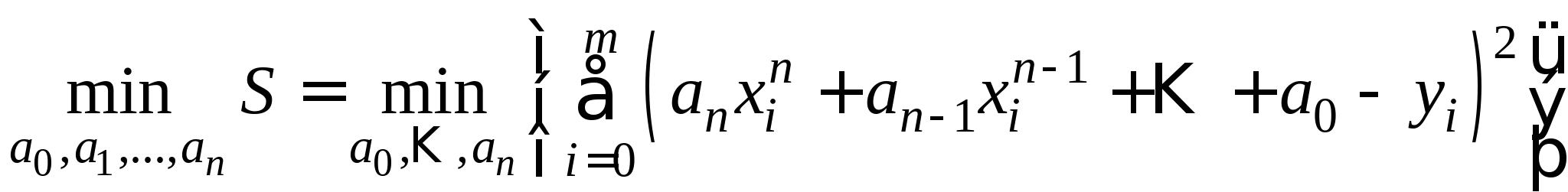 .
.
Необходимыми условиями экстремума функции ![]() является равенство нулю ее первой производной по всем переменным
является равенство нулю ее первой производной по всем переменным 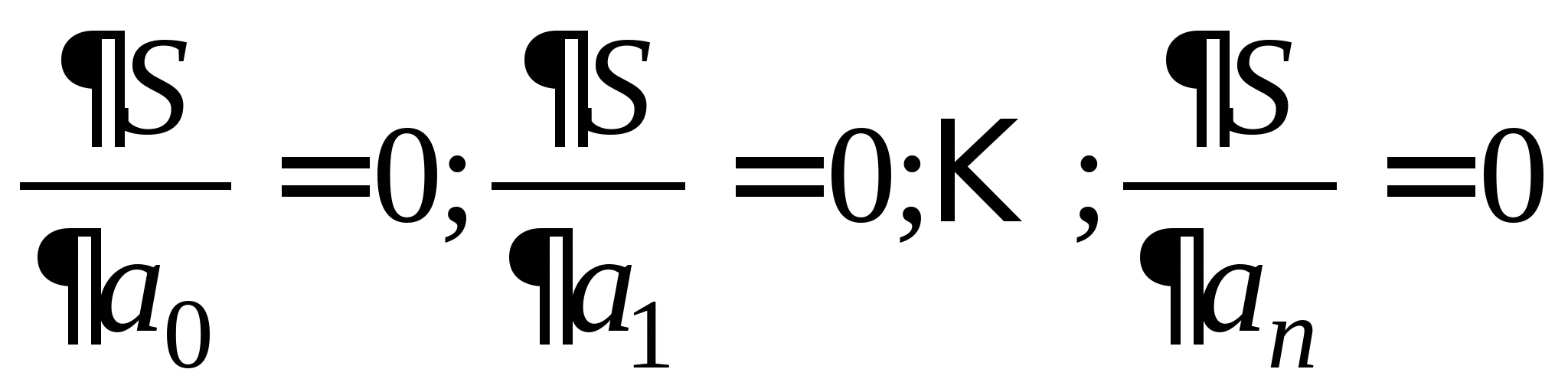 . Расписав эти условия, получим СЛАУ вида:
. Расписав эти условия, получим СЛАУ вида:
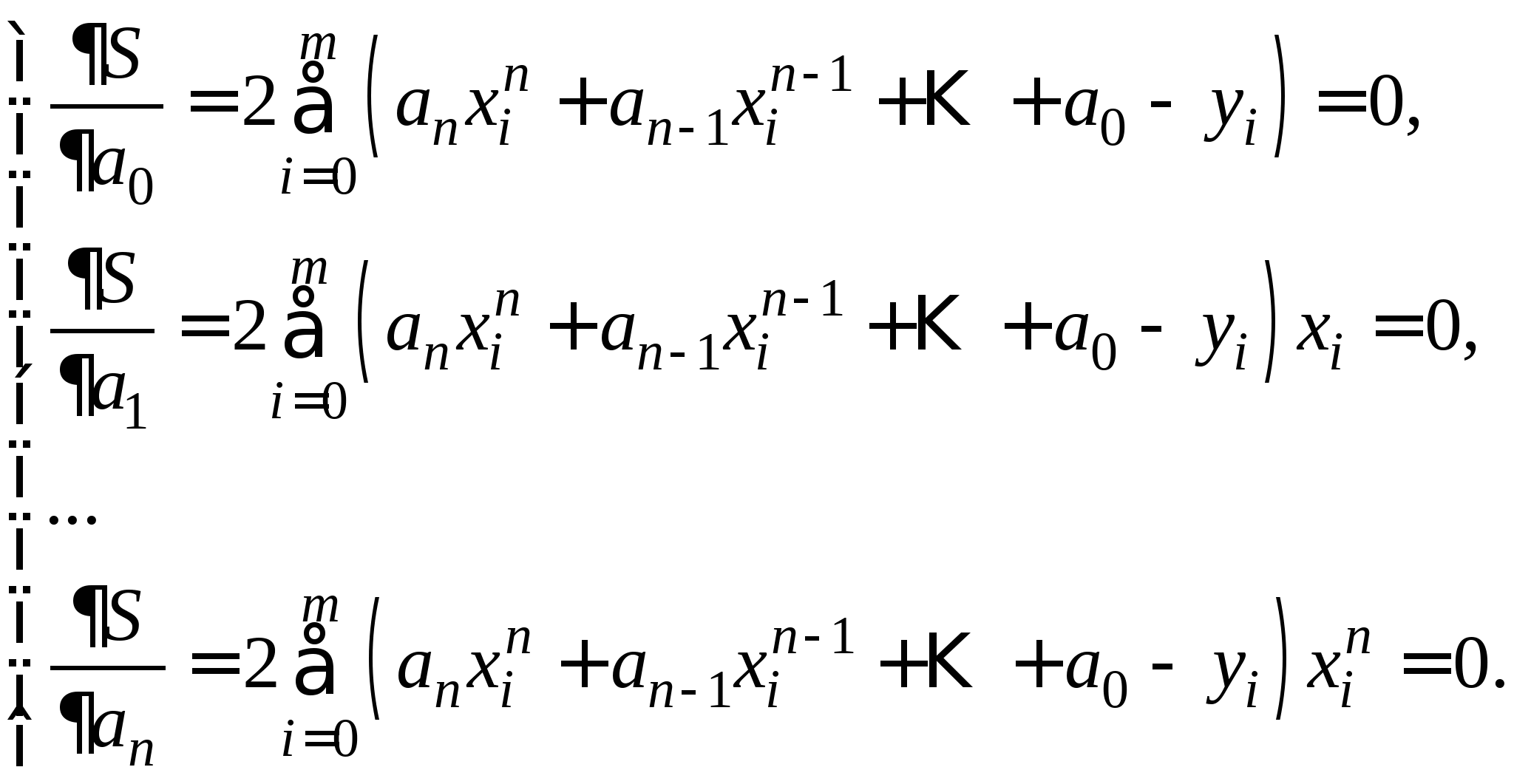
Запишем систему для определения ![]() в нормальной форме:
в нормальной форме:
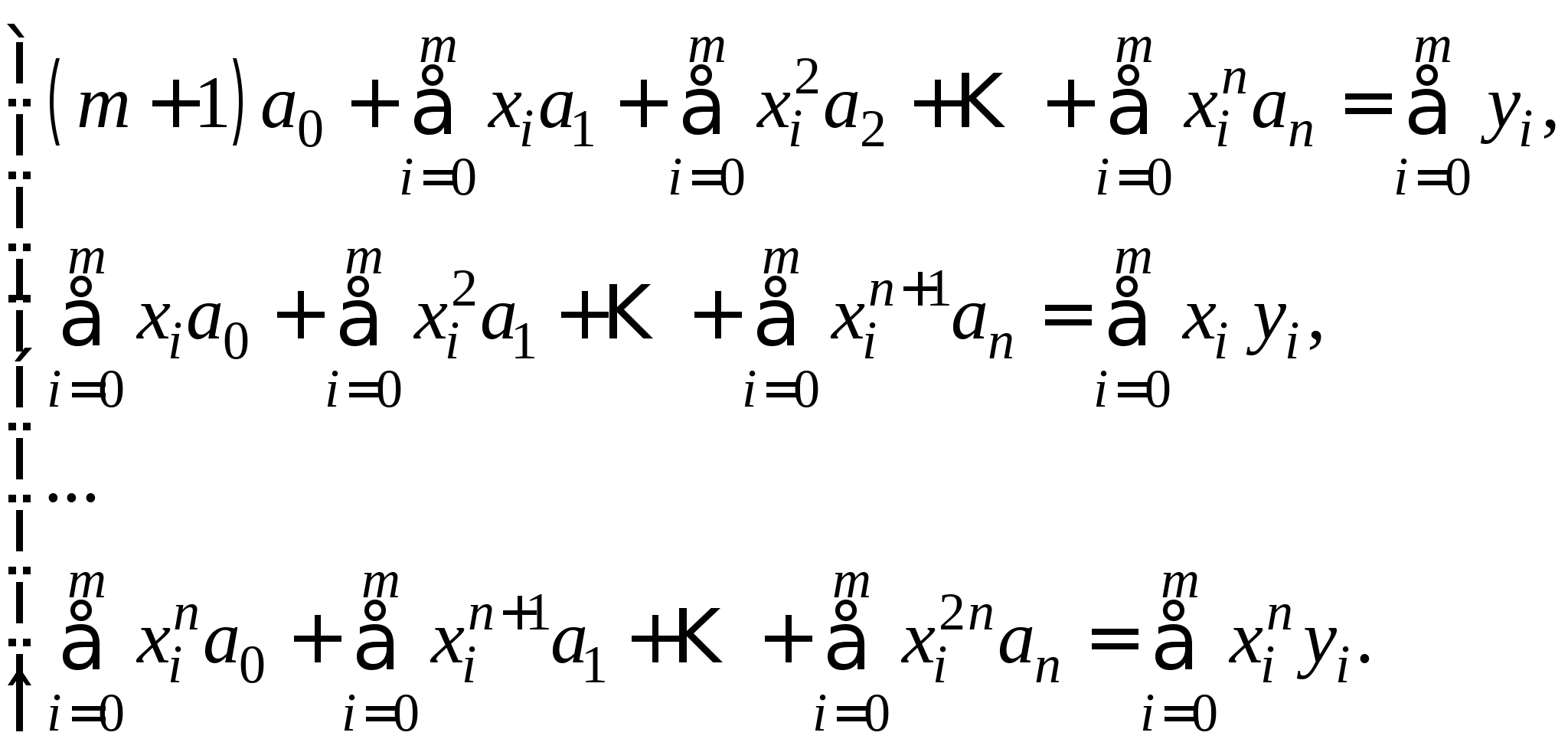
Решим систему одним из известных методов и найдем коэффициенты ![]() , которые затем подставим в искомый многочлен.
, которые затем подставим в искомый многочлен.
Запишем алгоритм метода наименьших квадратов.
Ввести таблицу чисел ![]() .
.
Вычислить ![]() .
.
Решить любым известным методом полученную систему линейных алгебраических уравнений и получить коэффициенты искомого многочлена ![]() .
.
Пример 5.2. По заданной системе точек (см. Табл.5.3) из примера 5.1 построить аппроксимационные многочлены первого ![]() и второго порядков
и второго порядков ![]() методом наименьших квадратов.
методом наименьших квадратов.
Для построения полинома первого порядка необходимо вычислить следующие суммы
![]() ,
,
и решить СЛАУ относительно неизвестных коэффициентов ![]() вида:
вида:
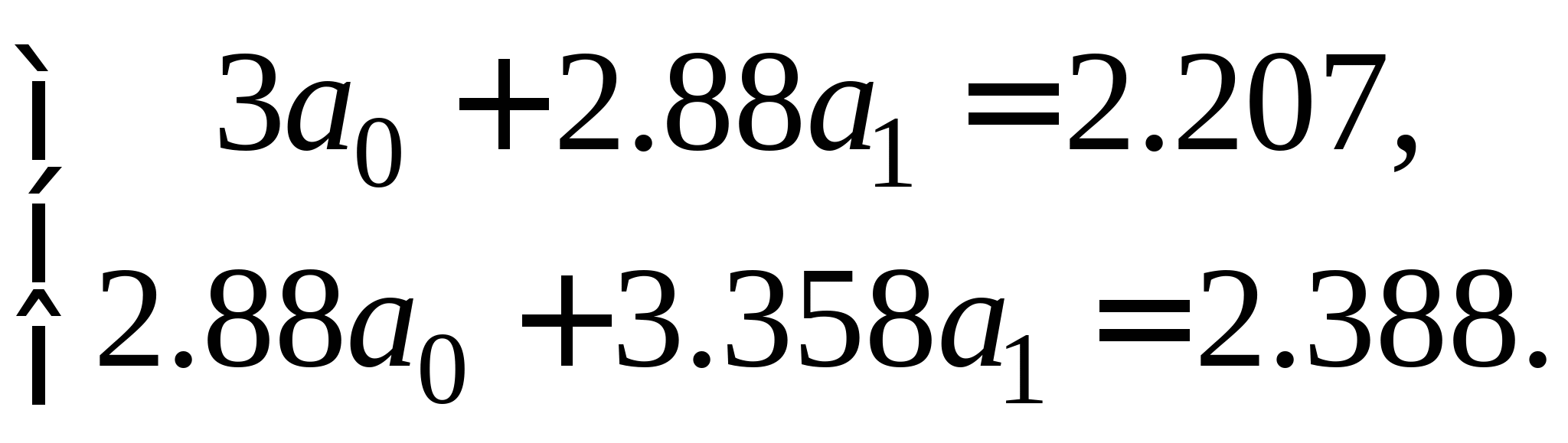
Значения неизвестных коэффициентов равны:
![]()
Тогда искомый многочлен первого порядка будет иметь вид:
![]() .
.
Погрешность вычислений по данной формуле в контрольной точке ![]() составляет
составляет
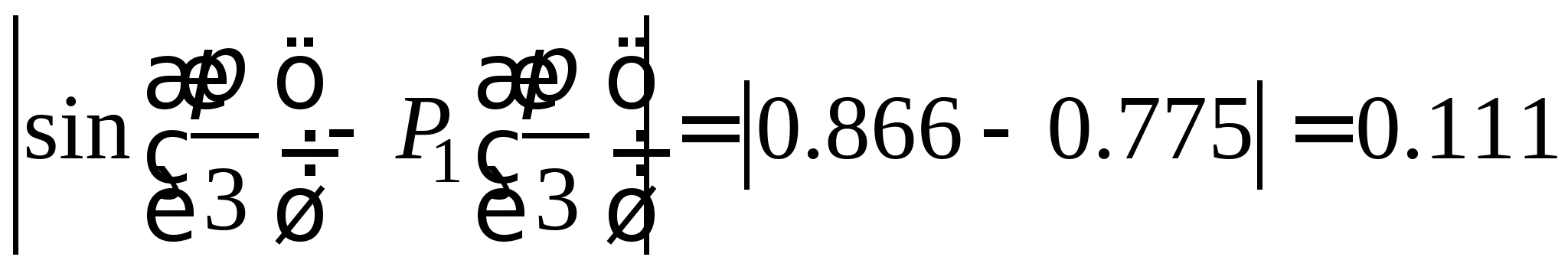 .
.
Для построения многочлена второго порядка дополнительно необходимо вычислить следующие суммы
![]() ,
,
и решить СЛАУ относительно неизвестных коэффициентов ![]() вида:
вида:
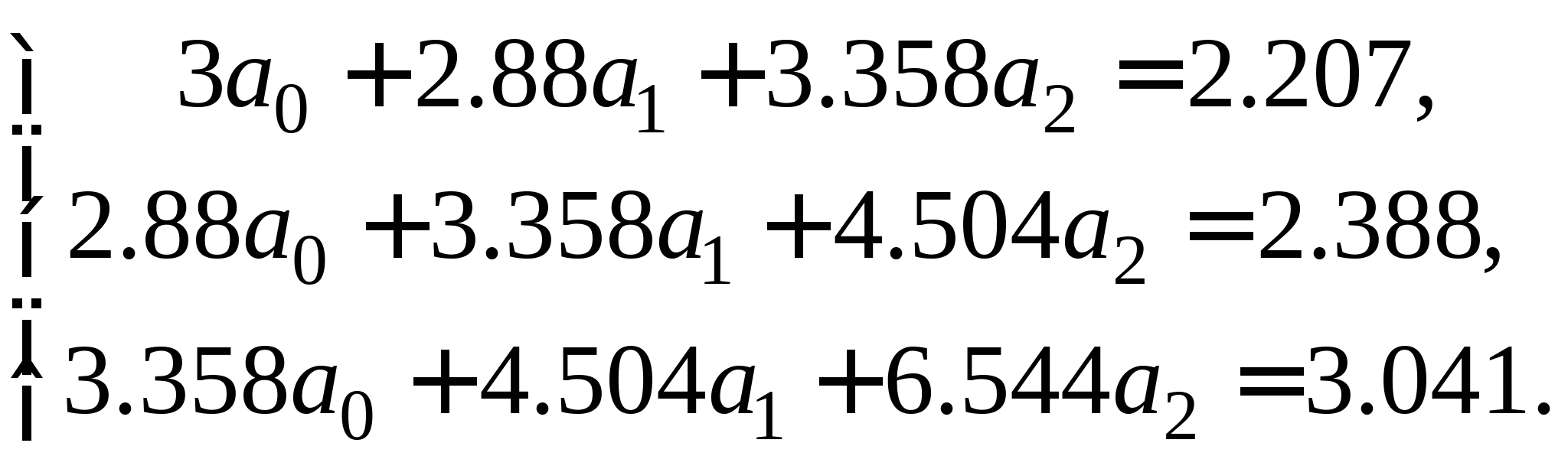
Значения неизвестных коэффициентов равны:
![]() .
.
Тогда искомый многочлен второго порядка будет иметь вид:
![]() .
.
На рисунке 5.2 приведены графики искомых полиномов и табличной функции. Погрешность вычислений по данной формуле в контрольной точке равна:
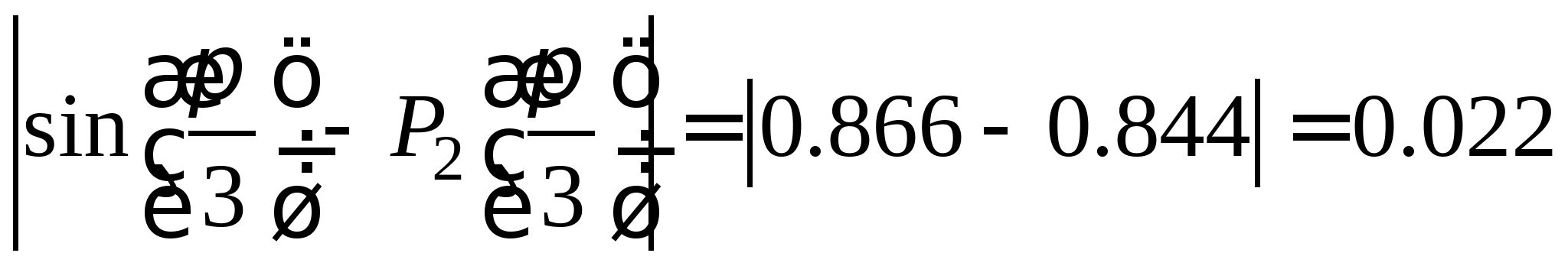
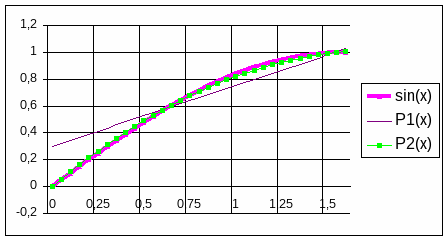
.
Рис.5.2.
§5.7. Обработка экспериментальных данных некоторыми другими функциями.
Во многих случаях экспериментальные данные могут быть аппроксимированы не только полиномами различных порядков. Это обусловлено физическими, экономическими и другими законами исследуемых процессов, а также опытом испытателя. Если, например, испытатель уверен, что параметры какого-либо прибора, снятые с испытательного стенда, по своим физическим характеристикам являются близкими к экспоненциальным, то нет смысла аппроксимировать их полиномами. Также экспериментальные данные могут быть аппроксимированы показательными, логарифмическими, тригонометрическими и другими функциями.
В качестве примера рассмотрим аппроксимацию экспериментальных данных, приведенных в таблице 5.3, экспоненциальной функцией ![]() , где
, где ![]() и
и ![]() - параметры искомой функции, которые требуется определить.
- параметры искомой функции, которые требуется определить.
Сформулированную задачу будем решать методом наименьших квадратов. Функция ![]() в этом случае запишется так:
в этом случае запишется так:
![]() .
.
Расписав необходимые условия экстремума этой функции по переменным ![]() и
и ![]() , и, сделав несложные преобразования, получим СЛАУ второго порядка вида:
, и, сделав несложные преобразования, получим СЛАУ второго порядка вида:
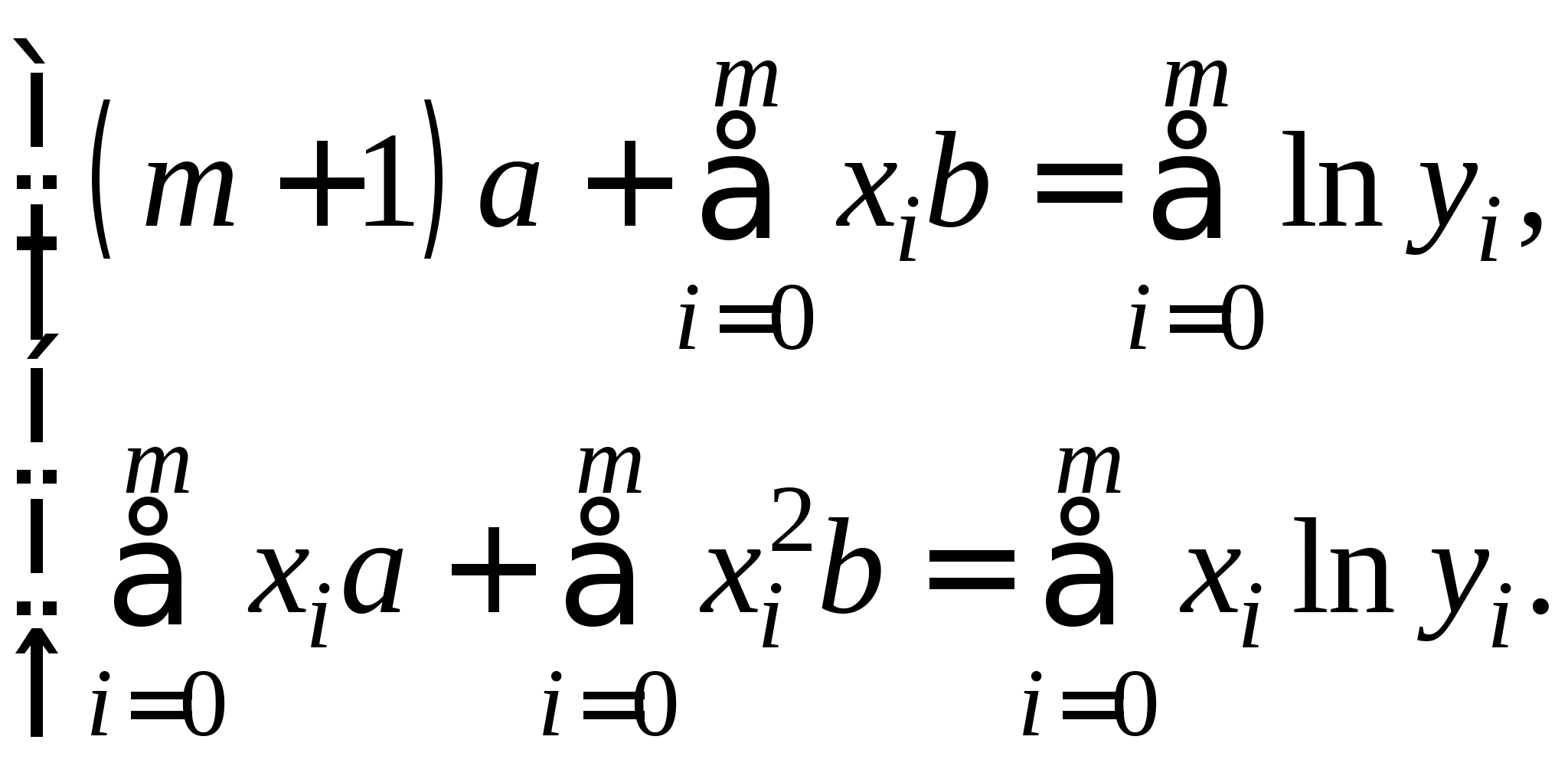
Решая эту систему любым известным методом, определим коэффициенты экспоненциальной функции ![]() и
и ![]() .
.
Пример 5.3. По заданной в таблице 5.4 системе точек
Таблица 5.4.
|
| 0 | 0,7 | 1,39 | 1,65 | 1,93 | 2,2 | 2,45 | 2,79 |
|
| 0,05 | 0,07 | 0,24 | 0,42 | 0,66 | 0,78 | 0,89 | 1,07 |
методом наименьших квадратов построить аппроксимационную экспоненциальную функцию вида:
![]() .
.
Для построения необходимо вычислить следующее суммы:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
и решить СЛАУ второго порядка относительно неизвестных коэффициентов ![]() и
и ![]() :
:
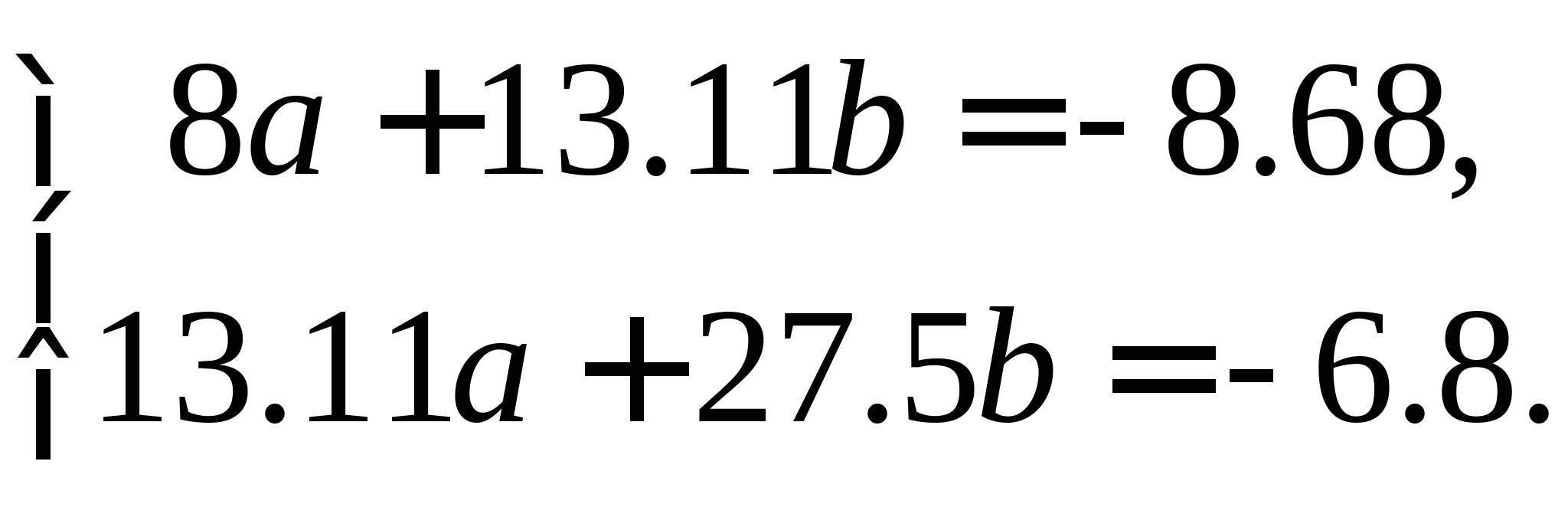
Значения неизвестных коэффициентов равны: ![]() ,
, ![]() .
.
Тогда искомая экспоненциальная функция будет иметь вид:
![]() .
.
График функции ![]() и ломаная
и ломаная ![]() , построенная по результатам, приведенным в таблице 5.4, изображены на рисунке 5.3.
, построенная по результатам, приведенным в таблице 5.4, изображены на рисунке 5.3.
Рис.5.3.
69
ГЛАВА 4. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
Пусть дана система линейных алгебраических уравнений (СЛАУ) вида
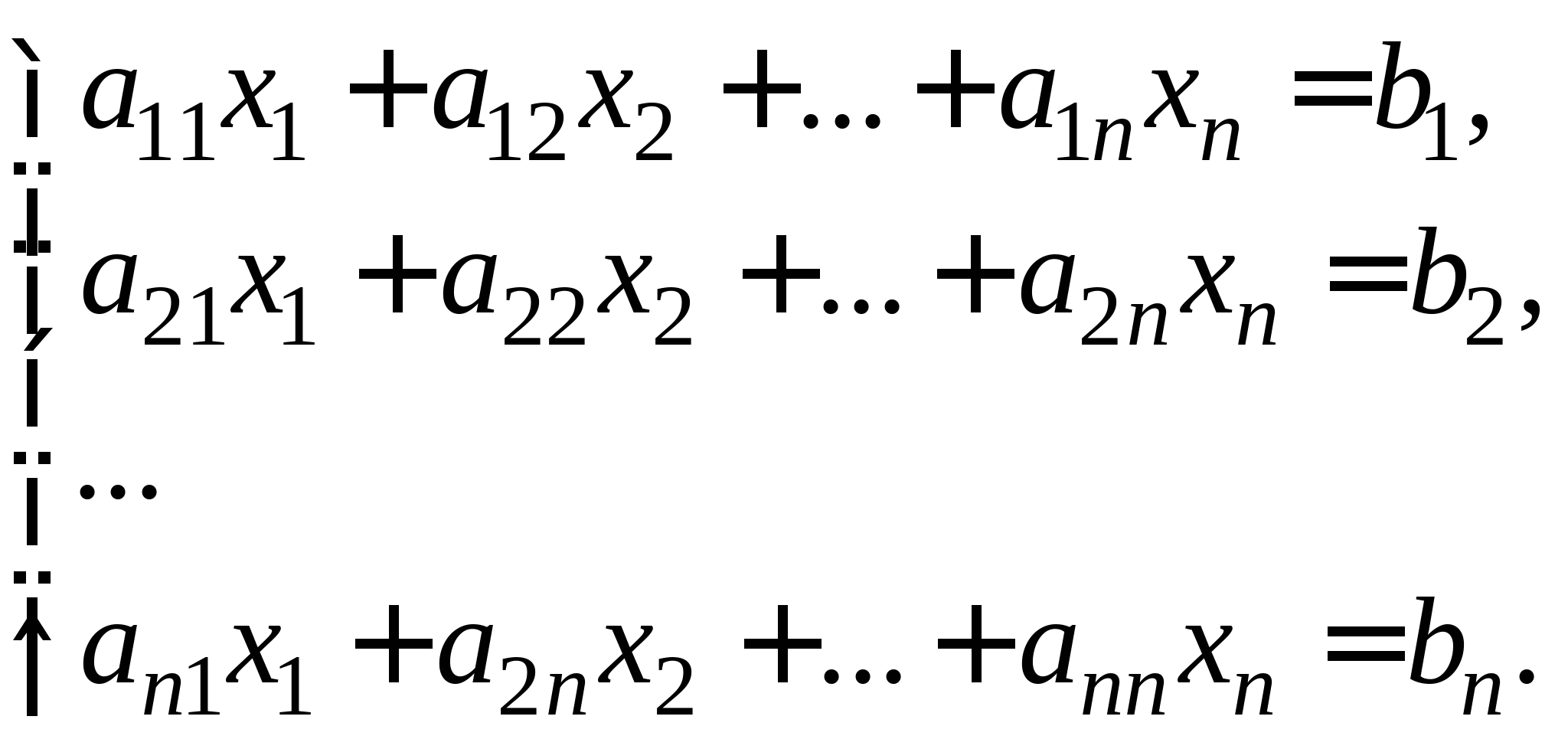 (4.1)
(4.1)
Вводя в рассмотрение матрицы
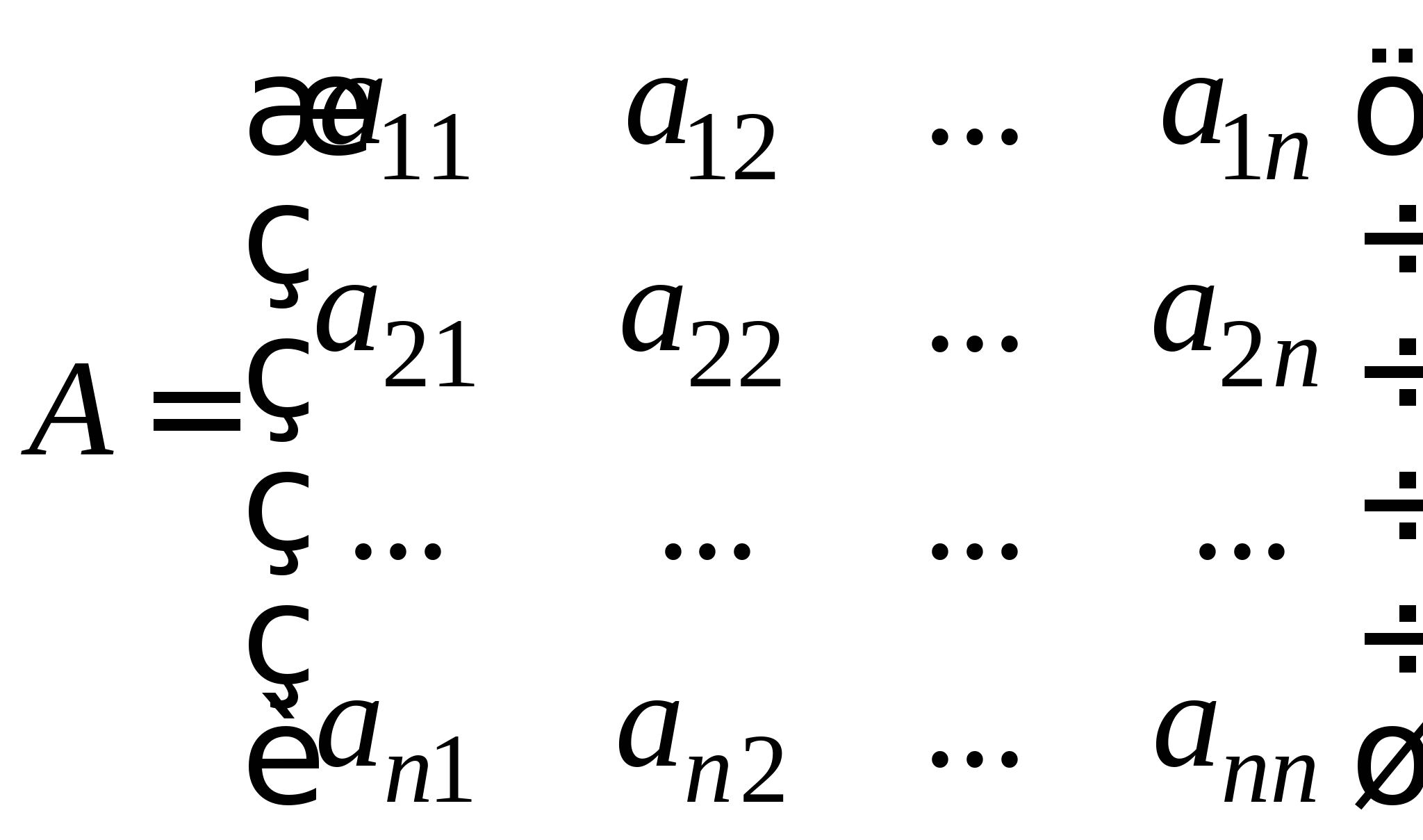 ,
, 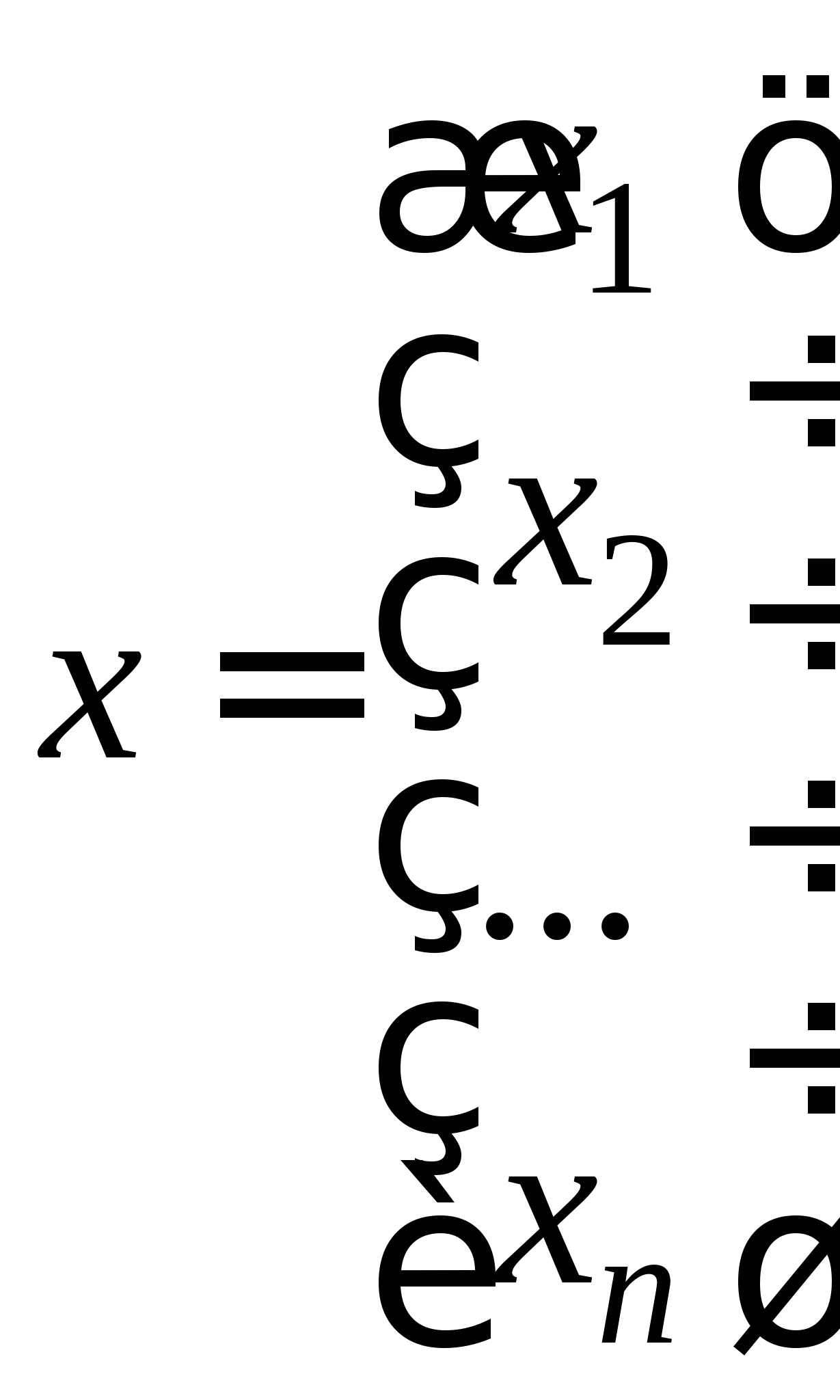 ,
, 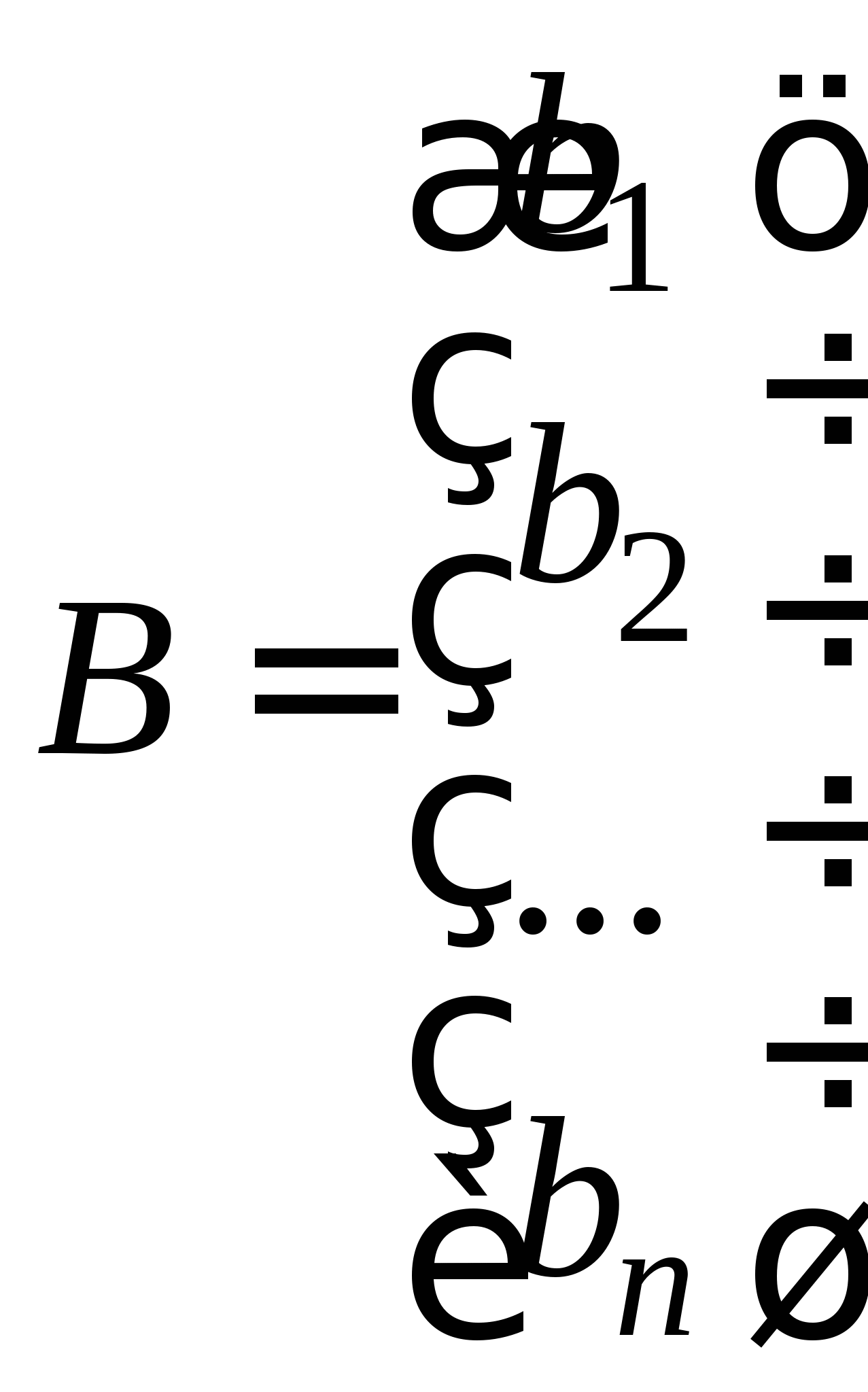 (4.2)
(4.2)
систему (4.1) можно записать в виде матричного уравнения
![]() . (4.3)
. (4.3)
Для решения систем линейных алгебраических уравнений существуют точные методы: метод Гаусса, с помощью обратной матрицы (матричный метод), по формулам Крамера. Однако, при большом числе неизвестных применение точных методов решения затруднено. В этом случае для нахождения корней системы (4.1) целесообразнее пользоваться приближенными (численными) методами, которые и будут рассмотрены в данной главе.
§4.1. Метод простых итераций для решения систем линейных алгебраических уравнений.
Пусть дана система линейных алгебраических уравнений вида (4.1).
Предположим, что диагональные элементы матрицы ![]() не равны нулю, т.е.
не равны нулю, т.е. ![]() (в случае равенства одного или нескольких из них нулю, с помощью перестановки уравнений или других эквивалентных преобразований можно добиться, чтобы они были отличны от нуля). Разделив
(в случае равенства одного или нескольких из них нулю, с помощью перестановки уравнений или других эквивалентных преобразований можно добиться, чтобы они были отличны от нуля). Разделив ![]() -ое уравнение системы на
-ое уравнение системы на ![]() , получим:
, получим:
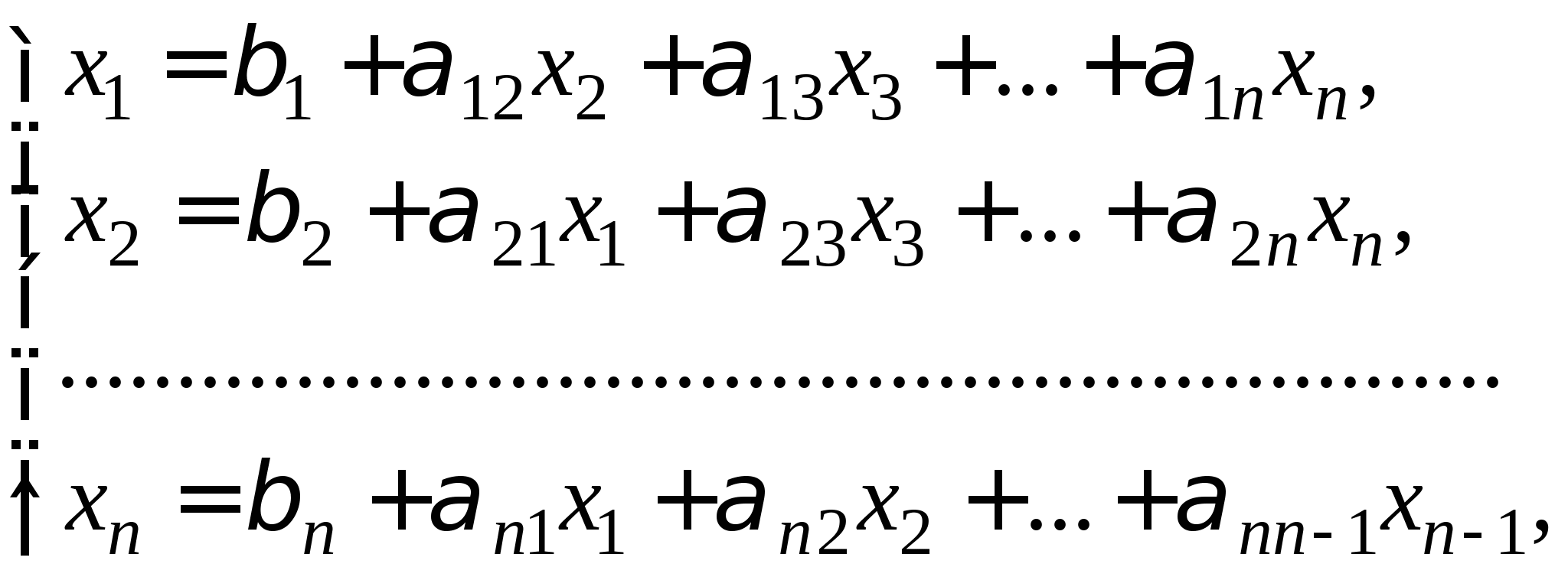 (4.4)
(4.4)
где коэффициенты 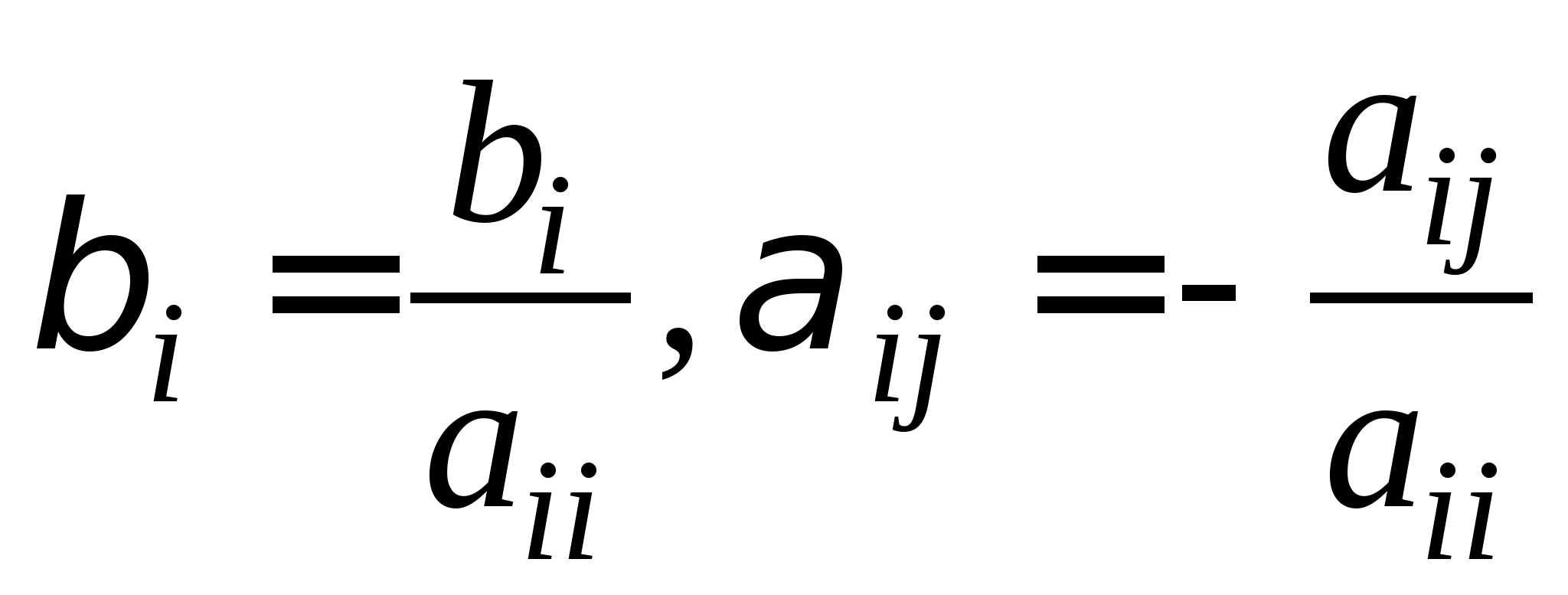 при
при ![]() .
.
Введем обозначения:
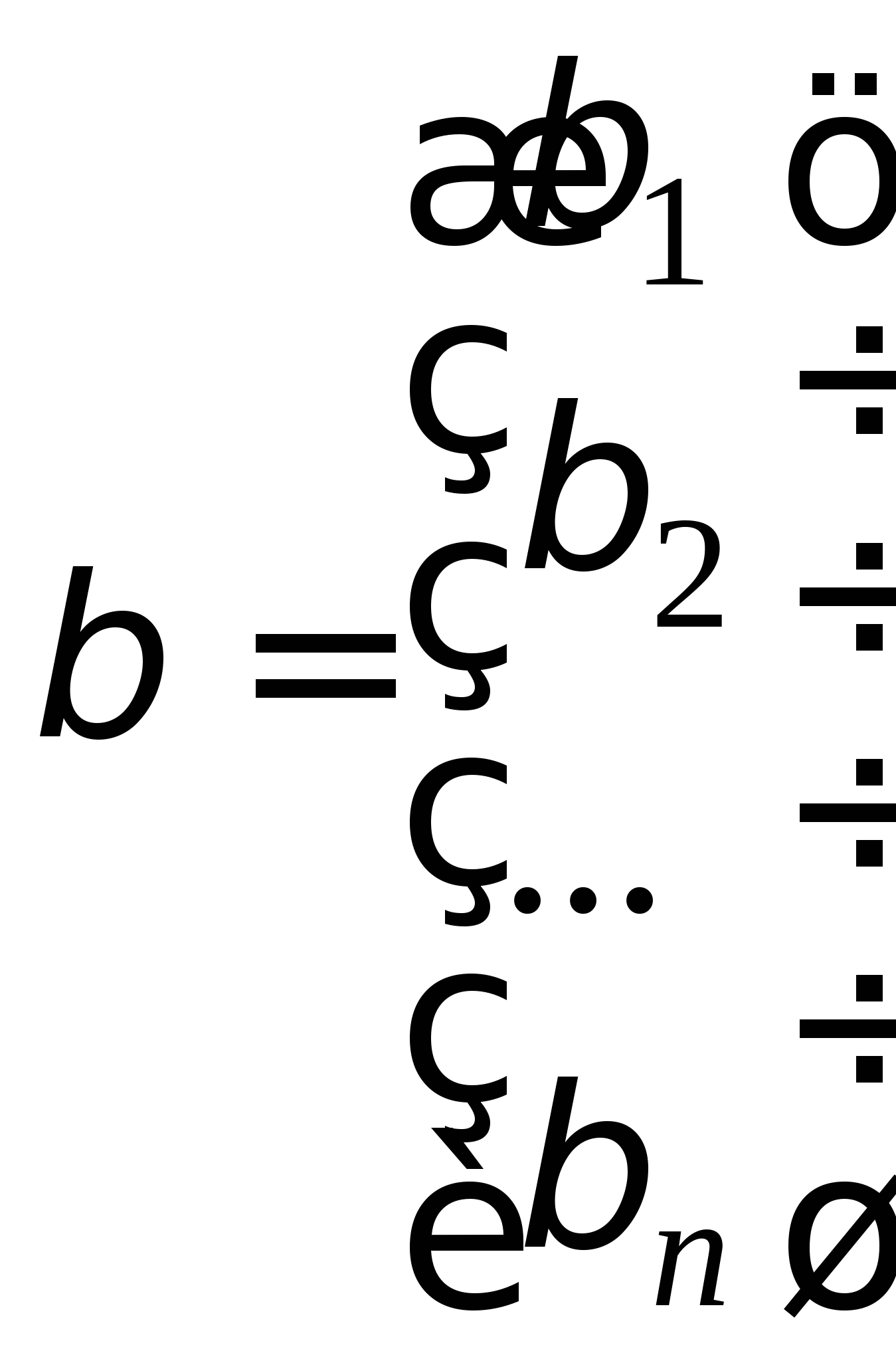 ,
, 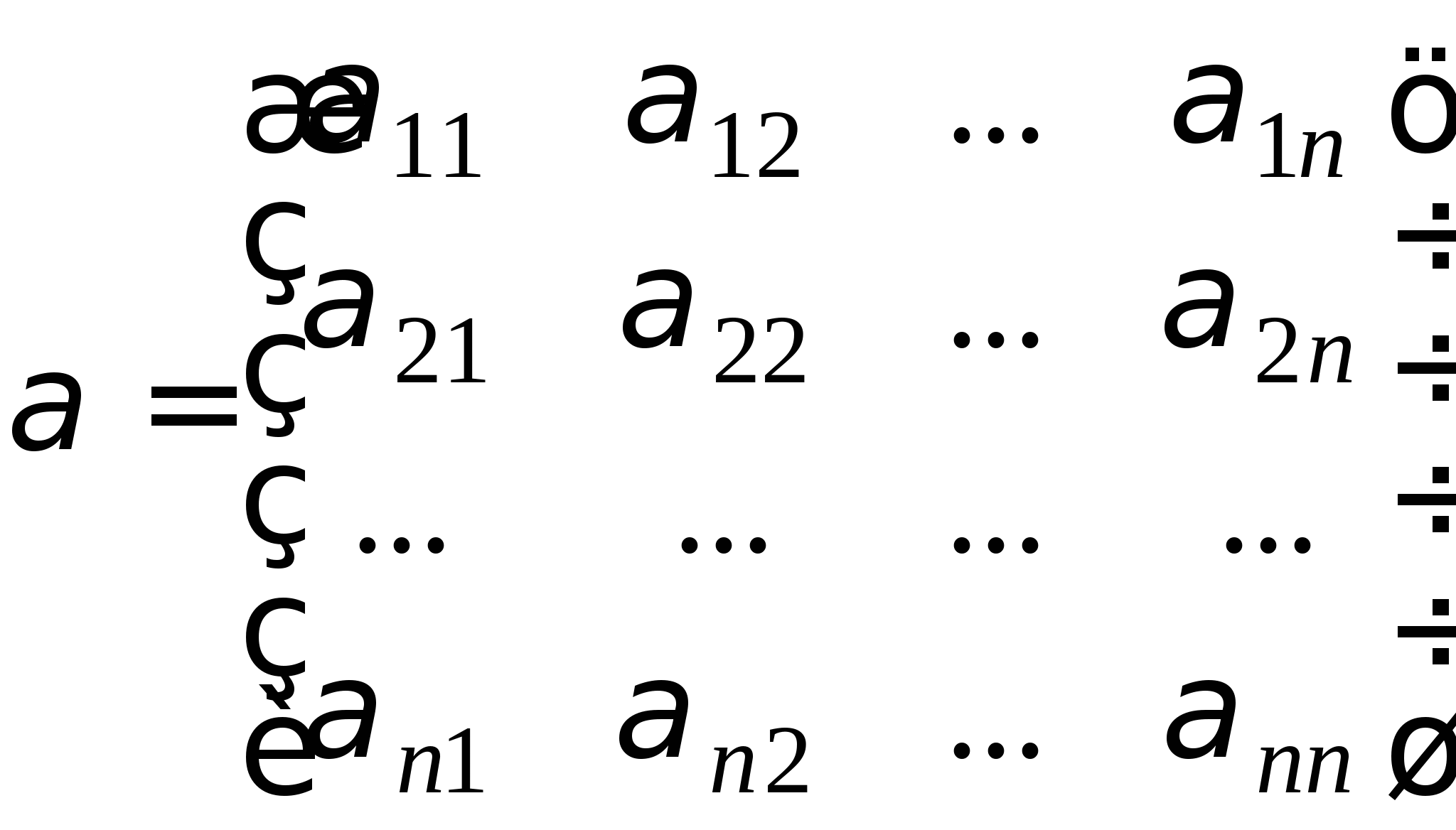 (4.5)
(4.5)
Тогда система (4.4) примет вид:
![]() (4.6)
(4.6)
Систему (4.6) будем решать методом последовательных приближений. Выбираем начальное приближение ![]() ; далее вычисляем следующие приближения:
; далее вычисляем следующие приближения:
![]() ,
, ![]() ,…,
,…, ![]() , … (4.7)
, … (4.7)
Если последовательность приближений ![]() является сходящейся, т.е. у нее существует предел
является сходящейся, т.е. у нее существует предел ![]() , то этот предел
, то этот предел ![]() является решением системы (4.6). Действительно,
является решением системы (4.6). Действительно,
![]() .
.
Получили ![]() , т.е.
, т.е. ![]() – является решением системы (4.6), а система (4.6) получена из системы (4.1), следовательно,
– является решением системы (4.6), а система (4.6) получена из системы (4.1), следовательно, ![]() будет являться решением исходной системы (4.1).
будет являться решением исходной системы (4.1).
Теорема 4.1 (достаточное условие сходимости итерационного процесса).
Если для приведенной системы ![]() выполнено хотя бы одно из условий:
выполнено хотя бы одно из условий:
а) 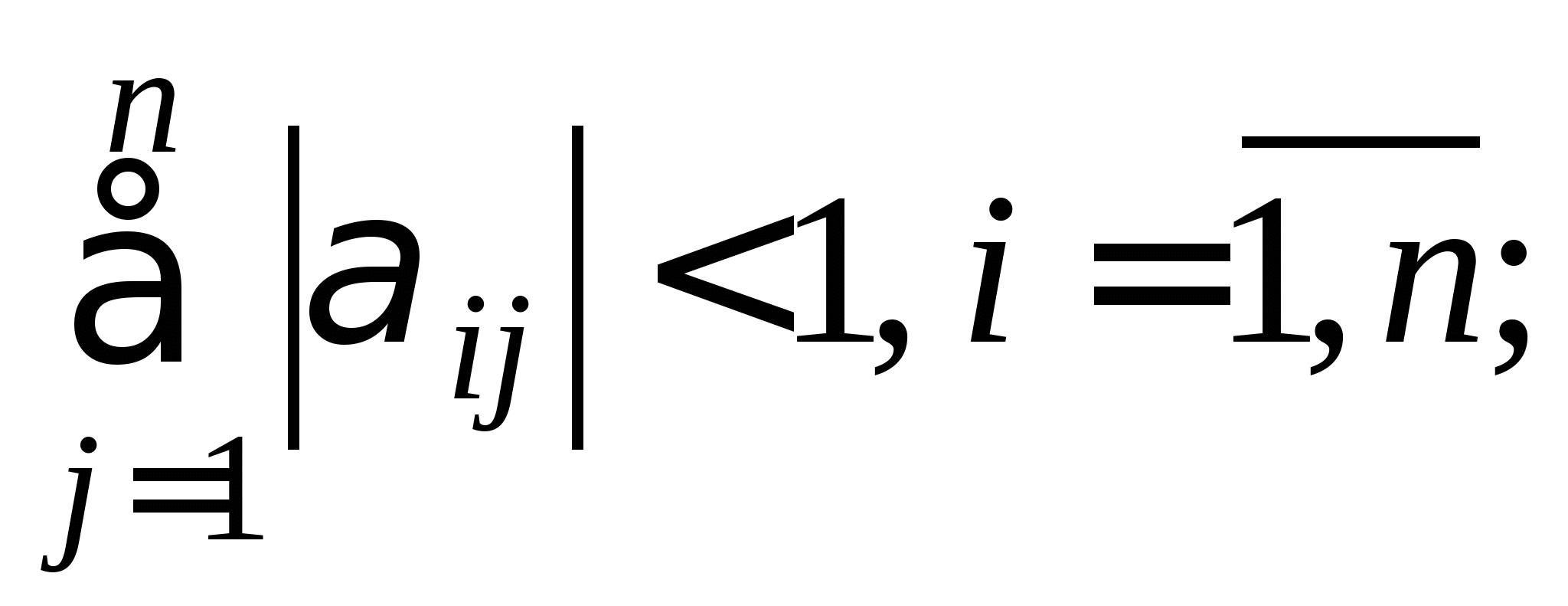
б) ![]() ,
,
то процесс итерации, заданный формулой ![]() , сходится к единственному решению этой системы, независимо от выбора начального приближения.
, сходится к единственному решению этой системы, независимо от выбора начального приближения.
В частности процесс итерации заведомо сходится, если элементы ![]() приведенной системы (4.4) удовлетворяют неравенству
приведенной системы (4.4) удовлетворяют неравенству ![]() , где
, где ![]() - число неизвестных системы.
- число неизвестных системы.
Следствие.
Для исходной системы (4.1) итерационный процесс сходится, если выполнены неравенства 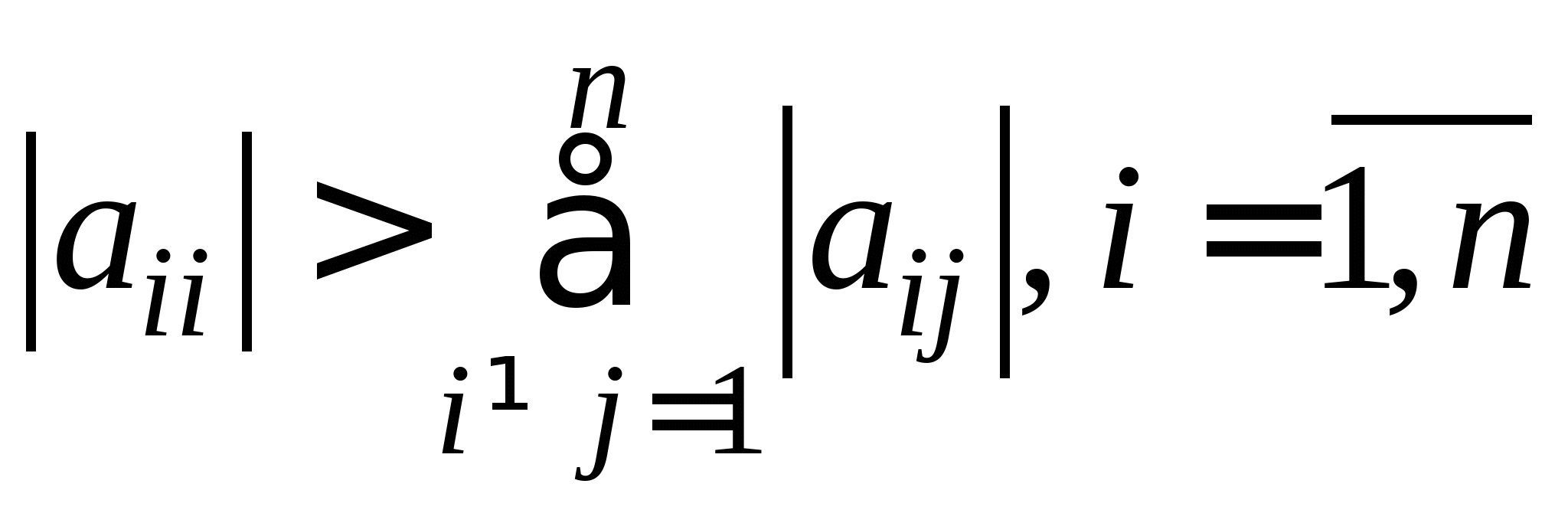 (то есть модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов, не считая свободных членов).
(то есть модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов, не считая свободных членов).
Теорема 4.2 (необходимое и достаточное условие сходимости процесса итерации для системы линейных уравнений).
Для сходимости процесса итераций ![]() при любом выборе начального приближения
при любом выборе начального приближения ![]() и любом свободном члене
и любом свободном члене ![]() необходимо и достаточно, чтобы собственные значения матрицы
необходимо и достаточно, чтобы собственные значения матрицы ![]() (т.е. корни характеристического уравнения
(т.е. корни характеристического уравнения ![]() ) были по модулю меньше единицы.
) были по модулю меньше единицы.
Приведение исходной системы к виду, удобному для применения сходящегося итерационного процесса.
Теорема сходимости итерационного процесса накладывает жесткие условия на коэффициенты системы (4.3). Однако, если ![]() , то с помощью элементарных преобразований системы (4.3) ее можно заменить эквивалентной системой
, то с помощью элементарных преобразований системы (4.3) ее можно заменить эквивалентной системой ![]() , такой, что условия теоремы сходимости будут выполнены.
, такой, что условия теоремы сходимости будут выполнены.
Умножим левую и правую часть соотношения (4.3) слева на матрицу ![]() , где
, где ![]() - матрица с малыми по модулю элементами.
- матрица с малыми по модулю элементами.
Проведем преобразования:
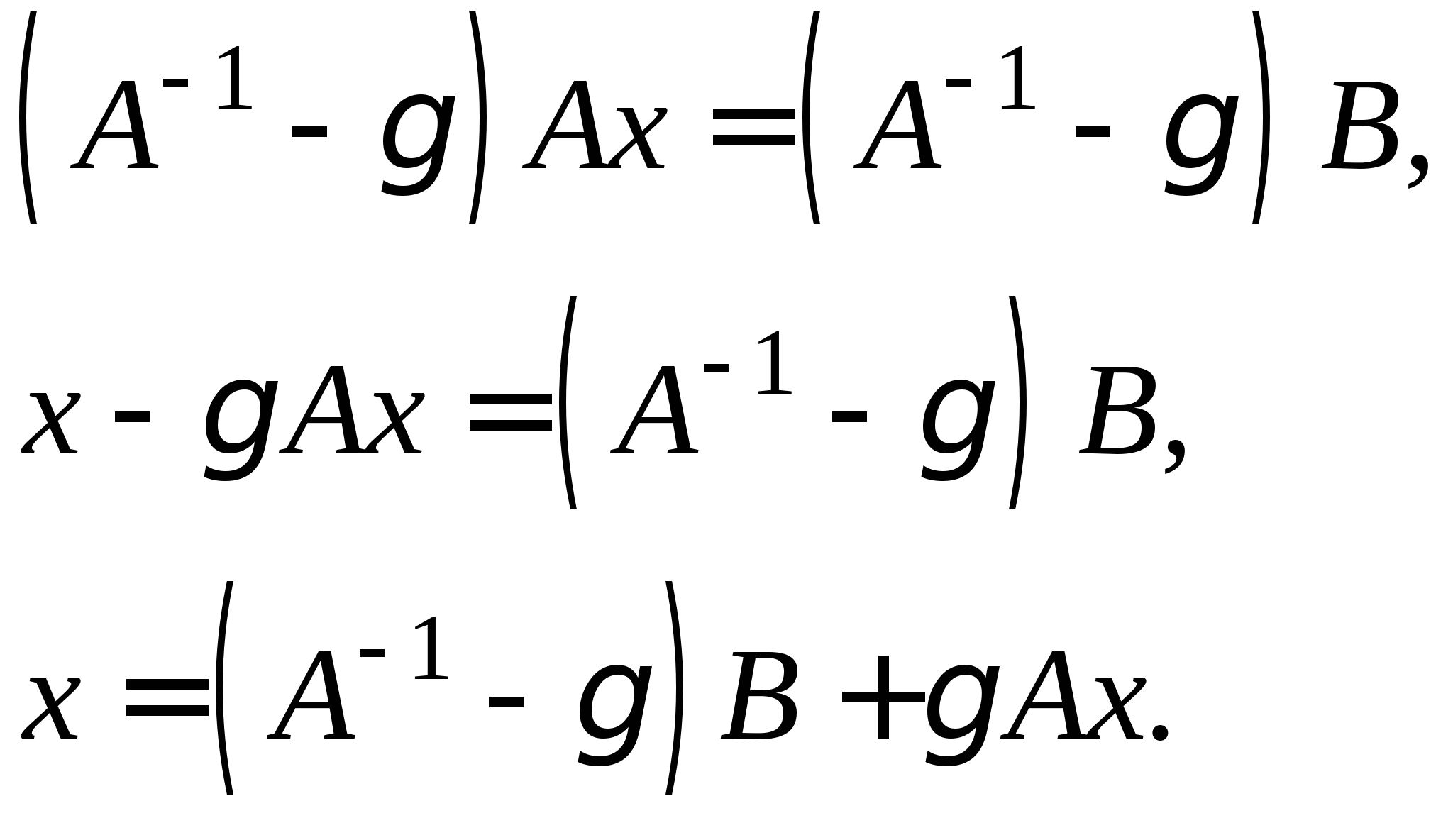
Если обозначить ![]() ,
, ![]() , то получим
, то получим ![]() .
.
Если элементы матрицы ![]() достаточно малы по модулю, т.е.
достаточно малы по модулю, т.е. ![]() , то элементы матрицы
, то элементы матрицы ![]() будут удовлетворять достаточному условию сходимости итерационного процесса.
будут удовлетворять достаточному условию сходимости итерационного процесса.
Итерационный процесс заканчивается, если для двух приближений ![]() и
и ![]() выполнено условие
выполнено условие 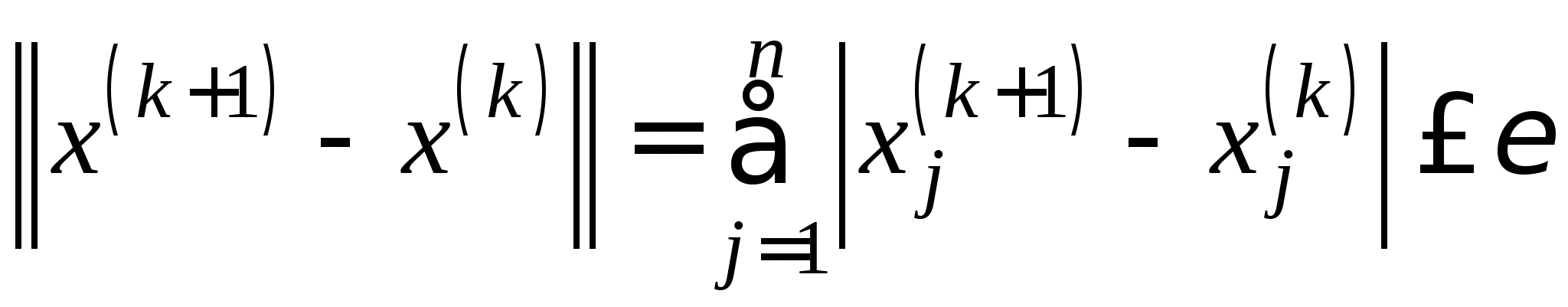 , где
, где ![]() - заданная точность.
- заданная точность.
§4.2. Метод Зейделя.
М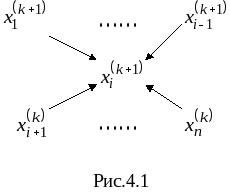
етод Зейделя представляет собой некоторую модификацию метода простых итераций. Основная его идея состоит в том, что при вычислении ![]() -го приближения неизвестной
-го приближения неизвестной ![]() учитываются уже вычисленные ранее
учитываются уже вычисленные ранее ![]() -е приближения неизвестных
-е приближения неизвестных ![]() . Т.е. найденное
. Т.е. найденное ![]() -е приближение сразу же используется для получения
-е приближение сразу же используется для получения ![]() -го приближения последующих координат (Рис.4.1).
-го приближения последующих координат (Рис.4.1).
Предполагая, что ![]() -е приближения
-е приближения ![]() корней системы (4.4) известны,
корней системы (4.4) известны, ![]() -е приближения корней будут находиться по следующим итерационным формулам метода Зейделя:
-е приближения корней будут находиться по следующим итерационным формулам метода Зейделя:
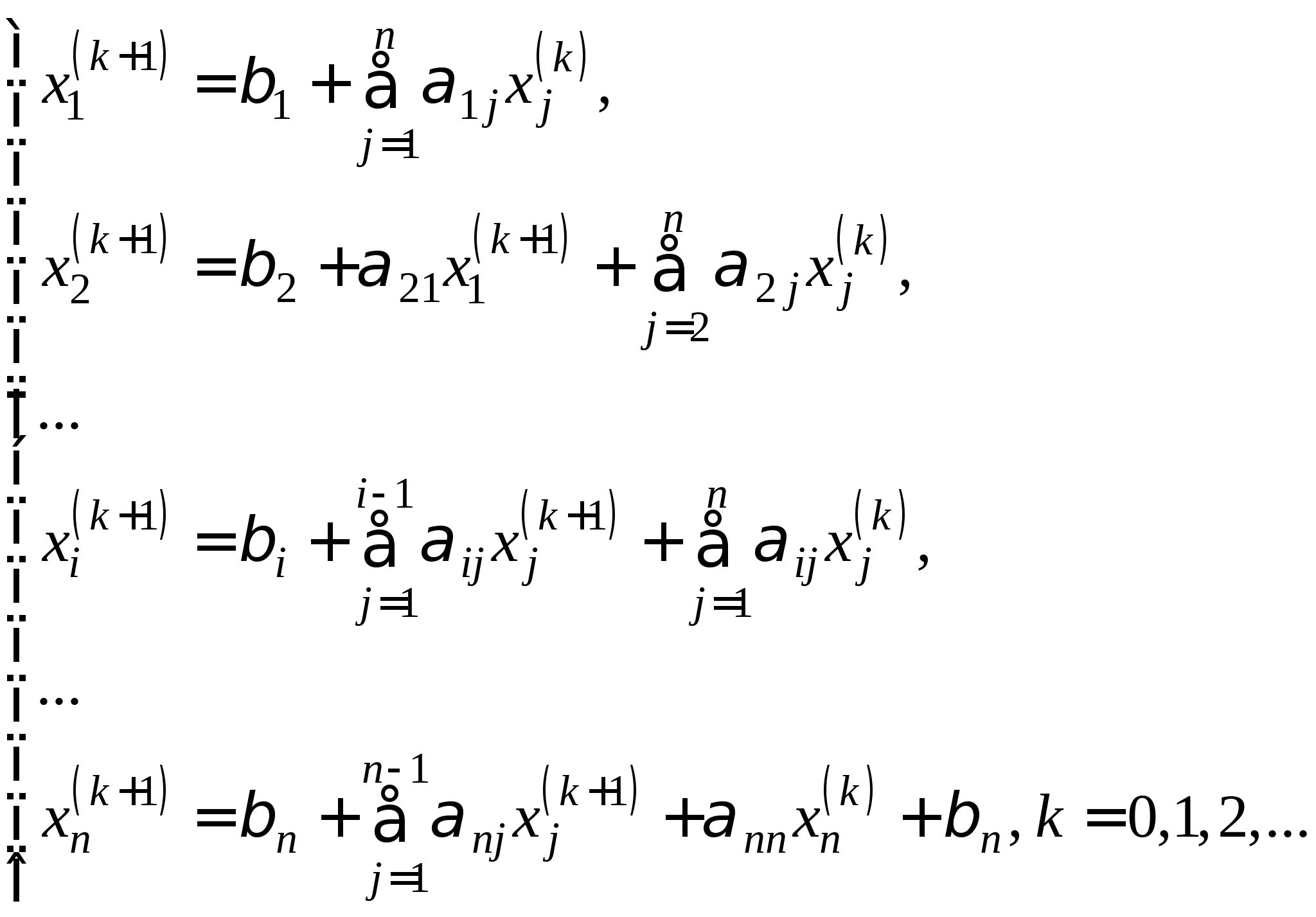 . (4.8)
. (4.8)
Теорема 4.3 (достаточное условие сходимости метода Зейделя).
Если для приведенной системы ![]() выполнено хотя бы одно из условий:
выполнено хотя бы одно из условий:
1) ![]() , где
, где 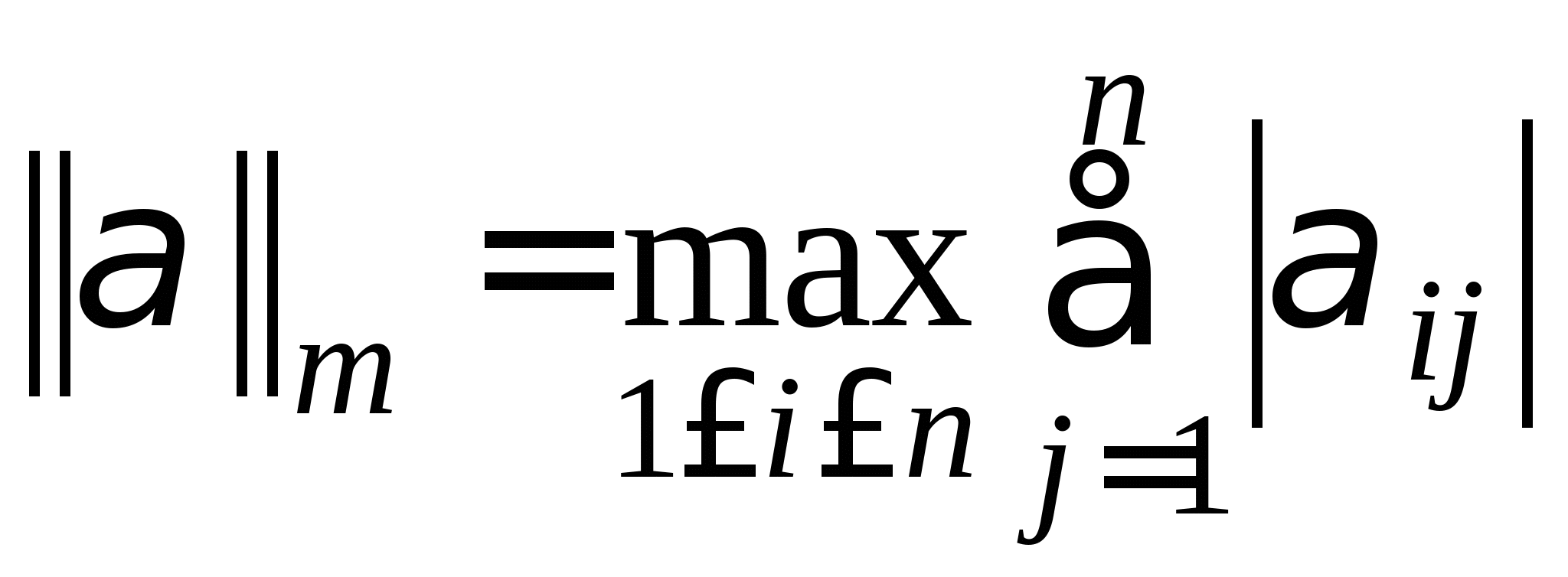 ;
;
2) ![]() , где
, где ![]() ;
;
3) ![]() , где
, где 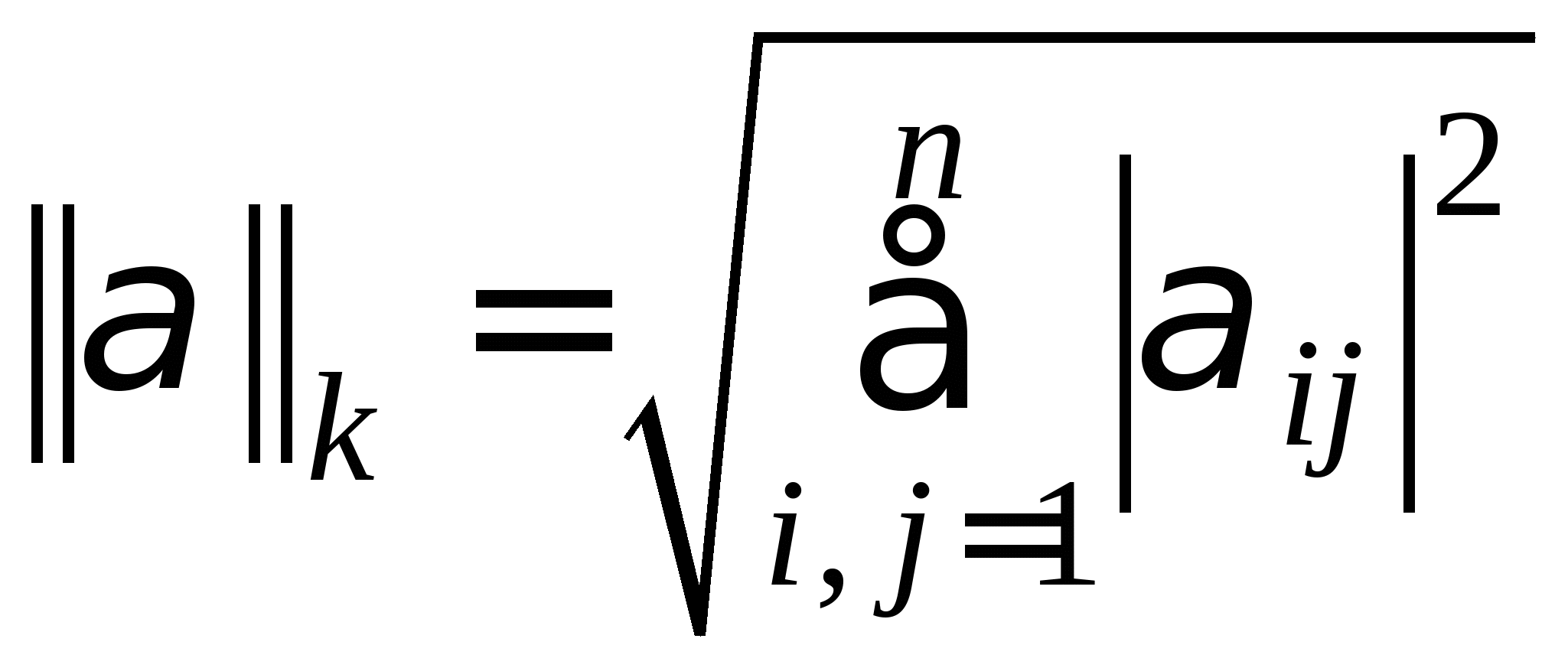 ,
,
то процесс Зейделя сходится к единственному решению системы при любом выборе начального вектора.
Запишем систему (4.8) в сокращенном виде:
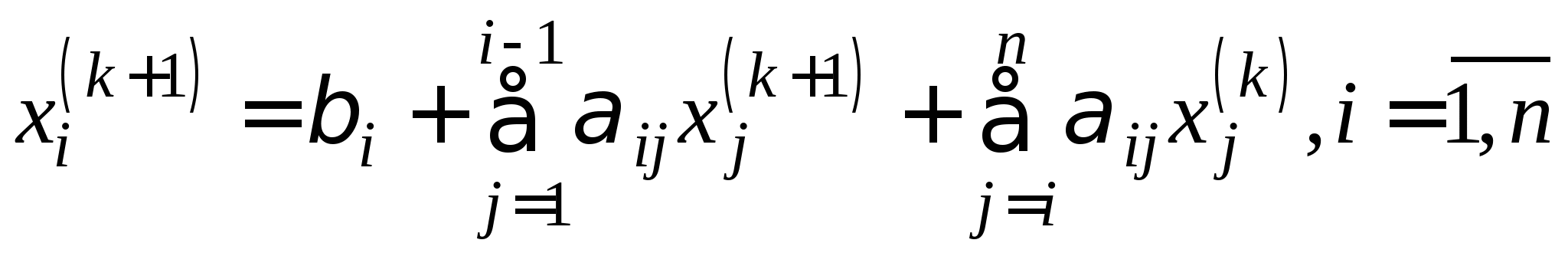 (4.9)
(4.9)
Введем обозначения: ![]() , где
, где
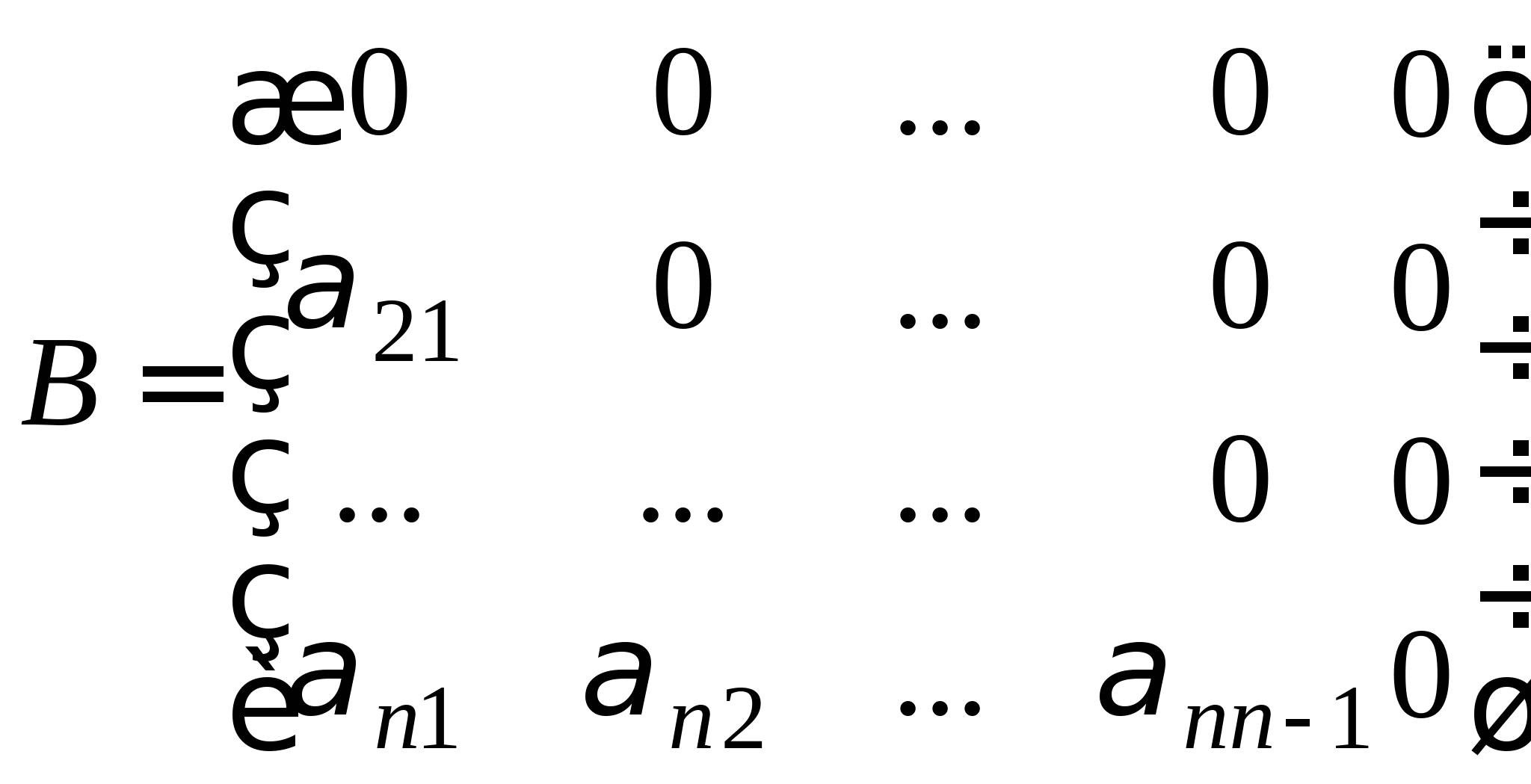 ,
,  .
.
Тогда формулу (4.9) можем переписать в матричном виде:
![]() , (4.10)
, (4.10)
где
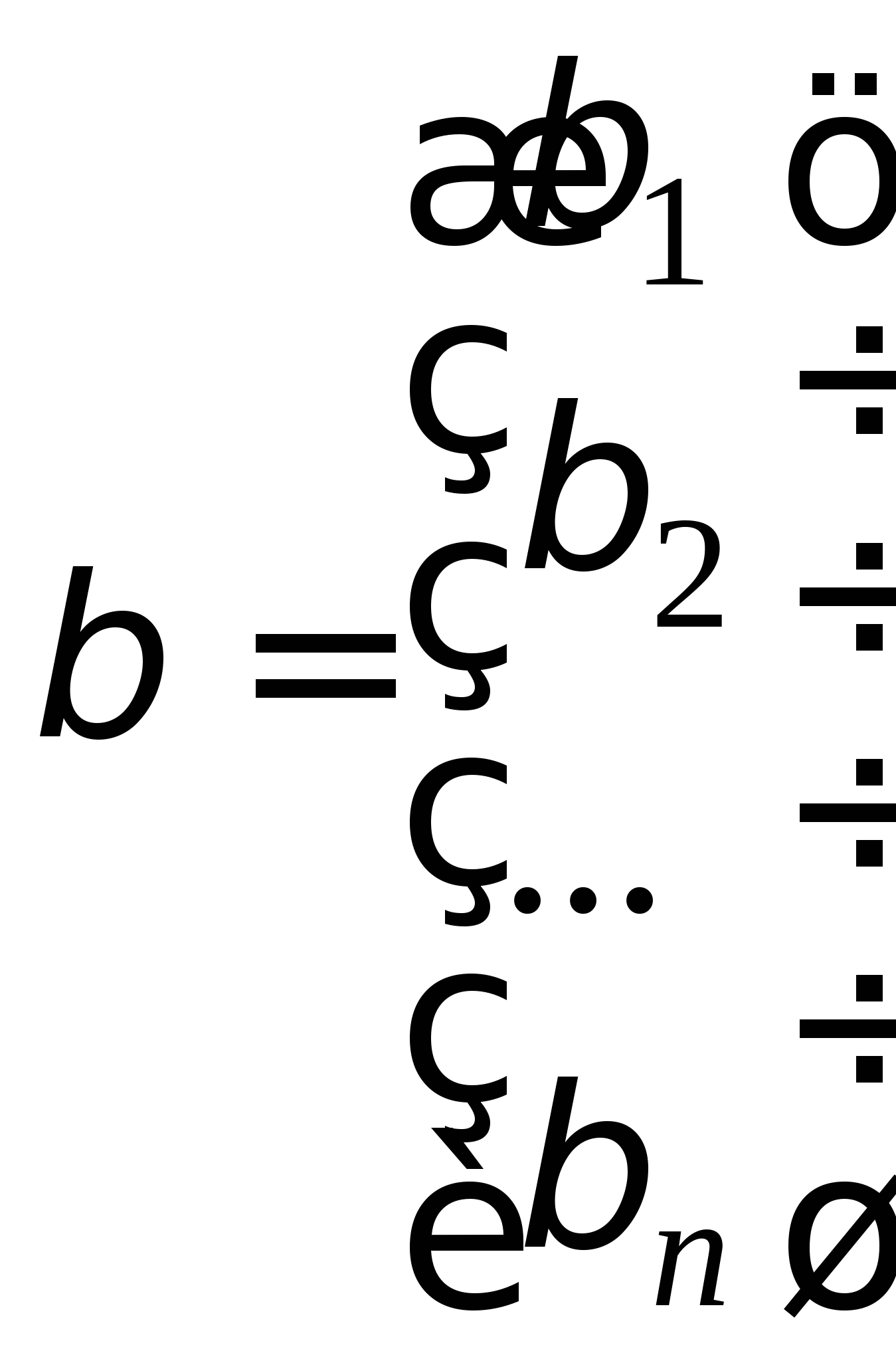 ,
, 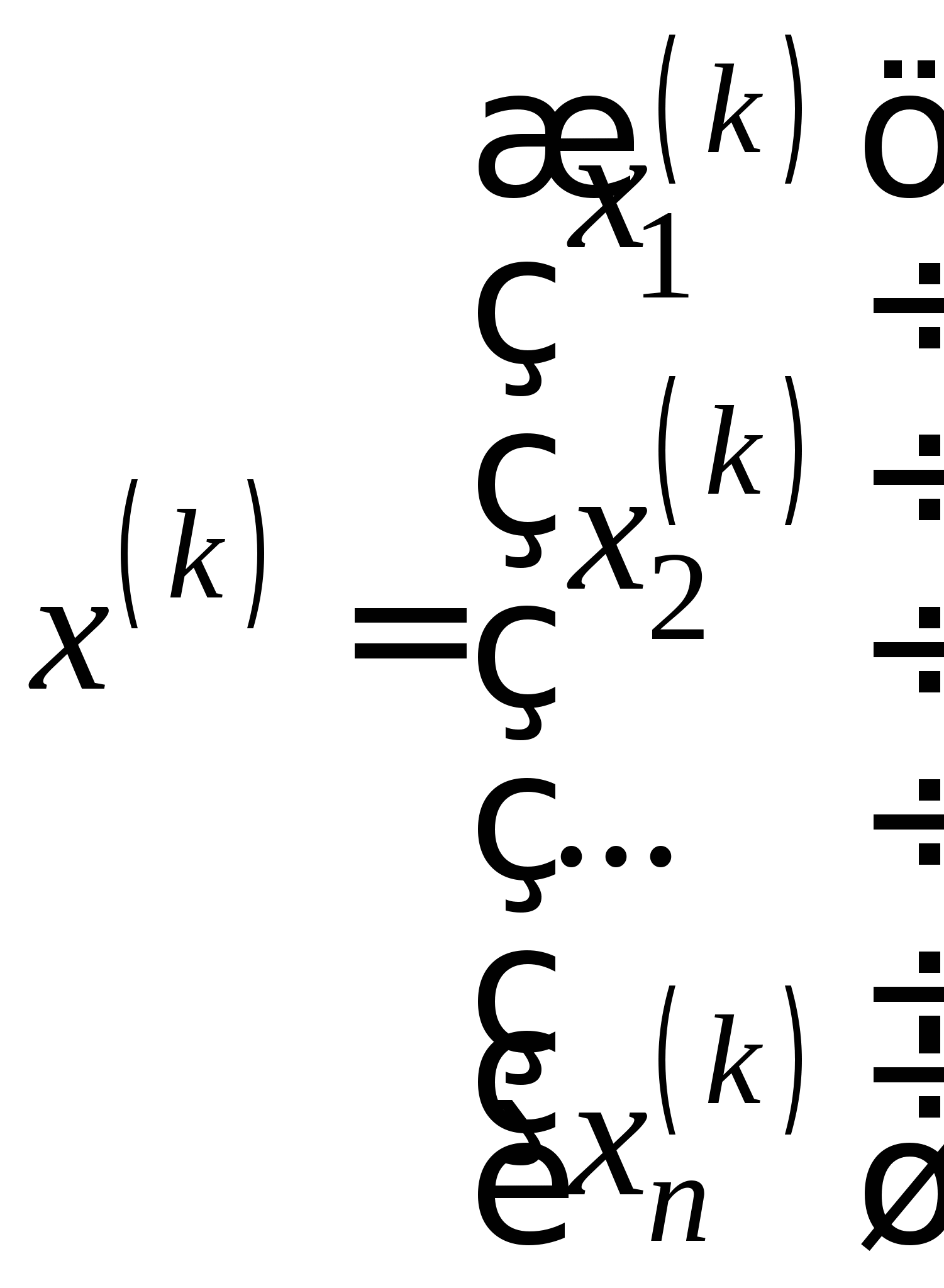 ,
, 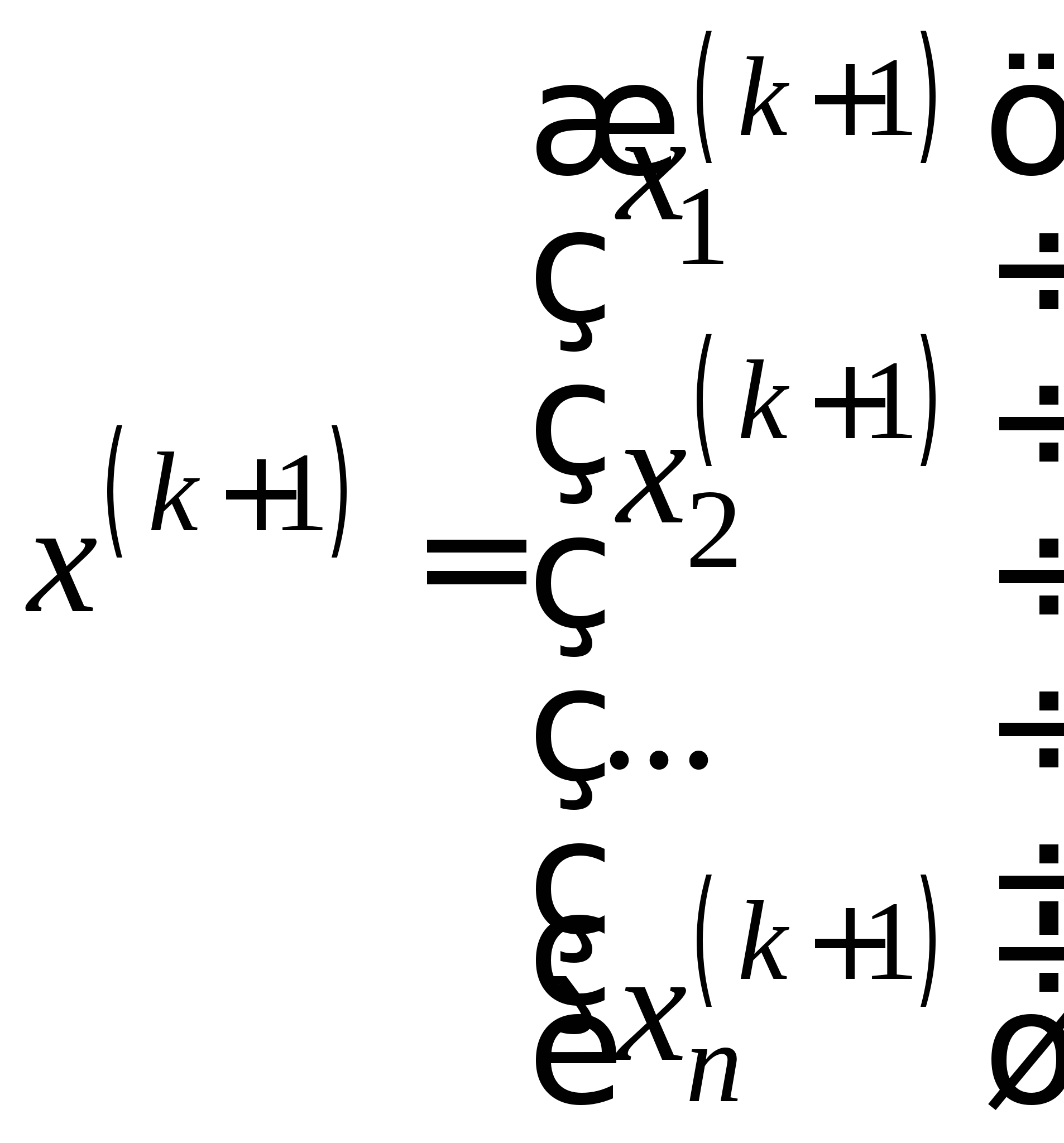 .
.
Теорема 4.4 (необходимые и достаточные условия сходимости метода Зейделя).
Для сходимости процесса Зейделя, заданного формулой (4.9), для приведенной системы линейных уравнений (4.4) при любом выборе свободного члена ![]() и начального вектора
и начального вектора ![]() необходимо и достаточно, чтобы все корни
необходимо и достаточно, чтобы все корни ![]() уравнения
уравнения ![]() были по модулю меньше единицы.
были по модулю меньше единицы.
Пример 4.1. Построить рабочие формулы метода простых итераций и метода Зейделя для численного решения СЛАУ вида:
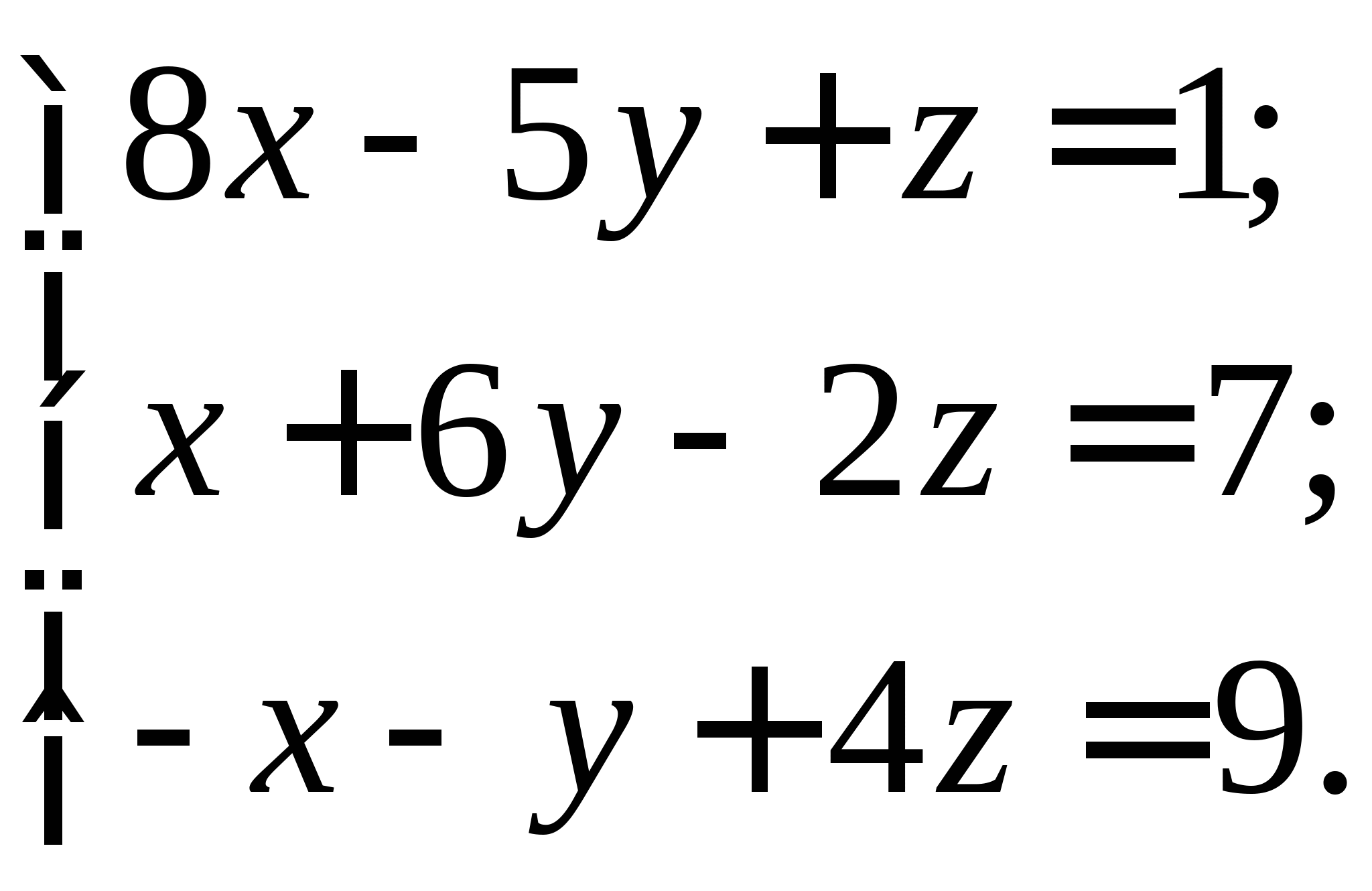 (4.11)
(4.11)
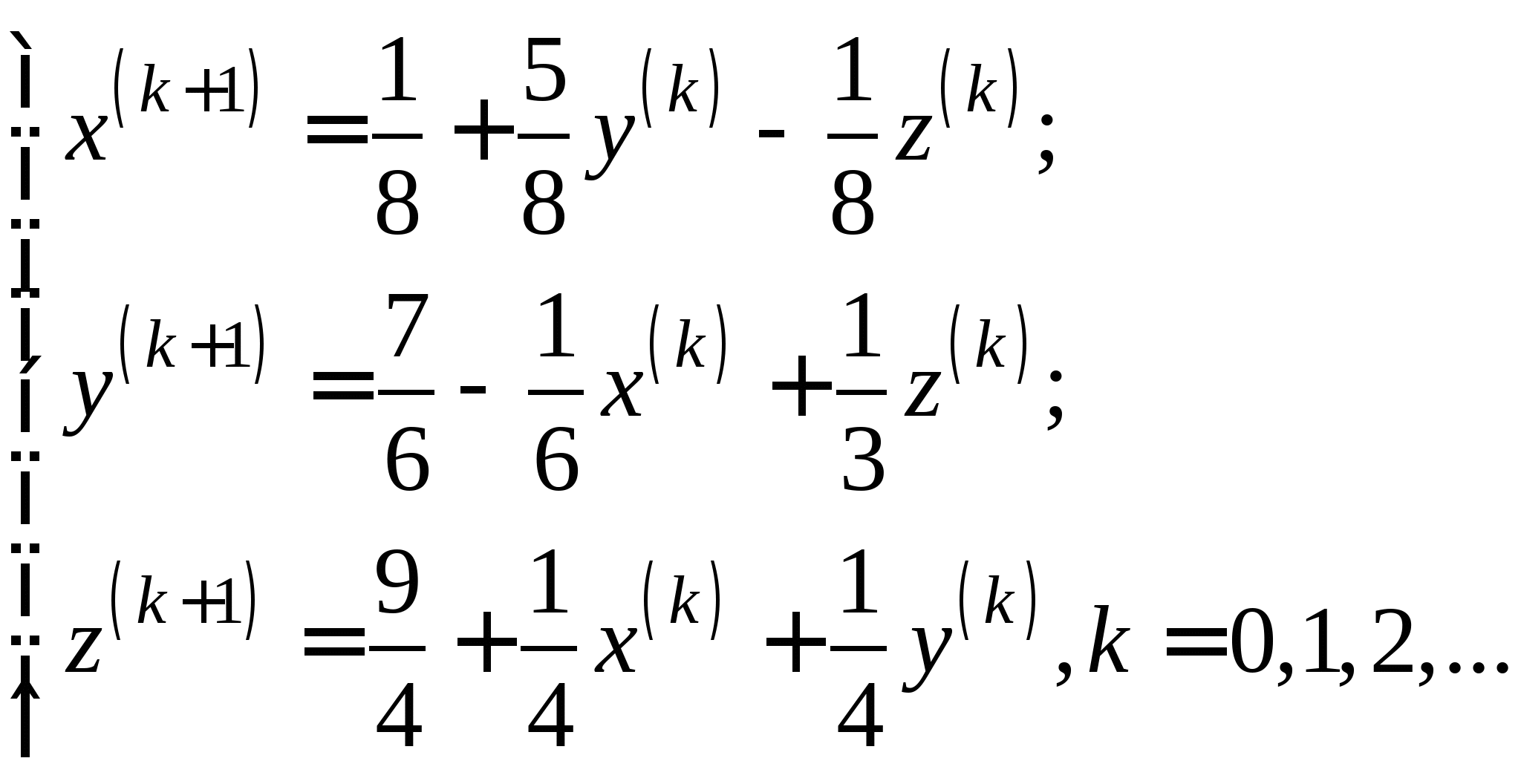
Начальное приближение обычно выбирают равным столбцу свободных членов преобразованной системы 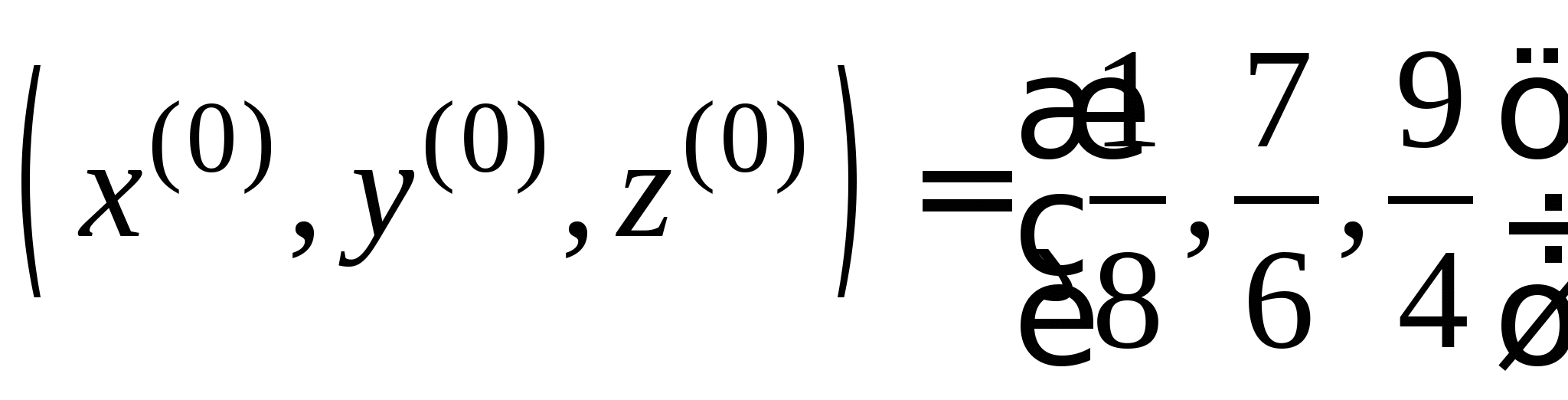 .
.
Рабочие формулы метода Зейделя запишутся так:
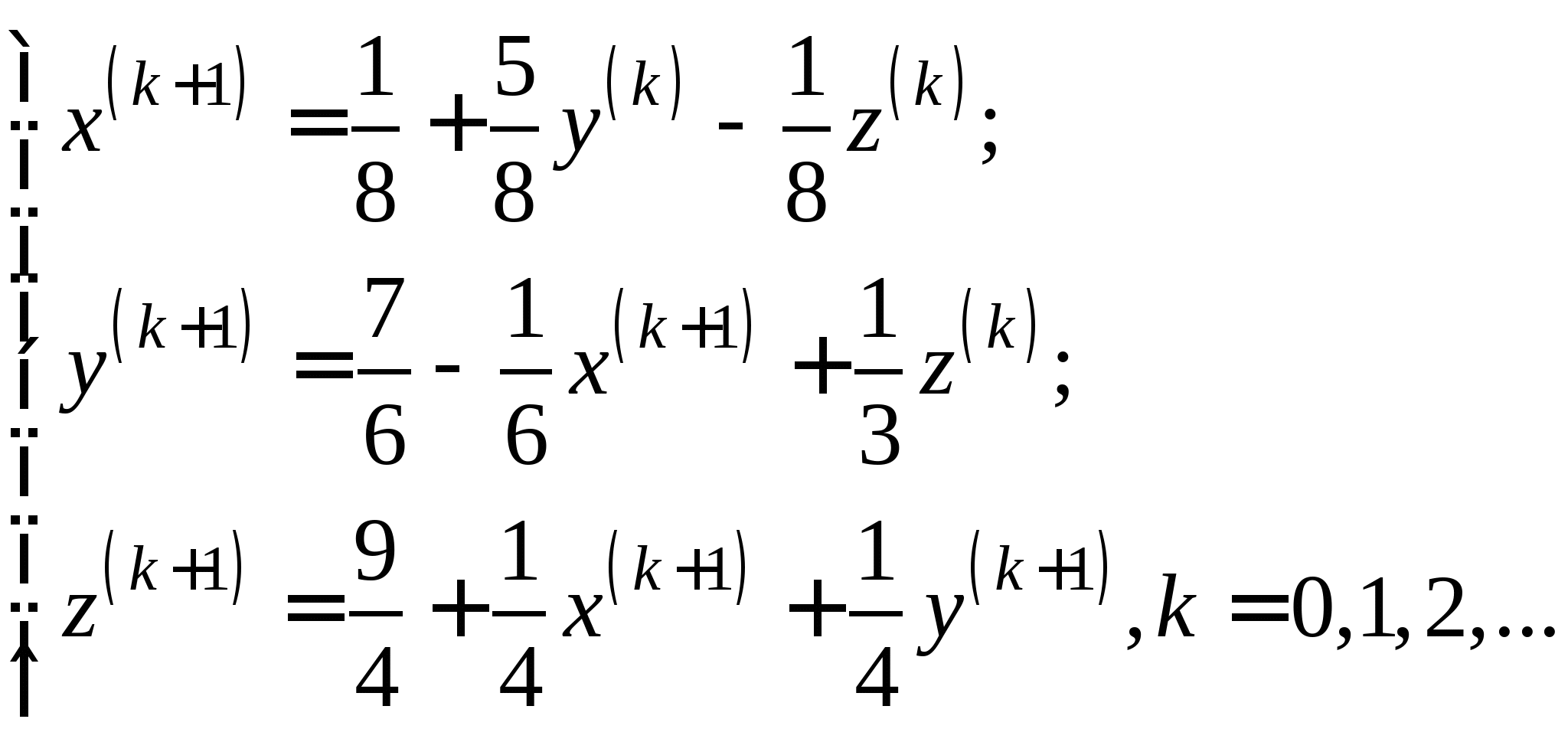
§4.3. Метод релаксации.
Рассмотрим систему линейных алгебраических уравнений (4.1)
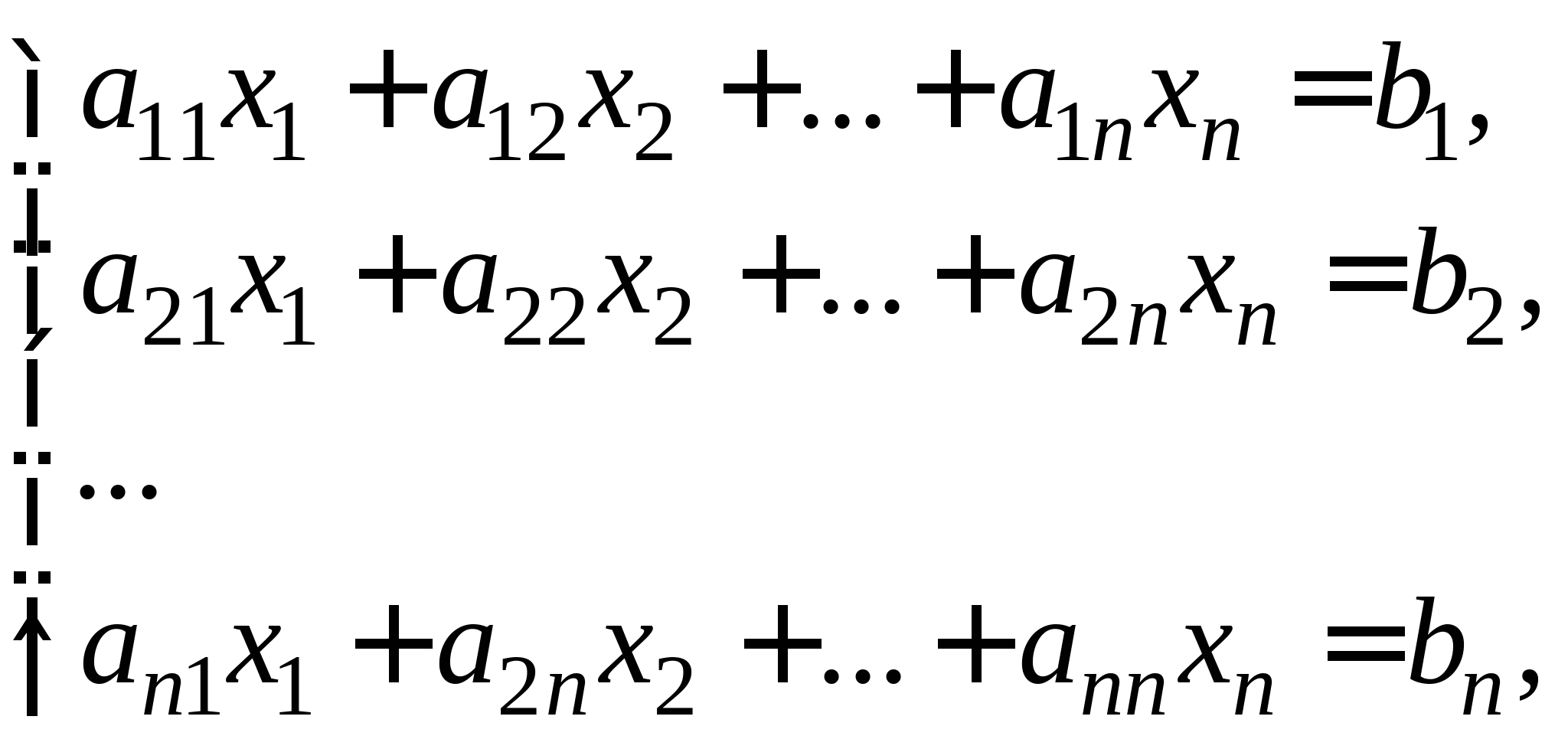
в которой ![]() .
.
Сделаем преобразования: свободные члены перенесем в левую часть и каждое ![]() -ое уравнение поделим на
-ое уравнение поделим на ![]() . Таким образом, получим систему, удобную для релаксации:
. Таким образом, получим систему, удобную для релаксации:
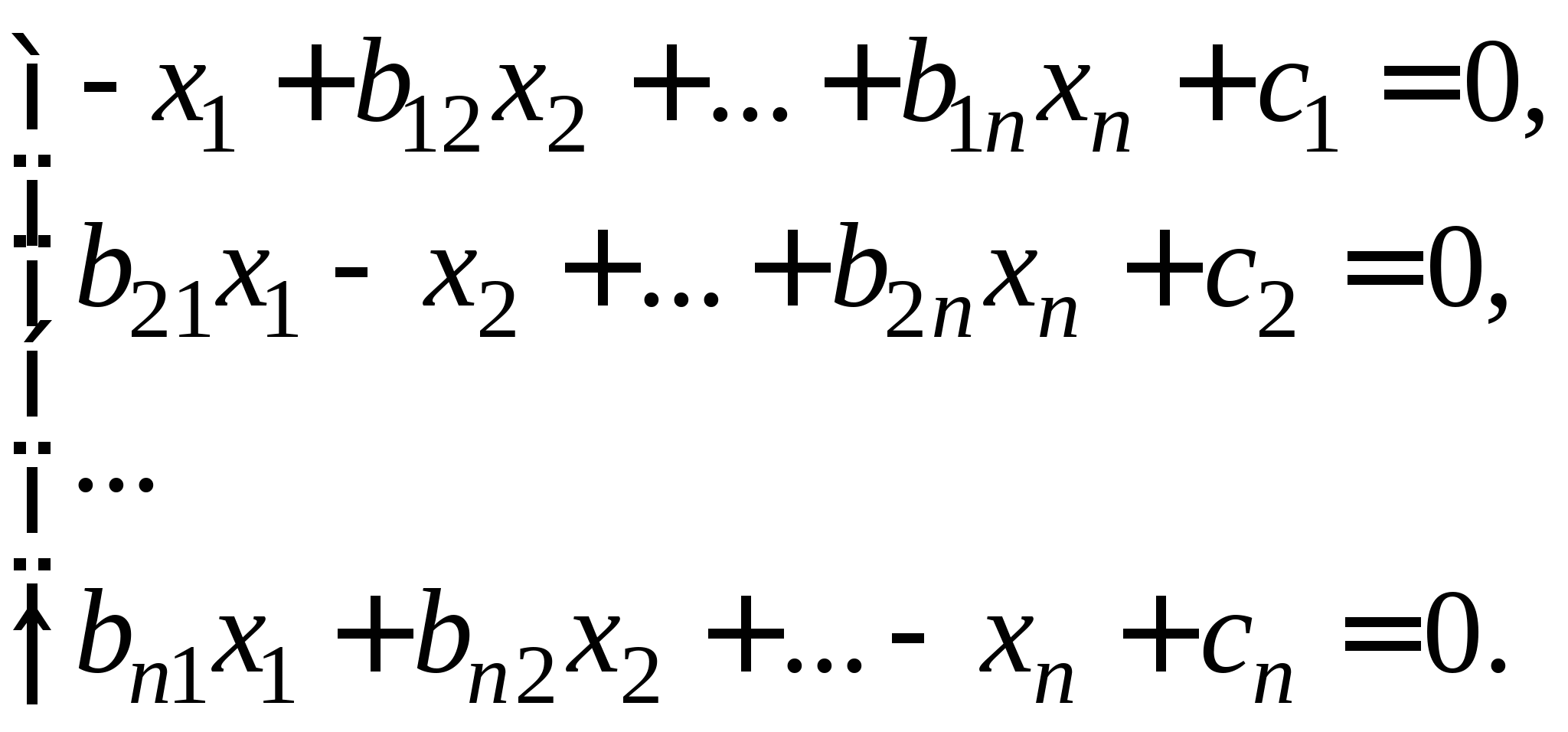 (4.12)
(4.12)
где 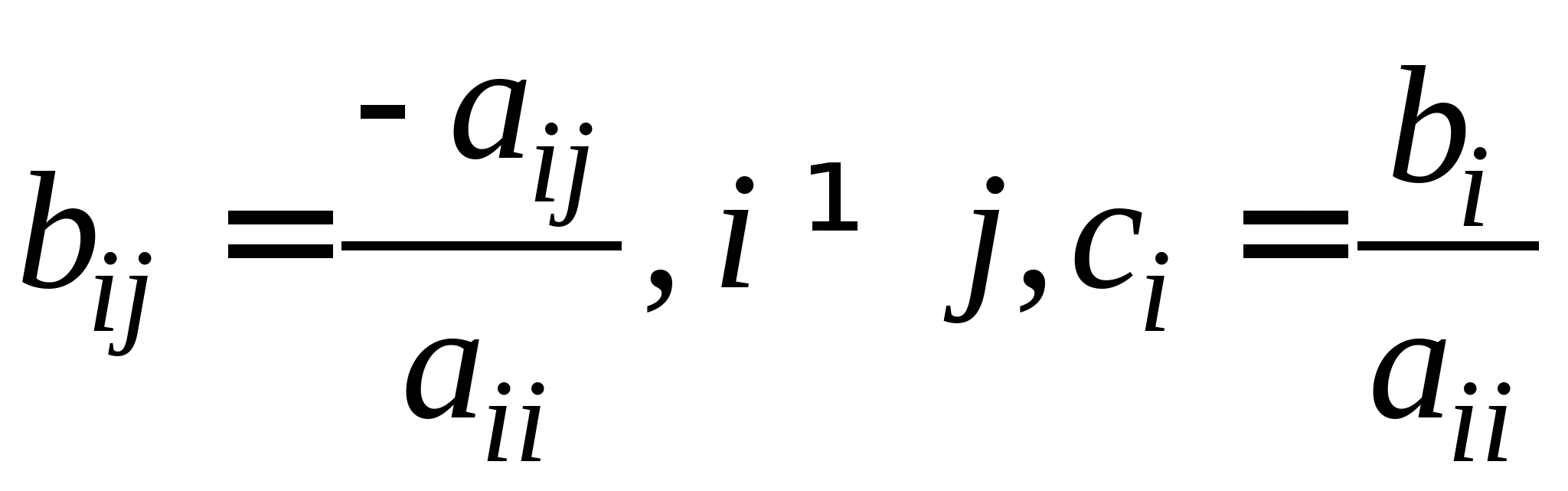 .
.
Введем понятие невязки для приближенного решения ![]() .
.
Пусть дана система ![]() , тогда точное решение
, тогда точное решение ![]() можно записать в виде
можно записать в виде ![]() , где
, где 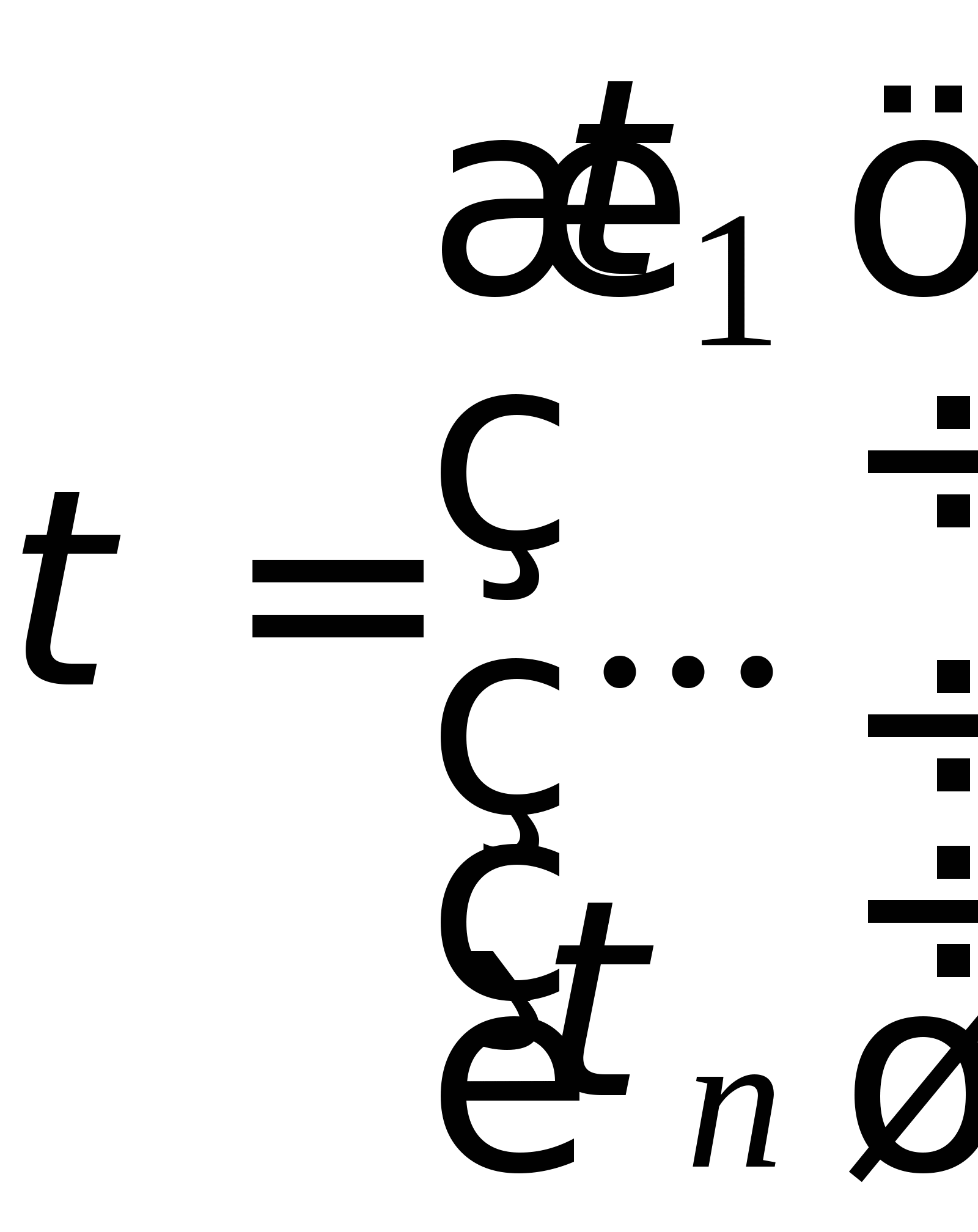 -правка корня
-правка корня ![]() . Подставим
. Подставим ![]() в систему, получим
в систему, получим
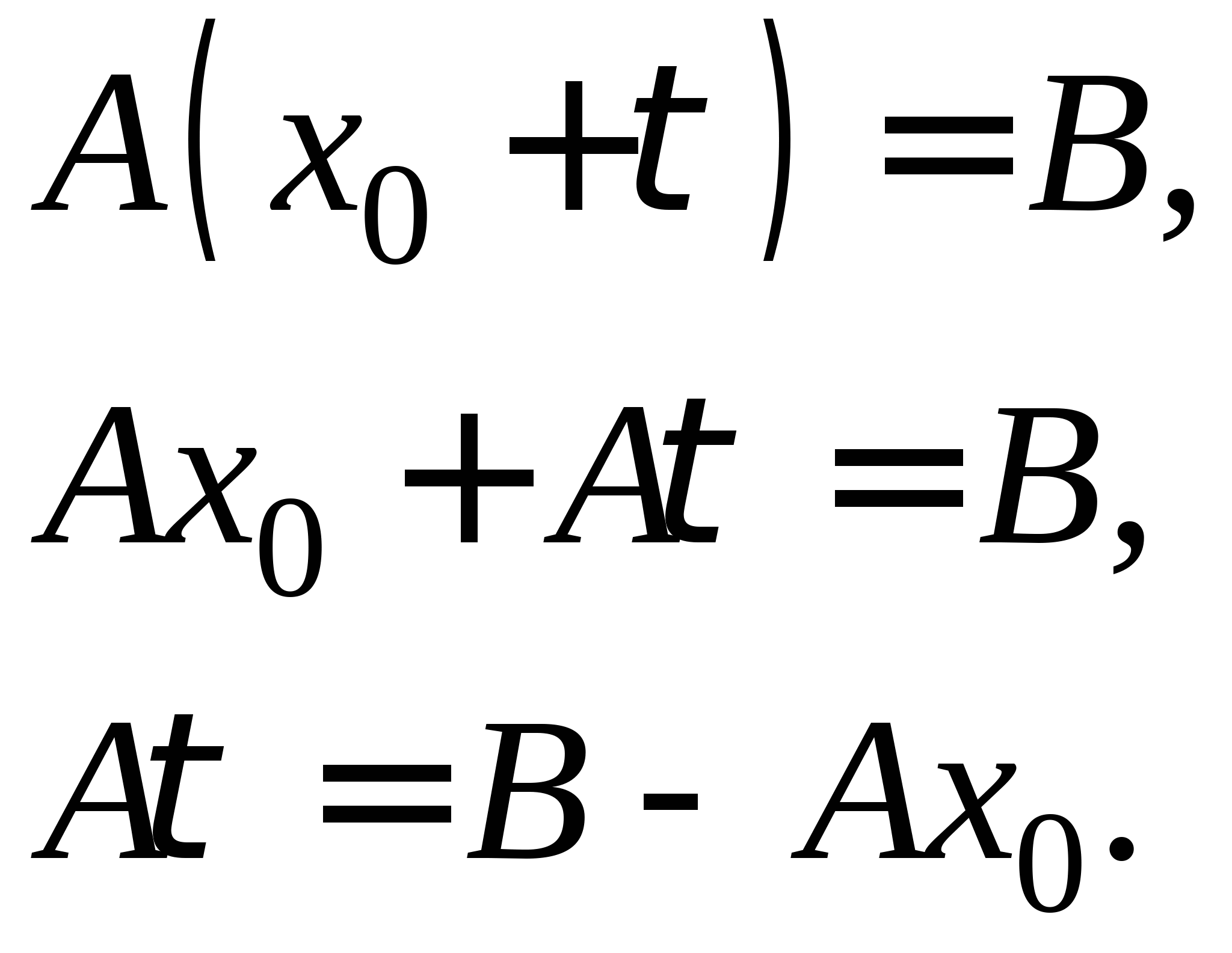
Введем обозначение ![]() . Тогда
. Тогда ![]() . Выражение
. Выражение ![]() называется невязкой для приближенного решения
называется невязкой для приближенного решения ![]() .
.
Пусть задано начальное приближение системы (4.12):
![]() .
.
Подставим данное приближение в систему (4.12) и получим невязки ![]() :
:
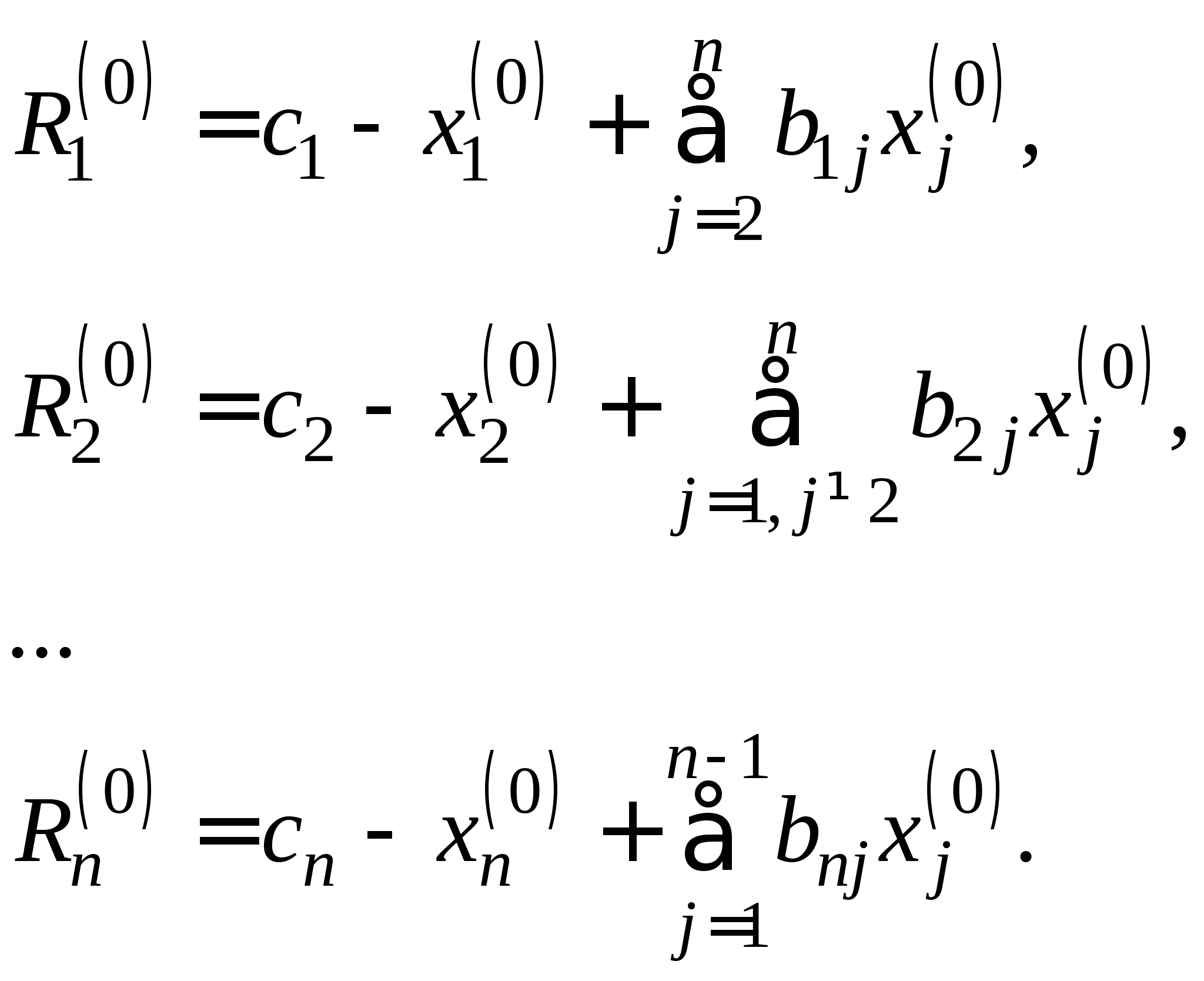 (4.13)
(4.13)
Если одной из неизвестных ![]() дать приращение
дать приращение ![]() , то соответствующая невязка
, то соответствующая невязка ![]() уменьшится на величину
уменьшится на величину ![]() , а все остальные невязки
, а все остальные невязки ![]() изменятся на величину
изменятся на величину ![]() . Чтобы обратить очередную невязку
. Чтобы обратить очередную невязку ![]() в нуль, нужно величине
в нуль, нужно величине ![]() дать приращение
дать приращение ![]() , следовательно,
, следовательно, ![]() , а остальные невязки будут равны
, а остальные невязки будут равны
![]() .
.
Метод релаксации (метод ослабления) заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точностью.
Пример 4.2. Решить систему методом релаксации, производя вычисления с двумя десятичными знаками.
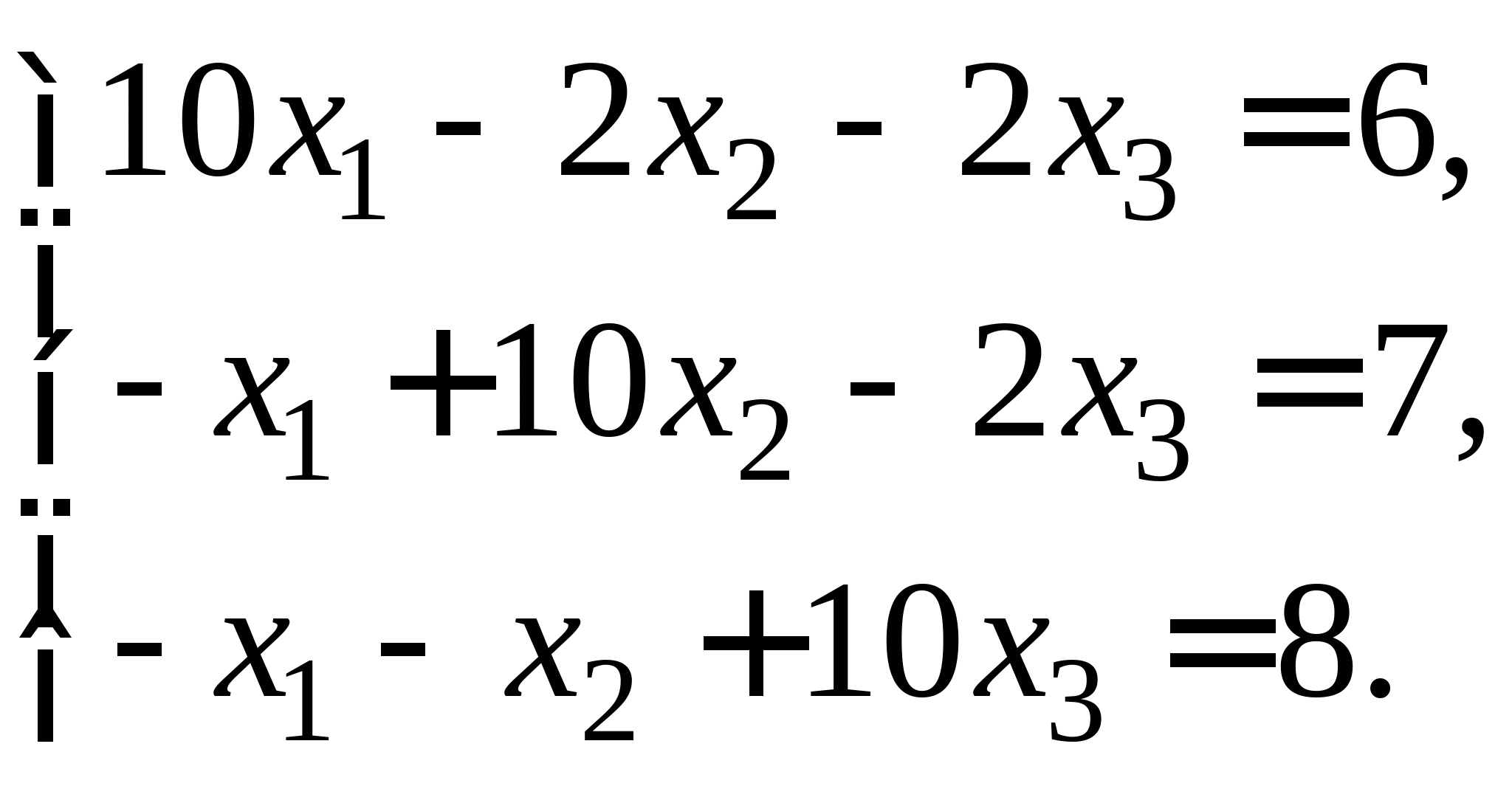 (4.14)
(4.14)
Решение.
Приведем систему (4.14) к виду, удобному для релаксации
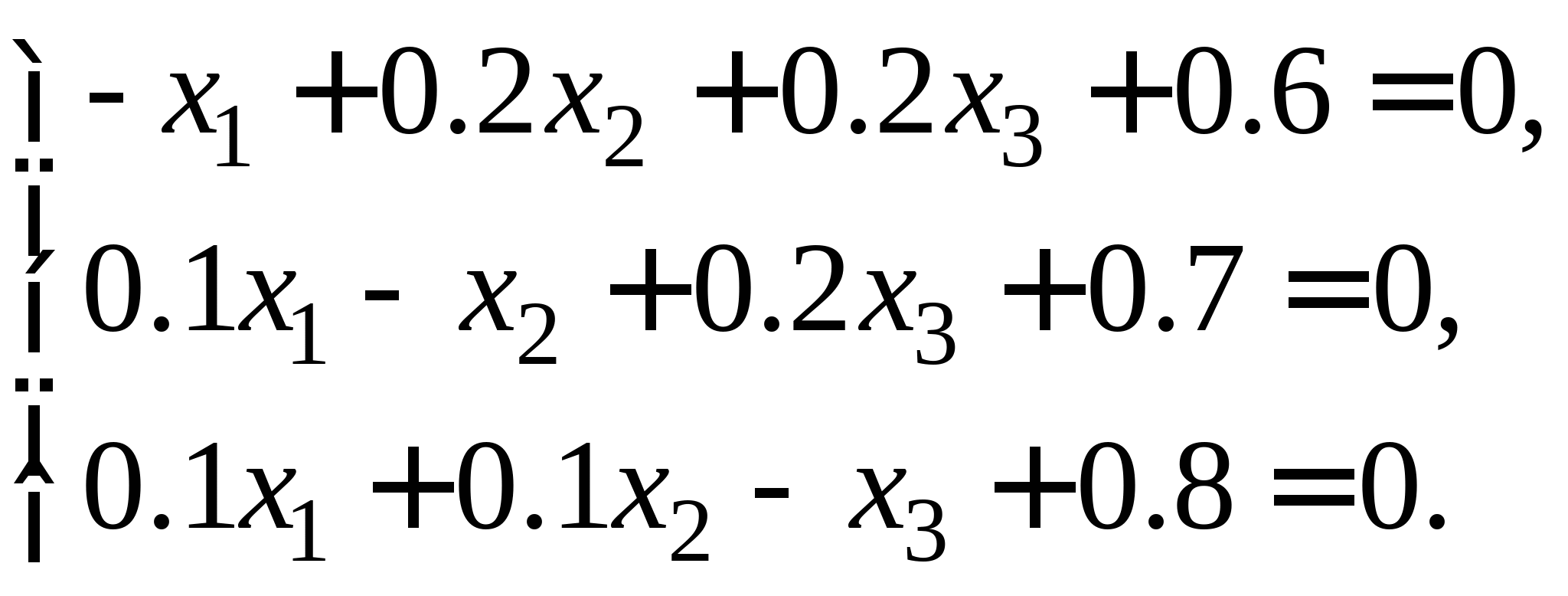 (4.15)
(4.15)
В качестве начального приближения выбираем
![]() .
.
Находим соответствующие невязки: ![]() ,
, ![]() ,
, ![]() . Выбираем максимальную невязку и полагаем
. Выбираем максимальную невязку и полагаем ![]() , тогда
, тогда
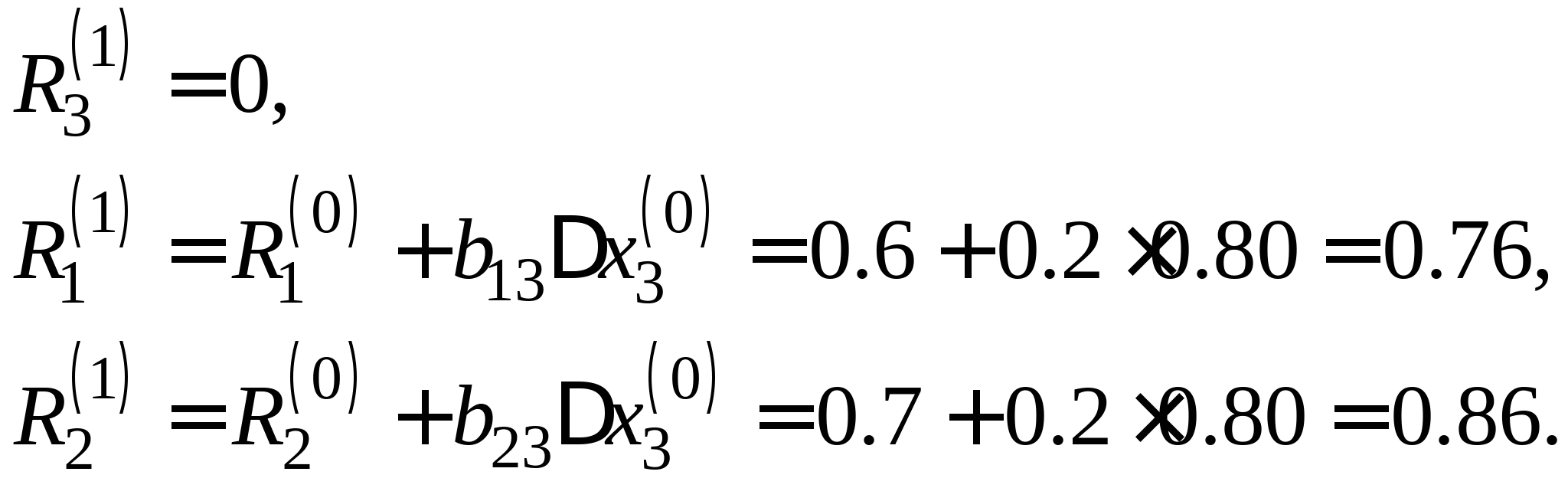
Опять выбираем максимальную невязку и полагаем ![]() , тогда
, тогда
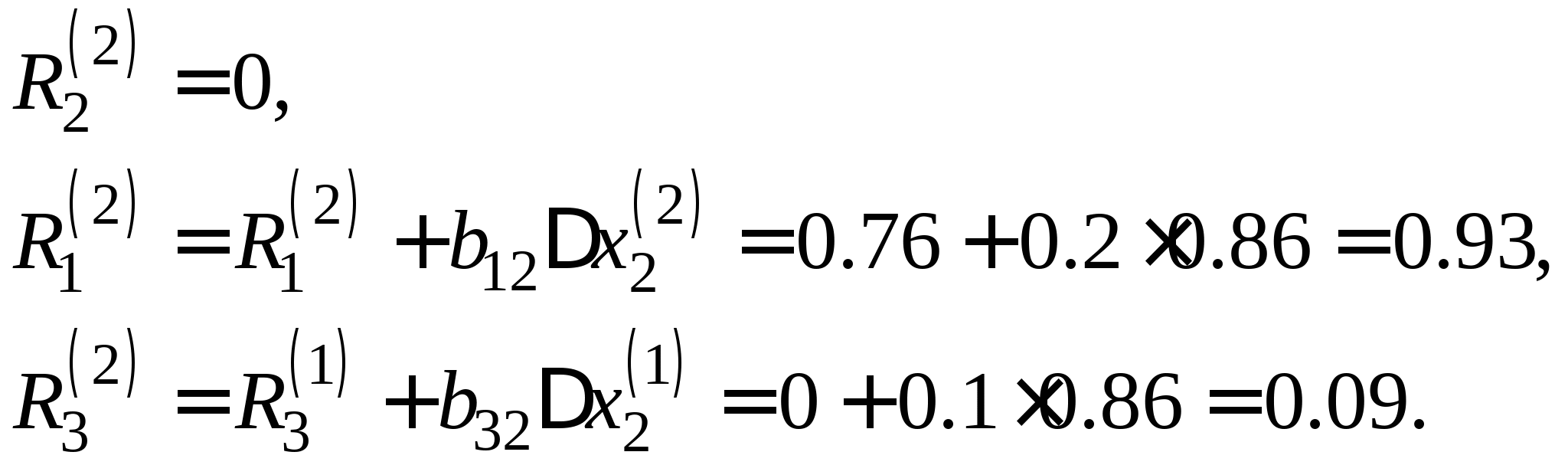
Далее ![]() и
и
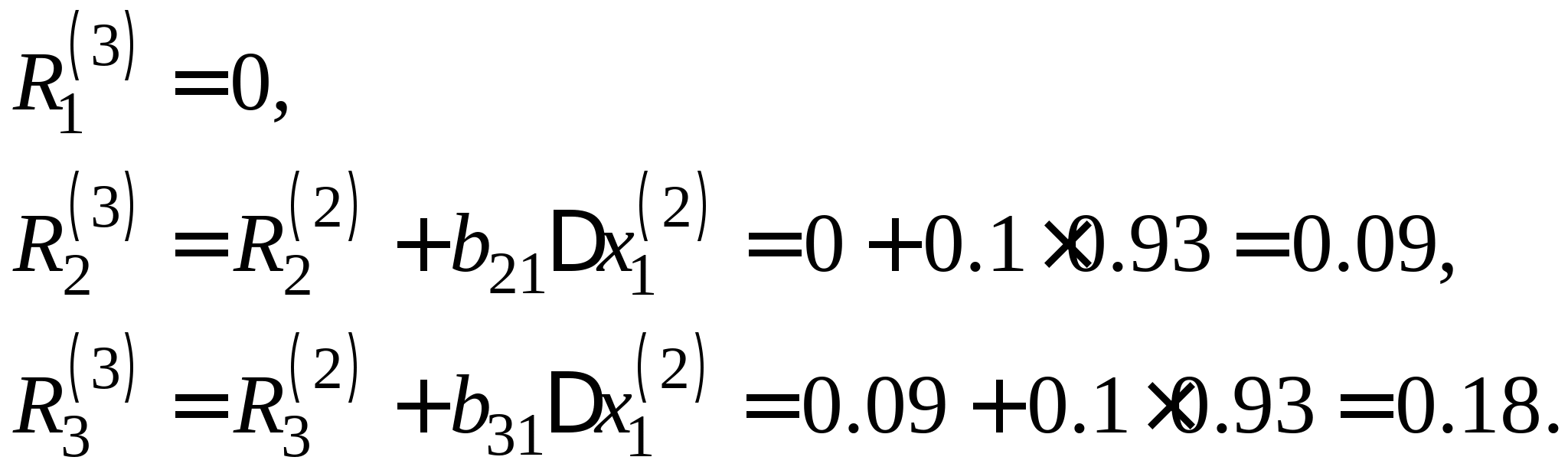
![]() ,
,
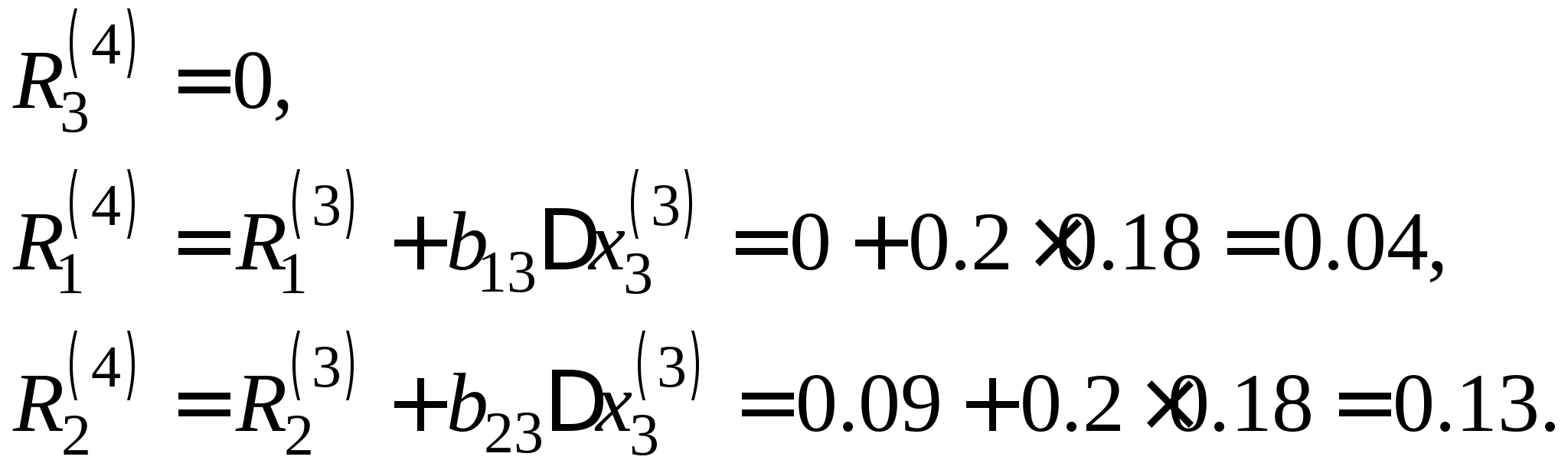
![]() ,
,
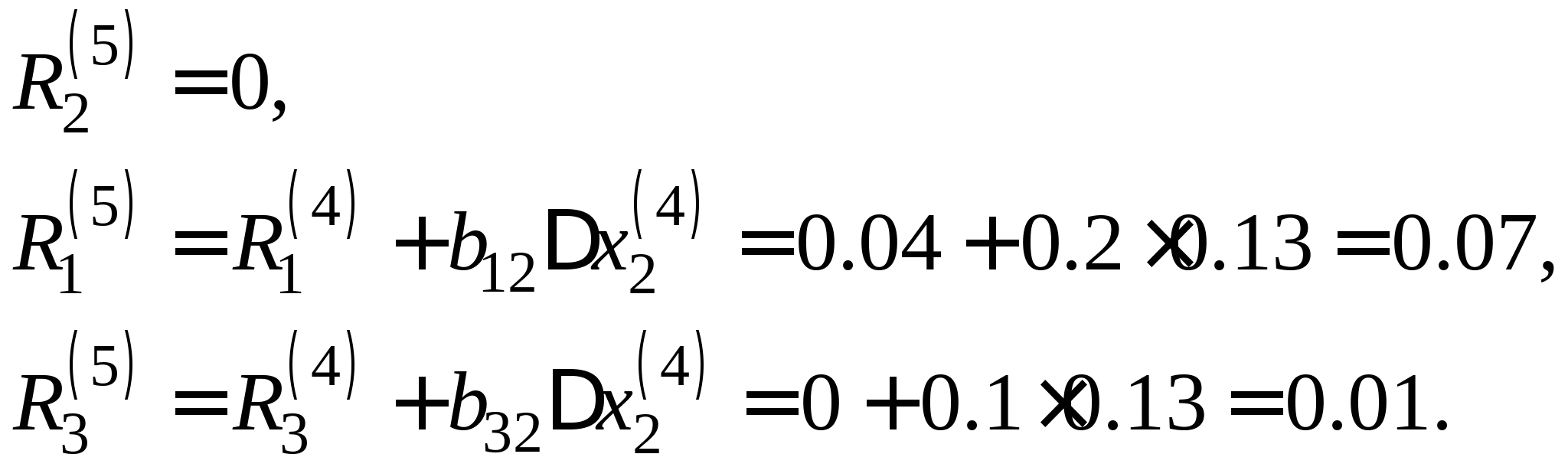
![]() ,
,
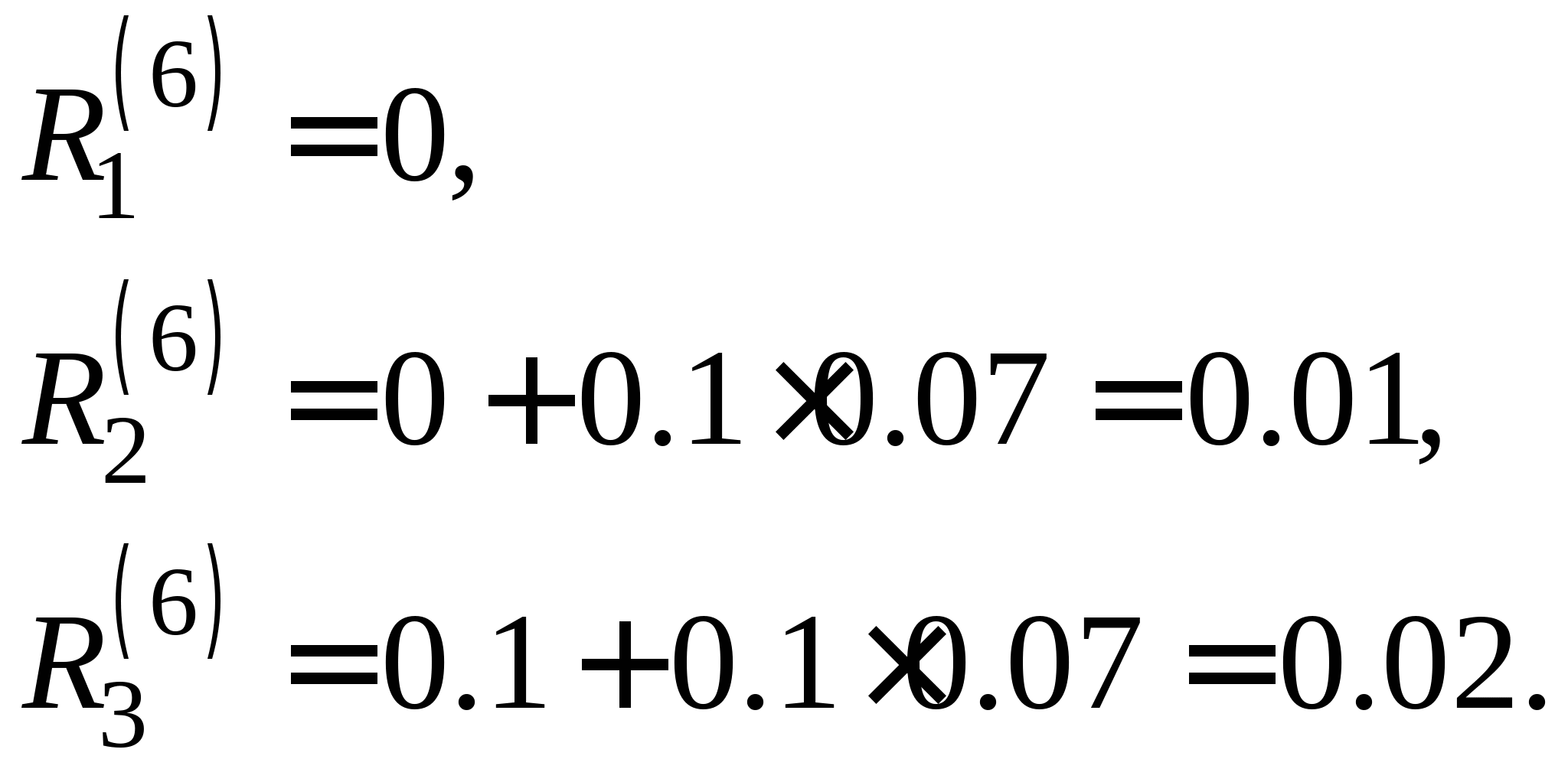
![]() ,
,
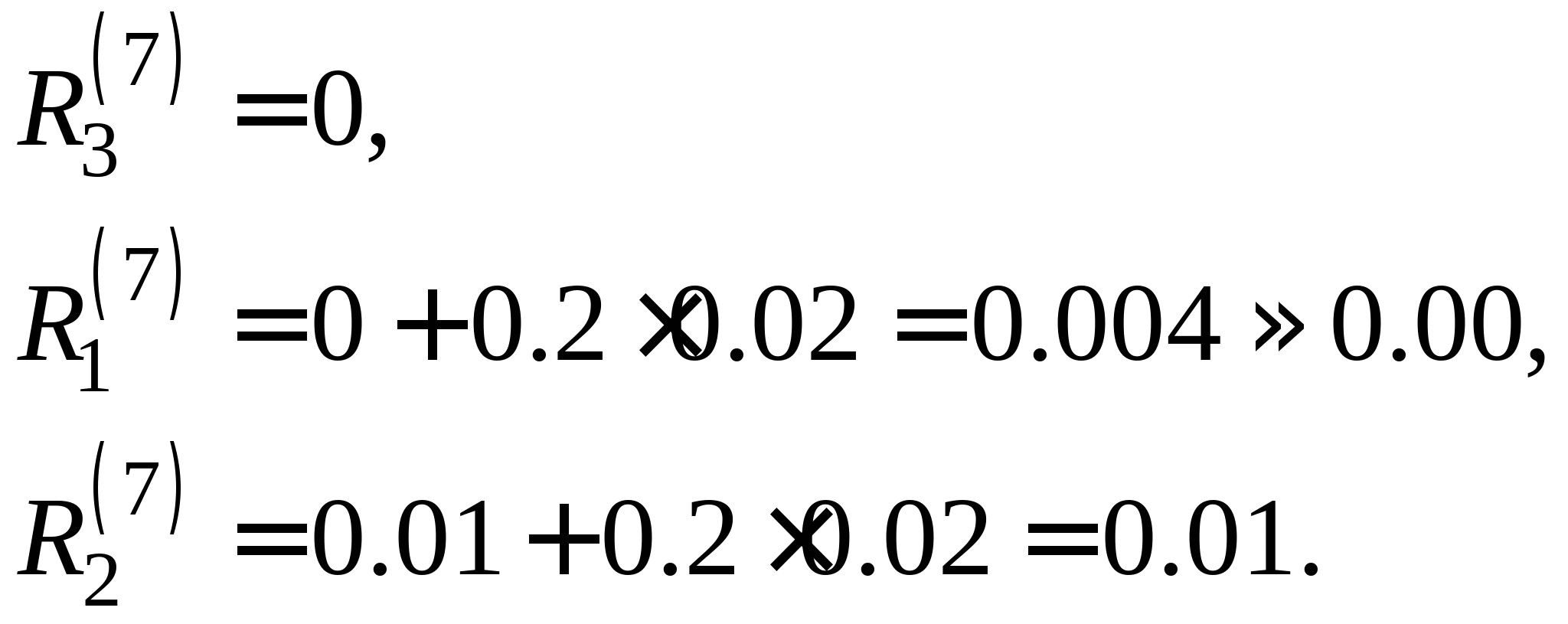
![]() ,
,
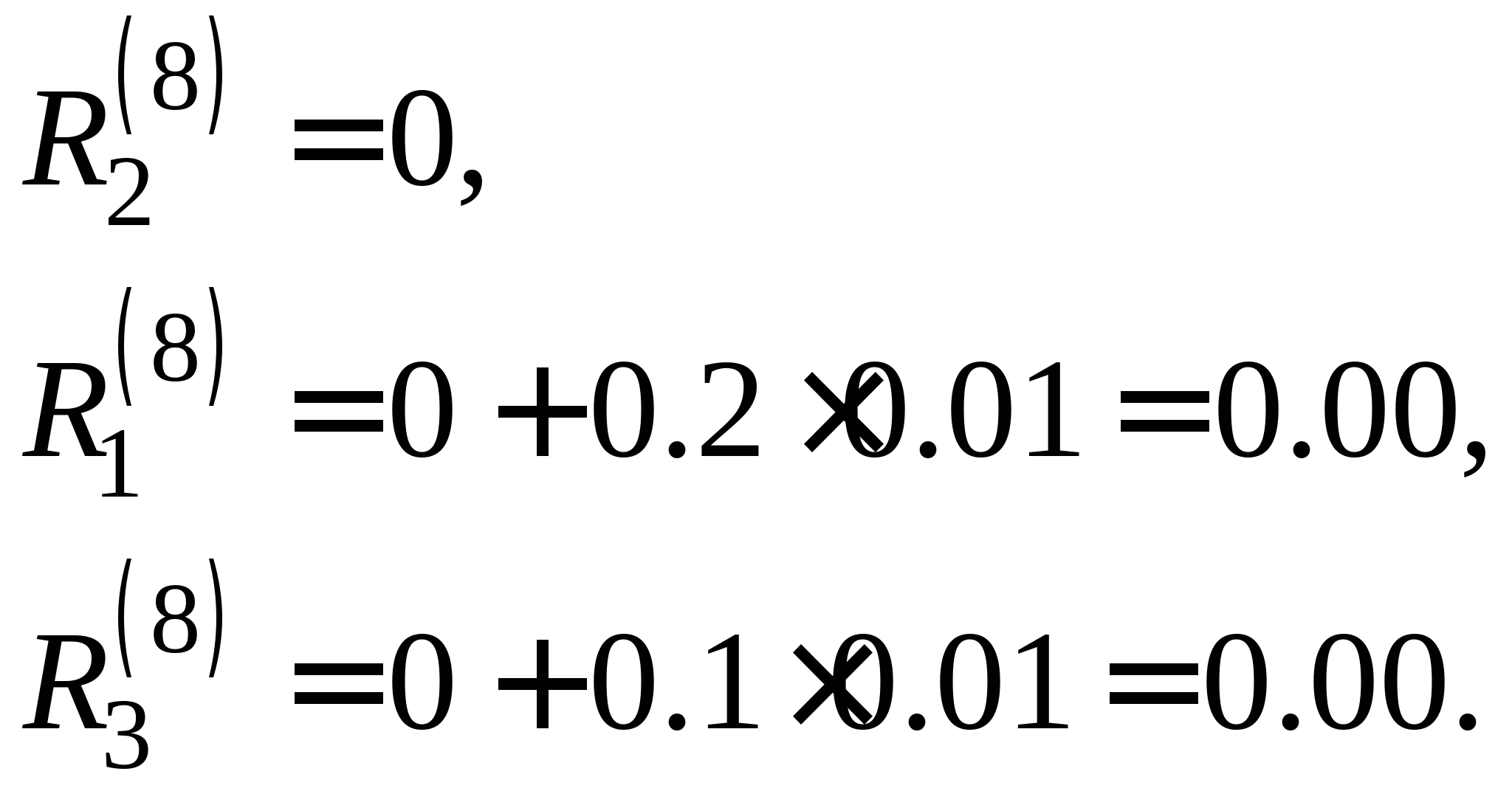
Окончательно получим:
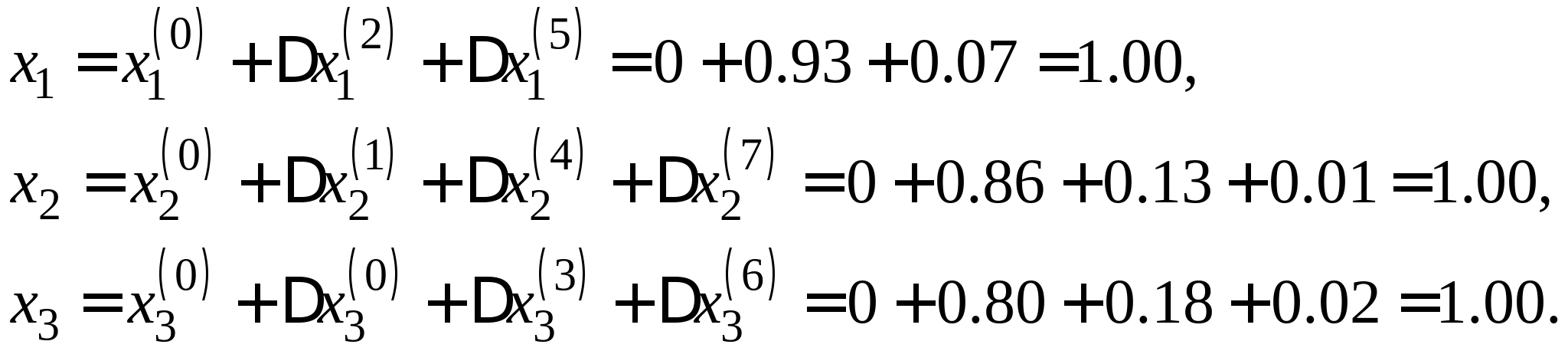
52
ГЛАВА 3. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Определение 3.1.
Системами нелинейных уравнений (СНУ) называются системы вида:
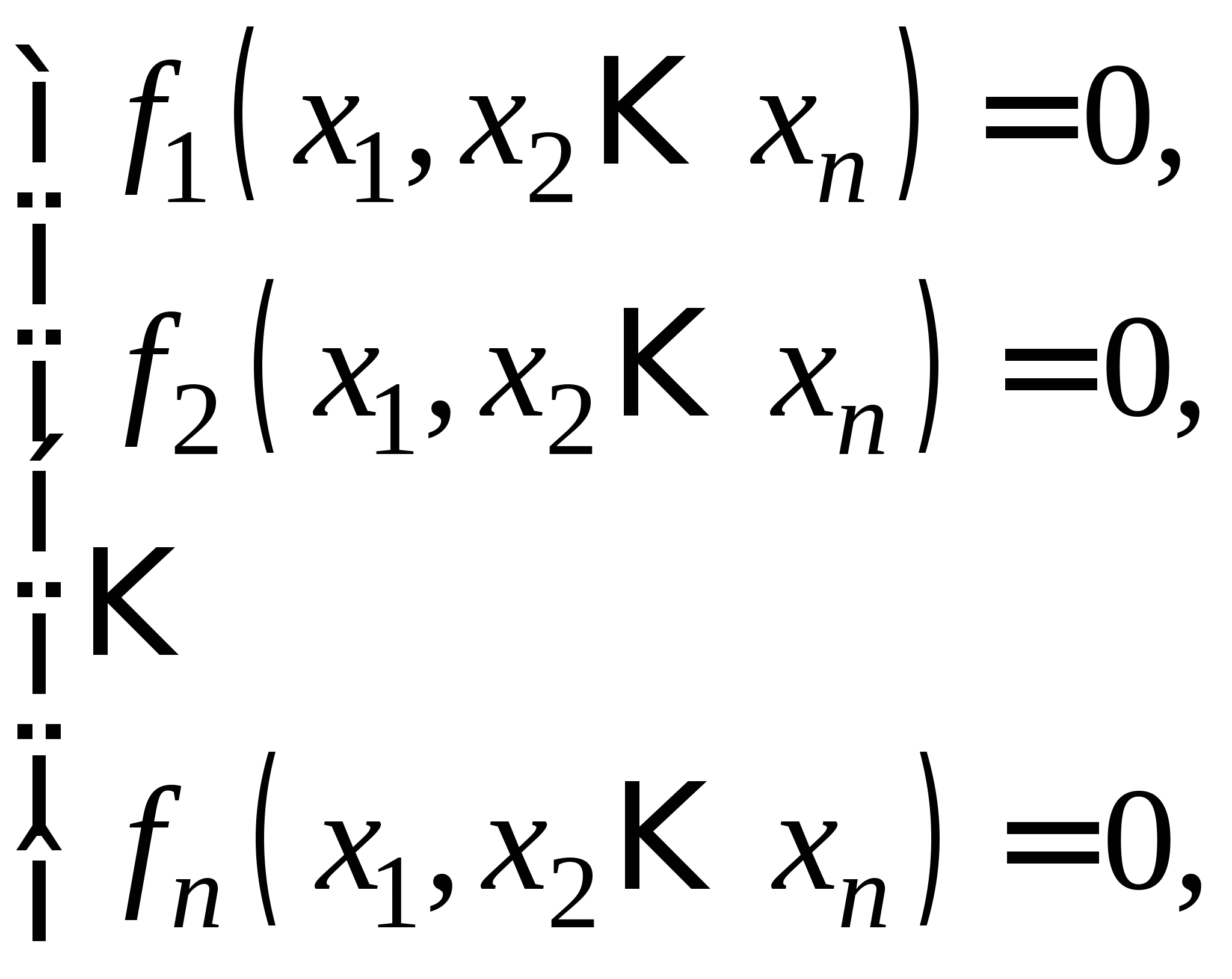 (3.1)
(3.1)
где хотя бы одна из функций ![]() нелинейна,
нелинейна, ![]() - неизвестные переменные.
- неизвестные переменные.
Решение систем нелинейных уравнений является в общем случае задачей более сложной, чем решение одного нелинейного уравнения. Не существует методов, которые гарантировали бы успех решения любой такой задачи.
Как и для отдельных уравнений, наибольшую проблему представляет задача отделения решений (корней). Для системы нелинейных уравнений с ![]() неизвестными необходимо, во-первых, выяснить, сколько у нее решений, а во-вторых, выделить области
неизвестными необходимо, во-первых, выяснить, сколько у нее решений, а во-вторых, выделить области ![]() -мерного пространства, в каждой из которых есть одно и только одно решение. Лишь после этого можно говорить о нахождении решений с заданной точностью.
-мерного пространства, в каждой из которых есть одно и только одно решение. Лишь после этого можно говорить о нахождении решений с заданной точностью.
Для отделения корней общих методов, гарантирующих успех, не существует. В реальных задачах, являющихся этапами моделирования, исследователь обычно догадывается, где примерно находятся корни системы.
Описанные ниже приемы исходят из того, что задача отделения корней решена и имеется достаточно малая область ![]() -мерного пространства, в которой находится корень, подлежащий уточнению. Пусть функции
-мерного пространства, в которой находится корень, подлежащий уточнению. Пусть функции ![]() определены в областях
определены в областях ![]() . Тогда область
. Тогда область 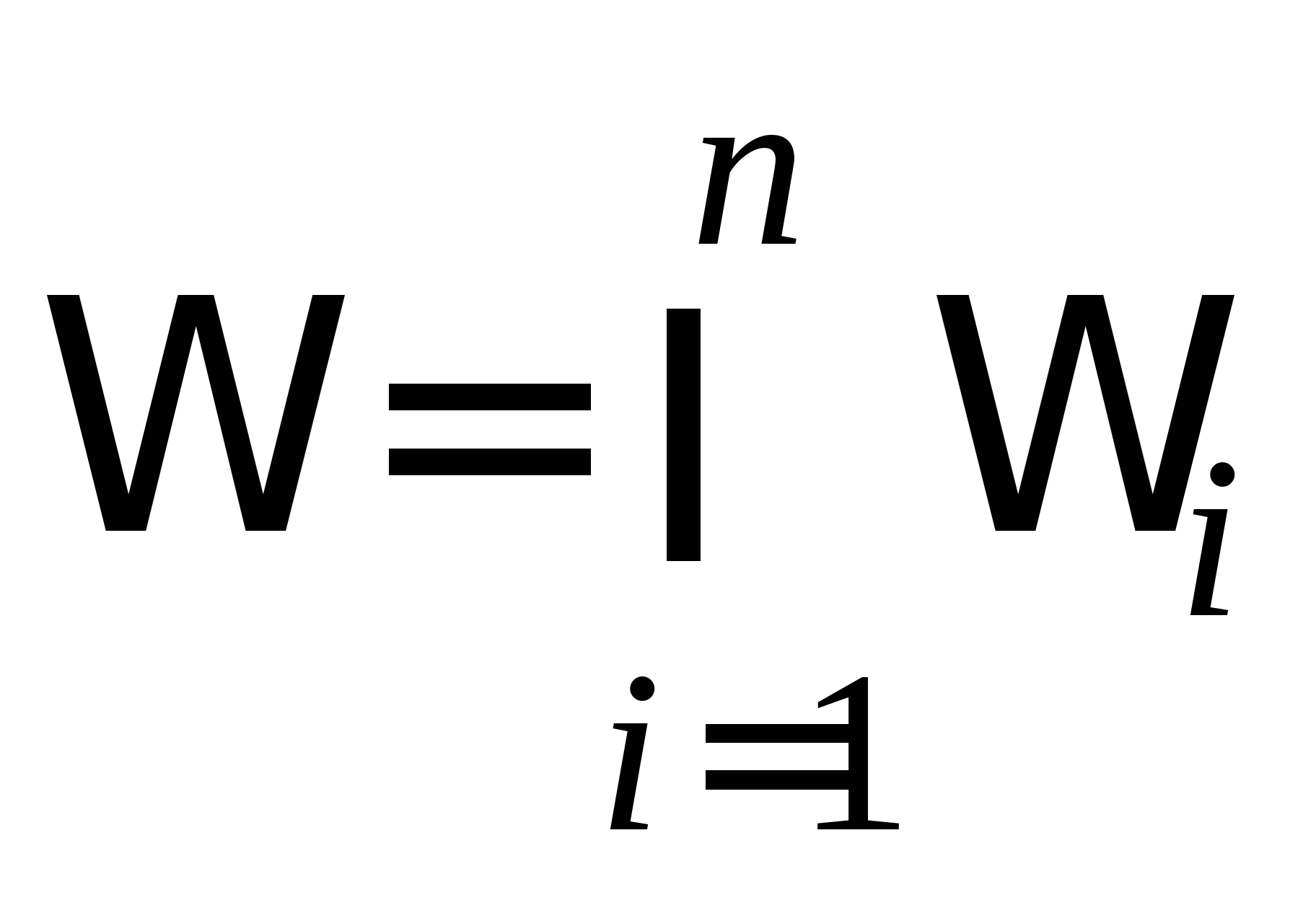 и будет той областью, где может находиться решение задачи.
и будет той областью, где может находиться решение задачи.
Наиболее распространенными методами уточнения решения являются метод простых итераций, метод Ньютона и его модификация.
§3.1. Метод простых итераций для решения систем нелинейных уравнений.
От исходной системы (3.1) путем элементарных преобразований переходим к эквивалентной системе вида:
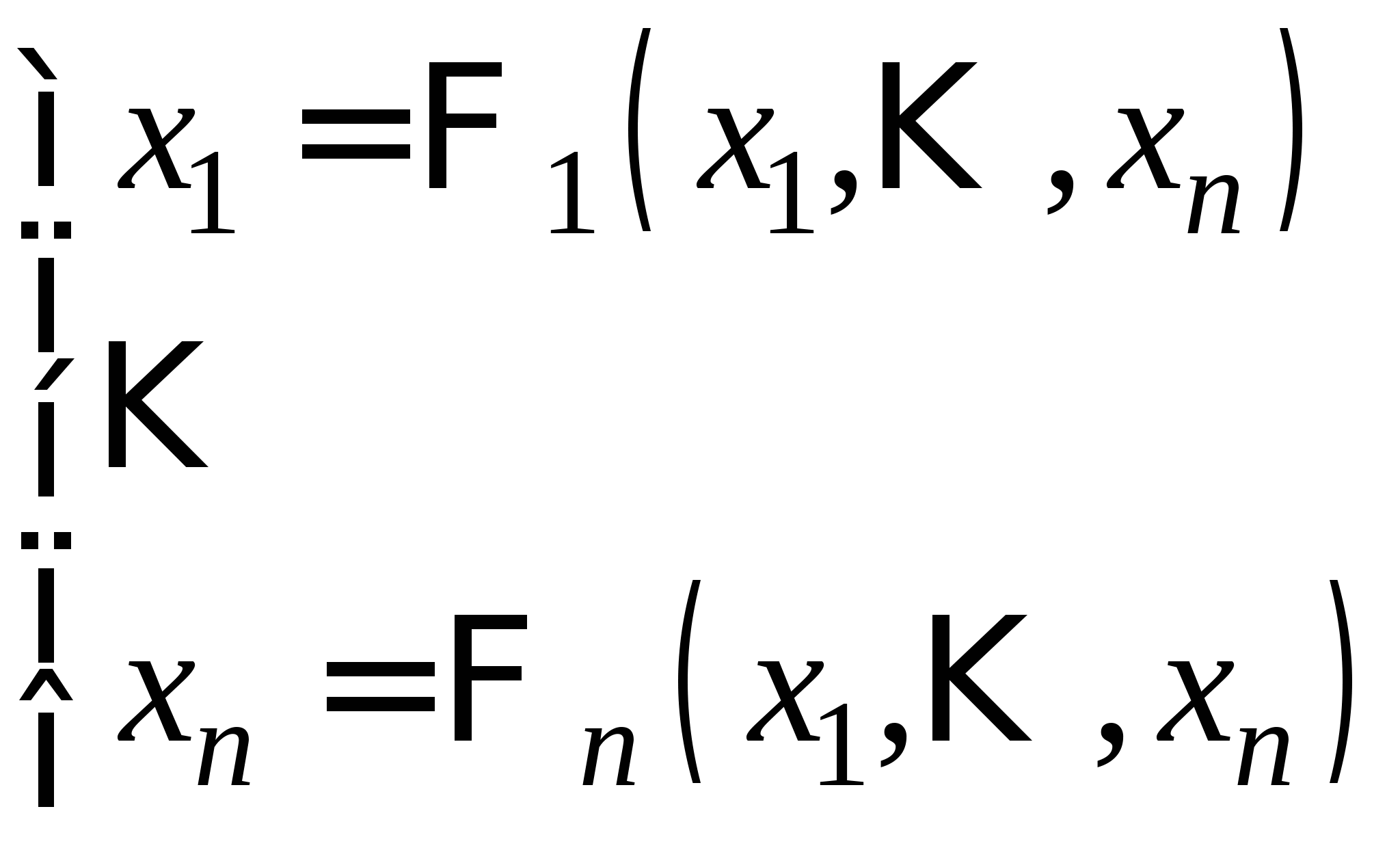 (3.2)
(3.2)
Итерационный процесс, определяемый формулами
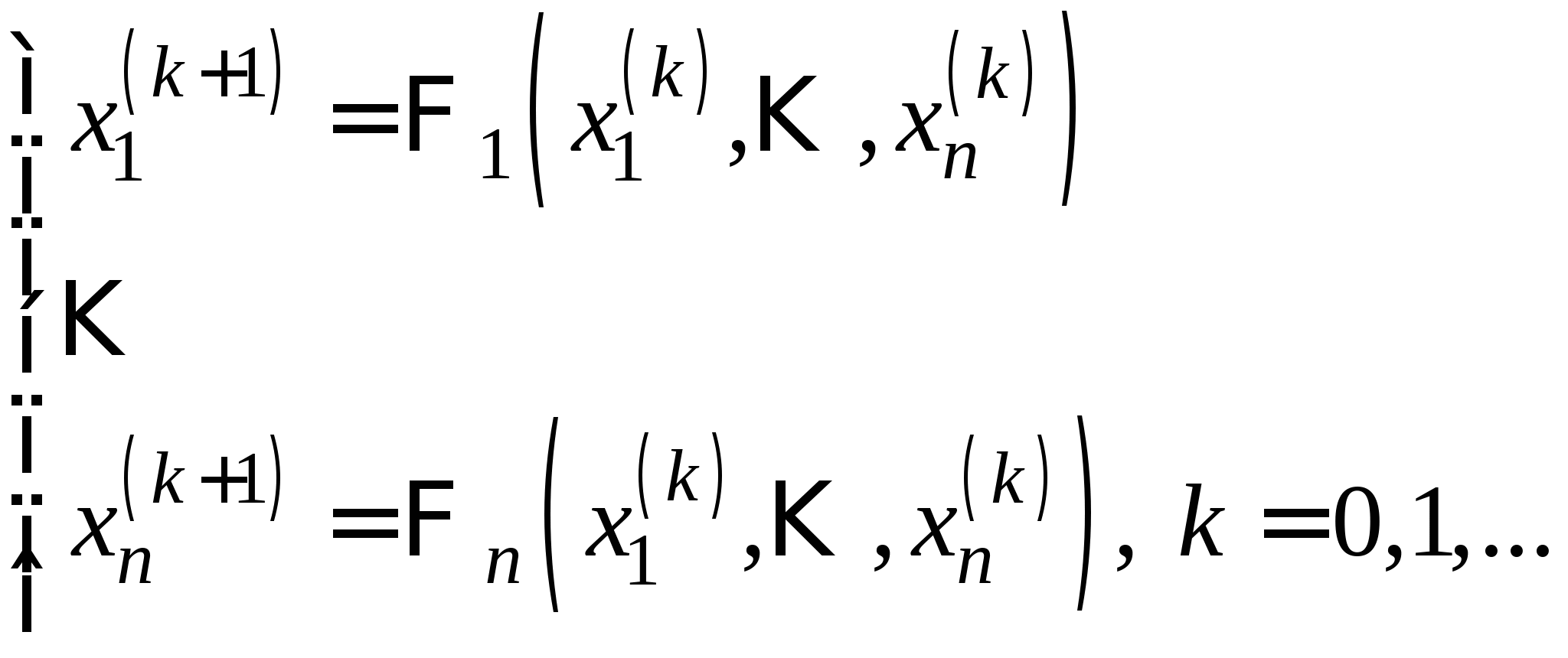
можно начать, задав начальное приближение ![]() .
.
Достаточным условием сходимости итерационного процесса является выполнение одного из двух условий:
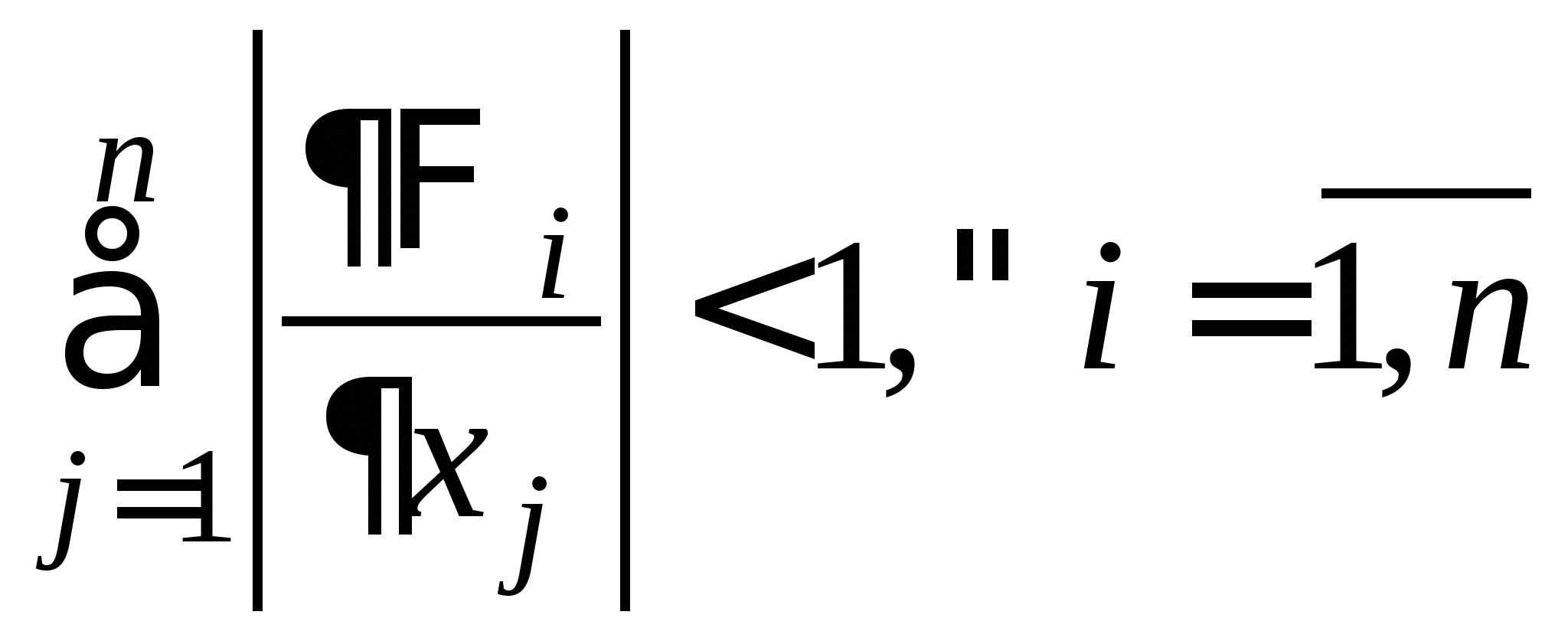
или
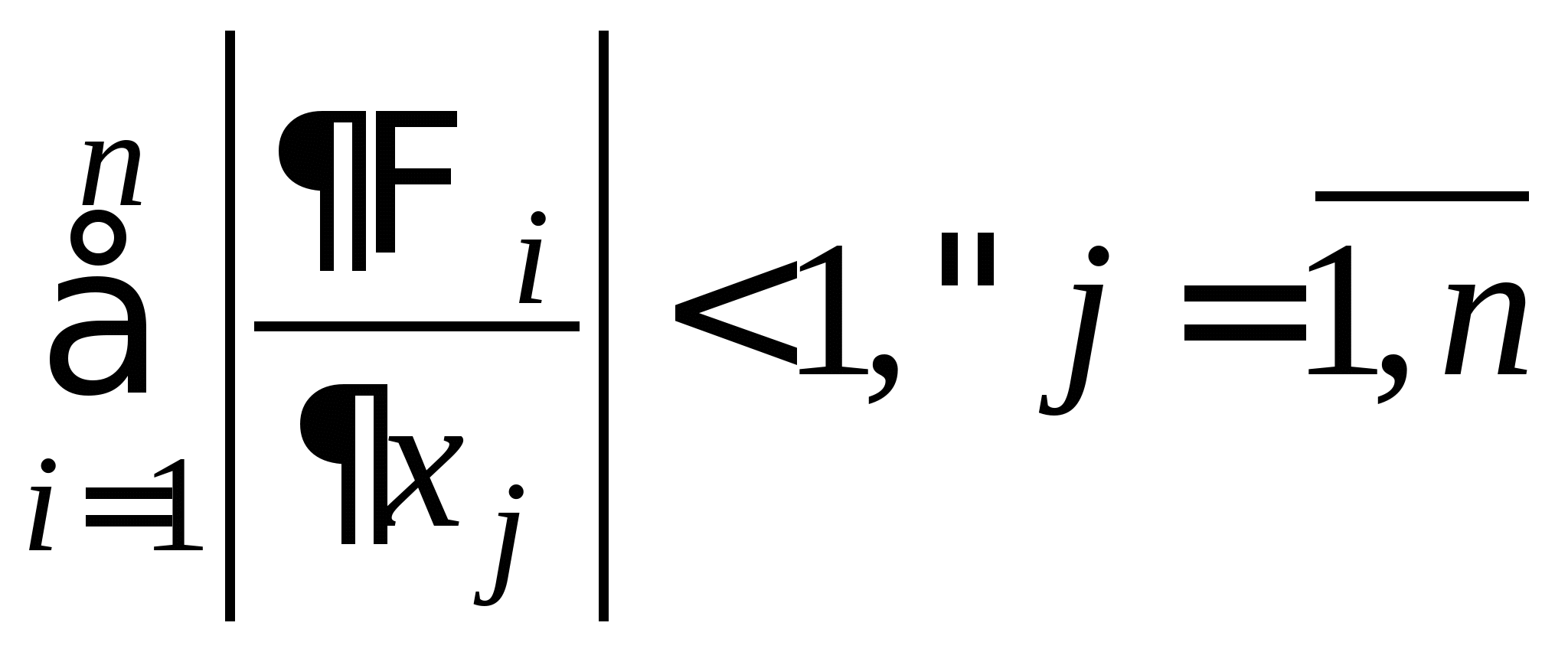 .
.
Распишем первое условие:
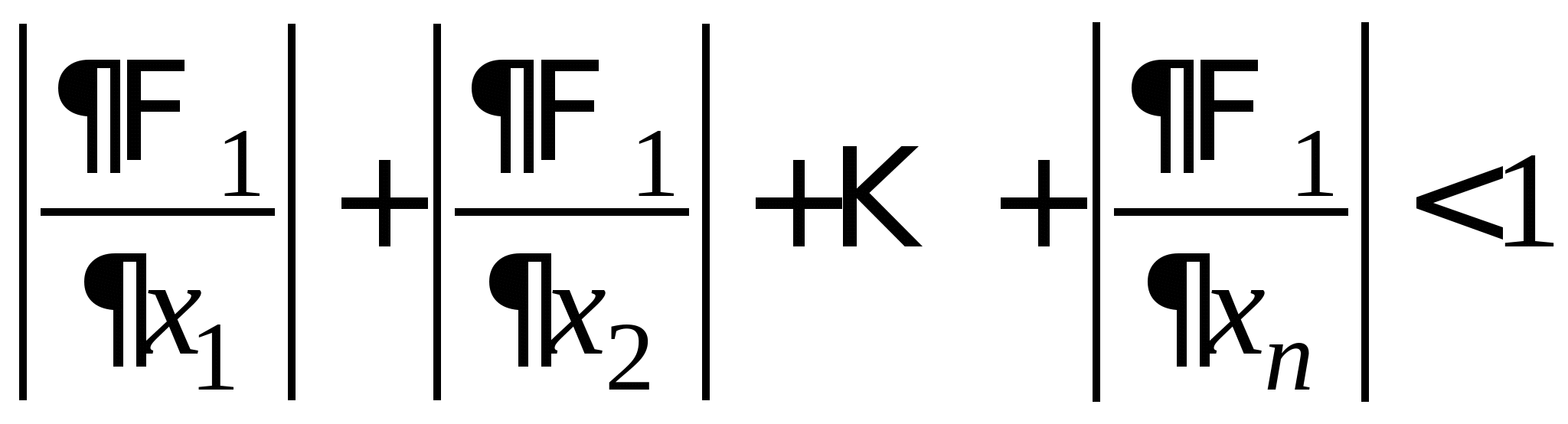 при
при ![]() ,
,
…
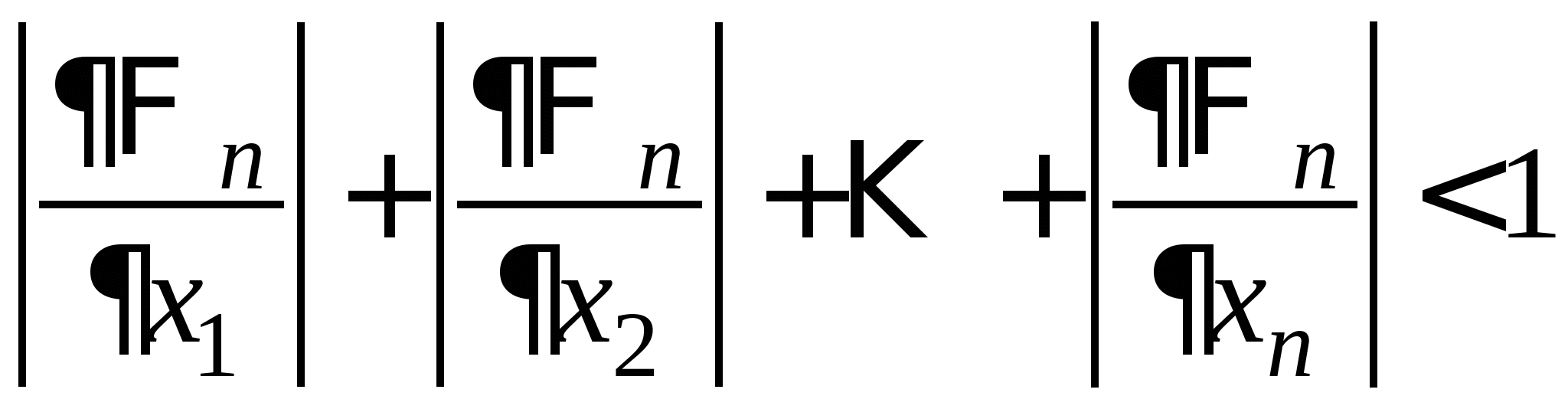 при
при ![]() .
.
Распишем второе условие:
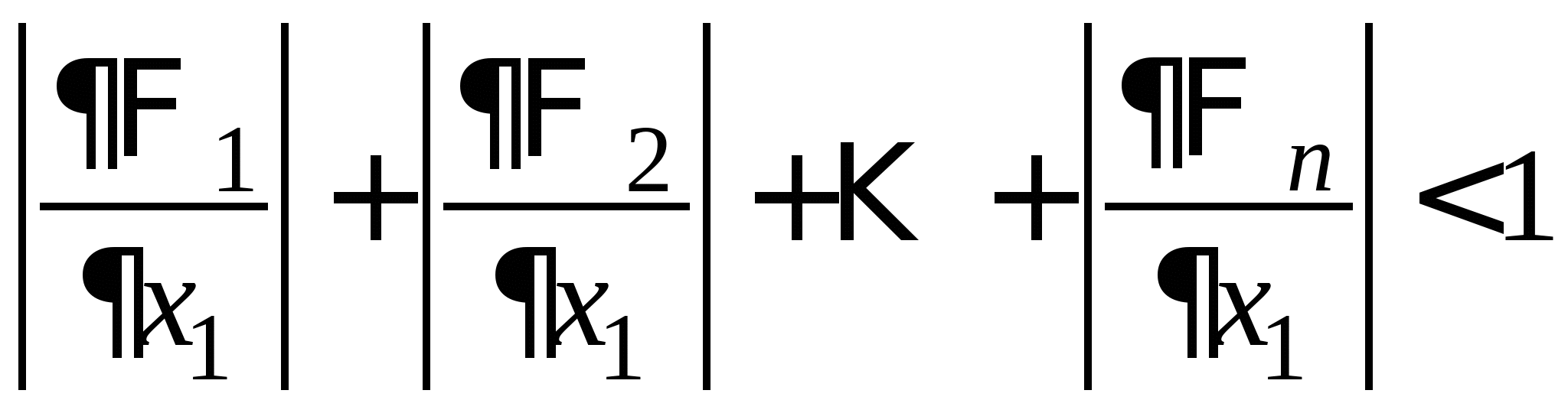 при
при ![]() ,
,
…
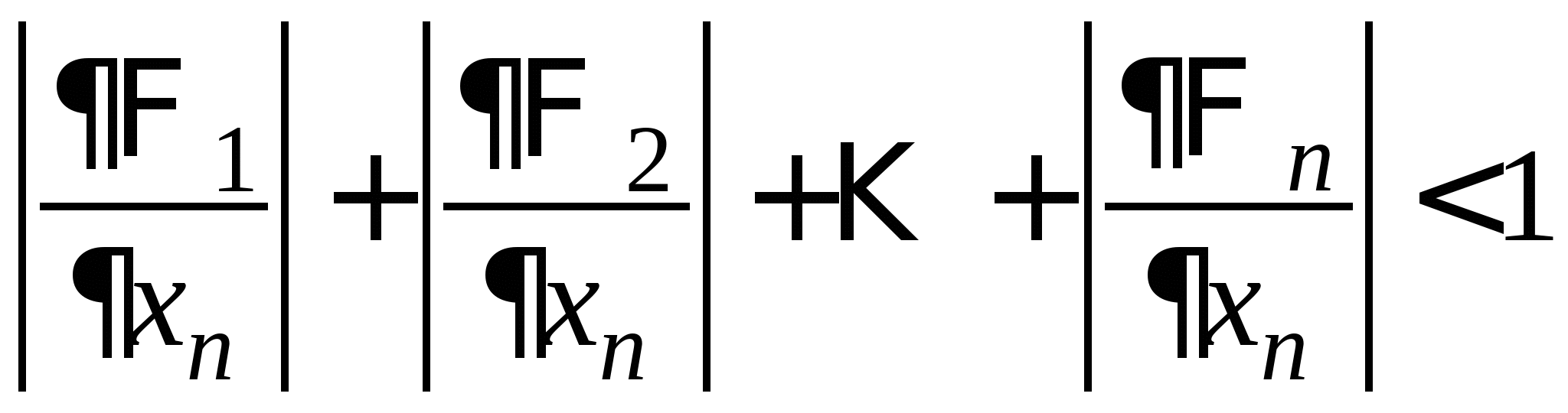 при
при ![]() .
.
Рассмотрим один из способов приведения системы (3.1) к виду (3.2), допускающему сходящийся итерационный процесс.
Пусть задана система второго порядка вида:
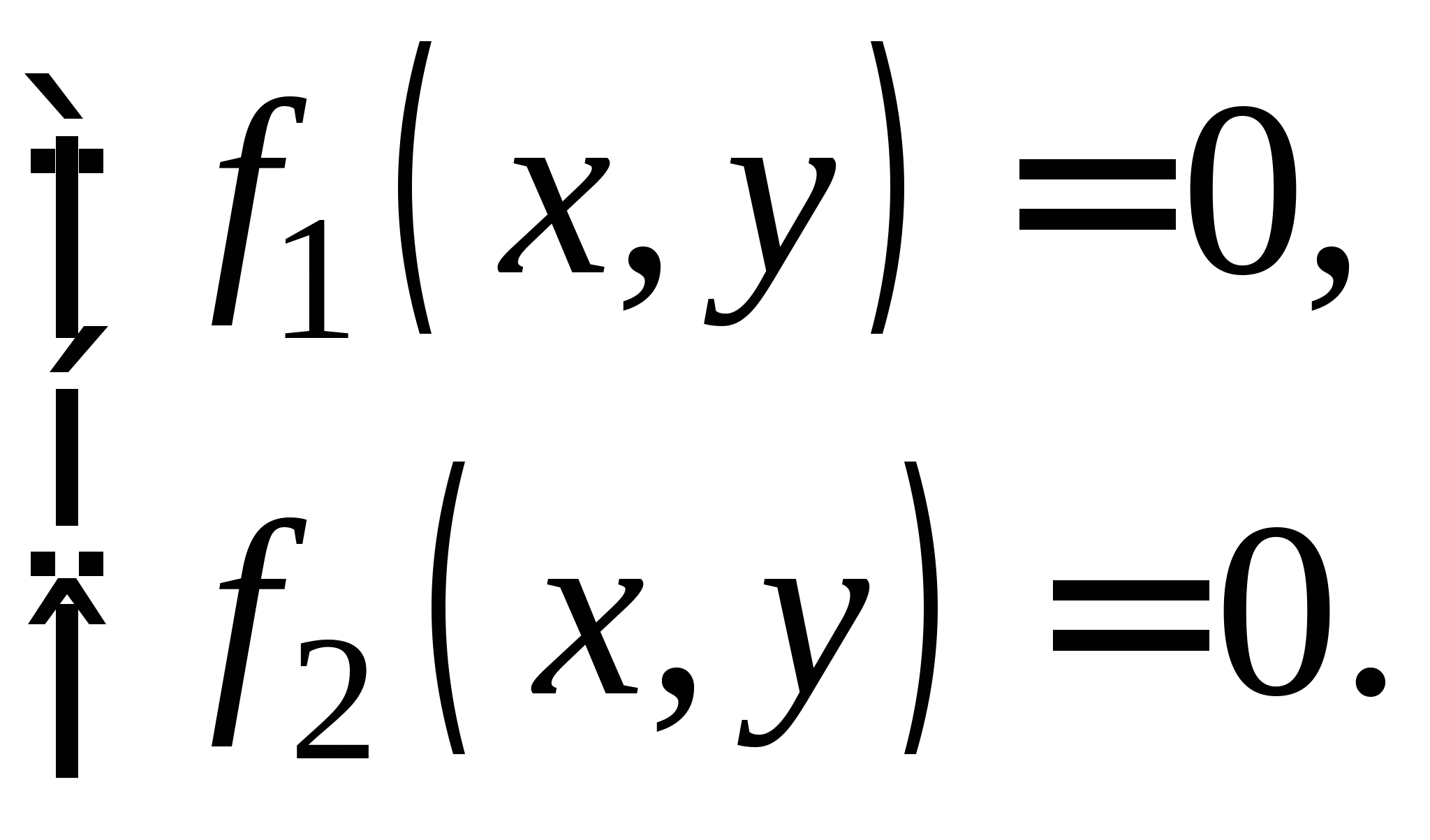 (3.3)
(3.3)
Требуется привести ее к виду:
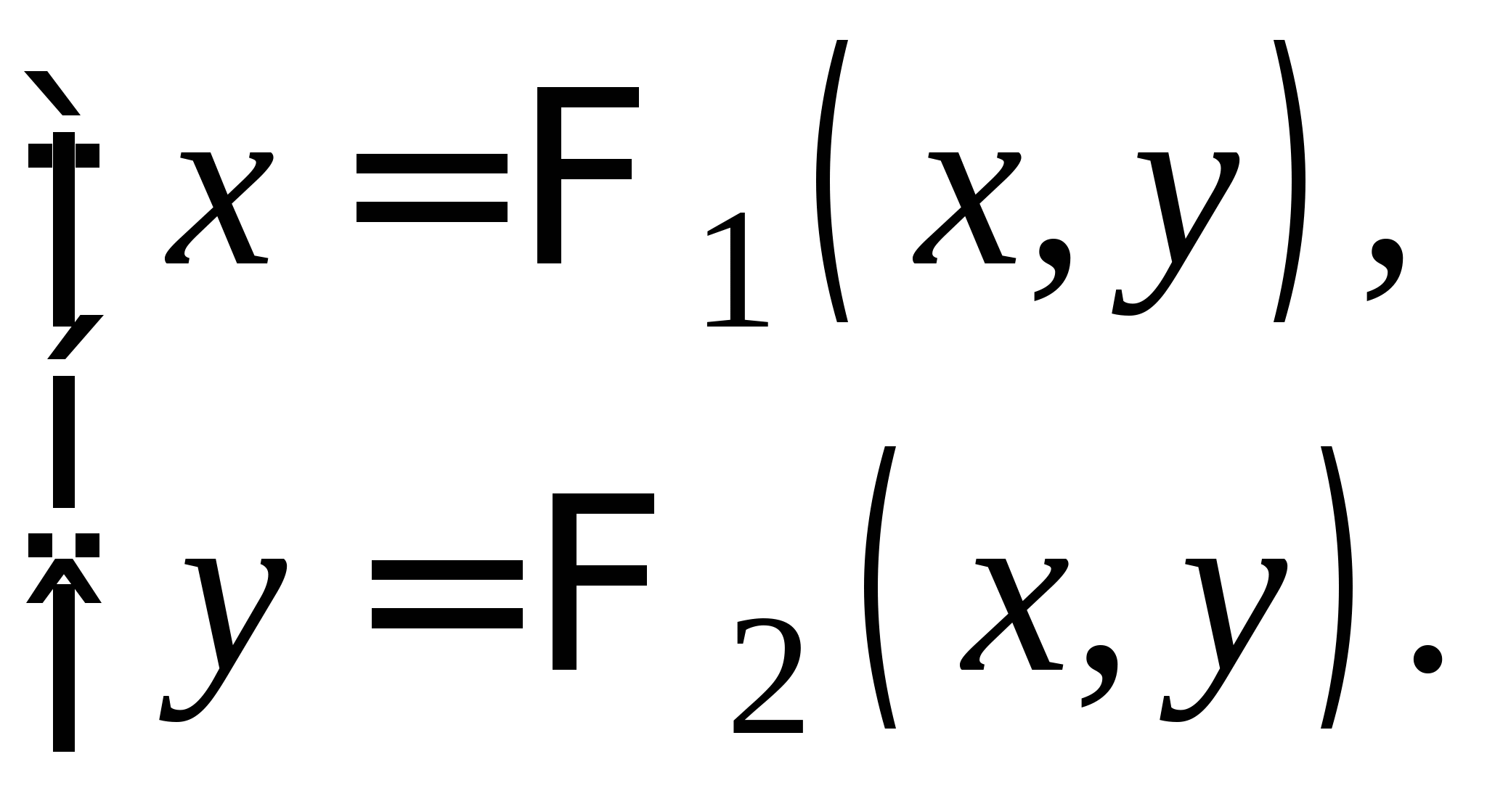 . (3.4)
. (3.4)
Умножим первое уравнение системы (3.3) на неизвестную постоянную ![]() , второе - на
, второе - на ![]() , затем сложим их и прибавим к обеим частям уравнения
, затем сложим их и прибавим к обеим частям уравнения ![]() . Получим первое уравнение преобразованной системы (3.4) в виде
. Получим первое уравнение преобразованной системы (3.4) в виде
![]()
где ![]() .
.
Далее, умножим первое уравнение системы (3.3) на неизвестную постоянную ![]() , второе - на
, второе - на ![]() , затем сложим их и прибавим к обеим частям уравнения
, затем сложим их и прибавим к обеим частям уравнения ![]() . Тогда второе уравнение преобразованной системы (3.4) будет иметь вид:
. Тогда второе уравнение преобразованной системы (3.4) будет иметь вид:
![]()
где ![]() .
.
Неизвестные постоянные ![]() определим из достаточных условий сходимости
определим из достаточных условий сходимости
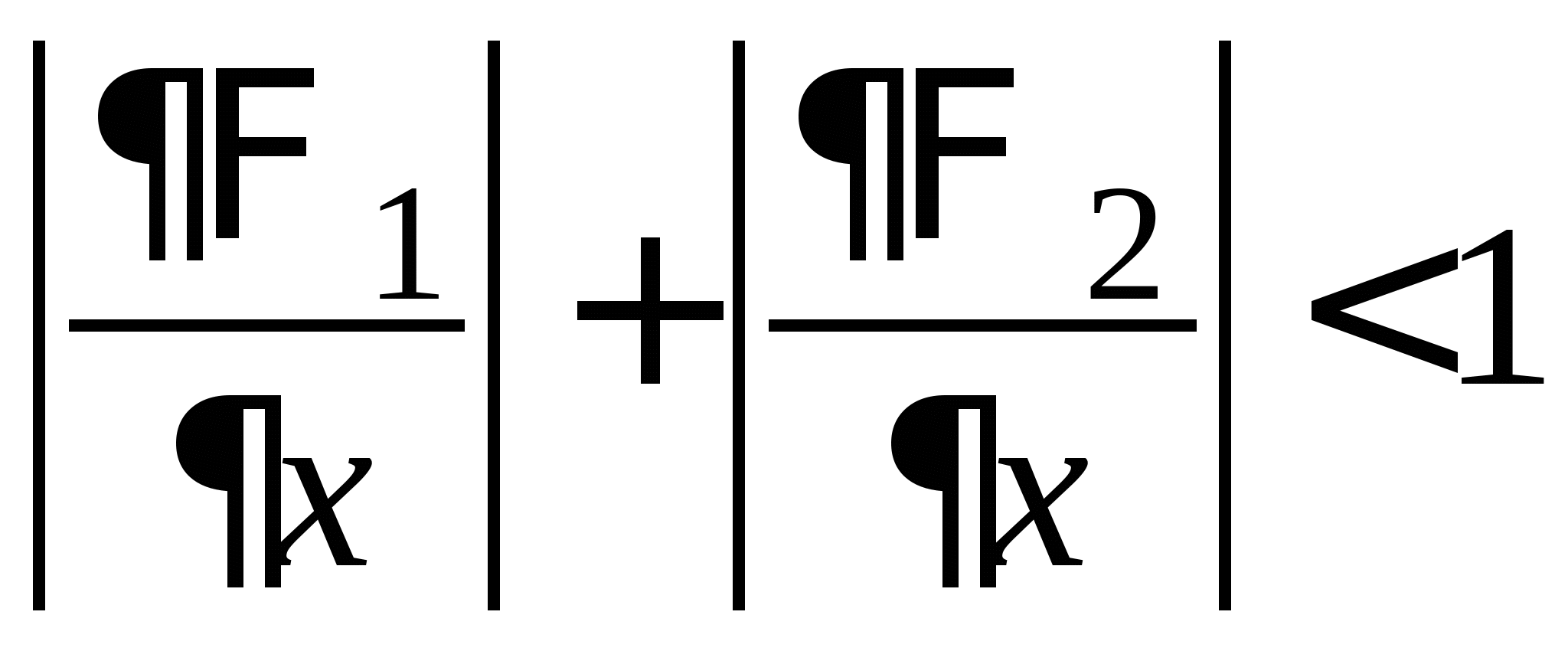 и
и 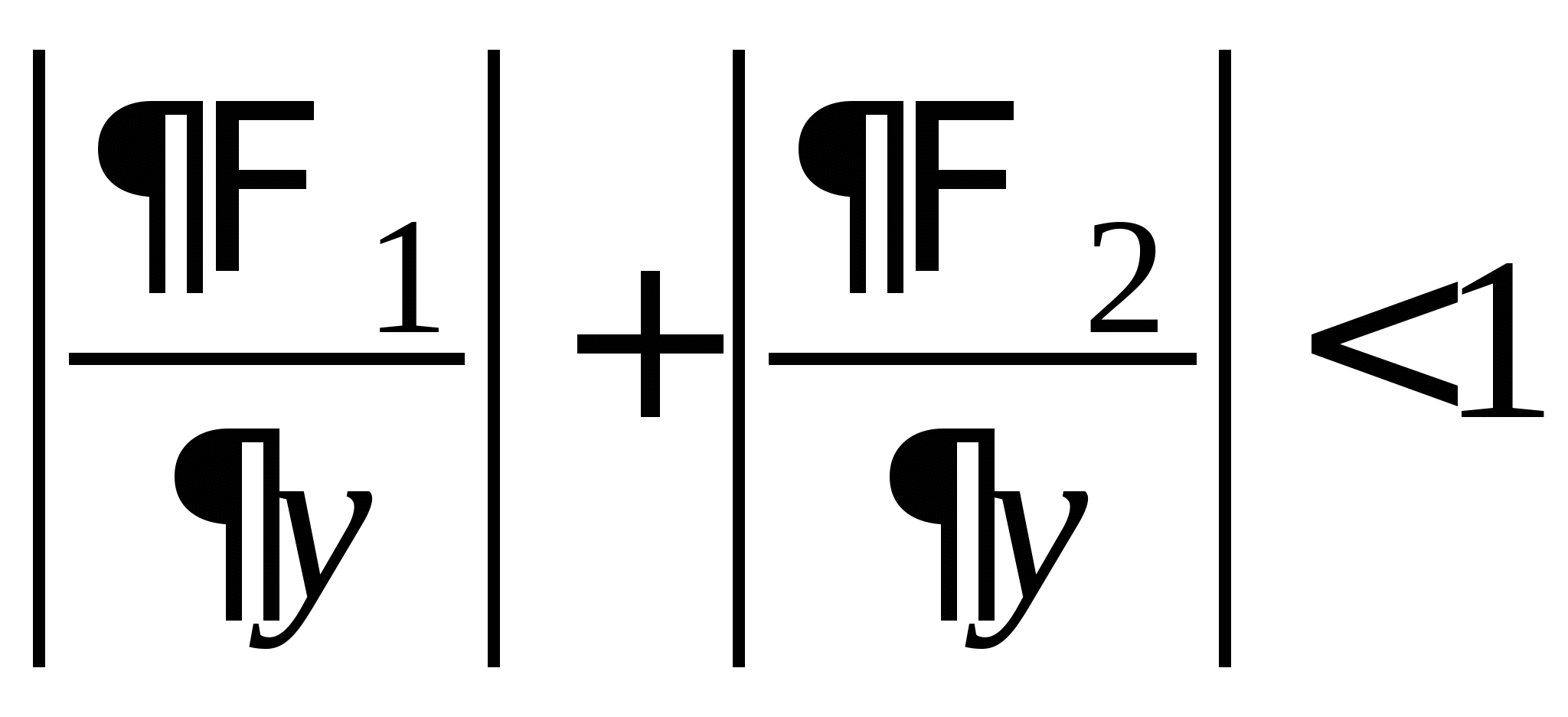 . (3.5)
. (3.5)
Запишем эти условия более подробно:
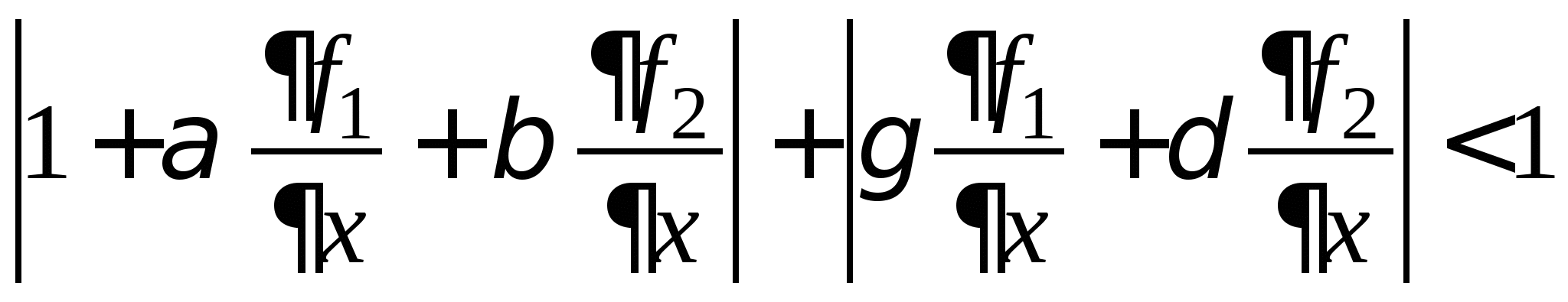 ,
,
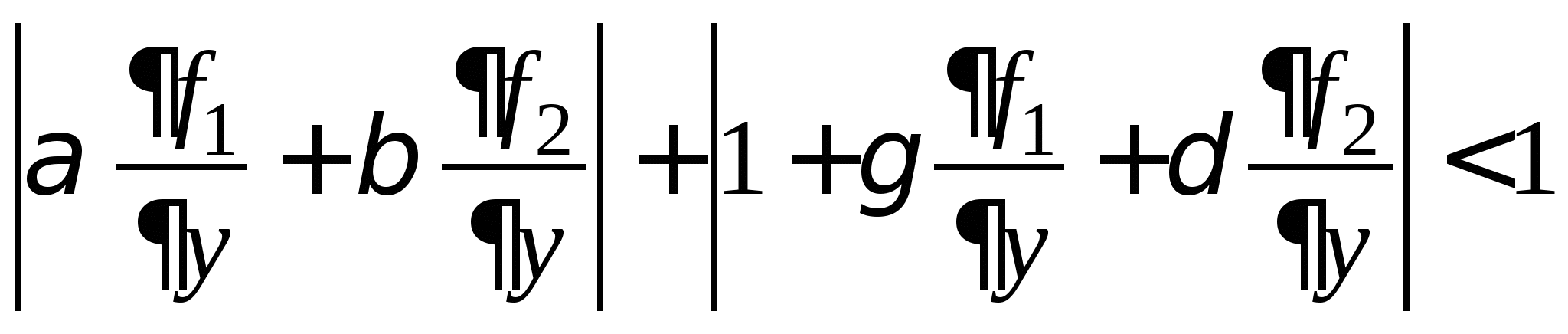 .
.
Полагая равными нулю выражения под знаком модуля, получим систему, состоящую из четырех линейных алгебраических уравнений с четырьмя неизвестными ![]() :
:
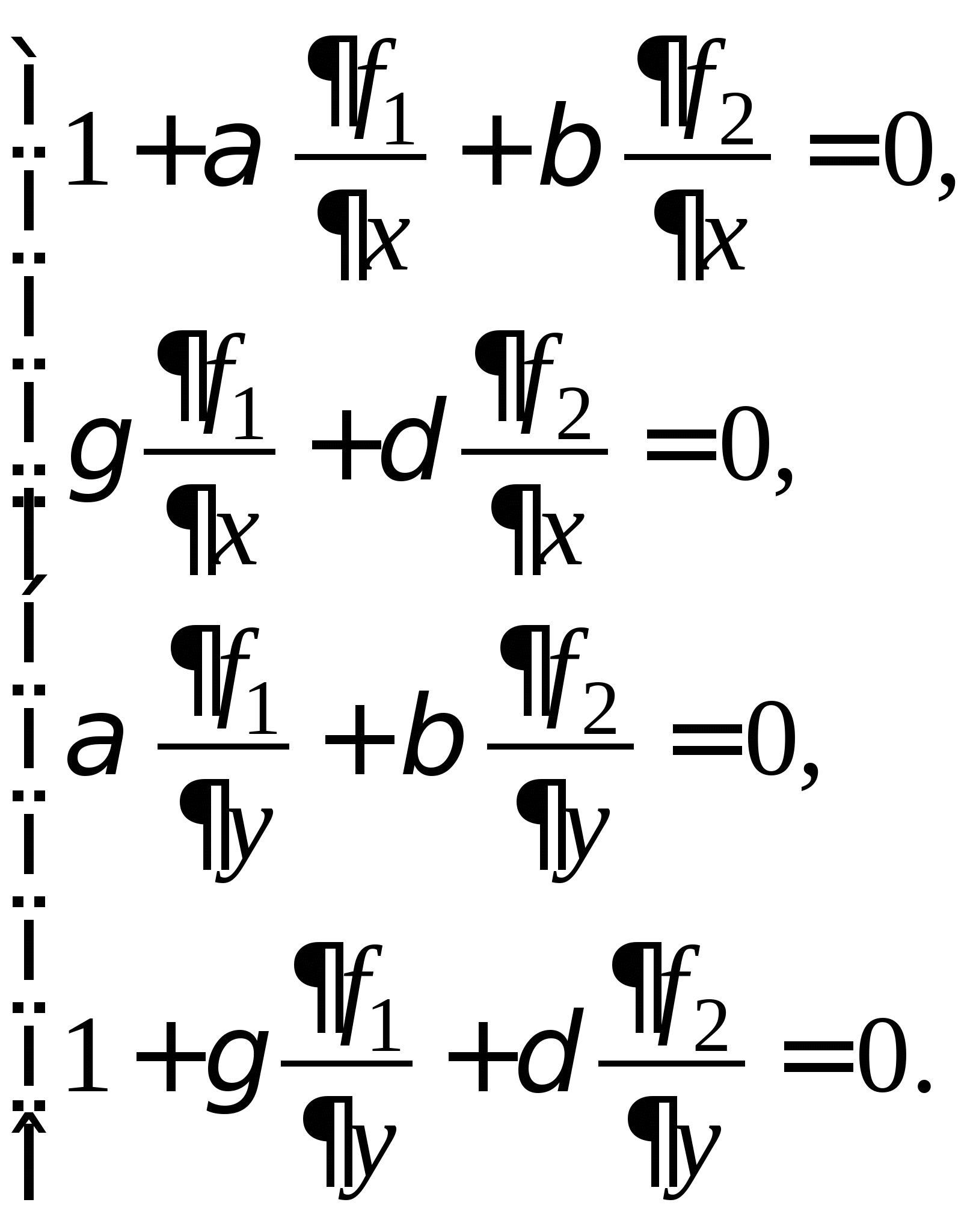 (3.6)
(3.6)
При таком выборе параметров условия сходимости будут выполнены, если частные производные функций ![]() и
и ![]() будут изменяться не очень быстро в окрестности точки
будут изменяться не очень быстро в окрестности точки ![]() . Тогда, для того, чтобы решить систему (3.1), нужно задать начальное приближение
. Тогда, для того, чтобы решить систему (3.1), нужно задать начальное приближение ![]() и вычислить значения производных
и вычислить значения производных 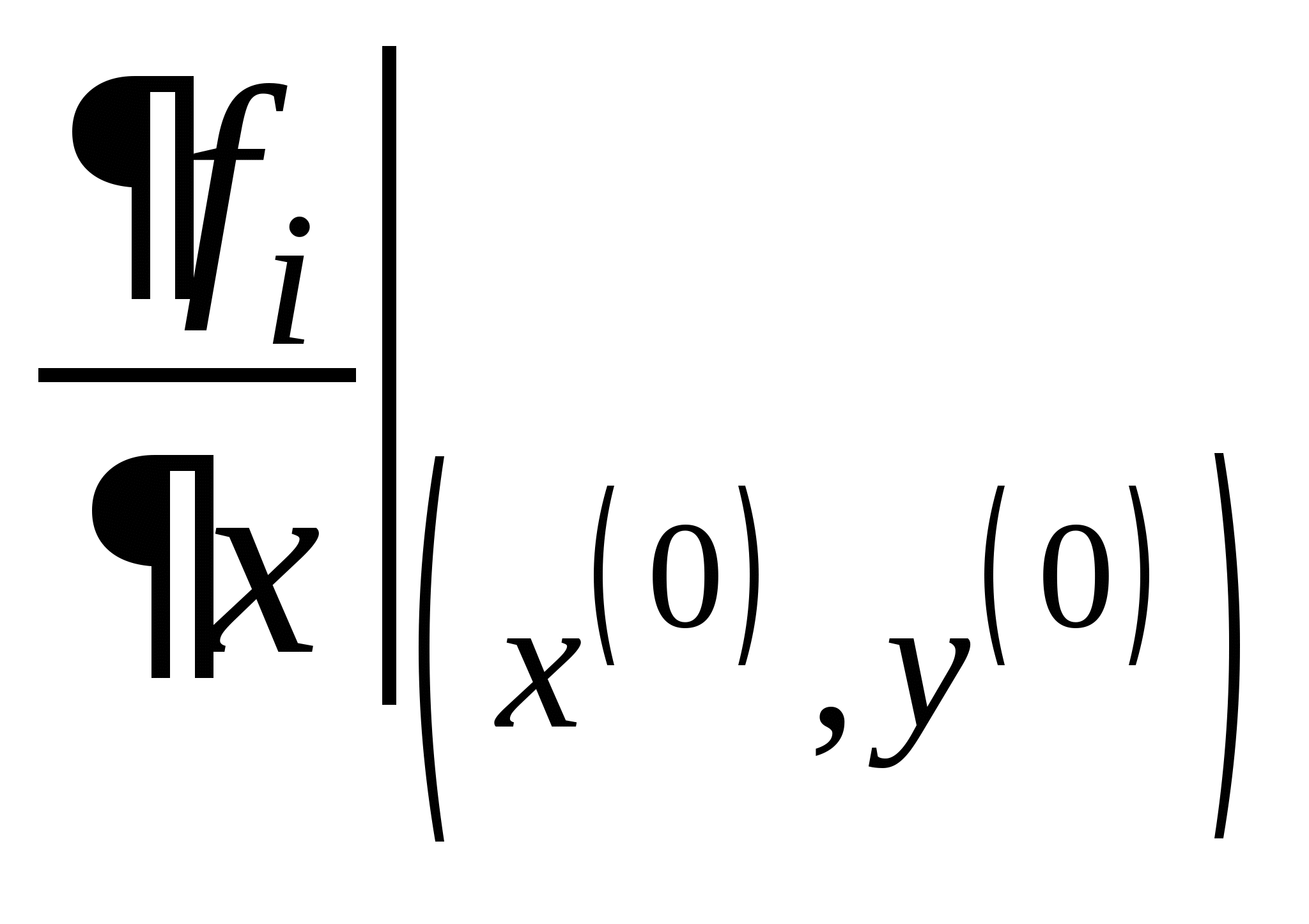 и
и 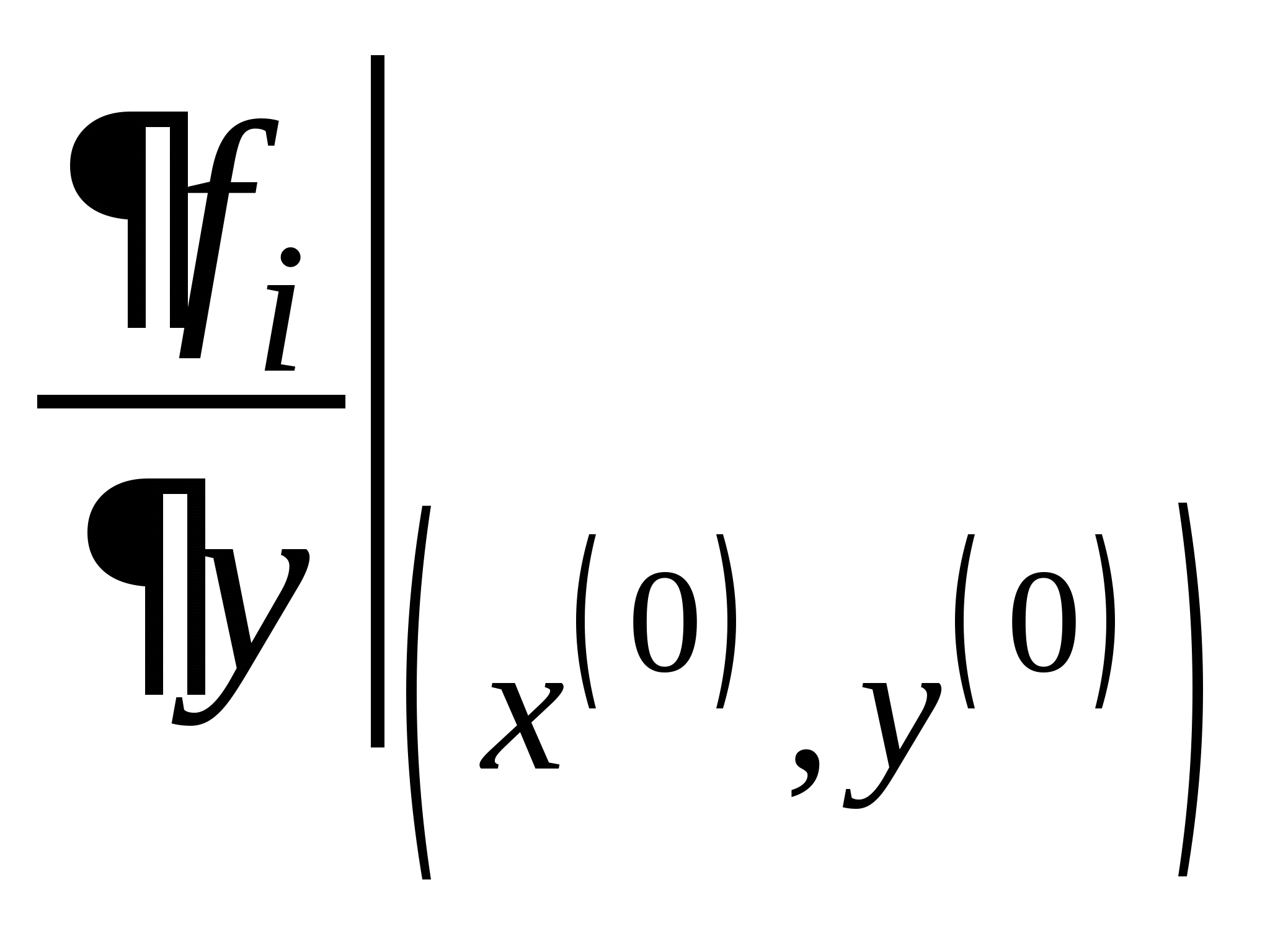 ,
, ![]() в этой точке. В противном случае, вычисление
в этой точке. В противном случае, вычисление ![]() осуществляется на каждом
осуществляется на каждом ![]() шаге итераций, при этом
шаге итераций, при этом 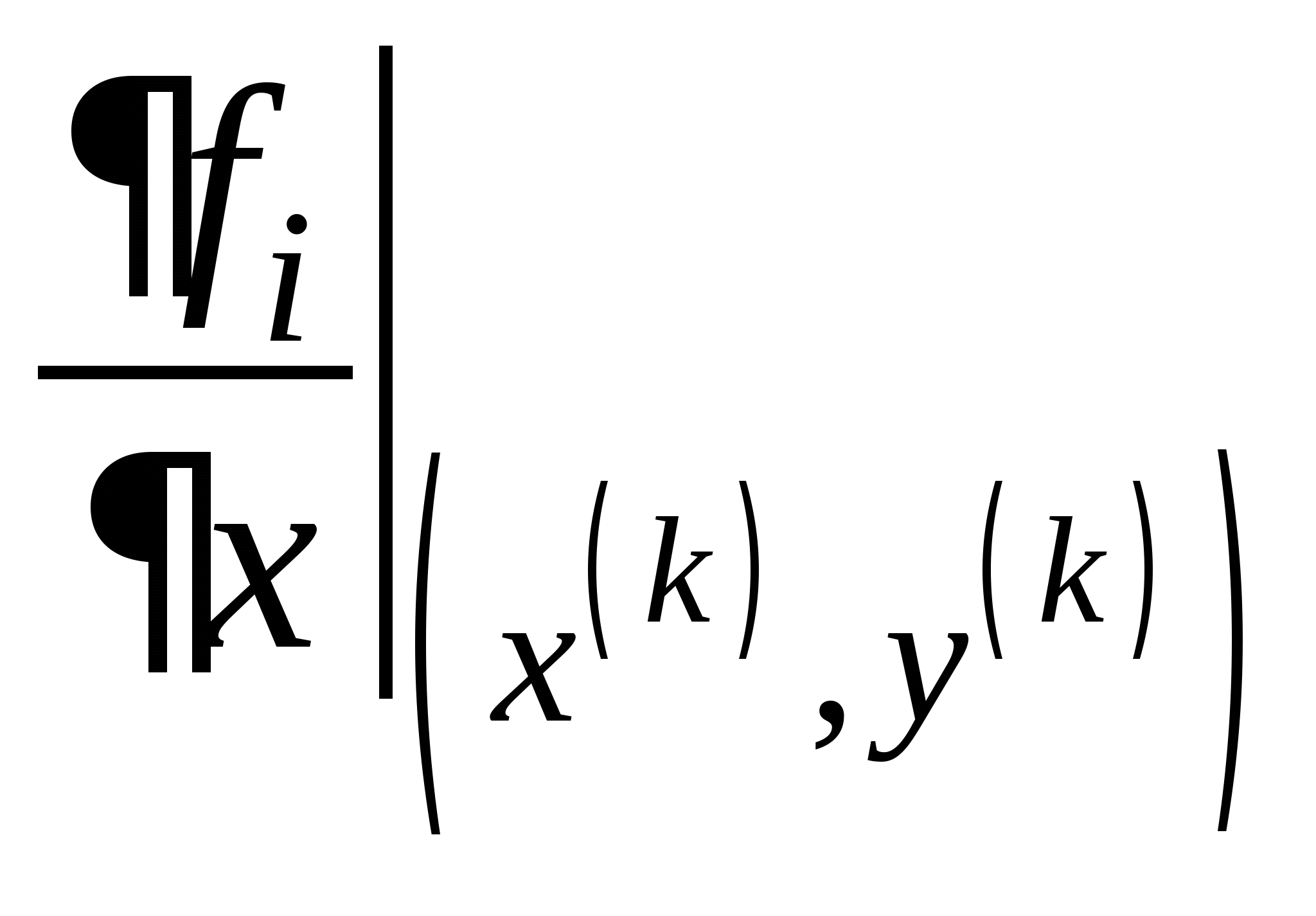 ,
, 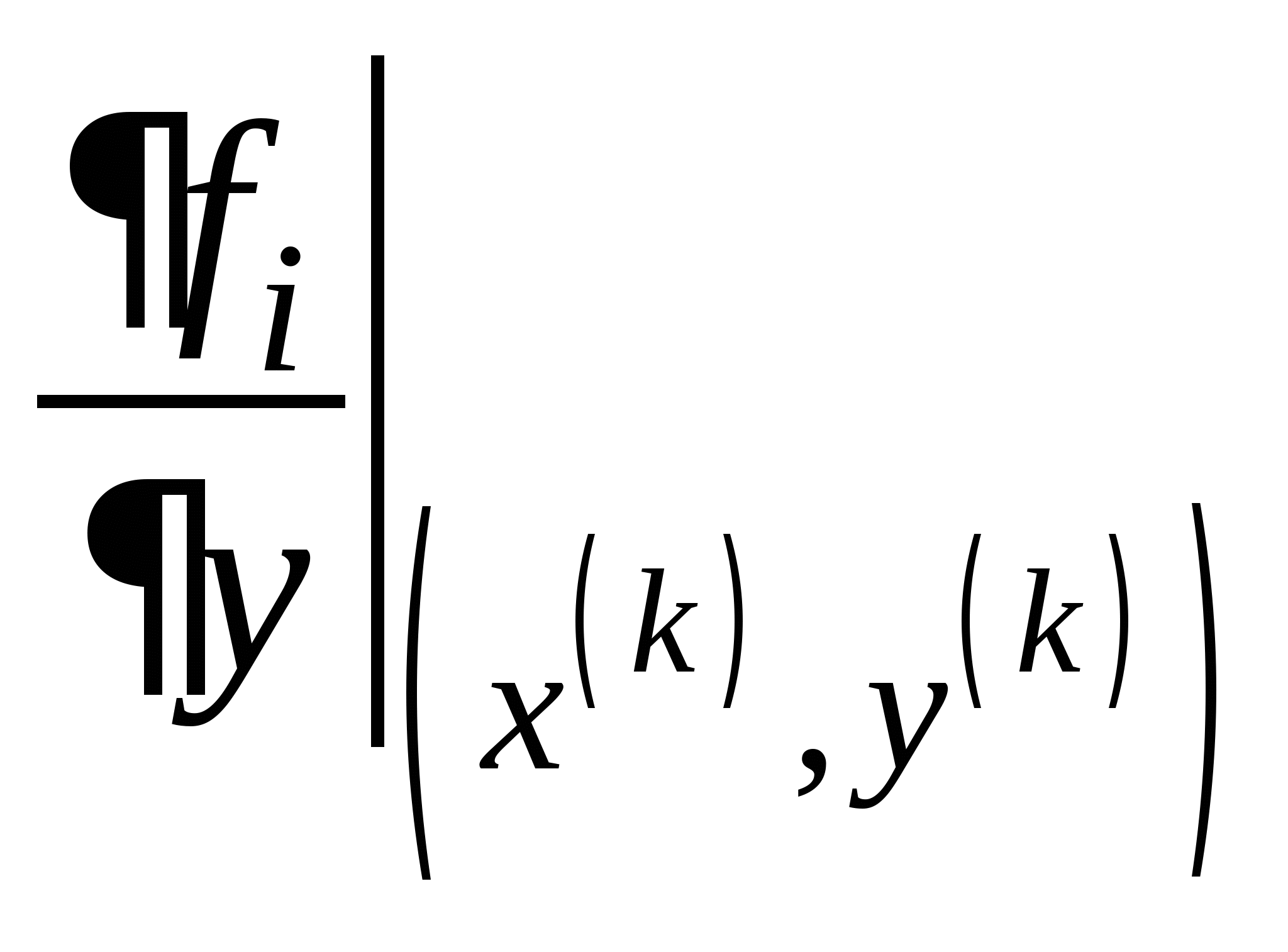 ,
, ![]() .
.
Метод простых итераций является самоисправляющимся, универсальным и простым для реализации на ЭВМ. Если система имеет большой порядок, то применение данного метода, имеющего медленную скорость сходимости, не рекомендуется. В этом случае, используют метод Ньютона, который имеет более высокую скорость сходимости.
Пример 3.1. Построить рабочие формулы метода простых итераций для численного решения СНУ вида:
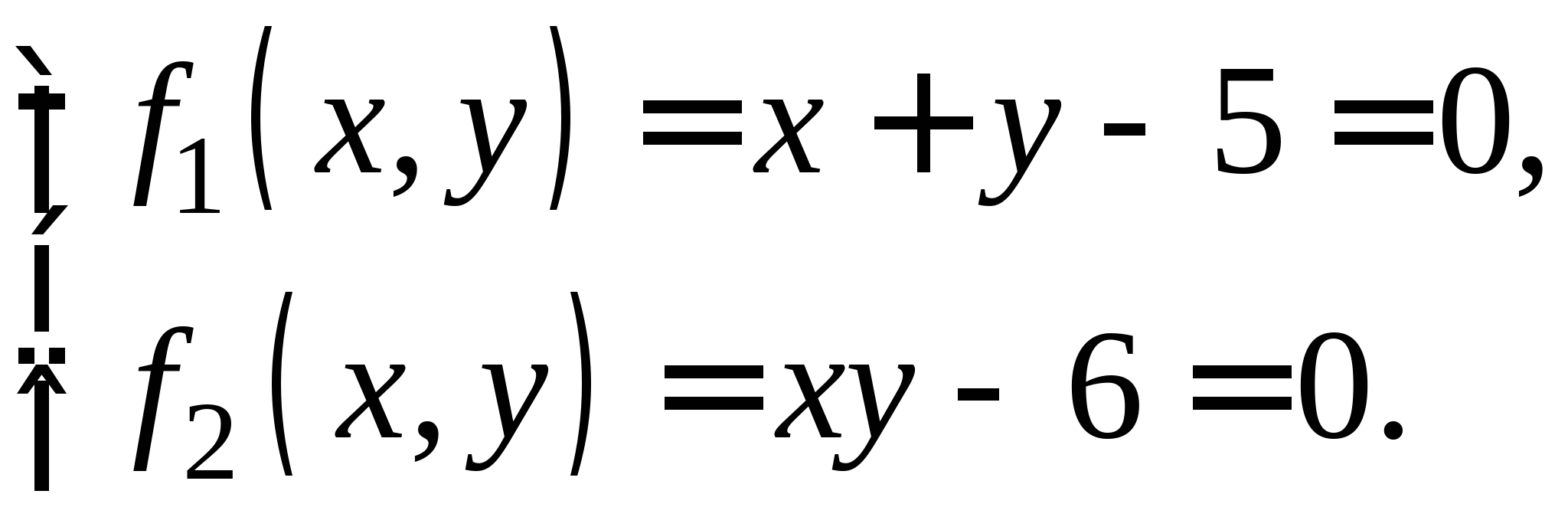 (3.7)
(3.7)
при начальном приближении
![]() . (3.8)
. (3.8)
Заметим, что аналитическим решением СНУ (3.7) являются точки ![]() и
и ![]() .
.
Для построения рабочих формул метода простых итераций для численного решения системы необходимо решить СЛАУ (3.6). Для ее решения необходимо вычислить частные производные 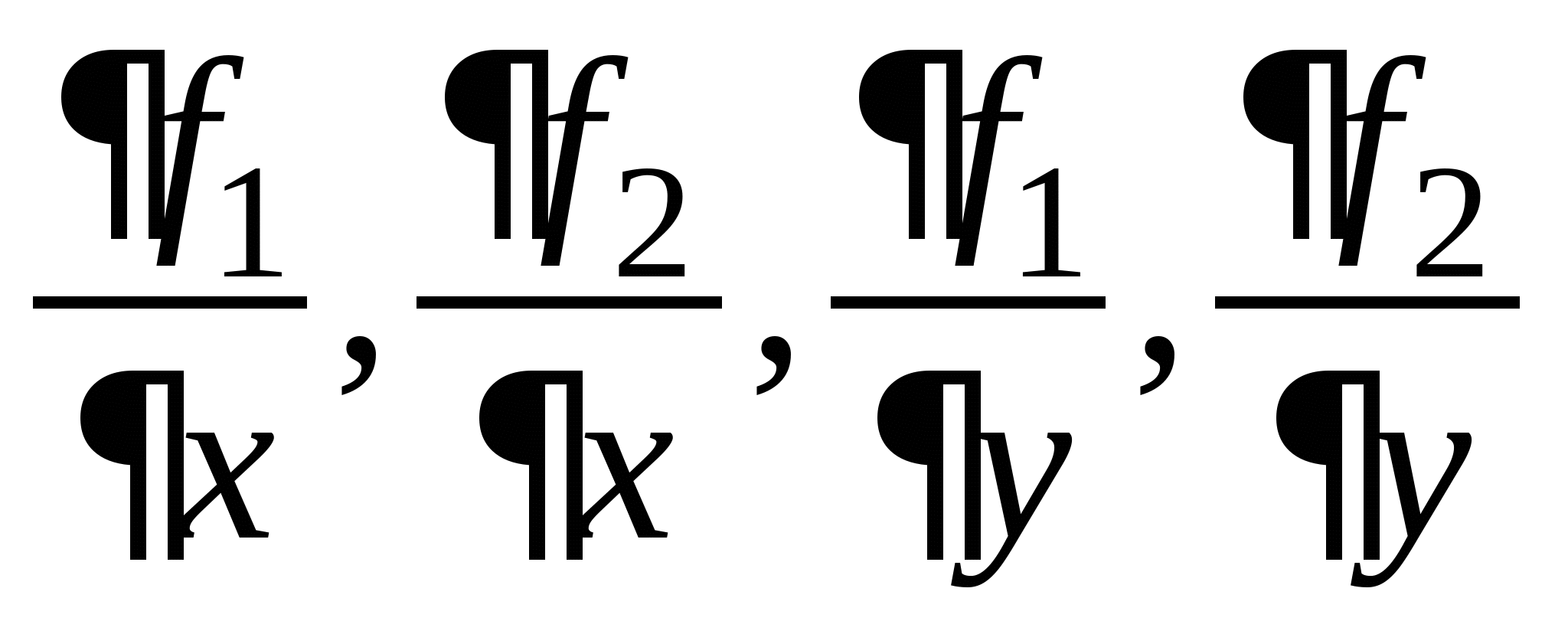 при начальном приближении (3.8):
при начальном приближении (3.8):
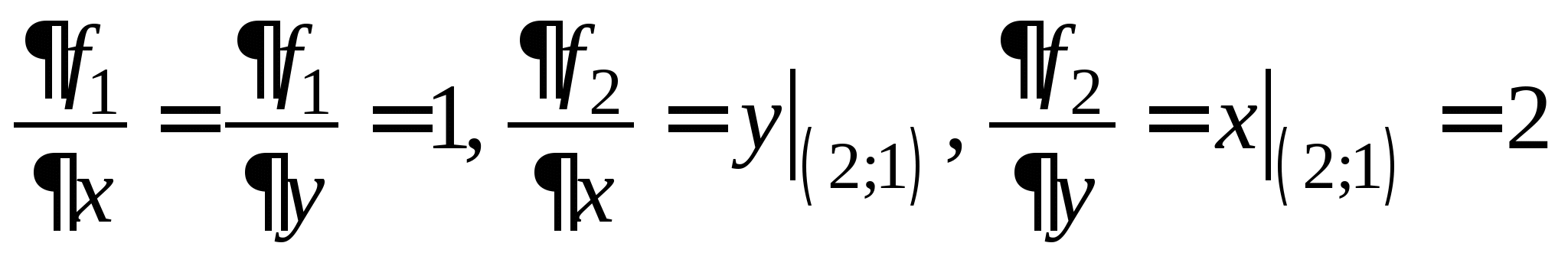 .
.
Тогда СЛАУ (3.6) запишется так:
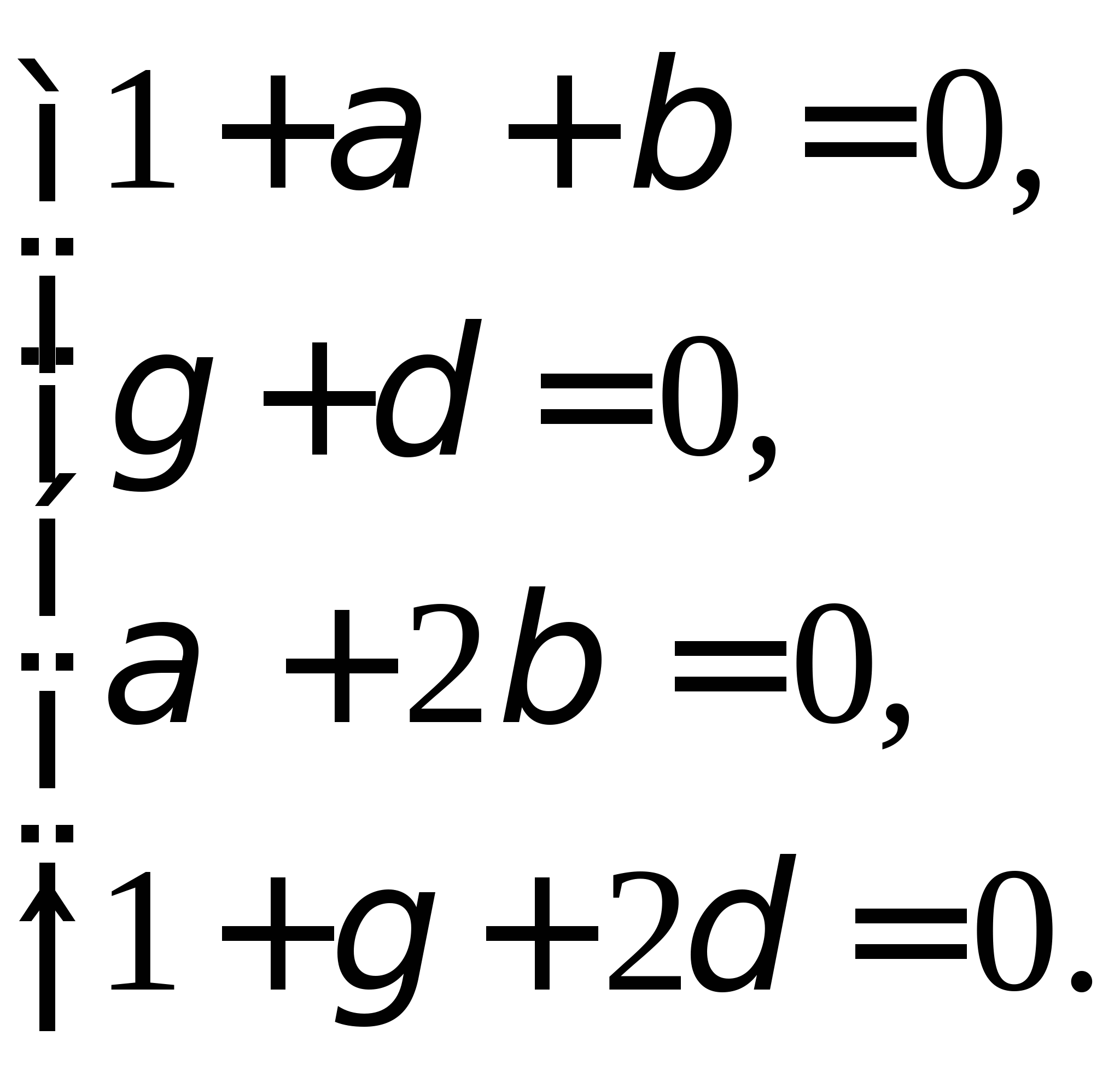
Решением этой системы являются ![]() ,
, ![]() ,
, ![]() . Тогда рабочие формулы метода простых итераций для решения СНУ (3.7) примут вид:
. Тогда рабочие формулы метода простых итераций для решения СНУ (3.7) примут вид:
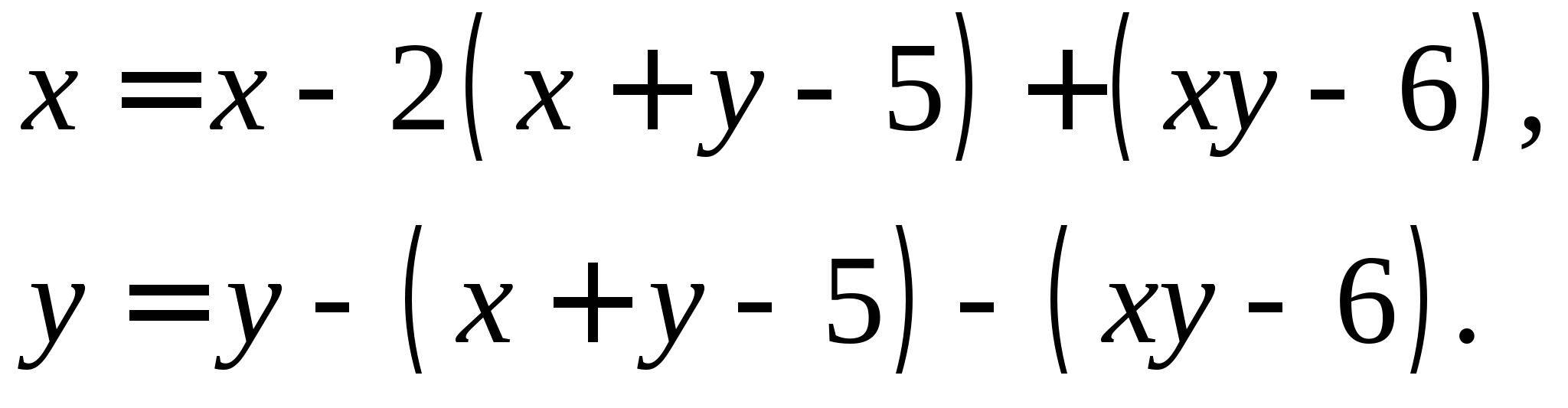
Для реализации на ЭВМ рабочие формулы можно переписать так:
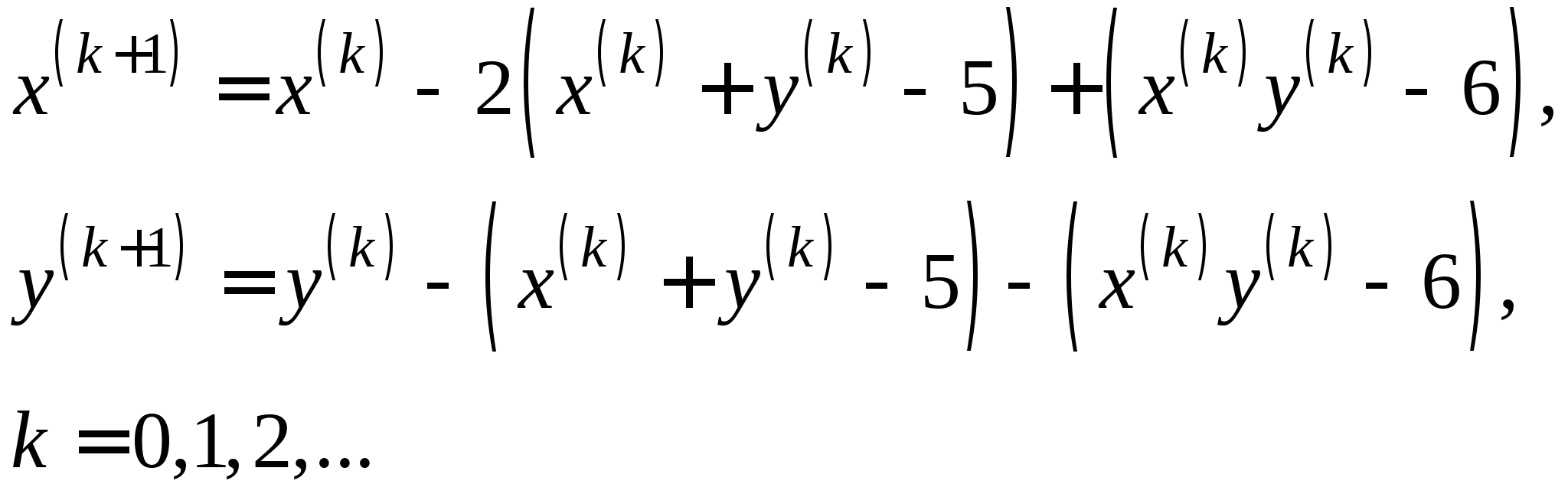
§3.2. Метод Ньютона для решения систем нелинейных уравнений.
Пусть требуется решить систему нелинейных уравнений с действительными левыми частями вида (3.1):
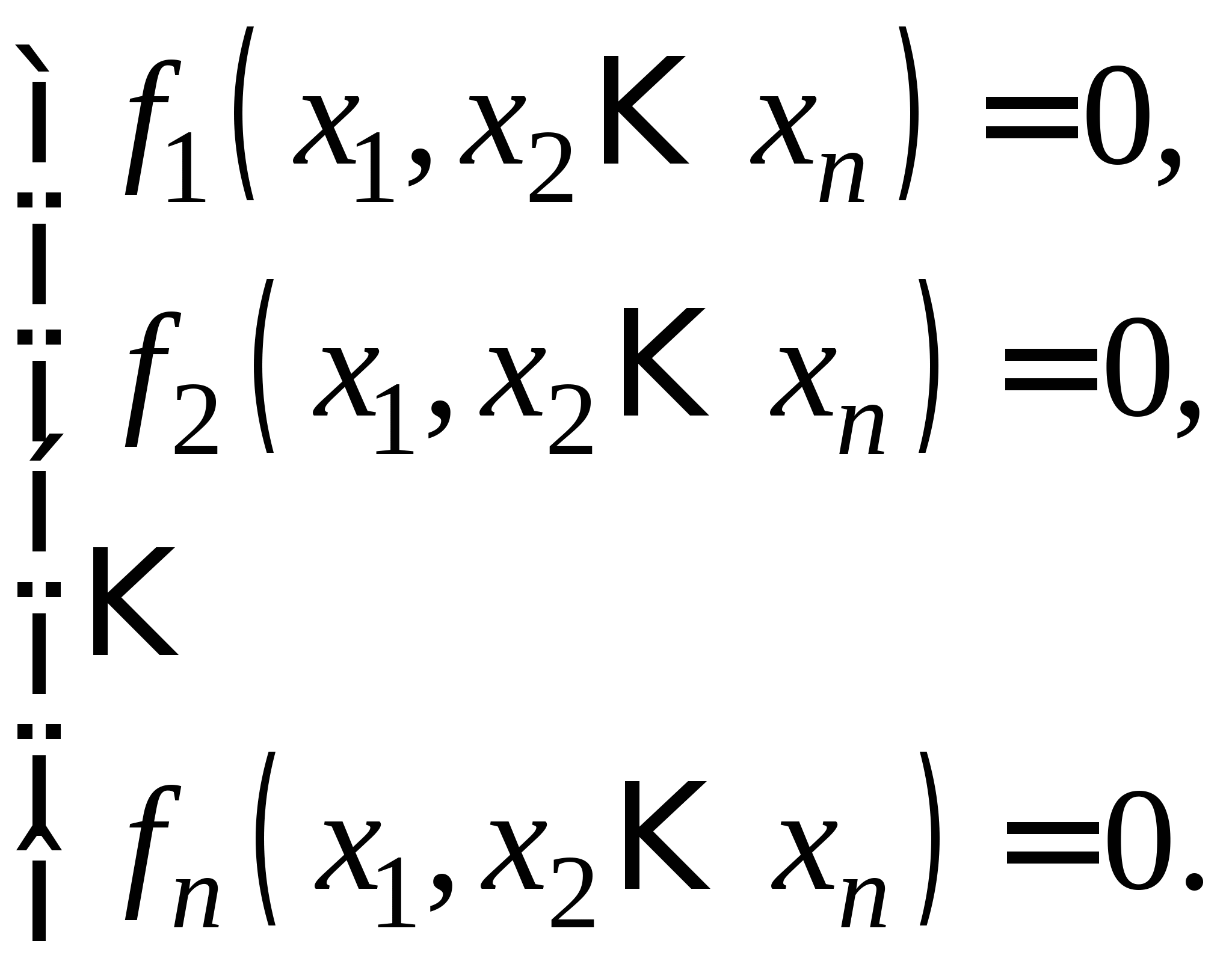
Введем обозначения.
Совокупность аргументов ![]() будем рассматривать как
будем рассматривать как ![]() -мерный вектор
-мерный вектор 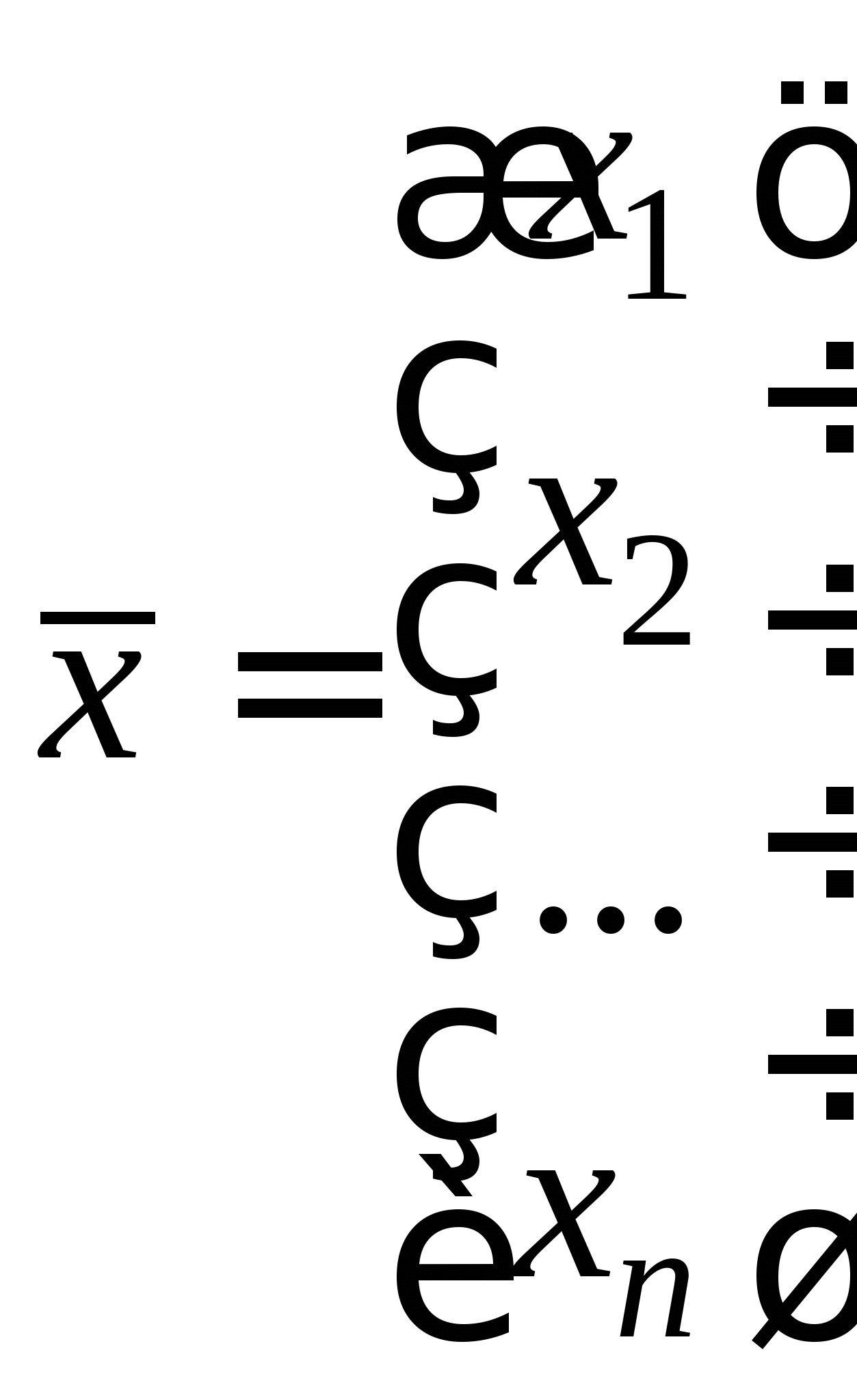 , а совокупность функций
, а совокупность функций ![]() как вектор-функцию
как вектор-функцию 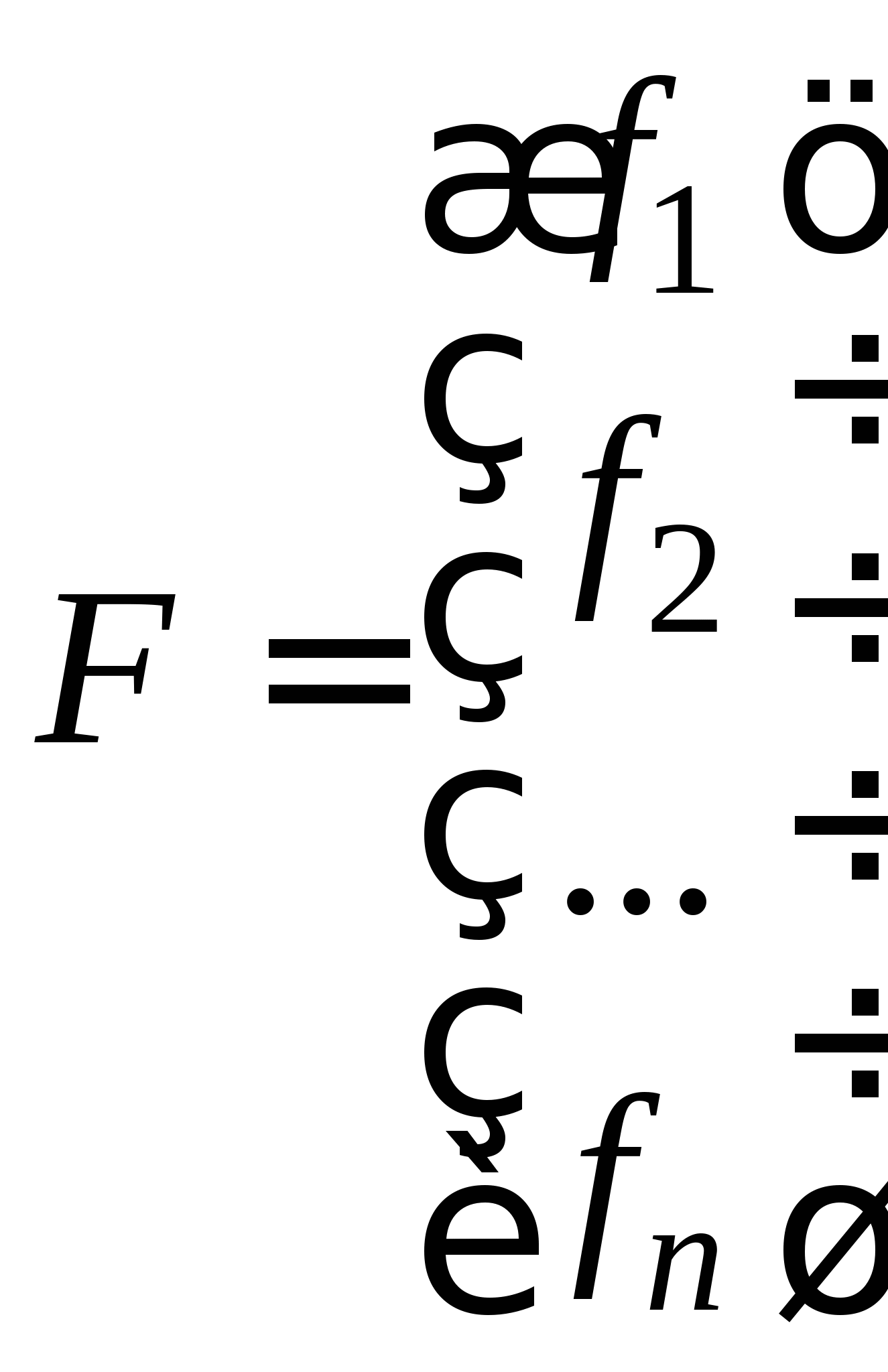 . Тогда система (3.1) в матричной форме запишется так:
. Тогда система (3.1) в матричной форме запишется так:
![]() . (3.9)
. (3.9)
Для решения системы (3.9) будем использовать метод последовательных приближений.
Предположим, что найдено ![]() -е приближение
-е приближение ![]() одного из изолированных корней
одного из изолированных корней ![]() векторного уравнения (3.9). Тогда точный корень уравнения (3.9) можно представить в виде:
векторного уравнения (3.9). Тогда точный корень уравнения (3.9) можно представить в виде:
![]() , (3.10)
, (3.10)
где ![]() погрешность корня (правка).
погрешность корня (правка).
Подставляя (3.10) в (3.9), получим:
![]() . (3.11)
. (3.11)
Предположим, что функция ![]() непрерывно дифференцируема в некоторой выпуклой области, содержащей
непрерывно дифференцируема в некоторой выпуклой области, содержащей ![]() и
и ![]() . Разложим левую часть уравнения (3.11) по степеням
. Разложим левую часть уравнения (3.11) по степеням ![]() , ограничиваясь линейными членами:
, ограничиваясь линейными членами:
![]() , (3.12)
, (3.12)
где 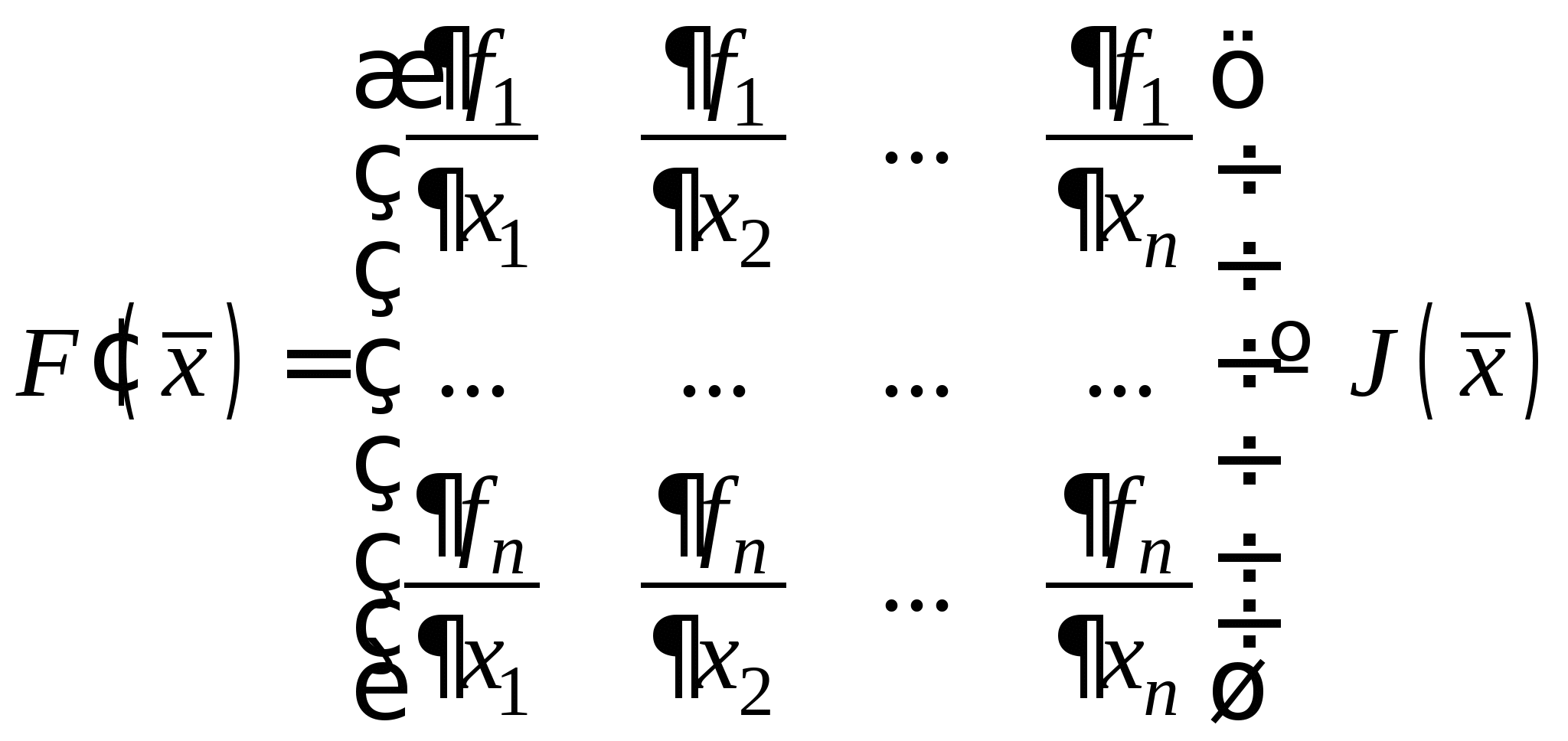 - матрица Якоби системы функций
- матрица Якоби системы функций ![]() относительно переменных
относительно переменных ![]() .
.
Система (3.12) представляет собой линейную систему относительно правок ![]() с матрицей
с матрицей ![]() , поэтому формулу (3.12) можно записать в виде:
, поэтому формулу (3.12) можно записать в виде:
![]() . (3.13)
. (3.13)
Если матрица ![]() невырожденная, то существует
невырожденная, то существует ![]() и тогда, умножив обе части соотношения (3.13) на
и тогда, умножив обе части соотношения (3.13) на ![]() слева, получим
слева, получим
![]() . (3.14)
. (3.14)
Следовательно,
![]() . (3.15)
. (3.15)
Соотношение (3.15) является итерационной формулой метода Ньютона для решения систем нелинейных уравнений.
Если начальное приближение ![]() выбрано достаточно близко к решению
выбрано достаточно близко к решению ![]() системы (3.9), то итерационная последовательность сходится к этому решению, и сходимость является квадратичной [10].
системы (3.9), то итерационная последовательность сходится к этому решению, и сходимость является квадратичной [10].
Недостатки метода Ньютона:
нахождение обратной матрицы ![]() на каждом итерационном шаге;
на каждом итерационном шаге;
возможность выхода приближения ![]() за пределы области
за пределы области ![]() и связанная с этим расходимость итерационного процесса.
и связанная с этим расходимость итерационного процесса.
Модифицированный метод Ньютона решает первую задачу. Если матрица ![]() непрерывна в окрестности искомого решения
непрерывна в окрестности искомого решения ![]() и начальное приближение
и начальное приближение ![]() достаточно близко к
достаточно близко к ![]() , то приближенно можно положить
, то приближенно можно положить ![]() . Тогда формула (3.15) принимает вид:
. Тогда формула (3.15) принимает вид:
![]() . (3.16)
. (3.16)
Формула (3.16) является рабочей формулой модифицированного метода Ньютона.
Достоинством данного метода является то, что обратная матрица вычисляется один раз. Но ответа на второй вопрос модифицированный метод Ньютона не дает.
Сходимость модифицированного процесса (метода) Ньютона исследовалась Л.В. Канторовичем [8].
Пример 3.2. Построить рабочие формулы метода Ньютона для численного решения СНУ (3.7) при начальном приближении (3.8).
Для нахождения обратной матрицы в формуле (3.15) необходимо:
1. Найти матрицу частных производных 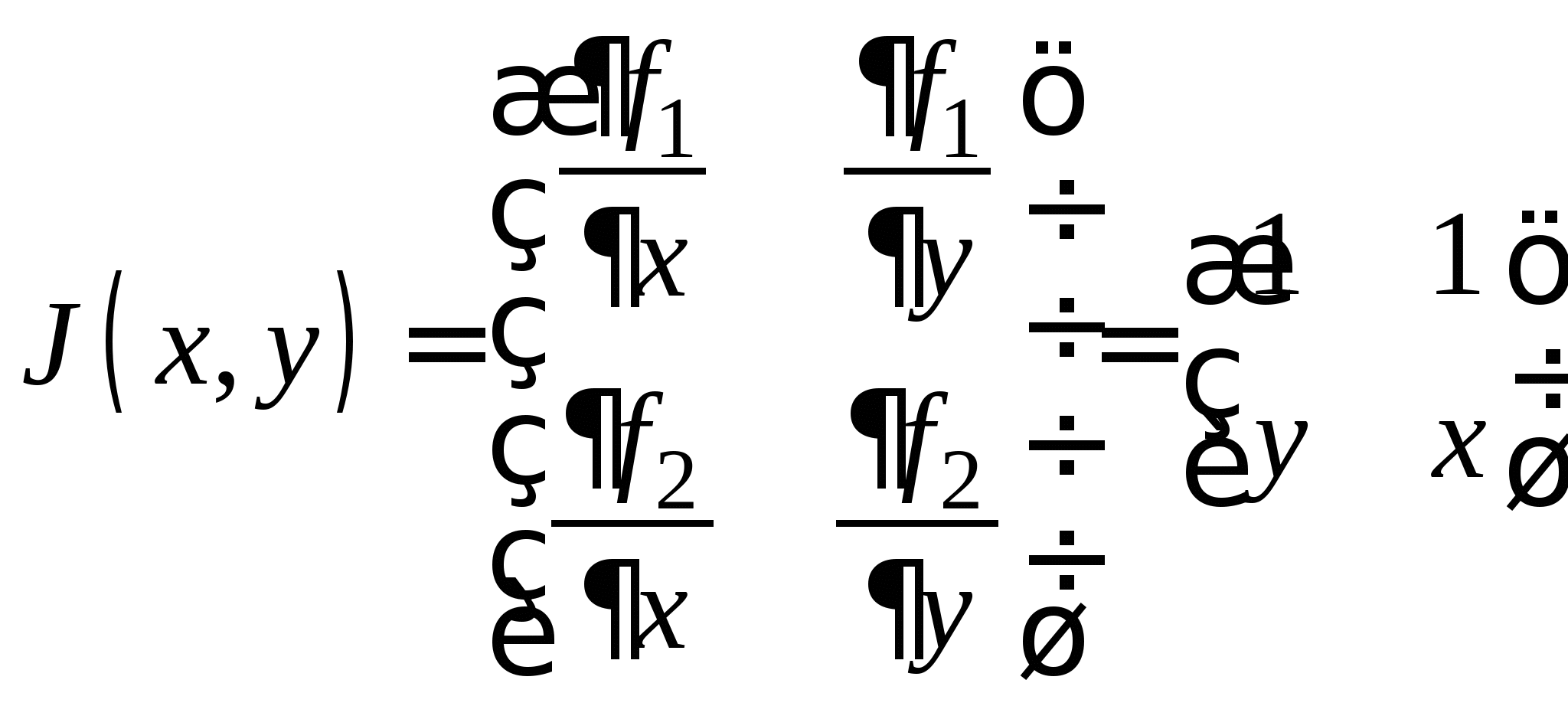 .
.
2. Найти определитель этой матрицы:
![]() .
.
3. Определить обратную матрицу:
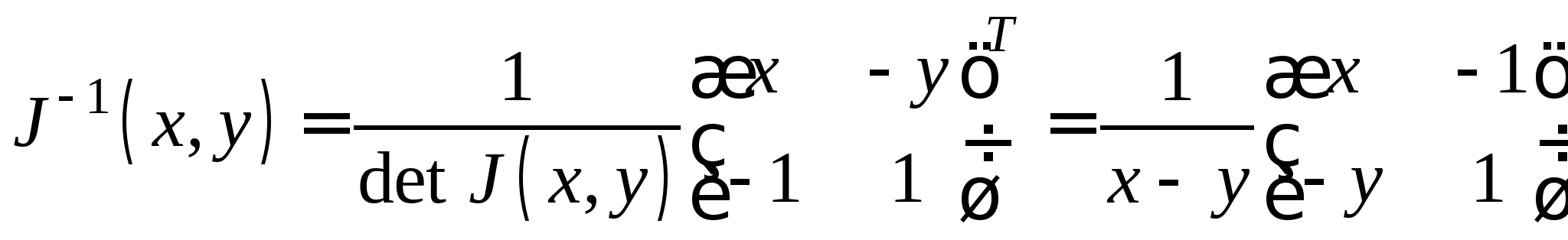 .
.
Проведя несложные преобразования с матрицами, получим рабочую формулу метода Ньютона (3.15) в виде:
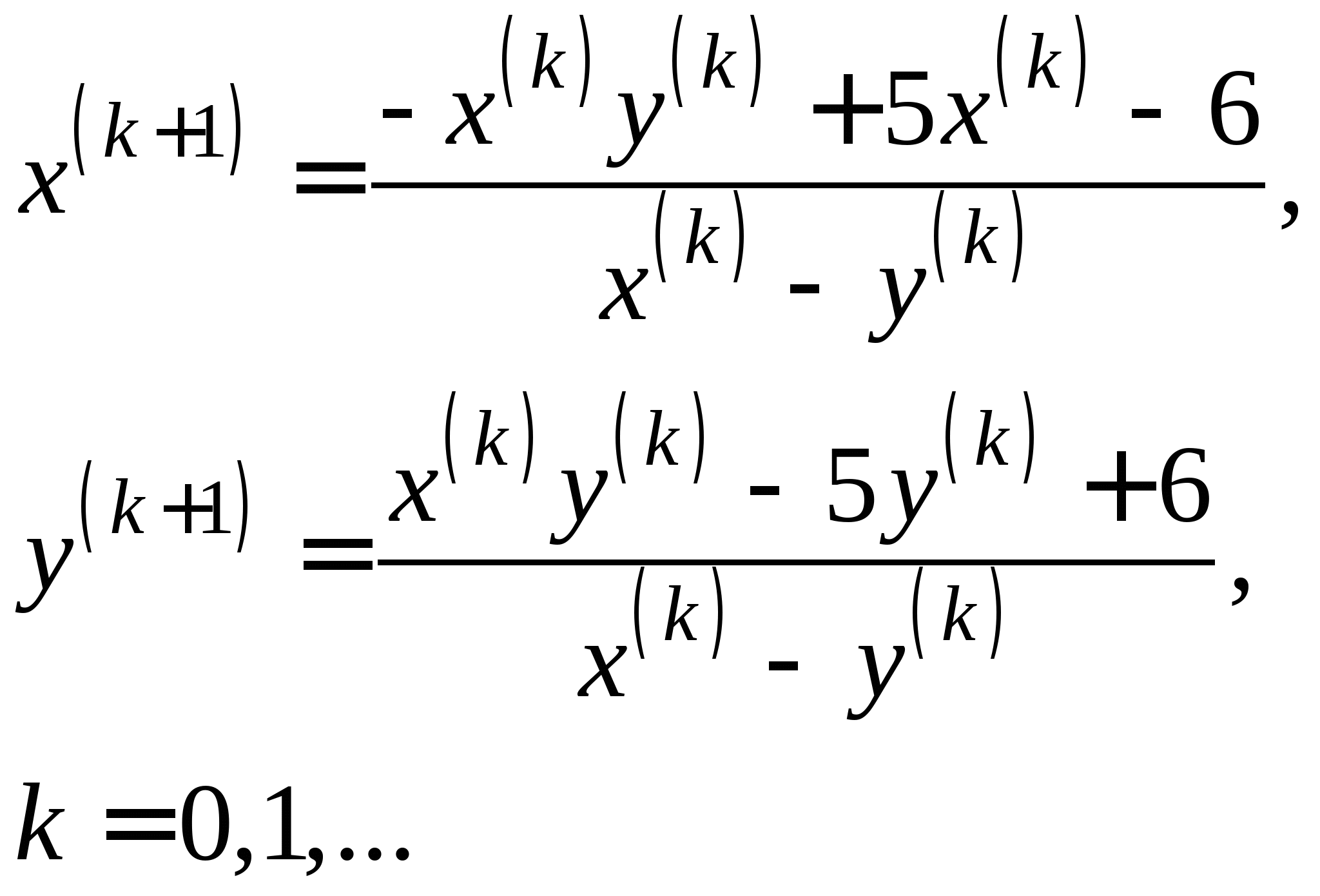
43
Глава 2. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
§2.1. Основные этапы решения нелинейных уравнений
Определение 2.1. Нелинейным уравнением называется уравнение вида
![]() , (2.1)
, (2.1)
где ![]() нелинейная функция вида:
нелинейная функция вида:
нелинейная алгебраическая функция (полином или многочлен) ![]() ;
;
трансцендентная функция – тригонометрическая, обратная тригонометрическая, логарифмическая, показательная, гиперболическая функция;
комбинирование этих функций, например ![]() .
.
Определение 2.2. Решением нелинейного уравнения (2.1) называется такое значение ![]() , которое при подстановке в уравнение (2.1) обращает его в тождество.
, которое при подстановке в уравнение (2.1) обращает его в тождество.
На практике не всегда удается найти точное решение. В этом случае решение уравнения (2.1) находят с применением приближенных (численных) методов.
Определение 2.3. Приближенным решением нелинейного уравнения (2.1) называется такое значение ![]() , при подстановке которого в уравнение (2.1) последнее будет выполняться с определенной степенью точности, т.е.
, при подстановке которого в уравнение (2.1) последнее будет выполняться с определенной степенью точности, т.е. ![]() , где
, где ![]() малая положительная величина.
малая положительная величина.
Нахождение приближенных решений составляет основу численных методов и вычислительной математики.
Решение нелинейных уравнений распадается на два этапа: отделение корней уравнений и уточнение корней нелинейных уравнений.
Н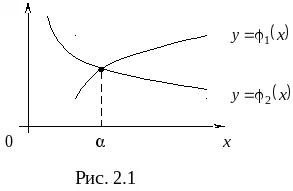 а первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то необходимо определить их количество и затем найти интервалы, в каждом из которых находится только один корень, т.е. отделить корни.
а первом этапе необходимо исследовать уравнение и выяснить, имеются корни или нет. Если корни имеются, то необходимо определить их количество и затем найти интервалы, в каждом из которых находится только один корень, т.е. отделить корни.
Первый способ отделения корней – графический. Данный метод позволяет определить количество корней на отрезке, но не единственность корня. Если ![]() имеет простой аналитический вид, то, исходя из уравнения (2.1), можно построить график функции
имеет простой аналитический вид, то, исходя из уравнения (2.1), можно построить график функции ![]() . Тогда точки пересечения графика функции с осью абсцисс будут являться приближенными значениями корней исходного нелинейного уравнения. Если
. Тогда точки пересечения графика функции с осью абсцисс будут являться приближенными значениями корней исходного нелинейного уравнения. Если ![]() имеет сложный аналитический вид, то можно представить ее в виде разности двух более простых функций
имеет сложный аналитический вид, то можно представить ее в виде разности двух более простых функций ![]() . Так как
. Так как ![]() , то выполняется равенство
, то выполняется равенство ![]() . Построим два графика
. Построим два графика ![]() ,
, ![]() (рис. 2.1). Тогда задача решения нелинейного уравнения (2.1) сводится к поиску абсцисс точек пересечения двух графиков, которые и будут являться приближенными значениями корней уравнения (2.1).
(рис. 2.1). Тогда задача решения нелинейного уравнения (2.1) сводится к поиску абсцисс точек пересечения двух графиков, которые и будут являться приближенными значениями корней уравнения (2.1).
П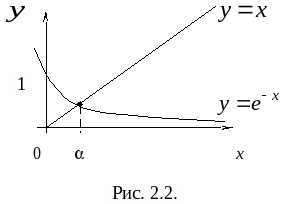 ример 2.1. Пусть дано нелинейное уравнение вида
ример 2.1. Пусть дано нелинейное уравнение вида ![]() . Для решения его графическим методом представим уравнение (2.1) в виде
. Для решения его графическим методом представим уравнение (2.1) в виде ![]() , где
, где ![]() ;
; ![]() . Графики функций
. Графики функций ![]() ;
; ![]() представлены на рис. 2.2, из которого видно, что исходное уравнение имеет единственный корень
представлены на рис. 2.2, из которого видно, что исходное уравнение имеет единственный корень ![]() .
.
П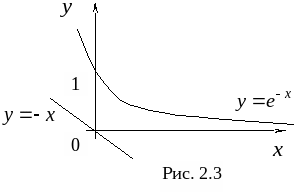 ример 2.2. Пусть задано нелинейное уравнение вида
ример 2.2. Пусть задано нелинейное уравнение вида ![]() или
или ![]() . Построив два графика функций
. Построив два графика функций ![]() и
и ![]() , нетрудно заметить, что исходное уравнение не имеет корней (рис. 2.3).
, нетрудно заметить, что исходное уравнение не имеет корней (рис. 2.3).
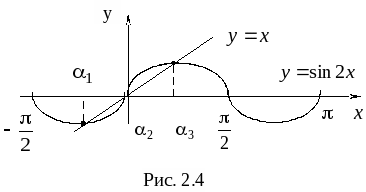
Пример 2.3. Для нелинейного уравнения вида ![]() с помощью аналогичных преобразований получим, что исходное уравнение имеет три корня (рис. 2.4).
с помощью аналогичных преобразований получим, что исходное уравнение имеет три корня (рис. 2.4).
Второй способ отделения корней нелинейных уравнений – аналитический. Процесс отделения корней здесь основывается на следующих теоремах.
Теорема 2.1. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() и на концах отрезка принимает значения разных знаков (т.е.
и на концах отрезка принимает значения разных знаков (т.е. ![]() ), то на
), то на ![]() содержится хотя бы один корень.
содержится хотя бы один корень.
Теорема 2.2. Если функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , выполняется условие вида
, выполняется условие вида ![]() и производная
и производная ![]() сохраняет знак на
сохраняет знак на ![]() , то на отрезке имеется единственный корень.
, то на отрезке имеется единственный корень.
Теорема 2.3. Если функция ![]() является многочленом
является многочленом ![]() -й степени и на концах отрезка
-й степени и на концах отрезка ![]() принимает значения разных знаков, то на
принимает значения разных знаков, то на ![]() имеется нечетное количество корней. Если на концах отрезка
имеется нечетное количество корней. Если на концах отрезка ![]() функция не меняет знак, то уравнение (2.1) либо не имеет корней на
функция не меняет знак, то уравнение (2.1) либо не имеет корней на ![]() , либо имеет четное количество корней.
, либо имеет четное количество корней.
При аналитическом методе исследований необходимо выявить интервалы монотонности функции ![]() . Для этого необходимо найти критические точки
. Для этого необходимо найти критические точки ![]() , т.е. точки, в которых первая производная
, т.е. точки, в которых первая производная ![]() равна нулю или не существует. Тогда вся числовая ось разбивается на интервалы монотонности
равна нулю или не существует. Тогда вся числовая ось разбивается на интервалы монотонности ![]() , на каждом из которых определяется знак производной
, на каждом из которых определяется знак производной ![]() , где
, где ![]() . Затем выделяются те интервалы монотонности
. Затем выделяются те интервалы монотонности ![]() , на которых функция
, на которых функция ![]() меняет знак, т.е. выполняется неравенство
меняет знак, т.е. выполняется неравенство ![]() . На каждом из этих интервалов для поиска корня используются методы уточнения корней.
. На каждом из этих интервалов для поиска корня используются методы уточнения корней.
Наиболее распространенными методами уточнения корня на отрезке являются итерационные (приближенные) методы: метод половинного деления (метод дихотомии), метод простых итераций, метод Ньютона (метод касательных) и его модификация.
§2.2. Метод половинного деления
Для уточнения корня нелинейного уравнения (2.1) на отрезке ![]() , где
, где ![]() , а производная сохраняет знак, применим метод половинного деления. Для этого разделим отрезок
, а производная сохраняет знак, применим метод половинного деления. Для этого разделим отрезок ![]() пополам и исследуем знак функции в полученной точке
пополам и исследуем знак функции в полученной точке ![]() , где
, где ![]() . Из двух отрезков
. Из двух отрезков ![]() и
и ![]() выбираем тот, на котором функция меняет знак. Уменьшая новый отрезок в два раза, повторяем процесс и т.д. Получим последовательность отрезков
выбираем тот, на котором функция меняет знак. Уменьшая новый отрезок в два раза, повторяем процесс и т.д. Получим последовательность отрезков ![]() , на концах которых выполняется неравенство
, на концах которых выполняется неравенство
![]() (2.2)
(2.2)
и длины этих отрезков равны
![]() . (2.3)
. (2.3)
Последовательность ![]() является монотонной неубывающей ограниченной последовательностью; а
является монотонной неубывающей ограниченной последовательностью; а ![]() монотонной невозрастающей ограниченной последовательностью. Следовательно, эти последовательности сходятся. Перейдем к пределу при
монотонной невозрастающей ограниченной последовательностью. Следовательно, эти последовательности сходятся. Перейдем к пределу при ![]() в левой и правой частях соотношения (2.3), получим
в левой и правой частях соотношения (2.3), получим
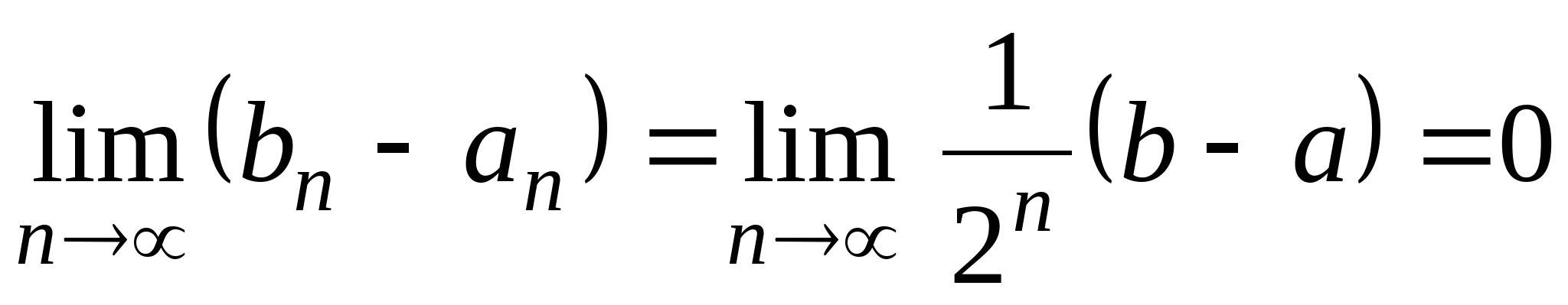 .
.
Тогда 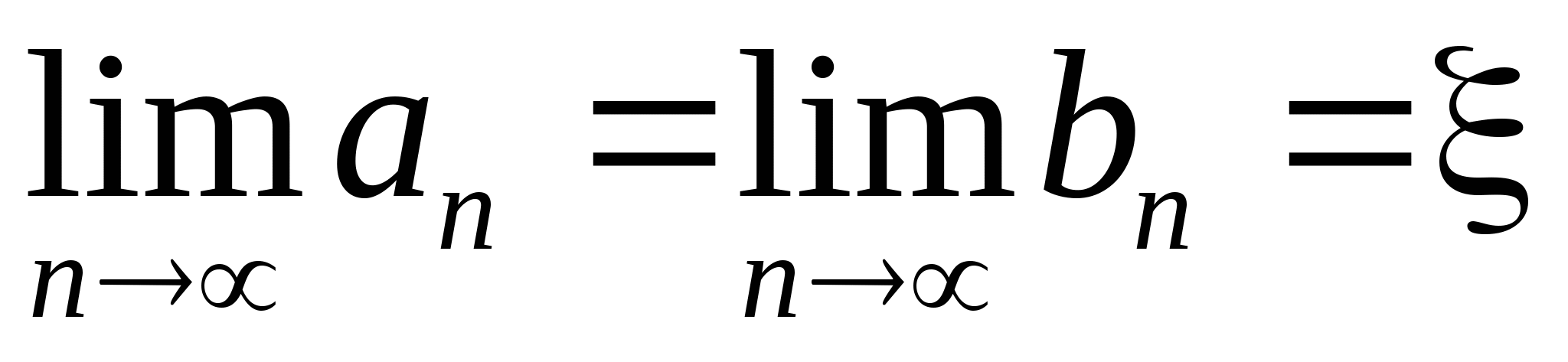 . С другой стороны, из неравенства (2.2) следует, что
. С другой стороны, из неравенства (2.2) следует, что 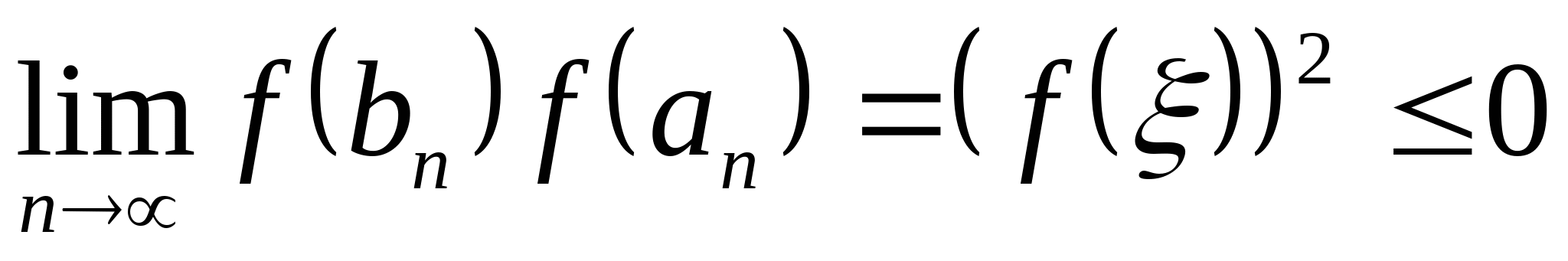 . Последнее неравенство возможно только тогда, когда
. Последнее неравенство возможно только тогда, когда ![]() . Следовательно,
. Следовательно, ![]() является корнем исходного уравнения (2.1).
является корнем исходного уравнения (2.1).
§2.3. Метод простых итераций
Пусть известно, что нелинейное уравнение ![]() , где
, где ![]() - непрерывная функция, имеет на отрезке
- непрерывная функция, имеет на отрезке ![]() единственный вещественный корень
единственный вещественный корень ![]() . Требуется найти этот корень с заданной точностью
. Требуется найти этот корень с заданной точностью ![]() . Применяя тождественные преобразования, приведем уравнение (2.1) к виду
. Применяя тождественные преобразования, приведем уравнение (2.1) к виду
![]() . (2.4)
. (2.4)
Выберем произвольно приближенное значение корня (начальное приближение) ![]() и вычислим первое приближение
и вычислим первое приближение ![]() . Найденное значение
. Найденное значение ![]() подставим в правую часть соотношения (2.4) и вычислим
подставим в правую часть соотношения (2.4) и вычислим ![]() , и так далее, т.е.
, и так далее, т.е.
![]() (2.5)
(2.5)
Продолжая процесс вычислений дальше, получим числовую последовательность ![]() . Если существует предел этой последовательности, то он и является приближенным значением корня уравнения (2.4). В самом деле, пусть
. Если существует предел этой последовательности, то он и является приближенным значением корня уравнения (2.4). В самом деле, пусть 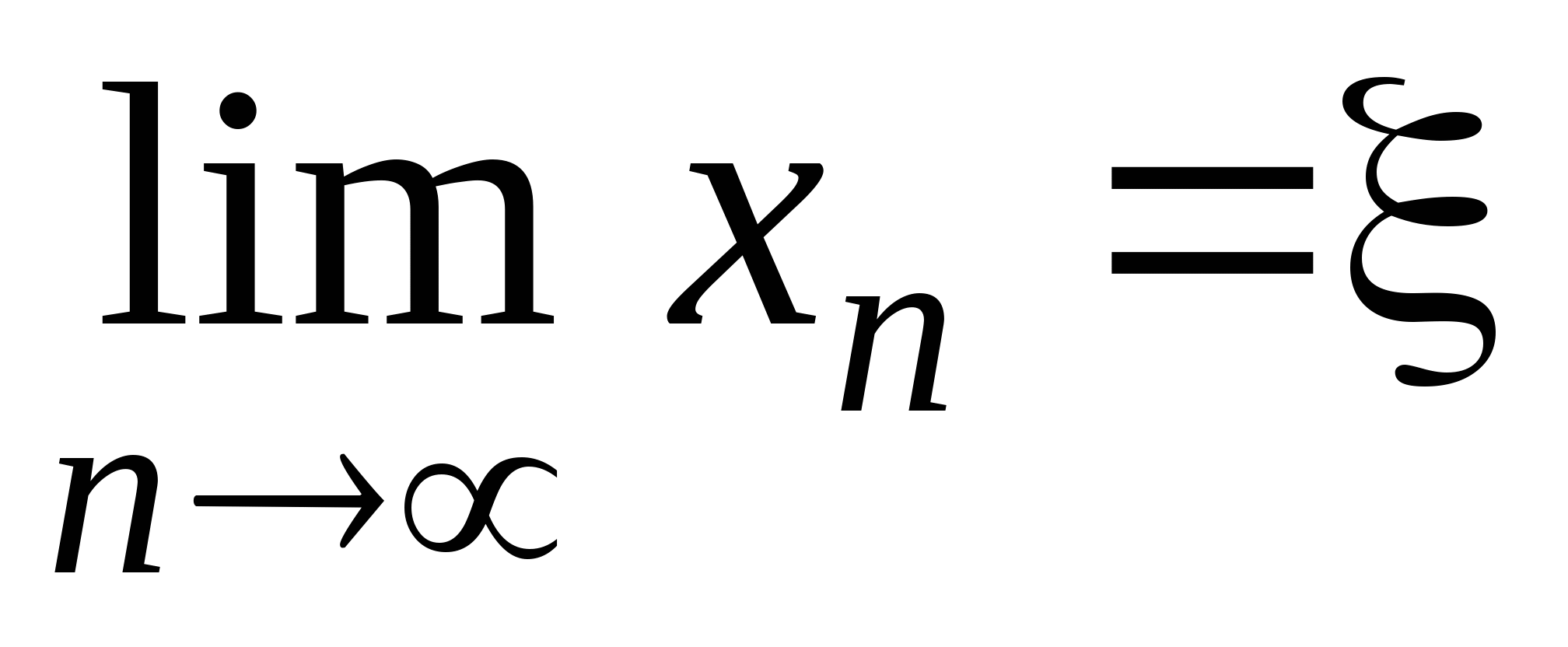 . Тогда, переходя к пределу в равенстве (2.5)
. Тогда, переходя к пределу в равенстве (2.5) 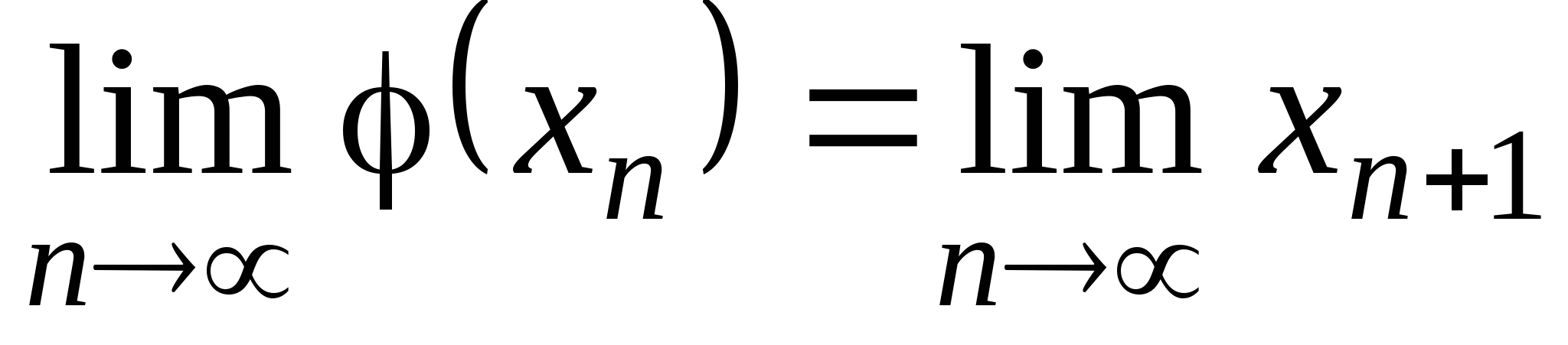 и учитывая непрерывность функции
и учитывая непрерывность функции ![]() на отрезке
на отрезке ![]() , получим
, получим 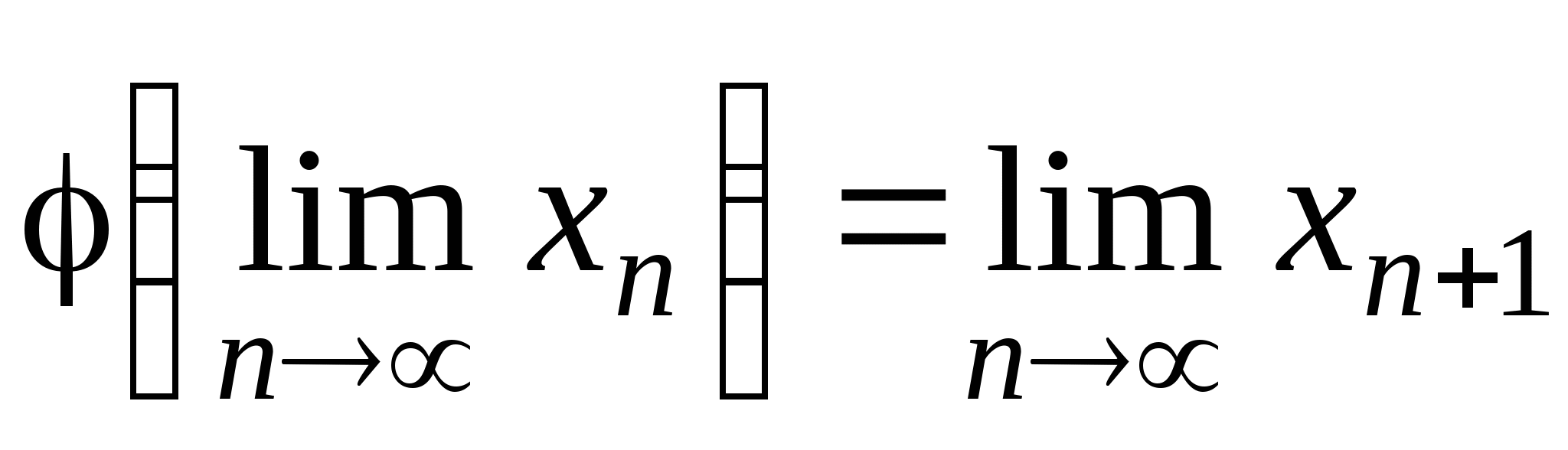 или
или ![]() . Следовательно, предел последовательности
. Следовательно, предел последовательности ![]() является корнем уравнения (2.4).
является корнем уравнения (2.4).
Таким образом, корень можно вычислить с заданной точностью по следующей итерационной формуле
![]()
Геометрическая интерпретация метода простых итераций
Г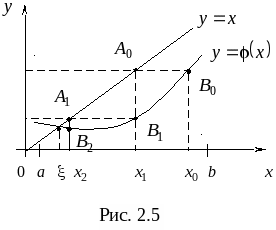
еометрически метод итерации может быть пояснен следующим образом. Построим на плоскости ![]() графики функций
графики функций ![]() и
и ![]() . Действительный корень
. Действительный корень ![]() уравнения (2.4) является абсциссой точки пересечения кривой
уравнения (2.4) является абсциссой точки пересечения кривой ![]() с прямой
с прямой ![]() (рис. 2.5).
(рис. 2.5).
Начиная процесс с некоторой точки ![]() , строим ломаную линию
, строим ломаную линию ![]() («лестница»), звенья которой попеременно параллельны оси
(«лестница»), звенья которой попеременно параллельны оси ![]() и оси
и оси ![]() , вершины
, вершины ![]() лежат на кривой
лежат на кривой ![]() , а вершины
, а вершины ![]() на прямой
на прямой ![]() . Общие абсциссы точек
. Общие абсциссы точек ![]() и
и ![]() ,
, ![]() и
и ![]() , … представляют собой соответственно последовательные приближения
, … представляют собой соответственно последовательные приближения ![]() корня
корня ![]() . В рассмотренном случае кривая
. В рассмотренном случае кривая ![]() пологая,
пологая, ![]() и
и ![]() .
.
В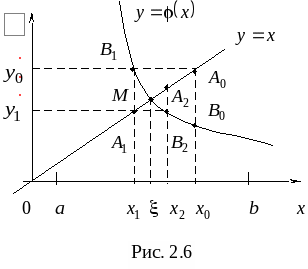
озможен другой вид ломаной ![]() («спираль») (рис. 2.6). В этом случае последовательные приближения
(«спираль») (рис. 2.6). В этом случае последовательные приближения ![]() стремятся к корню
стремятся к корню ![]() то с одной, то с другой стороны. В этом случае
то с одной, то с другой стороны. В этом случае ![]() , но
, но ![]() .
.
О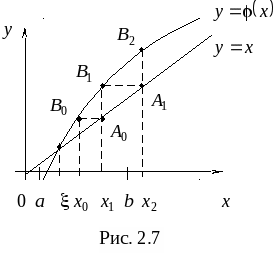
днако если рассмотреть случай, где ![]() (рис. 2.7), то процесс итераций расходится, т.е. последовательные приближения
(рис. 2.7), то процесс итераций расходится, т.е. последовательные приближения ![]() все дальше удаляются от корня
все дальше удаляются от корня ![]() и в какой-то момент могут выйти за пределы отрезка
и в какой-то момент могут выйти за пределы отрезка ![]() . Поэтому для практического применения метода простых итераций нужно определить достаточные условия сходимости итерационного процесса.
. Поэтому для практического применения метода простых итераций нужно определить достаточные условия сходимости итерационного процесса.
Достаточное условие, при котором итерационный процесс, заданный формулой (2.5), сходится, определяет следующая теорема.
Теорема 2.4. Пусть функция ![]() определена и дифференцируема на отрезке
определена и дифференцируема на отрезке ![]() , причем все ее значения
, причем все ее значения ![]() и выполняется условие
и выполняется условие
![]() при
при ![]() , (2.6)
, (2.6)
тогда процесс итераций, определяемый формулой (2.5), сходится независимо от выбора начального приближения ![]() и предельное значение
и предельное значение 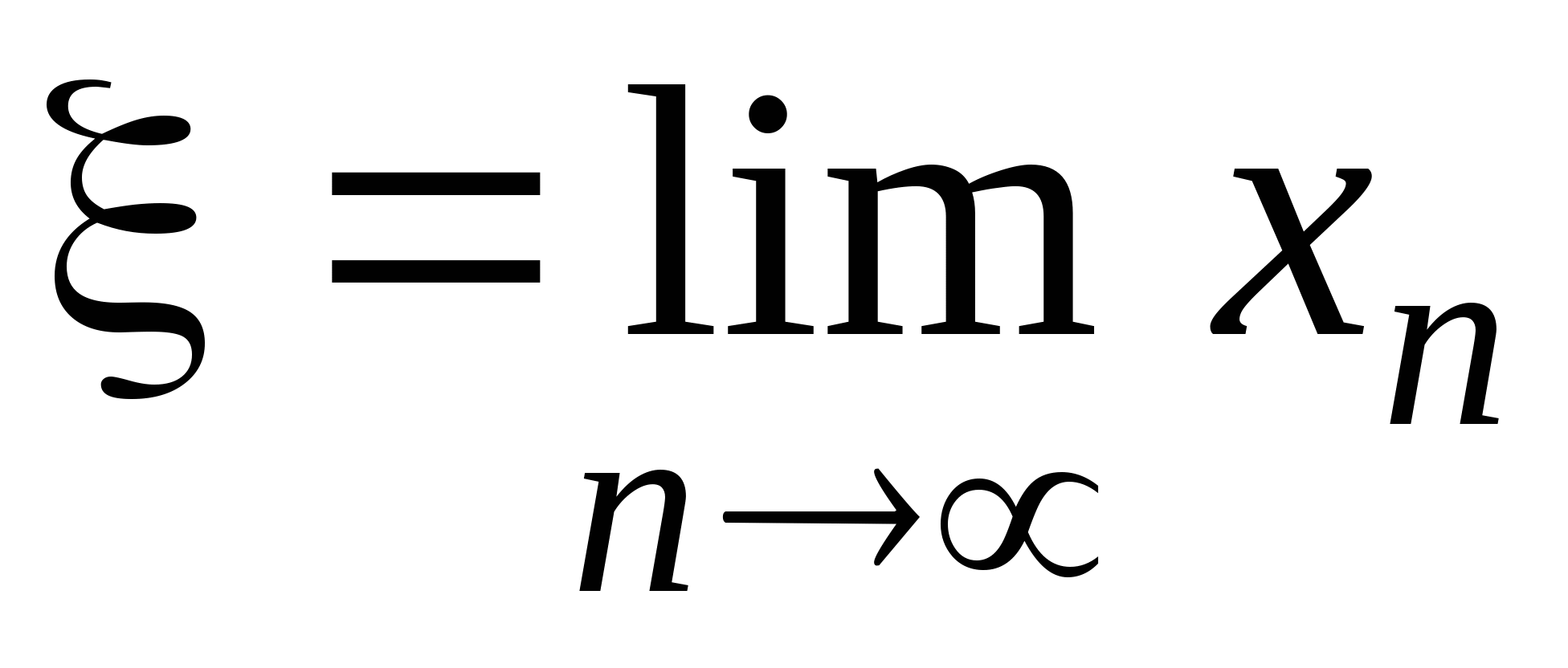 является единственным корнем уравнения (2.4) на отрезке
является единственным корнем уравнения (2.4) на отрезке ![]() .
.
Доказательство.
Рассмотрим два последовательных приближения ![]() и
и ![]() . По условию теоремы
. По условию теоремы ![]() принадлежат отрезку
принадлежат отрезку ![]() . Применяя теорему Лагранжа, получим:
. Применяя теорему Лагранжа, получим:
![]() ,
,
где точка ![]() лежит между
лежит между ![]() и
и ![]() . В силу условия (2.6)
. В силу условия (2.6)
![]() . (2.7)
. (2.7)
Придавая значения ![]() , получим
, получим
![]() ;
;
![]() ;
;
…
![]() . (2.8)
. (2.8)
Рассмотрим ряд
![]() , (2.9)
, (2.9)
для частичных сумм которого выполняется соотношение ![]() . Если докажем, что ряд (2.9) сходится, то тем самым будет доказана сходимость последовательности
. Если докажем, что ряд (2.9) сходится, то тем самым будет доказана сходимость последовательности ![]() .
.
Сравним два ряда:
![]() ; (2.10)
; (2.10)
![]() . (2.11)
. (2.11)
В силу соотношений (2.8) члены ряда (2.10) не превышают соответствующих членов ряда (2.11), которые являются членами геометрической прогрессии со знаменателем ![]() . Следовательно, ряд (2.10) сходится, а ряд (2.9) сходится абсолютно. Таким образом, существует
. Следовательно, ряд (2.10) сходится, а ряд (2.9) сходится абсолютно. Таким образом, существует
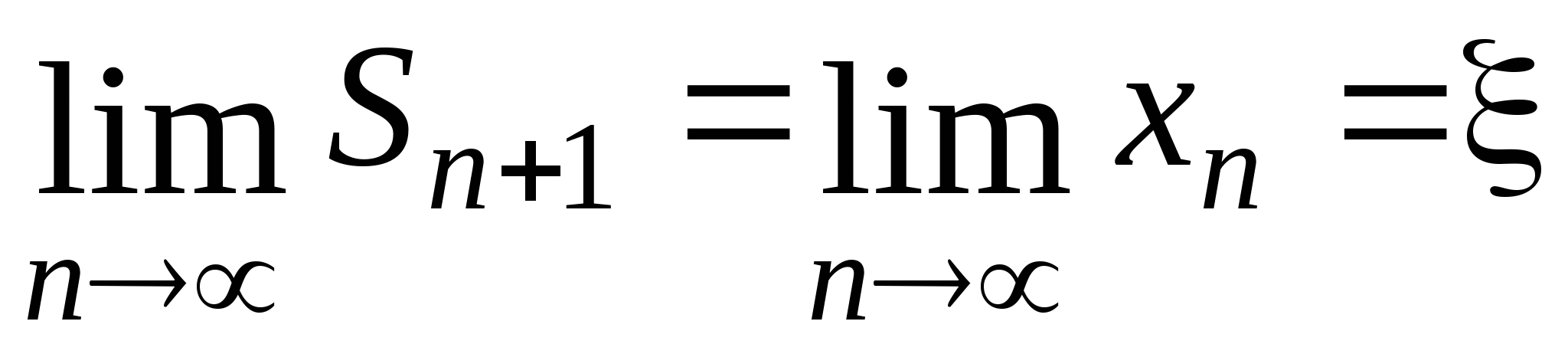 ,
,
причем ![]() .
.
Переходя к пределу в равенстве (2.5), в силу непрерывности функции ![]() получим
получим
![]() .
.
Следовательно, ![]() корень уравнения (2.4).
корень уравнения (2.4).
Докажем, что этот корень единственный. Предположим, что на отрезке ![]() существует еще один корень
существует еще один корень ![]() уравнения (2.4)
уравнения (2.4) ![]() . Тогда в силу теоремы Лагранжа
. Тогда в силу теоремы Лагранжа
![]() ,
,
где ![]() находится между
находится между ![]() и
и ![]() . Отсюда
. Отсюда ![]() . Но
. Но ![]() , поэтому выражение в квадратных скобках не равно нулю. Следовательно,
, поэтому выражение в квадратных скобках не равно нулю. Следовательно, ![]() , т.е.
, т.е. ![]() единственный корень уравнения (2.4).
единственный корень уравнения (2.4).
Точка ![]() при этом называется неподвижной точкой для уравнения (2.4).
при этом называется неподвижной точкой для уравнения (2.4).
Приведение нелинейного уравнения
Выполнения достаточного условия сходимости можно добиться путем перехода от исходного уравнения ![]() к эквивалентному виду
к эквивалентному виду ![]() следующим образом: умножим обе части уравнения (2.1) на неизвестную постоянную
следующим образом: умножим обе части уравнения (2.1) на неизвестную постоянную ![]() ,
, ![]() , затем прибавим к обеим частям переменную
, затем прибавим к обеим частям переменную ![]() , тогда получим
, тогда получим ![]() . Обозначим через
. Обозначим через ![]() , тогда
, тогда ![]() . Константа
. Константа ![]() выбирается так, чтобы выполнялось достаточное условие сходимости итерационного процесса (2.6), т.е.
выбирается так, чтобы выполнялось достаточное условие сходимости итерационного процесса (2.6), т.е. ![]() для всех
для всех ![]() . Это условие равносильно условию
. Это условие равносильно условию ![]() , отсюда:
, отсюда:
1) ![]() при
при ![]() ;
;
2) ![]() при
при ![]() .
.
Оценка приближения
Из формулы (2.8) имеем:
![]()
![]()
![]()
![]() .
.
Устремляя ![]() к бесконечности и учитывая, что
к бесконечности и учитывая, что 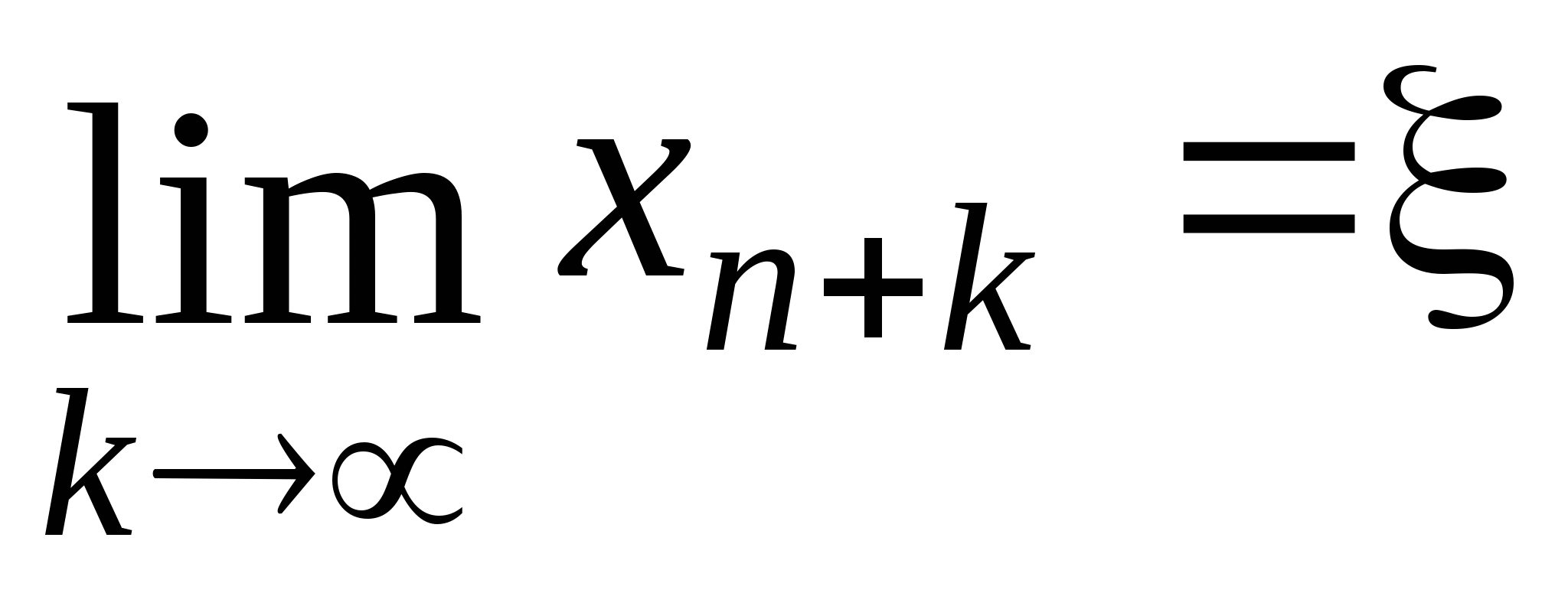 , окончательно получим:
, окончательно получим:
![]() . (2.12)
. (2.12)
Отсюда видно, что чем меньше ![]() , тем больше скорость сходимости итерационного процесса, заданного формулой (2.5).
, тем больше скорость сходимости итерационного процесса, заданного формулой (2.5).
Для оценки приближения можно использовать и другую формулу.
Пусть ![]() . Очевидно, что
. Очевидно, что ![]() . Учитывая, что
. Учитывая, что ![]() , получим:
, получим:
![]() ,
,
где ![]() находится между
находится между ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() , т.е.
, т.е.
![]() .
.
Используя формулу (2.7), получим:
![]() . (2.13)
. (2.13)
Если ![]() , то
, то ![]() . В этом случае из неравенства
. В этом случае из неравенства ![]() вытекает неравенство
вытекает неравенство ![]() , где
, где ![]() заданная точность.
заданная точность.
Условия окончания итерационного процесса
Процесс итераций заканчивается при одновременном выполнении двух условий:
если два последующих приближения отличаются между собой по модулю на величину, не превышающую заданной точности ![]() , т.е.
, т.е. ![]() . Отдельно этого критерия недостаточно, так как в случае крутизны графика, данное условие будет выполнено, но
. Отдельно этого критерия недостаточно, так как в случае крутизны графика, данное условие будет выполнено, но ![]() может находиться далеко от корня;
может находиться далеко от корня;
мера удовлетворения уравнению (2.1) последнего приближения корня: ![]() . Отдельно данного критерия недостаточно, так как при пологой функции
. Отдельно данного критерия недостаточно, так как при пологой функции ![]() это условие может быть выполнено, но
это условие может быть выполнено, но ![]() может находиться далеко от корня.
может находиться далеко от корня.
Метод простых итераций имеет два достоинства:
является универсальным, простым для реализации на ЭВМ и самоисправляющимся, т.е. любая неточность на каком - либо шаге итераций не отразится на конечном результате, а отразится лишь на количестве итераций. Подобные ошибки устойчивы даже по отношению к грубым ошибкам (сбоям ЭВМ), если только ошибка не выбрасывает очередное приближение за пределы области сходимости;
позволяет достигнуть любой заданной точности при любом начальном приближении ![]() .
.
Недостатки метода:
трудоемкость процесса приведения уравнения (2.1) к виду (2.4);
если начальное приближение ![]() выбрано достаточно далеко от корня, то число итераций, необходимых для достижения заданной точности, будет достаточно большое и объем вычислений возрастет.
выбрано достаточно далеко от корня, то число итераций, необходимых для достижения заданной точности, будет достаточно большое и объем вычислений возрастет.
Пример 2.4. Доказать графическим и аналитическим методами существование единственного корня нелинейного уравнения
![]() (2.14)
(2.14)
на отрезке ![]() и построить рабочие формулы метода простых итераций для поиска корня.
и построить рабочие формулы метода простых итераций для поиска корня.
1. Докажем графическим методом единственность корня нелинейного уравнения (2.14). Из графика функции ![]() на рис. 2.8 видно, что функция
на рис. 2.8 видно, что функция ![]() пересекает ось
пересекает ось ![]() в одной точке, являющейся приближенным значением корня нелинейного уравнения (2.14). Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение (2.14) к виду
в одной точке, являющейся приближенным значением корня нелинейного уравнения (2.14). Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение (2.14) к виду ![]() и построим два графика функций
и построим два графика функций ![]() и
и ![]() , имеющих более простой аналитический вид (рис. 2.9). Абсцисса точки пересечения графиков является приближенным значением корня.
, имеющих более простой аналитический вид (рис. 2.9). Абсцисса точки пересечения графиков является приближенным значением корня.
Д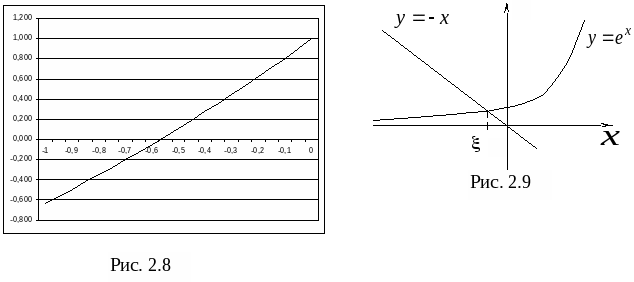
ля доказательства единственности корня на отрезке воспользуемся аналитическим методом. Функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , имеет на концах отрезка разные знаки (
, имеет на концах отрезка разные знаки (![]() ), а производная функции
), а производная функции ![]() не меняет знак на отрезке (
не меняет знак на отрезке (![]() ). Следовательно, нелинейное уравнение (2.14) имеет на указанном отрезке единственный корень.
). Следовательно, нелинейное уравнение (2.14) имеет на указанном отрезке единственный корень.
2. Для построения рабочей формулы перепишем уравнение (2.14) в виде: ![]() . Проверим, выполняется ли достаточное условие сходимости (2.6). Заметим, что в точке
. Проверим, выполняется ли достаточное условие сходимости (2.6). Заметим, что в точке ![]() из отрезка
из отрезка ![]() , значение
, значение ![]() , т.е. условие не выполняется. Построим функцию
, т.е. условие не выполняется. Построим функцию ![]() . Так как
. Так как ![]() всюду положительна на отрезке, то, конкретизируя значение производной в любой точке отрезка в неравенстве
всюду положительна на отрезке, то, конкретизируя значение производной в любой точке отрезка в неравенстве 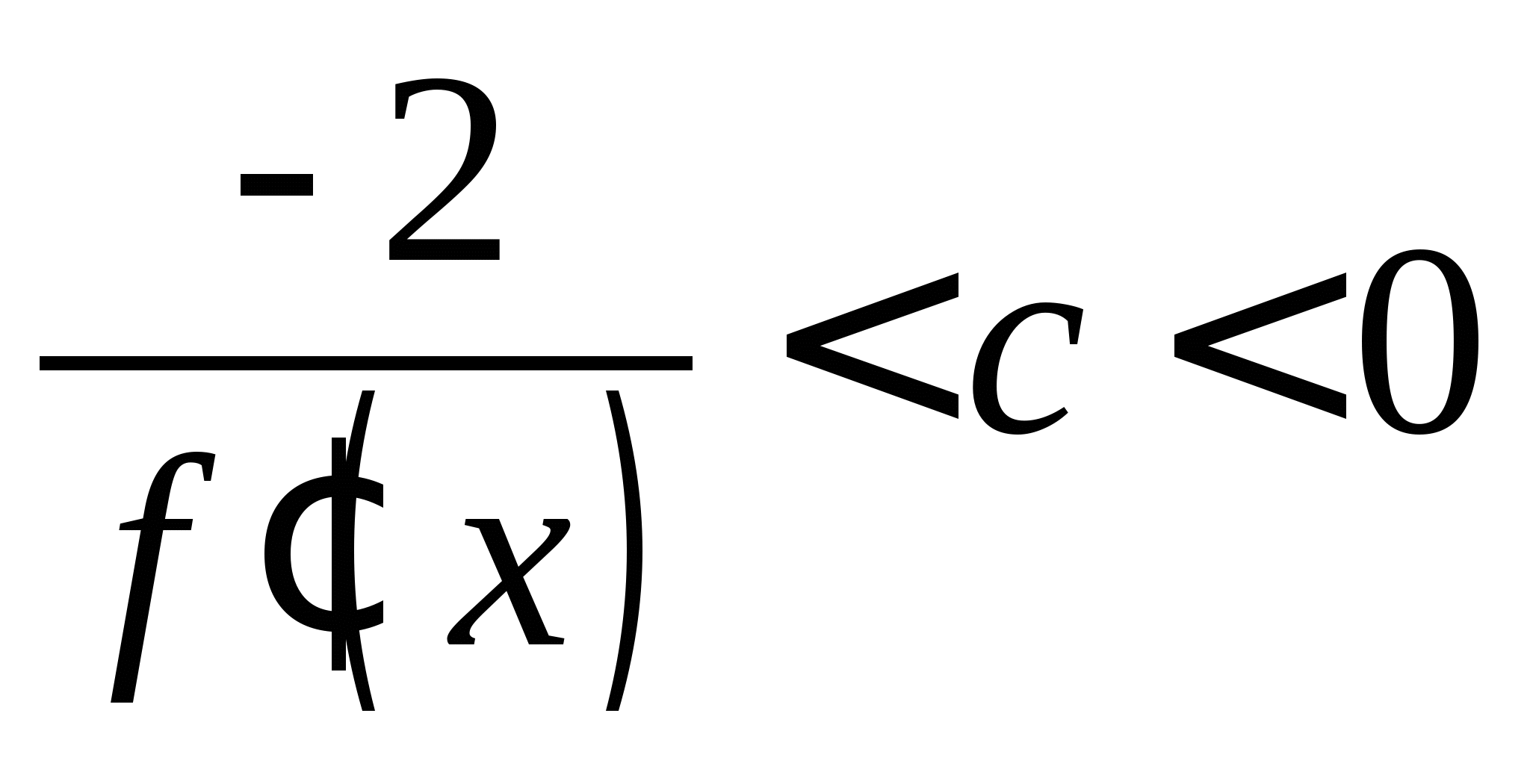 , значение
, значение ![]() определяется из интервала
определяется из интервала ![]() . Выбрав значение
. Выбрав значение ![]() , запишем рабочую формулу метода простых итераций:
, запишем рабочую формулу метода простых итераций:
![]() (2.15)
(2.15)
Итерационный процесс (2.15) можно начать, задав произвольное начальное приближение ![]() .
.
§2.4. Метод Ньютона (метод касательных)
Пусть известно, что нелинейное уравнение ![]() имеет на отрезке
имеет на отрезке ![]() единственный вещественный корень
единственный вещественный корень ![]() . Причем, производные
. Причем, производные ![]() – непрерывны и сохраняют определенные знаки на отрезке
– непрерывны и сохраняют определенные знаки на отрезке ![]() . Требуется найти этот корень с заданной точностью
. Требуется найти этот корень с заданной точностью ![]() . Найдем какое-либо
. Найдем какое-либо ![]() -е приближенное значение корня
-е приближенное значение корня ![]() (
(![]() ) и уточним его методом Ньютона следующим образом.
) и уточним его методом Ньютона следующим образом.
Пусть
![]() . (2.16)
. (2.16)
По формуле Тейлора получим
![]() .
.
Следовательно, 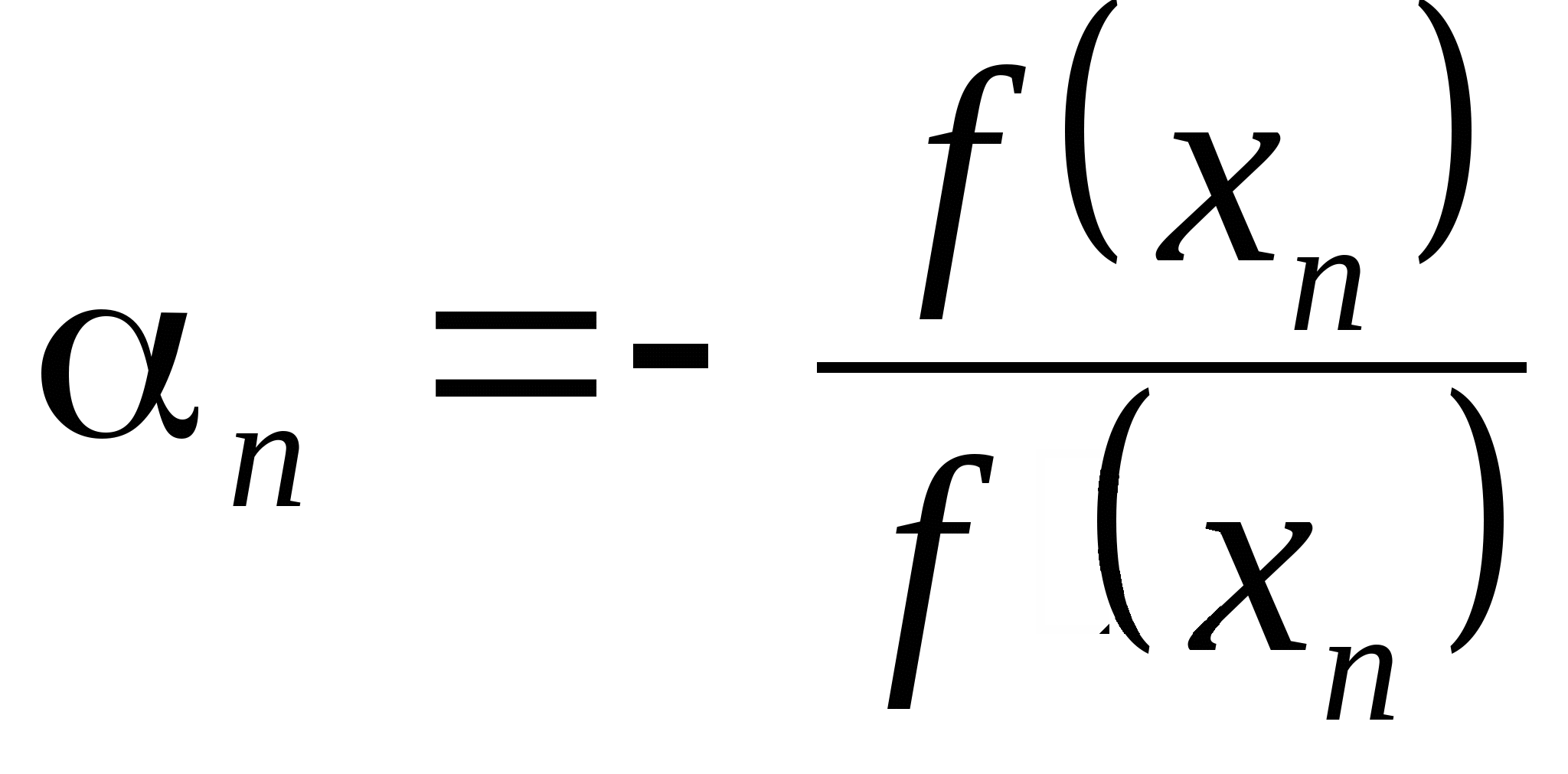 .
.
Внося эту правку в формулу (2.16), получим рабочую формулу метода Ньютона вида:
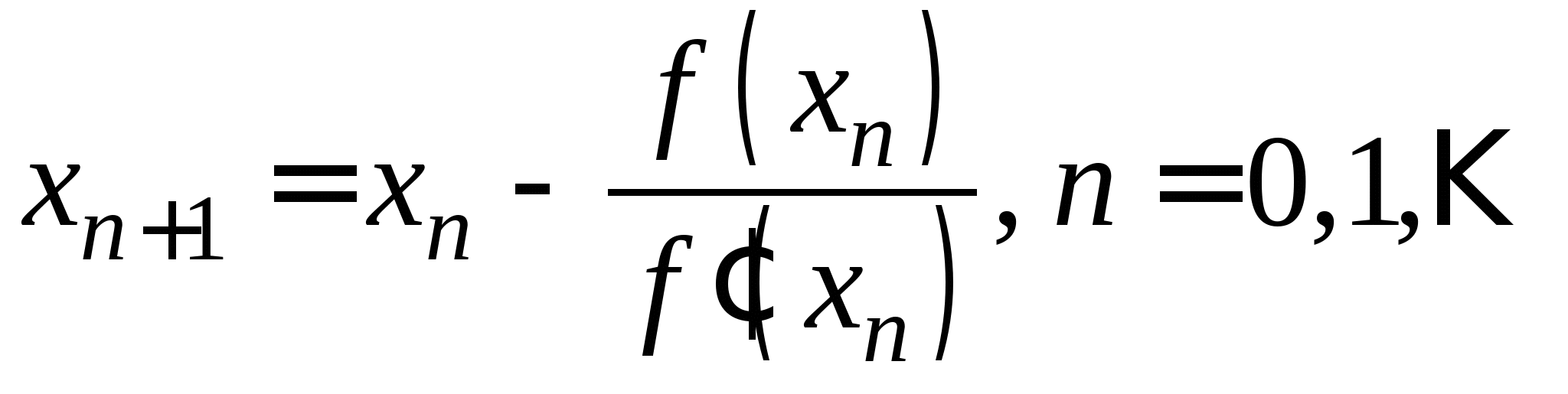 (2.17)
(2.17)
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой ![]() касательной, проведенной в некоторой точке
касательной, проведенной в некоторой точке ![]() этой кривой.
этой кривой.
Д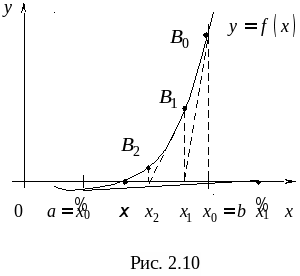
ля определенности положим ![]() и
и ![]() . Выберем начальное приближение
. Выберем начальное приближение ![]() , для которого
, для которого ![]() . Проведем касательную к кривой
. Проведем касательную к кривой ![]() в точке
в точке ![]() . За первое приближение
. За первое приближение ![]() берем точку пересечения касательной с осью
берем точку пересечения касательной с осью ![]() . На кривой определим точку
. На кривой определим точку ![]() и проведем касательную к кривой
и проведем касательную к кривой ![]() в этой точке. Найдем следующее приближение
в этой точке. Найдем следующее приближение ![]() и т.д. (рис. 2.10).
и т.д. (рис. 2.10).
Составим уравнение касательной в точке ![]() :
:
![]() .
.
Полагая ![]() , из уравнения касательной получим итерационную формулу метода Ньютона
, из уравнения касательной получим итерационную формулу метода Ньютона
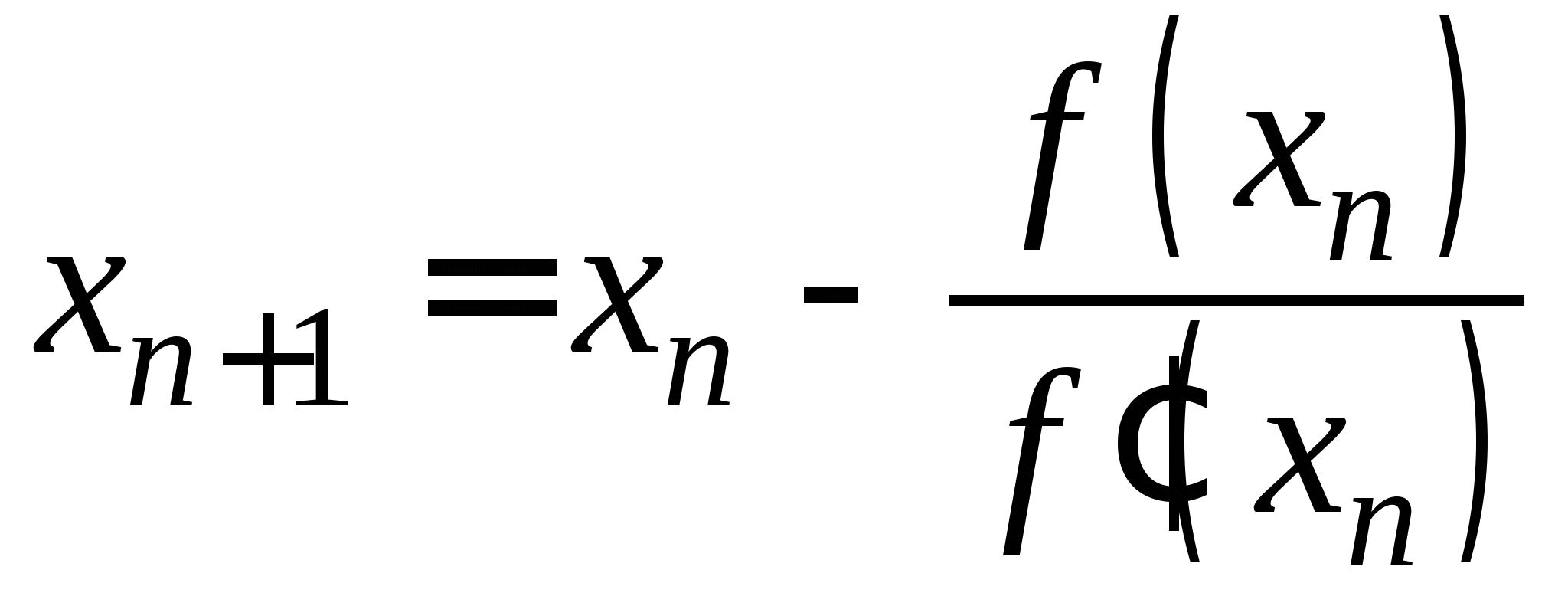 .
.
Если в качестве начального приближения взять другой конец отрезка ![]()
![]() , то следующее приближение
, то следующее приближение ![]() .
.
Теорема 2.5. Если ![]() и производные
и производные ![]() не равны нулю и сохраняют определенные знаки на отрезке
не равны нулю и сохраняют определенные знаки на отрезке ![]() , то исходя из начального приближения
, то исходя из начального приближения ![]() , удовлетворяющего неравенству
, удовлетворяющего неравенству ![]() , по методу Ньютона, заданному формулой (2.17), можно вычислить единственный корень
, по методу Ньютона, заданному формулой (2.17), можно вычислить единственный корень ![]() уравнения (2.1) с любой степенью точности.
уравнения (2.1) с любой степенью точности.
Доказательство.
Пусть для определенности ![]() ,
, ![]() ,
, ![]() при
при ![]() (остальные случаи рассматриваются аналогично).
(остальные случаи рассматриваются аналогично).
Из неравенства ![]() следует, что
следует, что ![]() , т.е.
, т.е. ![]() .
.
Докажем, что все приближения ![]() расположены правее
расположены правее ![]() , т.е.
, т.е. ![]() , а значит
, а значит ![]() .
.
Доказательство проведем методом индукции:
а) ![]() ;
;
б) предположим, что ![]() ;
;
с) докажем, что ![]() .
.
Точное решение уравнения (2.1) можно представить в виде
![]() .
.
Применяя формулу Тейлора, получим:
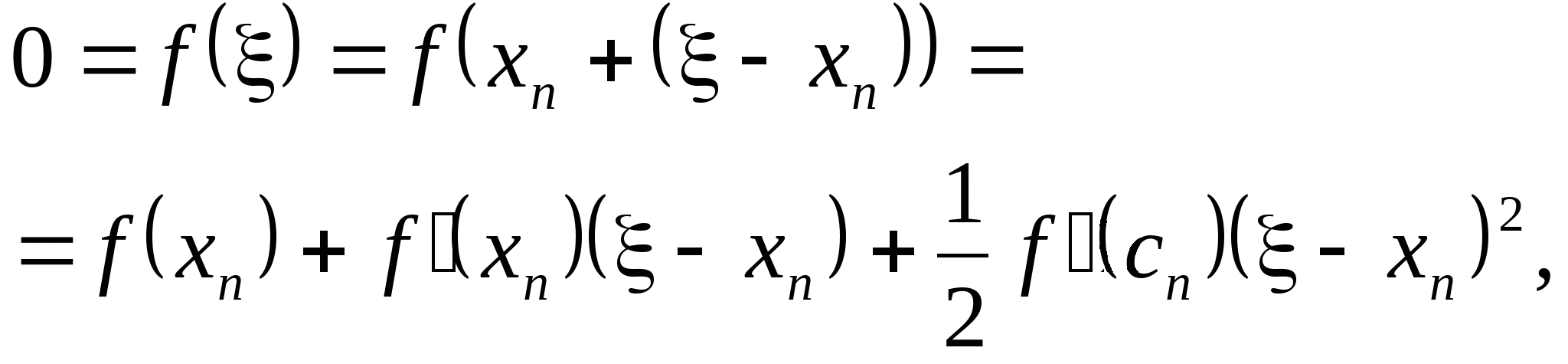 (2.18)
(2.18)
где ![]() .
.
Так как по условию теоремы ![]() , то последнее слагаемое в соотношении (2.18) положительное, следовательно,
, то последнее слагаемое в соотношении (2.18) положительное, следовательно,
![]() .
.
Отсюда, в силу того, что ![]() , получим:
, получим:
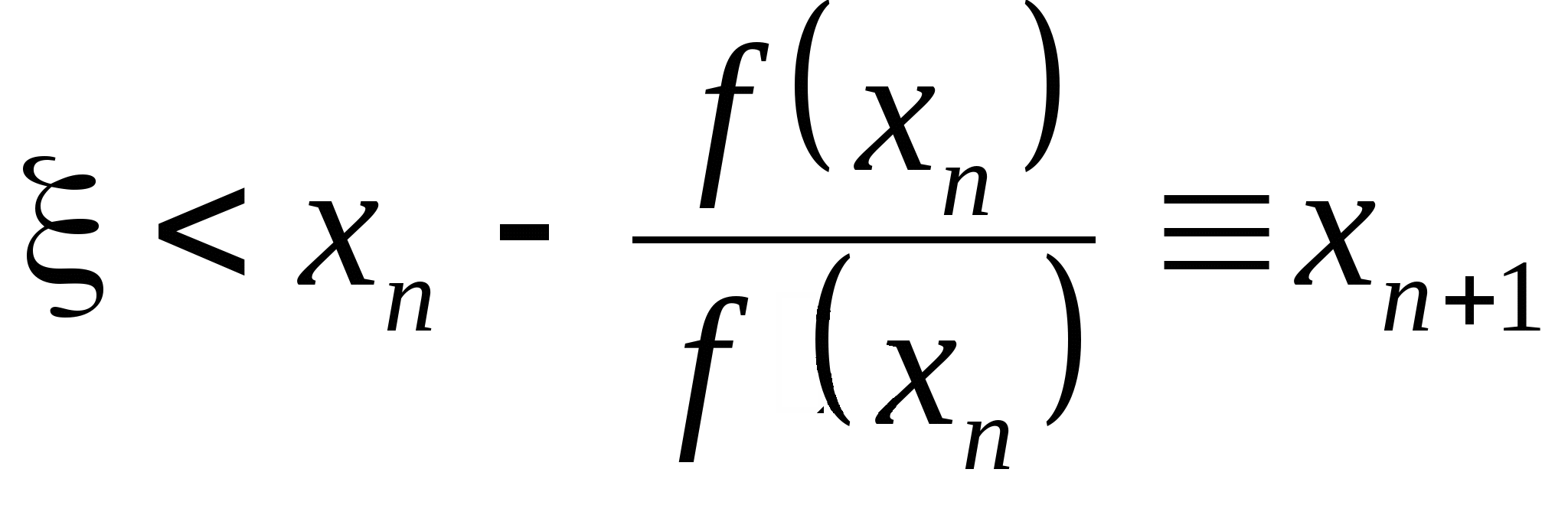 .
.
Таким образом доказали, что все последовательные приближения ![]() , т.е. находятся правее
, т.е. находятся правее ![]() , и, следовательно,
, и, следовательно, ![]() .
.
Из соотношения (2.17), учитывая знаки ![]() и
и ![]() , следует, что
, следует, что ![]() , т.е. последовательные приближения
, т.е. последовательные приближения ![]() образуют ограниченную монотонно убывающую последовательность. Иначе говоря, эта последовательность имеет конечный предел, который обозначим
образуют ограниченную монотонно убывающую последовательность. Иначе говоря, эта последовательность имеет конечный предел, который обозначим ![]() . Перейдем к пределу при
. Перейдем к пределу при ![]() в левой и правой частях соотношения (2.17), получим:
в левой и правой частях соотношения (2.17), получим:
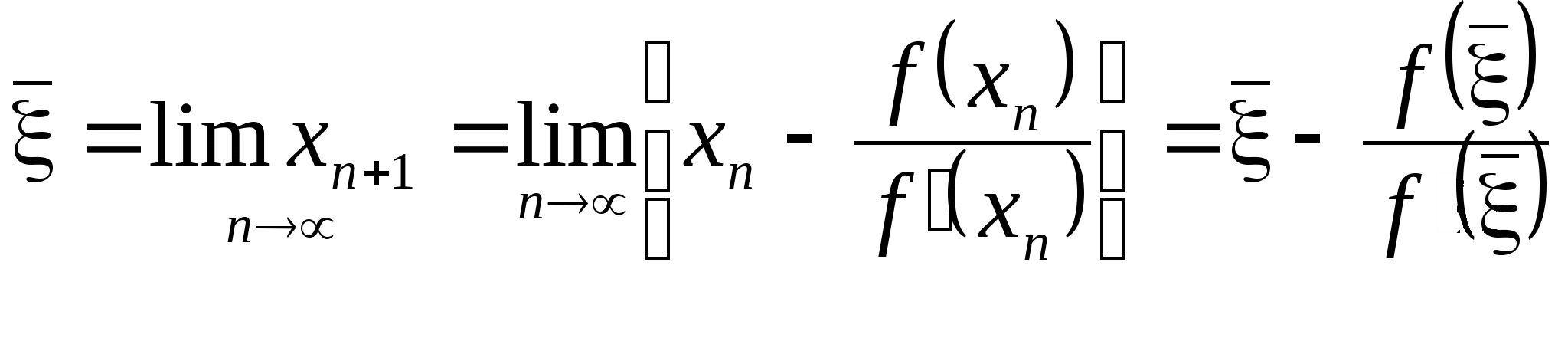 ,
,
т.е. 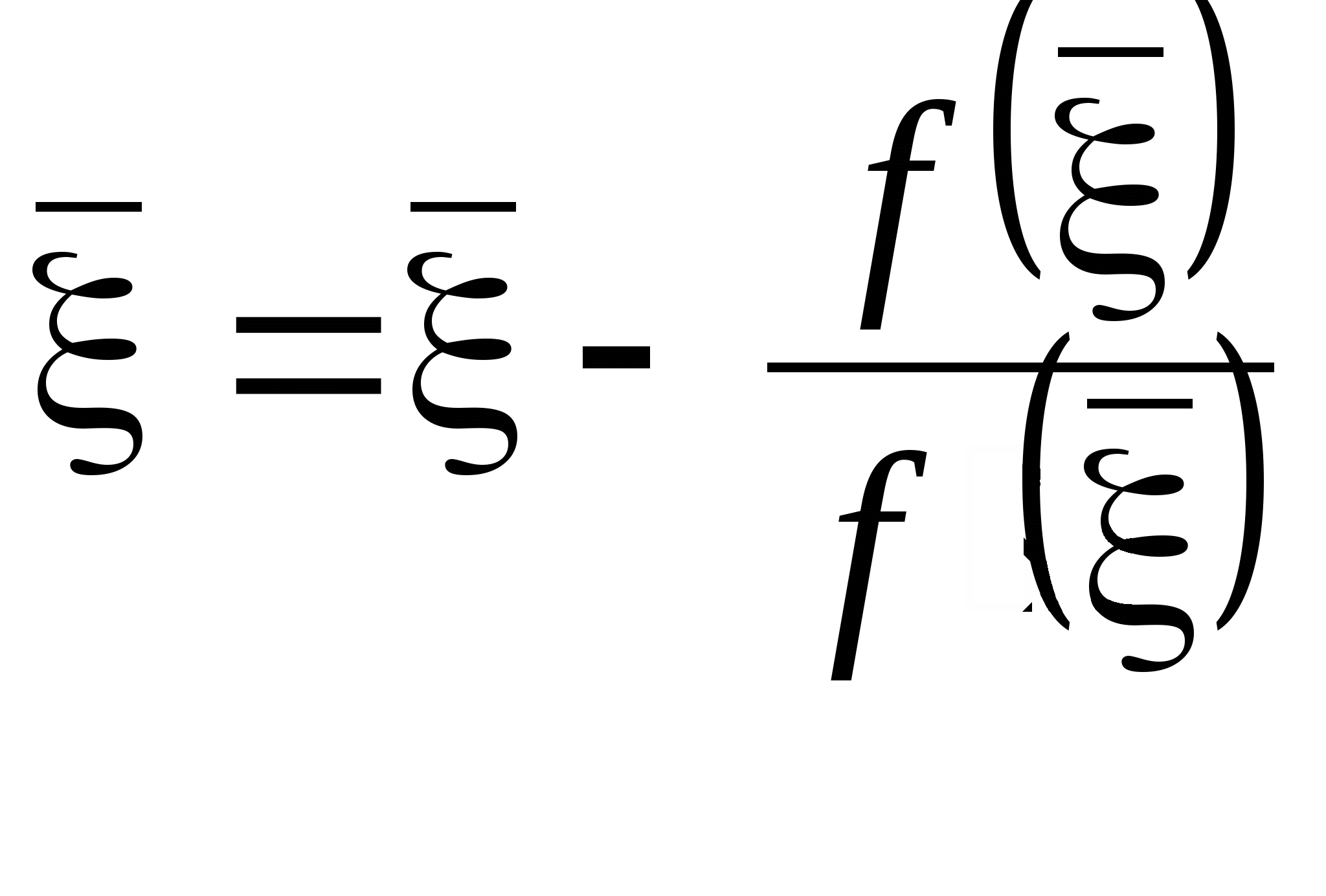 . Отсюда следует, что
. Отсюда следует, что ![]() , т.е.
, т.е. ![]() . А это означает, что последовательные приближения
. А это означает, что последовательные приближения ![]() сходятся к корню уравнения (2.1), что и требовалось доказать.
сходятся к корню уравнения (2.1), что и требовалось доказать.
Вывод: в методе Ньютона в качестве начального приближения ![]() выбирается тот конец отрезка
выбирается тот конец отрезка ![]() , которому отвечает ордината того же знака, что и
, которому отвечает ордината того же знака, что и ![]() , т.е. выполняется достаточное условие сходимости
, т.е. выполняется достаточное условие сходимости
![]() . (2.19)
. (2.19)
Замечание. Чем больше числовое значение ![]() в окрестности корня
в окрестности корня ![]() , тем меньше правка
, тем меньше правка ![]() . Поэтому методом Ньютона удобно пользоваться, когда в окрестности искомого корня
. Поэтому методом Ньютона удобно пользоваться, когда в окрестности искомого корня ![]() график функции
график функции ![]() имеет большую крутизну (т.е.
имеет большую крутизну (т.е. ![]() , тогда
, тогда 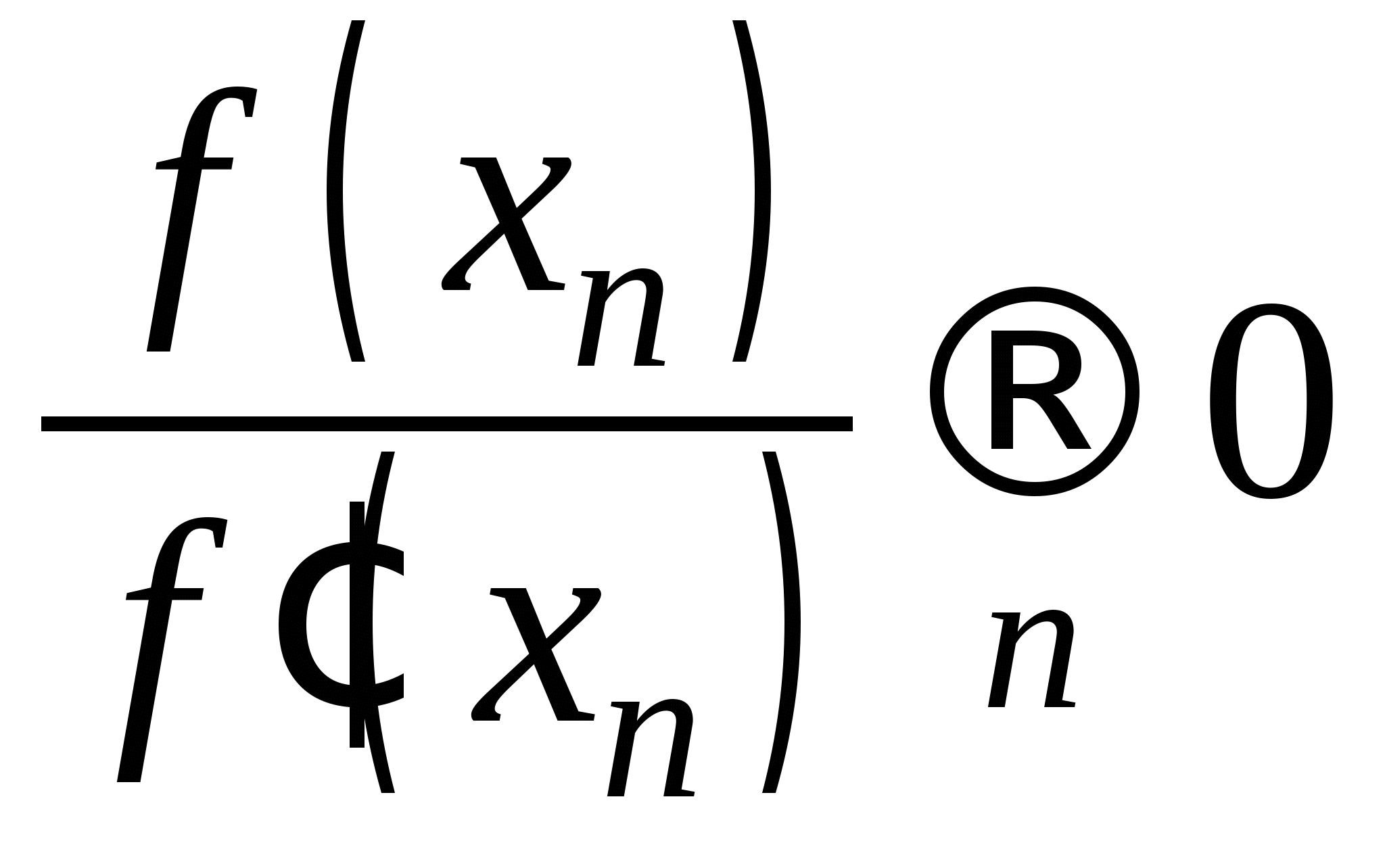 ). Если кривая
). Если кривая ![]() вблизи точки пересечения с осью
вблизи точки пересечения с осью ![]() почти горизонтальная (т.е.
почти горизонтальная (т.е. ![]() , тогда
, тогда 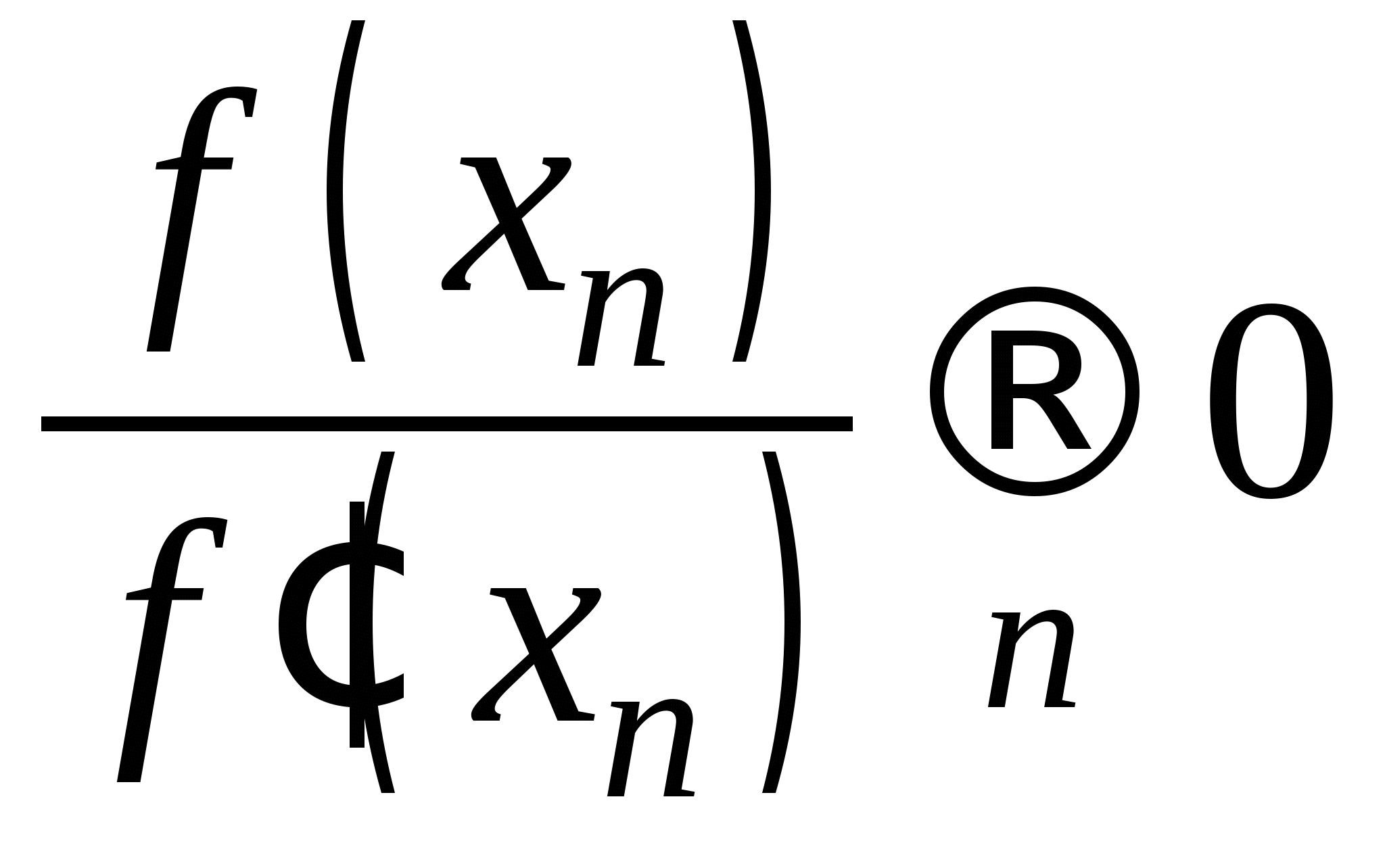 ), то применять метод Ньютона для решения уравнения (2.1) не рекомендуется.
), то применять метод Ньютона для решения уравнения (2.1) не рекомендуется.
Метод Ньютона можно рассматривать как частный случай метода простых итераций, если считать 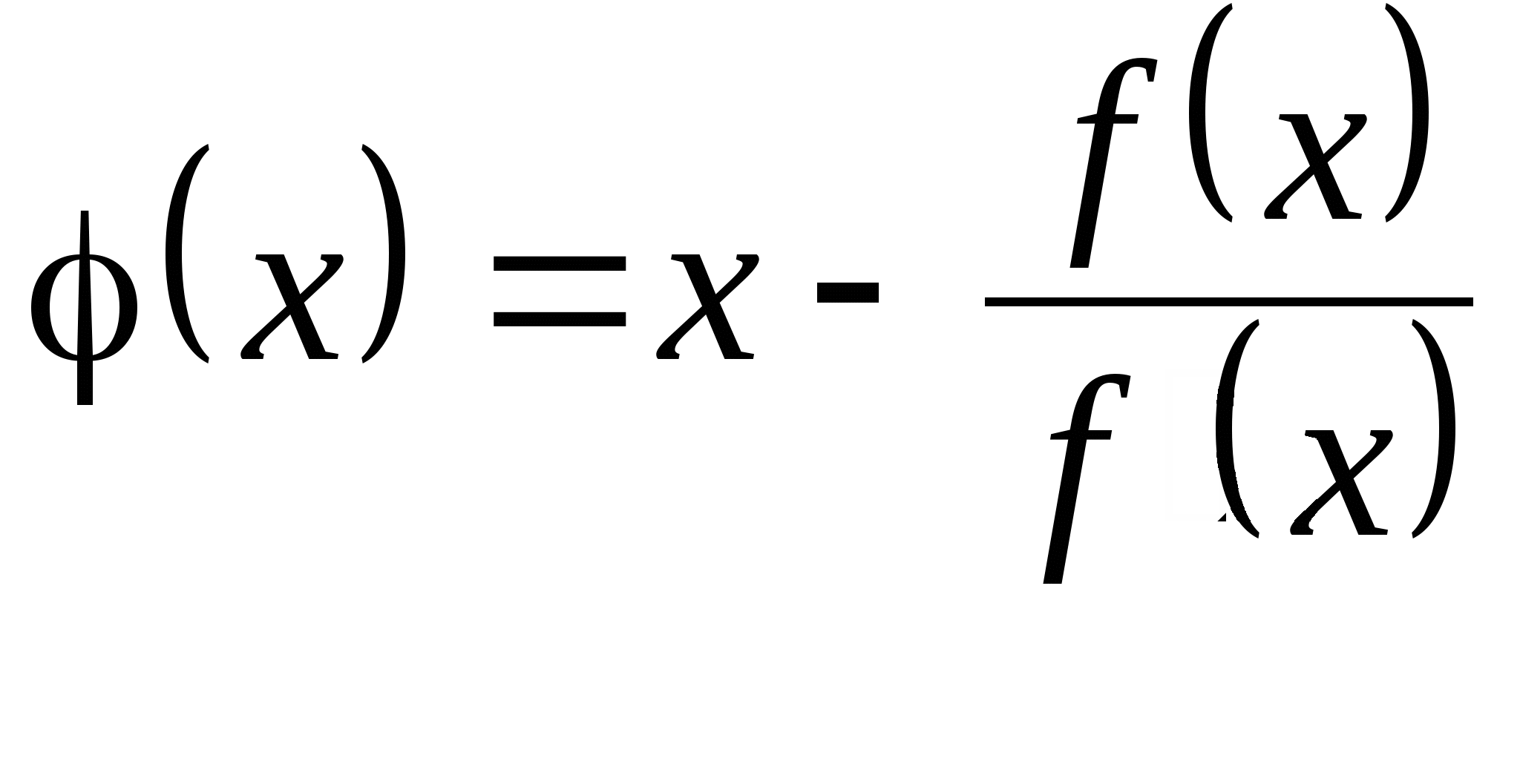 . Тогда достаточное условие сходимости метода простых итераций примет вид:
. Тогда достаточное условие сходимости метода простых итераций примет вид:
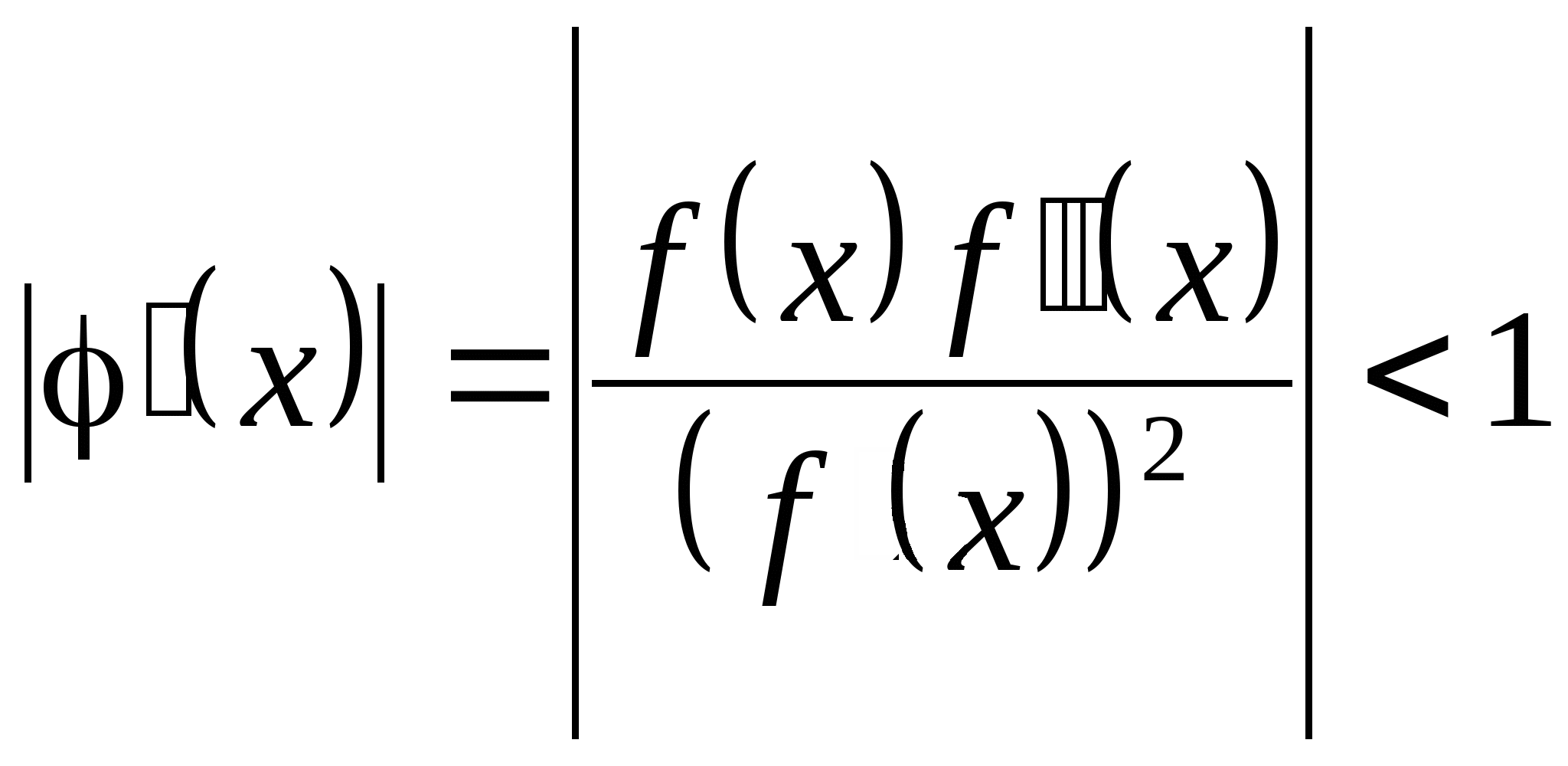 для всех
для всех ![]() . (2.20)
. (2.20)
Если выполнено условие (2.20), то итерационный процесс, заданный формулой (2.17), будет сходиться при произвольном выборе начального приближения ![]() .
.
Достоинства метода Ньютона:
обладает достаточно большой скоростью сходимости, близкой к квадратичной;
достаточно простое получение итерационной формулы (2.17).
Недостатки метода Ньютона:
сходится не при любом выборе начального приближения ![]() ;
;
применим только, когда ![]() для любого
для любого ![]() .
.
§2.5. Модифицированный метод Ньютона
Если производная ![]() мало изменяется на отрезке
мало изменяется на отрезке ![]() , то можно считать, что
, то можно считать, что ![]() . Заменив в формуле (2.17)
. Заменив в формуле (2.17) ![]() на
на ![]() , получим рабочую формулу модифицированного метода Ньютона:
, получим рабочую формулу модифицированного метода Ньютона:
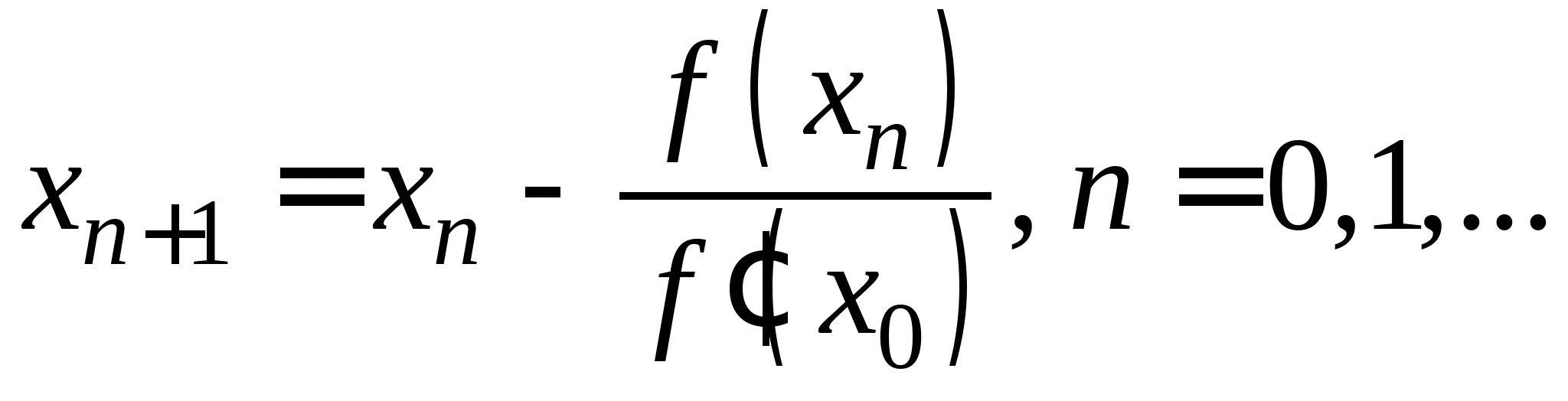 (2.21)
(2.21)
В
отличие от метода Ньютона, в модифицированном методе касательная заменяется на прямые, параллельные касательной, проведенной в точке ![]() (рис. 2.11).
(рис. 2.11).
Пример 2.5. Запишем рабочие формулы метода Ньютона и модифицированного метода Ньютона для нелинейного уравнения из примера 2.4. В качестве начального приближения ![]() здесь выбирается правый или левый конец отрезка, в зависимости от того, где выполняется достаточное условие сходимости метода Ньютона вида (2.19). Заметим, что в точке
здесь выбирается правый или левый конец отрезка, в зависимости от того, где выполняется достаточное условие сходимости метода Ньютона вида (2.19). Заметим, что в точке ![]() условие не выполняется, а в точке
условие не выполняется, а в точке ![]() - выполняется. Следовательно, в качестве начального приближения выбирается точка
- выполняется. Следовательно, в качестве начального приближения выбирается точка ![]() . Рабочая формула метода Ньютона (2.17) для данной задачи запишется так:
. Рабочая формула метода Ньютона (2.17) для данной задачи запишется так:
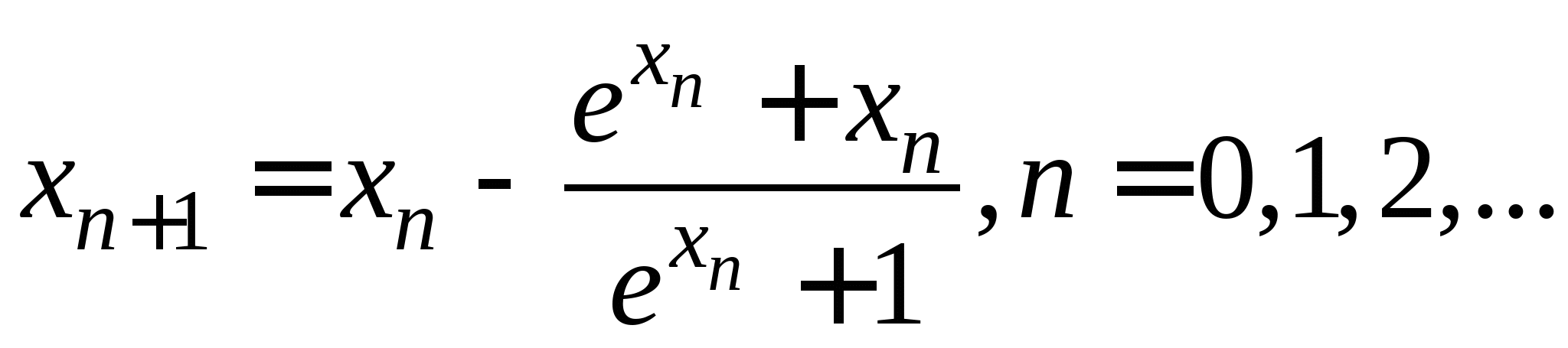
Рабочая формула модифицированного метода Ньютона (2.21) для данной задачи запишется в виде:
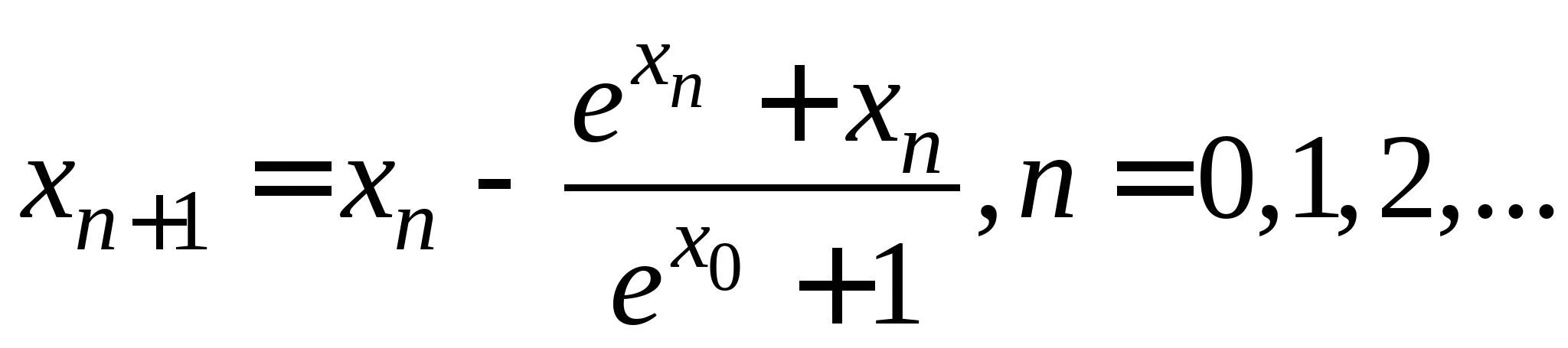
§2.6. Непрерывные схемы решения нелинейных уравнений
Итерационные методы решения нелинейного уравнения (2.1) можно разбить на две группы:
дискретные схемы решения;
непрерывные схемы решения.
Дискретные схемы решения были рассмотрены в §§2.2-2.5. Заметим, что основными недостатками перечисленных методов являются:
зависимость от начальных условий или от интервала нахождения корня;
сравнительно низкая скорость сходимости;
нет правил перехода от корня к корню уравнения (2.1) в случае, если их несколько.
При применении непрерывных схем для решения уравнения (2.1) [11] процесс нахождения корней осуществляется путем решения соответствующего обыкновенного дифференциального уравнения
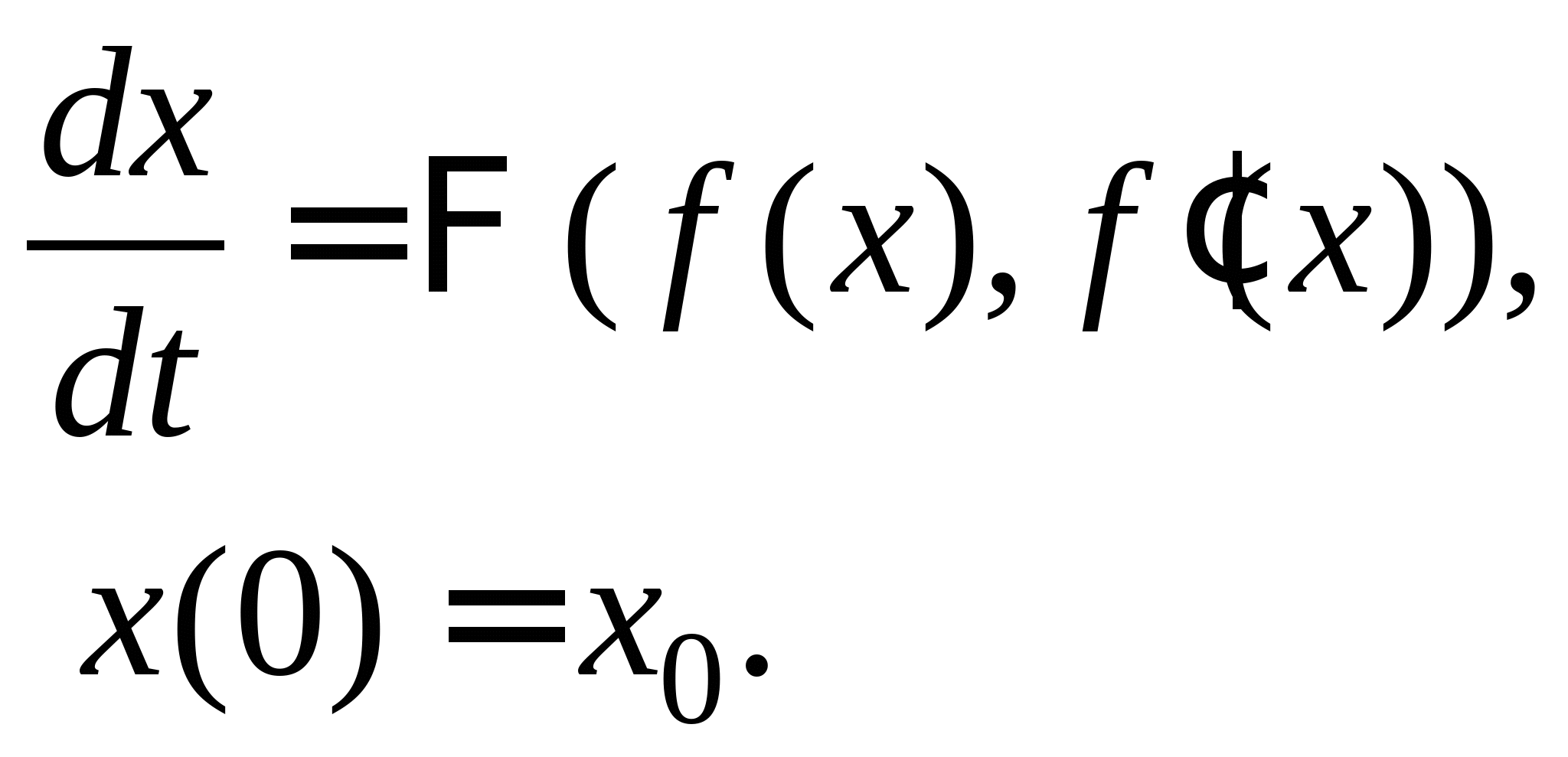 (2.22)
(2.22)
Пусть функция ![]() определена и монотонна при
определена и монотонна при ![]() и существует конечная производная
и существует конечная производная ![]() . Задачу нахождения корней уравнения (2.1), являющуюся непрерывным аналогом метода простых итераций, можно рассматривать как предел при
. Задачу нахождения корней уравнения (2.1), являющуюся непрерывным аналогом метода простых итераций, можно рассматривать как предел при ![]() решения задачи Коши
решения задачи Коши
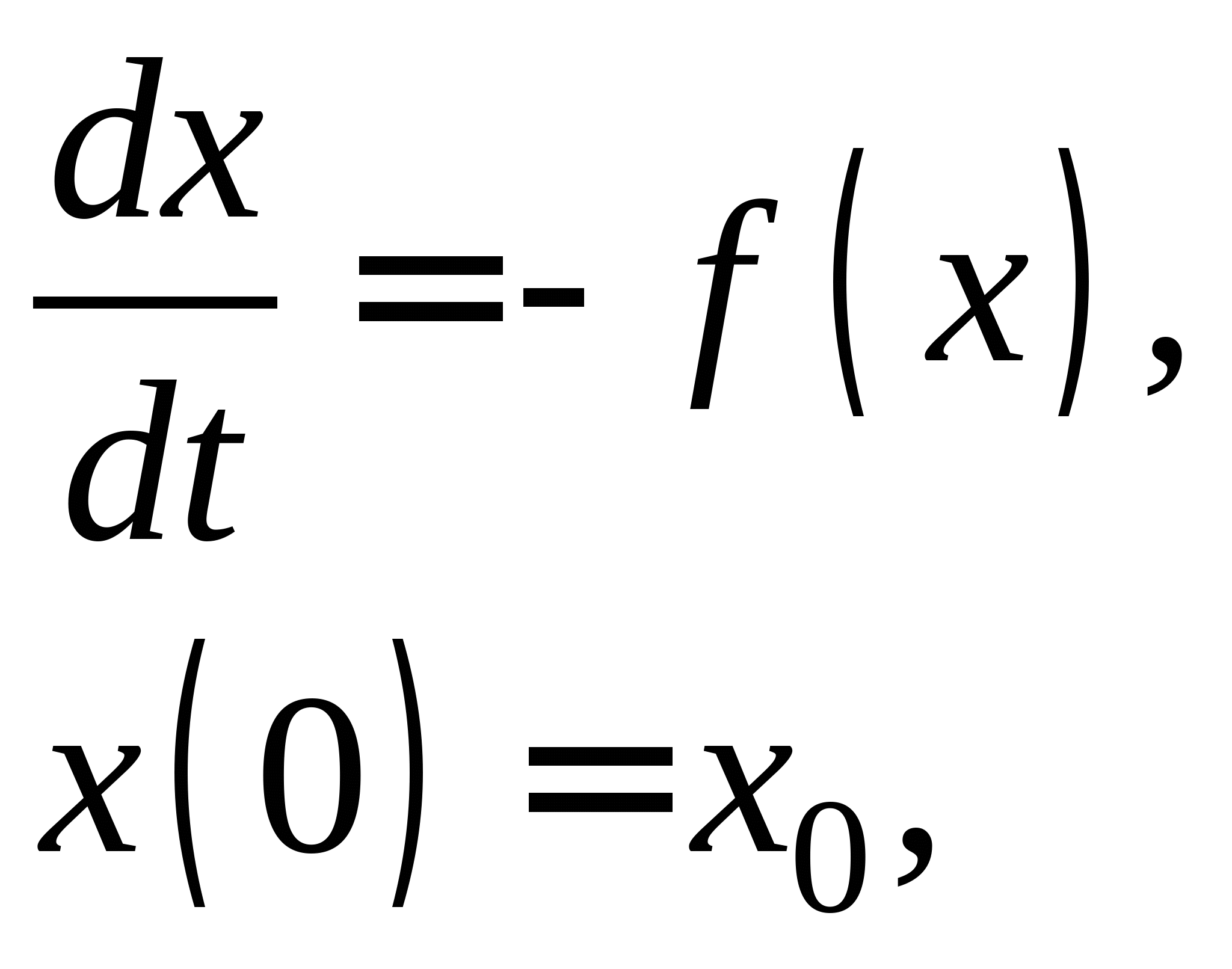 (2.23)
(2.23)
если этот предел существует. Обозначим через ![]() решение задачи Коши (2.23),
решение задачи Коши (2.23), ![]() искомое решение уравнения (2.1). Тогда должно иметь место тождество
искомое решение уравнения (2.1). Тогда должно иметь место тождество 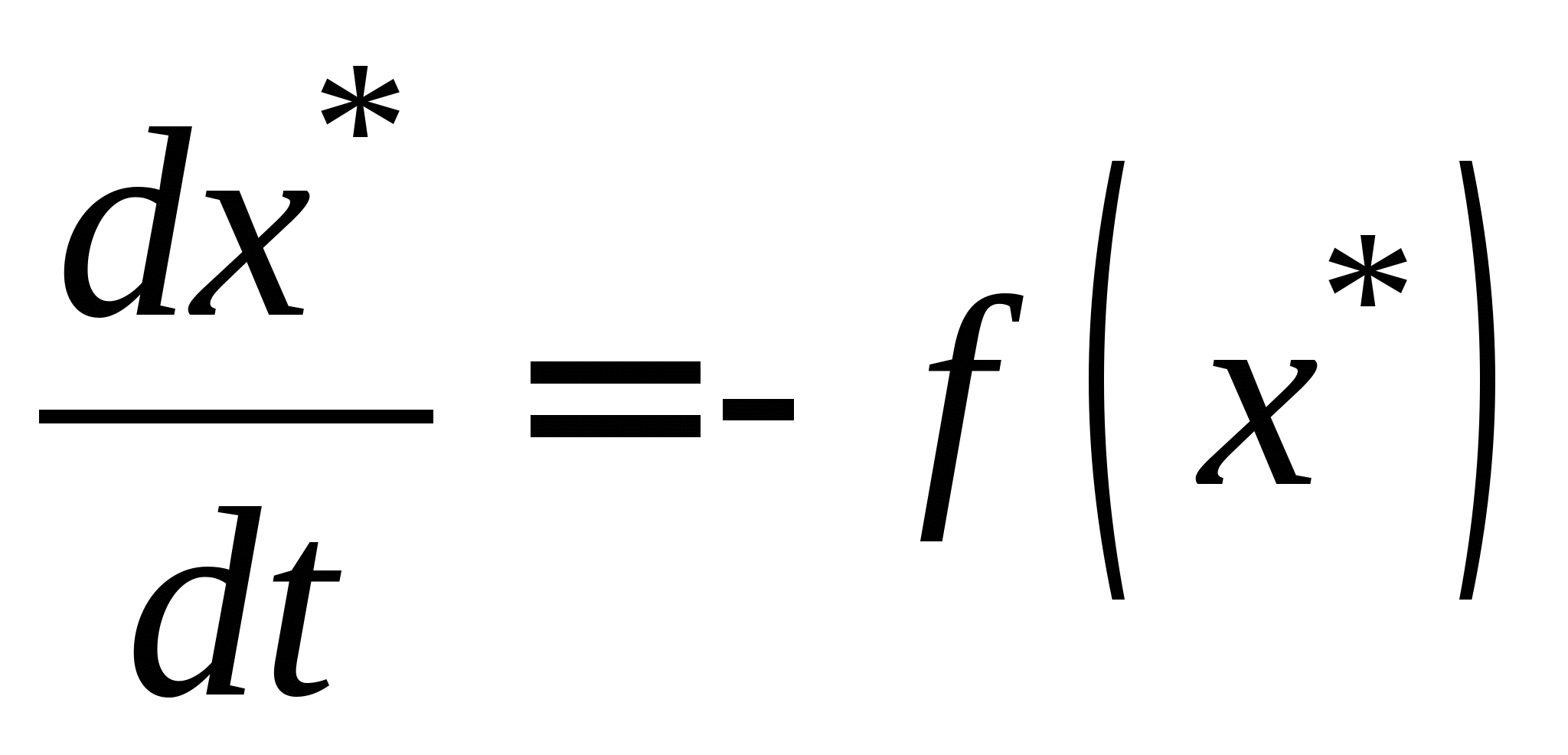 . Вводя обозначение для отклонения
. Вводя обозначение для отклонения ![]() и, вычитая из (2.23) последнее уравнение, имеем
и, вычитая из (2.23) последнее уравнение, имеем
![]() . (2.24)
. (2.24)
Разлагая ![]() в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки ![]() с сохранением линейных членов
с сохранением линейных членов ![]() и подставляя полученное выражение в уравнение (2.24), получаем дифференциальное уравнение в отклонениях
и подставляя полученное выражение в уравнение (2.24), получаем дифференциальное уравнение в отклонениях ![]() , решение которого имеет вид
, решение которого имеет вид
![]() . (2.25)
. (2.25)
Видим, что условием сходимости ![]() к корню
к корню ![]() является требование
является требование ![]() , так как в этом случае
, так как в этом случае ![]() при
при ![]() , и, следовательно,
, и, следовательно, ![]() . Считая, что
. Считая, что ![]() монотонна при
монотонна при ![]() , последнее уравнение можно распространить на всю рассматриваемую область. Таким образом, условием применения непрерывной схемы метода простых итераций для решения задачи Коши (2.23) является
, последнее уравнение можно распространить на всю рассматриваемую область. Таким образом, условием применения непрерывной схемы метода простых итераций для решения задачи Коши (2.23) является
![]() . (2.26)
. (2.26)
Непрерывные схемы решения обладают более высокой скоростью сходимости и более высокой точностью решения по сравнению с соответствующими дискретными схемами. Но проблема зависимости от начальных условий и отсутствие правил перехода от корня к корню в случае, когда уравнение (2.1) имеет более одного решения, остается открытой.
Как видно из дифференциального уравнения (2.23) и уравнения (2.1), левая часть последнего заменяется производной ![]() . Данная замена является грубым приближением решения задачи (2.23) к решению задачи (2.1). Это влечет за собой не только большую погрешность при вычислениях, но и к снижению скорости расчетов.
. Данная замена является грубым приближением решения задачи (2.23) к решению задачи (2.1). Это влечет за собой не только большую погрешность при вычислениях, но и к снижению скорости расчетов.
Перепишем уравнение (2.1) в виде
![]() , (2.27)
, (2.27)
где ![]() малый параметр,
малый параметр, ![]() .
.
Переход от задачи (2.1) к задаче (2.27) теоретически обоснован, так как интегральные кривые, являющиеся решением уравнения с малым параметром (2.27), проходят через все решения уравнения (2.1). Задачу нахождения корней этого уравнения непрерывным сингулярным аналогом метода простых итераций можно рассматривать как предел при ![]() и
и ![]() решения задачи Коши вида
решения задачи Коши вида
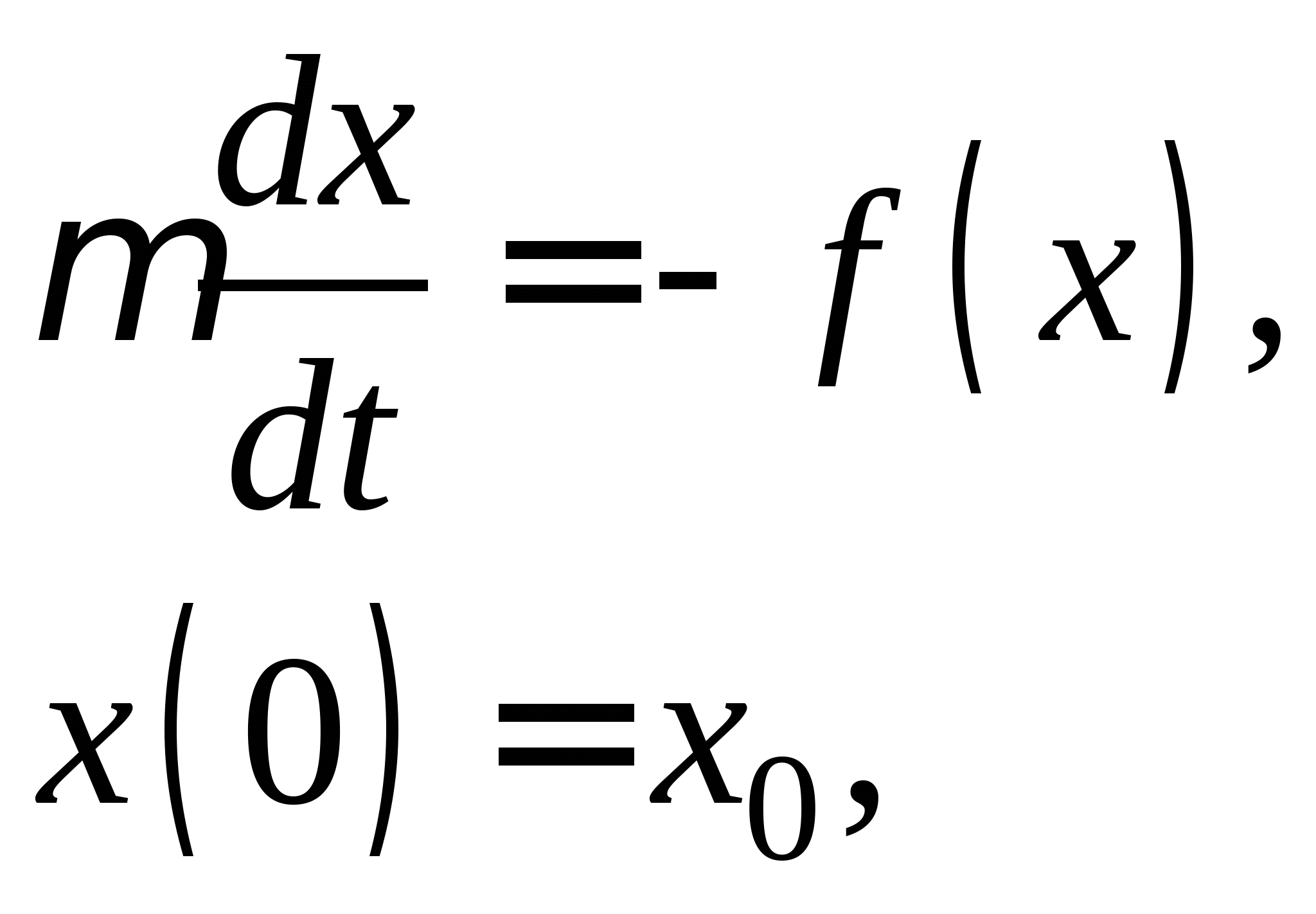 (2.28)
(2.28)
если этот предел существует.
Проводя рассуждения, аналогичные рассуждениям, приведенным выше, получим, что решение уравнения (2.27) в точке ![]() будет иметь вид:
будет иметь вид:
![]()
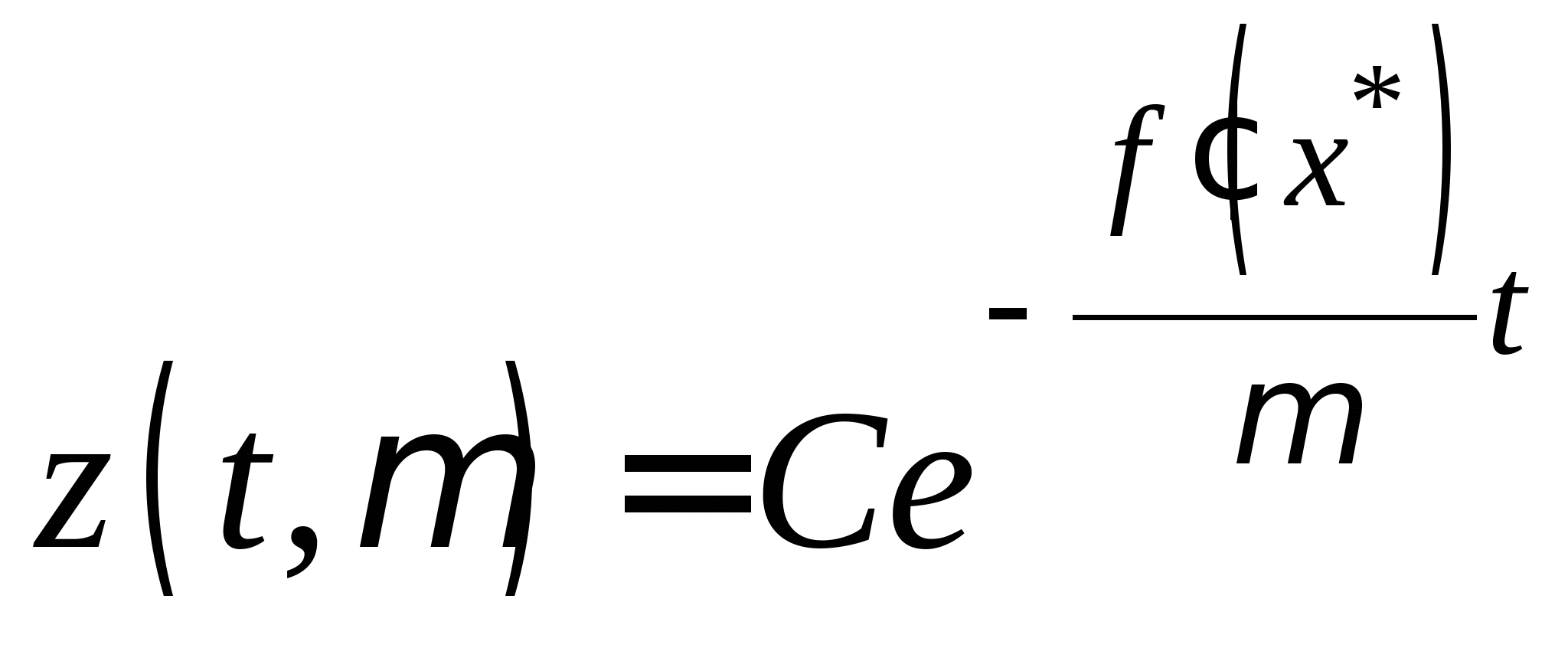 (2.29)
(2.29)
При этом, в силу того, что ![]() , условие сходимости (2.26) останется прежним.
, условие сходимости (2.26) останется прежним.
Полученная модификация классических схем решения не зависит от начальных условий и обладает более высокой точностью решения. Для доказательства более быстрой скорости сходимости предположим, что применение итерационных методов никогда не дает точного решения и введем точность решения ![]() . Моменты нахождения решений с точностью
. Моменты нахождения решений с точностью ![]() классическими и модифицированными методами обозначим как
классическими и модифицированными методами обозначим как ![]() и
и ![]() . Используя решения (2.25) и (2.29), запишем неравенства вида
. Используя решения (2.25) и (2.29), запишем неравенства вида
![]() ,
,
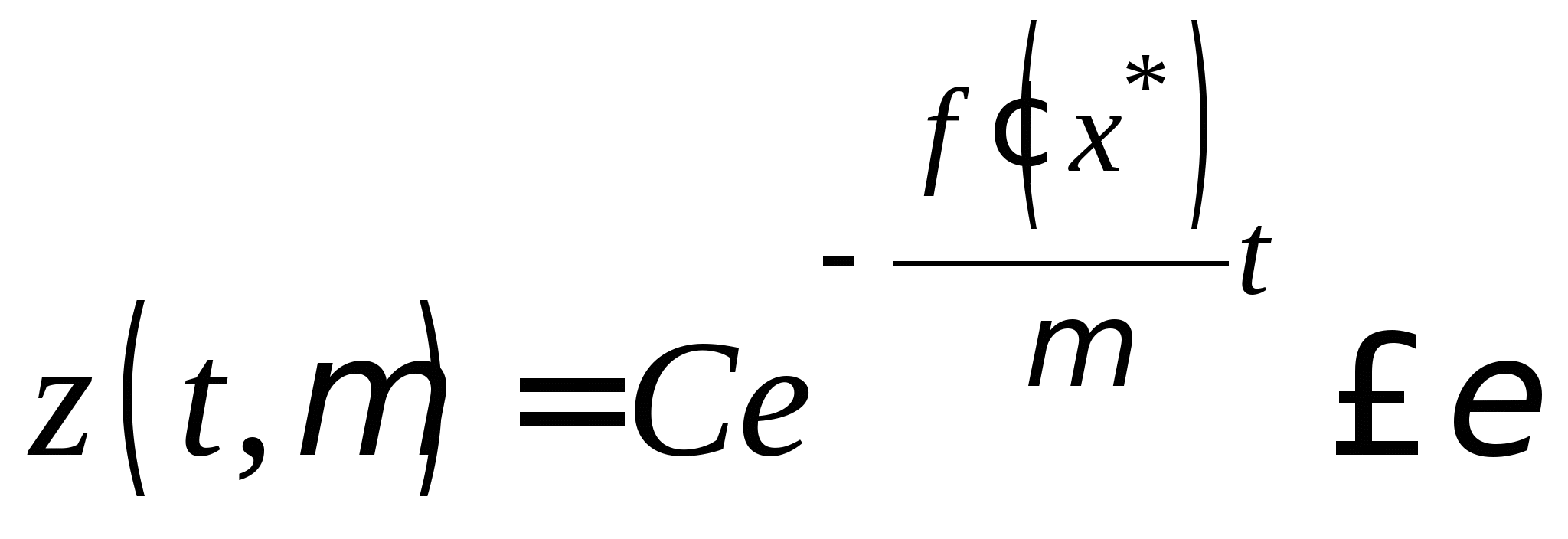 .
.
Из соотношений видно, что 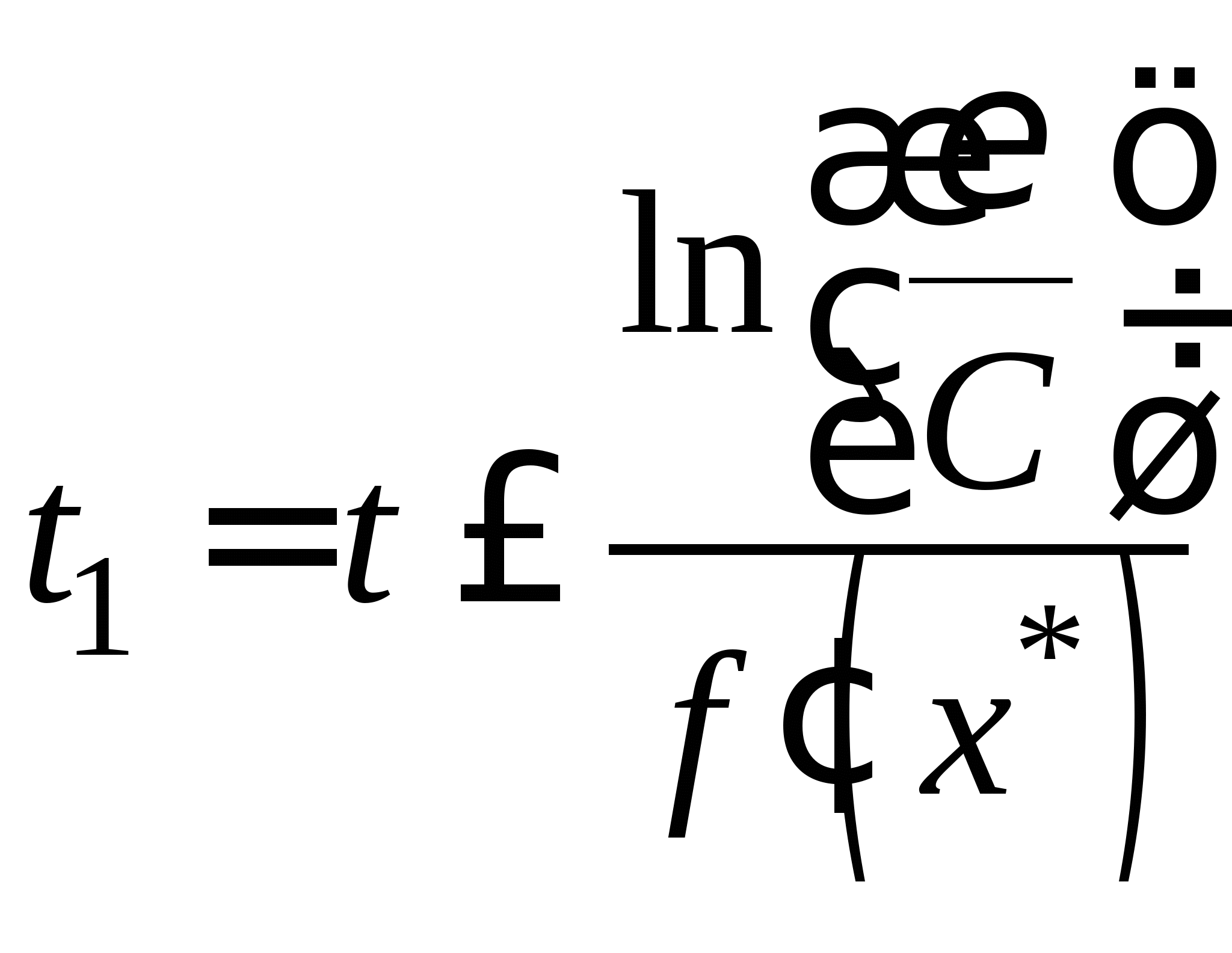 и
и 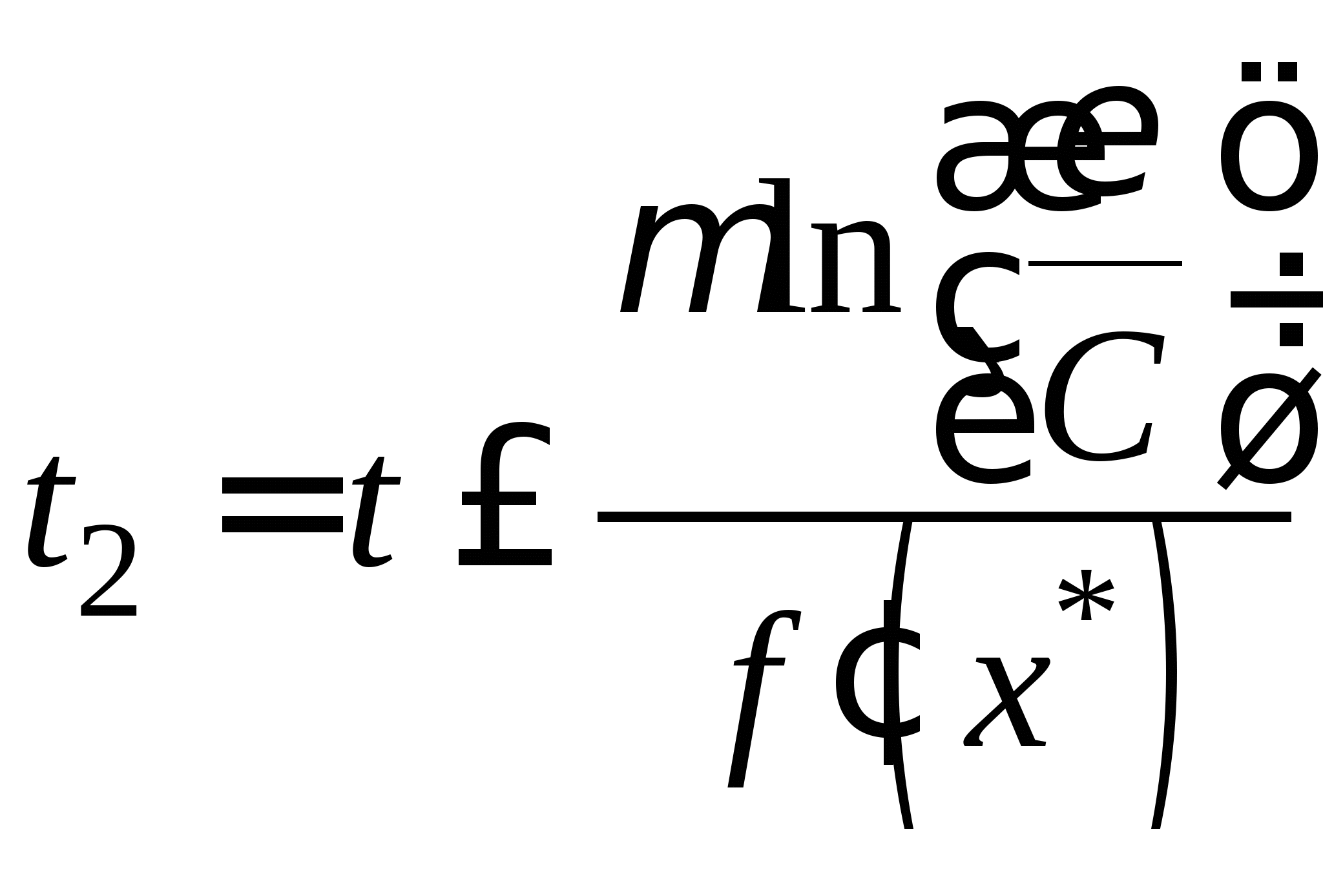 . Сопоставляя полученные значения
. Сопоставляя полученные значения ![]() и
и ![]() , видим, что
, видим, что 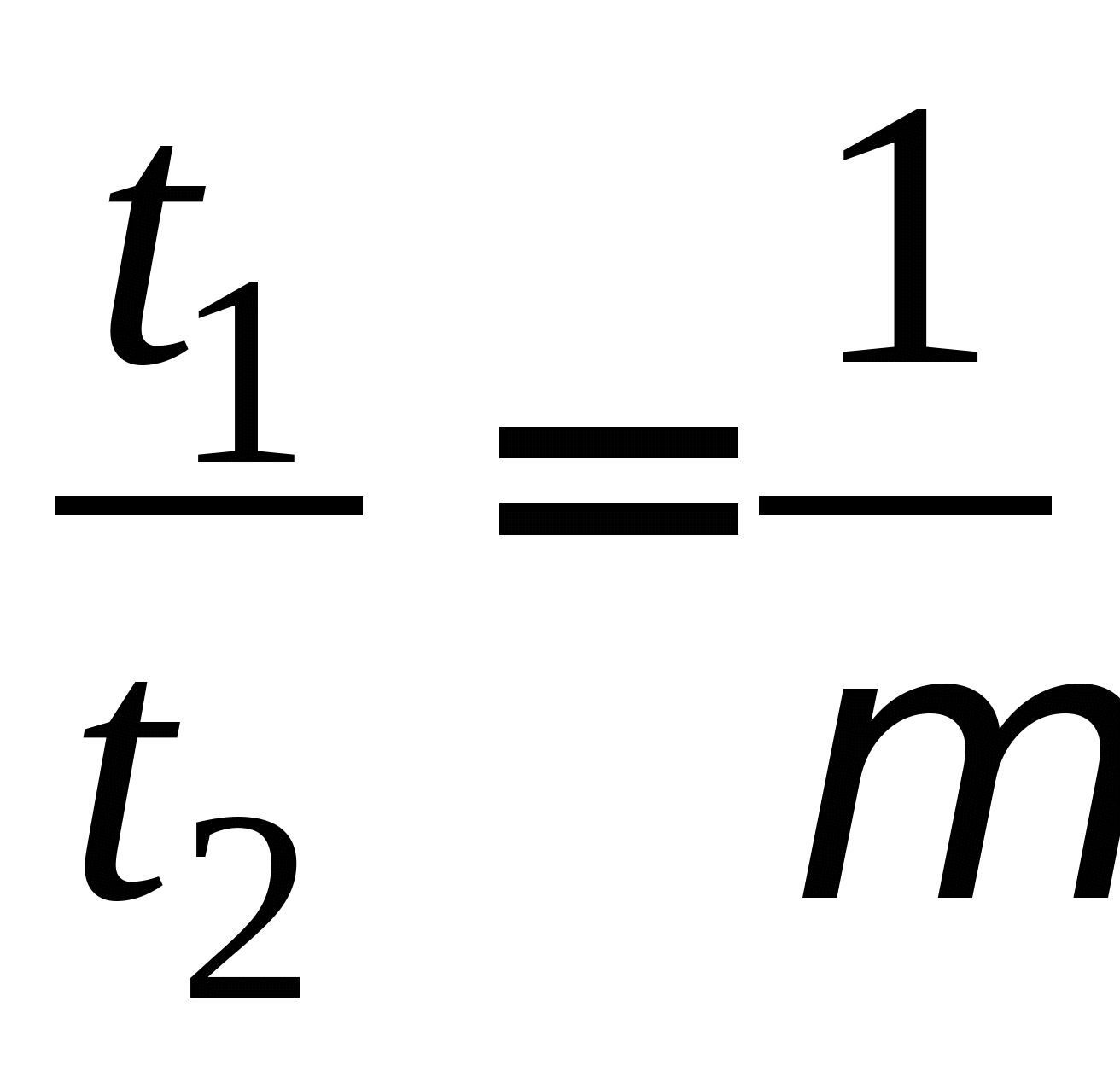 , т.е. скорость сходимости при решении задачи модифицированными методами в
, т.е. скорость сходимости при решении задачи модифицированными методами в ![]() раз выше, чем классическими.
раз выше, чем классическими.
ЛАБОРАТОРНАЯ РАБОТА №1-2. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
Цель работы: научиться решать нелинейные уравнения методом простых итераций, методом Ньютона и модифицированным методом Ньютона с помощью ЭВМ.
Содержание работы:
1. Изучить метод простых итераций, метод Ньютона и модифицированный метод Ньютона для решения нелинейных уравнений.
2. На конкретном примере усвоить порядок решения нелинейных уравнений с помощью ЭВМ указанными методами.
3. Составить программу (программы) на любом языке программирования и с ее помощью решить уравнение с точностью ![]() и
и ![]() . Сделать вывод о скорости сходимости всех трех методов.
. Сделать вывод о скорости сходимости всех трех методов.
4. Изменить ![]() и снова решить задачу. Сделать выводы о: скорости сходимости рассматриваемых методов; влиянии точности на скорость сходимости; влиянии выбора начального приближения в методе простых итераций на скорость сходимости.
и снова решить задачу. Сделать выводы о: скорости сходимости рассматриваемых методов; влиянии точности на скорость сходимости; влиянии выбора начального приближения в методе простых итераций на скорость сходимости.
5. Составить отчет о проделанной работе.
ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Задание.
1. Доказать графическим и аналитическим методами существование единственного корня нелинейного уравнения
![]() (1)
(1)
на отрезке ![]() .
.
2. Построить рабочие формулы метода простых итераций, метода Ньютона и модифицированного метода Ньютона, реализующие процесс поиска корня нелинейного уравнения (1) на указанном отрезке.
3. Составить программу (программы) на любом языке программирования, реализующие построенные итерационные процессы.
Решение.
1. Докажем графическим методом единственность корня нелинейного уравнения (1). Из графика функции ![]() на Рис.1 видно, что функция
на Рис.1 видно, что функция ![]() пересекает ось
пересекает ось ![]() в одной точке, являющейся приближенным значением корня нелинейного уравнения (1). Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение (1) к виду
в одной точке, являющейся приближенным значением корня нелинейного уравнения (1). Но так как данная функция имеет сложный аналитический вид, то преобразуем уравнение (1) к виду ![]() и построим два графика
и построим два графика ![]() и
и ![]() , имеющих более простой аналитический вид (Рис.2). Абсцисса точки пересечения графиков является приближенным значением корня. Заметим, что графический метод показывает количество корней исходного уравнения, но не доказывает единственность корня на отрезке.
, имеющих более простой аналитический вид (Рис.2). Абсцисса точки пересечения графиков является приближенным значением корня. Заметим, что графический метод показывает количество корней исходного уравнения, но не доказывает единственность корня на отрезке.
Р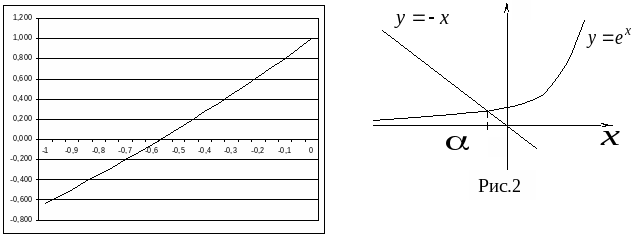
ис.1
Аналитический метод. Функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() , имеет на концах отрезка разные знаки (
, имеет на концах отрезка разные знаки (![]() ), а производная функции
), а производная функции ![]() не меняет знак на отрезке (
не меняет знак на отрезке (![]() ). Следовательно, нелинейное уравнение (1) имеет на указанном отрезке единственный корень.
). Следовательно, нелинейное уравнение (1) имеет на указанном отрезке единственный корень.
2. Метод простых итераций.
Построим функцию ![]() . Константа
. Константа ![]() выбирается из достаточного условия сходимости
выбирается из достаточного условия сходимости
![]() (2)
(2)
Если производная ![]() , то значение
, то значение ![]() выбирается из интервала
выбирается из интервала ![]() , если производная
, если производная ![]() , то – из интервала
, то – из интервала ![]() . Так как для рассматриваемого примера
. Так как для рассматриваемого примера ![]() всюду положительна на отрезке
всюду положительна на отрезке ![]() , то придавая переменной
, то придавая переменной ![]() различные значения из интервала
различные значения из интервала ![]() и выбирая наименьший интервал
и выбирая наименьший интервал ![]() , получим
, получим ![]() . Выбираем произвольное значение
. Выбираем произвольное значение ![]() из этого интервала. Пусть
из этого интервала. Пусть ![]() . Тогда рабочая формула метода простых итераций будет иметь вид:
. Тогда рабочая формула метода простых итераций будет иметь вид:
![]() (3)
(3)
Итерационный процесс (3) можно начать, задав произвольное начальное приближение ![]() . Итерационный процесс (3) заканчивается при одновременном выполнении двух условий:
. Итерационный процесс (3) заканчивается при одновременном выполнении двух условий:
![]() и
и ![]() . (4)
. (4)
В этом случае значение ![]() является приближенным значением корня нелинейного уравнения (1) на отрезке
является приближенным значением корня нелинейного уравнения (1) на отрезке ![]() .
.
Метод Ньютона. В качестве начального приближения ![]() здесь выбирается правый или левый конец отрезка, в зависимости от того, в котором выполняется достаточное условие сходимости метода Ньютона вида:
здесь выбирается правый или левый конец отрезка, в зависимости от того, в котором выполняется достаточное условие сходимости метода Ньютона вида:
![]() (5)
(5)
Заметим, что в точке ![]() условие (5) не выполняется, а в точке
условие (5) не выполняется, а в точке ![]() выполняется. Следовательно, в качестве начального приближения выбирается точка
выполняется. Следовательно, в качестве начального приближения выбирается точка ![]() . Рабочая формула метода Ньютона
. Рабочая формула метода Ньютона 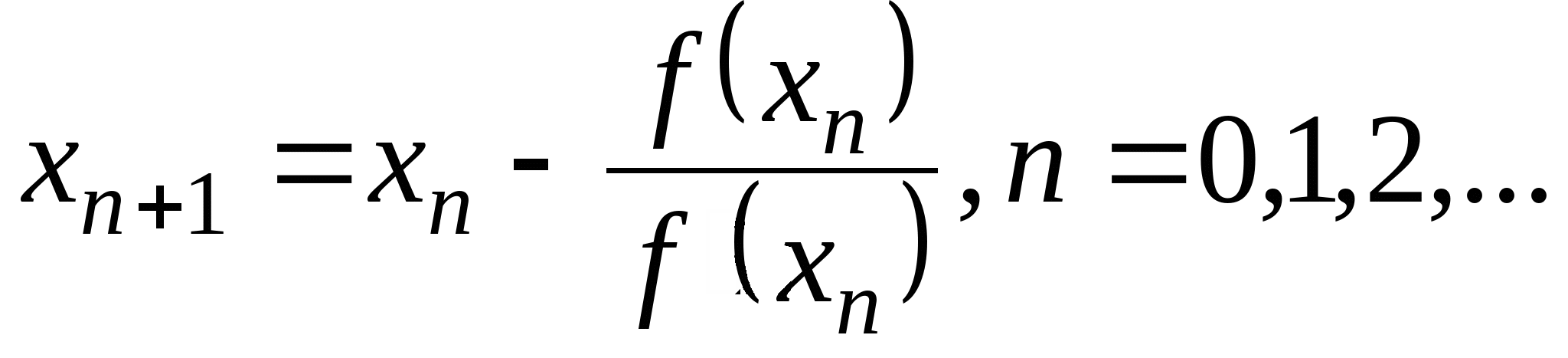 для данного уравнения запишется так:
для данного уравнения запишется так:
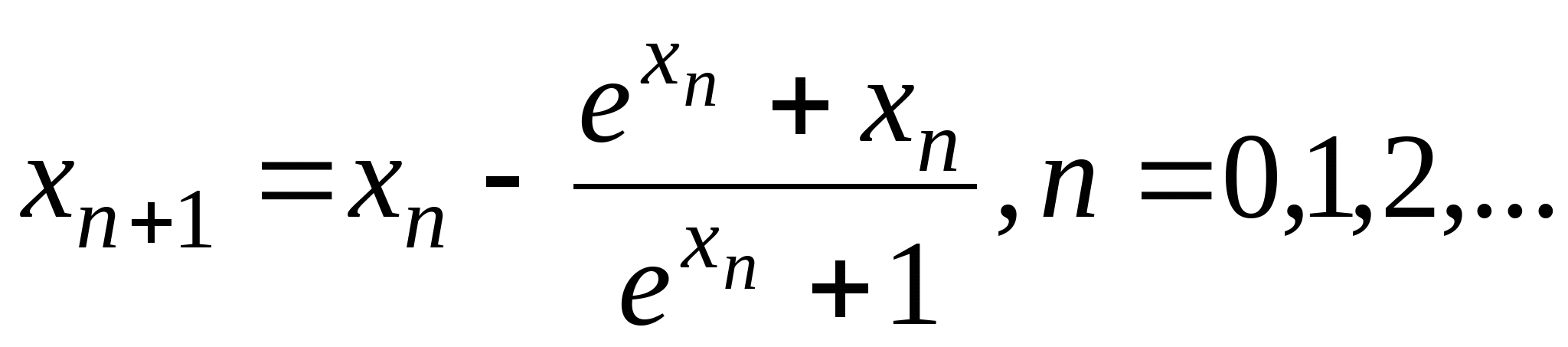 (6)
(6)
Условия выхода итерационного процесса (6) аналогичны условиям (4) метода простых итераций.
Модифицированный метод Ньютона. Начальное приближение ![]() выбирается аналогично методу Ньютона, т.е.
выбирается аналогично методу Ньютона, т.е. ![]() . Рабочая формула модифицированного метода Ньютона
. Рабочая формула модифицированного метода Ньютона 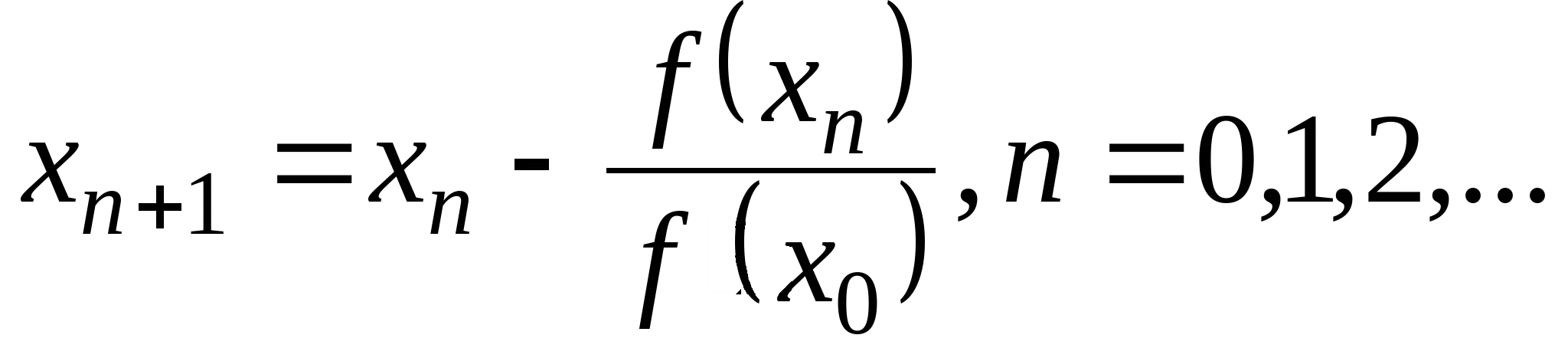 для данного примера запишется так:
для данного примера запишется так:
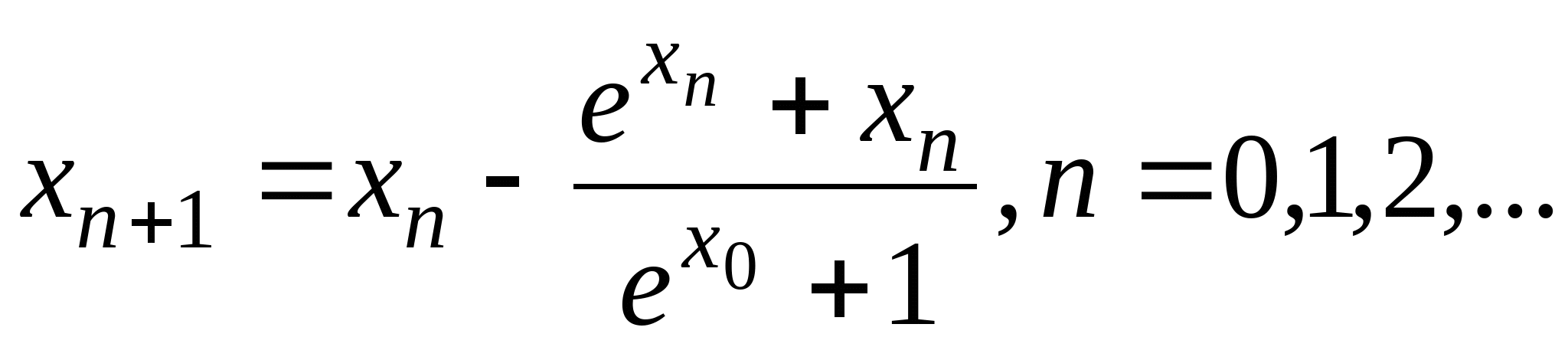 (7)
(7)
Условия выхода итерационного процесса (7) аналогичны условиям (4) метода простых итераций.
Замечание: для того, чтобы сделать вывод о скорости сходимости методов, необходимо в каждом методе выбирать одинаковое начальное приближение.
3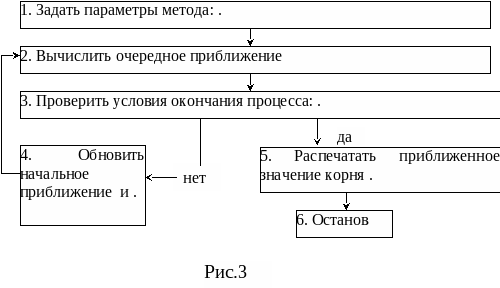
. Блок-схема метода простых итераций, метода Ньютона и модифицированного метода Ньютона приведена на рисунке 3.
Ниже в качестве примера приведены программы на языках программирования Паскаль и С, реализующие итерационный процесс метода простых итераций.
ПРИМЕР ПРОГРАММЫ НА ЯЗЫКЕ ПАСКАЛЬ
Program Pr_iter;
Uses Crt;
var n:integer;
x0,x,eps,d,y,z,c:real;
begin
clrscr;
n:=0;x0:=-1;c:=-0.1;x:=x0;eps:=0.001;d:=0.01;
repeat
y:=x+c*(exp(x)+x);
z:=x;
writeln(n:3,x:9:5,y:9:5,abs(y-x):9:5,abs(exp(y)+y):9:5);
x:=y;
n:=n+1;
until (abs(z-x)<=eps) and (abs(exp(x)+x)<=d);
end.
ПРИМЕР ПРОГРАММЫ НА ЯЗЫКЕ С
#include <stdio.h>
#include <math.h>
main()
{
int n=0;
float x,y,z,x0=-1,c=-0.1,eps=0.001;d=0.01;
x=x0;
clrscr();
do
{
y=x+c*(exp(x)+x);z=x;
printf(“%d %.4f %.4f %.4f %.4f\n”,n++,x,y,fabs(y-x),
fabs(exp(y)+y));
x=y;
}
while(fabs(z-x)>e || fabs(exp(x)+x)>d;
getch();
}
Решение: в результате решения нелинейного уравнения (1) на указанном отрезке тремя методами при начальном приближении ![]() с точностью
с точностью ![]() и
и ![]() получены следующие результаты: методом простых итераций
получены следующие результаты: методом простых итераций ![]() ; методом Ньютона
; методом Ньютона ![]() ; модифицированным методом Ньютона
; модифицированным методом Ньютона ![]() .
.
4. Содержание отчета.
Отчет о проделанной работе должен содержать: номер и название лабораторной работы; цель работы; содержание работы; задание на работу; теоретическую часть работы (вывод итерационных формул); листинг(и) программ(ы); таблицы результатов (в случае, если число итераций в таблице достаточно большое, в отчет занести две первых и две последних итерации); выводы о проделанной работе.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Определить количество корней исходного нелинейного уравнения графическим методом и построить график (пример приведен на рисунке 2).
2. Доказать аналитическим методом единственность корня исходного нелинейного уравнения на указанном отрезке.
3. Записать итерационные формулы, реализующие процесс поиска корня на отрезке методом простых итераций, методом Ньютона и модифицированным методом Ньютона.
4. Составить программу(ы) на любом языке программирования, реализующую(ие) построенные итерационные процессы, используя алгоритм методов, приведенный на рисунке. Печать результатов должна осуществляться на каждом шаге итераций в виде следующей таблицы:
|
|
|
|
|
|
5. Провести вычислительные эксперименты.
6. Сделать выводы.
7. Составить отчет о проделанной работе.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
| № варианта | Нелинейное уравнение | Отрезок |
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
120