| Похожие рефераты | Скачать .zip |
Реферат: Математический анализ
Числовые функции
Понятие функции является одним из основных в математике. С его помощью выражают зависимости между различными переменными величинами. Изучение свойств функций, основанное на методе пределов, составляет содержание математического анализа.
- Определение
Пусть
![]() -
некоторое
числовое множество,
и пусть каждому
элементу
-
некоторое
числовое множество,
и пусть каждому
элементу
![]() поставлено
в соответствие
число
поставлено
в соответствие
число
![]() .
Тогда говорят,
что на множестве
.
Тогда говорят,
что на множестве
![]() определена
числовая функция.
Функцию обозначают
некоторым
символом, например
определена
числовая функция.
Функцию обозначают
некоторым
символом, например
![]() ,
и пишут
,
и пишут
![]() .
(1)
.
(1)
Множество
![]() называется
областью
определения
функции
называется
областью
определения
функции
![]() ,
,
![]() - ее аргументом,
а
- ее аргументом,
а
![]() - значением
функции в точке
- значением
функции в точке
![]() .
Используются
также обозначения:
.
Используются
также обозначения:
![]() для области
определения
и
для области
определения
и
![]() для множества
значений функции.
для множества
значений функции.
Графиком
функции
![]() называется
множество всех
точек координатной
плоскости вида
называется
множество всех
точек координатной
плоскости вида
![]() ,
где
,
где
![]() .
График дает
наглядное
представление
о поведении
функции, однако
более удобным
в теоретических
исследованиях
является
аналитический
способ задания
функций с помощью
формул. На практике
используют
также табличный
способ, когда
значения функции
указываются
для отдельных
значений аргумента.
.
График дает
наглядное
представление
о поведении
функции, однако
более удобным
в теоретических
исследованиях
является
аналитический
способ задания
функций с помощью
формул. На практике
используют
также табличный
способ, когда
значения функции
указываются
для отдельных
значений аргумента.
В качестве области определения функции могут выступать различные числовые множества, например:
а) отрезок
![]() ;
;
б) интервал
![]() ;
;
в) полуинтервалы
![]() или
или
![]() ;
;
г) бесконечные
полуинтервалы
![]() или
или
![]() ;
;
д) множество
всех действительных
чисел R =![]() .
.
Под областью определения функции, заданной формулой, понимают обычно множество всех значений аргумента, для которых эта формула имеет смысл.
Примеры.
1) Для функции
![]() область определения
и множество
значений
область определения
и множество
значений
имеют
вид:
![]() ,
,
![]() ;
график функции
представлен
на рис. 1.
;
график функции
представлен
на рис. 1.
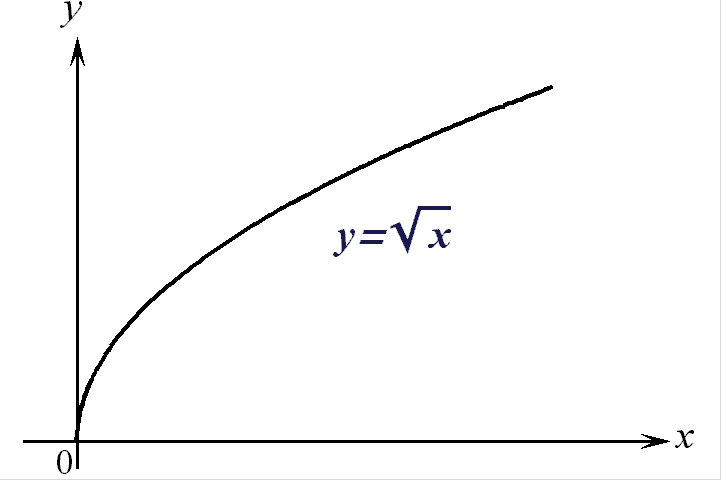
Рис. 1.
2)
Для функции
![]() имеем
имеем
![]() ,
,
![]() ;
график функции
изображен на
рис. 2.
;
график функции
изображен на
рис. 2.
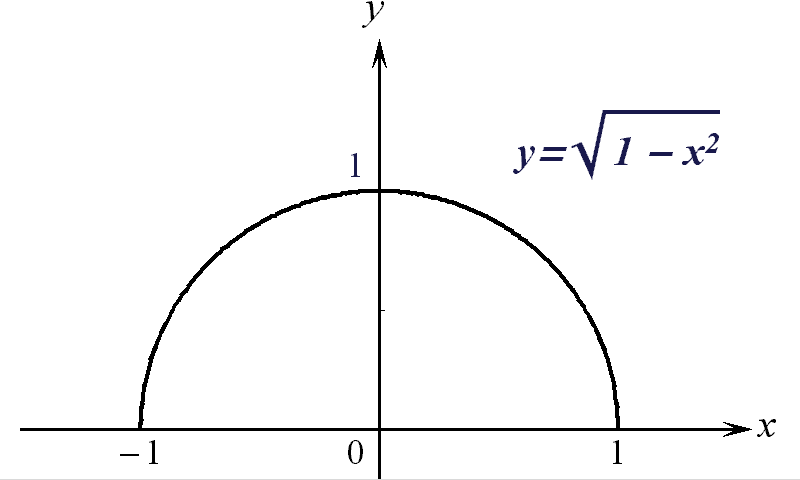
Рис. 2.
3) Для функции
![]() имеем:
имеем:
![]() ,
,
![]() ;
ее график приведен
на рис. 3.
;
ее график приведен
на рис. 3.
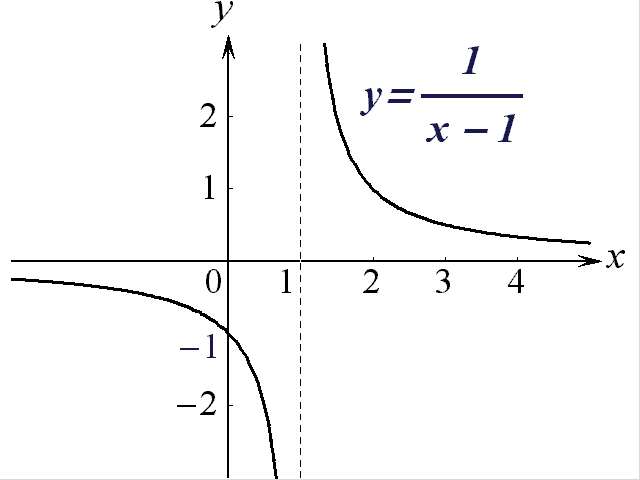
Рис. 3.
- Основные элементарные функций
Напомним определения и свойства некоторых элементарных функций, известные из школьного курса математики. В каждом случае укажем аналитическое выражение и область определения функции, приведем ее график.
а) Линейная функция:
![]() R,
R,
где
![]() и
и
![]() – некоторые
постоянные
(числа); график
– прямая с угловым
коэффициен-
– некоторые
постоянные
(числа); график
– прямая с угловым
коэффициен-
том
![]() (
(![]() ,
где
,
где
![]() – угол наклона
прямой к оси
– угол наклона
прямой к оси
![]() ):
):
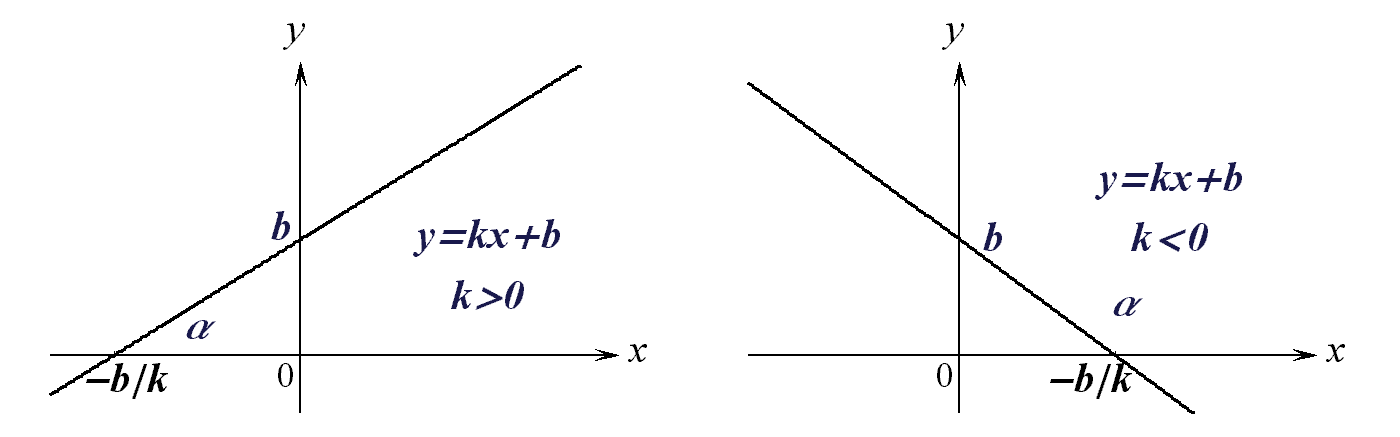
Рис.4.
б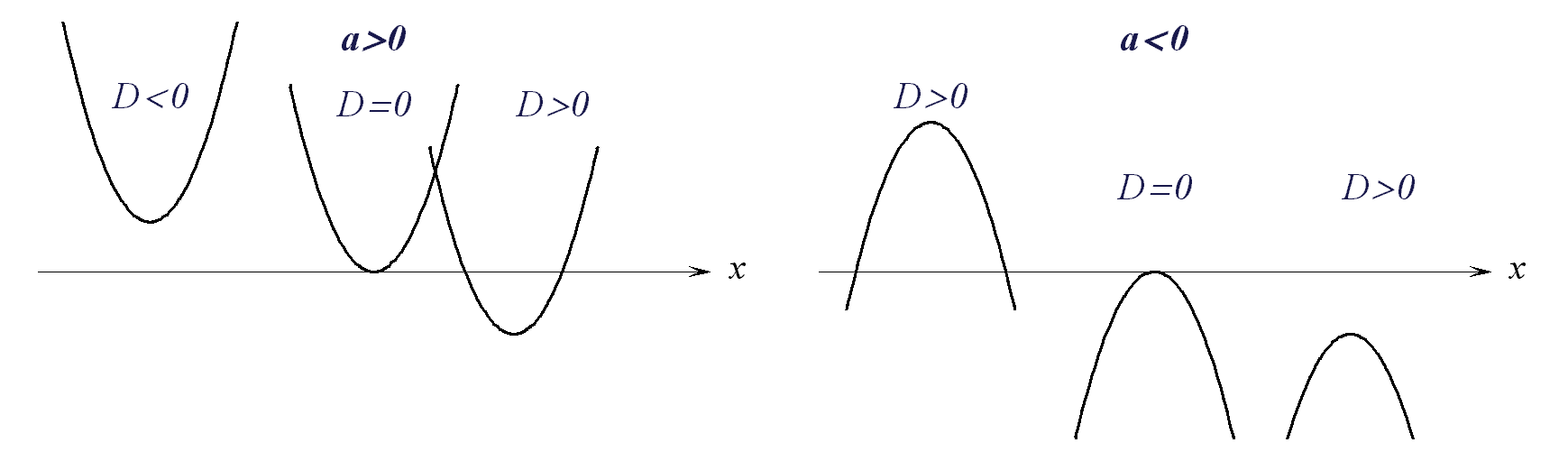
)
Квадратичная
функция:
![]() R,
R,
Рис. 5.
где
![]() ,
,
![]() ,
,
![]() - постоянные
коэффициенты;
график – парабола,
ее расположение
существенно
зависит от
величины
- постоянные
коэффициенты;
график – парабола,
ее расположение
существенно
зависит от
величины
![]() ,
,
называемой
дискриминантом
функции, и от
знака первого
коэффициента
![]() :
:
в) Обратно пропорциональная зависимость:
![]() ,
,
где
![]() - постоянная.
График – гипербола:
- постоянная.
График – гипербола:
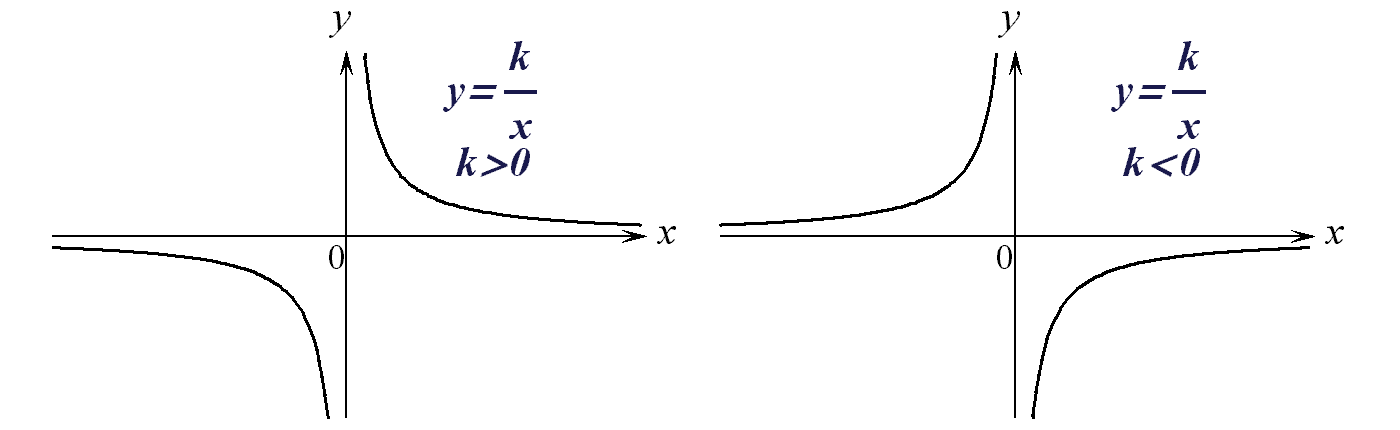
Рис. 6.
г) Степенная функция:
![]() ,
,
где
![]() и
и
![]() - постоянные;
область определения
существенно
зависит от
- постоянные;
область определения
существенно
зависит от
![]() .
В п. в) рассмотрен
случай
.
В п. в) рассмотрен
случай
![]() ,
а в примере 1 -
случай
,
а в примере 1 -
случай
![]() .
Приведем еще
графики функций
для
.
Приведем еще
графики функций
для
![]() и
и
![]() :
:
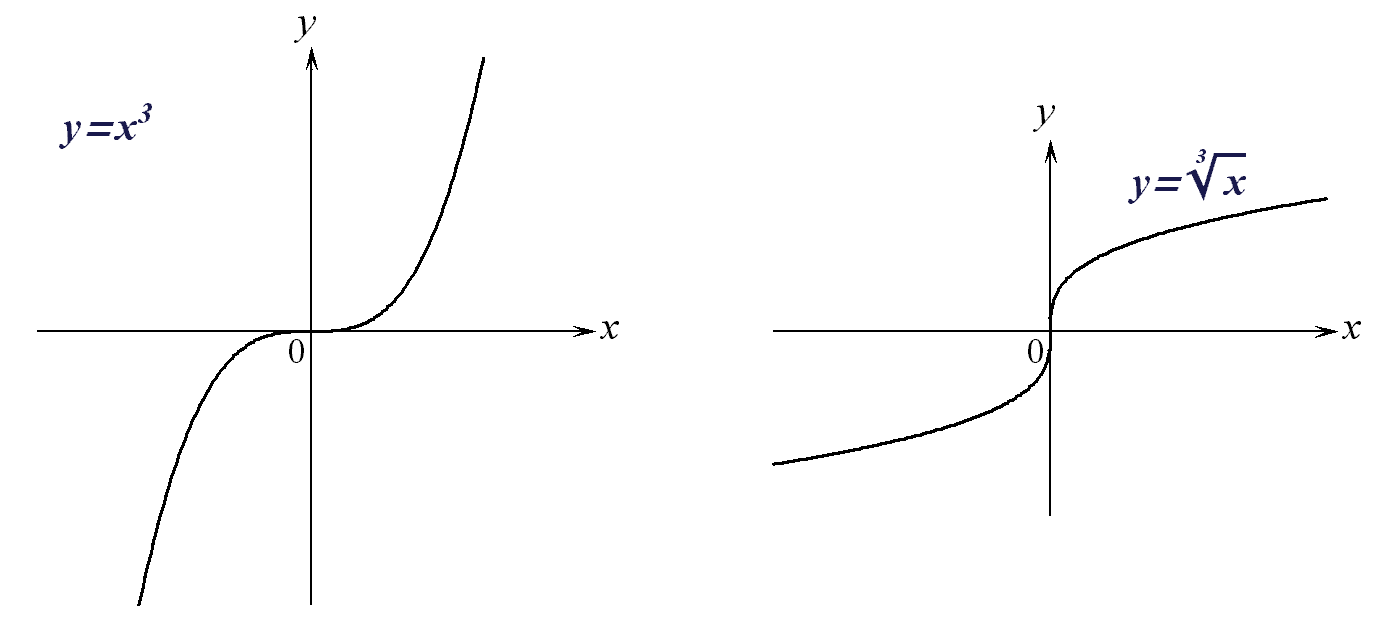
Рис. 7.
е) Показательная функция:
![]() R,
R,
где
![]() - постоянная;
график в зависимости
от значения
- постоянная;
график в зависимости
от значения
![]() имеет вид:
имеет вид:
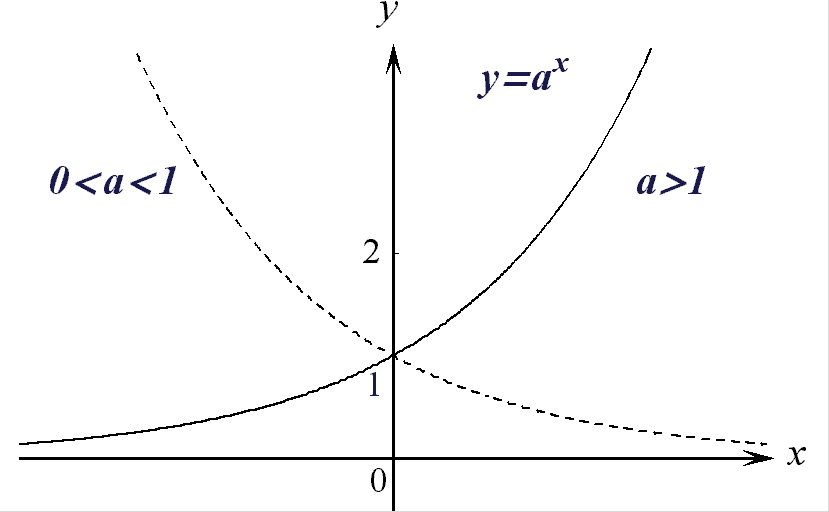
Рис. 8.
Все перечисленные здесь функции, а также логарифмическая, тригонометрические и обратные тригонометрические функции основными элементарными функциями.
- Сложная функция
Пусть заданы
функции
![]() и
и
![]() ,
причем множество
значений функции
,
причем множество
значений функции
![]() принадлежит
области определения
функции
принадлежит
области определения
функции
![]() :
:
![]() .
Тогда можно
определить
сложную функцию
.
Тогда можно
определить
сложную функцию
![]() ,
,
называемую
также композицией
функций
![]() и
и
![]() .
.
Пример.
Из функций
![]() и
и
![]() с помощью указанной
операции можно
составить две
сложные функции:
с помощью указанной
операции можно
составить две
сложные функции:
![]() и
и
![]() .
.
Используя операцию композиции, можно из основных элементарных функций, получать новые функции, также называемые элементарными. Вообще, элементарной функцией называют функцию, которую можно получить из основных элементарных функций с помощью конечного числа арифметических операций и композиций.
П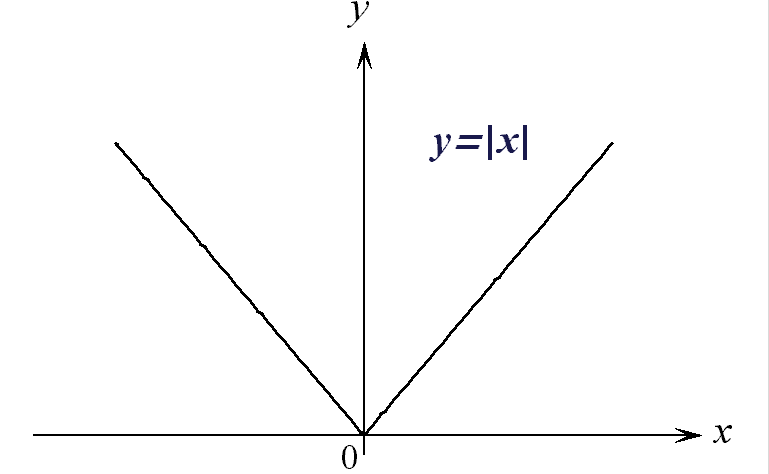
ример.
Функция
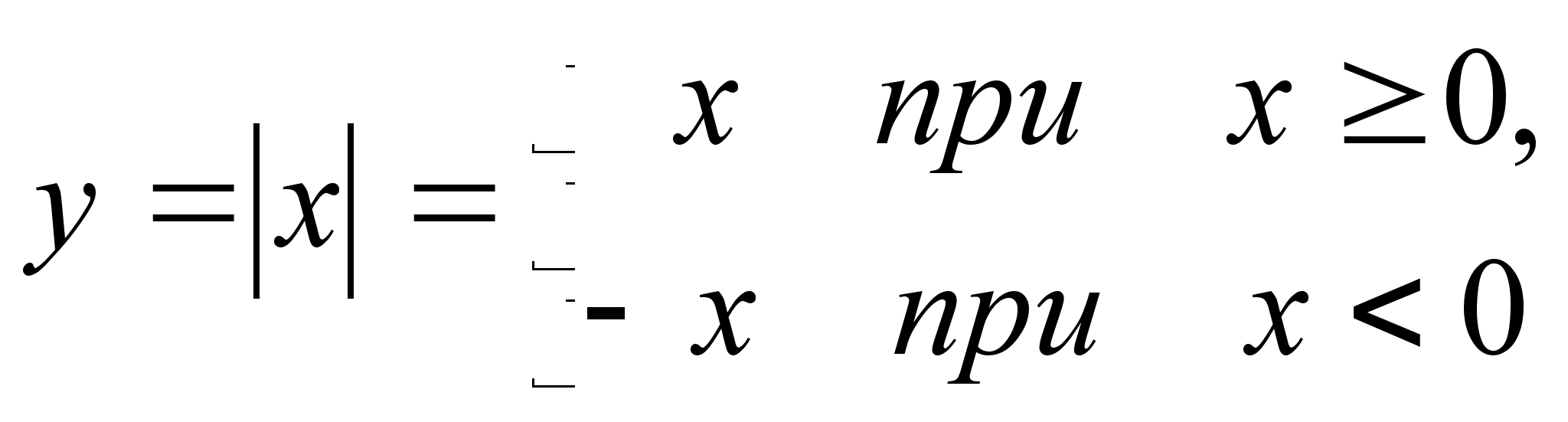 (читается: “модуль
(читается: “модуль
![]() ”)
является
элементарной,
так как для
всех
”)
является
элементарной,
так как для
всех
![]() R
справедливо
представление
R
справедливо
представление
![]() .
График этой
функции приведен
на рис. 9.
.
График этой
функции приведен
на рис. 9.
Рис. 9.
4. Обратная функция
Рассмотрим
функцию
![]() с областью
определения
с областью
определения
![]() и множеством
значений
и множеством
значений
![]() .
Предположим,
что для любого
.
Предположим,
что для любого
![]() уравнение
уравнение
![]() имеет единственное
решение
имеет единственное
решение![]() .
Тогда на множестве
.
Тогда на множестве
![]() можно определить
функцию, сопоставляющую
каждому
можно определить
функцию, сопоставляющую
каждому
![]() такое значение
такое значение
![]() ,
что
,
что
![]() .
Эту функцию
называют обратной
для функции
.
Эту функцию
называют обратной
для функции
![]() и обозначают
и обозначают
![]() :
:
![]() .
.
Функцию, у которой существует обратная функция, назовем обратимой.
Обозначая, как
обычно, аргумент
функции через
![]() ,
а значение
функции через
,
а значение
функции через
![]() ,
можно записать
,
можно записать
![]() .
.
Поскольку
взаимная перестановка
переменных
![]() и
и
![]() равносильна
переобозначению
координатных
осей, можно
показать, что
график функции
равносильна
переобозначению
координатных
осей, можно
показать, что
график функции
![]() симметричен
графику функции
симметричен
графику функции
![]() относительно
биссектрисы
первого и третьего
координатных
углов (то есть
относительно
прямой
относительно
биссектрисы
первого и третьего
координатных
углов (то есть
относительно
прямой
![]() ).
).
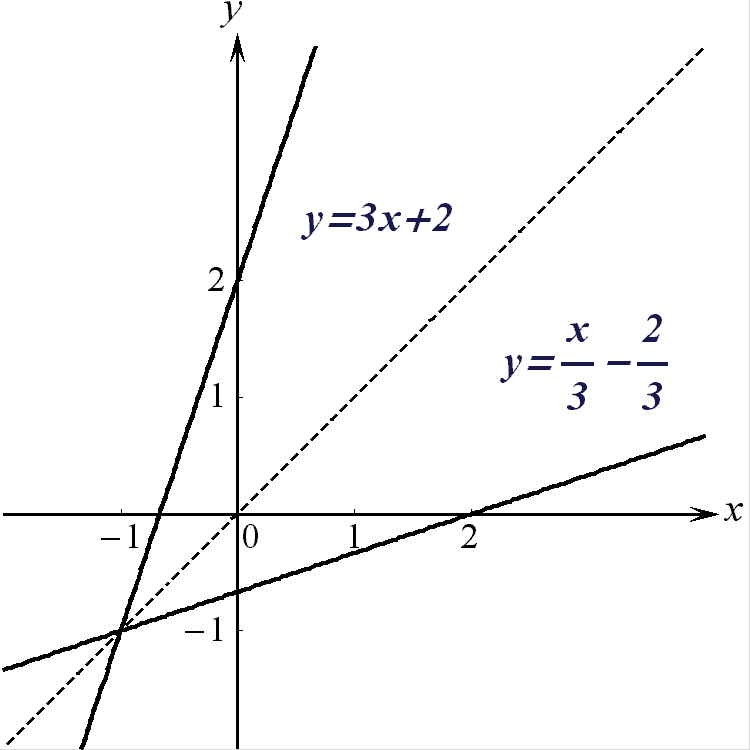
Примеры.
1) Для линейной
функции
![]() обратная функция
также линейна
и имеет вид
обратная функция
также линейна
и имеет вид
![]() .
Меняя местами
.
Меняя местами
![]() и
и
![]() ,
получаем
,
получаем
![]() .
Графики исходной
и обратной
функций приведены
на рис. 10.
.
Графики исходной
и обратной
функций приведены
на рис. 10.
Рис. 10.
2) Для функции
![]() ,
,
![]() ,
множество
значений имеет
вид
,
множество
значений имеет
вид
![]() .
Для каждого
.
Для каждого
![]() уравнение
уравнение
![]() имеет единственное
решение
имеет единственное
решение
![]() .
Поменяв местами
.
Поменяв местами
![]() и
и
![]() ,
получим
,
получим
![]() ,
,
![]() .
Графики функций
приведены на
рис. 11 .
.
Графики функций
приведены на
рис. 11 .
Рис. 11.
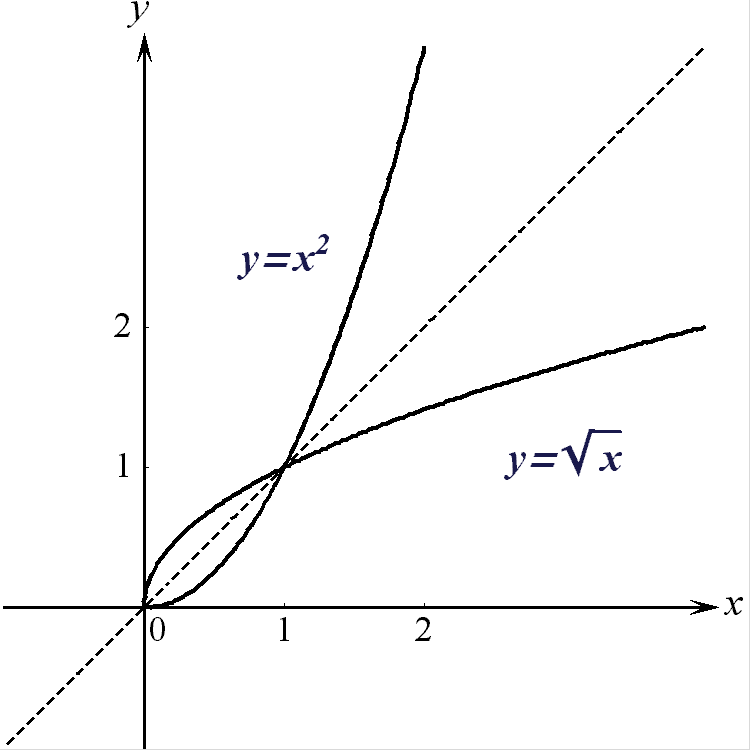
Рис. 11.
3) Обратной к
показательной
функции
![]() является
логарифмическая
функция
является
логарифмическая
функция
![]() .
На рис. 12 представлены
графики функций
.
На рис. 12 представлены
графики функций
![]() и
и
![]() .
.
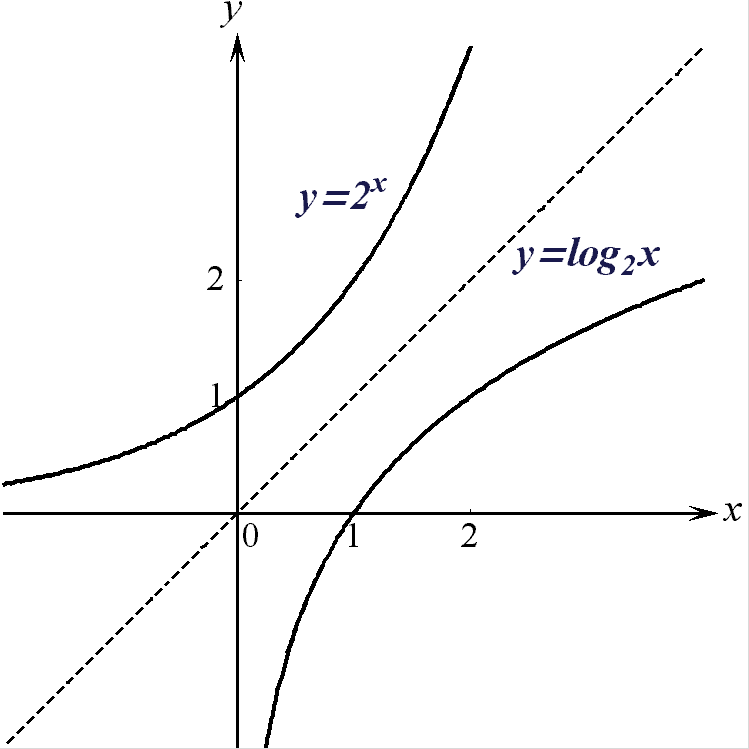
Рис. 12.
Упражнения
1. Найти области определения следующих функций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
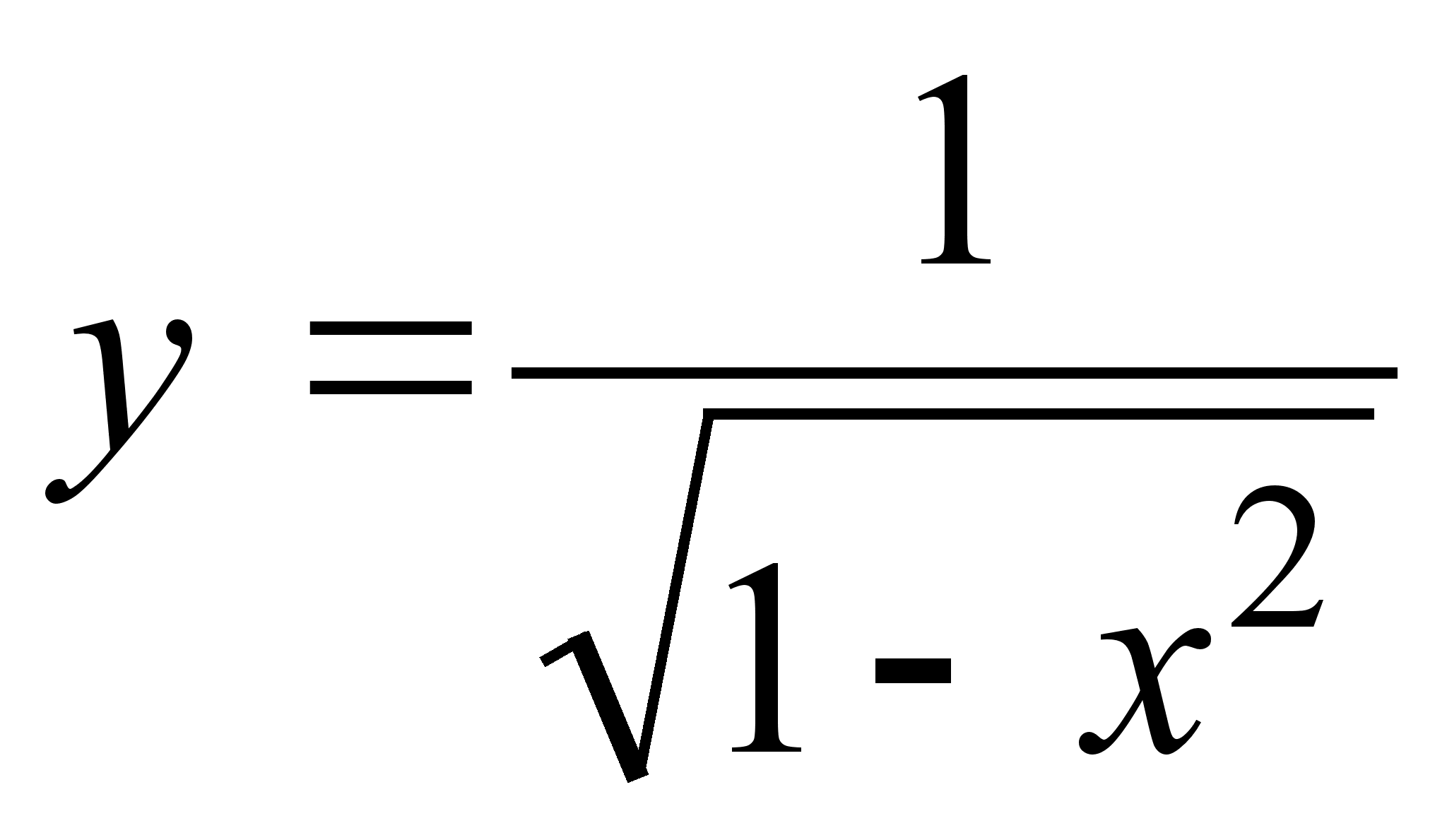 ;
;
18)
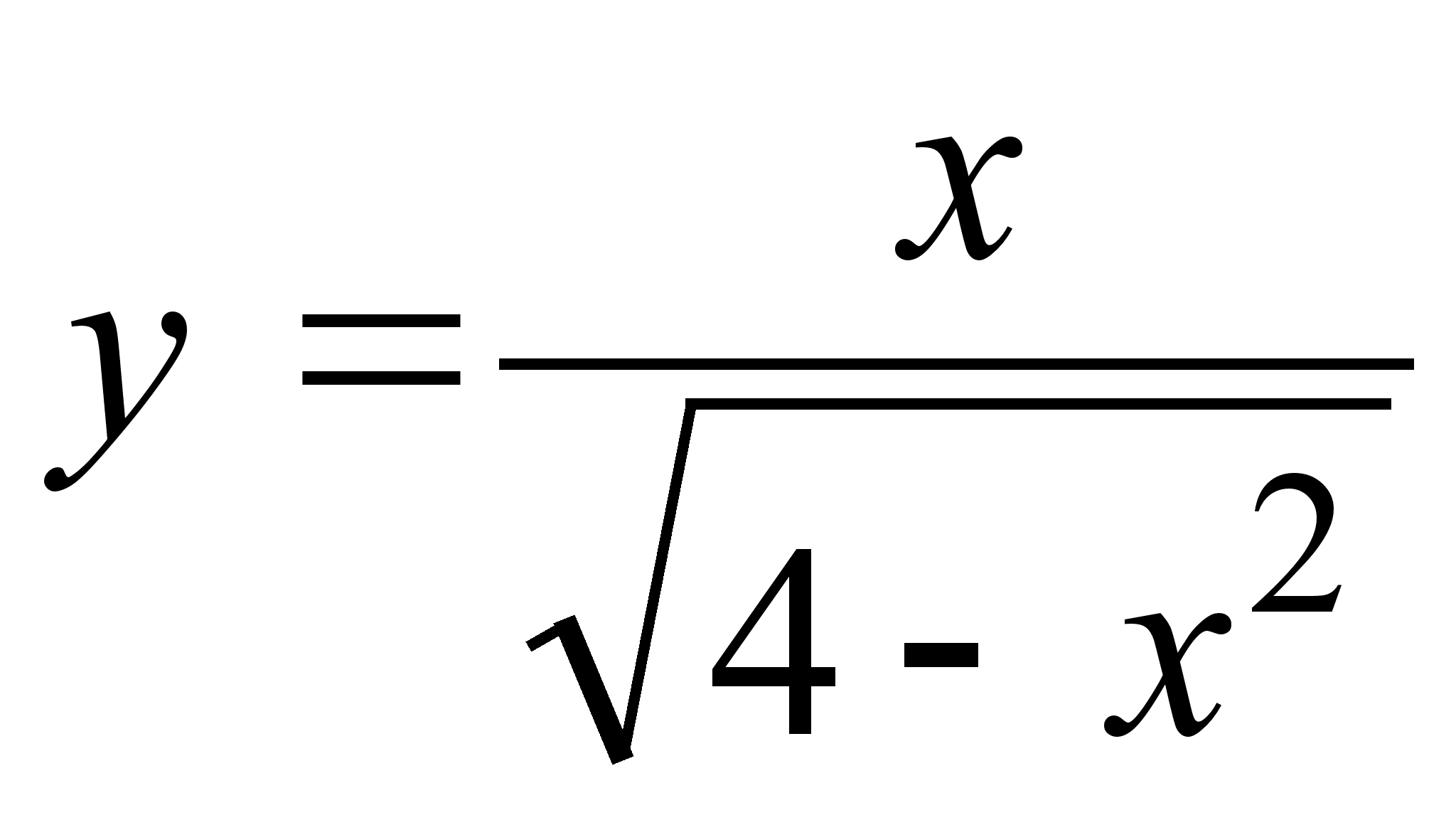 ;
;
19)
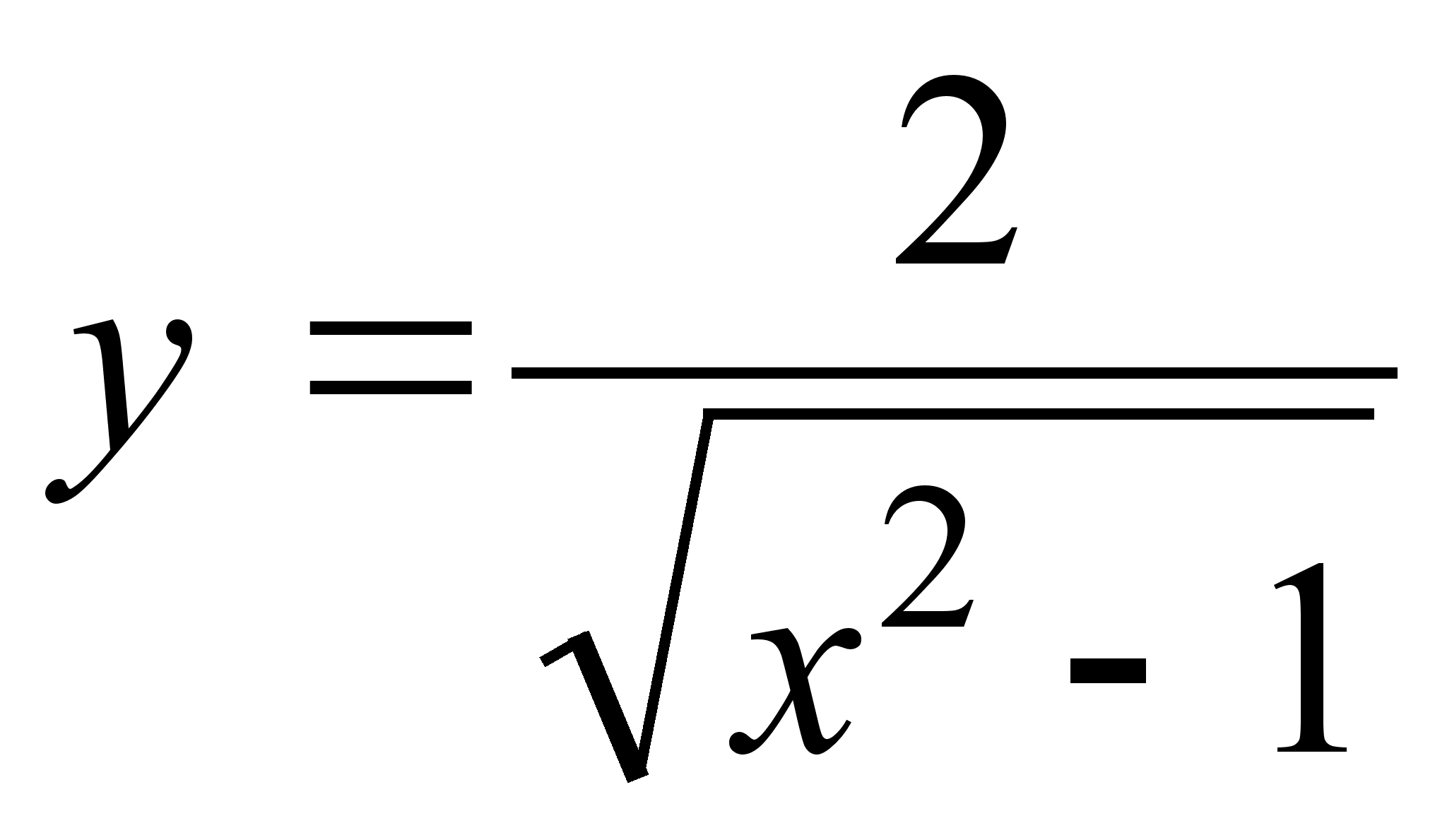 ;
;
20)
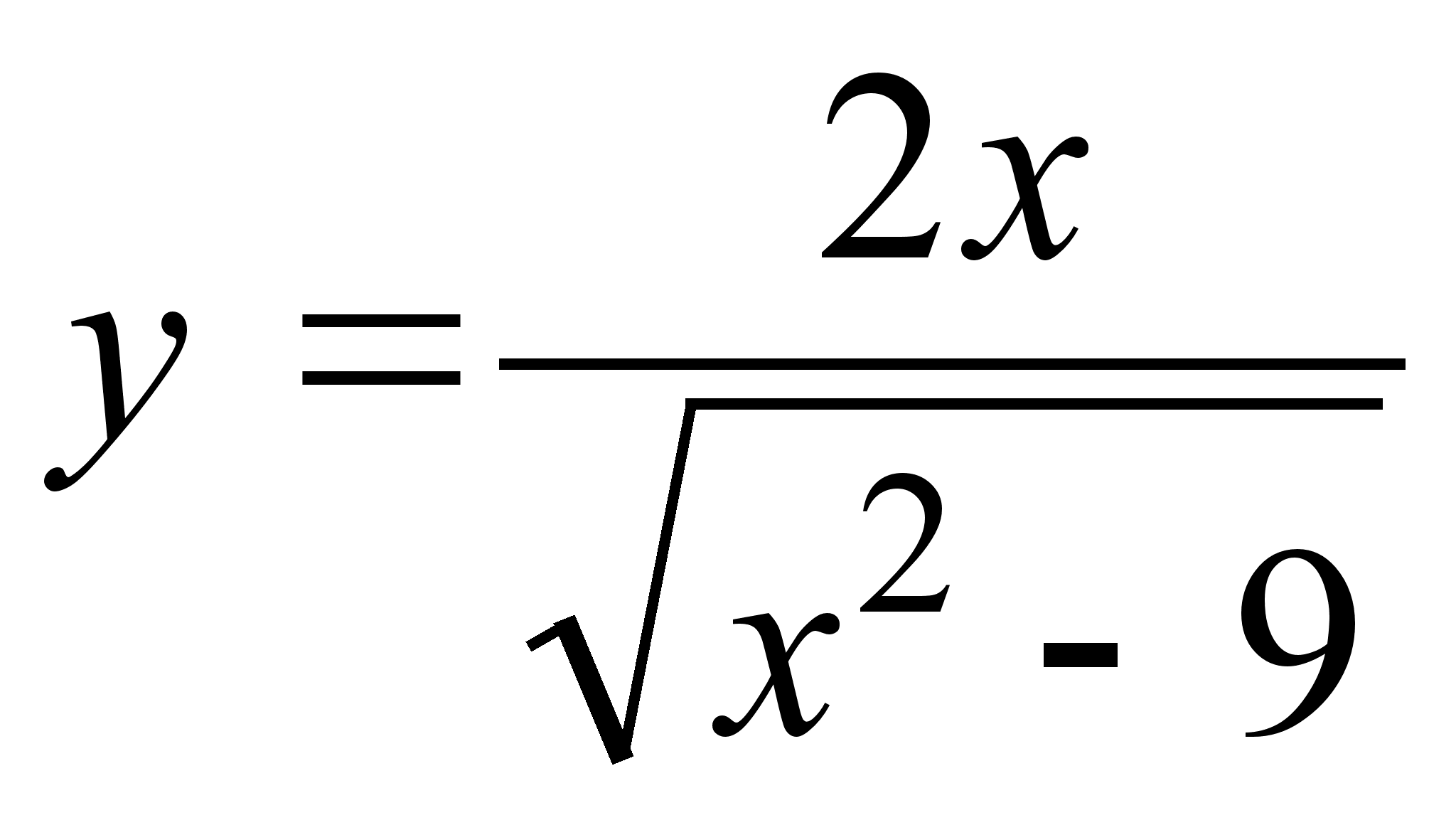 ;
;
21)
![]() ;
;
22)
![]() .
.
2. Построить графики функций:
1)
![]() ,
,
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ,
,
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() .
.
3.
Найти функции
обратные к
функции
![]() ,
указать их
области определения
и построить
графики:
,
указать их
области определения
и построить
графики:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
Ответы
1.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() R;
R;
6)
![]() R;
R;
7)
![]() ;
;
8);
![]()
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() R;
R;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
![]() ;
;
22)![]() .
.
.
3.
1)
![]() ,
,
![]() R;
R;
2)
![]() ,
,
![]() R;
R;
3)![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ;
;
6)
![]() ,
,
![]() ;
;
7)
![]() ,
,
![]() ;
;
8)
![]() ;
;
9)
![]() ,
,
![]() ;
;
10)
![]() ,
,
![]() R.
R.
§ 2. Предел и непрерывность функции
Пределом функции в точке называется число, к которому приближаются значения функции при приближении аргумента к этой точке. Строгое определение предела дается сначала для функций частного вида – последовательностей, а затем переносится на функции общего вида. На основе понятия предела определяются важнейшие понятия математического анализа – производная и интеграл.
- Предел последовательности
Последовательностью
называется
функция, определенная
на множестве
натуральных
чисел N =
![]() .
Значения этой
функции
.
Значения этой
функции
![]() ,
,
![]() N,
называются
элементами
или членами
последовательности,
число
N,
называются
элементами
или членами
последовательности,
число
![]() называется
номером элемента
называется
номером элемента
![]() .
Для последовательностей
используется
обозначение
.
Для последовательностей
используется
обозначение
![]() или более наглядная
запись
или более наглядная
запись
![]() .
Задать последовательность
можно с помощью
формулы, связывающей
.
Задать последовательность
можно с помощью
формулы, связывающей
![]() и
и
![]() .
.
Приведем примеры последовательностей, указав их различные представления:
а)
![]() ,
или
,
или
![]() ,
или
,
или
![]() ;
;
б)
![]() ,
или
,
или
![]() ,
или
,
или
![]() ;
;
в)
![]() ,
или
,
или
![]() ,
или
,
или
![]() .
.
Заметим,
что элементы
этих последовательностей
ведут себя
по-разному с
увеличением
номера
![]() :
в первом случае
убывают, приближаясь
к нулю; во втором
случае неограниченно
возрастают;
в третьем случае
не приближаются
ни к какому
определенному
числу, принимая
поочередно
значения
:
в первом случае
убывают, приближаясь
к нулю; во втором
случае неограниченно
возрастают;
в третьем случае
не приближаются
ни к какому
определенному
числу, принимая
поочередно
значения
![]() и
и
![]() .
Для описания
поведения
элементов
последовательности
при неограниченном
увеличении
n вводится
понятие предела.
.
Для описания
поведения
элементов
последовательности
при неограниченном
увеличении
n вводится
понятие предела.
Число а называется
пределом
последовательности
![]() ,
если для любого
положительного
числа
,
если для любого
положительного
числа
![]() существует
такой номер
существует
такой номер
![]() ,
что для всех
,
что для всех
![]() выполняется
неравенство
выполняется
неравенство
![]() (то есть
(то есть
![]() отличается
от
отличается
от
![]() менее, чем на
менее, чем на
![]() ).
).
Если предел
существует,
то говорят, что
последовательность
сходится, и
пишут
![]() (читается: “предел
(читается: “предел
![]() равен
равен
![]() ”)
или
”)
или
![]() при
при
![]() (“
(“![]() стремится к
стремится к
![]() при
при
![]() ,
стремящемся
к бесконечности”).
В противном
случае говорят,
что последовательность
расходится.
,
стремящемся
к бесконечности”).
В противном
случае говорят,
что последовательность
расходится.
Примеры. а)
Последовательность
![]() сходится,
ее предел равен
нулю:
сходится,
ее предел равен
нулю:
![]() .
Это непосредственно
следует из
определения
предела, поскольку
при любом
.
Это непосредственно
следует из
определения
предела, поскольку
при любом
![]() неравенство
неравенство
![]() выполняется
для всех
выполняется
для всех
![]() ,
и в качестве
,
и в качестве
![]() можно взять
любое натуральное
число, большее
можно взять
любое натуральное
число, большее
![]() .
.
б) Аналогично доказывается более общее утверждение:
![]() при любом
при любом
![]() .
.
Например,
![]() ,
,
![]() и т. д.
и т. д.
- Правила вычисления пределов последовательностей
При вычислении пределов последовательностей используются следующие правила:
I. Если
последовательности
![]() и
и
![]() сходятся, то
сходятся их
сумма, разность
и произведение,
причем:
сходятся, то
сходятся их
сумма, разность
и произведение,
причем:
1)
![]() ,
,
2)
![]() ,
,
3)
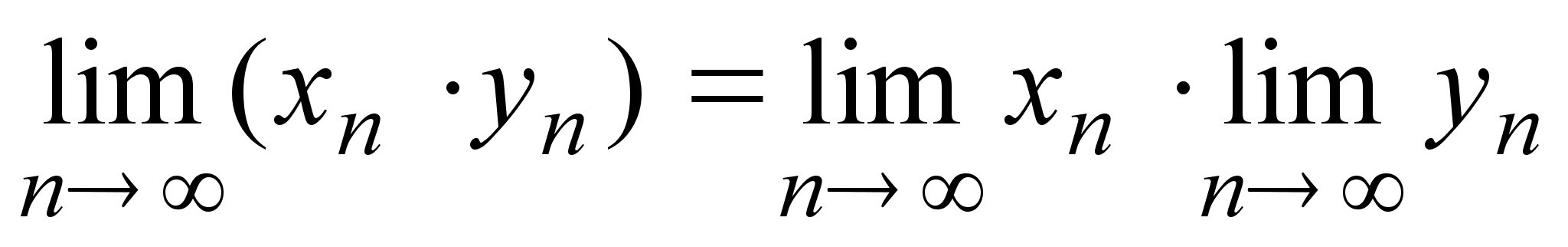 ;
;
если
![]() и
и
![]() ,
то сходится
также и частное:
,
то сходится
также и частное:
4)
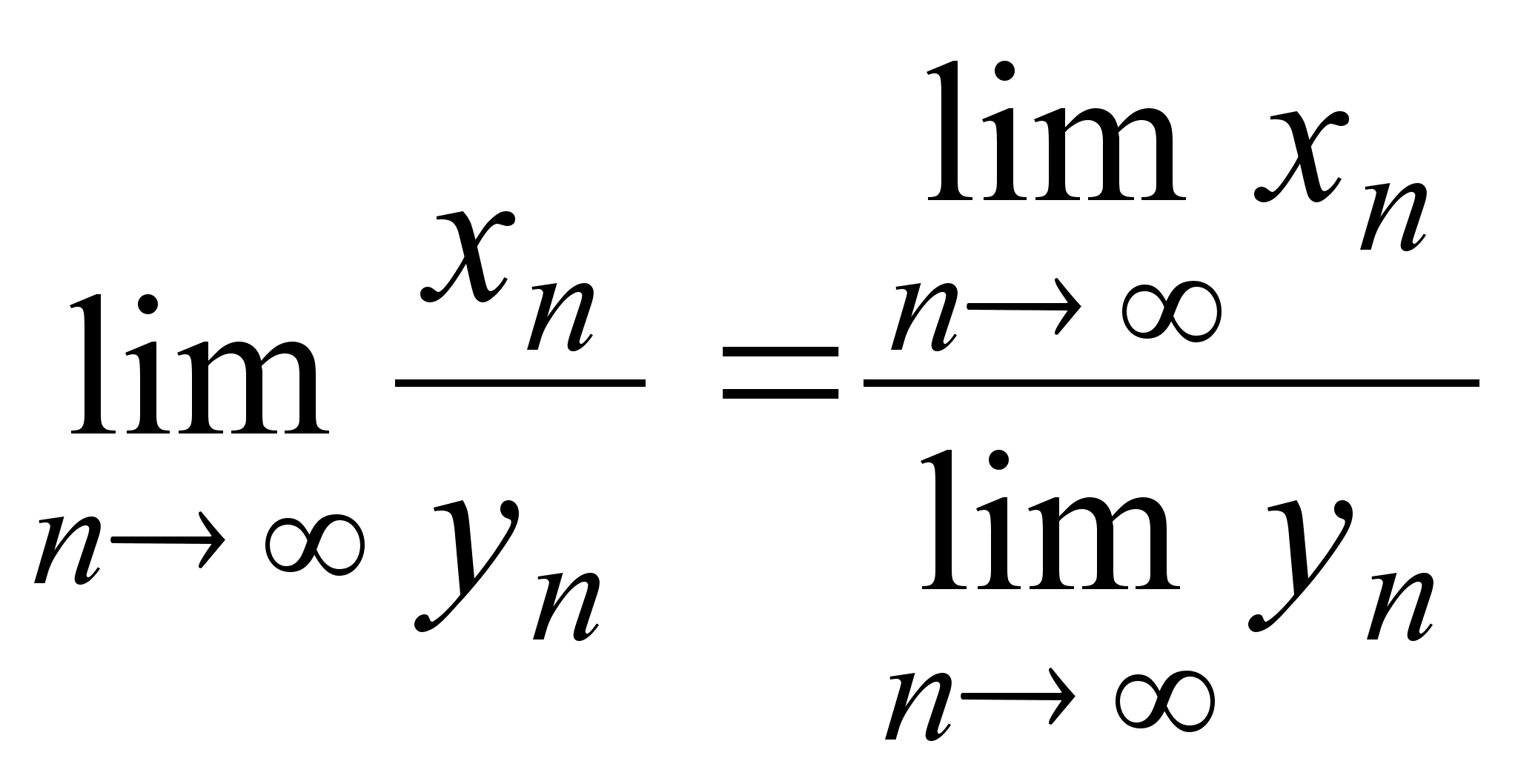 .
.
II. Предел
последовательности
![]() ,
где
,
где
![]() - постоянная,
равен этой
постоянной:
- постоянная,
равен этой
постоянной:
![]() .
.
III. Постоянный множитель можно выносить за знак предела:
![]()
(следствие правил I.3 и II).
Применению указанных правил часто предшествуют некоторые предварительные преобразования выражения, стоящего под знаком предела.
Примеры. а)
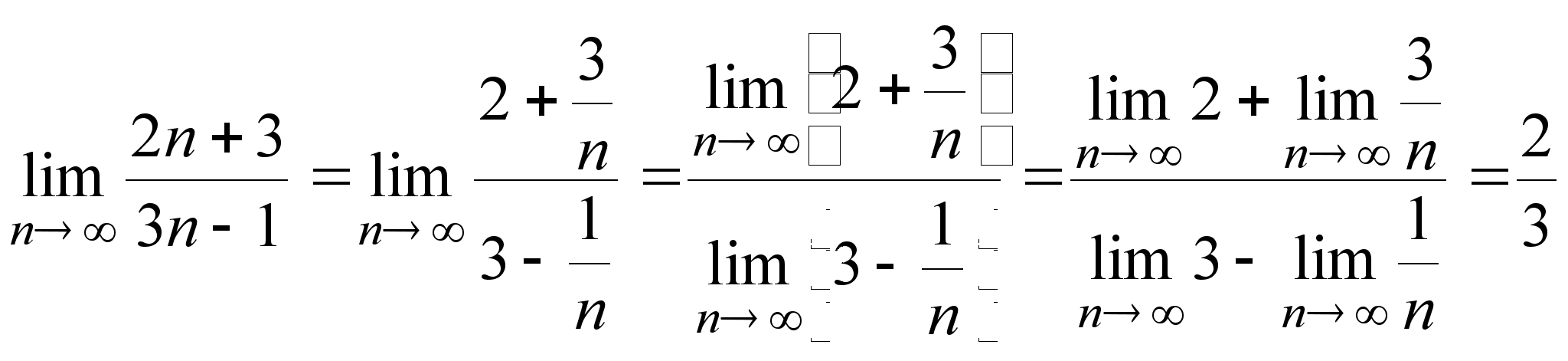 ;
;
б)
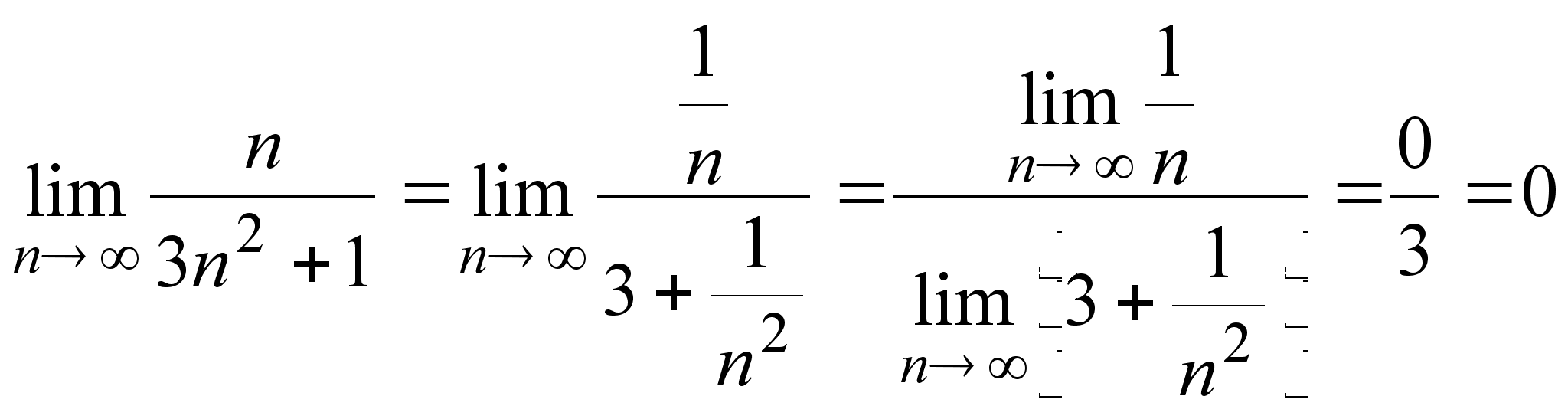 .
.
- Бесконечно малые и бесконечно большие последовательности
Последовательность
![]() называется
бесконечно
малой, если
называется
бесконечно
малой, если
![]() .
Это означает,
что для любого
.
Это означает,
что для любого
![]() найдется номер
найдется номер
![]() такой, что для
всех
такой, что для
всех
![]() выполняется
неравенство
выполняется
неравенство
![]() .
.
Последовательность
![]() называется
бесконечно
большой, если
для любого
числа
называется
бесконечно
большой, если
для любого
числа
![]() найдется такой
номер
найдется такой
номер
![]() ,
что для всех
,
что для всех
![]() справедливо
неравенство
справедливо
неравенство
![]() .
В этом случае
пишут
.
В этом случае
пишут
![]() (читается: “предел
(читается: “предел
![]() равен бесконечности”)
или
равен бесконечности”)
или
![]() при
при
![]() (“
(“![]() стремится к
бесконечности
при
стремится к
бесконечности
при
![]() ,
стремящемся
к бесконечности”).
Если при этом
все элементы
,
стремящемся
к бесконечности”).
Если при этом
все элементы
![]() положительны,
начиная с некоторого
номера, то пишут
положительны,
начиная с некоторого
номера, то пишут
![]() (“предел
(“предел
![]() равен плюс
бесконечности”),
а если отрицательны
- используют
запись
равен плюс
бесконечности”),
а если отрицательны
- используют
запись
![]() (“предел
(“предел
![]() равен минус
бесконечности”).
равен минус
бесконечности”).
Заметим, что
если
![]() ,
то
,
то
![]() (при
(при
![]() ),
то есть последовательность,
обратная к
бесконечно
большой, является
бесконечно
малой. Аналогично,
если
),
то есть последовательность,
обратная к
бесконечно
большой, является
бесконечно
малой. Аналогично,
если
![]() ,
то
,
то
![]() (при
(при
![]() ),
– последовательность,
обратная к
бесконечно
малой, является
бесконечно
большой.
),
– последовательность,
обратная к
бесконечно
малой, является
бесконечно
большой.
Справедливы также следующие утверждения:
сумма и произведение двух бесконечно малых последовательностей являются бесконечно малыми последовательностями;
произведение двух бесконечно больших последовательностей является бесконечно большой последовательностью;
если
оба предела
![]() и
и
![]() равны
равны
![]() (или
(или
![]() ),
то
),
то
![]() (соответственно
(соответственно
![]() ).
).
Примеры. а) Последовательности
![]() ,
,
![]() ,
,
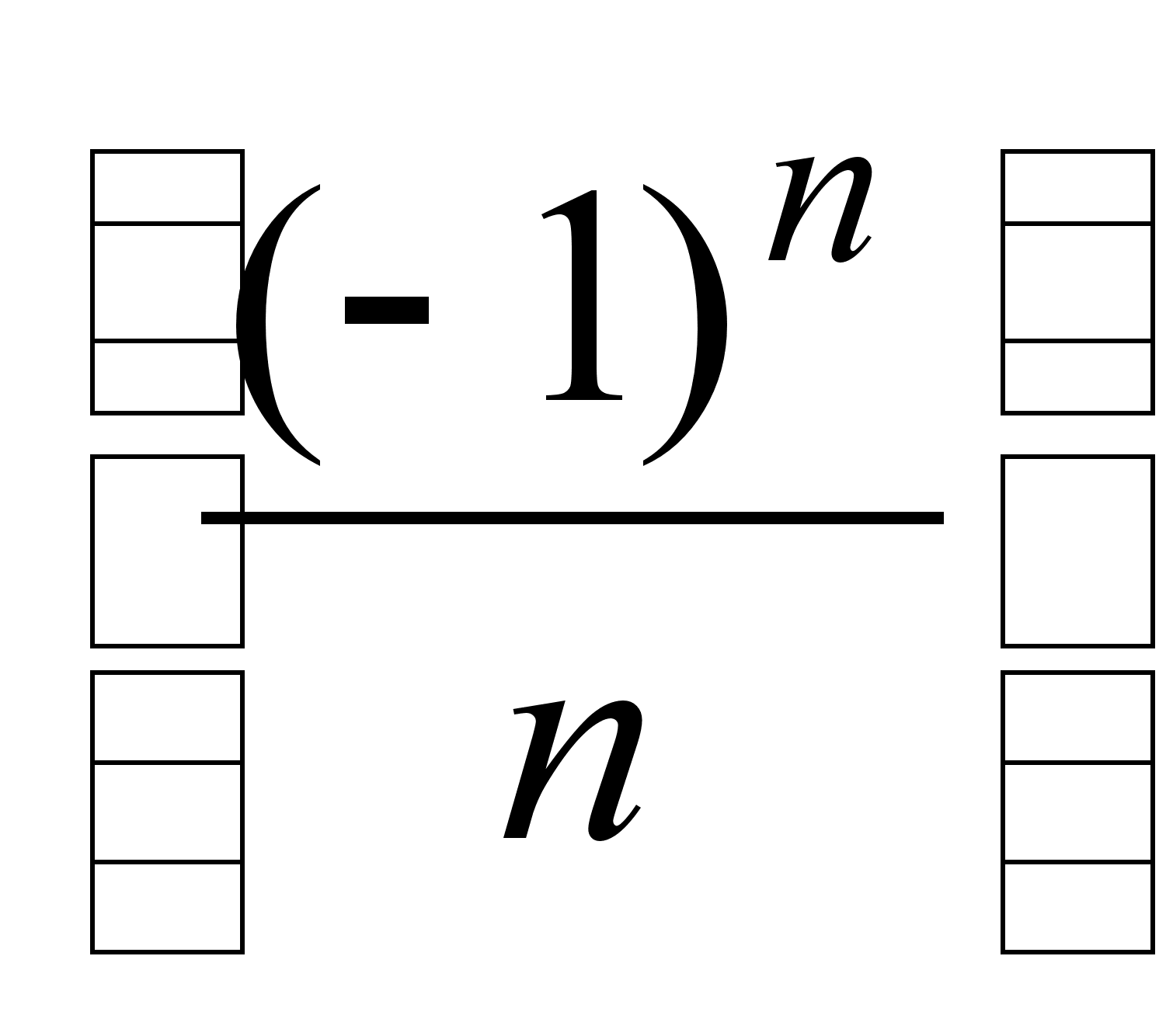 ,
,
![]() при
при
![]() ,
,
![]()
являются бесконечно малыми, а обратные к ним последовательности
{![]() },
{
},
{![]() },
{
},
{![]() },
{
},
{![]() }
при
}
при
![]() ,
{
,
{![]() }
}
– бесконечно большими.
б) Последовательности
![]() и
и
![]() бесконечно
большие, поэтому
их сумма
бесконечно
большие, поэтому
их сумма
![]() – также бесконечно
большая. Отсюда
следует, что
– также бесконечно
большая. Отсюда
следует, что
![]() – бесконечно
малая последовательность,
поскольку
– бесконечно
малая последовательность,
поскольку
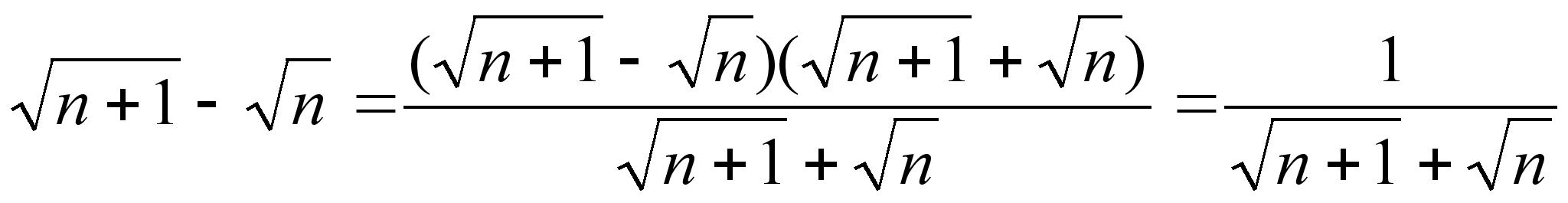 .
.
- Число e
Рассмотрим
последовательность
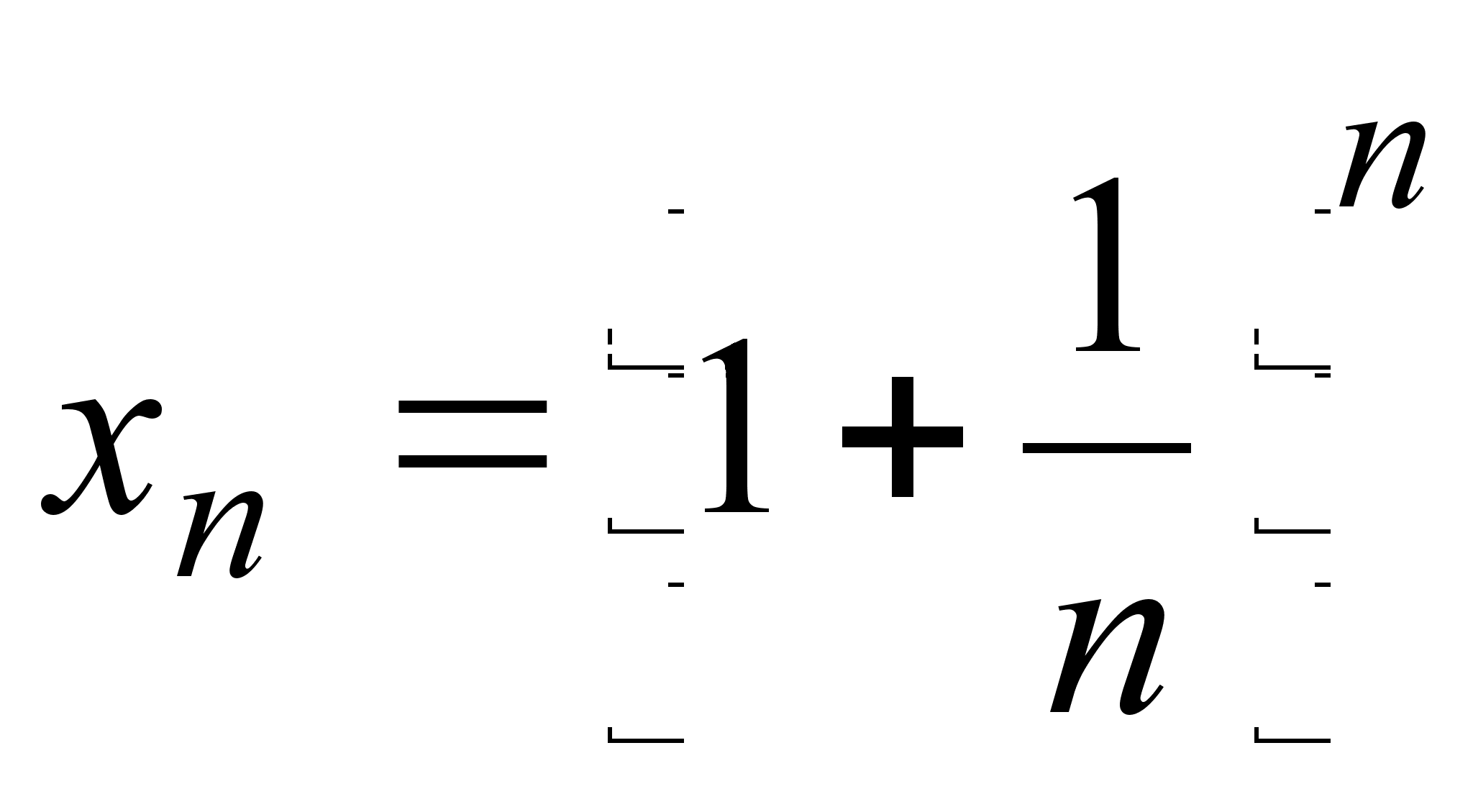 .
Можно показать,
что эта последовательность
сходится; ее
предел обозначается
буквой
.
Можно показать,
что эта последовательность
сходится; ее
предел обозначается
буквой
![]() :
:
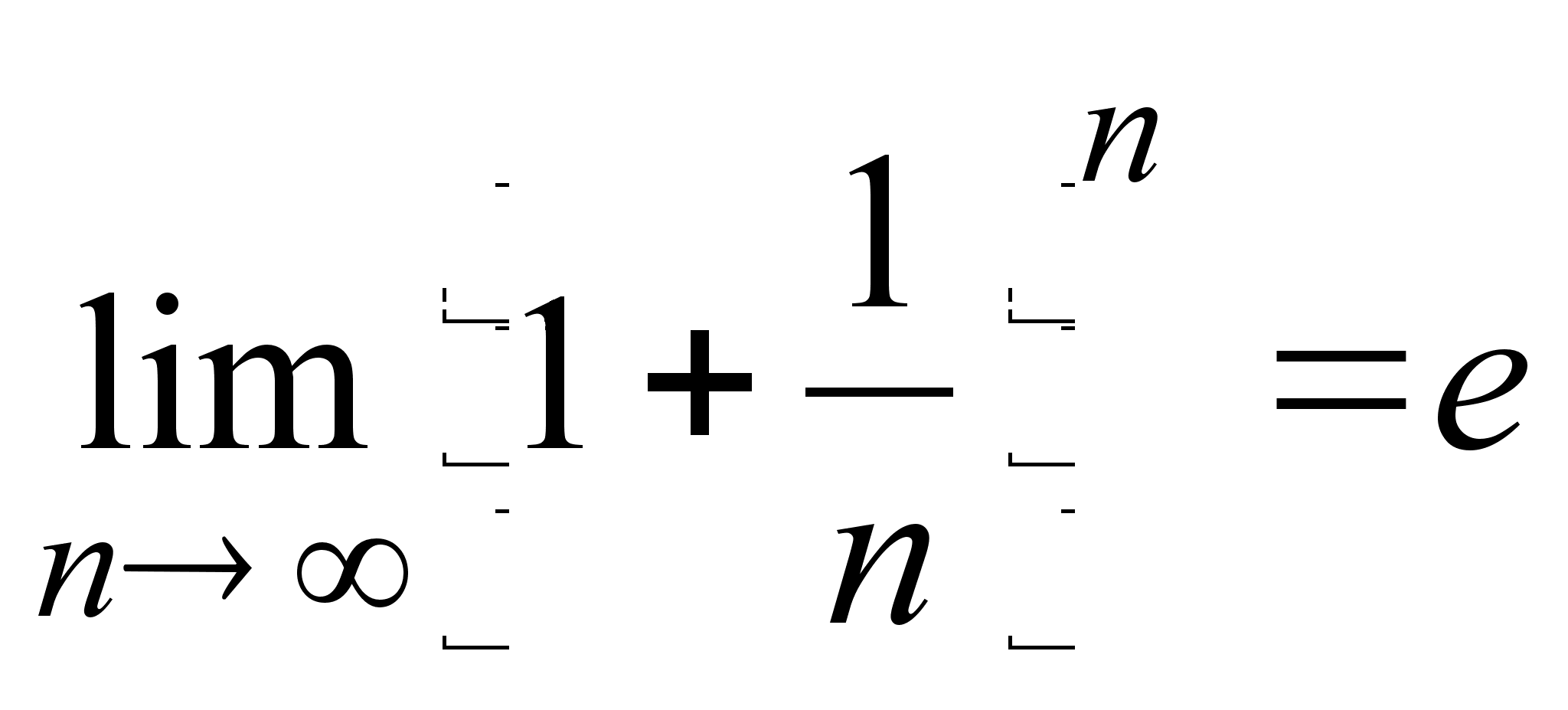 .
.
Число
![]() играет важную
роль в математике
(служит основанием
натуральных
логарифмов);
оно не является
рациональным
и приближенно
равно
играет важную
роль в математике
(служит основанием
натуральных
логарифмов);
оно не является
рациональным
и приближенно
равно
![]() .
.
Исходя
из определения
числа
![]() ,
можно получить
более общую
формулу:
,
можно получить
более общую
формулу:
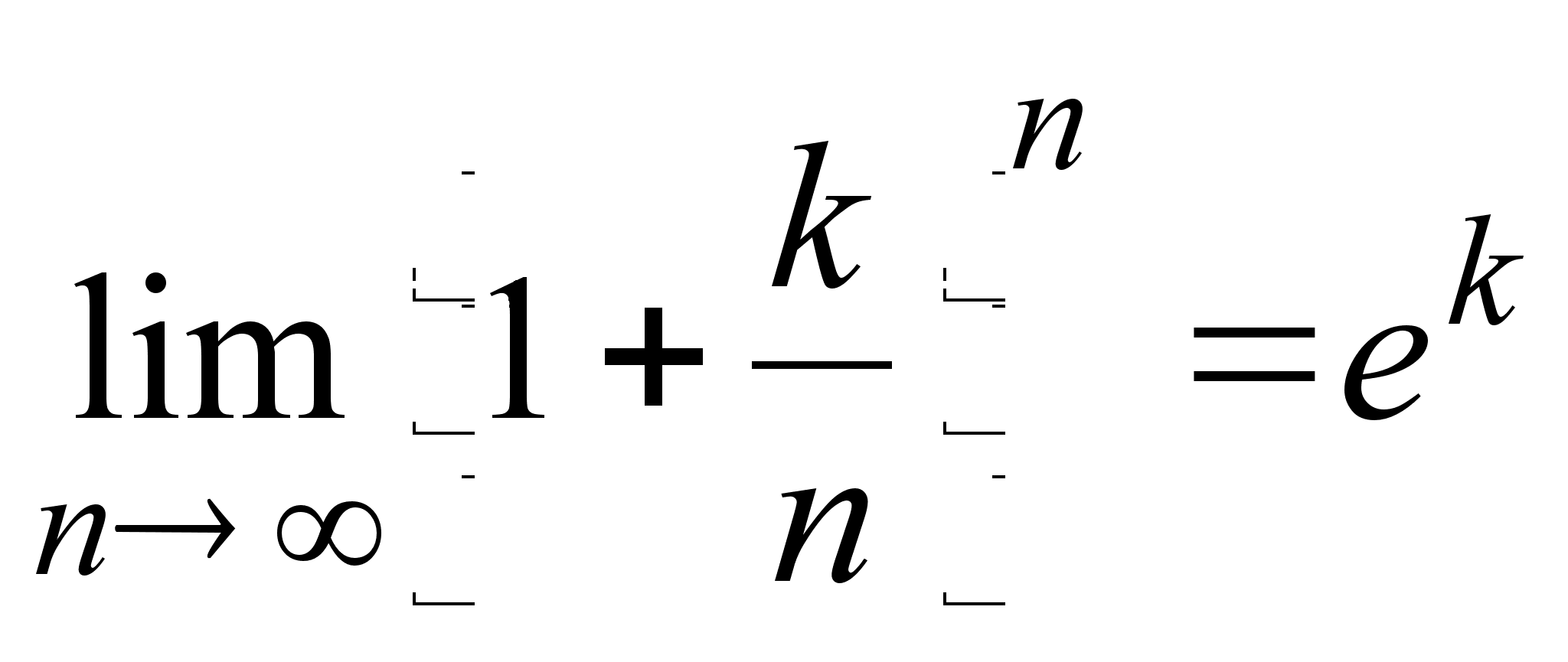 ,
,
справедливую
для любой постоянной
![]() .
.
Приведем пример
экономической
задачи, в которой
возникает число
![]() .
Предположим,
что в банк помещена
сумма
.
Предположим,
что в банк помещена
сумма
![]() под
под
![]() годовых. Тогда
через год сумма
вклада составит
годовых. Тогда
через год сумма
вклада составит
![]()
![]() ,
,
где
введено обозначение
![]() .
.
Предположим,
что вклад можно
снять по истечении
любого срока
в течение года,
и начисление
на вклад пропорционально
этому сроку,
т.е. за полгода
будет начислено
![]() ,
за месяц -
,
за месяц -
![]() ,
за один день
-
,
за один день
-
![]() .
Тогда к концу
года можно
получить доход
больший, чем
.
Тогда к концу
года можно
получить доход
больший, чем
![]() ,
действуя следующим
образом. Если,
например, в
середине года
закрыть счет
и полученную
сумму
,
действуя следующим
образом. Если,
например, в
середине года
закрыть счет
и полученную
сумму
![]() снова положить
в банк на оставшиеся
полгода, то в
конце года
сумма вклада
составит
снова положить
в банк на оставшиеся
полгода, то в
конце года
сумма вклада
составит
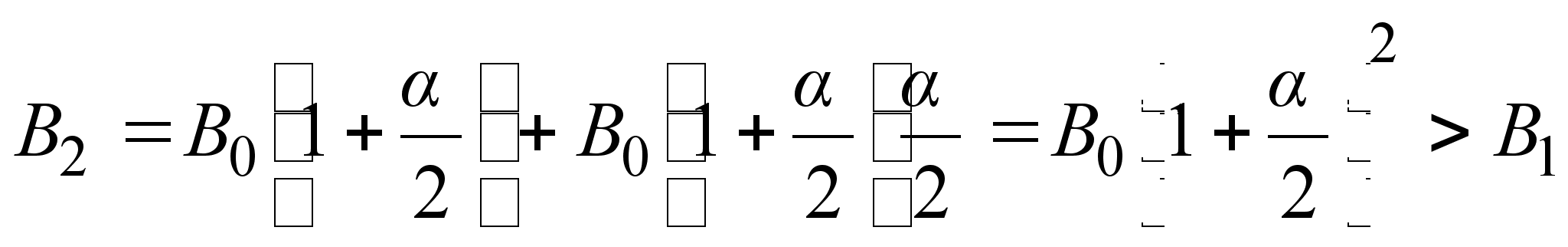 .
.
Если
повторять
операцию
закрытия-открытия
счета чаще,
например, каждый
месяц, то к концу
года будем
иметь
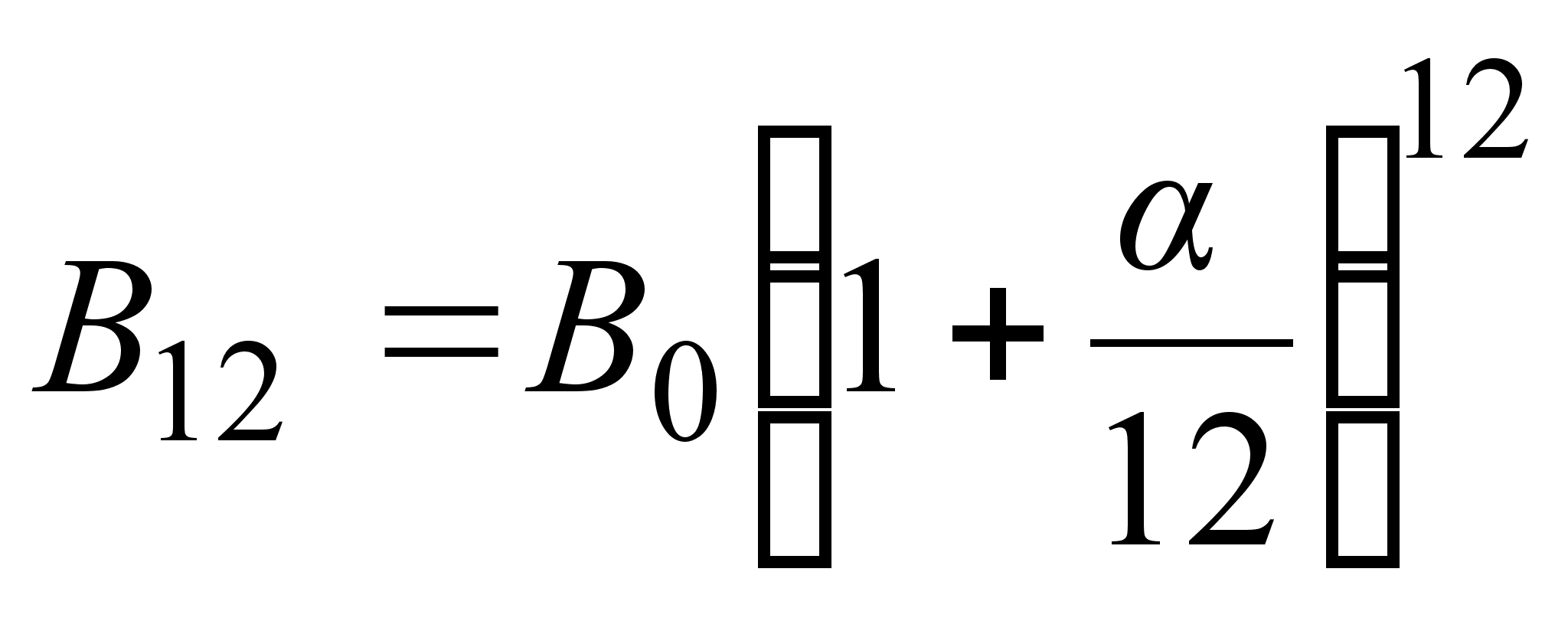 ,
а если каждый
день, то
,
а если каждый
день, то
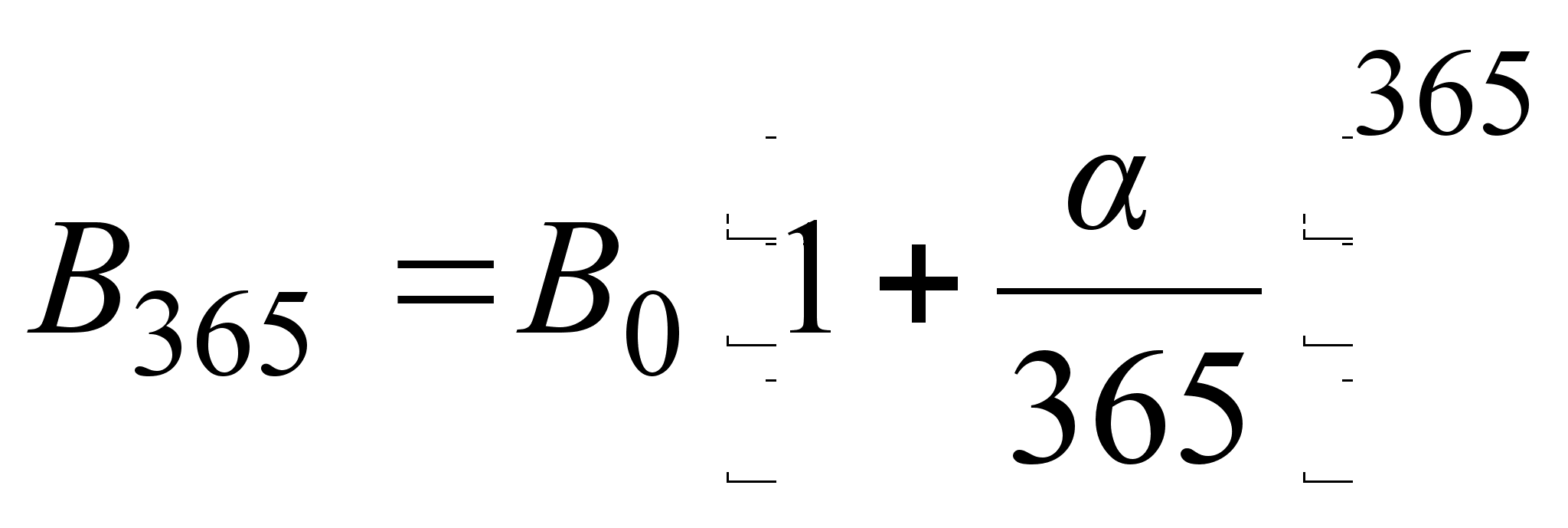 .
Если предположить,
что операция
закрытия-открытия
счета производится
.
Если предположить,
что операция
закрытия-открытия
счета производится
![]() раз в году через
равные промежутки
времени, то в
конце года
сумма вклада
составит
раз в году через
равные промежутки
времени, то в
конце года
сумма вклада
составит
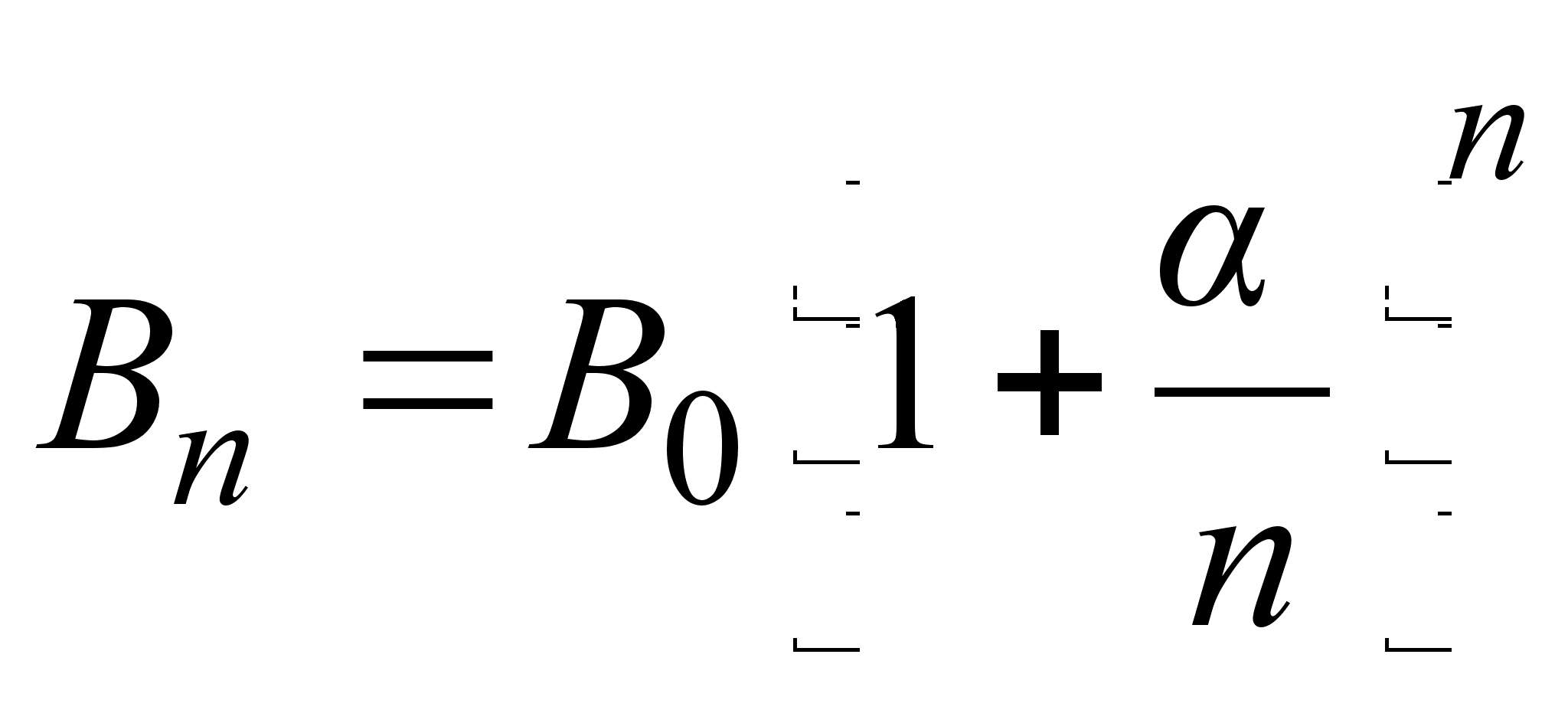 ,
а если представить,
что проценты
начисляются
непрерывно
(число операций
закрытия-открытия
счета неограниченно
растет), то
,
а если представить,
что проценты
начисляются
непрерывно
(число операций
закрытия-открытия
счета неограниченно
растет), то
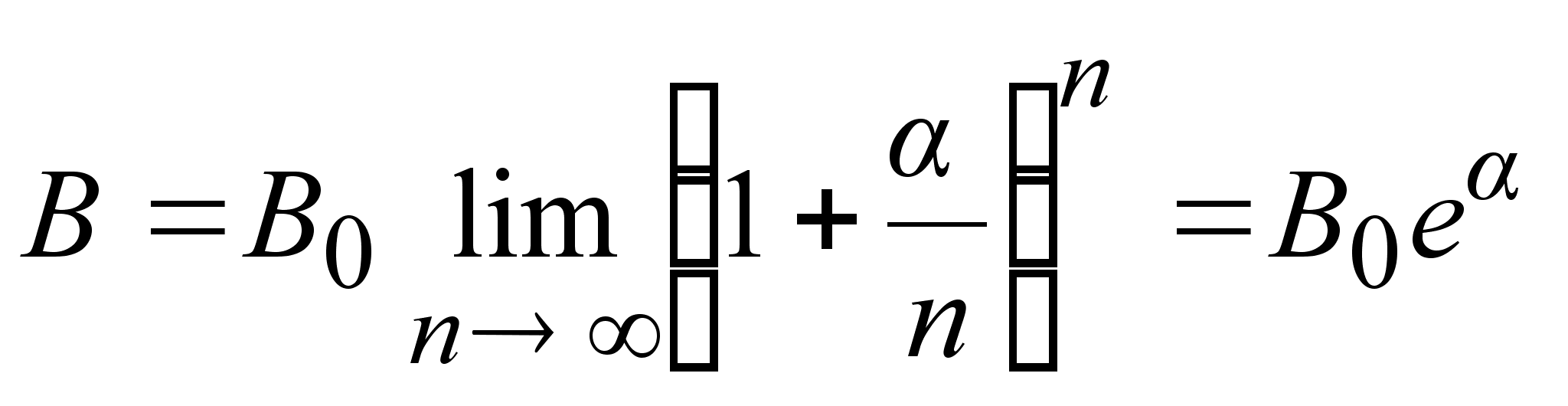 .
.
Таким образом,
максимальное
число процентов,
на которое
гипотетически
может увеличиться
вклад при данной
схеме начисления,
составляет
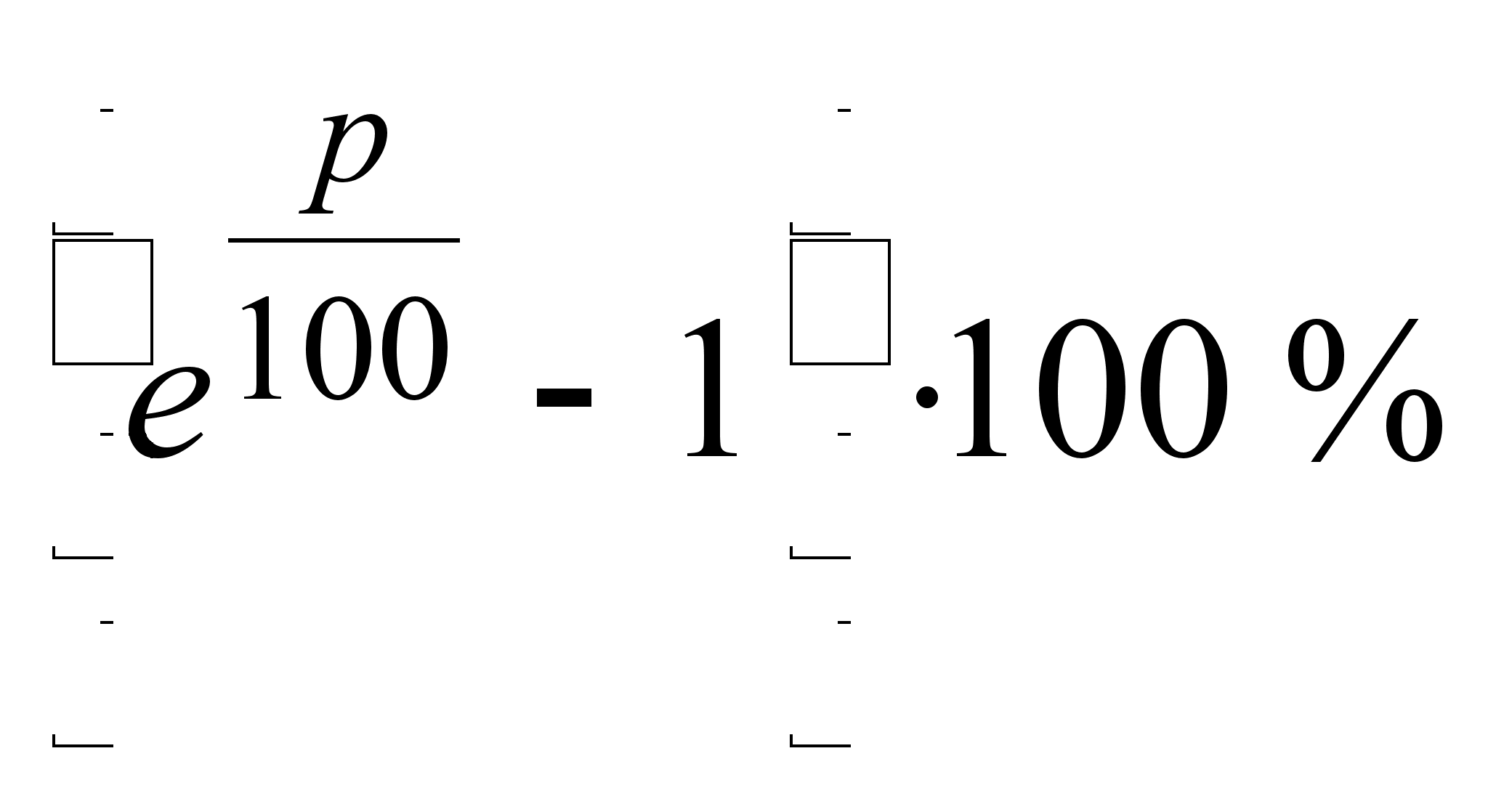 .
Например, при
номинальной
ставке 100 % (
.
Например, при
номинальной
ставке 100 % (![]() максимальная
эффективная
ставка составит
максимальная
эффективная
ставка составит
![]() .
.
- Предел функции
Пусть функция
![]() определена
на некотором
интервале
определена
на некотором
интервале
![]() ,
содержащем
точку
,
содержащем
точку
![]() ,
за исключением
быть может
самой этой
точки. В дальнейшем
любой интервал,
содержащий
некоторую точку
,
за исключением
быть может
самой этой
точки. В дальнейшем
любой интервал,
содержащий
некоторую точку
![]() ,
будем называть
окрестностью
данной точки.
,
будем называть
окрестностью
данной точки.
Число
![]() называется
пределом функции
называется
пределом функции
![]() в точке
в точке
![]() ,
если для любой
последовательности
,
если для любой
последовательности
![]() ,
,
![]() ,
сходящейся
к
,
сходящейся
к
![]() ,
последовательность
значений функции
,
последовательность
значений функции
![]() сходится к
сходится к
![]() .
Обозначения:
.
Обозначения:
![]() или
или
![]() при
при
![]() .
.
При вычислении
пределов функций
используются
те же правила,
что и при вычислении
пределов
последовательностей.
В частности,
если существуют
пределы
![]() и
и
![]() ,
то
,
то
![]() ;
;
![]() ;
;
![]() ;
;
если, кроме
того,
![]() (тогда
(тогда
![]() для всех
для всех
![]() ,
достаточно
близких к
,
достаточно
близких к
![]() ),
то
),
то
![]() .
.
Примеры.
а) Найдем предел
функции
![]() в точке
в точке
![]() .
Для произвольной
последовательности
.
Для произвольной
последовательности
![]() такой, что
такой, что
![]() ,
,
![]() ,
на основании
свойств пределов
последовательностей
имеем
,
на основании
свойств пределов
последовательностей
имеем
![]() .
.
Отсюда по определению предела функции получаем
![]() .
.
б) Найдем предел
функции
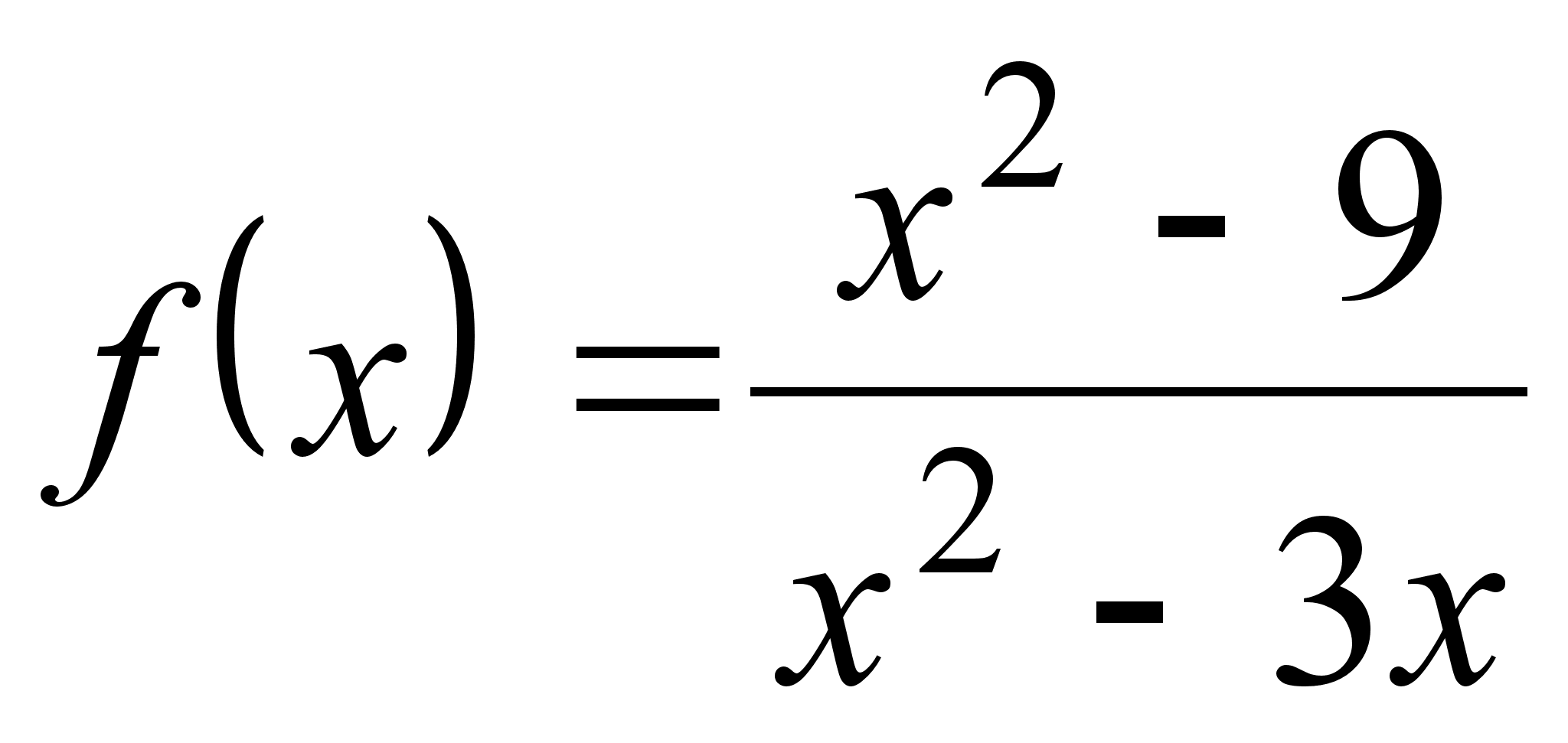 в точке
в точке
![]() ,
в которой функция
не определена.
Для произвольной
последовательности
,
в которой функция
не определена.
Для произвольной
последовательности
![]() такой, что
такой, что
![]() ,
,
![]() ,
имеем
,
имеем
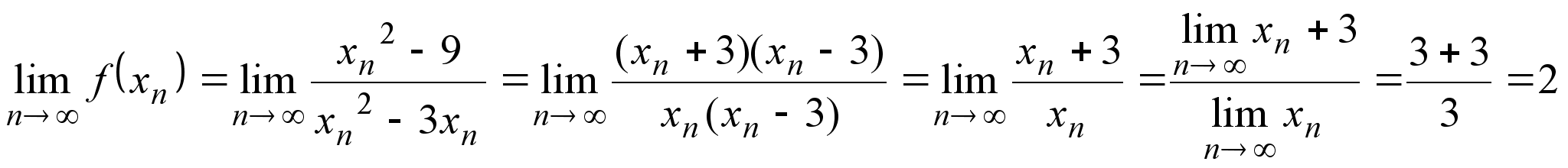 .
.
Отсюда получаем
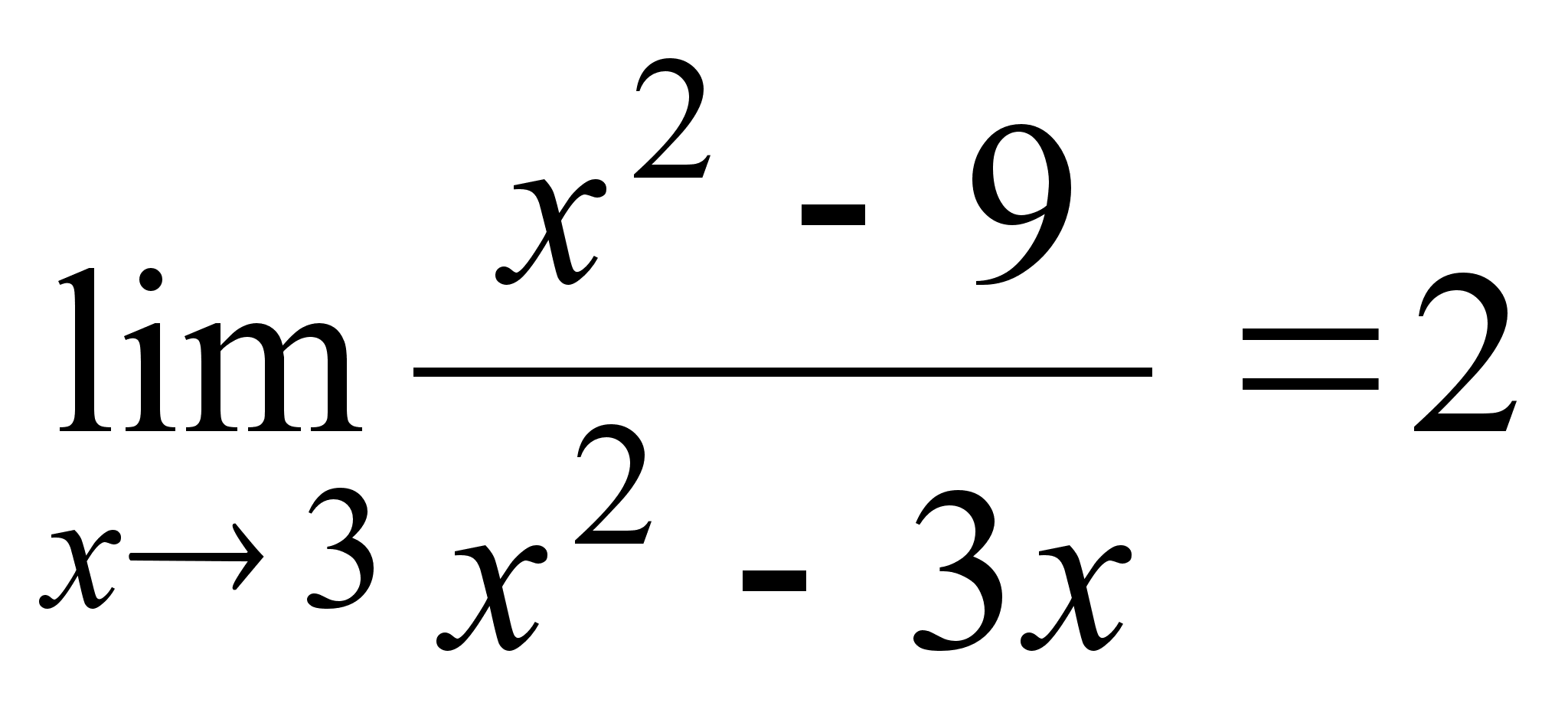 .
.
- Пределы в бесконечности. Бесконечные пределы
Данное
выше определение
предела функции
можно распространить
на случаи, когда
![]() или
или
![]() (по отдельности
или вместе)
являются не
числами, а символами
(по отдельности
или вместе)
являются не
числами, а символами
![]() ,
,
![]() или
или
![]() .
Так, например,
запись
.
Так, например,
запись
![]() ,
,
где
![]() - число, означает,
что для любой
бесконечно
большой последовательности
- число, означает,
что для любой
бесконечно
большой последовательности
![]() ,
стремящейся
к
,
стремящейся
к
![]() ,
последовательность
,
последовательность
![]() сходится к
сходится к
![]() .
Аналогично,
запись
.
Аналогично,
запись
![]() ,
,
означает,
что для любой
последовательности
![]() ,
стремящейся
к
,
стремящейся
к
![]() ,
последовательность
,
последовательность
![]() стремится к
стремится к
![]() .
.
Примеры.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
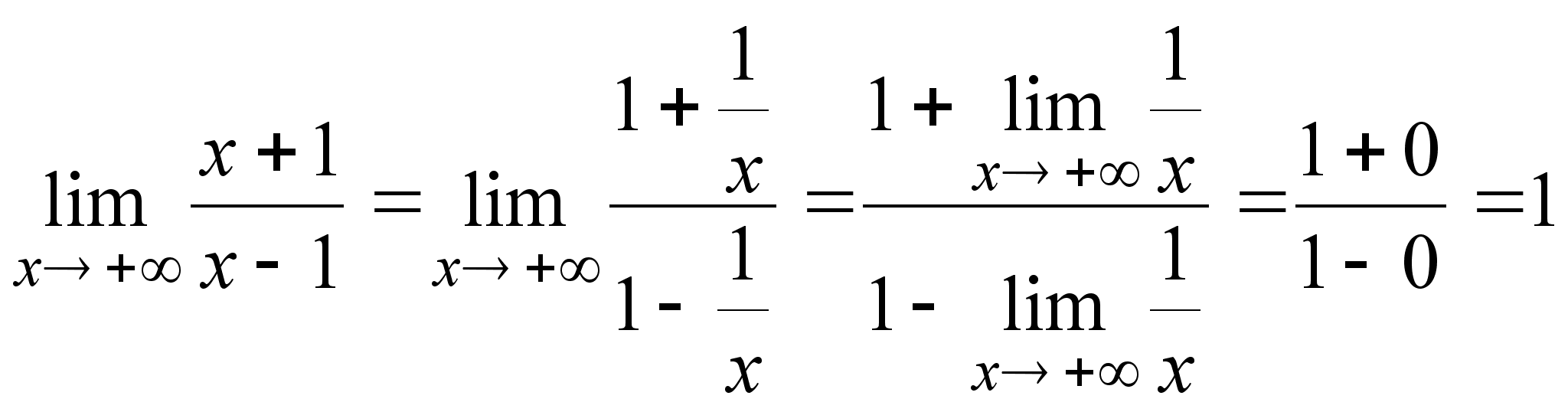 .
.
В качестве более сложного примера приведем равенство
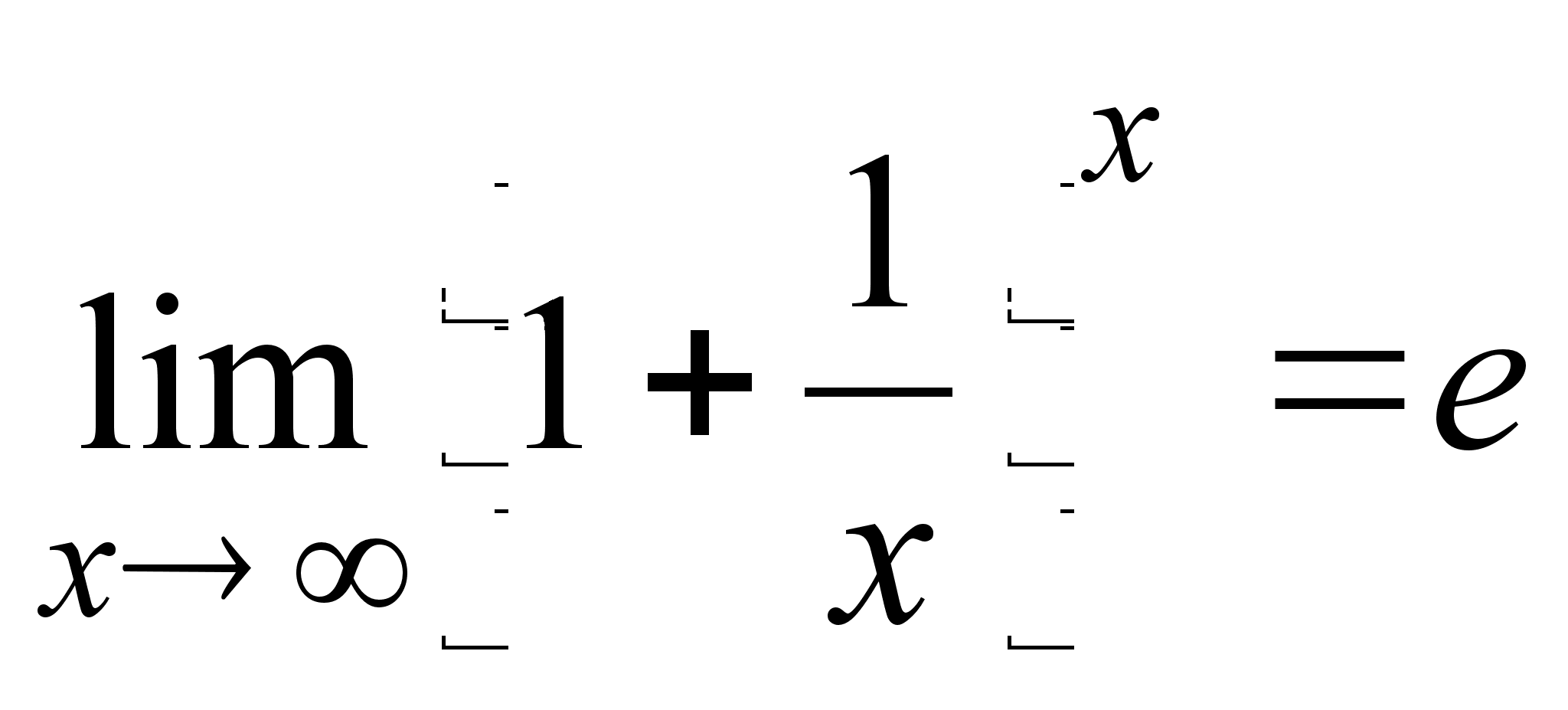 ,
,
которое
можно доказать,
исходя из определения
числа
![]() .
Заметим, что
этому равенству
можно придать
вид
.
Заметим, что
этому равенству
можно придать
вид
![]() .
.
- Непрерывность функции
Функция
![]() ,
определенная
в некоторой
окрестности
точки
,
определенная
в некоторой
окрестности
точки
![]() ,
называется
непрерывной
в точке
,
называется
непрерывной
в точке
![]() ,
если
,
если
![]() .
.
Если
ввести обозначения
![]() и
и
![]() (
(![]() называется
приращением
аргумента,
а
называется
приращением
аргумента,
а
![]() - соответствующим
приращением
функции), то
определению
непрерывности
можно придать
вид
- соответствующим
приращением
функции), то
определению
непрерывности
можно придать
вид
![]() .
.
Таким образом, непрерывность означает, что малым приращениям аргумента соответствуют малые приращения функции.
Функция называется
непрерывной
на множестве
![]() ,
если она непрерывна
в каждой точке
этого множества.
Справедливо
следующее
утверждение:
все основные
элементарные
функции непрерывны
на своих областях
определения.
,
если она непрерывна
в каждой точке
этого множества.
Справедливо
следующее
утверждение:
все основные
элементарные
функции непрерывны
на своих областях
определения.
Примеры. Следующие функции непрерывны на указанных множествах:
а) функция
![]() непрерывна
на R;
непрерывна
на R;
б) функция
![]() непрерывна
на
непрерывна
на
![]() ;
;
в) функция
![]() непрерывна
для всех
непрерывна
для всех
![]() ;
;
г) функция
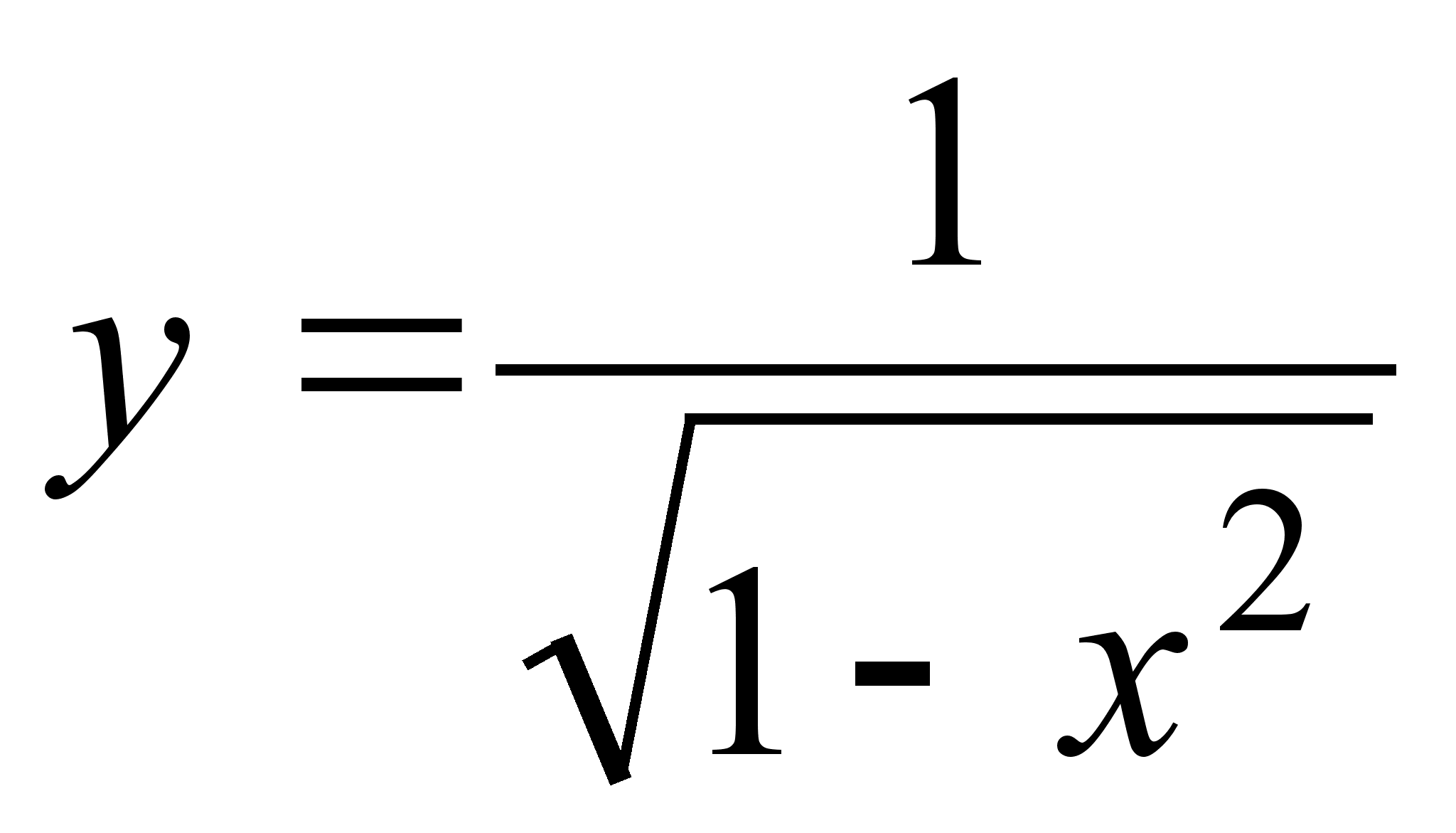 непрерывна
на
непрерывна
на
![]() .
.
Упражнения
1. Найти пределы последовательностей:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
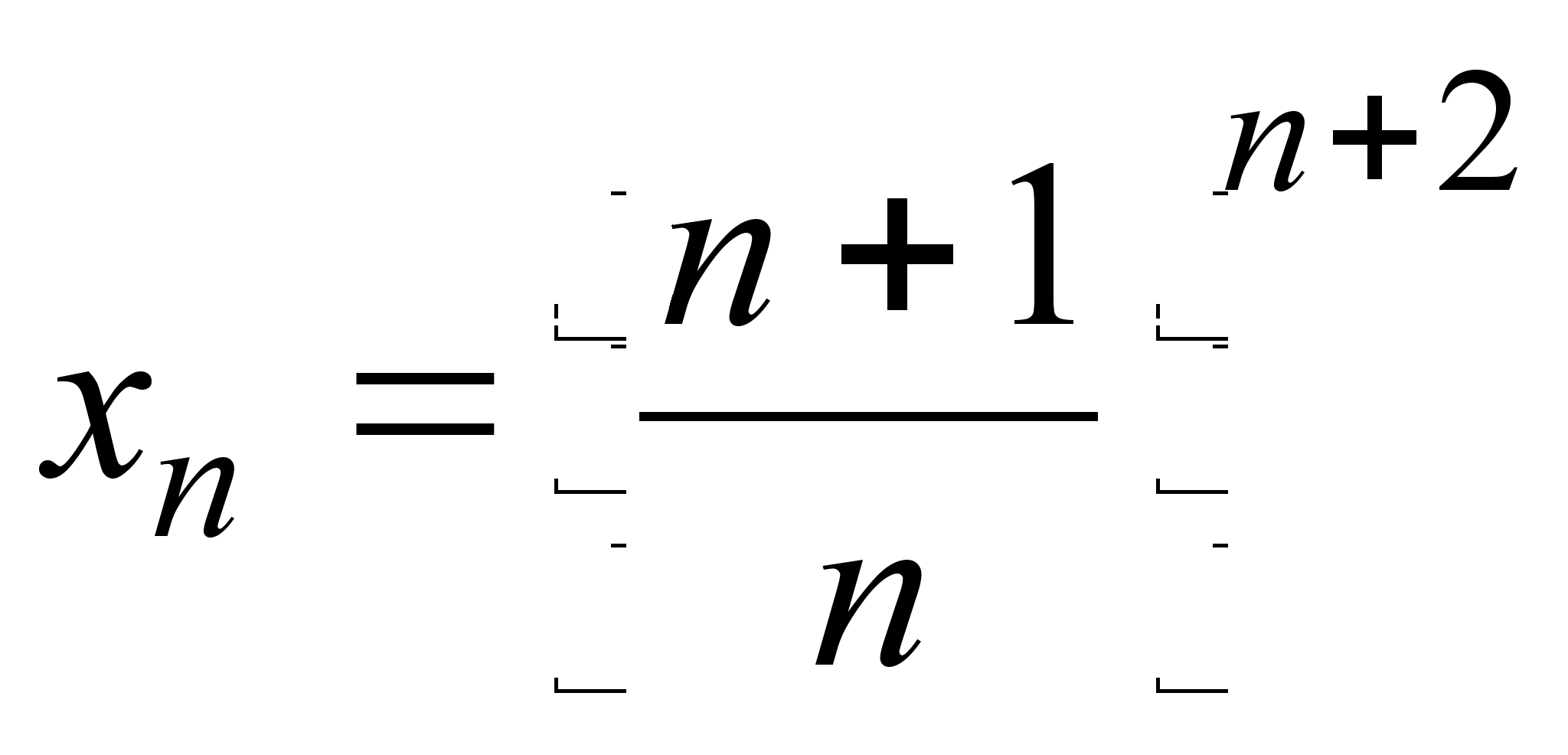 ;
;
18)
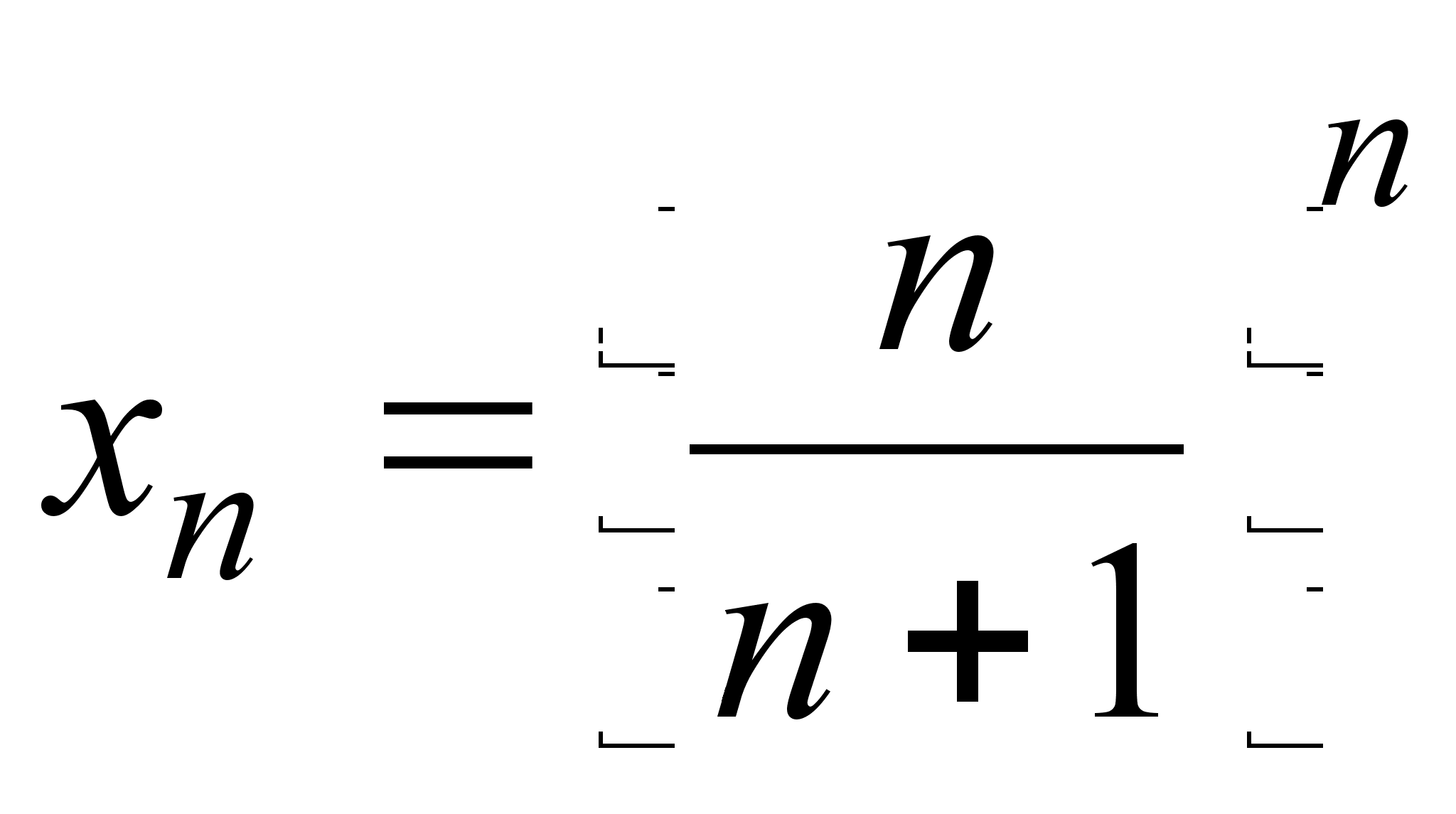 ;
;
19)
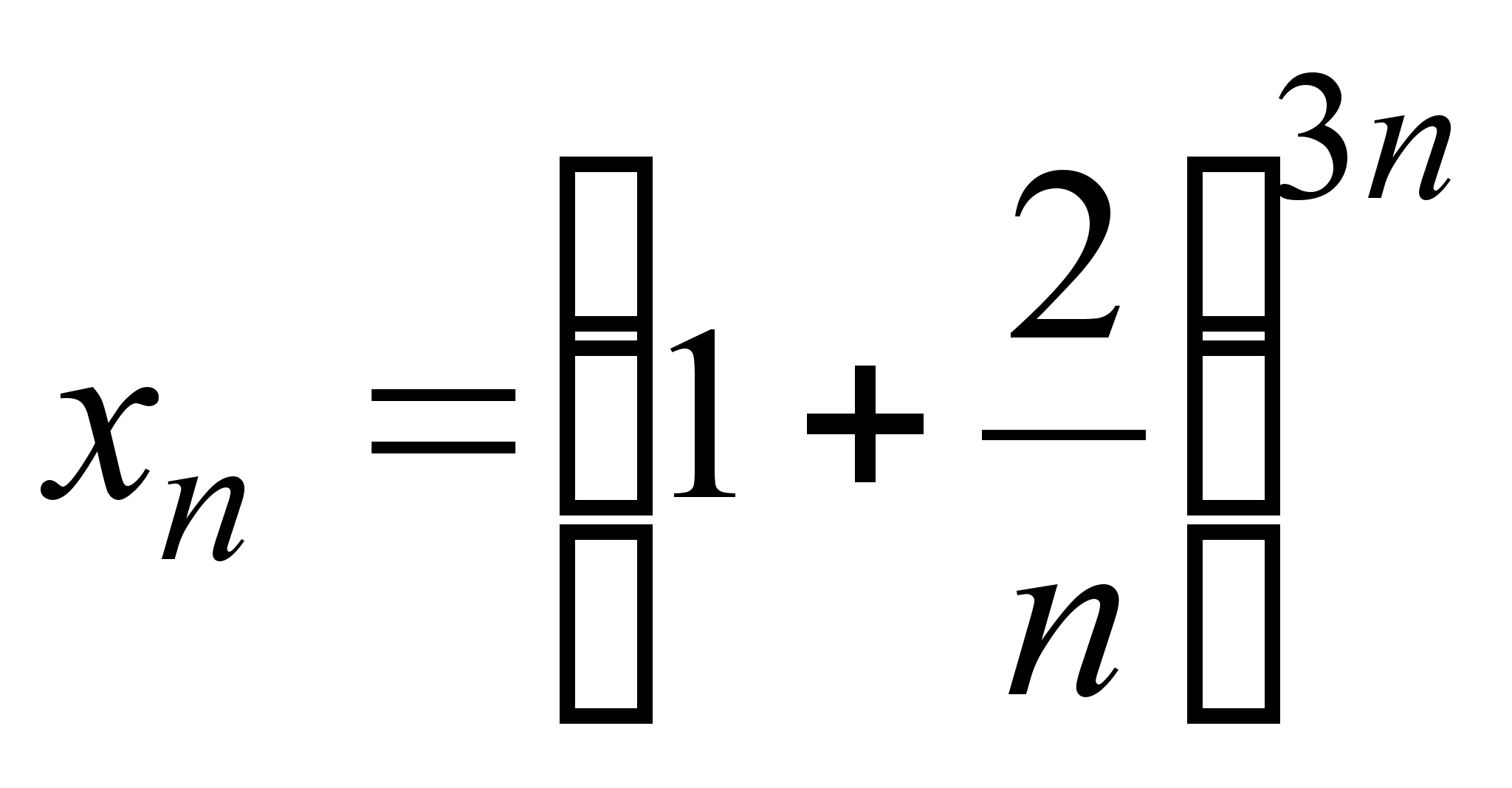 ;
;
20)
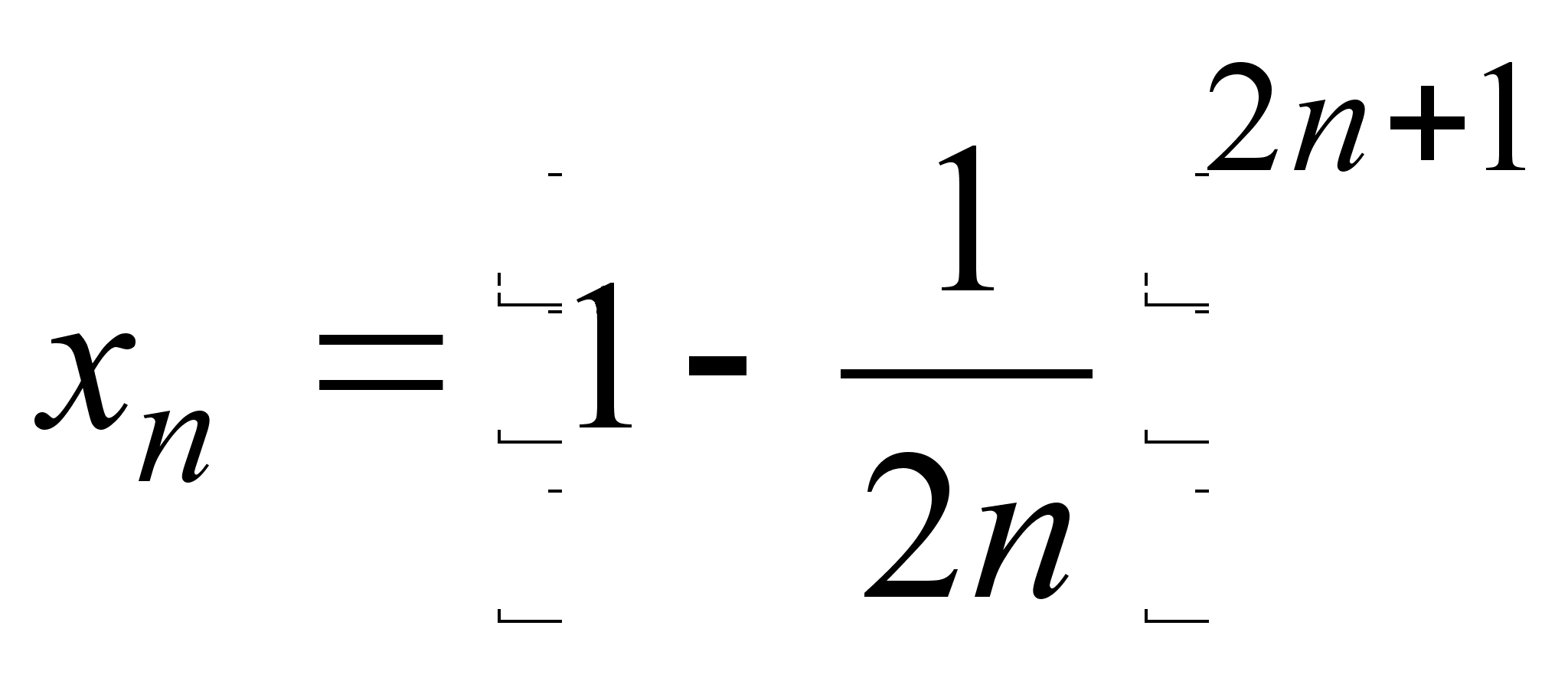 ;
;
21)
![]() ;
;
22)
![]() ;
;
23)
![]() ;
;
24)
![]() .
.
2. Найти пределы функций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
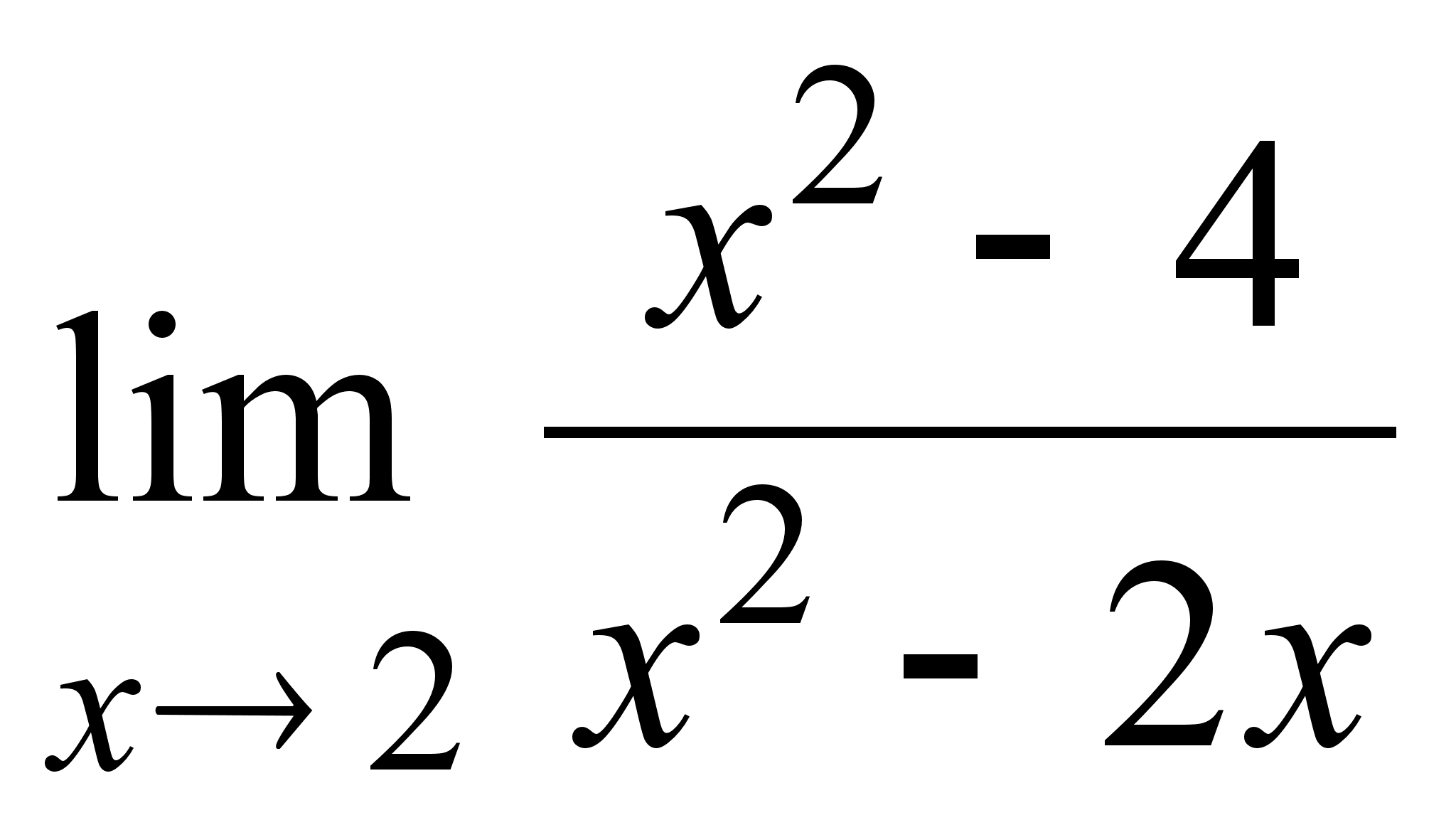 ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
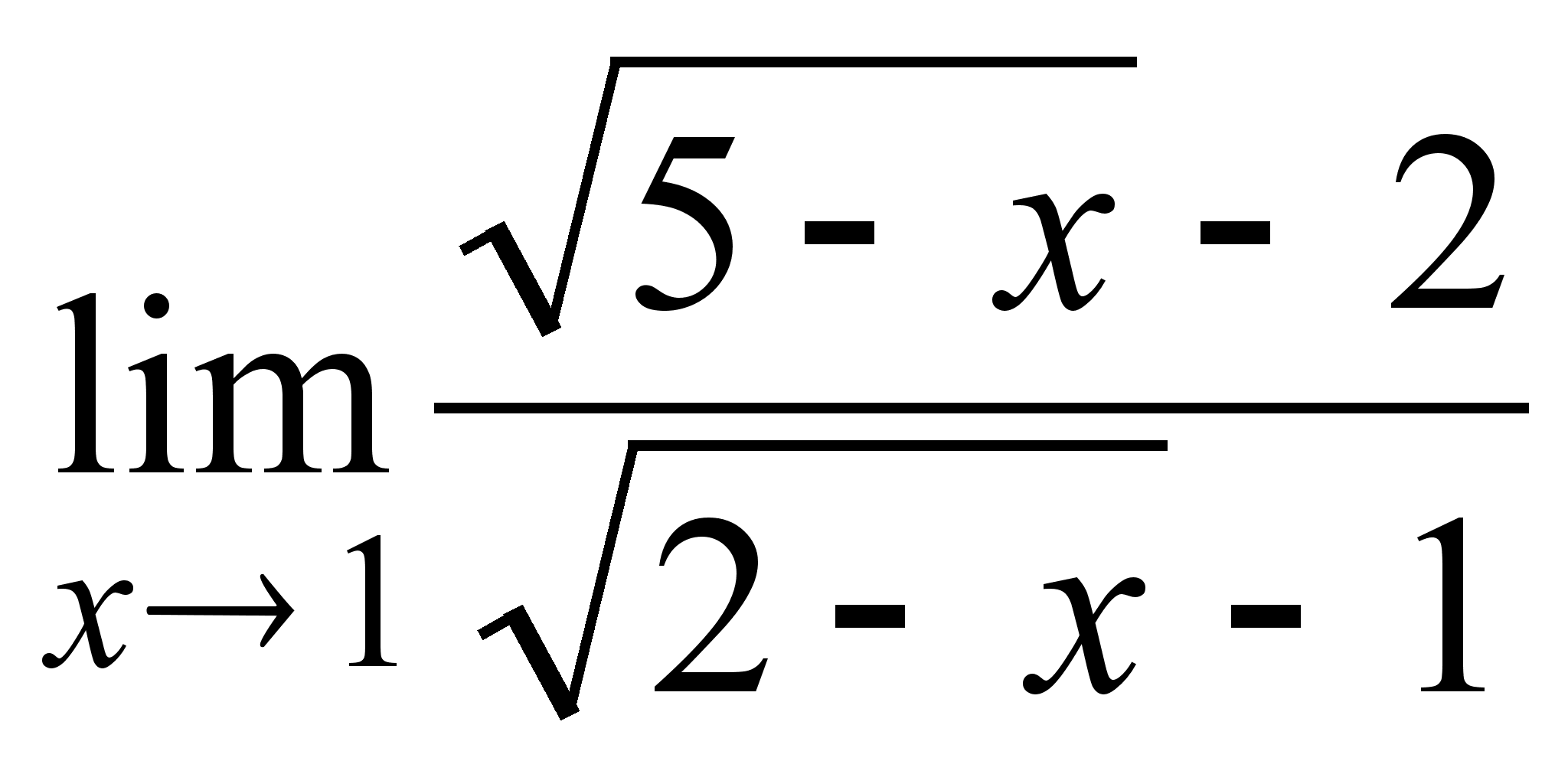 ;
;
8)
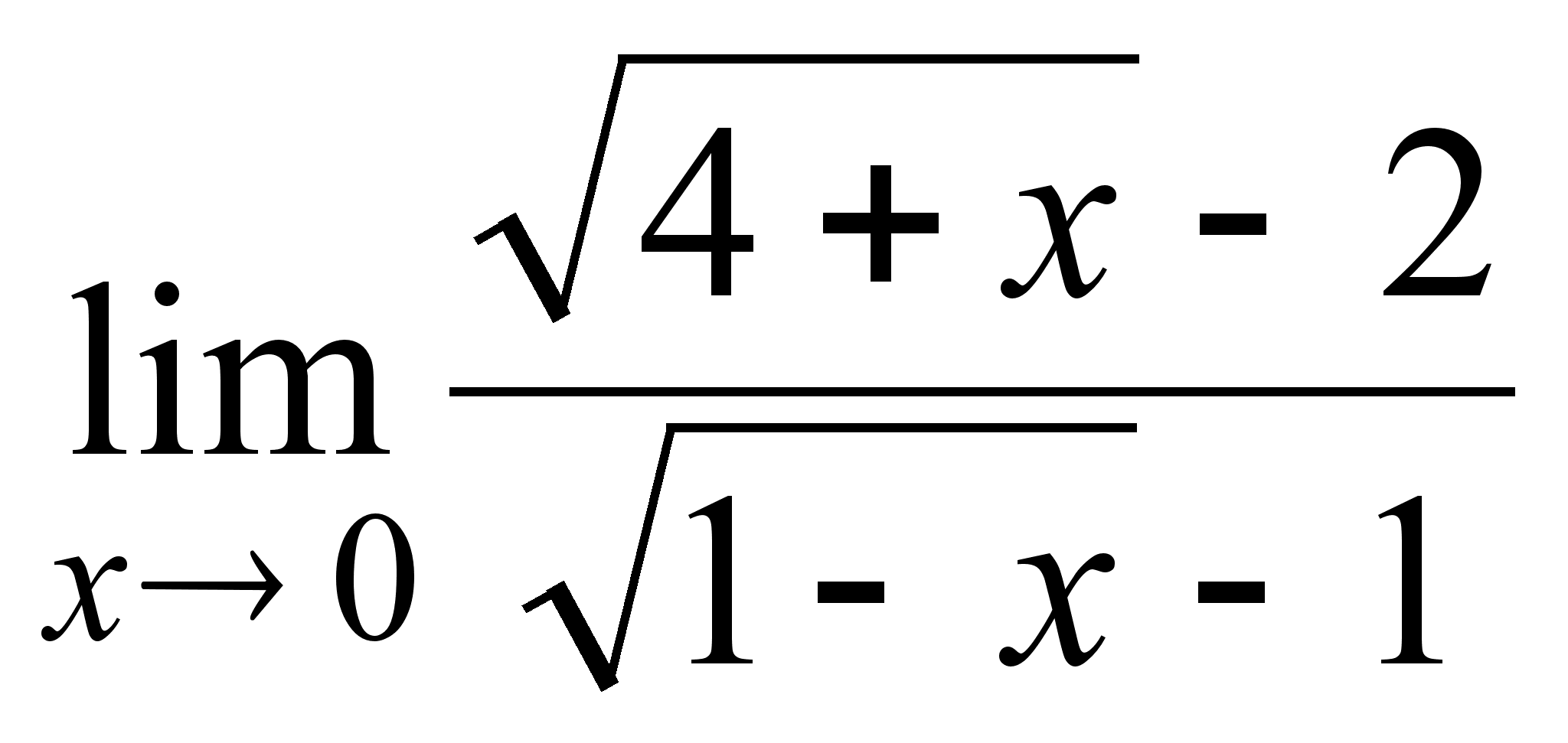 ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
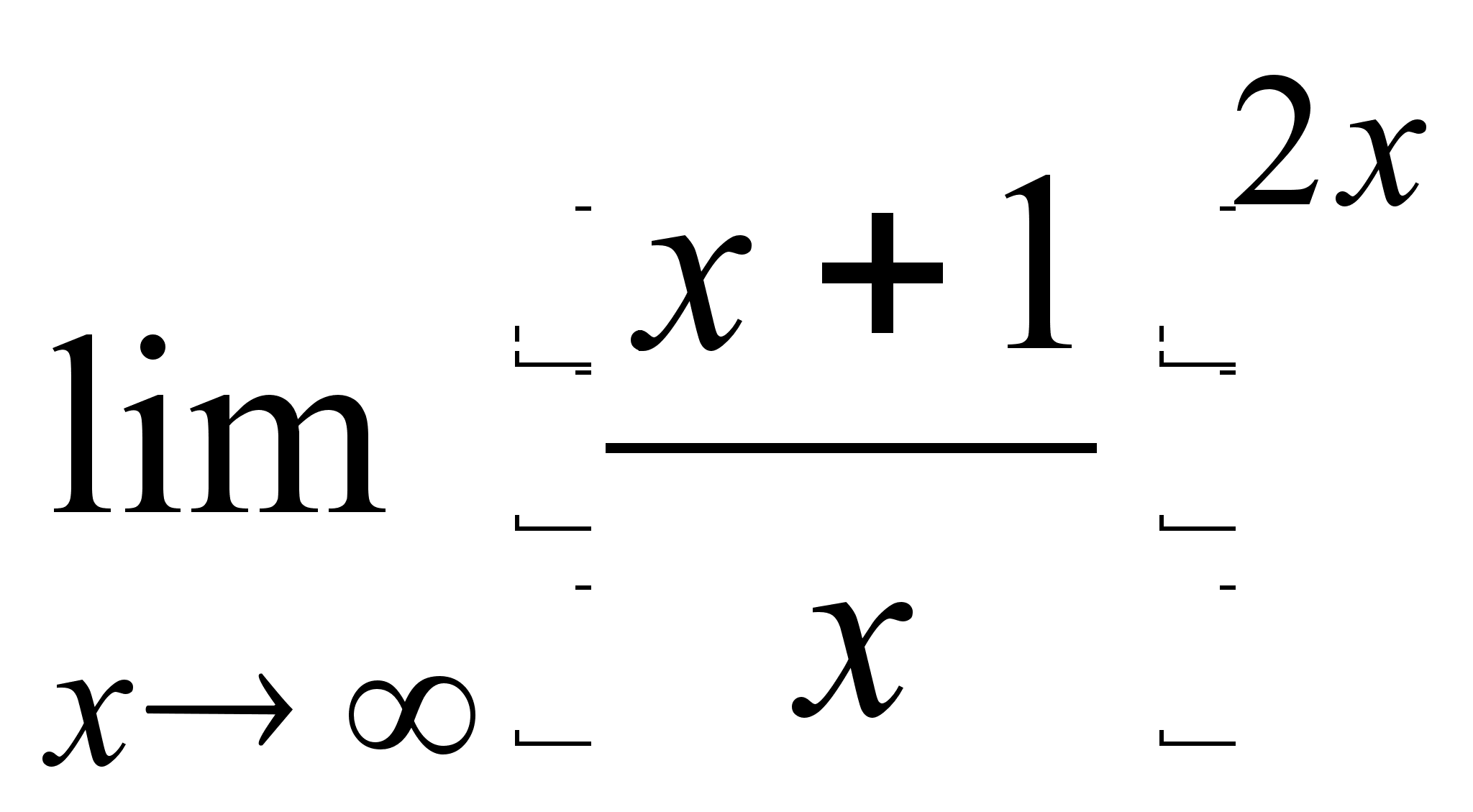 ;
;
18)
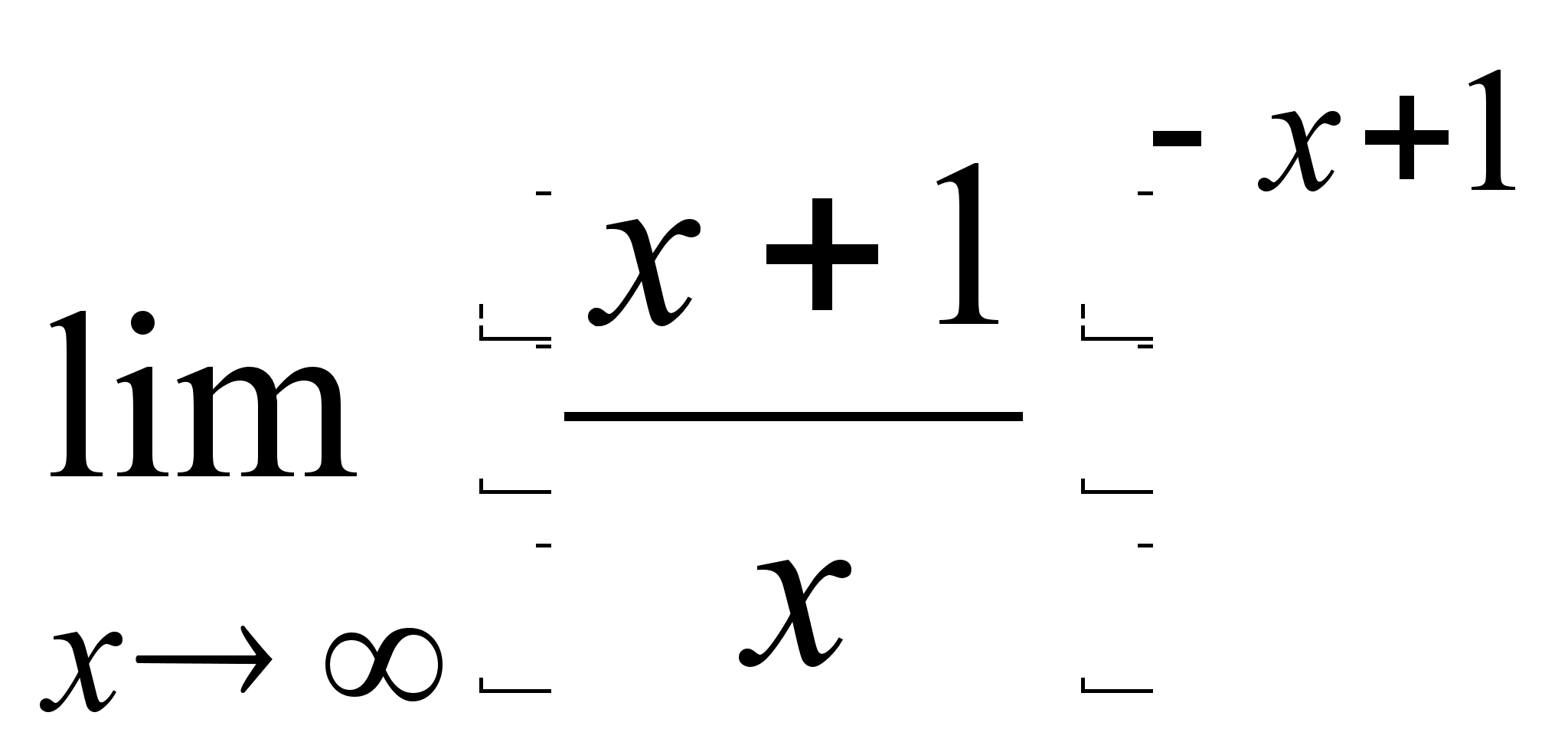 ;
;
19)
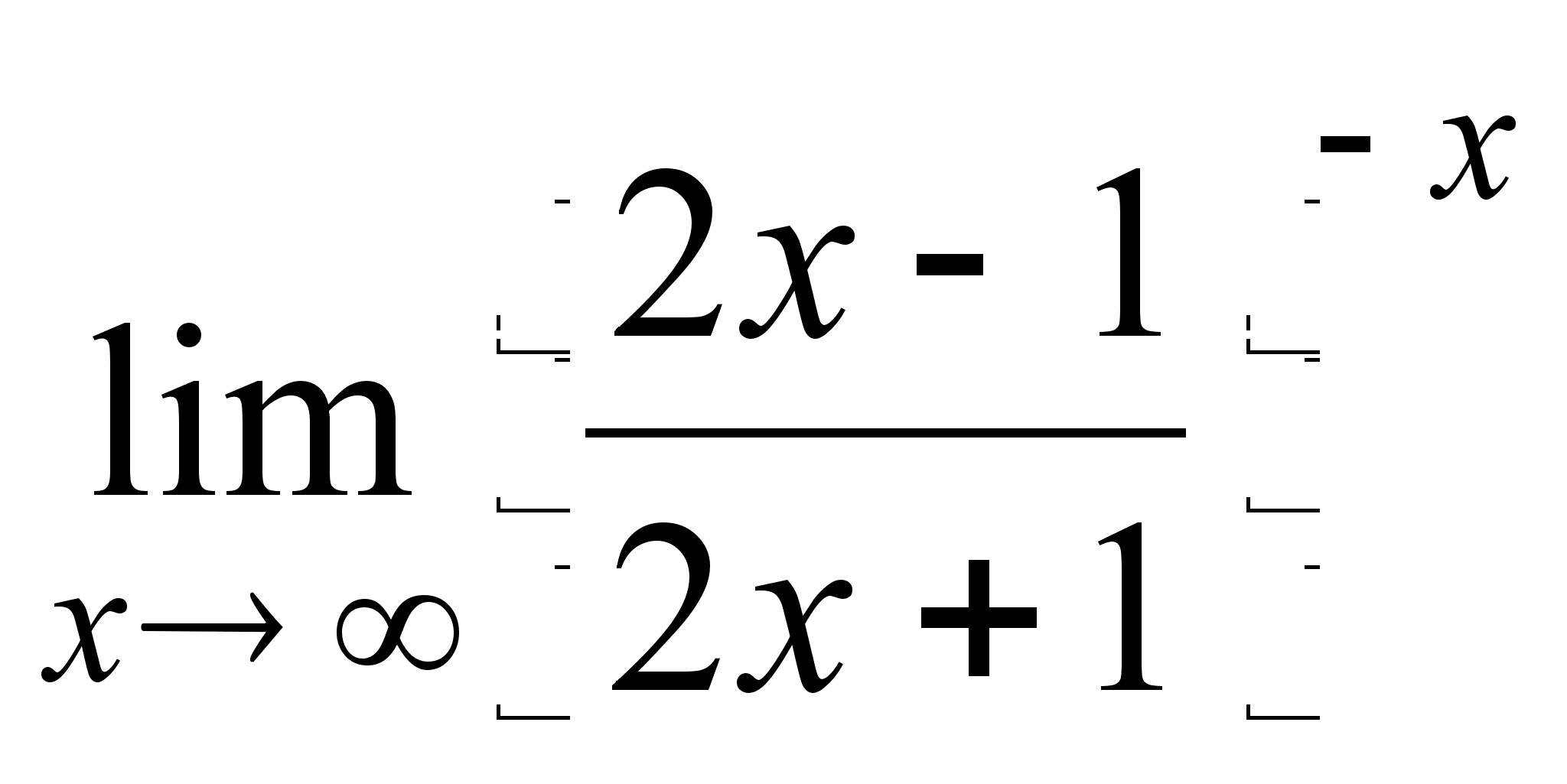 ;
;
20)
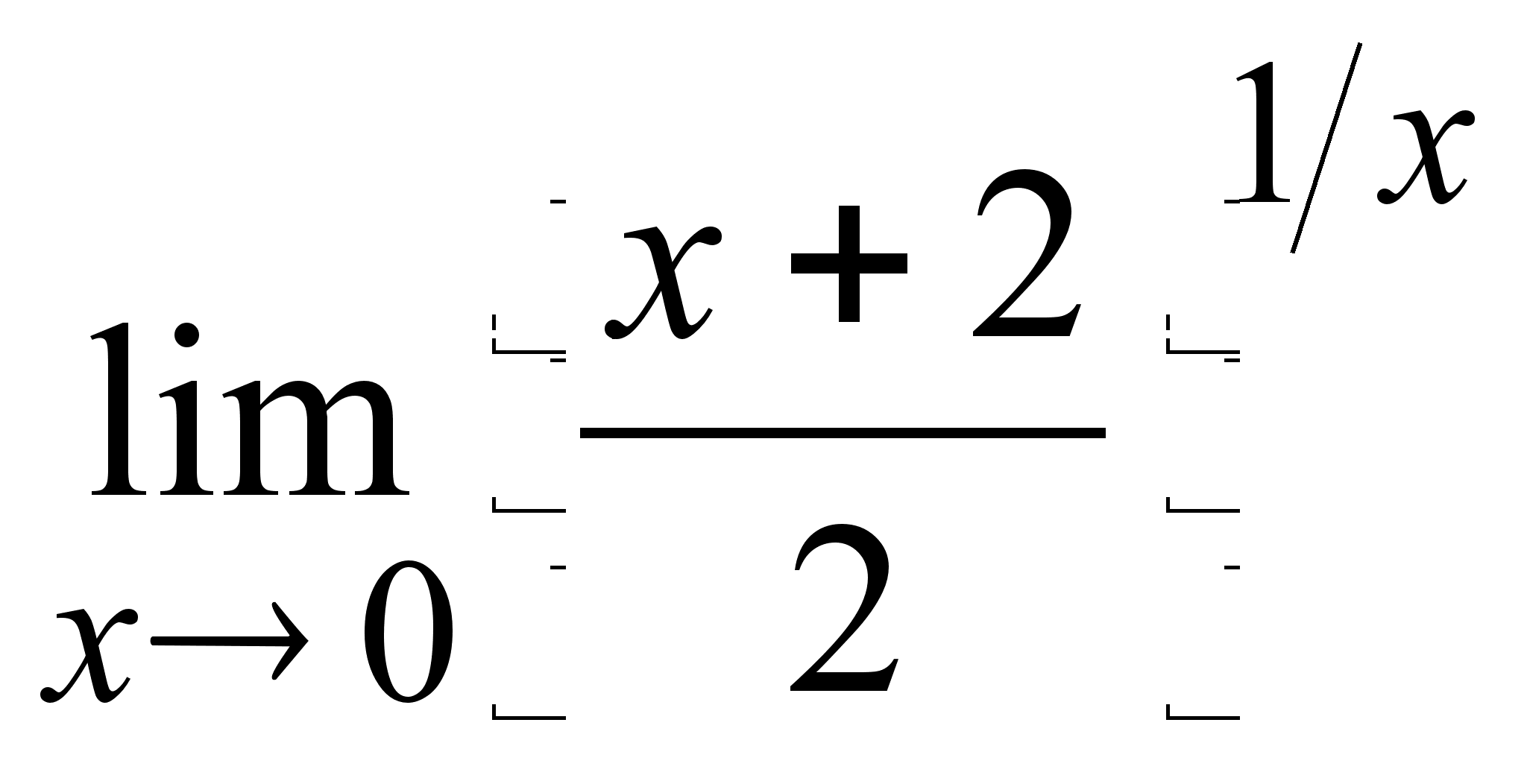
Ответы и указания к решению
1.
1) 0;
2) 0;
3) 1;
4)
![]() ;
;
5) 0;
6) 0;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13) 0;
14)
![]() ;
;
15) 0;
16)
![]() ;
;
17)
![]() ;
представить
;
представить
![]() в виде произведения
в виде произведения
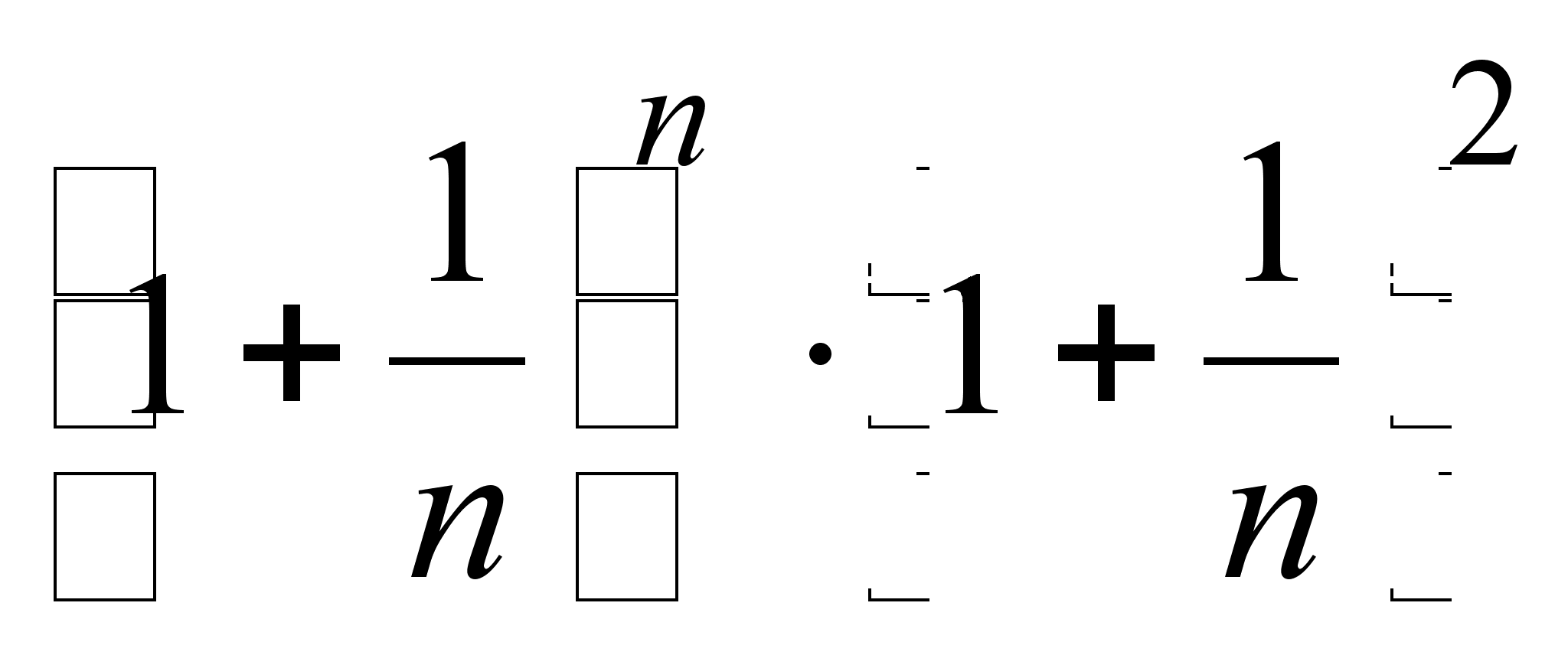 ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
0; преобразовать
![]() к виду
к виду
![]() ;
;
22) 0;
23)
![]() ;
;
24)
![]() .
.
2.
1) 2;
2) 1;
3) 2;
4) 2;
5) 3;
6) 4;
7)
![]() ;
;
8)
![]() ;
;
9) 2;
10) 0;
11)
![]() ;
;
12)
![]() ;
;
13)![]() ;
;
14)
![]() ;
;
15) 0;
16) 2;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() .
.
§ 3. Производная и ее применение
Производная характеризует скорость изменения функции при изменении ее аргумента. Она является основным инструментом исследования функций в математическом анализе, в частности, используется для отыскания точек экстремума: в этих точках производная либо равна нулю, либо не существует. Через производную определяется понятие эластичности функции, применяемое в экономических приложениях.
1. Определение производной и правила дифференцирования
Пусть функция
![]() определена
в некоторой
окрестности
точки
определена
в некоторой
окрестности
точки
![]() .
Пусть
.
Пусть
![]() – приращение
аргумента
в точке
– приращение
аргумента
в точке
![]() ,
а
,
а
![]() – соответствующее
приращение
функции. Составим
отношение
– соответствующее
приращение
функции. Составим
отношение
![]() этих приращений
и рассмотрим
его предел при
этих приращений
и рассмотрим
его предел при
![]() .
Если указанный
предел существует,
то он называется
производной
функции
.
Если указанный
предел существует,
то он называется
производной
функции
![]() в точке
в точке
![]() и обозначается
и обозначается
![]() ,
,
![]() или
или
![]() ,
то есть
,
то есть
![]() .
.
Операция вычисления
производной
называется
дифференцированием,
а функция, имеющая
производную
в точке, – дифференцируемой
в этой точке.
Если функция
имеет производную
в каждой точке
интервала
![]() ,
то она называется
дифференцируемой
на этом интервале.
,
то она называется
дифференцируемой
на этом интервале.
Примеры.
Найдем производные
функций в
произвольной
точке
![]() :
:
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
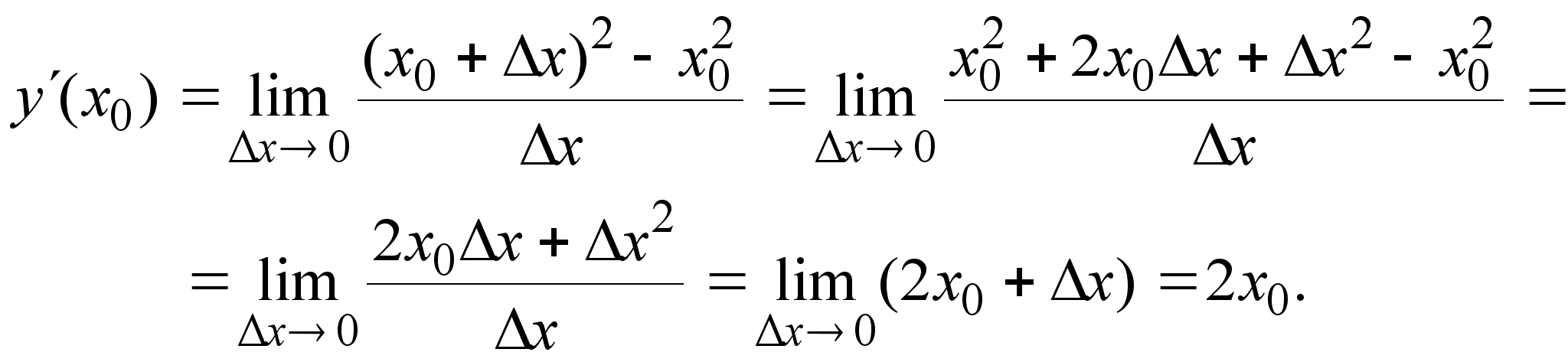
Заметим, что на практике при вычислении производных редко прибегают к определению. Вместо этого используют таблицу, содержащую выражения для производных всех основных элементарных функций, а также правила дифференцирования, позволяющие находить производную суммы, разности, произведения, частного и композиции функций.
Приведем таблицу производных некоторых основных элементарных функций и правила дифференцирования.
Таблица производных
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ,
,
где
![]() ,
,
![]() и
и
![]() - произвольные
постоянные,
- произвольные
постоянные,
![]() ,
,
![]() .
.
Примеры. Получим некоторые следствия формулы 2:
а)
![]() ,
,
б)
![]() ;
;
в)
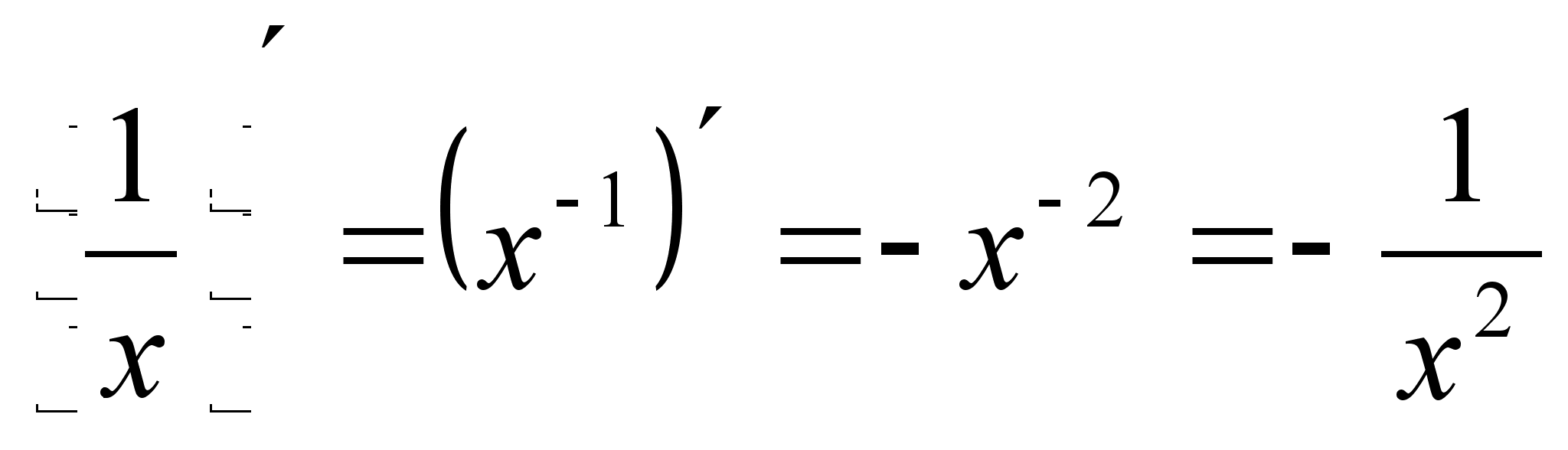 .
.
Правила дифференцирования
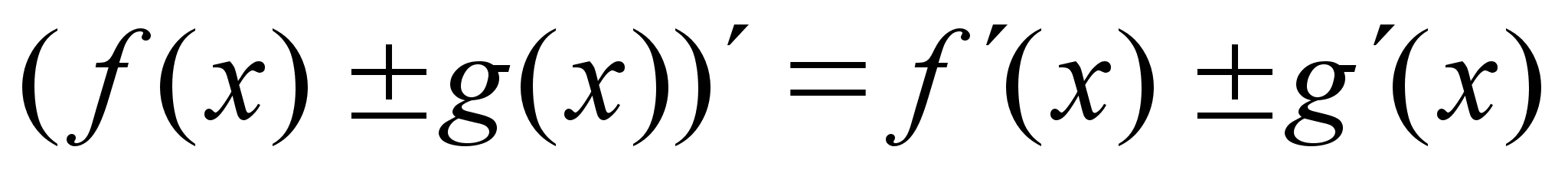 ;
;
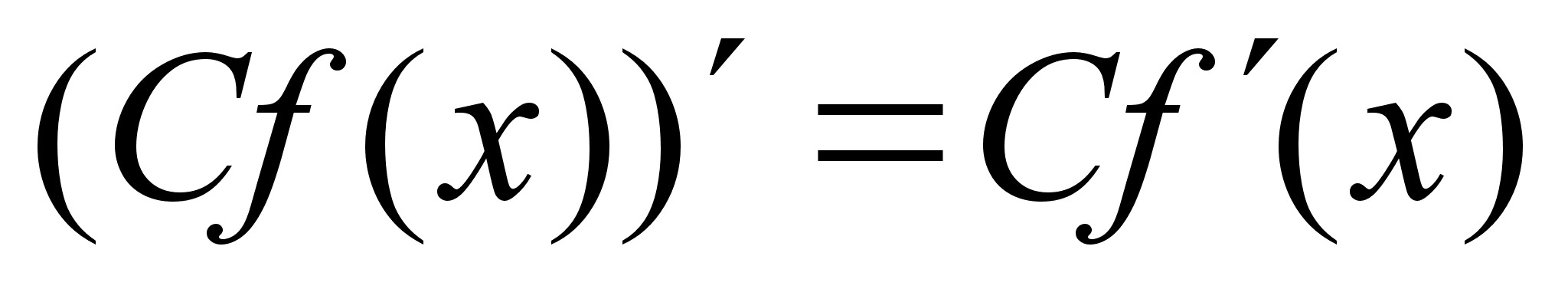 ,
где
,
где
 - постоянная;
- постоянная;
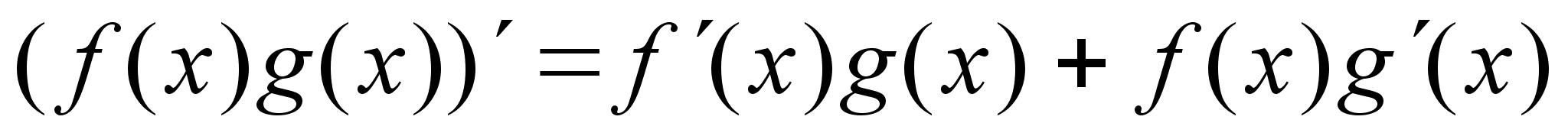 ;
; 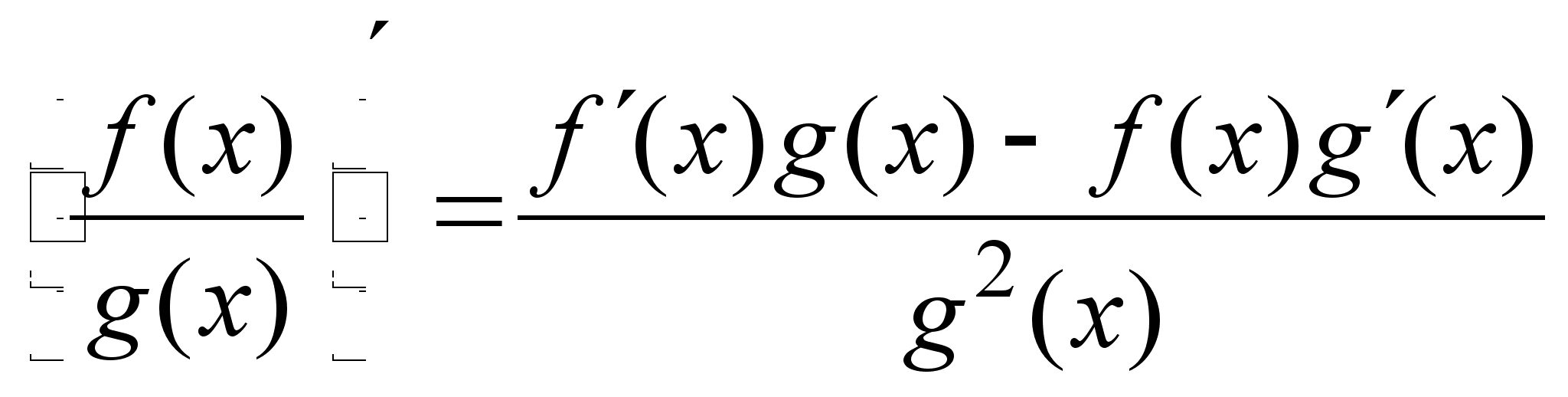 ;
;
если
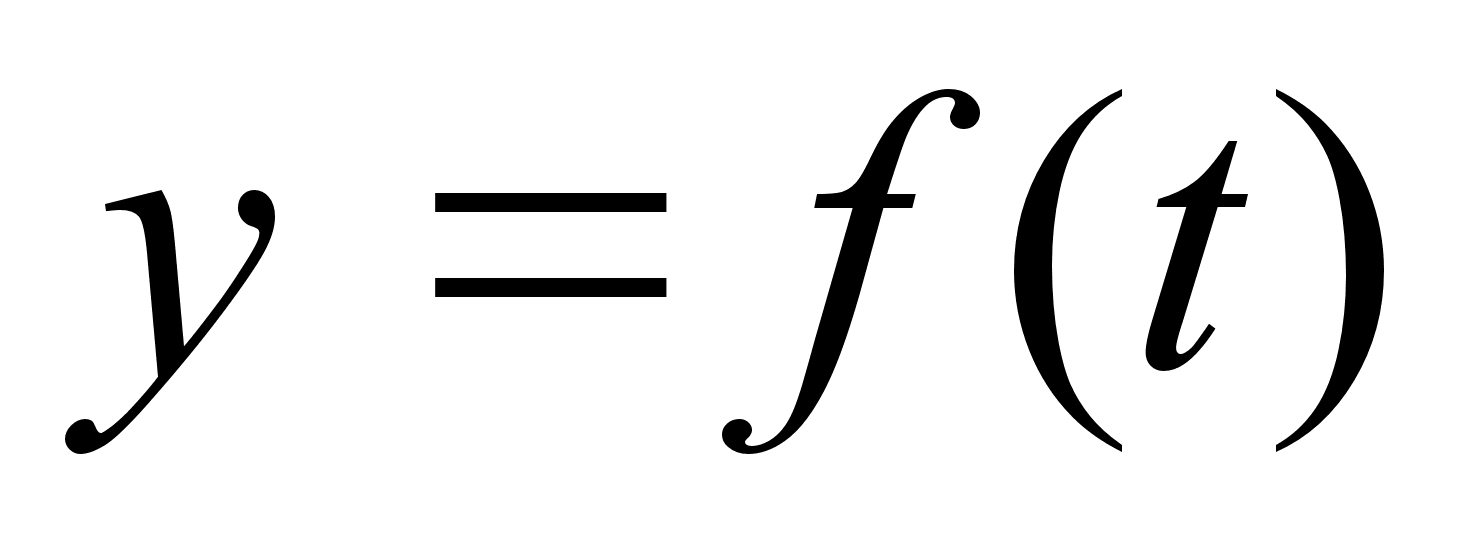 ,
а
,
а
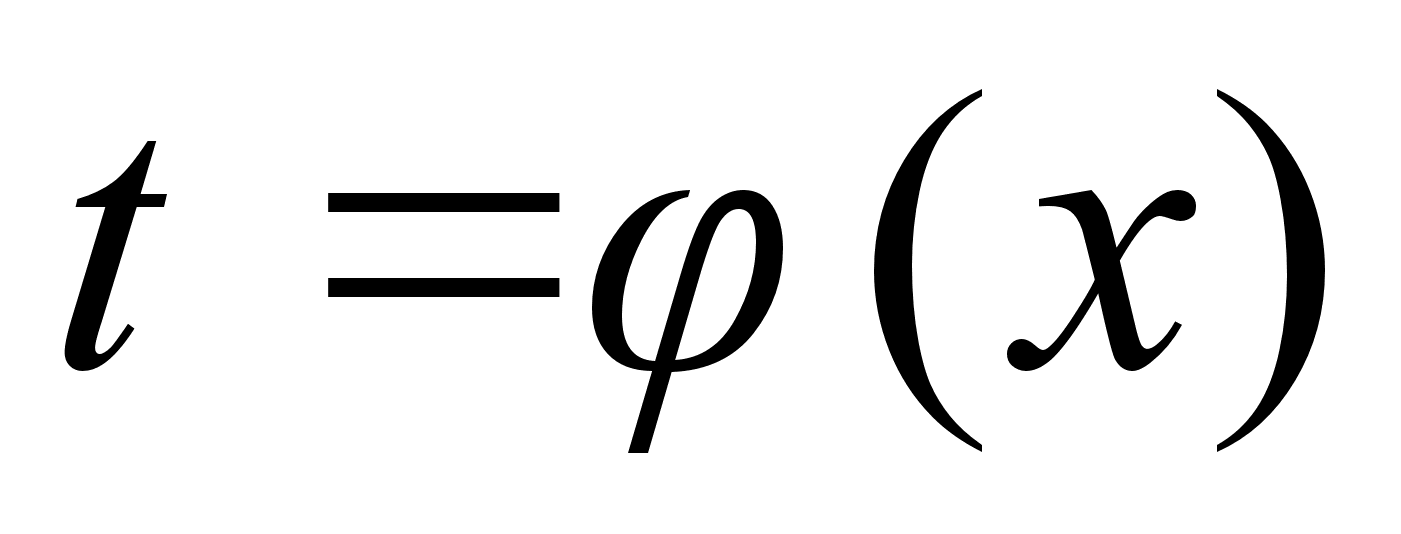 ,
то производная
сложной функции
,
то производная
сложной функции
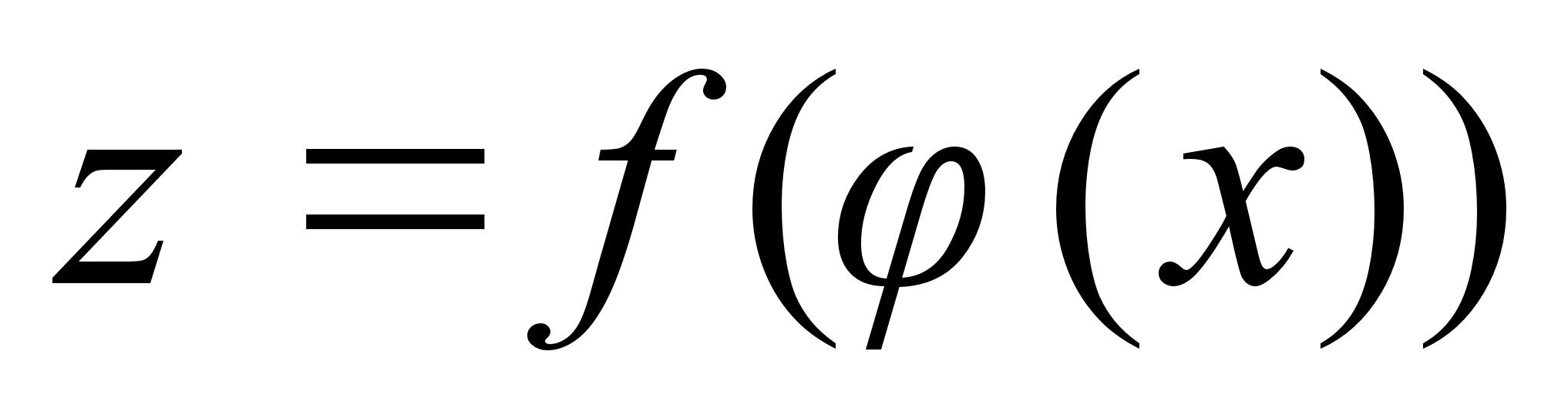 находится по
формуле
находится по
формуле
![]() ,
,
где индексы указывают, по какому аргументу производится дифференцирование.
Примеры. Найдем производные функций, используя правила 1-4:
а)
![]() ;
;
б)
![]() ;
;
в)
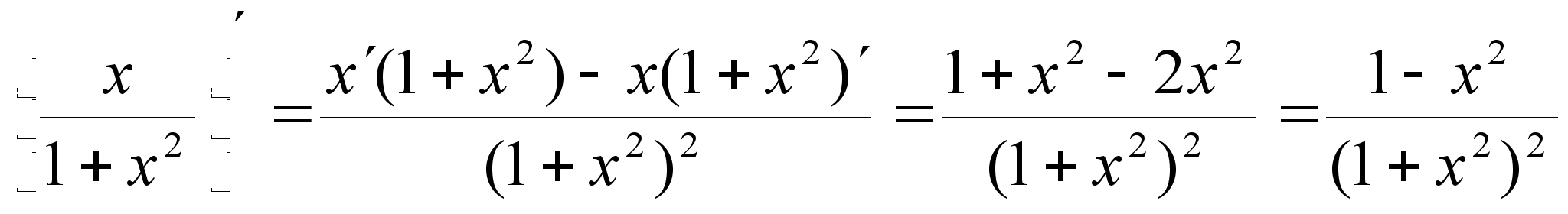 ;
;
Примеры. Найдем производные сложных функций по правилу 5:
а)
![]() ;
положим
;
положим
![]() ,
тогда
,
тогда
![]() ,
и, следовательно,
,
и, следовательно,
![]() ;
;
б)
![]() ;
положим
;
положим
![]() ,
тогда
,
тогда
![]() ,
и
,
и
![]() .
.
Заметим, что
производная
![]() ,
называемая
также первой
производной
функции
,
называемая
также первой
производной
функции
![]() ,
сама является
функцией аргумента
,
сама является
функцией аргумента
![]() .
Производная
этой функции
называется
второй производной
функции
.
Производная
этой функции
называется
второй производной
функции
![]() и обозначается
и обозначается
![]() ,
то есть
,
то есть
![]() .
Аналогично
можно ввести
третью и более
высокие производные.
.
Аналогично
можно ввести
третью и более
высокие производные.
Примеры. Найдем вторые производные:
а)
![]() ;
;
б)
![]() .
.
2. Геометрический и физический смысл производной
а) Геометрический
смысл производной.
Рассмотрим
график функции
![]() ,
дифференцируемой
в точке
,
дифференцируемой
в точке
![]() (рис. 13). Проведем
через точки
(рис. 13). Проведем
через точки
![]() и
и
![]() графика прямую
графика прямую
![]() ,
и пусть
,
и пусть
![]() - угол ее наклона
к оси
- угол ее наклона
к оси
![]() .
Тогда
.
Тогда
![]() .
(1)
.
(1)
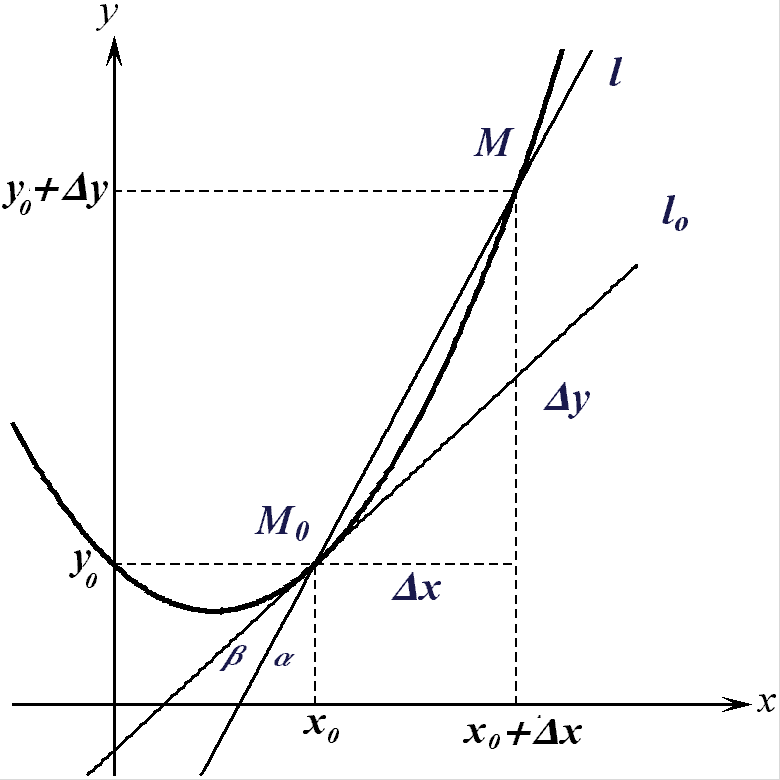
Рис. 13.
Если
![]() стремится к
нулю, то
стремится к
нулю, то
![]() также стремится
к нулю, и точка
также стремится
к нулю, и точка
![]() приближается
к точке
приближается
к точке
![]() ,
а прямая
,
а прямая
![]() - к касательной
- к касательной
![]() ,
образующей
с осью
,
образующей
с осью
![]() угол
угол
![]() .
При этом равенство
(1) принимает
вид:
.
При этом равенство
(1) принимает
вид:
![]() ,
(2)
,
(2)
откуда следует, что производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке.
Пример.
Найдем угол
![]() наклона касательной
к графику функции
наклона касательной
к графику функции
![]() в точке
в точке
![]() .
Поскольку
.
Поскольку
![]() ,
то в силу формулы
(2) получаем
,
то в силу формулы
(2) получаем
![]() .
Следовательно
угол
.
Следовательно
угол
![]() ,
то есть касательная
параллельна
оси
,
то есть касательная
параллельна
оси
![]() .
.
б) Физический
смысл производной.
Если
![]() - время движения,
а
- время движения,
а
![]() - путь, пройденный
за это время,
то отношение
- путь, пройденный
за это время,
то отношение
![]() есть средняя
скорость движения
на отрезке
есть средняя
скорость движения
на отрезке
![]() ,
а
,
а
![]() - мгновенная
скорость в
момент времени
- мгновенная
скорость в
момент времени
![]() .
.
3. Исследование функций с помощью производной
Функция
![]() называется
возрастающей
(убывающей)
на интервале
называется
возрастающей
(убывающей)
на интервале
![]() ,
если для любых
,
если для любых
![]() из
из
![]() следует
следует
![]() (
(![]() ).
).
Интервалы возрастания или убывания могут быть найдены на основании следующего утверждения.
![]()
Теорема 1. Если
![]() для всех
для всех
![]() ,
то функция
,
то функция
![]() возрастает
на интервале
возрастает
на интервале
![]() ;
если
;
если
![]() для всех
для всех
![]() ,
то функция
,
то функция
![]() убывает на
интервале
убывает на
интервале
![]() .
.
![]()
Точка
![]() называется
точкой локального
максимума
(минимума)
функции
называется
точкой локального
максимума
(минимума)
функции
![]() ,
если для всех
,
если для всех
![]() из некоторой
окрестности
точки
из некоторой
окрестности
точки
![]() ,
,
![]() ,
выполнено
неравенство
,
выполнено
неравенство
![]() (
(![]() ).
Точки максимума
и минимума
называются
точками экстремума
функции.
).
Точки максимума
и минимума
называются
точками экстремума
функции.
Для отыскания точек экстремума используются следующие теоремы.
![]()
![]()
Теорема 2 (необходимое
условие экстремума).
Если функция
![]() имеет экстремум
в точке
имеет экстремум
в точке
![]() и дифференцируема
в этой точке,
то
и дифференцируема
в этой точке,
то
![]() .
.
Из этой теоремы вытекает, что в точках экстремума функции производная либо равна нулю, либо не существует. Такие точки называются критическими. Экстремумы функции следует искать среди ее критических точек.
![]()
![]()
Теорема 3
(достаточное
условие экстремума).
Пусть
![]() - критическая
точка функции
- критическая
точка функции
![]() .
Если при переходе
через точку
.
Если при переходе
через точку
![]() производная
производная
![]() меняет знак
с "+" на "–",
то в точке
меняет знак
с "+" на "–",
то в точке
![]() функция
функция
![]() имеет максимум,
а если с "–"
на "+", то –
минимум. Если
производная
не меняет знак
при переходе
через точку
имеет максимум,
а если с "–"
на "+", то –
минимум. Если
производная
не меняет знак
при переходе
через точку
![]() ,
то в этой точке
экстремума
нет.
,
то в этой точке
экстремума
нет.
Проводимый на основе сформулированных теорем анализ поведения функций используют при построении их графиков.
Примеры. а) Найдем интервалы возрастания и убывания функции
![]() ,
,
и ее экстремумы.
Производная
рассматриваемой
функции существует
при любом
![]() и равна
и равна
![]() .
Приравняв
производную
нулю и решив
полученное
квадратное
уравнение,
найдем две
критические
точки:
.
Приравняв
производную
нулю и решив
полученное
квадратное
уравнение,
найдем две
критические
точки:
![]() и
и
![]() .
Ось
.
Ось
![]() разбивается
этими точками
на три интервала:
разбивается
этими точками
на три интервала:
![]() ,
,
![]() и
и
![]() ,
причем на каждом
из них
,
причем на каждом
из них
![]() сохраняет
знак. Определим
эти знаки, например,
вычислив
сохраняет
знак. Определим
эти знаки, например,
вычислив
![]() в произвольных
точках указанных
интервалов,
получим:
в произвольных
точках указанных
интервалов,
получим:
![]() на
на
![]() и
и
![]() ,
и
,
и
![]() на
на
![]() .
.
Отсюда в силу
теорем 1-3 заключаем,
что функция
![]() возрастает
на интервалах
возрастает
на интервалах
![]() и
и
![]() ,
убывает на
интервале
,
убывает на
интервале
![]() ,
в точке
,
в точке
![]() достигает
максимального
значения
достигает
максимального
значения
![]() ,
а в точке
,
а в точке
![]() - минимального
значения
- минимального
значения
![]() .
.
б) Пусть
![]() .
Тогда
.
Тогда
![]() ,
и единственной
критической
точкой является
,
и единственной
критической
точкой является
![]() .
Так как знак
производной
не меняется
при переходе
через эту точку,
то она не является
точкой экстремума.
График этой
функции приведен
в § 1 на рис. 7.
.
Так как знак
производной
не меняется
при переходе
через эту точку,
то она не является
точкой экстремума.
График этой
функции приведен
в § 1 на рис. 7.
в) Пусть
![]() ,
,
![]() .
Тогда
.
Тогда
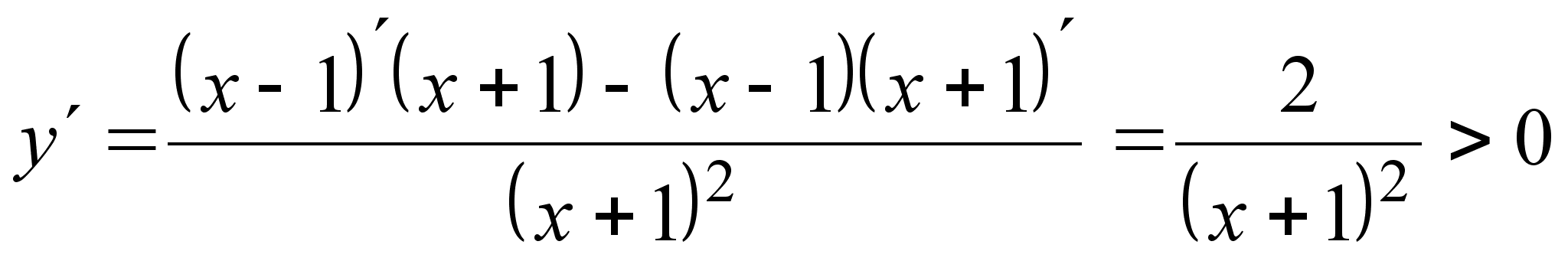 при всех
при всех
![]() .
Это означает,
что данная
функция возрастает
на интервалах
(
.
Это означает,
что данная
функция возрастает
на интервалах
(![]() )
и (
)
и (![]() ).
).
г) Точка
![]() является критической
точкой функции
является критической
точкой функции
![]() - производная
функции в этой
точке не существует.
Функция достигает
в этой точке
минимума, что
иллюстрирует
ее график (рис.
5).
- производная
функции в этой
точке не существует.
Функция достигает
в этой точке
минимума, что
иллюстрирует
ее график (рис.
5).
4. Эластичность функции
![]()
Пусть аргумент
![]() функции
функции
![]() получает приращение
получает приращение
![]() .
Тогда значение
функции изменяется
на величину
.
Тогда значение
функции изменяется
на величину
![]() .
Отношение
.
Отношение
![]() характеризует
среднее изменение
функции, приходящееся
на единицу
изменения ее
аргумента, а
предел этого
отношения при
характеризует
среднее изменение
функции, приходящееся
на единицу
изменения ее
аргумента, а
предел этого
отношения при
![]() равен производной
равен производной
![]() .
.
Рассмотрим
относительные
изменения
переменных
![]() и
и
![]() ,
выраженные,
например, в
процентах:
,
выраженные,
например, в
процентах:
![]() и
и
![]() .
Их отношение
.
Их отношение
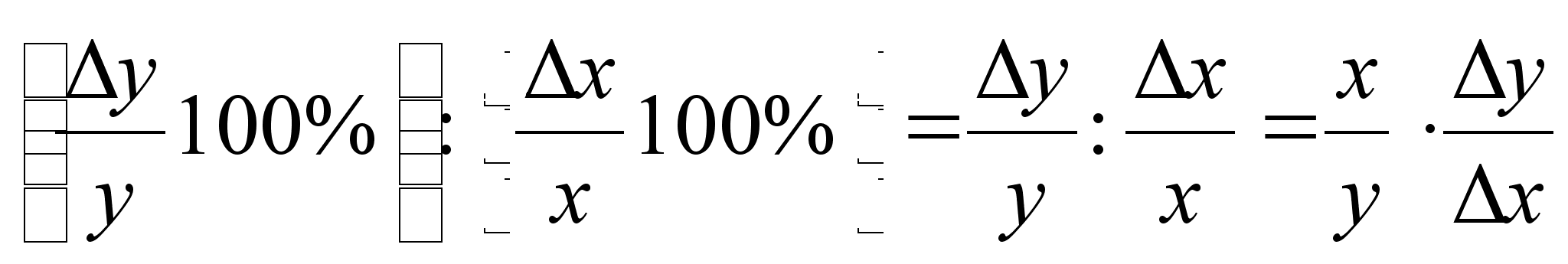
показывает,
на сколько
процентов в
среднем меняется
![]() при изменении
при изменении
![]() на
на
![]() .
Предел этого
отношения при
.
Предел этого
отношения при
![]() называется
эластичностью
функции
называется
эластичностью
функции
![]() и обозначается
и обозначается
![]() ,
то есть
,
то есть
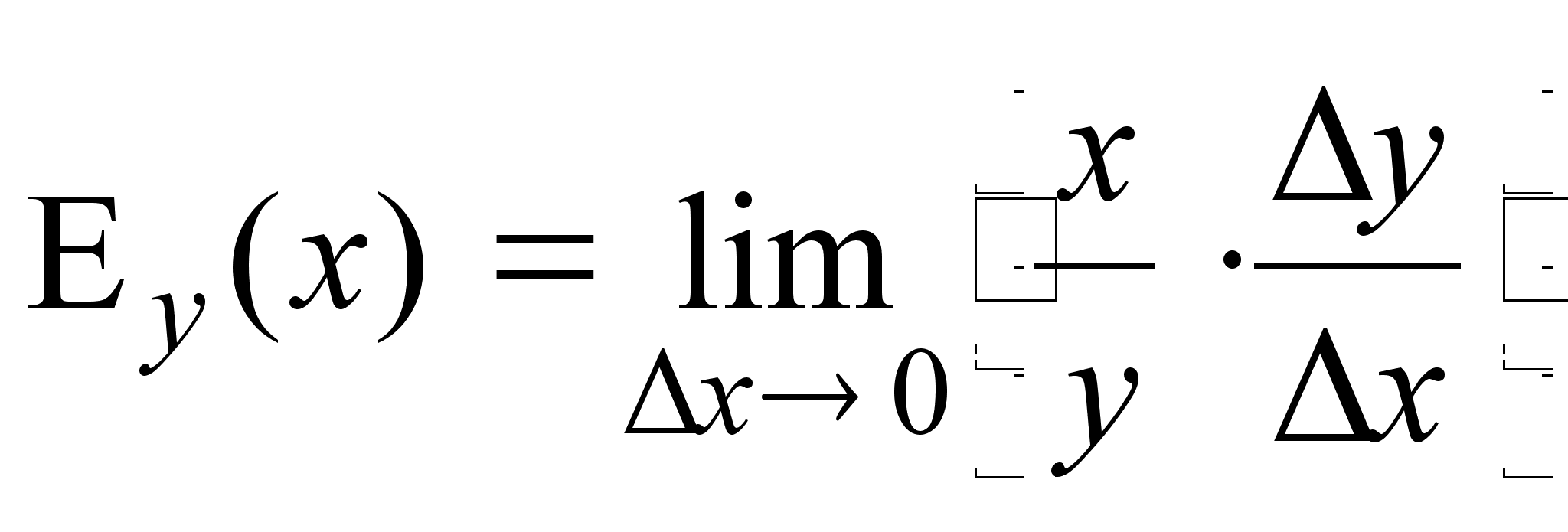 .
.
Так как
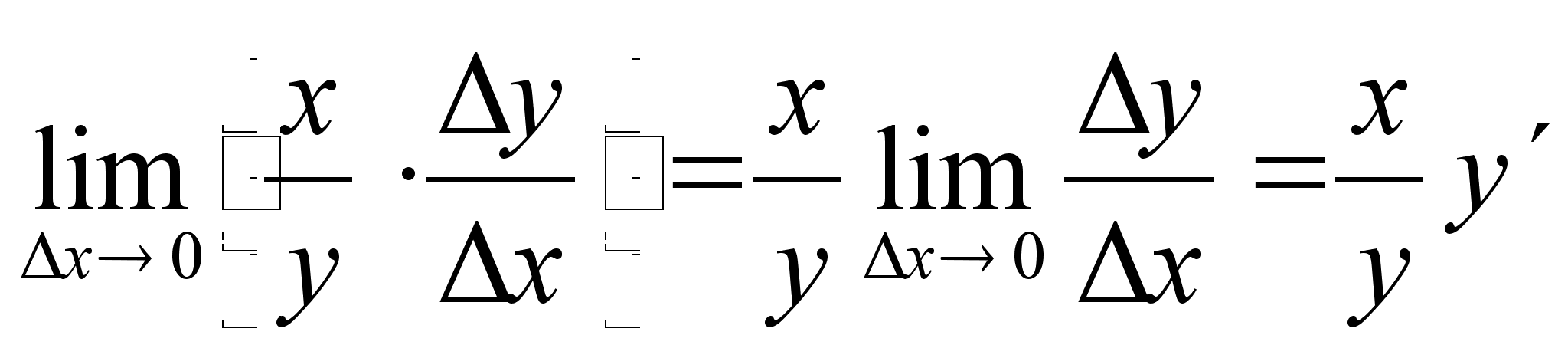 ,
,
то справедлива формула
![]() .
.
Примеры.
а) Пусть
![]() ,
тогда
,
тогда
![]() и, следовательно,
и, следовательно,
![]() .
При
.
При
![]() получаем
получаем
![]() ,
то есть при
увеличении
,
то есть при
увеличении
![]() от 2 до 2,02 (на 1%) значение
от 2 до 2,02 (на 1%) значение
![]() изменяется
примерно на
изменяется
примерно на
![]() .
.
б) Пусть
![]() ,
тогда
,
тогда
![]() и, следовательно,
и, следовательно,
![]() .
При
.
При
![]() получим
получим
![]() .
Следовательно,
увеличение
.
Следовательно,
увеличение
![]() от 3 до 3,03 ведет
к уменьшению
от 3 до 3,03 ведет
к уменьшению
![]() примерно на
примерно на
![]() .
.
в) Пусть
![]() ,
тогда
,
тогда
![]() и, следовательно,
и, следовательно,
![]() .
В этом случае
эластичность
постоянна и
равна
.
В этом случае
эластичность
постоянна и
равна
![]() ,
то есть при
любом значении
аргумента его
увеличение
на 1% ведет к
уменьшению
значения функции
также на
,
то есть при
любом значении
аргумента его
увеличение
на 1% ведет к
уменьшению
значения функции
также на
![]() .
.
Функция
![]() называется
эластичной
в точке
называется
эластичной
в точке
![]() ,
если
,
если
![]() ,
нейтральной,
если
,
нейтральной,
если
![]() ,
и неэластичной,
если
,
и неэластичной,
если
![]() .
.
Пример.
Дана зависимость
спроса
![]() от цены
от цены
![]() :
:
![]() .
.
Найдем
эластичность
спроса
![]() ,
и рассмотрим
ее значения
при некоторых
,
и рассмотрим
ее значения
при некоторых
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
При
.
При
![]() имеем
имеем
![]() ,
откуда
,
откуда
![]() ,
то есть спрос
неэластичен.
Если
,
то есть спрос
неэластичен.
Если
![]() ,
то
,
то
![]() ,
,
![]() ,
– спрос нейтрален.
При
,
– спрос нейтрален.
При
![]() получим
получим
![]() ,
то есть
,
то есть
![]() и, значит, спрос
эластичен.
и, значит, спрос
эластичен.
Эластичность спроса означает, что его относительное изменение по абсолютной величине превосходит относительное изменение цены; неэластичность означает меньшее относительное изменение спроса по сравнению с ценой; нейтральность – равенство этих изменений по абсолютной величине.
Пример.
Пусть зависимость
спроса от цены
представлена
функцией
![]() .
Величина
.
Величина
![]()
равна
выручке, получаемой
от продажи
товара в объеме,
равном спросу
на товар. Выясним,
как изменяется
спрос с увеличением
цены. Для этого
найдем производную
![]() :
:
![]() ,
,
откуда
![]() .
.
Будем предполагать,
что
![]() ,
поскольку, как
правило, спрос
уменьшается
с ростом цены.
В этом случае
,
поскольку, как
правило, спрос
уменьшается
с ростом цены.
В этом случае
![]() и, следовательно,
имеем
и, следовательно,
имеем
![]() .
.
Отсюда
видно, что если
спрос эластичен
(![]() ),
то
),
то
![]() ,
и с повышением
цены выручка
от продажи
товара снижается;
если спрос
нейтрален (
,
и с повышением
цены выручка
от продажи
товара снижается;
если спрос
нейтрален (![]() ),
то
),
то
![]() ,
и выручка
мало зависит
от изменения
цены; если спрос
неэластичен
(
,
и выручка
мало зависит
от изменения
цены; если спрос
неэластичен
(![]() ),
то
),
то
![]() ,
и выручка
увеличивается
с ростом цены.
,
и выручка
увеличивается
с ростом цены.
Упражнения
1. Найти
производные
![]() функций:
функций:
1)
![]() ;
;
2)![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
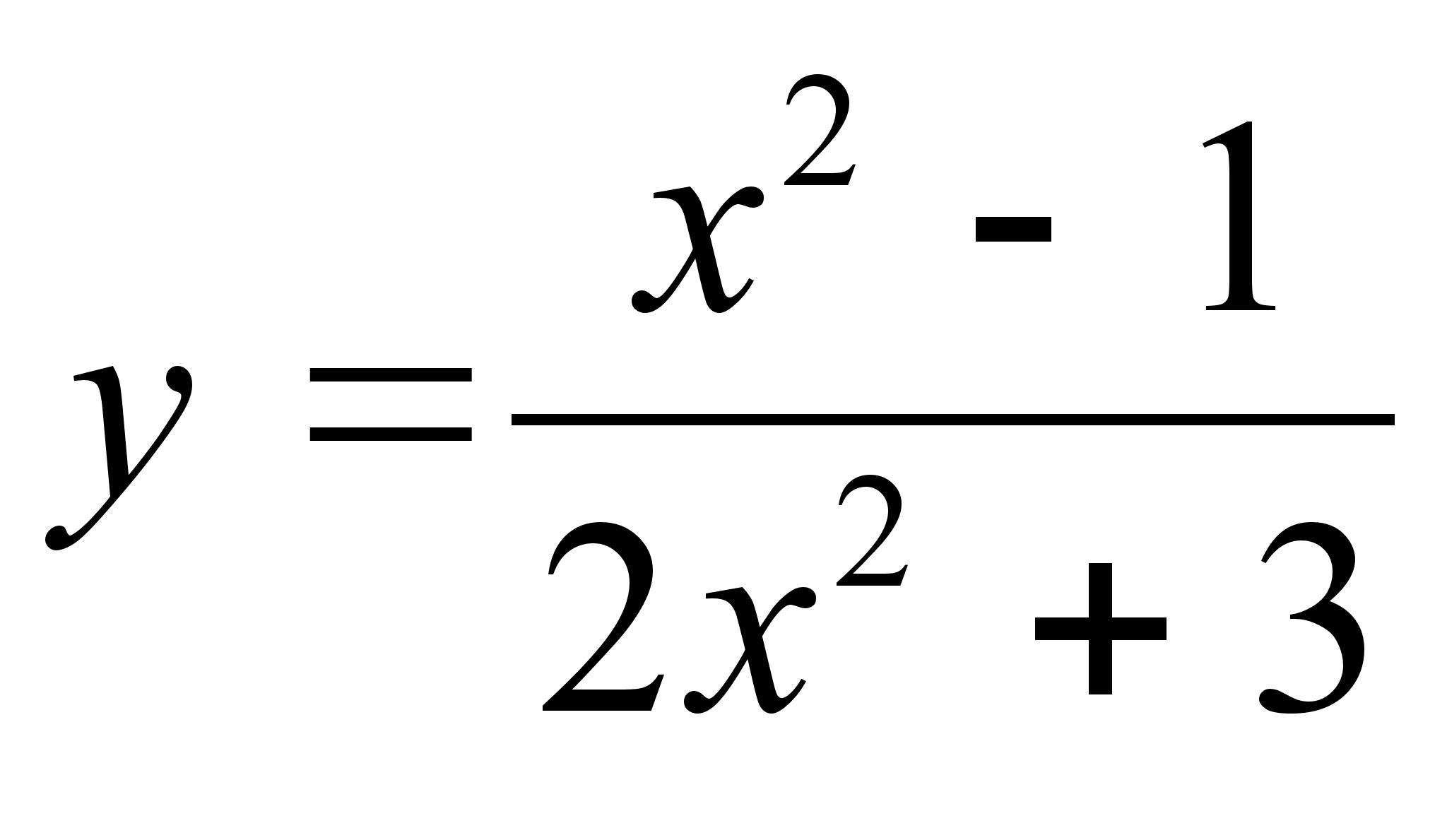 ;
;
13)
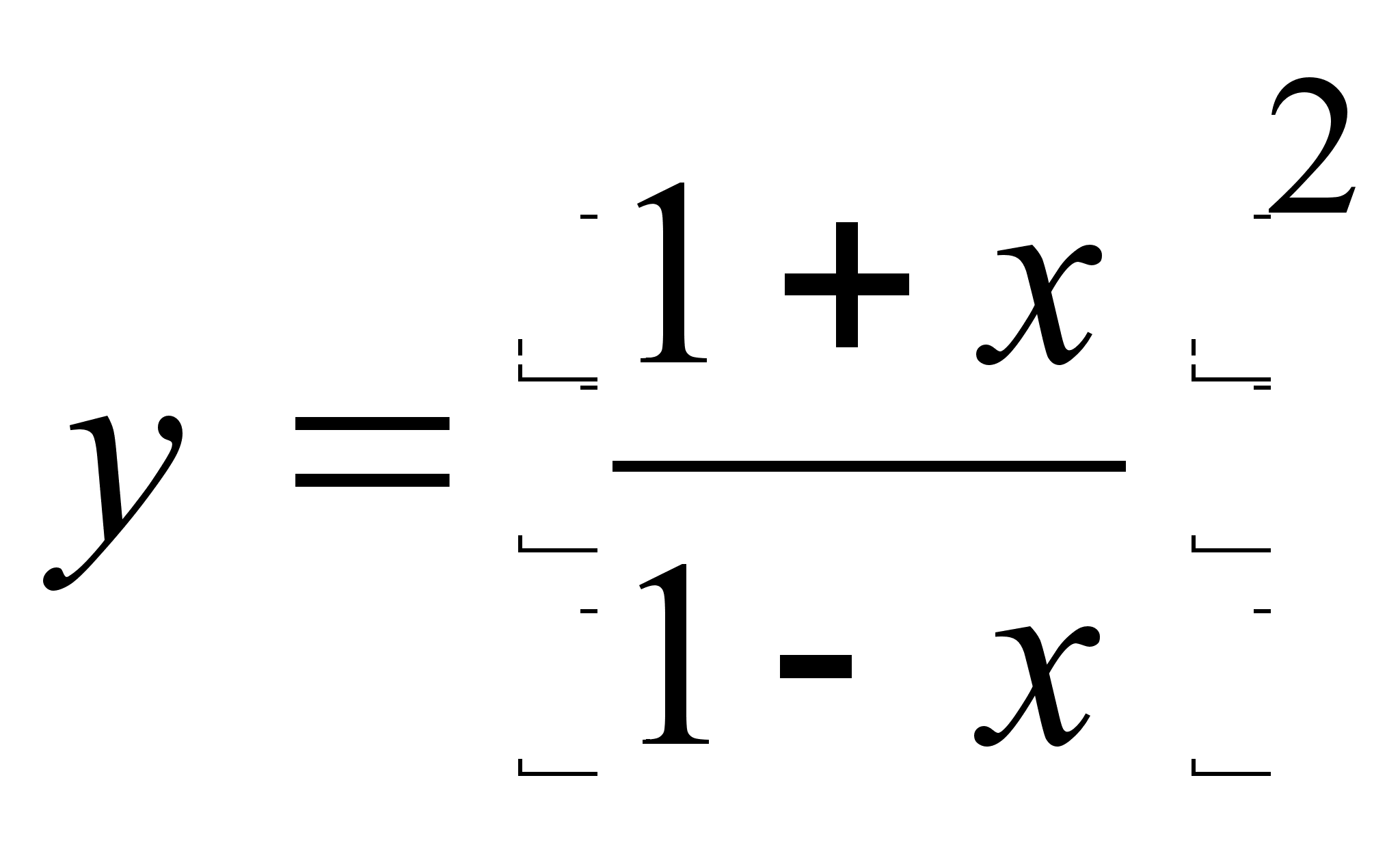 ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]()
21)
![]() ;
;
22)
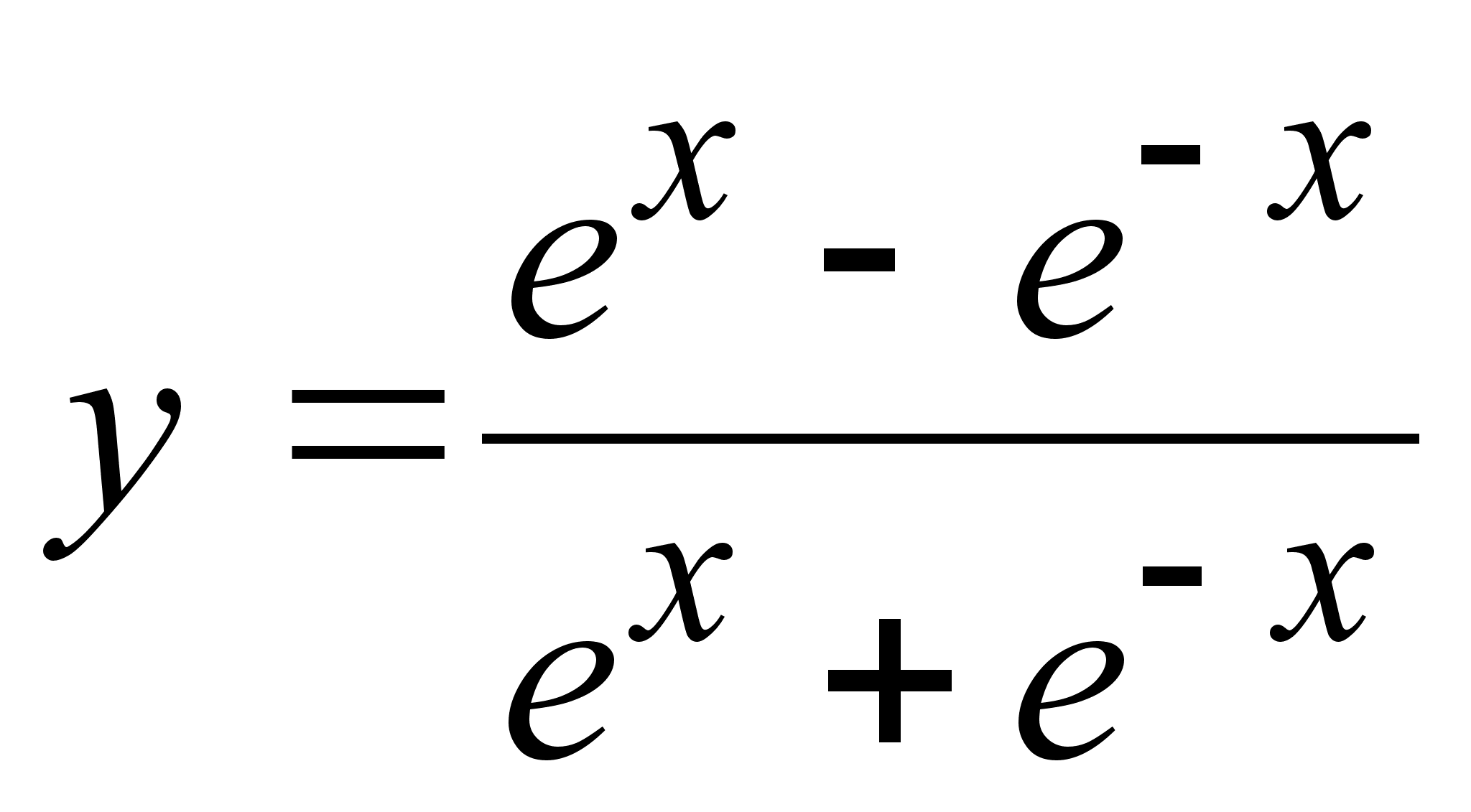 ;
;
23)
![]() ;
;
24)
![]() ;
;
25)
![]() ;
;
26)
![]() .
.
2. Определить угол наклона касательной к графику функции:
1)![]() при
при
![]() ;
;
2)
![]() при
при
![]() ;
;
3)![]() при
при
![]() ;
;
4)
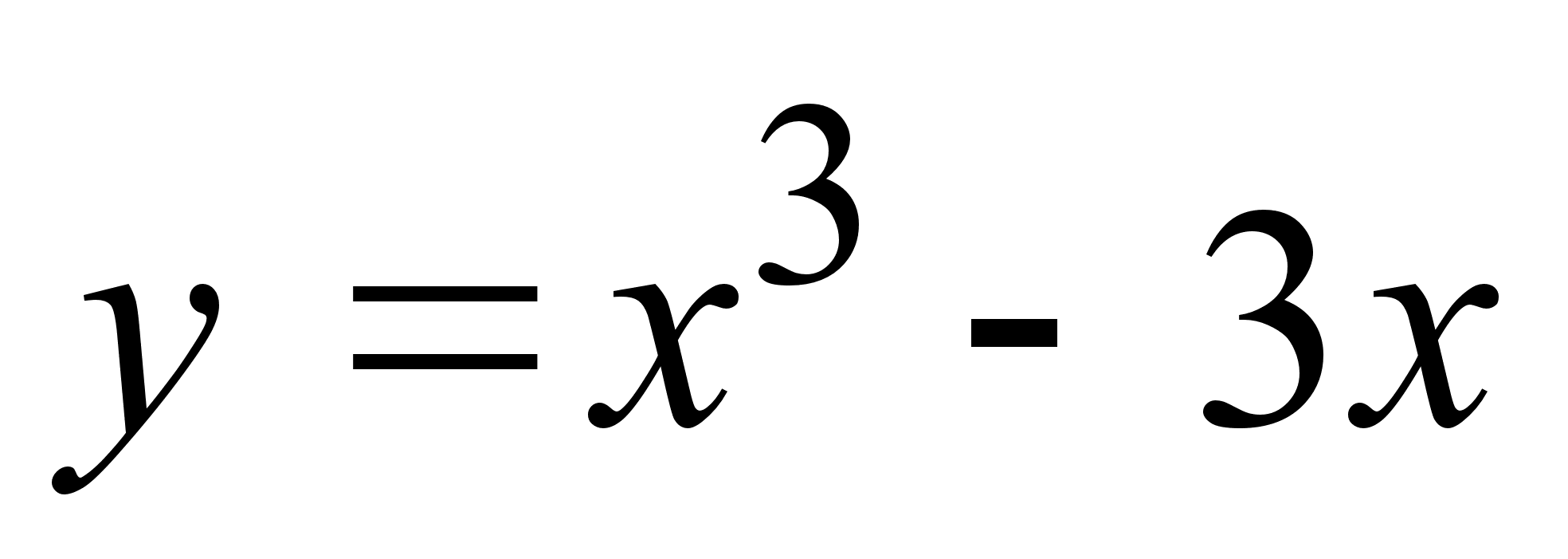 при
при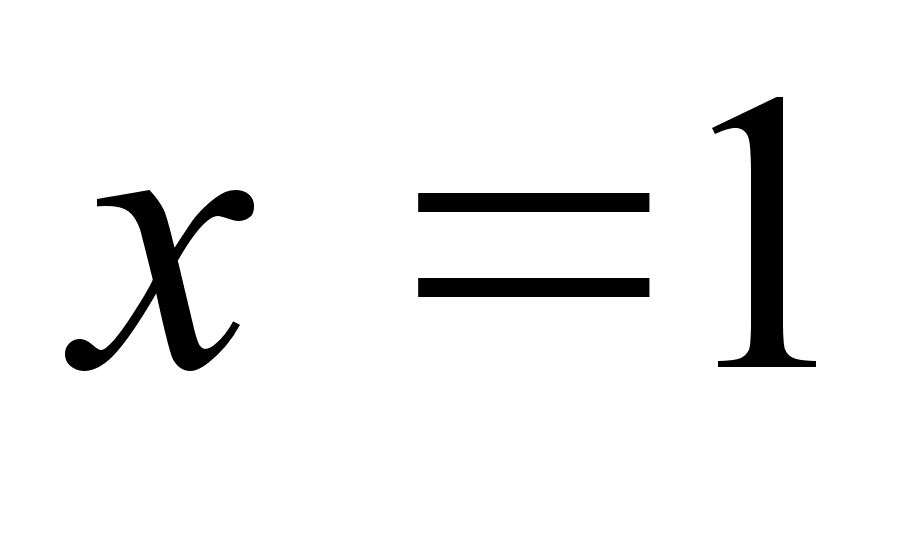 .
.
3. Найти промежутки возрастания и убывания функций и их экстремумы:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
4. Найти эластичность функций:
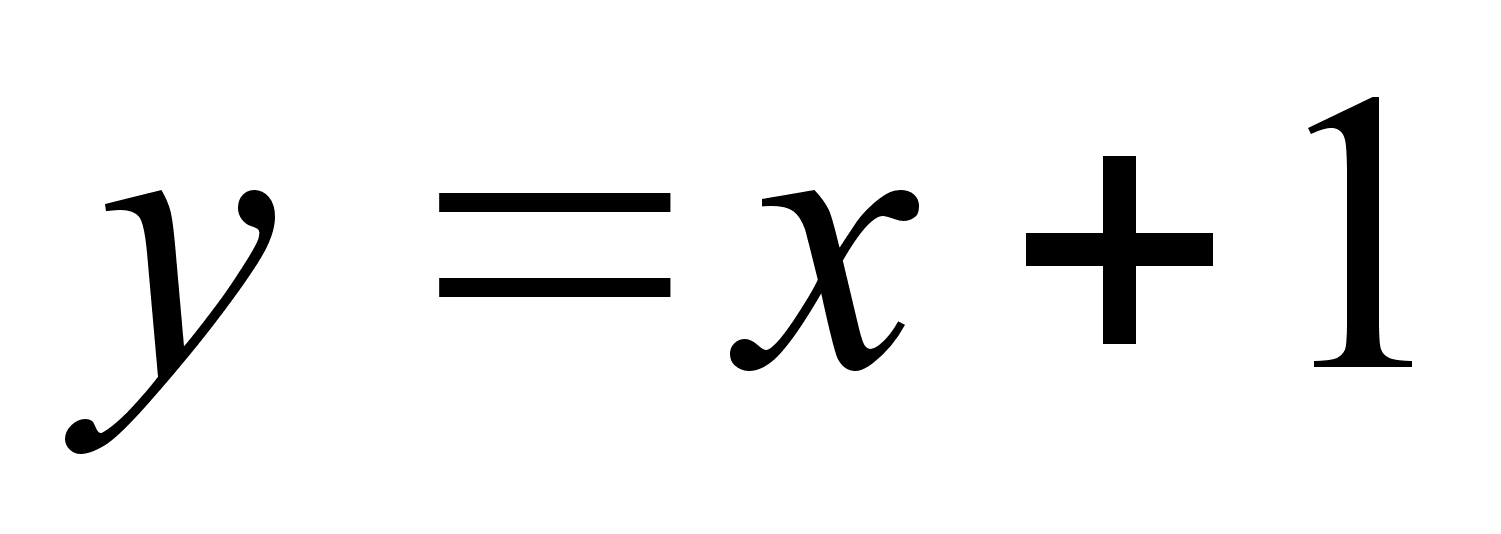 ;
;
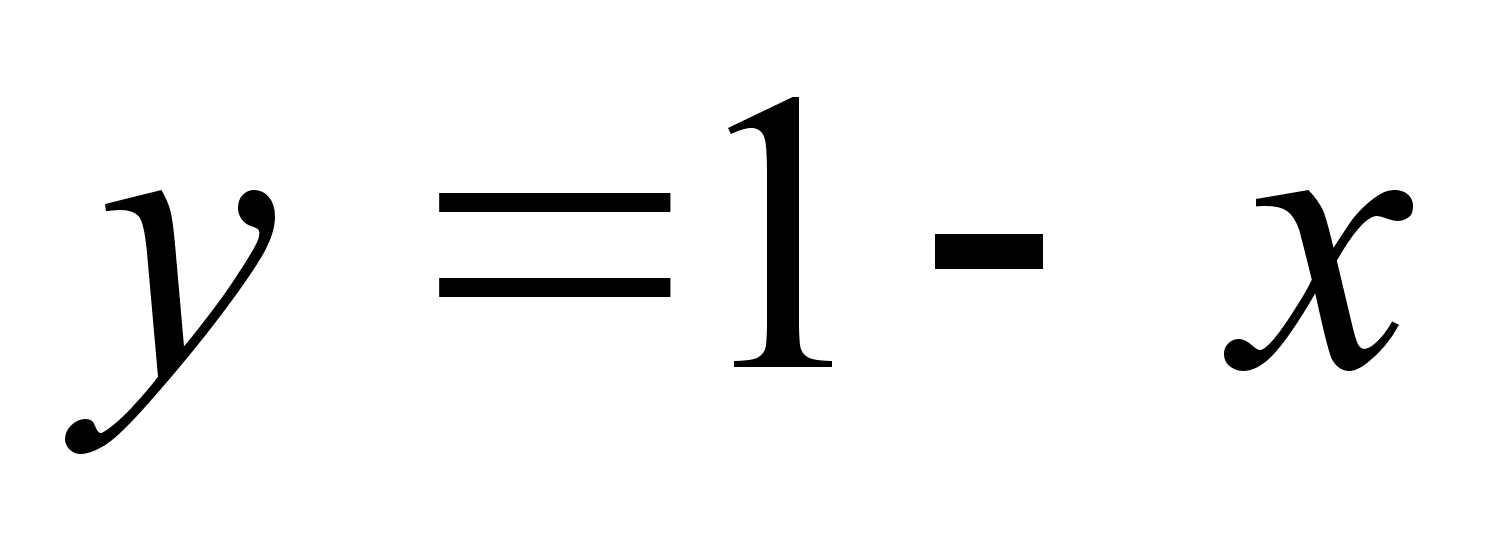 ;
;
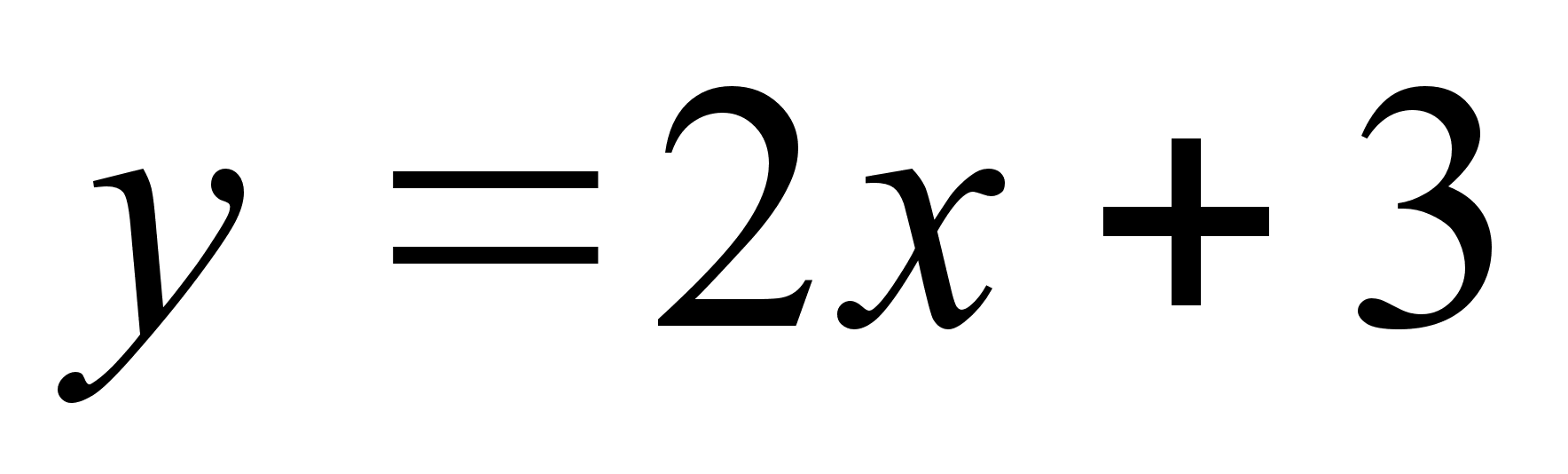 ;
;
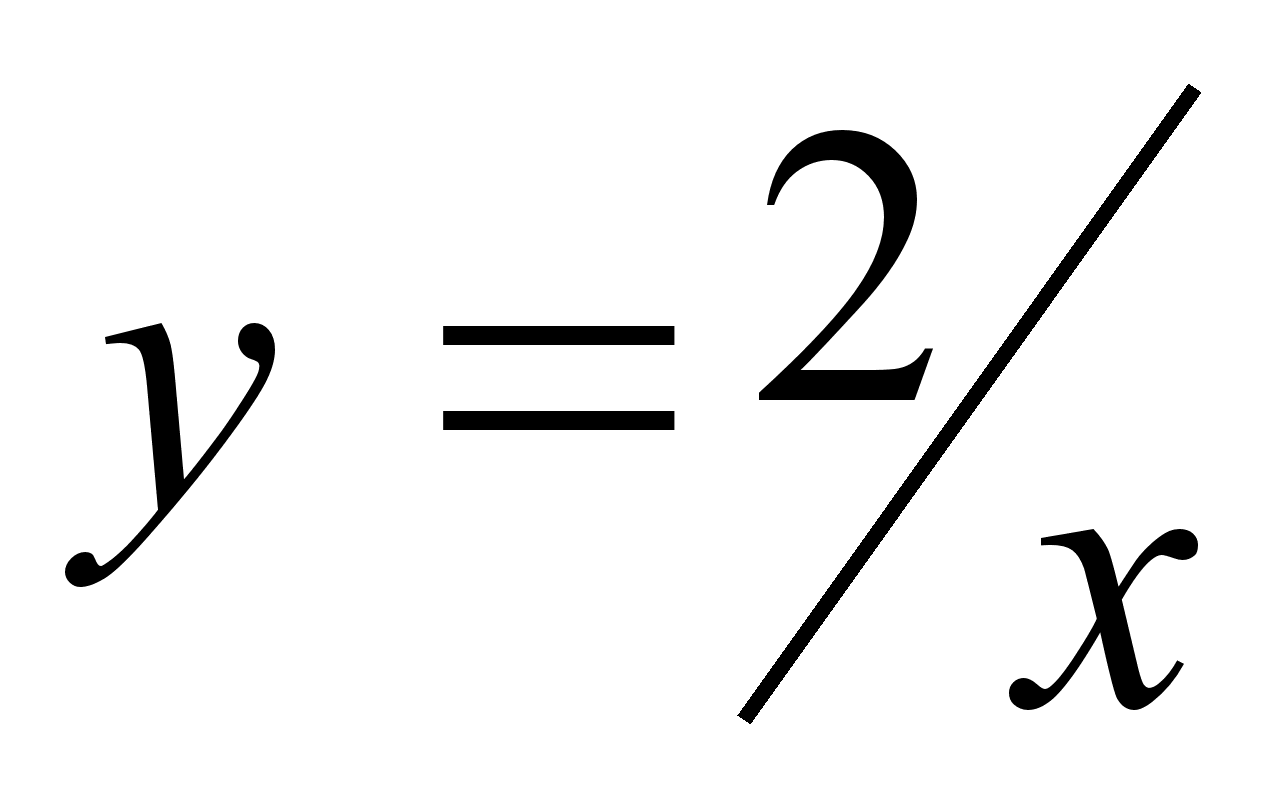 ;
;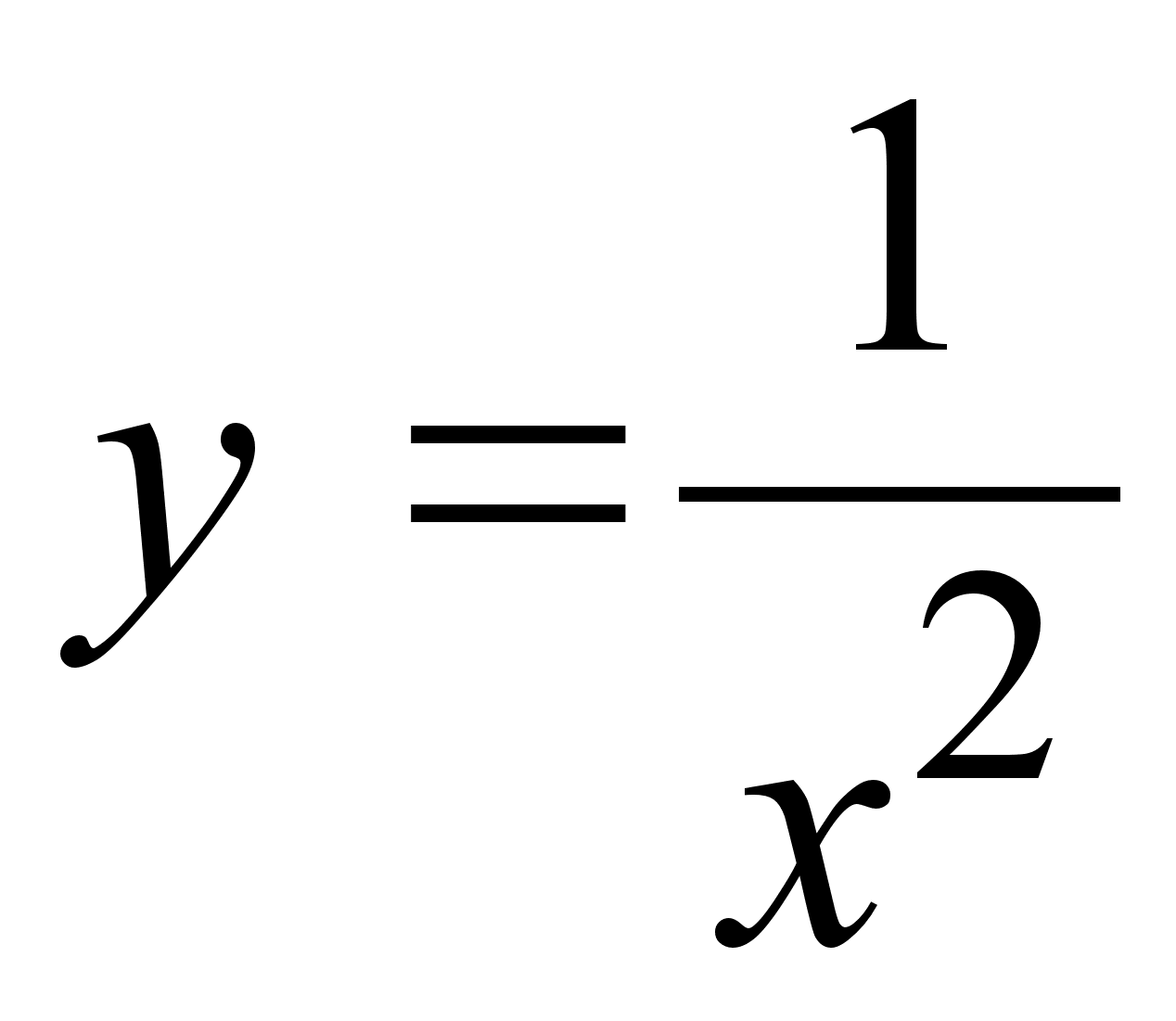 ;
;
6)
![]() .
.
5. Для
заданной зависимости
спроса
![]() от цены
от цены
![]() найти эластичность
спроса и вычислить
ее при заданном
значении
найти эластичность
спроса и вычислить
ее при заданном
значении
![]() :
:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
6. Для
заданной зависимости
спроса
![]() от цены
от цены
![]() найти значения
цены, при которых
выручка возрастает
с увеличением
цены:
найти значения
цены, при которых
выручка возрастает
с увеличением
цены:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Ответы и решения
1.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
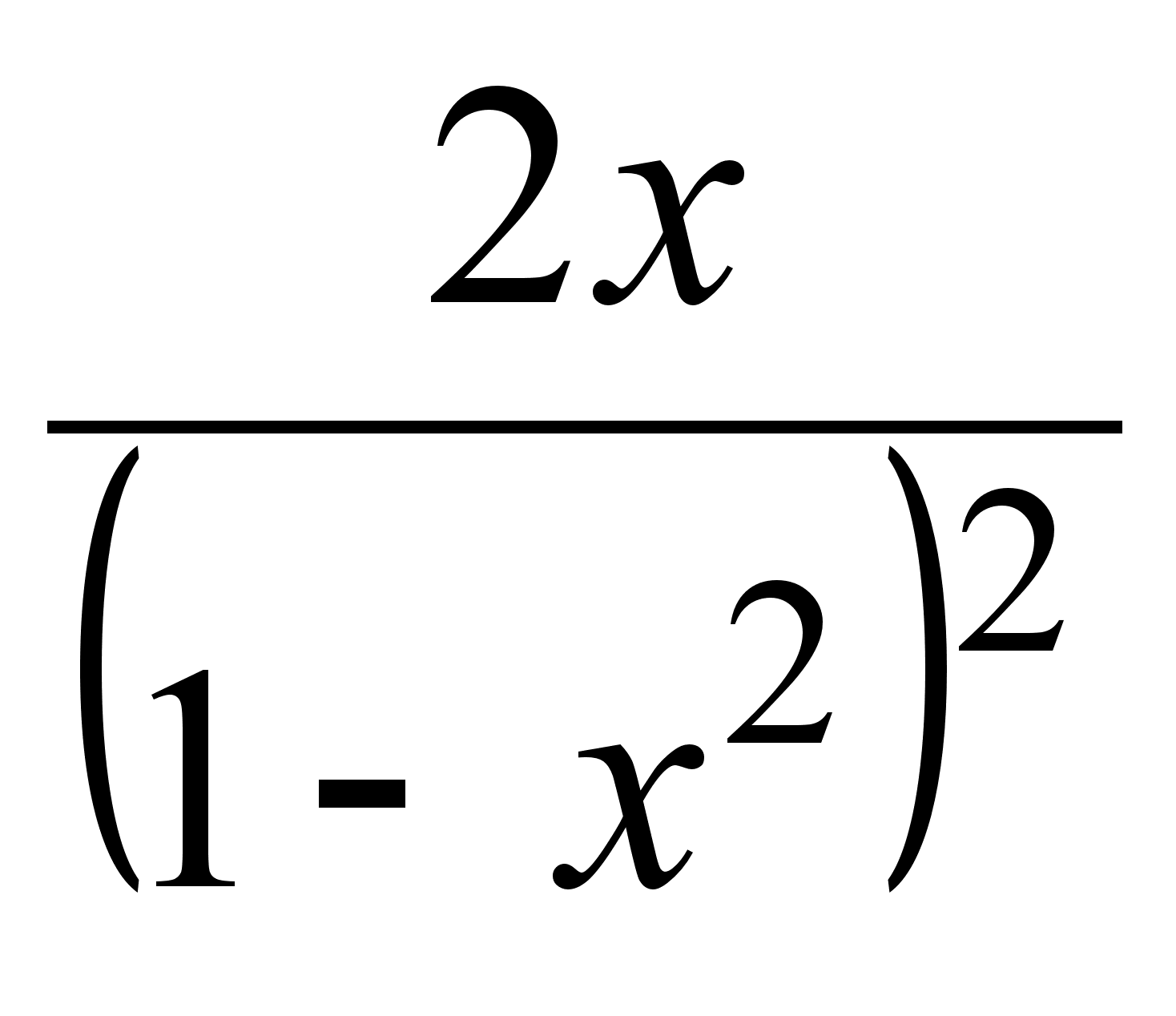 ;
;
11)
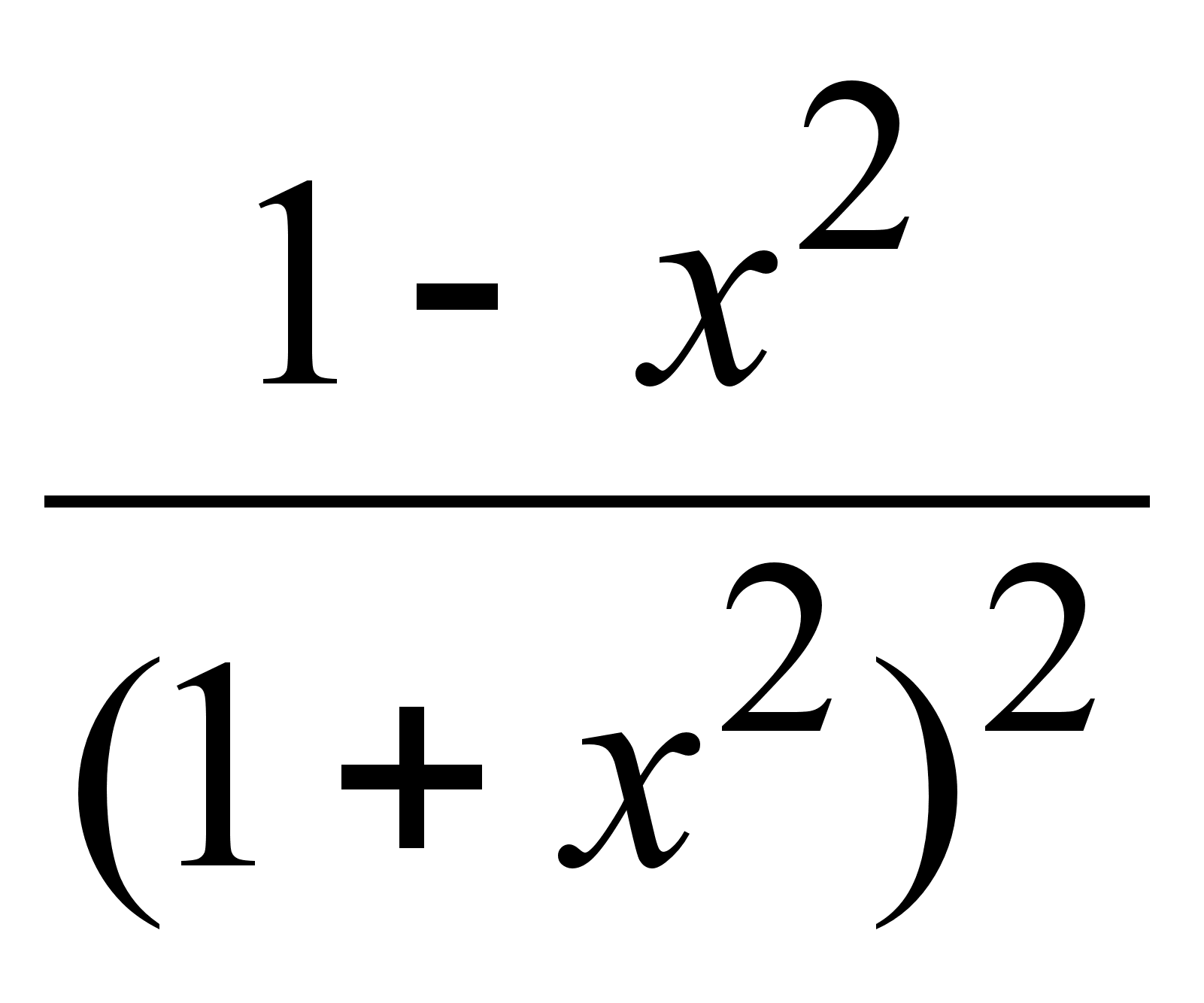 ;
;
12)
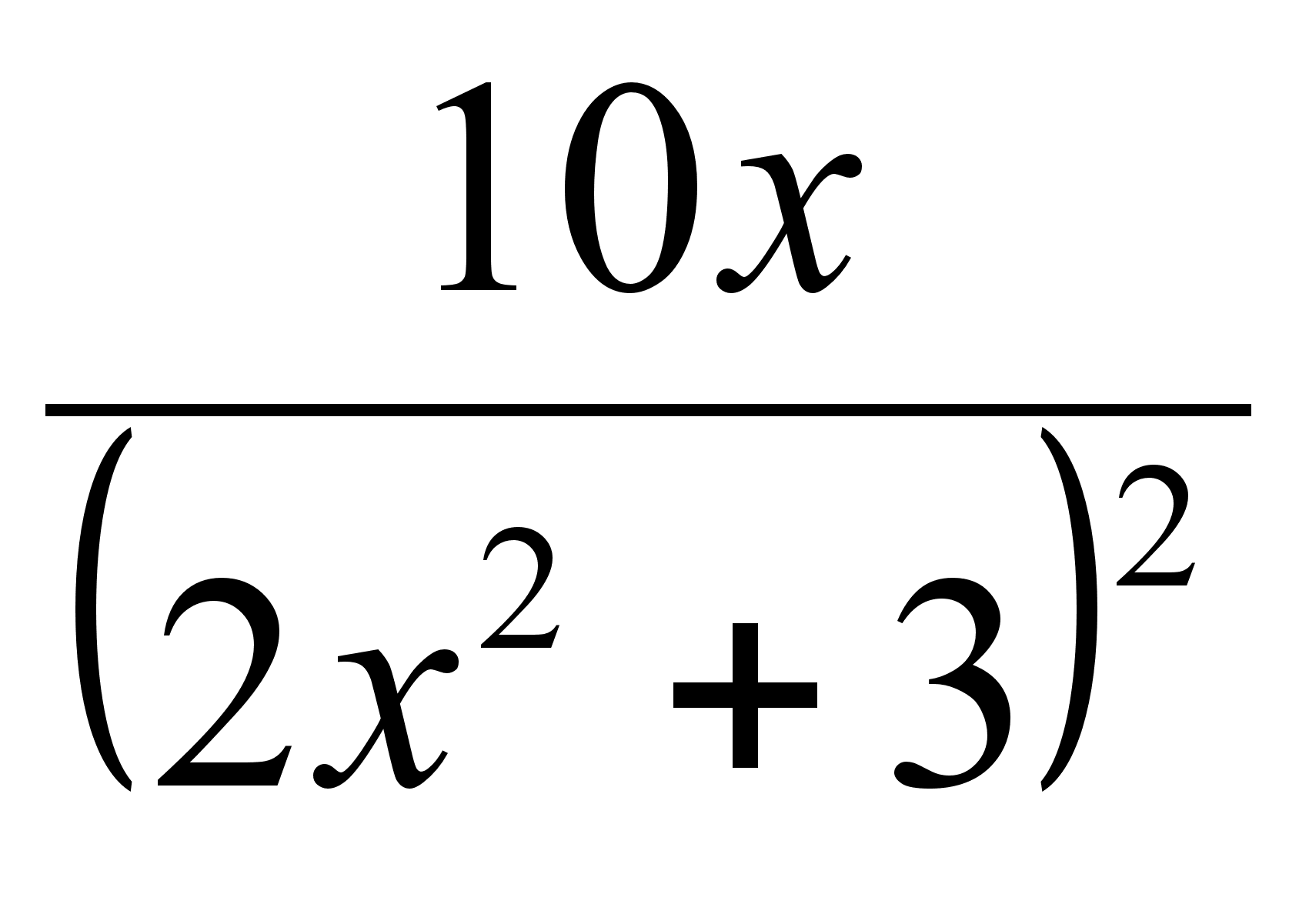 ;
;
13)
![]() ;
;
14)
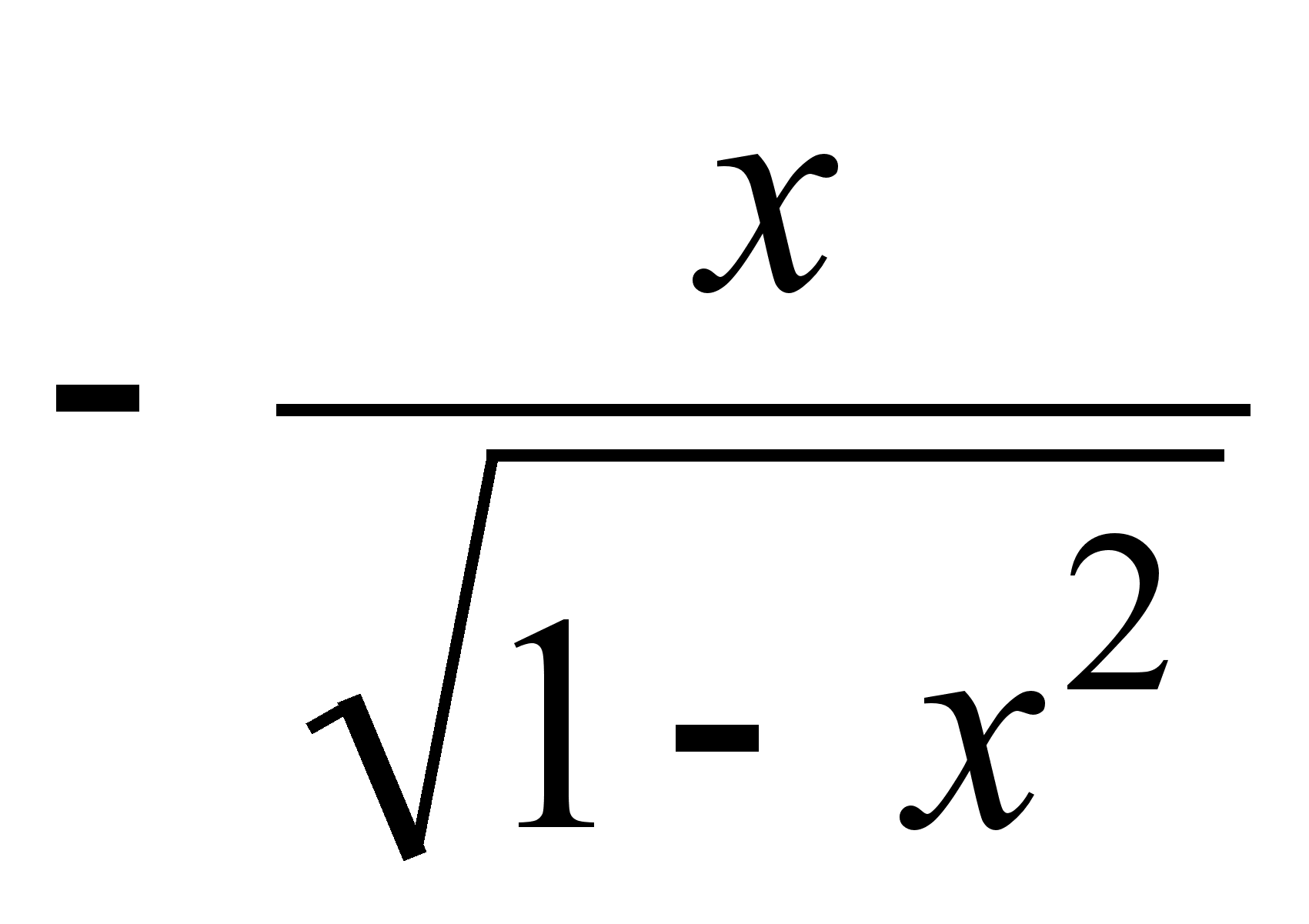 ;
;
15)
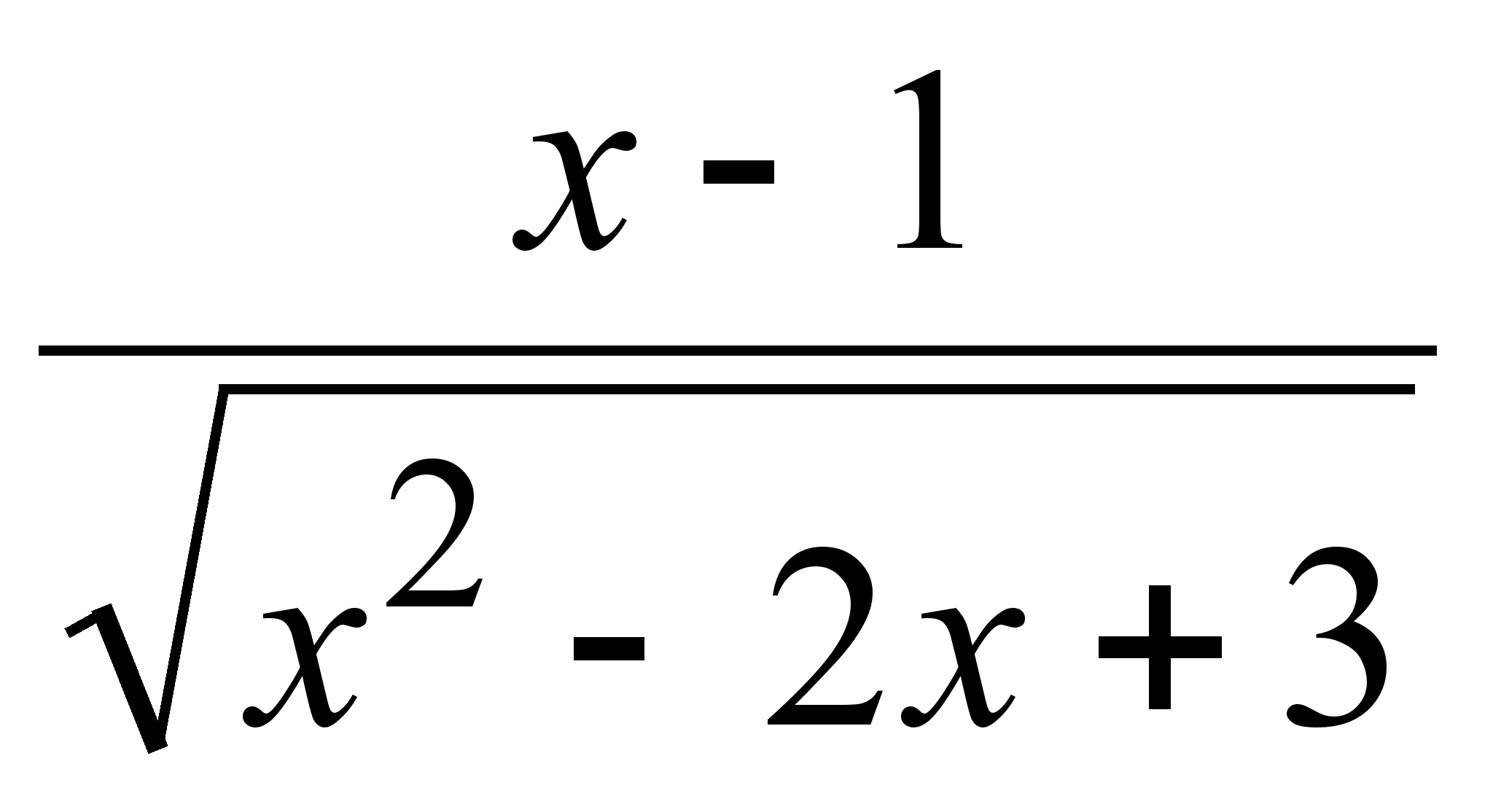 ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
![]() ;
;
22)
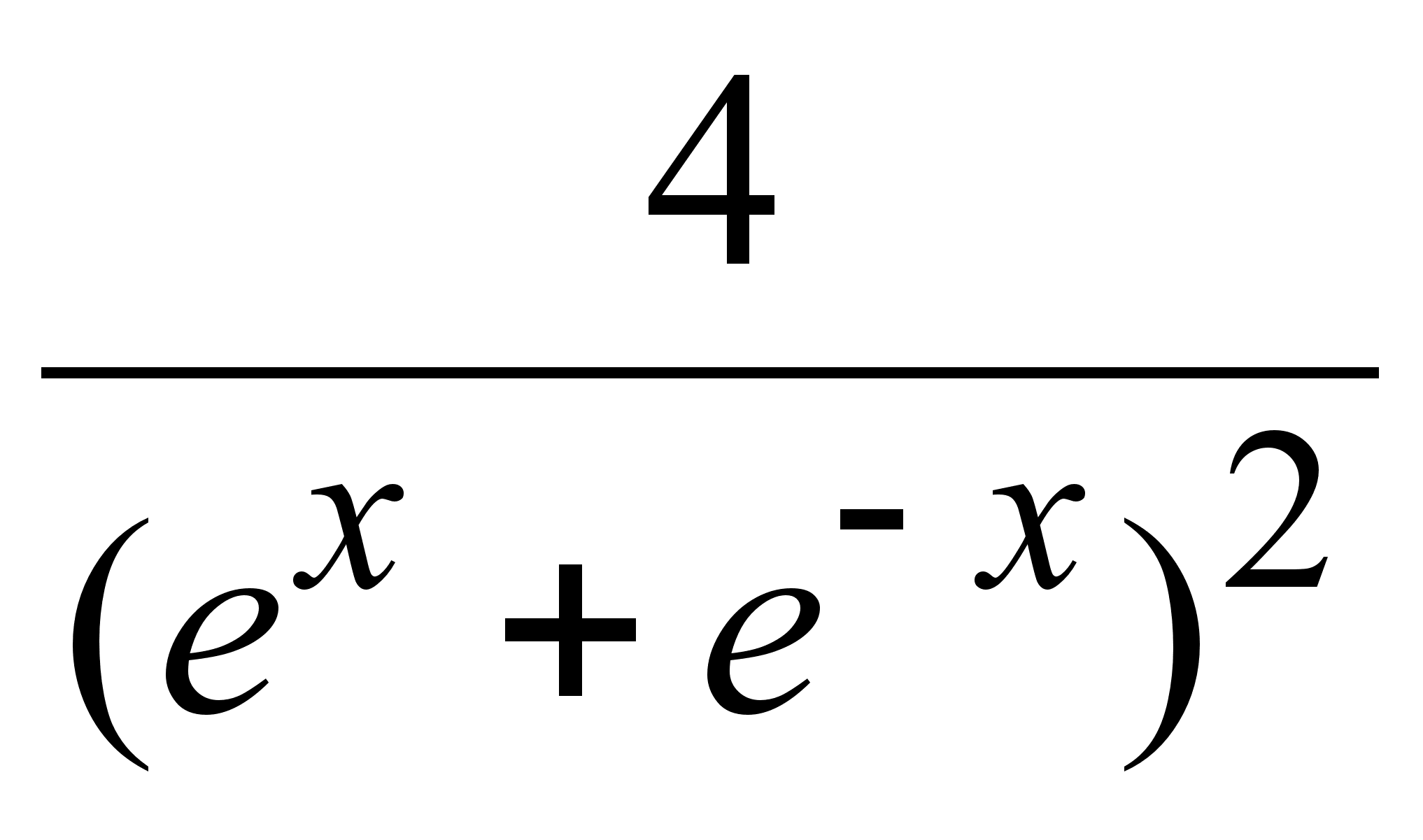 ;
;
23)
![]() ;
;
24)
![]() ;
;
25)
![]() ;
;
26)
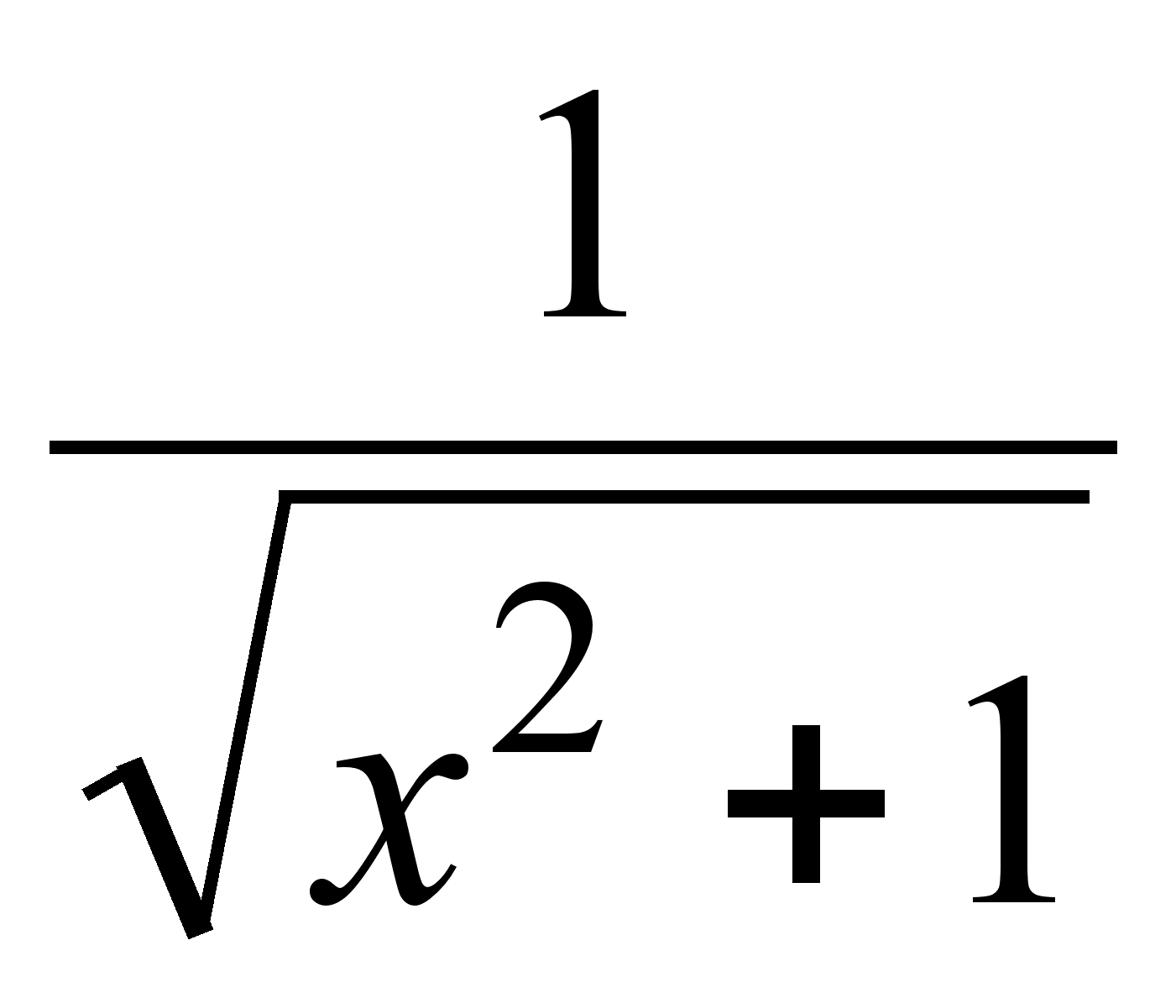 .
.
2.
1) Угол
наклона касательной
![]() поскольку
поскольку![]() ;
;
2)
![]() ;
3)
;
3)
![]() ,
4)
,
4)
![]() .
.
3.
1) При
![]() функция убывает,
при
функция убывает,
при
![]() - возрастает;
- возрастает;
![]() ;
;
2) Функция
возрастает
при
![]() и
и
![]() ;
убывает при
;
убывает при
![]() ;
;
![]() ;
;
![]() ;
;
3) Функция
убывает при
всех
![]() ;
4) Функция возрастает
при всех
;
4) Функция возрастает
при всех
![]() ;
;
5) Функция
убывает при
![]() ,
возрастает
при
,
возрастает
при
![]() ;
;
![]() ;
;
6) Функция
убывает при
всех
![]() ;
;
7) Функция
возрастает
при
![]() ,
убывает при
,
убывает при
![]() ;
;
![]() ;
;
8) Функция
убывает при
![]() и
и
![]() ,
возрастает
при
,
возрастает
при
![]() ;
;
![]() ,
,
![]() ;
;
9) Функция
возрастает
при
![]() ,
убывает при
,
убывает при
![]() ;
;![]() ;
;
10) Функция
убывает при
![]() ,
возрастает
при
,
возрастает
при
![]() ;
;
![]() ;
;
4.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() .
.
5.
1)
![]() ,
,
![]() ;
спрос нейтрален;
2)
;
спрос нейтрален;
2)
![]() ,
,
![]() ;
спрос эластичен;
3)
;
спрос эластичен;
3)
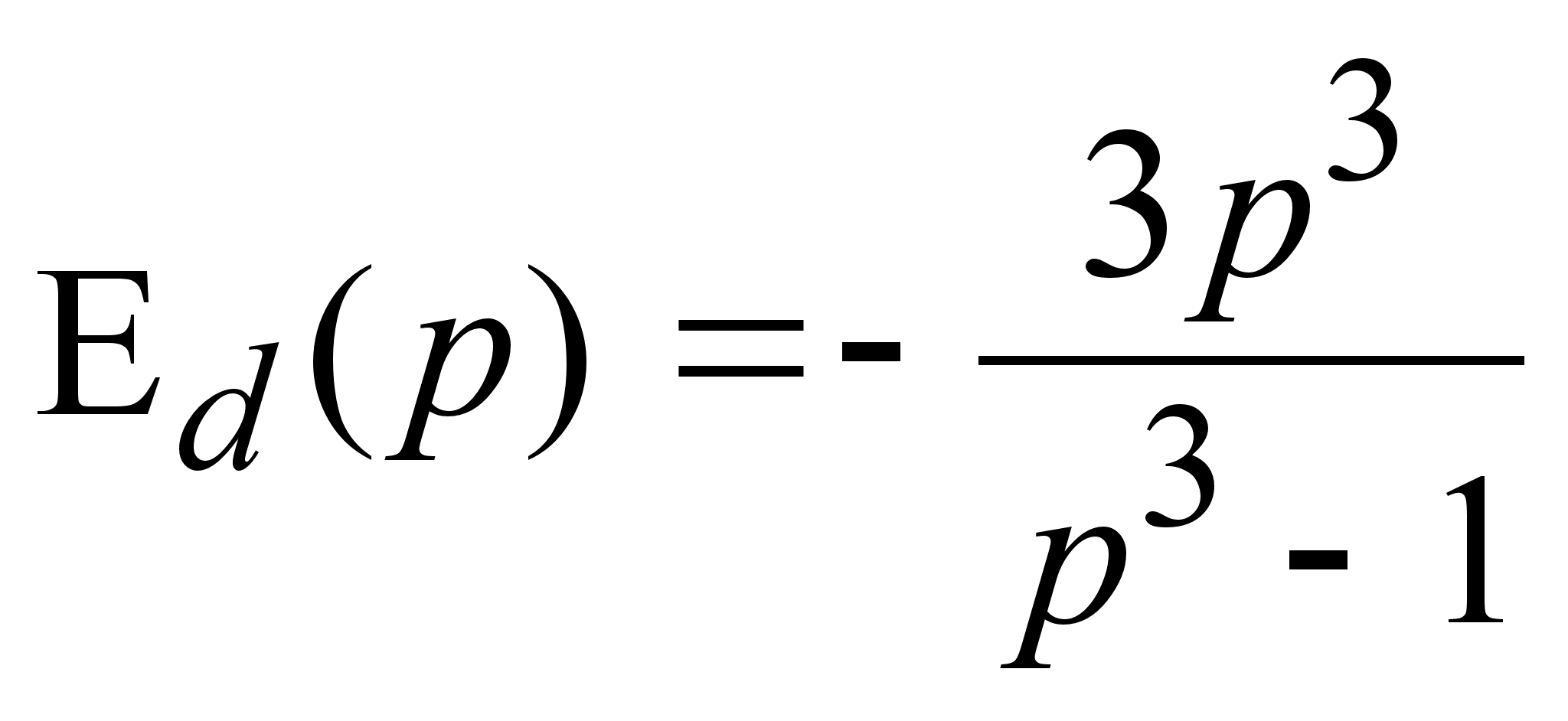 ,
,
![]() ;
спрос неэластичен.
;
спрос неэластичен.
6. 1)
![]() ;
2)
;
2)
![]() ;
3) Таких значений
цены нет; выручка
не меняется
с ростом цены.
;
3) Таких значений
цены нет; выручка
не меняется
с ростом цены.
§ 4. Неопределенный интеграл
К понятию неопределенного интеграла приводит задача о нахождении функции по ее производной. Эта задача решается с помощью операции интегрирования, обратной по отношению к операции дифференцирования.
1. Определение интеграла и правила интегрирования
Пусть для всех
![]() ,
принадлежащих
интервалу
,
принадлежащих
интервалу
![]() ,
выполнено
равенство
,
выполнено
равенство
![]() ,
,
тогда
функция
![]() называется
первообразной
функции
называется
первообразной
функции
![]() на
на
![]() .
.
Заметим,
что первообразная
функции
![]() определяется
не однозначно:
вместе с
определяется
не однозначно:
вместе с
![]() первообразными
являются функции
вида
первообразными
являются функции
вида
![]() ,
где
,
где
![]() –
произвольная
постоянная.
Справедливо
утверждение:
любая первообразная
функции представима
в виде
–
произвольная
постоянная.
Справедливо
утверждение:
любая первообразная
функции представима
в виде
![]() при некотором
значении
при некотором
значении
![]() .
.
Совокупность
всех первообразных
функции
![]() называется
ее неопределенным
интегралом
и обозначается
символом
называется
ее неопределенным
интегралом
и обозначается
символом
![]() :
:
![]() ;
;
при
этом
![]() называется
подынтегральной
функцией, а
называется
подынтегральной
функцией, а
![]() - переменной
интегрирования.
Операция нахождения
интеграла
называется
интегрированием.
- переменной
интегрирования.
Операция нахождения
интеграла
называется
интегрированием.
Пример. а) Из
равенства
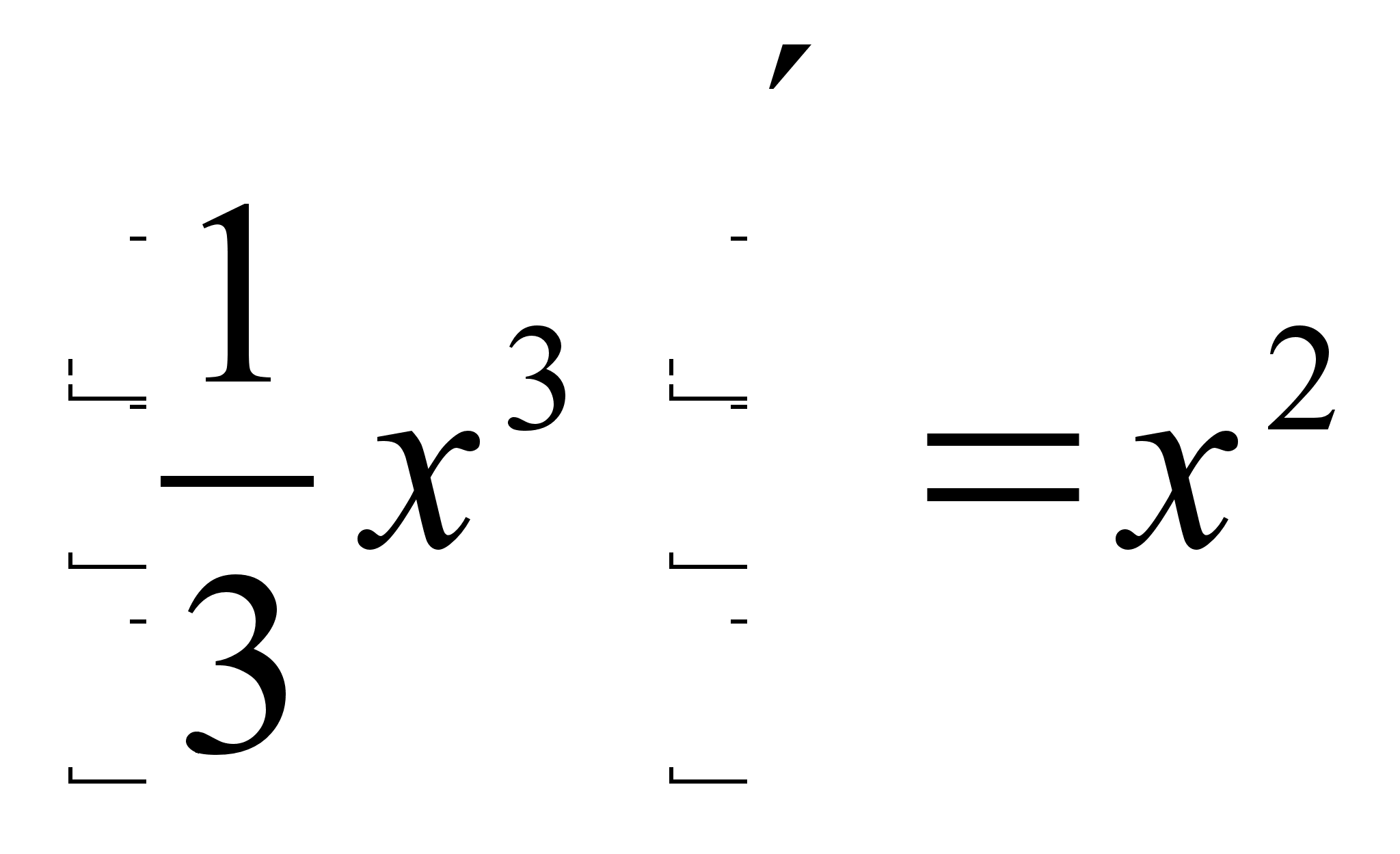 заключаем, что
функция
заключаем, что
функция
![]() является
первообразной
функции
является
первообразной
функции
![]() .
Следовательно,
можно записать
.
Следовательно,
можно записать
![]() .
.
б)
Аналогично,
из равенства
![]() следует
следует
![]() .
.
В отличие от
производной
интеграл элементарной
функции может
не быть элементарной
функцией. Это
относится,
например, к
интегралам
от
![]() ,
,
![]() ,
,
![]() .
Однако интегралы
всех основных
элементарных
функций выражаются
через элементарные
функции. Приведем
таблицу некоторых
из них, получаемую
из таблицы
производных,
и правила, по
которым можно
находить интегралы
других функций.
.
Однако интегралы
всех основных
элементарных
функций выражаются
через элементарные
функции. Приведем
таблицу некоторых
из них, получаемую
из таблицы
производных,
и правила, по
которым можно
находить интегралы
других функций.
Таблица интегралов
1)
![]() (
(![]() );
2)
);
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]()
![]() .
.
Правила интегрирования
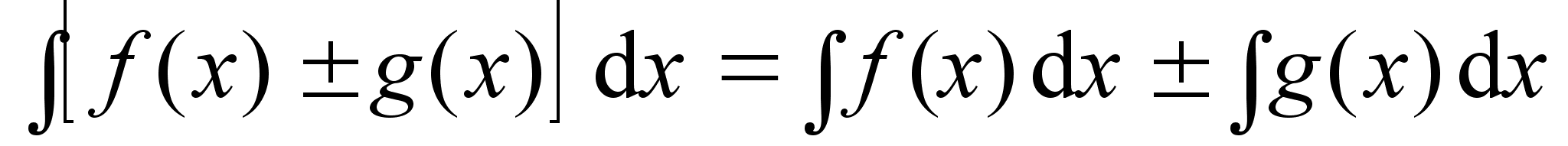 ;
;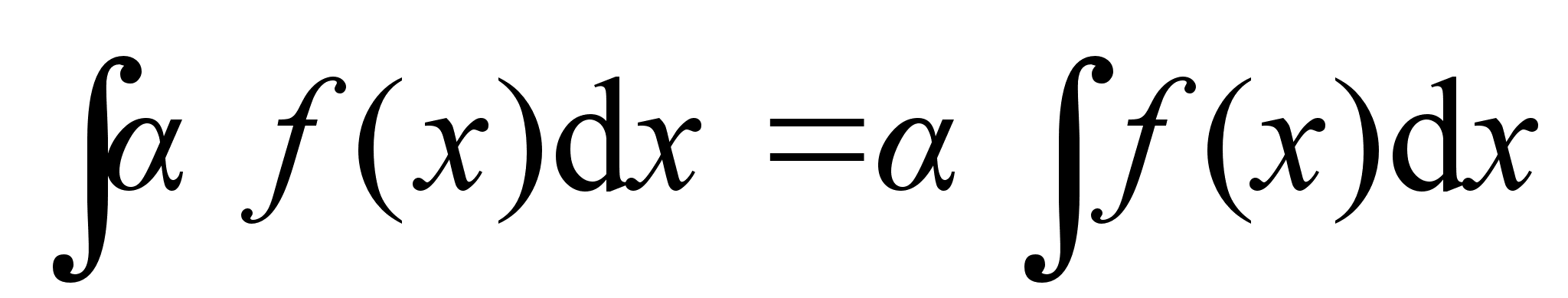 ,
где -
постоянная
,
где -
постоянная
Отметим, что приведенные правила аналогичны соответствующим правилам дифференцирования.
Примеры. Найдем интегралы, применяя указанные правила и таблицу:
а)
![]() ;
;
б)
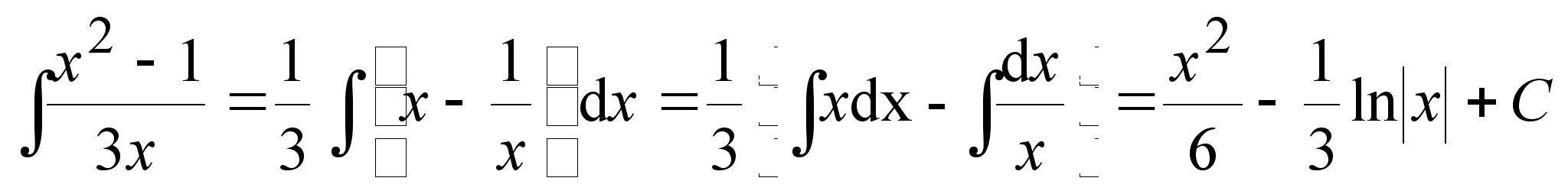 ;
;
в)
![]() .
.
2. Замена переменной в неопределенном интеграле
В некоторых
случаях нахождение
интеграла
упрощается
при переходе
к другой переменной
интегрирования.
При этом если
исходная и
новая переменные
![]() и
и
![]() связаны соотношением
связаны соотношением
![]() ,
где
,
где
![]() - обратимая
дифференцируемая
функция, то для
интегралов
справедливо
равенство
- обратимая
дифференцируемая
функция, то для
интегралов
справедливо
равенство
![]() ,
,
в правой
части которого
после вычисления
интеграла
следует сделать
обратную замену
![]() .
.
В частности,
используя
замену
![]() (или
(или
![]() ),
получаем формулу
),
получаем формулу
![]() ,
,
позволяющую обобщить табличные интегралы. Например:
![]() (
(![]() ),
),
![]() ,
,
![]() ,
,
где
![]() и
и
![]() - произвольные
постоянные,
- произвольные
постоянные,
![]() .
.
Примеры. Найдем интегралы, применяя полученные формулы:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
интеграл
![]() найдем, сделав
замену
найдем, сделав
замену
![]() ,
,
![]() .
Тогда
.
Тогда
![]() ,
,
где использован результат примера в);
д)
![]() .
.
Упражнения![]()
1. Найти интегралы:
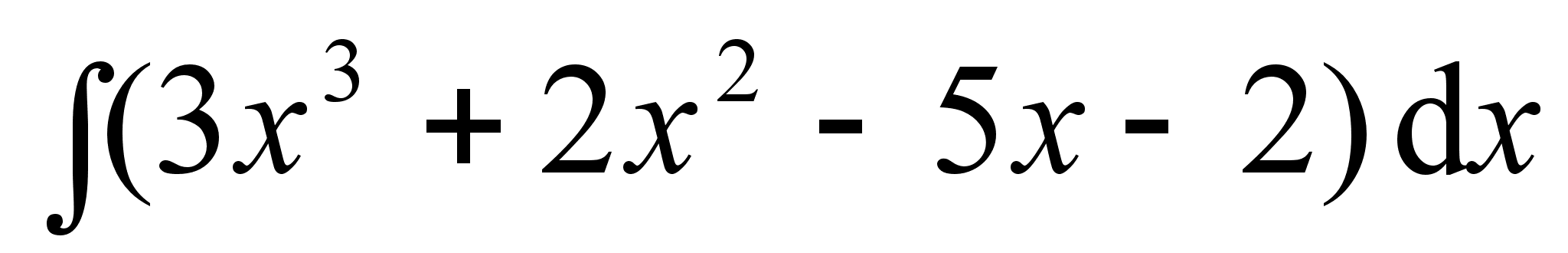 ;
;
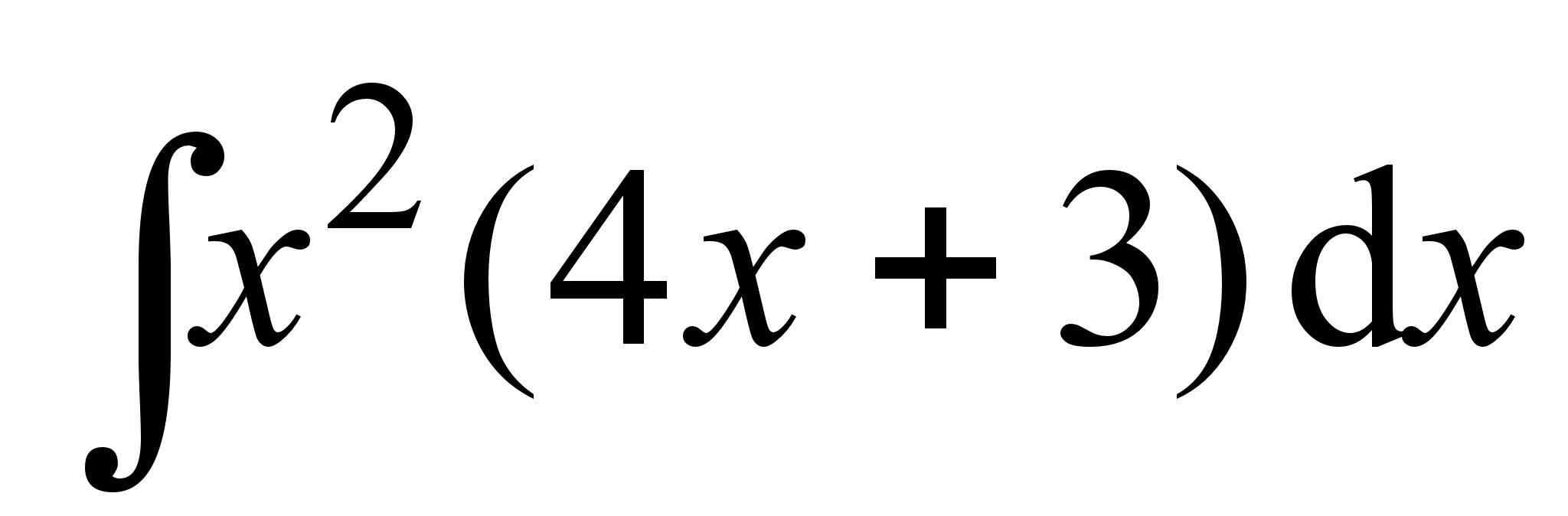 ;
;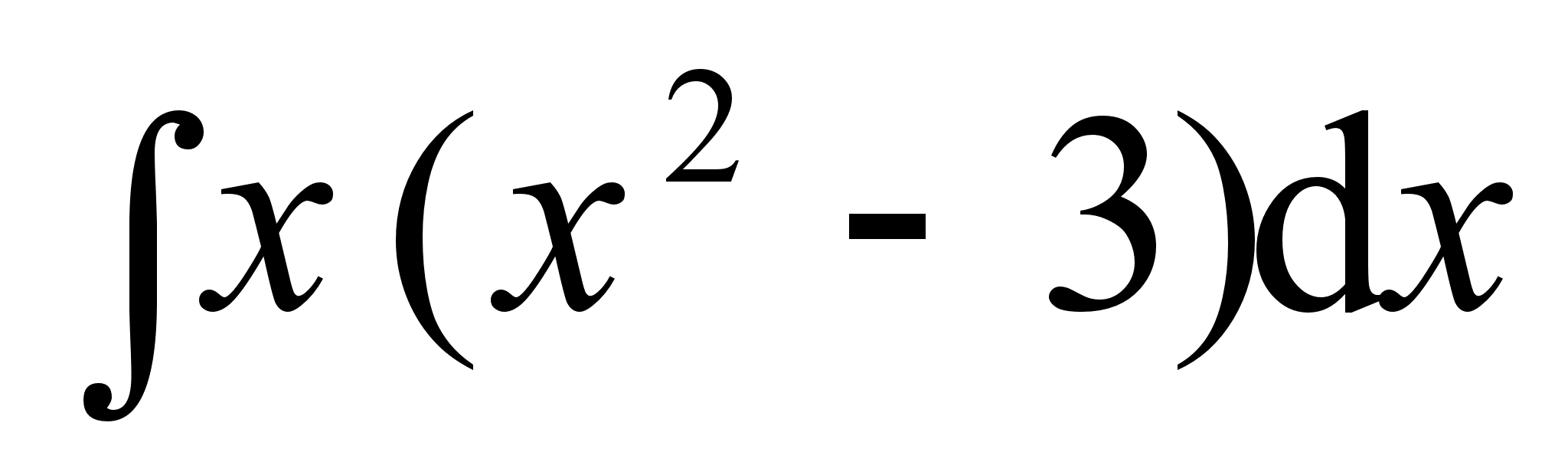
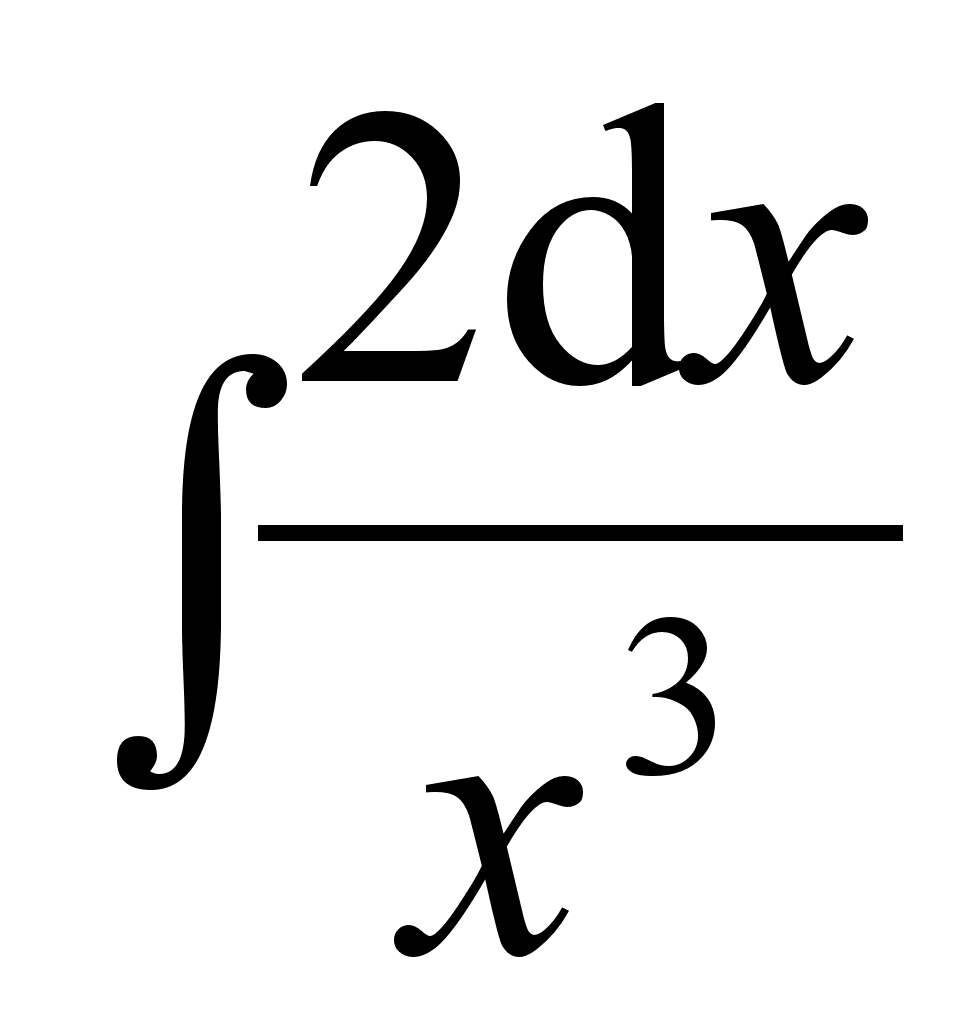 ;
; 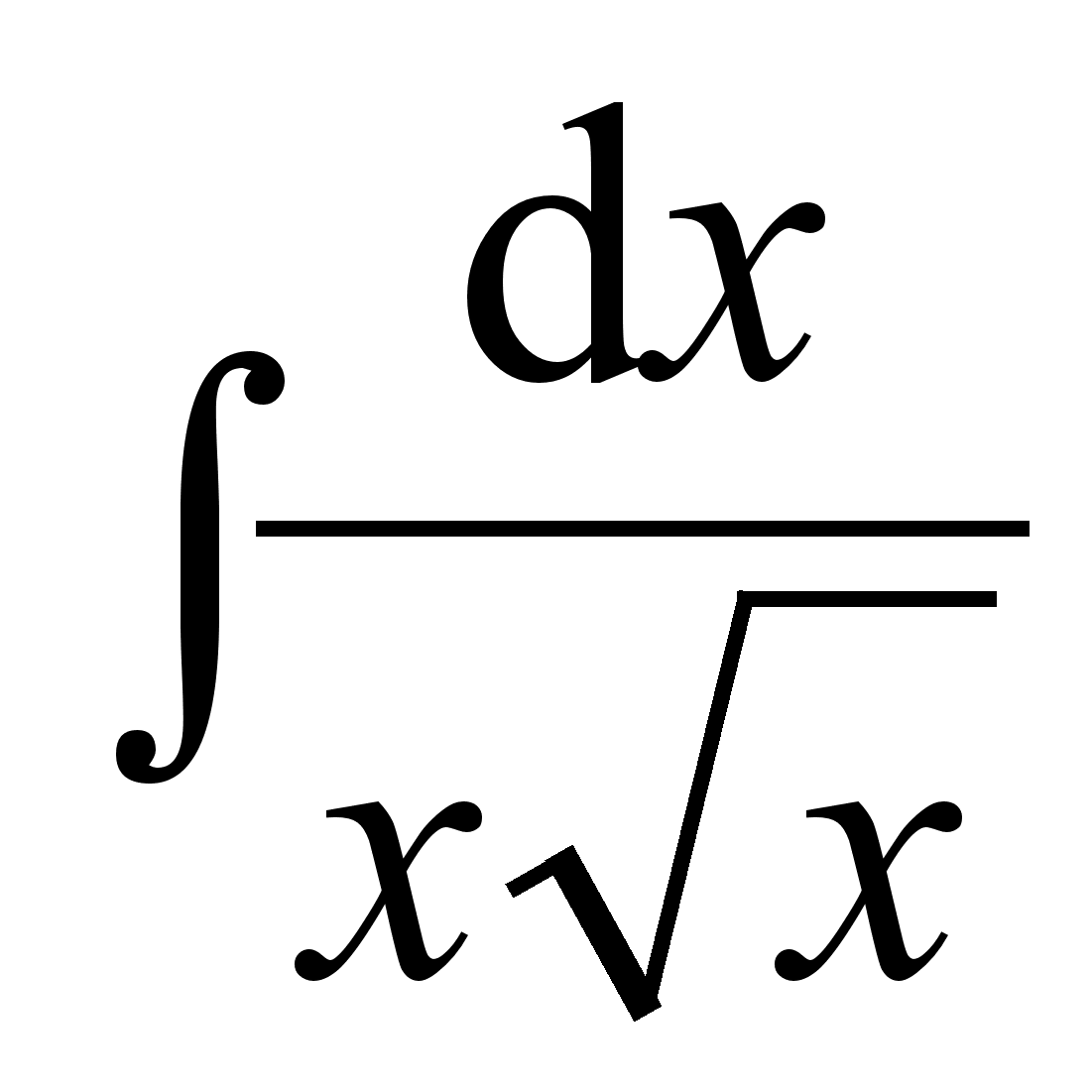 ;
;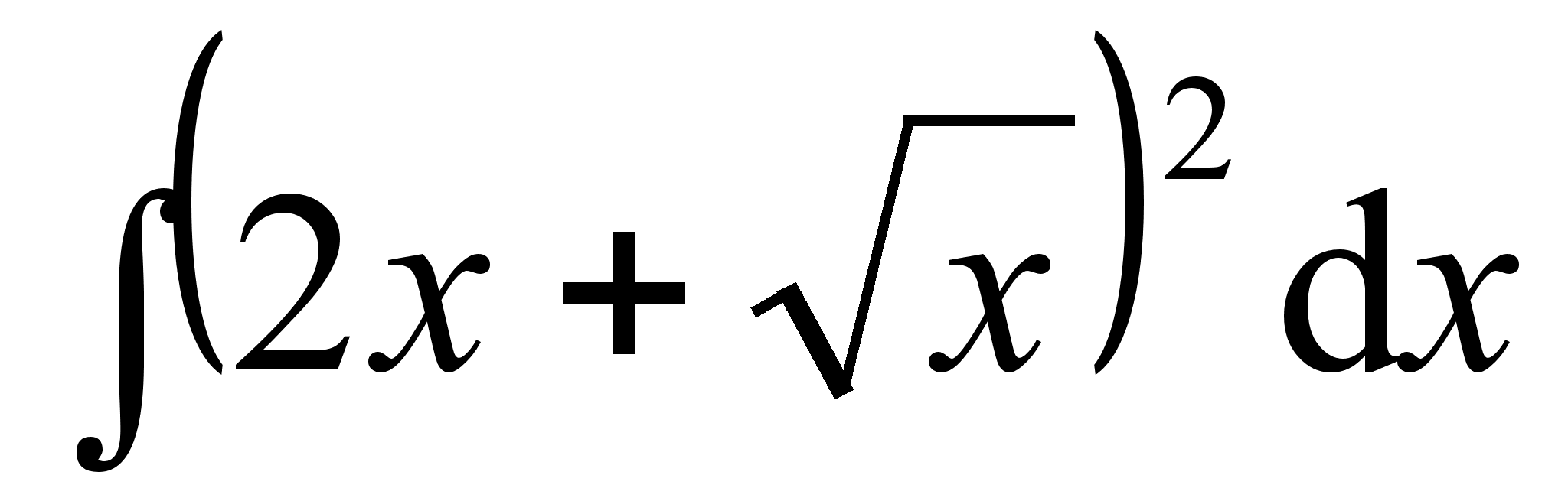 ;
;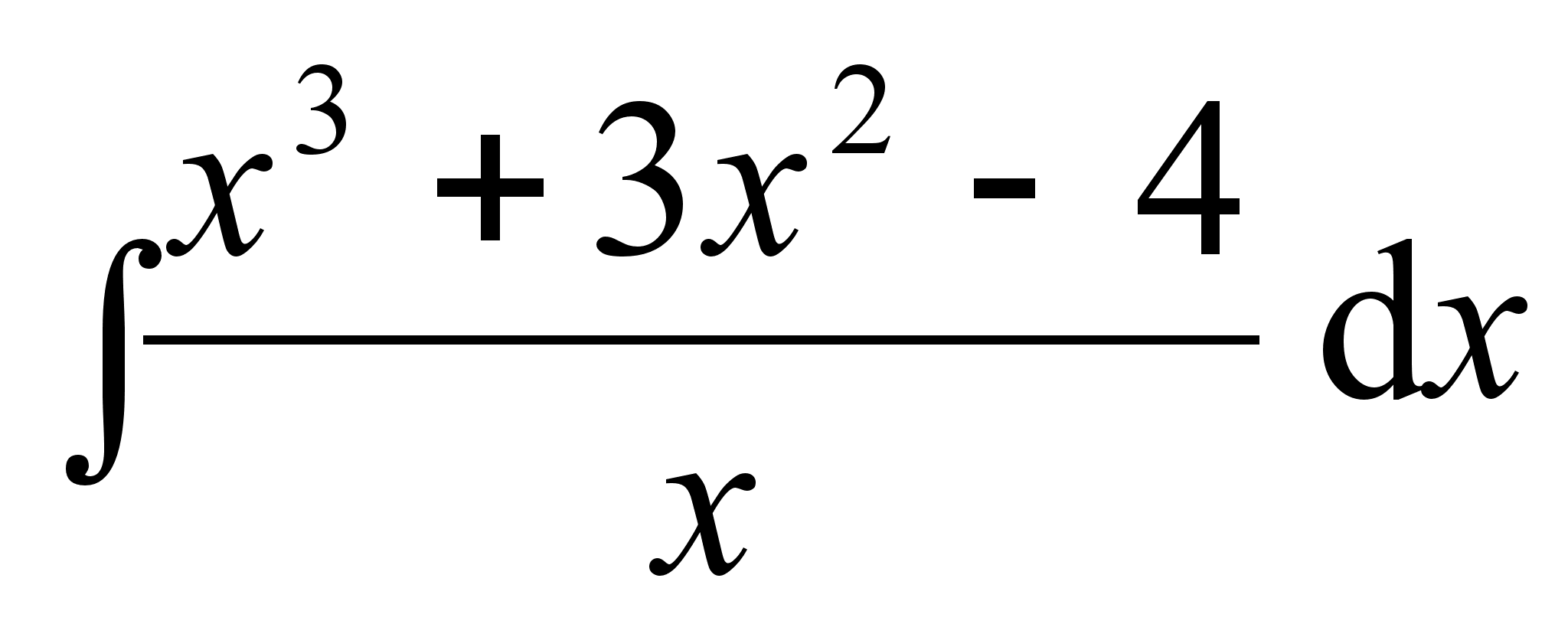
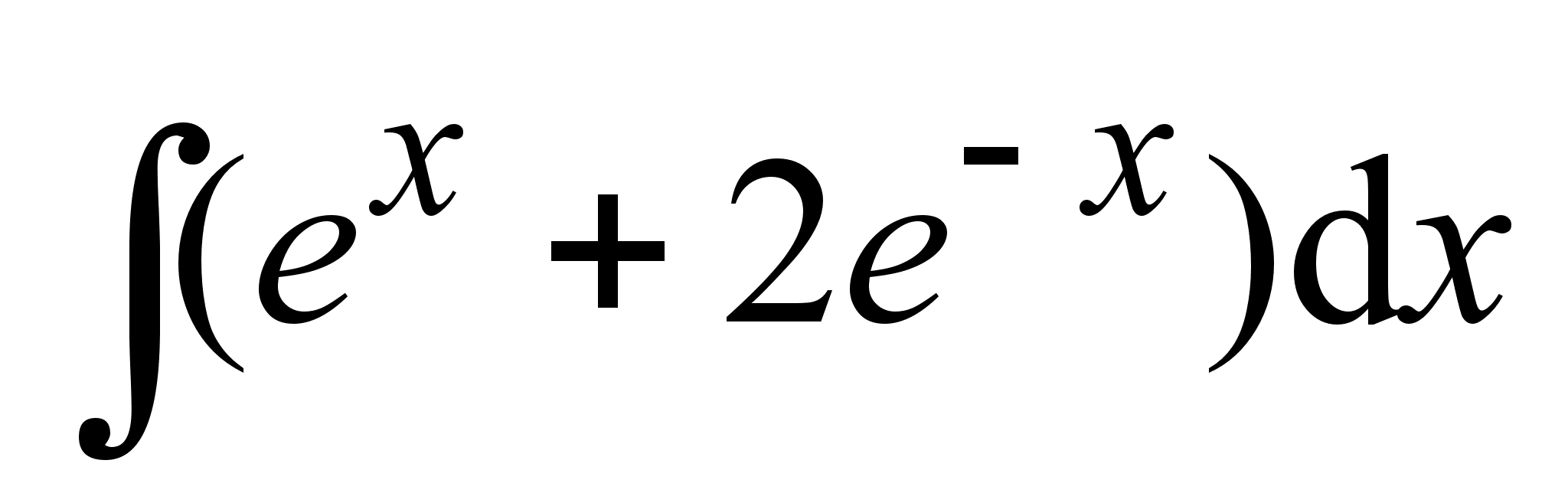 ;
;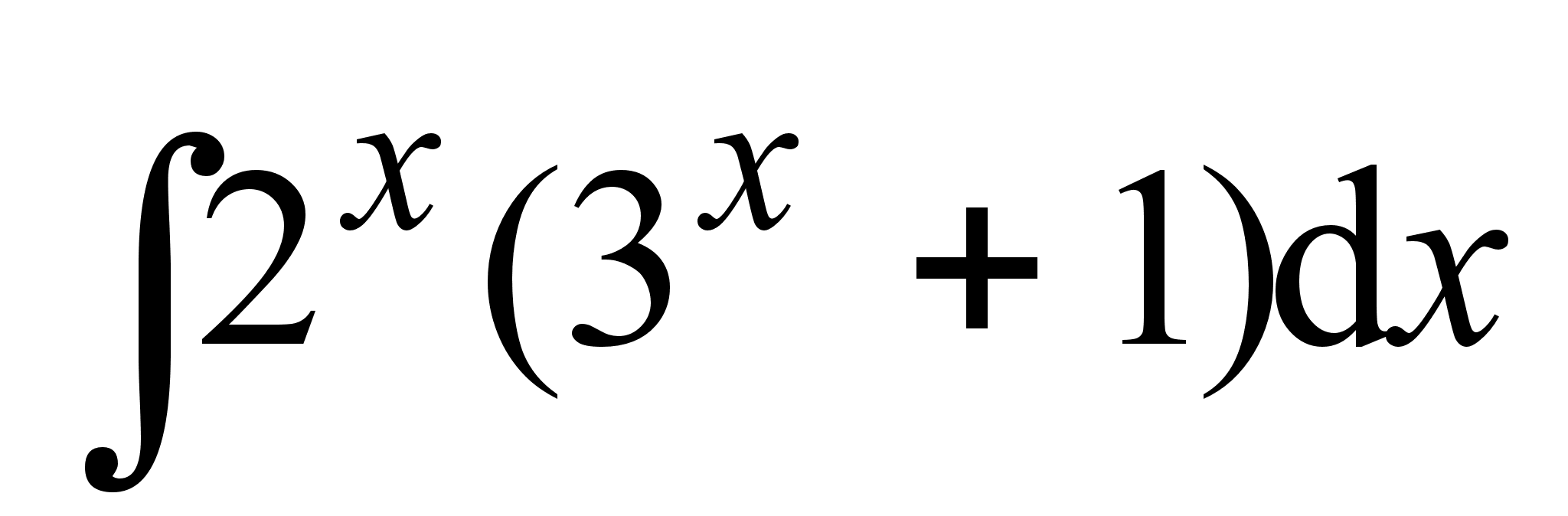 ;
;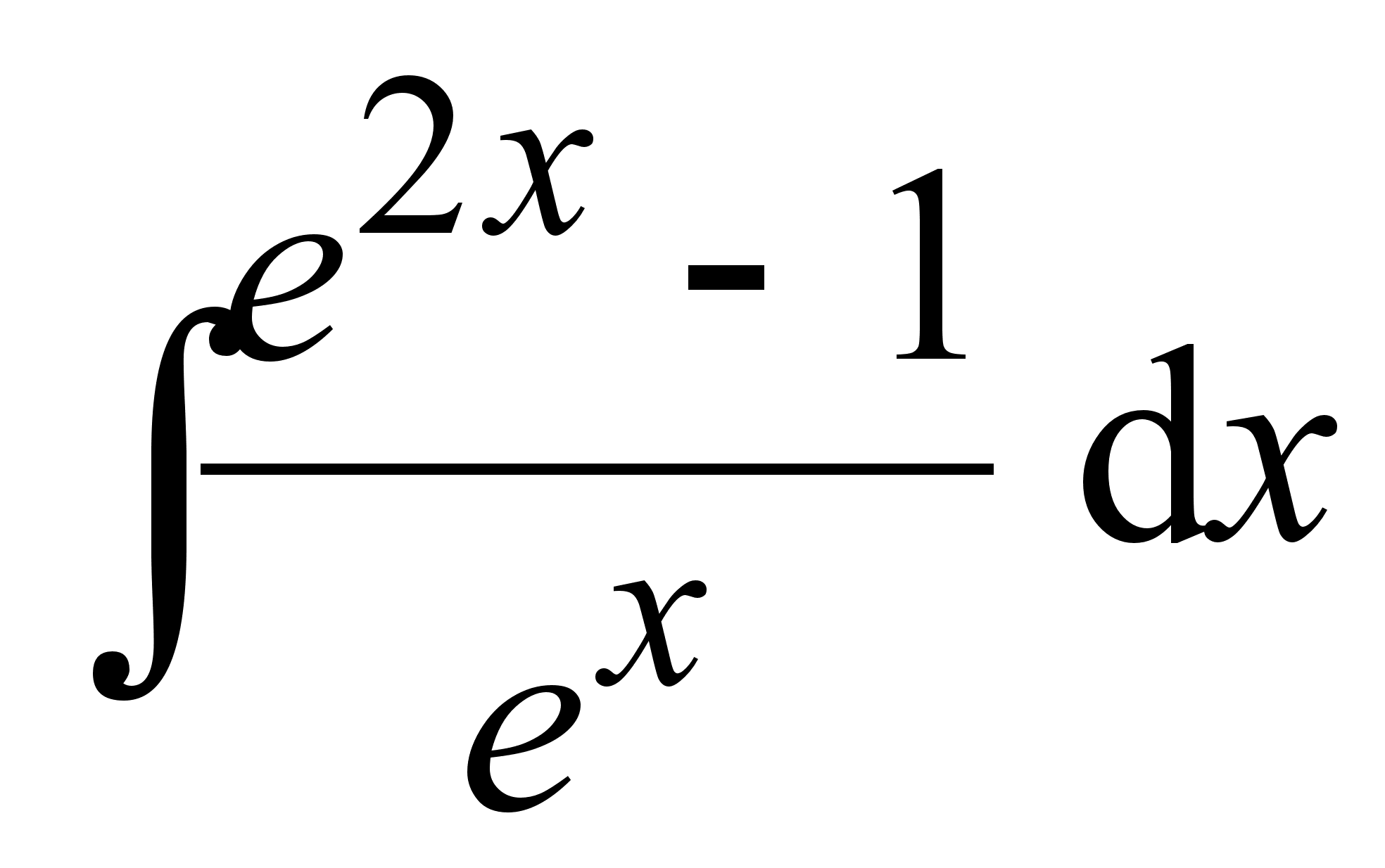 ;
;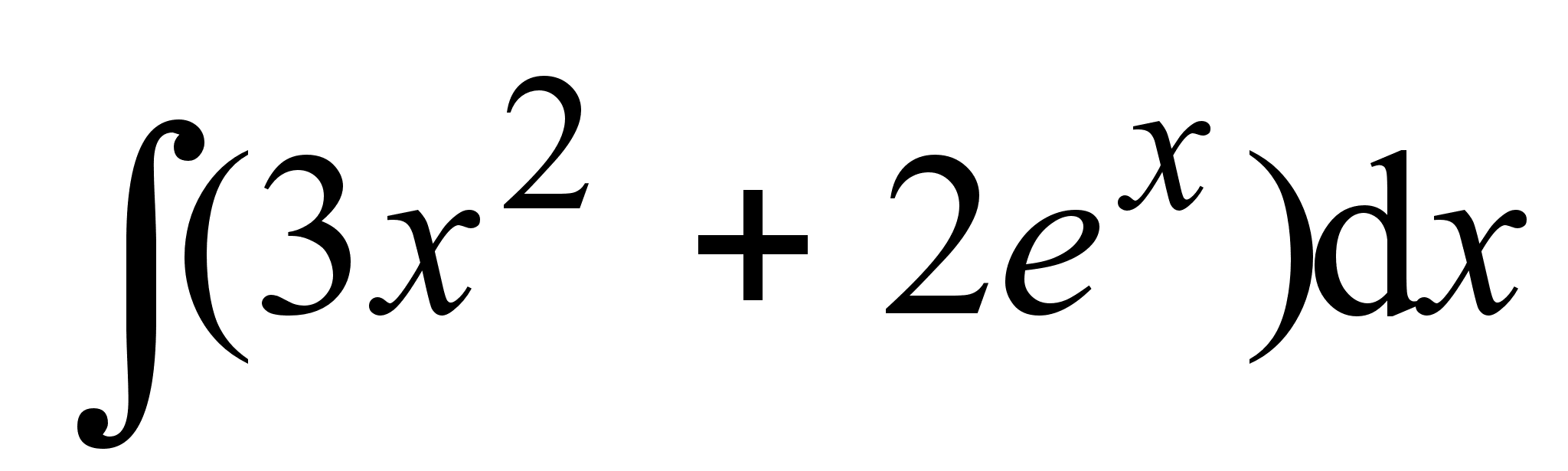 ;
;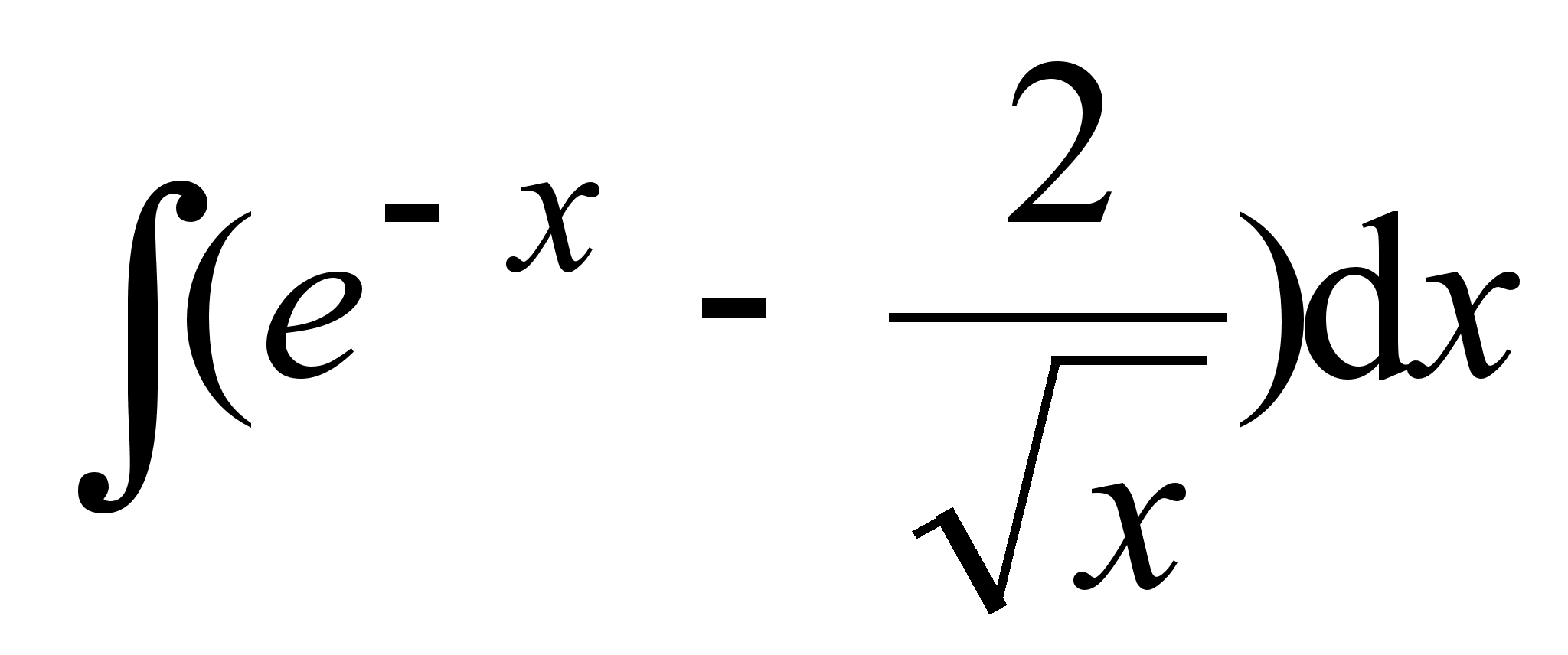 .
.
2. Найти интегралы:
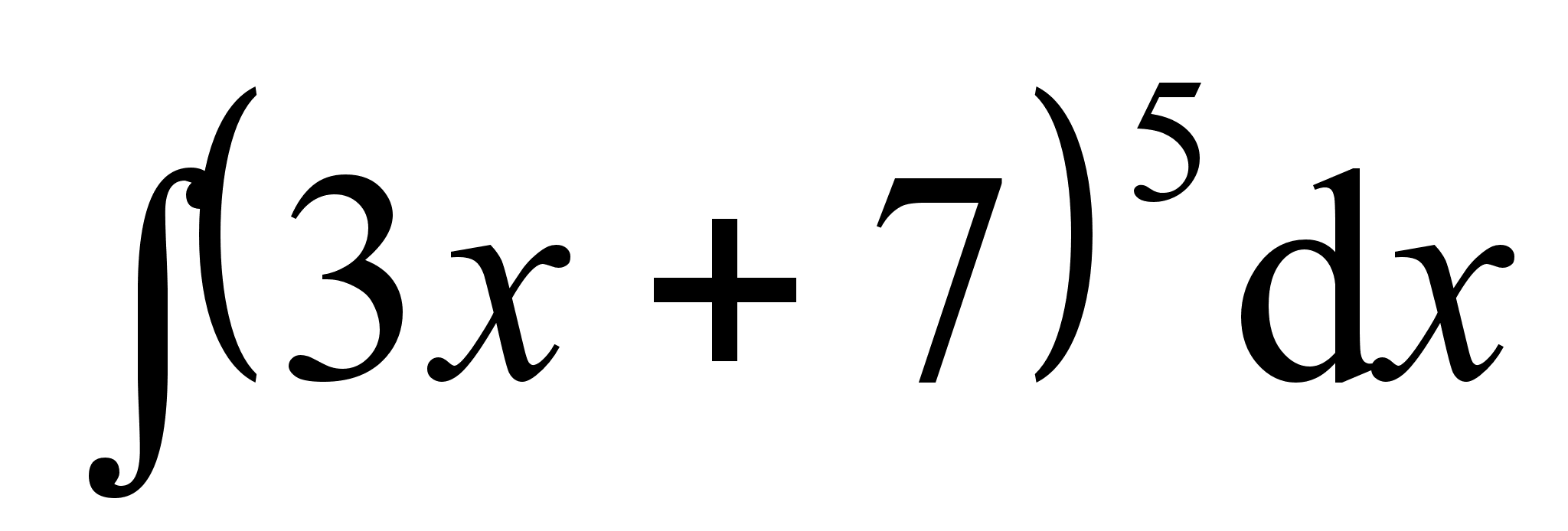 ;
;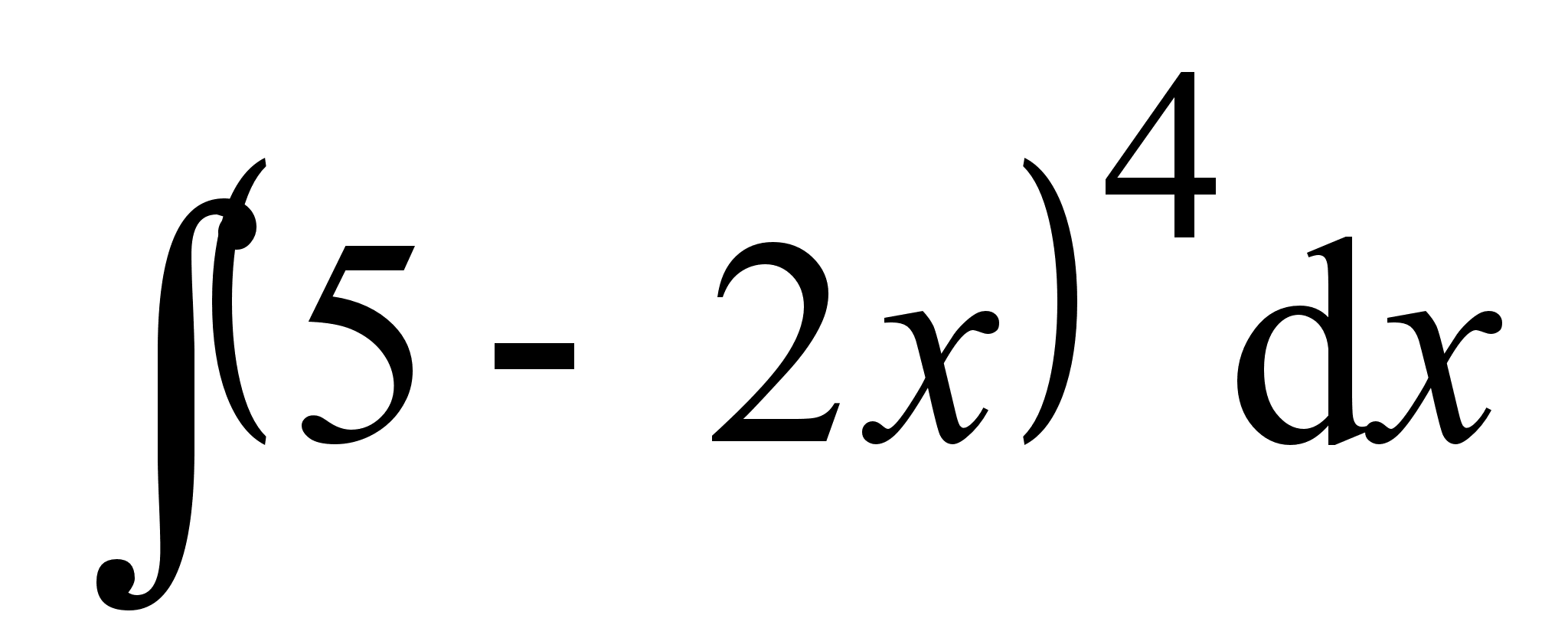 ;
;
![]() ;
;
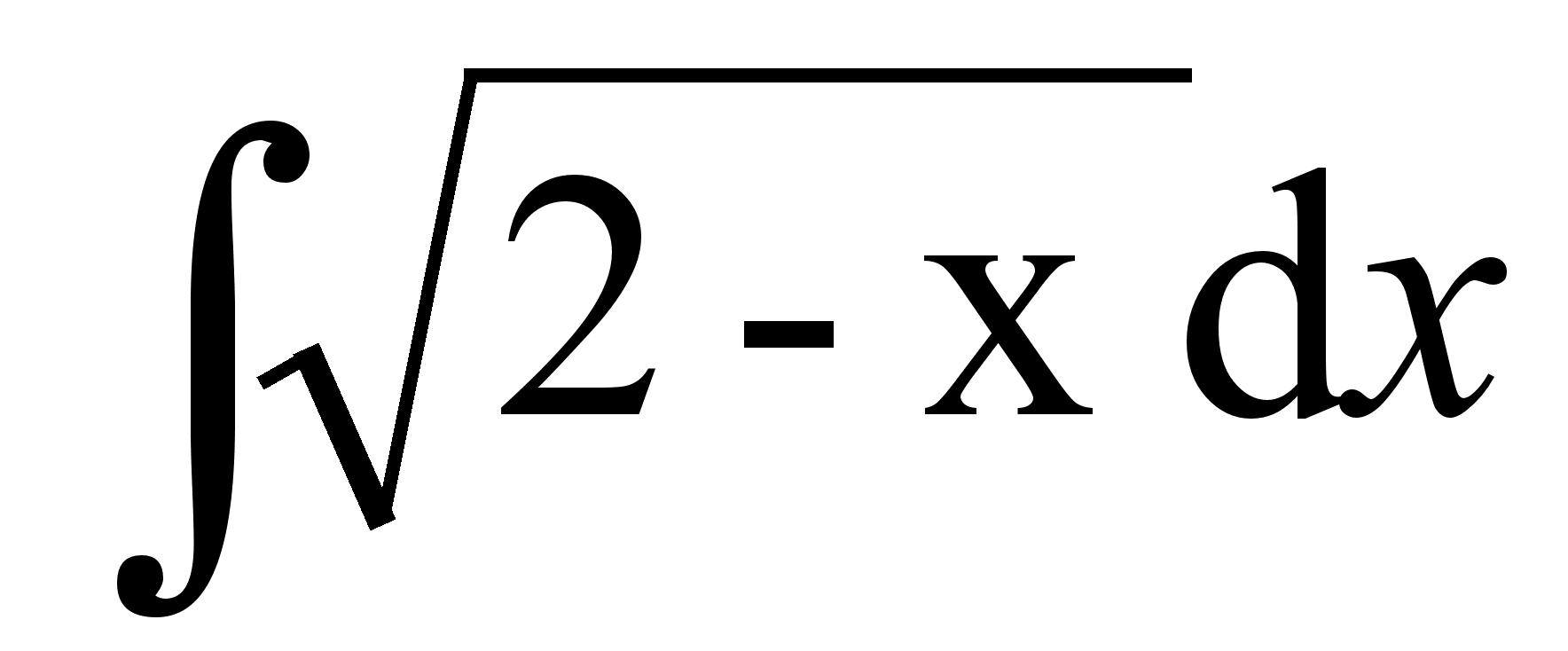 ;
;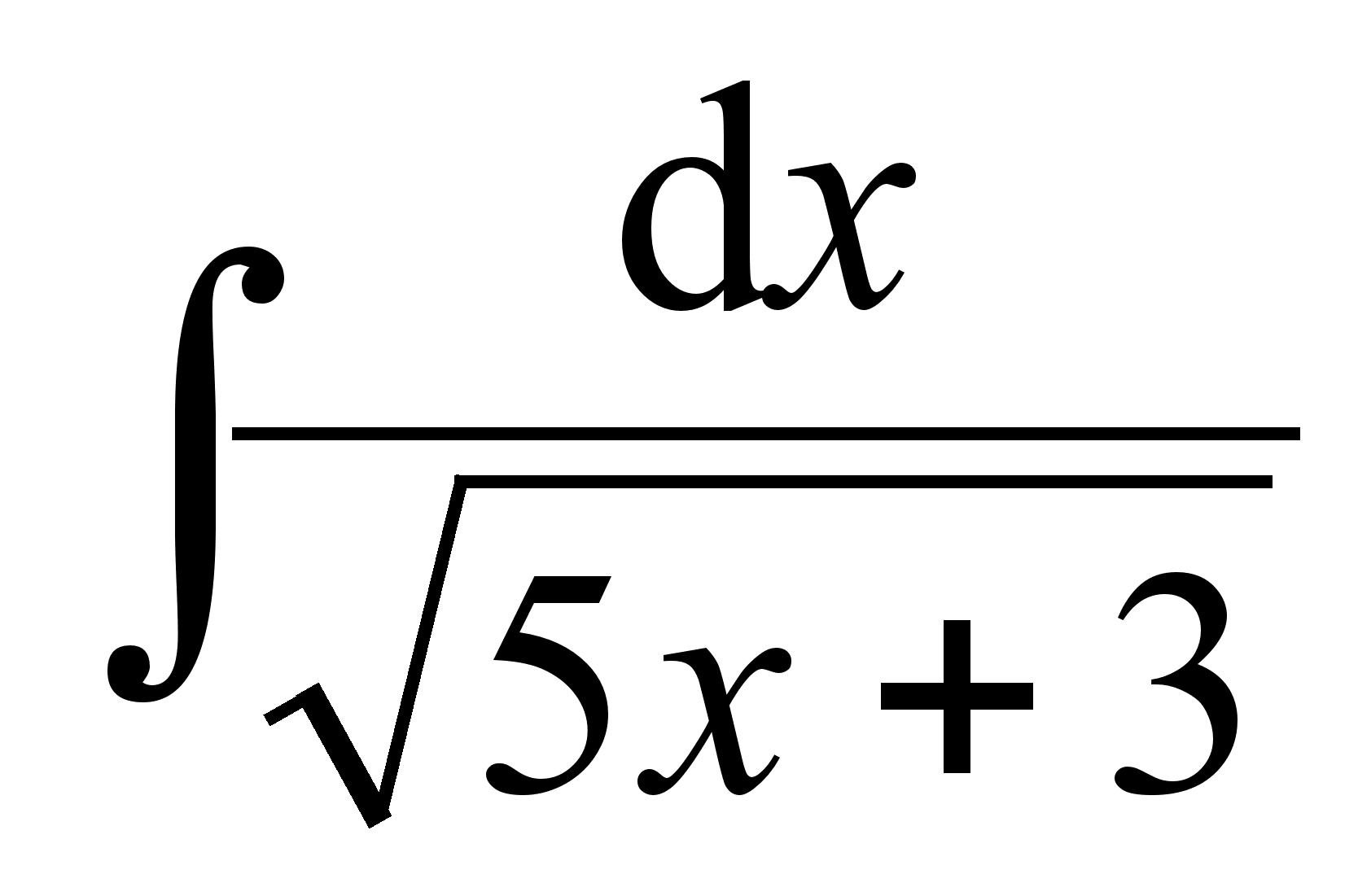 ;
;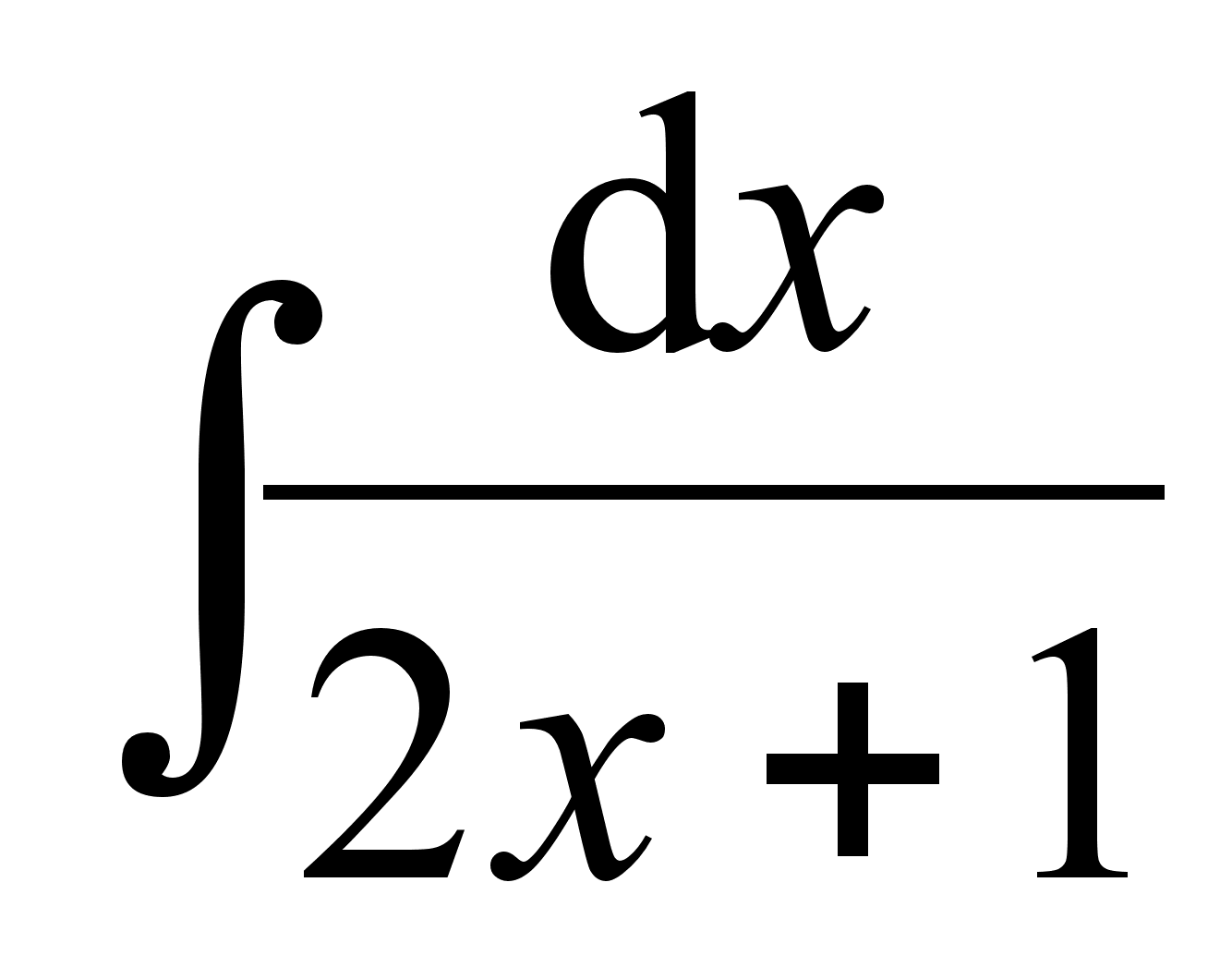 ;
;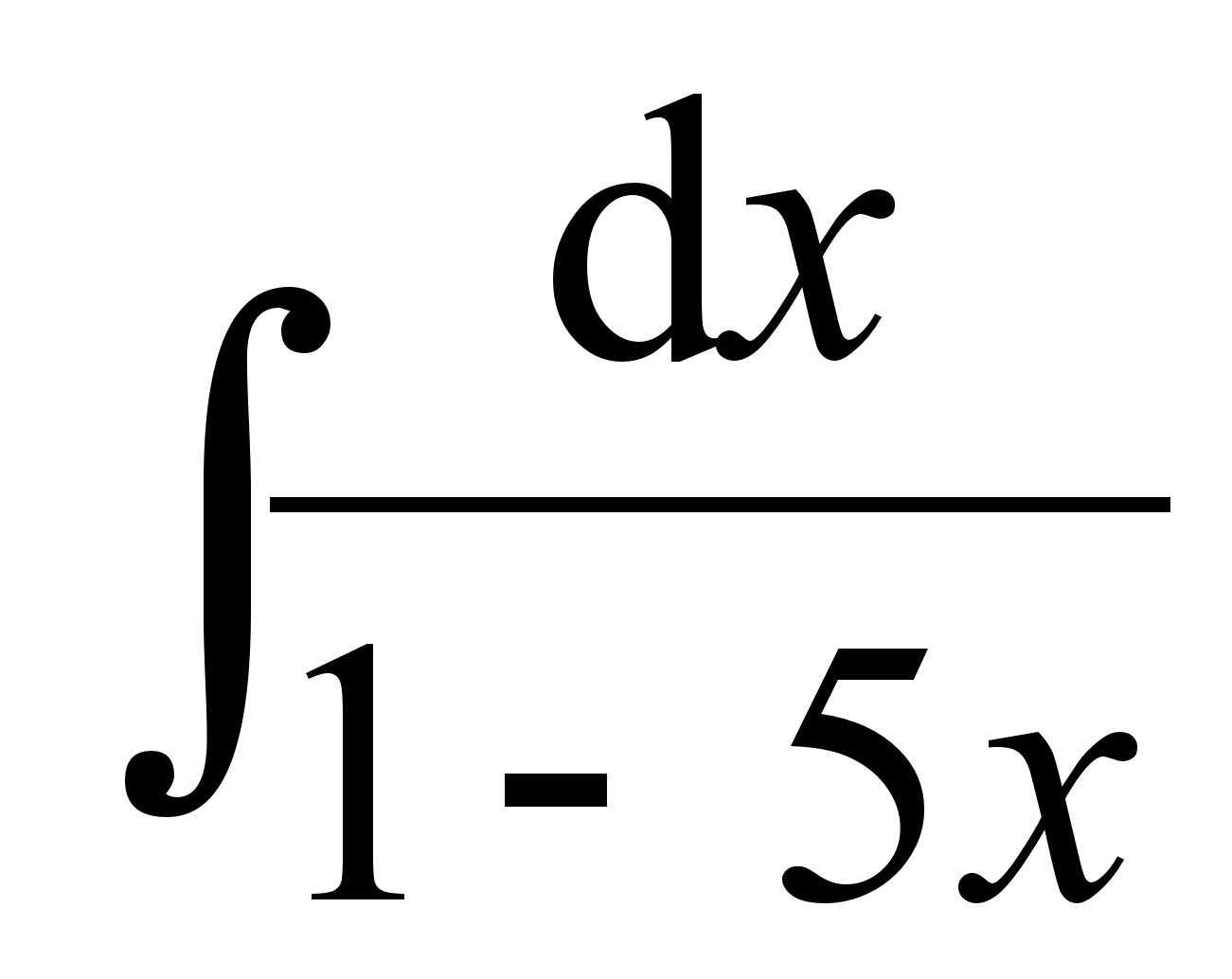 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
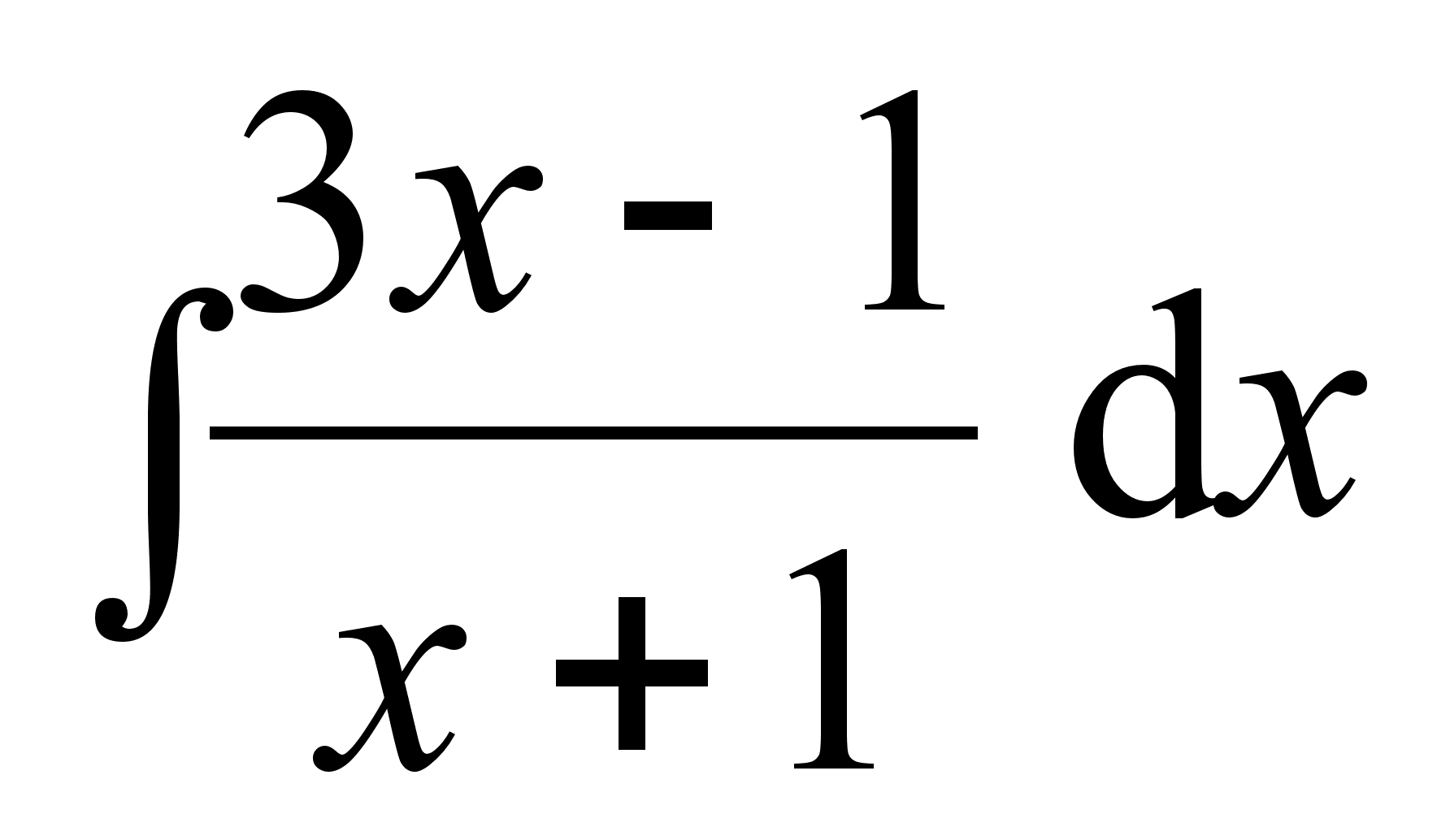 ;
;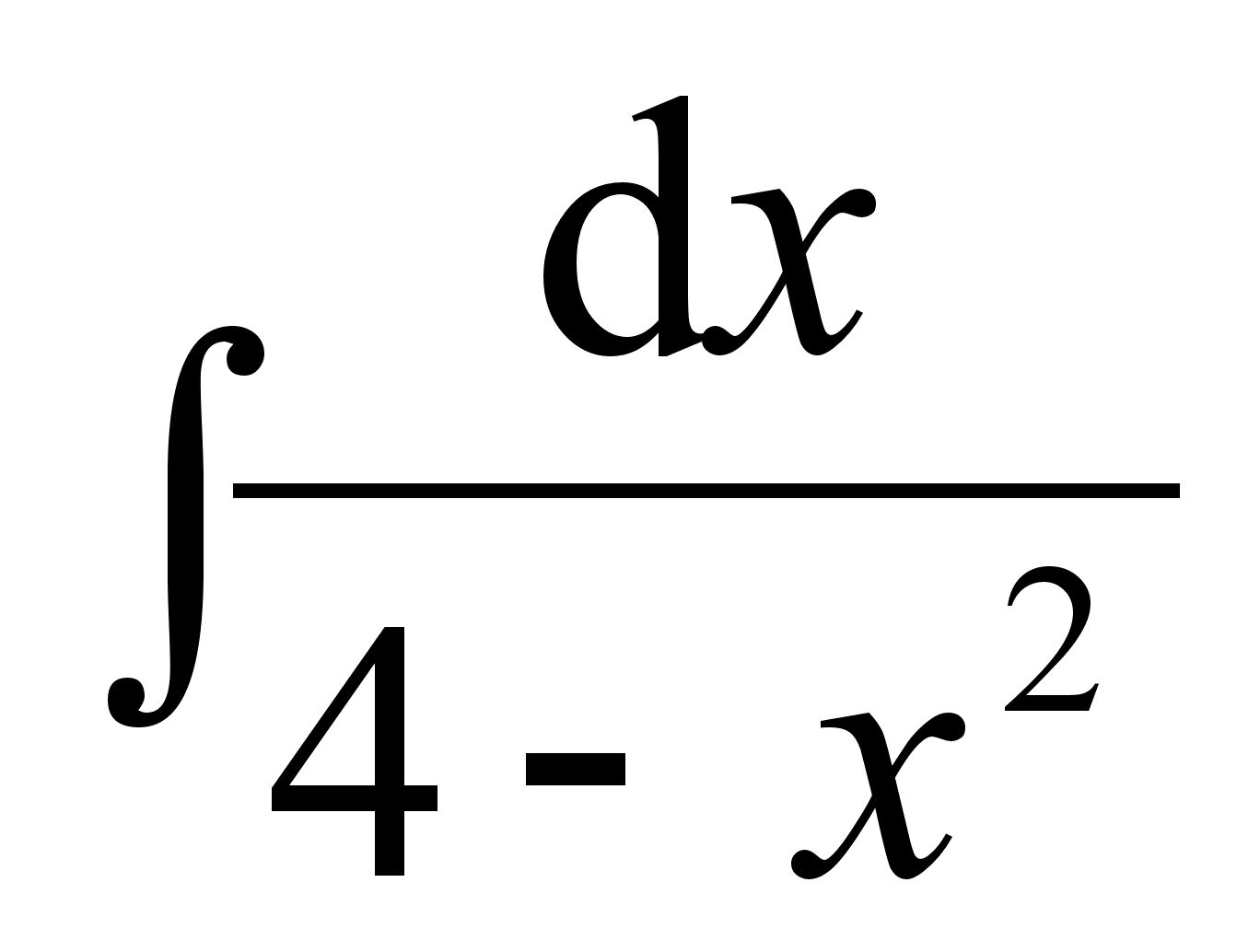 ;
;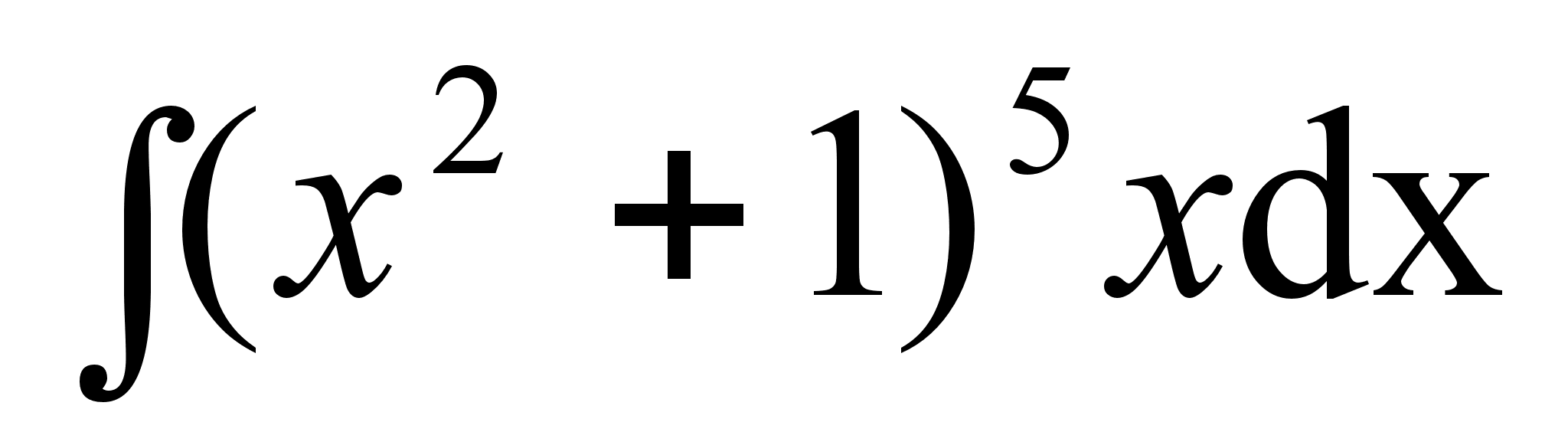 ;
;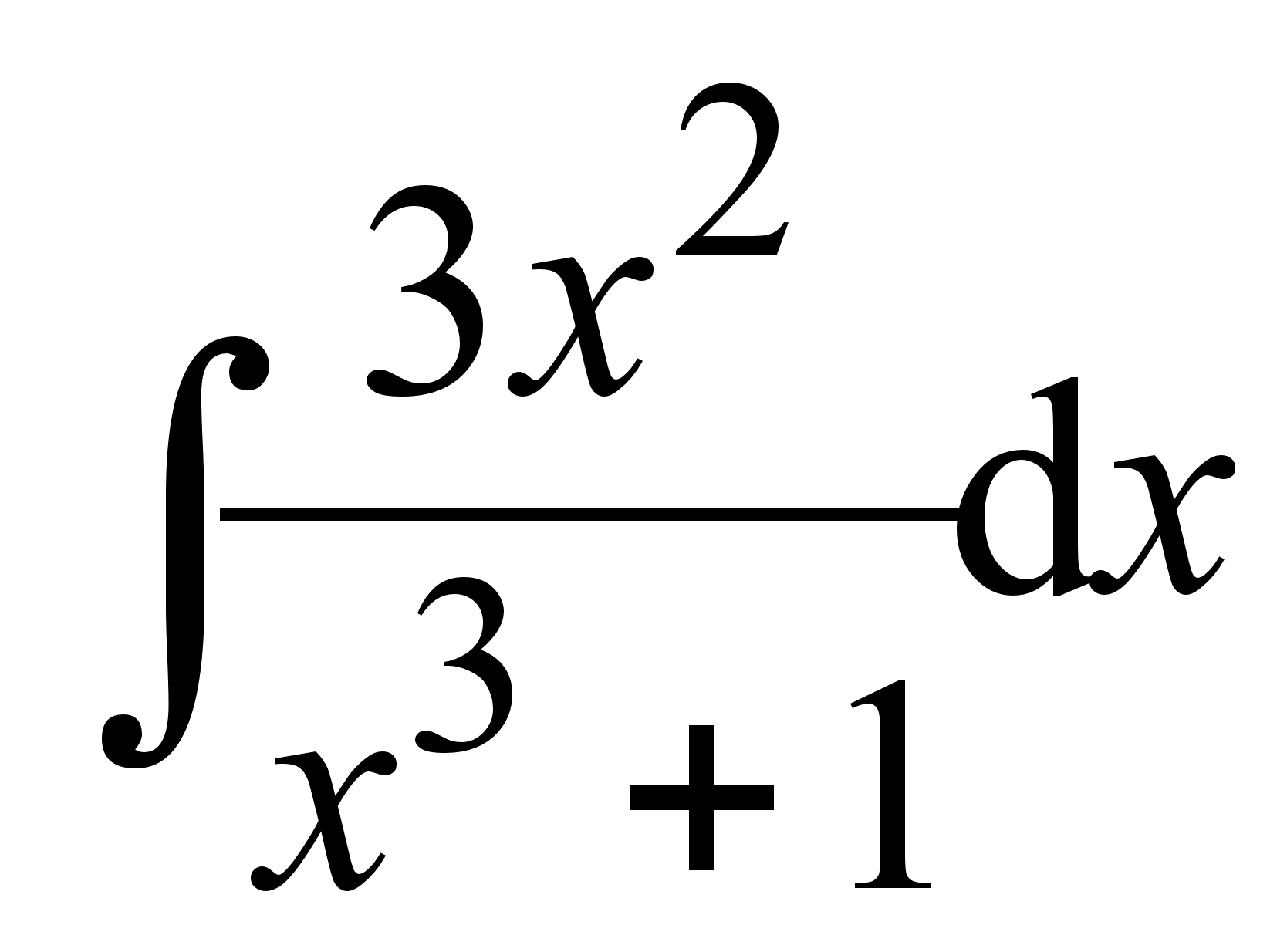 ;
;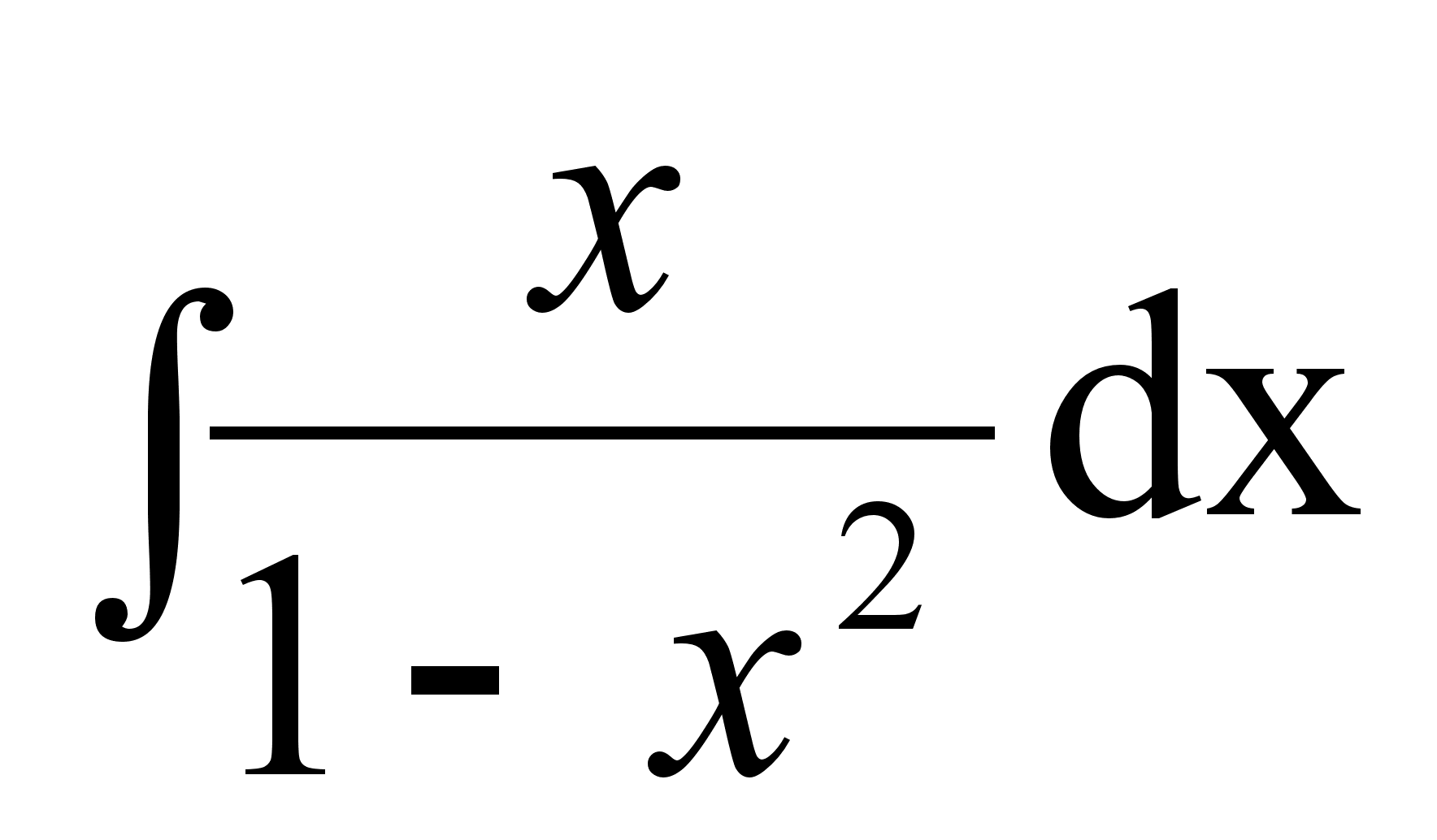 ;
;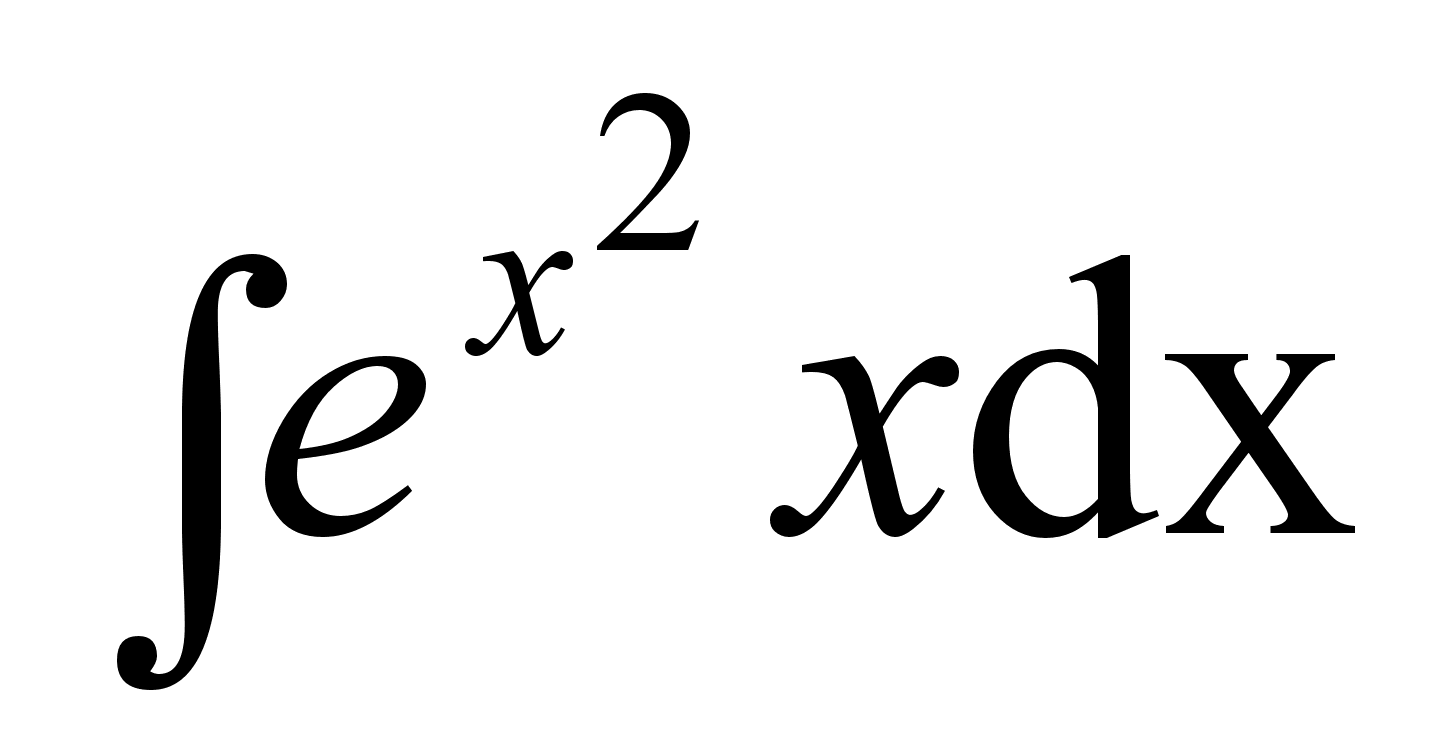 ;
;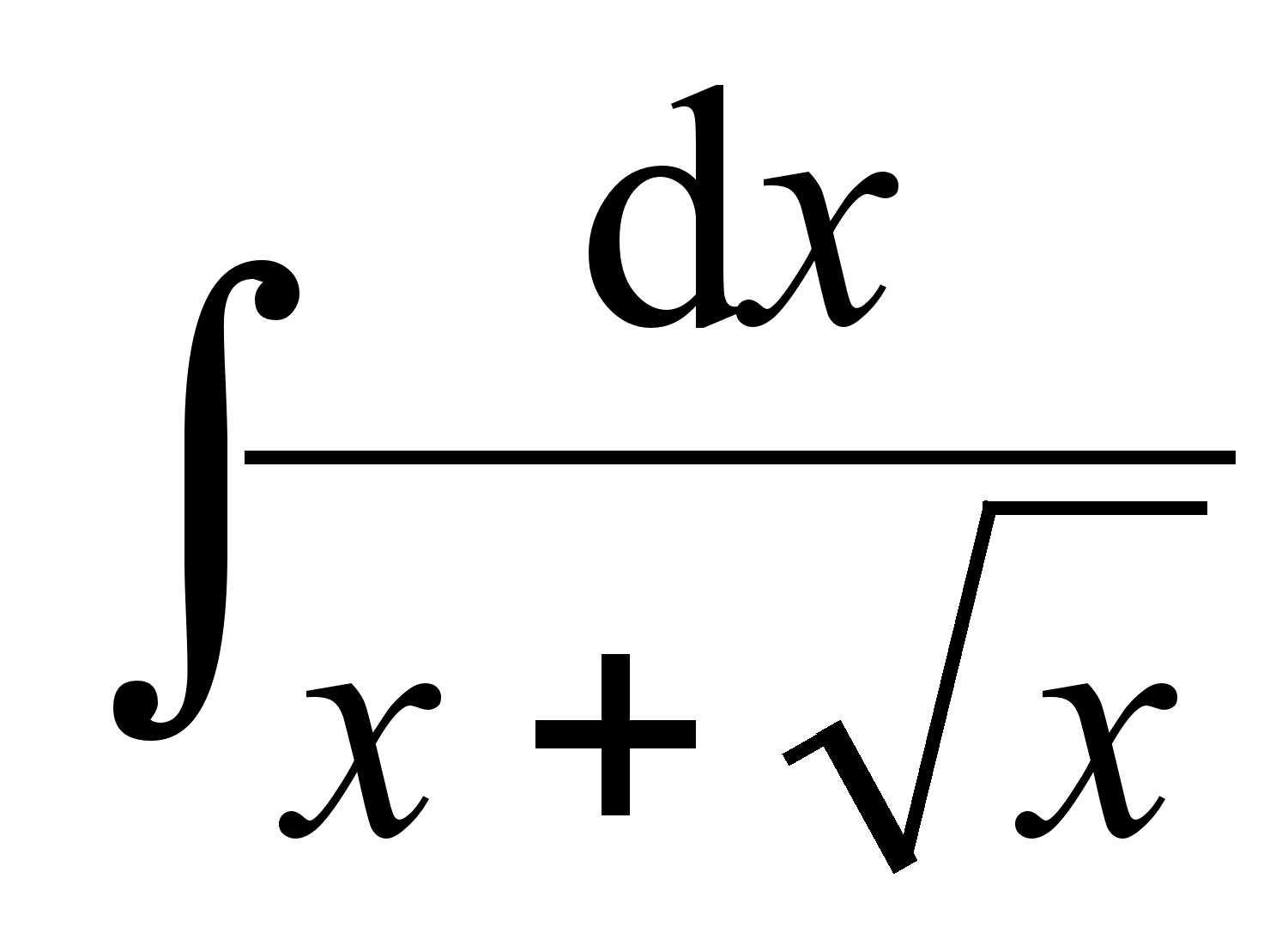 ;
;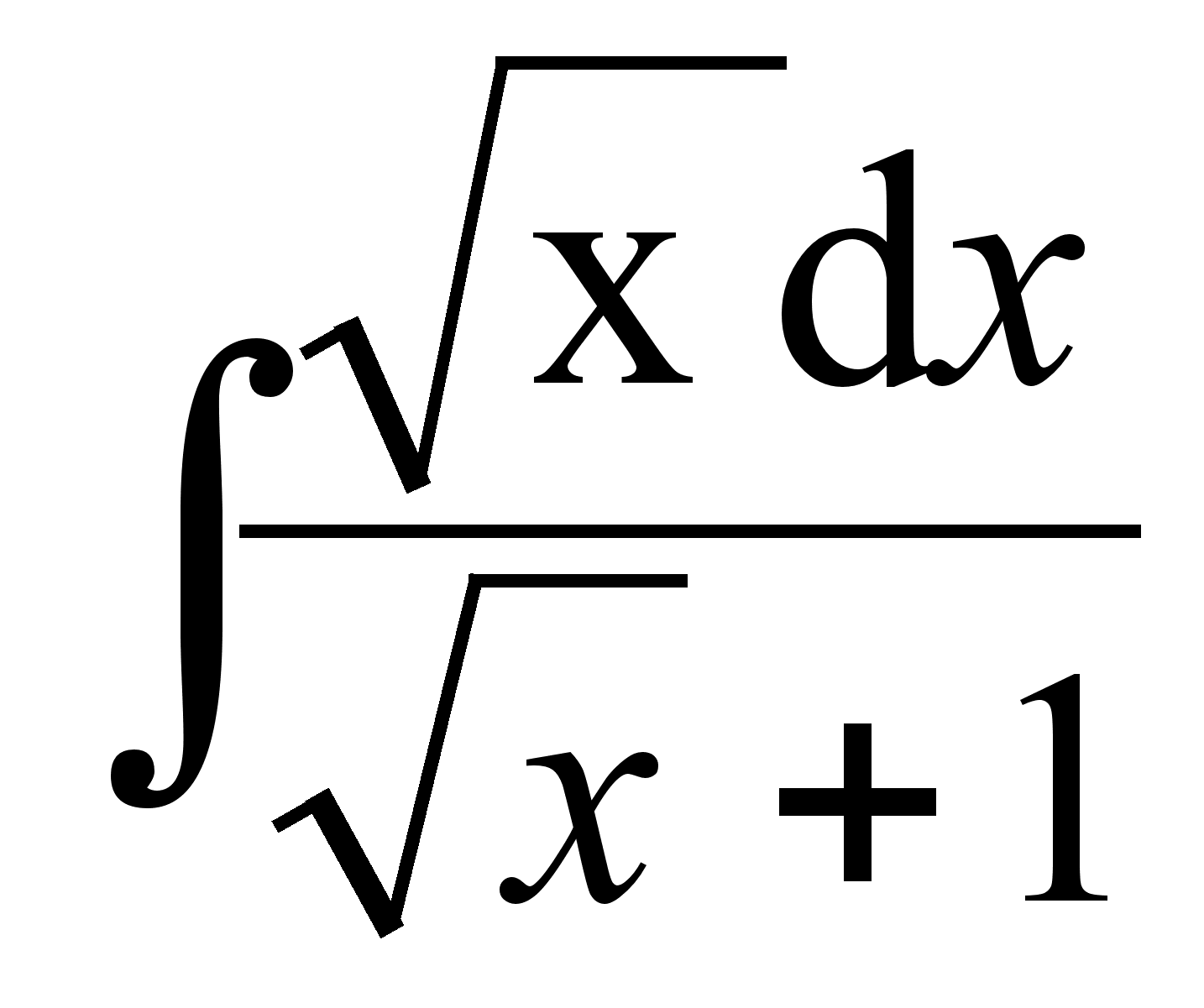 .
.
Ответы
1.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() .
.
2.
1)
![]() ;
;
2)
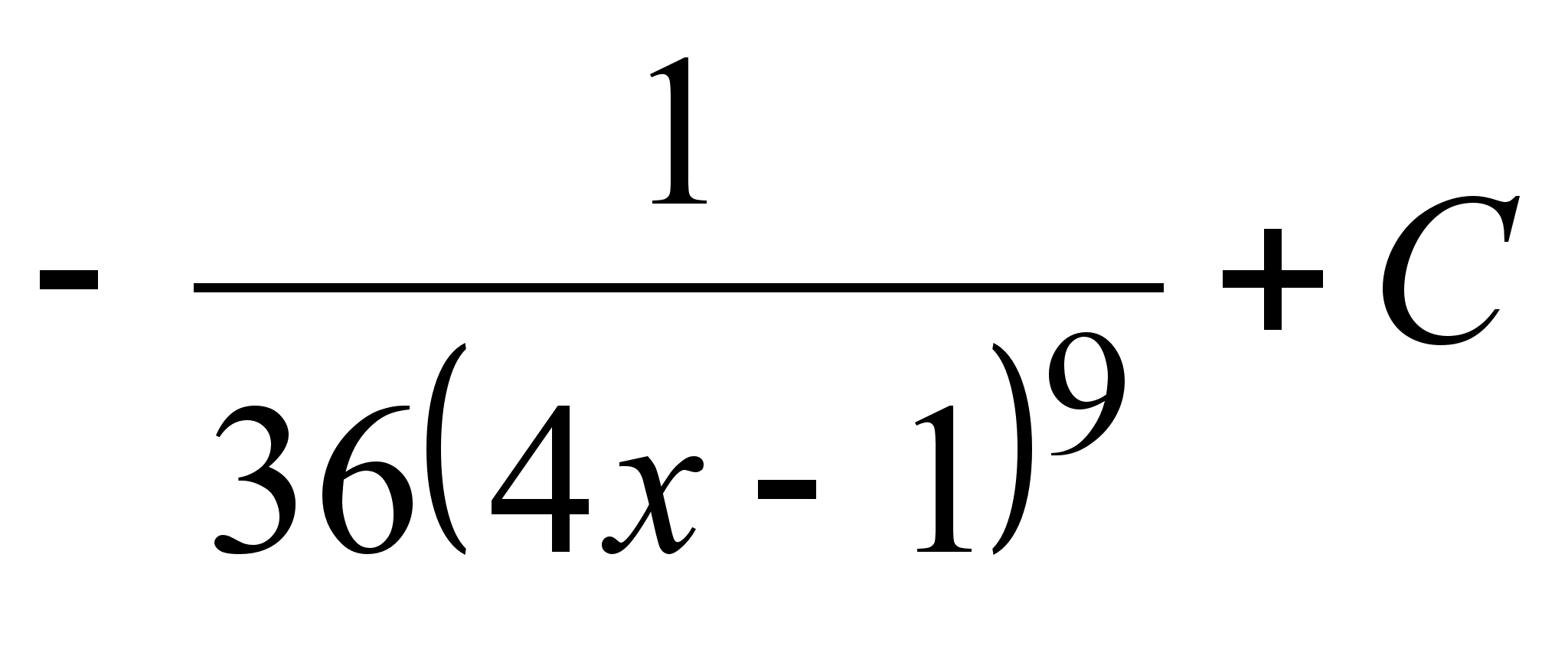 ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() .
.
§ 5. Определенный интеграл
Определенный
интеграл функции
равен пределу
интегральных
сумм, сопоставляемых
ей по некоторым
правилам. Для
непрерывной
неотрицательной
функции определенный
интеграл равен
площади фигуры,
заключенной
между графиком
функции и осью
![]() .
При вычислении
определенного
интеграла от
непрерывной
на отрезке
функции используется
формула Ньютона-Лейбница,
выражающая
определенный
интеграл через
первообразную
функции.
.
При вычислении
определенного
интеграла от
непрерывной
на отрезке
функции используется
формула Ньютона-Лейбница,
выражающая
определенный
интеграл через
первообразную
функции.
1. Определение
Пусть функция
![]() определена
на отрезке
определена
на отрезке
![]() .
Разобьем отрезок
на
.
Разобьем отрезок
на
![]() частей точками
частей точками
![]() (
(![]() )
такими, что
)
такими, что
![]() .
Длины полученных
отрезков обозначим
.
Длины полученных
отрезков обозначим
![]() (
(![]() ),
и пусть
),
и пусть
![]() – наибольшая
из этих длин.
Выберем на
каждом из отрезков
разбиения
произвольную
точку
– наибольшая
из этих длин.
Выберем на
каждом из отрезков
разбиения
произвольную
точку
![]() и составим
сумму
и составим
сумму
![]() ,
(1)
,
(1)
которую
назовем интегральной
суммой для
функции
![]() .
.
Рассмотрим
интегральные
суммы, соответствующие
разбиениям
отрезка
![]() при различных
значениях
при различных
значениях
![]() .
Если существует
предел таких
сумм при
.
Если существует
предел таких
сумм при
![]() ,
то он называется
определенным
интегралом
функции
,
то он называется
определенным
интегралом
функции
![]() на отрезке
на отрезке
![]() и обозначается
и обозначается
![]() ,
,
при
этом функция
![]() называется
интегрируемой
(по Риману) на
отрезке
называется
интегрируемой
(по Риману) на
отрезке
![]() ,
числа
,
числа
![]() и
и
![]() называются
соответственно
нижним и верхним
пределами
интегрирования.
называются
соответственно
нижним и верхним
пределами
интегрирования.
Заметим, что всякая непрерывная на отрезке функция интегрируема на этом отрезке.
Пример. Функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() и, следовательно,
интегрируема
на нем. Чтобы
вычислить
интеграл
и, следовательно,
интегрируема
на нем. Чтобы
вычислить
интеграл
![]() ,
достаточно
рассмотреть
любую последовательность
разбиений
отрезка
,
достаточно
рассмотреть
любую последовательность
разбиений
отрезка
![]() ,
для которой
,
для которой
![]() ,
и найти предел
соответствующей
последовательности
интегральных
сумм. При этом
промежуточные
точки
,
и найти предел
соответствующей
последовательности
интегральных
сумм. При этом
промежуточные
точки
![]() для каждого
разбиения можно
выбирать произвольно.
Рассмотрим
равномерные
разбиения вида
для каждого
разбиения можно
выбирать произвольно.
Рассмотрим
равномерные
разбиения вида
![]() ,
,
![]() ,
а в качестве
,
а в качестве
![]() выберем правые
концы отрезков
выберем правые
концы отрезков
![]() ,
то есть положим
,
то есть положим
![]() ,
,
![]() .
В этом случае
имеем
.
В этом случае
имеем
![]() ,
,
![]() ,
и интегральная
сумма (1) принимает
вид
,
и интегральная
сумма (1) принимает
вид
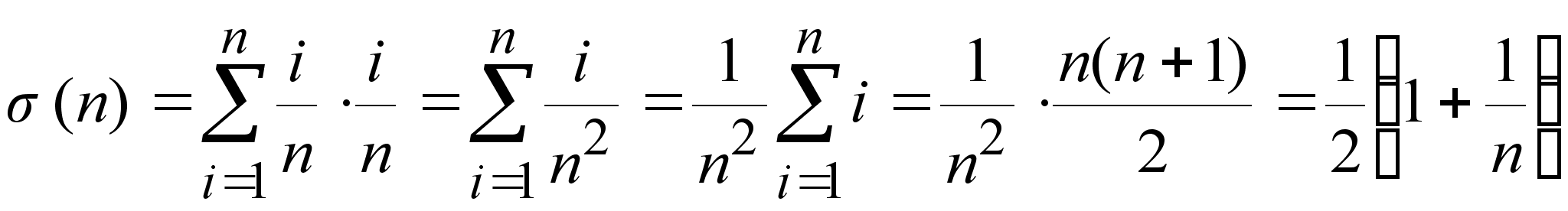 .
.
Переходя
к пределу при
![]() ,
получаем
,
получаем
![]() .
.
2. Геометрический смысл
Пусть функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() и неотрицательна:
и неотрицательна:
![]() .
Фигуру, ограниченную
графиком функции
.
Фигуру, ограниченную
графиком функции
![]() , вертикальными
прямыми
, вертикальными
прямыми
![]() и
и
![]() и осью
и осью
![]() ,
назовем криволинейной
трапецией.
Рассмотрим
разбиение
отрезка
,
назовем криволинейной
трапецией.
Рассмотрим
разбиение
отрезка
![]() ,
описанное в
предыдущем
пункте, и соответствующую
интегральную
сумму (1). Заметим,
что слагаемые
в (1) равны площадям
прямоугольников
с основаниями
,
описанное в
предыдущем
пункте, и соответствующую
интегральную
сумму (1). Заметим,
что слагаемые
в (1) равны площадям
прямоугольников
с основаниями
![]() и высотами
и высотами
![]() (
(![]() ),
а вся сумма
представляет
площадь ступенчатой
фигуры, образованной
этими прямоугольниками,
см. Рис. 14. Предел
интегральных
сумм (если он
существует),
то есть определенный
интеграл, естественно
принять в качестве
площади криволинейной
трапеции.
),
а вся сумма
представляет
площадь ступенчатой
фигуры, образованной
этими прямоугольниками,
см. Рис. 14. Предел
интегральных
сумм (если он
существует),
то есть определенный
интеграл, естественно
принять в качестве
площади криволинейной
трапеции.
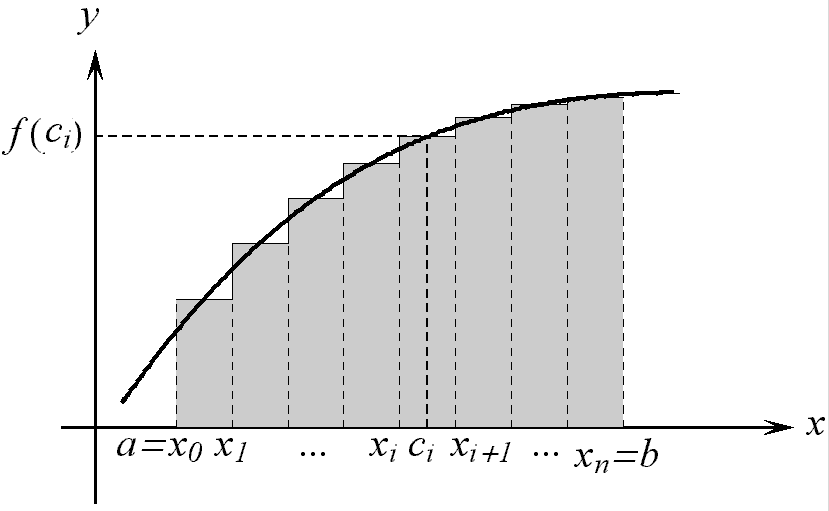
Рис. 14.
3. Формула Ньютона – Лейбница
Если функция
![]() непрерывна
на отрезке
непрерывна
на отрезке
![]() и
и
![]() - любая ее первообразная
на этом отрезке,
то справедлива
основная формула
интегрального
исчисления:
- любая ее первообразная
на этом отрезке,
то справедлива
основная формула
интегрального
исчисления:
![]() ,
,
называемая
формулой
Ньютона-Лейбница.
Используя
краткое обозначение
![]() ,
эту формулу
можно записать
в виде
,
эту формулу
можно записать
в виде
![]() .
.
Таким образом, вычисление определенного интеграла от непрерывной функции сводится к отысканию ее первообразной, то есть, по существу, неопределенного интеграла, что позволяет использовать методы, изложенные в § 4.
Пример.
Найдем интеграл
![]() .
Поскольку
.
Поскольку
![]() ,
то по формуле
Ньютона-Лейбница
получаем
,
то по формуле
Ньютона-Лейбница
получаем
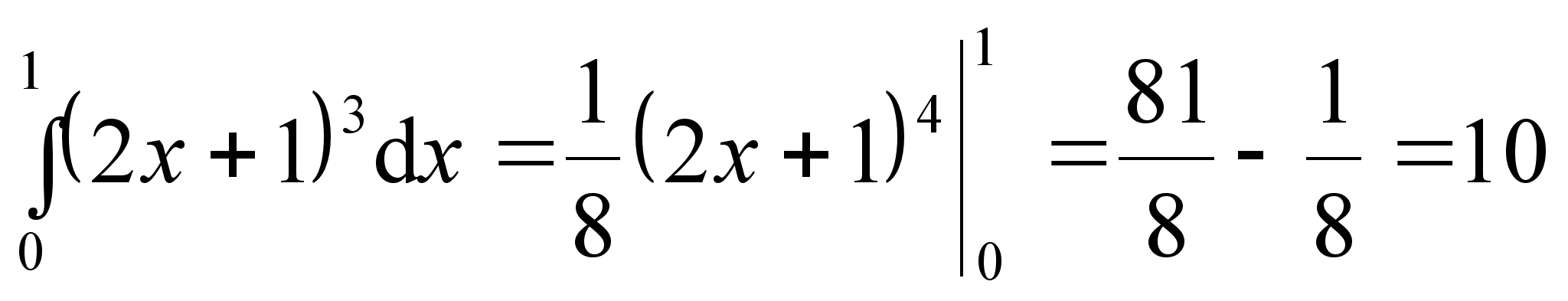 .
.
Пример.
Площадь
![]() криволинейной
трапеции,
ограниченной
графиком функции
криволинейной
трапеции,
ограниченной
графиком функции
![]() ,
осью
,
осью
![]() и прямыми
и прямыми
![]() и
и
![]() ,
равна
,
равна
![]() .
.
Упражнения
1. Вычислить определенные интегралы:
1)
![]() ;
6)
;
6)
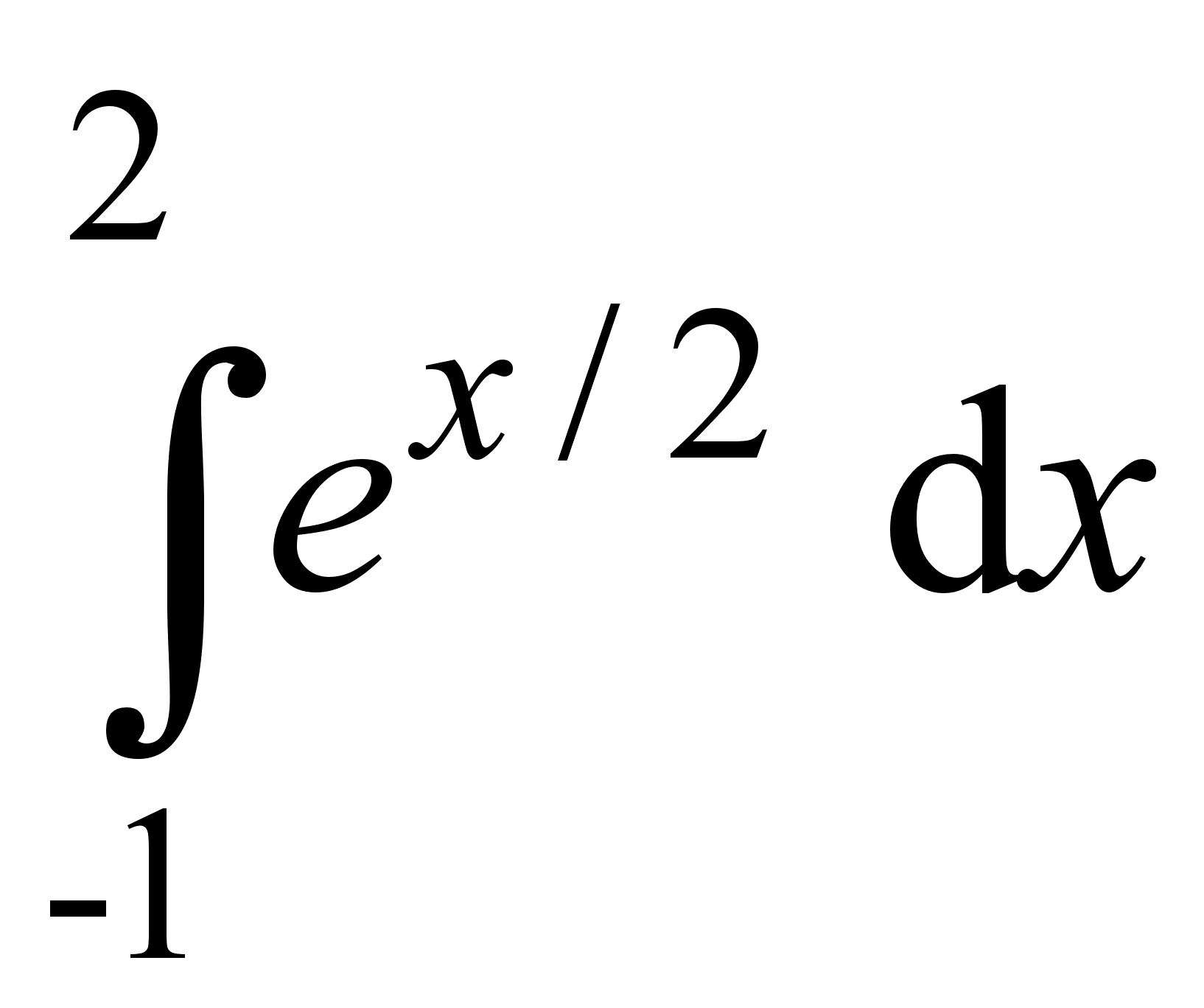 ; 11)
; 11)
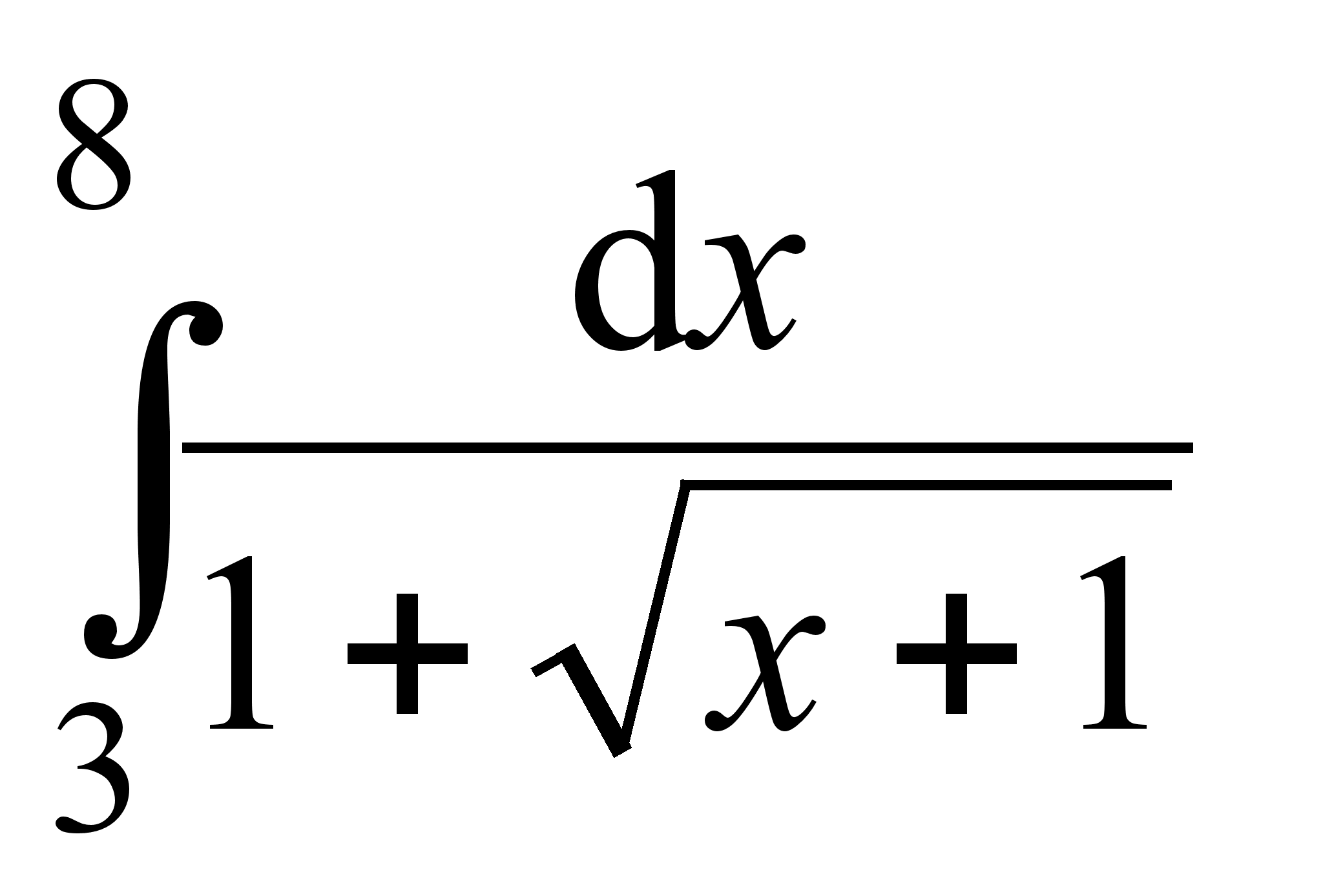 ;
;
2)
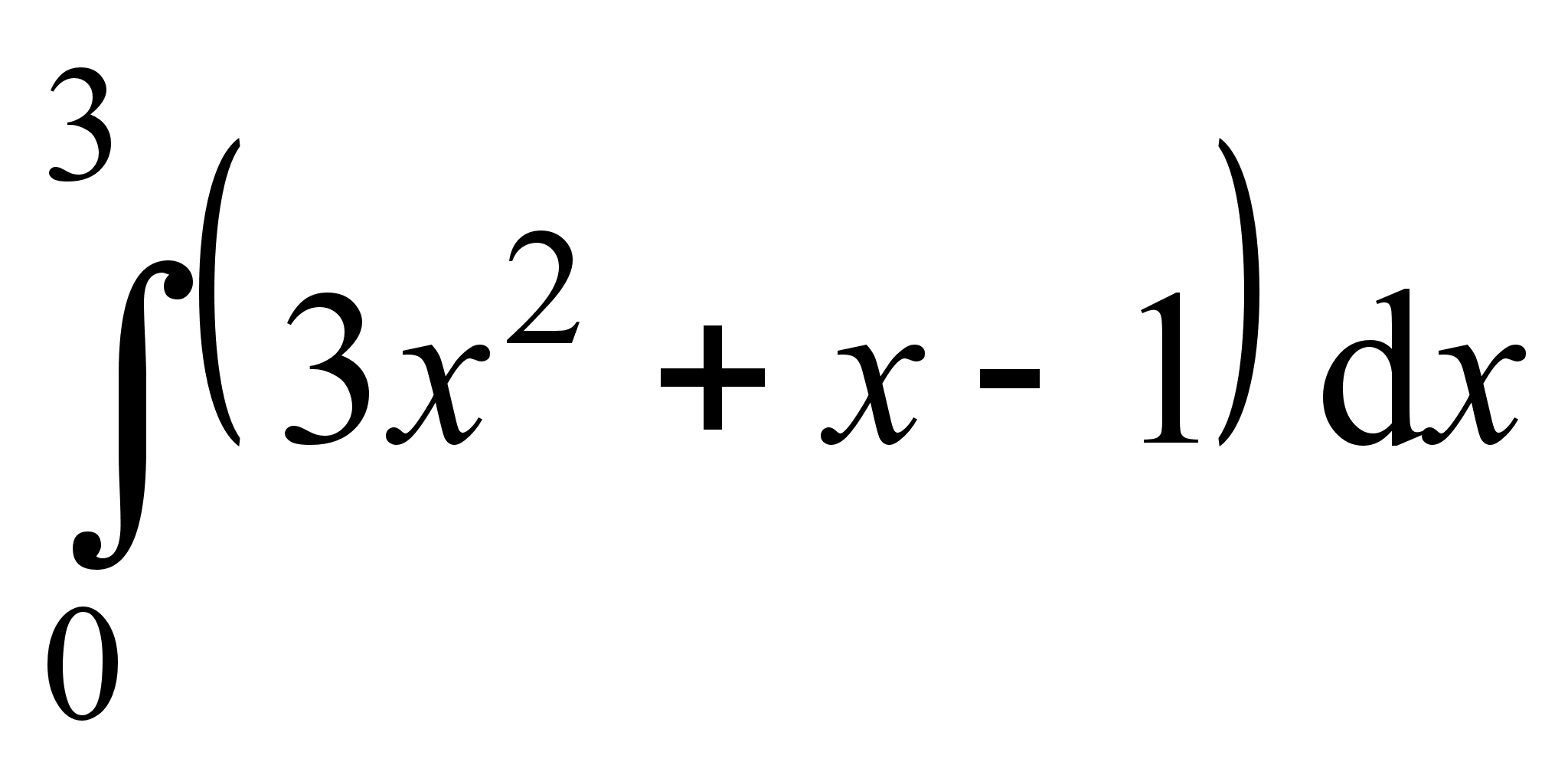 ;
7)
;
7)
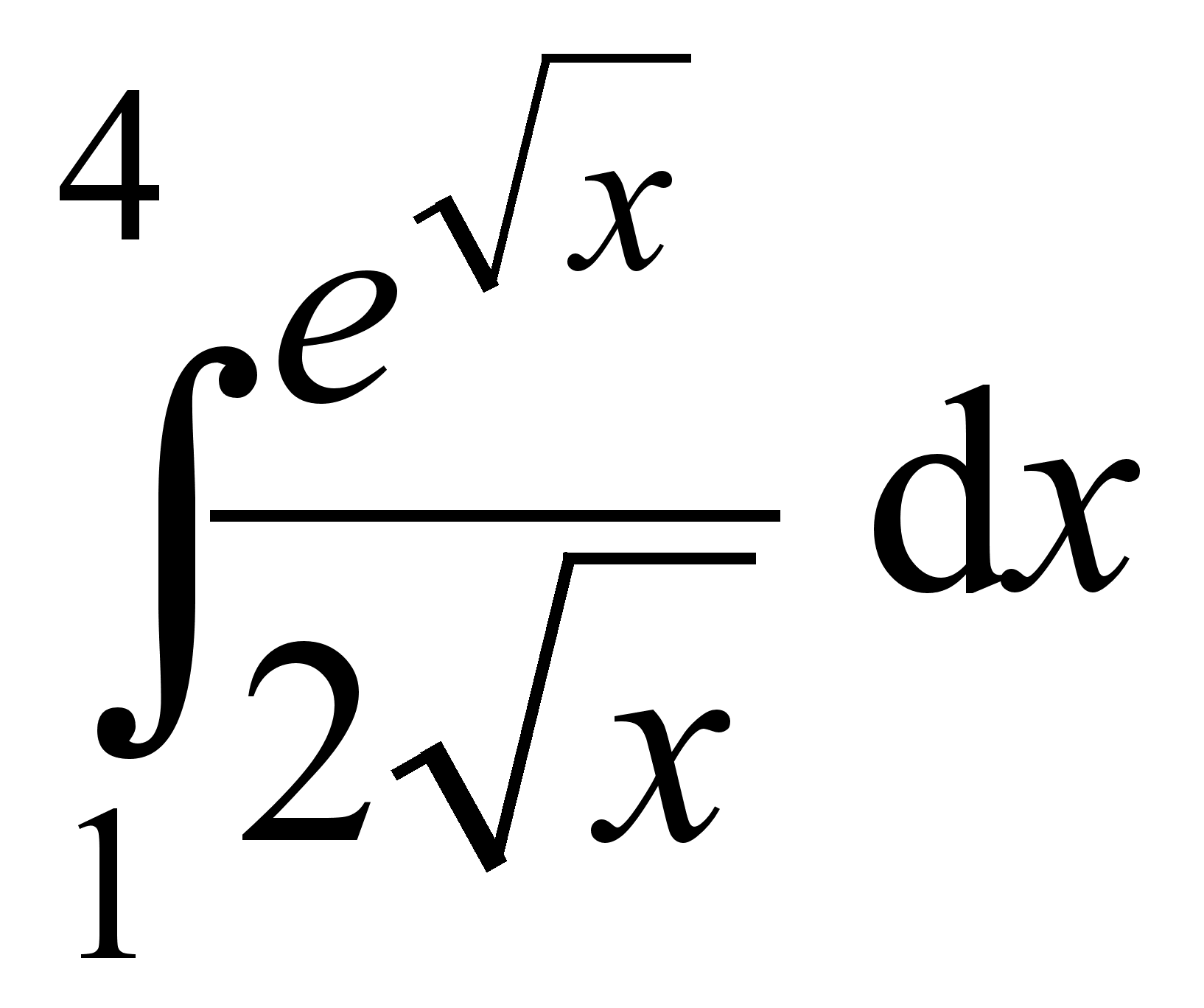 ; 12)
; 12)
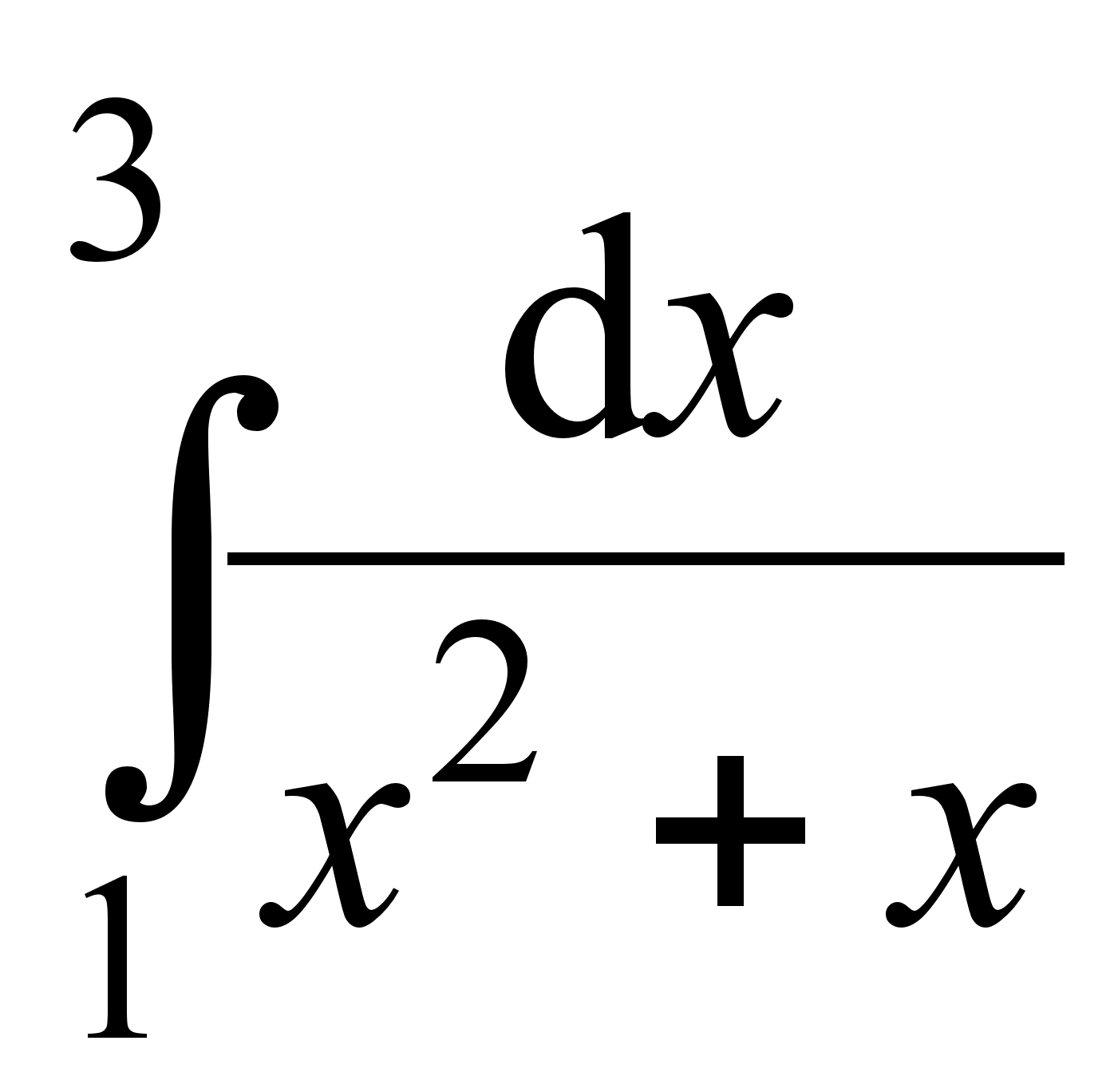 ;
;
3)
![]() ;
8)
;
8)
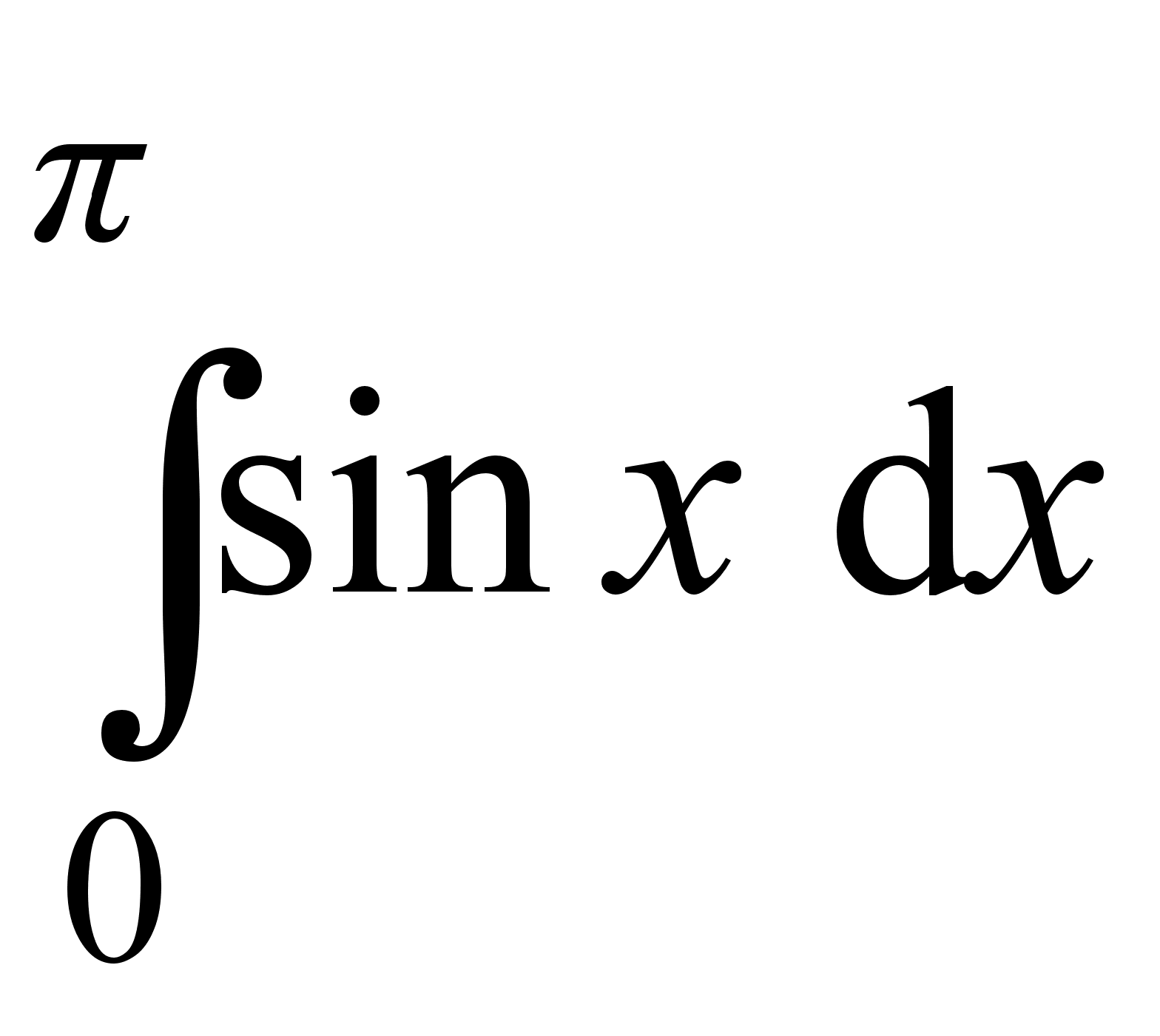 ; 13)
; 13)
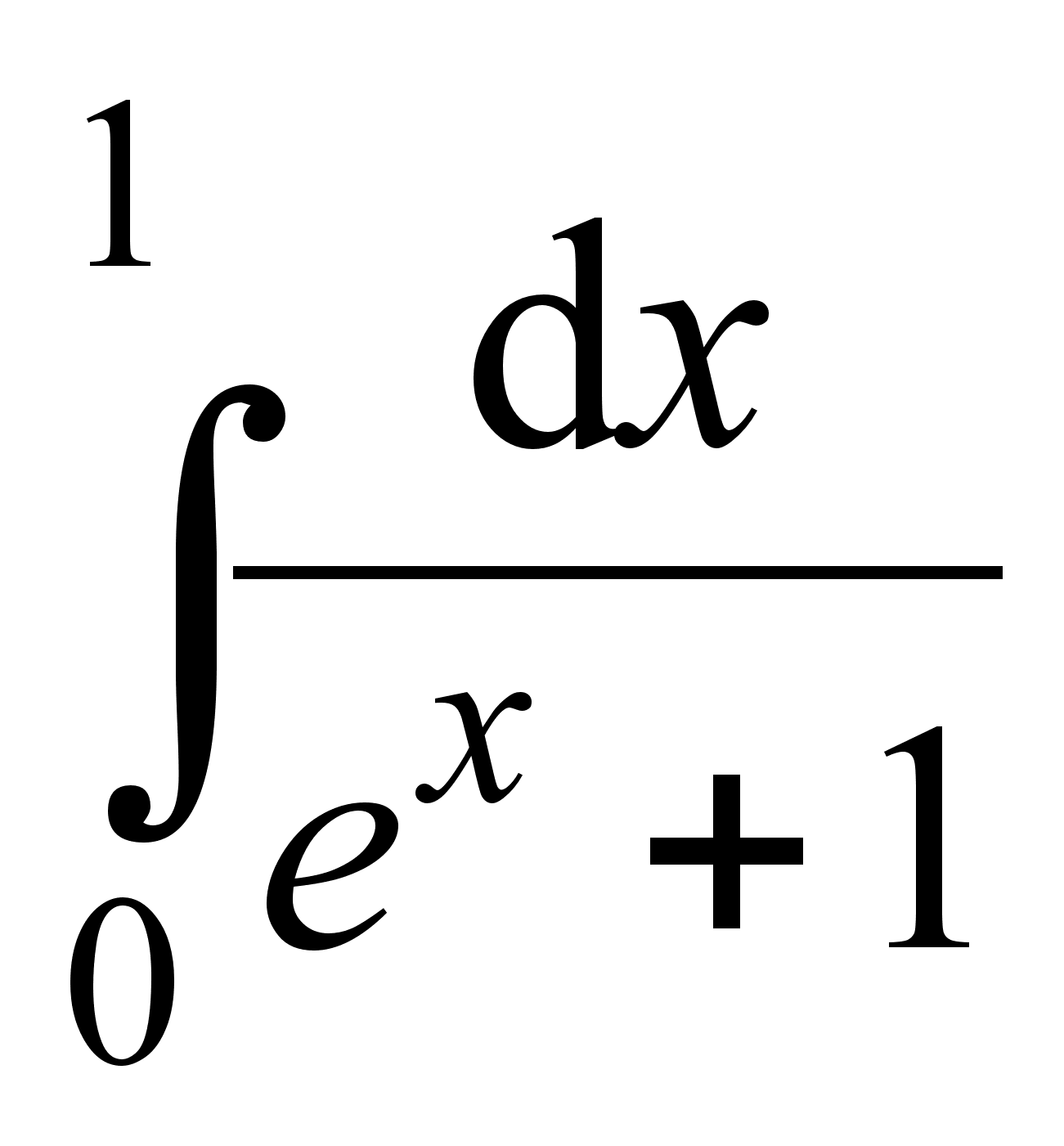 ;
;
4)
![]() ;
9)
;
9)
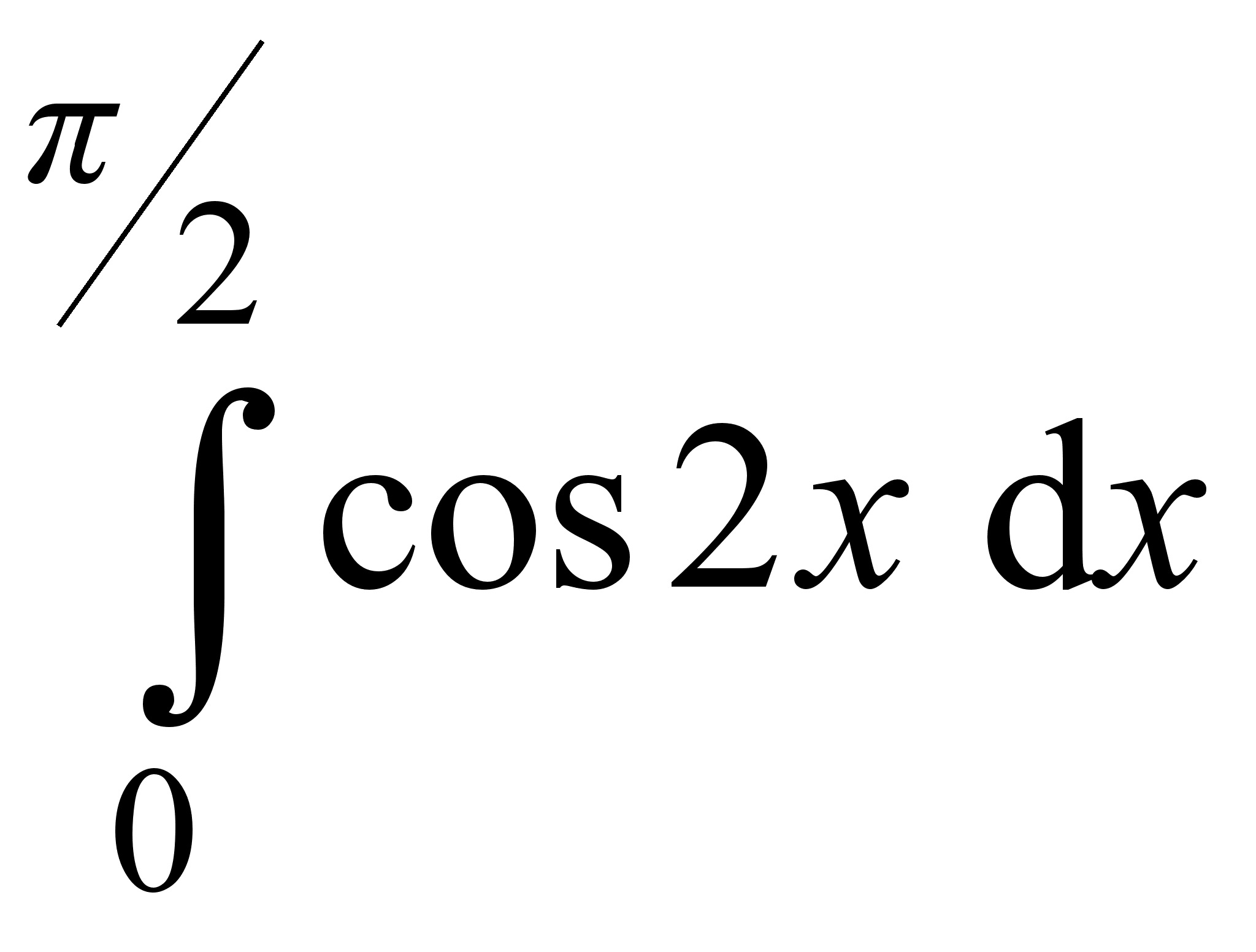 ; 14)
; 14)
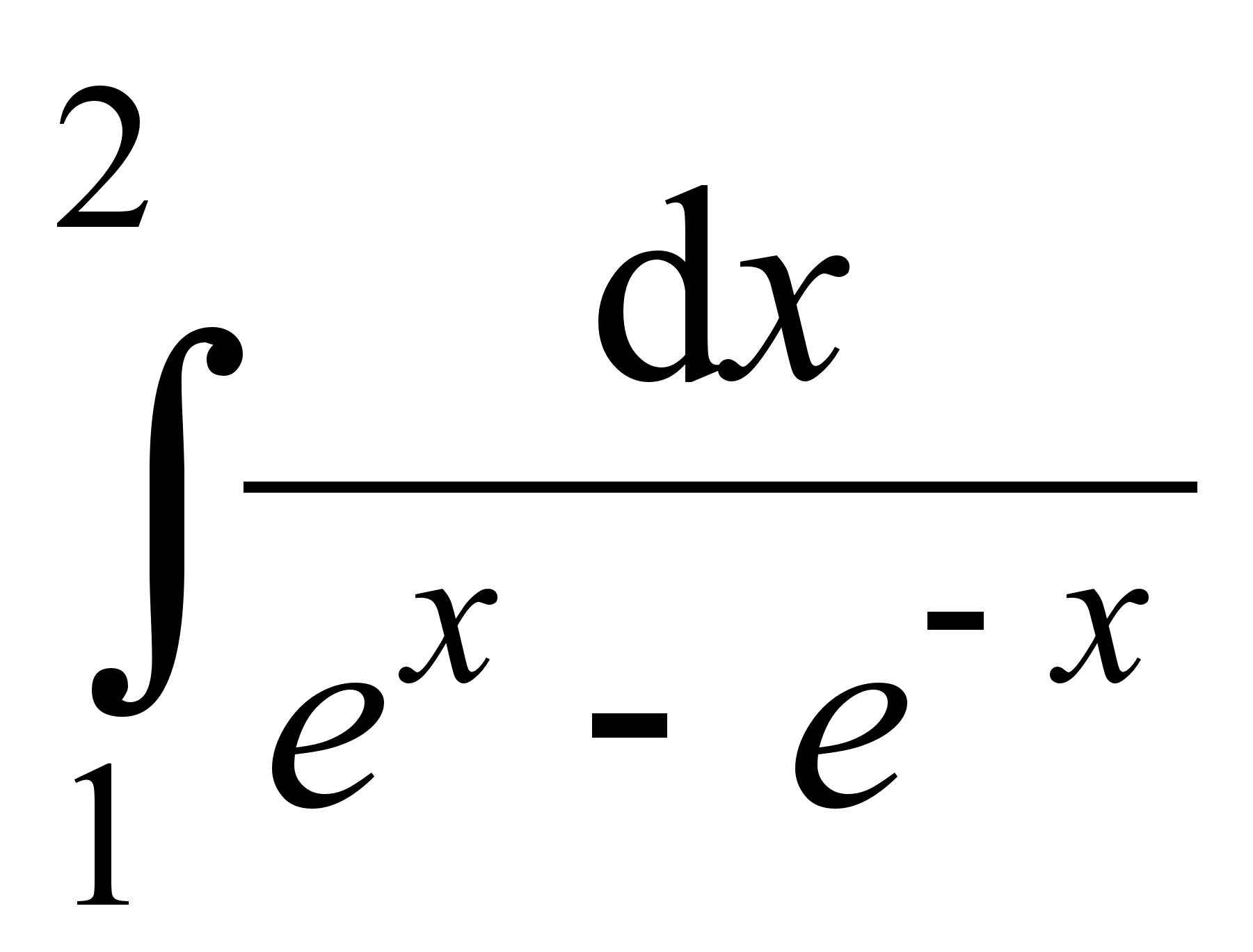 .
.
5)
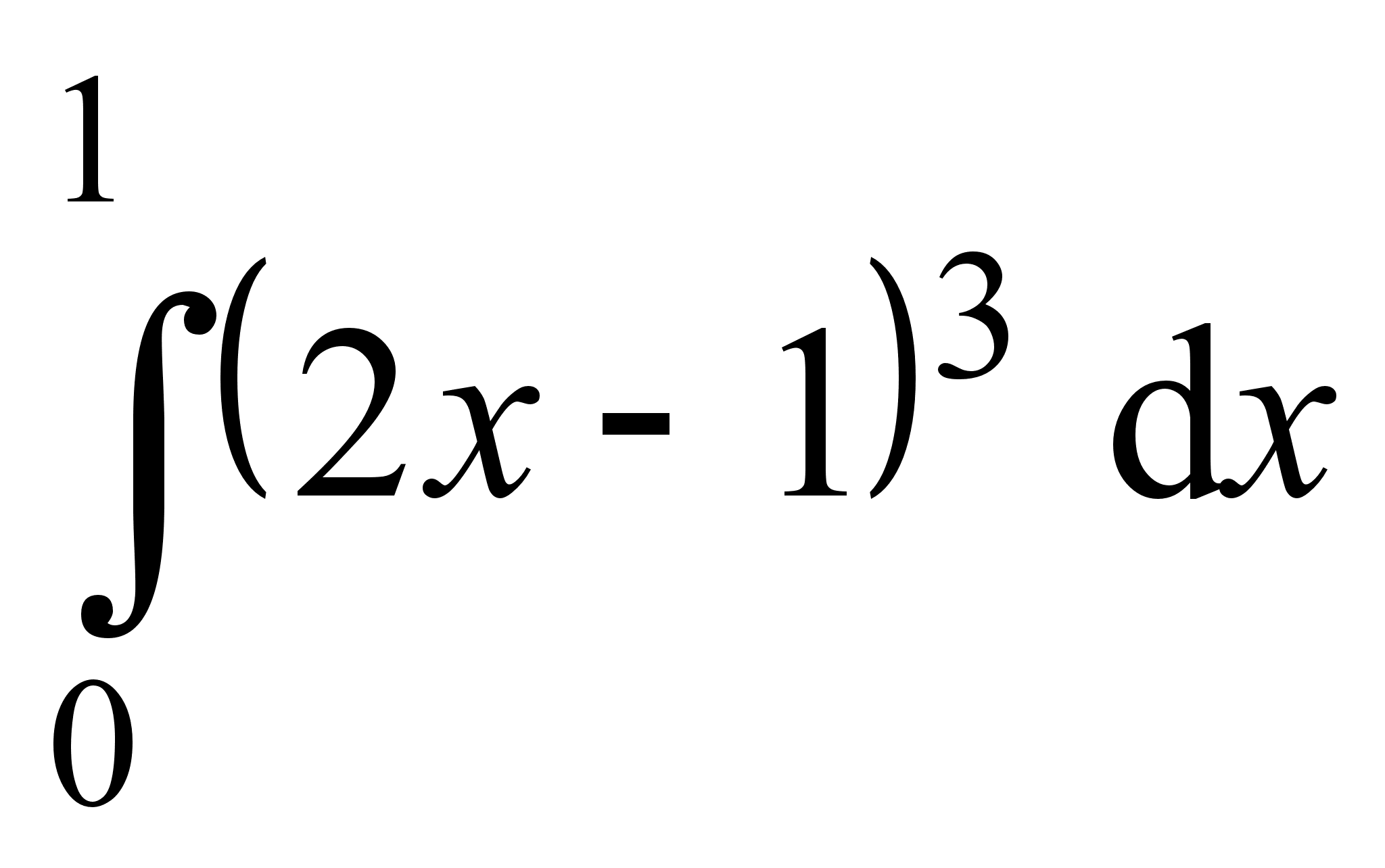 ; 10)
; 10)
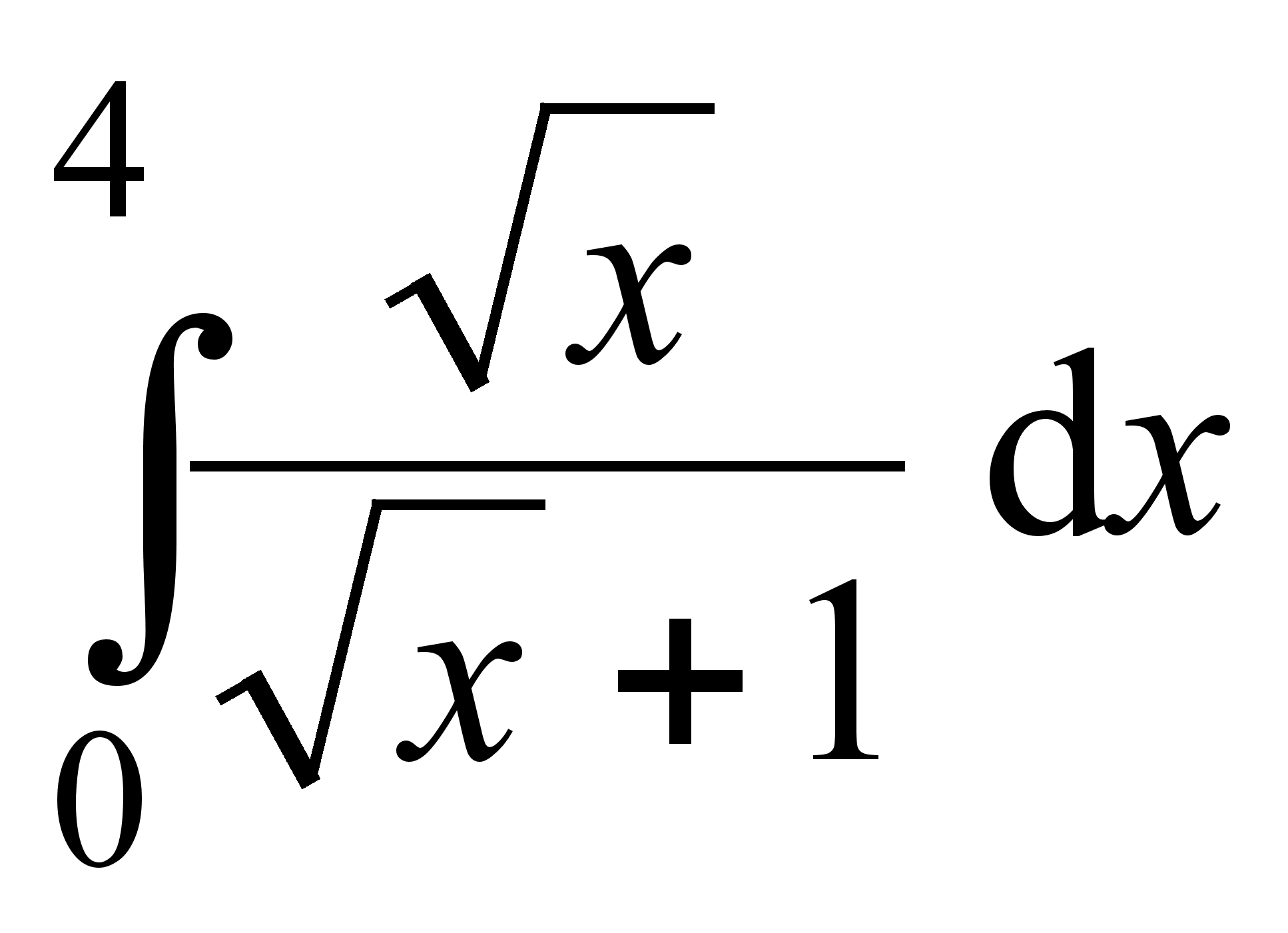 ;
;
2. Найти площади фигур, ограниченных линиями:
1)
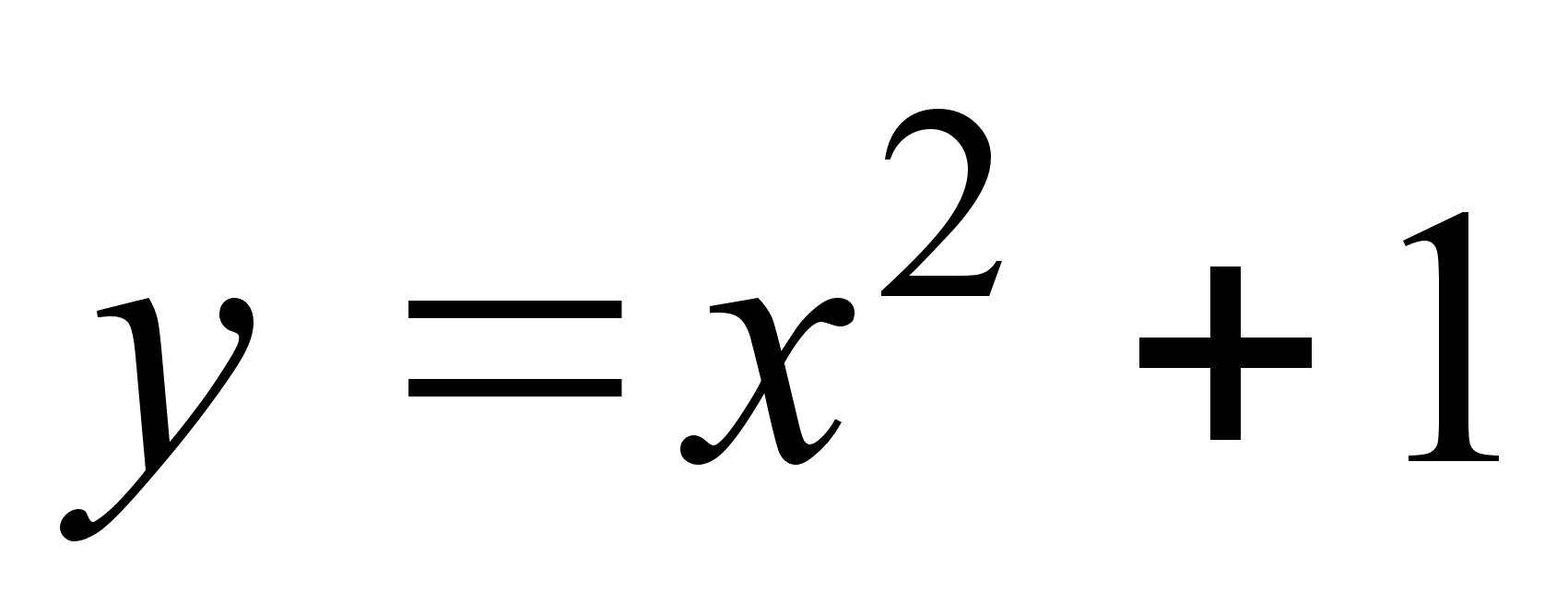 ,
,
 ,
,
 ,
,
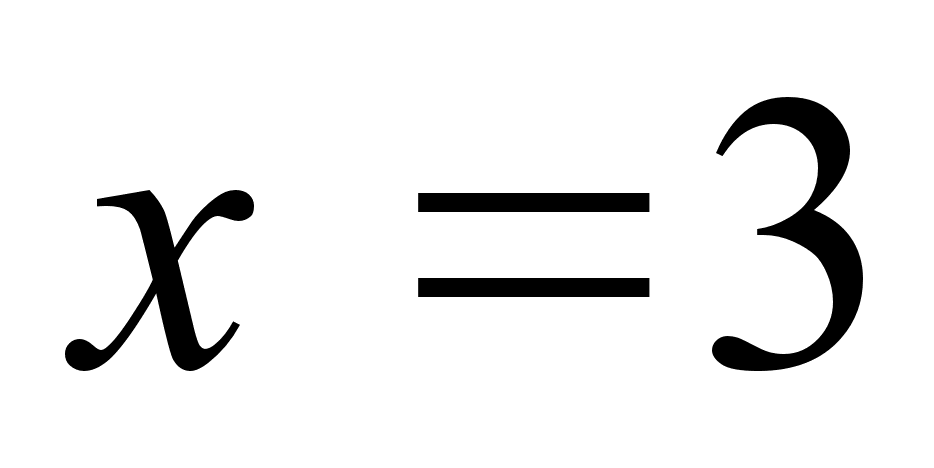 ;
;
2)
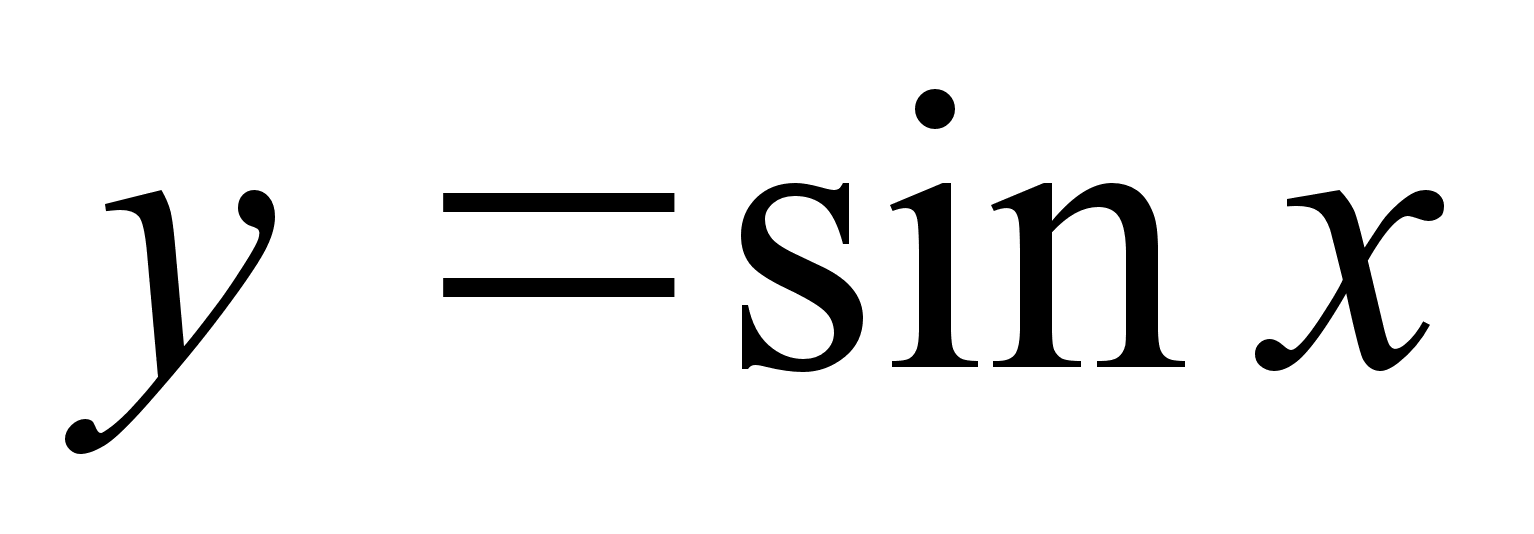 ,
,
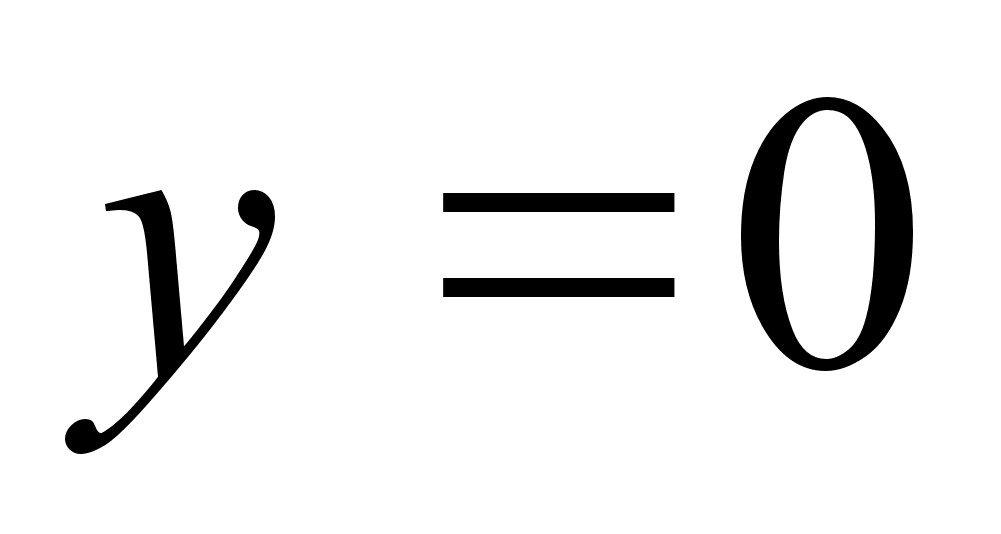 ,
,
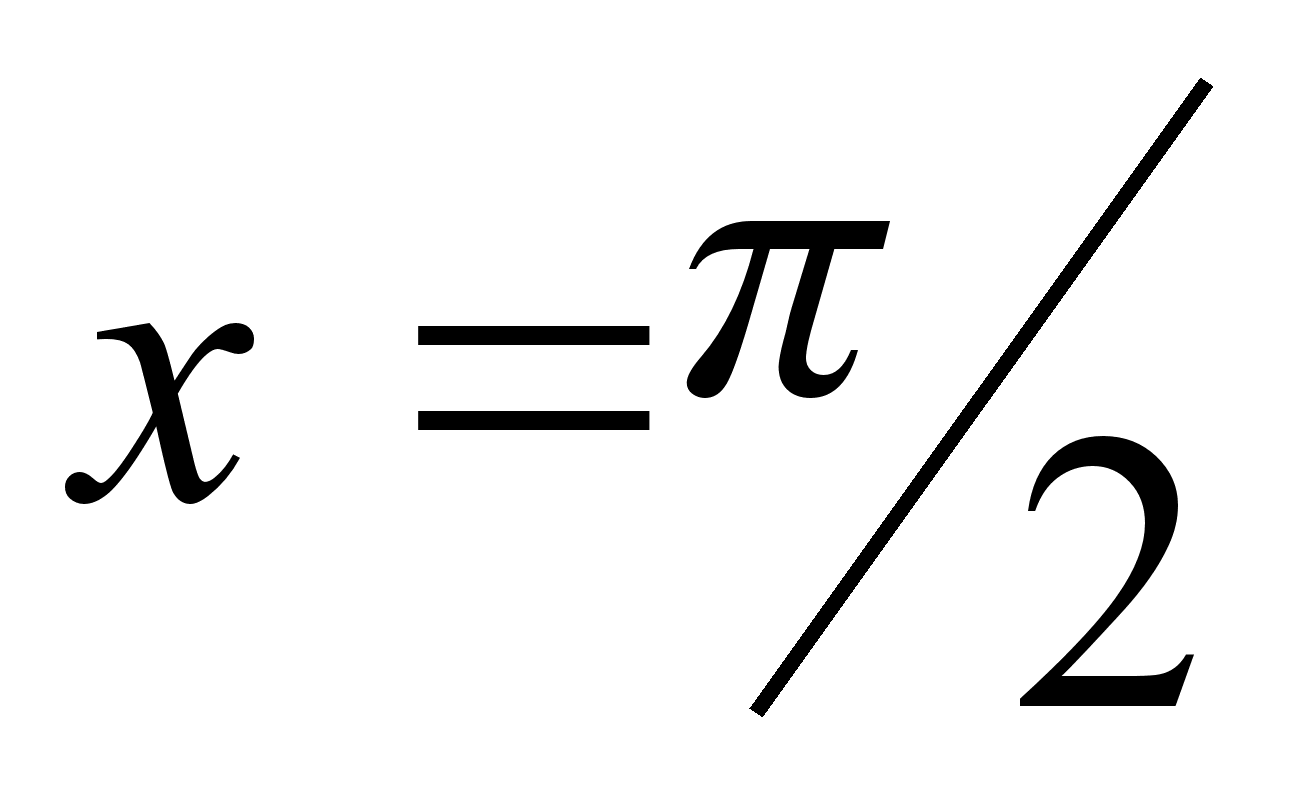 ,
,
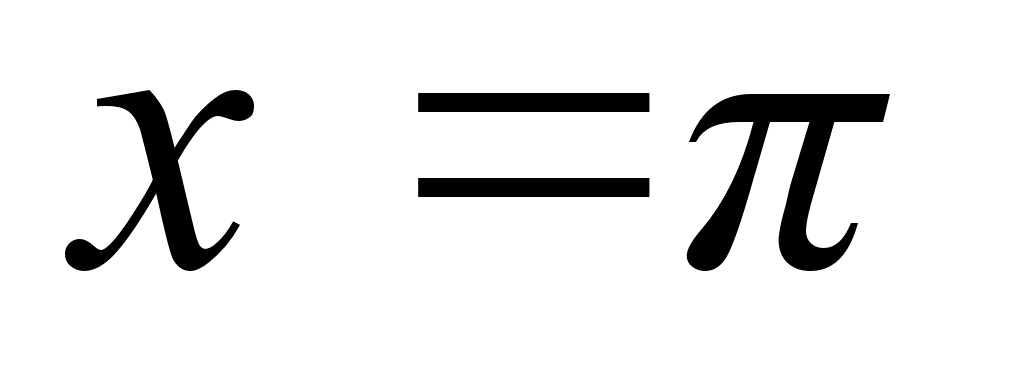 ;
;
3)
![]() ,
,
![]() .
.
Ответы
1. 1) 4; 2)
![]() ;
3)
;
3)
![]() ;
4) 1; 5) 0; 6) 2(
;
4) 1; 5) 0; 6) 2(![]() );
7)
);
7)
![]() ;
8) 2; 9) 0; 10)
;
8) 2; 9) 0; 10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() :
13)
:
13)
![]() ;
14)
;
14)
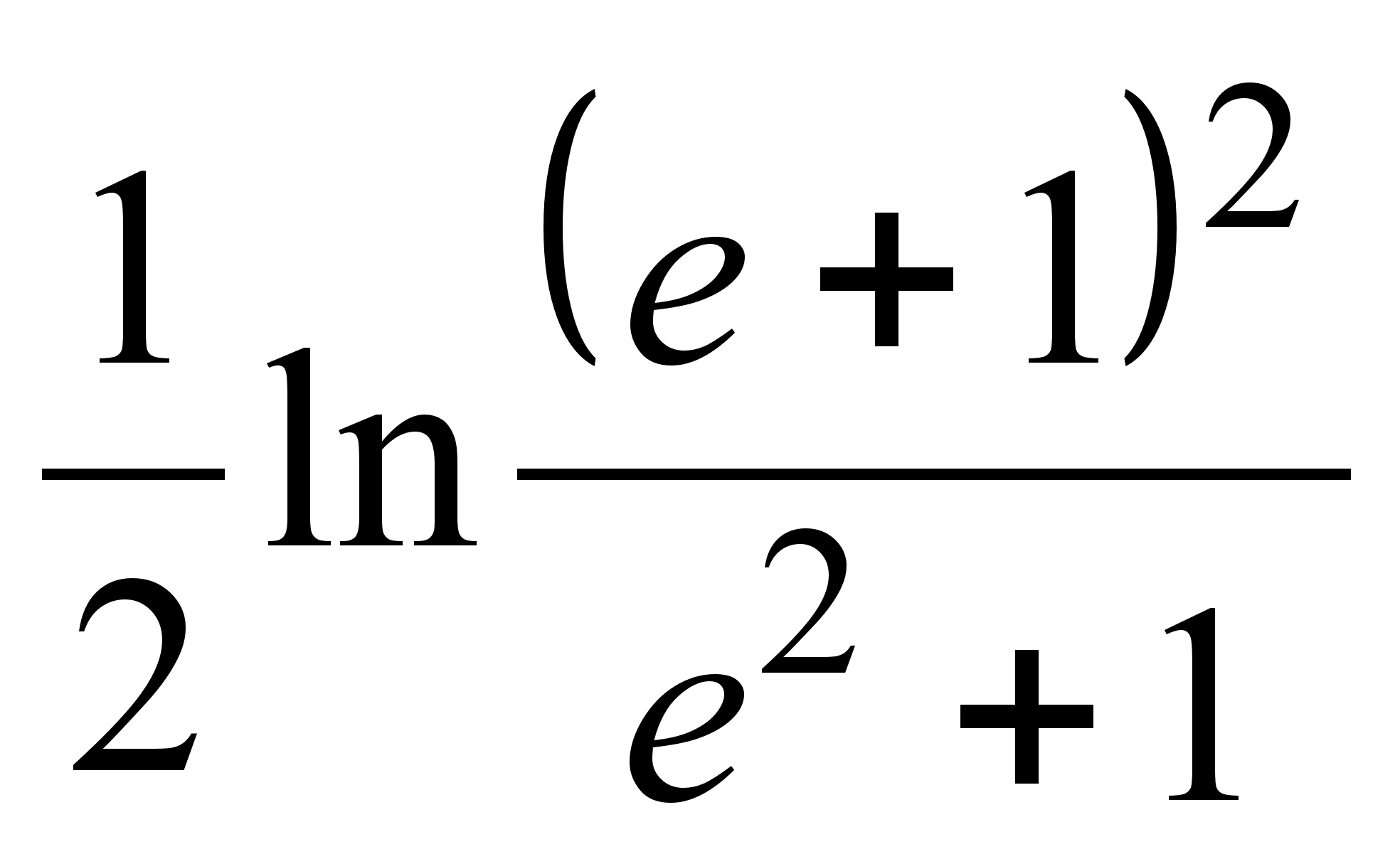 ;
;
2. 1) 12; 2) 1; 3)
![]() ;
Графики функций
;
Графики функций
![]() и
и
![]() пересекаются
в точках с абсциссами
пересекаются
в точках с абсциссами
![]() .
Площадь фигуры
может быть
вычислена как
разность двух
площадей:
.
Площадь фигуры
может быть
вычислена как
разность двух
площадей:
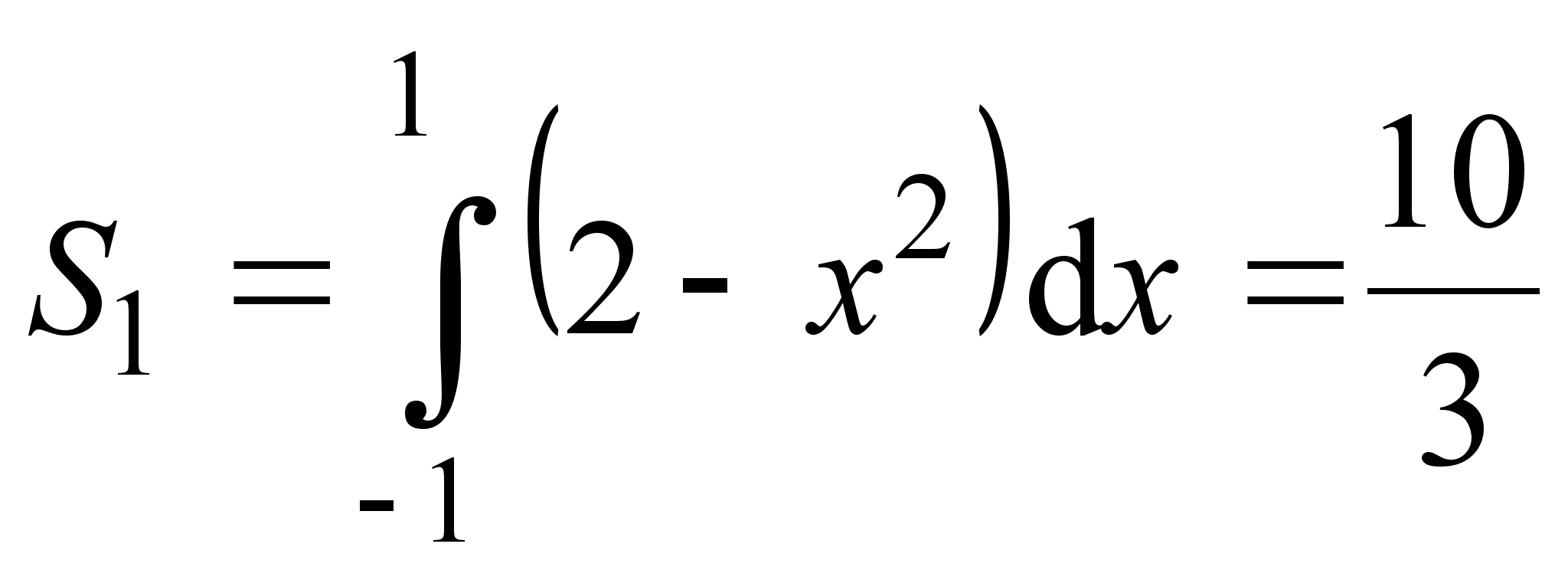 и
и
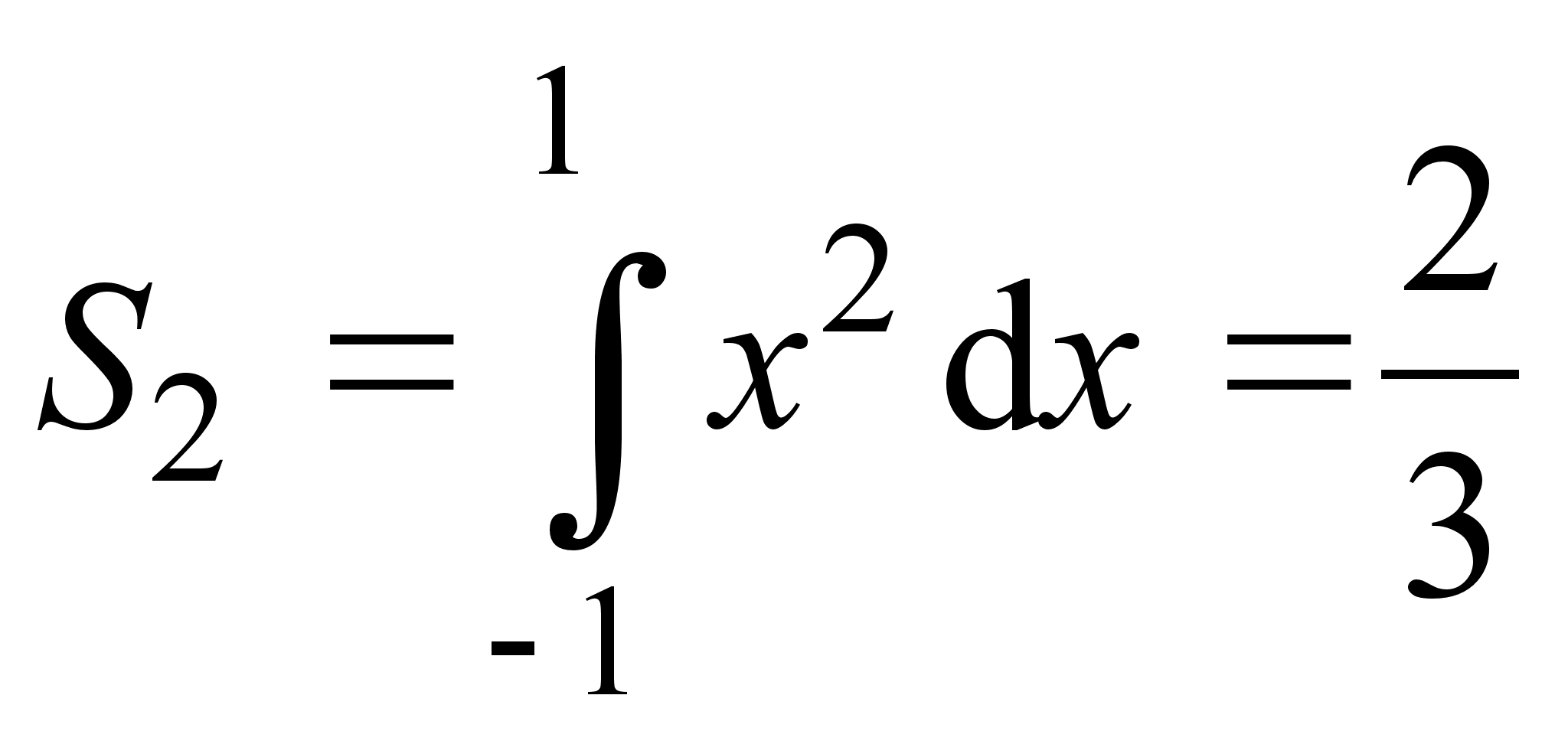 .
.
§ 6. Функции нескольких переменных
Функции нескольких переменных возникают при необходимости учета зависимости некоторой величины более чем от одного фактора. Многие понятия: предел, непрерывность, производная и другие, введенные для функций одной переменной, переносятся на случай функций нескольких переменных.
Мы ограничимся здесь рассмотрением функций двух переменных. Для функций большего числа переменных указанные понятия вводятся аналогично.
1. Определения
Пусть каждой
точке
![]() некоторого
множества
некоторого
множества
![]() плоскости
поставлено
в соответствие
число
плоскости
поставлено
в соответствие
число
![]() ,
тогда говорят,
что на множестве
,
тогда говорят,
что на множестве
![]() задана функция
двух переменных
задана функция
двух переменных
![]() .
Используется
также запись
.
Используется
также запись
![]() .
.
Пример. В экономических приложениях встречаются производственные функции, устанавливающие связь между затратами производственных ресурсов и объемом выпускаемой продукции. Производственные функции, как правило, зависят от многих переменных (факторов). В частности, рассматриваются двухфакторные функции
![]() ,
,
где
![]() - объем производственных
фондов,
- объем производственных
фондов,
![]() -
затраты труда,
-
затраты труда,
![]() -
объем выпускаемой
продукции.
Примером
двухфакторной
функции является
функция Кобба-Дугласа
-
объем выпускаемой
продукции.
Примером
двухфакторной
функции является
функция Кобба-Дугласа
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() - постоянные.
- постоянные.
Окрестностью
точки
![]() назовем внутренность
любого круга
с центром в
этой точке.
Пусть функция
назовем внутренность
любого круга
с центром в
этой точке.
Пусть функция
![]() определена
в некоторой
окрестности
точки
определена
в некоторой
окрестности
точки
![]() .
Зафиксируем
значение
.
Зафиксируем
значение
![]() и рассмотрим
функцию
и рассмотрим
функцию
![]() одной переменной
одной переменной
![]() .
Производная
функции
.
Производная
функции
![]() в точке
в точке
![]() (если она существует)
называется
частной производной
функции
(если она существует)
называется
частной производной
функции
![]() в точке
в точке
![]() по переменной
по переменной
![]() и обозначается
и обозначается
![]() .
Аналогично
определяется
частная производная
.
Аналогично
определяется
частная производная
![]() по переменной
по переменной
![]() .
.
Производные
![]() и
и
![]() функции
функции
![]() называются
частными производными
первого порядка.
Если они существуют
в некоторой
окрестности
точки
называются
частными производными
первого порядка.
Если они существуют
в некоторой
окрестности
точки
![]() ,
то частные
производные
от них по
,
то частные
производные
от них по
![]() и
и
![]() называются
частными
производными
второго порядка
и обозначаются
называются
частными
производными
второго порядка
и обозначаются
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
где, например,
,
где, например,
![]() ,
,
![]() .
Производные
.
Производные
![]() ,
,
![]() называются
смешанными
частными
производными.
называются
смешанными
частными
производными.
Аналогично можно ввести частные производные третьего и более высоких порядков. Из определения частных производных следует, что для их нахождения можно использовать все правила, справедливые для производных функций одной переменной.
Примеры. Найдем частные производные первого и второго порядков функций:
а)
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
б)
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Равенство смешанных производных, наблюдаемое в приведенных примерах, не случайно. Справедливо следующее общее утверждение.
Теорема. Если
производные
![]() ,
,
![]() существуют
в некоторой
окрестности
точки
существуют
в некоторой
окрестности
точки
![]() и непрерывны
в этой точке,
то справедливо
равенство
и непрерывны
в этой точке,
то справедливо
равенство
![]() .
.
2. Экстремумы
Точка
![]() называется
точкой локального
максимума
(минимума)
функции
называется
точкой локального
максимума
(минимума)
функции
![]() ,
если для всех
точек
,
если для всех
точек
![]() (
(![]() )
из некоторой
окрестности
этой точки
справедливо
неравенство
)
из некоторой
окрестности
этой точки
справедливо
неравенство
![]() (
(![]() ).
Точки локального
максимума и
минимума называются
точками экстремума
функции.
).
Точки локального
максимума и
минимума называются
точками экстремума
функции.
Пример. В экономическом анализе применяется функция прибыли
![]() ,
,
где
![]() – производственная
функция,
– производственная
функция,
![]() – цена выпускаемой
продукции,
– цена выпускаемой
продукции,
![]() и
и
![]() – факторные
цены. Пара чисел
(
– факторные
цены. Пара чисел
(![]() )
называется
оптимальным
планом, если
функция
)
называется
оптимальным
планом, если
функция
![]() достигает
максимума при
достигает
максимума при
![]() .
Таким образом,
поиск оптимального
плана сводится
к отысканию
точки экстремума
(максимума)
функции прибыли
.
Таким образом,
поиск оптимального
плана сводится
к отысканию
точки экстремума
(максимума)
функции прибыли
![]() .
.
Следующие теоремы позволяют находить точки экстремума функций.
Теорема (необходимое
условие экстремума).
Если функция
![]() имеет в точке
экстремума
имеет в точке
экстремума
![]() частные производные
первого порядка,
то они равны
нулю в этой
точке:
частные производные
первого порядка,
то они равны
нулю в этой
точке:
![]() .
(1)
.
(1)
Точки,
координаты
которых удовлетворяют
системе (1) называются
стационарными
точками функции
![]() .
Точки экстремума
функции следует
искать среди
ее стационарных
точек и тех
точек, в которых
частные производные
первого порядка
не существуют.
.
Точки экстремума
функции следует
искать среди
ее стационарных
точек и тех
точек, в которых
частные производные
первого порядка
не существуют.
Теорема (достаточное
условие экстремума).
Пусть функция
![]() имеет непрерывные
частные производные
второго порядка
в некоторой
окрестности
своей стационарной
точки
имеет непрерывные
частные производные
второго порядка
в некоторой
окрестности
своей стационарной
точки
![]() .
Положим
.
Положим
![]() .
.
Тогда:
а) если
![]() и
и
![]() ,
то
,
то
![]() - точка максимума
функции;
- точка максимума
функции;
б) если
![]() и
и
![]() ,
то
,
то
![]() - точка минимума
функции;
- точка минимума
функции;
в) если
![]() ,
то в точке
,
то в точке
![]() экстремума
нет.
экстремума
нет.
Пример.
Стационарная
точка
![]() ,
,
![]() функции
функции
![]()
является решением системы уравнений
![]() ,
,
![]() .
.
При этом
![]() ,
,
![]() ,
,
![]() и
и
![]() .
Следовательно,
в точке
.
Следовательно,
в точке
![]() функция имеет
локальный
минимум.
функция имеет
локальный
минимум.
Пример. Пусть
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
и, следовательно,
стационарная
точка
,
и, следовательно,
стационарная
точка
![]() не является
точкой экстремума.
не является
точкой экстремума.
Пример. Для
функции
![]() из системы
уравнений
из системы
уравнений
![]() ,
,
![]() ,
,
найдем
четыре стационарные
точки:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Поскольку
.
Поскольку
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
.
В точках
![]() и
и
![]() выполнено
условие
выполнено
условие
![]() ,
поэтому функция
имеет экстремумы
в этих точках:
минимум в
,
поэтому функция
имеет экстремумы
в этих точках:
минимум в
![]() ,
так как
,
так как
![]() ,
и максимум в
,
и максимум в
![]() ,
так как
,
так как
![]() .
В точках
.
В точках
![]() и
и
![]() экстремумов
нет, так как
экстремумов
нет, так как
![]() в этих точках.
в этих точках.
Упражнения
1. Найти частные производные первого порядка следующих функций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
2. Найти смешанные производные функций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
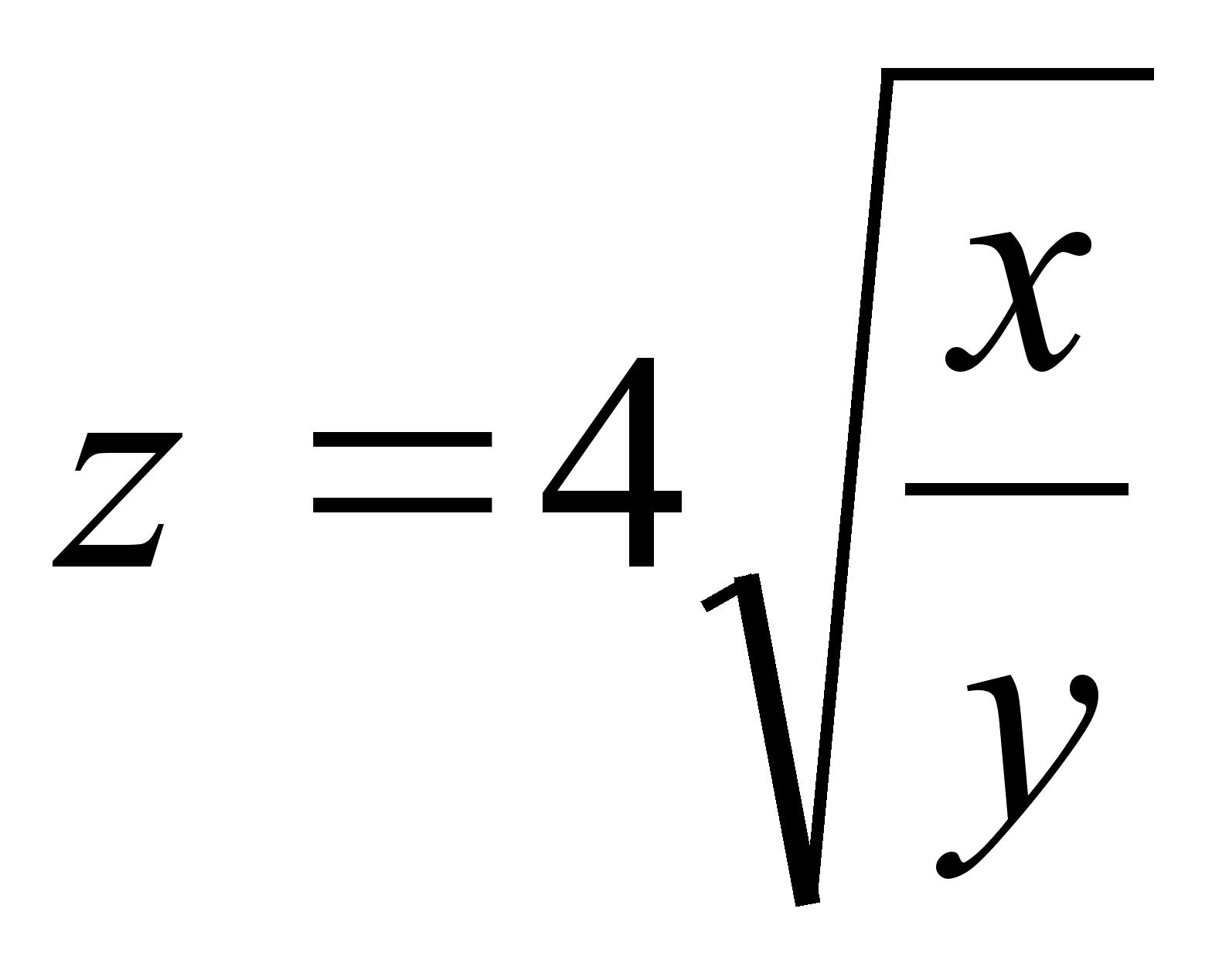 ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
3. Найти стационарные точки функций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;.
;.
6)
![]() );
);
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
4. Найти точки локального экстремума функций:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() .
.
Ответы
1.
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ;
;
6)
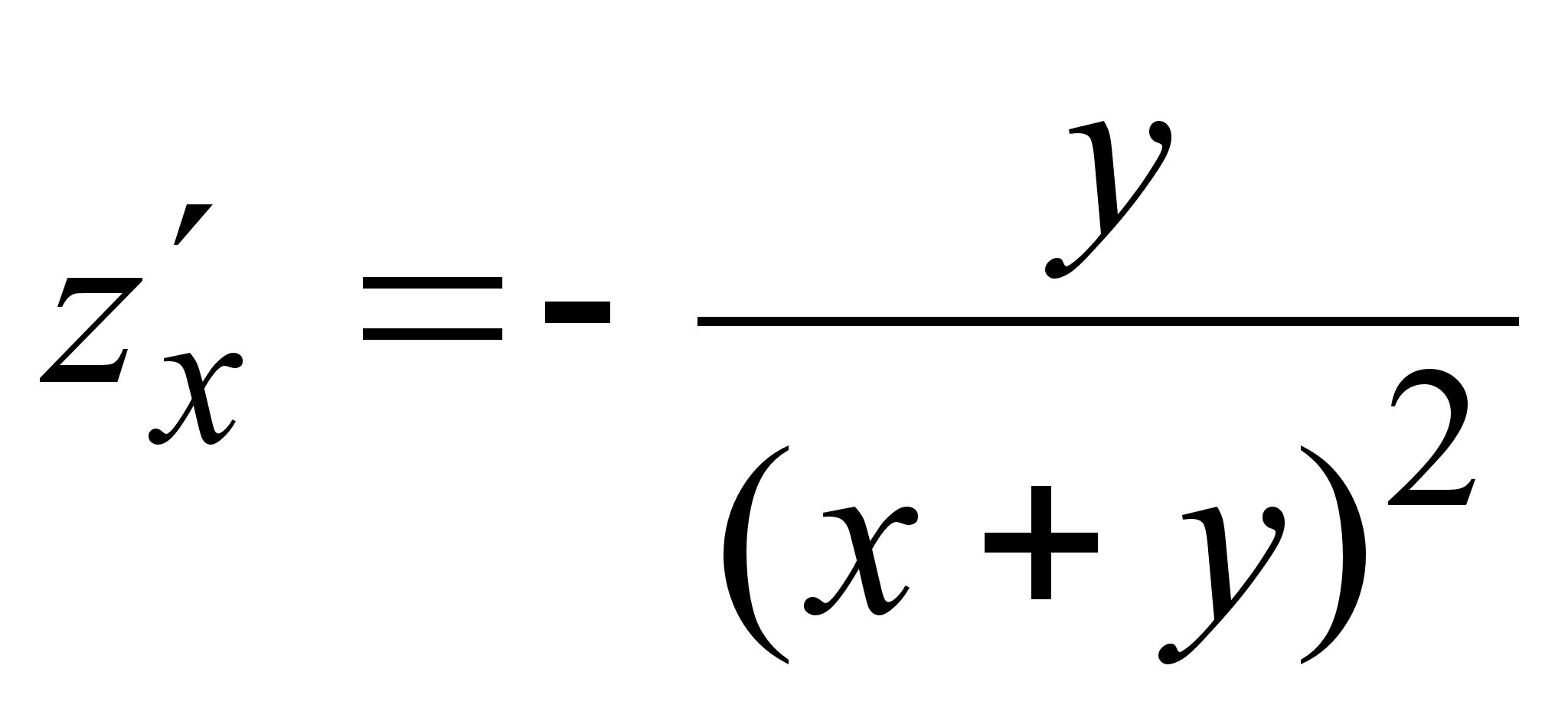 ,
,
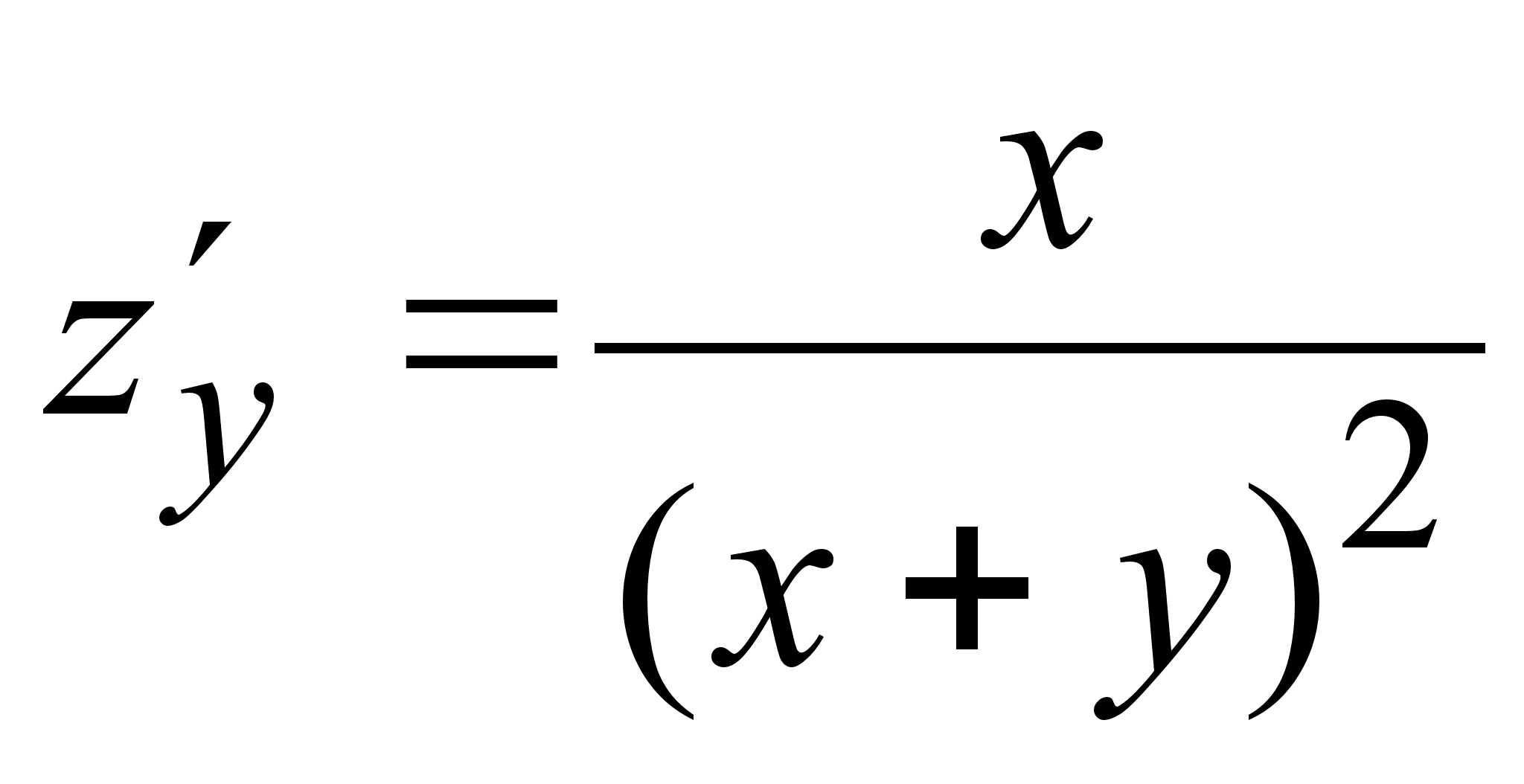 ;
;
7)
![]() ;
;
![]() ;
;
8)
![]() ,
,
 ;
;
9)
![]() ,
,
![]() ;
;
10)
![]() ,
,
![]() .
.
2.
1) 0;
2)
![]() ;
;
3)
![]() ;
;
4)
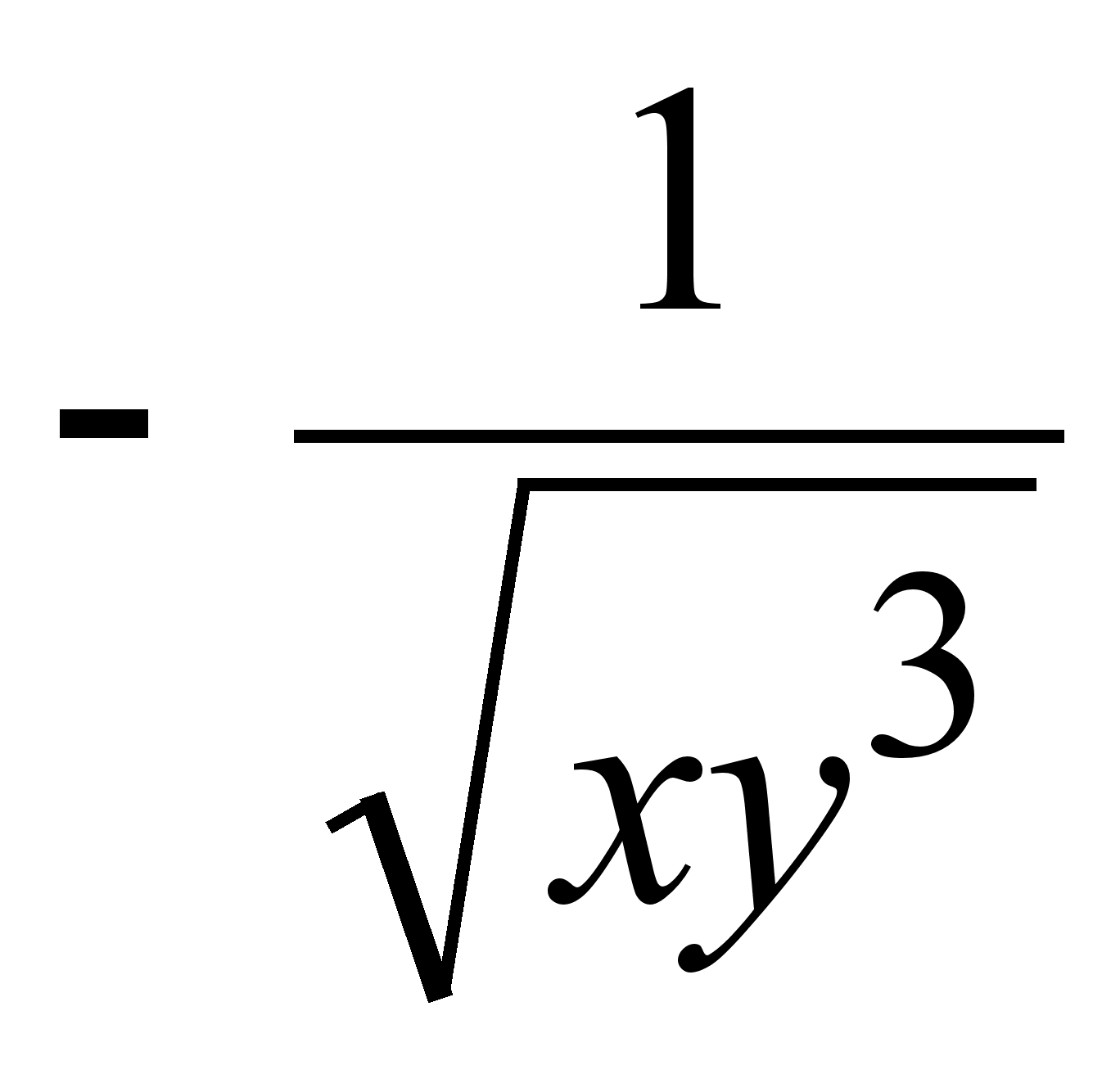 ;
;
5)
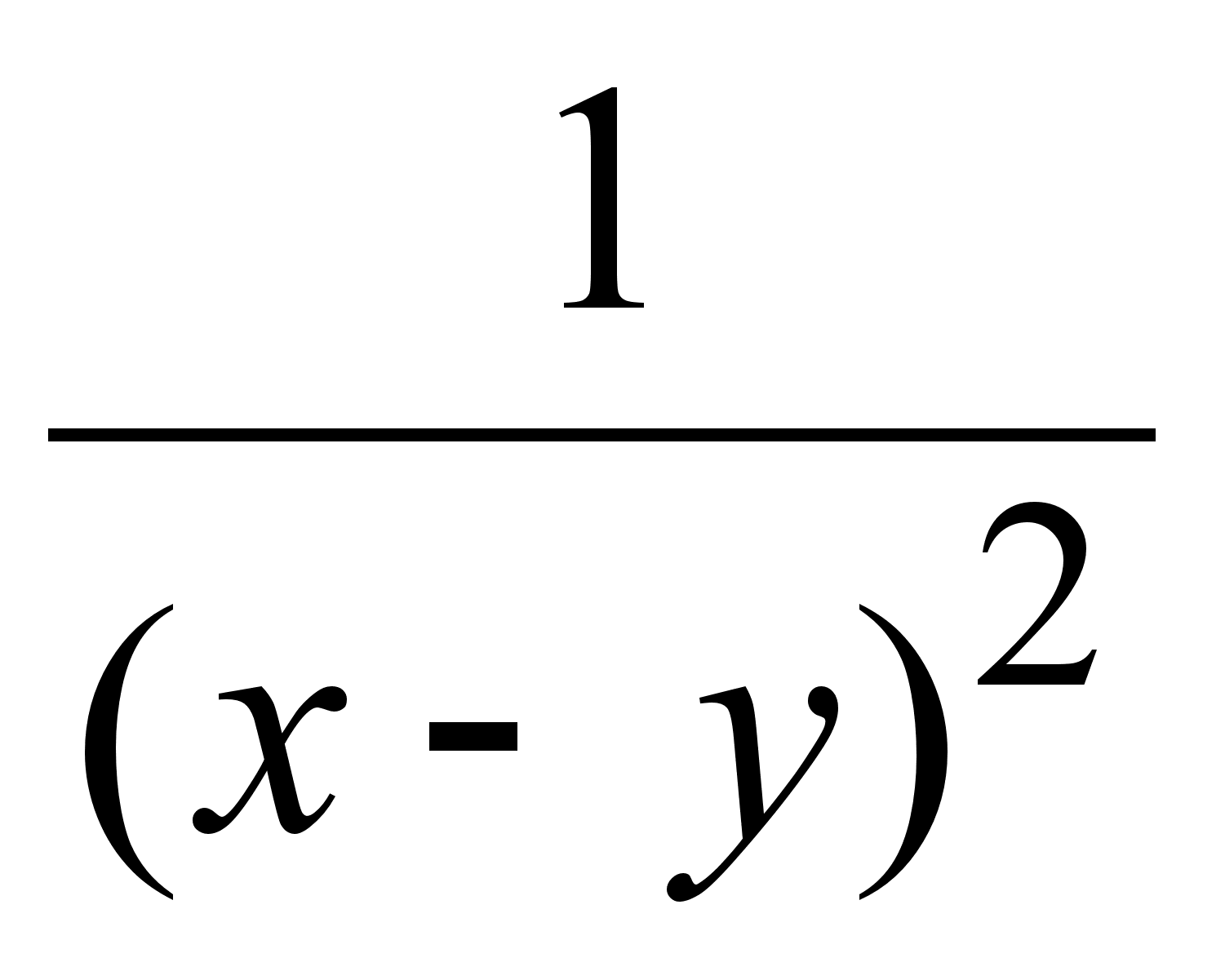 ;
;
6)
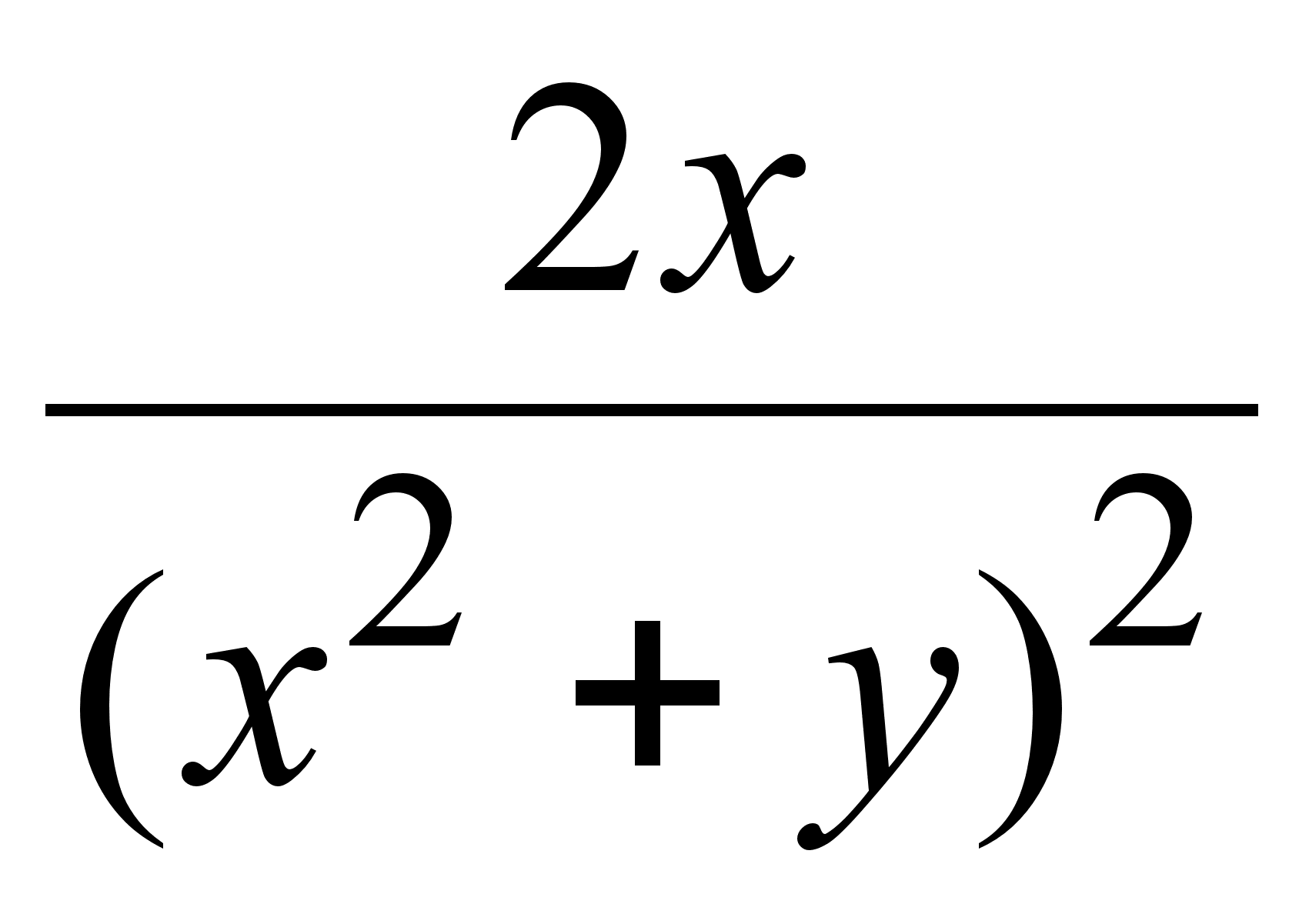 ;
;
7)
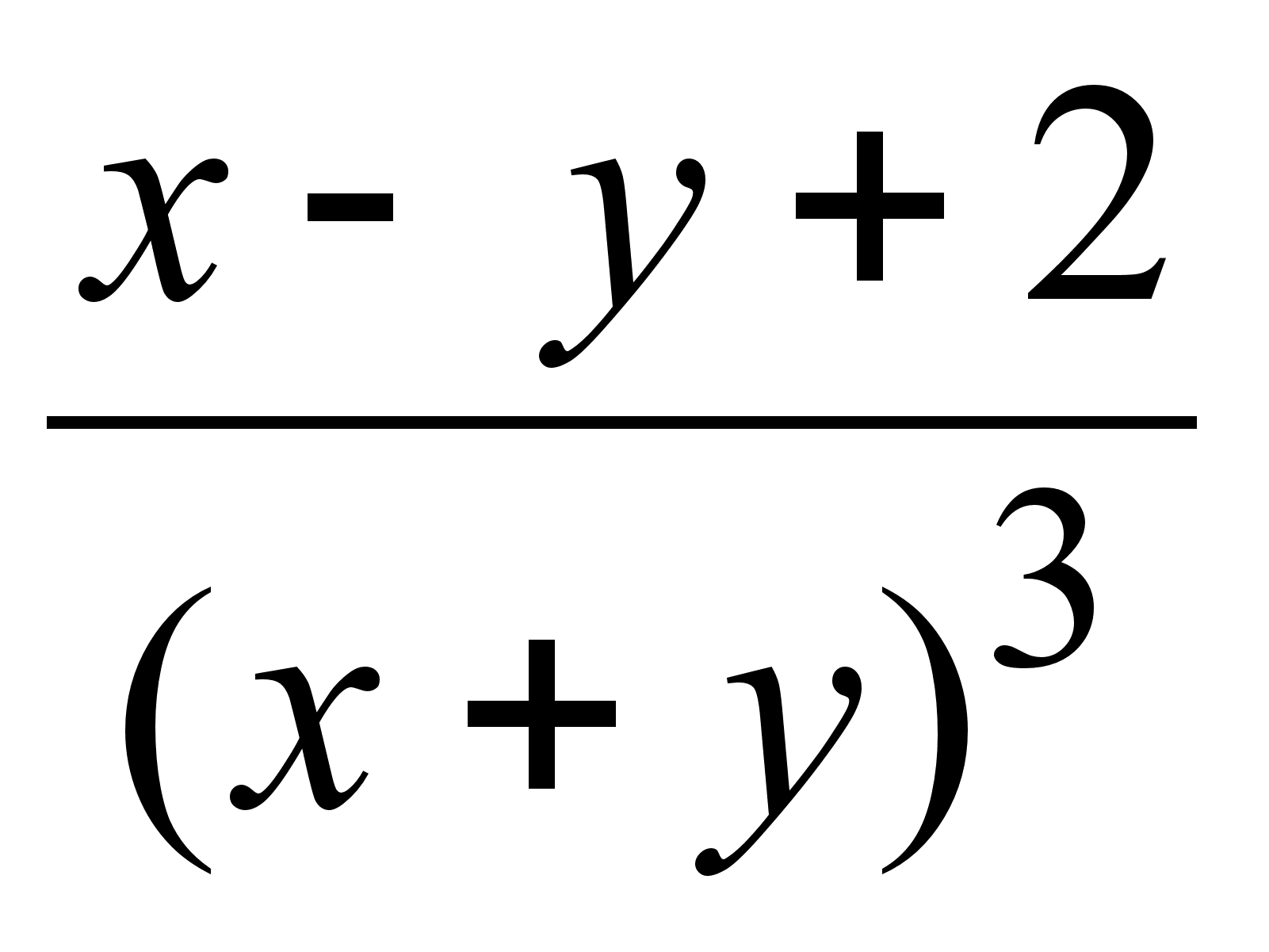 ;
;
8)
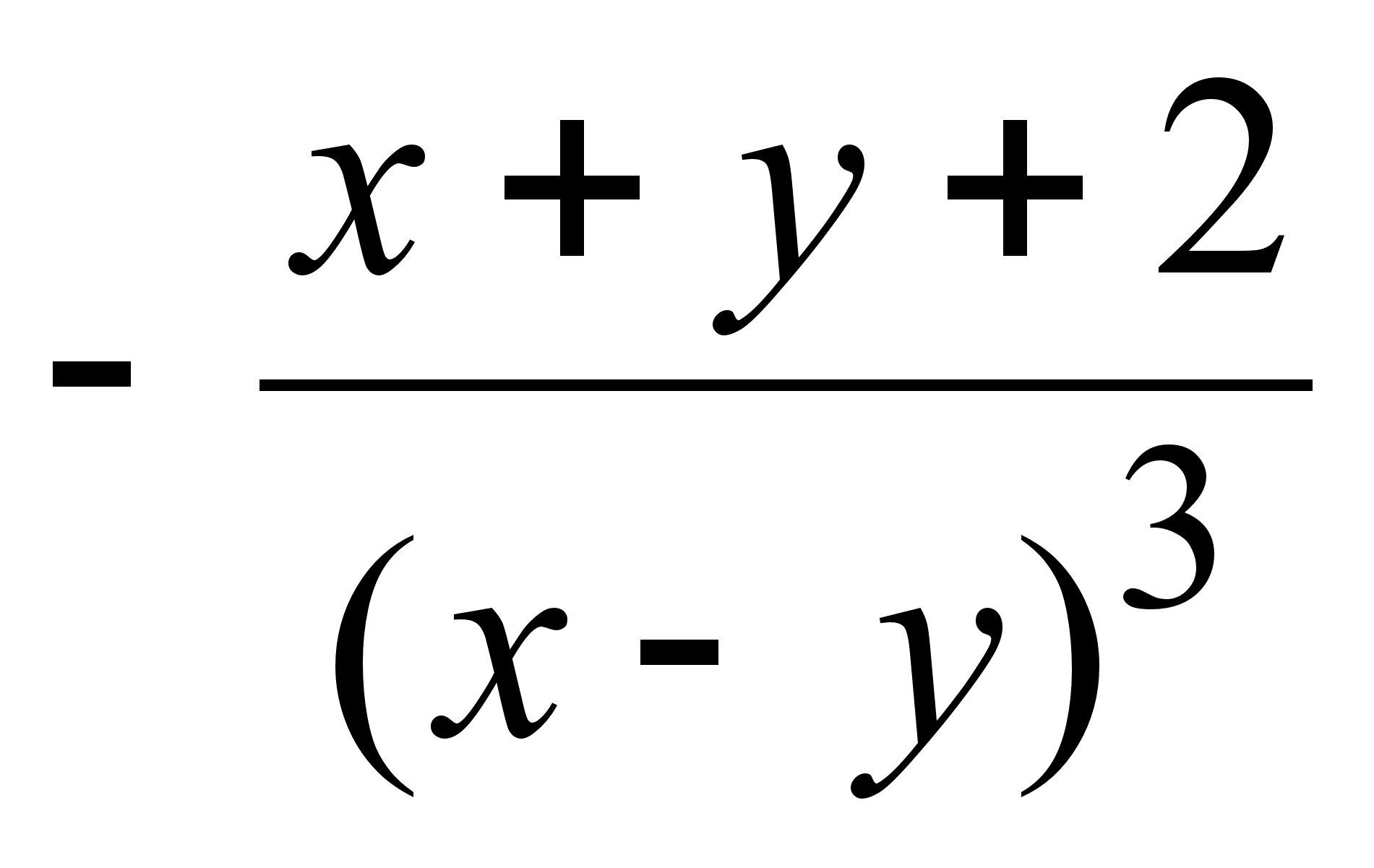 ;
;
9)
![]() ;
;
10)
![]() .
.
3.
1) (0,1);
2)
![]() ;
;
3) (1,2);
4)
![]() ;
;
5)
![]() и
и
![]() ;
;
6) стационарных точек нет;
7)
![]() ;
;
8)
![]() ;
;
9) стационарных точек нет;
10)
![]() .
.
4.
1)
![]() - точка минимума;
- точка минимума;
2)
![]() - точка минимума;
- точка минимума;
3)
![]() - точка максимума;
- точка максимума;
4) и 5) функция не имеет точек экстремума;
6)
![]() - точка минимума;
- точка минимума;
7)
![]() - точка минимума;
- точка минимума;
8)
![]() - точка максимума;
- точка максимума;
9) функция не имеет точек экстремума;
10)
![]() - точка минимума;
- точка минимума;
![]() - точка максимума.
- точка максимума.
§ 7. Обыкновенные дифференциальные уравнения
Математическое исследование многих реальных процессов основано на применении дифференциальных уравнений, содержащих производные искомых функций. Аппарат дифференциальных уравнений универсален: разнообразные процессы могут описываться одинаковыми уравнениями. Практика показывает, что даже простые математические модели, использующие дифференциальные уравнения, позволяют качественно изучить основные черты сложных явлений и оценить их количественные характеристики.
1. Определения
Порядком дифференциального уравнения называется наибольший порядок входящих в него производных. Этот параграф посвящен обыкновенным дифференциальным уравнениям первого порядка, то есть уравнениям вида
![]() ,
,
где
![]() - заданная функция,
- заданная функция,
![]() - независимая
переменная,
- независимая
переменная,
![]() - искомая функция,
- искомая функция,
![]() - ее производная.
Уравнения вида
- ее производная.
Уравнения вида
![]()
называются разрешенными относительно производной.
Функция
![]() называется
решением
дифференциального
уравнения, если
после ее подстановки
уравнение
обращается
в тождество.
Процесс нахождения
решений называется
интегрированием
уравнения.
Решить уравнение
значит найти
все его решения.
называется
решением
дифференциального
уравнения, если
после ее подстановки
уравнение
обращается
в тождество.
Процесс нахождения
решений называется
интегрированием
уравнения.
Решить уравнение
значит найти
все его решения.
Ниже рассматриваются
только уравнения,
разрешенные
относительно
производной.
В простейшем
случае, когда
правая часть
уравнения не
зависит от
![]() ,
то есть уравнение
имеет вид
,
то есть уравнение
имеет вид
![]() ,
,
любое его решение
является
первообразной
функции
![]() ,
а интегрирование
уравнения
сводится к
отысканию
неопределенного
интеграла от
,
а интегрирование
уравнения
сводится к
отысканию
неопределенного
интеграла от
![]() (см. § 4). Совокупность
всех решений,
то есть общее
решение уравнения,
можно представить
формулой
(см. § 4). Совокупность
всех решений,
то есть общее
решение уравнения,
можно представить
формулой
![]() ,
,
где
![]() - произвольная
постоянная.
При этом в данном
параграфе под
неопределенным
интегралом
функции условимся
понимать не
все множество
ее первообразных,
а любую фиксированную
первообразную.
- произвольная
постоянная.
При этом в данном
параграфе под
неопределенным
интегралом
функции условимся
понимать не
все множество
ее первообразных,
а любую фиксированную
первообразную.
Пример. Для уравнения
![]() ,
,
интегрируя, получим общее решение
![]() .
.
В следующем пункте рассматривается один класс уравнений, общее решение которых представляется в квадратурах, то есть с использованием интегралов от известных функций.
2. Уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
![]() ,
(1)
,
(1)
где
![]() и
и
![]() -
заданные функции.
-
заданные функции.
Заметим, что
если для некоторого
значения
![]() выполнено
выполнено
![]() ,
то функция
,
то функция
![]() является решением
уравнения (1).
является решением
уравнения (1).
Рассмотрим
случай
![]() .
Разделив левую
и правую части
уравнения на
.
Разделив левую
и правую части
уравнения на
![]() ,
получим
,
получим
![]() ,
откуда следует
соотношение
между первообразными
,
откуда следует
соотношение
между первообразными
![]() ,
где
,
где
![]() - произвольная
постоянная.
Используя
формулу замены
переменной
в неопределенном
интеграле (см.
§ 4), получаем
равенство
- произвольная
постоянная.
Используя
формулу замены
переменной
в неопределенном
интеграле (см.
§ 4), получаем
равенство
![]() ,
(2)
,
(2)
определяющее в неявном виде семейство решений уравнения (1), зависящее от произвольной постоянной.
Замечание. Чтобы из бесконечного множества решений дифференциального уравнения выделить частное решение нужно задать какое-либо дополнительное условие, например,
![]() ,
(3)
,
(3)
где
![]() ,
,
![]() - некоторые
постоянные.
Условие (2) называется
начальным,
а задача отыскания
решения, удовлетворяющего
такому условию,
называется
задачей Коши.
- некоторые
постоянные.
Условие (2) называется
начальным,
а задача отыскания
решения, удовлетворяющего
такому условию,
называется
задачей Коши.
Пример. Найдем общее решение уравнения
![]() .
.
Используя (2),
получаем
![]() ,
то есть
,
то есть
![]() ,
где
,
где
![]() - произвольная
постоянная.
Отсюда находим
семейство
решений
- произвольная
постоянная.
Отсюда находим
семейство
решений
![]() .
Кроме того,
имеется решение
.
Кроме того,
имеется решение
![]() ,
при котором
правая часть
уравнения
обращается
в ноль. Все найденные
решения можно
представить
одной формулой
,
при котором
правая часть
уравнения
обращается
в ноль. Все найденные
решения можно
представить
одной формулой
![]() ,
,
где
![]() - произвольная
постоянная.
- произвольная
постоянная.
Пример. Рассмотрим уравнение
![]() .
(4)
.
(4)
Как и в предыдущем
примере,
![]() является решением.
При
является решением.
При
![]() получаем
получаем
![]() или
или
![]() ,
откуда находим
бесконечное
семейство
решений
,
откуда находим
бесконечное
семейство
решений
![]() .
.
Пример. Решим задачу Коши
![]() ,
,
![]() .
.
Заметим, что
функция
![]() удовлетворяет
уравнению, но
не удовлетворяет
начальному
условию. Пусть
удовлетворяет
уравнению, но
не удовлетворяет
начальному
условию. Пусть
![]() ,
тогда общее
решение определяется
из равенства
,
тогда общее
решение определяется
из равенства
![]() ,
откуда
,
откуда
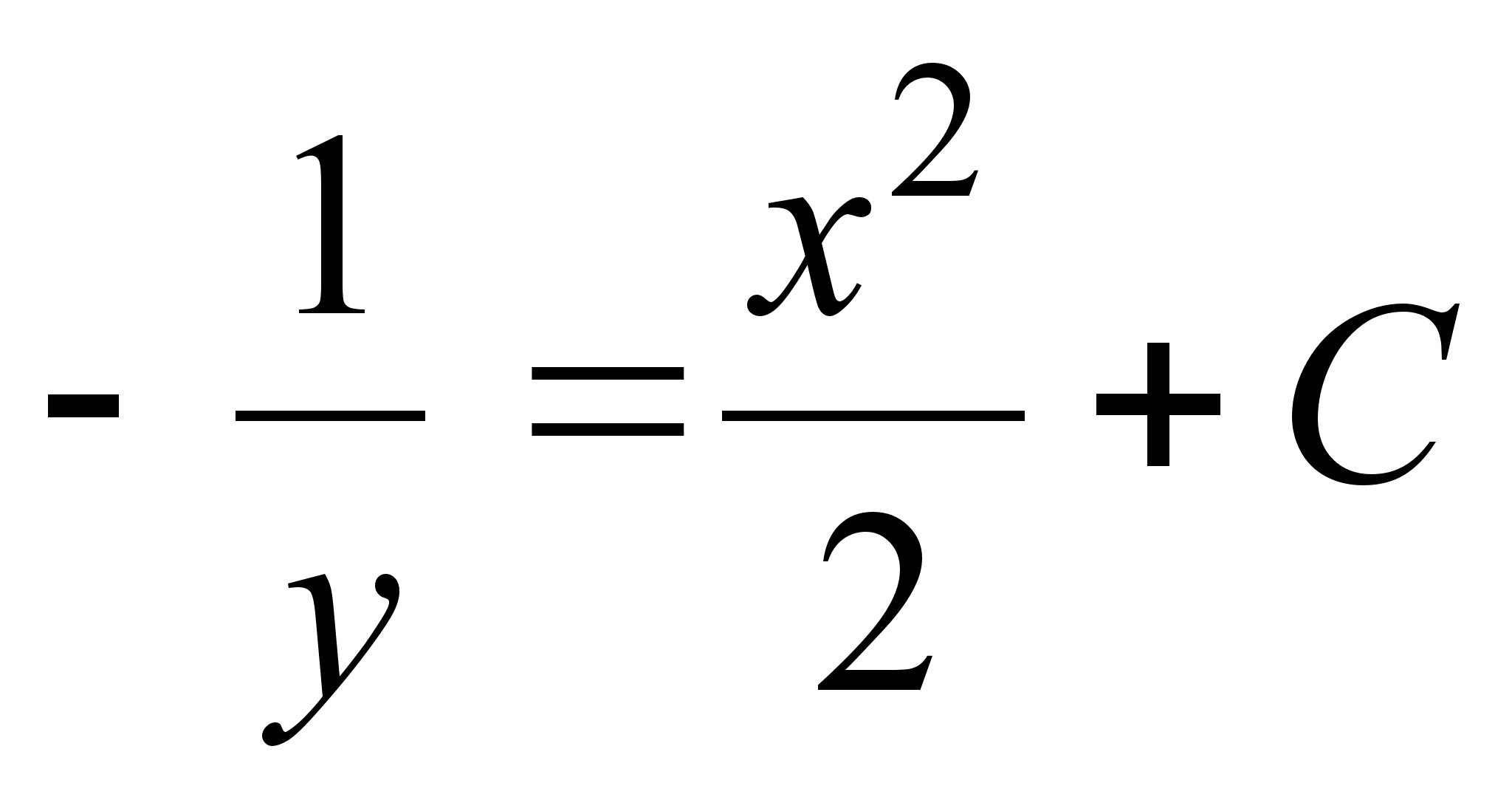 и, следовательно,
и, следовательно,
![]() .
.
При
![]() с учетом начального
условия получим
с учетом начального
условия получим
![]() ,
откуда
,
откуда
![]() .
Таким образом,
решением задачи
Коши является
функция
.
Таким образом,
решением задачи
Коши является
функция
![]() .
.
3. Математические модели некоторых процессов
Рассмотрим примеры задач, исследование которых проводится с использованием обыкновенных дифференциальных уравнений.
Пример (закон
роста населения
Земли). Пусть
![]() - число людей
на Земле в момент
времени
- число людей
на Земле в момент
времени
![]() .
Демографические
данные показывают,
что за небольшой
интервал времени
.
Демографические
данные показывают,
что за небольшой
интервал времени
![]() прирост населения
прирост населения
![]() пропорционален
квадрату числа
людей и интервалу
времени:
пропорционален
квадрату числа
людей и интервалу
времени:
![]() ,
,
где
![]() - некоторая
постоянная.
Разделив левую
и правую части
этого равенства
на
- некоторая
постоянная.
Разделив левую
и правую части
этого равенства
на
![]() и перейдя к
пределу при
и перейдя к
пределу при
![]() ,
получим уравнение
,
получим уравнение
![]() ,
(5)
,
(5)
где
![]() - дифференцируемая
функция, приближающая
функцию
- дифференцируемая
функция, приближающая
функцию
![]() .
Уравнение (5)
аналогично
уравнению (4),
рассмотренному
выше. Его общее
решение имеет
вид
.
Уравнение (5)
аналогично
уравнению (4),
рассмотренному
выше. Его общее
решение имеет
вид
![]() .
Заметим, что
известные
демографические
данные хорошо
согласуются
с частным решением
.
Заметим, что
известные
демографические
данные хорошо
согласуются
с частным решением
![]() ,
,
где время
![]() исчисляется
в годах от начала
нашей эры. Функция
исчисляется
в годах от начала
нашей эры. Функция
![]() не определена
при
не определена
при
![]() ,
поэтому закон
роста населения
в будущем должен
измениться.
,
поэтому закон
роста населения
в будущем должен
измениться.
Пример (модель
производства).
Пусть
![]() - интенсивность
выпуска продукции
некоторым
предприятием
в момент времени
- интенсивность
выпуска продукции
некоторым
предприятием
в момент времени
![]() ,
а
,
а
![]() - цена продукции.
Доход от продажи
этой продукции
составляет
- цена продукции.
Доход от продажи
этой продукции
составляет
![]() .
Пусть часть
вырученных
средств, равная
.
Пусть часть
вырученных
средств, равная
![]() , (6)
, (6)
где
![]() - некоторое
число, направляется
на расширение
производства.
Предположим,
что скорость
изменения
интенсивности
выпуска продукции
прямо пропорциональна
объему инвестиций:
- некоторое
число, направляется
на расширение
производства.
Предположим,
что скорость
изменения
интенсивности
выпуска продукции
прямо пропорциональна
объему инвестиций:
![]() ,
(7)
,
(7)
где
![]() -
постоянная.
Из (6) и (7) получаем
уравнение
-
постоянная.
Из (6) и (7) получаем
уравнение
![]() ,
(8)
,
(8)
общее решение
которого при
постоянном
![]() имеет вид
имеет вид
![]() ,
где
,
где
![]() .
Если задано
начальное
условие
.
Если задано
начальное
условие
![]() ,
(9)
,
(9)
то решением задачи Коши (8), (9) является функция
![]() .
.
Уравнение (8) называется уравнением естественного роста. Им описываются также процессы радиоактивного распада в физике и размножения бактерий в биологии.
На практике
с увеличением
выпуска продукции
происходит
насыщение рынка
и цена падает.
Если, например,
![]() ,
где
,
где
![]() и
и
![]() -
положительные
постоянные,
то вместо (8) получим
уравнение
-
положительные
постоянные,
то вместо (8) получим
уравнение
![]() ,
(10)
,
(10)
аналогичное уравнению, рассматриваемому в следующем примере.
Пример (модель
рекламы). Пусть
![]() - число людей,
знающих к моменту
времени
- число людей,
знающих к моменту
времени
![]() некоторую
новость, а
некоторую
новость, а
![]() -
общее число
людей. Будем
предполагать,
что скорость
распространения
новости
-
общее число
людей. Будем
предполагать,
что скорость
распространения
новости
![]() прямо пропорциональна
как числу людей
прямо пропорциональна
как числу людей
![]() ,
уже ее знающих,
так и числу
людей
,
уже ее знающих,
так и числу
людей
![]() ,
еще не знающих
новости, то
есть
,
еще не знающих
новости, то
есть
![]() ,
(11)
,
(11)
где
![]() -
постоянная.
Разделив переменные
в этом уравнении,
получим
-
постоянная.
Разделив переменные
в этом уравнении,
получим
![]() ,
,
откуда, используя результат последнего примера § 4, найдем
![]()
или
![]() .
.
График этой
функции называется
логистической
кривой. Для
случая
![]() ,
соответстщего
условию, что
в момент
,
соответстщего
условию, что
в момент
![]() половина людей
знает новость
(
половина людей
знает новость
(![]() ),
эта
),
эта
кривая представлена на рис. 15.
Рис.15.
Рассматриваемое
уравнение
обладает также
решениями
![]() и
и
![]() ,
обращающими
в ноль его правую
часть. Эти решения
соответствуют
ситуациям,
когда новость
не распространяется:
в первом случае
в начальный
момент ее никто
не знает, а во
втором - знают
все.
,
обращающими
в ноль его правую
часть. Эти решения
соответствуют
ситуациям,
когда новость
не распространяется:
в первом случае
в начальный
момент ее никто
не знает, а во
втором - знают
все.
Отметим, что уравнения (10) и (11), описывающие совершенно разные процессы, по существу, совпадают. Уравнения того же типа возникают при описании динамики эпидемий, процессов размножения бактерий в ограниченной среде обитания, применяются в математической теории экологии.
Упражнения
1. Решить уравнения:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() ;
;
21)
![]() ;
;
22)
![]() ;
;
23)
![]() ;
;
24)
![]() ;
;
25)
![]() ;
;
26)
![]() .
.
2. Решить задачи Коши:
1)
![]() ,
,
![]() ;
;
2)
![]() ,
,
![]() ;
;
3)
![]() ,
,
![]() ;
;
4)
![]() ,
,
![]() ;
;
5)
![]() ,
,
![]() ;
;
6)
![]() ,
,
![]() ;
;
7)
![]() ,
,
![]() ;
;
8)
![]() ,
,
![]() ;
;
9)
![]() ,
,
![]() ;
;
10)
![]() ,
,
![]() ;
;
11)
![]() ,
,
![]() ;
;
12)
![]() ,
,
![]() ;
;
13)
![]() ,
,
![]() ;
;
14)
![]() ,
,
![]() ;
;
15)
![]() ,
,
![]() ,
,
16)
![]() ,
,
![]() ;
;
17)
![]() ,
,
![]() ;
;
18)
![]() ,
,
![]() ;
;
19)
![]() ,
,
![]() ;
;
20)
![]() ,
,
![]() .
.
Ответы
1.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20) Общее решение находится
из
уравнения
![]() ;
;
21)
![]() ;
;
22)
![]() ;
;
23)
![]() ;
;
24 )
![]() ;
;
25)
![]() ;
;
26)
![]() .
.
2.
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
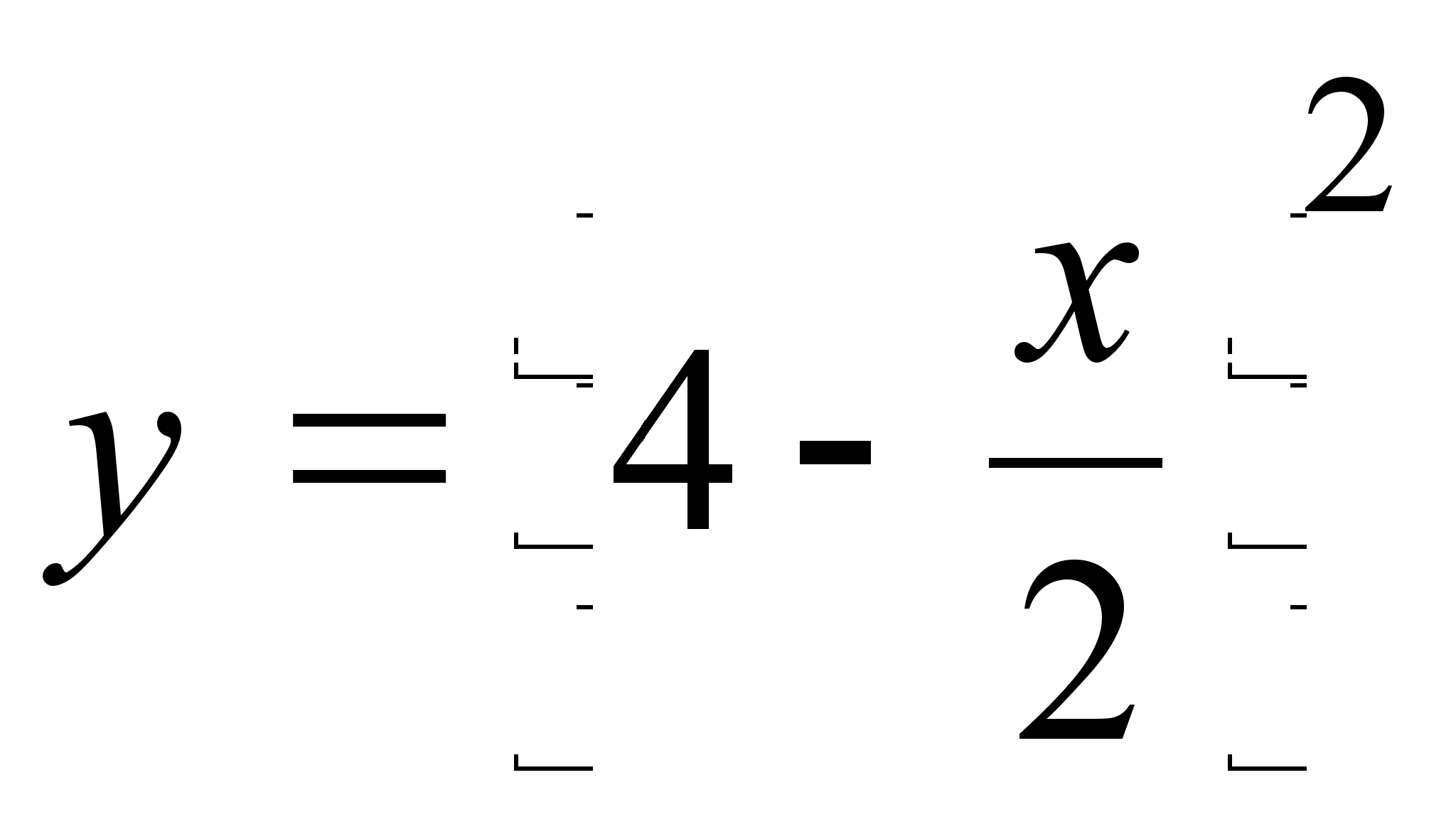 ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() и
и
![]() ;
;
16)
![]() ;
;
17)
![]() ;
;
18)
![]() ;
;
19)
![]() ;
;
20)
![]() .
.
Похожие рефераты:
Большая коллекция шпор для МАТАНа (1 семестр 1 курс)
Высшая математика для менеджеров
Шпаргалки по математическому анализу для 1-го семестра в МАИ
Лекции по Математическому анализу
Основы проектирования и конструирования
Методика решения иррациональных уравнений и неравенств в школьном курсе математики
Методы решения уравнений, содержащих параметр