| Скачать .docx | Скачать .pdf |
Реферат: Множина комплексних чисел
Чернігівський державний педагогічний університет імені Т.Г.Шевченка
фізико-математичний факультет
Курсова робота на тему:
Множина комплексних чисел
Підготувала студентка 45 групи
Петрова Наталія Олександрівна
Чернігів 2003
План
1. Виникнення та розвиток поняття комплексного числа.
2. Поняття комплексного числа.
3. Дії над комплексними числами.
4. Геометричне зображення комплексного числа.
5. Модуль і аргумент комплексного числа.
6. Тригонометрична форма комплексного числа.
7. Застосування комплексних чисел.
Виникнення та розвиток поняття комплексного числа.
“Помимо и даже против воли того или другого математика, мнимые числа снова и снова появляются на выкладках, и лишь постепенно по мере того как обнаруживается польза от их употребления, они получают более и более широкое распространение”
Ф. Клейн.
Древнегреческие математики считали “настоящими” только натуральные числа. Постепенно складывалось представление о бесконечности множества натуральных чисел.
В III веке Архимед разработал систему обозначения вплоть до такого громадного как . Наряду с натуральными числами применяли дроби - числа, составленные из целого числа долей единицы. В практических расчетах дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем Вавилоне. Долгое время полагали, что результат измерения всегда выражается или в виде натурального числа, или в виде отношения таких чисел, то есть дроби. Древнегреческий философ и математик Пифагор учил, что “… элементы чисел являются элементами всех вещей и весь мир в целом является гармонией и числом. Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной. Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с этого открытия начинается эра теоретической математики: открыть существование несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению, было невозможно.
Следующим важным этапом в развитии понятия о числе было введение отрицательных чисел - это было сделано китайскими математиками за два века до н. э. Отрицательные числа применяли в III веке древнегреческий математик Диофант, знавший уже правила действия над ними, а в VII веке эти числа уже подробно изучили индийские ученые, которые сравнивали такие числа с долгом. С помощью отрицательных чисел можно было единым образом описывать изменения величин. Уже в VIII веке было установлено, что квадратный корень из положительного числа имеет два значения - положительное и отрицательное, а из отрицательных чисел квадратный корень извлекать нельзя: нет такого числа , чтобы .
В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида кубические и квадратные корни: .
Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень (), а если оно имеет три действительных корня (), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически. Тем не менее всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены еще в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.
Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы. Он показал, что система уравнений , не имеющая решений во множестве действительных чисел, имеет решения вида , , нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что . Кардано называл такие величины “чисто отрицательными ” и даже “софистически отрицательными ”, считал их бесполезными и старался их не употреблять. В самом деле, с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены первые правила арифметических операций над такими числами, вплоть до извлечения из них кубических корней. Название “мнимые числа ” ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII века - Л. Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения числа (мнимой единицы). Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин “комплексные числа ” так же был введен Гауссом в 1831 году. Слово комплекс (от латинского complexus ) означает связь, сочетание, совокупность понятий, предметов, явлений и т. д. Образующих единое целое.
В течение XVII века продолжалось обсуждение арифметической природы мнимых чисел, возможности дать им геометрическое обоснование.
Постепенно развивалась техника операций над мнимыми числами. На рубеже XVII и XVIII веков была построена общая теория корней n-ых степеней сначала из отрицательных, а за тем из любых комплексных чисел, основанная на следующей формуле английского математика А. Муавра (1707): ![]() . С помощью этой формулы можно было так же вывести формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году замечательную формулу :
. С помощью этой формулы можно было так же вывести формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году замечательную формулу : ![]() , которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число e
в любую комплексную степень. Любопытно, например, что
, которая связывала воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера можно было возводить число e
в любую комплексную степень. Любопытно, например, что ![]() . Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.
. Можно находить sin и cos от комплексных чисел, вычислять логарифмы таких чисел, то есть строить теорию функций комплексного переменного.
В конце XVIII века французский математик Ж. Лагранж смог сказать, что математический анализ уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие уравнения встречаются, например, в теории колебаний материальной точки в сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял комплексные числа для решения интегралов.
Хотя в течение XVIII века с помощью комплексных чисел были решены многие вопросы, в том числе и прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще не было строго логического обоснования теории этих чисел. По этому французский ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, - только наведение, приобретающее характер настоящих истин лишь после подтверждения прямыми доказательствами.
“Никто ведь не сомневается в точности результатов, получаемых при вычислениях с мнимыми количествами, хотя они представляют собой только алгебраические формы иероглифы нелепых количеств” Л. Карно.
В конце XVIII века, в начале XIX века было получено геометрическое истолкование комплексных чисел. Датчанин К. Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили изобразить комплексное число ![]() точкой на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M
, а вектором , идущим в эту точку из начала координат. При таком истолковании сложение и вычитание комплексных чисел соответствуют эти же операции над векторами. Вектор можно задавать не только его координатами a и b, но так же длиной r и углом
который он образует с положительным направлением оси абсцисс. При этом , и число z принимает вид , который называется тригонометрической формой комплексного числа. Число r называют модулем комплексного числа z и обозначают . Число называют аргументом z и обозначают ArgZ. Заметим, что если , значение ArgZ не определено, а при оно определено с точностью до кратного . Упомянутая ранее формула Эйлера позволяет записать число z в виде
точкой на координатной плоскости. Позднее оказалось, что еще удобнее изображать число не самой точкой M
, а вектором , идущим в эту точку из начала координат. При таком истолковании сложение и вычитание комплексных чисел соответствуют эти же операции над векторами. Вектор можно задавать не только его координатами a и b, но так же длиной r и углом
который он образует с положительным направлением оси абсцисс. При этом , и число z принимает вид , который называется тригонометрической формой комплексного числа. Число r называют модулем комплексного числа z и обозначают . Число называют аргументом z и обозначают ArgZ. Заметим, что если , значение ArgZ не определено, а при оно определено с точностью до кратного . Упомянутая ранее формула Эйлера позволяет записать число z в виде ![]() (показательная форма комплексного числа).
(показательная форма комплексного числа).
Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения.
Стало ясно, что комплексные числа полезны во многих вопросах, где имеют дело с величинами, которые изображаются векторами на плоскости: при изучении течения жидкости, задач теории упругости.
После создания теории комплексных чисел возник вопрос о существовании “гиперкомплексных” чисел - чисел с несколькими “мнимыми” единицами. Такую систему вида , где , построил в 1843 году ирландский математик У. Гамильтон, который назвал их “кватернионами”.
Большой вклад в развитие теории функций комплексного переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее применениями к упругости, М. В. Келдыш и М. А. Лаврентьев - к аэро- и гидродинамике, Н. Н. Богомолов и В. С. Владимиров - к проблемам квантовой теории поля.
Поняття комплексного числа.
“Подобно тому, как всю область действительных величин можно представить с помощью бесконечной прямой, можно себе представить область всех величин, действительных и мнимых, с помощью бесконечной плоскости, где каждая точка, определенная своей абсциссой а и своей ординатой b , представляет в то же время величину a + ib” .
Гаусс
Рассмотрим множество чисел, каждое из которых определяется упорядоченной парой действительных чисел. Действительные числа будем обозначать буквами а, b, с, ..., а упорядоченные пары действительных чисел — буквами α, β, γ, ... и соответственно записывать α=(a, b), β =(c, d) и т. д. Такую упорядоченную пару действительных чисел (a,b) назовем комплексным числом.
Определим действия над упорядоченными парами действительных чисел. Суммой двух упорядоченных пар α= (а, b) и β = (с, d) назовем упорядоченную пару γ = (a+c, b+d):
(a, b) + (c, d) = (a + c, b + d), (1)
а произведением указанных пар — упорядоченную пару δ = (ас – bd, ad + bc):
(a, b)(c, d) = (ac – bd, ad + bc). (2)
Действия сложения и умножения упорядоченных пар действительных чисел определены аксиоматически.
Для этих действий существуют обратные действия — вычитание и деление (кроме деления на нуль). Разностью α — β двух упорядоченных пар α = (a, b) и β = (с, d) назовем такую упорядоченную пару (х, y), для которой (с, d) + (x, y) = (a, b). Принимая во внимание равенство (1), получаем с + х = a, d + y = b, откуда x = а – c, y = b – d. Разностью α — β упорядоченных пар α = (а, b) и β = (с, d) является упорядоченная пара (а – c, b – d):
(a, b) – (c, d) = (a – c, b – d). (3)
Нулем служит пара 0 = (0, 0). Упорядоченной парой, противоположной для упорядоченной пары α = (а, b) будет, пара - α = ( -а, -b), так как α + (-α) = (а, b) + (-а, -b) = (0,0) = 0.
Частным
от деления упорядоченной пары α = (а, b) на упорядоченную пару β = (с, d), где β ![]() 0 или с
0 или с![]() + d
+ d![]()
![]() 0 (т. е. хотя бы одно из чисел с, d отлично от нуля) должна быть упорядоченная пара (x, y) такая, что (с, d) (x, y) = (а, b). Отсюда на основании равенства (2) получаем cx – dy = a, cy – dx = b. Из этой системы уравнений находим x и y:
0 (т. е. хотя бы одно из чисел с, d отлично от нуля) должна быть упорядоченная пара (x, y) такая, что (с, d) (x, y) = (а, b). Отсюда на основании равенства (2) получаем cx – dy = a, cy – dx = b. Из этой системы уравнений находим x и y:
x = ![]() , y =
, y = ![]() .
.
Итак, если β![]() 0, то частное α/β двух упорядоченных пар α = (а, b), β = (с, d) существует и определяется формулой:
0, то частное α/β двух упорядоченных пар α = (а, b), β = (с, d) существует и определяется формулой:
![]() =
= ![]() . (4)
. (4)
Положив в этой формуле β = α (т. е. c = a, d = b), найдем, что единицей при умножении упорядоченных пар служит упорядоченная пара (1, 0). Полагая α = 1 = (1, 0), из формулы (4) получаем, что при β ![]() 0 упорядоченной парой, обратной для β, будет упорядоченная пара
0 упорядоченной парой, обратной для β, будет упорядоченная пара
![]() .
.
Таким образом, построено множество чисел, действия над которыми определяются по формулам (1) - (4). Это множество чисел называют множеством комплексных чисел.
Докажем, что множество комплексных чисел в качестве своего подмножества содержит все действительные числа. Рассмотрим упорядоченные пары вида (a, 0). Каждой паре (a, 0) поставим в соответствие действительное число а, в результате получим взаимно однозначное соответствие между множеством рассматриваемых упорядоченных пар и множеством всех действительных чисел. Применяя к указанным упорядоченным парам формулы (1) и (2), находим;
(а, 0) + (b, 0) = (а + b, 0); (а, 0) (b, 0) = (ab, 0).
Эти равенства означают, что упорядоченные пары вида (а, 0) складываются и умножаются так же, как действительные числа. Следовательно, множество указанных упорядоченных пар действительных чисел, рассматриваемое как подмножество множества комплексных чисел, по своим алгебраическим свойствам не отличается от множества действительных чисел. Это позволяет положить
(а, 0) = а, (5)
т. е. не различать упорядоченную пару (a, 0) действительных чисел и действительное число a. В частности, нуль (0, 0) и единица (1, 0) множества комплексных чисел оказываются обычными действительными числами 0 и 1.
Покажем, что среди комплексных чисел содержится корень уравнения х![]() + 1 = 0. Корнем уравнения х
+ 1 = 0. Корнем уравнения х![]() + 1 = 0 является такое число, квадрат которого равен действительному числу —1. Это число определяется упорядоченной парой (0, 1). В самом деле, применив формулу (2), получим
+ 1 = 0 является такое число, квадрат которого равен действительному числу —1. Это число определяется упорядоченной парой (0, 1). В самом деле, применив формулу (2), получим
(0, 1) (0, 1) = (-1, 0) = -1.
Обозначим эту упорядоченную пару через i , т. е. i = (0, 1), тогда
i![]() = - 1, i
=
= - 1, i
= ![]() , (6)
, (6)
число ί называют мнимой единицей .
Найдем произведение действительного числа b на упорядоченную пару (0, 1) = ί — мнимую единицу:
bi = (b, 0)(0, 1) = (0, b), i b = (0, 1)(b, 0) = (0, b). (7)
Если (а, b) - произвольная упорядоченная пара, то из очевидного равенства (а, b) = (a, 0) + (0, b) и формул (5), (7) получаем
(a, b) = a + bi . (8)
Следовательно, комплексное число α = (a, b) может быть записано в виде a + bi = a + i b, где a и b — действительные числа, ί — мнимая единица, определяемая соотношением (6). Выражение a + bi называют алгебраической формой комплексного числа . Число a называют действительной, число b — мнимой частью комплексного числа a + bi . Обозначая комплексное число a + bi одной буквой α, пишут:
a = Reα, b = Imα,
где Re — начальные буквы латинского слова realis (действительный), Im - начальные буквы латинского слова imaginarius (воображаемый). Кроме указанных обозначений, употребляются также и такие: a = R(α), b = I(α), где (a, b) = a + bi . Числа вида bi называют чисто мнимыми числами или просто мнимыми .
| 85 |
Комплексное число a + bi считают равным нулю тогда и только тогда, когда а = 0, b = 0:
![]()
![]() . (9)
. (9)
Два комплексных числа a + bi и c + di считают равными тогда и только тогда, когда равны между собой соответственно их действительные и мнимые части, т. е. a = с, b = d:
![]() . (10)
. (10)
Комплексное число a - bi
называют сопряженным
комплексному числу a + bi
. Обозначим число a - bi
буквой ![]() = a + bi
. Числу
= a + bi
. Числу ![]() будет сопряжено число a – (-bi
) = a + bi
= α. Вследствие этого числа α = a + bi
и
будет сопряжено число a – (-bi
) = a + bi
= α. Вследствие этого числа α = a + bi
и ![]() = a - bi
называют комплексно сопряженными числами
. Действительные числа и только они сопряжены сами себе. В самом деле, если α = a, где a - действительное число, то из формул (5) и (8) имеем: α = a + 0i
= a,
= a - bi
называют комплексно сопряженными числами
. Действительные числа и только они сопряжены сами себе. В самом деле, если α = a, где a - действительное число, то из формул (5) и (8) имеем: α = a + 0i
= a, ![]() = a – 0i
= a, т. е. α =
= a – 0i
= a, т. е. α = ![]() .
.
Например: комплексному числу 3 + 5i сопряжённым будет 3 – 5i ;
комплексному числу 4 - 7i сопряжённым будет 4 + 7i .
Действия над комплексными числами, заданными в алгебраической форме
Рассмотрим правила, по которым производятся арифметические действия над комплексными числами.
Если даны два комплексных числа α = a + bi и β = c + di , то
α + β = (a + bi ) + (c + di ) = (a + c) + (b + d)i ,
α – β = (a + bi ) – (c + di ) = (a – c) + (b – d)i . (11)
Это следует из определения действий сложения и вычитания двух упорядоченных пар действительных чисел (см. формулы (1) и (3)). Мы получили правила сложения и вычитания комплексных чисел: чтобы сложить два комплексных числа, надо отдельно сложить их действительные части и соответственно мнимые части; чтобы из одного комплексного числа вычесть другое, необходимо вычесть соответственно их действительные и мнимые части.
Число – α = – a – bi называют противоположным числу α = a + bi . Сумма двух этих чисел равна нулю: - α + α = (- a - bi ) + (a + bi ) = (-a + a) + (-b + b)i = 0.
Для получения правила умножения комплексных чисел воспользуемся формулой (6), т. е. тем, что i 2 = -1. Учитывая это соотношение, находим (a + bi )( c + di ) = ac + adi + bci + bdi 2 = ac + (ad + bc)i – bd, т.е.
(a + bi )( c + di ) = (ac - bd) + (ad + bc)i . (12)
Эта формула соответствует формуле (2), которой определялось умножение упорядоченных пар действительных чисел.
Отметим, что сумма и произведение двух комплексно сопряженных чисел являются действительными числами. В самом деле, если α = a + bi
,
![]() = a – bi
, то α
= a – bi
, то α![]() = (a + bi
)( a - bi
) = a2
– i
2
b2
= a2
+ b2
, α +
= (a + bi
)( a - bi
) = a2
– i
2
b2
= a2
+ b2
, α + ![]() = ( a + bi
) + (a - bi
) = (a + a) + (b - b)i
= 2a, т.е.
= ( a + bi
) + (a - bi
) = (a + a) + (b - b)i
= 2a, т.е.
α + ![]() = 2a, α
= 2a, α![]() = a2
+ b2
. (13)
= a2
+ b2
. (13)
При делении
двух комплексных чисел в алгебраической форме следует ожидать, что частное выражается также числом того же вида, т. е. α/β = u + vi
, где u, v ![]() R. Выведем правило деления комплексных чисел. Пусть даны числа α = a + bi
,
β = c + di
, причем β ≠ 0, т. е. c2
+ d2
≠ 0. Последнее неравенство означает, что c и d одновременно в нуль не обращаются (исключается случай, когда с = 0, d = 0). Применяя формулу (12) и второе из равенств (13), находим:
R. Выведем правило деления комплексных чисел. Пусть даны числа α = a + bi
,
β = c + di
, причем β ≠ 0, т. е. c2
+ d2
≠ 0. Последнее неравенство означает, что c и d одновременно в нуль не обращаются (исключается случай, когда с = 0, d = 0). Применяя формулу (12) и второе из равенств (13), находим:
![]() .
.
Следовательно, частное двух комплексных чисел определяется формулой:
![]() , (14)
, (14)
соответствующей формуле (4).
С помощью полученной формулы для числа β = с + di можно найти обратное ему число β-1 = 1/β. Полагая в формуле (14) а = 1, b = 0, получаем
![]() .
.
Эта формула определяет число, обратное данному комплексному числу, отличному от нуля; это число также является комплексным.
Например : (3 + 7i ) + (4 + 2i ) = 7 + 9i ;
(6 + 5i ) – (3 + 8i ) = 3 – 3i ;
(5 – 4i )(8 – 9i ) = 4 – 77i ;
![]() .
.
Свойства действий
над комплексными числами
Для любых комплексных чисел α = a + bi , β = с + di , γ = e + fi выполняются следующие свойства действий сложения и умножения:
1) α + β = β + α – переместительное (коммутативное) свойство сложения;
2) (α + β) + γ = α + (β + γ) – сочетательное (ассоциативное) свойство сложения;
3) αβ = βα – переместительное (коммутативное) свойство умножения;
4) (αβ)γ = α(βγ) – сочетательное (ассоциативное) свойство умножения;
5) (α + β)γ = αγ + βγ – распределительное (дистрибутивное) свойство умножения относительно сложения.
Докажем, например, первое и третье из этих свойств. По определению сложения получаем
α + β = (a + bi ) + (c + di ) = (a + c) + (b + d)i ,
β + α = (c + di ) + (a + bi ) = (c + a) + (d + b)i = (a + c) + (b + d)i = α + β,
так как с + a = a + с, d + b = b + d, т. е. для любых действительных чисел выполняется переместительное (коммутативное) свойство сложения. Далее,
αβ = (a + bi )(c + di ) = aс + adi + bci + bdi2 = (ac - bd) + (ad + bc)i ,
βα = (c + di ) (a + bi ) = сa + cbi + dai + dbi2 = (ca - db) + (cb + da)i = (ac - bd) + (ad + bc)i = αβ,
поскольку для любых действительных чисел ac = ca, bd = db, т. е. выполняется переместительное (коммутативное) свойство умножения.
Остальные свойства доказываются аналогично, с учетом соответствующих свойств операций над действительными числами.
Таким образом, операции над комплексными числами подчиняются тем же законам, что и операции над действительными числами.
Возведение в степень комплексного числа.
Извлечение корня из комплексного числа
При возведении в степень комплексного числа пользуются формулой бинома Ньютона:
![]() .
.
С помощью формулы бинома Ньютона получаем
![]() .
.
В правой части этого равенства заменяют степени мнимой единицы i их значениями и приводят подобные члены. Рассмотрим, как выражаются эти степени. Учитывая формулу i 2 = - 1 , получаем i 3 = i 2 ∙ i = -1 ∙ i = - i, i4 = i3 ∙ i = -i ∙ i = -i 2 = 1, i5 = i4 ∙ i = i, i6 = i5 ∙ i = i2 = - 1, i 7 = i 6 ∙ i = - i , i 8 = i 7 ∙ i = - i 2 = 1 и т. д. В общем виде полученный результат можно записать так:
i 4 k = 1, i 4 k +1 = i , i 4k+2 = -1, i 4 k +3 = - i (k = 0, 1, 2, …).
Например : (3 + 4i )2 = 32 + 2 ∙ 3 ∙ 4i + (4i )2 = 9 + 24i + 16i 2 = 9 + 24i – 16 = -7 + 24i ;
(1 + i )3 = 1 + 3i + 3i 2 + i 3 = 1 + 3i – 3 – i = - 2 + 2i .
Переходим к извлечению квадратного корни из комплексного числа a + bi . Квадратным корнем из комплексного числа называют такое комплексное число, квадрат которого равен данному комплексному числу. Обозначим это комплексное число через u + vi , т. е.
![]() .
.
Последнее равенство перепишем в следующем виде:
u2 + 2uvi + v2 i 2 = a + bi , u2 – v2 + 2uvi = a + bi .
Учитывая определение равенства комплексных чисел (см. (10)), получаем
u2 – v2 = a, 2uv = b. (15)
Возведем в квадрат обе части каждого из этих равенств, сложим их, преобразуем полученную левую часть и извлечем квадратный корень:
(u2
– v2
)2
+ 4u2
v2
= a2
+ b2
, (u2
+ v2
)2
= a2
+ b2
, u2
+ v2
= ![]() .
.
Это уравнение и первое из уравнений (15) дают возможность определить u2 и v2 :
![]()
![]() . (16)
. (16)
Из первого уравнения находим два значения u, отличающиеся друг от друга только знаком, второе уравнение дает два значения v. Все эти значения будут действительными, поскольку при любых a и b
![]()
![]()
![]() .
.
Знаки u и v следует выбирать так, чтобы выполнялось второе из равенств (15). Это дает две возможные комбинации значений u и v, т. е. два числа u1 + v1 i , u2 + v2 i , отличающиеся знаком.
Следовательно, извлечение квадратного корня из комплексного числа всегда возможно и дает два значения, отличающиеся друг от друга только знаком.
Например: пусть требуется извлечь квадратный корень из комплексного числа 3 — 4i , т. е. найти комплексное число u + vi такое, что (u + vi )2 = 3 – 4i . В данном случае a = 3, b = -4, поэтому уравнения (16) принимают вид
![]() ,
, ![]() .
.
Второе из равенств (15) запишется так: 2uv = - 4, uv =-2; это означает, что соответствующие значения u и v имеют разные знаки. Так как u2 = 4, v2 = 1, то с учетом равенства uv = -2 находим, что u1 = 2, v1 = -1, u2 = -2, v2 = 1, т.е. 2 – i и -2 + i – значения квадратного корня из комплексного числа 3 – 4i .
Геометрическое изображение комплексного числа
|
|
|
|
|
|
|
|
|
|
Комплексные числа и соответствующие им точки комплексной плоскости обозначают буквой z и пишут z = x + i y, где x – действительная часть (x = Rez), y – мнимая часть (y = Imz).
Модуль и аргумент комплексного числа
Комплексное число z = x + i
y изобразим точкой z комплексной плоскости; точка z имеет координаты (x, y). Рассмотрим радиус-вектор ![]() этой точки (рис. 2). Модулем
комплексного числа
z называют длину г радиус-вектора
этой точки (рис. 2). Модулем
комплексного числа
z называют длину г радиус-вектора ![]() данной точки. Модуль комплексного числа z обозначают через |z|. Следовательно, по определению
данной точки. Модуль комплексного числа z обозначают через |z|. Следовательно, по определению
r = |z|, |z|![]() 0. (17)
0. (17)
Поскольку г = ![]() (получено из формулы для расстояния между двумя точками на плоскости: 0 (0, 0) и z (x, y)), то
(получено из формулы для расстояния между двумя точками на плоскости: 0 (0, 0) и z (x, y)), то
|z| = ![]() . (18)
. (18)
|
|
|
|
|
|
|
|
|
|
Аргументом комплексного числа
z = x + i
y называют величину угла φ наклона радиус-вектора ![]() к положительной полуоси Ox. Аргумент комплексного числа z обозначают так: Argz. При изменении z этот угол может принимать любые действительные значения (как положительные, так и отрицательные; последние отсчитываются по часовой стрелке). Если модули двух комплексных чисел равны, а значения угла φ отличаются друг от друга на 2π, или на число, кратное 2π, то точки, соответствующие этим комплексным числам, совпадают; комплексные числа в этом случае равны между собой. Следовательно, аргумент комплексного числа z имеет бесконечное множество значений, отличающихся друг от друга на число, кратное 2π. Аргумент не определен лишь для числа 0, модуль которого равен нулю: |0| =0. Среди значений аргумента комплексного числа z
к положительной полуоси Ox. Аргумент комплексного числа z обозначают так: Argz. При изменении z этот угол может принимать любые действительные значения (как положительные, так и отрицательные; последние отсчитываются по часовой стрелке). Если модули двух комплексных чисел равны, а значения угла φ отличаются друг от друга на 2π, или на число, кратное 2π, то точки, соответствующие этим комплексным числам, совпадают; комплексные числа в этом случае равны между собой. Следовательно, аргумент комплексного числа z имеет бесконечное множество значений, отличающихся друг от друга на число, кратное 2π. Аргумент не определен лишь для числа 0, модуль которого равен нулю: |0| =0. Среди значений аргумента комплексного числа z![]() 0 существует одно и только одно значение, заключенное между —π, +π, включая последнее значение. Его называют главным значением аргумента и обозначают argz. Итак, модуль и аргумент комплексного числа z удовлетворяют следующим соотношениям:
0 существует одно и только одно значение, заключенное между —π, +π, включая последнее значение. Его называют главным значением аргумента и обозначают argz. Итак, модуль и аргумент комплексного числа z удовлетворяют следующим соотношениям:
|z|![]() 0, -π < argz
0, -π < argz ![]() π, Argz = argz + 2πn (n = 0,
π, Argz = argz + 2πn (n = 0, ![]() 1,
1, ![]() 2, …).
2, …).
Главное значение аргумента положительного действительного числа равно 0, главное значение аргумента действительного отрицательного числа равно π, главное значение аргумента мнимого числа bi (b > 0) равно π/2, главное значение аргумента мнимого числа –bi (b > 0) равно –π/2.
Выразим действительную и мнимую части комплексного числа z = x + i y через его модуль и аргумент. Пусть точка z изображает число z = x + i y (рис. 2). Из прямоугольного треугольника ОAz получаем
x = r cosφ, y = r sinφ, (19)
где r = |z|. Отсюда и из формул (17), (18) следует:
cosφ = ![]() , sinφ =
, sinφ = ![]() , tgφ =
, tgφ = ![]() .
.
Например
: 1) найдём аргумент числа z = 1 – i
.
Так как Re z = 1, Im z = -1, то точка z = 1 – i
лежит в IV четверти. Поэтому достаточно найти такое решение одного из последних уравнений , которое является углом в IV четверти. Рассмотрим уравнение cosφ = ![]() . Находим
. Находим
cos φ = ![]() , φ =
, φ = ![]() + 2kπ (k = 0,
+ 2kπ (k = 0, ![]() 1,
1, ![]() 2, …);
2, …);
2) найдём аргумент числа -1- i
. Точка -1-i
лежит в III четверти. Найдём такое решение уравнения tg φ = ![]() , которое является углом в III четверти. Находим
, которое является углом в III четверти. Находим
tg φ = 1, φ = ![]() + 2kπ (k = 0,
+ 2kπ (k = 0, ![]() 1,
1, ![]() 2, …).
2, …).
Тригонометрическая форма комплексного числа
Рассмотрим комплексное число
z = x + i y. (20)
Подставляя сюда выражения для x и y через модуль и аргумент комплексного числа (см. формулы (19)), получаем z = r cosφ + i r sinφ, или
z = r (cosφ + i
sinφ) (r![]() 0). (21)
0). (21)
Запись комплексного числа z в виде (21) называют тригонометрической формой этого числа.
Замечание. Не всякая запись комплексного числа через тригонометрические функции является тригонометрической формой этого числа. Например, запись числа ί в виде
i
= cos![]() + i
sin
+ i
sin![]() , или i =
(-1)(cos
, или i =
(-1)(cos![]() + i
sin
+ i
sin![]() )
)
не является тригонометрической формой числа i : в первом случае у косинуса и синуса разные аргументы, во втором - имеется отрицательный множитель. Поскольку аргументами комплексного числа i являются числа π/2 + 2kπ (k = 0, ±1, ±2, ...) и только они, и |i | = 1, то тригонометрическая форма числа i имеет вид
i
=
cos (![]() + 2kπ) + i
sin (
+ 2kπ) + i
sin (![]() + 2kπ) (k – любое целое число).
+ 2kπ) (k – любое целое число).
Очевидно, что
r (cosφ + i sinφ) = r (cos(φ +2kπ) + i sin(φ +2kπ)).
Два комплексных числа, заданных в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на величину, кратную 2π. Следовательно, если
r1 (cosφ1 + i sinφ1 ) = r2 (cosφ2 + i sinφ2 ), (22)
то
r1 = r2 , φ2 = φ1 + 2kπ (k = 0, ±1, ±2, ...). (23)
Если комплексное число z = x + i
y задано в тригонометрической форме (21), то комплексное число ![]() = x – i
y записывается в форме
= x – i
y записывается в форме
![]() = r (cos(-φ) + i
sin(-φ)),
= r (cos(-φ) + i
sin(-φ)),
поэтому
|z| = |![]() |, argz = -arg
|, argz = -arg![]() ,
,
т. е. при переходе от числа z к комплексно сопряженному числу ![]() модуль
модуль ![]() не меняется, а аргумент изменяет лишь знак (см. рис. 2).
не меняется, а аргумент изменяет лишь знак (см. рис. 2).
Покажем, как умножать и делить комплексные числа, заданные в тригонометрической форме. Пусть даны два комплексных числа
z1 = r (cosφ + i sinφ) , z2 = ρ (cosψ + i sinψ), (24)
где r = |z1 |, φ = Argz1 , ρ = |z2 |, ψ = Argz2 .
Пользуясь правилами действий над комплексными числами в алгебраической форме, находим
z1 z2 = r (cosφ + i sinφ) ρ(cosψ + i sinψ) = rρ(cosφcosψ + i cosφsinψ + i sinφcosψ + i 2 sinφsinψ ) = rρ(cosφcosψ – sinφsinψ) + i (cosφsinψ + sinφcosψ)),
или
z1 z2 = rρ (cos(φ + ψ) + i sin(φ + ψ) ). (25)
Из полученной тригонометрической формы произведения двух комплексных чисел следует, что
|z1 z2 | = rρ или |z1 z2 | = |z1 | |z2 |, (φ + ψ) = Arg(z1 z2 ),
т. е. модуль произведения равен произведению модулей множителей, а сумма аргументов множителей является аргументом произведения.
Предположив, что z2
![]() 0, т. е. ρ
0, т. е. ρ![]() 0, найдем частное двух комплексных чисел z1
и z2
, заданных формулами (24):
0, найдем частное двух комплексных чисел z1
и z2
, заданных формулами (24):
 или
или
![]() . (26)
. (26)
| Из формулы (26) следует, что |
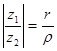 , или
, или  ; (27)
; (27)
φ – ψ = Arg![]() . (28)
. (28)
Формула (27) означает, что модуль частного равен модулю делимого, деленному на модуль делителя. Формула (28) показывает, что разность аргументов делимого и делителя является аргументом частного двух комплексных чисел.
Формула (26) позволяет найти модуль и аргумент комплексного числа, обратного данному числу. Полагая в этой формуле z1 = l = l (cos0 + i sin0), z2 = z = r (cosφ + i sinφ), получаем
z-1
= ![]() =
= ![]() (cos(0-φ) + i
sin(0-φ)),
(cos(0-φ) + i
sin(0-φ)),
z-1 = r-1 (cos(-φ) + i sin(-φ)), (29)
откуда |z-1 | = r-1 , argz-1 = -φ, т. е.
|z-1 | = |z|-1 , argz-1 = -argz.
Таким образом, модуль комплексного числа z-1 , обратного числу z, равен обратной величине модуля числа z, а его главное значение аргумента отличается от главного значения аргумента z лишь знаком.
Рассмотрим вопрос о возведении в степень комплексного числа z = r(cos φ + i sin φ), заданного в тригонометрической форме. Если n — целое положительное число, то с помощью формулы (25) получаем следующую формулу
zn = (r (cosφ + i sinφ))n = rn (cosnφ + i sinnφ), (30)
откуда |zn | = rn , Arg zn = nφ.
Итак, при возведении комплексного числа в натуральную степень модуль возводится в ту же степень, а аргумент умножается на показатель степени.
Формула (30) справедлива и для целых отрицательных показателей. В самом деле, так как z- n = (z-1 )n , то достаточно применить формулу (30) к числу z-1 , тригонометрическая форма которого определяется формулой (29).
Формулу (30) называют формулой Муавра. В частном случае, при r = 1, из этой формулы получаем
(cos φ + i sin φ)n = cos nφ + i sin nφ.
| ю; |
Извлечение корня n -й степени из комплексного числа
Извлечь корень n-й степени из комплексного числа z – это значит найти такое комплексное число α, что αn
= z. Представим числа z и α в тригонометрической форме: z = r (cosφ + i
sinφ), α = ρ (cosψ + i
sinψ), где r = |z|, φ = Argz; ρ = |α|, ψ = Αrgα. Обозначим корень n-й степени из комплексного числа z через ![]() , тогда по определению
, тогда по определению
![]() .
.
![]() .
.
Применяя формулу (30), получаем
![]() .
.
На основании формул (22) и (23) из этого равенства следует, что
ρn = r, nψ = φ + 2kπ (k = 0, ± 1, ± 2, …), откуда
![]() ,
, ![]() (k = 0, ± 1, ± 2, …). (31)
(k = 0, ± 1, ± 2, …). (31)
Полученные формулы определяют модуль ρ и аргумент числа α – корня степени n
из комплексного числа z. Обратно, если дано комплексное число ![]() , то при любом целом k
,
положительном или отрицательном, n-я степень этого числа равна числу z = r(cosφ + i
sinφ). Итак,
, то при любом целом k
,
положительном или отрицательном, n-я степень этого числа равна числу z = r(cosφ + i
sinφ). Итак,
![]() , (32)
, (32)
где ![]() - арифметическое значение корня из действительного неотрицательного числа, k – любое целое число. Так как k может принимать любые значения (положительные и отрицательные), то может показаться, что корень n-й степени из комплексного числа z имеет бесконечное множество различных значений. На самом деле различных значений будет только n. Полагая
- арифметическое значение корня из действительного неотрицательного числа, k – любое целое число. Так как k может принимать любые значения (положительные и отрицательные), то может показаться, что корень n-й степени из комплексного числа z имеет бесконечное множество различных значений. На самом деле различных значений будет только n. Полагая
k = 0, 1, 2, … , n – 1, (33)
получаем следующие n значений корня:
![]()
![]() ,
,
![]() ,
,
![]() , (34)
, (34)
……………………………….
![]() .
.
Докажем, что среди значений αi (i = 0, 1, ... , n – 1) нет равных между собой. Пусть p и q – любые различные числа из чисел k = 0, 1, 2, ... , n – 1, тогда
![]() .
.
Поскольку ![]() не является целым числом (p < n, q < n), то число
не является целым числом (p < n, q < n), то число ![]() 2π не будет кратным 2π. Таким образом, комплексные числа
2π не будет кратным 2π. Таким образом, комплексные числа
![]() ,
,
![]()
не равны между собой, потому что разность их аргументов не будет кратной 2π (см. (22) и (23)).
Предположим, что k – любое натуральное число, большее n – 1. Пусть k = nq + r, где 0 ≤ r ≤ n – 1, тогда ![]() , т. е. значение аргумента при этом значении k отличается от значения аргумента при k = r на число, кратное 2π. Следовательно, при этом значении k получаем такое же значение корня, как и при k = r, т. е. при значении k=0, 1, 2, ..., n – 1.
, т. е. значение аргумента при этом значении k отличается от значения аргумента при k = r на число, кратное 2π. Следовательно, при этом значении k получаем такое же значение корня, как и при k = r, т. е. при значении k=0, 1, 2, ..., n – 1.
Таким образом, извлечение корня n-й степени из комплексного числа z всегда возможно и дает n различных значений, определяемых формулами (34). Из этих формул видно, что все n значений корня n-й степени из комплексного числа z расположены на окружности радиуса ![]() с центром в точке нуль и делят эту окружность на n равных частей.
с центром в точке нуль и делят эту окружность на n равных частей.
Отметим, что корень n-й степени из действительного числа a
также имеет n различных значений. Среди этих значений действительных будет два, одно или ни одного, в зависимости от знака a
и четности n. Корень n-й степени из нуля имеет только одно значение, равное нулю, т. е. ![]() .
.
Рассмотрим важный частный случай извлечения корня, а именно извлечения корня n-й степени из числа 1. Представляя это число в тригонометрической форме 1=cos0+i sin0 и применяя формулу (34), получаем n значений корня из единицы:
![]() , k = 0, 1, 2, … , n – 1. (35)
, k = 0, 1, 2, … , n – 1. (35)
На комплексной плоскости корни n-й степени из единицы изображаются точками, расположенными на окружности радиуса R = 1 и делящими ее на n равных дуг. Одной из таких точек будет точка, изображающая число 1.
Например: найдем все значения корня шестой степени из единицы. По формуле (35), которая в данном случае принимает вид
![]() , k = 0, 1, 2, 3, 4, 5,
, k = 0, 1, 2, 3, 4, 5,
получаем шесть следующих значений:
|
|


![]()
|
|
|
|
|
![]()
|
|
|
Эти значения изображаются вершинами правильного шестиугольника, вписанного в единичную окружность (рис. 3).
Где применяются комплексные числа?
В течение последних двухсот лет комплексные числа находят многочисленные, а иногда и совершенно неожиданные применения. Так, например, с помощью комплексных чисел Гаусс нашел ответ на чисто геометрический вопрос: при каких натуральных n циркулем и линейкой можно построить правильный n-угольник? Из школьного курса геометрии известно, как циркулем и линейкой построить некоторые правильные многоугольники: правильный треугольник, квадрат, правильный шестиугольник (его сторона равна радиусу описанной около него окружности). Более сложным является построение правильных пятиугольника и пятнадцатиугольника. Научившись строить эти правильные многоугольники, легко перейти к построению соответствующих многоугольников с удвоенным числом сторон: восьмиугольника, десятиугольника и т. п. Все эти задачи на построение были решены еще в Древней Греции. Однако, несмотря на огромные усилия многих замечательных древнегреческих геометров и других ученых, никому не удалось построить ни правильный семиугольник, ни правильный девятиугольник. Не удалось также осуществить построение правильного р-угольника ни при каком простом числе р, кроме p = 3 и p = 5. Более двух тысяч лет никто не мог продвинуться в решении этой проблемы. В 1796 г. Карл Фридрих Гаусс, 19-летний студент-математик Геттингенского университета, впервые доказал возможность построения правильного семнадцатиугольника с помощью циркуля и линейки. Это было одно из самых удивительных открытий в истории математики. В течение нескольких последующих лет Гаусс полностью решил проблему построения правильных n-угольников.
Гаусс доказал, что правильный N–угольник с нечетным числом сторон (вершин) может быть построен с помощью циркуля и линейки тогда и только тогда, когда число N является простым числом Ферма или произведением нескольких различных простых чисел Ферма. (Числами Ферма называют числа вида Fn
= ![]() + 1 · При n = 0, 1, 2, 3, 4 эти числа являются простыми, при n = 5 число F5
будет составным. Из этого результата следовало, что построение правильного многоугольника невозможно при N = 7, 9, 11, 13.
+ 1 · При n = 0, 1, 2, 3, 4 эти числа являются простыми, при n = 5 число F5
будет составным. Из этого результата следовало, что построение правильного многоугольника невозможно при N = 7, 9, 11, 13.
Легко заметить, что задача о построении правильного n-угольника равносильна задаче о делении окружности радиуса R = 1 на n равных частей. Выше было показано, что корень n-й степени из единицы имеет точно n значений; почти все эти значения (за исключением одного, двух) являются комплексными. Точки, изображающие корни n-й степени из единицы, располагаются на окружности радиуса R = 1 и делят ее на n равных дуг, т. е. являются вершинами правильного n-угольника, вписанного в эту окружность (см. рис. 3). При доказательстве возможности построения правильного 17-угольника Гаусс пользовался свойствами корней 17-й степени из единицы.
|
|

|
|
|
|
|
|
|
Таким образом, каждая комплексная функция реализует однозначное в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции находят важные применения таких науках, как гидродинамика и аэродинамика, поскольку с их помощью удобно описывать движение объема жидкости (или газа).
С помощью теории функций комплексной переменной доказана следующая важная теорема, которую долгое время называли основной теоремой алгебры.
Теорема: Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
Рассмотрим многочлен степени n (n ≥ 1):
f(x) = a0 xn + a1 xn -1 + … + an -1 x + an . (36)
Корнем многочлена называют такое число с (в общем случае комплексное: с = a + bi ), которое обращает данный многочлен в нуль:
a0 cn + a1 cn-1 + … + an-1 c + an ≡ 0.
Другими словами, теорема утверждает, что алгебраическое уравнение n-й степени (n ≥ 1)
a0 xn + a1 xn -1 + … + an -1 x + an = 0 37)
имеет хотя бы один корень.
Отсюда следует, что любое алгебраическое уравнение n-й степени имеет ровно n корней. Действительно, если многочлен f(х) = a0 xn + a1 xn -1 + … + an -1 x + an , имеет корень α1 , то его можно представить в виде f(х) = (х – α1 )φ1 (x), где φ1 (x) – многочлен степени n – 1. Этот многочлен по данной теореме имеет хотя бы один корень. Обозначим корень многочлена φ1 (x) через α2 , тогда φ1 (x) = (х – α2 )φ2 (x), где φ2 (x) – многочлен степени n – 2. Продолжая аналогичные рассуждения, находим, что f(x) = a0 (x – a1 )(x – a2 )...(x – an ). Отсюда видно, что f(αi ) = 0 при i – 1, 2, ... , n, т. е. αi — корни многочлена (36) или уравнения (37). Таким образом, уравнение (37) имеет n корней.
Отметим, что комплексные корни всякого многочлена с действительными коэффициентами всегда сопряжены: если с = a - bi – корень уравнения, то с = а-bi – также корень данного уравнения. Иными словами, комплексные корни такого многочлена входят парами во множество его корней. Отсюда следует, что любое алгебраическое уравнение нечетной степени имеет хотя бы один действительный корень.
Замечание . Не всякое уравнение имеет корни, действительные или комплексные. Например, трансцендентное (неалгебраическое) уравнение аx = 0 (а > 0) не имеет никаких корней (ни действительных, ни комплексных).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|

Геометрическое преобразование, при котором величины углов между любыми двумя линиями, содержащимися в преобразуемой фигуре, не изменяются, называют конформным преобразованием или конформным отображением . (Под углом между двумя линиями, пересекающимися в некоторой точке, понимают угол между касательными к этим линиям, проведенными в этой точке.) Примерами конформных отображений могут служить сдвиг (параллельный перенос), гомотетия и поворот. Таким образом, можно сказать, что функция w = z + с осуществляет конформное отображение; это одна из таких функций.
Теория функций комплексной переменной находит широкое применение при решении важных практических задач картографии, электротехники, теплопроводности и др. Во многих вопросах, где речь идет, например, об электрическом потенциале в точках пространства, окружающего заряженный конденсатор, или о температуре внутри нагретого тела, о скоростях частиц жидкости или газа в потоке, движущемся в некотором канале и обтекающем при этом некоторые препятствия, и т. п., нужно уметь находить потенциал, температуру, скорости и т. п. Задачи такого рода могут быть решены без особых затруднений в случае, когда встречающиеся в них тела имеют простую форму (например, в виде плоских пластин или круговых цилиндров). Однако расчеты необходимо уметь производить и во многих других случаях. Например, чтобы сконструировать самолет, надо уметь вычислять скорости частиц в потоке, обтекающем крыло самолета. Разумеется, при полете самолета движутся и частицы воздуха, и само крыло. Однако, опираясь на законы механики, исследование можно свести к случаю, когда крыло неподвижно, а на него набегает и обтекает его поток воздуха. Крыло самолета в поперечном
|
 разрезе, (профиль крыла) имеет вид,
разрезе, (профиль крыла) имеет вид,  показанный на рисунке 7. Расчет скоростей производится достаточно просто, когда поперечный разрез обтекаемого тела есть круг (т. е. само тело является круглым цилиндром). Чтобы свести задачу о скоростях частиц потока
показанный на рисунке 7. Расчет скоростей производится достаточно просто, когда поперечный разрез обтекаемого тела есть круг (т. е. само тело является круглым цилиндром). Чтобы свести задачу о скоростях частиц потока 
 воздуха, обтекающего крыло самолета, к более простой задаче обтекания круглого цилиндра,
воздуха, обтекающего крыло самолета, к более простой задаче обтекания круглого цилиндра,  достаточно конформно отобразить часть плоскости, заштрихованную на рисунке 7, а (вне крыла), на другую фигуру, заштрихованную на рисунке 7, б (вне круга). Такое отображение осуществляется с помощью некоторой функции комплексной переменной.
достаточно конформно отобразить часть плоскости, заштрихованную на рисунке 7, а (вне крыла), на другую фигуру, заштрихованную на рисунке 7, б (вне круга). Такое отображение осуществляется с помощью некоторой функции комплексной переменной.
|
|
Конформное отображение, заданное соответствующей функцией комплексной переменной, аналогичным образом позволяет сводить решение задач о расчете электрического потенциала и температур от случая тел произвольной формы (любого профиля сечения) к простейшим случаям, для которых задачи решается легко.
Русский и советский ученый H. E. Жуковский (1847–1921) успешно применял теорию функций комплексной переменной к решению важных прикладных задач. Так, методами этой теории он доказал основную теорему о подъемной силе крыла самолета. В. И. Ленин назвал H. E. Жуковского «отцом русской авиации». В одном из своих выступлений H. E. Жуковский говорил: «...человек не имеет крыльев и по отношению веса своего тела к весу мускулов он в 72 раза слабее птицы; ...он почти и 800 раз тяжелее воздуха, тогда как птица тяжелее воздуха в 200 раз. Но, я думаю, что он полетит, опираясь не на силу своих мускулов, а на силу своего разума». (Жуковский H.E. Собрание сочинений. – М. – Л.: Гостехиздат, 1950. –T. 7. – С. 16.) С помощью теории функций комплексной переменной H.E. Жуковский решал задачи, относящиеся к вопросам просачивания воды через плотины.