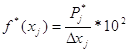| Скачать .docx | Скачать .pdf |
Реферат: Первичная статистическая обработка информации
ГОСУДАРСТВЕННАЯ СЛУЖБА ГРАЖДАНСКОЙ АВИАЦИИ РОССИИ
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ГРАЖДАНСКОЙ АВИАЦИИ
Кафедра Прикладной математики
Курсовая работа
защищена с оценкой
________________________
профессор Монсик В.Б.
_________________________
(подпись руководителя, дата)
Курсовая работа по дисциплине
“Теория вероятностей и математическая статистика”
Вариант №39
Тема: Первичная статистическая обработка информации.
Статистическая проверка гипотез
Выполнил студент группы ПМ 2-2
Митюшин М.С.
______________________________
(дата, подпись)
Москва - 2002
СОДЕРЖАНИЕ
Исходные данные 3
Задание 3
Выполнение первого задания 4
Выполнение второго задания 8
Литература 13
1. Исходные данные: исследуются трудозатраты на выполнение комплекса доработок на объекте (в человеко-часах). Результаты независимых измерений трудозатрат на 100 объектах приведены в таблице 1.
Таблица 1
| 431 | 394 | 362 | 436 | 343 | 403 | 483 | 462 | 395 | 467 |
| 420 | 411 | 391 | 397 | 455 | 412 | 363 | 449 | 439 | 411 |
| 468 | 435 | 313 | 486 | 463 | 417 | 369 | 377 | 409 | 390 |
| 389 | 386 | 409 | 379 | 412 | 370 | 391 | 421 | 459 | 390 |
| 415 | 415 | 366 | 323 | 469 | 399 | 486 | 393 | 361 | 407 |
| 392 | 353 | 432 | 406 | 409 | 391 | 371 | 401 | 321 | 359 |
| 472 | 352 | 446 | 367 | 384 | 371 | 426 | 487 | 454 | 371 |
| 394 | 401 | 408 | 393 | 373 | 327 | 429 | 360 | 401 | 412 |
| 392 | 338 | 398 | 461 | 403 | 418 | 520 | 448 | 440 | 433 |
| 362 | 406 | 342 | 441 | 391 | 390 | 432 | 374 | 280 | 395 |
Путем статической обработки результатов измерений выполнить следующие пункты задания:
Задание 1. Первичная статистическая обработка информации.
1. Построить вариационный статистический ряд.
2. Определить размах колебаний вариант.
3. Построить эмпирическую функцию распределения.
4. Выбрать число и длины разрядов (интервалов) и построить сгруппированный статистический ряд.
5. Построить статистический ряд распределения.
6. Построить полигон частот.
7. Построить гистограмму (эмпирическую плотность вероятности).
Задание 2. Статистическое оценивание параметров распределений. Статистическая проверка гипотез.
1. Вычислить точечные и интервальные оценки математического ожидания и дисперсии (с.к.о.) по данным таблицы 1 при доверительной вероятности 0,95.
2. Подобрать и построить на графике гистограммы сглаживающую кривую плотности вероятности, используя “метод моментов”.
3. Проверить гипотезу о нормальном распределении генеральной совокупности по критерию Пирсона (“хи-квадрат”) при уровне значимости 0,10.
4. Построить на графике эмпирической функции распределения сглаживающую кривую нормальной функции распределения, используя “метод моментов”.
5. Проверить гипотезу о нормальном распределении генеральной совокупности по критерию Колмогорова (“ламбда-критерий”) при уровне значимости 0,10.
6. Вычислить вероятность попадания случайной величины (трудозатраты на выполнение комплекса доработок на объекте) на интервал [МО - с.к.о.; МО + 2*с.к.о.].
2. Выполнение первого задания.
2.1. Для построения вариационного ряда необходимо результаты измерений трудозатрат расположить в порядке возрастания от ![]() до
до ![]() (по “ранжиру”). Этот ряд представлен в таблице 2.
(по “ранжиру”). Этот ряд представлен в таблице 2.
Таблица 2
| 280 | 359 | 371 | 390 | 393 | 401 | 411 | 421 | 440 | 463 |
| 313 | 360 | 371 | 390 | 394 | 403 | 411 | 426 | 441 | 467 |
| 321 | 361 | 371 | 390 | 394 | 403 | 412 | 429 | 446 | 468 |
| 323 | 362 | 373 | 391 | 395 | 406 | 412 | 431 | 448 | 469 |
| 327 | 362 | 374 | 391 | 395 | 406 | 412 | 432 | 449 | 472 |
| 338 | 363 | 377 | 391 | 397 | 407 | 415 | 432 | 454 | 483 |
| 342 | 366 | 379 | 391 | 398 | 408 | 415 | 433 | 455 | 486 |
| 343 | 367 | 384 | 392 | 399 | 409 | 417 | 435 | 459 | 486 |
| 352 | 369 | 386 | 392 | 401 | 409 | 418 | 436 | 461 | 487 |
| 353 | 370 | 389 | 393 | 401 | 409 | 420 | 439 | 462 | 520 |
2.2. Размах колебаний вариант равен разности максимального и минимального значений трудозатрат:
![]() = 520 – 280 = 240 (ч.час.)
= 520 – 280 = 240 (ч.час.)
2.3. Эмпирическая функция распределения F*(x) (рис.1) строится с использованием вариационного ряда на основании соотношения:
![]() ,
,
где ![]() – число точек, лежащих левее точки х
.
– число точек, лежащих левее точки х
.
2.4. Для построения сгруппированного статистического ряда размах J колебаний значений х делится на число разрядов – m , которое оценивается по формуле:
m =
![]() +1
, где n
– число измерений.
+1
, где n
– число измерений.
M =
![]() + 1 = 6
+ 1 = 6
Сгруппированный статистический ряд приведен в таблице 3.
Таблица 3
Разряды { |
[280..320] | (320..360] | (360..400] | (400..440] | (440..480] | (480..520] |
| Числа попаданий с.в. в разряды |
2 | 10 | 36 | 33 | 14 | 5 |
Рис.1.
2.5. Статистический ряд распределения строится на базе сгруппированного ряда. Для этого вычисляются частоты попадания значений x в соответствующие разряды по формуле:
![]()
Статистический ряд распределения представлен в таблице 4.
Таблица 4
Разряды
|
[280..320] | (320..360] | (360..400] | (400..440] | (440..480] | (480..520] |
Частоты
|
0.02 | 0.10 | 0.36 | 0.33 | 0.14 | 0.05 |
2.6. Графической иллюстрацией статистического ряда распределения является “полигон частот”, представленный на рис.2.
Рис.2.
2.7. Статистический ряд распределения является основой для вычисления и построения эмпирической плотности вероятности (рис.3). Гистограмма строится в виде прямоугольников, основания которых равны длинам разрядов, а высоты определяются из соотношения:

где ![]() длина j
-го разряда (j=1..m
).
длина j
-го разряда (j=1..m
).
Результаты расчетов по оценке эмпирической плотности вероятности ![]() приведены в таблице 5, а гистограмма на рис.3. (dx = 40)
приведены в таблице 5, а гистограмма на рис.3. (dx = 40)
Таблица 5
Разряды
|
[280..320] | (320..360] | (360..400] | (400..440] | (440..480] | (480..520] |
Значения
|
0.050 | 0.250 | 0.900 | 0.825 | 0.350 | 0.125 |
Рис.3.
3. Выполнение второго задания.
3.1. Вычислим точечные и интервальные оценки математического ожидания (выборочного среднего значения) и дисперсии (выборочной исправленной дисперсии) по данным таблиц 1 и 2. сначала определим точечные оценки.
![]()
![]()
![]()
Интервальную оценку математического ожидания (доверительный интервал) при заданной доверительной вероятности (надежности) ![]() и числе наблюдений (объеме выборки) n =100 определим по формуле:
и числе наблюдений (объеме выборки) n =100 определим по формуле:
![]() ,
,
где ![]() - точность вычисления МО по результатам наблюдений при заданных значениях n и
- точность вычисления МО по результатам наблюдений при заданных значениях n и ![]() .
. ![]() , где
, где ![]() определяется по таблицам Стьюдента:
определяется по таблицам Стьюдента:
![]() =
=![]() =1,984
=1,984
![]()
Интервальная оценка (доверительный интервал) для МО равна:
![]()
Этим отрезком с вероятностью 0,95 накрывается истинное (неизвестное) значение МО.
Интервальная оценка среднего квадратического отклонения (доверительный интервал) определяется по формуле:
![]() ,
,
где q определяется по таблице ![]()
q = q(100;0,95)=0,143
Доверительный интервал для оценки с.к.о. равен
42,493(1-0,143)< ![]() <42,493(1+0,143)
<42,493(1+0,143)
36,42<![]() <48,57
<48,57
Этим отрезком с вероятностью 0,95 накрывается истинное (неизвестное) значение с.к.о.
3.2. На основании изучения гистограммы (рис.3) выдвинем гипотезу ![]() о нормальном распределении генеральной совокупности случайных величин X
- трудозатрат на доработки на объекте. Нулевую гипотезу подвергнем статистической проверке на противоречивость данным, полученным из опыта (табл.1) по критериям
о нормальном распределении генеральной совокупности случайных величин X
- трудозатрат на доработки на объекте. Нулевую гипотезу подвергнем статистической проверке на противоречивость данным, полученным из опыта (табл.1) по критериям ![]() - Пирсона и
- Пирсона и ![]() - Колмогорова.
- Колмогорова.
В соответствии с методом моментов положим параметры нормального распределения равным оценкам:
3.3. На графиках гистограммы и эмпирической функции распределения (рис.1,3) построим сглаживающие функции (теоретические кривые) плотности вероятности и функции распределения в соответствии с их выражениями:

Для построения сглаживающих кривых используем таблицы нормированной нормальной плотности вероятности
![]()
и нормированной нормальной функции распределения

Для входа в таблицы нормируем случайную величину Х по формуле:
![]()
Значения нормированных величин ![]() на границах разрядов, численные значения сглаживающих кривых на границах разрядов приведены в таблице 6.
на границах разрядов, численные значения сглаживающих кривых на границах разрядов приведены в таблице 6.
Таблица 6
| Границы разрядов |
280 | 320 | 360 | 400 | 440 | 480 | 520 |
 |
-2,92 | -1,98 | -1,04 | -0,10 | 0,84 | 1,78 | 2,73 |
| 0,0056 | 0,0562 | 0,2341 | 0,3970 | 0,2803 | 0,0818 | 0,0096 | |
| 0,013 | 0,132 | 0,55 | 0,93 | 0,66 | 0,19 | 0,023 | |
| 0 | 0,024 | 0,14917 | 0,4602 | 0,79955 | 0,96246 | 0,99683 |
3.4. Статистическую проверку гипотезы ![]() о нормальном распределении случайной величины Х
по выборке из 100 значений осуществим по двум различным критериям.
о нормальном распределении случайной величины Х
по выборке из 100 значений осуществим по двум различным критериям.
1) Критерий
![]() - Пирсона.
- Пирсона.
Суммарная выборочная статистика ![]() - Пирсона рассчитывается по результатам наблюдений по формуле:
- Пирсона рассчитывается по результатам наблюдений по формуле:
 ,
,
где ![]() - числа попаданий значений х
в j
– й разряд (табл.3);
- числа попаданий значений х
в j
– й разряд (табл.3);
n – число наблюдений (объем выборки);
m – число разрядов;
![]() - вероятность попадания случайной величины Х
в j
– й интервал, вычисляемая по формуле:
- вероятность попадания случайной величины Х
в j
– й интервал, вычисляемая по формуле:
 ,
,
где ![]() ,
, ![]() - границы разрядов;
- границы разрядов;
Ф(u) – функция Лапласа.
Результаты расчетов выборочной статистики ![]() приведены в таблице 7.
приведены в таблице 7.
Таблица 7
| № | [280..320] | (320..360] | (360..400] | (400..440] | (440..480] | (480..520] | |
| 1 | 2 | 10 | 36 | 33 | 14 | 5 | |
| 2 | 0,0221 | 0,1276 | 0,3087 | 0,3393 | 0,1602 | 0,0421 | |
| 3 | 2,21 | 12,76 | 30,87 | 33,93 | 16,02 | 4,21 | |
| 4 | -0,21 | -2,76 | 5,13 | -0,93 | -2,02 | 0,79 | |
| 5 | 0,0441 | 7,6176 | 26,3169 | 0,8649 | 4,0804 | 0,6241 | |
| 6 | <5>:<3> | 0,02 | 0,597 | 0,853 | 0,025 | 0,2547 | 0,1482 |
| 7 | |||||||
Проверяем гипотезу ![]() о нормальном распределении генеральной совокупности значений Х
:
о нормальном распределении генеральной совокупности значений Х
:
1). По таблице ![]() - распределения по заданному уровню значимости
- распределения по заданному уровню значимости ![]() =0,10 и числу степеней свободы k=m-2-1=3
(m=6 – число разрядов, 2 – число параметров нормального распределения
=0,10 и числу степеней свободы k=m-2-1=3
(m=6 – число разрядов, 2 – число параметров нормального распределения ![]() ) определим критическое значение
) определим критическое значение ![]() , удовлетворяющее условию:
, удовлетворяющее условию:
![]() .
.
В нашем случае ![]()
2). Сравнивая выборочную статистику ![]() , вычисленную по результатам наблюдений, с критическим значением
, вычисленную по результатам наблюдений, с критическим значением ![]() , получаем:
, получаем:
![]() ,
, ![]()
![]() <
<![]()
![]()
![]() - согласуется с данными опыта (принимается).
- согласуется с данными опыта (принимается).
Вывод:
статистическая проверка по критерию ![]() - Пирсона нулевой гипотезы о нормальном распределении значений х
генеральной совокупности, выдвинутой на основании выборочных данных, не противоречит опытным данным.
- Пирсона нулевой гипотезы о нормальном распределении значений х
генеральной совокупности, выдвинутой на основании выборочных данных, не противоречит опытным данным.
2). Критерий
![]() - Колмогорова.
- Колмогорова.
Выборочная статистика ![]() - Колмогорова рассчитывается по формуле:
- Колмогорова рассчитывается по формуле:
![]()
где ![]()
модуль максимальной разности между эмпирической ![]() и сглаживающей функциями распределения.
и сглаживающей функциями распределения.
При заданном уровне значимости ![]() =0,10 критическое значение распределения Колмогорова
=0,10 критическое значение распределения Колмогорова ![]() Полученной на основании выражения:
Полученной на основании выражения:
![]()
функции распределения статистики ![]() - Колмогорова.
- Колмогорова.
Для проверки нулевой гипотезы проведем следующую процедуру:
1). Найдем максимальное значение модуля разности между эмпирической ![]() и сглаживающей F(x)
функциями распределения:
и сглаживающей F(x)
функциями распределения:
![]() =0,063.
=0,063.
2). Вычислим значение выборочной статистики ![]() по формуле:
по формуле:
![]() =0,063
=0,063![]() =0,63.
=0,63.
3). Сравнивая выборочную статистику ![]() и критическое значение
и критическое значение ![]() получаем:
получаем:
![]() =0,63<1,224=
=0,63<1,224=![]() .
.
Следовательно, гипотеза ![]() о нормальном распределении случайной величины Х
согласуется с опытными данными.
о нормальном распределении случайной величины Х
согласуется с опытными данными.
3.5. Вероятность попадания значений случайной величины Х на интервал [МО - с.к.о.; МО + 2*с.к.о.] вычислим по формуле:
P=(X
![]() [404,180-42,493;404,180+2*42,493])=P(X
[404,180-42,493;404,180+2*42,493])=P(X![]() [361,7;489,17])=
[361,7;489,17])=
=
![]() =Ф(2)+ Ф (1)=
=Ф(2)+ Ф (1)=
=0,477+0,341=0,818.
ЛИТЕРАТУРА
Монсик В.Б. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА: Пособие к выполнению курсовой работы. – М.: МГТУ ГА, 2002. – 24 с..