Реферат: Равногранный тетраэдр

Кировский Физико-математический лицей

Реферат на тему

''Свойства равногранного тетраэдра''

Выполнил : ученик 10 ''А'' класса Соболев Александр

Проверила : Прокашева Маргарита Анатольевна

Киров 2003 г.

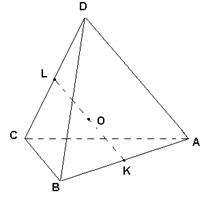
У любого тетраэдра 4 вершины, 6 рёбер, 4 грани, 4 трёхгранных угла, 6 двугранных углов, 12 плоских углов. Если все 6 рёбер равны, то равными будут и грани, и трёхгранные углы, и плоские; в этом случае тетраэдр - правильный. Из равенства всех 4 граней, однако, ещё не следует правильность тетраэдра; тетраэдр, у которого все грани равны, называется равногранным. Чтобы представить себе равногранный тетраэдр, отличный от правильного, возьмём произвольный остроугольный треугольник из бумаги и будем сгибать его по средним линиям. Тогда три вершины сойдутся в одну точку, а половинки сторон сомкнутся, образуя боковые рёбра тетраэдра (рис. 2).

Перечислим теперь свойства тетраэдра, каждое из которых является необходимым и достаточным условием равногранности, включая определение:

(0) Грани равны.

(1) Скрещивающиеся рёбра попарно равны (2) Трёхгранные углы равны.

(3) Противолежащие двугранные углы равны.

(4) Два плоских угла, опирающиеся на одно ребро, равны.

(5) Сумма плоских углов при каждой вершине равна 180.

(6) Развёртка тетраэдра - треугольник или параллелограмм

(7) Описанный параллелепипед - прямоугольный.

(8) Тетраэдр имеет три оси симметрии.

(9) Общие перпендикуляры скрещивающихся рёбер попарно перпендикулярны.

(10) Средние линии попарно перпендикулярны.

(11) Периметры граней равны.

(12) Площади граней равны.

(13) Высоты (тетраэдра) равны. 19=>18

(14) Отрезки, соединяющие вершины с центром тяжести пртивоположных граней, равны.

(15) Радиусы описанных около граней окружностей равны.

(16) Центр тяжести (тетраэдра) совпадает с центром описанной сферы.

(17) Центр тяжести (тетраэдра) совпадает с центром вписанной сферы.

(18) Центр вписанной сферы совпадает с центром описанной.

(19) Вписанная сфера касается граней в центрах описанных около них окружностей.

(20) Сумма внешних единичных векторов, перпендикулярных к граням, равна 0 (рис. 4).

(21) Сумма косинусов всех двугранных углов равна 2.

Все перечисленные условия являются одновременно и свойствами и признаками равногранного тетраэдра. Чтобы вывести равногранность из какого-нибудь условия, надо выстроить целую цепочку промежуточных условий, в которой каждое прямое следствие предыдущего.

Проще всего устанавливается, что (0)<=>(1)<=>(2)<=>(3)<=>(4).

Докажем (0)<=>(1).

(0)=>(1).

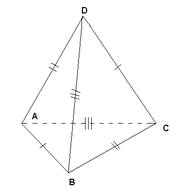
Все грани тетраэдра АВСD равны по условию. Рассмотрим треугольники АDВ и DАС: АD – общая, тогда АВ равна либо DС (если так, то из равенства треугольников АDВ и DАС следует АС=DВ; а из равенства треугольников АDВ и СВD следует АD=ВС, т.е. скрещивающиеся рёбра попарно равны), либо АС (если так, то из равенства треугольников АDВ и DАС следует DВ=DС, т.е. треугольник – равнобедренный, а остальные – нет, т.е. противоречие)

(0)<=(1).

По условию АВ=DС, ВС=АD, АС=ВD (рис.1), тогда треугольники АВD, СDВ, ВАС равны по третьему признаку равенства.

Докажем (1)<=>(2).

(1)=>(2).

Из (1) следует, что треугольники АВD, СDВ, ВАС (рис.1) равны (доказано выше). Тогда равны и соответствующие углы треугольников, т.е. трёхгранные углы ВАСD, АВСD, САВD, DАВС равны, т.к. любой трёхгранный угол однозначно определяется своими тремя плоскими углами.

Т.к. трёхгранный угол однозначно определяется своими тремя плоскими углами, то сдедующие доказательства будут аналогичны предудущему.

Дальше можно рассуждать по следующей схеме: (4)=>(5)=>(6)=>(1) (откуда уже следует равносильность первых шести условий).

Докажем (4)=>(5).

Из условия следует, что углы ADB=ACB, ADC=ABC, BDC=BAC. Тогда треугольники ABC, ADC, ADB, BCD подобны, но треугольники ADB и DAC имеют общую сторону, т.е. они равны, аналогично равны екжду собой и остальные треугольники, т.е. тетраэдр – равногранный.

Докажем (5)=>(6).

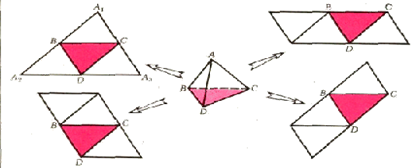Разрежем тетраэдр АВСD по рёбрам АВ, АС, АD и рассмотрим развёртку А₁ ВА₂ DА₃ С (рис. => ), тогда в точках В, С и D приложены по три угла, сумма которых 180°, поэтому углы А₁ ВА₂ , А₂ ОА₃ , А₃ СА₁ — развер­нутые; значит, А₁ А₂ А₃ — треугольник, содержащий точки В, С, D и являющийся разверткой тетраэдра АВСD, Для остальных разверток рассуждение аналогично.

Докажем (6)=>(1).

Посмотрев на рисунок можно увидеть, что на развёртке (например треугольник) скрещивающиеся рёбра являются противоположными сторонами параллелограмма, т.е. они равны.

Наш следующий шаг - доказательство равносильности (1)<=>(7).

Докажем (1)<=>(7).

В самом деле, поскольку скрещиваю­щиеся ребра тетраэдра — диагонали граней описанного параллелепипеда, из попарного равенства ребер следует, что грани опи­санного параллелепипеда — прямо­угольники и наоборот.

Теперь мы предлагаем рассуж­дать по схеме (7)=>(8)=>(9)=>(10)=>(7).

Докажем (7)=>(8).

Взглянув на (рис. =>), вы легко уста­новите, что осями симметрии явля­ются прямые, соединяющие центры симметрии противоположных граней описанного (прямоугольного) парал­лелепипеда, или, что здесь то же са­мое, общими перпендикулярами скре­щивающихся рёбер.

Докажем (8)=>(9).

Общими перпендикулярами скрещивающихся рёбер являются отрезки соединяющие середины противоположных граней описанного параллелограмма (прямоугольного) (рис. ^), а это значит, что эти отрезки попарно перпендикулярны (т.к. каждый из отрезков перпендикулярен граням, которые он соединяет).

Докажем (9)=>(10).

Отрезки, соединяющие середины скрещивающихся рёбер – перпендикулярны, но это и есть средние линии.

Докажем (10)=>(7).

Следующая цепочка рассуждений (0)=>(11),(12),(13),(14),(15). Мы докажем, что (11)=>(1), (12)=>(3), (13)=>(12), (14)=>(1), (4)=>(15); тем самым будет установлена равносильность первых 15 свойств.

Докажем (11)=>(1).

Запишем условие (11) в виде a₂ +b₂ +c₂ ⁽¹⁾ =a₂ +b₁ +c₁ ⁽²⁾ =b₂ +a₁ +c₁ ⁽³⁾ =c₂ +a₁ +b₁ ⁽⁴⁾ , где a₁ b₁ c₁ – длины рёбер тетраэдра, исходящих из одной вершины, a₂ b₂ c₂ – длины соответственно скрещивающихся с ними рёбер. (1)-(2)=(3)-(4) или b₂ +c₂ -b₁ -c₁ =b₂ +c₁ -c₂ -b₁ , т.е. 2с₂ =2с₁ или по-другому с₂ =с₁ , рассуждая аналогично для a₁ ,a₂ ,b₁ ,b₂ , получаем a₁ =a₂ , b₁ =b₂ , c₁ =c₂ , а это и есть запись условия (1).

Докажем (12)=>(3).

Для этого утверждения предварительно заметим, что S₄ =S₁ c₁₄ +S₂ c₂₄ +S₃ c₃₄ (**), где S_i - площади i-й грани, а с_ij – косинус двугранного угла между i-й и j-й гранью. Соотношение (**) сразу следует из теоремы о площади проекции, если спроектировать все грани тетраэдра на четвёртую грань. Написав ещё три таких соотношения (для трёх других граней) и воспользовавшись условием (12), приходим к системе с₁₄ +с₂₄ +с₃₄ =с₁₃ +с₂₃ +с₃₄ =с₁₂ +с₂₃ +с₂₄ =с₁₂ +с₁₃ +с₁₄ , которая решается точно так же как система из предыдущего утверждения. Получим с₁₄ =с₂₃ , с₂₄ =с₁₄ , с₃₄ =с₁₂ , откуда следует равенство соответствующих углов, т.е. (3).

Докажем (13)=>(12).

Утверждение очевидно следует из формулы для объёма тетраэдра V=Sh/3: S₁ h₁ /3=S₂ h₂ /3=S₃ h₃ =S₄ h₄ /3 S₁ =S₂ =S₃ =S₄ по условию => h₁ =h₂ =h₃ =h₄ .

Докажем (14)=>(1).

Обозначим через О_i центр тяжести i-й грани и выразим |DO₄ | через стороны /DA/=/a/, /DB/=/b/, /DC/=/c/ (рис. =>). /DO₄ / = =/DA/ + + /AO₄ / = /DA/ + 2/3*/AE/ = /DA/ + 2/3*1/2*(/AB/ + /AC/) = = 1/3*(/DA/ + /AB/) + 1/3*(/DA/ + /AC/) + 1/3*/DA/ = 1/3*/DA/ + + 1/3*/DB/ + 1/3*/DC/ = 1/3*(/a/+/b/+/c/). Отсюда находим скалярный квадрат вектора /DO₄ / : (DO₄ )² =1/9*(a² +b² +c² +2/a/*/b/+2/a/*/c/+2/b/*/c/). Обозначив a₁ =|a|, b₁ =|b|, c₁ =|c|, a₂ =|BC|, b₂ =|AC|, c₂ =|AB| и воспользовавшись тем, что /AB/=/b/-/a/, /BC/=/c/-/b/, /CA/=/a/-/c/, можно DO₄ выразить в виде ( DO₄ )² = 1/3*(( a₁ )² +( b₁ )² +( c₁ )² ) + 1/9*(( a₂ )² +( b₂ )² +( c₂ )² ) .

Напишем ещё три таких соотношения для трёх остальных граней:

(DO₃ )² =1/3*((a₂ )² +(b₂ )² +(c₁ )² ) + 1/9*((a₁ )² +(b₁ )² +(c₂ )² );

(DO₂ )² =1/3*((a₂ )² +(b₁ )² +(c₂ )² ) + 1/9*((a₁ )² +(b₂ )² +(c₁ )² );

(DO₁ )² =1/3*((a₁ )² +(b₂ )² +(c₂ )² ) + 1/9*((a₂ )² +(b₁ )² +(c₁ )² ).

По условию DO₁ =DO₂ =DO₃ =DO₄ приравняем, например, DO₁ =DO₂ , получаем :

1/3*((a₁ )² +(b₂ )² +(c₂ )² ) + 1/9*((a₂ )² +(b₁ )² +(c₁ )² ) = 1/3*((a₂ )² +(b₁ )² +(c₂ )² ) + 1/9*((a₁ )² +(b₂ )² +(c₁ )² ),

1/3*(a₁ )² + 1/3*(b₂ )² + 1/9*(a₂ )² + 1/9*(b₁ )² = 1/3*(a₂ )² + 1/3*(b₁ )² + 1/9*(a₁ )² + 1/9*(b₂ )² ,

2/9*(a₁ )² + 2/9*(b₂ )² = 2/9*(a₂ )² + 2/9*(b₁ )² ,

(a₁ )² + (b₂ )² = (a₂ )² + (b₁ )² (***),

Приравняв DO₃ =DO₄ , получаем :

1/3*((a₂ )² +(b₂ )² +(c₁ )² ) + 1/9*((a₁ )² +(b₁ )² +(c₂ )² ) = 1/3*((a₁ )² +(b₁ )² +(c₁ )² ) + 1/9*((a₂ )² +(b₂ )² +(c₂ )² ),

1/3*(a₂ )² + 1/3*(b₂ )² + 1/9*(a₁ )² + 1/9*(b₁ )² = 1/3*(a₁ )² + 1/3*(b₁ )² + 1/9*(a₂ )² + 1/9*(b₂ )² ,

2/9*(a₂ )² + 2/9*(b₂ )² = 2/9*(a₂ )² + 2/9*(b₁ )² ,

(a₂ )² + (b₂ )² = (a₁ )² + (b₁ )² вычитая из этого равенства (***) получаем :

(a₂ )² -(a₁ )² = (a₂ )² -(a₁ )² , т.е. получаем, что (a₂ )² =(a₁ )² , аналогично находим (b₂ )² =(b₁ )² , (c₂ )² =(c₁ )² , т.е. получим (1).

Докажем (4)=>(15).

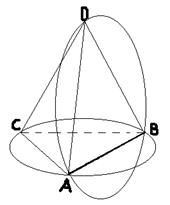
Углы ADB и АСВ опираются на равные хорды в равных окружностях, поэтому они равны или составляют в сумме 180°. Предположим сначала, что для каждой пары углов граней тет­раэдра, опирающихся на одно ребро, имеет место равенство углов. Тогда, например, сумма плоских углов при вершине D равна сумме углов треугольника АВС, т.e. равна 180°. Сумма плоских углов при любой вершине тетраэдра равна 180°, поэтому он равногранный (свойство (5)).

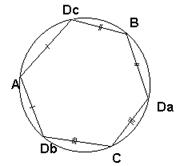Докажем теперь, что случай, когда углы ADB и АСВ не равны, невозможен. Предположим, что углы ADB + АСВ = 180° и угол ADB не = АСВ. Пусть для определенности угол ADB ту­пой. Поверхность тетраэдра ABCD можно так «развернуть» на плоскость АВС, что образы D_а , D_b и D_c точки D попадут па описанную окружность треугольника АВС; при этом направле­ние поворота боковой грани вокруг ребра основания выбирается в соответствии с тем, равны ли углы, опирающиеся на это ребро, или же они составляют в сумме 180°. В процессе разворачивания точка D движется по окружностям, плоскости которых пер­пендикулярны прямым АВ, ВС и СА. Эти ок ружности лежат в разных плоскостях, поэтому любые две из них имеют не более двух общих точек. Но две общих точки есть у каждой пары этих окружностей: точка D и точка, симметричная ей относительно плоскости АВС. Следовательно, точки D_а , D_b и D_c попарно раз­личны. Кроме того, AD_b =AD_c , BD_a =BD_c , CD_a =CD_b . Развертка выглядит следующим образом: в окружность вписан треугольник AD_c B с тупым углом D_c ; из точек А и В проведены хорды AD_b и BD_a , равные AD_c и BD_c соответственно; С — сере­дина одной из двух дуг, заданных точками D_a и D_b . Одна из се­редин этих двух дуг симметрична точке D_c относительно прямой, проходящей через середину отрезка АВ перпендикулярно ему; эта точка нам не подходит. Искомая развертка изображена на рис. . Углы при вершинах D_a , D_b и D_c шестиугольника AD_c BD_a CD_b дополняют до 180° углы треугольника АВС, по­этому их сумма равна 360°. Но эти углы равны плоским углам при вершине D тетраэдра ABCD, поэтому их сумма меньше 360°. Получено противоречие.

Докажем остальные пять свойств

Докажем (16).

Пусть К и L — середины ребер А В и CD, О — центр тяжести тетраэдра, т.e. середина отрезка KL.Так как О — центр описанной сферы тетраэдра, то треугольники АОВ и COD рав­нобедренные, с равными боковыми сторонами и равными ме­дианами ОК и OL. Поэтому треугольники АОВ = СОD, а значит, АВ =CD. Аналогично доказывается равенство других пар про­тивоположных ребер.

Докажем (19).

Пусть О₁ и О₂ — точки касания вписанной сферы с гра­нями АВС и ВСD. Тогда треугольник О₁ ВС=О₂ ВС. Из условия задачи следует, что O₁ и O₂ — центры описанных окружностей указан­ных граней. Поэтому угол ВАС = BO₁ C/2 == ВО₂ С/2 == BDC. Аналогичные рассуждения показывают, что каждый из плоских углов при вершине D равен соответствующему углу треуголь­ника АВС, а значит, их сумма равна 180°. Это утверждение справедливо для всех вершин тетраэдра.

Докажем (20).

Докажем это утверждение для любого многогранника. (задача, когда длина вектора = площади грани , которой он перпендикулярен)

Докажем, что сумма проекции всех данных векторов на любую прямую L равна 0. Рассмотрим для этого проекцию многогранника на плоскость, перпендикулярную L. Проекция многогранника покрыта проекциями его граней в два слоя (видимые сверху, видимые снизу). Приписав площадям проекций граней одного типа ''+'', другого типа ''–'', получим, что сумма площадей проекций с учётом знака равна 0. Заметим теперь, что площадь проекции грани равна длине проекции соответствующего вектора на прямую L, причём для граней разного типа проекции векторов противоположно направлены. Следовательно, сумма проекций векторов на прямую L тоже равна 0. Т.к. это утверждение справедливо для многогранника, то оно справедливо и для тетраэдра

Докажем (21).

Пусть ,e₁ , e₂ , e₃ , e₄ единичные векторы, перпендикулярные граням и направленные во внeшнюю сторону. Так как площади всех граней равны, то e₁ +e₂ +e₃ +e₄ == 0 (см. задачу выше). Следовательно, 0 = | e₁ +e₂ +e₃ +e₄ |2 =4+2*S(e_i ,e_j ) .Остается заме­тить, что скалярное произведение (e_i ,e_j ) равно —cosф_ij , где (ф_ij — двугранный угол между гра­нями с номерами i и j. Т.е. сумма косинусов двугранных углов равна 2 : -4 = -2*S(cosф_ij ) => S(cosф_ij )=2

Задачи

1. Рёбра равногранного тетраэдра равны a,b,c. Вычислите объём тетраэдра V, и радиус описанной сферы R.
2. В равногранном тетраэдре ABCD опущена высота AH; H₁ – точка пересечения высот грани BCD; h₁ , h₂ – длины отрезков, на которые одна из высот грани BCD делится точкой H₁ .

а) докажите, что точки H и H₁ симметричны относительно центра описанной окружности треугольника BCD.

б) докажите, что AH² =4h₁ h₂ .

Докажите, что в равногранном тетраэдре центры 4 вневписанных шаров являются вершинами тетраэдра равного данному и радиус вписанного шара в 2 раза меньше вневписанного шара.

Решения

1. Достроим данный тетраэдр до прямоугольного па­раллелепипеда; пусть х, у и z — ребра этого параллелепипеда. Тогда х² + у² = а² , у² + z² = b² и z² + х² == с² . Так как R == d/2, где d — диагональ параллелепи­педа, а d² = x² + y² + z² , то R² == (x² + y² + z2)/4 == (а² + b² +c² )/8.

Складывая равенства х² + у² = а² и z² + x² == с² и вычитая из них равенство y² + z² = b² , получаем x² = (a² +c² -b² )/2 . Аналогично находим у² и z² . Так как объем тетраэдра в три раза меньше объема параллелепипеда, то V² = (xyz)² /9 = (а² + b² — c² ) (а² + c² — b² ) (c² + b² — a² )/72

2. Достроим данный тетраэдр до прямоугольного парал­лелепипеда. Пусть AA₁ — его диагональ, О — его центр. Точка H₁ является проекцией точки A1 на грань BCD, а центр O₁ описанной окружности треугольника BCD — проек­цией точки О. Так как О — середина отрезка AA₁ , точки H и H₁ симметричны относительно O₁ .

Рассмотрим проекцию параллелепипеда на плоскость, пер­пендикулярную BD (рис. =>в дальнейшем решении исполь­зуются обозначения этого рисунка, а не обозначения в пространстве). Высота СС' треугольника BCD параллельна плоскости проекции, поэтому длины отрезков ВH₁ и СН₁ равны h₁ и h₂ , длины отрезков АН и А₁ Н₁ при проецировании не измени­лись. Так как АН : A1H1 = АС : А₁ В = 2 и A₁ H₁ : ВН₁ = CH₁ : A₁ H₁ , то АН² = 4(H₁ A₁ )² = 4h₁ h₂ .

3. Достроим данный тетраэдр до прямоугольного парал­лелепипеда. Точка пересечения биссекторных плоскостей двугранных углов тетраэдра (т. е. центр впи­санного шара) совпадает с центром О параллелепипеда. Рассмат­ривая проекции на плоскости, перпендикулярные ребрам тет­раэдра, легко проверить, что грани тетраэдра удалены от вер­шин параллелепипеда, отличных от вершин тетраэдра, вдвое больше, чем от точки О. Следовательно, эти вершины являются центрами вневписанных шаров. Этим доказаны оба утверж­дения.

Литература:

1. Энциклопедия для детей Аванта+ (том ''Математика'' )

2. Журнал ''Квант'' №7 1983 г.

3. ''Задачи по стереометрии'' Прасолов, Шарыгин.