| Скачать .docx | Скачать .pdf |
Реферат: Составление и решение нестандартных уравнений графоаналитическим методом
Фрунзенский район
Технологическая гимназия №13 г. Минска
Авторы:
Кравченко Арсений Борисович
ученик 9”Д” класса
ул. Горецкого 69-263
д.т. 215-84-33
Ермолицкий Алексей Александрович
ученик 9”Д” класса
ул. Сухаревская 7-46
д.т. 215-62-23
Тема:
Составление и решение нестандартных уравнений графоаналитическим методом
Секция: математика
Научный руководитель:
Кайданова Татьяна Юрьевна
учитель высшей категории
Минск 2003
Содержание
Теоретическая часть научной работы………..……………………3
Цель и задача научной работы……………………………………...4
Примеры решения нестандартных уравнений…………………...6
Трехуровневый тест на решение нестандартных уравнений…20
Ответы на тест……………………………………………………….21
Список литературы…………………………………………………22
Составление уравнения данной задачи есть основной прием, посредством которого математика применяется к естествознанию и технике. Без уравнения нет математики как средства познания природы.
П.С. Александров
Теоретическая часть
Пусть X и Y - два произвольных численных множества. Элементы этих множеств будем обозначать х и у соответственно и будем называть переменными.
Определение. Числовой функцией, определенной на множестве Х и принимающей значения во множестве Y , называется соответствие (правило, закон), которое каждому х из множества Х сопоставляет одно и только одно значение у из множества Y .
Переменную х называют независимой переменной или аргументом , а переменную у – зависимой переменной . Говорят также, что переменная у является функцией от переменной х . Значения зависимой переменной называют значениями функции .
Введенное понятие числовой функции является частным случаем общего понятия функции как соответствия между элементами двух или более произвольных множеств.
Пусть Х и Y – два произвольных множества.
Определение. Функцией, определенной на множестве Х и принимающей значения во множестве Y , называется соответствие, соотносящее с каждым элементом множества Х один и только один элемент из множества Y .
Задать функцию – это значит указать область ее определения и соответствие (правило), при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции.
Графический способ. пусть на координатной плоскости изображена некоторая линия АВ , пересекаемая любой прямой, перпендикулярной к оси абсцисс, не более чем в одной точке. Каждому значению абсциссы х поставим в соответствие значение ординаты у точки К этой линии. Следовательно, с помощью линии АВ определена функция y = f ( x ) , где х и у – координаты точки К линии АВ .
Часто самопишущие приборы на экране осциллографа, дисплея вычерчивают кривые, которые изображают графически функциональную зависимость. Например, в медицине электрокардиограф вычерчивает электрокардиограмму – кривую изменения электрических импульсов сердечной мышцы во времени.
Графическое задание удобно тем, что по графику функции можно установить общее впечатление о том, как протекает моделируемый процесс.
Возьмем на плоскости прямоугольную систему координат хОу и рассмотрим функцию y = f ( x ) , определенную на некотором числовом множестве Х. Придавая х последовательно значения х1 , х2 , …, х n из множества Х, получим соответствующие значения у1 , у2 , …, у n . Отметим на плоскости точки с координатами (х1 ; у1 ), (х2 ; у2 ), …, ( xn ; yn ).
Множество таких точек называют графиком данной функции.
Определение. Графиком функции
y
=
f
(
x
) называется множество всех точек {(
x
,
f
(
x
) |
x
D
(
f
)} координатной плоскости.
На практике для построения графика некоторых функций составляют таблицу значений функции для некоторых значений аргумента, затем наносят соответствующие точки на координатную плоскость и последовательно соединяют их линией. При этом предполагается, что точки достаточно точно показывают ход изменения функции.
Заметим, что так как функция
f
сопоставляет каждому
x
D
(
f
)
одно число
f
(
x
)
, то график функции
f
пересекается любой прямой, параллельной оси ординат, не более, чем в одной точке. И наоборот: всякое непустое множество точек плоскости, имеющее со всякой прямой, параллельной оси ординат, не более одной общей точки, является графиком некоторой функции.
Не всякое множество точек координатной плоскости является графиком какой-либо функции. Например, множество точек окружности не может быть графиком функции, поскольку значению абсциссы внутри окружности, соответствует два значения ординаты.
В общем случае уравнение с одной переменой х можно записать в виде:
f (x) = g (x)
где f ( x ) и g ( x ) – некоторые функции. Функция f ( x ) называется левой частью , а g ( x ) – правой частью уравнения.
Определение. Корнем (решением) уравнения f ( x ) = g ( x ) называется такое число, при подстановке которого в обе части уравнения вместо х получается верное числовое равенство.
Решить данное уравнение – значит найти множество всех его корней (решений). Множество корней (решений) может быть пустым , конечным или бесконечным .
На практике довольно часто оказывается полезным графический метод решения уравнений. Он заключается в следующем: для решения уравнения f ( x ) = 0 строят график функции y = f ( x ) и находят абсциссы точек пересечения графика с осью х ; эти абсциссы и являются корнями уравнения.
С графическим методом решения уравнения f ( x ) = g ( x ) связан функциональный метод решения уравнения, основанный на том, что если одна из функций f ( x ) или g ( x ) возрастает, а другая убывает, то уравнение f ( x ) = g ( x ) либо не имеет корней, либо имеет единственный корень.
Стандартный способ решения уравнений и неравенств в отдельных случаях приводит к сложным и утомительным преобразованиям. Процесс может быть тогда упрощен и, если применять так называемый графоаналитический метод .
ЦЕЛЬ : научиться составлять и решать нестандартные уравнения, которые содержат элементарные функции, проходимые по школьной программе, с использованием преобразования графиков на плоскости.
ЗАДАЧА : углубить свои знания в области математики
x 2 -6 x +6=2{ x }
Ответ:
x 1 =4-2 Ö 2
x 2 =4- Ö 10
Ö 2x=[x]+3
Ответ :
3{x}=|0.5x+0.5|
Ответ:
x 1 =1/6
x 2 =1 1/3
x 3 =2.5
x 4 =3 2/3
x 5 =4 5/6
( Ö x)2 =[x]
x Î [0;+ ¥ ) Ç Z =>
Ответ:
{0; N }
| x 2 -6 x +6|=-|( x -3)3 |+3
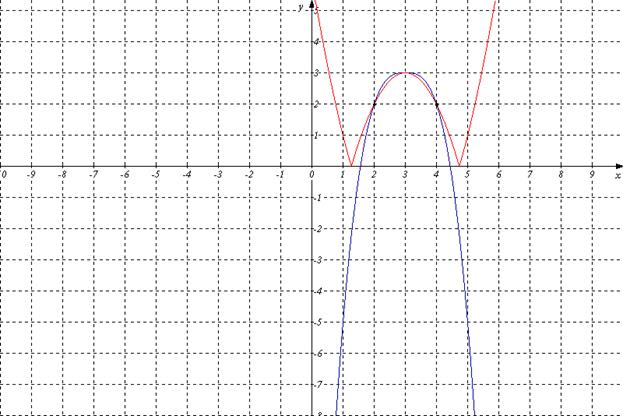
Ответ:
x 1 =2
x 2 =3
х3 =4
| x /2+ x |=2 x + Ö x
Ответ:
x =1
√(5- x )√(5+ x )=- x +5
 |
Ответ:
x 1 =0
x 2 =5
| x 2 +6| x |+2|-3=5 x 2
Ответ:
x2 -4x+5=√|x-2|+1
Ответ:
x 1 =1
x 2 =2
x 3 =3
-√(4- x 2 )=| x |-2
Ответ:
x 1 =-2
x 2 =0
x 3 =2
|(Öх-1)|²+2=x³+a
 |
при а=1 х=1
при а=3 х=0
при а>3 Æ
при а<3 один корень
Öх³=Ö|х|+а
 |
Ответ:
при а=0, х=0 х=1
при а>0 один корень
при а<0 Æ
3-|х-3|=3а-х
 |
при а=2 хÎ [3;+¥)
при а<2 один корень
при а>2 Æ
|(4/х)+3|=а
Ответ:
при а=0 один корень
при а=1 х=-2 х=-1
при а=3 один корень
при а>3 два корня
при аÎ (0;3) два корня
при а<0 Æy 2 = Ö - x +1
-x+|y|=1
Ответ:
(0;1)
1- x 2 = y
| x |+| y |=5
Ответ:
(-2;-3)
(2;-3)
| x +1|=1- y
-2 y = x 2 y +2 xy - y 2
Ответ:
(-2;2)
(-1;1)
(0;2)
TECT
I ypo вень
1.Корень уравнения х2 +4х=√х3 равен:
А) –2 Б) –1 В)0 Г) 1 Д) 2
2.Сумма корней уравнения x 2 - x -3=3 равна:
А) 4 Б) 2 В) –4 Г) 0 Д) –2
3.Произведение корней уравнения –0.5х2 +3=х2 -3
А) 2 Б) 1 В)6 Г) -2 Д) –4
4.Корни уравнения 2√ x =2 x принадлежат промежутку:
А) [0;1] Б) [–1;1] В)(0;1] Г) [1;3) Д) (2;5)
5.Система уравнений х2 +у2 =2х имеет:
Ö y =| x |
А)0 решений Б)1 решение В)2 решения Г)3 решения Д)4 решения
6.Система уравнений y 2 -| x |=0 не имеет решения:
| y +1|=| x +1|
А)(-4;-2) Б)(-1;-1) В)(0;0) Г)(4;-2) Д)(1;-1)
II ypo вень
1.Больший корень уравнения 2/х+1=х³+2 равен:
А) -3 Б) 4 В) 2 Г) 1 Д) –1
2.Сумма квадратов корней уравнения|х²-3|=|х³|+1 равна:
А) 4 Б) 8 В) 2 Г) 3 Д) 10
3.Сумма корней уравнения –0.25х²+1=|х²-6|х|+8| равна:
А) 0 Б) –1 В) 5 Г) 16 Д) -5
4.Разность большего и меньшего корней уравнения
|√|х-2|+1|=2 равна:
А) 8 Б) 1.5 В) 4 Г) 0 Д) 2
5.Уравнение - | х-1 | ³+2=а+1 имеет один корень при а, равном:
А) 2 Б) 0 В)5 Г) 1 Д) –3
III ypo вень
1. Произведение корней уравнения | x -2|-1=[ x ] равно:
А) -12 Б) 12 В) -6 Г) -9 Д) 8
2. Корни уравнения 4{ x }=2 принадлежат множеству:
А) Z Б) N +0.2 В) Z +0.5 Г) R Д) D
3. Сумма модулей корней уравнения-(√(5- x )√(5+ x ))+2=-1
равна:
А) 4 Б) 8 В)7 Г) 5 Д) 9
4. Корни уравнения x 4 =|(-| x |+1)2 -1| принадлежат множеству:
А)(-1;1) Б) [-1;1] В){4;11} Г){-1;0;1} Д) (0;2]
5.Значение а, при котором уравнение 2/ Ö х= | а- | х || имеет три корня, относится к промежутку:
А) (3;+ ¥ ) Б) [–1;12] В)(- ¥ ;1) Г) [1;3) Д) (- ¥ ;+ ¥ )
ОТВЕТЫ:
☻☻☻☻☻☻☻ ☻☻☻☻☻☻☻ |
№1 | №2 | №3 | №4 | №5 |
| 1-й уровень | В | Б | Д | А | В |
| 2-й уровень | Г | В | А | Д | Г |
| 3-й уровень | А | В | Б | Б | А |