| Скачать .docx | Скачать .pdf |
Реферат: Структура сходящихся последовательностей
Последовательность, у которой существует предел, называется сходящейся. Последовательность не являющаяся сходящейся называется расходящейся.
Определение: Последовательность {xn } называется сходящейся, если существует такое число а, что последовательность {xn -а} является бесконечно малой. При этом число а называется пределом последовательности {xn }.
В соответствии с этим определением всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число ноль.
Можно, также, дать еще одно определение сходящейся последовательности: Последовательность {xn } называется сходящейся, если существует такое число а, что для любого положительного числа e можно указать номер N такой, что при n³N все элементы xn этой последовательности удовлетворяют неравенству:
|xn -a|<e.
Некоторые свойства сходящихся последовательностей:
ТЕОРЕМА: Сходящаяся последовательность имеет только один предел.
Доказательство: Пусть a и b – пределы сходящейся последовательности {xn }. Тогда, используя специальное представление для элементов xn сходящейся последовательности {xn }, получим xn =а+an , xn =b+bn , где an и bn – элементы бесконечно малых последовательностей {an } и {bn }.
Вычитая данные соотношения, найдем an -bn =b-a. Так как все элементы бесконечно малой последовательности {an -bn } имеют одно и то же постоянное значение b-a, то (по теореме: Если все элементы бесконечно малой последовательности {an } равны одному и тому же числу с, то с=0) b-a=0, т.е. b=a. Теорема доказана.
ТЕОРЕМА: Сходящаяся последовательность ограничена.
Доказательство: Пусть {xn } - сходящаяся последовательность и а – ее предел. Представим ее в следующем виде:
xn =а+an ,
где an
- элемент бесконечно малой последовательности. Так как бесконечно малая последовательность {an
} ограничена (по теореме: Бесконечно малая последовательность ограничена.), то найдется такое число А, что для всех номеров n справедливо неравенство |an
|£А. Поэтому | xn
| £ |a| + A для всех номеров n, что и означает ограниченность последовательности {xn
}. Теорема доказана.
Ограниченная последовательность может и не быть сходящейся. Например, последовательность 1, -1, 1, -1, … - ограничена , но не является сходящейся. В самом деле, если бы эта последовательность сходилась к некоторому числу а, то каждая из последовательностей {xn -a} и {xn+1 -a} являлась бы бесконечно малой. Но тогда (по теореме: Разность бесконечно малых последовательностей есть бесконечно малая последовательность.) {(xn -a) – (xn+1 -a)}={xn – xn+1 } была бы бесконечно малой, что невозможно т.к. |xn – xn+1 | = 2 для любого номера n.
ТЕОРЕМА: Сумма сходящихся последовательностей {хn } и {yn } есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей {хn } и {yn }.
Доказательство: Пусть а и b – соответственно пределы последовательностей {хn } и {yn }. Тогда:
xn =а+an , yn =b+bn ,
где {an
} и {bn
) – бесконечно малые последовательности. Следовательно, (хn
+ yn
) - (а + b) =an
+bn
.
Таким образом, последовательность {(хn + yn ) - (а + b)} бесконечно малая, и поэтому последователдьность {хn + yn } сходится и имеет своим пределом число а+b. Теорема доказана.
ТЕОРЕМА: Разность сходящихся последовательностей {хn } и {yn } есть сходящаяся последовательность, предел которой равен разности пределов последовательностей {хn } и {yn }.
Доказательство: Пусть а и b – соответственно пределы последовательностей {хn
} и {yn
}.Тогда:
xn =а+an , yn =b+bn ,
где {an
} и {bn
) – бесконечно малые последовательности. Следовательно, (хn
- yn
) - (а - b) =an
-bn
.
Таким образом, последовательность {(хn - yn ) - (а - b)} бесконечно малая, и поэтому последователдьность {хn - yn } сходится и имеет своим пределом число а-b. Теорема доказана.
ТЕОРЕМА: Произведение сходящихся последовательностей {хn } и {yn } есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {хn } и {yn }.
Доказательство: Пусть а и b – соответственно пределы последовательностей {хn } и {yn }, то xn =а+an , yn =b+bn и xn ×yn =a×b+a×bn +b×an +an ×bn . Следовательно,
xn ×yn -а×b=a×bn +b×an +an ×bn .
(в силу теоремы: Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.) последовательность {a×bn
+b×an
+an
×bn
} бесконечно малая, и поэтому последовательность {xn
×yn
-а×b} тоже бесконечно малая, а значит последовательность {xn
×yn
} сходится и имеет своим пределом число а×b. Теорема доказана.
ЛЕММА: Если последовательность {yn
} сходится и имеет отличный от ноля предел b, то, начиная с некоторого номера, определена последовательность ![]() , которая является ограниченной.
, которая является ограниченной.
Доказательство: Пусть ![]() . Так как b¹0, то e>0. Пусть N – номер, соответствующий этому e, начиная с которого выполняется неравенство:
. Так как b¹0, то e>0. Пусть N – номер, соответствующий этому e, начиная с которого выполняется неравенство:
|yn
-b|<e или |yn
-b|<![]()
из этого неравенства следует, что при n³N выполняется неравенство |yn
|>![]() . Поэтому при n³N имеем
. Поэтому при n³N имеем ![]() . Следовательно, начиная с этого номера N, мы можем рассматривать последовательность
. Следовательно, начиная с этого номера N, мы можем рассматривать последовательность ![]() , и эта последовательность ограничена. Лемма доказана.
, и эта последовательность ограничена. Лемма доказана.
ТЕОРЕМА: Частное двух сходящихся последовательностей {xn } и {yn } при условии, что предел {yn } отличен от ноля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {xn } и {yn }.
Доказательство: Из доказанной ранее леммы следует, что, начиная с некоторого номера N, элементы последовательности {yn
} отличны от ноля и последовательность ![]() ограничена. Начиная с этого номера, мы и будем рассматривать последовательность
ограничена. Начиная с этого номера, мы и будем рассматривать последовательность ![]() . Пусть а и b – пределы последовательностей {xn
} и {yn
}. Докажем, что последовательность
. Пусть а и b – пределы последовательностей {xn
} и {yn
}. Докажем, что последовательность 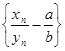 бесконечно малая. В самом деле, так как xn
=а+an
, yn
=b+bn
, то
бесконечно малая. В самом деле, так как xn
=а+an
, yn
=b+bn
, то
![]()
![]() .
.
Так как последовательность ![]() ограничена, а последовательность
ограничена, а последовательность ![]() бесконечно мала, то последовательность
бесконечно мала, то последовательность 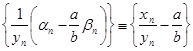 бесконечно малая. Теорема доказана.
бесконечно малая. Теорема доказана.
Итак, теперь можно сказать, что арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.
ТЕОРЕМА: Если элементы сходящейся последовательности {xn }, начиная с некоторого номера, удовлетворяют неравентству xn ³b (xn £b), то и предел а этой последовательности удовлетворяет неравенству а³b (a£b).
Доказательство: Пусть все элементы xn , по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ³b. Предположим, что а<b. Поскольку а – предел последовательности {xn }, то для положительного e=b-a можно указать номер N такой, что при n³N выполняется неравенство
|xn -a|<b-a.
Это неравенство эквивалентно
-(b-a)<xn -a<b-a
Используя правое из этих неравенств мы получим xn <b, а это противоречит условию теоремы. Случай xn £b рассматривается аналогично. Теорема доказана.
Элементы сходящейся последовательности {xn
} могут удовлетворять строгому неравенству xn
>b, однако при этом предел а может оказаться равным b. Например, если xn
=1/n, то xn
>0, однако ![]() .
.
Следствие 1: Если элементы xn и уn у сходящихся последовательностей {xn } и {yn }, начиная с некоторого номера, удовлетворяют неравенству xn £ уn , то их пределы удовлетворяют аналогичному неравенству
![]() .
.
Элементы последовательности {yn
-xn
} неотрицательны, а поэтому неотрицателен и ее предел ![]() . Отсюда следует, что
. Отсюда следует, что
![]() .
.
Следствие 2: Если все элементы сходящейся последовательности {xn } находятся на сегменте [a,b], то и ее предел с также находится на этом сегменте.
Это выполняется, так как а£xn £b, то a£c£b.
ТЕОРЕМА: Пусть {xn } и {zn }- сходящиеся последовательности, имеющие общий предел а. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {yn }удовлетворяют неравенствам xn £yn £zn . Тогда последовательность {yn } сходится и имеет предел а.
Доказательство: достаточно доказать, что {yn -a} является бесконечно малой. Обозначим через N’ номер, начиная с которого, выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполнятся также неравенства xn -а £ yn -а £ zn -а. Отсюда следует, что при n³N’ элементы последовательности {yn -a} удовлетворяют неравенству
|yn -a| £ max {|xn -a|, |zn -a|}.
Так как ![]() и
и ![]() , то для любого e>0 можно указать номера N1
и N2
такие, что при n³N1
|xn
-a|<e, а при n³N2
|zn
-a|<e. Итак последовательность {yn
-a} бесконечно малая. Теорема доказана.
, то для любого e>0 можно указать номера N1
и N2
такие, что при n³N1
|xn
-a|<e, а при n³N2
|zn
-a|<e. Итак последовательность {yn
-a} бесконечно малая. Теорема доказана.
Итак, мы показали неравенства, которым удовлетворяют элементы сходящихся последовательностей, в пределе переходят в соответствующие неравенства для пределов этих последовательностей.
ПРИМЕРЫ
1. Последовательность ![]() сходится и имеет своим пределом ноль. Ведь каково бы ни было e>0, по свойству Архимеда вещественных чисел существует такое натуральное число ne
, что ne
>
сходится и имеет своим пределом ноль. Ведь каково бы ни было e>0, по свойству Архимеда вещественных чисел существует такое натуральное число ne
, что ne
>![]() . Поэтому
. Поэтому ![]() для всех n³ne
, а это означает, что
для всех n³ne
, а это означает, что ![]() .
.
2. Последовательность ![]() сходится и
сходится и ![]() , что следует из того, что
, что следует из того, что
![]() , и того, что
, и того, что ![]() .
.
ЗАДАЧИ
ЗАДАЧА № 1
Пусть числовая последовательность а1 , а2 , а3 , … удовлетворяет условию
![]() (m, n = 1, 2, 3, … ),
(m, n = 1, 2, 3, … ),
тогда последовательность
![]() ,…
,…
должна либо расходиться к ![]() , причем предел этой последовательности будет равен ее нижней грани.
, причем предел этой последовательности будет равен ее нижней грани.
РЕШЕНИЕ:
Видим частный случай теоремы у M. Fekete. Достаточно рассмотреть случай, когда нижняя грань a конечна. Пусть e>0 и ![]() a+e. Всякое целое число n может быть представлено в форме n=qm+r, где r=0 или 1, или 2, …, или m-1. Полагая единообразие а0
=0, имеем:
a+e. Всякое целое число n может быть представлено в форме n=qm+r, где r=0 или 1, или 2, …, или m-1. Полагая единообразие а0
=0, имеем:
an =aqm+r £am +am +…+am +ar =qam +ar ,
![]() ,
,
![]()
ЗАДАЧА № 2
Пусть числовая последовательность а1 , а2 , а3 , … удовлетворяет условию
![]()
тогда существует конечный предел
![]() ,
,
причем
![]() (n = 1, 2, 3, … ).
(n = 1, 2, 3, … ).
РЕШЕНИЕ:
Из неравенств 2am -1<a2m <2am +1 получаем:
![]() (*)
(*)
Ряд
![]()
сходится, ибо в силу неравенства (*) он мажорируется сходящимся рядом:
|a1 |+2-1 +2-2 +2-3 +…
запишем целое число n по двоичной системе:
n=2m +e1 2m-1 +e2 2m-2 +…+em (e1 , e2 , …, em = 0 или 1)
согласно предположению
![]()
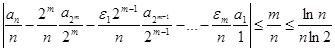 .
.
Применяя теорему (1) для данных:
s0
=0, s1
=![]() , sm-1
=
, sm-1
=![]() , sm
=
, sm
=![]() , …, pn0
=0, pn1
=
, …, pn0
=0, pn1
=![]() , …, pn, m-1
=
, …, pn, m-1
=![]() ,
,
![]() , pn, m+1
=0, …,
, pn, m+1
=0, …,
заключаем, что ![]() . Наконец, в силу (*) имеем:
. Наконец, в силу (*) имеем:
![]() .
.
ЗАДАЧА № 3
Если общий член ряда, не являющегося ни сходящимся, ни расходящимся в собственном смысле, стремится к нулю, то частичные суммы этого ряда расположены всюду плотно между их нижним и верхним пределами lim inf и lim sup.
РЕШЕНИЕ:
Нам достаточно рассмотреть случай, когда частичные суммы s1
, s2
, …, sn
, … ограничены. Пусть ![]() ,
, ![]() , l - целое положительное число, l>2 и
, l - целое положительное число, l>2 и ![]() .
.
Разобьем числовую прямую на l интервалов точками
-¥, m+d, m+2d, …, M-2d, M-d, +¥.
Выберем такое N, чтобы для n>N выполнялось неравенство |sn
-sn+1
|<d. Пусть, далее, sn1
(n1
>N) лежит в первом интервале и sn2
(n2
> n1
) – в последнем. Тогда числа конечной последовательности ![]() не смогут “перепрыгнуть” ни один из l-2 промежуточных интервалов длиной d. Аналогично рассуждаем и в том случае, когда последовательность будет не «медленно восходящей», а «медленно нисхожящей».
не смогут “перепрыгнуть” ни один из l-2 промежуточных интервалов длиной d. Аналогично рассуждаем и в том случае, когда последовательность будет не «медленно восходящей», а «медленно нисхожящей».
ЗАДАЧА № 4
Пусть для последовательности t1
, t2
, … , tn
, … существует такая последовательность стремящихся к нулю положительных чисел ![]() …, что для каждого n
…, что для каждого n
![]() .
.
Тогда числа t1
, t2
, … , tn
, …лежат всюду плотно между их нижним и верхним пределами.
РЕШЕНИЕ:
Существуют в сколь угодно большом удалении конечные последовательности ![]() , произвольно медленно нисходящие от верхнего предела последовательности к ее нижнему пределу.
, произвольно медленно нисходящие от верхнего предела последовательности к ее нижнему пределу.
ЗАДАЧА № 5
Пусть v1 , v2 , … , vn , … - положительные числа, v1 £ v2 £ v3 … Совокупность предельных точек последовательности
![]() , …
, …
заполняет замкнутый интервал (длина которого равна нулю, если эта последовательность стремится к пределу).
РЕШЕНИЕ:
![]()
ЗАДАЧА № 6
Числовая последовательность, стремящаяся к ![]() , имеет наименьший член.
, имеет наименьший член.
РЕШЕНИЕ:
Какое бы число мы ни задали, слева от него будет находиться лишь конечное число членов последовательности, а среди конечного множества чисел существует одно или несколько наименьших.
ЗАДАЧА № 7
Сходящаяся последовательность имеет либо наибольший член, либо наименьший, либо и тот и другой.
РЕШЕНИЕ:
При совпадении верхней и нижней граней рассматриваемой последовательности теорема тривиальна. Пусть поэтому они различны. Тогда по крайней мере одна из них отличается от предела последовательности. Она и будет равна наибольшему, соответственно наименьшему, члену последовательности.
ЗАДАЧА № 8
Пусть l1
, l2
, l3
, … , lm
, … - последовательность положительных чисел и ![]() , тогда существует бесконечно много номеров n, для которых ln
меньше всех предшествующих ему членов последовательности l1
, l2
, l3
, … , ln-1
.
, тогда существует бесконечно много номеров n, для которых ln
меньше всех предшествующих ему членов последовательности l1
, l2
, l3
, … , ln-1
.
РЕШЕНИЕ:
Пусть задано целое положительное число m и h – наименьшее из чисел l1 , l2 , l3 , … , lm ; h>0. Согласно предположению в рассматриваемой последовательности существуют члены, меньше чем h. Пусть n – наименьший номер, для которого ln <h. Тогда:
n>m; ln <l1 , ln <l2 , …, ln <ln-1 .
ЗАДАЧА № 9
Пусть l1
, l2
, l3
, … , lm
, … - последовательность положительных чисел и ![]() , тогда существует бесконечно много номеров n, для которых ln
превосходит все следующие за ним члены ln+1
, ln+2
, ln+3
,…
, тогда существует бесконечно много номеров n, для которых ln
превосходит все следующие за ним члены ln+1
, ln+2
, ln+3
,…
ЗАДАЧА № 10
Пусть числовые последовательности
l1 , l2 , l3 , … , lm , … (lm >0),
s1 , s 2 , s 3 , … , s m , … (s1 >0, sm+1 >sm , m=1, 2, 3, …)
обладают тем свойством, что
![]() ,
, ![]() .
.
Тогда существует бесконечно много номеров n, для которых одновременно выполняются неравенства
ln >ln+1 , ln >ln+2 , ln >ln+3 , …
ln sn >ln-1 sn-1, ln sn >ln-2 sn-2, … ln sn >l1 s1,
РЕШЕНИЕ:
Будем называть lm «выступающим» членом последовательности, если lm больше всех последующих членов. Согласно предположению в первой последовательности содержится бесконечно много выступающих членов; пусть это будут:
![]() ,…
,… ![]()
Каждый невыступающий член lv заключается (для v>n1 ) между двумя последовательными выступающими членами, скажем nr-1 <v<nr . Имеем последовательно:
![]() ,
,
значит
![]() (*)
(*)
отсюда заключаем, что
![]()
Действительно, в противном случае ![]() , значит, в силу (*) и вся последовательность
, значит, в силу (*) и вся последовательность
l1
s1
, l2
s2
, … были бы ограничены, что противоречит предположению. Теперь пусть задано целое положительное число m и h – наименьшее из чисел ![]() ,… ; h>0. Согласно предположению в рассматриваемой последовательности существуют члены, меньше чем h. Пусть k – наименьший номер, для которого
,… ; h>0. Согласно предположению в рассматриваемой последовательности существуют члены, меньше чем h. Пусть k – наименьший номер, для которого ![]() <h. Тогда:
<h. Тогда:
k>m; ![]() .
.
ЗАДАЧА № 11
Если числовая последовательность ![]() ,… стремится к
,… стремится к ![]() и А превышает ее наименьший член, то существует такой номер n (возможно несколько таких), n³1, что n отношений
и А превышает ее наименьший член, то существует такой номер n (возможно несколько таких), n³1, что n отношений
![]()
все не больше А, а бесконечное множество отношений
![]() ,…
,…
все не меньше А.
РЕШЕНИЕ:
Имеем ![]() . Пусть минимум последовательности
. Пусть минимум последовательности
L0 -0, L1 -A, L2 -2A, L3 -3A, …
Будет Ln -nA; тогда
Ln-u -(n-u)A³ Ln -nA; Ln+v -(n+v)A³ Ln -nA,
u=1, 2, …, n; v=1, 2, 3, …; n=0 исключено в силу предложений относительно А.
ЗАДАЧА № 12
Пусть относительно числовой последовательности l1 , l2 , l3 , … , lm , … предполагается лишь, что
![]() .
.
Пусть, далее, А>l1
. Тогда существует такой номер n, n ³ 1, что одновременно выполняются все неравенства
![]()
![]() .
.
Если А®¥, то также n®¥.
РЕШЕНИЕ:
Пусть
l1 +l2 +l3 +…+lm =Lm , m=1, 2, 3, …; L0 =0.
Так как L1 -A<0, то L0 -0 не является минимумом в предыдущем решении. ln+1 ³A; поэтому ln+1, а следовательно и n должны стремиться к бесконечности одновременно с А.
ЗАДАЧА № 13
Пусть числовая последовательность l1 , l2 , l3 , … , lm , … удовлетворяет условиям
![]() ,
, ![]()
Пусть, далее, l1
>A>0. Тогда существует такой номер n, n ³ 1, что одновременно выполняются все неравенства
![]()
![]() .
.
Если А®0, то также n®0.
РЕШЕНИЕ:
Положим
l1 +l2 +l3 +…+lm =Lm , m=1, 2, 3, …; L0 =0.
Тогда ![]() . Последовательность
. Последовательность
L0 -0, L1 -A, L2 -2A, L3 -3A, …, Lm -mA, …
стремится к -¥. Пусть ее наибольший член будет Ln -nA. Тогда интересующие нас неравенства будут выполняться для этого номера n.
В последовательности L0 , L1 , …, Lm , … содержится бесконечно много членов, превышающих все предыдущие. Пусть Ls будет один из них. Тогда числа:
![]()
все положительны: коль скоро А меньше наименьшего из них, соответствующий А номер n больше или равен s. Точки (n, Ln ) должны быть обтянуты теперь бесконечным выпуклым сверху полигоном.