| Скачать .docx | Скачать .pdf |
Реферат: Теорема сложения вероятностей. Закон равномерной плотности вероятностей
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТВЕРСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра: «____________________________________________»
Реферат
по дисциплине «Теория вероятностей»
Тема:
«Теорема сложения вероятностей.
Закон равномерной плотности вероятности»
Работу выполнила: студентка II курса
заочного отделения группы ПИЭ-1
Колосова Олеся
Шифр-01302
Работу проверил:
Тверь
2003
СОДЕРЖАНИЕ:
1. Введение………………………………………………………3-4с.
2. Теорема сложения вероятностей…………………………..4-7с.
3. Закон равномерной плотности вероятности……………..7-
4. Заключение……………………………………………………
1. ВВЕДЕНИЕ
Случай, случайность — с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находки, случайная ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут лет места для математики—какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности—они позволяют человеку уверенно чувствовать себя при встреча со случайными событиями.
Как наука теория вероятности зародилась в 17в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр. Слово «азарт», под которым обычно понимается сильное увлечение, горячность, является транскрипцией французского слова hazard , буквально означающего «случай», «риск». Азартными называют те игры, а которых выигрыш зависит главным образом не от умения игрока, а от случайности. Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных—алгебраиста Джероламо Кардана (1501- 1576) и Галилео Галилея (1564—1642). Однако честь открытия этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым—Блезу Паскалю (1623—1662) и Пьеру Ферма. Ещё в древности было замечено, что имеются явления, которые обладают особенностью: при малом числе наблюдений над ними не наблюдается никакой правильности, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность.
2. ТЕОРЕМА СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Непосредственный подсчёт случаев, благоприятствующих данному событию, может оказаться затруднительным. Поэтому для определения вероятности события бывает выгодно представить данное событие в виде комбинации некоторых других, более простых событий. Приведём теоремы, с помощью которых можно по вероятностям одних случайных событий вычислять вероятности других случайных событий, каким – либо образом связанных с первыми. Начнём с теорем, которые образуют группу с общим названием «теоремы сложения».
Теорема 1. Пусть А и В – два несовместных события. Тогда вероятность того, что осуществится хотя бы одно из этих двух событий, равна сумме их вероятностей: P ( A U B )= P ( A )+ P ( B ).
Доказательство.
Обозначим исходы, благоприятные для события А , через а1 ,а2 ,…,а m , а для события В – через b 1 , b 2 ,…, bn . Вероятности этих исходов обозначим соответственно через p 1 , p 2 ,…, pm иq 1 , q 2 ,…, qn . Тогда событию A UB благоприятны все исходы a 1 , a 2 ,…, am , b 1 , b 2 ,…, bn . В силу того что события А и В несовместны, среди этих исходов нет повторяющихся. Поэтому вероятность события А UB равна сумме вероятностей этих исходов. т.е.
P (A UB )=p1 +p2 +…+pm +q1 +q2 +…+qn .
Но p1 +p2 +pm=P (A), q1 +q2 +qn =P (B), а потому
P(A UB)=P(A)+P(B).
Теорема доказана.
Пример 1. Стрелок стреляет в мишень. Вероятность выбить 10 очков равна 0,3 , а вероятность выбить 9 очков равна 0,6. Чему равна вероятность выбить не менее 9 очков?
Решение. Событие А «выбить не менее 9 очков» является объединением событий В - «выбить 10 очков» и С – «выбить 9 очков». При этом события В и С несовместны, так как нельзя одним выстрелом выбить сразу и 9, и 10 очков.
Поэтому по теореме 1 имеем:
P(A)=P(B)+P(C)=0,3+0,6=0.9.
Если события А1 , А2 , … ,А n попарно несовместны, то событие A 1 U … UAn -1 несовместно с событием An . В самом деле,
(A1 U…UAn-1 ) I An =(A1 An )U…U(An-1 An ) .
Но при s<n имеемAs An = , ипотому(A1 U… UAn-1 ) An = . Пользуясь этим замечанием, получаем из теоремы 1 следствие:
Следствие. Если события А1 ,…, Аn попарно несовместны, то вероятность объединения этих событий равна сумме их вероятностей:
P(A1 U…UAn )=P(A1 )+… +P(An ).
Доказательство. Как было отмечено выше, события A1U … UAn-1 и An несовместны, а потому по теореме 1имеем:
P(A1 U…UAn-1 UAn )=P(A1U…UAn-1)+P(An).
Применяя это же рассуждение к первому слагаемому и продолжая далее, получаем после n-1 шага, что
P(A1 U … UAn )=P(A1 )+…+P(An ).
Пример 2. В цехе работает несколько станков. Вероятность того, что за смену потребует наладки ровно один станок, равна 0,2. Вероятность того, что за смену потребуют наладки ровно два станка, равна 0,13. Вероятность того, что за смену потребуют наладки больше двух станков, равна 0,07. Какова вероятность того, что за смену придётся проводить наладку станков?
Решение. В том примере опыт состоит в том, что прошла смена и отмечено, сколько станков за эту смену потребовало наладки. В этом опыте события: А – «за смену потребовал наладки ровно один станок», В – «за смену потребовали наладки ровно два станка» и С – « за сену потребовали наладки более двух станков» несовместны. Нас же интересует вероятность события A UB UC . По теореме 1: P(A UB UC )=P(A)+P(B)+P(C)=0,2+0,13+0,07=0,4.
Выведем теперь связь между вероятностями противоположных событий.
Теорема 2. Для любого события А имеем: P(A*)=1-P(A).
Для доказательства вспомним, что AUA*=U , P(U )=1 и A A*. Тогда по теореме 1 получаем: 1=P(U )=P(AUA*)=P(A)+P(A*), откуда следует требуемая формула.
Пример 3. Берётся наудачу трёхзначное натуральное число от 100 до 999. Какова вероятность того, что хотя бы две его цифры совпадают?
Решение. Опыт здесь состоит в том, что наудачу выбирается натуральное число от 100 до 999 и смотрят, есть ли у негосовпадающие цифры. События «взяли наудачу число N» (N= 100, 101, … , 999) равновероятны (в этом смысл слова «наудачу» ) и образуют множество исходов этого опыта. Число исходов n=900. Нас интересует событие А - «у выбранного числа совпадают хотя бы две цифры». Проще, однако, подсчитать вероятность противоположного события А* - «у выбранного числа все цифры различны». Каждое такое число есть размещение без повторений из 10 цифр по 3, не имеющее первым элементом нуль. Следовательно, m =(A10 )3 –(A9 )2 =10. 9. 8—9. 8=92 . 8 (из числа всех трёхэлементных размещений без повторений надо вычесть число тех, у которых на первом месте стоит нуль) и P(A*)=92. 8/900=0,72. Тогда по
теореме 2 P(A)=1-P(A*)=0,28.
Пример 4. В урне, содержащей n шаров белого, красного и чёрного цвета, находится k белых шаров и L красных. Какова вероятность вынуть шар не чёрного цвета?
Решение. Если событие А состоит в появлении белого, а событие В – красного шара, то появление шара не чёрного цвета означает появление либо белого, либо красного шара. Так как по определению вероятности
P (A)=k/n, P (B)=L/n,
То по теореме сложения вероятность появления шара не чёрного цвета равна: P (AUB)=k/(n+L)/n=(k+L)/n.
Эту задачу можно решить и так. Пусть событие С состоит в появлении чёрного шара. Число чёрных шаров равно n –(k+L), так что P(C)=(n—k—L)/n. 3
Появление шара не чёрного цвета является противоположным событием С* , поэтому на основании указанного выше следствия из теоремы сложения имеем: P(C*)=1—P(C )=1—(n—k—L)/n=(k+L)/n, как и раньше.
Пример 5. В денежно – вещевой лотерее на серию в 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Какова вероятность какого – либо выигрыша на один лотерейный билет?
Решение. Если обозначить через А событие, состоящее в выпадении денежного выигрыша, и через В — вещевого, то из определения вероятности следует P ( A ) =120/1000=0,12; P ( B ) =80/1000=0,08. Интересующее нас событие представляет (AUB), поэтому из теоремы сложения вытекает:
P(AUB)=P(A)+P(B)=0,20.
Таким образом, вероятность какого – либо выигрыша равна 0,2.
3. Закон равномерной плотности вероятности.
В некоторых задачах практики встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких случайных величинах говорят, что они распределяются по закону равномерной плотности .
Дадим определение: равномерным называется распределение непрерывной случайной величины Х все значения которой лежат на отрезке [a;b] и имеют при этом постоянную плотность распределения:
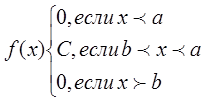
площадь под кривой распределения равна 1 и поэтому с(в-а)=1

вероятность попадания случайной величины Х на интервал от (α;β)
![]()
α=а, если α<а
β=в, если β>в
основные числовые характеристики закона распределения плотности вычисляются по общим формулам и они равны

Приведем примеры подобных случайных величин:
Пример 1.
Произведено взвешивание тела на точных весах, но в распоряжении взвешивающего имеются только разновески весом не менее 1г
.; результат взвешивания показывает, что вес тела заключен между k
и (
k+1/2)
граммам. Допущенная при этом ошибка X
, очевидно, есть случайная величина, распределенная с равномерной плотностью на участке  г.
г.
Пример 2. Вертикально поставленное симметричное колесо (см.Рисунок№1) приводится во вращение и затем останавливается вследствие трения. Рассматривается случайная величина θ –угол, который после остановки будет составлять с горизонтом фиксированный радиус колеса ОА. Очевидно величина θ распределена с равномерной плотностью на участке (0,2 π)
|

Пример 3. Поезда метрополитена идут с интервалом 2 мин. Пассажир выходит на платформу в некоторый момент времени. Время Т, в течении которого ему придется ждать поезда, представляет собой случайную величину, распределенную с равномерной плотностью на участке (0,2) минут.
Рассмотрим случайную величину X, подчиненную закону равномерной плотности на участке α до β (см.Рисунок №2), и напишем для нее выражение плотности распределения f( x) .
Плотность f(
x)
постоянна и равна с
на отрезке (α,β); вне этого отрезка она равна нулю: 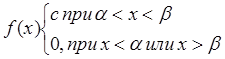 .
.
Так как площадь, ограниченная кривой распределения, равна единице: с (β- α)=1,
 ,
,
и плотность распределенияf( x) имеет вид: