| Скачать .docx | Скачать .pdf |
Реферат: Формирование понятия цилиндра
I этап: Введение понятия цилиндр. Математическое видение цилиндра.
Цель этапа : Формирование пространственного представления и логического мышления учащихся при изучении и формировании математического видения цилиндра его характерных элементов и изображений.
Дидактические средства:
- набор пространственных тел (прозрачных и непрозрачных);
- пластилин;
- деревянные палочки;
- цветные карандаши;
- модели изготовленные по рис. 3.
Перед началом урока учитель на своем столе располагает все пространственные тела: призмы, пирамиды, цилиндры, конусы, сферы и шары.
Рекомендуется начать урок со следующего упражнения.
Упражнение 1 . Из множества тел представленных выбрать те, которые были уже изучены (предполагается, что учащиеся выберут призмы и пирамиды).
Упражнение 2 . Оставшиеся тела сгруппируйте по внешним сходным признакам. (получили три группы: цилиндры, конусы, сферы и шары).
Упражнение 3 . Вызывается с каждого ряда по ученику. Им предлагается на интуитивном уровне к каждому пространственному телу сопоставить соответствующую табличку с названием данного тела. Предполагаемый ответ:
|
|
|
|||||||||
 |
|||||||||||
 |
 |
||||||||||
Упражнение 3 можно предложить выполнить стоящим ученикам. Затем, после того как кто-нибудь выполнит это упражнение верно, учитель говорит о том, что изучение этих пространственных тел они начнут с изучения цилиндра.
Упражнение 4 . Из пластилина учащиеся делают линию (KL). Затем деревянные палочки прикрепляют к пластилину, таким образом, чтобы эти палочки (АВ) как бы пересекали линию (KL) и были бы друг другу параллельны. В результате получилась бы поверхность которую назовем цилиндрической (рис. 1).
[Вывод : поверхность образованная движением прямой (АВ), которая во всех положениях параллельна данной прямой и пересекает линию (KL) назовем цилиндрической поверхностью ].
Соглашение 1 . Движущаяся прямая (АВ) – образующая; линия (KL) – направляющая.
Упражнение 5 . Предполагается соединить оба конца линии (KL) вместе (Получится цилиндрическая поверхность которая называется замкнутой ) (рис. 2).
|
|
Упражнение 6 . Учащиеся из пластилина делают две лепешки (плоскости) и с двух сторон прикрепляют к замкнутой цилиндрической поверхности и получают модель цилиндра.
[Вывод : Цилиндром назовем тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими цилиндрическую поверхность].
Соглашение 2 . В получившейся модели цилиндра параллельные плоскости, которые пересекает цилиндрическая поверхность назовем основаниями цилиндра .
Упражнение 7 . Учащимся предлагается из центра (приблизительно) верхнего основания цилиндра опустить перпендикуляр на нижнее основание (возможные варианты: а) высота проектируется точно в центр нижнего основания (прямой цилиндр ); б) пересекает нижнее основание, но не в центре; в) не пересекает нижнее основание (наклонный цилиндр )). Высотой может служить одна из деревянных палочек.
Соглашение 3 . Высотой цилиндра назовем кратчайшее расстояние между двумя основаниями цилиндра.
Упражнение 8 . Учащимся на урок принести модели по рис. 3 из спиц и проволки.
Всем предлагается сделать полный оборот вокруг оси. В результате, точки линии АМВ опишут окружности, которые назовем параллелями , они лежат в плоскостях, перпендикулярных оси вращения, а следовательно эти плоскости параллельны между собой.
|
[Вывод : Поверхностью вращения назовем поверхность, образованую линией, которая лежит в одной плоскости с осью и при вращении вокруг оси (Z) делает полный оборот].
Упражнение 9 . Назовите какой из пунктов в упражнении является цилиндрической поверхностью? (Ответ в)).
Учащиеся делают вывод :
При вращении прямоугольника вокруг прямой, содержащей одну из его сторон, получается, что во всех положениях АВ параллельна ОО1 , а поэтому при полном обороте описывает цилиндрическую поверхность (часть), а отрезки ОВ и О1 А опишут круги.
- ломанная опишет поверхность цилиндра О1 АВО
- основания круги;
- образующая АВ перпендикулярна основаниям.
Полученное тело назовем цилиндром вращения .
Упражнение 10 . (Самостоятельно). Предлагается учащимся вращать прямоугольник вокруг оси, проходящей через ось симметрии прямоугольника. Необходимо ли делать полный оборот в данном случае? (Ответ: нет, достаточно пол оборота).
Изображение цилиндра
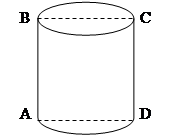
Обычно цилиндр изображают от руки:
1) основание изображают в виде эллипсов, лежащих в параллельных плоскостях;
2) двумя образующими соединяют концы больших диаметров эллипсов (оснований);
3) видимые линии рисуют сплошными, невидимые – контурными.
Соглашение 4. Под цилиндром будем понимать (подразумевать) цилиндр вращения .
Упражнение 11 . Ученикам предлагается провести всевозможные сечения цилиндра, плоскостью. Каждый ученики предлагает вариант, а затем все сведения систематизируются в следующую таблицу : (это упражнение выполняется на модели цилиндра сделанного полностью из пластилина, используя нож для резки пластилина).
 |
||||||||||||||||
|
|
|
|
|||||||||||||
 |
 |
 |
||||||||||||||
|
|
|
||||||||||||||
Соглашение 5 . Цилиндр осевое сечение (проходящее через ось вращения), которого – квадрат называется равносторонним цилиндром .
I этап: Введение понятия конус. Математическое видение конуса.
Цель этапа : сформировать ценностное представление у учащихся о конусе и его элементах. Развить пространственное воображение и логическое мышление через «видение конуса».
Дидактические средства:
- набор пространственных тел;
- пластилин;
- деревянные палочки;
- цветные карандаши;
модели изготовленные по рис. 3.
Упражнение 1 . Назовите уже изученные вами пространственные тела? (призма, пирамида, цилиндр). Назовите те которые еще не изучались? (конус, сфера (шар)).
Изучение данной темы по своей структурной схеме аналогично изучению темы «Цилиндр».
Упражнение 2 . Из пластилина изготовьте линию (KL). Пересеките ее деревянными палочками, таким образом, чтобы все эти палочки проходили через одну точку (S), не принадлежащую (KL). В результате получим поверхность, которую назовем конической поверхностью (рис. 1).
Соглашение 1 . Точка S – вершина, линия MN – направляющая, а прямая а – образующая.
Упражнение 3 . Соедините концы линии (KL) (получится замкнутая линия (KL) и коническая поверхность, которую назовем замкнутой ) (рис. 2).
|
|
Упражнение 4 . Из пластилина делается плоскость (лепешка) и коническую поверхность соединяют с этой плоскостью. Получилась модель конуса .
[конусом назовем тело, ограниченное замкнутой конической поверхностью и пересекающей ее плоскостью].
Соглашение 2 . Плоскость, пересекающая коническую поверхность назовем основанием .
Упражнение 5 . Учащимся предлагается из точки S опустить перпендикуляр. Это можно сделать при помощи деревянной палочки, протянув ее в модели конуса через вершину точку S.
(а) перпендикуляр опущен в центр основания, то есть конус прямой;
б) перпендикуляр пересекает основание или плоскость основания, но не в центре, то есть наклонный конус).
Соглашение 3 . Данный перпендикуляр назовем высотой конуса (кратчайшее расстояние от точки до плоскости).
Упражнение 6 . Учащиеся приходят на урок с моделями по рис. 3. Необходимо выполнить полный оборот вокруг оси.
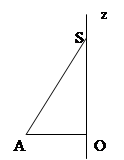 |
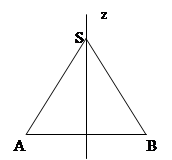 |
 |
 |
||||||
|
|
||||||||
|
|||||||||
[поверхностью вращения. Конусом вращения назовем тело полученное при вращении прямоугольного треугольника на полный оборот вокруг одного из катетов, в тогда другой катет опишет круг основание конуса, а образующая (гипотенуза) часть конической поверхности, или равнобедренного треугольника вокруг высоты опушенной из вершины) Достаточно пол оборота].
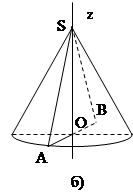
Соглашение 4 . Конус вращения – частный случай конуса, основание которого – круг и вершина проецируется в центр основания.
Изображение конуса

1) основание изображается в виде эллипса;
2) из точки вне плоскости основания проводятся две касательные (образующие) к концам большого диаметра эллипса.
Упражнение 7 . С помощью пластилиновой модели конуса и ножа для пластилина учащимся предлагается провести всевозможные сечения конуса. Результаты систематизируются в таблицу :
 |
||||||||
 |
 |
 |
||||||
|
||||||||

|
Упражнение 8 . Рассмотрим часть конуса заключенную между основанием конуса и плоскостью сечения параллельной основанию (рис. 4.1.)
|
[эту часть конуса назовем усеченным конусом ; круги с центрами в точках О и О1 – его основания; его образующие (АС, BD, …) равны между собой; прямая – ось; отрезок [ОО1 ] - высота].
|
|
|
|
|
|
 |
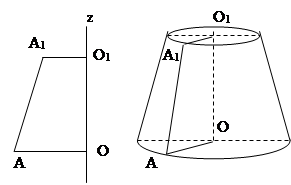 |
Усеченный конус можно рассматривать как тело полученное вращением прямоугольной трапеции вокруг оси, содержащей перпендикулярную сторону, или равнобокой трапеции вокруг оси симметрии.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()



 Упражнение 10
.Изобразите все возможные сечения усеченного конуса.
Упражнение 10
.Изобразите все возможные сечения усеченного конуса.
I этап: Введение понятия сфера и шар.
Цель этапа : Формирование понятия сфера (шар) развитие воображения, систематизация знаний по теме вращения. Формирование целостной системы.
Дидактические средства:
- набор пространственных тел;
- пластилин;
- надувные шарики (круглые!);
- цветные карандаши;
- модели заготовки (рис.1).
Упражнение 1 . Выполните вращение модельными заготовками. Если вращать полукруг, какое тело получится?
 |
 |
 |
Рис. 1
Соглашение . Поверхность образованная вращением полуокружности или окружности около диаметральной прямой называется сферой . Если же вращать полукруг или круг, то в результате получится тело вращения называемое шаром .
Упражнение 2 . Из пластилина вылепите тело вращения и надуйте шарик. Что сфера, а что шар? Воздух внутри шарика и он сам, что это за тело? (ответ: 1) пластилин – шар; шарик – сфера; 2) шар).
Упражнение 3 . Сфера – геометрическое место точек … (пространства), которые расположены на данном расстоянии от одной … (точки) называемой … (центром) … (сферы).
- отрезок, соединяющий центр с точкой сферы называется … (радиусом);
- тело, ограниченное сферой называется … (шаром);
- центром и радиусом шара называется … и … сферы.
Изображение сферы (шара)
1. Изображается круг;
2. Пунктиром рисуют два перпендикулярных диаметра;
3. Изображаются эллипсы на этих диаметрах, как больших диаметрах эллипса.
Упражнение 4 . Изобразите всевозможные сечения сферы (шара).
 |
 |
 |
Сечения сферы – окружности;
Сечения шара – круги.
Упражнение 5 . Выясните взаимное расположение сферы (шара) и плоскости?
(ответ: возможны три случая:
1) не пересекаются и не касаются, то есть нет общих точек;
2) касаются, существует одна общая точка, точка касания;
3) пересекаются, то есть для сферы – по окружности, для шара по кругу).
Упражнение 6 . Проверьте истинность утверждений:
1) Сечение шара плоскостями, равноудаленными от центра равны;
2) Сечение шара плоскостью тем больше, чем ближе она расположена к центру;
3) Rсеч
=![]() , где r – радиус сферы (шара),
, где r – радиус сферы (шара),
d – расстояние от центра сферы до центра сечения
4) Два больших круга пересекаются по диаметру;
5) Линия пересечения двух пересекающихся сфер – мерна линии центров сфер.
Упражнение 7 . Каково взаимное расположение сфер (шаров)?
(ответ: аналогично расположению окружностей:
1. Не касаются
1) расположены независимо друг от друга;
2) находятся одна внутри другой с общим центром или нет
2. Касаются
1) в одной точке
а) внешне
б) внутренне
2) в нескольких точках
а) пересекаются
Упражнение 8. На интуитивном уровне к каждому рисунку поставьте цифру, соответствующую изображенному на рисунке.
 |
 |
 |
 |
1. Шаровой слой
2. Сферический сегмент
3. Шаровой сегмент
4. Сферический пояс.