| Скачать .docx | Скачать .pdf |
Реферат: Элементарные частицы и космология
В работе с единой точки зрения рассмотрены вопросы организации живой и неживой материи, делается предположение об эквивалентности этих понятий. Делается попытка нового взгляда на такие понятия, как масса, пространство и время. В основе пересмотра этих понятий лежит предположение, что вакуум представляет собой 4-мерную жидкости. Данное предположение возникло при анализе возможных механизмов процесса движения элементарной частицы. Также сделаны выводы о единообразии микромира и макромира и на их основе попытка качественного анализа живых и информационных систем, как квантовых объектов.
На сегодняшний день в науке наблюдается определенный кризис. Кризис естественный и, по-видимому, связан с индустриализацией, точнее даже коммерциализацией, науки, превращения ее в отрасль народного хозяйства, ориентированной на производство ликвидных товаров. Это не хорошо и не плохо, но в такой ситуации главной становится технологическая сторона и прикладной характер любых научных исследований. В то же время, такие фундаментальные вопросы, как время, материя, жизнь и смерть и т.д., остаются в тени.
Интуитивно человек чувствует неслучайность существования мира и универсальность законов его устройства, но современные научные теории слишком разрознены, наука поделена на разделы, которые слабо связаны между собой. Особенно это видно на примере физики и медицинских наук или биологии, где даже не обосновывается, каким образом набор неживых элементов (молекул, атомов) образуют живой организм, жизнь для него воспринимается как данность. То же самое относительно других научных дисциплин. Тем не менее, внутреннее ощущение подсказывает, что должны существовать общие принципы и законы и одна основа для всех этих направлений. В частности, на определенные размышления наводит огромное количество элементарных частиц в физической теории, наверное, один из самых серьезных критических моментов в ней. Такие же чувства вызывает наличие в современных теориях таких понятий, как вакуум и силы взаимодействия. Собственно эти вопросы и ставятся в данной работе, и по мере возможности, делается попытка ответить на них.
Начнем с рассмотрения механизма движения объектов в пространстве. Будем считать объекты элементарными частицами, элементарными в классическом понимании, то есть в виде твердых бесструктурных шариков, размеры шариков могут быть и конечными и бесконечными, как увидим далее, это не влияет на характер движения.
Для этого рассмотрим такой пример. Пусть частица двигается из точки a в точку b с конечной скоростью (рис. 1). Подразумеваем, что частица в процессе движения будет находиться на линии траектории движения, правильнее, наверное даже сказать, что при движении частицы из a в b можно говорить о траектории движения. Действительно, считая, что время и пространство непрерывным, можем уменьшать расстояние dr между a и b и промежуток времени dt до бесконечно малых величин. Так как мы условились считать частицы бесструктурными, и кроме того, мы верим в законы сохранения материи и энергии, то в пределе рассмотрения, когда 
и 
, частица никогда не сможет покинуть точку a, либо должна находится в любой точке траектории своего движения, то есть “размазываться” по траектории, этот парадокс известен как “парадокс Зенона”. В чем же причина такого парадокса в отношении элементарных частиц, ведь опыт показывает обратное - частицы всегда находятся в движении? Причины, по-видимому, кроются в неправильности исходных предположений: либо предположение о непрерывности пространства-времени неверно, либо - движение частицы происходит без переноса материи в классическом понимании материи.
Если первое предположение неверно, то можно сделать вывод, что пространство-время имеет дискретную структуру. В этом случае должны существовать элементарные промежуток времени 
и расстояние 
, но тогда следует пересмотреть механизм движения частиц и само представление о материальной частице. Необходимо уточнить, что подразумевается под дискретным пространством - временем. Здесь также может быть несколько моделей такого пространства, но их, в принципе, можно свести к двум. Первая модель представляет пространство в виде решетки, а вторая предполагает непрерывное пространство при наличии квантов времени и длины.
В первой модели пространство-время или пространство и время в отдельности, не могут представлять собой жесткую сетку, в узлах которой только и могут находится частицы, так как в этом случае во-первых невозможно взаимодействие между частицами, во-вторых, ни элементарное расстояние 
, ни элементарный промежуток времени 
, не имеют никакого значения, так как пространство между узлами решетки не влияет на объекты в пространстве узлов решетки, в-третьих -- пространство становится анизотропным, причем анизотропные свойства должны зависеть от вида решетки (кубическая, октаэдровая и т.д.) и, в-четвертых, ни о каких волновых свойствах частиц не может быть и речи.
Рис.1 Движение частицы в дискретном пространстве-времени
Рассмотрим вторую модель, в которой пространство-время непрерывно, но имеется элементарные промежутки времени и расстояния. В таком пространстве, любая частица будет двигаться только “скачками”, то есть через определенные интервалы (кванты времени) частица появляется на расстоянии L от предыдущего своего положения (рис.1), причем появлению частицы в одной точке пространства должно предшествовать исчезновение её в предыдущей по времени точке пространства. Сейчас не имеет значения величины кванта времени и расстояния, важен процесс движения. Сразу возникают следующие вопросы: в каком направлении должна двигаться частица и что происходит с частицей в промежутке времени между исчезновением в точке a и появлением ее в точке b, чтобы не нарушались законы сохранения. Предположим, что в момент, следующий за исчезновением частицы в точке a, вся материя частицы на самом деле не исчезла, а перешла в иную форму. То есть мы предполагаем, что эта материя фактически, “растворилась” в вакууме, причем через некоторый элементарный промежуток, она снова должна возникнуть, но уже на элементарном расстоянии от предыдущего положения. При этом, в силу известной изотропии пространства, направления следующего появления частицы абсолютно эквивалентны, следовательно частица опять не сможет покинуть своего положения, а будет появляться в окрестностях точки a, что, опять-таки, противоречит наблюдениям. Из всех этих рассуждений можно сделать вывод о том, что и эти модели не отражают действительности. Но эти модели построены были исходя из представления о частицах, как бесструктурных элементах. Теперь можно сделать предположение, что частицы могут обладать некоторой структурой, то есть в такой модели, они уже не будут элементарными.
На сегодняшний день достоверно установлены, доказаны и используются в технике и науке волновые свойства материи, впрочем, дальше придется уточнить само понятие материи. Суть волновых свойств материи пока не выяснена, однако совершенно логично предполагать, что для распространения любой волны необходима какая-либо среда, причем обладающая структурой или, по-другому, локальными характеристиками. Иными словами эта среда должна быть материальной. Так как мы рассматриваем волны материи, естественно такой средой для них является вакуум; в этом нет ничего удивительного, вакуум в физике уже несколько десятилетий считается видом материи, правда весьма специфическим. Одной из характеристик вакуума, как известно, является его изотропия, в силу установленной изотропии пространства. Кроме того, в дальнейших рассуждениях, нам понадобиться такое явление, как универсальность волновых свойств материи, независимо от её вида. То есть то, что любой материальный объект должен обладать волновыми свойствами. Из этих исходных предположений, можно сделать вывод о том, что вакуум в действительности является сплошной средой, и, кроме того, обладает локальными характеристиками, то есть является средой, способной к распространению волн. Далее, сделаем еще одно небольшое, но очень важно предположение, будем считать, что физический вакуум обладает текучестью, то есть обладает свойствами жидкости.
Немного отвлечемся от вопроса природы вакуума и обратимся к теме измерения, точнее даже не измерения, а получения информации и восприятия. Этот вопрос очень интересен сам по себе и, как увидим далее, приводит к довольно интересным выводам. К тому же этот вопрос уж очень набил оскомину, и воспринимается как какое-то колдовство и магия.
Как уже было сказано, процесс измерения есть не что иное, как процесс получения информации об измеряемом объекте. Соответственно, в любом измерении должны участвовать как минимум два объекта: собственно объект измерения и измерительный прибор. Здесь нужно сделать одно замечание, касающееся прибора, принципиально ни один прибор не в состоянии определять значения величин с абсолютной точностью, в этом случае было бы необходимо наличие элементов прибора с “нулевыми” и элементов с “бесконечными” размерами, что противоречит природе физических объектов.
Рис.2 Иллюстрация к измерению длины объекта
Для изучения этого вопроса обратимся к самому простому и понятному примеру: измерению линейных размеров объекта [рис. \ref{vol_fig}]. В качестве прибора в данном случае выступает линейка. Прибор имеет две характеристики: первая - это цена деления l, вторая - это собственно размеры прибора (количество делений), обозначим ее как Z. Измеряемый объект будет характеризоваться единственной величиной - длиной L. В действительности у объекта может быть множество характеристик, но мы не сможем их измерить данным прибором (линейкой) непосредственно.
Теперь можно рассмотреть в подробности процесс измерения размера объекта. Предположим, что размер объекта L меньше размера прибора, тогда проведя измерение, можно установить, что размер объекта составляет L/l единиц. Обозначим m размер объекта в единицах прибора.
При этом реальный размер будет отличаться от измеренного на величину до l. То есть ошибка измерения составит l. Можно уменьшить ошибку измерения, уменьшая цену деления прибора, но в любом случае цена деления будет отлична от нуля, иначе нет смысла в измерении длины. Мало того, цена деления не может быть также и бесконечно малой, так как мы имеем дело с физическим прибором, то есть с реальной и материальной линейкой, то для такой линейки цена деления может быть уменьшена до конечных значений, а ограничения на величину деления может накладывать например размер молекул вещества из которой она сделана.
Так как размер измеряемого объекта меньше размера прибора, то в этом случае его длина может быть в принципе измерена.
Что касается ситуации, когда размер прибора меньше измеряемого размера объекта, то в этом случае вообще невозможно измерить объект и для прибора такой объект не будет иметь линейных свойств. Что это означает? Это означает, что поведение объекта (в данном случае его линейные размеры), зависит от того, с каким прибором он взаимодействует, при этом его собственные реальные свойства остаются неизменными. Действительно, если размер линейки меньше размера прибора - это вовсе не означает, что они отсутствуют, отсутствуют они только для данной конкретной линейки.
Если продолжить наши рассуждения дальше и считать любое взаимодействие двух и более объектов, как взаимное измерение, то можно предположить, что один и тот же объект будет проявлять себя по разному в различных взаимодействиях. Если говорить об элементарных частицах, то известный дуализм “волна-частица” в этом случае абсолютно нормальное явление, так как характеризует то, какое происходит взаимодействие, а не является свойством частицы.
В продолжение предыдущих рассуждений о процессе измерения и вакууме, попробуем теперь выяснить более общие закономерности и, по возможности, количественные характеристики этого процесса. Для этого в качестве объекта измерения примем некоторый сигнал, распространяющийся в “жидком” вакууме. Для начала рассмотрим характеристики сигналов и введем некоторые определения. Пусть имеем сигнал вида 
. Здесь 
- функция, описывающая шум, а 
- полезный сигнал. Как известно важной характеристикой сигнала при его детектировании (измерении), является отношение сигнал/шум, обозначим ее как 
и назовем эту величину качеством сигнала. Для детектирования важны энергетические составляющие сигнала и шума, так как измерение является процессом энергетического обмена. Тогда можно записать
(1)
где 
- интенсивность сигнала, а 
- интенсивность шума.
Кроме того известно, что для “белого шума” интенсивность 
, обозначим интенсивность “белого шума” как T и будем говорить об интенсивности “белого шума”, как о его температуре, то есть будем считать T температурой “белого шума”. Теперь можно посчитать интегральное выражение качества сигнала за промежуток времени измерения.
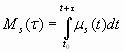(2)
(3)
Так как 
- интенсивность ''белого шума'', то в рассмотрении её можно считать величиной постоянной, и правильнее будет записать
. Тогда можно записать
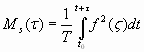(4)
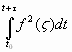(5)
выражает энергию чистого сигнала. Тогда выражение (4) запишется как
(6)
где 
- энергия сигнала в промежутке времени измерения. Назовем полученную величину 
“массой” сигнала, а величину - потенциалом.
Далее попробуем применить полученные выражение для оценки массы сигнала. В качестве сигнала рассмотрим звуковой сигнал в газе. Для идеального газа существует известная зависимость скорости звука от температуры идеального газа.
(7)
соответственно
(8)
Подставив в (6) выражение температуры из (8) запишем
(9)
или, иначе
(10)
Всегда можно подобрать систему единиц такую, что произведение kR будет равно единице и выражение примет вид
(11)
Пусть 
- некоторая функция распределения величин, полностью описывающая состояние системы в данный момент времени. Будем называть ее функцией состояния. Следующее состояние системы будет описано иной функцией. Условимся обозначать состояния системы натуральным числом n, а соседние состояния обозначать соответственно n+1 и n-1. Тогда переход системы из состояния с номером n в состояние n+1 можно записать
(12)
где F - оператор перехода. Тогда
(13)
где 
- дифференциальный оператор перехода.
Для дальнейших рассуждений нам понадобится выяснить, что считать переходом системы из одного состояния в другое.
Переход к уравнению (13) возможен при неизменных условиях преобразования, то есть в применении к системе, при условии неизменности внешнего воздействия. В общем случае будет зависеть от номера перехода.
Как уже было отмечено, переход из одного стационарного состояния в другое должно удовлетворять условию
(14)
или, исходя из (13)
(15)
(16)
Для дальнейших рассуждений необходимо сделать небольшие замечания. Как уже говорилось вначале главы, n - это порядковый номер события. При этом событием будем считать осреднение параметров в системе по всему набору элементов системы, точнее осреднение по сменам их состояний. На самом деле, смысл этого определения выясниться дальше, придется его уточнить и подкорректировать. Пока же будем рассуждать как условились. Теперь мы можем провести предельный переход в уравнении (13)
(17)
или
(18)
Что происходит при переходе из одного состояния системы в следующее на уровне ее составных частей? Допустим, мы рассматриваем газ бесструктурных частиц. Тогда можно утверждать, что при смене состояния произошло перераспределение энергии между частицами. Опять же будем рассматривать газ бесструктурных частиц. В этом случае в качестве момента перераспределения энергии можно считать характерное время свободного пробега элементов газа.
(19)
где - длина свободного пробега. Соответственно
(20)
Теперь обратимся к упорядоченному движению элементов газа. В этом случае на хаотическое движение элементов накладывается групповое движение и (20) запишется так
(21)
где V - групповая скорость элементов.
Теперь переходим к очень существенному и интересному моменту рассуждений. В данный момент мы ведем речь о собственном времени системы и о собственных масштабах системы и, вообще, о собственных характеристиках системы. Из этого следует, что собственная длина свободного пробега в газе не изменилась. Действительно, в групповой системе координат, связанной с групповой скоростью, каждый элемент проходит то же самое среднее расстояние, что и раньше. То есть справедливо следующее соотношение:
(22)
или
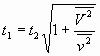(23)
Заметим, что среднеквадратичная скорость полностью хаотического движения элементов 
связана с температурой газа соотношением 
и также пропорциональна скорости звука в газе 
. Если внимательно посмотреть на правую часть (23), то можно заметить, что 
отражает энергию группового, упорядоченного, движения элементов. Таким образом (23) можно записать в виде:
(24)
В действительности, выражение (24) имеет более общий характер, нежели (23), так может быть применено не только для газа, но и вообще для любых мультисистем, если обобщить понятие температуры и считать ее относительной (масштабной) величиной. В таком виде время зависит от энтропии и особенно интересно для рассмотрения в качестве собственного времени в живых, информационных или даже социальных системах.
Что касается функции 
, то она отражает плотность энергии в данной точке пространства и по сути является энергетическим потенциалом. В случае, если соотношение
, выражение (24) можно представить в виде ряда
(25)
или, соответственно
(26)
Если учесть полученное в главе 3 выражение массы (6), в (26) можно заметить, что 
является локальной массой или, другими словами, плотностью массы. Из этих рассуждений вытекает, что темп времени прямо пропорционален плотности массы в этой точке. Еще раз надо отметить, что, используя эти понятия (масса, темп времени), всегда необходимо помнить о том, в каком масштабе они рассматриваются.
Возвращаясь к началу главы, найдем выражение изменения собственного времени в системе, считая, что оно является результатом осреднения времени по событиям со всеми элементами системы, то есть характерным временем перераспределения энергии. Для газа мы считаем его временем свободного пробега частиц газа.
(27)
здесь λ - приведенная длина свободного пробега.
соответственно
(28)
Если ввести новую величину n, характеризующую концентрацию элементов газа, то, используя статистическое выражение времени свободного пробега, можно переписать (27) и (28) в виде
(29)
где 
- плотность энергии, приходящаяся на один элемент, а ς - сечение взаимодействия.
Далее, продолжим развитие понятия времени как итеративного процесса в виде (18). Перепишем теперь (18) в виде
(30)
где τ - собственное время системы.
Попробуем поменять знак времени на противоположный. Что при этом произойдет с системой. В смысле (18) и (19) воздействие оператора на функцию состояния 
однозначно приведет систему к состоянию с функцией 
, следовательно,
(31)
Соотношение (31) будет справедливо только в том случае, если обе части в уравнении (31) являются чисто мнимыми. В то же время, оператор переводит систему из одного физического состояния в другое физическое состояние и, соответственно, должен быть эрмитовым, то есть
Данное соотношение очень важно, так как отражает фундаментальное свойство времени - необратимость. Теперь, на основе предыдущих рассуждений, можем записать следующее соотношение
(32)
или
(33)
Здесь W - энергия сигнала, а - энергетическая характеристика шума.
В частности, следует, что любую открытую динамическую или информационную систему можно рассматривать, как квантовый объект и, соответственно, применять для его описания математический аппарат квантовой механики, в дальнейшем, в главе, посвященной живым объектам, попробуем применить такой подход к изучению “живых” систем и вопроса самообучения. При этом нужно учитывать, что волновая функция ψ будет зависеть от времени в смысле (17), то есть должна быть нормирована для всякой системы и любую систему в этом случае необходимо описывать в терминах составляющих её элементов.
Здесь нужно сделать еще один важный вывод из приведенных рассуждений. В частности, из (18) и (11) следует, что течение времени системы возникает тогда, когда происходит изменение ее внутренней энергии. Следовательно, то обстоятельство, что любое изменение в системе приводит к изменению времени, выразится в следующем неравенстве
(34)
Продолжая те же рассуждения, нужно также учесть, что в такой записи возможно сколь угодно малое уменьшение влияния возмущения, что противоречит предположению о том, что любая физическая система состоит из элементов конечного масштаба. Так что, более точно выражение (34) должно быть записано как
(35)
где const - конечная величина, зависящая от масштаба восприятия и свойств системы. Как видим const имеет размерность действия, следовательно, можно сделать вывод, что любое изменение в системе происходит порциями конечной величины, определяемой соотношением (35). Собственно ничего экстраординарного в этом нет. Далее, попробуем подставить в (35) выражение для изменения собственного времени из (29), считая также 
.
сокращая n, получим
(36)
Если проводить аналогию с квантово-механическим описанием можно записать
(37)
или далее
из чего окончательно получим
(38)
где ħ нужно понимать в более широком смысле, чем в квантовой механике, так как из приведенных выше рассуждений ħ зависит от температуры системы.
Что из этого следует? Ничего особенного из этого не следует. Выражение (36) отражает лишь то, что минимальное воздействие, которое можно оказать на систему, может быть проведено лишь с одним её элементом как целым. А любое воздействие приводит к увеличению времени системы, точнее к увеличению ее возраста.
В принципе из (36) можно записать
(39)
Для изучения вопроса о пространстве вернемся к вопросу о его размерности. В начале статьи в ходе рассуждений мы пришли к выводу, что наше пространство должно обладать свойствами жидкости или газа, а материя представляет собой возмущения этой жидкости. Теперь обратимся к вопросу меры пространства, иными словами, каким образом мы оказались в трехмерном мире. Чисто феноменологически, нет оснований считать, что нет четвертого, пятого или какого-то еще измерения. Но тогда возникает вопрос о выделенности нашего трехмерного мира. То есть, если бы существовало измерение выше третьего, то мы могли бы наблюдать несоблюдение законов сохранения, но многолетней историей доказано обратное, по крайней мере в пределах доступных нам масштабов длин и времени.
Единственное, чем можно объяснить в рассматриваемой нами модели, выделенность трехмерного мира - это наличие границы раздела многомерной, конкретно 4-мерной, жидкости. Поэтому попробуем изучить некоторые поверхностные явления в такой жидкости. Для начала, чтобы получить наглядное представление о их,
рассмотрим некоторые поверхностные явления в трехмерной несжимаемой жидкости.
Самым характерным явлением в жидкости, как известно, являются вихри. В качестве системы координат возьмем поверхность жидкости, а третью координату будем считать нормалью к поверхности. То обстоятельство, что мы рассматриваем поверхностные явления, выражается в том, что третья координата представлена чисто мнимой.
Тогда запишем выражение вихря в жидкости. Условимся обозначать операции по действительным координатам символами κ, μ и λ, а символом ,3 и i,3 - если операция производится над 3-действительным и 4-комплексным векторами соответственно. Для общего случая n комплексных и m действительных осей комплексного пространства, обозначение будет выглядеть как ni,m.
Псевдотензор вихря, как известно [4], запишется
Или в развернутой записи
Рассмотрим каждую компоненту в отдельности. Из (2) можно получить выражение для dx
(40)
Граничное условие на поверхности раздела выразится в том, что распространение “звука” должно происходить внутрь жидкости, таким образом, из (41) получим
(41)
Тогда, следуя тем же рассуждениям, что и в [4], можно записать
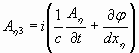
Где 
. Или, вводя новые обозначения
Окончательно, в таких обозначениях тензор поверхностного вихря запишется как
В случае 4-х мерной жидкости, рассуждения будут аналогичны и мы придем к выражению для тензора электромагнитного поля. Здесь не приведены эти выкладки, так как это известное выражение, к тому же все они аналогичны 3-х мерному случаю, в частности в [4], [6] приведены подробные выкладки. Просто запишем готовый результат
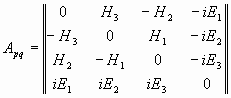(42)
Окончательно, теперь запишем (42) в векторных обозначениях
(43)
соответственно
(44)
(45)
Важно, что мы выполнили замену мнимой пространственной координаты на выражение ict, которое получено из предположений о 4-х мерной жидкости. Данный подход любопытен еще и тем, что в принципе позволяет изучать поверхностные явления в n-мерном пространстве путем замены его на комплексное пространство с действительными осями, принадлежащими изучаемой поверхности.
В главе, посвященной вопросу времени, мы пришли к тому, что для любой открытой, в том числе информационной системы, можно применить квантово-механическое описание. Тогда запишем выражение (32) для рассматриваемого нами живого объекта
(46)
Далее можно применять для нашего объекта те же рассуждения, что и для квантового. Как известно, из свойства эрмитовости оператора следует [6]
(47)
Из (47) следует, что у объекта должны существовать стационарные состояния. Физический смысл оператора в данном случае можно описать как воздействие внешней по отношению к объекту среды на него. Следовательно, в стационарном состоянии, внешнее воздействие среды на объект не приводит к изменению его внутреннего состояния. В связи с данным замечанием, будем считать, что стационарные состояния соответствуют обученной или адаптированной системе, а нестационарные - соответственно необученной и будем считать переходные процессы из одного стационарного состояния в другое обучением или адаптацией системы.
Так как функция ψ - есть функция состояния, то она является скаляром. В то же время в стационарных состояниях в системе должно оставаться неизменным не только полный интеграл от ψ, но и пространственное распределение скалярных величин, то есть должна сохраняться внутренняя структура объекта. Это требование, принимая во внимание (13), выразиться в следующем соотношении
(48)
То есть полная производная 
должна быть равна нулю. Рассматривая явления в жидкости (48), можно выразить через скалярный потенциал, а полную производную в (48) записать [2] как
(49)
(50)
Там же, в [2], говориться, что условие (49) - есть условие параллельного переноса, то есть из (48) в стационарных состояниях оператор является оператором полной производной состояния.
Вообще говоря, в (46) физический смысл оператора заключается в том, что система переходит из одного состояния в другое под воздействием некоторых факторов. Эти факторы делятся на две группы - внутренние и внешние по отношению к системе, так что можно выделить две составляющие оператора, обозначим соответственно внутренний оператор 
, а внешний - 
тогда
(51)
Естественно, (51) имеет смысл только в том случае, когда можно говорить о внутренних и внешних воздействиях.
Сравнивая (51) с (50), можно записать
(52)
соответственно
(53)
(54)
Введем представление вектора тока 
, такой что,
(55)
(56)
Теперь можно попробовать развернуть (53) и (54). Тогда из (53) получим
(57)
(58)
Раскрывая (58) получим для оператора потенциала
(59)
или используя (56)
(60)
Окончательно можно теперь переписать (51) в виде
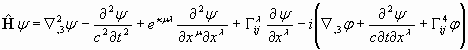(61)
Следуя обозначениям из [8, с.70] , 
, то (61) можно теперь записать в новых обозначениях
(62)
Для систем, удовлетворяющих (48) получим систему двух уравнений
(63)
(64)
При этом необходимо дополнительно выделить скалярные и векторные уравнения в (64). Для этого, однако, придется выделить скалярное и векторное слагаемое в тензоре 
.
Для чего мы все это проделали? Это нужно, в первую очередь, для того, чтобы попытаться раскрыть связь в уже известных, но, на первый взгляд, несвязанных явлениях. Как уже было сказано, (48) описывает стационарные системы, то есть такие системы, у которых не происходит изменения внутреннего состояния, или, по-другому, такие, которые можно рассматривать как твердые тела. Что касается другого класса систем, для которых несправедливо выражение (48), то такие системы по определению являются нестационарными. Это такие системы, в которых происходят фазовые превращения, сопровождающиеся изменением внутренней энергии и, соответственно, внутреннего времени. Очевидно, такие системы должны быть открытыми для того чтобы происходил энергетический обмен с внешней средой, однако обратное утверждение, вообще говоря, неверно, то есть определенный класс открытых систем может быть описан выражением (48).
Чтобы замкнуть (63), осталось выяснить как связан тензор 
c ψ-функцией. Здесь мы уже сделаем еще одно предположение - предположение о том, что H и E выражают соответственно магнитные и электрические поля. Очевидно, если связывать E и H с электромагнитным полем, то должен каким-то образом включать в себя выражения электрического заряда и тока, при этом, он, по определению, является тензором кривизны. Кроме того, выражение (42), полученное ранее, будет соответствовать, в таком случае, тензору электромагнитного поля.
Из (64) можно заметить, что в отсутствие искривления i,3 - пространства (64) вырождается и в таком пространстве должно отсутствовать электромагнитные поле.
(65)
Обратно, при наличии электромагнитного поля, возникает искривление - пространства. Ниже мы еще вернемся к обсуждению этого вопроса, и также вопроса о связи электромагнитного поля и гравитационной массы.
Система уравнений (63), вообще говоря, слишком неоднозначна. Для того, чтобы избавиться от неоднозначности в (63),необходимо также определить некоторые ограничения, налагаемые на функции, входящие в (63).
Прежде всего, рассмотрим, что представляет собой функция ψ, определенная ранее как функция состояния. Для этого определим плотность массы “жидкого” вакуума в (1), принимая во внимание и (22), как
(66)
В предположении малости плотности массы, то есть для случаев, когда
(67)
можно записать уравнение несжимаемости 4-мерной жидкости
(68)
Уравнение (68) - это, по сути своей, другая запись уравнения (49). Но в предыдущих рассуждениях, мы подразумевали под вакуумом 4-мерную жидкость и, соответственно, конечность скорости звука в этой жидкости. Следовательно, допущение о несжимаемости вакуума и, соответственно, наличия стационарных состояний (47), не является в общем случае верным, а верно только тогда, когда сжимаемостью вакуума можно пренебречь. Однако, мы можем записать другое уравнение исходя из условия изотропии вакуума, а именно
(69)
Применим известную формулу векторного анализа [9,с.32],
(70)
получим
(71)
где
(72)
и, исходя из (43)
(73)
и рассмотрим каждое слагаемое в правой части (75) по отдельности
(74)
(75)
Введем новые обозначения в (72)
(76)
Окончательно теперь, разделяя на комплексные и действительные слагаемые в (71), а также, на векторные и скалярные, запишем полученную систему уравнений
(77)
В простейшем случае, получим известные уравнения свободного электромагнитного поля
(78)
Подводя итоги этой главы, выпишем введенные здесь обозанчения
(79)
Как видно, мы получили известные уравнения электродинамики. Однако, существенно, что они были получены естественным образом исключительно из предположения о “жидком” вакууме, а точнее, существования некоторой комплексной потенциальной функции ψ, свойства которой определяются уже из предполагаемых свойств 4-мерной жидкости. Кроме того, было сделано предположение, что выражение (69) - верно. Что эквивалентно предположению о точечности источников электромагнитного поля, то есть в тех случаях, когда можно пренебречь линейными размерами возмущенных областей вакуума.
Глядя на уравнение (51) и вспоминая рассуждения о внешнем и внутреннем воздействии, остается непонятным однако, в чем между ними, внутренним и внешним воздействием, различия, так как остается неясным каким образом нужно отделять систему от ее окружения, особенно ярко это проявляется при рассмотрении явлений в жидкости. Здесь можно предположить, что элементы системы должны быть связаны между собой и вовлечены в совместное движение.
Математически это можно выразить локальной связностью множества элементов системы в стационарных состояниях. В общем случае можно записать определение системы используя оператор перехода F (12).
В стационарных состояниях системы, при условии локальной связности M, отображение F должно, кроме того, быть еще и непрерывным. Заметим, что (80) - есть определение фрактальной системы. На самом деле, под “стационарными”, везде в данной статье, подразумеваются такие состояния системы, в которых сохраняется её (системы) внутренняя структура, то есть для которых верно выражение, и, следовательно, сохраняется связность множества составляющих её элементов.
О системах, которые не отвечают этим требованиям, будем говорить как о трансформирующихся системах, находящихся в стадии фазовых переходов, или проще назовем их “транcформерами”.
В связи с введением данных понятий, естественно возникает следующий парадокс. Рассмотрим его на простом примере. Предположим, в процессе митоза из одной родительской клетки возникли две и мы затем отдалили их на значительное расстояние друг от друга, так что они не смогут взаимодействовать друг с другом. При этом в обеих из них находятся элементы родительской клетки и они абсолютно идентичны ей и друг другу соответственно. Можем ли мы сказать теперь, единая ли это система, или мы получили две новые системы, и, что самое важное, погибла ли при этом родительская клетка, а если нет, то что с ней стало? Если родительская клетка не погибла, то какая из двух клеток является родительской? Следуя определению (\ref{fractal_system1}) две новые клетки утратили локальную связность, следовательно, они есть две различные системы. Понимание данного вопроса очень важно с философской точки зрения, так как-то же самое можно говорить и о превращениях элементарных частиц и вообще о превращениях вещества. Важно определить границы, разделяющие различные состояния системы, например, те же самые рассуждения, касающиеся делящихся клеток живого организма, можно перенести на процессы деления атомных ядер или, двигаясь дальше, на процессы превращения одних элементарных частиц в другие. Конечно, все эти процессы сильно различаются, так как при делении ядер атомов, новые ядра не идентичны родительскому, а в случае элементарных частиц, вообще не происходит деления.
В заключение хотелось бы сделать некоторые предположения о возможных следствиях из представленной гипотезы, а также возможных возникающих вопросах.
В первую очередь хотелось бы отметить то обстоятельство, что полученные результаты относятся к любым мультисистемам, в том числе информационным, биологическим, физическим, социальным и т.д., и их описания необходимо задать функцию величин ψ. Единственная постулируемая и никак не осмысленная величина, или понятие, если хотите, является понятие энергии, она же является основой описания мультисистем. При этом, остается открытым вопрос откуда возникает энергия и что это такое.
Помимо всего выше сказанного, можно еще добавить одно важное замечание. В подобном описании систем проявляется общность ''живой'' и ''неживой'' природы и нам нет уже необходимости разграничивать эти два понятия, различие систем проявляется в том, в каком состоянии находятся системы - стационарном или нет, и какие процессы в них происходят.
То, что в описании систем обязательно присутствует температура, а следовательно в системах должна происходить диссипация энергии. В применении к вакууму, данное явление должно приводить либо к предположению о том, что в результате диссипации, в конце концов, наступит смерть Вселенной, либо о том, что во вселенной существует поток энергии в направлении четвертой координаты. Второй вариант мне лично нравится больше. По крайней мере, в этом случае думаю можно объяснить ячеистое распределение вещества во Вселенной. Можно пойти и дальше, и утверждать, что жизнь существует и на других планетах во Вселенной и даже больше, жизнь, подобная Земной. Это утверждение основано на предположении об изотропии жидкого вакуума.
Кроме того, силы и взаимодействия в таком описании имеют одну и ту же природу, а следовательно нет необходимости искусственно разделяют их отдельно на электромагнитные, ядерные, гравитационные, а они суть есть проявления единых взаимодействий.
Ландау Л.Д., Лифшиц Е.М.: Теоретическая физика: Учеб. пособие для вузов. В 10 т. Т. I. Механика. -- М.:ФИЗМАТЛИТ, 2002. -- 224 с. -- ISBN 5-9221-0055-6 (Т. I).
Ландау Л.Д., Лифшиц Е.М.: Теоретическая физика: Учеб. пособие. В 10 т. Т. II. Теория поля. -- М.:Наука. Гл. ред. физ-мат. лит., 1988, 512 с. -- ISBN 5-02-014420-7 (Т. II).
Ландау Л.Д., Лифшиц Е.М.: Теоретическая физика: Учеб. пособие для вузов. В 10 т. Т. III. Квантовая механика (нерелятивистская теория). -- М.:Наука. Гл. ред. физ-мат. лит., 1989, 768 с. -- ISBN 5-02-014421-5 (Т. III).
Астафьева Н.М.: УФН {\bf 166} 1145. N 11, стр.1151