Реферат: Безинерциальные заряды и токи. Гипотеза об эквивалентности 2-х калибровок

Кулигин В.А., Кулигина Г.А., Корнева М.В.

Введение

Исследуя проблемы калибровки уравнений Максвелла [1], [2], мы математически строго доказали следующее.

1. Задача Коши для уравнений в частных производных не имеет единственного решения. Решение зависит от выбора калибровки, т.е. калибровочная инвариантность и градиентная инвариантность в общем случае не имеют места.

2. Предельный переход в уравнениях Максвелла от волновых процессов к квазистатическим при v<<c является незаконным.

3. В силу этого, электромагнитные волны и квазистатические поля заряженных инерциальных частиц (электронов, протонов и т.д.) должны описываться разными группами уравнений. Электромагнитная волна должна удовлетворять волновому уравнению, а квазистатические поля должны описываться уравнением Пуассона.

Поскольку выводы опираются на строгое математическое доказательство и не содержат каких-либо гипотез, они подрывают основы не только классической электродинамики, но и квантовой электродинамики.

В то же время, хорошее согласие уравнений Максвелла с экспериментом (например, прекрасно подтвержденная экспериментом теория антенно-фидерных систем) и ряд важных результатов в квантовой электродинамике требуют поиска объяснения этих фактов.

В настоящей работе показано, что существует условие, при котором имеет место градиентная инвариантность, т.е. эквивалентность кулоновской калибровки и калибровки Лоренца. Рассмотрены также следствия, вытекающие из этого условия.

1. Токи в коаксиальной линии

Первым направлением наших исследований, нацеленным на решение поставленной проблемы, стал анализ различных калибровок уравнений Максвелла и попытки видоизменить эти уравнения так, чтобы сохранить положительные результаты и правильно описать явления. К сожалению, этот путь не привел нас к желаемым результатам.

Второе направление – анализ решений уравнений Максвелла для различных задач электродинамики. Именно этот путь позволил переосмыслить уравнения Максвелла и найти условие, при котором градиентная инвариантность имеет место.

В качестве иллюстрации рассмотрим распространение полей в коаксиальной линии (ТЕМ волна). Когда к линии подключается источник напряжения, между проводниками линии начинает со скоростью света распространяться электромагнитная энергия. Проводник, как известно, можно рассматривать как квазинейтральную систему, в которой заряды электронов и ионов создают суммарное поле, равное нулю при отсутствии сторонних источников полей. В рамках максвелловской теории имеет место закон сохранения заряда. Если заряды возникают (разделяются), то попарно (положительный и отрицательный) без нарушения этого закона.

Мы должны при объяснении процессов принять также во внимание то, что согласно современным воззрениям средняя скорость электронов проводимости в проводнике весьма мала.

Вернемся к полям в коаксиальной линии. Рассмотрим процесс распространения энергии при подключении к линии источника постоянного напряжения. В современной литературе нет ясного объяснения процесса распространения энергии от источника. Мы рассмотрим некоторые варианты.

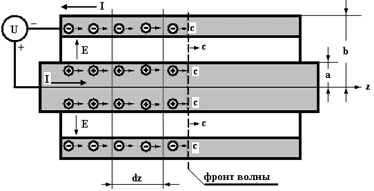
Рис.1

Вариант первый. Это наиболее распространенный вариант объяснения. В линии будет распространяться волна, которая на поверхности проводников образует заряды. Поверхностные заряды движутся и создают поперечное электрическое и магнитное поле.

Однако, если волна возбуждает эти заряды, то они возникают парами в соответствии с законом сохранения заряда (ион и электрон проводимости). Сразу после прохождения фронта волны заряды должны разделяться в обоих проводниках, причем так, чтобы на центральном проводнике существовали и двигались только положительные заряды, а на периферийном – только отрицательные заряды. В противном случае электрическое поле в коаксиальной линии существовать не может! В этом случае мы должны объяснить следующую проблему. Каким образом при рождении пары разноименных зарядов на каждом из проводников (ион и электрон проводимости) электрон проводимости может перескочить с центрального проводника на периферийный, чтобы обеспечить избыток отрицательных зарядов на внешнем проводнике и недостаток – на внутреннем (положительный ион, конечно же, не может!)? Такого механизма перехода не существует.

Вариант второй. Можно предположить другое. Вдоль проводников от источника напряжения и к нему по разным проводникам движутся электроны проводимости как показано на рис. 2. Однако и это положение не согласуется ни с теорией относительности (например, здесь скорость электронов проводимости должна быть равна скорости света), ни с современными представлениями о малой средней скорости перемещения электронов проводимости в проводнике.

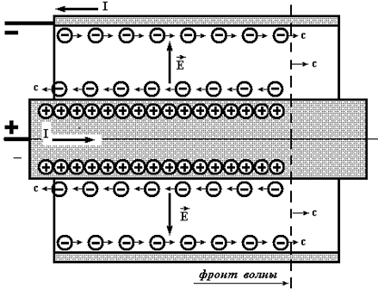
Рис. 2

Третий вариант. Второй вариант объяснения можно дополнить предположением, что электроны проводимости по какой-то причине “теряют” свои инерциальные свойства, т.е. их масса покоя становится равной нулю. Тогда они действительно могут двигаться со скоростью света вдоль поверхности металла. Но и этот вариант имеет дефект. Причина в том, что поверхностные токи на каждом из проводников образуются только электронами проводимости (положительные ионы неподвижны!). Следовательно, при распространении энергии вдоль линии даже при переменном напряжении внутри коаксиальной линии должна образовываться и существовать постоянная составляющая магнитного поля. Экспериментально она не была зафиксирована.

Новый вариант. По этой причине у нас остается единственный вариант объяснения. В проводнике должны существовать положительные и отрицательные заряды, не обладающие инерциальными свойствами. Но это не инерциальные электроны проводимости! Следовательно, не волна возбуждает заряды и токи в коаксиальных линиях, волноводах и т.д. на поверхностях проводников. Такие заряды создаются источником напряжения, и они движутся со скоростью света вдоль поверхности проводников. Именно они порождают в линии электромагнитные поля и переносят энергию; они – источник полей в длинных линиях.

Этот вывод настолько противоречит современным представлениям, что необходимо рассмотреть математическую сторону этого процесса.

Известно, что поля Er и H , которые существуют в коаксиальной линии, образуя ТЕМ волну, удовлетворяют волновым уравнениям.

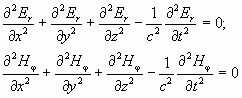(1.1)

Выделим кольца шириной dz на поверхностях коаксиальных цилиндров (см. рис. 1) и подсчитаем величину зарядов на этих кольцах:

Внешний коаксиальный цилиндр: dq1=2 b Er(b)dz.

Внутренний коаксиальный цилиндр: dq2=2 a Er(a)dz,  dq1 = dq2 =dq

Поверхностные токи этих проводников соответственно равны:

Внешний коаксиальный цилиндр: I1=2 bH (b).

Внутренний коаксиальный цилиндр: I2=2 aH (a),  I1 = I2 =I.

Принимая во внимание уравнения (2.1), мы можем записать уравнения для зарядов и токов:

. (1.2)

Из уравнений следует, что поверхностные заряды q, создающие поверхностные токи I, движутся вдоль коаксиальной линии с постоянной скоростью, равной скорости света! Эта скорость неизменна. Заряды не могут ускоряться или замедляться под действием каких-либо сил. Они не имеют инерциальных свойств. Масса покоя этих зарядов равна нулю. Мы еще раз хотим повторить, что единственным источником этих зарядов служит источник U.

Описанные выше токи и заряды не являются чем-то новым. Любой учебник, описывающий распространение волн в волноводах, коаксиальных линиях и т.д., содержит упоминание о поверхностных зарядах и токах. Однако авторы учебников по классической электродинамике старательно избегают обсуждать эту проблему. Причина тривиальная.

Ток в проводниках, согласно современным представлениям, обусловлен движением электронов проводимости. Признать, что эти электроны могут двигаться со скоростью света, означает признать несостоятельной Специальную теорию относительности. Добавим, что движение электронов с такой скоростью не согласуется с результатами электронной теории. По этим причинам авторы учебников “списывают” эти явления на электромагнитную волну, избегая подробностей объяснения.

Существование безинерциальных зарядов и токов – не гипотеза. Вся современная теория антенно-фидерных систем подтверждает их существование. Необходимо лишь отбросить предрассудки и догмы современных представлений и опереться на логику и здравый смысл. Нужно осознать и принять этот факт.

2. Условие выполнения “градиентной инвариантности”

Как мы установили в [1], [2], градиентная инвариантность в общем случае не имеет места. Для инерциальных зарядов кулоновская калибровка не эквивалентна калибровке Лоренца. Эквивалентность требует одновременного выполнения двух условий:

(2.1)

В общем случае, если мы рассматриваем движение зарядов с произвольной скоростью v, это условие не выполнимо. Два записанных уравнения несовместны.

Однако пример, рассмотренный в предыдущем параграфе, подсказывает единственное условие эквивалентности калибровок. Оно гласит:

Уравнения (2.1) являются совместными тогда и только тогда, когда плотность пространственного заряда удовлетворяет волновому уравнению.

(2.2)

Как следствие, токи тоже должны подчиняться этому уравнению

(2.3)

где с - вектор скорости, равный по величине скорости света.

Действительно, если заряд удовлетворяет волновому уравнению, то его потенциал удовлетворяет ему автоматически. Мы не будем останавливаться на простом доказательстве этого факта. Сформулированное нами условие, когда градиентная инвариантность имеет место, влечет за собой важнейшие следствия фундаментального характера.

Уравнения Максвелла имеют дело только с безинерциальными зарядами и токами.

Уравнения Максвелла не могут описывать поля инерциальных зарядов (электронов, позитронов, протонов и т.д.). Заметим, что, предельный переход к малым скоростям зарядов некорректен, как было математически строго установлено в [1] и [2]. К счастью, в таком переходе нет необходимости, поскольку безинерциальные заряды имеют постоянную скорость, равную скорости света.

Итак, в проводниках существуют токи двух видов: токи, образованные электронами проводимости, и токи, образованные безинерциальными зарядами.

Ниже мы будем многократно обсуждать свойства двух этих типов зарядов. Заметим, что безинерциальность поверхностных зарядов в проводниках позволяет объяснить высокую величину коэффициента отражения света от гладких металлических поверхностей и весьма быстрое (по отношению к периоду световых колебаний) выполнение граничных условий на поверхности металлов. Существующая электронная теория не в состоянии объяснить даже тысячной доли коэффициента отражения.

3. Заряды, их потенциалы и массы

Вернемся к потенциалам полей в кулоновской калибровке:

; ; (3.1)

Условие для градиентной инвариантности имеет вид:

(3.2)

Это условие можно заменить эквивалентным:

(3.3)

Поскольку ток связан с зарядом простым соотношением j=c , аналогичные уравнения мы можем записать и для тока:

(3.4)

Сопоставляя уравнения (3.1), (3.3) и (3.4) мы получим уравнение для векторного потенциала, описывающего электромагнитное излучение:

(3.5)

где Aw – векторный потенциал, описывающий электромагнитную волну.

Теперь мы можем обсудить полученные результаты и дать классификацию полей в классической электродинамике.

1. Инерциальные частицы (масса покоя отлична от нуля, индекс полей и потенциалов “k” , от слова “кирхгофовский”). В работе [3] мы показали, что любая заряженная частица, имеющая инерциальную массу покоя mo, обладает электромагнитной массой. Как известно, кулоновские силы стремятся “разорвать” заряженную частицу на части из-за сил кулоновского отталкивания частей заряда друг от друга. По этой причине учеными была выдвинута плодотворная гипотеза. Масса покоя заряженной частицы должна складываться из двух масс:

mo=me+mn

где: me – электромагнитная масса заряда; mn– масса неэлектромагнитного происхождения, которая отвечает за силы, удерживающие заряд от распада на части. Неэлектромагнитная масса может иметь отрицательный знак.

Поэтому мы можем записать для инерциальной заряженной частицы [3]:

mo=mek+mnk (3.6)

где: mnk– масса неэлектромагнитного происхождения, ответственная за устойчивость заряда; mek– электромагнитная масса, определяемая формулой:

(3.7)

Как показано в [3] , электромагнитная масса обладает всеми свойствами стандартной инерциальной массы.

(3.8)

Приведенные выше результаты справедливы, если потенциалы поля заряда описываются уравнениями Пуассона [3]:

(3.9)

Инерциальные заряды не могут непосредственно сами излучать электромагнитную волну. Это положение подтверждается результатами исследований, проведенных в [4].

2. Безинерциальные частицы (масса покоя равна нулю; индекс полей и потенциалов “n”, от слова “некирхгофовский”). Перейдем теперь к анализу безинерциального заряда. Для определенности мы будем считать, что размеры такого заряда значительно меньше размеров известных частиц. Мы имеем право применить к этим зарядам рассуждения, изложенные выше. Причина в том, что потенциалы этих зарядов также удовлетворяют уравнению Пуассона (уравнения (3.2) и (3.4)).

Поскольку безинерциальные частицы движутся с постоянной скоростью (скоростью света), мы можем предположить, что их масса покоя равна нулю. Отсюда следует вывод, что масса неэлектромагнитного происхождения этих зарядов имеет ту же величину, что электромагнитная, но знак неэлектромагнитной массы отрицательный.

mon=men+mnn=0 (3.10)

Именно это важное условие обеспечивает их “безинерциальность” и устойчивость от распада. В то же время, электрическое и магнитное поля этих зарядов не являются “запаздывающими” в обычном понимании этого термина. Поля этих зарядов движутся всегда синхронно с зарядом, не испытывая задержки, которая должна была бы зависеть от расстояния до движущегося заряда. Например, в рассмотренной картине распространения электромагнитной энергии в коаксиальной линии поля Е и Н имеют мгновеннодействующий характер. В этом смысле, свойства полей безинерциальных зарядов занимают “промежуточное” положение между свойствами полей инерциальных зарядов и свойствами полей электромагнитной волны в свободном пространстве.

Здесь классическая электродинамика смеется над язычески наивным постулатом “о конечной скорости распространения взаимодействий”. В работе [5] мы показали пустоту содержания этого постулата. Пока отсутствует четкое определение понятия “взаимодействие”, ни о каких “скоростях” его распространения не может идти речь. (см. Приложение).

Запишем уравнения для потенциалов полей безинерциальных зарядов.

; (3.11)

3. Электромагнитная волна (масса покоя равна нулю; индекс полей и потенциалов “w”). Электромагнитная волна это особый вид материи (или, если кому-то это больше по душе: особое состояние эфира, вакуума и т.д.), который после излучения существует самостоятельно, независимо от источников, которые излучили электромагнитную волну. В отличие от полей зарядов, которые были рассмотрены выше, поля и потенциалы электромагнитной волны являются всегда запаздывающими и вихревыми. Запишем уравнение для векторного потенциала электромагнитной волны.

(3.12)

где jсмещ– ток смещения, образованный электрическим полем.

Из этого уравнения следует, что источником электромагнитного излучения (волн) служит не ток из электронов проводимости, а электрическое поле, созданное безинерциальными зарядами. Это полевая модель излучения, которая противостоит токовой модели. В токовой модели электромагнитная волна формируется не полем, а током. Вне этого тока волна существует уже как самостоятельный объект.

Вернемся к уравнению (3.12). Подействуем на него оператором дивергенции (div). Левая часть уравнения обратится в нуль, поскольку divAw=0. Правая часть уравнения, как легко видеть, есть условие реализуемости градиентной инвариантности (2.1).

(3.13)

Уравнение (3.12) удовлетворяет закону сохранения пойнтинговского типа.

(3.14)

где: - плотность потока электромагнитного излучения; - плотность энергии электромагнитной волны; - плотность мощности.

Для полноты анализа запишем поля в калибровке Лоренца.

Поля безинерциальных зарядов.

;

(3.15)

Поля электромагнитной волны.

(3.16)

Нетрудно показать, что система уравнений (3.16) может быть приведена к уравнению (3.12). Систему уравнений (3.6) – (3.14) мы назовем 3КС калибровкой, а (3.6) – (3.10), (3.15) и (3.16) 3KL калибровкой.

Рассмотрим еще один широко распространенный предрассудок. Опираясь на представление о корпускулярно-волновом дуализме, некоторые физики пытаются безуспешно построить волновую модель заряженной частицы. Они записывают модель частицы в виде суперпозиции (суммы) электромагнитных волн. При этом они полагают, что групповая скорость волнового пакета из этих волн есть скорость перемещения заряженной частицы. Здесь они совершают две ошибки.

Во-первых, как показано в [6], групповая скорость есть скорость перемещения интерференционной картины, образованной группой волн. Никакого отношения к переносу энергии она не имеет.

Во вторых, масса покоя любой из волн, создающих волновой пакет, всегда равна нулю. Можно до бесконечности складывать эти нулевые массы, но кроме нулевого результата здесь нечего ждать (принцип суперпозиции!).

Заметим, что формула m=E/c2, хотя формально и позволяет вычислить массу, но ничего не говорит о ее характере (инерциальная или гравитационная, масса покоя или нет и т.п.). С тем же успехом мы могли бы искать, например, свою массу покоя у кинетической энергии (mv2/2(!)), у электромагнитной волны и т. д. Наличие инерциальных свойств (3.7), (3.8) было установлено математически строго только для полей, удовлетворяющих уравнению Пуассона [3]. Для полей, описываемых другими уравнениями (например, волновыми), таких доказательств пока не существует. Отсюда следует, что:

Ненулевой электромагнитной инерциальной массой покоя могут обладать только поля, удовлетворяющие уравнению Пуассона!

4. Граничные условия

Уравнения (3.6), (3.12) и (3.13) описывают потенциалы полей, создаваемых зарядами и процесс излучения электромагнитной волны. Эти уравнения должны быть дополнены двумя группами уравнений:

А) Уравнения, описывающие взаимодействие инерциальных зарядов с полями других инерциальных зарядов, с полями безинерциальных зарядов и электромагнитными волнами.

Б) Уравнения, описывающие рождение и уничтожение безинерциальных зарядов полями электромагнитной волны и полями других безинерциальных и инерциальных зарядов. Это самостоятельные темы для изложения.

Поставленные задачи являются весьма важными. Мы уже писали, что процесс “рождения” и “уничтожения” этих зарядов протекает весьма быстро. По этой причине даже для ультрафиолетовой части спектра справедливы граничные условия, приводимые во всех учебниках по классической электродинамике и волновым процессам.

Для металлов:  пов=(noE); jпов=[H no], где:  пов – поверхностная плотность пространственного заряда; jпов – поверхностная плотность тока; no – единичная нормаль к поверхности; Е и Н – поля у поверхности металла.

Для диэлектриков (без поверхностного заряда на границе раздела сред):

[E1 no]=[E2 no];  1(E1no)= 2(E2no)

[H1 no]=[H2 no];  1(H1no)= 2(H2no)

где: E1, E2, H1, H2 – поля в двух средах на границе раздела сред;  1,  2,  1,  2 – диэлектрическая и магнитная проницаемости двух сред.

Говоря о поверхностных токах и зарядах, мы должны понимать, что такое представление есть идеализация. Эта идеализация связана с макроскопическим описанием явлений на границе раздела сред. Реально заряды и токи занимают некоторый слой и имеют объемную плотность.

Процесс выполнения граничных условий на поверхности раздела сред достаточно быстр, поэтому кажется, что условия для соблюдения градиентной инвариантности практически не нарушаются даже в ультрафиолетовой части спектра. Однако это не означает, что поверхностные токи и заряды не имеют источников. Причина в том, что такие источники не оказывают заметного влияния на макропроцессы.

Только по мере уменьшения длины волны, когда длина волны становится соизмеримой с межатомными расстояниями ионной решетки металла или межмолекулярными расстояниями в диэлектрике, влиянием этих источников уже нельзя пренебрегать. Мы должны записать следующие уравнения:

(4.1)

где f и F – функции, характеризующие обильность соответствующих источников; они зависят как от электрических и магнитных полей, так и от длины волны и уменьшаются с ее ростом.

Записанные уравнения согласуются с задачами, поставленными в начале параграфа. Здесь можно было бы постулировать свойства микромира, задав f и F. Мы полагаем, для любых длин волн  условие эквивалентности (2.1) не выполняется. Безинерциальные заряды и токи не могут возникать без своих источников. Однако это “нарушение” еще не приводит к исчезновению реальной эквивалентности между кулоновской калибровкой и калибровкой Лоренца. Оно показывает, что существующие уравнения Максвелла не только имеют границу применимости и не полны. Введение функций f и F поможет расширить пределы применимости уравнений Максвелла, позволяя использовать их для описания явлений микромира. Но это уже другая тема.

Попутно заметим, что в соответствии с теорией познания объективной истины, эйнштейновская интерпретация преобразований Лоренца (СТО) некорректна, а преобразование Лоренца не имело и не имеет всеобщей значимости [5]. Если преобразование Лоренца и может применяться к некоторым явлениям электродинамики, то к довольно узкой области, которую еще предстоит найти. Можно предположить, что преобразование Лоренца справедливо только для полей безинерциальных зарядов.

Приложение

Используя матрицу Лоренца для преобразования 4-векторов, Эйнштейн ввел постулат о существовании "предельной скорости распространения взаимодействий". Этот постулат навязал физикам некорректную интерпретацию принципа причинности. Постулат, как бы, логически вытекал из "релятивистского множителя" (1-(v/c)2)-1/2, входящего в знаменатель некоторых компонент матрицы Лоренца. Рассмотрим содержание постулата о конечной скорости распространения взаимодействий. Что такое "взаимодействие"? Как и почему оно "распространяется"?

По нашему мнению, взаимодействие есть процесс (но не материальный объект!), который может занимать определенную область пространства (простираться) и длиться какой-то промежуток времени. Но ведь в постулате А.Эйнштейна речь идет не об изменении области, где проявляется взаимодействие, не об интенсивности этого процесса и не о времени его существования! Речь идет о скорости взаимного воздействия двух материальных объектов друг на друга!

С эйнштейновской точки зрения взаимодействие это волейбольный мяч, летающий от одной команды к другой через сетку.

С одной стороны, если это так, то тогда следовало бы отождествить взаимодействие с неким материальным объектом и рассматривать именно его скорость. Если взаимодействие есть материальный объект (например, электромагнитная волна), то нарушается симметрия при взаимодействии тел и нарушается принцип взаимности действия (симметрия и принцип равенства действия противодействию и т.д.). Какое-то тело должно начать взаимодействие первым (как у малышей: кто первый начал драку?)? Проверенная 200 летним опытом вся классическая (нерелятивистская) физика противоречит подобным представлениям о взаимодействии.

С другой стороны, подобное “взаимодействие” можно разбить на элементы. Пусть тело 1 взаимодействует с телом 2. Тогда:

А) Отделение от тела 1 электромагнитной волны можно рассматривать как акт элементарного взаимодействия.

Б) Движение этой волны к телу 2 не может рассматриваться как взаимодействие между телами.

В) Взаимодействие волны с телом 2 тоже акт элементарного взаимодействия.

Где же скорость распространения взаимодействий?

Некоторые ученые, понимая некорректность этого постулата, пытались "выправить" положение путем изменения терминологии. Они предлагали новую формулировку этого постулата: постулат о существовании предельной скорости распространения информации. Но ведь информация есть содержание, выражаемое с помощью символов [звуковых, графических т.п.]. Более того, передача информации всегда идет от генератора к приемнику, т.е. имеет все ту же асимметрию. По этой причине "изменение номенклатуры" не достигает своей цели. Без определения содержания понятия “взаимодействие” постулат о существовании предельной скорости распространения взаимодействий превратился в бессодержательную догму (постулат, не отвечающий сущности физических явлений и здравому смыслу).

В соответствии со сказанным выше, настоятельной задачей стал детальный анализ содержания причинно-следственных отношений и ревизия содержания причинно-следственных связей. Такой анализ отношений дан в [7].

Список литературы

Кулигин В.А., Кулигина Г.А.. Корнева, М.В. Калибровки и поля в электродинамике. /Воронеж. ун-т. - Воронеж, 1998. Деп. в ВИНИТИ 17.02.98, № 476-В98.

См. также: Кулигин В.А., Кулигина Г.А., Корнева М.В. Кризис релятивистских теорий, Часть 2 (Анализ основ электродинамики) http://www.n-t.org/tp/ns/krt.htm

Kuligin V.A., Kuligina G.A., Korneva M.V. Analisis of Lorentz’s gauge. Apeiron, vol.7, №1-2, 1996.

В.А.Кулигин, Г.А.Кулигина. Механика квазинейтральных систем заряженных частиц и законы сохранения нерелятивистской электродинамики. Воронеж. ун-т, Воронеж,1986. Деп. в ВИНИТИ 09.04.86, №6451-В86.

См. также: Кулигин В.А., Кулигина Г.А., Корнева, М.В. Кризис релятивистских теорий, Часть 5 (Электромагнитная масса) и Часть 6 (Магнитные взаимодействия движущихся зарядов) http://www.n-t.org/tp/ns/krt.htm

Сахаров Ю.К. Противоречия современных концепций излучения заряженных частиц и строения атома. //Проблемы пространства, времени и тяготения. Материалы IV международной конференции в С.-Петербурге, Политехника С.-П., 1997.

Кулигин В.А., Кулигина Г.А., Корнева М.В. Физика и философия физики / Воронеж. ун-т. - Воронеж, 2001. Деп. в ВИНИТИ 26.03.01, № 729-В2001.

См. эту статью также: http://www.n-t.ru/tp/ns/fff.htm

Кулигин В.А., Кулигина Г.А., Корнева М.В. Фазовая скорость и групповая скорость / Воронеж. ун-т. - Воронеж, 1997. Деп. в ВИНИТИ 24.12.97, № 3751-В 97

См также: Кулигин В.А., Кулигина Г.А., КорневаМ.В. “Фазовая скорость, групповая скорость и скорость переноса энергии” http://www.n-t.org/tp/ns/fs.htm

Кулигин В.А. Причинность и взаимодействие в физике.