| Скачать .docx | Скачать .pdf |
Реферат: Математическое ожидание и дисперсия для интервальных и пропорциональных шкал. Доверительные интервалы
.
С.В. Усатиков, кандидат физ-мат наук, доцент; С.П. Грушевский, кандидат физ-мат наук, доцент; М.М. Кириченко, кандидат социологических наук
Рассмотрим случай, когда в проводимом эксперименте числовая шкала имеет единицу измерения, т.е. про полученные числовые величины всегда можно сказать, насколько одно больше другого. Например, х - это число ошибок, допущенных при каком-либо тестировании, или число правильных ответов. Обозначим х1,...,хк деления этой шкалы, а n1,...,nk - частоты или число попаданий случайной величины х на каждое из этих делений. Например, в тестировании: шкала х1=0 правильных ответов, ..., хк=к-1 правильных ответов; n1 тестируемых не дали ни одного правильного ответа, ..., nk тестируемых дали к-1 правильных ответов.
Математическим ожиданием или просто средним называется число mx, вычисляемое по следующему правилу:
mx= ![]() (n1x1+.....+nkxk),
(n1x1+.....+nkxk),
где n=n1+...+nk - общее число испытаний
Дисперсией называется число , ![]() вычисляемое по следующему правилу:
вычисляемое по следующему правилу:
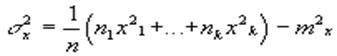 чаще используется число
чаще используется число ![]() , которое называется стандартным отклонением.
, которое называется стандартным отклонением.
Например, группу из n=11 учащихся опросили и получили следующее число правильных ответов:
| Шкала Xi | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Частоты ni | 0 | 1 | 0 | 1 | 1 | 2 | 2 | 2 | 1 | 0 | 1 | 0 |
Здесь 9 правильных ответов дал только один человек, 10 - ни одного, 13 правильных ответов дали 2 человека и т.п. Тогда:
![]()
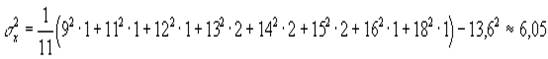 или
или ![]()
Таким образом, mx является обобщенным показателем достигнутого группой уровня в среднем, в виде одного числа, как меры центральной тенденции. Число же s x показывает, насколько испытуемые в группе отличаются по уровню развития изучаемого признака. Чем больше s x, тем больше различия у испытуемых, тем более разнородна по составу группа. Наоборот, чем меньше s x , тем однороднее группа и тем ближе по своему уровню испытуемые.
Дисперсия - весьма важный для исследователя-практика показатель. Анализируя ту или иную сторону учебно-воспитательного процесса, необходимо сравнивать большие наборы средних арифметических. Скажем, если опрос проводили в пяти классах параллели, а анкета содержала 15 вопросов с интервальной шкалой, каковой приписывались балльные значения, то общее число значений средних арифметических достигает 75. При этом самый опытный исследователь может запутаться в расчетах и пропустить какую-либо зависимость (или же обнаружить ее там, где она никогда не существовала). Это делать довольно легко, так как средняя арифметическая, как мера центральной тенденции, обладает рядом весьма капризных свойств. Понять их помогает приводимая ниже таблица.
“Удовлетворяют ли Вас результаты проведенной аттестации ?”
| Позиция вопроса | Да, в полной мере | В общем да, за исключением нес-кольких моментов | Скорее всего нет | Совершенно не удовлет-воряет | Трудно сказать |
| Балльное значение, приписанное позиции | +2 | +1 | -1 | -2 | 0 |
| Выборка 1 | 20% | 20% | 20% | 20% | 20% |
| Выборка 2 | 0% | 50% | 50% | 0% | 0% |
| Выборка 3 | 0% | 0% | 0% | 0% | 100% |
| Выборка 4 | 10% | 10% | 10% | 10% | 60% |
Если мы рассчитаем результаты этих четырех опросов, то получим, что во всех случаях mx=0. Разумеется, вероятность получить столь явно расходящиеся, как в нашей таблице, распределения, равна нулю - в практике возможны лишь какие-либо приблеженные варианы. Но наш пример носит чисто иллюстративный характер. Он позволяет понять почему в большинстве случаев исследователь, приводя значения mx по серии групп опрошенных, указывает и на размер дисперсии. В нашем примере при полном равенстве mх значения дисперсии будут разлисчаться очень сильно - от минимума в выборке 3 (дисперсия отсутствует вообще) до максимума в выборке 1.
Справедливости ради надо отметить, что неудобства причиняемые исследователю средним арифметическим, как мерой центральной тенденции, носят не только математический, но также и логический характер. Последнее обстоятельство не совсем относится к сути данной проблемы, но мы считаем необходимым о нем упомянуть, так как с ошибками такого рода сталкиваться приходится довольно часто. Проблема связана с тем, что ни в одной анкете не возможно дать вопросы, хотя бы приблизительно равные по степени сложности. На вопрос “Укажите Ваш разряд: 10,11,12,...15 (обведите кружком)” ответят практически все и ответы на 100% будут совпадать с действительностью. Вопрос о взаимоотношениях с администрацией вызовет большие сложности в заполнее и большее число уклонений от ответа. А оценить, например, преимущества методик школы Монтессори смогут весьма не многие, (да и с теми, кто такую оценку произвел, надо еще разобраться, используя “вопросы-фильтры” и “вопросы-ловушки” - не затесались ли туда те, чья информированность о Монтессори ограничивается газетной заметкой). Поэтому всегда возникает вопрос - включать ли в знаменатель формулы среднего арифметического тех, кто избрал вариант “Затрудняюсь ответить, не знаю” или нет ?
Расхождения могут быть весьма значительными. Например, если группа учителей оценивает какую-либо сторону педагогического процесса следующим образом:
| “отличную” | “хорошую” | “среднюю” | “ниже средней” | “плохую” | |
| балл | 5 | 4 | 3 | 2 | 1 |
| 2% | 16% | 25% | 22% | 10% |
При 25% не давших ответа, при внесении в знаменатель численности всей группы (100%), mx=2,03, при учете лишь тех, кто дал содержательные ответы, средняя оценка составит уже 2,70.
Есть кажущийся простым выход - в рамках одной анкеты в одних случаях считать от 100%, в других - от числа давших ответы, но тогда в итоге мы получим несопостовимые данные - оценки одних параметров могут оказаться резко завышенными, других - заниженными в сравнении с реальностью. Частично снять эту сложность можно, лишь оговаривая в итоговом документе исследования применяемые способы обработки и доказывая, почему был применен именно данный вариант. Это удлинит отчет, но избавит исследователя от возможной критики.
Однако, допустим, что в результате тщательной разоработки инструментария эта проблема перед нами не стоит, и мы можем без опсения сопостовлять среднии арифметические двух числовых рядов.
Рассмотрим ситуацию, когда необходимо сравнить две группы из n человек первая и N вторая: например, экспериментальную и контрольную - две группы детей, обучающихся по разным методикам. Правильность составления этих групп мы сейчас не будем подвергать сомнению и будем считать их случайными выборками.
В отличие от мышления на уровне обыденного сознания, склонного воспринимать полученную в результате опыта разность средних как факт и основание для вывода, более вдумчивый исследователь не будет торопиться. Ведь всегда остается возможность случайности различий и отсутствия значимой разницы в числах, например, средних mx и стандартных ошибок s x. Поэтому в начале придется выдвинуть статистическую гипотезу об отсутствии значимых различий, которую назовем нулевой гипотезой. По отношению к средним эта гипотеза следующая: и в первой и во второй группах mx=M, где число М можно назвать теоретическим средним.
Логика проверки подобных статистических гипотез определяется тем, что всегда есть риск ошибиться в выводах и неправильно отвергнуть правильную гипотезу. Обозначим a - вероятность ошибочно отвергнуть правильную гипотезу, или уровень значимости, а р=1- a назовем доверительной вероятностью. Величину a исследователь выбирает произвольно в зависимости от конкретной ситуации. Например, a =0,05 (или 5%) означает риск ошибиться в 5 случаях из 100.
Как известно, гипотеза отвергается, если в эксперименте наблюдается явление, противоречащее этой гипотезе. Наоборот, если в эксперименте встретилось явление, не противоречащее гипотезе, это еще не означает ее доказательства. Таким образом, отвержение гипотезы гораздо более надежно, в противном же случае можно говорить только, что наблюдения не противоречат гипотезе.
В статистике приходится считать явление противоречащим гипотезе, если вероятность его появления мала (а именно равна a ). Остается теперь только выяснить, чтоже это за явление.
Посмотрев на формулу для математического ожидания mx, можно увидеть, что эта величина есть не что иное, как сумма большого числа случайных величин - отдельных наблюдений. Поэтому в силу центральной предельной теоремы величина mx подчиняется нормальному закону (см. рис.1), со средним (теоретическим) М и неизвестным стандартным отклонением S. Можно доказать, что S в Ц n раз меньше стандартного отклонения каждого отдельного наблюдения, для оценки которого можно использовать величину s х. Поэтому по правилу “трех s “ для Z - закона получаем, что с доверительной вероятностью р=0,997:
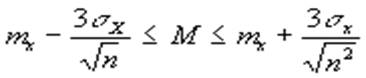
а для р=0,95 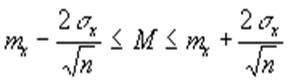
которые называются доверительными интервалами для теоретической средней М. Ясно, что если доверительные интервалы для М из двух групп не пересекаются, то нулевую гипотезу следует отвергнуть.
Например, опросили еще одну группу из N =9 человек и получили следующее число правильных ответов:
| шкала xi | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| частота ni | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 0 |
Аналогично расчетам для первой группы mx» 9,44 и d х» 2,18. По формуле для доверительного интервала, для первой группы при р=0,997:
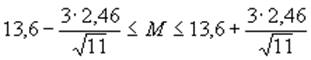
или 11Ј МЈ 16;
а для второй группы при р=0,997:
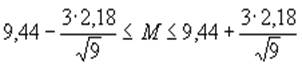
или 7 Ј М Ј 12
Таким образом, при уровне значимости 0,3% результаты тестирования этих двух групп не позволяют опровергнуть гипотезу о том, что среднее число правильных ответов в этих двух группах одинаково. По исследуемому параметру группы представляют практически единое целое. Предварительно выдвинутая гипотеза о том, что две разные методики должны представлять “на выходе” качественно различный уровень обученности, должна быть отвергнута. (Во всяком случае, такой вывод нельзя произвести, исходя из именно этих двух распределений. Возможно, что на полученном результате сказались случайные моменты, скажем, первую группу составили “звезды” одного класса, а вторую - в целом средние ученики. Но этот нюанс относится уже к несколько иной сфере - процедурам формирования выборки).
Следует отметить, что при уровне значимости 5% эту гипотезу уже следует отвергнуть, поскольку доверительные интервалы сужаются и не пересекаются в данном примере (проверьте).
Итак, обнаружилось одно важное обстоятельство: при одних a гипотеза отвергается, при других отвергать ее нет основания. Самое честное в таких ситуациях (когда выбор a не совсем ясен) указывать то “пограничное” значение уровня значимости, выше которого гипотеза отвергается, а ниже все еще остается не опровергнутой. Традиционно этот уровень колеблется в пределах 0,05>a >0,001, в социологической литературе не принято обсуждать результаты, подтверждаемые на уровне і 0,05.