| Скачать .docx |
Курсовая работа: Построение сетевого графика и определение резервов выполнения работы
Федеральное агентство по образованию
Курсовая работа
по дисциплине «Менеджмент»
САМАРА
Реферат
Курсовая работа
Расчётно-пояснительная записка: 19 с., 2 табл., 18 рис., 2 источника.
ГРАФ, РЕБРА, ВЕРШИНА, СЕТЬ, ПРОЕКТ, РАБОТА, СОБЫТИЕ, МОДЕЛЬ, РЕЗУЛЬТАТ, ТОПОЛОГИЯ, КОЭФФИЦИЕНТ СЛОЖНОСТИ, ПУТЬ,КОДИРОВАНИЕ, РЕЗЕРВ ВРЕМЕНИ, ОПТИМИЗАЦИЯ
Построена топология сетевого графика и закодированы работы (часть 1). Определен коэффициент сложности для данных работ (часть 1). Сделаны выводы по 1 части выполненной курсовой работы. Определена взаимосвязь работ во 2 части выполнения курсовой работы. Расписаны работы в виде таблицы исходных данных. Определено число путей в рассматриваемом графе. Подсчитаны продолжительность критического пути и срок окончания проекта. Приведены работы критического пути. Определены свободные резервы времени. Сделаны выводы по 2 части выполненной курсовой работы.
Содержание
Введение
1. Правила построения классических сетевых графиков
2. Построение сетевого графика
3. Анализ сетевой модели
3.1 Взаимосвязь работ и построение таблицы исходных данных
3.2 Определение числа путей
3.3 Определение сроков окончания проекта и продолжительности критического пути
3.4 Определение свободных резервов времени
3.5 Графическое изображение возможностей резерва
Заключение
Одной из основных проблем управления большими системами является проблема управления комплексами взаимосвязанных работ, которая получила название исследование операций. Известны 2 метода сетевого планирования: CPM – метод критического пути при фиксированном числе работ для составления расписания, и PERT – метод оценки и пересмотра программ.
Основным плановым документом в системе сетевого планирования и управления является сетевой график, представляющий собой информационно-динамическую модель, в которой изображаются взаимосвязи и результаты всех работ, необходимых для достижения конечной цели разработки. Другими словами, сетевая модель – конечный ориентированный граф, в котором одна вершина не имеет входных дуг (начальных вершин) и одна вершина не имеет исходных дуг (конечных вершин). Граф состоит из двух элементов: работа и событие. События являются результатами произведенных работ. Событие, не имеющее предшествующих работ, называется исходным. Событие, не имеющее последующих работ, называется завершающим. Любая последовательность работ в сетевом графике, которой конечное событие одной работы совпадает с начальным событием следующей за ней работы, называется путем. Всякая работа сетевого графика кодируется номерами ее начального (i) и конечного (j) событий.
В данной курсовой работе (часть 1) необходимо построить топологию сетевого графика и закодировать работы, согласно приведенным в методическом пособии, общим правилам построения. Результатом выполнения 1 части будет построение сети и краткий ее анализ. Результатом выполнения 2 части будет выполнение краткого анализа в представленной сетевой модели основных ее характеристик.
1. Правила построения классических сетевых графиков
При построении сетевого графика: рекомендуется направлять стрелки слева направо и изображать их по возможности горизонтальными линями без лишних пересечений.
Для правильного отображения взаимосвязи между работами сетевого графика при его построении необходимо соблюдать ряд правил.
Первое правило. Если работы А, Б и В выполняются последовательно, то на сетевом графике изображаются по горизонтали одна за другой (рисунок 1).
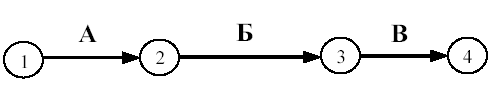
Рисунок 1
Второе правило. Если результат работы А необходим для выполнения работ Б и В, то на сетевом графике это отображается следующим образом (рисунок 2).

Рисунок 2
Третье правило. Если результат работ Г и Д необходим для выполнение работы Е, то на сетевом графике это изображается так (рисунок 3).

Рисунок 3
Четвертое правило . Работы сетевого графика не должны иметь одинакового кода. Если работы Б, В, Г выходят из одного события и выполнение необходимо для свершения одного и того же события, то вводятся дополнительные фиктивные работы (рисунок 4).
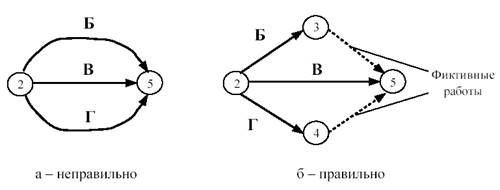
Рисунок 4
Пятое правило. Если работы Б, В и Г начинаются после частичного выполнения работы А, то работа А разбивается на части А1, А2 ... Аi и т.д., при этом каждая работа А в сетевом графике считается самостоятельной работой (рисунок 5).

Рисунок 5
Шестое правило. Если для начала работы Ж необходимо выполнение работ В и Г, а для начала работы Д выполнение работы Г, то в сетевой график вводится дополнительная фиктивная работа (рисунок 6).
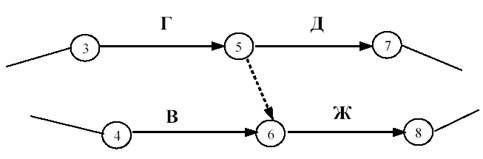
Рисунок 6
Седьмое правило. Если после окончания работы А можно начать работу Б, а после окончания работы В работу Г, а работа Д может быть начата только после окончания работ А и В, то на сетевом графике это изображается с помощью двух дополнительных фиктивных работ (рисунок 7).
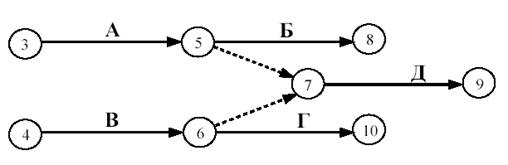
Рисунок 7
Восьмое правило. В сетевом графике не должно быть замкнутых контуров (циклов), т.е. цепочек работ, возвращающихся к тому событию, из которого они вышли. На рисунке 9 замкнутый контур (цикл) образовался из событий 3, 4, 2, 3. Наличие цикла в сети свидетельствует об ошибке в исходных данных или в неправильном изображении взаимосвязи работ.
Такая ситуация чаще возникает в больших и сложных сетях, которые разрабатываются несколькими исполнителями. При обнаружении подобной ошибки сетевой графика, после выяснения ее причины, необходимо исправить (рисунок 8).
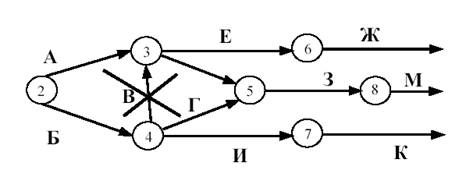
Рисунок 8
Девятое правило. События следует кодировать так, чтобы номер начального события данной работы был меньше номера конечного события этой работы (рисунок 9).

Рисунок 9
Десятое правило. В одноцелевом сетевом графике не должно быть "тупиков", т.е. таких событий, из которых не выходит ни одной работы (событие 2 на рисунке 10). Если в сети, кроме завершающего, появилось еще одно событие, из которого не выходит ни одной работы – это означает либо ошибку при построении сетевого графика, либо планирование ненужной работы Б, результат которой никого не интересует (рисунок 10).
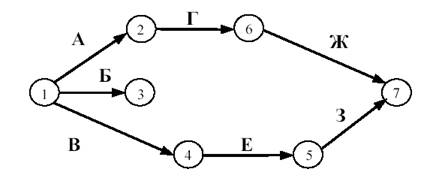
Рисунок 10
Одиннадцатое правило. В сетевом графике не должно быть "хвостов", т.е. событий, в которые не входит ни одной работы, если эти события не являются исходными для данного сетевого графика (событие 4 на рисунке 11).Если это правило нарушено, и в сети, кроме исходного, появилось еще одно событие, в которое не входит ни одной работы – это означает либо ошибку при составлении сетевого графика, либо отсутствие работы, результат которой необходим для начала работы (Г).
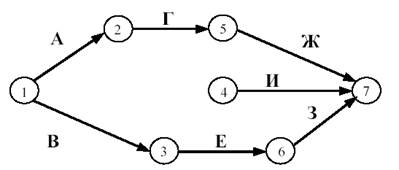
Рисунок 11
Двенадцатое правило. При укрупнении сетевых графиков группа работ может изображаться как одна работа, если в этой группе имеется одно конечное событие и если эти работы выполняются одним исполнителем при наличии в группе входных и выходных работ.
Продолжительность укрупненной работы равна продолжительности наибольшего пути от начального до конечного событий этой группы работ.
2. Построение сетевого графика
Изображение топологии сетевого графика начинаем с исходного события и работ, выходящего из него. В нашем примере исходными событиями являются работы А, Б и В. Работы Г и Д являются последующими работами относительно работы А. (рис. 12).

Рисунок 12
Работа Е зависит от выполнения работ Г и Д. Правильное отображение достигается путем введения фиктивных работы Г’ и Д’. Работа Л зависит от выполнения работ Б и В. Правильное отображение достигается путем введения фиктивных работы Б’ и В’.

Рисунок 13
Работа Е зависит от предшествующей ей работы Г. Работа З зависит от выполнения работы Б. Работа И зависит от выполнения работы З. Выполнение работы М зависит от работ И, Ж. Завершающим событием в данном примере является выполнение работы К, которое зависит от свершения работ Ж и К (рис. 14). Произведем кодирование работ топологии сетевого графика. Нумерация, при этом, должна соответствовать правилам нумерации, приведенным в методическом пособии.
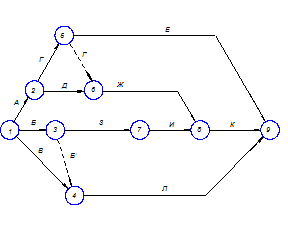
Рисунок 15
Подсчитаем число событий (n), число действительных (Д) и фиктивных (Ф) работ и число ожиданий (О).
n=9, Д=11, Ф=2, О=0.
Определим коэффициент сложности:
![]()
3. Анализ сетевой модели
3.1 Взаимосвязь работ и построение таблицы исходных данных
Объясним взаимосвязь работ, представленных на рисунке 16.

Рисунок 16
Как видно из рисунка 16 , работы А и Б являются исходными. Результат работы А
необходим для выполнения работ В и Г которые по отношению к работе А являются последующими. Результат работы Б необходим для выполнения работы К, которая по отношению к работе Б также является последующей. Работы Л и М выполняются последовательно и оказываются последующими для работы К. Работа Ж является результатом выполнения работы Г. Работы Д и И выполняются последовательно и оказываются последующими для работы В. Работа З происходит только после осуществления работ Е и Ж, где работа Е является последующей работе В. Работы Н, так же как и работа О выполняется только после осуществления работ З и И. После совершения работ М и Н выполняется работа Р. Работы С и Т выполняются последовательно и оказываются последующими для работы О. Завершающим событием, не имеющим последующих работ, является событие 14. Оно происходит после выполнения работ Р и Т. На основе объяснения взаимосвязи работ построим таблицу исходных данных (см. табл. 1).
Таблица 1 – Исходные данные
| № п/п | Работы, окончание которых является необходимым условием для начала рассматриваемой | Рассматриваемая работа |
| 1 | - | А |
| 2 | - | Б |
| 3 | А | В |
| 4 | А | Г |
| 5 | В | Д |
| 6 | В | Е |
| 7 | Г | Ж |
| 8 | Е, Ж | З |
| 9 | Д | И |
| 10 | Б | К |
| 11 | К | Л |
| 12 | Л | М |
| 13 | И, З | Н |
| 14 | И, З | О |
| 15 | М, Н | Р |
| 16 | О | С |
| 17 | С | Т |
3.2 Определение числа путей
В сетевой модели имеются пути, опирающиеся на исходное и
завершающее событие. Определим число путей в данной модели.
1. Цепь Б-К-Л-М-Р;
2. Цепь А-В-Д-И-Н-Р;
3. Цепь А-В-Е-З-Н-Р;
4. Цепь А-В-Е-З-О-С-Т;
5. Цепь А-В-Д-И-О-С-Т;
6. Цепь А-Г-Ж-З-О-С-Т; 7. Цепь А-Г-Ж-З-Н-Р.
Таким образом, в данном сетевом графике 7 путей.
3.3 Определение сроков окончания проекта и продолжительности критического пути
Существуют ненапряженные и критические пути. Они отличаются друг от друга продолжительностью времени. Наиболее протяженная по времени цепочка работ, ведущих от исходного к завершающему событию, носит название критического пути.
1. Цепь Б-К-Л-М-Р:17+8+30+19+24=98;
2. Цепь А-В-Д-И-Н-Р: 1+16+19+5+7+24=72;
3. Цепь А-В-Е-З-Н-Р: 1+16+12+8+7+24=68;
4. Цепь А-В-Е-З-О-С-Т: 1+16+12+8+6+19+12=74;
5. Цепь А-В-Д-И-О-С-Т:1+16+19+5+6+19+12=78;
6. Цепь А-Г-Ж-З-О-С-Т: 1+14+8+8+6+19+12=68; 7. Цепь А-Г-Ж-З-Н-Р: 1+14+8+8+7+24=62.
Цепь 1 представляет собой критический путь для данного сетевого графика, цепи 2-7 – подкритические пути, имеющие резервы времени.
Сроком окончания проекта принимаем продолжительность критического пути, как самой длинной цепочки. Для выбранной единицы измерения, например дни, проект завершится через 98 дней после своего начала.
Критическим путем, как было выяснено, будет являться путь, описываемый цепочкой 1. Работы, формирующие критический путь: Б-К-Л-М-Р.
3.4 Определение свободных резервов времени
Свободный резерв – это наибольшее время, на которое можно задержать выполнение данной работы, не меняя раннего начала последующей. Этот резерв возможен только тогда, когда в событие входят две или более работы (зависимости), т.е. на него направлены две или более стрелки (сплошные или пунктирные). Тогда лишь у одной из этих работ раннее окончание будет совпадать с ранним началом последующей работы, для остальных же это будут разные значения. Эта разница у каждой работы и будет ее свободным резервом.
Цепь Б-К-Л-М-Р является критическим путем, значит на нем не могут быть получены полные резервы времени. Значит, корректировке могут подвергнутся пути, описываемые цепочками А-В-Д-И-Н-Р, А-В-Е-З-Н-Р, А-В-Е-З-О-С-Т, А-В-Д-И-О-С-Т, А-Г-Ж-З-О-С-Т и А-Г-Ж-З-Н-Р . Свободный резерв времени в нашем случае можем получить, рассматривая процесс выполнения работы К. Составим таблицу, наиболее полно характеризующую
временные параметры в данной сетевой модели. При этом:
· ранний срок начала работы:
![]() ;
;
· поздний срок начала работы:
![]() ;
;
· ранний срок окончания работы:
![]() ;
;
· поздний срок окончания работы:
![]() ;
;
· полный резерв:
![]() ;
;
· свободный резерв:
![]() .
.
Процесс заполнения таблицы 2 произведем по следующему алгоритму:
1) Графа код работы заполняется на основе сетевого графика или перечня работ, расположенных в порядке их выполнения.
2) Количество предшествующих работ для исходного события равно 0, для остальных работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
3) Третья графа заполняется на основе сетевого графика или перечня работ с временными оценками.
4) Раннее начало работ, выходящих из исходного события, равно 0, а раннее окончание работ определяется путем выбора максимального их сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ, указанному в графе 1.
Таким образом, нельзя определить раннее начало последующих работ, не найдя раннего окончания предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы.
5) Продолжительность критического пути находится после заполнения граф 4 и 5, как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию. Найденная величина критического пути заносится в графу 7 (позднего окончания работ) для всех работ, ведущих к завершающему событию.
6) Заполнение графы 7 (кроме последней ее строки) – ведется снизу вверх следующим образом. Находятся все работы, последующие за рассматриваемой работой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из полученных величин заносится в графу 7 против рассматриваемой работы.
7) Данные графы 6 (позднее начало работы) находят как разность позднего окончания этих работ и их продолжительности (графа 7 - графа 3).
8) Полный резерв времени работы (графа 8) определяется разностью между значениями в графах 7 и 5 (или 6 и 4).
9) Резерв времени события j (графа 10) определяется следующим образом. В графе 7 отыскивается позднее окончание работы, заканчивающееся событием j. В графе 4 отыскивается раннее начало работы, начинающееся событием j. Разность этих величин является искомым резервом времени события j.
10) Свободный резерв времени работы Ксi , j определяется в результате вычитания значений графы 10 из значений граф 8.
Таблица 2 – Расчёт параметров работ
| Код работы | ||||||||
| 1,2 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1,3 | 17 | 0 | 17 | 0 | 17 | 0 | 0 | 0 |
| 2,4 | 14 | 1 | 15 | 61 | 75 | 60 | 0 | 60 |
| 2,5 | 16 | 1 | 17 | 61 | 77 | 60 | 0 | 60 |
| 3,9 | 8 | 17 | 25 | 17 | 25 | 0 | 0 | 0 |
| 4,6 | 8 | 15 | 23 | 51 | 59 | 36 | 60 | 24 |
| 5,6 | 12 | 17 | 29 | 47 | 59 | 30 | 60 | 30 |
| 5,7 | 19 | 17 | 36 | 47 | 62 | 30 | 60 | 30 |
| 6,8 | 8 | 29 23 |
37 31 |
59 | 67 | 30 36 |
30 36 |
0 0 |
| 7,8 | 5 | 36 | 41 | 62 | 67 | 26 | 26 | 0 |
| 8,11 | 7 | 41 37 31 |
48 44 38 |
67 | 74 | 26 30 36 |
26 30 36 |
0 0 0 |
| 8,12 | 6 | 41 37 31 |
47 43 37 |
67 | 73 | 26 30 36 |
26 30 36 |
0 0 0 |
| 9,10 | 30 | 25 | 55 | 25 | 55 | 0 | 0 | 0 |
| 10,11 | 19 | 55 | 74 | 55 | 74 | 0 | 0 | 0 |
| 11,14 | 24 | 74 48 44 38 |
98 92 68 62 |
74 | 98 | 0 26 30 36 |
0 26 30 36 |
0 0 0 0 |
| 12,13 | 19 | 47 43 37 |
66 62 56 |
67 | 86 | 26 30 36 |
20 24 30 |
6 6 6 |
| 13,14 | 12 | 66 62 56 |
78 74 68 |
86 | 98 | 20 24 30 |
20 24 30 |
0 0 0 |
Изобразим схематично сетевую модель расчёта (рис. 17).
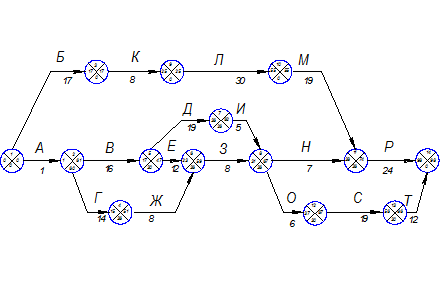
Рисунок 17
3.5 Графическое изображение возможностей резерва
Рассмотрим резервы полного и свободного времени для события 12-13.

Рисунок 18
На рисунке 18 величина Трi означает ранний срок начала события 12; Tni - ранний срок окончания события 12; Tpj - ранний срок начала события 13; Tnj - ранний срок окончания события 13.
Графически полный резерв времени может быть представлен как сумма двух отрезков АВ и СД. Каждый из этих отрезков охватывает величину резерва времени соответствующего события и величину возможного смещения начала или окончание работы. Эти последние величины зависят, естественно, от продолжительности самой работы. Сумма отрезков АВ и СF дает величину свободного резерва. Свободный резерв – это независимый резерв. Его использование на какой-либо работе не меняет величины свободных резервов остальных работ сети, так как при его исчислении в качестве плановых сроков начала выполнения всех работ приняты ранние сроки наступления событий.
Заключение
В результате выполненной 1 части работы был построен сетевой график по таблице исходных данных. Определен коэффициент сложности работ, который оказался невысоким. Его можно еще больше снизить уменьшением количества фиктивных работ, которых в данной модели четыре.
В результате выполненной 2 части работы был проанализирован сетевой график, представленный на рисунке 16. Для этой сетевой модели определены: количество путей; наличие и продолжительность критического и подкритических путей; определены свободные резервы времени. Наличие положительного резерва указывает на возможность опережения утвержденного календарного графика (избыток ресурсов). Наличие нулевого резерва указывает на возможность осуществления проекта точно по календарного графику (достаточное количество ресурсов). Наличие отрицательного резерва указывает на возможность отставания от календарного графика (недостаток ресурсов).
Таким образом, знания о наличии резервов времени позволяют оптимально руководить процессами начала или окончания каких-либо работ. Из таблицы 2 видно, что полный резерв времени на критическом пути равен 0, что соответствует истине. Важнейшее свойство полного резерва работы заключается в том, что если его использовать частично или полностью, то уменьшится полный резерв у работ, лежащих с ним на одних путях. Т.о. полный резерв времени принадлежит не одной данной работе, а всем работам, лежащим на путях, проходящим через эту работу. Используя свободные резервы времени, можно маневрировать в его пределах сроком начала данной работы или его продолжительностью.