Реферат: О вопросах звуковысотного интонирования

В 19 веке, с появлением работы Гельмгольца «Die Lehre von den Tonempfindungen als physiologiche Grundlage fur die Theorie der Music, Braunschweig, 1863[1] » было положено начало новому научному разделу в музыкальной теории – музыкальной психофизиологии. В последовавшей волне исследований, в этой области были сделаны важные открытия, среди которых на особом месте стоит теория Н. А. Гарбузова о зонной природе слухового восприятия звука. Она положила начало иному подходу к трактовке звуковысотных отношений в музыкальных системах, позволила качественно повысить воспитание музыкального слуха в образовательном процессе. В то же время в своих выводах Н. А. Гарбузов не в полной мере раскрыл содержание своего открытия в понимании звуковысотных функций музыкальных ступеней[2] .

Чтобы объяснить, в чем это проявилось, нам необходимо сделать небольшое отступление для краткого исторического обзора проблемы.

Музыкальный строй, как отражение уровня гармонического мышления для каждой эпохи, влиял на математический строй и заставлял его изменяться. Наглядным примером этому служит процесс трансформации математического строя в европейской музыке от пифагорова к 12-ступенному равномерно-темперированному. И в этом основную роль сыграла способность человеческого слуха к звуковысотному интонированию.

Первый теоретический музыкальный строй, обоснованный математическими расчетами, был создан Пифагором, по имени которого он называется и по настоящее время. В его основе лежат квинтовые отношения с интервальным коэффициентом 3/2. Выделяя одну ступень в качестве исходной и двигаясь от нее по квинтам, Пифагор определял настройку всех остальных двенадцати ступеней[3] . Его строй был единственным известным математическим строем, применявшимся в настройке музыкальных инструментов до появления чистого строя. Отметим, что любая музыкальная ступень, любой музыкальный интервал понимались только в том звуковысотном значении, на которое были настроены. Причем такое понимание звуковысотного содержания музыкальных интервалов и ступеней было перенесено и на музыкальную ладовую систему в целом, как для инструментов с фиксированным строем, так и с нефиксированным. То есть за каждой музыкальной ступенью, за каждым музыкальным интервалом закрепилось определенное звуковысотное значение, которое определяется музыкальным строем. Такой подход к звуковысотной трактовке музыкальных ступеней и интервалов Н. А. Гарбузов назвал точечным.

При невысоком уровне гармонического мышления пифагоров строй вполне удовлетворял музыкальным требованиям того времени. С появлением многоголосия произошел относительно резкий (в течение нескольких столетий) скачок в сторону повышения уровня гармонического мышления. Большую самостоятельность стала приобретать инструментальная музыка, шло усложнение вертикали, а главное, расширялась тонально-модуляционная сфера. И если в XVI веке в трактате «Додекахордон» Глареана «традиционная система восьми ладов была расширена до двенадцати»[4] , что еще в какой-то мере позволял пифагоров строй, то к XVIII веку он стал препятствием на пути дальнейшего развития гармонии. В первой половине XVIII века И. С. Бах стал использовать равномерно-темперированный строй на практике, чем обеспечил расширение тонально-модуляционной сферы до 24 ладотональностей.

Характерной особенностью пифагорова строя является то, что, в пределах семиступенной диатоники и ее расширениях, до определенного предела, он является равномерно-темперированным. То есть настройка всех одноименных интервалов одинакова[5] . Так, большие терции имеют настроечный интервальный коэффициент 82/64 (408 центов), большие секунды – 9/8 (204 цента) и т.д. Но при выходе за эти пределы положение меняется. Так, например, к большим терциям в 408 центов прибавляются большие терции в 384 цента[6] , у малых секунд – 114 и 90 центов, у больших секунд – 204 и 180 цента, у малых терций – 317 и 294 центов[7] . Такая двойственность стала помехой привычному звуковысотному интонированию, заставляя перестраивать слуховое восприятие, в зависимости от тональности, модуляционного движения или транспонирования. А также, проявлялась при настройке музыкальных инструментов. Объяснение данного явления через введение понятий уменьшенных и увеличенных интервалов (кварт, квинт, терций, секунд) не помогали слуховому восприятию.

Возможно, этот недостаток был выявлен еще современниками Пифагора, в частности Аристоксеном и его сторонниками. По крайней мере, можно предположить, что неполная равномерная темперация пифагорова строя выявлялась уже тогда, но не в такой мере, чтобы помешать его всеобщему распространению и практическому применению. Возможно, они просто более тонко чувствовали значительное расхождение между настройкой большой терции и звуковым интервалом с коэффициентом 5/4.

К недостаткам пифагорова строя и в первую очередь к вопросу о консонантности терций и чистоте их настройки теоретики вернулись в XII веке. Франко Кельнский сформулировал свое учение о консонансах[8] . Позже возник вопрос о точности настройки терций, в частности большой терции. Как консонантный интервал она должна настраиваться на звуковой интервал с коэффициентом 5/4, что расходилось ее настройкой в пифагоровом строе примерно на 23 цента. Процесс перехода от пифагорова строя к «чистому», где большая терция должна была настраиваться в звуковом значении 5/4, растянулся на века.

В XVI веке Дж. Царлино «окончательно ниспроверг систему Пифагора, доказал возможность использования больших терций как консонансов. Пифагорейская большая терция (81/64) была заменена «чистой» (без биений) большой терцией (5/4=80/64)»[9] .

Казалось бы, что музыкальная исполнительская практика должна была перейти к нему. Но этот строй в окончательном виде так и не был создан. С его появлением в еще большей мере проявился другой, до этого скрытый недостаток пифагорова строя – отсутствие полной равномерной темперации[10] . В течение столетия появлялись и исчезали разные виды темпераций[11] , пока И. С. Бах не использовал в своем творчестве 12-ступенной равномерно темперированный строй, который до того математически был определен Мерсенном.

Своим появлением равномерно-темперированнный строй нарушил стройное представление о природных основаниях музыкальной гармонии, ведь в нем отсутствуют природные феномены, даже настройка квинты отличается от чистой на 2 цента. Возникла неразрешимая дилемма – с одной стороны существовала функциональная система музыкального гармонического анализа, основы которой заложил Ж. Ф. Рамо, имеющая в своем основании природные феномены, и обеспечивающая достаточно подробный гармонический анализ практически любого музыкального произведения, с другой – музыкальная европейская практика, полностью перешедшая к равномерно-темперированному строю.

Решение данной проблемы было отложено до определенного времени, хотя со стороны отдельных теоретиков и экспериментаторов проводились попытки создания строя объединяющего в себе пифагоров, «чистый» и равномерно-темперированный строи. Все они имели в своем основании точечный подход к звуковысотной трактовке музыкальных ступеней и интервалов. Такой подход подразумевает, что любые музыкальные ступени, музыкальные интервалы воспринимается только в том звуковысотном значении, на которое настроены. До настоящего времени, в период полного господства 12-ступенного равномерно-темперированного строя, в некоторых теоретических исследованиях поднимается вопрос о том, какой строй более точно отражает звуковысотные отношения между музыкальными ступенями[12] .

С появлением в конце 19 века музыкальной психофизиологии (акустической психофизиологии) как науки, ученые снова вернулись к этому вопросу в своих исследованиях. Но вопрос уже был поставлен иначе – насколько необходима точная настройка отдельных интервалов на их характерные гармонические отношения. Свое окончательное решение он получил в созданной Н. А. Гарбузовым теории о зонной природе слуха. Следует отметить, что и после появления данной теории точечный подход к музыкальным акустическим явлениям остался. Об этом свидетельствует и объяснение обертонов на основе музыкального звукоряда во многих учебниках по элементарной теории музыкальной гармонии (см. сноску 2) и продолжающиеся попытки построить строй с «чистой интонацией», основываясь на «точечном» подходе к музыкальным ступеням. Число ступеней в одном из таких строев достигло 84[13] . Это заставляет нас подробно остановиться на исследованиях Н. А. Гарбузова и рассмотреть их результаты несколько с иных позиций.

Основной интерес для нас представляет работа «Зонная природа звуковысотного слуха» (4, с. 80-145), в которой Н. А. Гарбузов привел условия проведения экспериментов и результаты своих исследований по особенностям слухового восприятия музыкальных звуков и интервалов.

Вкратце рассмотрим суть и условия проводившихся исследований.

В первой главе ученый описывает исследования по абсолютному слуху, то есть точности определения высоты одиночного звука. В ходе исследований он определил, что испытуемые воспринимают высоту одиночного звука не с абсолютной точностью, а в некоторой звуковысотной зоне и данный вид слуха правильнее называть «зонным слухом». Ширина зоны абсолютного слуха «есть величина переменная, зависящая от регистра, в котором воспроизведен звук, тембра и громкости воспроизводимого звука, индивидуальности испытуемого, его психического состояния»[14] . Основываясь на опытах Абрагама, Гарбузов предположил, что наименьшая величина зоны абсолютного слуха (в среднем) равна 50 центам, причем, до этого значения ее можно сузить «путем упражнений»[15] .

Из этой части исследований Гарбузов сделал следующий вывод: «Так как у лиц, обладающих абсолютным слухом, эталоном высоты служат представления звуков, то можно утверждать, что нашим высотным представлениям звуков соответствуют не частоты, а полосы частот (зоны)»[16] .

Следующая глава посвящена исследованиям в области относительного (интервального) слуха и имеет для нас особое значение.

При проведении экспериментов Гарбузов рассматривал следующие интервалы[17] :

- прима (0 полутонов, 0 центов);

- м. секунда (1 полутон, 100 центов);

- б. секунда (2 полутона, 200 центов);

- м. терция (3 полутона, 300 центов);

- б. терция (4 полутона, 400 центов);

- кварта (5 полутонов, 500 центов);

- тритон (6 полутонов, 600 центов);

- квинта (7 полутонов, 700 центов);

- м. секста (8 полутонов, 800 центов)

- б. секста (9 полутонов, 900 центов);

- м. септима (10 полутонов, 1000 центов);

- б. септима (11 полутонов, 1100 центов);

При проведении испытаний с помощью специальной аппаратуры производились фиксируемые изменения настройки музыкальных интервалов и определялось когда испытуемый переставал воспринимать его гармоническое качество.

В ходе экспериментов Н. А. Гарбузов выявил наличие промежуточных интервалов, то есть таких, которые испытуемые не могли отнести ни к какому близлежащему музыкальному интервалу.

Результаты исследований Н. А. Гарбузов свел в таблицы, которые мы (объединив по разделам и опустив границы зон интервалов) приводим ниже – таблицы 1, 2. В таблице 1 приведены значения зон для интервалов, в которых они сохраняют свое гармоническое качество. В таблице 2 – значения для промежуточных зон, в которых музыкальные интервалы это качество теряют.

Таблица 1.

Таблица 2.

Как мы видим, в результатах исследований имеются некоторые несовпадения[18] . Они состоят в том, что зона сохранения индивидуальности интервала и промежуточная зона (с неопределенной индивидуальностью) в сумме не дают 100 центов (см. рис. 1[19] ).

Рисунок 1.

То есть в действительности, в ходе исследований Н. А. Гарбузова, определились три качественно различные зоны, первая – в которой ступень сохраняет свою индивидуальность, вторая – в которой звук определенно нельзя отнести ни к какой близлежащей ступени, и третья – в которой ступень «начинает терять свою индивидуальность», как бы переходная зона. Последняя зона образовалась в связи с большим количеством экспериментов и испытуемых, и ее можно рассматривать как статистический переходный процесс. Поэтому Гарбузов никак не определил ее. Мы же, для сохранения целостности октавы и интервалов в ней, звуки, не попавшие в зону сохранения индивидуальности музыкального интервала, отнесем к промежуточной зоне (см. рис 2).

Рисунок 2.

Зону, в которой сохраняется индивидуальность музыкального интервала мы будем называть зоной звуковысотного интонирования или просто зоной интонирования, и, в связи с относительной точностью[20] результатов исследований, будем считать ее равной 60 центов (± 30 центов от точки настройки ступени) (см. рис. 2).

Но музыкальный строй формирует также функциональную зону ступени (интервала) – зона в которую входят звуки (звуковые интервалы), чьи функции берет на себя ступень (интервал). Границы функциональной зоны определяются, как точки, делящие пополам интервалы между соседними ступенями. В 12-ступенном равномерно-темперированном строе функциональная зона ступени (интервала) равна 50 центам (см. рис. 3), и она существенно шире зоны интонирования.

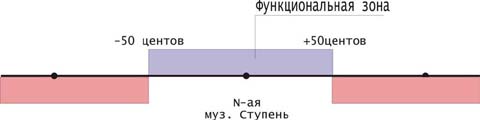
Рисунок 3.

Таким образом, мы можем взглянуть на результаты исследований Н. А. Гарбузова в несколько ином ракурсе.

Музыкальный интервал – есть понятие относительное, которое приобретает конкретное звуковое значение лишь в определенных гармонических условиях.

В связи с этим мы можем выделить музыкальные (абстрактные) и звуковые (конкретные) понятия. Музыкальная ступень – это область звукового спектра, в которую теоретически входит бесконечное число звуков. Соответственно, музыкальный интервал – есть бесконечное множество звуковых интервалов.

В определенном музыкальном строе музыкальная ступень и музыкальный интервал могут получить конкретное числовое значение или быть выраженными через интервальные коэффициенты, но это не будут истинные значения, так как являются только характеристиками данного строя для инструментов с фиксированным строем. Данные числовые значения определяются только количеством ступеней в строе и теми настройками, которые характерны для этого музыкального строя. Как пишет Ю. Н. Рагс: «… представление о высоте звука[21] ля первой октавы характеризуется тем, что оно находится в связи с представлениями о высоте разных звуков[22] (соль, фа или си, до и других), представлениями об их октавном положении; отсюда возникает и определенность, то есть отграниченность этого представления»[23] . Основное понимание музыкальной ступени проявляется в том, что, в принципе, она может принять любое звуковое воплощение в пределах зоны интонирования.

В то же время, при исполнении музыкальных интервалов и ступеней, мы слышим конкретный звук, а не зону – допустимый звуковой спектр. То есть в соответствии с определенными законами, при определенных условиях музыкальные понятия (интервал, ступень) превращаются в звуковые.

Музыкальный интервал несет в себе сравнение зон интонирования двух музыкальных ступеней. Реальное же звуковое значение музыкальный интервал получает «на более высоком уровне связей между «музыкальными ступенями»[24] , например на уровне ладовых связей в рамках тональности, этот представляемый звук или интервал «обрастает» функциями или отношениями к центральному тону, аккорду, или опорным тонам, аккордам»[25] . То есть, на уровне этих связей музыкальная ступень превращается в звук, музыкальный интервал – в звуковой. Вопрос о том, как это происходит, мы рассмотрим немного позже.

Как мы определили выше, музыкальная ступень характеризуется двумя зонами.

Первая – зона функционального применения ступени. Данная зона определяется музыкальным строем, применяемым для фиксированной настройки соответствующих музыкальных инструментов. Она вычисляется делением интервала между соседними ступенями пополам. В равномерно-темперированном строе она одинакова для всех ступеней и равна 100 центам (± 50 центов от высоты фиксированной настройки ступени). В пифагоровом строе функциональные зоны изменят свое количественное содержание и местоположение точки настройки, но, например, в рамках диатоники ладовые звуковысотные отношения останутся теми же. Функциональная зона является только продуктом деления октавы на определенное количество ступеней по определенному закону, который называется настройкой.

Вторая – зона интонирования. Ее основная особенность состоит в том, что звуковые интервалы, входящие в нее могут быть восприняты в своем звуковысотном качестве независимо от фиксированной настройки музыкального интервала, лишь бы они находились в его зоне интонирования.

Рассмотрим это все на примере большой терции.

Как известно, в равномерно-темперированном строе гармонически чистая большая терция с интервальным коэффициентом 5/4 звучит ниже на 14 центов по сравнению с ее настройкой. Но мы воспринимаем этот интервал именно в качестве гармонически чистой большой терции. Если же мы перестроим музыкальный интервал большой терции на 25 центов вверх, то нижняя область ее функциональной зоны увеличится до 62,5 центов, а расхождение между гармонически чистой большой терцией и настройкой музыкального интервала станет 39 центов. То есть гармонически чистый интервал выйдет за пределы зоны интонирования фиксированной настройки музыкального интервала, оставаясь в пределах функциональной зоны. И мы, в соответствии с результатами исследований Н. А. Гарбузова, не услышим музыкальный интервал в качестве гармонически чистого звукового или воспримем его как фальшивый, если приготовились слышать гармонически чистый[26] .

Это поясняет слова Н. А. Гарбузова о том, что нет необходимости абсолютно точно настраивать музыкальные интервалы на определенные звуковысотные значения, которые принято считать чистыми (для малой терции это 6/5, большой терции – 5/4, кварты – 4/3, квинты – 3/2, малой сексты – 8/5, большой сексты – 5/3). Достаточно чтобы музыкальный строй обеспечил их нахождение в зонах интонирования соответствующих музыкальных интервалов. Поэтому чистота настройки перестает быть основным требованием к строю и становится не более чем просто пожеланием, стремлением к лучшему.

В связи с этим основной недостаток 12-ступенного строя (любого) состоит не в том, что в нем нет достаточной точности в настройке определенных интервалов на характерные звуковые отношения, не то, что он рассчитан математически[27] , а то, что в нем функциональные зоны ступеней шире, чем их зоны интонирования. Это приводит к тому, что звуки (звуковые интервалы) расположенные между зонами интонирования не могут быть восприняты нами[28] . А это 30 - 45 % звуков (звуковых интервалов) из состава октавы.

В связи с вышесказанным на первый план выходят две задачи, с которыми связано дальнейшее развитие музыкальной гармонии:

- нахождение музыкального строя, в котором весь звуковой состав оказался бы воспринят с помощью зон интонирования;

- описание механизма звуковысотного интонирования, то есть, каким образом интонирование приводит нас к определенным звуковым интервалам, и какие гармонические свойства, какие гармонические качества присваивает наше слуховое восприятие «ошибочно» настроенным интервалам, входящим в зону гармонического действия музыкальной ступени.

Список литературы

[1] Первый русский перевод: «Учение о слуховых ощущениях как физиологическая основа для теории музыки» СПБ, 1875.

[2] В академическом понимании, с одной стороны для наглядности, каждый обертон представляется на примере их соответствия ступеням хроматического звукоряда (см., например, Способин В.В. «Учебник элементарной гармонии» издания до 1998 г.). С другой стороны, в рамках каждого строя (12-ступенного равномерно-темперированного, пифагорова, чистого) за каждым музыкальным интервалом закреплено определенное гармоническое значение, выражаемое в числовом виде (приведенная таблица):

То есть, за каждым интервалом закреплено конкретное гармоническое значение, что неправомерно, как будет показано в настоящей работе. Это значение определяет настройку ступеней в октаве для инструментов с фиксированным строем.

[3] На тему о древнегреческих строях имеется много публикаций, среди которых хотелось бы выделить работу Петра В. И. «О составах, строях и ладах в древнегреческой музыке» Киев, 1901 и работы Герцмана Е. (см. в библиографии).

[4] Пэрриш К., Оул Дж. Образцы музыкальных форм от григорианского хорала до Баха. Л., 1975, с. 51.

[5] Мы рассматриваем строи с учетом энгармонических замен, то есть до#=реb, ре#=миb и т.д.

[6] Очень часто такое интонационное значение большой терции называют уменьшенной квартой, но клавиша с таким названием отсутствует в 12-ступенном строе.

[7] Подробное описание возникновения одноименных интервалов с разной настройкой в Пифагоровом строе см. в приложении.

[8] Браудо Е. М. Всеобщая история музыки. Т. 1, Пб., 1922, с. 101-102.

[9] Переверзев Н. К. Проблемы музыкального интонирования. М., 1966. с. 56.

[10] Полная равномерная темперация определяется одинаковой настройкой одноименных интервалов во всем диапазоне звучания музыкального инструмента.

[11] Шерман Н. С. Формирование равномерно-темперированного строя. М., 1964.

[12] См., например, Переверзев Н. К. Проблемы музыкального интонирования. М., 1966.

[13] См. Рагс Ю. Н. Концепция зонной природы музыкального слуха Н. А. Гарбузова. // Н.А.Гарбузов - музыкант, исследователь, педагог. М., 1980, с. 16. В современных строях с «чистой интонацией» встречается разделение октавы на более чем 600 ступеней (см. музыкальную программу Scala по адресу http://www.xs4all.nl/~huygensf/scala/ и приложения к ней).

[14] Гарбузов Н.А. Зонная природа звуковысотного слуха. // Н.А.Гарбузов - музыкант, исследователь, педагог. М., 1980, с. 89.

[15] Там же.

[16] Там же.

[17] Н. А. Гарбузов, подразумевая, что они приняты музыкальной наукой, никак их не определяет, поэтому мы будем называть их «музыкальными» (кавычки будут опущены, но иметься в виду).

[18] Н. А. Гарбузов по-своему разъясняет их происхождение, но это не существенно для данной работы.

[19] Рисунок приведен из работы: Гарбузов Н.А. Зонная природа звуковысотного слуха. // Н.А.Гарбузов - музыкант, исследователь, педагог. М., 1980, с. 94.

[20] Результаты исследований не являются абсолютно точными в силу исследования субъективных восприятий.

[21] Точнее – музыкальной ступени.

[22] Музыкальных ступеней.

[23] Рагс Ю.Н. Концепция зонной природы музыкального слуха Н.А.Гарбузова. // Н.А. Гарбузов - музыкант, исследователь, педагог. М., 1980, с. 27.

[24] Замена в цитате «звуками» на «музыкальными ступенями» - моя (Автор).

[25] Рагс Ю.Н. Концепция зонной природы музыкального слуха Н.А.Гарбузова. // Н.А. Гарбузов - музыкант, исследователь, педагог. М., 1980, с. 27.

[26] Понятие «фальшивый» не совсем точно. Под этим подразумевается только то, что в данной настройке мы не услышим б. терцию в качестве звукового интервала с коэффициентом 5/4. Но при этой настройке мы можем услышать этот музыкальный интервал в качестве звукового с коэффициентом 9/7, что для современной (и даже более ранней) гармонии вполне естественно. Но об этом мы будем говорить позже.

[27] Пифагоров строй также рассчитан математически, просто в качестве исходного для расчетов интервала бралась квинта. Но ее природный феномен не заменяет природных феноменов других обертонов и, следовательно, не позволяет утверждать в полной мере природного происхождения пифагорова строя. Также и природный феномен большой терции не позволяет через нее определять звуковысотные значения для других музыкальных ступеней и интервалов в «чистом» строе.

[28] Они могут быть воспроизведены на инструментах с нефиксированным строем, но в современной теории музыкальной гармонии их гармонические (звуковысотные) функции необъяснимы.

Колебательные движения. Восприятие звуковых колебаний

Математические строи

Принцип минимизации

Универсальный музыкальный строй

Образование неустойчивости в аккордах

Развитие музыкального мышления у учащихся младших классов в условиях музыкальной школы

Развитие музыкально-сенсорных способностей у детей старшего дошкольного возраста средствами музыкально-дидактических пособий и игр

История развития музыкальной культуры Хакасии (ее взаимодействие и взаимообогащение с русской музыкальной культурой)

Влияние музыкальных и художественных символов на восприятие художественного (музыкального) произведения

Восприятие музыкального произведения в процессе выстраивания личностного значения символов

Когнитивное и личностное развитие старших подростков музыкальных школ

Методы позиционирования и сжатия звука

Музыкальные способности и методы их развития

Эстетические искания Б.В. Асафьева и его труд "Музыкальная форма как процесс"

Формирование музыкально- ритмической способности у учащихся (фортепиано)

Музыкальное воспитание школьников в детском оздоровительном лагере: проблемы и перспективы

Влияние фольклора на развитие музыкальных эмоций детей младшего школьного возраста

Музыкально-информационное поле в эволюционных процессах искусства

Развитие полифонических музыкальных способностей у учащихся младших классов общеобразовательной школы