| Скачать .docx |
Реферат: Учебное пособие: Методические указания по выполнению лабораторных работ для студентов высших учебных заведений по специальности 230101. 65 «Вычислительные машины, системы, комплексы и сети»
Калининградский Государственный Технический Университет
СХЕМОТЕХНИКА ЭВМ.
Методические указания по выполнению лабораторных работ для
студентов высших учебных заведений по специальности
230101.65 «Вычислительные машины, системы, комплексы и сети»
Калининград
Издательство КГТУ
2005
Базовые логические элементы. Реализация простейших логических функций.
Цель работы: изучение основных характеристик интегральных микросхем транзисторно-транзисторной логики; обучение навыкам проектирования и синтеза простейших комбинационных схем.
Литература: /1/, с. 6-25; /2/, с. 65-78; /3/, с. 87-118; /4/, с. 18-28; /7/, с. 542-552.
Приборы и оборудование: лабораторный стенд УМ11.
1.1 Общая часть.
1.1.1 Представление информации физическими сигналами.
Числовые данные и машинные команды представлены в ЭВМ в двоичной системе счисления. Физическими аналогами знаков 0 и 1 двоичного алфавита служат сигналы, способные принимать два хорошо различимых значения, например, напряжения (потенциал) высокого и низкого уровня, отсутствие или наличие электрического импульса в определённый момент времени, противоположные по знаку значения напряжённости магнитного поля и т.п.
В цифровых вычислительных устройствах обычно применяют два первых способа физического представления информации, в соответствии с чем, схемы цифровых устройств принято делить на потенциальные, импульсные и импульсно-потенциальные.
Потенциальный сигнал присутствует в определённой точке схемы в течение всего машинного такта и характеризуется величиной верхнего и нижнего уровня напряжения U1 и U0 .
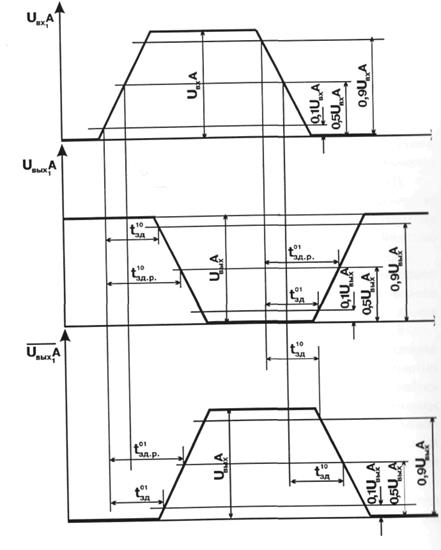
Наличие фронта и спада у потенциального сигнала связано с процессом перехода от нижнего к верхнему и от верхнего к нижнему уровню. Длительность этих процессов обозначается соответственно t01 и t10 (рис. 1.1), причём моменты перехода определяются тактовыми сигналами.
Импульсный сигнал, помимо перечисленных выше параметров, определяется также моментом своего появления и длительностью, не зависящей в общем случае от длительности машинного такта (рис. 1.1).
В транзисторной схемотехнике прошлых лет наибольшее распространение получили импульсные и импульсно-потенциальные системы элементов. Внедрение в аппаратуру серий ИС с потенциальными логическими элементами вытеснило другие цифровые структуры. Новые разработки, тем не менее, показали возможность очередного этапа развития импульсно-потенциальных систем на базе интегральных разностных преобразователей (РП). Такие РП формируют импульсные сигналы при заранее определённых видах переключений входных булевых переменных. Длительность выходного импульса синхронных РП определяется параметрами их компонентов, обеспечивающих задержку прохождения сигналов. В синхронных РП в качестве элемента задержки используются D-триггеры или регистры сдвига, поэтому длительность выходного импульса определяется периодом тактовых сигналов.
![]()

1.1.2 Системы логических элементов. Основные характеристики.
Системой (серией) логических элементов ЭВМ называется предназначенный для построения цифровых устройств функционально полный набор логических элементов, объединяемый общими электрическими, конструктивными и технологическими параметрами, использующие способ представления информации и одинаковый тип межэлементных связей. Система элементов включает элементы для выполнения логических операций, а также усиления, восстановления и формирования стандартной формы сигналов.
Основными параметрами систем логических элементов являются (табл. 1.1):
1. Напряжения питания и логических уровней. Система элементов характеризуется количеством используемых питающих напряжений и их номинальными значениями.
Для логических уровней указываются их полярность и величина. Если не оговорено особо, то логическому нулю соответствует низкий уровень напряжения, а логической единице - высокий (положительная логика).
2. Коэффициент разветвления по выходу (нагрузочная способность К раз) характеризует количество входов аналогичных элементов, которое может быть подключено к выходу логического ключа.
3. Помехоустойчивость. Помехой называется нежелательное электрическое воздействие (например, пульсации напряжения питания, действия паразитных ёмкостей) на логический элемент, которое может привести к искажению преобразуемых или хранимых данных. Помехоустойчивость есть способность элемента правильно функционировать при наличии помех, она определяется максимально допустимым напряжением помехи, при котором не происходит сбоя в его работе.
4. Быстродействие логических элементов является одним из важнейших параметров и характеризуется средним временем задержки распространения сигнала
 (1.1)
(1.1)
Время задержки распространения при включении t01 зд.р. , и выключении t10 зд.р. измеряют как интервал между уровнем 0,5UвхА входного сигнала и уровнем 0,5UвыхА выходного сигнала (рис. 1.2)
|
5. Потребляемая мощность также является немаловажным фактором, поскольку ее увеличение повышает затраты на создание и эксплуатацию цифровых устройств, а снижение уменьшает быстродействие и помехоустойчивость. В зависимости от типа компонентов наиболее широко распространённые серии элементов характеризуются следующими усреднёнными параметрами:
| Таблица 1.1 |
||||||||
| Тип-серия |
ТТЛ |
ДТЛ |
ЭСЛ |
кМОП |
n-МОП |
p-МОП |
||
| Характеристика |
155 |
158 |
131 |
511 |
500 |
176 |
172 |
108 |
| 1. Напряжение питания Напряжение лог. 0 Напряжение лог. 1 |
+5 0,4 2,4 |
+5 0,4 2,4 |
+5 0,4 2,5 |
+15 1,5 12 |
-5,2 -1,63 -0,98 |
+9,0 0,3 8,2 |
-27 -2,0 7,5 |
-27 0,85 -9,5 |
| 2. Коэффициент разветвления |
10 |
10 |
10 |
25 |
- |
100 |
15 |
10 |
| 3. Время задержки распространения, нс |
15 |
15 |
10 |
300 |
2,9 |
200 |
600 |
6000 |
| 4. Потребляемая мощность на элемент, мВт |
24 |
4,85 |
50 |
187 |
35 |
0,001 |
- |
100 |
1.1.3 Рекомендации по применению интегральных микросхем серии К155.
1.1.3.1 Подключение неиспользованных входов
Для обеспечения максимального быстродействия и помехоустойчивости неиспользуемые входы должны находиться под постоянным потенциалом. Это позволяет исключить перезарядку ёмкости разомкнутого эмиттера входного транзистора относительно выводов схемы, которая увеличивает задержку сигнала. Существует ряд методов создания данного потенциала. Напряжение питания, ограниченное до значения 4,5 В, позволяет подключать неиспользуемые входы непосредственно к источнику питания.
Если напряжение 4,5 В отсутствует, то возможно подключение до 20 неиспользуемых входов через резистор сопротивлением 1кОм к источнику питания +5 В. Неиспользуемые входы можно соединить с используемым, если логическая функция при этом не претерпит изменений и не будет превышена нагрузочная способность при входном напряжении, соответствующем уровню логической единицы.
Неиспользуемые входы могут быть подключены к выходу неиспользуемой инвертирующей микросхемы, на вход которой подаётся напряжение логического нуля. При необходимости на отдельные неиспользуемые входы микросхем серии К155 подаётся напряжение логического нуля, что определяется таблицей истинности соответствующей микросхемы.
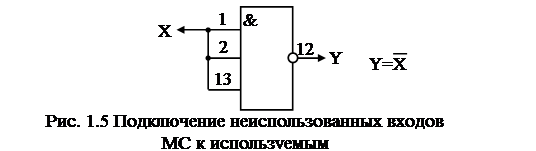
Рассмотрим возможность применения данных способов подключения неиспользуемых входов для получения инвертора на основе микросхемы К155 ЛА4 (3 элемента «ЗИ-НЕ») (рис. 1.3-1.5).


1.1.3.2 Допустимые значения фронта спада сигнала
Для микросхем серии К155 длительность фронта не должна превышать 150 нс (для ИС 155 ЛА8 длительность фронта и спада критична).
1.1.3.3 Обеспечение коэффициентов разветвления
Для обеспечения работоспособности логических микросхем друг от друга при условии сохранения их параметров, оговоренных в ТУ, необходимо выполнять следующие требования:
- выходные напряжения микросхем-генераторов в открытом и закрытом состояниях должны соответствовать входным напряжениям закрытого и открытого состояния микросхемы - нагрузки с учётом величины напряжения помехи,
- значение суммарных токов всех микросхем-нагрузок, подключённых к выходу микросхемы-генератора, не должно превышать значений выходных токов микросхемы-генератора в открытом и закрытом состояниях,
- значение суммарных ёмкостей входов микросхем-нагрузок, при которых регламентируются временные параметры, не превышает 15 пФ. При необходимости суммарная ёмкость нагрузки ИС-генератора с учётом ёмкости монтажа может достигать максимальной ёмкости нагрузки 200 пФ, но динамические параметры при этом не регламентируются.
Примечание. При объединении нескольких входов одного логического элемента, принадлежащих одному многоэмиттерному транзистору, ток I0 вх остаётся неизменным, ток I1 вх увеличивается пропорционально числу объединяемых входов.
1.1.3.4 Нумерация выводов микросхем
Микросхемы 155-й серии, применяемые в данном лабораторном практикуме, могут иметь 14 или 16 выводов. Нумерация выводов показана на рис. 1.6.

Устройство, преобразующее дискретную информацию, в общем случае имеет n-входов и k-выходов, на которые подаются и с которых снимаются электрические сигналы. Каждый из них представляет собой некоторый символ (букву) входного и выходного алфавита. Устройства, в которых совокупность выходных сигналов (выходное слово Y) в некоторый момент времени t, однозначно определяется входными сигналами (входным словом X), поступившими на входы в тот же момент времени, называются комбинационными схемами. В них результат обработки информации зависит только от комбинации входных сигналов и вырабатывается сразу при подаче входной информации.
Закон функционирования комбинационной схемы (КС) определён, если задано соответствие между словами ее входного и выходного алфавитов, что может быть осуществлено либо в виде таблицы, либо в аналитической форме, с использованием булевых функций. Таким образом, комбинационная схема, выполняющая соответствующее некоторой булевой функции преобразование информации, является её техническим аналогом. КС, реализующая элементарную логическую операцию, носит название логического элемента, причём число его входов соответствует числу аргументов воспроизводимой им булевой функции.
В состав элементов ТТЛ 155-й серии входит ряд элементов малой степени интеграции, выполняющих элементарные логические операции.
Базовым элементом, т.е. таким, посредством которого могут быть реализованы все остальные логические операции, является элемент И-НЕ. Технология производства позволяет число входов данного элемента варьировать от 2 до 8, при этом, в зависимости от данного числа, наименование элемента будет: 2И-НЕ, ЗИ-НЕ, 4И-НЕ, 8И-НЕ. Элементы с числом входов 5, 6, 7 - не изготавливаются. Схема базового элемента показана на рис. 1.7.
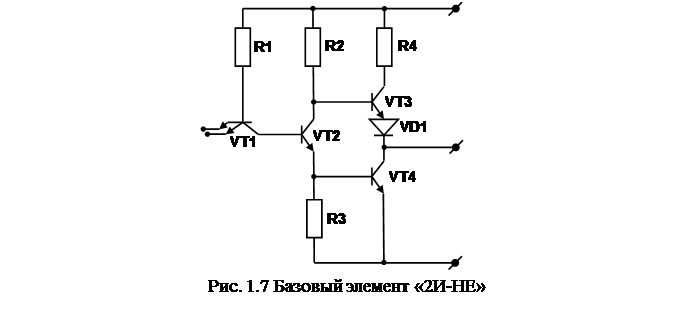
Основной его особенностью является использование многоэмиттерного транзистора, специфичного для интегрального исполнения логических элементов. При подаче на все его эмиттеры, выполняющие роль входов логического элемента, сигнала высокого уровня, ток коллектора смещается в прямом направлении и возникает ток базы транзистора VT2 . За счёт падения напряжений на резисторах R2 и R3 транзистор VT3 закрывается, VT4 - открыт, при этом напряжение на выходе не превышает 0,4 В. При подаче сигнала низкого уровня хотя бы на один вход - картина противоположная: транзисторы VT2 и VT4 закрываются, а VT3 - открыт. На выходе элемента устанавливается потенциал более 2,4В. Выходной каскад подобного вида иногда называется столбовым. Некоторым недостатком подобного принципа построения выходного каскада является невозможность создания "монтажной функции" путём соединения выходов определённых элементов. Указанное ограничение снимается при использовании микросхем с "открытым коллектором" (рис. 1.8).
![]()

Отсутствие транзистора, сходного по функции с VT3 согласно рис. 1.7, компенсируется наличием нагрузочного резистора Rн , за счёт которого при закрытом транзисторе VT3 на входах элементов, подключённых к данному, устанавливается единичный потенциал. Подключение к точке А выходов однотипных элементов, транзисторы VT3 которых закрыты, не изменяет состояние. Если же хотя бы один из указанных транзисторов открыт, в точке А устанавливается низкий потенциал.
Очевидно, что таблица истинности для данного типа микросхем будет включать одну строку, соответствующую случаю, когда на все входы поданы логические единицы, с нулём в графе выхода. В остальных 2N -1 случаях (где N - число входов) на выходе будет сохраняться высокий уровень.
1.2 Порядок выполнения работы
1. Ознакомиться с установкой УМ11. Разобраться с назначением всех гнёзд, имеющихся на наборном поле установки.
2. Экспериментальным путём получить таблицы истинности для следующих элементов:
2-И-НЕ,
3-И-НЕ,
4-И-НЕ,
2И-2ИЛИ-НЕ.
В отчёте для каждого элемента должно быть приведено его название, математическое представление реализуемой функции, графическое обозначение и таблица истинности.
3. Построить на основе элементов "2-И-НЕ" схему, реализующую функцию элемента "НЕ". Привести 2 различные схемы, их математические модели и графическое изображение.
4. Построить на основе элементов "2-И-НЕ" схему, реализующую функцию элемента "ИЛИ". Привести математическое описание работы схемы и её графическое изображение.
5. Построить на основе элементов "2-И-НЕ" схему, реализующую функцию элемента "И". Привести математическое описание работы схемы и её графическое изображение.
6. Построить на основе элементов "2-И-НЕ" схему, реализующую функцию, указанную преподавателем.
7. Определить свой вариант переключательной функции. Для этого необходимо номер варианта перевести в двоичную систему счисления и записать шесть его младших разрядов в виде слова α6 α5 α4 α3 α2 α1. Определив значение αi, записать их в табл. 1.2.
Например, если номер варианта 19 (010011), то α6=0, α5=1, α4=0, α3=0, α2=1, α1=1.
Для заданной функции и ее отрицания найти МДНФ. Представить функцию в форме И-НЕ.
Построить указанную схему, учитывая, что на входы могут подаваться с помощью тумблеров прямые и инверсные значения переменных.
| Таблица 1.2 |
||||
| X4 |
X3 |
X2 |
X1 |
y |
| 0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
α1 |
| 0 |
0 |
1 |
1 |
1 |
| 0 |
1 |
0 |
0 |
α2 |
| 0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
1 |
0 |
0 |
| 0 |
1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
α3 |
| 1 |
0 |
0 |
1 |
α4 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
| 1 |
1 |
0 |
0 |
0 |
| 1 |
1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
0 |
α5 |
| 1 |
1 |
1 |
1 |
α6 |
1.3 Вопросы для самостоятельной работы
1. Системы логических элементов (серии, комплексы), основные параметры системы логических элементов, значения основных параметров для логических элементов серии 155.
2. Подключение неиспользуемых входов элементов, работоспособность элемента с "висящими в воздухе" выводами.
3. Базовый элемент 155-й серии, реализация элемента "НЕ", "ИЛИ" многовходовых "И" и "ИЛИ", "ИСКЛЮЧАЮЩЕЕ ИЛИ".
4 Комбинационная схема, закон функционирования, способы его задания.
5. Управляемый инвертор.
6. Схемы с "открытым коллектором", "монтажное ИЛИ", возможность соединения логических элементов, минимальные и максимальные величины нагрузочных резисторов для элементов с открытым коллектором.
7. Система обозначения микросхем.
Комбинационные преобразователи логических сигналов. Дешифраторы.
Цели работы: изучение принципов построения дешифраторов для управления индикацией; синтез преобразователей кодов.
Литература: /4/, с. 38-41, 104-117, /6/, с. 124-186, /7/, с. 201 -211, /8/, с. 387-393.
2.1 Общая часть
Некоторые функции нескольких переменных встречаются достаточно часто, поэтому они нашли свое отражение в системе логических элементов 155-й серии. К числу подобных элементов можно отнести прежде всего дешифраторы-схемы, способные преобразовать логическую информацию из одного цифрового кода в другой. Двумя наиболее общими типами подобных дешифраторов являются дешифраторы типа "один-из-N" и семисегментные дешифраторы.
2.1.1 Дешифраторы "один-из-N"
В данном типе дешифраторов в каждый момент времени возможно наличие сигнала лишь на одном из выходов, причём номер выхода определяется двоичной комбинацией на соответствующих входах. Очевидно, что наиболее просто подобный дешифратор синтезирован с помощью схем совпадения, каждая из которых "настроена" на индивидуальную и единственную кодовую комбинацию.
2.1.2 Семисегментные дешифраторы
Более сложными по структуре являются устройства, осуществляющие процесс преобразования кодовых комбинаций с произвольным в общем случае числом нулей и единиц как на входе, так и на выходе. Синтез преобразователей подобного вида представляет весьма сложную задачу и распадается на два этапа:
1. Определение связей входов и выходов схем и генерация структуры системы в заданном классе базовых элементов, которая будет выполнять требуемые функции системы.
2. Решение задачи минимизации, т.е. выбор структуры системы, состоящей из минимального числа базовых элементов.
Минимизация особенно важна, если цифровая система производится серийно, когда желательно обеспечить использование минимального количества элементов. Минимизация числа элементов уменьшает стоимость и повышает быстродействие и надёжность разрабатываемой системы.
Минимизация может оказаться очень трудоёмкой процедурой, особенно при проектировании сложной системы, в связи с чем решение задачи синтеза проводится, как правило, на ЭВМ с помощью специального математического обеспечения.
Решение указанной задачи вручную проводится с учётом того, что подобные преобразователи можно представить в виде композиции стандартного дешифратора "один-из-N" (где N соответствует числу входов преобразователя), входы которого в соответствии с определённым законом подключены к выходам дешифратора.



Примеры преобразователей, выполняющих роль дешифраторов для семисегментных индикаторов, построенных на рассмотренных принципах, приведены на рис. 2.1 а,б.
Как показано на рис. 2.2, каждый из семи сегментов индикатора обозначается буквой латинского алфавита от а до g включительно. Любая цифра от 0 до 9 может быть высвечена в символьной форме на этом индикаторе, для чего необходимо включить соответствующие сегменты. Например, цифра 7 высвечивается, когда горят сегменты а, в, с.
| Таблица 2.1 |
||||||||
| 8 |
4 |
2 |
1 |
7 |
3 |
2 |
1 |
|
| X4 |
X3 |
X2 |
X1 |
Y |
X4 |
X3 |
X2 |
X1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
2 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
1 |
3 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
4 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
1 |
5 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
0 |
6 |
0 |
1 |
1 |
1 |
| 0 |
1 |
1 |
1 |
7 |
1 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
8 |
1 |
0 |
0 |
1 |
| 1 |
0 |
0 |
1 |
9 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
10 |
1 |
1 |
0 |
0 |
| 1 |
0 |
1 |
1 |
11 |
1 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
12 |
1 |
1 |
1 |
0 |
|
|
1 |
0 |
1 |
13 |
1 |
1 |
1 |
1 |
| Дешифратор |
Шифратор |
|||||||

| Таблица 2.2 |
||||||||
| 8 |
4 |
2 |
1 |
6 |
3 |
2 |
1 |
|
| X4 |
X3 |
X2 |
X1 |
Y |
X4 |
X3 |
X2 |
X1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
2 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
1 |
3 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
4 |
0 |
1 |
0 |
1 |
| 0 |
1 |
0 |
1 |
5 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
0 |
6 |
1 |
0 |
0 |
0 |
| 0 |
1 |
1 |
1 |
7 |
1 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
8 |
1 |
0 |
1 |
0 |
| 1 |
0 |
0 |
1 |
9 |
1 |
1 |
0 |
0 |
| 1 |
0 |
1 |
0 |
10 |
1 |
1 |
0 |
1 |
| 1 |
0 |
1 |
1 |
11 |
1 |
1 |
1 |
0 |
| 1 |
1 |
0 |
0 |
12 |
1 |
1 |
1 |
1 |

2.1.2 Задание на лабораторную работу
1. Построить и собрать на стенде схему двоично-десятичного дешифратора.
2. Заполнить перекодирующую таблицу 8421-ХХХХ, где ХХХХ-код.
3. Синтезировать преобразователь кодов из элементов, имеющихся на стенде.
4. Заполнить перекодирующую таблицу 8421-сегментный код.
5. Оформить отчёт, который должен содержать:
- схему двоично-десятичного шифратора,
- перекодирующую таблицу 8421-ХХХХ,
- схему преобразователи кодов в соответствии с вариантом, указанным в табл. 2.3,
| Таблица 2.3 |
|||||
| Входной код 8421 |
Вариант |
||||
| 1 |
2 |
3 |
4 |
5 |
|
| Выходной код |
2421 |
5221 |
Джонсона |
Грея |
8421+3 |
- рисунок семисегментного индикатора с обозначением сегментов,
- перекодирующую таблицу 8421-сегментный код, взаимное соответствие различных цифр различных кодов указано в табл. 2.4.
| Таблица 2.4 |
||||||
| Десятичная цифра |
Коды |
|||||
| 8421 |
2421 |
5221 |
Джонсона |
Грея |
8421+3 |
|
| 0 |
0000 |
0000 |
0000 |
00000 |
0010 |
0011 |
| 1 |
0001 |
0001 |
0001 |
00001 |
0110 |
0100 |
| 2 |
0010 |
0010 |
0010 |
00011 |
0111 |
0101 |
| 3 |
0011 |
0011 |
0011 |
00111 |
0101 |
0110 |
| 4 |
0100 |
0100 |
0110 |
01111 |
0100 |
0111 |
| 5 |
0101 |
1011 |
1000 |
11111 |
1100 |
1000 |
| 6 |
0110 |
1100 |
1001 |
11110 |
1101 |
1001 |
| 7 |
0111 |
1101 |
1010 |
11100 |
1111 |
1010 |
| 8 |
1000 |
1110 |
1011 |
11000 |
1110 |
1011 |
| 9 |
1001 |
1111 |
1110 |
10000 |
1010 |
1100 |
2.1.3 Вопросы для самостоятельной работы
1. Шифратор: назначение, принципы построения.
2. Дешифратор "один из N": назначение, принципы построения, работа микросхем К155 ИД1, К155 ИДЗ, К155 ИД4.
3. Семисегментный код, представление информации на семисегментных индикаторах.
4. Семисегментный дешифратор К155 ИД1, работа схемы.
5. Преобразователи кода на основе запоминающих устройств (ПЗУ).
6. Условные графические обозначения дешифраторов (УГО). Примеры схемных решений приведены на рис. 2.3; 2.4 и табл. 2.1; 2.2.
Последовательностные схемы. Триггеры, регистры.
Цель работы: изучение принципов построения интегральных триггеров; приобретение навыка синтеза триггеров, регистров и сдвигающих регистров.
Литература: /4/, с. 90-104; /6/, с. 124-186; /8/, с. 305-315.
3.1 Общая часть
Характерной особенностью последовательностных (многотактных) структур является зависимость состояния выходов не только от значений входных булевых переменных в данный момент времени, но и от внутренних состояний, определяемых тем, какие условия (последовательности) имели место в предшествующие моменты времени (номер такта).
Последовательностные структуры (логические автоматы с памятью), к числу которых относятся регистры, счётчики и другие системы цифровых устройств, обычно строятся на основе триггерных цепей с тем или иным законом функционирования.
Триггер является элементом, который может неограниченно долго находиться в одном из двух устойчивых состояний. Состояние триггера распознаётся по его выходному сигналу.
Логика работы определяется количеством входов и особенностями схемы. В зависимости от влияния, оказываемого на состояние триггера, его входы имеют следующие обозначения:
S - вход раздельной установки триггера в 1;
R - вход раздельной установки триггера в 0;
Т - счётный вход;
D - вход задержки;
J - вход для синхронизируемой установки в 1;
К - вход для синхронизируемой установки в 0;
С - вход синхронизации;
Y - вход разрешения.
Входы и выходы триггеров так же, как и других логических элементов, могут быть прямыми и инверсными, т.е. наличие сигнала определяется высоким или низким уровнем напряжений соответственно.
Часто в структуре триггера присутствуют элементы, реализующие функцию разностного преобразования. В таких случаях можно обеспечить переключение триггера по заранее определённому изменению входных переменных (т.е. по переходу из логического "О" в "1" или наоборот). С наибольшей эффективностью разностные преобразователи используются в цепях синхронизации. Синхровходы такого рода носят название динамических.
Триггер типа D имеет расширенную функциональную схему, представленную на рис. 3.1.

Триггер может работать в двух режимах: синхронном, при котором управление производится по входу D, и асинхронном - по R-S-входам.
Таблица переходов триггера в зависимости от сигнала на D-входе и синхроимпульса положительной полярности на входе С представлена в табл. 3.1.
| табл. 3.1 |
||
| C |
D |
Qt+1 |
| 0 |
0 |
Qt |
| 0 |
1 |
Qt |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
Уровни сигналов для представления 0 и 1 те же, что и для логических элементов "И-НЕ", "И-ИЛИ-НЕ".
Триггер переключается по переднему фронту сигнала синхронизации. Для организации счётного режима необходимо инверсный выход триггера подсоединить к входу D (см. пунктир на рис. 3.1).
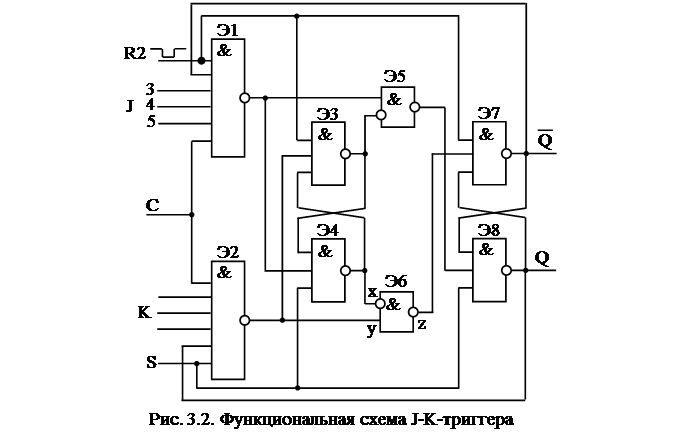
Триггер типа J-K имеет функциональную схему, представленную на рис. 3.2.
Триггер может работать в синхронном и асинхронном режимах. Таблица переходов J-K триггера приведена в таблице 3.2. J-K триггер по своей структуре является двухступенчатым. По переднему фронту положительного синхроимпульса переключается первая триггерная ступень, построенная на элементах Э3, Э4; по заднему фронту информация с первой ступени передаётся на вторую, оконечную триггерную ступень Э7, Э8. Можно сказать, что J-K триггер в синхронном режиме работает с задержкой на длительность синхроимпульса. По асинхронным R-S входам J-K триггер управляется аналогично асинхронным входам триггера D. При каскадировании однотипных триггеров получаются регистры, предназначенные для запоминания слов, а также для выполнения над словами некоторых логических преобразований.
| таблица 3.2 |
|||
| C |
J |
K |
Qt+1 |
| 0 |
0 |
0 |
Qt |
| 0 |
0 |
1 |
Qt |
| 0 |
1 |
0 |
Qt |
| 0 |
1 |
1 |
Qt |
| 1 |
0 |
0 |
Qt |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
ù Qt |
К числу операций, которые способны выполнять типичные регистры, относятся следующие:
- установка регистра в "0" ("сброс"),
- приём слова из другого устройства (регистра, сумматора и т.п.),
- передача слова в другой регистр,
- сдвиг слова вправо или влево на требуемое число разрядов; преобразование, таким образом, параллельного кода слова в последовательный и наоборот.
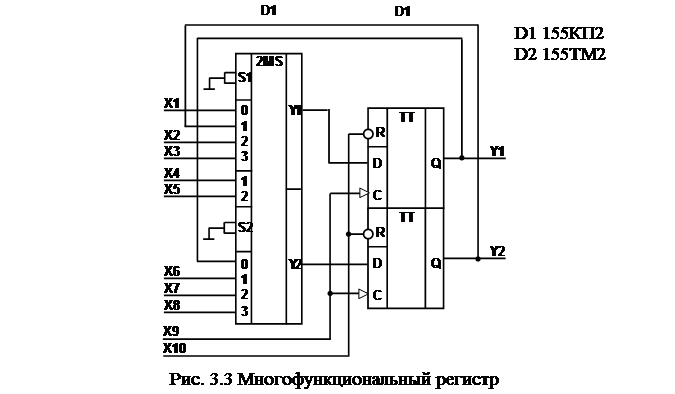
Поскольку один регистр выполняет чаще всего несколько из перечисленных операций, помимо триггеров в его состав входят вспомогательные комбинационные схемы, служащие, как правило, целям коммутации (подключающие, например, информационные входы триггеров к тем или иным источникам сигнала; позволяющие осуществлять управление процессом записи от того или иного синхросигнала).
Пример построения многофункционального регистра, реализующего вышеперечисленные операции, приведён на рис. 3.3. Синхровходы триггеров, как показано на схеме, являются динамическими.
Операции сдвига выполняются на регистрах сдвига. Регистр сдвига представляет собой схему на триггерах, соединения между которыми, называемые цепями сдвига, обеспечивают передачу двоичной информации от одних триггеров регистра к другим.
Регистр сдвига, в котором для хранения информации используется k триггеров, называется n-разрядным регистром сдвига.
По способу записи информации различают:
1) параллельные регистры, в которых запись числа осуществляется во все разряды одновременно параллельным кодом;
2) последовательные регистры с записью кода числа путём его последовательного сдвига тактирующими сигналами, начиная с младшего или старшего разряда;
3) параллельно-последовательные регистры, которые имеют входы для последовательной и параллельной записи кода.
По количеству входных каналов регистры подразделяются на:
1) парафазные с записью информации по двум каналам: прямому и инверсному;
2) однофазные с записью по одному каналу.
В зависимости от способа тактирования различают регистры однотактного и многотактного действия.
Одной из основных характеристик сдвигающего регистра является быстродействие, которое определяется временем сдвига на один или несколько разрядов одновременно. Время сдвига равно промежутку времени между моментом поступления импульса на шину сдвига и моментом окончания переходного процесса в схеме, вызванного этим импульсом.
3.2 Задание на лабораторную работу
1. Изучить и собрать асинхронный RS-триггер на элементах «2-И-НЕ» (рис. 3.4).
2. Преобразовать собранный триггер в синхронизируемый (рис. 3.5).
3. Построить двухтактный RS-триггер на элементах «2-И-НЕ» (рис. 3.6).
4. Ознакомиться с универсальным JK-триггером 155ТВ1 (рис. 3.7). На его основе получить RS-, D-,Т-триггеры (рис. 3.8-3.10).
5. Ознакомиться с другими триггерами 155-й серии, в частности ТМ2, ТМ5, ТМ7, ТМ8.
6. Построить схему, реализующую межрегистровую передачу двоичных чисел в единичном коде (рис.3.11).
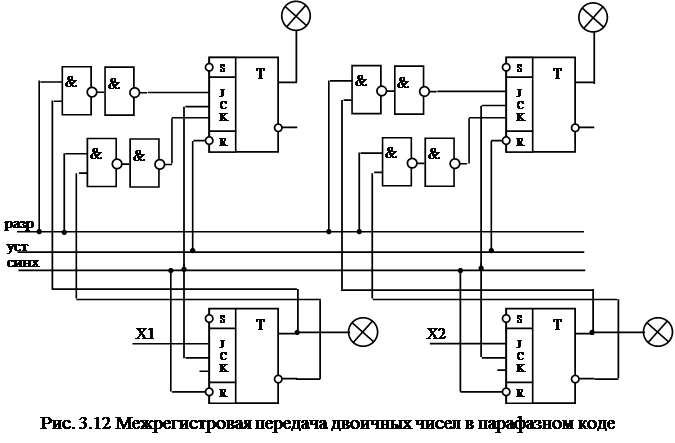
7. Построить схему, реализующую межрегистровую передачу двоичных чисел в парафазном коде (рис.3.12).
8. Построить схему сдвигающего регистра.
9. Оформить отчёт, который должен содержать схемы всех рассмотренных триггеров, их условные графические обозначения и соответствующие таблицы переходов, а также УГО микросхем 155 ТВ1, ТМ2, ТМ5, ТМ7, ТМ8.
3.3 Вопросы для самостоятельной работы
1. Взаимозаменяемы ли триггеры с динамическими синхровходами и фиксаторы?
2. Каким образом следует включать фиксаторы ТМ7, чтобы они по своим возможностям полностью соответствовали двухступенчатым триггерам ТМ8?
3. Что необходимо предпринять, чтобы триггер, срабатывающий по переднему фронту синхросигнала, стал срабатывать по его спаду?
4. Чем определяется быстродействие триггера?
5. Опишите работу триггеров К155ТВ1, ТМ2, ТМ7, ТМ8.
Опишите работу сдвигающего регистра К155 ИР1. Примеры схемных решений приведены на рис. 3.5-3.10.
| R |
S |
Qt+1 |
ùQt+1 |
| 0 |
0 |
- |
- |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 1 |
1 |
Qt |
Qt |

Рис. 3.4 Асинхронный RS-триггер
| C |
S |
R |
Qt+1 |
ùQt+1 |
| 1 |
0 |
0 |
Qt |
Qt |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
1 |
0 |
1 |
0 |
| 1 |
1 |
1 |
1 |
1 |
| 0 |
0 |
0 |
Qt |
ùQt |
| 0 |
0 |
1 |
Qt |
ùQt |
| 0 |
1 |
0 |
Qt |
ùQt |
| 0 |
1 |
1 |
Qt |
ùQt |
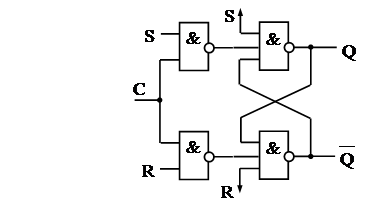
Рис. 3.5 Синхронный RS-триггер
 |
| S |
R |
C |
Qt+1 |
| 0 |
0 |
0 |
Qt |
| 0 |
1 |
0 |
Qt |
| 1 |
0 |
0 |
Qt |
| 1 |
1 |
0 |
Qt |
| 0 |
0 |
1 |
Qt |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
1 |
1 |
| 1 |
1 |
1 |
- |
| C |
J |
K |
Qt+1 |
| 0 |
0 |
0 |
Qt |
| 0 |
0 |
1 |
Qt |
| 0 |
1 |
0 |
Qt |
| 0 |
1 |
1 |
Qt |
| 1 |
0 |
0 |
Qt |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
ù Qt |

Рис. 3.7 JK-триггер
| C |
S |
R |
Qt+1 |
| 0 |
0 |
0 |
Qt |
| 0 |
0 |
1 |
Qt |
| 0 |
1 |
0 |
Qt |
| 0 |
1 |
1 |
Qt |
| 1 |
0 |
0 |
Qt |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
- |
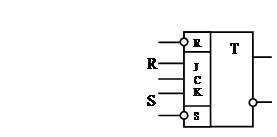
Рис. 3.8 RS-триггер
| C |
D |
Qt+1 |
| 0 |
0 |
Qt |
| 0 |
1 |
Qt |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
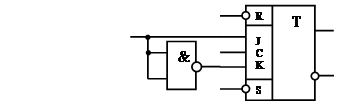
Рис. 3.9 D-триггер
| C |
T |
Qt+1 |
| 1 |
0 |
Qt |
| 1 |
1 |
ùQt |
| 0 |
0 |
Qt |
| 0 |
1 |
Qt |
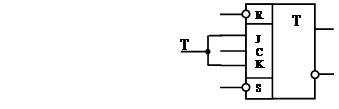
Рис. 3.10 T-триггер

Элементы операционных устройств. Мультиплексоры. Сумматоры
Цель работы: изучение принципов построения мультиплексоров и сумматоров; синтез блоков операционных устройств.
4.1 Общая часть
Процессоры любых ЭВМ включают в себя операционное и управляющее устройства. Операционное устройство предназначено для обработки операндов и команд, управляющее - для управления вычислительным процессом, состоящим в выборке команд из памяти, дешифрации и преобразовании их в управляющие и синхронизирующие сигналы, координирующие работу всех узлов ЭВМ.
В операционное устройство входят следующие узлы (рис. 4.1):
- операционные блоки, предназначенные для непосредственного исполнения микроопераций преобразования информации, поступающей на их входы;
- группы регистров, предназначенных для приёма и хранения информации, над которой производятся действия в операционных блоках;

Рис. 4.1 Структура типового операционного устройства
- блок формирования состояний, предназначенный для формирования арифметико-логических условий перехода, используемых в микропрограммном устройстве управления для изменения последовательности выборки микрокоманд.
Как видно из рисунка 4.1, важное место в структуре операционного устройства занимают мультиплексоры - узлы, предназначенные для коммутации логических сигналов, поступающих на АЛУ с других блоков.
Распространено использование мультиплексоров для реализации операций арифметического и логического сдвигов.
4.2 Мультиплексоры
Мультиплексор - устройство, сигнал на выходе которого определяется сигналом на одном из информационных входов заданным адресным кодом.
Наглядным примером мультиплексора является элемент К155 ЛРЗ. Очевидно, что адресный код в данном случае должен быть вида "один-из-четырёх" (рис. 4.2).


Рис. 4.3 Схема мультиплексора
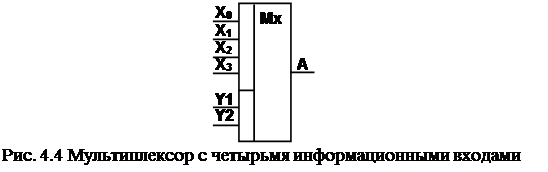
4.3 Сумматоры
Основным узлом АЛУ, входящего в состав операционного устройства, является сумматор - логический элемент, реализующий алгебраическое сложение двух чисел.
При сложении двух чисел независимо от системы счисления в каждом разряде производится сложение трёх цифр: цифры данного разряда первого слагаемого, цифры данного разряда второго слагаемого и цифры (1 или 0) переноса из соседнего младшего разряда. В результате сложения для каждого разряда получаются цифры суммы для этого разряда и цифры (1 или 0) переноса в следующий старший разряд.
Рассмотрим операцию сложения для одного какого-нибудь разряда складываемых чисел в двоичной системе счисления. В зависимости от значений складываемых цифр и наличия или отсутствия единицы переноса из предыдущего разряда результат сложения будет различным. В табл. 4.1 приведены восемь возможных вариантов, возникающих при сложении двух двоичных чисел.
| Таблица 4.1 |
||||
| Цифра переноса из предыдущего разряда, pi |
Первое слагаемое, Xi |
Второе слагаемое, Yi |
Сумма, Si |
Цифра переноса в старший разряд, pi +1 |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
1 |
По приведённой таблице можно составить булевы функции для описания одноразрядного сумматора - устройства, вырабатывающего на выходе сигналы суммы и переноса из предыдущего разряда.
Преобразуя выражения для цифры суммы цифры переноса с помощью правил булевой алгебры, можно получать различные соотношения для построения схем полных сумматоров на базе различных элементов.
Поскольку на практике приходится суммировать более чем одноразрядные числа, практический интерес представляют способы построения многоразрядных сумматоров.
Наиболее просто можно осуществить построение параллельных сумматоров, число которых равно числу разрядов слагаемых, путём соединения выхода, на котором фиксируется сигнал переноса данного разряда (рис. 4.5).

Рис. 4.5 Одноразрядный сумматор К155ИМ1
В сумматорах этого типа, называемых сумматорами с поразрядным последовательным переносом, перенос распространяется последовательно от разряда к разряду по мере образования цифры суммы в каждом отдельном разряде. При наиболее неблагоприятных условиях для распространения переноса будет иметь место "пробег" единицы переноса через весь сумматор от самого младшего к самому старшему разряду, поэтому время суммирования двух чисел с момента одновременной подачи слагаемых на входы такого сумматора определяется следующей формулой:
t ∑ = ts + n ∙ tp ,
где ts - время формирования сигнала суммы в одном разряде;
tp - время задержки сигнала переноса в одном разряде;
n - число разрядов параллельного сумматора.
Из приведённой формулы видно, что повысить быстродействие можно двумя способами: во-первых, уменьшением времени задержки сигнала переноса в одноразрядном сумматоре; во-вторых, уменьшением влияния числа разрядов на время распространения переноса.
Микросхемы 155ИМ2 и 155ИМЗ представляют собой соответственно двух- и четырёхразрядные сумматоры, построенные на указанных принципах.
Столь широкое использование последовательного переноса с одной инверсией обусловлено простотой с точки зрения построения цепей распространения переноса.
Второй способ реализуется в сумматорах с параллельным и с групповым переносом, причём сумматоры первого вида, в которых сигналы переноса каждого разряда формируются одновременно с помощью специальной комбинационной схемы, почти не находят применения в чистом виде в многоразрядных сумматорах вследствие значительности затрат на построение данной схемы, а используются для построения сумматоров с групповым переносом.
Сумматор с групповым переносом разбивается на несколько групп примерно равной длины. Сигнал переноса, поступающий на вход младшего разряда группы, при наличии условий распространения переноса во всех разрядах данной группы передаётся на вход младшего разряда соседней, более старшей группы.
4.4 Порядок выполнения работы
1. Собрать мультиплексор с четырьмя информационными входами (рис. 4.3-4.4).
2. Составить булевы функции для описания одноразрядного полного сумматора согласно табл. 4.1.
3. Собрать 2-х разрядный комбинационный сумматор.
4. Собрать 2-х разрядный сумматор накапливающего типа.
4.5 Вопросы для самостоятельной работы
Мультиплексор:
1. Назначение, принципы построения.
2. Реализация логических функций на основе мультиплексоров.
3. УГО.
4. Работа микросхем 155КР1, КР2, КР5, КРУ.
5. Каскадирование мультиплексоров.
Сумматор:
1. Назначение, принципы построения.
2. Булевы функции, описывающие работу одноразрядного полного сумматора.
3. Полные и неполные сумматоры.
4. Параллельные и последовательные сумматоры.
5. Последовательный, параллельный и групповой переносы.
6. Быстродействие многоразрядных сумматоров.
7. Работа микросхем 155ИМ1, ИМ2, ИМЗ.
Пример схемного решения 155ИМ1 приведен на рис. 4.5.
Счётчики
Цель работы: изучение принципов построения счётчиков; приобретение навыков синтеза цифровых автоматов.
Литература: /4/, с. 75-90; /8/, с. 324-348; /6/, с. 124-186.
5.1 Общая часть
Счётчиком в цифровой технике называется схема для хранения числа, представляющая собой совокупность триггеров и схем управления ими, позволяющая изменять это число на некоторую константу, а также имеющая, как правило, цепи установки заданной величины, в частности - нуля.
Модулем счётчика (М) называется число разрешённых устойчивых состояний.
Сигналы, поступающие на вход счётчика, называются считаемыми; они могут быть, в зависимости от знака, прибавляемыми или вычитаемыми и иметь обозначение +К и -К соответственно. В тех случаях, когда константа, на которую изменяется состояние счётчика, равна единице, указанные входы имеют обозначения +1 и -1.
Установка счётчика в исходное состояние может производиться либо подачей общего для всех триггеров сигнала (как правило сброс), либо путём установки каждого триггера в отдельности индивидуальным сигналом.
При создании счётчика с модулем М требуется не менее K=log2 M триггеров. Следовательно, двоично-десятичный счётчик должен содержать не менее, чем четыре триггера. Схема двоично-десятичного счётчика в коде 8421 (где 8, 4, 2, 1 - веса двоичных разрядов) приведена на рис. 5.1.
В этой системе кодирования каждая десятичная цифра записывается четырьмя двоичными (табл. 5.1).
Работа этого десятичного счётчика поясняется диаграммой (рис. 5.2).
Данный счётчик является синхронным. Можно представить и асинхронную организацию структуры счётчика, когда на синхронизирующие входы триггеров поступают не считываемые сигналы, а сигналы с входов логических элементов или соседних триггеров. Преимуществом асинхронной организации счётчиков является простота получаемой структуры. Но при проектировании асинхронных двоично-десятичных счётчиков возникают трудности, обусловленные различием во внутренней организации триггеров. Эти различия появляются только при асинхронной работе. Покажем это на примере асинхронного двоично-десятичного счётчика в коде 8421.
На рис. 5.3 приведена схема асинхронного счётчика на синхронных двухступенчатых JK-триггерах. На рис. 5.4 приведён также асинхронный двоично-десятичный счётчик в коде 8421, но с использованием JK-триггеров с динамическим управлением записью. При сравнении схем (см. рис. 5.3 и 5.4) ясно видны отличия в структурах асинхронного счётчика, построенных на основе различных типов JK-триггеров.

Рис. 5.1 Синхронный двоично-десятичный счётчик в коде 8421

Рис. 5.2 Временная диаграмма работы счётчика
| Таблица 5.1 |
|||||
| Номер п/п |
Состояние счётчика |
Состояние битов |
|||
| 4 |
3 |
2 |
1 |
||
| 1 |
0 |
0 |
0 |
0 |
0 |
| 2 |
1 |
0 |
0 |
0 |
1 |
| 3 |
2 |
0 |
0 |
1 |
0 |
| 4 |
3 |
0 |
0 |
1 |
1 |
| 5 |
4 |
0 |
1 |
0 |
0 |
| 6 |
5 |
0 |
1 |
0 |
1 |
| 7 |
6 |
0 |
1 |
1 |
0 |
| 8 |
7 |
0 |
1 |
1 |
1 |
| 9 |
8 |
1 |
0 |
0 |
0 |
| 10 |
9 |
1 |
0 |
0 |
1 |


Структура синхронного счётчика (см. рис. 5.1) останется неизменной, если двухступенчатые JK-триггеры заменить триггерами с динамическим управлением записью. Если для логического проектирования синхронных счётчиков существуют отработанные методы, то для проектирования асинхронно работающих счётчиков таких систематизированных методов нет. Всё осложняется тем, что различия во внутреннем строении триггеров появляются именно при асинхронной работе. Поэтому проектирующий схемы должен иметь совершенно чёткое представление о внутреннем строении используемого им типа триггеров и не ограничиваться таблицей переходов, которая описывает только синхронную работу триггера. Последовательным соединением n счётчиков с модулем М можно получить счётчик с модулем MS .=Mn .
5.2 Синтез синхронных счётчиков
На рис. 5.5 приведена обобщённая схема логической структуры синхронного счётчика. Из этой схемы можно уяснить принцип работы любого синхронного счётчика. Сигналы с выходов триггеров поступают на входы комбинационной схемы, которая преобразует поступившую информацию. Сигналы с выходов комбинационной схемы подают на входы триггеров. Преобразованная информация не воспринимается триггерами до тех пор, пока на синхронизирующие входы не поступит подсчитываемый сигнал V. Информация, находящаяся на входах каждого триггера, так преобразуется комбинационной схемой, чтобы с приходом очередного подсчитываемого сигнала осуществить требуемый переход счётчика из предыдущего состояния в следующее.
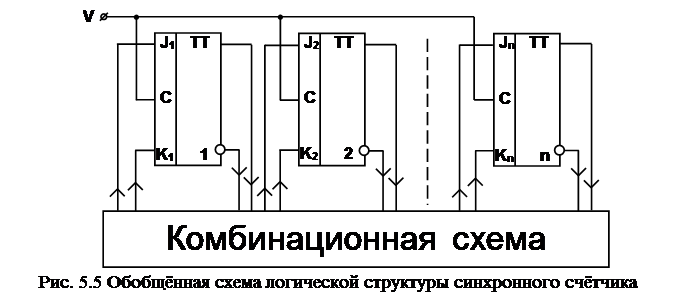
Таким образом, функции возбуждения входов триггера можно записать в виде:
![]() J1i
(t)=f1i
[Q1
(t), Q2
(t), ..., Qn
(t)];
J1i
(t)=f1i
[Q1
(t), Q2
(t), ..., Qn
(t)];
K2i (t)=f2i [Q1 (t), Q2 (t), ..., Qn (t)].
Значения всех переменных в этом выражении определены для одного и того же момента времени t. Поэтому функции возбуждения триггеров являются переключательными функциями, которым соответствуют комбинационные схемы, формирующие входные сигналы для триггеров. Следовательно, если задан тип триггера, то задача логического проектирования схемы счётчика заключается в составлении функции возбуждения каждого триггера и минимизации найденных функций в заданном базисе.
5.3 Пример синтеза синхронного счётчика
Спроектировать двухразрядный двоично-десятичный счётчик с системой кодирования 2421 (2, 4, 2, 1 - веса двоичных разрядов) на JK-триггерах. В этой системе кодирования вместо каждой десятичной цифры записываются четыре двоичные.
Кодированная таблица переходов одного разряда двоично-десятичного счётчика в коде 2421 представлена колонками 1-8 (табл. 5.2). Для составления функций возбуждения каждого триггера десятичного разряда счётчика на JK-триггерах воспользуемся матрицей переходов JK-триггера (рис. 5.6, 5.7).
| Таблица 5.2. Переходы и функции возбуждения счётчика |
|||||||||||||||||
| Деся тичные цифры |
Номер набора |
Значения прямых выходов триггеров |
Время |
||||||||||||||
| Время t |
Время t+1 |
Функции возбуждения триггеров |
|||||||||||||||
| T4 |
T3 |
T2 |
T1 |
||||||||||||||
| Q4 |
Q3 |
Q2 |
Q1 |
Q4 |
Q3 |
Q2 |
Q1 |
J4 |
K4 |
J3 |
K3 |
J2 |
K2 |
J1 |
K1 |
||
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
ai |
0 |
ai |
0 |
ai |
1 |
ai |
| 1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
ai |
0 |
ai |
1 |
ai |
ai |
1 |
| 2 |
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
ai |
0 |
ai |
ai |
0 |
1 |
ai |
| 3 |
3 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
ai |
1 |
ai |
ai |
1 |
ai |
1 |
| 4 |
4 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
ai |
ai |
1 |
1 |
ai |
1 |
ai |
| 5 |
11 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
ai |
0 |
1 |
ai |
ai |
1 |
ai |
1 |
| 6 |
12 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
ai |
0 |
ai |
0 |
0 |
ai |
1 |
ai |
| 7 |
13 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
ai |
0 |
ai |
0 |
1 |
ai |
ai |
1 |
| 8 |
14 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
ai |
0 |
ai |
0 |
ai |
0 |
1 |
ai |
| 9 |
15 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
ai |
1 |
ai |
1 |
ai |
1 |
ai |
1 |
| Время |
t |
t+1 |
|
| J |
K |
Q(t) |
Q(t+1) |
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
| Рис. 5.6. Матрица переходов триггера (составляется по таблице переходов этого триггера) |
|||
| Q(t)→Q(t+1) |
J |
K |
| 0→0 |
0 |
ai |
| 0→1 |
1 |
ai |
| 1→0 |
ai |
1 |
| 1→1 |
ai |
0 |
| Рис. 5.7. Матрица переходов JK-триггера |
||
Рассмотрим первую строку табл. 5.2. Счётчик из состояния Q4 =0, Q3 =0, Q2 =0, Q,=0 должен после поступления подсчитываемого импульса перейти в состояние Q4 =0, Q3 =0, Q2 =0, Q,=1, т.е. для триггеров Т4, ТЗ, Т2 необходимо реализовать переход типа "0-0", а для триггера Т1 - переход типа "0-1". В соответствии с матрицей переходов JK-триггеров в столбцах 9, 11, 13 (табл. 5.2) необходимо записать 0, в столбцах 10, 12, 14, 16 - а, а в столбце 15 - 1. Аналогично записываются остальные строки табл. 5.2.
Составленная таким образом таблица определяет функции возбуждения входов всех триггеров. Аргументы этих функций написаны в колонках 1-4.
Для представления функций возбуждения триггеров в минимальной дизъюнктивной нормальной форме составим диаграммы Вейтча (рис. 5.8). Чтобы облегчить процесс занесения функции возбуждения на диаграмму Вейтча, пронумеруем все двоичные наборы состояний счётчика соответствующими десятичными числами, в этом случае двоичная запись состояния счётчика воспринимается как двоичное число с естественными весами разрядов. При составлении диаграмм (рис. 5.8) неопределённые коэффициенты а i , i в каждой строке следует заносить с индексами, равными десятичному числу двоичного набора. Перед заполнением диаграмм Вейтча составим эталонную диаграмму, в которой обозначим все поля десятичными числами (рис. 5.9). Эти числа соответствуют десятичной записи двоичного набора конституанты единицы.
Из таблицы переходов (см. рис. 5.8) десятичного счётчика в коде 2421 видно, что из 16 возможных комбинаций используются только десять. Остальные шесть являются запрещёнными, при правильной работе счётчика. Это
`Q4Q3Q2Q1∙`Q4Q3Q2`Q1∙`Q4Q3`Q2Q1∙Q4`Q3`Q2Q1∙ Q4`Q3`Q2`Q1∙ Q4`Q3Q2`Q1
Им соответствуют незаполненные поля диаграмм Вейтча.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 5.8 Диаграммы Вейтча функций возбуждения JK-триггера
В некоторых случаях рассмотрение запрещённых комбинаций приводит к существенному упрощению структуры проектируемой схемы, поэтому избыточные комбинации на диаграммах Вейтча обозначены крестиками X.
В остальные клетки диаграмм Вейтча заносятся биты (0, 1, аi ) из колонок 9-16 (табл. 5.2) переходов и функций возбуждения счётчика. Клетка в диаграмме Вейтча выбирается по расположению в эталонной диаграмме (рис. 5.9) десятичного набора, которому соответствует строка в таблице.
| Q3 |
||||
| Q4 |
12 |
13 |
9 |
8 |
| 14 |
15 |
11 |
10 |
Q2 |
| 6 |
7 |
3 |
2 |
|
| 4 |
5 |
1 |
0 |
|
| Q1 |
||||
Рис. 5.9 Эталонная диаграмма Вейтча
| J 3 |
Q3 |
|||||
| Q4 |
ai |
ai |
X |
X |
J3 =Q1 ∙Q2 |
|
| ai |
ai |
1 |
X |
Q2 |
||
| X |
X |
1 |
0 |
|||
| ai |
X |
0 |
0 |
|||
| Q1 |
||||||
Рис. 5.10
В полученных диаграммах коэффициент аi , может принимать любое из двух логических значений "0" или "1". Варьируя этими коэффициентами, необходимо добиться того, чтобы функция, полученная по диаграмме Вейтча, имела наиболее простой вид и "накрыла" все клетки с логическими единицами, но не "покрывала" клетки с логическими нулями. Например, для входа J третьего триггера можно получить Q2 ∙Q1 (рис. 5.10).
Примечание. "Накрытая" область заштрихована. В данном случае полагается a15 =1.
Зная функции возбуждения каждого входа каждого JK-триггера, можно синтезировать схему счётчика.
Схема одноразрядного десятичного счётчика приведена на рис. 5.11. При реализации счётчика было учтено, что JK-триггеры имеют три входа J, связанных функцией конъюнкции, и три входа К, также связанных функцией конъюнкции. Это позволяет уменьшить число логических элементов в комбинационной схеме счётчика.

Рис. 5.11 Двоично-десятичный счётчик в коде 2421
Например, при реализации функции возбуждения входа триггера Т4, которая представляет собой элементарную (Q1 Q2 Q3 ) конъюнкцию (см. рис. 5.8), можно вообще обойтись без логических элементов, закоммутировав входы Q1 Q2 и Q3 на J-входы триггера Т4.
![]() Приведём ещё пример использования трёх входов J и К триггера. Преобразуем функцию возбуждения входа JK-триггера Т2 к следующему виду:
Приведём ещё пример использования трёх входов J и К триггера. Преобразуем функцию возбуждения входа JK-триггера Т2 к следующему виду:
![]()
![]() J2
= Q1+Q3·Q4 = (Q1+Q3)(Q1+Q4) = (Q1+Q3)(Q1+Q4) = `Q1·`Q3·`Q1·`Q4 =
J2
= Q1+Q3·Q4 = (Q1+Q3)(Q1+Q4) = (Q1+Q3)(Q1+Q4) = `Q1·`Q3·`Q1·`Q4 =
(`Q1/`Q3)( `Q1/`Q4).
Полученное выражение реализуется с помощью двух элементов И-НЕ, выходы которых поданы на входы J-триггера Т2.
Временные диаграммы с учётом задержек в срабатывании приведены на рис. 5.12. По ним можно определить быстродействие двухразрядного двоично-десятичного счётчика.
Быстродействие счётчика характеризуется промежутком времени между поступлением подсчитываемого сигнала на вход счётчика и моментом установления на выходах триггеров уровней напряжения, соответствующих двоичной единице или двоичному нулю. Данный параметр счётчика показывает, через какое время после подачи подсчитываемого сигнала можно опрашивать новое состояние триггеров счётчика.
Переход счётчика из одного состояния в другое (сопровождается переходным процессом, который может завершаться или установлением всех триггеров, или переключением логических элементов счётчика. Поэтому при определении быстродействия счётчика необходимо найти такое состояние, время перехода из которого в соседнее будет наибольшим.
Для нашей схемы быстродействие определяется временем срабатывания цепи переноса и триггера, т.е.
Туст .=tи+t+ з.ф.+ t- з.ф.+ t- з.ф.тр.+ t- з.тр..,
где tи - длительность импульса;
t- з.ф.тр - время задержки отрицательного фронта триггера;
t- з.ф.тp. - время отрицательного фронта триггера;
t+ з.ф.. - время задержки положительного фронта логического элемента.
При выводе формулы учтено, что в данной системе элементов задержка в срабатывании триггера будет наибольшей при переходе его из "1" в "0".

Рис. 5.12 Временные диаграммы двоично-десятичного счётчика в коде 8421
5.4 Порядок выполнения работы
1. В соответствии с полученным вариантом и табл. 5.8 синтезировать двоично-десятичный счётчик.
| Таблица 5.8 |
||||||
| Десятичная цифра |
Коды |
|||||
| 8421 |
2421 |
5221 |
Джонсона |
Грея |
8421+3 |
|
| 0 |
0000 |
0000 |
0000 |
00000 |
0010 |
0011 |
| 1 |
0001 |
0001 |
0001 |
00001 |
0110 |
0100 |
| 2 |
0010 |
0010 |
0010 |
00011 |
0111 |
0101 |
| 3 |
0011 |
0011 |
0011 |
00111 |
0101 |
0110 |
| 4 |
0100 |
0100 |
0110 |
01111 |
0100 |
0111 |
| 5 |
0101 |
1011 |
1000 |
11111 |
1100 |
1000 |
| 6 |
0110 |
1100 |
1001 |
11110 |
1101 |
1001 |
| 7 |
0111 |
1101 |
1010 |
11100 |
1111 |
1010 |
| 8 |
1000 |
1110 |
1011 |
11000 |
1110 |
1011 |
| 9 |
1001 |
1111 |
1110 |
10000 |
1010 |
1100 |
2. Оформить отчёт, который должен содержать:
- матрицу переходов JK-триггера,
- таблицу переходов и функций возбуждения счётчика,
- эталонную диаграмму Вейтча,
- диаграммы Вейтча для функций возбуждения JK-триггера,
- минимизированные при помощи диаграмм Вейтча функции возбуждения JK-триггеров (все конъюнкции из получившихся выражений необходимо исключить),
-принципиальную схему синтезированного счётчика.
5.5 Вопросы для самостоятельной работы
1. Счётчик, модуль счётчика.
2. Количество триггеров для счётчика с модулем М.
3. Двоично-десятичный счётчик.
4. Синхронные и асинхронные счётчики.
5. Двухступенчатые триггеры с динамическим управлением записью: различия в работе, возможности при построении синхронных и асинхронных счётчиков.
6. Последовательные соединения счётчиков, модуль полученного каскада.
7. Быстродействие счётчиков.
8. Порядок проектирования синхронного счётчика.
9. Как получена диаграмма Вейтча?
10. Сохраняется ли состояние счётчика при отключении питания
11. Временная диаграмма работы счётчика.
- Примеры схемных решений приведены на рис. 5.13, 5.14.
![]()
![]()
Управляющие автоматы
Цель работы: изучение принципов построения управляющих автоматов с "жёсткой" логикой, приобретение навыков синтеза и анализа их работы.
Литература: /4/, с. 75-90, /8/, с. 324-348, /6/, с. 124-186.
6.1. Общая часть
Любое цифровое устройство можно рассматривать как устройство, состоящее из двух частей: операционного и управляющего блоков. Операционный блок, например АЛУ, характеризуется совокупностью определённых в нём микроопераций, каждая из которых представляет собой некоторый выполняемый в данном операционном блоке акт передачи или преобразования информации. Часть цифрового вычислительного устройства, предназначенного для выработки последовательности управляющих функциональных сигналов, называется управляющим блоком или управляющим устройством (УУ).
Формально УУ можно рассматривать как конечный автомат, определяемый:
1) множеством двоичных выходных сигналов,
2) множеством входных сигналов,
3) множеством подлежащих реализации программ,
4) множеством внутренних состояний.
Управляющие блоки называются управляющими автоматами. Поскольку эти автоматы задаются микропрограммами, они часто именуются микропрограммными автоматами.
Существуют два метода построения логики управляющих автоматов:
- с жёсткой логикой,
- с хранимой в памяти логикой.
Управляющие автоматы с "жёсткой" логикой представляют собой логические схемы, вырабатывающие распределённые во времени управляющие функциональные сигналы. В отличие от управляющих устройств, с хранимой в памяти логикой, у этих автоматов можно изменить логику работы только путём переделок схем автомата.
ЭВМ высокой производительности управляются автоматами с "жёсткой" логикой. Типичным применением такого автомата является устройство управления АЛУ.
Произведём синтез цифрового автомата, заданного микропрограммой (рис. 6.1). По микропрограмме строится соответствующий управляющий автомат Мили или Мура. Синтезируем автомат Мили, так как он имеет число состояний, как правило, меньше, чем число состояний эквивалентного ему автомата Мура. С этой точки зрения автомат Мили предпочтительнее.
![]()
![]()
Переход от микропрограммы к автомату Мили иллюстрируется рис. 6.2, на котором показаны микропрограмма и граф интерпретирующего её автомата Мили. Начало и конец микропрограммы представляются начальным состоянием автомата Q0 .
Каждая дуга, выходящая из прямоугольника, представляющего микрокоманду, отмечается меткой X и символом состояния автомата. Исключение составляют дуги, идущие к конечной вершине, которые не отмечаются. Если несколько дуг с меткой X входят в один блок графа программы, то все они отмечаются одинаковым символом состояния. Условия перехода по микропрограмме от одной метки состояния к другой задают функции переходов. Эти условия записываются в виде конъюнкции осведомительных сигналов. Для каждого перехода фиксируется также набор выходных переменных, принимающих при переходе единичное значение (задание функции выходов).
От графа, интерпретирующего микропрограмму, можно перейти к её технической реализации. Зная число состояний автомата m, определим число триггеров, необходимых для реализации его памяти, K=log2 m.
Для приведённого примера m=3 => K=log2 3 º2 требуется два триггера. Выберем для определённости D-триггера. Для триггеров составим таблицы состояний и истинности (табл. 6.1-6.2). Схема дешифрации состояний состоит из элементов D3.1, D3.2, D3.3 (рис. 6.3).
Примечание. Состояние триггера D1=1, D2=1 является запрещённым.
| Таблица 6.1 |
Таблица 6.2 |
||||||||
| № |
Q |
D1 |
D2 |
№ |
D1 |
D2 |
Q0 |
Q1 |
Q2 |
| 1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
| 2 |
1 |
0 |
1 |
2 |
0 |
1 |
0 |
1 |
0 |
| 3 |
2 |
1 |
0 |
3 |
1 |
0 |
0 |
0 |
1 |
![]()
На элементах D1.3, D4 собрана схема, вырабатывающая управляющие сигналы состояний Q0 , Q1 , Q2 и множество входных сигналов {U}. Схема функционирует так, что на её выходах только одно логическое значение "0", все остальные - "1". Зная этот выход (в разные моменты времени он разный) и граф микропрограммы, можно точно определить текущие и следующие состояния автомата, выходные управляющие сигналы.
Поэтому тем, на какие элементы D1.1 или D1.2 заведён этот вывод (провод), и определяются следующие состояния автомата.
Объединение по "п" некоторых выводов этих элементов (D1.3, D4) согласно графу функционирования автомата даёт множество управляющих выходных сигналов.
Элементы D1.1, D1.2 служат для формирования функций возбуждения триггеров.
6.2. Порядок выполнения работы
1. Получите у преподавателя вариант индивидуального задания.
| Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
| Микропрограмма автомата (рис. 6.4-6.5) |
6.4 |
6.5 |
6.6 |
6.7 |
6.8 |
6.9 |
2. От микропрограммы перейдите к графу интерпретирующего автомата Мили.
3. По графу микропрограммы синтезируйте схему технической реализации.
4. Проверьте правильность функционирования автомата. Для этого:
- подайте кратковременно на вход R сигнал со значением логического "0". При этом произойдёт сброс их триггеров в "0",
- определите множество входных сигналов, определяющих переход автомата из одного состояния в другое.
6.3. Вопросы для самостоятельной работы
1) Чем определяется конечный автомат?
2) Что представляет собой автомат с "жёсткой " логикой?
3) Как перейти от микропрограммы к графу интерпретирующему автомат Мили?
4) В чём различие автомата Мили и Мура?
5) Объясните работу схемы технической реализации автомата Мили.
![]()
![]()
![]()
![]()
![]()
![]()
ЛИТЕРАТУРА
1. Балашов Е.П., Пузанков Д.В. Микропроцессоры и микропроцессорные системы. -М.: Радио и связь, 1981, 328 с.
2. Каган Б.М. Электронные вычислительные машины и системы. -М.: Энергия, 1979, 528 с.
3. Клингман Э., Проектирование микропроцессорных систем. -М.: Мир, 1980, 576 с.
4. Майоров С.А., Новиков Г.И., Структура цифровых вычислительных машин. - Л.: Машиностроение, 1970, 480 с.
5. Специализированные ЦВМ. Под ред. Смолова В.Б. -М.: Высшая школа, 1980, 816 с.
6. Тарабрин Б.В., Якубовский С.В., Барканов Н.А. и д.р., Справочник по интегральным микросхемам. - М.: Энергия, 1980, 816 с.
7.Справочник по полупроводниковым диодам, транзисторам и интегральным схемам. Под ред. Н.Н. Горюнова. -М.: Энергия, 1977, 744с.
8. Трачик В., Дискретные устройства автоматики. -М.: Энергия, 1978, 456 с.