referatmix.ru
  Скачать .docx  

Реферат: Ход работы программы заключение Список источников и литературы Введение

Реферат

ученицы 10 класса «Б»

Киракосовой Таисии

по теме:

«Множество Жулиа и Мандельброта»

Научный руководитель:

Таранов А.А.

Оглавление

Введение.………………………………………………………………………3

Глава 1. Фракталы

1.1. Определение фракталов …………………………………………………4

1.2. Типы фракталов …………………………………………………………4

1.3. Роль фракталов в современном мире……………………………………6

Глава 2. Множество Мандельброта

2.1.Общие сведения …………………………………………………………... 7

2.2. История……………………………………………………..………………8

2.3 Взаимодействие с множеством Жулиа……………………………………8

Глава 3.Описание программы

3.1 Операции над комплексными числами…………………………………... 9

3.2. Структура программы……………………………………………………..10

3.3. Ход работы программы …………………………………………………..11

Заключение .……………………………………………………………………12

Список источников и литературы……………………………………………..13

Введение

Актуальность : данная тема является очень важной в современном мире. В настоящее время фракталы широко применяются в компьютерной графике для построения изображений природных объектов. Так же используются у «трейдеров» для анализа курса фондовых бирж, валютных и торговых рынков. В физике фракталы естественным образом возникают при моделировании нелинейных процессов.

Целью моей работы являлось создание программы для изучения множества Мандельброта в программе Adobe Flash CS3. Из поставленной цели выделялись следующие задачи:

1) Изучение и сбор информации по темам «Фрактальные множества» и «Множество Мандельброта»;

2) Изучение комплексных чисел и математических операций над комплексными числами;

3) Изучение среды Flash и основ программирования на Action Script;

4) Создание программы для изображения множества Мандельброта в программе Adobe Flash CS3;

Глава 1. Фракталы

1.1.Определение фрактала [1]

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского "fractus" и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'‚ в его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.

Одним из основных свойств фракталов является самоподобие ‚ в самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.
Определение фрактала, данное Мандельброттом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому".

1.2 Типы фракталов

- Геометрические фракталы
Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

- Алгебраические фракталы
Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.
Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные нетривиальные структуры.

- Стохастические фракталы
Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

1.3 Роль фракталов в современном мире [2]
Одно из главных применений фракталов - это машинная графика. С помощью них можно создать поверхности очень сложной формы, а изменяя всего несколько коэффициентов в уравнении добиваться практически бесконечных вариантов исходного изображения. Фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Также фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста

1. неразветвляющееся бесконечное дерево, тождественные самим себе с любой итерации («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…», «Ложно утверждение, что истинно утверждение, что ложно утверждение…»)

2. неразветвляющиеся бесконечные тексты с вариациями («У Пегги был весёлый гусь…») и тексты с наращениями («Дом, который построил Джек»)

Глава 2. Множество Мандельброта

2.1 Общие сведения [3]

Одним из наиболее известных примеров может являться множество Мандельброта . В математике это фрактал, определённый как множество точек на комплексной плоскости, для которых итеративная последовательность

не уходит в бесконечность.

Визуально, внутри множества Мандельброта можно выделить бесконечное количество элементарных фигур, причём самая большая в центре представляет собой кардиоиду (плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом). Также есть набор кругов, касающихся кардиоиды, размер которых постепенно уменьшается, стремясь к нулю. Каждый из этих кругов имеет свой набор меньших кругов, диаметр которых также стремится к нулю и т. д. Этот процесс продолжается бесконечно, образуя фрактал. Также важно, что эти процессы ветвления фигур не исчерпывают полностью множество Мандельброта: если рассмотреть с увеличением дополнительные «ветки», то в них можно увидеть свои кардиоиды и круги, не связанные с главной фигурой. Самая большая фигура (видимая при рассматривании основного множества) из них находится в области от −1,78 до −1,75 на отрицательной оси действительных значений.

2.2 . История [4]

Впервые множество Мандельброта было описано в 1905 году Пьером Фату (Pierre Fatou), французским математиком, работавшим в области аналитической динамики комплексных чисел. Фату изучал рекурсивные процессы вида

Начав с точки на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу. Такая последовательность точек называется орбитой при преобразовании

Фату нашел, что орбита при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований — своё для каждого значения . В те времена компьютеров ещё не было, и Фату, конечно, не мог построить орбиты всех точек плоскости, ему приходилось всё делать вручную. Основываясь на своих расчётах, он доказал, что орбита точки, лежащей на расстоянии больше 2 от начала координат, всегда уходит в бесконечность.

Фату никогда не видел изображений, которые мы сейчас знаем как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную. Профессор Бенуа Мандельброт был первым, кто использовал для этого компьютер.

Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение. Эти феномены рождались при использовании рекурсивного алгоритма для получения какой-либо кривой или множества. Множество Мандельброта — один из таких феноменов, названный по имени своего исследователя.

2.3 Взаимодействие с множеством Жюлиа

Множество Мандельброта изначально было построено как каталог множеств Жулиа: каждой точке на комплексной плоскости соответствует своё множество Жюлиа. Точки, лежащие внутри множества Мандельброта, точно соответствуют связным множествам Жюлиа, а точки снаружи — несвязаным.

Отсюда понятно, что интересные варианты множества Жюлиа соответствуют точкам, лежащим на границе множества Мандельброта. Точки глубоко внутри образуют простые геометрические фигуры, а внешние выглядят как «пыль», окружающая цветные пятна. Некоторые программы, например, Fracint, позволяют пользователю прямо на экране указать точку, для которой необходимо построить соответствующее множество Жюлиа, упрощая поиск красивых изображений.

Множество Мандельброта и само содержит структуры, напоминающие множество Жюлиа: для любого область множества Мандельброта около напоминает центр множества Жюлиа с параметром .

Глава 3.Описание программы

3.1 Операции над комплексными числами

Для написания программы использованы комплексные числа. Эти операции выполняются следующим образом:

Сложение(a + bi ) + (c + di ) = (a + c ) + (b + d )i

Вычитание(a + bi ) − (c + di ) = (a − c ) + (b − d )i

Умножение(a + bi )(c + di ) = ac + bci + adi + bdi 2 = (ac − bd ) + (bc + ad )i Деление

Все указанные выше операции можно доказать с помощью выполнения действий на координатной плоскости. На приведенных ниже графиках показаны примеры действий над комплексными числами.

Сложение комплексных чисел

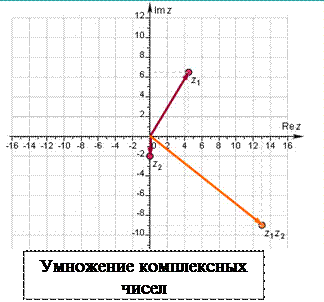3.2 Структура программы

Программа написана в программе Adobe Flash CS3. Состоит из двух Flash Action Script файлов.

В файле Complex создан класс Complex и пять функций для работы с комплексными числами:

1) Функция real возвращает в программу вещественную единицу комплексного числа;

2) Функция imag возвращает в программу мнимую единицу комплексного числа;

3) Функция add выполняет сложение комплексных чисел;

4) Функция mul выполняет умножение комплексных чисел;

5) Функция mod2 возводит комплексное число в квадрат;

Файл Test2 является исполняемым файлом. Включает в себя класс Test2 и 9 функций:

Основные функции:

1) Функция Test2;

2) Функция Mandelbrot, определяет принадлежность координаты к множеству Мандельброта и «число шагов» ( i ), за которое точка стала принадлежать множеству. В функцию передается значение координаты mx, my;

3) Функция onFrame к событию Event. Выполняет постепенное изображение множества Мандельброта на экране. В зависимости от высчитанных точек в функции Mandelbrot и цвета, определившегося функцией colour;

4) Функция colour определяет цвет пикселя на экране в зависимости от i, которое определяется в функции Mandelbrot;

Вспомогательные функции:

5) 5)Функция s2mX переводит экранные координаты X в математические координаты;

6) Функция s2mY переводит экранные координаты Y в математические

7) координаты;

Функции для увеличения выбранной области множества:

8) Функция mouseD при нажатой левой кнопке мыши рисует полупрозрачный прямоугольник, выделяя область множества. Левый верхний угол определяется местом нажатия левой кнопки мыши. Устанавливается обработчик MouseEvent.MOUSE_MOVE;

9) Функция mouseU снимает обработчик MouseEvent.MOUSE_MOVE и задает новую ширину и высоту области изображения;

10)Функция mouseM перерисовывает прямоугольник в зависимости от перемещения мыши. Правый угол определяется положением курсора.

11)Функция shiftPress передает в функции исходные параметры области;

3.3 Ход работы программы

При запуске программы срабатывает функция Mandelbrot, высчитывающая точки, принадлежащие множеству Мандельброта. В функции стоит счетчик i, который определяет за какое количество шагов точка стала принадлежать множеству. Функция onFrame постепенно показывает область множества: черным - точка не принадлежит множеству, цветным - принадлежит. Цвет точки определяется функцией colour, в которую передается счетчик i из функции Мандельброт. Чем больше значение счетчика, тем светлее цвет точки.

При нажатии кнопки мыши сначала срабатывает функция mouseD, рисующая полупрозрачный прямоугольник. При перемещении мыши, функция mouseM перерисовывает прямоугольник, в зависимости от передвижения мыши. При отпускании клавиши функция mouseU передает получившиеся параметры области в функцию onFrame. При нажатии клавиши Shift в программу передаются исходные параметры области.

Заключение

В результате проведенной работы была изучена теоретическая информация о множествах, в частности о множестве Жулиа и Мандельборота и была написана программа, реализующая графически множество Мандельброта, с возможным увеличением изображения:

Изначальный рисунок:

Рисунок, полученный с помощью увеличения:

Список используемой литературы:

1)Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002. ;

2)Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.;

3) Learning ActionScript 3.0 A beginner Guide, Adobe Developer Library;

4) Электронная энциклопедия Википедия. Фракталы. http://ru.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB#.D0.90.D0.BD.D0.B0.D0.BB.D0.B8.D0.B7_.D1.80.D1.8B.D0.BD.D0.BA.D0.BE.D0.B2

5) Электронная энциклопедия ВикиЗнание. Эвентологические фракталы.

http://www.wikiznanie.ru/ru-wz/index.php/%D0%AD%D0%B2%D0%B5%D0%BD%D1%82%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB%D1%8B


[1] http://www.wikiznanie.ru/ru-wz/index.php/%D0%AD%D0%B2%D0%B5%D0%BD%D1%82%D0%BE%D0%BB%D0%BE%D0%B3%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB%D1%8B

[2] http://ru.wikipedia.org/

[3] Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.;

[4] Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.