| Скачать .docx |
Реферат: Теории деформационного упрочнения монокристаллов
ТЕОРИИ ДЕФОРМАЦИОННОГО УПРОЧНЕНИЯ МОНОКРИСТАЛЛОВ
Среди многих неясных вопросов в проблеме пластичности монокристаллов вопрос о природе деформационного упрочнения, которое состоит в увеличении сопротивляемости кристалла пластической деформации при активном нагружении, является одним из самых трудных. По современным представлениям физики пластичности основная причина упрочнения - затруднение движения дислокаций по кристаллу вследствие увеличения их количества в кристалле и связанного с этим усиления взаимодействия дислокаций друг с другом. Для построения физической теории деформационного упрочнения необходимо описать эволюцию дислокационной структуры: увеличение плотности дислокаций, характер их расположения и взаимодействия в кристалле при увеличении внешнего напряжения и связать эти изменения с приростом пластической деформации кристалла. Наибольший успех в данном направлении достигнут для монокристаллов ГЦК металлов, в которых процесс пластической деформации обладает ярко выраженной стадийностью. Создано несколько теорий деформационного упрочнения для каждой отдельной стадии. Не давая полного обзора всех теорий, остановимся в основном на теории Зегера, которая является наиболее обоснованной как в плане сравнения с экспериментальными данными, так и с точки зрения логической последовательности. Однако начнем с рассмотрения самых первых теорий деформационного упрочнения Тейлора и Мотта, ставших теперь уже классическими, для того, чтобы внимательно проследить путь развития теории от первых ее шагов до современного состояния.
1. ТЕОРИЯ ТЕЙЛОРА
Первая теория деформационного упрочнения, оперирующая дислокационными представлениями, предложена Тейлором в 1934 г. К тому времени было установлено, что кривые упрочнения металлических кристаллов, таких, как алюминий, в первом приближении можно считать параболическими и это учитывалось при разработке теории.
Следуя Тейлору, рассмотрим кристалл, в котором при приложении внешнего напряжения t , действующего в плоскости скольжения в направлении скольжения, зарождаются и скользят бесконечные, прямолинейные, параллельные друг другу дислокации. Механизм зарождения конкретизировать не будем, а механизмом упрочнения будем считать упругое взаимодействие дислокаций друг с другом.
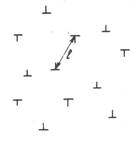
Если плотность дислокаций в кристалле r, то среднее расстояние между ними l= r -1/2 (рис.1 ) и средняя амплитуда случайного поля внутренних напряжений
tm = amb/e » ambr 1/2 (2.1)
где a равно 1/2p(1-n) и 1/2p для краевых и винтовых дислокаций соответственно; м. - модуль сдвига; n - коэффициент Пуассона; в -величина вектора Бюргерса.
|
Рисунок 1 Взаимодействие дислокаций (модель Тейлора) |
Из рис 1 видно, что с ростом плотности дислокаций растет и амплитуда случайного поля внутренних напряжений, противодействующего движению дислокаций.
Считая, что зарождение и движение дислокаций происходит со скоростью, намного большей скорости увеличения t, так что условие
t=tm (2.2)
выполняется в любой момент деформации. Из (2.1) и (2.2) получаем зависимость
r(t)=1/(a2 b2 )*(t/m)2 (2.3)
Если положить, что с момента зарождения до остановки дислокации проходят в среднем одинаковое расстояние L , то, используя известную формулу для пластического сдвига
g=rbL (2.4)
и выражение (2.3), получаем параболическое соотношение между напряжением t и сдвигом g. А при подстановке в это соотношение экспериментального значения длины линий скольжения мы получим неплохое совпадение кривой упрочнения параболической формы монокристаллов алюминия с экспериментальными данными.
Однако теория Тейлора не согласуется с экспериментами в том отношении, что высота ступенек на линиях скольжения составляет 10 — 100 b, и это говорит о движении большого числа дислокаций друг за другом по одной
и той же плоскости скольжения, а не о движении отдельных дислокаций. Кроме того, в теории Тейлора ничего не сказано о механизме, по которому происходит увеличение количества дислокаций в кристалле при увеличении t.
2. ТЕОРИЯ МОТТА
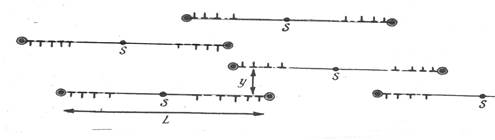
Мотт преодолел эти затруднения теории Тейлора (1952 г.). К тому времени был предложен оригинальный механизм размножения дислокаций, так называемый источник Франка - Рида. Мотт считал, что в кристалле хаотически располагаются источники дислокаций Франка — Рида, испускающие под действием внешнего напряжения V в плоскости скольжения группы дислокаций, которые после прохождения некоторого расстояния скапливаются у препятствий (рис. 2). Препятствиями могут быть субграницы, сидячие дислокации, и т.п.
|
Рисунок 2 Взаимодействие скоплений дислокаций в первичной системе скольжения |
Появление в кристалле таких групп дислокаций приводит к увеличению внутреннего напряжения tm . Для его расчета можно рассматривать скопление дислокаций как сверхдислокации с вектором Бюргерса nb, где n — число дислокаций в скоплении. Если предположить, что дислокации разных знаков, порождаемые одним источником, скапливаются по обе стороны от него, так что общая длина скопления составляет L (каждая дислокация продвигается на расстояние L/2), а расстояние между плоскостями равно y , то плотность сверхдислокации равна 2/Ly, а среднее расстояние между ними есть (Ly/2)1/2
Пластический сдвиг кристалла в таком случае определяется суммированием сдвигов от каждого скопления и согласно является произведением величины плотности сверхдислокации на их вектор Бюргерса nb на длину их пробега L/2. т.е.
g=nb/y
Эта теория так же, как теория Тейлора, дает параболическую связь между напряжением и деформацией монокристаллов. Однако, как показали экспериментальные исследования, выполненные после 1950 г., для ГЦК кристаллов характерна не параболическая, а трехстадийная кривая упрочнения, поэтому для ее описания потребовались более детализированные теории.
3. ТЕОРИЯ ЗЕГЕРА
В теории, предложенной Зегером, считается, что даже хорошо отожженные кристаллы содержат дислокации, которые образуют случайную пространственную сетку, состоящую из почти прямолинейных дислокационных сегментов, соединенных между собой тройными узлами. Средняя длина дислокационных сегментов сетки Lo » ro-1/2 где ro - плотность дислокаций. Большей частью сегменты сетки ростовых дислокаций неподвижны, и лишь некоторые из них при действии внешнего напряжения Т прогибаются между неподвижными узлами сетки. При достижении напряжения
t » mbro 1/2 (2.9)
в первичной системе скольжения соответствующие сегменты начинают действовать как источники Франка — Рида, образуя вокруг каждого систему концентрических замкнутых петель в плоскости скольжения - скопление дислокаций.
Дальнейшее движение дислокаций (расширение петель) ограничивается их взаимодействием с другими дислокациями, скользящими в параллельных плоскостях и с дислокациями леса. При деформации среднеориентированных кристаллов плотность дислокаций леса почти не меняется, поэтому Зегер
считает, что деформационное упрочнение обусловлено ростом плотности дислокаций в первичной системе скольжения и усилением их взаимодействия друг с другом. Следовательно, эта теория является развитием теорий деформационного упрочнения Тейлора и Мотта.
65
В заключение необходимо отметить, что теорию деформационного упрочнения Зегера, хотя она и является наиболее полной и детально разработанной из современных теорий, нельзя считать действительно законченной физической теорией деформационного упрочнения ГЦК металлов. В своей основе она является полуфеноменологической, так как использует экспериментально определяемые зависимости для длин пробега дислокаций, расстояния между плоскостями скольжения, числа дислокаций в скоплении. Основным результатом теории Зегера можно считать установление связи между характеристиками дислокационной структуры, определяемыми в процессе деформации по картинам следов.
Полная физическая теория деформационного упрочнения должна быть способной предсказать эволюцию дислокационной структуры и рассчитать кривую деформации кристалла, используя только данные о его исходной дефектной структуре и условиях деформации.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1 Аргон А.С. - В кн.: Физика прочности и пластичности. - М.: Металлургия, 1972,с. 186 - 214.
2 Берне Р., Кронмюллер Г. Пластическая деформация
монокристаллов. - М.:Мир, 1969.-272 с.
3 Горячев С.Б. Микроскопические механизмы деформационного
упрочнения. -М.: МИФИ 1984 61-с
77