Реферат: Экзаменационные билеты с вопросами за весенний семестр 2001 года по: математическое моделирование экономических систем

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ ЭКЗАМЕНАЦИОННЫХ ВОПРОСОВ

Математическое моделирование экономических систем

1. Сущность и значимость экономико-математического моделирования.

2. Этапы экономико-математического моделирования.

3. Основные экономические институты и их характеристики.

4. Область применения экономико-математических моделей.

5. Экономическая значимость каждого этапа моделирования.

6. Сущность критерия практики.

7. Обязательные элементы математической модели.

8. В задаче составления плана производства дать постановку экономической задачи.

9. Для задачи составления плана производства описать переменные и параметры задачи.

10. Для задачи составления плана производства описать основные экономические условия.

11. Для задачи составления плана производства сформулировать ограничения задачи.

12. Что принимается в качестве целевой функции в задаче составления плана производства?

13. Дать экономический смысл точного равенства в ограничении задачи составления плана производства.

14. Экономический смысл оптимального решения в задаче составления плана производства.

15. Экономический смысл строгого неравенства в ограничении задачи составления плана производства.

16. Для задачи составления плана производства записать двойственную задачу.

17. В двойственной задаче для задачи составления плана производства привести экономический смысл целевой функции.

18. В двойственной задаче для задачи составления плана производства привести экономический смысл ограничений.

19. В двойственной задаче для задачи составления плана производства привести экономический смысл переменных.

20. Проанализировать изменение целевой функции в линейной модели производства при изменении цен реализации продукции.

21. Проанализировать изменение целевой функции в линейной модели производства при изменении запаса дефицитного ресурса.

22. Проанализировать изменение целевой функции в линейной модели производства при изменении запаса недефицитного ресурса.

23. Привести экономический смысл связи целевых функций прямой и двойственной задач в линейной модели производства.

24. Постановка задачи управления запасами.

25. Основные положения задач управления запасами.

26. Описать виды издержек, учитывающихся в задачах управления запасами.

27. Основные модели управления запасами.

28. Формула Уилсона.

29. Геометрическая иллюстрация движения запасов для основных моделей управления запасами.

30. Привести принципы построения целевых функций в задачах управления запасами.

31. Дать геометрическую иллюстрацию изменения издержек в основной модели управления запасами.

32. Точка заказа. Понятие, геометрическая иллюстрация.

33. Транспортная задача: постановка.

34. Транспортная задача: экономическая значимость.

35. Транспортная задача: условия существования решения.

36. Постановка задач о найме, режиме работы энергосистемы, складе и смесях.

37. Производственная функция: основные понятия.

38. Производственная функция: экономическое содержание.

39. Производственная функция: предельные продукты. Определение, экономический смысл.

40. Производственная функция: экономическая и особая области.

41. Производственная функция: закон убывающей доходности.

42. Производственная функция: характер изменения при расширении масштабов производства.

43. Производственная функция: эластичность производства и эластичность выпусков по отношению к изменению факторов производства.

44. Производственная функция: средний и предельный доходы.

45. Характеристика производств в зависимости от соотношения средних и предельных доходов.

46. Предельная норма замены.

47. Производственная функция Кобба-Дугласа. Определение.

48. Производственная функция Кобба-Дугласа. Основные свойства.

49. Производственная функция Кобба-Дугласа. Экономический смысл средних и предельных показателей.

50. Производственная функция Кобба-Дугласа. Свойства показателей эластичности.

51. Производственная функция Кобба-Дугласа. Экономическая и особая области.

52. Производственная функция Кобба-Дугласа. Изокванты.

53. Задача фирмы в условиях совершенной конкуренции: экономическая постановка.

54. Задача фирмы в условиях совершенной конкуренции: математическая модель.

55. Задача фирмы в условиях совершенной конкуренции: условие максимума прибыли.

56. Изокоста. Понятие, экономический смысл, геометрическая иллюстрация.

57. Функции спроса на ресурсы в задаче фирмы, функционирующей в условиях совершенной конкуренции.

58. Функция предложения фирмы в условиях совершенной конкуренции. Обоснование.

59. Свойства функции предложения, геометрическая иллюстрация.

60. Пространство товаров. Отношение предпочтения.

61. Функция полезности. Определение, теорема Дебре.

62. Функция полезности. Предельная полезности.

63. Функция полезности. Основные предположения.

64. Функция полезности. Закон убывающей полезности.

65. Функция полезности. Кривая безразличия.

66. Задача потребителя. Постановка задачи.

67. Задача потребителя. Математическая модель.

68. Задача потребителя. Геометрическая иллюстрация.

69. Задача потребителя. Бюджетное множество.

70. Решение задачи потребителя.

71. Функции спроса на товары.

72. Компенсированное изменение цены.

73. Законы Госсена.

74. Товары Гиффина и нормальные товары.

75. Управление Слуцкого.

76. Эластичности спроса на товары по отношению к цене на товары.

77. Взаимозаменяемые и взаимодополняемые товары.

78. Ценные и малоценные товары.

79. Графическая иллюстрация компенсированного изменения цены.

80. Один товар: кривая спроса и предложения.

81. Один товар: понятие равновесной цены, дефицит и излишек.

82. Один товар: индивидуальный и рыночный спрос.

83. Один товар: эластичный и неэластичный спрос. Определение, свойства.

84. Один товар: спрос постоянной эластичности.

85. Один товар: реакция потребителя на изменение цен в зависимости от коэффициента эластичности.

86. Реакция производителя товара в зависимости от эластичности спроса.

87. Понятие равновесной цены.

88. Паутинообразная модель.

89. Частное и общее равновесие.

90. Равновесие по Вальрасу.

91. Равновесие по Маршаллу.

92. Межотраслевой баланс: основные положения.

93. Межотраслевой баланс: основные элементы.

94. Межотраслевой баланс: балансовые соотношения.

95. Межотраслевой баланс: матрица прямых затрат.

96. Межотраслевой баланс. Модель Леонтьева: постановка.

97. Межотраслевой баланс: матрица полных затрат.

98. Обобщенная модель Леонтьева.

99. Понятие магистрали. Элементы магистральной теории.

100. Фирма производит два вида продукции используя для этого два вида ресурсов. Цены реализации ― 120 д.е. и 90 д.е. Технологическая матрица задана в виде таблицы

Запас ресурсов ― 3000 ед. ресурса № 1, 3600 ед. ресурса № 2. Требуется определить план производства, максимизирующий доход.
Записать математическую модель.

101. Фирма производит два вида продукции используя для этого два вида ресурсов. Цены реализации ― 120 д.е. и 90 д.е. Технологическая матрица задана в виде таблицы

Запас ресурсов ― 3000 ед. ресурса № 1, 3600 ед. ресурса № 2. Требуется определить план производства, максимизирующий доход.
Найти наилучший план производства.

102. Фирма производит два вида продукции используя для этого два вида ресурсов. Цены реализации ― 120 д.е. и 90 д.е. Технологическая матрица задана в виде таблицы

Запас ресурсов ― 3000 ед. ресурса № 1, 3600 ед. ресурса № 2. Требуется определить план производства, максимизирующий доход.
Найти максимальный доход.

103. Фирма производит два вида продукции используя для этого два вида ресурсов. Цены реализации ― 120 д.е. и 90 д.е. Технологическая матрица задана в виде таблицы

Запас ресурсов ― 3000 ед. ресурса № 1, 3600 ед. ресурса № 2. Требуется определить план производства, максимизирующий доход.
Определить оценки стоимости ресурсов.

104. Производственная функция фирмы описывается функцией Кобба-Дугласа
, где x ― затраты капитала, y ― затраты труда.
Рассчитать выпуск при x = 243, y = 32.

105. Производственная функция фирмы описывается функцией Кобба-Дугласа
, где x ― затраты капитала, y ― затраты труда.
Рассчитать предельную и среднюю производительность труда при x = 243, y = 32.

106. Производственная функция фирмы описывается функцией Кобба-Дугласа
, где x ― затраты капитала, y ― затраты труда.
Рассчитать предельную и среднюю фондоотдачу при x = 243, y = 32.

107. Фирма работает в условиях совершенной конкуренции: выпускает один вид продукции, используя при этом два вида ресурсов. Производственная функция фирмы равна f(x,y) = 80xy, цена реализации продукции ― 120 д.е., ресурсы приобретаются по ценам W₁ = 20 д.е., W₂ = 15 д.е. соответственно.
Записать функцию прибыли.

108. Фирма работает в условиях совершенной конкуренции: выпускает один вид продукции, используя при этом два вида ресурсов. Производственная функция фирмы равна f(x,y) = 80xy, цена реализации продукции ― 120 д.е., ресурсы приобретаются по ценам W₁ = 20 д.е., W₂ = 15 д.е. соответственно.
Записать условия максимума прибыли.

109. Фирма работает в условиях совершенной конкуренции: выпускает один вид продукции, используя при этом два вида ресурсов. Производственная функция фирмы равна f(x,y) = 80xy, цена реализации продукции ― 120 д.е., ресурсы приобретаются по ценам W₁ = 20 д.е., W₂ = 15 д.е. соответственно.
Решить задачу фирмы максимизации прибыли.

110. Фирма работает в условиях совершенной конкуренции: выпускает один вид продукции, используя при этом два вида ресурсов. Производственная функция фирмы равна f(x,y) = 80xy, цена реализации продукции ― 120 д.е., ресурсы приобретаются по ценам W₁ = 20 д.е., W₂ = 15 д.е. соответственно.
Построить изокванту f(x,y) = 6400.

111. Фирма работает в условиях совершенной конкуренции: выпускает один вид продукции, используя при этом два вида ресурсов. Производственная функция фирмы равна f(x,y) = 80xy, цена реализации продукции ― 120 д.е., ресурсы приобретаются по ценам W₁ = 20 д.е., W₂ = 15 д.е. соответственно.
Построить изокосту C(x,y) = 3000.

112. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго ― 22 д.е. Функция полезности потребителя ― U(x,y) = 60x + 90y.
Записать задачу потребителя.

113. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго ― 22 д.е. Функция полезности потребителя ― U(x,y) = 60x + 90y.
Изобразить геометрически бюджетное множество, отметить бюджетную линию.

114. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго ― 22 д.е. Функция полезности потребителя ― U(x,y) = 60x + 90y.
Изобразить геометрически кривую безразличия U(x,y) = 4500.

115. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго ― 22 д.е. Функция полезности потребителя ― U(x,y) = 60x + 90y.
Какова предельная полезность потребителя по каждому товару?

116. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго ― 22 д.е. Функция полезности потребителя ― U(x,y) = 60x + 90y.
Решить задачу потребителя.

117. Потребитель выделил на приобретение двух товаров 3300 д.е. Цена первого товара 15 д.е., второго ― 22 д.е. Функция полезности потребителя ― U(x,y) = 60x + 90y.
Определить максимальную полезность потребителя от потребления этих двух товаров.

118. Спрос потребителя на некоторый товар в зависимости от цены определяется функцией d(p) = -0,3p + 60.
Определить коэффициент ценовой эластичности при p = 120, p = 60.

119. Спрос потребителя на некоторый товар в зависимости от цены определяется функцией d(p) = -0,3p + 60.
При какой цене коэффициент эластичности равен единице?

120. Спрос потребителя на некоторый товар в зависимости от цены определяется функцией d(p) = -0,3p + 60.
Эластичен ли спрос при p = 120, p = 60?

121. Исследовался спрос на товар двух групп потребителей. Функции спроса в зависимости от цены, предъявляемые каждой группой, имеют вид: d₁ (p) = -0,2p + 80, d₂ (p) = -0,4 + 60.
Построить совокупную функцию спроса.

122. Исследовался спрос на товар двух групп потребителей. Функции спроса в зависимости от цены, предъявляемые каждой группой, имеют вид: d₁ (p) = -0,2p + 80, d₂ (p) = -0,4 + 60.
Чему равен совокупный спрос при p = 100 д.е., p = 200 д.е.?

123. Исследовался спрос на товар двух групп потребителей. Функции спроса в зависимости от цены, предъявляемые каждой группой, имеют вид: d₁ (p) = -0,2p + 80, d₂ (p) = -0,4 + 60.
Изобразить геометрически спрос каждой группы и совокупный спрос.

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 1

1. Задача составления плана производства: критерий.

2. Как определяется максимум прибыли при постоянном уровне затрат?

3. Свойство постоянного дохода от расширения масштабов производства.

4. Экономические свойства кривых безразличия.

5. Способы измерения ценовой эластичности.

6. Производственная функция, описывающая выпуск при использовании двух ресурсов, имеет вид f(x₁ , x₂ ) = 50x₁ +40x₂ . Определить эластичность выпуска по первому ресурсу про x₁ =10, х₂ =25.

7. Функции спроса и предложения на товар имеют вид: d(p) = - 0,3p + 60 и S(p) = 9,7p+10, соответственно.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 2

1. В чем состоит связь целевых функций прямой и двойственной задач и что это значит для задачи составления плана производства?

2. Основные положения постановки задачи управления запасами.

3. Понятия среднего и предельного продукта.

4. Нормальные товары и товары Гиффина.

5. Типы экономического равновесия.

6. Имеются два вида продуктов, содержащих питательные вещества А и В. Содержание веществ А и В в 1 кг каждого вида продуктов приведены в таблице:


В ежемесячном рационе должно содержаться веществ А и В не менее 100 и 300 ед., соответственно. Продукты приобретаются по ценам 35 руб./кг и 40 руб./кг. Пусть х = (х₁ , х₂ ) – вектор количеств приобретаемых продуктов. Задача выбора рациона заключается в нахождении вектора х* = (х₁ *, х₂ *), минимизирующего стоимость покупки и обеспечивающего необходимое количество питательных веществ. Построить математическую модель.

7. Для приобретения трех товаров потребитель выделил 2500 у.е. Цены на товары равны р₁ = 80 у.е., р₂ = 70 у.е., p₃ = 100 у. е. Рассчитать затраты потребителя на покупку x = (8,15, 10). Уложится ли потребитель в бюджет при этой покупке? (ответ обосновать)

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 3

8. Задача составления плана производства: допустимый план.

9. Постановка задачи о смесях.

10. Особая область в пространстве затрат.

11. Свойство однородности функций спроса. Дать обоснование и экономическое значение.

12. Паутинообразная модель.

13. Фирма решает задачу обеспечения производства сырьем. Поставка сырья происходит со скоростью 200 ед/день, спрос на сырье непрерывен, с постоянной интенсивностью 100 ед/день. Перебои не допускаются (I_o = 0). Затраты на доставку партии сырья равны 1000 у.е. На хранение единицы сырья в единицу времени 0,5 у.е. Найти оптимальный уровень заказа.

14. Для приобретения двух товаров потребитель выделил 1800 у.е. Цены на товары равны р₁ = 90 у.е., р₂ = 75 у.е. Рассчитать затраты потребителя на покупку х = (5, 4). Уложится ли потребитель в бюджет при этой покупке? (ответ обосновать)

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 4

15. Задача составления плана производства: экономический смысл строгого неравенства в ограничении на оптимальном плане.

16. Определение точки заказа.

17. Изокванта. Понятие, экономический смысл.

18. Решение задачи потребителя. Свойство, экономический смысл.

19. Анализ структуры отраслей с помощью МОБ.

20. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Изобразить геометрически изокванту f(x, y) = 18000.

21. Для приобретения двух товаров потребитель выделил 1800 у.е. Цены на товары равны р₁ = 90 у.е., р₂ = 75 у.е. Построить бюджетную линию. Решение изобразить геометрически.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 5

22. Подготовка модели к эксплуатации.

23. Как определяется предельная норма замены одного ресурса другим в задаче фирмы. Экономическая значимость.

24. Производственная функция Кобба-Дугласа. Определение, экономический смысл, свойства.

25. Изменение спроса при компенсированном изменении цены от цены на этот товар.

26. Магистральная модель потребления. Общая постановка.

27. Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Доходность кредитов и ценных бумаг равны 20 % и 15 %, соответственно. Пусть х₁ – средства, размещенные в кредитах, х₂ – средства, вложенные в ценные бумаги. Распределить средства банка между кредитами и ценными бумагами таким образом, чтобы получить максимальный доход от кредитов и ценных бумаг.

28. Потребитель на приобретение двух товаров выделил 1500 рублей. Цена первого товара 50 рублей, 2- го - 70 рублей. Описать бюджетное ограничение потребителя, изобразить геометрически и указать на графике бюджетную линию.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 6

29. Для линейной модели производства привести связь между увеличением отдельного ресурса, двойственной оценкой этого ресурса и изменением дохода.

30. Общие принципы построения моделей с непрерывным спросом без допущения дефицита.

31. Привести свойства функции предложения фирмы.

32. Теорема Дебре.

33. Паутинообразная модель и экономическое равновесие.

34. Имеются два вида продуктов, содержащих питательные вещества А и В. Содержание веществ А и В в 1 кг каждого вида продуктов приведены в таблице:

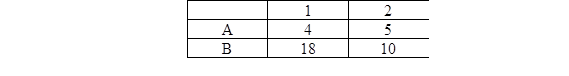
Какие количества питательных веществ А и В содержится в продуктах, приобретенных в количествах (10, 15)? Удовлетворяет ли такая покупка месячному рациону?

35. Функция полезности потребителя от потребления двух видов продукции равна: . Для приобретения товаров выделено 1800 у.е. Цены на товары равны р₁ = 90 у.е., р₂ = 75 у.е. Чему равен спрос на первый продукт, предъявляемый данным потребителем?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 7

36. Задача составления плана производства: экономический смысл целевой функции двойственной задачи.

37. Постановка задачи о рационе.

38. Свойство функции Кобба-Дугласа при рассмотрении расширения масштабов производства.

39. Привести условия Куна-Таккера для задачи потребителя.

40. Условия существования равновесия в паутинообразной модели.

41. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Пусть А – способ производства, при котором х = 32, y = 243.
Вычислить среднюю производительность труда при способе А.

42. Функция полезности потребителя от приобретения двух товаров имеет вид
U(x₁ ,x₂ ) = 150x₁ + 100x₂ . Каков уровень полезности при объемах покупок (10, 20). Какова предельная норма замены первого товара вторым при снижении потребления первого товара на единицу?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 8

43. Задача составления плана производства: экономический смысл строгого неравенства на оптимальном плане ограничения двойственной задачи.

44. Издержки хранения запасов в задачах управления запасами.

45. Обосновать равенство минимального уровня средних издержек предельным затратам.

46. Свойства отношения предпочтения товаров на пространстве товаров.

47. Кривая безразличия и норма замены.

48. Фирма решает задачу обеспечения производства сырьем. Поставка сырья происходит мгновенно, спрос на сырье непрерывен, с постоянной интенсивностью в 150 ед/день. Перебои не допускаются. Размер заказа составил 30000 ед. Чему будет равен уровень запаса через 5 дней?

49. Функция полезности потребителя от потребления двух видов продукции равна: . Определить уровень полезности потребителя при покупке х = (30, 40).

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 9

50. Проанализировать изменение целевой функции в линейной модели производства при изменении цен реализации выпускаемой продукции.

51. Постановка простой задачи о складе.

52. Предельная норма замещения в случае использования двух ресурсов. Геометрическая иллюстрация, экономический смысл, способ расчета.

53. Свойство решения задачи потребителя, выраженное в терминах предельных полезностей (II закон Госсена).

54. Понятие равновесной цены.

55. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Пусть А – способ производства, при котором х = 32, y = 243.
Вычислить предельную производительность труда при способе А.

56. Функция полезности потребителя от потребления двух видов продукции равна: . Построить кривую безразличия U(х₁ ,х₂ ) = 900. Решение изобразить геометрически.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 10

57. Что представляет собой математическая модель?

58. Привести функцию уровня запасов в зависимости от времени в классической модели наиболее экономичного размера партии.

59. Закон убывающей доходности.

60. Эластичности спроса на один товар по отношению к цене на другой (перекрестная эластичность). Способ расчета, экономический смысл.

61. Дать геометрическую иллюстрацию паутинообразной модели.

62. Фирма решает задачу обеспечения производства сырьем. Поставка сырья происходит со скоростью 200 ед/день, спрос на сырье непрерывен, с постоянной интенсивностью 100 ед/день. Перебои не допускаются (I_o = 0). Затраты на доставку партии сырья равны 1000 у.е. На хранение единицы сырья в единицу времени 0,5 у.е. Найти уровень затрат на доставку и хранение заказа объема q = 2000 ед. На сколько дней хватит запаса?

63. Потребитель на приобретение двух товаров выделил 2 тысячи рублей. Цена первого товара 50 рублей, 2- го - 70 рублей. Функция полезности потребителя U(x₁ , x₂ )= 100x₁ + 250x₂ . Решить задачу потребителя.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 11

64. Как определяются функции спроса фирмы на ресурсы в задаче фирмы в условиях совершенной конкуренции?

65. Основная модель управления запасами.

66. Эластичность выпуска по отношению к изменению затрат.

67. Задача потребителя.

68. Путь к экономическому общему равновесию по Вальрасу.

69. Фирма работает в условиях совершенной конкуренции; выпускает один вид продукции, используя для этого два вида ресурсов. Продукция реализуется по цене р = 580 у.е., ресурсы приобретаются по ценам w₁ = 30 у.е., w₂ = 45 у.е., соответственно. Производственная функция фирмы f(x₁ , x₂ ) = 15 x₁ ×x₂ , где х = (х₁ , х₂ ) – вектор объемов ресурсов. Построить функцию прибыли фирмы. Выписать условия максимума прибыли и найти максимальную прибыль.

70. Потребитель предъявляет спрос на некоторый товар в количествах d(p) = 120-10p, производитель производит данный товар в зависимости от цены в объемах S (p) = -10+2p. Геометрически изобразить схему нахождения равновесной цены по паутинообразной модели, начиная с р₀ =6.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 12

71. Задача составления плана производства: способ задания технологий.

72. Постановка задачи о режиме работы энергосистемы.

73. Дать геометрическую иллюстрацию решения фирмы в условиях совершенной конкуренции.

74. Привести примеры нормальных товаров, взаимозаменяемых и взаимодополняемых товаров. Дать обоснование.

75. Понятие о частном и общем равновесии.

76. Производственная функция, описывающая выпуск при использовании двух ресурсов (труд x и капитал y), является функцией Кобба - Дугласа

76. f(x, y) =. Определить предельную фондоотдачу при х =27, y=125.

77. Функция полезности потребителя от потребления трех видов продукции имеет вид: . Рассчитать предельную полезность потребителя по первому продукту при векторе потребления (27, 8, 1).

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 13

78. Задача фирмы в условиях совершенной конкуренции. Постановка задачи.

79. Общие принципы построения моделей с непрерывным спросом с допущением дефицита.

80. Эластичности выпуска по отношению к изменению затрат функции Кобба-Дугласа.

81. Товары Гиффина. Обоснование существования товаров Гиффина с помощью уравнения Слуцкого.

82. Матрица полных затрат. Понятие, способ расчета, экономический смысл.

83. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Пусть А – способ производства, при котором х = 32, y = 243.
Вычислить среднюю фондоотдачу при способе А.

84. Функция полезности потребителя от потребления двух видов продукции линейна. Полезности потребления единицы каждого вида продукции равны, соответственно, 10 ед. и 25 ед. полезности. Товары приобретаются по ценам 50 у.е. и 70 у.е., бюджет потребителя составляет 2000 у.е. Определить спрос потребителя на первый товар в данных условиях.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 14

85. Этапы построения математических моделей.

86. Постановка задачи управления запасами в случае аренды складов под хранение запасов.

87. Понятие малоценных ресурсов в задаче фирмы.

88. Свойства функций спроса.

89. Понятие эластичного (неэластичного) спроса на товар.

90. Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Доходность кредитов и ценных бумаг равны 20 % и 15 %, соответственно. Пусть х₁ – средства, размещенные в кредитах, х₂ – средства, вложенные в ценные бумаги. Привести пример средств, вложенных в кредиты и ценные бумаги, удовлетворяющих условиям задачи.

91. Функция полезности потребителя U(x₁ , x₂ ) = 200x₁ + 150x_2. Что из себя представляют кривые безразличия? Изобразить геометрически кривую безразличия U(x₁ , x₂ ) = 60000.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 15

92. Рассматривается задача составления плана производства как Задача линейного программирования: записать двойственную.

93. Определение оптимального размера заказа в классической модели без допущения дефицита.

94. Производственная функция с постоянной эластичностью замещения. Понятие, примеры.

95. Дать геометрическую иллюстрацию задачи потребителя и ее решения.

96. Принцип построения межотраслевого баланса.

97. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Пусть А – способ производства, при котором х = 32, y = 243.
Вычислить предельную норму замены труда капиталом при способе А.

98. Функция полезности потребителя от потребления двух видов продукции равна: . Цены на товары равны р₁ = 90 у.е., р₂ = 75 у.е. Записать второй закон Госсена.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 16

99. Задача составления плана производства: решение задачи.

100. Построить функцию затрат в классической задаче управления запасами без допущения дефицита.

101. Предельная и средняя производительности труда производственной функции Кобба-Дугласа.

102. Бюджетная прямая, определение и геометрическая иллюстрация, экономический смысл.

103. Производитель товара и эластичный (неэластичный) спрос на него.

104. Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Доходность кредитов и ценных бумаг равны 20 % и 15 %, соответственно. Пусть х₁ – средства, размещенные в кредитах, х₂ – средства, вложенные в ценные бумаги. Определить максимальный доход от кредитов и ценных бумаг.

105. Зависимости объема предложения товара и спроса на товар от цены р_t имеют вид:
S(p_t ) = 5 + 2p_{t -1}
d(p_t ) = 7 - p_t , соответственно. Полагая р_о =3, найти р₂ .

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 17

106. Область применения экономических моделей.

107. Привести функцию прибыли фирмы в условиях совершенной конкуренции.

108. Эластичность производства.

109. Бюджетное ограничение. Определение и геометрическая иллюстрация.

110. Спрос постоянной эластичности: функциональная зависимость, геометрическая иллюстрация.

111. Имеются два вида продуктов, содержащих питательные вещества А и В. Содержание веществ А и В в 1 кг каждого вида продуктов приведены в таблице:

В ежемесячном рационе должно содержаться веществ А и В не менее 100 и 300 ед., соответственно. Продукты приобретаются по ценам 35 руб./кг и 40 руб./кг. Пусть х = (х₁ , х₂ ) – вектор количеств приобретаемых продуктов. Задача выбора рациона заключается в нахождении вектора х* = (х₁ *, х₂ *), минимизирующего стоимость покупки и обеспечивающего необходимое количество питательных веществ. Какова наименьшая стоимость покупки.

112. Функция полезности потребителя от потребления трех видов продукции имеет вид: . Рассчитать предельную полезность потребителя по третьему продукту при векторе потребления (27, 8, 1).

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 18

113. Задача составления плана производства: экономический смысл равенства нулю некоторой компоненты оптимального вектора выпуска.

114. Построить функцию затрат в классической задаче управления запасами с допущением дефицита.

115. Функция спроса фирмы на ресурсы, построение, свойства, экономический смысл.

116. Функция полезности потребителя.

117. Модель Леонтьева. Постановка задачи, экономическая значимость.

118. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Пусть А – способ производства, при котором х = 32, y = 243.
Вычислить объем производства при способе А.

119. Спрос на товар в зависимости от цены описывается линейной функцией d(p) = -0,3р+60. Рассчитать коэффициент эластичности при р = 1204∙ℓ₀ . Эластичен ли спрос на товар при цене р = 120 у.е.? При какой цене на товар спрос на него характеризуется единичной эластичностью?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 19

120. Предложение фирмы в зависимости от цены р, если фирма выходит на рынок совершенной конкуренции. Дать обоснование, геометрическую иллюстрацию, экономическую зависимость.

121. Условия максимума прибыли, выраженные через предельные продукты.

122. Характеристика производства при отрицательном предельном доходе.

123. Экономический смысл компенсированного изменения цены.

124. Привести расчет дуговой ценовой эластичности.

125. Производственная функция, описывающая выпуск при использовании двух ресурсов (труд х₁ и капитал х₂ ), является функцией Кобба - Дугласа

125. f(x₁ , x₂ ) =. Определить предельную производительность труда при х₁ =27, х₂ =125.

126. Результаты анализа полезности апельсинов приведены в таблице:

Определить предельные полезности по мере увеличения потребления апельсинов.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 20

127. Для задачи фирмы в условиях совершенной конкуренции привести условие максимума прибыли.

128. Привести геометрическую иллюстрацию движения запасов в классической модели управления запасов с допущением дефицита.

129. Понятие и экономический смысл замещения.

130. Привести примеры функции полезности.

131. Матрица затрат в МОБ. Понятие, экономический смысл.

132. Фирма решает задачу обеспечения производства ресурсом. Поставка ресурса происходит мгновенно, спрос на ресурс постоянной интенсивности в 50 ед/день. Условия производства таковы, что допускается дефицит глубины в 200 ед. ресурса. В течении скольких дней производство может испытывать нехватку ресурса? Какова будет глубина дефицита через 10 дней при q = 350 ед.?

133. Полезность потребителя от приобретения трех видов товаров описывается закономерностью U(x₁ ,x₂ ,x₃ ) = 25 x₁ ² x₂ + 10x₂ x₃ + 15x₃ x_1. Рассчитать предельную полезность по третьему товару при приобретении набора товаров в количествах (15, 8, 10).

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 21

134. Сущность экономико-математического моделирования.

135. Привести транспортную задачу в жесткой постановке.

136. Дать геометрическую иллюстрацию предельных и средних кривых дохода, издержек фирмы в условиях совершенной конкуренции.

137. Предельные полезности. Понятие, свойства, экономический смысл.

138. Реакция потребителя на изменение цен при неэластичном спросе.

139. Фирма работает в условиях совершенной конкуренции, для производства использует один ресурс, производственная функция выпуска имеет вид q(x)=x² -100. Цена ресурса 4000 рублей, продажная цена единицы продукта 1000 рублей. Определить объем выпуска, максимизирующий прибыль.

140. Полезность потребителя от приобретения трех видов товаров описывается закономерностью U(x₁ ,x₂ ,x₃ ) = 25 x₁ ² x₂ + 10x₂ x₃ + 15x₃ x_1. Рассчитать предельную полезность по первому товару при приобретении набора товаров в количествах (15, 8, 10).

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 22

141. Этапы принятия решений.

142. Сформулировать цель в транспортной задаче, экономический смысл переменных и ограничений.

143. Дать геометрическую иллюстрацию изоквант линейной производственной функции, производственной функции «затрат-выпуск».

144. Как связаны функция полезности и аксиома ненасыщения?

145. Путь к экономическому общему равновесию по Маршаллу.

146. Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Доходность кредитов и ценных бумаг равны 20 % и 15 %, соответственно. Пусть х₁ – средства, размещенные в кредитах, х₂ – средства, вложенные в ценные бумаги. Определить объем средств, который следует разместить в ценных бумагах с целью получения максимального дохода от кредитов и ценных бумаг.

147. Рассчитать равновесную цену на товар для совокупных функций спроса d(p) = -0,3p+60 и предложения S(p) = 9,7p + 10

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 23

148. Сущность критерия практики.

149. Задача фирмы в условиях конкуренции. Понятие взаимозаменяемых и взаимодополняемых ресурсов.

150. Характеристика производства при превышении среднего дохода предельным.

151. Пространство товаров и отношение предпочтения на пространстве товаров. Понятие, экономический смысл.

152. Привести геометрическую иллюстрацию задачи фирмы и ее решения в условиях совершенной конкуренции.

153. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Пусть А – способ производства, при котором х = 32, y = 243.
Вычислить предельную фондоотдачу при способе А.

154. Спрос на некоторый товар описывается линейной функцией от цены d(p) = - 0,6p + 60. При какой цене коэффициент эластичности равен единице?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 24

155. Задача составления плана производства: ограничения.

156. Постановка транспортной задачи.

157. Геометрическая иллюстрация экономической и особой области, разделяющих линий. Экономический смысл.

158. Компенсированное изменение цены. Понятие, геометрическая иллюстрация.

159. Обобщенная модель Леонтьева.

160. Построить задачу составления плана производства фирмы, производящей два вида продукции, использующей два вида ресурсов и реализующей продукцию по ценам 450 рублей и 400 рублей соответственно. Технологическая матрица задана в виде таблицы

Фирма располагает 4000 ед. ресурсов №1 и 2300 ед. ресурс №2.

161. Функция полезности потребителя от потребления двух видов продукции равна: . Для приобретения товаров выделено 1800 у.е. Цены на товары равны р₁ = 90 у.е., р₂ = 75 у.е. Чему равен спрос на второй продукт, предъявляемый потребителем?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 25

162. Задача составления плана производства: экономический смысл строгой положительности оценки некоторого ресурса.

163. Построение модели найма, увольнения и обучения рабочих.

164. Понятие эластичности замещения.

165. Функции спроса потребителя. Определение, свойства.

166. Магистральная модель накопления. Общая постановка.

167. Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Пусть х₁ – средства, размещенные в кредитах, х₂ – средства, вложенные в ценные бумаги. Изобразить геометрически область допустимых планов.

168. Функция полезности потребителя от потребления двух видов продукции равна: . Для приобретения товаров выделено 1800 у.е. Цены на товары равны р₁ = 90 у.е., р₂ = 75 у.е. Решить задачу потребителя.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 26

169. В линейной модели производства дать экономический смысл ограничений двойственной задачи.

170. Что решают задачи управления запасами?

171. Производственная функция. Определение, экономическое содержание.

172. Кривые безразличия. Понятие, геометрическая иллюстрация, экономический смысл.

173. Кривые спроса и предложения на товар в зависимости от цены на этот товар,

174. Имеются два вида продуктов, содержащих питательные вещества А и В. Содержание веществ А и В в 1 кг каждого вида продуктов приведены в таблице:

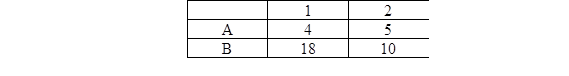
В ежемесячном рационе должно содержаться веществ А и В не менее 100 и 300 ед., соответственно. Продукты приобретаются по ценам 35 руб./кг и 40 руб./кг. Пусть х = (х₁ , х₂ ) – вектор количеств приобретаемых продуктов. Задача выбора рациона заключается в нахождении вектора х* = (х₁ *, х₂ *), минимизирующего стоимость покупки и обеспечивающего необходимое количество питательных веществ. Найти вектор х*.

175. Функция полезности потребителя от приобретения двух товаров имеет вид
U(x₁ ,x₂ ) = 100x₁ + 120x₂ . Каков уровень полезности при объемах покупок (10, 20). Какова предельная норма замены второго товара первым при снижении потребления второго товара на единицу?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 27

176. Основные экономические институты.

177. Классическая модель наиболее экономичного размера партии.

178. Кривые среднего и предельного продукта. Способ расчета, геометрическая иллюстрация.

179. Эластичность спроса на товар по отношению к доходу потребителя. Способ расчета, экономический смысл.

180. Реакция потребителя на изменение цен при эластичном спросе.

181. Производственный процесс описывается с помощью производственной функции типа Кобба-Дугласа: f(x, y) = 125 ´ x^0,8 ´ y^0,4 , где х – капитал, y – труд.
Пусть А – способ производства, при котором х = 32, y = 243.
Вычислить предельную норму замены капитала трудом при способе А.

182. Функция полезности потребителя от потребления двух видов продукции равна: . Для приобретения товаров выделено 1800 у.е. Цены на товары равны р₁ = 90 у.е., р₂ = 75 у.е. Записать задачу потребителя.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 28

183. Записать задачу составления плана производства как задачу линейного программирования.

184. Издержки, учитывающиеся в задачах управления запасами.

185. Характер изменения производственной функции при расширении масштабов производства.

186. Первый закон Госсена: закон убывающей полезности. Формулировка в терминах функции полезности и экономический смысл.

187. Основные элементы межотраслевого баланса.

188. Имеются два вида продуктов, содержащих питательные вещества А и В. Содержание веществ А и В в 1 кг каждого вида продуктов приведены в таблице:

В ежемесячном рационе должно содержаться веществ А и В не менее 100 и 300 ед., соответственно. Продукты приобретаются по ценам 35 руб./кг и 40 руб./кг. Пусть х = (х₁ , х₂ ) – вектор количеств приобретаемых продуктов. Задача выбора рациона заключается в нахождении вектора х* = (х₁ *, х₂ *), минимизирующего стоимость покупки и обеспечивающего необходимое количество питательных веществ. В чем состоит экономический смысл двойственных переменных? (Ответ обосновать).

189. Рассчитать коэффициент эластичности спроса по цене при цене р = 10 рублей, если функция спроса имеет вид d(p)= 420 - 30p.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 29

190. Классификация экономических моделей.

191. Привести геометрическую иллюстрацию движения запасов при мгновенном поступлении заказа и постоянном спросе на него.

192. Экономическая область в пространстве затрат.

193. Уравнение Слуцкого.

194. Область применения паутинообразной модели.

195. Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Доходность кредитов и ценных бумаг равны 20 % и 15 %, соответственно. Пусть х₁ – средства, размещенные в кредитах, х₂ – средства, вложенные в ценные бумаги. Какой объем средств следует разместить в кредитах, чтобы получить максимальный доход от кредитов и ценных бумаг?

196. Функция полезности потребителя от потребления двух видов продукции линейна. Полезности потребления единицы каждого вида продукции равны, соответственно, 10 ед. и 25 ед. полезности. Товары приобретаются по ценам 50 у.е. и 70 у.е., бюджет потребителя составляет 2000 у.е. Сформулировать задачу потребителя.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 30

197. Изокоста. Понятие. Экономический смысл, геометрическая иллюстрация в случае двух ресурсов.

198. Описать и дать геометрическую иллюстрацию зависимости издержек хранения запасов от размера заказа в основной модели управления запасами.

199. Предельная и средняя фондоотдача производственной функции Кобба-Дугласа.

200. Функция Лагранжа для задачи потребителя.

201. Понятие магистрали в динамических моделях макроэкономики.

202. Фирма работает в условиях совершенной конкуренции; выпускает один вид продукции, используя для этого два вида ресурсов. Продукция реализуется по цене р = 580 у.е., ресурсы приобретаются по ценам w₁ = 30 у.е., w₂ = 45 у.е., соответственно. Производственная функция фирмы f(x₁ , x₂ ) = 15 x₁ ×x₂ , где х = (х₁ , х₂ ) – вектор количеств ресурсов. Построить изокосту , если на приобретение ресурсов выделено 30000 у.е. Построить изокванту f(x₁ , x₂ ) = 4500 у. е. (решение изобразить графически).

203. Результаты анализа полезности пирожных приведены в таблице:

На сколько единиц возрастает полезность от потребления второго пирожного, третьего, четвертого?

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 31

204. Кривая предельного дохода фирмы в условиях совершенной конкуренции. Дать обоснование и геометрическую иллюстрацию.

205. Проиллюстрировать геометрически движение запасов в классической модели с допущением дефицита.

206. Связь эластичности производства и эластичностей выпуска по отношению к изменению затрат.

207. Функции спроса при компенсированном изменении цены.

208. Индивидуальный и рыночный спрос.

209. Имеются два вида продуктов, содержащих питательные вещества А и В. Содержание веществ А и В в 1 кг каждого вида продуктов приведены в таблице:

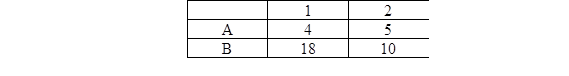
В ежемесячном рационе должно содержаться веществ А и В не менее 100 и 300 ед., соответственно. Продукты приобретаются по ценам 35 руб./кг и 40 руб./кг. Пусть х = (х₁ , х₂ ) – вектор количеств приобретаемых продуктов. Задача выбора рациона заключается в нахождении вектора х* = (х₁ *, х₂ *), минимизирующего стоимость покупки и обеспечивающего необходимое количество питательных веществ. Найти решение двойственной задачи.

210. Определить равновесную цену товара, если спрос на него описывается законом
d(p) = - 1/2500 p + 20, а предложение s(p) = 1/500p – 10.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 32

211. Обязательные элементы математической модели.

212. Формула Уилсона, экономический смысл и значимость.

213. Понятие предельного продукта.

214. Потребитель и пространство товаров.

215. Матрица коэффициентов прямых затрат. Продуктивность матрицы А: понятие, экономический смысл.

216. Собственные средства банка в сумме с депозитами составляют 200 млн. руб. Часть этих средств, но не менее 30 млн. руб. должна быть размещена в кредитах, не менее 35 % средств, размещенных в кредитах и ценных бумагах, составляют ценные бумаги. Доходность кредитов и ценных бумаг равны 20 % и 15 %, соответственно. Пусть х₁ – средства, размещенные в кредитах, х₂ – средства, вложенные в ценные бумаги. Записать математическую модель.

217. Для приобретения двух товаров потребитель выделил 2000 у.е. Цены на товары равны р₁ = 100 у.е., р₂ = 50 у.е. Изобразить геометрически бюджетное множество.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 33

218. Задача составления плана производства: экономический смысл двойственных переменных.

219. Классическая модель управления запасами с дискретным спросом.

220. Экономические свойства производственной функции Кобба-Дугласа.

221. Понятие компенсированного изменения цены в задаче потребителя.

222. Дать в общем виде постановку модели функционирования рынка.

223. Имеются два вида продуктов, содержащих питательные вещества А и В. Содержание веществ А и В в 1 кг каждого вида продуктов приведены в таблице:

В ежемесячном рационе должно содержаться веществ А и В не менее 100 и 300 ед., соответственно. Продукты приобретаются по ценам 35 руб./кг и 40 руб./кг. Пусть х = (х₁ , х₂ ) – вектор количеств приобретаемых продуктов. Задача выбора рациона заключается в нахождении вектора х* = (х₁ *, х₂ *), минимизирующего стоимость покупки и обеспечивающего необходимое количество питательных веществ. Какие количества питательных веществ А и В содержатся в покупке х* = (х₁ *, х₂ *)?

224. Исследовался спрос на товар в зависимости от цены двух групп потребителей. Функции спроса, предъявляемые каждой группой, имеют вид: d₁ (p) = - 0,3p + 60, 0 £ p £ 200 и
d₂ (p) = - 0,5p + 50, 0 £ p £ 100. Построить функцию совокупного спроса. Решение проиллюстрировать геометрически.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 34

225. Задача составления плана производства: экономический смысл нулевой оценки некоторого ресурса.

226. Определение оптимального размера заказа в классической модели с допущением дефицита.

227. Свойства функции предложения фирмы в условиях совершенной конкуренции.

228. Привести аксиому ненасыщения и ее экономический смысл.

229. Ценные и малоценные товары.

230. Фирма решает задачу обеспечения производства сырьем. Поставка сырья происходит со скоростью 200 ед/день, спрос на сырье непрерывен, с постоянной интенсивностью 100 ед/день. Перебои не допускаются (I_o = 0). Затраты на доставку партии сырья равны 1000 у.е. На хранение единицы сырья в единицу времени 0,5 у.е. Построить график движения уровня запаса при q = 2000 ед. В течение скольких дней будет поступать заказ?

231. Функция полезности потребителя от потребления двух видов продукции линейна. Полезности потребления единицы каждого вида продукции равны, соответственно, 10 ед. и 25 ед. полезности. Построить кривую безразличия, соответствующую наборам товаров, приносящих полезность в 750 ед.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ СИСТЕМ

Билет № 35

232. Задача составления плана производства: экономический смысл точного равенства в ограничении на оптимальном плане.

233. Издержки выполнения заказа в задачах управления запасами.

234. Дать геометрическую иллюстрацию изоквант производственной функции Кобба-Дугласа.

235. Что означает отношение безразличия для наборов товаров?

236. Взаимозаменяемые и взаимодополняемые товары.

237. Производственная функция, описывающая выпуск при использовании двух ресурсов, имеет вид f(x₁ , x₂ ) = 50x₁ +40x₂ . Определить эластичность выпуска по второму ресурсу про х₁ =10, х₂ =25.

238. Функция полезности потребителя от потребления двух видов продукции равна: . Для приобретения товаров выделено 2000 у.е. Цены на товары равны р₁ = 100 у.е., р₂ = 85 у.е. Каков уровень полезности потребителя при покупке х = (10, 12)? Может ли потребитель достигнуть данного уровня полезности?

Зав. кафедрой

--------------------------------------------------