| Похожие рефераты | Скачать .docx |
Дипломная работа: Измерения геометрических величин в курсе геометрии 7-9 классов
Оглавление
Введение
Глава 1. Психолого-педагогические и научно-методические основы изучения измерений геометрических величин в школе
§1. Практическая деятельность учащихся при изучении геометрии
§2. Этапы изучения измерений геометрических величин в школьном курсе математики
§3. Сравнительный анализ учебных пособий по геометрии для 7 – 9 классов
3.1 Учебник геометрии 7 – 9 (авторы Атанасян Л.С. и др.)
3.2 Учебник геометрии 7 – 11 (авторы Погорелов А.В. и др.)
3.3 Учебник геометрии 7 – 9 (авторы Шарыгин И.Ф. и др.)
3.4 Учебник геометрии 7 – 9 (авторы Смирнова И. М., Смирнов В.А.)
3.5 Учебники геометрии 7, 8 – 9 (авторы Александров А.Д. и др.)
§4. Измерительные инструменты в школе
4.1 Измерительные инструменты для измерения длин отрезков
4.2 Приборы для переноса измеряемого размера с объекта на линейку
4.3 Инструменты, с помощью которых можно измерить градусную меру угла
4.4 Инструменты для измерения площадей
§5. Различные направления использования измерений геометрических величин при обучении геометрии
5.1 Типология задач на измерения
5.1.1 Задачи на непосредственные измерения
5.1.2 Задачи на косвенные измерения
5.1.3 Задачи, в которых до методов косвенного измерения, применяются непосредственные измерения
5.1.4 Задачи на измерение геометрических величин средствами информационных технологий
5.2 Использование измерений геометрических величин на разных этапах урока геометрии
Глава 2. Измерения геометрических величин в курсе геометрии 7 – 9 классов
§1. Примеры использования измерений в обучении геометрии
1.1 Использование измерений при введении новой темы
1.1.1 Сумма углов треугольника
1.1.2 Площадь трапеции
1.1.3 Длина окружности
1.1.4 Теорема Пифагора
1.2 Использование измерений при решении задач
1.3 Использование измерений для опровержения каких-либо утверждений
1.4 Измерения, подчеркивающие практическую значимость геометрии
§2. Рекомендации по реализации основных направлений использования измерений в школьном курсе геометрии
§3. Элективный курс «Измерение расстояний на местности»
Заключение
Библиография
Введение
Выбор темы дипломной работы «Измерения геометрических величин в курсе геометрии 7 – 9 классов» обусловлен следующими факторами: идейно-содержательная линия «Измерения геометрических величин» входит в состав геометрической линии школьного курса математики и изучается с 5 по 11 класс.
Эта линия как бы пронизывает весь математический материал, изучаемый в школе.
Само слово «геометрия» в переводе с греческого означает «землемерие». С древних времен люди сталкивались с необходимостью находить расстояния между предметами, определять размеры участков земли, ориентироваться по расположению звезд на небе и т.п. Таким образом, зарождение геометрии было связано с различными измерительными работами, которые приходилось выполнять при разметке земельных участков, проведении дорог. При строительстве различных сооружений необходимо было рассчитывать, сколько материала пойдет на постройку, вычислять расстояния между точками, измерять углы между прямыми и др. В результате этой деятельности появились и постепенно накапливались различные правила, связанные с геометрическими измерениями и построениями. Таким образом, геометрия возникла на основе практической деятельности людей. До сих пор мы используем умения, связанные с измерением геометрических величин в повседневной жизни и профессиональной деятельности. Поэтому важной составляющей обучения геометрии является обучение использованию измерительных инструментов на практике.
При этом измерения могут оказать значительную помощь в изучении остальных тем геометрии и достижении целей обучения математике в школе. Без знания разнообразных измерительных инструментов, геометрических величин и без умения производить измерения этих величин обучение геометрии становится невозможным.
А в связи с тем, что в настоящее время возникает острая нехватка профессиональных инженеров, технических специалистов и руководителей среднего звена на производстве, вопрос об обучении школьников умениям, связанных с измерениями геометрических величин, занимает одно из первых мест.
Целью дипломной работы является выявление возможностей использования измерений геометрических величин при изучении различных тем курса геометрии 7 – 9 классов.
При достижении цели работы потребовалось решение следующих задач:
- изучение психологической и учебно-методической литературы по теме;
- анализ измерительных инструментов для школ
- проведение классификации измерений геометрических величин
- разработка методических рекомендаций для реализации основных дидактических функций на уроке математики с использованием измерений;
- разработка элективного курса «Измерение расстояний на местности».
Дипломная работа состоит из введения, двух глав, заключения, приложения и списка литературы, состоящего из 33 источников.
Первая глава работы содержит пять параграфов.
В первом параграфе рассматривается необходимость использования практической деятельности учащихся на уроках геометрии, а также принципы обучения, которые необходимо соблюдать и при организации практической деятельности учащихся.
Во втором – мы выделили этапы изучения измерений в школьном курсе геометрии.
Далее представлен анализ школьных учебников геометрии, различных подходов к введению определений геометрических величин, рассматриваемых авторами измерительных инструментов. Анализ содержания предлагаемого для изучения материала проводился по четырем вопросам: понятие измерения геометрической величины; измерение геометрических величин; вычисление геометрических величин; применение измерений геометрических величин на практике.
Четвертый параграф посвящен описанию различных измерительных инструментов, используемых в школе, и инструментов, которые полезно изучить в школе.
В пятом параграфе мы рассматриваем различные направления использования измерений при обучении геометрии.
Вторая глава отведена на различные примеры использования измерений при изучении различных тем геометрии, методических рекомендаций к урокам, а также описанию элективного курса «Измерение расстояний».
В заключении представлены основные выводы о работе. В приложении – краткий сравнительный анализ глубины и последовательности изучения отдельных содержательных вопросов измерения геометрических величин в школьных учебниках геометрии для 7 – 9 классов.
Глава 1. Психолого-педагогические и научно-методические основы изучения измерений в школе
§1. Практическая деятельность учащихся при изучении геометрии
Источником знания является практическая деятельность учащихся. Она обеспечивает не только закрепление и применение знаний, но и формирует опыт, умения, служит интеллектуальному, физическому и нравственному развитию.
Как если ни на практике повар узнает вкус той еды, которую он готовит; как если ни на практике инженеры проверят свои изобретения на работоспособность, - практическая деятельность важна не только в процессе обучения, но и в жизни каждого. С самого рождения человек познает окружающий его мир с помощью практической деятельности – он пробует сидеть, ходить, говорить… Ведь именно на практике ребенок узнает свои возможности, способности, узнает о совершенных ошибках и исправляет их. При изучении геометрии эта деятельность также важна.
Именно на практике школьнику выдается возможность прочувствовать всю красоту геометрии: это и связь с другими дисциплинами, и возможность применения ее в повседневной жизни, и разнообразие геометрических фигур, и интереснейшая история ее развития и многое другое.
Практическая деятельность школьников играет немалую роль при достижении целей изучения математики. Достижение образовательной цели: в процессе практической деятельности возрастает степень понимания учебного материала. Ученик, проделывая какую-либо работу, обдумывает каждое свое действие, усваивая при этом теоретический материал, связанный с выполняемым заданием. Также практическая деятельность способствует выполнению воспитательной и развивающей функций: ученики внимательнее относятся к выполнению заданий, развивается ответственность за свои действия, самостоятельность, аккуратность. Активизация практической деятельности позволит не только заинтересовать учащихся, но и проявить себя с лучшей стороны. Нередко ученик, который не может похвастаться своими теоретическими знаниями, на практике добивается успехов, при этом он может и не понимать того, что он все равно использует теорию. Достижение хороших результатов поднимает и самооценку школьников, появляется стремление к совершенствованию своих умений и навыков. В литературе [24] отмечается, что зачастую практическая деятельность связана с выполнением лабораторных работ, упражнений, исследованием, творческой деятельностью, что предполагает: положительную мотивационную активность; направленность и целеустремленность; высокий уровень интеллектуального развития; оригинальное мышление; развитие воображения и фантазии, самостоятельности и способности самооценки. Практическая деятельность помогает развивать познавательные интересы учащихся. У учителя в то же время есть возможность осуществить дифференциальный и индивидуальный подход к учащимся, в зависимости от темпа их работы, - выполнение контрольно – оценочной функции. Также практическая деятельность способствует развитию мотивации школьников к изучению геометрии [9].
Любой учебный материал по геометрии имеет практическую направленность. Например, третий признак равенства треугольников является теоретической основой «жесткости» треугольника, что широко используется при конструкции мостов, подъемных кранов и т.п. [29]. Поэтому для показа ученикам важности геометрии в повседневной жизни ученикам необходимо не просто рассказать об этих возможностях, но и показать, в каких именно областях знаний помогает эта наука, дать ученикам самим попробовать применить свои знания на практике. Занятия по геометрии должны сопровождаться практическими работами с привлечением всех учащихся. Это могут быть все виды моделирования, различные землемерные работы, лабораторные работы и т.д.
Несомненно, при организации практической деятельности учеников нельзя забывать об основных принципах обучения. В методической литературе по математике общепризнанной является следующая система дидактических принципов [14]:
1. Принцип воспитания в обучении математике. Практическая деятельность, как уже было сказано, способствует достижению воспитательных целей. Воспитание мировоззрения и морали способствует формированию характера каждого школьника. Чтобы учащийся мог действовать в соответствии с принципами мировоззрения и морали, он должен сформировать у себя такие черты характера, как принципиальность, сила воли, скромность, честность по отношению к самому себе и другим людям. Мировоззрение, базирующееся на научном знании и практическом жизненном опыте, связывает в единое целое эти свойства личности. Отсюда вытекают возможность и необходимость передачи всем людям знаний о закономерностях развития природы, общества и человеческого мышления, чтобы они могли сознательно осуществлять деятельность, направленную на построение общества.
2. Принцип научности в обучении математике. Одним из аспектов реализации принципа научности в обучении является выработка у учащихся учебно-исследовательских навыков и умений, что невозможно без практической деятельности школьников.
3. Принцип сознательности, активности и самостоятельности в обучении математике. Данный принцип заключается в целенаправленном активном восприятии изучаемых явлений, их осмыслении, творческой переработке и применении. Где же еще, как ни на практике у ученика есть возможность проявить свои знания, попробовать свои силы в решении задач.
4. Принцип доступности в обучении математике. Принцип доступности в обучении вытекает из требований учета возрастных особенностей учащихся. Он лежит в основе составления учебных планов и программ. Принцип доступности требует, чтобы объем и содержание учебного материала были по силам учащимся, соответствовали уровню их умственного развития и имеющемуся запасу знаний, умений и навыков. Ведь если перед учеником стоит задача, которую он не может решить из-за недостатка каких-либо знаний, то вскоре у него пропадает интерес к решению этой задачи и вообще к изучаемой теме и предмету.
5. Принцип наглядности в обучении математике. В обучении геометрии этот принцип очень важен, так как в геометрии присутствует множество фигур, теорем и др., которые требуют демонстрации для прочного усвоения их свойств и формулировок. Например, при изучении многогранников демонстрация и самостоятельное моделирование этих фигур способствуют развитию пространственного мышления, понимаю свойств моделируемого объекта.
6. Принцип индивидуального подхода к учащимся в обучении математике. Соблюдение этого принципа эффективно при использовании практических заданий на уроках геометрии. У учителя появляется возможность осуществить индивидуальный и дифференцированный подход в обучении. В зависимости от качества и скорости выполнения заданий преподаватель уделяет время каждому школьнику отдельно: объясняет процесс решения задачи, помогает в решении возникших проблем, обеспечивает дополнительными заданиями, более сложными или легкими, в зависимости от того «сильный» ученик или «слабый».
Практическая деятельность школьника обеспечивает вовлечение его в учебный процесс, достижение целей обучения математики и соблюдение основных дидактических принципов обучения. В обучении геометрии это очень важно. Где, если ни на геометрии учащиеся встречаются с формами, которые их окружают: квадраты, окружности, параллелепипеды и др. И именно на геометрии они учатся измерять, вычислять геометрические величины: площади, объемы и др. Поэтому очень важно чтобы весь процесс обучения геометрии сопровождался практической деятельностью учеников.
§2. Этапы изучения измерений геометрических величин в школьном курсе математики
Показ учащимся приложения математики к решению жизненно важных задач способствует повышению у них интереса к обучению, возбуждает творческую активность и самостоятельность в работе.
Одним из важных звеньев процесса обучения в школе является приобретение учащимися знаний, умений и навыков в измерении геометрических величин. В содержании Стандарта основного общего образования по математике [28] уделяется время измерению геометрических величин. А именно, туда относят следующие понятия: длина отрезка, длина ломаной, периметр многоугольника, расстояние от точки до прямой, расстояние между параллельными прямыми, длина окружности, число π; длина дуги, величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности, понятие о площади плоских фигур, площадь параллелограмма, треугольника и трапеции (основные формулы), формулы, выражающие площадь треугольника: через две стороны и угол между ними, через периметр и радиус вписанной окружности, формула Герона, площадь четырехугольника, площадь круга и площадь сектора, связь между площадями подобных фигур, объем тела, формулы объема прямоугольного параллелепипеда, куба, шара, цилиндра и конуса. Идейно-содержательная линия «Измерение геометрических величин» входит в состав геометрической линии школьного курса математики и изучается с 5 по 11 класс. В объяснительной записке и в тексте Программы [22] по математике говорится, что учащиеся в процессе обучения геометрии должны:
уметь:
- распознавать на чертежах и моделях пространственные формы: соотносить трехмерные объекты с их описаниями, изображениями;
- описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
- анализировать в простейших случаях взаимное расположение объектов в пространстве;
- изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
- строить простейшие сечения куба, призмы, пирамиды;
- решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
- использовать при решении стереометрических задач планиметрические факты и методы;
- проводить доказательные рассуждения в ходе решения задач;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
- исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
- вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Рассмотрим, какое место отводят авторы современных учебников по геометрии измерениям и измерительным приборам в своих книгах, и какие этапы изучения измерений в школе можно выделить.
Этапы изучения измерений в школе: пропедевтический курс (1-6 классы), основная школа (7-9 классы), старшая школа (10-11 классы).
В пропедевтическом курсе, который охватывает начальную школу и младшие классы среднего звена, учащиеся знакомятся с различными геометрическими фигурами, приобретают начальные навыки изображения этих фигур с помощью линейки, циркуля, угольника. С процессом измерения учащиеся знакомятся на наглядно-интуитивном уровне. Школьники приобретают опыт непосредственного измерения, нахождения и сравнения длины отрезка, площадей плоских фигур, а также знакомятся с различными единицами измерения и переводом из одних единиц измерения в другие. На этом же этапе учащимся приводятся формулы для косвенного измерения периметра многоугольника, площадей плоских фигур (квадрата, прямоугольника).
На втором этапе изучается большое число теоретических фактов, с помощью которых проводится косвенное измерение геометрических величин. Переходя к этому этапу необходимо мотивировать переход от непосредственного к косвенному измерению. Для этого полезно вспомнить об инструментах, с помощью которых измеряются длины отрезков (линейка), углы (транспортир) и др. Также на этом этапе изучается большинство теорем, позволяющих производить косвенные измерения геометрических величин (длин отрезков, углов, площадей).
В старшей школе от измерений длин отрезков, углов, площадей переходят к измерению объемов геометрических тел, применяя при этом знания начал математического анализа.
Для того, чтобы ответить на вопрос о месте измерений в курсе геометрии, проведем сравнительный анализ учебников по геометрии, используемых в школе.
§3. Сравнительный анализ учебных пособий по геометрии для 7 – 9 классов
Проведем сравнительный анализ как теоретического материала, так и задачного. Анализ содержания предлагаемого для изучения материала проведем по четырем вопросам:
- понятие измерения геометрической величины;
- измерение геометрических величин;
- вычисление геометрических величин;
- применение измерений геометрических величин на практике.
Выбраны именно такие аспекты, так как именно они охватывают всю теорию измерений. Первый аспект – понятие измерения геометрической величины, подразумевает ответ на вопрос о том, дается ли в учебнике определение понятия длины отрезка, градусной или радианной меры угла, понятия площади плоской фигуры. Измерение и вычисление геометрических величин подразумевают непосредственное (прямое) и опосредованное (косвенное) измерение длин отрезков, углов, площадей соответственно. Непосредственное измерение связано с применением измерительных приборов, а косвенное – с использованием формул. Последний аспект охватывает область применения измерений геометрических величин на практике, то есть использование измерений при решении практико-ориентированных задач, доказательстве теорем.
Для анализа были выбраны учебники геометрии, рекомендованные (допущенные) Министерством Образования и Науки Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2008/2009 учебный год [30]. Это такие учебники как Атанасян Л.С. и др. Геометрия 7- 9 [7]; Погорелов А.В. Геометрия 7 – 9 [20]; Шарыгин И.Ф. Геометрия 7 – 9 [31]; Смирнова И.М. и др. Геометрия 7 – 9 [26] (учебники, рекомендованные Министерством Образования и Науки РФ); Александров А.Д. и др. Геометрия 7, 8 – 9 [1, 2] (учебники, допущенные Министерством Образования и Науки РФ Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2008/2009 учебный год).
3.1 Учебник геометрии 7 – 9 (авторы Атанасян Л.С. и др.) [7]
В первой главе рассматриваются простейшие геометрические фигуры – точка, прямая, отрезок, луч, вопрос сравнения и измерения отрезков и углов. Введение основных понятий опирается на наглядные представления и на тот опыт, который накоплен учащимися при изучении математики в 1 – 6 классах.
Прежде, чем вводить понятие длины отрезка, авторы рассматривают решение задачи: с помощью данной линейки построить отрезок более длинный, чем сама линейка.
Авторы также поясняют, что для проведения длинных отрезков, прямых на местности, используется прием, который называется провешиванием прямой. Он широко используется на практике, например, при рубке лесных просек, при прокладывании трассы шоссейной или железной дороги, линий высоковольтных передач и т.д.
На практике часто приходится не только строить различные отрезки, но и измерять их, то есть находить их длины. Измерение отрезков основано на сравнении их с некоторым отрезком, принятым за единицу измерения (его также называют масштабным отрезком). Если, например, за единицу измерения принят сантиметр, то для определения длины отрезка узнают, сколько раз в этом отрезке укладывается сантиметр. Может оказаться так, что отрезок, принятый за единицу измерения, не укладывается целое число раз в измеряемом отрезке – получается остаток. Тогда единицу измерения делят на равные части, обычно на 10 равных частей, и определяют, сколько раз одна такая часть укладывается в остатке.
За единицу измерения можно принимать не только сантиметр, но и любой другой отрезок. Выбрав единицу измерения, можно измерить любой отрезок, то есть выразить его длину некоторым положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в измеряемом отрезке.
После этого в тексте учебника выделяются некоторые свойства длин отрезков: если два отрезка равны, то единица измерения и ее части укладываются в этих отрезках одинаковое число раз, то есть равные отрезки имеют равные длины. Если же один отрезок меньше другого, то единица измерения (или ее части) укладываются в этом отрезке меньшее число раз, чем в другом, то есть меньший отрезок имеет меньшую длину. Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков. Длина отрезка называется также расстоянием между концами этого отрезка.
Также авторы рассказывают о единицах измерения и измерительных инструментах, применяемых при измерении отрезков. Для измерения отрезков и нахождения расстояний на практике используют различные единицы измерения. В учебнике упоминается о таких единицах измерения как метр, сантиметр, миллиметр, дециметр, километр, морская миля, световой год, аршин, сажень.
Измерительные приборы, рассматриваемые в учебнике: масштабная миллиметровая линейка, используемая в техническом черчении; штангенциркуль – для измерения диаметра трубки; рулетка – для измерения расстояний на местности.
Измерение углов вводится аналогично измерению отрезков, основано на сравнении их с углом, принятым за единицу измерения. В параграфах «Измерение углов на местности» и «Построение прямых углов на местности» рассказывается о специальных приборах, предназначенных для измерения углов. Так, например, одним из таких приборов является астролябия. «Она состоит из двух частей: диска, разделенного на градусы, и вращающейся вокруг центра диска линейки (алидады). На концах алидады находятся два узких окошечка, которые используются для установки ее в определенном направлении».
Для построения прямых углов на местности также применяют специальные приборы, простейшим из которых является эккер. «Эккер представляет собой два бруска, расположенных под прямым углом и укрепленных на треножнике. На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны. Чтобы построить на местности прямой угол с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О; а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставлены на луче. Затем провешивают прямую линию по направлению другого бруска. Получается прямой угол АОВ.
В геодезии для построения прямых углов используют более современные приборы, например теодолит». Затем в учебнике уже при изучении признаков параллельных прямых рассматриваются способы построения параллельных прямых, также с использованием различных чертежных и измерительных инструментов. И уже в конце седьмого класса упоминается такой инструмент как уголковый отражатель и способы его применения, но данная тема не является обязательной.
Изучение геометрии в 8 классе начинается с рассмотрения понятия многоугольника и различных видов многоугольников и их свойств. Затем переходят к изучению темы «Площадь многоугольника». Измерение площадей проводится с помощью выбранной единицы измерения аналогично измерению отрезков. За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Так, если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной 1 см. Такой квадрат называется квадратным сантиметром и обозначается см2 . Аналогично определяется квадратный метр, квадратный миллиметр и т.д. [12].
При выбранной единице измерения площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в данном многоугольнике. Далее выводятся различные формулы для нахождения площади того или иного многоугольника. Но как можно заметить на непосредственное измерение площади времени не отводится, в учебнике также не рассматриваются приборы, предназначенные для измерения площади фигур.
Далее изучаются понятие подобия фигур, признаки подобия треугольников и рассматриваются практические приложения подобия треугольников: задачи на построение, измерительные работы на местности. Свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности. В учебнике рассматриваются две задачи: определение высоты предмета и расстояния до недоступной точки.
Затем уже в девятом классе вновь упоминается об измерительных работах на местности с использованием тригонометрических формул. И изучаются понятия длины окружности и площади круга.
Чтобы получить наглядное представление о длине окружности, представим себе, что окружность сделана из тонкой нерастяжимой нити. Если мы разрежем нить в какой-нибудь точке А и распрямим ее, то получим отрезок АА1 , длина которого и есть длина окружности (рис. 1).

Рис. 1
Затем выводится формула для вычисления длины окружности, длины дуги. Аналогично проводится изучение и площади круга, кругового сектора.
Авторы уделяют время на изучение нового понятия объема геометрического тела.
Итак, определения длины отрезка, градусной меры угла, площади, реализуемые в учебнике являются описательными [8], то есть перечисляются лишь основные свойства нового понятия [6]. Что касается задачного материала, предлагаемых в учебнике, то на непосредственное измерение приводится небольшое количество задач; на косвенное измерение геометрических величин отводится достаточное количество времени, так как научить школьников правильно измерять эти величины очень важно. Эти умения учащимся пригодятся и в дальнейшем изучении геометрии, физики, черчении, и в их повседневной жизни, и в будущей профессии. Содержание материала учебника отвечает требованиям стандарта.
3.2 Учебник геометрии 7 – 11 (авторы Погорелов А.В. и др.)
Рассмотрим теперь еще один учебник, предназначенный для обучения геометрии в российских школах: учебник геометрии 7 – 11 (авторы Погорелов А.В. и др) [20].
Учебник Погорелова А.В. также как и учебник Атанасяна Л.С. и др. начинается с изучения простейших геометрических фигур: точка, прямая, отрезок, угол, - и их свойств. Измерению отрезков уделяется меньше внимания, чем в уже рассмотренном учебнике, – авторы не дают определения длины, а вводят это понятие с помощью свойств измерения отрезков; не рассматривается задача о построении отрезка, длина которого будет больше, чем длина линейки, также не рассматриваются приборы, предназначенные для измерения длин отрезков и углов. В отличие от учебника Атанасяна Л.С. и др., в рассматриваемом учебнике нет ни одной задачи на непосредственное измерение длин отрезков и углов.
Затем автор подчеркивает, что углы измеряются в градусах при помощи транспортира. Вводятся основные свойства измерения углов.
Определение понятия площади вводится аксиоматически, то есть понятие задается через выполнение определенных свойств. Метрические свойства окружности традиционно связываются с изучением правильных многоугольников, вписанных в окружность или описанных около нее [16].
К применению измерений в изучении геометрии вновь автор обращается лишь при изучении тем «Соотношение между сторонами и углами в прямоугольном треугольнике» и «Решение треугольников».
Таким образом, автор не делает акцент на практической направленности геометрии.
3.3 Учебник геометрии 7 – 9 (авторы Шарыгин И.Ф. и др.)
Шарыгин И.Ф. [31] уже в начале книги указывает на то, что любое геометрическое тело имеет три измерения: длина, ширина, высота.
При изучении понятия отрезка подразумевается, что о понятии длины отрезка, единицах длины школьники уже знают. Отмечены лишь некоторые свойства:
- длина отрезка выражается положительным числом;
- два отрезка являются равными, если они имеют равную длину и др.
Поясняется, каким образом мы можем построить равные отрезки. Также небольшое внимание уделяется и измерению углов. Автор напоминает, что с этой мерой углов ученики уже знакомы, поэтому это понятие больше не вводится.
Простейшим инструментом измерения градусной меры угла служит транспортир. Также подробно описывается, как именно использовать этот измерительный инструмент. Совместив вершину угла с точкой О на транспортире и направив одну из его сторон по прямолинейной границе транспортира, мы увидим значение величины угла в точке пересечения его второй стороны со шкалой, указанной на транспортире. При этом подчеркивается, что каждому углу соответствует его единственная градусная мера. Рассмотрим какой-нибудь угол. Пусть одна его сторона неподвижна, а другая вращается вокруг вершины. Будем считать, что в начальном положении стороны угла совпадают, что соответствует углу 0° , а в конечном положении стороны образуют развернутый угол, величина которого равна 180° . Тогда любой угол, величина которого равна заданному числу градусов, при этом вращении появится лишь однажды.
Затем уже только в восьмом классе вводятся теоремы об измерении вписанного угла, угла с вершиной внутри и вне круга, угла между касательной и хордой. Заметим, что эти измерения являются косвенными, и в теоремах выводятся формулы, с помощью которых можно отыскать градусную меру упомянутых углов.
При изучении геометрии в девятом классе вводится понятие площади следующим образом: площадь – это некоторая характеристика геометрической фигуры, расположенной на плоскости или иной поверхности. Также приводятся свойства площади, аналогичные свойствам длины отрезка и градусной меры углов.
Таким образом, в учебнике Геометрия 7-9, Шарыгина И.Ф. должного внимания непосредственным измерениям не уделяется, не делается акцента на возможности применения измерительных инструментов в геометрии.
3.4 Учебник геометрии 7 – 9 (авторы Смирнова И.М., Смирнов В.А.) [26]
В данном учебнике поясняется, что измерение длины отрезка основано на сравнении его с отрезком, длина которого принимается за единицу (единичный отрезок). Авторы вводят определение понятия длины отрезка следующим образом: длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке. Подробно описывается процесс измерения отрезков: авторы говорят, что для измерения длины данного отрезка АВ последовательно откладывают единичный отрезок ОЕ на луче АВ от вершины А. Если при этом единичный отрезок целиком укладывается в отрезке АВ целое число раз без остатка, то процесс измерения на этом заканчивается и полученное число считается длиной отрезка АВ. Если единичный отрезок целиком укладывается в отрезке АВ с остатком, т.е. конец последнего единичного отрезка С не совпадает с концом отрезка АВ и остаток СВ меньше единичного отрезка, то полученное число n считается приближенным значением длины отрезка. В этом случае единичный отрезок разбивается на 10 равных частей. Уже откладывают одну десятую часть единичного отрезка и т.д. После этого рассматриваются свойства длины отрезка и приводятся некоторые исторические сведения о длине отрезка. Задачи на непосредственные измерения отрезков в учебнике не рассматриваются.
При изучении градусной меры угла поступают также, как и при изучении длин отрезков: вводится определение градусной меры угла и свойства. После приводятся краткие исторические сведения, где рассказывается об истории возникновения угломерного инструмента – астролябии. Помимо единицы измерения углов – градуса рассматриваются и такие: минуты и секунды.
В учебнике авторы вновь обращаются к измерениям только лишь при изучении темы «Углы, связанные с окружностью». Рассматривается такое понятие, как градусная мера дуги окружности. Также говорится о длине окружности, выводится формула для ее нахождения.
И в следующей главе учебника «Площадь» вводятся определение площади, как числа, получающегося в результате измерения и показывающего, сколько раз единичный квадрат и его части укладываются в данной фигуре. И приводятся свойства площадей, аналогичные свойствам длин отрезков. Выводятся формулы для нахождения площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, многоугольника, описанного около окружности, круга и его частей. В данном учебнике рассматривается изопериметрическая задача: какую наибольшую площадь ограничивают кривые заданной длины. В последней главе учебника авторы уделяют время на изучение площади поверхности и объема многогранника.
Определения, реализуемые в рассматриваемом учебнике, являются описательными. Приведено немало задач на косвенные измерения, не рассматриваются задачи на измерения на местности.
3.5 Учебники геометрии 7, 8 – 9 (авторы Александров А.Д. и др.) [1, 2]
Рассматриваемый учебник начинается с истории возникновения геометрии. Затем авторы вводят понятия отрезка, луча, прямой. При рассмотрении понятий длины отрезков, градусной меры углов и др. авторы поясняют, что длина отрезка – первая и самая важная из геометрических величин. Она характеризует его протяженность. Измерять длину постоянно приходится на практике. Длина используется при вычислении других геометрических величин – площадей, объемов, величин углов, показывая возможность косвенного измерения.
Геометрические величины характеризуют форму и размеры фигур. Измерение геометрических величин, по мнению авторов, - одна из важнейших задач геометрии.
Авторы обращаются к уже полученным знаниям учеников, и просто напоминают, что для измерения длины сначала надо выделить единичный отрезок. Также как и в других учебниках, перечисляются свойства длины.
После этого, рассматриваются два важных вопроса:
1. Как, имея измерительный инструмент, найти численное значение длины отрезка?
2. Как можно сделать инструмент для измерения длины?
Также в учебнике отмечается, что мера углов обладает теми же свойствами, что и длина отрезков. Измерение углов, как и отрезков, производится с помощью линейки, которая называется транспортиром. Авторы учебников подробно описывают такую линейку и рассказывают, как ей пользоваться.
Понятие площади многоугольника вводится уже в 8 классе, при этом дается определение площади. Также описывается процесс измерения этой геометрической величины.
И затем, только в конце 8 класса рассматриваются понятия длины окружности и площади круга.
Данный учебник предназначен для учащихся школ и классов с углубленным изучением математики, поэтому авторы уделили внимание как непосредственному измерению, так и косвенному измерению геометрических величин.
Мы рассмотрели пять учебников геометрии, рекомендованных (допущенных) Министерством Образования и Науки Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2008/2009 учебный год, и можем сделать следующие выводы: в учебниках Атанасяна С.Л. и др. и Александрова А.Д. и др. уделяется внимание непосредственному измерению площадей, различным измерительным инструментам и мерам длин, приводятся задачи как на непосредственное измерение, так и на косвенное измерение геометрических величин. Но в учебнике Александрова А.Д. практически не рассматриваются задачи, в которых отражалась бы значимость измерений в жизни. В отличие от этих учебников, у Погорелова А.В. и у Шарыгина И.Ф. и др. практически не уделяется время вопросам об измерительных инструментах и возможности применения их на практике. В учебнике Смирновых нет задач, показывающих практическую значимость измерений.
Также из проведенного анализа учебников, мы можем сделать вывод, что учащиеся знакомятся с такими методами геометрии как метод подобия, метод площадей, и используют другие методы: метод дополнительных построений, метод вспомогательного треугольника, координатный метод, метод геометрических мест [16].
Далее мы рассмотрим, с какими измерительными инструментами следует знакомить школьников, и как эти инструменты могут помочь в изучении геометрии.
§4. Измерительные инструменты в школе
Измерения являются не только неотъемлемой частью процесса обучения математике в школе, но и играют определенную роль в выборе будущей профессии. Уже сейчас возникает острая нехватка профессиональных инженеров, технических специалистов и руководителей среднего звена на производстве. В современном мире область применения измерений геометрических величин чрезвычайно широка.
Измерения являются одной из самых древнейших операций в процессе познания человеком окружающего материального мира. Вся история цивилизации представляет собой непрерывный процесс становления и развития измерений, совершенствования средств, методов измерений, повышения их точности и единообразия мер.
В процессе своего развития человечество прошло путь от измерений на основе органов чувств и частей человеческого тела до научных основ измерений и использования для этих целей сложнейших физических процессов и технических устройств. В настоящее время измерениями охватываются все физические свойства материи практически независимо от диапазона изменения этих свойств.
Несомненно, для того, чтобы измерять какие-либо геометрические величины, нам нужны специальные инструменты – измерительные инструменты.
В соответствии с действующими «Перечнем учебного оборудования по математике для общеобразовательных учреждений России» [19], утвержденными Министерством образования Российской Федерации кабинеты математики должны быть оснащены комплектом средств обучения, выпускаемых промышленностью,. В комплект инструментов классных входит: линейка (рис. 2), транспортир (рис. 3), угольник (30º, 60 º) (рис. 4), угольник (45º, 45º) (рис. 5), циркуль (рис. 6).

Рис. 2


Рис. 3 Рис. 4


Рис. 5 Рис. 6
Существует множество измерительных приборов, которые человек применяет в своей деятельности. Для более удобного их рассмотрения, разделим эти приборы на группы. За основание классификации примем измеряемую геометрическую величину. Итак, в школьном курсе геометрии средней школы необходимо уметь измерять: длины отрезков, углы, площади.
4.1 Измерительные инструменты для измерения длин отрезков
В первую группу инструментов отнесем инструменты, предназначенные для измерения длин отрезков:
- классная линейка;
- масштабная линейка;
- металлическая линейка;
- метр складной,
- мерная лента,
- рулетка и др.

Рис. 7 10 см – более длинными
На ребре классной линейки (рис. 7) нанесены сантиметровые деления. Каждые 5 см отделяются удлиненными штрихами, а каждые
Наименьшее деление линейки называется ценой деления. Измерения классной линейкой возможны лишь с точностью, не превышающей половины цены деления, то есть с точностью, не превышающей 0,5 см, при этом половина цены деления определяется визуально. Этот измерительный прибор является наиболее распространенным в школе. С помощью него удобно производить построения на классной доске на уроках математики, где точность измерения не всегда имеет значение.
Масштабная линейка является удобным инструментом для школьников. На одном ребре этой линейки нанесены миллиметровые деления. Каждые 5 мм отделяются удлиненными штрихами, а 10 мм – более длинными. Ценой деления масштабной линейки является 1 мм. Незаштрихованное ребро линейки используется для проведения на бумаге прямых линий, при построении различных прямолинейных фигур. Ребро линейки с делениями используется для измерения на бумаге длины отрезка.
Металлическая линейка используется для более тщательных измерений. Различают жесткие и упругие металлические линейки. На одном ребре жесткой линейки нанесены миллиметровые деления. Второе ребро оставлено свободным от делений и используется для проведения прямых линий. Упругая линейка может свертываться в кольцо, благодаря чему она применима для измерения длины кривой линии. Метр складной (рис. 8) обычно состоит из пяти или десяти звеньев, соединенных между собой шарнирами. На одном из ребер метра нанесены миллиметровые деления. Складные метры бывают стальные и деревянные. Стальной метр применяется в слесарном деле, а деревянный является измерительным инструментом плотника и столяра. Практически точность складного метра очень низкая из-за шарнирного соединения звеньев. В связи с этим складные метры применяются лишь в тех случаях, когда не требуется большой точности измерения.

Рис. 8
Существует еще несколько инструментов, предназначенных для измерения длин. Одним из них является мерная лента. Для измерения линейных размеров сравнительно больших предметов используются рулетки: стальная или матерчатая. На стальной ленте рулетки нанесены миллиметровые деления, а на матерчатой – сантиметровые. Матерчатые рулетки применяются в тех случаях, когда не требуется большой точности измерения. Стальная лента используется при измерении расстояний на местности и при съемке планов земельных участков. Ценой деления является дециметр.
Для измерения длин на планах и картах и определения затем расстояний на местности пользуются линейным масштабом. Для его построения необходимо на прямой линии отложить равные отрезки, принимая за единицу меры один сантиметр. Концы отрезков обозначить штрихами, против которых ставятся числа, соответствующие расстоянию на местности. Конец первого отрезка обозначается нулевым штрихом. Этот отрезок делится на десять равных частей. В этом случае точность измерения не будет превышать 1 мм, хотя на глаз она может быть повышена до 0,5 мм. Для получения точности измерения до 0,1 мм служит поперечный масштаб. Этот инструмент применяется в сельском хозяйстве при измерении длины и ширины земельных участков.
О таком измерительном инструменте, как линейка упоминается во всех рассмотренных учебниках. Помимо этого, в учебнике А.Д. Александрова и др. рассматривается вопрос о том, как можно самому сделать инструмент для измерения длин.
Для измерения диаметров поперечного сечения тел цилиндрической формы применяются такие приборы как диаметромер-центроискатель (рис. 9) или мерная вилка лесовода (рис. 10).
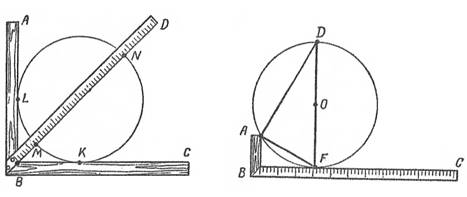
Рис. 9
Мерная вилка лесовода состоит из линейки с делениями, неподвижной планки, прикрепленной на конце линейки, и подвижной планки.
Все эти инструменты могут быть использованы при изучении понятия длины отрезка. Учащимся могут быть предложены разные виды задач на:
– измерение длины отрезков, изображенных на бумаге в различных положениях;

Рис. 10
- измерение длины, ширины и высоты прямоугольных параллелепипедов;
- измерение длины, ширины комнаты, коридора, двора;
- измерение расстояний на классном и индивидуальном полигонах;
- измерение расстояний на местности мерной лентой;
- измерение длины шага и измерение расстояний шагами;
- глазомерная оценка небольших расстояний с последующим измерением мерной лентой;
- измерение геометрических величин с помощью частей тела: фаланги пальца, локтя, стопы и др.
- измерение периметров прямолинейных фигур на местности и др.
4.2 Приборы для переноса измеряемого размера с объекта на линейку
Очень часто непосредственное измерение рассмотренными инструментами затрудняется или становится невозможным в связи со сложностью измеряемого предмета. В этом случае пользуются особыми инструментами для переноса измеряемого размера с объекта на линейку. Такие инструменты отнесем ко второй группе. Примерами рассматриваемых приборов являются циркуль, кронциркуль, нутромер, рейсмас. Рассмотрим их.
Различают несколько видов циркулей: переносный циркуль и кронциркуль (рис. 11). Переносный циркуль служит для перенесения линейных размеров с объекта на измерительную линейку, для нанесения окружности и дуг на объект. Точность измерения циркулем очень мала, так как она зависит от величины угла раствора ножек, исправности шарнирного соединения, заточки концов игл циркуля и от точности шкалы измерительной линейки.

Рис. 11
Кронциркуль служит для снятия размера диаметров цилиндров и шаров и перенесения его на измерительную линейку. Для снятия внутренних размеров деталей и перенесения их на измерительную линейку служит нутромер (рис. 12). Для более точного измерения диаметров отверстий и других внутренних размеров применяется микрометрический нутромер, дающий результаты с точностью до 0,01 мм. К переносным измерительным инструментам также можно отнести и рейсмас (рис. 13). Рейсмасы бывают разнообразных конструкций.

Рис. 12
Например, столярный рейсмас применяется в столярном деле и служит для перенесения и прочерчивания параллельных линий на устанавливаемом расстоянии. Процесс прочерчивания называется разметкой, а заостренный металлический стержень, прочерчивающий линию, называется чертилкой. Рейсмас с подвижной муфтой состоит из основания, стойки, подвижной муфты и чертилки. Благодаря подвижности муфты и прикрепленной к ней чертилки острие чертилки легко установить под нужным углом и на нужном расстоянии от разметочной плиты.
Рис. 13
Рассмотрение таких инструментов позволит ученикам получить более полное представление о возможностях измерений. При изучении этих приборов с учащимися можно разобрать следующие задачи:
- с помощью кронциркуля определить диаметры данных шаров, цилиндров;
- на деревянном бруске прочертить линию, параллельную ребру бруска на расстоянии нескольких миллиметров;
– определить внутренние размеры отверстий деталей: плиток, трубок и пр.
Для получения при измерении большей точности применяются инструменты с нониусом. В середине 16 века португалец Нуньес изобрел приспособление в виде дополнительной подвижной линейки с особыми делениями. Это приспособление и названо нониусом. Рассмотрим один из инструментов с нониусом: штангенциркуль (рис. 14). На линейке штангенциркуля нанесены миллиметровые деления. На длине рамки нониуса в 9 мм нанесено 10 равных делений. При таком делении нониуса измерения производятся с точностью до 0,1 мм.

Рис. 14
4.3 Инструменты, с помощью которых можно измерить градусную меру угла
В третью группу измерительных приборов отнесем те инструменты, с помощью которых можно измерить градусную меру угла – угломеры.
В некоторых современных учебниках геометрии упоминается о таком приборе, как малка (рис. 15). Рассмотрим этот инструмент подробнее.
Малки применяются при измерении и переносе углов с одной детали на другую, а также для проверки углов на изготовленных предметах. Малки бывают различных конструкций. Простая малка состоит из двух подвижных линеек, соединенных с одного конца шарнирным винтом. Такая малка служит для одновременного измерения, переноса и проверки только одного угла.

Рис. 15
Линейки малки устанавливаются под углом, заданным на рабочем чертеже детали, и закрепляются винтом. После этого малка накладывается на проверяемую деталь. В столярном производстве простые малки употребляются при изготовлении деревянных деталей с заданным углом и при разметке материала. Универсальная малка служит для одновременного переноса и проверки двух или трех углов.
Также при изучении темы «Измерение углов» учащиеся и учитель используют такой инструмент как транспортир (рис. 5). Соответственно различают классный и ученический транспортиры.
Классный транспортир используется для измерения и построения на классной доске углов до 180 градусов. Ценой деления такого транспортира является 1 градус. Ученический транспортир устроен также как и классный.
Для построения на местности углов в 45, 90, 135 градусов и других служат экеры (рис. 16). Они бывают различной конструкции: крестообразные, в виде прямоугольного треугольника, квадратной доски, цилиндрические и другие. Экеры применяются в практике не только для построения углов, но и для проведения параллельных и взаимно перпендикулярных линий, для проведения высот в треугольниках, при съемке планов земельных участков и др.

Рис. 16
Еще одним инструментом, упоминавшимся в школьных учебниках является астролябия (рис. 17). Она состоит из лимба с
градусным делением.
В центре лимба прикреплена подвижная алидада
с диоптрами на концах для визирования. Лимб
с алидадой надевается на штырь штатива. Для
ориентирования астролябия снабжается компасом
или буссолью. При помощи астролябии измеряются
и строятся углы в горизонтальной плоскости,
проводятся параллельные и перпендикулярные линии. Усовершенствованные астролябии на конце алидады имеют верньер (круговой нониус) для отсчета долей градуса.
Учащимся могут быть предложены следующие задачи:
- малкой измерить и перенести данный угол на деталь.
- с помощью классного транспортира измерить изображенные на доске углы различной величины.
- экером построить угол на местности в 45°, 90°, 135° и 180o .

Рис. 17
4.4 Инструменты для измерения площадей
В четвертую группу приборов можно отнести приборы, предназначенные для измерения площадей. Заметим, что непосредственное измерение площадей неудобно, поэтому для их нахождения удобно пользоваться известными математическими теоремами и формулами. Также можно использовать такой прибор как палетка (рис. 18). Это прозрачная пластинка с нанесенной на нее сеткой линий, предназначенная для вычисления площадей на планах и картах, для отсчета координат и т.д.
Ученикам могут быть предложены разные виды задач на:
- измерение с помощью палетки площадей плоских фигур, изображенных на бумаге;
- измерение площади поверхности многогранника и др.

Рис. 18
Мы рассмотрели измерительные инструменты, с которыми полезно знакомить в школе. Изучение некоторых из них является обязательным. Это такие инструменты как линейка, угольник, транспортир, циркуль. Без умения использовать их невозможно изучение геометрии, так как измерения являются одной из основных линий геометрии. И именно при изучении этой линии у школьников появляется возможность познакомится с разнообразными методами геометрии, например, метод площадей, знание которого важно при изучении других геометрических фактов. Вычислительные и измерительные задания формируют у учащихся навыки, необходимые в их будущей трудовой деятельности. Рассмотрение таких измерительных инструментов как астролябия, малка, штангенциркуль и др. дает возможность активизировать работу учащихся по формированию вычислительных навыков, навыков измерений и работы с единицами измерений [29].
§ 5. Различные направления использования измерений геометрических величин при обучении геометрии
Роль измерений в жизни человека невозможно преувеличить. Рассмотрим, какова же роль измерений в курсе геометрии.
Немало слов было сказано о прикладном значении геометрии и роли измерений в ней, как самостоятельного раздела для изучения. Также измерения могут быть использованы и как средство обучения.
5.1 Типология задач на измерения
Измерения могут быть использованы как при изучении нового материала, решении задач, доказательстве теорем, так и при закреплении материала. Но прежде чем перейти к рассмотрению способов применения измерений в том или ином случае, рассмотрим виды заданий на измерения:
- задания на непосредственные измерения;
- задания на косвенные измерения;
- задания на косвенные и непосредственные измерения;
- задания на измерения с помощью информационных технологий.
В результате проведенного сравнительного анализа школьных учебников по геометрии мы можем сделать вывод: в школьном курсе геометрии основное внимание уделяется вычислению геометрических величин: длин отрезков, градусной и радианной мер углов, площадей, объемов и т.п., – то есть опосредованному измерению. Но нельзя проигнорировать непосредственные измерения. Ведь геометрия возникла в глубокой древности в связи с необходимостью измерять, расстояния, площади земельных участков, возводить постройки и т.п. И в настоящее время любой человек в своей жизни сталкивается с необходимостью что-либо измерять.
5.1.1 Задачи на непосредственные измерения
Рассмотрим задачи на непосредственные измерения. К таким задачам относятся задачи, при решении которых используются только измерительные инструменты: линейка, транспортир и др.
- Найти длину отрезков АВ, CD, EF, GH (рис. 19).

Рис. 19
При этом учащиеся проявляют свои знания, умения пользоваться измерительными инструментами.
- Найти периметр многоугольника АВCDEF (рис. 20).
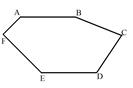
Рис. 20
- Найти градусные меры углов, указанных на рисунке 21.

Рис. 21
При решении подобных задач ученикам могут быть заданы вопросы:
- Что нам нужно измерить? (длину отрезка, градусную меру угла)
- Что мы знаем о длине отрезка, о градусной мере угла? (длина отрезка, градусная мера угла выражается некоторым положительным числом)
- Каким измерительным инструментом удобно пользоваться? (линейкой, транспортиром)
Также к задачам этого типа можно отнести и измерение площади плоской фигуры с помощью палетки. Важно отметить, что при непосредственных измерениях мы сталкиваемся с понятием погрешности измерения. Поэтому ученики должны понимать, что результаты, полученные при их измерениях неточны. Следующим типом задач, могут быть задачи, в которых использование измерительных инструментов недостаточно. Кроме них необходимо использование дополнительных средств.
Например, найти длину окружности (рис. 22).

Рис. 22 расстояния на местности
При решении подобной задачи возможно использование подручных средств, например, нити. С помощью нити и линейки можно измерить длину окружности.
Также могут быть решены задачи такого типа как измерение.
Например, измерить длину коридора в школе. Это можно сделать с помощью рулетки, мерной ленты, шагами или на глаз.
Измерения расстояний на местности могут быть выполнены непосредственно различными инструментами. В тех случаях, когда достаточны менее точные результаты измерения, могут быть применены измерения расстояний шагами. Рассмотрим, примеры таких измерений. Для шагомерного определения расстояний каждый ученик должен знать среднюю длину своего шага. Длина шага находится путем двух, трехкратного измерения шагами одного и того же расстояния, измеренного рулеткой. Делением расстояния, измеренного рулеткой, на среднее арифметическое числа шагов находится средняя длина шага. Чтобы найти длину шага точнее, можно измерить несколько расстояний. Для удобства может быть заполнена таблица:
Таблица 1
| Расстояние, измеренное рулеткой, м | Число сделанных шагов | Длина шага, м |
| Расстояние 1 |
Приведем пример заполнения такой таблицы (таблица 2).
Среднее арифметическое числа шагов: ![]()
Таким образом, длина шага: ![]()
Таблица 2
| Расстояние, измеренное рулеткой, м | Число сделанных шагов | Длина шага, м | |
| Расстояние 1 | 6 | 10 | 0,62 |
| 9 | |||
| 10 |
Развитие глазомера учащихся также имеет большое практическое значение. Привитие навыков в определении расстояний на глаз в различных условиях должно осуществляться в школе систематически. Только постоянной тренировкой в развитии глазомера можно добиться более или менее удовлетворительных результатов.
Начинать упражнения следует с определения на глаз малых расстояний, а по мере совершенствования глазомера переходить к определению больших расстояний. Определяемые на глаз расстояния необходимо проверять путем непосредственного измерения мерной лентой с целью убеждения в качестве глазомера.
В процессе непосредственных измерений, учащиеся поймут, как вычисляются те или иные геометрические величины, с помощью формул, а также смогут оценить все достоинства непосредственных и косвенных измерений. В школьном курсе геометрии большое внимание уделяется задачам на косвенное измерение величин. Косвенные измерения могут быть осуществлены на основании геометрических свойств фигур. Использование учащимися знаний, приобретенных на уроках геометрии, имеет большое образовательное и практическое значение. Учащиеся на личном опыте проведения измерительных работ убеждаются в ценности математических знаний, что несомненно способствует повышению у них интереса к изучению геометрии, а также математики, в целом.
5.1.2 Задачи на косвенные измерения
Рассмотрим, задачи на косвенные измерения, то есть в которых необходимо использовать теорему для нахождения геометрической величины.
Пример 1. Найти площадь прямоугольного треугольника, есди известны катеты а и b.
Для этого учащимся необходимо вспомнить определение прямоугольного треугольника и формулу, по которой удобно вычислить площадь рассматриваемого треугольника.
Итак, прямоугольным треугольником называется треугольник, у которого один из углов прямой. Площадь прямоугольного треугольника можно найти по формуле: ![]() , где а и b – катеты прямоугольного треугольника (рис. 23). Таким образом, по известным катетам ученики могут найти площадь треугольника, не прибегая к использованию измерительных инструментов.
, где а и b – катеты прямоугольного треугольника (рис. 23). Таким образом, по известным катетам ученики могут найти площадь треугольника, не прибегая к использованию измерительных инструментов.

Рис. 23
5.1.3 Задачи, в которых до методов косвенного измерения, применяются непосредственные измерения
Можно также выделить класс задач, в которых до методов косвенного измерения, применяются непосредственные измерения.
Пример 2. Найти площадь круга.
Для этого, ученикам необходимо применить формулу: ![]() . При этом, ученики путем непосредственного измерения могут найти радиус круга, а затем и площадь. Рассмотрим способ нахождения радиуса:
. При этом, ученики путем непосредственного измерения могут найти радиус круга, а затем и площадь. Рассмотрим способ нахождения радиуса:
1. Построим произвольную хорду окружности (рис. 24).
Рис. 24
2. Построим серединный перпендикуляр m к отрезку АВ.
3. Прямая m пересекает окружность в двух точках С и D. Середина этого отрезка О – центр окружности (рис. 25).

Рис. 25
Таким образом, ученикам необходимо измерить радиус ОА, а после найти по уже указанной формуле площадь круга.
Также к задачам на косвенные измерения можно отнести некоторые задачи на измерения на местности: например, измерение недоступного расстояния между доступными точками; измерение расстояния между недоступными точками; измерение расстояния до доступной точки.
Пример 3. Измерить ширину озера.

Рис. 26 задачи были использованы признаки равенства треугольников.
Строим произвольный треугольник ABC. На продолжениях АС и ВС откладываем А'С и В'С . Соединив точки А' и В', получим ∆А'В'С = ∆АВС по двум сторонам и углу между ними (рис. 26). Из равенства треугольников следует, что АВ = А'В'. Измерив непосредственно А'В', определим и равное ему недоступное расстояние АВ.
Заметим, что при решении данной
При измерениях на местности часто используют и другие известные теоремы, свойства и признаки:
- свойства равнобедренного треугольника;
- свойства прямоугольного треугольника;
- подобие треугольников;
- теорема Фалеса;
- теоремы синусов и косинусов и др.
5.1.4 Задачи на измерение геометрических величин средствами информационных технологий
Также при обучении измерениям в курсе геометрии могут быть использованы измерения с помощью информационных технологий. Одной из программ для наглядного иллюстрирования математических процессов является программа «Живая геометрия» [33]. Она является наиболее простым и легко доступным средством иллюстрации математических процессов и явлений.
С помощью этой программы возможно измерение следующих величин: длины отрезка; расстояния между двумя точками; периметра; длины окружности; углов; площади; длины дуги; радиуса. Использование данной программы возможно при решении различного рода задач.
Пример 4. Необходимо найти гипотенузу прямоугольного треугольника (рис. 27).

Рис. 27
Ученики могут самостоятельно построить прямоугольный треугольник с использованием данной программы, и измерить необходимые длины. Посмотреть, как изменяется длина гипотенузы в зависимости от изменения длины катетов. Также учащиеся могут проверить результат, путем вычислений. Это можно сделать самостоятельно: по теореме Пифагора: ![]() или с использованием программы (рис. 28):
или с использованием программы (рис. 28):
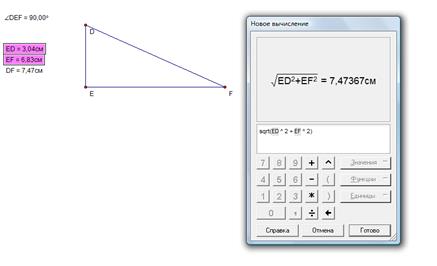
Рис. 28
Так же как и в случае непосредственных измерений мы работаем с приближенными значениями. Применение рассматриваемой программы не только показывает ученикам возможности ее использования и вызывает интерес у учащихся к предмету, в целом, к изучаемой теме, в частности. Также позволяет увидеть и «открыть» некоторые геометрические теоремы.
Таким образом, мы рассмотрели виды заданий на измерения. Теперь перейдем к рассмотрению различных направлений использования измерений в курсе геометрии.
5.2 Использование измерений геометрических величин на разных этапах урока геометрии
Как уже было сказано выше, измерения можно использовать на самых различных этапах обучения:
- при изучении нового материала;
- при закреплении полученных знаний;
- при решении задач, выводе формул или установлении каких-либо математических фактов;
- для установления межпредметных связей;
- для опровержения утверждений и др.
Использование измерений при изучении нового материала.
Например, при изучении площадей треугольника по формуле
![]() .
.
Ученикам могут быть розданы различные вырезанные из бумаги треугольники с отмеченными на них высотами (рис. 29).

Рис. 29
Учащиеся измеряют длины сторон а и b и длины высот, проведенных к стороне a, а также угол g. И вычисляют площадь треугольника по уже известной формуле.
Для удобства заносят результаты измерений в таблицу:
Таблица 3
| Длина стороны а | Длина стороны b | Длина высоты hа | sin g | Площадь треугольника |
| 1. | ||||
| 2. |
После нескольких таких измерений, учащиеся могут догадаться, что ![]() . Таким образом, сформулировать гипотезу. Ученики при этом пользовались непосредственными и косвенными измерениями.
. Таким образом, сформулировать гипотезу. Ученики при этом пользовались непосредственными и косвенными измерениями.
При изучении, например, теоремы о площади треугольника, вычисляемой по формуле: ![]() , могут быть использованы измерения с помощью информационных технологий (рис. 30).
, могут быть использованы измерения с помощью информационных технологий (рис. 30).

Рис. 30
Ученикам можно показать, что пока длина высоты и стороны, к которой проведена эта высота, не изменятся, площадь треугольника также не изменится (рис. 31).
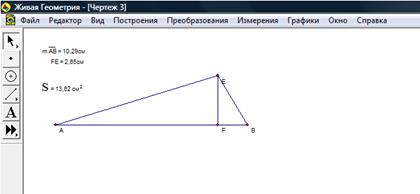
Рис. 31
Таким образом, учащиеся могут сделать вывод о том, что площадь треугольника зависит от стороны треугольника и высоты, проведенной к этой стороне. После некоторых исследований, учащиеся также смогут сделать вывод, что площадь треугольника вычисляется по формуле: ![]() .
.
Таким образом, измерения могут быть средством обнаружения каких-то математических фактов.
Помимо этого, измерения могут быть использованы для проверки достоверности или опровержения какого-то высказывания.
Например, в треугольнике сумма двух его сторон меньше третьей стороны.
Итак, учащиеся могут проверить правильность этого высказывания путем измерения сторон произвольного треугольника. Затем сделать вывод о недостоверности этого высказывания.
Или учитель предлагает ученикам выяснить верно, ли высказывание о том, что в любом треугольнике сумма двух его сторон больше третьей его стороны. Учащиеся, начертив каждый свой треугольник в тетради, убеждаются в том, что неравенство выполняется. После чего уже ищут доказательство этого утверждения.
Рассмотрим другой пример: пусть ученикам уже известно, что внешний угол треугольника больше каждого внутреннего угла этого треугольника, не смежного с ним. Для уточнения знаний о соотношении между величиной любого внешнего угла и величиной суммы внутренних углов треугольника, не смежных с ним, учащимся может быть предложено начертить произвольный треугольник АВС, построить три внешних угла и обозначить внутренние и внешние углы цифрами.
Затем убедиться в том, что внешний угол треугольника действительно равен сумме внутренних углов этого треугольника, несмежного с ним. После этого доказать соответствующую теорему.
Измерения могут быть использованы и для решения каких-либо задач.
Рассмотрим следующую задачу:
По данным катетам a и b прямоугольного треугольника найдите высоту, проведенную к гипотенузе: а = 5см, b = 12см.
Эту задачу можно решить с применением косвенных измерений площади треугольника, то есть, используя известную формулу: ![]() , и вычислив при этом гипотенузу прямоугольного треугольника. Также можно построить такой треугольник, и измерить необходимый отрезок. Таким образом, также пользуясь измерениями.
, и вычислив при этом гипотенузу прямоугольного треугольника. Также можно построить такой треугольник, и измерить необходимый отрезок. Таким образом, также пользуясь измерениями.
При этом все задачи, решаемые с использованием измерений можно разделить на две группы: задачи на местности, то есть для которых не составлена математическая модель для их решения и задачи, которые являются математической моделью некоторой реальной ситуации.
Итак, направления применения измерений в курсе геометрии, рассмотренные нами:
- использование измерений для обнаружения математических фактов;
- измерения для доказательства теорем или опровержения утверждений;
- использование измерений при решении задач;
- для установления межпредметных связей и др.
Таким образом, мы можем сделать вывод не только о практической значимости измерений, но и ценности их во всей геометрии.
Глава 2. Измерения геометрических величин в курсе геометрии 7 – 9 классов
§1. Примеры использования измерений в обучении геометрии
Мы рассмотрели различные направления использования измерений в курсе геометрии. Теперь приведем примеры использования измерений при изучении различных тем курса, при достижении различных дидактических целей.
1.1 Использование измерений при введении новой темы
Ученикам предлагается для изучения новая теорема или какой-либо математический факт. Важно, чтобы школьник усвоил и формулировку и все пункты доказательства, чтобы он был убежден в справедливости доказываемого утверждения, также важно, чтобы ученик понимал, для чего служит эта теорема. Использование измерений помогает добиться этого понимания. Также ученик в результате ряда измерений может самостоятельно прийти к формулировке гипотезы. При введении новой темы могут быть применены как непосредственные так и косвенные измерения. Они могут служить средством обнаружения математических фактов, средством для доказательства теоремы или опровержения утверждений.
Рассмотрим способ применения измерений при введении теоремы о сумме углов треугольника. Важно, чтобы ученики понимали, что сумма углов произвольного треугольника постоянна. И для того, чтобы они убедились в этом, им нужно самим измерить углы различных треугольников и найти их сумму. Таким образом, на уроке используются непосредственные измерения .
1.1.1 Сумма углов треугольника
Тема: «Сумма углов треугольника»
Цель: доказать теорему о сумме углов треугольника, добиться понимания этого факта, научить решать задачи с использованием полученных знаний.
В результате изучения данной темы учащиеся должны:
- знать формулировку и доказательство теоремы о сумме углов треугольника;
- уметь применять теорему при решении задач.
Оборудование: чертежные и измерительные инструменты: линейка, транспортир, учебник для 7 – 11 кл, Погорелов, А.В. [20].
Фрагмент урока.
1. Актуализация опорных знаний, умений и навыков.
Так как на этом уроке учащимся необходимо измерять углы, то нужно вспомнить, какая фигура называется углом, виды углов и способы их измерений. Ученикам могут быть предложены следующие задания и вопросы:
- Какая геометрическая фигура называется углом?
(Углом называется фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, - сторон угла.)
- Назовите виды углов?
(острый, тупой, прямой)
- Укажите на рисунке 32 тупые, острые и прямые углы.
-

а б в

д е ж
Рис. 32 (а – прямой угол, б – острый, в – прямой, д – тупой, е – острый, ж – тупой)
- С помощью какого измерительного инструмента мы можем измерить угол?
(с помощью транспортира)
Сегодня на уроке мы будем измерять углы треугольника.
- Что же такое треугольник?
(Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.)
- Укажите на рисунке 33 треугольники и вид треугольника:
-

а б в

Г д
Рис. 33
(а – остроугольный треугольник, в – тупоугольный, г – прямоугольный)
2. Изучение нового материала
Ученикам предстоит выяснить, что сумма углов в треугольнике постоянна и равна 180º.
Ученикам предлагается выполнить лабораторную работу:
1) Начертить треугольник АВС.
2) Измерить углы треугольника АВС.
3) Повторить опыт 3 раза.
Данные занести в таблицу:
Таблица 4
| ÐА | ÐВ | ÐС | ÐА+ÐВ+ÐС |
| Опыт 1 | |||
| Опыт 2 | |||
| Опыт 3 |
4) Вывод: сумма углов треугольника равна ___________________________________
Таким образом, учащиеся самостоятельно пришли к формулировке теоремы о сумме углов треугольника. Обсудив вопрос о необходимости доказательства, переходят его осуществлению.
3. Первичное закрепление полученных знаний. На данном этапе ученики применяют теорему о сумме углов треугольника при решении задач следующего типа:
1) Определите углы треугольника и его вид, если один его угол равен 25°, а другой – 75°. (ответ: 25°, 75°, 80°, остроугольный)
2) В треугольнике АВС угол А в 2 раза больше угла В, а ÐС = 45°. Определите ÐА и ÐВ. (ответ: ÐА = 90°, ÐВ = 45°)
Отметим, что большинство задач решается без использования измерительных инструментов, а с помощью уравнения ![]() ° (с помощью косвенных измерений).
° (с помощью косвенных измерений).
Здесь мы использовали измерение градусной меры углов при введении нового материала как средство обнаружения математического факта.
Также непосредственные измерения могут использоваться при введении таких тем, как «Смежные и вертикальные углы». Ученики при измерении вертикальных углов убеждаются, что такие углы равны, а сумма смежных углов равна 180°. При изучении темы «Равенство треугольников» школьникам могут быть выданы модели треугольников с равенством различных элементов: равны только углы, равны два/один угол, равны стороны, равны две стороны и угол между ними и т.п. При измерении элементов треугольника ученики «отбросят» варианты, которых недостаточно для равенства двух фигур. И останется только доказать достоверность оставшихся утверждений. Учащиеся могут самостоятельно прийти к формулировке свойств равнобедренных треугольников после ряда измерений: измерение углов, сторон равнобедренного треугольника.
Помимо непосредственных измерений при введении новой темы могут быть использованы и косвенные измерения . Рассмотрим способ их применения при изучении площади трапеции. Здесь удобно использовать именно косвенные измерения, так как большинство формул, связанных с площадями, ученикам уже известны: это и площадь треугольника, и площадь квадрата, параллелограмма.
1.1.2 Площадь трапеции
Тема: «Площадь трапеции»
Цель: сформулировать и доказать теорему о площади трапеции.
В результате изучения данной темы учащиеся должны:
- знать формулировку и доказательство теоремы о площади трапеции;
- уметь применять теорему при решении задач.
Оборудование: картонные геометрические фигуры: треугольники, квадрат, прямоугольник, трапеции, параллелограмм, учебник Геометрия 7 – 9, Л.С. Атанасян и др. [7].
Фрагмент урока:
1. Актуализация опорных знаний и умений.
- Какая фигура называется трапецией?
(Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие нет.)
Ученикам предлагаются следующие задачи:
- Укажите на рисунке 34 трапеции.
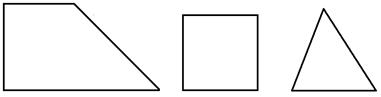
а б в

Г д
Рис. 34
(а, г - трапеции)
- Из каких фигур можно составить трапецию?
(из треугольника и параллелограмма (рис. 35, а), из треугольника и квадрата или прямоугольника (рис. 35, б), из двух трапеций (рис. 35, в), из нескольких треугольников и др.) Ученикам раздаются картонные фигуры, и они пробуют собрать из них трапецию.
а) 
б) 
в) 
Рис. 35
- Что такое площадь, и какими свойствами она обладает?
(Площадь многоугольника – это положительное число, которое показывает сколько раз единица измерения и ее части укладываются в данном многоугольнике.)
Свойства:
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.)
2. Введение нового материала.
После того, как ученики поняли, что трапецию можно разбить на несколько фигур, площади которых они могут найти, основываясь на известных им свойствах площадей, школьники найдут и площадь трапеции. Рассматривается задача: известно, что высота трапеции BH = 4 см, ВС = 8 см, AD = 16 см. Найти площадь трапеции.

Рис. 36
Учитель поясняет, что данную трапецию можно разбить на две фигуры: треугольник и параллелограмм (рис. 36), площади которых мы уже умеем находить. Таким образом, площадь трапеции АВСD равна сумме площадей треугольника и параллелограмма.
Ученикам предлагается самостоятельно решить эту задачу.
Решение:
1. Построим отрезок BF, параллельный отрезку CD.
2. Четырехугольник BCDF является параллелограммом, так как BC || FD (ABCD – трапеция, AD || BC) и BF || CD – по построению.
3. Найдем площадь параллелограмма BCDF: BC = FD = 8. BH = 4 – высота параллелограмма (так как BH – высота трапеции, то BH | ВС). S = BH*BC = 4*8=32
4. Найдем площадь треугольника ABF: BH – высота, AF – основание: BH = 4 cм, AF = AD – FD = 16 – 8 = 8 (cм). S = ![]() (см2
).
(см2
).
5. Площадь трапеции равна сумме площадей треугольника и параллелограмма: Sтрап =Sпар +Sтр = 32+16 = 48 (см2 ).
Ответ: 48 см2 )
После рассмотрения частного случая можно перейти к рассмотрению общего случая нахождения площади трапеции. Учитель задает школьникам вопрос:
- Любую ли трапецию можно разбить на треугольник и параллелограмм, как?
(да, нужно провести через одну из ее вершин прямую параллельную одному из боковых ребер, тогда эта прямая разобьет трапецию на параллелограмм и треугольник)
Итак, нам дана трапеция с основаниями AD = b, BC = a, высотой BH = h. Нужно найти площадь этой трапеции. Учащиеся уже ознакомлены с алгоритмом решения такой задачи:
1. Провести через одну из вершин трапеции прямую параллельную одному из боковых ребер, тогда эта прямая разобьет трапецию на параллелограмм и треугольник.
2. Найти площадь полученного параллелограмма: ![]() .
.
3. Найти площадь полученного треугольника: ![]()
4. Сложитьрезультаты:
![]()
Таким образом, ученики самостоятельно доказали и сформулировали теорему.
В этом случае косвенные измерения площадей треугольника и параллелограмма помогли при доказательстве теоремы. Косвенные измерения могут быть использованы при введении тем: Теорема Пифагора (доказательство этой теоремы происходит с помощью косвенных измерений – вычислений площадей треугольника и квадрата), признаки подобия, площадь круга и многое другое. Использовать именно косвенные измерения удобно при изучении тем, связанных с площадями, где можно применять уже известные формулы, к тому же непосредственное измерение площадей затрудняется в связи с неточностью измерительных инструментов (палетка). Эти недостатки исчезают при использовании информационных измерений, то есть измерений геометрических величин с помощью технических средств. Заметим, что они могут быть заменены и непосредственными и косвенными, так как компьютер выполняет лишь роль вычислителя. Информационные «измерения» могут быть использованы при введении многих тем: обнаружения фактов, доказательстве теорем. Рассмотрим использование такого вида измерений при введении формулы длины окружности.
1.1.3 Длина окружности
Тема: «Длина окружности»
Цели: вывести формулу для нахождения длины окружности.
В результате изучения данной темы учащиеся должны:
- знать формулу для нахождения длины окружности и ее вывод;
- уметь применять полученные знания при решении задач.
Оборудование: компьютер, приложение «Живая математика» [33], учебник Геометрия 7 – 9, Л.С. Атанасян и др. [7].
Фрагмент урока.
1. Актуализация опорных знаний.
Прежде чем перейти к выводу формулы для нахождения длины окружности необходимо вспомнить, какая фигура называется окружностью.
(Окружность – это геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки)
2. Введение нового материала.
Учащимся необходимо выполнить работу исследовательского характера, с целью определения формулы для нахождения длины окружности.
Им предлагается с помощью программы Живая геометрия провести ряд измерений и заполнить таблицу:
Таблица 5
| Длина окружности – C, см | Радиус окружности – R, см | |
| Измерение 1 | ||
| ………….. |
1. Запустить приложение Живая геометрия.
2. Выбрать элемент Циркуль, расположенный на панели инструментов: ![]()
3. С помощью выбранного инструмента начертить окружность.
4. Выполнить команду: Измерения – Длина окружности.
На экране появится поле, в котором будет отображаться длина начерченной окружности.
5. Выбрать элемент Линейка: ![]()
6. С помощью выбранного инструмента соединить центр окружности с точкой, лежащей на окружности.
7. Выполнить команду Измерения – Длина.
На экране появится поле, в котором указана длина отрезка, являющимся радиусом (рис. 37).

Рис. 37
8. Провести подобные измерения пять раз.
После заполнения таблицы учащиеся замечают, что в четвертом столбце у них получается примерно одно и тоже число, то есть чтобы найти длину окружности необходимо знать радиус окружности. Длина окружности равна удвоенному произведению радиуса окружности на полученное школьниками число.
Затем учитель поясняет, что число ![]() обозначается p (число «пи»), которое приближенно равно 3,14.
обозначается p (число «пи»), которое приближенно равно 3,14.
Затем учитель рассказывает историю открытия числа p.
Также можно объединить несколько видов измерений, так появляется косвенное и непосредственное измерение , то есть измерения, где нужно применять и умения использовать измерительные инструменты и знания различных формул. Рассмотрим применение таких измерений при введении темы «Теорема Пифагора».
1.1.4 Теорема Пифагора
Тема: «Теорема Пифагора»
Цель: сформулировать и доказать теорему Пифагора.
В результате изучения данной темы учащиеся должны:
- знать формулировку теоремы Пифагора и ее доказательство;
- уметь применять полученные знания при решении задач.
Оборудование: чертежные и измерительные инструменты: линейка, транспортир, учебник для 7 – 11 кл, Погорелов, А.В. [20].
Фрагмент урока.
1. Актуализация опорных знаний.
Учитель предлагает ученикам вопросы и задания для выполнения, позволяющие вспомнить необходимые для усвоения нового материала факты.
- Что такое треугольник?
(Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.)
- Как называется треугольник, если у него все углы острые? (если один из углов тупой, прямой?)
(остроугольный, тупоугольный, прямоугольный)
2. Введение нового материала.
Учитель предлагает школьникам высказать предположения о справедливости следующей формулы: с2 = а2 + b2 , где а и b – катеты прямоугольного треугольника, с – гипотенуза треугольника.
Ученикам выдаются модели прямоугольных треугольников.
Затем им предлагается провести измерения длин катетов прямоугольного треугольника и его гипотенузы и заполнить таблицу:
Таблица 6
| а | b | c | а2 | b2 | а2 + b2 | с2 |
Таким образом, ученики убедятся в истинности предположения, и уже после этого можно перейти к доказательству этого утверждения.
1.2 Использование измерений при решении задач
Еще одно направление использования измерений в геометрии, которое мы рассмотрим – это использование измерений при решении задач.
Часто решая какую-либо задачу, ученик сталкивается с рядом проблем: не знает с чего начать рассуждения, от чего отталкиваться и др. В таком случае может помочь непосредственное измерение . Школьник строит необходимый чертеж и измеряет элементы фигур, пытаясь найти какую-либо связь, зависимость между исходными данными и получаемыми результатами. Это помогает ученику найти способ решения задачи.
Пример 5. Дан треугольник АВС. Сторона АС равна 6 см. Высота, проведенная к АС, равна ![]()
![]() см см. Высота, проведенная к АВ, равна 3
см см. Высота, проведенная к АВ, равна 3![]() см. ÐС треугольника АВС равен 30°. Найти ÐА (рис. 38).
см. ÐС треугольника АВС равен 30°. Найти ÐА (рис. 38).
Рис. 38
При решении такой задачи дети могут не сразу догадаться, как же ее решить, им может потребоваться некоторая наводка. Они могут получить эту подсказку, если точно выполнят чертеж к задаче и найдут связь между исходными данными и неизвестными.
Дано:
∆АВС,
АС = 6 см,
ВМ = ![]()
![]() см – высота ∆АВС,
см – высота ∆АВС,
СН = 3![]() см – высота ∆АВС,
см – высота ∆АВС,
ÐС = 30°,
Найти: ÐА.
Уже при построении чертежа от учеников требуется умение строить такие отрезки, как ![]()
![]() см. Это построение может быть выполнено следующим образом:
см. Это построение может быть выполнено следующим образом:
1. Сначала построим отрезок, равный ![]() см. Для этого построим прямоугольный треугольник с гипотенузой 2 см, а катетом 1 см. Тогда второй катет этого треугольника будет равен
см. Для этого построим прямоугольный треугольник с гипотенузой 2 см, а катетом 1 см. Тогда второй катет этого треугольника будет равен ![]() см (по теореме Пифагора) (рис. 39).
см (по теореме Пифагора) (рис. 39).
2. Затем мы три раза откладываем полученный отрезок и делим его пополам.

Рис. 39
Таким образом, при использовании такого вида измерения в качестве средства поиска решения задачи, учащиеся должны хорошо владеть измерительными и чертежными инструментами.
Построение (рис. 40):
1. АС = 6 см;
2. ÐС = 30°;
3. ![]()
4. ![]() ;
;
5. КР = ВМ, КÎ а;
6. b || АС, Р Îb;
7. ![]()
Рис. 40
После того, как школьник построил такой треугольник, он может измерить угол, который необходимо найти. Измерив ÐА, ученики убедятся, что он равен 60°, таким образом, треугольник АВС – прямоугольный. У школьников появятся мнения о том, с чего начать решение этой задачи – найти АВ, после чего, показать, что треугольник, в самом деле, прямоугольный.
А уже после того, как ребенок нашел способ решения этой задачи, он ее решает с использованием косвенных измерений .
(Решение:
1. Найдем площадь треугольника АВС:
С одной стороны: ![]() (см2
);
(см2
);
С другой стороны: ![]() . Откуда АВ =
. Откуда АВ = ![]() (см)
(см)
2. ÐС = 30°, АС = 6 см, АВ = 3 см, сл-но, ∆АВС – прямоугольный, ÐВ = 90°, ÐА = 60°.
Ответ: ÐА = 60°.)
Непосредственные и косвенные измерения также могут помочь в решении задач.
Пример 6. Дана монета (монета имеет форму окружности) (рис. 41). Найти ее радиус.

Рис. 41
Ученики с помощью нити измеряют длину окружности, а затем вычисляют ее радиус по уже известной им формуле.
Заметим, что использование информационных измерений при решении задач возможно, но в большинстве случаев они помогают лишь вычислить что-то, не позволяют ученику понять ход решения. Использование информационных измерений при решении задач оказывают влияние в следующих случаях:
- для четкого построения чертежа. С помощью компьютерных технологий школьник может сделать правильный и точный чертеж к задаче, а после этого перейти к поиску решений.
- Решение задач на ГМТ.
- Решение задач исследовательского характера.
Пример 7. Дан равносторонний треугольник со стороной а и окружность с радиусом, равным стороне треугольника. Определить, сколько возможно точек пересечения окружности со сторонами треугольника.
В программе Живая геометрия ученики могут построить равносторонний треугольник и окружность. Передвигая эту окружность, школьники определят количество точек пересечения. Учитель может сделать это для демонстрации в классе, с использованием анимации, что также возможно в указанном компьютерном приложении.
- В решении задач на построение. На этапе анализа задачи ученики могут выполнить чертеж на компьютере, а уже после этого и к отысканию способа построения.
1.3 Использование измерений для опровержения каких-либо утверждений
Школьникам задается вопрос об истинности какого-то утверждения. Не каждый ребенок может сразу ответить верно, поэтому чтобы ученики убедились в правильности своего ответа, они проверяют выполнение факта на практике. Рассмотрим несколько примеров таких вопросов.
Ученикам предлагается высказать предположение о том, верно ли следующее утверждение: в треугольнике сумма двух сторон меньше, чем другая его сторона. Учащиеся высказывают свои догадки, после чего учитель предлагает построить в тетрадях произвольный треугольник и проверить выполняется ли это неравенство. После некоторых измерений ученики убеждаются в том, что это утверждение ложно. В этом им помогли непосредственные измерения .
Рассмотрим другой вопрос, для ответа на который понадобятся косвенные измерения
: всегда ли площадь квадрата, сторона которого равна диаметру круга, больше площади такого круга. Пусть сторона квадрата равна а, тогда его площадь равна а2
. Площадь круга с диагональю а равна ![]() . Ученикам нужно сравнить полученные площади: так как
. Ученикам нужно сравнить полученные площади: так как ![]() <1, то площадь квадрата будет больше, чем площадь круга, диаметр которого равен стороне квадрата. Таким образом, ученики получают ответ на вопрос. (ответ: да)
<1, то площадь квадрата будет больше, чем площадь круга, диаметр которого равен стороне квадрата. Таким образом, ученики получают ответ на вопрос. (ответ: да)
1.4 Измерения, подчеркивающие практическую значимость геометрии
Использование измерений в школьном курсе геометрии помогает при достижении различных целей, дает возможность организовывать урок и в форме лабораторной, исследовательской, практической работы, то есть разнообразить формы организации обучения, что поможет учителю и при контроле знаний и умений учащихся, и при организации индивидуального и дифференцированного подхода к обучению. Заметим, что помимо перечисленных нами направлений использования измерений, они так же существуют как самостоятельная единица. Существует множество разнообразнейших занимательных задач на измерения, подчеркивающих практическую направленность геометрии и межпредметную связь. Рассмотрим примеры таких задач.
Пример 8. Измерить высоту дерева.

Рис. 42
На некотором расстоянии (рис. 42) от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ED), во сколько раз расстояние ВС от зеркала до дерева больше расрасстояния CD от зеркала до наблюдателя. Способ основан на законе отражения света. Вершина А (рис. 43) отражается в точке А' так, что АВ = А'В. Из подобия же треугольников ВСА' и СЕВ следует, что A'B:ED = BC:CD. В этой пропорции остается лишь заменить A’В равным ему АВ, чтобы обосновать указанное в задаче соотношение.
Рис. 43
Пример 8. В тени серебристого тополя от его корней разрослась поросль. Сорвите лист и заметьте, как он велик по сравнению с листьями родительского дерева, особенно с теми, что выросли на ярком солнце. Теневые листья возмещают недостаток света размерами своей площади, улавливающей солнечные лучи. Определить, во сколько именно раз площадь листа поросли больше площади листа родительского дерева.
Оба листа, различные по величине, имеют все же одинаковую или почти одинаковую форму: другими словами, — это фигуры, геометрически подобные. Площади таких фигур, мы знаем, относятся, как квадраты их линейных размеров. Значит, определив, во сколько раз один лист длиннее или шире другого, мы простым возведением этого числа в квадрат узнаем отношение их площадей.
Пример 9. У одуванчика, выросшего в тени, лист имеет длину 31 см. У другого экземпляра, выросшего на солнцепеке, длина листовой пластинки всего 3,3 см. Во сколько примерно раз площадь первого листа больше площади второго? [18]
Отношение площадей равно ![]() . Значит, один лист больше другого по площади раз в 90.
. Значит, один лист больше другого по площади раз в 90.
Такие задачи могут быть использованы также при подготовке внеклассных мероприятий по математике или факультативов.
§2. Рекомендации по реализации основных направлений использования измерений в школьном курсе геометрии
В предыдущих параграфах мы рассмотрели виды измерений и направления их использования в обучении геометрии. В зависимости от направления использования измерений целесообразно применять тот или иной вид измерений. Рассмотрим, при изучении каких тем школьного курса геометрии, возможно использование измерений геометрических величин.
Применение непосредственных измерений, то есть измерений с помощью специальных инструментов, возможно при изучении таких тем как «Смежные и вертикальные углы», «Признаки равенства треугольников», «Свойства равнобедренных треугольников», «Параллельные прямые», «Соотношения между сторонами и углами треугольника», «Подобные треугольники» и др. На уроках при введении перечисленных тем, разделов ученикам предлагается с помощью измерений обнаружить какой-либо факт, убедиться в истинности утверждения. Это можно реализовать с помощью непосредственного измерения геометрических величин. При этом, ученикам нужно дать понять, что непосредственные измерения не всегда точны, и поэтому результат может не совпадать с ожидаемым. В этом случае школьников необходимо познакомить с такими понятиями как погрешности и приближенные значения величин. С погрешностью мы сталкиваемся при измерениях в связи с неточностью измерительного прибора, человеческим фактором, внешними воздействиями. О них следует рассказать ученикам и научить их определять погрешности измерений и работать с ними, если школьники углубленно занимаются математикой. В остальных случаях столь подробного рассмотрения этих понятий не требуется, так как вопрос об погрешности измерений очень сложен. Нам достаточно уметь находить приближенные значения величин.
Итак, при знакомстве с понятиями смежных и вертикальных углов школьники самостоятельно могут сформулировать утверждения: сумма смежных углов равна 180°, вертикальные углы равны. При изучении признаков равенства треугольников, свойств равнобедренных треугольников, признаков параллельности прямых ученики так же приходят к формулировке теорем. После ряда измерений учащиеся приходят к этому. Но после проведенной ими работы учитель должен объяснить необходимость в доказательстве нужной гипотезы: ведь измерения были неточны, и то, что утверждение верно в одном случае не означает, что оно верно всегда.
Использование измерений при изучении нового материала очень широко, но есть и такие темы, при которых применение измерений не требуется. К таким можно отнести следующие темы: «Векторы», «Метод координат», «Движения».
Также при введении нового материала возможно и использование косвенных измерений, то есть те, где необходимо использование известных ученикам формул. Но в отличие от непосредственных, которые помогали прийти к формулировке гипотезы, косвенные измерения могут помочь и в ее доказательстве. Применение косвенных измерений может быть реализовано при изучении таких тем как «Теорема Пифагора», «Подобие фигур», «Площади фигур». Ведь именно здесь ребята уже знакомы с некоторыми формулами, которые помогут им в дальнейшем. Так при изучении площадей четырехугольников они уже знают, как находится площадь треугольника. А так как любой четырехугольник можно разбить на несколько треугольников, то сложностей в нахождении их площадей не возникает.
Применение информационных «измерений» также играет немалую роль при изучении новых понятий. С помощью компьютерных технологий можно продемонстрировать всему классу ряд свойств или теорем. Так, например, при изучении темы «Площадь треугольника» можно показать ученикам, что площадь треугольника не изменится пока будут постоянными основание и высота треугольника.
Так как наглядность в геометрии играет важную роль, то применение информационных технологий на уроках также поможет при реализации принципа наглядности в обучении.
Следующим направлением использования измерений являются измерения при решении задач. Заметим, что непосредственные измерения здесь помогают в поиске решения. Так сделав чертеж к той или иной задаче и измерив необходимые величины, ученик может обнаружить связь между искомыми и данными значениями. Косвенные же измерения необходимы практически при решении любой геометрической задачи. А вот информационные измерения не всегда помогают в решении задач. Компьютер, как мы знаем, создан человек для ускорения вычислений, поэтому ни в поиске решения, ни на этапе осуществления плана решения, он не помогает ученику. При этом информационные технологии, как уже было отмечено выше, могут помочь в следующих случаях:
- для четкого построения чертежа.
- решение задач на ГМТ.
- решение задач исследовательского характера.
- решении задач на построение.
Помимо того, чтобы выбрать какой тип измерений использовать на каждом из этапов обучения, учитель должен организовать работу учащихся. Активизировать процесс обучения математике позволяет собственная практическая деятельность учащихся. Так как измерения тесным образом связаны с практической деятельностью, то необходимо правильно подобрать форму обучения. Одной из таких форм является лабораторная работа.
Хотя лабораторная работа обычно выполняется в группах это не всегда удобно. При введении темы, например, учащиеся должны быть сосредоточены на изучаемом материале и на работе, которую они выполняют. Работая в парах или группах, школьники могут отвлекаться, что помешает качественному усвоению темы. Поэтому ученикам нужно дать индивидуальные занятия, нацеленные на достижение одной цели. Например, при изучении признаков равенства треугольников, ученики могут быть разделены на группы, но при этом каждый должен выполнять свою функцию: к примеру, один человек измеряет стороны треугольников, розданных учителем, и заносит результаты в таблицу, второй – измеряет углы, третий путем наложения, проверяет равны ли треугольники. Таким образом, каждый из учеников играет важную роль в выполнении работы. Это подчеркивает их важность и позволяет не отвлекаться. Также при выполнении работы учителю следует продемонстрировать ход работы перед ее выполнением, или вместе с учениками проделывать все шаги. Не менее важным является обеспечение всех школьников нужными измерительными инструментами.
Помимо лабораторных работ могут быть использованы также и практические работы, и работы исследовательского или творческого характера.
Таким образом, измерения не только помогают при изучении геометрии, но и позволяют разнообразить формы обучения.
геометрия школьный курс измерение
§3. Элективный курс «Измерения расстояний на местности»
Пояснительная записка
Измерительные работы на местности связаны с измерением реальных расстояний, в том числе между недоступными предметами, высот, площадей участков, съемкой плана местности. Обучение выполнению таких работ способствует подготовке к моделированию разнообразных задач, а также к дальнейшей профессиональной деятельности.
Предлагаемый элективный курс предназначен для реализации в 9 классах средней школы. При изучении предложенных тем ученикам достаточно знаний, приобретенных на уроках математики, поэтому никакой дополнительной подготовки от школьников не требуется. При изучении элективного курса реализуются междпредметные связи с такими областями как физика, информационные технологии, черчение, технология и др.
Цель элективного курса: подготовить учащихся к дальнейшей профессиональной деятельности, повысить уровень понимания практической значимости предмета.
Задачами курса являются:
- формирование или развитие представлений учащихся об измерениях геометрических величин и расстояний на местности;
- применение знаний, полученных на уроках математики;
- выделение разных видов взаимосвязей математики с другими областями знаний;
Элективный курс имеет большой образовательный, воспитательный и развивающий потенциал:
- обучает разнообразным способам измерения расстояний на местности,
- воспитывает интерес к предмету;
- направлен на обучение школьников грамотному использованию измерительных инструментов.
На изучение курса целесообразно отвести 9 часов.
Тематическое планирование курса:
1. Меры длины, измерения расстояний подручными средствами – 1ч
2. Измерение расстояний шагами и на глаз – 1ч
3. Измерительные инструменты – 1ч
4. Измерение диаметра ствола дерева – 1ч
5. Измерение недоступного расстояния между доступными точками – 1ч
6. Применение свойств прямоугольного треугольника и осевой симметрии – 1ч
7. Измерение расстояний до недоступной точки – 1ч
8. Измерение расстояний между недоступными точками – 1ч
9. Итоговое занятие – 1ч
Содержание курса
| Номер занятия | Тема | Краткое содержание |
| 1 | Меры длины, измерения расстояний подручными средствами | Различные меры длины (ладонь, фаланги пальцев, пядь, аршин, сажень, сантиметр, метр, фут и др.). Измерение геометрических величин с помощью частей тела: ладонь, фаланги пальцев и т.п. |
| 2 | Измерение расстояний шагами и на глаз | Измерение расстояний на местности на глаз и шагами. Определение длины шага, измерение расстояния шагами. Определение расстояний на глаз. |
| 3 | Измерительные инструменты | Обучение школьников пользоваться измерительными инструментами: штангенциркуль, рулетка, мерная вилка лесовода. Определение расстояний с помощью разнообразных измерительных инструментов. |
| 4 | Измерение диаметра ствола дерева | Измерение диаметра ствола дерева различными инструментами (мерная вилка лесовода, диаметромер-центроискатель, нить) |
| 5 | Измерение недоступного расстояния между доступными точками | Рассмотрение возможности применения математических фактов на практике, в частности при измерении недоступного расстояния между доступными точками. Применение равенства и подобия треугольников при измерении недоступного расстояния между доступными точками. |
| 6 | Применение свойств прямоугольного треугольника и осевой симметрии | Применение свойств прямоугольного треугольника и осевой симметрии при измерении недоступного расстояния между доступными точками |
| 7 | Измерение расстояний до недоступной точки | Применение теоремы о зависимости между углами и сторонами треугольника при измерении расстояний до недоступной точки |
| 8 | Измерение расстояний между недоступными точками | Применение теорем синусов и косинусов при Измерение расстояний между недоступными точками |
| 9 | Итоговое занятие | Подведение итогов |
Занятие 1. Меры длины, измерения расстояний подручными средствами
Время, отведенное на это занятие, нужно отвести на рассмотрение возможности измерения расстояний подручными средствами. Важно дать понять школьникам, как производилось измерение геометрических величин раньше, когда еще не было таких понятий как сантиметр, метр и др. На уроках геометрии ученики уже знакомились с различными мерами длины: аршин, сажень и др. Учащиеся должны знать, что с древности мерой длины и веса был человек: на сколько он протянет руку, сколько сможет поднять на плечи и т.д. Для того, чтобы измерять маленькие величины использовали пядь. Пядь – это расстояние между концами расставленных большого и указательного пальцев. Еще одной древнерусской мерой была сажень – одна из наиболее распространенных на Руси мер длины, расстояние между концами пальцев широко расставленных рук взрослого мужчины. Также широко использовались такие меры как аршин, локоть, ладонь и др. Учитель рассказывает о происхождении этих мер, после чего учащиеся учатся измерять геометрические величины с помощью частей тела: ладонь, фаланги пальцев и т.п. Школьникам предлагаются задания на нахождение длины или ширины парты, книги и т.п. При этом ученикам нужно рассказать и о мерах длины, используемых в современном мире: сантиметр, метр, фут и др., о их происхождении. А также указать связь между древними и современными мерами длин:
1 аршин = 0,7112 м,
1 сажень = 2,1336 м и др.
Ученики могут произвести некоторые измерения и занести результаты в таблицу:
Таблица 7
| Измеряемая длина | Длина, аршин | Длина, ладонь | Длина, сантиметр | Длина, метр |
| 1. длина книги |
Таким образом, ребята научатся измерять расстояния без помощи измерительных инструментов, а также вспомнят некоторый материал, изучаемый на уроках геометрии и алгебры.
Ученики в конце занятия уже знают о различных способах измерений и поэтому на следующем занятии можно приступить к измерениям с помощью шагов или на глаз. У школьников появится возможность самим попробовать измерить расстояния на местности, используя при этом «старинные» меры длины.
Литература
1. Перельман Я.И. Живая математика. Математические рассказы и головоломки.– М.: Наука, 1967.– 160 с.: ил. [17]
2. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с.[23]
3. Шапиро, И.М. Использование задач с практическим содержанием в преподавании математики. Кн. для учителя.– М.: Просвещение, 1990.– 96 с.: ил.[32]
Занятие 2. Измерение расстояний шагами и на глаз
На данном занятии важно показать ученикам возможность измерения расстояния без применения измерительных инструментов, то есть измерение расстояний на глаз или шагами.
Для шагомерного определения расстояний каждый ученик должен знать среднюю длину своего шага. Длина шага находится путем 2-3 кратного измерения шагами одного и того же расстояния, измеренного рулеткой. Делением расстояния, измеренного инструментом, на среднее арифметическое числа шагов находится средняя дина шага. Для удобства ученикам выдаются инструкции, которые они должны выполнить, а также сдать отчет в конце работы.
Итак, первым заданием для учеников будет измерение длины своего шага.
Ученики должны быть поделены на группы, по два – три человека. Затем учитель вместе с учащимися выходит на школьную площадку. Школьники с помощью известного им из курса геометрии метода – провешивания прямой, измеряют некоторое расстояние. После этого учащиеся измеряют то же самое расстояние шагами. Затем ученикам предлагается проделать обратную операцию: сначала измерить некое расстояние шагами, а уже после этого, используя рулетку. После они сравнивают полученные результаты.
Также, имеет большое практическое значение развитие глазомера. Если занятия по определению расстояний на глаз ранее не осуществлялись, то следует начать с определения на глаз малых расстояний. Уже после этого переходить к определению больших длин. Так же, как и в случае с измерением шагами, определяемые расстояния на глаз необходимо проверять путем непосредственных измерений.
После выполнения ряда заданий учащиеся заполняют отчет и делают выводы.
В результате проведенной работы школьники научатся измерять расстояние шагами и на глаз, сделают вывод о целесообразности таких измерений.
Занятие строится следующим образом:
1. Измерение расстояния на местности рулеткой – провешивание прямой. Ученикам выдаются небольшие брусочки и измерительные инструменты.
2. Измерение длины своего шага.
3. Измерение расстояния на местности шагами.
4. Измерение этого же расстояния рулеткой.
5. Сравнение результатов.
6. Измерение расстояния на глаз.
7. Подведение итогов.
Отчет
ученика (цы) ____________________________________________
класса___________________________школы_______________________
Таблица 8
| № задания | Расстояние, измеренное рулеткой, м | Количество шагов, шт. | Длина шага, м |
| 1 | |||
| 2 |
На сколько отличаются длины, измеренные шагами и рулеткой?
_____________________________________________________________________________
Таблица 9
| № упражнения | Между какими предметами измеряется расстояние | Расстояние, измеренное на глаз, м | Расстояние, измеренное инструментом, м |
| 1 | Два бруса | ||
| 2 | Два дерева | ||
| 3 | ....... |
На сколько отличаются длины, измеренные на глаз и рулеткой?
_____________________________________________________________________________
_____________________________________________________________________________
Возможно ли измерение недоступного расстояния рассмотренными способами? (Например, измерить ширину озера, реки)
_____________________________________________________________________________
_____________________________________________________________________________
Будет ли измеренное расстояние точным?
_____________________________________________________________________________
_____________________________________________________________________________
В каких ситуациях можно прибегнуть к измерению расстояний шагами или на глаз?
_____________________________________________________________________________
_____________________________________________________________________________
Литература
1. Перельман Я.И. Живая математика. Математические рассказы и головоломки.– М.: Наука, 1967.– 160 с.: ил.[17]
2. Перельман Я.И. Занимательная геометрия.– М.: Гос. изд. технико-теоретической литературы, 1967.– 160 с.: ил. [18]
3. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с. [23]
Занятие 3. Измерительные инструменты
Учащиеся уже научились измерять расстояния без помощи измерительных инструментов. Теперь можно приступить к измерению длин, применяя различные приборы. Сначала ученикам нужно рассказать о том, что они измеряли и большие и малые расстояния, используя при этом разные меры длины. Например, для измерения малых расстояний были использованы фаланги пальцев, ладонь, измерения на глаз, а когда измеряли большие, то использовали шаги, аршин, сажень. И после этого уточнить, что существуют и различные измерительные инструменты: одни – для измерения малых длин, другие – больших, с некоторыми из которых школьники знакомы (линейка, рулетка, мерная лента).
На данном занятии нужно научить ребят пользоваться такими инструментами как штангенциркуль, рулетка, мерная вилка лесовода.
С рулеткой, линейкой и т.п. дети уже работали на предыдущих занятиях, поэтому отдельного внимания этим инструментам уделять не обязательно. А с такими приборами как штангенциркуль и мерная вилка лесовода стоит учеников познакомить. При этом важно всех ребят подготовить к этому занятию, проследить, чтобы у всех были нужные инструменты и т.д.
Учащиеся могут попробовать измерить диаметр детали: болт, гайка и др.
После этого учитель объясняет, как использовать инструмент для измерения больших длин. Одним из таких инструментов является мерная вилка лесовода.
Литература
1. Афонский, А.А. Измерительные приборы и массовые электронные измерения. Учеб. пособие / А.А. Афонский, В.П. Дьяконов.– М.: Солон-Пресс, 2007.– 544 с.: ил. [3]
2. Знаменский, М.А. Землеизмерительные инструменты и работа с ними в средней школе.– М.: Учпедгиз, 1933.– 39 с. [11]
3. Карасев, П.А. Сам измеряй и вычисляй. Линейные измерения, измерение площадей. Рабочая тетрадь по геометрии / П.А. Карасев, П.И. Попов.– Москва–Ленинград: ГИЗ, 1926.– 60 с.: ил. [13]
4. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с. [23]
Занятие 4. Измерение диаметра ствола дерева
Ученикам для размышлений предоставляется задача: измерить диаметр ствола дерева. Для этого можно применить такой инструмент как мерная вилка лесовода, с которым ученики знакомились на предыдущем занятии. С его помощью рассматриваемая задача легко решается. Также она может быть решена с использованием других средств: диаметромер-центроискатель, подручных средств (нить для измерения длины окружности). Учитель демонстрирует ученикам, как именно это делается, а затем ребята пробуют выполнить измерения сами.
Литература
1. Афонский, А.А. Измерительные приборы и массовые электронные измерения. Учеб. пособие / А.А. Афонский, В.П. Дьяконов.– М.: Солон-Пресс, 2007.– 544 с.: ил. [3]
2. Знаменский, М.А. Землеизмерительные инструменты и работа с ними в средней школе.– М.: Учпедгиз, 1933.– 39 с. [11]
3. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с. [23]
4. Перельман Я.И. Занимательная геометрия.– М.: Государственное издательство технико-теоретической литературы, 1950.– 296 с.: ил. [18]
Занятие 5. Измерение недоступного расстояния между доступными точками
Учащиеся уже знают о разных способах измерения: это и измерение подручными средствами, с помощью частей тела, и измерения на глаз, и измерения с помощью специальных инструментов. Но возникают ситуации, когда результата, полученного на глаз недостаточно, а использование приборов становится невозможным. В таких случаях требуется применение различных теорем.
На данных занятиях следует рассмотреть возможность применения теорем курса геометрии при измерении расстояний на местности.
Применение равенства и подобия треугольников.
Пусть требуется измерить ширину озера. Измерить ее с помощью рулетки или другого измерительного инструмента не предоставляется возможным. Нужно построить точку С, таким образом, чтобы расстояния АС и ВС были доступными. На продолжениях АС и ВС отложить А’C = АС и B’C = BC. Соединив точки А’ и B’, получим ∆A’B’C’ = ∆ABC, но расстояние A’B’ мы можем измерить. Таким образом, измерим расстояние АВ.

Рис. 44
После рассмотрения задачи ученикам предлагается проделать это на местности. Школьники заполняют отчет:
Таблица 10
| Построить | Измерить, м | Сравнить |
| Точку С | ||
| АС | ||
| А’С | ||
| ВС | ||
| B’C | ||
| A’B’ |
1. Ширина озера АВ равна ___________________________________________________
2. Какими теоремами курса геометрии вы пользовались?
____________________________________________________________________________________________________________________________________________________
3. Какими измерительными инструментами вы пользовались?
____________________________________________________________________________________________________________________________________________________
Литература
1. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с. [23]
2. Перельман Я.И. Занимательная геометрия.– М.: Государственное издательство технико-теоретической литературы, 1950.– 296 с.: ил. [18]
Занятие 6. Применение свойств прямоугольного треугольника
При рассмотрении задач в решении которых помогает знание свойств прямоугольных треугольников потребуется умение строить прямые углы. В этом помогут такие инструменты как угломер или экер, поэтому следует показать учащимся, как нужно пользоваться этими инструментами.
После объяснения школьникам предлагаются задания на построение углов на местности. А уже потом переходить к измерениям расстояний на местности.

Рис. 45
Решение задач на измерение недоступных расстояний сводится к построению углов.
Применение свойств осевой симметрии.

Рис. 46
Необходимо определить недоступное расстояние АВ. Для этого нужно построить прямую MN и точки A’ и B’, симметричные точкам А и В относительно прямой MN. И затем уже измерить расстояние, равное расстоянию АВ.
Ученикам также может быть предложено самим составить задачу, в которой необходимо измерить недоступное расстояние между доступными точками.
Литература
1. Афонский, А.А. Измерительные приборы и массовые электронные измерения. Учеб. пособие / А.А. Афонский, В.П. Дьяконов.– М.: Солон-Пресс, 2007.– 544 с.: ил. [3]
2. Знаменский, М.А. Землеизмерительные инструменты и работа с ними в средней школе.– М.: Учпедгиз, 1933.– 39 с. [11]
3. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с. [23]
Занятие 7. Измерение расстояний до недоступной точки.
После того, как со школьниками были рассмотрены различные способы измерения недоступных расстояний следует перейти к измерению расстояний до недоступной точки.
Для этого потребуется так же знание геометрии.
Применение теоремы о зависимости между углами и сторонами треугольника.

Рис. 47
Необходимо найти расстояние между доступной точкой А и недоступной точкой В. Для этого нужно построить произвольный острый угол ВАМ. Затем на луче АМ выбираем точку С так, чтобы полученный треугольник АВС был равнобедренным, с основанием ВС. В данной работе ученикам потребуется умение использовать эккер и угломер.
Литература
1. Афонский, А.А. Измерительные приборы и массовые электронные измерения. Учеб. пособие / А.А. Афонский, В.П. Дьяконов.– М.: Солон-Пресс, 2007.– 544 с.: ил. [3]
2. Знаменский, М.А. Землеизмерительные инструменты и работа с ними в средней школе.– М.: Учпедгиз, 1933.– 39 с. [11]
3. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с. [23]
Занятие 8. Измерение расстояний между недоступными точками.
Применение теорем синусов и косинусов.
Для этого занятия можно использовать следующую задачу: необходимо измерить расстояние между двумя предметами, находящимися на другой стороне реки.

Рис. 48
Итак, для того, чтобы измерить недоступное расстояние АВ, нужно выбрать такие точки C и D, между которыми можно измерить расстояние, и таким образом, чтобы из них можно было видеть точки А и В. После чего, нужно измерить расстояние CD, углы ACD, ADC, BDC, BCD. А затем из треугольника ACD по теореме синусов найти АС, из треугольника CDB – ВС. После чего из треугольника АВС по теореме косинусов мы сможем найти и АВ.
Литература
1. Афонский, А.А. Измерительные приборы и массовые электронные измерения. Учеб. пособие / А.А. Афонский, В.П. Дьяконов.– М.: Солон-Пресс, 2007.– 544 с.: ил. [3]
2. Знаменский, М.А. Землеизмерительные инструменты и работа с ними в средней школе.– М.: Учпедгиз, 1933.– 39 с. [11]
3. Прочухаев, В.Г. Измерения в курсе математики средней школы.– М.: Просвещение, 1965.– 140 с. [23]
Занятие 9. Итоговое занятие.
На последнем занятии с учениками подводят итоги работы и выполняют практические задания на закрепление пройденного. Также с учениками могут быть рассмотрены задания на нахождение площади комнаты, например. То есть те, которые связаны с измерением расстояний на местности.
В результате этих занятий ученики понимают важность измерений, а также математики в повседневной жизни. Ученики на личном опыте убеждаются в жизненности и ценности математических знаний.
Заключение
В данной работе рассмотрен вопрос о необходимости изучения измерений геометрических величин в курсе геометрии 7 – 9 классов. В результате работы были сделаны выводы о необходимости изучения измерений геометрических величин в школе, о необходимости обучения умению использовать различные измерительные инструменты.
Была достигнута поставленная цель: мы выявили возможности использования измерений геометрических величин при изучении различных тем курса геометрии 7 – 9 классов. При достижении цели работы мы решили следующие задачи: изучение психологической и учебно-методической литературы по теме; анализ измерительных инструментов для школ; проведение классификации измерений геометрических величин; разработка методических рекомендаций для реализации основных дидактических функций на уроке математики с использованием измерений; разработка элективного курса «Измерение расстояний на местности».
В результате изучения психологической и учебно-методической литературы по теме мы сделали вывод о необходимости практической деятельности учащихся на уроках геометрии: очень важно, чтобы весь процесс обучения геометрии сопровождался практической деятельностью учеников. В результате сравнительного анализа учебников геометрии, рекомендованных (допущенных) Министерством Образования и Науки Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2008/2009 учебный год мы выделили основные этапы изучения измерений геометрических величин: пропедевтический курс (1-6 классы), основная школа (7-9 классы), старшая школа (10-11 классы).
При изучении измерений школьники знакомятся с такими методами геометрии как метод подобия, метод площадей, и используют другие методы: метод дополнительных построений, метод вспомогательного треугольника, координатный метод, метод геометрических мест, которые играют немаловажную роль в дальнейшем обучении геометрии. В различных учебниках уровень ознакомления с этими методами различный.
Также нами рассмотрены измерительные инструменты, используемые в школах. В комплект классных инструментов входит: линейка, транспортир, угольник (30º, 60º), угольник (45º, 45º), циркуль. Но учащихся также полезно познакомить и с другими инструментами: мерная вилка лесовода, кронциркуль, штангенциркуль, диаметромер-центроискатель, астролябия, палетка и др.
В соответствии с тем, какие приборы мы используем при измерении геометрической величины, мы провели классификацию измерений геометрических величин: непосредственные, косвенные, измерения с помощью информационных технологий. Также мы рассмотрели возможность применения тех или иных измерений на разных этапах урока, при достижении дидактических целей. В соответствии с которыми, выдели направления использования измерений геометрических величин в школьном курсе геометрии: при изучении нового материала; при закреплении полученных знаний; при выводе формул или установлении математических фактов; для установления межпредметных связей; для опровержения утверждений или верификации гипотезы. Привели примеры фрагментов уроков по различным направлениям использования измерений и методические рекомендации к ним.
Помимо этого, разработали программу элективного курса «Измерение расстояний на местности», который направлен на подготовку учащихся к дальнейшей профессиональной деятельности, повышение уровня понимания практической значимости геометрии, который могут использовать учителя в своей деятельности. Курс состоит из девяти занятий, на каждом из которых учащиеся знакомятся с различными измерительными инструментами, учатся работать с ними, а также знакомятся с различными способами измерений расстояний на местности.
Библиография
1. Александров, А.Д. Геометрия [Текст]: Экспериментальное учебное пособие для учащихся VII класса средних учебных заведений / А.Д. Александров, А.Л. Вернер, В.И. Рыжик.– М.: Мирос, 1994.– 200 с.: ил.
2. Александров, А.Д. Геометрия для 8 – 9 кл. [Текст]: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики / А.Д. Александров, А.Л. Вернер, В.И. Рыжик.– М.: Просвещение, 1991.– 415 с.: ил.
3. Афонский, А.А. Измерительные приборы и массовые электронные измерения [Текст]: Учеб. пособие / А.А. Афонский, В.П. Дьяконов.– М.: Солон-Пресс, 2007.– 544 с.: ил.
4. Бескин, Н.М. Методика геометрии [Текст]: Учебник для пед. институтов / Н.М. Бескин.– М.: Учпедгиз, 1947.– 278 с.
5. Виноградова, Л.В. Методика преподавания математики в средней школе [Текст]: Учеб. пособие / Л.В. Виноградова.– Ростов н/Д.: Феникс, 2005.– 252 с.: ил.
6. Воронов, В.В. Педагогика школы в двух словах [Текст]: Учеб. пособие для студентов пед. вузов / В.В. Воронов.– М.: Педагогическое общество, 2000.– 192 с.: ил.
7. Геометрия, 7 – 9 [Текст]: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.– 16-е изд.– М.: Просвещение, 2006.– 384 с.: ил.
8. Геометрия в 7-9 классах [Текст]: Преподавание курса геометрии по учебнику А.В. Погорелова «Геометрия: 7-9» / Л.Ю. Березина, Н.Б. Мельникова, Т.М. Мищенко и др.– 2-е изд., перераб. и доп.– М.: Издательство «Экзамен», 2008.– 431с.
9. Гусев, В.А. Психолого-педагогические основы обучения математике [Текст] / В.А. Гусев.– М.: ООО «Издательство «Вербум-М», ООО «Издательский центр «Академия», 2003.– 432 с.
10. Дакацьян У.В. Проверка знаний учащихся по математике [Текст]: Пособие для учителей / У.В. Дакацьян.– М.: Академия педнаук, 1963.– 88 с.
11. Знаменский, М.А. Землеизмерительные инструменты и работа с ними в средней школе [Текст] / М.А. Знаменский.– М.: Учпедгиз, 1933.– 39 с.
12. Изучение геометрии в 7, 8, 9 классах [Текст]: Метод. рекомендации к учеб.: Кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков и др.– 6-е изд.– М.: Просвещение, 2003.– 255 с.: ил.
13. Карасев, П.А. Сам измеряй и вычисляй. Линейные измерения, измерение площадей [Текст]: Рабочая тетрадь по геометрии / П.А. Карасев, П.И. Попов.– Москва–Ленинград: ГИЗ, 1926.– 60 с.: ил.
14. Колягин, Ю.Г. Методика преподавания математики в средней школе [Текст]: Общая методика.: Учеб. пособие для студентов физ.-мат. фак. пед. институтов / Ю.Г. Колягин.– М.: Просвещение, 1975.– 462 с.
15. Методика и технология обучения математике [Текст]: Курс лекций: пособие для вузов / Н.Л. Стефанова, Н.С. Подходова, В.В. Орлов и др.– М.: Дрофа, 2005.– 416 с.: ил.
16. Методика преподавания математики в средней школе [Текст]: Частная методика: Учебное пособие для студентов пед. институтов по физ.-мат. спец. / А.Я. Блох, В.А. Гусев, Г.В. Дорофеев и др.; Сост. В.И. Мишин.– М.: Просвещение, 1987.– 416 с.: ил.
17. Перельман Я.И. Живая математика [Текст]: Математические рассказы и головоломки / Я.И. Перельман.– М.: Наука, 1967.– 160 с.: ил.
18. Перельман Я.И. Занимательная геометрия [Текст]: Занимательная геометрия / Я.И. Перельман.– М.: Государственное издательство технико-теоретической литературы, 1950.– 296 с.: ил.
19. Перечни учебного оборудования по кабинетам Российской Академии Образования [Электронный документ]: (http://www.ucheba.com/pos_rus/baza/baz_matem.htm) 23.11.2008.
20. Погорелов, А.В. Геометрия [Текст]: Учеб. для 7 – 11 кл. сред. шк. / А.В. Погорелов.– М.: Просвещение, 1992.– 383 с.: ил.
21. Преессман, Л.П. Методика и техника эффективного использования средств обучения в учебно-воспитательном процессе [Текст]: Книга для учителя / Л.П. Преесман.– М.: Просвещение, 1985.– 197 с.: ил.
22. Примерная программа среднего (полного) общего образования по математике [Электронный документ] / Министерство образования и науки РФ (http://window.edu.ru/window_catalog/files/r37204/08-1-s1.pdf). 20.11.2008.
23. Прочухаев, В.Г. Измерения в курсе математики средней школы [Текст] / В.Г. Прочухаев.– М.: Просвещение, 1965.– 140 с.
24. Саранцев, Г.И. Методика обучения математике в средней школе [Текст]: Учеб. пособие для студентов мат. спец. пед. вузов и ун-тов / Г.И. Саранцев.– М.: Просвещение, 2002.– 224 с.: ил.
25. Саранцев, Г. Современный урок математики [Текст] // Математика в школе.– 2006.– № 7.– С. 50-55
26. Смирнова, И.М. Геометрия [Текст]: 7-9 кл.: Учеб. для общеобразоват. учреждений / И.М. Смирнова, В.А. Смирнов.– 3-е изд., стереотип.– М.: Мнемозина, 2008.– 376 с.: ил.
27. Смирнова, И.М. Геометрия. 7 класс [Текст]: Методические рекомендации для учителя / И.М. Смирнова, В.А. Смирнов.– М.: Мнемозина, 2007.– 269 с.: ил.
28. Стандарт основного общего образования по математике [Электронный документ] / Министерство образования и науки РФ (http://window.edu.ru/window_catalog/files/r39261/11.pdf) 15.01.2009.
29. Темербекова, А.А. Методика преподавания математики [Текст]: Учеб. пособие для студ. высш. учеб. заведений / А.А. Темербекова.– М.: Гуманит. изд. центр Владос, 2003.– 176 с.
30. Федеральный перечень учебников на 2008-2009 учебный год. – Введ. 2007-12-13 [Электронный документ] / Министерство образования и науки Российской Федерации (http://fsu.edu.ru/p97aa1.html). 15.12.2008.
31. Шарыгин, И.Ф. Геометрия [Текст]: 7 – 9 кл.: Учеб. для общеобразоват. учреждений / И.Ф. Шарыгин.– 7-е изд., стереотип.– М.: Дрофа, 2004.– 368 с.: ил.
32. Шапиро, И.М. Использование задач с практическим содержанием в преподавании математики [Текст]: Кн. для учителя / И.М. Шапиро.– М.: Просвещение, 1990.– 96 с.: ил.
33. Thegeometer’ssketchpad [Электронный ресурс] Живая геометрия. Версия 4.04. Русскоязычная версия (http://math66.ucoz.ru/load/2-1-0-6). 07.03.2009.
Похожие рефераты:
Методические особенности изучения темы "Подобные треугольники" в средней общеобразовательной школе
Изучение геометрии на уроках математики в 5-6 классах
Групповая работа на уроках математики в начальной школе
Концепции современного естествознания
Геометрический материал на уроках математики
Методики датирования древних событий
Развитие логического мышления учащихся при решении задач на построение
Оборудование летательных аппаратов
Основы стандартизации, метрологии и сертификации