Реферат: Обобщающее повторение по геометрии на примере темы Четырехугольник

Содержание.

Введение.................................................................................... 2

Глава I. Психолого–педагогические особенности подросткового периода................................................................................................... 5

§1. Возрастные критерии........................................................ 5

§2. Повышение уровня обобщённости изучаемых знаний...... 12

Глава II. Обобщающее повторение по геометрии в 8 классе

(на примере темы: "Четырехугольники").................................. 16

§1. Значение повторения....................................................... 16

§2. Виды повторения............................................................ 17

§3. Содержание и методика обобщающего повторения на примере темы: «Четырехугольники»............................................................. 24

Глава III. Описание и результаты эксперимента........................ 42

ЗАКЛЮЧЕНИЕ........................................................................ 47

БИБЛИОГРАФИЯ.................................................................... 50

Введение.

В процессе обучения математике важное место отводится организации повторения изученного материала. Необходимость повторения обусловлена задачами обучения, требующими прочного и сознательного овладения ими.

Указывая на важность процесса повторения изученного материала, современные исследователи показали значительную роль при этом таких дидактических приёмов, как сравнение, классификация, анализ, синтез, обобщение, содействующее интенсивному протеканию процесса запоминания. При этом вырабатывается гибкость, подвижность ума, обобщённость знаний.

В процессе повторения память у учащихся развивается. Эмоциональная память опирается на наглядно–образные процессы, постепенно уступает памяти с логическими процессами мышления, которая основана на умении устанавливать связи между известными и неизвестными компонентами, сопоставлять абстрактный материал, классифицировать его, обосновывать свои высказывания.

Повторение учебного материала по математике осуществляется во всей системе учебного процесса: при актуализации знаний — на этапе подготовки и изучения нового материала, при формировании учителем новых понятий, при закреплении изученного ранее, при организации самостоятельных работ различных видов, при проверке знаний учащихся.

Необходимость повторения изученного ранее материала вызвано самой структурой программы учебного курса математики. Например, учащиеся проходят по учебной программе тему: «Четырёхугольники» в 8 классе, но пользуются ей в 10­­–11 классах при изучении темы: «Поверхность тел вращения», «Площадь поверхности», «Объёмы тел» и др. Школьная программа устроена так, что, не повторяя ранее изученного материала, трудно понять новый. Поэтому повторение пройденного материала необходимо учащимся. На практике чувствуется важность и полезность обобщающего повторения. Обобщающие уроки являются итогом большой работы учащихся по повторению, оказывают им практическую помощь в подготовке к экзаменам. Отзывы восьмиклассников об этих уроках, их осознанные, логически правильные ответы, с правильным использованием символической записи, умением применять теоретические знания при решении задач говорят о большой эффективности такого повторения.

Литературы по организации повторения не хватает. Важность обобщающего повторения и методических разработок определяют актуальность этой проблемы.

Проблема заключается в изучении влияния обобщающего повторения на качество знаний учащихся.

В связи с возникшей проблемой выдвигается гипотеза: предлагаемая методика обобщающего повторения способствует повышению качества знаний учащихся.

Объектом является учебно–воспитательный процесс в периоды повторения пройденного материала.

Предметом служит обобщающее повторение на уроках математики в 8 классе.

Для решения проблемы необходимо решить задачи:

Изучить научно–педагогический материал по психологии, по математике, по методике преподавания.

Изучить состояние обобщающего повторения в процессе работы, практику работы учителей, то есть, опыт их работы.

Проанализировать виды обобщающего повторения.

Разработать содержание и метод приёмов на примере темы: «Четырехугольники».

Провести экспериментально в средней школе.

Методы, использованные при экспериментировании гипотезы: теоретический анализ, педагогическое наблюдение, беседа, тестирование анкетирование, эксперимент. Аплобирование гипотезы проводилось в средней школе №46 (гимназия №4) под руководством Баязитовой Л.Ш. в 8^б и 8^г классах.

Глава I. Психолого–педагогические особенности подросткового периода.

§1. Возрастные критерии.

В настоящее время наблюдается усиленный интерес учителей математики к психолого–педагогическим проблемам, к психологическим знаниям. Этот интерес обусловлен тем, что учителя математики в своей повседневной практической деятельности встречаются с такими проблемами, которые можно разрешить лишь на основе психолого–педагогических знаний, а также при условии глубокого психологического осмысления сущности этих проблем.

1. Ученик как объект и субъект процесса обучения.

В процессе обучения математике непосредственно участвуют с одной стороны — учитель, с другой — ученик. Роли их в этом процессе представляются, по крайней мере на первый взгляд, достаточно ясными: учитель организует, направляет и руководит процессом обучения математике, а ученик должен учиться, выполнять все требования учителя.

Вот как, например, определяется процесс обучения в одном из учебников по педагогике: «Обучением называется двусторонний процесс, состоящий из деятельности учителя, когда он ученикам объясняет, рассказывает, показывает, заставляет их выполнять упражнения, исправляет их ошибки и т.д., и из деятельности учеников, которые под руководством учителя усваивают знания и соответствующие умения и навыки».

Основная роль учителя математики в современных условиях — это воспитание личности учащихся, формирование их потребностно–мотивационной сферы, воспитание их способностей, нравственных идеалов и убеждений. Обучение знаниям умениям и навыкам по математике является составной частью этого воспитания и тем процессом, в котором это воспитание осуществляется.

2. Возрастные психологические особенности ученика как объекта обучения математике.

О том, что надо учитывать возрастные особенности учащихся, говорится всюду, но не всегда указывается, что это означает, какие особенности надо учитывать и как их надо учитывать. Между тем, надо иметь в виду, что возрастные особенности — это не нечто неизменное и вечное, что присуще ученикам определённого возраста. Сами эти особенности довольно резко меняются со временем. Скажем, возрастные психологические особенности ученика младшего школьного возраста теперь и лет 30 тому назад совсем не одни и те же. Точно также современный подросток весьма существенно отличается от подростка довоенных лет.

Рассмотрим некоторые психологические особенности современного ученика, имея в виду лишь те его особенности, которые важно учитывать в процессе обучения математике.

Ученик — это растущий, развивающийся человек. Придя в школу в семь лет, он заканчивает её в 17 лет вполне сложившимся человеком юношеского возраста. За эти десять лет обучения ученик проходит огромный путь физического, психического и социально–нравственного развития.

Подростковый возраст — это весьма сложный, таящий в себе опасность кризисных явлений, период в жизни ученика. В этот период организм ребёнка претерпевает кардинальные изменения. Развёртывается процесс полового созревания. С этим процессом связано возникновение у подростка физического ощущения собственной взрослости. У него возникает представление о себе уже не как о ребёнке, он стремится быть и считаться взрослым. Отсюда у подростка возникает новая жизненная позиция по отношению к себе, к окружающим людям, к миру. Он становится социально активным, восприимчивым к усвоению норм ценностей и способов поведения, которые существуют среди взрослых.

Поэтому период подросткового возраста характерен тем, что здесь начинается формирование морально–нравственных и социальных установок личности ученика, намечается общая направленность этой личности.

Подросток стремится к активному общению со своими сверстниками, и через это общение он активно познаёт самого себя, овладевает своим поведением, ориентируясь на образцы и идеалы, почерпнутые из книг, кинофильмов, телевидения.

Подросток становится более независимым от взрослых ещё и потому, что у него возникают такие потребности, которые он должен удовлетворить только сам (потребность в общении со сверстниками, в дружбе, в любви). Родители и вообще взрослые при всём их желании не могут решить проблемы, встающие перед подростками в связи с возникновением у них новых потребностей, между тем как удовлетворение всех основных потребностей младших школьников зависит в основном от родителей. Всё это зачастую болезненно сказывается на отношении учащихся к учению. Вот как характеризует это известный психолог Н.С. Лейтес: «Дети 12–13 лет в подавляющем большинстве своём относятся к учению в основном благодушно: не утруждают себя излишними раздумьями, выполняют только уроки в пределах заданного, часто находят поводы для развлечения… Ослабление связи с учителем, снижение его влияния особенно дают о себе знать в недостатках поведения учеников на уроках. Теперь учащихся не только иногда позволяют себе игнорировать получаемые замечания, но могут и активно им противостоять. В средних классах можно столкнутся с изобретательными шалостями и проявлением самого легкомысленного поведения».

Общая картина работы учащихся–подростков на уроках по сравнению с младшими классами ухудшается. Ранее примерные и аккуратные ученики позволяют себе не выполнять задания. Тетради ведутся неряшливо. У многих учащихся меняется подчерк, он становится неразборчивым и небрежным. При решении математических задач многие подростки не проявляют нужной настойчивости и прилежания. Попытки учителя заинтересовать учеников занимательностью формы изложения или какими–либо другими способами зачастую не приносят ожидаемого результата.

В то же время эти же подростки весьма охотно участвуют в работе различных кружков, где, казалось бы, наиболее трудные подростки охотно выполняют все указания взрослого руководителя кружка, с интересом и усердием овладевают теоретическими знаниями, нужными для выполнения практических работ.

Если подростковый возраст есть начало внутреннего перехода ученика от положения объекта обучения и воспитания, которым он был в младшем школьном возрасте, к положению субъекта этого процесса, то в юношеском возрасте ученик становится (во всяком случае, должен становиться) уже подлинным субъектом своей деятельности в учебно–воспитательном процессе.

В то же время ученики ещё сохраняют материальную зависимость от родителей. Главным в их жизни становится подготовка к будущей самостоятельной, взрослой жизни, подготовка к труду, выбор жизненного пути, профессии.

В эти годы особую значимость для учеников приобретает ценностно–ориентационная деятельность. Ученик пытается произвести глубокую самооценку своей личности, своих способностей. Растёт и развивается рефлексия, познавательный интерес к философским проблемам, юноша пытается выяснить смысл жизни; оценить наблюдаемые явления с этой точки зрения.

Особо следует отметить стремление учеников старшего школьного возраста к автономии, к эмоциональной и ценностной самостоятельности, к независимости, к самоуважению, между тем как для подростков характерна зависимость от группы своих сверстников. Подросток весьма податлив влиянию сверстников. Внутренне отойдя от родителей, он ещё не пришёл к своей индивидуальности, которая обретается в юношеском возрасте. Если подростка волнует вопрос: «Неужели я не такой, как все?», то юношу: «Неужели я такой, как все?».

Учителю всё это надо иметь в виду и учитывать в своей работе.

3. Мотивация процесса учения.

Выше мы установили, что ученик в процессе обучения математике из объекта этого обучения постепенно становится его субъектом. Что это значит? В чём выражается различие между объектом и субъектом обучения? Ведь в том и в другом случае ученик как–то учится, приобретает знания, умения.

Действительно, и когда ученик является лишь объектом обучения математике, и когда он становится субъектом этого процесса он выполняет задания учителя, решает задачи, повторяет изученный материал и т.д., т.е. он учится. Все различия между учением ученика в роли объекта и его же учением в роли субъекта состоят в том, ради чего он это делает.

Человек, ученик есть деятельное существо. Он всегда что–то делает, участвует в какой–то деятельности. Но ученик участвует во многих различных деятельностях, совершает разные действия. Для того чтобы ученик эффективно учился, он должен совершать не любые действия, а вполне определённые. Встаёт вопрос: почему ученик совершает именно эти действия, а не другие, что побуждает совершать эти действия, что направляет и регулирует его деятельность в процессе обучения? Иными словами, что мотивирует — побуждает и направляет — деятельность ученика.

Только разобравшись в этом, мы сможем понять, в чём различия между объектом и субъектом процесса обучения. Кроме того, в этом надо разобраться ещё и потому, а может быть главным образом потому, что учитель должен научиться управлять деятельностью учащихся в процессе обучения, а для этого он должен формировать у них нужную мотивацию. Ведь в противном случае, если этого не делать, становится вполне реальной опасность, о которой говорил В.А.Сухомлинский:

«Все наши замыслы, все поиски и построения превращаются в прах, если нет у учащихся желания учиться.»

Поэтому учитель должен вызвать у учащихся такое желание, а это значит, что он должен формировать у них соответствующую мотивацию.

Что такое мотивация, как она формируется у человека? Под мотивацией понимают обычно совокупность побуждений к деятельности.

Однако когда деятельность уже началась, то она имеет определённую цель. Цель — это то, чего сознательно хочет достигнуть человек в результате этой деятельности. Но между целью деятельности и её побуждениями не всегда существует полное соответствие. Когда оно имеется, то говорят, что эта деятельность имеет смысл; в противном случае, когда цель деятельности и вызвавшие эту деятельность побуждения не соответствуют друг другу, то говорят, что деятельность не имеет смысла, лишена для данного человека смысла.

Например, ученики решают задачу. Цель у них одна — научиться решать подобные задачи. Побуждения же могут быть самые различные. Так, одни из них решают задачу потому, что привыкли выполнять требования учителя, у них ещё имеется достаточно стойкая установка на выполнение требований учителя, но некоторые из них, кроме того, хотят получить хорошую отметку, похвалу. Для других главное — получить хорошую отметку; третьи решают задачу ещё и потому, что их интересует сам процесс решения, он приносит эмоциональное удовольствие; наконец, есть и такие, у которых, кроме перечисленных побуждений, есть ещё и стремление овладеть общим способом решения подобных задач. Возможно, что у некоторых учащихся и другие побуждения.

Однако независимо от мотивов, которые побуждают учащихся решать задачу, объективно эта деятельность направлена на какие–то учебные цели, например, на то, чтобы каждый из них научился решать подобные задачи. Заметим, что сама задача с психологической точки зрения выступает лишь как материал, как средство этой деятельности.

Итак, ученик всегда является объектом деятельности в процессе обучения, а субъектом этой деятельности он становится тогда, когда сознательно принимает объективные цели деятельности за свои личные цели. Очевидно, что в последнем случае обучение является наиболее эффективном, только в этом случае учитель может легко и с удовольствием полностью осуществить цели и задачи обучения.

Учителю необходимо стремиться к тому, чтобы каждый ученик становился субъектом деятельности в процессе обучения. А для этого нужно, чтобы все стороны учебно–воспитательного процесса, его содержание, организация и методы содействовали такому становлению, были прямо направлены на воспитание ученика — субъекта своей деятельности. К описанию одного из путей построения процесса повторения математики мы и переходим.

§2. Повышение уровня обобщённости изучаемых знаний.

В настоящее время школьный курс математики далеко отстаёт от математики как науки по уровню обобщённости знаний. Если в современной математике уровень обобщённости очень высок, то в школьном курсе математики он пока ещё весьма низок. Его повышение (в разумных пределах) приведёт к повышению информационной ценности изучаемых знаний, и также к резкому сокращению времени на их усвоение.

Следует особо отметить, что только на этом пути можно избавиться от пресловутой перегрузки учащихся, ибо общими понятиями современный школьный курс математики, не только не перегружен, но явно не догружен.

Проблема развития самостоятельности мышления учащихся в процессе обучения математике является острой, ещё не разрешённой проблемой методики математики.

Анализ характера умственной деятельности учеников на различных уроках, в разных классах показал, что лишь 15–20% учебного времени тратится на самостоятельную работу, чем старше класс, тем самостоятельных работ меньше.

Создаётся ненормальное положение: с возрастом учащиеся, конечно, становятся более способными к самостоятельной работе, а им предоставляют для этого всё меньше времени.

Если в числе тренировочных упражнений преобладают однотипные, при решении которых ученик ограничивается лишь получением ответа и сверкой его с готовым ответом, то такие упражнения не направляют усилия ученика на разрешение иных нешаблонных заданий, с чем ему придётся встречаться в жизни.

Знания ученика будут прочными, если они приобретены не одной памятью, не заучены механически, а являются продуктом собственных размышлений и закрепились в результате его собственной творческой деятельности над учебным материалом.

Не случайно Леонид Эйлер полагал, что кроме описания результатов своих исследований, обогативших науку, ему надобно для общей пользы чистосердечно изложить ещё и процесс искания истины со всеми его исканиями и затруднениями.

Действующие учебники математики мало, чем могут помочь развитию творческих начал: в них по меткому выражению профессора Б.В Гнеденко, спрятаны все концы, дана уже готовая схема, знания представлены в статистическом состоянии, в завершённых формах.

Под обобщением будем понимать распространение, какого–либо суждения от частого понятия к общему (например, от «четырёхугольника» до «трапеции, ромба…»).

Суждения полученные по аналогии, будут проблематическими и подлежат дальнейшему исследованию и доказательству.

Умозаключения по аналогии являются непременной составной частью творческого мышления, так как этим путём мысль человека выходит за пределы известного, пролагая путь к неизвестному.

Умственное развитие учащихся, которые должны подготавливаться уже в период школьного обучения к роли творчески мыслящих активных деятелей, не может быть полноценным, если их не научат в школе специально применению приёма аналогии.

Простое применение аналогии даёт упражнение подобное, однопорядковое с исходным. От него следует отличать составление задачи обобщением, когда новая задача оказывается в том или ином отношении сложнее исходной.

Процесс обобщения основывается на применении аналогии, но не сводится полностью к ней.

Применение обобщения связано с преобразованием мыслей, с умственным экспериментированием; оно есть одно из самых важных средств самообучения, то есть, самостоятельного расширения и углубления имеющихся знаний.

Для достижения глубокого усвоения нового понятия, способа решения нельзя обходиться задачами одного уровня трудности, а нужно предложить обобщённую задачу, а ещё лучше дать учащимся возможность самим обобщить решённую задачу, чтобы затем решить таковую, видоизменяя, если нужно прежний способ.

В практике обучения общее классное задание рассчитано на среднего ученика, а для расширения познавательных способностей более сильных учащихся необходимы дополнительные задания по самостоятельному обобщению и решению составленных задач.

Если, скажем готовую задачу, решают все учащиеся в основном одинаковой последовательностью рассуждений, то с обобщением уже справляется не всякий. Результат обобщения зависит не столько от суммы знаний, примерно одинаковой для всех учащихся класса, а от умения комбинировать, связывать эти знания по–новому, заглядывать дальше обычных пределов.

Характер упражнений, выполняемых в классе, должен отразится и на характере контрольных и проверочных работ; чему обучают, то и следует проверять.

Всякая математическая задача неисчерпаема в своих связях с другими задачами; после решения задачи почти всегда можно найти предмет размышления, найти несколько направлений, в которых удаётся обобщить задачу, и найти затем решение созданных таким образом новых проблем.

Время и усилия, затраченные на обобщение знаний, окупаются той большой экономией мышления, в последующем, которые достигаются благодаря единообразным методам усвоения материала.

Глава II. Обобщающее повторение по геометрии в 8 классе (на примере темы: "Четырехугольники").

§1. Значение повторения.

Одним из важнейших вопросов, способствующих дальнейшему повышению успеваемости, достижению глубоких и прочных знаний у учеников является вопрос о повторении ранее пройденного материала.

Без прочного сохранения приобретенных знаний, без умения воспроизвести в необходимый момент, ранее пройденный материал, изучение нового материала всегда будет сопряжено с большими трудностями и не дает надлежащего эффекта.

"Обучение нельзя довести до основательности без возможно более частых и особенно искусно поставленных повторений и упражнений", — говорил Каменский.

Преподавать математику, не повторяя повседневно на каждом уроке ранее пройденный материал, это значит — передать, пересказать учащимся определенную сумму различных законов, теорем, формул и т. п. , совершенно не заботясь о том, насколько прочно и сознательно освоили этот материал наши питомцы; это значит не дать детям глубоких и прочных знаний. Работать так, это, по меткому выражению Ушинского, уподобиться "пьяному вознице с дурно увязанной кладью: он все гонит вперед, не оглядываясь назад, и привозит домой пустую телегу, хвастаясь только тем. что сделал большую дорогу".

Ранее пройденный материал должен служить фундаментом, на который опирается изучение нового материала, который в свою очередь, должен обогащать и расширять ранее изученные понятия.

"Старое должно подпирать новое, а новое обогащать старое".

Правильно организованное повторение помогает ученику увидеть в старом нечто новое; помогает установить логические связи между вновь изучаемым материалом и ранее изученным; обогащает память ученика; расширяет его кругозор; приводит знания ученика в систему; дисциплинирует ученика; приучает в нем уменье находить необходимого для ответа на поставленный вопрос материал; воспитывает в ученике чувство ответственности.

В связи с этимособо важное значение приобретают вопросы:

Что надо повторять? Как повторять? Когда повторять?

Большую и серьезную ошибку допускает тот учитель, который побуждает ученика повторять материал в том порядке, в котором он изучался. Повторение в этом случае сводится и механическому воспроизведению в памяти пройденного материала.

Ушинский воспитывал против механического повторения. "Нет никакой надобности повторять выученное в том порядке, в каком оно было пройдено, а напротив, ещё полезнее повторения случайные, сводящие выученное в новые комбинации", — говорил он.

Повторение пройденного материала должно стать необходимейшим элементом в преподавании математики, органической и неотъемлемой частью каждого урока.

§2. Виды повторения.

В связи с этим мы различаем следующие виды повторения ранее пройденного материала:

1. Повторение в начале учебного года.

2. Текущее повторение всего, ранее пройденного:

а) повторение пройденного в связи с изучением нового материала (сопутствующие повторению);

б) повторение пройденного вне связи с новым материалом.

3. Tематичеcкoе повторение (обобщающее и систематизирующее повторение законченных тем и разделов программы).

4. Заключительное повторение (организуемое при окончании прохождения большого раздела программы или в конце учебного года).

Цели и время повторения тесно связаны и взаимообусловлены и в свою очередь определяют методы и приемы повторения.

При планировании повторения необходимо отобрать материал, установить последовательность и время повторения, распределить отобранный материал по урокам, установить формы и методы для осуществления повторения, разумеется, надо учитывать и свойство памяти.

Основные требования к организации повторения должны исходить из целей повторения, специфики математики как учебного предмета, её методов.

Первое требование к организации повторения, исходящее из его целей, это определение времени: когда повторять? Оно должно осуществляться по принципу: "Учить новое, повторяя, и повторять, изучая новое" (В. П. Вахтеров).

Это не означает, однако, что нельзя специально отводить уроки для повторения, скажем, для таких вопросов программы, которые трудно увязать с текущим материалом.

План повторения и выбор тем для повторения учитель должен составлять в каждом отдельном случае на основании общих теоретических соображений с учетом того, как усвоен учащимся материал соответствующих разделов.

К сказанному добавим еще то, то характер урока в связи с переходом учащихся из одного класса в другой значительно меняется. В старших классах существенно перестраивается закрепление и повторение учебного материала. Увеличивается объем фактического материалами, выносимого на закрепление и повторение; поурочное закрепление в ряде случаев переходит и тематическое или перерастает в обобщающее повторение, увеличивается доля самостоятельности учащихся при закреплении и повторении.

Второе требование к организации повторения должно отвечать на вопрос: Что повторять? Исходя из высказываний классиков педагогики, можно выдвинуть следующие положения при отборе учебного материала по различным видам повторения:

1. Не следует повторять всеранее пройденное. Нужно выбрать для повторения наиболее важные вопросы и понятия, вокруг которых группируется учебный материал.

2. Выделять для повторения такие темы и вопросы, которые по трудности своей недостаточно прочно усваиваются.

3. Выделять для повторения надо то, что необходимо обобщить, углубить и систематизировать.

4. Не следует повторять все в одинаковой степени. Повторять основательно надо главное и трудное. При отборе материала для повторения необходимо учитывать степень его связи с вновь изучаемым материалом.

Третье требование к организации повторения математики должно отвечать на вопрос, как повторять, т. е. осветить те методы и приемы, которыми должно осуществляться повторение. Методы и приемы повторения должны находиться в тесной связи с видами повторения.

Приповторении необходимо применять различные приемы и методы, сделать повторениеинтересным путём внесения, как в повторяемый материал, так и в методы изучения некоторых элементов новизны. Только разнообразие методов повторения может устранить те противоречие, которое возникает ввиду отсутствия желания у части учащихся повторять то, что ими усвоено однажды.

Различные виды повторения тесно взаимодействуют; от своевременного и успешного проведения одного из видов повторения, например, тематическогоили текущего, зависит продолжительность и успешность повторения другого вида — заключительного повторения или повторения в конце года. Перейдём к краткой характеристике видов повторения.

1. Повторение пройденного в начале года.

При повторении в начале учебного года в первый план должно выдвигаться повторение тем, имеющих прямую связь с новым учебным материалом. Новые знания, приобретаемые на уроке, должны опираться на прочный фундамент уже усвоенных.

При повторении в начале года необходимо наряду с повторением тем, тесно связанных с новым материалом, повторить и другие разделы, которые пока не примыкают к вновь изучаемому материалу. Здесь необходимо сочетать обе задачи: провести общее повторение в порядке обзора основных вопросов из материала прошлых лет и более глубоко повторить вопросы, непосредственно связанные с очередным материалом по программе учебного года.

Само повторение следует проводить как в классе, так и дома. При решении вопроса, какой материал должен быть повторен в классе и какой оставлен учащимся для самостоятельного повторения дома, нужно исходить из особенности материала. Наиболее трудный материал повторили в классе, а менее трудный дали на дом для самостоятельной работы.

2. Текущее повторение пройденного.

Текущее повторение в процессе изучения нового материала — весьма важный момент в системе повторения. Оно помогает устанавливать органическую связь между новым материалом и ранее пройденным.

Текущее повторение может осуществляться в связи с изучением нового материала. В этом случае повторяется материал, естественно увязывающийся с новым материалом. Повторение здесь входит составной и неотъемлемой частью во вновь изучаемый материал.

Под руководством учителя ученики на уроке воспроизводят ранее изученный ими необходимый материал. В результате этого доказательство новой теоремы воспринимается учащимися легко, а дальнейшая работа учителя — воспроизведение доказанного и упражнения, обеспечивающие вторичное осмысление теоремы и её закрепление.

Во втором случае все связи с новым материалом, когда повторяемый материал не находит естественной увязки с новым и его приходится повторять на специальных уроках.

При текущем повторении вопросы и упражнения могут быть предложены учащимся из различных разделов программы.

Текущее повторение осуществляется в процессе разбора упражнений, включается в домашнее задание. Оно может быть проведено как в начале или в конце урока, так и во время опроса учащихся.

Текущее повторение дополняется сопутствующим повторением, которое нельзя строго планировать на большой период. Сопутствующее повторение не вносится в календарные планы, для него не выделяется специальное время, но оно является органической частью каждого урока. Сопутствующее повторение зависит от материала, привлекаемого для изучения очередного вопроса, от возможности установить связи между новым и старым, от состояния знаний учащихся в данный момент. Успех сопутствующего повторения в значительной степени обусловливается опытом и находчивостью учителя. Сопутствующим повторением учитель по ходу работы устраняет неточности в знаниях, напоминает вкратце давно пройденное, указывает их связь с новым.

3. Тематическое повторение.

В процессе работы над математическим материалом особенно большое значение приобретает повторение каждой законченной темы или целого раздела курса.

При тематическом повторении систематизируются знания учащихся по теме на завершающем этапе его прохождения или после некоторого перерыва.

Для тематического повторения выделяются специальные уроки, на которых концентрируется и обобщается материал одной какой-нибудь темы.

В процессе работы над темой вопросы, предлагаемые учащимся по каждому разделу, следует вновь пересмотреть; оставить наиболее существенные и отбросить более мелкие. Обобщающий характер вопросов при тематическом повторении отображается и на их количестве. Учителю приходится основной материал темы охватить в меньшем числе вопросов.

Повторение на уроке проводится путём беседы с широким вовлечением учащихся в эту беседу. После этого учащиеся получают задание повторить определённую тему и предупреждаются, что будет проведена контрольная работа.

Контрольная работа по теме должна включать все ее основные вопросы. После выполнения контрольной работы проводится разбор характерных ошибок и организуется повторение для их устранения.

При тематическом повторении полезно составить вопросник, а затем логический план по теме и завершить работу составлением итоговых схем. Таблица или схема экономно и наглядно показывает общее для понятий, входящих в данную тему, их взаимосвязь в логической последовательности.

Процесс составления таблиц в одних случаях, подбор и запись примеров после анализа готовой таблицы в других случаях является одновременно и формами письменных упражнений при обобщающем и систематизирующем повторении.

Последовательное изучение различных особых случаев при повторении весьма полезно закончить их классификацией, что поможет учащимся яснее различить отдельные случаи и группировать их по определенному признаку.

4. Заключительное повторение.

Повторение, проводящееся на завершающем этапе изучения основных вопросов курса математики и осуществляемое в логической связи с изучением учебного материала по данному разделу или курсу в целом, будем называть заключительным повторением.

Цели тематического повторения и заключительного повторения аналогичны, материал повторения (отбор существенного) весьма близок, а приемы повторения в ряде случаев совпадают.

Заключительное повторение учебного материала преследует цели:

1. Обозрение основных понятий, ведущих идей курса соответствующего учебного предмета; напоминания в возможно крупных чертах пройденного пути, эволюции понятий, их развития, их теоретических и практических приложений.

2. Углубления и по возможности расширения знаний учащихся по основным вопросам курса в процессе повторения.

3. Некоторой перестройки и иного подхода к ранее изученному материалу, присоединения к повторному материалу новых знаний, допускаемых программой с целью его углубления.

§3. Содержание и методика обобщающего повторения на примере темы: «Четырехугольники».

Решением одной из важных задач общеобразовательной и профессиональной школы являетсяусиление прикладной направленности обучения. В этой связи важно выработать у учащихся умение при решении конкретных вопросов ориентироваться на существенные свойства объектов и явлений. Большие возможности для формирования такого умения имеются при изучении темы "Четырёхугольники".

Предлагаемый материал представляет большие возможности для организации разных форм коллективной учебно-познавательской деятельности учащихся, формирования их диалектико–материалистического мировоззрения, закладывает фундамент для развитая умения применять геометрические знания при решении вопросов жизненно–практического и производственного характера.

В качестве ведущей идеи берем идею четкого разграничения свойств и признаков параллелограмма и его частных видов.

Прежде всего нужно добиться, чтобы учащиеся научились различать понятия "свойство фигуры" и "признак фигуры". Если дано, что фигура параллелограмм, и исходя из этой посылки доказывают некоторые соотношения между элементами рассматриваемой фигуры, то каждое из этих соотношений называется свойством фигуры, о которой речь идет в условии теоремы.

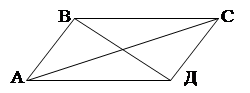Например, теорема: "У параллелограмма противоположные стороны равны, противоположные углы равны", кратко может быть записано так:

Дано: АВСД – параллелограмм.

Доказать: 1) АВ = СД; АД = ВС

2) ÐА = ÐС; ÐВ = ÐД

Каждое из соотношений (1), (2) заключения теоремы дает свойство параллелограмма.

В теореме же "Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм" указаны соотношения между элементами некоторого четырехугольника (АО=ОС, ВО=ОД) и доказывается, что при их выполнении четырехугольник будет принадлежать к классу параллелограммов (будет являться параллелограммом). В этом случае условия (АО=ОС, ВО=ОД) называют признаками параллелограмма, т. к. при их выполнении мы можем смело утверждать, что четырехугольник, для которого выполняются эти условия, обязательно будет параллелограммом (теорема).

Более глубокого и осознанного усвоения понятий "свойство" и "признак" можно добиться, если связать их с понятиями "необходимое условие", "достаточное условие", "необходимое и достаточное условие".

Сообщаем школьникам, что любая теорема может быть записана в виде АÞВ, гдеА — условие теоремы (что дано), а В — заключение теоремы (что требуется доказать).

Если доказана теорема АÞВ, то А является достаточным для В (как только есть А, то сейчас же будет и В), а В — необходимо для А, из А неизменно (необходимо) следует В.

Ещё более убедительное обоснование того, почему условие В считается необходимым для А, можно дать, если познакомить учащихся с вопросом о видах теорем и связи между ними. Записываем схему:

(1) АÞВ ВÞА (2)

(3) нет А Þ нет В нет В Þ нет А (4)

Сообщаем, что если утверждение (1) назвать прямым, то утверждение (2) будет к нему обратным, утверждение (3) — противоположным прямому, а (4)—противоположно обратному. Далее доказывается, что из справедливости утверждения (1) следует справедливость утверждения (4) [(1)Þ(4)] и наоборот, т. е. (4)Þ(1).

Сообщается, что если (1)Þ(4), то утверждения называются эквивалентными. Аналогично эквивалентны утверждения (2) и (3) [(2)Û(3)].

Словами формулу (1)Þ(4) можно расшифровать так: если из условия А следует (вытекает) условие В, то без в нет и А (из нет в нет А), иными словами В необходимо для А (без В не будет и А).

А далее сообщаем, что необходимое условие дает нам свойство, а если условие не только необходимо, но и достаточно, то получаем признак.

Иными словами, чтобы получить свойство В какого-нибудь объекта А, достаточно доказать теорему АÞВ, а чтобы убедиться, что рассматриваемое свойство В является признаком, следует ещё доказать теорему ВÞА (обратную).

Вместе с учащимися вспоминаем все свойства параллелограмма и составляем таблицу.

Дано: АВСД – параллелограмм

Доказать: 1) АВ || СД

2) 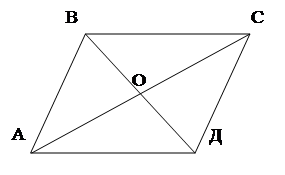ВС || АД

3) АВ = СД

4) ВС = АД

5) АО = ОС

6) ВО = ОД

7) ÐА = ÐС

8) ÐВ = ÐД

9) ÐА + ÐВ = 180⁰

10)ÐС + ÐВ = 180⁰

11)ÐС + ÐД = 180⁰

12)ÐА + ÐД = 180⁰

Обращаем внимание на тот факт, что каждое из условий 1–12 вытекает из того, что АВСД — параллелограмм, следовательно, каждое из них является необходимым условием того, чтобы четырехугольник АВСД был параллелограммом. Легко убедиться, что из каждого из условий 1–12 не следует, что АВСД — параллелограмм (например, если дано, что АВ II СД, что имеем трапецию, ибо ВС || АД).

Таким образом, каждое из условий 1–12, взятое в отдельности, признаком параллелограмма не является. Теперь начнём комбинировать свойства по два (Сколько таких комбинаций будет? Как сосчитать все комбинации, чтобы быть убеждённым, что ни одна не пропущена?). Убеждаемся, что некоторые из комбинаций дают признак параллелограмма. Какие из комбинаций по два дают известные уже вам признаки параллелограмма? [(1, 2), (1, 3), (2, 4), (5, 6)].

В то же время легко видеть, что не каждая из комбинаций по два дает признак параллелограмма. Например, из того что АВ II СД и ВС = АД следует, что фигура АВСД — равнобочная трапеция, а не параллелограмм.

Естественно встает вопрос, сколько же всего признаков у параллелограмма? Для ответа на этот вопрос нужно перебрать все возможные комбинации и либо доказать полученную теорему, либо привести пример, опровергающий её (контрпример). Ясно, что эта работа на уроке проделана быть не может. Она может быть дана в качестве индивидуальных заданий на дом хорошо успевающим учащимся, или еще лучше, предложена в качестве коллективной работы кружковцам. Здесь встают интересные вопросы о планировании работы, о разделении труда при решении этой проблемы, об организации самоконтроля и взаимоконтроля, о подведении окончательных итoгoв, т.e. вопросы, возникающие при организации любой трудовой деятельности.

Далее аналогичную работу можно провести по выяснению признаков прямоугольника и ромба. Но этой работе должно предшествовать уточнение определений прямоугольника и ромба. Действительно, достаточно потребовать, чтобы у параллелограмма был один прямой угол, т. к. из условия (АВСД — параллелограмм; ÐА=900) следует, что ÐВ=90⁰ , ÐС=90⁰ , ÐД=90⁰ . Для доказательства этого факта достаточно воспользоваться известными свойствами углов параллелограмма.

Аналогично, легко доказать теорему (АВСД — параллелограмм, АВ=ВСÞАВ=ВС=СД=АД), из которой следует, что ромбом называется параллелограмм, у которого две смежные стороны равны.

Можно не менять привычные учащимся избыточные определения, но обязательно подчеркнуть тот факт, что, чтобы убедиться, что рассматриваемый параллелограмм будет ромбом, достаточно проверить равенство двух смежных сторон, а чтобы убедиться, что он будет прямоугольником, достаточно доказать, что один из его углов прямой.

После этого отмечаемособые свойства диагоналей прямоугольника и ромба и опять ставим вопрос, будут ли эти условия не тольконеобходимыми, но и достаточными, т. е. являются ли эти условия признаками рассматриваемых фигур. Как это проверить? Учащиеся должны сообразить, что для ответа на поставленный вопрос следует сформулировать и доказать теоремы, обратные к теоремам, выражающим свойства диагоналей прямоугольника и ромба.

Запишем одну из этих теорем.

Дано: АВСД - прямоугольник. Доказать: АС=ВД.

Обратное к этой теореме утверждение записывается так:

Дано: в четырёхугольнике АВСД АС=ВД .

Доказать: АВСД — прямоугольник.

Легко убедиться, что это утверждение несправедливо. Приведите примеры, подтверждающие этот факт. Учащиеся могут вспомнить, что диагонали равны у равнобочной трапеции, или начертить произвольный четырехугольник с равными диагоналями. Таким образом, мы убеждаемся, что равенство диагоналей не выделяет прямоугольник из класса четырехугольников (среди четырёхугольников с равными диагоналями есть и не являющиеся прямоугольниками).

Здесь учитель знакомит учащихся с еще одним способом получения утверждений, обратных данному. Замечает, что условие прямой теоремы может быть разбито на две части.

Дано: 1) АВСД — параллелограмм.

2)ÐА=900.

Доказать: АС = ВД.

Если теперь поменять местами заключение и вторую часть условия, то мы получим утверждение:

Дано: АВСД — параллелограмм

АС=ВД.

Это утверждение легко доказать. Докажите самостоятельно.

Если учащиеся затрудняются, то можно "навести" их на мысль, обратив внимание, что ÐА + ÐД = 1800 (АВСД — параллелограмм ). Что осталось теперь доказать? (ÐА=ÐД).

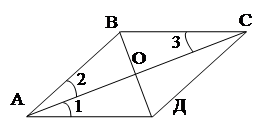Аналогичную работу проводим с установлением признаков ромба, основанных на свойствах его диагоналей. Вспоминаем теорему о свойствах диагоналей ромба.

Дано: АВСД — ромб.

Доказать: 1) ВД | АС;

2) ÐВАС =ÐСАД.

Для этой теоремы можно составить две обратные:

Теорема 1 Теорема 2

Дано: ВД | АС Дано: ÐВАС = ÐСАД

Доказать: АВСД — ромб. Доказать: АВСД — ромб.

Легко показать, что каждая из этих теорем несправедлива, приведя хотя бы по одному "контрпримеру";

Интересен вопрос. А как можно видоизменить первый чертеж чтобы его можно било использовать одновременно для "опровержения" и теоремы 1 и теоремы 2 (Достаточно взять АО=ОС и тогда ÐAВД=ÐДВС.

Используя второй способ образования обратных теорем, с которым учащиеся ознакомлены при установлении признака прямоугольника.

Имеем:

Прямая теорема: Дано:

АВСД –параллелограмм, АВ = ВС.

Доказать: ВД | АС

Обратная теорема:

Дано: АВСД –параллелограмм, ВД | АС.

Доказать: АВ=ВС

Вспоминая уточненное определение ромба, даем такую формулировку обратной теоремы: "Если в параллелограмме диагонали взаимоперпендикулярны, то этот параллелограмм — ромб".

Схема аналитического рассуждения при отыскании доказательства этой теоремы.

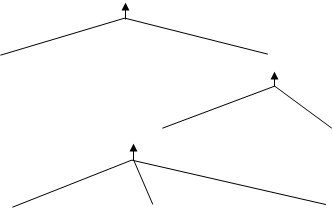АВСД – ромб

АВСД – параллелограмм АВ=ВС

DАВО = DСВО ÐАОВ = ÐСОВ

Ý ВД | АС

АО = ОС ВО – общая ÐАОВ = ÐСОВ

Ý

АВСД – параллелограмм ВД | АС

Аналогично формулируем второй признак ромба: "Если в параллелограмме диагональ делит угол пополам, то этот параллелограмм — ромб". Аналитическое рассуждение проводится аналогично.

Схематическая запись доказательства

АВСД — параллелограмм ÞАД II ВС Þ (Ð1 = Ð3, Ð1 = Ð2) Þ

ÞÐ2 = Ð3 Þ (АВ=BС, АВСД - параллелограмм) Þ АВСД — ромб.

Обобщая полученные результаты, полезно обратить внимание школьников на тот факт, что равенство диагоналей не выделяет прямоугольник из множества всех четырехугольников, но выделяет его из множества параллелограммов, и предложить им самостоятельно сформулировать аналогичные утверждения (их 2!) для ромба.

Для поверки того, владеют ли учащиеся признаками параллелограмма, ставим перед ними следующую проблему:

Как сформулировать признаки прямоугольника и ромба, основанные на свойствах их диагоналей, чтобы они выделяли прямоугольник и ромб из множества всех четырехугольников? Подсказка, если ученики не справляются: условие АВСД — параллелограмм, каким требованием относительно его диагоналей можно заменить.

Получаем признаки:

1. Если в четырехугольнике диагонали равны и точкой их пересечения делятся пополам, то этот четырехугольник — параллелограмм.

2. Если в четырехугольнике диагонали взаимноперпендикулярны и делятся точкой пересеченияпополам, то этот четырехугольник — параллелограмм.

3. Признак формулируем аналогично.

Переходя к выяснению признаков квадрата, подчеркиваем, что квадрат является как частным случаем прямоугольника, так и ромба и следовательно обладает всеми свойствами прямоугольника и всеми свойствами ромба. Ставится проблема: выделить комбинации свойств диагоналей, которые выделяли квадрат из множества прямоугольников, из множества ромбов, их множества параллелограммов, из множества четырехугольников.

Если ученики осмыслили рассмотренный материал о признаках прямоугольника и ромба, то они легко ответят на поставленные вопросы и сформулируют следующие признаки квадрата:

Квадратом является:

Прямоугольник с взаимно–перпендикулярными диагоналями,

Прямоугольник, у которого диагональ делит угол пополам.

Ромб с равными диагоналями.

Параллелограмм, у которого диагонали равны и взаимно–перпендикулярны.

Параллелограмм, у которого диагонали рваны и делят угол пополам.

Четырехугольник, у которого диагонали равны, взаимно–перпендикулярны и в точке пересечения делятся пополам.

После этого можно перейти к решению задач, требующих применения изученных признаков.

Для приведения в систему материала по теме "Параллелограмм и его виды» очень хороша задача: «Определить вид четырехугольника, который получится, если последовательно соединить отрезками прямых середины сторон произвольного четырехугольника».

После доказательства того факта, что полученный четырехугольник будет параллелограммом, ставится вопрос: «Каким должен быть исходный четырехугольник, чтобы полученный оказался прямоугольником, ромбом, квадратом?».

2) 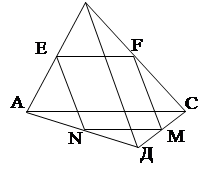Начертим произвольный четырехугольник.

3)

4) Соединим последовательно полученные точки E, F, M, N.

Вопрос: какой четырехугольник получился?

У разных учащихся ответ будет различным: параллелограмм, прямоугольник, ромб, квадрат. Учитель обращает внимание на то, что прямоугольник, ромб, квадрат — частные виды параллелограмма, поэтому всем придется доказывать, что четырехугольник EFMN — параллелограмм.

Дано: АЕ = ЕB, BF=FC, СМ=МД, ДN=NА.

Доказать: EFMN — параллелограмм.

Проводится анализ:

Вопрос: Для того, чтобы доказать, что EFMN — параллелограмм, что достаточно доказать?

Ответ; параллельность прямых EF и MN, а также ЕN и MF.

Вопрос: Как можно доказать? (или, если не отвечают: Используя какой признак параллельности прямых можно это доказать?).

Ответ: Первый признак параллельности прямых т.к. в других признаках участвуют углы, а в условии задачи об углах ничего не сказано.

Вопрос: В первом признаке параллельности прямых говорятся о трех прямых. Где взять третью прямую?

Ответ: Соединить точки А и С. Получим два треугольника — АВС и АДС.

Вопрос: Какое соотношение известно в этих треугольниках? Или: Чем являются ЕF и MN в DАВС и DАДС?

Ответ; ЕF является средней линией DАВС, ибо АЕ = FВ и ВГ = FC, а MN является средней линией DАДС, т.к. СМ = МД и ДN = NА.

Вопрос: Какой признак среднейлинии мы знаем?

Ответ: Средняя линия параллельна основанию.

Вопрос: Какой вывод можно сделать о ЕF и MN?

Ответ: ЕF || АС и МN || АС. Значит, по первому признаку параллельности прямых следует, что ЕF || MN.

Аналогично доказывается, что ЕN || FM.

Проведем так называемый «взгляд назад» и попробуем найти другое решение, более рациональное и короткое.

Вопрос: Как еще можно доказать, что четырехугольник EFMN — параллелограмм?

Или: Каким признаком параллелограмма можно воспользоваться, чтобы доказать, что четырехугольник EFMN — параллелограмм?

Ответ: Воспользоваться признаком параллелограмма, который заключается в том, что если в четырехугольнике противоположные стороны попарно параллельны и равны, то этот четырехугольник — параллелограмм. Значит надо доказать, что EF || MN и EF = MN.

Вопрос: Параллельность прямых EF и MN доказывается так, как это было сделано выше. Как доказать равенство ЕF и МN? или: Какое свойство средней линии мы знаем?

Ответ: Так как ЕF — средняя линия DАВС, то ЕF равна половине основания АС; MN средняя линия АДС и М равна половине основания АС. Значит ЕF = MN.

Это решение являетсяболее рациональным и коротким.

Теперь надо записать решение задачи. Для этого уже используется синтез.

АЕ = ЕВ ЕF || AC

BF = FC EF = 1/2 AC EF || MN Þ EFMN – парал–

СМ = МД MN || AC EF = MN лелограмм

ДN = NA MN = 1/2 AC

В классе всегда есть ученики, которые быстро найдут решение этой задачи. Для организации индивидуальной групповой деятельности более сильным учащимся можно дать дополнительные задания:

Какой вид должен иметь исходный четырехугольник, чтобы полученный был

а) прямоугольником?

б) ромбом?

в) квадратом?

В этом случае целесообразно подойти к распределению дифференцированно: наиболее сильным предложить вариант в), средним — вариант б), остальным — а).

Предлагая учащимся задачи с избыточной и неполной информацией, мы воспитываем в них готовность к практической деятельности. Рассматривая изящное решение той или иной математической задачи, мы способствуем эстетическому воспитанию школьников.

Мне хочется привести несколько примеров задач, возникших из рассмотрения шарнирной модели четырехугольника.

Убедившись вместе со школьниками в подвижности этой модели (не жёстко скрепленной в вершинах) учитель побуждает их к выводу, что четыре данные стороны не определяют четырехугольник однозначно,

Затем перед учащимися формируется сама задача.

Задача 1. Имеется модель шарнирного четырехугольника со сторонами определённой длины. Каким способами можно придать «жёсткость» данной модели четырехугольника, если его вершины не могут быть закреплены? Ответ обосновать.

В ходе обсуждения этой задачи предлагаются различные варианты её решения, которые проверяются опытными путями, например, скрепить две вершины четырехугольника планкой по диагонали, соединить планкой середины двух противоположных сторон и т. д.

Убедившись на опыте в разумности сделанных предложений, учащихся приходят к необходимости обосноватьтот или иней способ «наведения жесткости». С помощью учителя они приходят к возможности провести это обоснование, переформулировать задачу в виде соответствующей задачи на построение. Роли по заданным элементам можно построить единственную фигуру, то её модель будет жёсткой.

Возможность сведения конкретной задачи, определённой на модели, к решению абстрактной геометрической задачи на построение реализует одну из важнейших воспитывающих функций геометрических задач: связь обучения математике с жизнью, т.е. показывает реальное происхождение математических абстракций.

Учитывая «свойство жесткости» треугольника первое из вышеназванных решений обосновывается достаточно просто. Однако обоснование второго пути решения задачи не столь очевидно. Возникает уже чисто геометрическая абстрактная задача.

Задача 2. Построить 4-х угольник АВСД, зная длину его сторон и длину отрезка MN, соединяющего середины сторон АВ и ДС.

Допустим, что искомый 4-х угольник АВСД построен (рис. 3а). Выполним параллельный перенос (ДN) стороны ДА и || перенос (CN) стороны СВ, теперь из точки исходят 3 отрезка А₁ N, MN, NВ₁ известной длины.

Нетрудно показать, что точка М является серединой АВ₁ . В самом деле, длины отрезков АА₁ и ВВ₁ равны 1/2ДС, а сами отрезки || ДС.

Поэтому четырехугольник А₁ АВ₁ В является параллелограммом. Точка М — середина его диагонали АВ. Поэтому М принадлежит диагонали А₁ В₁ и является ее серединой.

Итак, в D NA₁ B₁ известны стороны NA₁ , В₁ N и заключённая между ними медиана. Для того, чтобы построить этот треугольник, отметим точку N₁ , симметрично относительно М. Очевидно, |АN| = |В₁ N|.

Треугольник N₁ NA₁ можно построить по трем известным сторонам: |NA₁ | = |ДА|, |A₁ N₁ | = |В₁ N| = |CB| и |NM₁ | = 2|NM|.

Теперь построим искомый четырехугольник. Делим отрезок N₁ N точкой М на два конгруэнтных отрезка, строим точку В₁ , симметричную А₁ относительно М. По трем сторонам построим треугольники А₁ МА и МВВ₁ . Перенеся отрезок А₁ А на вектор А₁ N, а отрезок ВВ₁ на вектор В₁ N, подучим все четыре вершины искомого 4-х угольника АВСД. Нетрудно показать единственность решения задачи.

Например, 4‑х угольник ДД₁ В₁ В — параллелограмм, стороны которого конгруэнтны диагоналям 4-х угольника АВСД, в углы конгруэнтны углами между этими диагоналями; длины диагоналей ДД₁ В₁ В вдвое больше длин отрезков, соединяющих середины противоположных сторон АВСД; расстояния от точки С до вершин этого параллелограмма равны соответственно длинам сторон 4-х угольника АВСД и т.д.

Таковы, например, следующие задачи:

Задача 3. В четырехугольнике АВСД известны длина отрезка М, соединяющего середины сторон АВ и СД, длина диагонали АС и длины сторон АВ, ВС и АД.

Является ли данная фигура жесткой?

Задача 4. Построить трапецию АВСД по данным диагоналям АС, ВД, стороне АД и отрезу МN, соединяющему середины её оснований.

Рассмотрение этого примера показывает, как достаточно широко можно использовать обучающие, развивающие и воспитывающие функции задач в их единстве. В самом деле, в ходе решения этих задач используются различные свойства геометрических фигур, активно работает метод параллельного переноса и прием построения вспомогательной фигуры с весьма интересными свойствами, тесно связанными со свойствами заданной (искомой) фигуры (реализуются различные развивающие функции), задача легко моделируется (дотекает опытные решения), возбуждает интерес школьников (реализуются воспитывающие функции). Задача такова, что может служить источником разнообразных аналогичных задач, многие из которых как показал опыт, успешно составляются самими школьниками, что способствует формированию у них творческой активности.

Опыт показывает, что успешность в реализации воспитывающих функций математических задач во многом определяется пробуждением у учащихся интереса к данной задаче, возникновением у них устойчивой потребности в её решении, наличием интереса к самому процессу решения задач на основе последнего часто возбуждается и формируется интерес учащихся к изучению самой математики и смежных учебных дисциплин, интерес к учению в целом.

Факторы, существенно влияющие на формирование у учащихся устойчивого интереса к решению математических задач, весьма разнообразны. К ним, например, относится доступность предложенной задачи, внешняя или внутренняя занимательность задачи, осознанная возможность проявить при этом творческую самостоятельность.

Глава III. Описание и результаты эксперимента.

Эксперимент проводится в СШ №46 (гимназия №4)

под руководством Баязитовой Л.Ш. в 8^б и 8^г .

Перед проведением уроков по обобщающему повторению в обоих классах была проведена самостоятельная работа с целью узнать их уровень знаний.

Проверочная самостоятельная работа.

Через точку пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AD и BC в точках Е и F соответственно. Найдите стороны параллелограмма, если его периметр равен 28 см, АЕ = 5 см, ВF = 3 см. [1. Биссектрисы углов А и D параллелограмма ABCD пересекаются в т. М лежащей на стороне ВС. Найдите стороны параллелограмма, если его периметр равен 36 см.]

Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10 см и 6 см, а один из углов 45^о [2. Найдите боковую сторону равнобедренной трапеции, основания которой равны 12 см и 6 см, а один из углов 60^о ]

Самостоятельная показала, что знания у учеников в обоих классах разрозненные, решают задания очень медленно. Оценки по самостоятельной работе низкие. (Это показано на графике.)

После самостоятельной работы, используя таблицу темы: «Четырехугольники», которая приведена в методическом пособии по геометрии (Гудвин и Гангнус ч.1). Перед учащимися можно поставить ряд вопросов, ответы на которые ученики не найдут в готовой форме в учебнике, а должны поработать головой, чтобы дать их.

Приведём некоторые вопросы, которые ставятся нами перед учащимися:

Как из равнобедренной трапеции получить квадрат? Какие дополнительные условия необходимы для этого?

Как из параллелограмма получить квадрат?

Как трапецию обратить в ромб?

Являясь параллелограммом, ромб имеет свои обычные свойства. Перечислите их. Тоже о квадрате.

Перечислите , какими свойствами параллелограмма обладает ромб? Квадрат? Прямоугольник? И т.д.

Наряду с использованием указанной таблицы перед учащимися были поставлены вопросы: в каком четырехугольнике:

Диагональ делит его на два равных треугольника?

Диагонали пересекаются в одной точке и делятся пополам?

Диагонали являются биссектрисами внутренних углов?

Диагонали взаимно перпендикулярны?

Диагонали служат осями симметрии?

Учащиеся должны были дать не только ответы на вопросы, но каждый ответ обосновать, ссылаясь на изученные теоремы.

Ответ считали малоценным, если он перечислял без системы отдельные виды четырехугольников, в которых диагонали обладают требуемым свойством. Так если на вопрос: «В каких четырехугольниках диагонали пересекаясь делятся пополам? »

Ученик отвечал: «Диагонали, пересекаются в одной точке, делятся пополам в параллелограмме, ромбе, квадрате ».

Не перебивая его давали возможность ученику высказаться, но по окончанию ответа ставили вопрос: «Следует ли для ответа на поставленный вопрос перечислять все виды четырехугольников? Нельзя ли дать полный и исчерпывающий ответ, но в более короткой формулировке? »

Если ученик затрудняется ответить на эти вопросы, перед ним ставились дополнительные вопросы: «Является ли прямоугольник параллелограммом? Почему?»

Подобные вопросы ставились и по отношению к ромбу и квадрату.

Следовательно, можно ли утверждать, что прямоугольник, квадрат, ромб — есть параллелограмм?

После этого учащимся не составляло затруднений дать такой ответ:

«Диагонали, пересекаются и точкой пересечения делятся пополам в параллелограммах».

Если учащихся давали сразу исчерпывающий ответ и при том в краткой форме, мы давали дополнительные вопросы с целью выяснить, на сколько сознательно усвоен материал.

Так если на вопрос: «В каком четырехугольнике диагональ делит его на два равных треугольника?»

Следовал ответ: «Диагональ делит четырехугольник на два равных треугольника в том случае, если он параллелограмм», то ученику ставился вопрос: «А в прямоугольнике, квадрате, ромбе диагональ не обладает тем же свойством?»

«Прямоугольник, квадрат, ромб — это параллелограммы, но каждый с особыми свойствами. Поэтому, когда говорил о параллелограмме, говорил и о них», — отвечал ученик.

Подобные ответы мы считали наиболее ценными, так как они показывают, что ученик действительно поработал сам над данным ему заданием, что материал не зазубрил, а усвоил сознательно.

Однако таких ответов было очень мало. Тогда в одном из классов (8^б ) было проведено обобщающее повторение. А в 8^г была пройдена тема «четырехугольники» и закреплена. После всего этого была проведена контрольная работа.

Контрольная работа. (1ч.)

Диагонали прямоугольника АВСД пересекаются в точке О. Найдите угол между диагоналями, если АВО = 30^о [1. Диагонали ромба КМНР пересекаются в точке О. Найдите углы треугольника КОМ, если угол МНР = 80^о ].

В параллелограмме КМНР проведена биссектриса угла МКР, которая пересекает сторону МН в точке Е.

а) Докажите, что треугольник КМЕ равнобедренный.

б) Найдите сторону КР, если МЕ = 10 см, а периметр параллелограмма = 52 см. [2. На стороне ВС параллелограмма АВСД взята точка М так, что АВ=ВМ. а) Докажите, что АМ — биссектриса угла ВАД. б) Найдите периметр параллелограмма, если СД=8 см, а СМ = 4 см].

Результаты контрольной работы можно показать диаграммой.

Проведённый эксперимент показывает, что класс, в котором было проведено обобщающее повторение, легко работает с материалом, быстро решает задачи, может ответить на любой дополнительный вопрос, пояснить, что и как решается, обосновать свой ответ.

Эффективность обобщающего повторения заметна сразу.

ЗАКЛЮЧЕНИЕ

Прочное усвоение знаний является главной задачей процесса обучения, это очень сложный процесс. В него входят восприятие учебного материала, его запоминание и осмысливание, а также возможность использования этих знаний в различных условиях.

1. Преподавание математики не может стоять на должном уровне, а знания учащихся не будут достаточно полными и прочными, если в работе учителя отсутствует система повторительно-обобщающихуроков.

Это объясняется психологическими особенностями процесса познания и свойств памяти. Только постоянное в определенной системе осуществляемое включение новых знаний в систему прежних знаний может обеспечить достаточно высокое качество усвоения предмета. Только через повторение можно приходить к логическим выводам. Без повторения невозможно, раскрыть сущность вещей и явлений, их развитие. Не даром говорят: «Повторение — мать учения».

2. Повторение математики необходимо как для учащихся с целью углубления, упрочнены и систематизации своих знания, так и для самого учителя в чётности совершенствование методов обучения и поднятия эффективности своей работы.

3. Повторение математики должно систематически проводиться на уроках, органически сочетаясь с основным содержанием урока.

При сообщении нового материала одновременно надо повторять ранее изучаемый материал. Учащиеся должны чувствовать потребность к повторений. Это достигается тем, что при изучении нового материала учитель сравнивает его, сопоставляет со старым, устанавливает аналогии между ними, проводит обобщение, углубление и систематизацию.

4. Перед началом учебного года или четверти необходимо тщательно спланировать материал для повторения, указать виды повторения, через которое оно может проводится, т.е. устанавливается, какой материал будет проводится параллельно с изучением новой темы и какой на специально отведенных уроках повторения.

5. Необходимо систематически практиковать текущее повторение. Необходимо и тематическое повторение по окончании темы, заключительное — по окончании раздела, курса в целом, на которых устанавливаютсяболее широкие логические связи между темами и разделами, подчеркиваются те основные и ведущие идеи, которые лежат в основе данной учебной дисциплины.

6. Для повышения интереса и активности учащихся при повторении необходимо применять различные приемы и методы работы, разнообразить повторяемый материал, старый материал рассмотреть с новых точек зрения, устанавливать все новые и новые логические связи, стимулировать самостоятельную работу учащихся.

Только таким путём можно устранить то противоречие, которое возникает, с одной стороны, ввиду отсутствия желания у части учащихся повторять то, что ими усвоено однажды, а с другой в силу необходимости повторять с целью углубления, обобщения и систематизации ранее изученного материала.

7. Необходима хорошо продуманная теоретическая и практически обоснованная система повторения, которая должна обеспечить высокое качество и прочность знаний учащихся. Только в этом случае преподаватель достигает тех целей, которые он преследует повторением.

8. Необходимо тщательно проанализировать теорию и практику повторения с целью установления положительных и отрицательных сторон работы школ при повторении.

Повторение учебного материала требует от учителя творческой работы. Он должен обеспечить четкую связь между видами повторения, осуществить глубоко продуманную систему повторения.

Овладеть искусством организации повторения — такова задача учителя, от её решения во многом зависит прочность знаний учащихся.

БИБЛИОГРАФИЯ

Аракелян О.А. «Некоторые вопросы повторения математики в средней школе» М. Учпедгиз, 1960.

Басова Л.А., Шубин М.А., Эпштейн Л.А. Лекции и задачи по математике: из опыта работы летней физико–математической школы в Карелии. М. 1981.

Беляев Е.А., Киселёва Н.А., Перминов В.Я. Некоторые особенности развития математического знания. М. 1975.

Бескин Н.М. «Методика геометрии». Учебник для педагогических институтов. Учпедгиз. 1947.

Библиотека учителя математики. Преподавание геометрии в 6-8 классах. Сборник статей составитель В.А. Гусев. Москва "Просвещение" 1979.

Богоявленский Д.Н., Менчинская Н.М. Психология усвоения знаний в школе. М., 1959.

Глейзер. История математики в школе (4–6 кл.). М. «Просвещение», 1981.

Жуков Н.И. Философские проблемы математики. Минск, 1977.

Кабанова–Меллер Е.Н. Психология формирования знаний и навыков. М. 1962.

Карри Х.Б. Основания математической логики. М. 1969.

Кедровский О.И. Методологические проблемы развития математического познания. Киев, 1977.

Кудрявцев Л.Д. Современная математика и её преподавание. М. 1981.

Менчинская А.А. Психологические вопросы развивающего обучения и новые программы. «Советская педагогика», 1968.

Методика преподавания математики в средней школе: Общая методика /Ю.М. Колягин и др. — М. Просвещение , 1980.

Методика преподавания математики. Составители: Р.С. Черкасов, А.А. Столяр.

Молодший В.Н. Очерки по философским вопросам математики. М. 1969.

Моноезон Е.И. Методика и результаты изучения знаний учащихся. «Советская педагогика», 1962.

Петров Ю.Н. Философские проблемы математики. М. 1973.

Поба Д. Математика и правдоподобные рассуждения. М. 1975.

Проверочные задания по математике для учащихся 5–8 и 10 классов средней школы. М. «Просвещение» 1992.

Реньи А. Диалоги о математике. М. 1969.

Рузавин Г.И. О природе математического знания. М. 1968.

Славков С. Аспекты на математические познания. София. 1971.

Срода Р.Б. "Повторение на уроках математики". Издательство газеты "Волга" Астрахань, 1950.

Школьный факультатив по математике. Межвузовский сборник. Издательство Саратовского педагогического института 1993.

Эрдниев П.М. Обучать математике активно, творчески, экономно. «Народное образование», 1962.

Эрдниев П.М. Сравнение и обобщение при обучении математике, М. Учпедгиз, 1960.

Фёдоров И.Г. Некоторые методологические проблемы математики. М. 1975.