| Скачать .docx |
Курсовая работа: Изучение темы Треугольники в курсе геометрии 7-9 классов средней школы
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
Математический факультет
Кафедра математического анализа и
методики преподавания математики
КУРСОВАЯ РАБОТА
Изучение темы "Треугольники"
в курсе геометрии 7-9 классов средней школы
Выполнила студентка математического
факультета группы М-41
Михеева М.А.
Научный руководитель Ошуева Е.С.
Киров 2003
Содержание
§ 1 Анализ школьных учебников по теме: "Треугольники" в 7-9 классе
п. 1 Содержание и порядок изложения материала
п. 2 Сравнительный анализ учебников по данной теме
п. п. 1 Определение треугольника
п. п. 2 Равнобедренный треугольник
п. п. 3 Признаки равенства треугольников
п. п. 4 Признаки подобия треугольников
§ 2 Конспекты итоговых уроков по теме "Треугольники" для 7-9 классов
п. 1 Обобщающий урок по теме "Признаки равенства треугольников"
п. 3 Итоговый урок по теме "Подобные треугольники"
п. 4 Итоговый урок повторения и обобщения по теме "Треугольники"
Введение
Треугольник является важнейшей фигурой планиметрии, и потому в первую очередь изучают свойства этой фигуры. С ним связаны многие методы, используемые при решении различных геометрических задач. Любой многоугольник может быть разделён на треугольники, а изучение свойств этого многоугольника, сводится к изучению составляющих его треугольников. В каком-то смысле изучаемая в школьном курсе геометрия - это геометрия треугольника. Поэтому очень важно представлять себе методику изложения этой темы в различных учебных пособиях для правильного построения курса и избежания методических ошибок.
Данная работа проведена с целью, проследить методику изложения темы "Треугольники" в курсе геометрии 7-9 класса средней школы, а также подготовить конспекты итоговых уроков по данной теме.
Анализ проводится по 4 основным учебникам, наиболее часто встречаемым в школьной практике. Это учебники А.В. Погорелова Геометрия 7-11 (8 издание), Л.С. Атанасяна, Б.Ф. Бутузова и др. Геометрия 7-9, А.П. Киселёва Геометрия 7-9, И.Ф. Шарыгина Геометрия 7-9.
Цель:
Проанализировать подходы и особенности изложения данной темы.
Проследить соответствие материала учебников содержанию обучения, принятого министерством образования Р.Ф.
Выявить достоинства и недостатки изложения этой темы.
Разработать 4 конспекта уроков итогового повторения.
§ 1 Анализ школьных учебников по теме: "Треугольники" в 7-9 классе
п. 1 Содержание и порядок изложения материала
Л.С. Атанасян и др. Геометрия 7-9 |
А.В. Погорелов Геометрия 7-11 |
А.П. Киселёв Геометрия 7-9 |
И.Ф. Шарыгин Геометрия 7-9 |
Начальные геометрические сведения Треугольники Параллельные прямые Соотношения между сторонами и углами Четырёхугольники Площадь Подобные треугольники Окружность Векторы |
Основные свойства простейших геометрических фигур Смежные и вертикальные углы Признаки равенства треугольников Сумма углов треугольника Геометрические построения Четырёхугольники Теорема Пифагора Декартовы координаты на плоскости Движение Векторы Подобие фигур Решение треугольников Многоугольники Площади фигур |
Прямая линия Углы Математические предложения Треугольники Основные задачи на построение Параллельные прямые Параллелограммы и трапеции Окружность Подобные фигуры Понятие об измерении величин Подобие треугольников Подобие многоугольников Подобие фигур произвольного вида Некоторые теоремы о пропорциональных отрезков Метрические соотношения между элементами треугольника Пропорциональные линии в круге тригонометрические функции острого угла |
Первые понятия геометрии Основные свойства плоскости Треугольник и окружность. Начальные сведения Виды геометри-ческих задач и методы их решения Параллельные прямые и углы Подобие Метрические соотношения в треугольнике и окружности Задачи и теоремы геометрии |
Содержание рассмотренных выше учебников соответствует содержанию образования и даже по некоторым вопросам превосходит её.
п. 2 Сравнительный анализ учебников по данной теме
п. п. 1 Определение треугольника
Существуют два подхода к определению треугольника:
1 подход. Понятие треугольника вводится конструктивно: как фигура, состоящая из трёх точек и трёх отрезков соединяющих эти точки. Такой подход реализован в учебнике Атанасяна и в учебнике Погорелова. При этом ничего не говорится о плоскости треугольника. Это делается с целью отступления от теоретико-множественной концепции и от определения равных геометрических фигур с помощью отображений, сохраняющих расстояния (перемещений и движений). Но и здесь есть существенные различия.
В книге Погорелова даётся следующее определение треугольника: "Треугольником называется фигура, которая состоит из трёх точек не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки". Смысл выражения "отрезок соединяет точки" нигде не объяснён. Хотя об этом и легко догадаться; но смысл слова "попарно" совсем не очевиден для семиклассника. Кроме того, определение существенно зависит от обозначений, чего явно в формулировке не указано. В целом, формулировка воспринимается как тяжеловесная и трудная для понимания. У Атанасяна определение чисто конструктивное, оно наглядно и легче воспринимается школьниками.
2 подход. Понятие треугольника даётся как частный случай многоугольника, но в этом понятии говорится не только о фигуре образованной замкнутой линией, но и о части плоскости ограниченной этой замкнутой линией. Этот подход реализован в учебниках Киселёва и Шарыгина. Здесь определение треугольника отдельно не рассматривается. Впоследствии Атанасян и Погорелов всё же обращаются ко второму подходу в теме "Многоугольники" т.к это понятие им потребуется для определения понятия площади.
Определение равенства треугольников во всех четырёх учебниках даётся через совмещение равных фигур путём наложения. Но в учебниках со вторым подходом подразумевается, что и плоскости треугольников также совмещаются наложением.
п. п. 2 Равнобедренный треугольник
Определение равнобедренного и равностороннего треугольника одинаковое во всех учебниках. Такое определение является общепринятым в математике.
В учебниках Киселёва и Шарыгина свойства равнобедренного треугольника рассматриваются в одной теореме. Доказательства проводятся аналогично, с использованием осевой симметрии относительно биссектрисы треугольника и определения равных треугольников. В силу того, что ни Атанасян, ни Погорелов не используют движения плоскости в 7 классе, основой для доказательства свойств равнобедренных треугольников являются признаки равенства треугольников.
Атанасян в доказательстве свойств равнобедренного треугольника пользуется первым признаком равенства треугольников. В книге Погорелова свойства равнобедренного треугольника доказываются с использованием определения треугольника как упорядоченной тройки точек, но ни где не поясняется, что ΔCAB и ΔCBA это разные треугольники, а не один и тот же по-разному обозначенный. Такое доказательство учениками 7 класса понимается довольно трудно. Автор, уклонившись от явной формулировки определения треугольника как ориентированного пути, ставит ученика лицом к лицу с рассуждениями, которые может понять только тот, кто совершенно чётко представляет себе треугольник как ориентированный путь (это хоть и не явное, но обращение к теоретико-множественному подходу, который так тщательно избегается). Поэтому такие доказательства воспринимаются учениками как цирковой фокус.
Признаки равнобедренного треугольника в учебнике Атанасяна не рассматриваются, хотя эти теоремы очень полезные. В учебнике Погорелова приводится один признак (через равенство углов при основании). Полностью все признаки рассмотрены только у Шарыгина.
п. п. 3 Признаки равенства треугольников
Во всех четырёх учебниках применяется один и тот же подход с использованием аксиомы существования треугольника равного данному. Но нигде ссылок на эту аксиому нет. Доказательства проводятся на основе наглядности с помощью наложения и приложения. В учебнике Погорелова эта аксиома формулируется, но непосредственно при доказательстве на неё ссылки не делаются. Лишь после доказательства первого признака равенства треугольников проводится подробный разбор его с указанием используемых в доказательстве аксиом. Это введено с целью, сделать доказательство более строгим, чем, например доказательство, приведённое у Киселёва. Как нам кажется, именно для этого автор вводит такое нетрадиционное определение треугольника.
Доказательства, приведённые в учебниках Атанасяна и Киселёва аналогичны. Но в учебнике Киселёва, исходя из введенного им определения треугольника, следовало бы ещё доказать, что плоскости треугольников так же совпадут при наложении (о чём в доказательствах даже не упомянуто). В учебнике Атанасяна аксиомы не являются основой, на которой строится школьный курс геометрии (вместе с тем, в приложении в конце учебника подробно изложен вопрос о системе аксиом в курсе геометрии). По нашему мнению, большое преимущество по сравнению с учебным пособием Киселёва, имеет использование в учебнике Атанасяна в качестве основного рабочего аппарата признаки равенства треугольников, а не свойства геометрических преобразований. Такой подход позволяет отработать общие приёмы доказательства теорем. Эти доказательства строятся по схеме: поиск равных треугольников → доказательство предполагаемого равенства → обоснование новых утверждений. Благодаря использованию признаков равенства треугольников легче усваиваются основные теоремы планиметрии (свойства и признаки серединного перпендикуляра, свойства равнобедренного треугольника, теорема о внешнем угле треугольника, свойства и признаки параллельных прямых и параллелограмма, теорема Фалеса, признаки подобия треугольников и т.п.). В учебнике Атанасяна первый признак рассматривается в отрыве от двух других. Это обосновано тем, что он является основой для доказательства свойств равнобедренного треугольника, облегчающих доказательство третьего признака равенства треугольников.
Лишь в учебниках Киселёва и Шарыгина все три признака изучаются последовательно т.к. там не требуется разбивать их для доказательства свойств равнобедренных треугольников.
В учебнике Шарыгина кроме наложения используются ещё и симметрия, что усложняет доказательства. Доказательство третьего признака проводится с использованием элементов построения. Кроме того, применяется движение называемое переносом, но нигде не указано как оно осуществляется и действительно ли переводит одну точку в другую. Кроме трёх традиционных признаков равенства треугольников приводится ещё один для тупого угла и двух не образующих его сторон. Доказательство вытекает из задачи о не существовании треугольника равного данному, если равны две стороны и не содержащийся между ними угол.
п. п. 4 Признаки подобия треугольников
Определение подобных треугольников даётся как треугольники, у которых соответственные углы равны, а соответственные стороны пропорциональны. Атанасян вводит понятие пропорциональных сходственных сторон. Аналогичное определение приведено в учебнике Киселёва. В учебнике Шарыгина понятие аналогично определению, приведённому у Погорелова, но оно ни как не связано с обозначениями.
Доказательство признаков подобия треугольников в учебнике геометрии А.В. Погорелова основывается на свойствах гомотетии, вывод которых использует формулу расстояния между точками на координатной плоскости и тем самым теорему Пифагора. А теорема Пифагора, в свою очередь, доказывается на основе тригонометрических функций угла, корректность определений которых проверяется с помощью обобщённой теоремы Фалеса, утверждающей, что параллельные прямые, пересекающие стороны угла, отсекают от них пропорциональные отрезки. Ясно, что теорема Фалеса является частью признаков подобия, здесь наблюдается нежелательный в методическом отношении отход от поступательного развития курса. Кроме того, при доказательстве теоремы Фалеса процесс измерения отрезков, и в случае, когда отрезки не соизмеримы, осознавание процесса их измерения происходит у учащихся со значительными трудностями. Этот материал занимает время всего курса геометрии в 8 классе. Теорема Фалеса рассматривается в самом начале 8 класса, а признаки подобия в самом конце 8 класса. В этом плане предпочтительнее расположение материала в учебном пособии Киселёва. Но и у него доказательство признаков подобия основано на такой лемме: прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному. При доказательстве этой леммы рассматриваются отдельно случаи, когда отношение сторон треугольников является либо рациональным, либо иррациональным числом, доказательство усложняется также использованием общей меры и аксиом. А у Атанасяна площади фигур, в отличие от трёх других учебников, рассматриваются раньше, и поэтому удаётся обойти указанную трудность. Фактически она преодолевается один раз при доказательстве свойств пропорциональных отрезков в прямоугольном треугольнике. В этом и состоит одно из преимуществ раннего введения понятия площади.
Как уже видно метод доказательства признаков подобия треугольников в учебнике Атанасяна является существенно другим. Так доказательство первого признака подобия треугольников в этом учебнике основывается на теореме об отношении площадей треугольников, утверждающей, что если в треугольниках ABC и A1
B1
C1
углы А и А1
равны, то  . Эта теорема не является традиционной для школьного курса и скорее всего носит вспомогательный характер. С другой стороны на основе этой теоремы весьма просто доказывается, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. По сути дела всё доказательство в одну строчку. Эта же теорема позволяет дать простое доказательство признаков подобия треугольников. В то же время её удалённость от места применения накладывает определённые трудности на усвоение учащимися доказательства признаков подобия треугольников. Здесь лучше модифицировать её, с тем, чтобы её можно было применить непосредственно в теме "Признаки подобия треугольников". У Погорелова такой теоремы нет, что делает невозможным решение его методами задач такого плана:
. Эта теорема не является традиционной для школьного курса и скорее всего носит вспомогательный характер. С другой стороны на основе этой теоремы весьма просто доказывается, что отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. По сути дела всё доказательство в одну строчку. Эта же теорема позволяет дать простое доказательство признаков подобия треугольников. В то же время её удалённость от места применения накладывает определённые трудности на усвоение учащимися доказательства признаков подобия треугольников. Здесь лучше модифицировать её, с тем, чтобы её можно было применить непосредственно в теме "Признаки подобия треугольников". У Погорелова такой теоремы нет, что делает невозможным решение его методами задач такого плана:
Треугольники АВС и А1 В1 С1 подобны, их соответствующие стороны относятся как 6: 5. Площадь Δ АВС больше площади Δ А1 В1 С1 на 77 см2 . Найдите площади треугольников.
В учебнике Шарыгина доказывается терема о пропорциональных отрезках и свойства параллельных прямых. Все три признака подобия формулируются друг за другом, и для всех приводится одно доказательство с некоторыми пояснениями для каждого из признаков. Применяются дополнительные построения для каждого, а дальше используется предыдущая теорема с некоторыми вариациями и признаки равенства треугольников.
Об отношении площадей подобных фигур так же ничего не говорится.
§ 2 Конспекты итоговых уроков по теме "Треугольники" для 7-9 классов
п. 1 Обобщающий урок по теме "Признаки равенства треугольников"
(По учебнику Погорелова А.В. Геометрия 7-11)
Цель :
повторить и систематизировать знания учащихся по данной теме;
применить полученные знания для решения задач связанных с треугольниками;
осуществить проверку полученных знаний.
План урока :
Организационный момент (2-3 мин).
Актуализация знаний (3-8 мин).
Тестирование (8-10 мин).
Групповая работа (10-15 мин).
Математический диктант (3-4 мин).
Подведение итогов урока. Постановка домашнего задания (2 мин).
Организационный момент. Формулируется тема урока. Цели урока сообщаются заранее. Класс настраивается на работу и получение хороших оценок.
Повторение признаков равенства треугольн6иков. Трое учеников доказывают признаки на доске, а трое других производят контроль и формулируют признаки.
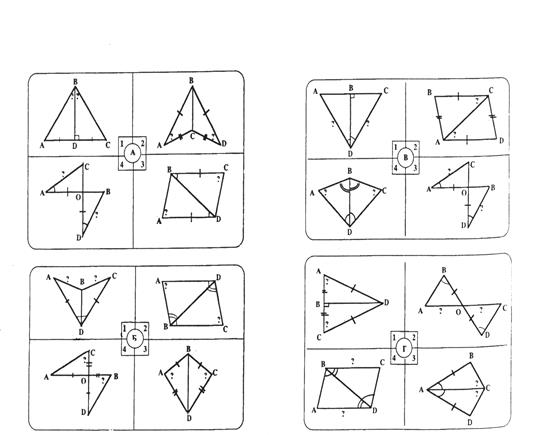
Тест на знание признаков равенства треугольников. Каждый из учащихся получает листочек с изображением 10 пар треугольников (см. приложение лист 1), на которых отмечены соответствующие равные элементы. Предлагается отыскать пары треугольников, о равенстве которых можно утверждать, опираясь на один из признаков. Выдаются маленькие листочки, на них в строчку по порядку записываются: в случае положительного ответа - номер соответствующего признака, в случае отрицательного - ставится ноль. В результате должен получится код из 10 цифр состоящий из 0,1,2 и 3 (1020103002). Совпадение ответа ученика и цифры кода отмечается знаком "+" (код заранее выписывается на доску). Сразу же подсчитывается количество заработанных баллов.
Работа тут же оценивается: 10-8 совпадений - "5";
7-6 совпадений - "4";
5-3 совпадений - "3".
После урока листочки сдаются на проверку.
Групповая работа. Работают в группе по 4 человека. Разбирают задачи (см. приложение лист 2). Каждый берёт на себя по одной задаче на объяснение. Учитель по выбору может спросить любого из группы или всех (всего 4 варианта). Остальные внимательно слушают, дополняют, исправляют. Внимание должно быть постоянно т.к на любом этапе объяснения задачу можно передать ученику в другой группе.
Математический диктант. Математический диктант позволяет за короткое время проверить глубину знаний учащихся, выставить оценки, проанализировать ошибки. Диктант проводится на месте под копирку: один экземпляр ученику сдают учителю для проверки, другую оставляют себе. Отвечать на вопросы нужно "да" или "нет".
Верно ли, что если треугольники равны, то каждый угол первого треугольника равен каждому углу второго треугольника? [Нет].
Верно ли, что каждому углу одного треугольника найдётся угол, равный ему во втором равном треугольнике? [Да].
Верно ли, что если сторона и два прилежащих к ней угла соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны? [Да].
Верно ли, что если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники равны? [Нет].
Верно ли, что две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны? [Нет].
Верно ли, что медианы в равных треугольниках, проведённые к равным сторонам равны? [Да].
Подведение итогов урока. Постановка домашнего задания.
Учащимся сообщают результаты их работы, поощряют лучшие ответы. Урок считается успешным, если оставляет у учащихся чувство удовлетворения собой, если их знания становятся систематизированными, а действия осознанными.
Методические рекомендации:
В случае не имения в наличии копирки математический диктант ученики проверяют друг у друга карандашом, выставляют оценки, а затем эти листочки сдаются на проверку учителю
При работе по группам в среднем может получиться от 6 до 10 групп, т.е.2-3 группы будут иметь одинаковые варианты. В этом случае работа организуется по усмотрению учителя.
п. 2 Обобщающий урок по теме "Равнобедренные треугольники. Высоты, медианы, биссектрисы треугольника"
(По учебнику Атанасяна Л.С., Бутузова Б.Ф. и др. Геометрия 7-9)
Цель: закрепить, обобщить, систематизировать, оценить знания по данной теме.
План урока :
Организационный момент (2-3 мин).
Актуализация знаний (3-8 мин).
Тестирование (8-10 мин).
Групповая работа (15-20 мин).
Подведение итогов урока. Постановка домашнего задания (2 мин).
Организационный момент. Сообщается тема, цель урока. Настраиваем класс на работу. Даём стимул на получение хороших оценок.
Повторение основных определений и свойств. Проводится фронтальный опрос учащихся, желательно слабых учеников по следующим вопросам: определения треугольника, медианы, биссектрисы, высоты, равнобедренного треугольника; его свойства, первый признак равенства треугольников.
Тест на знание определений и свойств равнобедренного треугольника (см. приложение лист 3). Каждому ученику выдаются листочки с заданиями. Ответы пишутся под копирку, один из листочков сдается учителю. Тест тут же проверяется, и ставятся оценки.
Групповая работа. Работают в группе по 4 человека. Разбирают задачи. Каждый берёт на себя по 1-2 задачи на объяснение. Учитель по выбору может спросить любого ученика. Объяснение задачи можно передавать другому ученику ответственному за эту же задачу. Ученики рассказывают решение с места. Учитель записывает на доске основные моменты. Остальные проверяют и дополняют ответы.
Вариант 1.
1. Запишите все треугольники, изображенные на рисунке
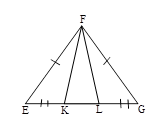
2. В Δ EFG EF=FG, EK=LG. Определите вид треугольников EFG и KFL.
3. Чем отличается биссектриса угла от биссектрисы треугольника?
4. В равнобедренном Δ ABCAB=BC. Докажите равенство его медиан AM и CN.
5. Периметр равнобедренного треугольника равен 36 см. Основание равно 6 см. Найти боковую сторону данного треугольника.
Вариант 2.
1. Какие линии совпадут, если треугольник, вырезанный из бумаги, перегнуть по его биссектрисе? Почему?
2. В равнобедренном Δ CEFCE=CF. Докажите равенство его биссектрис EL и FK.
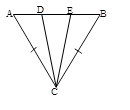
3. В Δ ABC (см. рис) AC=BC, ![]() . Определите вид Δ ABC и ΔDEC.
. Определите вид Δ ABC и ΔDEC.
4. Периметр равнобедренного треугольника равен 42 см., боковая сторона составляет 2/7 периметра. Найдите основание данного треугольника.
5. Треугольники ABC и OPQ равны. Периметр Δ ABC равен 40 см., AB=17см., PQ=5см. Найти остальные стороны треугольников.
Вариант 3.
1. Может ли треугольник быть выпуклым? Почему?
2. Может ли высота треугольника лежать:
внутри треугольника;
вне треугольника;
на его стороне?
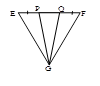
3. Сформулируйте второй признак равенства треугольников для равнобедренных треугольников.
4. В Δ EFGEP=FQ и ![]() Определите вид треугольников EFG и GPQ.
Определите вид треугольников EFG и GPQ.
5. Периметр равнобедренного треугольника равен 32 см., боковая сторона больше основания на 4 см. Найдите стороны данного треугольника.
V. Подведение итогов урока. Задание домашнего задания.
Учащиеся сообщают результаты их работы, поощряют лучшие ответы. Подводят итоги урока. Выясняют, что ещё не усвоено в чём возникли трудности.
п. 3 Итоговый урок по теме "Подобные треугольники"
(По учебнику Атанасяна Л.С., Бутузова Б.Ф. и др. Геометрия 7-9)
Цель:
обобщить изученный материал;
сформировать умения применять математические знания к решению задач;
выявить и устранить пробелы в знаниях учащихся.
План урока :
Организационный момент (2-3 мин).
Актуализация знаний (5-8 мин).
Фронтальная работа (7-9 мин).
Групповая работа (10-12 мин).
Математический диктант (3-4 мин).
Подведение итогов урока. Постановка домашнего задания (2 мин).
Организационный момент.
Цель: настроить класс на хорошую работу. Дать стимул для получения хороших отметок.
Повторение признаков подобия и теоремы об отношении площадей подобных фигур. Доска заранее разбивается на 4 части, в каждой из которых выполняется чертёж и записывается условие и заключение соответствующего признака или теоремы (см. приложение лист 4). Вызвать к доске четырёх учащихся, предложив каждому заполнить пробелы и выполнить, где это нужно дополнительные построения.
Коллективная работа с доской.
Пока учащиеся готовятся к ответу, класс решает (устно) задачи по готовым чертежам.
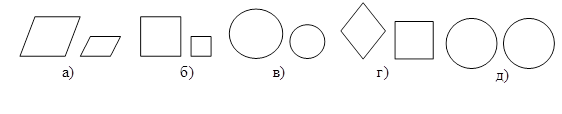
Дайте определение подобных фигур. Какие из приведённых на доске фигур являются подобными? Какие из приведённых параллельно треугольников являются подобными?

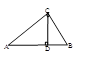

В трапеции АВСD проведены диагонали АС и ВD. В силу, какого признака подобия треугольников Δ COB~Δ AOD?
В прямоугольном треугольнике АВС из вершины прямого угла опущена на гипотенузу высота СD, AC=6, DB=9. Найти отношение площадей треугольников АСD и CDB.
Боковая сторона и основание одного равнобедренного треугольника соответственно равны 34 см. и 20 см., а другого 17 и 10. Определите подобные ли это треугольники.
Прослушать вызванных ранее учеников, которые доказывали один из признаков подобия треугольников, и выяснить, что в доказательстве каждого из двух последних признаков отличаются лишь признаки равенства треугольников в зависимости от данных.
Дополнительные вопросы отвечающим:
в прямоугольном треугольнике проекции катетов на гипотенузу равны 25 и 16. Найдите катеты, высоту.
Приведите примеры из жизни, которые приводят к понятию подобных фигур.
Групповая работа.
Класс разбивается на группы по 4 человека. Каждая группа решает задачи на выданной карточке. Через 8 мин. по вариантам спрашиваются задачи с места по выбору учителя. Если человек в группе не отвечает, спрашивают другую группу, у которой тот же вариант.
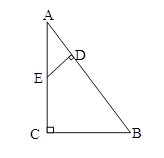
Вариант 1
Дано:
Δ АВС - прямоугольный;
DE^AB.
Докажите, что треугольники АВС и АЕD подобны;
Найдите катеты Δ АВС, если АВ=13 см., АЕ=5,2 см., DE=2 cм;
Найдите отношение площадей Δ ABC и Δ AED.
Вариант 2

Дано:
ABCD- параллелограмм;
BD- диагональ;
AF- произвольный отрезок;
BO=6 см;
OD=18 см.
Укажите подобные треугольники;
Определите коэффициент подобия;
Найдите отношение их площадей.
Вариант 3
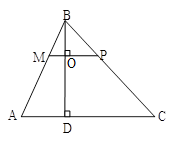
Дано:
Δ АВС;
BD- высота;
MP^BD; BM=5 см;
BP=8 см; BC=24см.
Доказать, что Δ BOP~Δ BDC;
Найти АВ;
Найти отношение площадей треугольников MPB и ABC.
Математический диктант.
Диктант пишется под копирку один вариант учителю, другой ученикам. Проверка осуществляется тут же.
Если вы согласны с утверждением то поставьте знак "+", если не согласны то знак "-".
Имеются два треугольника, они являются подобными, если
отношение их площадей равно 2;
одна сторона в два раза больше другой;
три угла равны, а одна сторона треугольника пропорциональна соответствующей стороне другого треугольника;
отношение соответствующих сторон равно 2;
отношение средних линий треугольников равно отношению оснований.
Подведение итогов урока. Постановка домашнего задания.
Учащимся сообщают результаты их работы, поощряются лучшие ответы.
Методические рекомендации:
Количество доказательства записанного на доске может варьироваться по усмотрению учителя.
В зависимости от времени можно также сократить число устных задач.
п. 4 Итоговый урок повторения и обобщения по теме "Треугольники"
( По учебнику Атанасяна Л.С., Бутузова Б.Ф. и др. Геометрия 7-9)
Цель :
закрепить умения и знания, полученные ранее;
применить полученные знания для решения задач связанных с треугольниками.
План урока :
Организационный момент (2-3 мин).
Актуализация знаний (3-4 мин).
Фронтальная работа с классом (10-13 мин).
Самостоятельная работа (17-20 мин).
Подведение итогов урока. Постановка домашнего задания (2 мин).
Организационный момент.
Настраиваем класс на работу. Сообщаем цель урока.
II. В начале урока проводится разминка фронтально с классом: повторение основных теоретических положений по данной теме.
1) Сформулируйте определение треугольника:
равнобедренного;
равностороннего;
прямоугольного.
2) Перечислите свойства равнобедренного треугольника.
3) Сформулируйте признаки равнобедренного треугольника.
4) Можно ли назвать равносторонний треугольник равнобедренным?
5) Какие треугольники называются равными?
6) Какие элементы называются соответственными?
7) Сформулируйте:
1-й признак равенства треугольников;
2-й признак равенства треугольников;
3-й признак равенства треугольников.
8) Какие треугольники называются подобными?
9) Что значит пропорциональные стороны?
10) Что такое коэффициент подобия?
11) Сформулируйте:
1-й признак подобия треугольников;
2-й признак подобия треугольников;
3-й признак подобия треугольников.
12) Назовите:
формулу для вычисления площади треугольника;
формулу Герона;
формулу площади треугольника, вписанного в окружность;
формулу площади треугольника, описанного вокруг окружности.
|
|
|
|
а) ![]()
![]() б)
б) ![]()
|
|
г) ![]()
д) ![]()
14) Что такое вектор?
18) Сформулируйте правило сложения векторов:
треугольника;
четырехугольника
Задача для общего разбора. По очереди ученики вызываются к доске или, по возможности, с места. Задача записана на доске.
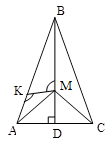
Дано:
ΔАВС-равнобедренный (АВ=ВС);
![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Докажите, что Δ АВМ=Δ ВМС;
Докажите, что Δ АКМ![]() ~Δ ВМС;
~Δ ВМС;
Найти КМ;
Найдите площадь Δ АВМ, Δ АКМ;
Найдите радиус окружности вписанной в Δ АВС;
Постройте Δ ВDС, уменьшив масштаб в 2 раза, и опишите около него окружность;
Выразите вектор ![]() через вектора
через вектора ![]() и
и ![]() ;
;
Найдите радиус окружности, описанной около Δ АВС;
IV. Задача для самостоятельной работы. Решение задачи в конце урока сдается.
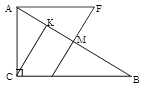
Дано:
Δ АВС - прямоугольный; ![]() =90о
;
=90о
;
АМ=МВ; DM![]() AB; AF||BC;
AB; AF||BC;
CK||DM; DM=6; MB=8.
Докажите, что Δ AFM=ΔDMB.
Докажите, что Δ AFM~ΔABC.
Найдите стороны Δ АВС.
Найдите СК.
Найдите отношение периметров Δ АСК и Δ СКВ.
Найдите СМ.
Выразите вектор ![]() через векторы
через векторы ![]() и
и ![]() .
.
Начертите тупоугольный треугольник и впишите в него окружность.
V. Постановка домашнего задания. Подведение итогов урока.
Методические рекомендации :
Проводится в конце 8 класса. Повторение по данной теме проводится как урок одной задачи.
С целью экономии времени можно актуализацию знаний проводить по мере необходимости непосредственно при разборе задачи.
Заключение
В данной работе был проведён методический анализ учебных пособий по геометрии для средней школы. Выделены подходы, достоинства и недостатки изложения данной темы в четырёх предложенных выше учебниках, а также приведены примерные конспекты уроков итогового повторения с методическими рекомендациями. Проанализированы базовые понятия и теоремы темы "Треугольники", что позволяет выбрать наиболее верный подход и методику изложения курса.
Данная курсовая будет полезна методистам, учителям, студентам педагогических ВУЗов.
Библиографический список
1. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина Геометрия: учебник для 7-9 класса средней школы. - М.: Просвещение, 1990 г.
2. А.В. Погорелов Геометрия: учебник для 7-11 класса общеобразовательных учреждений. - 8-е издание - М.: Просвещение, 1998 г.
3. А.П. Киселёв, Н.А. Рыбкин Геометрия: учебник - задачник для 7-9 класса. - М. изд-во "Дрофа", 1995 г.
4. И.Ф. Шарыгин Геометрия: учебник для 7-9 класса. - 2-е издание - М. изд-во "Дрофа", 1998 г.
5. Уроки итогового повторения 7-11 классы общеобразовательной школы \ Н. Гришкова, А. Илюхина \\ "Математика" приложение к газете "1 сентября" №13, 1999 г.
6. Л. Басова Признаки равенства треугольников \\ "Математика" приложение к газете "1 сентября" №34, 2000 г.
7. И. Смирнова, В. Смирнов Самостоятельные работы по геометрии 7 класс \\ "Математика" приложение к газете "1 сентября" №33, 2001 г.
8. В. Рыжик Тесты на экзамене. Геометрия 8-11 класс \\"Математика" приложение к газете "1 сентября" №1, 2002 г.
9. Л. Птичкина Тесты повторения по геометрии 7 класс \\"Математика" приложение к газете "1 сентября" №11, 2000 г.
10. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина О конкурсном учебнике геометрии для 7-9 классов \\ Математика в школе №1, 1989 г.
11. А.В. Гладкий О некоторых определениях в учебном пособии А.В. Погорелова \\ Математика в школе №6, 1990 г.
12. В.А. Смирнов О доказательствах признаков подобия треугольников \\ Математика в школе №6, 1990 г.
13. А.Н. Колмогоров Об учебном пособии Геометрия 6-10 А.В. Погорелова \\ Математика в школе №2, 1983 г.
14. А.С. Мищенко, А.С. Понтрягин О пробном учебнике Геометрия 6-8 \\ Математика в школе №2, 1983 г.
15. А.И. Медяник Научно - методические достоинства учебного пособия по геометрии А.В. Погорелова \\ Математика в школе №2, 1983 г.
16. В.В. Пикан О практической направленности пробного учебника Геометрия 6-8 \\ Математика в школе №2, 1983 г.
Приложение
Лист 1.
. 
Лист 2.
Докажите, что треугольники равны.
Докажите, что равны те элементы треугольников, которые отмечены знаком "?".
Лист 3,Тест
1.
|
ВС=10 см.
ВС=5 см.
ВС=15 см.
![]()
![]()
![]()
![]()
![]()
![]() 2.
2.
|
 |
![]()
|
3.
|

а) АС=10 м.
б) АС=20 м.
в) АС=5 м

а) ![]()
б) ![]()
в) ![]()
5. Доказать, что ![]()

а) 1) Рассмотрим Δ АВО и Δ ОСD;
2) АВ=ВО (дано);
3) DO=DC (дано);
4) AO=AB=BO (см. рисунок);
5) OD=DC=OC (см. рисунок);
6) из 2) - 5) следует, что Δ АВО и Δ ОCD равносторонние;
7) из 6) ![]()
![]()
8) ![]() (вертикальные углы);
(вертикальные углы);
9) из 7) и 8) ![]()
б) 1) Рассмотрим треугольники АВО и ОСD;
2) АВ=ВО (дано);
3) DO=DC (дано);
4) из 2) и 3) Δ АВО и Δ OCD- равнобедренные;
5) из 4) следует ![]() и
и ![]()
6) ![]() (вертикальные углы)
(вертикальные углы)
7) из 5) и 6) ![]() .
.
Лист 4
Дано: Δ АВС=Δ А1 В1 С1 ; ÐА=ÐА1 , ÐВ=ÐВ1 . Доказать, что Δ АВС~Δ А1 В1 С1 . Доказательство. По теореме о сумме углов треугольника… Аналогично используя равенство ÐА=ÐА1
, ÐВ=ÐВ1
, получаем Ч. т.д. |
Дано: Δ KLM=ΔK1 L1 M1 ; ÐK=ÐK1
; Доказать, что ΔPQR~ΔP1 Q1 R1 . Доказательство. Учитывая первый признак достаточно доказать ÐМ=ÐМ1 . Рассмотрим Δ КLM2 … Отсюда следует, что ÐМ=Ð2,а т.к Ð2=ÐМ1 , то ÐМ=ÐМ1 . Воспользуемся первым признаком Δ КLM~ΔK1 L1 M1. Ч. т.д. |
Дано: Δ PQR и ΔP1 Q1 R1 ;
Доказать, что Δ PQR~ΔP1 Q1 R1. Доказательство. Для этого, учитывая второй признак подобия треугольников достаточно доказать, что ÐP=ÐP1 . Рассмотрим треугольник PQR2 … Отсюда следует ÐP=Ð1, т.к Ð1=ÐP1 , то ÐP=ÐP1 Ч. т.д. |
Дано: Δ АВС~Δ А1 В1 С1 ; к - коэффициент подобия; S и S1 - площади треугольников АВС и А1 В1 С1 соответственно. Доказать, что
Доказательство. Воспользуемся теоремой об отношении площадей треугольников имеющих по равному углу… Ч. т.д. |
 . Итак, сходственные стороны треугольников АВС и А1
В1
С1
пропорциональные.
. Итак, сходственные стороны треугольников АВС и А1
В1
С1
пропорциональные.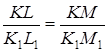 .
. ;
;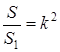 .
.