| Похожие рефераты | Скачать .docx |
Реферат: Сопротивление материалов
1. Введение и основные понятия
Ключевые слова : Прочность. Жесткость. Устойчивость. Надежность. Деформирование. Ресурс. Отказ.
Постановка задачи . Прикладная механика - это наука, интегрирующая, с одной стороны циклы общеобразовательных дисциплин таких как: физика, математика, теоретическая механика, материаловедение, инженерная графика, а с другой стороны - это первая инженерная дисциплина, которая преподается студентам технических специальностей. Прикладная механика, в принципе, охватывает две дисциплины: сопротивление материалов и основы конструирования. Ниже излагается цикл лекций по прикладной механике с расстановкой акцентов на наиболее сложно воспринимаемой части курса - сопротивлению материалов.
Сопротивление материалов - наука о прочности, жесткости и надежности элементов инженерных конструкций. Методами сопротивления материалов ведутся практические расчеты и определяются необходимые, как говорят, надежные размеры деталей машин, различных конструкций и сооружений.
Основные понятия сопротивления материалов опираются на законы и теоремы общей механики и в первую очередь на законы статики, без знания которых изучение данного предмета становится практически невозможным.
В отличие от теоретической механики сопротивление материалов рассматривает задачи, где наиболее существенными являются свойства деформируемых тел, а законы движения тела, как жесткого целого, не только отступают на второй план, но в ряде случаев являются попросту несущественными.
Сопротивление материалов имеет целью создать практически приемлемые простые приемы расчета типичных, наиболее часто встречающихся элементов конструкций. Необходимость довести решение каждой практической задачи до некоторого числового результата заставляет в ряде случаев прибегать к упрощающим гипотезам - предположениям, которые оправдываются в дальнейшем путем сопоставления расчетных данных с экспериментом.
Необходимо отметить, что первые заметки о прочности упоминаются в записках известного художника ЛЕОНАРДО Де ВИНЧИ, а начало науки о сопротивлении материалов связывают с именем знаменитого физика, математика и астронома ГАЛИЛЕО ГАЛИЛЕЯ. В 1660 году Р.ГУК сформулировал закон, устанавливающий связь между нагрузкой и деформацией: "Какова сила - таково и действие" . В XVIII веке необходимо отметить работы Л.ЭЙЛЕРА по устойчивости конструкций. XIX - XX века являются временем наиболее интенсивного развития науки в связи с общим бурным ростом строительства и промышленного производства при безусловно огромном вкладе ученых-механиков России.
Итак, мы будем заниматься твердыми деформированными телами с изучением их физических свойств .
Введем основные понятия, принимаемые при изучении дисциплины.
Прочность - это способность конструкции выдерживать заданную нагрузку, не разрушаясь.
Жесткость - способность конструкции к деформированию в соответствие с заданным нормативным регламентом.
Деформирование - свойство конструкции изменять свои геометрические размеры и форму под действием внешних сил
Устойчивость - свойство конструкции сохранять при действии внешних сил заданную форму равновесия.
Надежность - свойство конструкции выполнять заданные функции, сохраняя свои эксплуатационные показатели в определенных нормативных пределах в течение требуемого промежутка времени.
Ресурс - допустимый срок службы изделия. Указывается в виде общего времени наработки или числа циклов нагружения конструкции.
Отказ - нарушение работоспособности конструкции.
Опираясь на вышесказанное, можно дать определение прочностной надежности.
Прочностной надежностью называется отсутствие отказов, связанных с разрушением или недопустимыми деформациями элементов конструкции.
На рис.1 приведена структура модели прочностной надежности. Она включает известные модели или ограничения, которые априорно накладываются на свойства материалов, геометрию, формы изделия, способы нагружения, а также модель разрушения. Инженерные модели сплошной среды рассматривают материал как сплошное и однородное тело, наделенное свойством однородности структуры. Модель материала наделяется свойствами упругости, пластичности и ползучести.
Упругостью называется свойство тела восстанавливать свою форму после снятия внешних нагрузок.
Пластичностью называется свойство тела сохранять после прекращения действия нагрузки, или частично полученную при нагружении, деформацию.
Ползучестью называется свойство тела увеличивать деформацию при постоянных внешних нагрузках.
Основными моделями формы в моделях прочностной надежности, как известно, являются: стержни, пластины, оболочки и пространственные тела (массивы) (рис.2). Модели нагружения содержат схематизацию внешних нагрузок по величине, характеру распределения (сосредоточенная или распределенная сила или момент), а также воздействию внешних полей и сред.
После обоснованного выбора моделей формы, материала, нагружения переходят к непосредственной оценке надежности с помощью моделей разрушения. Модели разрушения представляют собой уравнения, связывающие параметры работоспособности элемента конструкции в момент разрушения с параметрами, обеспечивающими прочность. Эти уравнения (условия) называют условиями прочности. Обычно рассматриваются в зависимости от условий нагружения четыре модели разрушения:
статические,
длительно статические,
малоцикловые,
усталостные.
Как уже отмечалось, изучение дисциплины невозможно без знания основ теоретической механики. Поэтому свой остаточный ресурс знаний рекомендую проверить по разделу "Статика", используя систему входных тестов.
Поскольку изучение сопротивления материалов базируется прежде всего на таких известных понятиях как сила, пара сил, связи, реакции в связях, равнодействующая система внешних сил, то…
Вам рекомендуется решить простые задачи, указанные в ПРИЛОЖЕНИИ под разделом Т-1.
2. Метод сечений для определения внутренних усилий
Ключевые слова : Внешние силы. Внутренние усилия (силовые факторы). Следящая система координат. Нормальная сила. Внутренние крутящие и изгибающие моменты. Поперечная сила.
Деформации рассматриваемого тела (элементов конструкции) возникают от прохождения внешней силы. При этом изменяются расстояния между частицами тела, что в свою очередь приводит к изменению сил взаимного притяжения между ними. Отсюда, как следствие, возникают внутренние усилия. При этом внутренние усилия определяются универсальным методом сечений (или метод Разреза).
Известно, что различают силы внешние и силы внутренние. Внешние усилия (нагрузки) - это количественная мера взаимодействия двух различных тел. К ним относятся и реакции в связях. Внутренние усилия - это количественная мера взаимодействия двух частей одного тела, расположенных по разные стороны сечения и вызванные действием внешних усилий. Внутренние усилия возникают непосредственно в деформируемом теле.
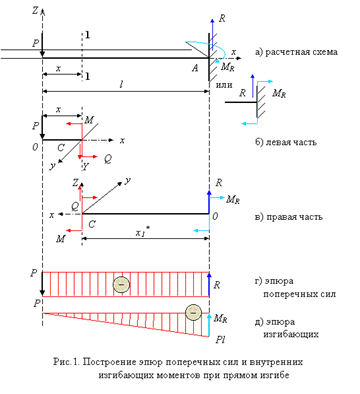
На рис.1 приведена расчетная схема бруса с произвольной комбинацией внешней нагрузки образующую равновесную систему сил:
![]() (1)
(1)
При этом, реакции связей определяются из известных уравнений равновесия статики твердого тела:
 ,
,  (2)
(2)
 ,
, 
 ,
, 
где х0 , у0 , z0 - базовая система координат осей.
Мысленное разрезание бруса на две части произвольным сечением А (рис.1 a), приводит к условиям равновесия каждой из двух отсеченных частей (рис.1 б,в). Здесь {S' } и {S" }- внутренние усилия, возникающих соответственно в левой и правой отсеченных частях вследствие действия внешних усилий.
При составлении мысленно отсеченных частей, условие равновесия тела обеспечивается соотношением:
![]()
Так как исходная система внешних сил (1) эквивалентна нулю, получаем:
{S'} = -{S"} (3)
Это условие соответствует четвертой аксиоме статики о равенстве сил действия и противодействия.
Используя общую методологию теоремы Пуансо
о приведении произвольной системы сил к заданному центру и выбрав за полюс приведения центр масс, сечения А'
, точку С'
, систему внутренних усилий для левой части {S'
} сводим к главному вектору ![]() и главному моменту
и главному моменту ![]() внутренних усилий. Аналогично делается для правой отсеченной части, где положение центра масс сечения А"
определяется, соответственно, точкой С"
(Рис.1 б,в).
внутренних усилий. Аналогично делается для правой отсеченной части, где положение центра масс сечения А"
определяется, соответственно, точкой С"
(Рис.1 б,в).
{S'} ~ {R',L'0 }; {S"} ~ {R",L"0 } (4)
Здесь в соответствие с четвертой аксиомой статики по-прежнему имеют место следующие соотношения:
R' = -R" (5)
L'0 = -L"0
Таким образом, главный вектор и главный момент системы внутренних усилий, возникающие в левой, условно отсеченной части бруса, равны по величине и противоположны по направлению главному вектору и главному моменту системы внутренних усилий, возникающих в правой условно отсеченной части.
График (эпюра) распределения численных значений главного вектора и главного момента вдоль продольной оси бруса и предопределяют, прежде всего, конкретные вопросы прочности, жесткости и надежности конструкций.
Определим механизм формирования компонент внутренних усилий, которые характеризуют простые виды сопротивлений: растяжение-сжатие, сдвиг, кручение и изгиб.
В центрах масс исследуемых сечений С' или С" зададимся соответственно левой (с', х', у', z' ) или правой (с", х", у", z" ) системами координатных осей (рис.1 в), которые в отличие от базовой системы координат x, у, z будем называть "следящими". Термин обусловлен их функциональным назначением. А именно: отслеживание изменения положения сечения А (рис.1 а) при условном смещении его вдоль продольной оси бруса, например при: 0 ≤ х'1 ≤ а, а ≤ x'2 ≤ b и т.д., где 0 , а и b - линейные размеры границ исследуемых участков бруса.
Зададимся положительными направлениями проекций главного вектора ![]() или
или ![]() и главного момента
и главного момента ![]() или
или ![]() на координатные оси следящей системы (рис.1 б, в):
на координатные оси следящей системы (рис.1 б, в):
![]() {N', Q'y
, Q'z
},
{N', Q'y
, Q'z
}, ![]() {M'x
, M'y
, M'z
} (6)
{M'x
, M'y
, M'z
} (6)
![]() {N", Q"y
, Q"z
},
{N", Q"y
, Q"z
}, ![]() {M"x
, M"y
, M"z
}
{M"x
, M"y
, M"z
}
При этом положительные направления проекций главного вектора и главного момента внутренних усилий на оси следящей системы координат соответствуют правилам статики в теоретической механике: для силы - вдоль положительного направления оси, для момента - против часовой стрелки при наблюдении со стороны конца оси. Они классифицируются следующим образом:
Nx - нормальная сила, признак центрального растяжения или сжатия;
Мx - внутренний крутящий момент, возникает при кручении;
Qz , Qу - поперечные или перерезывающие силы - признак сдвиговых деформаций,
Му , Мz - внутренние изгибающие моменты, соответствуют изгибу.
Соединение левой и правой мысленно отсеченных частей бруса приводит к известному (3) принципу равенства по модулю и противоположной направленности всех одноименных компонент внутренних усилий, а условие равновесии бруса определяется в виде:
{P1 , P2 , P3 , ... , N', N", Q'y , Q"y , Q'z , Q"z , M'x , M"x ,
M'y , M"y , M'z , M"z , ... , Pn-1 , Pn } ~ 0 (7)
С учетом эквивалентности нулю исходной системы сил (1) имеет место:
{N', N", Q'y , Q"y , Q'z , Q"z , М'x , M"x , M'y , M"y , М'z , M"z }~0 (8)
Как естественное следствие из соотношений 3,4,5 полученное условие является необходимым для того, чтобы одноименные компоненты внутренних усилий попарно образовали подсистемы сил эквивалентные нулю:
{N', N"} ~ 0 > N' = -N"
{Q'y , Q"y } ~ 0 > Q'y = -Q"y
{Q'z , Q"z } ~ 0 > Q'z = -Q"z
{М'x , M"x } ~ 0 > М'x = -M"x
{M'y , M"y } ~ 0 > M'y = -M"y
{М'z , M"z } ~ 0 > М'z = -M"z (9)
Общее число внутренних усилий (шесть) в статически определимых задачах совпадает с количеством уравнений равновесия для пространственной системы сил и связано с числом возможных взаимных перемещений одной условно отсеченной части тела по отношению к другой. Эти перемещения могут наблюдаться при разрушении тела по этому сечению.
Искомые усилия определяются из соответствующих уравнений для любой из отсеченных частей в следящей системе координатных осей. Так, для любой отсеченной части соответствующие уравнения равновесия приобретают вид;
![]() ix
= N + P1x
+ P2x
+ ... + Pkx
= 0 N
ix
= N + P1x
+ P2x
+ ... + Pkx
= 0 N
![]() iy
= Qy
+ P1y
+ P2y
+ … + Pky
= 0 Qy
iy
= Qy
+ P1y
+ P2y
+ … + Pky
= 0 Qy
![]() iz
= Q + P1z
+ P2z
+ ... + Pkz
= 0 Qz
iz
= Q + P1z
+ P2z
+ ... + Pkz
= 0 Qz
![]() x
(Pi
) = Mx
+ Mx
(Pi
) + ... + Mx
(Pk
) = 0 Mx
x
(Pi
) = Mx
+ Mx
(Pi
) + ... + Mx
(Pk
) = 0 Mx
![]() y
(Pi
) = My
+ My
(Pi
) + ... + My
(Pk
) = 0 My
y
(Pi
) = My
+ My
(Pi
) + ... + My
(Pk
) = 0 My
![]() z
(Pi
) = Mz
+ Mz
(Pi
) + ... + Mz
(Pk
) = 0 Mz
(10)
z
(Pi
) = Mz
+ Mz
(Pi
) + ... + Mz
(Pk
) = 0 Mz
(10)
Здесь для простоты обозначений системы координат с' х' у' z' и с" х" у" т" заменены единой оxуz .
Уважаемые коллеги! Таким образом, механизм предложенного автором лекций метода построения эпюр внутренних усилий, освобождающий Вас от механического запоминания "правил знаков" при построении эпюр внутренних усилий, заключается в следующем:
Определите реакции в связях по величине и направлению в базовой системе координат.
Определите количество участков бруса для использования метода сечений.
Мысленно рассеките брус в пределах исследуемого участка и изобразите на Ваше усмотрение левую или правую условно отсеченную часть.
Укажите пределы изменения положения сечения вдоль продольной оси в базовой системе координат на этом участке.
Введите в искомом сечении соответственно левую или правую следящую систему координатных осей.
Задайтесь положительными направлениями внутренних усилий в следящей системе координат.
Составьте уравнения равновесия для рассматриваемой условно отсеченной части бруса в следящей системе координат.
Определите из уравнений равновесия искомые внутренние усилия.
Вычислите искомые внутренние усилия на границах участков и при необходимости, - их экстремальные значения.
Выбрав масштаб усилий, выполните построение эпюры в соответствие с полученными их модульными значениями и знаками.
Указанная последовательность действий (кроме п.1) составляет суть метода сечений (разреза), единственного метода для определения внутренних усилий.
Не забываем, что при распределенной нагрузке в соответствие с теоремой Вариньона векторный момент равнодействующей рассматриваемой системы сил относительно любой точки равен сумме векторных моментов всех сил этой системы относительно той же точки.
Эпюры внутренних усилий позволяет визуально найти положение опасного сечения, где действуют наибольшие по модулю внутренние усилия. В этом сечении при прочих равных условиях наиболее вероятно разрушение конструкции при предельных нагрузках.
3. Эпюры внутренних усилий при растяжении-сжатии и кручении
Ключевые слова : Нормальное сечение. Нормальная сила. Внутренний крутящий момент.
Эпюры внутренних усилий при растяжении-сжатии
Растяжением или сжатием называется такой простой вид сопротивления, при котором внешние силы приложены вдоль продольной оси бруса, а в поперечном сечении его возникает только нормальная сила.
Рассмотрим расчетную схему бруса постоянного поперечного сечения с заданной внешней сосредоточенной нагрузкой Р и распределенной q , (рис.1).
Пусть ![]() . Прежде всего определим опорную реакцию R
, задавшись ее направлением вдоль оси х
.
. Прежде всего определим опорную реакцию R
, задавшись ее направлением вдоль оси х
.
![]()
Брус имеет 2 участка ![]() и
и ![]() .
.
В пределах первого участка мысленно рассечем брус на 2 части нормальным сечением и рассмотрим равновесие, допустим левой части, введя следующую координату х1 , рис.1 б:
![]()
Следовательно, в пределах первого участка брус претерпевает сжатие постоянной нормальной силой.
Аналогично поступим со вторым участком. Мысленно рассечем его сечением 2-2, и рассмотрим равновесие левой части (рис.1 в).Установим предварительно границы изменения х2 :

Подставляя граничные значения параметра х2 , получим:
![]()
Таким образом, в пределах второго участка брус растянут и нормальная сила изменяется по линейному закону.
Аналогичный результат получается и при рассмотрении правой отсеченной части (рис.1 г):

На основе полученных данных строится эпюра нормальных сил в виде графика распределения нормальной силы по длине бруса (рис.1 д). Характерно, что скачки на эпюре обусловлены наличием в соответствующих сечениях сосредоточенных сил R и Р .
Эпюры внутренних усилий при кручении
Кручением называется простой вид сопротивления, при котором к брусу (валу) прикладываются внешние пары сил в плоскостях, совпадающих с поперечным сечением вала, а в последних возникает только внутренний крутящий момент.
Рассмотрим расчетную схему вала, нагруженного двумя сосредоточенными моментами М и 2М и распределенными по длине: m , рис.2.
Методика построения эпюры аналогична только что рассмотренной методике при растяжении-сжатии.
В исходных сечениях № 1,2 и 3 задаются положительными значениями внутренних крутящих моментов М1 , М2 , М3 . Пусть М=ml .
Для первого участка (рис.2 б):

Для второго участка (рис.2 в):
![]()
Для третьего участка (рис.2 г):
![]()
Границы измерения параметра х3 в следующей системе координат:
![]()
Тогда:
![]()
Отмеченные значения ординат откладываются на эпюре внутренних крутящих моментов (рис.2 д).
4. Эпюры внутренних усилий при прямом изгибе
Ключевые слова : поперечная сила. Внутренний изгибающий момент.
Прямым изгибом называется такой вид простого сопротивления, когда внешние силы приложены перпендикулярно продольной оси бруса (балки) и расположены в одной из главных плоскостей в соответствие с конфигурацией поперечного сечения балки.
Как известно, при прямом изгибе в поперечном сечении возникают два вида внутренних усилий: поперечная сила и внутренний изгибающий момент.
Рассмотрим пример расчетной схемы консольной балки с сосредоточенной силой Р , рис. 1, а, но…
Предварительно рекомендую Вам вспомнить из раздела "Статика" теоретической механики методы расчета реакций в связях на примерах тестов, приведенных в ПРИЛОЖЕНИИ по разделом Т-2.
Прежде всего вычислим реакции в связи на базе уравнений равновесия:

После мысленного рассечения балки нормальным сечением 1-1 рассмотрим равновесие левой отсеченной части (рис.1, б), получим:

Таким образом, на первом участке поперечная сила отрицательная и постоянная, а внутренний изгибающий момент изменяется по линейному закону.
Для правой отсеченной части при рассмотрении ее равновесия результат аналогичен рис.1, в. А именно:

На основании полученных значений строятся эпюры поперечных сил (рис.1, г) и внутренних изгибающих моментов (рис.1, д).
Как следует из построенных эпюр ![]() , а
, а ![]() в сечении жесткой связи. Именно это сечение и является наиболее опасным в данной расчетной схеме.
в сечении жесткой связи. Именно это сечение и является наиболее опасным в данной расчетной схеме.
Продифференцируем выражение внутреннего изгибающего момента по координате х :
![]()
Как видим, после дифференцирования получено выражение для поперечной силы. Случайность это или закономерность? - Закономерность.
Дифференциальные зависимости между внутренними усилиями при изгибе
Рассмотрим расчетную схему балки с произвольной распределенной нагрузкой ![]() (рис.2).
(рис.2).
Составим уравнение равновесия:

![]()
Таким образом, действительно: первая производная от внутреннего изгибающего момента по линейной координате равна поперечной силе в сечении.
Это известное свойство функции и ее первой производной успешно используется при проверке правильности построения эпюр. Так, для расчетной схемы консольной балки (рис.1) эта связь дает следующие проверочные результаты: ![]() и М
убывает от 0
до -Pl
.
и М
убывает от 0
до -Pl
. ![]() и М
х
.
и М
х
.
Таким образом, для квалифицированной проверки Вам рекомендуется вспомнить из высшей математики раздел, связанный с вычислением производных функции. Считаю целесообразно решить тесты, приведенные в ПРИЛОЖЕНИИ под разделом Т-3.
Рассмотрим ВТОРОЙ ХАРАКТЕРНЫЙ ПРИМЕР ИЗГИБА двухопорной балки (рис.3).
Очевидно, что опорные реакции RA = RB
![]() :
:
для первого участка (рис.3, б)

для второго участка (рис.3, в)

Эпюры внутренних усилий представлены соответственно на рис.3, г и 3, д.
На основе дифференциальной связи Q и М , получим:
для первого участка:
Q > 0
и М
возрастает от нуля до ![]() .
.
Q = const и M x
для второго участка:
Q < 0
и М
убывает с ![]() до нуля.
до нуля.
Q = const и M также пропорционален х , т.е. изменяется по линейному закону.
Опасным в данном примере является сечение балки в центре пролета:
![]()
Третий характерный пример связан с использованием распределенной по длине балки нагрузки (рис.4). Следуя методике, принятой ранее, очевидно равенство опорных реакций:
![]() ,
,
а для искомого сечения (рис.4, б) выражения для внутренних усилий приобретают вид:

На обеих опорах изгибающий момент отсутствует. Тем не менее опасным сечением балки будет центр пролета при ![]() . Действительно, исходя из свойства функции и производной при
. Действительно, исходя из свойства функции и производной при ![]() , внутренний изгибающий момент достигает экстремума. Для нахождения исходной координаты х0
(рис.3 в) в общем случае приравняем выражение поперечной силы к нулю. В итоге получим
, внутренний изгибающий момент достигает экстремума. Для нахождения исходной координаты х0
(рис.3 в) в общем случае приравняем выражение поперечной силы к нулю. В итоге получим

После подстановки ![]() в выражение изгибающего момента получим:
в выражение изгибающего момента получим:

Таким образом,
![]() .
.
Необходимо отметить, что техника построения эпюр при изгибе наиболее трудно усваивается слушателями. Вам представляется возможность научиться "быстрому" построению эпюр на тесторе-тренажере, приведенном в ПРИЛОЖЕНИИ под грифом Т-4.
5. Понятие о напряжениях и деформациях
Ключевые слова : нормальное и касательное напряжения, линейная и угловая деформации, тензор напряжений.
Как отмечалось выше, внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Зафиксируем точку М в рассматриваемом сечении с единичным вектором нормали n . В окрестности этой точки выделим малую площадку F . Главный вектор внутренних сил, действующих на этой площадке, обозначим через P (рис. 1, а). При уменьшении размеров площадки соответственно уменьшаются главный вектор и главный момент внутренних сил, причем главный момент уменьшается в большей степени. В пределе при F 0 получим
![]()
Аналогичный предел для главного момента равен нулю. Введенный таким образом вектор рn называется вектором напряжений в точке . Этот вектор зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки F , характеризуемой вектором n . Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора n определяет напряженное состояние в этой точке.
В общем случае направление вектора напряжений рn не совпадает с направлением вектора нормали n . Проекция вектора рn на направление вектора n называется нормальным напряжением sn , а проекция на плоскость, проходящую через точку М и ортогональную вектору n, - касательным напряжением n (рис. 1 б).
Размерность напряжений равна отношению размерности силы к размерности площади. В международной системе единиц СИ напряжения измеряются в паскалях: 1 Па=1 Н/м2 .
При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.
Отнесем недеформированное тело к декартовой системе координат Oxyz (рис. 2). Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z) . В деформированном состоянии точка М займет новое положение М' , характеризуемое радиус-вектором r' (х, у, z) . Вектор u=r'-r называется вектором перемещений точки М . Проекции вектора u на координатные оси определяют компоненты вектора перемещений u(х, у, z), v(х, у, z), w(х, у, z) , равные разности декартовых координат точки тела после и до деформации.
Перемещение, при котором взаимное расположение точек тела не меняется, не сопровождается деформациями. В этом случае говорят, что тело перемещается как жесткое целое (линейное перемещение в пространстве или поворот относительно некоторой точки). С другой стороны, деформация, связанная с изменением формы тела и его объема, невозможна без перемещения его точек.
Деформации тела характеризуются изменением взаимного расположения точек тела до и после деформации. Рассмотрим, например, точку М и близкую к ней точку N , расстояние между которыми в недеформированном состоянии вдоль направления вектора s обозначим через s (рис. 2). В деформированном состоянии точки М и N переместятся в новое положение (точки М' и N' ), расстояние между которыми обозначим через s' . Предел отношения
![]()
называется относительной линейной деформацией в точке М в направлении вектора s . Рассматривая три взаимно перпендикулярных направления, например, вдоль координатных осей Ох, Оу и Oz , получим три компоненты относительных линейных деформаций ex, ey, ez , характеризующих изменение объема тела в процессе деформации.
Для описания деформаций, связанных с изменением формы тела, рассмотрим точку М и две близкие к ней точки N и Р , расположенные в недеформированном состоянии в направлении двух взаимно ортогональных векторов s1 и s2 . Расстояния между точками обозначим через s1 и s2 (рис. 4). В деформированном состоянии положение точек обозначим через М', N' и Р' . Угол между отрезками M'N' и М'Р' в общем случае будет отличным от прямого. При s1 0, s2 0 изменение угла 12 между двумя ортогональными до деформации направлениями называется угловой деформацией . Как видно из рис. 4, угловая деформация складывается из двух углов 1 и 2 , связанных с поворотами отрезков M'N' и М'Р' в плоскости, образованной векторами s1 и s2 , относительно этих векторов. Если заданы три взаимно ортогональных вектора, направленных вдоль координатных осей, то имеются три угловые деформации xy , xz и yz , которые вместе с тремя линейными деформациями ex, ey и ez полностью определяют деформированное состояние в точке.
Напряженное состояние в точке. Тензор напряжений
Вектор напряжений pn является физическим объектом, имеющим длину, направление и точку приложения. В этом смысле он обладает векторными свойствами. Однако этому объекту присущи некоторые свойства, не характерные для векторов. В частности, величина и направление вектора напряжений зависят от ориентации вектора n нормали бесконечно малого элемента поверхности dF . Совокупность всех возможных пар векторов n , рn в точке определяет напряженное состояние в данной точке. Однако для полного описания напряженного состояния в точке нет необходимости задавать бесконечное множество направлений вектора n , достаточно определить векторы напряжений на трех взаимно перпендикулярных элементарных площадках. Напряжения на произвольно ориентированных площадках могут быть выражены через эти три вектора напряжений. В дальнейшем лектор умышленно меняет ориентацию координат. Так, что ось Z - продольная ось бруса, а X и Y - координаты любой точки его поперечного сечения. Проведем через точку М три взаимно перпендикулярных плоскости с векторами нормалей, направления которых совпадают с направлениями координатных осей. Элементарные площадки образуем дополнительными сечениями, параллельными исходным плоскостям и отстоящими от них на бесконечно малые расстояния dx, dy, dz . В результате в окрестности точки М получим бесконечно малый параллелепипед, поверхность которого образована элементарными площадками dFх =dydz , dFн =dxdz , dFя =dxdy . Векторы напряжений px, py, pz , действующие на элементарных площадках, показаны на рис. 5.
Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 6). На каждой площадке действует одно нормальное напряжение x , y , z , где индекс обозначает направление вектора нормали к площадке и два касательных напряжения с двумя индексами, из которых первый указывает направление действия компоненты напряжения, второй-направление вектора нормали к площадке.
Совокупность девяти компонент напряжений (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой некоторый физический объект, называемый тензором напряжений в точке. Тензор можно представить в виде матрицы, соответствующим образом упорядочив девять компонент:

Для компонент тензора напряжений общепринятым является следующее правило знаков: компонента считается положительной, если на площадке с положительной внешней нормалью (т. е. направленной вдоль одной из координатных осей) эта компонента направлена в сторону положительного направления соответствующей оси. На рис. 6 все компоненты тензора напряжений изображены положительными. На площадках с отрицательной внешней нормалью (грани параллелепипеда, не видимые на рис. 5 и 6) положительная компонента направлена в противоположном направлении. Напряжения на трех взаимно ортогональных площадках с отрицательными направлениями нормалей также характеризуют напряженное состояние в точке. Эти напряжения, являющиеся компонентами тензора напряжений , определяются аналогично напряжениям на площадках с положительной нормалью. Они обозначаются теми же символами и имеют положительное направление, обратное изображенному на рис. 6.
6. Свойства тензора напряжений. Главные напряжения
Ключевые слова : шаровый тензор напряжений, инвариантность, характеристическое уравнение, девиатор.
Тензор напряжений обладает свойством симметрии. Для доказательства этого свойства рассмотрим приведенный в лекции 5 элементарный параллелепипед с действующими на его площадках компонентами тензора напряжений. Так как тело находится в равновесии, следовательно, находится в равновесии любая его часть, в том числе и элементарный объем. Запишем одно из шести уравнений равновесия этого объема, а имен но - сумму моментов всех сил относительно оси Ох . Все силы, кроме двух, либо не создают момента относительно ocи Ох , либо взаимно уничтожаются. Отличные от нуля моменты создают компоненты yz (верхняя грань) и zy (правая грань):
![]()
После сокращения на элемент объема dV =dxdydz получим
![]()
Аналогично, приравнивая нулю сумму моментов всех сил относительно осей Оу и Оz , получим еще два соотношения
![]()
Эти условия симметрии и тензора напряжений называются также условиями парности касательных напряжений : касательные напряжения, действующие по двум взаимно перпендикулярным площадкам в направлениях, ортогональных ребру, образованному пересечением этих площадок, равны по величине. С учетом этих свойств из девяти компонент тензора напряжений независимыми оказываются шесть компонент.
Покажем теперь, что компоненты тензора напряжений определенные для трех взаимно перпендикулярных площадок, полностью характеризуют напряженное состояние в точке, т. е. позволяют вычислить компоненты вектора напряжений на площадках, произвольно ориентированных относительно выбранной системы координат. Для этого рассмотрим элементарный объем, образованный сечением параллелепипеда, изображенного на рис. 1, плоскостью, пересекающей координатные оси и имеющей единичный вектор нормали n с компонентами nx , ny , nz .
На гранях полученного таким образом бесконечно малого тетраэдра действуют напряжения, показанные на рис. 1. При этом вектор напряжений pn на наклонной площадке разложен па составляющие рx , рy , рz вдоль координатных осей. Площади граней, ортогональных координатным осям и вектору нормали, обозначим соответственно dFx , dFy , dFz , dF. Эти площади связаны между собой соотношениями
dFx =dFnx , dFy =dFny , dFz =dFnz (1)
вытекающими из того, что грани, ортогональные координатным осям, есть проекции наклонной площадки на соответствующую координатную плоскость.
Проектируя силы, действующие на гранях элементарного тетраэдра, на координатные оси, получим уравнения равновесия для рассматриваемого объема. Например, проекции всех поверхностных сил на ось Ох дают
![]()
С учетом соотношений (1) после сокращения на dF получим уравнение, связывающее проекцию рx вектора напряжений с соответствующими компонентами тензора напряжений. Объединяя это уравнение с двумя аналогичными уравнениями, полученными проектированием сил на оси Оy и Оz , приходим к следующим соотношениям
 (2)
(2)
носящим название формул Коши . Эти формулы определяют вектор напряжений на произвольно выбранной площадке с вектором n через компоненты тензора напряжений.
Формулы (2) позволяют вычислить через компоненты тензора напряжений
полное напряжение
![]() (3)
(3)
нормальное напряжение
![]() (4)
(4)
и касательное напряжение :
![]()
Среди всех возможных направлений вектора нормали n существуют такие направления, для которых вектор напряжений pn параллелен вектору n . На соответствующих площадках действуют только нормальные напряжения, а касательные напряжения отсутствуют. Такие площадки называются главными , а нормальные напряжения на этих площадках называются главными напряжениями . Пусть площадка с единичным вектором нормали является главной. Условия коллинеарности векторов pn и n есть условия пропорциональности их компонент:
![]()
С учетом формул Коши получим систему линейных однородных уравнений относительно неизвестных компонент nx , ny , nz вектора нормали к главной площадке

Эта система уравнений имеет ненулевое решение, если определитель, составленный из коэффициентов уравнений, обращается в нуль:

Раскрывая определитель, приходим к кубическому уравнению относительно главного напряжения
![]()
Здесь введены обозначения

Уравнение (3) называется характеристическим уравнением для тензора напряжений. Коэффициенты (4) этого уравнения называются инвариантами тензора напряжений . Решение кубического уравнения (3) имеет три вещественных корня s1 , s2 , s3 , которые обычно упорядочиваются s1 s2 s3 .
Каждому значению j (j =1, 2, 3) соответствует вектор nj , характеризующий положение j -й главной площадки, с компонентами nj 1 , nj 2 , nj 3 . Для нахождения этих компонент достаточно в уравнения подставить найденное значение j и решить любые два из этих уравнений совместно с условием нормировки
Главные напряжения обладают важным свойством: по сравнению со всеми другими площадками нормальные напряжения на главных площадках принимают экстремальные значения. Для доказательства этого свойства достаточно исследовать на экстремум нормальное напряжение как функцию nx , ny , nz при дополнительном ограничении (5). Можно показать, что три главные площадки, соответствующие главным напряжениям s1 , s2 , s3 , взаимно перпендикулярны или, что то же самое, векторы nj и nk , соответствующие различным значениям j и k - ортогональны. Условие ортогональности имеет вид
![]()
Кубическое уравнение (3) можно переписать в виде
![]()
Приводя это уравнение к виду (3), получим следующие выражения для инвариантов (4) через главные напряжения:
![]()
Термин "инвариантность" обозначает независимость некоторой величины от выбора системы координат.
Введем среднее (гидростатическое) напряжение по формуле
![]()
Тензор напряжений можно представить в виде суммы двух тензоров ![]() , где
, где

Первый тензор называется шаровым , он характеризует изменение объема тела без изменения его формы. Второй тензор, называемый девиатором , характеризует изменение формы.
Особенностью девиатора напряжений является равенство нулю его первого инварианта:
![]()
Найдем положение площадок, на которых касательные напряжения принимают экстремальные значения. Для этого нужно отыскать экстремумы касательного напряжения при ограничении (5). Экстремальные касательные напряжения действуют на площадках, параллельных одной из главных осей и образующих с двумя другими осями угол /4. По величине эти напряжения равны
![]()
При этом на площадках с экспериментальными касательными напряжениями присутствуют нормальные напряжения, которые равны
![]()
Фигура, которую образуют площадки с экстремальными касательными напряжениями, изображена на рис. 2. Она принадлежит к классу параллелоэдров и представляет собой 12-гранник с гранями в виде ромбов, отношение диагоналей которых равно ![]() .
.
Таким образом, общая теория напряженного состояния позволяет охватывать, в целом, весь комплекс видов сопротивлений, как простого, так и сложного характера.
7. Упругость и пластичность. Закон Гука
Ключевые слова : упругость, пластичность, разрушение, коэффициент Пуассона, модуль Юнга, модуль сдвига, энергия деформации.
Действие внешних сил на твердое тело приводит к возникновению в точках его объема напряжений и деформаций. При этом напряженное состояние в точке, связь между напряжениями на различных площадках, проходящих через эту точку, определяются уравнениями статики и не зависят от физических свойств материала. Деформированное состояние, связь между перемещениями и деформациями устанавливаются с привлечением геометрических или кинематических соображений и также не зависят от свойств материала. Для того чтобы установить связь между напряжениями и деформациями, необходимо учитывать реальные свойства материала и условия нагружения. Математические модели, описывающие соотношения между напряжениями и деформациями, разрабатываются на основе экспериментальных данных. Эти модели должны с достаточной степенью точности отражать реальные свойства материалов и условия нагружения.
Наиболее распространенными для конструкционных материалов являются модели упругости и пластичности. Упругость-это свойство тела изменять форму и размеры под действием внешних нагрузок и восстанавливать исходную конфигурацию при снятии нагрузок . Математически свойство упругости выражается в установлении взаимно однозначной функциональной зависимости между компонентами тензора напряжений и тензора деформаций. Свойство упругости отражает не только свойства материалов, но и условия нагружения. Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим , если компоненты тензора напряжений и тензора деформаций связаны линейными соотношениями.
При высоких уровнях нагружения, когда в теле возникают значительные деформации, материал частично теряет упругие свойства: при разгрузке его первоначальные размеры и форма полностью не восстанавливаются, а при полном снятии внешних нагрузок фиксируются остаточные деформации. В этом случае зависимость между напряжениями и деформациями перестает быть однозначной. Это свойство материала называется пластичностью . Накапливаемые в процессе пластического деформирования остаточные деформации называются пластическими.
Высокий уровень нагружения может вызвать разрушение, т. е. разделение тела на части . Твердые тела, выполненные из различных материалов, разрушаются при разной величине деформации. Разрушение носит хрупкий характер при малых деформациях и происходит, как правило, без заметных пластических деформаций. Такое разрушение характерно для чугуна, легированных сталей, бетона, стекла, керамики и некоторых других конструкционных материалов. Для малоуглеродистых сталей, цветных металлов, пластмасс характерен пластический тип разрушения при наличии значительных остаточных деформаций. Однако подразделение материалов по характеру разрушения на хрупкие и пластичные весьма условно, оно обычно относится к некоторым стандартным условиям эксплуатации. Один и тот же материал может вести себя в зависимости от условий (температура, характер нагружены я, технология 'изготовления и др.) как хрупкий или как пластичный. Например, пластичные при нормальной температуре материалы разрушаются как хрупкие при низких температурах. Поэтому правильнее говорить не о хрупких и пластичных материалах, а о хрупком или пластическом состоянии материала.

Пусть материал является линейно-упругим и изотропным. Рассмотрим элементарный объем, находящийся в условиях одноосного напряженного состояния (рис. 1), так что тензор напряжений имеет вид

При таком нагружении происходит увеличение размеров в направлении оси Ох
, характеризуемое линейной деформацией ![]() , которая пропорциональна величине напряжения
, которая пропорциональна величине напряжения
Это соотношение является математической записью закона Гука , устанавливающего пропорциональную зависимость между напряжением и соответствующей линейной деформацией при одноосном напряженном состоянии. Коэффициент пропорциональности Е называется модулем продольной упругости или модулем Юнга . Он имеет размерность напряжений.
Наряду с увеличением размеров в направлении действия напряжения x происходит уменьшение размеров в двух ортогональных направлениях (рис. 1). Соответствующие деформации обозначим через y (x ) и z (x ), причем эти деформации отрицательны при положительных x и пропорциональны z :
Коэффициент пропорциональности называется коэффициентом Пуассона , который в силу изотропности материала одинаков для обоих ортогональных направлений.
Соотношения, аналогичные (1) и (2), в случае одноосного нагружения в направлении осей Оу , Оx напряжением y , z , соответственно имеют вид
![]() (3)
(3)
![]() (4)
(4)
При одновременном действии напряжений по трем ортогональным осям, когда отсутствуют касательные напряжения, для линейно-упругого материала справедлив принцип суперпозиции (наложения решений):
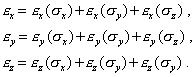
С учетом формул (1) - (4) получим
 (5)
(5)
Касательные напряжения вызывают угловые деформации, причем при малых деформациях они не влияют на изменение линейных размеров, и следовательно, на линейные деформации. Поэтому они справедливы также в случае произвольного напряженного состояния и выражают так называемый обобщенный закон Гука .
Угловая деформация xy обусловлена касательным напряжением xy , а деформации xz и yz - соответственно напряжениями xz и yz . Между соответствующими касательными напряжениями и угловыми деформациями для линейно-упругого изотропного тела существуют пропорциональные зависимости
которые выражают закон Гука при сдвиге . Коэффициент пропорциональности G называется модулем сдвига . Существенно, что нормальное напряжение не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними (рис.1).

Линейная зависимость существует также между средним напряжением, пропорциональным первому инварианту тензора напряжений, и объемной деформацией, совпадающей с первым инвариантом тензора деформаций:
Соответствующий коэффициент пропорциональности К называется объемным модулем упругости . В формулы (1) - (7) входят упругие характеристики материала Е, , G и К , определяющие его упругие свойства. Однако эти характеристики не являются независимыми. Для изотропного материала независимыми упругими характеристиками являются две, в качестве которых обычно выбираются модуль упругости Е и коэффициент Пуассона . Чтобы выразить модуль сдвига G через Е и , рассмотрим плоскую деформацию сдвига под действием касательных напряжений t (рис. 2). Для упрощения выкладок используем квадратный элемент со стороной а . Вычислим главные напряжения 1 = t , 3 = t . Эти напряжения действуют на площадках, расположенных под углом /4 к исходным площадкам. Из рис. 2 найдем связь между линейной деформацией 1 в направлении действия напряжения 1 и угловой деформацией . Большая диагональ ромба, характеризующая деформацию 1 , равна
![]()
Для малых деформаций tg
![]() ,
,
![]()
С учетом этих соотношений
![]()
До деформации эта диагональ имела размер АВ=а![]() . Тогда будем иметь
. Тогда будем иметь
![]()
Из обобщенного закона Гука (5) получим
![]()
![]()
Сравнение полученной формулы с записью закона Гука при сдвиге (6) дает
G=E /[2(1+)] (8)
Сложим три соотношения упругости (5)
В итоге получим
![]()
Сравнивая это выражение с объемным законом Гука (7), приходим к результату
![]()
Механические характеристики Е , , G и К находятся после обработки экспериментальных данных испытаний образцов на различные виды нагрузок. Из физического смысла все эти характеристики не могут быть отрицательными. Кроме того, из последнего выражения следует, что коэффициент Пуассона для изотропного материала не превышает значения 1/2. Таким образом, получаем следующие ограничения для упругих постоянных изотропного материала:
E >0, G >0, K >0, 01/2,
Предельное значение 1/2 приводит к предельному значению К , что соответствует несжимаемому материалу ( 0 при 0). В заключение выразим из соотношений упругости (5) напряжения через деформации. Запишем первое из соотношений (5) в виде
![]()
С использованием равенства (9) будем иметь
![]()
![]()
Аналогичные соотношения можно вывести для х и y . В результате получим
Здесь использовано соотношение (8) для модуля сдвига. Кроме того, введено обозначение
![]()
Потенциальная энергия упругой деформации
Рассмотрим вначале элементарный объем dV=dxdydz в условиях одноосного напряженного состояния (рис. 1). Мысленно закрепим площадку х =0 (рис. 3). На противоположную площадку действует сила x dydz . Эта сила совершает работу на перемещении x dx . При увеличении напряжения от нулевого уровня до значения x соответствующая деформация в силу закона Гука также увеличивается от нуля до значения x , а работа пропорциональна заштрихованной на рис. 4 площади: dA =0,5x x dV . Если пренебречь кинетической энергией и потерями, связанными с тепловыми, электромагнитными и другими явлениями, то в силу закона сохранения энергии совершаемая работа перейдет в потенциальную энергию , накапливаемую в процессе деформирования: dA=dU =0,5x x dV . Величина Ф=dU/dV называется удельной потенциальной энергией деформации , имеющей смысл потенциальной энергии, накопленной в единице объема тела. В случае одноосного напряженного состояния
![]()

При одновременном действии напряжений x , y и z на главных площадках (т. е. при отсутствии касательных напряжений) потенциальная энергия равна сумме работ, совершаемых силами x dydz , y dxdz , z dxdy на соответствующих перемещениях x dx , y dy , z dz . Удельная потенциальная энергия равна
![]() (2.47)
(2.47)
В частном случае чистого сдвига в плоскости Оху , изображенном на рис. 5, сила xy dxdz совершает работу на перемещении xy dy . Соответствующая этому случаю удельная потенциальная энергия деформации равна
![]()
Подобные соотношения будут иметь место при сдвиге в других плоскостях.
В общем случае напряженно-деформированного состояния будем иметь
Если деформации выразить через напряжения с помощью соотношений упругости (5) и (6), то получим эквивалентную форму записи через компоненты тензора напряжений
Выразив напряжения через деформации с использованием соотношений (6) и (10), получим еще одну форму записи для Ф - через компоненты тензора деформаций

Еще одну форму записи для удельной потенциальной энергии деформации получим, разложив тензоры напряжений и деформаций на шаровые тензоры и девиаторы. В результате (11) можно привести к одной из форм
 (13)
(13)
Здесь введены обозначения для - интенсивности касательных напряжений и - интенсивности деформаций сдвига , которые выражаются через вторые инварианты J2 (d) и J2 (d) девиаторов тензора напряжений и тензора деформаций следующим образом:
![]()
Первые слагаемые в (13) соответствуют произведению шаровых составляющих тензоров напряжений и деформаций, а вторые - произведению девиаторных составляющих. Так как шаровой тензор характеризует изменение объема, а девиатор - изменение формы, то соотношения (13) можно интерпретировать как разложение удельной потенциальной энергии на две составляющие: Ф=Ф0 + Фф , где Ф0 соответствует изменению объема без изменения формы, а Фф - изменению формы без изменения объема. Первая составляющая будет вычисляться через компоненты тензора напряжений следующим образом:
Удельную потенциальную энергию изменения формы проще найти не через интенсивность касательных напряжений, а как разность Ф - Ф0 . Вычитая (14) из (12), после преобразований получим

8. Механические характеристики конструкционных материалов
Ключевые слова : упругое состояние; пластичное состояние; пределы пропорциональности, упругости, текучести, прочности.
Механические характеристики определяются следующими факторами:
веществом, его структурой и свойствами;
конструктивными особенностями элемента, т. е, размерами, формой, наличием концентраторов, состоянием поверхности;
условиями при нагружении: температурой, скоростью, повторяемостью нагрузки и др.
Конструкционные материалы в процессе деформирования вплоть до разрушения ведут себя по разному. Пластичное поведение характеризуется существенным изменением формы и размеров, при этом к моменту разрушения развиваются значительные деформации, не исчезающие после снятия нагрузки. Такие материалы называют пластичными . При хрупком поведении разрушение наступает при весьма малых деформациях, и материалы с такими свойствами называют хрупкими . Однако одни и те же конструкционные материалы, находящиеся в различных условиях деформирования, ведут себя по разному: при одних условиях проявляют себя как пластичные материалы, при других - как хрупкие. В связи с этим, основные макромеханические характеристики материалов - упругость, пластичность, вязкость и др. правильнее относить не к их свойствам, а к состояниям материала.
Механические состояния деформирунмых тел
В упругом состоянии деформации обратимы, и вся энергия, затраченная на деформирование, при разгрузке возвращается (диссипация энергии отсутствует). Для любого твердого тела процесс деформирования начинается с упругой деформации. Изотропное тело имеет две константы упругости - модуль упругости Е и коэффициент Пуассона . Для анизотропных тел число упругих констант в общем случае равно 21. Из основных констант упругости можно получить их производные - модуль сдвига G , модуль объемной реформации К и постоянную Ламе .
Вязкое сопротивление - в некотором смысле противоположно упругому - работа внешних сил, уравновешенных силами вязкого сопротивления, полностью рассеивается в виде тепла.
Вязкое сопротивление определяется величиной касательной силы, необходимой для поддержания ламинарного скольжения слоев, или течения с определенной скоростью. Таким образом вязкость можно определить как сопротивление течению.
Представление о вязкоупругой деформации дает поведение моделей, сочетающих свойства вязкости и упругости в такой последовательности: при нагружении тела в нем возникает мгновенная упругая деформация, подчиняющаяся закону Гука; далее при том же максимальном напряжении наблюдается вязкая деформация, подчиняющаяся закону Ньютона.
Наиболее распространенными в теории линейной вязко-упругости являются реологические модели Максвелла и Фойгта, дающие связь между напряжениями и деформациями и скоростями их изменения:
![]() - модель Максвелла,
- модель Максвелла,
![]() - модель Фойгта,
- модель Фойгта,
тде - коэффициент вязкости.
Пластическое состояние
характеризуется наличием остаточных деформаций, фиксируемых после снятия внешних нагрузок. Объем тела при пластической деформации не изменяется; условие постоянства объема записывается в виде ![]() , (эксперименты показывают, что изменение объема не превышает 0,5%).
, (эксперименты показывают, что изменение объема не превышает 0,5%).
В случае, когда все напряжения изменяются пропорционально одной из составляющих, в процессе пластической деформации направления главных деформаций совпадают с направлениями главных нормальных напряжений, направления максимальных сдвигов - с направлениями максимальных касательных напряжений, а главные направления девиатора напряжений - с главными направлениями девиатора деформаций.
Одной из распространенных моделей поведения материала при упруго-пластических деформациях является модель пластичности, основанная на деформационной теории Генки-Ильюшина, описываемая уравнениями:

![]()
![]() - средняя деформация,
- средняя деформация,
![]() - среднее напряжение,
- среднее напряжение,
- безразмерный коэффициент, называемый параметром пластичности (с точностью до множителя он совпадает с интенсивностью касательных напряжений). При =1 эта модель описывает поведение упругого материала.
Высокоэластическое состояние - наиболее характерно для полимеров; особенностями этого состояния являются большая изменяемость формы и деформирование без изменения объема. Для материалов, находящихся в высокоэластическом состоянии, наблюдается существенная зависимость их свойств от длительности и скорости нагружения, температуры и т. д.
Состояние разрушения - состояние, при котором за счет интенсивного развития трещин в материале тела начинается нарушение его сплошности и непрерывности. Физический процесс разрушения материала представляется в виде двух основных стадий-стадии рассеянных разрушений (зарождение и развитие микроскопических трещин) и стадии развития магистральной трещины. Очаги зарождения микротрещин распределены по всему объему материала, находящегося в однородном напряженном состоянии, достаточно равномерно. Относительная длительность первой и второй стадии разрушения зависит от свойств материала, характера напряженного состояния и условий нагружения.
Диаграммы упруго-пластического деформирования конструкционных материалов
Основным опытом для определения механических характеристик конструкционных материалов является опыт на растяжение призматического образца центрально приложенной силой, направленной по продольной оси; при этом в средней части образца реализуется однородное напряженное состояние. Форма, размеры образца и методика проведения испытаний определяются соответствующими стандартами, например, ГОСТ 34643-81, ГОСТ 1497-73. По результатам испытаний строится зависимость ![]() между напряжениями
между напряжениями ![]() и деформациями
и деформациями ![]() , которая называется диаграммой деформирования. Опыты на растяжение образцов выявляют некоторые общие свойства конструкционных материалов-свойства упругости и пластичности. На рис. 1 показаны типичные кривые деформирования при растяжении образцов из материала сталь 30 и сталь 40Х.
, которая называется диаграммой деформирования. Опыты на растяжение образцов выявляют некоторые общие свойства конструкционных материалов-свойства упругости и пластичности. На рис. 1 показаны типичные кривые деформирования при растяжении образцов из материала сталь 30 и сталь 40Х.
Если напряжения не превышают пц
- предела пропорциональности
(точка / на диаграмме), и зависимость между напряжениями и деформациями линейна, то она описывается законом Гука ![]() , где Е - модуль продольной упругости материала
. Размерность модуля упругости-Н/м2 (Паскаль). Значение модуля упругости Е
на кривой деформирования
, где Е - модуль продольной упругости материала
. Размерность модуля упругости-Н/м2 (Паскаль). Значение модуля упругости Е
на кривой деформирования ![]() численно равно тангенсу угла наклона линейного участка:
численно равно тангенсу угла наклона линейного участка: ![]() . Таким образом, величину Е
можно рассматривать как характеристику упругого сопротивления или как характеристику интенсивности нарастания напряжения с увеличением деформации. Физический смысл коэффициента Е
определяется как напряжение, необходимое для увеличения длины образца в два раза. Такое толкование довольно искусственно, поскольку величина упругого удлинения у большинства твердых тел редко достигает даже 1 %.
. Таким образом, величину Е
можно рассматривать как характеристику упругого сопротивления или как характеристику интенсивности нарастания напряжения с увеличением деформации. Физический смысл коэффициента Е
определяется как напряжение, необходимое для увеличения длины образца в два раза. Такое толкование довольно искусственно, поскольку величина упругого удлинения у большинства твердых тел редко достигает даже 1 %.
Напряжения, являющиеся верхней границей проявления чисто упругих деформаций, соответствуют точке 2 диаграммы и называются пределом упругости упр .
Точка 3 диаграммы характерна тем, что при достижении напряжениями величины - предел текучести ), дальнейшее удлинение образца (для малоуглеродистых сталей) происходит практически без увеличения нагрузки. Это явление носит название текучести , а участок диаграммы, расположенный непосредственно правее точки 3, называется площадкой текучести . При этом полированная поверхность образца мутнеет, докрывается ортогональной сеткой линий (линии Чернова-Людерса), расположенных под углом 45° к продольной оси образца по направлению плоскостей действия максимальных касательных напряжений.
У многих конструкционных материалов площадка текучести не выражена столь явно, как у малоуглеродистых сталей. Для таких материалов вводится понятие условного предела текучести s ; это напряжение, которому соответствует остаточная (пластическая) деформация, равная s %. Обычно принимается s = 0,2%.
После площадки текучести для дальнейшего увеличения деформации необходимо увеличение растягивающей силы. Материал снова проявляет способность сопротивляться деформации; участок за площадкой текучести (до точки 4) называется участком упрочнения . Точка 4 соответствует максимальной нагрузке, выдерживаемой образцом. Соответствующее напряжение называется временным сопротивлением в (или пределом прочности пч ). Дальнейшая деформация образца происходит без увеличения или даже с уменьшением нагрузки вплоть до разрушения (точка 5). Точке 4 на диаграмме соответствует начало локального уменьшения размеров поперечного сечения образца, где, в основном, сосредоточивается вся последующая пластическая деформация.
Диаграмма, приведенная на рис.1, является диаграммой условных напряжений, условность состоит в том, что все силы относились к F0 - первоначальной площади поперечного сечения образца; в действительности же при растяжении площадь поперечного сечения образца уменьшается. Если учитывать текущее значение площади поперечного сечения при определении напряжений, то получим диаграмму истинных напряжений (рис. 2).
Если в некоторый момент нагружения (точка А на рис. 1) прекратить нагружение и снять нагрузку, то разгрузка образца пойдет по линии АВ, параллельной линейному участку диаграммы 0-1. При этом полная деформация в точке А равна:
![]()
где ![]() - упругая
деформация,
- упругая
деформация, ![]() - пластическая (остаточная деформация
). Это уравнение справедливо для любой точки диаграммы.
- пластическая (остаточная деформация
). Это уравнение справедливо для любой точки диаграммы.
После того как материал испытал воздействие осевого усилия одного знака (например, растяжение) в области пластических деформаций ( ) сопротивляемость этого материала пластической деформации при действии сил другого знака (сжатие) понижается. Это явление носит название эффекта Баушингера .
При растяжении образца происходит не только увеличение его длины, но и уменьшение размеров поперечного сечения, т. е. в упругой области деформация в поперечном направлении ![]() , где - деформация в продольном направлении, - коэффициент Пуассона
. Для изотропных материалов значения коэффициента Пуассона находятся в пределах 0 < 0,5.
, где - деформация в продольном направлении, - коэффициент Пуассона
. Для изотропных материалов значения коэффициента Пуассона находятся в пределах 0 < 0,5.
Таблица 1. Механические характеристики некоторых материалов
| Материал |
Характеристика |
||||
| Е, ГПа |
, МПа |
в , МПа |
, % |
, % |
|
| Сталь Ст.3 |
200 |
240/240 |
450/- |
26 |
50 |
| Сталь 15 |
200 |
210/210 |
350/- |
28 |
55 |
| Сталь 45 |
200 |
340/340 |
610/- |
24 |
45 |
| Сталь ЗОХГСА |
200 |
950/950 |
1200/- |
13 |
50 |
| Чугун СЧ15-32 |
150 |
- |
150/640 |
0,6 |
- |
| Медь прутковая |
110 |
250/250 |
320/- |
15 |
45 |
| Дюралюмин Д16 |
75 |
240/240 |
420/- |
18 |
- |
| Дельта-древесина |
20 |
- |
250/160 |
- |
- |
| Текстолит |
30 |
75/115 |
127/168 |
1,5 |
- |
Примечание. В знаменателе указана соответствующая характеристика при сжати.
Для сталей различных марок Е = 195-206 ГПа, G = 79-89 ГПа, = 0,23-0,31, для сплавов алюминия Е = 69-71 ГПа, G = 26-27 ГПа, = 0,30-0,33. Упругие свойства некоторых материалов даны в табл. 1.
Характеристиками пластичности материала являются относительное удлинение и относительное сужение при разрыве :
![]()
![]()
где l0 , F0 - длина рабочей части образца и площадь поперечного сечения до деформации; lк - длина рабочей части образца после разрыва; F0 - конечная площадь поперечного сечения в шейке образца после разрыва.
По величине относительного удлинения при разрыве проводится разделение состояния материалов на пластичное и хрупкое. Материалы, имеющие к моменту разрушения достаточно большие значения >10%), относят к пластическим материалам ; к хрупким относят материалы с относительным удлинением < 3%.
Оценка пластических свойств материала может быть проведена по такой характеристике, IKBK ударная вязкость –
KC=A/F,
где А - работа, затрачиваемая на ударное разрушение образца, Дж (или НЧм), F - площадь поперечного сечения образца в месте концентратора, м2 (или см2),
Работа А
деформации при разрушении образца может быть определена по диаграмме растяжения ![]() . Так, если первоначальная длина образца l0
, то работа деформации, совершаемая силой Р
на перемещении u
:
. Так, если первоначальная длина образца l0
, то работа деформации, совершаемая силой Р
на перемещении u
:

где uк
- перемещение в момент, предшествующий разрушению. Тогда по зависимости ![]() и
и ![]() , находим
, находим

где  - площадь диаграммы деформирования (работа деформации на единицу объема материала). Для сталей КС=50-100 Н м/см2. Материалы с ударной вязкостью КС < 30 Н м/см2 относят к числу хрупких.
- площадь диаграммы деформирования (работа деформации на единицу объема материала). Для сталей КС=50-100 Н м/см2. Материалы с ударной вязкостью КС < 30 Н м/см2 относят к числу хрупких.
Некоторые пластичные материалы в районе площадки текучести обнаруживают особенность (например титан), называемую "зубом текучести"; для таких материалов вводится понятие верхнего и нижнего предела текучести (т в , т н ).
Экспериментальное изучение свойств материалов при сжатии проводится на коротких образцах с тем, чтобы исключить возможность искривления образца. Для пластичных материалов характер диаграммы ![]() при сжатии примерно до возникновения текучести такой же, как и при растяжении. В процессе деформации сжатия образец укорачивается; при этом размеры поперечного сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается.
при сжатии примерно до возникновения текучести такой же, как и при растяжении. В процессе деформации сжатия образец укорачивается; при этом размеры поперечного сечения увеличиваются. Из-за трения между опорными плитами нагружающего устройства и торцевыми поверхностями образца он принимает бочкообразную форму. Для ряда пластичных материалов обнаружить напряжение, аналогичное временному сопротивлению при растяжении, не удается, так как образец сплющивается.
Хрупкие материалы проявляют значительно лучшую способность сопротивляться деформациям сжатия, чем деформациям растяжения; для них разрушающее напряжение при сжатии превышает предел прочности при растяжении в несколько раз. Разрушение хрупких материалов при сжатии происходит за счет образования трещин.
9. Растяжение (сжатие) призматических стержней
Ключевые слова : прочность, перемещение, концентрация напряжений, напряженное состояние.
Напряжение при растяжении (сжатии) призматических стержней. Расчет на прочность
Переходя к изучению введенных основных видов деформации стержней, ограничимся рассмотрением стержней постоянного поперечного сечения с прямолинейной осью, т. е. призматических стержней. Начнем с деформации растяжения (сжатия).
Напомним, что под растяжением (сжатием) понимают такой вид деформации стержня, при котором в его поперечном сечении возникает лишь один внутренний силовой фактор - продольная сила Nz . Поскольку продольная сила численно равна сумме проекций, приложенных к одной из отсеченных частей внешних сил на ось стержня (для прямолинейного стержня она совпадает в каждом сечении с осью Oz ), то растяжение (сжатие) имеет место, если все внешние силы, действующие по одну сторону от данного поперечного сечения, сводятся к равнодействующей, направленной вдоль оси стержня (рис. 1). Одна и та же продольная сила Nz при действии на различные части стержня (левую или правую) имеет противоположные направления. Знак Nz зависит от характера вызываемой ею деформации. Продольная сила считается положительной, если вызывает растяжение элемента (рис. 2, а), и она отрицательна, если вызывает сжатие (рис. 2, б).
Для того, чтобы сформулировать предпосылки теории растяжения (сжатия) призматического стержня, обратимся к эксперименту. Представим себе стержень, изготовленный из какого-либо податливого материала (например, резины), на боковую поверхность которого нанесена система продольных и поперечных рисок (рис. 3, а). Эта ортогональная система рисок остается таковой и после приложения растягивающей нагрузки (рис. 3, б). Поскольку поперечные риски являются следами поперечных сечений на поверхности стержня и остаются прямыми и перпендикулярными к оси стержня то это свидетельствует о выполнении гипотезы плоских сечений (Бернулли) . С учетом гипотезы об отсутствии поперечного взаимодействия продольных волокон приходим к выводу, что деформация растяжения стержня сводится к одноосному растяжению его продольных волокон, и в поперечном сечении стержня возникают лишь нормальные напряжения а (рис. 4), индекс г у которых опускаем. Ортогональность продольных и поперечных рисок свидетельствует также об отсутствии сдвигов, а, следовательно, и связанных с ними касательных напряжений т в поперечных и продольных сечениях стержня.
Тогда продольная сила N " равная сумме проекции внутренних сил, действующих в данном поперечном сечении площадью F (рис. 4) очевидно будет равна
![]()
Это соотношение является уравнением равновесия статики, связывающим продольную силу Nz , и нормальное напряжение , которое в общем случае является функцией координат х и у и поэтому не может быть найдено из одного лишь 1 уравнения статики . Таким образом, задача определения напряжений даже в самом простом случае деформирования стержня (растяжении или сжатии) оказывается статически неопределимой.
Необходимое для решения этой задачи дополнительное уравнение вытекает из гипотезы плоских сечений. Поскольку поперечные сечения стержня, оставаясь плоскими и перпендикулярными к оси стержня, в процессе деформирования лишь поступательно перемещаются вдоль оси стержня (что приводит к одинаковому удлинению всех продольных волокон), то приходим к уравнению =const, из которого ввиду однозначности связи и (для линейно-упругого материала это - закон Гука: =Е.) вытекает, что
= const .
Решая совместно уравнения получим, что Nz = F или
= Nz / F .
Таким образом, при растяжении (сжатии) призматического стержня нормальные напряжения равномерно распределены по поперечному сечению, а касательные напряжения в сечениях отсутствуют, что является следствием гипотезы плоских сечений. Указанное, несмотря на, казалось бы, очевидность и простоту, является фундаментальным результатом, справедливым, строго говоря, лишь для призматического стержня. Однако в инженерной практике его используют и для приближенной оценки нормальных напряжений в стержнях переменного сечения. При этом, чтобы погрешность формулы была невелика, необходимо, чтобы площадь поперечного сечения стержня изменялась достаточно плавно вдоль его оси.
Условие прочности при растяжении (сжатии) призматического стержня для стержня из пластического материала (т. е. материала, одинаково работающего на растяжение и сжатие) будет иметь вид:
где [] - допускаемое напряжение. Напряжение в условии (1) подставляется по модулю, так как знак в этом случае роли не играет. Для стержней из хрупких материалов, неодинаково сопротивляющихся растяжению и сжатию, знак напряжения имеет принципиальное значение, и условие прочности приходится формулировать отдельно для растяжения и сжатия

где р и с - напряжения растяжения и сжатия, а [р ] и [с ] - ответствующие им допускаемые напряжения.
В практике инженерных расчетов, исходя из условия прочности, решаются три основные задачи механики материалов конструкций. В применении к случаю растяжения (сжатия) призматического стержня эти задачи формулируются следующим образом.
Проверка прочности (поверочный расчет). Этот расчет проводится, если нагрузка (в нашем случае ее представляет Nz ), сечение стержня F и его материал [] заданы.
Необходимо убедиться, что выполняется условие прочности
![]()
Проверочный расчет заключается в том, что определяется фактический коэффициент запаса прочности n и сравнивается с нормативным коэффициентом запаса [n] :
![]()
где * - предельное (или опасное) напряжение, т. е. напряжение, вызывающее отказ элемента конструкции (напомним, что, например, для стержня из пластичного материала это-предел текучести sт или условный предел текучести 0,2 ).
Подбор сечения (проектный расчет). В этом расчете по Заданной нагрузке (Nz ) определяются размеры поперечного сечения стержня (F ) из заданного материала ([] дано). Минимальное значение F получим, если в условии прочности (1) принять знак равенства:
[F] = Nz / [ ]
Определение допускаемой нагрузки , то есть максимального значения нагрузки, которое допускает данный элемент конструкции (F и [] даны) при выполнении условия прочности (1)
[N] = [ ]F
Понятие о концентрации напряжений, принцип Сен-Венана
Даже для призматического стержня равномерное распределение напряжений по поперечному сечению не всегда имеет место. Так, отклонения от равномерного распределения напряжений наблюдаются в окрестности сечений, содержащих вырезы, выточки, отверстия, трещины, в местах резкого изменения поперечного сечения, а также в местах приложения сосредоточенных сил и т. п. Неравномерное распределение напряжений в указанных местах является следствием искажения плоскостей поперечных сечений или их депланации .
Поясним это явление на примере подверженной растяжению полосы из податливого материала с круговым отверстием, на поверхности которой нанесены продольные и поперечные риски (рис. 5, а). В зоне отверстия имеет место депланация поперечных сечений, вызванная неравномерным растяжением продольных волокон (рис.5, б). При этом наибольшие удлинения и соответственно напряжения max получают волокна возле отверстия. Такое местное увеличение напряжений возле вырезов, выточек, отверстий и т. п., а также в местах приложения сосредоточенных сил, называется концентрацией напряжений , а источники концентрации напряжений (вырезы, выточки, отверстия и т. п.) получили название концентраторов напряжений .
Рассмотренными методами механики деформированного тела, опирающимися на гипотезу плоских сечений, задачи о распределении напряжений в зонах концентрации напряжений не решаются. Такие задачи решаются методами теории упругости или исследуются экспериментально. При этом для практических расчетов вводится так называемый теоретический коэффициент концентрации напряжений к , представляющий собой отношение максимальных max и номинальных ном напряжений: к = max /ном , где номинальные напряжения определяются без учета концентрации напряжений. В приведенном примере растяжения полосы с отверстием ном = Nz / Fnt , a Fnt - площадь поперечного сечения полосы, уменьшенная за счет отверстия ("нетто"). Таким образом, к играют роль поправочных коэффициентов.
Однако, как показали эксперименты и точные решения задач теории упругости, местные отклонения от равномерного распределения напряжений, вызванные концентрацией напряжений, быстро затухают по мере удаления от сечения с концентратором, и на расстояниях порядка ширины сечения распределение напряжений можно считать практически равномерным (рис. 5, в). Отмеченное свойство является частным случаем широко используемого практически во всех разделах механики деформируемого твердого тела (в том числе и теории упругости) принципа Сен-Венана
Определение деформаций и перемещений
Как показывают эксперименты, при растяжении стержня размеры его поперечного сечения уменьшаются (см. рис. 6), а при сжатии - увеличиваются. Это явление получило название эффекта Пуассона .
По аналогии с продольной деформацией изменение размеров поперечного сечения b (на рис. 6 b <0) будем называть абсолютной поперечной деформацией , а '=b/b - относительной поперечной деформацией . Относительные продольная и поперечная деформа-ции, имеющие противоположные знаки, связаны между собой коэффициентом , являющимся константой материала и называемым коэффициентом поперечной деформации или коэффициентом Пуассона :
Формула (2) для удлинения стержня l применима только в случае, когда по длине стержня ни жесткость поперечного сечения, ни продольная сила не изменяются (EF =const, Nz =const). Удлинение стержня со ступенчатым изменением EF и Nz (рис. 7) может быть определено как сумма удлинений ступеней, у которых EF и Nz постоянны:

(индекс k у модуля продольной упругости означает, что участки стержня могут быть изготовлены из различных материалов). В случае, когда Nz и EF меняются по длине стержня l непрерывно и их можно считать постоянными лишь в пределах ступеней длиной dz , обобщая формулу эту, получаем

В качестве тестов для практики расчетов определенных интегралов рекомендую воспользоваться системой входных тестов Т-5, указанных в ПРИЛОЖЕНИИ.


С упругими продольными деформациями стержня при растяжении (сжатии) связаны продольные перемещения его сечений. На рис. 8 приведены три случая определения таких перемещений, откуда видно, что перемещения поперечных сечений численно равны удлинениям заштрихованных частей стержня:
перемещение свободного торцевого сечения 1-1 при неподвижном другом торцевом сечении (рис. 8, а) численно равно удлинению стержня;
перемещение промежуточного сечения 2-2 (рис. 8, б) численно равно удлинению части стержня, заключенной между данным сечением и сечением неподвижным;
взаимное перемещение сечений 3-3 и 4-4 (рис, 8, в) численно равно удлинению части стержня, заключенной между этими сечениями.
Напряженное состояние при растяжении (сжатии)
Напряженное состояние при растяжении стержня является одноосным (рис. 9, а). Поскольку на поперечных и продольных площадках касательные напряжения не возникают, то эти площадки являются главными.
Напряжения на площадках, наклоненных к оси стержня под углом , определяются по формулам для упрощенного плоского напряженного состояния:
![]()
Площадки с экстремальными касательными напряжениями 13 (рис. 9, б), как известно, наклонены по отношению к исходным под углами =±45° (следует и из формулы для ) и равны 13 =/2.
Именно с действием экстремальных связывается появление на боковой поверхности образца из малоуглеродистой стали, испытываемого на растяжение, линий скольжения, ориентированных под углом =±45° к оси образца. На площадках с экстремальными t действуют и нормальные напряжения, равные /2.
10. Составные балки и перемещения при изгибе
Ключевые слова : сварные двутавровые балки, уравнение упругой кривой, прогиб, угол поворота, граничные условия.
Понятие о составных балках
Работу составных балок проиллюстрируем на простом примере трехслойной балки прямоугольного поперечного сечения. Если слои между собой не связаны и силы трения между ними отсутствуют, то каждый из них деформируется как отдельная балка, имеющая свой нейтральный слой (рис. 1, а). Нагрузка между этими балками распределяется пропорционально их жесткостям при изгибе (в данном примере поровну). Это означает, что моменты инерции и моменты сопротивления трех независимо друг от друга деформирующихся балок должны быть просуммированы
![]()
Если скрепить балки сваркой, болтами или другим способом (рис. 1, б), то с точностью до пренебрежения податливостью наложенных связей сечение балки будет работать как монолитное с моментом инерции и моментом сопротивления, равным
![]()
Как видно, при переходе к монолитному сечению жесткость балки возрастает в девять раз, а прочность - в три раза. В инженерной практике наиболее распространены сварные двутавровые балки.
Дифференциальное уравнение прямого изгиба призматического стержня
Определено, что мерой деформации призматического стержня при прямом чистом изгибе является кривизна нейтрального слоя. Можно показать, что с достаточной для инженерных расчетов точностью этим тезисом можно пользоваться и в случае прямого поперечного изгиба стержня. Однако для практических целей кроме кривизны 1/ необходимо определить вертикальные перемещения центров тяжести отдельных поперечных сечений - прогибов балки v, а иногда и углы поворота этих сечений (рис. 2). Вследствие гипотезы плоских сечений угол поворота сечения ( оказывается равным углу наклона касательной к изогнутой оси балки, который в силу малости
![]()
Тогда возникает геометрическая задача: составить уравнение для функции прогиба ![]() , зная закон изменения ее кривизны.
, зная закон изменения ее кривизны.
Воспользуемся известным из дифференциальной геометрии выражением для кривизны в прямоугольных декартовых координатах:

Однако, учитывая, что в инженерной практике применяются достаточно жесткие балки, для которых наибольший прогиб f мал по сравнению с длиной (f / l << 1 ), а первая производная от прогиба имеет порядок
![]()
и, следовательно, величиной (dv / dz )2<<1, стоящей в знаменателе, можно пренебречь, выражение для кривизны упрощается
![]()
Тогда, подставив это выражение в полученную ранее связку кривизны и изгибающего мометна - ![]() , условившись что ось Oy
направлена вверх и согласовав знаки 1/ и Мх
, приходим к дифференциальному уравнению прямого изгиба балки
, условившись что ось Oy
направлена вверх и согласовав знаки 1/ и Мх
, приходим к дифференциальному уравнению прямого изгиба балки

известному также как дифференциальное уравнение упругой кривой .
Если учесть точное выражение для кривизны по формуле, то точное уравнение упругой кривой

является нелинейным дифференциальным уравнением. Поэтому линейное дифференциальное уравнение, описывающее малые прогибы балки, иногда называют линеаризованным уравнением упругой кривой .
Решение уравнения получаем путем двукратного почленного интегрирования. При первом интегрировании получаем выражение
![]()
которое с учетом ![]() , дает также закон изменения углов поворота поперечных сечений по длине балки. Повторным интегрированием получаем функцию прогиба
, дает также закон изменения углов поворота поперечных сечений по длине балки. Повторным интегрированием получаем функцию прогиба
![]()
Постоянные интегрирования С и D должны быть найдены из граничных условий.
Во всех приведенных выше уравнениях функция изгибающего момента Мх (г) предполагалась известной, что возможно лишь для статически определимых балок. Простейшие варианты статически определимых однопролетных балок и соответствующие граничные условия показаны на рис. 3.
Условия, накладываемые на прогиб и угол поворота сечения, получили название кинематических граничных условий . Как видно, для шарнирно опертой балки требуется, чтобы прогиб на опорах v(0) =v(l) =0 , а для консольной балки прогиб и угол поворота сечения в заделке
![]()

Дифференциальное уравнение неприменимо для расчета статически неопределимых балок, так как содержит неизвестный изгибающий момент Мx появившийся в результате двукратного интегрирования уравнения четвертого порядка

В этом уравнении нагрузка q известна, поэтому его можно получить, учитывая, что

При интегрировании уравнения необходимо задать четыре граничных условия (по два на каждом конце балки) в том числе так называемые силовые граничные условия - условия, накладываемые на силовые величины (изгибающий момент и поперечную силу), которые выражаются через производные от прогиба. Так как

а с учетом дифференциального соотношения Qy =dMx /dz , получаем

Вернемся к интегрированию уравнения второго порядка. Если имеется несколько участков, для которых правая часть уравнения исходного f(z)=Mx /EJx , содержит разные аналитические выражения, то интегрирование усложняется. На рис. 4 приведена эпюра Мx , содержащая n участков. Для каждого участка независимое интегрирование дает по две константы, а при п участках требуется определить 2n постоянных. Добавляя к двум граничным условиям на опорах 2(n-1) условия непрерывности и гладкости упругой кривой на границе; смежных участков, заключающиеся в равенстве прогибов v и углов поворота сечений dv/dz на этих границах
![]()
![]()
получим 2n граничных условий, необходимых для нахождения постоянных интегрирования.
Рекомендую для практики решения дифференциальных уравнений второго порядка воспользоваться системой входных тестов Т-6, приведенных в ПРИЛОЖЕНИИ.
11. Напряжения и деформации при кручении призматических стержней кругового поперечного сечения
Ключевые слова : чистый сдвиг, жесткость сечения при кручении, угол закручивания, вал, прочность, жесткость.
Кручением называется такой вид деформации, при котором в поперечном сечении стержня возникает лишь один силовой фактор - крутящий момент Мz . Крутящий момент по определению равен сумме моментов внутренних сил относительно продольной оси стержня Oz . Нормальные силы, параллельные оси Oz , вклада в крутящий момент не вносят. С силами, лежащими в плоскости поперечного сечения стержня (интенсивности этих сил - касательные напряжения xz и yz ) Мz связывает вытекающее из его определения уравнение равновесия статики (рис. 1)
![]()
Условимся считать Mz положительным, если со стороны отброшенной части стержня видим его направленным против часовой стрелки (см. рис. 2). Это правило проиллюстрировано на рис. 1 и в указанном соотношении, где крутящий момент Мz принят положительным. Численно крутящий момент равен сумме моментов внешних сил, приложенных к отсеченной части стержня, относительно оси Оz .
Рассмотрим кручение призматических стержней кругового поперечного сечения. Исследование деформаций упругого стержня с нанесенной на его поверхности ортогональной сеткой рисок (рис. 3) позволяет сформулировать следующие предпосылки теории кручения этого стержня:
поперечные сечения остаются плоскими (выполняется гипотеза Бернулли);
расстояния между поперечными сечениями не изменяются, следовательно z =0;
контуры поперечных сечений и их радиусы не деформируются. Это означает, что поперечные сечения ведут себя как жесткие круговые пластинки, поворачивающиеся при деформировании относительно оси стержня Оz . Отсюда следует, что любые деформации в плоскости пластинки равны нулю, в том числе и x = y =0;
материал стержня подчиняется закону Гука. Учитывая, что x =y = z =0, из обобщенного закона Гука в форме получаем x =y = z =0. Это означает, что в поперечных сечениях, стержня возникают лишь касательные напряжения , а вследствие закона парности касательных напряжений, равные им напряжения действуют и в сопряженных продольных сечениях. Следовательно напряженное состояние стержня - чистый сдвиг .
Выведем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения. Как видно, поворот правого торцевого сечения относительно неподвижного левого на угол j (назовем его углом закручивания стержня) вызывает поворот продольных волокон на угол (угол сдвига), поскольку на величину искажаются углы ортогональной сетки продольных и поперечных рисок модели. Двумя смежными сечениями вырежем элемент стержня длиной dz и, поскольку нас интересуют деформации элемента, левое сечение его будем считать неподвижным (рис. 4). При повороте правого сечения на угол d в соответствии с гипотезой о недеформируемости радиусов, правый конец волокна АВ (отстоящий от оси элемента на величину полярного радиуса ) будет перемещаться по дуге BB1 , вызывая поворот волокна на угол сдвига
![]()
Обратим внимание на то, что в соответствии с рис. 4 и рис. 5, а сдвиг и связанное с ним касательное напряжение перпендикулярны радиусу . Определим , воспользовавшись законом Гука для чистого сдвига
Здесь d /dz - погонный угол закручивания стержня, который остается пока неизвестным. Для его нахождения обратимся к условию статики, записав его в более удобной для данного случая форме (рис. 5, a)
![]() (2)
(2)
Подставляя (1) в (2) и учитывая, что
![]()
где Jp - полярный момент инерции поперечного сечения (для круга с диаметром d Jp =4 /32 ), получаем
Подставляя выражение (3) в (1), получаем формулу для касательных напряжений при кручении призматического стержня кругового поперечного сечения
Как видно из (4), сдвиги и касательные напряжения пропорциональны расстояний от оси стержня. Обратим внимание на структурные аналогии формул для нормальных напряжений чистого изгиба и касательных напряжений кручения.
Мерой деформации стержня при кручении является погонный угол закручивания стержня, определяемый по (3). Поскольку величина DJp стоит в знаменателе формулы и при заданной нагрузке (Mz через нее выражается) d /dz тем меньше, чем больше DJp , последнюю называют жесткостью поперечного сечения при кручении .
Пользуясь (3) для определения угла закручивания элемента длиной dz
![]()
найдем полный угол закручивания стержня длиной l
![]() (5)
(5)
В случае, если по длине стержня Мz и DJp постоянны, получаем
![]()
когда эти величины кусочно-постоянны, то:
![]() (6)
(6)
Отметим, что полученные формулы по структуре аналогичны формулам для деформаций при растяжении стержня.
Наибольшие касательные напряжения возникают у внешней поверхности стержня, т. е. при max =d/2
![]()
где Wр - момент сопротивления при кручении или полярный момент сопротивления
![]()
Полярный момент сопротивления, стоящий в знаменателе для максимальных касательных напряжений, очевидно, является геометрической характеристикой сечения, а условие прочности стержня при кручении принимает вид
где [] - допускаемое напряжение на кручение.
Как показали эксперименты и точное решение этой задачи в теории упругости, все гипотезы, сформулированные ранее для стержня со сплошным круговым сечением, остаются справедливыми и для стержня кольцевого поперечного сечения (рис. 6). Поэтому все выведенные ранее формулы пригодны для расчета стержня кольцевого сечения с той лишь разницей, что полярный момент инерции определяется как разность моментов инерции кругов с диаметрами D и d
![]()
где =d/D , а момент сопротивления определяется по формуле
![]()
Учитывая линейный характер изменения касательных напряжений по радиусу (рис. 6) и связанное с этим лучшее использование материала, кольцевое сечение следует признать наиболее рациональным при кручении стержня. Коэффициент использования материала тем выше, чем меньше относительная толщина трубы.
Как отмечено ранее, напряженное состояние при кручении стержня - чистый сдвиг, являющийся частным случаем плоского напряженного состояния. На площадках, совпадающих с плоскостью поперечного сечения и на парных им площадках продольных сечений возникают экстремальные касательные напряжения max-min , а главные напряжения 1,3 = ± действуют на площадках, наклоненных .коси стержня под углами ±45°; главное напряжение 2 = 0.
Особенности напряженного состояния при кручении нашли отражение в характере разрушения стержней. Так, разрушение стержня из дерева, плохо работающего на скалывание вдоль волокон, происходит от продольных трещин (рис. 7, a). Разрушение стержня из хрупкого металла (например, чугуна) происходит по винтовой линии, наклоненной к образующим под углом 45°, т. е. по траектории главного напряжения 3 (рис. 7,б).
Расчет валов
Рассмотрим расчет вала на прочность и жесткость. Пусть известна мощность W (кВт), передаваемая вращающимся с заданным числом оборотов в минуту (n ) валом от источника мощности (например, двигателя) к ее потребителю (например, станку), а момент m , передаваемый валом, требуется найти, так как численно равный этому моменту крутящий момент необходим для расчета вала.
Если число оборотов вала в минуту п и соответствующая угловая скорость (с-1 ) постоянны, а Ф - угол поворота вала в данный момент времени t , то работа вращательного движения А=mФ . Тогда передаваемая валом мощность будет равна
![]()
![]() кНм
кНм
где учтено, что ![]() .
.
Если мощность подается на вал через ведущий шкив, а раздается потребителям через несколько ведомых шкивов, то соответственно определяются моменты на шкивах, а затем строится эпюра крутящих моментов. Расчет вала на прочность и жесткость ведется, очевидно, по max Mz . Определение диаметра вала из условия прочности. Условие прочности при кручении вала имеет вид (7), где допускаемые напряжения [] принимаются пониженными по сравнению с допускаемыми напряжениями обычного статического расчета в связи с необходимостью учета наличия концентраторов напряжений (например, шпоночных канавок), переменного характера нагрузки и наличия наряду с кручением и изгиба вала.
Требуемое значение Wp =dз /16 получаем из условия (7), принимая в нем знак равенства
![]()
откуда получаем формулу для диаметра вала кругового сечения
![]()
Определение диаметра вала из условия жесткости. Условие жесткости состоит в наложении ограничения на погонный угол закручивания вала ![]() , так как недостаточно жесткие валы не обеспечивают устойчивой передачи мощности и подвержены сильным колебаниям:
, так как недостаточно жесткие валы не обеспечивают устойчивой передачи мощности и подвержены сильным колебаниям:
![]()
Тогда, учитывая, что Jp =d4 /32 , для диаметра вала из условия жесткости имеем

Аналогично проводятся расчеты и для вала кольцевого поперечного сечения.
Похожие рефераты:
Основы проектирования и конструирования
Физика в МГУ (билеты-вопросы-ответы) по лекциям Ремезовой Н.И. и лекторов из МГУ
Простейшие типы деформаций стержней. Допущения и определение деформаций
Внешние силы. Деформация и перемещение. Определение внутренних усилий
Оборудование летательных аппаратов
Основы теории и технологии контактной точечной сварки