Курсовая работа: Устойчивость систем автоматического управления

Елабужский Филиал ГОУ ВПО Казанского Государственного Технического Университета им. А.Н. Туполева

Курсовая работа по дисциплине:

«Теория автоматического управления»

На тему:

«Устойчивость систем автоматического управления»

Выполнил: студент гр. 22308

Зиннатуллин А.Ф.

Проверил: Конюхов М.И.

Елабуга 2010

Аннотация

В данной работе было представлено устойчивость систем автоматического управления. Устойчивость считается важнейшим и обязательным понятием, так как только в устойчивой системе могут быть удовлетворены другие требования к качеству.

Введение

Устойчивость АСУ характеризует способность системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Следовательно, только устойчивая система является работоспособной. Понятие "устойчивость" наглядно иллюстрирует рис. 1, на котором представлена физическая система шар – опорная поверхность. На рис. 1, а и б шар находится в положении равновесия. При отклонении от этого положения в любую сторону в первом случае (рис. 1,а) шар не может вернуться в исходное положение (неустойчивое равновесие), а во втором (рис. 1,б) – возвращается (устойчивое равновесие). Если опорная поверхность представляет собой горизонтальную плоскость, то шар движется по ней до тех пор, пока действует движущая сила F_д и после ее исчезновения останавливается в любой точке на плоскости (безразличное равновесие). Такая система иногда называется нейтральной (рис. 1,в).

Рис. 1. Физическая система шар – опорная поверхность

Говорят, что система устойчива в малом, если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы. Если границы устойчивости определены, т.е. границы области начальных отклонений, при которых система возвращается в состояние равновесия, известны (рис. 1,г), и выяснено, что реальные начальные отклонения принадлежат этой области, то система устойчива в большом. Когда система возвращается в состояние равновесия при любых начальных отклонениях, ее называют устойчивой в целом, т. е. в малом и большом.

Переходные процессы в АСУ.

В любой АСУ в результате воздействия возмущающих сил, с одной стороны, и восстанавливающего действия управляющего устройства, с другой, возникает переходный процесс: переход АСУ из одного состояния в другое. Рассмотрим различные типы переходного процесса.

Пусть АСУ описывается дифференциальным уравнением вида

(1)

характеристическое уравнение, которого

имеет корни

Решение ДУ описывает переходной процесс y(t) характер которого определяется коэффициентом x. Возможное расположение корней характеристического уравнения на комплексной плоскости р при различных значениях x показано на рис. 2. Рассмотрим переходные процессы, соответствующие различным значениям x.

Рис. 2. Расположение корней характеристического уравнения

x<-1. Переходная функция h(t) при подаче на вход единичного ступенчатого сигнала имеет вид: , при этом корни характеристического уравнения вещественные положительные (p_1,2 >0) и, следовательно, .В данном случае система не может восстановить равновесное состояние, значение управляемой координаты все больше отклоняется от заданного. Такой переходный процесс называется расходящимся монотонным (апериодическим) (рис. 3,а), а система неустойчивой (идет процесс накопления энергии из внешней среды).

Рис. 3. Виды переходного процесса

-1<x<0. При этом , а переходная функция имеет вид:

где , .

Характеристики системы те же, что и в предыдущем случае, но переходный процесс колебательный (рис. 3,б).

0<x<1. Переходная функция h(t) та же, что и в случае II, но при . При этом система возвращается в равновесное состояние, а значение управляемой координаты приближается к заданному. Такой переходный процесс называется сходящимся колебательным, а система устойчивой (происходит отдача энергии во внешнюю среду) (рис. 3,в).

x>1. Переходная функция h(t) имеет тот же вид, что и в случае I, но . Характеристика системы та же, что и в III случае, но переходный процесс монотонный (апериодический) (рис. 3,в). На этом же рисунке показана переходная функция при x=1, .

x=0. , , .

В системе устанавливается периодическое движение, процесс называется колебательным незатухающим, система находится на границе устойчивости (рис.3,д). Она является замкнутой (консервативной), автономной от внешней среды.

Все рассмотренные колебания (И, III и V случаи) относятся к классу свободных, их параметры A и jзависят от начальных условий, т. е. от привнесенной энергии. Для случаев II и III функция , где Т- период колебаний, и, следовательно, эти колебания непериодические. Периодические колебания наблюдаются только в случае V.

Сопоставление корней характеристического уравнения на комплексной плоскости р с соответствующими переходными процессами (рис. 3) показывает, что линейная система восстанавливает равновесное состояние только тогда, когда корни характеристического уравнения расположены слева от мнимой оси.

В общем случае условие устойчивости АСУ имеет вид

где у(0) – начальное значение управляемой величины;

– установившееся отклонение управляемой величины или статическая ошибка (в случае астатической системы e = 0).

Реальные системы всегда нелинейны, однако, если для анализа поведения системы можно произвести линеаризацию уравнений, то о ее устойчивости можно судить исходя из первого метода А.М. Ляпунова:

- Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то реальная система будет устойчива в малом.

- Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то реальная система всегда неустойчива.

- Если характеристическое уравнение линеаризованной системы имеет хотя бы один нулевой корень или пару чисто мнимых корней, то поведение реальной системы не может определяться ее линеаризованным уравнением. В этом случае отброшенные при линеаризации уравнения члены высшего порядка малости определяют поведение системы и могут превратить ее как в устойчивую, так и в неустойчивую.

Таким образом, анализ устойчивости линеаризованной системы сводится к нахождению расположения корней на комплексной плоскости, которое однозначно определяется коэффициентами характеристического уравнения. Однако не всегда можно вычислить корни характеристического уравнения в аналитическом виде. В соответствии с теоремой Абеля, корни уравнения выше четвертого порядка в общем случае не могут быть найдены аналитически в принципе. Поэтому желательно иметь такие критерии, с помощью которых можно было судить об устойчивости системы непосредственно по коэффициентам характеристического уравнения, зависящих от параметров систем, и определять влияние изменяемых параметров на расположение корней характеристического уравнения на комплексной плоскости. Эти критерии называют критериями устойчивости и подразделяются на алгебраические и частотные.

Алгебраические критерии устойчивости

Необходимое условие устойчивости. Характеристическое уравнение системы после определения его корней может быть представлено в виде

Если система устойчива и все ее корни имеют отрицательные вещественные части, то после раскрытия скобок в последнем выражении получим характеристическое уравнение системы

в котором все коэффициенты а_i , i=1,2,...n, будут строго больше нуля.

Для устойчивости системы необходимо, но недостаточно, чтобы все коэффициенты ее характеристического уравнения были строго больше нуля.

Понятие недостаточности означает, что если какой-либо коэффициент характеристического уравнения системы меньше нуля или равен нулю, то система неустойчива, но положительность всех коэффициентов еще не означает, что система устойчива. Нужны дополнительные исследования

Критерий устойчивости Гурвица

Пусть дано характеристическое уравнение системы вида

(2)

при а₀ > 0.

Гурвиц предложил алгебраический критерий, который основан на построении специальных определителей характеристического уравнения (2), называемых определителями Гурвица. Они составляются по следующим правилам:

по главной диагонали выписывают все коэффициенты от а₁ до а_n в порядке возрастания индекса;

дополняют столбцы определителя вверх от диагонали коэффициентами с последовательно возрастающими, а вниз – с последовательно убывающими индексами;

на место коэффициентов, индексы которых больше nи меньше 0, ставят нули.

В соответствии с этими правилами, определитель Гурвица n-го порядка для уравнения (2) имеет вид:

(3)

Определители Гурвица более низкого порядка являются диагональными минорами D_n . Например, при n = 3

; ;

Поскольку в последнем столбце определителя D_n стоят нули, за исключением, то

Критерий Гурвица формулируется следующим образом:

для того чтобы АСУ была устойчива необходимо и достаточно, чтобы все определители Гурвица

были положительными, и при этом выполнялось условие

a₀ >0.

Пример. Исследовать устойчивость системы стабилизации угла тангажа самолета и определить критическое значение передаточного числа автопилота по углу тангажа. Система задана структурной схемой.

На схеме обозначено:

k_u - передаточное число (коэффициент передачи) автопилота по углу тангажа;

передаточная функция рулевого привода;

передаточная функция самолета по угловой скорости тангажа w_z ;

k_w _z - передаточное число автопилота по угловой скорости тангажа.

Для передаточной функции разомкнутой системы можно записать

где

Передаточная функция замкнутой системы примет вид

где

Составим определитель Гурвица

Оценим устойчивость системы для следующих значений параметров:

При этих значениях для коэффициентов характеристического уравнения получим

Следовательно, все коэффициенты характеристического уравнения замкнутой системы положительны и

Условия устойчивости выполнены и система при избранных параметрах устойчива.

Определим критическое значение передаточного числа по углу тангажа, для чего приравняем третий диагональный определитель нулю и сделаем преобразования.

Отсюда

В последнем выражении только d₃ и d₄ являются функциями коэффициента k_u и подставив их в него, получим квадратное уравнение относительно этого коэффициента

Решив это уравнение, получим критическое значение передаточного числа по углу тангажа

Система устойчива, если ku<16.56.

Критерий устойчивости Рауса

Этот критерий представляет собой систему неравенств, составленных по особым правилам из коэффициентов характеристического уравнения замкнутой САУ.

Критерий Рауса требует несколько меньшего объема вычислений, чем критерий Гурвица и более удобен для программирования на ЭВМ. Для суждения об устойчивости системы по этому критерию необходимо составить таблицу Рауса.

Таблица Рауса

В первой строке таблицы записывают коэффициенты характеристического уравнения, имеющие четные индексы в порядке их возрастания. Во второй строке таблицы записывают коэффициенты с нечетными индексами в порядке их возрастания. В последующие строки вписывают коэффициенты, определяемые как

Условия устойчивости Рауса: Чтобы САУ была устойчивой необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса имели один и тот же знак, то есть были положительными. Если не все коэффициенты первого столбца таблицы Рауса положительны, то есть САУ неустойчива, число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.

Частотные критерии устойчивости

Принцип аргумента. Частотные критерии устойчивости используются в графоаналитическом виде и отличаются большой наглядностью при проведении расчетов. В основе всех частотных методов лежит принцип аргумента.

Рассмотрим характеристическое уравнение системы

Если l_i , i=1,2,...n- корни этого уравнения, то

Каждому корню на комплексной плоскости соответствует определенная точка, и геометрически на этой плоскости каждый корень можно изобразить в виде вектора с модулем ½l_i ½, проведенного из начала координат (рис.3.4). Сделаем замену s=jwи получим

В соответствием с правилом вычитания векторов получим, что конец каждого элементарного вектора (jw - l_i ) находиться на мнимой оси.

Аргумент вектора D(jw) равен сумме аргументов элементарных векторов

Направление вращения вектора (jw - l_i ) против часовой стрелки при изменении частоты от -¥ до +¥ принято считать положительным, а по часовой стрелке- отрицательным. Предположим, что характеристическое уравнение имеет m корней в правой полуплоскости и n - mкорней в левой полуплоскости. При изменении частоты от -¥ до +¥ каждый вектор (jw - l_i ), начало которого лежит в левой полуплоскости повернется на угол +p , а каждый вектор, начало которого лежит в правой полуплоскости - на угол -p. Изменение аргумента вектора D(jw) при этом будет

(3.14)

Это выражение и определяет принцип аргумента.

Изменение аргумента вектора D(jw) при изменении частоты от -¥ до +¥ равно разности между числом (n-m) корней уравнения D(s)=0, лежащих в левой полуплоскости, и числом m корней этого уравнения, лежащих в правой полуплоскости, умноженной на p .

Критерий устойчивости Михайлова

Пусть дано уравнение замкнутой системы

где – передаточная функция замкнутой системы.

Тогда дифференциальное уравнение системы, преобразованное по Лапласу можно записать в виде:

где – характеристический полином n-ной степени.

В соответствии с основной теоремой алгебры этот полином можно разложить на множители в виде:

(4)

где p₁ , p₂ , …, p_n - корни характеристического уравнения А(р) = 0.

Выражение (5) действительно при любых значениях p, в частности при p=jw. Тогда (5) можно переписать так:

(5)

Выражение (5) называется кривой Михайлова и обычно обозначается D(jw) = A(jw). Каждый сомножитель выражения (5) отображается на комплексной плоскости вектором, конец которого лежит на мнимой оси (рис.4).

В основу критерия Михайлова положен принцип аргумента: произведение комплексных чисел имеет аргумент, равный сумме аргументов всех его сомножителей.

В нашем случае при изменении wот -¥ до + ¥ векторы сомножителей (jw - p_i ), i = 1,n, поворачиваются на угол p (5). Если корни лежат в левой части полуплоскости, то изменение угла будет положительным, если в правой, то отрицательным. Вектор (jw - p_i ) поворачивается против часовой стрелки в левой полуплоскости и по часовой стрелке – в правой.

Запишем выражение (5) в показательной форме. Учтем, что

где ;

Тогда

(6)

Из (5) вытекает, что изменение аргумента вектора Михайлова D(jw) равно сумме изменений аргумента каждого сомножителя выражения (6), т.е.

Если все корни характеристического уравнения расположены слева от мнимой оси (т. е. система устойчива), то изменение аргумента каждого из сомножителей (jw - p_i ) при изменении wот –¥ до + ¥, равно +p, а изменение аргумента произведения всех сомножителей DargD(jw) = + pn.

Если хотя бы один корень будет расположен в правой полуплоскости (система неустойчива), то изменение аргумента вектора Михайлова DargD(jw) = + p(n – 2).

Заметим, что при изменении wот –¥ до + ¥ кривая Михайлова симметрична относительно оси абсцисс, что позволяет ограничиться изучением кривой в диапазоне изменения wот 0 до + ¥. Тогда условие устойчивости системы по Михайлову можно записать в виде

(7)

Годографы кривой Михайлова при изменении wот 0 до + ¥ для устойчивых систем при различных значениях nприведены на рис. 5.

В соответствии с (7) критерий Михайлова формулируется следующим образом: для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при изменении wот 0 до + ¥ вектор Михайлова D(jw) повернулся на угол .

Рассматривая расположение D(jw) на комплексной плоскости (рис.4), условие устойчивости можно сформулировать иначе: чтобы система была устойчива, необходимо и достаточно, чтобы годограф вектора D(jw) прошел на комплексной плоскости последовательно nквадрантов в положительном направлении (против часовой стрелки), не проходя через начало координат. Если годограф проходит через начало координат, то система находится на границе устойчивости. Расположение годографа на комплексной плоскости для различных систем иллюстрируется рис. 6.

Пример. Используя критерий Михайлова, оценить устойчивость системы стабилизации угла тангажа самолета и определить критическое значение передаточного числа k_u .

Характеристическое уравнение замкнутой системы было получено выше и имеет вид

Сделаем замену s=jwи выделим вещественную и мнимую части

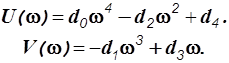
Построенная при заданных ранее параметрах системы кривая Михайлова имеет вид, показанный на рис.3.7.

Кривая начинается на вещественной положительной полуоси, проходит последовательно 4 квадранта и заканчивается в 4-м квадранте. Следовательно, при данных параметрах исследуемая система устойчива.

Для определения критического значения передаточного числа по углу тангажа составим систему уравнений

Из второго уравнения системы определяем частоту и подставив выражение для нее в первое уравнение, после преобразований получим квадратное уравнение относительно искомого значения передаточного числа

Полученное уравнение абсолютно идентично полученному при решении задачи по критерию Гурвица и результат таким же

Построение кривой Михайлова для систем высокого порядка может быть связано с громоздкими вычислениями и графическими построениями. В этих случаях может быть более просто оценить устойчивость по корням уравнений U(w)=0 и V(w)=0. Определим корни этих уравнений и расположим их на числовой оси

Корни вещественные и перемежаются между собой. Система стабилизации угла тангажа устойчива.

Критерий устойчивости Найквиста

Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по виду АФЧХ разомкнутой системы.

Пусть передаточные функции разомкнутой и замкнутой системы имеют вид:

Введем функцию

( 3.17)

где D(s)- характеристический полином замкнутой системы. Перейдя к частотным представлениям, получим

(3.18)

Вектор N(jw) называется вектором Найквиста. Очевидно, что числитель и знаменатель этого вектора имеют один и тот же порядок n. При использовании критерия Найквиста следует различать два случая.

1). Разомкнутая система устойчива и ее характеристическое уравнение A(s)=0 имеет все корни в левой полуплоскости. Тогда при изменении частоты от 0 до ¥

(3.19)

Изменение аргумента вектора D(jw) в общем случае равно

(3.20)

где m- число корней уравнения D(s)=0, лежащих в правой полуплоскости.

Изменение аргумента вектора Найквиста будет

(3.21)

Если замкнутая система устойчива, то m=0 и

Так как при w®¥, W(jw)®0, то N(jw)®1. Рассмотрим рисунок 3.8а, на котором показана кривая Найквиста, которую описывает вектор Найквиста при изменении частоты от 0 до ¥. Нетрудно убедиться, что вектор Найквиста опишет угол, равный нулю только в случае, если его годограф не охватывает начало координат. Перенесем начало координат в точку с координатами (1,j0) (рис.3.9б). Можно убедиться, что изменение аргумента вектора Найквиста будет равно нулю если АФЧХ W(jw) разомкнутой системы не охватывает критическую точку с координатами (-1,j0).

Критерий Найквиста для рассматриваемого случая формулируется следующим образом.

Система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчивой и в замкнутом состоянии, если АФЧХ W ( j w ) разомкнутой системы при изменении частоты от 0 до ¥ не охзватывает критическую точку с координатами (-1, j 0).

Особенности возникают, если разомкнутая система нейтрально-устойчива, т.е.

где полином A₁ (s) имеет все корни в левой полуплоскости. При w=0 АФЧХ разомкнутой системы W(jw)=¥ и проследить поведение кривой АФЧХ в окрестности этой точки невозможно. При изменении частоты от -¥ до +¥ наблюдается движение корней вдоль мнимой оси снизу вверх и при w=0 происходит бесконечный разрыв.

При этом движении обойдем нулевой корень (рис.3.10) по полуокружности бесконечно малого радиуса r так, чтобы этот корень остался слева, т.е. искусственно отнесем его к левой полуплоскости.

При движении по этой полуокружности в положительном направлении независимая переменная изменяется по закону

где фаза j(w) изменяется от -p / 2 до +p / 2. Подставив это выражение в передаточную функцию вместо множителя s в знаменателе, получим

где R®¥при r®0 , а фаза j(w) изменяется от +p / 2 до -p / 2. Следовательно, в окрестности нулевого корня годограф W(jw) представляет собой часть окружности бесконечно большого радиуса, движение по которой происходит при увеличении частоты в отрицательном направлении.

Для оценки устойчивости замкнутой системы, если разомкнутая система нейтрально устойчива, необходимо АФЧХ W ( j w ) разомкнутой системы дополнить дугой бесконечно большого радиуса, начиная с меньших частот, в отрицательном направлении и для полученной замкнутой кривой воспользоваться критерием Найквиста для систем, устойчивых в разомкнутом состоянии.

2).Разомкнутая система неустойчива. В этом случае

где р- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости.

Если замкнутая система устойчива, т.е. m=0, то

( 3.22)

т.е. АФЧХ разомкнутой системы охватывает критическую точку (-1,j0) в положительном направлении ровно p / 2 раз.

Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если АФЧХ W ( j с w ) разомкнутой системы при изменении частоты от 0 до ¥ охватывает критическую точку (-1, j 0) в положительном направлении ровно р/2 раз, где р- число правых полюсов разомкнутой системы.

Определение числа охватов критической точки- непростая задача, особенно в случае систем высокого порядка. Поэтому в практических приложениях нашла применение другая формулировка критерия Найквиста для рассматриваемого случая.

Переход годографа W(jw) через отрезок вещественной полуоси (-¥,-1), т.е. левее критической точки при увеличении частоты сверху вниз считается положительным, а снизу вверх- отрицательным.

Система, неустойчивая в разомкнутом состоянии, будет устойчивой в замкнутом состоянии, если разность между числом положительных и отрицательных переходов АФЧХ разомкнутой системы равна р/2.

(3.23)

где число положительных переходов, число отрицательных переходов.

Например, передаточная функция ракеты-носителя “Авангард” имеет два неустойчивых полюса и ее АФЧХ показана на рис. 3.11.

Очевидно, что для данной ракеты, как объекта управления, а и Замкнутая система будет устойчивой.

Пример. Используя критерий Найквиста оценить устойчивость замкнутой системы стабилизации угла тангажа и определить ее запасы устойчивости.

Передаточная функция разомкнутой системы была получена ранее и имеет вид

Численные значения коэффициентов заданы или вычислены ранее. Сделаем замену s=jw:

После преобразований получим

Изменяя частоту от 0 до ¥ построим кривую АФЧХ - рис. 3.13. Проведя дугу окружности единичного радиуса, определим, что запас устойчивости по фазе g=110⁰ . Для рассматриваемого примера получим, что h =3.3.

Запасы устойчивости

Устойчивость замкнутой САУ зависит от расположения годографа АФЧХ разомкнутой системы относительно критической точки. Чем ближе эта кривая проходит от критической точки, тем ближе замкнутая САУ к границе устойчивости. Для устойчивых систем удаление АФЧХ разомкнутой системы от критической точки принято оценивать запасами устойчивости по фазе и по модулю.

Допустим, что АФЧХ некоторой разомкнутой системы имеет вид, показанный на рис. 3.12.

Угол g , образуемый прямой, проходящей через точку пересечения АФЧХ с окружностью единичного радиуса, что соответствует частоте среза системы, и отрицательной вещественной полуосью называется запасом устойчивости системы по фазе.

(3.24)

Запасом устойчивости по модулю называется величина

(3.25)

где А(w_p )- значение АФЧХ при частоте w=w_p , при которой она пересекает вещественную ось.

Для всех систем должны выполняться требования:

Так как АФЧХ графически строится в определенном масштабе, то для вычисления запаса устойчивости по модулю можно просто измерить длины отрезков, соответствующих единице и ОВ, и разделить результат первого измерения на второй. Если увеличивать коэффициент усиления системы, то точка В будет смещаться влево и при ОВ=-1 коэффициент усиления примет критическое значение. Поэтому запас устойчивости по модулю можно определить и по формуле:

Оценка устойчивости по ЛЧХ

АФЧХ разомкнутой системы подразделяются на два типа:

АФЧХ первого рода, все точки, пересечения которых с вещественной осью расположены справа от критической точки (кривая 1, рис. 3.14);

АФЧХ второго рода, точки, пересечения которых с вещественной осью расположены как справа, так и слева от критической точки (кривая 2, рис. 3.14).

В системах первого рода увеличение коэффициента усиления ведет к сдвигу ветви кривой влево и приближению ее к критической точке. Запасы устойчивости при этом уменьшаются и при k=k_кр система попадает на границу устойчивости. Уменьшение коэффициента усиления стабилизирует систему. В системах 2-го рода переход системы на границу устойчивости может происходить как при увеличении коэффициента усиления, так и при его уменьшении. Из критерия Найквиста следует, что замкнутая система, имеющая в разомкнутом состоянии АФЧХ 1-го рода устойчива, если всем точкам АФЧХ, вплоть до точки пересечения ее с окружностью единичного радиуса (w=w_с ) , соответствуют значения фазы j(w), большие, чем -p, т.е. должно выполняться неравенство w_с <w_p . Этому определению легко дать интерпретацию на языке ЛЧХ.

Для того чтобы система, устойчивая в разомкнутом состоянии и имеющая АФЧХ первого рода, была устойчивой и в замкнутом состоянии, необходимо и достаточно, чтобы при всех частотах, при которых ЛАХ положительна, значения фазовой характеристики были больше, чем - p , т.е. w _с < w _p .

По ЛЧХ легко определяются и запасы устойчивости, причем запас устойчивости по усилению в логарифмическом масштабе должен удовлетворять условию ç Нê>6дб, что соответствует значениям h>2.

Для того, чтобы САУ неустойчивая в разомкнутом состоянии и имеющая АФЧХ 2-го рода, была устойчивой в замкнутом состоянии, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов фазовой характеристикой через линию - p была равна р/2, где р- число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости, при всех частотах когда L ( w )>0.

Необходимо подчеркнуть, что показанные способы оценки устойчивости по ЛЧХ и определения запасов устойчивости справедливы при таком расположении оси ординат относительно фазовой характеристики, когда с началом координат совмещена точка j(w)=-180⁰ .

По ЛЧХ можно определить и критический коэффициент усиления. Для этого необходимо сместить ЛАХ вдоль линий сопряжения параллельно самой себе так, чтобы выполнить условие w_с = w_p и вычислить коэффициент усиления для вновь полученной ЛАХ.

Определение критического коэффициента усиления для статической и астатической систем иллюстрируется рис. 3.17 а и 3.17б.

Некоторые особенности возникают при определении критического коэффициента усиления, если в состав передаточной функции разомкнутой системы входит колебательное звено с малым показателем затухания, причем начало асимптоты, соответствующей этому звену лежит ниже оси частот. В этом случае критический коэффициент усиления определяется в момент касания резонансного пика оси частот.

Пример. Построить ЛЧХ системы стабилизации угла тангажа и оценить ее устойчивость. Определить запасы устойчивости и рассчитать критическое значение передаточного числа по углу тангажа.

Передаточную функцию разомкнутой системы можно привести к виду

Корни характеристического уравнения разомкнутой системы имеют значения:

Следовательно, После преобразований получим

где

Определим частоты сопряжения и разобьем сетку координат.

Построим ЛАХ системы, учитывая, что коэффициент усиления разомкнутой системы равен Так как относительный показатель затухания мал, то необходимо полученную ЛАХ уточнить в окрестности частоты сопряжения w₀₃ .

Это можно сделать как по специальным графикам, так и расчетным путем по известной амплитудной частотной характеристике. АЧХ данной системы определяется выражением

Подставив несколько значений частоты в окрестности частоты сопряжения w₀₃ , получим значения АЧХ, рассчитаем значения ЛЧХ и построим уточняющую кривую. Фазовая частотная характеристика строится как сумма фазовых характеристик типовых звеньев, входящих в состав передаточной функции

где

Из графиков ЛЧХ следует, что w_с <w_p и, следовательно, замкнутая система устойчива. Запас устойчивости по фазе g=108⁰ . Для систем, в которые входят колебательные звенья с малым относительным коэффициентом затухания, запас устойчивости по модулю определяется в точке резонанса и в данном случае он равен » 10дб, что соответствует значению h=3.16. Полученные значения запасов устойчивости незначительно отличаются от значений рассчитанных в соответствии с критериями Гурвица и Михайлова.

В исследуемом случае критический коэффициент усиления определяется при касании L(w_р ) оси частот. Перенесем ЛАХ параллельно самой себе так, чтобы в точке w=w_р она касалась оси частот и продлим первую асимптоту до пересечения с осью частот. В этой точке k=w=7.244, что соответствует значению (k_u )_кр =16.74.

Выделение областей устойчивости

Среди физических параметров, характеризующих САУ, всегда имеется несколько, легко поддающихся изменению и использующихся для определенной настройки системы. При конструировании системы весьма важно знать диапазоны значений изменяемых параметров, допустимые с точки зрения сохранения устойчивости САУ. Об этих диапазонах можно судить, если в пространстве изменяемых параметров построить область устойчивости, т.е. выделить область значений параметров, при которых система сохраняет устойчивость.

Область устойчивости в теории автоматического управления принято называть D – областью, а представление области параметров в виде областей устойчивости и неустойчивости называют D – разбиением.

Построение области устойчивости по алгебраическим критериям

Допустим, что коэффициенты характеристического уравнения

зависят от двух изменяемых параметров m и l. Для построения области устойчивости прежде всего нужно, в соответствии с необходимым условием устойчивости, выделить область изменяемых параметров при нахождении в которой, коэффициенты характеристического уравнения положительны. Это можно сделать, решив систему уравнений

(3.26)

Для построения границы положительности коэффициентов а_i необходимо из решений уравнений (3.26) выбрать те, которые обеспечивают положительность всех коэффициентов. Из всех границ положительности только две одновременно могут быть и границами устойчивости. Такими являются границы, уравнениями которых являются

(3.27)

Доказано, что если d₀ и d_n приблизятся к нулю, то характеристическое уравнение будет иметь два действительных корня

(3.28)

При дальнейшем уменьшении коэффициенты d₀ и d_n перейдут через ноль, станут отрицательными, а корни (3.28) окажутся положительными. Так как вещественные корни определяют апериодические составляющие решения дифференциального уравнения, то границы (3.27) называют апериодическими границами устойчивости. На самих границах устойчивости корни (3.28) равны соответственно ±¥ и 0. Стороны кривых, d_i (m,l)=0, примыкающие к области положительности соответствующих коэффициентов, штрихуются в сторону положительности. Может случиться так, что какой либо из коэффициентов, d₀ или d_n не зависит от изменяемых параметров. Это означает отсутствие соответствующей апериодической границы устойчивости.

Колебательной границей устойчивости называется кривая в плоскости изменяемых параметров, при переходе через которую пара комплексно – сопряженных корней изменяет знак своей вещественной части на обратный. Доказано, что колебательная граница устойчивости определяется выражением

(3.29)

В этом выражении D_n _-1 – (n-1) – й определитель Гурвица. Колебательная граница устойчивости штрихуется в сторону положительности D_n _-1 .

Пример. Построить область устойчивости в плоскости параметров k_u и k_w _z системы стабилизации угла тангажа.

Характеристическое уравнение замкнутой системы имеет вид

Исследуем неравенства d₂ >0, d₃ >0, d₄ >0 . Из первого неравенства следует, что для положительности коэффициента d₂ необходимо, чтобы выполнялось условие

Неравенство d₄ >0 определяет, что для положительности этого коэффициента необходимо, чтобы k_u >0. Для выполнения неравенства d₃ >0 требуется, чтобы

При любых значениях передаточного числа по углу больших нуля, правая часть последнего выражения по модулю будет больше единицы. Таким образом, границами положительности коэффициентов будут

От изменяемых параметров зависит коэффициент d_n =d₄ и не зависит коэффициент d₀ . Поэтому уравнение k_u =0 одновременно является и апериодической границей устойчивости.

Составив определитель Гурвица, для его D_n _-1 минора получим

Подставим в это выражение значения коэффициентов d₂ , d₃ , d₄ , как функций параметров k_u и k_w , после преобразований получим квадратное уравнение, определяющее передаточное число по угловой скорости как функцию от передаточного числа по углу тангажа

По этому выражению строится колебательная граница устойчивости. График деления области исследуемых параметров на области устойчивости и неустойчивости показан на рис. 3.19.

Граница колебательной неустойчивости штрихуется в сторону положительности D_n _-1 - го определителя Гурвица, а прямая k_w _z =0 в сторону положительности этого коэффициента.

Для проверки полученных результатов выберем какие – либо значения параметров внутри заштрихованной области, например k_u =5, k_w _z =0.6, вычислим значения коэффициентов характеристического уравнения и оценим устойчивость замкнутой системы по критерию Гурвица.

Получим, что при выбранных значениях передаточных чисел система устойчива. Это означает, что и вся область, внутрь которой обращены штрихи, является областью устойчивости.

D – разбиение в плоскости одного параметра

Пусть нас интересует влияние какого – либо одного параметра на устойчивость САУ и этот параметр входит в характеристическое уравнение линейно, так что это уравнение можно представить в виде

(3.30)

Сделав замену s= jw , получим

(3.31)

Задавая значения частоты от -¥ до +¥, можно построить кривую m(w), отображающую мнимую ось плоскости корней на плоскость m. Эта граница D – разбиения симметрична относительно вещественной оси. Поэтому вычисления можно вести в диапазоне частот от 0 до +¥, а затем дополнить полученную кривую ее зеркальным отображением на диапазон частот от -¥ до нуля. При движении по мнимой оси от -¥ до +¥ на плоскости корней область устойчивости остается слева. Поэтому при движении по кривой D – разбиения в сторону увеличения частоты ее штрихуют слева. Область, внутрь которой обращены штрихи, является предполагаемой областью устойчивости. Для окончательного решения, необходимо взять какое – либо вещественное значение параметра m в исследуемой области и воспользоваться каким – либо критерием устойчивости. Если при избранном значении параметра система устойчива, то рассматриваемая область является областью устойчивости.

Пример. Построить область устойчивости системы стабилизации угла тангажа в плоскости передаточного числа k_u .

Характеристическое уравнение исследуемой системы можно записать в виде

где

В полученных выражения сделаем замену s=jw и получим

В этих выражениях

Построенная по этим выражениям кривая D – разбиения показана на рис. 3.20.

Так как необходимым условием устойчивости рассматриваемой системы является k_u >0, то мнимая ось также является границей устойчивости и штрихуется в сторону положительности k_u . Значение этого коэффициента, равное 5, находится внутри заштрихованной области и мы знаем, что при этом значении система устойчива. Значит и весь отрезок вещественной оси, расположенный внутри заштрихованной области, дает значения передаточного числа по углу, при которых система устойчива. Можно показать, что окончание этого отрезка находиться в точке, равной критическому значению коэффициента k_u =16.56.

D – разбиение в плоскости двух параметров

Пусть коэффициенты характеристического уравнения линейно зависят от двух параметров m и l так, что его можно записать в виде

(3.32)

После замены s=jwполучим

Так как равенство нулю всего преобразованного характеристического уравнения может выполняться только, если одновременно равны нулю его вещественная и мнимая части, то получим систему уравнений относительно изменяемых параметров

(3.33)

Разрешив систему (3.33) относительно m и l, получим

где

Задавая значения частоты от -¥ до +¥, определим совокупность точек на плоскости m - l, образующих кривую D – разбиения. Функции m(w) и l(w) являются четными, и поэтому, при изменении частоты в указанных выше пределах, кривая D – разбиения пробегается дважды. При построении кривой D – разбиения в плоскости двух параметров необходимо руководствоваться следующими правилами [8,14]:

1) если в системе (3.33) первое уравнение получено из вещественных частей, а второе – из мнимых частей функций P(jw), Q(jw) и S(jw) и если параметр m по написанию стоит первым, а l - вторым, то система координат должна быть правой, т.е. ось m является осью абсцисс с отсчетом положительных значений вправо, а ось l - осью ординат с отсчетом положительных значений вверх;

2)двигаясь по кривой D – разбиения при изменении частоты в сторону увеличения, ее штрихуют слева, если D(w)>0, и справа, если D(w)<0; в результате кривая штрихуется дважды с одной стороны, так как на концах кривой при w=0 и w=¥ знак главного определителя D(w) изменяется.

Может быть случай, когда при w=w^* ¹ 0,¥ одновременно D(w^* )= =Dm(w^* )=Dl(w^* )=0. Тогда система (3.33) становится линейно – зависимой и ее уравнения отличаются друг от друга только на постоянный множитель. В этом случае эта система сводится к одному уравнению, определяющему на плоскости m - l прямую линию, которая называется особой прямой.

Если особая прямая пересекает кривую D – разбиения в точке w=w^* и в этой точке определитель D(w) меняет знак, то эта прямая также является границей устойчивости и в указанной точке изменяется направление штриховки кривой и особой прямой. Если при w=w^* изменение знака главного определителя не происходит, то штриховка на особую прямую не наносится. Если свободный член характеристического уравнения d_n =d_n (m,l), то это соответствует существованию особой прямой для w=0 и ее уравнение будет

(3.34)

Уравнение особой прямой для w=¥ определяется выражением

(3.35)

Прямые (3.34) и (3.35) называются концевыми. Они штрихуются одинарной штриховкой, согласованной в точках w=0 и w=¥ с направлением штриховки основной линии. Предполагаемая область устойчивости находится внутри заштрихованного участка и проверяется аналогично предыдущему. Переход через кривую D – разбиения, заштрихованную дважды, соответствует переходу через границу устойчивости двух корней, а переход через особую концевую с одинарной штриховкой – переходу одного корня. Если концевые прямые не имеют общих точек с основной кривой, то штриховка на них наносится в сторону положительности параметров.

Пример. Построить область устойчивости системы стабилизации угла тангажа в плоскости параметров k_u и k_w _z .

Характеристическое уравнение замкнутой системы может быть представлено в виде (3.32), где

После подстановки s=jwи выделения вещественных и мнимых частей, получим

Составив систему уравнений (3.33) и решив ее, получим

Определив корни этих уравнений, можно сделать вывод, что общих корней, кроме нулевого корня, не существует.

Значит особых прямых нет, существует только концевая прямая, соответствующая уравнению d_n =k_c k_u =0. Руководствуясь выше приведенными правилами, построим кривую D – разбиения и заштрихуем ее и концевую прямую. Проверку осуществим в точке k_u =5, k_w _z =0.6.

уже ранее установили, что в этой точке система устойчива, а значит и заштрихованная область является областью устойчивости.

Заключение

Практическая пригодность САУ, определяется ее устойчивостью и приемлемым качеством процесса управления (регулирования). На любую САУ действуют различные внешние возмущения, которые могут нарушать ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.

В простейшем случае, понятие устойчивость системы связана со способностью ее возвращения к исходному состоянию после кратковременного внешнего воздействия. Если система неустойчивая, она не возвращается к состоянию равновесия, из которого по каким-то причинам вышла.

Только устойчивая система автоматического управления может выполнять возложенные на нее функции. Поэтому одной из основных задач САУ является обеспечение ее устойчивости.

Устойчивость считается важнейшим и обязательным понятием, так как только в устойчивой системе могут быть удовлетворены другие требования к качеству.

В своей работе я исследовал устойчивость системы стабилизации угла тангажа самолета и определял критическое значение передаточного числа автопилота по углу тангажа, используя различные критериями устойчивости. А именно:

- Критерием устойчивости Рауса-Гурвица;

- Критерием устойчивости Михайлова;

- Критерием устойчивости Найквиста.

Литература

1) Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002г. – 832с.

2) Харазов В.Г. Интегрированные системы управления технологическими процессами: Справочник. Издательство: ПРОФЕССИЯ, ИЗДАТЕЛЬСТВО, 2009. – 550с.

3) Брюханов В.Н. и др. Теория автоматического управления. – М: Высшая школа, 2000.

4) Ким Д.П., Дмитриева Н.Д. Сборник задач по теории автоматического управления. Линейные системы. ФИЗМАТЛИТ, 2007. – 168 с.

5) Лукас В.А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.

6) В.А. Бесекерского, Е.П. Попов Теория систем автоматического управления-747с.

7) Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 198 – 712 с.

Курсовая работа: Устойчивость систем автоматического управления

Частотные критерии устойчивости

Заключение

Похожие рефераты: