Курсовая работа: Визначення характеристик вала з дисками

Курсова робота: Визначення характеристик вала з дисками

Зміст

Введення

1. Визначення власних частот крутильних коливань вала з дисками

1.1 Постановка прямого спектрального завдання Коливання вала з одним диском

1.2 Рішення прямого завдання для вала з n-дисками

1.3 Коливання вала із трьома дисками

1.4 Коливання вала із чотирма дисками

1.5 Застосування методу рішення прямого завдання, програмна реалізація рішення

2. Діагностування характеристик вала з дисками по спектрі частот коливань

2.1 Постановка зворотної спектральної завдань

2.2 Діагностування коефіцієнтів твердості ділянок вала між дисками

2.3 Діагностування моментів інерції мас дисків

2.4 Застосування методу рішення зворотного завдання, програмна реалізація рішення

Висновок

Список літератури

Введення

Діагностування характеристик вала з дисками по спектрі частот його коливань є актуальною у зв'язку з необхідністю рішень завдань акустичної діагностики технічних конструкцій і віброзахисту механічних систем.

Завдання ж акустичної діагностики важливі у зв'язку зі збільшенням техногенних катастроф і небезпеками, пов'язаними зі зношеністю основних фондів. Зі збільшенням розмірів і швидкостей сучасних машин в інженерних розрахунках стає усе більше й більше важливим рішення завдань, пов'язаних з коливаннями. Добре відомо, що тільки на основі теорії коливань можуть бути повністю з'ясовані такі практично важливі проблеми, як зрівноважування машин, крутильні коливання валів і зубчастих передач, коливання турбінних лопаток і турбінних дисків, прецесія обертових валів, коливання рейкового шляху й мостів під дією вантажів, що рухаються, коливання фундаментів. Лише за допомогою цієї теорії можна встановити найбільш удалі пропорції конструкцій, що відсувають експлуатаційні умови роботи машин можливо далі від умов виникнення більших коливань.

Інше важливе використання завдань визначення характеристик вала з дисками - віброзахист механічних систем, у яких є вали з дисками. Коливання валів приводять часом до деренчання, зайвому шуму. Зв'язано це з тим, що спектри частот коливань іноді перебувають у небезпечному для здоров'я людини діапазоні. Для зміни частот коливань вала не завжди буває доцільно міняти його довжину або ж прикріплювати зосереджені маси. Тому виникає завдання визначення таких твердостей ділянок валів на крутінні або моментів інерції мас дисків, які забезпечували б потрібний діапазон частот коливань вала. Ця проблема пов'язана з науковими завданнями шумозаглушення, акустичної діагностики й теорії зворотних завдань математичної фізики. Рішенню подібної проблеми й присвячена представлена робота. Пряме завдання по визначенню спектра частот коливань вала з дисками розглянуті в підручниках по теорії коливань. Але зворотне завдання по діагностуванню характеристик вала з дисками не досліджені.

Завданням технічної діагностики присвячена велика кількість робіт. Процеси, що протікають у механізмах і двигунах, є джерелом шуму. Наука, що вивчає можливості розпізнавання характеристик елементів механічної системи по його шуму, зветься виброакустичною діагностикою. Завдання діагностики можуть бути різними. У роботі Кузьміна Р.В. [14], наприклад, розглядалися завдання виявлення дефектів у суднових механізмах по шуму, викликуваному пружними коливаннями від зіткнення сполучених деталей. Аналогічні завдання виявлення несправностей вирішені в роботах Бухтиярова И.Д., Алилуєва В.А.[9], але вже для пошуку дефектів в автотракторних двигунах. У працях Биргера И.А. [8], Артоболевського І.И., Бобровницкого Ю.И., Генкина М.Д.[1], Павлова Б.В.[16] також вирішувалися завдання акустичної діагностики механізмів.

Велика кількість робіт з діагностики присвячено не тільки виявленню стану двигуна по його шуму, але й також питанням шумозаглушення, це роботи, наприклад, Зинченко В. И.[12], Лапіна А.Д. [15]. Близькі проблемам діагностики завдання виникали також і в інших роботах. Так у роботі Kас М.[26] ставилося питання: чи можна по звучанню барабана встановити його форму? Стаття W. U. Qunli і F. Fricke [27] присвячена визначенню розміру об'єкта і його положення в камері по зрушеннях власних частот його коливань, а стаття Васильєва Н.А., Дворникова С.І. [10] - способу виявлення шпал, що втратили щільний контакт із баластом насипу, за допомогою ударного порушення коливань і аналізу акустичних сигналів. У роботах Frikha S., Coffignal G., Trolle J.L.[24, 25] досліджувалися умови на вході й виході вихлопних труб і трубопровідних систем, у працях Аксьонова А.Л., Тукмакова И.Б. [21,22] - завдання ідентифікації об'єктів по їхньому акустичному відгуку. Завдання акустичної діагностики закріплень по одному спектрі для струн, мембран, стрижнів, пластин розглядалися А.М. Ахтямовим [2-6, 23], а Г.Ф. Сафиной [18-20] - для порожніх труб і трубопроводів з рідиною. На відміну від всіх робіт з діагностики, у представленій роботі відшукуються не форма області, розміри об'єкта, його місце розташування або стан, а коефіцієнти пружних закріплень і моменти інерції мас дисків. Таке завдання для вала з дисками ставляться вперше.

Метою наукової праці є знаходження власних частот крутильних коливань вала з дисками й діагностування по спектрі частот моментів інерції мас дисків і твердості ділянок вала на крутінні. У відповідність із метою були поставлені й вирішені завдання:

дослідження завдання визначення власних частот крутильних коливань вала з різною кількістю дисків (із двома, трьома, чотирма, n- дисками) по відомих моментах інерції мас дисків і твердості ділянок вала на крутінні;

дослідження завдання діагностування моментів інерції мас дисків по власних частотах коливань вала;

дослідження завдання діагностування твердості ділянок вала на крутінні по власних частотах коливань вала.

розробка математичних моделей рішення поставлених завдань; аналітичне й чисельне дослідження моделей.

Наукова новизна отриманих результатів полягає в тому, що вперше досліджені й вирішені завдання діагностування по спектрі частот коливань вала з дисками таких характеристик, як моменти інерції мас дисків і твердості ділянок вала на крутінні.

Практична значимість результатів полягає в тому, що розроблені методи рішення завдань ставляться до акустичної діагностики недоступних для візуального огляду елементів механічних систем і технічних конструкцій, у яких є вали з дисками. Оскільки зміни величин коефіцієнтів твердості ділянок вала або моментів інерції дисків можуть характеризувати ступінь зношеності, несправності й т.п., те отримані результати за рішенням зворотних завдань застосовні для діагностування зазначених характеристик вала з дисками без дорогого розбирання всієї механічної системи

Отримані результати можна також використовувати для збереження заданого діапазону частот коливань вала з дисками. У роботі запропоноване збереження діапазону частот за допомогою змін значень моментів інерції мас дисків або коефіцієнтів твердості ділянок вала на крутінні.

Перший розділ роботи присвячений прямому завданню визначення власних частот крутильних коливань вала з дисками по відомих моментах інерції мас дисків і коефіцієнтів твердості ділянок вала на крутінні. Рішення зводиться до системи n - звичайних рівнянь щодо невідомих власних частот крутильних коливань вала. Із цієї системи отримані частотні рівняння для вала із двома, трьома, чотирма дисками. Зроблено відповідні обчислення, складена програма в математичному пакеті Maple.

У другому розділі наведена постановка зворотного спектрального завдання діагностування характеристик вала з дисками по спектрі частот його коливань. Алгоритм діагностування зведений до рішення систем алгебраїчних рівнянь. Розглянуто діагностування моментів інерції мас дисків по власних частотах коливань вала. Завдання вирішене для вала із трьома, чотирма дисками. У цій же главі діагностуються коефіцієнти твердостей ділянок вала при крутінні між дисками. Для рішення зворотних завдань складені програми в математичному пакеті Maple.

На закінчення роботи зроблені виводи за отриманими результатами рішень прямих і зворотних завдань. Проаналізовано практичну значимість отриманих результатів діагностування.

1. Визначення власних частот крутильних коливань вала з дисками

1.1 Постановка прямого спектрального завдання Коливання вала з одним диском

Пряме завдання: Визначити власні частоти крутильних коливань вала, що складає з п (п =1, 2, 3, 4,...) дисків з відомими моментами інерції мас, укріплених на сталевому валу з відомими твердостями.

Розгляд крутильних коливань почнемо з найпростішого випадку круглого вала постійного перетину, що несе на вільному кінці диск, верхній кінець вала забитий (мал. 1).

Нехай у силу яких-небудь причин диск (маховик), зображений на кресленні, одержав у площині обертання, який є площина, перпендикулярна кресленню, переміщення на кут . На той же кут повернеться й жорстко пов'язаний з диском вал. Представлена самої собі така система буде робити коливання, підтримувані силами пружності вала, що полягають у повторних обертових рухах.

Мал. 1 Вал з одним диском

Відомо, що коливання, що представляють ряд повторних обертальних переміщень від положення рівноваги, називаються коливаннями крутіння або, крутильними.Установимо величину навантаження, що викликає одиницю статичної деформації вала. Статичною деформацією вала в цьому випадку буде кут закручування, обумовлений по відомій формулі опору матеріалів

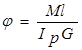(1.0)

де М - крутний момент;

-довжина вала;

I_{p -} полярний момент інерції вала;

— модуль дотичної пружності.

Навантаженням, що викликає одиницю статичної деформації, тобто кут закручування, рівний одному радіану, буде з формули (1.0) деякий момент; будемо позначати цей момент буквою k і називати твердістю вала на крутіння.

(1.1)

Якщо вал повернеться на кут , то в ньому виникне момент внутрішніх сил пружності, рівний

(1.1а)

Цей момент за принципом Даламбера повинен бути дорівнює моменту сил інерції диска. (Масою вала ми зневажаємо.) Якщо кутове прискорення позначити

і момент інерції диска щодо поздовжньої вертикальної осі вала

,

де Q - вага диска, D-Його діаметр, g- прискорення сили ваги.

У випадку кільцевого диска (шків, колесо)

те момент сил інерції диска буде дорівнює

(1.1b)

Рівняння руху тоді буде мати вигляд:

Звільняючись від коефіцієнта при диференціалі

і позначаючи

(1.2)

одержимо

(1.3)

Рішення цього рівняння може бути представлене у вигляді:

(1.4)

за аналогією одержуємо:

(1.5)

Очевидно, що ми в цьому випадку одержали просте гармонійне коливання.

Кругова частота цього коливання (рівна кутової швидкості) буде

(1.2а)

і період коливання

(1.6)

Формули (1.2а) і (1.6) справедливі в остаточному виді тільки для суцільного диска постійної товщини, у випадку якого-небудь іншого диска частоту й період варто визначати по формулах:

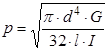(1.2)

. (1. )

Обчислюємо в них відповідний момент інерції диска по формулах теоретичної механіки.

Розглянемо тепер випадок коливань вала з диском (мал. 1), з урахуванням маси вала. Крім полярного моменту інерції перетину вала, скористаємося вираженням для екваторіального моменту інерції (маси) вала, відомим з теоретичної механіки.

де I₀ — екваторіальний момент інерції,

W - власна вага вала,

r - радіус вала.

Якщо вага одиниці об'єму вала, тобто його питома вага, позначити, то I₀ для круглого вала можна представити у вигляді:

(2.b)

і екваторіальний момент одиниці довжини вала

(2.c)

Для рішення вартої перед нами завдання зручніше за все скористатися рівняннями руху Лагранжа, тому, насамперед, знайдемо кінетичну й потенційну енергію нашої системи.

Кінетична енергія системи буде складатися з кінетичної енергії диска й кінетичної енергії вала. Кінетична енергія диска

Для знаходження кінетичної Енергії вала спочатку знайдемо кінетичну енергію елемента його dc. Якщо кут закручування в перетині з позначити, то кінетична енергія елемента dc буде

тому що якщо — момент інерції одиниці довжини, то I₀ 'dc момент інерції елемента dc.

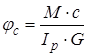Знайдемо залежність між кутом закручування в перетині з-с-і в перетині

і

Звідки

Підставляючи отримане значення у вираження кінетичної енергії елемента dc, одержимо:

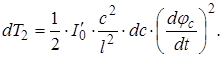
Повну кінетичну енергію вала знайдемо інтегруванням:

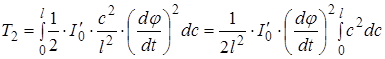
Або заміняючи на основі формул (b) і (с) на одержимо остаточно:

Повна кінетична енергія системи

коливання вад диск спектральний

Потенційна енергія системи

де M - крутний момент, прикладений до вала. Для крутний моменту маємо вираження:

(1.1а)

Підставляючи це значення у вираження для потенційної енергії, одержимо:

(2.1)

Тепер можемо скласти диференціальне рівняння коливального руху нашого вала, що зручніше за все зробити у формі Лагранжа. У нашім випадку за узагальнену координату необхідно прийняти кут закручування , тоді рівняння Лагранжа прийме вид:

у цьому рівнянні

Знаходимо значення часток похідних, що входять у це рівняння:

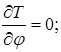
Підставимо отримані значення в рівняння Лагранжа

Звільняючись від коефіцієнта при диференціалі й думаючи

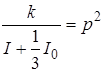
одержимо

відоме нам рівняння (1.3), рішення якого

.

Частота цього коливального руху

І період

(2.2)

Отже, для обліку власної маси вала, що має коливання, необхідно до моменту інерції диска, що сидить на валу, додати одну третину моменту інерції вала.

Розглянемо випадок вала, що лежить у двох підшипниках (вплив яких на коливання ми, у виді незначності, не враховуємо), що несе на кінцях два диски (маховика, шківа й т.д.) (малюнок 2).

Мал. 2 Вал із двома дисками

Вал буде випробовувати крутильні коливання тільки за умови обертання дисків у різні сторони, що може бути досягнуто додатком до дисків двох рівних і прямо протилежних моментів. Після видалення моментів у системі, що складається з вала й двох; дисків, виникнуть крутильні коливання. У кожний момент часу кутові швидкості дисків будуть спрямовані протилежно один одному. Лівий диск і деяка частина вала, що примикає до нього, буде обертатися, допустимо, за годинниковою стрілкою, а правий диск і його частина вала проти годинникової стрілки. У такому випадку на валу обов'язково повинне бути перетин, у якому немає ніякого обертання. Вал можна розглядати як жорстко забитий у перетині, причому, у нашім прикладі, ліва частина обертається по вартовий і права проти годинникової стрілки.

Перетин, що залишається під час коливання системи нерухливим, називається вузлом коливання.

Періоди коливань однакові для обох частин того самого вала можуть бути знайдені з формули (1.6),

(2.3)

Завдання, таким чином, зводиться до визначення розташування вузла коливань по довжині вала, тобто довжин l₁ і l₂ . Рівняння (2.3) показує, що вузол коливання ділить вал назад пропорційно моментам інерції дисків, тобто

або

Друге рівняння для визначення положення вузла коливань буде

З рівнянь одержимо

і

і період коливання прийме вид

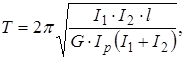(2.4)

частота коливань буде:

(2.5)

Для вивчення випадків коливання валів з більшим числом дисків, чим два, зручніше на відміну від вищенаведених випадків вала з однієї й двома масами знайти рівняння руху вала з довільною кількістю мас і потім застосовувати його для будь-якої частки випадку.

1.2 Рішення прямого завдання для вала з n-дисками

Розглянемо вал, що несе дисків. Нехай кути закручування вала в місцях насадки диска будуть відповідно Твердості I, II,..., n-1 ділянок вала, тобто на основі позначення (1.1) моменти, які можуть викликати кут закручування даної ділянки рівний одному радіану, позначимо: k₁ , k_2,…, k_п-1. Моменти інерції дисків як і раніше позначимо I₁ ,I₂ ,..,I_n . Для одержання рівняння коливального руху розглянутої нами системи застосуємо рівняння Лагранжа, при користуванні якими необхідно знати вираження для кінетичної й потенційної енергії системи. Кінетична енергія диска, що має момент інерції I і кут закручування , виражається формулою

Кінетична енергія нашої системи складається із суми кінетичної енергії всіх дисків (кінетичну енергію вала ми отут не враховуємо, уважаючи момент інерції диска більшим у порівнянні з моментом інерції вала).

Кінетична енергія всієї системи

(2.6)

Для знаходження потенційної енергії системи, що є в цьому випадку енергією крутіння, необхідно користуватися формулою

,

де М - крутний момент, що діє на даній ділянці, а - кут закручування тієї ж ділянки. Знайдемо крутний момент і кут закручування для першої ділянки нашої системи.

Якщо в місці насадки першого диска кут закручування , а в місці насадки другого диска — ₂ , то кут закручування на ділянці вала між дисками буде:

(2.7)

Для того щоб викликати кут закручування першої ділянки вала завбільшки I радіан, необхідно прикласти крутний момент величини k₁ , якщо ж, як у нашім випадку кут закручування має ₁ -₂ радіан, то на валу діє крутний момент величини

У нашім випадку кути закручування для ділянок вала будуть:

(2.8)

і крутний моменти:

(2.9)

Тепер можемо скласти вираження для потенційної енергії системи, підсумовуючи потенційну енергію ділянок.

(2.10)

(тому що те, підставляючи значення ₁ з (2.8) і M₁ з (2.9) і аналогічно для інших ділянок одержимо формулу (2.10)).

У цьому випадку система має п ступенів волі, чому відповідає п узагальнених координат. Узагальненими координатами є кути закручування вала в місцях насадки дисків. Рівняння Лагранжа, мабуть, прийде скласти по числу ступенів волі, тобто також п. Для користування рівнянням Лагранжа у вигляді

(2.11)

необхідно знайти частки похідні від кінетичної й потенційної енергії системи, по узагальнених координатах і частки похідні від кінетичної енергії по диференціалах узагальнених координат:

Диференціюючи рівняння (2.6) знайдемо:

;

і диференціюючи рівняння (2.10)

; ;

;……;

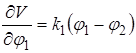Диференціюючи рівняння (2.6) по одержимо:

Отримані рівняння необхідно диференціювати за часом

Маючи у своєму розпорядженні знайденими вище величини, можемо скласти систему диференціальних рівнянь руху розглянутої системи.

(2.12)

Для рішення отриманої системи диференціальних рівнянь думаємо, що кожний коливальний рух системи (їх буде стільки ж, скільки й ступенів волі, тобто п) буде простим гармонійним. Приватні рішення системи (2.12), можна представити у вигляді:

. (2.13)

У цих рівняннях як і раніше М амплітуда коливання, і р частота. Знаходимо другу похідну від за часом:

.

Аналогічно,

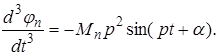
Підставляючи значення й у рівняння системи (2.12), одержимо систему звичайних рівнянь із багатьма невідомими для визначення частоти коливання р.

Скорочуючи в даних рівняннях на одержимо остаточно

(2.14)

Послідовно крім невідомого , одержимо рівняння для визначення частоти р. Рівняння для визначення частоти власних коливань, отримане в результаті виключення з рівнянь (2.14), називається характеристичним. Рівняння (2.14) можуть бути застосовані для визначення числа власних крутильних коливань системи з довільним числом дисків. У тих випадках, що коли вийшло характеристичне рівняння має високий ступінь відносно р² (що буває при системі з багатьма дисками), воно може бути вирішене графічно або яким-небудь наближеним методом.

1.3 Коливання вала із трьома дисками

Розглянемо коливання вала із трьома дисками (мал. 3). Тут I₁ , I₂ ,I₃ моменти інерції дисків, k₁ і k₂ твердості ділянок вала на крутінні, за аналогією з формулою (1.1) рівні:

і

Мал. 3 Вал із трьома дисками

Якщо амплітуди коливань дисків позначити то рівняння (2.14) для даного випадку приймуть вид:

. (2.15)

Складаючи ці рівняння одержимо

звідки

,

.

Квадрат частоти коливань р² нулю дорівнює бути не може, тому:

. (2.16)

Виразимо М₁ і М₃ через М₂ , що може бути зроблене з рівняння (2.15)

Підставимо отримані значення М₁ і М₃ у рівняння (2.16)

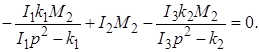
Скорочуючи на М₂ і приводячи до загального знаменника одержимо:

Робимо угруповання

Звільняючись від коефіцієнта при р⁴ і роблячи перетворення в круглих дужках одержимо остаточно:

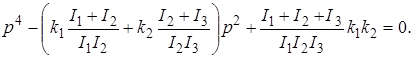(2.17)

Одержали біквадратне рівняння для визначення частоти. Корінь цього рівняння й відповідають двом головним видам коливань: нижчому, що має один вузол коливань (два сусідніх диски обертаються в одну сторону), і вищому, що має два вузли коливання (крайні диски обертаються в одну сторону).

1.4 Коливання вала із чотирма дисками

Розглянемо крутильні коливання вала із чотирма дисками. Нехай I₁ , I₂ ,I₃ ,,I₄ — моменти інерції дисків, k₁ ,k₂ ,,k₃ — твердості ділянок вала на основі формули (1.1) рівні:

; ;

Амплітуди коливань дисків позначимо як і раніше: М₁ ,М₂ ,,М₃ ,,М₄ .

Тоді рівняння (2.14) для даного випадку приймуть вид:

(2.18)

Складаючи отримані рівняння знайдемо:

З огляду на подібні доданки, одержимо

Квадрат частоти - р² нулю не дорівнює, отже:

(2.19)

Виразимо М₁ ,М₃ і М₄ через М₂ , що може бути зроблене за допомогою рівнянь (2.18).

За допомогою першого рівняння з (2.18) знайдемо:

(2.а)

Із другого рівняння нижченаведеними діями знайдемо:

,

або підставляючи замість М₁ його значення з (2.а)

,

,

,

. (2.d)

З рівняння четвертого знайдемо

Підставивши значення М₃ з (2.d)

(2.е)

Знайдені значення М₁ , М₃ і М₄ підставимо в рівняння (2.19)

Скорочуємо отримане рівняння на М₂ і приводимо ліву частину рівняння до загального знаменника, що і відкидаємо. Загальним знаменником, мабуть, буде вираження:

Робимо угруповання

Звільняючись від коефіцієнта при р⁶ , приведемо наше рівняння до виду:

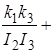
(2.20)

Таким чином, були розглянуті формули для знаходження власних частот коливання вала з різною кількістю дисків. Визначивши частоти, можна розрахувати критичні швидкості прямих валів, а, знаючи ці швидкості можна попередити надходження різного роду порушення нормального ходу машини, які звичайно виражаються в появі биттів вала або вібрації всієї установки в цілому.

1.5 Застосування методу рішення прямого завдання, програмна реалізація рішення

Розглянемо застосування методу рішення прямого завдання по визначенню власних частот крутильних коливань вала з дисками на конкретних прикладах.

Приклад 1

Визначити власні частоти системи, що складає із трьох дисків з моментами інерції мас: , укріплених на сталевому валу з жестокостями й .

При підстановці даних значень у рівняння (2.17) одержуємо біквадратне рівняння:

р⁴ -3.5p² +2.0=0.

Корінь даного рівняння, знайдені в пакеті Maple, мають вигляд:

p₁ =-1.667566013, p₂ =1.667566013, p₃ =-0.8480705122, p₄ =0.8480705122

Але нас цікавлять тільки позитивні величини, тому що частоти негативні значення приймати не можуть.

Приклад 2

Визначити власні частоти системи, що складає із трьох дисків з моментами інерції мас: , укріплених на сталевому валу з жестокостями й .

При даних значеннях фізичних величин рішення рівняння (2.17) має вигляд:

p₁ =-1,370821968, p₂ =-0,7879385321, p₃ =1,370821968, p₄ =0,7879385321

Приклад 3

Визначити власні частоти системи, що складає із чотирьох дисків з моментами інерції мас: , укріплених на сталевому валу з жестокостями , і .

При даних значеннях фізичних величин рішення рівняння (2.20) має вигляд:

p₁ =-2,417091066, p₂ =-1,581138830, p₃ =2,417091066, p₄ =1,581138830

Приведемо програмну реалізацію рішення прямого спектрального завдання, що використовує команди математичного пакета MAPLE

Рішення приклада 1:

> I1:=0.2;

> I2:=0.3;

> I3:=0.1;

> k1:=0.1;

> k2:=0.2;

> y:=p^4-(k1*(I1+I2)/(I1*I2)+k2*(I2+I3)/(I2*I3))*p^2+((I1+I2+I3)/(I1*I2*I3))*k1*k2=0;

Підставимо дані значення в рівняння (2.17)

> y:=p^4-(k1*(I1+I2)/(I1*I2)+k2*(I2+I3)/(I2*I3))*p^2+((I1+I2+I3)/(I1*I2*I3))*k1*k2=0;

> solve(y,p);

Рішення приклада 3:

> restart;

> i1:=0.2;

> i3:=0.3;

> i2:=0.1;

> i4:=0.2;

> k1:=0.1;

> k2:=0.2;

> k3:=0.3;

Підставимо дані значення в рівняння (2.20)

> y:=p^6-(k1*(i1+i2)/(i1*i2)+k2*(i2+i3)/(i2*i3)+k3*(i3+i4)/(i3*i4))*p^4+(k1*k2*(i1+i2+i3)/(i1*i2*i3)+k2*k3*(i2+i3+i4)/(i2*i3*i4)+k1*k3*(i1+i3+i4)/(i1*i3*i4))*p^2+k1*k2*k3(i1+i2+i3+i4)/(i1*i2*i3*i4)=0;

> fsolve(y,p);

2. Діагностування характеристик вала з дисками по спектрі частот коливань

2.1 Постановка зворотної спектральної завдань

Поставимо тепер до завдання визначення частот крутильних коливань вала з дисками зворотне спектральне завдання.

Оскільки зміни величин моментів інерції мас дисків і коефіцієнтів твердості ділянок вала на крутінні можуть характеризувати ступінь зношеності дисків, налипання до вала сторонніх предметів і так далі, те зворотне завдання полягає в діагностуванні характеристик вала з дисками по власних частотах коливань вала. Відомо, що зміни зазначених значень характеристик вала проявляються в змінах значень власних частот його коливань, що у свою чергу може привести до непотрібних вібрацій, збільшенню шуму й т.п.

Тому виникає також завдання збереження заданого (безпечного) діапазону частот крутильних коливань вала. Подібну проблему ми пропонуємо вирішити також при розгляді зворотного завдання.

Отже, відомі власні частоти р крутильних коливань вала з дисками. Необхідно визначити характеристики вала з дисками по спектрі частот його коливань. До характеристик ми віднесемо моменти інерції мас дисків і коефіцієнти твердості ділянок вала на крутінні.

Зупинимося на діагностуванні цих характеристик докладніше.

2.2 Діагностування коефіцієнтів твердості ділянок вала між дисками

При дослідженні завдання про коливання вала із трьома дисками отримане наступне частотне рівняння (2.17):

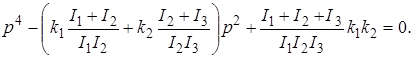
Тут, як і раніше, k₁ , k_2. – коефіцієнти твердості ділянок вала між дисками, р.– власна частота крутильних коливань вала, I₁ , I_2, I_3.. – моменти інерції мас трьох дисків відповідно.

Зворотне завдання: Відомі власні частоти коливань вала, моменти інерції дисків. Невідомі коефіцієнти твердості ділянок вала між дисками.

Перетворимо рівняння (2.17) до виду

.

Якщо розглянути дві власні частоти р₁ і р₂ , то останні рівняння являють собою систему алгебраїчних рівнянь із двома невідомими k₁ , k_{2 .}

(3.1)

Віднімаючи з першого рівняння системи (3.1) друге, одержимо

.

Розділимо обидві частини останньої рівності на :

Виразимо :

, (3.2)

і підставимо його в перше рівняння системи (3.1):

Перетворимо останню рівність до виду:

Вирішуючи останнє рівняння відносно , одержимо

, (3.3)

де

Таким чином, формули (3.2) і (3.3) однозначно визначають коефіцієнти твердості ділянок вала на крутінні для вала із трьома дисками.

Поставимо тепер подібне зворотне завдання для вала із чотирма дисками, частотне рівняння для крутильних коливань якого має вигляд (2.20):

Тут, знову, k₁ , k_2. k₃ – коефіцієнти твердості ділянок вала між дисками, р.– власна частота крутильних коливань вала, I₁ , I_2, I_3, I_4. - моменти інерції мас чотирьох дисків.

Зворотне завдання: Відомі власні частоти коливань вала, моменти інерції дисків. Невідомі коефіцієнти твердості ділянок вала між дисками.

Розглянемо знову дві власні частоти р₁ і р₂ крутильних коливань вала, тоді рівняння (2.20) являють собою систему алгебраїчних рівнянь із двома невідомими k₁ , k₂ при відомому коефіцієнті k_3. Обчислення, проведені в пакеті MAPLE, показують, що із системи (3.4) можна однозначно визначити коефіцієнти твердості двох будь-яких ділянок вала між дисками при відомому коефіцієнті твердості одного із трьох ділянок. Причому всі ці коефіцієнти пружних закріплень визначаються по двох власних частотах крутильних коливань вала.

2.3 Діагностування моментів інерції мас дисків

Розглянемо знову частотне рівняння (2.17), отримане для обчислення частот крутильних коливань вала із трьома дисками.

Зворотне завдання. Нехай відомі власні частоти р коливань вала, коефіцієнти твердості k₁ , k₂ ділянок вала між дисками. Необхідно визначити невідомі моменти інерції мас двох дисків при відомому моменті інерції третього диска.

Нехай, наприклад, відомий момент інерції другого диска. Тоді, якщо розглянути знову дві власні частоти р₁ і р₂ коливань вала, то рівняння (2.17) являють собою систему алгебраїчних рівнянь із двома невідомими I₁ , I_3.

(3.5)

Підставляючи вираження із другого рівняння системи (3.5) у перше рівняння, одержимо

.

З останньої рівності виразимо через :

(3.6)

.

Підставимо тепер вираження (3.6) у перше рівняння системи (3.5). Після перетворень маємо

(3.7)

де .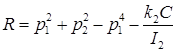

Вирішуючи рівняння (3.7) щодо невідомої , одержимо квадратне рівняння

дискримінант якого має вигляд

.

. (3.8)

Таким чином, моменти інерції мас двох дисків перебувають однозначно по формулах (3.7) і (3.8). Подібні формули можна одержати для моментів інерції будь-яких двох дисків при відомому моменті інерції одного із трьох дисків.

Аналогічне завдання діагностування розв'язуване й для вала із чотирма дисками, частотне рівняння якого отримане нами у вигляді (2.20).

Обчислення, проведені в пакеті MAPLE, показують, що із системи (3.4) можна однозначно визначити коефіцієнти твердості двох будь-яких ділянок вала між дисками при відомому коефіцієнті твердості одного із трьох ділянок. Причому всі ці коефіцієнти пружних закріплень визначаються по двох власних частотах крутильних коливань вала.

2.4 Застосування методу рішення зворотного завдання, програмна реалізація рішення

Розглянемо застосування методу рішення зворотного завдання по визначенню характеристик вала з дисками на конкретних прикладах.

Приклад 4

Відомі власні частоти крутильних коливань вала із трьома дисками: , . Момент інерції маси першого диска коефіцієнти твердості ділянок вала між дисками , .Знайти моменти інерції мас другого й третього дисків.

Рішення.

Підставляючи значення , у рівняння (2.20), одержимо систему двох рівнянь із двома невідомими . Рішення системи, знайдене в пакеті Maple, має вигляд: . Значення визначені вірно, тому що за рішенням прямого завдання саме цим моментам інерції відповідають дані значення власних частот.

Приклад 5

По двох власних частотах , крутильних коливань вала із трьома дисками й відомими моментами інерції діагностувати коефіцієнти твердості ділянок вала на крутінні.

Рішення

Рівняння (2.17) при заданих значеннях , являє собою наступну систему:

з якої одержуємо, що , . Цього ж значення коефіцієнтів виходять при підстановці значень власних частот в аналітичні формули (3.2) і (3.3). Коефіцієнти вірни, тому що саме цим коефіцієнтам при рішенні прямого завдання відповідали задані значення власних частот.

Приклад 6

Розглядається вал із чотирма дисками, для якого відомі , , . По частотах визначити моменти інерції мас перших трьох дисків.

Рішення

Підставляючи значення в рівняння (2.20), одержимо систему трьох рівнянь із трьома невідомими . Рішення системи має вигляд .Значення визначені вірно, тому що за рішенням прямого завдання саме цим моментам інерції відповідають дані значення власних частот.

Розглянемо програмні реалізації рішень зворотних завдань.

Рішення приклада 4

> restart;

> i1:=0.2;

> k1:=0.1;

> k2:=0.2;

> p:=.8480705122;

> p:=1.667566013;

> p:=-1.667566013;

> t1:=.5172825777-.7192235937e-1*(i1+i2)/i1/i2-.1438447187*(i2+i3)/i2/i3+.2e-1*(i1+i2+i3)/i1/i2/i3 = 0;

> t2:=7.732717430-.2780776408*(i1+i2)/i1/i2-.5561552816*(i2+i3)/i2/i3+.2e-1*(i1+i2+i3)/i1/i2/i3 = 0;

> t3:=7.732717430-.2780776408*(i1+i2)/i1/i2-.5561552816*(i2+i3)/i2/i3+.2e-1*(i1+i2+i3)/i1/i2/i3 = 0;

> solve({t1,t2,t3},{i2,i3});

Рішення приклада 5

> restart;

> i1:=0.2;

> i2:=0.3;

> i3:=0.1;

> p:=.8480705122;

> p:=1.667566013;

> t1:=p^4-(k1*(i1+i2)/(i1*i2)+k2*(i2+i3)/(i2*i3))*p^2+k1*k2*(i1+i2+i3)/(i1*i2*i3)=0;

> t2:=p^4-(k1*(i1+i2)/(i1*i2)+k2*(i2+i3)/(i2*i3))*p^2+k1*k2*(i1+i2+i3)/(i1*i2*i3)=0;

> solve({t1,t2},{k1,k2});

Рішення приклада 6

> restart;

> i4:=0.2;

> k1:=0.1;

> k2:=0.2;

> k3:=0.3;

> p:=1.581138830;

> p:=2.417091066;

> p:=-1.581138830;

> t1:=p^6-(k1*(i1+i2)/(i1*i2)+k2*(i2+i3)/(i2*i3)+k3*(i3+i4)/(i3*i4))*p^4+(k1*k2*(i1+i2+i3)/(i1*i2*i3)+k2*k3*(i2+i3+i4)/(i2*i3*i4)+k1*k3*(i1+i3+i4)/(i1*i3*i4))*p^2+k1*k2*k3(i1+i2+i3+i4)/(i1*i2*i3*i4)=0;

> t2:=p^6-(k1*(i1+i2)/(i1*i2)+k2*(i2+i3)/(i2*i3)+k3*(i3+i4)/(i3*i4))*p^4+(k1*k2*(i1+i2+i3)/(i1*i2*i3)+k2*k3*(i2+i3+i4)/(i2*i3*i4)+k1*k3*(i1+i3+i4)/(i1*i3*i4))*p^2+k1*k2*k3(i1+i2+i3+i4)/(i1*i2*i3*i4)=0;

> t3:=p^6-(k1*(i1+i2)/(i1*i2)+k2*(i2+i3)/(i2*i3)+k3*(i3+i4)/(i3*i4))*p^4+(k1*k2*(i1+i2+i3)/(i1*i2*i3)+k2*k3*(i2+i3+i4)/(i2*i3*i4)+k1*k3*(i1+i3+i4)/(i1*i3*i4))*p^2+k1*k2*k3(i1+i2+i3+i4)/(i1*i2*i3*i4)=0;

> solve({t1,t2,t3},{i1,i2,i3});

Висновок

У роботі досліджені й вирішені завдання визначення власних частот крутильних коливань вала з дисками по відомих моментах інерції мас дисків і коефіцієнтів твердості ділянок вала на крутінні. Рішення зведене до системи n звичайних рівнянь щодо невідомих власних частот крутильних коливань вала. Із цієї системи отримані частотні рівняння для вала із двома, трьома, чотирма дисками. Зроблено відповідні обчислення, складена програма в математичному пакеті Maple.

Уперше наведена постановка зворотного спектрального завдання діагностування характеристик вала з дисками по спектрі частот його коливань. Алгоритм діагностування зводиться до рішення систем алгебраїчних рівнянь. Розглянуто діагностування моментів інерції мас дисків по власних частотах коливань вала. Завдання вирішене для вала із трьома, чотирма дисками. Ці характеристики однозначно визначаються для двох дисків вала із трьома дисками при відомому моменті інерції маси третього диска. Показано, що для вала із трьома дисками достатнє знання двох власних частот коливань вала. Причому, чисельні рішення показують можливість визначення моментів інерції мас будь-яких двох дисків (при відомому моменті третього диска), незалежно від їхнього взаємного розташування.

Аналогічне завдання вирішене для вала із чотирма дисками.

Діагностуються також коефіцієнти твердості ділянок вала при крутінні між дисками. Для вала із трьома дисками коефіцієнти твердості відновлюються по двох власних частотах. Для рішення зворотних завдань складені програми в математичному пакеті Maple. Отримані результати зворотних завдань підтверджують справедливість рішень прямих завдань.

Список літератури

1. Введення в акустичну динаміку машин./ І.І. Артоболевський [і ін]. – К., 2004

2. Ахатов І.Ш., Ахтямов О.М. Визначення виду закріплення стрижня по власних частотах його коливань // Прикладна математика й механіка. – К., 2001.

3. Ахтямов, О.М. Діагностування закріплення кільцевої пластини по власних частотах її коливань. – К., 2005

4. Ахтямов, О.М. До одиничності рішення одного зворотного спектрального завдання / О.М. Ахтямов // Диференціальні рівняння. - 2003. - №8. - C. 1011-1015.

5. Ахтямов, О.М. Розпізнавання закріплення кільцевої мембрани по власних частотах її коливань / О.М. Ахтямов // Звістки РАЕН. Серія МММИУ. Т.5. -2001. - №3. - C. 103-110.

6. Бабаков, І.В. Теорія коливань /І.В. Бабаков –К., 2004.

7. Биргер, І.А. Технічна діагностика /І.А. Биргер – К., 2003

8. Васильєв, Н.О. Експериментальні дослідження коливальних характеристик залізничних шпал /Н.О.Васильєв// Акустичний журнал. - 2000. - №3. - C. 424-426.

9. Вібрації в техніку: Довідник. Т.1. Коливання лінійних систем. – К., 2003

10. Зниження шуму на судах. / В.І. Зинченко. – К., 2006

11. Коллатц. Л. Завдання на власні значення (з технічними додатками):. – К., 2006

12. Кузьмін Р.В. Дифектація суднових механізмів. – К., 2005

13. Лапін, А.Д. Резонансний поглинач хвиль у стрижнях і пластинах /А.Д.Лапін// Акустичний журнал. - 2002. - №2. - C. 277-280.

14. Павлов, Б.В. Акустична діагностика механізмів /Б.В.Павлов – К., 2005