| Скачать .docx |
Курсовая работа: Система управления положением бортового прожектора вертолёта
Пояснительная записка к курсовому проекту по дисциплине системы автоматического управления
Выполнил студент гр. 3410 Набиуллин А.Х.
Казанский Государственный Технический Университет им. А. Н. Туполева
Казань, 2006
Задание на курсовой проект
Необходимо разработать двухкоординатную систему дистанционного управления бортовым прожектором вертолёта в соответствии с техническими требованиями.
Технические требования представлены в таблице 1.
Таблица 1.
| Параметры прожектора | Обозначение | Значение |
| Габариты прожектора, мм | 150×200 | |
| Масса прожектора, кг | 2 | |
| Размеры органа управления | 70×35 | |
| Источник питания, В | 36(400) | |
| Время переходного процесса, сек | 0.15 | |
| Динамическая ошибка, % | 10 | |
| Диапазоны регулирования: | ||
| по азимуту, град | ±180 | |
| по углу места, град | +5, -90 | |
| Максимальное время перемещения в пределах полного диапазона, сек | 2 | |
| 1.8 |
Задание:
Построить математическую модель объекта (считая прожектор однородным телом).
Выбрать тип приводного двигателя и передаточное число редуктора, тип датчиков для органа управления.
Составить структурную схему каждого канала системы с указанием передаточных функций звеньев.
Синтезировать регулятор для каждого канала.
Разработать электрическую схему системы, включая регуляторы.
Конструкторская часть – по согласованию с преподавателем.
1. Построение математической модели объекта управления.
На рис.1 представлена схема бортового прожектора.

Рис.1 Схема бортового прожектора
Построим математическую модель системы методом Лагранжа.
В целях упрощения математической модели накладываем на систему некоторые допущения:
Все тела системы абсолютно жесткие;
Люфты в редукторе отсутствуют.
Запишем уравнения Лагранжа по следующей формуле
 .
.
Здесь:
![]() - сумма кинетических энергий всех тел системы,
- сумма кинетических энергий всех тел системы,
![]() - обобщенная координата,
- обобщенная координата,
![]() - обобщенная сила инерции,
- обобщенная сила инерции,
![]() - обобщенная скорость.
- обобщенная скорость.
Число степеней свободы рассматриваемой системы равно двум.
За обобщённые координаты принимаем угловые перемещения прожектора вокруг осей x и y. Таким образом, ![]() .
.
Запишем кинетические энергии системы.
Запишем кинетическую энергию второго двигателя
 ,
,
где: ![]() - передаточное отношение второго редуктора;
- передаточное отношение второго редуктора; ![]() - момент инерции второго двигателя.
- момент инерции второго двигателя.
Запишем кинетическую энергию вилки
 ,
,
где: ![]() - момент инерции вилки.
- момент инерции вилки.
Запишем кинетическую энергию первого двигателя.
 ,
,
где: ![]() - передаточное отношение первого двигателя;
- передаточное отношение первого двигателя; ![]() - момент инерции первого двигателя;
- момент инерции первого двигателя; ![]() - масса первого двигателя;
- масса первого двигателя; ![]() - расстояние от центра масс первого двигателя до оси
- расстояние от центра масс первого двигателя до оси ![]() .
.
Запишем кинетическую энергию прожектора
 ,
,
где: ![]() - момент инерции прожектора вокруг оси
- момент инерции прожектора вокруг оси ![]() ;
; ![]() - момент инерции прожектора вокруг оси
- момент инерции прожектора вокруг оси ![]() .
.
 ,
,
где: ![]() - радиус прожектора;
- радиус прожектора; ![]() - длина прожектора.
- длина прожектора.
![]() .
.
![]() .
.
 .
.
 .
.

Запишем сумму кинетических энергий всех тел системы

 .
.

 ;
;
 ;
;
 ;
;
 .
.

![]()
![]() .
.

Определяем работы при малых приращениях
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ниже представлены уравнения Лагранжа для исследуемой системы


![]() .
.
Проводим линеаризацию полученных уравнений.
Определяемся с номинальным движением
![]() .
.
Принимем
![]() ,
,
где ![]() ,
, ![]() - бесконечно малые приращения.
- бесконечно малые приращения.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Подставляем полученные соотношения в уравнения Лагранжа.
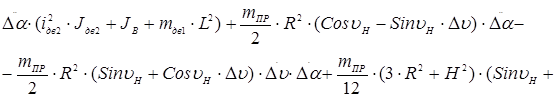


![]() .
.
Принимаем
![]() ;
;
![]() .
.
Переписываем уравнения относительно отклонений, оставляя только первый порядок малости
 ;
;
 .
.
Получаем окончательные уравнения
 ;
;
 .
.
2. Выбор типа приводного двигателя.
Требуемую мощность двигателя определяем по формуле
![]()
![]() ,
,
где: ![]() - требуемый вращающий момент на выходном валу двигателя;
- требуемый вращающий момент на выходном валу двигателя; ![]() - частота вращения объекта, приводимого в движение двигателем.
- частота вращения объекта, приводимого в движение двигателем.
![]() ,
,
где: ![]() - момент инерции всех тел, приводящихся в движение двигателем;
- момент инерции всех тел, приводящихся в движение двигателем; ![]() - угловое ускорение этих тел.
- угловое ускорение этих тел.
Зададим синусоидальное входное воздействие
![]() ;
;
![]() ;
;
![]() .
.
Требуемую мощность двигателя будем вычислять по формуле
![]() .
.
Вычисляем требуемую мощность первого двигателя
![]() .
.
 .
.
![]() - для первого двигателя равняется половине диапазона регулирования по углу места.
- для первого двигателя равняется половине диапазона регулирования по углу места.
![]() .
.
 .
.
![]() .
.
По найденной требуемой мощности двигателя из справочной литературы был выбран двигатель ДПМ-25-Н1-04 со следующими характеристиками:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вычисляем требуемую мощность второго двигателя.
![]()
Вычисляем момент инерции вилки. Конструкция вилки упрощённо показана на рис. 2.

Рис. 2 Схема вилки
Примерно определимся с размерами вилки.
Принимаем
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Вычисляем объём составных частей вилки
![]() ,
,
![]() .
.
Вычисляем массы составных частей вилки
![]() ,
,
![]() .
.
Момент инерции вилки найдём как сумму моментов инерции верхней части вилки и боковин.
Верхняя часть вилки показана на рис. 3.

Рис.3 Верхняя часть вилки
Определяем момент инерции верхней части вилки, при этом пользуемся известной теоремой Штейнера-Гюйгенса
 .
.

![]() .
.
Боковина вилки показана на рис.4.

Рис.4 Боковина вилки
Определяем момент инерции боковины вилки
![]() ,
,
![]() ,
,
 .
.
Определяем момент инерции вилки
![]() .
.
Масса вилки
![]() .
.
![]() .
.
![]() .
.
![]() .
.
По найденной требуемой мощности двигателя из справочной литературы был выбран двигатель ДПМ-25-Н1-07 со следующими характеристиками:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вычисляем скорости вращения валов прожектора.
Вычисляем скорость вращения прожектора вокруг оси x.

![]()
![]()

Вычисляем скорость вращения прожектора вокруг оси z.
 .
.
![]() .
.
![]() .
.
 .
.
3. Составление структурных схем каналов системы, синтез регуляторов.
3.1 Составление структурной схемы первого канала, синтез регулятора.
Применим преобразование Лапласа к полученному уравнению Лагранжа
![]() .
.
 .
.
Структурная схема канала 1 показана на рис. 5.

Рис.5 Структурная схема первого канала
На схеме обозначены:
 ;
;
 ;
;
 ;
;
![]() ;
;
 ;
;
 ;
;
 .
.
Подставляем найденные значения в структурную схему.
На рис.6 представлена блок-схема первого канала.

Рис.6 Блок-схема первого канала
На рис. 7 представлена упрощённая блок-схема первого канала.

Рис.7 Упрощённая блок-схема первого канала
Ещё более упростим систему, записав единое уравнение для части системы, замкнутой обратной связью с коэффициентом 29,4. Для этого запишем передаточную функцию ![]() по
по ![]() (
(![]() по
по ![]() ).
).
Уравнение разомкнутой системы ![]() .
.
 .
.
Уравнение замкнутой системы:

 .
.

Рис.8 Упрощённая блок-схема первого канала
Запишем окончательную передаточную функцию разомкнутой системы.
![]()


![]() ;
;
![]() ;
;
![]() .
.
Так как ![]() , то имеем колебательное звено. Учитывая что
, то имеем колебательное звено. Учитывая что ![]() , можно пользоваться асимптотическими ЛЧХ колебательного звена, колебания будут малы.
, можно пользоваться асимптотическими ЛЧХ колебательного звена, колебания будут малы.
Находим сопрягающую частоту
 ;
;
![]() .
.
На рис. 9 представлены ЛЧХ нескорректированного первого канала.
Рис.9 Нескорректированные ЛЧХ первого канала
По ЛАЧХ видно, что нескорректированная система первого канала устойчива, но предъявленные к систем требования по качеству не выполняются. Кривая ЛАЧХ пересекает ось абсцисс на очень низкой частоте, вследствие чего система имеет очень высокое время регулирования. Путём моделирования нескорректированной системы в среде Matlab было установлено, что время регулирования составляет порядка 15 секунд.
Введём в исследуемую систему корректирующие звенья. Рассчитаем их методом синтеза последовательной коррекции. Найдём желаемую частоту среза, исходя из заданных времени регулирования и величины перегулирования.

Желаемую ЛАЧХ построим исходя из следующих соображений. Среднечастотный участок желаемой ЛАЧХ образуется асимптотой с наклоном ![]() , проводимый так, чтобы она пересекала ось частот при
, проводимый так, чтобы она пересекала ось частот при ![]() . Этот участок проводится влево и вправо до достижения модулей, равных по крайней мере
. Этот участок проводится влево и вправо до достижения модулей, равных по крайней мере ![]() . Высокочастотную область можно пустить параллельно исходной ЛАХ. Низкочастотная область желаемой ЛАЧХ также должна по возможности повторять нескорректированную ЛАЧХ.
. Высокочастотную область можно пустить параллельно исходной ЛАХ. Низкочастотная область желаемой ЛАЧХ также должна по возможности повторять нескорректированную ЛАЧХ.
Построенная асимптотическая ЛАЧХ находится в приложении к пояснительной записке.
После построения желаемой ЛАЧХ и ЛФЧХ можно строить ЛАЧХ и ЛФЧХ коррекции, исходя из следующих соотношений:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ниже представлена вычисленная передаточная функция коррекции.
 .
.
На рис. 10 показаны ЛЧХ скорректированного первого канала.

Рис.10 ЛЧХ первого канала
Добавляем коррекцию к уже имеющейся системе, и, для получения переходного процесса, смоделируем её в программе Matlab.
На рис.11 показан переходной процесс для первого канала исследуемой системы.

Рис. 11 Реакция на единичный скачок первого канала
Было установлено:
![]() ;
;
![]() .
.
Таким образом, можно сказать, что скорректированная система удовлетворяет всем предъявленным требованиям по качеству и быстродействию.
Рассчитаем корректирующие звенья для первого канала. По виду передаточной функции коррекции определяем, что нам потребуется две одинаковых дифференцирующих цепочки. Также необходимо включить последовательно с ними некоторое количество усилителей, коэффициент усиления которых мы найдём позднее.
Схема пассивного дифференцирующего звена показана на рис.12.

Рис.12 Схема пассивного дифференцирующего звена
 , (
, (![]() ),
),
где,  - коэффициент передачи дифференцирующего звена.
- коэффициент передачи дифференцирующего звена.
![]() ;
;
 .
.
Пусть ![]() , тогда
, тогда
 ,
,
![]() ,
,
![]() ;
;
 ,
,
![]() ;
;
![]() .
.
Рассчитаем дополнительный коэффициент усиления, требуемый для сигнала, ослабленного дифференцирующим звеном
 .
.
Рассчитаем общий коэффициент усиления рассчитанного регулятора
![]() .
.
На рис. 13 показана схемная реализация рассчитанного регулятора.

Рис. 13 Схема регулятора
Распределим полученный коэффициент усиления по усилителям. Первый усилитель включён по вычитающей схеме, и также будет усиливать сигнал. Второй усилитель включён как повторитель, он нужен только для ослабления влияния второго дифференцирующего звена на первый, это достигается благодаря огромному входному сопротивлению операционных усилителей, на основе которых построены усилители. Третий усилитель представляет собой мощный операционный усилитель с высоким выходным током, достаточным для пуска двигателя.
Распределим вычисленный коэффициент усиления регулятора по двум усилителям
![]() .
.
3.2 Составление структурной схемы второго канала, синтез регулятора.
Применим преобразование Лапласа к полученному уравнению Лагранжа
![]() .
.
![]() .
.
Структурная схема канала 2 показана на рис. 14.

Рис. 14 Структурная схема второго канала
На схеме обозначены:
 ;
;
 ;
;
 ;
;
![]() ;
;
 ;
;
 ;
;
 .
.
Подставляем найденные значения в структурную схему.
На рис.15 представлена блок-схема второго канала.

Рис.15 Блок-схема второго канала
На рис. 16 представлена упрощённая блок-схема второго канала.

Рис.16 Упрощённая блок-схема второго канала
Ещё более упростим систему, записав единое уравнение для части системы, замкнутой обратной связью с коэффициентом 8,56. Для этого запишем передаточную функцию ![]() по
по ![]() (
(![]() по
по ![]() ).
).
Уравнение разомкнутой системы ![]() .
.
 ;
;
Уравнение замкнутой системы:

 .
.

Рис.17 Упрощённая блок-схема второго канала
Запишем окончательную передаточную функцию разомкнутой системы.
![]() ;
;

 ;
;
![]() ;
;
![]() ;
;
![]() .
.
Так как ![]() , то имеем колебательное звено. Учитывая что
, то имеем колебательное звено. Учитывая что ![]() , можно пользоваться асимптотической ЛАЧХ колебательного звена.
, можно пользоваться асимптотической ЛАЧХ колебательного звена.
Находим сопрягающую частоту

![]() .
.
На рис. 18 представлены ЛЧХ нескорректированного второго канала.

Рис. 18 ЛЧХ нескорректированного второго канала
По ЛЧХ видно что нескорректированная система второго канала устойчива, но предъявленные к систем требования по качеству не выполняются. Кривая ЛАЧХ нескорректированной системы пересекает ось абсцисс на очень низкой частоте, вследствие чего система имеет очень высокое время регулирования. Путём моделирования нескорректированной системы в среде Matlab было установлено, что время регулирования больше 4 секунд.
Как и в случае с первым каналом, рассчитаем корректирующие звенья методом синтеза последовательной коррекции.
Построенная асимптотическая ЛАЧХ находится в приложении к пояснительной записке.
Ниже представлена вычисленная передаточная функция коррекции
 .
.
На рис. 19 показаны ЛЧХ скорректированного второго канала.

Рис.19 ЛЧХ второго канала
На рис.20 показан переходной процесс для второго канала исследуемой системы.

Рис. 20 Реакция на единичный скачок второго канала
Было установлено:
![]() ;
;
![]() .
.
Таким образом, можно сказать, что скорректированная система удовлетворяет всем предъявленным требованиям по качеству и быстродействию.
Рассчитаем корректирующие цепья для второго канала. Как и случае с первым каналом нам потребуется два одинаковых дифференцирующих звена и усилители.
Схема пассивного дифференцирующего звена показана на рис.12.
 ,
,
![]() ;
;
 .
.
Пусть ![]() , тогда
, тогда
 ,
,
![]() ,
,
![]() ;
;
 ,
,
![]() ;
;
![]() .
.
Рассчитаем дополнительный коэффициент усиления, требуемый для сигнала, ослабленного дифференцирующим звеном
 .
.
Рассчитаем общий коэффициент усиления рассчитанного регулятора
![]() .
.
Схемная реализация рассчитанного регулятора для второго канала будет такой же и как для первого канала и показана на рис. 13.
Распределим вычисленный коэффициент усиления регулятора по двум усилителям
![]() .
.
В качестве датчика для первого канала был выбран потенциометрический датчик угла Megatron MP20. Датчик показан на рис. 21.

Рис. 21 MP20
Параметры:
Технология – проволока;
Электрический угол поворота - 320![]() ;
;
Диапазон сопротивлений – 1 кОм – 50 кОм;
Допуск на сопротивление - ![]() ;
;
Допуск на линейность - ![]() ;
;
Мощность – 0,8 Вт;
Диаметр корпуса - 22 мм;
Максимальный вращающий момент – 0,3 ![]() .
.
В качестве датчика для второго канала был выбран потенциометрический датчик угла Megatron AL1703/1903. Датчик показан на рис. 22.

Рис. 22 AL1703/1903
Параметры:
Технология – проволока;
Диапазон сопротивлений – 10 кОм – 100 кОм;
Допуск на сопротивление - ![]() ;
;
Допуск на линейность - ![]() ;
;
Число оборотов – 3.
5. Выбор элементов
5.1 Выбор операционных усилителей
Для построения усилителей, с обозначенными на рис.13 коэффициентами усиления К1, К2 были выбраны сдвоенные операционные усилители 140УД20А. они предназначены для использования в различных узлах радиоэлектронной аппаратуры – активных фильтрах, сумматорах, интеграторах и т.п. Использование сдвоенных ОУ позволяет экономить место на плате и облегчает разводку печатных проводников платы.
Основные параметры ИМС 140УД20А представлены в таблице 2.
Таблица 2.
| Напряжение питания, В | |
| Входной ток, нА | <200 |
| Усиление по напряжению, |
50000 |
| Максимальное напряжение на выходе, В | |
| Входное сопротивление, Мом | >0,4 |
| Максимальный выходной ток, мА | 8 |
| Минимальное сопротивление нагрузки, кОм | >2 |
Для построения выходных усилителей были использованы мощные сдвоенные операционные усилители OPA2544T фирмы “Texas Instruments”. Первый операционный усилитель усиливает сигнал для первого канала, а второй – для второго. При использовании этих ОУ отпадает необходимость в построении усилителей мощности на основе мощных транзисторов, следовательно, уменьшаются габариты проектируемой платы.
Основные параметры OPA2544T представлены в таблице 3.
Таблице 3.
| Напряжение питания, |
|
| Входной ток, пА | 50max |
| Усиление по напряжению, дб | 103 |
| Максимальное напряжение на выходе, В | |
| Максимальный выходной ток, А | 2 |
| Минимальное сопротивление нагрузки, Ом | 10 |
| Рабочая температура, |
5.2 Выбор резисторов
Выбор резисторов производится из рядов по следующим параметрам:
По номиналу;
По мощности;
По допуску (разбросу номиналов).
Первый ОУ в обоих каналах включён по вычитающей схеме, показанной на рис. 23.

Рис. 23 Вычитающая схема включения ОУ
При этом должны выполняться следующие соотношения номиналов резисторов
![]() ;
;
![]() .
.
При этом напряжение на выходе
![]() .
.
Схема электрическая принципиальная показана в конструкторской части курсового проекта.
В соответствии с найденными коэффициентами усиления, были выбраны следующие номиналы сопротивлений резисторов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Рассчитаем требуемые мощности этих резисторов
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Рассчитаем мощности резисторов корректирующих звеньев.
 ;
;
 ;
;
 .
.
Марки выбранных резисторов, их номиналы и пр. показаны в таблице 4.
Таблица 4.
| Тип | Номинал | Рассеиваемая мощность | Допуск | Ряд | |
| R1 | С2-33Н | 1910 | 0,125 | ±2% | Е96 |
| R2 | С2-33Н | 3090 | 0,125 | ±2% | Е96 |
| R3 | С2-33Н | 200000 | 0,125 | ±5% | Е24 |
| R4 | С2-33Н | 200000 | 0,125 | ±5% | Е24 |
| R5 | С2-33Н | 1910 | 0,125 | ±2% | Е96 |
| R6 | С2-33Н | 200000 | 0,125 | ±5% | Е24 |
| R7 | СП3-38б | 15000 | 0,125 | ±20% | Е6 |
| R8 | С2-33Н | 3090 | 0,125 | ±2% | Е96 |
| R9 | С2-33Н | 200000 | 0,125 | ±5% | Е24 |
| R10 | СП3-38б | 15000 | 0,125 | ±20% | Е6 |
| R11 | С2-33Н | 20500 | 0,125 | ±2% | Е96 |
| R12 | С2-33Н | 23700 | 0,125 | ±2% | Е96 |
| R13 | С2-33Н | 2200 | 0,125 | ±5% | Е24 |
| R14 | С2-33Н | 2200 | 0,125 | ±5% | Е24 |
| R15 | СП3-38б | 15000 | 0,125 | ±20% | Е6 |
| R16 | СП3-38б | 15000 | 0,125 | ±20% | Е6 |
| R17 | С2-33Н | 20500 | 0,125 | ±2% | Е96 |
| R18 | С2-33Н | 23700 | 0,125 | ±2% | Е96 |
| R19 | С2-33Н | 2200 | 0,125 | ±5% | Е24 |
| R20 | С2-33Н | 2200 | 0,125 | ±5% | Е24 |
| R21 | С2-33Н | 105000 | 0,125 | ±2% | Е96 |
| R22 | С2-33Н | 1000 | 0,125 | ±5% | Е24 |
| R23 | С2-33Н | 64900 | 0,125 | ±2% | Е96 |
| R24 | С2-33Н | 1000 | 0,125 | ±5% | Е24 |
5.3 Выбор прочих элементов
Для питания ИМС 140УД20А был использован интегральный двуполярный стабилизатор напряжения К142ЕН6А, параметры которого приведены в таблице 5.
Таблица 5.
| К142ЕН6А | 0,2 | 5 |
Список литературы
Никитин Н.Н. Курс теоретической механики: Учеб. Для машиностроит. и приборостроит. спец. Вузов. – 5-е изд., перераб. и доп. – М.: Высш. шк., 1990. – 607 с.
Прохоров С.Г., Хуснутдинов Р.А. Электрические машины: Учебное пособие: Для студентов очного и заочного обучения/ Казань: Изд-во казан. гос. техн. ун-та, 2002. – 164 с.
Копылов, Клоков Б.К.. Справочник по электрическим машинам: в 2т. – М.: Энергоиздат., 1988. – 456с.
Теория автоматического управления: Учеб. для вузов по спец. “Автоматика и телемеханика”. В 2-х ч. Ч.1. Теория линейных систем автоматического управления / Н.А. Бабаков, А.А. Воронов, А.А.Воронова и др.; Под ред. А.А. Воронова. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 367 с.
Чекмарёв А.А. Справочник по машиностроительному черчению/ А.А. Чекмарёв, В.К. Осипов. – 3-е изд., стер. – М.: Высш. шк. 2002. – 493 с.
Опадчий Ю.Ф., Глудкин О.П., Гуров А.И. Аналоговая и цифровая электроника (полный курс): Учебник для вузов. Под. ред. О.П. Глудкина. – М.: Горячая линия – Телеком, 2003. – 768 с.
Булычев А.Л., Галкин В.И.. Аналоговые интегральные схемы: справочник. 2-е изд – М.: Энергоиздат, 1988. – 456с.
Дубровский В.В., Иванов Д.М., Пратусевич Н.Я., под ред. Четверткова И.И. Резисторы: справочник 2-е изд. – М.: Радио и связь 1991. – 528с.
Цокур Е.И. Интегральные стабилизаторы постоянного напряжения: Учебное пособие по дисциплине “Системы и источники вторичного электропитания”. Казань: Изд-во Казан. гос. техн. ун-та, 1998. – 160 с.
Александров К.К., Кузьмина Е.Г. Электротехнические чертежи и схемы. – 2-е изд., испр. и доп. – М.: Издательство МЭИ, 2004. – 300 с.
http://focus.ti.com/lit/ds/symlink/opa2544.pdf (спецификация на OPA2544T)
http://focus.ti.com/lit/ml/mpzf003a/mpzf003a.pdf (габариты корпуса OPA2544T)
http://www.eximer.net/products/electron/switching/connectors/rus/mrn/mpn_1337.html (габариты разъёма МРН8-1)
http://www.eliks.ru/product/oem/angle1.htm, http://www.eliks.ru/product/oem/angle1.htm (потенциометрические датчики)