| Скачать .docx |
Реферат: Закономерности поведения биазеотропных смесей
Закономерности поведения биазеотропных смесей (систем)
Известно, что свыше 70% энергетических затрат в производствах основного органического и нефтехимического синтеза приходится на стадию выделения конечных продуктов требуемой степени чистоты. Такая высокая энергоемкость процессов разделения, и в первую очередь, процесса ректификации, обуславливает особо тщательный подход к синтезу их технологических схем. Основные ограничения, накладываемые фазовым равновесием на процесс ректификации, связаны с наличием азеотропов разного типа и порождаемых ими разделяющих многообразий (сепаратрис).
Разработанный на сегодня термодинамико-топологический анализ (ТТА) диаграмм парожидкостного равновесия ориентирован на моноазеотропию, когда на каждом элементе концентрационного симплекса находится не более одной азеотропной точки. Однако в сравнительно недавнее время были экспериментально исследованы девять бинарных систем с двумя бинарными азеотропами и одна – с тремя. Пять бинарных биазеотропных систем, образованных карбоновой кислотой и бутиловым эфиром одноименной кислоты, являются составляющими промышленной смеси, получающейся при этерификации бутанолом фракции кислот С5 -С7 . По мере накопления массива данных по азеотропии, особенно в широком диапазоне температур (давлений), количество биазеотропных смесей будет увеличиваться. Как правило, компоненты бинарных биазеотропных смесей сами являются сильными азеотропными агентами и при добавлении к ним третьего компонента возможно образование не только одного, но и двух тройных азеотропов. Правило азеотропии, лежащее в основе классификации диаграмм парожидкостного равновесия, не накладывает никаких ограничений на возможность образования двух азеотропов на одном и том же элементе концентрационного симплекса. Исследованию биазеотропии в тройных системах с двумя тройными азеотропами посвящена статья (Комар.). В этой статье на основе правила азеотропии разработана классификация структур диаграмм парожидкостного равновесия (ПЖР) в тройных системах с учетом возможности образованиядвух азеотропов как в бинарных, так и в тройных системах. Было показано, что два тройных азеотропа могут возникать и в тройных системах с моноазеотропными составляющими. Таким образом, одним из направлений дальнейшего развития термодинамико-топологического анализа является расширение существующей классификации диаграмм парожидкостного равновесия трехкомпонентных систем, насчитывающей 26 типов, за счет включения трехкомпонентных систем с двумя тройными азеотропами.
В [д.Ч.] проведен синтез структур диаграмм парожидкостного равновесия трехкомпонентных систем с двумя тройными азеотропами при моноазеотропных бинарных составляющих, проведен анализ эволюции тройной биазеотропии при изменении давления, выявлены с помощью расчетного эксперимента две трехкомпонентные системы с двумя тройными азеотропами.
Обзор немногочисленных работ, в которых приводятся отдельные диаграммы трехкомпонентных систем с двумя тройными азеотропами, показал, что в настоящее время отсутствует системный подход к выявлению всего множества диаграмм подобных систем, не выявлены и не проанализированы особенности этих диаграмм.
В [д.Ч.] показано, что физико-химические закономерности преобразования фазовых диаграмм и эволюции тройных азеотропов являются научной основой для выявления конкретных трехкомпонентных систем с двумя тройными азеотропами. Отмечена определяющая роль точек Банкрофта различного рода.
Биазеотропия может возникать двояким образом: как через стадию образования внутреннего тангенциального азеотропа, так и с образованием граничных тангенциальных азеотропов. Схема возникновения тройного азеотропа через тройной граничный тангенциальный азеотроп (ТГТА), возникающий в точке бинарного азеотропа, приведена на рис. Эта схема весьма наглядна, если, используя математическую абстракцмю, выйти за границу концентрационного симплекса в область отрицательных концентраций. Чтобы образовался ТГТА (рис.), необходимо, чтобы при значезначении параметра, отличном от бифуркационного, в области отрицательных концентраций находилось либо седло (рис.), либо узел (рис.).
В [д.Ч.] проведен теоретический анализ векторного поля нод жидкость – пар, содержащего сложную особую точку седло-узел, соответствующую тройному внутреннему тангенциальному азеотропу. Этот анализ позволил установить все возможные варианты взаимного расположения единичных К-линий и обосновать нетривиальный ход дистилляционных линий в трехкомпонентных системах с двумя тройными азеотропами, не встречающийся в моноазеотроных системах. Были синтезированы диаграммы дистилляционных линий (64 структуры) и единичных К-линий (144 структуры) трехкомпонентных систем с двумя тройными азеотропами. на примере трехкомпонентных систем перфторбензол – бензол – третий компонент выявлены условия образования двух тройных азеотропов;
- впервые выявлены две конкретные трехкомпонентные системы с двумя тройными азеотропами: перфторбензол – бензол – метилпропионат и перфторбензол – бензол – трет. амиловый спирт. При этом впервые обнаружен тройной отрицательный азеотроп и тройной внутренний тангенциальный азеотроп;
- сформулированы достаточные условия образования тройного внутреннего тангенциального азеотропа. В [1] проведен синтез диаграмм трехкомпонентных систем с двумя тройными азеотропами. Уже на первых этапах синтеза были получены многочисленные диаграммы с нетривиальным ходом дистилляционных и единичных К -линий, ранее не встречавшимся в системах с одним тройным азеотропом. Предварительный анализ показал, что неординарность хода этих линий связана с мало изученным явлением тройной внутренней тангенциальной азеотропии (ТВТА). В связи с этим возникла необходимость исследования закономерностей формирования структур диаграмм ПЖР с ТВТА и эволюции таких диаграмм при изменении внешних параметров.
Был выявлен тип особой точки, соответствующей ТВТА. Известно, что общий баланс индексов особых точек векторного поля нод жидкость-пар для трехкомпонентной смеси на замкнутом многообразии, гомеоморфном сфере размерности 2, определяется уравнением:
Si = 2. (1)
Возникновение сложной особой точки, соответствующей ТВТА, не должно нарушать алгебраической суммы индексов. Следовательно, при образовании внутренней сложной особой точки тип и количество всех простых особых точек остаются неизменными. Пусть на векторном поле нод возникает внутренняя сложная особая точка, индекс которой ic . Тогда общий баланс индексов будет представлен уравнением:
Si + ic = 2. (2)
Из уравнений (1) и (2) следует, что ic = 0, это соответствует сложной особой точке, представляющей собой «седло-узел» различной кратности. Показано, что с наибольшей вероятностью на векторном поле равновесных нод реализуются двукратные «седло-узлы». После бифуркации рассматриваемая сложная особая точка либо исчезает, либо распадается на две простые особые точки – «седло» и «узел» (рис.1). Оба вида бифуркаций приводят к изменению топологической структуры диаграмм ПЖР.

Рис. 1. Бифуркация сложной особой точки типа двухкратный «седло-узел»
Синтез структур диаграмм трехкомпонентных систем с двумя тройными азеотропами проводился двумя независимыми методами с учетом установленных особенностей хода единичных К -линий. Один метод основан на алгоритме, ранее примененном Л.А. Серафимовым для синтеза диаграмм моноазеотропных систем. Основным его этапом является построение диаграмм единичных K -линий. В основе второго метода лежат закономерности преобразования диаграмм ПЖР при изменении внешних параметров. При этом учитывалось, что тройная биазеотропия может возникать либо в системе, содержащей один тройной азеотроп, через стадию образования тройного граничного тангенциального азеотропа (ТГТА) в соответствии с правилами сопряжения, либо в системе, не содержащей тройного азеотропа, через стадию образования тройного внутреннего тангенциального азеотропа. Использование двух методов дало одинаковый результат: получены 64 диаграммы дистилляционных линий, которым соответствуют 144 диаграммы единичных К -линий (табл. 1). По механизму возникновения тройной биазеотропии эти диаграммы были разбиты на три группы.
К первой группе относятся пять диаграмм, в которых тройная биазеотропия может возникнуть только через стадию образования ТГТА. Эти диаграммы содержат два азеотропа одного и того же типа – либо два «уз-ла», либо два «седла» (рис. 4). В них каждый из тройных азеотропов имеет свой набор единичных К -линий.
Ко второй группе относятся 12 диаграмм, в которых тройная биазеотропия может возникать как через ТГТА, так и через ТВТА. Диаграммы этой группы содержат два тройных азеотропа разного типа – «седло» и «узел». Оба азеотропа имеют один и тот же набор единичных К -линий (рис. 5, 6).
Таблица 1. Типы и количество структур диаграмм ПЖР трехкомпонентных систем с двумя тройными азеотропами
| Класс | Тип | Особые точки диаграммы | Количество диаграмм дистилляционных линий | Количество диаграмм единичных К -линий | ||||||
| N0 | N1 | C1 | N2 | C2 | общее | получены только через ТВТА | с замкнутой сепаратрисой | |||
3.0.2 3.1.2 3.2.2 3.3.2 |
1 1 2 1 2 3 1 2 3 4 |
2 1 3 - 2 - 1 1 3 3 |
- 1 - - 1 2 - 2 1 3 |
- - 1 2 1 - 3 1 2 - |
1 1 1 2 1 1 2 1 1 - |
1 1 1 - 1 1 - 1 1 2 |
1 4 5 1 24 1 2 13 11 2 |
1 2 4 - 21 - - 11 8 - |
1 4 3 - 15 1 - 8 5 - |
2 14 5 6 51 6 4 41 13 2 |
В этой группе появляются диаграммы с нетривиальным ходом сепаратрис «седла», замкнутых в узловой особой точке (рис. 7).
Третья группа диаграмм, самая многочисленная (47 структур), характеризуется тем, что тройная биазеотропия может возникать в этих системах только через ТВТА. Диаграммы этой группы содержат так же тройные азеотропы разного типа. Характерная особенность диаграмм этой группы – нетривиальный ход одной или обеих сепаратрис «седла», когда сепаратриса либо замкнута в узловой точке, либо проходит из «седла» в «седло», либо в одной диаграмме представлены обе эти особенности (рис. 8). Еще одна отличительная черта диаграмм этой группы – в пределах одного и того же типа различным подтипам диаграмм дистилляционных линий могут соответствовать одинаковые структуры диаграмм единичных К -линий.
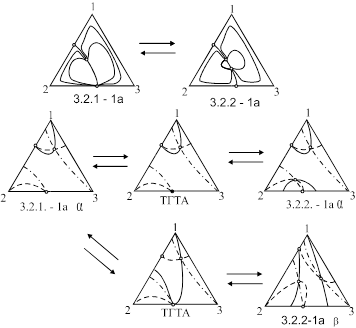
Рис. 4. Диаграммы дистилляционных линий и единичных K
-линий в тройной системе с двумя тройными узловыми азеотропами. 1, 2, 3 – компоненты, ![]() ,
, ![]() и
и ![]() - линии K
1
= 1, K
2
= 1 и K
3
= 1, соответственно;
- линии K
1
= 1, K
2
= 1 и K
3
= 1, соответственно; ![]() - точка азеотропа;
- точка азеотропа; ![]() - точечная K
1
- точечная K
1

Рис. 5. Возникновение биазеотропии в системах класса 3.2.2 – 2б

Рис. 6. Взаимное преобразование диаграмм единичных K -линий при возникновении биазеотропии в системах класса 3.2.2 – 2б. Обозначения те же, что и на рис. 4

Рис. 7. Взаимное преобразование диаграмм дистилляционных линий, приводящее к биазеотропии в системах класса 3.1.2-1а

Рис. 8. Диаграммы дистилляционных линий с нетривиальным ходом сепаратрис седла
Третья глава посвящена изучению эволюции тройной биазеотропии при изменении давления и выявлению трехкомпонентных систем, в которых возможно образование двух тройных азеотропов. Нами проанализированы основные типы эволюции тройной биазеотропии, являющиеся различной комбинацией типов эволюции тройной моноазеотропии. Новым типом эволюции является слияние двух тройных азеотропов с образованием ТВТА. Важной физико-химической характеристикой системы, определяющей эволюцию диаграмм ПЖР при изменении давления (температуры), является зависимость упругостей паров компонентов и азеотропов от температуры. Пересечению зависимостей P = f(T) соответствуют точки Банкрофта разного рода: компонент – компонент (r11 – 1 род); компонент – бинарный азеотроп (r12 – 2 род); бинарный азеотроп – бинарный азеотроп (r22 – 3 род); компонент – тройной азеотроп (r13 – 4 род); бинарный азеотроп – тройной азеотроп (r23 – 5 род).
В работах кафедры ХТООС МИТХТ им. М.В. Ломоносова показано, что достаточным условием возникновения азеотропа в бинарной системе является наличие точки Банкрофта первого рода (r11 ), а достаточным условием образования тройных азеотропов - точек Банкрофта второго (r12 ) либо третьего рода (r22 ), причем соответствующие особые точки диаграммы ПЖР должны быть соединены либо сепаратрисой, либо одним пучком дистилляционных линий. В системах с одним тройным азеотропом эти условия приводят к образованию второго тройного азеотропа и могут быть реализованы в пяти структурах диаграмм, которые до настоящего времени не обнаружены.
Вероятность наличия точек Банкрофта, приводящих к тройной биазеотропии, возрастает с увеличением количества особых точек на контуре концентрационного треугольника. В связи с этим мы перешли к рассмотрению трехкомпонентных систем, в которых одна из бинарных составляющих является биазеотропной. Для выявления конкретных систем с двумя тройными азеотропами в качестве базовой выбрана бинарная биазеотропная система перфторбензол (ПФБ) – бензол (Б). Далее для тройных систем ПФБ – Б – компонент 3 были синтезированы структуры диаграмм ПЖР, не содержащие тройных азеотропов (рис. 9). Рассмотрены разные варианты соотношений температур кипения чистых компонентов. Проведен анализ около 120 зависимостей P = f (T) с точками Банкрофта разного рода и проанализирована соответствующая этим зависимостям эволюция диаграмм ПЖР. Выявлено свыше 20 вариантов зависимостей P = f (T), в которых обязательно образование двух точек Банкрофта, приводящих к тройной биазеотропии, в том числе с эволюцией ее в ТВТА. На основе анализа многочисленных вариантов установлено, что достаточным условием эволюции тройной биазеотропии в ТВТА в трехкомпонентных системах с тремя азеотропными бинарными составляющими является одновременное наличие точек Банкрофта r23 ’ и r23 ” (рис. 10).

Рис. 9. Диаграммы дистилляционных линий тройной системы ПФБ - Б-3
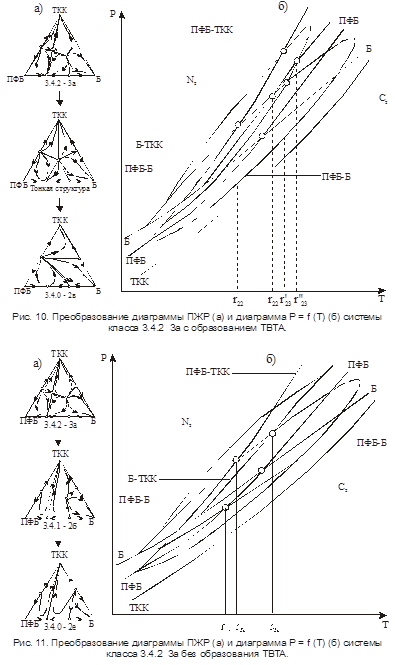
Отсутствие этих условий не приводит к образованию ТВТА (рис. 11).
Для последующего расчетного исследования конкретных тройных систем были выбраны два варианта зависимостей P = f (T), в которых реализуются условия образования тройной биазеотропии. Эти два варианта представляли для нас особый интерес, т.к. в одном из них может образоваться тройной отрицательный азеотроп, который до настоящего времени не обнаружен, в другом случае эволюция тройной биазеотропии проходит с образованием ТВТА.
Вариант, в котором один из двух тройных азеотропов является отрицательным узлом, должен удовлетворять условиям I : 1) T3 > TБ , TПФБ (третий компонент является тяжелокипящим); 2) Наличие точек Банкрофта 1 рода r11 в бинарных составляющих Б – 3, ПФБ - 3; 3) TПФБ – 3 > TПФБ - Б (третий компонент образует с ПФБ отрицательный азеотроп, кипящий в начале эволюции при более высокой температуре, чем отрицательный азеотроп ПФБ-Б); 4) TБ – 3 > TПФБ - Б (третий компонент образует с Б положительный азеотроп, кипящий в начале эволюции при более высокой температуре, чем положительный азеотроп ПФБ-Б). При этих условиях, как видно из диаграммы P = f (T) (рис. 12), неизбежно появление точек Банкрофта r22 между бинарными положительными азеотропами и r22 ’ между бинарными отрицательными азеотропами, приводящих к образованию двух тройных азеотропов (C2 и N2 ).
Из многочисленных вариантов, в которых обязательно образование двух тройных азеотропов с эволюцией их в ВТА, выбран в качестве примера вариант, удовлетворяющий условиям II : 1) T3 > TБ , TПФБ (третий компонент является тяжелокипящим); 2) Отсутствие точек Банкрофта 1 рода r11 в бинарных составляющих Б - 3, ПФБ – 3; 3) TПФБ – Б < TБ - 3 , TПФБ - 3 (положительный азеотроп ПФБ-Б в начале эволюции является более легкокипящим, чем положительные азеотропы ПФБ - 3 и Б - 3). В этом варианте образование седловинного азеотропа обусловлено точкой Банкрофта азеотропа ПФБ - 3 с Б (r12 ) либо с положительным азеотропом ПФБ – Б (r22 ). Образование второго тройного азеотропа связано с точкойБанкрофта второго рода между положительными азеотропами ПФБ - Б и Б – 3 (r22 ’) (рис.13).
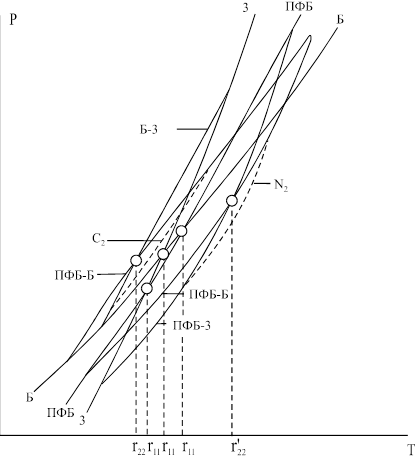
Рис. 12. Диаграмма P = f (T) системы ПФБ – Б – 3, удовлетворяющей условиям I.------ — тройные азеотропы
В итоге тяжелокипящим компонентом (3) в системе, удовлетворяющей условию I (рис. 12), выбран метилпропионат (МП); в системе, удовлетворяющей условию II (рис. 13) – третичный амиловый спирт (ТАС).
В четвертой главе с целью подтверждения результатов теоретического анализа проведено расчетное исследование азеотропии в двух тройныхсистемах ПФБ – Б – МП и ПФБ – Б – ТАС в широком диапазоне давлений.

Рис. 13. Диаграмма P = f (T) системы ПФБ – Б – 3, удовлетворяющей условиям II
Характеристики бинарных азеотропов определяли из данных по ПЖР, полученных по модели UNIFAC в программной реализации CHEMCAD. Затем при каждом выбранном давлении оценивали малые параметры уравнения Вильсона, которые использовали для определения состава и температуры кипения бинарных и тройных азеотропов. Задача решалась с применением пакета программ SIMRED-R, входящего в АСНИ МИТХТим. М.В. Ломоносова. При расчете характеристик тройных азеотропов важно правильно выбрать начальное приближение. Знание эволюции тройного азеотропа позволяет обоснованно сделать такой выбор. Оптимальной является следующая последовательность операций. Сначала проводится предварительный расчет для ориентировочного определения давления, при котором появляется тройной азеотроп. При этом в качестве начального приближения задается состав тройного раствора, близкий к составу сопряженного бинарного азеотропа, являющегося либо конечной, либо начальной точкой эволюции, лучше начальной. После определения этого давления проводится серия расчетов характеристик тройного азеотропа, причем при каждом последующем давлении в качестве начального приближения задаются характеристики тройного азеотропа, полученные на предыдущем этапе.
Парожидкостное равновесие в бинарной системе ПФБ - Б изучено многими исследователями в диапазоне давлений 106-900 мм рт. ст. Определение малых параметров уравнения Вильсона по этим данным показало, что по одним из них плохо предсказываются характеристики азеотропов, по другим описывается только один азеотроп в системе. Таким образом, имеющиеся экспериментальные данные не позволяют получить надежные параметры модели Вильсона при различных давлениях. Кроме того, использование экспериментальных данных разных авторов, характеризующихся большим разбросом, может в дальнейшем привести к некорректным результатам при расчете тройной биазеотропии. На рис. 14 приведены полученные нами расчетные составы двух бинарных азеотропов ПФБ - Б при различных давлениях и для сравнения экспериментальные данные, представленные в литературе. Средняя разница между экспериментальными и расчетными значениями состава пара и температуры кипения составляет для положительного азеотропа Δ yср. = 1,5% мол., Δ t ср. = 0,15о C, для отрицательного азеотропа Δ yср. = 1,7% мол., Δ t ср. = 0,14о C. Такая точность может считаться вполне удовлетворительной, особенно учитывая тот факт, что например, при 760 мм рт. ст. максимальная разница в составах азеотропов по данным различных авторовсоставляет 3,0% мол. для положительного азеотропа и 6,1% мол. для отрицательного.
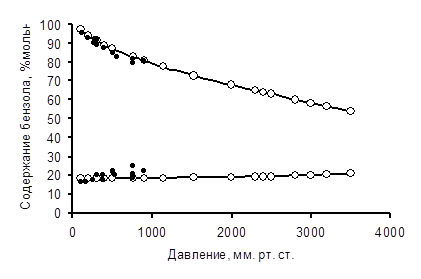
Рис. 14. Изменение составов положительного (1) и отрицательного (2) азеотропов ПФБ – Б в зависимости от давления
На рис. 15 приведена полученная нами зависимость составов тройных и сопряженных им бинарных азеотропов от давления в системе ПФБ – Б – МП. Расчеты тройной азеотропии проведены при 14-ти значениях давления в диапазоне 100-3500 мм рт. ст.
Как и предполагалось, ПФБ образует отрицательный азеотроп с МП, а между четырьмя бинарными азеотропами попарно имеются точки Банкрофта r22 , приводящие к образованию двух тройных азеотропов – отрицательного (N2 ) и седловинного (C2 ).
В тройной системе ПФБ – Б – ТАС спирт образует положительные азеотропы с Б и ПФБ. Расчетные данные показали, что в этой системе имеется 8 точек Банкрофта различного рода (рис. 12). Первым в системе появляется тройной седловинный азеотроп (C2 ). Появление второго тройного азеотропа – узлового (N2 ) - обусловлено точкой Банкрофта второго рода между азеотропами ПФБ - Б и Б - ТАС. При повышении давления оба тройных азеотропа двигаются навстречу друг другу и сливаются с образованием ТВТА (рис. 16). Расчеты тройной азеотропии проведены при 12 значениях давления в диапазоне 40-600 мм рт. ст.
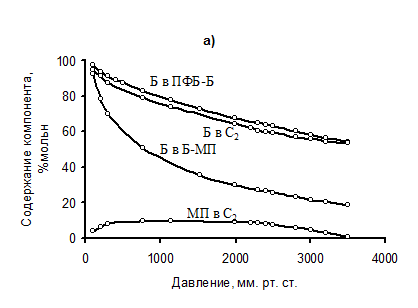

Рис. 15. Составы тройных седловинного (а), узлового (б) и бинарных азеотропов в системе ПФБ – Б – МП при различных давлениях
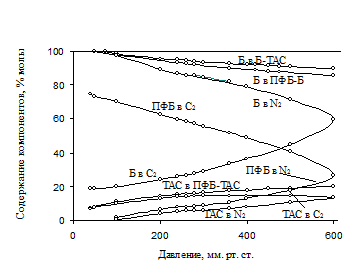
Рис. 16. Составы бинарных и тройных азеотропов в системе ПФБ – Б – ТАС при различных давлениях
На диаграмме P = f (T) имеются все точки Банкрофта, наличие которых является достаточным условием такого типа эволюции тройной биазеотропии, сформулированном при теоретическом анализе. После достижения точек Банкрофта r23 ’ (т.8 на рис. 12) и r23 ” (т.9 и т.10 на рис. 12) наблюдается нетривиальное соотношение между температурами кипения тройных и бинарных азеотропов, полностью идентичное аналогичным закономерностям эволюции бинарной биазеотропии.В диссертации приведены цепи преобразования структур диаграмм ПЖР и единичных K-линий в обеих тройных системах в расчетном диапазоне давлений, здесь же показаны диаграммы обеих тройных систем с двумя тройными азеотропами (рис. 17).

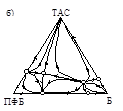
Рис. 17. Диаграммы дистилляционных линий систем класса 3.4.2 – 2 при Р = 2400 мм. рт. ст. (а) и класса 3.4.2. – 2 при Р = 500 мм. рт. ст.
Таким образом, сформулированные при теоретическом анализе закономерности эволюции тройных биазеотропов, условия их образования и возникновения ТВТА позволили однозначно синтезировать диаграммы конкретных тройных систем с двумя тройными азеотропами и нашли полное подтверждение при расчетном исследовании.
Значительная информативность диаграмм P = f (T) в плане предсказания образования тройных азеотропов и оптимизации диаграмм ПЖР при изменении давления является основанием для включения их в базовую информацию, необходимую для технолога при предпроектной разработке технологических схем разделения промышленных смесей.
Выводы
1. Осуществлено дальнейшее развитие термодинамико-топологического анализа диаграмм парожидкостного равновесия, заключающееся в распространении ТТА на тройные биазеотропные системы.
2. Синтезированы 64 диаграммы дистилляционных линий и 144 диаграммы единичных K-линий трехкомпонентных систем с моноазеотропными бинарными составляющими, содержащих два тройных азеотропа.
3. Выявлено значительное число диаграмм подобных систем с нетривиальным ходом дистилляционных и единичных K-линий, не характерным для тройных систем с одним тройным азеотропом.
4. Показано, что нетривиальный ход указанных линий характерен для систем, в которых возникновение или исчезновение тройной биазеотропии проходит через стадию образования тройного внутреннего тангенциального азеотропа.
5. Установлены основные типы эволюции двух тройных азеотропов при изменении давдения.
6. На основании закономерностей эволюции тройной биазеотропии предсказано наличие двух тройных азеотропов в системах перфторбензол – бензол – метилпропионат и перфторбензол – бензол – третичный амиловый спирт, подтвержденное расчетным исследованием в широком диапазоне давлений.
7. Сформулированы достаточные условия образования тройного внутреннего тангенциального азеотропа.
8. В связи со значительной информативностью диаграмм зависимостей P = f (T) для компонентов и азеотропов рекомендовано включать их в базовую информацию при предпроектной разработке технологических схем разделения промышленных смесей.
Основные результаты работы изложены в следующих публикациях:
1. Л.А. Серафимов, Т.М. Кушнер, Т.В. Челюскина Термодинамико-топологический анализ диаграмм парожидкостного равновесия в тройных системах с двумя тройными азеотропами // Вопросы термодинамики гетерогенных систем и теории поверхностных явлений. Издательство С.-Петербургского университета. – 1996. – вып. 10. – с. 26-55
2. Т.М. Кушнер, Т.В. Челюскина, Л.А. Серафимов. Термодинамико-топологический анализ диаграмм равновесия пар-жидкость в тройных системах с двумя тройными азеотропами // Журн. физ. химии. - 1999. - Т. 73, № 3. – с. 426-434
3. Т.В. Челюскина, Т.М. Кушнер. Диаграмма парожидкостного равновесия в системе бензол – перфторбензол – метилпропионат с двумя тройными азеотропами // Журн. физ. химии. - 2001. - Т. 75, № 7 – с. 1324-1330
Условные обозначения:
T – температура, о C;
P – давление, мм рт. ст.;
x – состав жидкой фазы, мол. дол.;
r – точка Банкрофта;
i, j, 1,2,3 – индексы компонентов;
K 1 , K 2 , K 3 – коэффициент распределения между паровой и жидкой фазами компонентов 1, 2, 3, соответственно;
N – особая точка типа «узел»;
С – особая точка типа «седло».