Главная / Рефераты / Промышленность, производство

Презентация: Теория надежности как наука и техническая дисциплина

ТЕОРИЯ НАДЕЖНОСТИ

• Теория надежности — наука, изучающая закономерности отказов технических систем.

Изучает:

• критерии и показатели надежности технических систем различного назначения;

• методы анализа надежности в процессе проектирования и эксплуатации технических систем;

• методы синтеза технических систем;

• пути обеспечения и повышения надежности технических систем ;

• научные методы эксплуатации техники, обеспечивающие ее высокую надежность.

ТЕОРИЯ НАДЕЖНОСТИ

Теория надежности как наука и техническая дисциплина имеет ряд особенностей:

-трудный для изучения предмет - широкое использование математики;

-случайный характер отказов и восстановлений. Эта особенность приводит к тому, что любые решения задач надежности имеют вероятностный характер;

-трудность математического моделирования объектов из-за отсутствия достоверных данных о надежности элементов системы, в частности, данных о законах распределения отказов и восстановлений;

-трудность, а во многих случаях невозможность статистических испытаний из-за технических и экономических ограничений;

-сложность современных систем и, как результат, большие размерности уравнений;

-необходимость применения компьютерных технологий решения практических задач.

ТЕОРИЯ НАДЕЖНОСТИ

Процессы, протекающие в сложных технических системах, в смысле их надежности, закономерны и не зависят от вида техники.

Разработанные в теории надежности методы анализа, синтеза, способы повышения надежности и научные методы эксплуатации техники являются общими для любых технических систем.

Технические системы с позиции надежности — это объект системного анализа.

Надежность технических систем зависит от многих факторов; критерии и показатели надежности устанавливаются в зависимости от вида технических систем и их применения; обеспечение надежности в процессе эксплуатации определяется системой обслуживания, квалификацией обслуживающего персонала, экономическими соображениями.

Надежностью называется свойство технического объекта сохранять свой характеристики (параметры) в определенных пределах при данных условиях эксплуатации.

Надежность — понятие объективное, независимое от нашего сознания.

Термины и определения

• Элемент — объект (материальный, информационный), обладающий рядом свойств, внутреннее строение (содержание) которого значения не имеет , т.е. рассматриваемый в данной задаче как нечто целое, неделимое.

В теории надежности под элементом понимают элемент, узел, блок, имеющий показатель надежности, самостоятельно учитываемый при расчете показателей надежности системы.

Примеры технических элементов: реле, датчик, линия связи, регулятор, регистрирующий (показывающий) прибор, исполнительный механизм, микроконтроллер, автоматическая система регулирования.

• Хк - вектор контролируемых (измеряемых) переменных;

• Хнк - вектор неконтролируемых (ненаблюдаемых) переменных;

• У - вектор выходных переменных.

• Каждая переменная y _i характеризует то или иное свойство элемента.

Термины и определения

Во время эксплуатации элемента имеют место случайные и регулярные изменения Хк и Хнк, что ведет к вариациям компонент у _i вектора Y во времени t.

При проектировании и изготовлении элемента устанавливают диапазон возможных (допустимых) изменений координат вектора Хк при некотором "обычном" уровне помех Хнк.

Термины и определения

Автоматическая система регулирования

Д - датчик; Р - регулятор; ИМ - исполнительный механизм; РО - регулирующий орган; ЛС1 ЛС2 - линии связи; ТОУ - технологический объект управления.

Множества X и Y для АСР

Термины и определения

• Система — совокупность связанных между собой элементов, обладающий свойством, отличным от свойств отдельных ее элементов.

Понятия элемента и системы трансформируются в зависимости от решаемой задачи.

Практически любой объект с определенной точки зрения может рассматриваться как система.

Структура системы — взаимосвязи и взаиморасположение составных частей системы, ее устройство.

Расчленение системы на группы элементов может иметь материальную, функциональную, алгоритмическую и другую основу.

Обычно понятие структура связывают с ее графическим отображением.

В зависимости от связей между элементами различают следующие виды структур: последовательные, параллельные, с обратной связью, сетевые и иерархические.

основных понятий и определений

Технический объект в процессе функционирования может находиться в различных состояниях.

Исправность — состояние объекта, при котором он соответствует всем требованиям, установленным нормативно-технической документацией (НТД).

Технический элемент считается исправным, если при нормальном режиме эксплуатации Хк Î Х имеет место допустимая работа элемента у Î Y , т.е. выполняются все неравенства:

y_I ^- ≤ y_I ≤ y_I ⁺ , i=1,n

Работоспособность — состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров, установленных НТД.

Технический элемент считается работоспособным, если при нормальном режиме эксплуатации Хк Î Х имеет место допустимая работа элемента у Î Y , т.е. выполняются все неравенства:

y _j ^- ≤ y _j ≤ y _j ⁺ , j=1,n

основных понятий и определений

Понятие исправности шире, чем понятие работоспособности.

Работоспособный объект обязан удовлетворять лишь тем требованиям НТД, выполнение которых обеспечивает нормальное применение объекта по назначению.

Работоспособная система удовлетворяет только тем требованиям, которые существенны для функционирования, и может не удовлетворять прочим требованиям (например, по сохранности внешнего вида элементов). Система, находящаяся в исправном состоянии, заведомо работоспособна.

Если объект неработоспособен, то это свидетельствует о его неисправности. С другой стороны, если объект неисправен, то это не означает, что он неработоспособен.

основных понятий и определений

Событие, заключающееся в нарушении работоспособности системы, т. е. в переходе ее из работоспособного в неработоспособное состояние, называется отказом .

Событие, заключающееся в переходе системы из исправного в неисправное, но работоспособное состояние, называется повреждением .

Восстановлением называется событие, заключающееся в переходе системы из неработоспособного в работоспособное состояние.

В связи с этим, объекты могут быть:

- невосстанавливаемые, для которых работоспособность в случае возникновения отказа не подлежит восстановлению, т.е. восстановление объекта непосредственно после отказа считается нецелесообразным или невозможным;

- восстанавливаемые, работоспособность которых может быть восстановлена, в том числе и путем замены.

основных понятий и определений

Один и тот же объект в различных условиях применения может быть отнесен к невосстанавливаемым (например, если он расположен в необслуживаемом помещении, куда запрещен доступ персонала во время работы технологического агрегата) и к восстанавливаемым, если персонал сразу же после отказа может начать восстановление.

Само понятие «восстановление» следует понимать не только как корректировку, настройку, пайку или иные ремонтные операции по отношению к тем или иным техническим средствам, но и как замену этих средств.

В принципе подавляющее большинство систем, применяемых для автоматизации технологических процессов, подлежит восстановлению после отказа, после чего они вновь продолжают работу. То же относится к большей части технических средств; к числу невосстанавливаемых можно отнести только такие их элементы, как интегральные схемы, резисторы, конденсаторы и т. п.

основных понятий и определений

Отказ

Отказом называется событие, после возникновения которого характеристики технического объекта (параметры) выходят за допустимые пределы.

Это понятие субъективно, т. к. допуск на параметры объекта устанавливает пользователь.

• По типу отказы подразделяются на:

-отказы функционирования, при которых прекращается выполнение объектом основных функций;

-отказы параметрические , при которых параметры объекта изменяются в недопустимых пределах.

• По своей природе отказы могут быть:

-случайные, обусловленные непредусмотренными перегрузками, дефектами материала, ошибками персонала, сбоями системы управления и т. п.;

-систематические , обусловленные закономерными явлениями, вызывающими постепенное накопление повреждений: усталость, износ, старение, коррозия материалов и т. п.

Отказ

• По виду отказы подразделяются на:

-зависимые отказы нескольких элементов вызваны одной ошибкой (дефектом);

Например, одновременное погасание осветительных ламп в жилом доме может быть вызвано отказом общего предохранителя на все здание.

-независимые отказы разных элементов вызваны разными причинами (ошибками), при этом вероятность одновременных отказов пренебрежимо мала;

-устойчивые отказы не исчезают сами по себе; после устойчивого отказа элемент заменяется на новый или ремонтируется;

-неустойчивые (перемежающиеся) отказы могут самопроизвольно исчезать, а затем возникнуть снова, ибо причина их не устранена.

Отказ

По характеру возникновения отказы могут быть:

- внезапный отказ — отказ, проявляющийся в резком (мгновенном) изменении характеристик объекта.

Внезапные отказ обычно проявляются в виде механических повреждений элементов (пробои изоляции, обрывы и т. п.) и не сопровождаются предварительными видимыми признаками их приближения. Внезапный отказ характеризую независимостью момента наступления от времени предыдущей работы, непрогнозируемый.

Отказ

-постепенный отказ —отказ, происходящий в результате медленного, постепенного ухудшения характеристик объекта из-за износа и старения материалов.

Характер изменения координаты y,(t) позволяет прогнозировать момент отказа элемента по тренду y,{t)

-перемежающиеся отказ - отказ самоустраняющийся (возникающий/исчезающий).

Отказ

• По причине возникновения отказы могут быть:

- конструкционный отказ- отказ появляющийся в результате недостат- ков и неудачной конструкции объекта;

- производственный отказ- отказ связан с ошибками при изготовлении объекта по причине несовершенства или нарушения технологии;

-эксплуатационный отказ – отказ, вызванный нарушением правил эксплуатации объекта.

• По признаку дальнейшего использования объекта отказы могут быть полные или частичные.

-полный отказ исключает возможность работы объекта до его устранения.

-частичный отказ –отказ при котором объект может частично использоваться.

• По признаку легкости обнаружения отказы бывают очевидные (явные) и скрытые (неявные).

• По времени возникновения отказы подразделяются на приработочные, возникающие в начальный период эксплуатации, отказы при нормальной эксплуатации, износовые отказы, вызванные необратимыми процессами износа , деталей, старения материалов и т.п.

основных понятий и определений

Рассмотрим элемент, начинающий функционировать в момент времени t=0, причем в этот момент элемент находится в работоспособном состоянии.

Предположим сначала, что элемент отключается только вследствие отказа. Обозначим через Т время, прошедшее от момента начала функционирования.

основных понятий и определений

Поток отказов называется стационарным, если вероятностные характеристики не зависят от времени.

В частности, закон распределения числа отказов на произвольном отрезке времени не зависит от его расположения на оси времени, а зависит только от длины отрезка.

основных понятий и определений

Величина t_j зависит от случайных отклонений технологических условий изготовления элементов от номинальных, различия условий транспортировки, монтажа, наладки и не будет одинаковой у различных элементах даже при абсолютно одинаковых условиях эксплуатации. К тому же сами условия эксплуатации (температура, вибрация, качество технического обслуживания, частота включения и т. д.) в определенной степени отличны друг от друга, поэтому величина t_j случайная.

Наработка до отказа в отличие от времени безотказной работы не всегда измеряется единицами времени; наработка до отказа может измеряться и числом включений (срабатываний, циклов). Однако для большей части систем наработка до отказа измеряется единицами времени.

основных понятий и определений

Наработка — продолжительность или объем работы объекта, измеряемые единицами времени, числом циклов нагружения, километрами пробега и т. п.

Наработка между отказами — наработка объекта от окончания восстановления его работоспособного состояния после отказа до возникновения следующего отказа.

Технический ресурс — наработка объекта от начала его эксплуатации (или ее возобновления после ремонта) до перехода в предельное состояние. Технический ресурс может быть также регламентирован, например, от начала эксплуатации до среднего или капитального ремонта, или от среднего до капитального ремонта, после которого требуется продление технического ресурса. Если регламентация отсутствует, то имеется в виду ресурс от начала эксплуатации до достижения предельного состояния после всех видов ремонтов.

Для невосстанавливаемых объектов понятия технического ресурса и наработки до отказа совпадают.

основных понятий и определений

• Назначенный ресурс — суммарная наработка объекта, при достижении которой эксплуатация должна быть прекращена независимо от его состояния.

• Срок службы — календарная продолжительность эксплуатации (в том числе хранение, ремонт и т. п.) от ее начала до наступления предельного состояния.

Для большинства объектов электромеханики в качестве критерия долговечности чаще всего используется технический ресурс.

• Время восстановления работоспособного состояния — продолжительность восстановления работоспособного состояния объекта.

основных понятий и определений

Безотказность — это способность объекта непрерывно сохранять работоспособность в течение некоторого времени.

Ремонтопригодность — способность объекта, заключающаяся в его приспособленности к предупреждению и обнаружению причин возникновения отказов, поддержанию и восстановлению работоспособного состояния путем проведения ремонтов и технического обслуживания.

Долговечность — способность объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.

Сохраняемость - свойство технического объекта сохранять свои характеристики (параметры) в процессе хранения.

Классификация технических систем

• Технические системы могут быть невосстанавливаемыми и восстанавливаемыми, длительного и короткого времени работы, резервированными и нерезервированными.

• Техническая система называется невосстанавливаемой (неремонтируемой), если ее отказ приводит к неустранимым последствиям и систему нельзя использовать по своему назначению. Работа после отказа невосстанавливаемой системы считается невозможной или нецелесообразной.

• Под восстанавливаемой (ремонтируемой) понимается система, которая может продолжать выполнение своих функций после устранения отказа, вызвавшего прекращение ее функционирования. Работа восстанавливаемой системы после отказа может быть возобновлена в результате проведения необходимых восстановительных работ. При этом под восстановлением системы понимается не только ремонт тех или иных элементов системы, а также полная замена отказавших элементов на новые.

• Существуют системы смешанного типа, у которых часть элементов может восстанавливаться, а другая — нет.

Классификация технических систем

• Резервированием называют способ повышения надежности путем включения резервных единиц, способных в случае отказа основного устройства выполнять его функции.

• Три метода резервирования: общей, раздельный (поэлементный) и комбинированный (смешанный).

-общим называется такое резервирование системы, при котором параллельно включаются идентичные системы;

-раздельным называется резервирование системы путем использования отдельных резервных устройств;

-при комбинированном резервировании в одной и той же системе применяется общее и раздельное резервирование.

Отношение числа резервных устройств к числу основных называется кратностью резервирования.

Если это отношение — число целое, то такое резервирование называется резервированием с целой кратностью, иначе — с дробной кратностью.

Классификация технических систем

Главными способами включения резервных устройств при отказах основных являются следующие:

- постоянное , при котором резервные объекты соединены с основными в течение всего времени работы;

- замещением , при котором резервные объекты замещают основные только после отказа последних.

При этом в обоих случаях резервные объекты могут находиться в трех режимах работы:

- нагруженн ом, при котором резервные объекты находятся в тех же условиях, что и основные;

- ненагруженном , при котором резервные объекты не включены и не могут отказывать;

- облегченном , при котором резервные объекты включены, но работают не на полную нагрузку, т. е. их надежность в резервном состоянии выше, чем в рабочем. Однако отказ элементов возможен.

КРИТЕРИИ НАДЕЖНОСТИ

Критерием называется признак (мерило), по которому оценивается надежность. Например, вероятность безотказной работы P(t), интенсивность отказов λ (t), средняя наработка на отказ Т .

Показателем надежности называется численное значение критерия.

Надежность является сложным физическим свойством, поэтому не существует одного обобщающего критерия и показателя.

Только семейство критериев позволяет оценить надежность сложных технических систем.

Критерии надежности невосстанавливаемых элементов

Невосстанавливаемые элементы работают до первого отказа.

Длительность безотказной работы J –го элемента есть наработка t_j до первого отказа.

В эксперименте над N одинаковыми элементами к моменту времени t,

0<t≤t _m , получены:

N(t) – число исправных элементов;

N – N(t) – число отказавших элементов;

ΔN – число отказов на малых отрезках времени Δt, расположенных на [0, t _m ];

t _m – длительность эксперимента, завершающегося при отказе всех N элементов

Функция ненадежности элемента

Q(t) = [N-N(t)] / N = 1 – N(t)/N – статистическая функция распределения отказов.

Доля или частота отказавших к моменту t элементов от общего их числа N

Критерии надежности невосстанавливаемых элементов

Интегральный закон распределения вероятностей отказов элемента до некоторого момента времени t Q(t)=Q (T<t)- функция ненадежности элемента .
Вероятность того, что элемент откажет в течение времени t или что время его работы до отказа меньше времени его функционирования Т

Функция ненадежности - в общем случае неубывающая непрерывная функция времени t , 0≤ t ≤ ∞.

Статистическая функция ненадежности Q( t ) является кусочно-постоянной неубывающей функцией времени.

Q(t) - неслучайная, a Q(t) - случайная функция.

В реальных условиях функция Q(t) нам не известна и мы всегда работаем с ее

оценкой Q(t).

0≤Q(t)≤1 Q(0)=0 Q(∞)=1

Критерии надежности невосстанавливаемых элементов

• Функция надежности элемента

Вероятностью безотказной работы называется вероятность того, что элемент не откажет в течение времени t или что время его работы до отказа больше времени его функционирования Т

Р(t) = P(T>t)

Вероятность безотказной работы является убывающей функцией времени, имеющей следующие свойства:

Критерии надежности невосстанавливаемых элементов

• Вероятность безотказной работы имеет следующие достоинства:

- характеризует надежность во времени, являясь интервальной оценкой;

- определяет многие важные показатели техники, например эффективность, безопасность, живучесть, риск;

- сравнительно просто вычисляется и определяется по статистическим данным об отказах техники;

- достаточно полно характеризует надежность невосстанавливаемой техники.

• Основной недостаток этого критерия — ограниченность применения.

Вероятность безотказной работы характеризует надежность невосстанавливаемого элемента или восстанавливаемого до первого его отказа.

Критерии надежности невосстанавливаемых элементов

• Интенсивность отказов

Функция интенсивности отказов

λ(t) = f(t) / P(t)

представляет условную плотность вероятности отказа элемента в момент t при условии, что до этого времени элемент не отказал.

Функцию интенсивности отказов λ(t) обычно называют лямбда-характерис

тикой.

Статистическая лямбда-характеристика определяется по результатам испытаний N одинаковых элементов на надежность:

гдеΔN – число отказов на интервала времени Δt;

N(t) – число отказавших элементов

Интенсивность отказов

Интенсивность отказов является основным показателем надежности элементов сложных систем. Это объясняется следующими обстоятельствами:

-надежность многих элементов можно оценить одним числом, т. к. интенсивность отказа элементов — величина постоянная;

-по известной интенсивности наиболее просто оценить остальные по
казатели надежности как элементов, так и сложных систем;

-обладает хорошей наглядностью;

-интенсивность отказов нетрудно получить экспериментально.

• Опыт эксплуатации сложных систем показывает, что изменение интенсивности отказов большого количества объектов описывается U-образной кривой

Интенсивность отказов

• Период приработки объекта имеет повышенную интенсивность отказов, вызванную приработочными отказами, обусловленными дефектами производства, монтажа и наладки. Иногда с окончанием этого периода связывают гарантийное обслуживание объекта, когда устранение отказов производится изготовителем.

• В период нормальной эксплуатации интенсивность отказов практически остается постоянной, при этом отказы носят случайный характер и появляются внезапно, прежде всего из-за случайных изменений нагрузки, несоблюдения условий эксплуатации, неблагоприятных внешних факторов и т. п. Именно этот период соответствует основному времени эксплуатации объекта.

• Возрастание интенсивности отказов относится к периоду старения объекта и вызвано увеличением числа отказов из-за износа, старения и других причин, связанных с длительной эксплуатацией.

Интенсивность отказов

Из формул для вычисления оценок и следует, что

для всех t, t≠0. При t=0 функции λ(0)=f (0), так как N(0)=N.

Рассмотренная особенность верна и для неслучайных функций λ(t) и f (t):

λ(t)>f (t) при 0≤ t ≤ ∞ и λ(0)=f (0).

Знание функции интенсивности позволяет находить любые другие характеристики надежности.

Критерии надежности невосстанавливаемых элементов

Числовые показатели надежности

Функциональные показатели надежности Q(t), P(t), f(t), λ(t) наиболее полно описывают поведение случайной величины Т - наработки до отказа элемента. Однако получение этих характеристик или хотя бы статистических аналогов вызывает значительные трудности, обусловленные длительными экспериментами с большим числом элементов, сложной математической обработкой данных и проверкой гипотез согласия. Поэтому при решении прикладных задач надежности шире используют числовые показатели надежности, оценки которых получают экспериментальным данным более просто, чем оценки функциональные показателей.

Численные показатели надежности: средняя наработка до отказа, дисперсия наработки до отказа, гамма-процентный ресурс надежности.

Числовые показатели надежности

• Средняя наработка до отказа

Средним временем безотказной работы называется математическое ожидание времени безотказной работы элемента: t _н =М {T₁ }

t _н - средняя наработка до отказа,

M - символ операции "математическое ожидание".

Оценка средней наработки до отказа определяется по известным из эксперимента значениям наработки до отказа

^ 1 N

t _н = ----∑ t_j

_N _j=1

Числовые показатели надежности

• Дисперсия наработки до отказа

Величина характеризует разброс значений наработок до отказа относительно средней наработки t_н :

唴 δ² = M{(t - t_н )² } =∫ (t - t_н )² f (t)dt

Оценка дисперсии определяется по экспериментальным наработкам до отказа t _j j=1,N

Числовые показатели надежности

Гамма-процентный ресурс надежности

t _γ – γ –процентный ресурс – наработка, в течение которой элемент не достигает состояния отказа с вероятностью γ/ 100

Вычислим значения λ(t).

На первом участке произошел 1 отказ, при этом в начале участка число исправных элементов N(0)=N=100, а в конце участка N(100)=N-1=99

На втором участке

Вычислим среднее время безотказной работы

Задача №2

Из 1000 одновременно включенных однотипных элементов к моменту времени 500 отказало 500 элементов.

• Найти оценки интенсивности отказа и средней наработки до отказа элемента.

Основные законы распределения наработки до отказа

Поведение случайной величины - наработки до отказа Т - может быть описано тем или иным теоретическим законом распределения вероятностей Q(t) или P(t).

Установлено, что поведение наработки до отказа Т технических средств автоматизации удовлетворительно описывается следующими законами распределения:

- экспоненциальным;

- Вейбулла;

- нормальным;

- усеченным нормальным;

- суперпозицией указанных законов

Экспоненциальное распределение

• Экспоненциальное (показательное) распределение относится к однопараметровым законам распределения вероятностей.

Экспоненциальное распределение

Экспоненциальное распределение выделяется среди других распределений свойством "отсутствия памяти".

Пусть X — время службы некоторого изделия с экспоненциальным законом распределения. "Отсутствие памяти" означает, что изделие, проработавшее время t , имеет такое же распределение, что и новое, только что начавшее работу.

Математически это свойство выражается в виде следующего равенства:

P(X>t+x/X>t) =P(X>x)

для любых t, x≥0.

Данное свойство как бы исключает износ и старение изделия.

Экспоненциальное распределение

• Экспоненциальным законом распределения можно аппроксимировать время безотказной работы большого числа элементов. Экспоненциальный закон распределения хорошо описывает наработки до внезапного отказа сложных элементов, которые состоят из большого числа М разнородных деталей (частей) с интенсивностями λ_β (t), β=1,2,…,M, имеющими экстремумы в разные моменты времени t_β β=1,2, ….M.

Примерами таких элементов могут служить электронные устройства, средства вычислительной техники, пневмоавтоматики и другие ТСА.

Экспоненциальное распределение удовлетворительно описывает надежность ТСА, обладающих малым периодом приработки элементов и почти не достигающих периода старения (износа) из-за относительно быстрого морального износа и замены на более совершенные.

Экспоненциальное распределение

Во многих прикладных задачах требуется знание вероятности безотказной работы элемента P(t_1, t₂ ) на интервале времени (t_1, t₂ ) при условии, что элемент был исправен до момента t_1,

Распределение Вейбулла

Функциональные показатели надежности случайной величины подчиняются двухпараметровому распределению Вейбулла вида

Распределение Вейбулла

Для распределения Вейбулла средняя наработка до отказа определяется достаточно сложно:

где Г( ) - гамма-функция

Удобнее находить значения Г( ) по таблицам гамма-функций, имеющимся в большинстве математических справочников.

Нормальное распределение

Согласно закону больших чисел, распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы. При большом времени работы элемента и наличии восстановления среднее число отказов имеет асимптотически нормальное распределение.

Нормальный закон распределения вероятностей описывает поведение случайных величин в диапазоне [ -∞, +∞] и обладает функциональными характеристиками

Нормальное распределение

Усеченное нормальное распределение

Усеченное нормальное распределение получается из нормального при ограни- чении интервала изменения случайной величины на промежуток [0, + оо).

Суперпозиции экспоненциальных распределений

Для приближения статистических распределений сложного вида известными ("хорошими") теоретическими распределениями применяют суперпозиции экспоненциальных законов

где …………………………………. с₁ ,с₂ - весовые множители, с₁ +с₂ =1,

величина с₁ подбирается наряду с интенсивностями λ₁ λ₂ из условий близости статистической плотности f (t) и нового закона f _с (t). Для подобной суперпозиции имеем

Суперпозиции экспоненциальных распределений

Вариацией параметров λ₁ λ₂ , с₁ можно добиться хорошей аппроксимация статистических интенсивностей λ_с на периодах приработки элемента. Если положить λ₂ >> λ₁ , то при при больших t имеем λ_с (t) → λ₁

Ремонтопригодность технических элементов

Техническая система называется невосстанавливаемой (неремонтируемой), если ее отказ приводит к неустранимым последствиям и систему нельзя использовать по своему назначению. Работа после отказа невосстанавливаемой системы считается невозможной или нецелесообразной.

Под восстанавливаемой (ремонтируемой) понимается система, которая может продолжать выполнение своих функций после устранения отказа, вызвавшего прекращение ее функционирования. Работа восстанавливаемой системы после отказа может быть возобновлена в результате проведения необходимых восстановительных работ. При этом под восстановлением системы понимается не только ремонт тех или иных элементов системы, а также полная замена отказавших элементов на новые.

Ремонтопригодность технических элементов

Продолжительность ремонта t_j в есть значение случайной величины T _в -

длительности восстановления.

В общем случае процесс восстановления элемента можно разделить на три последовательные операции:

-обнаружение (проявление) отказа; осуществляется чаще всего человеком-оператором за случайное время t ^обн , реже – автоматическим устройством
сигнализации;

-ожидание ремонтного персонала; характеризуется случайным временем
ожидания t ^ож ;

-поиск ошибки (дефекта) элемента, вызвавшей его отказ, и собственно
ремонт, выполняется ремонтным персоналом за случайное время t_рем

t ^в = t ^обн + t ^ож + t ^рем

• В некоторых системах математическое ожидание времени восстановления M{t} может быть пренебрежимо мало (относительно, например, t_н элемента). Это имеет место при автоматическом обнаружении отказов, при хорошем функционировании ремонтной службы и при замене отказавших элементов на аналогичные исправные устройства.

Ремонтопригодность технических элементов

Режим функционирования с мгновенным восстановлением связан со значительным удорожанием системы так как предполагает автоматизацию обнаружения отказов, повышения качества работы ремонтного персонала и создания парка резервных элементов. Поэтому подобные режимы функционирования экономически оправданы при эксплуатации ответственных элементов, отказы которых ведут к возникновению аварийных ситуаций или значительному экономическому ущербу.

Для большинства задач по расчету надежности не удается обосновать допущение о мгновенности восстановления элементов и поэтому необходимо учитывать продолжительность восстановления T_в и вводить функциональные числовые показатели ремонтопригодности.

Функциональные показатели ремонтопригодности

Дифференциальный закон распределения вероятностей своевременного завершения ремонта или функция плотности вероятности восстановления отказавшего элемента.

f (t^в ) =dQ(t^в )/dt

Интенсивность завершения ремонта характеризуется условной вероятностью своевременного восстановления элемента при условии, элемент еще не восстановлен к этому моменту времени t.

µ(t^в )= f (t^в )/ P(t^в )

Функциональные показатели ремонтопригодности

Статистические распределения ремонтопригодности имеют вид

Функциональные показатели ремонтопригодности

Комплексные показатели ремонтопригодности и безотказности

Самовосстанавливающаяся система часть времени находится в работоспособном состоянии, а часть (иногда значительную) - в состоянии восстановления. Система считается тем лучшей, чем больше доля времени, когда она работоспособна или готова к выполнению своих функций.

Функция готовности Кг(t) есть вероятность того, что система будет работоспособной в произвольный момент времени t₀ . Если этот момент времени t₀ достаточно удален от нуля и в системе имеет место установившийся или стационарный режим функционирования, то функция готовности Кг(t) превращается в коэффициент готовности Кг, численно равный средней доле времени, когда система работоспособна, от общего времени ее эксплуатации

Комплексные показатели ремонтопригодности и безотказности

Отметим, что стационарный коэффициент готовности Кг не зависит от вида распределений случайных величин ТиТв

Комплексные показатели ремонтопригодности и безотказности

В некоторых случаях ремонтопригодность и безотказность элемента характеризуют коэффициентом простоя К п:

Комплексные показатели ремонтопригодности и безотказности

Коэффициент Ког(τ) убывает с ростом времени τ и почти всегда меньше Кг, только при τ=0 имеем Ког(0) = Кг

Существует ряд ТСА, которые периодически выводятся на время tпр из эксплуатации, например, для тарировки, профилактики и др. Это время вынужденного "простоя" элемента не связано непосредственно с его безотказностью и ремонтопригодностью и не учитывается при определении tн и tнв а следовательно, и Кг и Ког. Если tпр - случайная величина и ее M{ tпр } соизмеримо с tн и tнв, то безотказность и ремонтопригодность элемента с вынужденными простоями следует характеризовать коэффициентом технического использования

Определение показателей надежности элементов по результатам испытаний

Анализ надежности сложной системы осуществляется путем расчетов. Рассчитать надежность системы это значит определить ее показатели по известным показателям надежности элементов структурной схемы, которые можно получить лишь путем статистических экспериментов. Наука еще не разработала методов определения интенсивностей отказов элементов методами расчетов.

Основными целями испытания элементов и систем на надежность являются:

- подтверждение соответствия данных анализа, полученных в процессе проектирования системы, с требуемыми показателями надежности;

- разработка рекомендаций по технической эксплуатации системы;

- получение показателей надежности элементов с целью их использования при расчетах надежности технических систем в процессе проектирования.

Статистические распределения и оценки параметров определяют только по результатам испытаний элементов на надежность и ремонтопригодность.

Испытаниям могут подвергаться АСУ ТП в целом, их подсистемы, технические средства и любые другие элементы АСУ ТП.

По целевому назначению испытания подразделяют на определительные и контрольные.

• По месту проведения испытания подразделяют - на лабораторные и эксплуатационные.

Определительные испытания

Кроме того, определительные испытания позволяют выявить

-типичные причины отказа элементов и закономерности возникновения отказов;

-конструктивные, технологические и эксплуатационные факторы, влияющие на надежность;

-наименее надежные элементы, узлы, блоки, технические средства;

-разработка мероприятия и рекомендации по повышению надежности; уточнить продолжительности и объем технического обслуживания, количества запасных частей и др.

Определительные испытания чаще всего проводят в лабораторных условиях, реже - в условиях эксплуатации.

Определительные испытания

Испытаниям надежности в лабораторных условиях (лабораторные) обычно подвергаются технические средства и некоторые локальные системы. Эти испытания обычно выполняют на заводах-изготовителях или в организациях—разработчиках технических средств.

При лабораторных испытаниях можно имитировать воздействия внешней среды на систему, в первую очередь условия эксплуатации. Для этого служат специальные установки: термокамеры для изменения температуры, барокамеры для изменения давления, вибростенды для создания вибраций и т. д.

Лабораторные испытания могут проходить при тех же воздействиях (температуре, влажности, вибрации и т. д.) и режимах работы, которые обычно имеют место при эксплуатации.

Основными этапами определительных испытаний являются выбор плана экспериментов и математическая (статистическая) обработка полученных данных.

Перед началом испытаний необходимо выработать правило, согласно которому следует проводить испытания. Выработку такого правила будем называть планированием испытаний. Выбор плана диктуется целями поставленных испытаний.

Проведение испытаний на надежность связано со значительными затратами средств, поэтому планирование испытаний включает в себя определение объема выборки и критериев завершения испытаний исходя из заданной точности и достоверности их результатов.

Формируют выборку таким образом, чтобы результаты ее испытаний могли быть распространены на совокупность систем или средств. Например, при лабораторных испытаниях на заводе-изготовителе образцы для испытаний выбирают из числа принятых отделом технического контроля и прошедших приработку; для формирования выборки используют таблицу случайных чисел.

Испытания проводятся для тех же условий эксплуатации, при которых в технической документации установлены показатели надежности.

Во время испытаний проводятся периодические проверки функционирования, измерение параметров, определяющих отказы и техническое обслуживание.

Планом испытаний называют правила, устанавливающие объем выборки, порядок проведения испытаний и критерии их прекращения.

Наименование плана принято обозначать тремя буквами (цифрами): первая из них обозначает число испытываемых систем, вторая — наличие R или отсутствие V восстановлений на время испытаний в случае отказа, третья — критерий прекращения испытаний.

Наиболее распространенные планы испытаний.

План [ NV Т] соответствует одновременному испытанию N систем. Эти системы после отказа не восстанавливаются (или же восстанавливаются, но данные о их поведении после первого отказа в испытаниях не рассматриваются). Испытания прекращают по истечении наработки каждой отказавшей системы – рис.а

Этот план обычно применяют для определения вероятности безотказной работы системы за время Т.

План [ NVr ] соответствует испытаниям N таких же невосстанавливаемых систем, однако в отличие от плана [ NV Т] испытания прекращают, когда число отказавших систем достигает r . - рис. б, r -й отказ имеет место у i-й системы.

Если r = N , то переходим к плану [ NVN ], когда испытания прекращают после отказов всех систем.

План [ NVr ] обычно применяют для определения средней наработки до отказа в случае экспоненциального распределения.

План [ NVN ] —в случае нормального распределения.

Испытания по плану [ NVN ] требуют значительных времени и числа испытываемых систем, но дают возможность полностью определить эмпирическую функцию распределения.

Планы [ NVr ] и [ NV Т] позволяют определить эмпирическую функцию распределения только для некоторого интервала времени, дают меньше информации, зато позволяют быстрее закончить испытания.

План [ NR Т] описывает испытания N систем, причем отказавшие во время испытаний системы заменяют новыми или восстанавливают. Испытания прекращают по истечении наработки Т — рис.в.

План [ NRr ] соответствует испытаниям N систем, когда отказавшие во время испытаний системы заменяют новыми или восстанавливают. Испытания прекращают, когда суммарное по всем позициям число отказавших систем достигает r - рис. г.

Задачами планирования является определение минимального объема наблюдений—выбор числа испытываемых систем N , а также продолжительности наблюдений Т для планов [ NV Т] и [ NR Т] или числа отказов r для планов [ NVr ] и[ NRr ] .

Во всех рассмотренных планах главной задачей является выбор числа испытуемых элементов N и длительности эксперимента Т или числа r .

При выборе учитывают стоимость элемента, наличие специализированных лабораторных стендов, стоимость испытания одной элемента, предварительные знания вида распределения P ( t ), величин tн , λ и т.д.

Результатами определительных испытаний должны являться точечные и интервальные оценки показателей надежности.

Точечные оценки.

Понятие точечная оценка в математической статистике вводится следующим образом. Пусть имеются результаты k наблюдений над некоторой случайной величиной Т (например, временем безотказной работы) с функцией распределения F(t,ϑ) при этом параметр ϑ этого распределения неизвестен. Необходимо найти такую функцию ϑ=g(t₁ ,…,t_k ) результатов наблюдений t₁ ,…,t_k , которую можно было бы рассматривать как оценку параметра ϑ. При таком выборе функции g каждой совокупности(t₁ ,…,t_k ) будет соответствовать точка ϑ на числовой оси, которую называют точечной оценкой параметра ϑ.

Точечная оценка являющаяся функцией результатов наблюдений,— так же случайная величина со своим собственным законом распределения, зависящим от закона распределения случайной величины Т, объема наблюдений k и вида функции g .

Для одного и того же неизвестного параметра ϑ обычно можно принять несколько функций g которые могут служить в качестве оценки.

Выбор требований к таким оценкам (состоятельность, несмещенность, эффективность) и методов нахождения оценки (максимального правдоподобия, моментов, квантилей, графические) описан в книгах по теории вероятностей и математической статистике

Одним из распространенных планов испытаний является план [ NVN ] когда выбирается относительно большое (для ТСА) число однотипных элементов N , N>80-100, отказавшие в моменты t_j элементы не восстанавливают, сам эксперимент длится до отказа всех N элементов, т.е. Т - max t_j 1≤j ≤ N .

Проведение опытов и обработка данных t_j ,j=l,2,..., N при этом упрощаются, но длительность Т может оказаться большой, что удорожает испытание.

Далее определяются несмещенные состоятельные оценки параметров распределений:

Строятся графики статистических распределений оценок

При определении оценок параметров, кроме их точечных значений, часто требуются их интервальные оценки, характеризующие точность найденных величин и/или.

Эти так называемые доверительные интервалы δ₁ , δ₂ для t_н определяют из равенства

Вер {t_н - δ₁ < t_н < t_н + δ₂ }= P _дов

• где P _дов - доверительная вероятность, задаваемая при расчете обычно из диапазона (0,80; 0,90). Кроме того, при решении задачи выбирают закон распределения случайной величины (обычно - нормальный) и затем по таблицам интеграла Лапласа находят δ₁ = δ₂ = δ_. Таким образом, истинное значение параметра t_н определено с погрешностью и найдены «пессиместичес- кое» и «оптимистическое» граничные значения средней наработки до отказа. Величина δ₁ = δ₂ = δ зависит от числа N используемых наработок на отказ t_j . Естественно, при росте N погрешность δ убывает.

Контрольные испытания

Эти испытания предназначены для установления соответствия (несоответствия) фактических показателей надежности (безотказности) элементов некоторым нормативным требованиям, задаваемым техническими паспортами, регламентами, отраслевыми стандартами.

Контрольным испытаниям подвергают элементы, показатели надежности которых ранее были изучены, но к моменту испытаний могли измениться.

Поэтому периодически (для ответственных ТСА через 3-4 года) требуется достаточно быстро и экономно определить фактически существующие в момент t показатели, сравнить их с нормативными величинами и принять решение о надежности или ненадежности элемента.

Контрольные испытания

Методика контрольных испытаний заметно отличается от методики определительных экспериментов. В частности, контрольные испытания проводят на меньшем, чем в определительных опытах, числе элементов; при этом обычно непосредственно испытывают только часть элементов из большой партии однородных элементов; наконец, контрольные опыты прекращаются как только принимается решение о соответствии или несоответствии показателей надежности элементов нормативным требованиям.

Процедура контрольных испытаний и принятия решений такова.

Перед испытаниями формируется большая партия однородных элементов, из которой случайным образом составляется небольшая выборка элементов. Эта выборка и подвергается испытаниям, по результатам которых принимается решение о соответствии (или несоответствии) показателей надежности всей партии известным нормативным показателям.

Контрольные испытания

Для принятия решения вводится так называемая нулевая гипотеза Но о том, что по результатам испытаний выборки вся партия удовлетворяет нормативным требованиям (или, проще, "вся партия надежна"). Помимо Но, существует альтернативная гипотеза Н₁ о том, что по результатам испытаний выборки вся партия ненадежна.

По результатам испытаний и проверки гипотез Н₀ , Н₁ возможна одна из следующих четырех ситуаций.

• Фактически партия элементов надежна; по результа-
там испытаний выборки принято считать всю партию надежной (т.е. гипотеза Но подтверждена). Данное решение - правильное.

Контрольные испытания

• Фактически партия элементов надежна; по результатам испытаний выборки принята гипотеза H ₁ . Принятое решение:
считать всю партию элементов ненадежной. Вероятность принятия ошибочного решения (ошибки первого рода или ошибки изготовителя элементов) равна α, 0 ≤α<1. Иногда α называют риском изготовителя. Понятно,что α зависит от величины выборки, точнее, от соотношения объемов выборки и партии.

• Фактически партия ненадежна, по результатам испытания выборки гипотеза Но не получила подтверждения, поэтому принята гипотеза H ₁ и решение о ненадежности всей партии. Это решение - правильное.

• Фактически партия ненадежна, по результатам испытаний гипотезаH ₀ "случайно" подтверждена, поэтому принято решение считать всю партию надежной. Это решение ошибочно, здесь допущена ошибка второго рода,
невыгодная пользователю элементов. Вероятность этой ошибки (или риска) пользователя обозначают β. Величина β также зависит от объемов выборки и партии.

Контрольные испытания

Контрольные испытания предназначены для установления соответствия фактических показателей надежности элементов некоторым нормативным требованиям.

Контрольные испытания проводят на части элементов из большой партии однородных элементов;

-контрольные опыты прекращаются как только принимается решение о соответствии или несоответствии показателей надежности элементов нормативным требованиям.

Для принятия решения вводится так называемая нулевая гипотеза Но о том, что по результатам испытаний выборки вся партия удовлетворяет нормативным требованиям.

Контрольные испытания

Кроме Но, существует альтернативная гипотеза Н₁ о том, что по результатам испытаний выборки вся партия не удовлетворяет нормативным требованиям.

По результатам испытаний и проверки гипотез Н₀ , Н₁ возможна одна из следующих четырех ситуаций.

• Фактически партия элементов надежна; по результатам
испытаний выборки принято считать всю партию надежной (т.е. гипотеза Но подтверждена). Данное решение - правильное .

Контрольные испытания

• Фактически партия ненадежна, принята гипотеза H₁ и решение о ненадежности всей партии. Это решение - правильное.

• Фактически партия ненадежна, принята гипотеза H₀ и решение о надежности всей партии. Это решение ошибочно, здесь допущена ошибка второго рода, невыгодная пользователю элементов. Вероятность этой ошибки (или риска) пользователя обозначают β.

При контрольных испытаниях стремятся снизить риски производителя и пользователя α и β. В идеальном случае можно потребовать, чтобы α=0 и β=0 .

Контрольные испытания

Примем за основной контролируемый показатель надежности элемента среднюю наработку t_н и обозначим вероятность приемки партии через F , а нормативный показатель через t_н ^норм . Зависимость F от t_н получила название оперативная характеристика плана контроля. На рис. показана эта характеристика для идеального приемочного контроля F=1.

Контрольные испытания

• Пусть, например, необходимо получить значение интенсивности отказа элемента, если λ=10^-6 час^-1 . При постановке такого опыта необходимо провести испытание миллиона элементов в течение одного часа или тысячи элементов в течение тысячи часов, чтобы получить один отказ. При этом достоверность такого испытания до первого отказа будет практически нулевой. Для получения данных об интенсивности отказа элемента с необходимой точностью объем и время испытаний должны быть значительно выше.

• В целях сокращения объема и времени испытаний разрабатывались ускоренные методы. Технически такие испытания реализуются путем повышения нагрузок на элементы и создания тяжелых условий работы.

• При этом делается много допущений. Вот одно из них: законы распределений отказов элементов при увеличении нагрузки не меняются, изменяются лишь моменты законов, например среднее значение и дисперсия. Подобные допущения не доказываются и не проверяются. Поэтому получаемые модели неадекватны объекту.

• Анализируя современные методы испытания, убеждаемся, что в большинстве случаев в лабораторных условиях практически невозможно получить данные о надежности элементов, которые бы позволили с требуемой точностью определить законы распределения отказов и их параметры. Подобные испытания требуют такого объема и времени проведения, которые разработчик физически и экономически реализовать не может.

обработка данных
об отказах техники в процессе эксплуатации

Анализ потока отказов технических систем в процессе их эксплуатации, когда функционирует большое количество техники в течение длительного времени в реальных условиях эксплуатации.

Такие испытания называют эксплуатационными наблюдениями за функционированием системы "элемент - обслуживающий персонал".

Наблюдения заключаются в регистрации в эксплуатационных журналах наработок на отказ t_j и длительностей восстановления t_j ^в одного и того же восстанавливаемого элемента или ряда однородных элементов. Для элементов с мгновенным восстановлением регистрируются только наработки до отказа t_j

Накопленные данные используются для нахождения "эксплуатационных" оценок и др.

обработка данных
об отказах техники в процессе эксплуатации

• Эксплуатационные наблюдения длятся обычно достаточно долго (особенно при малом числе подконтрольных элементов), поэтому при их проведении важен мониторинг условий работы элементов.

• Оценки показателей надежности и ремонтопригодности, полученные по результатам наблюдений за элементом на конкретном "рабочем месте", справедливы только для аналогичных условий применения элементов. Использование элементов в других условиях эксплуатации требует определения новых поправочных множителей Кп и пересчета найденных по эксплуатационным данным оценок показателей надежности и ремонтопригодности. При этом наибольшие затруднения возникают с пересчетом показателей ремонтопригодности существенно зависящих от характеристик обслуживающего персонала.

Надежность технических систем
Надежность простых технических систем
Основные понятия и классификация

Техническая система состоит из двух и более элементов,

взаимодействующих между собой при достижении той

или иной цели.

Система называется простой, если ее функционирование

можно описать конечным набором координат

y₁ (t), y₂ (t),…., y_i (t),…, y_n (t),

и ввести понятие работоспособности:

-система работоспособна (исправна) в момент времени t,

если при допустимых воздействиях x_к Î X справедливы

условия нормальной работы

y_i ^- ≤ y_i (t) ≤ y_i ⁺ , i=1,2,…,n

Надежность технических систем
Надежность простых технических систем

и понятие отказа:

система отказала (неисправна), если при x_к Î X нарушено хотя бы одно условие нормальной работы, т.е. имеет место

y_i (t) < y_i ^- или y_i (t) > y_i ⁺ , i=1,2,…,n

где y_i ^- , y_i ⁺ — заранее заданные границы области нормальной работы системы.

Сложная система - система для которой не удается ввести строгие понятия работоспособности и отказа и указать объективные значения y_i ^- ,y_i ⁺ , i=1,2,…,n и конечное натуральное число п.

Надежность технических систем

Формально понятия "отказ" и "работоспособность" простой системы совпадают с аналогичными понятиями технического элемента.

Простая система после ее отказа в случайный момент t_j заменяют на исправную ("мгновенное восстановление") или ремонтируют некоторое случайное время t_j ^в или снимают с эксплуатации (не восстанавливают).

Поведение восстанавливаемой простой системы характеризуют случайными величинами:

-наработка на отказ Т с реализацией {t_j j=1,2,…,N}

-длительность восстановления T^В с реализацией

{t_j ^в j=1,2,…,N}.

Надежность простых технических систем

Для невосстанавливаемой простой системы используют только случайную величину Т с реализацией {t_j j=1,2,…,N}.

Математическое описание поведения случайных величин Т и T^В

технического элемента и простой системы идентично:

P(t), f (t),λ(t), t_н ,Q(t^в ), μ(t^в ), t_н ^в , К_г , К_ог

Надежность простых технических систем

Элемент называется избыточным или резервным, если его отказ не ведет к отказу системы (формально резервный элемент -"лишний" и его можно удалить в целях упрощения системы и снижения ее стоимости).

Система, содержащая только основные элементы, называется безызбыточной или нерезервированной системой.

Система, содержащая избыточные элементы, является избыточной или резервированной.

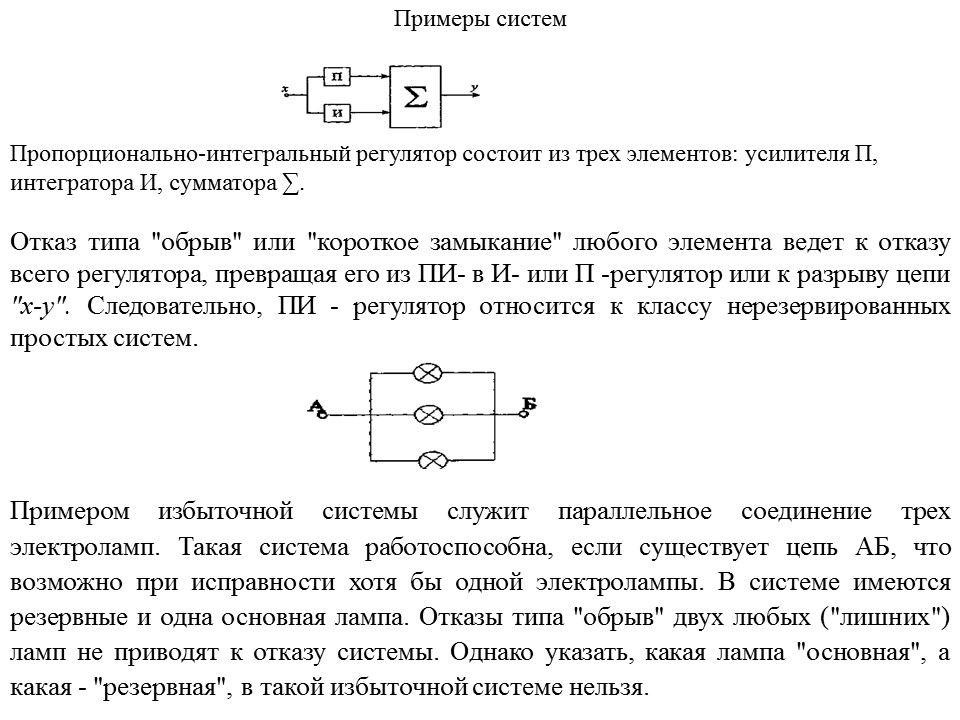
Примеры систем.

Примеры систем

Способы описания функционирования технических систем в смысле их надежности

Существуют следующие способы описания функционирования технической системы в смысле ее надежности:

- Структурная схема;

- Функции алгебры логики;

- Граф состояний;

- Дифференциальные и алгеброические уравнения;

- Интегральные уравнения.

Структурные схемы надежности систем

Из структурных схем наглядно видны условия работоспособности. Система на рис. работоспособна, если все ее элементы исправны. Отказ любого элемента нарушает работоспособность системы, наступает ее отказ.

Система на рис. работоспособна, если исправным является элемент 1 и любой один элемент дублированных пар, а также два любых элемента из трех резервированных с дробной кратностью т = 1/2 .

Структурные схемы надежности систем

При исследовании надежности простых систем используют графические представления функций и взаимосвязей элементов. При составлении надежностной структурной схемы некоторой системы все ее элементы соединяются между собой в цепи той или иной формы в зависимости от влияния элемента на работоспособность системы в целом. Так, если система безызбыточна, то ее структурная надежностная схема представляет собой последовательное соединение квадратиков-элементов с их номерами, именами или определяющими показателями надежности.

Примеры структурных надежностных схем безызбыточных систем

Структурные схемы надежности систем

На такой схеме не проставляют каких-либо стрелок, так как формально здесь нет передачи сигналов.

При анализе последовательного соединения служит аналогия с последовательным соединением электроламп: отказ типа "обрыв" i-го элемента ведет к отказу всей цепи АБ, по которой не будет протекать электроток.

Структура системы с избыточностью отображается надежностной схемой параллельного соединения элементов.

Показано несколько вариантов избыточных систем, считающихся работоспособными, если существует цепь АБ:

- резервированная система из двух элементов с разными
интенсивностями отказов λ₁ и λ₂ ;

-два последовательно включенных элемента с интенсивностями
отказов λ₁ и λ₂ резервируются третьим элементом с
интенсивностью отказа λ₃ ;

-два последовательно включенных элемента с интенсивностями
отказов λ₁ и λ₂ резервируются каждый индивидуально
элементами с интенсивностями отказов λ₃ и λ₄ .

Структурные схемы надежности систем

При составлении структурных надежностных схем следует иметь в виду, что они не всегда совпадают с функциональными схемами системы.

Например - ПИД -регулятор имеет следующую функциональную схему.

Функциональная схема ПИД - регулятора

У - усилитель; И - интегратор; Д - дифференциатор; ∑ - сумматор сигналов

Структурная схема надежности безызбыточного ПИД - регулятора

Структурные схемы надежности систем

Общая процедура построения структурных надежностных схем технических систем такова:

1). На физическом уровне проводится анализ функционирования технической системы и понятий "отказ" и "работоспособность".

2). Выделяются существенные (для конкретной задачи) элементы системы, каждому из которых присваивается имя или номер (условное обозначение).

3). Составляется традиционная функциональная схема системы, на которой с помощью стрелок показаны направления передачи информации и/или субстанции (связи между именованными элементами).

Структурные схемы надежности систем

4). На физическом уровне выполняется последовательный анализ влияния отказа (типа "обрыв" и/или КЗ) каждого элемента на работоспособность всей технической системы; цель анализа заключается в выявлении основных элементов и числа резервных элементов.

5). Составляется структурная схема надежности, на которой вначале все основные физические элементы изображаются в форме последовательно соединенных (линиями без стрелок) "прямоугольников", а затем к ним добавляются параллельно подключенные резервные элементы.

Каждому "прямоугольнику" на надежностной схеме присваивается имя или номер соответствующего элемента, при этом общее число "прямоугольников" должно быть равно количеству физических элементов.

Структурные схемы надежности систем

6). По надежностной схеме проверяется влияние отказов каждого элемента ("прямоугольника") на отказ всей схемы.

Количество основных и резервных элементов на надежностной и функциональной схемах должно быть одинаковым.

Построенная подобным образом структурная надежностная схема используется при анализе (синтезе) и расчете надежности простых технических систем.

Надежность нерезервированных систем

Надежность нерезервированных систем

Задача анализа безызбыточной системы заключается в определении

одной из ее характеристик P_с (t), f _с (t),λ_с (t), t_нс по известным показателям P_i (t), f_i (t),λ_i (t), t_н _i i=1,2,…,m.

Эта задача сводится к нахождению вероятности произведения независимых случайных событий -безотказностей элементов.

Согласно теореме о произведении независимых случайных событий

вероятность P_с (t) равна произведению вероятностей P_i (t) i=1,2,…,m.

Надежность нерезервированных систем

где λ_с (t) -интенсивность отказа системы

Надежность нерезервированных систем

Для повышения надежности нерезервированной системы следует:

• уменьшать число основных элементов m (там, где это возможно);

• применять равнонадежные элементы (напомним, что P_с (t) не
может быть больше функции P_i (t), самого ненадежного элемента);

• находить самый ненадежный элемент (с наибольшим λ_i (t) и
заменять его другим элементом с меньшим λ_i (t);

• использовать при конструировании системы более надежные
элементы с меньшими λ_i (t) .

Надежность нерезервированных систем

Нерезервированные системы часто применяют при автоматизации ТОУ, в частности при построении локальных АСР и информационных каналов АСУТП.

АСР, состоящая из датчика Д, нормирующего преобразователя НП, линий связи ЛС₁ и ЛСг ЛС₂ , задатчика ЗД, элемента сравнения ЭС, регулятора Р, исполнительного механизма ИМ, регулирующего органа РО.

Резервирование

Для повышения надежности систем и элементов применяют резервирование, основанное на использовании того или иного вида избыточности.

Разновидности резервирования: функциональное, временное, информационное, структурное.

Функциональное резервирование - резервирование для многофункциональных систем, выполняющих близкие функции.

Так, значение температуры пара на выходе котлоагрегата может быть определено по показаниям потенциометра, осуществляющего в комплекте с термоэлектрическим преобразователем и с помощью вызова этого параметра на экран монитора БЩУ.

Резервирование

Временное резервирование заключается в том, что допускается перерыв функционирования системы или устройства из-за отказа элемента. Временное резервирование осуществляется за счет введения аккумулирующих емкостей, из-за аккумулирующей способности технологического объекта.

Кратковременный перерыв в подаче топлива не приведет к прекращению генерации пара из-за аккумуляции теплоты поверхностям нагрева котлоагрегата.

Резервирование

Информационное резервирование связано с возможностью компенсации потери информации по одному каналу информацией по другому.

На большинстве технологических объектов, благодаря внутренним связям, имеет место информационная избыточность, которая часто используется для оценки достоверности информации.

Усредненный расход пара на выходе котла соответствует усредненному расходу воды на его входе, расход газа на котле определяет расход воздуха при фиксированном составе дымовых газов.

Для локальных систем наиболее характерно структурное резервирование. При использовании последнего повышение надежности достигается путем введения дополнительных элементов в структуру системы.

Резервирование

Резервированием называют способ повышения надежности путем включения резервных единиц, способных в случае отказа основного устройства выполнять его функции.

Три метода резервирования: общей, раздельный (поэлементный) и комбинированный (смешанный).

-общим называется такое резервирование системы, при котором параллельно включаются идентичные системы;

-раздельным называется резервирование системы путем использования отдельных резервных устройств;

Резервирование

Отношение числа резервных устройств к числу основных называется кратностью резервирования.

Главными способами включения резервных устройств при отказах основных являются следующие:

- постоянное , при котором резервные объекты соединены с основными течение всего времени работы;

- замещением , при котором резервные объекты замещают основные только после отказа последних.

Резервирование

Резервные объекты могут находиться в трех режимах работы: нагруженном, ненагруженном, облегченном

- нагруженном , при котором резервные объекты находятся в тех же условиях, что и основные.

В системе с нагруженным резервом все элементы постоянно находятся в работе и не делятся на основные и резервные.

При отказе одного из элементов система продолжает функционировать, при этом не требуется вводить в работу какие - либо дополнительные устройства, т.е. в системе с "горячим" резервом нет перерывов на подготовку и включение резервных элементов.

Резервирование

В промышленности и коммунальном хозяйстве широко применяются насосные станции для нагнетания жидкости в напорный коллектор НК

Резервирование

В общем случае структурная надежностная схема нагруженной системы из m элементов имеет вид.

Резервирование

Системы с недогруженным резервом имеют основной элемент, находящийся в работе до момента отказа t_j , и запасной или "холодный" (т.е. не готовый к работе). Этот элемент включается в работу автоматически или вручную после момента времени t_j .

Помимо основного и резервного (одного или нескольких) элементов в ненагруженной системе должны быть: контрольное устройство для определения момента отказа t_j , управляющее устройство для вывода из системы отказавшего элемента и ввода в момент времени t_j +τ, τ>0 в эксплуатацию резервного элемента.

Резервирование

При автоматическом обнаружении отказа и выводе-вводе элементов время простоя системы [t_j , t_j +τ] может быть малым относительно t^c _н и не учитываться при анализе функционирования нагруженной системы. При визуальном обнаружении отказа и ручном выводе-вводе элементов время простоя системы τ может быть значительным, что снижает качество функционирования нагруженной системы.

Резервирование

Системы с ненагруженным резервом достаточно широко применяются в различных отраслях промышленности, преимущественно в тех ситуациях, где удается реализовать надежный автоматический контроль отказов основных элементов и уменьшить время простоя τ .

Резервные объекты могут находиться в трех режимах работы: нагруженном, ненагруженном, облегченном

- облегченном , при котором резервные объекты включены, но работают не на полную нагрузку, т. е. их надежность в резервном состоянии выше, чем в рабочем. Однако отказ элементов возможен.

Системы с облегченным или "теплым" резервом содержат основной элемент, функционирующий до своего отказа в случайный момент t_j , и резервный элемент, подготовленный ("прогретый") к быстрому включению в работу в момент t_j +τ по сигналу устройства контроля отказов.

Резервирование

Термин "подготовленный" или "теплый" элемент означает частичное подключение резервного элемента или его эксплуатацию в режиме малой нагрузки ("холостой ход").

Главная цель использования облегченного резерва - значительное уменьшение времени простоя системы τ и соответственное увеличение коэффициента готовности.

Вместе с тем резервный элемент "стареет" и его надежностные характеристики ухудшаются (по сравнению с ненагруженным резервом). Возрастают при облегченном резерве и эксплуатационные расходы.

Резервирование

Поскольку структурное резервирование сопряжено с дополнительными затратами на резервные элементы, то последние должны окупаться за счет повышения надежности системы и снижения потерь от ее отказов.

Оценим качество резервированной системы набором показателей: время простоя τ, затраты капитальные ЗК и эксплуатационные ЗЭ, средняя наработка на отказ резервируемой системы t^c _н , средняя наработка на отказ нерезервируемой системы t^c _ннер , коэффициент готовности К г.

Резервирование

Наиболее простыми для определения показателями эффективности резервирования являются следующие:

В_t = t^c _н / t^c _ннер , В_p =P_н / P_{нер ,} В_Q =Q_н / Q_нер

где В_t —выигрыш за счет повышения средней наработки до отказа резервированной системы по сравнению с наработкой нерезервированной системы;

В_p ,В_Q — аналогичные показатели по повышению вероятности безотказной работы и снижению вероятности отказа.

Резервирование эффективно, если значение показателей В_t ,В_p ,В_Q больше единицы.

Введем нижние индексы, показывающие принадлежность к режиму резервирования:

• нр - нагруженный резерв,

• ннр - ненагруженный резерв,

• ор - облегченный резерв.

Резервирование

Сравнительный анализ эффективности функционирования систем с разными режимами резервирования

Резервирование

При нагруженном (горячем) резерве интенсивность отказов основного λ_о и резервного λ_г элементов одинакова, λ_о = λ_г .

У облегченного (теплого) резерва интенсивность отказов резервных элементов λ_об ниже, чем у основных работающих, λ_о > λ_об .

При ненагруженном (холодном) резерве вероятностью отказов элементов в состоянии резерва пренебрегают, λ_ох =0

Обобщенно с позиции надежности можно считать режим нагруженного резервирования наиболее тяжелым, а "холодного" резервирования - самым легким (при абсолютной надежности контролирующих и управляющих устройств); с экономической точки зрения наиболее выгодным считается нагруженный (иногда облегченный) режим резервирования ответственных элементов.

Резервирование

Основным способом повышения надежности является структурное резервирование. При этом наиболее эффективным считается раздельное (поэлементное) резервирование. Такой вывод следует из теории. Он безусловно верен, но без учета практической реализуемости раздельного резервирования.

Пусть необходимо защитить систему управления от отказа дифференцирующей цепи, обеспечивающей устойчивость системы.

Надежность систем с нагруженным резервом

Локальные системы включают в свой состав элементы, имеющие различный вид резерва, то для расчета надежности систем рассмотрим методы расчета надежности элементов при различных способах резервирования.

Простейший вариант этой задачи — определение показателей безотказности систем, содержащих резервированные невосста-навливаемые элементы.

Резервированная система состоит из т элементов с показателями надежности Q_i (t), P_i (t),λ_i (t),t_н _i i=1,2,…,m. Система работоспособна, если исправен один и более элементов, система находится в состоянии отказа при выходе из строя всех т элементов.

Надежность систем с нагруженным резервом

Структурная надежностная схема системы

Надежность систем с нагруженным резервом

На практике наиболее часто имеют место случаи, когда основная система и нее резервные одинаковы и имеют вероятность безотказной работы P(t)

P_c (t)=1-(1-P(t))ⁿ

Надежность систем с нагруженным резервом

Для экспоненциального закона распределения наработок имеем

Расчетные формулы для случая равнонадежных систем и постоянной интенсивности отказов элементов λ₁ =λ₂ =λ_m . В этом случае вероятность безотказной работы системы определяется по формуле:

Надежность систем с нагруженным резервом

Графики показывают, что постоянное резервирование эффективно на начальном участке работы системы, когда t≤τ

Надежность систем с нагруженным резервом

Из приведенного анализа следует, что с увеличением числа т резервных элементов наблюдается заметное снижение эффективности резервирования системы и прямо пропорциональное увеличение ее стоимости.

На практике чаще всего встречаются системы с одним или, реже, с двумя резервными элементами (т-2 или 3).

Резервирование

Расчет надежности локальных технических систем

Расчет надежности системы с двумя нагруженными элементами

В этой системе всего два элемента с интенсивностями отказов λ₁ и λ₂

Расчет надежности системы с двумя нагруженными элементами

Для равнонадежных элементов с λ₁ и λ₂ =λ

P_c (t)= 2P(t)-P² (t)=2e ^– ^λ ^t - e ^–2 ^λ ^t

Расчет надежности системы с двумя нагруженными элементами

Для равнонадежных элементов с λ₁ и λ₂ =λ

Расчет надежности системы с тремя нагруженными элементами

В системе имеется три элемента с интенсивностями λ₁ , λ₂ , λ₃

Расчет надежности системы с тремя нагруженными элементами

На втором этапе рассмотрим структурную схему расчета надежности

Расчет надежности системы с тремя нагруженными элементами

Средняя наработка на отказ системы

Расчет надежности системы с групповым нагруженным резервом

Средняя наработка на отказ системы с групповым резервом

Расчет надежности системы с индивидуальным резервом

Разделим систему на две подсистемы с номерами I и II

Расчет надежности системы с индивидуальным резервом

Для системы из равнонадежных элементов

Анализ эффективности систем с групповым и индивидуальным резервом

Введем критерий эффективности систем

Варианты I, II, III совпадают у обеих систем. Но система с индивидуальным резервом имеет еще два дополнительных варианта работоспособности IV и V.

При любых сочетаниях интенсивностей система с индивидуальным резервом более надежна, чем система с групповым резервом. Это утверждение справедливо при любом числе резервируемых элементов в обеих схемах.