| Скачать .docx | Скачать .pdf |
Курсовая работа: Привод к ленточному конвейеру для подачи формовочной земли в литейный цех
Московский Государственный Технический Университет МАМИ Кафедра «Детали машин и ПТУ» Курсовой проект
г. Москва 2002 год |
МГТУ «МАМИ» Кафедра «Детали машин и ПТУ»
Техническое задание на курсовой проект ДМ-ЗА
Тема: СПРОЕКТИРОВАТЬ ПРИВОД К ЛЕНТОЧНОМУ КОНВЕЙЕРУ ДЛЯ ПОДАЧИ ФОРМОВОЧНОЙ ЗЕМЛИ В ЛИТЕЙНЫЙ ЦЕХ
Задание:
РАЗРАБОТАТЬ;
1. Редуктор цилиндрический
2. Рабочие чертежи деталей;
3.  Муфту предохранительную;
Муфту предохранительную;
| ВАРИАНТ | 2 | |
| Натяжение ветвей конвейера | F1 , кН | 7,0 |
| F2 , кН | 2,6 | |
| Скорость ленты | V, м/с | 1,3 |
| Диаметр барабана | D, м | 0,5 |
| Ширина барабана | В, м | 0,6 |
| Высота центра приводного вала | Н, м | 0,7 |
| Ресурс работы, тыс. час. | Lh | 13,0 |
4. Приводной вал транспортера с барабаном и опорами; 5 Монтажный чертеж привода.
РЕЖИМ НАГРУЖЕНИЯ:

СОДЕРЖАНИЕ
ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ И КИНЕМАТИЧЕСКИЙ
РАСЧЁТ
РАСЧЁТ 1-Й ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
РАСЧЁТ 2-Й ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
РАСЧЁТ 3-Й ЦЕПНОЙ ПЕРЕДАЧИ
ПРЕДВАРИТЕЛЬНЫЙ РАСЧЁТ ВАЛОВ
КОНСТРУКТИВНЫЕ РАЗМЕРЫ ШЕСТЕРЕН И КОЛЁС
ПРОВЕРКА ПРОЧНОСТИ ШПОНОЧНЫХ (ШЛИЦЕВЫХ)
СОЕДИНЕНИЙ
КОНСТРУКТИВНЫЕ РАЗМЕРЫ КОРПУСА РЕДУКТОРА
![]()
![]() РАСЧЕТ РЕАКЦИЙ В ОПОРАХ
РАСЧЕТ РЕАКЦИЙ В ОПОРАХ
ПРОВЕРКА ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
УТОЧНЁННЫЙ РАСЧЁТ ВАЛОВ
ТЕПЛОВОЙ РАСЧЁТ РЕДУКТОРА
ВЫБОР СОРТА МАСЛА
ВЫБОР ПОСАДОК
КРАТКОЕ ОПИСАНИЕ ТЕХНОЛОГИИ СБОРКИ
РЕДУКТОРА
РАСЧЁТ ПРЕДОХРАНИТЕЛЬНОЙ МУФТЫ
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ И КИНЕМАТИЧЕСКИЙ РАСЧЕТ
КПД
По табл. 1.1 [1] примем следующие значения КПД:
- для закрытой зубчатой цилиндрической передачи: ηЗ1 = 0,97
- для закрытой зубчатой цилиндрической передачи: ηЗ2 = 0,97
- для открытой цепной передачи: ηЦ = 0,93 Общий КПД привода: η = ηЗ1 •ηЗ2 •ηЦ = 0,849
КПД подшипников учтено в КПД передач Угловая скорость на выходном валу: ωвых = 2•V/D = 5,2 рад/с
Требуемая мощность двигателя:
Pтреб = F•V/η = 6,739 кВт
В таблице П.1 [1](см. приложение) по требуемой мощности выбираем электродвигатель 132S4 ,с синхронной частотой вращения 1500,0 мин-1 , с параметрами: Pдв = 7,5 кВт и скольжением 3,0 % (ГОСТ 19523-81). Номинальная частота вращения Nдв = 1500,0-
1500,0•3,0/100= 1455,0 мин-1 , угловая скорость ωдв = π•Nдв / 30 = 152,367 рад/с.
общее передаточное отношение:
U = ωдв /ωвых = 29,301
Для передач выбрали следующие передаточные числа:
U1 = 3,55
U2 = 4,0
![]()
![]() U3
= 2,1
U3
= 2,1
Рассчитанные частоты и угловые скорости вращения валов:
| Вал 1-й | n1 = nдвиг = 1455,0 мин-1 . | ω1 = ωдв = 152,367 рад/c. |
| Вал 2-й | n2 = n1 /U1 = 409,859 мин-1 | ω2 = ω1 /U1 = 42,92 рад/c. |
| Вал 3-й | n3 = n2 /U2 = 102,465 мин-1 | ω3 = ω2 /U2 = 10,73 рад/c. |
| Вал 4-й | n4 = n3 /U3 = 48,793 мин-1 | ω4 = ω3 /U3 = 5,11 рад/c. |
Вращающие моменты на валах:
T1 = Pтреб /ω1 = 44230,684 Н•мм
T2 = T1 •U1 = 157018,93 Н•мм
T3 = T2 •U2 = 628075,72 Н•мм
T4 = T3 •U3 = 1318959,012 Н•мм
2. РАСЧЕТ 1-Й ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками (см. гл.3, табл.3.3 [1]): Для шестерни:
сталь: 45 термическая обработка: улучшение
твердость: HB 210 Для колеса: сталь: 40Л
термическая обработка: улучшение твердость: HB 180
Допустимые контактные напряжения (формула (3.9) [1]) , будут:
[σh] = σh_lim_b•KHL/[Sh], K - коэффициент долговечности. HL
[Sh ] - коэффициент безопасности.
По таблице 3.2 гл. 3 [1] имеем: для сталей с твердостью поверхностей зубьев менее HB 350:
σh_lim_b = 2•HRC + 70,
[Sh ]= 1.1;
![]() 6
N
6
N
HO
KHL = √ NHE
где N - базовое число циклов нагружения; для данных сталей
HO N = 17000000;
HO
N = 60•n•c• Lh•K = 797966741,25
HE HE
здесь: n - частота вращения шестерни, мин-1 .; c = 1,0 - число колёс, находящихся в зацеплении Lh = 13000 часов - срок службы передачи
KHE = Σ [(Mi /Mmax )3 •(ti /Lh)•(ni /nMmax )] = 0,234375 K - дополнительный множитель для эквивалентной циклической долговечности.
HE
В итоге получаем К = 0,527
HL
![]()
![]() Т.к. КHL< 1,0 , то принимаем КHL
= 1,0 для шестерни — [σh-1
] = 490,0 МПа; для колеса — [σh-2
] = 430,0 МПа.
Т.к. КHL< 1,0 , то принимаем КHL
= 1,0 для шестерни — [σh-1
] = 490,0 МПа; для колеса — [σh-2
] = 430,0 МПа.
Для косозубых колес расчетное допустимое контактное напряжение находим по формуле 3.10 гл.3 [1]:
[σh ] = 0,45•([σh-1 ] + [σh-2 ])
Тогда расчетное допускаемое контактное напряжение:
[σh ] = 376,364 МПа.
Требуемое условие выполнено: [σh ] < 1,23•[σh-2 ]
Принимаем коэффициент симметричности расположения колес относительно опор по таблице 3,5 [1]: Khb = 1,25.
Коэффициент ширины венца по межосевому расстоянию принимаем: ψba = b/aω = 0,4 , (см. стр.36 [1]). Межосевое расстояние
из условия контактной выносливости активных поверхностей зубьев по формуле 3.7 гл.3
[1]:
![]()
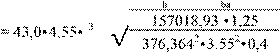 3 √T2•Khb =
3 √T2•Khb =
aω = Ka•(U + 1)•2•U2•ψ
[σ ]
= 127,211 мм.
где для косозубых колес Ка = 43,0, а передаточное число нашей передачи U = 3,55 Ближайшее значение межосевого расстояния по ГОСТ 2185-66 будет: aω = 125,0 мм.
1-й вариант расчёта модуля
Нормальный модуль зацепления берем по следующей рекомендации: mn = (0,01...0,02)•aw мм, для нас: mn = 1,25... 2,5 мм, принимаем:
по ГОСТ 9563-60 (см. стр. 36[1]) mn = 1,375 мм.
Принимаем предварительно угол наклона зубьев β = 10° и определим числа зубьев шестерни и колеса (см. формулу 30,16[1]):
z1 = 2•aw •сos(β)/((U + 1)•mn ) = 2•125•cos10°/(4,55•1,375) = 39 z2 = 3,55•z1 = 138
Уточненное значение угла наклона зубьев будет:
сos(β) = (z1 + z2 )•mn /(aw •2) = (39 +138)•1,375/(125•2) = 0,9735 β = 13,2198°
Основные размеры шестерни и колеса: диаметры делительные:
d1 = mn •z1 /сos(β) = 1,375•39/0,9735 = 55,085 мм; d2 = mn •z2 /сos(β) = 1,375•138/0,9735 = 194,915 мм.
Проверка: aw = (d1 + d2 )/2 = (55,085 + 194,915)/2 = 125,0 мм. диаметры вершин зубьев:
![]()
![]() da1
= d1
+ 2•mn
= 55,085 + 2•1,375 = 57,835 мм; da2
= d2
+ 2•mn
= 194,915 + 2•1,375 197,665 мм. ширина колеса: b2
= ψba
•aw
= 0,4•125 = 50,0 мм; ширина шестерни: b1
= b2
+ 5 мм = 50 + 5 = 55,0 мм; Определим коэффициент ширины шестерни по диаметру: ψb_d
= b1
/d1
= 55/55,085 = 0,998 Окружная скорость колес будет:
da1
= d1
+ 2•mn
= 55,085 + 2•1,375 = 57,835 мм; da2
= d2
+ 2•mn
= 194,915 + 2•1,375 197,665 мм. ширина колеса: b2
= ψba
•aw
= 0,4•125 = 50,0 мм; ширина шестерни: b1
= b2
+ 5 мм = 50 + 5 = 55,0 мм; Определим коэффициент ширины шестерни по диаметру: ψb_d
= b1
/d1
= 55/55,085 = 0,998 Окружная скорость колес будет:
V = ω1 •d1 /2 = 152•55,085•10-3 /2 = 4,197 м/c;
При такой скорости следует принять для зубчатых колес 8-ю степень точности. Коэффициент нагрузки равен:
Kh = Khb•Kha•Khv.
Коэффициент Khb = 1,11 выбираем по таблице 3.5[1], коэффициент Kha = 1,084 выбираем по таблице 3.4[1], коэффициент Khv = 1,02 выбираем по таблице 3.6[1], тогда: Kh = 1,227
Проверку контактных напряжений
проводим по формуле![]()
σh = ![]() ω b2
•U2
=
ω b2
•U2
=
= ![]() = 366,572 МПа. ≤ [σh
]
= 366,572 МПа. ≤ [σh
]
Силы действующие в зацеплении вычислим по формуле 8.3 и 8.4[1]:
окружная : Ft = 2•T2 /d2 = 2•157018,93/194,915 = 1605,914 Н; радиальная: Fr = Ft •tg(α)/cos(β) = 1605,914•tg20°/cos13,2198°= 600,416 Н; осевая : Fa = Ft•tg(β) = 600,416 •tg13,2198°= 377,249 Н.
Проверим зубья на выносливость по напряжениям изгиба по формуле 3.25[1]:
σF = Ft •Kf •Yf •Yβ •Kf α /(b•mn ) ≤ [σF ]
Здесь коэффициент нагрузки Kf = Kfb •Kfv (см. стр. 42[1]).
По таблице 3.7[1] выбираем коэффициент расположения колес Kfb = 1,23, по таблице 3.8[1] выбираем коэффициент Kfv = 1,3.
Таким образом коэффициент Kf = 1,598.
Yf - коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа zv (см. гл.3, пояснения к формуле 3.25[1]): у шестерни : zv1 = z1 /cos3 (β) = 42,272 у колеса : zv2 = z2/cos3 (β) = 149,579
Тогда : Yf1 = 3,691
Yf2 = 3,575
Допускаемые напряжения находим по формуле 3.24[1]:
[σf] = [σ°f_lim_b]KFL/[Sf].
K - коэффициент долговечности.
FL
![]() 6
N
6
N
FO
KFL = √ NFE
где N - базовое число циклов нагружения; для данных сталей N = 4000000;
FO FO
N = 60•n•c•Lh•K = 776697187,50
FE FE
здесь: n - частота вращения шестерни, мин-1 .; c = 1,0 - число колёс, находящихся в
зацеплении; Lh= 13000,0 - пордолжительность работы передачи в расчётный срок службы, ч.
![]()
![]() KFE = Σ[(Mi
/Mmax
)3
•(ti
/tΣ)•(ni
/nMmax
)] = 0,234375 - дополнительный множитель для эквивалентной циклической долговечности.
KFE = Σ[(Mi
/Mmax
)3
•(ti
/tΣ)•(ni
/nMmax
)] = 0,234375 - дополнительный множитель для эквивалентной циклической долговечности.
В итоге получаем К = 0,258
FL
Т.к. К <1,0 , то принимаем К = 1,0
FL FL
Для шестерни: [σ°f_lim_b ] = 378,0 МПа; для колеса : [σ° f_lim_b ] = 342,0 МПа.
Коэффициент [Sf ] безопасности находим по формуле 3.24[1]:
[Sf ] = [Sf `]•[Sf ``].
где для шестерни [Sf `] = 1,75 ;
[Sf ``] = 1,0 ; для колеса [Sf `] = 1,75 ; [Sf ``] = 1,0,
Допускаемые напряжения:
для шестерни: [σf_1 ] = 216,0 МПа; для колеса : [σf_2 ] = 195,429 МПа; Находим отношения [σf ]/Yf : для шестерни: [σf_1 ]/Yf1 = 58,522 для колеса : [σf_2 ]/Yf2 = 54,662
Дальнейший расчет будем вести для колеса, для которого найденное отношение меньше. Определим коэффициенты Yb и Kfa (см.гл.3, пояснения к формуле 3.25[1]):
Yb = 1 - β/140 = 0,906
Kf α = (4 + (εα -1)•(n - 5))/(4•εα )
Для средних значений торцевого перекрытия εα = 1,5 и для 8-й степени точности Kf α = 0,92.
Проверяем прочность зуба колеса по формуле 3.25[1]:
σf_2 = (Ft •Kf •Yf •Yb •Kfa )/(b2 •mn ) ≤ [σf ] σf_2 = 11,211 МПа < [σf ] = 195,429 МПа. Условие прочности выполнено.
2-й варинт расчёта модуля
Нормальный модуль зацепления берем по следующей рекомендации: mn = (0,01...0,02)•aω мм, для нас: mn = 1,25... 2,5 мм, принимаем:
по ГОСТ 9563-60 (см. стр. 36 [1]) mn = 2,0 мм.
Принимаем предварительно угол наклона зубьев β = 10° и определим числа зубьев шестерни и колеса (см. формулу 3.16 [1]):
z1 = 2•aω •сos(β)/((U + 1)•mn ) = 2•125•cos10°/(4,55•2,0) = 27 z2 = U•z1 3,55•27 = 96
Уточненное значение угла наклона зубьев будет:
сos(β) = (z1 + z2 )•mn /(aω •2) = (27 + 96)•2,0/(125,0•2) = 0,9840 β = 10,2631°
Основные размеры шестерни и колеса:
диаметры делительные:
d1 = mn •z1 /сos(β) = 2,0•27/cos10,2631° = 54.878 мм; d2 = mn •z2 /сos(β)= 2,0•96/cos10,2631° = 195,122 мм.
![]()
![]() Проверка: aω
= (d1
+ d2
)/2 = (54,878 + 195,122)/2 = 125,0 мм. диаметры вершин зубьев:
Проверка: aω
= (d1
+ d2
)/2 = (54,878 + 195,122)/2 = 125,0 мм. диаметры вершин зубьев:
da1 = d1 + 2•mn = 54,878 + 2•2,0 = 58,878 мм; da2 = d2 + 2•mn = 195,122 + 2•2,0 = 199,122 мм. ширина колеса: b2 = ψba •aω = 0,•125 = 50,0 мм; ширина шестерни: b1 = b2 + 5 мм = 50,0 + 5 = 55,0 мм; Определим коэффициент ширины шестерни по диаметру: ψb_d = b1 /d1 = 55,0/54,878 = 1,002 Окружная скорость колес:
v = ω1 •d1 /2 = 152,367•54,878•10-3 /2 = 4,181 м/c;
При такой скорости следует принять для зубчатых колес 8-ю степень точности. Коэффициент нагрузки равен:
Kh = Kh b•Kha •Khv .
Коэффициент Khb = 1,11 выбираем по таблице 3.5 [1], коэффициент Kha = 1,084 выбираем по таблице 3.4 [1], коэффициент Khv = 1,02 выбираем по таблице 3.6 [1], тогда: Kh = 1,228
Проверку контактных напряжений проводим по формуле 3.6 [1]:
σh = ![]() aω b2•U =
aω b2•U =
![]() = 366,664 МПа. ≤ [σh
]
= 366,664 МПа. ≤ [σh
]
Силы действующие в зацеплении вычислим по формуле 8.3 и 8.4 [1]:
окружная: Ft = 2•T2 /d2 = 2•157018,93 /195,122 = 1611,963 Н; радиальная: Fr = Ft •tg(α)/сos(β) = 1611,963•tg20°/cos10,2631° = 596,246 Н; осевая: Fa = Ft •tg(β)= 1611,963•tg10,2631° = 291,871 Н.
Проверим зубья на выносливость по напряжениям изгиба по формуле 3.25 [1]:
σF = Ft •Kf •Yf •Yβ •Kf α /(b•mn ) ≤ [σF ]
Здесь коэффициент нагрузки Kf = Kfb •Kfv (см. стр. 42 [1]).
По таблице 3.7 [1] выбираем коэффициент расположения колес Kfb = 1,231, по таблице 3.8 [1] выбираем коэффициент Kfv = 1,3.
Таким образом коэффициент Kf = 1,6.
Yf - коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа zv (см. гл.3, пояснения к формуле 3.25 [1]):
у шестерни: zv1 = z1 /сos3 (β) = 27/сos3 10,2631° = 28,339 у колеса: zv2 = z2 /сos3 (β)= 96/сos3 10,2631° = 100,759 Тогда: Yf1 = 3,833
Yf2 = 3,6
Допускаемые напряжения находим по формуле 3.24 [1]:
[σf] = [σ°f_lim_b]KFL/[Sf].
K - коэффициент долговечности.
FL
![]() 6
N
6
N
FO
KFL = √ NFE
![]()
![]()
где N - базовое число циклов нагружения; для данных сталей N = 4000000;
FO FO
N = 60•n•c•Lh•K = 797966741,25
FE FE
здесь: n - частота вращения шестерни, мин-1 ; c = 1,0 - число колёс, находящихся в
зацеплении; Lh = 13000 - продолжительность работы передачи в расчётный срок службы, ч. KFE = Σ [(Mi /Mmax )3 •(ti /tΣ )•(ni /nMmax )] = 0,234375
- дополнительный множитель для эквивалентной циклической долговечности.
В итоге получаем К = 0,555
FL
Т.к. К <1,0 , то принимаем К = 1,0
FL FL
Для шестерни: [σ°f_lim_b ] = 378,0 МПа; для колеса: [σ°f_lim_b ] = 324,0 МПа.
Коэффициент [Sf ] безопасности находим по формуле 3.24 [1]:
[Sf ] = [Sf `]•[Sf``].
где для шестерни [Sf `] = 1,75;
[Sf ``] = 1,0; для колеса [Sf `] = 1,75;
[Sf`` ] = 1,0,
Допускаемые напряжения:
для шестерни: [σf_1 ] = 216,0 МПа; для колеса: [σf_2 ] = 185,143 МПа; Находим отношения [σf ]/Yf : для шестерни: [σf_1 ]/Yf1 = 56,349 для колеса: [σf_2 ]/Yf2 = 51,434 Дальнейший расчет будем вести для колеса, для которого найденное отношение меньше. Определим коэффициенты Yb и Kfa (см.гл.3, пояснения к формуле 3.25 [1]):
Yb = 1 - β/140 = 0,927
Kf α = (4 + (εα -1)•(n - 5))/(4•εα )
Для средних значений торцевого перекрытия εα = 1,5 и для 8-й степени точности Kf α = 0,92.
Проверяем прочность зуба колеса по формуле 3.25 [1]:
σf_2 = (Ft •Kf •Yf •Yb •Kfa )/(b2 •mn ) ≤ [σf ] σf_2 = 79,151 МПа < [σf ] = 185,143 МПа.
Условие прочности выполнено.
Модуль, межосевое расстояние и числа зубьев шестерни и колеса выбираем из 2-го варианта расчёта из расчёта, что
1) при меньшем угле наклона зубьев, уменьшится осевая сила.
2) Режущий инструмент для зубчатых колёс с mn = 2,0 — дешевле.
3. РАСЧЕТ 2-Й ЗУБЧАТОЙ ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ
Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками (см. гл.3, табл.3.3 [1] ): Для шестерни: сталь: 30ХГС термическая обработка: улучшение
![]()
![]() твердость: HB 260 Для колеса: сталь: 40Л термическая обработка: улучшение
твердость: HB 260 Для колеса: сталь: 40Л термическая обработка: улучшение
твердость: HB 180
Допустимые контактные напряжения (формула (3.9) [1]) , будут:
[σh] = σh_lim_b•KHL/[Sh] ,
По таблице 3.2 гл. 3 [1] имеем: для сталей с твердостью поверхностей зубьев менее HB 350:
σh_lim_b = 2•HRC + 70,
[Sh ]= 1,1;
![]() 6
N
6
N
HO
KHL = √ NHE
где N - базовое число циклов нагружения; для данных сталей
HO N = 26400000;
HO
N = 60•n•c•Lh•K = 224779363,7324
HE HE
здесь: n - частота вращения шестерни, мин-1 .; c = 1,0 - число колёс, находящихся в зацеплении;
Lh = 13000 - продолжительность работы передачи в расчётный срок службы, ч.
KHE = Σ[(Mi /Mmax )3 •(ti /tΣ )•(ni /nMmax) ] = 0,234375 - дополнительный множитель для эквивалентной циклической долговечности.
В итоге получаем К = 0,7
HL
Т.к. КHL< 1,0 , то принимаем КHL = 1,0 для шестерни — [σh-1 ] = 590,0 МПа; для колеса — [σh-2 ] = 430,0 МПа.
Для косозубых колес расчетное допустимое контактное напряжение находим по формуле 3.10 гл.3 [1]:
[σh ] = 0,45•([σh-1 ] + [σh-2 ])
Тогда расчетное допускаемое контактное напряжение будет:
[σh ] = 417,273 МПа.
Требуемое условие выполнено: [σh ] < 1,23•[σh-2 ]
Принимаем коэффициент симметричности расположения колес относительно опор по таблице 3.5 [1]: Khb = 1,25.
Коэффициент ширины венца по межосевому расстоянию принимаем: ψba = b/aω = 0,4, (см. стр.36 [1]). Межосевое расстояние
из условия контактной выносливости активных поверхностей зубьев найдем по формуле
3.7 гл.3 [1]:
aω = Ka •(U + 1)•(T2 •Khb /[σh ]2 •U2 •ψba )1/3 = 191,311 мм. где для косозубых колес Ка = 43,0, а передаточное число нашей передачи U = 4,0 Ближайшее значение межосевого расстояния по ГОСТ 2185-66 будет: aω = 200,0 мм.
1-й вариант расчёта модуля
Нормальный модуль зацепления берем по следующей рекомендации: mn = (0,01÷0,.02)•aω мм, для нас: mn = 2,0÷4,0 мм, принимаем по ГОСТ 9563-60 (см. стр. 36 [1]):
mn = 2,0 мм.
![]()
![]() Принимаем предварительно угол наклона зубьев β = 10° и определим числа зубьев шестерни и колеса (см. формулу 3.16[1]):
Принимаем предварительно угол наклона зубьев β = 10° и определим числа зубьев шестерни и колеса (см. формулу 3.16[1]):
z1 = 2•aw •cos(β)/((U + 1)•mn ) = 2•200•cos10°/(5•2,0)= 35 z2 = U•z1 = 4•35 = 140
Уточненное значение угла наклона зубьев будет:
cos(β) = (z1 + z2 )•mn /(aw •2) = (35 + 140)• 2,25 /(200•2) = 0,9844 β = 10,1418°
Основные размеры шестерни и колеса: диаметры делительные:
d1 = mn •z1 /cos(β) = 2,25 •35/cos10,1418° = 80,0 мм; d2 = mn •z2 /cos(β)= 2,25 •140/cos10,1418° = 320,0 мм. Проверка: aw = (d1 + d2 )/2 = 200,0 мм. диаметры вершин зубьев:
da1 = d1 + 2•mn = 80,0 + 2•2,25 = 84,5 мм; da2 = d2 + 2•mn = 320,0 + 2•2,25 = 324,5 мм. ширина колеса: b2 = ψba •aw = 0,4•200,0= 80,0 мм; ширина шестерни: b1 = b2 + 5 мм = 85,0 мм;
Определим коэффициент ширины шестерни по диаметру: ψb_d = b1 /d1 = 85,0/80,0 = 1,063 Окружная скорость колес будет:
V = ω2 •d1 /2 = 42,92 •80,0•10-3 /2= 1,717 м/c;
При такой скорости следует принять для зубчатых колес 8-ю степень точности. Коэффициент нагрузки равен:
Kh = Khb•Kha•Khv.
Коэффициент Khb = 1,123 выбираем по таблице 3.5[1],
коэффициент Kha = 1,065 выбираем по таблице 3.4[1], коэффициент Khv = 1,02 выбираем по таблице 3.6[1], тогда: Kh = 1,22
Проверку контактных напряжений
проводим по формуле![]()
σh = ![]() ωb2
•U2
=
ωb2
•U2
=
![]() = 369,262 МПа. ≤ [σh
]
= 369,262 МПа. ≤ [σh
]
Силы действующие в зацеплении вычислим по формуле 8.3 и 8.4[1]:
окружная : Ft = 2•T3 /d2 = 2•628075,72/320,0 = 3925,473 Н; радиальная: Fr = Ft •tg(α)/cos(β) = 3925,473•tg20°/cos10,1418° = 1451,434 Н; осевая : Fa = Ft •tg(β) = 3925,473•tg10,1418° = 702,188 Н. Проверим зубья на выносливость по напряжениям изгиба по формуле 3.25[1]:
σF = Ft •Kf •Yf •Yβ •Kf α /(b•mn ) ≤ [σF ]
Здесь коэффициент нагрузки Kf = Kfb •Kfv (см. стр. 42[1]).
По таблице 3.7[1] выбираем коэффициент расположения колес Kfb = 1,252, по таблице 3.8[1] выбираем коэффициент Kfv = 1,1.
Таким образом коэффициент Kf = 1,377.
![]()
![]() Yf
- коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа zv (см. гл.3, пояснения к формуле 3.25[1]): у шестерни : zv1
= z1
/cos3
(β) = 36,693 у колеса : zv2
= z2
/cos3
(β) = 146,773
Yf
- коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа zv (см. гл.3, пояснения к формуле 3.25[1]): у шестерни : zv1
= z1
/cos3
(β) = 36,693 у колеса : zv2
= z2
/cos3
(β) = 146,773
Тогда : Yf1 = 3,8
Yf2 = 3,577
Допускаемые напряжен ия находим по формуле 3.24[1]:
[σf] = [σ°f_lim_b]•KFL/[Sf].
K - коэффициент долговечности.
FL
![]() 6
N
6
N
FO
KFL = √ NFE
где N - базовое число циклов нагружения; для данных сталей N = 4000000;
FO FO
N = 60•n•c•Lh•K = 218787940140,845
FE FE
здесь: n - частота вращения шестерни, мин-1.; c= 1,0 - число колёс, находящихся в зацеплении; Lh= 13000,0 - пордолжительность работы передачи в расчётный срок службы, ч.
K = Σ[(Mi /Mmax )3 •(ti /tΣ)•(ni /nMmax )] = 0,234375 - дополнительный множитель для
FE
эквивалентной циклической долговечности.
В итоге получаем К = 0,298
FL
Т.к. К <1,0 , то принимаем К = 1,0
FL FL
Для шестерни: [σ°f_lim_b ] = 414,0 МПа; для колеса : [σ°f_lim_b ] = 324,0 МПа.
Коэффициент [Sf ] безопасности находим по формуле 3.24[1]:
[Sf ] = [Sf `]•[Sf ``].
где для шестерни [Sf `] = 1,75 ;
[Sf ``] = 1,0 ; для колеса [Sf `] = 1,75 ; [Sf ``] = 1,0,
Допускаемые напряжения:
для шестерни: [σf_1 ] = 236,571 МПа; для колеса : [σf_2 ] = 185,143 МПа; Находим отношения [σf ]/Yf : для шестерни: [σf_1 ]/Yf1 = 62,256 для колеса : [σf_2 ]/Yf2 = 51,765
Дальнейший расчет будем вести для колеса, для которого найденное отношение меньше. Определим коэффициенты Yb и Kfa (см.гл.3, пояснения к формуле 3.25[1]):
Yb = 1 - β/140 = 0,928
Kf α = (4 + (εα -1)•(n - 5))/(4•εα )
Для средних значений торцевого перекрытия εα = 1,5 и для 8-й степени точности Kf α = 0,92.
Проверяем прочность зуба колеса по формуле 3.25[1]:
σf_2 = (Ft •Kf •Yf •Yb •Kfa )/(b2 •mn ) ≤ [σf ] σf_2 = 91,659 МПа < [σf ] = 185,143 МПа. Условие прочности выполнено.
![]()
![]() 2-й вариант расчёта модуля
2-й вариант расчёта модуля
Нормальный модуль зацепления берем по следующей рекомендации: mn = (0,01÷0,.02)•aω мм, для нас: mn = 2,0÷4,0 мм, принимаем по ГОСТ 9563-60 (см. стр. 36 [1]):
mn = 2,5 мм.
Принимаем предварительно угол наклона зубьев β = 10° и определим числа зубьев шестерни и колеса (см. формулу 3.16 [1]):
z1 = 2•aω •сos(β)/((U + 1)•mn ) = 2•200,0•cos10°/(5•2,5) = 32 z2 = U•z1 = 4•32 = 128
Уточненное значение угла наклона зубьев будет:
сos(β) = (z1 + z2 )•mn /(aω •2) = (32 + 128)•4,0/(200,0•2)= 1,0000 β = 0°
Основные размеры шестерни и колеса: диаметры делительные:
d1 = mn •z1 /сos(β) = 2,5•32/1 = 80,0 мм; d2 = mn •z2 /сos(β) = 2,5•128/1 = 320,0 мм.
Проверка: aω = (d1 + d2 )/2 = (80,0 + 320,0)/2 = 200,0 мм.
диаметры вершин зубьев:
da1 = d1 + 2•mn = 80,0 + 2•2,5 = 85,0 мм; da2 = d2 + 2•mn = 320,0 + 2•2,5 = 325,0 мм.
ширина колеса: b2 = ψba •aω = 4,0•200,0 = 80,0 мм; ширина шестерни: b1 = b2 + 5 мм = 80,0 + 5 = 85,0 мм; Определим коэффициент ширины шестерни по диаметру: ψb_d = b1 /d1 = 85,0/80,0 = 1,063
Окружная скорость колес будет:
V = ω2 •d1 /2 = 42,92 •80,0/2= 1,717 м/c;
При такой скорости следует принять для зубчатых колес 8-ю степень точности. Коэффициент нагрузки равен:
Kh = Khb•Kha•Khv.
Коэффициент Khb = 1,123 выбираем по таблице 3.5 [1], коэффициент Kha = 1,065 выбираем по таблице 3.4 [1], коэффициент Khv = 1,02 выбираем по таблице 3.6 [1], тогда: Kh = 1,22
Проверку контактных напряжений проводим по формуле 3.6 [1]:
σh = ![]() aω b2
•U2 =
aω b2
•U2 =
 = 369,262 МПа. ≤ [σh
]
= 369,262 МПа. ≤ [σh
]
Силы действующие в зацеплении вычислим по формуле 8.3 и 8.4 [1]:
![]()
![]() окружная: Ft
= 2•T3
/d2
= 2•628075,72/320,0= 3925,473 Н; радиальная: Fr
= Ft
•tg(α)/сos(β) = 3925,473•tg20°/1 = 1428,755 Н; осевая: Fa
= Ft
•tg(β) = 3925,473 tg0°= 0,0 Н. Проверим зубья на выносливость по напряжениям изгиба по формуле 3.25 [1]:
окружная: Ft
= 2•T3
/d2
= 2•628075,72/320,0= 3925,473 Н; радиальная: Fr
= Ft
•tg(α)/сos(β) = 3925,473•tg20°/1 = 1428,755 Н; осевая: Fa
= Ft
•tg(β) = 3925,473 tg0°= 0,0 Н. Проверим зубья на выносливость по напряжениям изгиба по формуле 3.25 [1]:
σF = Ft •Kf •Yf •Yβ •Kf α /(b•mn ) ≤ [σF ]
Здесь коэффициент нагрузки Kf = Kfb •Kfv (см. стр. 42 [1]).
По таблице 3.7 [1] выбираем коэффициент расположения колес Kfb = 1,252, по таблице 3.8 [1] выбираем коэффициент Kfv = 1,1.
Таким образом коэффициент Kf = 1,377.
Yf - коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа zv (см. гл.3, пояснения к формуле 3.25 [1]):
у шестерни: zv1 = z1 /cos3 (β) = 32/cos3 0° = 32,0 у колеса: zv2 = z2 /cos3 (β)= 128/cos3 0° = 128,0 Тогда: Yf1 = 3,8
Yf2 = 3,586
Допускаемые напряжения находим по формуле 3.24 [1]:
[σf] = [σ°f_lim_b]•KFL/[Sf].
K - коэффициент долговечности.
FL
![]() N
N
FO
KFL = √ NFE
где NFO- базовое число циклов нагружения; для данных сталей NFO = 4000000;
N = 60•n•c•Lh•K = 224779363,7324
FE FE
здесь: n - частота вращения шестерни, мин-1 ; c = 1,0 - число колёс, находящихся в зацеплении; Lh= 13000 - срок службы передачи;
KFE = Σ[(Mi /Mmax )3 •(ti /tΣ )•(ni /nMmax )] = 0,234375 - дополнительный множитель для эквивалентной циклической долговечности.
В итоге получаем К = 0,639
FL
Т.к. К < 1,0 , то принимаем К = 1,0
FL FL
Для шестерни: [σ°f_lim_b ] = 468,0 МПа; для колеса: [σ°f_lim_b ] = 324,0 МПа.
Коэффициент [Sf ] безопасности находим по формуле 3.24 [1]:
[Sf ] = [Sf `]•[Sf ``].
где для шестерни [Sf `] = 1,75;
[Sf ``] = 1,0;
для колеса [Sf `] = 1,75; [Sf ``] = 1,0,
Допускаемые напряжения:
для шестерни: [σf_1 ] = 267,429 МПа; для колеса: [σf_2 ] = 185,143 МПа; Находим отношения [σf ]/Yf : для шестерни: [σf_1 ]/Yf1 = 70,376 для колеса: [σf_2 ]/Yf2 = 51,629
Дальнейший расчет будем вести для колеса, для которого найденное отношение меньше. Определим коэффициенты Yb и Kfa (см.гл.3, пояснения к формуле 3.25 [1]): Yb = 1 - β/140 = 1,0
![]()
![]() Kf
α
= (4 + (εα
- 1)•(n - 5))/(4•εα
)
Kf
α
= (4 + (εα
- 1)•(n - 5))/(4•εα
)
Для средних значений торцевого перекрытия εα = 1,5 и для 8-й степени точности Kf α = 0,92.
Проверяем прочность зуба колеса по формуле 3.25 [1]:
σf_2 = (Ft •Kf •Yf •Yb •Kfa )/(b2 •mn ) ≤ [σf ] σf_2 = 89,169 МПа < [σf ] = 185,143 МПа.
Условие прочности выполнено.
Модуль, межосевое расстояние и числа зубьев шестерни и колеса выбираем из 2-го варианта расчёта из расчёта, что
3) при меньшем угле наклона зубьев, уменьшится осевая сила.
4) Режущий инструмент для зубчатых колёс с mn = 2,5 — дешевле.
4. РАСЧЕТ 3-Й ЦЕПНОЙ ПЕРЕДАЧИ
Выбираем приводную роликовую двухрядную цепь (cм. гл. VII [1], табл. 7.15). Передаточное число было принято ранее:
U = 2,1.
Число зубьев: ведущей звездочки (см. с.148 [1]):
z1 = 31 - 2•U3 = 26,8 = 26,8 = 27,0, ведомой звездочки:
z2 = z1 •U3 = 27,0•2,1 = 56,0,
Тогда фактическое передаточное число:
U3r = z2 / z1 = 56,0/27,0= 2,074. Отклонение:
(U3 - U3r )•100/U = 1,235%, что допустимо (отклонение не должно превышать 3%).
Расчетный коэффициент нагрузки (см. гл. VII [1], формулу 7.38 [1] и пояснения к ней): Кэ = kд •kа •kн •kр •kсм •kп . где:
kд = 1,0 - динамический при спокойной нагрузке;
ka = 1,0 - учитывает влияние межосевого расстояния [kа = 1 при ац ≤(30,..60)•t]; kн = 1,0 - учитывает влияние угла наклона линии центров kн = 1, если этот угол не
превышает 60°, в противном случае kн = 1.25; у нас: γ= 0°; kр = 1,25 - учитывает способ регулирования натяжения цепи, в нашем случае при
периодическом регулировании; kсм = 1,4 - учитывает способ смазки, в нашем случае - периодическая смазка kп = 1,5 - учитывает периодичность работы передачи, в нашем случае - 3 смены. Тогда:
Kэ = 2,625.
Для определения шага цепи
по формуле 7.38 гл. VII [1] надо знать допускаемое давление [p] в шарнирах цепи. В таблице 7.18 [1] допускаемое давление [p] задано в зависимости от частоты вращения ведущей звездочки и шага t. Поэтому для расчета по формуле 7.38 [1] величиной [p] следует задаваться ориентировочно. Ведущая звездочка имеет частоту вращения n1 = 102,465 мин-1 Среднее значение допускаемого давления примем [p]= 17, МПа. Тогда шаг цепи:
![]()
![]() T3
•K
T3
•K
t ≥ 2,8• z1 • =
![]()
![]()
![]() = 44,28 мм
= 44,28 мм
Подбираем по табл. 7.15 [1] цепь 2ПР-44,45-344,8 по ГОСТ 13568-75, имеющую t = 44,45 мм; разрушающую нагрузку Q = 344,8 кН; массу q = 14,4 кг/м; Аоп = 946, мм2 .
Скорость цепи:
v = z1 •t•n3 /(60•103 ) = 27•44,45•102,465 /60000= 2,05 м/с.
Окружная сила:
Ftц = T3 •ω4 = 62,8075•5,11 = 3288,186 H.
Давление в шарнире проверяем по формуле 7.39 [1]: p = Ftц •Kэ /Aоп = 3288,186•2,625/0,946 = 9,124 МПа. Уточняем по табл. 7.18 [1] допускаемое давление:
[p]= [p']•[1+0,01•(z1 -17)] = 17•106 •[1 + (27 - 17)] = 18,7 МПа.
Условие p<[p] выполнено.
В этой формуле [p']= 17,0 МПа - табличное значение допускаемого давления по табл.
7.18 [1] при n1 = 102,465 мин-1 и t = 44,45 мм.
Определяем число звеньев цепи по формуле 7.36 [1]:
Lt = 2•At + 0,5•z∑ + ∆2 /At = 122,033 , где
At = Aц /t = 40, (см. c. 148 [1]);
z∑ = z1 +z2 = 83,0;
∆ = (z2 - z1 )/2π = (56 - 27)/2π= 4,615.
Тогда:
Lt = 122,033 округляем до четного числа: Lt = 122,0,
Уточняем межосевое расстояние цепной передачи по формуле 7.37 [1]:
 Ац
= 0,25•t•(Lt
– 0,5•z =
Ац
= 0,25•t•(Lt
– 0,5•z =
= 2200,0 мм
Для свободного провисания цепи предусматриваем возможность уменьшения межосевого расстояния на 0,4%, т. е. на 2200,0•0,004 = 8,0 мм.
Определяем диаметры делительных окружностей звездочек (см. формулу 7.34 [1]): dд1 = t/sin(180°/z1 ) = 44,45/sin(180°/27) = 382,883 мм; dд2 = t/sin(180°/z2 ) = 44,45/sin(180°/56) = 792,753 мм.
![]()
![]() Определяем диаметры наружных окружностей звездочек
(см. формулу 7.35 [1]): de1
= (ctg(180/z1
) + 0,7) – 0,3•d1
= (ctg(180°/27) + 0,7) - 0,3•25,4 = 403,789 мм; de2
= (ctg(180/z2
) + 0,7) – 0,3•d2
= (ctg(180°/56) + 0,7) - 0,3•25,4 = 815,001 мм; где d1
= 25,4 мм - диаметр ролика цепи. Силы действующие на цепь:
окружная: Ftц
= 3288,186 Н; от центробежных сил: Fv
= q•v2
= 14,4•2,052
= 60,49 H; где q = 14,4 кг/м по табл.
Определяем диаметры наружных окружностей звездочек
(см. формулу 7.35 [1]): de1
= (ctg(180/z1
) + 0,7) – 0,3•d1
= (ctg(180°/27) + 0,7) - 0,3•25,4 = 403,789 мм; de2
= (ctg(180/z2
) + 0,7) – 0,3•d2
= (ctg(180°/56) + 0,7) - 0,3•25,4 = 815,001 мм; где d1
= 25,4 мм - диаметр ролика цепи. Силы действующие на цепь:
окружная: Ftц
= 3288,186 Н; от центробежных сил: Fv
= q•v2
= 14,4•2,052
= 60,49 H; где q = 14,4 кг/м по табл.
от провисания: Ff = 9,81•kf •q•Aц = 9,81•6,0•14,4•2,200 = 1864,685 H; где kf = 6,0 - коэффициент влияния наклона оси центров цепи (см. c. 151 [1]).
Расчетная нагрузка на валы:
Fв = Ftц + 2•Ff = 3288,186 + 2•1864,685 = 7017,555 H.
Проверяем коэффициент запаса прочности цепи по формуле 7.40 [1]:
s = Q/(Ftц •Кд + Fv + Ff ) = 344,8/(3288,186•1,0 + 60,49 + 1864,685 ) = 66,138.
Это больше, чем нормативный коэффициент запаса [s]= 8,1 (см. табл. 7.19 [1]); следовательно, условие прочности s> [s] выполнено. Толщина диска звёздочки 0,93•Ввн = 0,93•25,4 = 24,0 мм, где Ввн - расстояние между пластинками внутреннего звена (см. табл. 7.15 [1]).
ПРЕДВАРИТЕЛЬНЫЙ РАСЧЁТ ВАЛОВ
Предварительный расчёт валов проведём на кручение по пониженным допускаемым напряжениям.
Диаметр вала при допускаемом напряжении [τкр ] = 20 МПа вычисляем по формуле
8,16[1]:
dв = (16 × Tк / (π× [τк ]))1/3 Ведущий вал.
dв = 21,305 мм.
Под 1 - й элемент (муфту) выбираем диаметр вала: 25,000 мм.
Под 1 - й элемент (подшипник) выбираем диаметр вала: 35,000 мм. Под 1 - й элемент (ведущий) выбираем диаметр вала: 40,000 мм.
Под 1 - й элемент (подшипник) выбираем диаметр вала: 35,000 мм.
2 - й промежуточный вал. dв = 32,12 мм.
Под 2 - й элемент (подшипник) выбираем диаметр вала: 40,000 мм.
Под 2 - й элемент (ведущий) выбираем диаметр вала: 48,000 мм.
Под 2 - й элемент (ведомый) выбираем диаметр вала: 48,000 мм.
Под 2 - й элемент (подшипник) выбираем диаметр вала: 40,000 мм. Выходной вал. dв = 50,39 мм.
Под 3 - й элемент (подшипник) выбираем диаметр вала: 60,000 мм. Под 3 - й элемент (ведомый) выбираем диаметр вала: 63,000 мм.
Под 3 - й элемент (подшипник) выбираем диаметр вала: 60,000 мм.
![]()
![]() Под 3 - й элемент (муфту) выбираем диаметр вала: 58,000 мм.
Под 3 - й элемент (муфту) выбираем диаметр вала: 58,000 мм.
Диаметры участков валов назначаем исходя из конструктивных соображений.
КОНСТРУКТИВНЫЕ РАЗМЕРЫ ШЕСТЕРЕН И КОЛЁС
Цилиндрическая шестерня 1 - й передачи.
Цилиндрическая шестерня 1 - й передачи выполнена заодно с валом. Фаска: n = 0,5 × mn = 1,0 мм.
Цилиндрическое колесо 1 - й передачи.
Диаметр ступицы: dст = 1,6 × dв = 76,0 мм, где dв - диаметр вала.
Длина ступицы: Lст = 1,5 × dв = 72,0 мм.
Толщина обода: δ0 = 4 × mn = 8,0 мм.
Толщина диска: С = 3 × mn = 15,0 мм, где mn - модуль нормальный. Толщина рёбер: s = 0,8 × C = 12,0 мм.
Диаметр центровой окружности: Dотв = 0,5 × (D0 + dст ) = 126,0 мм, где D0 - внутренний диаметр обода.
Диаметр отверстий: Dотв = (D0 + dст ) / 4 = 24,0 мм. Фаска: n = 0,5 × mn = 1,0 мм.
Цилиндрическая шестерня 2 - й передачи.
Цилиндрическая шестерня 2 - й передачи выполнена заодно с валом. Фаска: n = 0,5 × mn = 1,0 мм.
Цилиндрическое колесо 2 - й передачи.
Диаметр ступицы: dст = 1,6 × dв = 112,0 мм, где dв - диаметр вала.
Длина ступицы: Lст = 1,0…1,5 × dв = 80,0 мм.
Толщина обода: δ0 = 4 × mn = 10,0 мм.
Толщина диска: С = 3 × mn = 24,0 мм, где mn - модуль нормальный. Толщина рёбер: s = 0,8 × C = 19,2 мм.
Диаметр центровой окружности: Dотв = 0,5 × (D0 + dст ) = 198,0 мм, где D0 - внутренний диаметр обода.
Диаметр отверстий: Dотв = (D0 + dст ) / 4 = 48,0 мм. Фаска: n = 0,5 × mn = 1,0 мм.
ПРОВЕРКА ПРОЧНОСТИ ШПОНОЧНЫХ СОЕДИНЕНИЙ
Шпонка входного вала.
Для данного элемента подбираем шпонку призматическую со скруглёнными торцами 8x7, Размеры сечений шпонки и пазов и длины шпонок по ГОСТ 23360 - 78 (см. табл. 8,9[1]).
Материал шпоноки - сталь 45 нормализованная.
Напряжение смятия и условие прочности проверяем по формуле 8,22[1].
σсм = ![]() (h - T2 )×× Т (l - b) =
(h - T2 )×× Т (l - b) = ![]() (7,0 – 4,0) 2 × 44230,684 × (40,0 - 8,0) = 0,921 МПа ≤ [σсм]
(7,0 – 4,0) 2 × 44230,684 × (40,0 - 8,0) = 0,921 МПа ≤ [σсм]
1
• где Т = 44230,684 Н×мм - момент на валу; d = 48,0 мм - диаметр вала; h = 7,0 мм - высота шпонки; b = 8,0 мм - ширина шпонки; l = 40,0 мм - длина шпонки; lр = l-b = 32 мм — рабочая длинна шпонки; T1 = 4,0 мм - глубина паза вала.
Допускаемые напряжения смятия при спокойной нагрузке и неподвижном соединении при стальной ступице [σсм ] = 120,0 МПа.
Проверим шпонку на срез по формуле 8,24[1].
![]()
![]() τср =
τср = ![]() d × b 2 ×× (l - b) Т =
d × b 2 ×× (l - b) Т = ![]() 48,0 ×2 14,0 × 44230,684 × (45,0 - 14,0) = 0,002 МПа ≤ [τср]
48,0 ×2 14,0 × 44230,684 × (45,0 - 14,0) = 0,002 МПа ≤ [τср]
Допускаемые напряжения среза при спокойной нагрузке и неподвижном соединении при стальной ступице [τср ] = 0,6 × [σсм ] = 72,0 МПа.
Все условия прочности удовлетворены.
ЦИЛИНЛРИЧЕСКОЕ КОЛЕСО 1 - Й ЦИЛИНДРИЧЕСКОЙ ПЕРЕДАЧИ.
Для данного элемента подбираем шпонку призматическую со скруглёнными торцами 14x9, Размеры сечений шпонки и пазов и длины шпонок по ГОСТ 23360 - 78 (см. табл.
8,9[1]).
Материал шпоноки - сталь 45 нормализованная.
Напряжение смятия и условие прочности проверяем по формуле 8,22[1].
σсм = ![]() (h - T21
)×× Т (l - b) =
(h - T21
)×× Т (l - b) = ![]() (9,0 - 5,5) 2 × 157018,93 × (45,0 - 14,0) = 2,894 МПа ≤ [σсм]
(9,0 - 5,5) 2 × 157018,93 × (45,0 - 14,0) = 2,894 МПа ≤ [σсм]
• где Т = 157018,93 Н×мм - момент на валу; d = 48,0 мм - диаметр вала; h = 9,0 мм - высота шпонки; b = 14,0 мм - ширина шпонки; l = 45,0 мм - длина шпонки; lр = l-b = 31 мм — рабочая длинна шпонки; T1 = 5,5 мм - глубина паза вала.
Допускаемые напряжения смятия при спокойной нагрузке и неподвижном соединении при стальной ступице [σсм ] = 120,0 МПа.
Проверим шпонку на срез по формуле 8,24[1].
τср = ![]() d × b 2 ×× (l - b) Т =
d × b 2 ×× (l - b) Т = ![]() 48,0 ×2 14,0 × 157018,93 × (45,0 - 14,0) = 0,015 МПа ≤ [τср]
48,0 ×2 14,0 × 157018,93 × (45,0 - 14,0) = 0,015 МПа ≤ [τср]
Допускаемые напряжения среза при спокойной нагрузке и неподвижном соединении при стальной ступице [τср ] = 0,6 × [σсм ] = 72,0 МПа.
Все условия прочности удовлетворены.
Цилинлрическое колесо 2 - й цилиндрической передачи.
Для данного элемента подбираем шпонку призматическую со скруглёнными торцами 18x11, Размеры сечений шпонки и пазов и длины шпонок по ГОСТ 23360 - 78 (см. табл.
8,9[1]).
Материал шпоноки - сталь 45 нормализованная.
Напряжение смятия и условие прочности проверяем по формуле 8,22[1]. σсм
= 2 × Т / ((h - T1
) × (l - b)) = 80,399 МПа ≤ [σсм
] σсм = ![]() (h - T2 )×× Т (l - b) =
(h - T2 )×× Т (l - b) = ![]() (11,0 - 7,0) 2 × 628075,72 × (70,0 - 18,0) = 6,039 МПа ≤ [σсм]
(11,0 - 7,0) 2 × 628075,72 × (70,0 - 18,0) = 6,039 МПа ≤ [σсм]
1
где Т = 628075,72Н×мм - момент на валу; d = 70,0 мм - диаметр вала; h = 11,0 мм - высота шпонки; b = 18,0 мм - ширина шпонки; l = 70,0 мм - длина шпонки; lр = l-b = 52 мм — рабочая длинна шпонки; T1 = 7,0 мм - глубина паза вала.
Допускаемые напряжения смятия при спокойной нагрузке и неподвижном соединении при стальной ступице [σсм ] = 120,0 МПа.
Проверим шпонку на срез по формуле 8,24[1].
τср = ![]() d × b 2 ×× (l - b) Т =
d × b 2 ×× (l - b) Т = ![]() 70,0 ×2 18,0 × 628075,72 × (70, - 18,0) = 0,019 МПа ≤ [τср]
70,0 ×2 18,0 × 628075,72 × (70, - 18,0) = 0,019 МПа ≤ [τср]
Допускаемые напряжения среза при спокойной нагрузке и неподвижном соединении при стальной ступице [τср ] = 0,6 × [σсм ] = 72,0 МПа.
Все условия прочности удовлетворены.
Шпонка выходного вала.
Для данного элемента подбираем шпонку призматическую со скруглёнными торцами 18x11, Размеры сечений шпонки и пазов и длины шпонок по ГОСТ 23360 - 78 (см. табл.
![]()
![]() 8,9[1]).
8,9[1]).
Материал шпоноки - сталь 45 нормализованная.
Напряжение смятия и условие прочности проверяем по формуле 8,22[1]. σсм = 2 × Т / ((h - T1 ) × (l - b)) = 80,399 МПа ≤ [σсм ]
σсм = ![]() (h - T21
)×× Т (l - b) =
(h - T21
)×× Т (l - b) = ![]() (11,0 - 7,0) 2 × 628075,72 × (60,0 - 18,0) = 7,477 МПа ≤ [σсм] где Т = 628075,72Н×мм - момент на валу; d = 53,0 мм - диаметр вала; h = 11,0 мм - высота шпонки; b = 18,0 мм - ширина шпонки; l = 60,0 мм - длина шпонки; lр
= l-b = 42 мм — рабочая длинна шпонки; T1
= 7,0 мм - глубина паза вала.
(11,0 - 7,0) 2 × 628075,72 × (60,0 - 18,0) = 7,477 МПа ≤ [σсм] где Т = 628075,72Н×мм - момент на валу; d = 53,0 мм - диаметр вала; h = 11,0 мм - высота шпонки; b = 18,0 мм - ширина шпонки; l = 60,0 мм - длина шпонки; lр
= l-b = 42 мм — рабочая длинна шпонки; T1
= 7,0 мм - глубина паза вала.
Допускаемые напряжения смятия при спокойной нагрузке и неподвижном соединении при стальной ступице [σсм ] = 120,0 МПа.
Проверим шпонку на срез по формуле 8,24[1].
τср = ![]() d × b 2 ×× (l - b) Т =
d × b 2 ×× (l - b) Т = ![]() 53,0 ×2 18,0 × 628075,72 × (60, - 18,0) = 0,031 МПа ≤ [τср]
53,0 ×2 18,0 × 628075,72 × (60, - 18,0) = 0,031 МПа ≤ [τср]
Допускаемые напряжения среза при спокойной нагрузке и неподвижном соединении при стальной ступице [τср ] = 0,6 × [σсм ] = 72,0 МПа. Все условия прочности удовлетворены.
КОНСТРУКТИВНЫЕ РАЗМЕРЫ КОРПУСА РЕДУКТОРА
Толщина стенки корпуса и крышки редуктора:
δ1 = 0,025 × aw + 3 = 6,15 = 7,0 мм; δ2 = 0,025 × aw + 3 = 8,0 мм.
Округляя, получим δ = 8,0 мм.
Принимаем δ2 = 8,0 мм.
Толщина верхнего пояса (фланца) корпуса: b = 1,5 ×δ = 12,0 мм.
Толщина нижнего пояса (фланца) крышки корпуса: b1 = 1,5 ×δ1 = 12,0 мм. = 12,0 мм.
Толщина нижнего пояса корпуса: без бобышки: p = 2,35 ×δ = 18,8 мм; при наличии бобышки: p1 = 1,5 ×δ = 12,0 мм; p2 = (2,25,..2,75) ×δ = 21,0 мм Толщина рёбер основания корпуса: m = (0,85,..1) ×δ = 8,0 мм.
Толщина рёбер крышки: m1 = (0,85,..1) ×δ1 = 8,0 мм.
Диаметр фундаментных болтов (их число і = 4): d1 = (0,3,..0,36) × AWт +12 = 6,0,..7,2 = 20,0 мм.
Диаметр болтов:
у подшипников: d2 = (0,6,..0,75) × d1 = 12,0 мм. соединяющих основание корпуса с крышкой: d3 = (0,5,..0,6) × d1 = 10,0 мм. Размеры, определяющие положение болтов d2 (см. рис. 10,18[1]):
eі (1,..1,2) × d2 = 17,0 мм; qі 0,5 × d2 + d4 = 14,0 мм; где крепление крышки подшипника d4 = 5,0 мм.
Высоту бобышки hб под болт d2 выбирают конструктивно так, чтобы образовалась опрная поверхность под головку болта и гайку. Желательно у всех бобышек иметь одинаковую высоту hб .
РАСЧЕТ РЕАКЦИЙ В ОПОРАХ
1 - Й ВАЛ.
Силы, действующие на вал, плечи сил Fa и углы контактов элементов передач:
![]()
![]() Fx3
= 593,13 H
Fx3
= 593,13 H
Fy3 = -1603,538 H
Fz3 = -290,345 H H3 = 27,439 H α3 = 27,439 H
Из условия равенства суммы моментов сил относительно 1 - й опоры:
Rx2 = (- Fa3 ×Hx3 ×N3 - Fx3 ×L3 )/(L2 +L3 ) = -188,53 H Ry2 = (- Fa3 ×Hy3 ×N3 - Fy3 ×L3 )/(L2 +L3 ) = 406,639 H
Из условия равенства суммы сил относительно осей X и Y:
Rx4 = Rx2 - Fx3 = -188,53 -290,345 = -478,875H Ry4 = - Ry2 - Fy3 = - 406,639 + 1603,538 = 1196,899 H Суммарные реакции о пор:
R2 = √ Rx2 2 + Ry2 2 = 448,217 H
R![]() = 1263,435 H
= 1263,435 H
2 - Й ВАЛ.
Силы, действующие на вал, плечи сил Fa и углы контактов элементов передач:
Fx2 = 1371,898 H
Fy2 = -3769,26 H
Fx3 = -593,13 H
Fy3 = -1603,538 H
Fz3 = 290,345 H
H3 = 97,561 H
Из условия равенства суммы моментов сил относительно 1 - й опоры:
Rx1 = (- Fa2 ×Hx2 ×N2 - Fa3 ×Hx3 ×N3 - Fx2 ×(L2 +L3 ) - Fx3 ×L3 )/(L1 +L2 +L3 ) = -847,203 H
Ry1 = (- Fa2 ×Hy2 ×N2 - Fa3 ×Hy3 ×N3 - Fy2 ×(L2 +L3 ) - Fy3 ×L3 )/(L1 +L2 +L3 ) = 2786,268 H Из условия равенства суммы сил относительно осей X и Y:
Rx4 = - Rx1 - Fx2 - Fx3 = 847,203 - 1371,898 + 593,13 = 68,435 H Ry4 = - Ry1 - Fy2 - Fy3 = - 2786,268 + 3769,26 + 1603,538 = 2586,529 H Суммарные реакции опор:
R![]() = 2912,223 H
= 2912,223 H
R4 = √ Rx4 2 + Ry4 2 = 2587,434 H
3 - Й ВАЛ.
Силы, действующие на вал, плечи сил Fa и углы контактов элементов передач:
Fx2 = -1371,898 H
Fy2 = -3769,26 H
Fx 4 = 6098,918 H
Из условия равенства суммы моментов сил относительно 1 - й опоры:
Rx1 = ( - Fa2 ×Hx2 ×N2 - Fx2 ×L2 )/(L1 +L2 ) = 2727,346 H
Ry1 = ( - Fa2 ×Hy2 ×N2 - Fy2 ×L2 )/(L1 +L2 ) = 2373,237 H
Из условия равенства суммы сил относительно осей X и Y:
Rx3 = - Rx1 - Fx2 -Fx4 = - 2727,346 + 1371,898 -6098,918 = -7454,366 H
![]()
![]() Ry3
= - Ry1
- Fy2
= - 2373,237 + 3769,26 = 1396,022 H Суммарные реакции опор:
Ry3
= - Ry1
- Fy2
= - 2373,237 + 3769,26 = 1396,022 H Суммарные реакции опор:
R![]() = 3615,339 H
= 3615,339 H
R3 = √ Rx3 2 + Ry3 2 = 7583,96 H
4-Й ВАЛ.
Силы, действующие на вал, плечи сил Fa и углы контактов элементов передач:
Fx1 = -6098,918 H
Fy1 = 0,0 H
Из условия равенства суммы моментов сил относительно 1-й опоры:
Rx2 = (-Fa1 ×Hx1 ×N1 -Fa4 ×Hx4 ×N4 - Fx1 ×(L1 +L2 )+Fx4 ×L3 )/L2 = 6743,661 H
Ry2 = (-Fa1 ×Hy1 ×N1 -Fa4 ×Hy4 ×N4 - Fy1 ×(L1 +L2 )+Fy4 ×L3 )/L2 = 0,0 H Из условия равенства суммы сил относительно осей X и Y:
Rx3 = -Fx1 - Rx2 = 6098,918 - 6743,661 = -644,743 H
Ry3 = -Fy1 - Ry2 = -0,0 - 0,0 = 0,0 H Суммарные реакции опор:
R![]() = 6743,661 H
= 6743,661 H
R3 = √ Rx3 2 + Ry3 2 = 644,743 H
1-Й

2 2 1/2 MΣ = (Mx + Mx ) , H*мм |
| Mкр(max) = Ткр, H*мм |
| My, H*мм |
| Mx, H*мм |
![]()
![]()
-21443,826
![]()
-29410,62
69921,857

66962,073
![]()
2-Й

2 2 1/2 MΣ = (Mx + Mx ) , H*мм |
| Mкр(max) = Ткр, H*мм |
| My, H*мм |
| Mx, H*мм |
![]()
![]()
3695,479
![]()
-66081,83
227153,39

139721,461
![]()
3-Й

2 2 1/2 MΣ = (Mx + Mx ) , H*мм |
| Mкр(max) = Ткр, H*мм |
| Mx, H*мм |
| My, H*мм |
![]()
![]()
218187,684 402528,581
![]()
402528,581
289227,082

![]()
| Mx, H*мм |
| My, H*мм |
| Mкр(max) = Ткр, H*мм |


![]()
![]()
 4-Й ВАЛ.
4-Й ВАЛ.
![]()
![]()
-451319,924
451319,924
2 2 1/2
MΣ = (Mx + Mx ) , H*мм
![]()
ПРОВЕРКА ДОЛГОВЕЧНОСТИ ПОДШИПНИКОВ
1 - Й ВАЛ.
Выбираем шарикоподшипник радиальный однорядный (по ГОСТ 8338 - 75) 107 особолегкой серии со следующими параметрами:
d = 35,0 мм; D = 62,0 мм;
C = 15900,0 Н; C0 = 8500,0 Н.
Радиальные нагрузки на опоры:
Pr1 = 513,271 H;
Pr2 = 1333,329 H.
Будем проводить расчёт долговечности подшипника по наиболее нагруженной опоре 2, Эквивалентная нагрузка вычисляется по формуле: Pэ = (Х × V × PR2 + Y × Pa ) × Кб × Кт ,
где - PR2 = 1333,329 H - радиальная нагрузка; Pa = Fa = 313,265 H - осевая нагрузка; V = 1,0 (вращается внутреннее кольцо подшипника); коэффициент безопасности Кб = 1,0 (см. табл.
9,19[1]); температурный коэффициент Кт = 1,0 (см. табл. 9,20[1]).
Отношение Fa / C0 = 0,037; этой величине (по табл. 9,18[1]) соответствует e = 0,233, Отношение Pa / (PR2 × V) = 0,235 > e; тогда по табл. 9,18[1]: X = 0,56; Y = 1,901,
Тогда: Pэ = (0,56 × 1,0 × 1333,329 + 1,901 × 313,265) × 1,0 × 1,0 = 1342,323 H.
Расчётная долговечность, млн. об. (формула 9,1[1]):
L = (C / Pэ )3 = 1342,323 млн. об.
Расчётная долговечность, ч.:
![]()
![]() Lh = L × 106
/ (60 × n1
) = 19037,337 ч,
Lh = L × 106
/ (60 × n1
) = 19037,337 ч,
что больше 10000 ч., установленных ГОСТ 16162 - 85 (см. также стр.307[1]), здесь n1 = 1455,0 об/мин - частота вращения вала.
2 - Й ВАЛ.
Выбираем шарикоподшипник радиальный однорядный (по ГОСТ 8338 - 75) 208 легкой серии со следующими параметрами:
d = 40,0 мм; D = 80,0 мм;
C = 32000,0 Н;
C0 = 17800,0 Н.
Радиальные нагрузки на опоры:
Pr1 = 3218,597 H; Pr2 = 2650,573 H.
Будем проводить расчёт долговечности подшипника по наиболее нагруженной опоре 1, Эквивалентная нагрузка вычисляется по формуле: Pэ = (Х × V × PR1 + Y × Pa ) × Кб × Кт ,
где - PR1 = 3218,597 H - радиальная нагрузка; Pa = Fa = - 313,265 H - осевая нагрузка; V = 1,0 (вращается внутреннее кольцо подшипника); коэффициент безопасности Кб = 1,0 (см.
табл. 9,19[1]); температурный коэффициент Кт = 1,0 (см. табл. 9,20[1]).
Отношение Fa / C0 = 0,018; этой величине (по табл. 9,18[1]) соответствует e = 0,198, Отношение Pa / (PR1 × V) = 0,097 ≤ e; тогда по табл. 9,18[1]: X = 1,0; Y = 0,0, Тогда: Pэ = (1,0 × 1,0 × 3218,597 + 0,0 × 313,265) × 1,0 × 1,0 = 3218,597 H.
Расчётная долговечность, млн. об. (формула 9,1[1]):
L = (C / Pэ )3 = 3218,597 млн. об.
Расчётная долговечность, ч.:
Lh = L × 106 / (60 × n2 ) = 39963,567 ч,
что больше 10000 ч., установленных ГОСТ 16162 - 85 (см. также стр.307[1]), здесь n2 = 409,859 об/мин - частота вращения вала.
3 - Й ВАЛ.
Выбираем шарикоподшипник радиальный однорядный (по ГОСТ 8338 - 75) 112 особолегкой серии со следующими параметрами:
d = 60,0 мм; D = 95,0 мм; C = 29600,0 Н;
C0 = 18300,0 Н.
Радиальные нагрузки на опоры:
Pr1 = 2817,154 H; Pr2 = 1510,648 H.
Будем проводить расчёт долговечности подшипника по наиболее нагруженной опоре 1, Эквивалентная нагрузка вычисляется по формуле: Pэ = (Х × V × PR1 + Y × Pa ) × Кб × Кт ,
где - PR1 = 2817,154 H - радиальная нагрузка; Pa = Fa = 0,0 H - осевая нагрузка; V = 1,0 (вращается внутреннее кольцо подшипника); коэффициент безопасности Кб = 1,0 (см. табл.
9,19[1]); температурный коэффициент Кт = 1,0 (см. табл. 9,20[1]).
Отношение Fa / C0 = 0,0; этой величине (по табл. 9,18[1]) соответствует e = 0,0, Отношение Pa / (PR1 × V) = 0,0 ≤ e; тогда по табл. 9,18[1]: X = 1,0; Y = 0,0, Тогда: Pэ = (1,0 × 1,0 × 2817,154 + 0,0 × 0,0) × 1,0 × 1,0 = 2817,154 H.
![]()
![]() Расчётная долговечность, млн. об. (формула 9,1[1]):
Расчётная долговечность, млн. об. (формула 9,1[1]):
L = (C / Pэ )3 = 2817,154 млн. об.
Расчётная долговечность, ч.:
Lh = L × 106 / (60 × n3 ) = 188676,445 ч,
что больше 10000 ч., установленных ГОСТ 16162 - 85 (см. также стр.307[1]), здесь n3 = 102,465 об/мин - частота вращения вала.
4-Й ВАЛ.
Выбираем шарикоподшипник радиальный однорядный (по ГОСТ 8338-75) 213 легкой серии со следующими параметрами:
d = 65,0 мм; D = 120,0 мм; C = 56000,0 Н;
C0 = 34000,0 Н.
Радиальные нагрузки на опоры: Pr1 = 10796,047 H; Pr2 = 6241,464 H.
Будем проводить расчёт долговечности подшипника по наиболее нагруженной опоре 1. Эквивалентная нагрузка вычисляется по формуле: Рэ = (Х × V × Pr1 + Y × Pa ) × Кб × Кт , где - Pr1 = 10796,047 H - радиальная нагрузка; Pa = Fa = 0,0 H - осевая нагрузка; V = 1,0 (вращается внутреннее кольцо подшипника); коэффициент безопасности Кб = 1,0 (см. табл.
9.19[1]); температурный коэффициент Кт = 1,0 (см. табл. 9.20[1]).
Отношение Fa / C0 = 0,0; этой величине (по табл. 9.18[1]) соответствует e = 0,0, Отношение Pa / (Pr1 × V) = 0,0 ≤ e; тогда по табл. 9.18[1]: X = 1,0; Y = 0,0, Тогда: Pэ = (1,0 × 1,0 × 10796,047 + 0,0 × 0,0) × 1,0 × 1,0 = 10796,047 H.
Расчётная долговечность, млн. об. (формула 9.1[1]):
L = (C / Рэ )3 = 10796,047 млн. об. Расчётная долговечность, ч.:
Lh = L × 106 / (60 × n4 ) = 47671,983 ч, что больше 10000 ч., установленных ГОСТ 16162-85 (см. также стр.307[1]), здесь n4 = 48,793 об/мин - частота вращения вала.
УТОЧНЁННЫЙ РАСЧЁТ ВАЛОВ
РАСЧЁТ 1 - ГО ВАЛА.
Крутящий момент на валу Tкр = 44230,684 H×мм. Для данного вала выбран материал: сталь 45, Для этого материала:
- предел прочности σb = 780,0 МПа;
- предел выносливости стали при симметричном цикле изгиба σ - 1 = 0,43 ×σb = 335,4
МПа;
- предел выносливости стали при симметричном цикле кручения τ - 1 = 0,58 ×σ - 1 = 194,532 МПа.
1 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 25,0 мм. Это сечение при передаче вращающего момента через муфту рассчитываем на кручение. Концентрацию напряжений вызывает наличие шпоночной канавки.
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ) , где:
- ![]()
![]() амплитуда и среднее напряжение отнулевого цикла:
амплитуда и среднее напряжение отнулевого цикла:
τv = τm = τmax / 2 = ![]() W0,5 к нетто
× T кр = 0,5
2785,722×44230,684
= 8,521 МПа
W0,5 к нетто
× T кр = 0,5
2785,722×44230,684
= 8,521 МПа
Здесь
Wк нетто = ![]() π×16 D 3
- b × T1
2 ×× (D - T D 1
)2
=
π×16 D 3
- b × T1
2 ×× (D - T D 1
)2
=
= 3,14 × 25,0 3 - 8,0 × 4,0 × (25,0 - 4,0) 2 = 2784,166 мм3
16 2 × 25,0
где b = 8,0 мм - ширина шпоночного паза; T1 = 4,0 мм - глубина шпоночного паза; - φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]. - kτ = 1,7 - находим по таблице 8,5[1]; - ετ = 0,77 - находим по таблице 8,8[1]; Тогда: Sτ = 9,608,
ГОСТ 16162-78 указывает на то, чтобы конструкция редукторов предусматривала возможность восприятия консольной нагрузки, приложенной в середине посадочной части вала. Величина этой нагрузки для редукторов должна быть 2,5 × Т1/2 ,
Приняв у ведущего вала длину посадочной части под муфту равной длине полумуфты l =
80 мм, получим Мизг = 2,5 × Tкр 1/2 × 80 / 2 = 21788,256 Н×мм.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (εσ ×β)) ×σv + φσ ×σm ) , где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 21788,256 г / 1251,741 = 17,406 МПа, здесь
π× D3 b × T1 × (D - T1 )2 =
Wнетто = ![]() 32 - 2 × D
32 - 2 × D
3,14 × 25,0 3 8,0 × 4,0 × (25,0 - 4,0) 2 3
= - = = 1251,741 мм
32 2 × 25,0
Wнетто = π× D3 / 32 - b × T1 × (D - T1 )2 / (2 × D) = 1251,741 мм3 , где b = 8,0 мм - ширина шпоночного паза; T1 = 4,0 мм - глубина шпоночного паза; - среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,638 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]; - kσ = 1,8 - находим по таблице 8,5[1];
- εσ = 0,88 - находим по таблице 8,8[1]; Тогда:
![]() Sσ
= σ- 1
/ ((kσ
/ (εσ
×β)) ×σv
+ φσ
×σm
)= 9,106, Результирующий коэффициент запаса прочности: S = √ SSσ×2 + S Sττ
2√ 9,106 9,106 +9,608 ×9,608 = 13,238
Sσ
= σ- 1
/ ((kσ
/ (εσ
×β)) ×σv
+ φσ
×σm
)= 9,106, Результирующий коэффициент запаса прочности: S = √ SSσ×2 + S Sττ
2√ 9,106 9,106 +9,608 ×9,608 = 13,238
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
2 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 35,0 мм. Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом (см. табл. 8,7[1]). Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (εσ ×β)) ×σv + φσ ×σm ) , где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 0,0 МПа, здесь
Wнетто = π× D3 3,14 × 35,0 3 3
- = 4209,243 мм
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,326 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ /εσ = 2,8 - находим по таблице 8,7[1]; Тогда:
Sσ = 5150,472,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: τt = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 2,82 МПа, здесь
Wк нетто = π× D3 - 3,14 × 35,03 = 8418,487 мм3
16 16
- φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ /ετ = 4,0 - находим по таблице 8,7[1]; Тогда:
Sτ = 23,101,
Результирующий коэффициент запаса прочности:
S = ![]() √ SSσσ
×2 + S Sττ
2√ 5150,4725150,472 +23,101 × 23,101 = 5150,524
√ SSσσ
×2 + S Sττ
2√ 5150,4725150,472 +23,101 × 23,101 = 5150,524
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
4 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 35,0 мм. Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом (см. табл. 8,7[1]). Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (εσ ×β)) ×σv + φσ ×σm ) , где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 0,0 МПа, здесь
Wнетто = π× D3 - 3,14 × 35,0 3 = 4209,243 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,326 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ /εσ = 2,8 - находим по таблице 8,7[1]; Тогда:
Sσ = 5150,472,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: τt = τm = τm ax / 2 = 0,5 × Tкр / Wк нетто = 2,82 МПа, здесь
Wк нетто = π× D3 3,14 × 35,03 3
- = 8418,487 мм
16 16
- φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ /ετ = 4,0 - находим по таблице 8,7[1]; Тогда:
Sτ = 23,101,
Результирующий коэффициент запаса прочности:
S = ![]() √ SSσ×
2 + S Sττ
2√ 5150,4725150,472 +23,101 × 23,101 = 5150,524
√ SSσ×
2 + S Sττ
2√ 5150,4725150,472 +23,101 × 23,101 = 5150,524
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
1 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 35,0 мм и d = 25,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8,2[1]). Проверку будем проводить по 0 - му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ) , где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 0,0 МПа, здесь
Wнетто = π× D3 3,14 × 25,0 3 3
- = 1533,981 мм
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,638 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]; - kσ = 2,15
- εσ = 0,88 - находим по таблице 8,8[1]; Тогда:
Sσ = 2627,792,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: σtv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 7,737 МПа, здесь
Wк нетто = π× D3 - 3,14 × 25,03 = 3067,962 мм3
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,6
- ετ = 0,77 - находим по таблице 8,8[1]; Тогда:
Sτ = 11,214,
Результирующий коэффициент запаса прочности:
![]() S = √ SSσσ
×2 + S Sττ
2√ 2627,7922627,792 +11,214 × 11,214 = 11,214
S = √ SSσσ
×2 + S Sττ
2√ 2627,7922627,792 +11,214 × 11,214 = 11,214
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
2 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 40,0 мм и d = 35,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8,2[1]). Проверку будем проводить по 0 - му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ) , где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 19,322 МПа, здесь
Wнетто = π× D3 - 3,14 × 35,0 3 = 4209,243 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,326 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]; - kσ = 2,05
- εσ = 0,85 - находим по таблице 8,8[1]; Тогда:
Sσ = 6,972,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла:
σtv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 2,82 МПа, здесь
Wк нетто = π× D3 - 3,14 × 35,03 = 8418,487 мм3
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,45
- ετ = 0,73 - находим по таблице 8,8[1]; Тогда:
Sτ = 32,124,
Результирующий коэффициент запаса прочности:
![]() S = √ SSσ×
2 + S Sττ
2√ 6,972 6,972 + 32,124 × 32,124 = 6,813
S = √ SSσ×
2 + S Sττ
2√ 6,972 6,972 + 32,124 × 32,124 = 6,813
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
3 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 40,0 мм и d = 35,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8,2[1]). Проверку будем проводить по 0 - му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 19,322 МПа, здесь
π× D3 3,14 × 35,0 3 3 Wнетто = - = 4209,243 мм
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,326 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ = 2,05
- εσ = 0,85 - находим по таблице 8,8[1]; Тогда:
Sσ = 6,972,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла:
σtv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 2,82 МПа, здесь
π× D3 3,14 × 35,03
Wк нетто = - = 8418,487 мм3
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,45
- ετ = 0,73 - находим по таблице 8,8[1]; Тогда:
Sτ = 32,124,
Результирующий коэффициент запаса прочности:
![]() S = Sσ× Sτ = 6,972 × 32,124 = 6,813
S = Sσ× Sτ = 6,972 × 32,124 = 6,813
6,972 + 32,124
Расчётное значениеполучилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
РАСЧЁТ 2 - ГО ВАЛА.
Крутящий момент на валу Tкр = 162672,11 H×мм. Для данного вала выбран материал: сталь 45, Для этого материала:
- предел прочности σb = 780,0 МПа;
- предел выносливости стали при симметричном цикле изгиба σ - 1 = 0,43 ×σb = 335,4
МПа;
- предел выносливости стали при симметричном цикле кручения τ - 1 = 0,58 ×σ - 1 = 194,532 МПа.
1 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 40,0 мм. Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом (см. табл. 8,7[1]). Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 0,0 МПа, здесь
Wнетто = π× D3 - 3,14 × 40,0 3 = 6283,185 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,249 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ /εσ = 2,8 - находим по таблице 8,7[1]; Тогда:
Sσ = 6727,147,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: τt = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 6,473 МПа, здесь
Wк нетто = π× D3 - 3,14 × 40,03 = 12566,371 мм3
16 16
- φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ /ετ = 4,0 - находим по таблице 8,7[1]; Тогда:
Sτ = 10,063,
Результирующий коэффициент запаса прочности:
![]() S = √ SSσ×
2 + S Sττ
2√ 6727,1476727,147 + × 10,063 10,063 = 6727,155
S = √ SSσ×
2 + S Sττ
2√ 6727,1476727,147 + × 10,063 10,063 = 6727,155
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
3 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 48,0 мм. Концентрация напряжений обусловлена наличием шпоночной канавки. Ширина шпоночной канавки b = 14,0 мм, глубина шпоночной канавки T1 = 5,5 мм.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ × β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений: σv = Mизг / Wнетто = 15,32 МПа, здесь
Wнетто = π×32 D 3 - b × T1 2× × (D - T D 1 ) 2 =
= 3,14 × 48,0 3 - 14,0 × 5,50 × (48,0 - 5,5)2 = 10593,933 мм3
32 2 × 48,0
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,173 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ = 1,8 = 1,8 - находим по таблице 8,5[1];
- εσ = 0,82 - находим по таблице 8,8[1]; Тогда:
Sσ = 9,665,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: τt = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 3,792 МПа, здесь
π× D3 b × T
Wк нетто = 16 - 1 2× × (D - T D 1 ) 2 =
= 3,14 × 48,0 3 - 14,0 × 5,50 × (48,0 - 5,5)2 = 21451,277 мм3
16 2 × 48,0
- φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,7 = 1,7 - находим по таблице 8,5[1];
- ετ = 0,7 - находим по таблице 8,8[1]; Тогда:
Sτ = 19,705,
Результирующий коэффициент запаса прочности:
![]() S = Sσ× Sτ = 9,665 × 19,705 = 21,947
S = Sσ× Sτ = 9,665 × 19,705 = 21,947
9,665 + 19,705
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
4 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 40,0 мм. Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом (см. табл. 8,7[1]). Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 0,0 МПа, здесь
Wнетто = π× D3 - 3,14 × 40,0 3 = 6283,185 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,249 МПа,
- φσ = 0,2 - см. стр. 164[1];
β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ /εσ = 2,8 - находим по таблице 8,7[1]; Тогда:
Sσ = 6727,147,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла:
τt = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 6,473 МПа, здесь
π× D3 3,14 × 40,03 3 Wк нетто = - = 12566,371 мм
16 16
- φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ /ετ = 4,0 - находим по таблице 8,7[1]; Тогда:
Sτ = 10,063,
Результирующий коэффициент запаса прочности:
![]() S = √ SSσ×
2 + S Sττ
2√ 6727,1476727,147 + × 10,063 10,063 = 6727,155
S = √ SSσ×
2 + S Sττ
2√ 6727,1476727,147 + × 10,063 10,063 = 6727,155
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
1 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 48,0 мм и d = 40,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8,2[1]). Проверку будем проводить по 0 - му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 37,907 МПа, здесь
Wнетто = π× D3 - 3,14 × 40,0 3 = 6283,185 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,249 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]; - kσ = 2,05
- εσ = 0,85 - находим по таблице 8,8[1]; Тогда:
Sσ = 3,557,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: σtv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 6,473 МПа, здесь
Wк нетто = π× D3 - 3,14 × 40,03 = 12566,371 мм3
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]. - kτ = 1,45
ετ = 0,73 - находим по таблице 8,8[1]; Тогда:
Sτ = 13,994,
Результирующий коэффициент запаса прочности:
S = √ SSσ×2 + S Sττ2 = √ 3,557 3,557 + 13,994 × 13,994 = 3,447
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
3 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 48,0 мм и d = 40,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8,2[1]). Проверку будем проводить по 0 - му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 25,831 МПа, здесь
Wнетто = π× D3 - 3,14 × 40,0 3 = 6283,185 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,249 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]; - kσ = 2,05
- εσ = 0,85 - находим по таблице 8,8[1]; Тогда:
Sσ = 5,218,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: σtv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 6,473 МПа, здесь
Wк нетто = π× D3 - 3,14 × 40,03 = 3
12566,371 мм
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,45
- ετ = 0,73 - находим по таблице 8,8[1]; Тогда:
Sτ = 13,994,
Результирующий коэффициент запаса прочности:
![]() S = √ SSσ×
2 + S Sττ
2√ 5,218 5,218 + 13,994 × 13,994 = 4,889
S = √ SSσ×
2 + S Sττ
2√ 5,218 5,218 + 13,994 × 13,994 = 4,889
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
РАСЧЁТ 3 - ГО ВАЛА.
Крутящий момент на валу Tкр = 628077,015 H×мм. Для данного вала выбран материал:
сталь 45, Для этого материала:
предел прочности σb = 780,0 МПа;
- предел выносливости стали при симметричном цикле изгиба σ - 1 = 0,43 ×σb = 335,4
МПа;
- предел выносливости стали при симметричном цикле кручения τ - 1 = 0,58 ×σ - 1 = 194,532 МПа.
2 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 63,0 мм. Концентрация напряжений обусловлена наличием шпоночной канавки. Ширина шпоночной канавки b = 18,0 мм, глубина шпоночной канавки T1 = 7,0 мм.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 8,65 МПа, здесь
π× D3 b × T1× (D - T1)2 = Wк нетто = 32 - 2 × D
3,14 × 63,0 3 18,0 × 7,0 × (63,0 - 7,0)2 3
= - = 24100,307 мм
32 2 × 63,0
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,0 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ = 1,8 = 1,8 - находим по таблице 8,5[1];
- εσ = 0,76 - находим по таблице 8,8[1]; Тогда:
Sσ = 15,88,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла:
τt = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 6,455 МПа, здесь π× D3 b × T1× (D - T1)2 = Wк нетто = 16 - 2 × D
= 3,14 × 63,0 3 - 18,0 × 7,0 × (63,0 - 7,0)2 = 24100,307 мм3
16 2 × 63,0
- φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,7 = 1,7 - находим по таблице 8,5[1];
- ετ = 0,65 - находим по таблице 8,8[1]; Тогда:
Sτ = 10,777,
Результирующий коэффициент запаса прочности:
S = √ SSσ×2 + S Sττ2 = √ 1515,88 ,88 + 10,777 × 10,777 = 19,192
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
4 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 58,0 мм. Это сечение при передаче вращающего момента через муфту рассчитываем на кручение. Концентрацию напряжений вызывает наличие шпоночной канавки.
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла:
τv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 8,706 МПа, здесь
π× D3 3,14 × 58,03
Wк нетто = - = 36072,359 мм3
16 16
где b = 16,0 мм - ширина шпоночного паза; T1 = 6,0 мм - глубина шпоночного паза; - φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]. - kτ = 1,7 - находим по таблице 8,5[1];
- ετ = 0,65 - находим по таблице 8,8[1]; Тогда: Sτ = 7,991,
ГОСТ 16162 - 78 указывает на то, чтобы конструкция редукторов предусматривала возможность восприятия консольной нагрузки, приложенной в середине посадочной части вала. Величина этой нагрузки для редукторов должна быть 2,5 × Т1/2 ,
Приняв у ведущего вала длину посадочной части под муфту равной длине полумуфты l =
80 мм, получим Мизг = 2,5 × Tкр 1/2 × 80 / 2 = 79251,31 Н×мм.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений: σv = Mизг / Wнетто = 4,685 МПа, здесь
b × T1 × (D -
Wнетто = π × D 3 - T1 )2 =
32 2 × D
3,14 × 63,03 16,0 × 6,0 × (58,0 -
= - 6,0)2 = 16917,283 мм3
32 2 × 58,0
где b = 16,0 мм - ширина шпоночного паза; T1 = 6,0 мм - глубина шпоночного паза; - среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,0 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]; - kσ = 1,8 - находим по таблице 8,5[1]; - εσ = 0,76 - находим по таблице 8,8[1]; Тогда:
Sσ = 29,322,
Результирующий коэффициент запаса прочности:
![]() S = Sσ× Sτ = 7,991 × 29,322 = 30,392
S = Sσ× Sτ = 7,991 × 29,322 = 30,392
7,991 + 29,322
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
1 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 63,0 мм и d = 60,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8,2[1]). Проверку будем проводить по 3 - му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 9,831 МПа, здесь
Wнетто = π× D3 3,14 × 60,0 3 3
- = 21205,75 мм
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,0 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ = 2,2
- εσ = 0,76 - находим по таблице 8,8[1]; Тогда:
Sσ = 11,432,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: σtv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 7,405 МПа, здесь
Wк нетто = π× D3 - 3,14 × 60,03 3
= 42411,501 мм
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,41
- ετ = 0,65 - находим по таблице 8,8[1]; Тогда:
Sτ = 11,245,
Результирующий коэффициент запаса прочности:
![]() S = √ SSσ×
2 + S Sττ
2√ 1111,432 ,432 + 11,245 × 11,245 = 14,017
S = √ SSσ×
2 + S Sττ
2√ 1111,432 ,432 + 11,245 × 11,245 = 14,017
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
2 - E СЕЧЕНИE.
Диаметр вала в данном сечении D = 63,0 мм и d = 60,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8,2[1]). Проверку будем проводить по 3 - му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ - 1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ), где: - амплитуда цикла нормальных напряжений:
σv = Mизг / Wнетто = 9,831 МПа, здес
π× D3 3,14 × 60,0 3
Wнетто = - = 21205,75 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,0 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ = 2,2
- εσ = 0,76 - находим по таблице 8,8[1]; Тогда:
Sσ = 11,432,
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ - 1 / ((kτ / (εt ×β)) ×τv + τt ×τm ), где:
- амплитуда и среднее напряжение отнулевого цикла: σtv = τm = τmax / 2 = 0,5 × Tкр / Wк нетто = 7,405 МПа, здесь
Wк нетто = π× D3 - 3,14 × 60,03 = 42411,501 мм3
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,41
- ετ = 0,65 - находим по таблице 8,8[1]; Тогда:
Sτ = 11,245,
Результирующий коэффициент запаса прочности:
S = √ SSσσ × 2 + S Sττ 2 = √ 1111,432 ,432 + 11,245 × 11,245 = 14,017
Расчётное значение получилось больше минимально допустимого [S] = 2,5, Сечение проходит по прочности.
РАСЧЁТ 4-ГО ВАЛА.
Крутящий момент на валу Tкр = 1316251,672 H×мм. Для данного вала выбран материал:
сталь 45. Для этого материала: - предел прочности σb = 780,0 МПа;
- предел выносливости стали при симметричном цикле изгиба σ-1 = 0,43 ×σb = 335,4 МПа; - предел выносливости стали при симметричном цикле кручения τ-1 = 0,58 ×σ-1 = 194,532 МПа.
2-E СЕЧЕНИE.
Диаметр вала в данном сечении D = 70,0 мм. Концентрация напряжений обусловлена посадкой подшипника с гарантированным натягом (см. табл. 8.7[1]). Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ-1 / ((kσ / (εσ ×β)) ×σv + φσ ×σm ) , где: - амплитуда цикла нормальных напряжений:
σv = Mизг. / Wнетто = 11,674 МПа, здесь
Wнетто = π× D3 3,14 × 70,0 3 3
- = 33673,946 мм
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,0 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1];
- kσ /εσ = 2,8 - находим по таблице 8.7[1]; Тогда:
Sσ = 6,967.
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ-1 / ((kτ / (ετ ×β)) ×τv + φτ ×τm ) , где: - амплитуда и среднее напряжение отнулевого цикла: τt = τm = τmax / 2 = 0,5 × Tкр. / Wк нетто = 9,772 МПа, здесь
Wк нетто = π× D3 - 3,14 × 70,03 = 67347,893 мм3
16 16
- φt = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ /ετ = 4,0 - находим по таблице 8.7[1]; Тогда:
Sτ = 6,665.
Результирующий коэффициент запаса прочности:
S = √ SSσσ × 2 + S Sττ 2 = √ 6,967 6,967 + 6,665 × 6,665 = 9,642
Расчётное значение получилось больше минимально допустимого [S] = 2,5. Сечение проходит по прочности.
1-E СЕЧЕНИE.
Диаметр вала в данном сечении D = 70,0 мм и d = 65,0 мм. Концентрация напряжений обусловлена галтелью (см. табл. 8.2[1]). Проверку будем проводить по 3-му сечению, где наибольший изгибающий момент.
Коэффициент запаса прочности по нормальным напряжениям:
Sσ = σ-1 / ((kσ / (σσ ×β)) ×σv + φσ ×σm ) , где: - амплитуда цикла нормальных напряжений:
σv = Mизг. / Wнетто = 14,581 МПа, здесь
Wнетто = π× D3 - 3,14 × 65,0 3 = 26961,246 мм3
32 32
- среднее напряжение цикла нормальных напряжений:
σm = Fa / (π× D2 / 4) = 0,0 МПа,
- φσ = 0,2 - см. стр. 164[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1]; - kσ = 1,75
- εσ = 0,76 - находим по таблице 8.8[1]; Тогда:
Sσ = 9,69.
Коэффициент запаса прочности по касательным напряжениям:
Sτ = τ-1 / ((kτ / (ετ ×β)) ×τv + φτ ×τm ) , где: - амплитуда и среднее напряжение отнулевого цикла:
σtv = τm = τmax / 2 = 0,5 × Tкр. / Wк нетто = 12,205 МПа, здесь
π× D3 3,14 × 65,03 3 Wк нетто = - = 53922,493 мм
16 16
- φτ = 0,1 - см. стр. 166[1];
- β = 0,97 - коэффициент, учитывающий шероховатость поверхности, см. стр. 162[1].
- kτ = 1,27
- ετ = 0,65 - находим по таблице 8.8[1]; Тогда:
Sτ = 7,539.
![]() Результирующий коэффициент запаса прочности: S = √ SSσ×
2 + S Sττ
2√ 9,69 9,69 + 7,539 × 7,539 = 5,95
Результирующий коэффициент запаса прочности: S = √ SSσ×
2 + S Sττ
2√ 9,69 9,69 + 7,539 × 7,539 = 5,95
σ
Расчётное значение получилось больше минимально допустимого [S] = 2,5. Сечение проходит по прочности.
ТЕПЛОВОЙ РАСЧЁТ РЕДУКТОРА
Для проектируемого редуктора площадь телоотводящей поверхности А = 0,796 мм2 (здесь учитывалась также площадь днища, потому что конструкция опорных лап обеспечивает циркуляцию воздуха около днища).
По формуле 10,1[1] условие работы редуктора без перегрева при продолжительной работе:
∆t = tм - tв = Ртр × (1 - η) / (Kt × A) [∆t], где Ртр = 7,306 кВт - требуемая мощность для работы привода.
Считаем, что обеспечивается нормальная циркуляция воздуха, и принимаем коэффициент теплоотдачи Kt = 15 Вт/(м2 ×°C). Тогда:
∆t = 47,5° ≤ [∆t], где [∆t] = 50°С - допускаемый перепад температур. Температура лежит в пределах нормы.
ВЫБОР СОРТА МАСЛА
Смазывание элементов передач редуктора производится окунанием нижних элементов в масло, заливаемое внутрь корпуса до уровня, обеспечивающего погружение элемента передачи примерно на 10 - 20 мм. Объём масляной ванны V определяется из расчёта 0,25 дм3 масла на 1 кВт передаваемой мощности:
V = 0,25 × 7,306 = 1,827 дм3 ,
По таблице 10,8[1] устанавливаем вязкость масла. При контактных напряжениях σH = 369,262 МПа и скорости v = 1,717 м/с рекомендуемая вязкость масла должна быть примерно равна 40,0×10 -6 м/с2 По таблице 10,10[1] принимаем масло индустриальное И - 40А (по ГОСТ 20799-75).
Выбираем для подшипников качения пластичную смазку ЦИАТИМ - 201 по ГОСТ 6267 - 74 (см. табл. 9,14[1]). Камеры подшинпиков заполняются данной смазкой и периодически пополняются ей.
ВЫБОР ПОСАДОК
Посадки элементов передач на валы - Н7/р6, что по СТ СЭВ 144-75 соответствует легкопрессовой посадке.
Посадки муфт на валы редуктора - Н8/h8,
Шейки валов под подшипники выполняем с отклонением вала k6,
Остальные посадки назначаем, пользуясь данными таблицы 8,11[1].
КРАТКОЕ ОПИСАНИЕ ТЕХНОЛОГИИ СБОРКИ РЕДУКТОРА
Перед сборкой внутреннюю полость корпуса редуктора тщательно очищают и покрывают маслостойкой краской. Сборку производят в соответствии с чертежом общего вида редуктора, начиная с узлов валов.
На валы закладывают шпонки и напрессовывают элементы передач редуктора.
Подшипники следует насаживать, предварительно нагрев в масле до 80 - 100 градусов по
Цельсию, последовательно с элементами передач. Собранные валы укладывают в основание корпуса редуктора и надевают крышку корпуса, покрывая предварительно поверхности стыка крышки и корпуса спиртовым лаком. Для центровки устанавливают крышку на корпус с помощью двух конических штифтов; затягивают болты, крепящие крышку к корпусу. После этого в подшипниковые камеры закладывают смазку, ставят крышки подшипников с комплектом металлических прокладок, регулируют тепловой зазор. Перед постановкой сквозных крышек в проточки закладывают войлочные уплотнения, пропитанные горячим маслом. Проверяют проворачиванием валов отсутствие заклинивания подшипников (валы должны проворачиваться от руки) и закрепляют крышку винтами. Затем ввертывают пробку маслоспускного отверстия с прокладкой и жезловый маслоуказатель. Заливают в корпус масло и закрывают смотровое отверстие крышкой с прокладкой, закрепляют крышку болтами. Собранный редуктор обкатывают и подвергают испытанию на стенде по программе, устанавливаемой техническими условиями.
РАСЧЁТ ПРЕДОХРАНИТЕЛЬНОЙ МУФТЫ.
1. Конструктивно принимаем: число кулачков Z = 6, рабочую высоту h = 10 мм
средний диаметр расположения кулачков dср = 3×dH = 2×53 =159 мм (dH = 53 мм – диаметр посадочного отверстия)
Окружная скорость на среднем диаметре:
V= π×dср ×n/60×103 = 3,14×116×102/60000 = 0,619208 м/с < 0,8 м/с допускаемое напряжение смятия для стали 40Х с закалкой рабочих поверхностей до
58…63HRC [σсм ] = 35 МПа. Коэффициент запаса β = 1,5 2. Вычисляем рабочую длинну кулачка:
2×T2×628075,72
b≥ = = 3,76 мм dср ×σсм ×h×Z 159×35×10×6
из [2] формула 9, стр 14. Принимаем b = 10 мм 3. Тогда: dср = (D+d)/2 = 159 мм , D = 169 мм, d = 149 мм
f = 0,15 - коэффициент трения между кулачками (смазка отсутствует — приимаем конструктивно).
φ = arctg f = 8,53° - угол трения на кулачках
f2 = 0,1 – приведённый коэффициент трения в осевых направляющих подвижной полумуфты 4. Для предотвращения самоторможения, мешающего срабатыванию муфты, должно соблюдаться условие:
f2 ×dср /dH < tg (α0 -φ) [2], стр 13 arctg (0,1× dср /dH ) < α0 - φ (α0 = 40°…65°) arctg (0,1× dср /dH ) = 16,7° < 31.46° при α0 = 40°
Конструктивно выбираем α0 = 40°
5. Расчётный вращающий момент для муфты:
Fx × dср
βT= 2[tg(α0-φ) – f2 ddсрH ]
Тогда:
β×T × 2[tg(α0 -φ) – f2 ×dср / dH ]
F x = dср =
2×628075,72×2 [tg(40°-8,53°)-0,1×3]
= 159 = 4930,78 Н
6. Силу срабатывания принимаем:
F3 = 1,2×Fx = 1,2×4930,78 = 5916,94 Н
Полная осадка пружины при срабатывании муфты:
fΣ3 = h×F3 /(F3 – Fx ) = 10×5916,94/(5916,94-4930,78) = 59,99 мм [2] формула 10 Используя одну центральную пружину, имеем расчётную силу сжатия:
Fр = F3 = 5916,94 Н
Используя рекомендацию [2] стр 19: C = 10; K= (4×C+2)/(4×C-3) = 42/37 = 1,135 Диаметр проволоки при [τ]к = 750 МПа:
d = ![]() π [τ] 3,14 750 = 14,9 мм
π [τ] 3,14 750 = 14,9 мм
По ряду Ra40 принимаем d = 15 мм Средний диаметр пружины:
D0 = C×d = 10×15 = 150 мм
Осадка одного витка при кручении:
8×Fx×D03 8×4930,78 ×1503
f2 = G×d4 = 8×104×154 = 32,87 мм
Необходимое число витков:
h10
n ≥f2 ×(F3/Fx – 1) +2 = 18,03×(5916,94/4930,78-1)+2 = 4,77 витков
В сжатом состоянии длина пружины составит:
H2 = [d +2]×n+h = [15 + 2]×5 + 10 = 95 мм Полная длинна пружины:
H = n×f2 = 5×32,87 = 164,35 мм
СПИСОК ИСПОЛЬЗОВАНОЙ ЛИТЕРАТУРЫ
1, Чернавский С.А., Боков К.Н., Чернин И.М., Ицкевич Г.М., Козинцов В.П. 'Курсовое проектирование деталей машин': Учебное пособие для учащихся. М.:Машиностроение, 1988 г.
2. Методическое пособие 1340 МАМИ; Москва 1996 г.
3. Чернавский С.А., Снесарев Г. А., Козинцев Б. С. «Проектирование механических передач». Учебно-справочное пособие для ВТУЗов. М.:Машиностроение, 1984 г.
