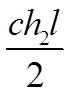| Скачать .docx |
Реферат: Определение перемещения методом Мора. Правило Верещагина
УО «БГУИР»
кафедра инженерной графики
РЕФЕРАТ
на тему:
«ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МОРА. ПРАВИЛО ВЕРЕЩАГИНА»
МИНСК, 2008
Рассмотрим теперь общий метод определения перемещений, пригодный для любой, линейно деформируемой системы при любой нагрузке. Этот метод предложен выдающимся немецким ученым О. Мором.
Пусть, например, требуется определить вертикальное перемещение точки А балки, представленной на рис. 7.13, а. Заданное (грузовое) состояние обозначим буквой к. Выберем вспомогательное состояние той же балки с единичной

силой, действующей в точке A и в направлении искомого перемещения. Вспомогательное состояние обозначим буквой i(рис. 7.13,6).
Вычислим работу внешних и внутренних сил вспомогательного состояния на перемещениях, вызванных действием сил грузового состояния.
Работа внешних сил будет равна произведению единичной силы на искомое перемещение ya
![]()
а работа внутренних сил по абсолютной величине равна интегралу
![]()
Имеем
![]()
или
![]() (1)
(1)
Формула (7.33) и есть формула Мора (интеграл Мора), которая дает возможность определить перемещение в любой точке линейно-деформируемой системы.
В этой формуле подынтегральное произведение MiMkположительно, если оба изгибающих момента имеют одинаковый знак, и отрицательно, если Miи Мк имеют разные знаки.
Если бы мы определяли угловое перемещение в точке А, то в состоянии iследовало бы приложить в точке А момент, равный единице (без размерности).
Обозначая буквой Δ любое перемещение (линейное или угловое), формулу (интеграл) Мора напишем в виде
![]() (2)
(2)

В общем случае аналитическое выражение Miи Мк может быть различным на разных участках балки или вообще упругой системы. Поэтому вместо формулы (2) следует пользоваться более общей формулой
![]() (3)
(3)
Если стержни системы работают не на изгиб, а на растяжение (сжатие), как, например, в фермах, то формула Мора имеет вид
![]() (4)
(4)
В этой формуле произведение NiNKположительно, если оба усилия растягивающие или оба сжимающие. Если стержни одновременно работают и на изгиб и на растяжение (сжатие), то в обычных случаях, как показывают сравнительные расчеты, перемещения можно определять, учитывая лишь изгибающие моменты, так как влияние продольных сил весьма мало.
По тем же соображениям, как отмечалось ранее, в обычных случаях можно не учитывать влияния поперечных сил.
Вместо непосредственного вычисления интеграла Мора можно пользоваться графо-аналитическим приемом «способом перемножения эпюр», или правилом Верещагина.
Рассмотрим две эпюры изгибающих моментов, из которых одна Мк имеет произвольное очертание, а другая Мi прямолинейна (Рис 7.14, а и б).
Сечение стержня на участке AВ будем считать постоянным. В этом случае
![]() (5)
(5)
Величина MKdzпредставляет собой элементарную площадь dωk эпюры Мк (заштрихована на рисунке). Таким образом,
 (6)
(6)
Но
![]() (7)
(7)
следовательно,
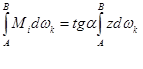 (8)
(8)
Но ![]() представляет собой статический момент площади эпюры Мк относительно некоторой оси у, проходящей через точку О, равный ωkzc, где ωk — площадь эпюры моментов; zс — расстояние от оси у до центра тяжести эпюры Мк. Из чертежа видно, что
представляет собой статический момент площади эпюры Мк относительно некоторой оси у, проходящей через точку О, равный ωkzc, где ωk — площадь эпюры моментов; zс — расстояние от оси у до центра тяжести эпюры Мк. Из чертежа видно, что
![]() (9)
(9)
где Мсi — ордината эпюры Mi, расположенная под центром тяжести эпюры Мк (под точкой С). Следовательно,
 (10)
(10)
т. е. искомый интеграл равен произведению площади эпюры Мк (любой по очертанию) на расположенную под ее центром тяжести ординату прямолинейной эпюры Мсi. Значение величины ωкМсi считается положительным, если обе эпюры располагаются по одну сторону стержня, и отрицательным, если они располагаются по разные стороны. Положительный результат перемножения эпюр означает, что направление перемещения совпадает с направлением единичной силы (или момента).
Необходимо помнить, что ордината Мсiберется обязательно в прямолинейной эпюре. В том частном случае, когда обе эпюры прямолинейные, можно умножить площадь любой из них на соответствующую ординату другой.
Для стержней переменного сечения правило Верещагина перемножения эпюр неприменимо, так как в этом случае уже нельзя выносить величину EJиз-под знака интеграла. В этом случае следует выразить EJкак функцию абсциссы сечения и затем уже вычислять интеграл Мора (1).
При ступенчатом изменении жесткости стержня интегрирование (или перемножение эпюр) производят для каждого участка отдельно (со своим значением EJ) и затем суммируют результаты.
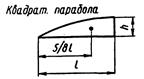
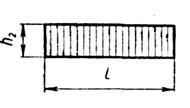
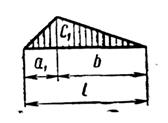
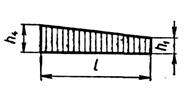
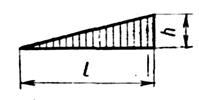
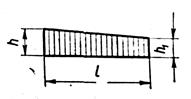
В табл. 1 приведены значения площадей некоторых простейших эпюр и координат их центра тяжести.
Таблица 1
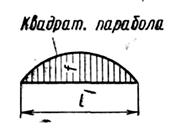
| Вид эпюры | Площадь эпюры | Расстояние до центра тяжести |
|
|
|
|
|
|
|
|
|
|
|
|
Для ускорения вычислений можно использовать готовые таблицы перемножения эпюр (табл.2).
В этой таблице, в клетках на пересечении соответствующих элементарных эпюр, приведены результаты перемножения этих эпюр.
При разбивке сложной эпюры на элементарные, представленные в табл. 1 и 7.2, следует иметь в виду, что параболические эпюры получены от действия только одной распределенной нагрузки.
В тех случаях, когда в сложной эпюре криволинейные участки получаются от одновременного действия сосредоточенных моментов, сил и равномерно распределенной нагрузки, во избежание ошибки следует сложную эпюру предварительно «расслоить», т. е. разбить ее на ряд самостоятельных эпюр: от действия сосредоточенных моментов, сил и от действия равномерно распределенной нагрузки.
Можно также применить другой прием, не требующий расслоения эпюр, а требующий лишь выделения криволинейной части эпюры по хорде, соединяющей крайние ее точки.
Покажем оба способа на конкретном примере.
Пусть, например, требуется определить вертикальное перемещение левого конца балки (рис. 7.15).
Суммарная эпюра от нагрузки представлена на рис. 7.15, а.
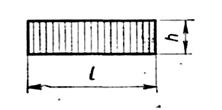
Таблица 7.2
Mi Mk |
|
|
|
|
|||||
 |
|
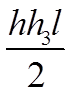 |
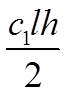 |
 |
|||||
 |
|
 |
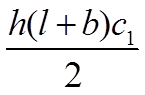 |
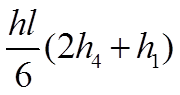 |
|||||
 |
 |
 |
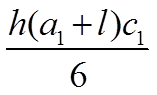 |
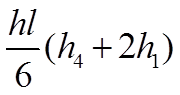 |
|||||
 |
 |
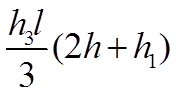 |
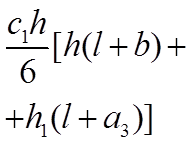 |
 |
|||||
|
|
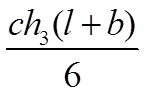 |
 |
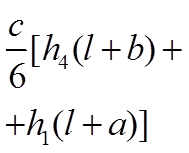 |
|||||
|
|
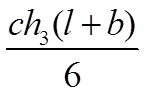 |
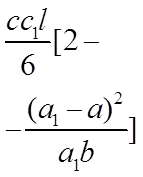 |
 |
|||||
 |
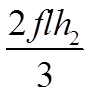 |
 |
 |
 |
|||||
|
 |
 |
 |
 |
|||||
Эпюра от действия единичной силы в точке А представлена на рис. 7.15, г.
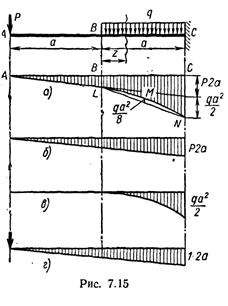
Для определения вертикального перемещения в точке А необходимо перемножить эпюру от нагрузки на эпюру от единичной силы. Однако замечаем, что на участке ВС суммарной эпюры криволинейная эпюра получена не только от действия равномерно распределенной нагрузки, но также и от действия сосредоточенной силы Р. В результате на участке ВС уже будет не элементарная параболическая эпюра, приведенная в таблицах 7.1 и 7.2, а по существу сложная эпюра, для которой данные этих таблиц недействительны.
Поэтому необходимо произвести расслоение сложной эпюры по рис. 7.15, а на элементарные эпюры, представленные на рис. 7.15, б и 7.15, в.
Эпюра по рис. 7.15, б получена только от сосредоточенной силы, эпюра по рис. 7.15, в — только от действия равномерно распределенной нагрузки.
Теперь можно перемножить эпюры, используя табл. 1 или 2.
Для этого необходимо перемножить треугольную эпюру по рис. 7.15, б на треугольную эпюру по рис. 7.15, г и добавить к этому результат перемножения параболической эпюры на рис. 7.15, в на трапециевидную эпюру участка ВС по рис. 7.15, г, так как на участке АВ ординаты эпюры по рис. 7.15, в равны нулю.
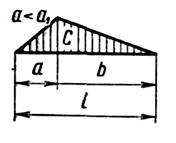
Покажем теперь второй способ перемножения эпюр. Рассмотрим снова эпюру по рис. 7.15, а. Примем начало отсчета в сечении В. Покажем, что в пределах кривой LMNизгибающие моменты могут быть получены как алгебраическая сумма изгибающих моментов, соответствующих прямой LN, и изгибающих моментов параболической эпюры LNML, такой же, как и для простой балки длиной а, загруженной равномерно распределенной нагрузкой q:
![]()
Наибольшая ордината посредине будет равна ![]() .
.
Для доказательства напишем фактическое выражение изгибающего момента в сечении на расстоянии zот точки В
![]() (А)
(А)
Напишем теперь выражение изгибающего момента в том же сечении, полученное как алгебраическая сумма ординат прямой LNи параболы LNML.
Уравнение прямой LN
![]()
где k— тангенс угла наклона этой прямой

Следовательно, уравнение изгибающих моментов, полученное как алгебраическая сумма уравнения прямой LNи параболы LNMNимеет вид
![]()
что совпадает с выражением (А).
При перемножении эпюр по правилу Верещагина следует перемножить трапецию BLNCна трапецию из единичной эпюры на участке ВС (см. рис. 7.15, г) и вычесть результат перемножения параболической эпюры LNML(площадью ![]() ) на ту же трапецию из единичной эпюры. Такой способ расслоения эпюр особенно выгоден, когда криволинейный участок эпюры находится на одном из средних участков балки.
) на ту же трапецию из единичной эпюры. Такой способ расслоения эпюр особенно выгоден, когда криволинейный участок эпюры находится на одном из средних участков балки.
Пример 7.7. Определить вертикальное и угловое перемещения консольной балки в месте приложения нагрузки (рис. 7.16).
Решение. Строим эпюру изгибающих моментов для грузового состояния (рис. 7.16, а).
Для определения вертикального перемещения выбираем вспомогательное состояние балки с единичной силой в точке приложения нагрузки.
Строим эпюру изгибающих моментов от этой силы (рис. 7.16, б). Определяем вертикальное перемещение по способу Мора
![]()
Значение изгибающего момента от нагрузки
![]()
Значение изгибающего момента от единичной силы
![]()
Подставляем эти значения МР и Miпод знак интеграла и интегрируем
![]()
Этот же результат был ранее получен другим способом.
Положительное значение прогиба показывает, что точка приложения нагрузки Р перемещается вниз (в направлении единичной силы). Если бы мы единичную силу направили снизу вверх, то имели бы Mi = 1zи в результате интегрирования получили бы прогиб со знаком минус. Знак минус показывал бы, что перемещение происходит не вверх, а вниз, как это и есть в действительности.
Вычислим теперь интеграл Мора путем перемножения эпюр по правилу Верещагина.
Так как обе эпюры прямолинейны, то безразлично, из какой эпюры брать площадь и из какой — ординату.
Площадьгрузовой эпюры равна
![]()
Центр тяжести этой эпюры расположен на расстоянии 1/3l от заделки. Определяем ординату эпюры моментов от единичной силы, расположенную под

центром тяжести грузовой эпюры. Легко убедиться, что она равна 1/3l.
Следовательно.
![]()
Тот же результат получается и по таблице интегралов. Результат перемножения эпюр положителен, так как обе эпюры располагаются снизу стержня. Следовательно, точка приложения нагрузки смещается вниз, т. е. по принятому направлению единичной силы.
Для определения углового перемещения (угла поворота) выбираем вспомогательное состояние балки, в котором на конце балки действует сосредоточенный момент, равный единице.
Строим эпюру изгибающих моментов для этого случая (рис. 7.16, в). Определяем угловое перемещение, перемножая эпюры. Площадь грузовой эпюры
![]()
Ординаты эпюры от единичного момента везде равны единице., Следовательно, искомый угол поворота сечения равен
![]()
Так как обе эпюры расположены снизу, то результат перемножения эпюр положителен. Таким образом, концевое сечение балки поворачивается по часовой стрелке (по направлению единичного момента).
Пример: Определить по способу Мора — Верещагина прогиб в точке Dдля балки, изображенной на рис. 7.17..
Решение. Строим расслоенную эпюру моментов от нагрузки, т. е. строим отдельные эпюры от действия каждой нагрузки. При этом для удобства перемножения эпюр целесообразно строить расслоенные (элементарные) эпюры относительно сечения, прогиб которого определяется в данном случае относительно сечения D.
На рис. 7.17, а представлена эпюра изгибающих моментов от реакции А (участок AD) и от нагрузки Р = 4 Т (участок DC). Эпюры строятся на сжатом волокне.
На рис. 7.17, б представлены эпюры моментов от реакции В (участок BD), от левой равномерно распределенной нагрузки (участок AD) и от равномерно распределенной нагрузки, действующей на участке ВС. Эта эпюра изображена на рис. 7.17, б на участке DCснизу.
Далее выбираем вспомогательное состояние балки, для чего в точке D, где определяется прогиб, прикладываем единичную силу (рис. 7.17, в). Эпюра моментов от единичной силы изображена на рис. 7.17, г.Теперь перемножим эпюры с 1 по 7 на эпюры 8 и 9, пользуясь таблицами перемножения эпюр, с учетом знаков.

При этом эпюры, расположенные с одной стороны балки, перемножаются со знаком плюс, а эпюры, расположенные по разные стороны балки, перемножаются со знаком минус.
При перемножении эпюры 1 и эпюры 8 получим
![]()
Перемножая эпюру 5 на эпюру 8, получим
![]()
Перемножение эпюр 2 и 9 дает
![]()
Перемножаем эпюры 4 и 9
![]()
Перемножаемэпюры 6 и 9
![]()
Суммируя результаты перемножения эпюр, получим
Знак минус показывает, что точка Dперемещается не вниз, как направлена единичная сила, а вверх.
Этот же результат был получен ранее по универсальному уравнению .
Конечно, в данном примере можно было расслоить эпюру только на участке AD, так как на участке DBсуммарная эпюра прямолинейная и ее незачем расслаивать. На участке ВС расслоения не требуется, так как от единичной силы на этом участке эпюра равна нулю. Расслоение эпюры на участке ВС необходимо для определения прогиба в точке С.
Пример. Определить вертикальное, горизонтальное и угловое перемещения сечения А ломаного стержня, представленного на рис. 7.18, а. Жесткость сечения вертикального участка стержня — EJ1 жесткость сечения горизонтального участка — EJ2.
Решение. Строим эпюру изгибающих моментов от нагрузки. Она представлена на рис. 7.18, б (см. пример 6.9). Для определения вертикального перемещения сечения А выбираем вспомогательное состояние системы, представленное на рис. 7.18, в. В точке А приложена единичная вертикальная сила, направленная вниз.
Эпюра изгибающих моментов для этого состояния представлена на рис. 7.18, в.
Определяем вертикальное перемещение по методу Мора, используя способ перемножения эпюр. Так как на вертикальном стержне во вспомогательном состоянии эпюра М1 отсутствует, то перемножаем только эпюры, относящиеся к горизонтальному стержню. Площадь эпюры берем из грузового состояния, а ординату — из вспомогательного. Вертикальное перемещение равно
![]()
Так как обе эпюры расположены снизу, то результат перемножения берем со знаком плюс. Следовательно, точка А перемещается вниз, т. е. так, как направлена единичная вертикальная сила.
Для определения горизонтального перемещения точки А выбираем вспомогательное состояние с горизонтальной единичной силой, направленной влево (рис. 7.18, г). Эпюра моментов для этого случая представлена там же.
Перемножаем эпюры МPи М2 и получаем
![]()
Результат перемножения эпюр положителен, так как перемножаемые эпюры располагаются на одной и той же стороне стержней.
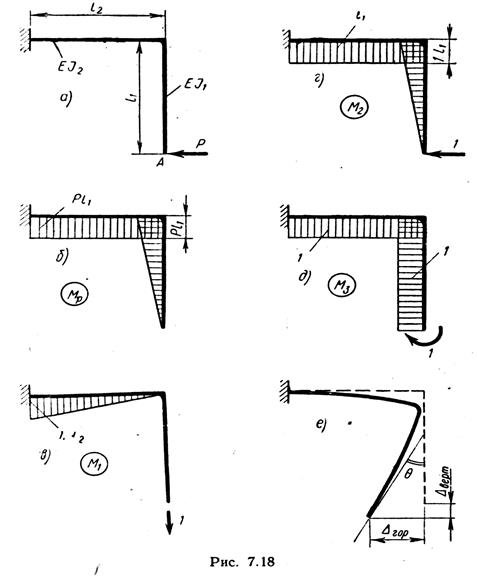
Для определения углового перемещения выбираем вспомогательное состояние системы по рис. 7.18,5 и строим эпюру изгибающих моментов для этого состояния (на том же рисунке). Перемножаем эпюры МР и М3:
![]()
Результат перемножения положителен, так как перемножаемые эпюры располагаются с одной стороны.
Следовательно, сечение Aповорачивается по часовой стрелке
Те же результаты получились бы и при использовании таблиц
перемножения эпюр.
Вид деформированного стержня показан на рис. 7.18, е, при этом перемещения сильно увеличены.
ЛИТЕРАТУРА
Феодосьев В.И. Сопротивление материалов. 1986
Беляев Н.М. Сопротивление материалов. 1976
Красковский Е.Я., Дружинин Ю.А., Филатова Е.М. Расчет и конструирование механизмов приборов и вычислительных систем. 1991
Работнов Ю.Н. Механика деформируемого твердого тела. 1988
Степин П.А. Сопротивление материалов. 1990