| Скачать .docx |
Реферат: Серия МОНАП: модели, методы, подходы
В работе описывается авторское средство проектирования интеллектуальных обучающих систем серии МОНАП. Процесс обучения рассматривается как управляемый и контролируемый процесс решения учебных задач. Подробно рассматривается математическая модель управления процессом обучения, реализованная в авторских средствах. Для идентификации знаний обучаемого используется Байесовский подход. Адекватное управление процессом обучения основано на стабилизации трудности учебных задач. В результате анализа ответа обучаемого МОНАП осуществляет на очередной шаг обучения задачу с оптимальным значением трудности для конкретного обучаемого.
В этой статье описывается история развития серии МОНАП: математической модели управления процессом обучения и авторских средств, основанных на этой модели. Описывается также ИОС GRAD, разработанная с помощью авторских средств, основанных на МОНАП.
Для некоторых предметных областей средства предоставляют полную автоматизацию разработки ИОС.
Рассматриваемые авторские средства включают подсистему моделирования, обеспечивающую педагогу возможность комфортного проведения дидактических экспериментов, направленных на выбор оптимальных значений параметров модели управления обучением.
Введение
Развитие и совершенствование архитектуры интеллектуальных обучающих систем (ИОС) находится в центре внимания многих исследователей [ConatiC. & VanLehnK., 1996; Kinshuk & Patel, 1997; GertnerA. etal., 1998; Yang & Akahory, 1999]. Одним из основных направлений проводимых работ является решение проблемы адаптивного управления процессом обучения. В случаях, когда в алгоритмах управления используются дидактические принципы обучения, инвариантные к предметной области (ПО) обучения, разрабатываются инструментальные средства проектирования ИОС. Педагог, использующий такие средства в конкретной ПО должен обеспечить параметрическую настройку этих принципов к ПО и конкретным обучаемым для обеспечения адекватности управления обучением в проектируемой ИОС.
Необходимая формализация основана на алгоритмическом подходе к процессу обучения. Этот подход направлен на решение следующих основных проблем:
разработка решающих алгоритмов конкретных учебных задач и изучение обучаемыми применение этих алгоритмов;
разработка алгоритмов адаптивного управления обучением, которые реализованы в ИОС.
Алгоритмы решения учебных задач, разработанные педагогом на основе анализа изучаемой предметной области и описанные посредством совокупности правил (операций): ЕСЛИ (условие), ТО (действие).
Инструментальные средства МОНАП предоставляют автоматизацию проектирования ИОС, реализуя алгоритмы адаптивного управления процессом обучения в выбранной ПО [GaleevI. etal., 1998; GaleevI., 1999]. Вместе с основной функцией МОНАП предоставляет автоматизацию проектирования подсистемы объяснений. Подсистема объяснений формирует ответ на вопрос обучаемого «ПОЧЕМУ?» в форме того правила в котором имела место ошибка, пока обучаемый решал учебную задачу. Здесь используется база данных, содержащая совокупность, сформулированных педагогом.
Для различных категорий обучаемых в одной и той же ПО целесообразно использовать различные среды, отличающиеся друг от друга дидактическими характеристиками в рамках единой модели обучения. В этом случае необходимо поддерживать механизм наследования свойств, обеспечивающий совместное использование данных различными ИОС. Требования реализованы в технологии формирования семейства ИОС как сети, которая по существу минимизирует трудность формирования новых ИОС, принадлежащих семейству.
В этой статье также описан подход к проектированию ИОС, который предлагает альтернативу разработке предметно-зависимых подсистем ИОС для некоторых ПО. Такой подход существенно уменьшает трудность проектирования новой ИОС.
Основные понятия
В результате анализа ряда теорий обучения выделен следующий ряд принципов организации обучения, инвариантных к ПО обучения.
Процесс обучения рассматривается как управляемый и контролируемый процесс решения учебных задач. Определение свойств учебных задач и выдача подкреплений должны осуществляться на основе идентификации знаний обучаемого на каждом шаге обучения. В процессе обучения должен соблюдаться принцип перехода от усвоения простого учебного материала к сложному. Переход к усвоению нового учебного материала осуществляется в случае успешного усвоения предыдущего материала. В процессе обучения должна осуществляться стабилизация субъективной степени трудности учебных заданий для каждого обучаемого.
Формализация выделенных принципов осуществляется следующим образом.
Экспертом-педагогом разрабатывается алгоритмическое предписание, описывающее пути решения учебных задач в заданной ПО обучения. Множество типов операций, выполняемых обучаемым при решении указанных задач и соответствующих алгоритмическому предписанию, обозначается через ![]() . Свойства конкретной задачи определяются вектором операций, используемых для ее решения:
. Свойства конкретной задачи определяются вектором операций, используемых для ее решения: ![]() , где
, где ![]() - число операций
- число операций ![]() , применение которых необходимо для решения задачи
, применение которых необходимо для решения задачи ![]() . Все задачи ПО обучения могут быть разделены на
. Все задачи ПО обучения могут быть разделены на ![]() классов, каждый из которых характеризуется соответствующим уникальным подмножеством типов операций
классов, каждый из которых характеризуется соответствующим уникальным подмножеством типов операций ![]() , используемых при выполнении задач, принадлежащих
, используемых при выполнении задач, принадлежащих ![]() -му классу. В свою очередь задачи, принадлежащие
-му классу. В свою очередь задачи, принадлежащие ![]() -му классу, могут быть разнотипными, то есть отличаться друг от друга тем, что их свойства описываются различными векторами
-му классу, могут быть разнотипными, то есть отличаться друг от друга тем, что их свойства описываются различными векторами ![]() и
и ![]()
![]() .
.
В качестве основного компонента модели обучаемого используется вектор ![]() , где
, где ![]() - вероятность правильного применения операции
- вероятность правильного применения операции ![]() на
на ![]() -м шаге обучения определяется как:
-м шаге обучения определяется как: ![]() . Мера трудности задания
. Мера трудности задания ![]() вводится как средняя доля ошибок, ожидаемых при выполнении задания:
вводится как средняя доля ошибок, ожидаемых при выполнении задания:
![]() , (1)
, (1)
где ![]() - математическое ожидание числа ошибок при выполнении задания (трудоемкость задания), то есть
- математическое ожидание числа ошибок при выполнении задания (трудоемкость задания), то есть ![]() , где
, где ![]() - вероятность неправильного применения операции
- вероятность неправильного применения операции ![]() на
на ![]() -м шаге обучения.
-м шаге обучения.
В соответствии с принципом стабилизации субъективной степени трудности учебных заданий необходимо стремиться к тому, чтобы на каждом шаге обучения выполнялось неравенство: ![]() , где
, где ![]() - оптимальная мера трудности;
- оптимальная мера трудности; ![]() - размер интервала.
- размер интервала.
С учетом введенных определений формулируется цель обучения:
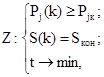 (2)
(2)
где ![]() - требуемое значение вероятности правильного применения операции;
- требуемое значение вероятности правильного применения операции; ![]() - требуемая сложность задачи в
- требуемая сложность задачи в ![]() -м классе задач;
-м классе задач; ![]() - время обучения.
- время обучения.
Если достигнут требуемый уровень обученности, то обучения успешно заканчивается. Предусматривается возможность аварийного окончания обучения в случае, когда процесс обучения не является эффективным, что оптимизирует затраты на его проведение. На каждом шаге обучения модель обеспечивает идентификацию знаний обучаемого и вынесение решения о продолжении обучения или его завершения (успешном или аварийном).
В настоящее время нами разрабатывается расширение модели. Это даст возможность адаптивно формировать теоретический материал для обучаемого.
Идентификация знаний обучаемого
Идентификация знаний обучаемого (определение значений ![]() ) осуществляется следующим образом. Для каждой операции
) осуществляется следующим образом. Для каждой операции ![]() вводится
вводится ![]() гипотез
гипотез ![]() , соответствующих
, соответствующих ![]() состояниям обученности. Каждому
состояниям обученности. Каждому ![]() -му состоянию обученности соответствует условная вероятность
-му состоянию обученности соответствует условная вероятность ![]() правильного применения операции
правильного применения операции ![]() в каждом из
в каждом из ![]() её применений, равная
её применений, равная ![]() .
.
Гипотезы ![]() образуют полную группу несовместных событий, то есть имеет место:
образуют полную группу несовместных событий, то есть имеет место: ![]() , где
, где ![]() - вероятность гипотезы
- вероятность гипотезы ![]() для операции
для операции ![]() .
.
На каждом шаге обучения наблюдается событие ![]() , состоящее в правильном применении
, состоящее в правильном применении ![]() -ой операции
-ой операции ![]() раз из
раз из ![]() заданных.
заданных.
Эта информация служит для пересчета распределения вероятностей гипотез ![]() с помощью формулы Байеса.
с помощью формулы Байеса.
Каждый ![]() -й шаг обучения характеризуется априорным и апостериорным распределениями вероятностей гипотез о состояниях обученности
-й шаг обучения характеризуется априорным и апостериорным распределениями вероятностей гипотез о состояниях обученности ![]() и
и ![]() , связанных между собой следующей зависимостью:
, связанных между собой следующей зависимостью:
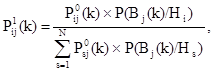 (3)
(3)
где ![]() - определяется по теореме Бернулли, то есть:
- определяется по теореме Бернулли, то есть:
![]() (4)
(4)
где ![]() - число сочетаний из
- число сочетаний из ![]() по
по ![]() .
.
Учитывая, что априорное распределение вероятностей гипотез на ![]() -м шаге совпадает с апостериорным распределением на
-м шаге совпадает с апостериорным распределением на ![]() -м шаге, то есть имеет место
-м шаге, то есть имеет место ![]() , формулу (3) можно переписать в виде который подчеркивает её рекурсивный характер (учитывается вся история обучения), а именно:
, формулу (3) можно переписать в виде который подчеркивает её рекурсивный характер (учитывается вся история обучения), а именно:
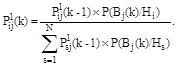 (5)
(5)
Вероятность правильного применения операции ![]() на
на ![]() -м шаге определяется по формуле полной вероятности:
-м шаге определяется по формуле полной вероятности:
![]() (6)
(6)
Окончательная оценка ![]() получается приведением значения, вычисленного по формуле (6), до введенных состояний обученности.
получается приведением значения, вычисленного по формуле (6), до введенных состояний обученности.
Осуществление на ![]() -м шаге обучения контроля ошибок и выдачи необходимых объяснений позволяет вести прогнозирование вероятности правильного применения операций
-м шаге обучения контроля ошибок и выдачи необходимых объяснений позволяет вести прогнозирование вероятности правильного применения операций ![]() на
на ![]() -й шаг обучения:
-й шаг обучения:
![]() где
где ![]() (7)
(7)
Адаптивное управление процессом обучения
При вынесении решения о необходимости продолжения обучения модель определяет задание, адекватное знаниям обучаемого, на очередной шаг обучения, то есть обеспечивает индивидуальную минимизацию времени обучения. Для этого используется алгоритм стабилизации меры трудности учебных заданий, который можно представить в виде следующей последовательности шагов:
Шаг 1. По результатам ![]() -го шага обучения определяются значения
-го шага обучения определяются значения ![]() для всех
для всех ![]() .
.
Шаг 2. Прогнозируются значения ![]() на
на ![]() -й шаг обучения:
-й шаг обучения: ![]() .
.
Шаг 3. В рассматриваемом классе задач пересчитывается прогнозируемое на ![]() -й шаг обучения значение трудности задач того же типа
-й шаг обучения значение трудности задач того же типа ![]() , что и на предыдущем шаге. Если выполняется условие:
, что и на предыдущем шаге. Если выполняется условие:
![]() (8)
(8)
то задача указанного типа вновь включается в учебное задание, формируемое на ![]() -й шаг обучения.
-й шаг обучения.
Шаг 4. Если условие (8) не выполняется, то для всех типов задач, рассматриваемого класса вычисляются отклонения их значений трудности от оптимального:
![]() . (9)
. (9)
Шаг 5. Если требуется уменьшить трудность, то есть имеет место: ![]() то в рассматриваемом классе осуществляется поиск задач такого типа, трудность которых
то в рассматриваемом классе осуществляется поиск задач такого типа, трудность которых ![]() имела бы минимально возможное отклонение от оптимальной:
имела бы минимально возможное отклонение от оптимальной:
![]() (10)
(10)
При этом трудоемкость задач искомого типа не должна возрастать, то есть: ![]() Кроме того, если для задач различных типов имеет место симметричное отклонение их значений трудности от оптимального:
Кроме того, если для задач различных типов имеет место симметричное отклонение их значений трудности от оптимального:
![]() (11)
(11)
то в задание, формируемое на ![]() -й шаг обучения, включается задача такого типа, значение трудности которой ближе к значению
-й шаг обучения, включается задача такого типа, значение трудности которой ближе к значению ![]() , то есть для которой, в рассматриваемом случае, дополнительно выполняется:
, то есть для которой, в рассматриваемом случае, дополнительно выполняется: ![]() .
.
В противоположном случае, когда требуется увеличить трудность, то есть имеет место: ![]() , так же используется критерий поиска (10). При этом должны соблюдаться противоположные ограничения. Трудоемкость задач искомого типа не должна уменьшаться, то есть
, так же используется критерий поиска (10). При этом должны соблюдаться противоположные ограничения. Трудоемкость задач искомого типа не должна уменьшаться, то есть ![]() Если имеет место симметрия отклонения трудностей (11), то дополнительно должно выполняться:
Если имеет место симметрия отклонения трудностей (11), то дополнительно должно выполняться: ![]() .
.
Ограничением на область применения модели выступает требование организации пооперационного контроля деятельности обучаемого по выполнению учебных заданий.
Проведенный анализ разработанной модели обучения показал, что она удовлетворяет основным требованиям, предъявляемым к математическим моделям (адекватности, сходимости, универсальности, экономичности) и может служить основой для разработки инструментальных средств проектирования подсистемы модели обучения в ИОС.
Авторские средства проектирования ИОС
МОНАП – ядро авторских средств проектирования подсистемы управления процессом обучением в ИОС. Подсистема управления процессом обучения, спроектированная посредством МОНАП на базе пооперационного контроля ответов обучаемого, рассчитывает уровни усвоения материала обучаемым для каждой операции (правила), используя Байесовский подход, который позволяет учитывать предысторию обучения. На основе анализа ответов обучаемых МОНАП определяет учебное задание с оптимальным значением трудности для конкретного обучаемого и отправляет эту информацию в подсистему формирования заданий. Эта подсистема генерирует или выбирает задание из базы данных на следующий шаг обучения. Таким образом, ИОС, спроектированная посредством МОНАП организует адаптивное управление процессом обучения, т.е. обеспечивает полную автоматизацию следующих интеллектуальных функций:
идентификацию знаний обучаемого;
принятие решения о продолжении обучения, достижении цели обучения, аварийное завершение;
определение свойств учебной задачи адекватной знаниям обучаемого на следующий шаг обучения.
Подсистема управления обучением построена на основе следующих моделей:
модель предметной области;
модель обучаемого;
модель управления процессом обучения.
В МОНАП могут быть выделены два основных компонента:
сервисные авторские средства, используемые для создания базы знаний и ее поддержки;
функциональные средства, используемые для обучающего диалога и управления.
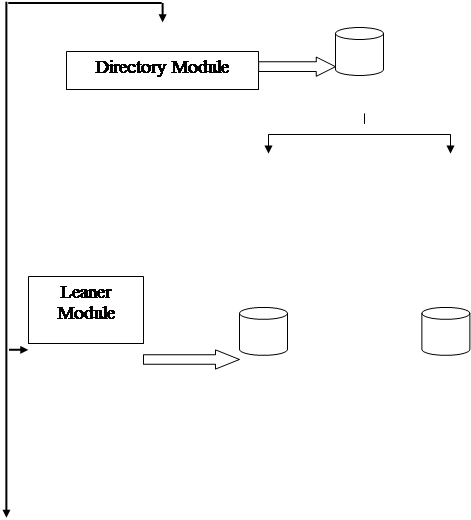
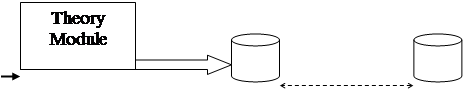
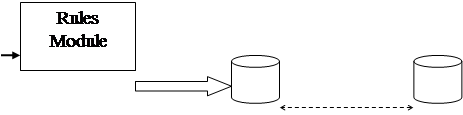
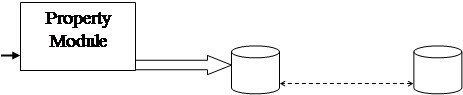
База знаний представляет собой совокупность сред обучения. Структура базы знаний представлена на рис. 1.
Каждая среда обучения, включенная в базу знаний содержит следующие знания:
знания о свойствах учебных задач (какого типа и сколько операций необходимо выполнить для решения учебного задания);
знания об обучаемом (имя, текущий шаг обучения, свойства учебного задания на следующий шаг обучения, вероятности правильного выполнения операций, вероятности гипотез об уровнях усвоения на текущий шаг);
знания об управлении процессом обучения определяемые соответствующими значениями параметров модели обучения (число гипотез об уровнях обученности, оптимальное значение трудности задания, минимальный уровень усвоения, "порог стресса" и т.д.).
|
|||||||||
 |
|||||||||
|
|
|
···
![]()
![]()
![]() Interchangeable components of
Interchangeable components of
ITS family information base
 |
|||||
 |
|||||
 |
|||||
|
|||||
Рис. 1. Структура базы знаний
Моделирование процесса обучения
В связи с тем, что невозможно дать точные и однозначные рекомендации по параметрической настройке модели управления обучением для произвольной ПО, возникает необходимость в расширении архитектуры ИОС, а соответственно и инструментальных средств проектирования ИОС за счет включения в них подсистемы моделирования процесса обучения.
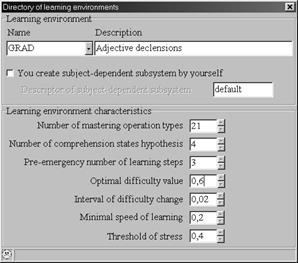 |
При проектировании конкретной ИОС преподаватель должен задать значения ряда параметров модели управления обучением (Рис. 2).
Рисунок 2.
 |
Значения некоторых из указанных параметров могут существенным образом влиять на то, какая задача будет выдана обучаемому в соответствии с его состоянием обученности. Практический опыт использования МОНАП-ПЛЮС для проектирования ИОС GRAD [GaleevI. etal., 1998] показал, что задание значений указанных параметров могут вызывать затруднения у педагогов несмотря на то, что встроенные средства помощи содержат рекомендации по их выбору. Для преодоления этих затруднений педагог может использовать режим моделирования. В этом режиме (Рис. 3) предоставляется возможность задавать любые результаты решения задач.
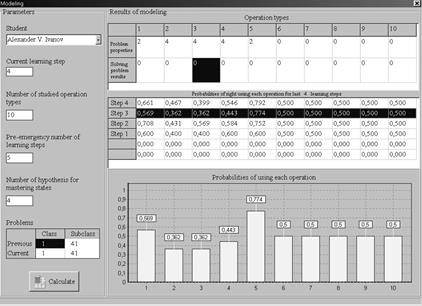
Рисунок 3.
Педагогу наглядно представляются итоги идентификации знаний обучаемого (используется байесовский подход) в цифровой и графической формах, а также тип текущей задачи, которая будет предложена обучаемому для выполнения на следующем шаге обучения в соответствии с его состоянием обученности и заданными значениями параметров модели обучения.
Варьируя результаты решения задач и значения параметров модели, педагог может подобрать такие значения, при которых модель обучения будет управлять процессом обучения оптимально с точки зрения педагога. В режиме моделирования доступны две различные формы графического представления итогов идентификации знаний обучаемого. В числовой форме эти же данные приведены в таблице, расположенной над графиком. Первый тип графика (Рис. 3) демонстрирует вероятности правильного применения обучаемым каждой операции на заданном количестве шагов обучения, то есть графически отображает данные, находящиеся в той или иной строке таблицы. Второй тип графика демонстрирует историю изменения состояния обученности обучаемого по конкретной операции (графическое изображение того или иного столбца таблицы). Переключиться между этими двумя типами представления графической информации можно щелкнув левой клавишей мыши на соответствующем заголовке строки или столбца цифровой таблицы соответственно.
В связи с тем, что процесс обучения является многофакторным, динамическим и слабо формализуемым процессом возникает необходимость в наличие инструментов, обеспечивающих педагогу возможность проведения дидактических экспериментов с целью такой настройки, модели управления обучением в ИОС, которая позволяет учитывать конкретные условия использования. Реализованная в МОНАП подсистема моделирования отвечает указанным требованиям.
Интеллектуальная обучающая система, основанная на МОНАП
Во многих научных исследованиях показано, что CALL системы более эффективны, чем традиционный человек-учитель [Yang & Akahory, 1999]. В результате анализа предметной области обучения (грамматики немецкого языка в части склонения имен прилагательных) разработаны структуры предметно-ориентированных подсистем соответствующей экспертной обучающей системы (ИОС GRAD) [GaleevI. etal., 1999]. Подсистема модели обучения спроектирована с помощью инструментальных средств МОНАП. В соответствии с разработанной ранее архитектурой проектируемых ИОС определен состав предметно-ориентированного расширения среды обучения в ИОС GRAD и разработаны программные средства, обеспечивающие её создание и обслуживание, в том числе и возможность построения семейства ИОС в рассматриваемой ПО обучения, имеющих сетевую архитектуру, т.е. использующих общие компоненты информационных баз. Разработанная ИОС GRAD обеспечивая адаптивный процесс освоения обучаемым грамматики немецкого языка в части склонения имен прилагательных представляет собой гибкую систему открытого типа, способную расширяться и изменяться по требованиям эксперта-педагога.
Актуальность усвоения грамматики немецкого языка в части склонения имен прилагательных обусловлена тем, что знания о прилагательном используются как при синтезе, так и при анализе немецкого предложения. В случае синтеза предложения основной задачей при изучении прилагательного является правильное определение его окончания. В случае анализа (понимания) немецкого предложения знания о прилагательном могут играть важнейшую роль при решении целого ряда задач анализа:
распознавание подлежащего;
различение числа;
распознавание распространенного предложения и т.д.
Таким образом, решая задачи синтеза, обучаемый приобретает знания, которые могут быть использованы и при решении задач анализа немецкого предложения. В связи с этим целесообразно проектирование ИОС GRAD (GR -Grammatik, AD - Adjektiv), в которой учебным заданием является набор предложений немецкого языка, содержащих основы прилагательных. Обучаемому необходимо правильно проставить требуемые окончания. Фрагмент учебного задания может выглядеть следующим образом:
Das klein... Kind trinkt warm... Milch.
На основе анализа морфологии прилагательного, а также учитывая результаты анализа морфологии определяемого существительного и артикля, сформулирован общий подход к формированию алгоритмических предписаний по определению окончаний прилагательных в виде набора правил (операций) типа: "ЕСЛИ (условие), ТО (действие)". Указанные предписания представляют собой реализации внешней формы представления знаний эксперта-педагога о грамматике немецкого языка в части склонения имен прилагательных. Очевидно, что может быть сформирован целый класс таких алгоритмических предписаний на ЕЯ. При этом алгоритмические предписания указанного класса могут существенно отличаться друг от друга. Возможны следующие основные различия:
по типам выделенных операций, входящих в алгоритмическое предписание;
по степени детализации выделенных операций, входящих в алгоритмическое предписание;
по указанной экспертом-педагогом последовательности выделенных операций;
по естественно-языковой форме представления алгоритмического предписания, обусловленного как многозначностью, так и синонимичностью ЕЯ.
В качестве примера, иллюстрирующего потенциальное многообразие алгоритмических предписаний в рассматриваемой ПО обучения можно привести ряд операций, описывающих то или иное подмножество правил склонения прилагательных в слабой форме:
ЕСЛИ перед прилагательным и существительным стоит определенный артикль der или одно из местоимений dieser, jener, solcher, jeder, welcher и определяемое существительное мужского рода, ТО окончанием прилагательного является -е;
ЕСЛИ перед прилагательным и существительным стоит определенный артикль der и определяемое существительное мужского рода, ТО окончанием прилагательного является -е;
В рамках сформулированного общего подхода разработано конкретное алгоритмическое предписание, для хранения которого используется файл «ПРАВИЛА». Эксперт-педагог может разработать свое, отличное от предложенного, алгоритмическое предписание, адекватно (как по естественно-языковой форме представления, так и по содержанию) отображающее его знания в анализируемой предметной области (ПО) обучения. Программные средства ИОС GRAD поддерживают такую возможность.
Определены следующие структуры предметно-ориентированных подсистем ИОС GRAD.
Подсистема формирования учебных заданий представляет собой совокупность банка учебных задач со средствами его создания и обслуживания, а также соответствующей программы, обеспечивающей предъявление обучаемому задачи, свойства которой определяются подсистемой модели обучения в соответствии с текущими знаниями обучаемого.
Подсистема решателя задач отсутствует в связи с отказом от построения генератора задач.
Подсистема диагностики обеспечивает:
ввод ответа обучаемого;
анализ ответа обучаемого;
выдачу диагностических сообщений;
представление помощи обучаемому;
определение типов и количества допущенных ошибок;
формирование обратной связи и возврат управления.
Подсистема объяснений представляет собой расширение подсистемы диагностики за счет включения в ее структуру файла «ПРАВИЛА», используемого для формирования ответов обучаемому на его вопрос “ПОЧЕМУ?”. Ответ формируется в естественно-языковой форме в виде “ЕСЛИ..., ТО...”.
Разработаны программные средства, обеспечивающие создание и обслуживание предметно-ориентированного расширения среды обучения ИОС GRAD. Указанные программные средства поддерживают уровень “открытости” ИОС, задаваемый инструментальными средствами проектирования МОНАП-ПЛЮС. Разработан предметно-ориентированный компонент учебного диалога, осуществляемый соответствующими предметно-ориентированными подсистемами ИОС GRAD при выполнении их основных функций. Кроме того, в процессе указанного диалога предусматривается анализ логической целостности (полноты и непротиворечивости) информационной базы ИОС GRAD, сопровождаемый выдачей аварийных сообщений в адрес эксперта-педагога в случаях ее нарушения.
ИОС GRAD, обеспечивая адаптивный процесс усвоения обучаемым грамматики немецкого языка в части склонения имен прилагательных, представляет собой гибкую систему открытого типа способную расширяться и изменяться по требованиям эксперта-педагога. Используя предоставляемые ему программные средства, эксперт-педагог может:
изменить существующую (поставляемую) ИОС;
построить набор независимых и существенно отличных друг от друга ИОС в рассматриваемой ПО обучения для различных категорий обучаемых;
построить семейство ИОС в рассматриваемой ПО обучения, имеющих сетевую архитектуру, то есть использующих общие компоненты информационных баз.
Дискуссия и выводы
В настоящее время, ведутся работы по созданию CALL системы по русскому языку в части склонения имени прилагательного посредством МОНАП. В будущем планируется апробировать предложенный подход в других ПО.
Общеизвестны преимущества Web-based интеллектуальных обучающих систем. Многие из существующих ОАС (обучающая адаптивная система) в Web, например, ELM-ART, CALAT, WITS и Belvedere, были разработаны на базе более ранних ИОС [BrusilovskyP., 1998]. В известных нам АОС в Web авторские средства проектирования курсов доступны только непосредственно на сервере разработчика системы. Это сильно сужает круг экспертов-педагогов, имеющих возможность создания своих авторских курсов в этих системах, что влечет за собой ограничение количества создаваемых курсов. Поэтому, одной из основных задач новых версий MONAP является разработка и реализация инструментальных средств проектирования сред обучения с помощь которых педагог с удаленного компьютера, подключенного к Internet, сможет создавать свои среды обучения. В результате появляется возможность множеству педагогов в одной ПО строить множество сред обучения с различными дидактическими характеристиками. Таким образом, система превращается в удобный инструмент для постановки широкомасштабных педагогических экспериментов и сбора большого количества полезной статистической информации, что расширяет ее возможности и в итоге увеличивает ценность для обучаемых.
Список литературы
[Conati C. & VanLehn K., 1996] Conati, C. & VanLehn, K., POLA: A student modeling framework for probabilistic on-line assessment of problem solving performance. In Proceedings of UM-96, Fifth International Conference on User Modeling. Kailua-Kona, HI: User Modeling Inc.
[Galeev I. et al., 1996] Galeev, I., Ivanov, V., Akhmadullin, M. A Learning Model in MONAP // Human-Computer Interaction. The 6th International Conference. EWHCI'96. Moscow, Russia, August 12-16, 1996. - P.320-323.
[Kinshuk & Patel, 1997] Kinshuk, Patel, A. “A Conceptual Framework for Internet based Intelligent Tutoring Systems” Knowledge Transfer, volume II, Ed. A. Behrooz, pAce, London, 1997, pp. 117-124
[Galeev I. et al., 1998] Galeev, I., Ivanov, V., Akhmadullin, M. The experience of development of intelligent tutoring systems, in proceeding of 27th International symposium "Ingenieurpädagogik'98”, Volume 2 "Padägogische Probleme in der Ingenieurausbildung" - pp. 255-258, Moscow, 1998.
[Brusilovsky P., 1998] Brusilovsky, P. Adaptive Educational Systems on the World-Wide-Web: A Review of Available Technologies, in proceedings of 4th International Conference on Intelligent Tutoring Systems (ITS'98), San Antonio, 1998.
[Gertner A. et al., 1998] Gertner, A., Conati, C., and VanLehn, K. Procedural help in Andes: Generating hints using a Bayesian network student model. In: Proceedings of the Fifteenth National Conference on Artificial Intelligence AAAI-98. Cambridge, MA: The MIT Press. pp.106-111
[Yang & Akahory, 1999] Yang, J. Ch., Akahory, K. An Evaluation of Japanese CALL Systems on the WWW Comparing a Freely Input Approach with Multiple Selection // Computer Assisted Languages Learning, 1999, Vol. 12, No. 1, pp. 59-79
[Galeev I., 1999] Galeev, I. “Automation of the ITS Design” Educational Technology journal, V. XXXIX, No. 5, September-October 1999, pp. 11-15.
[Galeev I. et al., 1999] Galeev, I., Tararina, L., Sosnovsky, S. “The structure and functions of ITS GRAD”, Proceedings of 8th International conference on Human-Computer Interaction (HCI’99) Volume 2 Munich, Germany, Lawrence Erlbaum Associate, Publishers, London, 22 – 26 of August, 1999, pp.682-685.