| Скачать .docx |
Реферат: Монолитное и сборное железобетонные перекрытия многоэтажного здания
 Федеральное агентство по образованию Российской Федерации
Федеральное агентство по образованию Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Южно-Уральский государственный университет»
Факультет «Архитектурно-строительный»
Кафедра «Строительные конструкции и инженерные сооружения»
Монолитное и сборное железобетонные перекрытия многоэтажного здания
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К КУРСОВОМУ ПРОЕКТУ
по дисциплине «Железобетонные и каменные конструкции»
ЮУрГУ-270102.2009.216.5432 ПЗ КП
Нормоконтролер Руководитель
С.А. Сонин С.А. Сонин
«__»_______2009г. «__»_______2009г.
Автор работы
студент группы АС-457
Абушахмина М.Р.
«__»_______2009г.
Работа защищена
с оценкой
_______________
«__»_______2009г.
Челябинск 2009г.
 АННОТАЦИЯ
АННОТАЦИЯ
Абушахмина М.Р. Монолитное и сборное железобетонные перекрытия многоэтажного здания. – Челябинск: ЮУрГУ, АС, 2009, ___с., библиогр. список – __ наименований.
В данном курсовом проекте рассчитывается монолитное и сборное перекрытие многоэтажного промышленного здания.
В первой части проекта рассчитывается монолитное перекрытие над подвалом, состоящее из плиты перекрытия второстепенных и главных балок.
Во второй части рассчитывается многопустотная панель перекрытия, которая представляет собой предварительно напряженную железобетонную конструкцию.
Графическая часть представлена в виде двух листов формата А1.
 ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ…………………………………………………………………….….4
1 РАСЧЕТ И КОНСТРУИРОВАНИЕ ПЛИТЫ И ГЛАВНОЙ БАЛКИ МОНОЛИТНОГО РЕБРИСТОГО ПЕРЕКРЫТИЯ
1.1 Исходные данные………………………………………………...…… 5
1.2 Компоновка перекрытия………………………………………….……5
1.3 Расчет и конструирование плиты…………………………………..…6
1.3.1 Расчетная схема плиты и нагрузок
1.3.2 Статический расчет плиты
1.3.3 Расчет на прочность нормальных сечений
1.3.4 Расчет на прочность наклонных сечений
1.4 Расчет главной балки…………………………………………………11
1.4.1 Расчетная схема балки и нагрузки
1.4.2 Статический расчет балки с учетом перераспределения
1.4.3 Перераспределение усилий
1.4.4 Проверка достаточности принятых размеров главной балки
1.4.5 Подбор продольной арматуры главной балки
1.4.6 Расчет наклонных сечений балки на поперечную силу
1.4.7 Расчет длин запусков обрываемых в пролете стержней за точки их теоретического обрыва
2 РАСЧЕТ И КОНСТРУИРОВАНИЕ МНОГОПУСТОТНОЙ ПАНЕЛИ ПЕРЕКРЫТИЯ
2.1 Исходные данные для проектирования…………………………..… 24
2.2 Компоновка перекрытия…………………………………………...…25
2.3 Нагрузки и расчетные воздействия……………………………….…26
2.4 Статический расчет панели в стадии эксплуатации………………..26
2.5 Подбор продольной рабочей напрягаемой арматуры из условия прочности сечения, нормального к продольной оси………………...…27
2.6 Геометрические характеристики поперечного сечения…………... 28
2.7 Предварительное натяжение арматуры……………………………. 28
2.8 Потери предварительного напряжения в напрягаемой арматуре…29
2.9 Проверка прочности панели по нормальному сечению………….. 30
2.10 Расчет прочности панели в стадии транспортирования……….…31
2.11 Расчет сечений, наклонных к продольной оси……………………32
2.12 Расчет на действие поперечной силы по наклонной сжатой полосе…………………………………………………………………..…33
2.13 Расчет панели по образованию трещин, нормальных к оси, в стадии эксплуатации………………………………………………..……33
2.14 Расчет по раскрытию трещин, нормальных к оси панели….…….34
2.15 Расчет прогиба панели в стадии эксплуатации……………………35
БИБЛИГРАФИЧЕСКИЙ СПИСОК……………………………………………37
 ВВЕДЕНИЕ
ВВЕДЕНИЕ
Железобетонные и каменные конструкции являются основной базой современного индустриального наземного и подземного строительства, они применяются при возведении промышленных, жилых и общественных зданий, инженерных сооружений, а также других объектов.
При проектировании железобетонных конструкций зданий основным нормативным документов является СНиП 2.03.01-84* «Бетонные и железобетонные конструкции».
В данном курсовом проекте рассчитывается монолитное и сборное перекрытие многоэтажного здания.
В первой части проекта рассчитывается монолитное перекрытие над подвалом, состоящее из плиты перекрытия второстепенных и главных балок. Сначала производится расчет монолитной плиты, подбираются арматурные сетки. Затем рассчитывается главная балка с учетом перераспределения усилий в ней и образования пластических шарниров. В результате построения эпюры материалов подбирается наиболее рациональное продольное армирование главной балки.
Во второй части рассчитывается многопустотная панель перекрытия, которая представляет собой предварительно напряженную железобетонную конструкцию. Панель рассчитывается по двум предельным состояниям: по прочности (по несущей способности) и по деформациям. Также производится расчет в стадии транспортирования. В результате подбирается сечение и количество напрягаемой арматуры. Расчет по деформациям ведется исходя из архитектурно-эстетических требований.
1 РАСЧЕТ И КОНСТРУИРОВАНИЕ ПЛИТЫ И ГЛАВНОЙ БАЛКИ МОНОЛИТНОГО РЕБРИСТОГО ПЕРЕКРЫТИЯ
1.1 Исходные данные
 Размеры здания в плане по крайним осям 21,6х26(м
).
Размеры здания в плане по крайним осям 21,6х26(м
).
Расстояние между продольными осями l 1 = 7,2 м.
Расстояние между поперечными осями l 2 = 5,2 м.
Толщина (кирпичных) наружных стен - 51 см .
Привязка внутренней грани наружных стен к осям здания - 20 см.
Материалы:
а) Бетон тяжелый класса В12,5: Rb =7,5 МПа ; Rbt =0,66 МПа ; γ b 2 =0,9; плотность ρ =25000 Н/м3
б) Арматура рабочая продольная:
для плиты – класса Вр- I ;
для главной балки – класса А- II ;
в) Арматура рабочая поперечная для главной балки класса А- I или A - III ;
г) Арматура монтажная:
для плиты – класса Вр-I;
для главной балки – класса А- I ;
Нагрузки (нормативные): временная (полезная) нагрузка на монолитное перекрытие V =13,0 кН/м2 ; кратковременно действующая Vsh = 2,5 кН/м2
Коэффициент надежности по назначению здания γ n =0,95.
1.2 Компоновка перекрытия
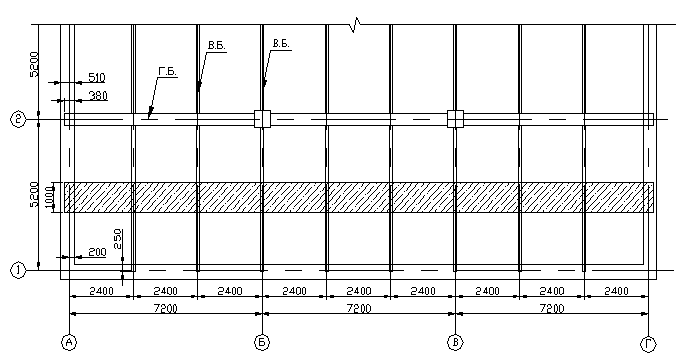
Рис. 1.1 Фрагмент плиты перекрытия
Вдоль поперечных осей здания расположим главные балки перекрытия с
шагом l 2 =5,2м , второстепенные балки параллельно продольным осям здания с шагом а по формуле (1):
![]() (1)
(1)
Предварительно зададимся размерами поперечных сечений элементов перекрытия:
- высота главной балки ![]() ; принимаем hr
= 60см.
; принимаем hr
= 60см.
- ширина главной балки![]() ; принимаем br
= 20см
.
; принимаем br
= 20см
.
- высота второстепенной балки ![]() ;
;
принимаем hB = 30см
– ширина второстепенной балки bB = (0,3...0,5). hB = 9…15см ;
принимаем bB = 12см
- толщина плиты перекрытия назначается по формуле (2):
![]() (2)
(2)
![]() ;
;
принимаем hп = 9см
 - глубина заделки главной балки в наружную стену здания Сr
= 38см; второстепенной балки СB
= 25см; плиты Сп
= 12см.
- глубина заделки главной балки в наружную стену здания Сr
= 38см; второстепенной балки СB
= 25см; плиты Сп
= 12см.
1.3 Расчет и конструирование плиты
1.3.1. Расчетная схема плиты и нагрузок
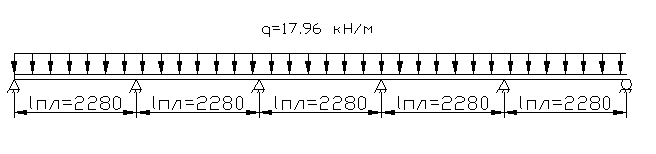 Рис. 1.2
Расчетная схема плиты
Рис. 1.2
Расчетная схема плиты
Так как отношение сторон плиты
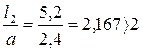 , (3)
, (3)
то плиту следует рассчитывать как балочную, то есть, работающую в одном коротком направлении. Для этого вырезаем полосу плиты шириной 1м и рассчитываем ее по многопролетной неразрезной схеме. Расчетный пролет плиты для средних пролетов вычисляется по формуле (4):
![]() (4)
(4)
Собственный вес плиты вычисляется в соответствии с формулой (5):
![]() (5)
(5)
Сбор нагрузок на плиту (Н/м)
Таблица 1
| Вид нагрузки |
Нормативные нагрузки |
Коэффициент надежности |
Расчетная нагрузка |
||||
| Постоянные: 1.Собственный вес плиты (hп =9 см; ρ = 25000 Н/м3 ) |
2250 |
1,1 |
2475 |
||||
| 2.Вес цементной стяжки δ = 20 мм; ρ = 22000 Н/м3 3.Вес керамической плитки δ = 13 мм; ρ = 18000 Н/м3 |
440 234 |
1,3 1,1 |
572 258 |
||||
| Итого |
Σ g =3305 |
||||||
| Временные: Полезная нагрузка V |
13000 |
1,2 |
15600 |
||||
| Итого |
Σ V = 15600 |
||||||
С учетом коэффициента надежности здания по назначению полная расчетная нагрузка на плиту:
![]() (6)
(6)
 |
 1.3.2 Статический расчет плиты
1.3.2 Статический расчет плиты
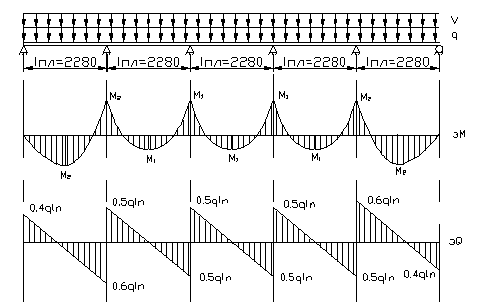
Рис. 1.3 Расчетная схема. Эпюры моментов и поперечных сил
 |
Расчетные значения изгибающих моментов в плите определяем с учетом распределения:
а) в средних пролетах и на средних опорах:
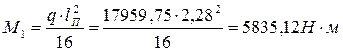 (7)
(7)
б) в крайних пролетах и на крайних промежуточных опорах:
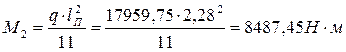 (8)
(8)
Максимальная поперечная сила в плите будет действовать на первой промежуточной опоре со стороны крайнего пролёта.
![]() (9)
(9)
1.3.3. Проверка прочности сечения на действие поперечных сил
![]() (10)
(10)
где γb 2 = 0,9 ; φ b 4 =0,6 – для тяжелого бетона;
![]()
Следовательно, прочность плиты на действие поперечных сил обеспечена.
1.3.4 Расчет на прочность нормальных сечений плиты
(подбор арматуры)
1. Подбор арматуры по M 1 .
Сечения рассчитываем как прямоугольные с единичной шириной b=1м и высотой h = h п =9см . Предполагая, что армирование плиты будет выполняться рулонными сетками. Для начала определим сечение основной сетки (С-1).
 Расчетный момент М1
=5835,12 (Н∙м). Принимаем рабочую арматуру сеток d=5 мм (Вр-I), тогда полезная высота сечения h01
=h-a=9,0-1,0-0,5/2=7,75см.
Расчетный момент М1
=5835,12 (Н∙м). Принимаем рабочую арматуру сеток d=5 мм (Вр-I), тогда полезная высота сечения h01
=h-a=9,0-1,0-0,5/2=7,75см.
Определяем требуемую высоту сжатой зоны бетона:
![]() (11)
(11)
Подбираем требуемую площадь сечения арматуры Вр-I (ds =5мм) при Rs =360МПа.
![]() (12)
(12)
Проверим полученную высоту сжатой зоны по предельной высоте:
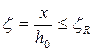 (13)
(13)
где ξ R – предельная высота сжатой зоны (для плит ξ R = 0,35)
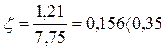
Требуемая площадь арматуры Вр-I:
![]() (14)
(14)
Примем:
для продольной арматуры
![]() (14Ǿ5мм Вр-
I
, шаг 75мм)
(14Ǿ5мм Вр-
I
, шаг 75мм)
для поперечной арматуры (Ǿ3мм Вр- I , шаг 250мм)
2. Подбор арматуры по M 2 .
Кроме основной сетки (C-1) необходимо подобрать дополнительную сетку(C-2). Расчетный момент М2 =8487,45(Н∙м). Полезная высота сечения h02 =h-a=9,0-1,75=7,25см. (а=1,0+0,05+0,05/2=1,75см)
Определяем требуемую высоту сжатой зоны бетона:
![]()
Подбираем требуемую площадь сечения арматуры Вр-I:
![]()
Проверим полученную высоту сжатой зоны по предельной высоте:
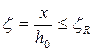
где ξ R – предельная высота сжатой зоны (для плит ξ R = 0,35)
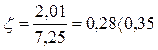
Требуемая площадь арматуры Вр-I:
![]()
7Ǿ5мм→1,37см2
7Ǿ4мм→0,88см2
Примем:
для продольной арматуры
![]() (7Ǿ5мм Вр-
I
, шаг 150мм)
(7Ǿ5мм Вр-
I
, шаг 150мм)
для поперечной арматуры (Ǿ3мм Вр- I , шаг 250мм)
1.3.5 Армирование плиты
Согласно расчета армирование выполняем сварными рулонными сетками с продольным расположением рабочей арматуры в рулоне. Ширину всех сеток принимаем равной 2500 мм.
Основная сетка С-1
![]()
Дополнительная сетка С-2
![]()
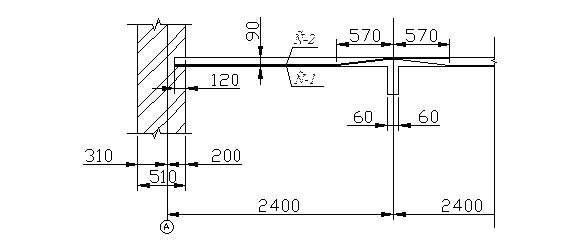
Рис 1.4 Армирование плиты монолитного перекрытия
 Спецификация арматуры плиты (на ячейку 3
L
1
xL
2
)
Спецификация арматуры плиты (на ячейку 3
L
1
xL
2
)
Табл.2
| Марка сетки и количество |
Назначение стержней сетки |
Длина, мм |
|
Количество стержней |
Общая длина, м |
|
| в сетке |
в плите |
|||||
| С-1 (2 шт) |
рабочая |
21440 |
5Вр-I |
34 |
68 |
1457,92 |
| расперед. |
2500 |
3Вр-I |
86 |
172 |
438,6 |
|
| С-2 (4 шт) |
рабочая |
2920 |
5Вр-I |
12 |
48 |
140,16 |
| распред. |
2500 |
3Вр-I |
17 |
68 |
173,4 |
|
Выборка арматуры на плиту
Табл.3
|
|
Общая длина, м |
Общая масса, кг |
| 5Вр-I |
1598,08 |
230,124 |
| 3Вр-I |
612 |
88,128 |
1.4 Расчет главной балки
1.4.1 Расчетная схема балки и нагрузки
Главная балка рассчитывается как трехпролетная неразрезная, нагруженная двумя сосредоточенными нагрузками в третях каждого пролета: постоянной G и временной V .
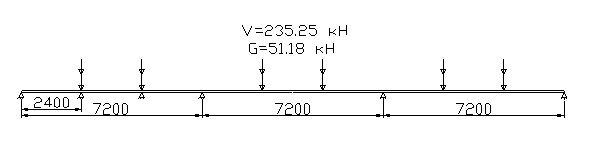
Рис.1.5 Расчетная схема главной балки
Постоянная нагрузка на балку рассчитывается по формуле:
. (15)
![]()
Временная нагрузка рассчитываются по формуле:
(16)
![]()
 1.4.2 Статический расчет балки с учетом перераспределения усилий
1.4.2 Статический расчет балки с учетом перераспределения усилий
Статический расчет главной балки с учетом перераспределения усилий выполняется в соответствии с требованиями пособия [2].
Расчет конструкции с учетом перераспределения усилий должен обеспечить образование пластических шарниров и в то же время не допустить преждевременного разрушения конструкции вследствие их образования. Поэтому должны быть выполнены следующие обязательные требования:
- в качестве рабочей растянутой арматуры должна применятся арматурная сталь с четко выраженной площадкой текучести. Этому требованию соответствуют арматурные стали классов A-I,A-II, A-III.
- изгибающий момент, действующий в пластическом шарнире, должен отличатся от момента в том же сечении, определенного по упругой стадии расчета, не более чем на 30% , т.е.
![]() (17)
(17)
Для определения величин изгибающих моментов в упругой стадии от действия постоянных нагрузок и различных схем временных нагрузок воспользуюсь расчетными коэффициентами k (k - для заданной расчетной точки балки, зависит от количества сил в пролете и вида загружения), таким образом, что моменты определяются по формуле:
М = k . m (18)
![]() (19)
(19)
l = l 1 = 7,2 м - пролет главной балки
F - сосредоточенная сила в главной балке.
Результаты расчета представлены в Таблице 5.
 Изгибающие моменты в расчетных сечениях главной балки (кНм)
Изгибающие моменты в расчетных сечениях главной балки (кНм)
Табл.5
| Вид нагружения |
Номер расчетной точки |
|||||||||
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
| П В1 В2 В3 В4 В5 В6 В7 |
0 0 0 0 0 0 0 0 |
90,08 414,04 489,32 -75,28 388,94 464,22 -50,19 25,09 |
57,32 263,48 414,04 -150,56 213,29 363,85 -100,37 50,19 |
-98,27 -451,68 -225,84 -225,84 -526,96 -301,12 -150,56 75,28 |
24,57 112,92 -225,84 338,76 163,11 -175,65 288,57 -50,186 |
24,57 112,92 -225,84 338,76 288,57 -50,186 163,11 -175,65 |
-98,27 -451,68 -225,84 -225,84 -150,56 75,28 -526,96 -301,12 |
57,32 263,48 414,04 -150,56 -100,37 50,19 213,29 363,85 |
90,08 414,04 489,32 -75,28 -50,19 25,09 388,94 464,22 |
0 0 0 0 0 0 0 0 |
| С1 =П+В1 С2 =П+В2 С3 =П+В3 С4 =П+В4 С5 =П+В5 С6 =П+В6 С7 =П+В7 |
0 0 0 0 0 0 0 |
504,12 579,4 14,8 479,02 554,3 39,89 115,17 |
320,8 471,36 -93,24 270,61 421,17 -43,05 107,51 |
-549,95 -324,11 -324,11 -625,23 -399,39 -248,83 -22,99 |
137,49 -201,27 363,33 187,68 -151,08 313,14 -25,62 |
137,49 -201,27 363,33 313,14 -25,62 187,68 -151,08 |
-549,95 -324,11 -324,11 -248,83 -22,99 -625,23 -399,39 |
320,8 471,36 -93,24 -43,05 107,51 270,61 421,17 |
504,12 579,4 14,8 39,89 115,17 479,02 554,3 |
0 0 0 0 0 0 0 |
| С1П С2П С3П С4П С5П С6П С7П |
0 0 0 0 0 0 0 |
541,55 541,55 -23,05 541,54 541,54 -23,05 111,98 |
395,66 395,66 -168,94 395,66 395,66 -168,94 101,13 |
-437,66 -437,66 -437,66 -437,66 -437,66 -437,66 -13,42 |
249,78 -314,82 249,78 249,78 -170,22 249,78 -38,38 |
249,78 -314,82 249,78 249,78 -38,38 249,78 -170,22 |
-437,66 -437,66 -437,66 -437,66 -13,42 -437,66 -437,66 |
395,66 395,66 -168,94 -168,94 101,13 395,66 395,66 |
541,55 541,55 -23,05 -23,05 111,98 541,54 541,54 |
0 0 0 0 0 0 0 |
1.4.3 Перераспределение усили
Таким образом, видно, что максимальный или критический момент возникает в 3-й расчетной точке (на опоре) т.е. четвертого сочетания нагрузок и он равен ![]() .
.
Опираясь на формулу получим:
![]()
![]()
Исходя из этого, будем перераспределять усилия таким образом, чтобы опорные моменты при любом сочетании нагрузок, были равны ![]()
Эпюры поперечных сил получаем из эпюр изгибающих моментов следующими дифференциальными зависимостями:
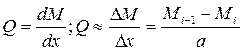 (20)
(20)
 Эпюры изгибающих моментов до и после перераспределения:
Эпюры изгибающих моментов до и после перераспределения:
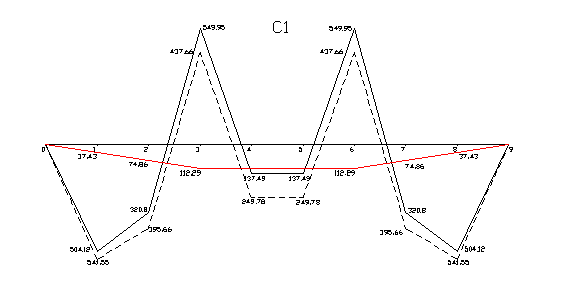
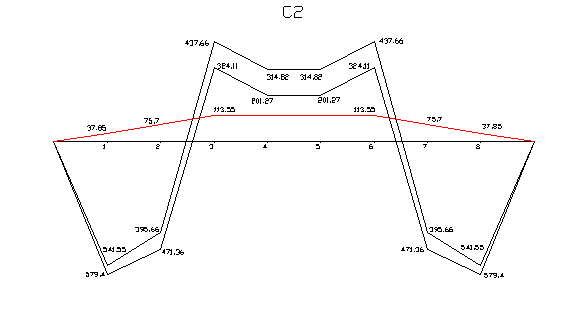
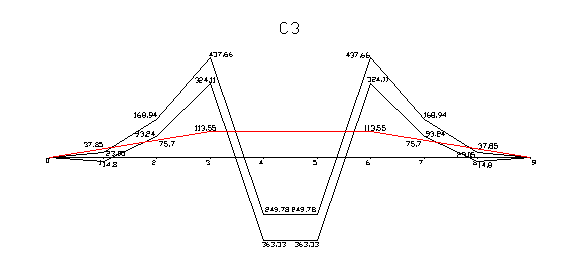
 |
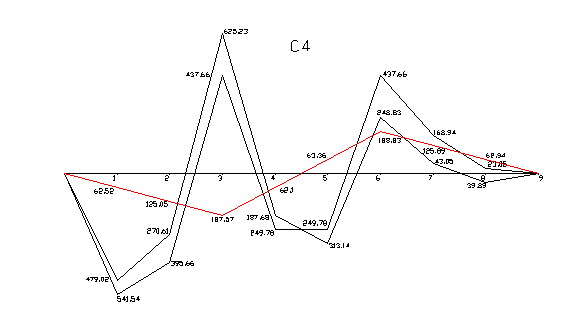

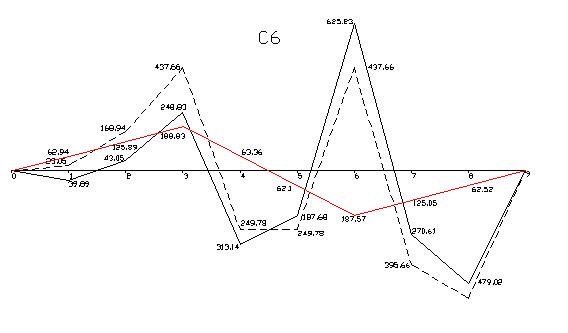

 |
 Огибающая эпюра моментов после перераспределения
Огибающая эпюра моментов после перераспределения
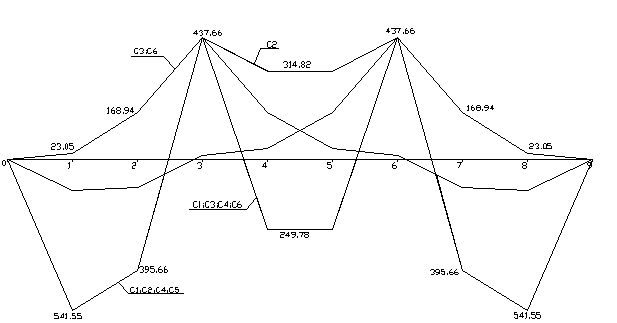
Эпюры поперечных сил и их огибающая после перераспределения
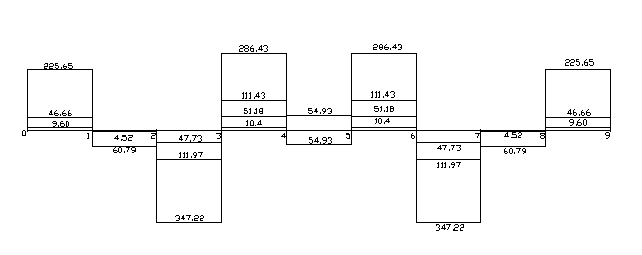 1.4.4 Проверка достаточности принятых размеров главной балки
1.4.4 Проверка достаточности принятых размеров главной балки
Главная балка на восприятие положительных изгибающих моментов работает как тавровое сечение со сжатой полкой, а на восприятие отрицательных моментов - как прямоугольное сечение. При расчете балки с учетом перераспределения усилий должно соблюдаться условие:
![]() (21)
(21)
Это условие дает гарантию, что разрушение конструкции произойдет в результате разрушения арматуры, а не бетона.
Наибольшая величина высоты сжатой зоны бетона будет в сечении с максимальным отрицательным моментом, то есть для нашего случая - на грани опирания балки на колонну. Принимаем размеры сечения колонны 60х60см , а затем считаем по формуле величину изгибающего момента на грани опоры балки на колонну, по которому и проверяют достаточность.
Мгр = Моп – 0,5. hk . Q оп = 437,66– 0,5. 0,6. 51,18 = 422,31кНм
Предполагая, что полезная высота сечения главной балки h0 = hг – а = 75 – 6 = 69 см, определяем высоту сжатой зоны бетона:
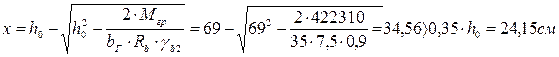
Следовательно, размеры сечения главной балки недостаточны.
Принимаем hг.б =80см; h0 = hг – а = 80 – 6 = 74 см, тогда
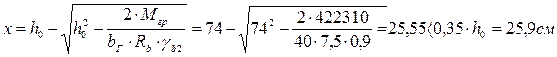
Принятые размеры главной балки достаточны.
 1.4.5 Подбор продольной арматуры главной балки и определение ординат эпюры материалов
1.4.5 Подбор продольной арматуры главной балки и определение ординат эпюры материалов
Сечение на средней опоре . На средней опоре главная балка работает со сжатой зоной в ее ребре. Поэтому расчет ведем для прямоугольного сечения балки на действие изгибающего момента:
М = Мгр
= 422,31 ![]() , x = 25,55см.
, x = 25,55см.
Требуемое сечение рабочей арматуры на опоре
![]()
![]() см2
.
см2
.
Принимаем Аs = 26,64 см2 (2ø36 + 2ø20 А-II)
Размещение арматуры в сечении принимаем согласно рис. 1.6
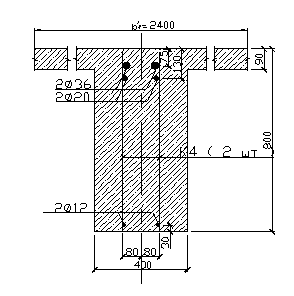
Рис. 1.6 Армирование главной балки на средней опоре
Проверяем несущую способность принятого сечения (вычисляем ординату эпюры материалов в опорном сечении балки):
Аs 1 = 20,36 см2 (2ø36 А-II), а1 = 7,5 см;
Аs 2 = 6,28 см2 (2ø20 А-II), а2 = 13 см;
![]() см;
см;
![]() см;
см;
![]() см;
см;
![]()
Теперь определяем несущую способность сечения после обрыва двух стержней ø20 мм:
![]() Аs
= As
1
= 20,36 см2
(2ø36 А-II), а = а1
= 7,5 см;
Аs
= As
1
= 20,36 см2
(2ø36 А-II), а = а1
= 7,5 см;
![]() см;
см;
![]()
![]() см;
см;
![]()
 Сечения в крайнем пролете.
При работе балки на восприятие положительных изгибающих моментов сечение балки работает как тавровое с полкой в сжатой зоне. Расчетная ширина сжатой полки сечения принимается в соответствии с требованиями пп. 6.2.12 [1] равной
Сечения в крайнем пролете.
При работе балки на восприятие положительных изгибающих моментов сечение балки работает как тавровое с полкой в сжатой зоне. Расчетная ширина сжатой полки сечения принимается в соответствии с требованиями пп. 6.2.12 [1] равной ![]() = lI
/3 = 720/3 = 240 см. Толщина полки
= lI
/3 = 720/3 = 240 см. Толщина полки ![]() см, М = 541,55кНм.
см, М = 541,55кНм.
Принимая ориентировочно полезную высоту сечения h0 = 74 см, определяем необходимую высоту сжатой зоны сечения:
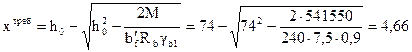 см <
см <
< ![]() см.
см.
Находим требуемое поперечное сечение нижней арматуры
![]() см2
.
см2
.
Принимаем Аs = 29,45 см2 (6ø25 А-II).
Размещение растянутой арматуры в крайнем пролете балки показано на рис. 1.7
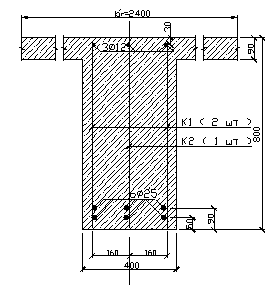
Рис. 1.7 Армирование главной балки в крайнем пролете
Выполним проверку несущей способности принятого сечения и подсчитаем ординаты эпюры материалов:
Аs 1 = 14,73 см2 (3ø25 А-II), а1 = 5 см;
Аs 2 = 14,73 см2 (3ø25 А-II), а2 = 9 см;
![]() см;
см;
![]() см;
см;
![]() см;
см;
Мсеч = 29,45. 280. 70,46 = 581,01кНм
 Обрываем верхний стержень ø25 среднего каркаса К-2 во втором ряду армирования и определим ординату эпюры материалов для этого сечения:
Обрываем верхний стержень ø25 среднего каркаса К-2 во втором ряду армирования и определим ординату эпюры материалов для этого сечения:
Аs 1 = 14,73 см2 (3ø25 А-II), а1 = 5 см;
Аs 2 = 9,82 см2 (2ø25 А-II), а2 = 9 см;
![]() см;
см;
![]() см;
см;
![]() см;
см;
Мсеч = (14,73+9,82)280. 71,28 = 489,98кНм
Теперь обрываем нижний стержень ø25 среднего каркаса К-2 в первом ряду армирования:
Аs 1 = 9,82 см2 (2 ø25 А-II), а1 = 5 см;
Аs 2 = 9,82 см2 (2ø25 А-II), а2 = 9 см;
![]() см;
см;
![]() см;
см;
![]() см;
см;
Мсеч = (9,82+9,82)280. 71,31 =392,15кНм
Далее обрываем оба стержня верхнего ряда в каркасах К-1:
Аs 1 = 9,82 см2 (2ø25 А-II), а1 = а = 5 см;
![]() см;
см;
![]() см;
см;
Мсеч = 9,82. 280. 74,16 = 203,91кНм.
Таким образом, получены ординаты эпюры материалов в крайнем пролете балки по положительным моментам.
В верхней зоне балки армирование выполняем из трех стержней ø12 А-II, входящих в состав верхней арматуры пролетных каркасов балки крайнего пролета К-1 (2 шт.) и К-2 (1 шт.). Определим несущую способность этой арматуры по отрицательным моментам:
Аs 1 = 3,39 см2 (3ø12 А-II), а1 = а = 4 см;
![]() см;
см;
![]() см;
см;
Мсеч = 3,39. 280. 74,24 = 70,47 Н. м.
 Сечения в среднем пролете.
Подбираем нижнюю
арматуру среднего пролета балки. Для этого ориентировочно принимаем полезную высоту балки h0
= 74 см. Определяем требуемую высоту сжатой зоны сечения при М = 249,78кНм:
Сечения в среднем пролете.
Подбираем нижнюю
арматуру среднего пролета балки. Для этого ориентировочно принимаем полезную высоту балки h0
= 74 см. Определяем требуемую высоту сжатой зоны сечения при М = 249,78кНм:
![]() см <
см <
< ![]() см.
см.
Находим требуемое сечение арматуры:
![]()
![]() см2
.
см2
.
Принимаем Аs = 12,56 см2 (4ø20 А-II).
Схема армирования балки в среднем пролете показана на рис. 1.8.
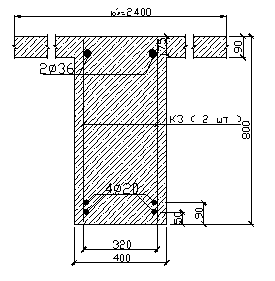
Рис. 1.8 Армирование главной балки в среднем пролете
Выполняем проверку прочности принятого сечения по положительным моментам:
Аs 1 = 6,28 см2 (2ø20 А-II), а1 = 5 см;
Аs 2 = 6,28 см2 (2ø20 А-II), а2 = 9 см;
![]() см;
см;
![]() см;
см;
![]() см;
см;
![]() 257,32кНм
257,32кНм
Теперь выполняем обрыв стержней второго ряда армирования в каркасах К-3 и определяем несущую способность такого сечения:
Аs 1 = Аs = 6,28 см2 (2ø20 А-II), а1 = а = 5 см;
![]() см;
см;
![]() см;
см;
Мсеч = 6,28. 280. 75,46 = 132,69кНм
 В среднем пролете балки могут действовать также отрицательные изгибающие моменты М = 314,82кНм (см. рис. 1.15). Для восприятия этих моментов в верхней зоне балки устанавливаем 2ø36 А-II. Выполним проверку несущей способности принятого армирования по отрицательным моментам:
В среднем пролете балки могут действовать также отрицательные изгибающие моменты М = 314,82кНм (см. рис. 1.15). Для восприятия этих моментов в верхней зоне балки устанавливаем 2ø36 А-II. Выполним проверку несущей способности принятого армирования по отрицательным моментам:
Аs 1 = 20,36 см2 (2ø36 А-II), а=а1 = 7,5 см;
![]() см;
см;
![]() см;
см;
![]() 353,14кНм > 314,82кНм.
353,14кНм > 314,82кНм.
Следовательно, несущая способность принятого сечения достаточна .
Теперь мы имеем все необходимые данные для построения эпюры материалов главной балки (см.Лист1 формата А1)
1.4.6 Расчет наклонных сечений балки на поперечную силу
Принимая для наклонных сечений балки полезную высоту h0 =74см, вычисляем параметр:
![]()
где φb 2 = 2 – коэффициент, учитывающий влияние вида бетона (тяжелый).
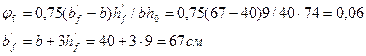
Так как балка нагружена сосредоточенными силами, длину проекции наклонных сечений принимаем равной расстоянию от опор балки до ближайшей к опоре сосредоточенной силы с=а=240см<3,33∙74=246,42см. Требуемая интенсивность поперечного армирования вычисляется по формуле:
![]()
Расчет поперечной арматуры на участке 1
Максимальная поперечная сила на этом участке равна Q1 = 225,65кН
Требуемая несущая способность поперечной арматуры на этом участке
![]()
![]() ,
,
В данном сечении поперечная арматура входит в состав двух каркасов К-1, поперечные стержни принимаем ø10 мм из стали класса А-I с шагом 150мм.
![]()
![]() >
> ![]()
![]() .
.
Расчет поперечной арматуры на участке 3
Максимальная поперечная сила на этом участке равна Q3 = 347,22 кН
Требуемая несущая способность поперечной арматуры на этом участке
![]()
![]()
 Поперечная арматура в этом сечении балки входит в состав двух каркасов К-1 и двух каркасов К-4. В каркасах К-1 принимаем ту же поперечную арматуру, что и на крайней опоре балки, а в каркасах К-4 поперечные стержни ø10 мм из стали класса А-I с шагом 200мм.
Поперечная арматура в этом сечении балки входит в состав двух каркасов К-1 и двух каркасов К-4. В каркасах К-1 принимаем ту же поперечную арматуру, что и на крайней опоре балки, а в каркасах К-4 поперечные стержни ø10 мм из стали класса А-I с шагом 200мм.
![]()
![]() >
> ![]()
![]() .
.
Расчет поперечной арматуры на участке 4
Максимальная поперечная сила на этом участке равна Q4 = 286,43 кН
Требуемая несущая способность поперечной арматуры на этом участке
![]()
![]()
Поперечная арматура в этом сечении балки входит в состав двух каркасов К-4 и двух каркасов К-3. В каркасах К-4 оставляем принятую поперечную арматуру, а в каркасах К-3 поперечную арматуру принимаем из стержней ø10 мм из стали класса А-I с шагом 250мм.Тогда
![]()
![]() >
> ![]()
![]() .
.
1.4.7 Расчет длин запуска обрываемых в пролете стержней
продольной арматуры за точки их теоретического обрыва
Для обеспечения прочности наклонных сечений главной балки по изгибающим моментам обрываемые в пролете стержни продольной арматуры необходимо завести за точку теоретического обрыва на расстояние
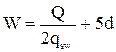 ,
,
где Q – поперечная сила в точке теоретического обрыва стержня;
qsw – несущая способность поперечного армирования балки в точке теоретического обрыва;
d – диаметр обрываемого стержня.
Кроме того, общая длина запуска стержня за точку теоретического обрыва должна быть не менее 20d и не менее 250 мм.
На участке 1 главной балки имеем:
Q = 225,65кН, qsw
= 18,32 ![]() .
.
Для d = 25 мм ![]()
На участке 2 главной балки имеем:
Q =60,79кН. Поперечная арматура на участке состоит из стержней ø10 мм из стали класса А-I с шагом 400мм, входящих в состав двух каркасов К-1 и одного каркаса К-2. Тогда
![]()
![]() .
.
Для d = 25 мм ![]()
 На участке 3 главной балки имеем:
На участке 3 главной балки имеем:
Q = 347,22кН, qsw
=32,1 ![]() .
.
Для d = 20 мм ![]()
Для d = 25 мм ![]()
Для d = 36 мм ![]()
На участке 4 главной балки имеем:
Q =286,43кН, qsw
= 24,73 ![]() .
.
Для d = 20 мм ![]()
Для d = 36 мм ![]()