| Скачать .docx |
Реферат: Проектирование монолитного ребристого перекрытия
1 ПРОЕКТИРОВАНИЕ МОНОЛИТНОГО ВАРИАНТА
Исходные данные:
Шаг колонн в продольном направлении, м.......................................... 5,80
Шаг колонн в поперечном направлении, м.......................................... 6,60
Временная нормативная нагрузка на перекрытие, кН/м2 .................... 4,00
Постоянная нормативная нагрузка от массы пола, кН/м2 ................... 1,00
Класс бетона монолитной конструкции и фундамента........................ B20
Класс арматуры монолитной конструкции и фундамента................... A-III
Влажность окружающей среды............................................................. 55%
Класс ответственности здания............................................................... II
Решение. Принимаем конструктивную схему монолитного ребристого перекрытия согласно рис.1.

Рис. 1. Конструктивная схема монолитного перекрытия:
1 – главные балки; 2 – второстепенные балки; 3 – условная полоса шириной 1 м для расчета плиты.
Назначаем предварительно следующие значения геометрических размеров элементов перекрытия:
1. высота и ширина поперечного сечения второстепенных балок
h = (1/12÷1/20)l = 1/15 × 5800 = 380 мм, b = (0,3÷0,5)h = 0,5 × 380 = 200 мм;
2. высота и ширина поперечного сечения главных балок
h = (1/8÷1/15)l = 1/12 × 6000 = 550 мм, b = 250 мм;
3. толщину плиты примем (1/25 ¸ 1/30)lпл 80 мм при максимальном расстоянии между осями второстепенных балок 2200 мм.
Вычисляем расчетные пролеты и нагрузки на плиту. Согласно рис. 1 и 2 получим в коротком направлении:
![]() мм;
мм;
![]() мм;
мм;
а в длинном направлении
![]() мм.
мм.
Поскольку отношение пролетов ![]() – плита балочного типа.
– плита балочного типа.

Рис. 2. К расчету неразрезной монолитной плиты:
а – расчетные пролеты и схема армирования; б – расчетная схема;
в – эпюра изгибающих моментов; г – расчетное сечение плиты
Для расчета плиты в плане перекрытия условно выделяем полосу шириной 1 м (рис.1). Плита будет работать как неразрезная балка, опорами которой служит второстепенная балка и наружные кирпичные стены. При этом нагрузка на 1 погонный метр плиты будет равна нагрузке на 1 м2 перекрытия. Подсчет нагрузок дан в табл. 1.
Таблица 1 - Нагрузки на 1 м2 монолитного перекрытия
| Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности по нагрузке |
Расчетная нагрузка, кН/м2 |
| Постоянная: |
|||
| от массы плиты h = 0,08 м (ρ = 2560 кН/м3 ) |
0,08×25 = 2,00 |
1,1 |
2,20 |
| от массы пола (по заданию) |
1,00 |
1,2 |
1,2 |
| Итого: |
— |
— |
g = 3,4 |
| Временная (по заданию) |
4,00 |
1,2 |
ν = 4,80 |
| Всего: |
7,00 |
— |
8,2 |
С учетом коэффициента надежности по назначению здания расчетная нагрузка на 1 м плиты q = (g + ν ) γ n = 8,2 – 0,95 = 7,76 кН/м.
Определим изгибающие моменты с учетом перераспределения усилий (рис. 2): в средних пролетах и на средних опорах
![]() кН × м;
кН × м;
в первом пролете и на первой промежуточной опоре
![]() кН × м.
кН × м.
Так как для плиты отношение ![]() , то в средних пролетах, окаймленных по всему контуру балками, изгибающие моменты уменьшаем на 20%, т. е. они будут равны 0,8 × 1,94 = 1,55 кН × м.
, то в средних пролетах, окаймленных по всему контуру балками, изгибающие моменты уменьшаем на 20%, т. е. они будут равны 0,8 × 1,94 = 1,55 кН × м.
Определим по [4] характеристики прочности бетона с учетом заданной влажности окружающей среды.
Бетон тяжелый, естественного твердения, класса В20, γ b 2 = 0,9; Rb = 11,5 × 0,9 = 10,35 МПа; Rbt = 0,9 × 0,9 = 0,81 МПа; Eb = 27000 МПа.
Выполним подбор сечений продольной арматуры сеток.
В средних пролетах окаймленных по контуру балками и на опорах:
![]() мм;
мм;
![]() ;
;
по приложениям 10, 11 находим ξ = 0,035 < ξ R = 0,628, ζ = 0,982, тогда
![]() Н;
Н;
по приложению 15 принимаем сетку С1 номер 34 марки ![]() с фактической несущей способностью продольной арматуры Rs
As
= 25030 Η > 23384 Η.
с фактической несущей способностью продольной арматуры Rs
As
= 25030 Η > 23384 Η.
В первом пролете и на первой промежуточной опоре
![]() мм;
мм;
![]() ;
;
ξ = 0,065 < ξ R ; ζ = 0,967;
![]() Н;
Н;
дополнительная сетка должна иметь несущую способность продольной арматуры не менее 41854 – 25030 = 16824 Н; принимаем сетку С2 номер 31 марки  c Rs
As
= 13310 Η > 16824 Η.
c Rs
As
= 13310 Η > 16824 Η.
2 ПРОЕКТИРОВАНИЕ СБОРНОГО ВАРИАНТА
2.1 Компоновка конструктивной схемы сборного перекрытия
При компоновке сборного балочного перекрытия необходимо:
1. выбрать сетку колонн;
2. выбрать направление ригелей, их форму поперечного сечения и размеры;
3. выбрать тип и размеры плит.
Сетка колонн назначается в зависимости от размеров плит и ригелей. Расстояние между колоннами должно быть, во-первых, кратно 100 мм, и, во-вторых, приниматься в пределах (4,2…6,6) м.
Направление ригелей может быть продольным и поперечным. Это обуславливается технико-экономическими показателями. Выбор типа поперечного сечения ригелей зависит от способа опирания на них плит. Высота ригеля  , где l
– пролет ригеля, его ширина bh
=20 см или 30 см.
, где l
– пролет ригеля, его ширина bh
=20 см или 30 см.
Тип плит перекрытия выбирается по архитектурно-планировочным требованиям и по величине действия временной нагрузки. Так при временной нагрузке J £ 5500 Н/м2 используются многопустотные плиты, высота которых равна (20…24) см.
Плиты выполняются преимущественно предварительно-напряженными, как более экономичные по расходу стали.
Количество типоразмеров плит должно быть минимальным: рядовые шириною (1,2…2,4) м, связевые плиты-распорки – (0,6…1,8) м, фасадные плиты-распорки – (0,6…0,95) м.
В данном случае принято следующее:
1. конструктивная схема с поперечным расположением ригелей и шагом колонн (5,8´6,6) м (рис. 3);
2. ригель таврового сечения шириною bh
=20 см и высотою ![]() см (рис. 4) без предварительного напряжение арматуры.
см (рис. 4) без предварительного напряжение арматуры.
3. плиты ребристые предварительно-напряженные высотою 22 см (рис.3) (ширина расчетной плиты 1,6 м, плиты-распорки 1,8 м, фасадной плиты-распорки 0,9 м);
4. величины действия временной нагрузки J = 1500 Н/м2 и J = 4500 Н/м2 .
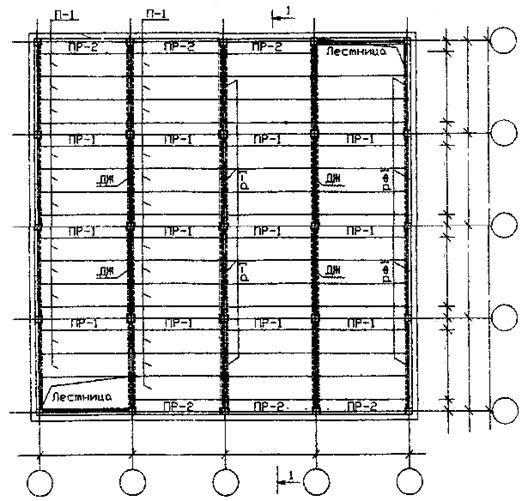

Рис. 3. Компоновка сборного перекрытия.
2.2 Расчет и конструирование многопустотной предварительно-напряженной плиты перекрытия при временной нагрузке 1500 Н/м2
Таблица 2 - Нагрузки на 1 м2 перекрытия
| Вид нагрузки |
Нормативная нагрузка, кН/м2 |
Коэффициент надежности по нагрузке, g f |
Расчетная нагрузка, кН/м2 |
| 1 |
2 |
3 |
4 |
| Постоянная нагрузка g d = 0,105м, r =19,9 кг/м3 |
19,9×0,105=2,09 |
1,1 |
2,3 |
| От массы пола |
1,0 |
1,2 |
1,2 |
| Итого g |
3,09 |
3,5 |
|
| Временная нагрузка J , в том числе: кратковременная J sh длительная J lon |
4,0 2,8 1,2 |
1,2 1,2 1,2 |
4,8 3,36 1,44 |
| Полная нагрузка (g + J ) |
7,09 |
8,3 |
|
| В т.ч. постоянная и длительная |
4,29 |
Нагрузка на 1 п. м. длины плиты при номинальной ее ширине 1,5 м с учетом коэффициента надежности по назначению здания (класс II ответственности) g n = 0,95;
1. расчетная постоянная g = 3,5 ´ 1,5 ´ 0,95 = 4,99 кН/м;
2. расчетная полная (g + J ) = 8,3 ´ 1,5 ´ 0,95 = 11,83 кН/м;
3. нормативная постоянная gn = 3,08 ´ 1,5 ´ 0,95 = 4,40 кН/м;
4. нормативная полная (g n + J n ) = 7,09 ´ 1,5 ´ 0,95 = 10,10 кН/м;
5. нормативная постоянная и длительная (g n + J lon , n ) = 4,29 ´ 1,5 ´ ´ 0,95 = 6,11 кН/м.
Материалы для плиты:
Бетон – легкий, класса по прочности на сжатие В30, плотность 1800.
Rbn = Rb , ser = 22 МПа,
Rbtn = Rbt , ser = 1,8 МПа,
Rb =17 МПа, Rbt = 1,3 МПа;
коэффициент условия работы бетона g b 2 = 0,9.
Плита подвергается тепловой обработке при атмосферном давлении. Начальный модуль упругости Eb = 19,552 ´ 103 МПа.
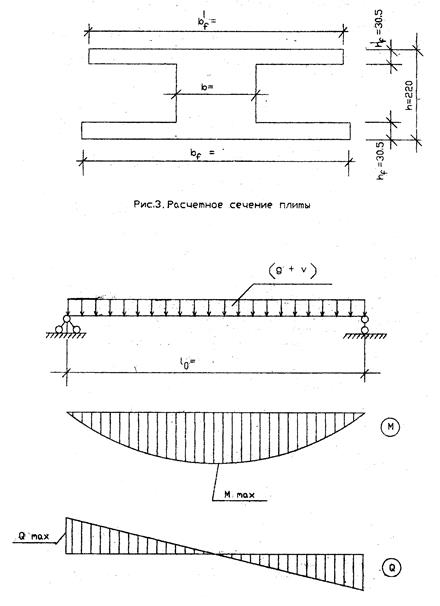
Рис.6. Расчетная схема плиты перекрытия
К трещиностойкости плиты предъявляются требования 3-ей категории. Технология изготовления плиты – агрегатно-поточная. Натяжение напрягаемой арматуры осуществляется электротермическим способом.
Арматура:
1. продольная напрягаемая класса BP-II
Rsn = Rs , ser = 1100 МПа,
Rs = 915 МПа,
Es = 20 ´ 104 МПа,
2. ненапрягаемая класса A-II,
Rs = 280 МПа,
Rsw = 225 МПа,
Е s = 21 × 104 МПа.
Расчет плиты по предельным состояниям первой группы
Определение внутренних усилий
Расчетный пролет плиты в соответствии с рис. 4
![]() м.
м.
Поперечное конструктивное сечение плиты заменяется эквивалентным двутавровым сечением (рис. 3).
h = 22 см;
h0 = h – a = 22 – 3 = 19 см;
h’ f = hf = (22 – 15,9) ´ 0,5 = 3,05 см;
bf = 159 см; b’ f = 159 – 3 = 156 см;
b = 159 – 15,9 ´ 7 = 47,7 см.
Плита рассчитывается как однопролетная шарнирно-опертая балка, загруженная равномерно-распределенной нагрузкой (рис. 6). Усилия от расчетной полной нагрузки:
1. изгибающий момент в середине пролета
![]() кН ´ м;
кН ´ м;
2. поперечная сила на опорах
![]() кН.
кН.
Усилия от нормативной нагрузки:
3. полной
![]() кН ´ м;
кН ´ м;
4. постоянной и длительной
![]() кН ´ м.
кН ´ м.
Расчет по прочности сечения, нормального к продольной оси плиты
При расчете по прочности расчетное поперечное сечение плиты принимается тавровым с полкой в сжатой зоне (свесы полок в растянутой зоне не учитываются).
При расчете принимается вся ширина верхней полки b ’ f =156 см, так как
![]() см,
см,
где l – конструктивный размер плиты.
Положение границы сжатой зоны определяется согласно (3.30) [1]:
![]() ;
;
44,57 ´ 105 £ 0,9 ´ 19,5 ´ 102 ´ 156 ´ 3,05 ´ (19 – 0,5´3,05)
44,57 ´ 105 £ 145,92 ´ 105 Н´см.
Следовательно, граница сжатой зоны проходит в полке и расчет плиты ведется как прямоугольного сечения с размерами b ` f и h .

По табл. 3.1 [1] и прил. 10 при a m = 0,045, x = 0,045 и z = 0,977. Граничная относительная высота сжатой зоны определяется по формуле (25) [4]:
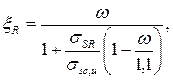
где ![]() ;
;
s
sc
,
u
=500 МПа при ![]() ;
;
![]()
Назначаем величину предварительного напряжения арматуры ![]()
Проверяем условие по формуле:
![]()
![]()
При ![]() (для механического способа натяжения арматуры).
(для механического способа натяжения арматуры).
Так как ![]() и
и ![]() следовательно, условие выполняется.
следовательно, условие выполняется.
Предварительное напряжение при благоприятном влиянии с учетом точности натяжения арматуры будет равно:
![]()
где ![]()
![]() =1-0,1=0,9
=1-0,1=0,9
ssp =0,9 ´ 1000=900 МПа.
При условии, что полные потери составляют примерно 30% начального предварительного напряжения, последнее с учетом полных потерь будет равно:
s sp = 0,7 ´ 900 = 630 МПа.
![]() МПа,
МПа,
s SR = 915 + 400 – 630 – 275,4 = 409,6 МПа;
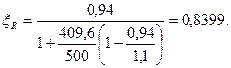
Так как x = 0,045 < x R = 0,8399, то площадь сечения растянутой арматуры определяется по формуле (3.15) [1]:
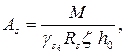
где ![]() – коэффициент условий работы арматуры, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести.
– коэффициент условий работы арматуры, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести.
По формуле (27) [4]:

Для арматуры класса B-II h = 1,15.
Поскольку ![]() , принимаем
, принимаем ![]() =1,15.
=1,15.
Тогда ![]() см2
.
см2
.
Принимаем по прил. 12: 5Æ8 с As =2,51 см2
Расчет по прочности сечения, наклонного к продольной оси плиты
Поперечная сила Q=32,47 кН.
Предварительно приопорные участки плиты заармируем в соответствии с конструктивными требованиями п. 5.27 [4]. Для этого с каждой стороны плиты устанавливаем по четыре каркаса длиной l
/4 с поперечными стержнями, шаг которых s
=10 см (по п. 5.27 [4] ![]() или
или ![]() мм).
мм).
По формуле (72) [4] проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами
![]()
Коэффициент, учитывающий влияние хомутов, j w 1 = 1 + 5a m w £ 1,3,
![]()
Коэффициент поперечного армирования
![]() ; Asw
= 0,5 см2
(4Æ4 Bp-I);
; Asw
= 0,5 см2
(4Æ4 Bp-I); ![]()
j w 1 = 1 + 5 ´ 8,71 ´ 0,001 = 1,04 < 1,3.
Коэффициент j b 1 = 1 – b g b 2 Rb = 1 – 0,02 ´ 0,9 ´ 19,5 = 0,649,
где b = 0,02 для легкого бетона.
Q = 32,47 кН < 0,3´1,04´0,649´0,9´19,5´47,7´19´100 = 322069 Н = 322,1 кН.
Следовательно, размеры поперечного сечения плиты достаточны.
Проверяем необходимость постановки расчетной поперечной арматуры из условия:
![]()
Коэффициент j b 3 = 0,5 для легкого бетона. Коэффициент, учитывающий влияние сжатых полок в двутавровых элементах:
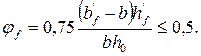
Учитывая, что ![]() ,
,
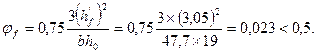
Коэффициент, учитывающий влияние продольной силы обжатия Р2 ,
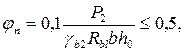
где Р2 (значение силы обжатия P2 см. ниже) принимается с учетом коэффициента g sp = 0,865.
![]()
Тогда ![]() ,
,
Q=32,47 кН < 0,5 ´ 1,42 ´ 0,9 ´ 1,3 ´ 47,7 ´ 19 ´ 100 = 75,29 кН.
Следовательно, условие удовлетворяется, поперечная арматура ставится по конструктивным требованиям. Армирование плиты см. рис. 7.
Расчет и конструирование однопролетного ригеля
Для опирания пустотных панелей принимается сечение ригеля высотой h
в
= 45 см или h
в
= 60 см, для опирания ребристых панелей принимается сечение ригеля высотой h
в
= 60см. Ригели могут выполняться обычными или предварительно напряженными. Высота сечения обычного ригеля  .
.
Исходные данные:
Нормативные и расчетные нагрузки на 1 м2 перекрытия принимаются те же, что и при расчете панели перекрытия. Ригель шарнирно оперт на консоли колонн, h в = 60 см. Расчетный пролет (рис. 3)
![]() мм = 6,02 м,
мм = 6,02 м,
где ld – пролет ригеля в осях; b – размер колонны; 20 – зазор между колонной и торцом ригеля, 140 – размер площадки опирания.
Расчетная нагрузка на 1 м длины ригеля определяется с грузовой полосы, равной шагу рам, в данном случае шаг рам 5,8 м.
Постоянная (g):
1. от перекрытия с учетом коэффициента надежности по назначению здания g n = 0,95; g = 3500 ´ 5,8 ´ 0,95 = 19290 Н/м = 19,29 кН/м;
2. от веса ригеля: g в n = 0,25 ´0,6 ´ 25000 = 3,75 кН/м,
где 2500 кг/м3 – плотность железобетона.
С учетом коэффициентов надежности по нагрузке g f = 1,1 и по назначению здания g n = 0,95; g в = 3,75 ´ 1,1 ´ 0,95 = 3,92 кН/м.
Итого: g + g в = 19,29 + 3,92 = 23,21 кН/м.
Временная нагрузка (J ) с учетом коэффициента надежности по назначению здания g n = 0,95 и коэффициента снижения временной нагрузки в зависимости от грузовой площади
 ,
,
где А 1 = 9 м2 [5]; А – грузовая площадь, A = 36 м2 .
 .
.
J = 4800 ´ 5,8 ´ 0,95 ´ 0,7 = 18,51 кН/м.
Полная нагрузка (g + J ) = 23,21 + 18,51 = 41,72 кН/м.
Определение усилий в ригеле
Расчетная схема ригеля – однопролетная шарнирно опертая балка пролетом l 0 . Вычисляем значения максимального изгибающего момента М и максимальной поперечной силы Q от полной расчетной нагрузки:
![]() кН ´ м;
кН ´ м;
![]() кН.
кН.
Характеристики прочности бетона и арматуры:
бетон тяжелый класса В30, расчетное сопротивление при сжатии Rb
= 17 МПа, при растяжении Rbt
= 1,2 МПа (табл. 13 [4], прил. 3); коэффициент условий работы бетона ![]() = 0,9;
= 0,9;
арматура продольная рабочая класса A-II диаметром 10-40 мм, расчетное сопротивление Rs = 280 МПа и поперечная рабочая класса A‑III диаметром 6-8 мм, Rsw = 225 МПа (прил. 7).
Расчет прочности ригеля по сечению, нормальному к продольной оси
Определяем высоту сжатой зоны x = x × h 0 , где h 0 – рабочая высота сечения ригеля; x – относительная высота сжатой зоны, определяемая по a m (прил. 10).
h 0 = (h в – 5) см = 55 см,
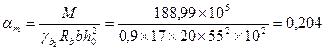 ,
,
где М = 188,99 кН ´ м; Rb =17 МПа; b – ширина сечения ригеля, b = 20 см.
По прил. 10 определяем x = 0,23 и z = 0,885, высота сжатой зоны
x = x × h 0 = 0,23 ´ 55 = 12,65 см.
Граница сжатой зоны проходит в узкой части сечения ригеля, следовательно, расчет ведем как для прямоугольного сечения.
Граничная относительная высота сжатой зоны определяется по формуле (25) [4]:
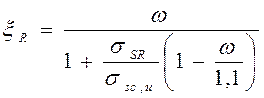 ,
,
где w – характеристика сжатой зоны бетона, по (26) [4]
![]() ,
,
для тяжелого бетона a = 0,85;
w = 0,85 – 0,008 ´ 0,9 ´ 17 = 0,728,
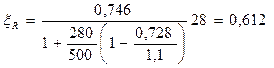 .
.
Аналогичное значение x R = 0,612 имеем согласно прил. 11.
Так как x = 0,23 < x R = 0,612, то площадь сечения растянутой арматуры можно определить по формуле
![]() см2
.
см2
.
Принимаем по прил. 12 2Æ22 A-II (As = 7,6 см2 ) и
2Æ25 A-II (A s = 9,28 см2 ),
общая площадь принятой арматуры As = 16,88 см2 .
Расчет прочности ригеля по сечению, наклонному к продольной оси
Расчет прочности ригеля по сечению, наклонному к продольной оси, выполняется согласно п.п. 3.29…3.33. [4].
Расчет производится рядом с подрезкой в месте изменения сечения ригеля.
Поперечная сила на грани подрезки на расстоянии 10 см от торца площадки опирания
![]() кН.
кН.
Проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами по формуле (72) [4]:
![]() .
.
Коэффициент, учитывающий влияние хомутов:
![]() ,
,
где
![]() ,
,
![]() – коэффициент поперечного армирования.
– коэффициент поперечного армирования.
Ориентировочно принимаем
m w = 0,001.
Тогда
![]() = 1 + 5 ´ 7,24 ´ 0,001 = 1,036 < 1,3.
= 1 + 5 ´ 7,24 ´ 0,001 = 1,036 < 1,3.
Коэффициент ![]() = 1 – b
g
b
2
Rb
,
= 1 – b
g
b
2
Rb
,
где m = 0,01 для тяжелого бетона.
![]() = 1 – 0,01 ´ 0,9 ´ 17 = 0,85.
= 1 – 0,01 ´ 0,9 ´ 17 = 0,85.
Q = 118,51 кН < 0,3 ´ 1,036 ´ 0,85 ´ 0,9 ´ 17 ´ 103 ´ 0,2 ´ 0,55 = 444,61кН.
Следовательно, условие прочности удовлетворяется.
Проверяем необходимость постановки расчетной поперечной арматуры из условия:
![]() .
.
Для тяжелого бетона ![]() = 0,6.
= 0,6.
![]() , так как рассчитывается ригель прямоугольного сечения без предварительного напряжения арматуры.
, так как рассчитывается ригель прямоугольного сечения без предварительного напряжения арматуры.
Так как Q = 118,51 кН > 0,6 ´ 0,9 ´ 1,2 ´ 103 ´ 0,2 ´ 0,55 = 71,28 кН, поперечная арматура необходима по расчету.
Расчет для обеспечения прочности по наклонной трещине производится по наиболее опасному наклонному сечению из условия:
Q < Qb + Qsw .
Поперечное сечение, воспринимаемое бетоном,
![]() ;
;
для тяжелого бетона g b 2 = 2,0.
Определяем максимальную длину проекции опасного наклонного сечения на продольную ось ригеля cmax .
![]() см.
см.
Поперечное усилие, воспринимаемое хомутами,
Qsw = Q – Qb min = 118,51 – 71,28 = 47,23 кН.
Приняв с 0 = с max , усилия в хомутах на единицу длины ригеля
![]() Н/см.
Н/см.
При этом должно выполняться условие:
![]() Н/см.
Н/см.
Так как q sw = 257,67 Н/см < 583,2 Н/см, принимаем qsw = 583,2 Н/см.
Определяем длину проекции опасной наклонной трещины на продольную ось ригеля
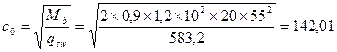 см.
см.
Поскольку 2h 0 = 2 ´ 55 = 110 см < 142,01 см < c max = 183,3 см, принимаем
c 0 = 110 см.
Уточняем величину Qsw , исходя из условия, что при с = с 0 = 2h0 = 110 см,
![]() кН.
кН.
При этом ![]() > 583,2 Н/см.
> 583,2 Н/см.
Окончательно принимаем qsw = 591,2 Н/см.
 см.
см.
Из условия сварки с продольной арматурой (d max = 20 мм) принимаем поперечную арматуру Æ10 А-II.
При двух каркасах Asw = 2 ´ 0,785 = 1,57 см2 . Шаг поперечных стержней на приопорных участках
![]() см.
см.
Из условия обеспечения прочности наклонного сечения в пределах участка между хомутами максимально возможный шаг поперечных стержней
![]() см.
см.
Кроме того, по конструктивным требованиям согласно п. 5.27 [4] поперечная арматура устанавливается:
на приопорных участках, равных 1/4 пролета, при h £ 60 см с шагом
![]() см;
см;
![]() см;
см;
на остальной части пролета при h > 30 см с шагом
![]() см;
см;
s £ 50 см.
Окончательно шаг поперечных стержней принимаем:
на приопорных участках длиной 1,5 м s = 20 см;
на приопорных участках в подрезке s = 10 см;
на остальной части пролета s = 45 см.
Построение эпюры материалов
Продольная рабочая арматура в пролете 2Æ22 А-II и 2Æ25 A-II. Площадь этой арматуры А s , определена из расчета на действие максимального изгибающего момента в середине пролета. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролете, а два других доводятся до опор. Если продольная рабочая арматура разного диаметра, например, 2Æ22 A-II и 2Æ25 A-II, то до опор доводятся два стержня большего диаметра.
Площадь рабочей арматуры As (2 Æ 22) = 7,6 см2 ,
As (2 Æ 25) = 9,28 см2 .
Определяем изгибающий момент, воспринимаемый ригелем с полной запроектированной арматурой, 2Æ22 А-II и 2Æ25 A-II (As = 16,88 см2 )
![]() ;
;
h 0 = 60 – 5 = 55 см (рис.7).
Из условия равновесия As Rs = bxRb , где x = x h 0 ;
![]() ;
;
по прил. 10 z = 0,86;
М (2 Æ 22+2 Æ 25) = 280 ´ 100 ´ 16,88 ´ 0,86 ´ 55 = 22355872 Н´см = 223,6кН´м.
Изгибающий момент, воспринимаемый сечением, больше изгибающего момента, действующего в сечении:
223,6 кН´м > 188,99 кН´м.
До опоры доводятся 2Æ25 А-II, As (2 Æ 25) = 9,28 см2 .
Вычисляем изгибающий момент, воспринимаемый сечением ригеля, заармированным 2Æ25 A-II:
![]() ; h
01
= 60 – 3 = 57 см (рис. 8);
; h
01
= 60 – 3 = 57 см (рис. 8);
![]() ;
;
по прил.10 z = 0,925; М (2 Æ 25) = 280 ´ 100 ´ 9,28 ´ 0,925 ´ 57 = 13700064Н×см = 137 кН×м.
Графически по эпюре моментов определяем место теоретического обрыва стержней 2Æ22 А-ΙΙ. Эпюра моментов для этого должна быть построена точно с определением значений изгибающих моментов в 1/8, в 2/8 и в 3/8 пролета.
Изгибающий момент в 1/8 пролета
![]() кН×м.
кН×м.
Изгибающий момент в 1/4 пролета
![]() кН×м.
кН×м.
Изгибающий момент в 3/8 пролета
![]() кН×м.
кН×м.
Откладываем на этой эпюре M (2Ø25) = 137 кН×м в масштабе. Точка пересечения прямой с эпюрой называются местом теоретического обрыва арматуры (рис. 8).
Момент, воспринимаемый сечением ригеля с арматурой 2Ø25 А-II и 2Ø22 А-II. также откладывается в масштабе на эпюре М .
Длина анкеровки обрываемых стержней определяется по следующей зависимости:
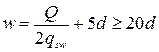 .
.
Поперечная сила Q определяется графически в месте теоретического обрыва, в данном случае Q = 60 кН.
Поперечные стержни Ø10 A-II с Asw = 2 × 0,785 = 1,57 см2 в месте теоретического обрыва имеют шаг 20 см.
![]() ;
;
![]() Н/см = 1,8 кН/см.
Н/см = 1,8 кН/см.
![]() см.
см.
20d = 44 см.
Принимаем w = 44 см. Шаг хомутов в приопорной зоне s 1 принимается равным 0,5·s на участке длиной 0,5 м.
Место теоретического обрыва арматуры можно определить аналитически. Для этого общее выражение для изгибающего момента нужно приравнять моменту, воспринимаемому сечением ригеля с арматурой 2Ø25 A-II М (2Ø25) = 137 кН×м.
![]() ;
;

переносим в левую часть свободный член, получаем
![]() ;
;
x 1 = 4,59 м, x 2 = 1,43 м – это точки теоретического обрыва арматуры. Длина обрываемого стержня будет равна 4,59 – 1,43 + 2 × w = 4,04 м. Принимаем длину обрываемого стержня равной 4 м.
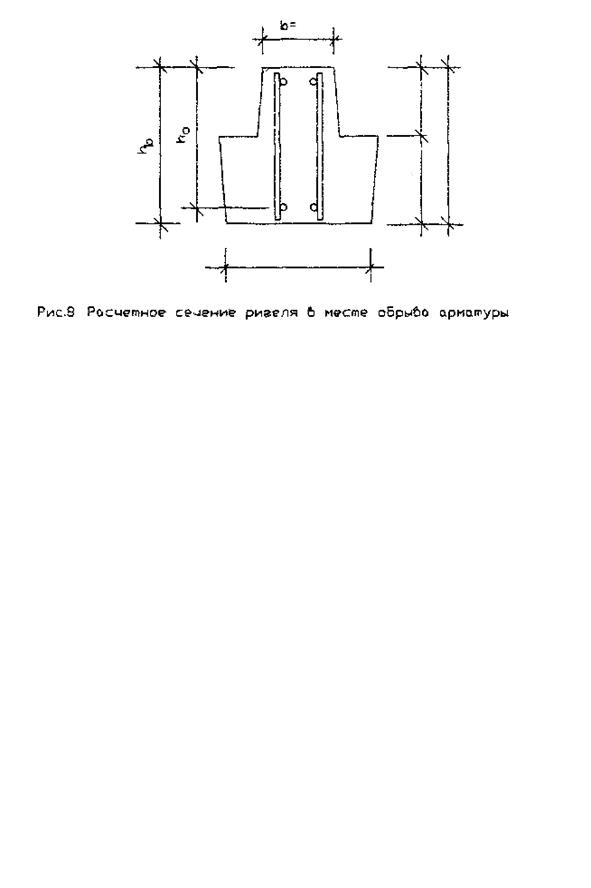 Рис. 9. Эпюра материалов
Рис. 9. Эпюра материалов
Расчет и конструирование колонны
Для колонн применяют бетон классов по прочности на сжатие не ниже В15, для сильно загруженных не ниже B25.
Колонны армируют продольными стержнями диаметром 12…40 мм, преимущественно из горячекатаной стали класса А-III и поперечными стержнями из горячекатаной стали классов А-III, А-II, A-I.
Насыщение поперечного сечения продольной арматурой оценивается коэффициентом ![]() или процентом армирования μ
× 100, где As
– суммарная площадь сечения всех продольных стержней.
или процентом армирования μ
× 100, где As
– суммарная площадь сечения всех продольных стержней.
В практике для сжатых элементов обычно принимают армирование не более 3%.
Если общее количество арматуры более 3%, то поперечные стержни необходимо устанавливать на расстоянии не более 10d и не более 300 мм.
При расчете по прочности бетонных и железобетонных элементов на действие сжимающей продольной силы должен приниматься во внимание случайный эксцентриситет ea , обусловленный неучтенными в расчете факторами. Эксцентриситет ea в любом случае принимается не менее 1/600 длины элемента или расстояния между его сечениями, закрепленными от смещения, 1/30 высоты сечения и 1 см для сборных конструкций.
Исходные данные:
Нагрузка на 1 м2 перекрытия принимается такой же, как и в предыдущих расчетах, нагрузка на 1 м2 покрытия приводится в таблице 3.
Характеристики прочности бетона и арматуры:
1. бетон тяжелый класса В30, расчетное сопротивление при сжатии Rb = 17 МПа = 1,7 кН/см2 (табл. 13 [4], прил. 3);
2. арматура продольная рабочая класса А-II (диаметр 12-40мм), расчетное сопротивление Rs = 280 МПа = 28 кН/см2 (прил. 7).
Принимаем размер сечения колонны 40×40 см, рис. 9.
Определение усилий в колонне
Грузовая площадь средней колонны А = 5,8×6,6 = 38,28 м2 . Постоянная нагрузка от перекрытия одного этажа с учетом коэффициента надежности по назначению здания g n = 0,95.
0,95 × 3500 × 38,28 = 127281 Н = 127,28 кН.
Нагрузка от ригеля: 5 × 6,2 = 31 кН,
где 5 кН/м – погонная нагрузка от собственного веса ригеля;
6,2 м – длина ригеля ври расстоянии между осями колонн 6,6 м.
Нагрузка от собственного веса колонны типового этажа:
0,4 × 0,4 × 3,6 × 2500 × 0,95 × 1,1 × 10-2 = 15,05 кН.
Нагрузка от собственного веса колонны подвала 15,05 кН.
Постоянная нагрузка на колонну с одного этажа:
127,28 + 31 + 15,05 = 173,05кН.
Постоянная нагрузка от покрытая, приходящаяся на колонну:
0,95 × 7224 × 38,28 = 262,7 кН.
Нагрузка от ригеля 31 кН.
Общая постоянная нагрузка на колонну от покрытия:
262,7 + 31 = 293,7 кН.
Временная нагрузка, приходящаяся на колонну с одного этажа:
0,95 × 4800 × 38,28 = 174,6 кН.
Временная нагрузка, приходящаяся на колонну с покрытия:
0,95 × 1400 × 38,28 = 50,9 кН.
Таблица 2 – Сбор нагрузок
| Вид нагрузки |
Нормативная нагрузка (γ f = 1), Н/м2 |
Коэффициент надежности по нагрузке, (γ f > 1) |
Расчетная нагрузка (γ f > 1), Н/м2 |
| 1 |
2 |
3 |
4 |
| Гидроизоляционный ковер 4 слоя |
190 |
1,3 |
247 |
| Армированная цементная стяжка δ =40 мм, ρ =2200 кг/м3 |
880 |
1,3 |
1144 |
| Пеностекло δ =120 мм, ρ =300 кг/м3 |
360 |
1,3 |
468 |
| Керамзит по уклону δ =100 мм, ρ =1200 кг/м3 |
1200 |
1,3 |
1560 |
| Пароизоляция 1 слой |
50 |
1,3 |
65 |
| Многопустотная плита перекрытия с омоноличиванием швов δ =220 мм |
3400 |
1,1 |
3740 |
| Постоянная нагрузка groof |
6080 |
– |
7224 |
| Временная нагрузка – снеговая s = s 0 μ , в т. ч. длительная* slon |
1000 300 |
1,4 1,3 |
1400 420 |
| Полная нагрузка (groof + s) |
7780 |
9394 |
Коэффициент снижения временных нагрузок в многоэтажных зданиях
![]() ,
,
где n – число перекрытий, от которых учитывается нагрузка; например, если здание имеет 6 этажей и подвал:
![]()
Нормальная сила в средней колонне на уровне подвала
N = 173,05× 8 + 293,7 + 174,6 × 8 × 0,522 + 50,9 + 15,05 = 3173,3 кН,
здесь 15,05 кН – собственный вес колонны подвала.
Расчет прочности колонны
Расчет прочности сжатых элементов из тяжелого бетона классов В15…В40 на действие продольной силы, приложенной со случайным эксцентриситетом, при l 0 < 20 hcol допускается производить из условия:
![]() ,
,
где φ – коэффициент, определяемый по формуле:
![]() ,
,
где φ
b
и φ
sb
– коэффициенты, принимаемые по прил. 17 в зависимости от ![]() и
и ![]() .
.
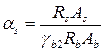 , где As
– площадь всей арматуры в сечении элемента;
, где As
– площадь всей арматуры в сечении элемента;
Rsc = Rs для арматуры классов A-I, A-II, A-III.
При α s > 0,5 можно принимать φ = φsb .
В первом приближении принимаем:
μ = 0,01;
Ab = 40 × 40 = 1600 см2 ;
As = 0,01 × 1600 = 16 см2 ;
![]() .
.
Свободная длина колонны подвала l 0 = 0,7 (3,6 + 0,15) = 2,625 м, h = 0,4м (размер сечения колонны),
![]() .
.
Nl – длительно действующая нагрузка на колонну (постоянная и длительно действующая часть временной), которая определяется по табл. 3 [5] или по согласованию с консультантом.
В данном случае временная длительно действующая нагрузка на перекрытие 1440 Н/м2 , кратковременно действующая 3360 Н/м2 , временная длительно действующая нагрузка на покрытие 420 Н/м2 , кратковременно действующая 980 Н/м2 (см. табл. сбора нагрузок).
Временная кратковременно действующая нагрузка на колонну с одного этажа:
0,95 × 3360 × 38,28 = 122,19 кН.
Временная кратковременно действующая нагрузка на колонну с покрытия:
0,95 × 980 × 38,28 = 35,64 кН.
Временная кратковременно действующая нагрузка на колонну:
122,19 × 6 × 0,522 + 35,64 = 418,34 кН.
Остальная нагрузка на колонну – длительно действующая
Nl = N – 418,34= 3173,3 – 418,34 = 2754,96 кН.
![]() .
.
Определяем коэффициенты φ b и φ sb по прил. 17
φ b = 0,92; φ sb = 0,92;
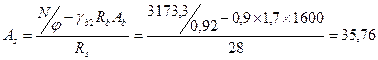 см2
.
см2
.
Принимаем по прил. 12 6Ø28 А-II (As = 36,95 см2 );
![]() , μ
% = 0,023 × 100 = 2,3%, что больше μ
min
= 0,4%.
, μ
% = 0,023 × 100 = 2,3%, что больше μ
min
= 0,4%.
Учитывая, что при таких отношениях ![]() и
и ![]() φ
b
и φ
sb
равны, уточнение делать не нужно, т. к. коэффициент армирования не влияет на φ
.
φ
b
и φ
sb
равны, уточнение делать не нужно, т. к. коэффициент армирования не влияет на φ
.
Расчет и конструирование фундамента под колонну
Исходные данные:
Условное расчетное сопротивление грунта R 0 = 0,25 МПа.
Бетон тяжелый класса В20, Rbt = 0,90 МПа.
Арматура класса A-III, Rs = 365 МПа.
Вес единицы объема бетона фундамента и грунта на его обрезах g m = 20 кН/м3 .
Высоту фундамента принимаем равной 150 см (кратной 30 см), глубина заложения фундамента Н 1 = 150 см. Расчетное усилие, передающееся с колонны на фундамент, N = 3173,3 кН. Усредненное значение коэффициента надежности по нагрузке g f = 1,15.
![]() кН.
кН.
Определение размера стороны подошвы фундамента
Площадь подошвы центрально загруженного фундамента определяем по условному давлению на грунт R 0 без учета поправок в зависимости от размеров подошвы фундамента и глубины его заложения:
 ,
,
где Nn – нормативное усилие, передающееся с колонны на фундамент;
R 0 – условное давление на грунт, зависящее от вида грунта;
g m – усредненная нагрузка от единицы объема фундамент и грунта на его уступах, g m = 20 кН/м3 ;
H 1 – глубина заложения фундамента.
![]() м2
.
м2
.
Размер стороны квадратной подошвы:
![]() м.
м.
Принимаем размер a = 3,6 м (кратным 0,3 м).
Давление на грунт от расчетной нагрузки:
![]() кН/м2
.
кН/м2
.
Рабочая высота из условия продавливания по подколоннику
![]() ,
,
где hc , bc – размеры подколонника.
![]() м.
м.
Полная высота фундамента устанавливается из условий
1) продавливания
H = h 0 + 0,04 = 0,27 + 0,04 = 0,31 = 31 см – высота части фундамента под подколонником.
2) заделки колонны в фундаменте
H = l,5hcol + 25 = 1,5 × 40 + 25 = 85 см (меньше высоты подколонника).
3) анкеровки сжатой арматуры
Н = 24d + 25 = 24 × 2,2 + 25 = 52,8 + 25 =77,8 см.
Принимаем полную высоту фундамента 150 см, в том числе высота подколонника 90 см, монолитной части 60 см (две ступени по 30 см) (рис. 11). Если высота части фундамента под подколонником получится больше 60 см, следует ее принять равной 60 см (две ступени по 30 см).
Проверяем, отвечает ли рабочая высота нижней части (или нижней ступени) h 02 = 60 – 4 = 56 см условию прочности при действии поперечной силы без поперечного армирования в наклонном сечении. Для единицы ширины этого сечения (b = 100 см) должно выполняться условие:
![]() .
.
Поперечная сила от давления грунта в сечении по грани подколонника:
![]() ,
,
где а – размер подошвы фундамента;
а 1 – размер подколонника;
h 0 – рабочая высота фундамента;
р – давление на грунт от расчетной нагрузки.
![]() кН.
кН.
Поперечная сила, воспринимаемая нижней ступенью фундамента без поперечного армирования:
![]() кН.
кН.
119,98 кН < 272,16 кН – условие прочности удовлетворяется.
Расчет на продавливание
Проверяем монолитную часть или нижнюю ступень монолитной части на прочность против продавливания:
![]() ,
,
где Rbt – расчетное сопротивление бетона осевому растяжению;
um – среднее арифметическое между периметрами верхнего и нижнего оснований пирамиды продавливания в пределах полезной высоты
![]() м;
м;
h 02 – рабочая высота нижней ступени фундамента или нижней части, если он состоит из одной ступени.
Продавливающая сила P = N – A 1 p ,
где N – расчетное усилие, передающееся с колонны;
A 1 – площадь нижнего основания пирамиды продавливания
A 1 = (1,2 + 2 × 0,56) × (1,2 + 2 × 0,56) = 4,64 м2 ;
р – давление на грунт.
Продавливающая сила
Р = 3173,3 – 4,64 × 244,85 = 2037,2 кН.
![]() = 0,9 × 0,90 × 103
× 0,56 × 7,04 = 3193,3 кН.
= 0,9 × 0,90 × 103
× 0,56 × 7,04 = 3193,3 кН.
Р = 2037,2 кН < 3193,3 кН, следовательно, прочность монолитной части или нижней ступени против продавливания обеспечена.
Окончательно принимаем фундамент, изображенный на рис. 10.
Определение площади арматуры фундамента
Расчетная схема нижней части фундамента принимается в виде консоли с равномерно распределенной нагрузкой, равной давлению на грунт.
Расчетный изгибающий момент по грани подколонника определяется по формуле:
![]() кН×м.
кН×м.
Нижняя часть фундамента имеет две ступени, поетому следует еще определить:
![]() кН×м.
кН×м.
где а 2 – размер верхней ступени.
Площадь сечения арматуры определяется по формуле.
![]() см2
.
см2
.
![]() см2
.
см2
.
Принимаем 14Ø18 А-III с As 1 = 35,62 см2 (см. прил. 12).
6Ø40 А-III с As 2 = 75,4 см2
![]() , что больше чем μ
min
= 0,05%
, что больше чем μ
min
= 0,05%
![]() , что больше чем μ
min
= 0,05%
, что больше чем μ
min
= 0,05%
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Байков В. Н., Сигалов Э. Е. Железобетонные конструкции: Общий курс: Учеб. для вузов: - 5-е изд., перераб. и доп. – М.: Стройиздат, 1991.
2. СНиП 2.03.01-84*. Бетонные и железобетонные конструкции / Госстрой СССР – М.: ЦИТП Госстроя СССР, 1996.
3. Пособие по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры (к СНиП 2.03.01-84). – М.: ЦИТП, 1986.
4. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов (к СНиП 2.03.01-84). Часть 1.– М.: ЦИТП, 1986
5. Пособие по проектированию предварительно напряженных железобетонных конструкций из тяжелых и легких бетонов (к СНиП 2.03.01-84). Часть 2.– М.: ЦИТП, 1986
6. СНиП П-22-81. Каменные и армокаменные конструкции.
7. СНиП 2.01.07-85*. Нагрузки и воздействия.
8. СНиП 2.01.07-85*. Нагрузки и воздействия. Дополнение. Раздел 10. Прогибы и перемещения. / Госстрой СССР – М.: ЦИТП Госстроя СССР, 2003.
9. СНиП 2.02.01-83. Основания зданий и сооружений.
10. Рекомендации по расчету прочности трещиностойкости узлов преднапряженных железобетонных ферм. – М.:НИИЖБ Госстроя СССР, 1987.
11. Бородачев Н.А. Программная система для автоматизированного обучения по дисциплине "Железобетонные и каменные конструкции", 1990.