Курсовая работа: Розрахунок рами методом сил

Номер розрахункової схеми визначається двома останніми цифрами номера залікової книжки, від яких треба відняти 24: 58-24-24=10. Отже, номер розрахункової схеми - 10.

Вихідні дані : l = 8 м; h = 12 м; = 1,2; q₂ = 12 кН/м; F₂ = 60 кН; F₄ = 20 кН.

1. Кінематичний аналіз заданої системи та визначення кількості невідомих методу сил

а). Визначимо ступінь свободи системи:

Л= - ,

де Д - кількість дисків;

Ш - кількість простих шарнірів;

В₀ - кількість опорних в’язей.

Ступінь статичної невизначеності системи .

Також ступінь статичної невизначності можна визначити за формулою:

Де К - кількість замкнутих контурів;

В_К - кількість в’язей, які розмикають замкнений контур.

Отже, дана рама є тричі статично невизначною (має 3 невідомих методу сил) і може бути геометрично незмінна.

б). Аналіз геометричної структури заданої рами.

Дана рама складається із одного диска, який опирається на нерухому основу за допомогою шести опорних в’язей і є геометрично незмінна.

2. Вибір основної системи методу сил

Основну систему методу сил вибираємо шляхом відкидання зайвих в’язей, навантаживши при цьому її зовнішніми силами та зусиллями відкинутих зайвих в’язей Х₁ , Х₂ , Х₃ .

Х₁ , Х₂ , Х₃ - основні невідомі методу сил.

Основна система методу сил.

Поверхова схема основної системи методу сил

3. Запис канонічних рівнянь методу сил

Для основної системи методу сил запишемо канонічні рівняння у вигляді системи лінійних алгебраїчних неоднорідних рівнянь:

(1)

Зміст канонічних рівнянь: першого - переміщення перерізу, де прикладена невідома Х₁ у напрямку невідомої Х₁ , від основних невідомих і зовнішнього навантаження дорівнює нулю; другого - переміщення перерізів, де прикладені невідомі Х₂ у напрямку невідомих Х₂ , від основних невідомих і зовнішнього навантаження дорівнює нулю; третього - аналогічно другому рівнянню. У матричному вигляді система (1) має вид: , де - матриця податливості; - вектор невідомих; - вектор вільних членів.

; ; .

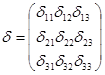4. Визначення коефіцієнтів канонічних рівнянь методу сил і їх перевірка

Коефіцієнти матриці податливості визначаємо за формулою:

; i, k =1,2,3.

Отже, маємо

Склавши епюри , , , одержимо епюру :

Перевірка коефіцієнтів матриці податливості:

Отже, коефіцієнти матриці податливості обчислені вірно.

5. Визначення вільних членів канонічних рівнянь методу сил і їх перевірка

Визначаємо вільні члени канонічних рівнянь методу сил (вектор вільних членів) за формулою:

- епюра згинальних моментів в основній системі від заданого навантаження;

;

Перевірка вільних членів канонічних рівнянь методу сил:

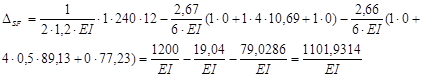
Отже, вільні члени канонічних рівнянь методу сил обчислені вірно.

6. Розв’язок системи канонічних рівнянь методу сил і його перевірка

Система канонічних рівнянь методу сил (1) має вид:

Після рішення системи (1) одержимо:

;

Перевірка рішення система канонічних рівнянь методу сил (1):

;

7. Побудова епюр внутрішніх зусиль для заданої системи та їх кінематична і статична перевірки

Побудову епюр внутрішніх зусиль для заданої системи починаємо з епюри згинаючих моментів.

1). Згідно принципу суперпозиції, епюру згинаючих моментів для заданої системи будуємо таким чином:

а). Кінематична перевірка згинаючих моментів для заданої системи:

Відносна похибка:

Висновок: епюру M побудовано вірно.

б). Статична перевірка.

2). Епюру поперечних зусиль (Q ) будуємо з використанням епюри згинаючих моментів для заданої системи, розглядаючи окремо кожен її елемент.

;

: ;

. Перевірка: : ; .

Ділянка ML: Ділянка LK:

; ;

. ;

Ділянка KF: Ділянка FA:

; ;

. .

: ;

; : .

Ділянка BE:

;

Ділянка CE:

;

Отже, епюра Q для заданої системи матиме вигляд:

Ділянка DA:

;

3). Епюра N для заданої системи матиме вигляд:

4). Статична перевірка поперечних та поздовжніх зусиль для заданої системи:

: ;

: ;.

Висновок: епюри Q та N побудовано вірно.

Література

1. Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика стержневых систем. - М.: Стройиздат, 1981.

2. Дарков А.В., Шапошников Н.Н. Строительная механика. - 8-е изд., перераб. и доп. - М.: Высшая школа, 1986.

3. Киселев В.А. Строительная механика, общий курс - 4-е изд., исправленное и доп. - М.: Стройиздат, 1986.

4. Бутенко Ю.И., Канн С.Н., Пустовойтов В.П. и др. Строительная механика стержневых систем и оболочек. - К.: Вища школа, 1980.

5. Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. - К.: Вища школа, 1989.

6. Руководство к практическим занятиям по курсу строительной механики (статически определимые и неопределимые системы) / Под ред. Г.К. Клейна. - 3-е изд., перераб. и доп. - М.: Высшая школа, 1973.

7. Методичні вказівки та контрольні завдання з дисципліни „Будівельна механіка (спецкурс) ” для студентів денної форми навчання. Частина 2 (статично невизначні системи) / Полтава: ПНТУ, 2003. Укладачі: О.А. Шкурупій, Б.П. Митрофанов, А.М. Пащенко.

Додатки

Додаток А

Розрахункова схема, епюри внутрішніх зусиль для заданої рами.

Розрахункова схема рами.

Основна система методу сил та епюри внутрішніх зусиль від одиничних значень невідомих та заданого навантаження в основній системі

Основна система методу сил.