Реферат: Задача по теории упругости

Задача №1

Использование плоского напряженного состояния балки-стенки с использованием степенных полиномов

Рисунок 1.

Решение:

Выделим из пластины бесконечно малый элемент aob и рассмотрим его равновесие:

, откуда t _xy = t _yx (1.1)

откуда после сокращения на ds

; (а)

откуда после упрощения

. (б)

Итак, (1.2)

Если заменить в формуле (а) угол a на 90 ° + a , то получим

. (в)

Исключая в формулах (1.2) угол a , получим уравнение круговой диаграммы Мора для плоского напряженного состояния (рис. 2)

. (1.3)

. (1.4)

Ориентация главных осей определяется из условия t _{x ¢ y ¢} = 0, откуда tg 2 a _o = 2 t _xy /( s _x - s _y ). (1.4)

Более удобна следующая формула:

. (1.5)

Экстремальные касательные напряжения равны по величине радиусу круговой диаграммы

. (1.6)

И действуют на площадках, равнонаклоненных к главным осям.

Частный случай - чистый сдвиг (рис. 3).

Так как s _x = s _y = 0, t _xy = t _yx = t , то по формулам (1.3) и (1.4) получим

Зависимости между напряжениями и деформациями определяются законом Гука:

- прямая форма

(1.7)

- обратная форма

(1.8)

Пользуясь законом Гука в обратной форме, находим напряжения

Для вычисления главных напряжений имеем следующую систему:

решая которую, найдем s ₁ = 60 МПа, s ₂ = 20 МПа.

Задача №2

Решение плоской задачи методом конечных разностей

Рисунок 4.

Решение:

1. Проверка существования заданной функции напряжений.

Подстановка полученных выражений в бигармоническое уравнение обращает его в тождество:

Функция может быть принята в качестве решения плоской задачи теории упругости.

2. Выражения для напряжений.

,

,

.

3. Распределение внешних нагрузок по кромкам пластинки (рис3.1,а).

Сторона 0-1 : ,

Вершина парабол при .

: ,

: .

Сторона 1-2 : ,

Экстремумы

.

:

:

:

Сторона 2 - 3 : ,

Экстремумы за границей стороны

:

: ,

: , .

Сторона 0-3: ,

Вершины парабол при х=0.

:

:

4. Проверка равновесия пластинки (рис.3.1,б).

Сторона 0-1 :

Расстояние до точки приложения :

.

Сторона 1-2 :

Расстояние до точки приложения :

Сторона 2-3:

.

Расстояние до точки приложения :

.

Сторона 0-3:

Расстояние до точки приложения :

5. Проверка равновесия пластинки:

Пластинка находится в равновесии.

Рис.3. Графическая часть задачи №2

Задача №3

Расчет тонкой плиты методом конечных элементов

Решение:

Построение эпюр изгибающих моментов.

Опорные реакции:

å m _D = 0,

R _A × 4 a = qa × 3 a + q × 2 a × 2 a + qa ² ,

R _A = 2 qa , å Y _i = 0, R _A + R _D = 3 qa , R _D = qa .

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С .

1. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка.

Участок АВ :

Участок ВС :

Участок С D :

Искомое перемещение

.

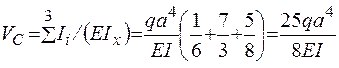2. Определение прогибов. Из условий опирания балки V _A = V _B = 0. Согласно первому условию V _о = 0, а из второго находим q _о :

,

откуда .

Следовательно, уравнения прогибов и углов поворота имеют вид

, .

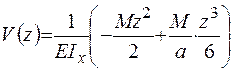Наибольший прогиб возникает в том сечении, где dv / dz = q = 0, т.е. при z = 2 a . Подставив в уравнение прогибов z = 2 a , вычислим наибольший прогиб

V _max = -2 Ma ² /(3 EI _x ).

прогиб посредине пролета плиты равен V _ср = V (1,5 a ) = -9 Ma ² /(16 EI _x ) и отличается от наибольшего на 15%. Угол поворота сечения В

q _B = q (3 a ) = 3 Ma /(2 EI _x ).

3. Определение главных напряжений. Напряжения в поперечном сечении определяются по формулам

,

.

Вычисляя ,

,

,

, находим

,

.

Величины главных напряжений

;

; ; .

Направление главного растягивающего напряжения s ₁ по отношению к продольной оси плиты z :

; ,

а напряжение s ₃ направлено перпендикулярно к s ₁