Курсовая работа: Система автоматического регулирования температуры воды на выходе теплообменника в тепломагистрал

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ НЕФТИ И ГАЗА

Кафедра Кибернетических систем

Курсовая работа

по дисциплине: «Теория автоматического управления»

на тему: «Система автоматического регулирования температуры

воды на выходе теплообменника в тепломагистрали »

Выполнил:

студент группы УИТС-07-1,

Хабибуллин А.Р.

Проверила:

Васькевич А.В.

Тюмень, 2010 г.

Содержание

Техническое задание……………………………………………………………...3

Введение…………………………………………………………………………...6

1. Анализ системы управления…………………………………………………..7

2. Синтез линейных САУ………………………………………………………..9

3. Динамический анализ скорректированной системы………………………..14

Заключение………………………………………………………………………21

Список использованной литературы…………………………………………..22

Техническое задание

Описание системы.

Объект регулирования (ОР): газоходный тракт (далее газоход) конвертера. Регулируемая величина y: давление газа в газоходе, измеряемое датчиком давления PT [Па]. Регулирующее воздействие u : перемещение заслонки (регулирующий орган РО) с помощью электрогидравлического серводвигателя EHS (исполнительное устройство ИУ). Требуется рассчитать устройство регулирования (с возможностью индикации и регистрации) давления PIC (рис. 1, поз. а ).

Рис. 1 Функциональная схема системы автоматического регулирования давления

Функциональная схема системы автоматического регулирования давления показана на рис.1, поз. б . Информация о давлении подается на датчик давления 2 с последующим преобразованием изменения давления в унифицированный токовый сигнал I , который поступает на вход корректирующего фильтра 5 и далее на вход регулятора 7 с типовым алгоритмом регулирования (ПИ- или ПИД- регулятор). Регулятор формирует сигнал управления u и через серводвигатель 8 и заслонку 9 воздействует на расход газа. Датчик с преобразователем 2 , серводвигатель 8 , фильтр 5 и регулятор 7 питаются от источника 4 , а сам источник и регулятор питаются от трансформатора 3 . Для индикации и регистрации давления используется автоматический потенциометр 6 .

Таблица 1.

п.п.	Название элемента	Передаточные функции
1	Теплообменник (ОР)	по управляющему воздействию: по возмущающему воздействию:
2	Термопара (ТП )
3	Измерительный мост
4	Измерительный преобразователь
5	Регулятор (R )	ПИ-регулятор : ПИД-регулятор :
7	Электропнев- матический серводвигатель (EPS)
8	Регулирующий вентиль (РВ)

Таблица 2

№ вар..												, %	t P	, рад/с	, %	М
20	0,05	0,012	0,007	40	-	0,08	7	1,5	5	0,07	0,1	-	-	0,01	0,018	1,45

Введение

Управление состоит в том, чтобы, оказывая на какой-либо объект воздействие, изменять протекающие в нем процессы для достижения определенной цели. Управление является автоматическим, если оно осуществляется без вмешательства человека с помощью специальных технических устройств. Разработка общих принципов создания этих устройств и является основной задачей теории автоматического управления. Теория должна давать единую базу для решения задач управления объектами различной физической, химической или биологической природы.

Целью курсового проектирования является приобретение практических навыков расчета и компьютерного моделирования типовых локальных систем автоматического управления (САУ). Основная задача курсовой работы - научиться на конкретных примерах и задачах применению приёмов и методов, применяемых при анализе и синтезе систем автоматического управления.

В качестве примера использована система автоматического регулирования давления газа в газоходе газопламенной печи.

1. Анализ системы управления

а) Составим структурную схему системы по функциональной схеме и по данным из таблицы 1.

Рис. 2 Структурная схема системы

б) Оценим устойчивость системы (при заданных параметрах элементов) по алгебраическому критерию Гурвица (коэффициент усиления и постоянную времени регулятора примем за единицу, экспоненту в передаточной функции газохода также примем за единицу).

Для оценки по критерию замкнём исследуемую систему:

Составим матрицу:

Разомкнутая система неустойчива, т.к. определитель меньше нуля.

в) Выберем необходимое значение коэффициента усиления разомкнутой системы по заданной точности системы, которая определяется коэффициентами ошибок С ₀ , С ₁ .

Так как максимальная допустимая ошибка не задана в условии, то и находить коэффициенты ошибок не имеет смысла.

г) Исследуем устойчивость замкнутой системы методом логарифмических частотных характеристик разомкнутой системы

Передаточная функция разомкнутой системы примет вид:

Устойчивость замкнутой системы определим по передаточной функции разомкнутой.

ЛЧХ системы представлены на Рис.3 (построена с помощью пакета MATLAB) , по которому видно, что система устойчива, а запасы по амплитуде и по фазе соответственно равны 77,4 дБ и 35,1^о .

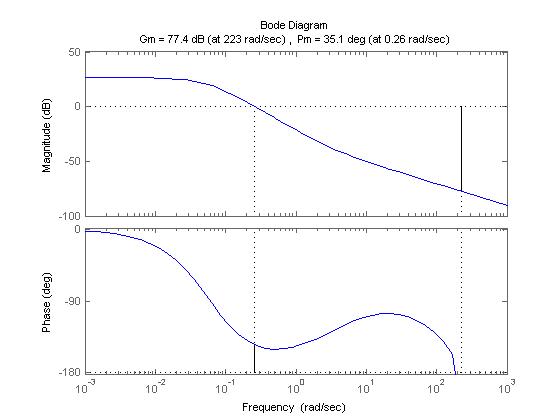
Рис.3 ЛЧХ системы

2. Синтез линейных САУ

Для заданной динамической системы управления с помощью частотного метода ЛАЧХ определим непрерывное корректирующее устройство, добавление которого в систему позволит получить необходимые показатели качества процесса управления.

Требуется выбрать корректирующее устройство, обеспечивающее получение следующих характеристик качества замкнутой системы:

1. длительность переходного процесса t_p не должна превышать 0,46 с;

2. относительное перерегулирование в переходном процессе не должно превышать 25%.

а) Передаточная функция нескорректированной системы имеет вид:

Коэффициент усиления выберем равным 6 - меньше, чем заданное значение, т.к. прямые показатели качества системы малы, и чтобы попасть в эти значения при синтезе, необходим небольшой коэффициент усиления.

б) Составим последовательную схему коррекции:

Рис. 4 Схема последовательной коррекции

где– передаточная функция корректирующего устройства,

- передаточная функция скорректированной системы.

в) Построим асимптотическую ЛАЧХ , для чего найдём величину начального усиления:

и частоты сопряжения:

Порядок астатизма системы равен двум, поэтому первичный наклон ЛАЧХ будет равен -40dB/dek.

г) Построим желаемую ЛАЧХ .

На низкочастотном участке , где вид определяется в основном требованиями к точности регулирования, а, следовательно, величиной коэффициента усиления системы, порядком ее астатизма, значением коэффициента ошибки и т.д. Статическая ошибка недопустима ( = 0), то скорректированная система должна быть астатической, поэтому в области НЧ желаемая ЛАЧХ будет иметь наклон -40dB/dek.

На среднечастотном участке желаемая ЛАЧХ в наибольшей степени зависит от требования к динамическим показателям качества регулирования. На этом участке находится частота среза и определяется запас устойчивости по фазе.

По заданной величине перерегулирования = 25 %, определим величину времени регулирования по первой номограмме Солодовникова.

Значению = 25 % на номограмме соответствует P макс = 1,2. Поскольку допустимое значение времени регулирования , то можно вычислить необходимую частоту среза:

Вид желаемой ЛАЧХ в среднечастотном диапазоне должен гарантировать необходимый запас устойчивости системы по фазе, что в максимальной степени обеспечивается, когда желаемая ЛАЧХ в районе частоты среза имеет достаточно протяженный участок с наклоном -20 дБ/дек.

Для желаемой ЛАЧХ примем следующие обозначения: – протяженность среднечастотного участка ; – протяженность участка желаемой ЛАЧХ, по которому сопрягаются низкочастотный и среднечастотный участки .

Выберем частоты и . Наложим ограничение на абсолютную величину и , которые должны быть не ниже значений, определенных по второй номограмме Солодовникова (Рис. 6), обычно эти значения находятся в пределах от 12 до 16 дБ.

Для заданного P макс по номограмме найдём необходимые значения запасов устойчивости по модулю h ⁺ и по фазе . При этом вначале вычислим P мин по формуле:

На второй номограмме Солодовникова для значений и найдены значения h ⁺ = 16 дБ и h ^- =-16 дБ. Необходимый запас устойчивости по фазе :

= 44⁰ .

Значения h ⁺ и h ^- определяют протяженность среднечастотного участка желаемой ЛАХ:

= 16 дБ, = -16 дБ.

На указанном интервале частот фазо-частотная характеристика скорректированной системы не должна заходить в запретную область:

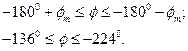
Сопряжённый участок желаемой ЛАЧХ оставим с наклоном равным желаемой ЛАЧХ в НЧ диапазоне – 40 дБ/дек.

Вид желаемой ЛАХ в высокочастотном диапазоне определяет, например, такой показатель, как помехоустойчивость системы, но на качество регулирования поведение в этой частотной области влияет в незначительной степени. Поэтому на участке высоких частот с целью упрощения корректирующего звена допустим совпадение наклонов асимптот желаемой ЛАЧХ и ЛАЧХ исходной нескорректированной системы.

Вид ЛЧХ показывает, что запасы отрицательны, поэтому сместим ЛАХ влево, на частоту среза

д) Построим ЛАЧХ корректирующего звена:

Произведем графическое вычитание ЛАЧХ нескорректированной системы из ЛАЧХ желаемой. Получили ЛАЧХ корректирующего звена.

е) Найдём ПФ корректирующего звена W_к (s):

Найдём постоянные времени:

С учётом постоянных времени ПФ корректирующего звена примет вид:

ж) Найдем ПФ скорректированной системы, для этого требуется выполнить произведение нескорректированного системы и корректирующего звена:

3.Динамический анализ скорректированной системы

а) Исследуем на устойчивость скорректированную замкнутую систему по логарифмическим характеристикам разомкнутой системы. Определим запасы устойчивости замкнутой системы. Построение ФЧХ было проведено с помощью пакета MATLAB.

Из ЛЧХ следует, что скорректированная замкнутая система устойчива и имеет запасы по амплитуде и по фазе 23,9 дБ и 56,1^о соответственно.

б) Построим переходный процесс замкнутой скорректированной системы по управляющему воздействию. Определим прямые показатели качества переходного процесса. Построение переходного процесса проведено в пакете MATLAB.

Рис.5 Переходный процесс замкнутой скорректированной системы

Переходный процесс является сходящимся, а перерегулирование и время процесса равны 5,55% и 0,103 с соответственно, что удовлетворяет заданным условиям. Из чего следует, что коррекция системы была проведена правильно.

в) Построим амплитудно-частотную характеристику скорректированной замкнутой системы. Определим показатель колебательности. Для построения амплитудно-частотной характеристики используем MATLAB.

Рис.6 АЧХ и ФЧХ замкнутой скорректированной системы

Показатель колебательности найдём по формуле:

г) Оценим, будет ли обеспечена заданная степень устойчивости системы во всех режимах работы. Если параметры системы К , Т имеют разброс .

При К=1,2(+20%) :

При K =0,8(-20%) :

Замкнём системы и построим переходные характеристики. Всё это сделаем с помощью MATLAB.

Рис.7 Переходная характеристика замкнутой скорректированной системы при увеличении K на 20%.

Рис.8 Переходная характеристика замкнутой скорректированной системы при уменьшении K на 20%.

Как видно из представленных графиков при разбросе параметра К

система остаётся устойчивой, при незначительном изменении качества переходного процесса.

Влияние на поведение системы разброса параметра Т проанализировать невозможно

д) На основе метода D-разбиения построим область устойчивости в плоскости параметра К .

Чтобы построить область устойчивости произведём замену:

;

Замкнём систему:

Получим характеристичекское уравнение и выразим из него К :

Произведём замену и получим:

Разделим выражение на реальную и мнимую составляющие:

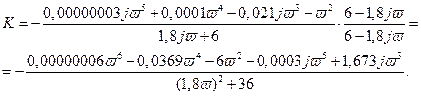
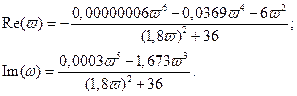
Изменяя w, построим границу D-разбиения.

Рис. 9 Граница D-разбиения

Граница получилась нестандартной формы, поэтому область устойчивости определить не удалось.

Заключение

В ходе курсовой работы был проведен анализ системы автоматического регулирования давлениягаза в газоходе газопламенной печи. Была проведена коррекция системы.

В результате была синтезирована устойчивая система с запасами по амплитуде m=23,9 dB и по фазе =56,1⁰ . Система имеет перерегулирование 5,55 %, показатель колебательности М=1,02 и время ругулирования .

Все показатели лежат в рамках заданных условий.

Список использованной литературы:

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. - Профессия – 2003 – 752с

2. Воронов А.А. ТАУ. Ч.1. Теория линейных систем. – Высшая школа - 1986 – 367с.

3. Воронов А.А. ТАУ. Ч.2. Теория нелинейных и специальных систем. – Высшая школа - 1986 – 504с.

4. Ким Д.П. ТАУ Ч.1. Линейные системы – Физматлит – 2003 – 288с.

5. Ким Д.П. ТАУ Ч.2. Многомерные, нелинейные, оптимальные и адаптивные системы – Физматлит – 2004 – 464с.