| Похожие рефераты | Скачать .docx |
Дипломная работа: Модернизация подвески автомобиля ЗАЗ1102 Таврия
СОДЕРЖАНИЕ
Введение и постановка задачи
Условные обозначения
1 Требования к подвеске
2 Подвеска на направляющих пружинах и амортизационных стойках
2.1 Преимущества и недостатки пружинных стоек
2.2 Кинематические свойства
2.3 Силы и трение
3 Силы в пятне контакта колеса с дорогой
3.1 Определение жесткости шин ЗАЗ – 1102 «Таврия»
3.2 Определение сил и коэффициентов
4 Определение статических нагрузок в пружине и шариках
5 Расчеты на прочность
5.1 Основные теоретические положения расчетов на прочность
5.1.1 Определение допускаемых напряжений
5.1.2 Напряжения при изгибе
5.2 Расчет на выносливость и сопротивление усталости
5.2.1 Определение верхних значений сил длительного действия
5.2.2 Определение нижних значений сил длительного действия
5.2.3 Определение сил в направляющей и на поршне амортизатора при верхних значениях сил длительного действия
5.2.4 Определение сил в направляющей и на поршне амортизатора при нижних значениях сил длительного действия
5.2.5 Преобразование знакопеременной нагрузки
5.2.6 Определение сил, действующих на резиновые шарниры рычага
5.2.7 Определение напряжений и деформаций резиновых втулок-шарниров
5.3 Расчет на прочность
5.3.1 Кратковременно действующие силы
5.3.2 Силы, возникающие при движении по дороге с выбоинами
5.3.3 Силы, возникающие при торможении
5.3.4 Силы, возникающие при преодолении железнодорожного переезда
5.3.5 Силы, действующие при полном ходе отбоя колеса
6 Подрессоривание передней оси
6.1 Вертикальные колебания, их действие на человека
6.2 Определение передаточных чисел
6.3 Построение кривой жесткости подвески
7 Расчет и проектирование стального упругого элемента
7.1 Пружинные стали и их свойства
7.2 Расчет винтовой пружины
8 Расчет характеристики амортизатора
9 Построение графика изменения колеи автомобиля в зависимости от хода колеса
10Охрана труда
10.1 Меры безопасности при эксплуатации автомобиля
10.2 Требования к рабочему месту водителя
10.3 Виброизоляция сиденья самоходной машины
10.4 Устойчивость легкового автомобиля
10.5 Противопожарная безопасность
Заключение
Список литературы
Введение и постановка задачи
Основными устройствами, защищающими автомобиль от динамических воздействий дороги и сводящими колебания и вибрации к приемлемому уровню, являются подвеска и шины.
Многолетний опыт показывает, что неровности дороги и вызываемые ими колебания кузова и колес автомобиля ведут, как правило, к ухудшению всех его эксплуатационно-технических качеств и к тем большему, чем хуже качество дороги.
Можно считать, что на дорогах с неровной поверхностью снижается производительность автомобиля вследствие уменьшения скоростей движения и увеличения простоев, возрастают расходы на техническое обслуживание и ремонты. Кроме этих прямых потерь есть и косвенные, вызванные, в частности, слабым использованием сети дорог с неровной поверхностью. Прямые и косвенные потери от эксплуатации различных автомобилей и автопоездов на дорогах с неровной поверхностью исчисляются значительными денежными суммами.
Есть два пути уменьшения этих потерь — строительство дорог с усовершенствованным покрытием и улучшение качества подвески. Оба направления дополняют друг друга, так как строительство дорог — процесс длительный и дорогостоящий. Кроме того, всегда требуется некоторое количество автомобилей повышенной и высокой проходимости, которым необходима совершенная подвеска.
Подвеской автомобиля называют совокупность устройств, связывающих колеса с рамой (кузовом) и предназначенных для уменьшения динамических нагрузок, передающихся автомобилю вследствие неровной поверхности дороги, а также обеспечивающих передачу всех видов сил и моментов, действующих между колесом и рамой (кузовом).
Разнообразные силы взаимодействия колеса и дороги можно свести к трем составляющим: вертикальной Z, продольной Х, поперечной или боковой У (рис.1). Передача этих сил и их моментов состоит из трех устройств: упругого, демпфирующего и направляющего.
Упругим устройством на подрессоренную массу передаются вертикальные силы, действующие со стороны дороги, уменьшаются динамические нагрузки и улучшается плавность хода.
Направляющее устройство — механизм, воспринимающий действующие на колесо продольные и боковые силы и их моменты. Кинематика направляющего устройства определяет характер перемещения колеса относительно несущей системы.
Демпфирующее устройство — предназначено для гашения колебаний кузова и колес путем преобразования энергии колебаний в тепловую и рассеивание ее в окружающую среду.
Кроме того задачи повышения плавности хода на автомобильном транспорте становятся актуальней потому как это связано не только с требованиями повышения ресурса динамически нагруженных узлов автомобиля, но и с причиной перемещения центра вопроса в область обеспечения высокой безопасности движения, комфортабельности водителя и пассажиров и защиты их от воздействия высокочастотных колебаний. Особенно это важно для легковых автомобилей, которые, как правило, эксплуатируются при более высоких скоростях, чем грузовые и значительно легче последних, а потому более полно воспринимают неровности дороги. Однако большая номенклатура существующих конструкций подвесок говорит об отсутствии, какой либо универсальной. Более того, зачастую, казалось бы, подходящая конструкция для конкретного типа автомобиля требует доработки, и переработки ввиду различного рода эксплуатационных факторов, морального старения, с учетом возможности дальнейшей модернизации, с целью повышения ресурса и уменьшения нагрузок на её детали и узлы. Последнее время распространение получают подвески с увеличенными ходами. Это способствует высокой плавности хода. Наиболее известной является подвеска на несущих пружинных стойках (типа «Макферсон»). При относительной простоте она позволяет приобрести массу положительных эффектов, о которых будет сказано ниже.
Целью настоящей работы является расчет силовых факторов подвески на направляющей пружинной стойке переднеприводного автомобиля ЗАЗ-1102 «Таврия» с введением изменений. А именно: смещения амортизатора относительно пружины на угол α=7º. Расчет основных геометрических параметров элементов и деталей, расчет их основных физических свойств, проведение кинематического и силового анализа, проверка адекватности используемой методики.
Условные обозначения
Силы, действующие в пятне контакта колеса с дорогой
F – сила упругости;
LА – сила тяги;
LВ – тормозная сила;
NV1 h – нагрузка от колеса (нормальная сила, равная половине допустимой нагрузки соответственно на переднюю или заднюю оси);
NV ′1h – нормальная нагрузка (вертикальная), действующая на кузов, в расчете соответственно на заднюю или переднюю оси;
± ∆N – колебания нагрузки на колесe;
± S1 – продолжительно действующая боковая сила;
± S2 – кратковременно действующая боковая сила;
U – вес неподрессоренных частей, отнесенный к оси.
Нижние индексы
h – задний;
v – передний;
о – верхний предел;
u – нижний предел;
ℓ – нагрузка продолжительного действия;
2 – при движении по железнодорожному переезду;
3, 4 – при движении по дороге с выбоинами;
5 – при торможении.
Моменты
Мbo – верхнее значение длительно действующего изгибающего момента;
Мbu – нижнее значение длительно действующего изгибающего момента;
Мbw – изгибающий момент при чистом знакопеременном изгибе.
Расчеты на прочность (по ДИН 1350 и ДИН 50100)
αА – соотношение напряжений;
αК – коэффициент концентрации напряжений;
βК – то же, обусловленный формат поверхности;
βN – то же, обусловленный посадкой;
γ – отношение предела текучести к временному сопротивлению;
δ – удлинение;
υ – запас прочности;
b1 – масштабный коэффициент, учитывающий влияние размеров;
b2 – масштабный коэффициент, учитывающий шероховатость обработанной поверхности;
σ – нормальное напряжение;
τ – касательное напряжение при срезе или кручении;
fw – коэффициент, учитывающий материал.
Нижние индексы
а – амплитудное значение действующих напряжений;
b – напряжение при изгибе;
m – среднее значение напряжений;
o – верхнее значение предельных напряжений;
t – напряжения при кручении;
u – нижнее значение предельных напряжений;
доп. – допускаемые напряжения;
А – допускаемое амплитудное значение напряжений (на испытуемом образце);
В – временное сопротивление.
Жесткость системы подрессоривания
С1 – жесткость шин при принятом для данного автомобиля давлении в шинах;
С2 – жесткость подвески кузова, приведенная к одному колесу, при равностороннем нагружении обеих (левой и правой) подвесок;
С2 А – жесткость подвески кузова, приведенная к оси, при равностороннем нагружении обеих подвесок;
С3 – жесткость стабилизатора, приведенная к одному колесу, при разностороннем нагружении подвесок;
СF – жесткость собственно упругого элемента, приведенная к месту его опоры;
CS – жесткость стабилизатора, измеряемая на концах рычагов при разностороннем нагружении подвесок.
Частота колебаний
nІ – частота недемпфированных колебаний оси в вертикальном направлении, мин.
nІ D – то же, демпфированных колебаний;
nІІ – частота недемпфированных колебаний кузова в вертикальном направлении;
nІІ D – то же, демпфированных колебаний.
Передаточные числа и числа витков пружин
if – число рабочих витков;
ig – общее число витков;
iw – передаточное отношение при поперечно-угловом подрессоривании;
ix – кинематическое передаточное число;
iy – силовое передаточное число.
1 Требования к подвеске
Подвеска, являясь промежуточным звеном между кузовом автомобиля и дорогой, должна быть легкой и наряду с высокой комфортабельностью обеспечить максимальную безопасность движения. Для этого необходимы точная кинематика колес, легкость поворота управляемых колес, а также изоляция кузова от дорожных шумов и жесткого качения радиальных шин. Кроме того, надо учитывать, что подвеска передает на кузов силы, возникающие в пятне контакта колеса с дорогой, поэтому она должна быть прочной и долговечной (рис. 1). Наиболее характерными требованиями к подвеске являются:
1. Обеспечение движения по неровным дорогам без ударов в ограничитель.
2. Ограничение поперечного крена автомобиля.
3. Обеспечение затухания колебаний кузова и колес.
4. Постоянство колеи и углов установки колес.
5. снижение массы неподрессоренных частей.
6. Общие требования.
 Детали, соединяющие опоры подшипника колеса с кузовом (рычаги, штанги и упругие элементы), должны удовлетворять этим требованиям. Применяемые шарниры должны легко поворачиваться, быть малоподатливыми и вместе с тем обеспечивать шумоизоляцию кузова. Рычаги должны передавать силы во всех направлениях, а также тяговые и тормозные моменты и быть при этом не слишком тяжелыми или дорогими. Упругие элементы при эффективном использовании материала должны быть простыми и компактными и допускать достаточный ход подвески.
Детали, соединяющие опоры подшипника колеса с кузовом (рычаги, штанги и упругие элементы), должны удовлетворять этим требованиям. Применяемые шарниры должны легко поворачиваться, быть малоподатливыми и вместе с тем обеспечивать шумоизоляцию кузова. Рычаги должны передавать силы во всех направлениях, а также тяговые и тормозные моменты и быть при этом не слишком тяжелыми или дорогими. Упругие элементы при эффективном использовании материала должны быть простыми и компактными и допускать достаточный ход подвески.
Рис. 1 Силы, действующие в точке контакта колеса с дорогой (левое переднее колесо):
Fb – сила сопротивления качению или тормозная сила;
Fn – вертикальная сила;
Fs – боковая сила.
Подвеска автомобиля и демпфирование в ней должны обеспечить комфортабельность движения (плавность хода); безопасность движения и устойчивость на поворотах.
Свойства самой подвески зависят от различных параметров и взаимодействия отдельных деталей, т. е. от типа и жесткости упругих элементов, стабилизаторов, шарниров рычагов, амортизаторов и их соединения, массы осей, типа подвески двигателя, колесной базы, колеи и особенно от шин.
· Тип и жесткость упругих элементов.
Мягкие пружины и большие хода подвески являются предпосылкой высокой плавности хода автомобиля, достаточной свободы продольных угловых колебаний кузова и хорошего держания, дороги шинами. Последнее условие необходимо и для обеспечения безопасности движения.
Если, например, колесо, нагруженное NV1 h = 2944 Н, попадает в выбоину глубиной 80 мм, то при мягкой подвеске с жесткостью упругого элемента С2 = 10 Н/мм в момент касания колесами дна выбоины остаточная сила
N′ = NV1 h - С2 f2 = 2944 – 10 х 80 = 2144 Н.
При жесткой («спортивной») подвеске с С2 = 20 Н/мм эта сила составила бы лишь 1344 Н. Более высокое значение остаточной силы означает лучшее сцепление с дорогой. Аналогичным образом можно рассмотреть переезд дорожной неровности высотой 40 мм. При более жесткой подвеске увеличение силы, передаваемой подвеской на кузов в виде удара, составит без учета демпфирования ∆N = 800 Н. При мягкой подвеске это увеличение нагрузки на колесо будет меньшим. Недостатком мягкой подвески будет больший крен кузова на поворотах и связанное с этим уменьшение способности шин воспринимать боковые силы. При независимой подвеске колеса наклоняются вместе с кузовом. Наружное по отношению к центру поворота колесо воспринимает основную часть боковых сил и приобретает положительный угол развала. В результате этого наклон шины увеличивается.
· Стабилизаторы.
Стремление автомобиля к крену может быть ослаблено благодаря применению стабилизаторов на обеих осях или только на передней. Недостатком в этом случае является большая жесткость подвески при воздействии неровностей с одной стороны автомобиля, когда уменьшается способность подвески к гашению ударов, создаваемых булыжной мостовой и неровностями дорожного покрытия.
· Шарниры рычагов.
К повышению жесткости подвески могут приводить также слишком жесткие шарниры рычагов направляющего устройства. Если речь идет о подшипниках скольжения, то в точках изменения направления колебаний необходимо учитывать появление силы сопротивления, которую следует рассматривать одновременно с повышением демпфирующего эффекта. Если же в качестве шарниров использованы резиновые элементы, запрессованные между внутренней и наружной втулками, то при повороте рычага в предварительно напряженной резине возникают напряжения сдвига, что приводит к увеличению общей жесткости подвески.
· Амортизаторы и их соединения.
Демпфирование оказывает на свойства подвески автомобиля аналогичное воздействие. «Жесткие» амортизаторы способствуют хорошему контакту колес с дорогой, но ухудшают плавность хода. Более «мягкие» амортизаторы делают движение более комфортабельным, но не способствуют повышению безопасности. Аналогичным образом слишком мягкие элементы соединения амортизаторов, хотя и способствуют изоляции от дорожного шума и обеспечивают необходимую свободу углового перемещения, но они приводят к запаздыванию срабатывания амортизатора, тем самым уменьшают его эффективность.
· Масса осей.
Для демпфирования колебаний легкой оси (т. е. для уменьшения колебаний колес) в большинстве случаев достаточно той регулировки амортизатора, которая предусмотрена для демпфирования колебаний кузова. Для тяжелого ведущего неразрезного моста, напротив, требуются более высокие силы демпфирования, которые в свою очередь снижают плавность хода.
· Подвеска двигателя.
Мягкая и по частоте собственных колебаний неправильно выбранная подвеска двигателя может привести к тому, что установленный без демпфирующих элементов силовой агрегат при определенных частотах вращения коленчатого вала будет колебаться с частотой собственных колебаний и вызовет неприятные вибрации кузова и рулевого управления. В таких случаях рекомендуется использовать гаситель колебаний двигателя.
· Колесная база.
Автомобиль с большой (по сравнению с общей длиной) колесной базой L имеет меньшую склонность опрокидывания в продольном направлении и продольным угловым колебаниям, чем автомобиль с малой базой.
· Колея.
Чем больше колея автомобиля, тем меньше крен кузова на поворотах и опасность опрокидывания при заносе.
· Шины.
Мягкие шины лучше поглощают толчки от коротких неровностей дороги. Однако недостатком таких шин является меньший коэффициент бокового сцепления на поворотах, а также замедленная реакция на резкий поворот рулевого колеса.
2 Подвеска на направляющих пружинных и амортизаторных стойках
Если упругие силы передаются вверху в зоне крепления штока, а внизу приходится на корпус амортизатора, то речь идет о направляющих пружинных стойках. Если же пружина установлена на нижнем рычаге либо с ним соединяется торсион или листовая рессора, такой вариант конструкции называется амортизаторной стойкой.
Применявшийся ранее термин «подвеска Макферсона» со временем был заменен термином «подвеска на направляющих и амортизаторных стойках».
2.1 Преимущества и недостатки пружинных стоек
Направляющая пружинная стойка представляет собой развитие подвески на двойных поперечных рычагах. Верхний рычаг здесь заменен точкой крепления на брызговике крыла кузова, где опирается шток стойки и пружина подвески. В этой точке воспринимаются силы во всех направлениях, которые, со своей стороны, вызывают нагружение штока на изгиб. Чтобы избежать нежелательного изменения развала и продольного наклона, обусловленных податливостью, диаметр штока должен быть увеличен с 11 мм хотя бы до 18мм; при сохранении прежнего диаметра поршня демпфирование осуществляется по двухтрубной схеме.
Основное преимущество направляющей пружинной стойки в том, что все детали, выполняющие упругую работу и направляющие функции, могут быть объединены в одну монтажную единицу. Имеются в виду следующие детали: чашка для опоры нижнего торца пружины, дополнительный упругий элемент или буфер сжатия, буфер отбоя, собственно демпфирующая часть и опора подшипника колеса (поворотный кулак).
Последняя деталь может жестко соединяться с корпусом посредством сварки, твердой пайки либо иметь разъемное болтовое соединение.
Другие преимущества, связанные с подвесками на направляющих стойках (рис. 2):
- меньшие усилия в точках крепления к кузову (A, D) за счет большого расстояния между ними;
- небольшое расстояние b между точками N и G, приложения нормальной реакции дороги и центра шаровой опоры соответственно;
- большие хода подвески;
- упразднение трех опорных точек;
- лучшая возможность создания передней зоны деформации.
Противостоящие им следующие неизбежные недостатки благодаря конструктивным мероприятиям в передних подвесках уже явно не проявляются:
- неблагоприятные кинематические характеристики;
- восприятие усилий и колебаний брызговиками, т. е. передней частью кузова;
- затрудненная изоляция от дорожных шумов;
- меньшая возможность достаточного противодействия продольному крену при торможении;
- трение между штоком и его направляющей, ухудшающее упругое действие;
- неблагоприятно длинные рулевые тяги при верхнем расположении реечного рулевого механизма;
- большая чувствительность передней подвески к дисбалансу и биению шин;
- иногда малый зазор между шиной и демпфирующей частью.
Последнее, однако, имеет значение только при переднем приводе, поскольку исключает возможность установки цепей противоскольжения. При ведомых колесах указанный недостаточный зазор не позволил бы лишь установку более широких шин. В случае безусловной необходимости таких шин следует применять колеса с меньшим вылетом С, которые, однако, неблагоприятно увеличивают плечо обкатки Ro (рис. 2.1)
В течение последних десяти лет направляющие пружины и амортизаторные стойки получили широкое применение в передних подвесках, однако их часто используют и для подвески задних колес переднеприводных автомобилей. Приподнятая из аэродинамических соображений задняя часть кузова позволяет использовать направляющую базу между направляющей штока и поршнем.
2.2 Кинематические свойства
Высокое расположение центра крена W может быть получено только за счет наклона стойки (т. е. нежелательно большого угла δо поперечного наклона оси поворота) или нежелательного наклона нижнего рычага (рис. 2). Таким образом, центр крена расположен не выше (как часто полагают), чем в подвеске на двойных поперечных рычагах; более того, при нагружении он опускается в большей степени. На изменение колеи, как и на изменение развала, здесь повлиять труднее, чем при двойных поперечных рычагах. Изменение развала становится особенно неблагоприятным, если для получения меньшего перераспределения колесных нагрузок на повороте центр крена (например на переднеприводном автомобиле) должен располагаться спереди низко или же для устойчивости прямолинейного движения желательно иметь лишь небольшое изменение колеи. Стойка располагается тогда почти вертикально, а нижний рычаг практически не имеет подъема от нагруженного шарнира к внутреннему (рис. 2.1).
 |
Рис. 2. Направляющая стойка с соосной пружиной.
Чем больше наклон нижнего рычага GD, тем выше расположены наклон Р и центр крена W, который определяется соединением точек Р и N. Недостатком такого решения может считаться большое изменение колеи. Приложенная в точке N вертикальная сила Fn дает на плече b момент, который должен восприниматься в стойке двумя скользящими опорами С и К.
При сохранении высоты hw центра крена кинематические свойства могут быть улучшены удлинением нижнего рычага до точки D2 вместо D1 . Однако такая возможность может быть осуществлена только в задних подвесках, спереди же наибольшую длину рычагов определяет ширина расположенных рядом двигателя и агрегатов.
Рис. 2.1 Схема для определения центра крена
Чем более отвесно установлена пружинная или амортизаторная стойка и чем ближе к горизонтали положение нижнего рычага GD, тем меньше высота hw центра крена W, следствием чего является неблагоприятное изменение развала при ходе сжатия. Удлинением нижнего рычага (GD2 вместо GD1 ) можно улучшить кинематические свойства. Для получения малого или отрицательного плеча обкатки Ro точка G должна быть смещена наружу, в пространство колеса; в результате благоприятно уменьшается плечо b действия вертикальной силы Fn (b = Ro + d tg δo ). Чем короче отрезок b, тем меньше опасность заклинивания в направляющей и на поршне и меньше силы в опорных точках D, А, G.
Экономичнее всего поручить исполнение функций нижнего направляющего элемента в продольном направлении стабилизатору. Однако плечи стабилизатора перемещаются по дуговым траекториям и поэтому при ходах подвески смещают поперечные рычаги подвески вперед или назад в точках прикрепления. Эти отклонения могут быть компенсированы применением длинных плеч стабилизатора, однако это связано с увеличением диаметра, т. е. повышенной массой и стоимостью.
Если стабилизатор расположен перед осью колес, то его спинка для обеспечения требуемого дорожного просвета размещается высоко. Направленные назад плечи стабилизатора опускаются от спинки к концам, что приводит к расположению центра продольного крена перед осью колес. В результате передняя часть кузова при торможении дополнительно подтягивается вниз. Этот недостаток можно было бы устранить размещением стабилизатора, выполняющего и направляющие функции, позади колес. Если стабилизатор не исполняет направляющих функций, как показатель экономичности, он может иметь короткие плечи и при меньшем диаметре – более высокую приведенную жесткость.
Изменение развала под действием боковых сил на повороте, приложенных в точке контакта колеса, меньше, чем в подвеске на двойных поперечных рычагах. Массовые обследования, выполненные в лаборатории шасси Высшего технического училища г. Кельна, дали следующую среднюю величину (при исключении податливости диска колеса): ∆γ5 = 22′ на 1 кН боковой силы. В подвесках на двойных поперечных рычагах это значение несколько выше: 25′.
2.3 Силы и трение
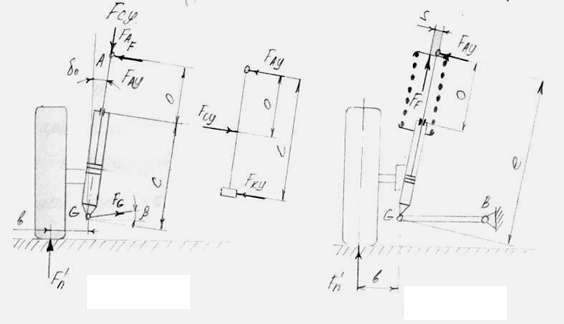
Когда колесо совершает ход сжатия или отбоя, то неподвижно соединенный с опорой подшипника колеса рабочий цилиндр демпфирующего элемента перемещается относительно поршня и штока. Если упругим элементом служат продольные торсионы, поперечная рессора или в верхней опорной точке фиксируется только шток, а не пружина подвески, то при повороте руля происходит относительное вращение, которое уменьшает или почти полностью устраняет трение в направляющей штока и на поршне. Пружины должны при этом иметь возможность поворота на неподвижной верхней опоре, в противном случае в результате их деформации в них появились бы дополнительные напряжения изгиба и возник бы возвратный момент. Если пружина установлена соосно с амортизатором, то как в статике, так и при прямолинейном движении без внешних воздействий в точке крепления А к кузову действует поперечная сила FАУ (рис. 2.3.1). Она вызывает на поршне реакцию того же направления, а на направляющей штока – приблизительно вдвое большую силу FСУ :
FСУ = FАУ + FКУ .
Поршень имеет большой диаметр, что обусловливает малое давление на поверхности, и, кроме того, скользит в амортизаторной жидкости; шток же имеет меньший диаметр и испытывает большую боковую нагрузку. Чем больше FСУ , тем больше сила трения Fч в направляющей; соответственно возрастает и требуемое для ее преодоления изменение нагрузки на колесо.
Силу FСУ легко рассчитать по размерам, обозначенным на рис. 2.3.3, массе Мv , приходящейся на ось, и неподрессоренной массе Мuv . Вертикальная сила F′n в Ньютонах: F′n = (Мv - Мuv ) / 2g, отсюда
![]()
Чем длиннее сама пружинная стойка (т.е. размер с) и чем короче размер b, тем меньше будет сила FСУ . Однако размер b складывается из двух отрезков: d tg δo и Ro , т. е. малое или отрицательное плечо обкатки позволяет уменьшить силу FСУ .
 |
|
| Рис. 2.3.1. Графическое определение сил в стойке где пружина соосна амортизатору | Рис. 2.3.2. Графическое определение сил в стойке где ось пружины смещена к колесу |
Кроме того, это усилие, грозящее заеданием, можно ограничить за счет смещения пружины к колесу (рис. 2.3.2). Если S – взаимное смещение осей пружины и амортизатора и FF – усилие пружины, то уравнение имеет вид:
![]()
Отсюда можно вычислить требуемую величину смещения S.
Если пружина подвески установлена с наклоном относительно оси амортизатора (рис. 2.3.3), так что ось ее проходит через точку М пересечения линии действия вертикальной силы Fn и продолжения линии GD, соединяющей точки поворота рычага, то сила FАУ в точке крепления А для рассматриваемого нагрузочного состояния полностью исчезает. Вместе с ней и сила FСУ , так что трение в направляющей приближается к нулю.
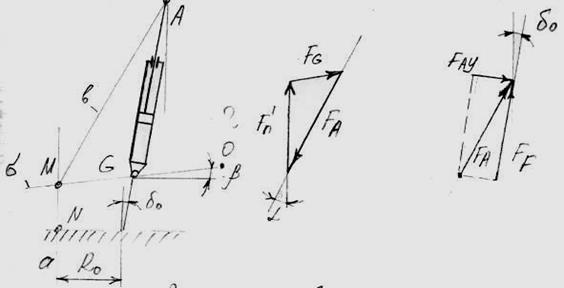
Рис. 2.3.3. Графическое определение силы FА в точке крепления А к кузову пружинной стойки.
Линия a(Рис. 2.3.3) вертикальной силы F′n и продолжение прямой σ, проведенной через точки G и D поворота рычага, пересекаются в точке М. Путем соединения точек М и А получается направление b силы FА и угол α относительно вертикали. На схеме все силы изображаются в масштабе с учетом их величины. Сила + FА действует на нижнюю чашку пружины, размещенную с наклоном на корпусе амортизатора; верхняя чашка на брызговике крыла нагружается реакцией - FА . Разложение с учетом угла δo дает FF и составляющую FАУ , которая в рассматриваемом положении подвески устраняет трение в стойке.
При переднем приводе в точке контакта колес кроме вертикальной и боковой сил присутствуют еще тяговые силы Fа . Как показано на рис. 2.3.5 эту силу нужно рассматривать приложенной к оси поворота ниже центра колеса; сила Fа ′′ вызывает в точке А, а также в направляющем маршруте G реакции FАХо и FGХо . За счет смещения пружины назад можно в некотором диапазоне скоростей (при вполне определенной тяговой силе) почти полностью устранить силу FАХо , также вызывающую трение в направляющей и на поршне.

Рис. 2.3.4 Силы действующие напрямолинейно катящееся колесо
Рис. 2.3.4 На прямолинейно катящемся колесе силу сопротивления качению FR нужно рассматривать в виде силы F′R , приложенной в центре колеса; она имеет плечо Rа относительно от поворота. Величина этого плеча продольной силы зависит от плеча обкатки Ro ; чем меньше последнее, тем выше на оси поворота приложена в виде F′R сила FR и тем равномернее нагружаются в продольном направлении точки А и G. Аналогичные статические соотношения справедливы и для тяговых сил, а также для тормозных в том случае, если тормоза расположены внутри, на главной передаче.
На рис. 2.3.5 приведены силы, действующие в статике в передней подвеске автомобиля, имеющей вынос колеса вперед – nτ и угол продольного наклона от поворота τ = 1˚ 20′. Пружина смещена на расчетное расстояние и относительно обеих вертикальных сил F′n и FGZ , чтобы получить пару горизонтальных сил FАХ1 и FGХ1 . Вторая из этих сил складывается с уже имеющейся на направляющем шарнире силой FGХо ; сила же FАХ1 при определенной скорости компенсирует действие противоположно направленной силы FАХо . При этой скорости в точке А практически отсутствуют продольные силы, вызывающие трение, а вместе с этим и силы на поршне К и в направляющей С.
За счет смещения пружины (сила FF рис. 2.3.5) на виде сбоку за ось колеса можно при определенной скорости устранить трение в направляющей С и на поршне К, вызванное продольной тяговой силой Fа на переднем колесе.
У автомобилей, имеющих тормоза наружного расположения в колесах, при торможении в верхней точке крепления А и в направляющем шарнире G возникают продольные силы FАХ2 и FGХ2 , противодействующие составляющим FАХ1 и FGХ1 , обусловленным смещением пружины. За счет этого при торможении малой интенсивности опасность заклинивания уменьшается (рис. 2.3.6). По причине отрицательного плеча обкатки Ro тормозную силу Fb следует рассматривать в виде F′b , приложенной на расстоянии а = Ro cos δo sin δo выше уровня дороги.
|
| Рис. 2.3.5 Статические силы в подвеске с выносом колеса вперёд | Рис. 2.3.6 Схема стойки со смещением оси пружины за ось колеса |
3 Силы в пятне контакта колеса с дорогой
Для расчета деталей шасси на прочность используют силы, действующие в пятне контакта колеса с дорогой при равномерном прямолинейном движении автомобиля. При определении долговечности выбирают дорожное покрытие среднего качества, а для расчета статической прочности используют движение по дороге с выбоинами, переезд препятствия или торможения с максимальным замедлением.
Подвеска автомобиля представляет собой колебательную систему, собственная частота колебаний которой определяется жесткостью шины С1 , жесткостью подвески кузова С2 и массой оси М1 . На неровной дороге амортизатор не может полностью погасить постоянно появляющиеся колебания нагрузки ± ∆N (рис. 3). Применив индекс V для переднего колеса, получим следующие верхние значения нормальной силы в пятне контакта колеса с дорогой:
NV0 = NV + ∆ NV ,
где NV равна половине допустимой нагрузки на ось, т.е. GV /2 . При проведении расчета цапфы или полуоси колеса из значения NV0 следует вычесть вес колеса и ступицы UR = 100 …150 Н. При рассмотрении других деталей подвески колеса используют половину веса неподрессоренных деталей UV , т.е.
N′V0 = NV + ∆N - (UV /2)
Многочисленные замеры показали, что изменения нагрузок длительного действия на колесо зависят как от нагрузки на колесо NV , так и от жесткости шины С1 . Для определения С1 следует установить в шине рекомендуемое для данного автомобиля давление. На рис. 3 приведен коэффициент динамической нагрузки на колесо К1 , который после умножения на NV дает верхнее значение нормальной нагрузки соответственно на передние колеса:
NV0 = К1 NV = NV + ∆ NV
Отсюда собственно амплитуда изменения нагрузки на передние колеса:
∆ NV = NV0 - NV .
 |
3.1 Определение жесткости радиальных шин 155 ⁄ 70 R 13
автомобиля ЗАЗ – 1102 «Таврия»
Шины автомобиля ЗАЗ – 1102 — радиальные, с универсальным рисунком протектора. Отношение высоты профиля к ширине Н/B = 0,7. Радиальное расположение нитей корда обеспечивает снижение числа слоёв корда по сравнению с диагональным расположением, высокую жесткость шин и повышает устойчивость и управляемость автомобиля, уменьшает теплообразование и сопротивление качению. Обозначение шин 155 ⁄ 70 R13, где 155 — ширина профиля в миллиметрах (или 6,1 дюймов), R — обозначает радиальную конструкцию, 13 — посадочный диаметр шины в дюймах (330 мм), 70 — отношение высоты профиля к ширине в процентах. Внутреннее давление воздуха в шинах передних колес 0,2…0,22 МПа (2,0…2,2 кгс/см²).
О жесткости шины судят по ее упругой характеристике, которая представляет собой зависимость между вертикальной нагрузкой и радиальной деформацией, измеряемой обычно при статическом нагружении. Жесткость шины С1 равна тангенсу угла наклона к средней линии, проведенной в точке, соответствующей статической нагрузке.
Для определения статической жесткости шины воспользуемся следующей формулой [ 1, стр. 263 ]:
 ,
,
где kB – поправочный коэффициент, учитывающий конструкцию шины;
F – нагрузка на шину, H;
D – наружный диаметр шины без нагрузки, мм;
rст – статический радиус шины с нагрузкой.
· Определяем осадку шины или статический прогиб:
tш = GК / (рш π √Dм В),
где GК – нагрузка на колесо, кг;
рш – внутреннее давление воздуха, кг/см² (Мпа);
tш = 294 / (2,1 · 3,14 √54,4 · 15,5) ≈ 1,506 см,
где 294 – половина допустимой нагрузки на переднюю ось данного автомобиля, кг.
3.2 Определение сил и коэффициентов
 |
Рис. 3.2. Коэффициенты динамической нагрузки на колесо К1 и К2 , применяемые соответственно при расчетах на выносливость и прочность. Значения обоих коэффициентов зависят от нагрузки на колесо и от жесткости шины С1 ; при С1 не учитывается коэффициент КF увеличения жесткости при увеличении скорости.
С1 =170,5 Н ∕ мм = 173,8 кгс/см =1,705 кН/см
С1 / NV = 173,8 / 294 ≈ 0,6 см ˉ¹.
Получаем по графику следующие коэффициенты:
К1 = 1,6, К2 = 2,6.
Верхнее значение нормальной нагрузки:
NV0 = К1 NV = 1,6∙ 2885 = 4616 Н; NV0 ≈ 4,616 кН.
Диапазон колебаний нагрузки составляет:
∆NV = NV0 – NV = 4,616 – 2885 = 1,731 кН
Нижнее значение нормальной нагрузки:
NVU = NV – ∆ NV = 2,885 – 1,731 = 1,154 кН.
В связи с использованием жестких шин отношение С1 / N h является достаточно высоким. При меньшем давлении воздуха в шине жесткость шины ниже, что равнозначно меньшему значению К1 .
В отличие от меняющейся только по величине (из-за неровностей дороги), но постоянной по направлению вертикальной силы NV боковая сила ± S1 (индекс 1 соответствует расчету на сопротивление усталости) действует в пятне контакта колеса с дорогой знакопеременно.
При равномерном прямолинейном движении следует исходить из статической нагрузки на колесо NV , умножая ее на коэффициент боковых сил µF1 , т. е. ± SV1 = µF1 NV .
Многочисленные измерения показали, что величина µF1 зависит только от нагрузки на колесо. На рис. 3.2.2 приведены значения µF1 , соответствующие дороге с покрытием среднего качества.
  |
Рис. 3.2.1. При равномерном прямолинейном движении неровности дороги вызывают поперечные силы переменного направления. Рис. 3.2.2. Коэффициенты боковых сил µF1 и µF2 , используемые соответственно при расчетах на выносливость (дорога с покрытием среднего качества) и на прочность (дорога с выбоинами), значения которых зависят только от нагрузки на колесо NV . |
Получаем µF1 = 0,34 и µF2 = 0,86.
± SV1 = 0,34 · 2,885 = ± 0,981 кН
± SV2 = 0,86 · 2,885 = ± 2,48 кН
4 Определение статических нагрузок в пружине и шарнирах
 |
Рис. 4. Принятая расчетная схема подвески.

Рис. 4.1 Схема обозначения основных размерных параметров
(а) – вид сбоку (б) – вид сзади
В качестве расчетной принят тип подвески изображенный на рис. 4 со следующими конструктивные параметры подвески (рис. 4.1, а, б):
· Угол поперечного наклона оси поворота δo = 15º позволяет сместить несущий шарнир b в пространство колеса и получить отрицательное плечо обкатки, а также укоротить отрезок b.
· Угол продольного наклона оси поворота ε = 3º обеспечивает возврат управляемых колес в нейтральное положение при повороте. Значение последнего угла обеспечивает благоприятное расположение центра продольного крена и связанную с этим 20%-ную компенсацию продольного крена при торможении.
· Угол α = 7° смещения оси амортизатора относительно оси поворота также способствует созданию отрицательного плеча обкатки.
· Плечо обкатки Ro ст = -5 мм позволяет уменьшить плечо действия вертикальных нагрузок, тормозных и тяговых сил на амортизаторную стойку, улучшить динамику и кинематику подвески и ее компактность.
· Расстояние dо = 0,18 м (180 мм) от поверхности дороги до центра шаровой опоры колеса, принимается при статическом положении автомобиля и максимально допустимой нагрузке.
· Угол наклона поперечного рычага β = 3º35′ принимается с учетом, что в движении при незначительных колебаниях подвески автомобиля на ровной дороге он (автомобиль) будет занимать наиболее устойчивое положение при колее передних колёс 1314 мм.
· Высота подвески от поверхности дороги до точки крепления штока амортизатора в крыле автомобиля при номинальной нагрузке на ось принимается равной Нⁿст = 771 мм (без нагрузки Нⁿст = 800 мм.)
· Расстояние (с + о), характеризующее длину амортизаторной стойки при статическом номинальном нагружении автомобиля принимается равной 612 мм.
· Длина рычага ВД принимается равной Lр =325 мм, это позволяет уменьшить зависимость изменения развала от хода колеса при более коротких рычагах, а также добиться относительно большого хода подвески S = 150 мм (рис. 4.2).

|
|
||||||
|
|
|||||
|
|
|||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Силу F пружины определяют для неподвижного автомобиля, рассчитывая ее по законам статики.
Колесо, поворотная цапфа колеса, наружная труба амортизатора и шток при анализе статического равновесия образуют единое целое по отношению к точке А крепления на брызговике и нижнему рычагу, закрепленному в точке В (рис. 4.3).

Рис.4.3 Виды подвески сбоку (а) и сзади (б), необходимые для определения сил, действующих в направлении оси Z.
Составляем уравнения моментов относительно оси Z и точки А.
Σ МОZА : NV ′ · b + Вy (c + o) sin δo – Bx (c + o) cos δo = 0;
где b = Ro ст + do tg δo + (c + o) sin δo ;
Bx = By ctg β;
NV ′ (Ro ст + do tg δo + (c + o) sin δo + By (c + o) sin δo – – By (c + o) cos δo ctg β = 0;

Bx = By ctg β = 56,4 · 15,97 = 900,71 Н
Сумма моментов относительно оси Х и точки А:
Σ МОХА : NV ′е + Вy t – BZ (c + o) cos δo = 0;
где t = (с + о) cos δo tg ε;
е = [(с + о) cos δo + dо – rст ] tg ε.

Āх + Вх = 0; Āy + Вy + NV ′ = 0; Āz + Вz = 0;
Ах – Вх = 0; – Аy + Вy + NV ′ = 0; Аz – Вz = 0;
Ах = Вх = 900,71 Н Аy = Вy + NV ′; Аz = Вz;
Аy = 56,4 +2596,5 = 2652,9 Н; Аz = 118,17 Н
Теперь необходимо эти силы разложить на составляющие в направлении линии оси амортизатора и перпендикулярно к ней.
Вертикальную силу Аy поэтому следует рассматривать отдельно и с учетом пространственного угла υ, разложить на составляющие в направлении осей U и V (рис. 5.2.). С учетом
tg υ = √tg² (δo – α) + tg² ε
tg υ = √tg² 8º + tg² 3° = √0,1405² + 0,0524² = 0,15
υ ≈ 8°32′.
получаем АYU = Аy sin υ = 2652,9 · 0,1484 = 393,69 Н
АYV = Аy cos υ = 2652,9 · 0,9889 = 2623,45 Н.
Силы Ах и Аz следует разложить и, учитывая угол æ на виде сверху системы сил на рис. 4.6, разложить на составляющие в направлении сил S и Т.
Поскольку
tg æ = tg (δo – α) / tg ε = 0,1405 / 0,0524 = 2,6813
æ = 69°33′.
Ахs = Ах · sin æ = 900,71 · 0,937 = 843,97 Н
Ахt = Ах · cos æ = 900,71 · 0,3494 = 314,71 Н
Аzs = Аz · cos æ = 118,17 · 0,3494 = 41,29 Н
Аzt = Аz · sin æ = 118,17 · 0,937 = 110,73 Н
Аs = Аzs + Ахs = 41,29 + 843,97 = 885,26 Н
Аt = Ахt – Аzt = 314,71–110,73 = 203,98 Н

| Рис. 4.4 Пространственная система сил (ПСС) действующих в т. А крепления штока амортизатора в крыле автомобиля | Рис. 5.2. Вид пространственной системы сил на плоскость АЕК (ось амортизатора совпадает с линией АК). |
Силу Аs следует далее разложить на составляющие в направлениях U и V (рис. 4.7).
ASU = As cos υ = 885,26 · 0,9889 = 875,43 H
ASV = As sin υ = 885,26 · 0,1484 = 131,37 H.
Силы AYV и ASV совместно определяют нагрузку на пружину:
F1 =AYV + ASV =2623,45+131,37 =2754,82 Н.
Вторая составляющая ASU , также перпендикулярна к прямой АВ, как и AYU , приложена к штоку поршня. Чтобы иметь возможность определить напряжение изгиба, на основе двух сил с учетом силы Аt , действующей под углом 90° к ним, следует найти поперечную составляющую
AU = ASU – AYU = 875,43 – 393,69 = 481,74 Н.
Aguer = √Au ² + At ² = √481,74² + 20
3,98² = 523,15 Н .
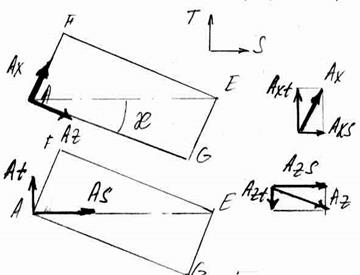

| Рис. 4.3. Видсверху на ПСС | Рис. 4.7 Разложение сил в направлении осей V и U |
Осуществляем проверку найденных сил:
√AX ² + AY ² + AZ ² = √Fω ² + AU ² + At ² ;
√900,71² + 2652,9² +118,17² = √2754,82² + 481,74² + 203,98² ;
2804,12 ≈ 2804,05.
Рис. 4.8 Силы изгибающие шток амортизатора |
Изгибающий момент в штоке амортизатора: МК = Aguer · 0′ = 523,15 · 0,136 = 71,15 Нм. Сила в направляющей втулке штока амортизаторной стойки С= Сила, действующая на поршень, К = С - Aguer =860,35–523,15=337,2 Н. |
|||||
На основе замеров характеристик упругости подвески с петлей гистерезиса сила трения, в данном случае, равная Сµ1 + Кµ2 , является одной из демпфирующих сил и способствует повышению жесткости подвески.
5 Расчеты на прочность
5.1 Основные теоретические положения расчетов на прочность
При расчетах на прочность сопоставляют фактические и допустимые напряжения, чтобы гарантировать долговечность детали и убедиться в том, что даже при максимальных нагрузках не произойдет ее пластической деформации. Это может иметь место при условии, если будет превышено временное сопротивление или предел текучести материала. Во всех случаях уравнения для расчета будут иметь вид:
σф = σдоп. и τ ф ≤ τ доп.
Фактически возникающие напряжения вызываются передаваемыми силами и моментами. Их величина зависит от размеров деталей, т. е. от внешних факторов. Допустимые напряжения зависят от тех характеристик материала, которые он будет иметь в данной детали, т. е. речь идет о возникающих в детали внутренних напряжениях.
5.1.1 Определение допускаемых напряжений
Напряжения, которые материал может выдерживать в течение длительного времени, зависят не только от его прочностных характеристик, но также от размеров детали в опасном сечении, от поверхности обработки детали и от наличия концентратов напряжений. Если деталь нагружена только крутящим моментом, то выражение для допускаемых касательных напряжений примет вид:
τ доп. D = τ tо b1 b2 / (βNt βК t υ).
При растягивающих, сжимающих и изгибающих нагрузках или при их совместном действии выражение будет иметь вид:
σдоп. D = σо b1 b2 / (βNb βК b υ).
Влияние концентратов напряжения при кручении и изгибе различно, поэтому в коэффициентах βN и βК введены индексы t (кручение) и b (изгиб).
В числителе на первом месте стоит максимально допустимое напряжение τ tо или σо , т. е. такое напряжение, которое может выдержать полированный круглый стержень диаметром 10 мм при соответствующем нагружении. Длительные испытания, проведенные с целью определения предела выносливости, показали, что при знакопеременной нагрузке сопротивление усталости связано с временным сопротивлением σb , а при знакопостоянной пульсирующей нагрузке – с пределом текучести σS .
Последнее условие справедливо только в том случае, когда отношение γ = σS / σb не превышает определенной величины. При более высоких значениях γ вновь имеет место зависимость от σb . Эта зависимость позволяет рассчитать прочностные показатели, необходимые для оценки долговечности, с помощью взятых из стандартов ДИН характеристик материалов (табл. 1.1. [1] ).
В случае применения поверхностного упрочнения (независимо от того, использована для этого цементация, высокочастотная или газопламенная закалка) напряжения, которые в течение длительного времени может выдерживать поверхностный слой, возрастает примерно на 20%, т. е. приведенные в таблице 1.1. [1] значения предела выносливости следует умножить на коэффициент 1,2. Предел прочности при изгибе и предел текучести при кручении, определяющие прочностные свойства детали, также возрастают и притом тем больше, чем больше глубина закаленного слоя.
На поверхности валов с целью повышения прочности стремятся добиться Еht = 3,0 . . . . . 4,5 мм, что позволяет выдерживать кратковременное перегружение до 50%. В первом случае упрочнение учитывается коэффициентом, равным 1,2, во втором – 1,5. Фирма БМВ, например, применив высокочастотную закалку глубиной 3 ……4 мм, добилась того, что задние полуоси могут выдерживать длительное увеличение напряжений на 15%, а кратковременное – на 60 …. 70%.
В соответствии с действующими напряжениями и видами нагрузки в приведенных выше уравнениях следует использовать при знакопеременном изгибе σbw ≈ 0,5σb и при нагружении пульсирующим знакопеременным крутящим моментом τо = 0,58σs или 0,5σb . Зависимость от σb и σs для различных видов сталей (конструкционная, улучшенная, цементуемая) не остается постоянной и может быть для различных случаев получена из табл. 1.1. [1]. В принципе, для временного сопротивления σb следует брать значение приведенного диапазона, т. е. σb min .
Определяя допускаемые напряжения при одновременном действии нескольких сил, следует учитывать нормальные напряжения.
В числителе появляется масштабный коэффициент b1 , который отражает снижение предела выносливости с увеличением диаметра, а также коэффициент b2 , который учитывает шероховатость поверхности, обусловленную технологией обработки. Коэффициент b1 можно получить из рис. 1.13. [1] в зависимости от диаметра d или толщины t в опасном сечении.
Коэффициент b2 приведен на рис. 1.14. [1] в зависимости как от высоты неровностей Rt , так и от минимального значения временного сопротивления σb min .
В знаменателе на первом месте стоит коэффициент концентрации напряжений βN прессовой посадки.
Стоящий на втором месте коэффициент концентрации напряжений βК учитывает влияние всех (кроме обусловленных шероховатостью поверхности) концентраторов напряжений, таких, как изменение диаметра, галтели, выточки, не округлость сечения.
Последним в знаменателе расчетной формулы стоит запас прочности υ, который при расчетах на сопротивление усталости принимается не ниже 1,2, а при поверочном расчете на прочность υ ≥ 1,5. В последнем случае при определении допустимых напряжений исключаются все коэффициенты концентрации напряжений. Однако посредством расчета следует убедиться, что даже под действием максимальных нагрузок не будут превышены ни временное сопротивление, ни предел текучести: τдоп. 2 = τо / υ; σдоп. 2 = σо / υ.
В качестве предельных значений τо и σо следует использовать при растяжении – сжатии σs , при изгибе σbs = 1,2 σs и при кручении τts = 0,58 σs .
5.1.2. Напряжения при изгибе.
Верхнее и нижнее значения направлений изгиба
σbо = Мbo / Wb ; σbu = Мbu / Wb.
При положительном значении σbu (и момента Мbu ) имеет место знакопостоянная нагрузка, а при отрицательном – знакопеременная. В первом случае расчет ведется только по σbо и σbsch = 1,2 σs или 0,86 σb для σо . При знакопеременной нагрузке с учетом знаков на основе σbо и σbu следует определять соответственно среднее значение напряжений и амплитуду их изменения:
σbm = (σbо + σbu ) / 2; (1)
σbа = σbо - σbm . (2)
Обе эти величины необходимы для сопоставления с пределом выносливости материала при изгибе. При определении σbm следует не упустить из виду отрицательный знак перед σbu .
Через углы 50, 45 и 40° на диаграмме предельных напряжений (рис. 1.12 [1] ) можно получить расчетным путем величины допускаемых предельных напряжений при переменной нагрузке:
σbа + 0,159 σbm = σbw (3)
Коэффициент 0,159 получен из выражения, составленного для трех функций углов sin 5° / (sin 50° sin 45°). Целесообразно убедиться, что сумма амплитудного и среднего значений напряжений не превышает предела текучести при изгибе σbs :
σbа + σbm ≤ σbs . (4)
При подстановке уравнений (1) и (2) в уравнение (3) можно непосредственно выразить σbw как функцию σbо и σbu :
σbw ф = 0,58 σbо – 0,42 σbu. (5)
После того, как получено σbw ф , вновь действует условие σф ≤ σдоп. D , что в данном случае означает:
σдоп. D = σbw b1 b2 / (βNb βКb υ). (6)
Значение σbw , полученное из табл. 1.1. [1], должно быть равно σbw ≈ 0,5 σb или, в случае применения поверхностной закалки, σbw = 0,6 σb .
При поверочном расчете на статическую прочность следует определить запас прочности υ для предела текучести σbs при изгибе. Для этого следует лишь провести расчет в соответствии с уравнениями изгибающих моментов по большему из них:
Мb2 (или Мb3 ) / Wb ≤ σbs / υ. (7)
Вводя σbs ≈ 1,2 σs (в случае применения поверхностного упрочнения умножая, кроме того, на коэффициент 1,2 ….. 1,5 в зависимости от глубины закаленного слоя), получаем:
υ ≥ 1,2 (или 1,44 ….. 1,8) σs ∙ 0,098 d³min / М b2 (или Мb3 ). Коэффициент должен быть по возможности близок к 1,5, но ни в коем случае не менее 1,2.
5.2 Расчет на выносливость и сопротивление усталости
Расчет на выносливость осуществляем для случая прямолинейного движения, а не при предельно допустимом сцеплении колес с дорогой при движении на повороте, так как при движении на повороте боковая сила на более нагруженное колесо направлена снаружи к центру поворота (т. е. она уменьшает момент Nо а (рис. 5.1). Кроме того, проведенные на дороге замеры показали, что на обычном легковом автомобиле боковые силы при прямолинейном движении вызывают более высокие усилия, чем при движении по кривой.
В последнем случае действует боковая сила, величина которой ограничена дорожным покрытием и шинами.
Несколько иная картина наблюдается в продольной плоскости, например, при резком торможении с начальной скоростью ниже V = 10 км/ч. На передних колесах имеет место очень сильное сцепление между широкими зонами контакта колес с дорогой благодаря низкой скорости автомобиля, в результате чего коэффициент сцепления в продольном направлении может достигать µL = 1,25.
Поэтому все детали оси должны быть дополнительно проверены расчетом, исходя из того, что может возникнуть продольная сила
LBV = µL NV = 1,25 NV .
При разгоне, напротив, происходит увеличение нагрузки на заднюю подвеску и уменьшение на переднюю. Вместе с верхним значением вертикальной силы следует включить в расчет тяговое усилие
LAV = µL NV при µL = 0,8
В качестве условий трогание с места при заблокированных тормозах не рассматривается.
5.2.1 Определение верхних значений сил длительного действия
При расчете долговечности следует исходить из допустимой нагрузки на мост. Ниже приведены допустимые нагрузки, силы и веса деталей, а также плечи действия сил и углы:
Нагрузка на передний мост GV = 5770 Н
Нагрузка на колеса NV = 2885 Н
Половина веса неподрессоренных частей UV /2 = 343,35 Н
Сила тяги на третьей передаче LА1 = 352,8 Н
Плечо обкатки Ro = – 7 мм; Ro ст = – 5 мм
Угол наклона оси поворота в поперечной плоскости δо = 15°
Угол продольного наклона оси поворота колеса ε = 3°
Схождение и развал колес γо = 0°
Расстояние между точками А и В в направлении оси с+о= 612 мм=0,612 м
Высота точки над поверхностью дороги d = 203мм, dо = 180 мм
Угол наклона рычага β β = 3°35′
Шины:
наружный диаметр D=588мм (544 c нагруз.)
статический радиус rст = 272 мм
диаметрический радиус rд = 282 мм
Так как рассматриваемый автомобиль имеет продольный угол наклона колеса и является переднеприводным, в направляющем устройстве передней подвески возникают дополнительные силы, действующие в продольном направлении.
Действующую в пятне катящегося колеса силу тяги LA1 , следует вначале перенести в центр колеса, обозначив ее L′A1 , а затем как L′′A1 перенести ее на ось поворота под прямым углом к последней. Это необходимо для расчета составляющих сил в направлении оси Z в точках А и В. Таким образом, сила тяги обозначаемая LA1 , оказывается смещенной от центра колеса вниз на величину аL (рис. 5.1.).
аL
= Ro
sin δo
![]() + rд
sin (δo
+ γ o
) sin δo
.
+ rд
sin (δo
+ γ o
) sin δo
.
При динамическом радиусе колеса rд = 282 мм плечо обкатки Ro уменьшается до Ro = – 7 мм.
аL
= – 0,007 · 0,2588 ![]() +0,282 · 0,2588² = =0,01701 м.
+0,282 · 0,2588² = =0,01701 м.
Дополнительно следует перенести боковую силу S1 , которую следует рассматривать действующей на ось поворота колеса над дорогой на высоте:
ns = rд sin² ε = 0,282 · 0,0523² = 0,00077 м.
Вертикальные направляющие сил, которые необходимы для определения , можно получить, используя приведенный на рисунке вид сзади, по зависимости Вхо = Вуо сtg β и с помощью уравнения моментов относительно точки А:

где NV ′О = К1 NV - UV /2 = 1,6 · 2885 – 288,5 =4327,5 Н≈4,33 кН.
![]() Рис. 5.1. Виды подвески сбоку (а) и сзади (б).
Рис. 5.1. Виды подвески сбоку (а) и сзади (б).

Вхо =Вуо ∙ctgβ=179,78 · 15,97 =2871,09 Н.
Направление действия силы Аzо , приведенной на виде сбоку, не очевидно. Поэтому, составляя уравнение моментов относительно точки А, вначале определяем:

где t = (с + о) cos δo tg ε = 0,612∙0,9659∙0,0524 = 0,031 ;
е = [(c + o) cos δo + d – rд ] tg ε = [0,612∙0,9659+0,203–0,282]∙0,0524 = 0,0268.

Bzo =521,43 Н.
В точке А действуют взаимно перпендикулярные силы:
- Ахо + Вхо - S1 = 0; Ауо = Вуо + NV ′O ; Аzо = Вzо - LA1
Ахо = Вхо - S1; Ауо = 179,78+4327,5; Аzо = 521,43–352,8
Ахо = 2871,09 –981= 1890,09 Н Ауо = 4507,28 Н Аzо =168,63 Н.
Эти силы раскладываем в направлении оси амортизатора и перпендикулярно ей аналогично статическому положению.
Ауu = Ayo · sin υ = 4507,28 · 0,1484 = 668,88 Н.
Ayv = Ayo · cos υ = 4507,28 · 0,9889 = 4457,25 Н.
Axs = Axo · sin æ = 1890,09 · 0,937 = 1771,01 Н.
Axt = Axo · cos æ = 1890,09 · 0,3494 = 660,4 Н.
Azs = Azo · cos æ = 168,63 · 0,3494 = 58,92 Н.
Azt = Azo · sin æ = 168,63 · 0,937 = 158,01 Н.
As = Azs + Axs = 58,92 + 1771,01 = 1829,93 Н.
At в = Axt – Azt = 660,4 – 158,01 = 502,39 Н.
Asu = As · cos υ = 1829,93 · 0,9889 = 1809,62 Н.
Asv = As · sin υ = 1829,93 · 0,1484 = 271,56 Н.
F1 = Ayv + Asv = 4457,25 + 271,56 = 4727,81 Н.
Au в = Asu – Ayu = 1809,62 – 668,88 = 1140,74 Н.
Aquer = √Au ² + At ² = √1140,74² + 502,39² = 1246,47 Н.
Осуществляем проверку разложения сил на составляющие:
√Ахо ² + Ауо ² + Аzo ² = √Au ² + At ² + F1 ² ;
√1890,09² + 4507,28² + 168,63² = √1140,74² + 502,39² + 4727,81² ;
4890,44 ≈ 4889,36
Следует дополнительно произвести расчет с использованием нижних значений нагрузки (знакопеременный или знакопостоянный), а также создание предпосылок для сложения всех сил, действующих в одной точке.
5.2.2. Определение нижних значений сил длительного действия
Нижнее значение нормальной нагрузки с учетом половины веса неподрессоренных масс:
![]()
В этом случае боковая сила S1 будет иметь противоположное направление, по сравнению с предыдущим расчетом. В этом случае силы в т.В:

Вхо =Byu ∙ctgβ=-64,66 · 15,97 = -1032,62 Н

Силы в т.А:
- Ахо + Вхо + S1 = 0; Ауо = Вуо + Nv ′u ; Аzо = Вzо - LA1
Ахо = Вхо + S1; Ауо = - 82,74 + 902 Аzо = 352,8 – 352,8
Ахо = - 1032,62 + 981 Ауо = 800,84 Н Аzо = 0 Н.
Ахо = - 51,62 Н.
Осуществляем разложение сил в направлении оси амортизатора и перпендикулярно к ней, согласно схеме, приведенной на рис. 4.4 – 4.7:
Ау u = Ay о · sin υ = 800,84 · 0,1484 = 118,84 Н.
Ayv = Ay о · cos υ = 800,84 · 0,9889 = 791,95 Н.
Axs = Ax о · sin æ = - 51,62 · 0,937 = - 48,37 Н.
Axt = Ax о · cos æ = - 51,62 · 0,3494 = - 18,04 Н.
Azs = Az о · cos æ = 0 · 0,3494 = 0 Н.
Azt = Az о · sin æ = 0 · 0,937 = 0 Н.
As = Azs + Axs = 0 – 48,37 = - 48,37 Н.
At н = Axt – Azt = - 18,04 – 0 = - 18,04 Н.
Asu = As · cos υ = - 48,37 · 0,9889 = - 47,83 Н.
Asv = As · sin υ = - 48,37 · 0,1484 = - 7,18 Н.
F1 = Ayv + Asv = 791,95 – 7,18 = 784,77 Н.
Au н = Asu – Ayu = - 47,83 – 118,84 = -166,67 Н.
Aquer = √Au ² + At ² = √(- 166,67)² + (- 18,04)² = 167,64 Н.
Осуществляем проверку разложения сил на составляющие:
√Ахо ² + Ауо ² + Аzo ² = √Au ² + At ² + F1 ² ;
√(-51,62)² + 800,84² + 0² = √(-166,67)² + (-18,04)² + 784,77² .
802,5=802,5
Теперь необходимо сложить все силы, действующие в одной точке.
5.2.3 Определение сил в направляющей и на поршне
амортизатора при верхних значениях сил длительного действия
![]()
РРис. 5.2. Силы в направляющей и на поршне амортизатора при верхних значениях сил
Изгибающий момент в штоке амортизатора будет складываться из двух составляющих: в направлении U и в направлении Т.
Силы в направляющей втулке штока амортизаторной стойки:
С u = А u · ℓ′ / (ℓ′ – о′) = 1140,74 ∙ 0,347 / (0,347 – 0,136) = 1876 Н
Сt = Аt ∙ ℓ′ / (ℓ′ – о′) = 502,39 ∙ 0,347 / (0,347 – 0,136) = 826,21 Н.
Силы, действующие на поршень:
Кu = С u - А u = 1876 – 1140,74 = 735,26 Н
Кt = Сt - Аt = 826,21 – 502,39 = 323,82 Н.
5.2.4 Определение сил в направляющей и на поршне
амортизатора при нижних значениях сил длительного действия
![]()
Рис. 5.3. Силы в направляющей и на поршне амортизатора при верхних значениях сил
Так как нижние значения сил в точке А в направлениях U и Т отрицательны, т. е. направлены противоположно соответствующим им силам верхних значений нагрузок, то сразу можно определить знакопеременный характер нагружения штока амортизатора. Учитывая истинное направление сил нижних значений нагрузок:
С u = А u · ℓ′ / (ℓ′ – о′) = 166,67 ∙ 0,347 / (0,347 – 0,136) = 274,1 Н;
Сt = Аt ∙ ℓ′ / (ℓ′ – о′) = 18,04 ∙ 0,347 / (0,347 – 0,136) = 29,67 Н.
Силы, действующие на поршень:
Кu = С u - А u = 274,1 – 166,67 = 107,43 Н
Кt = Сt - Аt = 29,67 – 18,04 = 11,63 Н.
5.2.5 Преобразование знакопеременной нагрузки
![]()
Рис. 5.4. Схема знакопеременных нагрузок действующих на шток и поршень
Определяем приведенные силы при знакопеременной нагрузке в направлениях U и Т (рис. 5.4).
Аuw = 0,58 Аuо + 0,42 Аu u = 0,58∙1140,74+0,42∙166,67 = 731,63 Н.
Аtw = 0,58 Аt o + 0,42 Аt u = 0,58 · 502,39 + 0,42 · 18,04 = 298,96 Н.
В формуле учтены отрицательные значения коэффициента 0,42 и противоположно направленных сил.
Результирующая знакопеременных нагрузок:
Аw = √Аuw ² + Аtw ² = √731,63² + 298,96² = 790,35 Н
Момент, изгибающий шток:
Млw = Аw · о′ = 790,35 · 0,136 = 107,49 Н∙м
В завершение следует определить минимальный для данного случая диаметр штока и убедиться, что имеющиеся напряжения не превышают допустимые.
В качестве материала штока применяем среднеуглеродистую, качественную сталь 40, обладающей следующими свойствами: σb min =568,98 Мпа, εs = 333,54 Мпа, δs =19% . Выбранная сталь дает отличные результаты при высокочастотной закалке, что для штоков амортизаторов весьма важно.
Допустимые напряжения:
σb = 0,6 σb min b1 b2 / (βКb · υ)=0,6 · 568,98 · 0,94 · 0,95 / (1 · 1,2) = 254,05 Мпа.
где 0,6 – коэффициент, справедливый для поверхностного упрочнения и вводится при использовании твердого хромирования штока амортизатора;
b1 = 0,94 – масштабный коэффициент, отражающий снижение предела выносливости с увеличением диаметра; определен для Ø 20 мм;
b2 – коэффициент, учитывающий шероховатость поверхности, обусловленную технологией обработки. При σb min = 700 МПа и высоте микронеровностей поверхности штока Rt = 6 мкм b2 = 0,95;
βКb = 1 – коэффициент концентрации напряжений;
υ = 1,2 – коэффициент запаса прочности, обусловленный способностью поверхностного слоя при его упрочнении выдерживать в течение длительного времени возросшие примерно на 20% напряжения.
σb =
Чтобы иметь шток, упрочненный закалкой ТВЧ на 3 мм, принимаем минимальный его диаметр dmin = 20 мм.
Фактические напряжения от изгиба:
![]()
σb ф =136,86< σb =254,05
Условие усталостной прочности выполнено.
5.2.6 Определение сил, действующих на резиновые
шарниры рычага
Благодаря тому, что рычаг не воспринимает действие пружины, действующие на него и шарниры силы можно рассмотреть в плоскости.
1. Определение верхних значений сил, действующих на резиновые шарниры.
При расчете рычага приняты следующие размеры (рис. 5.5 ): Lр = 325 мм; к = 120 мм.
Сумма моментов относительно точки D:
ΣМD : В′хуо ∙ к – В′zо Lр = 0;
Рис. 5.5Схема для определения верхних значений сил действующих на рычаг и резиновый шарнир. |
│В′хуо │= Вхуо = √ Вхо ² + Вуо ² = =√2871,09²+ 179,78² =2876,71 Н; │В′z о │= Вz о = 521,43 Н. ∑МB ’ =В’хуо ∙к–Dzo ∙Lp =0 |
 ;
;
∑MB ” =-B’zo ∙Lp +Dxyo ∙к=0

2 Определение нижних сил, действующих на резиновые шарниры
Рис. 5.6 Схема для определения нижних значений сил действующих на рычаг и резиновый шарнир. |
│В′x уu │= Вx у u = √ Вx u ² + Ву u ² = = √(- 1032,62)² + (- 64,66)² = 1034,62Н; │В′z u │= Вzu = 352,8 Н. ΣМВ´ = В′ху u ∙ к – Dzo ∙ Lp = 0; |

ΣMB ” =-В′zu ∙Lp +Dxyo ∙к= 0;

Расчет резинового шарнира будем производить по максимальной длительно действующей нагрузке в нем, т. е. при радиальной силе р = Dхуо = =1412,21 Н.
5.2.7 Определение напряжений и деформаций
резиновых втулок – шарниров
Исходя из конструктивных соображений и рассматривая конструкцию существующих резиновых втулок, принимает размеры втулок (рис. 5.7 ).
![]()
Рис. 5.7. Конструкция ручно-механической втулки рычага подвески.
1 – обойма рычага, 2 – резиновый элемент, 3 – внутренняя обойма.
Резиновая втулка работает на кручение и воспринимает радиальную и осевую нагрузки. Втулки такого типа можно отнести к шарнирам с равными касательными напряжениями.
Определяем крутильную жесткость шарнира по формуле:

где G = 0,9 МПа – модуль сдвига для радиан.
Напряжения сжатия при действии рациональной нагрузки:
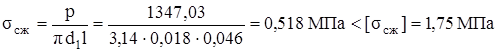
где [σсж ]=1,75 МПа – допускаемые статические напряжения сжатия для резины с твердостью по Шору 60 ед.
Как указывается в литературе [ 5 ], угловое пересечение по дуге наружного радиуса не должно превышать толщины элемента. Углы закрутки резиновых элементов определяются по кинематической схеме подвески. Наибольший угол при ходе колеса Sот (отбоя) = 85 мм составил:


сtg φ =3,8936 ; φ = 14°27′ или φ = 0,24906 рад.
Тогда угловое перемещение наружной поверхности резинового элемента составит:
![]()
Вывод: при принятых размерах резиновых элементов, напряжения при сжатии, деформации и скручивании не превышают допустимых значений — это обеспечивает долговечность шарниров.
5.3 Расчет на прочность
При расчетах на прочность сопоставляют фактические и допустимые напряжения, чтобы гарантировать долговечность детали и убедиться в том, что даже при максимальных нагрузках не произойдет ее пластической деформации. Это может иметь место при условии, если будет превышено временное сопротивление или предел текучести материала: σф £ σдоп .
При изгибе или совместном действии различных нагрузок: σдоп = σо / υ.
В качестве предельных значений следует использовать σbs = 1,2 σs .
При расчетах на прочность принимается υ ≥ 1,5.
5.3.1. Кратковременно действующие силы.
Для определения наибольших значений сил, действующих в подвеске «Макферсон», следует рассмотреть три случая: движение по дороге с выбоинами (случай 3 [1]); преодоление железнодорожного переезда (случай 2 [1]); торможение с блокировкой колес с начальной скорости V ≤ 10 км/ч (случай 5 [1]).
5.3.2. Силы, возникающие при движении по дороге с выбоинами.
В представленном в этом параграфе случае нагружения 3, подвеска вновь рассматривается в нормальном положении. По-прежнему используем вертикальную силу NV 'о = К1 NV – (Uv / 2) = 4,43 кН, однако вместо S1 использовать максимальное значение боковой силы S2 = µF2 Nv , а вместо продольной силы LА1 силу
LА4 = Mt 4 / rд = Md max i2 iD iгл ηтр / (4 rд ) = 80 · 2,056 · 3,588 · 0,9224 / (4 · ∙0,282) = 482,59 Н.
S2 = 2,48 кН.
Итак, методика расчета соответствует приведенной, с исключениями: вместо S1 действует S2 , а вместо LА1 - LА4 .
Используя приведенный на рис.5.1 вид сзади, учитывая, что Вх3 =Ву3 сtg β, уравнение моментов относительно точки А:

Вх3 =Ву3 ∙ctgβ=307,91 · 15,97 = 4917,32 Н.

где f = (с + о) cos δo tg ε = 0,612∙0,9659∙0,0524=0,030975;
е = [(с + о) cos δo + d – rд ] tg ε=(0,612∙0,9659+0,203-0,282)∙0,0524=0,026836.
В точке А действуют взаимно перпендикулярные силы:
Ах3 = В х3 - S2 ; Ау3 = Ву3 + NV ′о ; Аz3 = Вz3 - LA4
Ах3 = 4917,32 – 2480;Ау3 = 307,91 + 4327,5; Аz3 = 662,73 – 482,59;
Ах3 = 2437,32 Н Ау3 = 4635,41 Н Аz3 = 180,14 Н.
Эти силы раскладываем в направлениях оси амортизатора и перпендикулярно к ней, аналогично проводимым ранее:
Ау u = Ay3 · sin υ = 4635,41 · 0,1484 = 687,75 Н.
Ayv = Ay3 · cos υ = 4635,41 · 0,9889 = 4583,96 Н.
Axs = Ax3 · sin æ = 2437,32 · 0,937 = 2283,77 Н.
Axt = Ax3 · cos æ = 2437,32 · 0,3494 = 851,6 Н.
Azs = Az3 · cos æ = 180,14 · 0,3494 = 62,94 Н.
Azt = Az3 · sin æ = 180,14 · 0,937 = 168,79 Н.
As = Azs + Axs = 62,94 + 2283,77 = 2346,71 Н.
At = Axt – Azt = 851,6 – 168,79 = 682,81 Н.
Asu = As · cos υ= 2346,71 · 0,9889 = 2320,66 Н.
Asv = As · sin υ = 2346,71 · 0,1484 = 348,25 Н.
F1 = Ayv + Asv = 4583,96 + 348,25 = 4932,21 Н.
Au = Asu – Ayu = 2320,66 – 687,75 = 1632,91 Н.
Осуществляем проверку разложения сил:
√Ах3 ² + Ау3 ² + Аz3 ² = √Au ² + At ² + F1 ² ;
√2437,32² + 4635,41² + 180,14² = √1632,91² + 682,81² + 4932,21² ;
5240,23 ≈ 5240,16.
Aquer = √Au ² + At ² = √1632,91² + 682,81² = 1769,92 Н.
Силы, действующие на поршень:
К3
=  – Aquer
=
– Aquer
= 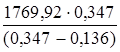 –1769,92 = 1140,8 Н.
–1769,92 = 1140,8 Н.
Изгибающий момент в штоке амортизатора:
Мк3 = Aquer · о′ = 1769,92 · 0,136 = 240,71 Н м.
σдоп. = σbs / υ = 1,2 σs / υ = 1,2 · 480 / 1,5 = 384 Мпа,
т. к. υ ≥ 1,5 при кратковременных перегрузках.
Проверим выбранный в п.5.2.5 диаметр штока амортизатора по условию прочности:
 .
.
Таким образом видно, что условие прочности для выбранногшо диаметра штока dmin = 20 — выполняется.
5.3.3 Силы, возникающие при торможении
Если тормозные механизмы передних колес расположены в колесе, то при коэффициенте сцепления шины с дорогой Мк = 1,25 в подвеске могут возникнуть бόльшие перегрузки, чем при движении по дороге с разбитым покрытием. Для расчета сил в рычаге подвески автомобиля в положении, соответствующем номинальной нагрузке, вычисляем продольную силу:
Lb = Мк NV = 1,25 ∙ 2885 = 3606,25 Н
и верхнее значение вертикальной силы NV 'о = 4327,5 Н. Боковые силы подвески и шин можно пренебречь.
Расчет сил, возникающих при торможении, предусматривает скорость близкую к нулю. К этому следует добавить уменьшение радиуса шины в результате увеличения нагрузки. Поэтому в расчете необходимо использовать статический радиус rст . Деформация шины приводит к уменьшению плеча обкатки.
Тормозную силу LА следует считать действующей на расстоянии:
![]() аb
= Ro
соs δo
sin δo
аb
= Ro
соs δo
sin δo
над поверхностью дороги при и над ней – при отрицательном плече обкатки.
Рис. 5.8. Силы возникающие в стойке при торможении
Рассматривая силы относительно оси Z и точки А:
Σ МОZА : NV ′о · b + Вy5 (c + o) sin δo – Bx5 (c + o) cos δo = 0;
b = Ro ст + d tg δo + (c + o) sin δo ; Bx5 = By5 ctg β NV ′ (Ro ст + do tg δo + (c + o) sin δo + By (c + o) sin δo – By (c + o) cos δo ctg β = 0;

Bx5 = By5 ctg β = 94·15,97 = 1501,1 Н
Сумма моментов относительно оси Х и точки А:
Σ МОХА : NV ′о · е + Вy5 · t – BZ5 (c + o) cos δo – Lb [(с + о) cos δo + d – аb ] = 0;
где t = (с + о) cos δo tg ε = 0,612∙0,9659∙0,0524 = 0,031;
е = [(с +о) cos δo + dо – rст ] tgε = (0,612∙0,9659+0,18–0,272)∙0,0524=0,0262.
аb =Ro ст cosδo sinδo = 0,005∙0,9659∙0,2588 =0,00125м.
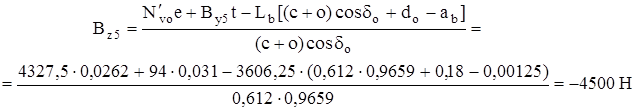
Силы в точке А:
Ах5 - Вх5 = 0; - Аy 5 + Вy 5 + NV ′о = 0; Аz 5 - Вz 5 - Lb = 0;
Ах5 = Вх5 ; Аy 5 = Вy 5 + NV ′о ; Аz5 = Вz5 + Lb ;
Ах5 = 1501,1 Н Аy5 = 94 + 4327,5; Аz5 = -4500 +3606,25;
Аy5 = 4421,5 Н Аz5 = -893,75 Н.
Раскладываем силы на составляющие:
Ау u = Ay 5 · sin υ = 4421,5 · 0,1484 = 656,15 Н.
Ayv = Ay5 · cos υ = 4421,5 · 0,9889 = 4372,42 Н.
Axs = Ax5 · sin æ = 1501,1 · 0,937 = 1406,53 Н.
Axt = Ax5 · cos æ = 1501,1 · 0,3494 = 524,48 Н.
Azs = Az5 · cos æ = - 893,75 · 0,3494 = - 312,28 Н.
Azt = Az5 · sin æ = - 893,75 · 0,937 = - 837,44 Н.
As = Azs + Axs = - 312,28 + 1406,53 = 1094,25 Н.
At = Axt – Azt = 524,48 – (- 837,44) = 1362,27 Н.
Asu = As · cos υ = 1094,25 · 0,9889 = 1082,06 Н.
Asv = As · sin υ = 1094,25 · 0,1484 = 162,38 Н.
F1 = Ayv + Asv = 4372,42 + 162,38 = 4534,8 Н.
Au = Asu – Ayu = 1082,06 – 656,15 = 425,91 Н.
Осуществляем проверку разложения сил:
√Ах5 ² + Ау5 ² + Аz 5 ² = √Au ² + At ² + F1 ² ;
√1501,1² + 4421,5² + (- 893,75)² = √425,91² +1362,27² + 4534,8² ;
4754,13≈4754,11
Aquer = √Au ² + At ² = √425,91² + 1362,27² = 1427,3 Н.
Сила в направляющей втулке штока амортизатора:
С5 = Аquer · ℓ′ / (ℓ′ – о′) = 1427,3 ∙ 0,347 / (0,347 – 0,136) = 2347,27 Н
Сила, действующая на поршень:
К5 = С5 – Аquer = 2347,27 – 1427,3 = 919,97 Н
Изгибающий момент в штоке амортизаторной стойки:
Мк5 = Аquer · о′ = 1427,3 · 0,136 = 194,11 Н м;
Т. к. изгибающий момент для этого случая меньше момента для случая движения по разбитой дороге (Мк5 < Мк3 ), то заведомо можно сказать, что условие прочности для данного случая выполняется.
По-прежнему фиксируем пока минимальный диаметр штока dmin = 20 мм.
5.3.4 Силы, возникающие в подвеске при
преодолении железнодорожного переезда
При расчете максимальных вертикальных нагрузок следует установить колесо в крайнее верхнее положение, сместив его на величину хода f1 (рис. 5.9). Это необходимо для определения изменившихся углов (с индексом 2) ε2 δ2 , β2 , а также изменившегося плеча обкатки Ro2 . При расчете на прочность используется положение автомобиля при допустимой полной загрузке. Используем действующие в пятне контакта силы:
NV ′2 = NV 2 – (U2 / 2) и S1 = µF1 NV .
NV ′2 = 2,6∙2885 – 288,5 = 7212,5 Н.
S1 = 981 Н.
![]()
![]()
Рис. 5.9 Изменение положения рычага при преодолении железнодорожного переезда
Определяем угол β2 :
sin β = a / Lp ; sin β2 = b / Lp ;
b = 65 – а = 65 - Lр sin β;

β2 = 8°08′.
Угол δ2 определяем графически через соотношение изменившегося расстояния между точками А и В и его проекцией на ось ОУ:
соs δ2 = 0,528 / 0,551 = 0,9583; δ2 ≈ 16°36′.
При ходе сжатия подвески существующее расстояние о (между направляющей с и точкой А в крыле) уменьшается до:
о′2 = о′ - f1 / ix = 0,136 – 0,065 / 1,0112 = 0,072 м.
Изменившийся угол ε2 :

ε2 ≈ 3°22′.
Изменившееся плечо обкатки:
Ro2 = - d tg δ2 + к = -0,203∙0,2934 + 0,025 = -0,035 м;
где к = 0,025 м.
аL 2 = Ro 2 · sin δ2 √(1 + tg²ε2 ) (1 + tg²ε2 + tg² δ2 ) + rд sin (δ2 + γ2 ) sin δ2 ;
гдеγ2 = δ2 – δо = 16º36′ – 15° = 1°36′

nS2 = rд sin²ε2 = 0,282 · 0,0587² = 0,001 м
По приведенному на рис. 5.10 виду сзади, используя зависимость Вх2 = Ву2 сtg β2 , составляем уравнение моментов относительно оси ОZ и точки А:
![]()
Рис. 5.10 Виды сбоку (а) и сзади (б).


Bx2 = Ву2 сtg β2 = 453,71 · 8,105 = 3677,32 Н.
Сумма моментов относительно оси ОХ и точки А:
Σ МОХА : NV ′2 · е2 +LA1 [(с+о)cosδo – f1 + d – (rд – aL2 )] – By2 · f2 – Bz2 ·[(с + о)cos δo – – f1 ] = 0;

Где е2 =[(с+о)cosδo –f1 +d–rд ]tgε2 =(0,612∙0,9659–0,065+0,203–0,282)∙0,0588=0,0263;
f2 = [(с + о)cosδo – f1 ] tg ε2 =(0,612∙0,9659–0,065)∙0,0588= 0,031.
В точке А действуют взаимно перпендикулярные силы:
- Ах2 + Вх2 - S1 = 0; - Аy2 + NV ′2 - Вy2 = 0; - Аz2 + Вz2 - LА1 = 0;
Ах2 = Вх2 - S1 ; Аy2 = NV ′2 - Вy2 ; Аz2 = Вz2 – LА1 ;
Ах2 = 3677,32 – 981; Аy2 = 7212,5 – 453,71; Аz2 = 643,08 – 352,8;
Ах2 = 2696,32 НАy2 = 6758,79 Н Аz2 = 290,28 Н
Раскладываем эти силы в направлении оси амортизатора и перпендикулярно ей аналогично предшествующим случаям.
Определяем пространственный угол υ2 :
tg υ2 = √tg² (δ2 – α) + tg² ε2
tg υ2 = √tg² 8°21′ + tg² 3°22′ = √0,1468² + 0,0588² = 0,15814.
υ ≈ 8°59′.
Определяем пространственный угол æ2 :
tg æ2 = tg (δ2 – α) / tg ε2 = 0,1468 / 0,0588 = 2,4966
æ = 68°10′.
Аyu = Аy2 · sin υ2 = 6758,79 · 0,1561 = 1055,05 Н
Аyv = Аy2 · cos υ2 = 6758,79 · 0,9877 = 6675,66 Н.
Ахs = Ах2 · sin æ2 = 2696,32 · 0,9283 = 2503 Н
Ахt = Ах2 · cos æ2 = 2696,32 · 0,3719 = 1002,76 Н
Аzs = Аz2 · cos æ2 = 290,28 · 0,3719 = 107,96 Н
Аzt = Аz2 · sin æ2 = 290,28 · 0,9283 = 269,47 Н
Аs = Аzs + Ахs = 107,96 + 2503 = 2610,96 Н
Аt = Ахt – Аzt = 1002,76 – 269,47 = 733,29 Н
Asu = As · cos υ2 = 2610,96 · 0,9877 = 2578,85 Н.
Asv = As · sin υ2 = 2610,96 · 0,1561 = 407,57 Н.
F1 = Ayv + Asv = 6675,66 + 407,57 = 7083,23 Н.
Au = Asu – Ayu = 2578,85 – 1055,05 = 1523,8 Н.
Осуществляем проверку разложения сил:
√Ах2 ² + Ау2 ² + Аz2 ² = √Au ² + At ² + F1 ² ;
√2696,32² + 6758,79² + 290,28² = √1523,8² + 733,29² + 7083,23² ;
7282,56 ≈ 7282,3.
Aquer = √Au ² + At ² = √1523,8² + 733,29² = 1691,06 Н.
Сила в направляющей втулке амортиизаторной стойки:
с2 = Aquer ℓ′ / (ℓ′2 - о′2 ) = 1691,06 · 0,347 / (0,347 – 0,072) = 2133,81 Н.
Сила, действующая на поршень:
К2 = с2 - Aquer = 2133,81 – 1691,06 = 442,75 Н.
Изгибающий момент в штоке амортизатора:
Мк2 = Aquer · о′2 = 1691,06 · 0,072 = 121,76 Н м.
Т. к. изгибающий момент для этого случая меньше моментов прочности для случая максимальной вертикальной нагрузки выполняется.
Минимальный диаметр штока dmin = 20 мм.
5.3.5 Силы, действующие при полном ходе отбоя колеса
Чтобы учесть все напряжения изгиба в штоке амортизатора, следует рассматривать действия боковых сил от поперечных составляющих неровностей дороги при крайнем нижнем положении колеса (рис. 5.11). При этом ограничитель хода отбоя, закрепленный на штоке амортизатора, упирается в направляющую втулку штока в зоне точки С.
Определяем угол β4 :
![]()
Рис. 5.11 Изменение положения рычага при полном ходе отбоя
 ; β4
=19º
; β4
=19º
Определение углов наклона оси поворота δ4 и развала колеса γ4 .
В этом случае не будем пренебрегать изменением угла α между осью поворота и осью амортизатора, как это было сделано в случае максимальной вертикальной нагрузки (случай 2 п.5.3.4) из-за ничтожного его изменения в сравнении с изменением угла δo → δ2 . Так как очень сложно учесть все факторы, влияющие на изменение развала γ, то единственными критериями оценки изменения угла α можно считать кратчайшее расстояние от центра шаровой опоры до оси амортизатора и угол δo – α = 8° между осью колеса и осью амортизатора, которые неизменны при любом положении подвески.
Угол δ4 определяем графически с учетом масштаба по рис. 5.12 через соотношение:
соs δ4 = j/q = 0,671 /0,685 = 0,9796,
что соответствует δ4 = 11°36′.
Аналогично определяем угол α4 :
sinα4 = t/q= 0,045 / 0,685 = 0,0571, α4 ≈ 3°44′.
Находим развал при полном ходе отбоя:
g4 =(d4 -a4 )-(d0 -a)=(11°36¢-3°44¢)-(15°-7°)= -0,08¢.
Составляем уравнение моментов относительно т.А:
SМА :S1 [d+fm+(c+o)cosd0 +f2 ]+BX4 [(c+o)cos d0 +f2 ]-
-BY4 [(c+o)cos d0 +f2 ]sin d4 /cosd4 =0
Учитывая, что BX4 =BY4 ∙Ctg b4 и sin d4 /cos d4 =tg d4 :

![]()
BX 4 = -469,96∙2,904= -1364,76 H.
Силы в точке А:
-Aх4 +Bх4 +S1 =0; -Aу4 +Bу4 =0;
Aх 4 =Bх 4 +S1 ; Aу 4 =Bу 4 ;
Aх 4 = -1364,76+981= -383,76 H; Aу 4 = -469,96 H.
Aу t =Aу 4 ∙cos (d4 -a4 )= -469,96∙0,9979= -468,97 H.
Aу s =Aу 4 ∙sin (d4 -a4 )= -469,96∙0,0651= -30,59 H.
Aх t =Aх 4 ∙sin (d4 -a4 )= -383,76∙0,0651= -24,98 H.
Aх s =Aх 4 ∙cos(d4 -a4 )= -383,76∙0,9979= -382,95 H.
As =Aх s –Aу s = -382,95–(-30,59)= -352,36 H.
At =Aу t +Aх t = -468,97+(-24,98)= -493,95 H.
![]()
Рис. 5.12 Схема сил в подвеске при полном ходе отбоя.
![]()
Рис. 5.13 Силы действующие на шток амортизатора при полном ходе отбоя.
Проверка:
![]()
![]()
606,74»606,75.
O¢4 =O¢+f2 /ix=0,136+0,085/1,0112=0,2186 м.
Сила в направляющей втулке амортизаторной стойки:
C4 =AS ∙l¢/(l¢-O¢4 )= -352,36∙0,347/(0,347- -0,2186) = -952,25 H.
Сила, действующая на поршень:
K4 =C4 -AS = -952,25–(-352,36)= -599,89 H.
Момент, изгибающий шток:
MK4 =AS ∙O¢4 = -352,36∙0,2186= -77,03 Hм.
Т. к. изгибающий момент для этого случая меньше всех рассчитанных раньше моментов, то условие прочности выполняется.
Окончательно имеем диаметр штока амортизаторной стойки d=20 mm.
6 Подрессоривание передней оси
Передняя подвеска легкового автомобиля с кузовом седан или универсал должна быть максимально мягкой. Это необходимо для обеспечения комфортабельности водителя и пассажиров, защиты перевозимых грузов от вибраций и хорошего сцепления колес с дорогой. При низких частотах колебаний (nII » 30 мин-1 ) восприимчивость человека к колебаниям и их скорости на 80% ниже, чем при использовании ранее жестких подвесок с частотами 100 мин-1 . Уменьшение жесткости подвески ограничено возможностью перемещения колес от среднего положения на ходе отбоя t1 +t2 , а также большим креном кузова на поворотах при мягкой подвеске. Для уменьшения крена следует использовать стабилизаторы. Замеры, проведенные на большом числе моделей легковых автомобилей, показали, что считающиеся комфортабельными (и оборудованные стальными упругими элементами) автомобили фирм “Даймлер – Бенц”, “Рено”, “Ауто юнион” и “Крайслер” имеют частоту колебаний подрессоренных масс передней подвески nIIV =55…65 мин-1 , а общий ход подвески около 200 мм.
6.1 Вертикальные колебания
Жесткость упругих элементов, входящую во все расчеты, приводят только к одному колесу.
Для кузова уравнение частоты колебаний [в мин-1 ] без учета демпфирования, а также влияния оси и шин имеет вид:
 (1)
(1)
а для колебаний неподрессоренных масс [в мин -1 ], связанных с одним колесом:
 (2)
(2)
где CIV,h – жесткость шины, KF – коэффициент повышения жесткости, который учитывает ее рост с увеличением скорости. После подстановки массы mI оси и жесткости СI шины уравнения частоты колебания кузова в мин-1 примет следующий вид:
 (3)
(3)
Из этого уравнения с опущенными индексами v, h соответственно для передней и задней осей можно заметить, что частота колебаний по сравнению с рассчитанной с помощью уравнения (1) будет тем меньше, чем больше отношение с2 /с1 . Это будет иметь место при жесткой подвеске кузова (большая величина с2 ) и мягких шинах (малая величина с1 ).
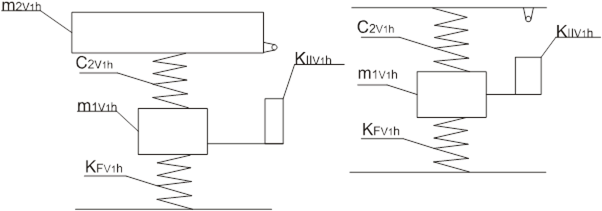 Рис. 6.1 Рис. 6.2
Рис. 6.1 Рис. 6.2
Собственная частота колебаний колеса nIV,h является функцией массы оси mIV,h , жесткости подвески C2V,h (см. рис. 6.1, 6.2), жесткости шины C1V,h и приведенного к колесу коэффициента сопротивления амортизатора KIIV,h . Дополнительно влияние оказывает скорость движения, которая учитывается с помощью коэффициента KF .
Частота колебаний кузова nIIV,h зависит не только от подрессоренной массы m2V,h и жесткости подвески C2V,h но также от массы оси m1V,h , жесткости шины C1V,h , коэффициента KF и коэффициента сопротивления амортизатора KIIV,h .
Частота колебаний подрессоренных масс у легковых автомобилей со стальными упругими элементами составляет для передней оси nIIV =55…80 мин-1 и для задней оси nIIh =68…100 мин-1 .
Для обеспечения комфортабельности следует стремиться к тому, что достижимо даже для подвесок относительно легких автомобилей (“Рено – 4”, “Рено – 6”). Однако, для задней подвески это возможно только в том случае, если автомобиль оборудован системой регулирования уровня кузова.
6.2 Определение передаточных чисел
Кинематическое передаточное число ix:
![]()
Силовое передаточное число iy:
iy=F1 /N¢V =2754,82/2596,5=1,061.
6.3 Построение кривой жесткости подвески
Для построения упругой характеристики подвески автомобиля ЗАЗ-1102 “Таврия” необходимо определить жесткость средней части подвески с1 .
Расчет жесткости подвески с1 проводится по выбранной частоте колебаний ω при условии среднего положения автомобиля. Динамическая деформация резиновых элементов в шарнирах приводит к повышению частоты по сравнению с расчетной до 10%.
По рис.3 [15] принимаем расчетную частоту колебаний ω=8,6 рад⁄с, тогда замеренная частота ω= 9,46 рад⁄с. Жесткость средней части характеристики, которая, обычно, постоянная по величине, определяется, исходя из условия обеспечения высокой плавности хода автомобиля:

Определим условный статический прогиб подвески по формуле:
![]() ,
,
что соответствует исходному положению.
Величина динаического хода подвески (хода сжатия sд ) должна быть выбрана из условия, что вероятность (степень риска) ударов в упоры не превосходила заданную. Если извесна характеристика микропрофиля дорожного полотна, то можно, задаваясь определенной скоростью движения автомобиля, рассчитать теоретически необходимую величину sд . Однако этот метод в связи с трудоемкими расчетами, а также в следствие отсутствия в настоящее время достаточно полных данных о микропрофиле дорожного полотна не может обеспечить требуемую достоверность расчетов. Поэтому для определения sд будем использовать опытные данные, полученные анализом существующих моделей автомобилей. В этом случае величину sд определим по формуле:
sд = ke ∙sст = 0,8∙135 = 108 мм,
где ke =0,6÷1 — для малых и средних легковых автомобилей [15, стр.4].
Величину хода подвески до касания буфера сжатия sсб определим по формуле:
sсб = ke ´∙sд = 0,6∙108 = 65 мм,
где ke ´= 0,6÷0,7 — для легковых автомобилей [15, стр.4].
Величина хода, до срабатывания буфера отдачи, sоб :
sоб = kоб ∙ sсб = 1,3∙65 = 85 мм,
где kоб = 0,7÷1,5 — для передних подвесок [15, стр.4].
Важным параметром упругой характеристики являетсязначение максимальной силы Nmax , возникающей в конце полного хода сжатия sд . Обычно принимают, что допустимая деформация буфера ограничителя хода подвески равна 2/3 номинальной его высоты [15, стр.4]. Потенциальная энергия деформации буфера должна быть достаточной для полного поглощения энергии удара при пробое подвески. Однако ввиду отсутствия разработанных теоретических методов определения характеристики буфера-ограничителя обычно используют рекомендации, полученные опытным путём. Величину Nmax определяем по формуле:
Nmax = kд ∙N´vo = 3∙2596,5 = 7789,5 Н,
где kд =3 — коэффициент динамичности для легковых автомобилей [15, стр.4].
Определив Nmax , можно найти основные параметры характеристики буфера-ограничителя хода подвески.
По минимальной и максимальной пробивочным нагрузкам на ось следует подобрать характеристики и размеры дополнительных упругих элементов, выполняемых из резины или ячеистого полиуретана.
Ограничители хода лучше выполнять из ячеистого полиуретана, т.к. в этом случае они будут более долговечны, чем резиновые и допускают большую деформацию.

Рис. 6.3 График изменения жесткости подвески в зависимости от хода колеса.
Жесткость при номинальной нагрузке на одно колесо С1 =19,576 [H/mm]
Частота колебаний ω=8,6 рад/с.

Рис 6.4 Конструкция и желаемая характеристика
ограничителя хода сжатия.

Рис 6.5 Конструкция и желаемая характеристика
ограничителя хода отбоя.
7 Расчет и проектирование стального упругого элемента
7.1 Пружинные (рессорные) стали и их свойства
В ГОСТ нормированы стали для автомобильных пружин и рессор, изготавливаемых горячим формообразованием. Винтовые пружины выполняются преимущественно из стальной проволоки классов I, II, IIa, III по ГОСТ 9389-75, а также из проволоки по ГОСТ 14963-78. В табл. 43 [8] приведены выдержки из стандарта ГОСТ 14959–69 для наиболее распространенных марок сталей. Марки сталей разбиты на группы в зависимости от прочности, что позволяет лучше видеть зависимость между временным сопротивлением, пределом текучести и удлинением. Добавка в качестве регулирующего элемента хрома или марганца улучшает прокаливаемость стали. Именно поэтому при большой толщине листов или при большем диаметре торсионов могут использоваться стали марок 50ХСА, 60С2Н2А, 60СГА и т.п.
В штампе чертежа указывается временное сопротивление, которое материал рессоры или пружины должен иметь после обработки с учетом поля допуска. Буква А после марки стали, означает, что сталь высококачественная, поэтому надпись в штампе чертежа будет иметь вид:
60С2А
σв =1500÷1600 Мпа.
Однако при расчете упругих элементов используется не временное сопротивление (σв ), а напряжения, которые может выдержать материал при данном типе нагружения, т.е. при изгибе или кручении. Эти величины считаются допускаемыми верхними напряжениями, являясь функцией также указанных в табл. 22.4 [1] значений текучести σт . Уравнения для расчета допускаемых напряжений с учетом запаса прочности n и коэффициента b0 (который учитывает уменьшение прочности при толщине свыше 10 mm рис 2.10.6 [1]) будут иметь вид:
σв доп0 »1,2 σт b0 /n;
ttдоп0 »0,63 σт b0 /n.
Для пружинных сталей предел текучести при кручении составляет около tt =0,63 σт в отличие от углеродистых улучшаемых сталей по стандарту ДИН 17200, для которых tt =0,58 σт .
Для создания легких конструкций при достаточно полном использовании возможностей материала следует принимать запас прочности на уровне всего n=1,05…1,1. Превышение напряжений при проседании пружин и уменьшении высоты кузова практически невозможно в связи с наличием ограничителей хода.
Круглые прутки, используемые для изготовления винтовых пружин и торсионов, шлифуются, что обеспечивает высокую точность (допуск h9 по стандарту ИСО) и гладкую металлическую поверхность без концентраторов напряжения с высотой микронеровностей Rt £15 мкм. Перед завершающей операцией нанесения ударопрочного антикоррозионного покрытия осуществляется дробеструйная обработка готовой пружины, что позволяет устранить последние имеющиеся концентраторы напряжений и обеспечить требуемое сопротивление усталости. При использовании высококачественной стали допускаемые напряжения ttA могут быть рассчитаны по формуле:
ttA =tt w –0,159 ttm .
Предположив, что при пробое подвески напряжения в упругом элементе достигают предела текучести при кручении, вместо ttm подставляем ttF -ttA . В соответствии с табл. 1.1. [1] при знакопеременных нагрузках предел прочности при кручении tt w »0,29db . Используя характерную для пружинных сталей величину ttF »0,63dS , а также отношение предела текучести к временному сопротивлению g=dS /db »0,92, получаем:
ttA =tt w –0,159(ttF –ttA ) »0,29 σв –0,159(0,63∙0,92∙ σв –ttA )»0,24 σв .
Кроме того, в расчет должны войти: запас прочности для защиты от поломок при усталости металла n=1,1, коэффициент уменьшения напряжений b1 , который учитывает снижение прочности при диаметре более 10 мм. Для винтовых пружин дополнительно учитывается коэффициент k. В окончательной форме уравнение имеет следующий вид:
ttдопА »0,24 σв min b1 /(nk).
Для определения прочности в него следует ввести минимальное значение указанного на чертеже поля допуска. При работе подвески редко используется весь ее ход. Преднамеренно учитывая при расчетах на прочность только часть зоны допускаемых нагрузок, принимают во внимание 90% хода подвески. Без этого пружины были бы слишком тяжелыми и неоправданно дорогими, что учитывается коэффициентом 0,9.
7.2 Расчет винтовой пружины
Винтовую пружину можно рассматривать как цилиндрический торсионный стержень, навитый на сердечник диаметром D1 . в процессе навивки проволока будет деформирована, в результате чего на внутренней (сжатой) стороне будут иметь место более высокие напряжения кручения. Величина этих напряжений, обозначенных ti , зависит от индекса пружины w=Dm /d, т.е. от отношения диаметра навивки к диаметру проволоки. С помощью коэффициента k, учитывающего влияние кривизны витка и приведенного на рис. 2.123. [1], можно рассчитать ti как функцию допускаемых верхних значений напряжений.
ti =ttдon0 /k.
Чем меньше Dm и, следовательно, индекс пружины w, тем большие значения будет принимать коэффициент k. В результате: напряжения, которые может выдержать пружина, будут снижены, а использование материала ухудшается. Кроме того, для пружины с малым диаметром Dm существует опасность потери устойчивости под нагрузкой. По этим причинам целесообразно предусматривать максимально возможный диаметр навивки.
![]()
![]()
Рис 7.1 При навивке спиральных пружин на внутренней (сжатой) стороне возникают повышенные напряжения кручения. А – зона повышенных напряжений.
ix – передаточное отношение по ходу;
iy – передаточное отношение по силам;
n0,1 – число пружинных витков (индекс 0 означает расчетное число, индекс 1фактическое);
n1 – общее число витков;
k – коэффициент уменьшения, учитывающий изгиб проволоки;
L0 – длина пружины без нагрузки, мм;
Lw - длина пружины под воздействием начальной нагрузки Fw , мм;
Lb1 – длина пружины при полной нагрузке (длина блока при плотном
прилегании всех витков), мм;
Ln – наименьшая рабочая длина;
Sa – сумма наименьших расстояний между пружинящими витками (зазор),мм;
w - степень навивки, w=Dm /d;
l - коэффициент гибкости пружины;
ti – допустимые напряжения сдвига с учетом изгиба проволоки, МПа.
Чтобы по среднему диаметру навивки Dm определить индекс пружины w и коэффициент k, следует вначале задаться диаметром d. ориентировочно, предположив, что d»1,4 см=14 мм и Dm =160 мм, определяем коэффициент k:
k=1+5/4∙d/Dm +7/8∙(d/Dm )2 +( d/Dm )3 ;
k=1,1167,
что равноценно уменьшению на 11,67% напряжений, которые может выдержать пружина.
Степень навивки:
ω= Dm ⁄d = 160 ⁄14 = 11,43.
В качестве материала, при диаметре проволоки меньше 40 мм в соответствии с табл. 2.4 [1], рассматривается сталь 60С2А [8, табл. 43]в группе прочности ІІ. При этом на чертеже должны быть указаны следующие характеристики: σв =1570 Мпа и σт ³1373 Мпа.
Используя запас прочности n=1,1 и определяя по рис. 2.106 [1] значение величины b0 =0,94 как функцию d=0,14 мм, получаем допускаемые максимальные напряжения:
ttдоп0 »0,63 σт ∙b0 /n»0,63∙1373∙0,94/1,1=739,17 Мпа.
При k=1,1167 идеальные касательные напряжения:
ti =ttдоп0 /k=739,17/1,1167=661,92 Мпа.
Допустимые амплитудные напряжения определяются как функция максимального временного сопротивления при n=1,1 и b1 =0,95 (рис. 1.13 [1]), а также с учетом k=1,1167:
ttдопА »0,24 σв ∙b1 /(n∙k)=0,24∙1570∙0,95/(1,1∙1,1167)=291,41 Мпа.
Вначале рассчитываются силы, действующие на пружину, и ее перемещения и, кроме того, жесткость CF . Затем по этим величинам определяем относительные величины y1 и y2 :
Fw =N¢V ∙iy= 2596,5∙1,061 = 2754,89 H .
f1F =f1 /ix=65/1,0112=64,28мм;
f2F =f2 /ix=85/1,0112=84,06 мм;
F1 =f1F ∙CF = 64,28∙20 = 1285,6 H,
где CF =с1 ∙ix∙iy= 19,576∙1,0112∙1,061 = 20 Н/мм;
Fmax =Fw +F1 = 2754,89+1285,6= 4040,49 H.
FA =[(f1 F +f2 F )∙0,9/2]CF =[(64,28+84,06)∙0,9/2]∙20=1335,06 H.
y2 =FA /tt доп A =1335,06 /291,41 = 0,045814 см2 ;
y1 =Fmax /ti =4040,49/661,92 = 0,061042 см2 .
Определяем минимальный диаметр проволоки с использованием большей из величин (в данном случае y1 ).
![]()
В результате расчета диаметр проволоки dmin оказался меньшим, чем диаметр, который был использован при первоначальном расчете dmin =1,4 см. Коэффициенты уменьшения допускаемых нагрузок b0 и b1 , определяемые диаметром, будут поэтому больше принятых при расчете, а коэффициент k, зависящий от кривизны витка, будет меньше. Идеальные напряжения среза будут больше и поэтому не требуется проведения повторного расчета.
С учетом допускаемых отклонений размеров (допуски на рис. 2.118 [1]) следует определить средний диаметр проволоки, который будет использован при дальнейших расчетах и является исходным для изготовления проволоки. При диаметре проволоки меньше 20 мм допускаемые отклонения равны ±0,08 мм, поэтому диаметр d с учетом поля допуска равен 14,08±0,08 мм. Следовательно, индекс пружины, необходимый в дальнейшем расчете, составляет w=11,36. Используя величину d, выраженную в см, определяем число рабочих витков:

Добавляя по концам пружины по ¾ витка, получаем общее число витков:
n1 =n+1,5=5+1,5=6,5.
Число витков должно быть кратным 0,5, т.к. при этом концы крайних витков будут развернуты в разные стороны.
После определения диаметра проволоки и числа витков следует найти размеры, имеющие значение для высоты автомобиля.
Одним из таких размеров является та высота Lw , которую пружина будет иметь под действием начальной нагрузки Fw . Нижний предел размера Lw зависит от наименьшей рабочей высоты Ln , т.е. от длины, которую будет иметь пружина, полностью сжатая до такого состояния, когда витки даже с учетом предусмотренного покрытия не касаются один другого. При определении величины Ln следует использовать максимально возможный диаметр проволоки dmax , т.е. средний диаметр с допускаемым положительным отклонением. В рассматриваемом примере dmax =14,08+0,08=14,16 мм. Длина пружины при полной нагрузке (длина блока при плотном прилегании всех витков), мм:
Lb1 =(n+1,1)dmax =(5+1,1)∙14,16= 86,376 мм.
Стоящая в скобках цифра 1,1 учитывает прижатые концевые витки.
Sa =cdmax n= 0,19∙14,16∙5 = 13,452 мм.
Ln =Lb 1 +Sa =86,376 +13,452 = 99,828 мм,
где коэффициент c определяется по рис. 2.125 [1] как функцию индекса пружины w. В приведенном примере при w=11,36 коэффициент c=0,19.
Высота пружины при начальной нагрузке:
Lw =f1F +Ln =64,28+99,828 = 164,108 мм.
Высота пружины в свободном состоянии без нагрузки:
L0 =Lw +Fw /CF = 164,108+2754,89/20 = 301,85 мм.
Используя L0 , следует проверить устойчивость пружины, т.е. ее продольный изгиб под нагрузкой. Коэффициент гибкости:
l=L0 /Dm =301,85/160=1,887.
Относительная упругость, приведенная на рис. 2.126 [1], определяется по уравнению:
(L0 –Lb1 )/L0 =(301,85–86,376)/301,85=0,7138.
В соответствии с рис. 2.126 [1] при коэффициенте гибкости l=1,887 и условии по относительной упругости: (L0 -Lb1 )/L0 =0,7138, опасность продольного изгиба — отсутствует.
Кроме того необходимо учитывать следующие соображения: пружина очень редко бывает максимально сжата, а в основном – на 0,9 величины хода подвески; от продольного изгиба пружину предохраняет корпус амортизатора; изменение Dm приводит к отсутствию продольного изгиба.
Для пружин, изготавливаемых в условиях крупносерийного производства, из шлифованных прутков изготовители указывают допуски Тр , исчисляемые в ньютонах в соответствие со следующей формулой:
TP =±(0,5[1,5 мм+0,03(L0 –Lb 1 )]∙CF +0,01Fω ).
TP =±(0,5∙[1,5+0,03∙(301,85–86,376)]∙20+0,01∙2754,89)=±107,19 H.
На чертеже с учетом округления должно быть указано:
Длина пружины 164 мм при 2755±107 Н.
Наносимый на чертеже наружный диаметр будет иметь значение:
Da =Dm +d=160+14,08=174,08 мм.
И принимая допуск, указанный в колонке “шлифованные прутки” (по табл. 2.5 [1]), получаем диаметр 174.08±1,5 мм, или округленно 174±1,5 мм.
8 Расчет характеристики амортизатора
Амортизатор, предназначенный для гашения колебаний колес и кузова, повышает плавность хода автомобиля, устойчивость движения,
Долговечность упругих элементов и шин. Решающее влияние на все указанные выше качества автомобиля оказывает правильный выбор характеристики амортизатора, т.е. правильный выбор зависимости силы на штоке амортизатора от скорости относительного перемещения штока и цилиндра. Математически эта зависимость устанавливается уравнением:
Pa =ka Vn n ,
Где Pa – сила на шток амортизатора;
Vn – скорость относительного перемещения штока и цилиндра амортизатора;
ka – коэффициент пропорциональности;
n – показатель степени, который обычно колеблется в пределах 1 – 2.
Конструктивно амортизатор в проектируемой подвеске располагается внутри направляющей пружинной стойки. Так как передаточное число iX =1,0112 близко к единице, то перемещение штока должно соответствовать величине, близкой к ходу колеса 150 мм.
На рис. 8.1 изображена линейная характеристика современного гидравлического амортизатора, которая обычно определяется следующими параметрами: коэффициентами сопротивления отбоя kao и сжатия kac при закрытых клапанах амортизатора; коэффициентами сопротивления k¢ao и k¢ac при открытых клапанах и силами на штоке амортизатора Рао и Рас , при которых открываются клапаны амортизатора.
Величины коэффициентов kao и kac определяются расчетом, исходя из требований к плавности хода или устойчивости движения автомобиля. Силы на штоке автомобиля могут быть определены по формулам:
Pao =kao Vxo и Pac =kac Vxc .
Скорости относительного движения штока и цилиндра амортизатора Vx0 и Vxc , соответствующие моменту открытия клапанов, обычно лежат в пределах 0,3 – 0,52 м/с.
Величины коэффициентов k¢ao и k¢ac обычно не рассчитываются. Однако, если имеется экспериментально определенная характеристика, то они могут быть рассчитаны по формулам:


В большинстве конструкций амортизаторов показатель степени n не равен единице, однако характеристика амортизатора для инженерных расчетов приводится к линейной.
При выборе характеристики амортизатора, обычно, задаются величиной парциального коэффициента апериодичности, рассматривая подвеску как одномассовую систему:

где kn – приведенный коэффициент сопротивления амортизатора;
g – ускорение силы тяжести;
Cn – жесткость подвески;
ТСТ – статическая нагрузка на подвеску.

Диапазон коэффициента апериодичности y=0,15…0,30. Жесткость подвески c1 =19576 Н/м (на одно колесо). Нагрузка на одно колесо Nv = 2885 Н. Принимая y=0,17, определяем kn :

При несимметричной характеристике необходимо, зная величину kn , установить приведенные коэффициенты сопротивления амортизатора при сжатии и отбое. С этой целью необходимо выбрать отношение a=kno /knc , которое для современных амортизаторов находится в пределах от 2 до 5. В этом случае принимая a=3, получим:

kno =a∙knc =3∙407,895=1223,685 Нс/м.
Действительные коэффициенты сопротивления амортизатора определяются из выражений:
kao =kno (dS/dfa )2 и kac =knc (dS/dfa )2 ,
где S – вертикальная деформация подвески;
fa – относительное перемещение поршня и цилиндра амортизатора.
Для данного случая dS/dfa является ни чем иным, как кинематическим передаточным числом подвески iX =1,0112.
kao =1223,685∙(1,0112)2 =1251,25 Нс/м;
kac =407,895∙1,01122 =417,08 Нс/м.
Силы на штоке амортизатора:
Pao =kao Vxo ;
Pac =kac Vxc ,
где Vxo и Vxc – скорости относительного движения штока и цилиндра амортизатора при ходах отбоя и сжатия, соответствующие моменту открытия клапанов.
Из диапазона 0,3…0,52 м/с принимаем скорость Vxo =Vxc =0,5 м/с в связи с тем, что подвеска довольно жесткая для легкового автомобиля, имеет большой ход и воспринимает высокие нагрузки.
Pao =1251,25∙0,5=625,625 H»626 H.
Pac =417,08∙0,5=208,54»209 H.
Величины коэффициентов сопротивления амортизатора при открытых клапанах принимаем:
– при отбое - k¢ao =400 Нс/м,
– при сжатии - k¢ac =300 Нс/м.
Относительная скорость перемещения штока и цилиндра V¢xo =V¢xc =0,8 м/с.
P¢ao =Pao +k¢ao (V¢xo -Vxo )=626+400∙(0,8–0,5)=746H.
P¢ac =Pac +k¢ac (V¢xc -Vxc )=209+300∙(0,8–0,5)=299 H.
Столь низкие на первый взгляд демпфирующие силы и коэффициенты рассчитаны с учетом того, что в направляющей втулке амортизатора создаются достаточно высокие нагрузки, вызывающие силу трения, также являющуюся демпфирующей и которую нужно учитывать при выборе характеристики амортизатора.
По результатам расчета строим характеристику амортизатора.
![]()
Рис 8.1 Характеристика амортизатора
9 Построение графика изменения колеи в зависимости от хода колеса
![]()
 |
|
Рис. 9.1
Очевидно, что изменение колеи Dd можно вычислять по формуле:
![]()
где Df – изменение хода колеса от горизонтального положения рычага, мм.
Для расчета достаточно взять Dfmax =85 мм, т.к. и для Df1 и для Df2 значения будут одинаковы. Для расчета возьмем 14 точек:
Изменение колеи, мм. Если считать, что колесо движется сверху вниз, то для участка В3 -В0 (рис.10.1 ) Db будет положительным, а для участка В0 -В8 – отрицательным.
Таблица 9.1
![]()
![]()
1 0 ОХРАНА ТРУДА.
Охрана труда в Украине регламентируется законом «Об охране труда», принятым в 1933 году.
Согласно ГОСТ 12.0.002–80. «Система стандартов безопасности труда. Термины и определения». Охрана труда — это система законодательных актов, социально-экономических, организационных, технических, гигиенических и лечебно-профилактических мероприятий и средств, обеспечивающих безопасность, сохранения здоровья и работоспособности человека в процессе труда.
Техника безопасности — это система организационных мероприятий и технических средств, предотвращающих или уменьшающих воздействие на работающих опасных производственных факторов.
Опасный производственный фактор — это производственный фактор, воздействие которого на работающего в определенных условиях приводит к травме или внезапному резкому ухудшению здоровья.
Вредный производственный фактор — это производственный фактор, воздействие которого на работающего в определенных условиях приводит к заболеванию или снижению работоспособности.
В соответствии с ГОСТ 12.0.003–74. опасные и вредные производственные факторы по природе их воздействия на организм человека подразделяют на четыре группы:
1) физические — движущиеся детали, элементы механизмов и машины в целом; недопустимая температура поверхностей машин и оборудования и воздуха в рабочей зоне; недопустимый уровень вибрации, производственных излучений (ионизирующих, лазерных, инфракрасных, ультрафиолетовых), электромагнитных полей; метеорологических колебаний в рабочей зоне; недостаточная или повышенная освещенность рабочей зоны;
2) химические — токсические, раздражающие, сенсибилизирующие, канцерогенные, мутагенные, влияющие на репродуктивную функцию;
3) биологические — микро- и макроорганизмы;
4) психофизиологические — физические нагрузки (статические, динамические, гиподинамия); нервно-психические перегрузки (умственные, эмоциональные, монотонность труда, перенапряжение анализаторов).
10.1 Меры безопасности при эксплуатации автомобиля.
10.1.1 Подготовка автомобиля к выезду на линию.
Автомобиль (автопоезд) перед выпуском на линию проходит проверку технического состоянии. Лицо, ответственное за выпуск автомобилей, после проверки их технического состояния делает отметку в путевом листе о готовности автомобиля к работе. Категорически запрещается выпуск на линию автомобилей с неисправностями, угрожающими безопасности движения и сохранности пассажиров и груза, а также грязного, без номеров и без опознавательных знаков автопоезда.
Водитель перед выездом на пинию должен иметь при себе: удостоверение на право управления автомобилем, выданное Государственной автомобильной инспекцией, талон технического паспорта, путевой или маршрутный лист. Перед выездом на линию, водитель проверяет техническую исправность автомобиля: отсутствие подтекания топлива, масла, воды, а у газобаллонных автомобилей герметичность газовой аппаратуры и магистралей; при этом особое внимание oн обращает на органы управления и механизмы, обеспечивающие безопасность движения — тормоза, рулевое управление, шины, фары, задний фонарь, стоп-сигнал, указатели поворотов, звуковой сигнал, крепление карданного вала. Кроме того, перед выездом водитель проверяет: давление воздуха в шинах и соответствие его нормам; наличие инструментов и инвентаря; заправку автомобиля топливом, маслом, водой и тормозной жидкостью; уровень электролита в аккумуляторной батарее.
В случае перевозки опасных грузов администрация грузоотправитель обязана до перевозки этих грузов каждый раз инструктировать водителя, экспедитора, грузчиков и других лиц, сопровождающих груз, и проверять наличие защитных средств и средств тушения пожара.
До направления водителя пассажирского транспорта на новый маршрут с ним проводится инструктаж о характере маршрута, и он должен быть направлен и специальный рейс для ознакомления с маршрутом.
До выезда в рейс водителю предоставляется отдых, предусмотренный законодательством. Водителю запрещается выезжать в рейс в болезненном состоянии или при такой степени утомления, которая может повлиять на безопасность движения.
10.1.2 Работа автомобиля на линии.
При работе на линии водителю категорически запрещается управлять автомобилем в состоянии даже самого легкого алкогольного опьянения или под воздействием наркотических средств; передавать управление автомобилем лицам, находящимся в нетрезвом состоянии, либо не указанным в путевом листе, или не имеющим при себе удостоверения на право управления автомобилем; самовольно отклоняться от маршрута, указанного в путевом листе, если это не вызывается ухудшением дорожных или климатических условий.
Во время работы водитель обязан выполнять правила безопасности движения, указания регулировщиков уличного движения; поддерживать скорость в соответствии с требованиями Правил дорожного движения с учетом состояния дороги, но не выше максимальной скорости, установленной технической характеристикой для данной модели автомобиля; наблюдать за показаниями контрольных приборов автомобиля, и правильностью работы всех механизмов.
Особые правила водитель должен соблюдать при перевозке людей. Перевозка пассажиров на грузовых автомобилях может осуществляться только при соблюдении следующих требований: в кузове автомобиля должен находиться старший, отвечающий за поведение пассажиров, и фамилия его записывается, в путевом листе; скорость движения автомобиля не должна превышать 60 км/ч. Регулярная перевозка людей на грузовом бортовом автомобиле, кузов которого не оборудован тентом, не разрешается. Перевозка детей на грузовых автомобилях может быть допущена как исключение, но с детьми в кузове должны находиться не менее двух взрослых. На грузовых автомобилях, не приспособленных для перевозки пассажиров, разрешается проезд лицам сопровождающим или получающим грузы, но не более шести человек, фамилии их указываются в путевом листе. Однако такой проезд запрещается на платформах без бортов, на грузе, размещенном на уровне или выше бортов кузова, на длинномерном грузе и рядом с ним, на цистернах, грузовых прицепах или полуприцепах всех типов.
В кабине, кузове и салоне автомобиля не разрешается нахождение большего числа людей, чем это указано в паспорте завода-изготовителя.
Категорически запрещается перевозка людей в кузове автомобиля-самосвала даже на самое короткое расстояние. Лица, сопровождающие эти автомобили, должны находиться только в кабине водителя.
В кузове автомобиля не разрешается перевозить лиц, не имеющих отношения к выполняемой работе. В путевом листе должны быть записаны фамилии и должности людей, направляемых с автомобилем на линию.
Лица, находящиеся на автомобиле, должны выполнять все требования водителя по соблюдению правил техники безопасности.
Движение автомобиля при нахождении людей на подножках, крыльях, буферах, бортах запрещается.
Ели во время работы на линии водитель или лица, сопровождающие автомобиль, находятся в условиях, опасных для жизни и здоровья (например, отсутствие механизации при погрузке тяжеловесных грузов, несоответствие автомобиля перевозимому грузу, невозможность оставления безопасных мест для грузчиков при погрузке, несоответствие погрузочно-разгрузочных площадок и подъездных путей установленным правилам и т, п.), водитель обязан немедленно остановить работу и сообщить в свое автотранспортное предприятие, а также сделать отметку о своем заявлении в путевом листе. Если сообщить в свое автотранспортное предприятие не представляется возможным, то водитель обязан поставить в известность администрацию того предприятия, в распоряжении которого находится автомобиль, и может продолжать работу только после устранения опасности. Из кабины автомобиля на проезжую часть дороги водитель может выходить, только предварительно убедившись в отсутствии движения во встречном и в попутном направлениях.
Если во время работы на линии в автомобиле обнаружится неисправности, угрожающая безопасности движения и сохранности людей, автомобиля и груза, водитель обязан принять необходимые меры к устранению неисправности, а если это невозможно, должен следовать на ближайшую ремонтную базу или возвратиться в гараж с соблюдением необходимых мер предосторожности.
10.2 Требования к рабочему месту водителя.
Работа по управлению автомобилем может быть отнесена к разряду, наиболее напряженных и утомительных форм трудовой деятельности. Эта работа протекает в условиях постоянного и значительного нервноэмоционального напряжения, углубляемого сознанием огромной ответственности за жизнь людей и материальные ценности. Быстрота реакции и точность рабочих движений водителя современного автомобилля являются важнейшими факторами обеспечения безопасности движения. Эти качества в большой степени зависят от удобства рабочего места водителя, которое должно создавать благоприятныеусловия труда и исключать возможность возникновения аварий, вызываемых перенапряжением при работе водителя.
Большое влияние на работу водителя оказывает правильная его посадка, которая определяется как «спокойное положение в состоянии готовности». Плоскость сиденья должна быть не горизонтальной, а слегка наклоненной назад (3–7° к горизонтальной плоскости). Спинка сиденья не должна быть фиксирована, сиденье должно регулироваться по высоте и в горизонтальном направлении. Обивка сиденья должна быть достаточно жесткой и шероховатой.
Рычаги управления автомобилем, перемещающиеся в горизонтальной плоскости к водителю и от него, должны быть рационально расположены на 230 мм выше сиденья, причем они должны быть удалены от спинки сиденья в первом случае на 560 мм, а во втором – на 600 мм. Сила сопротивления рычага должна составлять около 10 кгс, т. е. 20–25% максимальной (45 кгс). Оптимальный ход педалей при нажатии передней части пятки и середины стопы 100–150 мм. При компоновке рычагов управления должно быть соблюдено условие, чтобы основные рычаги располагались перед водителем с справа, а вспомогательные – с левой стороны. Всю компоновку рабочего места водителя выполняют так, чтобы водитель не находился длительное время в вынужденной неудобной позе.
Конструкция и внутренние размеры кабины должны обеспечивать водителю свободный вход в зимней одежде, нестесненное положение на сиденье, удобное действие рычагами и педалями.
С рабочего места водителя должна быть обеспечена максимальная обзорность. Под обзорностью автомобиля подразумевается одно из его конструктивных свойств, определяющее объективную возможность для водителя видеть рабочую зону, путь движения и объекты, которые могут помешать безопасному его движению. Обзорность рабочей зоны характеризуется величиной хорошо видимого водителем пространства в вертикальной и горизонтальной плоскостях. Водителю должны быть созданы такие условия, при которых он мог бы наблюдать путь движения и объекты, не совершая при этом излишне сложных движений. В противном случае работа водителя сопровождается дополнительным мышечным и нервным напряжением, вызывающим повышенную утомляемость.
Для обеспечения здоровых условий труда водителя большое значение имеет состояние воздушной среды в кабине автомобиля (микроклимат). Микроклимат — это физическое состояние воздушной среды в ограниченном пространстве, характеризуемое атмосферным давлением, температурой, влажностью и скоростью движения воздуха. Температура воздуха в кабине водителя определяется температурой наружного воздуха и тепловыделениями двигателя, если он расположен в передней части автомобиля. Температура, должна быть в пределах от +15 до +17°С.
Соотношение температуры, влажности и скорости движения воздуха в кабине автомобиля могут создавать различные зоны удобства работы водителя. Так, зона полного удобства при температуре воздуха 19–22°С и при влажности воздуха 50% достигается при скорости движения воздуха 0,15 м/с.
Скорость воздуха в кабине в теплое время года допускается от 1 до 2 м/с, а в холодное время — не свыше 0,5 м/с. Поступающий в кабину воздух должен быть очищен от пыли.
Теплоизоляция и отопление кабины в соответствии со СНиП II-Г. 7–62 должны обеспечивать при работе в холодное время года температуру в кабине от +14 до +16°С.
Вентиляционная система кабины должна обеспечить воздухообмен в холодное время года не менее 40 м3 /ч.
Воздухообмен при температуре наружного воздуха до 28°С должен обеспечить температуру воздуха в кабине не выше чем на 2–3°С по сравнению с температурой наружного воздуха.
Концентрация вредно действующих веществ, содержащихся в отработавших газах, в зоне дыхания не должна превышать предельно допустимого уровня: окиси углерода – 20 мг/м3 , акролеина – 0,7, тетра-этилсвинца – 0,05, углеводородов (в пересчете на углерод) – 300 мг/м3 .
Предельно допустимый уровень шума в кабине автомобиля и вибрация на рабочем месте водителя не должны превышать значений действующих санитарных норм и правил (СН245–71). С целью снижения шума в кабине автомобиля тщательно подгоняют соприкасающиеся части кабины, обивают кабину звукопоглощающим материалом.
Сиденье водителя является хорошим амортизатором вибраций, но радикальными мерами снижения отрицательного воздействия на водителя вибрации является устранение колебаний деталей кузова при длительной эксплуатации автомобиля и устранение возможности вибраций основных узлов автомобиля при его конструировании.
Кабины транспортных средств, предназначенных для работы в южных районах, должны быть окрашены светлыми красками. Световые проемы кабин изготовляют из небьющегося и безосколочного, но прозрачного материала.
В транспортных средствах, предназначенных для эксплуатации в условиях Cевера, стекла кабин необходимо обдувать теплым воздухом или делать двойное остекление и между стеклами помещать влагопоглотитель (силикагель). Внутри кабины устраивают отопитель кабины типа 0-30, работающий независимо от двигателя.
10.3 Виброизоляция сиденья самоходной машины.
Пассивная виброизоляция (виброзащита) – это виброизоляция, не использующая энергию дополнительного источника.
Сиденья в самоходных строительно-дорожных машинах, грузовых автомобилях и тракторах должны обеспечивать санитарно-гигиенические условия для длительной работы водителей. Сиденье должно смягчать толчки и удары и часть вибраций, превышающую гигиенические характеристики и нормы вибрации по ГОСТ 12.1.012-78*.
Учитывая, что утомляемость оператора во многом зависит от положения его во время работы, исследованиями установлено, что сидение должно быть регулируемым, мягким и подрессоренным. Горизонтальное, продольное перемещение должно быть не менее 150 мм, вертикальное не менее 80 мм, вертикальное перемещение спинки не менее 60 мм, а угол ее наклона не менее 10˚.
Типовая схема подрессоривания сиденья водителя (рис.4) состоит из следующих элементов: направляющего механизма 1, состоящего из параллелограмных рычагов и обеспечивающих стабильность вертикального положения корпуса водителя при колебании машины. Направляющий механизм, соединяющий посадочное место водителя с рамой ходовой части машины, выполняет роль кинематической и силовой связи; пружины 3, снижающей амплитуду колебаний сиденья от колебаний машины при передвижении по неровностям дороги; регулировочного винта 4 для изменения жесткости пружины в зависимости от массы тела водителя; гидроамортизатора 2, поглощающего колебания сиденья при передвижении машины по неровностям дороги.
Схема гидроамортизатора показана на рис.5. При переезде препятствий на неровностях пути возникают резкие колебания рамы ходовой части, в результате чего сопротивление гидроамортизатора возрастает. Это сопротивление вызвано тем, что жидкость в нем не успевает проходить через отверстия 1 в поршне 2. В результате возникающего гидравлического торможения колебания сиденья гасятся.
![]()
Схема гидроамортизатора.Рис.10.1
10.4 Устойчивость легкового автомобиля.
Исходные данные для расчета:
Легковой автомобиль ЗАЗ – 1102: Ga =5770 Н; a= 1390мм; b=930 мм; hG =464 мм; L=2320 мм.
10.4.1 Расчет на продольную устойчивость.
Продольная устойчивость автомобиля без прицепа обеспечивается тогда, когда подъем или уклон его (рис.1) не превышает предельного угла α, при которых заторможенный автомобиль не опрокинется. При подъеме он может опрокинуться вокруг точки 0. В этом случае возникает опрокидывающий момент силы тяжести М=Gsinαn b. Машина будет находиться в состоянии устойчивости в том случае, пока удерживающий момент силы тяжести М=Gcosαn b будет больше опрокидывающего момента, т.е.
Gsinαn hG ≤ Ga cosαn b,
где Ga – вес машины с грузом, Н;
hG – высота центра тяжести, м;
a,b – соответственно расстояние от передней и задней оси до вертикали, проходящей через центр тяжести, м;
αn – угол подъема, град.
На подъеме автомашина будет находиться в состоянии устойчивости, если соблюдается условие:
tgαn = b/hG = 930/464 =4,766; αn =63º30′.
На уклоне, аналогично предыдущей зависимости, имеем:
tgαn = b/hG =1390 /464 = 2,9957; αn =71º35′.
Расчетные углы, обеспечивающие устойчивость, будут значительно меньшими, если при спуске автомобиля водитель резко тормозит, а при подъеме делает резкий рывок с места.
В действительности автомобили крайне редко опрокидываются; чаще у них буксуют ведущие колеса, в результате чего машины сползают. В этом случае предельный угол автомобиля, при котором исключается буксование колес:

αбук =31º40′
где φx – коэффициент сцепления шин автомобиля;
L – база автомобиля;
10.4.2 Расчет на поперечную устойчивость.
Часто нарушение устойчивости проявляется в боковом скольжении колес или опрокидываний автомобиля в плоскости, перпендикулярной продольной оси. Возмущающими силами могут быть: составляющая силы инерции, поперечная составляющая силы тяжести Ga sinβ, возникающая в результате поперечного наклона дороги на угол β, аэродинамическая сила.
Поперечная устойчивость автомобиля характеризуется предельным углом (рис. 2) при движении машины поперек уклона:
![]()
Во избежание аварий при движении автомобилей по кривой необходимо выдерживать следующие радиусы поворота:
1) по условию, при которых возникает боковое скольжение колес:
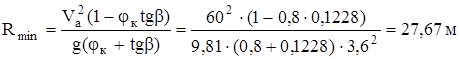
где Rmin – минимальный радиус поворота по кривой, м;
Va – скорость движения автомобиля, км/ч;
g– ускорение силы тяжести, м/с2 ;
β– угол бокового наклона дороги, град.
Если движение происходит на горизонтальной дороге, то β=0, тогда минимальный радиус поворота находится:

2). по условию, при которых происходит боковое опрокидывание:
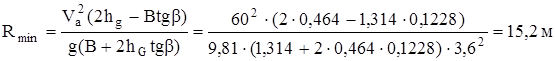
На горизонтальной дороге при β=0:

Если рассматривать круговое движение на горизонтальной дороге и учитывать смещение центра масс только в результате крена подрессоренной массы, не учитывая поперечного наклона за счет радиальных деформаций шин, то смещение центра масс автомобиля, вызванное креном подрессоренной массы, несколько отличается от смещения центра подрессоренной массы. Согласно нормативным требованиям, ψкр max <6º. C учетом крена подрессоренной массы получим:
10.5 Противопожарная безопасность.
Пожары и взрывы причиняют значительный материальный ущерб и в ряде случаев вызывают тяжелые травмы и гибель людей. Поэтому защита зданий, сооружений и других материальных ценностей от пожаров является обязанностью всех граждан и проводится в общегосударственном масштабе. Мероприятия по предупреждению возникновения и ограничению размеров пожаров, называемые пожарной профилактикой, являются составной частью мероприятий по охране труда, так как их главная цель – предупреждение несчастных случаев с людьми.
Пожарная безопасность (согласно ГОСТ 12.1.004–76 «Пожарная безопасность») – это такое состояние объекта, при котором исключается возможность пожара, а в случае возникновения предотвращается его опасное воздействие на людей и обеспечивается защита материальных ценностей.
Пожарная безопасность обеспечивается системами предотвращения пожара и пожарной защитой. Под системой предотвращения пожара имеется в виду комплекс организационных мероприятий и технических средств, направленных на исключение возможности возникновения пожара. Под системой пожарной защиты понимают комплекс организационных мероприятий и технических средств, направленных на предотвращение воздействия на людей опасных факторов пожара и ограничение материального ущерба от него.
Пожарная защита обеспечивается: ограниченным применением горючих и трудногорючих веществ и материалов; предотвращением распространения пожара с использованием средств его тушения, строительных конструкций с необходимыми пределами огнестойкости и горючести; эвакуацией людей; системой противодымной защиты; средствами пожарной сигнализацией или извещением о пожаре, а также организацией пожарной охраны объекта.
При эксплуатации строительных машин пожары в большинстве случаев возникают по следующим причинам: у строительных машин с электроприводом – из-за перегрузки электродвигателей, электрооборудования, электропроводов и электросетей, в результате чего они нагреваются свыше допустимых норм или искрят; у машин с двигателями внутреннего сгорания – из-за воспламенения оставшейся внутри двигателя горючей смеси; неправильного расположения баков с горюче-смазочными материалами, масло- и топливопроводов по отношению к трубопроводу выхлопных газов и глушителю; применение открытого огня для запуска двигателей при низких температурах; самовоспламенение разлитых масел и горючего под картером двигателя; отсутствие искрогасителей на выпускных трубах; курение при заправке машин топливом.
Для быстрого прекращения горения при пожарах необходимо выполнять два основных условия: прекратить доступ воздуха (кислорода) в зону горения, так как горение возможно при содержании кислорода в воздухе не менее 14% (всего в воздухе содержится до 21% кислорода); охладить зону горения ниже температуры самовоспламенения, тогда процесс горения прекращается даже при наличии достаточного доступа воздуха.
Вещества, введенные в зону горения и нарушающие процесс горения, называют огнетушащими. К ним относятся вода, водяной пар, химические средства тушения, песок. Воздействие этих веществ на процесс горения зависит от физико-химических свойств и способов применения.
Список литературы
1. Раймпель Й. Шасси автомобиля: элементы подвески. Пер. с нем. М.: Машиностроение, 1987. 288 с.
2. Раймпель Й. Шасси автомобиля: конструкции подвесок. Пер. с нем. М.: Машиностроение, 1983. 356 с.
3. Ротенберг Р.В. Подвеска автомобиля. Изд. 3-е, перераб. и доп. М., “Машиностроение”, 1972, стр. 392.
4. Дербаремдикер А.Д. Гидравлические амортизаторы автомобилей. М., “Машиностроение”, 1969, 263 стр.
5. Потураев В.Н. Резиновые и резиново – металлические детали машин.
6. Вахламов В.К. Автомобили ВАЗ. Учеб. Пособие для учащихся ПТУ. 2-е изд., стер., - М.: Транспорт, 1993. – 193 с.: ил.
7. Анурьев В.И. Справочник конструктора – машиностроителя. В 3-х т. Т. 1-2. – 5-е изд., перераб. и доп. – М.: Машиностроение, 190. – 559 с., ил.
8. Масино М.А., Алексеев В.Н., Мотовилин Г.В. Автомобильные материалы. Справочник инженера–механика. М.: Транспорт, 1971, стр. 296.
9. Осепчугов В.Р., Фрумкин А.К. Автомобиль: Анализ конструкций, элементы расчета.—М.: Машиностроение, 1989 –304 с.: ил.
10. Литвинов А.С., Форобин Я.Е. Автомобиль: Теория эксплуатационных свойств.—М.: Машиностроение, 1989.–240 с.: ил.
11. Гришкевич А.И., Бусел Б.У. и др. Проектирование трансмиссий автомобилей: Справочник.— М.: Машиностроение, 1984.–272 с., ил.
12. Лукин П.П., Гаспарянц Г.А., Радионов В.Ф. конструирование и расчет автомобиля.— М.: Машиностроение ,1984.–376 с., ил.
13. Гришкевич А.И. Автомобили: Теория.— Мн.: Вышэйша школа, 1986.–208 с.: ил.
14. Раймпель Й. Шасси автомобиля: Амортизаторы, шины и колёса ⁄пер. с нем. В.П. Агапова; под ред. О.Д. Златовратского.— М.: Машиностроение, 1986.–320 с.: ил.
15. Цимбалин В.Б., Успенский И.Н. и др. Шасси автомобиля. Атлас конструкций.— М.: Машиностроение, 1977.–108 с. с ил.
16. Фучаджи К.С. АвтомобильЗАЗ-1102 «Таврия». Устройство, техническое обслуживание и устранение неисправностей.
17. Филиппов Б. И. Охрана труда при эксплуатации строительных машин: Учебник для студентов вузов по спец. «Строительные и дорожные машины». — 3-е изд., перераб. и доп.— М. Высш. Шк., 1984.– 247 с., ил.
18. Охрана труда на предприятиях строительной индустрии. А.Ф. Бицаев, Ю.Н. Посяда, А.А. Чуканов, В.В. Сафонов. Киев, «Будівельник», 1976, стр. 144.
Похожие рефераты:
Анализ конструкции и методика расчета автомобиля ВАЗ-2108
Исследование особенностей технической эксплуатации ходовой части автомобилей "Toyota"
Оценка ассортимента и конкурентоспособности автомобилей
Развитие сервисного обслуживания автомобилей
Двухосный индикаторный стабилизатор телекамер на ВО
Передняя подвеска автомобиля ГАЗ-53А (L=1450 мм)
Проект автотранспортного парка для техобслуживания автомобилей
Основы проектирования и конструирования
Управляемость автомобиля. Параметры маневра
Проект легкового автомобиля, грузоподъемностью 4 человека, микрохэтчбэк



 .
.