| Похожие рефераты | Скачать .docx |
Реферат: Экономическое моделирование
Задача 1
Пусть имеется следующая модель регрессии, характеризующая зависимость x от y:
![]() .
.
Известно также, что, ![]() .
.
Задание
1. Постройте доверительный интервал для коэффициента регрессии в этой модели:
a. с вероятностью 90%;
b. с вероятностью 99%.
2. Проанализируйте результаты, полученные в п.1, и поясните причины их различий.
Решение.
Формула для расчета доверительного интервала для коэффициента регрессии имеет вид:
![]()
где ![]() - случайная ошибка параметра линейной регрессии. Оценка значимости коэффициента регрессии проводится путем сопоставления его значения с величиной случайной ошибки.
- случайная ошибка параметра линейной регрессии. Оценка значимости коэффициента регрессии проводится путем сопоставления его значения с величиной случайной ошибки.
![]()
где F – F-критерий Фишера и определяется из соотношения:
![]()
Тогда
![]()
При ![]() и числа степеней свободы
и числа степеней свободы ![]() табличное значение
табличное значение ![]() .
.
Сравнив его с расчетными значениями, получаем, что ![]() , из чего следует, что гипотезу о несущественности параметра b с вероятностью 90% (p = 1 – α) следует отклонить
, из чего следует, что гипотезу о несущественности параметра b с вероятностью 90% (p = 1 – α) следует отклонить
Для коэффициента регрессии в примере 90 %-ые границы составят:
-7 + 1,7143 · (-2,86) ≤ b ≤ -7 - 1,7143 · (-2,86)
-11,9 ≤ b ≤ -2,04
При ![]() и числа степеней свободы
и числа степеней свободы ![]() табличное значение
табличное значение ![]() .
.
Сравнив его с расчетными значениями, получаем, что ![]() , из чего следует, что гипотезу о несущественности параметра b с вероятностью 99% (p = 1 – α) следует принять и признается статистическая незначимость параметра b.
, из чего следует, что гипотезу о несущественности параметра b с вероятностью 99% (p = 1 – α) следует принять и признается статистическая незначимость параметра b.
Для коэффициента регрессии в примере 99 %-ые границы составят:
-7 + 2,8784 · (-2,86) ≤ b ≤ -7 – 2,8784 · (-2,86)
-15,23 ≤ b ≤ 1,232
Получили, что доверительный интервал для коэффициента корреляции с вероятностью 90% значительно меньше доверительного интервала с вероятностью 99%. Это объясняется тем, что при увеличении интервала вероятность попадания в него оцениваемого параметра растет и наоборот, с уменьшением интервала – вероятность снижается.
| № | Производительность труда рабочих, тыс.руб., y | ||||
| фактическая, y | расчетная, |
||||
| 1 | 12 | 10 | 0,167 | 4 | 0,16 |
| 2 | 8 | 10 | 0,250 | 4 | 12,96 |
| 3 | 13 | 13 | 0,000 | 0 | 1,96 |
| 4 | 15 | 14 | 0,067 | 1 | 11,56 |
| 5 | 16 | 15 | 0,063 | 1 | 19,36 |
| 6 | 11 | 12 | 0,091 | 1 | 0,36 |
| 7 | 12 | 13 | 0,083 | 1 | 0,16 |
| 8 | 9 | 10 | 0,111 | 1 | 6,76 |
| 9 | 11 | 10 | 0,091 | 1 | 0,36 |
| 10 | 9 | 9 | 0 | 0 | 6,76 |
| Итого: | - | - | 0,922 | 14 | 60,40 |
| Ср. значение | 11,6 | - | - | - | - |
Задача 2
Зависимость среднемесячной производительности труда от возраста рабочих характеризуется моделью ![]() . Ее использование привело к результатам, представленным в таблице:
. Ее использование привело к результатам, представленным в таблице:
| № | Производительность труда рабочих, тыс.руб., y | |
| фактическая | расчетная | |
| 1 | 12 | 10 |
| 2 | 8 | 10 |
| 3 | 13 | 13 |
| 4 | 15 | 14 |
| 5 | 16 | 15 |
| 6 | 11 | 12 |
| 7 | 12 | 13 |
| 8 | 9 | 10 |
| 9 | 11 | 10 |
| 10 | 9 | 9 |
Задание
Оцените качество модели, определив ошибку аппроксимации, индекс корреляции и F-критерий Фишера.
Решение
Значение средней ошибки аппроксимации находится по формуле:
![]()
![]()
Рассчитанное значение средней ошибки аппроксимации говорит о предельном качестве модели, поскольку близко подходит к критическому пределу в 10%.
Индекс корреляции (для нелинейной регрессии):

![]()
Найденное значение индекса корреляции говорит о наличии близкой зависимости среднемесячной производительности труда от возраста рабочих.
F-критерий Фишера:
 .
.
![]()
При уровне значимости α = 0,05, k1
= 1 (m) и k2
= 10 (n-m-1=10-1-1) степенях свободы табличное значение F-критерия Фишера ![]() .
.
![]() =26,5 >
=26,5 > ![]() =5,12, значит, H0
– гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность. Вывод: показатели рассчитанных коэффициентов позволяют предложить отобразить зависимость среднемесячной производительности труда от возраста рабочих выбором более точной модели путем введения дополнительных переменных, либо изменением уравнения регрессии.
=5,12, значит, H0
– гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность. Вывод: показатели рассчитанных коэффициентов позволяют предложить отобразить зависимость среднемесячной производительности труда от возраста рабочих выбором более точной модели путем введения дополнительных переменных, либо изменением уравнения регрессии.
Задача 3
регрессия аппроксимация корреляция спрос
Зависимость спроса на товар K от его цены характеризуется по 20 наблюдениям уравнением: ![]() . Доля остаточной дисперсии в общей составила 18%.
. Доля остаточной дисперсии в общей составила 18%.
Задание
1. Запишите данное уравнение в виде степенной функции.
2. Оцените эластичность спроса на товар в зависимости от его цены.
3. Определите индекс корреляции.
4. Оцените значимость уравнения регрессии через F-критерий Фишера. Сделайте выводы.
Решение.
1. Уравнение в виде степенной функции: ![]()
2. Эластичность степенной функции: ![]()
Фактором снижения спроса выступает его цена: с ростом цены на 1%, спрос снижается на 0,35%.
3. Индекс корреляции (для нелинейной регрессии):
Поскольку доля остаточной дисперсии в общей составила 18%, поэтому уравнение регрессии объясняется 82% дисперсии результативного признака, т. е. коэффициент детерминации равен R2 = 0,82.
Индекс корреляции находится: ![]() Величина индекса корреляции достаточно близка к 1 и означает наличие достаточно тесной связи объема спроса от размера цены.
Величина индекса корреляции достаточно близка к 1 и означает наличие достаточно тесной связи объема спроса от размера цены.
F –тест состоит в проверке гипотезы H0
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого сравнивается фактическое и критическое значение F-критерия Фишера. При уровне значимости α = 0,05, k1
= 1 (m) и k2
= 20 (n-m-1=20-1-1) степенях свободы табличное значение F-критерия Фишера ![]() :
:
 .
.
![]() >
> ![]() ,
,
то H0 – гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность.
Вывод: уравнение регрессии характеризует достаточно тесную зависимость спроса на товар K от его цены. Причем, наблюдается обратная зависимость: с увеличением цены, спрос падает.
Задача 4
Изучение влияния стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 12 торговым предприятиям были получены данные, приведенные в таблице:
| Номер предприятия | Валовой доход за год, млн.руб. | Среднегодовая стоимость, млн.руб. | |
| основных фондов | оборотных средств | ||
| 1 | 203 | 118 | 105 |
| 2 | 63 | 28 | 56 |
| 3 | 45 | 17 | 54 |
| 4 | 113 | 50 | 63 |
| 5 | 121 | 56 | 28 |
| 6 | 88 | 102 | 50 |
| 7 | 110 | 116 | 54 |
| 8 | 56 | 124 | 42 |
| 9 | 80 | 114 | 36 |
| 10 | 237 | 154 | 106 |
| 11 | 160 | 115 | 88 |
| 12 | 75 | 98 | 46 |
Задание
1. Постройте линейное уравнение множественной регрессии и поясните экономический смысл его параметров. Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия.
2. Рассчитайте средние коэффициенты эластичности.
3. Определите парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделайте выводы о силе связи результата и факторов.
4. Дайте оценку полученного уравнения на основе общего F-критерия Фишера.
5. Оцените качество уравнения через среднюю ошибку аппроксимации.
6. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
7. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение.
Построение линейной множественной регрессии сводится к оценке ее параметров – а, b1
и b2.
Для расчета параметров а, b1
и b2
уравнения регрессии ![]() решаем систему нормальных уравнений относительно а, b1
и b2
:
решаем систему нормальных уравнений относительно а, b1
и b2
:

По исходным данным произведем расчет предварительных параметров (табл. 4.1)
Таблица 4.1
| № | У | Х1 | Х2 | Х1 2 | Х2 2 | Х1 ·Х2 | У·Х1 | У·Х2 | ŷ |
| 1 | 203 | 118 | 105 | 13924,00 | 11025,00 | 12390,00 | 23954,00 | 21315,00 | 197,29 |
| 2 | 63 | 28 | 56 | 784,00 | 3136,00 | 1568,00 | 1764,00 | 3528,00 | 80,63 |
| 3 | 45 | 17 | 54 | 289,00 | 2916,00 | 918,00 | 765,00 | 2430,00 | 73,07 |
| 4 | 113 | 50 | 63 | 2500,00 | 3969,00 | 3150,00 | 5650,00 | 7119,00 | 100,80 |
| 5 | 121 | 56 | 28 | 3136,00 | 784,00 | 1568,00 | 6776,00 | 3388,00 | 44,39 |
| 6 | 88 | 102 | 50 | 10404,00 | 2500,00 | 5100,00 | 8976,00 | 4400,00 | 98,90 |
| 7 | 110 | 116 | 54 | 13456,00 | 2916,00 | 6264,00 | 12760,00 | 5940,00 | 110,97 |
| 8 | 56 | 124 | 42 | 15376,00 | 1764,00 | 5208,00 | 6944,00 | 2352,00 | 93,91 |
| 9 | 80 | 114 | 36 | 12996,00 | 1296,00 | 4104,00 | 9120,00 | 2880,00 | 80,01 |
| 10 | 237 | 154 | 106 | 23716,00 | 11236,00 | 16324,00 | 36498,00 | 25122,00 | 212,75 |
| 11 | 160 | 115 | 88 | 13225,00 | 7744,00 | 10120,00 | 18400,00 | 14080,00 | 167,62 |
| 12 | 75 | 98 | 46 | 9604,00 | 2116,00 | 4508,00 | 7350,00 | 3450,00 | 90,66 |
| Итого: | 1351,00 | 1092,0 | 728,0 | 119410,0 | 51402,0 | 71222,0 | 138957,0 | 96004,0 | 1351,00 |
Систему линейных уравнений удобно решать методом Крамера (метод определителей):
![]()


![]() - частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
- частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

частный определитель параметра а.
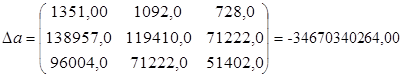

частный определитель параметра х1 .


частный определитель параметра х2 .

Теперь произведем расчет коэффициентов множественной регрессии:

Аналогичные результаты можно получить с помощью автоматической процедуры нахождения параметров «Анализ данных» → «Регрессия» MS Excel уравнения множественной регрессии:
Окончательно уравнение множественной регрессии, связывающее валовой доход за год (у) со средней стоимостью основных фондов (х1 ) и со средней стоимостью оборотных средств (х2 ) имеет вид:
![]()
Анализ данного уравнения позволяет сделать выводы – с увеличением среднегодовой стоимости основных фондов на 1 млн. руб. размер валового дохода возрастет в среднем на 380 тыс. руб., при том же стоимости оборотных средств. Увеличение среднегодовой стоимости оборотных средств на 1 млн. руб. при той же стоимости основных фондов предполагает дополнительное увеличение валового дохода за год на 1,68 млн. руб.
Для оценки статистической значимости коэффициентов регрессии рассчитываются t-критерий Стьюдента и доверительные интервалы для каждого из них. Выдвигается гипотеза H0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки по формулам:
![]() и
и ![]() .
.
Где случайные ошибки параметров линейной регрессии определяются следующим образом:
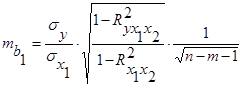 ;
; 
![]() средняя квадратическая ошибка i-го коэффициента регрессии (стандартная ошибка i-го коэффициента регрессии);
средняя квадратическая ошибка i-го коэффициента регрессии (стандартная ошибка i-го коэффициента регрессии);
![]() среднеквадратичное отклонение величины у;
среднеквадратичное отклонение величины у;
![]() среднеквадратичное отклонение величины х1
;
среднеквадратичное отклонение величины х1
;
![]() среднеквадратичное отклонение величины х2
;
среднеквадратичное отклонение величины х2
;

совокупный коэффициент множественной корреляции;

определитель матрицы парных коэффициентов корреляции;

определитель матрицы межфакторной корреляции. Как видно, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым их факторов, но и от межфакторной корреляции. Парный коэффициент корреляции между у и х1 рассчитывается по формуле:

Произведем расчет необходимых параметров в таблице 4.2
Таблица 4.2
| № | У | Х1 | |||||
| 1 | 203,0 | 118,0 | 90,4 | 27,0 | 2441,25 | 8175,17 | 729,00 |
| 2 | 63,0 | 28,0 | -49,6 | -63,0 | 3123,75 | 2458,51 | 3969,00 |
| 3 | 45,0 | 17,0 | -67,6 | -74,0 | 5001,17 | 4567,51 | 5476,00 |
| 4 | 113,0 | 50,0 | 0,4 | -41,0 | -17,08 | 0,17 | 1681,00 |
| 5 | 121,0 | 56,0 | 8,4 | -35,0 | -294,58 | 70,84 | 1225,00 |
| 6 | 88,0 | 102,0 | -24,6 | 11,0 | -270,42 | 604,34 | 121,00 |
| 7 | 110,0 | 116,0 | -2,6 | 25,0 | -64,58 | 6,67 | 625,00 |
| 8 | 56,0 | 124,0 | -56,6 | 33,0 | -1867,25 | 3201,67 | 1089,00 |
| 9 | 80,0 | 114,0 | -32,6 | 23,0 | -749,42 | 1061,67 | 529,00 |
| 10 | 237,0 | 154,0 | 124,4 | 63,0 | 7838,25 | 15479,51 | 3969,00 |
| 11 | 160,0 | 115,0 | 47,4 | 24,0 | 1138,00 | 2248,34 | 576,00 |
| 12 | 75,0 | 98,0 | -37,6 | 7,0 | -263,08 | 1412,51 | 49,00 |
| Итого | 1351,00 | 1092,00 | 16016,00 | 39286,92 | 20038,00 | ||
| Среднее значение | 112,6 | 91,0 |
Тогда коэффициент корреляции между у и х1 составит:
![]()
Парный коэффициент корреляции между у и х2 рассчитывается по формуле:

Произведем расчет необходимых параметров в таблице 4.3
Таблица 4.3
| № | У | Х2 | |||||
| 1 | 203,0 | 105,0 | 90,4 | 44,3 | 4008,47 | 8175,17 | 1965,44 |
| 2 | 63,0 | 56,0 | -49,6 | -4,7 | 231,39 | 2458,51 | 21,78 |
| 3 | 45,0 | 54,0 | -67,6 | -6,7 | 450,56 | 4567,51 | 44,44 |
| 4 | 113,0 | 63,0 | 0,4 | 2,3 | 0,97 | 0,17 | 5,44 |
| 5 | 121,0 | 28,0 | 8,4 | -32,7 | -274,94 | 70,84 | 1067,11 |
| 6 | 88,0 | 50,0 | -24,6 | -10,7 | 262,22 | 604,34 | 113,78 |
| 7 | 110,0 | 54,0 | -2,6 | -6,7 | 17,22 | 6,67 | 44,44 |
| 8 | 56,0 | 42,0 | -56,6 | -18,7 | 1056,22 | 3201,67 | 348,44 |
| 9 | 80,0 | 36,0 | -32,6 | -24,7 | 803,72 | 1061,67 | 608,44 |
| 10 | 237,0 | 106,0 | 124,4 | 45,3 | 5640,22 | 15479,51 | 2055,11 |
| 11 | 160,0 | 88,0 | 47,4 | 27,3 | 1296,06 | 2248,34 | 747,11 |
| 12 | 75,0 | 46,0 | -37,6 | -14,7 | 551,22 | 1412,51 | 215,11 |
| Итого | 1351,00 | 728,00 | 14043,33 | 39286,92 | 7236,67 | ||
| Среднее значение | 112,6 | 60,7 |
Тогда коэффициент корреляции между у и х2 составит:
![]()
Парный коэффициент корреляции между х1 и х2 рассчитывается по формуле:

Произведем расчет необходимых параметров в таблице 4.4
Таблица 4.4
| № | х1 | х2 | |||||
| 1 | 118,0 | 105,0 | 27,0 | 44,3 | 1197,00 | 729,00 | 1965,44 |
| 2 | 28,0 | 56,0 | -63,0 | -4,7 | 294,00 | 3969,00 | 21,78 |
| 3 | 17,0 | 54,0 | -74,0 | -6,7 | 493,33 | 5476,00 | 44,44 |
| 4 | 50,0 | 63,0 | -41,0 | 2,3 | -95,67 | 1681,00 | 5,44 |
| 5 | 56,0 | 28,0 | -35,0 | -32,7 | 1143,33 | 1225,00 | 1067,11 |
| 6 | 102,0 | 50,0 | 11,0 | -10,7 | -117,33 | 121,00 | 113,78 |
| 7 | 116,0 | 54,0 | 25,0 | -6,7 | -166,67 | 625,00 | 44,44 |
| 8 | 124,0 | 42,0 | 33,0 | -18,7 | -616,00 | 1089,00 | 348,44 |
| 9 | 114,0 | 36,0 | 23,0 | -24,7 | -567,33 | 529,00 | 608,44 |
| 10 | 154,0 | 106,0 | 63,0 | 45,3 | 2856,00 | 3969,00 | 2055,11 |
| 11 | 115,0 | 88,0 | 24,0 | 27,3 | 656,00 | 576,00 | 747,11 |
| 12 | 98,0 | 46,0 | 7,0 | -14,7 | -102,67 | 49,00 | 215,11 |
| Итого | 1092,00 | 728,00 | 4974,00 | 20038,00 | 7236,67 | ||
| Средне значение | 91,0 | 60,7 |
Тогда коэффициент корреляции между х1 и х2 составит:
![]()
При трех переменных для двухфакторного уравнения регрессии рассчитаем определители матрицы парной корреляции и межфакторной корреляции:
 ;
;

Тогда совокупный коэффициент множественной корреляции составит:

По данным из табл. 2, 3 рассчитаем теперь среднее квадратическое отклонение величин у, х1 и х2 по формулам:

Рассчитаем теперь средние квадратические ошибки коэффициентов регрессии b1 и b2

Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значений:

При уровне значимости α = 0,05, df = 11 (n-m-1=12-2-1) степенях свободы табличное значение t-критерия Стьюдента 2,26.
Сравнив его с расчетными значениями, получаем, что ![]() , из чего следует, что гипотезу о несущественности параметра b2
с вероятностью 95% (p = 1 – α) следует отклонить. А вот
, из чего следует, что гипотезу о несущественности параметра b2
с вероятностью 95% (p = 1 – α) следует отклонить. А вот ![]() из чего следует, что гипотезу о несущественности параметра b1
с вероятностью 95% (p = 1 – α) следует принять и признается статистическая незначимость параметра b1
.
из чего следует, что гипотезу о несущественности параметра b1
с вероятностью 95% (p = 1 – α) следует принять и признается статистическая незначимость параметра b1
.
2. Для характеристики относительной силы влияния х1 и х2 на у используя коэффициенты регрессии можно рассчитать средние коэффициенты эластичности. Как правило, их рассчитывают для средних значений факторов и результатов.

С увеличением среднегодовой стоимости основных фондов (х1 ) на 1% от его среднего уровня, средний объем валового дохода за год увеличится на 0,37% от своего среднего уровня; при повышении среднегодовой стоимости оборотных средств на 1% - увеличится на 0,53% от своего среднего уровня. Очевидно, что сила влияния средней стоимости оборотных средств (х2 ) на валовой доход (у) оказалась сильнее, чем сила влияния средней стоимости основных фондов (х1 ).
Рассчитаем линейные коэффициенты частной корреляции

Расчёт линейного коэффициента множественной корреляции и коэффициентов парной корреляции выполнен в п.1 Коэффициент множественной детерминации рассчитывается как квадрат коэффициента множественной корреляции:
![]() Зависимость у от х1
и х2
характеризуется как тесная, в которой 76% вариации валового дохода определяются вариацией учтенных в модели факторов: среднегодовой стоимости основных фондов и среднегодовой стоимости оборотных средств. Прочие факторы, не включенные в модель, составляют соответственно 14% от общей вариации у.
Зависимость у от х1
и х2
характеризуется как тесная, в которой 76% вариации валового дохода определяются вариацией учтенных в модели факторов: среднегодовой стоимости основных фондов и среднегодовой стоимости оборотных средств. Прочие факторы, не включенные в модель, составляют соответственно 14% от общей вариации у.
4. F –тест Фишера состоит в проверке гипотезы H0
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого сравнивается фактическое и критическое значение F-критерия Фишера. При уровне значимости α = 0,05, k1
= 2 (m) и k2
= 9 (n-m-1=12-2-1) степенях свободы табличное значение F-критерия Фишера: ![]()
![]()
Таблица 4.5
| № | у | ŷ | ||
| 1 | 203 | 197,29 | 7174,61 | 32,65 |
| 2 | 63 | 80,63 | 1020,85 | 310,91 |
| 3 | 45 | 73,07 | 1561,63 | 787,69 |
| 4 | 113 | 100,80 | 138,89 | 148,88 |
| 5 | 121 | 44,39 | 4650,78 | 5869,60 |
| 6 | 88 | 98,90 | 187,15 | 118,88 |
| 7 | 110 | 110,97 | 2,59 | 0,95 |
| 8 | 56 | 93,91 | 348,78 | 1437,00 |
| 9 | 80 | 80,01 | 1060,74 | 0,00 |
| 10 | 237 | 212,75 | 10033,02 | 588,14 |
| 11 | 160 | 167,62 | 3029,24 | 58,09 |
| 12 | 75 | 90,66 | 480,55 | 245,29 |
| Сумма | 1351,00 | 29688,8 | 9598,1 |
Тогда
![]()
![]() >
> ![]() , значит, H0
– гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность.
, значит, H0
– гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность.
Значение средней ошибки аппроксимации найдем по формуле:
![]()
Таблица.4.6 Расчет ошибки аппроксимации
№ |
у | ŷ | |
| 1 | 203,0 | 197,29 | 0,03 |
| 2 | 63,0 | 80,63 | 0,28 |
| 3 | 45,0 | 73,07 | 0,62 |
| 4 | 113,0 | 100,80 | 0,11 |
| 5 | 121,0 | 44,39 | 0,63 |
| 6 | 88,0 | 98,90 | 0,12 |
| 7 | 110,0 | 110,97 | 0,01 |
| 8 | 56,0 | 93,91 | 0,68 |
| 9 | 80,0 | 80,01 | 0,00 |
| 10 | 237,0 | 212,75 | 0,10 |
| 11 | 160,0 | 167,62 | 0,05 |
| 12 | 75,0 | 90,66 | 0,21 |
| 13 | 1351,0 | 1351,0 | 2,8 |
| 14 | 203,0 | 197,29 | 0,03 |
| Сумма | 63,0 | 80,63 | 0,28 |
![]()
Ошибка аппроксимации показала очень сильное отличие фактического значения результативного признака от теоретического, рассчитанного по множественному уравнению регрессии, что свидетельствует о плохом выборе уравнения регрессии.
Рассчитаем прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
Задача 5
Имеются данные об объемах продаж в перерабатывающей промышленности и торговле США в течение 5 лет в сопоставимых ценах в млрд. долл.
| Месяц | 1 год | 2 год | 3 год | 4 год | 5 год |
| Январь | 472,5 | 477,9 | 510,9 | 541,0 | 578,2 |
| Февраль | 482,1 | 467,5 | 484,7 | 512,3 | 539,4 |
| Март | 489,5 | 470,9 | 486,6 | 512,6 | 545,3 |
| Апрель | 493,6 | 469,1 | 488,4 | 511,5 | 551,9 |
| Май | 488,0 | 478,1 | 489,5 | 511,9 | 549,7 |
| Июнь | 490,6 | 480,6 | 486,6 | 513,9 | 550,1 |
| Июль | 492,5 | 479,3 | 491,8 | 520,0 | 554,0 |
| Август | 488,1 | 484,2 | 495,2 | 515,9 | 550,0 |
| Сентябрь | 493,1 | 484,9 | 491,8 | 524,2 | 565,6 |
| Октябрь | 484,5 | 485,6 | 496,1 | 527,1 | 564,7 |
| Ноябрь | 483,0 | 486,1 | 498,8 | 529,8 | 566,9 |
| Декабрь | 476,9 | 484,7 | 501,5 | 534,9 | 572,7 |
Задание
Рассчитайте трендовую и сезонную компоненты. Постройте мультипликативную модель этого ряда. Найдите наиболее целесообразный вариант построения уравнения авторегрессии через расчет коэффициентов автокорреляции первого, второго и третьего порядка. Охарактеризуйте структуру этого ряда.
Решение
1. Расчет оценок сезонной компоненты в мультипликативной модели
Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние. Используем эти оценки для расчета значений сезонной компоненты S. Для этого найдем средние за каждый месяц (по всем годам) оценки сезонной компоненты Sj . Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем месяцам должна быть равна числу периодов в цикле, т.е. двенадцати, так как в нашем случае число периодов одного цикла (год) равно 12 месяцам. Для данной модели имеем:
![]() .
.
Определим корректирующий коэффициент:
![]() .
.
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
![]() ,
,
где ![]() .
.
Проверим условие равенства двенадцати суммы значений сезонной компоненты:
![]() .
.
Таким образом, получены следующие значения сезонной компоненты:
Элиминируем влияние сезонной компоненты, разделив значение каждого уровня исходного временного ряда на соответствующие значения сезонной компоненты. Получим T∙E=Y/S, значения, которые содержат только тенденцию и случайную компоненту.
Таблица 5.3 Расчет выравненных значений Т и ошибок Е в мультипликативной модели
| t | y | S | y/S | T | T·S | E | |||
| 1 | 472,5 | 1,045 | 452,024 | 462,884 | 483,852 | 1223,600 | 0,977 | -11,352 | 128,866 |
| 2 | 482,1 | 0,992 | 486,039 | 464,396 | 460,632 | 644,144 | 1,047 | 21,468 | 460,863 |
| 3 | 489,5 | 0,995 | 492,032 | 465,908 | 463,510 | 323,280 | 1,056 | 25,990 | 675,460 |
| 4 | 493,6 | 0,994 | 496,428 | 467,419 | 464,757 | 192,654 | 1,062 | 28,843 | 831,923 |
| 5 | 488 | 0,996 | 490,190 | 468,931 | 466,836 | 379,470 | 1,045 | 21,164 | 447,915 |
| 6 | 490,6 | 0,993 | 494,071 | 470,443 | 467,138 | 284,934 | 1,050 | 23,462 | 550,462 |
| 7 | 492,5 | 1,000 | 492,362 | 471,955 | 472,087 | 224,400 | 1,043 | 20,413 | 416,700 |
| 8 | 488,1 | 0,997 | 489,587 | 473,466 | 472,028 | 375,584 | 1,034 | 16,072 | 258,315 |
| 9 | 493,1 | 1,000 | 493,166 | 474,978 | 474,915 | 206,784 | 1,038 | 18,185 | 330,712 |
| 10 | 484,5 | 0,997 | 485,935 | 476,490 | 475,083 | 528,080 | 1,020 | 9,417 | 88,688 |
| 11 | 483 | 0,997 | 484,563 | 478,001 | 476,459 | 599,270 | 1,014 | 6,541 | 42,783 |
| 12 | 476,9 | 0,994 | 479,676 | 479,513 | 476,738 | 935,136 | 1,000 | 0,162 | 0,026 |
| 13 | 477,9 | 1,045 | 457,190 | 481,025 | 502,814 | 874,976 | 0,950 | -24,914 | 620,722 |
| 14 | 467,5 | 0,992 | 471,320 | 482,537 | 478,626 | 1598,400 | 0,977 | -11,126 | 123,785 |
| 15 | 470,9 | 0,995 | 473,336 | 484,048 | 481,558 | 1338,096 | 0,978 | -10,658 | 113,586 |
| 16 | 469,1 | 0,994 | 471,787 | 485,560 | 482,794 | 1473,024 | 0,972 | -13,694 | 187,532 |
| 17 | 478,1 | 0,996 | 480,246 | 487,072 | 484,896 | 863,184 | 0,986 | -6,796 | 46,180 |
| 18 | 480,6 | 0,993 | 484,000 | 488,584 | 485,151 | 722,534 | 0,991 | -4,551 | 20,714 |
| 19 | 479,3 | 1,000 | 479,166 | 490,095 | 490,233 | 794,112 | 0,978 | -10,933 | 119,520 |
| 20 | 484,2 | 0,997 | 485,676 | 491,607 | 490,113 | 541,958 | 0,988 | -5,913 | 34,968 |
| 21 | 484,9 | 1,000 | 484,965 | 493,119 | 493,053 | 509,856 | 0,983 | -8,153 | 66,467 |
| 22 | 485,6 | 0,997 | 487,038 | 494,630 | 493,170 | 478,734 | 0,985 | -7,570 | 57,300 |
| 23 | 486,1 | 0,997 | 487,674 | 496,142 | 494,541 | 457,104 | 0,983 | -8,441 | 71,255 |
| 24 | 484,7 | 0,994 | 487,521 | 497,654 | 494,774 | 518,928 | 0,980 | -10,074 | 101,480 |
| 25 | 510,9 | 1,045 | 488,760 | 499,166 | 521,777 | 11,696 | 0,979 | -10,877 | 118,302 |
| 26 | 484,7 | 0,992 | 488,660 | 500,677 | 496,620 | 518,928 | 0,976 | -11,920 | 142,075 |
| 27 | 486,6 | 0,995 | 489,117 | 502,189 | 499,605 | 435,974 | 0,974 | -13,005 | 169,130 |
| 28 | 488,4 | 0,994 | 491,198 | 503,701 | 500,832 | 364,046 | 0,975 | -12,432 | 154,543 |
| 29 | 489,5 | 0,996 | 491,697 | 505,212 | 502,955 | 323,280 | 0,973 | -13,455 | 181,042 |
| 30 | 486,6 | 0,993 | 490,042 | 506,724 | 503,164 | 435,974 | 0,967 | -16,564 | 274,382 |
| 31 | 491,8 | 1,000 | 491,662 | 508,236 | 508,378 | 245,862 | 0,967 | -16,578 | 274,837 |
| 32 | 495,2 | 0,997 | 496,709 | 509,748 | 508,199 | 150,798 | 0,974 | -12,999 | 168,971 |
| 33 | 491,8 | 1,000 | 491,866 | 511,259 | 511,191 | 245,862 | 0,962 | -19,391 | 376,008 |
| 34 | 496,1 | 0,997 | 497,569 | 512,771 | 511,257 | 129,504 | 0,970 | -15,157 | 229,726 |
| 35 | 498,8 | 0,997 | 500,415 | 514,283 | 512,623 | 75,342 | 0,973 | -13,823 | 191,086 |
| 36 | 501,5 | 0,994 | 504,419 | 515,794 | 512,809 | 35,760 | 0,978 | -11,309 | 127,902 |
| 37 | 541 | 1,045 | 517,556 | 517,306 | 540,739 | 1123,590 | 1,000 | 0,261 | 0,068 |
| 38 | 512,3 | 0,992 | 516,486 | 518,818 | 514,613 | 23,232 | 0,996 | -2,313 | 5,351 |
| 39 | 512,6 | 0,995 | 515,251 | 520,330 | 517,652 | 26,214 | 0,990 | -5,052 | 25,526 |
| 40 | 511,5 | 0,994 | 514,430 | 521,841 | 518,869 | 16,160 | 0,986 | -7,369 | 54,300 |
| 41 | 511,9 | 0,996 | 514,197 | 523,353 | 521,015 | 19,536 | 0,983 | -9,115 | 83,079 |
| 42 | 513,9 | 0,993 | 517,536 | 524,865 | 521,178 | 41,216 | 0,986 | -7,278 | 52,965 |
| 43 | 520 | 1,000 | 519,854 | 526,376 | 526,524 | 156,750 | 0,988 | -6,524 | 42,562 |
| 44 | 515,9 | 0,997 | 517,472 | 527,888 | 526,284 | 70,896 | 0,980 | -10,384 | 107,836 |
| 45 | 524,2 | 1,000 | 524,270 | 529,400 | 529,329 | 279,558 | 0,990 | -5,129 | 26,308 |
| 46 | 527,1 | 0,997 | 528,661 | 530,912 | 529,344 | 384,944 | 0,996 | -2,244 | 5,035 |
| 47 | 529,8 | 0,997 | 531,515 | 532,423 | 530,705 | 498,182 | 0,998 | -0,905 | 0,820 |
| 48 | 534,9 | 0,994 | 538,014 | 533,935 | 530,845 | 751,856 | 1,008 | 4,055 | 16,443 |
| 49 | 578,2 | 1,045 | 553,144 | 535,447 | 559,701 | 5001,318 | 1,033 | 18,499 | 342,198 |
| 50 | 539,4 | 0,992 | 543,807 | 536,959 | 532,607 | 1018,886 | 1,013 | 6,793 | 46,148 |
| 51 | 545,3 | 0,995 | 548,120 | 538,470 | 535,700 | 1430,352 | 1,018 | 9,600 | 92,168 |
| 52 | 551,9 | 0,994 | 555,062 | 539,982 | 536,906 | 1973,136 | 1,028 | 14,994 | 224,816 |
| 53 | 549,7 | 0,996 | 552,167 | 541,494 | 539,074 | 1782,528 | 1,020 | 10,626 | 112,904 |
| 54 | 550,1 | 0,993 | 553,992 | 543,005 | 539,191 | 1816,464 | 1,020 | 10,909 | 119,009 |
| 55 | 554 | 1,000 | 553,845 | 544,517 | 544,670 | 2164,110 | 1,017 | 9,330 | 87,055 |
| 56 | 550 | 0,997 | 551,676 | 546,029 | 544,370 | 1807,950 | 1,010 | 5,630 | 31,698 |
| 57 | 565,6 | 1,000 | 565,676 | 547,541 | 547,467 | 3377,934 | 1,033 | 18,133 | 328,793 |
| 58 | 564,7 | 0,997 | 566,373 | 549,052 | 547,431 | 3274,128 | 1,032 | 17,269 | 298,224 |
| 59 | 566,9 | 0,997 | 568,735 | 550,564 | 548,788 | 3530,736 | 1,033 | 18,112 | 328,060 |
| 60 | 572,7 | 0,994 | 576,034 | 552,076 | 548,881 | 4253,648 | 1,043 | 23,819 | 567,361 |
| Итого | 52661,016 | 60,006 | 1,751 | 11202,95 |
Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (T∙E) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
Таким образом, имеем линейный тренд:
![]() .
.
Подставив в это уравнение значение t = 1, 2, …, 60, найдем уровни Т для каждого момента времени.
Найдем значения уровней ряда, полученные по мультипликативной модели, умножив уровни Т на значения сезонной компоненты для соответствующих месяцев.
Расчет ошибки в мультипликативной модели проводится по формуле:
![]() .
.
Численные значения ошибок приведены в таблице
Для оценки качества построения мультипликативной модели можно использовать сумму квадратов абсолютных ошибок![]() . Для данной мультипликативной модели сумма квадратов абсолютных ошибок равна 11202,95. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 52661,016, эта величина составляет 21,2%:
. Для данной мультипликативной модели сумма квадратов абсолютных ошибок равна 11202,95. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 52661,016, эта величина составляет 21,2%:
![]() .
.
Следовательно, можно сказать, что мультипликативная модель объясняет 78,8% общей вариации уровней временного ряда объема продаж в перерабатывающей промышленности и торговле США за последние 60 месяцев. Мультипликативная модель построена.
При этом при расчете коэффициента автокорреляции первого порядка параметрами будут являться значения исходного ряда ![]() и значения ряда с отставанием на 1
и значения ряда с отставанием на 1 ![]() .
.

 ;
; 
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков.
Таблица 5.4 Расчет коэффициента автокорреляции первого порядка
| t | y | ||||||
| 1 | 472,5 | - | - | - | - | - | - |
| 2 | 482,1 | 472,5 | -25,9729 | -33,8746 | 879,8204 | 674,5906 | 1147,4869 |
| 3 | 489,5 | 482,1 | -18,5729 | -24,2746 | 450,8488 | 344,9519 | 589,2551 |
| 4 | 493,6 | 489,5 | -14,4729 | -16,8746 | 244,2237 | 209,4643 | 284,7513 |
| 5 | 488 | 493,6 | -20,0729 | -12,7746 | 256,4226 | 402,9206 | 163,1898 |
| 6 | 490,6 | 488 | -17,4729 | -18,3746 | 321,0568 | 305,3016 | 337,6251 |
| 7 | 492,5 | 490,6 | -15,5729 | -15,7746 | 245,6556 | 242,5146 | 248,8373 |
| 8 | 488,1 | 492,5 | -19,9729 | -13,8746 | 277,1153 | 398,9160 | 192,5039 |
| 9 | 493,1 | 488,1 | -14,9729 | -18,2746 | 273,6231 | 224,1872 | 333,9601 |
| 10 | 484,5 | 493,1 | -23,5729 | -13,2746 | 312,9200 | 555,6807 | 176,2144 |
| 11 | 483 | 484,5 | -25,0729 | -21,8746 | 548,4587 | 628,6494 | 478,4971 |
| 12 | 476,9 | 483 | -31,1729 | -23,3746 | 728,6529 | 971,7485 | 546,3708 |
| 13 | 477,9 | 476,9 | -30,1729 | -29,4746 | 889,3329 | 910,4028 | 868,7506 |
| 14 | 467,5 | 477,9 | -40,5729 | -28,4746 | 1155,2956 | 1646,1587 | 810,8015 |
| 15 | 470,9 | 467,5 | -37,1729 | -38,8746 | 1445,0800 | 1381,8231 | 1511,2327 |
| 16 | 469,1 | 470,9 | -38,9729 | -35,4746 | 1382,5465 | 1518,8855 | 1258,4456 |
| 17 | 478,1 | 469,1 | -29,9729 | -37,2746 | 1117,2265 | 898,3736 | 1389,3940 |
| 18 | 480,6 | 478,1 | -27,4729 | -28,2746 | 776,7841 | 754,7592 | 799,4517 |
| 19 | 479,3 | 480,6 | -28,7729 | -25,7746 | 741,6088 | 827,8787 | 664,3288 |
| 20 | 484,2 | 479,3 | -23,8729 | -27,0746 | 646,3481 | 569,9145 | 733,0327 |
| 21 | 484,9 | 484,2 | -23,1729 | -22,1746 | 513,8488 | 536,9824 | 491,7118 |
| 22 | 485,6 | 484,9 | -22,4729 | -21,4746 | 482,5956 | 505,0304 | 461,1574 |
| 23 | 486,1 | 485,6 | -21,9729 | -20,7746 | 456,4773 | 482,8075 | 431,5830 |
| 24 | 484,7 | 486,1 | -23,3729 | -20,2746 | 473,8753 | 546,2916 | 411,0584 |
| 25 | 510,9 | 484,7 | 2,8271 | -21,6746 | -61,2766 | 7,9926 | 469,7873 |
| 26 | 484,7 | 510,9 | -23,3729 | 4,5254 | -105,7722 | 546,2916 | 20,4795 |
| 27 | 486,6 | 484,7 | -21,4729 | -21,6746 | 465,4156 | 461,0846 | 469,7873 |
| 28 | 488,4 | 486,6 | -19,6729 | -19,7746 | 389,0229 | 387,0223 | 391,0339 |
| 29 | 489,5 | 488,4 | -18,5729 | -17,9746 | 333,8397 | 344,9519 | 323,0854 |
| 30 | 486,6 | 489,5 | -21,4729 | -16,8746 | 362,3458 | 461,0846 | 284,7513 |
| 31 | 491,8 | 486,6 | -16,2729 | -19,7746 | 321,7893 | 264,8067 | 391,0339 |
| 32 | 495,2 | 491,8 | -12,8729 | -14,5746 | 187,6168 | 165,7111 | 212,4183 |
| 33 | 491,8 | 495,2 | -16,2729 | -11,1746 | 181,8426 | 264,8067 | 124,8712 |
| 34 | 496,1 | 491,8 | -11,9729 | -14,5746 | 174,4997 | 143,3499 | 212,4183 |
| 35 | 498,8 | 496,1 | -9,2729 | -10,2746 | 95,2749 | 85,9863 | 105,5669 |
| 36 | 501,5 | 498,8 | -6,5729 | -7,5746 | 49,7868 | 43,2028 | 57,3742 |
| 37 | 541 | 501,5 | 32,9271 | -4,8746 | -160,5058 | 1084,1951 | 23,7615 |
| 38 | 512,3 | 541 | 4,2271 | 34,6254 | 146,3658 | 17,8685 | 1198,9200 |
| 39 | 512,6 | 512,3 | 4,5271 | 5,9254 | 26,8251 | 20,4948 | 35,1106 |
| 40 | 511,5 | 512,6 | 3,4271 | 6,2254 | 21,3353 | 11,7451 | 38,7559 |
| 41 | 511,9 | 511,5 | 3,8271 | 5,1254 | 19,6156 | 14,6468 | 26,2700 |
| 42 | 513,9 | 511,9 | 5,8271 | 5,5254 | 32,1973 | 33,9553 | 30,5303 |
| 43 | 520 | 513,9 | 11,9271 | 7,5254 | 89,7566 | 142,2562 | 56,6320 |
| 44 | 515,9 | 520 | 7,8271 | 13,6254 | 106,6478 | 61,2638 | 185,6522 |
| 45 | 524,2 | 515,9 | 16,1271 | 9,5254 | 153,6176 | 260,0840 | 90,7337 |
| 46 | 527,1 | 524,2 | 19,0271 | 17,8254 | 339,1665 | 362,0312 | 317,7457 |
| 47 | 529,8 | 527,1 | 21,7271 | 20,7254 | 450,3037 | 472,0677 | 429,5432 |
| 48 | 534,9 | 529,8 | 26,8271 | 23,4254 | 628,4366 | 719,6943 | 548,7505 |
| 49 | 578,2 | 534,9 | 70,1271 | 28,5254 | 2000,4058 | 4917,8128 | 813,6998 |
| 50 | 539,4 | 578,2 | 31,3271 | 71,8254 | 2250,0836 | 981,3884 | 5158,8915 |
| 51 | 545,3 | 539,4 | 37,2271 | 33,0254 | 1229,4414 | 1385,8584 | 1090,6786 |
| 52 | 551,9 | 545,3 | 43,8271 | 38,9254 | 1705,9892 | 1920,8163 | 1515,1886 |
| 53 | 549,7 | 551,9 | 41,6271 | 45,5254 | 1895,0922 | 1732,8170 | 2072,5642 |
| 54 | 550,1 | 549,7 | 42,0271 | 43,3254 | 1820,8427 | 1766,2787 | 1877,0923 |
| 55 | 554 | 550,1 | 45,9271 | 43,7254 | 2008,1827 | 2109,3002 | 1911,9127 |
| 56 | 550 | 554 | 41,9271 | 47,6254 | 1996,7968 | 1757,8833 | 2268,1810 |
| 57 | 565,6 | 550 | 57,5271 | 43,6254 | 2509,6449 | 3309,3694 | 1903,1776 |
| 58 | 564,7 | 565,6 | 56,6271 | 59,2254 | 3353,7651 | 3206,6306 | 3507,6508 |
| 59 | 566,9 | 564,7 | 58,8271 | 58,3254 | 3431,1166 | 3460,6299 | 3401,8551 |
| 60 | 572,7 | 566,9 | 64,6271 | 60,5254 | 3911,5837 | 4176,6645 | 3663,3269 |
| Итого | 29973,6 | 29876,1 | 46980,9093 | 52640,2766 | 49558,8719 |

Рассчитав коэффициент автокорреляции второго порядка r2
, получим количественную характеристику корреляционной связи рядов ![]() ,
, ![]() :
: ![]() .
.
Аналогично рассчитаем коэффициент автокорреляции третьего порядка: ![]() .
.
Можно сделать вывод, что наиболее целесообразно построение уравнения авторегрессии так как значение ![]() свидетельствует о наличии очень тесной связи между уровнями ряда с лагом в 1 месяц.
свидетельствует о наличии очень тесной связи между уровнями ряда с лагом в 1 месяц.
Похожие рефераты:
Демографическая ситуация в Республике Бурятия
Линейный множественный регрессивный анализ
Построение математических моделей
Методы решения уравнений, содержащих параметр
Экономико-математические методы анализа
Составление и решение уравнений линейной регрессии
Особенности эконометрического метода