| Похожие рефераты | Скачать .docx |
Курсовая работа: Экономико-математические модели задач о смесях на примере СПК "Родина"
Министерство образования Республики Беларусь
Учреждение Образования
Гомельский государственный технический университет имени П.О. Сухого
Кафедра «Экономика и управление в отраслях»
Курсовая работа
по курсу: «Экономико-математические методы и модели»
на тему:
Экономико-математические модели задач о смесях на примере СПК «Родина»
Выполнил
студент гр. ОП-31
Градов Ю.И
Руководитель: Кожевников Е.А.
Гомель, 2008
Содержание
Введение
Глава 1. Теоретические основы экономико-математических задач о смесях
1.1 Общая классификация экономико-математических моделей
1.2 Принципы построения и структура интегрированной системы экономико-математических моделей
Глава 2.Методы решения экономико-математических задач о смесях
2.1Основные типы линейных экономико-математических моделей
2.2 Методы решения задач о смесях
Глава 3.Постановка и решение экономико-математических смесей на примере СПК «Родина»
3.1Организационно-экономическая характеристика СПК «Родина»
3.2Основныетехнико-экономических показатели работы СПК «Родина»
3.3Постановка и решение собственно задачи о смесях на примере СПК «Родина»
Заключение
Список использованной литературы
Введение
Успешность решения подавляющего большинства экономических задач зависит от наилучшего, наивыгоднейшего способа использования ресурсов. В процессе экономической деятельности приходится распределять такие важные ресурсы, как деньги, товары, сырье, оборудование, рабочую силу и др. И от того, как будут распределяться эти, как правило, ограниченные ресурсы, зависит конечный результат деятельности, бизнеса.
Суть методов оптимизации заключается в том, что исходя из наличия определенных ресурсов выбирается такой способ их использования (распределения), при котором обеспечивается максимум (или минимум) интересующего нас показателя.
При этом учитываются определенные ограничения, налагаемые на использование ресурсов условиями экономической ситуации.
Отличительными признаками оптимизационных моделей являются:
- наличие одного или нескольких критериев оптимальности (критерий оптимальности - это признак, по которому множество или одно решение задачи признается наилучшим); наиболее типичными критериями в экономических оптимизационных задачах являются: максимум дохода или прибыли, минимум издержек, минимальное время для выполнения задания и другие;
- система ограничений, которая формируется, исходя из содержательной постановки задачи, и представляет собой систему уравнений или неравенств.
В качестве методов оптимизации в экономике находят применение все основные разделы математического программирования (планирования): линейное, нелинейное и динамическое.
Линейное программирование (планирование) - математический метод отыскания максимума или минимума линейной функции при наличии ограничений в виде линейных неравенств или уравнений. (Линейное здесь означает, что на графике функции изображаются в виде прямых линий, обозначающих 1-е степени соответствующих величин.)
Максимизируемая (минимизируемая) функция представляет собой принятый критерий эффективности решения задачи, соответствующий поставленной цели. Она носит название целевой функции.
Ограничения характеризуют имеющиеся возможности решения задачи.
Существо решения задач линейного программирования заключается в нахождении условий, обращающих целевую функцию в минимум или максимум.[7. c.13]
Решение, удовлетворяющее условиям задачи и соответствующее намеченной цели, называется оптимальным планом.
Линейное программирование (планирование) служит для выбора наилучшего плана распределения ограниченных однородных ресурсов в целях решения поставленной задачи.
Этапы построения оптимизационных экономико-математических моделей.
1) Выбор объекта исследования. Ими могут быть различные производственно-экономические процессы: раскрой промышленного материала, загрузка производственных мощностей, перевозка грузов, размещение производства и т.д.
2) Определение цели исследования. Ее формулируют на основе задач, поставленных при изучении данного объекта.
3) Выбор критерия оптимальности. Отличительной особенностью оптимизационных моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функций.
Критериями оптимальности обычно служат: минимальная стоимость, максимальный доход, минимальные издержки и т.д. Неправильно выбранный критерий оптимальности может привести к решению, не отвечающему цели поставленной задачи.
4) Выявление основных ограничений. При построении моделей необходимо найти основные ограничения и включить их в модель. Реальная задача обычно содержит большое число ограничений, часть из которых вытекает из условия задачи, другие можно выявить лишь после решения, которое по каким-либо требованиям не устраивает.
Целью данной курсовой работы является изучениематематических моделей оптимального планирования производства на сельскохозяйственном предприятии, а также возможности их применения на реальном объекте хозяйственной деятельности.
Тема, рассматриваемая в данной курсовой работе, довольно широко освещена в литературе. При написании работы использовались, например, работы таких авторов, как: Гасс С.И., Вагин Е.А., Попов И.П., Барсов А.С. и других.
Данная курсовая работа состоит из введения, трех глав, списка использованной литературы и приложений. В первой главе описаны общая классификация экономико-математических моделей, принципы построения и структура интегрированной системы экономико-математических моделей.
Вторая глава состоит из двух подразделов, в которых описываются основные типы линейных экономико-математических моделей и методы решения задач о смесях.В третьей главе – организационно-экономическая характеристика и технико-экономические показатели работы СПК «Родина», постановка и решение задачи о смесях на примереСПК «Родина».
Решение задачи о рационе производилось при помощи ресурса Поиск решения MSExcel ввиду сложности построенной экономико-математической модели. Описание методики вычисления с помощью данного инструмента приведено в третьей главе.
Глава 1. Теоретические основы экономико-математических задач о смесях
1.1 Общая классификация экономико-математических моделей
Экономико-математические модели подразделяются на: статистические, балансовые и оптимизационные.
Статистические модели – это модели, в которых описываются корреляционно-регрессионые зависимости результата производства от одного или нескольких независимых факторов. Эти модели широко используются для построения производственных функций, а также при анализе экономических систем.
Балансовые модели представляют систему балансов производства и распределения продукции и записываются в форме шахматных квадратных матриц. Балансовые модели служат для установления пропорций и взаимосвязей при планировании различных отраслей народного хозяйства.
Оптимизационные модели представляют систему математических уравнений, линейных или нелинейных, подчиненных определенной целевой функции и служащих для отыскания наилучших (оптимальных) решений конкретной экономической задачи. Эти модели, в отличие от статистических и балансовых, относятся к классу экстремальных задач и описывают условия функционирования экономической системы.
Классификация экономико-математических моделей может быть различной и условной. Это зависит от того, на базе каких признаков строится модель. В основу классификации кладутся различные признаки. Так, по функциональному признаку модели подразделены на модели планирования, модели бухгалтерского учета, модели экономического анализа, модели информационных процессов.
По признаку размерности модели классифицируются на макромодели, локальные модели и микромодели. Макроэкономические модели строятся для изучения народного хозяйства республики в целом на базе укрупненных показателей. Цель таких моделей состоит в разработке более обоснованных перспективных планов народнохозяйственного развития на основе познания важнейших экономических пропорций и соотношений, темпов роста производства и уровней потребления, рациональной отраслевой структуры.
Макромодели в зависимости от принятых уровней детализации подразделяются на: односекторные, двухсекторные и многосекторные. В двухсекторной модели выделяется группа производства средств производства и группа производства предметов потребления. Однако двухсекторные модели в силу весовой агрегированности показателей не позволяют непосредственно решать задачи, которые возникают в процессе планирования.
Более полная информация о механизме взаимосвязей в народном хозяйстве представляется многосекторными моделями, в которых сфера материального производства представляется состоящей из десятков, а порой и сотен самостоятельных отраслей
В основе всех экономических макромоделей лежит уравнение баланса
X - F(Х) - W = Z,
где X- совокупный общественный продукт;
F(Х) - производственная функция (прямые затраты), показывающая долю совокупного общественного продукта, необходимую для его производства;
W- доля совокупного общественного продукта, идущая на потребление;
Z - доля совокупного общественного продукта, идущая на накопление.
Макромодели могут разрабатываться и для отдельных отраслей народного хозяйства, например, тракторостроения, машиностроения на ближайшую перспективу.
К локальным экономическим моделям можно отнести также модели, с помощью которых анализируются и прогнозируются некоторые показатели развития отрасли. Например, модель прогноза научно-технического прогресса, модель прогноза производительности труда и т. д.
Микромодели на предприятиях разрабатываются для углубленного анализа структуры производства. Они позволяют выявить резервы роста объемов производства продукции. При построении микромоделей широко используются методы математической статистики — корреляционный и регрессионный, индексный и выборочный методы.
Оптимизационные модели могут носить детерминированный и стохастический характер. В детерминированных моделях результат решения однозначно зависит от входных данных. В стохастических вероятностных моделях - определенный набор входных данных может дать, а может и не дать соответствующего результата. Стохастические модели описывают случайные процессы, в которых результат всегда остается неопределенным в отличие от детерминированных моделей, входная информация которых заранее предопределяет результат решения.
Наиболее разработаны и практически более применимы детерминированные модели, использующие аппарат математического программирования.
Поскольку экономико-математическая модель отражает объективные закономерности воспроизводства определенного объекта или отдельные стороны этого процесса с помощью различных математических средств, то любая модель характеризуется рядом признаков, часть которых относится к отражаемым свойствам моделируемого объекта (процесса), а часть связана с самим аппаратом моделирования.
В основу классификации положен следующий прием: выделены четыре признака объекта и три признака по средствам построения моделей.
Моделируемые объекты рассматриваются с позиций:
1) сущности моделируемых процессов воспроизводства;
2) временных характеристик процессов;
3) уровней управления процессами (объектами);
4) назначения моделей в управлении.
В основу классификации по средствам их построения положены:
1) средства моделирования и методы реализации моделей;
2) структура моделей и характер зависимости ее компонентов;
3) используемая информация.
Каждая из этих совокупностей классификационных процессов отражает математическую и информационную сторону моделей. Приведенная классификация моделей условна. Она проводится по вполне определенным общим признакам моделей.
Классификация моделей, их анализ являются предпосылкой для построения интегрированной системы моделей.
1.2 Принципы построения и структура интегрированной системы экономико-математических моделей
Динамичность развития общественного производства и повышения его эффективности требуют совершенствования методов управления. Одним из важнейших направлений современного состояния производства во всех отраслях народного хозяйства является разработка методологии интегрированной системы экономико-математических моделей.
Сущность интегрированной системы состоит в изучении объекта как сложной динамической системы, состоящей из множества функционирующих во взаимодействии элементов. При этом изменения, происходящие хотя бы с одним элементом, отражаются на эффективности в целом всей системы.
Интегрированная система экономико-математических моделей представляет совокупность логически, информационно и алгоритмически связанных моделей, отражающих экономические, организационные и технологические процессы воспроизводства в их объективно существующем единстве. Только во взаимосвязи всех моделей системы обеспечивается комплексное решение задач управления производством. В систему включаются различные модели, отражающие воспроизводство экономического объекта. Это модели по функционирующим показателям эффективности производства, таким, как производительность труда, себестоимость единицы продукции, валовая продукция, прибыль, рентабельность, объем капитальных вложений и другие показатели. К интегрированной системе можно отнести модели ценообразования, модели финансирования и кредитования, налогообложения.
Использование интегрированной системы моделей в управлении производством возможно только на основе широкого применения экономико-математических методов и ЭВМ.
Интегрированная система моделей строится с учетом общих методологических принципов. Это принципы развития, единства, относительной автономности, соответствия и адаптации.
Принцип развития требует постоянного совершенствования системы моделей, включения в ее состав новых моделей, использование которых становится необходимым и возможным по мере общего совершенствования методологии планирования и управления. Развитие системы моделей требует соответствующего развития информационного и математического обеспечения плановых и прогнозных расчетов.
Принцип единства означает представление всего комплекса экономико-математических моделей в единой структуре взаимосвязанных блоков. Существенным требованием является общность методологического подхода к построению однотипных моделей, используемых на разных уровнях управления производством. Важнейшим условием выступает единство математического обеспечения системы.
Принцип относительной автономности предусматривает возможность выделения из общей системы моделей относительно самостоятельных частей, которые можно разрабатывать и внедрять, не ожидая полного завершения работ по всей системе моделей. Этот принцип позволяет разрабатывать локальные системы плановых расчетов по конкретным показателям.
Принципы соответствия и адаптации в системе экономико-математических моделей означают соответствие системы моделей сложившимся уровням управления. Модели для каждого уровня отличаются степенью детализации отражаемых процессов. В зависимости от уровня управления выделяют следующие комплексы моделей:
1) регионального (республиканского, областного, районного);
2) предприятий и их подразделений.
Учитывая совершенствование организационной структуры управления и методологии планирования, изменения структуры плановых документов, необходимо, чтобы система моделей адаптировалась к изменяющимся условиям, что означает реализацию принципа соответствия.
Кроме рассмотренных общеметодологических принципов, выделяют ряд специфических принципов, имеющих важное значение для построения интегрированной системы моделей. Это такие принципы, как принцип ориентации на выходные плановые показатели, принцип необходимого разнообразия, принцип взаимного дополнения групп моделей, принцип увязки моделей.
Принцип ориентации на выходные плановые показатели означает, что система моделей и решение с ее помощью плановых задач должна обеспечить выход на утверждаемые и контролируемые плановые показатели. Это условие влияет на степень детализации моделей, на разрабатываемые алгоритмы и программы расчетов и в значительной мере на состав входной информации.
Принцип необходимого разнообразия состоит в том, что для адекватного отражения объективных процессов в состав системы моделей следует включать разнообразные модели, в том числе реализующие методы математической статистики и математического программирования, межотраслевого баланса, сетевые и имитационные модели. Выбор математического аппарата .для построения и реализации моделей должен определяться особенностью моделируемого процесса и возможностями программного и технического обеспечения расчетов.
Принцип взаимного дополнения групп моделей заключается в том, что для каждого из основных блоков системы моделей целесообразно выделять три взаимодополняющие группы моделей, имеющие специфическое направление. Модели первой группы предназначены для прогнозирования состояния ресурсов и ряда отправных показателей планирования. Модели этой подготовительной группы предназначены для обеспечения входной информацией расчета основных показателей плана. Вторая основная группа моделей включает модели для проведения основных оптимизационных и балансовых расчетов, для увязки плановых показателей производства, материально-технического обеспечения, финансирования. Модели этой группы обеспечивают выход на основные утверждаемые и контролируемые плановые показатели. И, наконец, модели третьей, заключительной, группы предназначены для дополнительных расчетов, например, для более детального представления ряда натуральных и стоимостных балансов, планов распределения ресурсов в объекте и других вспомогательных расчетов.
Принцип увязки моделей означает, что между моделями групп и блоками системы в целом должны устанавливаться три вида связей: логическая, информационная и алгоритмическая.
Логическая связь определяет общую последовательность реализации моделей в системе, логику взаимного согласования разнообразных моделей.
Информационная связь строится на базе того, что результативная информация этих моделей служит входной информацией для других. Информационная связь между моделями характеризуется горизонтальной и вертикальной связями. Горизонтальная - связывает модели для планирования в одном объекте. При этом поток информации от моделей долгосрочного планирования к моделям средне- и краткосрочного планирования называют ориентирующим потоком. Вертикальные связи между моделями служат отражением реальных связей в планировании производства между различными уровнями управления.
Алгоритмическая связь - совокупность алгоритмов и программ для преобразования входной и выходной информации по всей системе моделей.
Глава 2. Методы решения экономико-математических задач о смесях
2.1 Основные типы линейных экономико-математических моделей
Среди линейных моделей математического программирования особое место занимают четыре типа моделей:
1) модель общей задачи линейного программирования- применяют для решения задач на смеси, использования сырья, определение оптимального плана выпуска изделий и ряда других. В каждой из них отыскивается оптимум целевой функции
![]()
при линейных ограничениях
![]()
![]() ;
;
2) модель транспортной задачи линейного программирования- состоит в том, чтобы наивыгоднейшем образом прикрепить поставщиков однородного продукта ко многим потребителям этого продукта;
3) модель распределительной (лямбда) задачи линейного программирования - часто ее называют обобщенной транспортной задачей, которая заключается в использовании взаимозаменяемых ресурсов;
4) модель ассортиментной задачи линейного программирования- ее можно решать на основе системы ограничений общей или распределительной задачи линейного программирования. Особенность целевой функции состоит в том, что ставится задача максимизации количества комплектов изделий, т.е.
![]() С= X1
/K1
= X2
/K2
=…= Xn
/Kn
Max, где
С= X1
/K1
= X2
/K2
=…= Xn
/Kn
Max, где
C- количество комплектов;
Kj - количество j-х изделий, входящих в комплект (j=1,2,..,n)
Xj - количество производимых изделий j- го вида.
В общем виде задачи распределения характеризуются следующими условиями:
1. Существует ряд операций, которые должны быть выполнены.
2. Имеется достаточное количество ресурсов для выполнения всех операций.
3. Некоторые операции можно выполнять различными способами.
4. Некоторые способы выполнения операций лучше других.
5. Имеющегося в наличии количества ресурсов недостаточно для выполнения каждой операции наилучшим способом.
Рассмотрим более подробно задачи распределения, различающихся между собой видом математических моделей и объектами исследования: задачи о назначениях, задачи использования ресурсов (или задачи собственно распределения), задачи о смесях (о диете), задачи о раскрое, транспортные задачи. Так как я буду использовать при решении задачи задачу собственно распределения, то остановлюсь на ней более подробно[].
Задача о смесях (о диете)
К задачам о диете относятся задачи, в которых требуется выбрать самый дешевый пищевой рацион, содержащий необходимое количество указанных заранее питательных веществ. Предполагается, что:
1. известен перечень биологически необходимых питательных веществ и их минимальная норма (например, суточная);
2. задан набор продуктов, из которых требуется составить пищевой рацион;
3. имеются нормы содержания различных питательных веществ в единице соответствующего продукта;
4. известна цена единицы каждого продукта, который может быть использован в пищевом рационе. Подобная проблема возникает при выборе рационального корма для скота.
Формализуем описанную ситуацию:
Будем считать, что в рацион должно входить m биологически необходимых питательных веществ (индекс i). Таким образом, i=1,2,..,m.
Известно, что i-го питательного вещества в рационе должно быть не меньше, чем bi единиц. Предположим, что мы располагаем n различными продуктами, из которых составляется пищевой рацион (индекс j, j=1,2,…,n). Норму содержания i-го питательного вещества в j-ом продукте обозначим через aij . Нам известна таблица-матрица, состоящая из m×n чисел aij .
Таблица 2.1.1
| Пищевые продукты | |||||
| 1 | 2 | … | n | ||
| Питательные вещества | 1 | a11 | a12 | … | a1n |
| 2 | a21 | a22 | … | a21 | |
| ... | … | … | … | … | |
| … | … | … | … | … | |
| m | am1 | am2 | … | amn | |
Цены, которые установлены на продукты питания, обозначим cj за единицу j-го продукта. Количество j-го продукта, входящего в пищевой рацион, обозначим через xj .
В этих обозначениях выбор самого дешевого рациона, удовлетворяющего сформулированным выше требованиям, сводится к решению следующей математической задачи:
Найти вектор X = ( x1 , x2, …, xn ), удовлетворяющий системе ограничений:

и доставляющий целевой функции ![]() минимальное значение.
минимальное значение.
Ограничение для каждого i означает, что в выбираемом рационе i-го питательного вещества должно содержать не менее, чем bi единиц. Второе ограничение формализует тот факт, что j-ый продукт может либо входить в рацион, и тогда xi >0, либо не входить, и тогда xi =0.
2.2 Методы решения задач о смесях
экономическая математическая задача интегрированная
От того, как будут распределяться ограниченные ресурсы, зависит конечный результат деятельности бизнеса, т. е., успешность решения подавляющего большинства экономических задач зависит от наилучшего способа использования ресурсов.
В результате чего и разработали методы решения данных задач, называемых оптимизационными методами задач распределения, основные из них: симплекс-метод, двойственный симплекс-метод, метод искусственного базиса, графический метод и решение задач средствами Excel через «Поиск решений». Так как я во втором разделе буду использовать при решении задачи распределения симплекс-метод, то рассмотрю его подробнее.
Симплекс-метод
Классическим методом решения рада линейного программирования стал симплекс-метод, получившим также в литературе название метода последовательного улучшения плана. Этот метод был разработан в 1947 г. американским математиком Джорджем Данцигом. Этот метод может быть использован для решения большого комплекса задач внутризаводского планирования: формирование специфицированной годовой производственной программы выпуска предприятия, плана загрузки различных групп оборудования, календарное распределение производственной программы выпуска и т.д.
Сточки зрения рациональности и наглядности вычислительного процесса выполнение алгоритма симплекс-метода удобно оформлять в виде последовательности таблиц. В различных источниках приводятся разные модификации симплекс таблиц, отличающихся друг от друга расположением отдельных элементов. Однако все они базируются на одних и тех же принципах. Основная идея симплекс-метода состоит в следующем:
1) принимается за базу одна из возможных программ - отправная (опорный план);
2) осуществляется ее пошаговое улучшение, пока не будет получен оптимум по заданной критериальной функции.
Т.о. проблема сводится к определению отправного варианта программы и нахождению способа улучшения последнего. При этом при формировании начального варианта программы создается как бы запас, возможность реализации в виде резервов тех ресурсов, которые регламентируются в сложившейся производственной ситуации. В процессе преобразований одни переменные вводятся в план, другие исключаются из него. С каждым шагом план приближается к оптимальному и в конечном счете приходит к нему, если в условиях задачи нет противоречия. За счет пошагового распределения ресурсов между планируемыми на выпуск изделиями (деталями) находится такое сочетание номенклатуры и количества этих изделий, которое является наилучшим с точки зрения достижения заданного критерия оптимальности и использования имеющихся ресурсов.
Решение задач симплекс-методом предусматривает выполнение следующих процедур:
1) формирование целевой функции;
2) определение ограничительных условий – функциональных ограничений, которые могут иметь вид неравенств;
3) преобразование ограничений из неравенств в систему равенств путем ввода вспомогательных, свободных переменных (последние имеют экономическое содержание и характеризуют резерв, неиспользованный остаток тех ресурсов, по которым введено ограничение);
4) построение исходной симплексной таблицы, в которой в формируемый план входят только свободные переменные;
5) ввод в исходный вариант плана реальных переменных и прежде всего тех, которые в наибольшей степени реализуют целевую функцию;
6) определение числового значения вводимой переменной – величины программы.
При этом каждый из показателей, характеризующих ограничительное условие, делится на соответствующий коэффициент при вводимом переменном – удельный расход данного ресурса. Тогда наименьшее частное определит максимально возможное в условиях принятых ограничений использование ресурсов при заданном критерии оптимальности. Полученный результат вводится в соответствующую строку формируемого плана симплексной таблицы. На этой строке матрицы весь ресурс исчерпан, она является «узким местом» и подлежит выводу. На ее место вводится другая строка, предварительно пересчитанная. Формируется новый вариант симплексной таблицы.
После каждой симплексной таблицы анализируется оптимальность полученного решения. Если все элементы последней строки (Z-строки) положительны и задача на максимум, то решение оптимально. Если все элементы Z-строки отрицательны и задача на минимум, то решение оптимально. Если план неоптимальный, производится его дальнейшее улучшение.
Алгоритм решения задачи симплекс-методом. Формирование целевой функции и системы ограниченных условий.
1. Перевод неравенств в систему равенств.
2. Построение исходной симплекс-таблицы
Таблица 2.2.1
| Базис | Ci+n | C1 | C2 | … | Cn | Cn+1 | Cn+2 | … | Cn+m | Bj |
| x1 | x2 | … | xn | xn+1 | xn+2 | … | xn+m | |||
| xn+1 | Cn+1 | a11 | a12 | … | a1n | 1 | 0 | … | 0 | b1 |
| xn+2 | Cn+2 | a21 | a22 | … | a2n | 0 | 1 | … | 0 | b2 |
| … | … | … | … | ... | … | … | … | … | … | … |
| xn+m | Cn+m | am1 | am2 | … | amn | 0 | 0 | … | 1 | bn+m |
| Z0 | -- | -C1 | -C2 | … | -Cn | 0 | 0 | … | 0 | 0 |
3. 1-й столбец содержит базисные переменные (xn + m ). 2-й столбец содержит коэффициенты целевой функции при базисных переменных (Ci + n ). xi - переменные задачи i=1,2,…n. C1 , …,Cn – коэффициенты при x1 ,…, xn целевой функции соответственно. Остальные столбцы и строки (кроме последней) содержат коэффициенты переменных в ограничениях. В последнем столбце находятся свободные члены. Последняя строка определяется по формуле:
![]()
4. Если решение не оптимально, то выбираем максимальный по абсолютной величине из отрицательных (если целевая функция стремится к максимуму) или из положительных (в противном случае) элемент Z-строки. В результате получаем «ключевой» столбец. Затем находим минимальное отношение элемента B-столбца на соответствующий положительный элемент «ключевого» столбца, получаем «ключевую» строку. На пересечении «ключевого» столбца с «ключевой» строкой находится «ключевой» элемент.
5. Вводим соответствующую переменную полученного «ключевого» элемента в состав базисных и строим новую таблицу по следующим правилам:
· В «новой» таблице на месте «ключевого» элемента ставится 1. Все остальные строки данного столбца равны 0.
· Если в «ключевой» строке (столбце) «старой» таблицы есть элемент равный 0, то соответствующий столбец (строка) переписывается в «новой» таблице без изменений.
· Переменные «ключевой» строки в «новой» таблице равны соответствующим элементам «старой» таблицы, деленным на «старый» «ключевой» элемент.
· Элемент «новой» таблицы равен соответствующему элементу «старой» таблицы минус произведение соответствующего элемента «старого» «ключевого» столбца на соответствующий элемент «новой» «ключевой» строки.
· Такие таблицы строятся до тех пор, пока решение не будет оптимальным.
Глава 3 Постановка и решение экономико-математических смесей на примере СПК «Родина»
3.1 Организационно-экономическая характеристика ПСК «Родина»
В архивных документах упоминается, что в конце 1929 года в деревне Бобры Мозырского района создано коллективное хозяйство. В протоколе правления Мозырского Окрколхозсоюза от 22 марта 1930 года встречается упоминание о колхозе «Бобры». Есть отчет Белколхозцентра, в котором говорится, что в сентябре 1930 года в деревне Бобры Мозырского района создан колхоз им. Ворошилова.
Летом и осенью 1930 года были организованы колхоз «Пролетерский» в деревне Лучежевичи , им. Калинина – в Майском, им.Ленина в Телепунах, им. Фрунзе – в Дроздах, «Чырвоная зорка» - в Козенках, «Чырвоны араты» - в Норавчизне, «1 Мая» - в Боровиках. Все они в начале 50-х годов объединились с колхозом им. Ворошилова, хозяйство стало называться «Дружба», а позже – «Родина».
Трудны были первые шаги жизни коллективизированной социалистической деревни. Часть крестьян сознательно боролась за коллективную жизнь, другая просто примирилась, третья – затаилась в ожидании лучших времен.
Сегодня хозяйства – это производственный сельскохозяйственный кооператив «Родина», который находится на юго-восточной части области. Его хозяйственный центр – деревня Козенки – расположен в 2 км от города Мозыря. Общая земельная площадь составляет 3487 га, в том числе с/х угодья 2370 га, из них пашня – 1691га, сенокосы – 202 га, пастбища – 420 га, сад – 57 га. Удельный вес пашни в структуре сельскохозяйственных угодий составляет 68,9%, что характеризует высокую распаханность угодий. Средний бал с/х угодий составляет – 27,1, пашни – 28,1.
Таблица 3.1 Землепользование
| Наличие земельных угодий на 01.01.2006год | Площадь, га |
| Общая земельная площадь | 3487 |
| Сельскохозяйственные угодья, всего | 2370 |
| из них: пашня | 1691 |
| сенокосы – всего | 202 |
| из них сенокосы корен. улучшения | 6 |
| пастбища – всего | 420 |
| из них пастбища культурные, включая коренного улучшения | 391 |
| многолетние насаждения | 57 |
| Кустарники | 194 |
| Пруды и водоемы | 43 |
| Балл с/х угодий | 27,1 |
| балл пашни | 28,1 |
В хозяйстве имеется 2040 голов КРС, в том числе коров – 686 голов. Плотность скота на 100 га с/х угодий составляет 94 головы, в том числе коров –31 голова. Поголовье свиней составляет 372 головы.
Средний удой на корову равен 2143 кг, среднесуточные привесы достигают 357 гр.
В хозяйстве имеется молочно-товарная ферма «Козенки», комплекс «Майский», ферма по откорму и выращиванию КРС «Майская».
На фермах действует поточно-цеховая система производства молока, корм раздается механизированным путем и вручную.
А также в хозяйстве имеется СТФ, специализирующаяся на выращивании свиней и реализации поросят населению. На территории хозяйства находится автопарт, машинно-тракторный парк, механизированная мастерская, складские помещения, мойка.
Располагая относительно небольшой земельной площадью предприятие из года в год добивается неплохих результатов.
Управление деятельностью ПСК «Родина» осуществляет правление кооператива во главе председателя Жилин В.В., который назначается на должность общим собранием членов кооператива.
ПСК «Родина» является юридическим лицом, имеет самостоятельный баланс, расчетный и другие счета в банках, имеет круглую печать РБ со своим наименованием, другие необходимые штампы и бланки.
Хозяйственная деятельность осуществляется на основании Устава кооператива. Разработан коллективный договор между правлением ПСК «Родина» и членами кооператива, пересматриваемым ежегодно и утвержденным на общем собрании членов кооператива.
Каждый член кооператива работает и материально заинтересован в результатах личного и коллективного труда, в эффективности использования ресурсов.
Основным направлениями и целями деятельности ПСК «Родина» являются:
1. выращивание и реализация мяса КРС и свиней. В 2006 году выручка от реализации мяса КРС составила 450 млн. руб. и мяса свиней -- 158 млн. руб.
2. производство и реализация молока.
3. производство и реализация зерна, картофеля, рапса, овощей;
4. выполнение работ и оказания услуг;
5. иная деятельность, не запрещенная законодательством.
Среднесписочная численность работников составляет 145 человек.
Среднегодовая стоимость основных производственных средств сельскохозяйственного назначения составляет 2301 млн.руб.
3.2 Основные технико-экономические показатели работы СПК «Родина» за 2005-2007гг.
Таблица 3.2.1 Основные технико-экономические показатели
№ п\п |
Основные технико-экономические показатели | Ед. измер. | 2005 | 2006 | 2007 | % роста (2005-2006) |
% роста (2006-2007) |
| 1 | Валовая продукция с\х в СЦ, всего 10 | Млн.руб. | 1305 | 1869 | 2042 | 143,2 | 109,3 |
В том числе: Растениеводство,15 |
Млн.руб. | 691 | 799 | 937 | 115,6 | 117,3 | |
| Животноводство,20 | Млн.руб. | 614 | 1070 | 1105 | 174,3 | 109,4 | |
| 2 | Ср. спис. численность работников,30 |
Чел |
151 | 123 | 145 | 81 | 117 |
| В том числе занятых в с\х производстве | чел | 151 | 123 | 140 | 81 | 113.8 | |
| 3 | Затраты на прод., работы и услуги, всего,001 | Млн.руб. | 2291 | 2454 | 2713 | 107,1 | 110,6 |
| в т.ч. материалы,002 | Млн.руб. | 1693 | 1769 | 1882 | 104,5 | 106,4 | |
| 4 | Выручка от реали-зации продукции 010 | Млн.руб. | 1094 | 1652 | 1878 | 151 | 113,7 |
| 5 | Выручка от реали-зации продукции без налогов, 030 | Млн.руб. | 982 | 1485 | 1690 | 151,2 | 113,8 |
| 6 | Прибыль от реал. прод., работ, услуг 070 | Млн.руб. | 40 | 173 | 261 | 432,5 | 179 |
| 7 | Рентабельность, 211 | % | 38 | 35 | 38,4 | 92 | 110 |
| 8 | Коэф. текущей ликвидности | % | 1 | 1,45 | 2,1 | 145 | 144,8 |
| 9 | Коэф. обеспеч. собст.ОС | % | - | 0,13 | 0,4 | - | 307,8 |
| 10 | Коэф. платежесп. | % | 1 | 1,16 | 1,53 | 116 | 132 |
Анализируя данные в таблице, нужно отметить, что валовая продукция в сопоставимых ценах за 3 года (2005-2007 г.г.) увеличилась на 737 млн. руб. или в 1,56 раза. Если анализировать по годам, то нужно отметить, что темпы роста валовой продукции сократились с 143,2% до 109,3 %. Причиной этому стали неблагоприятные погодные условия, но кооператив все же увеличил объёмы валовой продукции. Так в 2007г. она составила 2042 млн.руб.
Выручка от реализации продукции без налогов и сборов соответственно тоже увеличилась за данный период на 708 млн. руб. или в 1,72 раза. Это же и следовало, т.к. объёмы валовой продукции также выросли.
В своё время увеличиваются и затраты на продукцию, работу и услуги. Так за данный период они выросли на 422 млн. руб. или в 1,18 раза. В основном увеличиваются затраты на покупку сырья и материалов, которые увеличились на 189 млн. руб.
Так прибыль от реализации продукции, работ и услуг с 2005 по 2007 увеличилась на 221 млн. руб. или в 6,525 раз.
Рентабельность предприятия в 2007 году составила 38.4 %, а в 2005 – 38%. Это связано с тем, что прибыль в своё очередь растет быстрее, чем себестоимость продукции.
Характеристика финансового состояния предприятия.
В настоящее время ПСК «Родина» находится в сложном финансовом положении. На 1 января 2006 года кредиторская задолженность –236 млн. руб., в тоже время предприятию должны другие организации 93 млн. руб.
Сложное финансовое положение предприятия обусловлено прежде всего тем, что денежная выручка от реализации продукции не обеспечивает покрытие затрат на ее производство и не позволяет своевременно погасить кредиторскую задолженность и кредиты банка.
Оплата труда.
В ПСК «Родина» тарификация работников производится на основе действующего ЕТКС по профессиям рабочих и работ, а также квалификационного справочника должностей руководителей, специалистов и служащих с учетом положений, инструкций и аттестаций работников.
На предприятии применяется сдельно-премиальная система оплаты труда. Рабочему кроме заработка по прямым сдельным расценкам, выплачивается премия за выполнение и перевыполнение установленных показателей. Премии определяются за фактически отработанное время на основании сдельного заработка.
Оплата труда руководителей, специалистов и других работников, относящихся к служащим, производится по повременной системе. Порядок исчисления заработка такой же, так и для рабочих-повременщиков, но устанавливается оклад согласно штатному расписанию. Должностной оклад формируется на основе тарифной ставки 1 разряда, тарифного разряда и коэффициента, а также установленных надбавок.
3.3 Постановка и решение собственно задачи о смесях на примере ПСК «Родина»
Данная задача возникает при составлении наиболее экономного (т.е. наиболее дешевого) рациона питания животных, удовлетворяющего определенным медицинским требованиям.
У кооператива есть возможность произвести или купить следующие корма для кормления стада коров:
1) сено по цене 62 рубля за килограмм;
2) сенаж - по 35 рублей;
3) силос - по 34 рубля;
4) корнеплоды - по 45 рублей;
5) комбикорм - по 250 рублей;
6) отруби кукурузные – по 180 рублей
Из зоотехнических справочников известно, что одной корове массой в среднем 500 кг и суточным удоем молока равным 10 кг в сутки необходимо дать не менее 10 кг кормовых единиц, 940 г перевариваемого протеина (белка) и 66 г кальция, 47 г фосфора, 440 мг каротина. Кроме того, в рационе коров должно содержаться около 1/3 сочных кормов и общее количество кормов в сутки на одну корову не должно превышать 40 кг.
Мы знаем стоимость (себестоимость) килограмма каждого корма, поэтому можем определить такой рацион кормления коров, при котором животное получило бы все необходимые ей вещества в нужном количестве и при этом стоимость рациона была бы минимальной
Для обеспечения разнообразия кормления введем ограничение по содержанию отдельных групп кормов в рационе:
1. Сочные корма (силос, корнеплоды) рекомендуется включать в рационы коров в размере 60-65% (1\3) от их общей питательности;
Данные по видам кормов, используемых в хозяйстве, их себестоимости и содержанию в них питательных веществ приведены в таблице 1 [Приложение 1.]
Построение экономико-математической модели.
Введем следующие обозначения:
xi - количество кормов i-гo вида в суточном рационе.
Сi -- стоимость (себестоимость) единицы i-гo корма;
aij — содержание j-гo вещества в единице i-гo корма;
Yj - необходимое содержание j-гo вещества в суточном рационе животного;
Р — общая суточная масса кормов;
IС — индексы подмножества сочных кормов в рационе;
К — коэффициент, определяющий содержание сочных кормов в суточном рационе (0 < К < 1).[9. c 73]
Таким образом, необходимо определить, сколько килограмм j-того корма необходимо взять, чтобы минимизировать стоимость рациона и в то же время удовлетворить потребность в питательных веществах.
Модель задачи в общем виде выглядит следующим образом:
 (2.1)
(2.1)
при ограничениях:
Совокупное количество i-того питательного вещества, содержащееся во всех используемых согласно рациону кормах, равно:
 (2.2)
(2.2)
ограничения на общую массу кормов:
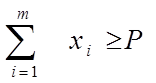 (2.3)
(2.3)
ограничение на необходимое количество кормов:
 (2.4)
(2.4)
xj ≥0 (2.5)
Тогда получаем следующую экономико-математическую модель задачи:
Найти оптимальное количество кормов
X1 + X2 + X3 + X4 + X5 + X6 ≥ 0, (2.6)
Тогда целевая функция может быть записана так:
![]() (2.7)
(2.7)
Ограничения по содержанию необходимых веществ [Приложение 2, табл. 1]:
По кормовым единицам:
0.5X1 + 0.17X2 +0.3X3 +0.14X4 + 0.96X5 + 0.89X6 >= 10 (2.8)
По перевариваемому протеину:
79X1 + 18X2 +29X3 +9.7X4 + 157X5 + 59X6 >= 940 (2.9)
По кальцию:
13X1 + 1.7X2 +3.8X3 +0.4X4 + 5.3X5 + 0.5X6 >= 66 (2.10)
По фосфору:
3.4X1 + 0.6X2 + X3 +0.4X4 + 8.7X5 + 4X6 >= 47 (2.11)
По каротину:
30X1 +15X2 + 20X3 >= 440 (2.12)
Легко запишется ограничение на общее количество кормов в сутки:
X1 + X2 + X3 + X4 + X5 + X6 <=40 (2.13)
Ограничение по сочным кормам; к которым относится силос (х2 ) и корнеплоды (х4 ):
X2 + X4 =1/3(X1 + X2 + X3 + X4 + X5 + X6 ) (2.14)
И обычное ограничение для задач распределения:
xj ≥0 (2.15)
Таким образом, выше была построена экономико-математическая модель для задачи о рационе, состоящая из целевой, минимизирующей затраты, функции и 16 ограничений
Решение задачи.
Данную задачу наиболее рационально решать прямым симплекс-методом, т.к. целевая функция минимизируется и в модели присутствуют ограничения со знаком ≥, ![]() ,=.
,=.
Сначала приведем систему ограничений к каноническому виду. Строим первую симплексную таблицу (Приложение 2, табл. 4 ). Затем:
1. Выбираем max по абсолютной величине из положительных элемент Z-строки, получаем ключевой столбец.
2. Находим min отношение свободных членов к положительным элементам ключевого столбца:
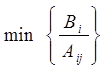 , (2.16)
, (2.16)
получаем ключевую строку, и на пересечении - ключевой элемент.
Соответствующую ключевому элементу переменную вводим в состав базисных и строим новую симплексную таблицу
3. когда все отрицательные элементы уйдут, получим допустимое решение.
Так как процесс нахождения решения для данной модели является довольно трудоемким, воспользуемся инструментом Поиск решения MSExcel .
Вводим в виде столбца произвольные значения переменных х1 , х2 …хп , удовлетворяющих всей системе ограничений.
1. В блок ячеек, размерностью n´m (где n - количество переменных х, m- количество ограничений при целевой функции) вводятся коэффициенты при переменных х в ограничениях.
2. В свободную строку вводятся коэффициенты при переменных целевой функции.
3. В виде столбца вводят формулы левых частей ограничений, используя адреса переменных из пункта 1 и значения коэффициентов п. 2. В соседний столбец вносятся правые части ограничений.
4. Поставив знак “=” в свободную ячейку, вводится формула целевой функции Z через адреса коэффициентов (п. 3) и адреса переменных (п.1).
Решение поставленной задачи выполняется следующим образом:
1.Выполняется команда СЕРВИС®ПОИСК РЕШЕНИЯ. В поле Установить целевую ячейку вводится ссылка на ячейку с целевой функцией (п. 4).
2.В группе Равной устанавливается соответствующая опция. В поле Изменить ячейки вводится диапазон ячеек с произвольными значениями переменных (п.1).
3. Нажимается кнопка Добавить для ввода ограничений. В окне «Добавление ограничения» в поле Ссылка на ячейку вводится ссылка на ячейку, содержащую формулу левой части текущего ограничения, выбирается в средней части поля нужное ограничение. В правую часть поля вводится значение правой части ограничения (п.4).
4. Щелкаем кнопкой Выполнить, чтобы произвести поиск решения. Когда решение будет найдено, появится окно «Результаты поиска решения». Устанавливаем в нем опцию Сохранить найденное решение. Для представления результатов поиска решения в форме отчета, указываем Тип отчета, например, выбрав опцию Результаты.
Получим следующий рацион кормления для коровы:
· сено – 17,1кг;
· силос кукурузный –8,547кг;
· общее количество кормовых единиц – 10.
Общая стоимость данного рациона составила 1350 руб.
В данной главе было проанализировано применение задачи о смесях на сельскохозяйственном предприятии – СПК «Родина».
Целью решения поставленной задачи было получение наиболее дешевого рациона кормления животных с удовлетворением потребности в необходимых питательных веществах. Задача была решена с помощью средства Поиск решения MSExсel, был получен наиболее дешевый рацион (стоимость составила рубля). Как видно, в данном рационе соблюдены все ограничения: и по содержанию питательных веществ, и по разнообразию кормов. Была получена минимальная по стоимости смесь кормов.
Заключение
Сельское хозяйство является благоприятной сферой использования экономико-математических методов и электронных вычислительных машин. Так, посредством применения методов линейного программирования можно установить рациональное сочетание отраслей в хозяйстве; определить наилучшую структуру кормовых культур и оптимальные рационы кормления скота; осуществлять оптимальное планирование капиталовложений.[4. c.14]
При организации кормления молочного скота па крупных фермах в колхозах и совхозах в настоящее время признано необходимым нормировать кормовые рационы корон но энергетическим кормовым единицам, сухому веществу, перевариваемому протеину, кальцию, фосфору, магнию, сере, калию, натрию, меди, цинку. В приусадебных и крестьянских хозяйствах на фермах, на которых содержится обычно не более 100 коров, очень трудно осуществить контроль за таким большим числом показателей. Поэтому здесь можно ограничиться нормированием рационов, по семи основным показателям — кормовым единицам, перевариваемому протеину, кальцию, фосфору. Необходимо только более строго соблюдать рекомендуемую структуру рационов по соотношению грубых, сочных и концентрированных кормов.
Некоторые животноводы с целью быстрого увеличения молочной продуктивности коров стараются включать в рационы как можно больше концентрированных кормов, не считаясь даже с их более высокой стоимостью.
В данной курсовой работе был предложен оптимальный рацион кормления КРС из смеси, которая состоит из сена лугового и силоса. В данной смеси учитывались следующие элементы:
· Перевариваемый протеин;
· Кальций;
· Фосфор;
Кроме этого были учтены кормовые единицы в каждом составляющем смеси.
Список использованной литературы
1.Акоф Р., Сасиени М. “Основы исследования операций”: - М .: «Мир», 1971.-536
2.Алексеенко П.П., Виткин Ю.В,“Применение пакетов прикладного программирования по экономико-математическим методам АСУ ” Под ред. - Б.Я. Курицкого: - М.:Статистика, 1986.-196
3.Барсов А.С. “ Линейное программирование в технико-экономических задачах”.- М.: «Наука», 1964.-280
4.Вагин Е.А. “ Скотоводство, свиноводство в приусадебных участках и крестьянских хозяйствах”.- М .: «Наука», 1992.-191
5.Гасс С. “Линейное программирование (методы и приложения)”.- пер. с англ. Е.П. Гольштейн и М.И. Сушкевич/ Под ред.Д.Б.Юдина- М .: 1961.-304
6. Гейл Д. “ Теория линейных экономических моделей”. Под ред. И.И. Воробьёва. - пер. с англ. Л.И. Горькова- М .: 1963.-419
7 .Данилина Н.И., Кротов В.Ф.” Оптимальное управление экономическим процессом ”. Уч. пособ..- М .: «Ротапринт МЭСИ», 1980.-147
8.Зайченко Ю.Л.“ Исследование операций ”.-Изд. объедин.: «Вища школа», 1975.-320
9.Карагодова Е.А. и др. “ Линейное и нелинейное програмирование”.-Изд. объедин.: «Вища школа», 1975.-372
10. Кархов А.Н. Щедрин Н.И. “Математические методы программирования в экономике ”.- М.:Статистика, 1974.-144
11.Министерство по ЧС РБ; Министерство с/х и продовольствия РБ; Академия аграрных наук. Руководство по ведению агропромышленного производства в условиях радиоактивного загрязнения земель РБ на 1997-2000 гг.- под ред. Академика ААН РБ И.М.Богдевича.- Мн, 1997.-76с
12.Морозов В.В. и др. .“ Исследование операций в задачах и упражнениях ”. Уч. пособ. для студентов ВУЗов, обучающихся по специальности прикладная математика- М .: «Высшая школа», 1986.-287
13.Попов И.Г. “Математические методы в планировании отраслей и предприятий ”. Уч. пособ. для экон. ВУЗов.- изд. 2-е, перераб. и дополн. –М .: «Экономика» 1981.-336
Похожие рефераты:
Социальные ограничения: содержание, структура, функции
Решение транспортной задачи линейного программирования в среде MS Excel
Теоретические основы математических и инструментальных методов экономики
Анализ факторов, влияющих на молочную продуктивность коров
Линейное программирование как метод оптимизации
Проектирование модели для составления оптимального рациона кормления скота
Решения задачи планирования производства симплекс методом
Классификация математических моделей, используемых в экономике и менеджменте
Задачи математического программирования
Применение линейного программирования для решения экономических задач (оптимизация прибыли)
Технология производства и переработки молока
Билеты на государственный аттестационный экзамен по специальности Информационные Системы
Методика математического моделирования программы развития сельскохозяйственного предприятия