Курсовая работа: Задача о движении снаряда

Курсовая работа

Задача о движении снаряда

Содержание

Введение

Постановка задачи

Решение поставленной задачи

Блок-схема

Результат работы программы

Заключение

Список литературы

Приложения

Введение

С середины XX в. в самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, как «математическая экономика», «математическая химия», «математическая лингвистика» и т. д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.

Математическая модель — это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования — исследовать эти объекты и предсказать результаты будущих наблюдений. Однако моделирование — это еще и метод познания окружающего мира, дающий возможность управлять им.

Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории, чтобы проверить, «что было бы, если бы...» Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.

Целью данной курсовой работы является моделирование движения снаряда.

модель параметр движение снаряд

Постановка задачи

Снаряд пущен с Земли с начальной скоростью v₀ под углом  к ее поверхности; требуется найти траекторию его движения (y), расстояние S между начальной и конечной точкой этой траектории, время движения (t) и максимальную высоту подъема снаряда (h).

Будем считать, что движение снаряда определяется полем тяготения. Сопротивлением воздуха, притяжением других планет Солнечной системы, наличием деформаций ствола орудия можно пренебречь. Можно считать также, что поверхность Земли на расстоянии полета снаряда плоская, поле притяжения не изменяется, а снаряд не имеет геометрических размеров, но имеет вполне определенную массу.

Решение поставленной задачи

Движение тела, брошенного с некоторой начальной скоростью V_о под углом α к горизонту, представляет собой сложное движение: равномерное по горизонтальному направлению и одновременно происходящее под действием силы тяжести равноускоренное движение в вертикальном направлении. Так движется лыжник при прыжке с трамплина, струя воды из брандспойта (рис. 12.1) и т.д.

Рис. 1

Изучение особенностей такого движения началось довольно давно, еще в XVI веке и было связано с появлением и совершенствованием артиллерийских орудий.

Представления о траектории движения артиллерийских снарядов в те времена были довольно забавными. Считалось, что траектория эта состоит из трех участков: А - насильственного движения, В - смешанного движения и С - естественного движения, при котором ядро падает на солдат противника сверху (рис. 12.2).

Рис. 2

Законы полета метательных снарядов не привлекали особого внимания ученых до тех пор, пока не были изобретены дальнобойные орудия, которые посылали снаряд через холмы или деревья - так, что стреляющий не видел их полета.

Сверхдальняя стрельба из таких орудий на первых порах использовалась в основном для деморализации и устрашения противника, а точность стрельбы не играла вначале особенно важной роли.

Близко к правильному решению о полете пушечных ядер подошел итальянский математик

Тарталья, он сумел показать, что наибольшей дальности полета снарядов можно достичь при направлении выстрела под углом 45° к горизонту. В его книге "Новая наука" были сформулированы правила стрельбы, которыми артиллеристы руководствовались до середины ХVII века.

Однако, полное решение проблем, связанных с движением тел брошенных горизонтально или под углом к горизонту, осуществил все тот же Галилей.

В своих рассуждениях он исходил из двух основных идей: тела, движущиеся горизонтально и не подвергающиеся воздействию других сил будут сохранять свою скорость; появление внешних воздействий изменит скорость движущегося тела независимо от того, покоилось или двигалось оно до начала их действия.

Галилей показал, что траектории снарядов, если пренебречь сопротивлением воздуха, представляют собой параболы.

Галилей указывал, что при реальном движении снарядов, вследствие сопротивления воздуха, их траектория уже не будет напоминать параболу: нисходящая ветвь траектории будет идти несколько круче, чем расчетная кривая.

Ньютон и другие ученые разрабатывали и совершенствовали новую теорию стрельбы, с учетом возросшего влияния на движение артиллерийских снарядов сил сопротивления воздуха.

Появилась и новая наука – баллистика. Прошло много-много лет, и теперь снаряды движутся столь быстро, что даже простое сравнение вида траекторий их движения подтверждает возросшее влияние сопротивления воздуха.

На нашем рисунке 12.3 идеальная траектория движения тяжелого снаряда, вылетевшего из ствола пушки с большой начальной скоростью, показана пунктиром, а сплошной линией - действительная траектория полета снаряда при тех же условиях выстрела.

Рис. 3

В современной баллистике для решения подобных задач используется электронно-вычислительная техника - компьютеры, а мы пока ограничимся простым случаем - изучением такого движения, при котором сопротивлением воздуха можно пренебречь. Это позволит нам повторить рассуждения Галилея почти без всяких изменений.

Полет пуль и снарядов представляет собой пример движения тел, брошенных под углом к горизонту. Точное описание характера такого движения возможно только при рассмотрении некоторой идеальной ситуации. Посмотрим, как меняется скорость тела, брошенного под углом α к горизонту, в отсутствие сопротивления воздуха. В течение всего времени полета на тело действует сила тяжести. На первом участке траектории (рис. 12.4) от точки А до точки В скорость тела уменьшается по величине и изменяется по направлению.

Рис. 4

В наивысшей точке траектории – в точке С - скорость движения тела будет наименьшей, она направлена горизонтально, под углом 90° к линии действия силы тяжести. На второй части траектории полет тела происходит аналогично движению тела, брошенному горизонтально. Время движения от точки А до точки С будет равно времени движения по второй части траектории в отсутствие сил сопротивления воздуха.

Если точки "бросания" и "приземления" лежат на одной горизонтали, то тоже самое можно сказать и о скоростях "бросания" и "приземления". Углы между поверхностью Земли и направлением скорости движения в точках "бросания" и "приземления" будут в этом случае тоже равны.

Дальность полета АВ тела, брошенного под углом к горизонту, зависит от величины начальной скорости и угла бросания. При неизменной скорости бросания V₀ с увеличением угла, между направлением скорости бросания и горизонтальной поверхностью от 0 до 45°, дальность полета возрастает, а при дальнейшем росте угла бросания - уменьшается. В этом легко убедиться, направляя струю воды под разными углами к горизонту или следя за движением шарика, выпущенного из пружинного "пистолета" (такие опыты легко проделать самому).

Траектория такого движения симметрична относительно наивысшей точки полета и при небольших начальных скоростях, как уже говорилось раньше, представляет собой параболу.

Максимальная дальность полета при данной скорости вылета достигается при угле бросания 45°. Когда угол бросания составляет 30 или 60°, то дальность полета тел для обоих углов оказывается одинаковой. Для углов бросания 75 и 15° дальность полета будет опять одна и та же, но меньше, чем при углах бросания 30 и 60°. Значит, наиболее "выгодным" для дальнего броска углом является угол в 45°, при любых других значениях угла бросания дальность полета будет меньше.

Если бросить тело с некоторой начальной скоростью V_о под углом 45° к горизонту, то его дальность полета будет в два раза больше максимальной высоты подъема тела, брошенного вертикально вверх с такой же начальной скоростью.

Пренебрегая размерами снаряда, будем считать его материальной точкой. Введем систему координат xOy, совместив ее начало O с исходной точкой, из которой пущен снаряд, ось x направим горизонтально, а ось y — вертикально (рис. 1).

Рис. 5

Тогда, как это известно из школьного курса физики, движение снаряда описывается формулами:

где t — время, g = 10 м/с² — ускорение свободного падения. Эти формулы и дают математическую модель поставленной задачи. Выражая t через x из первого уравнения и подставляя во второе, получим уравнение траектории движения снаряда:

Эта кривая (парабола) пересекает ось x в двух точках: x₁ = 0 (начало траектории) и (место падения снаряда).

Блок-схема

S=v² *sin(2*α);

Y=x*tgα-x² g/2*v₀ ² *cos² α;

H= v₀ ² *sin² α/2*g;

T= 2v₀ *sinα/g

Результат работы программы

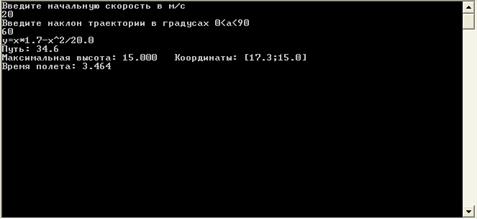
Заключение

Целью данной курсовой работы было написание программы, которая моделировала движение снаряда.

Результатом работы стали следующие параметры:

· Путь

· Максимальная высота (координаты)

· Время полета

· Уравнение траектории

При выполнении курсовой работы были выполнены основные этапы разработки модели:

· постановка задачи и определение целей моделирования;

· анализ методов построения модели;

· разработка алгоритма модели;

· написание и отладка программы;

Таким образом, в результате выполнения курсовой работы была получена модель, полностью удовлетворяющая потребностям поставленной задаче.

Список литературы

1. Мальханов С.Е. Общая физика (конспект лекций). – СПб.: СПбГТУ, 2001. – 438 с.

2. Смирнов М.С. Курс лекций по информатике – СПб., 1999 – 2002.

3. Мышкис А.Д. Лекции по высшей математике – М., 2000.

4. Панов Ю.Д., Егоров Р.Ф. Математическая физика. Методы решения задач. Учеб. пособие. – Екатеринбург, 2005. – 150 с.

5. Турчак Л.И., Плотников П.В. Основы численных методов: Учеб. пособие – 2-е изд., перераб. и доп. – М.: ФИЗМАТЛИТ, 2003. – 304 с.

6. Понамарев В.А. Visual Basic.NET. Экспресс курс. – СПб.: БХВ-Петербург, 2003.

7. Исаков В.Б. Элементы численных методов: Учебное пособие для студентов, обучающихся по специальности Математика группы Педагогические специал. – М.: Академия, 2003. – 192 с.

8. http://mathem.by.ru

Приложения

Листинг программы

program Project1;

{$APPTYPE CONSOLE}

uses

SysUtils,

Math,

InOut;

var

alpha,a,S,v,tg,tg2,t,h,h2:extended;

Key: Char;

Fok: Boolean;

const

g=10;

begin

Repeat

WriteLn(RusWD('Введите начальную скорость в м/с'));

ReadLn(v);

WriteLn(RusWD('Введите наклон траектории в градусах 0<a<90'));

ReadLn(a);

alpha:=Pi*a/180;

S:=sqr(v)*sin(2*alpha)/g;

tg:=tan(alpha);

tg2:=(2*sqr(v)*sqr(cos(alpha)))/g;

t:=2*v*sin(alpha)/g;

h:=sqr(v)*sqr(sin(alpha))/(2*g);

h2:=S/2;

Writeln('y=x*',tg:2:1,'-x^2/',tg2:2:1);

Writeln(RusWD('Путь: '),S:2:1);

Writeln(RusWD('Максимальная высота: '),h:3:3,' ',RusWD('Координаты: ['),h2:2:1,';',h:2:1,']');

Writeln(RusWD('Время полета: '),t:3:3);

Readln;

WriteLn(RusWD('Ввести данные повторно("Да"-[y]; "Нет"-Любая клавиша)?'));

ReadLn(Key);

until(Key<>'y') and (Key<>'Y');

WriteLn(RusWD('Для выхода нажмите - [Enter].'));

ReadLn;

end.

Курсовая работа: Задача о движении снаряда

Похожие рефераты: