| Похожие рефераты | Скачать .docx |
Реферат: Алгебра логики. Элементы цифровой схемотехники
Министерство образования и науки РФ
Государственное образовательное учреждение высшегопрофессионального образования
Белгородский государственный технологический университет
им. В.Г. Шухова
ИИТУС
Кафедра: «Техническая кибернетика»
Лабораторная работа №7
Дисциплина: Информатика
Тема:
Алгебра логики. Элементы цифровой схемотехники
Выполнил: студент группы УС-11
Лукьянов Л.В.
Принял: ст. препод. кафедры ТК
Крюков А.В.
Белгород 2010
Содержание
1. Цель работы
2. Список индивидуальных заданий
3. Примеры практической работы
3.1Задание 1
3.2Задание 2
3.3 Задание 3
Заключение
1. Цель работы
Изучение логических операций и правил их преобразований. Получение навыков практической работы по моделированию цифровых схем, состоящих из логических вентилей. Ознакомление с различными способами описания логики работы логического устройства – таблицами истинности, временными диаграммами, аналитическими функциями, цифровыми схемами.
2. Список индивидуальных задач
Задание 1
Задано булева функция от трех переменных:
![]()
А) Постройте таблицу истинности (в среде Microsoft Excel) для заданной булевой функции (таблицу истинности строить без каких-либо упрощений, пользуясь лишь встроенными логическими функциями И, ИЛИ, НЕ, ЕСЛИ).
Б) Смоделировать данную логическую функцию в среде Electronics Workbench. Построить соответствующую цифровую схему и временные диаграммы.
В) Упростить данное логическое выражение.
Задание 2
Используя пакет Electronics Workbench спроектировать схемы соответствующие обоим частям тождества (№2,№7,№16) (см. приложение), и с помощью проведения анализа доказать тождество. В отчет включить построенные схемы и диаграммы входных и выходных сигналов каждой из выполненных схем.
Приложение
| № | Логическое выражение | Формулировка |
| 1 | F1=X*0=0 | Логическое произведение любого аргумента на 0 равно 0 |
| 2 | F2=X*1=X | Логическое произведение любого аргумента на 1 равно значению аргумента |
| 3 | F3=X*X=X | Логическое произведение одних и тех же аргументов равно аргументу |
| 4 | F4=X*X’=0 | Логическое произведение аргумента с его инверсией равно 0 |
| 5 | F5=X+0=X | Логическая сумма любого аргумента с 0 равна аргументу |
| 6 | F6=X+1=1 | Логическая сумма любого аргумента с 1 равна 1 |
| 7 | F7=X+X=X | Логическая сумма аргумента с самим собой равна аргументу |
| 8 | F8=X+X’=1 | Логическая сумма аргумента с его инверсией равна 1 |
| 9 | F9=X’’=Х | Двойная инверсия аргумента дает его истинное значение |
| 10 | F10=X1*X2=X2*X1 | Переместительный закон |
| 11 | F11=X1+X2=X2+X1 | Переместительный закон |
| 12 | F12=(X1*X2)*X3=X1*(X2*X3) | Сочетательный закон |
| 13 | F13=(X1+X2)+X3=X1+(X2+X3) | Сочетательный закон |
| 14 | F14=X1*(X2+X3)=X1*X2+X1*X3 | Раскрытие скобок |
| 15 | F15=X1+(X2*X3)=(X1+X2)*(X1+X3) | Исключенное третье |
| 16 | F16=X1+X1*X2=X1 | Поглощение |
| 17 | F17=X1+X1’*X2=X1+X2 | Поглощение |
| 18 | F18=(X1*X2)’=X1’+X2’ | 1 правило де Моргана |
| 19 | F19=(X1+X2)’=X1’*X2’ | 2 правило де Моргана |
Задание 3
Спроектировать цифровую схему, выполняющая указанные действия и состоящую из простейших элементов И, ИЛИ, НЕ. Результаты подтвердить построением таблицы истинности и соответствующими временными диаграммами.
Спроектировать цифровую схему сравнения двухразрядных двоичных чисел А и В. На выходе схемы «1» – если А>B и «0» – в противном случае.
3. Примеры практической работы
3.1 Задание 1
Задано булева функция от трех переменных:
![]()
А) Постройте таблицу истинности (в среде Microsoft Excel) для заданной булевой функции (таблицу истинности строить без каких-либо упрощений, пользуясь лишь встроенными логическими функциями И, ИЛИ, НЕ, ЕСЛИ).
Б) Смоделировать данную логическую функцию в среде Electronics Workbench. Построить соответствующую цифровую схему и временные диаграммы.
В) Упростить данное логическое выражение.
Решение:
А) Для удобства разделим данное выражение на 5 частей: F1, F2, F3, F4, F5, где F1 = xxory, F2 = не z, F3 = F1 ![]() F2, F4 = не F3, F5 = xy+F4*x. Запишем данные формулы на языке MSExcel:
F2, F4 = не F3, F5 = xy+F4*x. Запишем данные формулы на языке MSExcel:
F1 = ЕСЛИ(x<>y,1,0); F2 = Ч(НЕ(z)); F3 = ЕСЛИ(И(F1=0,F2=0),1,0);
F4 = Ч(НЕ(F3)); =Ч(ИЛИ(И(x,y),И(F2,x))).
Построим таблицу истинности для данных функций:
логический операция цифровой моделирование

Рис. 3.1 Таблица истинности данной функции
Б) При моделировании будем использовать функцию
f(x,y,z)=![]() :
:

Рис. 3.2 Цифровая схема данной функции в среде Electronics Workbench
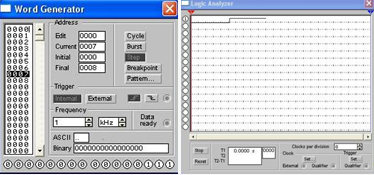
Рис.3.3 Временная диаграмма данной функции
В) ![]() =
=
![]()
![]()
3.2 Задание 2
Используя пакет Electronics Workbench спроектировать схемы соответствующие обоим частям тождества (№2,№7,№16) (см. приложение), и с помощью проведения анализа доказать тождество. В отчет включить построенные схемы и диаграммы входных и выходных сигналов каждой из выполненных схем.
Приложение
| № | Логическое выражение | Формулировка |
| 1 | F1=X*0=0 | Логическое произведение любого аргумента на 0 равно 0 |
| 2 | F2=X*1=X | Логическое произведение любого аргумента на 1 равно значению аргумента |
| 3 | F3=X*X=X | Логическое произведение одних и тех же аргументов равно аргументу |
| 4 | F4=X*X’=0 | Логическое произведение аргумента с его инверсией равно 0 |
| 5 | F5=X+0=X | Логическая сумма любого аргумента с 0 равна аргументу |
| 6 | F6=X+1=1 | Логическая сумма любого аргумента с 1 равна 1 |
| 7 | F7=X+X=X | Логическая сумма аргумента с самим собой равна аргументу |
| 8 | F8=X+X’=1 | Логическая сумма аргумента с его инверсией равна 1 |
| 9 | F9=X’’=Х | Двойная инверсия аргумента дает его истинное значение |
| 10 | F10=X1*X2=X2*X1 | Переместительный закон |
| 11 | F11=X1+X2=X2+X1 | Переместительный закон |
| 12 | F12=(X1*X2)*X3=X1*(X2*X3) | Сочетательный закон |
| 13 | F13=(X1+X2)+X3=X1+(X2+X3) | Сочетательный закон |
| 14 | F14=X1*(X2+X3)=X1*X2+X1*X3 | Раскрытие скобок |
| 15 | F15=X1+(X2*X3)=(X1+X2)*(X1+X3) | Исключенное третье |
| 16 | F16=X1+X1*X2=X1 | Поглощение |
| 17 | F17=X1+X1’*X2=X1+X2 | Поглощение |
| 18 | F18=(X1*X2)’=X1’+X2’ | 1 правило де Моргана |
| 19 | F19=(X1+X2)’=X1’*X2’ | 2 правило де Моргана |
Решение:
Для тождества
F2=X*1=X:

Рис.3.4 Логическая схема и временная диаграмма тождества №2
Для тождества
F7=X+X=X:


Рис.3.5 Логическая схема и временная диаграмма тождества №7
Для тождества
F16=X1+X1*X2=X1:


Рис.3.6 Логическая схема и временная диаграмма тождества №16
На основе данных временных диаграмм можно сделать вывод, что все тождества верны, так как результаты левой и правой частей совпадают.
3.3 Задание 3
Спроектировать цифровую схему, выполняющая указанные действия и состоящую из простейших элементов И, ИЛИ, НЕ. Результаты подтвердить построением таблицы истинности и соответствующими временными диаграммами.
Спроектировать цифровую схему сравнения двухразрядных двоичных чисел А и В. На выходе схемы «1» – если А>B и «0» – в противном случае.
Решение:
Пусть F1 и F2 числа А и В соответственно. А, В – старший и младший бит F1, aC,D – старший и младший бит F2. Если F1>F2 на выходе мы должны получить «1», иначе – «0». Составим таблицу истинности:

Рис.3.7. Таблица истинности
Составим логическое выражение на основе таблицы истинности:
![]()
![]()
Для полученной функции в среде Electronics Workbench составим логическую схему:

Рис.3.8 Логическая схема полученной функции

Рис.3.9 Временная диаграмма полученной функции
Данные полученной временной диаграммы и составленной таблицы истинности совпадают, следовательно, поставленная задача решена.
Заключение
В ходе данной работы мы получили навыки практической работы по моделированию цифровых схем, состоящих из логических вентилей. Ознакомились с различными способами описания логики работы логического устройства – таблицами истинности, временными диаграммами, аналитическими функциями, цифровыми схемами. Научились строить логические схемы и получать временные диаграммы в среде Electronics Workbench. Научились анализировать временные диаграммы, и синтезировать логические функции. В целом закрепили теоретические знания и научились применять их на практике, освоив специально ПО для решения данных задач.
Похожие рефераты:
Основы анализа и синтеза комбинационных логических устройств
Высшая математика для менеджеров
Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ)
Конспект лекций по дискретной математике