| Похожие рефераты | Скачать .zip |
Реферат: Проблемное обучение
Введение.
Вся жизнь человека постоянно ставит перед ним острые и неотложные задачи и проблемы. Возникновение таких проблем, трудностей, неожиданностей означает, что в окружающей нас действительности есть еще много неизвестного, скрытого. Следовательно, нужно все более глубокое познание мира, открытие в нем все новых и новых процессов, свойств и взаимоотношений людей и вещей. Поэтому какие бы новые веяния, рожденные требованиями времени, ни проникали в школу, как бы ни менялись программы и учебники, формирование культуры интеллектуальной деятельности учащихся всегда было и остается одной из основных общеобразовательных и воспитательных задач. Интеллектуальное развитие – важнейшая сторона подготовки подрастающих поколений.
Успех интеллектуального развития школьника достигается главным образом на уроке, когда учитель остается один на один со своими воспитанниками. И от его умения «и наполнить сосуд, и зажечь факел», от его умения организовать систематическую познавательную деятельность зависит степень интереса учащихся к учебе, уровень знаний, готовность к постоянному самообразованию, т.е. их интеллектуальное развитие, что убедительно доказывает современная психология и педагогика.
Большинство ученых признают, что развитие творческих способностей школьников и интеллектуальных умений невозможно без проблемного обучения.
Творческие способности реализуются через мыслительную деятельность.
Психологической основой концепции проблемного обучения является теория мышления, как продуктивного процесса, выдвинутая С.Л.Рубинштейном. Мышление занимает ведущую роль в интеллектуальном развитии человека.
Значительный вклад в раскрытие проблемы интеллектуального развития, проблемного и развивающего обучения внесли Н.А.Менчинская, П.Я.Гальперин, Н.Ф.Талызина, Т.В.Кудрявцев, Ю.К.Бабанский, И.Я.Лернер, М.И.Махмутов, А.М.Матюшкин, И.С.Якиманская и др.
Хотя данная проблема достаточно обстоятельно рассматривается в психолого-педагогической и методической литературе, но в практике школы должного внимания не получила. Поэтому мы и выбрали для своей дипломной работы следующую тему: «Проблемное обучение как фактор интеллектуального развития школьников».
Цель дипломной работы: изучить факторы интеллектуального развития школьников.
Объектом нашей работы является процесс обучения школьников.
Предметом – проблемное обучение как фактор интеллектуального развития школьников.
Исходя из объекта и предмета для достижения поставленной цели, нами были определены следующие задачи:
Изучить и проанализировать психолого-педагогическую и методическую литературу по теме исследования.
Раскрыть сущность интеллектуального развития и проблемного обучения.
Рассмотреть классификацию интеллектуальных умений.
Организовать исследовательскую работу.
Разработать уроки с элементами проблемного обучения и составить подборку проблемных заданий, способствующих интеллектуальному развитию школьников.
При реализации задач исследования использовались следующие методы:
изучение и анализ психолого-педагогической и методической литературы;
изучение и обобщение опыта работы передовых учителей;
анализ деятельности учителей по организации проблемного обучения;
анализ работы учащихся;
беседа с учащимися и учителями;
тестирование и анкетирование.
Наше исследование проводилось в течение двух лет, базой исследования служила школа № 67 Советского района. О ходе исследования и его результатах докладывалось на научной студенческой конференции физико-математического факультета СамГПУ 1 апреля 1999 года.
Глава I. Психолого-педагогические основы интеллектуального развития школьников в проблемном обучении.
1.1. Интеллект, интеллектуальное развитие и интеллектуальные умения.
Понятие «интеллект», перешедшее в современные языки из латыни в XVI веке и обозначавшее первоначально способность понимать, становится в последние десятилетия все более важной общенаучной категорией. В специальной литературе обсуждаются интеллектуальные ресурсы отдельных групп населения и интеллектуальные потребности общества в целом.
Можно без преувеличения сказать, что абсолютное большинство эмпирических исследований в психологии имеет отношение к изучению познавательной сферы личности.
Как известно, познавательная сфера личности исследуется при помощи тестов.
Понятие «теста» как системы коротких стандартизированных заданий, предназначенных для объективного измерения уровня развития тех или иных психических процессов и свойств личности, было впервые введено известным английским психологом Ф.Гальтоном. Идеи Ф.Гальтона получили дальнейшее развитие в работах американского психолога Д.Кеттела, разработавшего системы тестов для исследования различных видов чувствительности, времени реакции, объема кратковременной памяти.
Следующим шагом в развитии тестирования явился перенос метода тестов с измерения простейших сенсомоторных качеств и памяти на измерение высших психических функций, обозначаемых термином «ум», «интеллект». Этот шаг был сделан известным психологом А.Бине, разработавшим в 1905 году совместно с Т.Симоном систему тестов для измерения уровня развития интеллекта детей.
На основе тестовых методик получают показатель умственного развития – коэффициент интеллектуальности (англ. Intellectual quotient, сокр. IQ). Система тестов на определение IQ включает как задания, требующие словесного ответа на поставленные вопросы, так и задачи на манипулирование, например, складывание целостной фигуры по данным ее частям. Требуется решить (с ограничением времени) простые арифметические задачи и примеры, ответить на ряд вопросов, определить значение некоторых терминов и слов. Ответы оцениваются по определенной заранее установленной шкале. Общее количество баллов, полученное по всем заданиям переводится в соответствующий показатель IQ.
В 1921 году журнал «Психология обучения» организовал дискуссию, в которой приняли участие крупнейшие американские психологи. Каждого из них просили дать определение интеллекта и назвать способ, которым интеллект можно было бы лучше всего измерить. В качестве лучшего способа измерения интеллекта почти все ученые назвали тестирование, однако, их определения интеллекта оказались парадоксально противоречивыми друг другу. Интеллект определялся как «способность к абстрактному мышлению» (Л.Термен), «возможность давать хорошие ответы по критерию истинности, правды » (Э.Торндайк), совокупность знаний или способность к обучению, обеспечивающие возможности приспособления к окружающей действительности» (С.Колвин) и др.
В настоящее время в теории тестологии сохраняется примерно та же ситуация, что и в 20-е – 40-е годы. По-прежнему не достигнуто согласия по вопросу о том, что же должны измерять интеллектуальные тесты); по-прежнему тестологи строят свои диагностические системы на основе противоречащих друг другу моделей интеллекта.
Например, современный американский психолог Ф.Фримен строит теорию, в соответствии с которой интеллект состоит из 6 компонентов:
Способность к цифровым операциям.
Словарный запас.
Способность воспринимать сходство или различия между геометрическими фигурами.
Беглость речи.
Способность к рассуждению.
Память.
Здесь в качестве компонентов интеллекта берется и общая психическая функция (память), и такие способности, которые явно являются прямыми следствиями обучения (способность к цифровым операциям, словарный запас).
Английский психолог Г.Айзенк по сути дела сводит интеллект человека к скорости протекания умственных процессов.
Американские психологи Р.Кеттел и Дж.Хорн выделяют в интеллекте 2 компонента: «флюидный» и «кристаллизованный». «Флюидный» компонент интеллекта наследственно предопределен и проявляется непосредственно во всех сферах человеческой деятельности, достигая своего пика в раннем взрослом возрасте и после этого угасая. «Кристаллизованный» компонент интеллекта представляет собой фактически сумму прижизненно сформировавшихся навыков.
Автор одного из наиболее известных методов исследования интеллекта американский психолог Д.Векслер толкует интеллект как общую способность личности, которая проявляется в целенаправленной деятельности, правильном рассуждении и понимании, в приспособлении среды к своим возможностям. Для известного швейцарского психолога Ж.Пиаже сущность выступает в структурировании отношений между средой и организмом.
Немецкие ученые-педагоги Мельхорн Г. и Мельхорн Х.Г. называют интеллектом совокупность способностей, которые характеризуют уровень и качество мыслительных процессов личности. Они считают, что функция интеллекта состоит в умственном решении объективно существующих проблем. Выражением наиболее развитой формы интеллекта является направленное проблемное мышление. Оно создает новое знание для освоения окружающего мира. Проблемное мышление приводит к более или менее большому и качественному расширению горизонтов познания, которое делает возможным сознательное воздействие на природу и общество в соответствии с мыслями человека.[31].
Психодиагносты высказывают мысль, что коэффициенты интеллекта, которые выводятся из различных тестов, трудно сравнивать друг с другом, так как в основе разных тестов лежат различные концепции интеллекта, и в тесты входят различные задания.
В настоящее время многие психометристы все яснее видят несовершенство применяемых ими средств оценки интеллекта. Некоторые из них пытаются усовершенствовать процедуру тестирования, широко используя математические и статические методы уже не только при составлении систем тестов, но и при разработке лежащих в основе этих тестов моделей интеллекта. Так, в тестировании получило широкое распространение направление, представители которого при характеристике и измерении интеллекта пользуются методом факторного анализа.
Представители этого направления опираются на работы Ч.Спирмена, который еще в 1904 году, основываясь на анализе результатов прохождения испытуемыми ряда интеллектуальных тестов, выдвинул теорию, по которой интеллект состоит из общего фактора «G»-«общей умственной энергии»- участвующего в решении всех интеллектуальных тестов, и ряда специфических факторов-«S», каждый из которых действует в пределах данного теста и не коррелирует с другими тестами.
Идеи Спирмена были затем развиты в работах Л.Тэрстоуна и Дж.Гилфорда.
Представители факторного подхода в тестологии исходят из того реального наблюдения, что некоторые лица, хорошо выполняющие одни тесты, могут неудачно действовать при решении других. Следовательно, в решении разных тестов принимают участие различные компоненты интеллекта.
Гилфордом экспериментально выделено 90 факторов (способностей) интеллекта (из 120 факторов теоретически, по его мнению, возможных).
Для того, чтобы получить представление об интеллектуальном развитии испытуемого, необходимо, по Гилфорду, исследовать степень развития всех составляющих интеллект факторов.
Л. Терстоун, в свою очередь, разработал модель интеллекта, состоящую из 7 факторов:
Пространственная способность.
Скорость восприятия.
Легкость оперирования цифровым материалом.
Понимание слов.
Ассоциативная память.
Беглость речи.
Понимание или рассуждение.
Вообще, интеллект (от латинского intellektus – понимание, понятие) – в широком смысле вся познавательная деятельность человека, в более узком смысле – мышление. Мы в своей работе остановимся на определении интеллекта как совокупности познавательных процессов от ощущений и восприятий до мышления и воображения включительно.
Ведущую роль в структуре интеллекта занимает мышление, организующее любой познавательный процесс. Это выражается в целенаправленности и избирательности этих процессов: восприятие проявляется в наблюдении, память фиксирует существенные в том или ином отношении явления и избирательно «подает» их в процессе размышления, воображение входит как необходимое звено в решение творческой задачи, т.е. каждый из психических процессов органически включается в мыслительный акт субъекта.
Интеллект есть высший продукт мозга и представляет собой наиболее сложную форму отражения объективной реальности, возникшую на основе более простых отражения и включающую в себя эти более простые (чувственные) формы.
Качественный скачок в развитии интеллекта человека произошел с возникновением трудовой деятельности и появлением речи. Интеллектуальная деятельность тесно связана с человеческой практикой, служит ей, проверяется ею. Абстрагируясь от единичного, обобщая типичное и существенное, интеллект человека не отходит от реальности, но более глубоко и полно раскрывает закономерности существующего.
Общественный характер человеческой деятельности обеспечивает ее высокую интеллектуальную активность. Она направлена не только на познавание объективной реальности, но и на ее изменение в соответствии с общественными потребностями. Такой характер интеллектуальной деятельности обеспечивает единство собственно познания (мышление), отношения к познаваемому (эмоции) и практического осуществления (воля) данного действия.
Воспитание интеллекта ребенка требует всестороннего развития его познавательных способностей (широты и тонкости разнообразных ощущений, наблюдательности, упражнений разных видов памяти, стимуляции воображения), но в особенности развития мышления. Воспитание интеллекта – одна из центральных задач всестороннего гармонического развития личности. В педагогической энциклопедии подчеркивается, что «интеллектуальное воспитание – важнейшая сторона подготовки к жизни и труду подрастающих поколений, заключающийся в руководстве развитием интеллекта и познавательных способностей путем возбуждения интереса к интеллектуальной деятельности, вооружая знаниями, методами их добывания и применения на практике, привитию культуры интеллектуального труда»[38]. Забота о воспитании интеллекта растущего является задачей семьи, школы и педагогической науки на всем пути их исторического развития.
Доказано, что интеллектуальное развитие – непрерывный процесс, совершающийся в учении, труде, играх, жизненных ситуациях, и что оно наиболее интенсивно происходит в ходе активного усвоения и творческого применения знаний, т.е. в актах, которые содержат особенно ценные операции для развития интеллекта.
Можно выделить типичные черты развитого интеллекта, знание которых важно для понимания процесса интеллектуального воспитания. Первой такой чертой является активное отношение к окружающему миру явлений. Стремление выйти за пределы известного, активность ума находят выражение в постоянном стремлении к расширению знаний и творческому применению их в теоретических и практических целях. С активностью интеллектуальной деятельности тесно связана наблюдательность, способность выделять в явлениях и фактах их существенные стороны и взаимосвязи.
Развитой интеллект отличается системностью, обеспечивающей внутренние связи между задачей и средствами, необходимыми для наиболее рационального ее решения, что приводит к последовательности действий и поисков.
Системность интеллекта есть в тоже время и его дисциплинированность, обеспечивающая точность в работе и надежность получаемых результатов.
Развитой интеллект характеризуется также самостоятельностью, которая проявляется как в познании, так и в практической деятельности. Самостоятельность интеллекта неразрывно связанна с его творческим характером. Если человек привык в школе жизни к исполнительному труду и подражательным действиям, то ему очень трудно обрести самостоятельность. Самостоятельный интеллект не ограничивается использованием чужых мыслей и мнений. Он ищет новые пути изучения действительности, подмечает ранее не замеченные факты и дает им объяснения, выявляет новые закономерности.
В современной психологии считается общепризнанным, что обучение ведет за собой интеллектуальное развитие. Однако проблема связи и взаимодействия между учением школьника и его интеллектуальным развитием изучена еще не достаточно.
Само понятие интеллектуального (умственного) развития трактуется разными исследователями по-разному.
В числе первых с призывом заняться исследованием общего умственного развития, общего интеллекта выступили С.Л.Рубинштейн и Б.Г.Ананьев. Так, Ананьев говорил об этих категориях, как о такой сложной психической особенности человека, от которой зависит успех учения и труда.
Указанная проблема исследовалась в самых различных направлениях. Среди этих исследований следует отметить исследования Н.С.Лейтеса, отмечающего, что общие умственные способности, к которым относится прежде всего качество ума (хотя они могут существенно зависеть также от волевых и эмоциональных особенностей), характеризует возможность теоретического познания и практической деятельности человека. Самое существенное для человеческого интеллекта состоит в том, что он позволяет отражать связи и отношения предметов и явлений окружающего мира и тем самым дает возможность творчески преобразовать действительность. Как показал Н.С.Лейтес, в свойствах высшей нервной деятельности коренятся некоторые активности и саморегуляции, что собой существенные внутренние условия формирования общих умственных способностей.
Психологи пытаются раскрыть структуру общих умственных способностей. Например, Н.Д.Левитов считает, что общие умственные способности прежде всего включают в себя те качества, которые обозначаются как сообразительность (быстрота умственной ориентировки), вдумчивость, критичность.
Плодотворно исследовала проблему умственного развития Н.А.Менчинская с группой своих сотрудников. Эти исследования исходят из положения, сформированного Д.Н.Богоявленским и Н.А.Менчинской о том, что умственное развитие связанное с двумя категориями явлений. Во-первых, должно иметь место накопление фонда знаний – на это обращал внимание еще П.П.Блонский: «Пустая голова не рассуждает: чем больше опыта и знаний имеет эта голова, тем более способна она рассуждать» Таким образом, знание необходимое условие мышления. Во-вторых, для характеристики умственного развития важны те умственные операции, с помощью которых приобретается знание[9]. То есть характерной чертой умственного развития является накопление особого фонда хорошо отработанных и прочно закрепленных умственных приемов, которые можно отнести к интеллектуальным умениям. Словом умственное развитие характеризуется и тем, что отражается в сознании, и еще в большей степени тем, как происходит отражение.
В этой группе исследований с различных точек зрения анализируются умственные операции школьников. Намечаются уровни продуктивного мышления, определяемые уровнями аналитико-синтетической деятельности. В основе этих уровней лежит характеристика:
а) связи между анализом и синтезом,
б) средств, с помощью которых осуществляются эти процессы,
в) степени полноты анализа и синтеза.
Наряду с этим изучаются и умственные приемы как системы операций, специально формируемых для решения задач определенного типа в пределах одного школьного предмета или для решения широкого круга задач из разных областей знаний (Е.Н.Кабанова-Меллер).
Интерес представляет и точка зрения Л.В.Занкова. Для него решающим в плане умственного развития является объединение в определенную функциональную систему таких способов действия, которые характерны по своей природе [42]. Например, младших школьников на одних уроках учили анализирующему наблюдению, а на других обобщению существенных признаков. О прогрессе в умственном развитии можно говорить тогда, когда происходит объединение в одну систему, в единую аналитико-синтетическую деятельность этих разнохарактерных способов умственной деятельности.
В связи изложенным выше встает вопрос о содержательных критериях (признаках, показателях) умственного развития. Перечень таких самых общих критериев дает Н.Д.Левитов. По его мнению, умственное развитие характеризуется следующими показателями:
самостоятельностью мышления,
быстротой и прочностью усвоения учебного материала,
быстротой умственной ориентировки (находчивости) при решении нестандартных задач,
глубоким проникновением в сущность изучаемых явлений (умением отличить существенное от несущественного),
критичностью ума, отсутствием склонности к предвзятым, необоснованным суждениям.
Для Д.Б.Эльконина основным критерием умственного развития является наличие правильно организованной структуры учебной деятельности (сформированная учебная деятельность) с её компонентами - постановкой задачи, выбором средств, самоконтролем и самопроверкой, а также правильное соотношение предметных и символических планов в учебной деятельности.
Н.А.Менчинская рассматривает в этой связи такие особенности мыслительной деятельности, как:
быстроту (или, соответственно, замедленность) усвоения;
гибкость мыслительного процесса (т.е. лёгкость или, соответственно, трудность перестройки работы, приспособления к изменяющимся условиям задач);
тесную связь (или, соответственно, разрозненность) наглядных и отвлечённых компонентов мышления;
различный уровень аналитико-синтетической деятельности.
Е.Н.Кабанова-Меллер
основным критерием
умственного
развития считает
широкий и активный
перенос приёмов
умственной
деятельности,
сформированных
на одном объекте,
на другой объект.
Например, перенос
схемы мышления
при выводе
формулы
![]() на самостоятельный
вывод формулы
на самостоятельный
вывод формулы
![]() .
Высокий уровень
умственного
развития связан
с межпредметным
обобщением
умственных
приемов, открывающим
возможность
их широкого
переноса с
одного предмета
на другой.
.
Высокий уровень
умственного
развития связан
с межпредметным
обобщением
умственных
приемов, открывающим
возможность
их широкого
переноса с
одного предмета
на другой.
Особый интерес представляют критерии, разрабатываемые З.И.Калмыковой в лаборатории с Н.А.Менчинской. Это, во-первых, темп продвижения – показатель, который нельзя путать с индивидуальным темпом работы. Быстрота работы и быстрота обобщения – разные вещи. Можно работать медленно, но обобщать быстро, и наоборот. Темп продвижения определяется количеством однотипных упражнений, необходимых для формирования обобщения.
Другим критерием умственного развития школьников является так называемая «экономичность мышления», т. е. Количество рассуждений, на основании которых учащиеся выделяют новую для себя закономерность. При этом З.И.Калмыкова исходила из следующих соображений. Учащиеся с низким уровнем умственного развития слабо используют информацию, заложенную в условиях задачи, часто решают её на основе слепых проб или необоснованных аналогий. Поэтому путь их к решению оказывается малоэкономичным, он перегружен конкретизирующими, повторными и ложными суждениями. Таким учащимся постоянно требуется коррекция и помощь со стороны. Учащиеся с высоким уровнем умственного развития обладают большим фондом знаний и способов оперирования ими, полностью извлекают информацию, заложенную в условиях задачи, постоянно контролируют свои действия, поэтому их путь к решению проблемы отличается лаконичностью, краткостью, рациональностью.
Важная задача современной психологии – построить объективные, научно обоснованные индикаторные психологические методики, с помощью которых можно диагностировать уровень умственного развития школьников на различных возрастных этапах.
К настоящему времени разработаны некоторые методы диагностики интеллектуального развития школьников в процессе обучения. Эти методы связаны с оценкой и измерением таких параметров умственной деятельности, как:
приёмы умственной деятельности;
умение самостоятельно добывать знания и др.
Сущность интеллектуальных умений.
В педагогическом словаре понятие «умение» определяется следующим образом: «умения – подготовленность к практическим и теоретическим действиям, выполняемым быстро, точно и сознательно, на основе усвоенных знаний и жизненного опыта».
Учебные умения предполагают использование ранее полученного опыта, определенных знаний. Знания и умения – деве неотделимые и функционально взаимосвязанные части любого целенаправленного действия. Качество умений определяется характером и содержанием знаний о предполагаемом действии.
Изучение каждого учебного предмета, проведение упражнений и самостоятельных работ вооружает учащихся умением применять знания. В свою очередь, приобретение умений способствует углублению и дальнейшему накапливанию знаний. Совершенствуясь и автоматизируясь, умения превращаются в навыки. Умения тесно взаимосвязаны с навыками как способами выполнения действия, соответствующими целям и условиям, в которых приходится действовать. Но, в отличие от навыков, умение может образовываться и без специального упражнения в выполнении какого-нибудь действия. В этих случаях оно опирается на знания и навыки, приобретенные раньше, при выполнении действий, только сходных с данным. В месте с тем умение совершенствуется по мере овладения навыком. Высокий уровень умения означает возможность пользования разными навыками для достижения одной ми той же цели в зависимости от условий действия. При высоком развитии умения действие может выполняться в разнообразных вариациях, каждая из которых обеспечивает успех действия в данных конкретных условиях.
Образование умений представляет собой сложный процесс аналитико-синтетической деятельности коры больших полушарий головного мозга, в ходе которого создаются и закрепляются ассоциации между заданием, необходимыми для его выполнения знаниями и применением знаний на практике. Повторные действия укрепляют эти ассоциации, а вариации заданий делают их все более точными. Таким образом формируются черты и признаки умений: гибкость, т.е. способность рационально действовать в различных ситуациях, стойкость, т.е. сохранение точности и темпа, несмотря на некоторые побочные влияния, прочность (умение не утрачивается в тот период, когда оно практически не применятся), максимальная приближенность к реальным условиям и задачам.
В современной педагогической литературе нет единого подхода к классификации учебных умений. Некоторые ученые считают, что «умения и навыки подразделяются на обобщенные (межпредметные) и частные (специфические для отдельных предметов), интеллектуальные и практические, учебные и самообразовательные, общетрудовые и профессиональные, рациональные и нерациональные, продуктивные и репродуктивные и некоторые другие» [12]. Однако деление умений на виды является в определенной степени условным, т.к. часто нет резкой границы, различающей их. Поэтому мы решили, что более точной является следующая классификация, предложенная Н.А.Лошкаревой [12]. Согласно этой классификации, учебный труд школьников обеспечивается учебно-организационными, учебно-интеллектуальными, учебно-информационными и учебно-коммуникативными умениями. Такую же классификацию дает Ю.К.Бабанский [4]. Мы остановимся подробнее только на учебно-интеллектуальных умениях.
В своей работе Ю.К.Бабанский выделяет следующие группы интеллектуальных умений: мотивировать свою деятельность; внимательно воспринимать информацию; рационально запоминать; логически осмысливать учебный материал, выделяя в нем главное; решать проблемные познавательные задачи; самостоятельно выполнять упражнения; осуществлять самоконтроль в учебно-познавательной деятельности.
Как видим, Бабанский в основу свой классификации положим деятельный подход. Не отвергая данную классификацию, мы рассмотрим еще один класс интеллектуальных умений, в основу которого было положено понятие «интеллект». В данной классификации под интеллектуальными умениями будем понимать подготовленность человека к выполнению интеллектуальных действий. Интеллектуальными умениями здесь являются следующие умения:
воспринимать,
запоминать,
быть внимательным,
мыслить,
обладать интуицией.
Рассмотрим перечисленные группы интеллектуальных умений, включая те, которые выделяет Ю.К.Бабанский.
1. Мотивация учения.
Известно, что успех любой деятельности, в том числе и учебной, во многом зависит от наличия положительных мотивов учения.
Человеку от природы присущ безусловный ориентировочный рефлекс «почему?». Задача педагогов состоит в том, чтобы в течение всего периода школьного обучения создавать самые благоприятные условия для поддержания этого свойственного человеку любопытства, не гасить его, а дополнять новыми мотивами, идущими от самого содержания обучения, форм и методов организации познавательной деятельности, от стиля общения с учениками. Мотивацию надо специально формировать, развивать, стимулировать и, что особенно важно, учить школьников «самостимулировать» свои мотивы.
Среди многообразия мотивов учения можно выделить две большие группы: мотивы познавательного интереса и мотивы долга и ответственности в обучении. Мотивы познавательного интереса проявляются в повышенной тяге к познавательным играм, учебным дискуссиям, спорам и другим методам стимулирования обучения. Мотивы долга и ответственности связаны прежде всего с наличием у ученика сознательной учебной дисциплины, стремления охотно выполнять требования учителей, родителей, уважать общественное мнение класса.
Зная состояние мотивов ученика, педагог может своевременно подсказать ему, над устранением каких недостатков следует настойчиво поработать в ближайшее время. Ведь многие ученики вообще не задумываются над этой проблемой, и бывает достаточно обратить их внимание на это, как они невольно начинают заниматься самовоспитанием хотя бы в самых элементарных его формах. Другим школьникам приходится подсказывать и доступные приемы самовоспитания мотивов учения. Третьи нуждаются еще в более тщательном и систематическом контроле за ходом самовоспитания, в оказании им текущей помощи. Педагоги должны учить школьников понимать субъективную значимость учения – что может дать изучение этого предмета для развития его склонностей, способностей, для профессиональной ориентированности подведения вплотную для овладения интересующей профессией. Учителя должны помогать ученику осознать, что дает учение для подготовки к общению в пульсирующей среде, в трудовом коллективе. Все это вырабатывает у школьников рефлекс сомомотивации, самостимулирования. В учебных делах в качестве источников стимулирования обычно выступают, конечно, чувства долга, ответственности и сознательной дисциплины. Самовоспитание учебной дисциплины и волевой собранности связанно также и с выработкой «помехоустойчивости»; умения заставлять себя вновь и вновь браться за выполнение «неподдающегося» решения задачи. Не менее важное значение имеет четкое предъявление требований со стороны учителей, единство таких требований, ясная мотивировка выставляемых оценок.
Серьезного внимания заслуживает разумная система поощрения. Похвала ответа, похвальная запись в дневнике и на экране успеваемости – все это способствует зарождению общественно ценных мотивов, которые играют особо важную роль в учебной мотивации вообще.
Самое главное для учителя – это необходимость добиваться перевода внешнего стимулирования в самостимулирование у учеников внутренней мотивации. И здесь особенно важное значение имеет умелое слияние целеполагания и мотивации ученика. Продумывая задачи своей деятельности дома и на уроке, школьник, особенно старший, тем самым уже мотивирует свою деятельность. Школьники активнее занимаются самовоспитанием мотивов, если видят, что этот процесс интересует учителей, родителей, ученический актив, когда их поддерживают при возникающих затруднениях.
Итак, видим, что конкретно предполагает процесс самостоятельного стимулирования учения:
осознание учениками учения как общественного долга;
оценку теоретической и практической значимости предмета и изучаемого вопроса;
оценку субъективной значимости учения вообще и данного предмета для развития своих способностей, профессиональных устремлений или, наоборот, для целенаправленного устранения причин, мешающих сполна опираться на свои реальные учебные возможности;
стремление приобретать не только наиболее интересные, яркие, увлекательные, занимательные знания, а осваивать все содержание образования;
развитие умений подчиняться самоприказу, волевому стимулированию образования;
настойчивое преодоление учебных затруднений;
стремление понять, осознать, пережить, оценить, полезность для себя выполнения требования учителей, родителей, классного коллектива;
сознательное подавление чувства страха перед предстоящими ответами, классной работой или зачетом.
2. Умение воспринимать.
Восприятием называется отражение в сознании человека предметов или явлений при их непосредственном воздействии на органы чувств. В ходе восприятия происходит упорядочение и объединение отдельных ощущений в целостные образы вещей и событий. Восприятие отражает предмет в целом, в совокупности его свойств. При этом восприятие не сводится к сумме ощущений, а представляет собой качественно новую ступень чувственного познания с присущими ее особенностями.
Хотя восприятие возникает в результате непосредственного воздействия раздражителя на рецепторы, перцептивные образы всегда имеют определенное смысловое значение. Умение воспринимать у человека теснейшим образом связанно с мышлением, с пониманием сущности предмета. Умение сознательно воспринять предмет – это значит умение мысленно назвать его, т.е. отнести воспринятый предмет к определенной группе, классу предметов, обобщить его в слове. Даже при виде незнакомого предмета мы пытаемся уловить в нем сходство со знакомыми нам объектами, отнести его к некоторой категории. Умение воспринимать – это умение организовывать динамический поиск наилучшего толкования, объяснения имеющихся данных. Восприятие – активный процесс, в ходе которого человек производит множество действий для того, что бы сформировать адекватный образ предмета.
Многократные психолого-педагогические эксперименты показали, что мы не можем воспринимать прежде, чем научимся воспринимать. Восприятие – это система перцептивных действий, и овладение ими требует специального обучения и практики.
Наиболее важной формой умения воспринимать является умение наблюдать. Наблюдение можно охарактеризовать как преднамеренное, планомерное восприятие предметов или явлений окружающего мира. В наблюдении восприятие выступает как самостоятельная деятельность. Мы часто не различаем определенные звуки иностранного языка, не слышим фальши в исполнении музыкального произведения или не видим ее в передаче цветовых тонов картин. Умению наблюдать можно и нужно учиться.
Известный голландский ученый М.Миннарт говорил: «От вас самих зависит прозрение – вам стоит лишь дотронутся до своих глаз магическим жезлом под названием «знай, на что смотреть»». Действительно, успех наблюдения в значительной степени определяется постановкой задачи. Наблюдателю необходим «компас», указывающий направление наблюдения. Таким «компасом» и является задача, поставленная перед наблюдателем, план наблюдения.
Для успешного проведения наблюдения большое значение имеет предварительная подготовка к нему, прошлый опыт, знания наблюдателя. Чем богаче опыт человека, чем больше у него знаний, тем богаче его восприятие. Эти закономерности наблюдения должен учитывать учитель, организуя деятельность учащихся.
Формирование умения наблюдать у учащихся помогает обеспечить более эффективное усвоение новых знаний при применении принципа наглядности обучения. Очевидно, процесс обучения не должен строиться лишь по принципу, когда учащиеся принимают информацию, которую сообщает на уроке учитель; «процесс обучения должен быть организован как активная мыслительная деятельность учащихся» [2]. Экспериментальные исследования показали, что существенным компонентом процесса принятия решения является манипулирование образом ситуации, сложившейся на основе ориентировочно-исследовательской перцептивной деятельности. Необходимость перевода проблемной ситуации во внутренний план для процесса принятия решения свидетельствует о чрезвычайной важности правильного подхода к исследованию принципа наглядности обучения. Использование наглядности в обучении должно направлять не только процесс создания образа ситуации, но и процесс переструктурирования этого образа в соответствии со стоящей задачей. Последовательность использования наглядных пособий на уроке должна направлять деятельность учащихся по созданию модели изучаемого материала.
Такой подход к использованию принципа наглядности обучению, когда оно строится на активном наблюдении и активной умственной деятельности учащихся, должен обеспечивать эффективное и прочное усвоение знаний.
3. Умение быть внимательным.
Внимательность – важное и неотделимое условие эффективности всех видов деятельности человека, прежде всего трудовой и учебной. Чем сложнее и ответственнее труд, тем больше требований предъявляет он к вниманию. Для успешной организации учебно-воспитательной работы необходимо, чтобы у учащихся в должной мере было сформировано умение быть внимательным. Еще великий русский педагог К.Д.Ушинский, подчеркивая роль внимания в обучении, писал: «внимание есть именно та дверь, через которую проходит все, что только входит в душу человека из внешнего мира». Понятно, что научить детей держать эти двери открытыми очень важно для успеха всего учения.
В зависимости от объекта сосредоточения (воспринимаемые предметы, представления памяти, мысли, движения) выделяют следующие проявления внимания: сенсорное (перцептивное), интеллектуальное, моторное (двигательное). Внимание как познавательный процесс по характеру происхождения и по способам осуществления разделяют на два вида: непроизвольное внимание и произвольное. Непроизвольное внимание возникает и поддерживается независимо от сознательных намерений целей человека. Произвольное внимание – это сознательно направленное и регулируемое сосредоточение.
Поскольку в определении понятия «умение» подчеркивается необходимость сознательного выполнения действий, то, говоря об умении быть внимательным будем понимать сформированность произвольного внимания. Произвольное внимание развивается на основе непроизвольного. Умение быть внимательным формируется, когда в деятельности человек ставит перед собой определенную задачу и сознательно вырабатывает программу действий. Это интеллектуальное умение формируется не только посредством воспитания, но и в огромной мере посредством самовоспитания учащихся. В степени сформированности умения быть внимательным проявляется активность личности. При произвольном внимании интересы носят опосредованный характер (это интересы цели, результата деятельности). Если в целенаправленной деятельности для ребенка интересными и значительными становятся содержание и сам процесс деятельности, а не только ее результат, как при произвольном сосредоточении, то есть основание говорить о послепроизвольном внимании. Послепроизвольное внимание характеризуется длительной высокой сосредоточенностью, с ним обоснованно связывают наиболее интенсивную и плодотворную умственную деятельность, высокую производительность всех видов труда. Значение учебной деятельности особенно велико для формирования произвольного внимания, то есть умения быть внимательным. Школьный возраст является периодом его активного становления, некоторые психологи (П.Я.Гальперин и др.) считают, что невнимательность школьников связанна с неполноценным формированием функций контроля в условиях, когда он складывается стихийно. В связи с этим, задачи планомерного развития умения быть внимательным ведется как постоянное целенаправленное формирование автоматизированных действий умственного контроля. Интеллектуальное умение быте внимательным характеризуется различными качественными проявлениями. К ним относятся: устойчивость, переключение, распределение и объем внимания.
Анализ практики обучения позволяет выделить некоторые типичные недостатки, которые мешают ученикам внимательно слушать объяснение учителей. Прежде всего, это слабая концентрация внимания на главном, нарушение логики изложения, отсутствие хорошо продуманных, четких, однозначно трактуемых обобщений и выводов. Очень редко используются художественные, образные приемы, это снижает эмоциональный тонус объяснения. Вниманию учеников мешает порой неумение учителей обеспечить хорошую дисциплину на уроке.
Особое значение в целях поддержания внимания учащихся на должном уровне имеет разнообразие методов обучения: рассказ, беседа, самостоятельное разрешение проблемных ситуаций и др. при правильном их сочетании и чередовании можно активно развивать внимательность как черту личности.
4. Умение запоминать.
Важнейшая особенность психики состоит в том, что отражение внешних воздействий постоянно используется индивидом в его дальнейшем поведении. Постепенное усложнение поведения осуществляется за счет накопления индивидуального опыта. Формирование опыта было бы невозможно, если бы образы внешнего мира, возникающие в коре головного мозга, исчезали бесследно. Вступая в различные связи между собой, эти образы закрепляются, сохраняются и воспроизводятся в соответствии с требованиями жизни и деятельности.
Запоминание, сохранение и последующее воспроизведение индивидом его опыта называется памятью. Память – важнейшая, определяющая характеристика психической жизни личности, обеспечивающая единство и целостность человеческой личности. Совокупность умений запоминать, сохранять и воспроизводить различного рода информацию мы будем в дальнейшем называть интеллектуальным умением запоминать.
Память как психический процесс разделяют на отдельные виды в соответствии с тремя основными критериями:
по характеру психической активности, преобладающей в деятельности, память делят на двигательную, образную и словесно-логическую;
по характеру целей деятельности – на непроизвольную и произвольную;
по продолжительности закрепления и сохранения (в связи с его ролью и местом в деятельности) – на кратковременную, долговременную и оперативную.
Согласно определению интеллектуальных умений, под формированием умения запоминать будем понимать развитие произвольной образной или словесно-логической памяти, которая должна быть долговременной или оперативной.
Образная память – это память на представления, картины природы и жизни, а также на звуки, знаки, вкусы. Для усиленного обучения геометрии (и многим другим наукам) особенно важно развитие у учащихся памяти на представления.
Содержанием словесно-логической памяти являются наши мысли. Мысли не существуют без языка, поэтому память на них называется не просто логической, а словесно-логической. Поскольку мысли могут быть воплощены в различную языковую форму, то воспроизведение их возможно ориентировать на передачу либо только основного смысла материала, либо его буквального словесного оформления.
Умение запоминать словесно-логические формы – специфически человеческое умение в отличие от умения запоминать образы, которые в своих простейших вариантах может быть сформировано и у животных. Опираясь на развитие других видов памяти, словесно-логическая память становится ведущей по отношению к ним, и от ее развития зависит развитие всех других видов памяти. Умение запоминать словесно-логические формы принадлежит к ведущим интеллектуальным умениям, необходимым для усвоения знаний учащимися в процессе обучения.
Запоминание и воспроизведение, в которых присутствует специальная цель что-то запомнить или припомнить, называется произвольной памятью. Говорить о формировании умения запоминать можно лишь тогда, когда происходит развитие произвольной памяти.
Для долговременной памяти характерно длительное сохранение материала после многократного повторения и воспроизведения. Понятием «оперативная память» обозначают мнемические процессы, обслуживающие непосредственно осуществляемые человеком действия, операции. Когда человек выполняет какое-либо действие, например арифметическое, то осуществляет его по частям, кусками. При этом человек удерживает «в уме» некоторые промежуточные результаты до тех пор, пока имеет с ними дело. По мере продвижения к конечному результату конкретный «отработанный» материал может забываться. Аналогичное явление наблюдается при чтении, списывании, вообще при выполнении любого более или менее сложного действия. Куски материала, которыми оперирует человек, могут быть различными (процесс чтения у ребенка начинается со складывания отдельных букв). Объем этих кусков, так называемых оперативных единиц памяти, существенно влияет на успешность выполнения той или иной деятельности.
Кроме видов памяти выделяют и ее основные процессы. При этом в качестве основания рассматривают именно различные функции, выполняемые памятью в жизни и деятельности. К процессам памяти относят запоминание (закрепление), воспроизведение (актуализацию, возобновление) и сохранение материала. Кратко охарактеризуем соответствующие умения.
Умение запоминать (в узком смысле, как часть общего учебно-интеллектуального умения запоминать) можно определить как умение закреплять новое знание путем связывания его с приобретенным ранее.
Умение воспроизводить информацию – это умение актуализировать закрепленное ранее знание путем извлечения его из долговременной памяти и перевода в оперативную.
Уже в подростковом возрасте память должна стать объектом не только воспитания, но и самовоспитания. Самовоспитание памяти достигает значительных успехов тогда, когда оно основывается на знании закономерностей ее формирования. Основой развития смысловой памяти является содержательная познавательная активность личности.
5. Умение обладать интуицией.
«Интуиция (лат. Intuitio – созерцание, видение, пристальное всматривание) – термин, означающий то же самое, что и непосредственное созерцание, знание, полученное в ходе практического и духовного освоения объекта, наглядное представление» [17]. Интуиция хотя и отличается от умения мыслить дискурсивно (то есть логически выводить одно понятие из другого), но не противопоставлена ему. Созерцание предмета посредством органов чувств (то, что иногда называют чувственной интуицией) не дает нам ни достоверного, ни всеобщего знания. Такое знание достигается только с помощью рассудка и интеллектуальной интуиции. Под последней Декарт понимает высшую форму познания, когда разуму непосредственно, без помощи рассуждения, доказательства становятся ясной истинность того или иного положения, идеи (например, если две величины равны третьей, то они равны и между собой).
Научное познание не сводится к одному логическому, понятийному мышлению; в науке большую роль играет чувственная и интеллектуальная интуиция. Каким бы путем не было получено то или иное положение, его достоверность доказывается практической проверкой. Например, истинность многих аксиом математики и правил логики интуитивно усматриваются не в силу их врожденного характера, а потому, что, миллиарды раз проверяясь на практике, они приобрели для человека «прочность предрассудка».
6. Умение осуществлять самоконтроль в учении.
Известно, что без текущего и итогового контроля невозможно объективно оценить реальную эффективность учебного труда. Не проверив степени усвоения материала, точности решаемой задачи, грамотности написания сочинения, не выработав привычку всегда проверять свои действия, невозможно гарантировать из правильность.
Между тем, изучение степени развития у учащихся навыка самоконтроля показывает, что именно он формируется, как правило, слабо. Ученики не всегда правильно работают с контрольными вопросами учебника, с ответами в задачниках.
Опыт работы учителей города Москвы и Санкт-Петербурга показывает, что для развития у учащихся навыков самоконтроля полезно использовать специальные приемы. Во-первых, необходимо советовать школьникам при домашней подготовке обязательно проверять степень усвоения учебного материала путем составления плана прочитанного и пересказа главных мыслей его своими словами.
Следующим важным средством развития самоконтроля является приучение школьников систематически отвечать на контрольные вопросы учебника, а также на дополнительные контрольные вопросы, требующие размышления над текстом. В средних и старших классах предлагают ученикам самим составлять контрольные вопросы к тексту, если они отсутствуют в учебнике. В таком случае одновременно осуществляется самоконтроль над умениями выделять главное, существенное. Особенно ценным приемом самоконтроля является проверка правильности выполнения письменных заданий. Для этого применяются специфические для каждого учебного предмета приемы. Например, в математике, производится приближенная прикидка правильности решения задачи; оценивается жизненная реальность результатов; проводится проверка точности вычислений обратными действиями (умножение делением, сложение вычитанием и так далее).
Примечательной особенностью опыта современных учителей является приобщение школьников к взаимной проверке сочинений, самостоятельных работ. С внедрением в школьную практику кодоскопов значительно расширилась и такая форма работы над ошибками, как сравнение своего решения с образцом, который демонстрируется на экране.
Совокупность описанных выше приемов работы неизменно обеспечивает развитие умения осуществлять самоконтроль в учении.
7. Умение самостоятельно выполнять упражнения, решать проблемные и познавательные задачи.
Современная педагогика исходит из того, что ученик должен быть не только объектом обучения, пассивно воспринимающим учебную информацию учителя. Он призван одновременно быть активным субъектом его, самостоятельно владеющим знаниями и решающим познавательные задачи. Для этого у него необходимо вырабатывать не только навыки внимательного восприятия учебной информации, но и самостоятельность учения, умение выполнять учебные упражнения, проводить опыты, а также решать проблемные задачи.
Ценным средством развития навыков самостоятельного решения учебных задач являются задания по отысканию учениками сферы применения изучаемых вопросов в окружающей действительности и составлению на этой основе новых задач по физике, математике и другим предметам. Самостоятельное составление задач очень нравится ученикам, особенно если педагог организует затем их коллективное обсуждение, а также и решение лучших из них.
Ценнейшим средством развития самостоятельности мышления является проблемное обучение. При проблемном обучении школьникам высказывают предположения, ищут аргументы для их доказательства, самостоятельно формулируют некоторые выводы и обобщения, являющиеся уже новыми элементами знаний по соответствующей теме. Поэтому проблемное обучение не только развивает самостоятельность, но и формирует некоторые навыки учебно-исследовательской деятельности.
8. Умение мыслить.
Наиболее важное из всех интеллектуальных умений – умение мыслить – рассмотрим чуть более подробно. Академик А.В.Погорелов отмечал, что «…очень немногие из оканчивающих школу будут математиками. Однако, вряд ли найдётся хотя бы один, которому не придётся рассуждать, анализировать, доказывать» [40].Успешное овладение основами наук и орудиями труда не возможно без формирования культуры мышления. Ещё Т.А.Эддисон говорил, что основная задача цивилизации – научить человека мыслить.
Познавательная деятельность начинается с ощущений и восприятий, и затем может произойти переход к мышлению. Однако любое, даже наиболее развитое мышление всегда сохраняет связь с чувственным познанием, т. е. с ощущениями, восприятиями и представлениями. Весь свой материал мыслительная деятельность получает только из одного источника – из чувственного познания.
Через ощущения и восприятия мышление непосредственно связано с внешним миром и является его отражением. Правильность (адекватность) этого отражения непрерывно проверяется в ходе практики. Поскольку в рамках только чувственного познания (с помощью умения ощущать и воспринимать) невозможно до конца расчленить такой общий, суммарный, непосредственный эффект взаимодействия субъекта с познаваемым объектом, то необходима сформированность умения мыслить. При помощи этого интеллектуального умения осуществляется дальнейшее, более глубокое познание внешнего мира. В результате удаётся расчленить, распутать сложнейшие взаимозависимости между предметами, событиями, явлениями.
В процессе мышления, используя данные ощущений, восприятий и представлений, человек вместе с тем выходит за пределы чувственного познания, т. е. начинает познавать такие явления внешнего мира, их свойства и отношения, которые непосредственно вовсе не даны в восприятиях и потому непосредственно вообще не наблюдаемы.
Для мыслительной деятельности человека существенна её взаимосвязь не только с чувственным познанием, но и с языком, с речью. Только с появлением речи становится возможным отвлечь от познаваемого объекта то или иное его свойство и закрепить, зафиксировать представление или понятие о нём в специальном слове. Человеческое мышление – в каких формах оно не осуществлялось – не возможно без языка. Всякая мысль возникает и развивается в неразрывной связи с речью. Чем глубже и основательнее продумана та или иная мысль, тем более четко и ясно она выражается в словах, в устной или письменной речи. И наоборот, чем больше совершенствуется, оттачивается словесная формулировка какой-либо мысли, тем отчетливее и понятнее становится сама эта мысль.
Специальные наблюдения в ходе психолого-педагогических экспериментов показали, что многие школьники часто испытывают трудности в процессе решения задачи, пока не сформулируют свои рассуждения вслух. Когда же решающие начинают специально и все более четко формулировать, проговаривать одно за другим основные рассуждения (пусть даже в начале явно ошибочные), то такое думание вслух обычно облегчает решение задач.
Такое формулирование, закрепление, фиксирование мысли в словах означает чтение мысли, помогает задержать внимание на различных моментах и частях этой мысли и способствует более глубокому пониманию. Благодаря этому и становится возможным развернутое, последовательное, систематическое рассуждение, т.е. четкое и правильное сопоставление друг с другом всех основных мыслей, возникающих в процессе мышления. В слове, в формулировании мысли заключены, таким образом, важнейшие необходимые предпосылки формирования умения дискурсивно мыслить. Дискурсивное мышление – это мышление рассуждающее, логически расчлененное и осознанное. Мысль прочно фиксируется в речевой формулировке – устной или даже письменной. Поэтому всегда существует возможность в случае необходимости снова вернуться к этой мысли, еще глубже ее продумать, проверить и в ходе рассуждения соотнести с другими мыслями.
Формулирование мыслей в речевом процессе является важнейшим условием их формирования. Большую роль в этом процессе может играть и так называемая внутренняя речь: решая задачу, человек решает не в слух, а про себя, как бы разговаривая только с собой. Таким образом, формирование умения мыслить неразрывно связанно с развитием речи. Мышление необходимо существует в материальной, словесной оболочке.
Познание предполагает преемственность всех знаний, приобретаемых в ходе человеческой истории. Фиксация всех основных результатов познания осуществляется с помощью языка – в книгах, журналах и т.п. Во всем этом выступает социальная природа человеческого мышления. Интеллектуальное развитие человека необходимо совершается в процессе усвоения знаний, выработанных человечеством в ходе общественно-исторического развития. Процесс познания мира человеком обусловлен историческим развитием научного знания, результаты которого каждый человек осваивает в ходе обучения.
В течение всего периода школьного обучения перед ребёнком выступает уже готовая, сложившаяся, известная система знаний, понятий и т. д., открытых и выработанных человечеством в ходе всей предшествующей истории. Но то, что известно человечеству и не является для него новым, неизбежно оказывается неизвестным и новым для каждого ребёнка. Поэтому усвоение всего исторически накопленного богатства знаний требует от ребёнка больших усилий мышления, серьёзной творческой работы, хотя он осваивает уже готовую систему понятий, причём осваивает под руководством взрослых. Следовательно, тот факт, что дети усваивают уже известные человечеству знания и делают это с помощью взрослых, не исключает, а, наоборот, предполагает необходимость формирования умения самостоятельно мыслить у самих детей. Иначе усвоение знаний будет чисто формальным, поверхностным, бездумным, механическим. Таким образом, умение мыслить – необходимая основа и для усвоения знаний (например, детьми), и для добывания совсем новых знаний (прежде всего учёными) в ходе исторического развития человечества.
Умение мыслить предполагает умение использовать логические формы – понятия, суждения и умозаключения. Понятия – это мысль, в которой отражаются общие, существенные и отличительные (специфические) признаки предметов и явлений действительности. Содержание понятий раскрывается в суждениях, которые всегда выражаются в словесной форме. Суждения – это отражение связей между предметами и явлениями действительности или между их свойствами и признаками. Суждения образуются двумя основными способами:
непосредственно, когда в них выражают то, что воспринимается;
опосредованно – путем умозаключений или рассуждений.
В умозаключающей, рассуждающей (и, в частности, предсказывающей) работе мышления наиболее отчетливо проявляется его опосредованный характер. Умозаключение – это такая связь между мыслями (понятиями, суждениями), в результате которой из одного или нескольких суждений мы получаем другое суждение, извлекая его из содержания исходных суждений. Все логические формы совершенно необходимы для нормального протекания мыслительной деятельности. Благодаря им всякое мышление становится доказательным, убедительным, непротиворечивым и, значит, правильно отражает объективную действительность.
Процесс мышления – это прежде всего анализ, синтез, сравнение и обобщения. А значит, умение мыслить включает в себя умения анализировать, синтезировать, сравнивать и обобщать. Умение анализировать – это умение выделять в объекте те или иные стороны, элементы, свойства, связи, отношения и т.д.; расчленять познаваемый объект на различные компоненты. Умение синтезировать – это умение объединять выделенные анализом компоненты целого. Анализ и синтез всегда взаимосвязаны. Умение анализировать и синтезировать создают основу для формирования умения сравнивать различные объекты. Умение сравнивать – это умение сопоставлять объекты познания с целью нахождения сходства и различия между ними. Сравнение ведет к обобщению. В ходе обобщения в сравниваемых предметах – в результате их анализа – выделяется нечто общее. Эти общие для различных объектов свойства бывают двух видов:
общие как сходные признаки,
общие как существенные признаки.
Общие существенные признаки выделяются в ходе и в результате углубленного анализа и синтеза.
Закономерности анализа, синтеза, сравнения и обобщения – это основные, внутренние, специфические закономерности мышления. На их основе только и могут получить объяснение все внешние проявления мыслительной деятельности. Так, учитель часто наблюдает, что ученик решивший данную задачу или усвоивший определенную теорему, не может осуществить перенос, т.е. использовать это решение в других условиях, не может применить теорему для решения однотипных задач, если их содержание, чертеж и т.д. несколько видоизменяются. Например, учащийся, только что доказавший теорему о сумме внутренних углов треугольника на чертеже с остроугольным треугольником, нередко оказывается не в состоянии провести то же рассуждение, если уже знакомый чертеж повернуть на 90 или если дать школьнику чертеж с тупоугольным треугольником. Такая ситуация свидетельствует о недостаточной сформированности умений анализировать, синтезировать и обобщать. Варьирование условий задачи способствует тому, чтобы ученик осуществил анализ предложенной ему задачи, выделил в ней наиболее существенные компоненты и произвел их обобщение. По мере того, как он выделяет и обобщает существенные условия разных задач, он и совершает перенос решения из одной задачи в другую, существенно сходную с первой. Так за внешней зависимостью «варьирование условий – перенос решения» выступает внутренняя зависимость «анализ – обобщение».
Мышление имеет целенаправленный характер. Необходимость применения умения мыслить возникает прежде всего тогда, когда в ходе жизни и практики перед человеком проявляется новая цель, новая проблема, новые обстоятельства и условия деятельности. По самому своему существу умение мыслить необходимо лишь в тех ситуациях, в которых возникают эти новые цели, а старые средства и способы деятельности недостаточны (хотя и необходимы) для их достижения. Такие ситуации называют проблемными.
Умение мыслить – это умение искать и открывать новое. В тех случаях, где можно обойтись старыми навыками, проблемно ситуации не возникает и поэтому умения мыслить попросту не требуется. Например, уже ученика второго класса не заставляет мыслить вопрос типа: «Сколько будет 2х2?». Потребность в применении умения мыслить исчезает и в тех случаях, когда школьник хорошо овладел новым способом решения определенных задач или примеров, но вынужден снова и снова решать эти однотипные, уже ставшие ему известными задачи и примеры. Следовательно, далеко не всякая ситуация в жизни является проблемной, т.е. вызывающей мышление.
Мышление и решение задач тесно связанны друг с другом. Но нельзя сводить умение мыслить к умению решать задачи. Решение задачи осуществляется только при помощи умения мыслить, и не иначе. Но умение мыслить проявляется не только в решении уже поставленных, сформулированных задач (например, школьного типа). Оно необходимо и для самой постановки задач, для выявления и осознания новых проблем. Нередко нахождение и постановка проблемы требует даже больших интеллектуальных усилий, чем ее последующее разрешение. Умение мыслить нужно также для усвоения знаний, для понимания текста в процессе чтения и во многих других случаях, совсем не тождественных решению задач.
Хотя умение мыслить и не сводится к умению решать задачи, лучше всего формировать его именно в ходе решения задач, когда ученик наталкивается на посильные для него проблемы и вопросы и формулирует их.
Психологи и педагоги приходят к выводу, что не нужно устранять всех трудностей с пути ученика. Лишь в ходе их преодоления он сможет сформировать свои интеллектуальные умения. Помощь и руководство со стороны педагога состоят не в устранении этих трудностей, а в том, чтобы готовить учащихся к их преодолению.
В психологии распространена следующая простейшая и несколько условная классификация видов мышления: наглядно-действенное; наглядно-образное; абстрактное (теоретическое).
В соответствии с этим мы будем различать умение абстрактно мыслить и умение мыслить наглядно.
И в историческом развитии человечества, и в процессе развития каждого ребенка исходной является не чисто теоретическая, а практическая деятельность. Поэтому в преддошкольном и дошкольном возрасте формируется в основном умение мыслить наглядно. Во всех случаях ребенку необходимо отчетливо воспринимать и наглядно представлять объект. Иначе говоря, дошкольники мыслят лишь только наглядными образами и еще не владеют понятиями (в строгом смысле). На основе практического и наглядно-чувственного опыта у детей в школьном возрасте формируется – сначала в простейших формах – умение мыслить абстрактно, то есть умение мыслить в форме отвлеченных понятий. Мышление выступает здесь прежде всего в форме абстрактных понятий и рассуждений. Овладение понятиями в ходе усвоения школьниками основ различных наук – математики, физики, истории – имеет огромное значение в интеллектуальном развитии детей. Формирование умения абстрактно мыслить у школьников в ходе усвоения понятий вовсе не означает, что отпадает необходимость развития умения мыслить наглядно. Наоборот, это первичная форма умения мыслить по-прежнему продолжает совершенствоваться. Не только у детей, но и у взрослых постоянно развиваются – в той или иной степени – все виды и формы мыслительной деятельности.
К индивидуальным особенностям умения мыслить относятся такие качества как самостоятельность, гибкость, быстрота мысли. Умение мыслить самостоятельно проявляется прежде всего в умении увидеть и поставить новую проблему и затем решить ее своими силами. Гибкость мышления заключается в умении изменять первоначальный план решения задачи, если он не удовлетворяет тем условиям проблемы, которые постепенно вычленяются в ходе ее решения и которые не удалось учесть с самого начала.
Важнейшим признаком сформированности умения мыслить является сформированность умения выделять существенное, самостоятельно приходить ко все новым обобщениям. Когда человек мыслит, он не ограничивается констатацией того или иного факта или события, пусть даже яркого, нового, интересного и неожиданного. Мышление необходимо идет дальше, углубляясь в сущность данного явления и открывая общий закон развития всех более или менее однородных явлений, как бы внешне они не отличались друг от друга.
Ученики не только старших, но и младших классов вполне способны на доступном им материале выделять существенное в явлениях и отдельных фактах и в результате приходить к новым обобщениям. Многолетний психолого-педагогический эксперимент В.В.Давыдова, Д.Б.Эльконина, Л.В.Занкова и других психологов убедительно показывает, что даже младшие школьники в состоянии усваивать – причем в обобщенной форме – гораздо более сложный материал, чем это представлялось до последнего времени. Мышление школьников, несомненно, имеет еще очень большие и недостаточно используемые резервы и возможности. Одна из основных задач психологии и педагогики – до конца вскрыть все резервы и на их основе сделать обучение более эффективным и творческим.
К основным типам заданий, включение которых в систему работы учителя с учащимися будет способствовать формированию у них интеллектуальных умений, относятся прежде всего задания, носящие исследовательский характер (наблюдения, подготовка эксперимента, поиск ответа в научной литературе и т.п.), способствующие развитию пытливости, самостоятельности, индуктивного мышления. Имеется целый ряд заданий, направленных на развитие творческого мышления, среди которых чаще всего встречаются: написания сочинений, составление своих задач, «хитрых» заданий, где надо догадаться о каком-либо условии, содержащимся в неявной форме, задания по конструированию приборов или приспособлений и т.п.
Очень важны задания на установление причинно-следственных связей, способствующие развитию логического мышления, широко опирающиеся на анализ, обобщения.
Развитию аналитико-синтетической деятельности способствуют задания, требующие выбора решения (экономного, более точного или исчерпывающего) из числа предложенных. (Нахождение более короткого решения математической задачи).
Большую роль в развитии логического и обобщающего мышления играют задания на сравнение, начиная с простейших – «сильнее, чем…» – и кончая сравнениями, выявляющими сходство или отличие понятий, сложных явлений.
Наряду с заданиями, обеспечивающими сравнение, выбор и поиск наиболее рационального решения, правомерны задания, направленные на упорядочивание мыслительных действий, приучение учащихся к выполнению их в строгой последовательности, соблюдение которой обеспечивает получение правильных результатов, т.е. пользование алгоритмами или самостоятельное их составление. Элементы алгоритмического мышления формируются при изучении русского и иностранного языков, математики, физики, химии.
Отдельные трудности возникают в работе по развитию догадки и интуиции. В математике это доведение учащихся до «озарения», которое наступает тогда, когда на основе анализа условий и перебора возможных путей решения ученику становится ясным весь путь решения и уже не столь важной оказывается собственно вычислительная работа.
Формированию категориального и обобщающего мышления способствует целый ряд заданий, связанных с анализом и обобщением признаков для выделения явления в определенный класс или вид. В их числе: подведение задачи под уже известный тип, подбор к группе слов обобщающего понятия или подбор к обобщающему понятию видового, нахождения общности в группе понятий и отнесение к ним подходящего по этому общему признаку понятия.
Процесс любого, в том числе и школьного обучения должен удовлетворять две важные человеческие потребности. Одной из них является стремление к познанию мира, к приобретению знаний, другой – стремление к формированию собственной индивидуальности, к своему интеллектуальному развитию, к более глубокому познанию мира и более полному использованию собственных сил.
Развитие умственных способностей и самостоятельности мышления лежит в основе умственной деятельности. Самостоятельность мышления нельзя получить путем одностороннего изучения готовой информации. Поэтому способов изучения, обращенных к репродуктивному мышлению, вниманию и памяти, недостаточно. Наряду с ними необходимы способы, которые побуждают учащихся к непосредственному познанию действительности, к самостоятельному разрешению теоретических проблем.
Таким является проблемное обучение.
1.2. Сущность проблемного обучения.
Проблемное обучение это не абсолютно новое педагогическое явление. Элементы проблемного обучения можно увидеть в эвристических беседах Сократа, в разработках уроков для Эмилля у Ж.Ж.Руссо. Особенно близко подходил к этой идеи К.Д.Ушинский. Он, например, писал: «Лучшим способом перевода механических комбинаций в рассудочные мы считаем для всех возрастов, и в особенности для детского, метод, употреблявшийся Сократом и названный по его имени Сократовским. Сократ не навязывал своих мыслей слушателям, но, зная, какие противоречия ряда мыслей и фактов лежат друг подле друга в их слабо освещенных сознанием головах, вызывал вопросами эти противоречащие ряды в светлый круг сознания и, таким образом, заставлял их сталкивать, или разрушать друг друга, или примиряться в третьей их соединяющей и уясняющей мысли».
История собственно проблемного обучения начинается с введения так называемого исследовательского метода, многие правила которого в буржуазной педагогике были разработаны Джоном Дьюи.
Глубокие исследования в области проблемного обучения начались в 60-х годах. Идея и принципы проблемного обучения в русле исследования психологии мышления разрабатывались советскими психологами С.Л.Рубинштейном, Д.Н.Богоявленским, Н.А.Менчинской, А.М.Матюшкиным, а в применении к школьному обучению такими дидактами, как М.А.Данилов, М.Н.Скаткин. Много этими вопросами занимались Т.В.Кудрявцев, Д.В.Вилькеев, Ю.К.Бабанский, М.И.Махмутов и И.Я.Лернер. Исследования в этой области ведутся сейчас и другими представителями педагогической науки.
Задачей школы является формирование гармонически развитой личности. В современной педагогике исследуются вопросы общего развития детей в процессе обучения. Важнейший показатель всесторонне и гармонично развитой личности – наличие высокого уровня мыслительных способностей.
Развивающим обучением, то есть ведущим к общему и специальному развитию можно считать только такое обучение, при котором учитель, опираясь на знания закономерностей развития мышления, специальными педагогическими средствами ведет целенаправленную работу по формированию мыслительных способностей своих учеников в процессе изучения ими основ наук. Такое обучение и является проблемным.
Проблемное обучение возникло как результат достижений передовой практики и теории обучения и воспитания в сочетании с традиционным типом обучения является эффективным средством общего и интеллектуального развития учащихся.
В педагогической литературе имеется ряд попыток дать определение этому явлению.
Под проблемным обучением В.Оконь понимает «совокупность таких действий, как организация проблемных ситуаций, формулирование проблем, оказание ученикам необходимой помощи в решении проблем, проверка этих решений и, наконец, руководство процессом систематизации и закрепления приобретенных знаний» [36].
Д.В.Вилькеев под проблемным обучением имеет в виду такой характер обучения, когда ему придают некоторые черты научного познания [11].
Сущность проблемного обучения И.Я.Лернер видит в том, что «учащийся под руководством учителя принимает участие в решении новых для него познавательных и практических проблем в определенно системе, соответствующей образовательно-воспитатальным целям школы» [24].
Т.В.Кудрявцев суть процесса проблемного обучения видит в выдвижении перед учащимися дидактических проблем, в их решении и овладении учащимися обобщенными знаниями и принципами проблемных задач [22]. Такое понимание имеется и в работах Ю.К.Бабанского [3].
На основе обобщения практики и анализа результатов теоретических исследований М.И.Махмутов дает следующее определение понятия «проблемное обучение»: «Проблемное обучение – это тип развивающего обучения, в котором сочетаются систематическая самостоятельная поисковая деятельность учащихся с усвоением или готовых выводов науки, а система методов построена с учетом целеполагания и принципа проблемности; процесс взаимодействия преподавания и учения ориентирован на формирование познавательной самостоятельности учащихся, устойчивости мотивов учения и мыслительных (включая и творческие) способностей в ходе усвоения ими научных понятий и способов деятельности, детерминированного системой проблемных ситуаций» [30].
Сущность «активизации учения»
Каково соотношение между активизацией познавательной деятельности учащихся и проблемным обучением?
Некоторые педагоги отождествляют эти два понятия, предлагая ликвидировать и сам термин «проблемное обучение». Проблемное обучение является одним из наиболее эффективных средств активизации мышления ученика. Суть активности, достигаемой при проблемном обучении, заключается в том, что ученик должен анализировать фактический материал и оперировать им так, чтобы самому получить из него новую информацию. Другими словами это расширение, углубление знаний при помощи ранее усвоенных знаний или новое применение прежних знаний. Нового применения прежних знаний не может дать ни учитель, ни книга, оно ищется и находится учеником, поставленным в соответствующую ситуацию. Это и есть поисковый метод учения как антипод методу восприятия готовых выводов учителя (хотя последний метод тоже вызывает определённую активность ученика).
Умственный поиск – сложный процесс. Не всякий поиск связан с возникновением проблемы. Если учитель даёт задание ученикам и указывает, как его выполнять, то даже их самостоятельный поиск не будет решением проблемы. Ученики могут принимать активное участие в научно-исследовательской работе, собирая эмпирический материал, но не решая никаких проблем. Подлинная активизация учащихся характеризуется самостоятельным поиском решения проблем.
Цель активизации учащихся посредством проблемного обучения заключается в том, чтобы поднять уровень мыслительной деятельности ученика и обучать его не отдельным операциям в случайности, стихийно складывающемся порядке, а системе умственных действий, которая характерна для решения нестереотипных задач, требующего применения творческой мыслительной деятельности.
Суть активизации учения школьника посредством проблемного обучения состоит в активизации его мышления путём создания проблемных ситуаций, в формировании познавательного интереса и моделирования умственных процессов.
Проблемная ситуация и учебная проблема являются основными понятиями проблемного обучения, которое рассматривается не как механическое сложение деятельности преподавания и учения, а как диалектическое взаимодействие и взаимосвязь этих двух деятельностей.
Проблемное преподавание определяется как деятельность учителя по созданию системы проблемных ситуаций, изложению учебного материала с его (полным или частичным) объяснением и управлению деятельностью учащихся, направленной на освоение новых знаний – как традиционным путем, так и путем самостоятельной подготовки учебных проблем и их решения.
Проблемное учение – это учебно-познавательная деятельность учащихся по усвоению знаний и способов деятельности путем восприятия объяснений учителя в условиях проблемной ситуации, самостоятельного (или с помощью учителя) анализа проблемных ситуаций, формулировки проблем и их решения посредством выдвижения предложений, гипотез, их обоснования и доказательства, а также путем проверки правильности решения.
А.М.Матюшкин характеризует проблемную ситуацию как, «особый вид умственного взаимодействия объекта и субъекта, характеризующийся таким психическим состоянием субъекта (учащегося) при решении им задач, который требует обнаружения (открытия или усвоения) новых, ранее субъекту неизвестных знаний или способов деятельности». Иначе говоря, проблемная ситуация – это такая ситуация, при которой субъект хочет решить какие-то трудные для себя задачи, но ему не хватает данных и он должен сам их искать.
Проблемные ситуации можно подразделять по нескольким основаниям: по области научных знаний или учебной дисциплине (физике, математике и т.п.); по направленности на поиск недостающего нового (новых знаний, способов действия, выявления возможности применения известных знаний и способов в новых условиях); по уровню проблемности (очень острые противоречия, средней остроты, слабо или неявно выраженные противоречия); по типу и характеру содержательной стороны противоречий (например, между житейскими представлениями и научными знаниями, неожиданным фактом и неумением его объяснить и т.п.).
Дидактически и методически основанные способы создания проблемных ситуаций могут быть найдены только в том случае, если учителю известны общие закономерности их возникновения. В литературе по проблемному обучению встречаются попытки сформулировать эти закономерности в виде типов проблемных ситуаций.
Как показали исследования, можно выделить наиболее характерные для педагогической практики типы проблемных ситуаций, общее для всех предметов.
1. Его следует считать наиболее общим и распространенным: проблемная ситуация возникает при условии, если учащийся не знает способа решения поставленной задачи, не могут ответить на проблемный вопрос, дать объяснение новому факту в учебной или жизненной ситуации, то есть в случае осознания учащимися недостаточности прежних знаний для объяснения нового факта.
Учительница на уроке геометрии в 7 классе на тему «Трапеция» предложила учащимся задачу: в трапеции ABCD (BC||AD) проведена средняя линия MN. Основание |BC| равно 8 см. |AD|=14см, |AB|=5см. |CD|=9см. Вычислить периметр трапеции MBCN.
Решая задачу, ребята легко находят боковые стороны новой трапеции; одно основание им известно, а найти длину второго, которое является средней линией не могут (недостаточно знаний о трапеции). Возникает противоречие между потребностью в решении задачи и недостаточностью прежних знаний.
2. Проблемные ситуации возникают при столкновении учащихся с необходимостью использовать ранее усвоенные знания в новых практических условиях. Как правило, учителя организуют эти условия не только для того, чтобы учащиеся сумели применить свои знания на практике, но и столкнулись с фактом их недостаточности. Осознание этого факта учащимися возбуждает познавательный интерес и стимулирует поиск новых знаний.
Например, учитель накануне урока на тему «Объем усеченной пирамиды» дает учащимся домашнее задание – найти в окружающей жизни примеры применения усеченной пирамиды и попытаться определить ее объем. Он объясняет, что для сооружения, например, железнодорожной насыпи необходимо заранее рассчитать ее объем, чтобы определить необходимое количество строительных материалов, то есть, указывает на практическую значимость домашнего задания.
На следующий день урок начинается с беседы. Учащиеся в качестве примеров усеченной пирамиды называют формы насыпей песка, щебня, формы картонных коробок, башни, детали машин и т.д. Они рассказывают о своих попытках найти варианты решения, но вычислить объем усеченной пирамиды не могут. Возникает проблемная ситуация и потребность найти решения проблемы, имеющей (для учащихся) практическую значимость.
Таким образом, процесс формирования новых знаний начался в ходе выполнения задания учителя в домашних условиях, в жизненной ситуации, которая раскрыла главную проблему, выявила противоречия между возникшей познавательной потребностью и необходимостью ее удовлетворения при полученных ранее знаний. Здесь мы видим элемент перспективности обучения: домашнее задание рассчитано на подготовку к усвоению новых знаний; повторения пройденного происходит не форме повторного чтения указанных учителем страниц учебника или переписывания упражнений, а в форме самостоятельной работы, содержанием которой является решение возникшей проблемы-практической или теоретической задачи.
4. Проблемная ситуация легко возникает в том случае, если имеется противоречие между теоретически возможным путем решения задачи и практической неосуществимостью избранного способа.
5. Проблемная ситуация возникает тогда, когда имеется противоречие между практически достигнутым результатом выполнения учебного задания и отсутствием у учащихся знаний для его теоретического обоснования.
Возможности управления процессом учения состоит в том, что проблемная ситуация в своей психологической структуре имеет не предметно-содержательную, но и мотивационную, личностную сторону (интересы ученика, его желания, потребности, возможности и т.д.).
Какие дидактические цели преследует создание проблемных ситуаций в учебном процессе? Можно указать на следующие дидактические цели:
привлечь внимание ученика к вопросу, задаче, учебному материалу, возбудить у него познавательный интерес и другие мотивы деятельности;
поставить его перед таким познавательным затруднением, продолжение которого активизировало вы мыслительную деятельность;
помочь ему определить в познавательной задаче, вопросе, задании основную проблему и наметить план поиска путей выхода из возникшего затруднения; побудить ученика к активной поисковой деятельности;
помочь ему определить границы актуализируемых ранее усвоенных заданий и указать направление поиска наиболее рационального пути выхода из ситуации затруднения.
Способы создания проблемных ситуаций.
На основании обобщения передового опыта можно указать несколько основных способов создания проблемных ситуаций.
Побуждение учащихся к теоретическому объяснению явлений, фактов, внешнего несоответствия между ними. Это вызывает поисковую деятельность учеников и приводит к активному усвоению новых знаний.
Использование учебных и жизненных ситуаций, возникающих при выполнении учащимися практических заданий в школе, дома или на производстве, в ходе наблюдений за природой и т.д. Проблемные ситуации в этом случае возникают при попытке самостоятельно достигнуть поставленной перед ними практической цели. Обычно ученики в итоге анализа ситуации сами формулируют проблему.
На уроке геометрии в 6 классе по теме «Длина ломаной» ученикам была предложена работа в 2-х вариантах: первый – начертить ломанную, состоящую из двух звеньев; второй – начертить ломанную состоящую из 3-х звеньев. Путем измерений сравнить длину ломаной с расстоянием между ее концами. Учащиеся это задание легко выполнили. Учитель некоторые из полученных результатов записывает в 2 столбика на доске:
-
Длина ломаной Расстояние между ее концами 15 см 13 см 24 см 20 см
Результат у всех получается разный, но учитель просит ребят внимательно рассмотреть числа и сделать предположение о зависимости между длиной ломанной и расстоянием между ее концами. Ученик формулирует предположение: «Длина ломаной больше расстояния между ее концами» и переходит к решению его в общем виде.
Постановка учебных проблемных заданий на объяснение явления или поиск путей его практического применения. Примером может служить любая исследовательская работа учащихся на учебно-опытном участке, в мастерской, лаборатории или учебном кабинете, а также на уроках по гуманитарным предметам.
Побуждения учащегося к анализу фактов и явлений действительности, порождающему противоречия между житейскими представлениями и научными понятиями об этих фактах.
Выдвижение предположений (гипотез), формулировка выводов и их опытная проверка.
Побуждение учащихся к сравнению, сопоставлению фактов, явлений, правил, действий, в результате которых возникает проблемная ситуация.
Побуждение учащихся к предварительному обобщению новых фактов. Учащиеся получают задание рассмотреть некоторые факты, явления, содержащиеся в новом для них материале, сравнить их с известными и сделать самостоятельное обобщение. В этом случае, как сравнение выявляет особые свойства новых фактов, необъяснимые их признаки.
Ознакомление учащихся с фактами, несущими как будто бы необъяснимый характер и приведшими в истории науки к постановке научной проблемы. Обычно эти факты и явления как бы противоречат сложившимся у учеников представлениям и понятиям, что объясняется неполнотой, недостаточностью их прежних знаний.
Организация межпредметных связей. Часто материал учебного предмета не обеспечивает создания проблемной ситуации (при отработке навыков, повторения пройденного т.п.). В этом случае следует использовать факты и данные наук (учебных предметов), имеющих связь с изучаемым материалам.
Варьирование задачи, переформулировка вопроса.
Правила создания проблемных ситуаций.
Чтобы создать проблемную ситуацию, перед учащимися следует поставить такое практическое или теоретическое задание, выполнение которого требует открытия новых знаний и овладения новыми умениями; здесь может идти речь об общей закономерности, общем способе деятельности или общих условиях реализации деятельности.
Задание должно соответствовать интеллектуальным возможностям учащегося. Степень трудности проблемного задания зависит от уровня новизны материала преподавания и от степени его обобщения.
Проблемное задание дается до объяснения усваиваемого материала.
Проблемными заданиями могут быть:
усвоение;
формулировка вопроса;
практические здания.
Проблемное задание может привести к проблемной ситуации только в случае учета вышеупомянутых правил.
Одна и та же проблемная ситуация может быть вызвана различными типами заданий.
Очень трудную проблемную ситуацию учитель направляет путем указания учащемуся причин невыполнения данного ему практического задания или невозможности объяснения им тех или других фактов. Например: «Вы не могли построить треугольник с 3 известными углами, т.к. в этом задании было нарушено одно из важных правил, касающихся треугольников».
Подготовленность ученика к проблемному учению определяется прежде всего его умением увидеть выдвинутую учителем (или возникшую в ходе урока) проблему, сформулировать ее, найти пути решения и решить эффективными приемами.
Всегда ли ученик сам выходит из создавшегося познавательного затруднения? Как показывает практика, из проблемной ситуации может быть 4 выхода:
Учитель сам ставит и решет проблему;
Учитель сам ставит и решет проблему, привлекая учащихся к формулировке проблемы, выдвижению предположений, доказательству гипотезы и проверке решения;
Учащиеся самостоятельно ставят и решают проблему, но с участием и (частичной или полной) помощью учителя;
Учащиеся самостоятельно ставят проблему и решают ее без помощи учителя (но, как правило, под его руководством).
На основе лингвистического определения: проблема – задача, подлежащая разрешению, исследованию. Какова же природа проблемы возникающей в процессе обучения? Многие учителя понятие «проблема» отождествляют с понятием «вопрос» и «задача», проблему в обучении смешивают с проблемой в общеупотребительном ее значении.
Учебная проблема не тождественна задаче. И в жизни, и в школе встречается много задач, решение которых требует лишь механической деятельности, не только не способствующей развитию самостоятельности мышления, но и тормозящей это развитие.
Учебная проблема – форма реализации принципа проблемности в обучении. Учебная проблема – явление субъективное и существует в сознании ученика в идеальной форме, в мысли, так же как любое суждение, пока оно не станет логически завершенным. Задача – явление объективное, для ученика она существует с самого начала в материальной форме, и превращается задача в субъективное явление лишь после ее восприятия и осознания.
Основными элементами учебной проблемы являются «известное» и «неизвестное» (нужно найти «связь», «отношение» между известным и неизвестным). В условиях задачи обязательно содержатся такие элементы, как «данное» и «требования».
Учебная проблема – форма проявления логико-психологического противоречия процесса усвоения, определяющее направление умственного поиска, пробуждающее интерес к исследованию (объяснению) сущности неизвестного и ведущее к усвоению нового понятия или нового способа действия.
Основные функции учебной проблемы:
Определение направления умственного поиска, то есть деятельности ученика по нахождению способа решения проблемы.
Формирование познавательных способностей, интереса, мотивов деятельности ученика по усвоению новых знаний.
К выдвигаемой проблеме нужно предъявить несколько требований. Если хоть одно из них не выполнить, проблемная ситуация не будет создана.
Проблема должна быть доступной пониманию учащихся. Если до учащихся не дошел смысл задачи, дальнейшая работа над ней бесполезна. Следовательно, проблема должна быть сформулирована в известных учащимся терминах, чтобы все или, по крайней мере, большинство учеников уяснили сущность поставленной проблемы и средства для ее решения.
Вторым требованием является посильность выдвигаемой проблемы. Если выдвинутую проблему большинство учащихся не сможет решить, придется затратить слишком много времени или решать ее самому учителю; то и другое не даст должного эффекта.
Формулировка проблемы должна заинтересовать учащихся. Конечно, главным в создании интереса является математическая сторона дела, но весьма существенно подобрать и надлежащее словесное оформление. Развлекательность формы нередко способствует успеху решения проблемы.
Немалую роль играет естественность постановки проблемы. Если учащихся специально предупредить, что будет решатся проблемная задача, это может не вызвать у них интереса при мысли, что предстоит переход к более трудному.
Знание учителем основных требований к учебной программе является одним из важнейших условий успешной постановки проблемы и организации самостоятельной познавательной деятельности учащихся.
Постановка учебной проблемы осуществляется в несколько этапов:
а) анализ проблемной ситуации;
б) осознание сущности затруднения – видение проблемы;
в) словесная формулировка проблемы.
Учебная проблема не является проблемой для учителя. Учитель ставит перед учениками проблемный вопрос или проблемную задачу. Такая постановка ведет к возникновению проблемной ситуации принятию учеником проблемы, сформулированной и поставленной учителем.
Процесс постановки учебной проблемы должен осуществляться с учетом основных логических и дидактических правил:
отделение (ограничение) известного от неизвестного,
локализация (ограничение) неизвестного,
определение возможных условий для успешного решения,
наличие в формулировке проблемы неопределенности.
Процесс решения учебной проблемы.
Решение любой проблемы начинается с ее правильной и четкой формулировки. Процесс формулировки означает, что ученик уже понимает возникшую перед ним задачу и в известной мере видит, «нащупывает» пути ее решения, то есть, составляет план решения, затем осуществляет план и «оглядывается назад» (изучение полученного решения).
Существует три вида решения проблемы в зависимости от наличия у решающего определенного опыта в отношении данного класса проблемных задач.
Первый вид решения. Сюда относится случаи решения таких задач, относительно которых у решающего нет никакого прежнего опыта. В этих случаях субъект идет путем проб и ошибок до тех пор, пока одна из проб более или менее случайно не приведет к решению проблемы.
Второй вид решения. Сюда относятся ситуации, относительно которых у человека имеются некоторые формулы, схемы и другие виды опыта. Решение происходит здесь в форме узнавания в предложенной ситуации одной из имеющихся схем.
Третий вид решения проблем заключается в том, что у человека имеется некоторый опыт, но опыт этот во всей его совокупности не позволяет человеку решить данную проблему. Решение здесь состоит в том, что создаются на основе анализа условий задачи специально для данного случая новая, не имевшаяся ранее схема действий.
Существенной чертой процесса решения проблем является сбор информации о признаках и свойствах элементов, составляющих проблемную ситуацию.
Логика решения учебной проблемы:
а) составление плана решения проблемы (обязательно план включает в себя выбор вариантов решения),
б) выдвижение предположения и обоснование гипотезы, (возникает в результате «мысленного забегания вперед»);
в) доказательство гипотезы (осуществляется путем выведения из гипотезы следствий, которые проверяются);
г) проверка решения проблемы (сопоставление цели, требования задачи и полученного результата, соответствие теоретических выводов практике);
д) повторение и анализ процесса решения.
Решение учебной проблемы есть результат преодоления противоречий учебного процесса вообще и основного противоречия познавательной проблемы в частности, есть результат активного мыслительного процесса, при котором отбрасываются неверные гипотезы и выбираются правильные, обоснованные. Решение учащимися проблемы, пишет польский дидакт В.Оконь, имеет огромное преимущество перед простым заучиванием готовой информации. Преимущество заключается в том, что при решении проблемы учащийся активно мыслит. А это приводит не только к прочности и глубине знаний, приобретенных самостоятельно, но и к ценнейшему качеству ума – умению ориентироваться в любой ситуации и самостоятельно находить пути решения любой проблемы.
Факторы, препятствующие успешному решению проблемы.
Какие помехи стоят на пути решения проблемы? Начав с этого, ученик может успешнее вести поиск, а учитель управлять процессом поиска.
Во-первых, надо выяснить, не мешает ли функциональная фиксированность. Как только она будет обнаружена, ученик увидит новые возможности решения.
Во-вторых, важно избегать завышенной оценки определенного способа решения проблемы как помехи развитию поиска, т.е. целесообразна постановка вопроса:
«А нет ли другого, более рационального способа действия?»
В-третьих, часто одно и то же правило, один и тот же прием или способ решения входит как бы в навык и механически применяется учеником при решении разнотипных задач и проблем. (Иногда вспомнить прежнее решение – это значит пойти по ложному пути).
В-четвертых, учитель должен раскрыть перед учениками и такой метод, при котором ученики должны уметь отбрасывать отдельные признаки, пренебрегать некоторыми условиями задачи (механизм анаксиоматизации). Важно выделить существенное путем отбрасывания несущественного.
В-пятых, злоупотребление наводящими вопросами. Подсказка эффективна не перед решением проблемы, а после попыток ее решения. Это основные помехи, стоящие на пути решения проблем.
Проблемная ситуация, интерес и эмоциональность – взаимообусловленные явления, которые вместе с волевым усилием ученика отражают рациональную и чувственные стороны активизации его познавательной (мыслительной) деятельности. Дидактически познавательная активизация достигается через вопрос, задачу, задание, наглядность, речь, а чаще их сочетание. При определенных условиях эти элементы становятся в руках учителя инструментом создания проблемной ситуации, возбуждения интереса и эмоционального настроя учащихся, мобилизации их воли, побуждения к действию.
В активизации познавательной деятельности учащихся вопросы имеют едва ли не первостепенное значение. При объяснении нового материала учитель умелой постановкой вопросов создает противоречивые ситуации, которые, обостряют у учащихся, сознание необходимости найти ответ, снимающий противоречие.
Для организации проблемного обучения и управления мыслительной деятельностью ученика важное значение имеет деление вопросов на основе принципа проблемности: вопросы бывают информационные и проблемные.
Вопросы, задающиеся с целью получения ответов, содержащих известные знания есть информационные вопросы. Такие вопросы не возбуждают активную мыслительную деятельность учащихся, память без напряжения ума работает в поисках имеющейся в кладовых мозга готовой информации. Вопрос, на который учащийся должен искать готовый ответ, не имеет проблемного характера.
Проблемными являются те вопросы, которые вызывают интеллектуальные затруднения у учащихся, поскольку ответ на них не содержится не в прежних знаниях ученика, ни в предъявляемой учителем информации.
Проблемный вопрос содержит в себе еще не раскрытую (учащимися) проблему, область неизвестного, новые знания, для добывания которых необходимо какое-то интеллектуальное действие, определенный целенаправленный мыслительный процесс.
При каких условиях вопрос считается проблемным (для данного ученика)?
Он должен иметь логическую связь как с ранее усвоенными понятиями и представлениями, так и с теми, которые подлежат усвоению в определенной учебной ситуации; содержать в себе познавательную трудность и видимые границы известного и неизвестного; вызывать чувство удивления при сопоставлении нового с ранее известным, неудовлетворенность имеющимся запасом знаний, умений и навыков.
Проблемное обучение предполагает последовательное и целенаправленное выдвижение перед учащимися познавательных задач, решая которые они под руководством учителя активно усваивают новые знания. Чаще всего познавательные проблемы выдвигаются при помощи постановки задач, наиболее типичных для данного учебного предмета.
Задачи широко используются и при информационном обучении только дидактические цели использования задач различны.
При информационном (репродуктивном) подходе задачи применяются для иллюстрации теоретических положений, высказанных учителем, а также для закрепления их и применения на практике. При проблемном же обучении эти задачи в первую очередь применяются для того, чтобы подвести учащихся к новой теме и активизировать процесс познания. При проблемном подходе эти задачи обычно предшествуют сообщению теоретических положений, при информационном – следует за ними. Таким образом, задачи при проблемном обучении носят познавательный характер, а не только тренировочный.
Познавательные задачи, применяемые для активизации умственной деятельности учащихся, должны иметь свойство обобщенности. Это свойство обусловлено наличием в задаче определенного уровня сложности, которая определяется:
а) проблемным содержанием задачи;
б) методическим способом постановки задачи перед учащимися (например, способом ее речевой формулировки);
в) личностным, субъективным отношением ученика к поставленной учителем задаче.
Иначе говоря, если ученик воспринимает задачу как проблему и самостоятельно ее решает, то это есть главнейшее условие развития его мыслительных способностей.
Таким образом, проблемный вопрос, проблемная задача – различные формы выражения учебной проблемы и основные дидактические понятия, применение которых приводит к возникновению проблемной ситуации и поисковой деятельности учащихся. Поэтому организация проблемного обучения невозможна без систематизации вопросов и познавательных задач на материале каждого учебного предмета. Такая работа уже производится.
Отличительная черта теории проблемного обучения состоит в ее глубокой психологической обоснованности. Эта теория сознательно ставит своей целью использование собственно психологических закономерностей мышления для управления усвоением знаний.
Подлинной психологической основой концепции проблемного обучения стала теория мышления как продуктивного процесса, выдвинутая С.Л.Рубинштейном.
Раскроем центральное положение этой теории.
Человеческое бытие есть непрерывное взаимодействие субъекта с объектом, осуществляющиеся в форме целесообразной предметно-преобразующей деятельности субъекта. Объекты деятельности не даны человеку в завершенном и готовом виде. Они всегда содержат в себе определенные внутренние противоречия, проблемы, задачи которые объект должен разрешить в процессе их практического и мысленного преобразования. Предметный мир, таким образом, открывается человеку как исполненный проблемностью. Это и вызывает необходимость в мышлении.
«Мышление обычно начинается с проблемы или вопроса, с удивления или недоумения, с противоречия. Этой проблемной ситуацией определяется вовлечение личности в мыслительный процесс…» [43]. Там, где нет проблемной ситуации, нет и мышления в строгом смысле слова.
Подчеркнем, что речь идет не о выдумывании и нагромождении искусственных проблем, а об обнаружении и постановке реальных проблем. «…Первый признак мыслящего человека это умение видеть проблемы там, где они есть» [43]. При этом процесс выполнения, проблемы в объекте познания представляет собой вполне «завершенный» творческий мыслительный акт, так как он связан с предварительной ориентировкой, анализом и преобразованием ситуации.
Недаром о творческом потенциале ученого нередко судят не по тем идеям, которые он выдвинул, а по характеру проблем, которые он поставил и тем самым очертил контуры будущего науки, задал ее перспективную направленность.
В проблеме, по словам С.Л.Рубинштейна, имеется неизвестные, как бы незаполненные места. Для их заполнения, для превращения неизвестного в известное необходимы соответствующие знания и способы деятельности, которые у человека поначалу отсутствуют. Необходимость поиска этих знаний и способов выражается в познавательной потребности субъекта. Без осознания и переживания такой необходимости процесс мышления невозможен. Будучи же осознанной в таком качестве, познавательная потребность побуждает мыслительную активность человека.
На сегодняшний день существуют различные типы обучения. Приведем сравнительные черты сообщающего и проблемного обучения.
| Сообщающее | Проблемное |
| 1. Материал дается в готовом виде, учитель обращает внимание прежде всего на программу. | 1. новую информацию учащиеся получают в ходе решения теоретических и практических задач. |
| 2. В устной подаче или через учебник возникают проблемы, преграды и трудности вызванные временным выключением учащегося из дидактического процесса. | 2. В ходе решения проблемы учащийся преодолевает все трудности, его активность и самостоятельность достигает здесь высокого уровня. |
| 3. Темп передачи информации ориентирован на более сильных, средних или слабых учащихся. | 3. Темп передачи сведений зависит от учащегося или группы учащихся. |
| 4. Контроль школьных достижений только частично связан с процессом обучения; он не является его органической частью. | 4. Повышенная активность учащихся способствует развитию позитивных мотивов и уменьшает необходимость формальной проверки результатов. |
| 5. Отсутствует возможность обеспечения всем учащимся стопроцентных результатов; наибольшую трудность представляет применение информатизации в практике. | 5. Результаты преподавания относительно высокие и устойчивые. Учащиеся легче применяют полученные знания в новых ситуациях и одновременно развивают свои умения и творческие способности. |
В чем основное различие между проблемным и традиционным обучением?
Главным отличием двух видов обучения следует считать целеполагание и принцип организации педагогического процесса.
Цель сложившегося типа обучения: усвоение результатов научного познания, вооружения учащихся знанием обнов наук, привития им соответствующих знаний и навыков.
Цель проблемного обучения более широкая: усвоение не только результатов научного познания, но и самого пути, процесса получения этих результатов, она включает еще и формирование познавательной деятельности ученика, и развитие его творческих способностей (помимо овладения системой знаний, умений и навыков). Здесь акцент делается на развитие мышления.
В основе организации объяснительно-иллюстративного обучения лежит принцип передачи слушателям готовых выводов науки учащимся. В основе организации процесса проблемного обучения лежит принцип поисковой учебно-познавательной деятельности ученика (основанной на закономерности проблемности усвоения знаний), то есть открытия или выводов науки, способов действия, «изобретения» новых предметов или способов приложения знаний к практике и «художественного отображения действительности».
Основным отличаем проблемного обучения от объяснительно-иллюстративного является характер организации учебного процесса. Суть этого отличия в следующем.
При объяснительно-иллюстративном обучении учитель сообщает факты, сам анализирует их и, применяя наглядность, объясняет сущность новых понятий, сам формулирует определение новых теорем, правил, законов и так далее. Здесь доминирует информационное изложение учебного материала учителем и нет преднамеренного создания проблемных ситуаций.
Учащиеся слушают и воспринимают объяснения учителя и усваивает новое знание путем запоминания, а новые действия – путем подражания действиям учителя. Чем сложнее материал, тем подробнее учитель объясняет его. Усвоение закрепляется выполнением много численных упражнений, обычно также не требующих творческой деятельности.
При проблемном обучении деятельность учителя состоит в том, что он, давая в необходимых случаях объяснение содержания наиболее сложных понятий, систематически создает проблемные ситуации, сообщает учащимся факты и организует их учебно-познавательную деятельность. На основе анализа фактов учащиеся самостоятельно делают выводы и обобщения, формулируют (с помощью учителя) определение понятий, правила, теоремы, законы, или самостоятельно применяют известные знания в навой ситуации (изобретает, конструирует и др.).
При проблемном обучении учитель систематически организует самостоятельные работы учащихся по усвоению новых знаний, умений, повторению закрепленного и отработке навыков. Учащиеся сами добывают новые знания, у них вырабатываются навыки умственных операций и действий, развиваются внимание, творческое воображение, догадка, формируется способность открывать новые знания и находить новые способы действия путем выдвижения гипотез и их обоснования.
Основные функции проблемного обучения.
Исходя из задачи общеобразовательной школы и на основе выводов из сравнения традиционного типа обучения с проблемным можно сформулировать основные функции проблемного обучения. Их можно разделить на общее и специальное. Можно указать следующие общие функции проблемного обучения:
усвоение учениками системы знаний и способов умственной и практической деятельности,
развитие интеллекта учащихся, то есть их познавательной самостоятельности и творческих способностей,
формирование диалектического мышления школьников,
формирование всесторонне развитой личности.
Кроме этого, проблемное обучение имеет и следующие функции:
воспитание навыков творческого усвоения знаний (применение системы логических приемов или отдельных способов творческой деятельности),
воспитание навыков творческого применения знаний (применение усвоенных знаний в новой ситуации) и умение решать учебные проблемы,
формирование и накопление опыта творческой деятельности (овладение методами научного исследования, решение практических проблем и художественного отображения действительности),
формирование мотивов обучения, социальных, нравственных и познавательных потребностей.
Каждая из указанных функций осуществляется в разнообразной практической и теоретической деятельности школьника и зависит от учета характерных особенностей проблемного обучения, которые одновременно являются и отличительными признаками.
Каковы эти особенности?
Особенности проблемного обучения.
Первая и важнейшая особенность – это специфическая интеллектуальная деятельность ученика по самостоятельному усвоению новых понятий путем решения учебных проблем, что обеспечивает сознательность, глубину, прочность знаний и формирование логико-теоретического и интуитивного мышления. Только прочное знание становится действительным достоянием школьников, которые они могут осознанно применять в своей дальнейшей теоретической и практической деятельности.
Вторая особенность состоит в том, что проблемное обучение – наиболее эффективное средство формирования мировоззрения, поскольку в процессе проблемного обучения складываются черты критического, творческого и диалектического мышления. Самостоятельное решение проблем учащимися является и основным условием превращения знаний в убеждения, так как только диалектический подход к анализу всех процессов и явлений действительности формулирует систему прочных и глубоких убеждений.
Третья особенность вытекает из закономерностей взаимосвязи между теоретическими и практическими проблемами и определяется дидактическим принципом связи обучения с жизнью. Связь с жизнью служит важнейшим средством создания проблемных ситуаций и критерием оценки правильности решения учебных проблем.
Четвертой особенностью проблемного обучения является систематическое применение учителем наиболее эффективного сочетания разнообразных типов и видов самостоятельных работ учащихся. Указанная особенность заключается в том, что учитель организует выполнение самостоятельных работ, требующих как актуализации ранее приобретенных, так и усвоения новых знаний и способов деятельности.
Пятая особенность определяется дидактическим принципом индивидуального подхода. Суть различия между проблемным и традиционным обучением состоит в том, что при традиционном обучении потребность в индивидуализации – следствие диалектического противоречия между фронтальным изложением новых знаний учителем и индивидуальной формой их восприятия и усвоения учеником.
При проблемном обучении индивидуализация обусловлена главным образом наличием учебных проблем разной сложности, которые каждым учеником воспринимаются по-разному. Индивидуальное восприятие проблемы вызывает различие в ее формулировании, выдвижении многообразных гипотез и нахождении иных путей их доказательства.
Шестая особенность проблемного обучения состоит в его динамичности (подвижной взаимосвязи его элементов). Динамичность проблемного обучения заключается в том, что одна ситуация переходит в другую естественным путем на основе диалектического закона взаимосвязи и взаимообусловленности всех вещей и явлений материального мира.
Как указывают некоторые исследователи, в традиционном обучении динамичности нет, вместо проблемности там преобладает «категоричность».
Седьмая особенность заключается в высокой эмоциональной активности ученика, обусловленной, во-первых, тем, что сама проблемная ситуация является источником ее возбуждения, во-вторых, тем, что активная мыслительная деятельность ученика неразрывно органически связанна с чувственно-эмоциональной сферой психической деятельности. Всякая самостоятельная мыслительная деятельность поискового характера, связанная с индивидуальным «принятием» учебной проблемы, вызывает личное переживание ученика, его эмоциональную активность. В свою очередь, эмоциональная активность детерминирует активность мыслительной деятельности.
Восьмая особенность проблемного обучения заключается в том, что, оно обеспечивает новое соотношение индукции и дедукции (усиление значения второго пути познания) и новое соотношение репродуктивного и продуктивного, в том числе творческого, усвоения знаний, повышая роль именно творческой познавательной деятельности учащихся.
Таким образом, первая особенность проблемного обучения состоит в том, что оно обеспечивает прочность знаний и особый тип мышления, вторая – глубину убеждений, третья – творческое применение знаний в жизни. Эти три особенности имеют наибольшую социальную значимость и обеспечивают выполнение основной задачи советской школы. Основные пять особенностей имеют социально-дидактический характер и обуславливают эффективность действий первых трех.
Виды проблемного обучения.
Проблемное обучение не может быть одинаково эффективным в любых условиях. Практика показывает, что процесс проблемного обучения порождает различные уровни как интеллектуальных затруднений учащихся, так и их познавательной активности и самостоятельности при усвоении новых знаний, чем при применении прежних знаний в новой ситуации.
Виды проблемного обучения правильнее всего различать по соответствующим видам творчества. На этом основании можно выделить три вида проблемного обучения.
Первый вид («научное» творчество) – это теоретическое исследование, то есть поиск и открытие ученикам нового правила, закона, теоремы и т.д. В основе этого вида проблемного обучения лежит постановка и решение теоретических учебных проблем.
Второй вид (практическое творчество) – поиск практического решения, то есть поиск способа применения известного знания в новой ситуации, конструирование, изобретение. В основе этого вида проблемного обучения лежит постановка и решение практических учебных проблем.
Третий вид (художественное творчество) – это художественное отображение действительности на основе творческого воображения, включающее в себя литературные сочинения, рисование, написание музыкального произведения, игру, и т.д.
Все виды проблемного обучения характеризуются наличием репродуктивной, продуктивной и творческой деятельности ученика, наличие поиска и решения проблемы. Они могут осуществляться при различных формах организации педагогического процесса. Однако первый вид чаще всего встречается на уроке, где наблюдается индивидуальное, групповое и фронтальное решение проблем. Второй – на лабораторных, практических занятиях. Третий вид – на уроке и на внеурочных занятиях.
Вполне понятно, что каждый вид проблемного обучения как внутренне дифференцированная деятельность имеет сложную структуру, дающую в зависимости от множества факторов различную результативность обучения.
Каждый из перечисленных видов проблемного обучения может протекать различной степенью познавательной активности ученика. Определение этой степени имеет важное значение для управления процессом формирования познавательной самостоятельности школьников.
Каждый вид отвечает одному из важнейших условий проблемного обучения – наличие определенного уровня познавательной самостоятельности ученика.
Изучив психолого-педагогическую литературу по вопросам проблемного обучения мы выяснили, что проблемным оно называется не потому, что весь учебный материал учащиеся усваивают только путем самостоятельного решения проблем и «открытия» новых понятий. Здесь есть и объяснения учителя, и репродуктивная деятельность учителя, и постановка задач, и выполнение учащимися упражнений. Но организация учебного процесса базируется на принципе проблемности, а систематическое решение учебных проблем – характерный признак этого типа обучения. Поскольку вся система методов при этом направлена на всестороннее развитие школьника, развитие его познавательных потребностей, на формирование интеллектуально активной личности, проблемное обучение является подлинно развивающим.
Проблемное обучение строится на основе принципа проблемности, реализуемого через различные типы учебных проблем и через сочетание репродуктивной, продуктивной и творческой деятельности ученика.
Все ли обучение должно быть проблемным?
Нет не все, если под проблемным обучением иметь в виду только решение учебных проблем и только самостоятельное усвоение всего учебного материала. Все обучение должно быть развивающим, в котором самостоятельное усвоение знаний путем решения учебных проблем, путем открытий сочетается с репродуктивным усвоением знаний, излагаемых учителем или учеником. Ученик не может и не должен повторять весь исторический путь развития человеческого знания. Но принципы этого развития и обобщенные способы действия он должен повторить для того, чтобы усвоить их выработать у себя способы творческой деятельности.
Проблемное обучение означает понимать как тип обучения, обеспечивающей, в сочетании с традиционным, и тем новым, что было внесено в педагогику многими исследователями и практиками развитие всей совокупности чувств и разума, мышления школьника и его памяти, развитие целостной, интеллектуально активной личности.
Обучение не может считаться развивающим, если не используются закономерности проблемного обучения (принцип проблемности, проблемная ситуация).
Проблемный тип обучения не решает всех образовательных и воспитательных задач, поэтому он не может заменить собой всей системы обучения, включающей разные типы, способы, организации учебно-воспитательного процесса. Но также система обучения не может быть подлинно развивающей без проблемного обучения.
Всем ли учащимся доступно проблемное обучение?
Практически всем. Однако уровень проблемности и степень познавательной самостоятельности будут сильно различаться в зависимости от возрастных и индивидуальных особенностей учащихся, от степени их обученности методам проблемного обучения и т.д.
Организация проблемного обучения.
Организация проблемного обучения предполагает применение таких приемов и методов преподавания, которые приводили бы к возникновению взаимосвязанных проблемных ситуаций и предопределяли применение школьниками соответствующих методов учения.
Однако возникновение проблемных ситуаций и поисковой деятельности учащихся возможно не в любой ситуации. Оно, как правило, возможно в таких видах учебно-познавательной деятельности учащихся, как: решение готовых нетиповых задач; составление задач и их решение; логических анализ текста; ученическое исследование; сочинение; рационализация и изобретение; конструирование и др.
Поэтому создание учителем цепи проблемных ситуаций в различных видах творческой учебной деятельности учащихся и управление их мыслительной (поисковой) деятельностью по усвоению новых знаний путем самостоятельного (иди коллективного) решения учебных проблем составляет сущность проблемного обучения.
1.3. Организация проблемного обучения в средней школе
Исходя из идеи развития познавательной самостоятельности учащихся, все разновидности современного урока на основе принципа проблемности делятся на проблемные и не проблемные.
С точки зрения внутренней специфики (логико-психологической) проблемным следует считать урок, на котором учитель преднамеренно создает проблемные ситуации и организует поисковую деятельность учащихся по самостоятельной постановке учебных проблем и их решению (высший уровень проблемности) или сам ставит проблемы и решает их, показывая учащимся логику движения мысли в поисковой ситуации (низший уровень проблемности).
Дидактическим (внешним) показателем проблемного урока является его комплексность, синтетичность. Сущность синтетичного урока заключается в том, что повторение пройденного, как правило, сливается с введением нового материала, происходит непрерывное повторение знаний, умений и навыков в новых связях и сочетаниях, что характерно как раз для проблемного урока.
Структурными элементами современного урока являются:
актуализация прежних знаний учащихся (что означает не только воспроизведение ранее усвоенных знаний, но и применение их часто в новый ситуации, стимулирование познавательной активности учащихся, контроль учителя);
усвоение новых знаний и способов действия (в значении более конкретном, чем понятие «изучение нового материала»);
формирование умений и навыков (включающих и специальное повторение, и закрепление).
Эта структура отражает и основные этапы учения, и этапы организации современного урока. Но по отношению к мыслительной деятельности учащихся, являясь выражением целей образования, она выступает как внешний показатель учения, то есть не отражает процесса продуктивной познавательной деятельности учащихся и не может обеспечить управление этой деятельностью. Поскольку показателем проблемности урока является наличие в его структуре этапов поисковой деятельности, то естественно, что они и представляют внутреннюю часть структуры проблемного урока:
возникновение проблемной ситуации и постановка проблемы;
выдвижение предположений и обоснование гипотезы;
доказательство гипотезы;
проверка правильности решения проблемы.
Таким образом, структура проблемного урока, в отличие от структуры непроблемного, имеет элементы логики познавательного процесса (логики продуктивной мыслительной деятельности), а не только внешней логики процесса обучения. Структура проблемного урока, представляющая собой сочетание внешних и внутренних элементов процесса обучения, создает возможности управления самостоятельной учебно-познавательной деятельностью ученика.
В рамках проблемного обучения в педагогике исследуются не только общепедагогические проблемы, но и проблемы обучения отдельным предметам. Особенно это относится к проблемам педагогики математики.
Именно на уроках математики складывается благоприятная атмосфера для введения элементов проблемного обучения, так как проблемным способом целесообразно изучать такой материал, который содержит причинно-следственные связи и зависимости, который направлен на формирования понятий, законов и теорий.
Примерная схема организации урока математики в форме проблемного обучения.
Создание учебной проблемной ситуации (реальной или формализованной) с целью возбудить у учащихся интерес к данной учебной проблеме и мотивировать целесообразность ее рассмотрения.
Постановка познавательной задачи (или задач), возникающей из данной проблемной ситуации, четкая ее формулировка.
Изучение различных условий, характеризующих поставленную задачу, обсуждение возможностей моделирования ее условия или замены имеющейся модели более простой и наглядной.
Процесс решения поставленной задачи (обсуждение задачи в целом и деталях, выявление существенного и несущественного в ее условиях, ориентация в возможных трудностях при ее решении, вычисление подзадачи и последовательность ее решения, соотношение данной задачи с имеющимися знаниями и опытом. Разработка возможных направлений решений основной задачи, отбор, воспроизведение известных теоретических положений, могущих быть использованы в указанном направлении решения задачи, сравнительная оценка направления решения и выбор одного из них, разработка плана решения задачи в выбранном направлении и его реализация в целом, детальная реализация плана решения задачи и обоснование правильности всех шагов возникающего решения задачи).
Исследование получаемого решения задачи, обсуждение его результатов, выявление нового знания.
Применение нового знания посредством решения специально подобранных учебных задач для его усвоения.
Обсуждение возможных расширений и обобщений результатов решения задачи в рамках исходной проблемной ситуации.
Изучение полученного решения задачи и поиск других более экономичных или более изящных способов ее решения.
Подведение итогов проделанной работы, выявление существенного в содержании, способах решения, результатах, обсуждение возможных перспектив применения новых знаний и опыта.
Данный схематический план организации проблемного урока математики (как и любой другой) динамичен (в зависимости от конкретной характеристики той или иной учебной проблемы). Он выполняется полностью или частично, отдельные пункты плана могут объединяться вместе и т.п.
Рекомендации учителю при разработке им проблемного урока.
Учителю рекомендуется продумать:
Точное определение объема и содержания учебного материала, предназначенного для изучения на уроке.
Систематизация учебного материала в соответствии с логикой учебного предмета, его структурой, а так же в соответствии с принципами дидактики.
Деление учебного материала на легко усваиваемые и тесно между собой связанные части.
Усвоение частей, сопровождающихся контролем и корректированием результатов усвоения.
Учет индивидуальных темпов усвоения учебного материала школьниками и темпов работы группы.
Виды учебной работы школьников в условиях проблемного обучения.
Проблемное обучение позволяет эффективно сочетать как индивидуальную, так и групповую работу учащихся на уроке. В традиционном обучении групповая работа учащихся используется крайне редко. Между тем групповая-коллективная работа учащихся также является эффективным способом активного приобретения ими знаний, не говоря уже о ее воспитательном значении.
Как же сочетать групповую и индивидуальную работу учащихся в проблемном обучении?
В примерной схеме проблемного урока основное место естественно занимает решение проблемы.
На этом этапе работа с учениками может выступать в виде:
фронтальной работы со всем классом,
групповой работы,
индивидуальной работы.
На выбор того или иного вида работы влияет характер работы, имеющиеся учебные средства (комплекты учебных пособий и других материалов), а также время, имеющиеся в распоряжении учителя.
Групповая работа предполагает деление класса на группы как примерно одинаковые (по уровню) развития, так иногда и различных учащихся. Количественный состав групп может быть разнообразным.
Можно указать на некоторые принципы организации групповой работы.
Наиболее целесообразно создавать учебные группы из 4-6 человек.
Состав ученических групп не следует часто менять, лучше если он является постоянным, но дифференцированным. Это способствует проявлению активности всех членов группы и ускорению работы «слабых» учащихся.
Какой-либо из учащихся назначается руководителем группы. При этом на разных уроках работой группы руководят разные учащиеся.
Учебные группы ориентируются на работу примерно в одинаковом темпе, что дает возможность вести деловое обсуждение изучаемого материала.
Коллективная работа учащихся над решением какой-либо учебной проблемы никаким образом не исключает индивидуальной работы каждого из них, так как групповая работа по существу объединяет индивидуальную работу каждого из членов группы.
Умелое сочетание групповой и индивидуальной формы занятий обеспечивает всестороннее развитие активности и самостоятельности в обучении всех учащихся, дает возможность обсуждать изучаемую тему, оценивать результаты своих наблюдений, высказывать гипотезы.
Методы проблемного обучения.
Можно говорить о шести дидактических способах организации процесса проблемного обучения, представляющих собой три вида изложения учебного материала учителем и три вила организации им самостоятельной учебной деятельности учащихся. Рассмотри их.
Метод монологического изложения.
Учитель сообщает факты в определенной последовательности, дает им необходимые пояснение, демонстрирует опыты с целью их подтверждения. Использование средств наглядности и технических средств обучения сопровождается поясняющим текстом. Учитель вскрывает только те связи между явлениями и понятиями, которые требуются для понимания данного материала, вводя их в порядке информации. Чередование фактов строится в логической последовательности, однако, в ходе изложения внимания учащихся на анализе причинно-следственных связей не конкретизируется. Факты «за» и «против» не приводятся, сразу сообщается правильные окончательные выводы. Проблемные ситуации если и создаются, то только с целью привлечения внимания учащихся, заинтересовать их. После ее создания ответа на вопрос «почему так, а не иначе?», от учеников не требуется, а сразу идет сообщение фактического материала.
При использовании монологического метода обучения материал незначительно перестраивается. Учитель чаще всего только изменяет с целью создания проблемной ситуации порядок следования сообщаемых фактов, демонстраций, опытов, показа средств наглядности и в качестве дополнительных элементов содержания использует интересные факты из истории развития изучаемого понятия или факты, повествующие о практическом применении усваиваемых знаний в науке и технике.
Роль ученика при использовании данного метода довольно пассивна, необходимый для работы этим методом уровень познавательной самостоятельности невысок.
При такой организации процесса усвоения нового знания учитель соблюдает все основные требования к уроку, реализует дидактические принципы наглядности, доступности изложения, соблюдает строгую последовательность в порядке следования информации, поддерживает устойчивое внимание учащихся к изучаемой теме, однако избранный им метод преподавания превращает ученика в пассивного слушателя, не активизирует его познавательную деятельность. Используемый в данном случае информационно-сообщающий метод преподавания позволяет достичь лишь одной цели – пополнить запас знаний учащихся дополнительными фактами.
Рассуждающий метод обучения.
Если учитель ставит цель показать образец исследования постановки и решения целостной проблемы, то он использует рассуждающий метод. При этом материал разделяется на части, учитель к каждому этапу предусматривает системы риторических вопросов проблемного характера с целью привлечь учащихся к мысленному анализу проблемных ситуаций, обнажает объективные противоречия содержания, но сам же и разрешает используются предложения повествовательного и вопросительного типа, информационные вопросы (т.е. такие вопросы, отвечая на которые нужно воспроизводить уже известные знания, давать информацию об известном знании) не ставятся, повествование ведется в форме лекции.
Способ перестройки материала для работы этим методом отличается прежде всего тем, что в содержание в качестве дополнительного структурного элемента вводится система риторических вопросов. Порядок следования сообщаемых фактов выбирается таким, чтобы объективные противоречия содержания были представлены особенно подчеркнуто, выпукло, возбуждали познавательный интерес учащихся и желание их разрешить.
В изложении учителя преобладает уже не категоричность сведений, а элементы рассуждения, поиска выхода из возникающих в силу особенностей построения материала затруднений. Учитель, как это и предполагает М.И.Махмутов, «демонстрирует самый путь научного познавания, заставляя учеников следить за диалектическим движением мысли к истине» [29], он не только создает проблемные ситуации, но ставит и решает проблемы, показывает, как выдвигались и сталкивались различные гипотезы.
Выбрав рассуждающий метод обучения, учитель в процессе организации процесса усвоения пользуется объяснительным методом преподавания, сущность которого заключается в том, что он «включает сообщение учителем фактов данной науки, их описание и объяснение, то есть раскрывает сущности новых понятий с помощью слова, наглядности и практических действий» [29].
Диалогический метод изложения.
Если учитель ставит перед собой задачу привлечь учащихся к непосредственному участию в реализации способа решения проблемы с целью активизировать их, повысить познавательный интерес, привлечь внимание к уже известному в новом материале, он, используя то же построение содержания, дополняет его структуру информационными вопросами, ответы на которые дают учащиеся.
Использование диалогического метода обучения обеспечивает более высокий уровень познавательной активности учащихся в процессе познания, так как они уже непосредственно привлекаются к участию в решении проблемы под жестоким управляющим воздействием преподавателя.
Эвристический метод изложения.
Эвристический метод применяется там, где учитель ставит цель обучить учащихся отдельным элементам решения проблемы, организовать частичный поиск новых знаний и способов действия. Используя эвристический метод, учитель применяет то же построение учебного материала, что и при диалогическом методе, но несколько дополняет его структуру постановкой познавательных задач и заданий учащимся на каждом отдельном этапе решения учебной проблемы. Таким образом, формой реализации этого метода является сочетание эвристической беседы с решением проблемных задач и заданий.
Суть эвристического метода состоит в том, что открытие нового закона, правила и т.п. совершается не учителем при участии учащихся, а самими учащимися под руководством и с помощью учителя.
Исследовательский метод.
Понятие исследовательского метода наиболее полно раскрыл И.Я.Лернер, который к исследовательскому методу отнес метод, организующий процесс усвоения «решением проблем и проблемных задач. Сущность его в том, что учитель конструирует методическую систему проблем и проблемных задач, адаптирует ее к конкретной ситуации учебного процесса, предъявляет учащимся, тем самым управляя их учебной деятельностью, а учащиеся, решая проблемы, обеспечивают сдвиг в структуре и уровне умственной деятельности, постепенно овладевая процедурой творчества, а заодно творчески усваивают и методы познавания» [25].
При проведении урока исследовательским методом опять используется такое же построение материала и берутся элементов структуры эвристического метода и порядок следования вопросов, указаний, заданий. Если в процессе реализации эвристического метода эти вопросы, указания и задания носят упреждающий характер, то есть ставятся до решения подпроблемы, составляющей содержание данного этапа, или в процессе ее решения и выполняет направляющую функцию в процессе решения, то в случае использования исследовательского метода вопросы ставятся в конце этапа, после того как большинство учащихся с решением подпроблемы справились.
Метод программированных заданий.
Метод программированных заданий представляет собой постановку учителем системы программированных заданий. Уровень эффективности учения определяется наличием проблемных ситуаций и возможностью самостоятельной постановки и решения проблем. Применение программированных заданий заключается в следующем: каждое задание состоит из отдельных элементов-кадров; один кадр содержит часть изучаемого материала, сформулированного в виде вопросов и ответов, либо в виде изложения новых заданий, либо в виде упражнений.
Положение учителя при проблемном обучении.
Мастерство учителя проявляется больше всего в организации проблемных ситуаций.
При проблемном обучении учитель остается руководителем учебного процесса, но выходит из не всегда благодарной роли человека сообщающего знания в традиционной школе, и становится тем, кто будит развивает, наблюдает мыслительные операции учащихся, исправляет ошибки, разъясняет сомнения.
Наблюдая работу коллективов, он видит то, что не замечал часто, проводя работу со всеми, - ведь отдельного ученика можно наблюдать в моменты спокойной работы, в минуты творческих поисков, дискуссий.
Реализация проблемного обучения поднимает очень важный вопрос, который сам по себе является проблемой: «какую подготовку должны пройти учителя, чтобы успешно справится с такого рода обучением?»
Учитель должен владеть как объяснительным, так и исследовательским методами обучения. Выступая в роли организатора обучения на проблемной основе, учитель призван действовать скорее как руководитель и партнер, чем как источник готовых знаний и директив для учащихся. В процессе подготовки учитель должен приобрести опыт, который позволит ему:
Тонко чувствовать проблемность ситуации с которыми сталкиваются учащиеся и уметь ставить перед классом реальные учебные задачи в понятной для детей форме?
Выполнять функцию координатора и партнера. В ходе исследования различных аспектов проблемы помогать отдельным учащимся и группам, избегая директивных приемов
Стараться увлечь учащихся проблемой и процессом ее глубокого исследования, стимулировать творческое мышление при помощи умело поставленных вопросов.
Проявлять терпимость к ошибкам учеников, допускаемых или в попытках найти собственное решение, предлагая свою помощь или адресовать к нужным источникам информации только в тех случаях, когда учащийся начинает чувствовать безнадежность своего поиска.
Помещение учителя на второй план отнюдь не значит, что он утрачивает в какой-то мере свое значение. Это лишь формально второй план, хотя и идущий от ученика, несмотря на то, что учитель появляется на сцене реже ученика, фактически он является главным героем. От него зависит все то, что происходит или не происходит с учеником. Однако свою роль главного актера, а также режиссера школьной сцены он выполняет надлежащим образом только тогда, когда умеет вызвать в учениках силы и творческие возможности и использовать их в хорошо организованном процессе воспитания.
Роль и место проблемного обучения в учебном процессе.
Поскольку проблемное обучение применяется в структуре других методов, его нельзя рассматривать ни как особый метод обучения, ни как какую-то новую систему обучения. Правильнее всего будет его считать особым подходом к организации обучения, проявляющимся прежде всего в характере организации познавательной деятельности обучаемых.
Несомненно, не всякий материал может служить основой для создания проблемной ситуации. К непроблемным элементам учебного материала относится вся конкретная информация, содержащая цифровые и количественные данные, факты, даты и т.п. которые нельзя «открыть».
Проблемное обучение возможно применять для усвоения обобщенных знаний – понятий, правил, законов, причинно-следственных и других логических зависимостей. Оно нужно тогда, когда ставится задача специального обучения учащихся приемам и способам умственной деятельности, необходимым при добывании знаний и решении поисковых задач.
Проблемными, как правило, являются первые уроки любой темы, ибо они содержат в себе новые по сравнению с ранее изученным теоретические и практические положения.
Бесспорно, что проблемное обучение обладает рядом достоинств.
Проблемное обучение при правильной его организации способствует развитию умственных сил учащихся (противоречия заставляют задумываться искать выход из проблемной ситуации затруднения); самостоятельности (самостоятельное видение проблемы, формулировка проблемного вопроса, проблемной ситуации, самостоятельность выбора плана решения и т.д.); развитию творческого мышления (самостоятельное применение знаний, способов действия, поиск самостоятельного нестандартного решения). Проблемное обучение обеспечивает и более прочное усвоение знаний (то, что добыто самостоятельно лучше усваивается и на долго запоминается); развивает аналитическое мышление (проводится анализ условий, оценка возможных вариантов решений), логическое мышление (требует доказательств правильности выбираемого решения, аргументации).
Проблемное обучение вооружает школьников методами познания окружающей действительности, развивает умения и навыки целесообразного наблюдения, воспитывает способность к обобщениям и выводу основных закономерностей с обоснованием их, прививает вкус к доступной исследовательской работе.
Учащиеся быстрее осмысливают сущность изучаемого явления и дают обоснованные ответы. У них развиваются познавательные потребности и интерес, воспитывается убежденность в знаниях, так как учащиеся сами выдвигают гипотезы и сами доказывают их.
Но проблемное обучение имеет и недостатки. Не всегда легко сформулировать учебную проблему, не весь учебный материал можно построить в виде проблем; проблемное обучение не способствует отработке навыков, не экономично – требует больших затрат времени.
Условия применения проблемного обучения.
Проблемное обучение целесообразно применять когда:
Содержание учебного материала содержит причинно-следственные связи и зависимости, направлено на формирование понятий, законов, теорий.
Ученики подготовлены к проблемному изучению темы.
Ученики решают задачи на развитие самостоятельности мышления, формирование исследовательских умений, творческого подхода к делу.
У учителя есть время для проблемного изучения темы.
Учитель хорошо владеет соответствующими методами обучения.
Глава II. Из опыта организации интеллектуального развития школьников.
2.1. Методики исследования интеллектуальных умений школьников и анализ опытной работы.
Экспериментальная программа была проверена в 9 «б» классе.
В классе 28 учащихся, из них 15 мальчиков и 13 девочек. Физически и умственно все дети здоровы. С ослабленным здоровьем – Денис Ф.
Преобладающее большинство детей в классе – холерики. Отсюда их подвижность, энергия, шумливость, темперамент.
По способностям класс средний, заниматься на «4» и «5» могут большинство ребят. Слабы в учебе Паша А., Саша С., Дима Л., хорошие способности у Андрея Б., Сережи Б., Юли К., Оксаны К., Георгия К.
Совсем нет желания и интереса к учебе у Димы Л.
Саша С. и Дима Л. имеют слабые способности, не сосредоточены, рассеяны на уроке, не успевают за классом. Требуют особого, постоянного контроля со стороны учителя и родителей.
Желание учиться у большинства детей есть, и это радует.
Особую тревогу вызывают Саша С. и Дима Л., так как со стороны родителей нет должного контроля за этими детьми, за их занятиями, за их учебой. Мальчики недисциплинированны, постоянно приходят с невыученными уроками.
В целом класс очень активный, требует на уроках большой нагрузки и постоянной занятости в свободное время.
Проведенное исследование включало 3 серии эксперимента:
констатирующая;
обучающая;
контрольная.
Для того, чтобы успешно организовать исследовательскую работу, нам необходимо было изучить уровень интеллектуального развития учащихся. В своей дипломной работе мы уделили больше внимания одному компоненту интеллектуального развития, а именно мышлению. Мы использовали ряд методик по изучению уровня развития умения мыслить, которые позволили нам получить первоначальный результат.
С целью установления индивидуальных особенностей скорости протекания мыслительного процесса у учащихся была проведена методика 1.
Методика 1. Скорость протекания мыслительного процесса.
Ход выполнения задания.
Учащимся предъявляется написанная на плакате или доске таблица слов с пропущенными буквами. Ученики по команде начинают писать те полные слова, которые они сумели образовать, вставив пропущенные буквы. Учитель фиксирует время завершения работы каждым учеником.
Необходимый материал: секундомер, список слов с пропущенными буквами.
Список слов:
| п – ро | д – р – во | п – л – а |
| г – ра | з – м – к | о – р – г |
| п – ле | к – м – нь | к – р – он |
| к – са | с – р – й | з – р – о |
| т – ло | п – в – д | в – с – ок |
| п – ля | х – л – д | с – г – об |
| в – ра | п – с – к | в – т – а |
| с – ла | к – з – л | п – д – ак |
| д – ма | з – л – нь | п – р – а |
| р - ка | т – л – га | б – л – он |
| з – о – ок | с – я – о – ть | |
| к – н – а | к – с – а – ник | |
| с – е – ло | у – и – е – ль | |
| к – ы – а | а – е – ь – ин | |
| т – а - а | с – а – ц – я | |
| к – у – ка | ч – р – и – а | |
| с – а – ка | к – п – с – а | |
| т – у – а | с – а – о – ть | |
| с – а – а | с – е – о – а | |
| п – е – а | к – н – о - а |
Обработка данных.
На основе составления результатов отдельных испытуемых со среднегрупповым делается вывод о скорости протекания мыслительных процессов.
Результаты выполнения методики представлены в таблице 1.
Таблица 1.
| № | Учащиеся | Время | Скорость протекания мыслительного процесса | ||
| низкая | средняя | высокая | |||
| 1. | Павел А. | 19м.15с. | + | ||
| 2. | Андрей Б. | 14м.30с. | + | ||
| 3. | Яна Б. | 17м.10с. | + | ||
| 4. | Рома Б. | 17м.20с. | + | ||
| 5. | Сережа Б. | 14м.15с. | + | ||
| 6. | Аня Г. | 16м.45с. | + | ||
| 7. | Игорь Г. | 20м.10с. | + | ||
| 8. | Костя Е. | 14м.50с. | + | ||
| 9. | Аня И. | 17м.20с. | + | ||
| 10. | Вова К. | 17м.15с. | + | ||
| 11. | Юля К. | 14м.40с. | + | ||
| 12. | Оксана К. | 14м.10с. | + | ||
| 13. | Ксения К. | 17м.05с. | + | ||
| 14. | Георгий К. | 13м.50с. | + | ||
| 15. | Надя К. | 16м.45с. | + | ||
| 16. | Маша К. | 16м.40с. | + | ||
| 17. | Катя Л. | 17м.05с. | + | ||
| 18. | Дима Л. | 20м.15с. | + | ||
| 19. | Оксана Л. | 15м.40с. | + | ||
| 20. | Сережа П. | 16м.00с. | + | ||
| 21. | Эля Р. | 16м.05с. | + | ||
| 22. | Саша С. | 19м.55с. | + | ||
| 23. | Марина С. | 14м.20с. | + | ||
| 24. | Сережа С. | 16м.50с. | + | ||
| 25. | Миша С. | 16м.45с. | + | ||
| 26. | Денис Ф. | 20м.30с. | + | ||
| 27. | Женя Ф. | 15м.15с. | + | ||
| 28. | Аня Ч. | 16м.35с. | + | ||
| Среднегрупповое время | 16м.41с. | ||||
Как видно из таблицы, у 25% учащихся высокая скорость протекания мыслительного процесса, у 18% - низкая и у 57% - средняя.
С целью изучения индивидуальных особенностей уровней развития мыслительных операций: анализа, синтеза, обобщение была проведена методика 2.
Методика 2. Поиск закономерностей числовых рядов.
Ход выполнения задания.
Учащимся предъявляется таблица, на которой напечатаны 10 рядов чисел. Рассматривая в отдельности каждый из данных 10 рядов, испытуемый должен найти правило, по которому подобранны числа и написать справа от ряда еще 2 числа, которые продолжили бы этот ряд.
Необходимый материал: таблица с рядами чисел, секундомер.
| Таблица с числами | Ответы | |||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | |
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | |
| 4 | 5 | 8 | 9 | 12 | 13 | 16 | 17 | |
| 19 | 16 | 14 | 11 | 9 | 6 | 4 | 1 | |
| 29 | 28 | 26 | 23 | 19 | 14 | 8 | 1 | |
| 16 | 8 | 4 | 2 | 1 | 1/2 | 1/4 | 1/8 | |
| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | |
| 21 | 18 | 16 | 15 | 12 | 10 | 9 | 6 | |
| 3 | 6 | 8 | 16 | 18 | 36 | 38 | 76 | |
Обработка данных.
На основе сопоставления результатов отдельных испытуемых со среднегрупповыми делается вывод об уровне развития мыслительных операций.
Данные по выполнению задания представлены в таблице 2.
Таблица 2.
| № | Учащиеся | Время | Уровень развития мыслительных операций | ||
| низкий | средний | высокий | |||
| 1. | Павел А. | 8м.10с. | + | ||
| 2. | Андрей Б. | 4м.50с. | + | ||
| 3. | Яна Б. | 6м.05с. | + | ||
| 4. | Рома Б. | 4м.25с. | + | ||
| 5. | Сережа Б. | 4м.10с. | + | ||
| 6. | Аня Г. | 6м.10с. | + | ||
| 7. | Игорь Г. | 7м.35с. | + | ||
| 8. | Костя Е. | 4м.15с. | + | ||
| 9. | Аня И. | 6м.25с. | + | ||
| 10. | Вова К. | 6м.10с. | + | ||
| 11. | Юля К. | 5м.15с. | + | ||
| 12. | Оксана К. | 6м.30с. | + | ||
| 13. | Ксения К. | 6м.40с. | + | ||
| 14. | Георгий К. | 4м.35с. | + | ||
| 15. | Надя К. | 6м.30с. | + | ||
| 16. | Маша К. | 6м.35с. | + | ||
| 17. | Катя Л. | 6м.50с. | + | ||
| 18. | Дима Л. | 7м.45с. | + | ||
| 19. | Оксана Л. | 6м.05с. | + | ||
| 20. | Сережа П. | 6м.45с. | + | ||
| 21. | Эля Р. | 6м.45с. | + | ||
| 22. | Саша С. | 7м.20с. | + | ||
| 23. | Марина С. | 4м.55с. | + | ||
| 24. | Сережа С. | 6м.15с. | + | ||
| 25. | Миша С. | 7м.50с. | + | ||
| 26. | Денис Ф. | 7м.40с. | + | ||
| 27. | Женя Ф. | 8м.05с. | + | ||
| 28. | Аня Ч. | 6м.20с. | + | ||
| Среднегрупповое время | 6м.28с. | ||||
Из таблицы видно, что у 25% учащихся высокий уровень развития мыслительных операций, у 25%-низкий и у 50%-средний.
С целью определения способности выделять существенное (способности к абстрагированию) была проведена методика 3.
Методика 3. Исключение.
Ход выполнения задания.
Учащимся предлагается 5 рядов слов. В каждом из рядов даются в скобках, а одно – перед ними. Ученики должны за специально отведенное время (1,5 мин.) исключить из скобок (т.е. выделить) 2 слова, наиболее существенны для слова перед скобками.
Необходимый материал.
Сад (растение, садовник, собака, забор, земля).
Ответ: растение, земля.
Река (берег, рыба, вода, рыболов, тина).
Ответ: берег, вода.
Куб (углы, чертеж, сторона, камень, дерево).
Ответ: углы, сторона.
Чтение (глаза, книга, картина, печать, слово).
Ответ: глаза, печать.
Игра (шахматы, игроки, штрафы, правила, наказание).
Ответ: игроки, правила.
Обработка данных.
Учащиеся, которые правильно выполнили задание, очевидно обладают умением выделять существенное. Те, кто допустил ошибки (или просто не выполнил), не умеют отличить существенные и несущественные признаки, то есть такая способность у них не развита.
Результаты выполнения методики представлены в таблице 3.
Таблица 3.
| № | Учащиеся | Способность к абстрагированию | ||
| низкая | средняя | высокая | ||
| 1. | Павел А. | + | ||
| 2. | Андрей Б. | + | ||
| 3. | Яна Б. | + | ||
| 4. | Рома Б. | + | ||
| 5. | Сережа Б. | + | ||
| 6. | Аня Г. | + | ||
| 7. | Игорь Г. | + | ||
| 8. | Костя Е. | + | ||
| 9. | Аня И. | + | ||
| 10. | Вова К. | + | ||
| 11. | Юля К. | + | ||
| 12. | Оксана К. | + | ||
| 13. | Ксения К. | + | ||
| 14. | Георгий К. | + | ||
| 15. | Надя К. | + | ||
| 16. | Маша К. | + | ||
| 17. | Катя Л. | + | ||
| 18. | Дима Л. | + | ||
| 19. | Оксана Л. | + | ||
| 20. | Сережа П. | + | ||
| 21. | Эля Р. | + | ||
| 22. | Саша С. | + | ||
| 23. | Марина С. | + | ||
| 24. | Сережа С. | + | ||
| 25. | Миша С. | + | ||
| 26. | Денис Ф. | + | ||
| 27. | Женя Ф. | + | ||
| 28. | Аня Ч. | + | ||
Как видно из таблицы, 39% учащихся класса имеют высокую способность выделять существенное и 61% - среднюю
.
С целью установления уровня развития у учащихся способности классификации, была проведена методика 4.
Методика 4. Способность к классификации. Найди лишнее слово.
Ход выполнения задания.
Учащимся предъявляется 10 рядов слов по 5 слов в каждом ряду. Их модно классифицировать различным образом. При правильном «раскладе» остается лишнее слово, которое не подходит к остальным четырем. Существует один, наиболее верный способ, все остальные варианты менее очевидны. Имеется качество или характеристика, которому удовлетворяют 4 слова, но не удовлетворяет одно, которое и должно быть изъято из ряда. Учащимся предлагается подчеркнуть это слово.
Необходимый материал: листок с рядами слов:
Птица, самолет, пчела, машина, бабочка.
Смотреть, таращится, глядишь, наблюдаешь, моргать.
Дождь, снег, молния, град, изморозь.
Хлопок, шерсть, нейлон, лен, шелк.
Безжизненный, апатичный, вялый, оцепенелый, чувствительный.
Бук, ясень, ель, ива, клен.
Превосходный, поэтичный, величавый, грациозный, величественный.
Канатоходец, акробат, клоун, шут, жонглер.
Растирать, нарезать, толочь, измельчать, дробить.
Нарцисс, гладиолус, подснежник, хризантема, тюльпан.
Обработка данных.
Подчеркивается число правильно выделенных слов. Доля верно выделенных слов в процентах показывает уровень развития у ученика способности к классификации.
Результаты выполнения методики представлены в таблице 4.
Таблица 4.
| № | Учащиеся | Показатель, % | Уровень развития способности к классификации | ||
| низкий | средний | высокий | |||
| 1. | Павел А. | 80 | + | ||
| 2. | Андрей Б. | 90 | + | ||
| 3. | Яна Б. | 90 | + | ||
| 4. | Рома Б. | 100 | + | ||
| 5. | Сережа Б. | 100 | + | ||
| 6. | Аня Г. | 70 | + | ||
| 7. | Игорь Г. | 60 | + | ||
| 8. | Костя Е. | 80 | + | ||
| 9. | Аня И. | 80 | + | ||
| 10. | Вова К. | 80 | + | ||
| 11. | Юля К. | 90 | + | ||
| 12. | Оксана К. | 90 | + | ||
| 13. | Ксения К. | 90 | + | ||
| 14. | Георгий К. | 100 | + | ||
| 15. | Надя К. | 80 | + | ||
| 16. | Маша К. | 70 | + | ||
| 17. | Катя Л. | 60 | + | ||
| 18. | Дима Л. | 60 | + | ||
| 19. | Оксана Л. | 100 | + | ||
| 20. | Сережа П. | 70 | + | ||
| 21. | Эля Р. | 80 | + | ||
| 22. | Саша С. | 40 | + | ||
| 23. | Марина С. | 100 | + | ||
| 24. | Сережа С. | 80 | + | ||
| 25. | Миша С. | 90 | + | ||
| 26. | Денис Ф. | 50 | + | ||
| 27. | Женя Ф. | 70 | + | ||
| 28. | Аня Ч. | 80 | + | ||
Из таблицы видно, что из всего класса 39% учащихся имеют высокий уровень развития способности, 19% - низкий и 42% - средний.
С целью установления уровня развития у учащихся умения сравнивать предметы, понятия, была проведена методика 5.
Методика 5. Сравнение понятий.
Ход выполнения задания.
Испытуемому показываются пары слов и предлагается указать сходства и различия этих явлений или предметов, обозначаемых приведенными словами.
Необходимый материал.
Испытуемым дается два слова явно относящиеся к одной категории. Во вторых, предлагаются два слова, у которых общее найти трудно и которые гораздо больше отличаются друг от друга, чем в предыдущем случае. Третья группа задач еще сложнее – это задачи на сравнение и различение объектов, где различия выражены гораздо больше, чем сходство.
Корова – лошадь.
Ворона – рыба.
Всадник – лошадь.
Обработка данных.
Подсчитывается количество выделенных испытуемым в каждой паре черт сходства и различия. Высокий уровень развития операции сравнения отличается в том случае, когда школьник назвал 16-20 черт, средний – 10-15 черт, низкий – менее 10 черт. Важно учесть, какие черты отметил учащийся в большем количестве – черты сходства или различия.
Данные по выполнению задания представлены в таблице 5.
Таблица 5.
| № | Учащиеся | Число названных черт сходства и различия | Уровень развития операции сравнения | ||
| низкий | средний | высокий | |||
| 1. | Павел А. | 7 | + | ||
| 2. | Андрей Б. | 16 | + | ||
| 3. | Яна Б. | 13 | + | ||
| 4. | Рома Б. | 18 | + | ||
| 5. | Сережа Б. | 11 | + | ||
| 6. | Аня Г. | 11 | + | ||
| 7. | Игорь Г. | 8 | + | ||
| 8. | Костя Е. | 10 | + | ||
| 9. | Аня И. | 16 | + | ||
| 10. | Вова К. | 10 | + | ||
| 11. | Юля К. | 17 | + | ||
| 12. | Оксана К. | 16 | + | ||
| 13. | Ксения К. | 11 | + | ||
| 14. | Георгий К. | 17 | + | ||
| 15. | Надя К. | 10 | + | ||
| 16. | Маша К. | 11 | + | ||
| 17. | Катя Л. | 11 | + | ||
| 18. | Дима Л. | 6 | + | ||
| 19. | Оксана Л. | 16 | + | ||
| 20. | Сережа П. | 12 | + | ||
| 21. | Эля Р. | 12 | + | ||
| 22. | Саша С. | 7 | + | ||
| 23. | Марина С. | 13 | + | ||
| 24. | Сережа С. | 10 | + | ||
| 25. | Миша С. | 10 | + | ||
| 26. | Денис Ф. | 8 | + | ||
| 27. | Женя Ф. | 11 | + | ||
| 28. | Аня Ч. | 16 | + | ||
Как видно из таблицы, у 29% учащихся высокий уровень развития умения сравнивать предметы, понятия, у 18% - низкий и у 53% - средний.
С целью определения у учащихся уровня развития способности оперировать в мышлении пространственными образами, была проведена методика 6.
Методика 6. Пространственная сообразительность.
Ход выполнения задания.
Учащимся предлагается решить задачи на сообразительность, не требующие каких-либо громоздких вычислений, рассуждений. Задачи могли быть 3х типов.
«Движение». Особенность этих задач состоит в том, что они требуют от школьника учения совершать такие мыслительные преобразования, операции, которые видоизменяют лишь местоположение имеющихся у него в представлении образцов, перемещают их, но не затрагивают их структурных, композиционных, особенностей.
«Реконструкция».
При решении задач этого типа меняется не только местоположение имеющегося в представлении образа, но и его структура, строение.
«композиция».
Решение этих задач требует умения от школьника изменять образ и по местоположению, и по структуре одновременно и неоднократно совершать не одномоментные отдельные операции, а их композиции.
Ученику предлагается решить задачи всех трех типов, начиная с третьего.
Необходимый материал.
1) Укажите несколько букв (слов), запись которых имеет ось симметрии.
2) Сейчас 2ч. 45м. Сколько будет времени, когда минутная стрелка повернется на 210 градусов?
1) Разрезать прямоугольник со сторонами 4 и 9 ед. на две равные части таким образом, что бы, сложив их надлежащим образом, получить квадрат.
2) В квадрате через верхнюю левую вершину провели диагональ. Нижний прямоугольник оставили на месте, а верхний повернули вокруг этой вершины против часовой стрелки на 270 градусов. Какая фигура образовалась в результате?
Квадратный лист сложили вдвое по диагонали, затем еще раз вдвое так, что получился равнобедренный треугольник. Какая образуется фигура, если каждую вершину последнего треугольника отрезать по линии одинаковой длины, параллельной противоположным сторонам, и развернуть лист?
Обработка данных.
Решение задач определенного типа (первого, второго, третьего) соответствует определенному уровню пространственного мышления. Третий уровень самый высокий. Поэтому, если ученик решил задачу на третий тип ориентирования, то более простые задачи первого и второго типа ему уже можно не предлагать. Если он задачу третьего уровня не смог решить, то ему предлагают задачу второго уровня. Если и ее он не сможет решить, то дают задачу первого уровня.
Результаты выполнения методики представлены в таблице 6.
| № | Учащиеся | Уровень развития пространственного мышления | ||
| низкий | средний | высокий | ||
| 1. | Павел А. | + | ||
| 2. | Андрей Б. | + | ||
| 3. | Яна Б. | + | ||
| 4. | Рома Б. | + | ||
| 5. | Сережа Б. | + | ||
| 6. | Аня Г. | + | ||
| 7. | Игорь Г. | + | ||
| 8. | Костя Е. | + | ||
| 9. | Аня И. | + | ||
| 10. | Вова К. | + | ||
| 11. | Юля К. | + | ||
| 12. | Оксана К. | + | ||
| 13. | Ксения К. | + | ||
| 14. | Георгий К. | + | ||
| 15. | Надя К. | + | ||
| 16. | Маша К. | + | ||
| 17. | Катя Л. | + | ||
| 18. | Дима Л. | + | ||
| 19. | Оксана Л. | + | ||
| 20. | Сережа П. | + | ||
| 21. | Эля Р. | + | ||
| 22. | Саша С. | + | ||
| 23. | Марина С. | + | ||
| 24. | Сережа С. | + | ||
| 25. | Миша С. | + | ||
| 26. | Денис Ф. | + | ||
| 27. | Женя Ф. | + | ||
| 28. | Аня Ч. | + | ||
Из таблицы видно, что 25% учащихся имеют высокий уровень развития способности оперировать в мышлении пространственными образами, 36% - низкий и 39% - средний.
С целью установления наличия интуитивных способностей была проведена методика 7.
Методика 7. Сила интуиции.
Ход выполнения задания и необходимый материал.
Учащимся предлагается из двух вариантов ответа на вопросы выбрать тот, который ближе всего.
Если у меня нет готового ответа, я:
а) спокоен;
б) не спокоен.
В ситуации неопределенности я:
а) дезориентирован (пасую):
б) спокоен, собран.
В ситуациях соревнования я глубоко увлечен:
а) почти всегда;
б) редко.
Если моя интуиция противоречит фактам, обычно я:
а) верю чувствам;
б) следую логике.
Решая сложную проблему, я:
а) сосредоточен на поиске ее решения;
б) жду, когда придет решение.
Если я не согласен с мнением других людей, я:
а) заявляю об этом открыто;
б) держу свое мнение при себе.
В целом я:
а) предпочитаю (действовать наверняка) старые уже испытанные способы и пути;
б) люблю рисковать.
Решая проблему, я меняю стратегию:
а) редко;
б) часто.
Я предпочитаю, чтобы мне говорили:
а) как я должен делать;
б) что должно быть сделано.
Если ситуация осложняется, я:
а) оживляюсь;
б) волнуюсь.
Сталкиваясь с проблемой, обычно я:
а) сначала намечаю план и направление работы;
б) сразу погружаюсь в работу.
В большинстве случаев:
а) всякие изменения нервируют меня;
б) я рад неожиданным изменениям.
Я читаю:
а) о разных существах, в том числе и вымышленных;
б) фактический материал, относящийся к работе (занятиям).
Если мое мнение отличается от мнения специалиста, я обычно:
а) полагаюсь на себя;
б) считаюсь с авторитетом.
Когда по работе я сталкиваюсь одновременно с несколькими заданиями, я:
а делаю их параллельно;
б) делаю их последовательно.
В учебе (при усвоении нового) я:
а) сначала усваиваю правила и инструкции;
б) приступаю к самому материалу, а правила учу уже по ходу дела.
В работе я предпочитаю:
а) следовать установленным правилам и предписаниям;
б) создаю и следую собственному порядку.
В школе мне лучше даются:
а) ответы на открытые вопросы (типы сочинений, размышление и т.п.);
б) ответы на закрытые вопросы (краткие: да, нет, столько и т.п.).
В основном я:
а) идеалист;
б) реалист.
Когда я ошибаюсь, я:
а) проверяю себя еще раз;
б) забываю об этом и продолжаю дальше.
В разных ситуациях:
а) я обычно могу объяснить, откуда я знаю что-либо;
б) обычно не могу этого объяснить.
При описании и объяснении я больше опираюсь:
а) на аналогичные эпизоды;
б) на факты и примеры.
Меня обычно можно убедить:
а) обращаясь к смыслу;
б) обращаясь к эмоциям.
Если я не прав, я:
а) охотно признаю это;
б) защищаюсь.
Скорее всего, я:
а) фантазер;
б) практик.
Решая сложную проблему, я:
а) прошу совета;
б) стараюсь справится сам.
Непредсказуемые люди:
а) раздражают меня;
б) они мне интересны.
Получая задание на следующую неделю, я обычно говорю:
а) «Давайте договоримся о точном времени»;
б) «Сообщите мне за один день».
Если мои планы нарушаются, я:
а) расстраиваюсь;
б) спокойно принимаю новый план.
К своим догадкам я отношусь:
а) с энтузиазмом;
б) с недоверием.
Большинство моих друзей и коллег:
а) верят в интуицию;
б) относятся к ней скептически.
Меня считают:
а) человеком «идеи»;
б) человеком «детали».
Обработка данных.
Подчитывается общее число баллов. Если общая оценка 24 балла и больше, то испытуемый обладает тенденцией интуитивного подхода к принятию решения и проблемам. В основном этот человек полагается на свою интуицию и, возможно, она его не обманывает.
Оценка 16-23. Испытуемый склонен менять (варьировать) свой стиль, но преобладает интуиция, а не анализ и синтез. Интуиция чаще инстинктивна, чем ошибочна.
Оценка 8-15. У испытуемого смешанный стиль, но ближе к анализу и синтезу, рациональному. Интуиция может его подводить.
Оценка меньше 8. У испытуемого преобладает системно-рациональный подход к проблемам. Он не доверят своей интуиции, так как она в прошлом его подводила.
Данные по выполнению задания представлены в таблице 7.
Таблица 7.
| № | Учащиеся | Общий балл | Интуи-тивный подход | Смешанный стиль | Смешанно-рациональный подход | |
| Преобладает интуиция | Ближе к рациональ-ному | |||||
| 1. | Павел А. | 13 | + | |||
| 2. | Андрей Б. | 10 | + | |||
| 3. | Яна Б. | 23 | + | |||
| 4. | Рома Б. | 14 | + | |||
| 5. | Сережа Б. | 13 | + | |||
| 6. | Аня Г. | 10 | + | |||
| 7. | Игорь Г. | 23 | + | |||
| 8. | Костя Е. | 22 | + | |||
| 9. | Аня И. | 22 | + | |||
| 10. | Вова К. | 13 | + | |||
| 11. | Юля К. | 16 | + | |||
| 12. | Оксана К. | 21 | + | |||
| 13. | Ксения К. | 9 | + | |||
| 14. | Георгий К. | 17 | + | |||
| 15. | Надя К. | 13 | + | |||
| 16. | Маша К. | 13 | + | |||
| 17. | Катя Л. | 13 | + | |||
| 18. | Дима Л. | 11 | + | |||
| 19. | Оксана Л. | 8 | + | |||
| 20. | Сережа П. | 15 | + | |||
| 21. | Эля Р. | 8 | + | |||
| 22. | Саша С. | 14 | + | |||
| 23. | Марина С. | 10 | + | |||
| 24. | Сережа С. | 17 | + | |||
| 25. | Миша С. | 11 | + | |||
| 26. | Денис Ф. | 21 | + | |||
| 27. | Женя Ф. | 14 | + | |||
| 28. | Аня Ч. | 9 | + | |||
Как видно из таблицы, среди учащихся нет таких, кто полностью доверяет, либо не доверяет своей интуиции: у 68% учащихся смешанный стиль, ближе к рациональному, а 32% - больше преобладает интуиция, а не анализ и синтез.
С целью определения уровня творчества была проведена методика 8.
Методика 8. Диагностика творческого мышления учащихся.
Ход выполнения задания и необходимый материал.
- Разминочный блок.
Дается слово одуванчик. Необходимо из букв этого слова составить как можно больше новых слов. (Время выполнения 3 минуты). Два раза одну и туже букву в словах использовать нельзя. Высокий уровень развития способности – 9 и более слов.
Средний уровень – 7,8 слов.
Низкий уровень – 6 и менее слов.
Детям предлагается написать как можно больше предложений из пяти слов, в которых каждое слово начинается с указанной буквы.
Р – И – С – Н – К –
Для оценки гибкости конструирования фраз подсчитывается количество верно составленных предложений. Фраза должна обязательно выражать какой-либо смысл, а слова в предложении должны быть согласованны по родам, числам и падежам. Добавлять другие слова или предлоги не разрешается. Указанные буквы можно использовать в качестве предлогов. (Время выполнения 5 минут).
Экран оценки результатов задания
| Возраст детей | Уровни | ||
| высокий | средний | низкий | |
| 10-11 лет | 4 и более | 3 | 0-2 |
| 12 лет | 5 и более | 4 | 0-3 |
| 13 лет | 6 и более | 5 | 0-4 |
Из трех скороговорок выбрать одну и как можно быстрее ее проговорить (устно).
Ткет ткач ткани на платки Тане.
Топоры остры до поры, до поры остры топоры.
Свинья тупорылая весь двор перерыла, выросла на полрыла, до коры не доросла.
Быстро, чисто – 2 балла.
С погрешностями – 1 балл.
Выберите тот ответ, который соответствовал бы вашему поступку в предложенных ниже ситуациях.
Если бы я строил детский городок, то
а) построил такой городок, которого нет нигде – 2
б) построил городок, по предложенному типовому проекту – 0
в) построил городок, который видел в кино, журналах книгах – 1
Если я приглашаю друзей на свой день рождения, то
а) пишу сценарий и готовлю сюрпризы – 2
б) говорю им время и надеюсь на родителей – 0
в) участвую в приготовлении блюд для гостей – 1
На вопрос, поставленный учителем на уроке, я выбираю ответ:
а) простой – 0
б) сложный – 1
в) оригинальный – 2
Когда я чем-то сильно очарован то:
а) пишу стихи – 2
б) просто любуюсь объектом очарования – 1
в) чувствую умиротворенность – 0
Когда я провожу исследовательскую работу по моему любимому предмету, то:
а) читаю много дополнительной литературы – 2
б) подбираю материал попроще – 1
в) надеюсь на помощь учителя – 1
Для меня в общении самое главное:
а) возможность узнавать яркое нешаблонное, неординарное – 2
б) поделится своими бедами с друзьями – 1
в) просто провести время – 0
Если бы я стал ученым, то:
а) ездил часто за границу – 0
б) написал бы много полезных книг – 1
в) совершил бы открытия на пользу всему человечеству – 2
Из трех тропинок, оказавшихся перед вами в лесу, вы выбрали ту:
а) которая вам удобна – 0
б) о которой вам рассказывали знакомые – 1
в) которая является неизвестной тропинкой – 2
Мне хочется, чтобы в школе:
а) все учились в меру своих возможностей – 1
б) все были дружны – 0
в) узнавали как можно больше нового – 2
Произнесите громко, отчетливо три скороговорки:
а) Жужжит над жимолостью жук. Зеленый на жуке кожух.
б) Два дровосека, два дроворуба, два дровокола дрова рубили, дрова кололи, дрова секли.
в) Карл у Клары украл кораллы, а Клара у Карла украла кларнет.
Согласны ли вы со следующими высказываниями великих. Обозначьте в карточке следующими символами ваши ответы:
полностью согласен – 0,
не согласны – 2,
не готов оценить данное высказывание – 1.
Идеи могут быть обезврежены только идеями (О. Бальзак).
Разум человека сильнее его кулаков (Ф. Рабле).
Способности, как и мускулы, растут при тренировке (И. Тимирязев).
Только глупцы и покойники не меняют своих мнений (Д. Оруэлл).
Беда, коль пироги начнет печь сапожник, а сапоги тачать пирожник. (И. Крылов).
Льстят тем, кого боятся (А. Чехов).
Быть смелым на слова легко, когда не собираются говорить всей правды (Р. Тагор).
Всякий обладает достаточной силой, чтобы исполнить то, в чем он убежден (В. Гете).
Стыд перед людьми – хорошее чувство, но лучше всего стыд перед самим собой (Л. Толстой).
Самый счастливый человек тот, кто дает счастье наибольшему числу людей (Д. Дидро).
Величайшая слабость ума заключается в недоверчивости к силам ума (В. Белинский).
Способность преобразовывать структуру объекта.
В первой строке каждого вопроса есть пара слов, между которыми существует некая связь или какое-то соотношение. Вы должны определить какая связь или какое соотношение существует между этими двумя словами и выбрать из четырех предложенных ответов пару слов, между которыми существует та же связь или то же соотношение. (Правильный ответ – 2 балла).
МОРЕ – БАССЕЙН
река – труба
река – душ
река – лука
река – вода
ВОЗРОЖДЕНИЕ – ПОБЕДИТЕЛЬ
подъем – высота
подъем – учитель
подъем – гора
подъем – спуск
ПЧЕЛА – МЕД
собака – шерсть
кабан – мясо
коза – молоко
лошадь – хвост
Представлена исходная пара слов, которые назодятся в определенном соотношении, и пять других слов, из которых только одно находится в таком же отношении к исходному слову (правильный выбор – 2 балла).
БОЛЬНИЦА – ЛЕЧЕНИЕ
Институт
а) профессор
б) преподавание
в) обучение
г) учреждение
д) студент
МУХА – ПАУТИНА
Рыба
а) паук
б) треска
в) сеть
г) удочка
д) плавание
СМЕХ – ПЕЧАЛЬНЫЙ
Горе
а) легкий
б) клоун
в) апатия
г) радостный
д) мрачный
Словесные ассоциативные способности.
Найдите выход из ситуации:
Вас избрали губернатором области. Ваши первоочередные действия.
Вы купались в реке. У вас похитили одежду. Вам нужно найти выход из положения.
Вы оказались в африканском племени аборигенов. Ваши действия?
Экспериментатор оценивает ответ следующим образом:
отсутствие ответа – 0
тривиальный ответ – 1
оригинальный ответ – 2.
Перечислите как можно больше способов применения каждого предмета.
Велосипедная спица
Зубная щетка.
Полиэтиленовая бутылка.
(контрольный блок).
Да – 2 балла, трудно сказать – 1, нет – 0.
Мне приятно ощущать чувство новизны.
Мне удается представить то, чего не бывает в действительности.
Хорошо ориентируюсь в трудных ситуациях.
Часто ощущаю прилив творческих сил.
Могу аргументировать свое пристрастие к чему-либо.
Оригинальные идеи часто посещают меня.
Умею разграничить в сложных задачах главное и второстепенное.
Всегда рад услышать оценку своего труда от окружающих.
Я научился распознавать причины своих неудач.
Мне часто не хватает школьного учебного материала для удовлетворения моих познавательных потребностей.
Я верю в свои способности и возможности.
Обработка данных.
Более 67% выполненных заданий с баллом 2 – высокий уровень творчества; не менее 50% выполненных заданий с баллом 2 – средний уровень творчества.
Результаты выполнения методики представлены в таблице 8.
Таблица 8.
| № | Учащиеся | Количество заданий выполненных с высшим баллом, % | Уровень творчества | ||
| низкий | средний | высокий | |||
| 1. | Павел А. | 49 | + | ||
| 2. | Андрей Б. | 53 | + | ||
| 3. | Яна Б. | 64 | + | ||
| 4. | Рома Б. | 64 | + | ||
| 5. | Сережа Б. | 62 | + | ||
| 6. | Аня Г. | 45 | + | ||
| 7. | Игорь Г. | 43 | + | ||
| 8. | Костя Е. | 57 | + | ||
| 9. | Аня И. | 51 | + | ||
| 10. | Вова К. | 45 | + | ||
| 11. | Юля К. | 64 | + | ||
| 12. | Оксана К. | 85 | + | ||
| 13. | Ксения К. | 66 | + | ||
| 14. | Георгий К. | 90 | + | ||
| 15. | Надя К. | 55 | + | ||
| 16. | Маша К. | 66 | + | ||
| 17. | Катя Л. | 43 | + | ||
| 18. | Дима Л. | 38 | + | ||
| 19. | Оксана Л. | 62 | + | ||
| 20. | Сережа П. | 49 | + | ||
| 21. | Эля Р. | 55 | + | ||
| 22. | Саша С. | 53 | + | ||
| 23. | Марина С. | 66 | + | ||
| 24. | Сережа С. | 38 | + | ||
| 25. | Миша С. | 47 | + | ||
| 26. | Денис Ф. | 43 | + | ||
| 27. | Женя Ф. | 49 | + | ||
| 28. | Аня Ч. | 62 | + | ||
Из таблицы видно, что только 7% учащихся имеют высокий уровень творчества; 39% - низкий и 54% - средний.
С целью определения уровня сформированности интеллектуальных умений, была проведена методика 9.
Методика 9. Сформированность интеллектуальных умений.
Ход выполнения задания.
Данная методика предлагается учителям для оценки учеников и может быть использована учениками для самоанализа уровня сформированности у них интеллектуальных умений по предметам, наиболее и наименее трудным для усвоения.
Предполагаемые баллы имеют следующее описание:
2 – умение ярко выражено;
1 – умение имеет место;
0 – умение не сформировано.
Следует обвести балл, соответствующий мнению испытуемого.
Необходимый материал.
Ученик умеет слушать:
объяснение учителя, не опирающиеся на средства наглядности 2 1 0
объяснения учителя, опирающиеся на средства наглядности 2 1 0
вопросы учителя к средствам наглядности 2 1 0
вопросы учителя о связях между явлениями, представленными в наглядной форме 2 1 0
ответы товарищей во время опроса 2 1 0
оценивать свой ответ, то есть слушать самого себя 2 1 0.
Ученик умеет работать с наглядностью:
формулировать вопросы к иллюстрируемым фактам 2 1 0
схематизировать текст, представить его в таблице, схеме 2 1 0
самостоятельно изготовить пособие на основании чтения 2 1 0
объяснить, когда наглядное пособие может быть использовано 2 1 0
давать наглядное и логическое объяснение материала на основании самостоятельного изготовленного наглядного пособия 2 1 0
формировать вопросы к наглядным пособиям и оценивать их 2 1 0.
Умеет работать с текстом:
излагать текст своими словами 2 1 0
разделять текст на логические части и составлять план 2 1 0
систематизировать учебный материал 2 1 0
делать вступление к своему сообщению 2 1 0
строить логически законченный рассказ 2 1 0
раскрывать материал в сравнении 2 1 0.
Умеет оперировать знаниями:
пользоваться справочной литературой 2 1 0
на основании ряда изложенных фактов делать обобщения 2 1 0
формулировать познавательную задачу, содержащуюся в тексте 2 1 0
высказывать собственное отношение к фактам и событиям 2 1 0
самостоятельно формулировать вопросы 2 1 0
сопоставлять новый материал с уже известными фактами 2 1 0.
Умеет проявлять творческую самостоятельность:
при решении задач, предлагаемых учителем на уроке 2 1 0
при решении учебных задач, выполняя домашнее задание 2 1 0
проводя анализ, сравнения, сопоставления 2 1 0
делая выводы 2 1 0
делая обобщения на основании ряда фактов 2 1 0.
Умеет применять знания на практике:
формулируя гипотезу в исследовательском поиске 2 1 0
намечая пути ее проверки 2 1 0
проводя элементарное исследование с привлечением дополнительного материала по этой теме 2 1 0
осуществляя перенос знаний на рассмотрение текущих событий 2 1 0
применяя знания в общественной работе 2 1 0.
Обработка данных.
Подсчитывается общее число баллов. Если общая оценка 50 баллов и более – высокий уровень сформированности интеллектуальных умений; оценка 35-49 – средний уровень.
Данные по выполнению задания приведены в таблице 9.
Таблица 9.
| № | Учащиеся | Общий балл | Уровень сформированности интеллектуальных умений | ||
| низкий | средний | высокий | |||
| 1. | Павел А. | 19 | + | ||
| 2. | Андрей Б. | 61 | + | ||
| 3. | Яна Б. | 44 | + | ||
| 4. | Рома Б. | 58 | + | ||
| 5. | Сережа Б. | 58 | + | ||
| 6. | Аня Г. | 40 | + | ||
| 7. | Игорь Г. | 30 | + | ||
| 8. | Костя Е. | 62 | + | ||
| 9. | Аня И. | 45 | + | ||
| 10. | Вова К. | 48 | + | ||
| 11. | Юля К. | 60 | + | ||
| 12. | Оксана К. | 63 | + | ||
| 13. | Ксения К. | 49 | + | ||
| 14. | Георгий К. | 65 | + | ||
| 15. | Надя К. | 43 | + | ||
| 16. | Маша К. | 45 | + | ||
| 17. | Катя Л. | 34 | + | ||
| 18. | Дима Л. | 34 | + | ||
| 19. | Оксана Л. | 44 | + | ||
| 20. | Сережа П. | 43 | + | ||
| 21. | Эля Р. | 43 | + | ||
| 22. | Саша С. | 32 | + | ||
| 23. | Марина С. | 63 | + | ||
| 24. | Сережа С. | 40 | + | ||
| 25. | Миша С. | 42 | + | ||
| 26. | Денис Ф. | 33 | + | ||
| 27. | Женя Ф. | 47 | + | ||
| 28. | Аня Ч. | 49 | + | ||
Как видно из таблицы, у 29% учащихся класса высокий уровень сформированности интеллектуальных умений, у 21% - низкий и у 50% - средний.
Констатирующая серия эксперимента показала следующий результат (данные по умению мыслить совпали с данными таблицы 9): 29% учащихся имеют высокий уровень умения мыслить, 21% - низкий и 50% - средний.
Целью обучающей серии эксперимента стала организация интеллектуального развития школьников посредством проблемного обучения.
Обучающая серия была проведена на материале геометрии «Подобие и площади фигур». На каждом уроке особое внимание уделялось решению задач проблемного характера.
После обучающей серии эксперимента, с целью выяснения, насколько эффективно была организованна работа по развитию интеллекта учащихся, была проведена контрольная серия эксперимента, результаты которой представлены на диаграмме.

Из диаграммы видно, что изменения произошли незначительные, но и они говорят об эффективности проблемного обучения для интеллектуального развития.
2.2. Организация уроков математики с элементами проблемного обучения.
Курс геометрии своей строгостью и логической последовательностью создает большие возможности для проблемного обучения. Отдельные темы курса настолько связанны между собою, что сознательное усвоение одной из них создает условия для предвидения проблемы, которые возникают при изучении последующих.
Основой проблемного обучения на уроках геометрии является знакомство учащихся с новыми геометрическими фактами путем создания проблемных ситуаций, способствующих выдвижению гипотезы о свойствах рассматриваемых объектов и с последующим поиском доказательства справедливости выдвинутого предположения.
Наведению ученика на догадку может способствовать удачно подобранная система подготовительных упражнений, включающих в себя выполнение практических работ по измерению, построению, моделированию, рассмотрению наглядных пособий и чертежей, проведению эксперимента.
Во время педагогической практики у меня была возможность разнообразить уроки элементами проблемного обучения.
Соотношение между тригонометрическими функциями одного и того же аргумента.
Если учащиеся убеждены в существовании неизвестного математического объекта или неизвестных математических соотношений, то, естественно, возникает интерес к поиску этих объектов и соотношений – их открытию.
Целесообразно создать проблемную ситуацию, мотивирующую обязательное существование каких-то соотношений между двумя тригонометрическими функциями одного и того же аргумента. Вместе с тем получим ситуацию, мотивирующую тему и цель урока: открыть и изучить эти соотношения.
Краткое содержание проблемной беседы:
Если нам известно значение одной какой-либо тригонометрической функции, острого угла, то можно найти значения любой иной тригонометрической функции того же угла. Как, например, зная, что sin =3/5, найти cos , tg и т.д.?
Учащиеся указывают два приема:
найти по таблицам угол и затем по тем же таблицам cos , tg и т.д.
можно построить угол и измерить стороны полученного прямоугольного треугольника и т.д.
А нельзя ли решить задачу, если нет возможности пользоваться таблицами и построениями?
Здесь учащиеся испытывают затруднение. В этот момент уже возникает проблемная ситуация, мотивирующая постановку темы и цели урока: вывести такие формулы, которые позволяют решить поставленную задачу.
Поисковую проблемную ситуацию можно создать с помощью таких вспомогательных задач.
Катет прямоугольного треугольника равен 20 см., гипотенуза 25 см. Найти второй катет и его отношение к гипотенузе. Найти отношение первого катета к гипотенузе. Найти сумму квадратов обоих отношений.
Отношение одного катета к гипотенузе равно 4/5. Найти отношение второго катета к гипотенузе. Найти сумму квадратов обоих отношений.
Синус острого угла равен 4/5.найти косинус этого угла.
Отношение одного катета к гипотенузе равно m, а второго – n. Докажите, что сумма квадратов этих отношений равна 1.
Такое (или сходное) задание способствует успешному самостоятельному поиску и открытию искомого отношения.
В более подготовленном классе достаточно (для создания поисковой ситуации) предложить учащимся решить при помощи теоремы Пифагора задачу: «По данному синусу угла (sin =m/n), найти его косинус». В процессе решения этой задачи и будет открыто искомое соотношение.
Теорема об отрезках хорд, пересекающихся внутри круга.
C B
A
D


 Перед изучением
темы учащимися
предлагается
дома решить
следующую
задачу:
Перед изучением
темы учащимися
предлагается
дома решить
следующую
задачу:
Хорда AB, пересеклась с хордой CD в точке О, делится на отрезки АО=45 мм. и ОВ=30 мм. определить отрезок CD, если OD=90 мм.
Урок начинается с проверки выполнения домашнего задания. Выясняется, что большинство учеников справились с работой, притом различными способами.
Одни построили отрезок АВ=75 мм, отметили на нем точку О и отложили отрезок OD=90 мм. по трем точкам A, B, D построили окружность. Точка С была найдена как точка пересечения прямой OD с этой окружностью.
Другие построили круг произвольного радиуса, в нем хорду АВ=75 мм и на последней точку О. На окружности отметили точку D так, что OD=90 мм. Точка С была найдена как точка пересечения прямой OD с окружностью.
Третьи построили чертеж и нашли отрезок СО из подобия треугольников AOC и BOD.
Каждый способ решения задачи ученики объясняли по своим же чертежам. Последний способ решения задачи отмечается учителем как самый рациональный.
Учеников очень удивило то, что, несмотря на произвольность угла пересечения хорд (в первом случае), радиуса круга (во втором случае) и различия способов решения задачи, они получили один и тот же результат: СО=15 мм. Это убедило их в существовании определенной зависимости между отрезками пересекающихся в круге хорд. Еще раз обратившись к третьему случаю решения задачи, ученики сформулировали проблему: найти свойство отрезков пересекающихся хорд. Затем учитель называет тему урока и записывает ее. Построив чертеж, ученики составили пропорцию из отношения сходственных сторон подобных треугольников. Используя основное свойство пропорции, они дали формулировку теоремы.
Таким образом, проблемная ситуация возникла в результате рассмотрения способов решения конкретной задачи.
Тема урока заранее не объявляется, а вытекает из проблемной ситуации. Она принимается учащимися как своя, поскольку ими выстрадана, заработана в процессе умственной деятельности. Так, тема урока становится проблемой, разрешение которой увлекает учащихся.
Еще один вариант создания проблемной ситуации.
Учитель предлагает классу лабораторную работу: каждый учащийся строит в тетради окружность и две-три пересекающиеся в одной точке внутри окружности хорды, измеряет миллиметровой линейкой (с точностью до 1 мм) отрезки хорд, находит произведение длин отрезков каждой хорды и сравнивает эти произведения.
Учащиеся с интересом замечают, что все произведения оказываются приблизительно равными.
Учитель отличает, что обнаруженная закономерность не случайна, т.к. имеет место соответствующая теорема. Формулировку теоремы могут дать сами учащиеся.
Сумма внутренних углов выпуклого многоугольника.
Для создания поисковой проблемной ситуации можно использовать метод неполной индукции в сочетании с методом нацеливающих задач.
Вот серия упражнений, которые должны выполнить учащиеся, чтобы самостоятельно открыть формулу, выражающую сумму всех внутренних углов выпуклого многоугольника через число n его сторон.
Внутренняя точка выпуклого четырехугольника соединена с его вершинами. Сколько получилось треугольников и какова сумма углов всех треугольников? На сколько эта сумма больше суммы всех внутренних углов четырехугольника?
Решите такую же задачу для выпуклого пятиугольника.
Найдите сумму внутренних углов: а) четырехугольника; б) пятиугольника.
Вычислить сумму внутренних углов выпуклого стоугольника.
После успешного выполнения учащимися этих упражнений смело предлагаем им решить задачу 4) для произвольного выпуклого n-угольника.
Можно построить вспомогательную серию задач, ведущую учащихся по иному пути вывода формулы: п-угольник разбивается на треугольники диагоналями, выходящими из одной вершины. В этом случае необходимо индуктивным путем подвести учащихся к самостоятельному открытию закономерности: число треугольников разбиения равно n – 2.
Если учащиеся самостоятельно выведут формулу S=180(n-2) одним способом, то они смогут вывести ее (без вспомогательных упражнений) другим.
Длина окружности.
Учащиеся 6 класса получают домашнее задание: каждый измеряет, пользуясь ниткой и миллиметровой линейкой, длину С окружности и диаметр D какого-либо круглого тела и вычисляет отношение первого результата ко второму.
Несколько учащихся вызываются к доске и вписывают в начерченную там таблицу результаты своих измерений. Можно поручить одному-двум учащимся аккуратно начертить такую таблицу для всего класса и уже заполненную принести на урок.
Изучая
на уроке эту
таблицу, учащиеся
открывают
закономерность:
отношение длины
окружности
к ее диаметру
остается почти
постоянным.
Учителю остается
добавить: в
математике
доказано, что
это отношение
строго постоянно
и может быть
вычислено с
любой точностью;
до 0.01 равно
![]() .
Каждый учащийся
получает возможность
оценить, насколько
точно он провел
измерения
(сопоставляя
это число со
своим результатом).
.
Каждый учащийся
получает возможность
оценить, насколько
точно он провел
измерения
(сопоставляя
это число со
своим результатом).
В таблице можно отразить тот факт, что с увеличением диаметра в n раз (nN) длина окружности увеличивается также в n раз (специально раздаем учащимся круги, диаметры которых равны 1, 2, 3 дм.). Таблица покажет, что длина окружности с диаметром 1дм приближенно равна 3.14 дм, и что остальные окружности имеют длину соответственно в 2 и 3 раза большую.
Перед домашним заданием (лабораторной работой) полезно создать проблемную ситуацию, мотивирующую необходимость научиться вычислять длину окружности по известному диаметру (радиусу) или диаметр (радиус) окружности по известной длине. С этой целью можно использовать, например, такие проблемные задачи:
Нужно построить цилиндрическую цистерну диаметром в 20 м и высотой в 8 м. Сколько квадратных метров содержит боковая поверхность этой цистерны?
Это потребуется знать при определении количества строительных материалов, которые необходимы для постройки боковых стенок цистерны. Может возникнуть, например, такая частная проблема: сколько эмалевой краски потребуется для покраски боковой поверхности цистерны, если на каждый квадратный метр расходуется 50 г?
Учитель с помощью развертки цилиндра легко убеждает учащихся в том, что для нахождения его боковой поверхности нужно длину окружности умножить на высоту. Возникает задача: как по известному диаметру окружности (20 м) найти ее длину? ( Ведь мы не можем «развернуть» цистерну).
Нужно построить цилиндрическую цистерну высотой 5 м. Каким должен быть поперечник (диаметр) цистерны, чтобы для обшивки ее боковой поверхности хватило 785 кв. м. железа?
С помощью учителя учащиеся убеждаются в том, что для решения этой задачи необходимо умение находить диаметр окружности по известной длине (785:5=157 м).
После изучения нового материала (формула длины окружности) учащиеся доводят решение проблемных задач до конца.
Развернутый угол.
На доске дан чертеж.
B
E


![]()
C
A
B
D

A
D




О
А
С
C


B
В
D
A
B
А
Учитель обращается к классу с вопросами:
Какие фигуры изображены на доске?
(лучи, отрезки, углы)
Сколько лучей изображено на (1)?
Сколько на (2)?
Сколько углов построено на рисунке (4)?
Сколько всего углов на доске?
Предположительный ответ на последний вопрос – 8 углов.
Учитель: «Нет, ребята, здесь не 8, а гораздо больше углов! Какие же углы вы сосчитали? Чтобы найти потерянные вами углы, вспомните, как строится угол («…из точки провести два луча»), и постарайтесь увидеть на доске все новые углы».
По завершению работы учащиеся дают определение. Угол называется развернутым, если его стороны являются дополнительными полупрямыми одной прямой.
2.3. Подборка заданий проблемного характера.
При выполнении дипломной работы мы поставили перед собой ряд задач. Одна из них состоит в подборке заданий проблемного характера.
Перед рассмотрением проблемных задач кратко остановимся на некоторых общих вопросах и задачах.
Математической задачей называют требование осуществить некоторую математическую деятельность в указанных условиях. По роли, которую играют учебные задачи, их делят на:
репродуктивные;
задачи с известным алгоритмом;
проблемные.
Репродуктивные задачи ставят своей целью припомнить то, что учащиеся узнали на предыдущих занятиях. Обычно их предлагают в виде вопросов, например: «Как формулируется теорема Пифагора?», «Чему равна сумма синусов двух углов?». Они важны потому, что без знания теоретического материала нельзя приступать к решению поставленной задачи. Задачи репродуктивного характера в некоторой мере помогают учащимся систематизировать пройденное. Однако, укрепляя память, они совершенно не развивают мышление, поэтому не могут считаться основными.
В задачах второй группы речь идет об использовании учащимися полученных ранее знаний. При этом общий план решения поставленной задачи ясен, остается только выбрать из числа изученных теорем или формул пригодные для достижения намеченной цели. Принципиальных трудностей при решении задач второй группы обычно не возникает. Они помогают лучше разобраться в изученном, систематизировать пройденное. Таких задач на уроке математики большинство. Однако задачи с известными алгоритмами не знакомят нас с новыми математическими фактами, с приемами математической деятельности, не способствуют математическому развитию.
Проблемная задача характерна тем, что алгоритм ее решения до начала решения неизвестен, трудно даже установить, достаточно ли знаний и умений учащегося для выполнения задания. Главная задача – открыть способ решения и убедиться в его пригодности. Следует иметь в виду, что определить, является ли данная задача проблемной или нет, можно только относительно конкретного школьника, только с учетом его знаний и умений в момент постановки задачи.
Д.З.Кнебельман называет следующие особенности проблемных задач:
а) задача должна вызывать интерес своей необычностью, неожиданностью, нестандартностью. Информация особенно привлекает учащихся, если она содержит противоречивость, хотя бы кажущуюся. Проблемное задание должно вызвать удивление, создать эмоциональный фон;
б) проблемные задачи обязательно должны содержать посильное познавательное или техническое затруднение. Казалось бы, видимому решению «мешает» досадное затруднение, и неизбежно возникает всплеск мыслительной активности;
в) проблемное задание предусматривает элементы исследования, поиск различных способов его выполнения, их сравнения. Удовлетворив познавательную пытливость учащихся, задачи эти должны пополнить багаж их знаний новыми методами, новой информацией и т. п.
Важно отметить: ни слишком легкая, ни слишком трудная для ученика задача не может вызвать активную мыслительную деятельность, то есть стать для школьника проблемной. Вызвать проблемную ситуацию. Легкую задачу ученик решит на основе так называемого репродуктивного мышления, которое предполагает прямое, не требующее поиска применение уже имеющихся знаний. Слишком трудная задача так же не вызовет у ученика мыслительной активности. Если даже он и сделает ряд попыток решить такую задачу, то очень скоро, убедившись в их малой эффективности, займет позицию пассивного слушателя, ожидающего от других готового решения.
Выбор проблемной задачи зависит от наличия у учащихся исходного минимума знаний или возможности за относительно короткий срок до постановки проблемы сообщить учащимся необходимые для самостоятельного решения сведения. Вместе с тем надо помнить, что эти знания должны служить опорой для поисков пути решения, а не «наводить», не подсказывать этот путь, иначе задача перестанет быть проблемной.
Итак, задача становится проблемной, если она удовлетворяет следующим требованиям:
представляет познавательную трудность, т. е. Требует размышлений над изучаемой проблемой;
вызывает познавательный интерес;
опирается на прежний опыт и знания учащихся.
К проблемным задачам относятся задачи, в которых условие либо противоречиво, либо решение невозможно при конкретных данных, либо они имеют еще какой-то «изъян», сводящий на нет саму задачу, делающий ее неверной по сути. Такие задач учат думать, сомневаться, искать, находить.
Задача 1. Докажите, что четырехугольник, у которого две стороны параллельны, а две другие равны – параллелограмм.
Ответ: утверждение задачи неверно. Это может быть и равнобокая трапеция.
Задача 2. Большая сторона треугольника ABC, равная 10 см, лежит против угла 45. Найдите радиус описанной около треугольника ABC окружности.
Ответ:
нет необходимости
применять
формулу
![]() ,
т. к. задача не
имеет смысла.
Действительно,
против большей
стороны треугольника
лежит больший
угол, а он должен
превышать 60
(иначе сумма
углов треугольника
будет меньше,
чем 180).
,
т. к. задача не
имеет смысла.
Действительно,
против большей
стороны треугольника
лежит больший
угол, а он должен
превышать 60
(иначе сумма
углов треугольника
будет меньше,
чем 180).
Задача 3. Решите треугольник ABC, если AB:AC:BC=1:3:6,а периметр равен 20 см, угол B равен 110.
Д
![]()

C
B
ано: ABCAB:AC:BC=1:3:6
P
A
=20 см,Найти:
AB, BC, AC,
![]() A,
A,
![]() C.
C.
Решение:
По следствию теоремы синусов в треугольнике против большего угла лежит большая сторона.
В ABC есть тупой угол

 B
- больший.
B
- больший.Из п. 1, 2 - большая.
По условию AB:AC:BC=1:3:6 BC - большая сторона.
Из п. 3, 4 противоречие сформулированная задача имеет нереальные условия.
Если эту задачу начать решать, предварительно не проанализировав ее условие, то можно получть неверное, но кажущееся правильным решение.
В этой задаче надо не только разбить условие задачи на данные и требования, но и установить связи между данными задачи, определить, нет ли противоречий в условии задачи.
Такие задачи относятся к проблемным потому, что содержат в себе противоречивость, тем самым вызывая удивление и интерес учащихся.
Задача 4. Разделите данный треугольник на три равновеликие части прямыми, проходящими через одну вершину.
B
![]()

![]()

![]()
A
C
![]()
K
D
E
Решение:
AD=DE=EC.
 .
.
![]() .
.
![]() .
.
п.1, п.2
 .
.п.3 BD и BE – искомые прямые, делящие треугольник на три равные части.
Задача 5. Разделите параллелограмм на три равновеликие части прямыми, проходящими через одну вершину.
B
E
K
C





L
![]()
M
A
D
Решение:
BE=EK=KC.
CL=LM=MD.
 (см предыдущую
задачу).
(см предыдущую
задачу).п.3 прямые AK и AL разделяют параллелограмм на три равновеликие части.
Задача 6. Докажите, что любой треугольник можно разрезать на несколько равнобедренных треугольников.
Доказательство:
Хоть одна из высот треугольника находится внутри треугольника. Такая высота делит треугольник на два прямоугольных треугольника. Таким образом, треугольник можно разделить на любое число n2 прямоугольных треугольников. А каждый прямоугольный треугольник делится медианой, проведенной к гипотенузе, на два равновеликих треугольника.




![]()
C
Задача 7. Докажите, что пятиугольник и можно разрезать на 3 трапеции.![]()

M
N
Д![]()
В
K
оказательство:П


О
D
 роводим
BKAE,
ENDC
роводим
BKAE,
ENDC
B
 KEN=0
KEN=0О
А
Е
МВСА
 ВОЕ,
ОМDE, ОВСМ –
трапеции.
ВОЕ,
ОМDE, ОВСМ –
трапеции.
Так как все элементы построения осуществимы, утверждение о возможности построения верно.
Задача 8. Как через вершину выпуклого четырехугольника провести прямую, которая разделяет четырехугольник на две равные части?
![]()
![]()
![]()

В
С
Р![]()

М
ешение:
![]()
![]()
![]()
О
А
 Если точка О
– середина
диагонали BD,
то ломаная АОС
делит четырехугольник
на две равновеликие
части. Если
провести ОМАС,
то SABCM=SAMD.
Если точка О
– середина
диагонали BD,
то ломаная АОС
делит четырехугольник
на две равновеликие
части. Если
провести ОМАС,
то SABCM=SAMD.
D
Задача 9. Как через данную точку на основании треугольника провести прямую, которая разделяет треугольник на две равновеликие части?
В
Р
Х
ешение:
![]()


Ао
Медиана ААо делит треугольник на две равновеликие части.


А
Если провести АХМАо, то SABXM=SMXC.
М
С
Задача 10. Как через данную точку на основании треугольника провести две прямые, которые, разделяют треугольник на три равновеликие части?
Решение:





![]()

В
Т
Если AD=DE=EC и TDBM, KEBM, то прямые МТ и МК – искомые.
К
![]()

А
С
![]()
Е
М
D
Задача
11. В треугольнике
АВС дано, что
![]() .
Каким должен
быть угол С:
тупым или острым?
.
Каким должен
быть угол С:
тупым или острым?
Решение:
S-площадь АВС.
 ,
,
 ,
, ,
, (по условию)
(по условию)
![]()
по теореме косинусов:
![]()
п.5, п.6
 .
.п.7 С – острый.
Ответ: С – острый.
Задача
12. В треугольнике
АВС угол А в
два раза больше
угла В. доказать,
что
![]() .
.
С
Дано:


b
a
АВСА=2В
2
Доказать:
![]()
![]()
В
А
c
.Доказательство:
По теореме косинусов
![]() .
.
По теореме синусов:
![]() .
.
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
 .
.
![]() В=С
В+С=А
А=90
В=С
В+С=А
А=90
![]() .
.
Ч.т.д.
Задача 13. Прямая проходящая через вершину прямого угла треугольника, образует с меньшим катетом угол 30 и пересекает гипотенузу в точке, которая делит ее в отношении 1:2. Найти длину гипотенузы, если длина меньшего катета равна 3.
В
D
Дано:

АВС (С – прямой),DCB=30,
BD:DA=1:2,
B
А
С
Найти : АВ.Решение:
А= В=90- (по теореме о сумме углов в треугольнике),
0<<45
Из ACD и BCD
По теореме синусов:
![]()
![]() .
.
П.2

![]()
П.3.
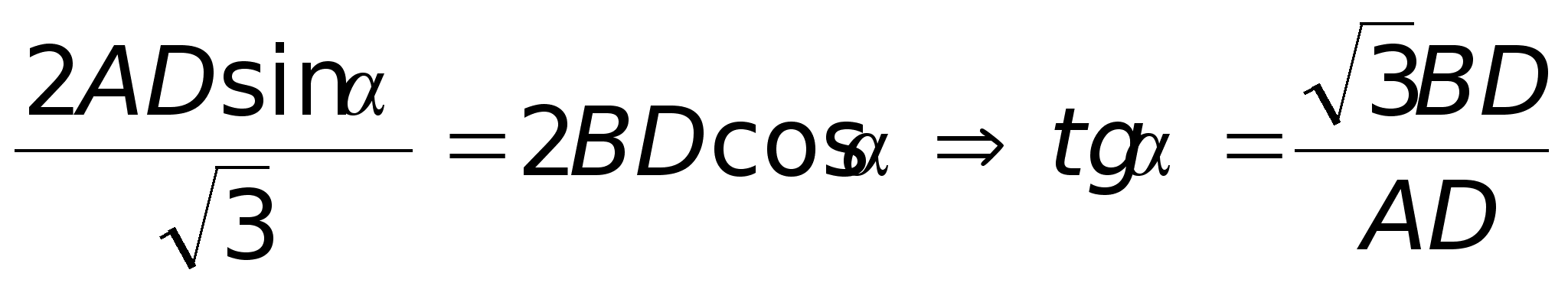 .
.П.4.
 .
.

Из АВС по теореме Пифагора
![]()
Ответ: 7
Задача 14. Три хорды окружности радиуса R образуют вписанный в эту окружность треугольник. Найти длину третьей хорды, если две другие равны R3 и R/2.
С

![]()
Дано:

А
АВС – вписан в окружность,В
С=R3,С
В
А=R/2.Найти: АВ.
Решение:
Найдем синус и косинус углов и .
По теореме синусов:


=180-- (по теореме о сумме углов треугольника)
sin=sin(180-(+))=sin(+).
Углы и могут быть острыми либо один из них тупой. Рассмотрим все случаи.
, - острые:
cos=1/2; cos=15/4,
sin=sincos+cossin=(3/2)(15/4)+1/8=(35+1)/8,
По теореме синусов:
АВ=2R sin=R(35+1)/8.
-тупой, -острый.
cos=-1/2, cos=15/4,
sin=(35-1)/8,
AB=R(35+1)/8.
-острый, -тупой.
cos=1/2 ,cos= -15/4,
sin=(-35+1)/8<0, а это невозможно для внутреннего угла треугольника.
Возможные случаи представлены на рисунках.
С
А
С


![]()
![]()

![]()
![]()

А
О
О
В
В
Задача 15. Показать что во всяком прямоугольном треугольнике сумма диаметров описанной окружности и вписанной окружностей равна сумме его катетов.
А
 Дано:
Дано:
c
b
Доказать:
2
![]()
К
L
R+2r=a+b, где R – радиус описанной окружности,
а![]()
![]()
В
С
r – радиус вписанной окружности.
M
Доказательство:
По свойству отрезков касательных имеем
a+b=AK+KL=CM+MB=AL+r+r+LB=2r+AB=2r+c=2r+2R.
Ч.т.д.
Задача 16. В треугольник АВС вписана окружность. К окружности в точке Е проведена касательная, пересекающая сторону АВ в точке К, а сторону ВС – в точке М. Найти периметр треугольника КВМ, если стороны треугольника АВС равны а,b,c.
B


c
a
Дано:
![]()
M
E
K
АВС описан около окружности,
К
Р
М – касательная.
L
Найти:РКВМ.
С
А
N
b
Решение:
РКВМ=ВК+КМ+МВ.
По свойству отрезков касательных
КР=РЕ,
МЕ=ML,
BP=BL,
AP=AN,
CL=CN.
П.1, п.2.РКВМ=ВК+КЕ+ЕМ+МВ=(ВК+КР)+(ML+MB)=BP+LB=2BP.
a+c=AB+BC=BP+PA+BL+LC=(BP+BL)+(PA+LC)=2BP+9AN=CN)=2BP+b.
П.3, п.4. a+c=PKBM+b PKBM=a+c-b.
Ответ: a+c-b.
Задача 17. В равнобедренный треугольник АВС с основание АС вписана окружность. Прямая, параллельная стороне АВ и касающаяся окружности, пересекает сторону АС в такой точке М, для которой МС=2/5АС. Найти радиус окружности, если периметр треугольника АВС равен 20.
В

![]() Дано:
Дано:
АВС (АВ=ВС),
М
Q
КАВ, точка Lокружности,МС=2/5АС,
Р![]()
О
K
АВС=20.
L
Найти: r.
С
А
H
M
Решение.
r=OH
MKC АВС (по углам)
 .
.С другой стороны, по свойству отрезков касательных
РМКС=MC+ML+LK+KC=MC+HM+KQ+KC=CH+CQ=2CH=AC.
П.3 АС=8.
АВ=ВС=1/2(20-8)=6.
Из АВН по теореме Пифагора
![]()
в АВН АО-биссектриса
по
свойству биссектрисы
![]()
п.7. ОН=2/5 ВН=45/5.
Ответ: (45)/5.
Задача
18. Медиана BK
и биссектриса
CL треугольника
ABC пересекаются
в точке .доказать
равенство
![]() .
.


![]()
B
L
Доказательство:L

 MBK.
MBK.

P
A
ALM ABK  .
.
M
K
PCK LCM  .
.

C
(по свойству биссектрисы).п.2, п.4
 .
. .
.
Ч.т.д.
Задача 19. В треугольнике ABC известно, что угол A в два раза больше угла C, сторона BC на 2 см больше стороны AB а AC=5 см. Найти AB и BC.
B
Дано:
![]()
 ABC,
ABC,
D
A=2C,
B C=AB+2
см,
C=AB+2
см,
AC=5 см.
![]()
С
А
Найти: AB, BC.Решение:
AD – биссектриса угла BAC.
П.1 BAD=DAC=ACD ADC – равнобедренный.
Обозначим AB=x, AD=DC=y.
П.3 BC=x+2, BD=x+2-y.
ABD ABC (по углам)
 ,
,
 .
.x и y найдем из системы
![]()
![]() , 5x=xy+2y,
, 5x=xy+2y,
![]() ; 5x+10-5y=xy;
; 5x+10-5y=xy;
5y-10=2y;
y=![]() ,
,
![]() ,
,
x=4.
AB=4см, BC=6см.
Ответ: 4 см, 6 см.
Задача 20. В правильный треугольник вписан квадрат так, что две его вершины лежат на одной стороне треугольника, а две другие вершины – на двух других сторонах треугольника. Найти отношение их периметров.
B
Дано:
![]() ABC
( AB=BC=AC ),
ABC
( AB=BC=AC ),
MNPQ – квадрат, вписан в ABC,
N
P
N
E
AB, PBC, M,QAC.
C
A
Найти:
M D Q
Решение:
BD – высота ABC.
Обозначим AB=a, MN=x.
NPAC (по условию) BNP=BPN=A=C=60.
П.3 BNP – равносторонний.
BE – высота BNP.
DE=MN=x.
Из BDC по теореме Пифагора BD=
 .
.П.7 BE=BD-ED=
 .
.BNP BAC (по углам)
 ,
,
 x=
x=
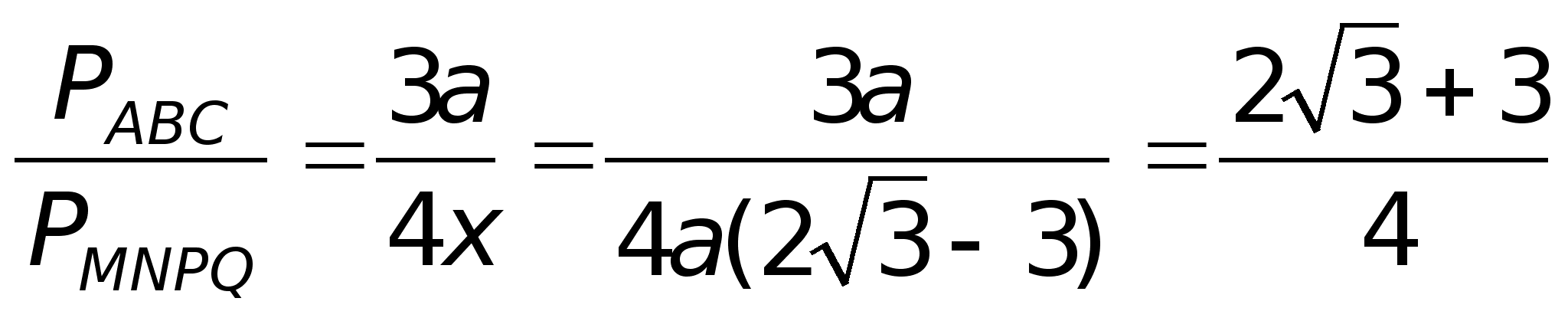 .
.
Ответ:
![]() .
.

![]()
 Задача 21. Площадь
треугольника
ABC равна P.
Прямая DE,параллельная
основанию AC,
отсекает от
треугольника
ABC треугольник
BED площадью
Q. На стороне
AC взята
произвольная
точка M и
соединена
отрезками
прямых с точками
D и E.Чему
равна площадь
четырехугольника
BEMD?
Задача 21. Площадь
треугольника
ABC равна P.
Прямая DE,параллельная
основанию AC,
отсекает от
треугольника
ABC треугольник
BED площадью
Q. На стороне
AC взята
произвольная
точка M и
соединена
отрезками
прямых с точками
D и E.Чему
равна площадь
четырехугольника
BEMD?
B
![]() Дано:
Дано:
АВС,
SABC=P,
D
E
EAC,S
D
BED=Q,() МАС.
Найти:
S
C
M
A
BEMD.Решение:
з
В
аметим, что четырехугольник BEMD состоит из фиксированного треугольника BED и подвижного, зависящего от выбора точки M, треугольника DEM. Но где бы на AC мы не выбрали точку М, высота DEM, проведенная к его основанию DE из точки М, не изменяется по его длине, значит, не изменяется и площадь треугольника DEM. Следовательно, точку М мы можем расположить на АС наиболее выгодным для нас способам, например, совместить ее с точкой А. И тогда речь будет идти об отыскании площади четырехугольника BEMD, а треугольника BEA с той же площадью.

Е
D
![]()

С
А
Рассмотрим ABE BDE:
![]() (т.к. у треугольников
общая высота,
а, значит, их
площади относятся
как основания).
(т.к. у треугольников
общая высота,
а, значит, их
площади относятся
как основания).
![]() .
.
ABC BDE (по углам)
 (свойство площадей
подобных фигур)
(свойство площадей
подобных фигур)
 .
.
п.2, п.3
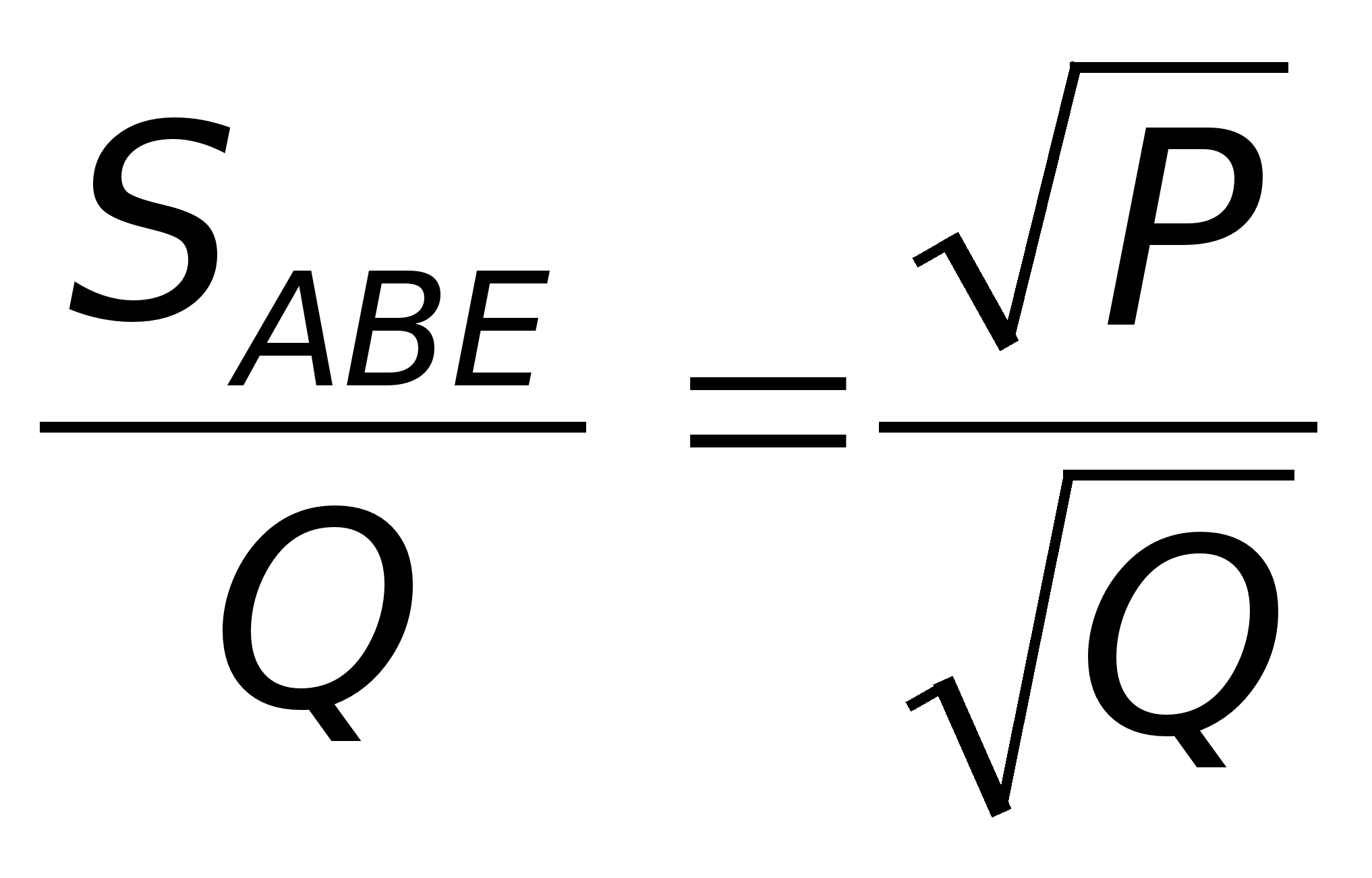 S
S =
= .
.
Ответ:
![]() .
.
Задача 22. В прямоугольном треугольнике биссектриса прямого угла отсекает на гипотенузе длиной a и c. Найдите площадь квадрата, стороной которого является эта биссектриса.

B
Решение:CM – биссектриса
AC : a = BC : c AC = aBC/c.
П


M
о теореме Пифагора из ABC:
A
A
B
C
H
(a+c)
B![]() C
C![]() =(a+c)
=(a+c)![]() /(a
/(a![]() /c
/c![]() +1)=
+1)=
=c![]() (a+c)
(a+c)![]() /(a
/(a![]() +c
+c![]() )
)
BC=c(a+c)/![]() .
.
MHC – прямоугольный, MCH=45,тогда MC=
 MH.
MH.MHBC AHM и ACM подобны по двум углам
MH : BC=AM : AB MH : BC = a : (a+c)
MH = aBC/(a+c).
п.2. 4 MH = ac/
 .
.п.3, 5 MC = ac
 /
/ .
.S = MC
 = 2a
= 2a c
c /(a
/(a +c
+c ).
).
Ответ:
![]() .
.
Задача формирует умения разбивать условие задачи на данные и требования, находить связи между данной задачей и теоремами, обобщать, вводить новые неизвестные, контролировать каждый шаг решения задачи, формулировать ответ.
Задача 23. Отношение величин двух углов треугольника равно 2, а разность длин противоположных им сторон равна 2 см; длина третьей стороны треугольника равна 5 см. вычислить площадь треугольника.
Решение:
п


В
усть А=В. проведем биссектрису АК.Р
К
5
ассмотрим треугольники АВС и АКС.
 АВС=КАС
(т.к. АК – биссектриса).
АВС=КАС
(т.к. АК – биссектриса).

С
А
АКС=180-КАС-ВАС ВАС=180-АВС-ВСА п.3.АКС=ВАС.П.3,4 треугольники АВС и КАС подобны ( по двум углам)
П.5АС/ВС=СК/АС
 =ВССК
(*).
=ВССК
(*).АК- биссектриса АС/СК=АВ/ВК, АВ=5 см АС/СК=5/ВК.
ВК=ВС-СК
П.7,8АС/СК=5/(ВС-СК)
5СК=АСВС-АССК
СК=АСВС/(5+АС) (**).
(*),(**)АС
 =АСВС/(АС+5)
=АСВС/(АС+5)
АС+5АС=ВС.
ВС=АС+2 (по усл.), п.10,АС
 +5АС=АС
+5АС=АС +4АС+4
+4АС+4
АС=4см, ВС=6см.
 .
.p=(AB+BC+AC)/2=(5+6+4)/2=7.5 см.
 см
см .
.
Ответ:
![]() .
.
Данная задача направлена на формирование умений находить связи между данными и требованиями задачи, переносить знания в новую ситуацию, сравнивать, контролировать каждый шаг решения задачи.
Задача 24. Диагонали четырехугольника равны, а длины его средних линий равны а и с. Найдите площадь четырехугольника.
Решение:
п






С
Т
Р
В
К
А
Н
усть К, Н, Т, М - соответственно середины сторон АВ, ВС, СР, АР четырехугольника АВСР.К

М
Н – средняя линия АВСКН=0,5АС (по свойству средней линии треугольника).Аналогично, МТ=0,5АС.
П.2.3КН=МТ=0,5АС.
Аналогично, НТ=КМ=0.5ВР.
АС=ВР (по условию).
П.4,5,6КН=МТ=НТ=КНКНТМ – ромб.
КНТМ - ромб НМКТ. (по свойству ромба).
НМКТSKNTM=0,5НМКТ.
НМ=а, КТ=с (по условию).
П.9,10SKHTM=0,5ас.
Обозначим площадь четырехугольника через S.

 ,
т.к. площади
подобных фигур
относятся как
квадраты их
линейных размеров
(КВН и
АВС
подобны по
двум углам,
т.к. КН- средняя
линия АВС).
,
т.к. площади
подобных фигур
относятся как
квадраты их
линейных размеров
(КВН и
АВС
подобны по
двум углам,
т.к. КН- средняя
линия АВС).Аналогично, SМНР=0,25SAPC.

п.14,15,16

Аналогично,
 .
.П 13,18,19 S=0,5ac+0,25S+0,25SS=ac.
Ответ: ас.
Данная задача формирует умения разбивать условие задачи на данные и требования, находить связи между данной задачей и задачей с известным решением, применять аналогию преобразовывать данные элементы, разбивать задачу на более частные задачи, переносить знания в новую ситуацию, грамотно оформлять решение задачи, проверять ход решения задачи
Задача 25. Площадь треугольника АВС S1; площадь треугольника АОВ, где О – точка пересечения высот, равна S2. На прямой СО взята точка К такая, что треугольник АВК – прямоугольный. Докажите, что площадь треугольника АВК есть среднегеометрический между S1 и S2.
Решение:
П



В
усть АВС-остроугольный, т.е. т.О лежит внутри АВС.



С
А
Н
М
АВК – прямоугольный, КМ- высота =АММВ
(т.к. в прямоугольном
треугольнике
высота, опущенная
на гипотенузу,
равна среднему
геометрическому
между отрезками,
на которые ее
основание
делит гипотенузу.
=АММВ
(т.к. в прямоугольном
треугольнике
высота, опущенная
на гипотенузу,
равна среднему
геометрическому
между отрезками,
на которые ее
основание
делит гипотенузу.
МАН=90-АВН=ВСМ, АМО=СМВ=90АОМ и СВМ подобны АМ:МО=СМ:МВАММВ=МОСМ.
п.2,3КМ
 =МОСМ.
=МОСМ.
=
В


С (О, К)
А
М
Пусть АВС – прямоугольный (С=90), тогда точки С, О и К совпадают, т.е.








О
К
А
М
В
Н
С
Пусть треугольник АВС – тупоугольный, тогда точки О и К лежат вне АВС. Проведем рассуждения аналогичные доказательству, проведенному для остроугольного треугольника. Получим: .
.
Данная задача направлена на формирование умений делать схематическую запись условия задачи, разбивать условие задачи на данные и требования, находить связи между данными и требованиями задачи, находить связи между задачей и теоремами, разбивать задачу на более частые задачи, проверять ход решения задачи, грамотно оформлять решение задачи, исследовать задачу.
Предложенные задачи взяты из различных сборников. Хороший, но не легкий путь составить задачу самому. Полезно подбирать вопросы проблемного характера и к стандартным задачам.
Самую обычную задачу можно сделать творческой, если создать в классе атмосферу поиска, размышления, когда ученики начинают искать и находят несколько способов решения одной и той же задачи; подать эту задачу так, чтобы каждый этап ее решения заставлял их обдумывать свои действия.
Нелегко требовать переделки всех задач в проблемные. Стандартные задачи, позволяющие закрепить навык, формулу, алгоритм необходимы. Но важно избегать единообразия, чаще предлагать ребятам задачи проблемные.
Говоря о значении проблемных задач, хочется отметить, что только такие задачи ведут к приобретению учащимися по-настоящему глубоких знаний.
Заключение.
Рассматривая проблемное обучение как фактор интеллектуального развития школьников, мы изучили и проанализировали психолого-педагогическую и методическую литературу по интересующим нас вопросам. В нашей работе мы опирались на труды Ю.К.Бабанского, П.Я.Гальперина, Н.А.Менчинской, А.М.Матюшкина, М.И.Махмутова и других авторов.
Исходя из анализа литературы, мы раскрыли сущность проблемного обучения и интеллектуального развития. Мы рассмотрели возможность интеллектуального развития в условиях проблемного обучения, его организацию и руководство в процессе обучения. Раскрывая эти вопросы, мы пришли к выводу, что проблемное обучение – фактор интеллектуального развития школьников.
Нами была разработана система уроков с элементами проблемного обучения и составлена подборка проблемных заданий. Каждый урок не только на изучение теоретического материала и формирование умений решать задачи, но и на организацию умственной деятельности учащихся, которая способствует интеллектуальному развитию.
Кроме обучающей серии, наш эксперимент состоял из констатирующей и контрольной серий. Для их проведения были отобраны методики исследования интеллектуальных умений, определяющие уровень интеллектуального развития.
Разработанные уроки и опытная работа были проведены в средней школе № 67 Советского района города Самары. Результаты проведенного исследования показали эффективность разработанной системы уроков и составленной подборки задач.
Проблема организации интеллектуального развития школьников на уроках с элементами проблемного обучения меня очень заинтересовала, и в будущей своей педагогической деятельности планирую и дальше ей заниматься.
Библиография.
Анастази А. Психологическое тестирование. Ч.1-2.-М.,1982.
Бабанский Ю.К. Интенсификация процесса обучения.-М.:Знание, 1987.
Бабанский Ю.К. Методы обучения в современной общеобразовательной школе.-М.:Просвещение, 1985.
Бабанский Ю.К. Оптимизация учебно-воспитательного процесса.-М.:Просвещение, 1982.
Бабанский Ю.К. Проблемное обучение как средство повышение эффективности учения школьников.-Ростов-на-Дону, 1970.
Бабанский Ю.К. Рациональная организация учебной деятельности.-М., 1981.
Блейхер В.М., Бурлачук Л.Ф. Психологическая диагностика интеллекта и личности.-Киев.: «Вища школа», 1978.
Богданова Т.Г., Корнилова Т.В. Диагностика познавательной сферы ребенка.-М.:Роспедагентство, 1994.
Богоявленский Д.Н., Менчинская Н.А. Психология усвоения знаний в школе.-М.,1959.
Величковский Б.М. Как устроен естественный интеллект.//Природа.- 1988.-№ 12.
ВилькеевД.В. Познавательная деятельность учащихся при проблемном характере обучения основам наук в школе.-Казань, 1967.
Воспитание ученика. Сборник программно-методических материалов. Сост.В.М.Коротов, Н.А.Лошкарева, В.Н.Зайцев..-М., 1990.
Гальперин П.Я. Методы обучения и умственное развитие ребенка.-М.:Изд-во МГУ, 1985.
Гузик Н.П. Учить учиться.-М.: Педагогика, 1981.
Доровской А.И. Сто советов по развитию одаренности детей. Родителям, воспитателям, учителям.-М., Роспедагентство, 1997.
Коротяев Б.И. Учение – процесс творческий : Кн. для учителя: Из опыта работы.-М.:Просвещение, 1989.
Краткий словарь по философии /Под ред. И.В.Блауберга, И.К.Пантина.-М.:Политиздат,1982.
Крутецкий В.А. Основы педагогической психологии.-М.:Просвещение, 1972.
Крутецкий В.А. Психология математических способностей школьников.-М.:Просвещение, 1968.
Крутецкий В.А. Психология обучения и воспитания школьников.-М., 1976.
Кудрявцев Т.В. Исследование и опыт проблемного обучения. В кн.: «О проблемном обучении»: Вып. 2.-М.:Высшая школа, 1969.
Кудрявцев Т.В. Проблемное обучение: истоки, сущность, перспективы.-М.:Знание, 1991.
Кулько В.А., Цехмистрова Т.Д. Формирование у учащихся умений учиться: Пособие для учителей.-М.:Просвещение, 1983.
Лернер И.Я. Вопросы проблемного обучения на Всесоюзных педагогических чтениях.//Советская педагогика.- 1968.-№ 7.
Лернер И.Я. Система методов обучения.-М.:Знание, 1976.
Людмилов Д.С.,Дышинский Е.А.,Лурье А.М. Некоторые вопросы проблемного обучения математике: Пособие для учителей.-Пермь, 1975.
Лоповок Л.М. Тысяча проблемных задач по математике: Кн. для учащихся.-М.:Просвещение, 1995.
Матюшкин А.М. Проблемные ситуации в мышлении и обучении.-М.:Педагогика, 1972.
Махмутов М.И. Организация проблемного обучения в школе. Книга для учителей.-М.:Просвещение, 1977.
Махмутов М.И. Проблемное обучение. Основные вопросы теории.-М.:Педагогика, 1975.
Мелхорн Г, Мелхорн Х.-Г. Гениями не рождаются: общество и способности человека: Кн. для учителя.-М.:Просвещение, 1989.
Менчинская Н.А. Проблемы учения и умственного развития школьника.-М, 1989.
Мочалова Н.М. Методы проблемного обучения и границы их применения.-Казань, 1978.
Обухова Л.Ф. Этапы развития детского мышления.-М.,1972.
Оконь В. Введение в общую дидактику.-М.:Высш.шк., 1990.
Оконь В. Основы проблемного обучения.-М.:Просвещение, 1968.
Паламарчук В.Ф. Школа учит мыслить.-М.:Просвещение, 1987.
Педагогическая энциклопедия/ Под ред. И.Я.Каирова, Ф.Н.Петрова, Т. 3.-М.: «Советская энциклопедия», 1966.
Педагогический словарь/ Под ред. Г.М.Воловниковой, Л.И.Генсиоровской, Т. 2.-М.: Изд-во АПН РСФСР, 1959.
Погорелов А.В. Элементарная геометрия.-М., 1977.
Поиски рациональных способов преподавания математики (из опыта учителей Татарии).-М.:Просвещение, 1968.
Развитие учащихся в процессе обучения: Под ред. Л.В.Занкова.-М., 1963.
Рубинштейн С.Л. О мышлении и путях его исследования.-М., Изд-во АН СССР, 1958.
Рубинштейн С.Л. Основы общей психологии.-М., 1989.
Супрун В.П. Избранные задачи повышенной сложности по математике:-Мн:Полымя, 1998.
Талызина Н.Ф., Карпов Ю.В. Педагогическая психология: Психодиагностика интеллекта.-М.: Изд-во МГУ,1987.
Талызина Н.Ф. Формирование познавательной деятельности учащихся.-М.:Знание, 1983.
Формирование умений и навыков учебного труда в процессе обучения школьников. Сборник научных трудов. Под ред. В.В.Краевского, А.В.Усовой.-М., 1981.
Фридман Л.М. Психологические основы обучения математике в школе: Учителю математики о педагогической психологии.-М.:Просвещение, 1983.
Шамова Н.В. Активизация учения школьников.-М.:Просвещение, 1982.
Юркевич В.С. Одаренный ребенок: иллюзии и реальность: Кн. для учителей и родителей.-М.:Просвещение, 1996.
Похожие рефераты:
Развитие логического мышления учащихся при решении задач на построение
Управление образовательным процессом в ДОУ с приоритетом интеллектуального развития детей
Художественно-конструкторская деятельность как основа формирования элементов дизайнерского мышления
РАЗВИТИЕ И ДИАГНОСТИКА МЫШЛЕНИЯ В ПОДРОСТКОВОМ ВОЗРАСТЕ
Словесно-логическое мышление успевающих и слабоуспевающих студентов
Дидактические игры в начальном курсе математики
Диагностика и коррекция уровня развития познавательных процессов младших школьников
Обогащение словарного запаса на уроках развития речи в младших классах вспомогательной школы
Детская практическая психология
Коррекция мышления трудовой деятельностью у детей с ЗПР младшего школьного возраста
Использование компьютерных технологий в изучении наглядной геометрии
Особенности развития одарённых детей в процессе обучения математике в 5-6 классах