Курсовая работа: Математические модели потребительского поведения и спроса

ТЕМА МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПОТРЕБИТЕЛЬСКОГО ПОВЕДЕНИЯ И СПРОСА

Содержание

Введение

1 Модели распределения доходов

2 Количественный подход к анализу полезности и спроса

3 Отношение предпочтения и функция полезности

4 Кривые безразличия. Решение задачи об оптимальном выборе потребителя

5 Функции спроса. Коэффициент эластичности

6 Изменение цен и компенсация

Заключение

Введение

Микроэкономика – основа всей современной экономической науки. Ее главная задача – выяснение того:

· как принимают решения и ведут себя субъекты хозяйственной деятельности – отдельные потребители (домашние хозяйства) и производители (предприятия), которые имеют специфические стимулы (интересы) и руководствуются определенными принципами;

· как устанавливаются на рынке цены на различные блага и услуги;

· как, исходя из цен, осуществляется распределение ресурсов.

Микроэкономику иногда называют «теорией цен», поскольку ее предметом является механизм распределения ресурсов, главными индикаторами которого выступают цены. В центре внимания микроэкономического анализа – достижение равновесия между спросом и предложением на рынке посредством цен. Спрос и предложение определяются производством и потреблением, за которыми, в свою очередь, стоят индивидуальные планы потребления и производства. Первые составляются отдельными потребителями, преследующими цель максимизировать полезный эффект потребления. Планы производства разрабатывают предприятия, стремящиеся максимизировать прибыль. Необходимые предпосылки микроэкономического анализа – предположения о существовании свободного рынка и о рациональном характере поведения индивидов.

1 Модели распределения доходов

Рыночный спрос определяется на базе решений, которые принимаются множеством отдельных лиц, исходя из их потребностей и располагаемых доходов. Но чтобы распределить средства между разнообразными потребностями необходимо их как-то сопоставить. В качестве основы для сопоставления различных потребностей в конце ХIХ века экономисты приняли полезность. Сам термин «полезность» был введен английским философом И. Бентамом (1748-1832). Согласно Бентаму максимизация полезности является руководящим психологическим принципом поведения людей. Категория полезности была взята на вооружение экономистами и легла в основу теории потребительского поведения, которая в свою очередь базируется на гипотезе о сопоставимости полезности самых разнообразных благ. Считалось, что при заданных ценах потребители стремятся так распределить свои средства на покупку различных благ, чтобы максимизировать ожидаемое удовлетворение или полезность от их потребления. При этом они руководствуются своими личными вкусами и представлениями.

Экономистами во второй половине ХIХ века было выдвинуто два подхода к сравнению и соизмерению полезности различных благ – количественный и порядковый.

Практически одновременно английский экономист Стенли Джевонс, австрийский экономист Карл Менгер (1840-1921) и швейцарский экономист Леон Вальрас предложили количественную теорию полезности. В основе этой теории лежала гипотеза о возможности соизмерения различных благ. Эту теорию разделял А. Маршалл.

Однако, эта теория встретила серьезную критику. Английский экономист Френсис Эджуорт (1845-1926), Вильфредо Парето и американский экономист Ирвинг Фишер предложили альтернативную количественной порядковую теорию полезности, которая в настоящее время является наиболее распространенной.

В основе моделей потребительского поведения и спроса лежат модели распределения доходов и теория полезности. Рассмотрим вначале модели распределения доходов.

В основе построения моделей личного потребления лежит принцип распределения потребителей по группам, для формирования которых используются как данные о социальном положении семей, так и сведения об их доходах. В соответствии с этим подходом все множество потребителей, т.е. население страны или региона, рассматривается как совокупность нескольких групп семей, каждая их которых характеризуется определенным уровнем дохода и примерно одинаковым социальным статусом (служащие, рабочие, крестьяне и т.п.). При этом считается, что каждая такая группа обладает некоторой общностью в выборе и предпочтении тех или иных потребительских благ. При разбиении потребителей на группы по различным уровням дохода обычно используют модели распределения доходов различных типов.

Для характеристики равномерности распределения доходов в обществе часто используется т.н. кривая Лоренца. Она строится следующим образом: все множество потребителей данной страны или региона разбивается на некоторое количество групп, обычно равных по численности, но различных по доходам. Затем подсчитывается, какую долю национального дохода получает каждая такая группа, причем счет ведется, начиная с группы с наименьшим доходом в сторону его увеличения.

Далее на диаграмме (рис. 5.1.) наносятся точки, соответствующие вычисленным долям в процентах. Очевидно, что совершенно равномерному распределению дохода отвечает прямая линия (биссектриса угла на диаграмме), если же распределение неравномерное, то возникает кривая линия, причем ее кривизна и отклонение от биссектрисы будет тем более, чем менее равномерным оказывается распределение доходов.

На рис. 1.1 представлены три случая распределения доходов в случае, когда население разделено на 5 равных по численности (по 20% каждая) групп. Прямая ОА соответствует равномерному распределению, кривая ОВ иллюстрирует следующее распределение доходов:

Рис. 1.1. Кривые Лоренца

1 группа имеет 15% дохода, 2 группа – 18%, 3 группа – 20%, 4 группа – 22% и 5 группа – 25%.

Кривая ОС отвечает еще более неравномерному распределению доходов.

1 группа получает 10% , 2 группа 15%, 3 группа 18%, 4 группа 20%, 5 группа 37%.

Модель распределения доходов, принадлежащая В.Парето, также предназначена для анализа характера неравномерности доходов в обществе. Она строится следующим образом:

Обозначим через I_m – наименьший доход, который может получать семья в данном обществе. Тогда для характеристики относительного числа семей (в процентах) N(I) , получающих доход не менее, чем I, может быть использовано соотношение:

которое является модификацией формулы В.Парето.

Исследования, проведенные в различных странах и в разные периоды времени дают основание полагать, что указанное соотношение вполне применимо и в том случае, когда речь идет о доходах от недвижимости и капитальных вложений. При этом показатель a обычно находится в интервале от 1.2 до 2. Очевидно, что меньшие значения a соответствуют более равномерному распределению доходов в обществе, а высокое значение a свидетельствует о резкой дифференциации доходов. В литературе можно встретить мнение о том, что при a = 1,5 имеет место сравнительно справедливое распределение доходов (рис. 1.2.).

Рис. 1.2. Модель распределения доходов В. Парето

Здесь линия АВ соответствует распределению дохода с a = 1.5, линии АС и АД значениям a = 2 и a =1,2.

Разбиение на доходные группы в случае a =1.5 может быть выполнено следующим образом:

· первая группа, имеет доход от I_m до 2I_m , состоит из 65% потребителей;

· вторая группа, имеет доход от 2I_m до 3I_m , включает 17% потребителей;

· третья группа с доходом 3I_m до 4I_m , в нее входят 7% потребителей и т.д. (рис. 1.3.).

Рис. 1.3. Доходные группы населения при a=1.5

Результаты исследований, проведенных в обществах, где основным источником доходов является заработная плата, показывает, что эти доходы распределяются скорее по нормальной кривой, впрочем, не совсем симметричной и с урезанными концами (рис. 1.4.).

Такой вид кривой объясняется наличием как нижнего, так и верхнего предела заработков; причем возможность получения высокой заработной платы ограничена вследствие воздействия многих факторов, совокупное влияние которых и приводит к квазинормальной кривой распределения доходов.

Рис. 1.4. Нормальная кривая распределения доходов

Разбиение на доходные группы в этом случае имеет вид, представленный на рис. 1.5.

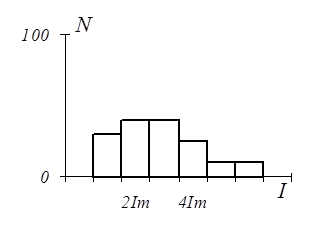
Рис. 1.5. Квазинормальное распределение доходов

Выбор конкретной модели распределения доходов, а следовательно и способ формирования доходных групп определяется в результате анализа данных о доходах потребителей в рассматриваемом обществе или регионе.

В дальнейшем изложении основ теории потребления мы будем исходить из того, что указанное формирование групп произведено и множество потребителей представлено как совокупность m групп с номерами i =1,...,m .

При этом, как уже отмечалось выше, предполагается, что члены группы достаточно схожи в определении своих предпочтений, и, следовательно, вся группа может рассматриваться как единый потребитель в вопросах формирования спроса на товары и услуги, выступающие на потребительском рынке.

2 Количественный подход к анализу полезности и спроса

Исходным пунктом функционирования любой экономической системы являются потребности людей. Потребление – процесс удовлетворения потребностей. Благо – средство удовлетворения потребностей. Существует огромное количество благ, удовлетворяющих потребности. Какое именно благо, и в каком количестве следует производить, определяет потребитель. В условиях рыночной экономики допускается производство только таких благ, которые могут быть проданы по цене, превышающей затраты на их производство. Потребители, покупая такие блага, оценивают работу производителей. Каждый потребитель принимает решение самостоятельно. Считается, что единой шкалы оценки благ не существует. Но у каждого потребителя есть своя шкала предпочтений. Каждый потребитель стремится выбрать максимально предпочтительный для себя набор благ в пределах своего дохода. Это предположение – гипотеза о рациональном поведении потребителя.

Если товар или услуга удовлетворяет желания и нужды потребителя, то они обладают полезностью. Полезность – удовлетворение или удовольствие, полученное человеком от потребления того или иного товара или услуги.

Концепция полезности изучает удовлетворение или удовольствие, получаемое от владения, использования, употребления или извлечения выгод из товара или услуги. Полезность заключается в качественных характеристиках, благодаря которым они удовлетворяют потребности. Это результат индивидуального вкуса и восприятия. Одни и те же товары имеют разную полезность для разных потребителей.

Общая полезность – всё количество удовлетворения, полученное от данного количества товара за определённый промежуток времени. Общая полезность возрастает по мере потребления, но всё более медленными темпами. Такая её динамика объясняется тем, что полезность каждой дополнительной единицы товара убывает.

Существует два основных подхода к измерению полезности: кардиналистский (количественный) и ординалистский (порядковый).

Количественный подход к анализу полезности основан на представлении о возможности измерения полезности различных благ в гипотетических единицах – ютилах (utility – полезность). Предполагается, что потребитель может сравнивать разные товары с точки зрения их предпочтений и упорядочить их по определённой шкале предпочтительности, то есть потребитель может определить разницу полезностей разных товаров или их набора. Это означает, что конкретный потребитель может сказать, что потребление одной чашки кофе приносит ему удовлетворение в 30 ютилов, двух чашек кофе – 56 ютилов, двух чашек кофе и одной сигареты – 70 ютилов и т.д. Этот подход лежит в основе потребительского выбора, целью которого является максимизация общей полезности при ограниченном доходе.

Следует иметь в виду, что количественные оценки полезности того или иного товара имеют исключительно индивидуальный, субъективный характер. Один и тот же товар может представлять большую ценность для одного потребителя и никакой ценности для другого. Для некурящего и непьющего кофе человека, их потребление не имеет никакой полезности, скорее наоборот приносит вред. Следовательно, количественный подход не имеет возможности объективно измерить полезность того или иного товара в ютилах. Невозможно также сравнить размеры удовлетворения, получаемые различными потребителями. Предполагается, что только конкретный потребитель может дать количественную оценку в ютилах полезности любого потребляемого им товарного набора.

Количественная функция общей полезности (TU) вначале возрастающая, имеет точку максимума (S), после которой она становится убывающей. Для конкретных потребителей очень важно почувствовать точку максимума полезности и прекратить избыточное потребление благ. Поэтому и говорят, что самое ценное чувство, это чувство меры.

TU

S

Q_A

MU

Q_A

Рис.5.6. График функции общей (вверху) и предельной полезности

Предельная полезность (MU) – это прирост общей полезности товарного набора при увеличении объема потребления данного товара на единицу:

Чаще всего, как видно на нижнем графике предельная полезность падает и в точке максимума становится равной нулю, а далее – отрицательной.

Однако, возможности человека оценивать полезность того или иного товарного набора в определенном количестве единиц полезности подвергнуты сомнению. Более распространенной считается точка зрения, что человеку присущи отношения предпочтения при оценке или полезности тех или иных товаров.

3 Отношение предпочтения и функция полезности

В отличие от предыдущего, второй подход не требует измерения полезности в каком-либо количестве. Потребитель здесь может сравнить полезность отдельных товаров или их набора и упорядочить их по степени предпочтения. Теория оптимального выбора потребителя исходит из того, что он осуществляет право сравнения и свободного выбора на некотором множестве X потребительских наборов, в каждый из которых включаются все виды продукции, являющиеся предметами потребления для данной группы семей. Не умаляя общности, можно считать, что всякий такой набор состоит из фиксированного числа ( n ) элементов и имеет вид:

x = (x₁ , . . . , x_j , . . . , x_n ) ,

где элементы x_j ³ 0 , поскольку они выражают количество потребляемой продукции.

Далее предполагается, что сравнительная оценка различных наборов данным потребителем с точки зрения его вкусов, привычек, традиций и т.д., может быть выражена при помощи т.н. бинарного отношения слабого предпочтения.

Это отношение определено на множестве потребительских наборов X , выражается формулой «предпочтительнее чем ...или равноценен», записывается при помощи знака «=« .

Формула «x= y» , где x и y суть потребительские наборы означает, что данный потребитель (группа семей) в равных условиях либо предпочтет набор x набору y , либо не видит различия между ними, т.е. считает их равноценными. На базе отношения слабого предпочтения вводится отношение безразличия (равноценности): два набора x и y безразличны для потребителя, если одновременно выполняются условия «x= y» и «y= x» . Факт равноценности двух наборов обычно записывается при помощи «y ~ x» . Понятие строгого (сильного) предпочтения определяется следующим образом: «x y» тогда и только тогда, когда «x= y» , а соотношение «y= x» не имеет места.

В теории потребления обычно исходят из того, что отношение слабого предпочтения удовлетворяет важным предположениям, которые называются аксиомами теории потребления. Таким образом, основой служит использование следующих аксиом:

· Транзитивности : если первая величина сравнима со второй, а вторая – с третьей, то первая сравнима с третьей;

· Полной или совершенной упорядоченности . Согласно ей, потребитель способен упорядочить всевозможные товары или их наборы с помощью отношений предпочтения и безразличия;

· Ненасыщения : если к любому набору товаров добавить дополнительную единицу товара, то полученный набор всегда предпочтительнее прежнего, так как обладает большей полезностью.

Первая аксиома гласит, что рассматриваемое отношение является совершенным, транзитивным и рефлексивным. Совершенность отношения означает для любых двух наборов из множества X обязательно имеет место либо соотношение «x = y» , либо «y = x» , либо оба вместе, т.е. «x ~ y» .

Это означает, что не существует таких наборов, которые потребитель не мог бы сравнить с другими. Транзитивность отношения состоит в том, что из соотношений «x = y» и «y = z» , следует, что «x = z» , где x, y, z – потребительские наборы. Это требование отражает совместимость (непротиворечивость) оценок потребителей и вызывает обычно много дополнительных обсуждений. Рефлексивность отношения, т.е. выполнение для любого набора соотношения «x = x» , вытекает из его совершенства.

Следует заметить, что вследствие выполнения первой аксиомы соответствующее отношение безразличия ~ оказывается т.н. отношением эквивалентности. Это означает, что все множество X потребительских наборов распадается на попарно непересекающиеся множества – классы эквивалентности, каждый из которых называется множеством безразличия.

Рассмотрим два примера отношений предпочтения и соответствующих множеств безразличия.

1) Пусть n = 2 и количества продуктов в наборе x=(x₁ , x₂ ) выражены в весовых единицах (кг), а потребитель строит свою сравнительную оценку следующим образом: «набор x предпочтительнее набора y или равноценен ему, если его суммарный вес больше или равен весу второго набора», т.е. «x = y» ; если x₁ +x₂ = y₁ +y₂ .

Нетрудно видеть, что это отношение удовлетворяет первой аксиоме, и каждый класс безразличия будет состоять из наборов одинакового веса.

2) лексикографическое предпочтение: количества продуктов в наборе x=(x₁ , x₂ ) выражены в любых единицах, потребитель считает первый продукт чрезвычайно ценным и сравнивает наборы по правилу «набор x предпочтительнее набора y , если количество первого продукта в этом наборе больше его количества в наборе y , а если количества первого продукта в обеих наборах равны, то предпочтение определяется по количеству второго продукта».Этот способ сравнительной оценки определяется формулой:

«x y» , еслиx₁ > y₁

или, если x₁ = y₁ и x₂ >y_2.

Это отношение также удовлетворяет первой аксиоме, и каждый набор образует свой собственный класс безразличия.

Для множества безразличия, состоящего из наборов, которые равноценны некоторому набору x , используется обозначение:

C_x = { y Î X ½ y ~ x }.

Обозначим множество всех слабо предпочтительных по отношению к x наборов через , а множество всех слабо не предпочитаемых наборов через .

Вторая аксиома теории потребления состоит в том, что для любого набора x оба множества и являются замкнутыми подмножествами векторного пространства R_n . Это означает, что оба множества содержат все свои предельные точки и множество безразличия:

,

т.е. определяется как пересечение этих множеств. Отношение предпочтения, обладающее таким свойством, называется непрерывным.

Из выполнения этих двух основных аксиом вытекает, что существует непрерывная скалярная функция u(x) , определенная на связном множестве X потребительских наборов и являющаяся индикатором предпочтения, поскольку она обладает следующим характеристическим свойством:

«x = y» тогда и только тогда, когда u(x) u(y).

Таким образом, если потребитель слабо предпочитает набор x набору y , то значение функции u в точке x будет иметь не меньшее значение, чем в точке y , и наоборот, если значение индикатора для некоторого набора x не меньше, чем для набора y , то потребитель слабо предпочитает набор x набору y .

Индикатор предпочтения функции – функция u(x) – обычно называется функцией полезности потребительских наборов. Нетрудно видеть, что любое монотонное преобразование функции полезности, например функции , или (где a>0), опять являются функциями полезности, поскольку они обладают указанным характеристическим свойством. Таким образом, функция полезности не является измерителем какой-то конкретной «полезности», но лишь дает представление о ранжировании (порядке) различных наборов, почему она и называется часто функцией порядковой или ординальной полезности.

Заметим, что каждому множеству С_x безразличия соответствует свое постоянное значение функции полезности : u(x) = const .

Рассмотрим с точки зрения построения функций полезности приведенные выше примеры:

1) «весовое» предпочтение удовлетворяет обеим аксиомам теории потребления, а в качестве функции полезности можно использовать сам вес набора, т.е.

u(x) = u(x₁ ,x₂ ) = x₁ +x₂ ;

2) лексиграфическое упорядочение не является непрерывным, поскольку предпочтительное множество () и непредпочтительное множество () не пересекаются между собой. В связи с этим функция полезности (индикатор предпочтения) здесь не существует.

Порядковый подход к анализу полезности является наиболее распространенным. От потребителя не требуется, чтобы он умел соизмерять блага в каких-то искусственных единицах измерения. Достаточно, чтобы потребитель был способен упорядочить все возможные товарные наборы по их «предпочтительности». В порядковой теории полезности понятие «полезность» означает не что иное, как порядок предпочтения. Утверждение: «Набор А предпочтительнее для данного потребителя, чем набор В», – тоже самое, что и утверждение: «Набор А полезнее для данного потребителя, чем набор В». Вопрос на сколько единиц полезнее набор А, чем набор В не ставится. Потребитель выбирает предпочтительный набор товаров из всех доступных для него.

4 Кривые безразличия . Решение задачи об оптимальном выборе потребителя

Основой изучения личного потребления (индивидуальных потребителей и домашних хозяйств) служат кривые безразличия. Кривая безразличия – линия, каждая точка которой представляет собой такую комбинацию двух товаров, что потребителю безразлично, которую из них выбрать. Кривые безразличия графически отражают систему предпочтений потребителя.

Для удобства воспроизведения используется двумерное пространство, т.к. выводы, полученные для двумерного случая (для двух товаров), справедливы для сколь угодно большого количества товаров.

Рассмотрим простой пример. Допустим, домашнее хозяйство может потреблять два вида благ (благо 1 и благо 2). Пусть в течение некоторого периода первое благо потребляется в количестве y₁ , а второе – в количестве Y₂ . Двумерный вектор (y₁ , y₂ ) назовем планом потребления. Домашнее хозяйство сравнивает вектор потребления (набор потребляемых благ) А= (Y₁ ^A , Y₂ ^A ) с другим вектором потребления, В = (Y₁ ^B , Y₂ ^B ) и выносит одно из следующих суждений:

а) вектор А предпочтительнее, чем вектор В;

б) вектор В предпочтительнее, чем вектор А;

в) векторы А и В равно предпочтительны (потребителю безразлично, какой из векторов А или В выбрать).

Кривая безразличия здесь – это все планы потребления, которые находятся в отношениях безразличия с рассматриваемым планом потребления.

Если обозначить через U = U(y₁ , y₂ ) функцию, или, иначе говоря, индекс полезности, которую можно получить от потребления благ, заданных вектором (y₁ , y₂ ), то кривая безразличия это набор значений
(y₁ , y₂ ), которые приводят к одному и тому же значению U.

Существуют различные виды кривых безразличия, определяемые способом задания функции полезности. Но существуют также и общие свойства кривой безразличия , независимо от её вида:

· через любую точку в графическом пространстве товаров всегда можно провести соответствующую кривую безразличия, т.к. для любой комбинации двух товаров всегда найдётся множество других комбинаций, полезность которых будет такой же, как у этой точки. Данное свойство основано на том, что потребитель может сравнить все товары или их набор с помощью отношений предпочтения или безразличия (аксиома полной упорядоченности);

· кривые безразличия никогда не пересекаются (аксиома транзитивности и аксиома ненасыщения);

· на основании первых двух свойств можно построить карту кривых безразличия, содержащую информацию о системе предпочтений потребителя. Кривая, более отдалённая от начала координат, имеет большую общую полезность: более предпочтительна;

· кривая безразличия имеет отрицательный наклон, так как сокращение количества одного товара должно быть компенсировано или заменено увеличением количества другого товара, чтобы была сохранена общая полезность набора;

· кривая безразличия в широком смысле вогнута по отношению к началу координат: наклон кривой безразличия уменьшается при движении вдоль горизонтальной оси от начала координат. Это объясняется тем, что готовность потребителя замещать один товар другим при этом падает.

Чтобы построить кривую безразличия, необходимо выразить один из аргументов функции полезности через другой аргумент и значение функции полезности U. Так, для функции полезности (1) получаем:

,

а для функции (2) – получаем:

.

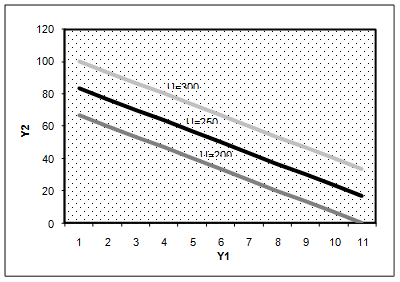
Рис. 5.7. Кривые безразличия

Данный тип кривой (Рис. 5.7.)присущ товарам-субститутам, причём, абсолютным. Это значит, что увеличение спроса на одно из двух благ (товаров) сопровождается падением спроса на другое благо: эти два блага находятся в отношениях взаимозаменяемости. В качестве примера можно привести кофе и чай.

Касательно последнего свойства кривой безразличия – при замене строгого неравенства на нестрогое в условии вогнутости функции приходим к понятию вогнутой линейной функции.

Рис.5.8. Кривые безразличия

Тип этих кривых (Рис. 5.8.), строго говоря, является одним из смешанных, так как существует ещё тип кривых безразличия для комплементарных товаров (благ). При увеличении спроса на одно из двух таких благ растет спрос и на второе благо: они находятся в отношениях взаимодополнения. Например, кофе и сахар.

Рассмотрим наборы только из двух товаров C и U . (Товары C и U можно рассматривать как комбинированные товары).

Отношения предпочтения, характерные для каждого индивида, отражают посредством кривой безразличия (рис.5.9.).

Кривая безразличия отражает множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. Наборы А и В с точки зрения данного потребления равноценны и лежат на одной и той же кривой безразличия. Для нашего потребителя любой набор, лежащий на кривой II, предпочтительнее любого набора, лежащего на кривой I и т.д.

Рис. 5.9. Кривые безразличия

В зависимости от функций полезности различают следующие типы кривых безразличия:

1). Функция полезности с полным взаимозамещением благ (чай и кофе) имеет вид:

,

гдеa, b – параметры;

U – полезность;

X, Y – товары.

Из функции полезности можно найти Y :

и построить кривые безразличия линейного типа (рис. 5.10.).

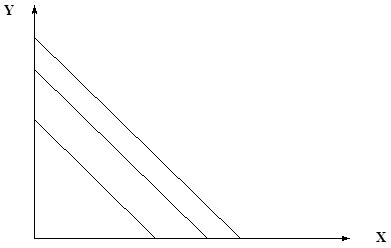
Рис. 5.10. Кривые безразличия линейного типа

2).Неоклассическая функция полезности имеет вид:

, где a+ b £ 1

Чтобы построить кривые безразличия необходимо найти Y:

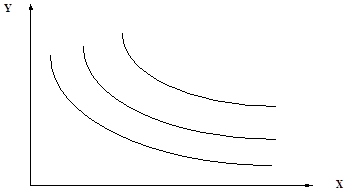
Рис. 5.11. Кривые безразличия неоклассического типа

3) Функции с полным взаимодополнением благ (при увеличении спроса на одно из двух благ растет спрос и на второе благо, например, сахар и чай, бензин и моторное масло) имеют кривые безразличия в виде точки на пересечении двух прямых. Избыток одного блага не имеет значения. Полезность достигается лишь при определенной комбинации обеих благ.

математическая модель потребительский спрос

Рис. 5.12. Кривые безразличия функций с полным взаимодополнением благ

Основными понятиями теории потребления являются предельная полезность и предельная норма замещения. Пусть U(Y₁ , Y₂ ) —функция полезности. Достигаемый при фиксированном уровне потребления первого блага и незначительном изменении уровня потребления второго блага прирост функции полезности называется предельной полезностью (marginalutility) второго блага. То есть предельная полезность – полезность, получаемая от потребления дополнительной единицы блага.

Величина, определяющая наклон кривой безразличия, называется предельной нормой замещения (marginalrateofsubstitution; MRS) потребительских благ. Она показывает, в какой степени потребитель готов заменить один товар другим, чтобы получить при этом ту же общую полезность.

Другими словами, предельной нормой замещения блага X блага Y (MRS_xy ) называют количество блага Y , которое должно быть сокращено «в обмен» на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным:

при условии, чтоU= const

Согласно аксиоме ненасыщения, любая точка, лежащая выше кривой безразличия, всегда более предпочтительна для потребителя, обладая большей общей полезностью. А любая точка, лежащая ниже, кривой безразличия, соответственно, менее предпочтительна для потребителя.

Если использовать функцию полезности неоклассического типа, то можно убедиться в существовании закона убывающей предельной нормы замещения. Этот закон явился результатом интерпретации закона убывающей предельной полезности с позиций теории выбора (теории порядковой полезности, ординалистского подхода) и считается одной из центральных идей современной микроэкономической теории. Закон убывающей предельной нормы замещения может быть сформулирован следующим образом: при стремлении поддерживать неизменным уровень полезности путем замещения первого блага вторым субъективное удовлетворение, получаемое от предельного потребления первого блага, в сравнении с удовлетворением, получаемым от предельного потребления второго блага, будет неуклонно уменьшаться.

Естественно потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Однако, это не всегда возможно, т.к. потребительское поведение ограничивается средствами, которыми он располагает.

Если обозначать рыночные цены блага X через Р_х , а блага Y через P_y , а его доход через I , то бюджетное ограничение потребителя можно записать в виде уравнения:

.

Доход потребителя равен сумме его расходов на покупку товаров X и Y.

Преобразуем уравнение и получим уравнение бюджетной линии, которая имеет вид прямой линии (рис. 5.13.). Чем выше доход, тем дальше от начала координат находится линия бюджетного ограничения.

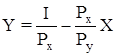
Рис. 5.13. Бюджетная линия

Пусть задана линия бюджетного ограничения и несколько кривых безразличия. Какой товарный набор выбирает потребитель?

Рис. 5.14. Оптимальный выбор потребителя

Оптимум потребителя будет в точке С . В рамках бюджетного ограничения индивид постарается так распределить свой доход между различными благами, чтобы максимизировать полезность U . Соответствующий набор благ называется оптимальным планом потребления и обычно обозначается точкой касания бюджетной линии и кривой безразличия. Итак, в условиях, когда рыночные цены и доход индивида заданы извне, оптимальный план потребления индивида определяется на основе принципа максимизации полезности. Оптимальный план потребления изменяется в зависимости от цен и дохода (рис. 5.14.).

В точке оптимума выполняется равенство:

Соотношение цены блага X к цене блага Y равно предельной норме замещения блага X блага Y .

В общем случае рассмотрим потребителя (группу семей) с определенным доходом I, предназначенным для приобретения набора товаров X=(x₁ ,..., x_j ,..., x_n ) , цены которых соответственно равны P=(p₁ ,..., p_j ,..., p_n ).

Здесь X, P – неотрицательные векторы.

Ограниченность возможного выбора потребителя выражается с помощью бюджетного ограничения

Постановка задачи оптимального выбора потребителя может быть сформулирована двояко: а) в терминах отношения предпочтения: наилучшим (оптимальным) считается набор , который является «наиболее предпочтительным по отношению «= « среди всех неотрицательных векторов x , удовлетворяющих бюджетному ограничению. Наиболее предпочтительным на множестве R обычно называется набор, обладающий тем свойством, что он удовлетворяет условию

«= x» для всех x Î R

Очевидно, что единственность такого набора, вообще говоря, не обеспечена,

б) в терминах функции полезности: оптимальный набор соответствует наибольшему значению u(x) в указанных выше условиях, т.е. является решением задачи:

u(x) = u(x₁ ,..., x_j ,..., x_n ) ® max

при условиях

; x_j ³ 0 ( j = 1, ... , n)

При анализе задачи оптимального выбора обычно применяется еще одно важное предположение теории потребления, которое носит название гипотезы ненасыщения потребителя и состоит в том, что для любых двух наборов x и y справедливо соотношение:

если x ³ y , то «x = y».

Также считается справедливым и более точное соотношение:

если x ³ y и x ¹ y , то «x > y».

Это означает, что для «ненасыщаемого» потребителя всякий набор x , который содержит любого продукта столько же, либо (хотя бы по одной позиции) несколько больше, чем набор y , оказывается более предпочтительным. Предположение о ненасыщении при помощи функции полезности выражается следующим образом:

· если x ³ y, то u(x) ³ u(y).

· если x ³ y и x ¹ y, то u(x) > u(y).

Таким образом, функция полезности является монотонно возрастающей по каждому аргументу x_j .

Если функция полезности имеет производные по своим аргументам, то из предположения о ненасыщаемости (и монотонности u(x) ) следует, что все первые частные производные функции полезности являются положительными, т.е.:

(j = 1, ..., n)

для любого набора потребительских благ. Величина частной производной:

имеет следующий экономический смысл: она показывает, на сколько увеличится полезность набора, если количество потребляемого блага увеличится на «малую единицу». В связи с этим указанная производная носит название предельной (маргинальной, дифференциальной) полезности.

В экономических исследованиях, как правило, используются некоторые конкретные виды выпуклых функций полезности, причем подбор вида функции и оценка числовых значений параметров производится на основе наблюдений и анализа поведения потребителей. Чаще всего применяются линейная, квадратическая и логарифмическая функция вида:

В пространстве двухэлементных наборов x=(x₁ , x₂ ) поверхности безразличия (т.е. линии u(x₁ , x₂ )=const ) обычно называются кривыми безразличия.

Например, для логарифмической функции:

u(x₁ , x₂ )= log x₁ + log x₂

кривые безразличия имеют вид:

log x ₁ + log x ₂ = log ( x ₁ x ₂ ) = const ,

т.е. являются просто гиперболами в положительном ортанте, удовлетворяющими уравнениям:

(x₁ × x₂ ) = const

Рис. 5.15. Кривые безразличия

На рис. 5.15 C₂ > C₁ , т.е. более высокая кривая безразличия соответствует большему уровню полезности тех наборов, которые составляют кривую безразличия.

Рассмотрим задачу оптимального выбора потребителя для ненасыщаемого потребителя:

Нетрудно заметить, что оптимальный набор ( , , ) необходимо должен удовлетворять бюджетному ограничению как точному равенству. В самом деле, если бы оптимальный набор достигался бы при условии:

,

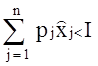то потребитель мог бы купить на оставшиеся деньги некоторое количество любого блага, и тем самым получить новый набор с большей полезностью. Это означает, что внутренняя точка множества не может быть оптимальным набором.

Таким образом, задача об оптимальном наборе имеет вид:

u(x) = u(x₁ ,..., x_j ,..., x_n ) ® max

.

Решение этой задачи на условный экстремум находится при помощи метода множителей. Оптимальный набор определяется путем решения следующей системы из (n+1) уравнения:

относительно (n+1)- го неизвестного, а именно элементов оптимального набора ( , , ) и множителя Лагранжа .

Таким образом, при заданной системе цен потребитель должен выбрать такой набор, а котором все предельные полезности пропорциональны ценам. При этом оптимальное значение множителя Лагранжа часто называют «предельной полезностью денег» и трактуют как прирост максимальной полезности при увеличении дохода I на малую единицу. Заметим, что соотношения оптимальности могут быть представлены в виде:

,

который допускает любопытную интерпретацию: в оптимальной точке величина дополнительной полезности в расчете на одну денежную единицу должна быть одинакова для всех товаров и услуг. Необходимо также отметить, что для некоторых товаров могут быть выполнены соотношения:

,

которые означают, что такие товары сравнительно мало полезны и относительно дороги, а поэтому и не должны быть включены в оптимальный набор потребителя, максимизирующего свою полезность при ограниченном доходе.

Рассмотрим простой пример.

Пусть n=2 , функция полезности:

u(x₁ , x₂ ) = ln x₁ + ln x₂ ,

бюджетное ограничение:

p₁ x₁ + p₂ x₂ = I .

Решение задачи оптимального выбора

отсюда:

Используя бюджетное ограничение, имеем:

Как видно из приведенного решения оптимальный выбор потребителя имеет очень естественный вид: количество потребляемого блага прямо пропорционально доходу (I) и обратно пропорционально его цене. Геометрическая интерпретация решения задачи оптимального выбора приведена на рис. 5.14.

В более реалистичных вариантах постановки задачи оптимального выбора при помощи дополнительных условий могут быть учтены ограничения по ассортименту потребляемых товаров и услуг, возможность взаимной замены различных продуктов и т.п.

5 Функции спроса. Коэффициент эластичности

В результате решения задач оптимального выбора оказывается возможным проследить связь между изменением систем цен и доходов группы потребителей, с одной стороны, и спросом этой группы на товары и услуги, с другой; и построить, таким образом, функцию оптимального спроса.

В достаточно общей форме оптимальный спрос выражается при помощи функций вида:

.

В ряде случаев функции оптимального спроса имеют особенно простой вид. Так, если функция полезности имеет логарифмический вид, то оптимальный спрос выражается формулой:

, где .

В подавляющем большинстве случаев, однако, конкретная форма функции спроса определяется путем статистической обработки результатов специальных наблюдений за доходами и расходами представителей различных социальных групп. В результате изучения функции спроса обычно устанавливаются некоторые классификационные признаки товаров.

Если для некоего товара выполняется условие:

то товар называется нормальным, так как спрос на него снижается по мере увеличения его цены. Однако существуют товары, спрос на которые повышается, невзирая на повышение цены. Эта парадоксальная ситуация возникает тогда, когда при повышении цены на малоэффективный товар (например, картофель) группа потребителей с низким доходом просто не может приобретать более высококалорийный продукт (мясо) и вынуждена компенсировать нехватку калорий усиленной покупкой картофеля.

Товары, для которых имеет место неравенство:

,

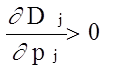называются аномальными или товарами Гиффина .

При фиксированном доходе и в практических целях для нормальных товаров используются, как правило, функции спроса двух видов:

1) линейная функция спроса

,

где a₀ > 0 , a₁ > 0 , статистически оцениваемые параметры модели.

2) степенная функция спроса:

.

Во многих прикладных исследованиях значительную роль играет коэффициент эластичности .

Мера реагирования эндогенной переменной на изменение экзогенной переменной называется эластичностью. Однако это определение слишком общее. Конкретнее, эластичность можно определить как предел соотношения между относительным приращением функцииy:

(зависимой переменной) и относительным приращение независимой переменной x:

,

когда и обозначается E_x ( y) .

Таким образом эластичность можно выразить формулой:

при

или в непрерывном случае:

Из практических соображений эластичность относят к проценту прироста независимой переменной. В этом случае эластичность показывает, насколько процентов повышается или понижается эндогенная переменная Y, если независимая переменная X изменяется на 1%.

Различают дуговую эластичность, то есть среднюю на каком-то отрезке кривой, и точечную эластичность – значение производной в заданной точке. Для практического вычисления эластичности используется формула английского математика и экономиста Рой Аллена (1906 – 1983). Он предложил использовать среднюю точку интервала, по которому происходит изменение в качестве знаменателя дроби. Тогда вычисляются:

· относительное изменение эндогенной переменной

;

· относительное изменение экзогенной переменной

.

Затем вычисляется отношение первого ко второму. Необходимо помнить, что формула Аллена, хотя и популярная, но не единственно возможная. Однако ее не следует применять к очень широким интервалам, так как в этом случае она может ввести в заблуждение.

Для определения эластичности спроса от цены можно воспользоваться формулой:

при

или

,

Коэффициент эластичности спроса по цене показывает, на сколько процентов уменьшится (увеличится) спрос, если цена товара увеличится (уменьшится) на 1%.

Для линейной функции спроса принимается, что:

,

где - среднее значение цены, - среднее значение спроса по использованной выборке.

Очевидно, что для cтепенной функции спроса:

.

Если коэффициент эластичности близок к нулю, то спрос на товар практически не зависит от его цены. В этом случае говорят, что спрос неэластичен по цене. Это относится в основном к предметам первой необходимости. Спрос называется нормально эластичным, если E_dp » 1 , что имеет место для товаров длительного пользования. Для предметов роскоши обычно E_dp > 1 , т.е. спрос является суперэластичным.

При постоянных ценах товары различаются по характеру изменения спроса в зависимости от величины дохода I . Товар j называется ценным (или товаром высшего ряда), если

,

т.е. спрос на него возрастает по мере перехода от менее доходных групп потребителей к более доходным. Для малоценного товара имеет место противоположное неравенство:

,

что означает вытеснение этого товара из потребительского набора группы потребителей по мере увеличения ее категории доходности.

На основе введенной выше классификации товаров по трем группам можно представить изменение спроса в зависимости от повышения дохода при помощи графика, представленного на рис. 5.16.

Рис. 5.16. Изменение спроса в зависимости от дохода

Здесь по горизонтальной оси (I) отложены относительные величины дохода, а по вертикали доли расходов по указанным трем группам товаров.

Нетрудно видеть, что доля спроса на товары первой необходимости падает с 70% (при малых доходах) до 35% (при доходе в 10 раз большем); сравнительно стабильна (в пределах от 20% до 27%) доля расходов на товары второй группы и значительно возрастает доля расходов на предметы роскоши (от 10% до 43%). Для изучения изменения спроса в зависимости от дохода различных потребительских групп применяются в основном модели двух типов:

1) Модели степенного вида (функции Энгеля ):

.

Здесь показатель g имеет смысл коэффициента эластичности: т.к. он показывает на сколько процентов увеличится спрос на товар, если доход увеличится на 1%. Коэффициент эластичности спроса от дохода находится как:

при

Для предметов первой необходимости показатель g < 1 , т.е. при увеличении дохода дополнительные затраты на эти товары этой категории, составляют все убывающую долю. Для предметов длительного пользования показатель эластичности g приблизительно равен 1, что означает примерное постоянство доли расходов на эти предметы в дополнительном доходе. Для предметов роскоши показатель эластичности g > 1 . Это означает, что при значительном увеличении дохода все большая часть его прироста тратится именно на товары этой группы.

2) Идея разделения потребляемых товаров и услуг на ряд различных групп развита далее при конструировании так называемых функций Торнквиста . Для товаров первой необходимости эта функция ищется в виде:

,

где a₁ , b₁ – параметры модели.

Заметим, что при очень большом доходе, условно представляемом как (I®¥) величина спроса , что выражает факт асимптотического насыщения потребителя предметами первой необходимости.

Функция спроса Торнквиста для товаров длительного пользования отражает тот факт, что спрос на эти товары возникает лишь с некоторого (достаточно высокого) уровня дохода I₂ . Соответствующее выражение имеет вид:

, если I ³ I₂ ,

где a₂ , b₂ – параметры модели,

, если I < I₂ .

Как видно, спрос на товары этой группы также имеет асимптотическую тенденцию к насыщению, поскольку

Для предметов роскоши используется формула, в которой отсутствует тенденция к насыщению, а спрос начинается с еще более высокого уровня дохода I₃ :

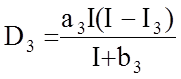, если I ³ I₃ ;

, еслиI < I₃ .

Легко видеть, что при достаточно больших значениях дохода I :

.

Это означает, что в этой ситуации практически весь прирост дохода тратится на предметы роскоши. Графическое изображение функций Энгеля и Торнквиста представлено на рис 5.17. и 5.18.

Pис. 5.17. Кривые Энгеля: рост спроса на различные группы товаров в зависимости от дохода

Рис. 5.18. Кривые Торнквиста

Графики функций Торнквиста для трех групп товаров.

6 Изменение цен и компенсация

Проблема компенсации путем увеличения дохода потребителя возникает во всех тех случаях, когда происходит повышение цен на один или несколько потребляемых товаров. При этом возможны различные подходы к решению этой проблемы. Наиболее прямой из них использует понятие функции спроса в достаточно общей форме и опирается на понятие компенсации как на такое увеличение дохода, которое позволяет оставить спрос на товар на том уровне, который определялся прежней ценой. Таким образом, применяется функция спроса

D = D(I, p),

где

I – исходный уровень дохода,

p – исходный уровень цены.

Обозначим новый уровень цены:

,

а компенсирующее изменение дохода

.

Легко видеть, что спрос остается неизменным, если выполняется условие

.

Для нормальных и ценных товаров и , поэтому при повышении цены (Dp>0 ), для сохранения уровня спроса необходимо увеличение дохода в размере

.

В конкретном случае, когда функция спроса имеет вид:

,

получаем следующее простое соотношение между повышением цены и компенсацией

или .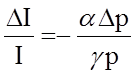

Это означает, что относительное увеличение дохода должно быть пропорционально относительному изменению цены с коэффициентом пропорциональности, равным отношению эластичностей этих факторов.

В более сложном случае многих товаров указанный подход основан на использовании функций спроса вида:

Повышение цены одного из товаров (например, с номером n ) изменяет, вообще говоря, спрос на каждый товар. Если для некоторого товара j имеет место соотношение:

,

т.е. при повышении цены на товар n падает спрос на товар j , то продукты n и j являются взаимодополняющими (например, автомобили и бензин).

Нетрудно видеть, что, если среди перечня товаров имеются взаимодополняющие, то в общем случае невозможно точно решить задачу компенсации путем увеличения дохода.

Если же для товара j справедливо неравенство:

,

т.е. повышение цены на товар «n » вызывает увеличение спроса на товар «j », то они называются взаимозаменяемыми (масло и маргарин). Функция спроса обладает свойством сильной валовой заменимости, если все товары являются взаимозаменяемыми. Нетрудно видеть, что в этом случае повышение цены на один товар приводит к снижению спроса только на этот товар, но увеличивает спрос на все остальные. В этой ситуации для расчета необходимой компенсации можно использовать подход, рассмотренный выше для случая одного товара. Однако при этом получается слишком высокий уровень компенсации, поскольку повысится потребление практически всех товаров.

В связи с этим применяется более экономный способ оценки размера компенсации, основанный на использовании понятия функции полезности. При таком подходе объемы спроса на различные товары рассматриваются как решение задачи об оптимальном выборе потребителя в условиях ограниченности дохода:

u(x₁ , ..., x_n ) ® max

x_j ³ 0 (j = 1, ..., n)

Решение этой задачи:

определяет максимально достижимый уровень функции полезности , который очевидно, зависит и от системы цен p = (p₁ , ..., p_n ) и от уровня дохода I .

Пусть теперь, как и прежде, повышена цена p_n товара «n ». Решение модифицированной задачи будет таково, что максимальный уровень понизится. В связи с этим возникает естественный вопрос: насколько нужно увеличить доход I , чтобы восстановить прежнее значение , а следовательно, и прежний уровень удовлетворения потребителя. В достаточно общей форме ответ на этот вопрос дает уравнение Слуцкого, основные выводы из которого будут далее рассмотрены на простом примере.

Пусть n=2 , функция полезности:

.

Решение задачи оптимального выбора имеет вид:

.

Максимальный уровень функции полезности:

Условие сохранения максимального уровня имеет вид:

или .

Отсюда получаем выражение для компенсации в случае изменения цен:

.

Таким образом, если цена p₂ возрастает (dp₂ > 0 ), а цена p₁ остается неизменной (dp₁ = 0 ), то спрос на второй товар упадет, а спрос на первый товар не изменится. Размер компенсации определяется в этом случае отношением

Таким образом, достигнутый уровень удовлетворения будет сохранен, если доход будет увеличен ровно настолько, чтобы потребитель мог приобрести прежний объем второго товара. Однако, нетрудно показать, что на самом деле потребитель использует компенсацию следующим образом: его спрос на товар с повышенной ценой (товар 2) уменьшится, но возрастет объем закупок первого товара. При этом уровень полезности останется тем же, каким он был до повышения цен и получения компенсации. Иллюстрацию этого перехода можно найти на рисунке 5.19.

Рис. 5.19. Оптимальный набор при изменении цен и компенсации

Здесь:

· линия С – кривая безразличия, соответствующая максимальному уровню полезности;

· линия АВ – бюджетная линия до повышения цен;

· точка D – оптимальный набор;

· линия FВ – бюджетная линия после повышения цены p₂ , но до выплаты компенсации;

· линия А¢B¢ – бюджетная линия после выплаты компенсации (А ¢В ¢ || FВ ), точка D ¢ – оптимальный набор в новых условиях.

В более общем случае, когда задача оптимального выбора имеет вид:

,

можно показать, что компенсационная доплата, сохраняющая прежний уровень максимальной полезности, связана с изменением цен соотношением:

,

где – оптимальный спрос на j – товар до изменения цен, а – изменение цены на j -тый товар.

Заключение

Итак, экономическая наука, как и любая другая имеет свою специфику, которая определяется общей спецификой наук о человеке. Все общественные науки изучают самую сложную и высокоорганизованную форму движения – социальную. На современном этапе экономические взаимоотношения между субъектами образуют экономические системы со сложной структурой, большим количеством элементов и связей между ними, которые и являются причиной почти всех особенностей экономических задач.

В данном разделе описан механизм функционирования экономической системы со стороны потребления. Неотъемлемой категорией теории потребления является понятие полезности. Существуют различные разработки методов измерения полезности. Но главным критерием применимости того или иного метода является проверка результатов исследования на практике. Уже поэтому полезность можно считать достаточно сложным компонентом данной теории – измерить его реально не представляется возможным. То же можно сказать, соответственно, и о понятии предельная полезность.

Поведение потребителя определяют, во-первых, отношения предпочтения потребителя, а, во-вторых, ограничением выступает бюджетное ограничение. Отношения предпочтения описывают кривые безразличия, тип которых зависит от вида потребляемых товаров. Бюджетное ограничение отражает бюджетная линия, зависящая от уровня дохода и уровня цен на товары. В этих условиях оптимальный план потребления определяется, исходя из максимизации общей полезности. Выражая оптимальный план потребления через зависимость от цен и дохода, получили функцию спроса отдельного домашнего хозяйства.

Кроме того, следует учитывать то, что экономические системы развиваются и усложняются сами, изменяется их структура, а иногда и содержание, обусловленное научно-техническим прогрессом. Это делает устаревшими многие методы, применявшиеся ранее, или требует их корректировки. В то же время научно-технический прогресс влияет и на сами математические методы, поскольку появление и усовершенствование электронно-вычислительных машин сделало возможным широкое использование методов, ранее описанных лишь теоретически, или применявшихся лишь для небольших прикладных задач.

Курс микроэкономики

Приложения производной

Учебник по микроэкономике

Математические методы экономики

Политэкономия

Некоторые задачи оптимизации в экономике

Микроэкономика

История экономических учений

Экономическая прибыль. Ценовая эластичность спроса

Высшая математика для менеджеров

Основы общей экономической теории

Лекции по экономической теории

Экономическая наука и общество

Теория предельной полезности

Общая и предельная полезность. Законы Госсена

Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ)