| Похожие рефераты | Скачать .docx |
Дипломная работа: Расчёт на прочность закрытой цилиндрической одноступенчатой передачи и её проектирование
Российской Федерации
Санкт-Петербургский государственный горный институт им. Г. В. Плеханова (технический университет)
Курсовой проект
По дисциплине
Прикладная механика
Тема
Расчёт на прочность закрытой цилиндрической одноступенчатой передачи и её проектирование
Автор
Сметанина А. И.
Техническое задание
2. Исходные данные к проекту: Вариант I-7, N=4кВт, n=600об /мин , К=1,5 Т=20000 прямозубая, вертикальная компановка
2. Содержание пояснительной записки: Полный расчёт на прочность с детальными пояснениями
3. Перечень графического материала: 1 лист формата А1, 3 вида, отдельные еобходимые узлы.
4. Срок законченной работы 28.05.2008г.
В курсовом проекте выполнен расчёт, и на основе его спроектирован одноступенчатый цилиндрический косозубый редуктор, предназначенный для понижения угловых скоростей и увеличения крутящего момента и имеющий широкое применение в горной промышленности.
При проектировании редуктора были приняты следующие конструктивные решения: корпус редуктора составлен из трёх частей и отливается из чугуна марки СЧ 15-32 , что позволяет получить сложные геометрические формы корпусных деталей, быстроходный вал спроектирован как вал-шестерня. Пояснительная записка выполнена в объёме 62 страниц, дополнена 4-мя иллюстрациями. К пояснительной записке прилагается один сборочный чертёж формата А1 и спецификация к сборочному чертежу в объёме трех листов.
Оглавление
Введение
1. Выбор электродвигателя и кинематический расчет
2. Расчет редуктора
2.1 Выбор материалов зубчатых колес и определение допускаемых напряжений
2.2 Определение параметров передачи
2.3 Определение основных размеров зубчатой пары
2.4 Определение окружной скорости и сил, действующих в зацеплении
2.5 Проверочный расчет на контактную и изгибную выносливость зубьев
2.6Ориентировочный расчет валов
2.7 Конструктивные размеры элементов корпуса и крышки редуктора
2.8 Конструктивные размеры валов, подшипниковых узлов
2.9 Первый этап эскизной компоновки редуктора
2.10 Проверка прочности валов
2.11 Второй этап эскизной компоновки редуктора
2.12 Подбор шпонок и проверочный расчет шпоночных соединений
2.13 Подбор подшипников
2.14 Уточненный расчет валов
2.15 Определение массы редуктор
3. Вычерчивание редуктора
4. Посадки основных деталей
5. Смазка зубчатых колес, подшипников. Выбор сорта масла
Список использованных источников
Приложения
Введение
Во всех отраслях промышленности производственные процессы осуществляются машинами или аппаратами с машинными средствами механизации. Поэтому уровень промышленности в большей степени определяется уровнем машиностроения. Современные машины многократно превышают производительность физического и умственного труда человека. В данном курсовом проекте нашли надлежащее отражение основные, связанные с конструированием одноступенчатого цилиндрического прямозубого редуктора, производственные проблемы и соответствующие решения:
1. Повышение надёжности и ресурса редуктора, достигаемое путём обеспечения его необходимого технического уровня, применения деталей и узлов, надёжных и долговечных по своей природе.
2. Уменьшение материалоёмкости конструкции путём её оптимизации, выбора оптимальных материалов.
3. Уменьшение энергозатрат путём обеспечения совершенного трения и повышения КПД редуктора.
В курсовом проекте реализуются основные принципы диалектики.
В соответствии с принципом детерминизма, т.е. всеобщей закономерной связи всех явлений, осуществляется переход от условных и независимых расчётов деталей редуктора к расчётам по истинным критериям работоспособности и к расчётам как элементам единой системы.
В соответствии с филосовскими категориями необходимость и случайность, все рассмотренные в курсовом проекте явления, позволяющие их удовлетворительное описание детерминистическими зависимостями, рассчитаны с помощью этих зависимостей. Вместе с тем применялись вероятностные расчёты для учёта таких недостаточно определённых и изученных факторов, как ресурсы деталей, интенсивность изнашивания, механические характеристики материалов.
В курсовом проекте закон диалектики - переход количественных изменений в качесвенные - очень ярко иллюстрируются основным критерием прочности - сопротивлением усталости.
1. Выбор электродвигателя и кинематический расчет
1. Вычерчиваем кинематическую схему проектируемого редуктора (рис.1).
 |
Рис.1
2. Определяем КПД редуктора. По источнику [3, с. 304] общий КПД редуктора равен произведению КПД последовательно соединенных подвижных звеньев, КПД смазки и определяется по формуле
η = η1 2 η2 η 3 (1)
где η 1 – КПД одной пары подшипников;
η 2 – КПД одной пары зубчатых колес;
η 3 – КПД смазки;
Принимая ориентировочно для одной пары подшипников η 1 = 0,99, для одной
пары зубчатых колес η 2 = 0,98,КПД смазки η3 =0,98, получаем общий КПД редуктора
η = 0,992 ·0,98·0,98=0,94
3. Определяем требуемую мощность электродвигателя при соединении муфтой быстроходного вала редуктора с валом электродвигателя:
P1 = P2 / η, (2 )
где P2 – мощность на тихоходном валу, кВт;
η – КПД редуктора;
P1 – требуемая мощность электродвигателя, кВт.
Тогда по формуле (2) получаем
P1 =4 /0,94 = 4,2 κВт.
4. Выбираем электродвигатель. Согласно рекомендациям [3, табл. П61], принимаем асинхронный электродвигатель общего назначения в закрытом обдуваемом исполнении типа 4А132М6У3, для которого n1 = 960 мин –1 – расчетная частота вращения; PЭ = 5,5кВт.
5. По формуле [3, стр.23] определяем передаточное отношение редуктора:
i = n1 / n2 ,(3)
где n1 – частота вращения ведущего (быстроходного) вала, мин -1 ;
n2 – частота вращения ведомого (тихоходного) вала, мин –1 .
Тогда по формуле (3) получаем
i = 960 / 600 = 1,6 = u
6. Вычисляем вращающий момент на быстроходном (ведущем) валу редуктора [3, стр.22] по формуле
T1 = 9,55P1 / n1 , (4)
где P1 - требуемая мощность электродвигателя, кВт;
n1 – частота вращения ведущего вала, мин –1 .
T1 = 9,55·4,2·103 /960 = 41,8Н·м.
2.1 Выбор материалов зубчатых колес и определение допускаемых напряжений
1.Согласно рекомендациям [3, стр.304,табл. П21 и П28], назначаем для изготовления зубчатых колес сталь 45 с термической обработкой: нормализация – для колеса, улучшение – для шестерни.
2. Допускаемое контактное напряжение определяется по формуле [3, стр. 97]
σНР = σ0 НР KHL , (5)
где σ0 НР – допускаемое контактное напряжение, МПа;
KHL – коэффициент циклической долговечности.
Допускаемое напряжение при расчете на выносливость зубьев при изгибе определяется по формуле
σFP = σ0 FР KFL , (6)
где σ0 FР – допускаемое напряжение при расчете на выносливость зубьев при изгибе, МПа;
KFL – коэффициент циклической долговечности.
Принимаем [3, табл. П28] для стали 45, нормализация, твердость рабочих поверхностей НВ180…200: допускаемое контактное напряжение σ0 НР = 420 МПа; база испытаний напряжений, соответствующая длительному пределу выносливости NHO = 107 ; допускаемое напряжение при расчете на выносливость зубьев при изгибе σ0 FР = 110 МПа для реверсивной передачи; база испытаний напряжений NFO = 4·106 – для колеса.
Назначая ресурс передачи tч = 20000ч, находим число циклов перемены напряжений [3, с.97] по формуле
NH Е = NF Е = 60 tч n2 , (7)
где NH Е , NF Е – относительное эквивалентное число циклов напряжения;
tч – наработка передачи в часах;
n2 – частота вращения тихоходного вала, мин –1 .
Тогда по формуле (7) получаем
NH Е = NF Е = 60· 20000·600 = 72·107
Так как NH Е > NHO и NF Е > NFO , то значения коэффициентов долговечности KHL = 1 и KFL = 1.
Допускаемые напряжения определяются по формулам (5) и (6):
для колеса
σ′′ НР = 420∙1 = 420 МПа;
σ′′ FP = 110∙1 = 110 МПа;
для шестерни
σ′ НР = 600∙1 = 600 МПа;
σ′ FP = 130∙1 = 130 МПа.
2.2 Определение параметров передачи
1.Параметры зубчатой передачи начнем определять с вычисления межосевого расстояния [3, с.92]. Межосевое расстояние определяем по формуле
aw
= Ka
(u + 1)  , (8)
, (8)
где T1 – вращающий момент на быстроходном валу, Н∙м;
u – передаточное отношение редуктора;
σHP – допускаемое напряжение на контактную выносливость зубьев колеса, МПа.
Находим значения коэффициентов: Ка = 4950Па1/ 3 – для стальных прямозубых колес по [3, табл. П22]; коэффициенты ширины зубчатых колес ψba = 0,4 по [3, с.95]; ψb д определяем согласно рекомендациям [3, с.96] по формуле
ψb д = 0,5 ψba (u + 1), (9)
где u – передаточное отношение редуктора.
Подставляя числовые значения в формулу (9), получаем
ψb д = 0,5·0,4(1,6+1) = 0,52.
Согласно рекомендациям [3,табл. П25] коэффициент распределения нагрузки
по ширине венца KHβ = 1,02. Подставляем числовые значения в формулу (8) и определяем межосевое расстояние
aw
= 4950(1,6 +1)  =
=
=12870·![]() = 0,093 м.
= 0,093 м.
По СТ СЭВ 229 – 75 [3, с.302] принимаем aw = 90мм.
2. Определяем нормальный модуль при известном межосевом расстоянии из соотношения по [3, с. 93 ]
mn = (0,01…0,02) aw , (10)
где aw – межосевое расстояние, мм.
Тогда по формуле (10) получаем
mn = (0,01…0,02)∙90 = 0,9…1,8 мм.
По СТ СЭВ 310 – 76 принимаем mn = 1,5 мм.
3. Определяем число зубьев шестерни и колеса по [3, с.91]. Межосевое расстояние связано с числом зубьев шестерни следующим соотношением
aw = 0,5mn z1 (u + 1), (11)
где aw – межосевое расстояние, мм;
mn – модуль, мм;
u – передаточное число;
z1 – число зубьев шестерни;
Выразив из формулы (11) число зубьев шестерни, получим:
z1 = 2 aw /[ mn (u + 1)] (12)
По формуле (12) определяем число зубьев шестерни
z1 = 2· 90/[1,5∙ (1,6 +1)] = 46,1.
Принимаем z1 = 46. Тогда, согласно рекомендациям [3, с. 305], определяем число зубьев колеса по формуле
z2 = u · z1 , (13)
где u – передаточное число;
z1 – число зубьев шестерни.
Подставляем числовые значения в формулу (13) и определяем число зубьев колеса
z2 = 1,6 · 46 = 73,6;
принимаем z2 = 74.
4. Уточняем передаточное число, выразив его из формулы (13)
u = z2 / z1 (14)
u = 74 / 46 = 1,6 – стандартное.
Уточняем частоту вращения, выразив ее из формулы (3)
n2 = n1 /i(15)
n2 = 960/1,6 = 600 мин –1 .
Определяем угловую скорость тихоходного (ведомого) вала по формуле
ω2 = π n2 /30, (16)
где n2 – частота вращения тихоходного вала, мин –1 .
Тогда по формуле (16) получаем
ω2 = 3,14∙ 600/30 = 62,8 c-1 .
2.3 Определение основных размеров зубчатой пары
Согласно рекомендациям [3, с.108], вычисляем делительные диаметры, диаметры вершин зубьев и диаметры впадин зубчатого колеса и шестерни.
1. Делительный диаметр определяется по формуле
d = mt z, (17)
где mt –окружной модуль косозубой передачи, мм;
z – число зубьев зубчатого колеса или шестерни.
Подставляем числовые значения в формулу (17) и определяем делительные диаметры шестерни и зубчатого колеса:
d1 = 1,5∙46 = 69 мм;
d2 = 1,5∙74 = 111 мм.
2.Определяем диаметры вершин зубьев зубчатого колеса и шестерни по формуле
dа = d + 2 mn , (18)
где d – делительный диаметр зубчатого колеса или шестерни, мм;
mn – нормальный модуль , мм.
Подставляем числовые значения в формулу (18) и определяем диаметры вершин зубьев шестерни и зубчатого колеса:
dа1 = 69 + 2∙1,5 = 72 мм;
dа2 = 111 + 2∙1,5 = 114 мм.
3. Определяем диаметры впадин зубчатого колеса и шестерни по формуле
df = d – 2,5 mn , (19)
где d – делительный диаметр зубчатого колеса или шестерни, мм;
mn – нормальный модуль прямозубой передачи , мм.
Подставляем числовые значения в формулу (19) и определяем диаметры впадин шестерни и зубчатого колеса:
df 1 = 69 – 2,5∙1,5 = 65,25 мм;
df 2 = 111 – 2,5∙1,5 = 107,25 мм.
4. Согласно рекомендациям [3, с. 108], уточняем межосевое расстояние по формуле
aw = 0,5(d1 + d2 ) , (20)
где d1 – делительный диаметр шестерни, мм;
d2 – делительный диаметр колеса, мм.
Тогда подставляя числовые значения в формулу (20) получаем
aw = 0,5(69+111) = 90 мм.
5. Согласно рекомендациям [3, с. 306], определяем ширину венца зубчатых колес по формуле
b = ψba ∙ aw , (21)
где ψba – коэффициент ширины зубчатых колес;
aw – межосевое расстояние, мм.
Тогда подставляя значения ψba и aw в формулу (21) определяем ширину венца зубчатых колес
b = 0,4 ∙ 90 = 36 мм,
принимаем b1 = 39 мм для шестерни, b2 = 36 мм для колеса.
2.4 Определение окружной скорости и сил, действующих в зацеплении
1. Определяем окружную скорость и назначаем степень точности передачи. Согласно рекомендациям [3, с. 306], окружную скорость определяем по формуле
υ = πn1 d1 /60, (22)
где n1 – частота вращения быстроходного вала, мин -1 ;
d1 – делительный диаметр щестерни , м.
Подставляем числовые значения в формулу (22) и определяем окружную скорость
υ = 3,14 · 960∙69∙10 –3 / 60 = 3,4 м/с.
Источник [3, табл. 2] рекомендует 9-ю степень точности передачи: υ < 4 м/с, однако для уменьшения динамической нагрузки на зубья принимаем 8-ю степень точности..
2. Вычисляем силы, действующие в зацеплении по [3, с. 306].Окружная сила, изгибающая зуб определяется по формуле
Ft = P1 / υ, (23)
где P1 – мощность электродвигателя, кВт;
υ– окружная скорость, м/с.
Тогда по формуле (23) получаем
Ft = P1 / υ = 41,8 · 103 / 3,4 = 1,2· 103 Н.
Осевая сила, согласно рекомендациям [3, с. 109], определяется по формуле
Fа = Ft tgβ, (24)
где Ft – окружная сила, Н;
β – угол наклона линии зуба.
Тогда по формуле (24) получаем
Fа = 1,2 · 103 ∙ tg 0○ = 0 Н.
Определяем радиальную (распорную) силу по формуле
Fr = Ft tgα(25)
где Ft – окружная сила, Н;
α – угол профиля (зацепления).
Тогда по формуле (25) получаем
Fr = 1,2 · 103 ∙ tg 20○ = 1,2 · 103 · 0,364 = 0,4·103 Н
2.5 Проверочный расчет на контактную и изгибную выносливость зубьев
1. Проверяем рабочие контактные напряжения по формуле
σН
= ZН
· ZМ
· ZЕ
·  < σНР
, (26)
< σНР
, (26)
где ZН – коэффициент, учитывающий форму сопряженных поверхностей зубьев (ZН = 1,76 по [3, табл. 3]);
ZМ – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес (ZМ = 274 · 103 Па1/2 по [3, табл. П22]);
ZЕ – коэффициент, учитывающий суммарную длину контактных линий;
КН – коэффициент нагрузки;
Ft – окружная сила, Н;
u – передаточное число;
d – делительный диаметр шестерни, мм;
b – ширина венца зубчатого колеса, мм;
σНР – допускаемое контактное напряжение, МПа (σНР = 420МПа).
Согласно [3, стр.96] коэффициент ZЕ , учитывающий суммарную длину контактных линий, определяется по формуле
ZЕ
= ![]() , (27)
, (27)
где Еα – коэффициент торцового перекрытия, определяется по формуле
Еα = [1,88 – 3,2∙ (1/ z1 + 1/ z2 )] ∙ cosβ, (28)
где z1 – число зубьев шестерни;
z2 – число зубьев зубчатого колеса.
Подставляем числовые значения в формулу (28) и определяем коэффициент торцового перекрытия
Еα = [1,88 – 3,2∙ (1/ 46 +1/ 74)] ∙ cos0○ = 1,77.
Подставляем значение коэффициента торцового перекрытия в формулу (27)
ZЕ
= ![]() = 0,86
= 0,86
Коэффициент нагрузки определяем по формуле
KH = KH β · KH υ , (29)
где KH β – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (KHβ = 1,02 по [3, табл. П25]);
KHυ – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении (KHυ = 1,13 по [3, табл. П26]).
Подставляем коэффициенты KHυ , KHβ в формулу (29) и находим коэффициент нагрузки
KH = 1,02 · 1,13 = 1,15.
По формуле (26) проверяем контактную выносливость зубьев:
σН
= 1,76·274·103
·0, 86· = 393·106
Па < σНР
= 420Мпа.
= 393·106
Па < σНР
= 420Мпа.
2. Проводим проверочный расчет зубьев на их выносливость при изгибе. Согласно рекомендациям [3, с. 307], выносливость зубьев по напряжениям изгиба
проверим по уравнению
σF
= ![]() < σFР
(30)
< σFР
(30)
где YF – коэффициент формы зубьев;
KF – коэффициент нагрузки;
Ft – окружная сила, Н;
b – ширина венца зубчатого колеса, мм;
mn – нормальный модуль, мм;
σFP – допускаемое напряжение при расчете на выносливость зубьев при изгибе, Мпа.
(σFP =110 Мпа).
Коэффициент нагрузки определяем по формуле
KF = KF β · KFυ (31)
где KF β – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (KF β = 1,04 по [3, табл. П25]);
KFυ – коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении; для прямозубых колес (KFυ = 1,26 по [3, табл.П26];
Следовательно, подставляем коэффициенты KFυ , KFβ в формулу (31) и находим коэффициент нагрузки
KF = 1,04 · 1,26= 1,31.
Согласно рекомендациям [3, с. 110], вычисляем эквивалентные числа зубьев шестерни и колеса по формуле
zυ = z/cos3 β, (32)
где z – число зубьев шестерни (z1 ) или колеса (z2 );
β – угол наклона линии зуба.
Тогда по формуле (34) получаем
z′ υ = 46/cos3 (0) = 46;
z′′ υ = 74/ cos3 (0) = 74.
Согласно рекомендациям [3, табл. П27], интерполируя, определяем коэффициент формы зуба шестерни Y′ F = 3,52 при z′ υ = 46 и колеса Y′′ F = 3,72
при z′′ υ = 74.
Сравнительная оценка прочности зуба шестерни и колеса при изгибе:
σ′ FP /Y′ F = 130/3,52 = 36,9 МПа,
σ′′ FP / Y′′ F = 110/3,72 = 29,56 МПа.
Прочность зубьев колеса оказалась ниже, чем зубьев шестерни, поэтому проверку на выносливость по напряжениям изгиба следует выполнить для зубьев колеса.
По формуле (30) проверяем выносливость зубьев при изгибе:
σF
= ![]() =
= ![]() 108 МПа < σFP
= 110 МПа.
108 МПа < σFP
= 110 МПа.
2.6 Ориентировочный расчет валов
Диаметр выходного конца вала определим грубо приближенно (ориентировочный расчет) из расчета на прочность при кручении по заниженным допускаемым касательным напряжениям: [τК ] = 20…40 МПа. Согласно рекомендациям [3, с. 307], принимаем [τК ]' = 25 МПа для стали 45 (при df 1 = 65,25мм целесообразно изготовить быстроходный вал вместе с шестерней) и [τК ]'' = 20 МПа для стали 35, которую назначаем для изготовления тихоходного вала.
1. Согласно рекомендациям [3, с. 194], для ведущего (быстроходного) вала редуктора уравнение прочности записывается в виде
τК = Т/WР < [τК ]' , (33)
где Т – крутящий момент на быстроходном валу, Н∙м;
WР – полярный момент сопротивления круглого сечения вала, м3 ;
[τК ]' - допускаемое напряжение на кручение для валов из углеродистой стали, МПа.
Полярный момент сопротивления круглого сечения вала определяется по формуле
WР = π d3 /16, (34)
где d – диаметр вала, мм.
Следовательно, уравнение прочности (33) имеет вид
τК = Т/WР = 16 Т1 /( π d3 ) < [τК ]' . (35)
Тогда для быстроходного вала редуктора при [τК ]' = 25 МПа из уравнения прочности (35) получаем
![]() d =
d =  2,04∙10-2 м.
2,04∙10-2 м.
Согласно рекомендациям [3, с. 196], в соответствии с рядом Rα 40 (СТ СЭВ 514 – 77) принимаем dВ1 = 24 мм.
Назначаем посадочные размеры под уплотнения и подшипники. Принимаем диаметр вала под манжетное уплотнение d1 ' = 28 мм (необходимо оставить высоту буртика примерно в 1…3 мм для упора торца втулки полумуфты); диаметр вала под подшипник d1 '' = 30 мм.
Диаметр d1 ''' примем равным 38 мм, чтобы обеспечить высоту упорного буртика 4,5 мм для посадки ориентировочно назначаемого конического роликоподшипника средней серии. Так как диаметр впадин шестерни df 1 = 65,25 мм незначительно превышает диаметр вала под подшипник d1 '' = 30 мм, то, как уже и указывалось, шестерню целесообразно изготовить заодно с валом.
2. Для ведомого вала редуктора при Т2 = iT1 = 1,6 · 41,8 = 66,8 Н∙м без учета КПД передачи определяем диаметр вала по формуле
d =  , (36)
, (36)
где Т2 – крутящий момент на тихоходном валу, Н∙м;
[τК ]′′ – допускаемое напряжение на кручение для валов из углеродистой стали, МПа ([τК ]′′ = 20 МПа).
Тогда для тихоходного вала редуктора при [τК ]'' = 20 МПа из формулы (36)
получаем
d = ![]() 2,57∙10-2 м.
2,57∙10-2 м.
Согласно рекомендациям [3, с. 196], в соответствии с рядом Rα 40 (СТ СЭВ 514 – 77) принимаем диаметр вала dВ2 = 28 мм; диаметр вала под уплотнение d2 ' = 32 мм; диаметр вала под подшипник d2 '' = 35 мм, диаметр вала под посадку ступицы зубчатого колеса d2 ''' = 38 мм.
3. Конструктивные размеры зубчатого колеса. Диаметр ступицы определяем по формуле
d2 '''' = (1,5…1,7) d2 ''' , (37)
где d2 ''' – диаметр вала под посадку ступицы зубчатого колеса, мм.
Тогда диаметр ступицы по формуле (37) равен:
d2 '''' = (1,5…1,7) ∙38= 57…64,6 мм,
принимаем диаметр ступицы d2 '''' = 60 мм.
Длина ступицы, согласно рекомендациям [3, с.307], определяется по формуле
lСТ = (0,7…1,8) d2 ''' , (38)
где d2 ''' – диаметр вала под посадку ступицы зубчатого колеса, мм.
Тогда по формуле (38) получаем
lСТ = (0,7…1,8) ∙38 = 26,6…68,4 мм,
принимаем длину ступицы lСТ = 36 мм.
Толщина обода определяется по формуле
δО = (2,5…4)mn , (39)
где mn – нормальный модуль, мм.
Тогда толщина обода
δО = (2,5…4) ∙1,5 = 3,75…6 мм,
принимаем толщину обода δО = 4 мм.
Колесо изготовляем из поковки, конструкция дисковая. Толщина диска определяется по формуле
е = (0,2…0,3)b2 , (40)
где b2 – ширина венца зубчатого колеса, мм.
Тогда толщина диска
е = (0,2…0,3) ∙36 = 7,2…10,8 мм,
принимаем е = 9 мм.
Согласно рекомендациям [3, с.308], диаметр отверстий в диске назначается конструктивно, но не менее 15…20 мм.
2.7 Конструктивные размеры элементов корпуса и крышки редуктора
Корпус и крышку редуктора изготовим литьем из серого чугуна.
1. Толщина стенки корпуса, согласно рекомендациям [3, с.308], определяется по формуле
δ = 0,025 aw + 1…5 мм, (41)
где aw – межосевое расстояние, мм.
Тогда толщина стенки корпуса
δ = 0,025 aw + 1…5 мм = 0,025∙90 + 1…5 мм = 3,25…7,25 мм,
принимаем толщину стенки δ = 6 мм.
2.Согласно рекомендациям [3, с.308], толщина стенки крышки корпуса редуктора, определяется по формуле
δ1 = 0,02 aw + 1…5 мм, (42)
где aw – межосевое расстояние, мм.
Тогда толщина стенки крышки корпуса по формуле (42)
δ1 = 0,02 aw + 1…5 мм = 0,02∙90 + 1…5 мм = 2,8…6,8 мм,
принимаем толщину стенки крышки редуктора δ 1 = 5 мм.
3. Толщина верхнего пояса корпуса редуктора определяется по формуле
s = 1,5 δ, (43)
где δ – толщина стенки корпуса, мм.
Тогда
s = 1,5 δ = 1,5 ∙ 6 = 9 мм.
Принимаем s = 9 мм.
4. Толщина пояса крышки редуктора, согласно рекомендациям [3, с.308], определяется по формуле
s1 = 1,5 δ1 , (44)
где δ 1 - толщина стенки крышки корпуса, мм.
Тогда
s1 = 1,5 δ1 = 1,5 ∙ 5 = 7,5 мм.
Принимаем s1 = 7 мм.
5. Согласно рекомендациям [3, с. 308], толщина нижнего пояса корпуса
редуктора определяется по формуле
t = (2…2,5) δ , (45)
где δ - толщина стенки корпуса, мм.
Тогда
t = (2…2,5) δ = (2…2,5) ∙ 6 = 12…15 мм.
Принимаем t = 14мм.
6. Согласно рекомендациям [3, с.308], толщина ребер жесткости корпуса редуктора, определяется по формуле
С = 0,85 δ, (46)
где δ – толщина стенки корпуса, мм.
Тогда
С = 0,85 δ = 0,85 ∙ 6 = 5,1 мм.
Принимаем С = 5 мм.
7. Диаметр фундаментальных болтов, согласно рекомендациям [3, с.308], определяется по формуле
dФ = (1,5…2,5)δ, (47)
где δ - толщина стенки корпуса, мм.
Тогда
dФ = (1,5…2,5)δ = (1,5…2,5) ∙ 6 = 9…15 мм.
Принимаем dФ = 12 мм.
8. Ширина нижнего пояса корпуса редуктора (ширина фланца для крепления редуктора к фундаменту), согласно рекомендациям [3, с.308], определяется по формуле
К2 = 2,1 dФ , (48)
где dФ – диаметр фундаментных болтов, мм.
Тогда
К2 = 2,1 dФ = 2,1· 12 = 25,2 мм.
Принимаем К2 = 25 мм.
9. Диаметр болтов, соединяющих корпус с крышкой редуктора, определяется по формуле
dК = (0,5…0,6) dФ , (49)
где dФ – диаметр фундаментных болтов, мм.
Тогда
dК = (0,5…0,6) dФ = (0,5…0,6) ∙ 12 = 6…7,2 мм.
Принимаем dК = 6 мм.
10. Ширина пояса (ширина фланца) соединения корпуса и крышки редуктора около подшипников определяется по формуле
К = 3 dК , (50)
где dК – диаметр болтов, соединяющих корпус с крышкой редуктора, мм.
Тогда
К = 3 dК = 3 ∙ 6 = 18 мм.
Принимаем К = 18 мм.
Ширину пояса К1 , согласно рекомендациям [3, с.309], назначаем на 2…8 мм меньше К, принимаем К1 = 13 мм.
11. Диаметр болтов, соединяющих крышку и корпус редуктора около подшипников, определяется по формуле
dК.П = 0,75 dФ , (51)
где dФ – диаметр фундаментных болтов, мм.
Тогда
dК.П = 0,75 dФ = 0,75 ∙12 = 9 мм.
Принимаем dК.П = 8 мм.
12. Диаметр болтов для крепления крышек подшипников к редуктору, согласно рекомендациям [2, с.309], определяется по формуле
dП = (0,7…1,4)δ, (52)
где δ - толщина стенки корпуса, мм.
Тогда
dП = (0,7…1,4) δ = (0,7…1,4) ∙ 6 = 4,2…8,4 мм.
Принимаем dП ' и dП '' = 6 мм для быстроходного и тихоходного валов.
13. Диаметр отжимных болтов принимаем из диапазона 8…16 мм (d = 8).
14. Диаметр болтов для крепления крышки смотрового отверстия dК.С , согласно рекомендациям [3, с.309], принимается от 6 до 10 мм. Принимаем dК.С = 8 мм.
15. Диаметр резьбы пробки (для слива масла из корпуса редуктора), согласно рекомендациям [3, с.309], определяется по формуле
dП. Р = (1,6…2,2) δ, (53)
где δ - толщина стенки корпуса, мм.
Тогда по формуле (53) получаем
dП. Р = (1,6…2,2) δ = (1,6…2,2) · 6 = 9,6…13,2 мм.
Принимаем dП. Р = 12 мм.
2.8 Конструктивные размеры валов, подшипниковых узлов
1. Зазор между внутренней боковой стенкой корпуса и торцом шестерни определяется из соотношения
y = (0,5…1,5) δ, (54)
где δ - толщина стенки корпуса, мм.
Тогда по формуле (54) получаем
y = (0,5…1,5) ∙ 6 = 3…9 мм.
Принимаем y = 6 мм.
Так как lСТ < b1 , то размер y берем от торца шестерни.
2. Расстояние между внутренней стенкой корпуса редуктора и окружностью вершин зубьев колеса и шестерни определяется из соотношения
y1 = (1,5…3) δ, (55)
где δ - толщина стенки корпуса, мм.
Тогда по формуле (55) получаем
y1 = (1,5…3) ∙ 6 = 9…18 мм.
Принимаем y1 = 14 мм.
Для обеспечения достаточной вместимости масляной ванны картера редуктора расстояние от окружности dа2 до внутренней стенки картера ориентировочно назначаем из соотношения
y1 ' = (3…4) δ, (56)
где δ - толщина стенки корпуса, мм.
Тогда по формуле (56) получаем
y1 ' = (3…4) · 6 = 18…24 мм.
Принимаем y1 ' = 21 мм.
3. Длины выходных концов быстроходного l1 и тихоходного l2 валов определяются из соотношения
l = (1,5…2) dВ , (57)
где dВ – диаметр вала, мм.
Тогда длина выходного конца быстроходного вала
l1 = (1,5…2) ∙ 24 = 36…48 мм.
Принимаем . l1 = 42 мм.
Длина выходного конца тихоходного вала
l2 = (1,5…2) ∙ 28 = 42…56 мм.
Принимаем . l2 = 48 мм.
4. Назначаем тип подшипников качения для быстроходного и тихоходного валов и определяем конструктивные размеры подшипниковых узлов.
Предварительно назначаем родиальные роликоподшипники воспринемающие только радиальную нагрузку .
При значительной разнице диаметров посадочных участков валов под подшипники (d1 '' = 30 мм, а d2 '' = 35 мм) следует ожидать , что для тихоходного вала подойдет более легкая серия подшипника, чем для быстроходного. Здесь типоразмеры подшипников намечаем ориентировочно для возможности компоновки редуктора; в дальнейшем при подборе подшипников по динамической грузоподъемности их параметры будут уточнены.
Ориентируясь на среднюю серию подшипника для быстроходного и легкую серию для тихоходного валов, согласно рекомендациям [3, табл. П41], получаем:
d= d1 ′′ = 30 мм, Т′ max = 19 мм, D1 = 72 мм;
d= d2 ′′ = 35 мм, Т′′ max = 17 мм, D2 = 72 мм.
Размер Х определяется по формуле
Х = 2 dП , (58)
где dП – диаметр болтов для крепления крышек подшипников к редуктору, мм.
Тогда для быстроходного вала
Х' = 2 dП ' = 2 ∙ 6=12 мм.
Для тихоходного вала
Х'' = 2 dП ′′ = 2 ∙6 =10 мм.
Размеры l1 ' и l2 ' определяем по формуле
l = 1,5Тmax , (59)
где Тmax – ширина подшипника, мм.
Тогда по формуле (59) получаем
l1 ' = 1,5 Т′ max = 1,5 ∙ 19 = 28,5 мм,
l2 ' = 1,5 Т′′ max = 1,5 ∙ 17 = 25,5 мм.
Принимаем l1 ' = 28 мм, l2 ' = 25 мм.
Расстояние от торца подшипника быстроходного вала до торца шестерни l1 '' = 8…18 мм, принимаем l1 '' = 12 мм. Размер l1 ''' = 8…18 мм, принимаем l1 ''' = 12 мм.
Осевой размер глухой крышки подшипника тихоходного вала l2 '' = 8…25 мм, принимаем l2 '' = 15 мм.
5. Определяем расстояния a1 и a2 по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно примем на уровне внутренних торцов подшипников в точках А и В оси вала.
Для тихоходного вала расстояние a2 определяется по формуле
a2 = y + 0,5lСТ , (60)
где y – зазор между внутренней боковой стенкой корпуса и торцом шестерни, мм;
lСТ – длина ступицы, мм.
Тогда по формуле (60) получаем
a2 = 6 + 0,5 ∙ 36 = 24 мм.
Принимаем a2 = 25 мм.
Для быстроходного вала расстояние a1 определяется по формуле
а1 = l1 '' + 0,5b1 , (61)
где l1 '' – расстояние от торца подшипника быстроходного вала до торца шестерни, мм;
b1 – ширина венца шестерни, мм.
Тогда по формуле (61) получаем
а1 = 12 + 0,5 ∙ 39 = 31,5 мм.
Принимаем a1 = 32 мм.
6. Определяем габаритные размеры редуктора. Ширину редуктора определяем по формуле
ВР = l2 + l2 ' + Т′′ max + y + lСТ + y+ l1 '' + Т′ max +l1 ' + l1 , (62)
где l2 – длина выходного конца тихоходного вала, мм;
где Т′′ max – ширина подшипника тихоходного вала, мм;
Т′ max – ширина подшипника быстроходного вала, мм;
y – зазор между внутренней боковой стенкой корпуса и торцом шестерни, мм;
lСТ – длина ступицы, мм;
l1 '' – расстояние от торца подшипника до торца шестерни, мм;
l1 – длина выходного конца быстроходного вала, мм.
Тогда по формуле (62) получаем
ВР = 48+25+17+6+36+6+12+19+28+42=239 мм.
Принимаем ширину редуктора ВР = 240 мм.
Длину редуктора определяем по формуле
LР = К1 + δ + y1 + 0,5 dа2 + aw + 0,5 dа1 + y1 + δ + К1 , (63)
где К1 – ширина пояса, мм;
δ – толщина стенки корпуса, мм;
y1 – расстояние между внутренней стенкой корпуса редуктора и окружностью вершин зубьев колеса и шестерни, мм;
dа1 , dа2 – диаметры вершин зубьев шестерни и зубчатого колеса, мм;
aw – межосевое расстояние, мм.
Тогда по формуле (63) получаем
LР = 2∙ (13 + 6 + 14) + 0,5∙ (114 + 72) + 90 = 249 мм.
Принимаем длину редуктора LР = 250мм.
Высоту редуктора определяем по формуле
НР = δ1 + y1 + dа1 + dа2 + y1 1 + t, (64)
где δ1 – толщина стенки крышки корпуса редуктора, мм;
y1 – расстояние между внутренней стенкой корпуса редуктора и окружностью вершин зубьев колеса и шестерни, мм;
dа1 – диаметр вершин зубьев шестерни колеса, мм;
dа2 – диаметр вершин зубьев зубчатого колеса, мм;
y1 1 – расстояние от окружности dа2 до внутренней стенки картера, мм;
t – толщина нижнего пояса корпуса редуктора, мм.
Тогда по формуле (64) получаем
НР = 5 + 14 + 72+114 + 21 + 14 = 240 мм.
Принимаем высоту редуктора НР = 240 мм.
2.9 Первый этап эскизной компоновки редуктора
Этот этап эскизной компоновки имеет целью установить приближенно положение зубчатых колес относительно опор, чтобы иметь возможность определить опорные реакции и подобрать подшипники.
Эскизную компоновку ведем на одной проекции – разрезе по осям валов (в масштабе 1: 1).
Порядок вычерчивания (рис. П. 1.1).
1. Посередине листа проводим горизонтальную осевую линию – ось симметрии редуктора, затем две вертикальные осевые линии, соответствующие осям валов на расстоянии аw = 90 мм.
2. Вычерчиваем без разреза шестерню и зубчатое колесо вместе со ступицей.
3. Очерчиваем внутреннюю стенку корпуса; при этом принимаем:
а) зазор между торцом и внутренней стенкой корпуса y = 6 мм;
б) расстояние между внутренней стенкой корпуса и окружностью вершин зубьев колеса и шестерни y1 = 14 мм.
4. Размещаем подшипники валов, нанося на чертеж их габариты.
2.10 Проверка прочности валов
Прочность валов проверим по гипотезе наибольших касательных напряжений.
Быстроходный (ведущий) вал.
1.Так как быстроходный вал изготовляют вместе с шестерней, то его материал известен – сталь 45, для которой предел выносливости определяется по формуле
σ-1 = 0,43σВ , (65)
σВ – предел прочности, МПа. Согласно рекомендациям [3, табл. П3], предел прочности σВ = 700 МПа.
Тогда по формуле (65) предел выносливости
σ-1 = 0,43 ∙ 700 = 301 МПа.
2. Допускаемое напряжение изгиба при симметричном цикле напряжений, согласно рекомендациям [3, с. 195], определяется по формуле
[σИ ]-1 = [σ-1 /([n]Kσ ] kРИ , (66)
где σ-1 – предел выносливости, МПа;
n – коэффициент запаса прочности (n = 2,2 по [3,с.195]);
Kσ – эффективный коэффициент концентрации напряжений (Kσ = 2,2 по [3, с. 310]); kРИ – коэффициент режима нагрузки при расчете на изгиб (kРИ = 1 по [3, с. 195]).
Тогда по формуле (66) получаем
[σИ ]-1 = [σИ ]-1 = [301 / (2,2 ∙ 2,2)] ∙1 = 62,1 МПа.
3. Вычерчиваем схему нагружения вала и строим эпюры изгибающих и крутящих моментов (рис 2):
а) определяем реакции опор в вертикальной плоскости zOyот сил Fr и Fа
∑МА = – Fr a1 – Fa ∙0,5∙d1 + YB ·2 a1 = 0, (67)
a1 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Fr – радиальная сила, сжимающая зуб, Н;
Fa – осевая сила, Н
d1 –делительный диаметр шестерни,мм.
Выразив из уравнения (67) YB получим
YB
= ![]() (68)
(68)
Подставив значения в уравнение (68) получим
YB
= ![]() = 200 Н.
= 200 Н.
∑МВ = – YА ·2 a1 – Fa 0,5d1 + Fr a1 = 0, (69)
где a1 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Fr – радиальная сила, сжимающая зуб, Н;
Fa – осевая сила, Н.
Выразив из уравнения (69) YА получим
YА
= ![]() (70)
(70)

Рис. 2.
Подставив значения в уравнение (70) получим
YА
=![]() = 200-0 = 200 Н.
= 200-0 = 200 Н.
б) определяем реакции опор в горизонтальной плоскости xOy от силы Ft :
∑МА = – Ft a1 + ХB ·2 a1 = 0 (71)
где a1 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала,
Ft – окружная сила, изгибающая зуб, Н.
Выразив из уравнения (71) ХВ получим
ХВ
= ![]() =
=![]() (72)
(72)
Подставив известные величины в уравнение (72) получим
ХВ = 1,2·103 /2 = 600 Н,
ХА = ХВ =600 Н;
в) для построения эпюр определяем размер изгибающих моментов в характерных точках (сечениях) А, С и В;
в плоскости yOz
МА = МВ = 0; (73)
МС ЛЕВ = YА · a1 , (74)
МС ПРАВ = YВ · a1 , (75)
где a1 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентироыочно приняты на уровне внутренних торцов подшипников в точках А и
В оси вала;
YА , YВ – опорные реакции, Н.
Тогда по формуле (74) имеем
МС ЛЕВ = 200 ∙ 0,032 = 6,4 Н ∙ м;
Тогда по формуле (75)
МС ПРАВ = YВ · a1 = 200 · 0,032= 6,4 Н ∙ м;
(МFrFa )max = 6,4 Н ∙ м;
в плоскости хOz
МА = МВ = 0; (76)
МС = ХА · a1 , (77)
где a1 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
ХА – опорная реакция, Н.
Тогда по формуле (77) получаем
МС = 600 · 0,032= 19,2 Н ∙ м;
МFt = 19,2 Н ∙ м;
г) крутящий момент
Т = Т1 = 41,8 Н ∙ м;
д) выбираем коэффициент масштаба и строим эпюры (рис.2).
4. Вычисляем наибольшие напряжения изгиба и кручения для опасного сечения С. Суммарный изгибающий момент по [3, с. 311], определяется по формуле
МИ
= ![]() , (78)
, (78)
где МFr и MFt – изгибающие моменты, Н ∙ м.
Тогда
МИ
= ![]() = 20,2 Н∙м.
= 20,2 Н∙м.
Напряжение изгиба по [3, с. 311], определяется по формуле
σИ = МИ /WX = 32 МИ /(πdf 1 3 ), (79)
где МИ – суммарный изгибающий момент, Н∙м;
WX – осевой момент сопротивления круглого сечения вала, м3 ;
WX = πdf 1 3 /32, (80)
df 1 – диаметр впадин шестерни, мм.
Подставив известные величины в формулы (79) и (80) получим
σИ = 32 МИ /(πdf 1 3 ) = 32·20,2 / (3,14· (65,25·10-3 )3 ) = 0,74·106 Па.
Допускаемое касательное напряжение на кручение определяется по формуле
τК = Т/ WР , (81)
где Т – крутящий момент, Н∙м;
WР – полярный момент сопротивления круглого сечения вала, м3 ;
WР = πdf 1 3 /16 (82)
df 1 – диаметр впадин шестерни, мм.
Подставив известные величины в формулы (81) и (82) получим
τК = 16·41,8 / (3,14· (65,25·10-3 )3 ) = 0,77·106 Па.
5. Согласно рекомендациям [3, с. 194], определяем эквивалентное напряжение по гипотезе наибольших касательных напряжений:
σЭ
= ![]() ≤ [σИ
]-1
, (83)
≤ [σИ
]-1
, (83)
где σИ – напряжение изгиба, Па;
τК – касательное напряжение на кручение, Па;
[σИ ]-1 – допускаемое напряжение, МПа.
Тогда
σЭ
= ![]() = 1,7 МПа,
= 1,7 МПа,
что значительно меньше [σИ ]-1 = 62,1 МПа.
Тихоходный вал.
1. Материал для изготовления тихоходного вала – сталь 35 , для которой по [3, табл. П3] при d < 100 мм предел прочности σВ = 510 МПа.
Предел выносливости, согласно рекомендациям [3, с.195] определяется по формуле
σ-1 = 0,43σВ , (84)
σВ – предел прочности, МПа.
Тогда по формуле (84) предел выносливости
σ-1 = 0,43 ∙510 = 219МПа.
2. Допускаемое напряжение изгиба при симметричном цикле напряжений, согласно рекомендациям [3, с. 195], определяется по формуле
[σИ ]-1 = [σ-1 / ([n]Kσ ] kРИ , (85)
где σ-1 – предел выносливости, МПа;
n – коэффициент запаса прочности (n = 2,2);
Kσ – эффективный коэффициент концентрации напряжений (Kσ = 2,2 по [3, с. 310]); kРИ – коэффициент режима нагрузки при расчете на изгиб (kРИ = 1 по [3, с. 310]).
Тогда по формуле (85) получаем
[σИ ]-1 = [219/(2,2 ∙ 2,2)] ∙1 = 45,25 МПа.
3. Вычерчиваем схему нагружения вала и строим эпюры изгибающих и крутящих моментов (рис. 3.):
а) определяем реакции опор в вертикальной плоскости yOzот сил Fr и Fа
∑МА = – Fr a2 – Fa 0,5d2 + YB ·2 a2 = 0, (86)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Fr – радиальная сила, сжимающая зуб, Н;
Fa – осевая сила, Н.
Тогда из уравнения (86) следует, что
YB
= ![]() (87)
(87)
Подставив известные величины в формулу (87) получим
YB
= ![]() = 200 Н
= 200 Н
∑МВ = – YА ·2 a2 – Fa 0,5d2 + Fr a2 = 0, (88)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Fr – радиальная сила, сжимающая зуб, Н; Fa – осевая сила, Н.
Выразив из уравнения (88) YА получим
YА
= ![]() (89)
(89)
Подставив известные величины в формулу (89) получим
YА
= ![]() = 200 Н.
= 200 Н.
б) определяем реакции опор в горизонтальной плоскости xOz от силы Ft :

Рис. 3.
∑МА = – Ft a2 + ХB ·2 a2 = 0, (90)
a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
Ft – окружная сила, изгибающая зуб, Н.
Выразив из уравнения (90) ХВ получаем
ХВ = Ft a2 /2 a2 (91)
Подставив известные величины в формулу (91) получим
ХВ = 1200/2 = 600 Н,
ХА = ХВ = 600 Н;
в) для построения эпюр определяем размер изгибающих моментов в характерных точках (сечениях) А, С и В;
в плоскости yOz
МА = МВ = 0; (92)
МС ЛЕВ = YА · a2 , (93)
МС ПРАВ = YВ · a2 , (94)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
YА , YВ – опорные реакции, Н.
Тогда по формуле (93) получаем
МС ЛЕВ = 200 ∙ 0,024 = 4,8 Н ∙ м;
По формуле (94) имеем
МС ПРАВ = 200 · 0,024 = 4,8 Н ∙ м;
(МFrFa )max = 4,8 Н ∙ м;
в плоскости хOz
МА = МВ = 0; (95)
МС = ХА · a2 , (96)
где a2 – расстояние по длине оси вала от точки приложения сил, возникающих в зубчатом зацеплении, до точек приложения опорных реакций, которые ориентировочно приняты на уровне внутренних торцов подшипников в точках А и В оси вала;
ХА – опрная реакция, Н.
Тогда по формуле (96) получаем
МС = 600 · 0,024 = 14,4 Н ∙ м;
МFt = 14,4 Н ∙ м;
г) крутящий момент Т = Т2 = 66,8 Н∙м;
д) выбираем коэффициент масштаба и строим эпюры (рис. 3.).
4. Вычисляем наибольшие напряжения изгиба и кручения для опасного сечения С. Суммарный изгибающий момент, согласно рекомендациям [3, с. 311], определяется по формуле
МИ
= ![]() , (97)
, (97)
где МFrFa и MFt – изгибающие моменты, Н ∙ м.
Подставляем значения изгибающих моментов в формулу (97) получаем
МИ
= ![]() = 15,1Н∙м.
= 15,1Н∙м.
Диаметр вала в опасном сечении d2 ''' = 38 мм ослаблен шпоночной канавкой. Поэтому в расчет вводим значение d, меньшее на 8…10% d2 ''' . Принимаем расчетный диаметр вала в опасном сечении d = 35 мм.
Напряжение изгиба по [3, с. 311], определяется по формуле
σИ = МИ /WX (98)
где МИ – суммарный изгибающий момент, Н•м;
WX – осевой момент сопротивления круглого сечения вала, м3
WX - расчетный диаметр вала в сечении С, мм.
WX = πd3 /32, d(99)
Тогда подставляя значения суммарного изгибающего момента и расчетного диаметра вала в формулу (98) и (99) получаем
σИ = 32·15,1∙103 / (3,14∙ (35)3 ) = 3,58 МПа.
Допускаемое касательное напряжение на кручение определяется по формуле
τК = Т / WР , (100)
где Т – крутящий момент, Н∙м;
WР – полярный момент сопротивления круглого сечения вала, м3 ;
WР = πd3 /16 (101)
d – расчетный диаметр вала в сечении С, мм.
Тогда подставляя значения крутящего момента и расчетного диамера вала в формулы (100) и (101) получаем
τК = 16·66,8·103 / (3,14· (35)3 ) = 7,9 МПа.
5. Согласно рекомендациям [3, с. 194], определяем эквивалентное напряжение по гипотезе наибольших касательных напряжений и сравниваем его значение с допускаемым:
σЭ
= ![]() ≤ [σИ
]-1
, (102)
≤ [σИ
]-1
, (102)
где σИ – напряжение изгиба, Па;
τК – касательное напряжение на кручение, Па;
[σИ ]-1 – допускаемое напряжение, МПа.
Тогда по формуле (102) получаем
σЭ
= ![]() = 16,2 МПа,
= 16,2 МПа,
что значительно меньше [σИ ]-1 = 45,25 МПа.
2.11 Второй этап эскизной компоновки редуктора
Задача второго этапа компоновки – конструктивно оформить механизм редуктора (шестерню, зубчатое колесо, валы, корпус, подшипники) для последующей проверки прочности валов и других деталей (рис.П.1.2). Вычерчивание производится в одной проекции (разрез по осям валов при снятой крышке редуктора в масштабе 1:2).
1. Оформляем конструкции шестерни и зубчатого колеса (разрез) по конструктивным размерам, найденным ранее.
2. Разрабатываем конструкцию узла ведущего вала:
а) оставив неизменным зазор y = 6 мм между торцом шестерни и внутренней стенкой корпуса, очерчиваем часть этой стенки, разрывая ее в соответсвующих местах на величину, равную наружному диаметру подшипников;
б) вычерчиваем подшипники в разрезе. Для экономии времени в разрезе вычерчиваем одну половину подшипника, а для второй наносим лишь габариты;
в) далее вычерчиваем вал, крышки подшипников и т.д.
3. Разрабатываем конструкцию узла ведомого вала:
а) для фиксации зубчатого колеса от осевых перемещений предусматриваем утолщение вала с одной стороны и установку распорного кольца – с другой;
б) сохраняя намеченный в первом этапе компоновки зазор между торцом ступицы зубчатого колеса и внутренней стенкой корпуса, очерчиваем часть этой стенки, разрывая ее в соответсвующих местах на величину, равную наружному диаметру подшипников;
в) вычерчиваем вал, подшипники, крышки подшипников с болтами крепления крышек и.т.д.
2.12 Подбор шпонок и проверочный расчет шпоночных соединений
Шпонки подбираем по таблицам ГОСТа в зависимости от диаметра вала и проверяем расчетом соединения на смятие.
Быстроходный вал. Для консольной части вала при dВ1 = 24 мм по [3, табл. П49] подбираем призматическую шпонку b × h = 8 × 7 мм. Длину шпонки принимаем из ряда стандартных длин так, чтобы она была меньше длины посадочного места вала l1 = 42 мм на 3…10 мм и находилась в границах предельных размеров длин шпонок.
Согласно рекомендациям [3, с 312], принимаем l = 36 мм – длина шпонки со
скругленными торцами. Расчетная длина шпонки определяется по формуле
lР = l – b, (103)
где l – длина шпонки, мм;
b – ширина шпонки, мм.
Тогда по формуле (103) получаем
lР = 36 – 8 = 28 мм.
Допускаемые напряжения смятия в предположении посадки полумуфты, изготовленной из стали, [σСМ ] = 100…150 МПа.
Согласно рекомендациям [3, с. 234] вычисляем расчетное напряжение смятия по формуле
σСМ = 4,4Т1 /(dlР h), (104)
где Т1 – крутящий момент, Н∙м;
d – диаметр вала, мм;
lР – расчетная длина шпонки, мм;
h – высота шпонки, мм.
Тогда подставляя значения крутящего момента, диаметра вала, длины и высоты шпонки в формулу (104) получаем
σСМ = 4,4Т1 /(dlР h) = 4,4·41,8 / (24·28·7·10 –9 ) = 39 МПа < [σСМ ].
Итак, принимаем шпонку 8×7×36 (СТ СЭВ 189 – 75).
Тихоходный вал. 1.Для выходного конца вала при dВ2 = 28 мм по [3, табл. П49] подбираем призматическую шпонку b × h = 8 × 7 мм. Длину шпонки принимаем из ряда стандартных длин так, чтобы она была меньше длины посадочного места вала l2 =48 мм на 3…10 мм и находилась в границах предельных размеров длин шпонок.
Согласно рекомендациям [3, с 312], принимаем l = 40 мм – длина шпонки со скругленными торцами. Расчетная длина шпонки определяется по формуле (103)
lР = 40 – 8 = 32 мм.
Допускаемые напряжения смятия в предположении посадки полумуфты, изготовленной из стали, [σСМ ] = 100…150 МПа.
Согласно рекомендациям [3, с. 234] вычисляем расчетное напряжение смятия по формуле
σСМ = 4,4Т2 /(dlР h), (105)
где Т2 – крутящий момент, Н∙м;
d – диаметр вала, мм;
lР – расчетная длина шпонки, мм;
h – высота шпонки, мм.
Тогда по формуле (108) имеем
σСМ = 4,4·66,8 / (28·32·7·10 –9 ) = 46,8 МПа < [σСМ ].
Принимаем шпонку 8×7×40 (СТ СЭВ 189 – 75).
2. Для вала под ступицу зубчатого колеса при d2 ''' = 38 мм по [3, табл. П49] подбираем призматическую шпонку b × h = 10 × 8 мм. Так как lСТ = 36 мм, то принимаем длину призматической шпонки l = 30 мм со скругленными торцами. Расчетная длина шпонки определяется по формуле (103)
lР = 30 – 10 = 20 мм.
Допускаемые напряжения смятия в предположении посадки полумуфты, изготовленной из стали, [σСМ ] = 100…150 МПа. Согласно рекомендациям [3, с. 234] вычисляем расчетное напряжение смятия по формуле (105)
σСМ = 4,4Т2 /( d2 ''' lР h) d2 ''' = 4,4·66,8 / (38·20·8·10 –9 ) = 48,3 МПа < [σСМ ].
Под ступицу колеса принимаем шпонку 10×8×30 (СТ СЭВ 189 – 75).
2.13 Подбор подшипников
Подшипники качения подбираем по таблицам ГОСТа в зависимости от размера и направления действующих на подшипник нагрузок; диаметра цапфы, на которую насаживается подшипник; характера нагрузки; угловой скорости вращающегося кольца подшипника; желательного срока службы подшипника и его наименьшей стоимости.
Быстроходный (ведущий) вал.
1 Определяем нагрузки, действующие на подшипники:
осевая сила
Fa = 0 Н;
определяем результирующие радиальные реакции подшипников, согласно рекомендациям [3, с. 313], по формулам
FrA
= ![]() , (106)
, (106)
Fr
В
= ![]() , (107)
, (107)
где XA и YA – опорные реакции, Н.
Тогда по формулам (106) и (107) получаем
FrA
= ![]() = 632 Н.
= 632 Н.
Fr
В
= ![]() = 632Н.
= 632Н.
2. Выбираем тип подшипников. Так как у нас отсутсвует осевая сила Fa ,а присутствует только радиальная, то следует применить родиальные роликоподшипники с кароткими цилиндрическими роликами [3, с. 208].
3. Согласно рекомендациям [3, с. 313], вычисляем требуемую динамическую грузоподъемность подшипника по формуле
СТР = (XVFr )Kб KT (6·10 –5 nLh )1/ α , (108)
где X, Y – коэффициенты радиальной и осевой нагрузок соответственно;
Fr – фактическая радиальная нагрузка подшипника, Н;
Fа – осевая нагрузка подшипника, Н;
V – коэффициент вращения;
Kб – коэффициент безопасности, зависящий от типа механизма, в котором подшипник установлен;
KT – температурный коэффициент;
n – частота вращения, мин -1 ;
Lh – требуемая долговечность подшипника, ч;
α – величина, зависящая от формы кривой контактной усталости.
Принимаем: V = 1 по [3, табл. П45]; Kб = 1,2 по [3, табл. П46]; KT = 1 по [3, табл. П47]; согласно рекомендациям [3, с. 213], коэффициент радиальной нагрузки X = 1; для роликовых подшипников по [3, с. 214] α = 10/3; требуемая долговечность подшипников Lh = 20000 ч.
По формуле (108) вычисляем динамическую грузоподъемность подшипника:
СТР = (1·1·632)·1,2·1·(6·10-5 ·960·20·103 )0,3 = = 6285,4 Н = 6,3 кН.
Согласно рекомендациям [3, табл. П41], окончательно принимаем роликоподшипник 2206 легкой серии для которого d = 30 мм, D = 62, Тmax = 16 мм,
С = 16,9 кН., что >> СТР требуемой.
Тихоходный (ведомый) вал.
1 Определяем нагрузки, действующие на подшипники:
осевая сила
Fa = 0 Н;
определяем результирующие радиальные реакции подшипников, согласно рекомендациям [3, с. 313], по формулам (106) и (107)
FrA
= ![]() = 632 Н.
= 632 Н.
Fr
В
= ![]() = 632 Н
= 632 Н
2. Выбираем тип подшипников. Так как у нас отсутсвует осевая сила Fa ,а присутствует только радиальная, то следует применить родиальные роликоподшипники с кароткими цылиндрическими роликами [3, с. 208].
3. Согласно рекомендациям [3, с. 313], вычисляем требуемую динамическую грузоподъемность подшипника по формуле (108).
Принимаем: V = 1 по [3, табл. П45]; Kб = 1,2 по [3, табл. П46]; KT = 1 по [3, табл. П47]; согласно рекомендациям [3, с. 213], коэффициент радиальной нагрузки X = 1; для роликовых подшипников по [3, с. 214] α = 10/3; требуемая долговечность подшипников Lh = 20000 ч.
По формуле (108) вычисляем динамическую грузоподъемность подшипника:
СТР = (1·1·632)·1,2·1·(6·10-5 ·600·20·103 )0,3 = 15458,8 Н =5,4 кН.
Согласно рекомендациям [3, табл. П41], принимаем конический роликоподшипник 2207 легкой серии для которого d = 35 мм, D = 72, Тmax = 17 мм, С = 25 кН. ,что>> СТР требуемой.
2.14 Уточненный расчет валов
Определение коэффициентов запаса прочности производим для особо опасных сечений каждого из валов, принимая при этом, что нормальные напряжения изменяются по симметричному циклу, а касательные по пульсирующему.
Ведущий вал
Так как быстроходный вал изготовляют вместе с шестерней, то его материал известен – сталь 45, для которой предел выносливости σ-1 = 301 МПа.
Определяем предел выносливости при симметричном цикле кручения по формуле
τ-1 = 0,58 σ-1 , (109)
где σ -1 – предел выносливости, МПа.
Тогда подставляя значение предела выносливости в формулу (109) получаем
τ-1 = 0,58∙301 = 174,158МПа.
1. Рассмотрим сечение в точке А (рис.2). Считаем, что эта часть вала при передаче вращающего момента через муфту от электродвигателя работает только на кручение. Концентрацию напряжений вызывает наличие шпоночной канавки.
Коэффициент запаса прочности по касательным напряжениям определяется по формуле
n = nτ
=  , (110)
, (110)
где τ-1 – предел выносливости при симметричном цикле кручения, МПа;
τυ и τm – амплитуда и среднее напряжение цикла касательных напряжений;
ψτ – коэффициент, отражающий соотношения пределов выносливости при пульсирующем цикле кручения [ 2, с. 166];
κτ – коэффициент концентрации напряжения кручения [2,табл.8.5];
ετ – масштабный фактор для нормальных и касательных напряжений [2, табл. 8.1].
Амплитуда и среднее напряжение цикла касательных напряжений определяются по формуле
τυ = τm = Т1 / 2Wк нетто , (111)
где Т1 – крутящий момент, Н∙м;
Wк нетто – момент сопротивления кручению по сечению нетто, м3 .
Момент сопротивления кручению по сечению нетто определяется по формуле
Wк нетто
= ![]() , (112)
, (112)
где b – ширина шпоночной канавки, мм;
d – диаметр вала, мм;
t – глубина шпоночной канавки в ведущем вале, мм.
Тогда подставляя значения ширины, высоты шпоночной канавки и значение диаметра вала в формулу (112) получаем
Wк нетто
= ![]() = 2,3·10 –6
м3
.
= 2,3·10 –6
м3
.
По формуле (111) определяем амплитуду и среднее напряжение цикла касательных напряжений
τυ = 41,8/(2·2,3·10-6 ) = 9,1 МПа.
Согласно рекомендациям [2, с.345], принимаем коэффициенты снижения пределов выносливости: ψτ = 0,1 по [2, с. 158]; ετ = 0,88 по [2, табл. 8.1]; κτ = 1,6 по [2, табл. 8.5].
Тогда по формуле (110) определяем коэффициент запаса прочности
n = nτ
= 
Ведомый вал.
Материал для изготовления тихоходного вала – сталь 35 , для которой предел выносливости σ-1 = 219МПа. Определяем предел выносливости при симметричном цикле кручения по формуле (109)
τ-1 = 0,58 σ-1 = 0,58·219 = 127 МПа.
Рассмотрим сечение в точке А (рис.3). В этом сечении возникает наибольший изгибающий момент. Концентрация напряжений в данном сечении обусловлена наличием шпоночной канавки.
1. Суммарный изгибающий момент МИ = 15,1 Н·м.
2. Определяем момент сопротивления сечения нетто по формуле
Wнетто
= ![]() , (113)
, (113)
где b – ширина шпонки, мм;
d – диаметр вала, мм;
t – глубина шпоночной канавки, мм.
Тогда по формуле (113) получаем
Wнетто
= ![]() 1,8·10-6 м3
.
1,8·10-6 м3
.
3. Амплитуда номинальных напряжений изгиба определяется по формуле
συ = σmax = МИ / Wнетто , (114)
где МИ – суммарный изгибающий момент, Н∙м; Wнетто – момент сопротивления сечения нетто, м3 .
Тогда по формуле (114) получаем
συ = 15,1/1,8·10-6 = 8,39 МПа.
4. По формуле (111) определяем амплитуду и среднее напряжение цикла касательных напряжений
τυ = τm = Т2 / 2Wк нетто = 66,8/(2·1,8·10-6 ) = 18,5 МПа.
5. Согласно рекомендациям [2, с.158], принимаем коэффициенты снижения пределов выносливости: ψτ = 0,1 по [2, с. 158]; εσ = 0,86 по [2, табл. 8.1]; κσ = 1,51 по [2, табл. 8.5].
6. Определяем коэффициент запаса прочности по нормальным напряжениям по формуле
nσ
=  , (115)
, (115)
где σ-1 – предел выносливости, МПа;
τυ и τm – амплитуда и среднее напряжение цикла касательных напряжений;
ψτ – коэффициент, отражающий соотношения пределов выносливости при пульсирующем цикле кручения [2, с.158];
κτ – коэффициент концентрации напряжения кручения [2, табл. 8.5];
ετ – масштабный фактор для нормальных и касательных напряжений [2, табл. 8.1].
nσ
= 
7. Коэффициент запаса прочности по касательным напряжениям определяется по формуле (110)
n = nτ
= 
8. Общий коэффициент запаса прочности определяется по формуле
n= 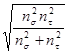 , (116)
, (116)
где nσ – коэффициент запаса прочности по нормальным напряжениям;
nτ –коэффициент запаса прочности по касательным напряжениям.
Тогда по формуле (116) определяем общий коэффициент запаса прочности
n = =
= ![]() = 3,3.
= 3,3.
Сечение в точке Б (рис.3). Считаем, что эта часть ведомого вала при передаче вращающего момента от редуктора через муфту работает только на кручение. Концентрацию напряжений вызывает наличие шпоночной канавки.
1. Момент сопротивления кручению по сечению нетто определяется по формуле (112)
Wк нетто
= ![]() = 4·10-6 м3
= 4·10-6 м3
2. По формуле (111) определяем амплитуду и среднее напряжение цикла касательных напряжений
τυ = τm = 66,8/(2·4·10-6 ) = 8,3 МПа.
3.Согласно рекомендациям [2, с.158], принимаем коэффициенты снижения пределов выносливости: ψτ = 0,1 по [2, с. 167]; ετ = 0,86 по [2, табл. 8.1]; κτ =1,51 по [2, табл. 8.5].
4. Коэффициент запаса прочности по касательным напряжениям определяется по формуле (110)
2.15 Определение массы редуктора
Согласно рекомендациям [1, с.262], масса редуктора вычисляется по формуле:
m=jrV·10-9 (117)
где j - коэффициент заполнения редуктора, согласно рекомендациям [1, с.263]
j=0,46;
r=7300 кг/м3 - плотность чугуна;
V – условный обьем редуктора, определяемый по формуле:
V=LBH (118)
Подставив известные величины в формулу (118) получим:
V=150·250·170=6,4·106 мм3
По формуле (117) найдем массу редуктора
m=0,46·7300·6,4·10-3 = 21,5 кг
3. Вычерчивание редуктора
Редуктор вычерчиваем в двух проекциях на листе формата А1 (594×841 мм) в масштабе 1:1. В нижнем правом углу вычерчиваем основную надпись. Спецификация всех деталей составлена по стандартному образцу и приведена в таблицах П.2.1., П.2.2., П.2.3.
4. Посадки основных деталей
Внутренние кольца подшипников насаживаются на вал с натягом, значение которого соответствует полю допуска κ6, а наружные кольца в корпус – по переходной посадке, значение которой соответствует полю допуска Н7. Для концов валов, на которые насаживаются муфты принимаем посадки с натягом К7.
Для ступицы зубчатого колеса принимаем посадку с натягом Н7. Для сопряжения упорного кольца ведомого вала применяем посадку с натягом Н7/р6.
5. Смазка зубчатых колес, подшипников. Выбор сорта масла
Зубчатое зацепление смазывается окунанием зубчатого колеса в масло, заливаемое внутрь корпуса до уровня, обеспечивающего погружение колеса приблизительно на 11 мм, но не менее чем на высоту зуба. Согласно рекомендациям [2, с.351], объем масляной ванны определяется из расчета 0,25-0,5 л масла на 1 квт передаваемой мощности. В нашем случае, объем равен примерно 1,05 л. По [2, табл. 11.9] устанавливаем вязкость масла. При υ = 3,4 м/с рекомендуемая кинематическая вязкость ν = 85 сст.Учитывая рекомендации [2, табл.11.11] выбираем автотракторное масло АК 15.
Подшипники качения смазываются из общей масляной ванны редуктора путем разбрызгивания масла вращающимся зубчатым колесом.
Список использованных источников
1. Шейнблид А.Е. Курсовое проектирование деталей машин: Учебное пособие для техникумов. – М.: Высш. Школа, 1991.-432 с.
2. Ицкович Г.М., Киселев В.А. Курсовое проектирование деталей машин: Учебно-справочное пособие для учащихся техникумов. – М., Изд-во Машиностроение, 1970. – 560 с.
3. Устюгов И.И. Детали машин: Учебное пособие для учащихся техникумов. – М.: Высш. Школа, 1981. – 399 с.
Приложение
Таблица П.2.1. Спецификация
| Формат | Зона | Поз. | Обозначение | Наименование | Кол. | Примечание |
| Документация | ||||||
| А1 | КП-ДМ. 981319.00.00.00.СБ. | Сборочный чертеж | ||||
| Сборочные единицы | ||||||
| 1 | КП-ДМ. 981319.00.00.01. | Маслоуказатель | 1 | |||
| Детали | ||||||
| 2 | КП-ДМ. 981319.00.00.02 | Вал | 1 | |||
| 3 | КП-ДМ. 981319.00.00.03. | Вал-шестерня | 1 | |||
| 4 | КП-ДМ. 981319.00.00.04. | Колесо зубчатое | 1 | |||
| 5 | КП-ДМ. 981319.00.00.05. | Кольцо распорное | 1 | |||
| 6 | КП-ДМ. 981319.00.00.06. | Корпус редуктора | 1 | |||
| 7 | КП-ДМ. 981319.00.00.07. | Крышка редуктора нижняя | 1 | |||
| 8 | КП-ДМ. 981319.00.00.08. | Крышка редуктора верхняя | 1 | |||
| 9 | КП-ДМ. 981319.00.00.09. | Крышка смотравая | 1 | |||
| 10 | КП-ДМ. 981319.00.00.10. | Крышка подшипника | 1 | |||
| 11 | КП-ДМ. 981319.00.00.11. | Крышка подшипника | 1 | |||
| 12 | КП-ДМ. 981319.00.00.12. | Крышка подшипника | 1 | |||
| 13 | КП-ДМ. 981319.00.00.13. | Крышка подшипника | 1 | |||
| 14 | КП-ДМ. 981319.00.00.14. | Прокладка в наборе | 1 | |||
| 15 | КП-ДМ. 981319.00.00.15. | Прокладка в наборе | 1 | |||
| 16 | КП-ДМ. 981319.00.00.16. | Прокладка в наборе | 2 | |||
| 17 | Прокладка в наборе | 1 | ||||
| Стандартные изделия | ||||||
| 18 | Болт М 6×10 | 4 | ||||
| ГОСТ 7798-70 |
Таблица П.2.2.
| Формат | Зона | Поз. | Обозначение | Наименование | Кол. | Примечание |
| 19 | Болт М 6×25 | 8 | ||||
| ГОСТ 7798-70 | ||||||
| 20 | Болт М 6×10 | 12 | ||||
| ГОСТ 7798-70 | ||||||
| 21 | Болт М 6×10 | 4 | ||||
| ГОСТ 7798-70 | ||||||
| 22 | Болт М 8×65 | 4 | ||||
| ГОСТ 7798-70 | ||||||
| 23 | Болт М 8×55 | 4 | ||||
| ГОСТ 7798-70 | ||||||
| 24 | Гайка М 6.5 | 8 | ||||
| ГОСТ 5915-70 | ||||||
| 25 | Гайка М 8.5 | 8 | ||||
| ГОСТ 5915-70 | ||||||
| 26 | Пробка М 12×1,5 | 1 | ||||
| СТП С25-4 | ||||||
| 27 | Роликоподшипник 2206 |
2 | ||||
| ГОСТ 8328-75 | ||||||
| 28 | Роликоподшипник 2207 |
2 | ||||
| ГОСТ 8328-75 | ||||||
| 29 | Сальниковые войлочные Кольца |
2 | ||||
| 30 | Шайба пружинная 6. 65Г 05 |
20 | ||||
| ГОСТ 6402-70 | ||||||
| 31 | Шайба пружинная 8. 65Г 05 |
8 | ||||
| ГОСТ 6402-70 | ||||||
| 32 | Шпонка 8×7×36 | 1 | ||||
| СТ СЭВ 189-75 |
Таблица П.2.3.
| Формат | Зона | Поз. | Обозначение | Наименование | Кол. | Примечание |
| 33 | Шпонка 8×7×40 | 1 | ||||
| СТ СЭВ 189-75 | ||||||
| 34 | Шпонка 10×8×30 | 1 | ||||
| СТ СЭВ 189-75 | ||||||
| 35 | Рым-болт М 8×18 | 2 | ||||
| ГОСТ 4751-52 |
Похожие рефераты:
Методические указания по технической механике
Проектирование привода пресс-автомата с плавающим ползуном
Проектирование механического привода с цилиндрическим соосным редуктором
Расчет и проектирование коническо-цилиндрического редуктора
Проектирование электродвигателя
Расчет зубчатых и червячных передач в курсовом проектировании
Проектирование привода цепного конвейера
Седельный тягач с колесной формулой 4*2 с разработкой дифференциала повышенного трения
Основы проектирования ленточного конвейера
 .
.